Abstract
Effective drug delivery requires ample dosing at the target tissue while minimizing negative side effects. Drug delivery vehicles such as polymeric nanoparticles (NPs) are often employed to accomplish this challenge. In this work, drug release of numerous drugs from surface eroding polymeric NPs was evaluated in vitro in physiologically relevant pH 5 and neutral buffers. NPs were loaded with paclitaxel, rapamycin, resiquimod, or doxorubicin and made from an FDA approved polyanhydride or from acetalated dextran (Ace-DEX), which has tunable degradation rates based on cyclic acetal coverage (CAC). By varying encapsulate, pH condition, and polymer, a range of distinct drug release profiles were achieved. To model the obtained drug release curves, a mechanistic mathematical model was constructed based on drug diffusion and polymer degradation. The resulting diffusion-erosion model accurately described drug release from the variety of surface eroding NPs. For drug release from varied CAC Ace-DEX NPs, the goodness of fit of the developed diffusion-erosion model was compared to several conventional drug release models. The diffusion-erosion model maintained optimal fit compared to conventional models across a range of conditions. Machine learning was then employed to estimate effective diffusion coefficients for the diffusion-erosion model, resulting in accurate prediction of in vitro release of dexamethasone and 3′ 3’-cyclic guanosine monophosphate–adenosine monophosphate from Ace-DEX NPs. This predictive modeling has potential to aid in the design of future Ace-DEX formulations where optimized drug release kinetics can lead to a desired therapeutic effect.
Keywords: Polyanhydride, Acetalated dextran, pH responsive, Fickian diffusion, Machine learning, Neural network
1. Introduction
For drugs with a narrow therapeutic index, traditional systemic administration can harm the patient due to dose limiting toxicities. At lower doses, an insufficient amount of drug arrives at the intended delivery site, rendering the treatment ineffective. At higher doses, therapeutic effects can be achieved, but increased systemic drug concentrations can cause adverse off-target effects. These dosing problems are observed for a variety of therapeutics and are especially prevalent with chemotherapeutics and immunotherapies [1–6]. In order to overcome these shortcomings and improve therapeutic outcome, drug delivery vehicles are often employed to enhance the local delivery of drug while reducing adverse off-target effects [7]. Various drug delivery platforms have been shown to protect sensitive drugs from premature degradation in the body and provide controlled release of the drug over time, resulting in less frequent dosing [7].
While there are a multitude of drug delivery platforms, polymeric nanoparticles (NPs) are one of the most common [7]. NPs are commonly comprised of degradable polymers that break down through bulk degradation or surface erosion. Bulk degrading NPs lose their density and become porous over time whereas surface eroding NPs maintain their density with the radius decreasing as the surface erodes. An example of a bulk degrading polymer is the FDA approved biodegradable polymer poly(lactic-co-glycolic acid) (PLGA) [8]. Two examples of surface eroding polymers are polyanhydrides and acetalated dextran (Ace-DEX).
As PLGA bulk degrades it does so through an autocatalytic reaction mediated by its acidic degradation products [9]. The degradation rate of PLGA is somewhat tunable based on the ratio of lactic to glycolic acid with most formulations degrading on the order of months [8,10]. While sustained drug release on this timeline can be favorable in some instances, there are other instances where quicker release or combined fast and slow kinetics are more favorable [10,11].
Surface eroding behavior has been previously documented for hydrophobic polymers such as polyanhydrides due to minimal fluid penetration into the polymer matrix [12]. FDA approved polyanhydrides have also been evaluated for the formulation of NPs [13,14]. Compared to PLGA, polyanhydrides maintain their bulk material properties during degradation, but they have limited storage options and a poor shelf life [15,16]. As a result, polyanhydrides have had limited commercial applications, with the most notable being larger implants such as Gliadel: a chemotherapeutic-loaded wafer made of 20:80 poly (1,3-bis-(p-carboxyphenoxy propane)-co-(sebacic anhydride) (20:80 poly(CPP:SA)) [15,16].
Ace-DEX has been used pre-clinically and degrades by surface erosion. Iťs pH-neutral degradation products and stability under various storage conditions make Ace-DEX ideal for a variety of cargoes [17,18]. Furthermore, Ace-DEX uniquely has tunable degradation kinetics that range from hours to months, allowing for a range of drug release profiles to meet a variety of clinical needs. Reaction time during polymer synthesis determines the ratio of cyclic to acyclic acetal groups, where a longer reaction time yields a higher cyclic acetal coverage (CAC) and a slower degrading polymer [18,19]. Furthermore, Ace-DEX is acid sensitive, making it an ideal biopolymer for enhanced drug delivery in the endosome of phagocytic cells, tumor microenvironments (TMEs), and sites of inflammation [18]. Due to its unique acid sensitivity and range of degradation kinetics, Ace-DEX has been applied in numerous therapeutic elements including drug and vaccine delivery as well as tissue engineering [20].
Applications using Ace-DEX have illustrated favorable outcomes in both vaccine and chemotherapeutic delivery because of the polymer's tunable and more rapid degradation kinetics. For example, ovalbumin (OVA) loaded Ace-DEX NPs with a degradation half-life () of 1.7 h demonstrated increased antigen cross presentation compared to OVA loaded NPs made with slower degrading Ace-DEX (), PLGA, and iron oxide [10]. Chen et al. reported similar findings when OVA, universal influenza antigen Matrix 2 ectoprotein (M2e), and adjuvants cGAMP and murabutide were individually encapsulated in Ace-DEX NPs with varied CAC. Antibody production, cellular responses, and survival after challenge were observed to be dependent on degradation rate (at pH 5: 20% CAC , 40% CAC , 60% CAC ) [21,22]. Additionally, drug release from Ace-DEX scaffolds used to treat glioblastoma have demonstrated varying efficacy based on drug delivery kinetics. In this instance, the combination of a quick degrading scaffold and a slow degrading scaffold resulted in improved survival, perhaps due to an initial burst of drug to immediately treat the present tumor as well as sustained drug release to prevent recurrence [11]. The quick degrading scaffold released 14.1% of loaded drug per day while the slow degrading scaffold released 1.3% per day [11]. Due to the high versatility of Ace-DEX as a drug delivery platform, there is value in developing a mathematical model to aid in optimization of drug-loaded Ace-DEX formulations.
Various mathematical models have been developed previously to model drug release from degradable NPs. These models have been employed to gain insight to the role of individual inputs of an experimental system [23,24]. As such, an effective model can be used to predict the behavior of similar systems and reduce future experimental trial and error, saving time and resources. A robust model can also aid in translation from in vitro to in vivo experiments [25]. Five of the most employed drug release models include the zero order, first order, Korsmeyer-Peppas, Higuchi, and Hixson-Crowell models [26–28]. In general, each of these models focuses primarily on either diffusion effects or carrier degradation [27,29–36]. While each of these models are well established, and have advantages, they were based on various assumptions and they may not fully encompass the release mechanisms of both diffusion and polymer degradation needed to describe surface eroding NPs.
In this work, a mechanistic model was derived to primarily describe drug release from surface eroding NPs. The rate of diffusion of drug out of the polymer matrix is expected to vary based on drug properties [37,38], and further drug release is expected to be reliant on polymer degradation, which for Ace-DEX occurs at a rate dependent on CAC [19]. A similar mechanistic approach has previously been utilized to model drug release from PLGA NPs [9,23]; however, these models contain parameters reliant on bulk degradation effects and are therefore not mechanistically appropriate for surface eroding polymers. Other drug release models have previously been employed to describe surface eroding polyanhydride drug carriers [12,39,40], but they do not characterize both diffusion and degradation effects. As such, these models may not adequately apply to a broad range of drug encapsulates with varied diffusivities or to alternate polymer formulations. Indeed, it has been previously shown that different polyanhydride polymers as well as varied drug cargo can produce drug release curves with unique kinetic profiles [40,41]. Furthermore, most applications of mathematical modeling to polyanhydride systems appear to focus on larger implants and may not always translate to NP systems [12,39,40]. As such, the model derived herein aims to overcome these challenges by encompassing the surface erosion of a variety of polymeric NPs as well as simple diffusion of numerous drugs through the polymer matrix. The development of this mechanistic model addresses a gap in the field in modeling drug release from polyanhydride NPs, and to our knowledge, this work is the first application of mathematical modeling to describe drug release from Ace-DEX.
In order to evaluate the developed model, herein referred to as the diffusion-erosion model, drug release curves were obtained for a variety of polymeric formulations, including NPs made with 20:80 poly(CPP: SA) and with varied CAC Ace-DEX achieving a range of degradation profiles on the order of minutes to months [13,18,19]. 20:80 Poly(CPP: SA) NPs were loaded with resiquimod (R-848), and Ace-DEX NPs were loaded with paclitaxel (PTX), rapamycin (Rapa), R-848, doxorubicin (DXR), and dexamethasone (DXM). The selected drugs have varied physicochemical properties and have been successfully applied in Ace-DEX platforms overcoming drug delivery challenges [11,42–47]. Drug release was evaluated in vitro in neutral pH buffer to mimic the extracellular space as well as pH 5 buffer to mimic the endosome, sites of inflammation, or TMEs. The diffusion-erosion model was then fit against PTX, Rapa, R-848, and DXR release curves. The goodness of fit of the developed model was then compared to commonly employed drug release models. The variety of conditions applied to the drug release curves and the multiple model comparisons allowed for a high level of rigor in evaluating the diffusion-erosion model for drug release from surface eroding NPs. Machine learning was then employed to increase predictive power of the diffusion-erosion model. Predicted drug release curves were compared to DXM release and previously published 3′ 3’-cyclic guanosine monophosphate–adenosine monophosphate (cGAMP) release [47] from varied CAC Ace-DEX NPs in vitro. Overall, the work herein encompasses the generation of experimental drug release data, derivation of the diffusion-erosion model, selection of the best fit drug release model, and implementation of machine learning for predictive modeling (Supplemental Fig. 1).
2. Materials and methods
Unless otherwise noted, all materials were obtained from Sigma Aldrich (St. Louis, MO).
2.1. Acetalated dextran synthesis
Ace-DEX was synthesized as previously described [18]. As such, 71 kDa dextran was dissolved in dimethyl sulfoxide (DMSO) along with catalyst pyridinium p-toluenesulfonate before being reacted with 2-ethoxypropene (Matrix Scientific, Columbia, SC) under anhydrous conditions. This reaction was quenched with triethylamine (TEA) after 3 min, 20 min, and 8 h for 20%, 40%, and 60% CAC Ace-DEX, respectively (CAC confirmed by Inova 400 MHz NMR). Each of these Ace-DEX polymers are herein referred to as 20, 40, and 60 CAC. Ace-DEX was then precipitated in basic water (0.04% v/v TEA in water) and lyophilized. On day 2, Ace-DEX was dissolved in ethanol and centrifuged to spin down impurities. Ace-DEX was then re-precipitated from the supernatant in basic water before being lyophilized again and stored at −20 °C.
2.2. Synthesis of 20:80 poly(1,3-bis-(p-carboxyphenoxy propane)-co-(sebacic anhydride)
20:80 poly(CPP-SA) was synthesized by a two-step method, as previously reported [13,14,48]. Sebacic acid (SA) and 1,3-bis-(4-carboxy-phenoxy)propane (CPP) monomers were first oligomerized and acetylated at their terminal carboxylic acids (Supplemental Fig. 2). SA and CPP were each refluxed in a 1:10 w/v mixture with acetic anhydride at 140 °C for 20 min. Excess acetic anhydride was removed under vacuum at 60 °C using a rotary evaporator. The resulting prepolymers (pSA and pCPP) were dissolved in dry toluene and precipitated in a 1:1 v/v solution of dry petroleum ether and ethyl ether. The precipitate was left overnight in the ether solution before being vacuum filtered then dried by lyophilization. Successful acetylation was confirmed via Inova 400 MHz H NMR, and degree of oligomerization was quantified (Supplemental Fig. 3A–B). pSA and pCPP prepolymers were then reacted in a melt polycondensation to prepare poly(CPP:SA). A 20:80 M mixture of pCPP:pSA was heated at 180 °C for 90 min under vacuum and flushed with nitrogen every 15 min. The copolymer was precipitated in dry petroleum ether from DCM, washed twice with diethyl ether, and lyophilized for 24 h. Copolymerization was assessed via Inova 400 MHz H NMR, and the 20:80 CPP:SA ratio was confirmed in the final polymer (Supplemental Fig. 3C). pSA, pCPP, and 20:80 poly(CPP:SA) were stored at −80 °C.
2.3. Formation and characterization of nanoparticles
Varied CAC Ace-DEX NPs were made with target weight loadings: blank, 1% Rapa, 1% R-848, 1% DXR, 1% PTX, 5% PTX, and 1% DXM. For 20:80 poly(CPP:SA) NPs, blank, 1% wt/wt R-848, and 5% wt/wt R-848 were made. All NPs were all made via homogenization, utilizing a previously described double emulsion procedure [42]. Ace-DEX was dissolved in ethyl acetate (EA) then homogenized at 18,000 rpm (IKA T25 Digital Ultra-Turrax, Cole Parmer, Vernon Hills, IL) with a small volume of phosphate buffered saline (PBS). Drugs were either included in the EA or the PBS where applicable. The resulting emulsion was homogenized again with 3% polyvinyl alcohol (PVA) in PBS. The final emulsion was stirred in 0.3% PVA in PBS at room temperature to allow the EA to evaporate. NPs were washed with basic water before being frozen and lyophilized. 20:80 poly(CPP:SA) NPs were fabricated similarly to the Ace-DEX NPs, but with DCM instead of EA and water instead of basic water. Emulsions containing R-848 or DXR were protected from light. The encapsulation efficiency (EE) of Rapa, PTX, and DXM were determined with high performance liquid chromatography (HPLC, 1100 Series, Agilent Technologies, Santa Clara, California) with a C18 column (Aquasil 77,505–154,630 C18 Column, 5 μm Pore; 150 mm L x 4.6 mm ID, Thermo Fisher Scientific). Conversely, the EE of R-848 and DXR were determined via plate reader (SpectraMax M2, Molecular Devices, San Jose, CA) with excitation/emission (ex/em) 260/370 and 480/580 for R-848 and DXR, respectively. The morphology of all NPs was assessed via scanning electron microscopy (SEM, Hitachi S-4700 Cold Cathode Field Emission). SEM images were then analyzed in ImageJ 1.52a to determine initial radii. Ace-DEX NPs were stored at −20 °C, and 20:80 poly(CPP:SA) NPs were stored at −80 °C.
2.4. Assessment of nanoparticle degradation
Blank Ace-DEX degradation was assessed at neutral and acidic pH. 1 mg/mL suspensions with 20, 40, and 60 CAC NPs were prepared in pH 7.4 PBS or in pH 5 0.3 M sodium acetate buffer. Suspensions were prepared in triplicate in Eppendorf tubes and placed on a shaker plate at 37 °C. At each timepoint (0, 0.5, 2, 4, 8, 24, 48, 72, 96, 168, 336, 504, 672, and 840 h) suspensions were vortexed briefly, then aliquots were taken and centrifuged. Supernatant was collected and degraded Ace-DEX was measured by bicinchoninic acid assay (BCA, Thermo Scientific, Rockford, IL). BCA data was normalized to fully degraded samples for each CAC and buffer. The degradation of PTX-loaded NPs was visualized by SEM at 0, 0.5, and 168 h for 40 CAC NPs at pH 7.4. Blank 20:80 poly(CPP:SA) degradation was similarly assessed at pH 7.4. To quantify degradation, SA was measured in the supernatant via HPLC with a PRP-1 column (Hamilton, 4.1 × 150 mm, 5 μm), UV detection at 210 nm, and a mobile phase of 50:50 acetonitrile:water with 1% phosphoric acid. Data was graphed as percent degraded over time, and a nonlinear fit was done to a one phase decay model in GraphPad 7.00 to determine .
2.5. Assessment of drug release from nanoparticles
Release curves for PTX were obtained at pH 7.4. PTX-loaded Ace-DEX NPs were suspended in triplicate at 1 mg/mL in PBS in a Slide-A-Lyzer Mini Dialysis Unit with a 7 MW cut off. One dialysis unit was prepared for each timepoint and placed into 1 L of PBS at 37 °C with sink conditions maintained. At each timepoint, aliquots were taken from the dialysis unit and centrifuged. The supernatant was removed and the remaining PTX in the NPs was measured from the pellet via HPLC. Release curves for Rapa, R-848, DXR, and DXM from Ace-DEX NPs were obtained at neutral pH, and additional release curves for Rapa, R-848, and DXR were obtained at pH 5. Suspensions were prepared in triplicate and samples were taken at each timepoint as done in the assessment of blank degradation. After centrifuging, the supernatant was separated from the pellet. The remaining drug in the Rapa NPs was measured from the pellet, and the drug released from the R-848, DXR, and DXM NPs was measured from the supernatant. R-848 release from 20:80 poly(CPP:SA) NPs was assessed at pH 7.4 similarly to drug release from Ace-DEX NPs.
2.6. Development of mathematical model
The constitutive equations for the mathematical model developed herein were derived manually. The first constitutive equation describes drug diffusion, and the second constitutive equation describes degradation. The following simplifying assumptions were made: (1) the drug is evenly incorporated throughout the polymer matrix, (2) diffusion only occurs in the radial direction, (3) diffusion cannot be negligible, (4) once the drug leaves the it falls away from the surface under sink conditions, and (5) the system has symmetry.
The first constitutive equation, representing drug diffusion, was developed similarly to previously described Fickian models [9,49–51]. In brief, the continuity equation in spherical coordinates with one-dimensional motion in the radial direction combined with Fick's first law of diffusion yields Fick's second law in spherical coordinates:
| (1) |
where is the concentration of drug in the at time , is the effective diffusion coefficient for drug moving through polymer, and is the radial coordinate. An initial condition and boundary conditions were defined to develop the model (Table 1).
Table 1.
Initial condition (IC) and boundary conditions (BCs) for diffusion-erosion model derivation based on the simplifying assumptions. is the radius, is the radial coordinate, is the concentration of drug in the at time , and is initial concentration of drug in the .
| Diffusion-Erosion Model IC and BCs | |||
|---|---|---|---|
| IC: | |||
| BC1: | |||
| BC2: | |||
Separation of variables and conditions (Table 1) were applied to yield the first constitutive equation of the diffusion-erosion model, the unsteady state Fickian diffusion equation:
| (2) |
where is the mass of drug remaining in the at time , and is the initial mass loading. The percent of drug released from the is then calculated as follows, yielding the first constitutive equation:
| (3) |
To develop the second constitutive equation, the degradation mechanism and kinetics observed for Ace-DEX NPs was considered. For simplicity, in a surface eroding system, it can be assumed that the size decreases proportionally to the mass [52], and the density can be considered constant. As a result, the effective diffusion coefficient was considered to be constant while the radius of the decreased over time. In line with the observed blank Ace-DEX degradation, the change in the radius was considered to follow first order degradation. As a result, the second constitutive equation of the model is as follows:
| (4) |
where is the degradation coefficient of the based on polymer CAC and the pH of the system. This equation was then simulated in tandem with the first constitutive equation.
Except for the effective diffusion coefficient, all model parameters and initial values were determined empirically based on standard characterization and blank degradation data. More detail on model derivation can be found in the supplementary materials.
2.7. Model simulations in MATLAB
The diffusion-erosion model as well as the zero order, first order, Korsmeyer-Peppas, Higuchi, and Hixson-Crowell models were simulated in MATLAB R2017b. For the diffusion-erosion model, the ode15s command was utilized on the second constitutive equation followed by the arrayfun command for the first constitutive equation. For the remaining models, an equation was manually developed to represent percent release and inputted into the MATLAB script. Parameters with unknown values at the time of simulation were determined with weighted least squares regression analysis using the nlinfit command and the drug release experimental data. Data points were weighted with the inverse of the variance at each timepoint. For previously published cGAMP release, where select data points had a reported standard deviation of 0, the value 0.1 was used as a proxy to calculate an approximate variance to return real numbers for weighting. The residual sum of squares (RSS) of each model was then calculated at the end of the script. The method was the same for models applied to 20:80 poly(CPP:SA), except that the nlinfit command was unweighted due to observed increases in error skewed to later timepoints for the polyanhydride system.
2.8. Statistical analysis
The mean square error () was calculated for each simulation and used to manually calculate the Akaike Information Criterion () and the Bayesian Information Criterion () according to the following equations:
| (5) |
| (6) |
where is the number of parameters in the model, and is the number of experimental data points. To calculate and , represented the number of unknown parameters at the time of MATLAB simulation. Any parameters determined empirically, independently of the drug release experimental data, were not counted. In order to compare the goodness of fit of the diffusion-erosion model against alternate, previously established models, an difference was calculated for each drug release curve where the of the diffusion-erosion model was subtracted from the of each alternate model. Positive values for the difference were considered an indication that the diffusion-erosion model was favorable over the alternate model. Conversely, negative values were considered an indication that the alternate model was a better choice. differences of zero were considered an indication that the models were comparable. After assessing the differences of all models at all drug release curves, the unknown parameters of the optimal models at both pHs were correlated with drug properties. This was done for high and low CAC (20 and 60) NPs at both pHs with Rapa, R-848, and DXR. Drug properties were obtained from PubChem, and a Pearson's correlation was conducted in GraphPad Prism 7.00.
2.9. Machine learning in MATLAB
Supervised learning models were explored in MATLAB R2020b. The neural network (NN) model was selected to predict new effective diffusion coefficients. A NN was constructed with 4 hidden neurons, 2/3 the number of model inputs. In order to develop the NN, information was provided to the model from all PTX, Rapa, R-848, and DXR release curves from Ace-DEX (22 unique release curves). The following inputs were provided: drug polar surface area, drug logP, drug MW, polymer CAC, initial drug loading, and pH. Estimated effective diffusion coefficients were provided as outputs. The corresponding inputs and outputs from all 22 release curves were passed into the NN together where 70% was randomly assigned as training data, 15% as validation data, and 15% as test data. Due to its efficiency as a training function, Levenberg-Marquadt backpropagation was performed with the trainlm command. Input-output processing functions were also applied to increase efficiency. For inputs, ‘mapminmax’ and ‘processpca’ were employed. For outputs, ‘mapminmax’ was employed. ‘Mapminmax’ normalizes inputs/outputs to fall in the range [−1,1], and ‘processpca’ applies principal component analysis. Model performance for each portion of the provided data (training, validation, and test) was measured as . The finalized NN resulted from the epoch with the best validation performance. To further evaluate performance, a regression between predicted and actual outputs from the pooled training, validation, and test data was performed. The NN was then applied to predict effective diffusion coefficients for DXM and cGAMP release from varied CAC Ace-DEX NPs at pH 7.4. For cGAMP release from Ace-DEX NPs, previously published data was used [47].
3. Results and discussion
3.1. Acetalated dextran nanoparticles degrade by surface Erosion and first order kinetics
Polymeric NPs are expected to degrade by either surface erosion or bulk degradation. In the case of surface eroding polymers like polyanhydrides, the size of the decreases over time but the polymer molecular weight (MW) remains constant [12,52]. By comparison, NPs made from bulk-degrading polymers such as PLGA develop pores due to the decreasing polymer MW and density [9]. The degradation mechanism of 40 CAC NPs was visualized by SEM (Fig. 1A). Prior to incubation at pH 7.4, the spherical NPs displayed a largely smooth surface (Fig. 1A1). After 0.5 h, the surface is no longer smooth, and after 168 h, layers of polymer appear to be sloughing off the surface (Fig. 1A2–3). Additionally, no visible pore formation was observed even after 168 h. Based on these observations, it was concluded that Ace-DEX NPs degrade primarily via surface erosion. As a result, polymer hydrolysis is expected to occur at a rate faster than fluid penetration into the polymer matrix, making bulk effects negligible [12,52].
Fig. 1.
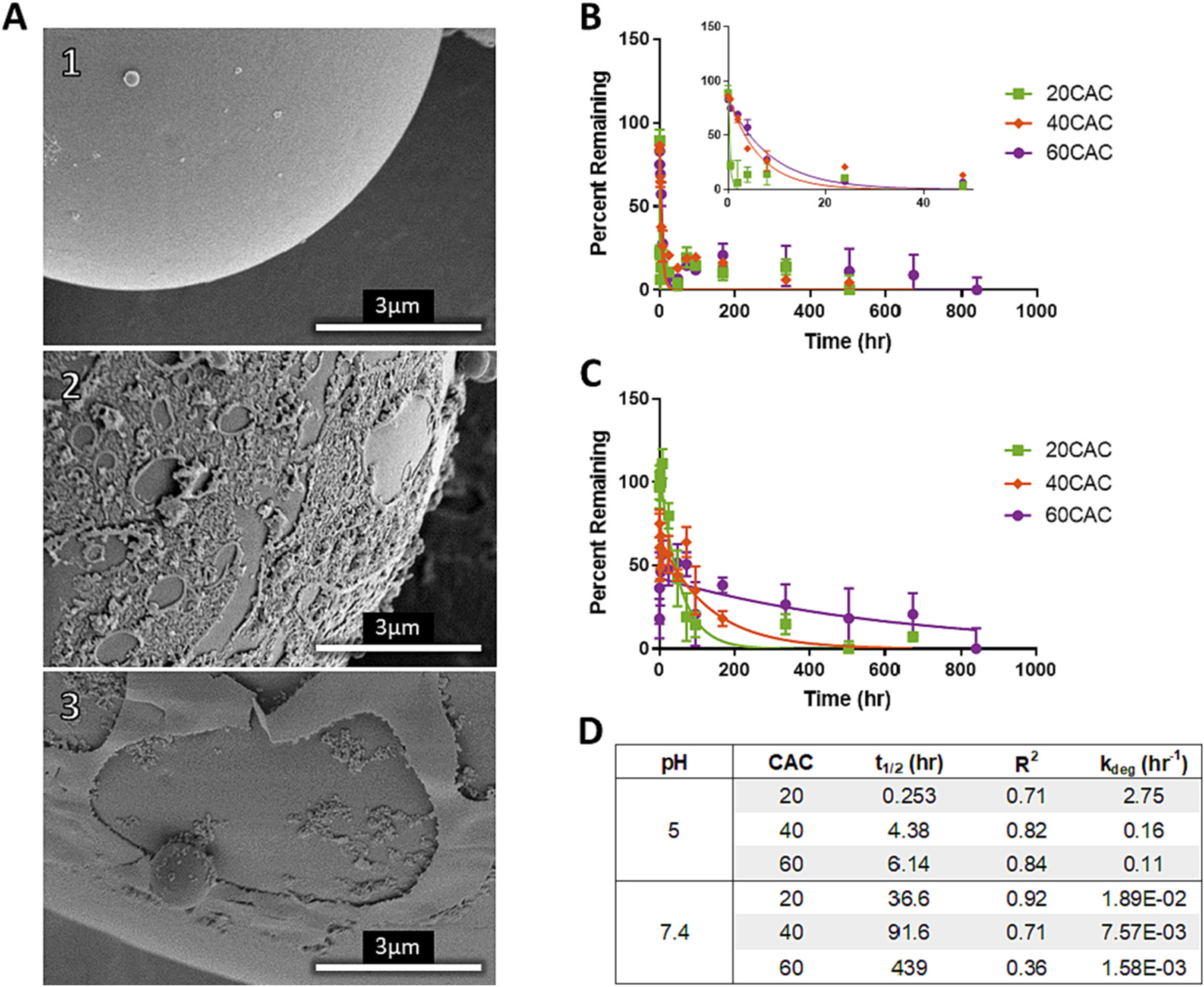
Visualization of degradation and measurement of blank degradation rates at varied CACs. (A) surface at pH 7.4 for (A1) , (A2) , and (A3) . (B,C) Percent of Ace-DEX s remaining and nonlinear fit of one phase decay of 20, 40, and 60 CAC NPs in (B) pH 5 and (C) pH 7.4 buffer at sink conditions and 37 ◦C. Percent remaining represents the percent of original polymer remaining and is calculated by 100% minus percent degraded as measured by BCA. (D) Summary of estimated in hours and R2 values from the one phase decay model. degradation coefficients for the diffusion-erosion model are calculated from via the Arrhenius equation.
The degradation kinetics of blank 20, 40, and 60 CAC Ace-DEX NPs was assessed at pH 5 (Fig. 1B) and pH 7.4 (Fig. 1C). All six of these degradation profiles could be fit with a one phase decay model (Fig. 1B–C). The estimated ranged from minutes to weeks across all three CACs at both pHs, with each CAC degrading more rapidly at pH 5 compared to pH 7.4 (Fig. 1D). These results are in agreement with previous reports of the of sonicated Ace-DEX NPs [19]. Furthermore, this wide range of degradation rates allows for greater optimization of drug delivery kinetics compared to NPs made from PLGA or polyanhydrides. Compared to Ace-DEX, 80:20 poly(CPP:SA) NPs also follow first order degradation with a comparable to 20 CAC NPs at pH 7.4 () (Supplemental Fig. 3, Fig. 1D).
Characterization of blank degradation kinetics informed the development of the diffusion-erosion model. It is widely accepted that drug can diffuse through polymer matrices [27,28,32,34], and the degradation of the can mediate further drug release [52]. The diffusion-erosion model developed herein encompasses both concepts. As a result, the first constitutive equation of the model was developed to encompass drug diffusion through the polymer matrix, while the second equation was developed to model surface erosion of NPs in a (or CAC for Ace-DEX) dependent manner at physiologically relevant pH 7.4 and 5 (Eqs. 3 and 4).
3.2. The diffusion-erosion model accurately fits drug release data from surface eroding nanoparticles under neutral and acidic conditions
Surface eroding NPs were made with 20:80 poly(CPP:SA) and with 20, 40, and 60 CAC Ace-DEX, encapsulating a variety of drugs with distinct physicochemical properties (Table 2). 20:80 poly(CPP:SA) NPs encapsulating 1% or 5% by weight (wt/wt) R-848 and varied CAC Ace-DEX NPs encapsulating 1% or 5% wt/wt PTX were made for evaluation at neutral pH. Additionally, varied CAC Ace-DEX NPs encapsulating 1% wt/wt Rapa, R-848, or DXR were made for evaluation at both neutral and acidic pH. All NPs demonstrated a spherical morphology (Supplemental Fig. 4), and the final drug loading and average size for each batch was characterized (Supplemental Table 1, Supplemental Fig. 4). The empirically determined parameters and initial values applied to the diffusion-erosion model were obtained from a combination of drugloaded characterization and blank-MP degradation kinetics (Supplemental Table 1, Fig. 1D, and Supplemental Fig. 3F).
Table 2.
Summary of selected drugs. Values for logP, molecular weight (MW), and polar surface area were obtained from PubChem. PTX = paclitaxel, Rapa = rapamycin, R-848 = resiquimod, DXR = doxorubicin, DXM = dexamethasone, cGAMP = 3′ 3’-cyclic guanosine monophosphate–adenosine monophosphate.
| Drug | LogP | MW (g/mol) | Polar Surface Area (Å2) | Application |
|---|---|---|---|---|
| PTX | 2.5 | 853.9 | 221.3 | Chemotherapeutic |
| Rapa | 6.0 | 914.2 | 195.0 | Immunosuppressant |
| R-848 | 1.3 | 314.4 | 86.2 | Vaccine Adjuvant |
| DXR | 1.3 | 543.5 | 206.1 | Chemotherapeutic |
| DXM | 1.9 | 392.5 | 94.8 | Immunosuppressant |
| cGAMP | −5.9 | 674.4 | 325.0 | Vaccine Adjuvant |
MPs of 20:80 poly(CPP:SA) or Ace-DEX of different CACs were loaded with R-848 (1%) or PTX (1% and 5%) and release determined (Fig. 2). For the most part, release followed degradation kinetics for both drugs and polymers. Unexpectantly, the PTX release rate from 40 CAC NPs 1% PTX was the slowest among 20 and 60 CAC 1% PTX group (Fig. 2B1). This discrepancy may be attributed to variable diffusivity of each drug through each polymer. With PLGA NPs, it has been postulated that polymer/drug interactions, drug solubility in the bulk phase, and structural differences in the polymer matrix can affect the diffusivity of the cargo through the [53]. Since Ace-DEX NPs are hydrophobic and appear to degrade via surface erosion, water penetration is expected to be minimal [12]. As such, any suspected variation in PTX diffusivity through varied CAC Ace-DEX is more likely due to intermolecular interactions between the drug and each CAC Ace-DEX and not solely on the degradation rate. The diffusion-erosion model was then applied to each of the release curves from NPs with varied drug loading. In all cases, the model output appeared to follow the same trends as the experimental data and demonstrated moderate to very high Pearson's correlations (Fig. 2, Supplemental Table 2).
Fig. 2.
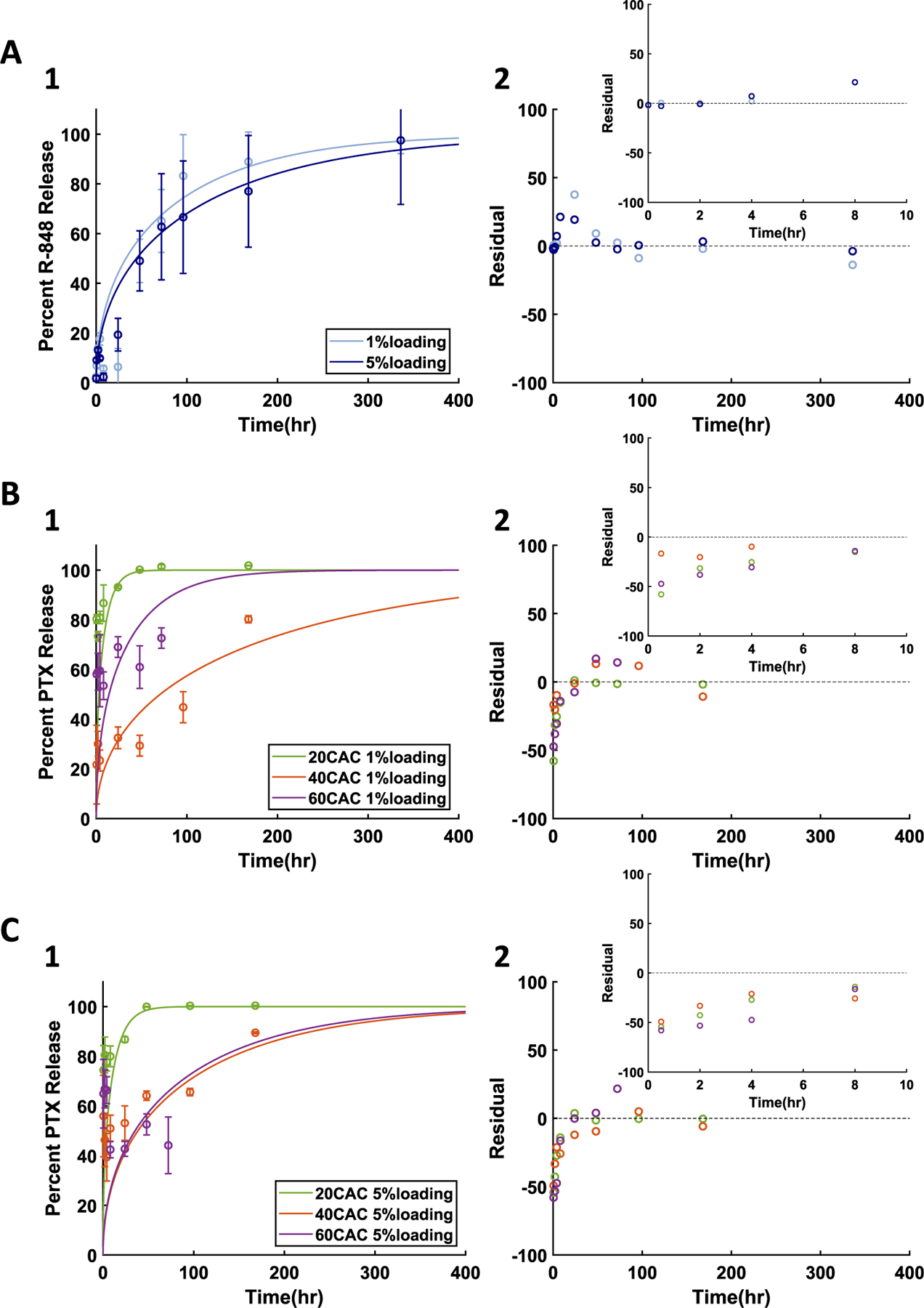
Diffusion-erosion model applied to drug release from surface eroding NPs with varied initial loading at pH 7.4 for A) 1% and 5% R-848 NPs made with 20:80 poly(CPP:SA), B) 1% PTX NPs made with varied CAC Ace-DEX, and C) 5% PTX NPs made with varied CAC Ace-DEX. 1) Experimental results (data points and error bars representing average ± standard deviation) and diffusion-erosion model simulations (lines) of drug release from NPs. 2) Residual plots for each model simulation compared to average experimental values.
Once the diffusion-erosion model was confirmed to adequately fit the release from surface eroding NPs with varied loading and polymer, release curves from a broader selection of drugs were obtained from varied CAC Ace-DEX NPs all fabricated with 1% wt/wt initial drug loading of R-848, DXR, or Rapa (Fig. 3). For all three drugs at neutral pH, release kinetics were notably quicker from 20 than 60 CAC NPs, in agreement with previous reports of drug release from varied CAC Ace-DEX formulations [10,11,19]. Additionally, release rates appeared to vary across drugs, likely as a result of the drugs' varied physicochemical properties [37,38,40]. The variation in drug physicochemical properties likely contributes to observed release kinetics from 40 CAC polymer, where some drugs appear to demonstrate stronger intermolecular interactions with 40 compared to 60 CAC. Simulations with the diffusion-erosion model appeared to follow the same trends as the neutral pH release data for all three drugs, and significant (p < 0.05) high to very high Pearson's correlations were observed (Fig. 3A–C, Supplemental Table 2). The successful characterization of drug release kinetics from a variety of Ace-DEX NPs at neutral pH is an essential step in optimizing drug delivery kinetics as in vitro drug release at neutral pH can mimic drug release kinetics in the extracellular space [19].
Fig. 3.
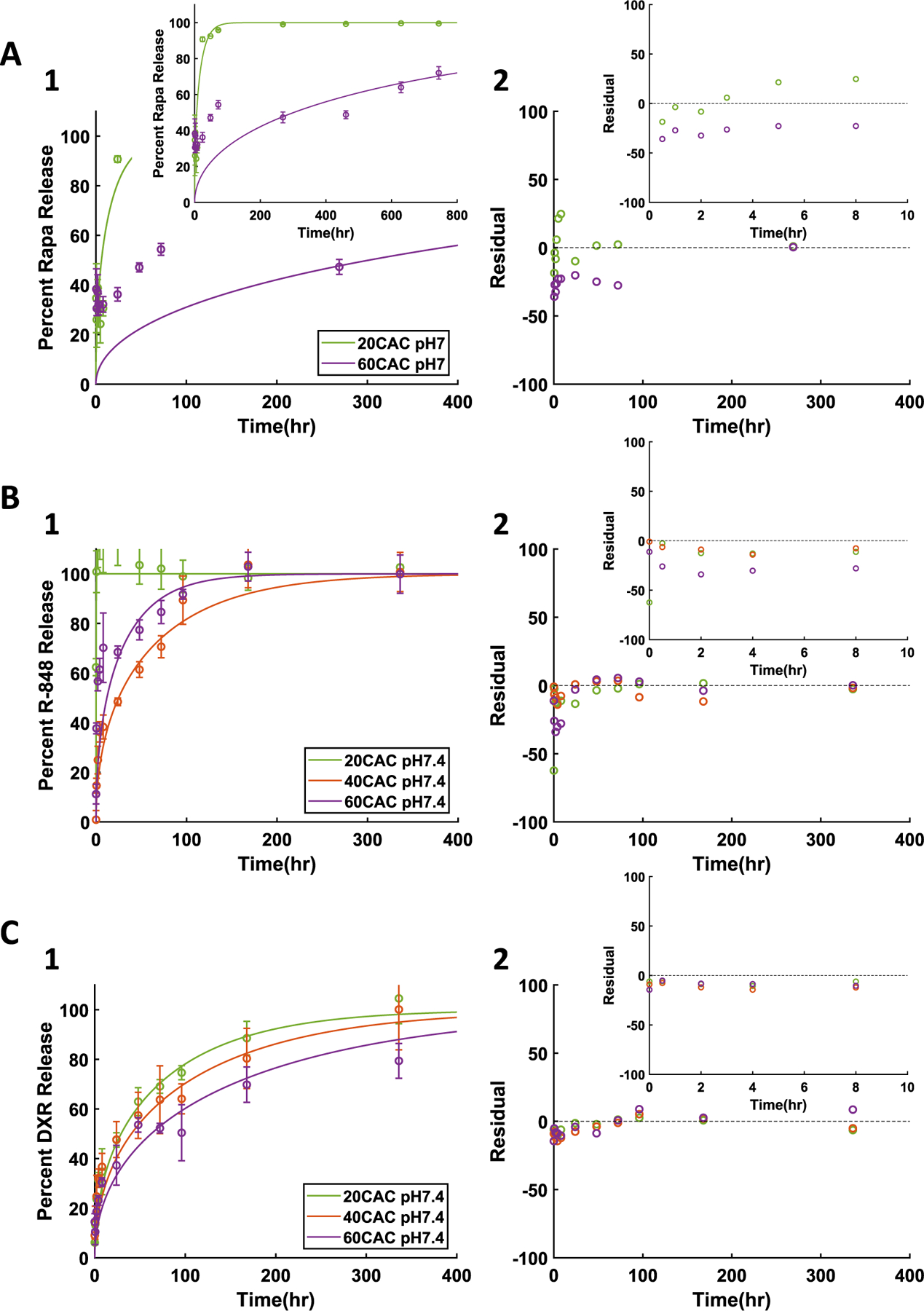
Diffusion-erosion model at neutral pH for A) 1% Rapa, B) 1% R-848, and C) 1% DXR NPs. 1) Experimental results (data points and error bars representing average ± standard deviation) and diffusion-erosion model simulations (lines) of drug release from varied CAC NPs. 2) Residual plots for each model simulation compared to average experimental values.
In order to further assess applications of the diffusion-erosion model for Ace-DEX NPs, release curves for the varied CAC NPs containing Rapa, R-848, or DXR were obtained at pH 5, mimicking physiologically relevant acidic conditions of common target delivery sites. Compared to the results at neutral pH (Fig. 3), all three drugs demonstrated notably quicker release kinetics (Fig. 4A1, B1, C1). The increase in release rates can be attributed to the acid sensitivity of Ace-DEX. Indeed, the increased polymer degradation has been previously shown to influence increased drug release kinetics [19]. Additionally, the correlations between release data at pH 5 and the diffusion-erosion model output were all significant (p < 0.05) (Supplemental Table 2). In vitro drug release at pH 5 mimics drug release in the endosome, sites of inflammation, and the TME of some tumors [19]. This is especially critical to characterize as these are target delivery sites for many applications [11,42–45].
Fig. 4.
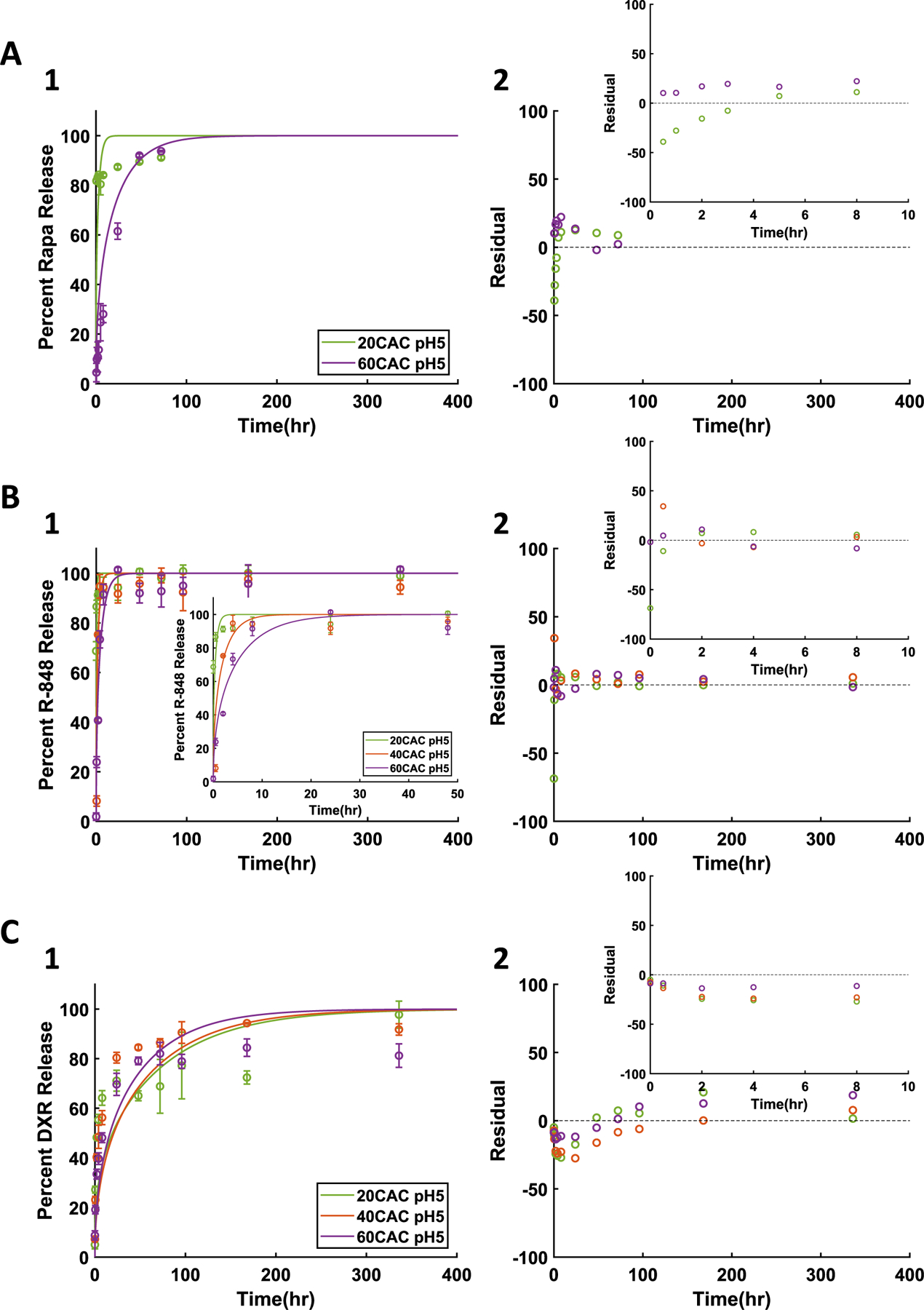
Diffusion-erosion model at acidic pH for A) 1% Rapa, B) 1% R-848, and C) 1% DXR NPs. 1) Experimental results (data points and error bars representing average ± standard deviation) and diffusion-erosion model simulations (lines) of drug release from varied CAC NPs. 2) Residual plots for each model simulation compared to average experimental values.
Taken together, the successful model fits of drug release from surface eroding NPs with varied loading concentrations, cargo, polymer, and pH demonstrate the utility of the diffusion-erosion model. Across the conditions assessed herein, the diffusion-erosion model correlated with the experimental drug release data with most correlations being very high, and these correlations were significant (p < 0.05) for all data sets except for PTX release from 60 CAC (Supplemental Table 2). Based on the residual plot of each model simulation (Fig. 2–4), it appears as though most of the error in the model is associated with earlier data points. This early error is likely due to burst release where there is a rapid release of drug incorporated at or near the surface. Burst release is a common phenomenon for matrix drug delivery systems, and its behavior is often difficult to accurately predict [54,55]. To address this challenge, others have employed highly robust mechanistic models that incorporate a burst step [50,51], but these models also introduce more unknown parameters. For the diffusion-erosion model, simplicity was prioritized to allow for greater predictive potential, and despite burst release, the Pearson's correlations and overall residual plot behavior indicate that the diffusion-erosion model adequately describes the drug release from surface eroding NPs across a variety of conditions.
In addition to correlating with drug release data, the diffusion-erosion model was used to determine effective diffusion coefficients of the encapsulated drugs through each polymer (Supplemental Table 3). Effective diffusion coefficients are often determined experimentally or estimated from existing release curves, with most available characterizations of drug-polymer diffusion focusing on PLGA systems [9,53]. In evaluating drug release from Ace-DEX, it is notable that the estimated effective diffusion coefficient of each drug varies somewhat with polymer CAC. It has been shown previously in PLGA systems that polymer MW and other factors affecting the structure of the polymer matrix have an effect on the effective diffusion coefficient of the cargo [23,53,56]. Thus, it is possible that each CAC forms NPs with distinct polymer matrices. Additionally, it is possible that each CAC has varied intermolecular forces with each drug. In cases where the drug release mechanism is more heavily influenced by diffusion than polymer erosion, these effects may be more noticeable. As such, it is possible that the slower release kinetics observed from some of the 40 compared to 60 CAC NPs can be a result of lower diffusivity and a predominantly diffusion-based release mechanism, though more work is warranted to elucidate the roles of degradation and diffusion in drug release kinetics from Ace-DEX NPs.
3.3. Quality of fit of diffusion-erosion model was compared to alternative drug release models to describe drug release behavior from acetalated dextran nanoparticles
The diffusion-erosion model developed herein was compared to five models conventionally applied to drug delivery systems: the zero order, first order, Korsmeyer-Peppas, Higuchi, and Hixson-Crowell models (Supplemental Table 4). The alternate models were applied to all release curves from Ace-DEX NPs (Supplemental Fig. 5–12), and parameter estimates were generated for each model at each release curve (Supplemental Table 5). In addition to the diffusion-erosion model, the first order and Korsmeyer-Peppas models appeared to trend with the experimental data (Supplemental Fig. 5–12) Furthermore, for some of the drug release curves, the associated with the first order and Korsmeyer-Peppas models were comparable to the diffusion-erosion model (Supplemental Table 6). Conversely, the zero order, Higuchi, and Hixson-Crowell models did not adequately capture drug release behavior from Ace-DEX NPs. Their underperformance aligns with the proposed mechanism of drug release from Ace-DEX NPs – diffusion paired with surface erosion. Zero order release kinetics is often exhibited by NPs with uneven drug distribution or layered structures [29,30]; however, the drug loaded into homogenized Ace-DEX NPs is expected to be evenly distributed. The Higuchi model has been developed for diffusion mediated release from spherical matrix systems [34]; however, this model does not account for degradation of the polymer matrix. Finally, the Hixson-Crowell model describes release from the decreasing surface area of the drug delivery device, but it does not emphasize diffusion effects [27,35,36,39].
3.4. Statistical analysis supports diffusion-erosion model as optimal to describe drug release from acetalated dextran nanoparticles
The goodness of fit of the alternate models was compared to the diffusion-erosion model by taking a difference of the and values for each release curve, where the diffusion-erosion or is subtracted from that of the alternate model. A positive or difference indicates that the diffusion-erosion model is the preferred model, and a negative difference indicates that the alternate model is preferred. Though the formula issues a higher penalty for the number of unknown parameters compared to , both model selection criteria agreed across all conditions (Supplemental Fig. 13). Of note, the Korsmeyer-Peppas model had two unknown parameters while all other models had one. For the drug release of 1% and 5% wt/wt PTX at neutral pH, the diffusion-erosion model outperformed all alternate models except for the Korsmeyer-Peppas model (Fig. 5A). The differences between the diffusion-erosion model and Korsmeyer-Peppas model were within error of zero, indicating that the two models demonstrate comparable fits of the drug release data. Similarly, the Korsmeyer-Peppas model was the only alternate model comparable to the diffusion-erosion model in fitting the drug release curves for Rapa, R-848, and DXR at neutral pH as this was the only alternate model with differences within error of zero (Fig. 5B). However, at acidic pH, both the Korsmeyer-Peppas and first order model were comparable to the diffusion-erosion model based on differences (Fig. 5B). Although, compared to the diffusion-erosion model, the Korsmeyer-Peppas model demonstrated a weaker fit at acidic pH than it did at neutral pH (Fig. 5B).
Fig. 5.
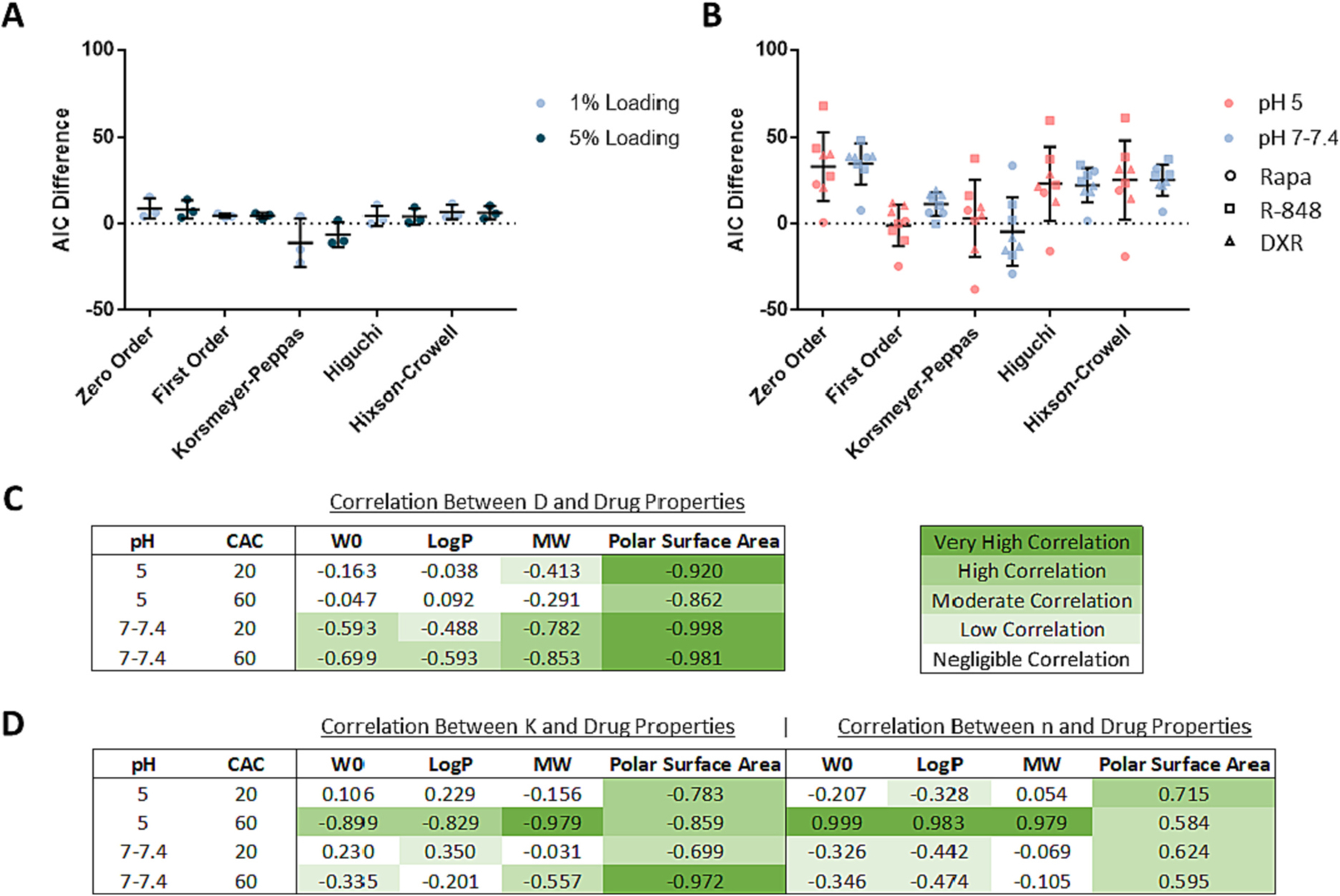
Drug release model comparisons. A) difference for PTX data sets by loading. B) difference for Rapa, R-848, and DXR data sets together at pH 5 and at pH 7–7.4. difference describes the of the alternate model minus the of the diffusion-erosion model. The average and standard deviations of difference is presented per alternate model. C) Correlation of initial loading or drug properties to estimated effective diffusion coefficients and D) to estimated Korsmeyer-Peppas model parameters. W0 refers to initial drug loading, and MW refers to drug molecular weight. Correlations are represented with Pearson's coefficients and are highlighted in green such that darker pigment indicates higher correlation and no pigment indicates negligible correlation. Each Pearson's coefficient represents correlations for Rapa, R-848, and DXR together at one release condition at a time (per CAC per pH). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
The pH dependence of the accuracy of the Korsemeyer-Peppas and first order models may provide insight to drug delivery kinetics of Ace-DEX NPs. Notably, the value in the Korsmeyer-Peppas model can indicate drug release mechanism. It has been reported that values of indicate Fickian release while between 0.43 and 0.85 indicate a non-Fickian mechanism [32,33,57–59]. Except for one release curve – 40 CAC 1% wt/wt PTX NPs at pH 7.4 – all of the values estimated for drug release from Ace-DEX NPs were <0.43 (Supplemental Table 5). This indicates that drug release from a variety of Ace-DEX NPs relies on Fickian diffusion. Additionally, the increased accuracy of the first order model at pH 5 may indicate an increased contribution of polymer erosion on drug release kinetics at acidic pH. Considering the acid sensitivity of the polymer and the observed first order degradation kinetics of blank Ace-DEX NPs, it seems appropriate that the first order model can capture drug release from some formulations under acidic conditions. Conversely, the subpar fit of the first order model at neutral pH could indicate that drug release kinetics are more heavily influenced by diffusion under neutral conditions. Understanding the pH effects on drug release kinetics from Ace-DEX NPs can provide insight to drug delivery kinetics in target tissues. The acid sensitivity of the polymer can allow for triggered first-order drug release in the endosome of phagocytic cells, sites of inflammation, or the TME, making Ace-DEX an optimal delivery system for chemotherapeutics and immunotherapies. In contrast, in the pH-neutral extracellular space, drug release more reliant on diffusion may be tunable based on drug properties.
While both the diffusion-erosion and Korsmeyer-Peppas models provided adequate fit to drug release data from a variety of Ace-DEX NPs, the diffusion-erosion model has a greater potential to be employed as a predictive model. Utilizing the effective diffusion coefficient to evaluate the drug release kinetics is simpler than utilizing two unknown parameters such as and . Furthermore, the effective diffusion coefficient may be considered a function of the interaction between physicochemical properties of the polymer matrix and the drug cargo. Indeed, in a Pearson's correlation comparing estimated model parameters against drug properties and loading, the effective diffusion coefficient had higher correlations to drug polar surface area than any other parameter comparison (Fig. 5C–D), which is in agreement with previous reports. It has previously been shown that higher drug polar surface area can allow for stronger dipole moments with the surrounding polymer matrix, slowing down release kinetics [60]. This effect may explain the differences in DXR and R-848 release kinetics from Ace-DEX NPs. Though some of the physicochemical properties of these two drugs are comparable, DXR has a notably higher polar surface area than R-848 (Table 2). This difference in polar surface area likely influenced the slower release kinetics observed for DXR compared to R-848.
3.5. Machine learning via a predictive neural network can be used to determine effective diffusion coefficients for further applications of the diffusion-erosion model
Effective diffusion coefficients for drug delivery systems are often determined experimentally, and in instances where mathematical modeling is employed, the models often rely on curve fitting, limiting further applications of these models to new systems [9,53]. For example, some previously reported modeling approaches to estimate effective diffusion coefficients have been dependent on parameters describing material interactions on an atomic level [61], which are not practical to characterize for a variety of drug delivery systems. Other modeling approaches have employed parameters relying on obstructive effects, requiring characterization of the structure and mesh size of the polymer matrix, while leaving out relevant effects from intermolecular forces [62]. The shortcomings of these approaches demonstrate the challenge in predicting accurate effective diffusion coefficients from measurable inputs.
In order to overcome modeling challenges and enhance the predictive potential of the diffusion-erosion model, a machine learning approach was employed to estimate effective diffusion coefficients of drugs through Ace-DEX NPs. Due to its utility in pattern recognition, a NN model was developed with inputs and outputs from all 22 of the previously discussed release curves from Ace-DEX NPs (Supplemental Fig. 14A, Supplemental Table 7). The final NN demonstrates low in the training, validation, and test data, indicating strong performance across the available data (Supplemental Fig. 14B). To avoid overfitting the training data upon indefinitely repeated training loops, the best performance on the validation data was used as a stopping point, occurring at epoch 42 (Supplemental Fig. 14C). From the resulting NN, the predicted effective diffusion coefficients were comparable to the actual effective diffusion coefficients estimated from fitting the 22 release curves. Indeed, the regression between the predicted versus actual outputs was approximate to the ideal case (Supplemental Fig. 14D).
To assess the utility of the NN, effective diffusion coefficients were predicted for DXM and cGAMP release from 20, 40, and 60 CAC Ace-DEX NPs at pH 7.4 (Supplemental Table 8). The predicted effective diffusion coefficients were inputted into the diffusion-erosion model along with empirically determined parameters based on characterization (Supplemental Table 1). The model output demonstrated distinct DXM and cGAMP release curves at each CAC and appeared to accurately fit the experimental release data (Fig. 6A–B). At each CAC, the predicted model achieved significant () high to very high correlation to the experimental release data (Supplemental Table 2). Furthermore, the plot of residuals demonstrates good fit of the predicted model, though some early error is observed for select curves, (Fig. 6A–B), likely due to higher burst release. The correlation between the predicted and actual effective diffusion coefficients is very high based on the Pearson's coefficient, and for the 4 release curves from 40 and 60 CAC NPs, the effective diffusion coefficient predictions appear nearly ideal (Fig. 6C, Supplemental Table 8). Overall, the NN predictions applied to the diffusion-erosion model were able to accurately describe DXM and cGAMP release from Ace-DEX NPs in vitro.
Fig. 6.
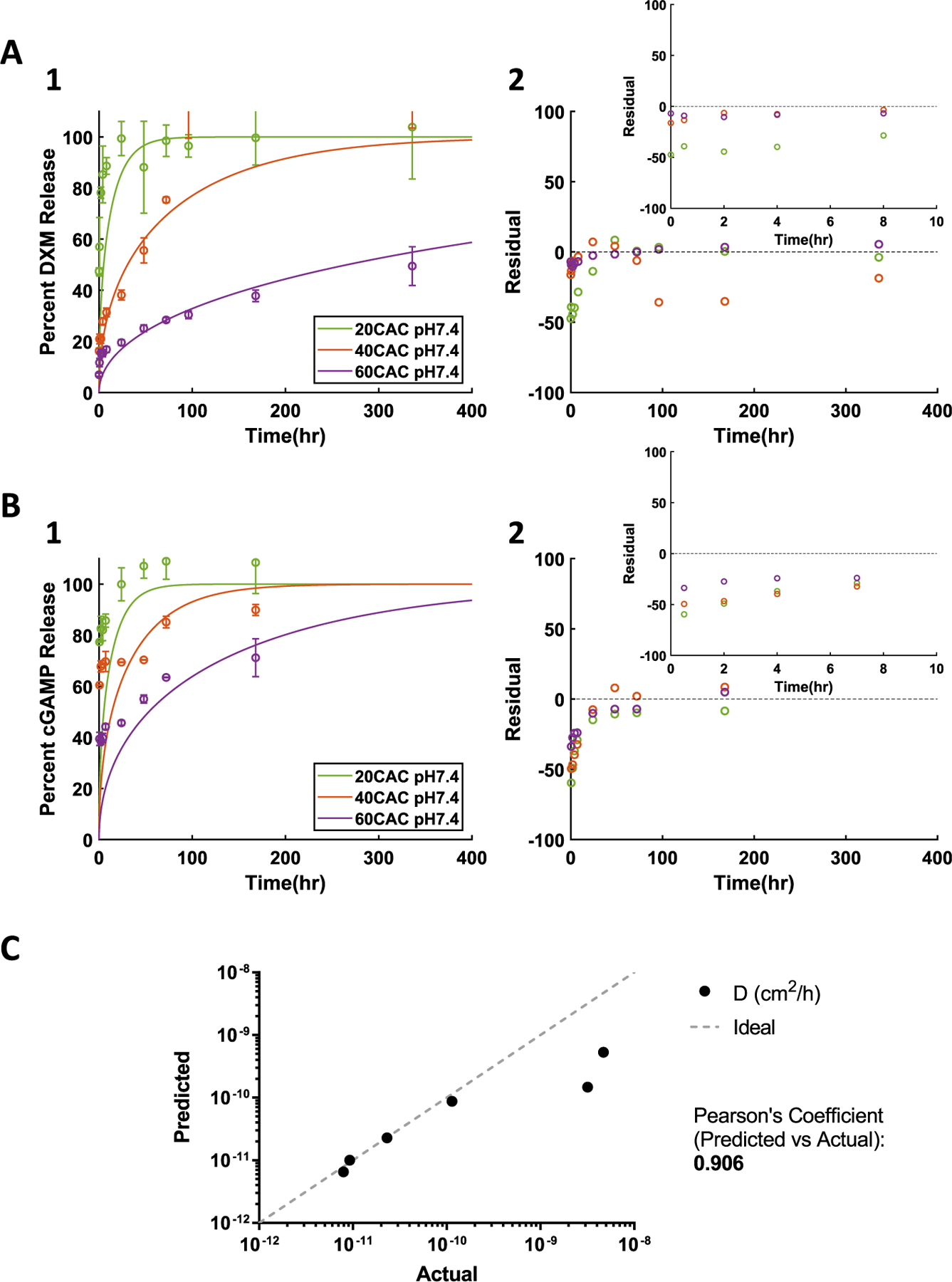
Application of NN to predict drug release from Ace-DEX NPs containing A) DXM or B) cGAMP. 1) Release experimental results (data points and error bars) and model simulations (lines) with NN predicted D parameter values. 2) Residual plot. C) Predicted vs actual (curve fit) effective diffusion coefficients. The “Ideal” line represents a perfect prediction where predicted = actual.
To further evaluate the NN results, the predicted output from the diffusion-erosion model was compared to curve fittings of alternate models (Supplemental Fig. 15–16). Compared to these ideal fits, the predicted output from the diffusion-erosion model largely outperformed the zero order, first order, Higuchi, and Hixson-Crowell models based on and differences (Supplemental Fig. 15G, 16G). The predictive diffusion-erosion model also outperformed the Korsmeyer-Peppas curve fit for DXM, but it did not for cGAMP (Supplemental Fig. 15G, 16G). Of note, cGAMP is far more hydrophilic than any of the other cargoes evaluated herein (Table 2), yet the NN prediction resulted in sufficient model fits for this cargo. Accuracy of the effective diffusion coefficient predictions for hydrophilic cargoes may be further improved with additional training of the NN as more release data becomes available. Overall, the predictive diffusion-erosion model largely outperformed the ideal curve fits of alternate standard drug release models.
Though the utility and accuracy of the NN and diffusion-erosion model can be further increased as more drug release data becomes evaluated, the work described herein highlights the predictive potential of the diffusion-erosion model and fulfills a necessary step towards optimizing the controlled release of therapeutics from future Ace-DEX formulations. Future models can build upon the diffusion-erosion model developed herein to explore the roles of alternate degradation assumptions, drug-drug interactions, crystallization, drug-polymer interactions, and more. Additionally, future work is planned to apply the diffusion-erosion model to in vivo drug release and additional geometries of Ace-DEX drug delivery systems.
4. Conclusion
This work describes the first report of mathematical modeling applied to Ace-DEX drug delivery systems. Upon evaluating the degradation mechanism of Ace-DEX NPs, the diffusion-erosion model was developed to fit a variety of drug release curves from surface eroding NPs. Relatively fast-degrading 20:80 poly(CPP:SA) NPs were loaded with 1% and 5% wt/wt R-848. Ace-DEX NPs were made with varied degradation rates based on polymer CAC, achieving fast, medium, and slow degrading acid sensitive polymer at 20, 40, and 60 CAC, respectively. Varied CAC NPs were successfully loaded with two different concentrations of PTX as well as 1% wt/wt Rapa, R-848, DXR, or DXM. In addition to evaluating drug release from NPs with varied polymer, loading, and drug cargo, drug release from Ace-DEX NPs was evaluated at both neutral and acidic pH. Across all conditions, the diffusion-erosion model was able to accurately fit drug release data. When compared to five of the most common drug release models applied to Ace-DEX NPs, the diffusion-erosion model outperformed the zero order, Higuchi, and Hixson-Crowell models for all conditions and outperformed the first order model at neutral pH. The diffusion-erosion model fit the drug release curves comparably to the Korsmeyer-Peppas model; however, the diffusion-erosion model had higher predictive potential. Subsequently, a NN model was developed from PTX, Rapa, R-848, and DXR release data in order to predict effective diffusion coefficients for DXM release. With the addition of the NN, the diffusion-erosion model was able to successfully predict DXM and cGAMP release curves from varied CAC Ace-DEX NPs. These results are encouraging for the diffusion-erosion model. Further work may result in applications in vivo and aid in the optimization of drug delivery from future Ace-DEX formulations.
Supplementary Material
Acknowledgements
This work was funded by the following: National Academies of Science Engineering and Medicine Ford Foundation Pre-Doctoral Fellowship, NIH NIAID R01AI141333, NIH NIAID T32AI007273, and NIH NIAID R01AI137525. This work was also supported in part by the University of North Carolina Summer of Learning and Research (UNC SOLAR) Program. The authors would like to acknowledge Dr. Guari Rao (Division of Pharmacotherapy and Experimental Therapeutics, Eshelman School of Pharmacy, University of North Carolina at Chapel Hill, USA) for advisement during the UNC SOLAR Program. SEM micrographs were performed at the Chapel Hill Analytical and Nanofabrication Laboratory, CHANL, a member of the North Carolina Research Triangle Nanotechnology Network, RTNN, which is supported by the National Science Foundation, Grant ECCS-1542015, as part of the National Nanotechnology Coordinated Infrastructure, NNCI. Figures were made with BioRender.
Footnotes
Declaration of Competing Interest
Drs. Ainslie and Bachelder serve on the advisory board for IMMvention Therapeutix, Inc. Although a financial conflict of interest was identified for management based on the overall scope of the project and its potential benefit to IMMvention Therapeutix, Inc., the research findings included in this publication may not necessarily be related to the interests of IMMvention Therapeutix, Inc.
Appendix A. Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jconrel.2022.09.067.
Data availability
Data will be made available on request.
References
- [1].Amreddy N, Babu A, Muralidharan R, Panneerselvam J, Srivastava A, Ahmed R, Mehta M, Unshi A, Ramesh R, Recent advances in nanoparticle-based cancer drug and gene delivery, Adv. Cancer Res 137 (2018) 115–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Riley R, June C, Langer R, Mitchell M, Delivery technologies for cancer immunotherapy, Nat. Rev. Drug Discov 18 (2019) 175–196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Martin J, Cabral H, Stylianopoulos T, Jain R, Improving cancer immunotherapy using nanomedicines: progress, opportunities and challenges, Nat. Rev. Clin. Oncol 17 (2020) 251–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Wadhwa A, Aljabbari A, Lokras A, Foged C, Thakur A, Opportunities and challenges in the delivery of mRNA-based vaccines, Pharmaceutics 12 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Pati R, Shevtsov M, Sonawane A, Nanoparticle vaccines against infectious diseases, Front. Immunol 9 (2018) 2224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Pearson R, Podojil J, Shea L, King K, Miller S, Getts D, Overcoming challenges in treating autoimmuntity: development of tolerogenic immune-modifying nanoparticles, Nanomedicine 18 (2019) 282–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Singh A, Biswas A, Shukla A, Maiti P, Targeted therapy in chronic diseases using nanomaterial-based drug delivery vehicles, Nat.: Sig. Transduct. Target. Therapy 4 (2019), 33 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Makadia H, Siegel S, Poly lactic-co-glycolic acid (PLGA) as biodegradable controlled drug delivery carrier, Polymers 3 (2011) 1377–1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Siepmann J, Elkharraz K, Siepmann F, Klose D, How autocatalysis accelerates drug release from PLGA-based microparticles: a quantitative treatment, Biomacromolecules 6 (2005) 2312–2319. [DOI] [PubMed] [Google Scholar]
- [10].Broaders K, Cohen J, Beaudette T, Bachelder E, Frechet J, Acetalated dextran is a chemically and biologically tunable material for particulate immunotherapy, Proc. Natl. Acad. Sci. U. S. A 106 (2009) 5497–5502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Graham-Gurysh E, Moore K, Schorzman A, Lee T, Zamboni W, Hingtgen S, Bachelder E, Ainslie K, Tumor responsive and tunable polymeric platform for optimized delivery of paclitaxel to treat glioblastoma, ACS Appl. Mater. Interfaces 12 (2020) 19345–19356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].You S, Yang Z, Wang C-H, Toward understanding drug release from biodegradable polymer microspheres of different erosion kinetics modes, J. Pharm. Sci 105 (6) (2016) 1934–1946. [DOI] [PubMed] [Google Scholar]
- [13].Lee W-C, Chu I-M, Preparation and degradation behavior of polyanhydrides nanoparticles, J Biomed Mater Res B Appl Biomater 84 (1) (2008) 138–146. [DOI] [PubMed] [Google Scholar]
- [14].Chu I-M, Liu T-H, Chen Y-R, Preparation and characterization of sustained release system based on polyanhydride microspheres with core/shell-like structures, J. Polym. Res 26 (2018), 1 (2019). [Google Scholar]
- [15].Snyder B, Mohammed H, Samways D, Shipp D, Drug delivery and drug efficacy from amorphous poly(thioether anhydrides), Macromol. Biosci 20 (5) (2020) e1900377. [DOI] [PubMed] [Google Scholar]
- [16].Jain J, Chitkara D, Kumar N, Polyanhydrides as Localized Drug Delivery Carrier (an update), 2008. [DOI] [PubMed]
- [17].Kanthamneni N, Sharma S, Meenach S, Billet B, Zhao J-C, Bachelder E, Ainslie K, Enhanced stability of horseradish peroxidase encapsulated in acetalated dextran microparticles stored outside cold chain conditions, Int. J. Pharm 431 (1–2) (2012) 101–110. [DOI] [PubMed] [Google Scholar]
- [18].Kauffman K, Do C, Sharma S, Gallovic M, Bachelder E, Ainslie K, Synthesis and characterization of acetalated dextran polymer and microparticles with ethanol as a degradation product, ACS Appl. Mater. Interfaces 4 (2012) 4149–4155. [DOI] [PubMed] [Google Scholar]
- [19].Chen N, Collier M, Gallovic M, Collins G, Sanchez C, Fernandes E, Bachelder E, Ainslie K, Degradation of acetalated dextran can be broadly tuned based on cyclic acetal coverage and molecular weight, Int. J. Pharm 512 (2016) 147–157. [DOI] [PubMed] [Google Scholar]
- [20].Bachelder E, Pino E, Ainslie K, Acetalated dextran: a tunable and acid-labile biopolymer with facile synthesis and a range of applications, Chem. Rev 117 (2017) 1915–1926. [DOI] [PubMed] [Google Scholar]
- [21].Chen N, Gallovic MD, Tiet P, Ting JP, Ainslie KM, Bachelder EM, Investigation of tunable acetalated dextran microparticle platform to optimize M2e-based influenza vaccine efficacy, J. Control. Release 289 (2018) 114–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Chen N, Johnson MM, Collier MA, Gallovic MD, Bachelder EM, Ainslie KM, Tunable degradation of acetalated dextran microparticles enables controlled vaccine adjuvant and antigen delivery to modulate adaptive immune responses, J. Control. Release 273 (2018) 147–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Hines D, Kaplan D, Poly (lactic-co-glycolic acid) controlled release systems: experimental and modeling insights, Crit. Rev. Ther. Drug Carrier Syst 30 (3) (2013) 257–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Ford Versypt A, Pack D, Braatz R, Mathematical modeling of drug delivery from autocatalytically degradable PLGA microspheres — A review, J. Control. Release 165 (2013) 29–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].D’Aurizio E, Sozio P, Cerasa L, Vacca M, Brunetti L, Orlando G, Chiavaroli A, Kok R, Hennink W, Di Stefano A, Biodegradable microspheres loaded with an anti-Parkinson prodrug: an in vivo pharmacokinetic study, Mol. Pharm 8 (2011) 2408–2415. [DOI] [PubMed] [Google Scholar]
- [26].Mohapatra S, Kar R, Sahoo S, Goodness of fit model dependent approaches of controlled release matrix tablets of zidovudine, Indian J. Pharmac. Educ. Res 50 (2016). [Google Scholar]
- [27].Gouda R, Baishya H, Qing Z, Application of mathematical models in drug release kinetics of carbidopa and levodopa ER tablets, J. Develop. Drugs 6 (2017). [Google Scholar]
- [28].Varma M, Kaushal A, Garg A, Garg S, Factors affecting mechanism and kinetics of drug release from matrix-based oral controlled drug delivery systems, Healthc. Technol. Rev 2 (2004) 43–57. American Journal of Drug Delivery. [Google Scholar]
- [29].Cerea M, Foppoli A, Palugan L, Melocchi A, Zema L, Maroni A, Gazzaniga A, Non-uniform drug distribution matrix system (NUDDMat) for zero-order release of drugs with different solubility, Int. J. Pharm 581 (2020) 119217. [DOI] [PubMed] [Google Scholar]
- [30].Zhao Y, Gu J, Jia S, Guan Y, Zhang Y, Zero-order release of polyphenolic drugs from dynamic, hydrogen-bonded LBL films, Soft Matter 12 (2016) 1085–1092. [DOI] [PubMed] [Google Scholar]
- [31].Zhang W, Wang X, Wang J, Zhang L, Drugs adsorption and release behavior of collagen/bacterial cellulose porous microspheres, Int. J. Biol. Macromol 140 (2019) 196–205. [DOI] [PubMed] [Google Scholar]
- [32].Ritger P, Peppas N, A simple equation for description of solute release I. Fickian and non-fickian release from non-swellable devices in the form of slabs, spheres, cylinders or discs, J. Control. Release 5 (1987) 23–26. [PubMed] [Google Scholar]
- [33].Peppas N, Narasimhan B, Mathematical models in drug delivery: how modeling has shaped the way we design new drug delivery systems, J. Control. Release 190 (2014) 75–81. [DOI] [PubMed] [Google Scholar]
- [34].Siepmann J, Peppas N, Higuchi equation: derivation, applications, use and misuse, Int. J. Pharm 418 (2011) 6–12. [DOI] [PubMed] [Google Scholar]
- [35].Jahromi L, Ghazali M, Ashrafi H, Azadi A, A comparison of models for the analysis of the kinetics of drug release from PLGA-based nanoparticles, Heliyon 6 (2) (2020) e03451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Hixson A, Crowell J, Dependence of Reaction Velocity upon Surface and Agitation, ACS Publications, 1931.
- [37].Varshosaz J, Hajian M, Characterization of drug release and diffusion mechanism through Hydroxyethylmethacrylate/methacrylic acid pH-sensitive hydrogel, Drug Deliv 11 (2008) 53–58. [DOI] [PubMed] [Google Scholar]
- [38].Liu C, Quan P, Fang L, Effect of drug physicochemical properties on drug release and their relationship with drug skin permeation behaviors in hydroxyl pressure sensitive adhesive, Eur. J. Pharm. Sci 93 (2016) 437–446. [DOI] [PubMed] [Google Scholar]
- [39].Geraili A, Mequanint K, Systematic studies on surface Erosion of Photocrosslinked Polyanhydride tablets and data correlation with release kinetic models, Polymers (Basel) 12 (5) (2020) 1105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Park E-S, Maniar M, Shah J, Biodegradable polyanhydride devices of cefazolin sodium, bupivacaine, and taxol for local drug delivery: preparation, and kinetics and mechanism of in vitro release, JCR 52 (1–2) (1998) 179–189. [DOI] [PubMed] [Google Scholar]
- [41].Kipper M, Shen E, Determan A, Narasimhan B, Design of an injectable system based on bioerodible polyanhydride microspheres for sustained drug delivery, Biomaterials 23 (22) (2002) 4405–4412. [DOI] [PubMed] [Google Scholar]
- [42].Chen N, Kroger C, Tisch R, Bachelder E, Ainslie K, Prevention of type 1 diabetes with Acetalated dextran microparticles containing rapamycin and pancreatic peptide P31, Adv. Healthc. Mater 7 (18) (2018) e1800341. [DOI] [PubMed] [Google Scholar]
- [43].Chen N, Peine K, Collier M, Gautam S, Jablonski K, Guerau-de-Arellano M, Ainslie K, Bachelder E, Co-delivery of disease associated peptide and rapamycin via acetalated dextran microparticles for treatment of multiple sclerosis, Adv. Biosyst 1 (2017). [Google Scholar]
- [44].Collier M, Junkins R, Gallovic M, Johnson B, Johnson M, Macintyre A, Sempowski G, Bachelder E, Ting J, Ainslie K, Acetalated dextran microparticles for codelivery of STING and TLR7/8 agonists, Mol. Pharm 15 (2018) 4933–4946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Graham-Gurysh E, Moore K, Satterlee A, Sheets K, Lin F, Bachelder E, Miller C, Hingtgen S, Ainslie K, Sustained delivery of doxorubicin via acetalated dextran scaffold prevents glioblastoma recurrence after surgical resection, Mol. Pharm 15 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Peine K, Guerau-de-Arellano M, Lee P, Kanthamneni N, Severin M, Probst G, Peng H, Yang Y, Vangundy Z, Papenfuss T, Lovett-Racke A, Bachelder E, Ainslie K, Treatment of experimental autoimmune encephalomyelitis by codelivery of disease associated peptide and dexamethasone in acetalated dextran microparticles, Mol. Pharm 11 (2014) 828–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Chen N, Gallovic M, Tiet P, Ting J, Ainslie K, Bachelder E, Investigation of tunable acetalated dextran microparticle platform to optimize M2e-based influenza vaccine efficacy, J. Control. Release 289 (2018) 114–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Domb A, Langer R, Polyanhydrides. I. Preparation of high molecular weight polyanhydrides, J. Polym. Sci. A Polym. Chem 25 (12) (1987) 3337–3386. [Google Scholar]
- [49].Crank J, The Mathematics of Diffusion, Clarendon Press, Oxford, 1975. [Google Scholar]
- [50].Lucero-Acuna A, Gutierrez-Valenzuela C, Esquivel R, Guzman-Zamudio R, Mathematical modeling and parametrical analysis of the temperature dependency of control drug release from biodegradable nanoparticles, RSC Adv 9 (2019) 8728–8739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Lucero-Acuna A, Guzman R, Nanoparticle encapsulation and controlled release of a hydrophobic kinase inhibitor: three stage mathematical modeling and parametric analysis, Int. J. Pharm 494 (1) (2015) 249–257. [DOI] [PubMed] [Google Scholar]
- [52].Zhang M, Yang Z, Chow L, Wang C, Simulation of drug release from biodegradable polymeric microspheres with bulk and surface erosions, J. Pharm. Sci 92 (2003) 2040–2056. [DOI] [PubMed] [Google Scholar]
- [53].Casalini T, Rossi F, Lazzari S, Perale G, Masi M, Mathematical modeling of PLGA microparticles: from polymer degradation to drug release, Mol. Pharm 11 (2014) 4036–4048. [DOI] [PubMed] [Google Scholar]
- [54].Rodrigues de Azevedo C, Von Stosch M, Costa M, Ramos A, Cardoso M, Danhier F, Preat V, Oliveira R, Modeling of the burst release from PLGA micro- and nanoparticles as function of physicochemical parameters and formulation characteristics, Int. J. Pharm 532 (2017) 229–240. [DOI] [PubMed] [Google Scholar]
- [55].Bhattacharjee S, Understanding the burst release phenomenon: toward designing effective nanoparticulate drug-delivery systems, Ther. Deliv 12 (1) (2020) 21–36. [DOI] [PubMed] [Google Scholar]
- [56].Hoare T, Kohane D, Hydrogels in drug delivery: progress and challenges, Polymer 49 (2008) 1993–2007. [Google Scholar]
- [57].Gao Y, Zuo J, Bou-Chacra N, Pinto T, Clas S, Walker R, Lobenberg R, In vitro release kinetics of antituberculosis drugs from nanoparticles assessed using a modified dissolution apparatus, Biomed. Res. Int 2013 (2013), 136590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Lisik A, Musial W, Conductomeric evaluation of the release kinetics of active substances from pharmaceutical preparations containing Iron ions, Materials (Basel) 12 (2019) 730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Wu I, Bala S, Skalko-Basnet N, Pio di Cagno M, Interpreting non-linear drug diffusion data: utilizing Korsmeyer-Peppas model to study drug release from liposomes, Eur. J. Pharm. Sci 138 (2019). [DOI] [PubMed] [Google Scholar]
- [60].Chaparro F, Presley K, Coutinho da Silva M, Lannutti J, Sintered electrospun polycaprolactone for controlled model drug delivery, Mater. Sci. Eng. C 99 (2019) 112–120. [DOI] [PubMed] [Google Scholar]
- [61].Gautieri A, Vesentini S, Redaelli A, How to predict diffusion of medium-sized molecules in polymer matrices. From atomistic to coarse grain simulations, J. Mol. Model 16 (12) (2010) 1845–1851. [DOI] [PubMed] [Google Scholar]
- [62].Hadjiev N, Amsden B, An assessment of the ability of the obstruction-scaling model to estimate solute diffusion coefficients in hydrogels, J. Control. Release 199 (2015) 10–16. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be made available on request.


