Carbon–cement supercapacitors as a scalable bulk energy storage solution

Significance

The extent and pace of the transition from our current fossil fuel-based economy to one based on renewable energy will strongly depend on the availability of bulk energy storage solutions. Herein, we investigate one such candidate technology, using chemical precursors which are inexpensive, abundant, and widely available, specifically cement, water, and carbon black. The energy storage capacity of these carbon-cement supercapacitors is shown to be an intensive quantity, and their high rate capability exhibits self-similarity. These properties point to the opportunity for employing these structural concrete-like supercapacitors for bulk energy storage in both residential and industrial applications ranging from energy autarkic shelters and self-charging roads for electric vehicles, to intermittent energy storage for wind turbines.

Abstract

The large-scale implementation of renewable energy systems necessitates the development of energy storage solutions to effectively manage imbalances between energy supply and demand. Herein, we investigate such a scalable material solution for energy storage in supercapacitors constructed from readily available material precursors that can be locally sourced from virtually anywhere on the planet, namely cement, water, and carbon black. We characterize our carbon-cement electrodes by combining correlative EDS–Raman spectroscopy with capacitance measurements derived from cyclic voltammetry and galvanostatic charge-discharge experiments using integer and fractional derivatives to correct for rate and current intensity effects. Texture analysis reveals that the hydration reactions of cement in the presence of carbon generate a fractal-like electron-conducting carbon network that permeates the load-bearing cement-based matrix. The energy storage capacity of this space-filling carbon black network of the high specific surface area accessible to charge storage is shown to be an intensive quantity, whereas the high-rate capability of the carbon-cement electrodes exhibits self-similarity due to the hydration porosity available for charge transport. This intensive and self-similar nature of energy storage and rate capability represents an opportunity for mass scaling from electrode to structural scales. The availability, versatility, and scalability of these carbon-cement supercapacitors opens a horizon for the design of multifunctional structures that leverage high energy storage capacity, high-rate charge/discharge capabilities, and structural strength for sustainable residential and industrial applications ranging from energy autarkic shelters and self-charging roads for electric vehicles, to intermittent energy storage for wind turbines and tidal power stations.

The successful large-scale transition from a fossil fuel-based economy to one based on renewable energy hinges on the widespread availability of energy storage solutions (1, 2). In fact, in contrast to fossil fuel energy, for which energy source and carrier coincide, the production of electrical energy from renewable sources such as sun, wind, and tidal waves at one time for use at a later one requires energy storage to reduce imbalances between energy demand and energy production. Unfortunately, the scarcity of mineral precursors used in current battery technologies defies mass scalability for energy storage (3–6), and motivates us to look into alternative material solutions for bulk supercapacitors using inexpensive and readily available material precursors that can be locally sourced at a global scale.

To approach this challenge, we focused on the world’s two most consumed materials, water and cement, which we then doped with a relatively low concentration of disordered microporous carbon black to produce high-rate capability supercapacitors. In contrast to batteries, which involve chemical energy conversion for energy storage, supercapacitors rely on storage of electrical charge on high specific surface area electron-conducting materials, such as porous carbons (7). In these systems, the charge is transported via an electrolyte to the storage sites and can be recovered by changes in the potential difference between the electrodes. More specifically, high-rate capability supercapacitors rely on three critical elements (8, 9): i) an electron-conductive network for charging the electrodes; ii) a storage porosity of high specific surface area onto which an oppositely charged surface layer adsorbs; and iii) a reservoir porosity for charge transport by ion-diffusion through a saturating electrolyte to or away from the surface layer. Herein, we argue that carbon-doped cement composites naturally combine these three attributes by leveraging the synergy between the hydration of hydrophilic cement in the presence of hydrophobic carbon black. This synergy makes our materials good candidates for bulk energy storage for residential and industrial applications. Moreover, we expect that the benefits of such structural capacitor elements in electrical energy storage systems could help offset the significant environmental footprint of cement production, which currently accounts for ca. 8% of global CO₂ emissions (10, 11).

Our material design departs from previous investigations of the electrical conductivity of carbon-cement composites and their resistive heating potential (Joule effect) (15–17), which was attributed to the development of a carbon network at a percolation threshold of a mere 3 to 4 Vol% (17). For our supercapacitors, this percolated carbon network likely results from a competition between particle aggregation of hydrophobic carbon black (18–20), and water demand by the hydration reactions of hydrophilic cement, which we explain as follows: The hydration of anhydrous clinker dissolves calcium oxide, freeing calcium ions to react with water to form various cement hydration products (Fig. 1B). In our carbon-cement composites, the short-range aggregation of nonpolar carbon black occurs via attractive Van der Waals interactions (18) as the ionic strength of free calcium ions (20) is reduced via hydration reactions in the high pH cement environment (19). We propose that this disaggregation of carbon black particles leads to the formation of an electron-conductive network composed of high specific surface area carbon black that can be directly leveraged for electrode charging. It is important to note, however, that electron conductivity alone, while important, is not sufficient to develop energy storage capabilities, since supercapacitors also require a reservoir or interparticle porosity for ion diffusion (8, 21). We therefore surmise that the hydration reactions hold the key to generating this reservoir porosity. These assumptions are based on the characteristic stoichiometry of the hydration reactions (22–24), which limits the maximum amount of water that can be chemically bound into calcium hydroxide (CH) and calcium-silica-hydrates (C-S-H), (24), and adsorbed onto the surface of C-S-H nanoparticles (23). Therefore, water in excess of this stoichiometric water limit (typically 42% in mass of cement) can lead to the formation of the micrometer/submicrometer-sized hydration porosity (22), which could in turn function as a template for the reservoir porosity of the saturating electrolyte, thus enabling the creation of a high-rate capability supercapacitor.

Fig. 1.

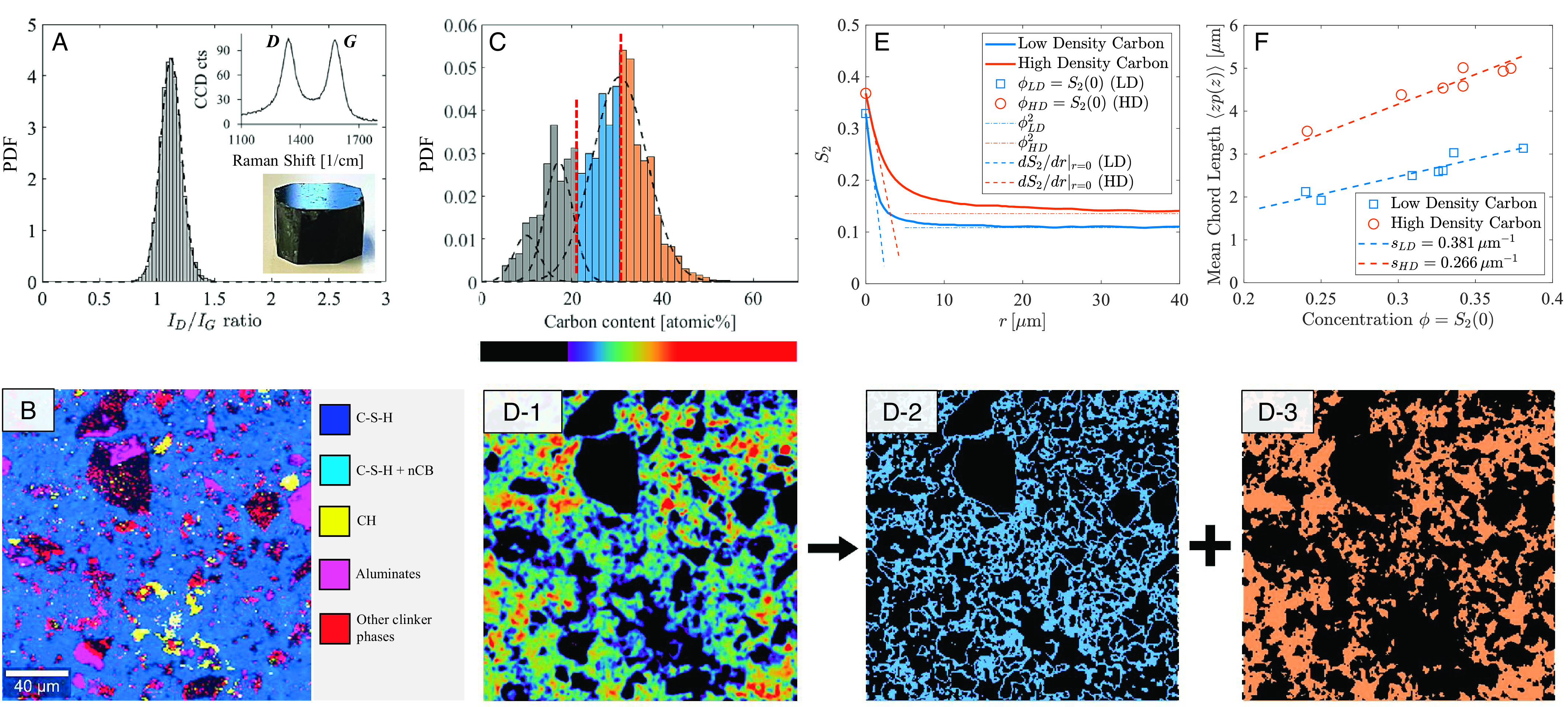
Correlative EDS–Raman Spectroscopy analysis: (A) Raman carbon intensity ratios I_D/I_G obtained from a 200 × 200 μm region of a carbon-cement sample [PBX55 (12), W/C=0.42, nCB/C=0.101; SI Appendix]. The inset displays the D and G bands of the carbon black (PBX55) powder associated, respectively, with defects in the C–C lattice structure, and the graphitized carbon structure, which allows us to distinguish carbon black particles from background carbon products resulting from cement carbonation. (B) Raman map from a polished section with their constituent major phases indicated. (C) Deconvolution of carbon content (in atomic %) from EDS mapping data identifies three distinct phases: the low carbon content phase (in gray) is background carbon which is also found in the control cement samples, whereas the dominating phase (in blue and orange) is correlated to the I_D/I_G ratio (shown in A). (D-1) By deconstructing our EDS data, we can subsequently map the distributions of (D-2) A low-density carbon phase (below mean value in C, blue bars), and (D-3) A high-density carbon phase (above mean value in C, orange bars). (E) The two-point correlation function, S₂(r = |r_i − r_j|) = ⟨I(r_i)I(r_j)⟩ (with I(r_j) the indicator function, I(r_j)=1 if r_j ∈ V_k, k = LD, HD, else I(r_j)=0), of the two phases permits determination of phase concentration, ϕ = S₂(0), mean chord length, ℓ = ⟨zp(z)⟩ = −S₂(0)/S₂′(0) (with p(z) the chord length probability distribution, and S₂′(0)=dS₂/dr|_r = 0 the slope of S₂(r) at r = 0 shown in the figure), and specific surface area, s = −πS₂′(0) of low- and high-density carbon phase. (F) Applied to seven samples of different mix design and carbon black constituents (12–14), a linear scaling of mean chord length with phase concentration is indicative of a unique specific (texture) surface of low- and high- density carbon phase, s_i = πϕ_i/ℓ_i, for i = LD, HD.

To test these material design hypotheses, we synthesized a representative set of electrode samples with different mix proportions (water, cement, carbon black), different types of carbon black with different specific surface areas (12–14), and different electrode thicknesses (SI Appendix, section SI-1). Using a correlative EDS–Raman spectroscopy-based approach, we visualized for the first time the texture of the carbon network in our electrodes, and spatially resolved carbon content and intensity from its Raman spectra, to perform spatial correlation analysis (SI Appendix, section SI-2). We further combined this texture analysis with cyclic voltammetry (CV) and galvanostatic charge-discharge (GCD) cycles to derive the capacitance properties of the electrodes and quantified the maximum amount of energy that can be stored in the electrodes (SI Appendix, section SI-3). Finally, by means of dimensional analysis, we show that the so-obtained capacitance of our materials can be reduced to an intensive quantity which exhausts the storage capacity of the high specific surface area carbon black (SI Appendix, section SI-4). Based on these observations, we argue that this intensive nature is the key to scaling our bulk electrode solutions to structural residential and industrial applications for massive bulk energy storage.

Results

Correlative EDS–Raman Mapping and Spatial Correlations.

We start with a quantitative assessment of the texture of the percolated network of carbon particles. This is a challenging task since carbon is always present in cement pastes due to the carbonation of cement hydration products from exposure to atmospheric CO₂ during sample preparation or after casting (see comparison with reference cement sample in SI Appendix, section SI-2). We address this challenge by using recently developed correlative EDS–Raman techniques (25, 26) which can be used to effectively distinguish different carbon phases. To gain insight into the carbon texture, we spatially resolved the carbon black by the Raman peak intensity ratio, I_D/I_G (Fig. 1 A and B), using the characteristic D- and G-bands (Inset of Fig. 1A), which can distinguish carbon black from other carbon-containing compounds in the sample (Fig. 1C). The fact that the in situ Raman intensity ratio, I_D/I_G, matches the one of the pure carbon black powder (inset of Fig. 1A) provides clear evidence of the nonreactivity of carbon black in the alkaline environment of cement-based materials. After background removal (SI Appendix, section SI-2), this Raman-enabled phase identification permits the mapping of the carbon intensity distribution obtained by high-vacuum EDS (Fig. 1C and D-1 ) into low-density (Fig. 1 D-2) and high-density carbon phases (Fig. 1 D-3). In order to quantify concentration, size, and surface area of the space-filling texture, we applied correlation analysis to the low- and high-density carbon phases using a two-point correlation function, S₂(r), which gives the probability of finding two points at a distance r = |r₁ − r₂| in one of the phases, and which has been widely applied to characterize and reconstruct random heterogeneous microstructures (27–29). More specifically, from the exponential decay of S₂(r) from the initial value, corresponding to the phase concentration ϕ = S₂(r = 0), to its asymptotic value, S₂(∞)=ϕ² (Fig. 1E), we determine the mean chord length, ℓ = −ϕ/S₂′(0) with S₂′(0) the slope of S₂(r) at r = 0, which reflects the effective size of the particles, and the specific surface area, s = πϕ/ℓ (27, 30). We applied this procedure to seven samples of different mix designs, different carbon black type and concentration, and found a linear scaling of mean chord length and volumetric concentration, ℓ_i = πϕ_i/s_i, of 2–3 μm for the low-density carbon phase, and 3–5 μm for the high-density phase (Fig. 1F). These values are well above the pixel resolution of ∼0.5 μm, and hence significant as texture properties at the micrometer scale of the investigated electrode materials (for a detailed discussion, see SI Appendix, section SI-2). Moreover, in contrast to the chord length measurements, the specific surface area (derived from the linear scaling) is the same for all samples, s_LD = 0.381 μm⁻¹ and s_HD = 0.266 μm⁻¹. This finding is significant for two reasons: First, these specific surface area values relate to the texture of the percolated carbon phase in the carbon-cement composite and are quite distinct from the specific surface area of the employed carbon black powders in the samples, ranging from ϕ_Cρ_CS_BET=7–9 μm⁻¹ for samples prepared with PBX 55 (12), to ϕ_Cρ_CS_BET = 32 μm⁻¹ for Vulcan carbon black (13), and ϕ_Cρ_CS_BET = 93 μm⁻¹ for Ketjen carbon black (14), with ϕ_Cρ_C the experimentally deduced mass density of carbon black in the composite materials, and S_BET the specific surface of the carbon black determined independently by gas adsorption measurements and application of the B.E.T. method (SI Appendix, section SI-1). This difference in the measured specific surface area of both the texture and the nanocarbon black particles is indicative of the multiscale nature of the carbon network. These observations suggest that texture patterns at the micrometer scale mediate the charge transfer from the electrolyte to the storage porosity in the carbon particles in the subnanometer range (SI Appendix, section SI-1). Second, this unique texture provides strong evidence that the carbon black particles develop a characteristic template, independent of mix proportions and the type of carbon black. That is, the texture-specific surface areas of the low- and high-density carbon networks are intrinsic texture properties of carbon-cement composites. While more advanced investigation methods are required to fully resolve the origin of this intrinsic texture, a good candidate to explain this observation is the disaggregation of carbon black particles by calcium ion and water consumption in the high pH-environment that occurs during cement hydration (18–20).

Capacitance Measurements and Analysis.

The second pillar of our investigation is the capacitance measurements. Building upon conventional electrochemical cyclic voltammetry (CV) and galvanostatic charge-discharge (GCD) cycles applied to supercapacitor devices (32–37), measurements were carried out with an electric double layer capacitor (EDLC) system, which hosted two carbon-cement electrodes of thickness d, saturated by an electrolyte (1M KCl), and separated by an insulator (Fig. 2A, 1–4). With our overall focus on scaling the energy storage capacity, we were interested in experimentally assessing the maximum energy storage capacity of our electrodes, by combining CV test results with GCD test results. More specifically, in a CV test, the electrodes are connected to an outside potential difference, U, charging one electrode with a positive charge, and the other with a negative charge, while current I is measured (Figs. 2 B-1, and B-2). A cyclic voltage scan rate, u = U₀/t₀, is applied to a maximum voltage of U₀ = 1 V, in order to limit Faradeic effects related to water-splitting in the aqueous-based electrolytes at a theoretical value of 1.23 V (38). In contrast, in a GCD test, a current, I₀, is applied and maintained constant in time until a target voltage, U(t = t₀)=1 V, is attained, at which state the current is instantaneously reversed until the potential difference is zero, U(t = t₀ + t_d)=0 (Fig. 2C-1).

Fig. 2.

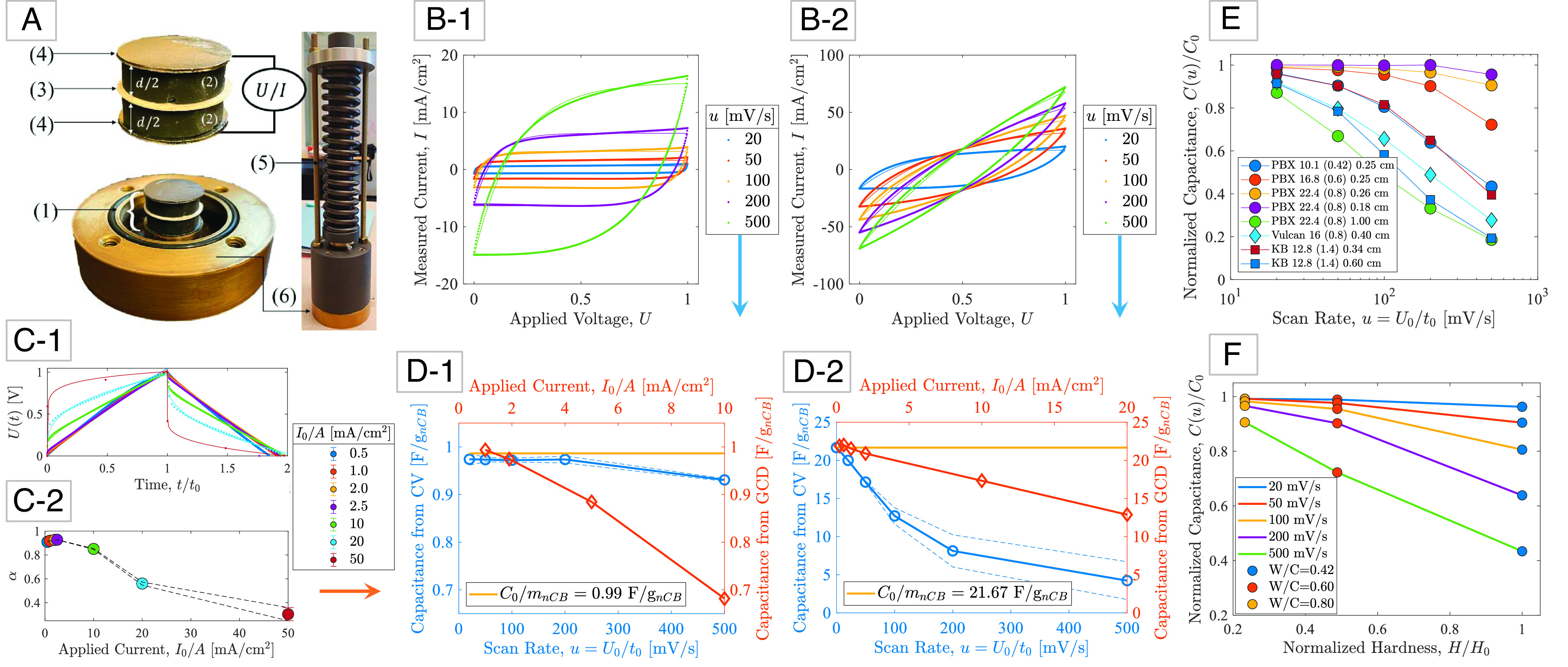
Capacitance measurements and analysis: (A) (1) An electric double layer capacitor (EDLC) composed of (2) two polished, electrolyte saturated carbon-cement electrodes (thickness d) separated by (3) a glassy fiber membrane soaked in the same electrolyte (1M KCl), and covered by (4) conductive graphite paper. The electrodes are (5) prestressed in (6) a closed cell to improve contact between the charge collectors and the electrodes (31). (B-1/B-2) Steady-state cyclic voltammetry (CV) measurements of current, I, during cyclic charge/discharge at different scan rates, u = U₀/t₀, for two carbon-cement electrode samples prepared with different carbon blacks, water-to-cement ratios, and electrode thickness: (B-1) PBX 22.4 (0.8) 0.18 cm, and (B-2) Ketjenblack 12.8 (1.4) 0.60 cm (SI Appendix, section SI-1). (C-1) Steady-state galvanostatic charge-discharge (GCD) measurements of voltage U when a constant current I₀ is applied and held constant over time t₀, and then removed until U = 0. (C-2) Fractional exponent α as a function of applied current in GCD experiments (error bars represent =/− 1 SD for 500 cycles). (D-1/D-2) Convergence of capacitance measurements from CV-tests and GCD-tests toward a rate-independent specific capacitance C₀/m_nCB, with m_nCB the mass of carbon black in the electrode. The dashed lines represent a 95% CI. (E) Applied to eight different carbon-cement electrode materials of different carbon blacks (12–14), mix designs, and electrode thickness, a characteristic scaling of the rate-dependent CV capacitance is obtained, indicative of the high-rate capability of the electrode materials. (F) Hardness vs. capacitance plot demonstrating that high-rate capability can be achieved with high water-to-cement electrode materials, but at the expense of the material strength.

While the experimental setup and measurements are straightforward, the extraction of the capacitance as a material property from the measured CV-curves (Fig. 2 B-1 and B-2) or GCD-curves (Fig. 2 C-1) is more involved and requires to correct either for rate effects in CV-tests or for the influence of the current magnitude in GCD-tests. Both phenomena stem from the diffusion control of the charge storage in a double-layer capacitor and its impact on ion conductivity, as well noted and analyzed at the electrode scale (32–37) and the scale of ion diffusion, dissociation, solvation, and charge storage (39, 40). To address this challenge, our approach is based upon the consideration that if capacitance exists as a standalone electrode property characterizing an EDLC, this capacitance should be independent of the experimental condition by which it is obtained. Once such a test-independent capacitance measure is available, it becomes possible to scale the rate capability of our electrodes.

With this focus in mind, we consider an equivalent R-C circuit in which a resistor, R, representative of all resistances present (interstitial solution and solids), is in series with a capacitor, C. We frame the problem in the context of Boltzmann’s integrodifferential equations, which has been employed for a large range of time-dependent phenomena, ranging from “elastic aftereffects” in the theory of viscoelasticity of solids (41) and fluids (42) to hereditary epidemiology to predict COVID-19 fatality trends (43). Following this approach, we link current I to potential difference U by means of the convolution integral:

$$\begin{array}{c}\hfill U(t)={\int }_{-\infty }^t\mathcal{R}(t-t^{\prime })\frac{\text{d}I}{\text{d}{t}^{\prime }}\text{d}{t}^{\prime },\end{array}$$ [1]

where the kernel, ℛ(t − t′), is the time-dependent resistance function, accessible in a GCD test carried out at constant current I(t)=I₀. We make use of the versatility of this linear input–output response theory to derive steady-state solutions for the cyclic testing for both the CV-curve and its integral representative of the area of the CV–hysteresis loop (SI Appendix, section SI-3.B):

$$\begin{array}{cc}\hfill I& =\lambda uC(u)\left(1-\frac{2(1-exp(-{\overline{t}}_0))}{1-exp(-2{\overline{t}}_0)}exp(-\lambda {\overline{t}}_0\mathrm{\Delta }\overline{U})\right),\hfill \end{array}$$ [2]

$$\begin{array}{cc}\hfill C(u)& =\frac{\oint I\text{d}U}{2u{U}_0}{\left(1-\frac{1}{{\overline{t}}_0}\frac{2{(1-exp(-{\overline{t}}_0))}^2}{1-exp(-2{\overline{t}}_0)}\right)}^{-1},\hfill \end{array}$$ [3]

where ${\overline{t}}_0=t_0/\tau$ is the ratio of charge time, t₀, to the characteristic time of the double layer capacitor defined by τ = RC, whereas $\mathrm{\Delta }\overline{U}=U/U_0-(1-\lambda )/2$ stands for the dimensionless voltage difference prescribed during charge (λ = +1) and discharge (λ = −1), respectively. Applied to CV-tests, the output of this dual-fit for each scan rate is the rate-dependent capacitance C(u) shown in Fig. 2 D-1 and D-2 (curve labeled “Capacitance from CV”) for two electrode samples prepared with different carbon blacks, mix proportions, and electrode thicknesses. The so-obtained results show that the model-based approach is able to translate the visible difference in CV-curves (Fig. 2 B-1 and B-2) into capacitance values (Fig. 2 D-1 and D-2) that differ by more than one order of magnitude. This difference is a hallmark of the versatility of our electrode materials.

We proceed in a similar fashion for the GCD-tests to extract from the recorded voltage history (Fig. 2 C-1) the capacitance, with one subtle difference. Instead of integer rate equations, we employ fractional derivatives to capture the visible impact of high applied currents on the model response. That is, instead of Eq. 1, we employ a fractional integral (44, 45):

$$\begin{array}{c}\hfill U(t)=U^{+}+\frac{R{\tau }^{\alpha }}{{\mathrm{\Gamma }}_{1-\alpha }}{\int }_{-\infty }^t{(t-t^{\prime })}^{-\alpha }\frac{\text{d}I}{\text{d}{t}^{\prime }}\text{d}{t}^{\prime },\end{array}$$ [4]

with Γ_x = Γ(x) the complete Gamma function. Herein, U⁺ represents the voltage after instantaneous charge or discharge, while the second term is the noninstantaneous part of the potential difference stored into the electrodes, defined by the fractional exponent, α ∈ [0, 1]. For a constant applied current, I(t)=I₀, integration of the fractional derivatives provides (SI Appendix, section SI-3.C):

$$\begin{array}{c}\hfill U(t)=U^{+}+\lambda \frac{R{I}_0}{{\mathrm{\Gamma }}_{1+\alpha }}\left\{\begin{array}{c}{\overline{t}}^{\alpha };\text{for}0\le t/t_0\le 1\hfill \\ {(\overline{t}-{\overline{t}}_0)}^{\alpha };\text{for}1\le t/t_0\le 2\hfill \end{array}\right.,\end{array}$$ [5]

with U⁺ = U(t = 0⁺)=RI₀ for charge (λ = +1) and $U^{+}=U(t_0^{+})=R{I}_0{\overline{t}}_0^{\alpha }/{\mathrm{\Gamma }}_{1+\alpha }$ for discharge (λ = −1), while $\overline{t}=t/\tau$ is dimensionless time. From fitting the recorded GCD-voltage for different applied current (Fig. 2 C-1), the fractional exponent is found to converge to α = 1 for low applied current (Fig. 2 C-2), for which the capacitance is readily obtained from C = I₀t_d/U(t₀⁺), with t_d the discharge time, and U(t₀⁺) the measured voltage after instantaneous voltage drop at time t₀. Sample results of the capacitance vs. applied current are displayed in Fig. 2 D-1 and D-2 (curve labeled “Capacitance from GCD”) for two electrode samples. Last, in SI Appendix, section SI-3.D and Fig. S9, we show that this capacitance is stable for at least n = 10,000 charge-discharge cycles in terms of both the capacitance retention, C(n)/max_nC, and the Coulombic efficiency, CE = t_d(n)/t₀(n), in the range of I₀/A = 5 − 30 mA/cm² (with A the electrode surface).

We thus obtain two series of capacitance measurements, one from the CV measurements, the other from the GCD measurements, which converge at respectively low scan rates in CV-tests (u → 0) and low current values in GCD tests (I₀ → 0) to a single value, C₀ (Fig. 2 D-1 and D-2). To appreciate its significance, we remind ourselves that the total power of a supercapacitor, P = IU, to estimate the energy, E_tot = ∫_(t)P dt, includes both an instantaneous and a noninstantaneous contribution, whereas the actual energy storage capacity in the electrodes is the potential difference associated with only the noninstantaneous charge storage in the EDLC system (the second term in Eq. 4). The capacitance, C₀, we thus obtain by correcting for rate and current intensity effects in CV and GCD measurements (Fig. 2 D-1), eliminates the instantaneous response, and can be viewed, therefore, as representative of the maximum (noninstantaneous) energy storage capacity of the electrodes in either test when considering the asymptotes in CV and GCD, respectively (the proof is given in SI Appendix, section SI-3.E):

$$\begin{array}{c}\max E_{\text{tot}}=\frac{1}{2}{C}_0{U}_0^2;C_0=\underset{u\to 0}{\lim }C(u);U_0=\underset{I_0\to 0}{\lim }U(t_0^{+}).\end{array}$$ [6]

That is, capacitance C₀ is a rate-independent electrode property independent of testing conditions, ion conductivity, and so on. The relevance of this rate-independent capacitance is readily understood from the distinct scaling behavior of the normalized rate-dependent CV capacitance of all our electrode materials, C(u)/C₀ (Fig. 2E). This scaling with respect to the maximum energy storage capacity permits evaluating the high-rate capability of our materials for fast energy storage. Specifically, electrodes prepared at high water-to-cement (W/C) ratios, which exhibit a large hydration porosity, approach the rate-independent capacitance even at high scan rates, and achieve close to the maximum energy storage in the shortest time. In contrast, as the thickness of the electrodes is increased, the rate capability diminishes requiring longer charge times to realize the full energy storage potential of the electrode materials. Moreover, the normalized capacitance, C(u)/C₀, allows us to identify the potential of our materials for structural electrodes, specifically for applications that focus on dual functionality, i.e., high rate capability energy storage when an external power supply is applied, and strength capacity to safely sustain mechanical load. Specifically, we find that high-rate capability is achieved with high W/C-ratio electrodes to the detriment of the cohesive strength of the materials, here determined by hardness measurements (Fig. 2F). This comes as no surprise: the increase in hydration porosity leads to stress concentrations around micrometer-sized pores, and hence to a lower strength performance for high W/C materials (22, 46). There exists thus a trade-off between energy storage properties and strength properties, specifically for structural electrode applications.

Discussion: Scaling of Energy Storage Capacity

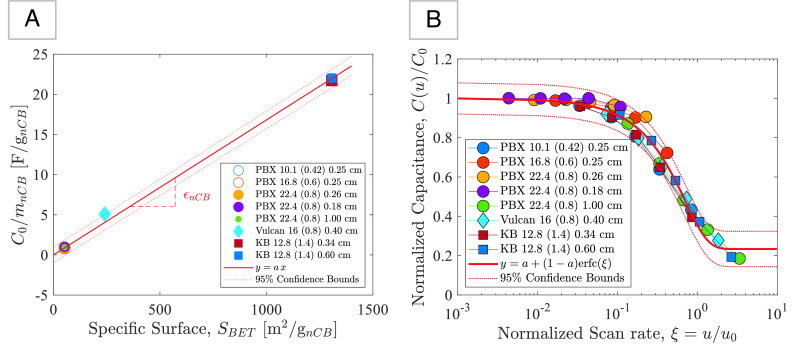
The availability and experimental accessibility of a rate-independent capacitance are invaluable to investigate the scalability of our electrode system for massive energy storage in structural carbon-cement supercapacitor systems. Such a scaling requires that 1) the rate-independent capacitance can be reduced to an intensive quantity, whose magnitude is independent of the size of the system, while 2) providing a measure for the high rate capability as a function of electrode dimensions and constituent properties. The first challenge is addressed here by means of a dimensional analysis of the asymptotic state of maximum energy storage (Eq. 6). In this asymptotic state, the surface of the carbon black can be considered to be entirely surrounded by an oppositely charged surface layer of ions. It is thus readily shown from a dimensional analysis (SI Appendix, section SI-4.A) that the rate-independent capacitance values of eight carbon-cement electrode samples (C₀ ∈ [0.11, 3.57] F) of different thickness (d ∈ [0.18, 1] cm) prepared with carbon black materials of different specific surface areas (S_BET = (52, 241, 1307) m²/g), different concentrations (ϕ_Cρ_C ∈ [0.071, 0.179] g/cm³) and water-to-cement mass ratios (W/C ∈ [0.42, 1.4]) can be reduced to a linear scaling of the rate-independent specific capacitance (Fig. 3A):

$$\begin{array}{c}\hfill \frac{C_0}{dA{\varphi }_C{\rho }_C}={ϵ}_{\text{nCB}}{S}_{\text{BET}},\end{array}$$ [7]

Fig. 3.

Experimentally derived scaling relations: (A) Rate-independent capacitance of eight different carbon-cement electrode materials showing the intensive nature of the energy storage capacity of our electrode systems. (B) Rate-dependent capacitance scaled along the horizontal axis by means of the classical dimensionless diffusion variable ξ = d²/(D t₀). All measured capacitance values for eight different electrodes and 5 different scan rates collapse onto a master curve.

with ϵ_nCB = 1.68 × 10⁻² F/m² [with 95% CI (1.63; 1.73)×10⁻²] the fitted aerial capacitance of carbon black. This scaling corroborates the intensive nature of the energy storage capacity of our electrode systems.

We proceed in a similar way for the rate capability, by considering a scaling of the scan rate, u = ξu₀, to achieve a single dimensionless relation, C(u)/C₀ = ℱ(ξ). From the asymptotic solution, Eq. 7, we retain that the energy storage capacity is an adsorption process of charged ions, for which reason we adopt for ξ the classical dimensionless diffusion variable ξ = d²/(D t₀). For diffusivity D, we make use of our texture analysis, recognizing that the tortuosity of the ion diffusion path through the hydration porosity is mediated by the chord length ratio of the texture, ℓ_nCB/ℓ_LD/HD ∼ (ϕ_Cρ_CS_BET/s_LD/HD), with s_LD/HD the texture-specific surface (Fig. 1F). These few considerations permit collapsing all test results onto a single master curve (Fig. 3B):

$$\begin{array}{c}\hfill \xi =\frac{d^2{\varphi }_C{\rho }_C{S}_{\text{BET}}}{s_{\mathit{LD}}{t}_0\gamma D_0}{\left(\frac{W}{C}\right)}^{-3}.\end{array}$$ [8]

This master curve is well approximated by a complementary error function of the form C(u)/C₀ = a + (1 − a)erfc(ξ), with γD₀ = 6.654 × 10⁻⁴ m²/s [with 95% CI (5.956, 7.352)×10⁻⁴ m²/s] a fitted diffusion coefficient, and a = 0.234 (0.191, 0.277) an asymptotic value for ξ >  > 1. While dimensional analysis provides us with the value of the diffusivity D₀ of the electrolyte only close to a multiplying factor γ [here, for 1M KCl, D₀ = 2.0 × 10⁻⁹m²/s (47), and γ = 3.33 × 10⁻⁵], the self-similar nature of the scaling relation is of great interest to evaluate the high rate capability of carbon-cement electrodes. For example, for ξ <  0.1, the electrodes exhibit a high-rate capacitance, C(u)/C₀ >  0.91 ± 0.05, whereas for ξ >  1 the capacitance drops below C(u)/C₀ <  0.35 ± 0.05. That is, the scaling relations (7) and (8) provide a rational means to fine-tune the material design of a carbon-cement composite for specific applications.

In summary, our material design of porous carbon-cement composites provides a scalable material solution for energy storage to support the urgent transition from fossil fuels to renewable energies. Key to scalability is the intensive nature of the volumetric capacitance, which originates from the unique texture of the space-filling carbon network. This intensive nature allows us to envision a mass scaling of the energy storage capacity density, maxE_tot/V = (1/2V) C₀U₀²≈20–220 Wh/m³ depending on the specific surface area of carbon black, from electrode to structural scales (of volume V); for example 45 m³ of high specific surface area carbon black-doped concrete for the average daily residential energy consumption of ∼10 kWh. More generally, while the results presented here are a step toward the development of scalable bulk energy storage solutions, we expect that the availability, scalability, and further developments of porous carbon-concrete supercapacitors open perspectives on multifunctional design of sustainable structures that leverage high energy storage capacity, high rate charge/discharge capability related to ion diffusion, and structural strength, for applications ranging from energy autarkic shelters and self-charging roads for electric vehicles (48), to intermittent energy storage for wind turbines and tidal power stations.

Materials and Methods

Carbon-cement pastes were prepared as a dry mix of Portland cement and nanocarbon black, and combined with water and superplasticizer (SI Appendix, section SI-1). Sealed during the hydration process, electrode samples were cut and prepared for correlative EDS-Raman investigation and correlation analysis (SI Appendix, section SI-2). Electrodes were saturated by electrolyte (1M KCl), and prepared for capacitance measurements and analysis (SI Appendix, section SI-3). A dimensional analysis was then performed to derive scaling relations (SI Appendix, section SI-4).

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.