Inferring Human Immunodeficiency Virus 1 Proviral Integration Dates With Bayesian Inference

Abstract

Human immunodeficiency virus 1 (HIV) proviruses archived in the persistent reservoir currently pose the greatest obstacle to HIV cure due to their evasion of combined antiretroviral therapy and ability to reseed HIV infection. Understanding the dynamics of the HIV persistent reservoir is imperative for discovering a durable HIV cure. Here, we explore Bayesian methods using the software BEAST2 to estimate HIV proviral integration dates. We started with within-host longitudinal HIV sequences collected prior to therapy, along with sequences collected from the persistent reservoir during suppressive therapy. We built a BEAST2 model to estimate integration dates of proviral sequences collected during suppressive therapy, implementing a tip date random walker to adjust the sequence tip dates and a latency-specific prior to inform the dates. To validate our method, we implemented it on both simulated and empirical data sets. Consistent with previous studies, we found that proviral integration dates were spread throughout active infection. Path sampling to select an alternative prior for date estimation in place of the latency-specific prior produced unrealistic results in one empirical data set, whereas on another data set, the latency-specific prior was selected as best fitting. Our Bayesian method outperforms current date estimation techniques with a root mean squared error of 0.89 years on simulated data relative to 1.23–1.89 years with previously developed methods. Bayesian methods offer an adaptable framework for inferring proviral integration dates.

Introduction

Human immunodeficiency virus 1 (HIV) remains an ongoing pandemic with more than 30 million current infections (Feehan and Apostolopoulos 2021). However, due to the effectiveness of combined antiretroviral therapy (cART) in reducing viral replication, progression to acquired immunodeficiency syndrome (AIDS), morbidity, and HIV transmission, HIV infection is now a manageable illness (Hogg et al. 1998; Palella et al. 1998). Despite this, cART alone cannot cure HIV infection, even over long timescales, because of the presence of persistent reservoirs of integrated HIV within host cells. As cART inhibits viral replication, it cannot eliminate latently integrated proviruses (Chun et al. 1997; Finzi et al. 1997, 1999). As proviruses in the persistent reservoir can reactivate at any time to reseed HIV infection, cART must be maintained for life (Chun et al. 1997; Finzi et al. 1997, 1999; Sneller et al. 2020). Thus, an effective, durable HIV cure must eliminate or permanently suppress the HIV in the persistent reservoir.

Obtaining a complete understanding of the composition and dynamics of the persistent reservoir is of the utmost importance for developing cure strategies. For example, it is pertinent to understand the distribution of both timings of proviral integration and lengths of proviral persistence because viruses of different ages may offer varying immune evasion or drug resistance phenotypes (Shankarappa et al. 1999; Clavel and Hance 2004; Sudderuddin et al. 2020). The reservoir is established early in infection (Chun et al. 1998; Whitney et al. 2014; Colby et al. 2018; Brooks et al. 2020) and is continuously seeded throughout untreated infection, where it persists after cART suppression (Brodin et al. 2016; Jones et al. 2018; Abrahams et al. 2019) with the majority of persistent proviruses seemingly having been integrated in the period directly preceding cART initiation (Brodin et al. 2016; Abrahams et al. 2019). These properties were ascertained by estimating the integration dates of proviral sequences using genetic and phylogenetic methods. For example, the presence of proviruses dating close to the infection date indicates that the reservoir is established early in infection; whereas a concentration of integration dates near cART initiation suggests that there is a large amount of proviral turnover or alternatively that cART influences viral latency. A wide distribution of integration dates suggests a reservoir that is actively contributed to and persists on therapy. Finally, estimated dates that fall within periods of cART administration are evidence for ongoing replication during therapy.

Since HIV proviruses integrated into the persistent reservoir do not replicate, and hence do not evolve, the sequence of a provirus will be identical (or nearly identical) to the genome of the original virus that infected the cell, and will therefore have the same “genetic age” as this original virus (Chun et al. 1995; Finzi et al. 1997). Thus, we can estimate the integration dates of individual proviruses by identifying where they fit into the within-host HIV evolutionary tree. Brodin et al. (2016) produced a genetic method to estimate HIV integration dates by comparing each proviral sequence to the motifs of sequences collected longitudinally from plasma pre-cART. Jones et al. (2018) developed a method that infers a linear regression between root-to-tip phylogenetic divergence and sampling time of pre-cART plasma sequences and uses the regression to estimate proviral integration dates. Subsequently, Abrahams et al. (2019) used an evolutionary placement algorithm (EPA) that places a proviral sequence in a phylogenetic tree inferred from the participant's pre-cART plasma sequences and estimates the proviral integration date by using the dates of the nearby plasma sequences. They also compared a nearest neighbor and a clade-based approach using phylogenies inferred from both pre-cART plasma and proviral sequences. Recently, we compared, using simulated HIV sequences (Jones and Joy 2020), several methods of inferring proviral integration dates including the nearest neighbor method, clade-based method, linear regression, node.dating (Jones and Poon 2017), and least squares dating (LSD) (To et al. 2016)—which infer dates for internal nodes and proviral tips in a tree using maximum likelihood and least squares, respectively. In that study, LSD produced the most accurate results on simulated data (Jones and Joy 2020).

Existing methods, however, have a number of shortcomings. For the method in Brodin et al. (2016) and the three methods described in Abrahams et al. (2019), the estimated proviral integration dates are restricted to the sampled dates of sequences collected from plasma. This can be problematic if plasma was sampled infrequently or over a restricted time frame. Phylogeny-based methods are generally implemented on a single tree topology, which may not have high support values, though linear regression has been applied to a Bayesian sampling of trees (Jones et al. 2020). Linear regression, node.dating, and LSD methods all rely on a mostly strict molecular clock that is unlikely to be the best-fitting model. These shortcomings can be addressed with Bayesian methods where a distribution of compatible dates can be estimated from a sample of tree topologies employing relaxed clock models. Recently, Bayesian methods have been developed to estimate proviral integration dates in HIV. Nagel and Rannala (2023) extended the software MCMCTree (Stadler and Yang 2013) to include tip sampling, and Ferreira et al. (2023) developed Bayesian-informed root-to-tip regression.

The last decades have seen a proliferation in software available to analyze sequence data utilizing a variety of phylogenetic models in Bayesian frameworks. These software are developed for multifarious purposes including inferring phylogenetic tree topologies, analyzing population structure, estimating epidemic reproductive numbers, molecular dating, and quantifying speciation (Huelsenbeck and Ronquist 2001; Lartillot et al. 2009; Suchard et al. 2018; Bouckaert et al. 2019). Additionally, Bayesian methods can be used to estimate the dates of sequences with otherwise unknown dates using tip date sampling (Shapiro et al. 2011).

The main challenge with Bayesian phylogenetic analysis is the large number of parameters that need to be considered. This leads to likelihood functions with complex shapes containing many peaks and valleys that are challenging for Bayesian methods to resolve. One way to overcome the estimation of many parameters at once is the fixation of the tree topology instead of sampling multiple trees; however, this limits the scope of the results and fails to account for phylogenetic uncertainty. A further complication of Bayesian phylogenetic analysis is selection of the appropriate prior distributions. In Bayesian analysis, the prior distribution should reflect our existing assumptions about the system. To achieve this, we can employ an informative prior that imposes our a prior knowledge (Nowak et al. 2013). Alternatively, we can select a prior that best fits our data with model selection through, for example, path sampling/stepping-stone sampling strategies (Fan et al. 2011; Xie et al. 2011; Bouckaert et al. 2019) or nested sampling (Skilling 2006; Russel et al. 2019).

Here, we develop and explore the use of Bayesian analysis with BEAST2 (Bouckaert et al. 2019) for estimating the integration dates of HIV proviral sequences. We apply our methodology to simulated and empirical data sets. We compare the merits of using informative priors versus applying model selection with path sampling. Finally, we compare our results to previously developed date estimation methods.

New Approaches

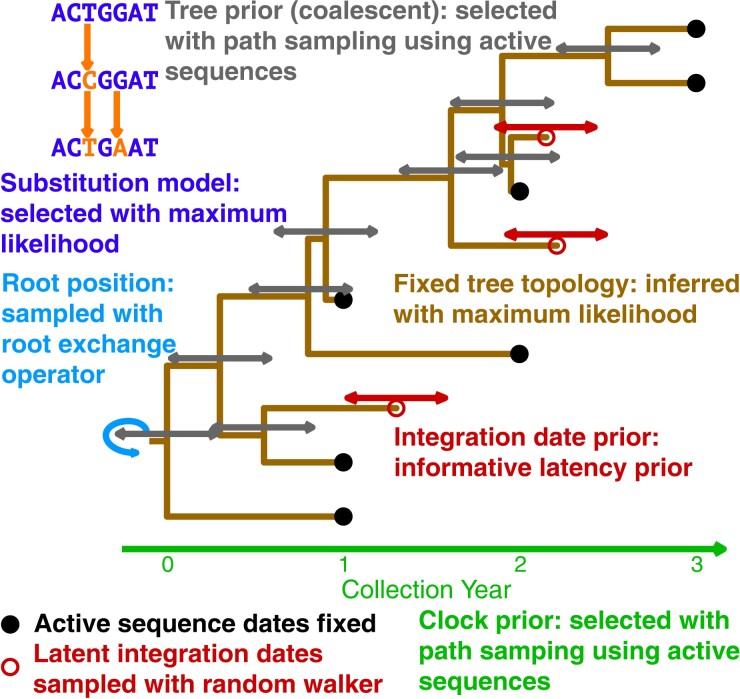
We detail a new Bayesian approach to estimate proviral integration dates of HIV using BEAST2. Though tip date sampling, in which sequence dates are adjusted between states of a Markov chain Monte Carlo (MCMC) simulation, is not new (Shapiro et al. 2011), it has only recently been used to estimate proviral integration dates. We combine tip date sampling with a latency-specific prior to estimate the dates (see fig. 1 for a visual outline of the model). This latency-specific prior accounts for the time since infection and the sampling time and is an informative prior that models HIV latency dynamics. We employ our new BBD package for BEAST2 that includes the latency-specific among other date priors and operators to assist in unknown sequence date estimation.

Fig. 1.

Diagram of BEAST2 model for proviral integration date estimation. Within a coalescent framework, tip date sampling is performed on the latent sequences to estimate their integration dates keeping the dates of active sequences fixed. The diagram is colored by each component of the model. The method to determine the prior for each component is detailed.

We employ a new RootExchange operator in our BBD package to estimate the root position without changing the tree topology. This allows us to use a fixed tree in our analyses without having to also fix the root position. Some data sets require using a fixed-tree topology in order to achieve convergence due to the complexity of simultaneously estimating tree topology and model parameters. Being able to infer the root position allows us to overcome the biases of a fixed root that may result from an outgroup sequence or root-to-tip regression.

We explore simultaneously inferring the tree topology and the integration dates in our framework. However, we could only reliably execute this on simulated data. This is an advance over previous methods which can be biased by a single tree inferred through maximum likelihood approaches. Simultaneous inference of tree topology and date estimation allows us to overcome the low-supported trees of within host HIV data sets (Capoferri et al. 2019; Miller et al. 2019).

Results

Estimating Proviral Integration Dates

We estimate proviral integration dates by using tip date sampling (Shapiro et al. 2011). With tip date sampling, an operator is added to a BEAST2 model that can adjust the date of the proviral sequences with a random walk across MCMC samplings. A latency-specific prior distribution, called the Latent prior, is assigned to the proviral integration dates and through MCMC, we achieve a sample of the posterior distribution of the proviral integration dates.

We applied our method to three data sets, one simulated and two empirical. To fashion the model, we applied model selection to determine the substitution, clock, and tree models (see Materials and Methods). The substitution model selected for each data set is shown in the Bayesian Information Criterion (BIC) column of supplementary table S1, Supplementary Material online. Uncorrelated relaxed clocks with log-normally distributed rates and coalescent tree priors with exponential population growth were selected for all data sets (see supplementary tables S2 and S3, Supplementary Material online).

Simulated Data

First, to assess method accuracy, we applied our Bayesian approach to simulated data with known latent sequence integration dates. Our simulated data set represents a single individual living with HIV who initiated cART 10 years following infection, and remained on suppressive cART for another 10 years, from whom we sampled 100 active sequences at ten pre-cART time points (10 per year for 10 years) and 50 latent sequences at five time points during suppressive cART (10 each at 2-year intervals); see Materials and Methods for details. After deduplication, we were left with 99 active sequences and 49 latent sequences. For this data set, the real integration dates of the latent sequences are known; the distribution of integration dates for the 49 distinct sequences are shown in supplementary figure S1, Supplementary Material online.

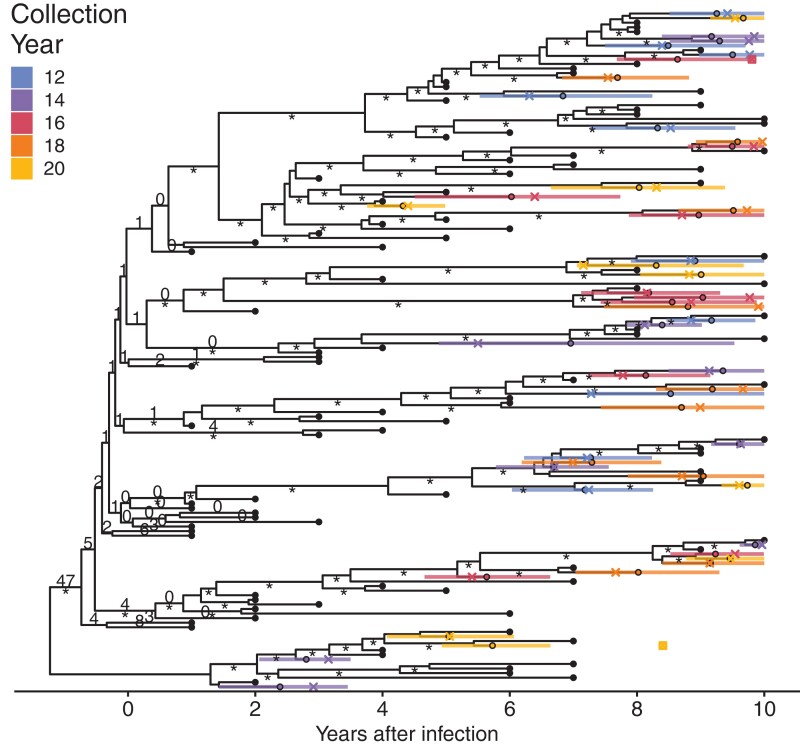
Estimated latent sequence integration dates and their 95% highest posterior densities (HPDs) of the estimates are displayed on the phylogenetic tree depicted in figure 2. All but two of the actual integration dates fell within the HPD of the BEAST2 sample's estimated dates (indicated in fig. 2 with small squares). For both sequences, the real dates were later than the HPD. Consistent with previous studies of real individuals (Abrahams et al. 2019), the integration dates of our simulated data are concentrated in the period immediately preceding therapy (see supplementary fig. S1, Supplementary Material online). This is suggestive of either a short reactivation period or cART-mediated integration (Abrahams et al. 2019). Our BEAST2 method was able to recover these dates to infer the same conclusion. However, six of the estimated integration dates were during cART. Some of these estimates had wide HPDs, with all HPDs including the actual integration date. These results are similar to the results of the linear regression method of Jones et al. (2018), where wide confidence intervals on late estimated dates were observed.

Fig. 2.

Phylogeny of date estimation analysis on simulated data. Nodes of the phylogeny are placed at their mean date. Black circles indicate active sequences. Colored circles indicate the mean integration dates (i.e., estimated dates) and colored bars indicate 95% HPD intervals for the integration dates. Crosses indicate real integration dates. The small squares indicate the two sequences whose real integration dates fell outside the 95% HPD interval. Numbers on edges show the percentage of times that edge was sampled as the root after burn-in. Edges without numbers were not sampled as the root. Edges with at least 70% maximum likelihood bootstrap support are marked with an “asterisk.”

For our integration date estimation, we used a fixed-tree topology inferred by maximum likelihood methods as described in the Materials and Methods and sampled the root position in our MCMC. This was performed to assist convergence of the runs, since it reduces the number of parameters to integrate over. We re-performed our analyses on simulated data estimating the tree topology simultaneously with the date estimation. Overall, results with an unfixed tree topology were comparable to the results with a fixed-tree topology (see supplementary fig. S2, Supplementary Material online). However, integration date estimates using an unfixed tree topology were slightly more accurate with lower root mean squared error (RMSE) (0.89 vs. 0.87 years) and higher concordance (0.890 vs. 0.893).

Empirical Data

Next, we applied our method to an empirical data set from an individual living with HIV. We acquired 122 HIV nef sequences from participant 1 from Jones et al. (2018). We will call this data set P1. This participant had been living with HIV for more than a decade before initiating suppressive cART, after which their viral load remained largely suppressed for the next decade (see Jones et al. 2018 for details). This participant's long infection history and breadth of sampling make them ideal for phylogenetic dating.

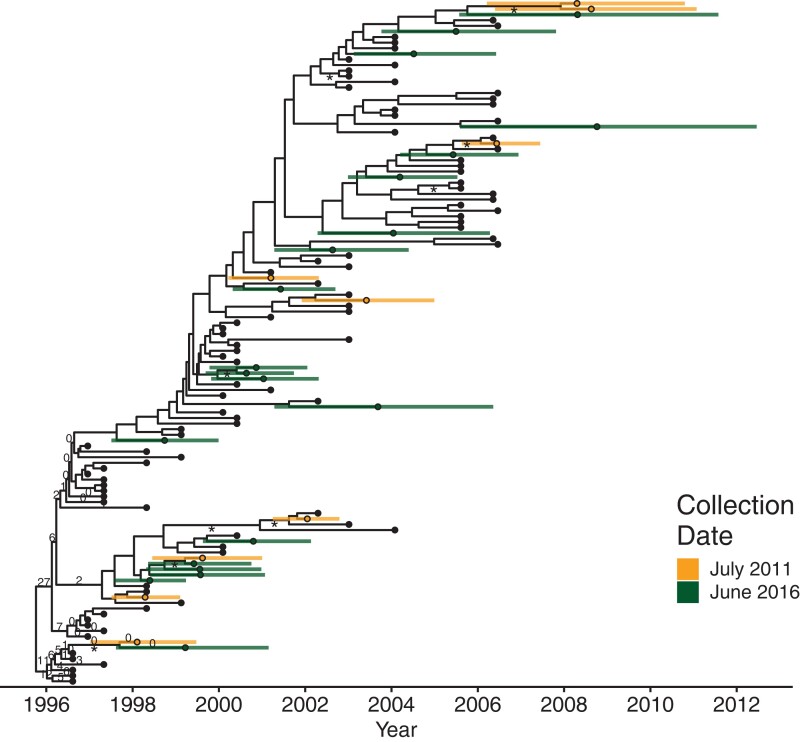
Figure 3 shows a maximum clade credibility tree of the BEAST2 run with the Latent prior. As in previous studies of this participant's proviral age distribution (Jones et al. 2018, 2020; Jones and Joy 2020), the estimated proviral integration dates spanned the infection period. This suggests that there is continual seeding of the persistent reservoir. Of note, we found four of the latent sequences had estimated integration dates later than the last plasma sequence collection date and the onset of suppressive therapy. This is possibly the same artifact as with the simulated data. However, this participant had two episodes of viral rebound following therapy initiation, the first in 2007 and the second in 2008 (see Jones et al. 2018). These proviruses could be descendants of reactivated viruses from these events. However, our date estimates are subject to the assumption that the mutation rate is held relatively constant (specifically it follows a log-normal distribution) and the later dates suggest that these sequences are fairly divergent from the latest plasma sequences. Dates in this range were observed previously using linear regression to estimate the integration dates (Jones et al. 2018).

Fig. 3.

Phylogeny of date estimation analysis on P1. Nodes of the phylogeny are placed at their mean date. Colored circles indicate mean integration dates (i.e., estimated dates) and colored bars indicated their 95% HPD intervals for the integration dates. Black circles denote active sequences. Numbers on edges show the percentage of times that edge was sampled as the root after burn-in. Edges without numbers were not sampled as the root. Edges with at least 70% maximum likelihood bootstrap support are marked with an “asterisk.”

Our last data set, N133M, consists of 97 HIV env sequences from participant N133M of Brooks et al. (2020). This participant had <3 years of untreated infection before going on suppressive cART. An important feature of this participant is that we have a lower bound for when they were infected via a negative HIV test result, which was 92 days before the first sample was collected (see Brooks et al. 2020 for details).

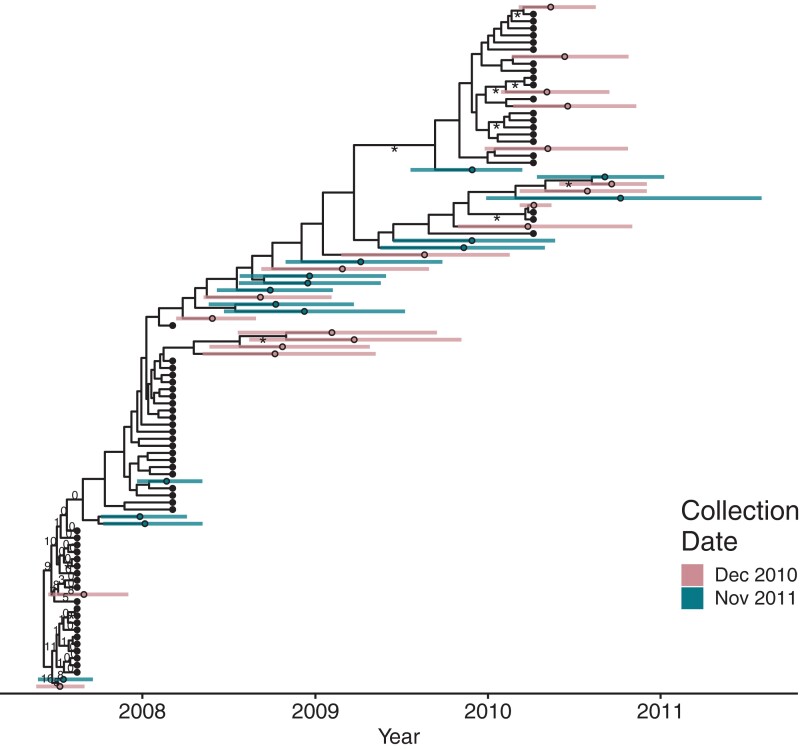
As with the other data sets, the estimated integration dates for N133M are spread throughout infection including some dates that fall within the treatment interval. Notably, there are two sequences from both sampling time points that date very close to infection (bottom left corner of fig. 4), which is compatible with early seeding of the persistent reservoir (Chun et al. 1998; Whitney et al. 2014; Colby et al. 2018; Brooks et al. 2020). Proviral sequences nicely bridge the sequences from the different plasma sampling time points in the tree showing the constant within-host evolution of the participant's viral population (see fig. 4).

Fig. 4.

Phylogeny of date estimation analysis on N133M. Nodes of the phylogeny are placed at their mean date. Colored circles indicate the mean integration dates (i.e., estimated dates) and colored bars indicated their 95% HPD intervals for the integration dates. Black circles denote active sequences. Numbers on edges show the percentage of times that edge was sampled as the root after burn-in. Edges without numbers were not sampled as the root. Edges with at least 70% maximum likelihood bootstrap support are marked with an “asterisk.”

Other Date Priors and Path Sampling

Next, we wanted to see what effect using different tip date priors would have on the estimated dates. We performed the tip date sampling using ten additional priors (see supplementary table S4, Supplementary Material online and the methods for details). The priors each depend on the sampling times of the plasma and latent sequences and are shown in supplementary figures S3–S5, Supplementary Material online. We then performed path sampling to determine which priors best fit the data.

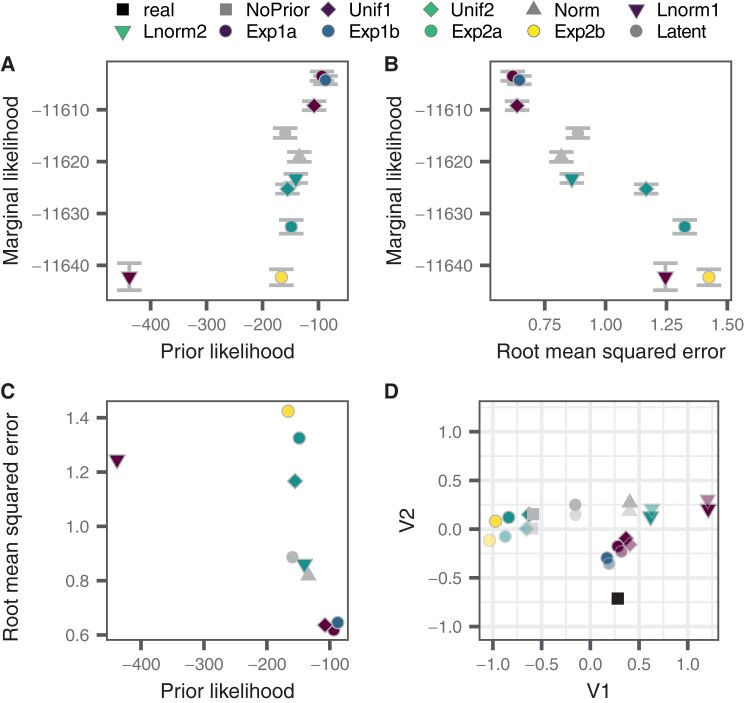
Path sampling revealed the best-fitting prior for the simulated data to be Exp1a, an exponential distribution acting on years before the latest active sampling date with a fixed mean. The next best-fitting prior was Exp1b, an exponential distribution acting on years before the latest active sampling date with an exponential prior on the mean of the distribution. The marginal likelihood of the models with the fixed and unfixed means were within 2 standard deviations (SDs) of their estimates, suggesting that the prior with the variable mean may be the better fitting model. The Exp1a and Exp1b priors also had the highest prior probability density of the actual integration dates (see fig. 5A and C) together with the lowest RMSE (see fig. 5B and C and supplementary table S5, Supplementary Material online). The Lnorm1 prior, a log-normal distribution on years before the latest active sequence, had a low prior posterior density, which resulted in a poor marginal likelihood and RMSE (see fig. 5A–C and supplementary table S5, Supplementary Material online). The Exp2b prior however, an exponential prior on years before latent sequence collection with an estimated mean, had a higher prior posterior density but a comparable marginal likelihood and higher RMSE than the Lnorm1 prior (see fig. 5A–C and supplementary table S5, Supplementary Material online). Overall, marginal likelihood correlated negatively with the RMSE (Pearson correlation coefficient: −0.941, P < 0.01), suggesting that the better fitting priors offer more accurate results for simulated data. Histograms of the estimated integration dates for each prior are shown in supplementary figures S6 and S7, Supplementary Material online.

Fig. 5.

Comparison of marginal likelihood, prior likelihood, and RMSE of simulated data. (A) The likelihood of the real integration dates using a specific date prior (prior probability density) versus the marginal likelihood of the BEAST2 run using that date prior. Error bars show twice the range of the SD of the estimate of the marginal likelihood. (B) RMSE (in years) of the date estimation of a BEAST2 run using a specific prior versus the marginal likelihood using that date prior. Error bars show twice the range of the SD of the estimate of the marginal likelihood. (C) The likelihood of the real integration dates using a specified date prior (prior probability density) versus the RMSE (in years) of the date estimation of the BEAST2 run using that date prior. (D) Sammon MDS of the root mean squared deviation between the estimates using each prior and the actual (real) dates. Faded points correspond to estimates achieved without using a fixed-tree topology. Axes units for V1 and V2 are time in years.

The model with the Unif1 prior had the highest marginal likelihood of the models with unfixed tree topologies for simulated data. However, the model with the Exp1a prior (which was selected in the fixed-tree analyses) had the greatest accuracy, with a lower RMSE and higher concordance. The uncertainty in estimating the marginal likelihood was much higher in the unfixed tree analyses than the fixed-tree analyses. In fact, marginal likelihoods of all models fell within the error of the marginal likelihood of the best-fitting model (see supplementary table S6 and fig. S8, Supplementary Material online).

For P1, the Latent prior had the highest marginal likelihood (see supplementary table S7, Supplementary Material online). Interestingly, with exponential priors and the Unif2 and Lnorm1 priors, two proviral sequence dates predated the earliest active collection time point (see supplementary figs. S9 and S10, Supplementary Material online). Previous analysis using linear regression did not yield these results (Jones et al. 2018) and were not observed with the Unif1, Norm, Lnorm2, and Latent priors, but were seen with the other six priors (see supplementary figs. S9 and S10, Supplementary Material online). The Norm, Lnorm2, and Latent priors have lower likelihoods for early dates than the other priors and the Unif1 prior has zero likelihood for early dates. A previous Bayesian estimate of this participant's infection date yielded December 1995 (Jones et al. 2018); however, this estimate only included the sequences derived from plasma in its analysis. The actual infection date of the participant is unknown.

In N133M, path sampling chose the Exp1a prior as in the simulated data (see supplementary table S8, Supplementary Material online). Supplementary figure S11, Supplementary Material online shows a maximum clade credibility tree of the BEAST2 run with the Exp1a prior. Although it was the best-fitting model, the results using the Exp1a prior are unrealistic. The earliest estimated dates were in August 2005, but the participant's latest negative HIV test result was in May 2007. The root in this tree was sampled between the second and third plasma times points, which is indicative of dual infection (see supplementary fig. S11, Supplementary Material online). However, dual infection s unlikely for this participant as their viral phylogenetic divergence is relativity low given HIV's mutation rate and the time span. The results of this model contradicting our prior understanding of the participant suggest that path sampling may be inappropriate for this participant. Most priors exhibit the same behavior and estimate early integration dates; however, the Unif1, Norm, Lnorm2, Latent, and NoPrior do not exhibit this result (see supplementary figs. S12 and S13, Supplementary Material online). These priors have low or zero density before the first plasma time point.

Comparison to Other Dating Methods

To assess the performance of the Bayesian methods, we compared Bayesian-derived estimates of proviral integration dates to those estimated using other methods. Specifically, we compared the EPA employed by Abrahams et al. (2019), the linear regression approach we used previously (Jones et al. 2018) and LSD as implemented in LSD (To et al. 2016). We recently showed that the least squares method, with a slight variation in the rooting method, was the most accurate at estimating proviral integration dates when compared against similar tip date estimation software on simulated HIV genomes using a rooted phylogenetic tree (Jones and Joy 2020). The EPA method was not included in that study.

We compared the results of our BEAST2 date estimation software to EPA, linear regression, and LSD on both data sets using each of three tree building software: FastTree, IQ-Tree, and RAxML. Our method using BEAST2 substantially outperformed the other methods (see table 1 and supplementary table S9, Supplementary Material online) with almost half the RMSE compared to LSD, the next most accurate method.

Table 1.

Comparison of Alternate Dating Methods (simulated data).

Method	RMSE	Concordance
BEAST2 (Latent prior)	0.89	0.890
EPA (FastTree)	1.64a	0.453a
Linear Regression (IQ-Tree)	1.89	0.572
LSD (IQ-Tree)	1.23	0.805

Note.—Only results using the tree inference software that produced the highest score (i.e., had the best fit; see supplementary table S7, Supplementary Material online) are shown. RMSE, root mean squared error and is in years.

^aRMSE and concordance for the EPA method were calculated over sequences where dates were computable.

The estimates of three alternate methods were relatively different from each other, residing in different regions of the multidimensional scaled (MDS) plot shown in supplementary figure S14, Supplementary Material online. The choice of tree inference software (FastTree, IQ-Tree, or RAxML) had little effect of the estimates for each method (see supplementary fig. S14 and table S9, Supplementary Material online). The BEAST2 analyses with different integration date priors and the real integration dates were clustered in two groups in the MDS plot with the LSD estimates separating Exp2 priors and the Unif2 prior from the rest of the priors and the real integration dates (see supplementary fig. S14, Supplementary Material online).

For the empirical data set P1, the choice of tree inference software had a greater effect on the estimated integration dates than for the simulated data where the results were comparable. This was especially true for the LSD method where there were 415–1,248 day root mean square differences between the estimates using different tree inference software (see supplementary fig. S15, Supplementary Material online). The scoring values to assess model fitness also varied by tree inference software for P1 (see supplementary table S10, Supplementary Material online), whereas the simulated data had similar scores across tree inference software (see supplementary table S9, Supplementary Material online). The BEAST2 analyses clustered together in the MDS plot (see supplementary fig. S15, Supplementary Material online).

In N133M, the choice of tree inference had an even greater effect on the results for the alternate methods than it did in P1. The EPA method estimates were distributed around the BEAST2 estimates and the LSD estimates derived from a tree inferred with FastTree clustered with the LR estimates (see supplementary fig. S16 and table S11, Supplementary Material online). The BEAST2 method estimates were grouped in two clusters based on whether early dates were detected or not. The later clustered with the LR method estimates since the LR method selects its root only based on the plasma-derived sequences and thus will preserve the appearance of a mono-infection with subsequent “linear” evolution.

Discussion

Our Bayesian method using BEAST2 was capable of recovering HIV proviral integration dates. It produced more accurate results than previous non-Bayesian methods employing optimization.

Nagel and Rannala (2023) recently described an alternative Bayesian method to estimate HIV proviral integration dates building upon the software MCMCTree (Stadler and Yang 2013). As with our method using BEAST2, their method uses HIV sequences collected longitudinally from plasma together with HIV sequences collected from the persistent reservoir and employs tip date sampling to estimate proviral integration dates. Their method uses a fixed rooted tree without integrating over the root position, a strict molecular clock instead of a relaxed clock, and in place of using a coalescent model, a prior is imposed on the root date to inform divergence times. Their method however includes the ability to combine multiple gene segments to improve accuracy. Multigene analyses are possible with our approach, but for now, we begin with our proof of concept using a single-gene analysis.

Ferreira et al. (2023) also recently developed a Bayesian method to estimate HIV proviral integration dates using root-to-tip regression with the same kind of data set. Their approach does not employ tip date sampling, but instead uses root-to-tip distances to estimate the integration dates. The advantage of this is that the proviral sequences do not bias the model estimate as they are not used to tune model parameters except through the tree construction. A disadvantage however is that their model does not leverage any biological insights that the proviral sequences may provide. As with our method, they used a fixed phylogenetic tree and estimate the root position. However, their model is based around root-to-tip regression instead of the coalescent framework utilized in our BEAST2 model.

The two recent approaches described above were applied to a greater number of data sets than in our study [over 1,000 simulated data sets and 3 empirical data sets for Nagel and Rannala (2023) and 100 simulated data sets for Ferreira et al. (2023)]. For our study, we chose to explore the depth of the intricacies of our method over its application to large numbers of data sets.

Our method uses a fixed-tree topology when estimating proviral integration dates. Likely due to the complexity of resolving a tree topology with intrahost HIV sequences (Capoferri et al. 2019; Miller et al. 2019), we were unable to achieve convergence with the empirical data sets when simultaneously estimating integration dates and tree topology. On simulated data, there was little difference between the estimates using a fixed-tree topology or estimating the tree topology. However, integrating over different topologies may have a greater effect with empirical data, evident when comparing the alternate dating methods with different tree inference software. Our dating method is dependent on the tree topology because divergence times and tip dates are highly associated with the dates of neighboring nodes and tips. Thus, the topology imposes a bias on the estimates and a poor topology may result in incorrect date estimates.

Despite using a fixed-tree topology, we integrate over the possible root positions allowing us to overcome potential biases imposed by using an outgroup or root-to-tip regression. The root position has a significant effect on estimating tip dates as divergence from the root is typically highly correlated with estimated tip date in phylogenetic dating methods. Over the three data sets, we found that although the support for any particular node being selected as root was low, the alternatively sampled root positions were always nearby (see figs. 2–4). Given the utility of Bayesian methods, it is not difficult to integrate the possible root positions.

In all three data sets, some of the estimated dates fell within the period of cART administration. Though it is possible for viral genomes to integrate during this period, there is typically no viral replication and hence likely no proviral integration during suppressive cART (Brodin et al. 2016; Van Zyl et al. 2017). For simulated data, these late estimates were observed, despite it being unlikely for integration to occur during cART. This behavior is not unique to the BEAST2 method as it also occurs for linear regression and LSD, where estimates can actually be later than the sampling date (Jones et al. 2018, 2020). This artifact is likely caused by highly divergent sequences that are difficult to date. One way to fix this would be to use a different prior that implements a low or zero likelihood of integration during cART, for example, the Exp1a prior.

There were marked differences between the results from our simulated data versus empirical data set. There was a greater degree of variability between the estimates with different integration date priors on the empirical data, especially when using different tree inference software for the alternate dating methods. Our simulation is a simplification of the complexities of within-host HIV evolution and thus produces data more amenable to phylogenetic analysis relative to empirical data. Despite this, the simulated data provide a proof of concept for our Bayesian integration date estimation method. It may be valuable in the future to explore how more sophisticated simulations affect the estimates of our method.

Although marginal likelihoods estimated via path sampling correlated with the RMSE of the integration dates in the simulated data, the unrealistic results estimated by the best-fitting Exp1a prior in the N133M data sets suggest that path sampling is not appropriate for empirical data. In both empirical data sets, the Exp1a prior estimated early integration dates that likely preceded the participants' infection date. This highlights the importance of carefully selecting priors when performing Bayesian analysis to reflect actual prior knowledge of the system. Here, the Latent prior best encapsulates this because it models the process of viral latency. The Latent prior was selected by path sampling for P1 and gave consistent estimates to alternative methods and the Latent prior for the simulated data had comparable RMSE to the best-fitting model (0.89 vs. 0.62 years). This RMSE is still lower than the RMSE of the alternative methods. Overall, we recommend using the Latent prior for integration date estimation without performing path sampling.

In the empirical data sets, the estimates using the Latent or NoPrior models were quite similar [concordance: 0.999 (P1) and 0.993 (N133M)]. This reveals that the prior on the root dates has a great effect on the integration date estimates. Nagel and Ranalla used a prior on the root dates to help inform the integration date estimates in their Bayesian method (Nagel and Rannala 2023). For the simulated data set and P1, we used a relatively tight prior on the root date for the Latent and NoPrior models. It would be interesting in the future to look at relaxing this prior given that we do not know the infection date of P1. The root date prior for N133M was informed by the participant's HIV test history and thus reflects our prior knowledge.

Two of our data sets feature a long period, approximately one decade, of untreated infection. This is at the upper end of the infection duration as untreated persons living with HIV typically go 6–10 years before progressing to AIDS. We chose these data sets to have this duration of untreated infection in order to ensure there were enough data and dispersion of data throughout time to get adequate model fit and to allow reservoir sequences to be distributed through the longer period of time so that we could analyze integration during different infection stages. N133M had a shorter period of untreated infection, <3 years, with only three time points of plasma samples. It is possible that the shorter interval with fewer time points led the path sampling to choose the Exp1a prior and with more data, a better prior would have fit or the Exp1a would have produced more appropriate results.

Being integrated into the BEAST2 framework provides an avenue of extensibility for our method allowing, for example, inclusion of correlated relaxed clocks, skyline/skygrid models, and birth death priors with the bdsky package (Stadler et al. 2013). BEAST2 also includes support for multiple genomic regions, but currently BEAST2 cannot date tips across multiple trees. Through a Bayesian framework, it is possible to incorporate additional prior information including from nongenetic sources such as viral load, T-cell quantity, and administration of therapy into the proviral date estimation model. Our method could be used to estimate proviral integration dates from different anatomical sites; lymph nodes (Finzi et al. 1999), brain (Rose et al. 2016), reproductive tissue (Shen et al. 2009; Miller et al. 2019), etc. (Churchill et al. 2016; Wong and Yukl 2016); possibly including dynamic models of migration (Vaughan et al. 2014). This would allow us to investigate genetic compartmentalization of proviruses in space and time as in Jones et al. (2020). Another avenue of future study is to estimate the “ages” of HIV emerging during viral rebound after treatment interruption or to compare the integration dates of intact and defective proviruses.

Latency is exhibited by other viruses including herpesvirus (Cohen 2020) and nonhuman viruses which can have significant ecological impacts (Biggs et al. 2021). Estimating latency periods in these viruses may provide useful insights. It is also possible to use our approach of tip date sampling to estimate dates of fossil samples from molecular data or morphological traits (Bapst et al. 2016; Froese et al. 2017) substituting latent sequences for fossil samples. We can also use tip date sampling to recover unknown collection dates of samples from an epidemiological outbreak, provided sufficient evolution occurred during the outbreak (Kuhnert et al. 2011; Didelot et al. 2018). Imposing prior information on the estimated collection dates may improve the epidemiological statistics computed.

In summary, we developed and implemented a method to estimate proviral integration dates from within-host HIV sequences using Bayesian analysis with BEAST2. Our method yielded accurate and precise results on both simulated and empirical data sets. Bayesian methods will yield a more accurate, granular, and complete understanding of persistent reservoir dynamics, ultimately contributing to development of durable HIV cure strategies.

Materials and Methods

Simulated Data Generation

Simulated HIV sequence data were generated using a modified SANTA-SIM, which allows multiple compartments (Jariani et al. 2019; Jones and Joy 2020) following the model described in Jones and Joy (2020). with the following alterations from Jones and Joy (2020): 1) instead of a full-length HIV sequence, the nef gene of the ancestral HIV subtype B strain HXB2 (GenBank accession: K03455) was used as the seed, after replacing the adenine (A) at position 371 with a guanine (G) to correct the premature stop codon at nef codon 124 to a tryptophan (W) and 2) neutral fitness was assumed, but nonstart codons at codon position 1 were given a fitness of 0.001 and stop codons were given zero fitness as before. This simulation model simulates longitudinal within-host HIV nef sequences with an active and latent compartment. HIV mutates and replicates freely in the active compartment and moves to and from the latent compartment where mutations do not occur. The simulation samples ten genomes from the active compartment each year over 10 years, at which point the initiation of antiretroviral therapy is simulated by setting the fitness of the active compartment to zero, thus clearing the active compartment. Ten more years are simulated on therapy during which time ten genomes are sampled from the latent compartment every 2 years. This results in 150 simulated sequences (100 active and 50 latent). The alignment was deduplicated using a custom R script that utilizes the R package seqinr (Charif and Lobry 2007) retaining duplicated sequences from the earliest collection time point.

Empirical Data Acquisition

We curated HIV nef sequences from participant 1 of Jones et al. (2018) available on GenBank (accessions: MG822918, MG822919, MG822923–MG822933, MG822935–MG822997, MG822999–MG823015, and MG823144–MG823170). Specifically, we used the alignment from Jones and Joy (2020), which was deduplicated and checked for hypermutation and recombination previously. This alignment includes 93 HIV RNA nef sequences derived from plasma from 14 time points during which the participant was not receiving antiretroviral therapy and 29 proviral nef sequences derived from peripheral blood mononuclear cells (PBMCs) from two time points while the participant was receiving cART.

We curated 99 sequences from participant N133M of Brooks et al. (2020) available on GenBank (accessions: MT195425-195535). The sequences were deduplicated using a custom R script that utilizes the R package seqinr (Charif and Lobry 2007) retaining duplicated sequences from the earliest collection time point. Hypermutated sequences were detected and removed using a custom R script based on HYPERMUT (https://www.hiv.lanl.gov/content/sequence/HYPERMUT/hypermut.html) and recombinants were identified and removed using OpenRDP (https://github.com/PoonLab/OpenRDP). This resulted in 63 HIV RNA nef sequences derived from plasma from three time points during which the participant was not receiving antiretroviral therapy and 34 proviral nef sequences derived from PBMCs from two time points while the participant was receiving cART.

For consistency with the simulated data, we will refer to the plasma-derived sequences from empirical data sets as “active sequences” and those derived from PBMCs as “latent sequences.”

Substitution Model Selection

Substitution model selection was performed using ModelTest-NG v0.1.6 (Darriba et al. 2020) considering all 203 substitution schemes, equal/unequal base frequencies, and uniform rate heterogeneity/discrete Gamma rate heterogeneity (GAMMA)/proportion of invariant sites (pInv)/GAMMA and pInv; and using all the distinct sequences for each data set. For the discrete Gamma rate heterogeneity, we employed four rate categories. The model with the lowest BIC was selected.

Prior Selection

We compared 6 BEAST2 models for each data set using only the sequences collected during active infection (99 simulated sequences and 93 empirical sequences) to determine the most appropriate clock and tree prior to use in the ultimate analyses. The specific clock and tree priors considered are given in supplementary table S2, Supplementary Material online. Clock priors for simulated data used a mean rate of 0.013 sub./site/year (Cuevas et al. 2015) and clock prior for empirical data used a mean rate of 8.2E−5 sub./site/day (Zanini et al. 2017). These models used the substitution model selected with ModelTest-NG under the default priors. A maximum likelihood phylogeny generated by IQ-TREE v1.6.1 (Nguyen et al. 2015) from the active sequences was used as a starting tree. All model XML files were generated via a custom R script.

Each model was run in BEAST v2.6.2 (Bouckaert et al. 2019) with a chain length of 100 million iterations, sampling every 10,000 iterations. We used the same operators for each run; except, we used larger operator weights and scales on the tree scale operator for models with a relaxed clock with exponential rate variation and coalescent with constant population size to facilitate convergence. Ten percentage of burn-in was discarded from each run and the parameters were checked for convergence by ensuring their effective sampling sizes (ESS) were all >200 and by inspection of parameter traces with Tracer v1.7.1 (Rambaut et al. 2018).

For each run, we performed path sampling using the BEAST package MODEL_SELECTION v1.5.3 (Leache et al. 2014). The model specifications were identical to the original run with 50 steps, 10 threads, alpha equal to 0.3, burn-in of 10,000,000 iterations and chain length of 11,000,000 iterations. We then ran the PathSampleAnalyser app included with MODEL_SELECTION with 100 cross-validations to compute the marginal likelihood and its SD.

Bayesian tip Date Sampling

We used our selected best-fitting BEAST2 model of clock and tree priors for each data set to generate BEAST2 models for the estimation of HIV proviral sequence integration dates. To our best model, we added latent sequences to the underlying data set and then extended our model adding the Latent prior on the integration date of the latent sequences. The Latent prior used the LatencyPrior class in the package BBD. Tip dates were sampled using the TipDatesRandomWalkerPadded operator in the BBD package with the padding set to 0. A maximum likelihood phylogeny generated by IQ-TREE including both active and latent sequences was used as a starting tree. The topology of the tree was fixed to aid run convergence and the root of the tree was sampled using the RootExchange operator from the BBD package. A diagram of the model is given in figure 1.

We developed a new prior in BEAST2 to serve as an informative prior based on our understanding of HIV latency dynamics. We call this prior the Latent prior. This prior models the likelihood that an HIV sequence underwent latency and was sampled before it could reactivate. The likelihood of the sequence becoming latent is given by an exponential distribution over the number of years/days since infection (the root of the tree), and likelihood of latent sequence reactivation is given by an exponential distribution over the number of years/days since proviral integration. Thus, the Latent prior is given by the following equation:

$$P(I=t):=P(L=t-T_{\mathrm{r}}|\overline{R\le T_{\mathrm{s}}-t})$$

where I is the integration date, L is the time till integration after infection, R is the time to reactivation after integration, $T_{\mathrm{r}}$ is the infection date, and $T_{\mathrm{s}}$ is the sampling date. This results in the likelihood function:

$$I(t)={\displaystyle \frac{(\rho -\lambda ){\mathrm{e}}^{(\rho -\lambda )t}}{{\mathrm{e}}^{(\rho -\lambda )T_{\mathrm{s}}}-{\mathrm{e}}^{(\rho -\lambda )T_{\mathrm{r}}}}}$$

where λ is the latency rate and $\rho$ is the reactivation rate. The values of these parameters are set the same as in the simulation (Jones and Joy 2020), which were based on Rong and Perelson (2009) and Strain et al. (2005). We also include a prior on the root date, a log-normal prior in the number of years/days the root was before first sampled sequence. See supplementary table S4, Supplementary Material online for details.

We ran the model in BEAST v2.6.2. To facilitate convergence, each run had variable chain lengths and operator scales. The specific values for each run are shown in supplementary table S12, Supplementary Material online. Ten percentage of burn-in was discarded from each run and the parameters were checked for convergence by ensuring that their ESS were all >200 and through inspection of parameter traces with Tracer. For some data sets (see supplementary table S12, Supplementary Material online) to achieve convergence, we split the analysis into 10 parallel runs with chain lengths of 1 or 5 billion iterations, sampling every 1,000,000 or 5,000,000 iterations. Ten percentage of burn-in was discarded from each run, the runs were combined using LogCombiner v2.6.2 (Bouckaert et al. 2019) and the combined runs were checked for convergence as above. The mean sampled date of each latent sequence was used as the estimate of the proviral integration for that sequence.

Path Sampling tip Date Priors

We performed the same analyses as above with ten additional priors on the integration dates and used path sampling to find the best-fitting priors. These priors are listed in supplementary table S4, Supplementary Material online and shown in supplementary figures S3–S5, Supplementary Material online. The priors which employed uniform or normal distributions used the MRCAPrior class in BEAST2, the log normal and exponential priors used the BBDPrior class in the package BBD v1.0.15 (available at https://github.com/brj1/BBD).

Each prior was selected and parametrized in an attempt to model the integration dates. The Unif1 and Unif2 use a uniform distribution bounded by the sampling times of the plasma sequences or the collection time of latent sequence and sometime before infection. These are meant to encapsulate nonpreferential seeding of the reservoir during active infection and nonpreferential seeding during the entire infection. The Norm prior uses a normal distribution centered at the midpoint of plasma sampling times with SD set to a quarter of the sampling interval of the plasma sequences. This prior is unrealistic in that it allows sequences to date later than their collection time, but it has most of its density within the period of sampling from plasma during active infection when we expect the majority of proviral integration to take place. We included this model to see if an unrealistic model will be selected by the path sampling. The Lnorm1 and Lnorm2 priors use log-normal priors on the number of days before the last sampled active sequence or collection date of the latent sequence. This distribution biases the dates to fall within the sampling period of plasma sequences during active infection in the absence of therapy. The Exp1a and Exp1b priors use exponential priors on the number of days before the last sampled active sequence or collection date of the latent sequence. These priors model a waiting time to proviral integration before collection. We also included Exp1b and Exp2b priors which had an estimated mean. We included these priors to see if we could infer the waiting time or “remain latent rate” from the data. Finally, we performed our analysis without specifying any prior for the integration dates. For these models, we also include the same prior on the root date as in the Latent prior; this prior on the root date was not included for the other runs. These runs are called the NoPrior runs.

The Unif2, Lnorm2, Exp2a, Exp2b, and Latent prior all depend upon the collection time of the latent sequence and thus for those priors each time point of latent sequences has its own prior. The other priors and the models with no prior on the integration dates do not depend on collection time and thus, those models have the same prior for each latent sequence.

We ran each model in BEAST v2.6.2 as described in the previous section. For each run except for runs with no prior on the integration dates, we performed path sampling with the BEAST2 package MODEL_SELECTION. We cannot use path sampling for the NoPrior runs because their likelihood function is improper. As before, the model specifications were identical to the original run with 50 steps, 10 threads, alpha equal to 0.3. We used the same burn-in as the original run and then sampled 100 times the sampling frequency of the original run, sampling the likelihood 1,000 times. We then ran the PathSampleAnalyser app included with MODEL_SELECTION with 100 cross-validations to compute the marginal likelihood and its SD.

Other Date Estimation Methods

For comparison, three other methods were used to infer proviral integration dates: EPA, linear regression, and LSD. EPA was performed as described in Abrahams et al. (2019). The alignment of unique active sequences was used to infer a maximum likelihood phylogeny using each of three software: FastTree v2.1.11—compiled with double precision (Price et al. 2010), RAxML v8.2.11 (Stamatakis 2014), or IQ-TREE v1.6.1 (Nguyen et al. 2015). Then EPA was used to find the most likely position in the phylogeny of each latent sequence using the scripts found at https://github.com/veg/ogv-dating running in HYPHY v2.5.8 (Kosakovsky Pond et al. 2020). For the empirical data, nucleotide position 34 was removed from the alignment as one sequence had a deletion.

Linear regression was performed as described in Jones et al. (2018). The alignment of all (including active and latent) distinct sequences was used to infer maximum likelihood phylogenies using the same three software packages. The phylogeny was rooted using root-to-tip regression maximizing the correlation between the active sequence dates and their phylogenetic distance from the root of the phylogeny using the R package ape. With R, a linear regression between sequence date and phylogenetic distance from the root was fit using only the active sequences. The latent sequence dates were then inferred from the linear regression using their phylogenetic distance from the root.

LSD was performed using the software LSD v2.3 (To et al. 2016). The same three maximum likelihood phylogenies inferred for the linear regression were used for LSD. The phylogeny was reduced to contain only active sequences using a custom R script and the root of the reduced phylogeny was inferred using LSD. The position of the root was then inferred in the complete phylogeny (active and latent sequences) from the position of the root in the reduced phylogeny using a custom R script. The integration dates of the latent sequences were then inferred using LSD with the rooted phylogeny containing all the sequences.

Statistical Analyses and Data Visualization

Statistical analyses and data visualization were performed in R v4.1.2. Specifically, the R packages: tidyverse (Wickham et al. 2019), magrittr, seqinr (Charif and Lobry 2007), and treeio (Wang et al. 2020) were used for data reading, writing, and manipulation. The R package optparse was used for script parameterization. The R package DescTools was used for statistical tests including RMSE and Lin's concordance coefficient (Lin 1989). The R package MASS (Venables and Ripley 2002) was used to perform Sammon MDS (Sammon 1969). The R packages ape (Paradis and Schliep 2019), phytools (Revell 2012), and tidytree were used for statistical analyses on trees. Finally, the R packages ggpubr, ggtree (Yu et al. 2017), and patchwork were used for producing graphics.

Edge bootstrap support values for phylogenies were computed by generating 1,000 bootstrap trees with IQ-Tree (Nguyen et al. 2015) using the “-bo” command and then assigning bootstrap values with the “prop.clades” function in the R package ape (Paradis and Schliep 2019).

Supplementary Material

Supplementary data are available at Molecular Biology and Evolution online.

Data Availability

Data available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.qfttdz0mj including simulated data XML specification file, BEAST2 XML specification files, scripts, and data.