Abstract
Hepatocellular carcinoma (HCC) is one of the most fatal cancers in the world. There is an urgent need to understand the molecular background of HCC to facilitate the identification of biomarkers and discover effective therapeutic targets. Published transcriptomic studies have reported a large number of genes that are individually significant for HCC. However, reliable biomarkers remain to be determined. In this study, built on max-linear competing risk factor models, we developed a machine learning analytical framework to analyze transcriptomic data to identify the most miniature set of differentially expressed genes (DEGs). By analyzing 9 public whole-transcriptome datasets (containing 1184 HCC samples and 672 nontumor controls), we identified 5 critical differentially expressed genes (DEGs) (ie, CCDC107, CXCL12, GIGYF1, GMNN, and IFFO1) between HCC and control samples. The classifiers built on these 5 DEGs reached nearly perfect performance in identification of HCC. The performance of the 5 DEGs was further validated in a US Caucasian cohort that we collected (containing 17 HCC with paired nontumor tissue). The conceptual advance of our work lies in modeling gene-gene interactions and correcting batch effect in the analytic framework. The classifiers built on the 5 DEGs demonstrated clear signature patterns for HCC. The results are interpretable, robust, and reproducible across diverse cohorts/populations with various disease etiologies, indicating the 5 DEGs are intrinsic variables that can describe the overall features of HCC at the genomic level. The analytical framework applied in this study may pave a new way for improving transcriptome profiling analysis of human cancers.
Keywords: Hepatocellular carcinoma, gene-gene interaction, batch effect, competing risk, transcriptome, differentially expressed genes (DEGs)
Introduction
Hepatocellular carcinoma (HCC) is the third most common cause of cancer death globally.1 -3 Hepatitis B virus (HBV) is a major cause of HCC in East Asians, while alcoholic/nonalcoholic fatty liver disease and chronic hepatitis C are the most common etiologies in the U.S. and European populations.4,5 In the U.S., the incidence of HCC has more than doubled over the past 2 decades and is anticipated to continue increasing due to a growing number of patients with alcoholic/non-alcoholic steatohepatitis (ASH/NASH) and advanced hepatitis C virus (HCV) infection.1,3 The development of HCC is a multistep process that involves the accumulation of genetic and epigenetic alterations.6 -10
Transcriptome profiling analysis is instrumental in understanding disease initiation and progression in HCC. 11 Over the past decade, microarray-based gene expression profiling studies have been performed to elucidate hepatocarcinogenesis and disclose molecular mechanisms underlying complex clinical features of HCC,8 -10,12 including comparative analysis of cancer versus non-cancerous samples, 13 early-stage versus late-stage, 14 good prognosis versus poor prognosis, 13 and HBV versus HCV infection. 15 With the advance of next-generation sequencing technologies, RNA sequencing (RNA-seq) has become a powerful tool in defining the transcriptomic changes related to HCC. Several RNA-seq studies have been performed on human HCC samples, predominantly in Asian populations.16 -19 Our recently RNA-seq study in a U.S. Caucasian cohort suggest oxidative phosphorylation and the associated DNA damage as a major driving pathophysiological feature in HCC. 20 Based on gene-expression profiles that are predictive of tumor metastasis, vascular invasion, and prognostic outcomes, several molecular classification schemes have been proposed,9,10 although they have not been applied in the clinical management of HCC patients yet.
To date, the majority of transcriptomic studies have relied on conventional analytical methods, which involve examining fold changes of individual genes between tumor and control tissues or conducting pathway enrichment analysis based on the existing knowledge of genes and biological processes. These methods have limitations in estimation accuracy and prediction power. As a result, a substantial number of genes/transcripts have been reported to be significant for HCC. However, their sensitivity and specificity in cancer identification/classification are not optimal, and the reproducibility of the findings across different studies is only moderate. Moreover, the conventional analytical models have not adequately addressed gene-gene interactions. Thus, there is a pressing need to develop novel methodologies that can identify critical differentially expressed genes (DEGs) with high sensitivity and specificity for disease identification/classification. Recent advances in the machine learning community have shown a great promise in addressing these challenges.21 -23
To this end, we sought to develop a new machine learning framework for analyzing transcriptome profiling data, aiming to identify a sparse selection of critical DEGs for HCC. Our approach builds upon the max-linear competing structure introduced in recently developed models, namely the max-linear competing factor models, 21 max-linear regression models, 22 and max-linear logistic models. 23 The key distinction between max-linear competing models and traditional regression models lies in the replacement of the original linear combination of predictors with the maximum value derived from multiple competing factors or competing-risk factors, also known as signatures. By considering interactions and competing relationships among the covariates in predicting the outcome variable, the max-linear competing factor models address a crucial aspect neglected by traditional regression models. The competing factor models have been proven to outperform the existing deep learning methods (such as random forest, support vector machine, and group LASSO-based method) in estimation accuracy and prediction power under broad data structures.21,22 In our early efforts, critical DEGs were successfully identified for lung cancer, 24 breast cancer 25 and COVID-19 23 using the max-linear competing factor models.
In this work, we applied the max-linear competing risk factor models to analyze 10 gene expression profiling datasets, including our own dataset from a U.S. Caucasian cohort. Through this analysis, we identified 5 critical DEGs (CCDC107, CXCL12, GIGYF1, GMNN, and IFFO1) that exhibit remarkable sensitivity and specificity for HCC identification. Importantly, these results are both interpretable and robust, demonstrating reproducibility across diverse cohorts and populations.
Material and Methods
Data acquisition and processing
A total of 10 whole-transcriptome datasets were analyzed, including 9 publicly available datasets and one RNA-seq dataset that we collected at the University of Wisconsin-Madison. The public datasets were obtained by searching the Cancer Genome Atlas (TCGA) Liver Cancer (LIHC) database and the Gene Expression Omnibus (GEO) database using the keywords of “hepatocellular carcinoma” and “Homo sapiens.” Since the primary purpose of our study was to identify critical DEGs for HCC in general, we deliberately included datasets representing diverse populations/ethnicities (eg, North American and European Caucasians, blacks, Chinese, Japanese, and Korean) with varying disease etiologies (eg, alcohol abuse, metabolic syndrome, HBV, and HCV). Moreover, these datasets were generated using different techniques and platforms, such as microarrays and RNA-seq. Relevant clinical and pathological information, such as age, sex, and TNM tumor stages, was also collected whenever it was available (Table 1).
Table 1.
Distribution of basic clinical and pathological characteristics in the TCGA dataset.
| Subgroup | Age (years) | Sex | BMI (kg/m2) | TNM tumor stage | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Median | Range | Male | Female | Median | Range | I | II | III | IV | |
| 1 | 66 | 64-69 | 1 | 1 | 21.28 | 18.61-23.94 | 2 | 0 | 0 | 0 |
| 2 | 57 | 46-74 | 3 | 4 | 27.00 | 16.98-37.88 | 2 | 2 | 2 | 0 |
| 3 | 66 | 20-80 | 16 | 5 | 29.94 | 18.20-35.92 | 8 | 5 | 5 | 0 |
| 4 | 62 | 16-85 | 98 | 56 | 23.70 | 14.53-56.14 | 55 | 35 | 49 | 1 |
| 5 | 61 | 17-85 | 79 | 25 | 25.28 | 16.30-131.84 | 63 | 22 | 13 | 1 |
| 6 | 58 | 20-90 | 56 | 30 | 23.88 | 15.81-41.10 | 43 | 23 | 16 | 2 |
Abbreviations: BMI, body mass index (kg/m2).
The first public dataset was obtained from a RNA-seq study performed in the TCGA LIHC cohort (https://xenabrowser.net/datapages/?dataset=TCGA-LIHC.htseq_fpkm.tsv&host=https://gdc.xenahubs.net&removeHub=https://xena.treehouse.gi.ucsc.edu:443) using the Illumina HiSeq platform. This dataset contained 60 484 identifiers (genes/transcripts) and 424 samples (374 HCC and 50 normal controls). Data from the same sample but different vials/portions/analytes/aliquotes was averaged. Data from different samples were combined into genomicMatrix. The gene expression data were log2(fpkm+1) transformed.
The second dataset (GSE54236) was obtained from a transcriptome profiling study performed in an Italian cohort using the Agilent-014850 Whole Human Genome Microarray 4x44K G4112F platform. 26 The dataset included 161 samples (81 HCC samples and 80 paired nontumor samples). The gene expression data were applied a transformation of (−20)/(Quantile normalized log2 signal intensity).
The third dataset (GSE6764) was obtained from a transcriptome profiling study of HCV-induced HCC using the Affymetrix human U133 plus 2.0 Array platform. 27 The dataset contained 75 samples from 48 patients, including 13 samples from cirrhotic tissue, 17 dysplastic nodules, 35 HCC samples, and 10 normal controls. The samples were collected in 3 hospitals, one in the United States (Mount Sinai Hospital, New York, NY) and 2 in Europe (Hospital Clínic, Barcelona, Spain, and National Cancer Institute, Milan, Italy). The gene expression data was applied a transformation of −50/(MAS probe set signal intensity).
The fourth dataset (GSE41804) was obtained from a transcriptome profiling study of HCV-related HCC performed in a Japanese cohort using the Affymetrix Human Genome U133 Plus 2.0 Array platform. 28 The dataset included 20 HCC samples and 20 nontumor controls with chronic hepatitis C. The gene expression data were log2 normalized signal intensity.
The fifth dataset (GSE25097) was obtained from a transcriptome profiling study of HBV-related HCC performed in a Chinese cohort using the Affymetrix 1.0 microarray platform. 29 The dataset included 268 HCC samples and 289 nontumor controls (243 adjacent non-tumor, 40 cirrhotic and 6 healthy liver samples). The gene expression data were normalized intensity.
The sixth dataset (GSE63898) was obtained from a transcriptome and methylome profiling study of HCC. 30 RNA profiling was conducted on 228 HCC and 168 nontumor adjacent cirrhotic liver tissues using the Affymetrix Human Genome U219 Array. The samples were collected from 2 institutions: IRCCS Istituto Nazionale Tumori (Milan, Italy) and Hospital Clínic (Barcelona, Spain). The gene expression data were normalized and logged-2 transformed using the RMA algorithm.
The seventh dataset (GSE101685) was obtained from a transcriptome profiling study of HCC in Taiwan using the Affymetrix Human Genome U133 Plus 2.0 Array. The dataset included 24 HCC samples and 8 normal controls.
The eighth dataset was obtained from a RNA-seq study of HCC in liver transplant livers in South Korea using Illumina HiSeq 2000. 31 RNA profiling analysis was conducted on 54 HCC samples and 15 nontumor samples.
The ninth dataset was obtained from a transcriptomic study of NASH-related HCC using the Affymetrix Human Genome U219 Array. 32 RNA profiling analysis was conducted on 53 NASH-HCC samples and 6 healthy liver samples.
Our dataset was collected at the University of Wisconsin-Madison from a U.S. Caucasian cohort. 20 The dataset contained 17 HCC samples and 17 paired nontumor samples. The patients provided “written” informed consent before sample collection. The majority of the patients had at least one risk factor for metabolic syndrome and some had a history of alcohol abuse. Few patients had a history of treated chronic hepatitis C. Through RNA-seq analysis, we identified oxidative phosphorylation and its associated DNA damage as the primary driving carcinogenic feature in HCC. 20 The gene expression data were subjected to log2(fpkm+1) transformation.
Analytical methodology
We implemented the max-linear logistic regression model to build a competing risk factor classifier. The competing factor classifier has an advantage over existing models in nonlinear predictions and classifications. In brief, the task is to discover the parsimonious number of critical genes for disease prediction. The theoretical foundation of competing risk factor models was recently described elsewhere.21,22,33 To identify the critical DEGs across the 9 public datasets and our own RNA-seq dataset, the heterogeneous extension of the max-linear logistic regression was applied. We started with 3 competing risk factors in the max-linear logistic regression models, with each factor having only 3 genes randomly drawn from the genes/transcripts in each dataset. A Monte Carlo method with extensive computation was applied to finalize model with the best performance of sensitivity and specificity and the smallest number of genes. The basic ideas of competing risk classifiers for heterogeneous populations are described below.
Suppose there are primary outcome variables where
| (1) |
Each of the , ( may be related to groups of genes
| (2) |
where is the th individual in the sample, is the number of genes in th group. The competing (risk) factor classifier for the th outcome variable is defined as
| (3) |
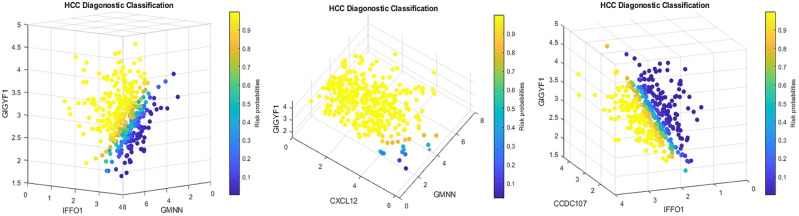
where ’s are intercepts, is a observed vector, is a coefficient vector which characterizes the contribution of each predictor to the outcome variable in the th group to the risk, and + is called the th competing risk factor, that is, th signature. In Figure 2, G = 3 corresponds to 3 competing factors, that is, as long as a patient falls in the yellow color range in any of the 3 subfigures, the patient is classified as an HCC patient.
Figure 2.
Four-dimension plot illustrating the signature patterns defined by each classifier in the TCGA dataset.
Remark 1: With , (3) is reduced to the classical logistic regression classifier. It is clear that compete against each other to win out to take the final effect. As such, they are called competing (risk) factors.
The unknown parameters are estimated from
| (4) |
where 0.5 is a probability threshold value that is commonly used in machine learning classifiers, is an indicator function, is defined in equation (3), is the index set of all genes, , , …, are index sets corresponding to (2), and is the final gene set selected in the final classifiers.
To introduce sparsity for both the number of variables (genes) and the number of groups (competing factors, signatures) into the model, the following optimization problem with penalties is considered:
| (5) |
where is the union set of , is the cardinality. Tuning parameters and are both non-negative. is monotone decreasing in both and . Additional properties of this bivariate function was described elsewhere. 22
Remark 2: In (2), and can be measured under different scales for even if they correspond to the same genes (variables), that is, from heterogeneous populations or cohort studies.
Remark 3: (5) is a completely new machine learning classifier with completely different penalization from existing ones, such as LASSO, SCAD, and MCP.
Next, we show a unique theoretical and computational property of the new competing risk factor classifier. The optimization problem (5) is designed to guarantee that, with suitable choices of and , the solution of problem (5) will lead to the smallest number of subsets of variables ( ) and the smaller number of signatures (S4) ( ) while achieving the best possible minimal misclassification rate.
The rationale is as follows:
1. Suppose the underlying best classifier is a “perfect classifier,” with then with this classifier
Problem (5) is equivalent to
Since , , problem (5) is equivalent to first minimizing and then , which leads to the smallest possible and
2. Suppose the underlying best classifier is not a perfect classifier, with the minimal misclassification number , then there exists and such that
Therefore, problem (5) will first minimize, ,then , and finally , which will again lead to the smallest possible and .
Remark 4. The S4 property of (5) and its capability to simultaneously classify multiple heterogeneous populations with common variables (genes) make the new competing risk factor classifier different from existing ones.
Remark 5. When and , (5) is equivalent to the classifier introduced by Zhang. 23 The details of computational steps were described early 23 and demo Matlab codes are publicly available online.
Note that equation (5) is integration of integer programing, combinatorial optimization, and continuous optimization. Its computational complexity level is extremely high. In this study, we adopted the following Monte Carlo approach:
- Randomly selecting a cohort (population), say without loss of generality.
- (a) Randomly draw sets of genes with each set having genes;
- (b) Use any optimization procedures (eg, Nelder–Mead method, genetic algorithm, simulated annealing) to solve minimizing
- (c) Repeat the above 2 steps for and until an acceptable best solution is reached.
- Using the genes selected from the cohort, for , repeat the above 2 steps (b) and (c) for until an acceptable best solution is reached.
- Remark 6. For the data used in this study, a nearly perfect classifier was achieved using the above Monte Carlo approach.
We adopted the following criteria to define critical DEGs:
(1) The number of genes should be as small as possible (smaller than 15).
(2) This set of genes should lead to overall accuracy of >95% in at least 3 different study cohorts with a total number of patients/subjects being at least 1000.
(3) This set of genes should lead to an overall 100% accuracy for at least one study cohort with at least 10 subjects.
(4) At least one gene functions and shows the same sign (+ or −) in each study cohort.
(5) This set of genes should lead to at least 80% accuracy for any cohort with either sensitivity or specificity of >75%.
(6) In each competing classifier, the number of genes should be as small as possible, and it must be less than six.
(7) The number of competing classifiers should be as small as possible and without redundancy, that is, every classifier cannot be replaced.
Results
Identification of critical DEGs
Using a probability higher than 50% as the threshold, we identify 5 critical DEGs: namely CCDC107 (Protein Coding: Coiled-Coil Domain Containing 107), CXCL12 (Protein Coding: C-X-C Motif Chemokine Ligand 12), GIGYF1 (Protein Coding: GRB10 Interacting GYF Protein 1), GMNN (Protein Coding: Geminin DNA Replication Inhibitor), and IFFO1 (Protein Coding: Intermediate Filament Family Orphan 1).
Identification of classifiers based on five critical DEGs
The final classifiers were the combination of the 3 competing factors ( as shown in Table 2. The risk probabilities were calculated using the logistic function of for the combined classifiers in each dataset, and of for each individual classifier .
Table 2.
The 5 critical DEGs and the classifiers in the 7 datasets.
| Dataset | Data source | Tumor | Non-tumor | Classifier | Intercept | CCDC107 | CXCL12 | GIGYF1 | GMNN | IFFO1 | Accuracy % | Sensitivity % | Specificity % |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | TCGA | 374 | 50 | CF1 | −11.185 | 6.992 | 2.072 | −7.164 | 68.87 | 64.71 | 100 | ||
| CF2 | −10.186 | 3.028 | −6.986 | 10.801 | 58.25 | 52.67 | 100 | ||||||
| CF3 | 3.311 | −2.582 | 1.925 | 1.923 | 97.88 | 97.59 | 100 | ||||||
| CFmax | 100 | 100 | 100 | ||||||||||
| Stage 1 | 173 | 50 | CFi | −6.536 | 2.954 | 96.86 | 97.69 | 94 | |||||
| Stage 1 | 173 | 50 | CFi | 4.707 | −1.036 | 91.48 | 94.8 | 80 | |||||
| 2 | GSE54236 | 81 | 80 | CF1 | 21.724 | 4.879 | −2.086 | 9.677 | 78.88 | 61.73 | 96.25 | ||
| CF2 | 15.893 | −5.440 | 0.355 | 14.239 | 78.26 | 64.2 | 95 | ||||||
| CFmax | 90.06 | 85.19 | 95 | ||||||||||
| 3 | GSE6764 | 35 | 10 | CF1 | 13.3 | 5.098 | 2.756 | 5.33 | 92 | 92.31 | 90 | ||
| CF2 | 8.3 | 5.336 | 21.878 | 0.454 | 72 | 67.69 | 100 | ||||||
| CFmax | 100 | 100 | 100 | ||||||||||
| 35 | 13 CI | CF1 | 0.983 | 4.182 | −12.002 | −6.002 | 95.83 | 94.29 | 100 | ||||
| CF2 | 10.090 | 3.002 | 2.502 | 10.154 | 89.58 | 85.71 | 100 | ||||||
| CFmax | 100 | 100 | 100 | ||||||||||
| 17 DN | 10 | CF1 | 9 | 8.5 | −18.928 | 26.26 | 92.59 | 88.24 | 100 | ||||
| CF2 | 2.2 | 12.686 | −44.914 | −0.974 | 81.48 | 70.59 | 100 | ||||||
| CFmax | 100 | 100 | 100 | ||||||||||
| 4 | GSE41804 | 20 | 20 | CF1 | 1.936 | −4.931 | −7.614 | 11.438 | 92.5 | 90 | 95 | ||
| CF2 | −49.690 | 6.308 | −3.712 | 0.894 | 85 | 75 | 95 | ||||||
| CFmax | 97.25 | 100 | 95 | ||||||||||
| 5 | GSE25097 | 268 | 249 | CF1 | −1.697 | −0.531 | −3.858 | 13.330 | 83.75 | 70.15 | 98.39 | ||
| CF2 | −2.834 | −5.803 | 10.392 | −6.829 | 96.13 | 92.54 | 100 | ||||||
| CFmax | 98.65 | 98.88 | 98.39 | ||||||||||
| 6 | GSE63898 | 228 | 168 | CF1 | −6.129 | 7.782 | −8.426 | 3.364 | 97.47 | 96.49 | 98.81 | ||
| Stage 1 | 19 | 168 | CFi | −11.295 | 1.202 | 95.19 | 63.16 | 98.81 | |||||
| Stage 1 | 19 | 168 | CFi | 14.587 | −1.719 | 97.33 | 84.21 | 98.81 | |||||
| 7 | GSE101685 | 24 | 8 | CF1 | −1.377 | −5.030 | 6.625 | 100 | 100 | 100 | |||
| 8 | GSE148355 | 54 | 15 | CF1 | 3.557 | −0.865 | 5.825 | 100 | 100 | 100 | |||
| 9 | GSE164760 | 53 | 6 | CF1 | −11.425 | −3.300 | 2.306 | 2.815 | 49.15 | 43.40 | 100 | ||
| CF2 | −3.909 | −4.797 | 9.897 | −2.595 | 84.75 | 83.02 | 100 | ||||||
| CFmax | 94.92 | 94.34 | 100 | ||||||||||
| 10 | Our RNA-seq data | 17 | 17 | CF1 | 6.432 | 6.587 | −2.235 | 5.964 | −14.586 | 97.06 | 100 | 94.12 | |
| Total | 1184 | 672 | 97.79 | 97.47 | 98.27 |
Abbreviations: DN, dysplastic nodule; CI, cirrhosis.The final classifiers are combined classifiers of individual competing factors.
As shown in Table 2, the classifier (CFmax) had decent performance in differentiating tumor from nontumor tissue, with an overall sensitivity/specificity/accuracy of >97%. Applying CF1, CF2, and CF3 simultaneously could increase the power of cancer detection. In general, the risk probability of HCC was determined by the direction/sign and absolute value of the coefficient of the classifier. A positive coefficient indicated a higher gene expression value was associated with higher risk probability of HCC. On the contrary, a negative coefficient suggested a lower gene expression value was associated with higher risk probability of HCC.
In the first dataset (TCGA), CF1 and CF2 had moderate sensitivity and accuracy for identification of HCC, but simultaneous use of all 3 classifiers (CF1, CF2, and CF3) achieved 100% sensitivity/specificity/accuracy. In the datasets 2, 3, 4 and 5, CF1 and CF2, had overall high sensitivity (>85%), specificity (>90%), and accuracy (>90%) of identifying HCC patients and thus additional CFs were not required for cancer identification. Given the availability of tumor staging information in the datasets 1 and 6, analyses were performed for stage 1 HCC as well. It can be seen stage 1 HCC could be identified by one classifier CF1 defined by CXCL12 or GMNN alone with decent sensitivity/specificity/accuracy, suggesting CXCL12 and GMNN could be powerful biomarkers for early-stage HCC. However, CXCL12 appeared to be the winner if applying Hill’s criteria.
In the third dataset, since the 75 samples included 35 HCC, 13 cirrhotic tissue, 17 dysplastic nodules, and 10 normal controls, separate analyses were performed for HCC versus normal controls, HCC versus cirrhotic tissue, and dysplastic nodules versus normal controls. It can be seen the CFmax achieved 100% sensitivity/specificity/accuracy for each subgroup analysis.
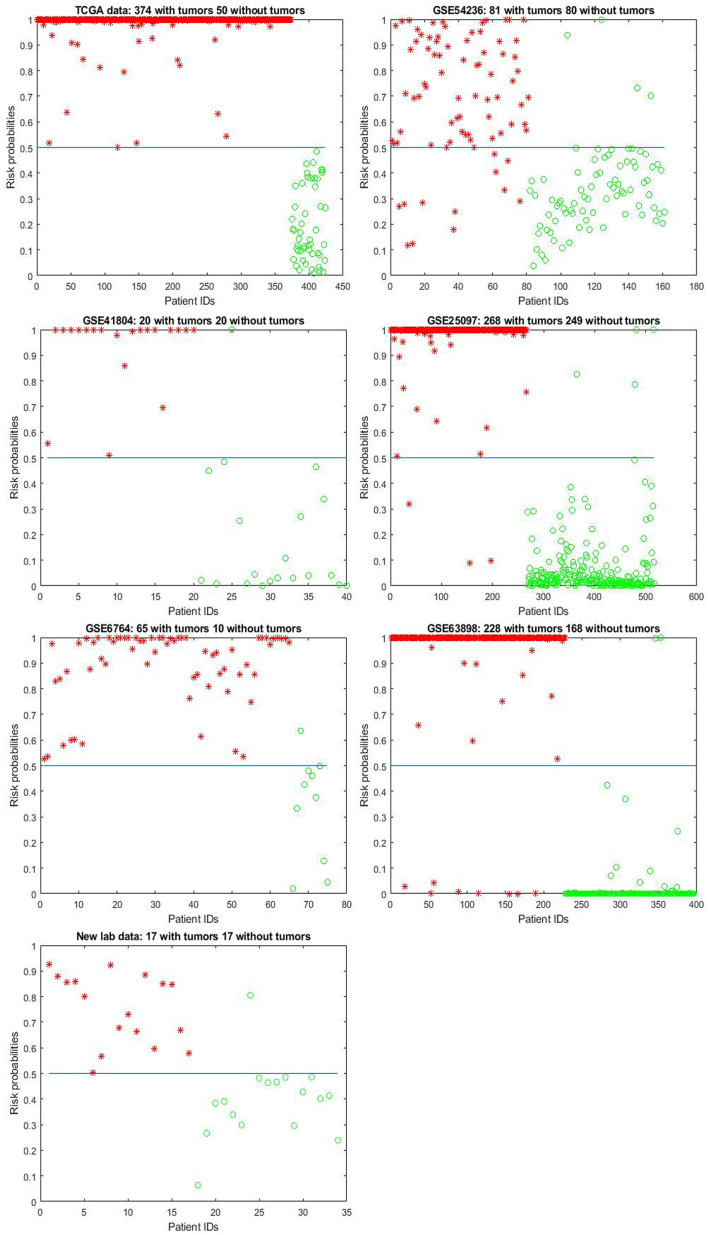
For illustration, Figure 1 shows the model-estimated risk probabilities evaluated from the final classifiers in all the datasets.
Figure 1.
Model-estimated risk probabilities evaluated from the final classifiers in the 7 datasets.
The plot designates hepatocellular carcinoma (HCC) samples by asters and the nontumor controls (NC) by circles. A 0.5 (50%) horizontal line (probability threshold value) is plotted in each panel.
Figure 2 is a four-dimension plot illustrating the signature patterns defined by each classifier in the TCGA data. The figure clearly shows how 5 critical DEGs interact with each other to form different signature patterns (shapes). In the figure, colors and their intensity indicates how patients were classified to HCC (yellow color) or cancer free (green and blue colors).
The Venn diagram (Figure 3) demonstrates patient subgroups classified by the classifiers in the TCGA data. In this North American cohort, HCC patients could be classified into 6 subgroups based on the above classifiers. The subgroup I contained the patients who were only detected by the CF1, the subgroup II contained the patients who were only detected by the CF2, the subgroup III contained the patients who were only detected by CF3, the subgroup IV contained the patients who were detected by CF1 and CF2 simultaneously but not CF3, the subgroup V contained the patients who were detected by CF2 and CF3 simultaneously but not CF1, and the subgroup V contained the patients who were detected by all the 3 classifiers simultaneously. The patients in one subgroup may possess different genetic features from other subgroups.
Figure 3.
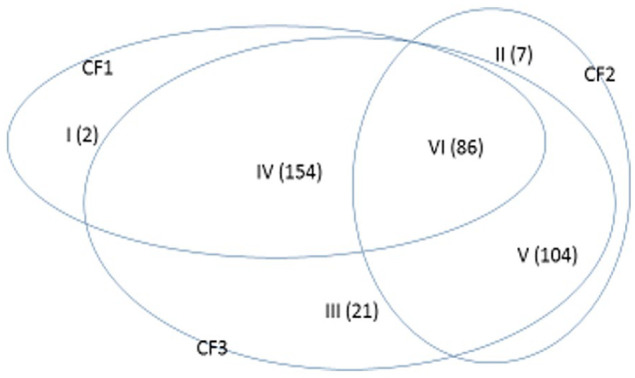
Venn diagram demonstrating patient subgroups classified by the classifiers in the TCGA dataset.
Table 3 shows gene expression values of the 5 critical DEGs in a small portion of the samples from the TCGA dataset. The full data with original gene expression values and the computed values are available online.
Table 3.
Gene expression values, competing factors, and risk probability in a small portion of the samples in the TCGA dataset.
| Ensembl_ID | Tumor status | CCDC107 | CXCL12 | GIGYF1 | GMNN | IFFO1 | CF1 | CF2 | CF3 | CFmax | Pmax |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TCGA-DD-A4NG-01A | 1 | 2.240 | 1.082 | 3.587 | 3.216 | 2.188 | 4.892 | −4.837 | 13.612 | 13.612 | 1 |
| TCGA-G3-AAV4-01A | 1 | 3.046 | 1.682 | 3.134 | 3.879 | 2.402 | 1.558 | 3.091 | 12.467 | 12.467 | 1 |
| TCGA-2Y-A9H1-01A | 1 | 3.323 | 0.708 | 2.354 | 2.243 | 1.807 | −3.021 | 2.948 | 10.330 | 10.330 | 1 |
| TCGA-BC-A10Y-01A | 1 | 2.620 | 0.849 | 2.331 | 3.828 | 2.395 | −4.106 | 7.326 | 12.974 | 12.974 | 0.98 |
| TCGA-DD-A3A2-11A | 0 | 1.446 | 4.903 | 2.212 | 1.863 | 1.205 | −0.489 | −8.244 | −1.503 | −0.489 | 0.40 |
| TCGA-BD-A2L6-11A | 0 | 1.624 | 5.677 | 2.755 | 1.575 | 2.211 | −4.495 | −0.637 | −3.014 | −0.637 | 0.41 |
| TCGA-EP-A12J-11A | 0 | 2.023 | 5.247 | 1.935 | 2.429 | 1.244 | −1.536 | −4.138 | −1.841 | −1.536 | 0.01 |
| TCGA-DD-A3A6-11A | 0 | 1.734 | 3.363 | 1.531 | 1.228 | 0.857 | −4.072 | −6.379 | −0.062 | −0.062 | 0.12 |
| TCGA-EP-A26S-11A | 0 | 1.617 | 4.070 | 1.683 | 1.797 | 1.050 | −3.218 | −5.702 | −0.500 | −0.500 | 0.06 |
In the column “Tumor status,” value “0′” stands for normal control sample, while value “1” stands for HCC. Column Pmax corresponds to Data_i, and the risk probability (truncated to 3 decimal digits for illustration purpose) of a HCC sample evaluated from the ith dataset.
Analysis of the U.S. Caucasian cohort (dataset 7)
We assessed the performance of the 5 critical DEGs identified in the 9 public datasets in our U.S. Caucasian cohort. Setting and solving equation (5), the classifiers were obtained (Table 2). It can be seen the classifier achieved an overall accuracy of 97.06%, sensitivity of 100%, and specificity of 94.12%.
Characterization of clinical and pathological features
To further characterize the differences between subgroups defined by classifiers, we examined the general clinical and pathological attributes, including age, sex, BMI (body mass index, kg/m2), and AJCC tumor stages in the first dataset (Table 1). Data are not shown for other datasets due to incomplete information. In the TCGA dataset, it appeared the patients in subgroup 3 had higher BMI than other subgroups.
Discussion
In this study, we analyzed datasets encompassing HCC patients from diverse populations/ethnicities with varying etiologies and spanning different tumor stages. The identification of the 5 critical DEGs (CCDC107, CXCL12, GIGYF1, GMNN, and IFFO1) exhibiting consistent high performance across all datasets suggests that they may represent intrinsic variables that capture the overarching genomic characteristics of HCC. Importantly, our model stands out by effectively addressing the challenge posed by batch effect, as it enables simultaneous modeling of heterogeneous populations (as demonstrated in equation (4)) and disease subtypes (as shown in equation (3)) within our framework. Consequently, there is no need for batch effect correction in our approach. In contrast, classical cross-validation (CCV) commonly employed for model fitting and inference is limited to homogeneous datasets and cannot handle the complexities of our model.
It should be noted gene-gene interactions defined in our model are different from interaction effects widely used in traditional experimental designs, such as row-column interaction effects or laboratory-chemical formula interaction effects in agriculture and industry. It is also different from the interaction term in linear regression analysis, that is, using the multiplication of 2 covariates (predictors) to form an additional covariate to study the interaction effects of these 2 covariates in existing statistical models and machine learning. Using TCGA data in Table 2 as an illustration, there are 3 combinations (3 competing classifiers, CF1, CF2, and CF3). In CF1, 3 genes GIGFY1, GMNN, IFFO1 form a combination (signature) with the coefficient signs of the first 2 being positive while the third one being negative. In CF2, 3 genes CCDC10, GIGYF1, IFFO1 form a different combination (signature) with the coefficient signs of the second gene being negative while the other 2 being positive. In CF3, 3 genes CXCL12, GIGYF1, GMNN form another combination (signature). Taking GIGYF1 as an example, its coefficient signs depend on which combination this gene falls into, that is, how this gene interacts with other genes. The same is true with IFFO1. Using a basketball team as an analog, these 5 genes correspond to 5 basketball players in a team. The team has 3 main teammate combinations for scoring. A positive coefficient associated with a player in a teammate scoring combination means that the longer the ball-controlling time by the player, and the higher chance the team to score. On the contrary, a negative coefficient associated with a player means that the shorter the ball-controlling time by the player, and the higher chance the team to score. A question is which scoring combination is going to score. As displayed in Figure 2 (Venn Diagram), in some scenarios, only one combination can score, whereas in some other scenarios, 2 of the 3 combinations or any combination can score. Using TCGA data as an example, there are interactions between competing factors (CF1, CF2, CF3) mainly mediated by GIGYF1.
Functional relevance of the 5 critical genes to HCC has been described in the literature. CXCL12 expression increases following acute or chronic liver injury. 34 CXCL12-dependent signaling contributes to modulating acute liver injury and subsequent tissue regeneration.35,36 The CXCL12 pathway is linked to development of HCC by promoting tumor growth, invasion, and metastasis.37,38 Down-regulation of CXCL12 was observed in HCC.39 -43 GMNN plays a key role in cell cycle regulation. 44 Increased expression of GMNN was reported in several malignancies such as HCC, colorectal, pancreatic and breast cancer.45 -49 Amplification of GMNN was associated with HCC and colorectal cancer, suggesting the role of GMNN as a common tumor driver gene in human malignancies, 50 which is consistent with its role in cell cycle regulation. 51 Suppression of geminin activity may selectively kill cancer cells. 45 GIGYF1 binds growth factor receptor bound 10 (GRB10) which is an adaptor protein that binds activated insulin-like growth factor 1 (IGF1) and insulin receptors and regulates receptor signaling. 52 Loss of GIGYF1 function is associated with clonal mosaicism and adverse metabolic health, such as higher susceptibility to type 2 diabetes, higher fat mass and lower serum IGF1 levels. 53 High expression of GIGYF1 is unfavorable in HCC. 54 IFFO1 is a member of the intermediate filament family. 55 Inactivating IFFO1 leads to increases in both the mobility of broken ends and the frequency of chromosome translocation. 56 The destruction of this nucleoskeleton accounts for the elevated frequency of chromosome translocation in many types of cancers including HCC. 56 CCDC107 encodes a membrane protein which contains a coiled-coil domain in the central region. CCDC107 expression was found to be decreased in colorectal cancer, 57 yet its significance in liver metabolism has not be described. Although these 5 genes have been described in molecular cellular levels studies of human malignancies, none of them has been reported to be individually significant in whole-transcriptome profiling studies of HCC. In other words, these 5 genes, which were individually insignificant at the level of whole-transcriptome profiling, stand out to be the key players for HCC as a group.
Our study has several limitations. First, this is a retrospective study analyzing large transcriptome datasets. It is necessary to perform additional analysis to assess their value in predicting disease prognosis, which yet is impossible due to lack of complete clinical follow-up data (such as disease recurrence, metastasis, and survival outcomes) in the public datasets. Therefore, further studies incorporating comprehensive clinical information are warranted to explore the clinical significance of molecular classification based on the 5 critical DEGs. Second, since the diagnosis of HCC is largely based on patients’ symptoms and clinical workups (eg, serology, radiology, and tissue biopsies), the 5 genes do not have immediate clinical significance in the diagnosis of HCC diagnosis. However, investigating molecular subtypes based on transcriptomic patterns is necessary for reveling the underlying molecular mechanisms of carcinogenesis. Incorporating reliable genomic biomarkers such as the 5-gene based classifiers in the HCC diagnosis algorithm may enhance the accuracy of disease identification and classification of patients and eventually personalized medicine. Third, whether the 5-gene based classifiers are applicable to the general population in blood samples await further validation, which can be done in a study cohort where the patients have both HCC tissues and blood samples available for analyses. Finally, while DEGs might be a chance finding due to a variety of reasons, such as linkage, epigenetic processes, strong signals from certain patients, and confounding factors, we consider the likelihood of this possibility to be low in our study since we have implemented highly stringent criteria to define critical DEGs. Moreover, the genes identified by our method consistently demonstrate efficacy across all cohorts, reinforcing our view of them as intrinsic variables.
In summary, our work for the first time describes the interaction effects of the 5 critical DEGs in determining the status of HCC. The findings could be a starting point for further work such as gene network analysis, testing other related genes and their functional interaction, and discovering causal effects. Our study is not merely reanalysis of public data and identifying genes with known functions to HCC, but it represents a pioneering effort in applying conceptually new max-linear competing risk factor models to identify transcriptomic signatures of human malignancies.
Footnotes
Author Contributions: ZZ and YJL contributed study design, data analysis and paper writing. YX contributed data analysis and paper writing. HZ, DPA, and MMY contributed to results interpretation and paper revision.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by Departmental R&D funding at the University of Wisconsin-Madison to Dr. Yongjun Liu, and NSF-DMS-2012298 to Dr. Zhengjun Zhang.
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Data Availability: The links of the public datasets are provided in Section “Data Description.” The dataset obtained from the independent U.S. Caucasian cohort will be made available upon the request from readers.
References
- 1. Bosch FX, Ribes J, Díaz M, Cléries R. Primary liver cancer: worldwide incidence and trends. Gastroenterology. 2004;127:S5-S16. [DOI] [PubMed] [Google Scholar]
- 2. El-Serag HB. Hepatocellular carcinoma. New Engl J Med. 2011;365:1118-1127. [DOI] [PubMed] [Google Scholar]
- 3. Njei B, Rotman Y, Ditah I, Lim JK. Emerging trends in hepatocellular carcinoma incidence and mortality. Hepatology. 2015;61:191-199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. McGlynn KA, Petrick JL, El-Serag HB. Epidemiology of hepatocellular carcinoma. Hepatology. 2021;73 Suppl 1:4-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Kwong AJ, Kim WR, Lake E, JR al. OPTN/SRTR 2019 annual data report: liver. Am J Transplant. 2021;21:208-315. [DOI] [PubMed] [Google Scholar]
- 6. Thorgeirsson SS, Grisham JW. Molecular pathogenesis of human hepatocellular carcinoma. Nat Genet. 2002;31:339-346. [DOI] [PubMed] [Google Scholar]
- 7. Farazi PA, DePinho RA. Hepatocellular carcinoma pathogenesis: from genes to environment. Nat Rev Cancer. 2006;6:674-687. [DOI] [PubMed] [Google Scholar]
- 8. Calderaro J, Couchy G, Imbeaud S, et al. Histological subtypes of hepatocellular carcinoma are related to gene mutations and molecular tumour classification. J Hepatol. 2017;67:727-738. [DOI] [PubMed] [Google Scholar]
- 9. Calderaro J, Ziol M, Paradis V, Zucman-Rossi J. Molecular and histological correlations in liver cancer. J Hepatol. 2019;71:616-630. [DOI] [PubMed] [Google Scholar]
- 10. Zucman-Rossi J, Villanueva A, Nault JC, Llovet JM. Genetic landscape and biomarkers of hepatocellular carcinoma. Gastroenterology. 2015;149:1226-1239.e4. [DOI] [PubMed] [Google Scholar]
- 11. Wang XW, Thorgeirsson SS. Transcriptome analysis of liver cancer: ready for the clinic? J Hepatol. 2009;50:1062-1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Maass T, Sfakianakis I, Staib F, Krupp M, Galle PR, Teufel A. Microarray-based gene expression analysis of hepatocellular carcinoma. Curr Genomics. 2010;11:261-268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Xu XR, Huang J, Xu ZG, et al. Insight into hepatocellular carcinogenesis at transcriptome level by comparing gene expression profiles of hepatocellular carcinoma with those of corresponding noncancerous liver. Proc Natl Acad Sci USA. 2001;98:15089-15094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Nam SW, Park JY, Ramasamy A, et al. Molecular changes from dysplastic nodule to hepatocellular carcinoma through gene expression profiling. Hepatology. 2005;42:809-818. [DOI] [PubMed] [Google Scholar]
- 15. Iizuka N, Oka M, Yamada-Okabe H, et al. Comparison of gene expression profiles between hepatitis B virus- and hepatitis C virus-infected hepatocellular carcinoma by oligonucleotide microarray data on the basis of a supervised learning method. Cancer Res. 2002;62:3939-3944. [PubMed] [Google Scholar]
- 16. Huang Q, Lin B, Liu H, et al. RNA-Seq analyses generate comprehensive transcriptomic landscape and reveal complex transcript patterns in hepatocellular carcinoma. PLoS One. 2011;6:e26168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Huang Y, Pan J, Chen D, et al. Identification and functional analysis of differentially expressed genes in poorly differentiated hepatocellular carcinoma using RNA-seq. Oncotarget. 2017;8:35973-35983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Okrah K, Tarighat S, Liu B, et al. Transcriptomic analysis of hepatocellular carcinoma reveals molecular features of disease progression and tumor immune biology. NPJ precis oncol. 2018;2:25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Pan Q, Long X, Song L, et al. Transcriptome sequencing identified hub genes for hepatocellular carcinoma by weighted-gene co-expression analysis. Oncotarget. 2016;7:38487-38499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Liu Y, Al-Adra DP, Lan R, et al. RNA sequencing analysis of hepatocellular carcinoma identified oxidative phosphorylation as a major pathologic feature. Hepatol Commun. 2022;6:2170-2181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Cui Q, Zhang Z. Max-Linear Competing Factor Models. Max-Linear Compet Factor Models. 2018;36:62-74. [Google Scholar]
- 22. Cui Q, Zhang Z, Chan V. Max-linear regression models with regularization. J Econom. 2021;222:579-600. [Google Scholar]
- 23. Zhang Z. Five critical genes related to seven COVID-19 subtypes: A Data Science Discovery. Data Sci J. 2021;19:142-150. [Google Scholar]
- 24. Zhang Z. Functional effects of four or fewer critical genes linked to lung cancers and new subtypes detected by a new machine learning classifier. J Clin Trials. 2021;11:S14. [Google Scholar]
- 25. Zhang Z. Lift the veil of breast cancers using four or fewer critical genes. Cancer Inform. 2022;21:11769351221076360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Villa E, Critelli R, Lei B, et al. Neoangiogenesis-related genes are hallmarks of fast-growing hepatocellular carcinomas and worst survival. Results from a prospective study. Gut. 2016;65:861-869. [DOI] [PubMed] [Google Scholar]
- 27. Wurmbach E, Chen YB, Khitrov G, et al. Genome-wide molecular profiles of HCV-induced dysplasia and hepatocellular carcinoma. Hepatology. 2007;45:938-947. [DOI] [PubMed] [Google Scholar]
- 28. Hodo Y, Honda M, Tanaka A, et al. Association of interleukin-28B genotype and hepatocellular carcinoma recurrence in patients with chronic hepatitis C. Clin Cancer Res. 2013;19:1827-1837. [DOI] [PubMed] [Google Scholar]
- 29. Tung EK, Mak CK, Fatima S, et al. Clinicopathological and prognostic significance of serum and tissue Dickkopf-1 levels in human hepatocellular carcinoma. Liver Int. 2011;31:1494-1504. [DOI] [PubMed] [Google Scholar]
- 30. Villanueva A, Portela A, Sayols S, et al. DNA methylation-based prognosis and epidrivers in hepatocellular carcinoma. Hepatology. 2015;61:1945-1956. [DOI] [PubMed] [Google Scholar]
- 31. Yoon SH, Choi SW, Nam SW, Lee KB, Nam JW. Preoperative immune landscape predisposes adverse outcomes in hepatocellular carcinoma patients with liver transplantation. NPJ Precis Oncol. 2021;5:27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Pinyol R, Torrecilla S, Wang H, et al. Molecular characterisation of hepatocellular carcinoma in patients with non-alcoholic steatohepatitis. J Hepatol. 2021;75:865-878. [DOI] [PubMed] [Google Scholar]
- 33. Malinowski A, Schlather M, Zhang Z. Intrinsically weighted means and non-ergodic marked point processes. Ann Inst Stat Math. 2016;68:1-24. [Google Scholar]
- 34. Hao NB, Li CZ, Lü MH, et al. SDF-1/CXCR4 axis promotes MSCs to repair liver injury partially through trans-differentiation and fusion with hepatocytes. Stem Cells Int. 2015;2015:960387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Kostallari E, Shah VH. Angiocrine signaling in the hepatic sinusoids in health and disease. Am J Physiol Gastrointest Liver Physiol. 2016;311:G246-G251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Lalor PF, Lai WK, Curbishley SM, Shetty S, Adams DH. Human hepatic sinusoidal endothelial cells can be distinguished by expression of phenotypic markers related to their specialised functions in vivo. World J Gastroenterol. 2006;12:5429-5439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Sun X, Cheng G, Hao M, et al. CXCL12 / CXCR4 / CXCR7 chemokine axis and cancer progression. Cancer Metastasis Rev. 2010;29:709-722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Sutton A, Friand V, Brulé-Donneger S, et al. Stromal cell-derived factor-1/chemokine (C-X-C motif) ligand 12 stimulates human hepatoma cell growth, migration, and invasion. Mol Cancer Res. 2007;5:21-33. [DOI] [PubMed] [Google Scholar]
- 39. Begum NA, Coker A, Shibuta K, et al. Loss of hIRH mRNA expression from premalignant adenomas and malignant cell lines. Biochem Biophys Res Commun. 1996;229:864-868. [DOI] [PubMed] [Google Scholar]
- 40. He K, Liu S, Xia Y, et al. CXCL12 and IL7R as novel therapeutic targets for liver hepatocellular carcinoma are correlated with somatic mutations and the tumor immunological microenvironment. Front Oncol. 2020;10:574853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Shibuta K, Begum NA, Mori M, Shimoda K, Akiyoshi T, Barnard GF. Reduced expression of the CXC chemokine hIRH/SDF-1alpha mRNA in hepatoma and digestive tract cancer. Int J Cancer. 1997;73:656-662. [DOI] [PubMed] [Google Scholar]
- 42. Shibuta K, Mori M, Shimoda K, Inoue H, Mitra P, Barnard GF. Regional expression of CXCL12/CXCR4 in liver and hepatocellular carcinoma and cell-cycle variation during in vitro differentiation. Jpn J Cancer Res. 2002;93:789-797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Shirota Y, Kaneko S, Honda M, Kawai HF, Kobayashi K. Identification of differentially expressed genes in hepatocellular carcinoma with cDNA microarrays. Hepatology. 2001;33:832-840. [DOI] [PubMed] [Google Scholar]
- 44. De Marco V, Gillespie PJ, Li A, et al. Quaternary structure of the human cdt1-geminin complex regulates DNA replication licensing. Proc Natl Acad Sci USA. 2009;106:19807-19812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Zhu W, Depamphilis ML. Selective killing of cancer cells by suppression of geminin activity. Cancer Res. 2009;69:4870-4877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Ananthula S, Sinha A, El Gassim M, et al. Geminin overexpression-dependent recruitment and crosstalk with mesenchymal stem cells enhance aggressiveness in triple negative breast cancers. Oncotarget. 2016;7:20869-20889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Kushwaha PP, Rapalli KC, Kumar S. Geminin a multi task protein involved in cancer pathophysiology and developmental process: A review. Biochimie. 2016;131:115-127. [DOI] [PubMed] [Google Scholar]
- 48. Salabat MR, Melstrom LG, Strouch MJ, et al. Geminin is overexpressed in human pancreatic cancer and downregulated by the bioflavanoid apigenin in pancreatic cancer cell lines. Mol Carcinog. 2008;47:835-844. [DOI] [PubMed] [Google Scholar]
- 49. Montanari M, Boninsegna A, Faraglia B, et al. Increased expression of geminin stimulates the growth of mammary epithelial cells and is a frequent event in human tumors. J Cell Physiol. 2005;202:215-222. [DOI] [PubMed] [Google Scholar]
- 50. Kim HE, Kim DG, Lee KJ, et al. Frequent amplification of CENPF, GMNN and CDK13 genes in hepatocellular carcinomas. PLoS One. 2012;7:e43223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Zhu W, Chen Y, Dutta A. Rereplication by depletion of geminin is seen regardless of p53 status and activates a G2/M checkpoint. Mol Cell Biol. 2004;24:7140-7150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Giovannone B, Lee E, Laviola L, Giorgino F, Cleveland KA, Smith RJ. Two novel proteins that are linked to insulin-like growth factor (IGF-I) receptors by the grb10 adapter and modulate IGF-I signaling. J Biol Chem. 2003;278:31564-31573. [DOI] [PubMed] [Google Scholar]
- 53. Zhao Y, Stankovic S, Koprulu M, et al. GIGYF1 loss of function is associated with clonal mosaicism and adverse metabolic health. Nat Commun. 2021;12:4178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Uhlen M, Zhang C, Lee S, et al. A pathology atlas of the human cancer transcriptome. Science. 2017;357:eaan2507. [DOI] [PubMed] [Google Scholar]
- 55. Steinert PM, Roop DR. Molecular and cellular biology of intermediate filaments. Annu Rev Biochem. 1988;57:593-625. [DOI] [PubMed] [Google Scholar]
- 56. Li W, Bai X, Li J, et al. The nucleoskeleton protein IFFO1 immobilizes broken DNA and suppresses chromosome translocation during tumorigenesis. Nat Cell Biol. 2019;21:1273-1285. [DOI] [PubMed] [Google Scholar]
- 57. Ghanizade P, Oroujalian A, Peymani M. Differential expression analysis of CCDC107 and RMRP lncRNA as potential biomarkers in colorectal cancer diagnosis. Nucleosides Nucleotides Nucleic Acids. 2021;40:1144-1158. [DOI] [PubMed] [Google Scholar]