Abstract

We describe an instrument to measure the speed of sound in liquids based on the dual-path, pulse-echo technique; it covers a temperature range of 228.15–423.15 K, with pressures of up to 93 MPa. It differs from similar instruments in the method of mounting the quartz-crystal transducer, a path-length ratio of 2.5:1, and automated data-collection protocols. The path-length difference was calibrated with measurements on high-purity propane. The performance of the instrument was verified by comparison with recent literature data on p-xylene. We present new liquid-phase measurements for the halogenated-olefin refrigerants 2,3,3,3-tetrafluoroprop-1-ene [R1234yf], trans-1,3,3,3-tetrafluoroprop-1-ene [R1234ze(E)], trans-1-chloro-3,3,3-trifluoroprop-1-ene [R1233zd(E)], and cis-1,1,1,4,4,4-hexafluorobut-2-ene [R1336mzz(Z)]. These measurements cover a combined temperature range of 230 to 420 K, with pressures of up to 50 MPa; these data are compared to literature data (where available) and multiproperty equations of state. The average relative expanded uncertainty in the speed of sound ranged from 0.035 to 0.088% for the different fluids.
1. Introduction
We describe an apparatus to measure the speed of sound based on the dual-path pulse-echo technique. Our instrument is intended for fluid property measurements of chemicals of industrial interest. It operates over a temperature range of 228.15–423.15 K, with pressures of up to 93 MPa. We describe the instrument in some detail, describe calibration measurements with propane and water, and report measurements on p-xylene as well as four “new” halogenated-olefin refrigerants that have very low values of the global warming potential (GWP).
Speed of sound is a thermodynamic property that is important for numerous applications, such as flow metering with ultrasonic flow meters or critical flow venturis. Speed of sound is more generally applicable for its use in developing multiproperty equations of state (EOS). Heat capacity is a useful input in fitting an EOS, and speed of sound w is related to isochoric heat capacity CV through
| 1 |
where p is pressure and ρ is density. But in contrast to the difficult measurement of the heat flows and small temperature differences involved in a calorimetric determination of heat capacity, the measurement of the speed of sound involves the measurement of a characteristic length and a time or frequency, both of which can be measured with very low uncertainties.
Modern EOS are often expressed in terms of the Helmholtz free energy, and the speed of sound provides information on the first and second derivatives of the Helmholtz free energy
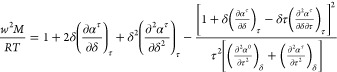 |
2 |
where the dimensionless Helmholtz energy α = A/RT is a function of the dimensionless density δ = ρ/ρcrit and dimensionless inverse temperature τ = Tcrit/T; α0 and αr are the ideal-gas and residual contributions to α, R is the molar gas constant, and M is the molar mass. Lemmon and Jacobsen1 provide a description of the Helmholtz-form EOS as well as additional thermodynamic relationships along the lines of eqs 1 and 2.
Vapor-phase speed-of-sound data at low pressures can yield the ideal-gas heat capacity, which is related to α0. At higher pressures and in the liquid phase, speed-of-sound data provide information on the slope and curvature of the Helmholtz energy. Trusler and Lemmon2 demonstrate how the entire liquid-phase EOS could be based on speed-of-sound data together with single datums for density and heat capacity at a reference temperature and pressure. Thus, speed of sound is a very valuable supplement to other types of data, such as density and vapor pressure, in defining an EOS.
Techniques for measuring speed of sound can be broadly divided into (1) resonator techniques, where the frequency of a standing wave in a cavity of simple geometry (e.g., a sphere or cylinder) is measured;3−6 (2) optical techniques, such as dynamic light scattering, where the frequency shift of Brillouin peaks is measured;7,8 and (3) time-of-flight techniques, which involve timing an ultrasonic burst as it traverses a defined path length.9,10 Time-of-flight techniques are most applicable to dense fluids. The instrument described here complements the spherical acoustic resonator at NIST (Perkins and McLinden11), which has been used to measure the vapor-phase speed of sound of numerous fluids.12−15
2. Description of Experimental Apparatus
2.1. Measuring Principle
The dual-path, pulse-echo-type instrument was first introduced by Kortbeek et al.16 In such an instrument, a piezoelectric transducer is located within a sample volume filled with the test fluid. A function generator excites the transducer (e.g., a quartz crystal) with a sinusoidal burst; ultrasonic pulses are thus emitted from each face of the crystal, which travel through the fluid sample, reflect off of planar surfaces at each end of the sample volume, and return to the transducer, which also serves as the detector. The experiment is schematically represented in Figure 1.
Figure 1.
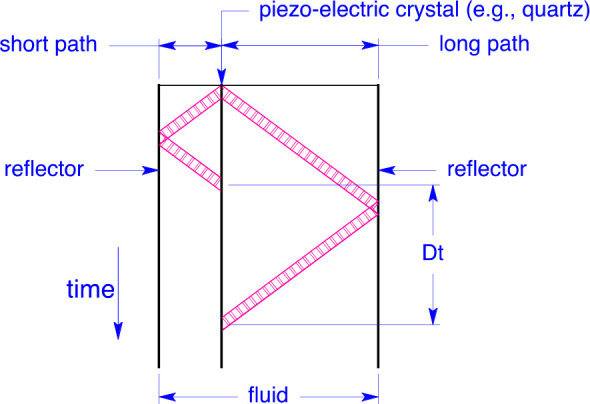
Principle of the dual-path pulse-echo experiment.
The difference in the arrival times of the echo signals gives the speed of sound by
| 3 |
where w is the speed of sound, L1 and L2 are the path lengths, Δt is the measured time difference, and δtd is a correction accounting for diffraction effects, as described in section 2.7. The differential nature of this technique cancels the end effects and improves the accuracy. This “single-burst method” has been described by Ball and Trusler,17 among others. An alternative method employing two burst signals separated by a Δt chosen to result in cancellation of the first burst traversing the long path with the second burst traversing the short path was the method originally proposed by Kortbeek et al.16 and has been adopted by others.10,18 We chose the single-burst method because it was much simpler to automate the data acquisition process. Furthermore, it allows for the off-line analysis of the data (as opposed to needing to determine the Δt in real time as a single-burst experiment is carried out).
2.2. Description of Instrument: Pulse-Echo Cell
A quartz crystal with a diameter of 24 mm, thickness of 0.36 mm, and resonant frequency of 8.00 MHz served as the ultrasonic transducer. The quartz crystal was “X-cut,” which means that its thickness expands and contracts when a voltage is applied to electrodes on opposite faces of the crystal. The electrodes were 10 mm in diameter and consisted of gold films plated onto the faces of the crystal; the electrical leads were connected to a keyhole extension of each electrode that extended to the edge of the crystal. The crystal was excited with a 10-cycle sinusoidal burst from an arbitrary function generator. The fluid path lengths on the opposite faces of the crystal were 30 mm and 12 mm (ratio of 2.5:1); the separations of the crystal and the reflectors were maintained by tubular spacers fabricated of a machinable ceramic (Macor, Corning Inc. Certain trade names and products are given to adequately document the experimental equipment and procedures. This does not constitute a recommendation or endorsement of these products by the National Institute of Standards and Technology nor does it imply that the products are necessarily the best available for the purpose.)
The crystal, spacers, and reflectors were assembled into a “stack” that was then inserted into a close-fitting support tube; these components were held in place with springs located at the ends of the support tube. Figure 2 gives a schematic diagram of the measuring cell (along with the pressure vessel and thermostat described in section 2.3), and Figure 3 shows an exploded view of the components. With this design, the individual components are of simple geometries, simplifying the fabrication of, for example, planar faces for the reflectors and parallel ends for the spacers. Our measuring cell was fabricated primarily of brass, which was chosen for ease of fabrication in prototype testing. A more corrosion-resistant cell made of stainless steel is planned. (Corrosion resistance is important because if the faces of the reflectors were to corrode during measurements the path lengths would be continually changing.)
Figure 2.
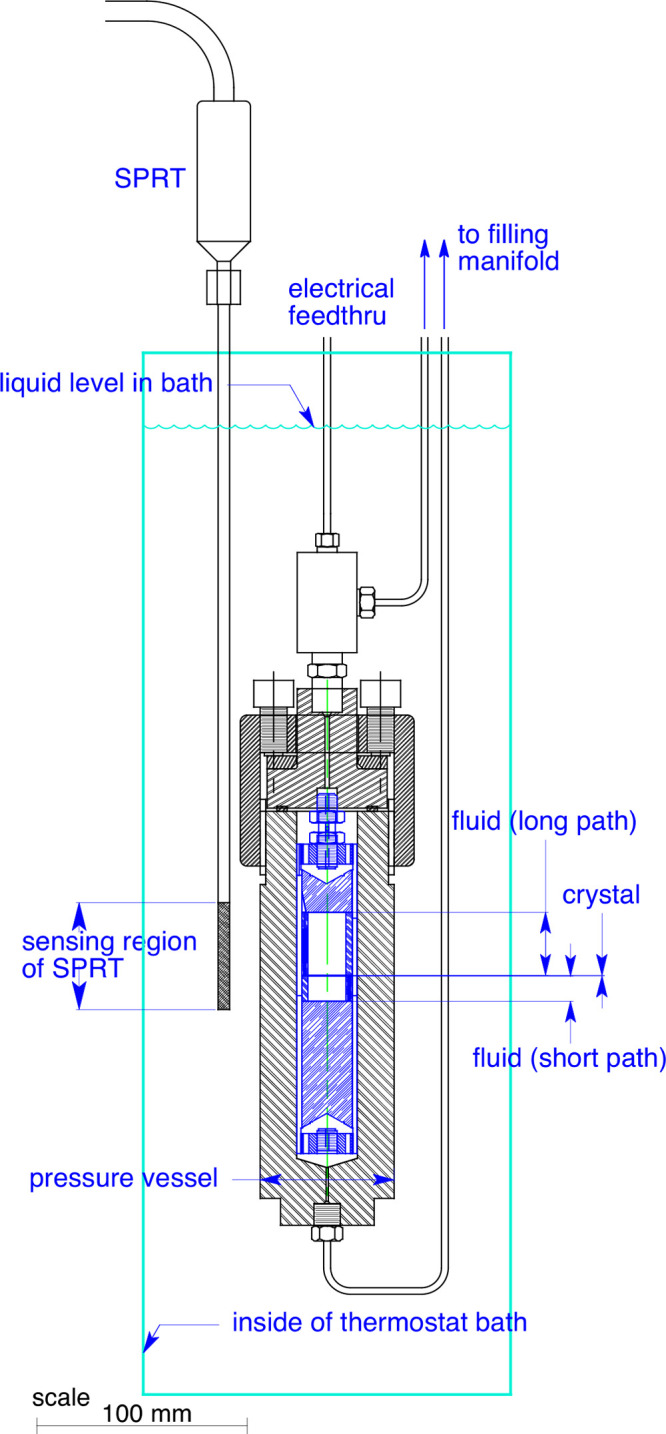
Schematic of the measuring cell and pressure vessel.
Figure 3.

Exploded view of the measuring cell showing the components.
The electrical connections to the crystal were made with spring-loaded pins contacting the keyhole extensions of the electrodes. These pins were located in holes drilled into the (electrically insulated) ceramic spacers. One of these pins connected to the reflector and then on to the support tube and pressure vessel, which was at electrical ground. The signal wire from the electrical feedthrough connected to the other pin; see Figure S1 in the Supporting Information.
The electrical feedthrough passed the signal to/from the crystal and served as a pressure seal into the pressure vessel; it also isolated the signal wire from the fluid of the thermostatting bath. This was accomplished with a custom-made assembly; this is shown in Figure S2 of the Supporting Information. The main portion of the feedthrough consisted of a coaxial assembly of the signal wire, PTFE sleeving (serving as the dielectric), and a 3.2-mm-diameter stainless steel tube (serving as the outer ground). The pressure seal of the signal wire was effected by a polyimide ferrule replacing the usual stainless-steel ferrule of a standard high-pressure fitting (High Pressure Equipment Company, 1/16 in. taper seal); the stainless tubing was brazed into the high-pressure nut to effect a seal against the bath fluid. At the top end of the feedthrough (which was above the level of the bath fluid), a standard SMA-coax fitting was modified to connect to the stainless tubing rather than the braid of the usual coaxial cable. This feedthrough maintained the coaxial electrical characteristics of the signal cable until it was inside the pressure vessel, and we observed substantially lower noise with this assembly compared to that of the twisted-pair connections that we used in early prototype testing.
An inductor, consisting of turns of PTFE-insulated wire wound around a 3.2 mm o.d. stainless-steel post, was in series with the signal wire inside the pressure vessel. The number of turns was adjusted to obtain an impedance of 50 Ω for the transducer/measuring cell assembly, thus matching the impedance of the oscilloscope and coax cable.
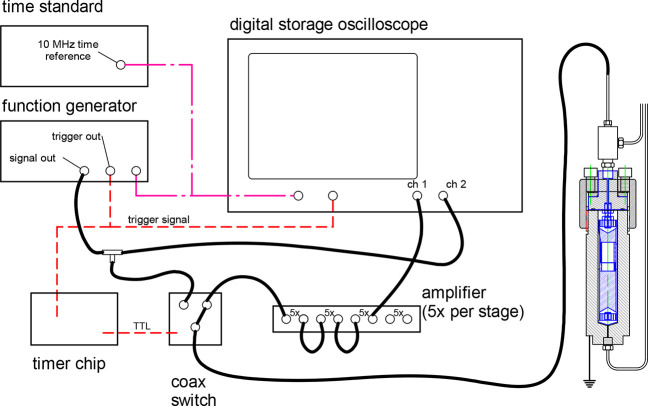
An electrical schematic is shown in Figure 4: A high-speed switch connected the crystal to the function generator during the input sinusoidal burst, and then, after a delay of 6 μs, it switched the crystal to the input of a three-stage amplifier (5× per stage for a total of 125×), which then fed into a digital storage oscilloscope (Keysight model DSO-X 4022A). Note that any noise was also amplified; the purpose of the 125× amplifier was to bring weak signals into the range of the oscilloscope. The echo signals were recorded for off-line analysis.
Figure 4.
Electrical schematic of the dual-path pulse-echo instrument.
A key feature of the pulse-echo technique is the unequal path lengths L1 and L2, and most authors have employed a path-length ratio of 1.5:1.10 Here, we chose a path-length ratio of 2.5:1. The larger ratio yields a longer time difference and, thus, greater time resolution for the arrival time of the two pulses for a given sample volume. It also allows a longer time for the short-path echo to damp out before the arrival of the long-path echo; this is a particular advantage for measurements on fluids, where damping is low. On the other hand, for fluids or conditions with significant damping, the long-path echo can be very weak with the 2.5:1 ratio. Thus, there is no single optimum path-length ratio.
There is the possibility of an overlap of echoes. The sound burst traverses the fluid sample and is reflected back to the crystal; the noninteger path-length ratio ensures that the reflected signals are well separated upon arriving back at the crystal. This time difference is the primary measurement of the experiment. A portion of the sound energy, however, is transmitted into the body of the reflector, bounces off the back face of the reflector, and is re-emitted into the fluid. Depending on the path lengths and fluid speed of sound relative to the reflector lengths and speed of sound in the reflector material, there is a range of fluid speeds of sound where the re-emitted short-path signal can overlap with the long-path echo. The magnitude of any overlap can be reduced in two ways. First, one wants to maximize the fraction of the sound energy that is reflected. This is done by maximizing the mismatch in acoustic impedance between the fluid sample and reflector material, which implies a reflector made of a very dense and stiff material, and most metals are adequate in this regard. The second way to minimize overlap is to have a coned (rather than flat) back surface of the reflector, thus scattering the sound burst transmitted into the reflector; this has been discussed by numerous authors.10,17,19 With these two considerations, we were not able to observe any signal returning from the back side of the reflector and consider the uncertainty arising from any potental overlap to be negligible.
2.3. Description of the Instrument: Thermostat and Pressure Measuring System
The measuring cell holding the crystal and fluid sample was contained in a commercial stainless-steel pressure vessel rated to 93 MPa (High Pressure Equipment Company, model GC-1); see Figure S3 in the Supporting Information. This, in turn, was held in a thermostated oil bath operating from −45 to 150 °C (228.15 to 423.15 K). A schematic of the measuring cell and pressure vessel in the thermostat is shown as Figure 2. A photograph of the thermostated bath is shown in the Supporting Information as Figure S4. A photograph of the instruments (which were located in the adjacent room) is shown as Figure S5.
The temperature of the oil bath was measured with a long-stem 25 Ω standard platinum resistance thermometer (SPRT); the temperature-sensing portion of the SPRT was located immediately adjacent to the pressure vessel, as indicated in Figure 2. The resistance of the SPRT was ratioed to a standard resistor with an AC resistance bridge. The 25 Ω reference resistor for the bridge was thermostated at 37.0 ± 0.1 °C in a small enclosure. The SPRT, standard resistor, and resistance bridge were calibrated as a system on ITS-90 over the range of 234.316 to 505.078 K with fixed-point cells (mercury triple point, water triple point, and indium and tin freezing points). The standard uncertainty in the fixed-point/SPRT/resistor/bridge system was estimated as 3 mK. The short-term (minute-to-minute) variations in the oil-bath temperature were 2 mK or less. No long-term (hour-to-hour) variation was observed. The temperature gradients in the oil bath were less than 3 mK over the region of the pressure vessel. Any uncertainty associated with measuring the bath temperature (as opposed to having the SPRT in the pressure vessel) is included in the 3 mK uncertainty associated with the bath gradients. The combined standard (k = 1) uncertainty in the temperature measurement, including the effects of the SPRT, standard resistor, resistance bridge, calibration standards, stability of the oil bath, and temperature gradients in the oil bath, was 5 mK.
The pressure was measured with a vibrating-quartz-crystal pressure transducer with a maximum pressure of 138 MPa. The transducer was held at room temperature and was calibrated by the manufacturer with piston gages; this calibration included a temperature-compensation term. The zero of the transducer was checked regularly (while the system was evacuated between samples), and readings were corrected for any drift in the zero. The standard uncertainty in pressure was 26 × 10–6p + 0.007 MPa.
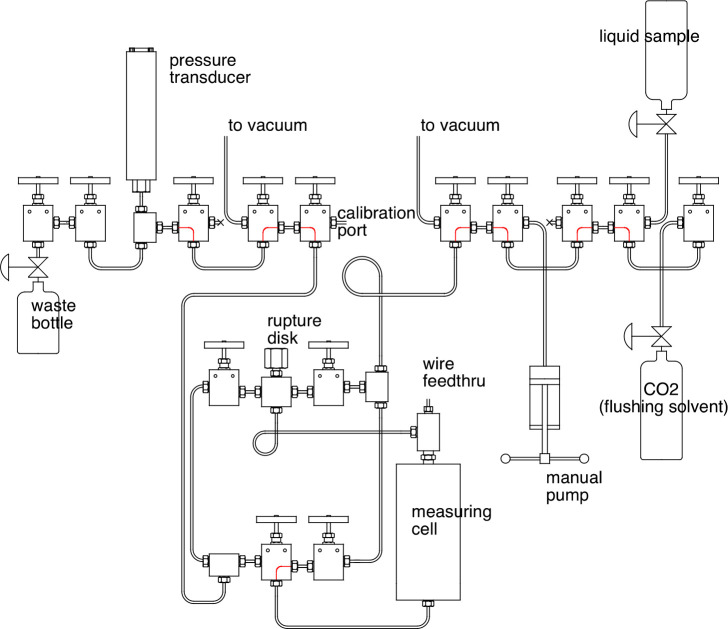
The pressure manifold for sample handling and pressure measurement is shown in Figure 5. It was built up from 1/8 in. high-pressure, coned-and-threaded-type valves and fittings rated to a pressure of 204 MPa. The design provided considerable flexibility in loading samples, and fluid ports on the top and bottom of the measuring cell allowed for flushing of the system between samples. During the course of an experiment, the sample was loaded from the right-hand side of the manifold, and the general “flow” of sample was toward the waste bottle on the left-hand side. The entire system was flushed with solvent and evacuated between samples, but there was the possibility of trapping nonvolatile samples or sample residues in the dead volumes formed by the safety rupture disk and the pressure transducer. These were both on the “downstream” side of the manifold so that any trapped sample that might diffuse out was carried toward the waste bottle as the pressure was adjusted during the course of measurements.
Figure 5.
Schematic of the pressure/filling manifold; red lines indicate valve ports that are always interconnected.
A manual, piston/cylinder-type pump could be used to pressurize the sample. (However, as described in section 2.6, this pump was not typically required for a measurement sequence.) The total volume of fluid sample, including the filling manifold and pressure transducer (but not the manual pump), was 30 mL.
The pressure manifold was operated at room temperature for most of the measurements reported here. The measurements on p-xylene, however, required heating the manifold to 40 °C to avoid freezing of the sample at a high pressure. This was done by wrapping tubing around the valves and pressure transducer through which water from a thermostated bath was circulated; insulation was then wrapped around the water tubing.
2.4. Typical Echoes
The description of the experiment presented above implied a single ultrasonic burst. In fact, we continuously excited the crystal with sinusoidal bursts at a frequency of 100 Hz (i.e., bursts of 10 sinusoids separated by 10 ms). The crystal was driven with a signal of 2.0 V peak to peak; higher voltages were found to overdrive the switch (although the received echo signals appeared normal and undistorted). The periodic excitation of the crystal enabled the averaging of the signal and other signal processing by the oscilloscope. We typically averaged 256 echo signals, although the oscilloscope would allow averaging of up to 10 000.
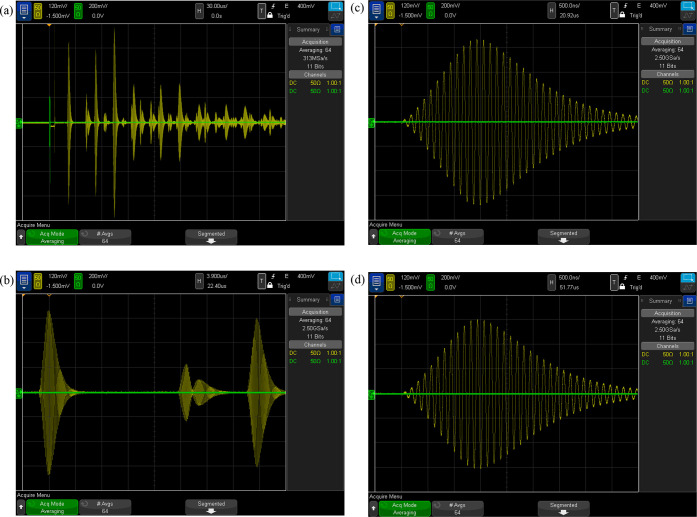
Figure 6(a) shows a screen shot of the oscilloscope for propane at T = 285 K, p = 35 MPa, and w = 1164 m·s–1. The input burst is shown in green on the left at t = 0 μs. A transient associated with switching the signal from the function generator to the oscilloscope is observed at t ≈ 6 μs. The echo signals are shown in yellow, and multiple echoes are observed. (Note the different voltage scales for the green and yellow traces.) The short-path echo arrives at t ≈ 21 μs, and the long-path echo arrives at t ≈ 52 μs. The bursts traversing the short path two and three times are seen at t ≈ 41 μs and at t ≈ 62 μs; these echoes have distorted shapes resulting from reflections off of both faces of the crystal and resulting interference. The strongest echo is seen at t ≈ 72 μs, corresponding to 3.5 times the arrival time of the short-path echo; we consistently observe this echo, and it is sometimes the strongest echo for highly compressed liquid states. We cannot associate this echo with any particular mode and surmise that it arises from constructive interference. It does not enter into the analysis, but it does present a slight complication for data recording, as discussed in section 2.5. All of the echoes have damped back down to noise level at t ≈ 1000 μs, well before the next burst is generated at t = 10 ms.
Figure 6.
Oscilloscope screen shots showing representative echo signals for propane at T = 285 K, p = 35 MPa, and w = 1164 m·s–1: (a) signal for t = (0–270) ms; each division represents 30 μs; (b) phase envelopes for short-path, 2 × short-path, and long-path echos, where each division represents 3.9 μs and the time scale is offset by 22.40 ms; (c) short-path echo, where each division represents 500 ns and the time scale is offset by 20.92 μs; (d) long-path echo where each division represents 500 ns and the time scale is offset by 51.77 μs.
Figure 6(b) shows the phase envelopes of the short-path, 2× short-path, and long-path echoes; these are the data of interest for the analysis. Figure 6(c,d) show zoomed-in images of the short-path and long-path echoes, respectively; they are virtually identical in shape, but with the long-path echo slightly attenuated compared to the short-path echo. Note that the maximum signal occurs on the 12th oscillation, although the input burst consisted of only 10 cycles. Note that these screen shots are an average of 64 echo signals taken over 0.64 s, which reduces the noise; this averaging was carried out by the oscilloscope itself. An example of much weaker echo signals is shown as Figure S6 in the Supporting Information.
2.5. Recording of Echo Signals
We used our control program (described in section 2.6) together with the signal-processing capabilities of the oscilloscope to automate the detection and recording of the echo signals. In brief, the oscilloscope operated on the portion of the signal displayed on its screen, and we adjusted the time and voltage scales of the oscilloscope multiple times to identify the short-path and long-path echoes and recorded them in a file for off-line analysis.
When the control program triggered a measurement, a time offset was used to push the input burst and switch transient off the left side of the screen; the maximum signal in the resulting window was found, and the voltage was rescaled accordingly. The average voltage was also computed, and this was used to adjust the voltage offset or zero. The maximum signal could be either the short-path echo at techo_short or the unidentified echo (discussed in section 2.4) at ∼3.5 × techo_short; resetting the window time scale to 0.4 times the time to the maximum signal then revealed either the short-path echo or a signal at noise level (in which case, the first signal was the short-path echo). Having identified the time to the short-path echo, the maximum signal in the time interval (2.3 × techo_short < t < 2.8 × techo_short) was the long-path echo at techo_long. The time scale was adjusted to place techo_short at the 10% position and techo_long at the 90% position in the window (i.e., the data shown in Figure 6(b)); the averaging was reset to 256, and 16 000 data points were written to the output file. The window was reset to span 10 μs (80 cycles) centered first around techo_short and then techo_long to separately record 16 000 data points for each of the echoes (i.e., the data shown in Figure 6(c,d)). (This final step was implemented after we saw that for fluid speeds of sound less than about 600 m·s–1 not enough points were being recorded for the actual echo signals; i.e., most of the 16 000 data points recorded the noise between the echoes. This separate recording was not done for all of the fluids reported here.)
2.6. Measurement Sequence
The sample was loaded into the measuring cell in one of two ways. For fluids with a room-temperature vapor pressure of more than a few kPa (including all of the fluids measured in this work), the fluid sample was loaded directly from the sample cylinder into the evacuated measuring cell. The sample cylinder was heated to increase the vapor pressure. This avoided any possibility of contamination that a pump might introduce.
For fluids with very low vapor pressures (such as the lubricants reported in ref (20)), the fluid sample was loaded into a manual piston-type pump and degassed by pulling a vacuum on the head space of the pump. The sample was then pushed into the measuring cell (which had been evacuated), the pump was valved off, the oil bath was set to the first set-point temperature, and the experimental run begun.
The entire experiment was controlled by a computer running a custom control program written in Visual Basic 6. The pressure of the fluid sample and the temperature of the oil bath were scanned every 30 s. The approach to equilibrium conditions was determined by monitoring three quantities: (1) the difference in the average bath temperature computed over the previous eight scans compared to the set-point temperature; (2) the standard deviation of the previous eight temperature scans; and (3) the rate of change of pressure with time, computed with a linear fit of the previous eight pressure readings. When all three of these were within preset tolerances, a “converged” flag was set in the control program, and an additional equilibration time of 30 min was allowed before starting the measurements. A single measurement set comprised recording three sets of echo signals and the four temperature and pressure readings made at the start and end of the set and between the recordings of the echoes. Four such sets, spaced 10 min apart, were recorded before moving to the next (T, p) state point. These raw data were analyzed with a separate program (described in section 2.8) to generate the (T, p, and w) data points.
When measurements at the first (T, p) state point were completed, the temperature was increased by (5 or 10) K, and since the cell was liquid-filled, this increased the pressure. Measurements continued along this pseudoisochore (line of approximately constant density) until either the desired maximum temperature or maximum pressure was reached. The bath was then cooled to a temperature (10 to 20) K above the initial temperature of the isochore, and the total quantity of sample in the measuring cell was reduced by venting sample into a waste bottle to achieve a starting pressure for the next isochore of approximately 1 MPa or slightly above the saturation pressure, whichever was greater. The next isochore then commenced. This process was repeated to cover the liquid surface of the fluid sample, within the operating limits of the instrument. Since the thermostatic bath was under computer control, an entire isochore could be carried out automatically; manual adjustment of the fluid charge was required only between isochores.
Replicate isochores were regularly measured by cooling the bath to a near-ambient temperature and adding a small amount of additional sample to again completely fill the system with liquid. These repeat isochores served to check the stability of the pulse-echo system and to check for any possible degradation in the fluid sample.
Some of the measurements on p-xylene were carried out along isotherms. The procedures were the same except that the pump was also partially filled along with the measuring cell. The pump was then used to adjust the pressure between points along an isotherm.
2.7. Diffraction Correction
The time difference was corrected for diffraction effects; these are due to a phase advance of the actual sound wave compared to a perfect plane wave.21 The electrodes on the quartz crystal cover only the central region (0 ≤ r ≤ b) of the crystal. Application of a voltage to the electrodes causes the thickness of the crystal to increase in the region between the electrodes. Since the quartz is stiff, there must also be some increase in the crystal thickness for some radial distance outside of the electrodes. This is obviously a simplification, and other functional forms for the vibration amplitude have been considered; for example, Meier9 considered four models for the deformation of the crystal, namely, a (1) piston source, (2) simply supported source, (3) clamped source, and (4) Gaussian source. The simplest model for the diffraction correction is based on a piston source that has a uniform amplitude of vibration in the active region of the electrodes. Meier et al. demonstrated that there were only small differences of less than 0.001% in the speed of sound between the diffraction corrections from each of these source models. We will base our diffraction correction on the piston source (uniform amplitude) model.
The development of the piston source model was originally described by Williams22 in 1951. The model is further discussed by Trusler21 as a diffraction correction for pulse-echo measurements of the speed of sound in fluids. The model assumes that the sound source is a plane that oscillates uniformly over its entire cylindrical surface with radius b. The sound is detected by a cylindrical surface of the same radius b that is located a distance z from the source and is centered on the same axis as the source. The detector response is proportional to the average acoustic pressure over its surface. The average acoustic pressure is given by
| 4 |
where
| 5 |
z is the distance and θ is the angle normal to the transducer, and
| 6 |
A is the amplitude, ϕ is the phase advance in radians due to diffraction, and f is the frequency of the tone burst. For path lengths greater than several times the source radius (which is to say about 20 mm for our system),
| 7 |
where
| 8 |
Equations 7 and 8 were evaluated for our transducer with complex numerical integration in Mathematica.23 These results are shown in Figure 7 along with a simple power law fit given by
| 9 |
which well represents eqs 7 and 8.
Figure 7.
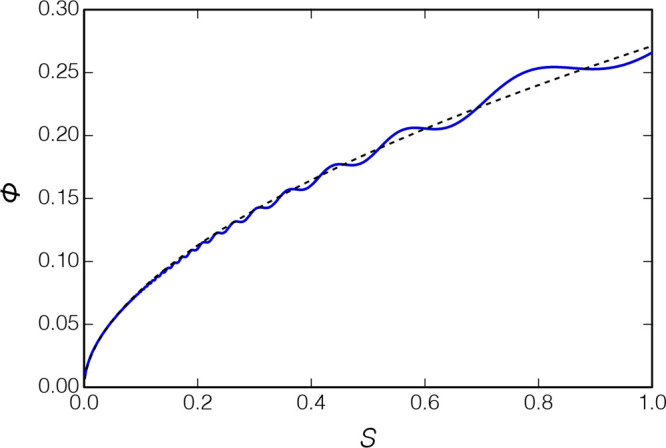
Diffraction phase advance calculated with eqs 7 and 8 (solid line); the dotted line shows a simple power law representation (eq 9), which represents these results with a correlation coefficient of R2 = 0.9977.
The diffraction correction is applied to the measured differential time between the return tone bursts along the short path and the long path. The time shift due to the diffraction correction is given by
| 10 |
with ϕ calculated from eq 9 and with S from eq 8 for each path length (i.e., z is set to 2Ls or 2Ll). From the above equations, it is seen that the diffraction correction becomes smaller as the frequency increases. The characteristics of our instrument are summarized in Table 1, which indicates that the diffraction correction ranges from 3.9 ppm for the long path at w = 200 m·s–1 to 207 ppm for the short path at w = 2000 m·s–1. But we are concerned with the difference in δtd between the short and long paths, which ranges from 2.5 ppm (0.0025%) at w = 200 m·s–1 to 88 ppm (0.0088%) at w = 2000 m·s–1. Although the diffraction correction is very small, it is non-negligible at low speeds of sound and long path lengths.
Table 1. Diffraction Correction Parameters for Our Transducer (f = 8 MHz with b = 5 mm) at Several Representative Values for Liquid Speeds of Sound.
| Speed of Sound: | w = 200 m·s–1 | w = 800 m·s–1 | w = 2000 m·s–1 |
|---|---|---|---|
| L = 2 × Ls = 24 mm | |||
| S | 0.024 | 0.096 | 0.240 |
| ϕ | 0.0355 | 0.0756 | 0.125 |
| Δt/μs | 120 | 30 | 12 |
| δtd/μs | 0.000706 | 0.00150 | 0.00249 |
| L = 2 × Ll = 60 mm | |||
| S | 0.060 | 0.240 | 0.600 |
| ϕ | 0.0585 | 0.125 | 0.205 |
| Δt/μs | 300 | 75 | 30 |
| δtd/μs | 0.00116 | 0.00248 | 0.00408 |
2.8. Data Analysis
The experimental data were written to a file for off-line analysis as described in section 2.6. The file was first parsed to identify and separate the echo, temperature, and pressure data.
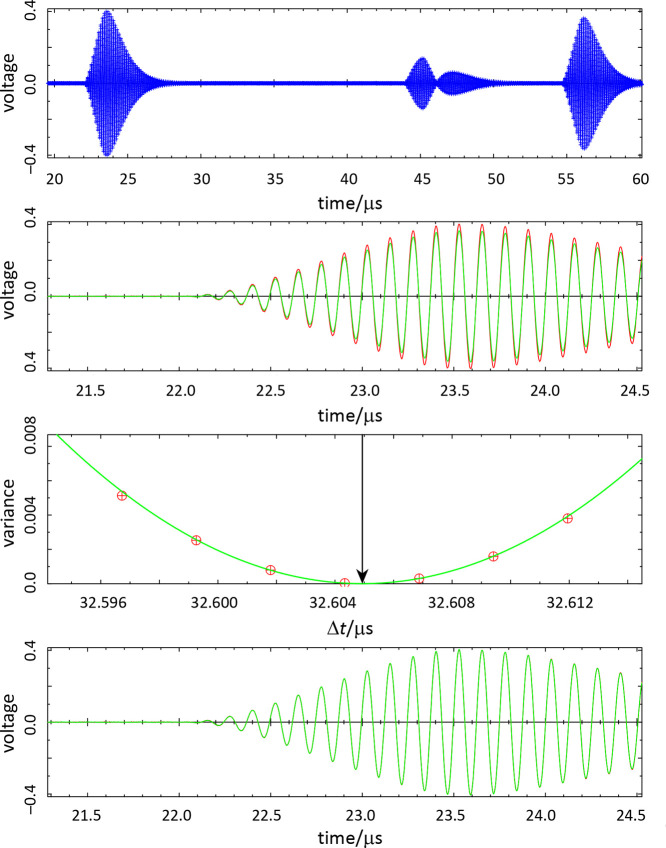
All of the echo data are depicted in the top panel of Figure 8. The basic idea of the analysis is to find a “best” superimposition of the short-path and long-path echo signals V by adjusting the amplitude ratio A and Δt according to
| 11 |
Figure 8.
Schema for the analysis of the echo data: (top) phase envelope for the 16 000 recorded data points; (second from top) approximate superposition of the short-path (red) and long-path (green) signals; (second from bottom) determination of the Δt giving the minimum variance for the superposition; and (bottom) final superposition. Data shown are for propane at T = 250.004 K, p = 6.403 MPa.
This general approach was developed by Ball and Trusler.17 Signal processing carried out by the oscilloscope provided the times to the maxima in the short-path and long-path echoes, from which an initial estimate of the Δt was obtained. An approximate superposition of the two echoes using this initial estimate is shown in the second panel. Here the attenuation of the long-path signal (green) relative to the short-path signal (red) can be clearly seen. A slight mismatch in the time overlap is also present although less apparent. A regression for A and Δt is carried out over ±12 cycles from the peak amplitude (±1.5 μs for our 8.00 MHz frequency); the variance in the fit for each cycle is plotted versus Δt as shown in the third panel of Figure 8. A parabola is fitted to the variance, and the minimum in this parabola defines the optimal Δt. Note that this approach allows a resolution in Δt that is smaller than that of the sample period. The final superposition with optimal Δt and A is shown in the bottom panel of Figure 8. With strong signals, the superposition is nearly perfect—while Figure 8 seems to show only the green of the long-path echo, a few pixels of red from the short-path signal are seen.
Figure 8 depicts the situation with strong echo signals (the data shown are for propane well away from the critical point). Figure S6 in the Supporting Information depicts signals that are much weaker and also with substantial attenuation; the same process successfully finds the optimal superposition. We note, however, that occasionally with weak signals the Δt is in error by one or two cycles (0.125 or 0.25 μs); these can be detected (and the points discarded) by manually examining the superposition plots. The case of weak signals emphasizes the advantage of basing the Δt on a superposition of the entire echo signal rather than attempting to find the difference between the rising edge of the echoes—the “time zero” of the long-path signal would be very difficult to ascertain in the case of weak echoes. The Δt obtained from this superposition was then adjusted by the diffraction correction of eqs 9 and 10.
This analysis contrasts with the analysis carried out by others using the dual-path pulse echo technique. We are not applying any sort of Fourier transform21 or Hilbert transform24 to deal with noisy data. Rather, we obtained signals with a good signal/noise ratio by averaging 256 echo signals; this was done with a few simple commands on the digital oscilloscope. The off-line analysis presented here contrasts with the real-time determination of the Δt obtained with the double-pulse method, a technique that requires sophisticated signal processing at the time of the measurement, often by a human operator as done by Meier.10 The present single-pulse method is much easier to automate, and the off-line analysis permits a closer examination of the data in cases of weak signals. The continuously rising or falling signal is advantageous in the present analysis: if the signal were to reach a steady-state amplitude, then the superposition would be much harder to identify, and the Δt could easily be in error by an integer number of cycles.
Our analysis could be improved for weak signals. We averaged 256 echo signals for the present measurements, but averaging a larger number of echoes could improve the signal-to-noise ratio and we have averaged as many as 4096 echoes for some subsequent measurements. A Fourier transform can function as a digital bandpass filter. We applied both of these techniques to mixtures of carbon dioxide and R1132a, which have very weak signals.25 An analog bandpass filter might also be helpful, but we were not able to locate a suitable commercial unit.
The temperature data were recorded as raw resistance ratios from the AC resistance bridge; these were converted to resistance, and then the SPRT calibration on ITS-90 was applied to obtain the temperature of the oil bath. Similarly, the signals from the pressure transducer were recorded as the vibration periods of the pressure and temperature crystals in the transducer, and calibration equations were applied to obtain the pressure. Four measurements of temperature and pressure were recorded for each set of three echo measurements, and the average of these four was assigned as the (T, p) for the three echo measurements.
3. Results
Measurements of the speed of sound of seven fluids were carried out. The path-length difference was calibrated with measurements on propane; measurements on water were used to confirm the calibration. Verification of the instrument was carried out on p-xylene by comparing our results to literature data. Finally, data for four “new” halogenated-olefin refrigerants are reported; the literature data for these fluids are very limited, and thus, comparisons are made primarily to reference-quality equations of state.
3.1. Experimental Samples
The experimental samples are detailed in Table 2. For all of the fluids, the samples were used as received, except that they were degassed with multiple cycles of freezing the sample, evacuating the vapor space, and thawing. The pressure over the frozen material on the final freeze–pump–thaw cycle was 1 × 10–4 Pa or lower. We also carried out our own analysis of the refrigerant samples by gas chromatography/mass spectrometry (carried out according to the protocols of Bruno and Svoronos26,27).
Table 2. Sample Information.
| Name | IUPAC Name | Source | Initial Purity/Mol Frac. | Purification Method | Final Purity/Mol Frac. | Analysis Method |
|---|---|---|---|---|---|---|
| propane | propane | Scott | 0.99999 | degassing | 0.99999 | GC/MSa |
| water | water | b | >0.99999 | b | >0.99999 | resistivity |
| p-xylene | p-xylene | Sigma-Aldrich | 0.997 | degassing | 0.997 | none |
| R1234yf | 2,3,3,3-tetrafluoroprop-1-ene | Honeywell | 0.9996 | degassing | 0.9996 | GC/MS |
| R1234ze(E) | trans-2,3,3,3-tetrafluoroprop-1-ene | Honeywell | 0.99993 | degassing | 0.99993 | GC/MS/IRc |
| R1233zd(E) | trans-1-chloro-3,3,3-trifluoroprop-1-pene | Honeywell | 0.99985 | degassing | 0.99985 | GC/MS |
| R1336mzz(Z) | cis-1,1,1,4,4,4-hexafluorobut-2-ene | Chemours | 0.9999 | degassing | 0.9999 | GC/QToF-MSd |
Gas chromatography/mass spectrometry.
The water sample was obtained from a commercial ultrapure laboratory water system that consisted of two ion-exchange stages, ultraviolet light dosing (to photo-oxidize organics), a third ion-exchange stage, and an ultrafiltration membrane; the resistivity of this water was 18.2 MΩ·cm.
Gas chromatography/mass spectrometry/infrared spectroscopy.
Gas chromatography/quadrupole time-of-flight mass spectroscopy.
3.2. Calibration of Path-Length Difference with Propane
The path-length difference was calibrated with measurements on propane spanning the operating range of temperature and pressure by taking the propane speed of sound as a known quantity and inverting eq 3 to obtain ΔL for each measurement
| 12 |
where the propane speed of sound was calculated with the equation of state (EOS) of Lemmon et al.28 Note that the diffraction correction δtd to the measured transit time must also be included. These data were fitted to an emprical function representing the temperature and pressure variation of the path-length difference
| 13 |
where ΔL is in mm, T is in K, and p is in MPa and the parameters are ΔL293 = 17.9546 mm, a1 = 7.843 × 10–6, a2 = 8.499 × 10–9, and a3 = −8.38 × 10–6. These parameters were obtained strictly from fitting the propane data, and while we did not expect any systematic temperature and pressure effects associated with our mounting of the crystal, such effects would be accounted for, in contrast with parameters developed from the material properties.
The propane EOS of Lemmon et al. was fitted to a wide range of data, including vapor pressure, p–ρ–T, saturation densities, isochoric and isobaric heat capacities, enthalpy of vaporization, second and third virial coefficients, and speed of sound. It fits the speed-of-sound data of Meier and Kabelac18 within 0.06% over their entire temperature and pressure range (240 to 420 K, with pressures of up to 100 MPa), with an RMS deviation of 0.013%. Thus, our instrument is, in effect, calibrated to the speed of sound data of Meier and Kabelac, who estimated the expanded uncertainty in their measurements to be 0.019 to 0.022%. Details of the Meier and Kabelac instrument are given by Meier;9 their path-length difference was based on a combination of material properties of their quartz transducer and stainless-steel measuring cell and calibrations carried out with water at p = 0.10 MPa over a temperature range of 1 to 95 °C. Propane was selected here as the calibration fluid largely because of the excellent data of Meier and Kabelac (which covered temperature and pressure ranges similar to those of our instrument) and the EOS of Lemmon et al.; furthermore, the availability of high-purity propane minimizes sample purity effects.
Figure 9 presents the path-length difference obtained from 1319 data points on propane measured along 10 isochores spanning a temperature range of (230 to 420) K with pressures to 52 MPa. The path-length correlation of eq 13 is shown for p = 0 and 60 MPa. The RMS deviation between the experimental points and eq 13 is 0.0021 mm, or 0.012%. The propane data are presented in the Supporting Information, including a comparison of our data with the data of Meier and Kabelac18 as Figures S7 and S8. Also shown in Figure 9 are similar results for water (discussed in section 3.4).
Figure 9.
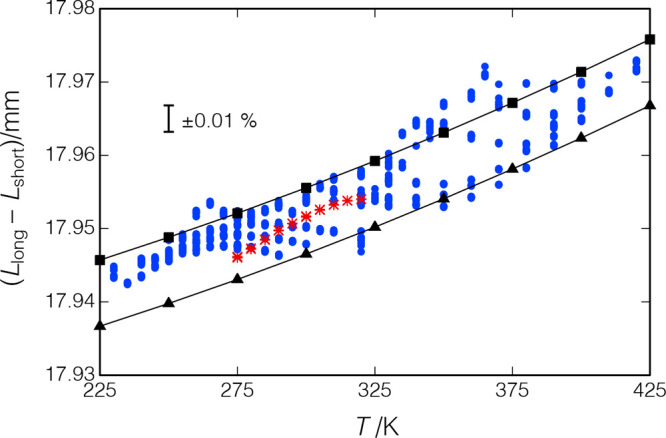
Propane calibration of the path-length difference; ●, propane data; −■–, eq 13 with p = 0; −▲–, eq 13 with p = 60 MPa; and *, water data.
3.3. Direct Measurement of Path-Length Difference
The path-length difference was also determined directly by measuring the lengths of the ceramic spacers before assembly. This was done with digital micrometers; the resolution of the micrometer used for the short-path spacer was 0.001 mm, and the one for the long-path spacer was 0.0025 mm. The calibration of the micrometers was checked with gage blocks immediately prior to measuring the spacers. Six to eight measurements were made of each spacer with average values and standard deviations of Lshort = 12.0096 mm, σ = 0.0066 mm and Llong = 29.9585 mm, σ = 0.0069 mm or (Llong – Lshort) = 17.949 mm at T = 293 K. This value is 0.0056 mm or 0.031% smaller than the path-length difference determined by the propane calibration. The standard deviation in this determination was 0.04%, with a somewhat larger uncertainty. This is a larger uncertainty than the path-length calibration with propane (as discussed in section 4.3), and thus, the calibrated path-length difference was used in the analysis. Nevertheless, this direct measurement served as a powerful consistency check.
3.4. Verification of Path-Length Difference with Water
The calibration of the path-length difference was repeated with water. These measurements were carried out on isochores over a temperature range of (275 to 420) K, with pressures of up to 68 MPa. For measurements at low temperatures along the first isochore (T = 275 to 320 K, p to 16.8 MPa), the results are seen to be consistent with the propane data and eq 13 as shown in Figure 9; the RMS deviation with eq 13 was 0.0039 mm or 0.022%. At higher temperatures and for subsequent isochores, however, the results were not repeatable, even at low temperatures or with a fresh sample.
The cell was disassembled, and we found that the ceramic spacers had been attacked by water; the surface appeared powdery. The spacers were swollen and had to be hammered out of the support tube. The quartz crystal, brass reflectors, and brass support tube, on the other hand, showed no visible degradation. It was not possible to determine when the spacers were attacked, and thus, we did not use the water data in calibrating the path lengths. Nevertheless, the low-temperature water data confirm the propane calibration.
We should note that the water measurements were the last ones carried out in the present work because we were concerned about the potential corrosivity of water at high temperatures. This is the reason that we measured propane first. After repairs, subsequent measurements with this instrument required a full repetition of the path-length calibration (which was different than the one reported here), as discussed by Rowane et al.29
3.5. Verification Measurements with p-Xylene
p-Xylene was chosen for verification measurements so that we could compare with the recent high-accuracy data of Al Ghafri et al.30 Our measurements began with isotherms at T = (373.7, 422.8, and 323.5) K; these measurements were limited to a pressure of 20 MPa to avoid freezing of the sample in the room-temperature manifold. We then heated the manifold, as described in section 2.3, and loaded a fresh sample of p-xylene. The isotherm at T = 323.5 K was repeated but with pressures of up to 43.1 MPa. The liquid phase was then measured along 11 isochores covering an overall (T, p) range of (288.1 K, 0.065 MPa) to (423.2 K, 53.7 MPa).
The measured data are summarized in Figure 10 and reported in Table 3. The most recent equation of state available for p-xylene, that of Zhou et al.,31 was developed with only limited speed-of-sound data, and its uncertainty in the speed of sound is estimated to be 0.3%. Thus, we compare to an empirical fit of the present data; we adopt the same implicit equation used by Al Ghafri et al.,30 namely,
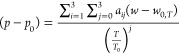 |
14 |
| 15 |
where p0 = 0.1 MPa, T0 = 286.4 K is the triple point of p-xylene, w0,T is the speed of sound at p0, and the coefficients are listed in Table 4.
Figure 10.
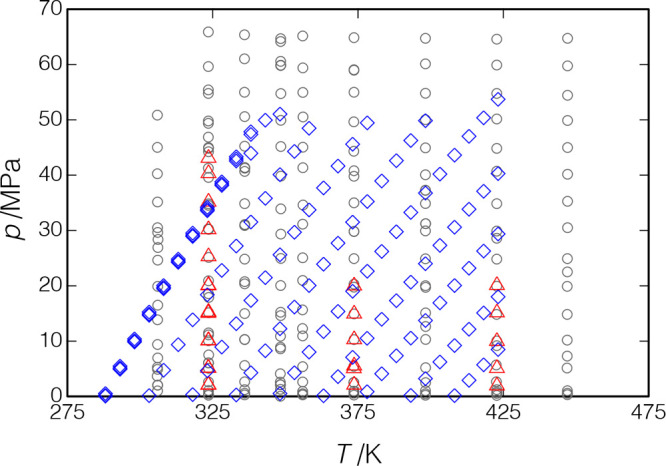
Measured points for p-xylene; Δ, present results, measurements along isotherms; ◇, present results, measurements along isochores; ○, Al Ghafri et al.30
Table 3. Experimental Liquid-Phase Speeds of Sound, w, for p-Xylene, with the Combined Expanded (k = 2) Relative Uncertainty in the Speed of Sound, Uc, Also Given along with Relative Deviations from the Empirical Fit to the Data (Equations 14 and 15)a,b.
| T (K) | P (MPa) | W (m·s–1) | Uc (k = 2) (%) | 100(w/wfit – 1) |
|---|---|---|---|---|
| 373.657 | 5.567 | 1053.42 | 0.038 | –0.071 |
| 373.657 | 2.096 | 1028.64 | 0.039 | –0.083 |
| 373.657 | 10.297 | 1085.31 | 0.037 | –0.062 |
| 373.657 | 14.943 | 1114.79 | 0.036 | –0.058 |
| 373.657 | 20.015 | 1145.20 | 0.035 | –0.055 |
| 422.819 | 1.934 | 851.85 | 0.048 | –0.062 |
| 422.818 | 5.097 | 880.82 | 0.045 | –0.061 |
| 422.819 | 10.008 | 922.22 | 0.042 | –0.060 |
| 422.819 | 15.148 | 961.81 | 0.040 | –0.061 |
| 422.818 | 20.102 | 997.06 | 0.038 | –0.063 |
| 373.566 | 5.088 | 1050.49 | 0.038 | –0.064 |
| 323.520 | 2.074 | 1218.73 | 0.035 | –0.015 |
| 323.520 | 5.173 | 1236.45 | 0.034 | –0.013 |
| 323.521 | 10.089 | 1263.47 | 0.034 | –0.009 |
| 323.520 | 15.068 | 1289.56 | 0.034 | –0.009 |
| 323.520 | 20.059 | 1314.60 | 0.033 | –0.009 |
| 288.105 | 0.193 | 1353.53 | 0.033 | –0.004 |
| 293.099 | 5.121 | 1357.32 | 0.033 | –0.005 |
| 298.114 | 10.045 | 1361.30 | 0.033 | 0.000 |
| 303.105 | 14.897 | 1365.23 | 0.033 | 0.005 |
| 308.106 | 19.706 | 1369.10 | 0.033 | 0.008 |
| 313.122 | 24.482 | 1372.93 | 0.033 | 0.009 |
| 318.107 | 29.176 | 1376.67 | 0.033 | 0.008 |
| 323.125 | 33.839 | 1380.33 | 0.033 | 0.006 |
| 328.113 | 38.419 | 1383.89 | 0.033 | 0.005 |
| 333.111 | 42.938 | 1387.33 | 0.033 | 0.005 |
| 338.126 | 47.351 | 1390.43 | 0.033 | 0.006 |
| 323.526 | 2.131 | 1219.18 | 0.035 | –0.004 |
| 323.524 | 5.138 | 1236.36 | 0.035 | –0.003 |
| 323.526 | 10.156 | 1263.86 | 0.034 | –0.005 |
| 323.525 | 15.284 | 1290.69 | 0.034 | –0.006 |
| 323.527 | 20.136 | 1314.97 | 0.033 | –0.007 |
| 323.526 | 25.306 | 1339.82 | 0.033 | –0.008 |
| 323.526 | 30.208 | 1362.47 | 0.033 | –0.010 |
| 323.527 | 35.192 | 1384.69 | 0.033 | –0.012 |
| 323.526 | 40.338 | 1406.86 | 0.033 | –0.014 |
| 323.527 | 43.121 | 1418.63 | 0.033 | –0.008 |
| 288.105 | 0.514 | 1354.98 | 0.033 | –0.017 |
| 293.099 | 5.467 | 1358.84 | 0.033 | –0.019 |
| 298.114 | 10.394 | 1362.78 | 0.033 | –0.016 |
| 303.105 | 15.243 | 1366.64 | 0.033 | –0.012 |
| 308.106 | 20.054 | 1370.46 | 0.033 | –0.011 |
| 313.122 | 24.829 | 1374.25 | 0.033 | –0.011 |
| 318.108 | 29.522 | 1377.96 | 0.033 | –0.012 |
| 323.127 | 34.194 | 1381.64 | 0.033 | –0.012 |
| 328.113 | 38.783 | 1385.24 | 0.033 | –0.012 |
| 333.112 | 43.330 | 1388.78 | 0.033 | –0.011 |
| 338.127 | 47.837 | 1392.28 | 0.033 | –0.007 |
| 343.115 | 49.951 | 1386.07 | 0.033 | –0.002 |
| 348.129 | 51.039 | 1375.73 | 0.033 | 0.000 |
| 303.103 | 0.145 | 1290.58 | 0.034 | 0.013 |
| 308.104 | 4.751 | 1294.89 | 0.034 | 0.009 |
| 313.119 | 9.345 | 1299.28 | 0.034 | 0.008 |
| 318.106 | 13.864 | 1303.59 | 0.034 | 0.008 |
| 323.125 | 18.369 | 1307.86 | 0.033 | 0.007 |
| 328.113 | 22.798 | 1312.04 | 0.033 | 0.006 |
| 333.111 | 27.193 | 1316.15 | 0.033 | 0.003 |
| 338.127 | 31.541 | 1320.15 | 0.033 | 0.003 |
| 343.115 | 35.827 | 1324.07 | 0.033 | 0.001 |
| 348.129 | 40.091 | 1327.96 | 0.033 | 0.001 |
| 353.128 | 44.302 | 1331.78 | 0.033 | 0.002 |
| 358.140 | 48.478 | 1335.54 | 0.033 | 0.004 |
| 318.104 | 0.331 | 1230.52 | 0.034 | 0.014 |
| 323.123 | 4.656 | 1235.36 | 0.034 | 0.010 |
| 328.110 | 8.921 | 1240.17 | 0.034 | 0.009 |
| 333.109 | 13.153 | 1244.90 | 0.034 | 0.009 |
| 338.126 | 17.348 | 1249.50 | 0.034 | 0.008 |
| 343.115 | 21.484 | 1254.02 | 0.034 | 0.006 |
| 348.128 | 25.604 | 1258.49 | 0.034 | 0.003 |
| 353.128 | 29.675 | 1262.87 | 0.034 | 0.000 |
| 358.140 | 33.716 | 1267.19 | 0.034 | –0.002 |
| 363.155 | 37.719 | 1271.43 | 0.033 | –0.003 |
| 368.133 | 41.651 | 1275.54 | 0.033 | –0.002 |
| 373.167 | 45.589 | 1279.63 | 0.033 | –0.001 |
| 378.156 | 49.458 | 1283.64 | 0.033 | 0.003 |
| 333.109 | 0.265 | 1170.63 | 0.035 | 0.015 |
| 338.123 | 4.287 | 1175.87 | 0.035 | 0.013 |
| 343.112 | 8.268 | 1181.10 | 0.035 | 0.013 |
| 348.126 | 12.237 | 1186.27 | 0.035 | 0.011 |
| 353.126 | 16.157 | 1191.32 | 0.035 | 0.009 |
| 358.138 | 20.050 | 1196.28 | 0.034 | 0.005 |
| 363.153 | 23.911 | 1201.14 | 0.034 | 0.002 |
| 368.132 | 27.706 | 1205.85 | 0.034 | –0.001 |
| 373.167 | 31.509 | 1210.53 | 0.034 | –0.004 |
| 378.156 | 35.238 | 1215.07 | 0.034 | –0.005 |
| 383.175 | 38.958 | 1219.55 | 0.034 | –0.004 |
| 388.181 | 42.631 | 1223.93 | 0.034 | –0.003 |
| 393.183 | 46.269 | 1228.24 | 0.034 | –0.001 |
| 398.191 | 49.865 | 1232.42 | 0.034 | 0.003 |
| 348.121 | 0.524 | 1114.17 | 0.036 | 0.014 |
| 353.122 | 4.274 | 1119.85 | 0.036 | 0.015 |
| 358.135 | 8.011 | 1125.50 | 0.036 | 0.016 |
| 363.150 | 11.718 | 1131.03 | 0.036 | 0.015 |
| 368.129 | 15.368 | 1136.40 | 0.035 | 0.012 |
| 373.165 | 19.025 | 1141.71 | 0.035 | 0.008 |
| 378.154 | 22.638 | 1146.95 | 0.035 | 0.003 |
| 383.173 | 26.220 | 1151.99 | 0.035 | –0.001 |
| 388.180 | 29.762 | 1156.94 | 0.035 | –0.003 |
| 393.182 | 33.270 | 1161.78 | 0.035 | –0.005 |
| 398.191 | 36.755 | 1166.55 | 0.034 | –0.004 |
| 403.194 | 40.202 | 1171.21 | 0.034 | –0.003 |
| 408.202 | 43.623 | 1175.79 | 0.034 | –0.003 |
| 413.209 | 47.019 | 1180.31 | 0.034 | –0.001 |
| 418.209 | 50.385 | 1184.77 | 0.034 | 0.000 |
| 423.215 | 53.729 | 1189.18 | 0.034 | –0.002 |
| 363.146 | 0.122 | 1054.28 | 0.038 | 0.003 |
| 368.125 | 3.588 | 1060.34 | 0.038 | 0.009 |
| 373.161 | 7.079 | 1066.42 | 0.037 | 0.012 |
| 378.150 | 10.512 | 1072.31 | 0.037 | 0.012 |
| 383.170 | 13.932 | 1078.06 | 0.037 | 0.011 |
| 388.176 | 17.318 | 1083.68 | 0.036 | 0.009 |
| 393.179 | 20.674 | 1089.17 | 0.036 | 0.006 |
| 398.187 | 24.010 | 1094.55 | 0.036 | 0.003 |
| 403.191 | 27.316 | 1099.81 | 0.036 | 0.002 |
| 408.200 | 30.599 | 1104.97 | 0.035 | 0.001 |
| 413.207 | 33.856 | 1110.04 | 0.035 | 0.001 |
| 418.208 | 37.086 | 1115.02 | 0.035 | 0.002 |
| 423.215 | 40.299 | 1119.96 | 0.035 | 0.004 |
| 378.147 | 0.838 | 1003.71 | 0.040 | 0.004 |
| 383.168 | 4.100 | 1010.13 | 0.039 | 0.012 |
| 388.175 | 7.341 | 1016.46 | 0.039 | 0.016 |
| 393.177 | 10.553 | 1022.62 | 0.038 | 0.017 |
| 398.186 | 13.746 | 1028.63 | 0.038 | 0.016 |
| 403.190 | 16.913 | 1034.50 | 0.038 | 0.014 |
| 408.200 | 20.062 | 1040.25 | 0.037 | 0.012 |
| 413.207 | 23.190 | 1045.89 | 0.037 | 0.010 |
| 418.207 | 26.294 | 1051.43 | 0.037 | 0.010 |
| 423.215 | 29.386 | 1056.90 | 0.036 | 0.012 |
| 393.176 | 0.195 | 943.46 | 0.042 | 0.009 |
| 398.185 | 3.214 | 950.34 | 0.042 | 0.019 |
| 403.189 | 6.215 | 957.08 | 0.041 | 0.025 |
| 408.199 | 9.192 | 963.58 | 0.040 | 0.028 |
| 413.206 | 12.154 | 969.96 | 0.040 | 0.028 |
| 418.207 | 15.096 | 976.20 | 0.039 | 0.028 |
| 423.215 | 18.026 | 982.34 | 0.039 | 0.030 |
| 408.198 | 0.138 | 888.35 | 0.046 | 0.034 |
| 413.205 | 2.928 | 895.52 | 0.045 | 0.043 |
| 418.206 | 5.706 | 902.59 | 0.044 | 0.051 |
| 423.215 | 8.486 | 909.57 | 0.043 | 0.055 |
| 288.103 | 0.065 | 1353.04 | 0.033 | 0.007 |
| 293.098 | 4.921 | 1356.50 | 0.033 | 0.007 |
| 298.114 | 9.839 | 1360.39 | 0.033 | 0.007 |
| 303.104 | 14.686 | 1364.27 | 0.033 | 0.009 |
| 308.105 | 19.475 | 1368.06 | 0.033 | 0.011 |
| 313.120 | 24.231 | 1371.83 | 0.033 | 0.012 |
| 318.107 | 28.910 | 1375.53 | 0.033 | 0.012 |
| 323.125 | 33.569 | 1379.20 | 0.033 | 0.011 |
| 328.112 | 38.145 | 1382.79 | 0.033 | 0.011 |
| 333.111 | 42.563 | 1385.81 | 0.033 | 0.011 |
| 338.126 | 43.961 | 1376.15 | 0.033 | 0.017 |
The listed data are averaged from 12 measured echo-delay times (4 sets of 3 replicates each); see Supporting Information for unaveraged data. The data are listed in the order measured; blank lines separate isotherms and isochores.
The standard (k = 1) uncertainties in T and p are 0.005 K and (26 × 10–6p + 0.016 MPa), respectively.
Table 4. Coefficients to the Empirical Fit of the p-Xylene Data (Equations 14 and 15).
| a10 | –0.50585 | a11 | 1.57213 | a12 | –1.29872 | a13 | 0.425685 | |||
| a20 | 2.41506 × 10–4 | a21 | –3.93517 × 10–4 | a22 | 3.34927 × 10–4 | a23 | 0.0 | |||
| a30 | –6.82551 × 10–7 | a31 | 1.84037 × 10–6 | a32 | 1.15418 × 10–6 | a33 | 0.0 | |||
| b0 | 3.20442 × 103 | b1 | –2.71050 × 103 | b2 | 1.11379 × 103 | b3 | –2.47322 × 102 |
Deviations of the measured data from eqs 14 and 15 are shown in Figure 11. Our data are seen to be self-consistent and well-fit by eqs 14 and 15 except for the two isotherms at T = (373.7 and 422.8) K, which are systematically lower by 0.058 to 0.069%. The RMS deviation of all of the data from eqs 14 and 15 is 0.022%; it is 0.015% dropping the two isotherms. Replicates of the T = (288 to 338) K isochore measured at the beginning and end of the testing showed a systematic difference of up to 0.021%, indicating a possible slight degradation of the sample.
Figure 11.
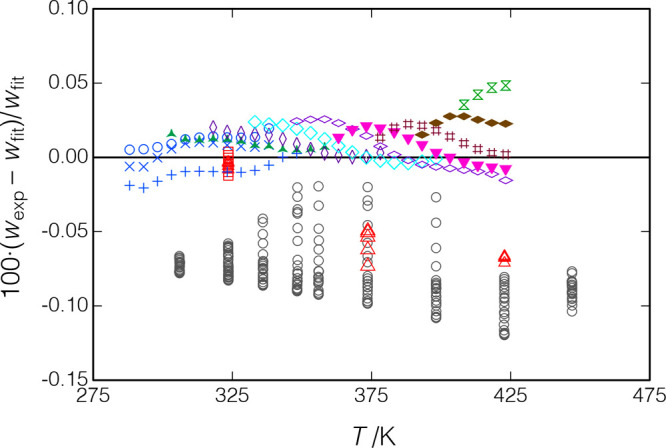
Deviations between the measured speed of sound for p-xylene and the fit of the present data (eq 14); ○, Al Ghafri et al.;30 Δ, □, present results for measurements along isotherms; replicates of the isochore starting at T = 288 K are indicated by ×, +, and ○ in blue (measured in that order); and other symbols indicate measurements along isochores.
Al Ghafri et al.30 measured along isotherms from T = (306 to 447) K, with pressures to 66 MPa; this is the only literature source covering a wide range of temperature and pressure. Their data are shown in Figures 10 and 11; they are quite self-consistent but are systematically lower than our data by an average of 0.077%. The NIST TDE database32 lists 57 additional sources of literature data for the liquid-phase speed of sound, but all report data only at atmospheric pressure (mostly at near-ambient temperatures) or for the saturated liquid and only three of these sources report more than six data points. As the present paper is not intended to review the literature on p-xylene, we will not consider these other sources further.
Al Ghafri et al.30 estimate their expanded uncertainty in speed of sound to range from 0.023 to 0.104%, and thus, our data and the data of Al Ghafri et al. are consistent within mutual uncertainties. (Our uncertainties are discussed in section 4.) It is instructive to discuss the differences and similarities in our two instruments: We both employ the dual-path pulse-echo technique with a single ultrasonic burst. We have a path-length difference of 18 mm with a 2.5:1 ratio, while the Al Ghafri et al. instrument has a path-length difference of 10 mm with a 1.5:1 ratio. We employ a quartz crystal with a resonant frequency of 8.00 MHz versus a piezoelectric element at 5.00 MHz. Our reflectors extend to the edges of the fluid volume while those of Al Ghafri et al. are of a “post-type” design that sits away from the edges of the fluid volume.
Our calibration procedures differ from those of Al Ghafri et al.30 As discussed in section 3.2, we calibrated with propane over a range of temperatures and pressure. Al Ghafri et al. calibrated with water at (T = 306.1 K, p = 0.1 MPa) and calculated the path-length difference as a function of T and p by use of the material properties of their Invar-36 spacers. They did carry out verification measurements on water at temperatures of up to 421 K and pressures of up to 60 MPa.
Our p-xylene sample had an overall purity of 99.7% according to the supplier’s certificate of analysis, with impurities of 0.18% m-xylene and 0.07% ethylbenzene (specified as “GC area percentage”, which we take as approximately equivalent to a molar basis). These impurities are chemically similar to those of p-xylene and have speeds of sound that differ by less than 1%. Calculating the liquid-phase speed of sound (over the range of T and p of our measurements) with the equations of state of Zhou et al.31 for each of the pure fluids and mixing coefficients given by Bell and Lemmon33 (as implemented in the REFPROP database34) gives speeds of sound for our sample that are 0.006 to 0.010% lower than for pure p-xylene.
The p-xylene sample of Al Ghafri et al.30 had an overall purity of 99.8%, with a water content of 0.01% (mass basis) according to the supplier’s certificate of analysis; other impurities were not listed but would likely contribute a systematic effect similar to the impurities in our sample. Calculating the p-xylene/water mixture with REFPROP yields a speed of sound 0.050 to 0.067% lower than that of pure p-xylene. It must be noted that there are no mixture data for p-xylene/water, and this calculation assumed mixing coefficients of octane/water. There is considerable uncertainty in the effect of a small water impurity on the speed of sound, but this result suggests that a significant fraction of the systematic difference between our data and the data of Al Ghafri et al. could be due to sample purity effects.
Given the differences in our instruments, procedures, and samples, our agreement with the data of Al Ghafri et al.30 is quite remarkable; this result serves to verify both of our instruments and indicates the robustness of the pulse-echo technique.
3.6. Speed of Sound of Halogenated-Olefin Refrigerants
Four “new” halogenated-olefin refrigerants were measured. These fluids have very low values of the global warming potential (GWP) due to the presence of a carbon–carbon double bond. They have been developed and recently commercialized as replacements for high-GWP hydrofluorocarbon (HFC) and hydrochlorofluorocarbon (HCFC) refrigerants currently in use. Some of these fluids are also used as solvents or foam-blowing agents. Table 5 lists some of the basic properties of these fluids, including the normal-boiling-point and critical-point temperatures and the global warming potential relative to CO2 on a 100-year integration time horizon (GWP100).35
Table 5. Characteristics of the Halogenated-Olefin Refrigerants Measured Here.
| Name | TNBP/K | Tcrit/K | GWP100 | ASHRAE Safety Class |
|---|---|---|---|---|
| R1234yf | 243.7 | 367.9 | <1 | A2L |
| R1234ze(E) | 254.2 | 382.5 | <1 | A2L |
| R1233zd(E) | 291.4 | 439.6 | 1 | A1 |
| R1336mzz(Z) | 306.5 | 444.4 | 2 | A1 |
Also listed in Table 5 is the safety classification under ANSI/ASHRAE Standard 34;36 the rating is divided into a toxicity part (A or B) and a flammability part (1, 2L, 2, or 3). A toxicity rating of “A” designates “lower toxicity” as indicated by an occupational exposure limit of 400 ppm (parts per million) or higher on a volume basis in air; all four fluids studied here have received an “A” rating. A flammability rating of “1” indicates “no flame propagation” in the ASTM E-681 test;37 a rating of “2L” indicates marginal flammability, defined as a heat of combustion of less than 19 MJ/kg, a lower flammability limit of greater than 0.10 kg·m–3, and a maximum burning velocity of less than 10 cm·s–1. Ratings of “2” and “3” indicate higher flammability. The fluids studied here are rated 1 or 2L. The R numbers used here as shorthand notation are also specified by ANSI/ASHRAE Standard 34. ISO Standard 81738 is substantially the same in both the designation and safety classification of these fluids.
Only very limited literature data for the liquid-phase speed of sound are available for these fluids, so we compare primarily to recent reference equations of state. For the refrigerants measured here, we provided the present data to the EOS developers of three of these EOS, who used our data in their fitting, and thus such comparisons cannot independently verify the measurements—they can only indicate their internal consistency. However, the ability of an EOS to fit the present speed-of-sound data as well as other data types (including vapor pressure, p–ρ–T, vapor-phase speed of sound, and heat capacity data), all nearly within experimental uncertainties (as will be shown below), strongly suggests that all of the data are thermodynamically consistent, as discussed by Lemmon and Jacobsen.1
3.6.1. R1234yf-2,3,3,3-Tetrafluoroprop-1-ene
R1234yf, also known as HFO-1234yf (“HFO” = “hydrofluoroolefin”), was developed as a replacement for R134a (1,1,1,2-tetrafluoroethane) in automotive air-conditioning systems,39 and it now accounts for the majority of new automotive systems. It is also a component in at least 29 refrigerant blends classified by ANSI/ASHRAE Standard 34.36
Measurements of the speed of sound of R1234yf were carried out along 19 isochores at temperatures from (235 to 380) K, with pressures of up to 50 MPa. The measured points are shown in Figure 12 and reported in Table 6. The initial set of four isochores was measured to a maximum (T, p) of 370 K and 50.3 MPa; upon venting the sample at the conclusion of these tests, a few milligrams of polymer was collected. Earlier testing indicated the possibility of polymerization at high pressures,40 and the second series of isochores (which comprises the main data set) was limited to a maximum pressure ranging from 15.9 MPa for the highest-density (i.e., lowest temperature) isochore to 7.1 MPa for the lowest-density isochore, which extended to T = 370 K. Upon completion of this series of isochores, the same sample was then measured along two additional isochores (referred to as series 3) up to (T = 370 K, p = 25.8 MPa) and (T = 380 K, p = 17.4 MPa); each of these tests was followed by a replicate of the isochore (measured in the second series) that extended from (T = 290 K, p = 1.0 MPa) to (T = 310 K, p = 11 MPa). Upon flushing the cell with acetone following these tests, less than 1 mg of residue was collected, indicating very limited or no polymerization.
Figure 12.
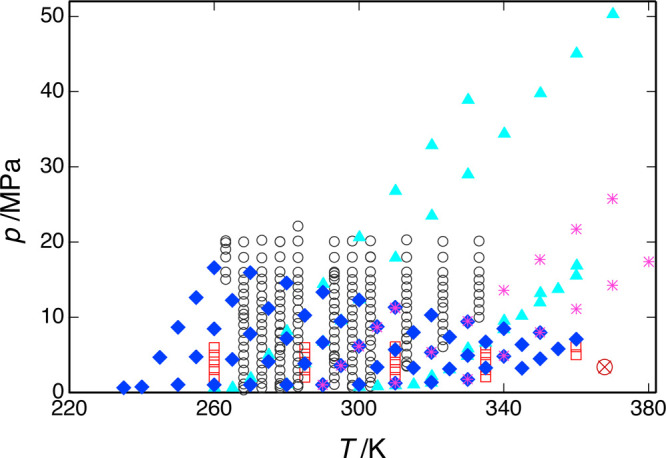
Measured speed-of-sound data for R1234yf; ▲, present work (series 1); ◆, present work (series 2); *, present work (series 3); □, Lago et al.;43 and ○, Yoshitake.42 The critical point is indicated by a red ⊗.
Table 6. Experimental Speeds of Sound, w, for R1234yf (2,3,3,3-Tetrafluoroprop-1-ene), with the Combined Expanded (k = 2) Relative Uncertainty in the Speed of Sound, Uc, Also Given along with Relative Deviations from the Equation of State of Lemmon and Akasaka41a,b.
| T (K) | P (MPa) | W (m·s–1) | Uc (k = 2) (%) | 100(w/wEOS – 1) |
|---|---|---|---|---|
| 260.090 | 0.641 | 617.92 | 0.055 | 0.034 |
| 265.117 | 0.638 | 595.66 | 0.058 | 0.067 |
| 270.098 | 1.895 | 585.39 | 0.059 | 0.059 |
| 275.100 | 5.020 | 592.64 | 0.056 | 0.033 |
| 280.107 | 8.149 | 599.84 | 0.054 | 0.015 |
| 290.111 | 14.430 | 614.11 | 0.050 | –0.012 |
| 300.105 | 20.638 | 627.61 | 0.047 | –0.016 |
| 310.108 | 26.784 | 640.41 | 0.045 | –0.011 |
| 320.146 | 32.869 | 652.60 | 0.043 | –0.001 |
| 330.159 | 38.879 | 664.28 | 0.041 | 0.006 |
| 280.103 | 1.080 | 533.39 | 0.071 | 0.058 |
| 285.089 | 3.892 | 541.30 | 0.067 | 0.035 |
| 290.106 | 6.728 | 549.09 | 0.063 | 0.014 |
| 295.105 | 9.540 | 556.58 | 0.060 | 0.001 |
| 300.105 | 12.350 | 563.88 | 0.057 | –0.008 |
| 310.109 | 17.923 | 577.75 | 0.053 | –0.010 |
| 320.133 | 23.485 | 591.08 | 0.050 | –0.004 |
| 330.123 | 28.982 | 603.71 | 0.047 | 0.003 |
| 340.118 | 34.401 | 615.63 | 0.045 | 0.017 |
| 350.119 | 39.760 | 627.01 | 0.043 | 0.028 |
| 360.126 | 45.057 | 637.89 | 0.042 | 0.035 |
| 370.138 | 50.278 | 648.27 | 0.040 | 0.037 |
| 300.100 | 0.715 | 437.61 | 0.109 | –0.016 |
| 305.118 | 0.821 | 415.20 | 0.123 | –0.059 |
| 310.104 | 0.938 | 392.78 | 0.140 | –0.108 |
| 315.115 | 1.068 | 370.05 | 0.161 | –0.162 |
| 320.127 | 2.166 | 365.95 | 0.161 | –0.116 |
| 330.125 | 5.839 | 384.76 | 0.130 | –0.025 |
| 340.116 | 9.517 | 401.52 | 0.108 | –0.009 |
| 350.135 | 13.197 | 416.80 | 0.094 | 0.003 |
| 360.143 | 16.855 | 430.86 | 0.083 | 0.019 |
| 319.979 | 1.289 | 349.60 | 0.185 | –0.174 |
| 324.983 | 3.063 | 359.82 | 0.163 | –0.071 |
| 329.992 | 4.846 | 369.35 | 0.146 | –0.023 |
| 334.981 | 6.621 | 378.20 | 0.132 | –0.010 |
| 339.983 | 8.403 | 386.62 | 0.121 | –0.007 |
| 344.992 | 10.185 | 394.64 | 0.111 | 0.000 |
| 349.990 | 11.966 | 402.33 | 0.103 | 0.004 |
| 355.010 | 13.754 | 409.76 | 0.095 | 0.007 |
| 359.996 | 15.527 | 416.85 | 0.089 | 0.015 |
| 235.010 | 0.637 | 729.97 | 0.043 | –0.050 |
| 240.002 | 0.734 | 708.26 | 0.045 | –0.023 |
| 245.003 | 4.676 | 714.03 | 0.044 | –0.032 |
| 250.005 | 8.663 | 720.22 | 0.043 | –0.036 |
| 254.995 | 12.624 | 726.36 | 0.042 | –0.035 |
| 259.990 | 16.592 | 732.57 | 0.041 | –0.033 |
| 250.001 | 1.049 | 666.04 | 0.049 | 0.004 |
| 254.996 | 4.746 | 672.67 | 0.047 | –0.012 |
| 259.990 | 8.460 | 679.43 | 0.046 | –0.024 |
| 264.997 | 12.253 | 686.64 | 0.044 | –0.038 |
| 269.992 | 15.942 | 693.26 | 0.043 | –0.032 |
| 259.988 | 1.012 | 621.58 | 0.054 | 0.031 |
| 264.995 | 4.401 | 628.57 | 0.052 | 0.007 |
| 269.992 | 7.791 | 635.56 | 0.050 | –0.010 |
| 274.996 | 11.181 | 642.49 | 0.048 | –0.019 |
| 280.000 | 14.563 | 649.33 | 0.047 | –0.023 |
| 269.990 | 1.011 | 577.43 | 0.061 | 0.049 |
| 274.995 | 4.113 | 584.90 | 0.058 | 0.022 |
| 280.000 | 7.177 | 591.96 | 0.056 | 0.009 |
| 285.002 | 10.248 | 598.98 | 0.053 | –0.005 |
| 290.020 | 13.339 | 606.04 | 0.051 | –0.011 |
| 279.999 | 1.014 | 533.15 | 0.071 | 0.059 |
| 285.001 | 3.836 | 541.08 | 0.067 | 0.034 |
| 290.004 | 6.660 | 548.85 | 0.063 | 0.016 |
| 294.999 | 9.483 | 556.46 | 0.060 | 0.004 |
| 300.000 | 12.305 | 563.88 | 0.057 | –0.003 |
| 290.002 | 1.002 | 488.16 | 0.085 | 0.045 |
| 294.998 | 3.566 | 496.79 | 0.079 | 0.030 |
| 300.003 | 6.159 | 505.32 | 0.074 | 0.007 |
| 305.000 | 8.776 | 513.87 | 0.069 | –0.002 |
| 310.001 | 11.331 | 521.56 | 0.065 | 0.000 |
| 289.998 | 1.065 | 488.94 | 0.085 | 0.042 |
| 294.995 | 3.618 | 497.39 | 0.079 | 0.030 |
| 299.997 | 6.182 | 505.63 | 0.073 | 0.015 |
| 304.996 | 8.743 | 513.59 | 0.069 | 0.006 |
| 309.999 | 11.304 | 521.30 | 0.065 | 0.000 |
| 299.996 | 1.063 | 443.13 | 0.105 | 0.000 |
| 304.996 | 3.365 | 452.31 | 0.096 | 0.005 |
| 310.002 | 5.680 | 461.14 | 0.089 | –0.001 |
| 314.994 | 7.997 | 469.68 | 0.082 | –0.001 |
| 320.002 | 10.294 | 477.62 | 0.077 | –0.002 |
| 309.996 | 1.242 | 398.58 | 0.134 | –0.061 |
| 314.993 | 3.278 | 408.13 | 0.121 | –0.023 |
| 320.003 | 5.328 | 417.23 | 0.110 | –0.007 |
| 325.008 | 7.377 | 425.86 | 0.101 | –0.001 |
| 329.998 | 9.417 | 434.05 | 0.093 | 0.004 |
| 320.001 | 1.356 | 351.05 | 0.183 | –0.112 |
| 325.006 | 3.135 | 361.18 | 0.161 | –0.027 |
| 330.014 | 4.921 | 370.57 | 0.144 | –0.010 |
| 335.002 | 6.722 | 379.65 | 0.130 | –0.016 |
| 340.006 | 8.495 | 387.97 | 0.119 | 0.025 |
| 330.012 | 1.732 | 306.16 | 0.256 | –0.207 |
| 335.000 | 3.267 | 316.98 | 0.221 | –0.016 |
| 340.007 | 4.814 | 327.03 | 0.193 | 0.106 |
| 345.011 | 6.373 | 336.21 | 0.172 | 0.084 |
| 350.008 | 7.969 | 345.18 | 0.153 | –0.019 |
| 289.995 | 1.008 | 488.27 | 0.085 | 0.044 |
| 294.990 | 3.578 | 496.95 | 0.079 | 0.028 |
| 299.991 | 6.155 | 505.37 | 0.074 | 0.016 |
| 309.992 | 1.278 | 399.22 | 0.133 | –0.054 |
| 319.997 | 5.380 | 418.02 | 0.109 | 0.001 |
| 329.995 | 9.489 | 434.97 | 0.093 | 0.008 |
| 340.005 | 13.584 | 450.38 | 0.081 | 0.017 |
| 350.007 | 17.663 | 464.70 | 0.073 | 0.029 |
| 359.997 | 21.713 | 478.08 | 0.066 | 0.050 |
| 369.991 | 25.751 | 490.77 | 0.061 | 0.068 |
| 289.991 | 0.994 | 488.14 | 0.085 | 0.052 |
| 294.989 | 3.557 | 496.76 | 0.079 | 0.038 |
| 299.991 | 6.128 | 505.12 | 0.074 | 0.025 |
| 304.991 | 8.697 | 513.20 | 0.069 | 0.015 |
| 309.993 | 11.264 | 521.00 | 0.066 | 0.010 |
| 329.995 | 1.753 | 307.02 | 0.255 | –0.132 |
| 340.003 | 4.867 | 328.07 | 0.192 | 0.100 |
| 350.006 | 7.987 | 345.96 | 0.153 | 0.117 |
| 359.996 | 11.113 | 361.70 | 0.127 | 0.023 |
| 369.991 | 14.242 | 376.38 | 0.109 | 0.019 |
| 380.020 | 17.378 | 390.06 | 0.095 | 0.027 |
| 289.992 | 1.010 | 488.35 | 0.085 | 0.054 |
| 294.990 | 3.561 | 496.83 | 0.079 | 0.042 |
| 299.987 | 6.117 | 505.04 | 0.074 | 0.029 |
| 304.990 | 8.666 | 512.92 | 0.069 | 0.022 |
| 309.993 | 11.224 | 520.64 | 0.066 | 0.016 |
The listed data are averaged from 12 measured echo-delay times (4 sets of 3 replicates each); see Supporting Information for unaveraged data. The data are listed in the order measured; blank lines separate measured isochores.
The standard (k = 1) uncertainties in T and p are 0.005 K and (26 × 10–6·p + 0.016 MPa), respectively.
The measured data are compared to the EOS of Lemmon and Akasaka41 in Figure 13; the present data were included in the fitting of this EOS. Figure 13(a) plots the deviations of the present data versus temperature, and there are no obvious trends except for a somewhat larger scatter at higher temperatures. (Note that the figure plots the deviations of all of the replicate measurements, which are tabulated in the Supporting Information, while Table 6 reports only average values.) The overall RMS deviation is 0.056%, which is not surprising given that these data were included in the EOS fitting. Figure 13(b) plots deviations versus pressure, and series 1 and 3 show small (less than 0.068%), but systematically increasing, deviations as the pressure is increased. Five replicates of the isochore extending from (T = 290.0 K, p = 1.0 MPa) to (T = 310.0 K, p = 11 MPa) were measured during the course of series 2 and 3; the speed of sound systematically increased by a maximum of 0.0087% between the middle and end of series 2 and 0.024% between series 2 and the end of series 3. These results indicate that the sample was stable, except for a slight degradation when it was taken to the higher pressures of series 3.
Figure 13.
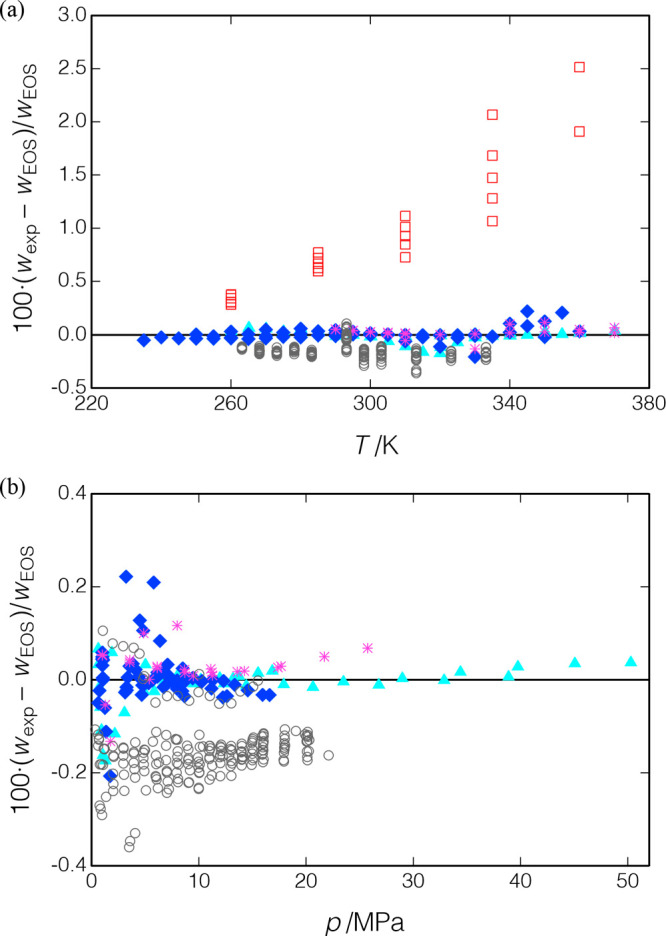
Deviations between data for R1234yf and the EOS of Lemmon and Akasaka;41 ▲, present work (series 1); ◆, present work (series 2); *, present work (series 3); □, Lago et al.;43 and ○, Yoshitake.42 (a) Deviations versus temperature and (b) deviations versus pressure (most of the data of Lago et al. would be off-scale and are not shown).
Figure 12 also shows the measured points of Yoshitake42 and Lago et al.,43 and these data are compared to the equation of state in Figure 13. (Note that ref (42) does not tabulate the measured data; Yositake provided these data directly to E. Lemmon of NIST for his EOS fitting.) Yositake measured to a maximum pressure of 22 MPa, and the data of Lago et al. extend to 6.1 MPa; nevertheless, there is considerable overlap in the measured temperature and pressure ranges of the three data sets. The data of Yoshitake are generally consistent with the EOS and the present data with a systematic bias of −0.152%; the RMS deviation to the EOS is 0.166%. The data of Lago et al., on the other hand, are systematically higher than the present data with an RMS deviation of 1.153% and maximum deviation of 2.516% at (T = 360.0 K, p = 5.0 MPa).
3.6.2. R1234ze(E)—trans-1,3,3,3-Tetrafluoroprop-1-ene
R1234ze(E) or HFO-1234ze(E) has been approved by the Significant New Alternatives Program (SNAP) of the U.S. Environmental Protection Agency44 for use in chillers, as a foam-blowing agent for polyurethane foams, and as an aerosol propellant. R1234ze(E) was measured along 14 isochores covering a temperature range of 230 to 420 K, with pressures of up to 37 MPa. The measured points are displayed in Figure 14 and reported in Table 7. Also shown are the liquid-phase data of Lago et al.,43 who measured R1234ze(E) along five isotherms from 260 to 360 K with pressures of up to 10 MPa.
Figure 14.
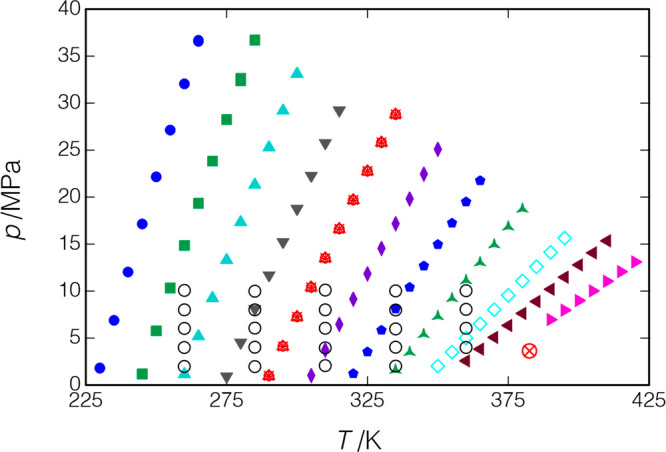
Measured points for R1234ze(E); ○, data of Lago et al.;43 other symbols indicate the measured isochores of the present work; replicates of the isochore starting at T = 290 K are indicated by ×, +, ○, and Δ in red (measured in that order). The critical point is indicated by a red ⊗.
Table 7. Experimental Speeds of Sound, w, for R1234ze(E) (trans-1,3,3,3-Tetrafluoroprop-1-ene) and the Combined Expanded (k = 2) Relative Uncertainty in the Speed of Sound, Uc, Given along with Relative Deviations from the Equation of State of Thol and Lemmon45a,b.
| T (K) | P (MPa) | W (m·s–1) | Uc (k = 2) (%) | 100(w/wEOS – 1) |
|---|---|---|---|---|
| 230.002 | 1.805 | 847.82 | 0.037 | 0.277 |
| 235.012 | 6.881 | 853.01 | 0.037 | 0.374 |
| 240.003 | 12.028 | 858.85 | 0.036 | 0.445 |
| 245.005 | 17.145 | 864.67 | 0.036 | 0.497 |
| 250.006 | 22.154 | 870.10 | 0.036 | 0.529 |
| 254.998 | 27.124 | 875.51 | 0.035 | 0.545 |
| 259.993 | 32.041 | 880.81 | 0.035 | 0.552 |
| 264.997 | 36.619 | 884.72 | 0.035 | 0.548 |
| 245.003 | 1.182 | 775.98 | 0.040 | 0.032 |
| 250.007 | 5.761 | 782.25 | 0.039 | 0.114 |
| 254.998 | 10.323 | 788.57 | 0.039 | 0.170 |
| 259.991 | 14.852 | 794.77 | 0.038 | 0.205 |
| 264.997 | 19.343 | 800.79 | 0.038 | 0.225 |
| 269.994 | 23.820 | 806.84 | 0.037 | 0.234 |
| 274.997 | 28.251 | 812.71 | 0.037 | 0.236 |
| 280.001 | 32.627 | 818.38 | 0.036 | 0.233 |
| 280.000 | 32.381 | 817.18 | 0.036 | 0.230 |
| 285.003 | 36.704 | 822.70 | 0.036 | 0.223 |
| 259.989 | 1.156 | 708.39 | 0.044 | –0.171 |
| 264.995 | 5.196 | 715.06 | 0.043 | –0.113 |
| 269.993 | 9.253 | 721.91 | 0.042 | –0.076 |
| 274.996 | 13.299 | 728.68 | 0.041 | –0.055 |
| 280.001 | 17.324 | 735.32 | 0.040 | –0.046 |
| 285.003 | 21.311 | 741.75 | 0.040 | –0.045 |
| 290.020 | 25.289 | 748.09 | 0.039 | –0.048 |
| 295.000 | 29.203 | 754.21 | 0.038 | –0.054 |
| 300.001 | 33.114 | 760.26 | 0.038 | –0.060 |
| 274.993 | 0.898 | 639.06 | 0.051 | –0.375 |
| 279.999 | 4.509 | 646.83 | 0.049 | –0.336 |
| 285.000 | 8.093 | 654.31 | 0.048 | –0.317 |
| 290.019 | 11.680 | 661.66 | 0.046 | –0.310 |
| 294.999 | 15.217 | 668.73 | 0.045 | –0.308 |
| 300.001 | 18.747 | 675.61 | 0.044 | –0.312 |
| 305.015 | 22.268 | 682.33 | 0.043 | –0.315 |
| 310.002 | 25.743 | 688.82 | 0.042 | –0.318 |
| 315.013 | 29.216 | 695.18 | 0.041 | –0.319 |
| 290.015 | 0.982 | 572.03 | 0.062 | –0.621 |
| 294.997 | 4.109 | 580.28 | 0.059 | –0.592 |
| 299.999 | 7.253 | 588.39 | 0.056 | –0.574 |
| 305.014 | 10.390 | 596.19 | 0.054 | –0.562 |
| 310.002 | 13.502 | 603.73 | 0.052 | –0.553 |
| 315.012 | 16.618 | 611.09 | 0.050 | –0.546 |
| 319.989 | 19.688 | 618.09 | 0.048 | –0.539 |
| 324.995 | 22.761 | 624.94 | 0.047 | –0.531 |
| 330.003 | 25.816 | 631.57 | 0.046 | –0.526 |
| 334.988 | 28.795 | 637.70 | 0.045 | –0.520 |
| 290.014 | 0.944 | 571.63 | 0.062 | –0.628 |
| 294.994 | 4.096 | 580.17 | 0.059 | –0.592 |
| 299.995 | 7.242 | 588.31 | 0.056 | –0.574 |
| 305.010 | 10.355 | 595.92 | 0.054 | –0.562 |
| 309.998 | 13.457 | 603.39 | 0.052 | –0.554 |
| 315.010 | 16.569 | 610.72 | 0.050 | –0.546 |
| 319.987 | 19.641 | 617.76 | 0.048 | –0.539 |
| 324.992 | 22.709 | 624.58 | 0.047 | –0.532 |
| 330.000 | 25.760 | 631.20 | 0.046 | –0.527 |
| 334.987 | 28.739 | 637.33 | 0.045 | –0.522 |
| 305.009 | 1.027 | 503.60 | 0.079 | –1.029 |
| 309.995 | 3.735 | 512.66 | 0.074 | –0.935 |
| 315.008 | 6.454 | 521.38 | 0.070 | –0.858 |
| 319.987 | 9.153 | 529.70 | 0.066 | –0.799 |
| 324.991 | 11.840 | 537.55 | 0.063 | –0.755 |
| 330.001 | 14.544 | 545.32 | 0.060 | –0.724 |
| 334.987 | 17.175 | 552.35 | 0.057 | –0.702 |
| 339.993 | 19.815 | 559.28 | 0.055 | –0.685 |
| 344.996 | 22.457 | 566.10 | 0.053 | –0.675 |
| 349.994 | 25.085 | 572.73 | 0.051 | –0.669 |
| 319.983 | 1.220 | 434.73 | 0.108 | –1.548 |
| 324.988 | 3.522 | 444.60 | 0.100 | –1.271 |
| 329.997 | 5.829 | 453.94 | 0.092 | –1.074 |
| 334.985 | 8.099 | 462.43 | 0.086 | –0.942 |
| 339.991 | 10.397 | 470.82 | 0.081 | –0.855 |
| 344.996 | 12.681 | 478.77 | 0.076 | –0.799 |
| 349.994 | 14.956 | 486.37 | 0.072 | –0.771 |
| 355.015 | 17.243 | 493.80 | 0.068 | –0.758 |
| 359.999 | 19.492 | 500.79 | 0.065 | –0.757 |
| 365.017 | 21.752 | 507.64 | 0.062 | –0.760 |
| 334.981 | 1.596 | 365.02 | 0.164 | –1.955 |
| 339.988 | 3.498 | 375.73 | 0.147 | –1.428 |
| 344.992 | 5.402 | 385.62 | 0.133 | –1.100 |
| 349.990 | 7.311 | 394.92 | 0.122 | –0.909 |
| 355.012 | 9.227 | 403.71 | 0.112 | –0.805 |
| 359.999 | 11.128 | 411.99 | 0.103 | –0.760 |
| 365.017 | 13.040 | 419.93 | 0.096 | –0.751 |
| 370.011 | 14.940 | 427.50 | 0.090 | –0.762 |
| 375.012 | 16.836 | 434.75 | 0.084 | –0.784 |
| 380.024 | 18.733 | 441.77 | 0.080 | –0.808 |
| 290.010 | 0.987 | 572.11 | 0.062 | –0.621 |
| 294.990 | 4.125 | 580.45 | 0.059 | –0.591 |
| 299.993 | 7.261 | 588.49 | 0.056 | –0.572 |
| 305.008 | 10.401 | 596.32 | 0.054 | –0.560 |
| 309.994 | 13.507 | 603.81 | 0.052 | –0.551 |
| 315.006 | 16.616 | 611.10 | 0.050 | –0.543 |
| 319.984 | 19.688 | 618.13 | 0.048 | –0.535 |
| 324.988 | 22.759 | 624.95 | 0.047 | –0.530 |
| 329.996 | 25.809 | 631.55 | 0.046 | –0.525 |
| 334.984 | 28.790 | 637.67 | 0.045 | –0.520 |
| 349.991 | 2.014 | 289.93 | 0.299 | –2.015 |
| 355.013 | 3.504 | 301.63 | 0.256 | –1.204 |
| 359.998 | 4.997 | 312.10 | 0.223 | –0.809 |
| 365.016 | 6.511 | 321.87 | 0.196 | –0.636 |
| 370.009 | 8.024 | 330.90 | 0.175 | –0.598 |
| 375.012 | 9.546 | 339.54 | 0.158 | –0.593 |
| 380.023 | 11.071 | 347.63 | 0.144 | –0.653 |
| 385.014 | 12.589 | 355.45 | 0.132 | –0.672 |
| 390.042 | 14.118 | 363.02 | 0.121 | –0.690 |
| 395.039 | 15.639 | 369.99 | 0.113 | –0.781 |
| 370.004 | 5.068 | 266.62 | 0.325 | –0.448 |
| 375.008 | 6.337 | 276.38 | 0.279 | –0.415 |
| 380.020 | 7.616 | 285.78 | 0.243 | –0.352 |
| 385.011 | 8.895 | 294.24 | 0.215 | –0.460 |
| 390.041 | 10.189 | 302.49 | 0.192 | –0.517 |
| 395.039 | 11.476 | 310.22 | 0.174 | –0.590 |
| 400.047 | 12.770 | 317.49 | 0.159 | –0.710 |
| 405.054 | 14.063 | 324.76 | 0.146 | –0.714 |
| 410.052 | 15.354 | 331.36 | 0.135 | –0.827 |
| 395.036 | 7.969 | 241.00 | 0.334 | 0.350 |
| 400.044 | 8.987 | 248.17 | 0.293 | –0.145 |
| 405.053 | 10.011 | 255.60 | 0.260 | –0.340 |
| 410.052 | 11.036 | 262.98 | 0.233 | –0.393 |
| 415.069 | 12.067 | 269.54 | 0.211 | –0.626 |
| 420.072 | 13.099 | 276.34 | 0.192 | –0.643 |
| 290.007 | 0.972 | 571.98 | 0.062 | –0.620 |
| 294.987 | 4.102 | 580.26 | 0.059 | –0.590 |
| 299.990 | 7.250 | 588.40 | 0.056 | –0.573 |
| 305.004 | 10.400 | 596.32 | 0.054 | –0.560 |
| 309.991 | 13.492 | 603.71 | 0.052 | –0.550 |
| 315.002 | 16.613 | 611.10 | 0.050 | –0.542 |
| 319.980 | 19.679 | 618.07 | 0.048 | –0.537 |
| 324.986 | 22.751 | 624.90 | 0.047 | –0.531 |
| 329.994 | 25.805 | 631.52 | 0.046 | –0.525 |
| 334.981 | 28.789 | 637.67 | 0.045 | –0.522 |
The listed data are averaged from 12 measured echo-delay times (4 sets of 3 replicates each); see Supporting Information for unaveraged data. The data are listed in the order measured; blank lines separate measured isochores.
The standard (k = 1) uncertainties in T and p are 0.005 K and (26 × 10–6p + 0.016 MPa), respectively.
Deviations of the present measurements from the EOS of Thol and Lemmon45 are shown in Figure 15; the RMS deviation is 0.68%, with an average deviation (bias) of −0.50%. The deviations range from −2.07 to +0.67%. Systematic deviations are observed for the individual isochores. The deviations are very smooth with temperature for the initial isochores. Significant scatter is observed only for the three isochores at the highest temperatures; these isochores were closer to the critical point, where the speed of sound was lower, the fluid was much more compressible, and the echo signals were much weaker. Four replicates of the isochore extending from (T = 290 K, p = 1.0 MPa) to (T = 335 K, p = 29 MPa) were measured, including one at the end of the testing; the speed of sound varied over a total range of 0.005% for replicate (T, p) state points, except at T = 290 K, where the total range was slightly higher at 0.013%. These results indicate the stability and repeatability of the pulse-echo system and negligible degradation of the fluid sample.
Figure 15.
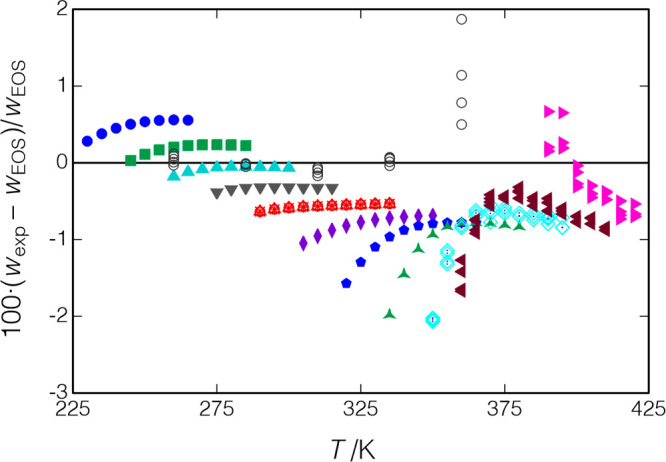
Deviations between data for R1234ze(E) and the EOS of Thol and Lemmon;45 ○, Lago et al.43 Other symbols indicate the measured isochores of the present work and are the same as in Figure 14.
The data of Lago et al.43 were included in the EOS fit of Thol and Lemmon,45 and these data are fitted well (deviations of less than 0.17%) for T = (260 to 335) K, but the isotherm at 360 K shows deviations of up to 1.84%; the overall RMS deviation is 0.48%. At temperatures of 260 to 310 K, the data of Lago et al. are consistent with the present data, but at T = 360 K, p = 10 MPa, they are systematically higher by 2.62%. Similar deviations with our data were observed for the Lago et al. data for R1234yf. Lago et al. report a purity “assay” for their sample of 99.5% (mass basis) but details on the impurities were not provided, and thus the effect of impurities on the measured speed of sound cannot be determined.
3.6.3. R1233zd(E)—trans-1-Chloro-3,3,3-trifluoroprop-1-ene
R1233zd(E) or HCFO-1233zd(E) (“HCFO” = “hydrochlorofluoroolefin”) contains chlorine and has a small, but nonzero, ozone depletion potential (ODP) of 0.00024–0.00034.44 It has been SNAP-approved44 for use in centrifugal-type chillers, as a foam-blowing agent for polyurethane foams, as a cleaning solvent, and as a fire-suppression agent. R1233zd(E) was measured at temperatures from (230 to 420) K, with pressures of up to 25.6 MPa. Measurements were carried out along 22 isochores, including 4 replicates of the isochore extending from (T = 300 K, p = 0.9 MPa) to (T = 325 K, p = 18.7 MPa). The measured points are displayed in Figure 16.
Figure 16.
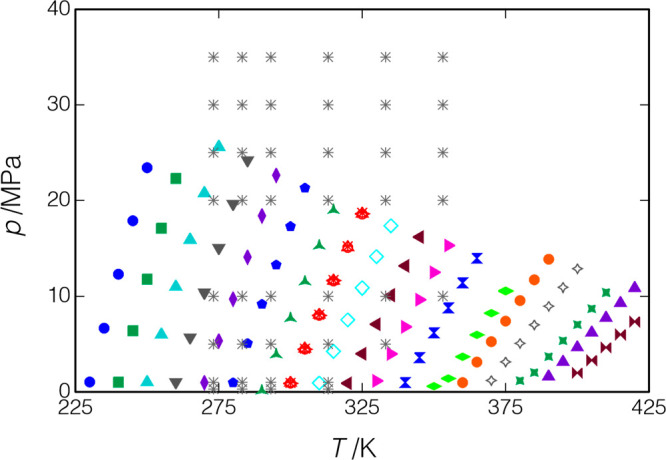
Measured points for R1233zd(E) and *, data of Lago et al.19 Other symbols indicate the isochores measured in the present work. Replicates of the isochore starting at T = 300 K are indicated by × , + , ○, and Δ in red (measured in that order). The critical point of 438.86 K, 3.358 MPa is off the scale of the plot.
Deviations of the present measurements from the EOS of Akaska and Lemmon46 are shown in Figure 17 and reported in Table 8. The EOS was fitted to these data. The RMS deviation is 0.054%, with a range of −0.189 to +0.122%. The deviations show a small systematic deviation with the temperature and increasing scatter at higher temperatures. The replicate isochores show a total range of 0.050% compared to the EOS. The final two replicates measured in the latter half of the testing were systematically 0.024% higher compared to the first replicate. While this is well within the uncertainty of the measurements (see section 4), we observed smaller differences for replicate measurements on other fluids, thus this difference could indicate a possible slight thermal degradation of the sample as the measurements progressed.
Figure 17.
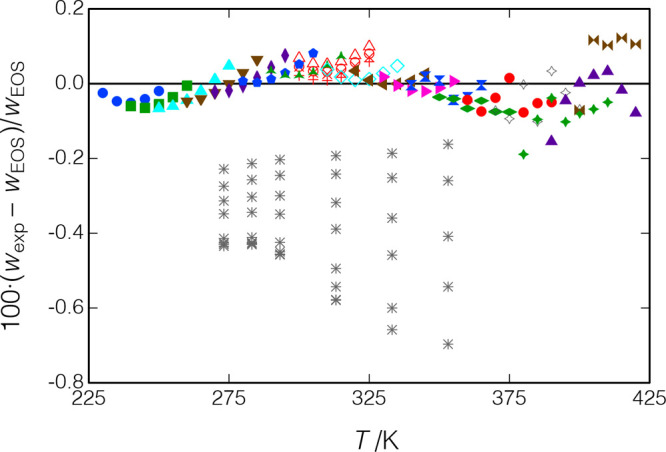
Deviations between the present data for R1233zd(E) and the EOS of Akasaka and Lemmon.46 *, Data of Lago et al.19 Other symbols indicate the measured isochores and are the same as in Figure 16.
Table 8. Experimental Speeds of Sound, w, for R1233zd(E) (trans-1-Chloro-3,3,3-trifluoroprop-1-ene), with the Combined Expanded (k = 2) Relative Uncertainty in the Speed of Sound, Uc, Given along with Relative Deviations from the Equation of State of Akasaka and Lemmon46a,b.
| T (K) | P (MPa) | W (m·s–1) | Uc (k = 2) (%) | 100(w/wEOS – 1) |
|---|---|---|---|---|
| 229.999 | 1.036 | 970.99 | 0.035 | –0.025 |
| 235.011 | 6.670 | 975.48 | 0.034 | –0.047 |
| 240.001 | 12.266 | 980.12 | 0.034 | –0.051 |
| 245.002 | 17.859 | 984.91 | 0.034 | –0.041 |
| 250.004 | 23.418 | 989.74 | 0.034 | –0.020 |
| 240.000 | 1.016 | 929.25 | 0.035 | –0.060 |
| 245.003 | 6.402 | 934.58 | 0.035 | –0.065 |
| 250.006 | 11.749 | 939.92 | 0.035 | –0.055 |
| 254.996 | 17.092 | 945.40 | 0.035 | –0.036 |
| 259.991 | 22.289 | 950.41 | 0.034 | –0.005 |
| 250.002 | 1.018 | 888.18 | 0.036 | –0.066 |
| 254.997 | 6.009 | 893.60 | 0.036 | –0.060 |
| 259.991 | 10.962 | 898.98 | 0.036 | –0.044 |
| 264.996 | 15.882 | 904.29 | 0.035 | –0.020 |
| 269.992 | 20.762 | 909.57 | 0.035 | 0.011 |
| 274.996 | 25.613 | 914.80 | 0.035 | 0.048 |
| 259.988 | 1.008 | 847.69 | 0.038 | –0.047 |
| 264.995 | 5.702 | 853.49 | 0.037 | –0.041 |
| 269.992 | 10.366 | 859.26 | 0.037 | –0.024 |
| 274.996 | 15.008 | 864.99 | 0.036 | –0.001 |
| 280.000 | 19.622 | 870.65 | 0.036 | 0.029 |
| 285.002 | 24.192 | 876.19 | 0.036 | 0.064 |
| 269.990 | 0.978 | 807.48 | 0.039 | –0.022 |
| 274.994 | 5.348 | 813.49 | 0.038 | –0.018 |
| 280.000 | 9.715 | 819.54 | 0.038 | –0.005 |
| 285.001 | 14.055 | 825.51 | 0.037 | 0.016 |
| 290.019 | 18.383 | 831.41 | 0.037 | 0.043 |
| 294.999 | 22.635 | 837.09 | 0.037 | 0.076 |
| 279.997 | 0.966 | 767.78 | 0.041 | 0.007 |
| 285.000 | 5.086 | 774.31 | 0.040 | 0.003 |
| 290.018 | 9.191 | 780.73 | 0.039 | 0.012 |
| 294.999 | 13.240 | 786.97 | 0.039 | 0.029 |
| 300.000 | 17.281 | 793.11 | 0.038 | 0.052 |
| 305.014 | 21.304 | 799.11 | 0.038 | 0.081 |
| 290.016 | 0.135 | 722.65 | 0.044 | 0.035 |
| 294.996 | 3.925 | 729.48 | 0.043 | 0.022 |
| 299.999 | 7.725 | 736.27 | 0.042 | 0.023 |
| 305.014 | 11.514 | 742.89 | 0.041 | 0.031 |
| 310.001 | 15.258 | 749.32 | 0.040 | 0.049 |
| 315.012 | 18.995 | 755.60 | 0.039 | 0.074 |
| 299.997 | 0.945 | 689.34 | 0.047 | 0.045 |
| 305.012 | 4.532 | 696.52 | 0.045 | 0.029 |
| 309.999 | 8.085 | 703.49 | 0.044 | 0.026 |
| 315.011 | 11.663 | 710.45 | 0.043 | 0.030 |
| 319.989 | 15.192 | 717.17 | 0.042 | 0.047 |
| 324.994 | 18.697 | 723.60 | 0.041 | 0.071 |
| 299.994 | 0.972 | 689.38 | 0.046 | 0.021 |
| 305.011 | 4.569 | 696.66 | 0.045 | 0.011 |
| 309.996 | 8.135 | 703.72 | 0.044 | 0.009 |
| 315.009 | 11.684 | 710.51 | 0.043 | 0.017 |
| 319.986 | 15.203 | 717.15 | 0.042 | 0.033 |
| 324.991 | 18.698 | 723.52 | 0.041 | 0.059 |
| 309.996 | 0.943 | 650.36 | 0.051 | 0.038 |
| 315.008 | 4.261 | 657.77 | 0.049 | 0.018 |
| 319.987 | 7.551 | 664.96 | 0.047 | 0.010 |
| 324.990 | 10.850 | 672.02 | 0.046 | 0.013 |
| 330.000 | 14.120 | 678.78 | 0.044 | 0.027 |
| 334.986 | 17.345 | 685.24 | 0.043 | 0.048 |
| 319.984 | 0.903 | 611.20 | 0.056 | 0.034 |
| 324.989 | 3.994 | 619.12 | 0.053 | 0.009 |
| 329.998 | 7.080 | 626.79 | 0.051 | –0.001 |
| 334.986 | 10.109 | 633.92 | 0.049 | 0.000 |
| 339.991 | 13.140 | 640.87 | 0.048 | 0.008 |
| 344.995 | 16.157 | 647.63 | 0.046 | 0.026 |
| 329.996 | 1.155 | 574.60 | 0.062 | 0.018 |
| 334.984 | 3.984 | 582.58 | 0.059 | –0.005 |
| 339.990 | 6.814 | 590.25 | 0.056 | –0.018 |
| 344.994 | 9.647 | 597.76 | 0.054 | –0.021 |
| 349.992 | 12.459 | 604.95 | 0.052 | –0.011 |
| 355.013 | 15.270 | 611.92 | 0.050 | 0.007 |
| 339.987 | 0.985 | 533.73 | 0.072 | –0.004 |
| 344.992 | 3.593 | 542.40 | 0.067 | 0.019 |
| 349.991 | 6.187 | 550.40 | 0.064 | 0.008 |
| 355.012 | 8.793 | 557.90 | 0.060 | –0.044 |
| 359.998 | 11.371 | 565.32 | 0.058 | –0.036 |
| 365.015 | 13.949 | 572.55 | 0.055 | –0.004 |
| 349.988 | 0.584 | 488.94 | 0.086 | –0.036 |
| 355.010 | 1.410 | 479.10 | 0.089 | –0.041 |
| 359.996 | 3.686 | 487.77 | 0.083 | –0.067 |
| 365.015 | 5.976 | 496.29 | 0.077 | –0.046 |
| 370.008 | 8.250 | 504.10 | 0.073 | –0.075 |
| 375.010 | 10.538 | 511.85 | 0.069 | –0.076 |
| 299.989 | 0.917 | 689.16 | 0.047 | 0.046 |
| 305.006 | 4.481 | 696.21 | 0.045 | 0.033 |
| 309.993 | 8.021 | 703.12 | 0.044 | 0.032 |
| 315.004 | 11.566 | 709.92 | 0.043 | 0.040 |
| 319.983 | 15.067 | 716.48 | 0.042 | 0.057 |
| 324.987 | 18.566 | 722.89 | 0.041 | 0.080 |
| 359.996 | 0.972 | 453.06 | 0.102 | –0.043 |
| 365.014 | 3.122 | 461.95 | 0.094 | –0.074 |
| 370.008 | 5.264 | 470.67 | 0.087 | –0.038 |
| 375.010 | 7.413 | 479.13 | 0.081 | 0.015 |
| 380.022 | 9.558 | 486.46 | 0.076 | –0.077 |
| 385.011 | 11.689 | 493.96 | 0.072 | –0.052 |
| 390.040 | 13.831 | 501.11 | 0.068 | –0.050 |
| 370.003 | 1.195 | 414.41 | 0.125 | –0.071 |
| 375.006 | 3.136 | 423.65 | 0.113 | –0.094 |
| 380.019 | 5.084 | 432.90 | 0.104 | –0.002 |
| 385.011 | 7.023 | 440.82 | 0.096 | –0.101 |
| 390.040 | 8.970 | 449.37 | 0.089 | 0.034 |
| 395.038 | 10.905 | 456.68 | 0.084 | –0.024 |
| 400.044 | 12.843 | 463.75 | 0.079 | –0.068 |
| 380.015 | 1.176 | 369.80 | 0.165 | –0.189 |
| 385.007 | 2.027 | 364.11 | 0.167 | –0.095 |
| 390.037 | 3.700 | 373.82 | 0.150 | –0.038 |
| 395.035 | 5.368 | 382.54 | 0.136 | –0.102 |
| 400.044 | 7.044 | 391.16 | 0.124 | –0.080 |
| 405.054 | 8.720 | 399.29 | 0.114 | –0.068 |
| 410.051 | 10.389 | 407.03 | 0.106 | –0.049 |
| 390.002 | 1.618 | 332.75 | 0.213 | –0.155 |
| 394.999 | 3.140 | 342.91 | 0.188 | –0.045 |
| 400.009 | 4.675 | 352.43 | 0.167 | 0.002 |
| 405.019 | 6.213 | 361.31 | 0.151 | 0.023 |
| 410.017 | 7.755 | 369.76 | 0.137 | 0.033 |
| 415.034 | 9.309 | 377.67 | 0.126 | –0.017 |
| 420.037 | 10.856 | 385.08 | 0.116 | –0.078 |
| 400.006 | 1.995 | 292.98 | 0.293 | –0.071 |
| 405.015 | 3.322 | 303.52 | 0.253 | 0.117 |
| 410.015 | 4.657 | 312.94 | 0.222 | 0.103 |
| 415.033 | 6.005 | 322.01 | 0.197 | 0.122 |
| 420.037 | 7.355 | 330.51 | 0.177 | 0.106 |
| 299.986 | 0.956 | 689.62 | 0.047 | 0.069 |
| 305.000 | 4.539 | 696.79 | 0.045 | 0.054 |
| 309.989 | 8.080 | 703.68 | 0.044 | 0.052 |
| 315.001 | 11.604 | 710.32 | 0.043 | 0.060 |
| 319.977 | 15.110 | 716.90 | 0.042 | 0.076 |
| 324.984 | 18.616 | 723.34 | 0.041 | 0.099 |
| 314.999 | 11.602 | 710.35 | 0.043 | 0.066 |
| 324.983 | 18.590 | 723.19 | 0.041 | 0.100 |
| 299.985 | 0.892 | 689.14 | 0.047 | 0.069 |
| 309.988 | 8.010 | 703.20 | 0.044 | 0.051 |
| 305.001 | 4.456 | 696.20 | 0.045 | 0.056 |
The listed data are averaged from 12 measured echo-delay times (4 sets of 3 replicates each); see Supporting Information for unaveraged data. The data are listed in the order measured; blank lines separate measured isochores.
The standard (k = 1) uncertainties in T and p are 0.005 K and (26 × 10–6p + 0.016 MPa), respectively.
Lago et al.19 measured R1233zd(E) along six isotherms from 273 to 353 K with pressures of up to 35 MPa, as shown in Figure 16. The Lago et al. data are consistently lower than the present data and the EOS of Akaska and Lemmon46 as shown in Figure 17; the average deviation is −0.383%.
3.6.4. R1336mzz(Z)—cis-1,1,1,4,4,4-Hexafluorobut-2-ene
R1336mzz(Z) is of interest as a refrigerant in chillers and as a working fluid in organic Rankine-cycle power systems. It has also been SNAP approved44 as a foam-blowing agent and cleaning solvent. R1336mzz(Z) (also known as HFO-1336mzz(Z)) is a component of the azeotropic mixture with trans-1,2-dichloroethene, which is designated as R514A in ANSI/ASHRAE Standard 34;36 this blend has been commercialized for use in centrifugal-type refrigeration compressors.
Here, we report speed-of-sound measurements for R1336mzz(Z) at temperatures from (230 to 420) K, with pressures of up to 46 MPa. The measurements were carried out along 15 isochores, including 4 replicates of the isochore extending from (T = 290 K, p = 0.9 MPa) to (T = 350 K, p = 42.9 MPa). The measured points are displayed in Figure 18 and reported in Table 9.
Figure 18.
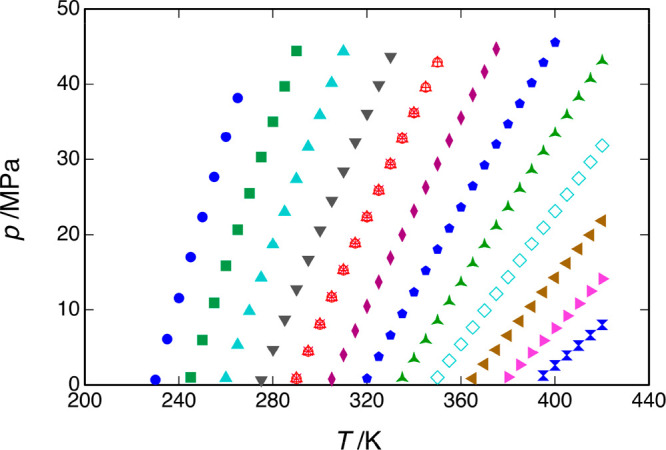
Measured points for R1336mzz(Z). Different symbols indicate the measured isochores. Replicates of the isochore starting at T = 290 K are indicated by × , + , ○, and Δ in red (measured in that order). The critical point of 444.5 K, 2.903 MPa is off the scale of the plot.
Table 9. Experimental Speeds of Sound, w, for R1336mzz(Z) (cis-1,1,1,4,4,4-Hexafluorobut-2-ene), with the Combined Expanded (k = 2) Relative Uncertainty in the Speed of Sound, Uc, Also Given along with Relative Deviations from the Equation of State of McLinden and Akasaka15a,b.
| T (K) | P (MPa) | W (m·s–1) | Uc (k = 2) (%) | 100(w/wEOS – 1) |
|---|---|---|---|---|
| 230.001 | 0.690 | 890.80 | 0.036 | –0.033 |
| 235.011 | 6.133 | 895.90 | 0.035 | –0.015 |
| 240.003 | 11.557 | 901.15 | 0.035 | –0.006 |
| 245.011 | 16.982 | 906.51 | 0.035 | 0.000 |
| 250.008 | 22.349 | 911.84 | 0.035 | 0.005 |
| 255.000 | 27.667 | 917.13 | 0.034 | 0.009 |
| 259.991 | 32.983 | 922.55 | 0.034 | 0.013 |
| 264.998 | 38.176 | 927.57 | 0.034 | 0.019 |
| 245.008 | 1.010 | 832.01 | 0.037 | –0.025 |
| 250.007 | 6.001 | 837.95 | 0.037 | –0.020 |
| 254.997 | 10.946 | 843.83 | 0.036 | –0.015 |
| 259.991 | 15.845 | 849.60 | 0.036 | –0.011 |
| 264.998 | 20.691 | 855.19 | 0.036 | –0.008 |
| 269.994 | 25.507 | 860.77 | 0.035 | –0.007 |
| 274.997 | 30.284 | 866.25 | 0.035 | –0.006 |
| 280.002 | 35.027 | 871.66 | 0.035 | –0.005 |
| 285.003 | 39.722 | 876.95 | 0.035 | –0.003 |
| 290.021 | 44.391 | 882.16 | 0.034 | –0.001 |
| 259.987 | 0.901 | 773.45 | 0.039 | –0.010 |
| 264.995 | 5.359 | 779.58 | 0.039 | –0.010 |
| 269.993 | 9.820 | 785.85 | 0.038 | –0.012 |
| 274.996 | 14.257 | 792.04 | 0.037 | –0.012 |
| 280.002 | 18.657 | 798.09 | 0.037 | –0.014 |
| 285.003 | 23.020 | 803.99 | 0.037 | –0.017 |
| 290.022 | 27.366 | 809.81 | 0.036 | –0.020 |
| 295.001 | 31.638 | 815.43 | 0.036 | –0.024 |
| 300.003 | 35.903 | 821.00 | 0.036 | –0.025 |
| 305.017 | 40.140 | 826.46 | 0.035 | –0.025 |
| 310.003 | 44.320 | 831.80 | 0.035 | –0.022 |
| 274.993 | 0.674 | 715.73 | 0.042 | 0.001 |
| 279.998 | 4.721 | 722.55 | 0.041 | –0.003 |
| 285.001 | 8.744 | 729.24 | 0.040 | –0.005 |
| 290.019 | 12.752 | 735.79 | 0.040 | –0.010 |
| 294.999 | 16.677 | 741.98 | 0.039 | –0.018 |
| 300.001 | 20.612 | 748.17 | 0.038 | –0.025 |
| 305.016 | 24.544 | 754.28 | 0.038 | –0.032 |
| 310.003 | 28.423 | 760.22 | 0.037 | –0.038 |
| 315.015 | 32.292 | 766.05 | 0.037 | –0.040 |
| 319.991 | 36.101 | 771.69 | 0.037 | –0.042 |
| 324.996 | 39.899 | 777.24 | 0.036 | –0.040 |
| 330.003 | 43.670 | 782.67 | 0.036 | –0.035 |
| 290.015 | 0.889 | 662.22 | 0.046 | 0.008 |
| 294.995 | 4.513 | 669.38 | 0.044 | 0.004 |
| 299.998 | 8.136 | 676.40 | 0.043 | –0.002 |
| 305.013 | 11.751 | 683.25 | 0.042 | –0.010 |
| 309.999 | 15.324 | 689.89 | 0.042 | –0.020 |
| 315.013 | 18.901 | 696.42 | 0.041 | –0.028 |
| 319.990 | 22.419 | 702.67 | 0.040 | –0.036 |
| 324.996 | 25.937 | 708.82 | 0.039 | –0.042 |
| 330.003 | 29.430 | 714.81 | 0.039 | –0.046 |
| 334.988 | 32.848 | 720.44 | 0.038 | –0.048 |
| 339.993 | 36.281 | 726.10 | 0.038 | –0.048 |
| 290.013 | 0.799 | 661.60 | 0.046 | 0.009 |
| 294.994 | 4.420 | 668.78 | 0.044 | 0.007 |
| 299.996 | 8.044 | 675.82 | 0.043 | –0.001 |
| 305.011 | 11.658 | 682.70 | 0.042 | –0.009 |
| 309.998 | 15.228 | 689.33 | 0.042 | –0.019 |
| 315.010 | 18.798 | 695.84 | 0.041 | –0.027 |
| 319.988 | 22.316 | 702.11 | 0.040 | –0.035 |
| 324.994 | 25.829 | 708.26 | 0.039 | –0.041 |
| 330.001 | 29.322 | 714.26 | 0.039 | –0.045 |
| 334.988 | 32.737 | 719.89 | 0.038 | –0.047 |
| 339.994 | 36.162 | 725.52 | 0.038 | –0.047 |
| 344.998 | 39.569 | 731.06 | 0.037 | –0.046 |
| 349.994 | 42.948 | 736.46 | 0.037 | –0.043 |
| 305.008 | 0.774 | 607.69 | 0.051 | 0.010 |
| 309.995 | 4.014 | 615.20 | 0.049 | 0.009 |
| 315.008 | 7.255 | 622.52 | 0.048 | 0.005 |
| 319.985 | 10.473 | 629.65 | 0.046 | –0.004 |
| 324.990 | 13.691 | 636.60 | 0.045 | –0.014 |
| 329.999 | 16.885 | 643.29 | 0.044 | –0.022 |
| 334.986 | 20.007 | 649.50 | 0.043 | –0.032 |
| 339.992 | 23.149 | 655.74 | 0.042 | –0.039 |
| 344.997 | 26.279 | 661.86 | 0.041 | –0.045 |
| 349.994 | 29.390 | 667.84 | 0.041 | –0.048 |
| 355.016 | 32.494 | 673.69 | 0.040 | –0.049 |
| 360.000 | 35.557 | 679.36 | 0.040 | –0.049 |
| 365.018 | 38.617 | 684.91 | 0.039 | –0.047 |
| 370.011 | 41.647 | 690.34 | 0.039 | –0.042 |
| 375.013 | 44.656 | 695.63 | 0.038 | –0.036 |
| 319.980 | 0.866 | 555.63 | 0.059 | 0.019 |
| 324.986 | 3.756 | 563.45 | 0.056 | 0.024 |
| 329.995 | 6.644 | 571.05 | 0.054 | 0.023 |
| 334.982 | 9.488 | 578.17 | 0.052 | 0.013 |
| 339.988 | 12.349 | 585.23 | 0.050 | 0.003 |
| 344.993 | 15.196 | 592.07 | 0.049 | –0.008 |
| 349.991 | 18.022 | 598.66 | 0.047 | –0.017 |
| 355.012 | 20.849 | 605.11 | 0.046 | –0.026 |
| 359.998 | 23.645 | 611.36 | 0.045 | –0.032 |
| 365.016 | 26.444 | 617.48 | 0.044 | –0.036 |
| 370.010 | 29.215 | 623.42 | 0.043 | –0.037 |
| 375.013 | 31.980 | 629.24 | 0.042 | –0.037 |
| 380.024 | 34.723 | 634.88 | 0.042 | –0.034 |
| 385.014 | 37.440 | 640.35 | 0.041 | –0.032 |
| 390.043 | 40.164 | 645.76 | 0.040 | –0.027 |
| 395.040 | 42.854 | 651.01 | 0.040 | –0.021 |
| 400.047 | 45.534 | 656.16 | 0.039 | –0.014 |
| 334.976 | 0.903 | 503.45 | 0.070 | 0.027 |
| 339.983 | 3.459 | 511.60 | 0.066 | 0.038 |
| 344.988 | 6.011 | 519.44 | 0.063 | 0.039 |
| 349.986 | 8.552 | 526.97 | 0.060 | 0.033 |
| 355.008 | 11.097 | 534.26 | 0.058 | 0.024 |
| 359.994 | 13.616 | 541.26 | 0.055 | 0.014 |
| 365.012 | 16.141 | 548.06 | 0.053 | 0.003 |
| 370.006 | 18.645 | 554.63 | 0.052 | –0.006 |
| 375.009 | 21.136 | 560.96 | 0.050 | –0.013 |
| 380.021 | 23.625 | 567.27 | 0.049 | –0.002 |
| 385.012 | 26.090 | 573.17 | 0.048 | –0.021 |
| 390.041 | 28.574 | 579.14 | 0.046 | –0.020 |
| 395.039 | 31.008 | 584.79 | 0.045 | –0.017 |
| 400.047 | 33.444 | 590.36 | 0.045 | –0.014 |
| 405.055 | 35.871 | 595.83 | 0.044 | –0.008 |
| 410.053 | 38.283 | 601.17 | 0.043 | –0.002 |
| 415.070 | 40.695 | 606.44 | 0.042 | 0.006 |
| 420.073 | 43.086 | 611.57 | 0.042 | 0.016 |
| 290.007 | 0.841 | 662.08 | 0.046 | 0.033 |
| 294.988 | 4.444 | 669.12 | 0.044 | 0.031 |
| 299.990 | 8.064 | 676.14 | 0.043 | 0.025 |
| 305.006 | 11.675 | 682.99 | 0.042 | 0.017 |
| 309.992 | 15.247 | 689.63 | 0.042 | 0.007 |
| 315.004 | 18.819 | 696.16 | 0.041 | –0.002 |
| 319.982 | 22.342 | 702.45 | 0.040 | –0.010 |
| 324.986 | 25.860 | 708.61 | 0.039 | –0.016 |
| 329.994 | 29.353 | 714.61 | 0.039 | –0.020 |
| 334.982 | 32.769 | 720.24 | 0.038 | –0.023 |
| 339.986 | 36.195 | 725.86 | 0.038 | –0.024 |
| 344.991 | 39.587 | 731.33 | 0.037 | –0.022 |
| 349.989 | 42.900 | 736.44 | 0.037 | –0.018 |
| 349.988 | 0.989 | 451.60 | 0.087 | 0.021 |
| 355.010 | 3.232 | 460.37 | 0.081 | 0.104 |
| 359.995 | 5.457 | 468.15 | 0.076 | 0.055 |
| 365.013 | 7.692 | 476.00 | 0.072 | 0.079 |
| 370.006 | 9.916 | 483.41 | 0.068 | 0.068 |
| 375.009 | 12.137 | 490.42 | 0.065 | 0.029 |
| 380.020 | 14.355 | 497.39 | 0.062 | 0.032 |
| 385.011 | 16.553 | 504.08 | 0.060 | 0.039 |
| 390.040 | 18.764 | 510.43 | 0.058 | 0.005 |
| 395.038 | 20.952 | 517.16 | 0.056 | 0.095 |
| 400.045 | 23.136 | 523.02 | 0.054 | 0.050 |
| 405.054 | 25.316 | 528.73 | 0.052 | 0.005 |
| 410.052 | 27.482 | 534.50 | 0.051 | 0.006 |
| 415.070 | 29.651 | 540.09 | 0.050 | –0.007 |
| 420.072 | 31.808 | 545.71 | 0.048 | 0.014 |
| 365.004 | 0.867 | 396.29 | 0.116 | 0.029 |
| 369.999 | 2.778 | 404.95 | 0.107 | 0.042 |
| 375.002 | 4.698 | 413.34 | 0.099 | 0.066 |
| 380.015 | 6.619 | 421.23 | 0.092 | 0.054 |
| 385.006 | 8.531 | 428.90 | 0.086 | 0.072 |
| 390.036 | 10.453 | 435.85 | 0.081 | –0.014 |
| 395.034 | 12.362 | 443.06 | 0.077 | 0.028 |
| 400.042 | 14.273 | 449.83 | 0.073 | 0.020 |
| 405.052 | 16.182 | 456.57 | 0.069 | 0.056 |
| 410.050 | 18.083 | 462.79 | 0.067 | 0.027 |
| 415.069 | 19.987 | 468.91 | 0.064 | 0.013 |
| 420.072 | 21.883 | 475.13 | 0.061 | 0.060 |
| 380.013 | 1.047 | 343.10 | 0.162 | 0.006 |
| 385.005 | 2.664 | 352.08 | 0.146 | 0.040 |
| 390.034 | 4.300 | 360.80 | 0.133 | 0.092 |
| 395.033 | 5.930 | 368.75 | 0.122 | 0.053 |
| 400.041 | 7.565 | 376.40 | 0.113 | 0.025 |
| 405.051 | 9.202 | 383.58 | 0.105 | –0.039 |
| 410.050 | 10.838 | 390.90 | 0.098 | 0.010 |
| 415.068 | 12.483 | 397.86 | 0.092 | 0.020 |
| 420.072 | 14.116 | 404.49 | 0.087 | 0.033 |
| 394.998 | 1.269 | 288.13 | 0.250 | 0.072 |
| 400.007 | 2.607 | 297.47 | 0.219 | 0.100 |
| 405.017 | 3.953 | 306.20 | 0.194 | 0.092 |
| 410.016 | 5.305 | 314.36 | 0.174 | 0.043 |
| 415.035 | 6.669 | 322.32 | 0.158 | 0.047 |
| 420.038 | 8.032 | 329.88 | 0.144 | 0.052 |
| 290.006 | 0.858 | 662.20 | 0.046 | 0.033 |
| 294.988 | 4.472 | 669.31 | 0.044 | 0.031 |
| 299.989 | 8.097 | 676.34 | 0.043 | 0.022 |
| 305.004 | 11.707 | 683.18 | 0.042 | 0.014 |
| 309.991 | 15.254 | 689.68 | 0.041 | 0.007 |
| 315.003 | 18.816 | 696.14 | 0.041 | –0.001 |
| 319.981 | 22.331 | 702.40 | 0.040 | –0.008 |
| 324.986 | 25.839 | 708.51 | 0.039 | –0.015 |
| 329.993 | 29.326 | 714.48 | 0.039 | –0.020 |
| 334.980 | 32.736 | 720.08 | 0.038 | –0.023 |
| 339.986 | 36.158 | 725.69 | 0.038 | –0.024 |
| 344.990 | 39.534 | 731.08 | 0.037 | –0.021 |
| 349.987 | 42.803 | 735.99 | 0.037 | –0.017 |
The listed data are averaged from 12 measured echo-delay times (4 sets of 3 replicates each); see Supporting Information for unaveraged data. The data are listed in the order measured; blank lines separate measured isochores.
The standard (k = 1) uncertainties in T and p are 0.005 K and (26 × 10–6p + 0.016 MPa), respectively.
Deviations of the present measurements from the EOS of McLinden and Akasaka15 are shown in Figure 19. The present data were included in the fitting of this EOS, which was also fitted to the vapor pressure, p–ρ–T, saturated liquid density, heat capacity, and vapor-phase speed-of-sound data. The RMS deviation to the EOS is 0.033%, with an average offset of −0.0005%. The overall range of the deviations is −0.049 to +0.104%. The individual isochores show smooth and systematic deviation patterns except for larger scatter for the higher-temperature isochores; these could arise from small systematic errors in the present measurements, small inconsistencies between the different data types used in the EOS fitting, or small defects in the form of the EOS, such that it was not able to simultaneously fit the different data types. The final replicate of the T = (290 to 350) K isochore was systematically 0.025% higher than the first replicate, indicating possible slight degradation of the sample as the measurements progressed. There are no literature data for comparison.
Figure 19.
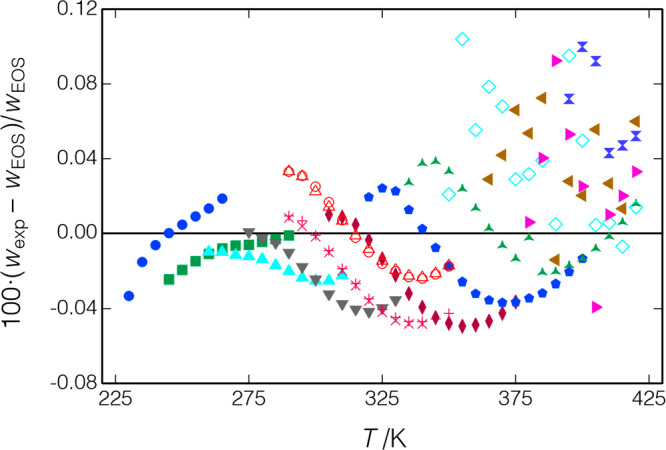
Deviations between present data for R1336mzz(Z) and the EOS of McLinden and Akasaka.15 Different symbols indicate the measured isochores and are the same as in Figure 18.
4. Uncertainty of the Measurements
The measurement of the speed of sound essentially reduces to the measurement of geometry (i.e., the difference in the path lengths) and time (i.e., the difference in the arrival time of the short-path and long-path echoes). Both geometry and time can be measured with extremely low uncertainties, and the potential for low uncertainties is one of the major advantages of measuring the speed of sound over other quantities (such as heat capacity) that would yield similar thermodynamic information for the purposes of fitting an equation of state. But other factors increase the uncertainties in the measurement and must be considered carefully. These can be grouped into uncertainties resulting from the analysis of the echo signals; determination of the geometry (i.e., the calibration and stability of the path length difference); correction for diffraction and dispersion effects; the determination of the thermodynamic (T, p, x) state point; and effects related to the purity and stability of the fluid sample. In this discussion, we consider standard (k = 1) uncertainties and apply a coverage factor when combining the individual uncertainty components to arrive at a combined expanded uncertainty.
4.1. Uncertainty of the Measured Echo Signals
The echo signals were detected and recorded with a digital storage oscilloscope. The time bases of the oscilloscope and function generator were synchronized to a 10 MHz rubidium frequency standard (Stanford Research Systems DG645) with a relative short-time stability of 1 × 10–10 and long-term stability of 5 × 10–10 per year. The uncertainty in the speed of sound is directly proportional to this uncertainty, so the uncertainty from timing was negligible.
An additional uncertainty is associated with the determination of the Δt between the two echoes. The time delay for the 12 replicate echo measurements carried out at each (T, p) state point was typically consistent within a few parts in 106. Occasionally (most often near the critical point), a larger variance was observed; this occurred because the data analysis algorithm superimposed the short-path and long-path echoes, and this could be in error by one or two cycles (i.e., 0.125 or 0.250 μs) with echo signals that were weak or noisy or where low damping in the fluid resulted in prolonged resonance of the crystal. State points with a large variance were manually examined, and faulty replicates were discarded. This effect was observed at speeds of sound lower than about 600 m·s–1, i.e., near the critical point, but only for propane, R1234yf, and R1234ze(E) for which 11 to 19% of the echoes were suspect. These three fluids were the first ones measured. No such problems were observed for p-xylene, R1233zd(E), or R1336mzz(Z), for which we separately recorded the short-path and long-path echoes, as described in section 2.5; for these fluids, the speed of sound was as low as 292 m·s–1. The estimated relative uncertainty associated with the determination of the time difference (after discarding suspect signals) was estimated to be 0.001%.
4.2. Path-Length Difference
As discussed in section 3.2, the path-length difference was calibrated as a function of the temperature and pressure with measurements on propane. The propane equation of state28 was fitted to the liquid-phase speed-of-sound data of Meier and Kabelac,18 and thus, the uncertainty in the path-length calibration is dependent on the uncertainties in the Meier and Kabelac18 data. Their data have an estimated expanded relative uncertainty of 0.019–0.022%, including purity effects. The propane EOS28 fits these data with an RMS deviation of 0.013%. The RMS deviation of our propane data from the path-length correlation (eq 13) was 0.0035%. Combining these three effects in quadrature yields a standard uncertainty of 0.017% due to the propane calibration.
Related to the uncertainty in the calibration of the path-length difference is the mechanical stability of the overall assembly comprising the crystal, spacers, and reflectors. Repeated measurements on propane taken over the course of 25 months revealed average differences of less than 0.005% as reported by Rowane et al.,29 and we take 0.005% as the standard uncertainty associated with the mechanical stability of the path lengths.
Any corrosion of the reflector faces, especially corrosion that affected one reflector more than the other, would alter the effective path length difference. We did not observe any corrosion on our brass reflectors upon disassembly after the completion of all of the tests reported here, and we consider any uncertainty associated with corrosion to be negligible.
4.3. Diffraction Correction
The time difference was corrected for diffraction effects, as discussed in section 2.7. Meier9 reported a difference of 0.001% among the different models used to calculate this correction for his (similar) pulse-echo instrument, and we take 0.001% as the uncertainty in this correction.
4.4. Possible Dispersion Effects
Dispersion can present problems; it occurs when the vibration period of the ultrasonic pulse is short relative to the relaxation time of the molecule’s internal degrees of freedom, resulting in a measured speed of sound that is not equal to the thermodynamic value. Dispersion was observed, for example, by El Hawary et al.48 for their measurements on isopentane, characterized by a significant damping of the echo signal.
Dispersion is more common with higher operating frequencies. Our frequency of 8 MHz is near the upper end of the pulse-echo instruments; lower frequencies would result in a longer pulse duration and the possibility of overlap between the short- and long-path echoes and the attendant need for longer path lengths. Thus, there is a design compromise, and we opted for a compact cell.
We did not observe any evidence of dispersion in the present measurements and considered the effects of dispersion to be negligible.
4.5. State-Point Uncertainty
The uncertainty in the temperature measurement system (SPRT and its calibration, resistance bridge, and standard resistor) was estimated to be 3 mK. The SPRT was calibrated with fixed-point cells on ITS-90. The uncertainty in the temperature of the fluid sample also included the effects of temperature gradients and short-term variations in the thermostat bath, and we estimated the total temperature uncertainty to be 5 mK. The uncertainty in the pressure measurement arose from the calibration of the transducers, their repeatability and zero (vacuum) drift, and the uncertainty in the hydrostatic head correction. We estimated the standard uncertainty in the pressure transducer to be (26 × 10–6p + 7 kPa), based on the uncertainties of the piston-gage pressure standards used for the calibration and the fit of the transducer coefficients to the piston-gage calibration points. The observed vacuum drift of the transducer adds (in quadrature) an additional 7 kPa. We estimate the uncertainty in the hydrostatic head correction to be 10% of the correction. The standard deviations in the observed temperature and pressure readings taken before, during, and after recording the echo signals were added to these uncertainty estimates as a type A uncertainty.
The effect of these state-point uncertainties on the speed of sound is given by
| 16 |
where the derivatives are estimated from the equation of state for the fluid being measured. The temperature effect was relatively constant from 0.008 to 0.011 m·s–1; the pressure effect ranged from 0.013 to 0.093 m·s–1 and increased as the critical point was approached.
4.6. Sample Purity and Stability
The state point also depends on the composition of the sample. This includes not only impurities in the fluid sample but also contamination that might be introduced by the system and possible decomposition of the sample during the course of the testing. This uncertainty component varied from fluid to fluid. The impurities in the propane and water samples were negligible. But, as noted in section 3.4, the water measurements resulted in corrosion and the sample removed following the first series of tests was discolored, but any corrosion was assumed to occur only at high temperatures and such points were not included in the analysis. Degradation of the p-xylene was observed upon measurement of replicate isochores at the level of 0.021%; also, as noted in section 3.5, impurities in the p-xylene sample resulted in a systematic error in the speed of sound of 0.006 to 0.010%. Replicate measurements of the refrigerants indicated stability effects of 0.013 to 0.025%. All of these were the maximum differences among replicates, which we take as expanded uncertainties with a coverage factor of 3. This effect was added as a linear function of the time that the sample was in the instrument. We had insufficient knowledge of impurities in the refrigerant samples to estimate this effect with any certainty, and we assign a conservative standard uncertainty of 0.005%. These effects are summarized in Table 10.
Table 10. Summary of Errors and Resulting Uncertainty in the Speed of Sound.
| Range of Uncertainties in Speed of Sound/(m·s–1, unless Indicated) |
||||||
|---|---|---|---|---|---|---|
| Source | Magnitude of Error (k = 1) | p-xylene | R1234yf | R1234ze(E) | R1233zd(E) | R1336mzz(Z) |
| State Point | ||||||
| Temperature | 0.005 Ka | 0.008 to 0.010 | 0.010to 0.011 | 0.009 to 0.010 | 0.008 to 0.011 | 0.010 to 0.010 |
| Pressure | 26 × 10–6p + 10 kPaa | 0.014 to 0.036 | 0.023to 0.088 | 0.016 to 0.093 | 0.013 to 0.083 | 0.017 to 0.074 |
| Path-Length Difference | ||||||
| ΔL (T, p) | 0.017% | 0.145 to 0.241 | 0.045 to 0.124 | 0.039 to 0.150 | 0.050 to 0.168 | 0.050 to 0.158 |
| ΔL (t) (stability) | 0.005% | 0.043 to 0.071 | 0.013 to 0.037 | 0.012 to 0.044 | 0.015 to 0.049 | 0.014 to 0.046 |
| Fitting of and Corrections to Echo Data | ||||||
| Δt | 0.001% | 0.009 to 0.014 | 0.003 to 0.007 | 0.002 to 0.009 | 0.003 to 0.010 | 0.003 to 0.009 |
| Diffraction | 0.001% | 0.009 to 0.014 | 0.003 to 0.007 | 0.002 to 0.009 | 0.003 to 0.010 | 0.003 to 0.009 |
| Sample Purity and Stability | ||||||
| Sample impurities | (Varies with fluid) | (0.006 to 0.010)% | 0.005% | 0.005% | 0.005% | 0.005% |
| Sample instability | (Varies with fluid) | 0.007% | 0.008% | 0.004% | 0.008% | 0.008% |
| Combined and Expanded Uncertainties | ||||||
| Relative combined expanded (k = 2.2) uncertainty | (0.033 to 0.048)% | (0.040 to 0.256)% | (0.035 to 0.334)% | (0.034 to 0.293)% | (0.034 to 0.250)% | |
| Average relative combined expanded (k = 2.2) uncertainty | 0.035% | 0.088% | 0.086% | 0.068% | 0.055% | |
Plus Type A uncertainty arising from standard deviation of multiple temperature or pressure readings
4.7. Summary of Uncertainties
The relative combined expanded standard uncertainty Uc,i for a given measurement i, expressed as a percentage, is given by
| 17 |
where the summation is over the individual uncertainty components discussed in sections 4.1 through 4.6 and 2.20 is a coverage factor corresponding to a 95% confidence interval, based on 12 echo signals measured at each state point. A tabulation of the individual uncertainty components for each measured point is given in the Supporting Information, and a summary of the uncertainties for each of the fluids is given in Table 10. The average Uc ranged from 0.035 to 0.088% for the different fluids and increased as the critical point was approached; we measured the refrigerants as close to the critical point as the signal strength allowed, and these had the highest uncertainties. All of the measurements on p-xylene (Tcrit = 616.2 K) were well below the critical point, and this fluid had the lowest average uncertainty.
5. Discussion and Conclusions
A dual-path, pulse-echo apparatus has been developed at NIST for measurement of the liquid-phase speed of sound. It operates over a temperature range of 228.15 to 423.15 K, with pressures of up to 93 MPa. While it implements a standard and well-proven technique, our instrument has several unique features. We employ a 2.5:1 ratio of path lengths compared to the more typical 1.5:1 ratio; the larger ratio gives a greater time resolution and allows a longer time for the short-path echo to damp out before the arrival of the long-path echo. The quartz crystal transducer is clamped between ceramic spacers. This simple mounting arrangement has proven to be reliable and yielded repeatable time-of-flight measurements. This mounting method, together with the design of the electrical contacts, results in a smaller sample volume compared with some other designs. The electrical feed through is a custom design.
The echo signals were automatically detected and recorded with custom instrument control software; this made extensive use of the signal processing capabilities of our modern digital oscilloscope. We averaged many echo signals (typically 256), again using the capability of the oscilloscope, and this reduced the noise in the signal and allowed a simple fitting of the data to evaluate the time delay; other authors using a single echo often require a fast Fourier transform (FFT) analysis to deal with a noisy signal. Our data analysis was done entirely off-line, and this simplified the automation of the instrument compared to the double-pulse/cancellation-of-echoes method.
We calibrated the path lengths of the instrument with measurements on propane. This calibration was nearly identical to the one based on a direct measurement of the spacer lengths at room temperature. The propane calibration also compared closely with a calibration (over a more limited range of temperatures) with water. We verified the overall performance of the instrument by comparing to recent, high-accuracy measurements on p-xylene. The average expanded combined uncertainty in the speed of sound for this instrument ranged from 0.035 to 0.088% for the different fluids based on a detailed analysis.
This instrument was used to determine the liquid-phase speed of sound of four “new” low-GWP refrigerants over a combined temperature and pressure range of (230 to 430) K with pressures of up to 50 MPa. There are very limited liquid-phase speed-of-sound data reported in the literature for these fluids, and the present data are the first reported for R1336mzz(Z). These data were used in developing high-accuracy, wide-ranging equations of state for three of the fluids.
Acknowledgments
We gratefully acknowledge Robert Gomez and Michael Rybowiak of NIST for fabricating the instrument described here. We found the habilitation thesis of Karsten Meier9 of Helmut-Schmidt-Universität to be a very helpful textbook on the pulse-echo technique. We appreciate helpful discussions with Martin Trusler of Imperial College London as we developed this instrument. We carried out the measurements on p-xylene in cooperation with Saif Al Ghafri of the University of Western Australia during his visit to NIST. Robin Wegge of Ruhr-Universität Bochum assisted with the setup and automation of the instrument during his visit to NIST. Finally, we thank Honeywell and Chemours for the donation of the refrigerant samples. This work was funded by the National Institute of Standards and Technology and was carried out in the normal course of our duties as research staff.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.iecr.3c01720.
Author Contributions
Contribution of the National Institute of Standards and Technology. Not subject to copyright in the United States.
The authors declare no competing financial interest.
Supplementary Material
References
- Lemmon E. W.; Jacobsen R. T. A new functional form and fitting techniques for equations of state with application to pentafluoroethane (HFC-125). J. Phys. Chem. Ref. Data 2005, 34, 69–108. 10.1063/1.1797813. [DOI] [Google Scholar]
- Trusler J. P. M.; Lemmon E. W. Determination of the thermodynamic properties of water from the speed of sound. J. Chem. Thermodynamics 2017, 109, 61–70. 10.1016/j.jct.2016.10.028. [DOI] [Google Scholar]
- Moldover M. R.; Mehl J. B.; Greenspan M. Gas-filled spherical resonators: Theory and experiment. J. Acoust. Soc. Am. 1986, 79, 253–272. 10.1121/1.393566. [DOI] [Google Scholar]
- Kano Y. Multi-property evaluation for a gas sample based on the acoustic and electromagnetic resonances measurement in a cylindrical cavity. J. Chem. Thermodynamics 2021, 159, 106448. 10.1016/j.jct.2021.106448. [DOI] [Google Scholar]
- Zhang K.; Feng X. J.; Zhang J. T.; Duan Y. Y.; Lin H.; Duan Y. N. Determination of T–T90 from 234 to 303 K by acoustic thermometry with a cylindrical resonator. Metrologia 2020, 57, 024004. 10.1088/1681-7575/ab7171. [DOI] [Google Scholar]
- Younglove B. A.; Frederick N. V. Sound speed measurements on gas mixtures of natural gas components using a cylindrical resonator. Int. J. Thermophys. 1990, 11, 897–910. 10.1007/BF00503582. [DOI] [Google Scholar]
- Fröba A. P.; Will S.; Leipertz A. Thermophysical properties of binary and ternary fluid mixtures from dynamic light scattering. Int. J. Thermophys. 2001, 22, 1349–1368. 10.1023/A:1012832701996. [DOI] [Google Scholar]
- Wang S.; Zhang Y.; He M.-G.; Zheng X.; Chen L.-B. Thermal diffusivity and speed of sound of saturated pentane from light scattering. Int. J. Thermophys. 2014, 35, 1450–1464. 10.1007/s10765-014-1718-x. [DOI] [Google Scholar]
- Meier K.The Pulse-Echo Method for High Precision Measurements of the Speed of Sound in Fluids. Postdoctoral Thesis, Helmut-Schmidt-University, Hamburg, Germany, 2006. [Google Scholar]
- Meier K.; Kabelac S. Speed of sound instrument for fluids with pressures up to 100 MPa. Rev. Sci. Instrum. 2006, 77, 123903. 10.1063/1.2400019. [DOI] [Google Scholar]
- Perkins R. A.; McLinden M. O. Spherical resonator for vapor-phase speed of sound and measurements of 1,1,1,2,2,3,3-heptafluoro-3-methoxypropane (RE347mcc) and trans-1,3,3,3-tetrafluoropropene [R1234ze(E)]. J. Chem. Thermodyn. 2015, 91, 43–61. 10.1016/j.jct.2015.07.005. [DOI] [Google Scholar]
- McLinden M. O.; Perkins R. A.; Lemmon E. W.; Fortin T. Thermodynamic properties of 1,1,1,2,2,4,5,5,5-nonafluoro-4-(trifluoromethyl)-3-pentanone. J. Chem. Engr. Data 2015, 60, 3646–3659. 10.1021/acs.jced.5b00623. [DOI] [Google Scholar]
- Wegge R.; McLinden M. O.; Perkins R. A.; Richter M.; Span R. Speed-of-sound measurements in (argon + carbon dioxide) over the temperature range from (275 to 500) K at pressures up to 8 MPa. J. Chem. Thermodyn. 2016, 99, 54–64. 10.1016/j.jct.2016.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mondejar M. E.; McLinden M. O.; Lemmon E. W. Thermodynamic Properties of trans-1–chloro–3,3,3–trifluoro-propene (R1233zd(E)): Vapor Pressure, p-ρ-T Data, Speed of Sound Measurements and Equation of State. J. Chem. Engr. Data 2015, 60, 2477–2489. 10.1021/acs.jced.5b00348. [DOI] [Google Scholar]
- McLinden M. O.; Akasaka R. Thermodynamic Properties of cis-1,1,1,4,4,4-tetrafluorobutene [R-1336mzz(Z)]: Vapor pressure, (p, ρ, T) Behavior and Speed of Sound Measurements and Equation of State. J. Chem. Engr. Data 2020, 65, 4201–4214. 10.1021/acs.jced.9b01198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kortbeek P.; Muringer M.; Trappeniers N.; Biswaw S. Apparatus for the measurement of compressibility isotherms of gases up to 10 kbar: Experimental data for argon at 298.15 K. Rev. Sci. Instrum. 1985, 56, 1269. 10.1063/1.1137990. [DOI] [Google Scholar]
- Ball S. J.; Trusler J. P. M. Speed of sound of n-hexane and n-hexadecane at temperatures between 298 and 373 K and pressures up to 100 MPa. Int. J. Thermophys. 2001, 22, 427–443. 10.1023/A:1010770730612. [DOI] [Google Scholar]
- Meier K.; Kabelac S. Thermodynamic Properties of Propane. IV. Speed of Sound in the Liquid and Supercritical Regions. J. Chem. Engr. Data 2012, 57, 3391–3398. 10.1021/je300466a. [DOI] [Google Scholar]
- Lago S.; Giuliano Albo P. A.; Brown J. S.; Bertinetti M. High-Pressure Speed of Sound Measurements of trans-1-Chloro-3,3,3-trifluoropropene (R1233zd(E)) in Liquid Region for Temperature from (273.15 to 353.15) K. J. Chem. Engr. Data 2018, 63, 4039–4045. 10.1021/acs.jced.8b00427. [DOI] [Google Scholar]
- Bruno T. J.; Fortin T. J.; Huber M. L.; Laesecke A.; Lemmon E. W.; Mansfield E.; McLinden M. O.; Outcalt S. L.; Perkins R. A.; Urness K. N.; Widegren J. A.. Thermophysical Properties of Polyol Ester Lubricants; Natl. Inst. Stand. Technol. Report 8263: 2019.
- Trusler J. P. M.Physical Accoustics and Metrology of Fluids; Adam Hilger: Bristol, U.K., 1991; p 255. [Google Scholar]
- Williams A. O. The piston source at high frequencies. J. Accoust. Soc. Am. 1951, 23 (1), 1–6. 10.1121/1.1906722. [DOI] [Google Scholar]
- Wolfram Research, I. Mathematica, version 12; Champaign, IL, 2018.
- Audoin B.; Roux J. An innovative application of the Hilbert transform to time delay estimation of overlapped ultrasonic echoes. Ultrasonics 1996, 34, 25–33. 10.1016/0041-624X(95)00088-K. [DOI] [Google Scholar]
- Menegazzo D.; Rowane A. J.; Fedele L.; Bobbo S.; Lombardo G.; McLinden M. O.. Compressed liquid density and speed of sound measurements and correlation of the binary mixture {carbon dioxide (CO2) + 1,1-difluoroethene (HFO-1132a)} at temperatures from 220 to 350 K. 26th International Congress of Refrigeration, 21–26 August, 2023, Paris.
- Bruno T. J.; Svoronos P. D. N.. CRC Handbook of Basic Tables for Chemical Analysis, 3rd ed.; Taylor and Francis/CRC Press: Boca Raton, FL, 2011. [Google Scholar]
- Bruno T. J.; Svoronos P. D. N.. CRC Handbook of Fundamental Spectroscopic Correlation Charts; Taylor and Francis/CRC Press: Boca Raton, FL, 2005. [Google Scholar]
- Lemmon E. W.; Wagner W.; McLinden M. O. Thermodynamic properties of propane. III. Equation of state. J. Chem. Eng. Data 2009, 54, 3141–3180. 10.1021/je900217v. [DOI] [Google Scholar]
- Rowane A. J.; Rasmussen E. G.; McLinden M. O. Liquid-phase speed of sound and vapor-phase density of difluoromethane. J. Chem. Engr. Data 2022, 67, 3022–3032. 10.1021/acs.jced.2c00441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al Ghafri S. Z. S.; Matabishi E. A.; Trusler J. P. M.; May E. F.; Stanwix P. L. Speed of sound and derived thermodynamic properties of para-xylene at temperatures between (306 to 448) K and pressures between saturation and 66 MPa. J. Chem. Thermo. 2019, 135, 369–381. 10.1016/j.jct.2019.03.022. [DOI] [Google Scholar]
- Zhou Y.; Lemmon E. W.; Wu J. Thermodynamic properties of o-xylene, m-xylene, p-xylene, and ethylbenzene. J. Phys. Chem. Ref. Data 2012, 41, 023103. 10.1063/1.3703506. [DOI] [Google Scholar]
- Diky V.; Muzny C.; Smolyanitsky A.; Bazyleva A.; Chirico R.; Magee J.; Paulechka Y.; Kazakov A.; Townsend S.; Lemmon E.; Frenkel M.; Kroenlein K.. ThermoData Engine (TDE). NIST Standard Reference Database 103b, version 10.1 (Pure Compounds, Binary Mixtures, Ternary Mixtures, and Chemical Reactions), Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, 2016.
- Bell I. H.; Lemmon E. W. Automatic fitting of binary interaction parameters for multi-fluid helmholtz-energy-explicit mixture models. J. Chem. Eng. Data 2016, 61, 3752–3760. 10.1021/acs.jced.6b00257. [DOI] [Google Scholar]
- Lemmon E. W.; Bell I. H.; Huber M. L.; McLinden M. O.. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties—REFPROP, version 10.0; National Institute of Standards and Technology: Gaithersburg, MD, 2018. [Google Scholar]
- Myhre G.; Shindell D.; Bréon F.-M.; Collins W.; Fuglestvedt J.; Huang J.; Koch D.; Lamarque J.-F.; Lee D.; Mendoza B.; Nakajima T.; Robock A.; Stephens G.; Takemura T.; Zhang H.. Anthropogenic and Natural Radiative Forcing. In Climate Change 2013: The Physical Science Basis, Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, U.K., 2013. [Google Scholar]
- ASHRAE ANSI/ASHRAE Standard 34–2022 Designation and Safety Classification of Refrigerants; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Atlanta, GA, 2022.
- ASTM International ASTM E-681, Standard Test Method for Concentration Limits of Flammability of Chemicals (Vapors and Gases). ASTM International: West Conshohocken, PA, 2009.
- ISO, Standard 817:2014(E). Refrigerants — Designation and Safety Classification. International Organization for Standardization: 2014.
- Booten C.; Nicholson S.; Mann M.; Abelaziz O.. Refrigerants: Market Trends and Supply Chain Assessment; National Renewable Energy Laboratory Technical Report NREL/TP-5500-70207: 2020.
- Richter M.; McLinden M. O.; Lemmon E. W. Thermodynamic properties of 2,3,3,3-tetrafluoroprop-1-ene (R1234yf): p-ρ-T measurements and an equation of state. J. Chem. Eng. Data 2011, 56, 3254–3264. 10.1021/je200369m. [DOI] [Google Scholar]
- Lemmon E. W.; Akasaka R. An International Standard Formulation for 2,3,3,3-Tetrafluoroprop-1-ene (R1234yf) Covering Temperatures from the Triple Point Temperature to 410 K and Pressures Up to 100 MPa. Int. J. Thermophys. 2022, 43, 119. 10.1007/s10765-022-03015-y. [DOI] [Google Scholar]
- Yoshitake M.; Matsuo S.; Sotani T.. Density and Speed of Sound Measurements of HFO1234yf. 30th Japan Symposium on Thermophysical Properties, Oct 28–30, 2009; paper A303.
- Lago S.; Giuliano Albo P. A.; Brignolo S. Speed of sound results in 2,3,3,3-tetrafluoropropene (R-1234yf) and trans-1,3,3,3-tetrafluoropropene and (R-1234ze(E)) in the temperature range of (260 to 360) K. J. Chem. Eng. Data 2011, 56, 161–163. 10.1021/je100896n. [DOI] [Google Scholar]
- U.S. Environmental Protection Agency Significant New Alternatives Policy (SNAP): SNAP Regulations. https://www.epa.gov/snap/snap-regulations#notices (accessed Dec 28, 2022).
- Thol M.; Lemmon E. W. Equation of State for the Thermodynamic Properties of trans-1,3,3,3-Tetrafluoropropene [R1234ze(E)]. Int. J. Thermophys. 2016, 37, 28. 10.1007/s10765-016-2040-6. [DOI] [Google Scholar]
- Akasaka R.; Lemmon E. W. An International Standard Formulation for trans-1-Chloro-3,3,3-trifluoroprop-1-ene [R1233zd(E)] Covering Temperatures from the Triple-Point Temperature to 450 K and Pressures up to 100 MPa. J. Phys. Chem. Ref. Data 2022, 51, 023101. 10.1063/5.0083026. [DOI] [Google Scholar]
- El Hawary A.; Mirzaev S. Z.; Meier K. Speed-of-sound measurements in liquid n-pentane and isopentane. J. Chem. Eng. Data 2020, 65, 1243–1263. 10.1021/acs.jced.9b00602. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Diky V.; Muzny C.; Smolyanitsky A.; Bazyleva A.; Chirico R.; Magee J.; Paulechka Y.; Kazakov A.; Townsend S.; Lemmon E.; Frenkel M.; Kroenlein K.. ThermoData Engine (TDE). NIST Standard Reference Database 103b, version 10.1 (Pure Compounds, Binary Mixtures, Ternary Mixtures, and Chemical Reactions), Standard Reference Data Program; National Institute of Standards and Technology: Gaithersburg, MD, 2016.