Abstract
The hallmark of spintronics has been the ability of spin–orbit interactions to convert a charge current into a spin current and vice versa, mainly in the bulk of heavy metal thin films. Here, we demonstrate how a light metal interface profoundly affects both the nature of spin–orbit torques and its efficiency in terms of damping-like (HDL) and field-like (HFL) effective fields in ultrathin Co films. We measure unexpectedly HFL/HDL ratios much larger than 1 by inserting a nanometer-thin Al metallic layer in Pt|Co|Al|Pt as compared to a similar stacking, including Cu as a reference. From our modeling, these results evidence the existence of large Rashba interaction at the Co|Al interface generating a giant HFL, which is not expected from a metallic interface. The occurrence of such enhanced torques from an interfacial origin is further validated by demonstrating current-induced magnetization reversal showing a significant decrease of the critical current for switching.
Keywords: Rashba-Edelstein effect, Spin−orbit torques, Spintronics, Magnetization switching
In modern nanomagnetism, spin–orbit
coupling (SOC) at interfaces is exploited to generate strong interfacial
perpendicular anisotropy (PMA) or antisymmetric exchange interactions.1 In spintronics, SOC is the key interaction to
generate spin-current via the spin Hall effect (SHE) in heavy metals,
enabling magnetization switching2−6 and driving skyrmions7 and domain walls.
In atomically thin layers with broken inversion symmetry, the interplay
of low-dimensionality and SOC may also lead to a Rashba spin-splitting8−10 modifying the electronic ground state, thus affecting the spin transport
via the Rashba–Edelstein (REE)11 or orbital Rashba effects (ORE).12,13 These phenomena,
namely, SHE5,14,15 and REE (or ORE),5,10,11,15,16 may convert
a charge current 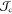 into either an out-of-equilibrium spin-current
into either an out-of-equilibrium spin-current 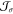 or spin accumulation μ̂ (out-of equilibrium spin-density) carrying an angular momentum.
Upon current injection, those can, in turn, transfer their angular
momentum to the adjacent ferromagnetic layer by precessing around
the exchange field.
or spin accumulation μ̂ (out-of equilibrium spin-density) carrying an angular momentum.
Upon current injection, those can, in turn, transfer their angular
momentum to the adjacent ferromagnetic layer by precessing around
the exchange field.
Both 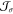 and μ̂ may exert
spin–orbit torques (SOTs) onto a magnetization vector
and μ̂ may exert
spin–orbit torques (SOTs) onto a magnetization vector 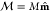 with two components: damping-like torque
(DLT), τ̂DL ∝ m̂ ×
(μ̂ × m̂), and field-like
torque (FLT), τ̂FL ∝ μ̂ × m̂. The nature and strength of the corresponding
DL (HDL) and FL (HFL) effective fields strongly depend on the relaxation of the
transverse spin i.e. on the spin decoherence length, which is predicted
to be a few atomic lattice parameters.17,18 Manipulating
the magnetization via SOTs and disentangling the exact origin of SOTs
to use them adequately are still challenging today for writing processes
in magnetoelectronic devices.
with two components: damping-like torque
(DLT), τ̂DL ∝ m̂ ×
(μ̂ × m̂), and field-like
torque (FLT), τ̂FL ∝ μ̂ × m̂. The nature and strength of the corresponding
DL (HDL) and FL (HFL) effective fields strongly depend on the relaxation of the
transverse spin i.e. on the spin decoherence length, which is predicted
to be a few atomic lattice parameters.17,18 Manipulating
the magnetization via SOTs and disentangling the exact origin of SOTs
to use them adequately are still challenging today for writing processes
in magnetoelectronic devices.
In the pioneer experiments by Miron et al. in Pt|Co|AlOx,2 SOT was discussed in terms of dominating FLT arising from REE at the Co|Oxide interface, larger than SHE-DLT from Pt, suggesting the crucial role of a large interfacial electric field at the ferromagnet/oxide interface. Although, in metals, SHE is largely considered as the primary source of DLT,3,19−21 a significant interfacial REE has been recently observed in Ir|ferromagnetic|Ta contributing to DLT.22 In the limit of atomically thin magnetic layers, additional mechanisms might also influence the strength of the SOTs: spin-filtering or charge quantum confinement,23−27 surface states of topological insulators (TIs)28 and 2D electron gases.29
Moreover, recent theory has evidenced additional orbital currents in light elements from orbital Hall effects (OHE) and/or orbital Rashba effects (ORE) superimposing to the spin currents.30 These orbital currents may result in the generation of orbital torques12,31 and orbital Rashba magnetoresistance.13,32 This questions the actual origin of the magnetic torques in multilayers with light elements.
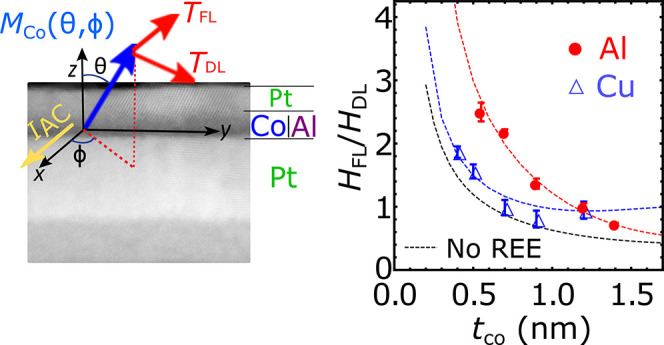
In this study, we investigate the properties of SOTs in atomically thin metallic structures, namely, Co layers ranging from 1.4 nm down to 0.4 nm, sandwiched between Pt and light element overlayers, i.e., Al or Cu. Using the second harmonic Hall measurement technique,33,34 we precisely determine the amplitude of the SOT vs the ferromagnetic film thickness, the light-element overlayer, and the heavy-element. Compared to the best-reported results,34 we find an increase of the DLT by ∼30% together with a drastic rise in the FLT by more than ∼190%. With the help of our spin-dependent Boltzmann calculations, we explicitly demonstrate the occurrence of enhanced SOT due to a strong REE in asymmetric Pt|Co|Al|Pt stacks, from a FLT over DLT ratio as large as 2.5 for 0.55 nm thick Co, one of the highest values ever reported in metals.
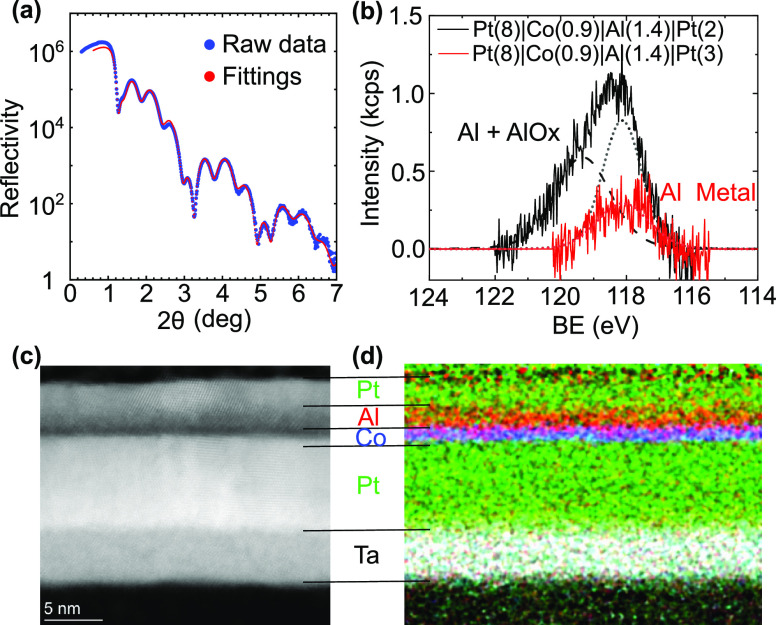
Samples were grown using magnetron sputtering at the base pressure 6 × 10–8 mbar. In Figure 1a, we show X-ray reflectivity (XRR) measurements (blue) and fit (red) on a Ta(5)|Pt(8)|Co(0.7)|Al(1.4)|Pt(3) sample where the layer thicknesses are found to be in good agreement with nominal values (<3% error). The XRR measurements reveal 0.29 and 0.12 nm roughness at Pt|Co and Co|Al interfaces, respectively, comparable with the SiO2|Ta interface (0.45 nm). We have also performed X-ray photoelectron spectroscopy (XPS) on Pt(8)|Co(0.7)|Al(1.4)|Pt(tPt) with tPt = 2 and 3 nm to probe the chemistry of Al underneath Pt (Figure 1b with black and red colors respectively). As the Al 2p peak (71 eV) is totally screened by the 4f Pt peaks, the 2s Al bonds are probed. The peak for the 2 nm Pt capping can be fitted with two contributions attributed to AlOx (dashed) and metallic Al (dotted) respectively whereas the 3 nm Pt capping sample only reveals a single metallic state of Al thus discarding any oxidization state. In Figure 1c and d, we show the energy dispersive X-ray spectroscopy (EDX) measurements in scanning transmission electron microscopy (STEM). The Ta, Pt Co, and Al layers can be clearly distinguished by bright and black Z-contrasts in high-angle annular dark-field (HAADF) image. In Figure 1d, we show elemental distribution of Ta (white), Pt (green), Co (blue), and Al (red). Together with XRR, the HAADF and EDX characterizations clearly show homogeneous and flat interfaces without any sign of oxidation of the Al film.
Figure 1.
(a) XRR measurements (blue) and fittings (red) on Pt(8)|Co(0.7)|Al(1.4)|Pt(3) sample. (b) Measurements of XPS on similar samples are shown by red color together with a reduced Pt capping (2 nm) with oxidized Al (in black). (c) HAADF image in STEM of the sample with corresponding EDX elemental map shown in (d).
To evaluate the two components of the SOTs, we
employed the harmonic
Hall measurement technique on 5 μm wide Hall bars with an AC
excitation of 727 Hz (SI-I). First, we
compare the results from the two series of multilayers with Al and
Cu light element interfaced with Co: Pt(8)|Co(tCo)|Al(1.4)|Pt(3) and Pt(8)|Co(tCo)|Cu(1.4)|Pt(3). Starting from negligible torques in a fully symmetric
Pt(8)|Co(0.9)|Pt(8) stack as expected (SI-V), the asymmetric “control” sample Pt(8)|Co(0.9)|Pt(3)
gives HDL = 0.80 ± 0.05 mT and HFL 0.58 ± 0.15 mT for a current density 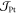 in Pt = 1011 A/m2 (later used as a reference value). To obtain integrated torques
over the whole ferromagnetic layer of thickness tCo and hence to be able to make an accurate comparison,
we define a normalized quantity by multiplying HDL,FL with tCo for a 1011 A/m2 current density
in Pt. This corresponds to the equivalent torque values for an applied
electric field
in Pt = 1011 A/m2 (later used as a reference value). To obtain integrated torques
over the whole ferromagnetic layer of thickness tCo and hence to be able to make an accurate comparison,
we define a normalized quantity by multiplying HDL,FL with tCo for a 1011 A/m2 current density
in Pt. This corresponds to the equivalent torque values for an applied
electric field 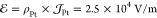 owing to the Pt resistivity ρPt = 25 μΩ·cm (SI-III). Our analyses mainly depend on the anisotropy field Hk, but not on the saturation magnetization
at the limit of thin Co Ms = 1.1 ±
0.1 MA/m, remaining however quite independent of the Co thickness tCo for both the Al and Cu series (SI-IV).
owing to the Pt resistivity ρPt = 25 μΩ·cm (SI-III). Our analyses mainly depend on the anisotropy field Hk, but not on the saturation magnetization
at the limit of thin Co Ms = 1.1 ±
0.1 MA/m, remaining however quite independent of the Co thickness tCo for both the Al and Cu series (SI-IV).
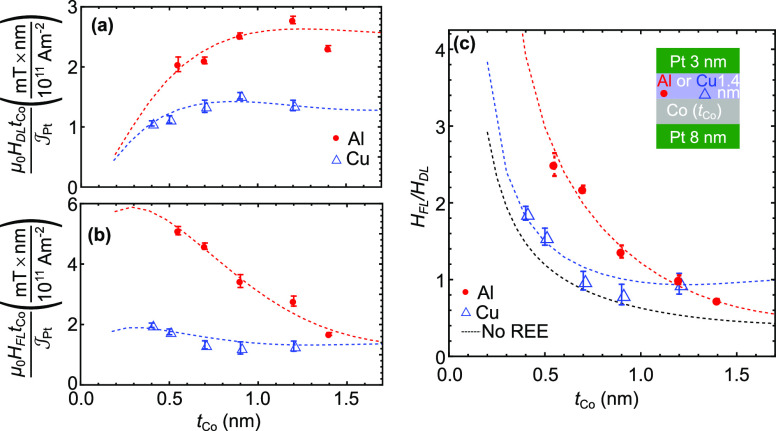
Several features may be highlighted with similarities and differences
between the Al and Cu series. First, as shown in Figure 2a, the integrated DL component 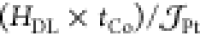 is about 65% larger in Pt|Co|Al(1.4)|Pt
samples compared to Pt|Co|Cu(1.4)|Pt for almost the whole Co thickness.
At tCo = 0.9 nm, the value of DLT is about
2.5 mT × nm/(1011 A·m–2) for
Al and 1.5 mT × nm/(1011 A·m–2) for Cu. We note however that the
is about 65% larger in Pt|Co|Al(1.4)|Pt
samples compared to Pt|Co|Cu(1.4)|Pt for almost the whole Co thickness.
At tCo = 0.9 nm, the value of DLT is about
2.5 mT × nm/(1011 A·m–2) for
Al and 1.5 mT × nm/(1011 A·m–2) for Cu. We note however that the 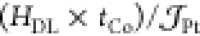 product exhibits in each case a similar
maximum close to tCo = 1.0–1.2
nm that we ascribe to the spin decoherence length at small thickness.
Second, we find that the FLT exhibits an increase in reducing tCo (Figure 2b) in both series, resulting in a dominating FLT component
at small tCo. Nevertheless, their SOT
magnitude strongly differs. We observe a substantial increase of the
FLT for Al(1.4), i.e., from 1.7 mT × nm/(1011 A·m–2) for tCo = 1.4 nm to
5.2 mT × nm/(1011 A·m–2) for tCo = 0.55 nm, whereas the maximum value of FLT
reaches only 2 mT × nm/(1011 A·m–2) for Cu. Such a large FLT increase in the atomically thin Co layer
has never been reported to our knowledge. This striking result manifests
also by a rise of the FLT to DLT ratio
product exhibits in each case a similar
maximum close to tCo = 1.0–1.2
nm that we ascribe to the spin decoherence length at small thickness.
Second, we find that the FLT exhibits an increase in reducing tCo (Figure 2b) in both series, resulting in a dominating FLT component
at small tCo. Nevertheless, their SOT
magnitude strongly differs. We observe a substantial increase of the
FLT for Al(1.4), i.e., from 1.7 mT × nm/(1011 A·m–2) for tCo = 1.4 nm to
5.2 mT × nm/(1011 A·m–2) for tCo = 0.55 nm, whereas the maximum value of FLT
reaches only 2 mT × nm/(1011 A·m–2) for Cu. Such a large FLT increase in the atomically thin Co layer
has never been reported to our knowledge. This striking result manifests
also by a rise of the FLT to DLT ratio 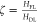 for Pt|Co|Al|Pt that we will consider as
a new figure of merit (see Figure 2c).
for Pt|Co|Al|Pt that we will consider as
a new figure of merit (see Figure 2c).
Figure 2.
(a) Damping-like (DL) field and (b) field-like (FL) field
multiplied
by tCo for 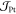 = 1011 A/m2 in Pt(8)|Co(0.55–1.4)|Al(1.4)|Pt(3)
and Pt(8)|Co(0.4–1.2)|Cu(1.4)|Pt(3). (c) tCo dependence of ζ = HFL/HDL. Red and blue dashed lines are fits
to experimental data points using our theoretical model, and black
dashed line in (c) is calculated ζ values without any Rashba
interface (see SI-VII).
= 1011 A/m2 in Pt(8)|Co(0.55–1.4)|Al(1.4)|Pt(3)
and Pt(8)|Co(0.4–1.2)|Cu(1.4)|Pt(3). (c) tCo dependence of ζ = HFL/HDL. Red and blue dashed lines are fits
to experimental data points using our theoretical model, and black
dashed line in (c) is calculated ζ values without any Rashba
interface (see SI-VII).
Such a behavior is expected either for SHE when tCo becomes smaller than the spin-decoherence
length (black
curve in Figure 2c
from our modeling (SI-VII) or for an increased
weight of REE (red dotted line for Al and blue for Cu in Figure 2c). We find that  saturates for tCo ≳ 1.2 nm with a magnitude ζ ≈ 0.7 in the “thick”
ferromagnet limit for SHE.19 This corresponds
also to the case of the Cu series with moderate Rashba effects. Similar
value of ζ ≃ 0.7 were also obtained on 4 nm thick Co|Ni
multilayers.35 Here, on reducing tCo below 1.2 nm, ζ increases sharply for
the Pt|Co|Al|Pt series (Figure 2c) and eventually reaches 2.5 for tCo = 0.55 nm. This ratio remains smaller than unity down to tCo = 0.7 nm for Pt|Co|Cu|Pt. Such FLT enhancement
by a factor larger than three from tCo = 1.4 nm to tCo = 0.55
nm strongly challenges the SHE (and/or OHE) origin of SOT with Al.
saturates for tCo ≳ 1.2 nm with a magnitude ζ ≈ 0.7 in the “thick”
ferromagnet limit for SHE.19 This corresponds
also to the case of the Cu series with moderate Rashba effects. Similar
value of ζ ≃ 0.7 were also obtained on 4 nm thick Co|Ni
multilayers.35 Here, on reducing tCo below 1.2 nm, ζ increases sharply for
the Pt|Co|Al|Pt series (Figure 2c) and eventually reaches 2.5 for tCo = 0.55 nm. This ratio remains smaller than unity down to tCo = 0.7 nm for Pt|Co|Cu|Pt. Such FLT enhancement
by a factor larger than three from tCo = 1.4 nm to tCo = 0.55
nm strongly challenges the SHE (and/or OHE) origin of SOT with Al.
In Figure 3, we
present the evolution of 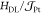 (Figure 3a),
(Figure 3a), 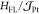 (Figure 3b), and their ratio
(Figure 3b), and their ratio 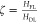 vs Al (red points) and Cu (blue points)
thickness (Figure 3c). Both DLT and FLT exhibit a strong enhancement with tAl in the 1–3 nm window, particularly pronounced
for the FLT. We find that FLT (respectively DLT) increases from ∼0.65
mT/1011 A·m–2 (∼0.8 mT/1011 A·m–2) for tAl = 0 nm to a saturation value of ∼7 mT/1011 A·m–2 (∼4.4 mT/1011 A·m–2) for tAl = 3 nm. This
corresponds to a boost of the FLT by more than a factor of 10 upon
inserting 3 nm of Al on top of 0.9 nm Co. Conversely, the ratio ζ
is also enhanced with tAl (Figure 3c) from ζ = 0.8 for tAl = 0 to ζ = 1.6 for tAl ≥ 3 nm. First, we comment the behavior of DLT.
Based on the results from our fits (SI-VII), we assign the rise of DLT vs tAl to the decrease of
the transmission coefficient
vs Al (red points) and Cu (blue points)
thickness (Figure 3c). Both DLT and FLT exhibit a strong enhancement with tAl in the 1–3 nm window, particularly pronounced
for the FLT. We find that FLT (respectively DLT) increases from ∼0.65
mT/1011 A·m–2 (∼0.8 mT/1011 A·m–2) for tAl = 0 nm to a saturation value of ∼7 mT/1011 A·m–2 (∼4.4 mT/1011 A·m–2) for tAl = 3 nm. This
corresponds to a boost of the FLT by more than a factor of 10 upon
inserting 3 nm of Al on top of 0.9 nm Co. Conversely, the ratio ζ
is also enhanced with tAl (Figure 3c) from ζ = 0.8 for tAl = 0 to ζ = 1.6 for tAl ≥ 3 nm. First, we comment the behavior of DLT.
Based on the results from our fits (SI-VII), we assign the rise of DLT vs tAl to the decrease of
the transmission coefficient 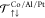 at the top of the structure varying linearly
from
at the top of the structure varying linearly
from 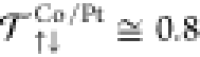 for tAl = 0
nm to
for tAl = 0
nm to 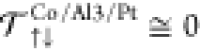 when tAl >
3 nm. This results in the quenching of the opposite SHE from the top
Pt. However, part of the DLT enhancement also originates from the
conversion of the FLT into the DLT in the Co thickness via the spin
precession mechanism. This trend is very different in the “reference”
Cu series vs tCu as we find that
when tAl >
3 nm. This results in the quenching of the opposite SHE from the top
Pt. However, part of the DLT enhancement also originates from the
conversion of the FLT into the DLT in the Co thickness via the spin
precession mechanism. This trend is very different in the “reference”
Cu series vs tCu as we find that 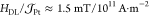 and ζ ≈ 0.7 remain roughly
constant vs tCu (blue open triangles in Figure 3a and b).
and ζ ≈ 0.7 remain roughly
constant vs tCu (blue open triangles in Figure 3a and b).
Figure 3.
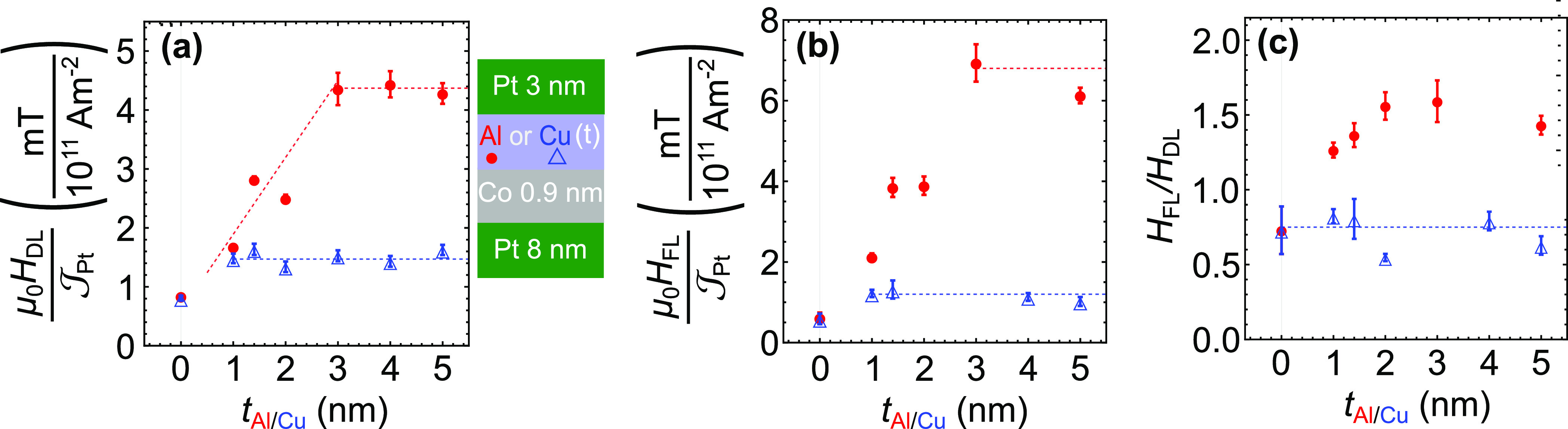
(a) HDL vs Al (red) and Cu (blue) layer
thickness. The variation in HDL is fitted
by the dashed red lines (SI-VII). We used lsfPt = 1.5 nm, r̃s = 2, 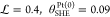 and the transmission coefficient
and the transmission coefficient 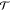 varying linearly from
varying linearly from 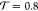 for tAl = 0
nm to
for tAl = 0
nm to 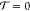 when tAl >
3 nm. (b) HFL vs Al (red) and Cu (blue)
layer thickness. (c) ζ = HFL/HDL vs Al (red) and Cu (blue) layer thickness.
Thick and constant blue lines are a guide to the eye.
when tAl >
3 nm. (b) HFL vs Al (red) and Cu (blue)
layer thickness. (c) ζ = HFL/HDL vs Al (red) and Cu (blue) layer thickness.
Thick and constant blue lines are a guide to the eye.
Two important conclusions may then be drawn for the DLT: (i) a progressive extinction of the SHE action from the top Pt on increasing the thickness of Al through the quench of the electron transmission at the Co|Al|Pt interfaces and (ii) a larger electronic transmission across Co|Cu|Pt36,37 partially compensating the SHE torque from the bottom Pt (irrespective of tCu). Considering both bottom and top Pt layers, the effective spin Hall angle (SHA) (θSHEeff) is
| 1 |
where θSHEbulkPt is the bare SHA of bulk Pt, 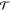 is the effective transmission coefficient
at the top, and
is the effective transmission coefficient
at the top, and 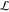 is the spin-loss.36,38,39 The function
is the spin-loss.36,38,39 The function 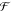 :
:
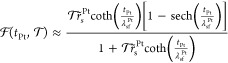 |
2 |
describes the spin back-flow in Pt with λsfPt ≈ 1.5
nm being its spin-diffusion length (SDL) in Pt as in ref (37) and r̃s ≈
2 is its spin-resistance in the unit of the inverse of the Sharvin
conductance (SI-VII). From our fitting
procedure (Figure 3a), we could extract 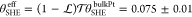 using θSHEbulkPt ≈ 0.225 ± 0.025 in
agreement with the literature for a Pt resistivity of ρ = 25
μΩ·cm.37,40 Similar values of θSHE were determined
from AHE.40 We considered here
using θSHEbulkPt ≈ 0.225 ± 0.025 in
agreement with the literature for a Pt resistivity of ρ = 25
μΩ·cm.37,40 Similar values of θSHE were determined
from AHE.40 We considered here 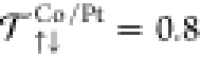 and
and  . Our fitting procedure applied to AHE (SI-IV) uses the same set of parameter values
as for SOTs. The SHE compensation from the top injection then approaches
75% in our ’control’ Pt(8)|Co(0.9)|Pt(3) structure and
60% in the Pt(8)|Co(0.9)|Cu|Pt(3) series. This implies that the expected
increase of the DLT is 25% (0.75/0.6) from Pt(8)|Co(0.9)|Pt(3) to
Pt(8)|Co(0.9)|Cu|Pt(3) and by a factor ×2.5 to Pt(8)|Co(0.9)|Al(3)|Pt(3)
(Figure 3a).
. Our fitting procedure applied to AHE (SI-IV) uses the same set of parameter values
as for SOTs. The SHE compensation from the top injection then approaches
75% in our ’control’ Pt(8)|Co(0.9)|Pt(3) structure and
60% in the Pt(8)|Co(0.9)|Cu|Pt(3) series. This implies that the expected
increase of the DLT is 25% (0.75/0.6) from Pt(8)|Co(0.9)|Pt(3) to
Pt(8)|Co(0.9)|Cu|Pt(3) and by a factor ×2.5 to Pt(8)|Co(0.9)|Al(3)|Pt(3)
(Figure 3a).
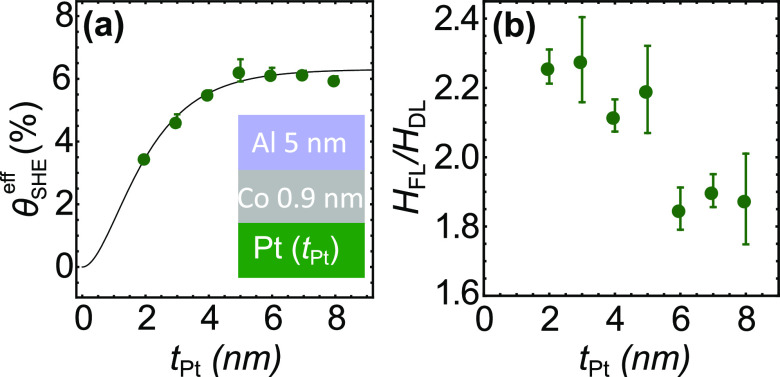
In order to highlight any additional REE (or ORE) arising from
Co|Al, we reduced the bottom Pt thickness in the Pt(tPt)|Co(0.9)|Al(5) series to attenuate the SOTs originating
from SHE. We first quantified this SHE contribution by extracting
θSHE from HDL according
to  (e is the electron charge).
In Figure 4a, we observe
that θSHEeff increases with tPt according to
(e is the electron charge).
In Figure 4a, we observe
that θSHEeff increases with tPt according to 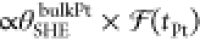 (eq 2) before reaching its saturation value for tPt ≥ 5 nm. From the fitting procedure, the spin-diffusion
length (SDL) and θSHE are, respectively, ≃1.5 nm and ≃0.08,
in agreement with data of Figure 3. In Figure 4b, we show the impact of the additional REE (or ORE) occurring
from Co|Al on the SOTs for tCo = 0.9 nm.
First, the FLT clearly dominates the DLT for all the Pt thicknesses.
In addition, a remarkable increase of ζ is observed at the lowest tPt = 2–5 nm thickness range, i.e., where
SHE has not yet reached its maximum efficiency. This undoubtedly supports
the role of a significant Rashba interaction (i.e., REE and/or ORE)
superimposed to SHE. Our data also yield a clear quantitative understanding
of how the Rashba effects at metallic interfaces may strongly affect HFL in chemically asymmetric Pt|Co|Al|Pt stacks
(see Figures 2 and 3).
(eq 2) before reaching its saturation value for tPt ≥ 5 nm. From the fitting procedure, the spin-diffusion
length (SDL) and θSHE are, respectively, ≃1.5 nm and ≃0.08,
in agreement with data of Figure 3. In Figure 4b, we show the impact of the additional REE (or ORE) occurring
from Co|Al on the SOTs for tCo = 0.9 nm.
First, the FLT clearly dominates the DLT for all the Pt thicknesses.
In addition, a remarkable increase of ζ is observed at the lowest tPt = 2–5 nm thickness range, i.e., where
SHE has not yet reached its maximum efficiency. This undoubtedly supports
the role of a significant Rashba interaction (i.e., REE and/or ORE)
superimposed to SHE. Our data also yield a clear quantitative understanding
of how the Rashba effects at metallic interfaces may strongly affect HFL in chemically asymmetric Pt|Co|Al|Pt stacks
(see Figures 2 and 3).
Figure 4.
a) Effective θSHEeff vs tPt (green points). The solid line is the fit enabling to extract lsf = 1.5 nm, Pt bulk θSHEbulk Pt = 0.225 ± 0.025 (effective θSHE = 0.075 ± 0.01), and r̃sPt = 2 using eq 2. (b) Plot of the ζ ratio vs tPt.
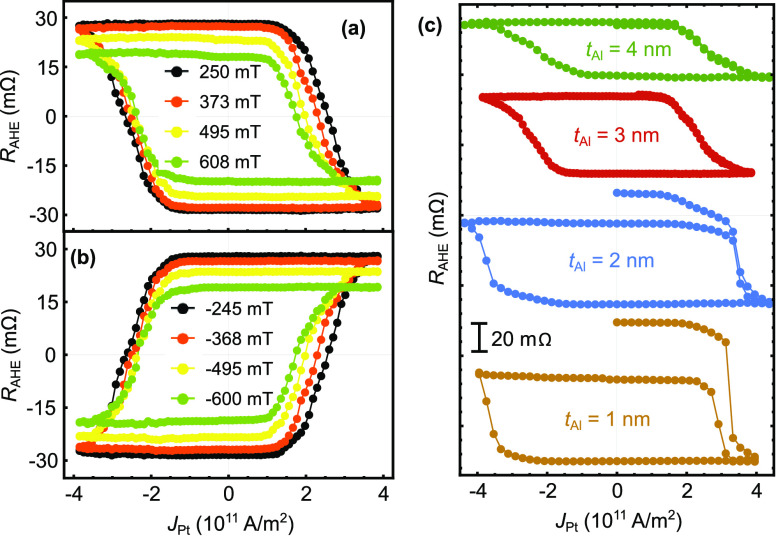
We then performed SOT-driven magnetization switching experiments on Pt(8)|Co(0.9)|Al(tAl)|Pt(3) Hall cross-bars. A magnetic field Hx, either positive or negative, is applied along the current direction to break the mirror symmetry, and RAHE is measured vs the current. Typical results of SOT-induced magnetization reversal are shown in Figure 5 for respective positive μ0Hx = +250, 373, 495, and 608 mT (Figure 5a) and equal negative μ0Hx = −240, −368, −495, and −600 mT (Figure 5b) fields for tAl = 3 nm. A complete magnetization reversal is observed for Jc ≈ ±2–2.5 × 1011 A·m–2 with the polarity of the magnetization reversal cycle depending on the sign of μ0Hx as expected. We also find that the critical current density decreases as |μ0Hx| increases as observed in refs (35) and (41) with the typical current density reaching Jc = 3–3.5 × 1011 A·m–2. In Figure 5c, we compare magnetization reversal cycles for different tAl = 1, 2, 3, and 4 nm, acquired under a field μ0Hx = +250 mT much smaller than the anisotropy field HK (SI-IV). Despite a larger HK and larger coercive field, we find that a complete switching of magnetization (between P and AP states) may be achieved in devices with tAl = 3 and 4 nm, whereas the ones with tAl = 1 and 2 nm exhibit only partial reversal, thus in agreement with the enhanced SOT shown in Figure 3. We hence conclude that increasing the Al thickness in the Pt(8)|Co(0.9)|Al(tAl)|Pt(3) series increases the SOT allowing a reduction of the critical current density for complete magnetization switching by more than 30%.
Figure 5.
Current-induced magnetization reversal in Pt(8)|Co(0.9)|Al(3)|Pt(3) for different (a) positive and (b) negative μ0Hx. (c) RAHE as a function of pulsed current in the Pt(8)|Co(0.9)|Al(tAl)|Pt(3) series of samples for μ0Hx = +250 mT. The pulse width was 100 μs.
The ensemble of the results highlighting the existence
of a large
interfacial Rashba effect from the Co|Al is supported by our modeling
(SI-VII). In the case of thick ferromagnet,
it is known that SOT from SHE is determined via the complex spin-mixing
conductance.21,42,43 For tCo smaller than the dephasing length,
the description is far more complex owing to the remaining outgoing
spin-currents and additional electronic reflections. We developed
numerical analyses gathering most of the ingredients discussed above
based on generalized drift-precession-diffusion equations20,44−46 able to express the profile of the vectorial spin-accumulation μ̂F. We thus provide
subsequent insights for HDL and HFL, the integrated value of the torque τSOT, by considering the precessing and dephasing
processes via the s–d exchange coupling (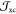 ). In particular, this implies a complex
value of the propagating length in Co. The SOT acting on the Co layer
by the out-of equilibrium spin μ̂F then writes:47
). In particular, this implies a complex
value of the propagating length in Co. The SOT acting on the Co layer
by the out-of equilibrium spin μ̂F then writes:47
| 3 |
where 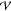 is the volume of Co and μF is expressed in the same unit (
is the volume of Co and μF is expressed in the same unit (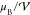 ) as
) as 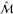 and
and 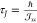 is the precession time. In our treatment,
the interfaces are described by their proper interfacial Gs or spin-mixing G↑↓ (between Co and the nonmagnetic material) conductances normalized
by their Sharvin values Gsh, or using
corresponding transmission coefficients (spin-mixing transmission).
It generally leads to possible spin-backflow processes48 and additional spin-accumulation within the
different layers. We considered:
is the precession time. In our treatment,
the interfaces are described by their proper interfacial Gs or spin-mixing G↑↓ (between Co and the nonmagnetic material) conductances normalized
by their Sharvin values Gsh, or using
corresponding transmission coefficients (spin-mixing transmission).
It generally leads to possible spin-backflow processes48 and additional spin-accumulation within the
different layers. We considered:
(i) a typical precession (or Larmor) length λJ = 2πvFτJ = 4.7 nm for the transverse part of the spin accumulation and spin-current and a transverse spin-decoherence length λ⊥ of 1.7 nm in the range of the values given in ref (45) for Co.
(ii) a large spin-mixing transmission coefficient 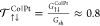 at the Co|Pt interface40,49 with G↑↓ and Gsh being, respectively, the spin-mixing conductance and
the Sharvin conductance.
at the Co|Pt interface40,49 with G↑↓ and Gsh being, respectively, the spin-mixing conductance and
the Sharvin conductance.
(iii) a mean spin-mixing transmission
coefficient 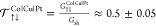 through Cu.36,37
through Cu.36,37
(iv)
a mean spin-mixing transmission coefficient 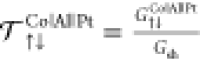 varying from 0.8 to 0 when the Al thickness
is increased from 0 to 3 nm and greater.
varying from 0.8 to 0 when the Al thickness
is increased from 0 to 3 nm and greater.
Based on our present knowledge for the Co|Pt interface,36,49,50 the predicted SOT fields are in excellent agreement with the experimental ones for both DL and FL (see dashed lines in Figures 2 and 3). We accounted for a spin-accumulation μF = μREE at the Co|Al(Cu) interface due to REE. For Pt|Co|Cu|Pt, we consider that μREE is homogeneous in Co and constant for all tCo. We quantify that REE (SHE) contributes ≈ 45% to the FLT (≈ 55%) for tCo = 0.4 nm in the reference Cu samples. The important result is that, for the Pt|Co|Al|Pt series, a much larger spin accumulation μREE is required to fit the data with a certain dependence on tCo varying within a length scale of the order of 0.75 nm. Consequently, the FLT contribution from REE (and/or ORE) reaches ≈75% for tCo = 0.55–1.2 nm (≈ 25% from SHE), whereas it contributes only 60% for tCo = 1.4 nm (≈ 40% from SHE).
Finally, we point out that, at this stage, and owing to the same symmetry of torques possibly generated by an ORE13 compared to the one by spin Rashba effect, we cannot distinguish between the two mechanisms and thus cannot discard that a large part of the FLT increase in Al-based samples may indeed originate principally from ORE. Note, however, we can discard the role of the OHE in the Al light element (nonetheless calculated to be small30,51) from our results displayed in Figure 4 on the basis of the same arguments discussed for the spin Hall effect.
In conclusion, we have demonstrated that, in atomically thin Co, the SOT amplitudes, both for damping- and field-like symmetries, vary significantly when a light element such as Al is deposited on top of Co, exceeding the values existing in the literature. In particular, we find a large increase of the field-like component and the corresponding ratio of HFL/HDL at Co|Al|Pt interfaces within the single atomic Co thickness range. This demonstrates the occurrence of interfacial Rashba interactions, leading to significant conversion effects at the Co|Al interface. Beyond the fundamental interest, these results in all-metallic systems in the limit of atomically thin ferromagnets also open a new research direction for CMOS-compatible and cost-effective spinorbitronic based technology.
Acknowledgments
This work has been supported by DARPA TEE program grant (MIPRHR - 0011831554), ANR grant STORM (ANR-22-CE42-0013-02), the FLAG - ERA SographMEM (ANR-15-GRFL-0005) and the Horizon2020 Framework Program of the European Commission, under FETProactive Grant agreement No. 824123 (SKYTOP) (H2020 FET proactive 824123). This research was funded by the French National Research Agency under the project “ORION” ANR-20-CE30-0022-02 and as part of the “Investissements d’Avenir” program (Labex NanoSaclay, reference: SPiCY ANR-10-LABX-0035). N. Sebe benefits from a France 2030 government grant managed by the French National Research Agency (ANR-22-PEPR-0009 Electronique-EMCOM).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.2c05091.
(Detailed analysis of harmonic Hall measurements, measurements of resistivity and estimation of current shunt effects in the each layer of multilayers, theoretical modeling of anomalous Hall effect and spin–orbit torques PDF)
Author Present Address
§ Department of Physics and Center for Advanced Nanoscience, University of California, San Diego La Jolla, CA, 92093, USA
The authors declare no competing financial interest.
Supplementary Material
References
- Soumyanarayanan A.; Reyren N.; Fert A.; Panagopoulos C. Emergent phenomena induced by spin–orbit coupling at surfaces and interfaces. Nature 2016, 539, 509–517. 10.1038/nature19820. [DOI] [PubMed] [Google Scholar]
- Miron I. M.; Garello K.; Gaudin G.; Zermatten P.-J.; Costache M. V.; Auffret S.; Bandiera S.; Rodmacq B.; Schuhl A.; Gambardella P. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 2011, 476, 189–193. 10.1038/nature10309. [DOI] [PubMed] [Google Scholar]
- Liu L.; Lee O. J.; Gudmundsen T. J.; Ralph D. C.; Buhrman R. A. Current-induced switching of perpendicularly magnetized magnetic layers using spin torque from the spin Hall effect. Phys. Rev. Lett. 2012, 109, 096602. 10.1103/PhysRevLett.109.096602. [DOI] [PubMed] [Google Scholar]
- Razavi A.; Wu H.; Shao Q.; Fang C.; Dai B.; Wong K.; Han X.; Yu G.; Wang K. L. Deterministic spin–orbit torque switching by a light-metal insertion. Nano Lett. 2020, 20, 3703–3709. 10.1021/acs.nanolett.0c00647. [DOI] [PubMed] [Google Scholar]
- Manchon A.; Železný J.; Miron I. M.; Jungwirth T.; Sinova J.; Thiaville A.; Garello K.; Gambardella P. Current-induced spin-orbit torques in ferromagnetic and antiferromagnetic systems. Rev. Mod. Phys. 2019, 91, 035004. 10.1103/RevModPhys.91.035004. [DOI] [Google Scholar]
- Wu H.; Nance J.; Razavi S. A.; Lujan D.; Dai B.; Liu Y.; He H.; Cui B.; Wu D.; Wong K.; Sobotkiewich K.; Li X.; Carman G. P.; Wang K. L. Chiral symmetry breaking for deterministic switching of perpendicular magnetization by spin–orbit torque. Nano Lett. 2021, 21, 515–521. 10.1021/acs.nanolett.0c03972. [DOI] [PubMed] [Google Scholar]
- Fert A.; Reyren N.; Cros V. Magnetic skyrmions: advances in physics and potential applications. Nature Reviews Materials 2017, 2, 17031. 10.1038/natrevmats.2017.31. [DOI] [Google Scholar]
- Bychkov Y. A.; Rashba É. I. Properties of a 2D electron gas with lifted spectral degeneracy. Soviet Journal of Experimental and Theoretical Physics Letters 1984, 39, 78. [Google Scholar]
- Mihai Miron I.; Gaudin G.; Auffret S.; Rodmacq B.; Schuhl A.; Pizzini S.; Vogel J.; Gambardella P. Current-driven spin torque induced by the Rashba effect in a ferromagnetic metal layer. Nat. Mater. 2010, 9, 230–234. 10.1038/nmat2613. [DOI] [PubMed] [Google Scholar]
- Manchon A.; Koo H. C.; Nitta J.; Frolov S. M.; Duine R. A. New perspectives for Rashba spin-orbit coupling. Nat. Mater. 2015, 14, 871–882. 10.1038/nmat4360. [DOI] [PubMed] [Google Scholar]
- Edelstein V. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 1990, 73, 233–235. 10.1016/0038-1098(90)90963-C. [DOI] [Google Scholar]
- Ding S.; Ross A.; Go D.; Baldrati L.; Ren Z.; Freimuth F.; Becker S.; Kammerbauer F.; Yang J.; Jakob G.; Mokrousov Y.; Kläui M. Harnessing orbital-to-spin conversion of interfacial orbital currents for efficient spin-orbit torques. Phys. Rev. Lett. 2020, 125, 177201. 10.1103/PhysRevLett.125.177201. [DOI] [PubMed] [Google Scholar]
- Ding S.; Liang Z.; Go D.; Yun C.; Xue M.; Liu Z.; Becker S.; Yang W.; Du H.; Wang C.; Yang Y.; Jakob G.; Kläui M.; Mokrousov Y.; Yang J. Observation of the orbital rashba-edelstein magnetoresistance. Phys. Rev. Lett. 2022, 128, 067201. 10.1103/PhysRevLett.128.067201. [DOI] [PubMed] [Google Scholar]
- Hirsch J. E. Spin Hall effect. Phys. Rev. Lett. 1999, 83, 1834–1837. 10.1103/PhysRevLett.83.1834. [DOI] [Google Scholar]
- Sinova J.; Valenzuela S. O.; Wunderlich J.; Back C. H.; Jungwirth T. Spin Hall effects. Rev. Mod. Phys. 2015, 87, 1213–1260. 10.1103/RevModPhys.87.1213. [DOI] [Google Scholar]
- Sánchez J. C. R.; Vila L.; Desfonds G.; Gambarelli S.; Attané J. P.; De Teresa J. M.; Magén C.; Fert A. Spin-to-charge conversion using Rashba coupling at the interface between non-magnetic materials. Nat. Commun. 2013, 4, 2944. 10.1038/ncomms3944. [DOI] [PubMed] [Google Scholar]
- Taniguchi T.; Yakata S.; Imamura H.; Ando Y. Penetration depth of transverse spin current in ferromagnetic metals. IEEE Trans. Magn. 2008, 44, 2636–2639. 10.1109/TMAG.2008.2003036. [DOI] [Google Scholar]
- Ghosh A.; Auffret S.; Ebels U.; Bailey W. E. Penetration depth of transverse spin current in ultrathin ferromagnets. Phys. Rev. Lett. 2012, 109, 127202. 10.1103/PhysRevLett.109.127202. [DOI] [PubMed] [Google Scholar]
- Stiles M. D.; Zangwill A. Anatomy of spin-transfer torque. Phys. Rev. B 2002, 66, 014407. 10.1103/PhysRevB.66.014407. [DOI] [Google Scholar]
- Haney P. M.; Lee H.-W.; Lee K.-J.; Manchon A.; Stiles M. D. Current induced torques and interfacial spin-orbit coupling: Semiclassical modeling. Phys. Rev. B 2013, 87, 174411. 10.1103/PhysRevB.87.174411. [DOI] [Google Scholar]
- Amin V. P.; Stiles M. D. Spin transport at interfaces with spin-orbit coupling: Phenomenology. Phys. Rev. B 2016, 94, 104420. 10.1103/PhysRevB.94.104420. [DOI] [Google Scholar]
- Dutta S.; Bose A.; Tulapurkar A. A.; Buhrman R. A.; Ralph D. C. Interfacial and bulk spin Hall contributions to fieldlike spin-orbit torque generated by iridium. Phys. Rev. B 2021, 103, 184416. 10.1103/PhysRevB.103.184416. [DOI] [Google Scholar]
- Qiu X.; Narayanapillai K.; Wu Y.; Deorani P.; Yang D.-H.; Noh W.-S.; Park J.-H.; Lee K.-J.; Lee H.-W.; Yang H. Spin-orbit-torque engineering via oxygen manipulation. Nat. Nanotechnol. 2015, 10, 333–338. 10.1038/nnano.2015.18. [DOI] [PubMed] [Google Scholar]
- Emori S.; Nan T.; Belkessam A. M.; Wang X.; Matyushov A. D.; Babroski C. J.; Gao Y.; Lin H.; Sun N. X. Interfacial spin-orbit torque without bulk spin-orbit coupling. Phys. Rev. B 2016, 93, 180402. 10.1103/PhysRevB.93.180402. [DOI] [Google Scholar]
- Amin V. P.; Zemen J.; Stiles M. D. Interface-generated spin currents. Phys. Rev. Lett. 2018, 121, 136805. 10.1103/PhysRevLett.121.136805. [DOI] [PubMed] [Google Scholar]
- Wang W.; Wang T.; Amin V. P.; Wang Y.; Radhakrishnan A.; Davidson A.; Allen S. R.; Silva T. J.; Ohldag H.; Balzar D.; Zink B. L.; Haney P. M.; Xiao J. Q.; Cahill D. G.; Lorenz V. O.; Fan X. Anomalous spin-orbit torques in magnetic single-layer films. Nat. Nanotechnol. 2019, 14, 819–824. 10.1038/s41565-019-0504-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han B.; Zhang B.; Sun S.; Wang B.; Guo Y.; Cao J. The thickness dependence of the field-like spin–orbit torque in heavy metal/CoFeB/MgO heterostructures. J. Appl. Phys. 2021, 130, 213902. 10.1063/5.0068373. [DOI] [Google Scholar]
- DC M.; Grassi R.; Chen J.-Y.; Jamali M.; Reifsnyder Hickey D.; Zhang D.; Zhao Z.; Li H.; Quarterman P.; Lv Y.; Li M.; Manchon A.; Mkhoyan K. A.; Low T.; Wang J.-P. Room-temperature high spin-orbit torque due to quantum confinement in sputtered BixSe1–x) films. Nat. Mater. 2018, 17, 800–807. 10.1038/s41563-018-0136-z. [DOI] [PubMed] [Google Scholar]
- Noël P.; Trier F.; Vicente Arche L. M.; Bréhin J.; Vaz D. C.; Garcia V.; Fusil S.; Barthélémy A.; Vila L.; Bibes M.; Attané J.-P. Non-volatile electric control of spin-charge conversion in a SrTiO3 Rashba system. Nature 2020, 580, 483–486. 10.1038/s41586-020-2197-9. [DOI] [PubMed] [Google Scholar]
- Jo D.; Go D.; Lee H.-W. Gigantic intrinsic orbital Hall effects in weakly spin-orbit coupled metals. Phys. Rev. B 2018, 98, 214405. 10.1103/PhysRevB.98.214405. [DOI] [Google Scholar]
- Kim J.; Go D.; Tsai H.; Jo D.; Kondou K.; Lee H.-W.; Otani Y. Nontrivial torque generation by orbital angular momentum injection in ferromagnetic-metal/Cu/Al2O3 trilayers. Phys. Rev. B 2021, 103, L020407. 10.1103/PhysRevB.103.L020407. [DOI] [Google Scholar]
- Ding S.; Noël P.; Krishnaswamy G. K.; Gambardella P. Unidirectional orbital magnetoresistance in light-metal-ferromagnet bilayers. Phys. Rev. Res. 2022, 4, L032041. 10.1103/PhysRevResearch.4.L032041. [DOI] [Google Scholar]
- Krishnia S.; Haltz E.; Berges L.; Aballe L.; Foerster M.; Bocher L.; Weil R.; Thiaville A.; Sampaio J. a.; Mougin A. Spin-orbit coupling in single-layer ferrimagnets: Direct observation of spin-orbit torques and chiral spin textures. Phys. Rev. Applied 2021, 16, 024040. 10.1103/PhysRevApplied.16.024040. [DOI] [Google Scholar]
- Garello K.; Miron I. M.; Avci C. O.; Freimuth F.; Mokrousov Y.; Blügel S.; Auffret S.; Boulle O.; Gaudin G.; Gambardella P. Symmetry and magnitude of spin–orbit torques in ferromagnetic heterostructures. Nat. Nanotechnol. 2013, 8, 587–593. 10.1038/nnano.2013.145. [DOI] [PubMed] [Google Scholar]
- Figueiredo-Prestes N.; Krishnia S.; Collin S.; Roussigné Y.; Belmeguenai M.; Chérif S. M.; Zarpellon J.; Mosca D. H.; Jaffrès H.; Vila L.; Reyren N.; George J.-M. Magnetization switching and deterministic nucleation in Co/Ni multilayered disks induced by spin–orbit torques. Appl. Phys. Lett. 2021, 119, 032410. 10.1063/5.0050641. [DOI] [Google Scholar]
- Rojas-Sánchez J.-C.; Reyren N.; Laczkowski P.; Savero W.; Attané J.-P.; Deranlot C.; Jamet M.; George J.-M.; Vila L.; Jaffrès H. Spin pumping and inverse spin Hall effect in platinum: The essential role of spin-memory loss at metallic interfaces. Phys. Rev. Lett. 2014, 112, 106602. 10.1103/PhysRevLett.112.106602. [DOI] [PubMed] [Google Scholar]
- Zhang W.; Han W.; Jiang X.; Yang S.-H.; Parkin S. S. P. Role of transparency of platinum-ferromagnet interfaces in determining the intrinsic magnitude of the spin Hall effect. Nat. Phys. 2015, 11, 496–502. 10.1038/nphys3304. [DOI] [Google Scholar]
- Berger A. J.; Edwards E. R. J.; Nembach H. T.; Karis O.; Weiler M.; Silva T. J. Determination of the spin Hall effect and the spin diffusion length of Pt from self-consistent fitting of damping enhancement and inverse spin-orbit torque measurements. Phys. Rev. B 2018, 98, 024402. 10.1103/PhysRevB.98.024402. [DOI] [Google Scholar]
- Zhu L.; Ralph D. C.; Buhrman R. A. Spin-orbit torques in heavy-metal-ferromagnet bilayers with varying strengths of interfacial spin-orbit coupling. Phys. Rev. Lett. 2019, 122, 077201. 10.1103/PhysRevLett.122.077201. [DOI] [PubMed] [Google Scholar]
- Dang T. H.; Barbedienne Q.; To D. Q.; Rongione E.; Reyren N.; Godel F.; Collin S.; George J. M.; Jaffrès H. Anomalous Hall effect in 3d/5d multilayers mediated by interface scattering and nonlocal spin conductivity. Phys. Rev. B 2020, 102, 144405. 10.1103/PhysRevB.102.144405. [DOI] [Google Scholar]
- Rojas-Sánchez J.-C.; Laczkowski P.; Sampaio J.; Collin S.; Bouzehouane K.; Reyren N.; Jaffrès H.; Mougin A.; George J.-M. Perpendicular magnetization reversal in Pt/[Co/Ni]3/Al multilayers via the spin Hall effect of Pt. Appl. Phys. Lett. 2016, 108, 082406. 10.1063/1.4942672. [DOI] [Google Scholar]
- Brataas A.; Bauer G. E.; Kelly P. J. Non-collinear magnetoelectronics. Phys. Rep. 2006, 427, 157–255. 10.1016/j.physrep.2006.01.001. [DOI] [Google Scholar]
- Cosset-Chéneau M.; Vila L.; Zahnd G.; Gusakova D.; Pham V. T.; Grèzes C.; Waintal X.; Marty A.; Jaffrès H.; Attané J.-P. Measurement of the spin absorption anisotropy in lateral spin valves. Phys. Rev. Lett. 2021, 126, 027201. 10.1103/PhysRevLett.126.027201. [DOI] [PubMed] [Google Scholar]
- Zhang S.; Levy P. M.; Fert A. Mechanisms of spin-polarized current-driven magnetization switching. Phys. Rev. Lett. 2002, 88, 236601. 10.1103/PhysRevLett.88.236601. [DOI] [PubMed] [Google Scholar]
- Petitjean C.; Luc D.; Waintal X. Unified drift-diffusion theory for transverse spin currents in spin valves, domain walls, and other textured magnets. Phys. Rev. Lett. 2012, 109, 117204. 10.1103/PhysRevLett.109.117204. [DOI] [PubMed] [Google Scholar]
- Kim K.-W. Spin transparency for the interface of an ultrathin magnet within the spin dephasing length. Phys. Rev. B 2019, 99, 224415. 10.1103/PhysRevB.99.224415. [DOI] [Google Scholar]
- Nikolić B. K.; Dolui K.; Petrović M. D.; Plecháč P.; Markussen T.; Stokbro K.. First-principles quantum transport modeling of spin-transfer and spin-orbit torques in magnetic multilayers. In Handbook of Materials Modeling: Applications: Current and Emerging Materials; Andreoni W., Yip S., Eds.; Springer International Publishing: Cham, 2018; pp 1–35. [Google Scholar]
- Han B.; Zhang B.; Sun S.; Wang B.; Guo Y.; Cao J. The thickness dependence of the field-like spin–orbit torque in heavy metal/CoFeB/MgO heterostructures. J. Appl. Phys. 2021, 130, 213902. 10.1063/5.0068373. [DOI] [Google Scholar]
- Dang T. H. J.; Hawecker E.; Rongione G.; Baez Flores D. Q.; Rojas-Sanchez J. C.; Nong H.; Mangeney J.; Tignon J.; Godel F.; Collin S.; Seneor P.; Bibes M.; Fert A.; Anane M.; George J.-M.; Vila L.; Cosset-Cheneau M.; Dolfi D.; Lebrun R.; Bortolotti P.; Belashchenko K.; Dhillon S.; Jaffrès H. Ultrafast spin-currents and charge conversion at 3d-5d interfaces probed by time-domain terahertz spectroscopy. Applied Physics Reviews 2020, 7, 041409. 10.1063/5.0022369. [DOI] [Google Scholar]
- Hawecker J.; Dang T.-H.; Rongione E.; Boust J.; Collin S.; George J.-M.; Drouhin H.-J.; Laplace Y.; Grasset R.; Dong J.; Mangeney J.; Tignon J.; Jaffrès H.; Perfetti L.; Dhillon S. Spin injection efficiency at metallic interfaces probed by THz emission spectroscopy. Advanced Optical Materials 2021, 9, 2100412. 10.1002/adom.202100412. [DOI] [Google Scholar]
- Salemi L.; Oppeneer P. M. First-principles theory of intrinsic spin and orbital Hall and Nernst effects in metallic monoatomic crystals. Phys. Rev. Mater. 2022, 6, 095001. 10.1103/PhysRevMaterials.6.095001. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.