Causal isotonic calibration for heterogeneous treatment effects

Abstract

We propose causal isotonic calibration, a novel nonparametric method for calibrating predictors of heterogeneous treatment effects. In addition, we introduce a novel data-efficient variant of calibration that avoids the need for hold-out calibration sets, which we refer to as cross-calibration. Causal isotonic cross-calibration takes cross-fitted predictors and outputs a single calibrated predictor obtained using all available data. We establish under weak conditions that causal isotonic calibration and cross-calibration both achieve fast doubly-robust calibration rates so long as either the propensity score or outcome regression is estimated well in an appropriate sense. The proposed causal isotonic calibrator can be wrapped around any black-box learning algorithm to provide strong distribution-free calibration guarantees while preserving predictive performance.

1. Introduction

Estimation of causal effects via both randomized experiments and observational studies is critical to understanding the effects of interventions and informing policy. Moreover, it is often the case that understanding treatment effect heterogeneity can provide more insights than overall population effects (Obermeyer & Emanuel, 2016; Athey, 2017). For instance, a study of treatment effect heterogeneity can help elucidate the mechanism of an intervention, design policies targeted to subpopulations who can most benefit (Imbens & Wooldridge, 2009), and predict the effect of interventions in populations other than the ones in which they were developed. These necessities have arisen in a wide range of fields, such as marketing (Devriendt et al., 2018), the social sciences (Imbens & Wooldridge, 2009), and the health sciences (Kent et al., 2018). For example, in the health sciences, heterogeneous treatment effects (HTEs) are of high importance to understanding and quantifying how certain exposures or interventions affect the health of various subpopulations (Dahabreh et al., 2016; Lee et al., 2020). Potential applications include prioritizing treatment to certain sub-populations when treatment resources are scarce, or individualizing treatment assignments when the treatment can have no effect (or even be harmful) in certain subpopulations (Dahabreh et al., 2016). As an example, treatment assignment based on risk scores has been used to provide clinical guidance in cardiovascular disease prevention (Lloyd-Jones et al., 2019) and to improve decision-making in oncology (Collins & Varmus, 2015; Cucchiara et al., 2018).

A wide range of statistical methods are available for assessing HTEs, with recent examples including Wager & Athey (2018), Carnegie et al. (2019), Lee et al. (2020), Yadlowsky et al. (2021), and Nie & Wager (2021), among others. In particular, many methods, including Imbens & Wooldridge (2009) and Dominici et al. (2020), scrutinize HTEs via conditional average treatment effects (CATEs). The CATE is the difference in the conditional mean of the counterfactual outcome corresponding to treatment versus control given covariates, which can be defined at a group or individual level. When interest lies in predicting treatment effect, the CATE can be viewed as the oracle predictor of the individual treatment effect (ITE) that can feasibly be learned from data. Optimal treatment rules have been derived based on the sign of the CATE estimator (Murphy, 2003; Robins, 2004), with more recent works incorporating the use of flexible CATE estimators (Luedtke & van der Laan, 2016). Thus, due to its wide applicability and scientific relevance, CATE estimation has been of great interest in statistics and data science.

Regardless of its quality as a proxy for the true CATE, it is generally accepted that predictions from a given treatment effect predictor can still be useful for decision-making. However, theoretical guarantees for rational decision-making using a given treatment effect predictor typically hinge on the predictor being a good approximation of the true CATE. Accurate CATE estimation can be challenging because the nuisance parameters involved can be non-smooth, high-dimensional, or otherwise difficult to model correctly. Additionally, a CATE estimator obtained from samples of one population, regardless of its quality, may not generalize well to different target populations (Frangakis, 2009). Usually, CATE estimators (often referred to as learners) build upon estimators of the conditional mean outcome given covariates and treatment level (i.e., outcome regression), the probability of treatment given covariates (i.e., propensity score), or both. For instance, plug-in estimators such as those studied in Künzel et al. (2019) — so-called T-learners — are obtained by taking the difference between estimators of the outcome regression obtained separately for each treatment level. T-learners can suffer in performance because they rely on estimation of nuisance parameters that are at least as non-smooth or high-dimensional as the CATE, and are prone to the misspecification of involved outcome regression models; these issues can result in slow convergence or inconsistency of the CATE estimator. Doubly-robust and Neyman-orthogonal CATE estimation strategies like the DR-learner and R-learner (Wager & Athey, 2018; Foster & Syrgkanis, 2019; Nie & Wager, 2021; Kennedy, 2020) mitigate some of these issues by allowing for comparatively fast CATE estimation rates even when nuisance parameters are estimated at slow rates. However, while less sensitive to the learning complexity of the nuisance parameters, their predictive accuracy in finite-samples still relies on potentially strong smoothness assumptions on the CATE. Even when the CATE is estimated consistently, predictions based on statistical learning methods often produce biased predictions that overestimate or underestimate the true CATE in the extremes of the predicted values (van Klaveren et al., 2019; Dwivedi et al., 2020). For example, the ‘pooled cohort equations’ (Goff et al., 2014) risk model used to predict cardiovascular disease has been found to underestimate risk in patients with lower socioeconomic status or chronic inflammatory diseases (Lloyd-Jones et al., 2019). The implications of biased treatment effect predictors are profound when used to guide treatment decisions and can range from harmful use to withholding of treatment (van Calster et al., 2019).

Due to the consequence of treatment decision-making, it is essential to guarantee, under minimal assumptions, that treatment effect predictions are representative in magnitude and sign of the actual effects, even when the predictor is a poor approximation of the CATE. In prediction settings, the aim of bestowing these properties on a given predictor is commonly called calibration. A calibrated treatment effect predictor has the property that the average treatment effect among individuals with identical predictions is close to their shared prediction value. Such a predictor is more robust against over-or-under estimation of the CATE in extremes of predicted values. It also has the property that the best predictor of the ITE given the predictor is the predictor itself, which facilitates transparent treatment decision-making. In particular, the optimal treatment rule (Murphy, 2003) given only information provided by the predictor is the one that assigns the treatment predicted to be most beneficial. Consequently, the rule implied by a perfectly calibrated predictor is at least as favorable as the best possible static treatment rule that ignores HTEs. While complementing one another, the aims of calibration and prediction are fundamentally different. For instance, a constant treatment effect predictor can be well-calibrated even though it is a poor predictor of treatment effect heterogeneity (Gupta et al., 2020). In view of this, calibration methods are typically designed to be wrapped around a given black-box prediction pipeline to provide strong calibration guarantees while preserving predictive performance, thereby mitigating several prediction challenges mentioned previously.

In the machine learning literature, calibration has been widely used to enhance prediction models for classification and regression (Bella et al., 2010). However, due to the comparatively little research on calibration of treatment effect predictors, such benefits have not been realized to the same extent in the context of heterogeneous treatment effect prediction. Several works have contributed to addressing this gap in the literature. Brooks et al. (2012) propose a targeted (or debiased) machine learning framework (van der Laan & Rose, 2011) for within-bins calibration that could be applied to the CATE setting. Zhang et al. (2016) and Josey et al. (2022) consider calibration of marginal treatment effect estimates for new populations but do not consider CATEs. Dwivedi et al. (2020) consider estimating calibration error of CATE predictors for subgroup discovery using randomized experimental data. Chernozhukov et al. (2018) and Leng & Dimmery (2021) propose CATE methods for linear calibration, a weaker form of calibration, in randomized experiments. For causal forests, Athey & Wager (2019) evaluate model calibration using a doubly-robust estimator of the ATE among observations above or below the median predicted CATE. Lei & Candès (2021) propose conformal inference methods for constructing calibrated prediction intervals for the ITE from a given predictor but do not consider calibration of the predictor itself. Xu & Yadlowsky (2022) propose a nonparametric doubly-robust estimator of the calibration error of a given treatment effect predictor, which could be used to detect uncalibrated predictors. Our work builds upon the above works by providing a nonparametric doubly-robust method for calibrating treatment effect predictors in general settings.

This paper is organized as follows. In Section 2, we introduce our notation and formally define calibration. There we also provide an overview of traditional calibration methods. In Section 3, we outline our proposed approach, and we describe its theoretical properties in Section 4. In Section 5, we examine the performance of our method in simulation studies. We conclude with a discussion of our proposed approach in Section 6.

2. Statistical setup

2.1. Notation and definitions

Suppose we observe $n$ independent and identically distributed realizations of data unit $O≔(W,A,Y)$ drawn from a distribution $P$, where $W\in 𝒲\subset {\mathbb{R}}^d$ is a vector of baseline covariates, $A\in \{0,1\}$ is a binary indicator of treatment, and $Y\in 𝒴\subset \mathbb{R}$ is an outcome. For instance, $W$ can include a patient’s demographic characteristics and medical history, $A$ can indicate whether an individual is treated (1) or not (0), and $Y$ could be a binary indicator of a successful clinical outcome. We denote by ${𝒟}_n≔\{O_1,O_2,\dots ,O_n\}$ the observed dataset, with $O_i≔(W_i,A_i,Y_i)$ representing the observation on the $i\mathrm{th}$ study unit.

For covariate value $w\in 𝒲$ and treatment level $a\in \{0,1\}$, we denote by ${\pi }_0(w)≔P(A=1\mid W=w)$ the propensity score and by ${\mu }_0(a,w)≔E(Y\mid A=a,W=w)$ the outcome regression. The individual treatment effect is $Y_1-Y_0$, where $Y_a$ represents the potential outcome obtained by setting $A=a$. Without loss of generality, we assume that higher values of $Y_1-Y_0$ are desirable. We also assume that the contrast ${\tau }_0(w)≔{\mu }_0(1,w)-{\mu }_0(0,w)$ equals the true CATE, $E(Y_1-Y_0\mid W=w)$, which holds under certain causal assumptions (Rubin, 1974). Throughout, we denote by $\Vert \cdot \Vert$ the $L^2(P)$ norm, that is, ${\Vert f\Vert }^2=\int {[f(w)]}^{2}d{P}_W(w)$ for any given $P_W$-square integrable function $f:𝒲\in \mathbb{R}$, where $P_W$ is the marginal distribution of $W$ implied by $P$. We deliberately take as convention that the median median $\{x_1,x_2,\dots ,x_k\}$ of a set $\{x_1,x_2,\dots ,x_k\}$ equals the ${\lfloor k∕2\rfloor }^{\mathit{th}}$ order statistic of this set, where $\lfloor k∕2\rfloor ≔\max \{z\in \mathbb{N}:z\le k∕2\}$.

Let $\tau :𝒲\in \mathbb{R}$ be a treatment effect predictor, that is, a function that maps a realization $w$ of $W$ to a treatment effect prediction $\tau (w)$. In practice, $\tau$ can be obtained using any black-box algorithm. Below, we first consider $\tau$ to be fixed, though we later address situations in which $\tau$ is learned from the data used for subsequent calibration. We define the calibration function ${\gamma }_0(\tau ,w)≔E[Y_1-Y_0\mid \tau (W)=\tau (w)]$ as the conditional mean of the individual treatment effect given treatment effect score value $\tau (w)$. By the tower property, ${\gamma }_0(\tau ,w)≔E[{\tau }_0(W)\mid \tau (W)=\tau (w)]$, and so, expectations only involving ${\gamma }_0(\tau ,W)$ and other functions of $W$ can be taken with respect to $P_W$.

The solution to an isotonic regression problem is typically nonunique. Throughout this text, we follow Groeneboom & Lopuhaa (1993) in taking the unique càdlàg piece-wise constant solution of the isotonic regression problem that can only take jumps at observed values of the predictor.

2.2. Measuring calibration and the calibration-distortion decomposition

Various definitions of risk predictor calibration have been proposed in the literature — see Gupta & Ramdas (2021) and Gupta et al. (2020) for a review. Here, we outline our definition of calibration and its rationale. Given a treatment effect predictor $\tau$, the best predictor of the individual treatment effect in terms of MSE is $w\mapsto {\gamma }_0(\tau ,w)≔E[Y_1-Y_0\mid \tau (W)=\tau (w)]$. By the law of total expectation, this predictor has the property that, for any interval $[a,b)$,

$$E\{[{\tau }_0(W)-{\gamma }_0(\tau ,W)]I({\gamma }_0(\tau ,W)\in [a,b))\}=0.$$ (1)

Equation 1 indicates that ${\gamma }_0(\tau ,\cdot )$ is perfectly calibrated on $[a,b)$. Therefore, when a given predictor $\tau$ is such that $\tau (W)={\gamma }_0(\tau ,W)$ with $P$-probability one, $\tau$ is said to be perfectly calibrated (Gupta et al., 2020) for the CATE — for brevity, we omit “for the CATE” hereafter when the type of calibration being referred to is clear from context.

In general, perfect calibration cannot realistically be achieved in finite samples. A more modest goal is for the predictor $\tau$ to be approximately calibrated in that $\tau (w)$ is close to ${\gamma }_0(\tau ,w)$ across all covariate values $w\in 𝒲$. This naturally suggests the calibration measure:

$$CAL(\tau )≔\int {[{\gamma }_0(\tau ,w)-\tau (w)]}^{2}d{P}_W(w).$$ (2)

This measure, referred to as the ${\ell }_2$-expected calibration error, arises both in prediction (Gupta et al., 2020) and in assessment of treatment effect heterogeneity (Xu & Yadlowsky, 2022). We note that $\mathrm{CAL}(\tau )$ is zero if $\tau (w)$ is perfectly calibrated. Additionally, averaging in $\mathrm{CAL}(\tau )$ with respect to measures other than $P_W$ could be more relevant in certain applications; such cases can occur, for instance, when there is a change of population that results in covariate shift and we are interested in measuring how well $\tau$ is calibrated in the new population.

Interestingly, the above calibration measure plays a role in a decomposition of the mean squared error (MSE) between the treatment predictor and the true CATE, in that

$$\mathrm{MSE}(\tau )≔{\Vert {\tau }_0-\tau \Vert }^2=\mathrm{CAL}(\tau )+\mathrm{DIS}(\tau ),$$ (3)

with $\mathrm{DIS}(\tau )≔E\{\mathit{var}[{\tau }_0(W)\mid \tau (W)]\}$ a quantity we term the distortion of $\tau$. We refer to the above as a calibration-distortion decomposition of the MSE. A consequence of the calibration-distortion decomposition is that MSE-consistent CATE estimators are also calibrated asymptotically. However, particularly in settings where the covariates are high-dimensional or the CATE is nonsmooth, the calibration error rate for such predictors can be arbitrarily slow — this is discussed further after Theorem 4.6.

To interpret $\mathrm{DIS}(\tau )$, we find it helpful to envision a scenario in which a distorted message is passed between two persons. The goal is for Person 2 to discern the value of ${\tau }_0(w)$, where the value of $w\in 𝒲$ is only known to Person 1. Person 1 transmits $w$, which is then distorted through a function $\tau$ and received by Person 2. Person 2 knows the functions $\tau$ and ${\tau }_0$, and may use this information to try to discern ${\tau }_0(w)$. If $\tau$ is one-to-one, ${\tau }_0(w)$ can be discerned by simply applying ${\tau }_0\circ {\tau }^{-1}$ to the received message $\tau (w)$. More generally, whenever there exists a function $f$ such that ${\tau }_0=f\circ \tau$, Person 2 can recover the value of ${\tau }_0(w)$. For example, if $\tau ={\tau }_0$ then $f$ is the identity function. If no such function $f$ exists, it may not be possible for Person 2 to recover the value of ${\tau }_0(w)$. Instead, they may predict ${\tau }_0(w)$ based on $\tau (w)$ via ${\gamma }_0(\tau ,w)$. Averaged over $W\sim P_W$, the MSE of this approach is precisely $\mathrm{DIS}(\tau )$. See Equation 3 in Kuleshov & Liang (2015) for a related decomposition of $E[{\{Y-\tau (X)\}}^2]=\mathrm{MSE}(\tau )+E[{\{Y-{\tau }_0(X)\}}^2]$ derived in the context of probability forecasting.

The calibration-distortion decomposition shows that, at a given level of distortion, better-calibrated treatment effect predictors have lower MSE for the true CATE function. We will explore this fact later in this work when showing that, in addition to improving calibration, our proposed calibration procedure can improve the MSE of CATE predictors.

2.3. Calibrating predictors: desiderata and classical methods

In most calibration methods, the key goal is to find a function $\theta :\mathbb{R}\to \mathbb{R}$ of a given predictor $\tau$ such that $\mathrm{CAL}(\theta \circ \tau )<\mathrm{CAL}(\tau )$, where $\theta \circ \tau$ refers to the composed predictor $w\mapsto \theta (\tau (w))$. A mapping $\theta$ that pursues this objective is referred to as a calibrator. Ideally, a calibrator ${\theta }_n$ for $\tau$ constructed from the dataset ${𝒟}_n$ should satisfy the following desiderata:

Property 1:

$\mathrm{CAL}({\theta }_n\circ \tau )$ tends to zero quickly as $n$ grows;

Property 2:

${\theta }_n\circ \tau$ and $\tau$ are comparably predictive of ${\tau }_0$.

Property 1 states the primary objective of a calibrator, that is, to yield a well-calibrated predictor. Property 2 requires that the calibrator not destroy the predictive power of the initial predictor in the pursuit of Property 1, which would occur if the calibration term in decomposition (3) were made small at the cost of dramatic inflation of the distortion term.

In the traditional setting of classification and regression, a natural aim is to learn, for $a\in \{0,1\}$, a predictor $w\mapsto {\nu }^a(w)$ of the outcome $Y$ among individuals with treatment $A=a$. The best possible such predictor is given by the treatment-specific outcome regression $w\mapsto {\mu }_0(a,w)$. For $a\in \{0,1\}$, ${\nu }^{(a)}$ is said to be calibrated for the outcome regression if ${\nu }^{(a)}(w)\approx E(Y\mid {\nu }^{(a)}(W)={\nu }^{(a)}(w))$, $A=a$ for $P_0$-almost every $w$. Such a calibrated predictor can be obtained using existing calibration methods for regression (Huang et al., 2020), which we review in the next paragraph. It is natural to wonder, then, whether existing calibration approaches can be directly used to calibrate for the CATE. As a concrete example, given predictors ${\nu }^{(1)}$ and ${\nu }^{(0)}$ of ${\mu }_0(1,\cdot )$ and ${\mu }_0(0,\cdot )$, a natural CATE predictor is the T-learner $\tau ≔{\nu }^{(1)}-{\nu }^{(0)}$. However, even if ${\nu }^{(1)}$ and ${\nu }^{(0)}$ are calibrated for their respective outcome regressions, the predictor $\tau$ can still be poorly calibrated for the CATE. Indeed, in settings with treatment-outcome confounding, T-learners can be poorly calibrated when the calibrated predictors ${\nu }^{(1)}$ and ${\nu }^{(0)}$ are poor approximations of their respective outcome regressions. As an extreme example, suppose that ${\nu }^{(a)}$ equals the constant predictor $w\mapsto E(Y\mid A=a)$ for $a\in \{0,1\}$, which is perfectly calibrated for the outcome regression. Then, the corresponding T-learner $\tau (\cdot )=E(Y\mid A=1)-E(Y\mid A=0)$ typically has poor calibration for the CATE in observational settings.

In classification and regression settings (Huang et al., 2020), the most commonly used calibration methods include Platt’s scaling (Platt et al., 1999), histogram binning (Zadrozny & Elkan, 2001), Bayesian binning into quantiles (Naeini et al., 2015), and isotonic calibration (Zadrozny & Elkan, 2002; Niculescu-Mizil & Caruana, 2005). Broadly, Platt’s scaling is designed for binary outcomes and uses the estimated values of the predictor to fit the logistic regression model

$$\mathrm{logit}P(Y=1\mid \tau (W)=t)=\alpha +\beta t$$

with $\alpha$, $\beta \in \mathbb{R}$. While it typically satisfies Property 2, Platt’s scaling is based on strong parametric assumptions and, as a consequence, may lead to predictions with significant calibration error, even asymptotically (Gupta et al., 2020). Nevertheless, Platt’s scaling may be preferred when limited data is available. Histogram binning, also known as quantile binning, involves partitioning the sorted values of the predictor into a fixed number of bins. Given an initial prediction, the calibrated prediction is given by the empirical mean of the observed outcome values within the corresponding prediction bin. A significant limitation of histogram binning is that it requires a priori specification of the number of bins. Selecting too few bins can significantly degrade the predictive power of the calibrated predictor, whereas selecting too many bins can lead to poor calibration. Bayesian binning improves upon histogram binning by considering multiple binning models and their combinations; nevertheless, it still suffers from the need to pre-specify binning models and prior distributions.

Isotonic calibration is a histogram binning method that learns the bins from data using isotonic regression, a nonparametric method traditionally used for estimating monotone functions (Barlow & Brunk, 1972; Martino et al., 2019; Huang et al., 2020). Specifically, the bins are selected by minimizing an empirical MSE criterion under the constraint that the calibrated predictor is a nondecreasing monotone transformation of the original predictor. Isotonic calibration is motivated by the heuristic that, for a good predictor $\tau$, the calibration function ${\gamma }_0(\tau ,\cdot )$ should be approximately monotone as a function of $\tau$. For instance, when $\tau ={\tau }_0$, the map ${\tau }_0\mapsto {\gamma }_0({\tau }_0,\cdot )={\tau }_0$ is the identity function. Despite its popularity and strong performance in practice (Zadrozny & Elkan, 2002; Niculescu-Mizil & Caruana, 2005; Gupta & Ramdas, 2021), to date, whether isotonic calibration satisfies distribution-free calibration guarantees remains an open question (Gupta, 2022). In this work, we will show that isotonic calibration satisfies a distribution-free calibration guarantee in the sense of Property 1. We further establish that Property 2 holds, in that the isotonic selection criterion ensures that the calibrated predictor is at least as predictive as the original predictor up to negligible error.

3. Causal isotonic calibration

In real-world experiments, Dwivedi et al. (2020) found empirically that state-of-the-art CATE estimators tend to be poorly calibrated. However, strikingly, the authors found that such CATE predictors can often still correctly rank the average treatment effect among subgroups defined by bins of the predicted effects. These findings support the heuristic that the calibration function ${\gamma }_0({\tau }_0,\cdot )$ is often approximately monotone as a function of the predictor $\tau$. This heuristic makes extending isotonic calibration to the CATE setting especially appealing since the monotonicity constraint ensures that the calibrated predictions preserve the (non-strict) ranking of the original predictions.

Inspired by isotonic calibration, we propose a doubly-robust calibration method for treatment effects, which we refer to as causal isotonic calibration. Causal isotonic calibration takes a given predictor trained on some dataset and performs calibration using an independent (or hold-out) dataset. Mechanistically, causal isotonic calibration first automatically learns uncalibrated regions of the given predictor. Calibrated predictions are then obtained by consolidating individual predictions within each region into a single value using a doubly-robust estimator of the ATE. In addition, we introduce a novel data-efficient variant of calibration which we refer to as cross-calibration. In contrast with the standard calibration approach, causal isotonic cross-calibration takes cross-fitted predictors and outputs a single calibrated predictor obtained using all available data. Our methods can be implemented using standard isotonic regression software.

Let $\tau$ be a given treatment effect predictor assumed, for now, to have been built using an external dataset, and suppose that ${𝒟}_n$ is the available calibration dataset. In general, we can calibrate the predictor $\tau$ using regression-based calibration methods by employing an appropriate surrogate outcome for the CATE. For both experimental and observational settings, a surrogate outcome with favorable efficiency and robustness properties is the pseudo-outcome ${\chi }_0(O)$ defined via the mapping

$${\chi }_0:o\mapsto {\tau }_0(w)+\frac{a-{\pi }_0(w)}{{\pi }_0(w)[1-{\pi }_0(w)]}[y-{\mu }_0(a,w)],$$ (4)

with $o≔(w,a,y)$ representing a realization of the data unit. This pseudo-outcome has been used as surrogate for the CATE in previous methods for estimating ${\tau }_0$, including the DR-learner (Luedtke & van der Laan, 2016; Kennedy, 2020). If ${\chi }_0$ were known, an external predictor $\tau$ could be calibrated using ${𝒟}_n$ by isotonic regression of the pseudo-outcomes ${\chi }_0(O_1),{\chi }_0(O_2),\dots ,{\chi }_0(O_n)$ onto the calibration sample predictions $\tau (W_1),\tau (W_2),\dots ,\tau (W_n)$. However, ${\chi }_0$ depends on ${\pi }_0$ and ${\mu }_0$, which are usually unknown and must be estimated.

A natural approach for calibrating treatment effect predictors using isotonic regression is as follows. First, define ${\chi }_n$ as the estimated pseudo-outcome function based on estimates ${\mu }_n$ and ${\pi }_n$ derived from ${𝒟}_n$. Then, a calibrated predictor is given by ${\theta }_n\circ \tau$, where the calibrator ${\theta }_n$ is found via isotonic regression as a minimizer over ${ℱ}_{\mathit{iso}}≔\{\theta :\mathbb{R}\to \mathbb{R};\theta \text{is monotone nondecreasing}\}$ of the empirical least-squares risk function

$$\theta \mapsto \frac{1}{n}\sum _{i=1}^n{[{\chi }_n(O_i)-\theta \circ \tau (W_i)]}^2.$$

However, this optimization problem requires a double use of ${𝒟}_n$: once, for creating the pseudo-outcomes ${\chi }_n(O_i)$, and a second time, in the calibration step. This double usage could lead to over-fitting (Kennedy, 2020), and so we recommend obtaining pseudo-outcomes via sample splitting or cross-fitting. Sample splitting involves randomly partitioning ${𝒟}_n$ into ${ℰ}_m\cup {𝒞}_{\ell }$, with ${ℰ}_m$ used to estimate ${\mu }_0$ and ${\pi }_0$, and ${𝒞}_{\ell }$ used to carry out the calibration step — see Algorithm 1 for details. Cross-fitting improves upon sample splitting by using all available data to estimate ${\mu }_0$ and ${\pi }_0$ as well as to carry out the calibration step. Algorithm 4, outlined in Appendix B, is the cross-fitted variant of Algorithm 1.

Algorithm 1 Causal isotonic calibration

$$\begin{array}{cc}\hfill & \mathrm{Require}:\text{predictor}\tau ,\text{training data}{ℰ}_m,\text{calibration data}{𝒞}_{\ell }\hfill \\ \hfill & 1:\text{obtain estimate}{\chi }_m\text{of}{\chi }_0\text{using}{ℰ}_m;\hfill \\ \hfill & 2:\text{perform isotonic regression to find}\hfill \\ \hfill & {\theta }_n^{\ast }=\underset{\theta \in {ℱ}_{\mathit{iso}}}{\mathrm{argmin}}\sum _{i\in {ℐ}_{ell}}{[{\chi }_m(O_i)-\theta \circ \tau (W_i)]}^2\hfill \\ \hfill & \text{with}{ℐ}_{ell}\text{the set of indices for observations in}{𝒞}_{\ell }\subset {𝒟}_n;\hfill \\ \hfill & 3:\text{set}{\tau }_n^{\ast }={\theta }_n^{\ast }\circ \tau .\hfill \\ \hfill & \mathbf{Ensure}:{\tau }_n^{\ast }\hfill \end{array}$$

In practice, the external dataset used to construct $\tau$ for input into Algorithm 1 is likely to arise from a sample splitting approach wherein a large dataset is split in two, with one half used to estimate $\tau$ and the other to calibrate it. This naturally leads to the question of whether there is an approach that fully utilizes the entire dataset for both fitting an initial estimate of ${\tau }_0$ and calibration. Algorithm 2 describes causal isotonic cross-calibration, which provides a means to accomplish precisely this. In brief, this approach applies Algorithm 1 a total of $k$ times on different splits of the data, where for each split an initial predictor of ${\tau }_0$ is fitted based on the first subset of the data and this predictor is calibrated using the second subset. These $k$ calibrated predictors are then aggregated via a pointwise median. Interestingly, other aggregation strategies, such as pointwise averaging, can lead to uncalibrated predictions (Gneiting & Ranjan, 2013; Rahaman & Thiery, 2020). A computationally simpler variant of Algorithm 2 is given by Algorithm 3. In this implementation, a single isotonic regression is performed using the pooled out-of-fold predictions; this variant may also yield more stable performance in finite-samples than Algorithm 2 — see Section 2.1.2 of Xu & Yadlowsky (2022) for a related discussion in the context of debiased machine learning.

Algorithm 2 Causal isotonic cross-calibration (unpooled)

$$\begin{array}{cc}\hfill & \mathrm{Require}:\text{dataset}{𝒟}_n,\#\text{of cross-fitting splits}k\hfill \\ \hfill & 1:\text{partition}{𝒟}_n\text{into datasets}{𝒞}^{(1)},{𝒞}^{(2)},\dots ,{𝒞}^{(k)};\hfill \\ \hfill & 2:\mathbf{for}s=1,2,\dots ,k\mathbf{do}\hfill \\ \hfill & 3:\text{set}{ℰ}^{(s)}≔{𝒟}_n\backslash {𝒞}^{(s)};\hfill \\ \hfill & 4:\text{get initial predictor}{\tau }_{n,s}\text{of}{\tau }_0\text{using}{ℰ}^{(s)};\hfill \\ \hfill & 5:\text{get calibrated predictor}{\tau }_{n,s}^{\ast }\text{via Alg.}1\text{using predictor}\hfill \\ \hfill & {\tau }_{n,s},\text{training data}{ℰ}^{(s)},\text{and calibration data}{𝒞}^{(s)};\hfill \\ \hfill & 6:\mathbf{end}\mathbf{for}\hfill \\ \hfill & 7:\text{set}{\tau }_n^{\ast }:w\mapsto \text{median}\{{\tau }_{n,1}^{\ast }(w),{\tau }_{n,2}^{\ast }(w),\dots ,{\tau }_{n,k}^{\ast }(w)\}.\hfill \\ \hfill & \mathbf{Ensure}:{\tau }_n^{\ast }\hfill \end{array}$$

4. Large-sample theoretical properties

We now present theoretical results for causal isotonic calibration. We first obtain results for causal isotonic calibration described by Algorithm 1 applied to a fixed predictor $\tau$. We also establish MSE guarantees for the calibrated predictor and argue that the proposed calibrator satisfies Properties 1 and 2. We then extend our results to the procedure described by Algorithm 2.

For ease of presentation, we only establish theoretical results for the case where the nuisance estimators are obtained using sample splitting. With minor modifications, our results can be readily extended to cross-fitting by arguing along the lines of Newey & Robins (2018). In that spirit, we assume that the available data ${𝒟}_n$ is the union of a training dataset ${ℰ}_m$ and a calibration dataset ${𝒞}_{\ell }$ of sizes $m$ and $\ell$, respectively, with $n=m+\ell$ and $\min \{m,\ell \}\to \infty$ as

Algorithm 3 Causal isotonic cross-calibration (pooled)

$$\begin{array}{cc}\hfill & \mathrm{Require}:\text{dataset}{𝒟}_n,\#\text{of cross-fitting splits}k\hfill \\ \hfill & 1:\text{partition}{𝒟}_n\text{into datasets}{𝒞}^{(1)},{𝒞}^{(2)},\dots ,{𝒞}^{(k)};\hfill \\ \hfill & 2:\mathbf{for}s=1,2,\dots ,k\mathbf{do}\hfill \\ \hfill & 3:\text{let}j(i)=s\text{for each}i\in {𝒞}^{(s)};\hfill \\ \hfill & 4:\text{set}{ℰ}^{(s)}≔{𝒟}_n\backslash {𝒞}^{(s)};\hfill \\ \hfill & 5:\text{get estimate predictor}{\chi }_{n,s}\text{of}{\chi }_0\text{from}{ℰ}^{(s)};\hfill \\ \hfill & 6:\text{get initial predictor}{\tau }_{n,s}\text{of}{\tau }_0\text{using}{ℰ}^{(s)};\hfill \\ \hfill & 7:\mathbf{end}\mathbf{for}\hfill \\ \hfill & 8:\text{perform isotonic regression using pooled out-of-fold predictions to find}\hfill \\ \hfill & {\theta }_n^{\ast }=\underset{\theta \in {ℱ}_{\mathit{iso}}}{\mathrm{argmin}}\sum _{i=1}^n{[{\chi }_{n,j(i)}(O_i)-\theta \circ {\tau }_{n,j(i)}(W_i)]}^2\hfill \\ \hfill & 9:\text{set}{\tau }_{n,s}^{\ast }≔{\theta }_n^{\theta }\circ {\tau }_{n,s}\text{for}s=1,2,\dots ,k;\hfill \\ \hfill & 10:\text{set}{\tau }_n^{\ast }:w\mapsto \text{median}\{{\tau }_{n,1}^{\ast }(w),{\tau }_{n,2}^{\ast }(w),\dots ,{\tau }_{n,k}^{\ast }(w)\}.\hfill \\ \hfill & \mathbf{Ensure}:{\tau }_n^{\ast }\hfill \end{array}$$

$n\to \infty$. Let ${\tau }_n^{\ast }$ be the calibrated predictor obtained from Algorithm 1 using $\tau$, ${ℰ}_m$ and ${𝒞}_{\ell }$ where the estimated pseudo-outcome ${\chi }_m$ is obtained by substituting estimates ${\pi }_m$ and ${\mu }_m$ of ${\pi }_0$ and ${\mu }_0$ into (4).

Condition 4.1 (bounded outcome support). The $P$-support $𝒴$ of $Y$ is a uniformly bounded subset of $\mathbb{R}$.

Condition 4.2 (positivity). There exists $ϵ>0$ such that $P(ϵ<{\pi }_{0}W)<1-ϵ)=1$.

Condition 4.3 (independence). Estimators ${\pi }_m$ and ${\mu }_m$ do not use any data in ${𝒞}_{\ell }$.

Condition 4.4 (bounded range of ${\pi }_m$, ${\mu }_m$, $\tau$). There exist $0<\eta$, $\alpha <\infty$ such that $P(\eta <{\pi }_m(W)<1-\eta )=P(\mid {\mu }_m(A,W)\mid <\alpha )=P(\mid \tau (W)\mid <\alpha )=1$ for $m=1,2,\dots$

Condition 4.5 (bounded variation of best predictor). The function ${\theta }_0:\mathbb{R}\mapsto \mathbb{R}$ such that ${\theta }_0\circ \tau ={\gamma }_0(\tau ,\cdot )$ is of bounded total variation.

It is worth noting that the initial predictor and its best monotone transformation can be arbitrarily poor CATE predictors. Condition 4.1 holds trivially when outcomes are binary, but even continuous outcomes are often known to satisfy fixed bounds (e.g., physiologic bound, limit of detection of instrument) in applications. Condition 4.2 is standard in causal inference and requires that all individuals have a positive probability of being assigned to either treatment or control. Condition 4.3 follows as a direct consequence of the sample splitting approach, because the estimators are obtained from an independent sample from the data used to carry the calibration step. Condition 4.4 requires that the estimators of the outcome regression and propensity score be bounded; this can be enforced, for example, by threshholding when estimating these regression functions. Condition 4.5 excludes cases in which the best possible predictor of the CATE given only the initial predictor $\tau$ has pathological behavior, in the sense that it has infinite variation norm as a (univariate) mapping of $\tau$. We stress here that isotonic regression is used only as a tool for calibration, and our theoretical guarantees do not require any monotonicity on components of the data-generating mechanism — for example, ${\gamma }_0(\tau ,w)$ need not be monotone as a function of $\tau (w)$.

The following theorem establishes the calibration rate of the predictor ${\tau }_n^{\ast }$ obtained using causal isotonic calibration.

Theorem 4.6 (${\tau }_n^{\ast }$ is well-calibrated). Under Conditions 4.1–4.5, as $n\to \infty$, it holds that

$$\mathrm{CAL}({\tau }_n^{\ast })=O_P\left({\ell }^{-2∕3}+{\Vert ({\pi }_m-{\pi }_0)({\mu }_m-{\mu }_0)\Vert }^2\right).$$

The calibration rate can be expressed as the sum of an oracle calibration rate and the rate of a second-order cross-product bias term involving nuisance estimators. Notably, the causal isotonic calibrator rate can satisfy Property 1 at the oracle rate ${\ell }^{-2∕3}$ so long as $\Vert ({\pi }_m-{\pi }_0)({\mu }_m-{\mu }_0)\Vert$ shrinks no slower than ${\ell }^{-1∕3}$, which requires that one or both of ${\pi }_0$ and ${\mu }_0$ is estimated well in an appropriate sense. If ${\pi }_0$ is known, as in most randomized experiments, the fast calibration rate of ${\ell }^{-2∕3}$ can be achieved even when ${\mu }_m$ is inconsistent, thereby providing distribution-free calibration guarantees irrespective of the smoothness of the outcome regression or dimension of the covariate vector. When π0 is unknown, the oracle rate of ${\ell }^{-2∕3}$ may not be achievable if the propensity score and outcome regression are insufficiently smooth relative to the dimension of the covariate vector (Kennedy, 2020; Kennedy et al., 2022).

It is interesting to contrast the calibration guarantee in Theorem 4.6 with existing MSE guarantees for DR-learners (Kennedy, 2020) since, in view of (3), they also provide calibration guarantees. While the MSE estimation rates for the CATE depend on the dimension and smoothness of ${\tau }_0$, the curse of dimensionality for our calibration rates only manifests itself in the doubly-robust cross-remainder term that involves nuisance estimation rates. For instance, when $\ell =m=n∕2$, if ${\pi }_0$ and ${\mu }_0$ are known to be Hölder smooth with exponent $\alpha \ge 1$, the calibration rate implied by Theorem 4.6 with minimax optimal nuisance estimators is, up to logarithmic factors, ${\ell }^{-2∕3}+{\ell }^{-4\alpha ∕(2\alpha +d)}$. In contrast, if ${\tau }_0$ is known to be Hölder smooth with exponent $\beta \ge 1$, a minimax optimal estimator of ${\tau }_0$ is only guaranteed to achieve an MSE, and therefore calibration, rate of ${\ell }^{-2\beta ∕(2\beta +d)}+{\ell }^{-4\alpha ∕(2\alpha +d)}$ (Kennedy et al., 2022). Moreover, when the nuisance smoothness satisfies $\alpha \ge d∕4$, causal isotonic calibration can achieve the oracle calibration rate of ${\ell }^{-2∕3}$, whereas a minimax optimal CATE estimator is only guaranteed to achieve the same calibration rate under the stringent condition that the smoothness of ${\tau }_0$ satisfies $\beta \ge d$.

The following theorem states that the predictor obtained by taking pointwise medians of calibrated predictors is also calibrated.

Theorem 4.7 (Pointwise median preserves calibration). Let ${\tau }_{n,1}^{\ast },{\tau }_{n,2}^{\ast },\dots ,{\tau }_{n,k}^{\ast }$ be predictors, and define pointwise ${\tau }_{n,k}^{\ast }(w)≔\text{median}\{{\tau }_{n,1}^{\ast }(w),{\tau }_{n,2}^{\ast }(w),\dots ,{\tau }_{n,k}^{\ast }(w)\}$. Then

$$\mathrm{CAL}({\tau }_n^{\ast })\le k\sum _{s=1}^k\mathrm{CAL}({\tau }_{n,s}^{\ast }),$$

where the median operation is defined as in Section 2.1.

Under similar conditions, Theorem 4.7 combined with a generalization of Theorem 4.6 that handles random $\tau$ (see Theorem C.5 in Appendix C.4) establishes that a predictor ${\tau }_{n,k}^{\ast }$ obtained using causal isotonic cross-calibration (Algorithm 2) has calibration error $\mathrm{CAL}({\tau }_{n,k}^{\ast })$ of order

$$O_P\left(n^{-2∕3}+\underset{1\le s\le k}{\max }{\Vert ({\pi }_{n,s}-{\pi }_0)({\mu }_{n,s}-{\mu }_0)\Vert }^2\right)$$

as $n\to \infty$, where ${\mu }_{n,s}$ and ${\pi }_{n,s}$ are the outcome regression and propensity score estimators obtained after excluding the $s^{\mathit{th}}$ fold of the full dataset. In fact, Theorem 4.7 is valid for any calibrator of the form ${\tau }_n^{\ast }:w\mapsto {\tau }_{n,s_n(w)}^{\ast }(w)$, where $s_n(w)$ is any random selector that may depend on the covariate value $w$. This suggests that the calibration rate for the median-aggregated calibrator implied by Theorem 4.7 is conservative as it also holds for the worst-case oracle selector that maximizes calibration error.

We now establish that causal isotonic calibration satisfies Property 2, that is, it maintains the predictive accuracy of the initial predictor $\tau$. In what follows, predictive accuracy is quantified in terms of MSE. At first glance, the calibration-distortion decomposition appears to raise concerns that causal isotonic calibration may distort $\tau$ so much that the predictive accuracy of ${\tau }_n^{\ast }$ may be worse than that of $\tau$. This possibility may seem especially concerning given that the ouput of isotonic regression is a step function, so that there could be many $w$, $w^{\prime }\in 𝒲$ such that $\tau (w)\ne \tau (w^{\prime })$ but ${\tau }_n^{\ast }(w)={\tau }_n^{\ast }(w^{\prime })$. The following theorem alleviates this concern by establishing that, up to a remainder term that decays with sample size, the MSE of ${\tau }_n^{\ast }$ is no larger than the MSE of the initial CATE predictor $\tau$. A consequence of this theorem is that causal isotonic calibration does not distort $\tau$ so much as to destroy its predictive performance. To derive this result, we leverage that ${\tau }_n^{\ast }$ is in fact a misspecified DR-learner of the univariate CATE function ${\gamma }_0(\tau ,\cdot )$. While isotonic calibrated predictors are calibrated even when ${\gamma }_0(\tau ,\cdot )$ is not a monotone function of $\tau$, we stress that misspecified DR-learners for ${\gamma }_0(\tau ,\cdot )$ are typically uncalibrated.

In the theorem below, we define the best isotonic approximation of the CATE given the initial predictor $\tau$ as

$${\tau }_0^{\ast }≔\underset{\theta \circ \tau :\theta \in {ℱ}_{\mathit{iso}}}{\mathrm{argmin}}\Vert {\tau }_0-\theta \circ \tau \Vert .$$

Theorem 4.8 (Causal isotonic calibration does not inflate MSE much). Under Conditions 4.1—4.5,

$$\Vert {\tau }_n^{\ast }-{\tau }_0^{\ast }\Vert =O_P\left({\ell }^{-1∕3}+\Vert ({\pi }_m-{\pi }_0)({\mu }_m-{\mu }_0)\Vert \right)$$

as $n\to \infty$. As such, as $n\to \infty$, the inflation in root MSE from causal isotonic calibration satisfies

$$\sqrt{\mathrm{MSE}{\tau }_n^{\ast }}-\sqrt{\mathrm{MSE}(\tau )}\le O_P\left({\ell }^{-1∕3}+\Vert ({\pi }_m-{\pi }_0)({\mu }_m-{\mu }_0)\Vert \right).$$

A similar MSE bound can be established for causal isotonic cross-calibration as defined in Algorithm 2.

5. Simulation studies

5.1. Data-generating mechanisms

We examined the behavior of our proposal under two data-generating mechanisms. The first mechanism (Scenario 1) includes a binary outcome whose conditional mean is an additive function (on the logit scale) of non-linear transformations of four confounders with treatment interactions. The second mechanism (Scenario 2) includes instead a continuous outcome with conditional mean linear on covariates and treatment interactions, with more than 100 covariates of which only 20 are true confounders. In both scenarios, the propensity score follows a logistic regression model. All covariates were independent and uniformly distributed on (−1, +1). Sample sizes 1,000, 2,000, 5,000 and 10,000 were considered. Further details are given in Appendix D.1.

5.2. CATE estimation

In Scenario 1, to estimate the CATE, we implemented gradient-boosted regression trees (GBRT) with maximum depths equal to 2, 5, and 8 (Chen & Guestrin, 2016), random forests (RF) (Breiman, 2001), generalized linear models with lasso regularization (GLMnet) (Friedman et al., 2010), generalized additive models (GAM) (Wood, 2017), and multivariate adaptive regression splines (MARS) (Friedman, 1991). In Scenario 2, we implemented RF, GLMnet, and a combination of variable screening with lasso regularization followed by GBRT with maximum depth determined via cross-validation. We used the implementation of these estimators found in R package sl3 (Coyle et al., 2021). Causal isotonic cross-calibration was implemented using the variant outlined in Algorithm 3. Further details are given in Appendix D.2.

5.3. Performance metrics

We compared the performance of the causal isotonic calibrator to its uncalibrated version in terms of three metrics: the calibration measure defined in (1), MSE, and the calibration bias within bins defined by the first and last prediction deciles. The calibration bias within bins is given by the measure in (2) standardized by the probability of falling within each bin. For each simulation iteration, the metric was estimated empirically using an independent sample $𝒱$ of size $n_{𝒱}={10}^4$. These metric estimates were then averaged across 500 simulations. Additional details on these metrics is provided in Appendix D.3.

5.4. Simulation results

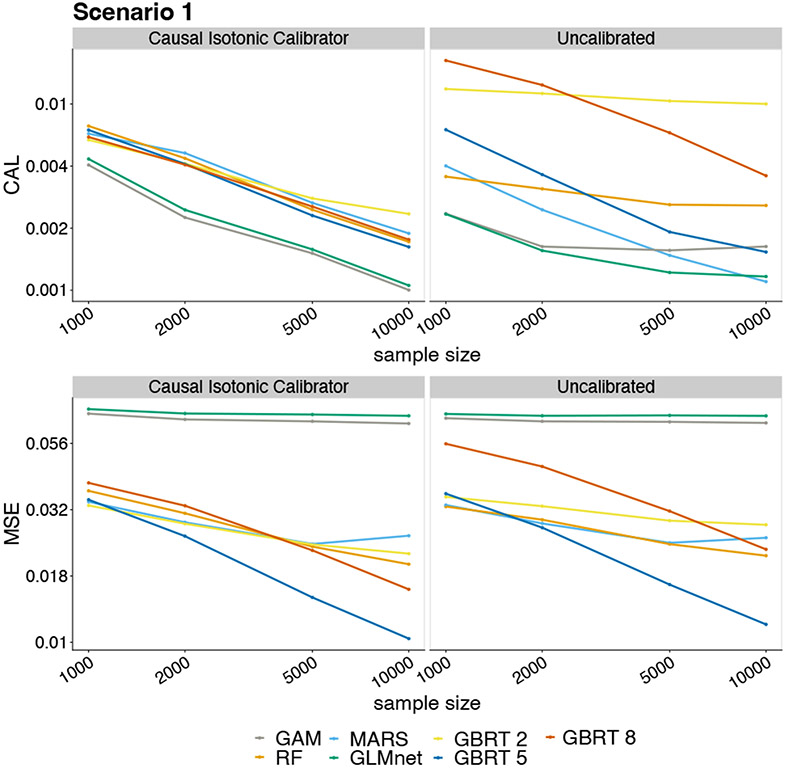
Results from Scenario 1 are summarized in Figure 3. The predictors based on GLMnet, RF, GAM, and MARS happened to be well-calibrated, and so, causal isotonic calibration did not lead to noticeable improvements in calibration error. In contrast, causal isotonic calibration of GBRT substantially decreased its calibration error, regardless of tree depth and sample size. In terms of MSE, calibration improved the predictive performance of GBRT and GAM, and preserved the performance of GLMnet and MARS. The calibration bias within bins of prediction was generally smaller after calibration, with a more notable improvement on GBRT — see Table 2 in Appendix E.

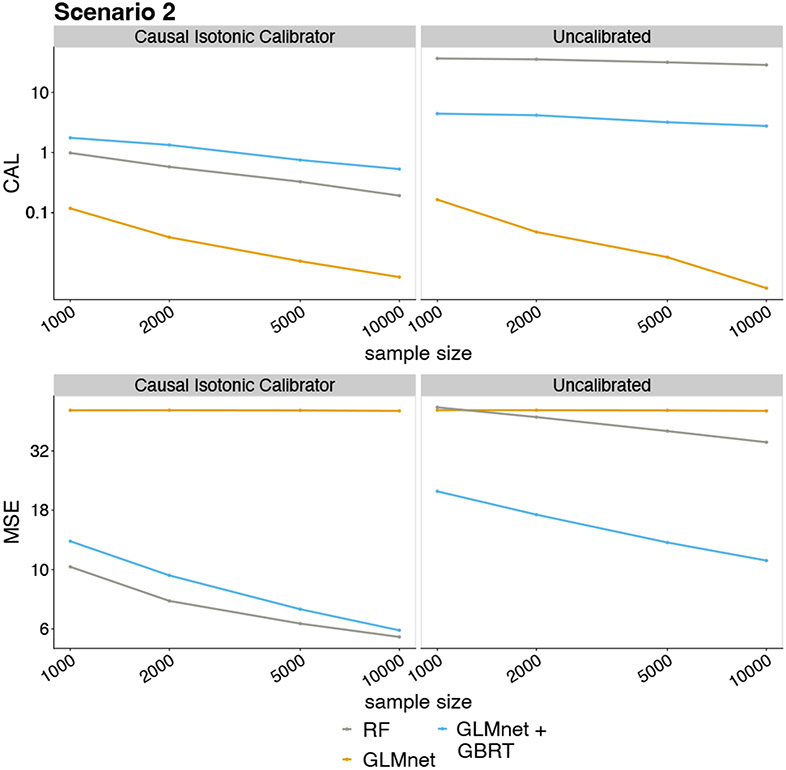
Results from Scenario 2 are summarized in Figure 2. The predictors based on RF and GBRT with GLMnet screening were poorly calibrated, and causal isotonic calibration substantially reduced their calibration error. Calibration did not noticeably change the already small calibration error of the GLMnet predictions; however, calibration substantially reduced the calibration error within quantile bins of its predictions — see Table 3 in Appendix E. Finally, with respect to MSE, causal isotonic calibration improved the performance of RF and GBRT with variable screening, and yielded similar performance to GLMnet.

Figure 2.

Calibration error and MSE in Scenario 2. The panels show the calibration error (top) and MSE (bottom) using the calibrated (left) and uncalibrated (right) predictors as a function of sample size. The y-axes are on a log scale.

In Figure 4 of Appendix E, we compared calibration performance using hold-out sets to cross-calibration. We found substantial improvements in MSE and calibration by using cross-calibration over conventional calibration.

6. Conclusion

In this work, we proposed causal isotonic calibration as a novel method to calibrate treatment effect predictors. In addition, we established that the pointwise median of calibrated predictors is also calibrated. This allowed us to develop a data-efficient variant of causal isotonic calibration using cross-fitted predictors, thereby avoiding the need for a hold-out calibration dataset. Our proposed methods guarantee that, under minimal assumptions, the calibration error defined in (2) vanishes at a fast rate of ${\ell }^{-2∕3}$ with little or no loss in predictive power, where $\ell$ denotes the number of observations used for calibration. This property holds regardless of how well the initial predictor $\tau$ approximates the true CATE function. To our knowledge, our method is the first in the literature to directly calibrate CATE predictors without requiring trial data or parametric assumptions. Potential applications of our method include data-driven decision-making with strong robustness guarantees. In future work, it would be interesting to study whether pairing causal isotonic cross-calibration with conformal inference (Lei & Candès, 2021) leads to improved ITE prediction intervals, and whether causal isotonic calibration and shape-constrained inference methods (Westling & Carone, 2020) can be used to construct confidence intervals for the calibration function ${\gamma }_0({\tau }_n^{\ast },\cdot )$.

Our method has limitations. Its calibration guarantees require that either ${\mu }_0$ or ${\pi }_0$ be estimated sufficiently well. Flexible learning methods can be used to satisfy this condition. If ${\pi }_0$ is known, this condition can be trivially met. Hence, our method can be readily used to calibrate CATE predictors and characterize HTEs in clinical trials. For proper calibration, our method requires all confounders to be measured and adjusted for. In future work, it will be important to study CATE calibration in the context of unmeasured confounding. Our strategy could be adapted to construct calibrators for general learning tasks, including E-learning of the conditional relative risk (Jiang et al., 2019; Qiu et al., 2019), proximal causal learning (Tchetgen et al., 2020; Sverdrup & Cui, 2023), and instrumental variable-based learning (Okui et al., 2012; Syrgkanis et al., 2019).

In simulations, we found that causal isotonic cross-calibration led to well-calibrated predictors without sacrificing predictive performance; benefits were especially prominent in high-dimensional settings and for tree-based methods. This is of particularly high relevance given that regression trees have become popular for CATE estimation due to their flexibility (Athey & Imbens, 2016) and interpretability (Lee et al., 2020). We also found that cross-calibration substantially improved the MSE of the calibrated predictor relative to hold-out set calibration approaches and can even improve the MSE of the original predictor.

Though our focus was on treatment effect estimation, our theoretical arguments can be readily adapted to provide guarantees for isotonic calibration in regression and classification problems. Hence, we have provided an affirmative answer to the open question of whether it is possible to establish distribution-free calibration guarantees for isotonic calibration (Gupta, 2022).

Figure 1.

Calibration error and MSE in Scenario 1. The panels show the calibration error (top) and MSE (bottom) using the calibrated (left) and uncalibrated (right) predictors as a function of sample size. The y-axes are on a log scale.