Multiset correlation and factor analysis enables exploration of multi-omics data

Summary

Multi-omics datasets are becoming more common, necessitating better integration methods to realize their revolutionary potential. Here, we introduce multi-set correlation and factor analysis (MCFA), an unsupervised integration method tailored to the unique challenges of high-dimensional genomics data that enables fast inference of shared and private factors. We used MCFA to integrate methylation markers, protein expression, RNA expression, and metabolite levels in 614 diverse samples from the Trans-Omics for Precision Medicine/Multi-Ethnic Study of Atherosclerosis multi-omics pilot. Samples cluster strongly by ancestry in the shared space, even in the absence of genetic information, while private spaces frequently capture dataset-specific technical variation. Finally, we integrated genetic data by conducting a genome-wide association study (GWAS) of our inferred factors, observing that several factors are enriched for GWAS hits and trans-expression quantitative trait loci. Two of these factors appear to be related to metabolic disease. Our study provides a foundation and framework for further integrative analysis of ever larger multi-modal genomic datasets.

Graphical abstract

Highlights

• •Rapid, unsupervised multi-modal data integration with self-inferred tuning parameters
• •614 ancestry-diverse participants from MESA/TOPMed with 5 omics types
• •Top shared components capture ancestry, even without genetic information
• •Further components are enriched for GWAS hits and related to metabolic disease

Brown, Wang et al. introduce MCFA, an approach to multi-modal dataset integration that generalizes canonical correlation analysis. MCFA is broadly applicable to data integration challenges but has been designed to handle issues in population-scale multi-omics data. A variety of analyses on the TOPMed/MESA multi-omics pilot demonstrate the power of this method.

Introduction

Recent years have seen an explosion in multi-omics data, with studies simultaneously profiling RNA expression, protein levels, chromatin accessibility, and more.¹ By providing complementary views into the underlying biology, these datasets promise to illuminate molecular processes and disease states that cannot be gleaned from any lone modality.² However, joint inference methods are lacking in either the number or type of modes that can be used or in flexibility and efficiency.¹ Multi-omics data bring substantial challenges: distributions differ between modes, the sample size is typically small relative to features, efficient algorithms are needed, and each mode has contributions from factors that are shared between modes and unique to itself.^3,4 Canonical correlation analysis (CCA) is a statistical technique that infers shared factors between two data modes by finding correlated linear combinations of the features in each.⁵ CCA has enjoyed substantial attention in genomics^6,7,8,9; however, extending CCA to additional modes is fraught: at least 10 different formulations are equivalent in the two-mode case,¹⁰ and many are challenging to fit.¹¹ Equivalently, CCA can be conceptualized as a probabilistic model (pCCA), revealing a connection to factor analysis.¹²

We have developed multi-set correlation and factor analysis (MCFA; Figures 1A and S1), an unsupervised integration method that generalizes pCCA and factor analysis, enabling fast inference of shared and private factors in multi-modal data. MCFA is designed to overcome challenges that are common with genomics data such as the large number of features relative to the sample size, the disparate data types, and the unknown contributions of dataset-specific technical factors. MCFA is based on two insights: (1) unlike traditional CCA, pCCA has only one natural extension to multi-modal data, which is both conceptually elegant and efficient to fit, and (2) after fitting pCCA, the residual in a mode represents private structure, which is well modeled by factor analysis. Our method combines these insights to fit factors that are shared across modalities and are private to each simultaneously. For efficiency and regularization, MCFA uses the top principal components (PCs) of each mode.^6,7 It allows the use of random matrix techniques¹³ to choose the shared dimensionality and number of PCs, eliminating tuning parameters. Finally, MCFA is a natural approach to integration: as detailed in Methods S1, there is a theoretical connection between our model and multi-set CCA.

Figure 1.

Overview of MCFA integration results

(A) The MCFA model. Each observed data mode (Ym) has contributions from two latent factors, one private to it (Xm) and one shared with other modes (Z).

(B) Breakdown of the variance in four omics types captured by the inferred space, as well as the per-mode contribution to each shared factor.

(C) UMAP embedding of the shared and private spaces, annotated with the most relevant feature set. Broadly, the top shared factors capture demographics, while the top private factors capture technical variation.

(D) Variance in sample metadata explained by each learned space. This shows that the shared space also captures inferred cell-type composition estimates as well as clinical biomarkers.

We have applied MCFA to 614 ancestry-diverse individuals from the Multi-Ethnic Study of Atherosclerosis (MESA).¹⁴ The Trans-Omics for Precision Medicine (TOPMed)¹⁵ program instituted a multi-omics pilot study to evaluate the utility of long-term stored samples for discovery related to heart, lung, blood, and sleep disorders. MESA provided samples for five omics types: (1) whole-genome sequencing (WGS), (2) RNA sequencing of peripheral blood mononuclear cells (PBMCs), (3) DNA methylation array profiling from whole blood, (4) protein mass spectrometry of blood plasma, and (5) metabolite mass spectrometry of blood plasma. In addition, MESA has collected comprehensive phenotypic metadata. These data include demographic markers such as self-reported ancestry (SRA), sex, age, and education level; morphological features including height, weight, and hip circumference; clinical measures including those related to atherosclerosis, lipid levels, kidney function, and inflammatory biomarkers; and behavioral features regarding smoking, drinking, and exercise frequency.

Results

We integrated RNA sequencing, methylation, protein, and metabolite data using MCFA, which inferred a 14-dimensional shared space. We found that shared structure explained a large proportion of the variance in each mode (Figure 1B, right). Protein levels had the highest sharing with 29.2% of the variance explained (VE) by the shared space, followed by RNA and metabolite levels (16.6% and 17.1%, respectively). Methylation showed the least sharing, with only 8.1% VE by the shared space. Due to the high dimensionality of the data and the limited sample size, about half of the variance in each dataset is unmodeled to reduce overfitting. Using MCFA, it is possible to further infer the variance in each modality explained by the individual factors, thus determining which modalities contribute to each (Figure 1B, left). Our top factor has contributions from all modalities, but their respective contributions to the other factors vary substantially.

We used uniform manifold approximation and projection (UMAP)¹⁶ to construct a 2D embedding of the shared and private spaces (Figure 1C). We noticed a striking clustering of the individuals by SRA and sex in the shared space, even though the top PCs of individual modes do not cluster by these factors (Figure S2), and the shared space was inferred without genetic or sex chromosome features. Shared factor 1 separates Black and White individuals, with Hispanic individuals in between, while factor 3 separates Chinese individuals, and factor 2 differentiates by sex (Figures S2 and S3). We validated this structure via leave-one-out cross-validation, indicating our PC selection strategy mitigated over-fitting (Figure S4).

Next, we evaluated the total phenotypic VE by each of our inferred spaces (Figures 1D and S2; Tables S1, S2, and S3). The shared space captured 95.3% of the variation in sex, 83.3% in site, 80.0% in SRA, and 60.2% in age. The shared space also captured anthropomorphic differences such as BMI (51.0% VE) and clinical measures including those related to kidney function (creatine, 64.8% VE) and inflammation (tumor necrosis factor (TNF)-alpha receptor-1 69.1% VE). We used CIBERSORT¹⁷ and the Houseman method¹⁸ to estimate the cell-type composition of our RNA (PBMC) and methylation (whole blood) samples, respectively. Both shared and privates spaces contributed to the relative proportions of PBMC-abundant cell types (e.g., T cells and natural killer (NK) cells) estimated from both data modalities, while the proportion of PBMC-depleted types (e.g., neutrophils) estimated from the methylation data was only captured by the methylation private space. Modality-private spaces frequently captured technical factors: 100% of the variance in sequencing center and 71.6% of the variance in 3′ bias are captured by the RNA private space, while 76.8% of the methylation array batch is captured by its private space. Many phenotypes that are themselves measurements of metabolites were captured by the metabolite private space; however, the strongest association was with the month of sample collection (85.8% VE). We noticed no large associations between the protein private space and any of our metadata, despite several of our phenotypes being clinical protein markers; however, several of these factors are partially captured by the shared space.

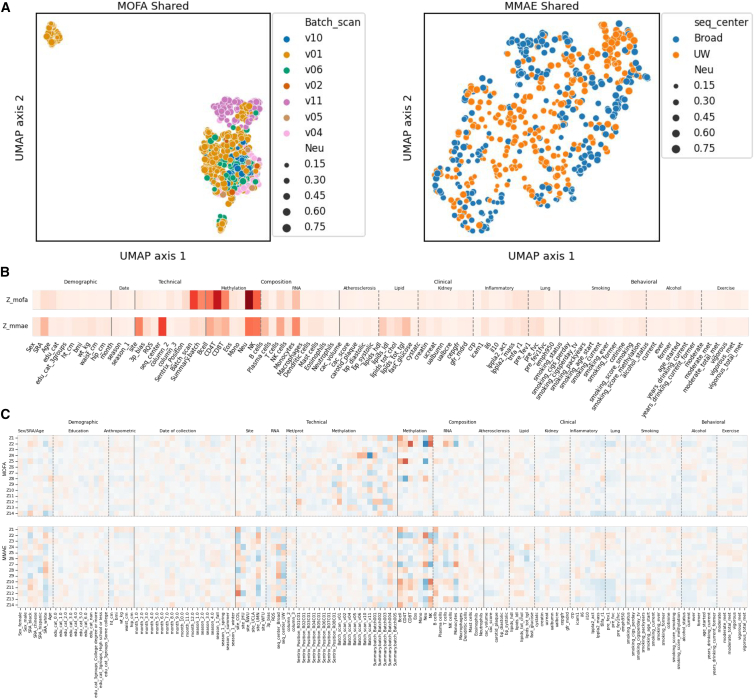
We compared the results obtained on MESA using MCFA with other multi-modal analysis approaches. We focused on two alternative methods: (1) MOFA2⁴ and (2) a multi-modal auto-encoder (MMAE, see STAR Methods and Figure S5). In the MOFA2 analysis, the methylation batch and cell-type proportions dominated the inferred shared space, likely owing to the very large number of features in that modality compared with the other modalities (Figure 2). The MMAE mitigated this over-focus on methylation somewhat and additionally captured RNA sequencing center and RNA cell-type proportions (Figure 2). Thus, neither MOFA2 nor the MMAE were able to infer shared variation while discarding dataset-specific technical artifacts. Moreover, using up to 8 cores of an Intel Xeon E5-2697v3 CPU on our cluster, MOFA2 took approximately 56 min to run when set to “medium” tolerance, while our MMAE took approximately 109 min to converge. In contrast, MCFA is able to process the same dataset in around 2 min.

Figure 2.

Comparison of MCFA with other methods

(A) UMAP embeddings of MOFA (left) and MMAE (right) shared space show that these methods fail to separate meaningful information from technical variation.

(B) Variance in sample metadata explained by the MOFA2 (top) and MMAE (bottom) shared spaces. MOFA2 primarily learns factors related to the methylation dataset, while the MMAE additionally incorporates some factors related to RNA sequencing.

(C) Correlation of each inferred factor with each metadata sample for MOFA (top) and the MMAE (bottom).

Finally, we integrated WGS data by conducting a genome-wide association study (GWAS) of the inferred factors while controlling for site, age, sex, and 11 genotype PCs. We hypothesized that genetic associations with our inferred factors, which represent major axes of molecular variation, may be enriched for known GWAS hits or trans-expression quantitative trait loci (eQTLs). We obtained a list of 10,174 such associations from the eQTLgen consortium,¹⁹ of which 3,854 are trans-eQTLs, and further defined a more limited set of 1,107 “influential” trans-eQTLs that affect at least 10 genes. We tested the GWAS of each factor for enrichment of these three categories and found 9 significant enrichments (mean ${\chi }_{cat}^2>1$, false discovery rate [FDR] 5%; Figures 3A and S6).

Figure 3.

Factor interpretation and integration with GWAS data

(A) QQ-plot of a GWAS for factors 1, 2, 6, and 7. Genetic associations with these factors are enriched for known GWAS loci (1, 6, and 7), trans-eQTLs (1 and 7), or highly influential trans-eQTLs (2 and 7).

(B and C) Correlation of factors 6 (B) and 7 (C) with morphological, immune-composition, and clinical metadata reveals that factor 6 is related to body composition and lipid profile, while factor 7 is related to body composition, inferred blood cell-type composition, and inflammatory biomarkers.

(D) Z-transformed correlation of individual protein and metabolite data with factor 6 reveals genes and metabolites related to insulin resistance and metabolic syndrome.

(E) Z-transformed correlation of individual methylation values with factor 7. Many genes colocated to these CpGs are involved in lipid metabolism.

Factor 7 showed the strongest enrichment for reported GWAS hits and trans-eQTLs. The top SNPs associated with factor 7 are from blood lipid studies and are located primarily around the FADS1 and FADS2 genes, which are known to regulate lipid metabolism.²⁰ These include rs174541 ($\mathrm{p}=4.3\times {10}^{-5}$ for factor 7 association), which is also reported in GWASs of type 2 diabetes²¹; rs174549 ($\mathrm{p}=5.6\times {10}^{-5}$), which is also reported in GWASs of white blood cell count²²; and rs1535 ($\mathrm{p}=8.3\times {10}^{-5}$), which is also reported in a GWAS of inflammatory bowel disease²³ (Table S4). Factor 7 explains 6.7% of the modeled variation in methylation, the largest of any factor, and is anti-correlated with sample proportion of CD8⁺ T cells and NK cells estimated from methylation data ($\rho =-0.41$ and $-0.25$), and correlated with BMI ($\rho =0.25$) and measures of inflammation including TNF-R1 ($\rho =0.33$) and interleukin-6 ($\rho =0.20$) (Figure 3B).

To assess the contribution of individual CpGs, we calculated the Z-transformed correlation of individual CpG values with factor 7 (Figure 3C). As epigenome-wide association studies remain small, generally little is known about the effects of individual CpGs and their associations with traits. Instead, we linked each gene to the CpGs falling in a window from 1.5 kb upstream of the transcription start site to the transcription termination site. Many of the genes colocated to CpGs with high weights for factor 7 have been implicated in lipid metabolism GWASs including IQCG and TMEM178A (cg01328500 and cg02571055; phosphatidylcholine levels²⁴), DSCAML1 (cg02571055; triglyceride levels²⁵), PTK2 (cg02153245; ApoB and low-density lipoprotein [LDL] levels²⁶); TULP4 (cg02571055; lipoprotein A levels²⁷), and C7orf50 (cg20054412; LDL, high-density lipoprotein [HDL], and total cholesterol levels²⁸). Interestingly, our second strongest hit, cg00697440, is colocated with CD86. Recent work has suggested that B7 molecules including CD86 play an important role in regulating CD8⁺ T cell population dynamics.²⁹ While further research is needed to establish causal relationships of these genetic effects and methylation patterns in cis and trans on gene regulation and diverse traits, DNA methylation patterns have been previously associated with lipid metabolism and metabolic disease.^30,31 Further research is required to determine whether the immune-cell component of this factor is related to the lipid metabolism component or whether these are simply independent biological functions captured by the same factor.

We used the same strategy to interpret factor 6. Factor 6 is correlated with fasting glucose, waist circumference, and triglycerides ($\rho =0.36,0.34$, and $0.32$, respectively) and anti-correlated with HDL cholesterol ($\rho =-0.25$; Figure 3D). Factor 6 explains 6% of the variance in protein levels and 4.1% of the variance in metabolite levels. Many of the top-weighted metabolites are uncharacterized products from untargeted metabolomics, but the two top characterized targets are 2-hydroxybutyric acid, a known marker of insulin resistance and glucose intolerance,^32,33 and glucose itself (Figure 3E). Several of the top-weighted proteins in this factor have known roles in growth and development including BMP1, GHR, IGFBP2, and FGFR1. GWASs have implicated BMP1 in coronary artery disease,^34,35 IGFBP2 in type 2 diabetes and BMI,³⁶ and FGFR1 in triglyceride levels²⁸ and waist-hip ratio.³⁷ Other notable highly weighted proteins include TFPI, which is involved in blood coagulation and is associated with BMI-adjusted waist-hip ratio,³⁸ and ADIPOQ, which is involved in regulating glucose levels³⁹ (Figure 3E). Many of the top GWAS hits associated with this factor corroborate these observations, including rs4805885, which is associated with adiponectin (ADIPOQ) levels⁴⁰; rs9787485, which is associated with insulin-carbohydrate interaction⁴¹; and rs7679, which is associated with HDL, LDL, and triglyceride levels⁴² (Table S5).

Interestingly, the strongest genetic association with this factor comes from GWASs of schizophrenia (rs112973353; $\mathrm{p}=1.6\times {10}^{-4}$ for factor 6 association), and we find 5 independent schizophrenia risk loci with factor 6 association p values below 0.01 (Table S5). Insulin resistance and schizophrenia have been consistently associated for nearly 100 years,⁴³ and while the association signal of each locus with factor 6 is relatively weak, the probability of finding 5 independent loci with these p values under the null is approximately $4\times {10}^{-13}$. While further research is needed, our results suggest that these particular loci may confer schizophrenia risk via insulin resistance. Another notable signal in our GWAS associations is related to erythrocyte and platelet traits. These hits include rs12451471 ($\mathrm{p}=8\times {10}^{-4}$; mean corpuscular hemoglobin concentration⁴⁴; platelet count⁴⁵) and rs13224082 ($\mathrm{p}=9\times {10}^{-4}$; platelet distribution width, platelet count, plateletcrit⁴⁴), among others (Table S5). Again, further research is required to establish causality and direction of effect between genetics, metabolite and protein levels, and traits, but we note that there is an established link between insulin resistance and platelet dysfunction.⁴⁶

Discussion

MCFA has several advantages compared with other multi-omics integration approaches. Compared with group factor analysis methods,⁴ MCFA separates modality-specific from dataset-shared factors. Compared with non-negative matrix factorization-based methods that share a feature weight set across modalities,³ MCFA is able to use all data types. As we have shown, MCFA is also substantially faster and is able to handle datasets with unbalanced numbers of features across the modes.

While our top factors captured ancestry and sex, these factors are usually observed and considered confounding in clinical applications. In that context, one could fit the model conditional on known confounding factors. Since we see exploratory data analysis as a primary application of MCFA, our goal instead was to map the primary axes of biological variation contained within these population-scale multi-omics data. It is important that these factors are a primary driver of variation within such data, as it implies that sampling across race and sex is critical for equitable discovery in medical genomics. Still, because these factors are captured by the top components, and the components themselves are orthogonal, further components can still capture disease-relevant information.

Integration with GWAS is biased toward well-powered studies that will typically have more hits, some of which may be acting indirectly through another phenotype.⁴⁷ Interpretability of factors is also biased toward the metadata collected in the study. In MESA, the goal was evaluation of risk factors for heart disease, and thus MESA focused metadata collection on lipid phenotypes, inflammatory biomarkers, and body morphology. It is therefore unsurprising that we are most easily able to interpret factors related to metabolic syndrome, lipid metabolism, and immune function in this study. Still, the ability of MCFA to produce results that are correlated with these factors demonstrates the utility of broad-scale sample metadata when interpreting results from multi-omics studies.

Careful consideration is required when analyzing multi-omics datasets that include WGS or genotype data. There are two primary ways that one can think about integrating these data: (1) include genetic information as a mode in the fit model, interpretable as inferring a latent state that affects genotype as well as molecular factors, or (2) look for genetic associations with inferred molecular factors, interpretable as mapping QTLs for inferred molecular phenotypes. In this study, we chose the latter due to the improved causal interpretation and to demonstrate the utility of surrogate molecular phenotypes. In other cases, for example the analysis of genetic copy-number variation data in tumor samples, the former analysis approach may be preferred. Future work with larger sample sizes may allow for network inference and Mendelian randomization methods to generate directed hypotheses.^47,48 Genetic associations are particularly valuable in this, with the inferred axes of molecular variation providing promising future traits for GWAS and phenome-wide association studies. TOPMed is among the most ambitious current efforts to collect multi-omics population-level data; thus, given the results of this pilot analysis, we expect future integration studies in this cohort to be fruitful.

Limitations of the study

Due to the use of observational data and unsupervised methods, all analyses should be considered exploratory; they can find structure in the data while generating hypotheses but cannot be used to make causal claims and may reflect technical properties of the underlying data. For example, in MESA, the sample collection site is strongly correlated with SRA. We repeated our analysis of the VE by the learned space while additionally controlling for site (Table S3) and noticed a small decrease in the proportion of VE in SRA (from 80.0% to 71.6%).

We observed that estimated cell-type composition had a strong association with both shared and private spaces. Since cell-type composition was inferred from the data, there may be circularity in composition estimation itself. In addition, complex interactions exist between cell-type composition in tissue samples and clinical, environmental factors as well as technical factors related to biospecimen collection. Thus, caution is necessary for biological interpretation in this aspect of the analysis.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
MESA TOPMed multi-omics pilot data	dbGaP	dbGaP: phs001416.v3.p1
Software and algorithms
Multiset Correlation and Factor Analysis	Zenodo	https://doi.org/10.5281/zenodo.7951370
MOFA2	github	https://github.com/bioFAM/MOFA2
eQTLgen trans-eQTL summary statistics	eQTLgen	https://www.eqtlgen.org/trans-eqtls.html

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Dr. Brielin Brown (bbrown@nygenome.org).

Materials availability

This study did not generate new unique reagents.

Method details

Multiset correlation and factor analysis

Let $Y={\left\{Y_m\right\}}_{m=1}^M$ be a set of $N\times p_m$ observed data matrices: $N$ individuals measured in $M$ data modalities consisting of $p_m$ features each. We model each observed mode as having contributions from two low-dimensional hidden factors (Figures 1A and S8)

$$z_n\sim N\left(0,I_d\right)$$

$$x_n^m\sim N\left(0,I_{k_m}\right)$$

$$y_n^m\sim N\left(W_m{z}_n+L_m{x}_n^m,{\Psi }_m\right)$$

where $d$ is the shared hidden dimensionality, $k_m$ are the dataset-private hidden dimensionalities, $W_m$ are $p_m\times d$ shared space loading matrices, $L_m$ are $p_m\times k_m$ private space loading matrices and ${\Psi }_m=diag\left({\psi }_m^1,\dots ,{\psi }_m^{p_m}\right)$ are the diagonal residual covariance matrices. Given $Y$, $d$ and $k_m$, our goal is to infer the hidden factors $Z$ and $X_m$ and loading matrices $W_m$ and $L_m$. This can be accomplished using a straightforward application of expectation maximization (EM).⁴⁹ For a derivation of the EM update equations, as well as a more detailed exposition including the relationship to pCCA, factor analysis and other multiset CCA (MCCA) methods, see Methods S1. In practice, we center and scale all data variables. This is not strictly required, however it enables simple estimation of the number of PCs to include and simplifies explained variance calculations, see below.

Model initialization

An important aspect of EM optimization is choosing a good initialization. We benchmarked three approaches to initializing $W$: random initialization and two versions of MCCA that correspond to maximizing the sum of pairwise correlations with the average variance and average norm constraints. These MCCA formulations can be solved via simple eigendecompositions. We found that the sum of pairwise correlations with average variance constraint produced the best initial estimates (Figure S7). This can be solved with a simple two step procedure: 1) whiten each data matrix using the singular value decomposition (SVD), 2) perform a second SVD on the concatenated whitened data matrices⁵⁰:

Input: $Y_1,\dots ,Y_M,d$

Result: $\hat{\mathit{W}}={\left[{\mathit{W}}_{\mathbf{1}}^{\top }:\dots :{\mathit{W}}_{\mathit{M}}^{\top }\right]}^{\top }$

$U_{all}\leftarrow$ concatenate(SVD($Y_1$). $U,\dots \text{,}$ SVD($Y_M$). $U$);

$\hat{W}\leftarrow$ SVD($U_{all}$). $V\left[:,0:d\right]$;

$\hat{\rho }\leftarrow$ SVD($U_{all}$). $\lambda \left[0:d\right]$;

return $\hat{\mathit{W}},\hat{\mathit{\rho }}$

We initialize $L$ and $\Psi$ using probabilistic PCA on the residual data matrices after fitting MCCA. Specifically:

Input: ${\mathit{Y}}_{\mathit{i}},{\mathit{W}}_{\mathit{i}},\mathit{N},{\mathit{k}}_{\mathit{i}}$

Result: ${\hat{\mathit{L}}}_{\mathit{i}},{\hat{\mathit{\Psi }}}_{\mathit{i}}$

${\Sigma }_{\mathit{i}}^{\perp }\leftarrow {\mathit{Y}}_{\mathit{i}}^{\top }{\mathit{Y}}_{\mathit{i}}/\mathit{N}-{\mathit{W}}_{\mathit{i}}{\mathit{W}}_{\mathit{i}}^{\top }$;

${\hat{L}}_i\leftarrow$ eigh(${\Sigma }_i^{\perp }$). $V\left[:,0:k_i\right]\text{;}$

${\sigma }^2\leftarrow$ mean(eigh(${\Sigma }_i^{\perp }$). $\lambda \left[k_i\text{:}\right]$);

${\hat{\Psi }}_i\leftarrow {\sigma }^2{1}_{k_i}$;

return ${\hat{L}}_i,{\hat{\Psi }}_i$

High dimensionality and selection of hyperparameters

There are two primary approaches to control for over-fitting in applications of CCA-type methods to high-dimensional ($N\ll p$) problems. The first is to use penalized optimization techniques, where the objective function additionally contains an $l_1$ constraint on the weight matrices.⁵¹ The second is to project each dataset onto its informative principal components.^6,7,11 In this application, we choose the latter approach in order to find components with broad effects on the structure of the data, rather than specific effects on small numbers of molecular features.¹¹ We choose the number of principal components of each dataset using the Marchenko-Pasteur law,¹³ which states that for mean $0$, variance $1$ data, principal components with corresponding eigenvalues above ${\lambda }_m=1+\sqrt{p_m/N}$ should be considered non-noise. We are not aware of a corresponding law for the cross-covariance matrices used in CCA, however, the empirical spectral distribution of the cross-covariance of matrices of random noise can be easily estimated in practice:

Input: $N,k={\left\{k_m\right\}}_{m=1}^M,n_{it}$

Result: $\underset{\_}{\rho }$

for $it\leftarrow 0$ to $n_{it}$ do

  for $k_m\in k$ do

  ${\left[Y_m\right]}_{i=1,j=1}^{N,k_m}\sim N\left(\mathrm{0,1}\right)\text{;}$

  end

 $\rho \left[\mathit{i}\mathit{t}\right]\leftarrow$ max(InitializeMCFA($Y_1,\dots ,Y_M$). $\rho$

end

return mean($\rho$)

Then we keep all components where ${\rho }_{init}>\underset{\_}{\rho }$.

Calculating the variance explained

The linear-Gaussian nature of the model simplifies estimation of the variance explained. That is, if the features of each mode $Y_m^{\left(:,j\right)}$ are normalized to variance $1$, the model $Y_m^{\left(:,j\right)}=\sum _d{W}_m^{\left(j,d\right)}{Z}^{\left(:,d\right)}+\sum _{k_m}{L}_m^{\left(j,k_m\right)}{X}_m^{\left(:,k_m\right)}+ϵ$ implies that the variance in feature $j$ of mode $m$ explained by shared factor $d$ is $W_m^{\left(j,d\right)2}$. Likewise, the variance explained by the $k_m$-th private factor of mode $m$ is $L_m^{\left(j,k_m\right)2}$. The total variance in mode $m$ explained by a given shared factor $d$ (respectively, private factor $k_m$) is thus given by $\sum _j{W}_m^{\left(j,d\right)2}$ (respectively, $\sum _j{L}_m^{\left(j,k_m\right)2}$), and the total variance in the mode explained by the factors are $\sum _{j,d}{W}_m^{\left(j,d\right)2}$ and $\sum _{j,k_m}{L}_m^{\left(j,k_m\right)2}$, respectively. Note that when working in PC-space, the raw $W$ and $L$ features correspond to variance in PCs explained, rather than modality features. Thus, we calculate the variance explained after projecting back into the original feature space $W_m\leftarrow V_m{W}_m,L_m\leftarrow V_m{L}_m$ where $V_m$ are the right singular vectors of mode $m$.

To calculate the variance in a metadata feature explained by a particular space, we regressed the trait value $T$ on the shared or private space, $T\sim Z$ or $T\sim X_m$. For continuous-valued traits we used linear regression as implemented in SciKitLearn v1.0 linear_model.LinearRegression and report the coefficient of determination.⁵² For discrete-valued traits, we used multinomial logistic regression as implemented in SciKitLearn v1.0 linear_model.LogisticRegression.⁵² We fit two models: a null model including only intercept or intercept and site, and one including the factor variables. We report the variance explained as the McFadden pseudo-$R^2$, $1-\frac{l{l}_{alt}}{l{l}_{null}}$, with $l{l}_{null}$ and $l{l}_{alt}$ being the model negative log likelihood for the null and alternative model respectively.⁵³

Calculating relative feature importance

Feature importance in traditional CCA is defined by the correlation of the variables in the reduced space $\rho =cor\left(Y_1{f}_1,Y_2{f}_2\right)$. Unfortunately this notion breaks down in higher dimensions. As we discuss further in Methods S1, the degree of sharing in MCCA is defined by functions of the cross-correlation matrix in the reduced space,

$$S=cor\left(Y_1{f}_1,\dots ,Y_m{f}_m\right)\in R^{m\times m}\text{.}$$

We seek to define an analogous quantity for our graphical model. In MCFA, the data in the reduced (shared) space is given by the posterior mean of $Z$, $\hat{Z}=E\left[Z|W,\Psi ,L,Y\right]=Y{\left(W{W}^{\top }+L{L}^{\top }\Psi \right)}^{-1}W$. We can also calculate the posterior mean of $Z$ conditional on observing a single mode, ${\hat{Z}}_m=E\left[Z|W_m,{\Psi }_m,L_m,Y_m\right]=Y_m{\left(W_m{W}_m^{\top }+L_m{L}_m^{\top }{\Psi }_m\right)}^{-1}{W}_m$. This latter quantity is analogous to the reduced variables $Y_m{f}_m$ in MCCA. Thus we can summarize the importance of each dimension of the shared space by calculating functions of the cross-correlation of columns of ${\hat{Z}}_m$,

$$S_d=cor\left({\hat{Z}}_1^{\left(:,d\right)},\dots ,{\hat{Z}}_m^{\left(:,d\right)}\right)\text{.}$$

The relevant function in our model is the generalized variance $\left|S\right|$, see Methods S1. The determinant of a correlation matrix is bounded between $0$ and $1$, with lower values indicating more correlation, and higher values less. Thus to aid interpretability, we report ${\rho }_d=-log\left|S_d\right|$ and reorder columns of $Z$ and $W$ with decreasing ${\rho }_d$.

SNP set enrichment analysis

For SNP set enrichment analysis, we broadly follow the approach of CAMERA.⁵⁴ In brief, enrichment statistics can be inflated due to correlations in the sample - in this case, linkage disequilibrium between two GWAS SNPs. This results in an under-estimate of the standard error of the enrichment test statistic and an increase in false positives. We calculate the variance inflation factor by using plink v $1.9$⁵⁵ to estimate linkage disequilibrium between annotation SNPs in $\mathrm{337,781}$ unrelated individuals from the UK Biobank.⁵⁶ The variance inflation factor is $\nu =1+\left(p_A-1\right){\rho ¯}_A$, with ${\rho ¯}_A$ the average person correlation between features in set $A$. We test the known GWAS mean ${\chi }^2$ statistic $h_0:{\chi ¯}_A^2=1$ against the alternative $h_1:{\chi ¯}_A^2>1$. The standard error of the test statistic is ${\sigma }_t=\sigma \sqrt{\frac{\nu }{p_A}-\frac{1}{p_m}}$ with $\sigma$ the pooled empirical standard deviation of the test statistics.

The MESA multi-omics pilot

The Multi-Ethnic Study of Atherosclerosis (MESA) is a prospective cohort study with the goal to identify progression of subclinical atherosclerosis.¹⁴ MESA recruited 6,814 participants, ages 45–84 years and free of clinical cardiovascular disease, during 2000–2002. The participants are 53% female, 38% non-Hispanic white, 28% Black, 22% Hispanic and 12% Asian-American. The Multi-Omics pilot dataset includes 30x whole genome sequencing (WGS) through the Trans-Omics for Precision Medicine (TOPMed) Project.¹⁵

Blood samples for multi-omic analysis of participants were collected at two time points (exam 1 and exam 5). RNA expression was profiled using poly-A RNA sequencing of PBMCs, and methylation was quantified by the Illumina 750K EPIC array in whole blood. The levels of 1,305 proteins were measured from plasma samples using the standard SOMAscan DNA aptamer–based platform, and metabolite levels were determined from targeted and untargeted mass spectrometry of blood plasma. The MESA Multi-Omics pilot biospecimen collection, molecular phenotype data production and quality control (QC) are described in detail in Kasela et al.⁵⁷

Cross-validation

We used leave-one-out cross-validation (CV) to evaluate our model. The primary reason we chose leave-one-out CV over $k$-fold CV is that our hyperparameter selection method depends on the sample size. With $n-1$ individuals, the same parameters used for the full inference procedure are likely to be valid. For small $k$, fitting with $\frac{k-1}{k}n$ individuals while using the same number of PCs may result in over-fitting in the training set, and using a smaller number of PCs may not capture the same variation as the full model.

To perform cross-validation we hold out a set of individuals, fit the MCFA model, then project the held out individuals into the learned space. If $W_{tr},L_{tr}$ and ${\Phi }_{tr}$ are the model parameters learned from the training set, the projections of the test data into the learned spaces are given by

$${\hat{Z}}_{te}=Y_{te}{\left(W_{tr}{W}_{tr}^{\top }+L_{tr}{L}_{tr}^{\top }{\Psi }_{tr}\right)}^{-1}{W}_{tr}{\hat{X}}_{te}=Y_{te}{\left(W_{tr}{W}_{tr}^{\top }+L_{tr}{L}_{tr}^{\top }{\Psi }_{tr}\right)}^{-1}{L}_{tr}$$

The full data reconstruction is

$${\hat{Y}}_{te}={\hat{Z}}_{te}{W}_{tr}^{\top }+{\hat{X}}_{te}{L}_{tr}^{\top }$$

We evaluate model fit by calculating the normalized root mean squared error (NRMSE). In order to provide a fair evaluation across modes with a highly variable number of features, we calculate NRMSE on a per mode basis

$$NRMSE=\sqrt{\frac{1}{p_m}\sum _{i=1}^{p_m}\frac{{\left(Y_m^{\left(:,i\right)}-{\hat{Y}}_m^{\left(:,i\right)}\right)}^2}{var{Y}_m^{\left(:,i\right)}}}$$

and potential over-fitting can be assessed by comparing the median training set NRMSE against the median test set NRMSE over many cross-validation iterations.

Comparison to MOFA2 and MMAE

We installed MOFA2 version 0.6.7 using pip install mofapy2. We used the options scale_groups = False, scale_views = False, ard_weights = True and spikeslab_weights = True. We set the convergence tolerance to convergence_mode = ’medium’. For comparison purposes we set the number of factors equal to the hidden dimensionality inferred by MCFA (factors = 14).

Our multi-modal auto-encoder architecture is visualized in Figure S4. We used two hidden layes per dataset, with the first layer having dimensionality equal to 8 times that modalities MCFA-inferred number of PCs, and the second layer having dimensionality equal to that modalities MCFA-inferred number of PCs. These layers are then concatenated, and sent through an additional hidden layer with 8 times the MCFA-inferred number of shared dimensions to the final 14-dimensional encoded representation. All layers except the final encoder layer consist of a linear transform followed by ReLU activation, while the final encoder layer omits the ReLU activation. The decoder had identical architecture to the encoder only reversed. The network was implemented in pytorch v1.11.0 and optimized with Adagrad using 10 batches per epoch until the NRMSE change relative to the total loss was less than ${10}^{-6}$.

Quantification and statistical analysis

We analyzed individuals from Exam 1 where all five data types were collected and passed QC. All data modalities were inverse rank normalized prior to sample filtering based on the availability of other data types. There were 614 individuals with observations of WGS, RNA-seq, methylation, metabolomics and proteomics that all pass QC. We further removed all features (CpGs, genes, proteins) located on sex-chromosomes, $0$-variance features, CpGs with missing data, and CpGs where the probe was within 5 bases of an SNP, leaving us with $\mathrm{6,042}$ metabolites, $\mathrm{1,222}$ proteins, $\mathrm{19,034}$ genes, and $\mathrm{724,210}$ CpGs. We analyzed $28$ PCs of RNA expression, $39$ PCs of methylation, $27$ PCs of protein expression and $63$ PCs of metabolite, as determined using the aforementioned method. For sample metadata, we leveraged the rich phenotype data available in MESA that were harmonized by the TOPMed Data Coordinating Center.⁵⁸ For details on the estimation of sample cell-type proportions from methylation and RNA-seq data, see Kasela et al.⁵⁷ Genetic association analyses were conducted using plink v 1.9⁵⁵ while controlling for site, age, sex and 11 genotype PCs; reported $p$-values are uncorrected and tested against a null of $0$ effect. SNP set enrichment significance was defined as having an FDR $q$-value below $0.05$ when corrected for 3 tested sets across 14 factors tested against the null hypothesis that the mean ${\chi }^2$ test statistic is 1.

Published: July 10, 2023

Data and code availability

The MESA TOPMed multi-omics pilot data have been deposited on dbGap and are publicly available as of the date of publication. The accession number is listed in the key resources table. All original code has been deposited on zenodo and is publicly available as of the date of publication. The DOI is listed in the key resources table. The code is also available on github at https://github.com/collinwa/MCFA. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.