Abstract
Although women demonstrate higher levels of rumination than men, it is unknown whether instruments used to measure rumination have the same psychometric properties for women and men. To examine this question, we evaluated measurement invariance of the brooding and reflection subscales from the Ruminative Responses Scale (RRS) by gender, using data from four samples of undergraduates from three universities within the United States (N = 4,205). A multigroup confirmatory factor analysis revealed evidence for configural, metric, and scalar invariance of the covariance structure of the 10-item version of the RRS. There were statistically significant latent mean differences between women and men, with women scoring significantly higher than men on both brooding and reflection. These findings suggest that the 10-item version of the RRS provides an assessment of rumination that is psychometrically equivalent across gender. Consequently, gender differences in brooding and reflection likely reflect valid differences between women and men.
Keywords: brooding, gender, measurement invariance, reflection, Response Styles Questionnaire, rumination, Ruminative Responses Scale
Beginning in adolescence, rates of depression in women are greater than in men, and by adulthood, women are twice as likely as men to become depressed (for reviews, see Girgus & Yang, 2015; Kessler, 2006); compared to men, women also report higher levels of depressive symptoms (for a meta-analysis, see Wang et al., 2016). One popular theory that has been advanced to explain the gender difference in depression is the Response Styles Theory (Nolen-Hoeksema, 1987, 1991), which proposes that women have a greater tendency to ruminate on their depressive symptoms and distress than do men, and this contributes to greater rates of depression in women relative to men. According to the Response Styles Theory, rumination involves repetitively and passively focusing on symptoms of distress and on the possible causes and consequences of these symptoms. Because rumination enhances the effects of depressed mood on thinking, impairs effective problem solving, interferes with instrumental behavior, and erodes social support, the initial symptoms of depression among people who chronically ruminate are likely to become more severe and evolve into episodes of major depression, and rumination may also prolong current depressive episodes (Nolen-Hoeksema, Wisco, & Lyubomirsky, 2008).
A large literature supports the hypothesis advanced in the Responses Styles Theory that women are more likely to ruminate than men. A meta-analysis reported significant gender differences in rumination in children (d = 0.14), with girls significantly more likely to ruminate than boys; in adolescence, this gender difference is significant and larger in magnitude (d = 0.36) (Rood, Roelofs, Bögels, Nolen-Hoeksema, & Schouten, 2009). Another meta-analysis examined gender differences in coping mechanisms and included 10 studies reporting on gender differences in rumination in children and adults (Tamres, Janicki, & Helgeson, 2002). Findings revealed a significant gender difference in rumination (d = 0.19), with women more likely to ruminate than men. Finally, a meta-analysis of gender differences in rumination in adults found that women were more likely than men to ruminate (d = 0.24) (Johnson & Whisman, 2013). There is also some evidence that the gender difference in rumination remains statistically significant after adjusting for potential confounds that could account for this gender difference. For example, one study found that gender was significantly associated with rumination, adjusting for neuroticism, masculinity, and depressive symptoms (Wupperman & Neumann, 2006).
Depressive rumination is most commonly measured with the 22-item Ruminative Responses Scale (RRS) of the Response Styles Questionnaire (Nolen-Hoeksema & Morrow, 1991). However, researchers have criticized this measure as including items that may overlap in content with measures of depressive symptoms (e.g., Roberts, Gilboa, & Gotlib, 1998; Segerstrom, Tsao, Alden, & Craske, 2000). Treynor, Gonzalez, and Nolen-Hoeksema (2003) eliminated 12 items from the RRS that may overlap with symptoms of depression. They then conducted a principal components analysis of the remaining 10 items in a community sample of 1,131 adults, and results suggested the presence of two components measuring subtypes of rumination: 5 items assessing “a passive comparison of one’s current situation with some unachieved standard,” which they labeled brooding, and 5 items measuring a “purposeful turning inward to engage in cognitive problem solving to alleviate one’s depressive symptoms,” which they labeled reflection (Treynor et al., 2003, p. 256). Support for the importance of the distinction between brooding and reflection comes from research suggesting that compared to the reflection subscale, the brooding subscale of the RRS is more strongly associated with depression and other forms of psychopathology. For example, a meta-analysis of correlational studies and clinical group comparison studies found that relative to the reflection subscale, the brooding subscale was more strongly associated with depression and anxiety (Olatunji, Naragon-Gainey, & Wolitsky-Taylor, 2013). Further evidence for the distinction between brooding and reflection comes from research indicating that brooding (but not reflection) correlates with other risk factors for depression (e.g., Debeer, Hermans, & Raes, 2009; Joormann, Dkane, & Gotlib, 2006) and moderates (e.g., Cox, Funasaki, Smith, & Mezulis, 2012; Olson & Kwon, 2008) and mediates (e.g., Mezulis, Simonson, McCauley, & Vander Stoep, 2011; Raes & Hermans, 2008) the association between other risk factors and depression. Researchers have also examined gender differences in these two subtypes of rumination. Results from a meta-analysis of adults indicated that women score higher than men on both brooding (d = 0.19) and reflection (d = 0.17) (Johnson & Whisman, 2013). The effect sizes for gender differences in the brooding and reflection subscales of rumination, as well as those for rumination in general, are comparable in magnitude to the effect size observed for gender differences in depressive symptoms found in the general population. For example, a meta-analysis of 91 studies examining gender differences on the Beck Depression Inventory (BDI) in non-clinical populations, involving over 29,000 women and 23,000 men, found a mean effect size (d) of 0.19 (Wang et al., 2016). Similarly, a study providing normative data on the Beck Depression Inventory – Second Edition (BDI-II) in a pooled sample of over 15,000 undergraduates from 17 universities, weighted to match the gender and race/ethnicity of students in degree-granting institutions in the United States, yielded a comparable effect size (d = 0.19) (Whisman & Richardson, 2015).
In evaluating gender differences in rumination, including gender differences in brooding and reflection, it is presumed that the measurement of the construct is comparable for women and men. However, because the meaning of items may differ for women and men, measurement invariance of rumination should be established. Measurement invariance (also sometimes labeled as measurement equivalence) is defined as “the mathematical equality of corresponding measurement parameters for a given factorially defined construct (i.e., the loadings and intercepts of a construct’s multiple manifest indicators) across two or more groups” (Little, 1997, p. 55). Without evidence of measurement invariance, it cannot be concluded that gender differences in rumination reflect true differences between women and men on the underlying construct, as they may be due to systematic biases in the way women and men respond to items on measures of rumination. As such, “demonstration of measurement equivalence is a logical prerequisite to the evaluation of substantive hypotheses regarding group differences” (Vandenberg & Lance, 2000, p. 9), because “if factors differ in their nature across groups, then cross-group comparisons on the factors have no meaning or interpretation” (Widaman & Grimm, 2014, p. 547). To date, there are no published studies on measurement invariance of the RRS (or other measures of depressive rumination) across gender. The present study was conducted to examine measurement invariance of Treynor et al.’s (2003) 10-item version of the RRS across gender in college students, using pooled data from four samples obtained from three universities.
Methods
Participants
To increase sample size and enhance generalizability, we used data from four studies from three universities to examine measurement invariance of the 10-item RRS. These four studies were selected because they included large samples of undergraduates; the studies were also diverse with respect to race and ethnicity. Participants who were missing data on >2 items (i.e., more than half the items) on the brooding or reflection scale were excluded from analyses. In addition, because there is some evidence that there are age differences in rumination (Nolen-Hoeksema & Aldao, 2011), we excluded people if they were univariate outliers on age to reduce the likelihood of potential gender differences being confounded with age; data on age were not collected in one study. Finally, we examined each data set for univariate and multivariate outliers and excluded participants who were multivariate outliers (Mahalanobis distance with p < .001; Tabachnick & Fidell, 2001); there were no univariate outliers in any of the studies.
Chan, Miranda, and Surrence (2009) sample.
Participants were undergraduates at a public university in the northeastern United States. From an initial sample of 1,011 people, 3 people were excluded because of missing demographic data and 11 people were excluded because of missing data on the RRS, 19 people were excluded because they were outliers on age, and 4 people were excluded because they were multivariate outliers on the RRS. The final sample used in the current study consisted of 974 participants (669 women and 305 men). The racial/ethnic composition of the sample was 37% White, 35% Asian, 13% Latino, 7% Black, and 8% other, and the mean age was 19.0 (SD = 1.7; range = 18 – 28) years.
Cheref, Lane, Polanco-Roman, Gadol, and Miranda (2015) sample.
Participants were undergraduates at a public university in the northeastern United States. From an initial sample of 1,179 people, 7 people were excluded because of missing demographic data, 27 people were excluded because they were outliers on age, and 2 people were excluded because they were multivariate outliers on the RRS. The final sample used in the current study consisted of 1,143 participants (842 women and 301 men). The racial/ethnic composition of the sample was 34% Asian, 34% White, 12% Latino, 7% Black, and 14% other, and the mean age was 18.9 (SD = 1.5; range = 18 – 27) years.
Fresco, Frankel, Mennin, Turk, and Heimberg (2002) sample.
Participants were undergraduates at a public university in the northeastern United States (Study 2). From an initial sample of 744 people, 173 were excluded because they were missing demographic data and 4 people were excluded because they were multivariate outliers on the RRS. The final sample used in the current study consisted of 567 participants (373 women and 194 men). The racial/ethnic composition of the sample was 51% White, 26% Black, 10% Asian, 2% Latino, and 11% other.
Valderrama, Miranda, and Jeglic (2016) sample.
Participants were undergraduates at a public university in the northeastern United States (Study 2). From an initial sample of 1,611 people, 42 people were excluded because of missing demographic data and 66 people were excluded because of missing data on the RRS, 27 people were excluded because they were outliers on age, and 29 people were excluded because they were multivariate outliers on the RRS. The final sample used in the current study consisted of 1,447 participants (1,047 women and 400 men). The racial/ethnic composition of the sample was 39% Latino, 24% White, 15% Asian, 11% Black, and 11% other, and the mean age was 20.2 (SD = 2.8; range = 18 – 33) years.
Measures
The Ruminative Responses Scale (RRS), which was originally developed as a subscale of the 71-item Response Styles Questionnaire (RSQ; Nolen-Hoeksema & Morrow, 1991), asks respondents to rate how frequently they think the described thought or do the described behavior when they feel “down, sad, blue, or depressed;” items are rated on a 4-point scale ranging from 1 (almost never) to 4 (almost always). Items are summed to yield a total score, with higher scores representing greater self-reported levels of ruminative thinking. As critically reviewed by Luminet (2004), the RRS has high internal consistency and test-retest stability and well-supported predictive validity; relatively few studies have been conducted to evaluate the discriminant validity of the scale. The brooding and reflection component scales of the 10-item version of the RRS identified by Treynor et al. (2003) have acceptable internal consistency and test-retest reliability.
Analysis
Measurement invariance of the 10-item version of the RRS was tested within the framework of multigroup confirmatory factor analysis modeling using procedures outlined elsewhere (e.g., Byrne, 2006; Vandenberg & Lance, 2000; Widaman & Reise, 1997). Analyses were conducted using EQS 6.1 (Bentler, 2005). Because data were missing for a small percentage of participants (see below), maximum likelihood (ML) estimation was used; EQS uses the expectation maximization (EM) type of ML estimation procedure. Estimation was based on the Yuan-Bentler scaled χ2 (Y-Bχ2) (Yuan & Bentler, 2000) test, permitting appropriate goodness-of-fit indices and standard errors for data that are non-normally distributed and that include missing data. Multivariate normality was investigated through Yuan, Lambert, and Fouladi’s (2004) extension of Mardia’s (1970) multivariate kurtosis coefficient and normalized estimate of multivariate kurtosis; the Yuan et al. (2004) value is provided in EQS when missing data are present. Mardia’s normalized multivariate kurtosis estimates can be interpreted like z scores, and Bentler and Wu (2002) suggest that estimates >3 will lead to chi-square and standard error biases.
We tested equivalence across groups of men and women by imposing a series of increasingly stringent between-group constraints. Our first model specified configural invariance (Vandenberg & Lance, 2000), meaning that the same factor structure (i.e., same pattern of fixed and free factor loadings) was estimated simultaneously in both groups but no between-group constraints were placed on parameter estimates. Given support for the configural model, we proceeded to test Model 2, in which we forced equal factor loadings across groups. Metric invariance or weak factorial invariance (Meredith & Teresi, 2006; Vandenberg & Lance, 2000) in the sense of a common factor structure and loadings is met if this model does not result in a deterioration of model fit. Although testing for invariance of error variances is generally considered unnecessary because it is extremely stringent (Widaman & Reise, 1997), any correlated error terms that are freely estimated because of model re-specification are important parameters in the baseline models. Therefore, in Model 3, we followed Byrne’s (2006) recommendation and tested for invariance across the two groups for any correlated error terms that were freely estimated for both women and men (i.e., we tested invariance for common error covariance). Finally, Model 4 added the additional constraint of equal item intercepts in the two groups. This model, known as scalar invariance or strong factorial invariance (Meredith & Teresi, 2006; Vandenberg & Lance, 2000), is met if it does not result in a deterioration of model fit, which would imply that any mean differences between groups are due to mean differences in the latent underlying construct rather than to mean differences that vary from item to item.
Measurement invariance was evaluated by examining overall model fit for each model and differences in model fit between models. We used several indices for evaluating overall model fit. First, we used the Y-Bχ2 (Yuan & Bentler, 2000) test for non-normal missing data because it incorporates a scaling correction for the χ2 when distributional assumptions are violated and data are missing; it parallels the Satorra-Bentler scaled χ2 (S-Bχ2) (Satorra & Bentler, 1988) test for non-normal complete data. Like the χ2 statistic, use of the Y-Bχ2 is sensitive to sample size. Consequently, we also evaluated model fit with the Comparative Fit Index (CFI), the Standardized Root Mean Square Residual (SRMR), the McDonald’s Non-centrality Index (NCI; labeled as McDonald’s Fit Index in EQS), and the Root Mean Square Error of Approximation (RMSEA) and its 90% confidence interval (CI). CFI values ≥ .95, SRMR values ≤ .08, NCI values ≥ .90, and RMSEA values ≤ .06 are viewed as evidence for a well-fitting model (Hu & Bentler, 1999), with CFI values of .92 – .94 and RMSEA values ≤ .08 considered as indicators of reasonable model fit (Byrne, 2008). For CFI, NCI, and RMSEA, we report the robust versions of these indices (i.e., *CFI, *NCI, and *RMSEA), which are robust to violations of the normality assumption.
The various models we tested are nested under each other, in the sense that as more between-group restrictions are included, the models are hierarchically nested. Nested models can be compared in pairs by calculating the differences in their overall χ2 values and the related degrees of freedom; the χ2-difference value (Δχ2) is distributed as χ2, with the degrees of freedom equal to the difference in degrees of freedom (Δdf); similar comparisons can be made based on the Y-Bχ2 (or S-Bχ2), except that a correction to this difference value is needed because it is not distributed as χ2 (Satorra & Bentler, 2001). Historically, if the Δχ2 value is significant, it suggests that the constraints in the more restrictive model do not hold and therefore that the two models are not equivalent across groups. However, the use of the Δχ2 has come under criticism because it is highly sensitive to sample size. Consequently, researchers have based decisions of invariance on alternative fit indices. Cheung and Rensvold (2002) recommended that ΔCFI should not exceed −.01 and ΔNCI should not exceed −.02. More recently, Chen (2007) recommended several criteria sets for rejecting measurement invariance, the most conservative of which is: (a) ΔCFI ≤ −.010 supplemented by ΔRMSEA ≥ .015 or ΔSRMR ≥ .030 for testing loading (i.e., metric) invariance; and (b) ΔCFI ≤ −.010 supplemented by ΔRMSEA ≥ .015 or ΔSRMR ≥ .010 for testing intercept (i.e., scalar) invariance. Finally, Meade, Johnson, and Braddy (2008) recommended a cutoff of −.002 for ΔCFI and condition-specific cutoff values for ΔNCI that differ by the number of factors and the number of items (e.g., a cutoff of −.008 for 10 items and 2 factors for the current study). For comparisons between all nested models, we report the appropriately scaled χ2 difference value [ΔY-Bχ2 – based on the Yuan-Bentler correction] and its degrees of freedom. However, because the sample size for our analyses were large, we relied on four alternative fit indices (ΔCFI, ΔSRMR, ΔNCI, and ΔRMSEA), using the robust versions of three of these indices (i.e., Δ*CFI, Δ*NCI, and Δ*RMSEA).
Results
We tested for measurement invariance of the 10-item RRS in the combined sample of data from the four studies. Only 1.8% of participants had missing data on one or more items; data were missing for ≤ 0.4% of participants for each individual item. According to the Missing Completely at Random (MCAR) test (Little & Rubin, 2002), missing items were distributed completely at random, χ2(166) = 187.41, p = .122.
The final pooled sample (N = 4,205) included 2,982 women and 1,223 men. The racial/ethnic distribution of the sample was 29% White, 23% Latino, 22% Asian, 16% Black, and 11% other. The mean age for the 3,638 people for whom data on age were collected was 19.4 years (SD = 2.2 years); women and men did not significantly differ on age, t(3636) = 0.68, p = .499.
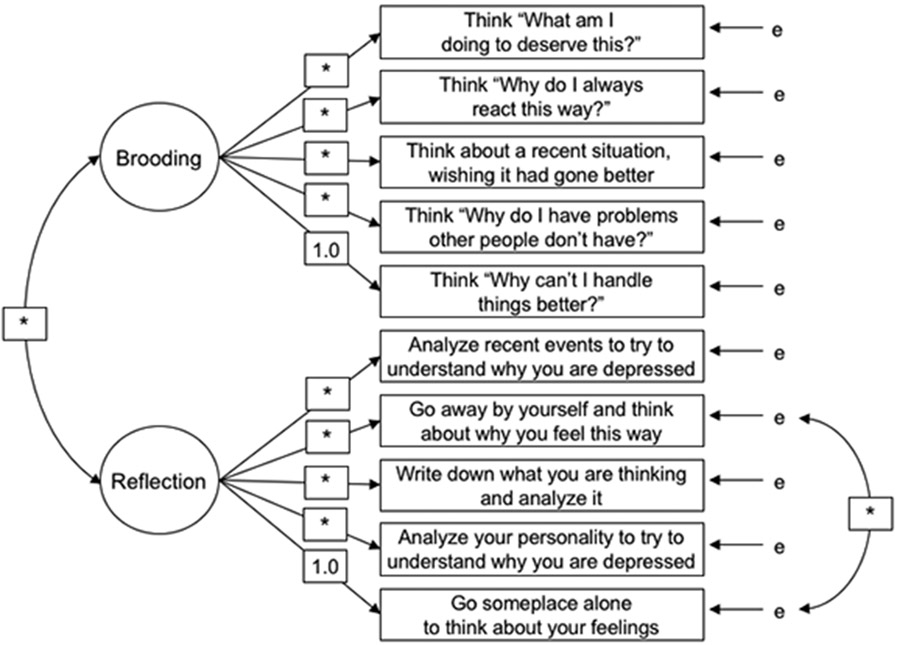
Prior to conducting the invariance analysis, we first needed to establish a well-fitting baseline model for the 10-item version of the RRS. We compared a single-factor model with Treynor et al.’s (2003) two-factor model for the pooled sample, with data from women and men combined. The Yuan et al. (2000) extension of Mardia’s multivariate kurtosis coefficient and its normalized estimate were 16.79 and 35.21, respectively; the substantial multivariate kurtosis supports the use of robust statistics. The single-factor model provided a relatively poor fit with the data, Y-Bχ2(35) = 2662.07, p < .001, *CFI = .777, SRMR = .086, *NCI = .731, *RMSEA = .134, 90% CI = .130, .138. Model fit for the two-factor model, S-Bχ2(34) = 1516.17, p < .001, *CFI = .874, SRMR = .061, *NCI = .838, *RMSEA = .102, 90% CI = .098, .106, was significantly better than model fit for the one-factor model, ΔS-Bχ2(1) = −671.08, p < .001. However, the fit statistics for the two-factor model did not generally meet the cutoffs for a well-fitting model. A review of the Lagrange Multiplier (LM) test statistics revealed the error covariance between Item 11 (“Go away by yourself and think about why you feel this way”) and Item 21 (“Go someplace alone to think about your feelings”) to be markedly misspecified. As the item content for these items is quite similar, covariance between the two items seems reasonable. Similarly, a CFA of the Dutch version of the 10-item RRS in a sample of Dutch-speaking undergraduates in Belgium found a significant improvement in model fit if the error terms between these two items was allowed to covary (Schoofs, Hermans, & Raes, 2010). Therefore, the two-factor model was re-specified, freely estimating the error covariance between these two items. The re-parameterization resulted in a better fitting model, Y-Bχ2(33) = 611.23, p < .001, *CFI = .951, SRMR = .041, *NCI = .933, *RMSEA = .065, 90% CI = .060, .069. The re-specified two-factor model for the 10-item RRS is shown schematically in Figure 1.
Figure 1.
Model of the Covariance Structure of the 10-item Ruminative Responses Scale
We then tested Treynor et al.’s (2003) two-factor model, re-specified to allow the error terms between Item 11 and Item 20 to be freely estimated, in separate CFAs of data from women and men. The test of the re-specified model resulted in a reasonable fit with the data for women, Y-Bχ2(33) = 451.19, p < .001, *CFI = .950, SRMR = .043, *NCI = .932, *RMSEA = .065, 90% CI = .061, .071, and men, Y-Bχ2(33) = 207.45, p < .001, *CFI = .949, SRMR = .041, *NCI = .931, *RMSEA = .066, 90% CI = .057, .074.
Having established that the re-specified model adequately fit the data for both women and men, we proceeded to test for measurement invariance; results from the tests of measurement invariance are presented in Table 1. Our first model specified configural invariance, meaning that the same factor structure (i.e., same pattern of fixed and free factor loadings and correlated error terms) was estimated for women and men, but no between-group constraints were placed on the parameter estimates. Although the Y-Bχ2 was statistically significant, the *CFI, SRMR, and *NCI values all fell within Hu and Bentler’s (1999) recommended cutoffs for a well-fitting model, and the *RMSEA value (and its 90% confidence interval) fell within Byrne’s (2008) recommended cutoff for reasonable model fit. Given support for the configural model, we proceeded to test Model 2, in which we forced equal factor loadings across groups. As can be seen in Table 1, the resulting ΔY-Bχ2 was not statistically significant, and the Δ*CFI, ΔSRMR, Δ*NCI, and Δ*RMSEA values fell well below the recommended values for rejecting measurement invariance. The additional constraint of a common error covariance (i.e., the one correlated error term that was freely estimated for both women and men) was added in Model 3. As can be seen in Table 1, there was little change in the Y-Bχ2 or the alternate fit indexes for this model. Finally, Model 4 added the additional constraint of equal item intercepts in the two groups. As can be seen in Table 1, although the ΔY-Bχ2 was statistically significant, the Δ*CFI, ΔSRMR, Δ*NCI, and ΔRMSEA values were all well below the recommended values for rejecting measurement invariance, the SRMR and *NCI values were within Hu and Bentler’s (1999) recommended cutoffs for a well-fitting model, and the *CFI and *RMSEA values fell within Byrne’s (2008) recommended cutoff for a reasonable model fit. In summary, results support the configural, metric, and scalar invariance (as well as invariance of one common error covariance) of the re-specified two-factor model of the Treynor et al. (2003) 10-item version of the RRS1. Given evidence of scalar invariance, we proceeded to test for latent factor mean differences in the two (i.e., brooding and reflection) factors. The latent variable means were fixed at zero in the male sample and estimated in the female sample. The latent factor means for women were estimated as .155 for brooding (Factor 1) and .063 for reflection (Factor 2), which are significantly higher than the mean of zero set for men on brooding (Z = 5.57, p < .001) and reflection (Z = 3.38, p < .001).
Table 1.
Tests of Measurement Invariance of the 10-item Ruminative Responses Scale
| Model Number & Description |
Y-Bχ2 (df) |
*CFI | SRMR | *NCI | *RMSEA | *RMSEA 90% CI |
ΔY-Bχ2 (df) |
Δ*CFI | Δ SRMR | Δ*NCI | Δ*RMSEA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 Configural | 652.91* (66) | .950 | .042 | .932 | .065 | .061, .070 | ----- | ----- | ----- | ----- | ----- |
| 2 Factor loadings invariant | 672.28* (74) | .949 | .044 | .931 | .062 | .058, .066 | 11.82 (8) | −.001 | .002 | −.001 | −.003 |
| 3 Factor loadings & common error covariance invariant | 673.34* (75) | .949 | .044 | .931 | .062 | .057, .066 | 0.03 (1) | .000 | .000 | .000 | .000 |
| 4 Factor loadings, common error covariance, & item intercepts invariant | 786.77* (85) | .949 | .045 | .929 | .063 | .058, .067 | 119.53* (10) | .000 | .001 | −.002 | .001 |
Note. Y-Bχ2 = Yuan-Bentler Scaled χ2; *CFI = Robust Comparative Fit Index; SRMR = Standardized Root Mean Square Residual; *NCI = Robust McDonald’s Non-centrality Index; *RMSEA = Robust Root Mean Square Error of Approximation; 90% CI = 90% Confidence Interval.
p < .001.
Discussion
The present study was conducted to test for measurement invariance of the two-factor model of the 10-item RRS, measuring brooding and reflection, across gender in data from a large, pooled sample of undergraduates from three universities selected from four studies. Results from the CFA for the pooled sample, collapsed across gender, indicated that Treynor et al.’s (2003) two-factor model provided a relatively poor fit to the data, although it provided a significantly better fit than a single-factor model. These results are consistent with the results from two other CFA studies of the 10-item RRS. Relatively poor fit for the two-factor model of the Dutch version of the 10-item RRS was found in a Dutch-speaking, Belgian undergraduate sample (Schoofs et al., 2010) and community sample (Griffith & Raes, 2015). In the current sample, there was a significant improvement in model fit if the error terms between two items on the reflection scale (i.e., items 11 and 21) were allowed to covary for both women and men. Similar results were obtained by Schoofs et al. (2010), who found that model fit improved by allowing the error terms between these two items (and two items on the brooding scale) to covary. The re-specified model, allowing these two items to covary, provided evidence for a well-fitting model in the current sample.
Turning to the findings from the multigroup CFA testing measurement invariance of the re-specified two-factor model for the 10-item RRS, the configural model (Model 1) was supported, which confirms that similar latent factors were present in groups of women and men. Thus, it appears that rumination is conceptualized similarly across gender, as reflected by two factors measuring brooding and reflection. In addition, there was support for metric (i.e., weak) invariance (Model 2, invariance in factor loadings), which means that “a one-unit change on a latent variable will translate into the identical predicted change in the particular manifest variable in all groups” (Widaman & Grimm, 2014, p. 548). Metric invariance implies that the unit of measurement for the underlying factors is comparable for women and men (i.e., that there are equal metrics or scale intervals across gender). Results also supported Model 3, which provides evidence for similarity between women and men in one correlated error term (between Item 11 and Item 21). Finally, there was support for scalar (i.e., strong) invariance (Model 4, invariance in item intercepts), which means that “a given score on a latent variable will translate into the identical predicted score on a particular manifest variable in all groups” (Widaman & Grimm, 2014, p. 548). Said differently, individuals who have the same score on the latent construct will have the same score on the observed (i.e., manifest) variable, regardless of their group membership (i.e., irrespective of whether the participant is a women or a man). Evidence for scalar invariance is necessary to establish that mean differences between women and men are due to differences in the latent underlying construct rather than to differences that vary from item to item. Given evidence for scalar invariance (i.e., invariance in both factor loadings and item intercepts, which implies that the measurement scales not only have similar intervals but also similar origins across groups), then the latent brooding and reflection variables can be viewed as unbiased predictors of brooding and reflection manifest variables, and mean differences between women and men in brooding and reflection manifest variables are accounted for by gender differences on the latent variables. Provided with evidence of invariant factor loadings and intercept, we were able to test for gender differences in the latent factor means. A test of the latent mean differences indicated that relative to men, women scored significantly higher on the latent brooding and reflection factors of the 10-item RRS, which is consistent with what has been observed regarding gender differences in manifest (i.e., observed) means on the RRS brooding and reflection subscales (Johnson & Whisman, 2013). The current findings extend this body of research in demonstrating mean differences between women and men in brooding and reflection, adjusted for measurement error.
In interpreting the results from the study, several strengths and weaknesses are noted. Strengths of the studies include examination of measurement invariance using data pooled from four studies collected at three separate universities, which was done in part to enhance generalizability. The resulting sample was diverse not only with respect to being drawn from separate universities (i.e., location), but also with respect to race and ethnicity. Furthermore, there were no significant differences in mean age between women and men, although data on age were not collected in one study. Therefore, it is unlikely that the results were confounded with group differences in age, which is important given that prior research has found evidence that there are age differences in rumination (Nolen-Hoeksema & Aldao, 2011). Furthermore, pooling data from several studies increased sample size and, therefore, statistical power. Meade et al. (2008) concluded that power is adequate for testing changes in alternative fit indices of measurement invariance when sample sizes are 400 per group or larger. Because the current results were based on a pooled sample of over 1,200 people per group, the size of the sample was more than adequate for testing measurement invariance. However, the data from the studies come from unscreened samples of college students. Prior research that has examined gender differences in rumination have included studies that are based on samples of undergraduates (e.g., Butler & Nolen-Hoeksema, 1994; Cheung, Gilbert, & Irons, 2004), and a meta-analysis of gender differences in rumination and adults found no evidence for heterogeneity of effect sizes (Johnson & Whisman, 2013), suggesting that the size of the gender difference in rumination did not differ significantly across studies, including across studies that did versus those that did not involve undergraduates. Furthermore, one study found evidence for metric invariance of a Brazilian version of the 10-item RRS across three samples of women (i.e., a college student sample, a general population sample, and a medical population sample of women in treatment for weight loss) (Lucena-Santos, Pinto-Gouveia, Carvalho, & Oliveira, 2018), which supports our decision to test for measurement invariance of the 10-item RRS in college students. However, the possibility remains that the results obtained in this study may not generalize to young adults who are not in college, or who have clinically elevated levels of depression, and research on measurement invariance of the RRS in these samples is warranted. Furthermore, research is needed to examine measurement invariance of the brooding and reflection subscales of the RRS in samples of middle-aged and older adults. In addition, research on children is needed to examine measurement invariance of the brooding and reflections subscales of the RRS in younger individuals, as prior studies have found gender differences in rumination in youth (Rood et al., 2009; Tamres et al., 2002). Finally, although the RRS is the most frequently used measure of rumination, there are other measures of rumination, and research on the measurement invariance of these other measures across gender is needed.
In conclusion, results from this study provide support for the configural, metric, and scalar invariance (as well as invariance of one common error covariance) of the re-specified two-factor model of the Treynor et al. (2003) 10-item version of the RRS, measuring brooding and reflection, in college students. These results imply that gender comparisons on these subscales are likely to be valid and that gender differences on the subscales can be meaningfully interpreted. Consequently, gender differences in brooding and reflection found in prior studies (for a meta-analysis, see Johnson & Whisman, 2013) support a key hypothesis of the Response Styles Theory (Nolen-Hoeksema, 1987, 1991), a widely studied theoretical model for understanding well-established gender differences in depression.
Acknowledgments
This research was supported by grants from the National Institute of Aging (AG045301) and the National Institute of Mental Health (MH091873), and the Hunter College Gender Equity Project, National Science Foundation ADVANCE Institutional Transformation Award (0123609).
Footnotes
We also evaluated the structural (i.e., construct-level) invariance of the 10-item RRS (i.e., invariance of the factor covariance; Byrne, 2006) by adding the additional constraint of equal factor covariances in the two groups. Results indicated that the overall model provided a reasonable fit, Y-Bχ2(35) = 788.77, p < .001, *CFI = .949, SRMR = .045, *NCI = .929, *RMSEA = .062, 90% CI = .058, .067. Furthermore, in comparison with Model 4, the ΔY-Bχ2 was 0.06, which was not statistically significant, and the values for Δ*CFI (= .000), Δ*NCI (= .000), and ΔRMSEA (= −.001) were all well below recommended values for rejecting invariance. Factor covariance invariance implies that the two latent variables have the same relationship for women and men.
Contributor Information
Mark A. Whisman, University of Colorado Boulder
Regina Miranda, Hunter College.
David M. Fresco, Kent State University
Richard G. Heimberg, Temple University
Elizabeth L. Jeglic, John Jay College of Criminal Justice
Lauren M. Weinstock, The Warren Alpert Medical School of Brown University and Butler Hospital
References
References marked with an asterisk indicate studies providing data included in the current study.
- Bentler PM (2005). EQS 6 structural equations program manual. Encino, CA: Multivariate Software. [Google Scholar]
- Bentler PM, & Wu EJC (2002). EQS for Windows user's guide. Encino, CA: Multivariate Software, Inc. [Google Scholar]
- Byrne BM (2006). Structural equation modeling with EQS: Basic concepts, applications, and programming (2nd ed.). Mahwah, NJ: Lawrence Erlbaum Associates. [Google Scholar]
- Byrne BM (2008). Testing for multigroup equivalence of a measuring instrument: A walk through the process. Psicothema, 20, 872–882. [PubMed] [Google Scholar]
- Butler LD, & Nolen-Hoeksema S (1994). Gender differences in responses to depressed mood in a college sample. Sex Roles, 30, 3331–346. doi: 10.1007/BF01420597 [DOI] [Google Scholar]
- *Chan S, Miranda R, & Surrence K (2009). Subtypes of rumination in the relationship between negative life events and suicidal ideation. Archives of Suicide Research, 13, 123–135. doi: 10.1080/13811110902835015 [DOI] [PubMed] [Google Scholar]
- Chen FF (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling, 14, 464–504. doi: 10.1080/10705510701301834 [DOI] [Google Scholar]
- * Cheref S, Lane R, Polanco-Roman L, Gadol E, & Miranda R (2015). Suicidal ideation among racial/ethnic minorities: Moderating effects of rumination and depressive symptoms. Cultural Diversity and Ethnic Minority Psychology, 21, 31–40. doi: 10.1037/a0037139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung GW, & Rensvold RB (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling, 9, 233–255. doi: 10.1207/S15328007SEM0902_5 [DOI] [Google Scholar]
- Cheung MSP, Gilbert P, & Irons C (2004). An exploration of shame, social rank and rumination in relation to depression. Personality and Individual Differences, 36, 1143–1153. doi: 10.1016/S0191-8869(03)00206-X [DOI] [Google Scholar]
- Cox S, Funasaki K, Smith L, & Mezulis AH (2012). A prospective study of brooding and reflection as moderators of the relationship between stress and depressive symptoms in adolescence. Cognitive Therapy and Research, 36, 290–299. doi: 10.1007/s10608-011-9373-z [DOI] [Google Scholar]
- Debeer E, Hermans D, & Raes F (2009). Associations between components of rumination and autobiographical memory specificity as measured by a Minimal Instructions Autobiographical Memory Test. Memory, 17, 892–903. doi: 10.1080/09658210903376243 [DOI] [PubMed] [Google Scholar]
- * Fresco DM, Frankel AN, Mennin DS, Turk CL, & Heimberg RG (2002). Distinct and overlapping features of rumination and worry: The relationship of cognitive production to negative affective states. Cognitive Therapy and Research, 26, 179–188. doi: 10.1023/A:1014517718949 [DOI] [Google Scholar]
- Girgus JS, & Yang K (2015). Gender and depression. Current Opinion in Psychology, 4, 53–60. doi: 10.1016/j.copsyc.2015.01.019 [DOI] [Google Scholar]
- Griffith JW, & Raes F (2014). Factor structure of the Ruminative Responses Scale: A community-sample study. European Journal of Psychological Assessment, 31, 247–253. doi: 10.1027/1015-5759/a000231 [DOI] [Google Scholar]
- Hu LT, & Bentler PM (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling, 6, 1–55. doi: 10.1080/10705519909540118 [DOI] [Google Scholar]
- Johnson DP, & Whisman MA (2013). Gender differences in rumination: A meta-analysis. Personality and Individual Differences, 55, 367–374. doi: 10.1016/j.paid.2013.03.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joormann J, Dkane M, & Gotlib IH (2006). Adaptive and maladaptive components of rumination? Diagnostic specificity and relation to depressive biases. Behavior Therapy, 37, 269–280. doi: 10.1016/j.beth.2006.01.002 [DOI] [PubMed] [Google Scholar]
- Kessler RC (2006). The epidemiology of depression among women. In Keyes CLM & Goodman SH (Eds.), Women and depression: A handbook for the social, behavioral, and biomedical sciences (pp. 22–37). New York: Cambridge University Press. [Google Scholar]
- Little RJA, & Rubin DB (2002). Statistical analysis with missing data, (2nd edition). New York: Wiley. [Google Scholar]
- Little TD (1997). Mean and covariance structures (MACS) analyses of cross-cultural data: Practical and theoretical issues. Multivariate Behavioral Research, 32, 53–76. doi: 10.1207/s15327906mbr3201_3 [DOI] [PubMed] [Google Scholar]
- Lucena-Santos P, Pinto-Gouveia J, Carvalho SA, & Oliveira MDS (2018). Is the widely used two-factor structure of the Ruminative Responses Scale invariant across different samples of women? Psychology and Psychotherapy: Theory, Research and Practice. Advance online publication. doi: 10.1111/papt.12168 [DOI] [PubMed] [Google Scholar]
- Luminet O (2004). Measurement of depressive rumination and associated constructs. In Papageorgiou C & Wells A (Eds.), Depressive rumination: Nature, theory and treatment (pp. 187–215). New York: Wiley. [Google Scholar]
- Mardia KV (1970). Measures of multivariate skewness and kurtosis with applications. Biometrika, 57, 519–530. doi: 10.1093/biomet/57.3.519 [DOI] [Google Scholar]
- Meade AW, Johnson EC, & Braddy PW (2008). Power and sensitivity to alternative fit indices in tests of measuremt invariance. Journal of Applied Psychology, 93, 568–592. doi: 10.1037/0021-9010.93.3.568 [DOI] [PubMed] [Google Scholar]
- Meredith W, & Teresi JA (2006). An essay on measurement and factorial invariance. Medical Care, 44, S69–77. doi: 10.1097/01.mlr.0000245438.73837.89 [DOI] [PubMed] [Google Scholar]
- Mezulis A, Simonson J, McCauley E, & Vander Stoep A (2011). The association between temperament and depressive symptoms in adolescence: Brooding and reflection as potential mediators. Cognition & Emotion, 25, 1460–1470. doi: 10.1080/02699931.2010.543642 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nolen-Hoeksema S (1987). Sex differences in unipolar depression: Evidence and theory. Psychological Bulletin, 101, 259–282. doi: 10.1037/0033-2909.101.2.259 [DOI] [PubMed] [Google Scholar]
- Nolen-Hoeksema S (1991). Responses to depression and their effects on the duration of depressive episodes. Journal of Abnormal Psychology, 100, 569–582. doi: 10.1037/0021-843X.100.4.569 [DOI] [PubMed] [Google Scholar]
- Nolen-Hoeksema S, & Aldao A (2011). Gender and age differences in emotion regulation strategies and their relationship to depressive symptoms. Personality and Individual Differences, 51, 704–708. doi: 10.1016/j.paid.2011.06.012 [DOI] [Google Scholar]
- Nolen-Hoeksema S, & Morrow J (1991). A prospective study of depression and posttraumatic stress symptoms after a natural disaster: The 1989 Loma Prieta Earthquake. Journal of Personality and Social Psychology, 61, 115–121. doi: 10.1037/0022-3514.61.1.115 [DOI] [PubMed] [Google Scholar]
- Nolen-Hoeksema S, Wisco BE, & Lyubomirsky S (2008). Rethinking rumination. Perspectives on Psychological Science, 3, 400–424. doi: 10.1111/j.1745-6924.2008.00088.x [DOI] [PubMed] [Google Scholar]
- Olatunji BO, Naragon-Gainey K, & Wolitzky-Taylor KB (2013). Specificity of rumination in anxiety and depression: A multimodal meta-analysis. Clinical Psychology: Science and Practice, 20, 225–257. doi: 10.1111/cpsp.12037 [DOI] [Google Scholar]
- Olson ML, & Kwon P (2008). Brooding perfectionism: Refining the roles of rumination and perfectionism in the etiology of depression. Cognitive Therapy and Research, 32, 788–802. doi: 10.1007/s10608-007-9173-7 [DOI] [Google Scholar]
- Raes F, & Hermans D (2008). On the mediating role of subtypes of rumination in the relationship between childhood emotional abuse and depressed mood: Brooding versus reflection. Depression and Anxiety, 25, 1067–1070. doi: 10.1002/da.20447 [DOI] [PubMed] [Google Scholar]
- Roberts JE, Gilboa E, & Gotlib IH (1998). Ruminative response style and vulnerability to episodes of dysphoria: Gender, neuroticism, and episode duration. Cognitive Therapy and Research, 22, 401–423. doi: 10.1023/A:1018713313894 [DOI] [Google Scholar]
- Rood L, Roelofs J, Bögels SM, Nolen-Hoeksema S, & Schouten E (2009). The influence of emotion-focused rumination and distraction on depressive symptoms in non-clinical youth: A meta-analytic review. Clinical Psychology Review, 29, 607–616. doi: 10.1016/j.cpr.2009.07.001 [DOI] [PubMed] [Google Scholar]
- Satorra A, & Bentler PM (1988). Scaling corrections for chi square statistics in covariance structure analysis. American Statistical Association 1988 Proceedings of the Business and Economic Sections (pp. 308–313). Alexandria, VA: American Stastistical Association. [Google Scholar]
- Satorra A, & Bentler PM (2001). A scaled difference chi-square test statistic for moment structure analysis. Psychometrika, 66, 507–514. doi: 10.1007/BF02296192 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segerstrom SC, Tsao JCI, Alden LE, & Craske MG (2000). Worry and rumination: Repetitive thought as a concomitant and predictor of negative mood. Cognitive Therapy and Research, 24, 671–688. doi: 10.1023/A:1005587311498 [DOI] [Google Scholar]
- Tabachnick BG, & Fidell LS (2001). Using multivariate statistics (4th ed.). Boston: Allyn and Bacon. [Google Scholar]
- Tamres LK, Janicki D, & Helgeson VS (2002). Sex differences in coping behavior: A meta-analytic review and an examination of relative coping. Personality and Social Psychology Review, 6, 2–30. doi: 10.1207/S15327957PSPR0601_1 [DOI] [Google Scholar]
- Treynor W, Gonzalez R, & Nolen-Hoeksema S (2003). Rumination reconsidered: A psychometric analysis. Cognitive Therapy and Research, 27, 247–259. doi: 10.1023/A:1023910315561 [DOI] [Google Scholar]
- * Valderrama J, Miranda R, & Jeglic E (2016). Ruminative subtypes and impulsivity in risk for suicidal behavior. Psychiatry Research, 236, 15–21. doi: 10.1016/j.psychres.2016.01.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenberg RJ, & Lance CE (2000). A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Organizational Research Methods, 3, 4–70. doi: 10.1177/109442810031002 [DOI] [Google Scholar]
- Wang K, Lu H, Cheung EFC, Neumann DL, Shum DHK, & Chan RCK (2016). “Female preponderance” of depression in non-clinical populations: A meta-analytic study. Frontiers in Psychology, 7, 1398. doi: 10.3389/fpsyg.2016.01398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whisman MA, & Richardson ED (2015). Normative data on the Beck Depression Inventory – Second Edition (BDI-II) in college students. Journal of Clinical Psychology, 71, 898–907. doi: 10.1002/jclp.22188 [DOI] [PubMed] [Google Scholar]
- Widaman KF, & Grimm KJ (2014). Advanced psychometrics: Confirmatory factor analysis, item response theory, and the study of measurement invariance. In Reiss HT & Judd CM (Eds.), Handbook of research methods in social and personality psychology (2nd ed., pp. 534–570). New York: Cambridge University Press. [Google Scholar]
- Widaman KF, & Reise SP (1997). Exploring the measurement invariance of psychological instruments: Applications in the substance use domain. In Bryant KJ, Windle M, & West SG (Eds.), The science of prevention: Methodological advances from alcohol and substance abuse research (pp. 281–324). Washington, DC: American Psychological Association. [Google Scholar]
- Wupperman P, & Neumann CS (2006). Depressive symptoms as a function of sex-role, rumination, and neuroticism. Personality and Individual Differences, 40, 189–201. doi: 10.1016/j.paid.2005.05.017 [DOI] [Google Scholar]
- Yuan K-H, & Bentler PM (2000). Three likelihood-based methods for mean and covariance structure analysis with nonnormal missing data. Sociological Methodology, 30, 165–200. doi: 10.1111/0081-1750.00078 [DOI] [Google Scholar]
- Yuan K-H, Lambert PL, & Fouladi RT (2004). Mardia's multivariate kurtosis with missing data. Multivariate Behavioral Research, 39, 413–437. doi: 10.1207/S15327906MBR3903_2 [DOI] [Google Scholar]