Summary
Nonignorable technical variation is commonly observed across data from multiple
experimental runs, platforms, or studies. These so-called batch effects can lead to
difficulty in merging data from multiple sources, as they can severely bias the outcome of
the analysis. Many groups have developed approaches for removing batch effects from data,
usually by accommodating batch variables into the analysis (one-step correction) or by
preprocessing the data prior to the formal or final analysis (two-step correction).
One-step correction is often desirable due it its simplicity, but its flexibility is
limited and it can be difficult to include batch variables uniformly when an analysis has
multiple stages. Two-step correction allows for richer models of batch mean and variance.
However, prior investigation has indicated that two-step correction can lead to incorrect
statistical inference in downstream analysis. Generally speaking, two-step approaches
introduce a correlation structure in the corrected data, which, if ignored, may lead to
either exaggerated or diminished significance in downstream applications such as
differential expression analysis. Here, we provide more intuitive and more formal
evaluations of the impacts of two-step batch correction compared to existing literature.
We demonstrate that the undesired impacts of two-step correction (exaggerated or
diminished significance) depend on both the nature of the study design and the batch
effects. We also provide strategies for overcoming these negative impacts in downstream
analyses using the estimated correlation matrix of the corrected data. We compare the
results of our proposed workflow with the results from other published one-step and
two-step methods and show that our methods lead to more consistent false discovery
controls and power of detection across a variety of batch effect scenarios. Software for
our method is available through GitHub (https://github.com/jtleek/sva-devel) and will be available in future
versions of the  R package in the Bioconductor
project (https://bioconductor.org/packages/release/bioc/html/sva.html).
R package in the Bioconductor
project (https://bioconductor.org/packages/release/bioc/html/sva.html).
Keywords: Batch effect, ComBat, Generalized least squares, Sample correlation adjustment, Two-step batch adjustment
1. Introduction
Because of the high cost of high-throughput profiling experiments or the difficulty in collecting a good number of samples, data sets are often processed in small batches, at different times, or in different facilities. These processing strategies often introduce unwanted technical variation into the data, commonly referred to as batch effects. RNA quality, lab protocol or experimenter, reagent batch, and other known and unknown factors affect the magnitude of batch effects and can often lead to significant technical heterogeneity and non-ignorable variation across batches (Leek and Storey, 2007; Leek and others, 2010; Johnson and others, 2007). It is well-established that batch effects will reduce statistical power and induce substantial bias for detecting differences between study groups (Leek and others, 2010; Johnson and others, 2007; Zhang and others, 2018). It is therefore common to perform some form of batch effect adjustment before the data are used for downstream analyses such as differential expression analysis (Leek and Storey, 2007).
There are many existing batch effect correction strategies, which can be classified as either “one-step” or “two-step” methods. One-step methods perform batch correction and data analysis simultaneously, by integrating the batch correction directly in the statistical model, prediction tool, or inference process. For example, a one-step strategy in a differential expression setting could be to include a batch indicator covariate in a linear model using common differential expression software tools (Smyth, 2005; Law and others, 2014; Robinson and others, 2010; Love and others, 2014). One-step approaches have the advantage of removing batch effects directly and succinctly in the modeling and analysis step. However, the batch correction is limited by the specific modeling approach, which in some cases may not adequately capture the batch effects. In addition, one-step approaches may lead to inconsistent models or handling of the batch effects if multiple downstream steps are desired.
In contrast, two-step methods perform batch correction as a data preprocessing step that is separate from the other steps of the analysis, outputting batch-corrected data for downstream tasks such as clustering, modeling, or prediction are applied to the data. There are several common methods for performing two-step batch correction, including ComBat (Johnson and others, 2007; Zhang and others, 2018; 2020), SVA (Leek and others, 2012), or RUV (Gagnon-Bartsch and Speed, 2012). Two-step methods such as ComBat are popular because they output “clean” data with batch effects removed, making the application of even complex downstream analyses more straightforward. Furthermore, adjusting for batch effects in a two-step process allows for the application of a richer model for batch adjustment (mean, variance, or other moments), which is often needed for combining highly heterogeneous batches of data or data from multiple studies. It is also important to note RUV/SVA and ComBat have different workflows and assumptions: RUV/SVA uses estimated factors of unwanted variation in a model based on the unadjusted data whereas ComBat first adjusts the data and uses a separate model for analysis based on the adjusted data. In addition, ComBat assumes the batch design is known while RUV/SVA does not make such an assumption. In this article, we assume the batch design is known and focus on workflows similar to ComBat, i.e., two-step batch adjustment based on known batches. Our purpose in this article is to understand and correct the impact of two-step batch adjustment on downstream differential expression analysis based on linear models and known batch design, as is the context where ComBat can be applied.
The main drawback of two-step batch effect adjustment using methods such as ComBat is that it may lead to exaggerated significance if downstream modeling is not appropriately conducted, especially for unbalanced group-batch designs where the samples of a study group are distributed unevenly across batches (Nygaard and others, 2016). Consequently, the actual false-positive rates (FPR) and false discovery rates (FDR) for some naïve downstream methods can be much higher than their nominal values, which renders results misleading. The root cause of exaggerated significance is the first step: removing batch effects with two-step methods (such as ComBat) introduces a correlation structure into the adjusted data. In a typical batch adjustment, the batch mean and/or variance are estimated using all the data points in the particular batch, and then this estimated batch mean is subtracted from each data point in the batch. This means that the adjusted data points within each batch are correlated with each other, because they are functions of all the other data from the batch. In addition to the exaggeration of significance established in previous work, we will show that in some circumstances this correlation structure can also result in diminished significance or power. Most researchers are unaware of these phenomena or are otherwise unable to incorporate this correlation structure into their models, which often leads to inappropriate downstream analyses that assume independent data points after batch correction.
Focusing on log-normalized microarray or log-normalized or variance-stabilized RNA-seq data (e.g., voom normalized) (Law and others, 2014), we provide a basic theoretical explanation of the impacts of a naïve two-step batch correction strategy on downstream gene expression inference and provide a heuristic demonstration and illustration of more complex scenarios using both simulated and real-data examples. We show that the group-batch design balance, i.e., whether the study/biological group design is correlated with the batch design, has a profound impact on the correlation structure induced by batch effect removal and thus on downstream analyses. We discuss the impact of the group-batch design balance on biological effect estimation and inference, and point out situations where we expect both exaggerated significance as well as diminished significance and power. We also propose a potential solution for mitigating the impacts of two-step batch correction on downstream analyses. Specifically, we show that the sample correlation matrix can be estimated for batch-corrected data and can be used in regression-based differential expression analysis (ComBat+Cor). This is equivalent to generalized least square (GLS) estimation based on the estimated sample correlation matrix in batch-corrected data. The ComBat+Cor approach, combined with an appropriate variance estimation approach that is built on the group-batch design matrix, proves to be effective in addressing the exaggerated significance problem in ComBat-adjusted data.
2. Methods
2.1. Two-step batch adjustment and sample correlation
To illustrate the correlation structure introduced by two-step batch adjustment methods, we describe a simplified problem with a mean/additive batch effect only. Based on ComBat (Johnson and others, 2007), we describe gene expression data with only batch effects in the mean with the following linear model:
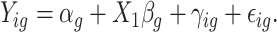 |
(2.1) |
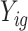 denotes the gene
expression of gene
denotes the gene
expression of gene 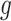 for samples from batch
for samples from batch
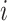 , which is the sum of the background
expression
, which is the sum of the background
expression 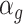 , the vector of biological effects
, the vector of biological effects
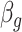 corresponding to a biological group
design matrix
corresponding to a biological group
design matrix 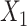 , the mean batch effects
, the mean batch effects
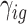 for batch
for batch
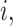 and the residual term
and the residual term
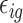 . Without loss of generality,
we reformulate the above equation in matrix form:
. Without loss of generality,
we reformulate the above equation in matrix form:
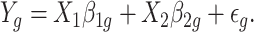 |
(2.2) |
For the model above, we define 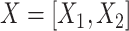 such that the
matrix
such that the
matrix 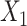 consists of the indicators of
biological groups (the group design) and the matrix
consists of the indicators of
biological groups (the group design) and the matrix 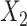 consists of the indicators of batches (the batch design). Therefore,
consists of the indicators of batches (the batch design). Therefore,
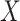 represents the group-batch design and is
of central interest in this article. In this case we will assume the errors
represents the group-batch design and is
of central interest in this article. In this case we will assume the errors
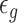 follows a Normal distribution
follows a Normal distribution
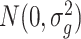 . The model (2.2) can be used to adjust for mean
batch effects and we refer to this approach as the “one-step” approach. Alternatively,
batch effect adjustment can be done by a two-step approach. In the first step, the batch
effects are estimated by
. The model (2.2) can be used to adjust for mean
batch effects and we refer to this approach as the “one-step” approach. Alternatively,
batch effect adjustment can be done by a two-step approach. In the first step, the batch
effects are estimated by 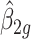 based on the regression
(2.2) above and the
batch-adjusted data
based on the regression
(2.2) above and the
batch-adjusted data 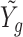 is obtained by removing the
estimated batch effects from
is obtained by removing the
estimated batch effects from 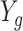 , i.e.,
, i.e., 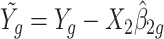 .
The variance of the adjusted data
.
The variance of the adjusted data 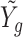 is
is
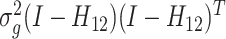 , where
, where
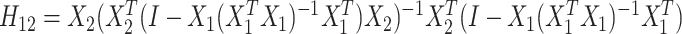 .
For a reference batch (Zhang and others,
2018), the matrix
.
For a reference batch (Zhang and others,
2018), the matrix 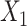 should also include the all-ones vector
should also include the all-ones vector
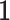 (see the Supplementary material available at
Biostatistics online for derivation).
(see the Supplementary material available at
Biostatistics online for derivation).
In the second step of the two-step approach using a similar linear modeling approach, the
biological effect 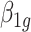 is estimated based on the
adjusted values
is estimated based on the
adjusted values 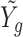 :
:
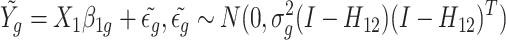 |
(2.3) |
As derived above (and in the Supplementary material available at Biostatistics online), the
samples in adjusted data 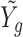 are correlated, with the
correlation matrix defined by
are correlated, with the
correlation matrix defined by 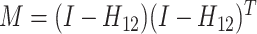 . Its important to
point out that (2.2) and (2.3) lead to different inferences of
. Its important to
point out that (2.2) and (2.3) lead to different inferences of
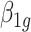 despite their point estimates of
despite their point estimates of
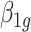 are the same, due to the sample
correlations induced by batch effect adjustment in
are the same, due to the sample
correlations induced by batch effect adjustment in 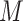 . One
interesting result is that in balanced group-batch designs, i.e., samples of a biological
group are uniformly distributed across batches, the correlations of the adjusted data
values are only dependent on the batch design, and not the group design (see Supplementary Methods available at
Biostatistics online, Section 3 for derivation). However, in unbalanced
group-batch designs, the correlations among individual adjusted values, both within and
across batches, depend also on the group design, which may have an influential impact on
downstream analysis. Regardless of whether or not the group-batch design is balanced,
researchers need to apply downstream analyses that are appropriate for correlated data, as
these correlations may in some cases have profound impact on statistical inference of the
biological effects if not properly modeled.
. One
interesting result is that in balanced group-batch designs, i.e., samples of a biological
group are uniformly distributed across batches, the correlations of the adjusted data
values are only dependent on the batch design, and not the group design (see Supplementary Methods available at
Biostatistics online, Section 3 for derivation). However, in unbalanced
group-batch designs, the correlations among individual adjusted values, both within and
across batches, depend also on the group design, which may have an influential impact on
downstream analysis. Regardless of whether or not the group-batch design is balanced,
researchers need to apply downstream analyses that are appropriate for correlated data, as
these correlations may in some cases have profound impact on statistical inference of the
biological effects if not properly modeled.
2.2. Impact of the design balance on biological effect estimation
One important implication of the covariance structure defined above is that the
correlation matrix 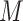 may depend on the biological group design
may depend on the biological group design
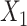 , resulting in possible correlations
between the residuals and the covariate itself, a concept often termed as
endogeneity. In this section, we will show that this issue is related
to the balance of the group-batch design, i.e., whether or not the group design is
correlated with the batch design. To start, we derive the formula of
, resulting in possible correlations
between the residuals and the covariate itself, a concept often termed as
endogeneity. In this section, we will show that this issue is related
to the balance of the group-batch design, i.e., whether or not the group design is
correlated with the batch design. To start, we derive the formula of
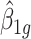 for the one-step approach
(i.e., the model (2.2)) as (see the
Supplementary material
available at Biostatistics online):
for the one-step approach
(i.e., the model (2.2)) as (see the
Supplementary material
available at Biostatistics online):
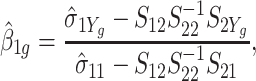 |
(2.4) |
where 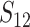 is the covariance
matrix between the group design
is the covariance
matrix between the group design 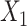 and the batch design
and the batch design
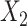 ,
, 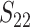 is
the covariance matrix of
is
the covariance matrix of 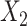 ,
, 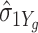 is the sample covariance
of
is the sample covariance
of 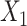 and the outcome
and the outcome
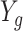 , and
, and 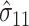 is the sample variance of
is the sample variance of
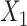 . The critical piece in (2.4) from an endogeneity perspective is
. The critical piece in (2.4) from an endogeneity perspective is
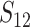 . We will now consider cases where
the batch-covariate design is balanced and unbalanced.
. We will now consider cases where
the batch-covariate design is balanced and unbalanced.
2.2.1. Balanced designs
If the group-batch design is balanced, 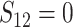 , and the
expression in (2.4) can be
simplified to
, and the
expression in (2.4) can be
simplified to 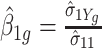 .
Thus it is only important to accurately estimate the residual variance using the
adjusted data. We note that this still requires knowledge of the batch design
.
Thus it is only important to accurately estimate the residual variance using the
adjusted data. We note that this still requires knowledge of the batch design
 . However, in gene expression
analysis, the correlation structure for balanced designs is the same for all genes,
providing ample data to estimate the correlation structure even if the overall sample
size is small. It follows that the biological effect estimates
. However, in gene expression
analysis, the correlation structure for balanced designs is the same for all genes,
providing ample data to estimate the correlation structure even if the overall sample
size is small. It follows that the biological effect estimates 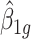 are the same for the
following three models:
are the same for the
following three models:
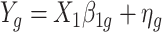 |
(2.5) |
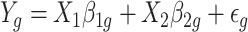 |
(2.6) |
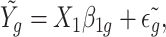 |
(2.7) |
where 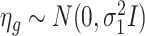 ,
,
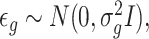 and
and
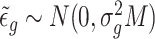 .
We use
.
We use 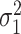 to denote residual variance
associated with (2.5) where one performs T-test on unadjusted data. This suggests that
the biological effect estimate
to denote residual variance
associated with (2.5) where one performs T-test on unadjusted data. This suggests that
the biological effect estimate 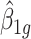 is not
affected by batch effect and therefore the endogeneity issue does not
exist in balanced batch-group design. This is because for balanced batch-group designs
the adjusted data correlations do not depend on the group design
is not
affected by batch effect and therefore the endogeneity issue does not
exist in balanced batch-group design. This is because for balanced batch-group designs
the adjusted data correlations do not depend on the group design
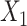 . We make two important observations
here: First, the variance for
. We make two important observations
here: First, the variance for 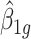 in the
first model will be larger than the variance in the second model, especially if the
batch effect is significant. This means that excluding the batch effect term from the
model will not bias the estimate of the biological effect, but it will inflate the
estimate for the residual standard deviation, leading to a reduction in power. Second,
the variance of
in the
first model will be larger than the variance in the second model, especially if the
batch effect is significant. This means that excluding the batch effect term from the
model will not bias the estimate of the biological effect, but it will inflate the
estimate for the residual standard deviation, leading to a reduction in power. Second,
the variance of 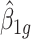 in the third equation
can be estimated using ordinary least squares with the appropriate mean squared error
estimate, or using GLS to directly estimate the residual variance across all genes.
in the third equation
can be estimated using ordinary least squares with the appropriate mean squared error
estimate, or using GLS to directly estimate the residual variance across all genes.
2.2.2. Endogeneity in unbalanced designs
In unbalanced design, the expressions in (2.3) and (2.4) have clear implications in batch correction contexts that must be
considered carefully. First, because the columns of the group design
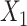 and the batch design
and the batch design
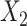 are not linearly independent, and the
are not linearly independent, and the
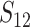 covariance matrix is nonzero,
unlike the balanced design case. Second, the adjusted data correlations are dependent on
both the batch and group designs, and the correlation structure will depend on the
nature and magnitude of the biological effects. Therefore, this correlation structure
will be different across the genes and cannot be easily estimated in gene expression
data with small sample sizes.
covariance matrix is nonzero,
unlike the balanced design case. Second, the adjusted data correlations are dependent on
both the batch and group designs, and the correlation structure will depend on the
nature and magnitude of the biological effects. Therefore, this correlation structure
will be different across the genes and cannot be easily estimated in gene expression
data with small sample sizes.
2.3. Exaggerated and diminished significance in differential expression analysis
The endogeneity in unbalanced designs can bias the biological effect and variance
estimates in gene expression analysis, often leading to incorrect
p-values for downstream differential expression. In general, the
correlation structure induced by two-step adjustments leads to the underestimation of the
residual error if correlation is ignored. As a result, the two-step approach for the model
in (2.1) usually results in
artificially smaller p-values, and inflates the FPR or FDR if the
correlation not properly modeled. Typically, the level of FPR inflation increases as the
group-batch design becomes more unbalanced. This phenomenon is often referred to as
exaggerated significance (Nygaard
and others, 2016). To overcome the exaggerated significance
problem, the correlation matrix 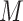 needs to be computed and
accounted for in the two-step analyses.
needs to be computed and
accounted for in the two-step analyses.
Some batch correction methods, such as ComBat, use a richer model than that of (2.1), in that they model and correct
for both mean batch effects 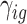 , and variance batch effects
, and variance batch effects
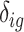 :
:
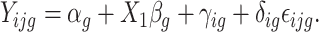 |
(2.8) |
If variance batch effects are not present or negligible, i.e., 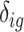 are all close to 1, the model in
(2.8) is equivalent to the
mean-only batch model in (2.1), for
which we have derived the correlation matrix
are all close to 1, the model in
(2.8) is equivalent to the
mean-only batch model in (2.1), for
which we have derived the correlation matrix  for batch-corrected
data. In this case, using ComBat for batch correction will also result in exaggerated
significance for unbalanced designs, as previously described, if methods for correlated
data or the correlation matrix
for batch-corrected
data. In this case, using ComBat for batch correction will also result in exaggerated
significance for unbalanced designs, as previously described, if methods for correlated
data or the correlation matrix 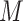 are not used in
downstream modeling.
are not used in
downstream modeling.
However, if variance batch effects are large, i.e., 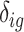 are significantly different among
batches and genes, failure to consider the correlation can have very different effects,
possibly leading to either exaggerated or diminished significance. In this case, the
sample correlation matrix
are significantly different among
batches and genes, failure to consider the correlation can have very different effects,
possibly leading to either exaggerated or diminished significance. In this case, the
sample correlation matrix 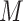 may not be adequate to fully characterize
the sample correlations brought by the two-step batch adjustment described earlier.
Intuitively, one factor that could drive this phenomenon is an underestimation or
overestimation of the residual variance. Specifically, for the ComBat model, the residual
variance estimate is given by the following (Johnson
and others, 2007):
may not be adequate to fully characterize
the sample correlations brought by the two-step batch adjustment described earlier.
Intuitively, one factor that could drive this phenomenon is an underestimation or
overestimation of the residual variance. Specifically, for the ComBat model, the residual
variance estimate is given by the following (Johnson
and others, 2007):
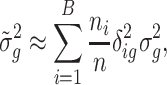 |
(2.9) |
where 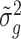 is the
ComBat estimate for the residual variance,
is the
ComBat estimate for the residual variance, 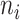 is the size of
is the size of
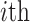 batch, and the total sample size
is
batch, and the total sample size
is 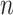 . For identifiability, the ComBat model
calibrates the
. For identifiability, the ComBat model
calibrates the 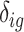 so that their products are
equal to 1. The variance estimate
so that their products are
equal to 1. The variance estimate 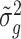 may be
smaller than expected if some or all
may be
smaller than expected if some or all 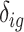 are
significantly less than 1 due to estimation error. In this case, this underestimation
would lead to exaggerated significance. On the other hand,
are
significantly less than 1 due to estimation error. In this case, this underestimation
would lead to exaggerated significance. On the other hand, 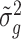 would be overestimated if
most of the
would be overestimated if
most of the 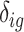 are larger than 1, which likely
leads to a conservative FPR and potentially a significant loss of statistical power.
Therefore, variance batch effects mainly affect the estimate of residual variance
are larger than 1, which likely
leads to a conservative FPR and potentially a significant loss of statistical power.
Therefore, variance batch effects mainly affect the estimate of residual variance
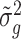 , as evidenced by the
contrast between (2.1) and (2.8), and large variance batch effects
likely lead to a different and much more complicated expression of
, as evidenced by the
contrast between (2.1) and (2.8), and large variance batch effects
likely lead to a different and much more complicated expression of
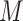 . For the inference of biological effect,
this means the statistical significance can be either exaggerated or diminished using
ComBat, depending on the distributions of
. For the inference of biological effect,
this means the statistical significance can be either exaggerated or diminished using
ComBat, depending on the distributions of 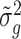 among
batches and genes. We caution readers to be specific about variance batch effects when
discussing the exaggerated significance problem for ComBat.
among
batches and genes. We caution readers to be specific about variance batch effects when
discussing the exaggerated significance problem for ComBat.
2.4. Computing the correlation matrix
We propose additional steps to appropriately address the correlation structure in
two-step adjusted data: first, the sample correlation matrix introduced by batch effect
removal needs to be estimated. Then, any downstream analysis based on batch-corrected data
needs to utilize the sample correlation matrix in their correlated data models. Obtaining
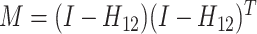 is straightforward
given both the batch and biological design matrices,
is straightforward
given both the batch and biological design matrices, 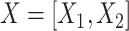 , except that it may not be not
full rank due to the batch correction. Thus,
, except that it may not be not
full rank due to the batch correction. Thus, 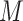 needs to be approximated
by another full rank matrix
needs to be approximated
by another full rank matrix 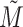 in order to make it usable for
downstream analysis. We note that
in order to make it usable for
downstream analysis. We note that 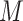 is not gene-specific and
does not consider the differences among gene-specific covariance matrices in unbalanced
group-batch design.
is not gene-specific and
does not consider the differences among gene-specific covariance matrices in unbalanced
group-batch design.
We propose to use the following steps to obtain an approximated sample correlation matrix
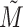 : (i) Apply a spectral
decomposition
: (i) Apply a spectral
decomposition 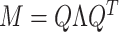 , where
, where
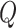 consists of the of eigenvectors of
consists of the of eigenvectors of
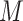 and
and 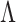 is the diagonal matrix with eigenvalues of
is the diagonal matrix with eigenvalues of 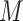 as its diagonal
elements; (ii) Since the batch-corrected data are obtained by removing mean batch effect
estimates from every observation,
as its diagonal
elements; (ii) Since the batch-corrected data are obtained by removing mean batch effect
estimates from every observation, 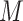 is not full rank and has
some zero eigenvalues. We will replace those zero eigenvalues by a small non-zero number,
is not full rank and has
some zero eigenvalues. We will replace those zero eigenvalues by a small non-zero number,
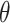 (Cheng and Higham, 1998; Zusmanovich,
2013). Conceptually, this is equivalent to adding a small amount of random noise to
the data set to make it full rank. We will denote the modified set of eigenvalues, with
zeros replaced by
(Cheng and Higham, 1998; Zusmanovich,
2013). Conceptually, this is equivalent to adding a small amount of random noise to
the data set to make it full rank. We will denote the modified set of eigenvalues, with
zeros replaced by 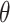 , as
, as 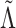 ; (iii) The approximated
sample correlation matrix is computed by
; (iii) The approximated
sample correlation matrix is computed by 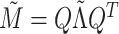 . To enhance
interpretability, we will redefine
. To enhance
interpretability, we will redefine 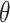 as the product of
the sum of nonzero eigenvalues and
as the product of
the sum of nonzero eigenvalues and 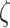 , in which
, in which
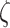 represents the percentage of noise
added by the user. It is recommended that
represents the percentage of noise
added by the user. It is recommended that 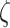 should be chosen as
a value between
should be chosen as
a value between 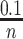 and
and 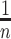 (Knol and ten Berge, 1989), where
(Knol and ten Berge, 1989), where 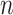 is the total sample
size of the combined batches, as both underadjustment and overadjustment may negatively
influence statistical power. We will demonstrate the impact of
is the total sample
size of the combined batches, as both underadjustment and overadjustment may negatively
influence statistical power. We will demonstrate the impact of 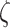 on
batch effect adjustment using our simulation studies below.
on
batch effect adjustment using our simulation studies below.
2.5. Use the sample correlation matrix in differential expression analysis
Based on 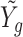 and
and 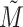 , the linear model for differential
expression analysis becomes:
, the linear model for differential
expression analysis becomes:
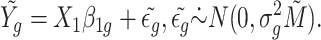 |
(2.10) |
The biological group effects can then be estimated through methods for correlated data,
such as GLS. This will require a Cholesky decomposition of 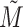 . Linear transformation of both
. Linear transformation of both
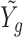 and
and 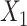 based on the Cholesky decomposition are also required but will be straightforward. Given
that
based on the Cholesky decomposition are also required but will be straightforward. Given
that 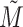 informs the sample correlations
brought by the unbalanced design, the batch-corrected data is no longer correlated via the
transformation based on
informs the sample correlations
brought by the unbalanced design, the batch-corrected data is no longer correlated via the
transformation based on 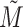 and therefore GLS estimation
should lead to proper statistical significance.
and therefore GLS estimation
should lead to proper statistical significance.
Here, we propose an enhanced version of ComBat, ComBat+Cor (the ComBat approach that includes a correlation adjustment). Incorporating the above procedure will mitigate downstream impacts such as exaggerated p-values (and q-values) for unbalanced group-batch designs. ComBat+Cor comprises the following three steps:
Use the original ComBat approach to obtain batch-adjusted data.
Obtain the sample correlation matrix
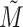 based on
the design matrix
based on
the design matrix 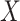 and the noise parameter
and the noise parameter
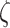 .
.Use downstream analysis methods that accommodate correlated data. For example, estimate the group effect(s) and variance estimates using GLS based on
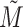 .
.
2.6. Simulation design
To illustrate the effectiveness of ComBat+Cor in addressing the exaggerated significance problem for unbalanced designs, we first performed experiments on simulated data with batch effects. Data sets were simulated with mean and variance batch effects at different levels in order to examine the impact of batch effect sizes on the effectiveness of ComBat+Cor.
In our experiments, we simulated data sets based on the experimental design of a
previously evaluated bladder cancer data set, henceforth denoted as the
bladderbatch data (Dyrskjøt and
others, 2004; Leek and
others, 2010). The simulated bladderbatch data sets followed the
original study design for batches and cancer status, which was highly unbalanced with
respect to status and batch. There were five batches in total, and the numbers of
cancer/control samples in each batch were 11/0, 14/4, 0/4, 0/5, and 15/4, respectively.
For comparison, we also simulated data sets based on a balanced group-batch design. The
number of treated/control samples in the balanced design in each batch were 6/6, 9/9, 2/2,
3/3, and 10/10, respectively. We simulated the expression of 20 000 genes, of which 2000
were set to be differentially expressed between the groups (treatment versus control).
Group effects for the 2000 differentially expressed genes were chosen as 2 (500 genes), 1
(500 genes),  1 (500 genes),
1 (500 genes),  2 (500
genes), reflecting scenarios when the group effect was strongly positive, positive,
negative, and strongly negative. The remaining 18 000 genes were not differentially
expressed between biological groups (“null” genes).
2 (500
genes), reflecting scenarios when the group effect was strongly positive, positive,
negative, and strongly negative. The remaining 18 000 genes were not differentially
expressed between biological groups (“null” genes).
Our simulation method follows the hierarchical linear model assumed in ComBat given in
Equation 2.8 (Johnson and others, 2007). We also specified the number
of samples, batches, and genes in the data, and the distributions of mean and variance
batch effects are given as 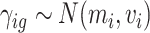 and
and
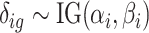 for batch
for batch  . We then sampled
. We then sampled
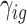 and
and 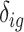 from their hyperparameter
distributions. The background average expression
from their hyperparameter
distributions. The background average expression 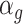 was set to be 3, and the gene-wise variation followed a gamma distribution
was set to be 3, and the gene-wise variation followed a gamma distribution
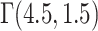 . For the residuals
. For the residuals
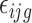 , the variances
, the variances
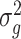 were randomly drawn from a gamma
distribution
were randomly drawn from a gamma
distribution 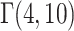 and we randomly sampled
and we randomly sampled
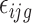 from
from
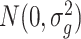 . The above parameters were
chosen based on the ComBat estimates for the original bladderbatch data
and were later modified to reflect scenarios where the batch effects were much larger than
the original estimates (see Table 1). With
simulated batch effects, the final gene expression
. The above parameters were
chosen based on the ComBat estimates for the original bladderbatch data
and were later modified to reflect scenarios where the batch effects were much larger than
the original estimates (see Table 1). With
simulated batch effects, the final gene expression 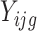 was calculated as
was calculated as 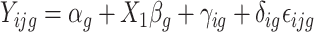 .
To set a benchmark for simulation, we generated data without batch effect as
.
To set a benchmark for simulation, we generated data without batch effect as
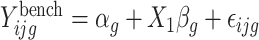 .
.
Table 1.
Hyperparameters of the mean and variance batch effects used in the simulation studies. The “Data” column refers to the parameter values estimated based on the original data. The “Small” and “Large” columns refer to the parameter values used for simulating data with small and large batch effects, respectively
| Batch |
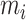
|
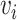
|
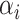
|
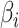
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data | Small | Large | Data | Small | Large | Data | Small | Large | Data | Small | Large | |
| 1 | –0.04 | –0.04 | –0.4 | 0.15 | 0.15 | 0.15 | 60 | 60 | 100 | 60 | 60 | 100 |
| 2 | 0.15 | 0.15 | 1.5 | 0.35 | 0.35 | 0.35 | 100 | 100 | 120 | 100 | 100 | 40 |
| 3 | –0.15 | –0.15 | –1.5 | 0.82 | 0.82 | 0.82 | 56 | 56 | 100 | 50 | 50 | 60 |
| 4 | –0.1 | –0.1 | 1.0 | 0.46 | 0.46 | 0.46 | 30 | 30 | 60 | 30 | 30 | 100 |
| 5 | –0.08 | –0.08 | –0.8 | 0.12 | 0.12 | 0.12 | 100 | 100 | 40 | 100 | 100 | 120 |
We ran a differential expression analysis using a linear model on data without batch
effects, and used the p/q-values obtained in this
approach as the benchmark for the uncorrected and batch-corrected data. After including
the batch effects, we compared ComBat and ComBat+Cor in terms of their distributions of
p-values and FDR. ComBat+Cor, as mentioned earlier, relies on the value
of the noise parameter 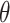 . Therefore, we ran ComBat+Cor with
different values of
. Therefore, we ran ComBat+Cor with
different values of 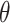 to check the sensitivity of
ComBat+Cor with regard to the choice of
to check the sensitivity of
ComBat+Cor with regard to the choice of 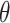 . T-tests based on
the unadjusted raw data were conducted in order to illustrate the necessity of batch
effect adjustment. Results based on the one-step approach, which controls for both the
group and batch indicators in regression model, were also included.
. T-tests based on
the unadjusted raw data were conducted in order to illustrate the necessity of batch
effect adjustment. Results based on the one-step approach, which controls for both the
group and batch indicators in regression model, were also included.
2.7. Empirical examples
In addition to the simulation study based on the bladderbatch data, we provide three real data examples that have unbalanced group-batch designs. The first example is a data set from Towfic and others (2014), which is used to compare the effects of Copaxone and Glatimer. The second example is a data set from Johnson and others (2007), which is used for comparison of TAL1 inhibited cells. The first and second examples were actually used by Nygaard and others (2016) to illustrate the exaggerated significance problem in ComBat. The third example is from several tuberculosis (TB) gene expression studies (Zak and others, 2016; Suliman and others, 2018; Leong and others, 2018), and we compare the gene expressions of progressors versus nonprogressors in TB. For each example, we compare the p/q-values of ComBat and ComBat+Cor. We also conduct simulations based on mean and variance batch effects estimated by ComBat for all three examples, and for each simulation we compare the p-values based on the benchmark approach (data set without batch effects), ComBat and ComBat+Cor, to illustrate the effectiveness of ComBat+Cor in these examples.
3. Results
We provide results for our primary bladderbatch simulation experiment (Example 1), re-analyses of two examples described by Nygaard and others (2016) (Examples 2 and 3), and an additional case in TB gene expression with pronounced variance batch effects (Example 4).
3.1. Example 1: Simulated bladderbatch datasets
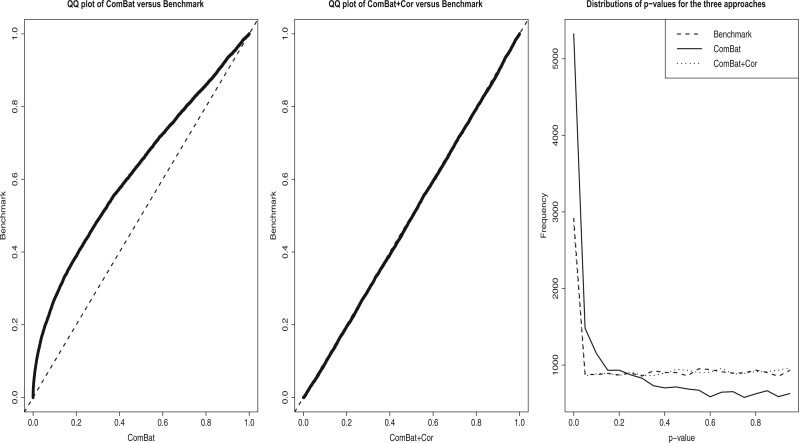
For data sets simulated based on the original bladderbatch data, we found that ComBat
generated exaggerated p-values compared to the benchmark
p-values (Figure 1(a)). The FPR
for ComBat was 18.3% which was much higher than the nominal rate of 5% (Table 2). In contrast, ComBat+Cor (with
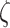 = 1%) was able to appropriately
control the false positive rate (Figure 1(b)). The
FPR for ComBat+Cor (with
= 1%) was able to appropriately
control the false positive rate (Figure 1(b)). The
FPR for ComBat+Cor (with 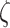 = 1%) was 4.8%. The distributions of
p-values for the benchmark, ComBat and ComBat+Cor are depicted in Figure 1(c). Unsurprisingly, ComBat also yielded an
exaggerated FDR that was much higher than the nominal one. We identified 3264 genes as
differentially expressed using ComBat and an FDR = 5% as the threshold. Of these genes,
1978 were truly differentially expressed, yielding a detection power of 98.9%. The
remaining 1,286 were actually ænullž genes (i.e., genes not differentially expressed),
meaning the actual FDR was inflated to 39.4%. Using ComBat+Cor with
= 1%) was 4.8%. The distributions of
p-values for the benchmark, ComBat and ComBat+Cor are depicted in Figure 1(c). Unsurprisingly, ComBat also yielded an
exaggerated FDR that was much higher than the nominal one. We identified 3264 genes as
differentially expressed using ComBat and an FDR = 5% as the threshold. Of these genes,
1978 were truly differentially expressed, yielding a detection power of 98.9%. The
remaining 1,286 were actually ænullž genes (i.e., genes not differentially expressed),
meaning the actual FDR was inflated to 39.4%. Using ComBat+Cor with
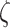 = 1%, 2001 genes were identified as
significant using the same FDR cutoff, 1926 of which were truly differentially expressed
(power = 96.3%). Only 75 of the genes identified as differentially expressed were null
genes, yielding an actual FDR for ComBat+Cor of 3.7%. Therefore, the ComBat+Cor method
provided considerably improved FDR control while retaining high detection power as
compared to ComBat.
= 1%, 2001 genes were identified as
significant using the same FDR cutoff, 1926 of which were truly differentially expressed
(power = 96.3%). Only 75 of the genes identified as differentially expressed were null
genes, yielding an actual FDR for ComBat+Cor of 3.7%. Therefore, the ComBat+Cor method
provided considerably improved FDR control while retaining high detection power as
compared to ComBat.
Fig. 1.
Three figures are used to illustrate that ComBat+Cor reduces the exaggerated
significance seen when ComBat is applied based on simulated data that mimics the
bladderbatch experimental design. Note that the original
bladderbatch data has unbalanced group-batch design and small (mean
and variance) batch effects. The benchmark approach refers to the approach that
applies ordinary differential expression analysis to data without any batch effects.
(a) QQ plot of p-values using ComBat and the
p-values using the benchmark approach. The line falls above the
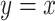 identity line, suggesting that
p-values generated by ComBat concentrate at smaller values than
those generated on the data without batch effect. (b) QQ plot of
p-values using ComBat+Cor (
identity line, suggesting that
p-values generated by ComBat concentrate at smaller values than
those generated on the data without batch effect. (b) QQ plot of
p-values using ComBat+Cor (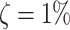 ) and
p-values using the benchmark approach. (c) line chart comparing the
distributions of p-values using ComBat, ComBat+Cor, and the benchmark
approach.
) and
p-values using the benchmark approach. (c) line chart comparing the
distributions of p-values using ComBat, ComBat+Cor, and the benchmark
approach.
Table 2.
Results from bladderbatch simulation with unbalanced design. For each approach, results were obtained under the conditions where the mean and variance batch effects could be null (N), small (S), or large (L). For each condition, the results are formatted as FPR (TPR)
| Approach | Mean(N) | Mean(S) | Mean(L) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Var(N) | Var(S) | Var(L) | Var(N) | Var(S) | Var(L) | Var(N) | Var(S) | Var(L) | |
| T-test | 4.9% | 4.8% | 4.2% | 34.0% | 33.3% | 22.6% | 37.8% | 38.0% | 31.2% |
| (99.7%) | (99.9%) | (95.9%) | (97.8%) | (97.3%) | (93.1%) | (78.9%) | (79.1%) | (76.8%) | |
| Benchmark | 4.9% | 4.8% | 5.3% | 5.3% | 5.0% | 5.1% | 4.8% | 5.0% | 5.0% |
| (99.7%) | (99.9%) | (99.8%) | (99.7%) | (99.9%) | (99.9%) | (99.9%) | (99.7%) | (99.8%) | |
| One-step | 4.9% | 5.0% | 8.4% | 5.2% | 5.1% | 8.1% | 4.9% | 5.0% | 8.3% |
| (99.1%) | (99.0%) | (89.0%) | (98.8%) | (98.5%) | (90.0%) | (98.7%) | (99.1%) | (89.7%) | |
| ComBat | 5.6% | 10.9% | 1.0% | 14.6% | 18.3% | 3.4% | 15.5% | 18.5% | 3.5% |
| (99.7%) | (99.9%) | (98.4%) | (99.7%) | (99.6%) | (98.2%) | (99.6%) | (99.6%) | (98.2%) | |
ComBat+Cor(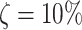 ) ) |
0.0% | 0.0% | 0.0% | 0.2% | 0.2% | 0.0% | 0.2% | 0.3% | 0.0% |
| (94.8%) | (96.1%) | (78.8%) | (94.9%) | (95.7%) | (78.1%) | (94.7%) | (95.3%) | (78.4%) | |
ComBat+Cor(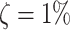 ) ) |
0.4% | 1.6% | 0.2% | 2.7% | 4.8% | 0.6% | 3.0% | 4.7% | 0.6% |
| (99.0%) | (99.2%) | (93.2%) | (98.7%) | (98.6%) | (94.0%) | (98.6%) | (99.1%) | (93.4%) | |
ComBat+Cor(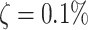 ) ) |
0.2% | 1.1% | 0.1% | 1.3% | 6.3% | 0.3% | 2.1% | 6.6% | 0.3% |
| (97.4%) | (99.1%) | (92.1%) | (98.3%) | (98.8%) | (92.4%) | (98.2%) | (99.4%) | (92.1%) | |
ComBat+Cor(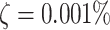 ) ) |
0.0% | 0.0% | 0.0% | 0.0% | 1.3% | 0.0% | 0.0% | 2.5% | 0.0% |
| (23.8%) | (51.3%) | (21.7%) | (17.8%) | (97.9%) | (23.0%) | (33.6%) | (98.8%) | (28.8%) | |
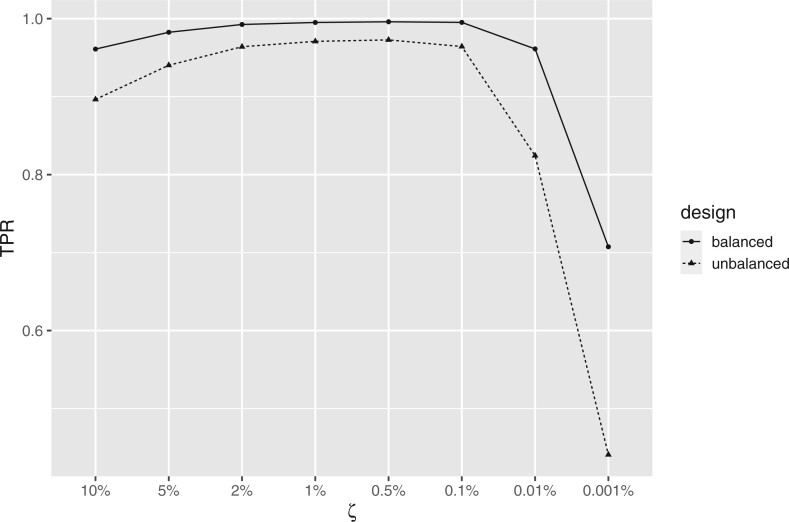
In addition, we conducted a sensitivity analysis using multiple values of
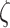 . Our earlier recommendations for
. Our earlier recommendations for
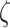 (between
(between 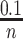 and
and 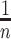 for sample size
for sample size
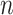 ) yield values in the [0.17%, 1.7%] range
for the sample size of this study (
) yield values in the [0.17%, 1.7%] range
for the sample size of this study (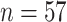 ). We ran ComBat+Cor
with different values of
). We ran ComBat+Cor
with different values of 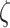 in order to evaluate the recommended
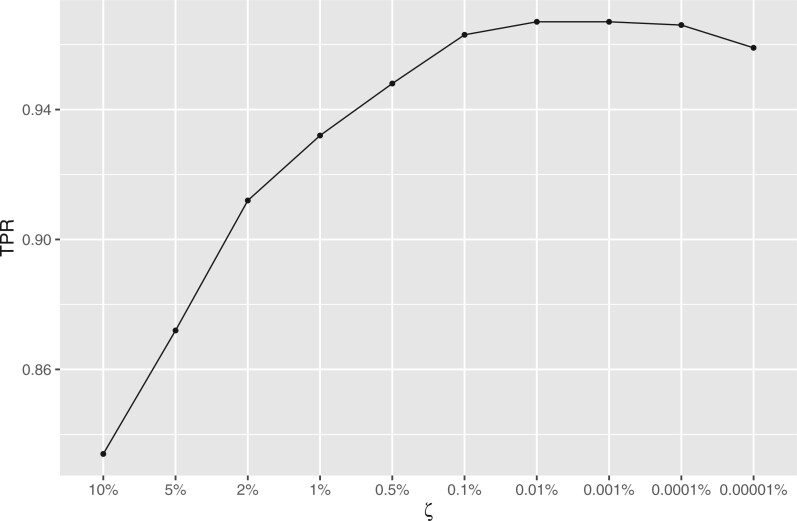
range, as well as check the sensitivity of ComBat+Cor to values outside the range. Figure 2 presents the true positive rate (TPR) associated
with different
in order to evaluate the recommended
range, as well as check the sensitivity of ComBat+Cor to values outside the range. Figure 2 presents the true positive rate (TPR) associated
with different 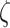 values. These results suggest that
when
values. These results suggest that
when 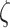 is smaller than 2% and larger than
0.1% (consistent with the recommended range), ComBat+Cor achieved acceptable power
(
is smaller than 2% and larger than
0.1% (consistent with the recommended range), ComBat+Cor achieved acceptable power
(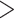 95% for both unbalanced and balanced
designs) for detecting differentially expressed genes. ComBat+Cor lost power when
95% for both unbalanced and balanced
designs) for detecting differentially expressed genes. ComBat+Cor lost power when
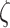 was either above or below the
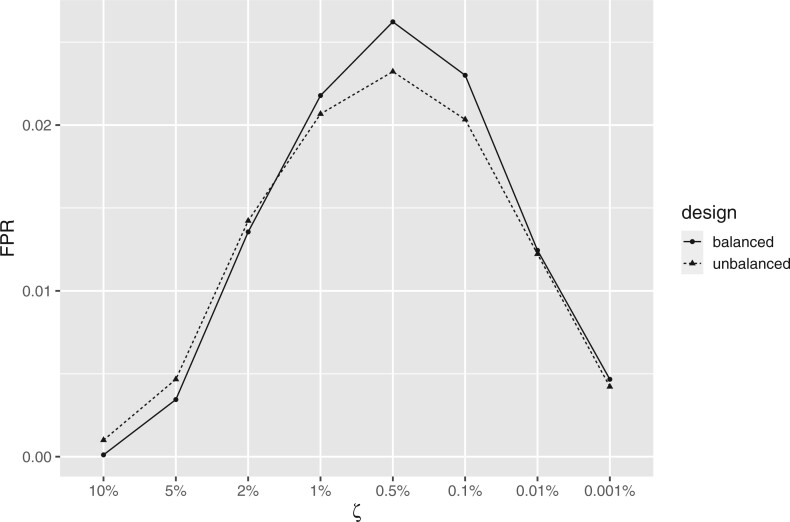
recommended range. Meanwhile, the FPR was consistently below 5% across this range of
was either above or below the
recommended range. Meanwhile, the FPR was consistently below 5% across this range of
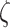 values, signaling that Combat+Cor
will produce conservative results regardless of choice of
values, signaling that Combat+Cor
will produce conservative results regardless of choice of 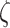 (Figure 3).
(Figure 3).
Fig. 2.
Plot of TPR for different choices of 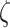 for ComBat+Cor.
The results were simulated based on the unbalanced/balanced group-batch design for the
bladderbatch study.
for ComBat+Cor.
The results were simulated based on the unbalanced/balanced group-batch design for the
bladderbatch study.
Fig. 3.
Plot of FPR for different choices of 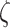 for ComBat+Cor.
The results were simulated based on the unbalanced/balanced group-batch design for the
bladderbatch study.
for ComBat+Cor.
The results were simulated based on the unbalanced/balanced group-batch design for the
bladderbatch study.
Because the mean and variance batch effects were small in the original data, we conducted
a second simulation with the bladderbatch data where we introduced large
mean and variance batch effects to examine the performance of ComBat and ComBat+Cor
(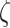 = 1%) under more difficult conditions
(see Table 2). We have two key observations: first,
ComBat led to exaggerated significance in all cases where mean batch effects existed in an
unbalanced design, and the level of exaggeration did not appear to have a relationship
with the size of mean batch effects. Second, the size of variance batch effects had a
strong impact on the performance of both ComBat and ComBat+Cor. When the variance batch
effects were small, ComBat+Cor had much lower FPR than ComBat, which was clearly
exaggerated in this case, in exchange for slightly worse TPR. This suggested that
ComBat+Cor was a better choice than ComBat for small variance batch effects. When the
variance batch effects were large, the TPR of ComBat+Cor reduced significantly while the
exaggerated significance problem of ComBat disappeared, which suggested ComBat+Cor was
overly conservative and less desirable than ComBat in this case. This is probably due to
the advantage that ComBat has in dealing with variance batch effects and the fact that
large variance batch effects would inflate the residual variance estimate and thus reduce
statistical power.
= 1%) under more difficult conditions
(see Table 2). We have two key observations: first,
ComBat led to exaggerated significance in all cases where mean batch effects existed in an
unbalanced design, and the level of exaggeration did not appear to have a relationship
with the size of mean batch effects. Second, the size of variance batch effects had a
strong impact on the performance of both ComBat and ComBat+Cor. When the variance batch
effects were small, ComBat+Cor had much lower FPR than ComBat, which was clearly
exaggerated in this case, in exchange for slightly worse TPR. This suggested that
ComBat+Cor was a better choice than ComBat for small variance batch effects. When the
variance batch effects were large, the TPR of ComBat+Cor reduced significantly while the
exaggerated significance problem of ComBat disappeared, which suggested ComBat+Cor was
overly conservative and less desirable than ComBat in this case. This is probably due to
the advantage that ComBat has in dealing with variance batch effects and the fact that
large variance batch effects would inflate the residual variance estimate and thus reduce
statistical power.
For the comparison among all the approaches included in simulation, we found that for
unbalanced design (Table 2), ComBat+Cor
(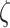 = 1%) consistently had FPR lower than
5% while maintaining a good statistical power. Notably, ComBat+Cor
(
= 1%) consistently had FPR lower than
5% while maintaining a good statistical power. Notably, ComBat+Cor
(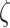 = 1%) was a better choice than the
one-step approach as the one-step approach also tended to have exaggerated significance
and decreased power when variance batch effects were large. The T-test without batch
correction predictably performed the worst among all the candidates, which demonstrated
the necessity for adjusting for batch effects in the data. When the group-batch design was
balanced (Table 3) there were no significant
differences among all approaches, except that the unadjusted T-test was still the worst
performing approach. In general, we observed that ComBat+Cor was a safer choice than
ComBat across all scenarios and protected against large FPR and consequent exaggerated
significance for unbalanced group-batch designs.
= 1%) was a better choice than the
one-step approach as the one-step approach also tended to have exaggerated significance
and decreased power when variance batch effects were large. The T-test without batch
correction predictably performed the worst among all the candidates, which demonstrated
the necessity for adjusting for batch effects in the data. When the group-batch design was
balanced (Table 3) there were no significant
differences among all approaches, except that the unadjusted T-test was still the worst
performing approach. In general, we observed that ComBat+Cor was a safer choice than
ComBat across all scenarios and protected against large FPR and consequent exaggerated
significance for unbalanced group-batch designs.
Table 3.
Results from bladderbatch simulation with balanced design. For each approach, results were obtained under the conditions where the mean and variance batch effects could be null (N), small (S), or large (L). For each condition, the results were formatted as FPR (TPR)
| Approach | Mean(N) | Mean(S) | Mean(L) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Var(N) | Var(S) | Var(L) | Var(N) | Var(S) | Var(L) | Var(N) | Var(S) | Var(L) | |
| T-test | 5.0% | 5.3% | 4.9% | 0.9% | 0.9% | 1.9% | 0.0% | 0.0% | 0.2% |
| (99.9%) | (99.9%) | (97.9%) | (99.9%) | (99.9%) | (97.5%) | (98.0%) | (97.4%) | (93.7%) | |
| Benchmark | 5.0% | 5.3% | 5.1% | 4.9% | 5.0% | 4.8% | 5.2% | 5.1% | 5.2% |
| (99.9%) | (99.9%) | (99.9%) | (99.9%) | (99.9%) | (100%) | (99.9%) | (100%) | (99.9%) | |
| One-step | 5.0% | 5.2% | 4.6% | 4.9% | 4.8% | 4.6% | 5.2% | 4.9% | 4.8% |
| (99.9%) | (99.9%) | (97.8%) | (99.9%) | (99.9%) | (97.9%) | (99.9%) | (100%) | (97.6%) | |
| ComBat | 5.2% | 6.9% | 0.0% | 4.6% | 6.8% | 0.1% | 5.4% | 6.9% | 0.0% |
| (99.9%) | (99.9%) | (99.4%) | (99.9%) | (99.9%) | (99.2%) | (99.9%) | (100%) | (98.8%) | |
ComBat+Cor(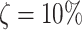 ) ) |
0.0% | 0.1% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| (98.5%) | (99.1%) | (91.2%) | (99.0%) | (99.0%) | (91.0%) | (99.0%) | (98.8%) | (89.3%) | |
ComBat+Cor(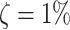 ) ) |
2.6% | 3.9% | 0.0% | 2.3% | 4.0% | 0.0% | 2.8% | 4.0% | 0.0% |
| (99.8%) | (99.8%) | (99.0%) | (99.9%) | (99.9%) | (98.8%) | (99.9%) | (100%) | (98.4%) | |
ComBat+Cor(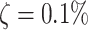 ) ) |
1.2% | 3.6% | 0.0% | 1.1% | 6.2% | 0.1% | 2.1% | 6.4% | 0.0% |
| (99.3%) | (99.8%) | (98.9%) | (99.9%) | (99.9%) | (99.2%) | (99.9%) | (100%) | (98.7%) | |
ComBat+Cor(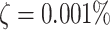 ) ) |
0.0% | 0.0% | 0.0% | 0.0% | 1.7% | 0.0% | 0.0% | 2.5% | 0.0% |
| (41.5%) | (69.6%) | (47.1%) | (32.9%) | (99.9%) | (94.9%) | (54.2%) | (100%) | (96.6%) | |
3.2. Example 2: Towfic and others (2014)
Towfic and others (2014) conducted
an experiment to compare the effects of Copaxone and Glatimer, which are immunomodulators
used to treat multiple sclerosis, and that was also used by Nygaard and others (2016) to illustrate how ComBat can
lead to exaggerated significance for an unbalanced batch-group design. There were 34
samples treated with Copaxone that were compared with 11 samples treated with Glatimer. In
total, there were 17 batches and the batch-group design was highly unbalanced. Following
the data processing and analysis procedure of Nygaard
and others (2016), there were 1928 genes found to be
significant at the 5% FDR threshold using ComBat adjusted data. We subsequently used
ComBat+Cor (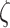 = 1%) to adjust for correlations
introduced by the unbalanced batch-group design and found no genes were significant at 5%
FDR level. However, we recognize that different models for differential expression,
including mixed effects effects models, have led to deferentially expressed genes in this
data set (Towfic and others, 2017;
Nygaard and others, 2017). These
can be further explored in the future with ComBat+Cor, but for the sake of this work, our
goal was to recreate the work of Nygaard and
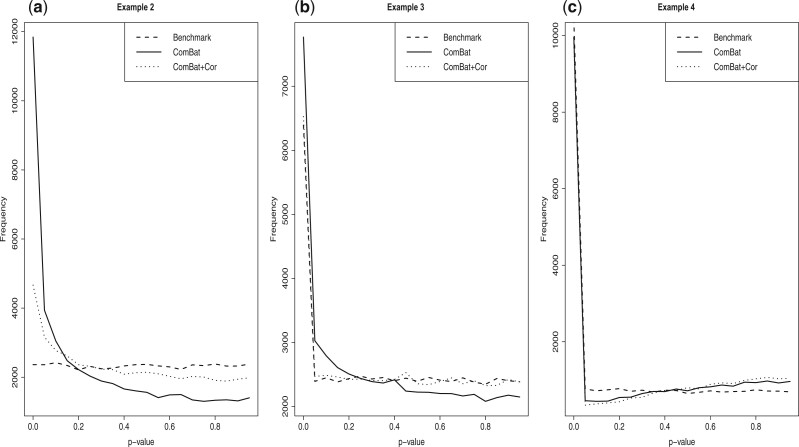
others (2016). The simulation results based on this data (Figure 4(a)) uncovered that the statistical significance
was highly exaggerated by ComBat and there was a strong need of adjustment for the
unbalanced design, which is also consistent with the finding of Nygaard and others (2016).
= 1%) to adjust for correlations
introduced by the unbalanced batch-group design and found no genes were significant at 5%
FDR level. However, we recognize that different models for differential expression,
including mixed effects effects models, have led to deferentially expressed genes in this
data set (Towfic and others, 2017;
Nygaard and others, 2017). These
can be further explored in the future with ComBat+Cor, but for the sake of this work, our
goal was to recreate the work of Nygaard and
others (2016). The simulation results based on this data (Figure 4(a)) uncovered that the statistical significance
was highly exaggerated by ComBat and there was a strong need of adjustment for the
unbalanced design, which is also consistent with the finding of Nygaard and others (2016).
Fig. 4.
Simulation results for examples 2, 3, and 4. In each plot, we illustrate the distributions of the p-values for the benchmark approach, ComBat, and ComBat+Cor. (a) Simulation results based on Towfic and others (2014). (b) Simulation results based on Johnson and others (2007). (c) Simulation results based on the TB data for comparing progressors versus nonprogressors.
3.3. Example 3: Johnson and others (2007)
Johnson and others (2007)
demonstrated ComBat using a data set on the comparison of TAL1 inhibited cells. The
experiment has 30 samples and 3 batches. The number of treated/control samples in each
batch is batch 1: 6/2, batch 2: 3/4, and batch 3: 9/6. Importantly, Batch 3 consisted of
technical replicates of the samples from Batches 1 and 2. Nygaard and others (2016) also used this experiment to
illustrate the exaggerated significance problem in ComBat. Following their processing
procedure, we found 730 significant genes at 5% FDR using ComBat, but only 269 genes
significant at 5% FDR using ComBat+Cor (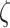 = 1%). Simulation
results (Figure 4(b)) suggested that ComBat had a
mild exaggerated significance problem due to the unbalanced design, which is consistent
with the finding of Nygaard and others
(2016). ComBat+Cor provides better control of the FDR and corrects the previously
reported exaggerated significance problem.
= 1%). Simulation
results (Figure 4(b)) suggested that ComBat had a
mild exaggerated significance problem due to the unbalanced design, which is consistent
with the finding of Nygaard and others
(2016). ComBat+Cor provides better control of the FDR and corrects the previously
reported exaggerated significance problem.
3.4. Example 4: progressors versus non-progressors in TB
We present a final example of TB gene expression data sets which have been used to detect
differentially expressed genes that distinguish progressors from non-progressors in TB
(Zak and others, 2016; Suliman and others, 2018; Leong and others, 2018). This data
example had three batches with each batch from a separate study. The ratios of the number
of progressors and the number of nonprogressors in each batch were 77/104, 95/304, and
0/19. We chose 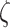 as 0.1% as guided by the recommended
range and the sample size, and simulation results supported this choice (Figure 5). Of 24 391 genes, We found 9659 significant
genes at 5% FDR using ComBat and 8403 significant genes at 5% FDR using ComBat+Cor
(
as 0.1% as guided by the recommended
range and the sample size, and simulation results supported this choice (Figure 5). Of 24 391 genes, We found 9659 significant
genes at 5% FDR using ComBat and 8403 significant genes at 5% FDR using ComBat+Cor
(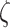 = 0.1%). We observed that the
significant genes found by ComBat contained all the genes found by ComBat+Cor. Our
simulation results (Figure 4(c)) showed that most of
the discovered genes were expected to be differentially expressed, as both ComBat and
ComBat+Cor had diminished significance in the simulated data due to large variance batch
effects. We also included SVA and RUV in our simulation and found that they were not
effective in terms of removing large variance batch effects in this case, as they both led
to exaggerated significance and reduced statistical power (see results in the Supplementary material available at
Biostatistics online).
= 0.1%). We observed that the
significant genes found by ComBat contained all the genes found by ComBat+Cor. Our
simulation results (Figure 4(c)) showed that most of
the discovered genes were expected to be differentially expressed, as both ComBat and
ComBat+Cor had diminished significance in the simulated data due to large variance batch
effects. We also included SVA and RUV in our simulation and found that they were not
effective in terms of removing large variance batch effects in this case, as they both led
to exaggerated significance and reduced statistical power (see results in the Supplementary material available at
Biostatistics online).
Fig. 5.
Plot of TPR for different choices of 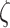 for ComBat+Cor.
The results were simulated based on the original TB data set.
for ComBat+Cor.
The results were simulated based on the original TB data set.
4. Discussion
ComBat is an established tool for batch effect adjustment, but we have shown it can often lead to inflated (or deflated) significance in gene expression studies, particularly for unbalanced group-batch designs. The exaggerated significance of ComBat results from the fact that samples are correlated after batch adjustment, because removing the estimated mean batch effect from the original data relies on all observations within a batch. To avoid this problem, downstream analysis must account for the correlation induced by batch adjustment.
We have shown that the sample correlation matrix can be derived based on the group-batch
design and should be incorporated into downstream analyses. Because the derived sample
correlation matrix is not full-rank, we proposed a procedure that adds a small amount of
random noise into the data using a parameter 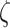 . This recovers
approximate estimability of the covariance structure and enables approximation through a
spectral decomposition approach. The ComBat three-step approach with a correlation
adjustment, ComBat+Cor, is defined as follows: (i) use the original ComBat to obtain
batch-corrected data; (ii) compute the approximated sample correlation matrix; (iii) conduct
downstream modeling with appropriate accommodations for correlated data, such as GLS, using
the estimated sample correlation matrix.
. This recovers
approximate estimability of the covariance structure and enables approximation through a
spectral decomposition approach. The ComBat three-step approach with a correlation
adjustment, ComBat+Cor, is defined as follows: (i) use the original ComBat to obtain
batch-corrected data; (ii) compute the approximated sample correlation matrix; (iii) conduct
downstream modeling with appropriate accommodations for correlated data, such as GLS, using
the estimated sample correlation matrix.
Our simulation results based on a real data set with substantial group-batch imbalance and
both mean and variance batch effects demonstrate that accounting for the sample correlation
matrix via Combat+Cor provides consistent control of the false positive rate for
differential expression analysis. This is especially important considering the exaggerated
significance problem of ComBat in unbalanced group-batch designs. ComBat+Cor is consistently
more conservative than ComBat regardless of the choice of 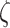 and
thus protects against inflated FDR. For a recommended choice of
and
thus protects against inflated FDR. For a recommended choice of 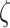 (i.e., between
(i.e., between 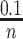 and
and 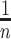 ), ComBat+Cor can also achieve good
statistical power, making it more desirable than ComBat for unbalanced group-batch designs
without large variance batch effects. It is also noteworthy that ComBat+Cor maintains a
better balance between TPR and FPR and is more flexible than the one-step approach for
unbalanced group-batch designs, as the one-step approach is not always available. We still
recommend using ComBat for balanced group-batch designs, as it consistently yields higher
statistical power and has no signs of exaggerated significance in the balanced designs.
), ComBat+Cor can also achieve good
statistical power, making it more desirable than ComBat for unbalanced group-batch designs
without large variance batch effects. It is also noteworthy that ComBat+Cor maintains a
better balance between TPR and FPR and is more flexible than the one-step approach for
unbalanced group-batch designs, as the one-step approach is not always available. We still
recommend using ComBat for balanced group-batch designs, as it consistently yields higher
statistical power and has no signs of exaggerated significance in the balanced designs.
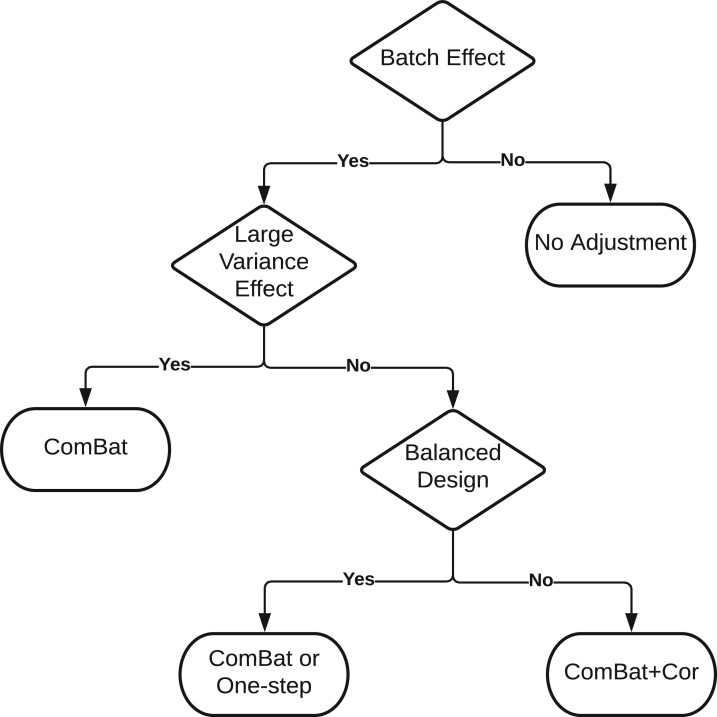
We caution readers that ComBat+Cor is less desirable for data with large variance batch effects, as it may become too conservative and underreport the number of truly significant features. The exaggerated significance problem for ComBat may not always be present in data examples where batches have large variance batch effects. Given ComBat+Cor actually loses TPR in exchange for a reduction in FPR, such a tradeoff would be undesirable when the ComBat approach does not lead to exaggerated significance. Therefore, we recommend using ComBat for data with large variance batch effects and ComBat+Cor for data with small variance batch effects. BatchQC, an interactive R shiny app, could be used to detect the existence and the degree of batch effects based on statistical significance tests and data visualizations (Manimaran and others, 2016). The one-step approach is also a good alternative for differential expression analysis when variance batch effect is small. To facilitate the decision-making process, we illustrate the guidance about the choice of ComBat and ComBat+Cor in Figure 6.
Fig. 6.
Guidance about the choice of ComBat and ComBat+Cor for addressing the exaggerated significance problem in batch correction.
In this article, we focus on log- or variance-normalized data where the exaggerated significance issue is well-known. However, this issue is not well-studied for unnormalized RNA-seq data and thus beyond the scope of this article. In the absence of future studies on raw RNA-seq data, the exaggerated significance issue indeed appears in batch-adjusted RNA-seq data as long as RNA-seq data is normalized (plausibly normal-distributed). For unnormalized RNA-seq data, there are three possible options to leverage our theoretical framework to address it: First, one can transform the raw data (such as logCPM) to make them more appropriate for Gaussian-based models such as ComBat. Second, one can define a working correlation structure where the samples are clustered based on both the batch and group designs for differential expression analysis based on generalized estimating equations. Third, one can choose the one-step approach based on GLM with known batches. Further research is needed for investigating the impact of exaggerated significance in batch-adjusted unnormalized RNA-seq data, and also for customary solutions for popular RNA-seq methods such as DESeq (Anders and Huber, 2010; Love and others, 2014), limma (Smyth, 2005), or edgeR (Robinson and others, 2010).
Future research is needed in the following three directions: First, more in-depth
discussions about the role of variance batch effects in downstream analyses as well as the
inference of biological effects are needed. Second, correlations in the batch-corrected data
given by ComBat may be partially due to empirical Bayes (EB) processing, and therefore
learning the impact of EB processing is necessary for a comprehensive understanding of the
sample correlations induced by ComBat. Its noteworthy that the sample correlation matrix
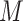 is an approximation of the underlying sample
correlation matrix whose expression is difficult to derive as it is intertwined with all
different processing steps in ComBat. However, via the simulation, we have shown that such
approximation is adequate for addressing the exaggerated significance problem brought by
unbalanced group-batch design and given recommendations about finding such approximations
based on empirical results (i.e., choice of
is an approximation of the underlying sample
correlation matrix whose expression is difficult to derive as it is intertwined with all
different processing steps in ComBat. However, via the simulation, we have shown that such
approximation is adequate for addressing the exaggerated significance problem brought by
unbalanced group-batch design and given recommendations about finding such approximations
based on empirical results (i.e., choice of 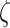 ). Third, further
investigations regarding the impact of batch adjustment on downstream machine learning
applications, such as classification or clustering, are needed.
). Third, further
investigations regarding the impact of batch adjustment on downstream machine learning
applications, such as classification or clustering, are needed.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
Contributor Information
Tenglong Li, Academy of Pharmacy, Xi’an Jiaotong-Liverpool University, 111 Ren’ai Road, Dushu Lake Higher Education Town, Suzhou Industrial Park, Suzhou 215123, Jiangsu Province, PRC.
Yuqing Zhang, Clinical Bioinformatics, Gilead Sciences, Inc., 333 Lakeside Dr, Foster City, CA 94404.
Prasad Patil, Department of Biostatistics, School of Public Health, 801 Massachusetts Ave. Boston, MA 02118, USA.
W Evan Johnson, Division of Computational Biomedicine, School of Medicine, 72 E. Concord Street, Boston, MA 02118, USA and Department of Biostatistics, School of Public Health, 801 Massachusetts Ave. Boston, MA 02118, USA.
5. Software and code
Software in the form of R code, together with a sample input data set and complete
documentation is available online at GitHub (https://github.com/tenglongli/ComBatCorr). Function for outputting the
adjusted p-values or the 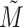 matrix (function
name:
matrix (function
name: 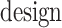 ) is also available in
GitHub (https://github.com/jtleek/sva-devel) and will be available in future versions
of the
) is also available in
GitHub (https://github.com/jtleek/sva-devel) and will be available in future versions
of the  package in Bioconductor
(https://bioconductor.org/packages/release/bioc/html/sva.html).
package in Bioconductor
(https://bioconductor.org/packages/release/bioc/html/sva.html).
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
This work was supported by funds from the National Institutes of Health, namely the National Cancer Institute (5U01CA220413) and the National Institute of General Medical Sciences (5R01GM127430).
References
- Anders, S. and Huber, W. (2010). Differential expression analysis for sequence count data. Genome Biology 11, R106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng, S. H. and Higham, N. J. (1998). A modified Cholesky algorithm based on a symmetric indefinite factorization. SIAM Journal on Matrix Analysis and Applications 19, 1097–1110. [Google Scholar]
- Dyrskjøt, L., Kruhøffer, M., Thykjaer, T., Marcussen, N., Jensen, J. L., Møller, K. and Ørntoft, T. F. (2004). Gene expression in the urinary bladder: a common carcinoma in situ gene expression signature exists disregarding histopathological classification. Cancer Research 64, 4040–4048. [DOI] [PubMed] [Google Scholar]
- Gagnon-Bartsch, J. A. and Speed, T. P. (2012). Using control genes to correct for unwanted variation in microarray data. Biostatistics 13, 539–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson, W. E., Li, C. and Rabinovic, l. (2007). Adjusting batch effects in microarray expression data using empirical Bayes methods. Biostatistics 8, 118–127. [DOI] [PubMed] [Google Scholar]
- Knol, D. L. and ten Berge, J. M. F. (1989). Least-squares approximation of an improper correlation matrix by a proper one. Psychometrika 54, 53–61. [Google Scholar]
- Law, C. W., Chen, Y., Shi, W. and Smyth, G. K. (2014). voom: precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biology 15, R29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek, J. T., Johnson, W. E., Parker, H. S., Jaffe, A. E. and Storey, J. D. (2012). The SVA package for removing batch effects and other unwanted variation in high-throughput experiments. Bioinformatics 28, 882–883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek, J. T., Scharpf, R. B., Bravo, H. C., Simcha, D., Langmead, B., Johnson, W. E., Geman, D., Baggerly, K. and Irizarry, R. A. (2010). Tackling the widespread and critical impact of batch effects in high-throughput data. Nature Reviews Genetics 11, 733–739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leek, J. T. and Storey, J. D. (2007). Capturing heterogeneity in gene expression studies by surrogate variable analysis. PLoS Genetics 3, e161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leong, S., Zhao, Y., Joseph, N. M., Hochberg, N. S., Sarkar, S., Pleskunas, J., Hom, D., Lakshminarayanan, S., Horsburgh C. R., Jr, Roy, G.. and others. (2018). Existing blood transcriptional classifiers accurately discriminate active tuberculosis from latent infection in individuals from South India. Tuberculosis 109, 41–51. [DOI] [PubMed] [Google Scholar]
- Love, M. I., Huber, W. and Anders, S. (2014). Moderated estimation of fold change and dispersion for RNA-seq data with deseq2. Genome Biology 15, 550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manimaran, S., Selby, H. M., Okrah, K., Ruberman, C., Leek, J. T., Quackenbush, J., Haibe-Kains, B., Bravo, H. C. and Johnson, W. E. (2016). Batchqc: interactive software for evaluating sample and batch effects in genomic data. Bioinformatics 32, 3836–3838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nygaard, V., Rødland, E. A. and Hovig, E. (2016). Methods that remove batch effects while retaining group differences may lead to exaggerated confidence in downstream analyses. Biostatistics 17, 29–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nygaard, V., Rødland, E. A. and Hovig, E. (2017). Reply to Towfic and others letter to the editor. Biostatistics 18, 586–587. [DOI] [PubMed] [Google Scholar]
- Robinson, M. D., McCarthy, D. J. and Smyth, G. K. (2010). edger: a bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 26, 139–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smyth G. K. (2005). limma: Linear Models for Microarray Data. In: Gentleman R., Carey V.J., Huber W., Irizarry R.A., Dudoit S. (editors), Bioinformatics and Computational Biology Solutions Using R and Bioconductor. Statistics for Biology and Health. New York, NY: Springer. 10.1007/0-387-29362-0_23 [DOI] [Google Scholar]
- Suliman, S., Thompson, E. G., Sutherland, J., Weiner J., 3rd, Ota, M. O. C., Shankar, S., Penn-Nicholson, A., Thiel, B., Erasmus, M., Maertzdorf, J.. and others. (2018). Four-gene Pan-African blood signature predicts progression to tuberculosis. American Journal of Respiratory and Critical Care Medicine 197, 1198–1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Towfic, F., Funt, J. M., Fowler, K. D., Bakshi, S., Blaugrund, E., Artyomov, M. N., Hayden, M. R., Ladkani, D., Schwartz, R. and Zeskind, B. (2014). Comparing the biological impact of glatiramer acetate with the biological impact of a generic. PLoS One 9, e83757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Towfic, F., Kusko, R. and Zeskind, B. (2017). Letter to the editor response: Nygaard et al. Biostatistics 18, 197–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zak, D. E., Penn-Nicholson, A., Scriba, T. J., Thompson, E., Suliman, S., Amon, L. M., Mahomed, H., Erasmus, M., Whatney, W., Hussey, G. D.. and others. (2016). A blood RNA signature for tuberculosis disease risk: a prospective cohort study. The Lancet 387, 2312–2322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Y., Jenkins, D., Manimaran, S. and Johnson, W. E. (2018). Alternative empirical Bayes models for adjusting for batch effects in genomic studies. BMC Bioinformatics 19, 1–15. 10.1186/s12859-018-2263-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, Y., Parmigiani, G. and Johnson, W. E. (2020). Combat-seq: batch effect adjustment for RNA-seq count data. NAR Genomics and Bioinformatics 2. lqaa078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zusmanovich, P. (2013). On near and the nearest correlation matrix. Journal of Nonlinear Mathematical Physics 20, 431–439. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.