Abstract
Fluorescence lifetime imaging microscopy (FLIM) is a popular modality to create additional contrast in fluorescence images. By carefully analyzing pixel-based nanosecond lifetime patterns, FLIM allows studying complex molecular populations. At the single-molecule or single-particle level, however, image series often suffer from low signal intensities per pixel, rendering it difficult to quantitatively disentangle different lifetime species, such as during Förster resonance energy transfer (FRET) analysis in the presence of a significant donor-only fraction. In this article we investigate whether an object localization strategy and the phasor approach to FLIM have beneficial effects when carrying out FRET analyses of single particles. Using simulations, we first showed that an average of ∼300 photons, spread over the different pixels encompassing single fluorescing particles and without background, is enough to determine a correct phasor signature (SD < 5% for a 4-ns lifetime). For immobilized single- or double-labeled dsDNA molecules, we next validated that particle-based phasor-FLIM-FRET readily allows estimating fluorescence lifetimes and FRET from single molecules. Thirdly, we applied particle-based phasor-FLIM-FRET to investigate protein-protein interactions in subdiffraction HIV-1 viral particles. To do this, we first quantitatively compared the fluorescence brightness, lifetime, and photostability of different popular fluorescent protein-based FRET probes when genetically fused to the HIV-1 integrase enzyme in viral particles, and conclude that eGFP, mTurquoise2, and mScarlet perform best. Finally, for viral particles coexpressing FRET-donor/acceptor-labeled IN, we determined the absolute FRET efficiency of IN oligomers. Available in a convenient open-source graphical user interface, we believe that particle-based phasor-FLIM-FRET is a promising tool to provide detailed insights in samples suffering from low overall signal intensities.
Why it matters
Phasor-FLIM is an extraordinarily popular tool for fluorescence lifetime imaging analysis. However, it remains susceptible for low signal intensities, operational challenges and therefore required informed users and a clear analysis understanding. In this work we developed a convenient all-graphical workflow for quantitative phasor-FLIM in heterogenous and low-signal samples and applied it to quantifying absolute FRET efficiencies from protein-protein interactions inside single viral particles. Moreover, containing a well-illustrated theoretical introduction to the phasor approach to FLIM, our paper helps novice users to correctly implement phasor-FLIM in standard microscopy practice.
Introduction
Fluorescence lifetime imaging microscopy (FLIM) exploits the excited state fluorescence lifetime of fluorophores to generate image contrast (1,2,3). For FLIM data recorded using pulsed lasers and photon counting (i.e., time-domain FLIM), pixel-based analysis is typically performed via (multicomponent) fluorescence decay fitting (4,5) or, more recently, the phasor approach to FLIM (from here on referred to as phasor-FLIM) (6).
The mathematical concepts behind phasor-FLIM were first introduced by Weber et al. (7) and applied by Jameson et al. in analysis of heterogenous fluorescent samples (8). The polar (phasor) plot representation of frequency-domain fluorescence lifetime data was originally introduced by Redford et al. (9). In the original phasor-FLIM paper by Digman et al. phasor analysis was carried out on lifetime data obtained via a classic time-domain FLIM microscope equipped with pulsed excitation and time-correlated single-photon counting (TCSPC) (6). In the more recent digital frequency domain FLIM, pulsed lasers are also employed, but the phase and modulation information needed for phasor representation are directly available in the resulting data (10).
Applications of phasor-FLIM vary widely from biosensors based on FRET (11,12,13,14), analyzing sample autofluorescence signatures (15,16,17,18,19,20), or investigating the nanoscale diversity of crystalline materials (21), to name just a few. In addition, new techniques sprouted using phasor principles such as spectral phasor focused on unmixing (22), phasor S-FLIM focused on species photophysics (23), and several others (24,25,26).
The broad applicability of FLIM comes with some limitations, the most notable of which is heterogeneity in FLIM data. Lifetime heterogeneity in FLIM data between individual pixels, in general, is extracted and utilized by a per-pixel lifetime analysis. Heterogeneity within one pixel, on the other hand, presents a complication for quantitative FLIM regardless of whether decay fitting or phasor-transformation-based analysis is used. In these approaches, the unmixing of contributing species is executed in different manners, each with benefits and drawbacks. While global lifetime fitting can provide an analysis for the whole FLIM image, it requires critical user input such as the number of exponentials and the fitting boundaries (27,28). The phasor approach to FLIM attempts the unmixing of contributing factors in a graphical way but equally requires user input such as the instrumental referencing (29), characterization of the autofluorescence contribution, and correct location of pure species in the phasor plot (6,19). Nonetheless, it is generally accepted that phasor-FLIM allows for an easy identification of data clusters and species assignment combined with convenient data representation using the image-phasor reciprocity (30). Indeed, one can select pixels from within the image and analyze these in phasor space or, inversely, one can select a region of interest in phasor space, and false-color these in the image.
Despite the relative ease of use, the application of phasor-FLIM has primarily focused on bright dyes, abundant label-free autofluorescence (such as nicotinamide adenine dinucleotide, NADH) or overexpressed fluorescent protein (FP) systems (12,19,31,32). Lower photon yields, subpixel species heterogeneity, and other experimental complications (e.g., fluorophore maturation, photobleaching) present, however, quite common experimental situations that render quantitative phasor-FLIM analysis challenging (33,34). For example, while FP-based biosensors generally offer high signal intensities due to strong subcellular expression (35,36,37,38,39), FLIM-based Förster resonance energy transfer (FRET) protein-protein interaction studies at physiological cellular concentrations are conversely often carried out at much weaker overall fluorescence signals. Methodologies that facilitate quantitative analysis under such conditions of low photon budget and/or signal/noise, e.g., the recently developed particle-based phasor-FLIM approach, are therefore highly desirable (40).
As a specific low-signal example, we focus here on FP-based FLIM-FRET of homo-interactions of human immunodeficiency virus 1 (HIV-1) integrase (IN) enzymes inside single viral particles. The subresolution HIV-1 particles can incorporate only a limited number of FPs/fluorescently labeled IN molecules. As such, they present a challenge for quantitative FRET analysis because of the overall low signal intensities. We previously employed acceptor photobleaching intensity-based FRET studies on the HIV-1 and murine leukemia virus IN enzyme to show that the multimerization state of IN functionally changes during nuclear entry or after drug treatment of infected cells (41,42,43). However, since the IN-labeled donor (D) and acceptor (A) could oligomerize in different combinations in the FRET system used, intensity-derived FRET values are significantly underestimated by the presence of D-D homodimers, which in turn limited the overall FRET dynamic range. Furthermore, the intensity-based FRET analyses used was completely blind to possible subparticle species heterogeneity.
In this paper, we quantitatively explore the effect of grouping pixels from a single particle. In particular, we investigate the advantages such grouping might present during the analysis of dim photon-limited samples that would render normal pixel-based phasor-FLIM analysis difficult. In addition, we present phasor-FLIM analysis in conjunction with the phasor theory to clarify phasor-FLIM for novice users. In doing so we finally present a fair evaluation of FRET data on the oligomerization of HIV-1 IN.
Theory
Phasor approach to FLIM
Frequency-domain FLIM utilizes a modulated excitation source at an angular frequency . The frequency-dependent demodulation and phase shift are characteristics of the emitted fluorescence, and each quantity can be related to the fluorescence lifetime (44,45):
| (1) |
| (2) |
where the phase () and modulation () lifetimes are equal for high-signal and pure-species data (see also Figs. S1 A and S2). Next to this, every lifetime can also be represented in a polar plot as a vector with length equal to the demodulation and an angle with respect to the abscissa equal to . This vector is called the phasor, a portmanteau of phase vector. The point determined by the phasor is described using the Cartesian coordinates and, which are the first cosine and sine Fourier coefficients, respectively, of the time-dependent fluorescence signal , normalized for the total intensity of the sample (Fig. S1 A) (7):
| (3) |
| (4) |
The parts between brackets, stemming from the time domain, were added merely for comparative purposes. A direct relation between and is found when investigating a monoexponential decay, where Eqs. 1 and 2 result in the same lifetime:
| (5) |
and can subsequently be written as:
| (6) |
| (7) |
which allows rewriting Eq. 5 in the Cartesian coordinates of the polar plot:
| (8) |
Eq. 8 describes the so-called semicircle, on which all monoexponential signals will be spread out, with the phasors for shorter lifetimes lying closer to the point (1,0), and larger lifetimes closer to (0,0) at the origin of the semicircle (see also Fig. S1 D). Combining Eq. 8 with Eqs. 3 and 4 subsequently allows calculating the and coordinates using the angular frequency and the monoexponential lifetime.
| (9) |
| (10) |
All multiexponentials, which are a sum of monoexponentials, are linear vector combinations of the constituent phasors, and thus will be found inside the described semicircle. For a combination of species the resulting phasor coordinates are calculated by the sum of fractional (photon-weighted) contributions () of every pure species (see Fig. S1, A and E):
| (11) |
| (12) |
Phasor-FLIM using TCSPC
When using pulsed excitation and TCSPC detection, as in time-domain FLIM, is no longer the modulation frequency but is rather determined by the TCSPC range (, in units of time), i.e., the total time period in which photons are timed. In this case, the angular frequency used for phasor transformations is given by:
| (13) |
When calculating the phasor for a pixel, or by extension, an image, the idealized scenario where monoexponential components are directly positioned on the semicircle does not hold true. Most importantly, the fluorescence decay and TCSPC range do not start at the same point relative to the TR, and even for a pure species, the mathematical monoexponential decay determined by its lifetime, will be convoluted with the instrument response function (IRF) of the measuring device, both effects significantly throwing off any phasor determination. Therefore, a reference measurement is necessary of a stable, well characterized, and monoexponentially decaying dye with a lifetime similar to the measured lifetime. The reader is referred to Ranjit et al. (46) and Michalet (47) for more information on referencing and phasor transformations, and data corrections to maintain transformations of monoexponentially decaying phasor data on the semicircle. Alternatively, the pure IRF signal can be used, representing a lifetime of 0. The reference’s known fluorescence lifetime is first used to calculate (using Eqs. 6, 7, 9, and 10) the expected demodulation and phase shift values for the reference (see Fig. S1 B):
| (14) |
| (15) |
These values are subsequently used to calculate the phasor values for the instrument:
| (16) |
| (17) |
where is the total number of time channels within the TCSPC range and the normalized intensity of the experimentally measured reference in time bin . These instrumental phasor coordinates can subsequently be used to calculate the phase and demodulation of the instrument, and via Eqs. 6 and 7. This finally allows to convert (instrument-dependent time-domain data from) the TCSPC range to (instrument-independent phasor data in) a polar plot:
| (18) |
| (19) |
Every photon is assigned such coordinates depending on its arrival time channel in the TCSPC range, and depending on the subsequent analysis, photon phasors were either averaged per pixel or per identified object. An overview figure of the phasor approach to FLIM illustrating pulse frequency impact and reference implementation is provided as Figs. S1, B–D and S3.
Resolving mixtures of pure species
Pixels containing photons that originate from a single type of pure (monoexponentially decaying) fluorophore translate to phasor values that lie on the semicircle. Phasors from samples containing a mixture of two pure fluorescent species, with each having a different fluorescence lifetime, on the other hand, are located on a straight “fraction line” connecting the two constituent pure phasors. The location of this phasor on this line is determined by the number of photons contributed by each species (Eqs. 11 and 12). Therefore, for a two-component mixture, the phasor (or fluorescence lifetime) of at least one species has to be known a priori. Finally, the concentration fraction of each species is determined from the lifetimes and the intensity fraction as follows:
| (20) |
where is the intensity fraction of species 1. For the derivation of this formula, a conceptual illustration and a proof-of-concept simulation, the reader is referred to Note S1 and Figs. S1 E and S4, respectively. Practically, the fraction line is manually drawn, starting at the phasor value of one species (which can be a mixture itself) and through the center-of-mass of the mixture’s phasor value. This then renders the fractions and the lifetime of all species.
Phasors in the presence of background signal
Background signals (autofluorescence from impurities, detector dark counts, Rayleigh or Raman scattering, laser reflections, etc.) will cause the phasor value of a pure species to be shifted away from the semicircle. The average phasor location of the background () needs to be determined in a separate experiment. In further experimental analyses, a fraction line can then be drawn through the background phasor and the measured sample phasor. The lifetime of the pure species is subsequently determined from the intersection of the fraction line and the semicircle. In this way, for FRET analyses, the location of the phasor within the semicircle was quantified via the fraction. This concept is illustrated in Figs. 2 D and S1 G.
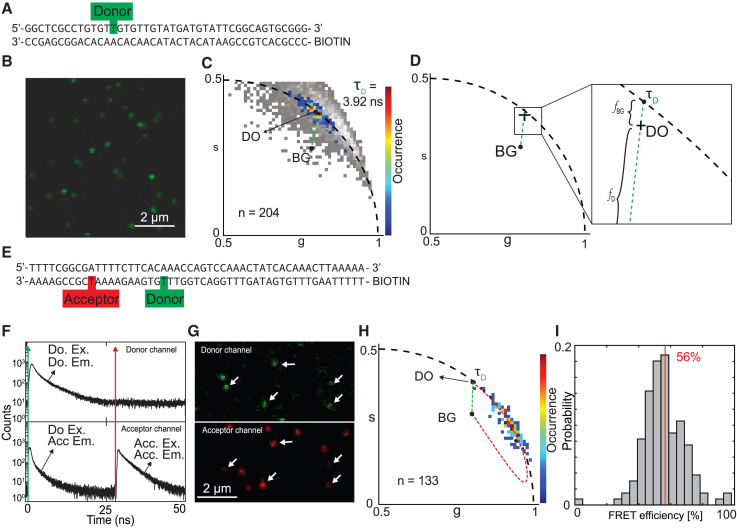
Figure 2.
Determination of FRET-labeled dsDNA FRET efficiency. (A) dsDNA strand with a single donor label on the sense strand. (B) Microscopy image using 485-nm excitation revealing single particles. (C) Pixel-binned particle phasor analysis on the donor-labeled dsDNA reveals its photon-weighted center of mass () revealing the donor lifetime of 3.92 ns ( upon extension of the fraction line to reveal its pure contributing species. Pixel-based phasor with a 10-photon/pixel threshold shown in gray. (D) Illustration of the contributing species to the phasor () location ( and ) of the donor-only-labeled dsDNA. (E) dsDNA with on the antisense strand both donor and acceptor present and a biotin tag on the 5′ end used for immobilization on the glass. (F) Pulsed interleaved excitation (PIE) measurement of FRET-labeled dsDNA used for colocalization. (G) Intensity image of double-labeled dsDNA showing a single region of interest for both donor and acceptor channel as determined by colocalization of both donor and acceptor channels for donor and acceptor excitation, respectively. White arrows indicate colocalized particles. (H) Phasor plot of imaged FRET-labeled dsDNA strands showing the autofluorescence phasor (), the donor-only phasor , and the quenching trajectory (red dashes) connecting the phasor with the phasor (see Eqs. 22 and 23). The fraction line between en (green dashes). (I) FRET efficiency histogram derived from the FRET trajectory. Vertical red line visualizes the average value.
Quenching trajectory of FRET species
In the case of a pure fluorophore that is quenched by FRET, its phasor describes a trajectory starting from the species (no FRET) along the semicircle to approximate a 0-ns lifetime (100% FRET) as described by the resulting monoexponential lifetimes on the semicircle by the formula:
| (21) |
as illustrated in Fig. S1 F. Here, is the quenched lifetime upon FRET, is the pure donor lifetime, and is the FRET efficiency (i.e., the quantum yield of the Förster transfer process depopulating the fluorophore’s excited state). In reality, however, and a possible contribution from donor molecules with no nearby acceptor (passive donors) will cause this trajectory to deviate from the semicircle. For points resembling higher FRET states the fluorescence quantum yield of the involved species decreases leading to increased fluorescence contribution of passive donors and , which maintain a constant brightness (i.e., fluorescence quantum yield in the case of fluorescing species). Taking this into consideration, the quenching trajectory in a nonperfect condition folds back and the trajectory ends at the phasor determined by the remaining passive donors and (Fig. S1 G). The quenching trajectory connecting all possible FRET efficiency states for a given and passive donor can therefore be determined by fraction lines between all monoexponential points on the semicircle < and the & phasor. The and coordinates of the quenching line are given by:
| (22) |
| (23) |
in which and , the coordinates of the pure quenched form on the semicircle, can be found using Eqs. 9 and 10 in which the lifetime of the quenched form is . and are the coordinates of the mixture of contributions by and . is the summed fractional contribution of and at the starting point (no FRET). The term scales the fractional contribution of the quenched species given the fluorescence quantum yield drops with increasing E. From the formulation it is clear that, with increasing FRET of the pure quenched state, the fractional contribution of the phasor becomes larger. Construction of the quenching line and its contributing factors are displayed in Fig. S1, F–I. A more in-depth explanation of Eqs. 22 and 23 can be found in note S2.
Materials and methods
Analysis software
All analysis of imaging data (simulated or experimental .ptu files) was done in the open source pulsed interleaved excitation (PIE) analysis with MATLAB (PAM) software, a versatile software package offering a variety of analysis tools, including phasor analysis of FLIM data (48). The software is available as a source code, requiring MATLAB to run, or as compiled standalone software compatible with Windows or MacOS at http://www.cup.uni-muenchen.de/pc/lamb/software/pam.html or hosted in Git repositories under http://www.gitlab.com/PAM-PIE/PAM and http://www.gitlab.com/PAM-PIE/PAMcompiled. Sample data are provided under http://www.gitlab.com/PAM-PIE/PAM-sampledata. A detailed manual is found under http://pam.readthedocs.io. The workflow of the software as applied in this paper is described in Fig. S5. Simulated photon data were generated by a subsection of PAM. This module is illustrated in Fig. S6. Simulation input parameters included: TCSPC range (50 ns), pixel intensity (defined by the number of frames pixel dwell time and the particle brightness ε), fluorescence lifetime, background intensity (0 kHz), diffusion coefficient D, number of species and their concentration, simulation box size, pixel size (50 nm) and image size, and (Gaussian) IRF width (250 ps). For the single-particle simulations, a single species of D = 0 μm2/s was used. For the concentration fraction line simulations, D = 100 μm2/s for both species and the fluorescence lifetime and brightness of one species was four times larger than that of the other species (4 and 1 ns, respectively), mimicking a species and its 75% quenched form. Particle detection was performed using the particle detection functionality within PAM, which localizes particles in the fluorescence intensity images using eccentricity (0.5), counts (>300), size in pixels (min, 15; max, 100), and a wavelet depth of 3, using the simple wavelet method (40). Colocalization of dsDNA particles was performed using the centroid positions of particles in the FRET donor and directly excited FRET acceptor images as input via a nearest-neighbor search with a maximum distance tolerance of 5 pixels for successful colocalization. Statistical analysis was performed using GraphPad Software version 9.4.1. For particle intensity tests and comparison of photobleaching, a Shapiro-Wilk test was first used to check normality of data. When no normality was found, a nonparametric (one-way ANOVA, Kruskal-Wallis) test was used to compare data sets of each IN-FP.
Phasor cloud center positions
The shape of a given phasor “cloud” at low signal intensities is determined by inherent shot noise on the one hand, and the spectroscopic contribution of the different emissive species, i.e., the background and the different lifetime species in the observed spectral window. To determine the center position, we calculated a “center of mass,” where the average phasor location of all pixels within the phasor cloud is determined, with each pixel weighed for the photon content of that point.
Background and passive donor fraction
Background samples are measured specifically per experimental case and aim to determine the contributing component of background, stray light, dark counts, and autofluorescence. The phasor analysis is performed identical to a normal sample analysis to determine the resulting background phasor location (). From all resulting phasor positions the photon weighted average position is determined and used as general background phasor. For DNA measurements, the prepared nonlabeled surface functionalized with PEG is imaged. In case of virus measurements, the viral particle itself is the main source of background and autofluorescence. Therefore, a photobleached region is imaged where viral particles are present in the scanned frame. The passive donor contribution in a FRET experiment skews the phasor to the pure donor phasor position, this is the fraction of donors that does not participate in FRET and has the same phasor location as a sample with only donors ().
FRET histograms
Using the phasor analysis tools of PAM, a FRET trajectory was drawn with the respective passive donor () and () contributions starting from the center-of-mass of a measurement only containing donor labels at the location. Using a MATLAB routine, we determined the nearest point of the FRET trajectory to every particle phasor location. From these FRET trajectory points a FRET histogram was made.
DNA strand hybridization
All DNA strands were purchased from IBA LifeSciences (Göttingen, Germany). For the single-color dsDNA experiments, the sense strand that was used is 5′-GGCTC GCCTG TGTXG TGTTG TATGA TGTAT TCGGC AGTGC GGG-biotin in which the X marks the 14th position that is labeled with ATTO 488 and biotin-labeled at its 3′ end. A compatible unlabeled antisense strand was used (5′-CCCGC ACTGC CGAAT ACATC ATACA ACACA GGCGA GCC) for annealing into a single-labeled dsDNA. For our double-labeled dsDNA, the antisense strand (5′-biotin-TTTTT AAGTT TGTGA TAGTT TGGAC TGGTT YGTGA AGAAA AZCGC CGAAA A, with Y and Z an Alexa Fluor 488 and ATTO 647N label, respectively) is covalently labeled with Alexa Fluor 488 on the 31st position followed by an ATTO647N-label 11 nucleotides further. In addition, the antisense strands are labeled with biotin on the 5′ end. The complementary sense strand (5′-TTTTC GGCGA TTTTC TTCAC AAACC AGTCC AAACT ATCAC AAACT TAAAA A) is unlabeled. Sense and antisense DNA strands were hybridized by centrifuging the lyophilized strands for 1 min at 1000 × g. Next, phosphate-buffered saline (PBS) (Merck, 806552, Sigma-Aldrich, Darmstadt, Germany) was used to dilute to a final concentration of 100 μM. The solution was homogenized by resuspension and vortexing. Afterward, the top and bottom strands were annealed using a PCR machine (Doppio, VWR-thermocyclerseries, VWR, part of Avantor, Radnor, USA) increasing the temperature to 95°C (3 min) and cooling down from 85 to 4°C at 1 min per degree to allow specific hybridization toward a final concentration of 10 μM. Finally, the PCR product was transferred to a –80°C Eppendorf (cat. no. 0030125215, Eppendorf, Hamburg, Germany) and directly flash frozen in liquid nitrogen. Afterward, the product was stored at –80°C. To remove the excess free dye as revealed by fluorescence correlation spectroscopy (FCS), a PD-10 desalting column was used.
DNA experiments
The glass surface immobilization protocol involved surface cleaning and surface functionalization. Firstly, the chamber glass coverslips (no. 1.0 chambered coverglass, Lab-Tek, cat. no. 155411) was cleaned by an incubation with 10 mM SDS for 1 h at room temperature. Next, the surface was washed several times with Milli-Q followed by surface activation with UV-ozone for 15 min. Functionalization was performed by adding 10 μg/mL of the passivation agent (PLL-PEG, SuSoS, Dübendorf, Switzerland) together with PLL-biotin-PEG in a 1:1 ratio and left to incubate at room temperature for 30 min. After this, the surface was rinsed three times with DNA resuspension buffer (150 mM STE buffer, BP2478-1, Thermo Fisher Scientific, Geel, Belgium) without letting the surface dry out. This was applied after each incubation step of the functionalization. Once the surface contained biotin, 10 μg/mL Neutravidin (Thermo Fisher Scientific) was added and incubated for 30 min followed by another three wash steps with 150 mM STE buffer. Finally, DNA was diluted to the picomolar range using 150 mM STE buffer and incubated for 30 min, after which excess DNA was washed away. Colocalization of DNA particles was done using a MATLAB routine in which particle centers are determined in both donor and acceptor channels. Particles are considered colocalized when a donor center position is equal or less than 5 pixels of the nearest acceptor center position.
Microscope
The microscope presented in this work is a custom-built confocal microscope. Its schematic is shown in Fig. S7. The base microscope is an Olympus IX70 modified with external pulsed excitation lasers, a scan unit, and multichannel single-photon detection. Five laser lines are available, of which four are diode pulsed lasers (LDH Series, PicoQuant, Berlin, Germany) and one supercontinuum laser (Solea, PicoQuant). Laser pulsing and synchronization was set in the acquisitioning software SymphoTime 64 “1 + 2” (PicoQuant). A multichannel diode laser driver (PDL 828 Sepia2, PicoQuant) controls the laser frequency at 20 MHz to ensure full fluorescence decay when measuring donor and acceptor fluorophores with PIE. Dichroic mirrors guide the laser lines into a polarization-maintaining single mode optical fiber (PMC-400Si-2.6-NA012-3-APB-150-P, Schäfter + Kirchhoff, Hamburg, Germany) via a lens-based coupler (60FC-4-RGBV11-47, SuK). Light is collimated again via a lens-based collimator (60FC-L-4-RGBV11-47, SuK). Excitation light is directed at a dichroic quadband mirror (zt405/488/561/640rpc or zt440/510/561/640rpc depending on needed excitation line, AHF, Tübingen-Pfrondorf, Germany) held in place by a kinematic fluorescence filter cube (DFM1/M, 30-mm cage compatible, Thorlabs, Bergkirchen, Germany) for easy optics switching, and reflecting the excitation beam to the scanhead (TILL Yanus IV digital scanner, FEI Munich, Gräfelfing, Germany) mounted straight onto the backport of the IX70. Scan motion is controlled with in-house software in C# Microsoft Visual Studio in combination with a National Instruments box (USB-6361 Multifunction I/O Device, NI, Austin, TX) that steers the xy galvo axis via a TILL photonics Scan Control Unit (SCU, FEI Munich, Munich, Germany). Pixel dimensions, number, and dwell time are controlled by this software. Upon transmission of emission light through the quadband dichroic, the light is focused (150 mm AC254-15-A-ML, Thorlabs) onto a 50-μm pinhole (PS50S, Thorlabs), after being collimated again using a 50=mm AC254-050-A-ML (Thorlabs). Detection is arranged over three detection channels, splitting the bundle with dichroic mirrors. For DNA experiments, both the 485- and 640-nm laser diodes (LDH-D-C-485 and LDH-D-C-640, PicoQuant) were used in PIE mode using the zt405/488/561/640rpc quadband. Emission light is split on a 560-nm longpass (H560LPXR, AHF). Reflected light is cleaned up using a 530/50m (HQ, AHF) and recorded on an avalanche photo diode (APD) (τ-SPAD, PicoQuant). Passing light is cleaned up using a 705/100 (ET bandpass, AHF analysentechnik, Tübingen-Pfrondorf). For mNeongreen, mClover3, and eGFP the 485-nm excitation source was used (LDH-D-C-485, PicoQuant) and emission detected identically to the ATTO 488-labeled DNA. mTFP1 and mTurquoise2 were excited using a 440-nm diode (LDH-D-C-440, PicoQuant) in combination with the zt440/510/561/640rpc quandband BS. Emission light was reflected on the 560 nm longpass and detected using an APD (τ-SPAD, PicoQuant) after passing a cleanup filter (480/40, Brightline HC, AHF analysentechnik). mVenus was excited using a 510-nm diode (LDH-D-C-510, PicoQuant) in combination with the zt440/510/561/640rpc quandband BS. Emission light was reflected on the 560-nm longpass and detected by an APD (τ-SPAD, PicoQuant) after passing a cleanup filter (540/15, Brightline HC, AHF analysentechnik). mCherry and mScarlet2 were excited using a 560-nm supercontinuum laser (Solea, PicoQuant) in combination with the zt440/510/561/640rpc quandband BS. Emission light was passed through the 560-nm longpass and detected using an APD (τ-SPAD, PicoQuant) after passing a cleanup filter (600/37, Brightline HC, AHF analysentechnik). For FRET experiments with mTurquoise2-mVenus, all mission light of donor and acceptor is reflected on the 560-nm longpass and split on a 507-nm longpass dichroic (H507LPXR, AHF analysentechnik) after which 480/40 and 540/15 cleanup filters are used for mTurquoise2 and mVenus, respectively, before detection. In the case of eGFP-mScarlet, the eGFP emission reflected on the 560-nm longpass is detected after cleanup with a 530/50m filter. For mScarlet, the emission passes the 560-nm longpass and is cleaned up using a 600/37 filter.
APD detectors were powered by a dedicated power supply (DSN-102, PicoQuant). APD NIM signals are directed toward the HydraHarp 400 (PicoQuant) to supply it with photon timing information. For all data acquired on the microscope a 60× water objective (Olympus UPlanSApo 60×/1.20 W Ꝏ/0.13–0.21/FN26.5) was used. The microscope was positioned on a vibration-free isolated optical table (S-2000 series Stabilizer, Newport Spectra-Physics BV, Utrecht, the Netherlands).
Frequent system checks, setup alignment, and quantifying confocal volume parameters were performed with FCS using ATTO425-COOH, ATTO488-COOH, Alexa Fluor 546, or ATTO655-COOH (ATTO-TEC, Siegen, Germany) (Alexa Fluor, Thermo Fisher Scientific). Data were analyzed using PAM-FCSfit (Fig. S8). As references for phasor-FLIM, organic dyes were measured using the same optical setup for the assigned detection channel. Reference lifetimes were experimentally determined via PAM-Taufit (Fig. S8), where the decay was fit using a reconvolution fit for a monoexponential with loaded IRF. Dyes used were ATTO488-COOH, ATTO425-COOH, Alexa Fluor 546, and ATTO 647N-maleimide.
Fluorescent HIV-1 particles
HIV-1-derived viral particles (vesicular stomatitis virus glycoprotein [VSV-G]- pseudotyped) with FP-labeled IN were synthesized using Vpr-mediated trans-incorporation (49,50). HEK293T cells (6.5 × 106) were seeded in 10-cm petri dishes with DMEM supplemented at 2% FBS and 50 μg/mL gentamicin (Invitrogen, Thermo Fisher Scientific, Waltham, Massachusetts, USA). For transfection, medium was replaced with Opti-MEM (Life Technologies, Thermo Fisher Scientific) supplemented with gentamicin (Invitrogen, Thermo Fisher Scientific). Cells were transfected with branched polyethylenimine (10 μM stock solution, Sigma-Aldrich, Merck Life Science BV, Hoeilaart, Belgium) when 90% confluency was reached. A three-plasmid system, consisting of 5 μg pVSV-G, 15 μg pNL4–3.Luc.R−.E−, and Vpr-IN-FP-encoding plasmid (5 μg for single FP viruses, twice 2.5 μg for viruses containing two FPs) was used in transfection. pVpr-IN-FP constructs with mTFP1, mTurquoise2, mNeongreen, mClover3, mScarlet, mRuby3, eGFP, and mCherry were used. pVpr-IN-FP constructs for mTFP1 and mVenus were made according to Borrenberghs et al. (50). Other pVpr-IN-FP constructs were made by starting from the original pVpr-IN-eGFP plasmid (49). Transfection lasted for 6 h at 37°C and was terminated by replacing the medium with fresh 37°C Opti-MEM (Life Technologies, Thermo Fisher Scientific) supplemented with 50 μg/mL gentamycin (Invitrogen, Thermo Fisher Scientific). Virus supernatant was collected 48 h after initiating transfection, filtered through a 0.45-μm filter (Minisart Syringe Filter, Sartorius, Göttingen, Germany), and concentrated by several washing steps in FBS-free Opti-MEM and virus particles were concentrated by ultracentrifugation on a 60% (w/V) iodixanol cushion at 21°C (131,500 × g, 90 min, SW28 rotor, Beckman Coulter Belgium, Suarlée, Belgium) to a final volume of 1 mL. Iodixanol was removed by ultrafiltration (Vivaspin, MWCO 50K, Merck, Overijse, Belgium). All generated viral particles were kept up to 2 months at –80°C, without thaw-freeze cycles.
Glass coating and viral particle plating
Glass coverslips used for viral particle imaging were coated with poly-D-lysine. This was done by incubating the wells for 20 min at 37°C in a 0.4 mg/mL solution (4×) of poly-D-lysine (Merck, P7280-5MG, Sigma-Aldrich, Merck Life Science BV, Hoeilaart, Belgium), made from a 1-mg/mL stock, and followed by washing three times with PBS. Coverslip coating was finished by removing all PBS, and coverslips were air dried in a sterile flow for 30 min. For imaging purposes, concentrated virus particles were freshly thawed and diluted in PBS (Merck, 806552, Sigma-Aldrich) based on the p24 antigen concentration in the supernatant, as determined by the p24-specific enzyme-linked immunosorbent assay. Then, 200 μL of the virus dilution containing 1–3 μg p24 antigen was transferred to a poly-D-lysine-coated glass coverslip (no. 1 chambered coverglass, Nunc Lab-Tek, cat. no. 155411, Thermo Fisher Scientific) and incubated at 37°C for 3–5 h. The virus particles were gently washed twice with PBS, after which 200 μL PBS was added to each well and the wells were sealed with parafilm to avoid evaporation.
Photobleaching of viral particles
Plated viral particles were imaged until photobleached. Particle tracking was performed across all image frames following total particle counts per frame using the particle detection module of PAM. Using a separate MATLAB routine, an exponential was fitted onto the decaying fluorescence intensity. All photobleaching rates are the determined b coefficients of (see also Fig. S9).
Results
Particle-detection-based pixel binning improves phasor-FLIM of dim particles
As the quality of a phasor-FLIM experiment depends on the photon content of the fluorescence data, we first quantified the effect of pixel binning on phasor-FLIM data. Specifically, we examined the effect of grouping pixels from the same subresolution object on the accuracy of the estimated lifetimes. Practically, we simulated confocal FLIM data of nondiffusing fluorophores exhibiting a 4-ns fluorescence lifetime. Because of their random axial location in the simulation box, the resulting image displayed particles with varying intensity in the image plane (Fig. 1 A).
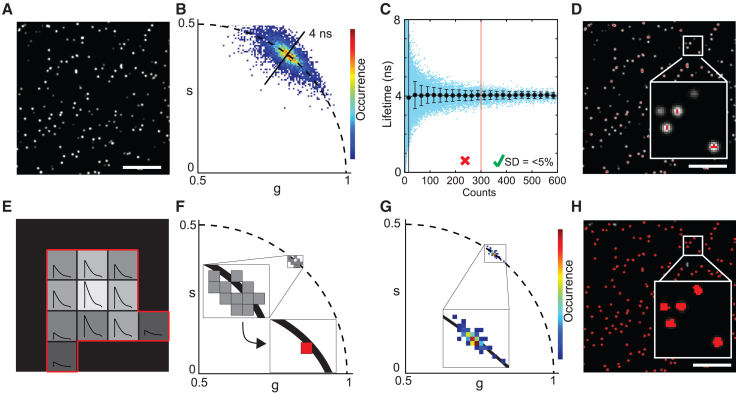
Figure 1.
Pixel binning for particle phasor-FLIM. (A) Intensity image of simulated subresolution single particles with variety of intensities but a constant lifetime of 4 ns. (B) Phasor analysis of the simulated photon data results in a wide spread on the phasor plot where every pixel (threshold for pixels with more than five counts) is assigned one phasor. (C) In blue: scatterplot of the pixel counts against the phase lifetime determined from the phasor plot. In black: standard deviation and mean lifetime per bin. Bins are defined as 25 counts wide, mean and standard deviation are plotted in the center coordinate of each bin. (D) Intensity image color coded in red if the pixel counts >300, inset is a 2.5- × 2.5-μm box. (E) Schematic of a single particle consisting of pixels from the same subresolution origin and showing identical decay lifetime composition but different amplitudes. (F) Pixel binning improves the particle phasor. (G) Simulated data from (A–D) analyzed in phasor with particle-based pixel binning show a compact phasor distribution. (H) Particles color coded if the particle counts are >300 counts. Scale bars, 5 μm.
Due to the overall low intensity per pixel, the resulting phasor plot exhibited a relatively large data spread (Fig. 1 B). When plotting the phasor-determined lifetime (average of phase and modulation lifetime, Eqs. 1 and 2) for every pixel, we observed an increase in lifetime precision for increased photon counts of the pixel (Fig. 1 C). We determined that a count of 300 photons was ideally needed to obtain lifetime values within a 5% deviation range of the true value. This value can therefore be considered a lower limit, acknowledging that a higher photon count is advised for more complex phasor component deconvolutions. Using this 300-photon count threshold, we false-color-coded the intensity image for the pixels that met this threshold and observed that relatively few pixels from the imaged particles were, in fact, colored (Fig. 1 D). Of note, multiple pixels share the signal originating from the same subresolution emitter with varying amplitudes but identical lifetime signature. Grouping of pixels originating from the same particle therefore should enhance the phasor coordinate calculation (Fig. 1, E and F). When we applied this pixel binning strategy to the simulated data, we noticed a greatly reduced spread and a highly concentrated particle datapoint population in the phasor plot, now clearly centered on the 4-ns semicircle location. (Fig. 1 G). Subsequent color coding of the simulated image for the particles that are detected with a sum of ≥300 photons showed that almost all particles were included into the analysis (Fig. 1 H). In summary, grouped single-particle phasor analysis helps robustly and accurately determine phasors from dim emitters, such as subresolution particles. In addition, 300 photons per pixel binned particle is a recommended minimum total pixel count target for reliable phasor lifetime determination.
Particle-based phasor-FLIM resolves individual DNA molecule lifetimes
Next, we investigated whether particle-based phasor-FLIM could successfully allow determining the fluorescence lifetime of single molecules. Therefore, we imaged a model system containing PEG-biotin immobilized DNA molecules labeled either with only a FRET donor (Fig. 2, A–D) or with both a FRET donor and acceptor spaced at a distance of 11 nucleotides as reported before (51,52) (Fig. 2, E–I). All particles were identified, and particle phasor positions were analyzed in the phasor plot for the average lifetime. A donor-only lifetime () of 3.92 ns was found with a background () contribution of 1.2%, resulting from the measured phasor position (). Autofluorescence of the particles themselves, here called , dragged an otherwise perfect monoexponential measurement inward of the semicircle due to the complex lifetime signature of the background. The position was determined (see materials and methods) and was used to measure the pure lifetime of the donor on the semicircle using fractionality (Fig. 2, C and D). With this no-FRET control measured we continued with a double-labeled (donor-acceptor) dsDNA system, in which donor and acceptor labels are separated by 11 nucleotides (Fig. 2 E). These double-labeled single molecules were imaged using PIE, whereby the donor laser was pulsed at the beginning and our acceptor in the middle of our detection window in between pulses (53,54). This way quasi synchronously measured both the donor and acceptor without suffering from spectral cross talk (Fig. 2 F). Colocalization was confirmed in a subset of single molecules using both donor and acceptor channel information. Using a maximum distance of 5 pixels between colocalization candidate centers, 133 single-molecule dsDNA particles were found. From the colocalized particles (Fig. 2 G), the donor signal upon donor excitation was used to calculate all phasor positions per particle using particle pixel binning. From the average position of the single (donor)-labeled single dsDNA molecules () and the previously measured BG coordinates (Fig. 2 B), a FRET trajectory was formed describing all possible FRET states ranging from 0% (phasor position equals the position) to 100% FRET (phasor position equals the only remaining signal of ; all donor signal is quenched) (Fig. 2 G). Finally, the FRET histogram resulting from projection of phasor positions onto the FRET trajectory showed an average value of 56% FRET (Figs. 2, H, I, and S1 G). Taking into account a Förster radius of 50.3 Å for Alexa 488 and ATTO 647N, the estimated donor-acceptor distance from our FRET measurement was determined to be 39 Å.
Performance comparison of single FP-labeled IN
With our positive FRET control in place, we connect to the open research field of HIV-1 IN multimerization, previously conducted in our lab. Earlier, the FRET readout of recombinant HIV-1 particles containing FP-labeled IN (mTFP1-mVenus FRET pair) was investigated with intensity-based acceptor photobleaching FRET methods throughout the replication cycle (41,42,43). To extend this study using our particle-based phasor-FLIM approach we explored which FP labels for IN performed superior for further application in FRET measurements involving donor FP- and acceptor FP-labeled IN monomers. Moreover, since an HIV-1 particle is a highly condensed environment and this might affect the fluorescence lifetime and overall FP performances, we furthermore decided to determine the optimal FRET pair directly in an HIV-1 particle context (55).
Practically we generated HIV-1 particles incorporating a single type of FP-labeled IN, allowing us to quantitatively compare several FRET donor and acceptor labels. First, we analyzed the HIV-1 particles for their brightness. We observed that especially particles containing IN-mTurquoise2 easily yielded more than 300 photons as the frequency distribution peaks less in the low photon range (<100 counts). Conversely, mNeongreen-particle preparations did not result in many high photon count particles as the frequency distribution peaked at 30–40 photons (Fig. 3 A). For acceptor candidates the photon distributions were rather similar (Fig. 3 E).
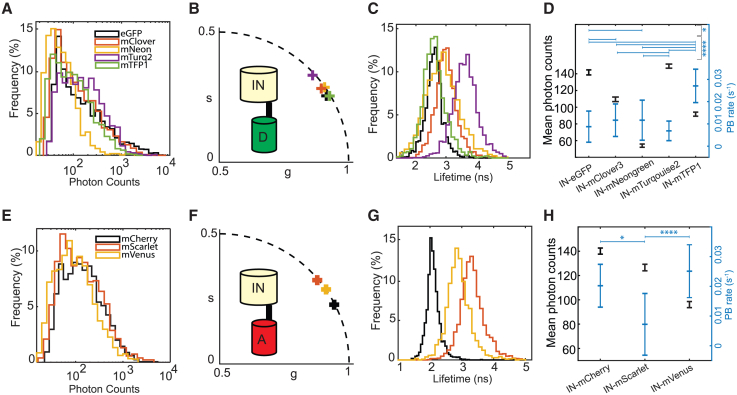
Figure 3.
Lifetime, photon count, and photobleaching study of single-FP HIV-IN-labeled virions on glass. (A and E) Count distributions of donor-labeled (A) and acceptor-labeled (E) HIV-IN-FP virions. (B and F) Photon-weighted centroid position of the phasor clouds of all respective donor and acceptor HIV-IN-FP virions. (C and G) Monoexponential phase lifetime distribution of the donor and acceptor HIV-IN-FP virions using a particle threshold of 10 counts to evaluate broadness of lifetime distribution. (D and H) Geometric mean photon counts normalized for excitation efficiency and the associated mean photobleaching rate of all donor and acceptor HIV-IN-FP particles. All geometric mean photon counts are significantly different from each other (p < 0.05), significance levels for photobleaching rates are determined by a one-way ANOVA nonpaired nonparametric Kruskal-Wallis test with multiple comparison (∗p < 0.05, ∗∗∗∗p < 0.001).
Next, we verified whether all IN-FP candidates, especially the donors, exhibited a monoexponential lifetime, which would enable us to use semicircle-derived lifetime values (phase or modulation lifetime would work) for evaluation. The plotted centroid positions of all measured particles in the phasor plot indicate that there is indeed a dominant monoexponential behavior (Fig. 3, B,F). Plotting all semicircle-derived phase lifetimes and their respective lifetime spread in a lifetime histogram shows their peak values and variability; introduced by the FP itself, the photon statistics per particle or shot noise. Histogram means for each fluorophore were: eGFP 2.66 ± 0.31 ns (n = 2675), mTFP1 2.62 ± 0.41 ns (n = 1769), mNeongreen 2.90 ± 0.60 ns (n = 1972), mClover3 3.01 ± 0.39 ns (n = 2219), mTurquoise2 3.68 ± 0.45 ns (n = 2375), mCherry 2.10 ± 0.22 ns (n = 2164), mScarlet 3.34 ± 0.4 ns (n = 2309), and mVenus 2.71 ± 0.39 ns (n = 2125). With a variability of more than 0.5 ns, IN-mNeongreen particles are most unfavorable (Fig. 3, C and G). Measured photobleaching rates of the FPs indicated a high rate for mTFP1 (0.0280 ± 0.0075, n = 29), while other donor candidates have a more favorable photobleaching rate: eGFP (0.0097 ± 0.0072, n = 143), mTurquoise2 (0.0078 ± 0.0044, n = 265), mClover3 (0.0127 ± 0.0073, n = 638), and mNeongreen (0.0126 ± 0.0090, n = 112) (Fig. 3 D). When comparing the geometric mean photon counts all particles were significantly different from each other (p < 0.001) and again eGFP (144.7, n = 2675) and mTurquoise2 (148.1, n = 2375) were best performing, while mNeongreen (56.5, n = 1972), mClover3 (111.5, n = 2219), and mTFP1 (94.2, n = 1769) were significantly lower (all p < 0.001) (Fig. 3 D). Regarding the measured acceptor photobleaching rates, mCherry (0.0202 ± 0.0072, n = 15) and mVenus (0.0251 ± 0.0089, n = 17) exhibited a significantly larger photobleaching rate compared with mScarlet (0.0072 ± 0.0104, n = 14) (p < 0.05 and p < 0.001, respectively) (Fig. 3 H). Mean photon counts were again all significantly different (p < 0.001) and mCherry (118.7, n = 2164) and mScarlet (110.5, n = 2309) outperformed mVenus (90.1, n = 2125) (Fig. 3 H). Based on these results, we selected eGFP and mTurquoise2 as they appear to be favorable donor candidates that can be paired with acceptors from our assay that also scored adequately. Due to its favorable photostability, mScarlet was shown to be the most promising acceptor compared with mCherry and mVenus. In summary, we have identified suitable FRET donors and acceptors attached to IN in the HIV-1 viral particles. The mTurquoise2-mVenus and eGFP-mScarlet pairs were selected for further single-particle FRET experiments.
Graphical phasor analysis reveals IN multimers in HIV-1 viral particles
IN is known to adopt different oligomeric states depending on the step in the replication cycle. Methods to quantify this oligomeric state of IN at the level of single viral particles and viral complexes are highly desired by virologists. In earlier work, the oligomeric state of IN was quantified with acceptor photobleaching intensity-based FRET. There, the dynamic range of the FRET quantifications was unavoidably lowered by the presence of (variable amounts of) FRET donor-only labeled complexes. Using phasor-FLIM in the present work, we sought to further disentangle the actual FRET species from any non-FRET species and background.
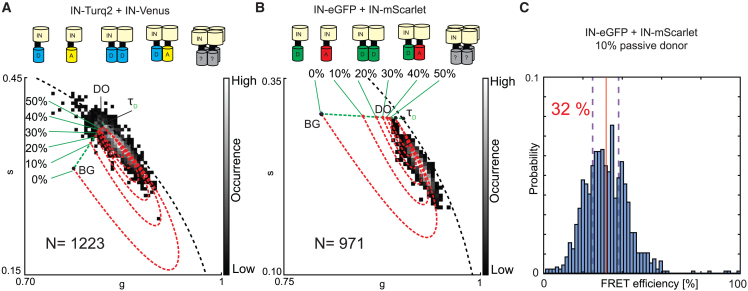
Now, we employ the particle-based phasor-FLIM methodology on the FRET measurements for our previously selected fluorescent FRET pairs. Each pair covers other sections of the visible spectrum, exhibits a slightly different Förster distance (58.3 Å for mTurquoise2-mVenus and 56.7 Å for eGFP-mScarlet from calculations assuming κ2 to be 2/3 and refractive index n of 1.33 with the donor quantum yields being 0.93 and 0.60, respectively, see also Note S3) and encompass a FRET donor with substantially different lifetimes. Ultimately, regardless of the fluorescent labels on IN, we wanted to evaluate the FRET state of IN complexes in the assembled virus particles to gain further insight into IN multimerization. Assuming a system where only monomeric IN and dimeric IN is present, in any combination possible (A, D, D:D, D:A, A:D, A:A), in a matured HIV-1 particle, there will be a passive donor intensity fraction between 50% (all IN complexes are dimers, the donor-only signal intensity fraction constitutes 50% of the total donor signal intensity) and 100% (all IN complexes are monomers, no FRET occurs). It is only when higher-order multimers such as tetramers are formed, leading to a range of different combinations between D and A (e.g., DDDA, DDAD, DADD, ADDD, ADAD, DADA), that the fraction of passive donors in IN complexes is further lowered, simultaneously increasing the overall FRET signal of a single HIV-1 particle. Since at the particle level both FRET and the passive donor fraction are unknown, no direct FRET readout can be provided. However, matching the particle phasor data with the possible FRET trajectories constructed by a range of passive donor contributions, should still give insights into the multimer composition. Practically, as shown in Fig. 4, A and B, we recorded FLIM data of FRET donor/acceptor double-labeled immobilized viral particles at photon counts compatible with single-particle phasor-FLIM and performed particle detection on the resulting FRET donor images. FRET trajectories are constructed using a background reference (see materials and methods) and the HIV-1 particle measurements with only the donor label (HIV-1 containing only IN-mTurquoise2 or IN-eGFP, see Fig. S10). Again, the signal intensity contribution of in the measured donor signal draws the phasor position away from the semicircle and serves as starting position for the FRET quenching line (as is previously illustrated in Fig. 2 D). For particles with IN-mTurquoise2 and IN-mVenus, had a 7.5% contribution and for IN-eGFP/IN-mScarlet particles 10.5%, as determined graphically from the phasor plot. Subsequently, HIV-1 particles containing both donor- and acceptor-labeled IN were measured and the particle-based phasor distribution was calculated. On top, we plotted all possible FRET trajectories for passive donor contributions between 0 and 50% and found that, for IN-eGFP+IN-mScarlet particles, a 0–20% passive donor contribution resulted in FRET trajectories that described the data well (see also Fig. S12). The smaller phasor shift for FRET particles containing IN-mTurquoise+IN-mVenus relative to the D-only population, on the other hand, did not allow us to pinpoint a reasonable range of passive donor contribution. Critically, pixel-based phasors of the IN-eGFP+IN-mScarlet particles also did not enable narrowing down the passive donor-contribution (Fig. S11). Finally, by projecting the phasor data of IN-eGFP+IN-mScarlet particles onto the FRET trajectory we determined average FRET efficiency distributions between 26 and 39% (in Fig. 4 C the FRET efficiency distribution for the 10% passive donors is shown) with an average FRET of 32%.
Figure 4.
FRET trajectory analysis of HIV-1 particles containing donor-labeled IN and acceptor-labeled IN using particle-based pixel binning. (A) Phasor analysis of viral HIV-1 particles containing both donor- and acceptor-labeled IN (IN-Turquoise2+IN-mVenus) forming an unknown mix of multimers including monomers and dimers and potentially higher-order multimers. The donor-only (DO) phasor (g = 0.82, s= 0.37 and background (BG) phasor (g = 0.78, s= 0.31) determine the starting point and end of the FRET trajectory. Variations of the donor-only signal contribution in the analyzed particles result in a variety of FRET trajectories and FRET trajectory end points (red dotted line). (B) Phasor analysis of viral HIV-1 particles containing both donor- and acceptor-labeled IN (IN-eGFP+IN-mScarlet) forming an unknown mix of multimers including monomers and dimers and potentially higher-order multimers. The DO (g = 0.90, s = 0.29) and BG (g = 0.79, s = 0.31) determine the starting point and end of the FRET trajectory. Variations of the donor-only signal contribution in the analyzed particles result in a variety of FRET trajectories and FRET trajectory end points (red dotted line). In both (A) and (B) the pure monoexponential lifetime of the donor () and BG determine by intensity fraction the position of DO on their connecting fraction line (green dotted line). (C) FRET histogram for (B) extracted from the 0, 10, and 20% passive donor contribution FRET trajectories of which the 0 and 20% histogram averages are indicated by purple dashed lines and the 10% passive donor histogram (shown) average is depicted as a vertical full red line with its value.
Discussion
In this paper, we demonstrate the usage of time domain phasor-FLIM in combination with grouped pixel analysis for subresolution single particles. We applied this method on FRET-labeled DNAs and on viral HIV-1 particles that contain single (donor)- or double (donor and acceptor)-labeled IN, the latter exhibiting FRET upon multimerization as demonstrated before using intensity-based approaches (43,50).
First, we studied the effect of grouping pixels to obtain a higher quality phasor determination, optimizing the analysis to utilize all available photons of a particle. In a perfect setting (no background) our simulations showed that 300 photons is the lower limit for proper particle photon statistics leading to a phasor determination within a 5% error range of the true lifetime of a single component. Therefore, when measuring with considerable background or working with complex multicomponent samples, effects which can quantitatively be studied via similar simulations, it is advised to maximize the number of successfully detected and timed photons per object. This requirement is the weak point of every FLIM-FRET analysis compared with intensity-based FRET approaches. On the other hand, the photon detection and timing efficiency is continuously improved with newer FLIM methodologies (e.g., digital frequency domain (10), Leica Falcon (56), PicoQuant rapidFLIM (57), etc.), with ultralow detection dead times or allowing to detect more than one photon per excitation pulse. At the same time, using FLIM with PIE would additionally allow the simultaneous readout of intensity-based and FLIM-FRET, as is routinely done in smFRET burst measurements using multiparameter fluorescence detection with PIE (52,58). In addition, PIE would allow multiplexing of (FRET) probes, as in three or even four color immobilized FRET (59) or using dark acceptor probes (60). Single object FLIM analysis was first used by Qian et al. (40) for viral particle FLIM analysis and now further explored here with complex FRET behavior. We envision that this technique could be further applied in small organelles, protein complexes, immobilized single molecules, or any system where signals originate from a subresolution entity (and are therefore measured as average, potentially spread over multiple pixels). Using object pixel binning allows for more precise analysis as one can oversample the image and later bin the pixels of desired structures. In this paper we have shown the importance of our particle-based analysis given the increased resolution to utilize phasor in a graphical manner. As a remark, we measured our FLIM data using a 20-MHz pulse rate, combining both acceptor and donor pulsing in a 50-ns pulse window, to ensure full decays were considered in phasor analyses. For an illustration of the effects of decay truncation, larger lifetimes, and used TAC range on the resulting phasor cloud shape, the reader is referred to Fig. S13. When PIE is not required, the used pulsing frequency can be changed to optimize the usage of the phasor space for graphical purposes. A formula was provided by Redford and Clegg in 2005 for frequency-domain phasor analysis (9):
| (24) |
which would result in an optical frequency of ∼46–50 MHz for a 4-ns lifetime. However, for time domain phasor applications the main improvement on the resolution of calculated s and g values will arise from a lowered TCSPC bin size.
Next, we tested the effect of pixel grouping on labeled DNA structures, with two fluorescent dyes set 11 nucleotides apart, to evaluate the detection and quantification of FRET by using the graphical phasor approach to FLIM. The obtained value of 39 Å is in close agreement with the literature, which described a value of 40 Å, determined by FRET restrained positioning and screening simulations (52). Since a broad cross-lab study on dye-labeled DNAs pointed out their robustness, we deem our measurements as a validation of the analysis performance (51). We confirmed that the object-binning strategy, together with the phasor plot analysis, allowed for determination of single-molecule FRET via their lifetime signatures. This DNA sample provided a double-labeled single-molecule structure exhibiting a FRET signal from a known donor-acceptor stoichiometry, not complicating the measurement with a donor-only fraction.
Thirdly, we analyzed the performance of several FPs as fusion proteins to IN inside viral particles, as it is difficult to predict the effect of IN coupling and the dense viral particle environment on the fluorescence brightness, lifetime, and FP maturation.
The donor fluorescence lifetimes were comparable with the known monoexponential lifetimes found in literature for these FPs except mTFP1 which was 0.6 ns lower compared with the literature value of 3.2 ns (Table 1). The mCherry lifetime was also found to be inconsistent with literature, which could not be explained by the shifted ratios of the two exponential factors normally involved in an mCherry decay. Wu et al. described two-component lifetimes for mCherry of 0.9 and 1.9 ns, which are both lower than the measured 2.1 ns (61). mVenus and mScarlet on the other hand both measured 0.4 and 0.5 ns, which was above the normal literature values. In general, longer lifetimes are preferred for FRET because of higher dynamic range given a limited time resolution on the hardware side (62). Indeed, it is more straightforward to measure a 2-ns difference compared with a 0.5-ns difference to determine a 50% FRET efficiency in a donor with respective lifetimes of 4 and 1 ns. Furthermore, we expected a photostability double as good for mNeongreen compared with mClover3 (63). However, we recorded a similar photostability, which could be hinting to a photophysical problem for mClover3 or a gained benefit for mNeongreen in the HIV-1 particle environment. Evaluating the particle photon counts, mClover3 and mNeongreen both underperformed while having the highest literature described brightness, further strengthening our belief that the emission of mClover3 is hampered in the viral particles. mTurquoise2 and mCherry performed well considering a generally low brightness. These findings lead us to conclude that fluorescent behaviors of IN-labeled proteins in HIV-1 are difficult to predict. We note that, for some FPs of similar spectra, identical filters were used and that the slightly different treatment of the filter of the emission spectrum could have introduced a small bias into our data.
Table 1.
Overview of measured single-label IN in HIV-1 viral particles
| FP | Literature lifetime (ns) |
Measured lifetime (ns) | Measured photobleaching rate | Maturation (min) | Literature brightness | Measured geomean photon count | References |
|---|---|---|---|---|---|---|---|
| EGFP | 2.6 | 2.61 ± 0.31 | 0.0097 ± 0.0073 | 25 | 33.54 | 144.7 | (64,62) |
| mClover3 | 3.2 | 3.01 ± 0.39 | 0.0127 ± 0.0073 | 43.5 | 85.02 | 111.5 | (62,65) |
| mNeongreen | 3.1 | 2.90 ± 0.60 | 0.0126 ± 0.0090 | 10 | 92.8 | 56.5 | (65) |
| mTurquoise2 | 4.0 | 3.68 ± 0.45 | 0.0078 ± 0.0044 | 33.5 | 27.9 | 148.1 | (66) |
| mTFP1 | 3.2 | 2.62 ± 0.41 | 0.0280 ± 0.0075 | 76.5 | 54.4 | 94.2 | (67) |
| Cherry | 1.49a | 2.10 ± 0.22 | 0.0202 ± 0.0072 | 15 | 15.6 | 118.7 | (68,69) |
| Scarlet | 3.86 | 3.34 ± 0.41 | 0.0072 ± 0.0104 | 174 | 71 | 110.5 | (65,70) |
| Venus | 3.1 | 2.71 ± 0.39 | 0.0251 ± 0.0089 | 17.6 | 66.56 | 90.1 | (71) |
Averaged two-component lifetime.
Finally, we studied viral particles using FRET. For both viral particle types used in our final FRET experiment with HIV-1 particles, the phasor was calculated. Based on the position of the phasor clouds on the plotted array of FRET trajectories, it can be safely concluded that, for IN-eGFP+IN-mScarlet particles, only 0–20% passive donors are present in the particles. With that, a scenario in which only monomers are present (in equal numbers D and A) is already excluded. Even a combination of only monomers or dimers in the particles cannot result in our experimentally observed FRET readout, as this would still require the passive donor fraction to be close to 50% passive donor signal (D, A, DA, AD, DD, and AA results in ∼50% passive donor signal). Furthermore, owing to the quantification of the FRET trajectory incorporating the range of acceptable passive donor fractions, we narrowed the possible FRET values down to 26–39%. In samples with roughly equal numbers of IN-donor and IN-acceptor molecules this can only be explained by the presence of higher-order multimers, which reduce the overall pure donor species since more are involved in FRET-active oligomers. For particles containing IN-mTurquoise+IN-mVenus, narrowing down the FRET values by FRET trajectory analysis proved more challenging. It is anticipated that the particles contain too large amounts of passive donors as a result of more donor- than acceptor-labeled IN in the particles. Even though, at least for IN-eGFP/IN-mScarlet, phasor-FLIM did provide novel insights into the oligomeric state of IN inside viral particles, this graphical analysis of phasor plots remains challenging for a variety of reasons. Firstly, there remains a large error on the precise fraction of passive donors present in the particles, together with between-particle variation of that number. In addition, every multimer formed in the imaged particles has its own FRET efficiency since it consists of a variable content of unlabeled and labeled (donor or acceptor) resulting in an extra variability in FRET readouts. Furthermore, the composition of unlabeled, donor-labeled and acceptor-labeled content cannot be verified, adding to difficulty of data interpretation. Overall, we can assume that measuring close to or more than 1000 particles provides a strong averaged readout with valuable information on the FRET state and therefore insight into the multimeric state of HIV-IN in assembled virus particles. One possible avenue of further investigation is redesigning particles with variable D/A ratios, variable total amounts of labels per particle, or non-FP labeling strategies altogether. In addition, because the number of FPs per particle is limited, the photon output is low and contributions of background and shot noise are considerable. We clearly show that taking the fraction of passive donors into account is essential. This factor is often overlooked because estimating the donor-only fraction is difficult. Using the phasor analysis, we acknowledged the presence of passive donors in our viral particles, which will in any case, lower the apparent FRET signal measured. Given a more precise technique to determine the number of passive donors, researchers would be able to pinpoint which FRET trajectory is suitable and derive more absolute FRET efficiency values. At the same time, determining the number of passive donors present in a mixture of FRET displaying IN multimers remains a variable that can change particle to particle and can therefore not be fully generalized. Although we cannot pinpoint the exact oligomerization state of every IN complex per particle, we can give a founded ensemble evaluation of the in vitro oligomeric state and expect to improve further when photon yield of such experiments becomes more efficient, increasing our phasor data quality. By trying to deconvolve the passive donor contribution we increase out analysis sensitivity to FRET changes, since the significant contribution can overshadow it otherwise. Optimization of the viral particle production to eliminate passive donor molecules as much as possible is a future research target.
Several additional tools can be used when working with phasor representations of FLIM. In our work we chose to work with unfiltered phasor data, but a median or wavelet filter can concentrate the phasor cloud even more, although caution is advised in using these tools (see also Fig. S14). In addition, to disentangle contributions from shot noise and FRET heterogeneity, phasor analysis could be combined with photon distribution analysis (72).
Conclusion
Having presented our work on phasor-FLIM using our particle-based analysis on FRET in viral particles, we aim to contribute in future research lines further enhancing the phasor methodology. The fit-free character of the phasor should not pose a restraint for analyzing data in-depth and with great care. Used correctly, the phasor approach allows for very streamlined analysis and benefits from a highly interesting pixel-phasor reciprocity allowing to select parts of the image based on phasor locations (or clusters) or vice versa. Qualitatively, a phasor is a superior tool to dissect FRET-FLIM data. Quantitatively, it requires thought and challenging parameters such as the contribution of passive donors. Combined with the graphical nature of phasor analysis, the number of photons per analyzed pixel is crucial to establish solid photon arrival statistics and/or estimate FRET values or lifetime values. In this regard, the proposed particle-based phasor can strongly improve analysis in comparison with pixel-based when the sample allows for it. Using FRET-labeled dsDNA we have shown the potential of quantitative FRET analysis extracting a FRET histogram from the phasor plot and in doing so match previous experiments determining the FRET in these single molecules. Particle-based FRET analysis on labeled IN in HIV-1 viral particles proved challenging. However, we provide a particle FRET range which would not be feasible in a straightforward manner using intensity-based FRET, as passive donors would obscure the value since they are unaccounted for.
Author contributions
G.S.F., J.He., and Q.C. designed, built, and aligned the microscope. Q.C. and J.He. performed simulations. N.P. imaged the DNA. Z.D. produced the viral particles. N.P. and Q.C. imaged viral particles. Q.C., C.Q., and J.He. adapted the PAM software for the specific analyses. N.P. performed preliminary analyses. Q.C., N.P., and J.He. performed all analyses. Q.C. and J.He. wrote the manuscript. All authors reviewed and edited the manuscript.
Acknowledgments
Jens de Wachter is thanked for assistance with the DNA experiments. Dr. Waldemar Schrimpf is thanked for implementing phasor analysis in PAM and evaluating the manuscript. Namjoo Vanderveken is acknowledged for assistance in producing the viral particle preparations. Rik Nuyts, Carine Jackers, and Débora Linhares are gratefully acknowledged for assistance in the lab and essential logistics. Dr. Kris Janssen is thanked for writing the software for galvanometric mirror scanning. Dr. Irena Zurnic Bönisch is acknowledged for critically reading the manuscript. J. Hofkens acknowledges financial support from the Research Foundation - Flanders (FWO grant nos. G0F2322N and ZW15_09-GOH6316), the Flemish government through long-term structural funding Methusalem (CASAS2, Meth/15/04), and the MPI as MPI fellow. J. Hendrix acknowledges Research Foundation - Flanders (FWO, projects G0B4915, G0B9922N, and G0H3716N) and KU Leuven Special Research Fund (C14/16/053).
Declaration of interests
The authors declare no competing interests.
Editor: Jorg Enderlein.
Footnotes
Quinten Coucke and Nagma Parveen contributed equally to this work.
Supplemental information can be found online at https://doi.org/10.1016/j.bpr.2023.100122.
Supporting material
References
- 1.Heaster T.M., Sharick J.T., et al. Skala M.C. Fluorescence lifetime imaging microscopy: fundamentals and advances in instrumentation, analysis, and applications. J. Biomed. Opt. 2020;25:1–43. doi: 10.1117/1.JBO.25.7.071203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chen Y.C., Spring B.Q., Clegg R.M. Fluorescence lifetime imaging comes of age how to do it and how to interpret it. Methods Mol. Biol. 2012;875:1–22. doi: 10.1007/978-1-61779-806-1_1. [DOI] [PubMed] [Google Scholar]
- 3.Berezin M.Y., Achilefu S. Fluorescence Lifetime Measurements and Biological Imaging. Chem. Rev. 2010;110:2641–2684. doi: 10.1021/cr900343z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Verveer P.J., Squire A., Bastiaens P.I. Global analysis of fluorescence lifetime imaging microscopy data. Biophys. J. 2000;78:2127–2137. doi: 10.1016/S0006-3495(00)76759-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Verveer P.J., Bastiaens P.I.H. Evaluation of global analysis algorithms for single frequency fluorescence lifetime imaging microscopy data. J. Microsc. 2003;209:1–7. doi: 10.1046/j.1365-2818.2003.01093.x. [DOI] [PubMed] [Google Scholar]
- 6.Digman M.A., Caiolfa V.R., et al. Gratton E. The phasor approach to fluorescence lifetime imaging analysis. Biophys. J. 2008;94:L14–L16. doi: 10.1529/biophysj.107.120154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Weber G. Resolution of the fluorescence lifetimes in a heterogeneous system by phase and modulation measurements. J. Phys. Chem. 1981;85:949–953. [Google Scholar]
- 8.Jameson D.M., Gratton E., Hall R.D. The measurement and analysis of heterogeneous emissions by multifrequency phase and modulation fluorometry. Appl. Spectrosc. Rev. 2007;20:55–106. doi: 10.1080/05704928408081716. [DOI] [Google Scholar]
- 9.Redford G.I., Clegg R.M. Polar plot representation for frequency-domain analysis of fluorescence lifetimes. J. Fluoresc. 2005;15:805–815. doi: 10.1007/s10895-005-2990-8. [DOI] [PubMed] [Google Scholar]
- 10.Colyer R.A., Lee C., Gratton E. A novel fluorescence lifetime imaging system that optimizes photon efficiency. Microsc. Res. Tech. 2008;71:201–213. doi: 10.1002/jemt.20540. [DOI] [PubMed] [Google Scholar]
- 11.Hinde E., Digman M.A., et al. Gratton E. Biosensor Förster resonance energy transfer detection by the phasor approach to fluorescence lifetime imaging microscopy. Microsc. Res. Tech. 2012;75:271–281. doi: 10.1002/jemt.21054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lou J., Solano A., et al. Hinde E. Phasor Histone FLIM-FRET Microscopy Maps Nuclear-Wide Nanoscale Chromatin Architecture With Respect to Genetically Induced DNA Double-Strand Breaks. Front. Genet. 2021;12:770081. doi: 10.3389/fgene.2021.770081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Celli A., Sanchez S., et al. Mauro T. The epidermal Ca2+ gradient: Measurement using the phasor representation of fluorescent lifetime imaging. Biophys. J. 2010;98:911–921. doi: 10.1016/j.bpj.2009.10.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Levitt J.A., Poland S.P., et al. Ameer-Beg S.M. Quantitative real-time imaging of intracellular FRET biosensor dynamics using rapid multi-beam confocal FLIM. Sci. Rep. 2020;10:5146. doi: 10.1038/s41598-020-61478-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liu Z., Pouli D., et al. Georgakoudi I. Mapping metabolic changes by noninvasive, multiparametric, high-resolution imaging using endogenous contrast. Sci. Adv. 2018;4:eaap9302. doi: 10.1126/sciadv.aap9302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Davis R.T., Blake K., et al. Lawson D.A. Transcriptional diversity and bioenergetic shift in human breast cancer metastasis revealed by single-cell RNA sequencing. Nat. Cell Biol. 2020;22:310–320. doi: 10.1038/s41556-020-0477-0. [DOI] [PubMed] [Google Scholar]
- 17.Datta R., Alfonso-Garciá A., et al. Gratton E. Fluorescence lifetime imaging of endogenous biomarker of oxidative stress. Sci. Rep. 2015;5:1–10. doi: 10.1038/srep09848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stringari C., Wang H., et al. Gratton E. In Vivo Single-Cell Detection of Metabolic Oscillations in Stem Cells. Cell Rep. 2015;10:1–7. doi: 10.1016/j.celrep.2014.12.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wright B.K., Andrews L.M., et al. Gratton E. Phasor-flim analysis of NADH distribution and localization in the nucleus of live progenitor myoblast cells. Microsc. Res. Tech. 2012;75:1717–1722. doi: 10.1002/jemt.22121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Stringari C., Edwards R.A., et al. Gratton E. Metabolic trajectory of cellular differentiation in small intestine by Phasor Fluorescence Lifetime Microscopy of NADH. Sci. Rep. 2012;2:568. doi: 10.1038/srep00568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schrimpf W., Jiang J., et al. Wuttke S. Chemical diversity in a metal-organic framework revealed by fluorescence lifetime imaging. Nat. Commun. 2018;9:1647. doi: 10.1038/s41467-018-04050-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fereidouni F., Bader A.N., Gerritsen H.C. Spectral phasor analysis allows rapid and reliable unmixing of fluorescence microscopy spectral images. Opt Express. 2012;20:12729–12741. doi: 10.1364/OE.20.012729. [DOI] [PubMed] [Google Scholar]
- 23.Scipioni L., Rossetta A., et al. Gratton E. Phasor S-FLIM: a new paradigm for fast and robust spectral fluorescence lifetime imaging. Nat. Methods. 2021;18:542–550. doi: 10.1038/s41592-021-01108-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ranjit S., Lanzano L., Gratton E. Mapping diffusion in a living cell via the phasor approach. Biophys. J. 2014;107:2775–2785. doi: 10.1016/j.bpj.2014.08.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Scipioni L., Gratton E., et al. Lanzanò L. Phasor Analysis of Local ICS Detects Heterogeneity in Size and Number of Intracellular Vesicles. Biophys. J. 2016;111:619–629. doi: 10.1016/j.bpj.2016.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chiu C.L., Gratton E. Axial super resolution topography of focal adhesion by confocal microscopy. Microsc. Res. Tech. 2013;76:1070–1078. doi: 10.1002/jemt.22267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Verveer P.J., Squire A., Bastiaens P.I. Global Analysis of Fluorescence Lifetime Imaging Microscopy Data. Biophys. J. 2000;78:2127–2137. doi: 10.1016/S0006-3495(00)76759-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pelet S., Previte M.J.R., et al. So P.T.C. A Fast Global Fitting Algorithm for Fluorescence Lifetime Imaging Microscopy Based on Image Segmentation. Biophys. J. 2004;87:2807–2817. doi: 10.1529/biophysj.104.045492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ranjit S., Malacrida L., et al. Gratton E. Fit-free analysis of fluorescence lifetime imaging data using the phasor approach. Nat. Protoc. 2018;13:1979–2004. doi: 10.1038/s41596-018-0026-5. [DOI] [PubMed] [Google Scholar]
- 30.Rahim M.K., Zhao J., et al. Haun J.B. Phasor Analysis of Fluorescence Lifetime Enables Quantitative Multiplexed Molecular Imaging of Three Probes. Anal. Chem. 2022;94:14185–14194. doi: 10.1021/acs.analchem.2c02149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Albertazzi L., Arosio D., et al. Beltram F. Quantitative FRET analysis with the E0GFP-mCherry fluorescent protein pair. Photochem. Photobiol. 2009;85:287–297. doi: 10.1111/j.1751-1097.2008.00435.x. [DOI] [PubMed] [Google Scholar]
- 32.De Los Santos C., Chang C.W., et al. Cardullo R.A. FRAP, FLIM, and FRET: Detection and analysis of cellular dynamics on a molecular scale using fluorescence microscopy. Mol. Reprod. Dev. 2015;82:587–604. doi: 10.1002/mrd.22501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Maus M., Cotlet M., et al. Seidel C.A. An experimental comparison of the maximum likelihood estimation and nonlinear least-squares fluorescence lifetime analysis of single molecules. Anal. Chem. 2001;73:2078–2086. doi: 10.1021/ac000877g. [DOI] [PubMed] [Google Scholar]
- 34.Cotlet M., Masuo S., et al. De Schryver F. Probing conformational dynamics in single donor-acceptor synthetic molecules by means of photoinduced reversible electron transfer. Proc. Natl. Acad. Sci. USA. 2004;101:14343–14348. doi: 10.1073/pnas.0406119101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kuimova M.K., Botchway S.W., et al. Ogilby P.R. Imaging intracellular viscosity of a single cell during photoinduced cell death. Nat. Chem. 2009;1:69–73. doi: 10.1038/nchem.120. [DOI] [PubMed] [Google Scholar]
- 36.Okabe K., Inada N., et al. Uchiyama S. Intracellular temperature mapping with a fluorescent polymeric thermometer and fluorescence lifetime imaging microscopy. Nat. Commun. 2012;3:705. doi: 10.1038/ncomms1714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Agronskaia A.V., Tertoolen L., Gerritsen H.C. 2004. Fast fluorescence lifetime imaging of calcium in living cells. [DOI] [PubMed] [Google Scholar]
- 38.Goryashchenko A.S., Pakhomov A.A., et al. Deyev I.E. FLIM-Based Intracellular and Extracellular pH Measurements Using Genetically Encoded pH Sensor. Biosensors. 2021;11 doi: 10.3390/bios11090340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lin H.J., Herman P., Lakowicz J.R. Fluorescence Lifetime-Resolved pH Imaging of Living Cells. Cytometry A. 2003;52:77–89. doi: 10.1002/cyto.a.10028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Qian C., Flemming A., et al. Lamb D.C. Dynamics of HIV-1 Gag Processing as Revealed by Fluorescence Lifetime Imaging Microscopy and Single Virus Tracking. Viruses. 2022;14 doi: 10.3390/v14020340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Desimmie B.A., Schrijvers R., et al. Debyser Z. LEDGINs inhibit late stage HIV-1 replication by modulating integrase multimerization in the virions. Retrovirology. 2013;10:57. doi: 10.1186/1742-4690-10-57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Borrenberghs D., Thys W., et al. Hendrix J. 2014. HIV Virions as Nanoscopic Test Tubes for Probing Oligomerization of the Integrase Enzyme. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Borrenberghs D., Dirix L., et al. Debyser Z. Dynamic Oligomerization of Integrase Orchestrates HIV Nuclear Entry. Sci. Rep. 2016;6:36485. doi: 10.1038/srep36485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lakowicz J.R. In: Principles of Fluorescence Spectroscopy. Lakowicz J.R., editor. Springer US; 2006. Fluorescence-lifetime imaging microscopy; pp. 741–755. [Google Scholar]
- 45.Gadella T.W., Jovin T.M., Clegg R.M. Fluorescence lifetime imaging microscopy (FLIM): Spatial resolution of microstructures on the nanosecond time scale. Biophys. Chem. 1993;48:221–239. [Google Scholar]
- 46.Ranjit S., Malacrida L., Gratton E. Differences between FLIM phasor analyses for data collected with the Becker and Hickl SPC830 card and with the FLIMbox card. Microsc. Res. Tech. 2018;81:980–989. doi: 10.1002/jemt.23061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Michalet X. Continuous and discrete phasor analysis of binned or time-gated periodic decays. AIP Adv. 2021;11:035331. doi: 10.1063/5.0027834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Schrimpf W., Barth A., et al. Lamb D.C. PAM: A Framework for Integrated Analysis of Imaging, Single-Molecule, and Ensemble Fluorescence Data. Biophys. J. 2018;114:1518–1528. doi: 10.1016/j.bpj.2018.02.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Albanese A., Arosio D., et al. Cereseto A. HIV-1 Pre-Integration Complexes Selectively Target Decondensed Chromatin in the Nuclear Periphery. PLoS One. 2008;3:2413. doi: 10.1371/journal.pone.0002413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Borrenberghs D., Thys W., et al. Hendrix J. HIV virions as nanoscopic test tubes for probing oligomerization of the integrase enzyme. ACS Nano. 2014;8:3531–3545. doi: 10.1021/nn406615v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hellenkamp B., Schmid S., et al. Hugel T. Precision and accuracy of single-molecule FRET measurements—a multi-laboratory benchmark study. Nat. Methods. 2018;15:669–676. doi: 10.1038/s41592-018-0085-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Vandenberk N., Barth A., et al. Hendrix J. Evaluation of Blue and Far-Red Dye Pairs in Single-Molecule Förster Resonance Energy Transfer Experiments. J. Phys. Chem. B. 2018;122:4249–4266. doi: 10.1021/acs.jpcb.8b00108. [DOI] [PubMed] [Google Scholar]
- 53.Hendrix J., Schrimpf W., et al. Lamb D.C. Pulsed interleaved excitation fluctuation imaging. Biophys. J. 2013;105:848–861. doi: 10.1016/j.bpj.2013.05.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Müller B.K., Zaychikov E., et al. Lamb D.C. Pulsed interleaved excitation. Biophys. J. 2005;89:3508–3522. doi: 10.1529/biophysj.105.064766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Toseland C.P. Fluorescent labeling and modification of proteins. J. Chem. Biol. 2013;6:85–95. doi: 10.1007/s12154-013-0094-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Alvarez L.A.J., Widzgowski B., et al. Hecht F. SP8 FALCON: a novel concept in fluorescence lifetime imaging enabling video-rate confocal FLIM. Nat. Methods. 2019;20:2–4. [Google Scholar]
- 57.Orthaus-Müller S., Krämer B., et al. Erdmann R. rapidFLIM : The New and Innovative Method for Ultra fast FLIM Imaging. Micron. 2016;88:1–6. [Google Scholar]
- 58.Hendrix J., Lamb D.C. 1st ed. Elsevier Inc; 2013. Pulsed interleaved excitation: Principles and applications. [DOI] [PubMed] [Google Scholar]
- 59.Ratzke C., Hellenkamp B., Hugel T. Four-colour FRET reveals directionality in the Hsp90 multicomponent machinery. Nat. Commun. 2014;5:4192. doi: 10.1038/ncomms5192. [DOI] [PubMed] [Google Scholar]
- 60.Laskaratou D., Fernández G.S., et al. Mizuno H. Quantification of FRET-induced angular displacement by monitoring sensitized acceptor anisotropy using a dim fluorescent donor. Nat. Commun. 2021;12:1–12. doi: 10.1038/s41467-021-22816-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wu B., Chen Y., Müller J.D. Fluorescence fluctuation spectroscopy of mCherry in living cells. Biophys. J. 2009;96:2391–2404. doi: 10.1016/j.bpj.2008.12.3902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Martin K.J., McGhee E.J., et al. Anderson K.I. Accepting from the best donor; analysis of long-lifetime donor fluorescent protein pairings to optimise dynamic FLIM-based FRET experiments. PLoS One. 2018;13 doi: 10.1371/journal.pone.0183585. e0183585–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Shaner N.C., Lambert G.G., et al. Wang J. A bright monomeric green fluorescent protein derived from Branchiostoma lanceolatum. Nat. Methods. 2013;10:407–409. doi: 10.1038/nmeth.2413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Cormack B.P., Valdivia R.H., Falkow S. FACS-optimized mutants of the green fluorescent protein (GFP) Gene. 1996;173:33–38. doi: 10.1016/0378-1119(95)00685-0. [DOI] [PubMed] [Google Scholar]
- 65.McCullock T.W., MacLean D.M., Kammermeier P.J. Comparing the performance of mScarlet-I, mRuby3, and mCherry as FRET acceptors for mNeonGreen. PLoS One. 2020;15 doi: 10.1371/journal.pone.0219886. e0219886–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Goedhart J., Von Stetten D., et al. Royant A. Structure-guided evolution of cyan fluorescent proteins towards a quantum yield of 93. Nat. Commun. 2012;3:751. doi: 10.1038/ncomms1738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Guerra P., Vuillemenot L.A., et al. Milias-Argeitis A. Systematic in Vivo Characterization of Fluorescent Protein Maturation in Budding Yeast. ACS Synth. Biol. 2022;11:1129–1141. doi: 10.1021/acssynbio.1c00387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Mukherjee S., Manna P., et al. Jimenez R. Directed Evolution of a Bright Variant of mCherry: Suppression of Nonradiative Decay by Fluorescence Lifetime Selections. J. Phys. Chem. B. 2022;126:4659–4668. doi: 10.1021/acs.jpcb.2c01956. [DOI] [PubMed] [Google Scholar]
- 69.Shaner N.C., Campbell R.E., et al. Tsien R.Y. Improved monomeric red, orange and yellow fluorescent proteins derived from Discosoma sp. red fluorescent protein. Nat. Biotechnol. 2004;22:1567–1572. doi: 10.1038/nbt1037. [DOI] [PubMed] [Google Scholar]
- 70.Bindels D.S., Haarbosch L., et al. Gadella T.W.J. MScarlet: A bright monomeric red fluorescent protein for cellular imaging. Nat. Methods. 2017;14:53–56. doi: 10.1038/nmeth.4074. [DOI] [PubMed] [Google Scholar]
- 71.Kremers G.J., Goedhart J., et al. Gadella T.W.J. Cyan and yellow super fluorescent proteins with improved brightness, protein folding, and FRET förster radius. Biochemistry. 2006;45:6570–6580. doi: 10.1021/bi0516273. [DOI] [PubMed] [Google Scholar]
- 72.Antonik M., Felekyan S., et al. Seidel C.A.M. Separating structural heterogeneities from stochastic variations in fluorescence resonance energy transfer distributions via photon distribution analysis. J. Phys. Chem. B. 2006;110:6970–6978. doi: 10.1021/jp057257+. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.