Optimal cell traction forces in a generalized motor-clutch model

Abstract

Cells exert forces on mechanically compliant environments to sense stiffness, migrate, and remodel tissue. Cells can sense environmental stiffness via myosin-generated pulling forces acting on F-actin, which is in turn mechanically coupled to the environment via adhesive proteins, akin to a clutch in a drivetrain. In this “motor-clutch” framework, the force transmitted depends on the complex interplay of motor, clutch, and environmental properties. Previous mean-field analysis of the motor-clutch model identified the conditions for optimal stiffness for maximal force transmission via a dimensionless number that combines motor-clutch parameters. However, in this and other previous mean-field analyses, the motor-clutch system is assumed to have balanced motors and clutches and did not consider force-dependent clutch reinforcement and catch bond behavior. Here, we generalize the motor-clutch analytical framework to include imbalanced motor-clutch regimes, with clutch reinforcement and catch bonding, and investigate optimality with respect to all parameters. We found that traction force is strongly influenced by clutch stiffness, and we discovered an optimal clutch stiffness that maximizes traction force, suggesting that cells could tune their clutch mechanical properties to perform a specific function. The results provide guidance for maximizing the accuracy of cell-generated force measurements via molecular tension sensors by designing their mechanosensitive linker peptide to be as stiff as possible. In addition, we found that, on rigid substrates, the mean-field analysis identifies optimal motor properties, suggesting that cells could regulate their myosin repertoire and activity to maximize force transmission. Finally, we found that clutch reinforcement shifts the optimum substrate stiffness to larger values, whereas the optimum substrate stiffness is insensitive to clutch catch bond properties. Overall, our work reveals novel features of the motor-clutch model that can affect the design of molecular tension sensors and provide a generalized analytical framework for predicting and controlling cell adhesion and migration in immunotherapy and cancer.

Significance

Adherent cells produce mechanical forces on their environment to mediate cell adhesion and signaling in development and disease progression. Despite recent progress, cell-generated force measurements across a wide range of extracellular stiffnesses and cell states have faced numerous technical challenges. Our mean-field study provides a new generalized analysis of regulation of force transmission by modulation of cellular components and extracellular rigidity. Here, we identify the existence of an intermediate stiffness of cell adhesion molecules for maximum force transmission and find that maximal force transmission on rigid environments depends on myosin motor properties. The generalized analysis provides important insights to aid design of novel molecular tension sensors and therapeutic strategies for cancers and other diseases.

Introduction

Cell migration plays a pivotal role in many biological processes, such as embryonic morphogenesis, wound healing, and cancer progression. A major challenge in cell biology is to understand how cells within an organism migrate through different environments. During migration, cells undergo a complex series of events that occur in a highly dynamic fashion (1,2). According to the motor-clutch hypothesis (3), cells start off the migration cycle by the extension of cell membrane protrusions driven by actin polymerization, followed by the formation of complex adhesion structures and generation of traction forces (4). Adhesion complexes function as molecular clutches by mechanically coupling the actin cytoskeleton to the extracellular substrate via membrane-bound receptors. Clutches cooperatively resist the forces arising from the rearward flow of actin filaments and transmit them to the substrate, allowing the cell to move forward (5,6,7). The flow of F-actin away from the leading edge, known as retrograde flow, emerges as actin filaments are subject to rearward forces produced by the leading-edge membrane due to actin polymerization (8) as well as by myosin motors as they bind and pull filaments away from the leading edge (9). Actin polymerization, adhesion formation, and myosin forces are therefore mechanically coordinated allowing cells to migrate and explore their extracellular environment.

How cells sense and respond to the mechanical features of their environment has been the focus of many studies (10,11,12,13,14,15). According to the motor-clutch model, coupling between the extracellular substrate and the actin cytoskeleton by molecular clutches permits the transmission of actomyosin-generated forces to the substrate, allowing cells to sense the mechanical properties of the environment (2,16). The motor-clutch model exhibits rigidity sensing, which emerges from load-dependent clutch-bond dissociation rates and load-dependent myosin motor force generation (2,10,17,18), and captures the reported biphasic dependence of cell migration on substrate adhesion strength, first postulated by DiMilla et al. (19) and later confirmed experimentally (20,21). Cell motility (12,21,22,23,24,25,26,27) and traction forces (12,13) have been reported to exhibit a biphasic dependence on substrate adhesivity/stiffness. Some cells, however, deviate from the biphasic force-rigidity relationship at physiological substrate stiffnesses through force-mediated clutch reinforcement (14,28). Also, some cells produce higher traction forces on stiffer substrates (29,30,31,32), whereas other cells produce higher traction forces on softer substrates (2). Together, these studies suggest the existence of an optimal substrate stiffness for maximal traction force, as observed experimentally (12,14).

Previous mean-field model studies addressed the production of traction forces on infinitely rigid substrates (33,34,35,36) and in compliant linearly elastic (17) and viscoelastic (37) substrates. Motor-clutch studies (2,10,17) identified the existence of three different traction force production regimes: a stalled regime characterized by clutch-dominated protrusions, a balanced regime characterized by a motor-clutch balanced protrusion, and a free-flowing regime characterized by motor-dominated protrusions. In this study, we introduce a mean-field representation of the motor-clutch model (2) with the aim of gaining a more general theoretical understanding of traction force production from individual cellular protrusions on elastic substrates that does not assume that motors and clutches are balanced. In addition, we included force-dependent clutch reinforcement (14,28) and catch bonding (38,39). In particular, we apply scaling analysis to our model with the purpose of deriving an analytical expression for the optimum substrate stiffness (i.e., the substrate stiffness that maximizes traction forces). In this work, we relax the adjustable parameter assumption made in (17) and derive a more general expression for the optimum substrate stiffness that is applicable to all motor-clutch ratio regimes. Our generalized mean-field model results allow us to identify the existence of an optimum clutch stiffness for maximal cellular traction force. In addition, we capture a biphasic dependence of force transmission on motor activity on rigid substrates and identify an intermediate myosin load-free velocity parameter for maximum traction force. Finally, we find that load-dependent clutch reinforcement can significantly shift the optimum substrate and clutch stiffnesses to larger values, increasing substantially the traction force produced by protrusions that display load-and-fail dynamics, whereas catch bond properties can modulate force transmission but do not affect the optimum substrate stiffness for maximum force. Our mean-field approach additionally allowed us to carry out an in-depth exploration of the distribution of clutch force states during the loading cycle as a function of all parameters grouped together to define new dimensionless variables and parameters.

Materials and methods

The developed mean-field theory is a generalization of the model by Bangasser and Odde (17), where a probability that each existing clutch in the protrusion is mechanically linking the actin cytoskeleton and the extracellular substrate was introduced. In this work, we introduce a multibond probability density of finding any clutch with a given extension at any instantaneous time and derive its conservation equation (see supporting material). Our approach relaxes the previous assumption that motors and clutches are balanced, without requiring an unknown parameter to define the optimum, and analytically investigates previously uncharacterized optimality of clutch stiffness, clutch catch bond behavior, and load-dependent clutch-bond reinforcement behavior, the latter two of which are common features of motor-clutch cellular systems. The present treatment allowed us to make a more complete and generalized analysis of cellular force transmission and further explored the entire motor-clutch model parameter space.

According to the motor-clutch hypothesis, myosin motors bind and pull actin filaments retrogradely away from the leading edge producing retrograde forces (Fig. 1 A). Forces on actin filaments are transmitted to the extracellular matrix through protein complexes, commonly called clutches, that mediate the production of traction forces on the surrounding compliant substrate allowing the cell body to propel forward. Molecular clutches bind—that is, couple—actin filaments to the compliant substrate in an unloaded state at a force-independent rate ${\mathrm{k}}_{\mathrm{o}\mathrm{n}}$ (see Table 1 for a summary of all parameters and estimated base values). Clutches form slip bonds and unbind with an effective dissociation rate that increases exponentially with force according to Bell’s law ${\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}={\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}{\mathrm{e}}^{\left|{\mathrm{F}}_{\mathrm{c}}\right|/{\mathrm{F}}_{\mathrm{b}}}$ (52), where ${\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}$ is the unloaded clutch dissociation rate, ${\mathrm{F}}_{\mathrm{b}}$ is the characteristic bond rupture force, and ${\mathrm{F}}_{\mathrm{c}}$ is the force on the clutch. The simplest motor-clutch description is to consider molecular clutches and the surrounding substrate as Hookean elastic materials. Accordingly, the clutch force is given by Hooke’s law ${\mathrm{F}}_{\mathrm{c}}={\kappa }_{\mathrm{c}}{\mathrm{x}}_{\mathrm{c}}$, where ${\kappa }_{\mathrm{c}}$ is the effective clutch stiffness and ${\mathrm{x}}_{\mathrm{c}}$ is the clutch extension, measured with respect to its resting value. To study clutch elongation dynamics, we introduce a probability density function ${\mathrm{P}}_{\mathrm{b}}\left({\mathrm{x}}_{\mathrm{c}},\mathrm{t}\right)$ of finding a bound clutch with elongation ${\mathrm{x}}_{\mathrm{c}}$ at time $\mathrm{t}$. Conservation of ${\mathrm{P}}_{\mathrm{b}}$ implies (see supporting material):

$$\frac{\partial {\mathrm{P}}_{\mathrm{b}}}{\partial \mathrm{t}}={\mathrm{k}}_{\mathrm{o}\mathrm{n}}\left({\mathrm{n}}_{\mathrm{c}}-{\mathrm{n}}_{\mathrm{b}}\right)\delta \left({\mathrm{x}}_{\mathrm{c}}\right)-{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}^{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}{\mathrm{P}}_{\mathrm{b}}-{\mathrm{v}}_{\mathrm{e}}\frac{\partial {\mathrm{P}}_{\mathrm{b}}}{\partial {\mathrm{x}}_{\mathrm{c}}}\text{.}$$ (1)

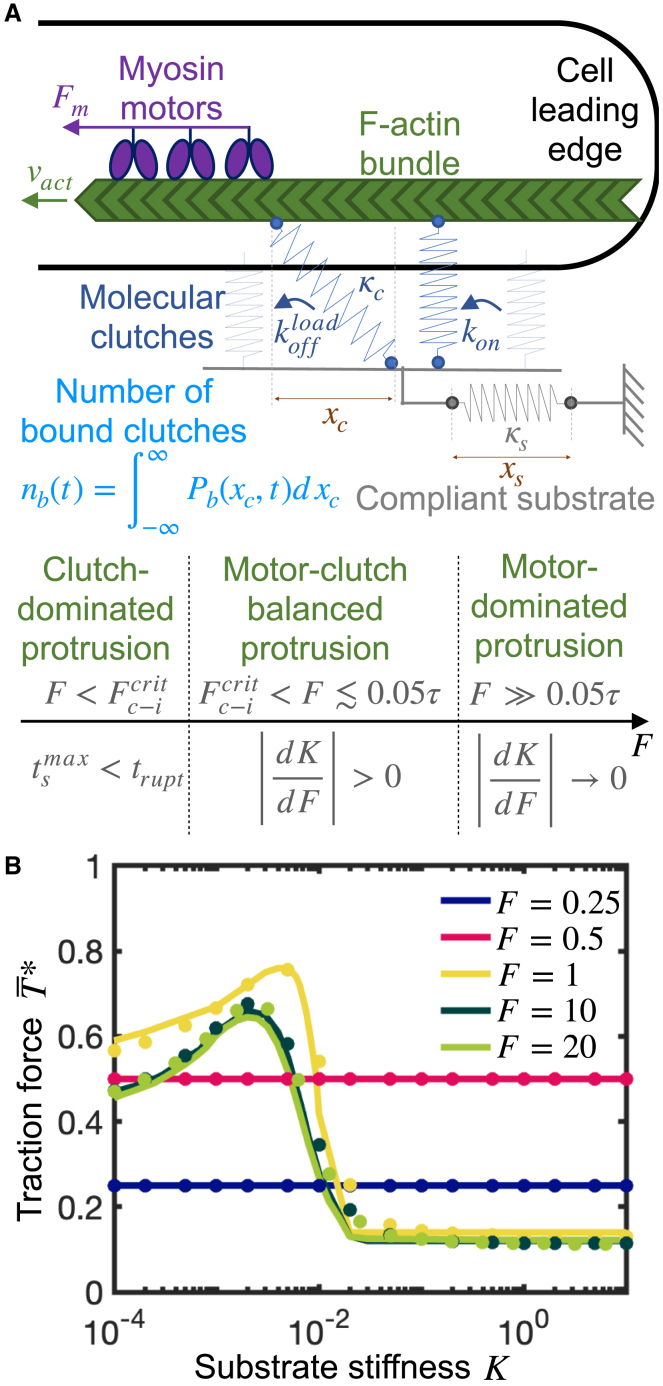
Figure 1.

Traction force production of individual cellular protrusions exhibit three different regimes: a motor-dominated regime, an intermediate motor-clutch balanced regime, and a clutch-dominated regime. Mean-field motor-clutch model captures force transmission sensitivity to substrate compliance. (A) Sketch of the model and required conditions for the protrusion to operate at each traction force production regime. (B) Dimensionless time-averaged traction force ${\overline{\mathrm{T}}}^{\ast }=\overline{\mathrm{T}}/{\mathrm{n}}_{\mathrm{c}}{\mathrm{F}}_{\mathrm{b}}$ as a function of the dimensionless substrate stiffness $\mathrm{K}$ for various values of the myosin activity parameter $\mathrm{F}$. Protrusions can belong to three different regimes: a motor-dominated regime characterized by the existence of an optimum stiffness for maximal traction that is largely independent of myosin activity ($\mathrm{F}=10$ and $\mathrm{F}=20$), a clutch-dominated regime characterized by stiffness-independent traction forces ($\mathrm{F}=0.25$ and $\mathrm{F}=0.5$), and an intermediate regime characterized by an optimum stiffness sensitive to motor activity ($\mathrm{F}\sim 1$). The three regimes are analyzed in detail in the main text. Solid lines are the numerical solution of the mean-field model Eqs. 3 and 4, and circular solid symbols are the mean statistics obtained from the numerical solution of the stochastic model. There is a very good agreement between the mean-field model solution and stochastic model solution. Parameter values: $\tau =10,\omega =2000$. To see this figure in color, go online.

Table 1.

Dimensional Model Parameters

Symbol	Description	Estimated Values	Legend/Referencesa
${\mathrm{n}}_{\mathrm{m}}$+	number of myosin motors in the cellular protrusion	$550$	A
${\mathrm{F}}_{\mathrm{m}}$+	single myosin motor stall force	$0.6-2.3\mathrm{p}\mathrm{N}$	Chan and Odde (2); Molloy et al. (40); Ishijima et al. (41); Kishino and Yanagida (42); Tyska et al. (43)
${\mathrm{v}}_{\mathrm{u}}$+	myosin unloaded velocity	$120-240$$\mathrm{n}\mathrm{m}·{\mathrm{s}}^{-1}$	Chan and Odde (2); Bangasser et al. (10); Bangasser and Odde (17); Stark et al. (44)
${\mathrm{n}}_{\mathrm{c}}$∗	number of clutches in the cellular protrusion	$470$	B
${\mathrm{k}}_{\mathrm{on}}$∗	clutch association rate constant	$0.1-6$${\mathrm{s}}^{-1}$	Chan and Odde (2); Bangasser et al. (10); Bangasser and Odde (17); Litvinov et al. (45)
${\mathrm{k}}_{\mathrm{off}}$∗	unloaded clutch dissociation kinetic rate constant	$0.1-6.5$${\mathrm{s}}^{-1}$	Chan and Odde (2); Bangasser et al. (10); Bangasser and Odde (17); Litvinov et al. (45); Le et al. (46)
${\mathrm{F}}_{\mathrm{b}}$∗	characteristic clutch-bond rupture force	$1.7\mathrm{p}\mathrm{N}$	C
${\kappa }_{\mathbf{c}}$∗	molecular clutch stiffness	$\left[0.1-2\right]\mathrm{p}\mathrm{N}·{\mathrm{n}\mathrm{m}}^{-1}$	D
$\theta$∗	load-dependent clutch reinforcement strength	adjusted	–
${\mathrm{F}}_{\mathrm{th}}$∗	load-dependent clutch reinforcement threshold force	$5-10$$\mathrm{p}\mathrm{N}$	Yao et al. (47); Yan et al. (48); Yu et al. (49); Yao et al. (50); Mekhdjian et al. (51)
${\mathrm{k}}_{\mathrm{off}}^{\mathrm{catch}}$∗	unloaded clutch catch bond dissociation kinetic rate constant	adjusted	–
${\mathrm{F}}_{\mathrm{b}}^{\mathrm{catch}}$∗	characteristic clutch catch bond rupture force	adjusted	–
${\kappa }_{\mathbf{s}}$#	compliant substrate stiffness	$\left[3.5-3.5\times {10}^4\right]\mathrm{p}\mathrm{N}·{\mu \mathrm{m}}^{-1}$	E

^aParameter values are estimated in the supporting material. Motor parameters (plus symbol), clutch parameters (asterisk), cell environment parameters (hash symbol).

The first term on the right-hand side (RHS) of Eq. 1 corresponds to the rate of change of the probability density due to clutch binding kinetics, where$\delta \left({\mathrm{x}}_{\mathrm{c}}\right)$ is the Dirac delta function, which enforces clutches to engage in an unloaded configuration. The number of bound clutches that mechanically connect the cytoskeletal filaments with the substrate is denoted by ${\mathrm{n}}_{\mathrm{b}}\left(\mathrm{t}\right)$, and ${\mathrm{n}}_{\mathrm{c}}$ is the total number of available clutches in the cellular protrusion. The second term on the RHS of Eq. 1 is the rate of change of the probability density due to clutch dissociation kinetics, and the last term of Eq. 1 accounts for the rate of change of the probability density due to force-mediated clutch extension, where the clutch elongation rate is ${\mathrm{v}}_{\mathrm{e}}={\mathrm{v}}_{\mathrm{a}\mathrm{c}\mathrm{t}}-\mathrm{d}{\mathrm{x}}_{\mathrm{s}}/\mathrm{d}\mathrm{t}$, where ${\mathrm{v}}_{\mathrm{a}\mathrm{c}\mathrm{t}}$ is the actin filament velocity and ${\mathrm{d}\mathrm{x}}_{\mathrm{s}}/\mathrm{d}\mathrm{t}$ is the substrate deformation rate. We therefore follow the standard motor-clutch view and assume that all bound clutches equally deform at any time, where the actin-binding domains of clutches move at the actin retrograde flow velocity ${\mathrm{v}}_{\mathrm{a}\mathrm{c}\mathrm{t}}$ and their substrate-binding domains move rigidly with the substrate. Furthermore, myosin motors obey a linear force-velocity relation; thus, the total force exerted by myosin motors on the actin filament bundle is ${\mathrm{F}}_{\mathrm{a}\mathrm{c}\mathrm{t}}={\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}\left(1-{\mathrm{v}}_{\mathrm{a}\mathrm{c}\mathrm{t}}/{\mathrm{v}}_{\mathrm{u}}\right)$, where ${\mathrm{n}}_{\mathrm{m}}$ is the total number of myosin motors in the protrusion, ${\mathrm{F}}_{\mathrm{m}}$ is the stall force exerted by one myosin motor, and ${\mathrm{v}}_{\mathrm{u}}$ is the load-free velocity of myosin motors. For convenience, we define the first two moments of the probability density over all possible clutch extensions: ${\mathrm{n}}_{\mathrm{b}}\left(\mathrm{t}\right)=\underset{-\infty }{\overset{\infty }{\int }}{\mathrm{P}}_{\mathrm{b}}\left({\mathrm{x}}_{\mathrm{c}},\mathrm{t}\right)\mathrm{d}{\mathrm{x}}_{\mathrm{c}}$ and ${\mathcal{\ell }}_{\mathrm{b}}\left(\mathrm{t}\right)=\underset{-\infty }{\overset{\infty }{\int }}{\mathrm{x}}_{\mathrm{c}}{\mathrm{P}}_{\mathrm{b}}\left({\mathrm{x}}_{\mathrm{c}},\mathrm{t}\right)\mathrm{d}{\mathrm{x}}_{\mathrm{c}}$, where ${\mathrm{n}}_{\mathrm{b}}$ is the above-mentioned number of bound clutches and ${\mathcal{\ell }}_{\mathrm{b}}$ is the sum of clutch extensions. Governing equations for the first two moments can be obtained from quadrature of the conservation equation for the probability density function, yielding $\frac{\mathrm{d}{\mathrm{n}}_{\mathrm{b}}}{\mathrm{d}\mathrm{t}}={\mathrm{k}}_{\mathrm{o}\mathrm{n}}\left({\mathrm{n}}_{\mathrm{c}}-{\mathrm{n}}_{\mathrm{b}}\right)-{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}\underset{-\infty }{\overset{\infty }{\int }}{\mathrm{e}}^{\frac{{\kappa }_{\mathrm{c}}\left|{\mathrm{x}}_{\mathrm{c}}\right|}{{\mathrm{F}}_{\mathrm{b}}}}{\mathrm{P}}_{\mathrm{b}}\mathrm{d}{\mathrm{x}}_{\mathrm{c}}$, and $\frac{\mathrm{d}{\mathcal{\ell }}_{\mathrm{b}}}{\mathrm{d}\mathrm{t}}=-{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}\underset{-\infty }{\overset{\infty }{\int }}{\mathrm{x}}_{\mathrm{c}}{\mathrm{e}}^{\frac{{\kappa }_{\mathrm{c}}\left|{\mathrm{x}}_{\mathrm{c}}\right|}{{\mathrm{F}}_{\mathrm{b}}}}{\mathrm{P}}_{\mathrm{b}}\mathrm{d}{\mathrm{x}}_{\mathrm{c}}+{\mathrm{v}}_{\mathrm{e}}{\mathrm{n}}_{\mathrm{b}}$. A force balance on the substrate allows calculation of the traction force exerted on the substrate $\mathrm{T}$ as a function of the first-order moment of the probability density: $\mathrm{T}={\kappa }_{\mathrm{s}}{\mathrm{x}}_{\mathrm{s}}={\kappa }_{\mathrm{c}}{\mathcal{\ell }}_{\mathrm{b}}$, where ${\kappa }_{\mathrm{s}}$ is the substrate stiffness constant and ${\mathrm{x}}_{\mathrm{s}}$ is the substrate deformation. We take the time-derivative of the traction force to obtain an expression for the clutch elongation rate

$${\mathrm{v}}_{\mathrm{e}}=\frac{1}{{\kappa }_{\mathrm{s}}+{\mathrm{n}}_{\mathrm{b}}{\kappa }_{\mathrm{c}}}\left[{\mathrm{v}}_{\mathrm{u}}{\kappa }_{\mathrm{s}}\left(1-\frac{{\kappa }_{\mathrm{c}}{\mathcal{\ell }}_{\mathrm{b}}}{{\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}}\right)+{\kappa }_{\mathrm{c}}{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}\underset{-\infty }{\overset{\infty }{\int }}{\mathrm{x}}_{\mathrm{c}}{\mathrm{e}}^{{\kappa }_{\mathrm{c}}\left|{\mathrm{x}}_{\mathrm{c}}\right|/{\mathrm{F}}_{\mathrm{b}}}{\mathrm{P}}_{\mathrm{b}}\mathrm{d}{\mathrm{x}}_{\mathrm{c}}\right]\text{.}$$ (2)

For convenience, we use dimensionless equations where we scale variables using ${\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}^{-1}$ as timescale, ${\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}/{\mathrm{n}}_{\mathrm{c}}{\kappa }_{\mathrm{c}}$ as length scale, ${\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}/{\mathrm{n}}_{\mathrm{c}}{\kappa }_{\mathrm{c}}$ as velocity scale, and ${\mathrm{n}}_{\mathrm{c}}{\mathrm{F}}_{\mathrm{b}}$ as force scale: ${\mathrm{t}}^{\ast }=\mathrm{t}{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}},{\mathrm{x}}^{\ast }=\mathrm{x}{\mathrm{n}}_{\mathrm{c}}{\kappa }_{\mathrm{c}}/{\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}},{\mathrm{v}}_{\mathrm{e}}^{\ast }={\mathrm{v}}_{\mathrm{e}}{\mathrm{n}}_{\mathrm{c}}{\kappa }_{\mathrm{c}}/{\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}},{\mathrm{P}}_{\mathrm{b}}^{\ast }={\mathrm{P}}_{\mathrm{b}}{\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}/{\mathrm{n}}_{\mathrm{c}}^2{\kappa }_{\mathrm{c}},{\mathrm{T}}^{\ast }=\mathrm{T}/{\mathrm{n}}_{\mathrm{c}}{\mathrm{F}}_{\mathrm{b}}$, where we have additionally normalized the probability density function by the total number of clutches ${\mathrm{n}}_{\mathrm{c}}$. The fraction of bound clutches is denoted as ${\mathrm{n}}_{\mathrm{b}}^{\ast }={\mathrm{n}}_{\mathrm{b}}/{\mathrm{n}}_{\mathrm{c}}$. Henceforth, any variable accompanied by an asterisk is dimensionless. Nondimensionalization of the governing equations yields four dimensionless groups (Table 2): $\mathrm{F}={\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}/{\mathrm{n}}_{\mathrm{c}}{\mathrm{F}}_{\mathrm{b}},\tau ={\mathrm{k}}_{\mathrm{o}\mathrm{n}}/{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}},\omega ={\mathrm{v}}_{\mathrm{u}}{\kappa }_{\mathrm{c}}/{\mathrm{F}}_{\mathrm{b}}{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}},\mathrm{K}={\kappa }_{\mathrm{s}}/{\mathrm{n}}_{\mathrm{c}}{\kappa }_{\mathrm{c}}$. The myosin activity parameter $\mathrm{F}$ is the ratio of the total myosin stall force ${\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}$ over the characteristic maximum clutch elastic force ${\mathrm{n}}_{\mathrm{c}}{\mathrm{F}}_{\mathrm{b}}$. The clutch kinetic parameter $\tau$ is the ratio of the clutch association constant ${\mathrm{k}}_{\mathrm{o}\mathrm{n}}$ over the clutch unloaded dissociation constant ${\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}$. The parameter $\omega$ represents the ratio of the characteristic clutch unloaded dissociation time over the characteristic clutch loaded dissociation time. The parameter $\omega$ can also be described as the dimensionless myosin load-free velocity, or as the ratio of the characteristic elongation that a single clutch undergoes in the absence of cooperative clutch effects over the characteristic clutch rupture length. Notice that only large $\omega$ values are physiologically relevant ($\omega \gg 1)$. Finally, the parameter $\mathrm{K}$ is the ratio of the substrate stiffness ${\kappa }_{\mathrm{s}}$ over the maximum effective clutch stiffness ${\mathrm{n}}_{\mathrm{c}}{\kappa }_{\mathrm{c}}$. With these scalings, the conservation equation (1) and dimensionless clutch strain rate ${\mathrm{v}}_{\mathrm{e}}^{\ast }$ read

$$\frac{\partial {\mathrm{P}}_{\mathrm{b}}^{\ast }}{\partial {\mathrm{t}}^{\ast }}=\tau \left(1-{\mathrm{n}}_{\mathrm{b}}^{\ast }\right){\delta }^{\ast }\left({\mathrm{x}}_{\mathrm{c}}^{\ast }\right)-{\mathrm{e}}^{\mathrm{F}\left|{\mathrm{x}}_{\mathrm{c}}^{\ast }\right|}{\mathrm{P}}_{\mathrm{b}}^{\ast }-{\mathrm{v}}_{\mathrm{e}}^{\ast }\frac{\partial {\mathrm{P}}_{\mathrm{b}}^{\ast }}{\partial {\mathrm{x}}_{\mathrm{c}}^{\ast }}\text{,}$$ (3)

$${\mathrm{v}}_{\mathrm{e}}^{\ast }=\frac{1}{\mathrm{K}+{\mathrm{n}}_{\mathrm{b}}^{\ast }}\left[\frac{\omega \mathrm{K}}{\mathrm{F}}\left(1-{\mathcal{\ell }}_{\mathrm{b}}^{\ast }\right)+\underset{-\infty }{\overset{\infty }{\int }}{\mathrm{x}}_{\mathrm{c}}^{\ast }{\mathrm{e}}^{\mathrm{F}\left|{\mathrm{x}}_{\mathrm{c}}^{\ast }\right|}{\mathrm{P}}_{\mathrm{b}}^{\ast }\mathrm{d}{\mathrm{x}}_{\mathrm{c}}^{\ast }\right]$$ (4)

where the first moment of the probability density over clutch extensions takes the form ${\mathcal{\ell }}_{\mathrm{b}}^{\ast }=\underset{-\infty }{\overset{\infty }{\int }}{\mathrm{x}}_{\mathrm{c}}^{\ast }{\mathrm{P}}_{\mathrm{b}}^{\ast }\mathrm{d}{\mathrm{x}}_{\mathrm{c}}^{\ast }$. Notice that the traction force exerted on the compliant substrate is ${\mathrm{T}}^{\ast }=\mathrm{F}{\mathcal{\ell }}_{\mathrm{b}}^{\ast }\text{.}$ Note, throughout the manuscript we use an overline symbol acting on a variable to denote the long time-averaged value of the variable.

Table 2.

Dimensionless Model Parameters

Symbol	Definition	Description	Estimated Valuea
$\mathrm{F}$	${\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}/{\mathrm{n}}_{\mathrm{c}}{\mathrm{F}}_{\mathrm{b}}$	myosin activity parameter	$1.38$
$\tau$	${\mathrm{k}}_{\mathrm{o}\mathrm{n}}/{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}$	clutch kinetic parameter	$1$
$\omega$	${\mathrm{v}}_{\mathrm{u}}{\kappa }_{\mathrm{c}}/{\mathrm{F}}_{\mathrm{b}}{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}$	dimensionless myosin unloaded velocity	$140$
$\mathrm{K}$	${\kappa }_{\mathrm{s}}/{\mathrm{n}}_{\mathrm{c}}{\kappa }_{\mathrm{c}}$	dimensionless substrate stiffness	$\sim \left[{10}^{-5}-{10}^{-1}\right]$
$\theta$	$\theta$	clutch reinforcement strength	adjusted
$\Delta$	${\mathrm{F}}_{\mathrm{t}\mathrm{h}}/{\mathrm{F}}_{\mathrm{b}}$	dimensionless clutch reinforcement threshold force	$2.9$
${\mathrm{K}}_{\mathrm{off}}$	${\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}^{\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}/{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}$	dimensionless catch bond dissociation kinetic rate constant	adjusted
${\chi }_{\mathbf{b}}$	${\mathrm{F}}_{\mathrm{b}}^{\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}/{\mathrm{F}}_{\mathrm{b}}$	dimensionless clutch catch bond rupture force	adjusted
${\beta }_{\mathbf{c}}$	${{\kappa }_{\mathrm{c}}\propto \beta }_{\mathrm{c}}$	clutch stiffness parameter	adjusted
${\mathbf{\omega }}^{\prime }$	$\omega /{\beta }_{\mathrm{c}}$	–	adjusted
${\mathrm{K}}^{\text{'}}$	$\mathrm{K}{\beta }_{\mathrm{c}}$	–	adjusted

^aParameter values are estimated in the supporting material.

Results

Production of traction forces in individual cellular protrusions exhibit three different regimes

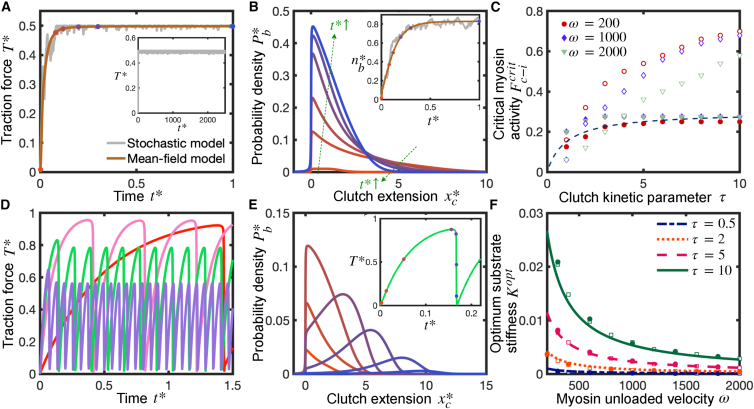
Cellular protrusions can generate traction forces and operate over three distinct regimes: a motor-dominated regime, a motor-clutch balanced regime, and a clutch-dominated regime. Previous analysis has focused only on the motor-clutch balanced regime (17). We have derived analytical expressions for the three key timescales that control traction force production: the characteristic time for available clutches to bind (i.e., mechanically couple actin filaments to the extracellular substrate) ${\mathrm{t}}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}$, the characteristic time for clutches to rupture due to force ${\mathrm{t}}_{\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}}$, and the characteristic time for the substrate to reach its maximal deformation ${\mathrm{t}}_{\mathrm{s}}^{\max }$. These three timescales depend on the different model parameters, dictate the cellular regime at which the protrusion operates, and are essential to understand traction force production and optimality conditions. We explored the high-dimensional parameter space by solving the governing equations of the mean-field model (Eqs. 3 and 4) using a finite-difference algorithm (see supporting material) and compared the numerical mean-field solution with the stochastic motor-clutch model version (2). We find a very good agreement between the mean-field solution and its stochastic counterpart for all the model parameters tested (Figs. 1, 2, and 3). We explore the three different cellular regimes in detail below.

Figure 2.

Clutch-dominated protrusions produce maximum possible traction forces and do not exhibit clutch failure avalanches, whereas cellular protrusions that operate in the intermediate regime features load-and-fail dynamics and produce maximum traction forces at an intermediate substrate stiffness. Temporal evolution of the dimensionless traction force (A), probability density function (B), and fraction of bound clutches (B, inset) in a clutch-dominated protrusion. The dimensionless probability density function is obtained by the mean-field model and sampled at the time points marked by symbols in (A and B inset). Color schemes of symbols in (A and B inset) and lines in (B) correspond to the same time points. In the clutch-dominated regime, long-time traction force and fraction of bound clutches approach the total myosin stall force $\mathrm{T}={\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}$ and unloaded equilibrium fraction of bound clutches ${\mathrm{n}}_{\mathrm{b}}={\mathrm{n}}_{\mathrm{c}}{\mathrm{k}}_{\mathrm{o}\mathrm{n}}/\left({\mathrm{k}}_{\mathrm{o}\mathrm{n}}+{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}\right)$, respectively. Brown, mean-field model solution; gray, a single-trajectory of the stochastic model. (A, inset) Long-time stochastic single-trajectory. Parameter values: $\mathrm{F}=0.5,\tau =10,\omega =500,\mathrm{K}=1$. (C) Critical motor activity parameter ${\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$, which sets the border between the clutch-dominated regime and the intermediate regime, as a function of the clutch kinetic parameter $\tau$, for three values of the dimensionless myosin load-free velocity $\omega$. Protrusions with $\mathrm{F}<{\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ belong to the clutch-dominated regime and produce maximum available traction forces. Solid and open symbols correspond to the critical activity parameter in soft and rigid substrates, respectively. The dashed line is our analytical solution for soft substrates obtained via scaling analysis (Eq. 5). (D) Time evolution of dimensionless traction force for four different substrate stiffnesses: $\mathrm{K}=0.001$ (red), $\mathrm{K}=0.005$ (pink), $\mathrm{K}=0.008$ (green), and $\mathrm{K}=0.01$ (purple). Parameter values: $\mathrm{F}=1$, $\tau =10,\omega =2000$. (E) Temporal evolution of the dimensionless probability density function ${\mathrm{P}}_{\mathrm{b}}^{\ast }$ and dimensionless traction force (inset). Symbols and color scheme in inset correspond to the time points where ${\mathrm{P}}_{\mathrm{b}}^{\ast }$ is sampled. Parameter values: $\mathrm{F}=1$, $\tau =10,\omega =2000,\mathrm{K}=0.005$. (F) Dimensionless optimum substrate stiffness ${\mathrm{K}}^{\mathrm{o}\mathrm{p}\mathrm{t}}={\kappa }_{\mathrm{s}}^{\mathrm{o}\mathrm{p}\mathrm{t}}/{\mathrm{n}}_{\mathrm{c}}{\kappa }_{\mathrm{c}}$ as a function of the dimensionless myosin load-free velocity, $\omega$, for four different values of the clutch kinetic parameter $\tau$. The dimensionless clutch binding timescales as ${\mathrm{t}}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}^{\ast }\sim 1/\left(\tau +1\right)$, whereas the dimensionless clutch rupture timescales as ${\mathrm{t}}_{\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}}^{\ast }\sim \left({\mathrm{C}}_2/\mathrm{F}+1/\mathrm{K}\omega \right)/\left(1+1/\tau \right)$. Solid lines correspond to our derived analytical solution (Eq. 6), open symbols correspond to the numerical solution of the mean-field model (Eqs. 3 and 4), and closed symbols correspond to the numerical solution of the stochastic model. Parameter value: $\mathrm{F}=2$. To see this figure in color, go online.

Figure 3.

Traction force transmission is maximum at intermediate values of clutch stiffness. (A and B) Dimensionless time-averaged traction force ${\overline{\mathrm{T}}}^{\ast }$ as a function of the clutch stiffness parameter ${\beta }_{\mathrm{c}}$ (notice that ${\kappa }_{\mathrm{c}}\propto {\beta }_{\mathrm{c}}$) for different values of the clutch kinetic parameter $\tau$ and for two values of the substrate stiffness parameter $K^{\prime }$ ($\mathrm{K}={\mathrm{K}}^{\prime }/{\beta }_{\mathrm{c}})$: (A) ${\mathrm{K}}^{\prime }=0.01$ and (B) ${\mathrm{K}}^{\prime }=1$. Cellular traction forces on rigid substrates are very sensitive to clutch stiffness. The optimum clutch stiffness (optimum ${\beta }_{\mathrm{c}}$) increases with the value of the clutch kinetic parameter. Parameter values: $\mathrm{F}=1$, ${\omega }^{\prime }=200$ ($\omega ={\omega }^{\prime }{\beta }_{\mathrm{c}})$. (C) Time evolution of traction force for four different values of the clutch stiffness parameter. Parameter values: $\mathrm{F}=1$, ${\omega }^{\prime }=200,{\mathrm{K}}^{\prime }=0.01,\tau =1$. (D) Dimensionless time-averaged traction force as a function of the effective clutch stiffness parameter for three different values of the myosin activity parameter $\mathrm{F}$. Parameter values: ${\omega }^{\prime }=200$, ${\mathrm{K}}^{\prime }=1$, $\tau =10$. Solid lines correspond to the numerical solution of the mean-field model (Eqs. 3 and 4), and symbols correspond to the numerical solution of the stochastic motor-clutch model. To see this figure in color, go online.

Clutch-dominated stalled regime

A distinct feature of the clutch-dominated regime, previously identified as the stalled regime (10,17), is that clutches dominate over motors. In this regime, the protrusion operates at its maximum efficiency by producing the maximum possible traction force, i.e., the total myosin stall force $\overline{\mathrm{T}}={\mathrm{T}}_{\max }={\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}$ (${\overline{\mathrm{T}}}^{\ast }=\mathrm{F}$ in dimensionless form), throughout a wide range of substrate stiffnesses (see Fig. 1 B, $\mathrm{F}=0.25$ and $\mathrm{F}=0.5$); hence, no single optimum substrate stiffness for maximum traction force exists. The clutch-dominated regime is therefore characterized by stiffness-independent traction forces as well as stiffness-independent clutch binding/unbinding kinetics, as shown in Fig. 2 by both the mean-field and stochastic motor-clutch model solutions of the time-averaged traction force (Fig. 2 A) and time-averaged fraction of bound clutches (Fig. 2 B, inset). The mean-field model captures the time-averaged traction force dynamics. In an unloaded protrusion, actin filaments flow rearward at the myosin load-free velocity. The first clutches that connect the fast-moving actin filaments with the deformable substrate undergo large extensions, since there is not enough elastic resistance against myosin pulling forces. This is shown in Fig. 2 B by the fat tail of the probability density function at short times. As time goes by, more clutches mechanically couple the actin cytoskeleton with the compliant substrate (Fig. 2 B, inset), which is manifested by the rise of the area under the probability density curve in Fig. 2 B, and elastic energy builds up in both substrate and bound clutches, slowing down actin retrograde flows. Low actin filament velocities lead clutches to dissociate stochastically before they can reach very large elongations, as demonstrated in Fig. 2 B by a reduction in the skewness of the probability distribution function at longer times (see green arrows in Fig. 2 B).

During loading, clutch binding dominates clutch unbinding in strong-clutch protrusions, there are enough bound clutches resisting myosin pulling forces at any instant in time, and the clutch complex never undergoes load-and-fail dynamics, as confirmed by Fig. 2 A and B. Clutch-dominated protrusions strain the substrate to its maximum deformation before clutch bonds break due to force (${\mathrm{t}}_{\mathrm{s}}^{\max }<{\mathrm{t}}_{\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}}$); that is, F-actin retrograde flows vanish and the protrusion stalls. This inequality is satisfied (see derivation below) for protrusions with a motor activity parameter $\mathrm{F}$ lower than a threshold ($\mathrm{F}<{\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$). Here, ${\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ is the critical motor activity parameter that sets the border between the clutch-dominated regime ($\mathrm{F}<{\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$) and the motor-clutch balanced regime ($\mathrm{F}>{\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$). Numerical values for ${\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ are displayed in Fig. 2 C as a function of $\tau$ and $\omega$ for both soft and rigid substrates, and an analytical expression for the critical activity parameter ${\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ has been estimated for soft substrates (see derivation below). The critical parameter ${\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ monotonically increases as the parameter $\tau$ increases, as high-clutch-binding-rate protrusions require higher myosin forces to cause a clutch failure avalanche, an event that takes places when clutch bonds break in a runaway process giving rise to a failure of the entire clutch complex.

The dependence of ${\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ on the dimensionless myosin load-free velocity $\omega$ is less straightforward. At the beginning of the loading cycle, stronger retrograde flows exist for larger values of $\omega$. On very soft substrates, loading is slow, the initial strong retrograde flows largely deform the substrate, and clutches dissociate stochastically at long times. Therefore, clutch dynamics are not affected by the strength of actin filament retrograde flows and, accordingly, ${\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ on soft substrates is nearly independent of $\omega$, as shown in Fig. 2 C. On rigid substrates, on the other hand, clutches build up elastic energy very fast; thus, higher values of $\omega$ enhance clutch deformations at the onset of the loading cycle favoring load-and-fail dynamics over stall conditions. As a result, lower myosin forces are required for load-and-fail dynamics to occur on high-$\omega$ protrusions; that is, ${\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}$ decreases with increasing $\omega$ on rigid substrates, as shown in Fig. 2 C.

Motor-clutch balanced regime

As its name suggests, the intermediate regime is a transitional regime between the free-flowing motor-dominated regime and the clutch-dominated stalled regime, where motors and clutches balance each other. The intermediate regime is characterized by load-and-fail dynamics (2) with stochastic transitions of slow and fast actin flows, also called stick-slip dynamics (34,36,53,54), and by the existence of a motor-sensitive optimum substrate stiffness for maximum traction force, as depicted in Fig. 1 B for $\mathrm{F}\sim 1$. Cycles of loading and failure are illustrated in Figs. 2 D and S2 for different substrate stiffnesses. The mean frequency between two consecutive clutch cascading failure events decreases with substrate compliance, as shown in Fig. 2 D, and in agreement with Chan and Odde (2). At the beginning of loading, the elastic energy built up in the system is undertaken by the substrate/clutches on soft/stiff environments, respectively. Therefore, clutch lifetimes depend inversely on substrate rigidity, and higher frequency of clutch failures is observed on more rigid environments, as shown in Fig. S1 B. In the beginning of the loading cycle, the number of bound clutches is nearly independent of substrate stiffness, being mainly governed by clutch binding kinetics, as Fig. S2 A shows, where the four curves with different stiffnesses practically lie on top of each other at short times at the beginning of the first loading cycle. During this early phase, protrusions produce larger traction forces on more rigid substrates (Fig. 2 D). Later in the loading cycle, some clutches cannot sustain load any longer and eventually their clutch bonds break. The net clutch unbinding rate becomes greater than the clutch binding rate and the number of bound clutches begins to drop (Fig. S2 A), leading to an increase in clutch elongation rate (Fig. S2 B) and a reduction in substrate deformation rate (Fig. 2 D). As clutches gradually dissociate, the total load is redistributed among the remaining bound clutches, with an increase of load per clutch (Fig. 2 E). Eventually, the load cannot be sustained by the remaining clutches, and an instability occurs that eventuates in the rupture of all clutch bonds, a sudden fall in traction force (2), and the beginning of a new loading cycle. Notice that the duration of the clutch unbinding phase $\left(\mathrm{d}{\mathrm{n}}_{\mathrm{b}}/\mathrm{d}\mathrm{t}<0\right)$ is much longer than that of the clutch binding phase $\left(\mathrm{d}{\mathrm{n}}_{\mathrm{b}}/\mathrm{d}\mathrm{t}>0\right)$, especially on very soft substrates.

The boundary between the clutch-dominated stalled regime and the balanced regime is set by the condition ${\mathrm{t}}_{\mathrm{s}}^{\max }\sim {\mathrm{t}}_{\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}}$; that is, the time required to reach stall conditions matches the time needed for clutch bonds to break due to force. We perform scaling analysis (see supporting material) and find that, on soft substrates, the protrusion operates in the clutch-dominated regime when

$$\mathrm{F}<{\mathrm{F}}_{\mathrm{c}-\mathrm{i}}^{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}}={\mathrm{C}}_1\frac{\tau }{\tau +1}\text{,}$$ (5)

where ${\mathrm{C}}_1=0.4$ is a constant that we estimate by fitting Eq. 5 with our numerical results. Fig. 2 C shows a very good agreement between our theoretical formula and numerical results.

Motor-dominated regime

Motor-dominated protrusions are characterized by a myosin-independent optimum stiffness, as shown in Fig. 1 B. Any changes in motor activity do not appreciably affect the dynamics of the protrusion (i.e., traction forces, clutch binding/unbinding kinetics, etc.). This is shown in Figs. 1 B and S1, where traction force, fraction of engaged clutches, and cycling time curves for $\mathrm{F}=10$, $\mathrm{F}=20$, and $\mathrm{F}=100$ lie on top of each other. Before any clutch links the actin cytoskeleton with the substrate, actin filaments flow rearward at the myosin load-free velocity. Once an individual clutch engages, it provides elastic resistance slowing down actin flows. In the high myosin limit, clutches are overpowered by motors and a further increase in motors does not alter actin flow speeds. Both clutch elongation and substrate elongation rates are myosin independent (see supporting material), which implies that motor-dominated protrusion dynamics are myosin insensitive. Motor-dominated protrusions also undergo load-and-fail dynamics and are still capable of sensing the rigidity of the environment. The previously identified free-flowing cellular state (10,17) is a particular case of the motor-dominated regime for motor-dominated protrusions on sufficiently rigid substrates, where traction forces build up at a fast rate, clutches reach a high tensional state very rapidly, and a state of frictional slippage takes place where clutches continually dissociate by force before additional clutches can associate and share the load with the already bound clutches, limiting traction force production. We show that protrusions belong to the strong-motor regime when the condition $\mathrm{F}\gg 0.05\tau$ is satisfied (see supporting material).

Optimum substrate stiffness for maximum traction force is reached when the clutch binding time equals the clutch rupture time

In this section, we apply scaling analysis to the mean-field model with the purpose of deriving an analytical expression for the optimum substrate stiffness (i.e., the substrate stiffness that maximizes traction forces). Previously, we found that optimum conditions for maximum traction force are reached when the time needed for available clutches to bind equals the cycle time (10,17). Here, we identify the cycle time as the characteristic time for clutches to rupture due to load; thus, we hypothesize that optimum conditions are reached when ${\mathrm{t}}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}\sim {\mathrm{t}}_{\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}}$. We apply scaling analysis to estimate ${\mathrm{t}}_{\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{d}}$ and ${\mathrm{t}}_{\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}}$ (see supporting material); we get:

$${\kappa }_{\mathrm{s},\mathrm{i}}^{\mathrm{o}\mathrm{p}\mathrm{t}}={\mathrm{C}}_2\frac{{\mathrm{n}}_{\mathrm{c}}{\mathrm{F}}_{\mathrm{b}}{\mathrm{k}}_{\mathrm{o}\mathrm{n}}}{{\mathrm{v}}_{\mathrm{u}}}\frac{1}{1-{\mathrm{C}}_3\frac{{\mathrm{k}}_{\mathrm{o}\mathrm{n}}}{{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}}\frac{{\mathrm{n}}_{\mathrm{c}}{\mathrm{F}}_{\mathrm{b}}}{{\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}}}\text{.}$$ (6)

where ${\mathrm{C}}_2=0.4,{\mathrm{C}}_3=0.05$. Figs. 2 F and S3 show that our theoretical expression is in very good agreement with our numerical results for all the motor-clutch dimensionless parameters. The optimum substrate stiffness in a protrusion that belongs to the intermediate regime, ${\kappa }_{\mathrm{s},\mathrm{i}}^{\mathrm{o}\mathrm{p}\mathrm{t}}$, is myosin sensitive and independent of the effective clutch stiffness ${\kappa }_{\mathrm{c}}$, as previously reported in other studies (10,17). Here, we explain this apparent counterintuitive result by realizing that both the characteristic clutch rupture length ${\mathcal{l}}_{\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}}$ and the characteristic clutch extension rate scale inversely to clutch stiffness. This implies that clutch rupture time is independent of clutch stiffness. Since neither the clutch binding rate nor the clutch rupture time depend on clutch stiffness, the substrate stiffness that maximizes traction forces does not depend on clutch stiffness, as Eq. 6 shows. We expect this result to hold for all physiologically relevant parameter values. In the non-physical situation where clutches dissociate stochastically instead of by force (small $\omega$), the characteristic clutch rupture length would not be ${\mathrm{F}}_{\mathrm{b}}/{\kappa }_{\mathrm{c}}$ anymore, and optimum substrate stiffness would a priori depend on clutch stiffness. The optimum stiffness in motor-dominated protrusions reduces to ${\kappa }_{\mathrm{s},\mathrm{m}}^{\mathrm{o}\mathrm{p}\mathrm{t}}={\mathrm{C}}_2{\mathrm{n}}_{\mathrm{c}}{\mathrm{F}}_{\mathrm{b}}{\mathrm{k}}_{\mathrm{o}\mathrm{n}}/{\mathrm{v}}_{\mathrm{u}}$, where we have taken the limit ${\mathrm{C}}_3{\mathrm{k}}_{\mathrm{o}\mathrm{n}}{\mathrm{n}}_{\mathrm{c}}{\mathrm{F}}_{\mathrm{b}}/{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}{\mathrm{n}}_{\mathrm{m}}{\mathrm{F}}_{\mathrm{m}}\to 0$. We also find very good agreement between our theoretical prediction, the numerical solution of the mean-field model, and the solution of the dimensionless version of the stochastic motor-clutch model (2) for motor-dominated protrusions, as shown in Fig. S3, right. Our theoretical solution indicates that, in the high-motor regime, the optimum substrate stiffness is myosin insensitive, as depicted in Fig. 1 B ($\mathrm{F}=10$, $\mathrm{F}=20$). Overall, our results indicate that substrate stiffness optimality in motor-dominated protrusions can be shifted by tuning clutch activity but not motor activity, whereas optimality in motor-clutch balanced protrusions is sensitive to both myosin activity and clutches.

Traction force production is maximal at intermediate clutch stiffnesses

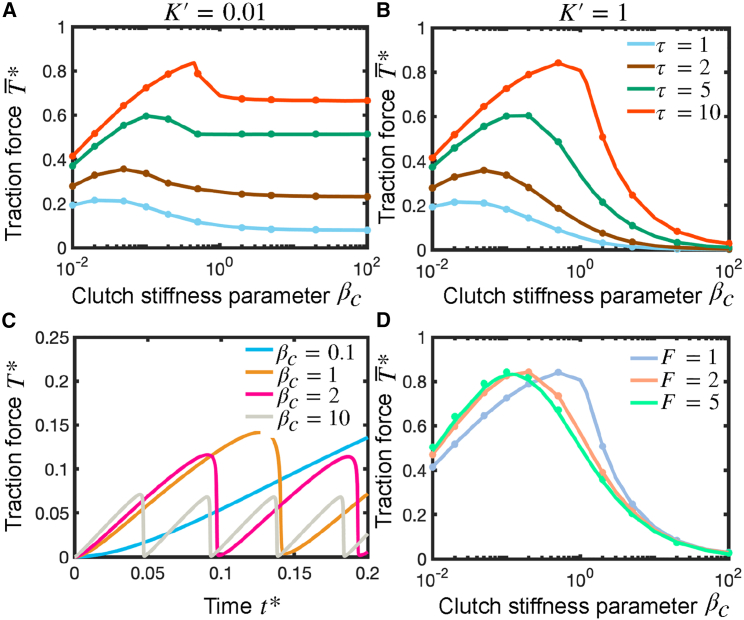
Since clutch stiffness is potentially a key mechanical property that the cell can control, and that can be engineered, e.g., via molecular tension sensors, we were interested in understanding the dependence of force transmission on clutch stiffness. In the previous section we showed that the optimum substrate stiffness ${\kappa }_{\mathrm{s}}^{\mathrm{o}\mathrm{p}\mathrm{t}}$ is insensitive to changes in clutch stiffness, ${\kappa }_{\mathrm{c}}$. Force transmission, however, could a priori depend on clutch stiffness when the substrate stiffness differs from the optimum. To investigate this effect, we notice that among the four dimensionless parameters introduced, only two depend on ${\kappa }_{\mathrm{c}}$: the parameter $\omega$, which is proportional to ${\kappa }_{\mathrm{c}}$, and the dimensionless substrate stiffness $\mathrm{K}$, which depends inversely on ${\kappa }_{\mathrm{c}}$. Accordingly, we introduce a new parameter, the clutch stiffness parameter ${\beta }_{\mathrm{c}}$, such that $\omega ={\omega }^{\prime }{\beta }_{\mathrm{c}}$ and $\mathrm{K}={\mathrm{K}}^{\prime }/{\beta }_{\mathrm{c}}$, where ${\omega }^{\prime }$ and ${\mathrm{K}}^{\prime }$ are, respectively, the values of the parameter $\omega$ and the dimensionless substrate stiffness $K$ when ${\beta }_{\mathrm{c}}=1$. Consequently, by definition, increasing the value of the clutch stiffness parameter ${\beta }_{\mathrm{c}}$ is equivalent to proportionally increasing the effective clutch stiffness ${\kappa }_{\mathrm{c}}$.

We investigated the dependence of the time-averaged force transmission on clutch stiffness by numerically solving our mean-field model equations. Our numerical results identified the existence of an optimum clutch stiffness for maximum traction force production (Fig. 3 A and B). Near-perfect agreement is found between the mean-field model solutions and the stochastic solutions. In the stiff-clutch limit, clutches provide enhanced elastic resistance to deformations, decreasing their strain rates. Their characteristic clutch rupture length, however, is inversely proportional to their stiffness (assuming that the clutch rupture force is constant). In the stiff-clutch limit, clutch lifetimes are low, especially on non-compliant substrates, and this is reflected in a low time-averaged number of bound clutches, as shown in Fig. S4. Even though the traction force buildup in stiff-clutch protrusions is extremely fast at the beginning of loading, the strong dependence of clutch lifetimes on their stiffness becomes the dominant effect and the resulting traction forces transmitted to the substrate are also low. In the soft-clutch limit, clutch extension rates are higher, but clutches disengage before high traction forces are produced, since the soft-clutch limit is associated with a slow buildup of traction forces, as shown in Fig. 3 C. Consequently, there exists an optimum clutch stiffness that maximizes force transmission. Under the assumption that ${\mathrm{v}}_{\mathrm{u}}=120\mathrm{n}\mathrm{m}·{\mathrm{s}}^{-1}$, ${\mathrm{F}}_{\mathrm{b}}=2\mathrm{p}\mathrm{N}$, ${\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}=1{\mathrm{s}}^{-1}$, and $\tau =10$ (${\mathrm{k}}_{\mathrm{o}\mathrm{n}}=10{\mathrm{s}}^{-1}$), the mean-field model predicts that the optimum clutch stiffness is ${\kappa }_{\mathrm{c}}^{\mathrm{o}\mathrm{p}\mathrm{t}}\approx 3.3\mathrm{p}\mathrm{N}·{\mathrm{n}\mathrm{m}}^{-1}$, a clutch stiffness that is within the range of physiological clutch stiffness values.

Interestingly, the sensitivity of force transmission on clutch stiffness is significantly higher for protrusions on rigid substrates than for protrusions on soft substrates, as shown in Fig. 3 A and B. This can be explained by noticing that, on stiff substrates, the load-and-fail dynamics are largely governed by the mechanical properties of clutches. Consequently, the sensitivity of traction forces to changes in clutch stiffness is expected to be higher on this type of substrate. The optimum clutch stiffness increases for higher values of the clutch kinetic parameter $\tau$, as shown by the shift in the optimum toward the right in Fig. 3 A and B and decreases with increasing values of the myosin activity parameter $F$, as shown in Fig. 3 D. Faster clutch recruitment or lower myosin activity strengthens clutches over motors, and stiffer clutches accelerate the buildup of traction forces, increasing the overall force transmission. This is consistent with Eqs. S51 and S52, where we show that the production of traction forces on rigid substrates in the limit of low myosin activity increases as the clutch stiffness increases. Direct comparison of Fig. 3 A and B indicates that the optimum clutch stiffness is barely sensitive to substrate compliance. Overall, these results show that there is an optimal clutch stiffness at which traction force is maximal.

Traction forces produced by protrusions on rigid substrates are maximal at intermediate myosin levels and unloaded myosin velocities

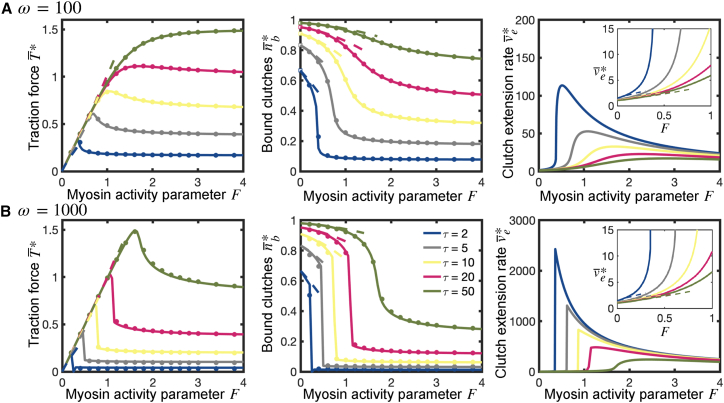
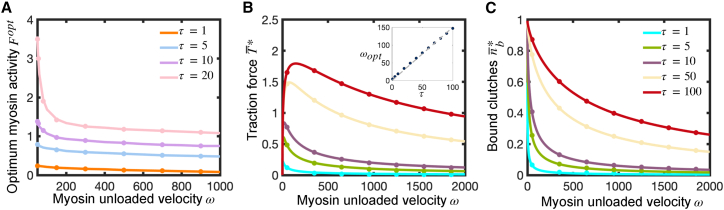
Although traditional traction force microscopy requires measurement of deformations in a compliant microenvironment (55,56,57,58), emerging molecular tension sensor technology is enabling measurement of traction forces on rigid substrates (59,60,61), significantly extending the range of potential traction force measurements to include stiff materials such as bone and medical devices. To characterize this rigid substrate regime in terms of optimal clutch stiffness, we investigated force transmission on rigid substrates and determined the time-averaged traction force $\overline{\mathrm{T}}$, mean number of bound clutches ${\overline{\mathrm{n}}}_{\mathrm{b}}$ and mean clutch strain rate ${\overline{\mathrm{v}}}_{\mathrm{e}}$ (see supporting material for more details). We find very good agreement between our mean-field semi-analytical solutions and the solution from the stochastic model, as shown in Fig. 4. We find that traction forces on rigid environments exhibit a biphasic dependence on motor activity (Fig. 4, left), where the maximum time-averaged traction force is reached at an intermediate value of the myosin activity parameter ${\mathrm{F}}^{\mathrm{o}\mathrm{p}\mathrm{t}}$, which monotonically decreases with $\tau$ and $\omega$ (Fig. 5 A). The time-averaged clutch extension rate also exhibits a maximum at a value of $\mathrm{F}$ that is greater than ${\mathrm{F}}^{\mathrm{o}\mathrm{p}\mathrm{t}}$ (Fig. 4, right).

Figure 4.

Force transmission on rigid substrates ($\mathrm{K}\to \infty$) exhibits a biphasic dependence on motor activity. Time-averaged dimensionless traction force, fraction of bound clutches, and clutch strain rate as a function of the myosin activity parameter $\mathrm{F}$ for five different values of the clutch kinetic parameter $\tau$, and two different values of the parameter $\omega$ ((A) First row, $\omega =100$; (B) second row, $\omega =1000$). Traction force and fraction of bound clutches monotonically increase with $\tau$, whereas clutch strain rate decreases with $\tau$. Traction force exhibits a maximum at an intermediate value of the myosin activity parameter ${\mathrm{F}}^{\mathrm{o}\mathrm{p}\mathrm{t}}$ (see Fig. 5A for further analysis). Clutch extension rate also exhibits a maximum at an intermediate value of the myosin activity parameter $\mathrm{F}>{\mathrm{F}}^{\mathrm{o}\mathrm{p}\mathrm{t}}$. Curves reach $\mathrm{F}$-independent asymptotic values at high myosin activity (large $\mathrm{F}$) (see Fig. 5B and C for additional details). Solid lines correspond to the numerical solution of the mean-field model (Eqs. S31–S36) and symbols correspond to the numerical solution of the stochastic model. Dashed lines correspond to our low-$\mathrm{F}$ asymptotic solutions (Eqs. S51, S46, and S49). To see this figure in color, go online.

Figure 5.

Traction force produced by a strong-motor protrusion on rigid substrates reaches a maximum at an intermediate value of the myosin load-free velocity parameter $\omega$. (A) Optimum myosin activity parameter for maximum traction force on rigid substrates as a function of $\omega$ for four different values of the clutch kinetic parameter $\tau$. The optimum activity ${\mathrm{F}}^{\mathrm{o}\mathrm{p}\mathrm{t}}$ monotonically decreases with $\tau$ and $\omega$. (B and C) Dimensionless time-averaged traction force (B) and average fraction of bound clutches (C) for a strong-motor protrusion ($\mathrm{F}\to \infty$) on rigid substrates ($\mathrm{K}\to \infty$), as a function of $\omega$ for five different values of $\tau$. Force transmission shows a biphasic dependence on the parameter $\omega$, with an optimum ${\omega }^{\mathrm{o}\mathrm{p}\mathrm{t}}$ that increases linearly with $\tau$ (see inset in (B)). Number of bound clutches increases monotonically with $\tau$ and $\omega$. Solid lines correspond to the analytical solutions of the mean-field model (Eqs. S55 and S57), and symbols are the solutions of the stochastic model. Near-perfect agreement is found between analytical and stochastic solutions. To see this figure in color, go online.

We additionally use perturbation theory to derive analytical expressions for the time-averaged clutch elongation rate, number of bound clutches, and traction force by low-motor ($\mathrm{F}\to 0$) and high-motor ($\mathrm{F}\to \infty$) activity protrusions (see supporting material for additional details). The derived analytical expressions for low-motor protrusions and high-motor protrusions agree very well with our numerical solutions, as shown in Figs. 4 and 5, respectively. Interestingly, the ${\overline{\mathrm{T}}}^{\ast }\left(\tau ,\omega \right)$ high-motor curves reach a maximum value at an optimum value ${\omega }^{\mathrm{o}\mathrm{p}\mathrm{t}}$, as shown in Fig. 5 B. This optimum dimensionless load-free velocity exhibits a nearly linear dependence with $\tau$, as shown in the inset of Fig. 5 B. In dimensional form, it implies that an intermediate value of ${\kappa }_{\mathrm{c}}{\mathrm{v}}_{\mathrm{u}}/{\mathrm{F}}_{\mathrm{b}}{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}$ exists that maximizes traction forces, and it scales linearly with the ratio ${\mathrm{k}}_{\mathrm{o}\mathrm{n}}/{\mathrm{k}}_{\mathrm{o}\mathrm{f}\mathrm{f}}$. Thus, our model can help guide molecular tension sensor design and prediction of traction forces on rigid surfaces such as bone and implantable medical devices.

Load-dependent clutch reinforcement increases the optimum substrate stiffness and optimum clutch stiffness

So far, we have assumed that clutches behave as slip bonds. However, since many cell types exhibit adhesion reinforcement, we added load-dependent clutch adhesion reinforcement on force transmission into our analysis (14,28,51,62,63,64). We assumed that the effective clutch association rate linearly depends on the actual fraction of clutches that are bound and whose load exceeds the clutch reinforcement threshold force ${\mathrm{F}}_{\mathrm{t}\mathrm{h}}$ (51). The conservation equation for the probability density thus reads:

$$\frac{\partial {\mathrm{P}}_{\mathrm{b}}^{\ast }}{\partial {\mathrm{t}}^{\ast }}=\tau \left(1+\theta {\int }_{\Delta /\mathrm{F}}^{\infty }{\mathrm{P}}_{\mathrm{b}}^{\ast }{\mathrm{d}\mathrm{x}}_{\mathrm{c}}^{\ast }\right)\left(1-{\mathrm{n}}_{\mathrm{b}}^{\ast }\right){\delta }^{\ast }\left({\mathrm{x}}_{\mathrm{c}}^{\ast }\right)-{\mathrm{e}}^{\mathrm{F}\left|{\mathrm{x}}_{\mathrm{c}}^{\ast }\right|}{\mathrm{P}}_{\mathrm{b}}^{\ast }-{\mathrm{v}}_{\mathrm{e}}^{\ast }\frac{\partial {\mathrm{P}}_{\mathrm{b}}^{\ast }}{\partial {\mathrm{x}}_{\mathrm{c}}^{\ast }}\text{,}$$ (7)

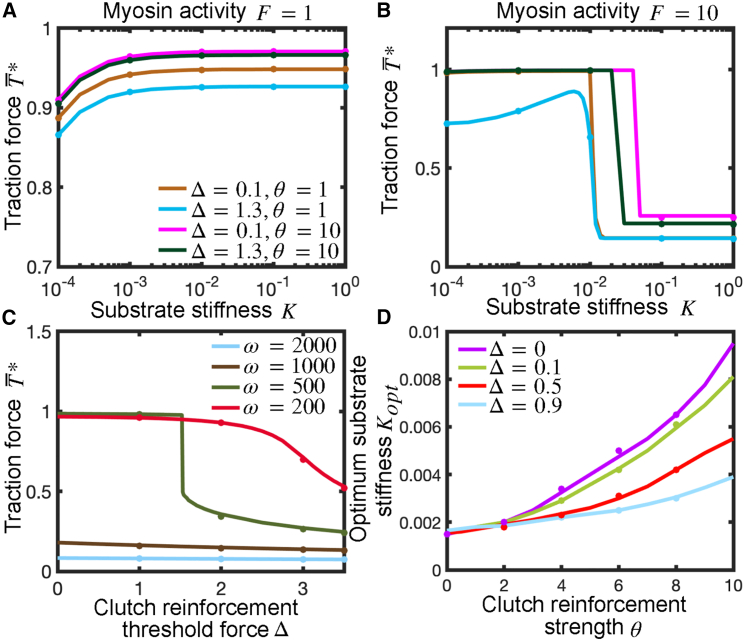
where we have introduced a clutch reinforcement strength parameter $\theta$ and dimensionless clutch reinforcement threshold force $\Delta ={\mathrm{F}}_{\mathrm{t}\mathrm{h}}/{\mathrm{F}}_{\mathrm{b}}$, so that Δ>>1 favors bond rupture under load and Δ<<1 favors reinforcement over rupture. We numerically solved Eq. 7 and found that, in protrusions with a small unloaded myosin velocity parameter ω and low number of myosin motors over clutches, i.e., low $\mathrm{F}$, clutch reinforcement prevents frictional slippage on rigid substrates and force transmission increases monotonically with substrate stiffness, as shown in Fig. 6 A. By contrast, motor-dominated protrusions, i.e., high $\mathrm{F}$, are associated with large clutch force loading rates due to large myosin pulling forces and require an anomalously high clutch reinforcement parameter to strengthen clutches, prevent frictional slippage, and allow the production of substantial traction forces on rigid substrates, as manifested by the low traction force transmitted on rigid substrates (Figs. 6 B and S6 D). For larger values of the unloaded myosin velocity parameter, ω (i.e., ω = 2000 instead of 200), the traction vs. substrate stiffness curves are monotonically increasing for sufficiently high values of the clutch reinforcement strength parameter $\theta$, whereas they display a biphasic behavior for low values of $\theta$, as shown in Fig. S5 A. Force transmission on rigid substrates monotonically decreases with an increase in the characteristic clutch reinforcement force $\Delta$, and it can be strongly influenced by the value of $\Delta$, particularly for sufficiently high $\theta$ values and low enough $\omega$ values, as shown in Figs. 6 C and S5 B. Clutch reinforcement shifts the optimum substrate stiffness for maximal force production to stiffer substrates, as shown in Figs. 6 D and S5 D, and this optimum stiffness shift is significant only for low values of the unloaded myosin velocity parameter $\omega$, as Fig. S5 C shows. Our mean-field model with clutch reinforcement also shows that adhesion reinforcement on rigid substrates shifts the optimum unloaded velocity parameter to larger values and the optimum clutch stiffness to higher stiffnesses, as depicted in Fig. S6 (parts B and C, respectively). Finally, we investigated the role of clutch catch bond behavior on force transmission, modeled as described in the supplement, and find nearly independent traction force generation on catch properties as shown in Fig. S7). Altogether, the inclusion of load-dependent clutch-bond reinforcement increases the optimal substrate stiffness and optimal clutch stiffness, but inclusion of clutch catch bonds has relatively little effect on optimal substrate stiffness.

Figure 6.

Influence of clutch reinforcement on traction force and optimal substrate stiffness. Force transmission on rigid substrates results from a competition between load-dependent clutch reinforcement and myosin-mediated clutch loading rates. (A and B) Dimensionless time-averaged traction force as a function of substrate stiffness for different values of the clutch reinforcement parameter $\theta$ and clutch reinforcement threshold force $\Delta$. Parameter values: $\tau =1$, $\omega =200$, (A) $\mathrm{F}=1$ and (B) $\mathrm{F}=10$. (C) Dimensionless time-averaged traction force on rigid substrates ($\mathrm{K}\to \infty$) as a function of $\Delta$ for four different values of the unloaded velocity parameter $\omega$. Parameter values: $\theta =10,\mathrm{F}=1,\tau =5$. (D) Optimum substrate stiffness as a function of $\theta$ for different values of $\Delta$. Parameter values: $\omega =200,\mathrm{F}=1,\tau =1$. Solid lines are the numerical solution of the developed mean-field model (Eq. 7), and symbols are the numerical solutions of the stochastic motor-clutch model. To see this figure in color, go online.

Discussion

In the present study, we developed a generalized mean-field motor-clutch model that provides new insights of force transmission of adhesion-based cellular protrusions on compliant elastic substrates and provides a quantitative analysis of regulation of force transmission by modulation of cellular components and extracellular rigidity. Unlike prior studies, the developed model explores motor-clutch imbalanced regimes, investigates novel traction optimality conditions, studies load-dependent reinforcement and catch bond behaviors, and quantifies traction force sensitivity to all the model parameters through the identification of key dimensionless parameters. Our model results indicate that shifting substrate stiffness optimality in cells that operate in the motor-dominated regime can be achieved by tuning clutch activity, whereas changes in motor activity will not produce any substrate mechanical optimality alterations. Motor-clutch balanced protrusions, on the other hand, are characterized by an optimum substrate stiffness sensitive to both myosin activity and clutches, whereas clutch-dominated stalled protrusions are characterized by substrate stiffness-insensitive traction forces, as previously shown (10). Our theoretical results additionally give the necessary and sufficient conditions required for the cell to operate at each regime. Determining the traction force production regime at which cells operate in physiological conditions would be a major step toward identifying the key cell molecular candidates and/or stromal components to target with the aim of controlling cell traction force production and substrate stiffness optimality and, in turn, cell adhesion-based migration (11,12).

We additionally found that traction force generation away from optimality is strongly influenced by clutch stiffness, especially on rigid substrates, and discovered the existence of an intermediate clutch stiffness for maximum force transmission. Our results strongly suggest that cells containing very soft or very stiff clutches will have reduced cell migration capabilities, especially on rigid substrates. Suboptimal cell migration conditions in the soft-clutch and stiff-clutch limits are caused by a slow buildup of traction forces and by frequent frictional slippage behavior, respectively. These results could be important for understanding cell behavior on stiff materials such as tissue culture plastic or glass, implanted biomedical devices, and bone. Furthermore, the biphasic dependence of traction force generation on clutch stiffness predicted here is reminiscent of the reported biphasic cell migration dependence on clutch component expression levels in an ex vivo disease model (11), and it could have important implications in the development of therapeutic strategies to treat cancer. One possible plan of action could involve molecular engineering by inserting deformable domains between two molecular clutch components with the aim of arresting cancer cell migration, in a similar fashion to the insertion of molecular tension sensors with controlled stiffness in focal adhesion complexes (65). Optimization of the mechanical properties of these domains would require cell-specific parameterization of the different model parameters, including the development of new techniques to accurately measure the effective clutch complex stiffness and the identification of the softest clutch bonds that largely contribute to the effective clutch complex softening. Although the stiffness of some clutch components has been estimated in multiple studies (47,66,67), clutch stiffness data are scarce (68) (Table 1). Our clutch stiffness results also suggest that the insertion of molecular tension sensors to measure cellular traction forces might alter traction force generation for sufficiently soft tension sensors delivering inaccurate traction force measurements. A specific example of such molecular tension sensors is digital readout sensors based on disruption of DNA duplexes with high force (>20 pN) thresholds (69,70,71). Consequently, accurate traction force measurements via molecular tension sensors require the design and engineering of stiff sensors, much stiffer than molecular clutches. Molecular tension sensors typically rely on a tension sensor module that is composed of two fluorophores connected by a force-sensitive linker peptide that extends reversibly in response to mechanical forces. The ideal fabrication strategy would be to design the force-sensitive linker peptide to be as stiff as possible to enhance measurement accuracy without penalizing sensor sensitivity and range. Our work also provides a physical explanation for why the optimum substrate stiffness for maximal force transmission is independent of clutch stiffness (10,17), since clutch rupture times are independent of clutch stiffness near the optimum. Our findings also show that motor-dominated protrusions shift the clutch stiffness optimum toward softer clutch rigidities, whereas clutch-dominated protrusions shift it toward stiffer clutch rigidities. Our work potentially suggests that clutch stiffness could play an important role not only in cell migration speed but also in changes in cell polarization direction by modulating clutch association and dissociation kinetics and/or actin retrograde flow strengths and, in turn, protein transport (72).

In addition, we found that protrusions on rigid substrates display a biphasic dependence of force transmission on motor activity. This is particularly interesting since motor activity levels can be modulated by the internal cellular state as well as by environmental cellular conditions (73,74). Our model predicts that a significant increase in motor activity can dramatically diminish adhesion-based traction forces and potentially suppress adhesion-based cell motility. Consequently, cells might require alternative mechanisms to efficiently migrate within highly confined spaces or within other mechanochemical environments that promote high-motor activity levels. Our mean-field model also predicts that traction force produced by a strong-motor protrusion on rigid substrates reaches a maximum at an intermediate value of the myosin load-free velocity parameter. This novel result could have important implications in understanding the contribution of different myosin motor types on force transmission, as different myosin motors produce distinct force-velocity curves and have different myosin load-free velocities (75,76,77). It would also be interesting to test this prediction experimentally, and it encourages the design of motor-oriented therapeutic strategies to modulate traction force production and potentially migration of cells that operate in a high-motor activity cellular state. The reported biphasic dependence of force transmission on motor activity and unloaded motor velocity could be potentially tested via novel molecular tension sensor experiments and opens new research avenues in biological systems with stiff cellular environments. Unraveling the mechanics of cellular force production and migration in stiff cellular environments is crucial in many aspects of health and human physiology. Cell migration dysregulation in stiff environments is associated with many processes in development and human diseases, such as clinical complications, tissue remodeling and immune modulation in inflammatory responses near implanted medical devices (78,79), bone cancer metastasis (80), fibrosis in cancer (81,82), calcified bone remodeling processes and homeostasis (83), and dental lamina development and degradation processes (84). The high stiffness regime is also important for understanding cell interactions with rigid implantable biomedical devices.

Our findings also predict that load-dependent clutch reinforcement can substantially increase the traction force produced by protrusions that display load-and-fail dynamics, and it can significantly shift the optimum substrate and clutch stiffnesses to larger values. Although traction force-substrate stiffness curves were found to be monotonically increasing functions in reinforced protrusions with small unloaded myosin velocities and relatively low number of myosin motors over clutches, motor-dominated protrusions displayed a biphasic dependence of force transmission on substrate stiffness for the clutch reinforcement strengths explored, requiring anomalously high clutch reinforcement strengths to prevent frictional slippage and to allow the production of significant traction forces on rigid substrates. These results provide key insights to effectively design novel cell and stromal engineering strategies to strengthen or weaken clutch reinforcement with the aim of, respectively, enhancing or decreasing traction force production and potentially cell migration capabilities.

Our current study has some limitations. We have addressed cycles of extension and retraction of single-cell protrusions and adhesion dynamics at the cell edge and did not study either cell polarization or cell migration. Existing biophysical models in compliant (12) and non-compliant (53,54) substrates and experimental work (72,85,86,87,88,89,90,91,92) have captured spontaneous symmetry breaking and a great diversity of cell migration patterns, including persistent migration and bipedal locomotion, that emerge from fluctuations in cellular components that spatially modulate force generation and resisting forces. Our developed mean-field model can be further extended to elucidate biophysical mechanisms underlying differential coordinated actin dynamics and traction force generation among cellular protrusions that cause cell symmetry breaking/polarization and to better understand 2D and 3D adhesion-based cell migration capabilities on compliant cellular microenvironments. We have assumed that the mechanical properties of clutches are those of the weakest link in the adhesion complex, a standard assumption in the motor-clutch framework. The constitutive adhesion proteins that form clutch complexes flow retrogradely at different speeds (93,94), with actin-binding proteins flowing at high speeds and more coherently, matrix-binding proteins flowing at low speeds and mostly incoherently, and core clutch proteins linking actin-binding and matrix-binding proteins flowing at intermediate speeds and with somewhat coherent motion. The reported differences in retrograde flow speeds agree well with the motor-clutch hypothesis, and this could imply the absence of a clear “weakest link” and that the constitutive protein-protein adhesion bonds may have similar mechanical properties with multiple bonds influencing force transmission. The reported differential coherence could suggest that adhesion complex links undergo slippage and do not maintain robust connections (59), which could limit force transmission and efficiency. We have also assumed that the substrate is a Hookean elastic material. However, tissues and extracellular fibril networks are not linearly elastic but display complex mechanical behaviors, including nonlinear elasticity such as stress stiffening and stress softening (95,96), mechanical plasticity (97), and viscoelasticity (98,99). Force loading rates are very slow in soft substrates and viscous dissipation provides additional resistance to retrograde myosin pulling forces, which increases the initial force loading rate (37,100), reducing actin retrograde flows, and increasing membrane front speeds and cell migration, consistent with enhanced experimental and computational cell migration speeds reported on soft substrates with faster stress relaxation times (100). The mechanical response of the extracellular space to cellular forces plays a critical role in force transmission and cell migration, and determining the constitutive mechanical model that better describes the extracellular space is a potential opportunity for future experimental and theoretical studies. In addition, our model does not account for spatial density gradients of myosin motors, molecular clutches, and actin filaments. Low traction stresses produced by epithelial cells were measured at the leading edge (lamellipodium) and cell body, whereas traction stresses peaked in the region between the lamellipodium base and the cell body where focal adhesions maturate (101,102). F-actin speeds reached a maximum at the leading edge and inversely correlated with distance from the cell edge. Traction forces and F-actin flows were therefore found to be inversely related in the lamellipodium and focal adhesion region, consistent with the motor-clutch framework. Focal adhesion disassembly and reduced myosin activity in the lamella or cell body region (103) can explain the drastic drop in traction stresses and F-actin speeds in those areas further away from the leading edge. Finally, additional studies are needed to identify the main adhesion clutch constituents, as well as the key mechanisms for efficient cellular force transmission/migration and activation of mechanotransduction pathways in different complex mechanochemical microenvironments. The mechanotransduction of cellular forces transmitted to the extracellular fibril network into biochemical signals leads to transcriptional regulation in the nucleus (104,105,106) that can modulate force transmission, thus influencing cell migration in non-trivial ways. Further understanding will speed up the discovery of new therapeutic strategies to treat human disease for improved patient outcomes.

Author contributions

R.A.M. designed research, developed the biophysical model, performed mathematical derivations and numerical simulations, and wrote the manuscript. P.P.P and D.J.O. secured funding, oversaw all aspects of the study, and provided edits to the manuscript.

Editor: Alex Mogilner.