Effect Measure Modification by Covariates in Mediation: Extending Regression-Based Causal Mediation Analysis

Abstract

Existing methods for regression-based mediation analysis assume that the exposure–mediator effect, exposure–outcome effect, and mediator–outcome effect are constant across levels of the baseline characteristics of patients. However, investigators often have insight into how these underlying effects may be modified by baseline characteristics and are interested in how the resulting mediation effects, such as the natural direct effect (NDE), the natural indirect effect (NIE), and the proportion mediated, are modified by these baseline characteristics. Motivated by an empirical example of anti-interleukin-1 therapy’s benefit on incident anemia reduction and its mediation by an early change in an inflammatory biomarker, we extended the closed-form regression-based causal mediation analysis with effect measure modification (EMM). Using a simulated numerical example, we demonstrated that naive analysis without considering EMM can give biased estimates of NDE and NIE and visually illustrate how baseline characteristics affect the presence and magnitude of EMM of NDE and NIE. We then applied the extended method to the empirical example informed by pathophysiologic insights into potential EMM by age, diabetes, and baseline inflammation. We found that the proportion modified through the early post-treatment inflammatory biomarker was greater for younger, non-diabetic patients with lower baseline level of inflammation, suggesting differential usefulness of the early post-treatment inflammatory biomarker in monitoring patients depending on baseline characteristics. To facilitate the adoption of EMM considerations in causal mediation analysis by the wider clinical and epidemiologic research communities, we developed a free and open-source R package, regmedint.

INTRODUCTION

Causal mediation analysis has been gaining popularity in the last decade. Several estimation methods have been proposed to date^1–6 that share a foundation in the counterfactual potential outcome framework, though these methods differ in their estimation approaches and resulting interpretations. One of the most popular approaches is closed-form regression-based causal mediation analysis, introduced in a landmark paper by Valeri and VanderWeele with accompanying SAS and SPSS macros^5,7. This approach involves fitting simple parametric models for the mediator and for the outcome. Closed-form variance estimation by delta method is computationally straightforward, compared to other major estimation approaches that require simulation or weighted data construction^1,4,8.

In this article, we develop generalized methods for mediation analysis that allow the inclusion of effect measure modification (EMM). Existing methods and software for regression-based mediation analysis assume that the exposure–mediator effect, the exposure–outcome effect, and the mediator–outcome effect are constant across levels of the controlled covariates. This is a limitation because researchers may be interested in investigating how mediation varies across these covariates. For example, in the Canakinumab Anti-Inflammatory Thrombosis Outcome Study (CANTOS) trial, canakinumab (anti-interleukin-1 [IL-1] medication) demonstrated beneficial estimated effects on cardiovascular disease as well as other outcomes^9,10, including incident anemia¹¹. Causal mediation analysis has been conducted for some of the outcomes^11,12 to examine the mediating role of early post-treatment change in high-sensitivity C-reactive protein (hsCRP) biomarker, which relates to the activity of the IL-1 biologic pathway targeted by canakinumab. Moderate to high levels of mediation were observed confirming the relevance of the early post-treatment changes in the IL-1 pathway and the usefulness of the hsCRP biomarker in assessing canakinumab benefits on subsequent clinical outcomes^11,12. The total benefit of canakinumab on incident anemia appeared somewhat greater among older individuals, diabetic individuals, and individuals with higher baseline hsCRP¹¹. However, to our knowledge the corresponding EMM of mediation by these variables was not previously investigated. The framework and software developed in this paper allow for formal investigation of potentially varying magnitudes of mediation through the early suppression of the IL-1 pathway across different baseline patient profiles.

The rest of the article is structured as follows. First, we extend the regression-based causal mediation approach to allow for the inclusion of EMM terms. Second, we develop closed-form formulas for the natural direct effect (NDE) and natural indirect effect (NIE) under four model specifications: (1) linear mediator model, linear outcome model; (2) logistic mediator model, linear outcome model; (3) linear mediator model, non-linear outcome model; (4) logistic mediator model, non-linear outcome model. We also describe settings when these conditional estimates: (a) coincide with marginal estimates, such that they can be interpreted as population average effects; and (b) are constant across levels of the covariates. Third, we use numerical examples to illustrate the EMM of the NDE and NIE. Fourth, we investigate the consequences of model misspecification in which the mediator and outcome models omit product terms when in fact EMM or causal interaction are present. Last, we revisit the above empirical example from the CANTOS trial to examine how EMM can impact NDE and NIE, and proportion mediated.

DEFINITIONS, NOTATIONS, AND ASSUMPTIONS

We use the same notational convention as in Valeri and VanderWeele (2013)⁵. We denote the exposure as $\mathrm{A}$, the mediator as $\mathrm{M}$, the outcome as $\mathrm{Y}$, and the vector of covariates as $\mathbf{C}$. We assume the causal structure represented in the directed acyclic graph ($\mathrm{D}\mathrm{A}\mathrm{G}$) in Figure 1. The effects of interest are the total effect ($\mathrm{T}\mathrm{E}),\mathrm{N}\mathrm{D}\mathrm{E}$ and $\mathrm{N}\mathrm{I}\mathrm{E}$, as defined below^4,5,7,10:

$$\mathrm{T}\mathrm{E}\left(\mathbf{c}\right)=g\left(\mathrm{E}\left[Y_a∣\mathbf{C}=\mathbf{c}\right]\right)-g\left(\mathrm{E}\left[Y_{a^{\mathrm{*}}}∣\mathbf{C}=\mathbf{c}\right]\right),$$

$$\mathrm{N}\mathrm{D}\mathrm{E}\left(\mathbf{c}\right)=g(\mathrm{E}\left[Y_{a{M}_{a^{\mathrm{*}}}}∣\mathbf{C}=\mathbf{c}\right])-g(\mathrm{E}\left[Y_{a^{\mathrm{*}}{M}_{a^{\mathrm{*}}}}∣\mathbf{C}=\mathbf{c}\right]),$$

$$\mathrm{N}\mathrm{I}\mathrm{E}\left(\mathbf{c}\right)=g(\mathrm{E}[Y_{a{M}_a}|\mathbf{C}=\mathbf{c}])-g(\mathrm{E}\left[Y_{a{M}_{a^{\mathrm{*}}}}∣\mathbf{C}=\mathbf{c}\right]),$$

where $g$ is a general link function. We assume the same four identification assumptions as in Valeri and VanderWeele (2013)⁵. Detailed definitions and assumptions are in Section 1 of the eSupplement.

Figure 1.

Assumed causal structure.

EMM-Extended Closed-Form Regression-Based Causal Mediation Analysis Approach

To accommodate EMM by $\mathbf{C}$ in both the mediator and outcome models, we specify the following extended parametric models that include product terms for EMM (underlined):

$$\text{M1.}{g}_M[\mathrm{E}(\mathrm{M}\mid \mathrm{A}=\mathrm{a},\mathbf{C}=\mathbf{c})]={\mathrm{\beta }}_0+{\mathrm{\beta }}_{1}a+{\mathrm{\beta }}_2\mathit{c}+\underset{¯}{{\mathrm{\beta }}_3}\underset{¯}{a\mathit{c}},$$

$$\text{M2.}{g}_Y\left[\mathrm{E}\right(\mathrm{Y}\mid \mathrm{A}=\mathrm{a},\mathrm{M}=\mathrm{m},\mathbf{C}=\mathbf{c}\left)\right]={\mathrm{\theta }}_0+{\mathrm{\theta }}_{1}a+{\mathrm{\theta }}_{2}m+{\mathrm{\theta }}_{3}am+{\mathrm{\theta }}_4\mathit{c}+\underset{¯}{{\mathrm{\theta }}_5}\underset{¯}{a\mathit{c}}+\underset{¯}{{\mathrm{\theta }}_6}\underset{¯}{m\mathit{c}},$$

where $g_{M}and{g}_Y$ are the link functions and ${\mathrm{\beta }}_2,{\mathrm{\beta }}_3,{\mathrm{\theta }}_4,{\mathrm{\theta }}_5$ and ${\mathrm{\theta }}_6$ are row vectors. In this article, we focus on identity and logit link functions, because the resulting formulas for these types of models can accommodate a wide range of outcome models, including survival outcomes.^5–7 Note that logistic and Cox proportional hazards model require rare outcome²⁵. Details are in the Supplement (Section 2.1).

The extended models include several product terms. Product terms can be used to model either causal interaction or EMM¹⁴, but there are critical differences in the interpretation and assumptions. Causal interaction entails a joint intervention on the two variables, while EMM entails heterogeneity in the causal effect of one variable across subgroups of the other¹⁴. Stronger assumptions regarding control of confounding will be required to identify causal interaction, compared to EMM¹⁴. Under the assumptions required for mediation analysis (A1-A4), the product term between the exposure and mediator represents causal interaction, but additional assumptions would be required for exposure–covariate or mediator–covariate product terms to represent causal interactions rather than mere EMM^5,7,8,13. Throughout this paper, we use the same identification assumptions as are required for mediation analysis^5,7,8,13, and so we describe product terms involving covariates as representing EMM rather than causal interaction.

EMM OF NATURAL DIRECT AND INDIRECT EFFECTS BY COVARIATES

Based on Models M1 and M2, we derive closed-form formulas for NDE and NIE (Table 1). When ${\mathrm{\beta }}_3={\mathrm{\theta }}_5={\mathrm{\theta }}_6=0$ (i.e., no EMM product terms are included in either the mediator or the outcome models), the formulas reduce to the original formulas in VV2013⁵. The extended formulas in Table 1 are implemented in the R regmedint package (version 1.0.0 and later)^15–17.

Table 1.

Closed-form formulas for NDE and NIE with different mediator and outcome models.

NDE
Linear mediator model, Linear outcome model	$\left(a-a^{\text{*}}\right)\left[{\theta }_1+{\theta }_3\left({\beta }_0+{\beta }_1{a}^{\text{*}}+{\beta }_{2}c+{\beta }_3{a}^{\text{*}}c\right)+{\theta }_{5}c\right]$
Logistic mediator model, Linear outcome model	$\left(a-a^{\text{*}}\right)\left[{\theta }_1+{\theta }_3\cdot \text{expit}\left({\beta }_0+{\beta }_1{a}^{\text{*}}+{\beta }_{2}c+{\beta }_3{a}^{\text{*}}c\right)+{\theta }_{5}c\right]$
Linear mediator model, Non-linear outcome model	$\text{exp}\left(\left[a-a^{\text{*}}\right]\cdot \left[{\theta }_1+{\theta }_{5}c+{\theta }_3\left({\beta }_0+{\beta }_1{a}^{\text{*}}+{\beta }_{2}c+{\beta }_3{a}^{\text{*}}c\right)+\frac{1}{2}{\sigma }^2{\theta }_3\left(2{\theta }_2+{\theta }_{3}a+{\theta }_3{a}^{\text{*}}+2{\theta }_{6}c\right)\right]\right)$
Logistic mediator model, Non-linear outcome model	$\text{exp}\left[\left({\theta }_1+{\theta }_{5}c\right)\left(a-a^{\text{*}}\right)\right]\frac{1+\text{exp}\left({\beta }_0+{\beta }_1{a}^{\text{*}}+{\beta }_{2}c+{\beta }_3{a}^{\text{*}}c+{\theta }_2+{\theta }_{3}a+{\theta }_{6}c\right)}{1+\text{exp}\left({\beta }_0+{\beta }_1{a}^{\text{*}}+{\beta }_{2}c+{\beta }_3{a}^{\text{*}}c+{\theta }_2+{\theta }_3{a}^{\text{*}}+{\theta }_{6}c\right)}$
NIE
Linear mediator model, Linear outcome model	$\left({\theta }_2+{\theta }_{3}a+{\theta }_{6}c\right)\left({\beta }_1+{\beta }_{3}c\right)\left(a-a^{\text{*}}\right)$
Logistic mediator model, Linear outcome model	$\left({\theta }_2+{\theta }_{3}a+{\theta }_{6}c\right)\left[\text{expit}\left({\beta }_0+{\beta }_{1}a+{\beta }_{2}c+{\beta }_{3}ac\right)-\text{expit}\left({\beta }_0+{\beta }_1{a}^{\text{*}}+{\beta }_{2}c+{\beta }_3{a}^{\text{*}}c\right)\right]$
Linear mediator model, Non-linear outcome model	$\text{exp}\left\{\left({\theta }_2+{\theta }_{3}a+{\theta }_{6}c\right)\left({\beta }_1+{\beta }_{3}c\right)\left(a-a^{\text{*}}\right)\right\}$
Logistic mediator model, Non-linear outcome model	$\frac{1+\text{exp}\left({\beta }_0+{\beta }_{1}a+{\beta }_{2}c+{\beta }_{3}ac+{\theta }_2+{\theta }_{3}a+{\theta }_{6}c\right)}{1+\text{exp}\left({\beta }_0+{\beta }_1{a}^{\text{*}}+{\beta }_{2}c+{\beta }_3{a}^{\text{*}}c+{\theta }_2+{\theta }_{3}a+{\theta }_{6}c\right)}\cdot \frac{1+\text{exp}\left({\beta }_0+{\beta }_1{a}^{\text{*}}+{\beta }_{2}c+{\beta }_3{a}^{\text{*}}c\right)}{1+\text{exp}\left({\beta }_0+{\beta }_{1}a+{\beta }_{2}c+{\beta }_{3}ac\right)}$

The formulas for non-linear outcome model accommodate logistic, log-linear, Poisson, negative binomial, accelerated failure time model and a Cox proportional hazards model, with appropriate link functions and modeling assumptions. Note that logistic and Cox proportional hazards model require the outcome to be rare. Details are in the Supplement (Section 2.1). NDE=natural direct effect; NIE=natural indirect effect.

Proportion mediated, which most studies are interested in reporting, is defined as $\frac{NIE}{NDE+NIE}$ when the outcome model is linear and $\frac{\exp \left(NDE\right)\cdot [\exp \left(NIE)-1\right]}{\exp \left(NDE\right)\cdot \exp \left(NIE\right)-1}$ when the outcome model is non-linear. Derivations of point estimates and standard errors by the delta method are given in the eSupplement Section 3.

Due to the way that mediator and outcome models are constructed (eSupplement Section 2.1), these formulas provide conditional effect estimates of $\mathrm{N}\mathrm{D}\mathrm{E}$ and $\mathrm{N}\mathrm{I}\mathrm{E}$. That is, these natural effect formulas contain the covariate vector $\mathbf{C}$ in their expressions, indicating that these natural effects are potentially modified by covariates. It is tempting to interpret the conditional effect estimates evaluated at the mean covariate level as the corresponding population average (marginal) effect estimates. However, this marginal interpretation does not generally hold. Most of the time, numerical integration is necessary to obtain marginal effects from the conditional mediator and outcome models^1–3,8. With the extended formulas in Table 1, we first examine the model specifications under which conditional natural effect estimates evaluated at the mean covariate levels coincide with the marginal effect estimates. Further, we discuss model specifications under which conditional effect estimates are constant.

When do conditional NDE and NIE estimates at the mean covariate levels coincide with the marginal estimates?

Conditional NDE and NIE estimates evaluated at the mean covariate levels coincide with corresponding marginal estimates when their effect formulas (Table 1) are linear in C. From Table 1, we see that the outcome model must be linear, because a non-linear outcome model cannot give NDE or NIE estimates that are linear in C due to the exponentiation, regardless of the type of the mediator model.

Table 2 summarizes, for different specifications of the outcome and mediator models, the conditions under which the NDE or NIE evaluated at the mean covariate level will have a marginal interpretation. If the outcome model is linear, then the NDE estimate evaluated at the mean covariate level will have a marginal interpretation if the mediator model is also linear. However, if the mediator model is logistic rather than linear, then the conditional NDE estimate will not have a marginal interpretation unless ${\mathrm{\theta }}_3=0$ (no exposure–mediator causal interaction [A×M]). Again for a linear outcome model, the NIE estimate evaluated at the mean covariate level may not have a marginal interpretation unless (1) the mediator model is also linear and either ${\mathrm{\beta }}_3=0$ (no EMM of the exposure effect by covariates [A×C] on mediator) or ${\mathrm{\theta }}_6=0$ (no modification of the mediator effect by covariates [M×C] on outcome); or (2) the mediator model is logistic and ${\mathrm{\beta }}_2={\mathrm{\beta }}_3=0$ (no covariate effects in the mediator model). These conditions are sufficient, but not necessary, conditions because some perfect cancellations can also eliminate covariates from the formulas in Table 1.

Table 2.

Sufficient conditions for conditional natural direct effect (NDE) and natural indirect effect (NIE) estimates at the mean covariate level to coincide with the marginal NDE and NIE estimates.

NDE	Linear outcome model	Non-linear outcome model*
Linear mediator model	Always	Never
Logistic mediator model	θ3 = 0
NIE	Linear outcome model	Non-linear outcome model*
Linear mediator model	β3 = 0 or θ6 = 0	Never
Logistic mediator model	β2 = β3 = 0

Abbreviations. EMM: effect measure modification; A: exposure; C: covariates; M: mediator.

Coefficients.

θ₅ = 0: no EMM of the exposure effect by covariates [A×C] on outcome

θ₃ = 0: no A×M interaction

β₂ = 0: no confounder in mediator outcome

β₃ = 0: no EMM of the exposure effect by covariates [A×C] on mediator

θ₆ = 0: no EMM of the mediator effect by covariates [M×C] on outcome

^*: The non-linear outcome model accommodates logistic, log-linear, Poisson, negative binomial, accelerated failure time model and a Cox proportional hazards model, with appropriate link functions and modeling assumptions. Note that logistic and Cox proportional hazards model require the outcome to be rare. Details are in the Supplement (Section 2.1).

When are conditional NDE and NIE estimates constant?

Table 3 shows the model specifications for which the conditional NDE and NIE are constant with respect to covariates, where the conditional NDE and NIE can be interpreted without reference to covariates. The conditions given are again sufficient, but not necessary, conditions because some perfect cancellations can also eliminate covariates from the formulas in Table 1.

Table 3.

Sufficient conditions for constant conditional natural direct effect (NDE) and natural indirect effect (NIE) estimates with respect to covariates.

NDE	Linear outcome model	Non-linear outcome model*
Linear mediator model	θ5 = 0 AND {θ3 = 0 OR β2 = β3 = θ6 = 0}
Logistic mediator model	θ5 = 0 AND β2 = β3 = θ6 = 0
NIE	Linear outcome model	Non-linear outcome model*
Linear mediator model	β3 = θ6 = 0
Logistic mediator model	β2 = β3 = θ6 = 0

Abbreviations. EMM: effect measure modification; A: exposure; C: covariates; M: mediator.

Coefficients.

θ₅ = 0: no EMM of the exposure effect by covariates [A×C] on outcome

θ₃ = 0: no A×M interaction

β₂ = 0: no confounder in mediator outcome

β₃ = 0: no EMM of the exposure effect by covariates [A×C] on mediator

θ₆ = 0: no EMM of the mediator effect by covariates [M×C] on outcome

^*: The non-linear outcome model accommodates logistic, log-linear, Poisson, negative binomial, accelerated failure time model and a Cox proportional hazards model, with appropriate link functions and modeling assumptions. Note that logistic and Cox proportional hazards model require the outcome to be rare. Details are in the Supplement (Section 2.1).

NUMERICAL ILLUSTRATIONS

To provide intuition, we use numerical examples to illustrate how the conditional NDE and NIE change when conditioning on different choices of covariate levels and when using different link functions for the mediator and outcome models. We outline the data generating, examine the true conditional NDE and NIE, and illustrate the bias in estimates of NDE and NIE when EMM terms are omitted.

Data Generating Process

We randomly generated data for $\mathrm{C},\mathrm{A},\mathrm{M}$, and $\mathrm{Y}$ in the following order. We generated one continuous covariate:

$$\mathrm{C}~\mathrm{Normal}\left(0,2^2\right).$$

We generated a binary exposure:

$$\mathrm{A}~\mathrm{B}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{i}\left(\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{t}\left(\mathrm{C}+{\mathrm{C}}^2\right)\right.\text{).}$$

For the link functions for mediator and outcome models, we consider the following four model specifications:

1. Linear mediator model, linear outcome model

2. Logistic mediator model, linear outcome model

3. Linear mediator model, logistic outcome model

4. Logistic mediator model, logistic outcome model

We generated continuous or binary mediators and outcomes as follows:

$$\begin{gathered} {\mathrm{M}}_{\text{cont}}=0.2+0.4\mathrm{A}+0.5\mathrm{C}+{\mathrm{\beta }}_3\mathrm{A}\mathrm{C}+\mathrm{\epsilon },\text{where}\mathrm{\epsilon }~\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\left(0,{0.5}^2\right), \\ \text{or}{\mathrm{M}}_{\text{bin}}~\mathrm{B}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{i}\left(\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{t}\left(0.2+0.4\mathrm{A}+0.5\mathrm{C}+{\mathrm{\beta }}_3\mathrm{A}\mathrm{C}\right)\right.\text{),} \\ {\mathrm{Y}}_{\text{cont}}=0.5+0.3\mathrm{A}+0.2\mathrm{M}+{\mathrm{\theta }}_3\mathrm{A}\mathrm{M}+0.1\mathrm{C}+{\mathrm{\theta }}_5\mathrm{A}\mathrm{C}+{\mathrm{\theta }}_6\mathrm{M}\mathrm{C}+\mathrm{\epsilon },\text{where}\mathrm{\epsilon }~\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\left(0,{0.5}^2\right), \\ {\mathrm{Y}}_{\text{bin}}~\text{Bernoulli}\left(\text{expit}\left(-5+0.3\mathrm{A}+0.2\mathrm{M}+{\mathrm{\theta }}_3\mathrm{A}\mathrm{M}+0.1\mathrm{C}+{\mathrm{\theta }}_5\mathrm{A}\mathrm{C}+{\mathrm{\theta }}_6\mathrm{M}\mathrm{C}\right)\right),\text{for}\text{scenarios}1-4, \\ \mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}1,2\mathrm{a}\mathrm{n}\mathrm{d}4. \\ {\mathrm{Y}}_{\mathrm{b}\mathrm{i}\mathrm{n}}~\mathrm{B}\mathrm{e}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{l}\mathrm{i}(\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{t}\left(-10\left.+0.3\mathrm{A}+0.2\mathrm{M}+{\mathrm{\theta }}_3\mathrm{A}\mathrm{M}+0.1\mathrm{C}+{\mathrm{\theta }}_5\mathrm{A}\mathrm{C}+{\mathrm{\theta }}_6\mathrm{M}\mathrm{C}\right)\right),\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{s}1-4, \\ \mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}3. \end{gathered}$$

We varied the magnitude of ${\mathrm{\beta }}_3$ (i.e., EMM by the covariate of the exposure’s effect on the mediator), ${\mathrm{\theta }}_3$ (i.e., causal interaction between the exposure and the mediator on the outcome), ${\mathrm{\theta }}_5$ (i.e., EMM by the covariate of the exposure’s effect on the outcome), and ${\mathrm{\theta }}_6$ (i.e., EMM by the covariate of the mediator’s effect on the outcome). We had a total of 48 settings representing all possible combinations of the 4 scenarios (i.e., inclusion of product terms), the 4 link function specifications, and the 3 parameter variations (Table 4). We then examined how the conditional NDE and NIE depend on the choice of conditioned covariate levels by evaluating them at levels of the covariate that ranged from −2 to +2 with a step size of 0.1.

Table 4.

Parameter settings under four simulation scenarios.

Scenario	Product terms in mediator and outcome models	θ3	β3	θ5	θ6
1	A×M in outcome model	{0, 0.5, 0.8}	0	0	0
2	A×M in outcome model, A×C in mediator model	0.5	{0.1, 0.4, 0.7}	0	0
3	A×M in outcome model, A×C in mediator model, A×C in outcome model	0.5	0.2	{0.2, 0.5, 0.8}	0
4	A×M in outcome model, A×C in mediator model, A×C in outcome model, M×C in outcome model	0.5	0.2	0.3	{0.3, 0.6, 0.9}

Coefficients.

θ₃: A×M causal interaction in outcome model

β₃: A×C effect measure modification in mediator model

θ₅: A×C effect measure modification in outcome model

θ₆: M×C effect measure modification in outcome model

Behavior of True Conditional NDE and NIE

In this section, we consider the true conditional NDE and NIE given the data generating process outlined above. Regarding the inclusion of product terms in the mediator and outcome models, we considered the following four possible model specifications, all of which were correctly specified. In Scenario 1, the model included an A×M product term but not any other product terms. In Scenarios 2–4, other possible product terms were nonzero, corresponding to A×C in the mediator model, A×C in the outcome model, and/or M×C in the outcome model (Table 4). The true NDE, NIE and total effects (TE) were calculated by directly plugging in the true coefficients ($\mathrm{\beta }$’s and $\mathrm{\theta }$’s) in the mediator and the outcome models from the data generating process in the previous section.

Figure 2 shows a special case of Scenario 1 $\left({\mathrm{\theta }}_3=0\right)$ in which neither regression model contained any of the possible product terms $\left({\mathrm{\theta }}_3={\mathrm{\beta }}_3={\mathrm{\theta }}_5={\mathrm{\theta }}_6=0\right)$.

Figure 2.

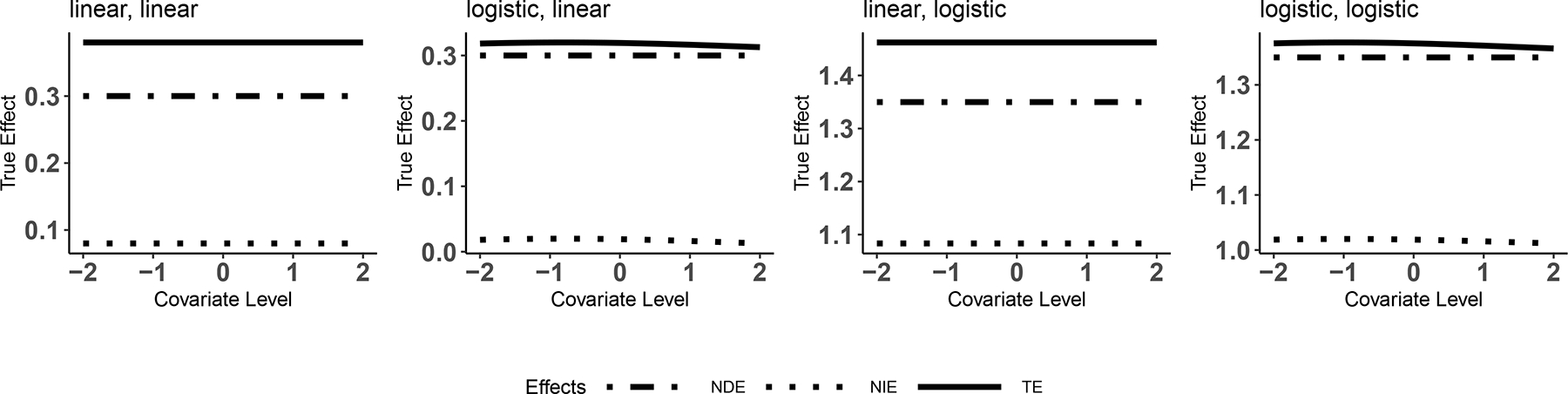
Effect measure modification (EMM) of conditional natural effects by covariates despite having no product terms in mediator or outcome regression model (i.e., Scenario 1).

In this case, the conditional NDE, NIE, and TE are all constant when the mediator model is linear. However, the conditional NIE varies slightly by the covariate level when the mediator model is logistic, despite having no explicit EMM terms in either mediator or outcome model.

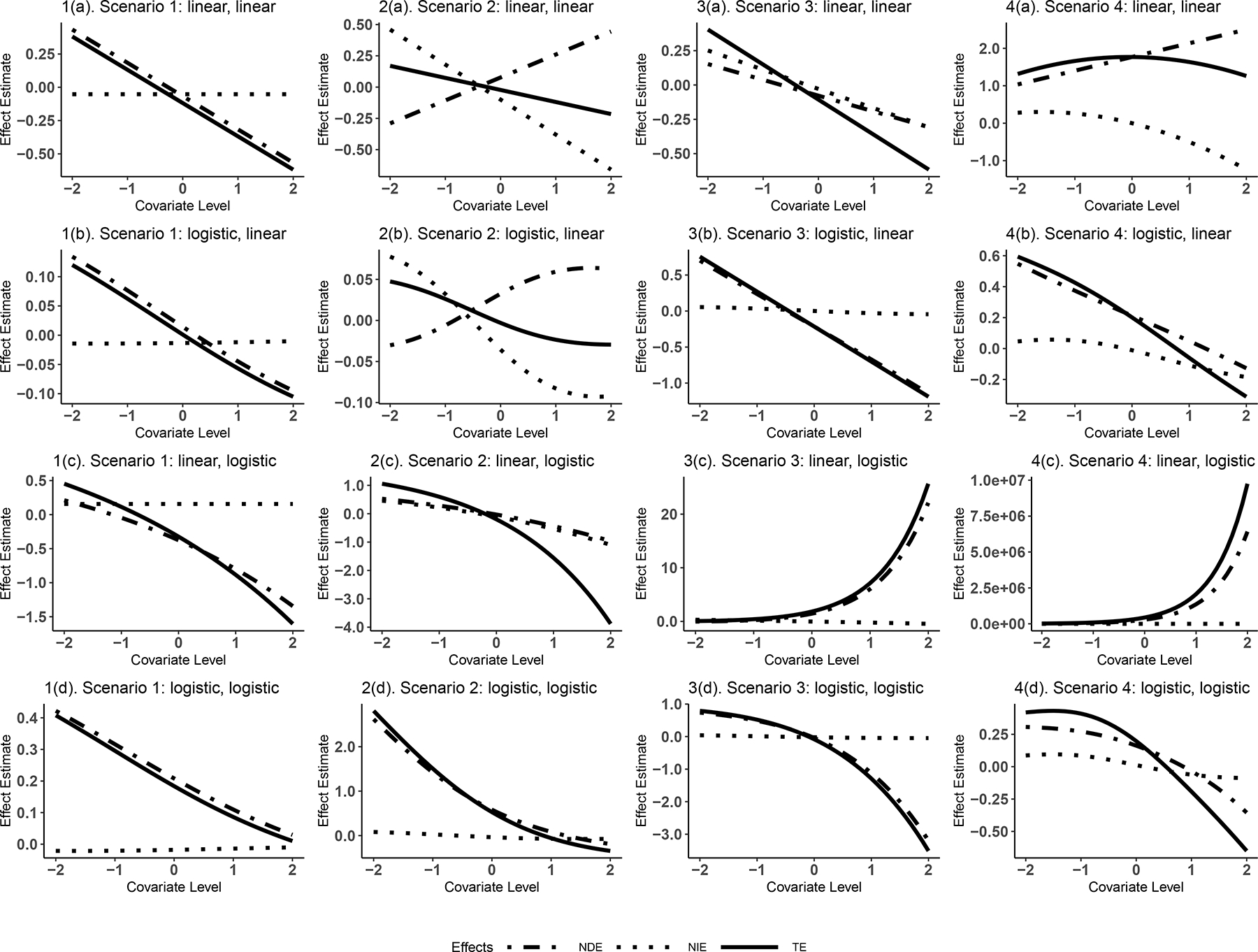
Figure 3 shows 16 selected settings with ${\mathrm{\theta }}_3\ne 0$ (A×M causal interaction is present) and with the middle coefficient values from Table 4. Each row represents one choice of mediator and outcome link functions. The remaining settings are in the eSupplement (Sections 4.1–4.4, the three columns on the left).

Figure 3.

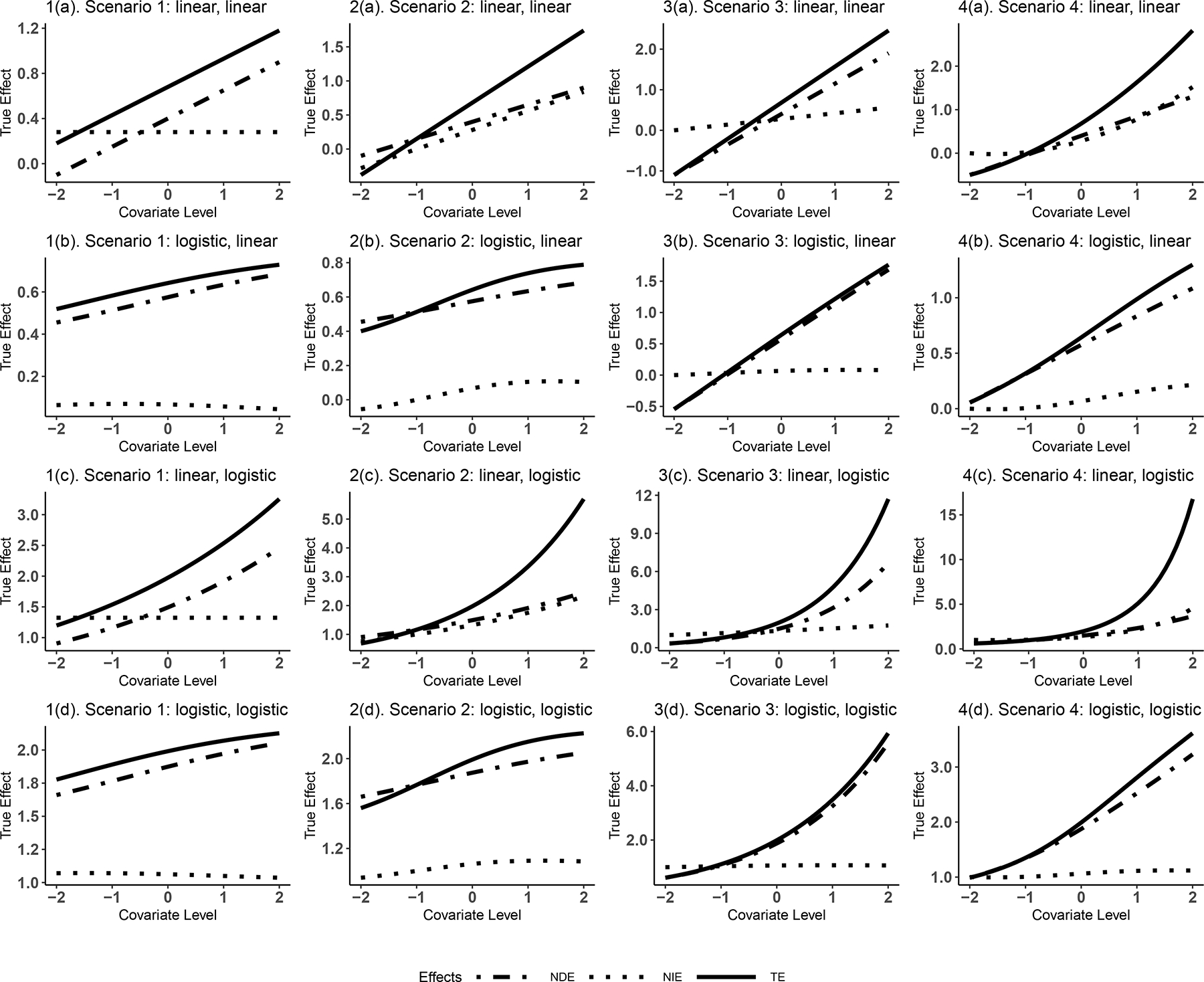
Selected plots across combinations of scenarios and link functions for the true NDE, NIE and TE effects.

The true conditional NDE is dependent on covariate levels in all settings when ${\mathrm{\theta }}_3\ne 0$. In the “linear, linear” case (i.e., a linear mediator model and a linear outcome model), the conditional NDE is always linearly dependent on covariate levels. As a result, as noted above, the conditional NDE evaluated at the mean covariate level coincides with the marginal NDE in this case. This marginal interpretation at the mean covariate level does not generally hold for other choices of link functions (i.e., cases other than the “linear, linear” case). In the “logistic, linear” case, the marginal interpretation does not hold in general, but may hold approximately if the effect of the covariate on the mediator is very weak (1(b), 2(b), 3(b) and 4(b) in Figure 3). The dependence on covariates of NDE and NIE stratified by the combination of mediator and outcome models’ link function and the inclusion of product term is summarized in Table 5.

Table 5.

Summary of effect modification by covariates, stratified by combinations of scenarios and link functions.

Model 1: linear mediator model, linear outcome model
Simulation	Coefficient	Inclusion of product terms	Dependence on covariates
Scenario			NDE	NIE
1	β3 = θ5 = θ6 = 0	only A×M	linearlya	constant
2	θ5 = θ6 = 0	adding A×C in mediator model	linearly	linearly
3	θ6 = 0	adding A×C in outcome model	linearly	linearly
4		adding M×C in outcome model	linearly	non-linearly
Model 2: logistic mediator model, linear outcome model
Simulation	Coefficient	Inclusion of product terms	Dependence on covariates
Scenario			NDE	NIE
1	β3 = θ5 = θ6 = 0	only A×M	non-linearlya	non-linearly
2	θ5 = θ6 = 0	adding A×C in mediator model	non-linearly	non-linearly
3	θ6 = 0	adding A×C in outcome model	non-linearly	non-linearly
4		adding M×C in outcome model	non-linearly	non-linearly
Model 3: linear mediator model, non-linear outcome model b
Simulation	Coefficient	Inclusion of product terms	Dependence of covariates
Scenario			NDE	NIE
1	β3 = θ5 = θ6 = 0	only A×M	non-linearlya	constant
2	θ5 = θ6 = 0	adding A×C in mediator model	non-linearly	non-linearly
3	θ6 = 0	adding A×C in outcome model	non-linearly	non-linearly
4		adding M×C in outcome model	non-linearly	non-linearly
Model 4: logistic mediator model, non-linear outcome model b
Simulation	Coefficient	Inclusion of product terms	Dependence of covariates
Scenario			NDE	NIE
1	β3 = θ5 = θ6 = 0	only A×M	non-linearlya	non-linearly
2	θ5 = θ6 = 0	adding A×C in mediator model	non-linearly	non-linearly
3	θ6 = 0	adding A×C in outcome model	non-linearly	non-linearly
4		adding M×C in outcome model	non-linearly	non-linearly

^a: NDE is constant when θ₃ = 0. This is corresponding to the special case shown in Figure 2.

^b: The non-linear outcome model accommodates logistic, log-linear, Poisson, negative binomial, accelerated failure time model and a Cox proportional hazards model, with appropriate link functions and modeling assumptions. Note that logistic and Cox proportional hazards model require the outcome to be rare. Details are in the Supplement (Section 2.1).

Abbreviations. NDE: natural direct effect; NIE: natural indirect effect.

Coefficients.

θ₃: A×M causal interaction in outcome model

β₃: A×C effect measure modification in mediator model

θ₅: A×C effect measure modification in outcome model

θ₆: M×C effect measure modification in outcome model

The true conditional NIE is constant in the “linear, linear” and “linear, logistic” cases (i.e., linear mediator model) when no EMM terms are involved (1(a) and 1(c) in Figure 3). However, if there are EMM terms, the conditional NIE is also modified by covariates even in the “linear, linear” and “linear, logistic” cases (2(a), 3(a), 4(a), 2(c), 3(c) and 4(c)). In the “linear, linear” case, the conditional NIE is linearly dependent on covariates, allowing for the conditional NIE at the mean covariate level to coincide with the marginal NIE, unless all three forms of EMM are present. Otherwise, such a marginal interpretation generally does not hold. In the “logistic, linear” case, approximate linearity and marginal interpretation holds if there is very weak covariate effect on the mediator.

Estimation of conditional NDE and NIE with misspecified regression models

Here we demonstrate the influence of misspecifying the regression models by omitting EMM terms (when they in fact exist in the data generating process) on the estimation of conditional NDE and NIE. Importantly, such misspecification could arise if one uses existing statistical methods and software tools for regression-based mediation analysis, which do not accommodate product terms involving the covariates, if in fact such EMM is present. We used the same data generating process in the previous section that included EMM terms. One large $(\mathrm{n}=\mathrm{5,000})$ dataset was simulated for each one of the 48 settings. In Scenario 1, we omitted the A×M causal interaction in the fitted outcome model despite its presence in the data-generating process. In Scenarios 2–4, we included the A×M causal interaction, but omitted all A×C and M×C terms in the fitted models, despite their presence in the data-generating process.

Figure 4 shows 16 selected settings, corresponding to Figure 3 (true conditional NDE, NIE and TE). The remaining settings are in the eSupplement (Sections 4.1–4, the three columns on the right). Figure 5 shows how much misspecified models biases the estimated NDE and NIE away from the true effects, comparing the 16 selected settings in Figures 3 and 4. In Figure 5, we see that omitting EMMs severely biases the conditional effects at most covariate levels, especially in “linear, logistic” cases when at least exposure–covariate product term is in both mediator and outcome models (3(c), 3(d), 4(c), 4(d)). The magnitude of bias is substantive, compared to the range of true effects.

Figure 4.

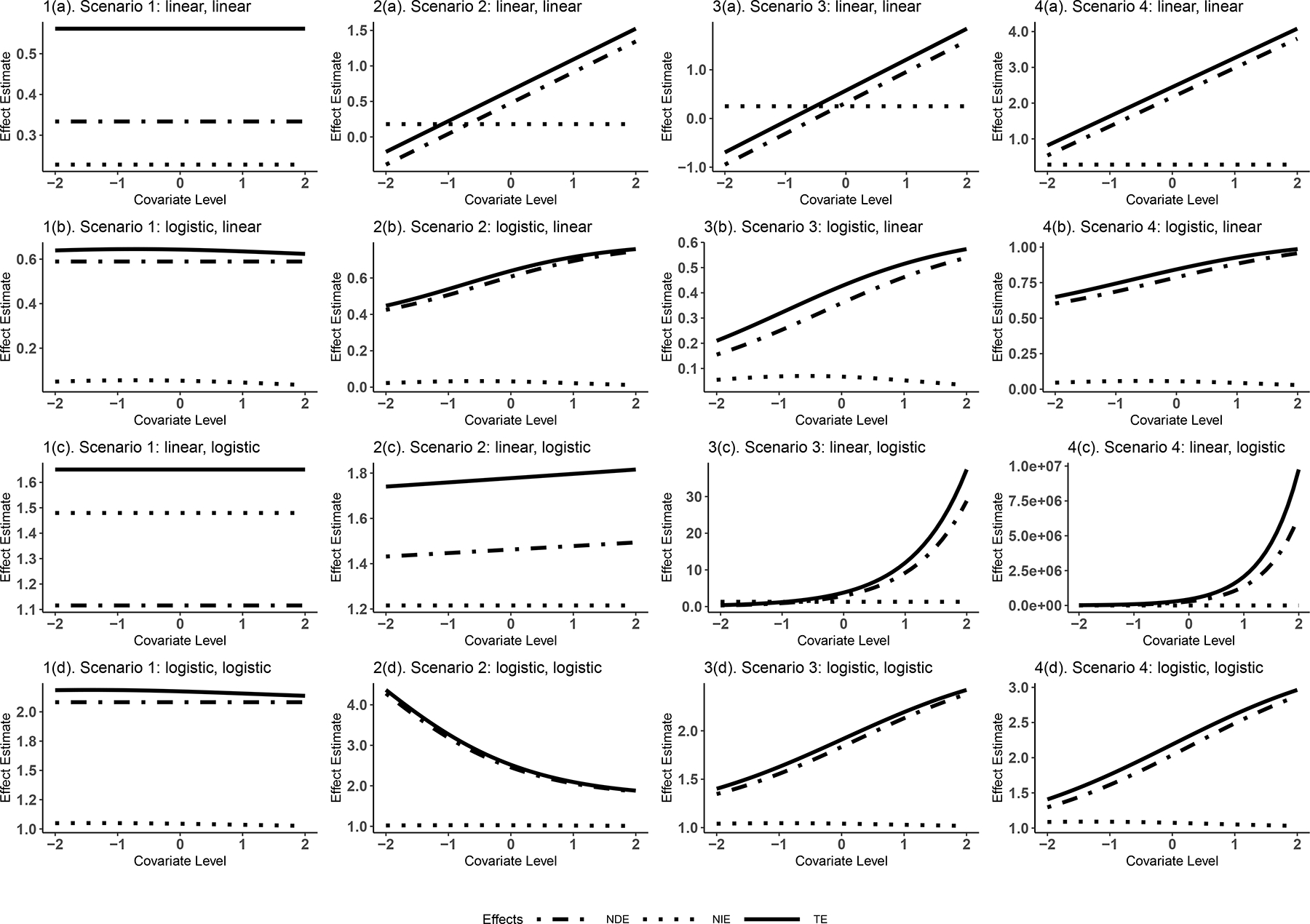
Selected plots across combinations of scenarios and link functions when models are misspecified.

Figure 5.

Selected plots showing bias, comparing true effects versus estimated effects from misspecified models.

Not only the magnitude of effects, but also their direction, can be estimated incorrectly. For instance, in Scenario 1 in the “linear, linear” case, the true conditional NDE at covariate level = 2 is negative (1(a) in Figure 3), while the estimated NDE when omitting A×M causal interaction is positive (1(a) in Figure 4). In Scenario 3 in the “logistic, linear” case, the true conditional NDE at covariate level = −2 is negative (3(b) in Figure 3), while the estimated NDE when omitting A×C term in both mediator and outcome models is positive. Although the bias in Scenario 1 (i.e., from omitting the exposure–mediator interaction) can be resolved using existing methods for mediation analysis that accommodate exposure–mediator interaction⁶, it is critical to note that the bias in Scenarios 2–4 (i.e., from omitting product terms involving the covariates) can only be resolved using the proposed extended method.

Additionally, omitting A×M causal interaction and EMM terms can also lead one to: (1) Falsely conclude constant conditional effects; (2) Falsely conclude conditional effects coincide with marginal effects. For (1), in Scenario 1 (omitting A×M causal interaction), for all mediator and outcome models, the conditional NDEs in Figure 4 are all falsely constant. For “linear, linear” case, Scenarios 2–4, the NIEs in Figure 4 are falsely constant. In both cases, the natural effect estimates should vary with C, as seen in the corresponding panels in Figure 3. For (2), when all three EMM terms are present, the conditional NIEs at the mean covariate level from the correctly specified model do not correspond to the marginal counterparts under “linear, linear” and “linear, logistic” cases. Omitting them gives the false impression of a marginal interpretation.

EMPIRICAL EXAMPLE DEMONSTRATION

The previously published analysis from the CANTOS trial found that the observed reduction in anemia associated with use of canakinumab (anti-interleukin-1 [IL-1] medication) was strongly mediated through the change in hsCRP in the first three months among 8,683 patients without anemia at trial entry¹¹. Here we examined whether this previously reported mediation is modified by clinically plausible modifiers of the underlying mechanisms.

Baseline hsCRP, age, and diabetes are three effect modifiers of interest¹¹ (Figure 6). Baseline hsCRP is a potential effect modifier of canakinumab’s impact on the change in hsCRP (mediator) because those with a higher baseline inflammation is expected to experience a greater decline in hsCRP due to the biological impact of IL-1 blockade as well as regression to the mean. As aging and diabetes both have detrimental influence on hematopoietic stem cell functions^18–22, we hypothesized that the beneficial impact of early reduction in hsCRP (mediator) on incident anemia is decreased by a higher age and diabetes.

Figure 6.

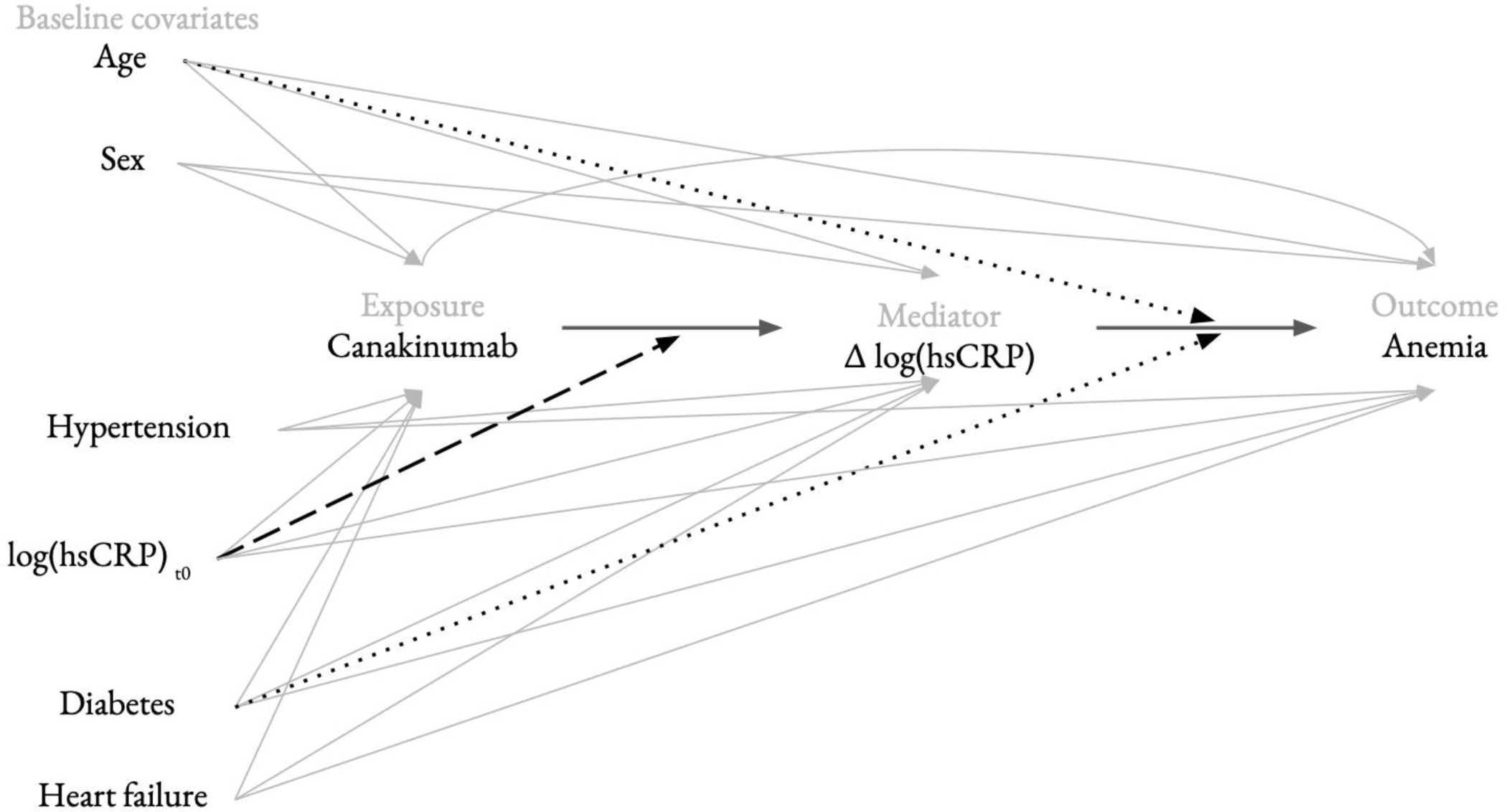
Effect measure modification graph for the CANTOS trial example

Long-dashed arrow: baseline log(CRP) modifies exposure–mediator relationship

Dotted arrow: Age and diabetes modify mediator-outcome relationship

Informed by the above clinical reasoning, the regression models were constructed as follows. The exposure was binary canakinumab use (treatment vs. placebo; treatment group: all doses combined), the continuous mediator was the change in log hsCRP (a negative value means improvement) from baseline to the 3^rd month, and the outcome was time to incident anemia. We adjusted for the same baseline covariates as the previous paper (age, sex, log hsCRP, heart failure status, diabetes status, and hypertension status)¹¹. We fit a linear mediator model and a Weibull accelerated failure time outcome model. We included baseline log hsCRP, age, diabetes as effect measure modifiers, where log hsCRP modifies the treatment’s effect on the mediator, and age and diabetes modify the mediator’s effect on the outcome. We evaluated the extent of mediation with the “lower anemia risk” profile, i.e. those who are younger (within 25^th percentile value of age), having lower baseline log hsCRP (within 25^th percentile value of baseline log hsCRP), and having no diabetes, to the “higher anemia risk” profile, i.e. those who are older (within 75^th percentile value of age), having higher log hsCRP (within 75^th percentile value of log hsCRP), and having diabetes. The R code is available at the Github repository https://github.com/einsley1993/emm-ext-med-cantos and the eSupplement Section 5.

We analyzed data from 8,302 subjects without anemia at baseline after excluding subjects with missing values. The trial protocol was approved by institutional review boards or ethics committees in the 39 countries involved in the study. All participants provided written informed consent to participate, and the trial underwent surveillance by an independent data and safety monitoring committee. Table 6 shows the causal mediation results. For the “lower anemia risk” profile, 64.0% of the canakinumab effect on the incident anemia outcome was mediated by the change of log hsCRP in the first 3 months. For the “higher anemia risk” profile, the proportion mediated was 48.7%. Although the total effect estimates were similar, we observed a greater proportion mediated for the lower anemia risk profile compared to the higher anemia risk profile.

Table 6.

Results of mediation analyses for the CANTOS trial example.

Subgroup	Effect	Point Estimate	95% CI
Lower anemia risk profilea	NDE	1.149	(0.951, 1.388)
	NIE	1.230	(1.137, 1.330)
	TE	1.413	(1.182, 1.689)
	PM	63.96%	(30.05%, 97.87%)
Higher anemia risk profileb	NDE	1.210	(1.012, 1.447)
	NIE	1.164	(1.065, 1.273)
	TE	1.409	(1.162, 1.708)
	PM	48.65%	(21.06%, 76.23%)

Abbreviations. EMM: effect measure modification; NDE: natural direct effect; NIE: natural indirect effect; PM: proportion mediated; CI: confidence interval.

The effects are on the mean time ratio scale, a value greater than 1.0 indicates a protective effect of canakinumab on the incident anemia outcome.

^a: Conditioning on 25^th percentile value of age, 25^th percentile value of baseline logarithm of high-sensitivity C-reactive protein, and having no diabetes.

^b: Conditioning on 75^th percentile value of age, 75^th percentile value of logarithm of high-sensitivity C-reactive protein, and having diabetes.

Table 7 shows the coefficients from the underlying mediator and outcome models, which can give further insights into the lower proportion mediated in the “higher anemia risk” profile. The coefficient of the Canakinumab×baseline log(hsCRP) in the mediator model was negative, although the magnitude of coefficients was small, confirming a greater canakinumab-driven reduction in hsCRP among individuals with a higher baseline hsCRP. The coefficient of change in log(hsCRP) on the survival time was negative, indicating that the effect of reduction in log(hsCRP) was protective. The coefficients of product terms $\mathrm{\Delta }$ log(hsCRP)×Age and $\mathrm{\Delta }$ log(CRP)×Diabetes were both positive, suggesting that the benefit of early reduction in hsCRP (mediator) on incidence anemia weakens with increasing age or diabetes, although the magnitude of coefficients was small.

Table 7.

Coefficients in the fitted mediator and outcome models in the CANTOS trial example

Mediator model
	Estimate	SE
(Intercept)	0.423	0.069
Canakinumab	−0.604	0.047
Age	−0.001	0.001
Sex (female)	0.013	0.021
Baseline log(hsCRP)	−1.437	0.023
Heart failure	0.093	0.019
Hypertension	0.016	0.023
Diabetes	0.043	0.023
Canakinumab×Baseline log(hsCRP)	−0.031	0.028
Outcome model
	Estimate	SE
(Intercept)	7.401	0.536
Canakinumab	0.082	0.149
Δ log(hsCRP)a	−0.484	0.205
Age	−0.048	0.008
Sex (female)	−0.009	0.090
Baseline log(hsCRP)	−0.734	0.089
Heart failure	−0.639	0.082
Hypertension	−0.067	0.106
Diabetes	−0.214	0.170
Canakinumab×Δ log(hsCRP)	−0.045	0.062
Δ log(hsCRP)×Age	0.004	0.003
Δ log(hsCRP)×Diabetes	0.047	0.064

^a: Δ log(hsCRP) = log(hsCRP) at month 3 - log(hsCRP) at month 0

DISCUSSION

Motivated by an empirical example on the causal mediation of canakinumab’s beneficial effect on incident anemia through early reduction in an inflammatory marker hsCRP, we extended the regression-based causal mediation approach to allow for EMM. EMM is a well-studied topic in the context of total effect estimation, but has not gained much attention in the context of causal mediation. Our methodologic results show that in many cases, existing methods will provide biased estimates of the NIE or NDE if there is exposure–covariate or mediator–covariate EMM by the covariates in the exposure–mediator effect, the exposure–outcome effect, or the mediator–outcome effect. The empirical example illustrates how substantive knowledge can inform the modeling process of the EMM in causal mediation. In the empirical analysis, we found that the level of mediation through the reduction in the hsCRP in the early post-treatment was higher for “low anemia risk” profile than for “higher anemia risk” profile. This finding may indicate that the usefulness of early post-treatment hsCRP as a therapeutic monitoring biomarker is greater among individuals with the “low anemia risk” baseline patient profile, providing a more nuanced understanding of hsCRP monitoring adding to the previous mediation investigation without EMM assessment¹¹. To facilitate the adoption of EMM considerations for applied researchers, we provided the free and open-source R package, regmedint.

Our EMM-extended regression-based causal mediation generalizes Valeri and VanderWeele’s closed-form regression-based approach⁵. However, it is beneficial to make a brief comparison to other causal mediation analysis approaches, including Imai et al.^1–3,8 and Lange et al.,⁴ and discuss how they address EMM. Imai et al.’s approach relies on the same set of mediator and outcome regression models, but supports the evaluation of EMM (discussed as “moderated mediation”, the common terminology used in the social science literature). However, their method gives NDE and NIE estimates only on the difference scale, whereas our proposed methods can provide such estimates on either the difference or the ratio scale. Additionally, our approach that uses closed-form formulas can be more computationally efficient than Imai et al.’s simulation-based approach²⁶. Lange et al.’s approach is a modification of the inverse probability weighted estimation of marginal structural model^4,23. This method accommodates EMM of the conditional NDE and NIE by including two product terms, one between the covariate and the reference exposure level, and the other between the covariate and the new exposure level, in the weighted counterfactual outcome model. The advantages of this approach are that users can read off NDE and NIE and how much they are modified by covariates directly from the coefficients of the model. Nevertheless, a downside of this approach is that inverse probability of weighting may give less-stable estimates for continuous exposures and mediators than the regression-based approach.

There are nonetheless a few limitations in our extended models. First, we consider only the cases when the additional product terms represent EMMs. To interpret the exposure–covariate and mediator–covariate product terms as causal interactions, we need further identification assumptions. Indeed, a covariate can be an effect modifier and causally interacts with exposure or mediator simultaneously¹⁴. Our intention is to extend the original closed-form mediation approach, so we extend the underlying mediator and outcome models without introducing additional assumptions. Hence, the limitations of Valeri and VanderWeele (2013)⁵ such as untestable cross-world independency assumptions still remain in our extended models. To accommodate the violation of the assumption of no exposure-induced mediator–outcome confounding^24,25, the randomized interventional analogue approach has been developed where the mediator values are sampled from a distribution, instead of fixed to the natural value it would take when treated or untreated. However, the natural direct and indirect effects redefined under a randomized interventional analogue are different from the classical NDE and NIE¹⁰. Although there is continued interest in developing mediation methods in the natural effects framework in recent years^27–35, some have also criticized the use of natural effects because the cross-world independency assumptions do not have corresponding real-world implications^36–42, though these views are not universal^7,43. A new approach called “separable treatment effect approach” (or “interventionist approach”) has been proposed that could mitigate the concerns around implausible cross-world assumptions by decomposing the treatment to two components to make the natural direct and indirect paths have an empirical meaning from the interventional perspective in the real world^36–42. If the investigators can build a story around treatment decomposition, the identification formulas provided in our paper also apply to the separable treatment effect approach.

In conclusion, we extended the regression-based causal mediation method^5–7 with EMM terms in the underlying mediator and outcome regressions models. Given the influence of covariates on conditional NDE and NIE, investigators are encouraged to consider EMM terms in the underlying regression models if substantive knowledge justifies these as exemplified by the CANTOS trial analysis. Our free and open-source R package regmedint is a convenient tool to conduct the EMM-extended closed-form regression-based causal mediation analysis and investigate the nature of covariate dependence of NDE and NIE.