Expanding use of digital mammography and repeated screening provides opportunities for risk assessment. To use these images for risk estimates and guide risk management in real time requires efficient processing. Evaluating the contribution of different views to prediction performance can guide future applications for risk management in routine care.
Abstract
Mammographic percentage of volumetric density is an important risk factor for breast cancer. Epidemiology studies historically used film images often limited to craniocaudal (CC) views to estimate area-based breast density. More recent studies using digital mammography images typically use the averaged density between craniocaudal (CC) and mediolateral oblique (MLO) view mammography for 5- and 10-year risk prediction. The performance in using either and both mammogram views has not been well-investigated. We use 3,804 full-field digital mammograms from the Joanne Knight Breast Health Cohort (294 incident cases and 657 controls), to quantity the association between volumetric percentage of density extracted from either and both mammography views and to assess the 5 and 10-year breast cancer risk prediction performance. Our results show that the association between percent volumetric density from CC, MLO, and the average between the two, retain essentially the same association with breast cancer risk. The 5- and 10-year risk prediction also shows similar prediction accuracy. Thus, one view is sufficient to assess association and predict future risk of breast cancer over a 5 or 10-year interval.
Prevention Relevance:
Expanding use of digital mammography and repeated screening provides opportunities for risk assessment. To use these images for risk estimates and guide risk management in real time requires efficient processing. Evaluating the contribution of different views to prediction performance can guide future applications for risk management in routine care.
Introduction
Mammographic breast density is well established as a risk factor for breast cancer. The classic studies used film mammograms and identified density as a risk factor. In 2005, Boyd wrote a classic article making the case for density as an intermediate phenotype (1). Because then it has been used as an endpoint for prevention trials (2), consistent with it being accepted as an intermediate phenotype. Although assessment of breast density in the film-screen era was qualitative and based on the radiologist's subjective evaluation of the presence of dense glandular tissue, widespread use of digital mammography created the potential for quantitative assessment of breast density. Older methods were area-based using two-dimensional (2D) film images, which has advanced to volumetric assessment with advent of digital images. The association of breast density with breast cancer risk is consistent across a range of methods used to estimate density as percent density (amount of dense glandular tissue compared with total breast tissue; refs. 3, 4). More specifically, the percentage of volumetric density (often %VD) and its association with breast cancer risk has been widely studied in the literature (3, 5–7). Volumetric density assessment is an established risk factor and is incorporated into existing risk assessment models, including Tyrer–Cuzick version 8 (8). Furthermore, a continuous measure of breast density shows low concordance with the 77 SNP polygenetic breast cancer risk scores (Spearman r = 0.024) and also a summary breast cancer–risk factor score derived from questionnaire risk factor data (Spearman r = 0.054; ref. 9). As risk models are implemented in broader clinical use, breast density is commonly included (10, 11).
However, debate in the epidemiologic literature still asks if the view used to assess breast density changes the magnitude of association or model performance for risk prediction (12). We note that approaches to process images and automatically remove pectoral muscles are described as more accurate for craniocaudal (CC) views than those for mediolateral oblique (MLO) mammograms (12). Previous meta-analysis of largely film-based studies suggests that the CC view shows a stronger association with future breast cancer risk than the MLO (13). With the advent of digital mammography, easier access to images has facilitated extension from consideration of density to define or mask lesions to now use the CC and MLO views for 5- and 10-year risk prediction (14, 15) consistent with NCCN guidelines (16) and providing sufficient interval for intervention to reduce risk (16).
To quantify the benefits of multiple views of breast density on predicting risk of future breast cancer as opposed to diagnosis, we draw on prospective data from the Joanne Knight Breast Health Cohort (JKBHC; ref. 17). We focus on the longer-term 5- or 10-year risk in this article in contrast with diagnosis of breast lesions, where more views (including tomosynthesis) may generate more precise identification to suspicious lesions (18). Few studies have investigated this issue thoroughly in the context of digital mammograms (4, 19, 20). We aim to investigate the association and risk prediction of CC, MLO, and the average of both in this study using the JKBHC comprised of 3,804 full-field digital mammograms.
Materials and Methods
Study population
The JKBHC is comprised of over 10,000 women ages 30 to 84 undergoing repeated mammography screening at Siteman Cancer Center and followed since 2010 (17). All women had a baseline mammogram at entry and completed a risk factor questionnaire. Mammograms are obtained using the same technology (Hologic). Women were excluded from the cohort if they had a history of cancer at baseline (other than nonmelanoma skin cancer). Women with breast implants were excluded from the cohort. Follow-up through October, 2020 was maintained through record linkages to electronic health records and pathology registries. 80% of participants had a medical center visit (mammography and other health visits) within the past 2 years. All analyses performed in this study use the nested case–control cohort within JKBHC where the pathology confirmed breast cancer cases were matched to two controls sampled from the perspective cohort. We sampled 2 control women for each case based on age at entry to the cohort and year of enrollment as previously described (17, 21). We identified 347 cases and 694 controls. After linkage to screening mammogram files, we excluded 8 women with breast implants and the rest without screening mammograms retrieved, we retained 294 cases diagnosed through October, 2020 and 657 controls. Supplementary Fig. S1 demonstrates the cohort selection and case identification. All women had 4 mammogram images and both the CC and MLO views are used in this study. Thus we used 3,804 images. We assessed the baseline characteristics of cases who did not have mammogram images retrieved (53) against those case who did (294) and observed comparable risk factor distribution, age (56.6 vs. 57.5), and breast density categories defined by BI-RADS clinical reports (48.8% vs. 49.0%).
Ethical approval for this prospective nested case–control cohort study was obtained from the Washington University in St Louis institutional review board. Participants provided informed written consent under the US Common Rule.
Breast cancer–risk factor collection
Women self-reported breast cancer–risk factors on entry to the cohort. These are drawn from established and validated measures (22). The questionnaire at entry assessed height, current weight, parity, age at first birth, menses ceased (yes/no), age at menopause (natural or with surgical removal of uterus, with removal of ovaries or without removal of ovaries), age at hysterectomy, family history of breast cancer (mother and/or sister), personal history of benign breast biopsy, and race.
Volumetric mammographic breast density assessment
As previously described (21), the volumetric percentage of breast density (VPD) within each digital mammogram is estimated with an automated pixel-thresholding algorithm developed and implemented at Washington University on processed images that directly takes in the full digital mammograms. The skin around the breast in CC and MLO views is removed and the pectoral muscle in MLO views is automatically removed using the boundary detection algorithm before estimating the dense volume. The VPD is then estimated using the volume of dense glandular tissue divided by the total breast volume that normalizes the difference in breast size across women and is consistent with other density estimation methods in the literature (23, 24). The correlation between VPD generated from our algorithm with the commercially available and widely used Volpara 4th edition (Volpara Solutions, Matakina Technology Limited, Wellington, New Zealand), is 0.81 based on an out-of-sample study with 375 women recruited from the mammography service at Washington University with mean age 47 (sd = 4.8; Supplementary Fig. S2; refs. 25, 26). Volpara reports the percentage of volumetric density that corresponds to BI-RADS as: A, <3.5%, Fatty; B, 3.5% to <7.5%, Scattered; C, 7.5% to <15.5%, Heterogeneously dense; D, 15.5% or more, Extremely dense. We refer to the CC view VPD as CC-VPD, MLO view VPD as MLO-VPD, and the average of the two as Full-VPD from here on.
Statistical analysis
We first assessed the Pearson correlation between the VPDs using different views. To estimate the 5 and 10-year breast cancer risk, we adopted the Cox proportional hazards model adjusting for baseline age in single years, BMI (continuous), family history of breast cancer (mother and/or sister), personal history of biopsy confirmed benign breast disease, parity (1+ vs. 0), and menopausal status (menses ceased; yes/no). This approach is consistent with routine practice as the loglikelihood for a conditional logistic regression model is statistically proven to be equivalent to the loglikelihood from a Cox model (27–29). Three different Cox regressions have been fitted that use CC-VPD, MLO-VPD, and Full-VPD on their original percent scale to investigate the model performance using different views.
The proportional hazards assumption has been formally checked using statistical tests and graphical diagnostics based on the scaled Schoenfeld residuals. The linearity assumption was checked by the Martingale residuals. We report the hazard ratios (HR), the 95% confidence interval (CI), and P value under all three Cox regressions. The 5 and 10-year prediction accuracy is assessed by the AUC using Uno's estimator (30) that considers censoring, under a 10-fold cross-validation study.
Data availability
All datasets were accessed and used under IRB-approved protocols and are available from the corresponding author upon reasonable request. The density estimation pipeline developed at Washington University is available upon request.
Results
The participant characteristics by case and control status are presented in Table 1. Among controls, the mean age was 56.6, mean BMI was 27.4 kg/m2, 81.1% were white and 12.9% were black, 82.8% of women reported having 1 or more children, and 68.8% were postmenopausal.
Table 1.
Risk factors at baseline by case–control status within the Joanne Knight Breast Health Cohort.
| Cases (n = 294) | Controls (n = 657) | |||
|---|---|---|---|---|
| Risk factors | Mean (sd) | Median (Range) | Mean (sd) | Median (Range) |
| Age, y | 56.56 | 57.19 | 56.62 | 56.68 |
| (8.75) | (35.38–76.80) | (8.67) | (35.27–76.84) | |
| BMI (kg/m2) | 29.25 | 28.45 | 27.38 | 25.82 |
| (6.37) | (17.47–54.54) | (6.19) | (14.14–50.96) | |
| CC-VPD (%) | 6.31 | 5.59 | 6.19 | 5.22 |
| (3.46) | (1.82–19.16) | (3.89) | (1.66–24.46) | |
| MLO-VPD (%) | 6.78 | 6.41 | 6.52 | 5.77 |
| (2.81) | (2.01–18.53) | (3.19) | (1.91–22.54) | |
| Full-VPD (%) | 6.48 | 6.20 | 6.28 | 5.45 |
| (2.78) | (1.92–16.44) | (3.23) | (1.87–20.27) | |
| n (%) | ||||
| Family history of breast cancer | 92 (31.30%) | 156 (23.74%) | ||
| Race | ||||
| White | 232 (78.91%) | 533 (81.13%) | ||
| Black | 57 (19.39%) | 85 (12.93%) | ||
| Others | 5 (1.70%) | 39 (5.94%) | ||
| Biopsy confirmed benign breast disease | 88 (29.93%) | 179 (27.25%) | ||
| Parity (1+) | 232 (78.91%) | 544 (82.80%) | ||
| Postmenopausal | 199 (67.69%) | 452 (68.80%) | ||
| Diagnosis (years since entry mammogram) | ||||
| 0 ≤ 5 | 104 (35.4%) | |||
| 5 ≤ 10 | 176 (60.0%) | |||
| 10+ | 14 (1.02%) | — | ||
Note: Continuous covariates are reported with mean and standard deviation (sd); binary covariates are reported by the number of positive responses and their corresponding percentage.
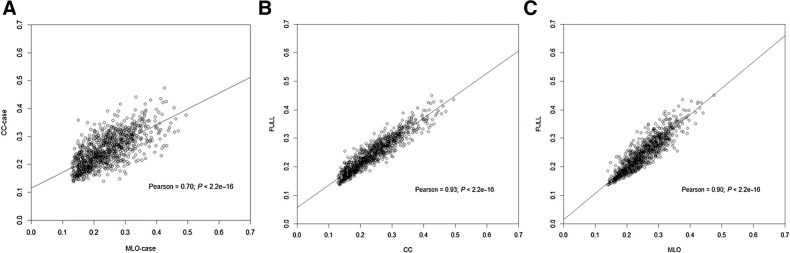
As shown in Fig. 1, the CC-VPD and MLO-VPD retain a significant positive linear relationship with each other (Pearson correlation of 0.70). The correlation between Full-VPD averaged between both views and CC-VPD is 0.93, and for MLO-VPD is 0.90. The correlation between BMI and CC-VPD is −0.48 and between age and CC-VPD is −0.22 where similar correlations are seen under both MLO- and Full-VPD. Additional correlation plots by case and control status are included in Supplementary Fig. S3.
Figure 1.
Linear correlation and scatter plots; all variables are square root transformed. A, MLO-VPD and CC-VPD. B, CC-VPD and Full-VPD. C, MLO-VPD and Full-VPD.
In Table 2, we summarize the associations between baseline risk factors and breast cancer risk using CC-, MLO-, and Full-VPD. We observe that each year increase in baseline age is associated with an increase of 2.3% in breast cancer risk and each unit increase in BMI (kg/m2) with a 5.0% increase in breast cancer risk in all three models. Women with family history of breast cancer are at significantly higher risk of breast cancer than those without. In all three models, the VPD measure was statistically significant, and an increase in VPD is positively associated with breast cancer risk. Subgroup analyses by menopausal status are shown in Supplementary Tables S1–S6. Results were largely unchanged in postmenopausal women, though family history had a somewhat stronger in premenopausal women.
Table 2.
Multivariate-adjusted hazards ratios (and 95% Confidence Intervals) summarizing breast cancer–risk factor associations with breast cancer incidence using different mammogram images CC, MLO, and combined.
| Risk factorsa | Measure of mammographic breast density used in breast cancer incidence model | |||||
|---|---|---|---|---|---|---|
| CC-VPD | MLO-VPD | Full-VPD | ||||
| Model | HR (95% CI) | P | HR (95% CI) | P | HR (95% CI) | P |
| Age | 1.02 (1.00–1.05) | 0.04 | 1.02 (1.00–1.05) | 0.07 | 1.02 (1.00–1.05) | 0.04 |
| BMI (kg/m2) | 1.05 (1.03–1.08) | <0.01 | 1.05 (1.03–1.07) | <0.01 | 1.05 (1.03–1.07) | <0.01 |
| Family history (yes vs. no) | 1.43 (1.11–1.83) | <0.01 | 1.44 (1.12–1.84) | <0.01 | 1.42 (1.11–1.83) | <0.01 |
| Biopsy confirmed benign breast disease | 1.01 (0.78–1.32) | 0.92 | 1.04 (0.80–1.35) | 0.76 | 1.02 (0.78–1.32) | 0.91 |
| Parity (1+ vs. 0) | 0.96 (0.72–1.28) | 0.78 | 1.01 (0.76–1.35) | 0.92 | 0.99 (0.74–1.31) | 0.92 |
| Menopause (post vs. pre) | 0.67 (0.45–1.01) | 0.05 | 0.68 (0.46–1.03) | 0.07 | 0.68 (0.45–1.02) | 0.06 |
| CC-VPD (per 1% increase) | 1.05 (1.01–1.09) | 0.01 | — | — | — | — |
| MLO-VPD (per 1% increase) | — | — | 1.05 (1.01–1.09) | 0.02 | — | — |
| Full-VPD (per 1% increase) | — | — | — | — | 1.06 (1.02–1.11) a | <0.01 |
Note: Findings from 294 women diagnosed with breast cancer and 657 controls from a cohort of 10,481 women.
aRisk factors entered as continuous in the model except for family history, history of benign breast biopsy, party and menopause that are binary.
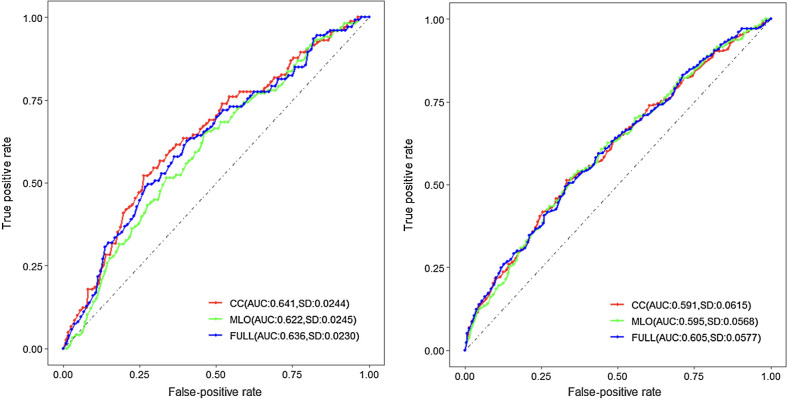
We further show in Fig. 2, the 5 and 10-year breast cancer prediction performance using the three VPD measures. To avoid over-optimism, the reported AUCs are based on Uno's integrated 5-year AUC estimated by averaging over a 10-fold cross-validation. As a benchmark, we see that the conventional Full-VPD achieved an AUC of 0.636 (sd = 0.023). When we separately estimated the 5-year AUC using CC-VPD and MLO-VPD, we observe an AUC of 0.641 (sd = 0.024) and AUC of 0.622 (sd = 0.025). For 10-year risk, we observe an AUC of 0.591 (sd = 0.062) for CC; an AUC of 0.595 (sd = 0.057) for MLO and an AUC of 0.605 (sd = 0.058) for Full-VPD. Although these AUCs are not statistically different from each other at either 5 or 10 years, we see that using one view (either CC- or MLO-VPD) can be as efficient as using both. The linearity assumption checked by the Martingale residuals was deemed reasonable in this study (Supplementary Fig. S4) and proportional hazards assumption was satisfactory under the model with CC, MLO, and the average of both (Supplementary Figs. S5–S7).
Figure 2.
5 and 10-year breast cancer–risk prediction for three different models. The reported AUCs are based on Uno's cumulative 5 and 10-year AUC estimated by averaging over a 10-fold cross-validation.
Discussion
In this study, which used data from 3,804 full-field digital mammography scans obtained from the JKBHC, we demonstrated that using the craniocaudal (CC)-view, the MLO view, and the average of both views, exhibit comparable associations with breast cancer risk. In addition, we found that using only one view (either CC or MLO) performs just as effectively as combining both views when it comes to predicting the risk of breast cancer over a 5- or 10-year period. Prior report from a meta-analysis of older film-based mammography with 13 case–control studies shows that absolute dense area and the percentage of dense area in the CC view had stronger associations with breast cancer (percentage of dense area summary OR 1.59 per SD; 95% CI, 1.46–1.69) compared with the MLO view measures (percentage of dense area summary OR 1.40 per SD; 95% CI, 1.28–1.54). 12 of the 13 studies used cumulus to estimate measures of breast density (13).
Combined cross-sectional data from 22 countries show that measures and changes of breast density with age are consistent across a diverse set of women worldwide, suggesting that breast density is an intrinsic biologic feature of women and that change across the life course is an inherent biologic feature (31). With the goal of incorporating breast density into risk prediction models (10, 32, 33) to improve risk management (16), efficient automated measures have become increasingly important. Machine-derived measures of breast density remove non-constant reader-specific differences (4). Although machine-derived approaches have become standard in clinical practice the value for prediction of future risk is less well studied. Others have compared performance of automated measures against clinical classification for BI-RADS showing comparable association with breast cancer (34–36). A number of studies compare approaches with estimation of density by different machines/technologies and show no important variation (4, 7, 19). Furthermore, the approach reported here for density estimation is related to breast cancer risk in prospective data, and change in density over up to 10 years in the breast developing breast cancer shows decline in density more slowly than in women who remain free from breast cancer (21).
We consider strengths and limitations of this study. Our population is diverse and all measures are consistent with routine screening services. Images are all obtained from a single system and were processed over a week for this comparison within the images. On the other hand, performance over 10 or more years for risk prediction may vary in ways not yet detected. We note that VPD is estimated from the 2D mammography. Thus, the estimated VPD is a surrogate to the true three-dimensional mammography. This approach is consistent with Volpara and Libra for estimating the VPD (37). However, it routinely shows strong association with breast cancer risk (3).
As others evaluate the implementation of digital image assessment for risk into routine clinical practice to develop risk classification that can guide risk management and maximize population health (10, 38), issues of efficiency become paramount for total population coverage (10). Further research is needed to determine optimal screening frequency and risk management strategies and how best to use images in this context.
Conclusion
We show that the association between VPD from CC, MLO, and the average between the two, retain similar association with breast cancer risk, and that solely using any one view mammography performs as well as or better than combining CC and MLO views when predicting future risk of breast cancer over a 5 and 10-year intervals.
Supplementary Material
Supplementary Table S1: Hazards ratio for association between baseline risk factors and breast cancer risk among postmenopausal women using CC-VPD only.
Supplementary Table S2: Hazards ratio for association between baseline risk factors and breast cancer risk among postmenopausal women using MLO-VPD only.
Supplementary Table S3: Hazards ratio for association between baseline risk factors and breast cancer risk among postmenopausal women using Full-VPD only.
Supplementary Table S4: Hazards ratio (95% Confidence Interval) for association between baseline risk factors and breast cancer risk among pre-menopausal women using CC-VPD only.
Supplementary Table S5: Hazards ratio (95% Confidence Interval) for association inure-menopausal women between baseline risk factors and breast cancer risk utilizing MLOL-VPD
Supplementary Table S6: Hazards ratio of association among premenopausal women for baseline risk factors and breast cancer risk utilizing FULL-VPD
Supplementary Figure S1: Cohort recruit and follow up chart.
Supplementary Figure S2: Pearson correlation between our algorithm and Volpara shows strong positive linear relationship of 0.81.
Supplementary Figure S3: Pearson correlation separated by view and case control status.
Supplementary Figure S4: The linearity assumption is checked with Martingale residual plots.
Supplementary Figure S5: The proportional hazards assumption is deemed reasonable by checking the Schoenfeld residuals plot for CC-VPD.
Supplementary Figure S6: The proportional hazards assumption is deemed reasonable by checking the Schoenfeld residuals plot for MLO-VPD.
Supplementary Figure S7: The proportional hazards assumption is deemed reasonable by checking the Schoenfeld residuals plot for Full-VPD.
Acknowledgments
This work was supported by Breast Cancer Research Foundation grant number (BCRF 21–028; to G.A. Colditz), and in part by NCI (R37 CA256810; to S. Jiang).
The publication costs of this article were defrayed in part by the payment of publication fees. Therefore, and solely to indicate this fact, this article is hereby marked “advertisement” in accordance with 18 USC section 1734.
Footnotes
Note: Supplementary data for this article are available at Cancer Prevention Research Online (http://cancerprevres.aacrjournals.org/).
Authors' Disclosures
R.M. Tamimi reports grants from NIH/NCI during the conduct of the study. G.A. Colditz reports a patent for ADAPT: Automated Volumetric Mammographic Density Assessment by Pixel Thresholding for Individual Breasts pending. S. Jiang reports a patent for ADAPT: Automated Volumetric Mammographic Density Assessment by Pixel Thresholding for Individual Breasts pending. No disclosures were reported by the other authors.
Authors' Contributions
S. Chen: Data curation, software, formal analysis, writing–original draft, writing–review and editing. R.M. Tamimi: Investigation, writing–review and editing. G.A. Colditz: Resources, data curation, supervision, funding acquisition, investigation, methodology, project administration, writing–review and editing. S. Jiang: Conceptualization, resources, data curation, software, formal analysis, supervision, funding acquisition, validation, investigation, methodology, project administration, writing–review and editing.
References
- 1. Boyd NF, Rommens JM, Vogt K, Lee V, Hopper JL, Yaffe MJ, et al. Mammographic breast density as an intermediate phenotype for brea cancer. Lancet Oncol 2005;6:798–808. [DOI] [PubMed] [Google Scholar]
- 2. Eriksson M, Eklund M, Borgquist S, Hellgren R, Margolin S, Thoren L, et al. Low-dose tamoxifen for mammographic density reduction: a randomized controlled trial. J Clin Oncol 2021;39:1899–908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Kleinstern G, Scott CG, Tamimi RM, Jensen MR, Pankratz VS, Bertrand KA, et al. Association of mammographic density measures and breast cancer "intrinsic" molecular subtypes. Breast Cancer Res Treat 2021;187:215–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Burton A, Byrnes G, Stone J, Tamimi RM, Heine J, Vachon C, et al. Mammographic density assessed on paired raw and processed digital images and on paired screen-film and digital images across three mammography systems. Breast Cancer Res 2016;18:130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Warner ET, Rice MS, Zeleznik OA, Fowler EE, Murthy D, Vachon CM, et al. Automated percent mammographic density, mammographic texture variation, and risk of breast cancer: a nested case–control study. NPJ Breast Cancer 2021;7:68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Gastounioti A, Kasi CD, Scott CG, Brandt KR, Jensen MR, Hruska CB, et al. Evaluation of LIBRA software for fully automated mammographic density assessment in breast cancer risk prediction. Radiology 2020;296:24–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Brandt KR, Scott CG, Miglioretti DL, Jensen MR, Mahmoudzadeh AP, Hruska C, et al. Automated volumetric breast density measures: differential change between breasts in women with and without breast cancer. Breast Cancer Res 2019;21:118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Rice MS, Bertrand KA, VanderWeele TJ, Rosner BA, Liao X, Adami HO, et al. Mammographic density and breast cancer risk: a mediation analysis. Breast Cancer Res 2016;18:94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Rosner B, Tamimi RM, Kraft P, Gao C, Mu Y, Scott C, et al. Simplified breast risk tool integrating questionnaire risk factors, mammographic density, and polygenic risk score: development and validation. Cancer Epidemiol Biomarkers Prev 2021;30:600–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Brooks JD, Nabi HH, Andrulis IL, Antoniou AC, Chiquette J, Despres P, et al. Personalized risk assessment for prevention and early detection of breast cancer: integration and implementation (PERSPECTIVE I&I). J Pers Med 2021;11:511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Vilmun BM, Vejborg I, Lynge E, Lillholm M, Nielsen M, Nielsen MB, et al. Impact of adding breast density to breast cancer risk models: a systematic review. Eur J Radiol 2020;127:109019. [DOI] [PubMed] [Google Scholar]
- 12. Schmidt DF, Makalic E, Goudey B, Dite GS, Stone J, Nguyen TL, et al. Cirrus: an automated mammography-based measure of breast cancer risk based on textural features. JNCI Cancer Spectr 2018;2:pky057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Pettersson A, Graff RE, Ursin G, Santos Silva ID, McCormack V, Baglietto L, et al. Mammographic density phenotypes and risk of breast cancer: a meta-analysis. J Natl Cancer Inst 2014;106:dju078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Jiang S, Cao J, Rosner B, Colditz GA. Supervised two-dimensional functional principal component analysis with time-to-event outcomes and mammogram imaging data. Biometrics 2023;79:1359–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Jiang S, Cao J, Colditz GA, Rosner B. Predicting the onset of breast cancer using mammogram imaging data with irregular boundary. Biostatistics 2023;24:358–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Bevers TB, Ward JH, Arun BK, Colditz GA, Cowan KH, Daly MB, et al. Breast cancer risk reduction, version 2.2015. J Natl Compr Canc Netw 2015;13:880–915. [DOI] [PubMed] [Google Scholar]
- 17. Colditz GA, Bennett DL, Tappenden J, Beers C, Ackermann N, Wu N, et al. Joanne knight breast health cohort at siteman cancer center. Cancer Causes Control 2022;33:623–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Libesman S, Zackrisson S, Hofvind S, Seidler AL, Bernardi D, Lang K, et al. An individual participant data meta-analysis of breast cancer detection and recall rates for digital breast tomosynthesis versus digital mammography population screening. Clin Breast Cancer 2022;22:e647–e54. [DOI] [PubMed] [Google Scholar]
- 19. Busana MC, Eng A, Denholm R, Dowsett M, Vinnicombe S, Allen S, et al. Impact of type of full-field digital image on mammographic density assessment and breast cancer risk estimation: a case–control study. Breast Cancer Res 2016;18:96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Habel LA, Lipson JA, Achacoso N, Rothstein JH, Yaffe MJ, Liang RY, et al. Case-control study of mammographic density and breast cancer risk using processed digital mammograms. Breast Cancer Res 2016;18:53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Jiang S, Bennett DL, Rosner BA, Colditz GA. Longitudinal analysis of change in mammographic density in each breast and its association with breast cancer risk. JAMA Oncol 2023;9:808–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Colditz GA, Hankinson SE. The Nurses' health study: lifestyle and health among women. Nat Rev Cancer 2005;5:388–96. [DOI] [PubMed] [Google Scholar]
- 23. Keller BM, Nathan DL, Wang Y, Zheng Y, Gee JC, Conant EF, et al. Estimation of breast percent density in raw and processed full field digital mammography images via adaptive fuzzy c-means clustering and support vector machine segmentation. Med Phys 2012;39:4903–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Lee HN, Sohn YM, Han KH. Comparison of mammographic density estimation by Volpara software with radiologists' visual assessment: analysis of clinical-radiologic factors affecting discrepancy between them. Acta Radiol 2015;56:1061–8. [DOI] [PubMed] [Google Scholar]
- 25. Mintz R, Wang M, Xu S, Colditz GA, Markovic C, Toriola AT. Hormone and receptor activator of NF-kappaB (RANK) pathway gene expression in plasma and mammographic breast density in postmenopausal women. Breast Cancer Res 2022;24:28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Alimujiang A, Imm KR, Appleton CM, Colditz GA, Berkey CS, Toriola AT. Adiposity at age 10 and mammographic density among premenopausal women. Cancer Prev Res 2018;11:287–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Gail M, Lu JH, Rubinstein L. Likelihood calculations for matched case–control studies and survival studies with tied death times. Biometrika 1980;68:703–7. [Google Scholar]
- 28. Peng C, Gao C, Lu D, Rosner BA, Zeleznik O, Hankinson SE, et al. Circulating carotenoids and breast cancer among high-risk individuals. Am J Clin Nutr 2021;113:525–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Therneau TM, Lumley T, Atkinson E, Cynthia C. Package “survival.” 3–11–2023. Available from: https://cran.r-project.org/web/packages/survival/survival.pdf.
- 30. Uno H, Cai T, Tian L, Wei L-J. Evaluating prediction rules for t-year survivors with censored regression models. J Am Statist Assoc 2007;102:527–37. [Google Scholar]
- 31. Burton A, Maskarinec G, Perez-Gomez B, Vachon C, Miao H, Lajous M, et al. Mammographic density and ageing: a collaborative pooled analysis of cross-sectional data from 22 countries worldwide. PLoS Med 2017;14:e1002335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Brentnall AR, Cuzick J, Buist DSM, Bowles EJA. Long-term accuracy of breast cancer–risk assessment combining classic risk factors and breast density. JAMA Oncol 2018;4:e180174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Brentnall AR, Harkness EF, Astley SM, Donnelly LS, Stavrinos P, Sampson S, et al. Mammographic density adds accuracy to both the tyrer-cuzick and gail breast cancer risk models in a prospective UK screening cohort. Breast Cancer Res 2015;17:147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Brandt KR, Scott CG, Ma L, Mahmoudzadeh AP, Jensen MR, Whaley DH, et al. Comparison of clinical and automated breast density measurements: implications for risk prediction and supplemental screening. Radiology 2016;279:710–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Jeffers AM, Sieh W, Lipson JA, Rothstein JH, McGuire V, Whittemore AS, et al. Breast cancer risk and mammographic density assessed with semiautomated and fully automated methods and BI-RADS. Radiology 2017;282:348–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Kerlikowske K, Scott CG, Mahmoudzadeh AP, Ma L, Winham S, Jensen MR, et al. Automated and clinical breast imaging reporting and data system density measures predict risk for screen-detected and interval cancers: a case–control study. Ann Intern Med 2018;168:757–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Maghsoudi OH, Gastounioti A, Scott C, Pantalone L, Wu F-F, Cohen EA, et al. Deep-LIBRA: an artificial-intelligence method for robust quantification of breast density with independent validation in breast cancer risk assessment. Med Image Anal 2021;73:102138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Evans DGR, van Veen EM, Harkness EF, Brentnall AR, Astley SM, Byers H, et al. Breast cancer risk stratification in women of screening age: incremental effects of adding mammographic density, polygenic risk, and a gene panel. Genet Med 2022;24:1485–94. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Table S1: Hazards ratio for association between baseline risk factors and breast cancer risk among postmenopausal women using CC-VPD only.
Supplementary Table S2: Hazards ratio for association between baseline risk factors and breast cancer risk among postmenopausal women using MLO-VPD only.
Supplementary Table S3: Hazards ratio for association between baseline risk factors and breast cancer risk among postmenopausal women using Full-VPD only.
Supplementary Table S4: Hazards ratio (95% Confidence Interval) for association between baseline risk factors and breast cancer risk among pre-menopausal women using CC-VPD only.
Supplementary Table S5: Hazards ratio (95% Confidence Interval) for association inure-menopausal women between baseline risk factors and breast cancer risk utilizing MLOL-VPD
Supplementary Table S6: Hazards ratio of association among premenopausal women for baseline risk factors and breast cancer risk utilizing FULL-VPD
Supplementary Figure S1: Cohort recruit and follow up chart.
Supplementary Figure S2: Pearson correlation between our algorithm and Volpara shows strong positive linear relationship of 0.81.
Supplementary Figure S3: Pearson correlation separated by view and case control status.
Supplementary Figure S4: The linearity assumption is checked with Martingale residual plots.
Supplementary Figure S5: The proportional hazards assumption is deemed reasonable by checking the Schoenfeld residuals plot for CC-VPD.
Supplementary Figure S6: The proportional hazards assumption is deemed reasonable by checking the Schoenfeld residuals plot for MLO-VPD.
Supplementary Figure S7: The proportional hazards assumption is deemed reasonable by checking the Schoenfeld residuals plot for Full-VPD.
Data Availability Statement
All datasets were accessed and used under IRB-approved protocols and are available from the corresponding author upon reasonable request. The density estimation pipeline developed at Washington University is available upon request.