Abstract
Microbial strategies for resource use are an essential determinant of their fitness in complex habitats. When facing environments with multiple nutrients, microbes often use them sequentially according to a preference hierarchy, resulting in well-known patterns of diauxic growth. In theory, the evolutionary diversification of metabolic hierarchies could represent a mechanism supporting coexistence and biodiversity by enabling temporal segregation of niches. Despite this ecologically critical role, the extent to which substrate preference hierarchies can evolve and diversify remains largely unexplored. Here, we used genome-scale metabolic modeling to systematically explore the evolution of metabolic hierarchies across a vast space of metabolic network genotypes. We find that only a limited number of metabolic hierarchies can readily evolve, corresponding to the most commonly observed hierarchies in genome-derived models. We further show how the evolution of novel hierarchies is constrained by the architecture of central metabolism, which determines both the propensity to change ranks between pairs of substrates and the effect of specific reactions on hierarchy evolution. Our analysis sheds light on the genetic and mechanistic determinants of microbial metabolic hierarchies, opening new research avenues to understand their evolution, evolvability, and ecology.
Keywords: microbial evolution, genotype–phenotype maps, metabolic hierarchies
Introduction
When presented with an environment with multiple nutrients, many microbes tend to use them one at a time in a preferred order. This phenomenon of hierarchical substrate use was famously characterized by Monod in the decade of 1940 (Monod 1942) when he coined the term “diauxie” to describe the experimentally observed double growth curve pattern. Despite the foundational role of Monod's work in molecular biology (Jacob and Monod 1961; Belliveau et al. 2018), we still know surprisingly little about the evolution and diversity of resource hierarchies across bacterial species (Perrin et al. 2020). For instance, are some hierarchies easier to evolve than others? And what determines how easy it is to evolve a preference for a given substrate?
The questions about the ecology and evolution of metabolic hierarchies have received renewed attention in recent years (Bajic and Sanchez 2020; Okano et al. 2021), as part of the ongoing effort to understand the drivers of microbial community assembly and coexistence (Chang et al. 2022; Estrela et al. 2022; Gralka et al. 2022; Schäfer et al. 2023). Recent theoretical work (Posfai et al. 2017; Goyal et al. 2018; Pacciani-Mori et al. 2020; Wang et al. 2021; Bloxham et al. 2023) and experiments with model communities (Pacciani-Mori et al. 2020; Bloxham et al. 2022) have shown that differences in metabolic hierarchies can impact ecology, for example by allowing species to segregate their metabolic niches and avoid competition. Although these studies carry the implicit assumption that metabolic preferences will readily diversify provided the ecological opportunity (e.g., in an environment with multiple nutrients), it is unclear in which cases this assumption will hold true. Systematic empirical analyses are lacking, and available evidence remains scarce and anecdotal. For example, the deep conservation of some preferences, for example the almost universal preference for glucose in fermentative microbes (Görke and Stülke 2008), would suggest that metabolic hierarchies are hard to rewire. If this is the case, we would expect metabolic hierarchies to be deeply conserved in the phylogenetic tree and act as a mechanism of coexistence only between distantly related species. However, other studies report divergent resource preferences in closely related species (Tuncil et al. 2017), implying that metabolic hierarchies can quickly diversify. In this scenario, we might expect resource hierarchies to promote the coexistence of closely related strains and possibly also lead to eco-evolutionary feedbacks (Bajić et al. 2018; Pacciani-Mori et al. 2020). Thus, in order to better understand the role of metabolic hierarchies in structuring coexistence within microbial communities, it is imperative to understand in a systematic way their potential to diversify.
A central determinant of the evolution of biological systems is the underlying genotype–phenotype (G–P) map (Fontana and Schuster 1998; Stadler et al. 2001). The architecture of this map determines the amount of phenotypic variation that can be accessed via mutations, which ultimately fuels evolution. Even in the presence of selection, evolution often follows lines of “least genetic resistance” (Schluter 1996), which are in principle determined by the G–P map. In the case of metabolic traits, the structure of the metabolic network is a central determinant of this map. The structure of metabolism has been shown to influence the evolution of individual enzymes (Papp et al. 2004; Vitkup et al. 2006; Notebaart et al. 2014; Aguilar-Rodríguez and Wagner 2018), metabolic innovation (Barve and Wagner 2013), or eco-evolutionary interactions (Bajić et al. 2018). Importantly, recent work has demonstrated that the structure of the metabolic network is also a key determinant of the strategy microbes adopt in mixed substrate environments, for example their choice to use them sequentially versus simultaneously (Wang et al. 2019). Because preferential substrate use represents an optimal metabolic strategy (Salvy and Hatzimanikatis 2021), the presence of one pathway or another will fundamentally determine which substrates an organism prefers, as different pathways have a different balance of benefits and costs when processing a substrate (Noor et al. 2016; Waschina et al. 2016; Wortel et al. 2018). However, how precisely the structure of the metabolic networks determines and constrains the evolution of metabolic hierarchies remain unexplored.
Here, we asked how the metabolic G–P map determines the evolutionary flexibility of microbial metabolic hierarchies using genome-scale metabolic modeling. Metabolic modeling techniques such as Flux Balance Analysis (FBA) enable accurate predictions of metabolic phenotypes from genotypes (Orth et al. 2011; Bordbar et al. 2014; O’Brien et al. 2015) and are widely used as a workhorse for the comprehensive exploration of metabolic G–P maps (Segrè et al. 2005; Barve and Wagner 2013; Notebaart et al. 2014; Szappanos et al. 2016; Goldford et al. 2017). Using FBA, we first show that a handful of “typical” resource hierarchies appear much more commonly across genotype space than other configurations. Hierarchies are easier to rewire for substrates that are more metabolically different. However, their evolutionary flexibility strongly depends on the presence or absence of a small number of central metabolic reactions that determine the behavior of the metabolic network across substrates. Our study provides the first systematic analysis of how metabolic networks determine the evolution of metabolic hierarchies, and we end by proposing new testable hypotheses, null expectations, and potential directions for future studies.
Results
How Easily Can Metabolic Hierarchies Evolve and Diversify?
We began by asking whether metabolic hierarchies could readily evolve and diversify through changes in the set of reactions encoded in a bacterial genome. To address this question, we employed the Markov chain Monte Carlo method, a widely used technique to uniformly sample multidimensional spaces (Metropolis and Rosenbluth 1953) that has also been applied to sample G–P maps (Samal et al. 2010). Using this procedure, we obtained 9,974 genotypes that are randomly and distributed across metabolic genotype space (see Materials and Methods). Briefly, to obtain each genotype, we started from the Escherichia coli metabolic model iJO1366 (Orth et al. 2011) and performed 10,000 random reaction swaps, removing a reaction from the model and adding another one from a universal set of prokaryotic reactions (fig. 1A; see Materials and Methods). We restricted our random walk to the space of genotypes capable of growth on seven sugars whose growth ranks are well predicted by performing FBA on the E. coli model (glucose, fructose, mannose, fucose, melibiose, galactose, and ribose; supplementary fig. S1A, Supplementary Material online; see Materials and Methods). Because sequential substrate use is an optimal strategy aimed at maximizing the growth benefit from a substrate (Beg et al. 2007; Kremling et al. 2015; de Groot et al. 2019; Wang et al. 2019; Salvy and Hatzimanikatis 2021), the preference hierarchy usually matches the hierarchy in growth rates (Aidelberg et al. 2014). To confirm this point, we used a global resource allocation constraint (see Materials and Methods), which is known to reproduce experimentally observed patterns of sequential substrate use (Beg et al. 2007; Salvy and Hatzimanikatis 2021). This confirmed that our substrates are not coutilized but sequentially used according to their growth rate hierarchy (supplementary fig. S1B, Supplementary Material online). Thus, in the rest of the paper, we use the growth hierarchy as a proxy for resource use hierarchy in our seven sugars.
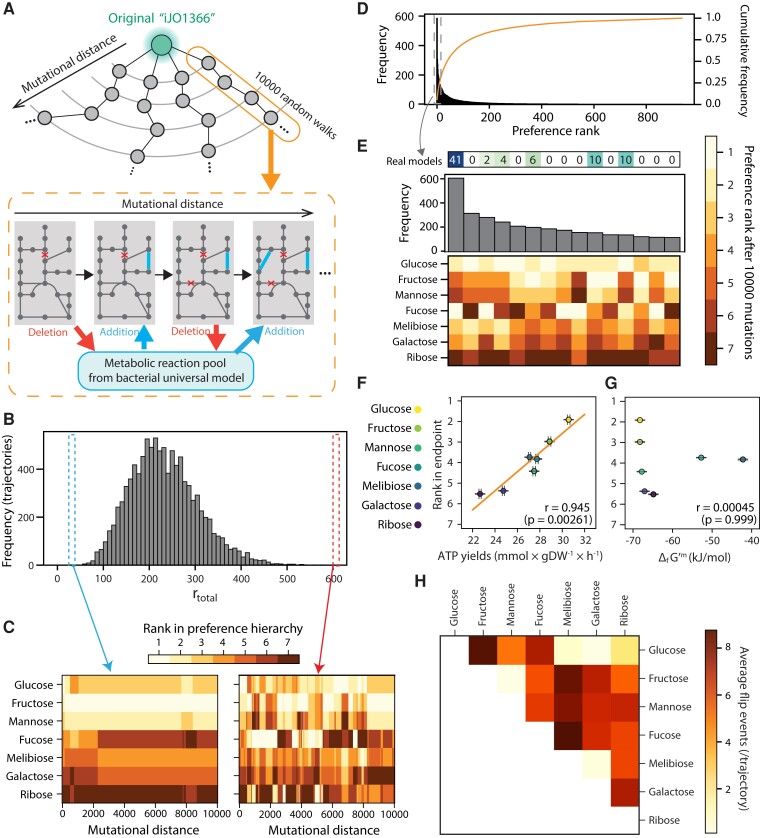
Fig. 1.
Some sugar hierarchies are easier to evolve than others. (A) A schematic of random walk trajectories through genotype space. At each step, a reaction from the model is exchanged by a new reaction from a universal bacterial reaction set (“universal model,” see Materials and Methods). (B) Large variation in metabolic hierarchy rewiring among random walk trajectories. The histogram shows the frequency of total rank flip events (rtotal) during random walks in the 9,974 trajectories. (C) Changes in metabolic hierarchy along an example random-walks trajectory. We show two cases, where the rank swaps rarely (left) or frequently (right) occurred. The preference rank of each sugar at each mutational distance is shown as a heatmap. (D) Convergence of the preference rank to small subsets among all possible preference ranks after random walks. The histogram shows the frequency of each preference rank at the end of the random walks in the 9,974 evolutionary trajectories. The line shows the cumulative distribution of the frequency of preference rank. (E) Zoom of the top 15 most frequent metabolic hierarchies, representing the final point of 3,068 of 9,974 trajectories (histogram), or about ∼30% of the total. We displayed the number of a real organism's models whose preference rank matches each rank configuration. (F) Correlation between the average rank of seven sugars and the average ATP yields at the end of random walks (n = 1,000 genotypes; see Materials and Methods). (G) Correlation between Gibbs free energy of a sugar and the average ranks at the end point in seven sugars. Gibbs free energy was normalized by the number of carbons. In both panels, Pearson's correlations were displayed with P-value obtained using a permutation test (see Materials and Methods). (H) Average number of rank flip events between pairs of sugars during random walks in 9,974 evolutionary trajectories. Sugars are ordered by their initial preference rank in the E. coli model.
An important driver of the evolution of any trait is the availability of enough phenotypic variation accessible by mutations (Besnard et al. 2020). In our trajectories, in absence of selection, rewiring of hierarchies occurred on average fairly often, implying that there is substantial accessible phenotypic variation across the G–P map (fig. 1B and C). However, the outcomes of our trajectories were quite nonuniformly distributed. Namely, 3,068 trajectories (≈30% of all trajectories, N = 9,974) ended in 1 of ∼15 configurations, of the 7! = 5,040 theoretically possible (fig. 1D). To give a sense of the magnitude of this bias, under a null model in which every hierarchy has equal chance to appear, the top 15 most frequent hierarchies would be expected to appear in only 51.5 ± 1.95 (SD) trajectories (N = 10,000; supplementary fig. S2, Supplementary Material online).
The most frequent outcomes among our randomly sampled genotypes were strongly reminiscent of established empirical observations. For instance, glucose was among the top ranked substrates in many of these frequently occurring hierarchy configurations. In addition, we found that these typical hierarchies also appeared recurrently in genome-derived models of real organisms (fig. 1E and supplementary fig. S3, Supplementary Material online). For example, 73 of 81 genome-derived models correspond to 1 of the 14 hierarchies most frequently found in randomly sampled metabolic genotypes (supplementary fig. S3, Supplementary Material online). In addition, a phylogenetic analysis of genome-derived models revealed a striking degree of conservation in metabolic hierarchies (supplementary fig. S4, Supplementary Material online). For the most phylogenetically distant species in our dataset (belonging to different phyla), the Spearman correlation coefficient was on average 0.73 (supplementary fig. S5A, Supplementary Material online). This contrasted with the comparatively low conservation of growth rates in individual sugars (supplementary fig. S5B, Supplementary Material online). The preference rank of three taxonomically distant bacterial groups also exhibited common trends, for example glucose and fructose were universally preferred to galactose or ribose (supplementary fig. S4, Supplementary Material online). Altogether, these results suggest that the metabolic G–P map is strongly biased toward a reduced number of resource hierarchy configurations.
Is there a possible biochemical explanation to the observed conservation of metabolic hierarchies? To address this question, we computed the average ATP yield of each sugar across genotypes. This typical ATP yield was strongly correlated to the average rank of the sugars in the hierarchy across genotypes (fig. 1F). However, the energy of formation of the different sugars (ΔfG’m) was not correlated to the hierarchy rank (fig. 1G). The fact that sugars with very similar ΔfG’m, for example glucose, fructose, or mannose, have a different average rank, suggests that stoichiometry (i.e., the ability to transform ΔG into ATP) plays a dominant role in determining resource hierarchies.
A particularly important aspect of hierarchy evolution is the ability of two substrates to switch their ranks in the hierarchy. If two substrates’ ranks can be easily switched, this would allow an easy evolution of metabolic specialization through differential resource preference. When we examined the evolutionary flexibility in the ranks of specific substrate pairs, we found again a very biased distribution in which some sugar pairs swapped their ranks much more often than others in our mutational trajectories (fig. 1H).
Finally, we also noticed that different trajectories give distinctly idiosyncratic growth rate changes during random walks among seven sugars (supplementary fig. S6A, Supplementary Material online), which resulted in markedly different degrees of metabolic hierarchy rewiring (mean = 233.2 total hierarchy changes per trajectory, SD = 73.5; fig. 1B and C and supplementary fig. S7, Supplementary Material online). This suggests that specific characteristics of the genetic background could modify the amount of accessible variation and thus the evolutionary flexibility of metabolic hierarchies (Rutherford and Lindquist 1998; Bergman and Siegal 2003; Richardson et al. 2013; Geiler-Samerotte et al. 2019; Poyatos 2020).
Overall, these patterns suggest that the architecture of metabolic networks strongly affects the evolution of metabolic hierarchies by 1) biasing the outcomes of metabolic rewiring toward specific hierarchy configurations, 2) making the rewiring easier for some pairs of substrates than others, and 3) modifying the amount of phenotypic variation accessible to mutations. In the following sections, we study the structural and mechanistic determinants of these patterns.
Metabolic Dissimilarity Predicts Hierarchy Swaps in Pairs of Substrates
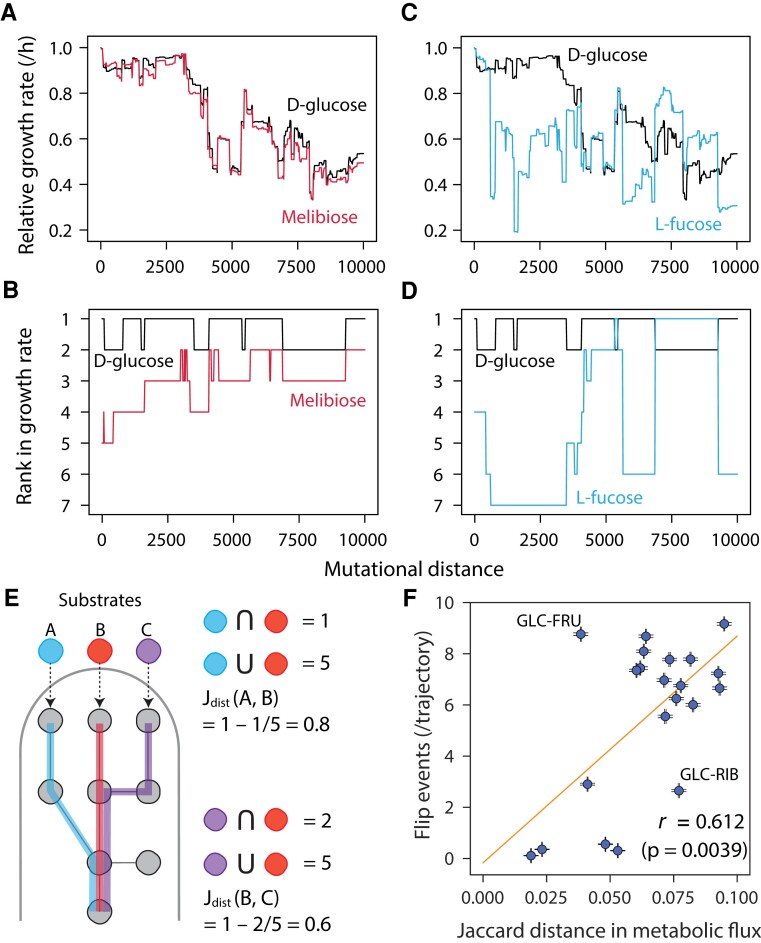
Why are the ranks in some pairs of substrates more easy to change than in others? We reasoned that a primary requirement for two substrates to flip their ranks is the existence of mutations that will affect each of them independently. If two substrates are processed largely by the same pathways, the same mutations should affect their growth similarly (e.g., glucose/melibiose, fig. 2A) resulting in a lower propensity to flip their ranks (fig. 2B). In contrast, substrates that are processed by different pathways have more opportunities to evolve independently and thus swap their hierarchy (e.g., glucose/fucose, fig. 2C and D). Thus, we hypothesized that the metabolic distance between two substrates will predict their propensity to swap their ranks.
Fig. 2.
Metabolic dissimilarity predicts hierarchy flips in pairs of substrates (A) and representative random walk trajectories (C). Two trajectories are compared for a metabolically similar (glucose and melibiose, A) and dissimilar (glucose and fucose, C) pairs of sugars. (B) and (D) Resource preference trajectories in the same trajectories shown in (A) and (C). (E) A schematic of calculating Jaccard distance in processing metabolic pathways between two sugars. The number of commonly used reactions for processing both two sugars was divided by the total metabolic reactions used to process each sugar (i.e., Jaccard similarity), and this value was subtracted from 1. In this scheme, we show examples in two pairs of sugars. (F) The dissimilarity in metabolic pathway (Jaccard distance) predicts the rank-flip events in 21 pairs of sugars. An orange line shows linear regressions, the error bars indicate ±SEM, and r stands for Pearson's correlations (N = 9,974) with Mantel test (106 permutations).
To test this hypothesis, we first need to quantify the metabolic distances between substrate pairs. Because two substrates partially share the pathways and reactions through which they are catabolized, we computed metabolic distance using a weighted Jaccard distance between the sets of reactions used by each metabolite (fig. 2E; see Materials and Methods). Although this distance will be genotype-specific (supplementary fig. S8A, Supplementary Material online), we observed that the distances between two substrates quickly converged to a typical value across genotypes during random walks (supplementary fig. S8, Supplementary Material online). Confirming our hypothesis, these “typical” pairwise metabolic distances predicted the propensity of two substrates to rewire their ranks (fig. 2F). Note that some of the outliers of this correlation (e.g., the glucose–ribose pair, supplementary fig. S6B, Supplementary Material online) can be explained by their large difference in average growth rates, leading to infrequent rank flips despite a large metabolic dissimilarity. However, in contrast to metabolic dissimilarity, this effect showed no explanatory power across all pairs (supplementary fig. S6C, Supplementary Material online). Thus, we conclude that the evolutionary flexibility in the hierarchy of two substrates is fundamentally determined by their metabolic dissimilarity.
The Architecture of Central Metabolism Controls the Evolutionary Flexibility of Metabolic Hierarchies
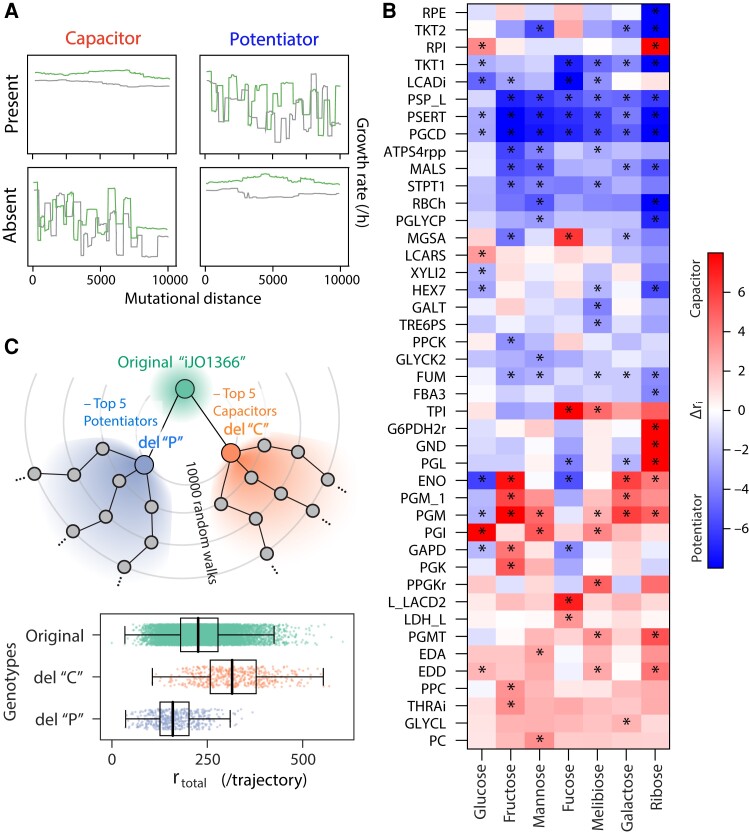
As shown in figure 1B and C, our random walk trajectories differed markedly in the frequency of shifts in metabolic hierarchies. Although part of this variation is expected because of stochastic sampling of mutations, the presence of specific reactions could also affect the evolvability of metabolic hierarchies by either buffering (capacitors) or potentiating (potentiators) the phenotypic effect of other mutations (Rutherford and Lindquist 1998; Bergman and Siegal 2003; Richardson et al. 2013; Geiler-Samerotte et al. 2019; Poyatos 2020). Can we pinpoint the observed differences in the evolutionary flexibility of metabolic hierarchies to the presence or absence of specific metabolic reactions in the genetic background?
To examine this question, we first compared the number of rank shifts (ri) between trajectories in which a focal reaction was present (TR+) or absent (TR−) along the most part of the trajectory (fig. 3A; see Materials and Methods). Our analysis revealed 43 reactions, which were associated with differences in the evolvability of the metabolic rank of at least one sugar (P < 0.01, Wilcoxon test with false discovery rate [FDR] correction, fig. 3B). To test whether these reactions did indeed alter the phenotypic variation in metabolic hierarchies, we ran two additional sets of 500 random walks, starting from a model either lacking capacitors (“del C”) or potentiators (“del P,” see Materials and Methods). As expected, these trajectories exhibited an opposite trend in terms of the number of rank swap events (fig. 3C). Thus, the presence of specific metabolic reactions critically determines the evolvability of metabolic hierarchies in our trajectories.
Fig. 3.
Propensity of rank flips strongly depends on the genetic background. (A) A schematic of the mutational effect of evolutionary capacitors and potentiators on growth-rate trajectories and propensity of rank flips. If the presence of the reaction of interest caused little effect on growth rate and the preference rank (top left) but its deletion caused their frequent changes (bottom left), such reaction was regarded as a “capacitor.” On the other hand, if the growth rate changes and rank flips were prevented by the deletion of the reaction (bottom right) but promoted in its presence, such reaction was regarded as a “potentiator.” Briefly, we screened those evolutionarily important reactions by computing the difference in rank flips (ri) between its presence [ri (TR+)] or absence [ri (TR−)] (Δri, see Materials and Methods). (B) Screened evolutionary capacitors and potentiators in metabolic networks by statistical analysis (P-value <0.01, FDR corrected). Δri in each metabolic reaction was shown as a heatmap. We put asterisks for significant reaction–sugar pairs. The shown metabolic reaction IDs correspond to BiGG ID. (C) Opposite effect on the propensity of rank flips between the deletions of capacitors or potentiators. We deleted 5 potentiators (“del P”) or capacitors (“del C”) from iJO1366 and performed 10,000 random walks by starting from each of them. Box and strip plots show the number of total rank flip events across 7 sugars during random walks (N = 500) in the displayed genetic backgrounds. Bold black lines indicate medians of each data.
The Mechanisms Controlling the Evolutionary Flexibility of Metabolic Hierarchies
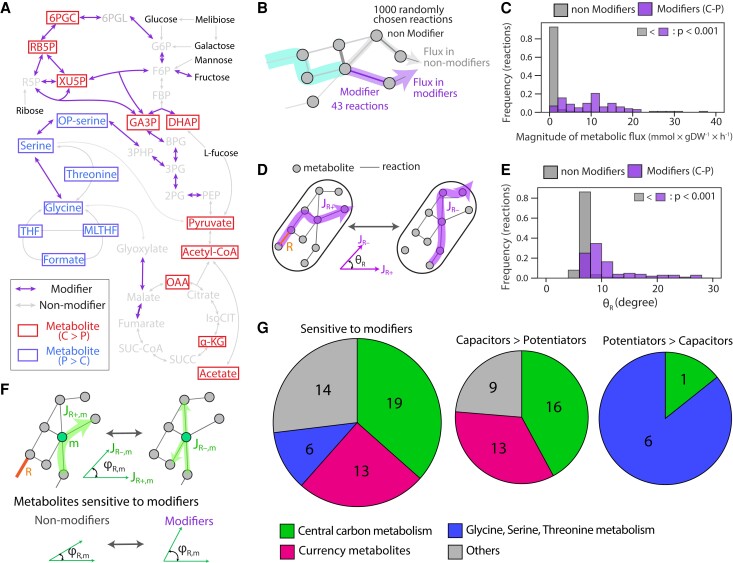
How do specific reactions modify the evolutionary flexibility of metabolic hierarchies? We hypothesized that modifiers (i.e., capacitors and potentiators) act by disproportionately impacting metabolites used by multiple sugars. By doing this, mutations in modifiers can decouple and reconnect sugars with one another, allowing them to evolve more or less independently. This hypothesis is supported by the fact that modifiers generally belong to central metabolism, for example glycolysis, tricarboxylic acid (TCA) cycle, or pentose phosphate pathway (PPP, fig. 4A). These reactions tend to carry flux across genotypes and resources (fig. 4B–C), and their disruption heavily alters the distribution of fluxes across the rest of the network (fig. 4D–E).
Fig. 4.
Specific reactions and metabolites govern the effects of mutations on resource hierarchies. (A) The locations of evolutionary modifiers and sensitive metabolites to the modifiers in a metabolic network. Here, we mapped them on the central carbon metabolic pathways, that is PPP, glycolysis, glycine/serine/threonine pathway, and TCA cycle, where many of those are involved. Metabolites that were more strongly affected by capacitors or potentiators are colored by red and blue, respectively. (B) and (C) Comparison of magnitude of flux between modifiers and nonmodifiers. We randomly picked out 1,000 evolved models and calculated the average flux carried by 43 reactions screened as modifiers (purple) and randomly chosen 1,000 nonmodifier reactions (gray) across 7 sugars (7301 reaction-sugar pairs). Among those, we selected the pairs working as modifiers (marked with asterisks in fig. 3B, N = 107) and compared them with other pairs (nonmodifier pairs, N = 7,194). Comparison of mean value and statistical significance level were indicated (Wilcoxon rank-sum test). (D) A schematic of “flux sensitivity” analysis. For randomly picked 1,000 evolved models, we added or deleted the target reaction R depending on whether it exists or not. Then, we calculated the cosine similarity of the total flux distribution between presence (JR+) or absence (JR−) of the reaction (θR). Similarly to (B) and (C), we calculated θR of 43 modifiers and 1000 nonmodifiers for each of 7 sugars, and θR is used as the proxy for flux sensitivity for the reaction R on each sugar. (E) Comparison of flux sensitivity (θR) among nonmodifiers (non C-P) or modifiers (C-P). Among 7,301 reaction-sugar pairs, we selected the pairs exhibiting statistically significant effects (marked with asterisks in fig. 3B). Then, we checked whether θR is significantly larger in modifiers than nonmodifiers (Wilcoxon rank-sum test, P-value is shown in the panel). (F) A schematic of flux sensitivity analysis for metabolites. For each metabolite m, influx and efflux to m were analyzed before and after a deletion or addition of a reaction of interest R. Then, cosine similarity between JR+,m, and JR−,m was calculated (φR,m). By comparing φR,m, we screened the metabolites that are significantly more sensitive to the modifiers. (G) Typical metabolites whose flux is sensitive to modifiers. We categorized the screened metabolites, which are sensitive to either capacitors or potentiators (supplementary fig. S9 and supplementary table S1, Supplementary Material online) into four groups: central carbon metabolism (green), currency metabolites (red), glycine/serine/threonine metabolism (blue), and others (gray) and shown its ratio as a pie chart (left pie chart). We also showed the number of metabolites that are more sensitive to capacitors (middle pie chart) or potentiators (right pie chart) in each category.
To investigate more in detail which specific fluxes are affected by modifiers, we devised a score φR, m quantifying the effect of a mutation in reaction R on the flux of a metabolite m (fig. 4F). As expected, metabolites associated with central metabolic pathways (glycolysis, PPP, or TCA cycle) were strongly affected (fig. 4G), especially in the case of capacitors (fig. 4G). As these pathways are in general the most efficient routes for sugar use, their disruption surfaces other alternatives that might be different for each sugar, thus revealing new mutational targets for the rewiring of metabolic hierarchies. Our analysis also revealed the metabolism of glycine/serine/threonine as an important pathway modulating the flexibility of metabolic hierarchies (fig. 4A and G). Because this pathway can serve as an alternative route from 3-phosphoglycerate to the TCA cycle in our models, its disruption limits the available metabolic alternatives. For this reason, metabolites in the glycine/serine/threonine pathway appear in general associated with potentiator reactions (fig. 4G and supplementary fig. S9, Supplementary Material online). The above logic also suggests that capacitors will more often tend to carry flux than potentiators, and they will also more strongly modify fluxes across the rest of the metabolic network when mutated. This was indeed the case (supplementary fig. S10, Supplementary Material online).
Altogether, these results suggest that by shaping the available metabolic alternatives for different substrates and/or their efficiency, the architecture of central metabolism critically determines the evolutionary flexibility of metabolic hierarchies.
Discussion
The strategies that microorganisms use to metabolize resources have a significant impact on their interactions and coexistence (Bajic and Sanchez 2020; Estrela et al. 2022). Theoretically, having different preferences for the same substrates could enhance biodiversity by allowing temporal niche segregation (Goyal et al. 2018; Bloxham et al. 2023). However, how easily microbial populations evolve alternative metabolic hierarchies remains unclear. In this study, we utilized genome-scale metabolic modeling to investigate how the structure of empirical metabolic G–P maps affects the evolution and diversity in the hierarchical use of sugars by microbes. Our findings indicate that the architecture of the metabolic network only permits the evolution of a limited set of hierarchy configurations. Moreover, the evolution of alternative strategies is restricted to substrates that can be processed through substantially different reactions and pathways. Overall, these findings suggest that the diversity of optimal metabolic hierarchies in natural populations may be in general limited.
The evolutionary flexibility of metabolic hierarchies (within the available alternatives) depended on a small set of reactions belonging to central metabolic pathways. From a genetic point of view, these reactions appear as strongly pleiotropic, as they are often active across different sugars. Because of this, they introduce strong genetic correlations in the growth of different sugars (Falconer and Mackay 1996), preventing to an extent the independent variation in their growth rates and thus “locking” the evolution of metabolic hierarchies. At the same time, these central metabolic reactions act as evolutionary modifiers—capacitors and potentiators that modulate the ability of the genetic system to generate variability and fuel evolution (Rutherford and Lindquist 1998; Bergman and Siegal 2003; Richardson et al. 2013; Geiler-Samerotte et al. 2019; Poyatos 2020). One prediction of this result is that sugar hierarchies will show different degrees of conservation across different clades, depending on the architecture of their central carbon metabolism. This suggests a possible explanation to why some phylogenetically distant species show similar metabolic preferences (e.g., the almost universal preference for glucose over other sugars [Monod 1942; Görke and Stülke 2008]), whereas at the same time for some species and substrates, we find differences between closely related species (Tuncil et al. 2017). Going beyond these anecdotal cases and understanding the evolution and conservation of resource hierarchies will require a more systematic empirical approach. From an ecological standpoint, our observation that some pairs of resources (e.g., glucose–fructose) are much more easily rewired than others (e.g., glucose–galactose), leads to the experimentally testable prediction that coexistence will evolve more often in environments containing the former than the latter (Bloxham et al. 2022; Bloxham et al. 2023). Altogether, we believe that our computational results provide a useful guide and well-defined set of expectations for future empirical studies.
A key assumption of our study is related to optimality in cell behavior. First, FBA operates under a strong assumption of optimality: phenotypes are predicted by assuming that the kinetic parameters of the metabolic enzymes and their regulation are optimal in a particular environment. Although this is generally accepted as a valid approximation (Dykhuizen et al. 1987; Elena and Lenski 2003; Dekel and Alon 2005; Schuetz et al. 2007; Schuetz et al. 2012), it might not be accurate across all conditions (Towbin et al. 2017). Additionally, we assumed that metabolic hierarchies mirror the hierarchy of growth rates. This is reasonable given previous empirical studies (Aidelberg et al. 2014) and, more generally, fits the established view that sequential substrate use represents an optimal “economic” strategy that maximizes the benefit obtained from the investment of costly cellular resources in processing a substrate (Beg et al. 2007; Kremling et al. 2015; de Groot et al. 2019; Wang et al. 2019; Salvy and Hatzimanikatis 2021). However, there are possible exceptions to this rule (Okano et al. 2021), for example if cells have evolved mechanisms to “prepare” for environmental uncertainty at the cost of optimality in certain environments (Schmidt et al. 2016; Balakrishnan et al. 2021). Deviations from optimality might be especially strong in organisms in which nonmetabolic functions (e.g., motility, biofilm formation, persistence) constitute major components of fitness.
An important caveat of our method is the inability to consider the effect of regulatory mutations. For example, E. coli implements the preference of some substrates over others through repression of their respective operons at different cAMP (cyclic adenosine monophosphate) concentration thresholds (Okano et al. 2020). Mutations in this regulatory system, for example promoter mutations changing the binding strength of the repressor, could therefore represent targets in the evolution of metabolic hierarchies. However, these repression thresholds typically evolve to implement a hierarchy matching the growth rates supported by the substrate. In other words, regulation does not define which metabolic strategy is optimal but evolves as a means to implement it. We might therefore expect that regulatory mutations driving the hierarchy away from growth optimality will be typically purged by selection (given that regulatory mechanisms evolve fast compared with their regulation targets (Lozada-Chávez et al. 2006; Price et al. 2008; Aguilar-Rodríguez et al. 2017). However, exceptions to this rule may emerge under certain ecological contexts. For example, regulatory rewiring to prefer suboptimal resources may evolve when resources are supplied sequentially in a nonoptimal order, or when an ecological competitor is able to monopolize the most optimal resource.
We want to note that a core result of this work, the strong bias toward a specific set of hierarchies in the genotype, was obtained using a method that relies only on stoichiometry. Our intuition is that other factors (e.g., thermodynamics, regulatory suboptimality) should overall only additionally constrain the available phenotypes but never “free” them from the yoke imposed by stoichiometry. If this logic is true, our work is providing only a null baseline for phenotypic bias in metabolic hierarchies, which might be in reality even stronger.
In summary, our study describes with mechanistic detail how the metabolic G–P map influences and constrains the evolution of microbial metabolic hierarchies. This mechanistic perspective has proven to be essential in advancing the field of evolutionary biology, as well as other disciplines (Wagner et al. 2000; de Visser et al. 2003). Future research will be required to explore how the patterns and mechanisms outlined in our study contribute to the phylogenetic and ecological distribution of microbial metabolic hierarchies, as well as their implications for natural and synthetic communities.
Materials and Methods
Reconstruction of the Genome-Scale Metabolic Model with Constrained Allocation
We used E. coli genome-scale metabolic model iJO1366 as a reference (Orth et al. 2011). For random walks of metabolic models through genotype space, we constructed bacterial “universal” models as previously described (Bajić et al. 2018). Briefly, we assembled metabolic reactions in prokaryotic metabolic models posted on the BiGG database, which consist of potential novel reactions in addition to the originally existing reactions in the E. coli model. We modified the directionality of metabolic reactions and removed erroneous energy-generating cycles as previously described. This generates the “universal” prokaryotic model, consisting of 5,584 reactions and 3,476 metabolites.
Because the cell has limited internal resources, inefficient but “cheap” pathways result in a higher growth rate than more efficient but expensive ones, by allowing for allocation of larger fractions of the proteome to uptake (Basan et al. 2015). We partially account for this using a global resource allocation constraint (CAFBA, “Constrained Allocation Flux Balance Analysis”, [Mori et al. 2016]) and saturating sugar concentrations. To this end, we implemented the CAFBA constraint as in the original paper. Briefly, partitioning of cellular resources (i.e., proteome) associated with ribosome, biosynthetic enzymes, carbon transport, and basic biological processes (i.e., housekeeping reactions) was introduced as φR, φE, φC, and φQ, respectively. The sum of those proteome fractions should be 1 (i.e., φR + φE + φC + φQ = 1), and each fraction except for φQ can be altered by environmental conditions and physiological states. Previous studies phenomenologically demonstrated dependencies of each fraction on environmental factors: ribosome sector φR is proportionally changed by the growth rate λ (i.e., ΔφR = wRλ); biosynthetic enzymes sector φE changes proportional to the metabolic flux vi such that ΔφE = ∑iwi|vi|; carbon transport sector φC alters proportional to the carbon intake flux vc (i.e., Δφc = wcvc). CAFBA maximizes objective function while optimally partitioning those flexible proteome fractions, φmax = ΔφR + ΔφE + ΔφC. By incorporating those schemes into FBA, we computed flux distribution to maximize growth rate λ with optimally allocating cellular resources to those three partitions. Then, the optimization problem of CAFBA is formulated as follows:
where λmax denotes the maximum growth rate, and v is a metabolic flux vector with the lower and upper bounds (i.e., vlb and vub). b is the vector of objective function. S denotes the stoichiometric matrix of metabolic networks. wR and wc are coefficients for φR and φC, respectively. ∑wi|vi| is the sum of metabolic flux catalyzed by enzymes except for transport and exchange reactions.
Metabolic Simulation of Growth
All FBA simulations were performed using the COBRApy package (Ebrahim et al. 2013). To simulate the growth of bacteria where the limiting factor is only the carbon source, we ran all the simulations under the condition that inorganic ions and gases (ca2_e, cl_e, cobalt2_e, cu2_e, fe2_e, fe3_e, h2O_e, h_e, k_e, mg2_e, mn2_e, mobd_e, na1_e, nh4_e, ni2_e, pi_e, so4_e, zn2_e, o2_e) were present in excess (i.e., the lower bound for exchange reactions for those metabolites was set to −1,000 mmol × gDW−1 × h−1). The lower bound of the exchange reaction for each sugar is set, so that the influx in C atoms is −120 mmol × gDW−1 × h−1 (i.e., if the given sugar is a hexose such as glucose, there are six carbon atoms per molecule, so the lower limit is set to −20 mmol × gDW−1 × h−1). In all simulations, the objective function is the biomass function of iJO1366 (i.e., BIOMASS_Ec_iJO1366_core_53p95M). Optimization problems were solved with Gurobi or CPLEX optimizer.
Simulation of the Repressive Effect on Sugar Influx by Metabolic Hierarchy
The repressive effect on the influx of sugar (i.e., flux in exchange reaction) by the presence of other sugar was simulated by parsimonious FBA (pFBA, supplementary fig. S1, Supplementary Material online) (Lewis et al. 2010). The influx of sugar i, where no other sugars are present is first computed, which is denoted as Ji. Then, the influx in sugar i in the presence of sugar j, denoted as Ji,j, is simulated. The repressive effect of sugar j on the influx of sugar i, which is denoted as Ri,j is formulated as follows:
Ji should always be larger than Ji,j, because the influx of sugar generally should be maximal when that sugar is used as a sole carbon source for the growth. Then, Ri,j < 1. If Ri,j ≈ 1, the influx in sugar i was barely affected by sugar j, indicating that sugar i is ranked higher than sugar j in metabolic hierarchy. On the other hand, if Ri,j ≈ 0, the influx of sugar i is strongly repressed by the presence of sugar j, indicating that sugar i is ranked lower than sugar j. The lower bound of the exchange reaction for sugars is set, so that the influx in Catoms is −120 mmol × gDW−1 × h−1.
Random Walks in Genotype Map
To explore the evolvability of metabolic hierarchy in sugars, we performed random walks by deleting and adding metabolic reactions one by one starting from the iJO1366 model. Because we focused on the effect of mutations in the intracellular metabolic network, we did not add or delete transport reactions. Exchange and sink reactions were also excluded as possible mutations. Starting from the iJO1366 model, in each step of a random walk, we randomly deleted an existing metabolic reaction and then randomly selected one from the universal model to be added one novel reaction from the universal model. This method, known as Markov chain Monte Carlo sampling, is a widely used technique to uniformly sample multidimensional spaces (Metropolis and Rosenbluth 1953) and has also been used in the past to sample G–P maps (Samal et al. 2010).
Once the reaction-swap event was accomplished, the deleted reaction from a model was added to the members of the prokaryotic reaction pool and regarded as a possible novel reaction that could be added at later steps. Similarly, the reaction appended to the model was removed from the prokaryotic reaction pool (fig. 1A). This random swap was performed 5,000 times, resulting in 10,000 additions and deletions of reactions. During random walks, the coexistence of following pairs of reactions was avoided: SHSL2 and SHSL2r, DHORD_NAD and DHORDi, ENO and HADPCOADH, LEUTA and LLEUDr, and P5CRx and PRO1y, because it leads to CO2 or H2 limitation (Bajić et al. 2018).
To prevent our random walks to end up in genotypes that have lost the ability to grow on most sugars, we imposed the constraint that every step during the random walk should result in a model that is still able to grow on all seven sugars. This constraint could however introduce bias in our sampling of genotype space. To relax this constraint, we performed an additional set of 21,000 simulations, this time constraining the models to grow on just two sugars at a time (1,000 random walks per pair of sugars). These simulations reproduce figure 1H to a large extent (supplementary fig. S11, Supplementary Material online), suggesting that our results are robust to changes in this constraint.
Estimation of the Rank in Metabolic Hierarchy by Growth Rate
Since the ranks of seven sugars in the metabolic hierarchy correspond to the ranks in growth rate when each sugar is used as a sole carbon source (for details, see supplementary fig. S1 and supplementary text, Supplementary Material online), we computed the growth rate on every seven sugars during random walks and used this metric for estimating the rank in the hierarchy. We compared the growth rate on each sugar and regarded that sugar i is ranked higher than sugar j if the log10 ratio of the growth rate on sugar i (denoted as gi) and j (denoted as gj) is more than 10−5 as follows:
For sugar i, j, in the metabolic hierarchy,
if
Estimation of Gibbs Free Energy of Formation for Substrates
Estimation of Gibbs free energy of formation (ΔfG’m) for sugars was done using eQuilibrator (Flamholz et al. 2012), a web interface for calculating thermodynamic properties of biochemical compounds. The estimated ΔfG’m for each sugar was normalized by the number of carbons.
Estimation of ATP Yields for Substrates
For estimating ATP yields, we first computed flux distributions for 1,000 randomly evolved models when each of 7 sugars is used by pFBA. Then, we estimated ATP yields for sugars by calculating total flux of metabolic reactions involving ATP except for transport, sink, and biomass reactions as follows:
Here, jk, ATP is the flux in reaction k, and εk, ATP is the coefficient of ATP in reaction k. Positive or negative value for this coefficient means that ATP is produced or consumed through that reaction, respectively. For figure 1F, we calculated the average of the ATP yield (JATP) in 1,000 randomly evolved models for each sugar.
Computation of Preference Ranks in Genome-Derived Models
Using the same criteria as above, we computed the rank in the metabolic hierarchy in the prokaryotic metabolic models constructed by the CarveMe pipeline (Machado et al. 2018). We started from a sample of 5,587 metabolic models available at https://github.com/cdanielmachado/embl_gems (Machado et al. 2018). To obtain a meaningful statistical sample, we searched for the set of sugars able to individually support the growth of a maximum number of models. This resulted in 5 sugars (glucose, fructose, mannose, galactose, ribose) that were able to support the growth of 81 models in total (glucose, fructose, mannose, galactose, ribose). These models are taxonomically broad, spanning three phyla: Bacillota (Firmicutes), Pseudomonadota (Proteobacteria), and Actinomycetota (Actinobacteria).
For the construction of a maximum likelihood phylogenetic tree, we first performed a multiple sequencing alignment (MSA) of the bacterial marker genes by align command in GTDB-tk (version 1.5.0) (Chaumeil et al. 2019). The resulting MSA file from GTDB-tk was further used for a reconstruction of a phylogenetic tree by iqtree (version 2.0.3) (Nguyen et al. 2015) with ModelFinder (Kalyaanamoorthy et al. 2017) for searching the best-fit model (we used “LG + F + I + G4,” here). We used the ETE toolkit (Huerta-Cepas et al. 2016) for visualizing the estimated phylogenetic tree.
Permutation Test for Pearson's Correlation
To check the statistical significance level of a correlation between two parameters, for example supplementary Figure S3B, Supplementary Material online, we performed a random permutation test to check the statistical significance levels of Pearson's correlation. We shuffled two parameters and computed Pearson's correlation using those shuffled data for 100,000 times. The displayed P-value is the probability that the correlations between shuffled data were larger than that observed in the original data.
Computation of Dissimilarity between Pairs of Sugars in Processing Metabolic Pathways
We estimated dissimilarity in used metabolic pathways between two sugars by calculating Jaccard distance in the set of active reactions where the sugar of interest is used for growth as a sole carbon source. We first simulated the flux distribution in intracellular metabolic reactions (i.e., transport reactions were not included) when the model grows on sugar i by pFBA. Then, the set of active reactions Ri, whose flux is more than 10−6 mmol × gDW −1 × h−1, was picked out. The Jaccard distance between sugar i and j in the processing pathways [Jdist(i, j)] was formulated as follows:
Screening of evolutionary modifiers
To screen the reactions whose presence or absence greatly affects the evolvability of the hierarchy during random walks, we selected two types of random walk trajectories: TR+, where the reaction of interest R is present in over 70% of genotypes among first 7,000 mutations; TR−, where the reaction of interest was not present in over 70% of genotypes among last 7,000 mutations. Then, we statistically tested whether ri (propensity of rank flips) was significantly different between TR+ and TR− for each reaction R by t-test using scipy.stats.ttest_ind function with P-value correction for multiple tests by Holm–Sidak method using statsmodels.stats.multitest.multipletests. We screened the reaction showing P-value < 10−6 after correction. We also calculated the magnitude of changes in ri between TR+ and TR− as follows:
If Δri is positive, the absence of reaction R increases the evolutionary flexibility of metabolic hierarchies of the hierarchy by mutations, which means that the reaction R, as it were, masks the effect of mutations during its presence. Then, such a reaction is defined as a “capacitor” for rewiring the metabolic hierarchy. On the other hand, if Δri is negative, the presence of reaction R increases the propensity of rewiring the hierarchy and thus is defined as a “potentiator”. We screened such reactions for two metrics and for each seven sugars. Of note, changing the threshold for TR+ and TR− to 50% or 90% did not produce substantial differences in the score of Δri (supplementary fig. S12A, Supplementary Material online) and the screened reactions as evolutionary modifiers (supplementary fig. S12B, Supplementary Material online), indicating that this analysis is robust to the imposed threshold.
Random Walks Using the Models Lacking Capacitors or Potentiators
To confirm the effect of modifiers on the evolutionary flexibility of the metabolic hierarchy, we removed five representative capacitors or five potentiators from the original iJO1366 before performing additional random walks. We first selected reactions which solely work as either capacitor or potentiator (i.e., not dual ways like “ENO,” which works as a potentiator for glucose but also works as a capacitor for fructose). In each case of potentiator or capacitor, the reactions were sorted by the number of significantly affected substrates. Then the reactions were deleted from the iJO1366 continuously from the top of the list up to five as long as the model can grow on all seven sugars. (i.e., If the reaction is essential for the growth on either of seven sugars, that deletion is canceled.) This gives us the models lacking five capacitors, “PGM,” “PGI,” “TPI,” “L_LACD2,” and “LCARS,” (“del C” in fig. 3C) or five potentiators, “PSERT,” “PGCD,” “PSP_L,” “FUM,” and “MALS” (“del P” in fig. 3C) and being capable of utilizing all seven sugars. Then, we performed 500 independent random walks in each case.
Flux Sensitivity Analysis
The impact of mutation to reaction i (i.e., deletion or addition of the reaction) on the intracellular metabolic flux is estimated by calculating cosine similarity in the flux distribution between before and after the mutation. For randomly mutated models (i.e., models after 10,000 random walks in genotype space), we added or deleted the reaction of interest (denoted as R) if that reaction is absent or present, respectively. We first computed the intracellular flux distribution by pFBA before or after the mutation to R, which is denoted as JR+ or JR−, and normalized it by the growth rate (i.e., the magnitude of biomass flux) as follows:
Here, gR + and gR− are growth rates in the presence or absence of reaction R, respectively. Then, we computed the cosine similarity between those normalized flux distribution matrices as follows:
As a metric of the distance, we used θR (degree). ΔJR is converted to θR as follows:
We computed θR across seven sugars, and the average value of that is used as the metric for flux sensitivity.
For computing the impact on the metabolic flux in a specific metabolite, we picked out fluxes of reactions where the target metabolite m is involved from the normalized intracellular metabolic flux, which are denoted as and , respectively. Then the impact of mutation to reaction R on the flux in metabolite m is as follows:
Experimental Quantification of Growth Hierarchy in E. Coli
E. coli MG1655 was streaked from glycerol on a TSA plate and grown at 37 °C for 24 h. A single colony was used to inoculate 5 mL of TSB medium in a 50 mL Falcon tube. After 24 h incubation at 37 °C, this preculture was then diluted 1:1,000 in M9 minimal medium supplemented with each of 7 carbon sources (glucose, fructose, mannose, fucose, melibiose, galactose, and ribose), at a final concentration of 0.07 moles of carbon per liter. E. coli growth was monitored in a 384-well plate (100 μL/well, 6 replicates each) at 37 °C by optical density (OD) measurements. The maximal exponential growth rate was computed by first smoothing the log(OD620) with a generalized additive model with an adaptive smoother, using the gam function from the mgcv package in R. This method allows for extraction of estimates of growth rate that are not biased by underlying assumptions when fitting parametric models such as logistic or Gompertz. The maximum of the derivative was taken as the exponential growth rate. The first 1 h of growth as well as all of the timepoints in the beginning of the curve that showed an OD < 0.01 were excluded to avoid artifacts derived from measurement and fitting noise.
Supplementary Material
Acknowledgments
We want to thank members of the Sanchez, Bajic, and Miyazaki groups for their helpful discussion.
Contributor Information
Sotaro Takano, Department of Ecology and Evolutionary Biology, Yale University, New Haven, CT, USA; Microbial Sciences Institute, Yale University, New Haven, CT, USA; Bioproduction Research Institute, National Institute of Advanced Industrial Science and Technology (AIST), Tsukuba, Japan.
Jean C C Vila, Department of Ecology and Evolutionary Biology, Yale University, New Haven, CT, USA; Microbial Sciences Institute, Yale University, New Haven, CT, USA; Department of Biology, Stanford University, Stanford, CA, USA.
Ryo Miyazaki, Bioproduction Research Institute, National Institute of Advanced Industrial Science and Technology (AIST), Tsukuba, Japan; Computational Bio Big Data Open Innovation Laboratory (CBBD-OIL), AIST, Tokyo, Japan.
Álvaro Sánchez, Department of Ecology and Evolutionary Biology, Yale University, New Haven, CT, USA; Microbial Sciences Institute, Yale University, New Haven, CT, USA; Department of Microbial Biotechnology, CNB-CSIC, Campus de Cantoblanco, Madrid, Spain.
Djordje Bajić, Department of Ecology and Evolutionary Biology, Yale University, New Haven, CT, USA; Microbial Sciences Institute, Yale University, New Haven, CT, USA; Section of Industrial Microbiology, Department of Biotechnology, Technical University Delft, Delft, The Netherlands.
Supplementary material
Supplementary data are available at Molecular Biology and Evolution online.
Authors’ Contributions
D.B. and A.S. conceived the idea and designed the study. S.T. carried out the simulations, formal analysis, and figure preparation. J.C.C.V and R.M. provided materials and technical assistance. S.T., J.C.C.V, R.M., A.S, and D.B. discussed the results and drafted the paper. S.T. and D.B. wrote the final version of the paper.
Data Availability
All code for simulations, data analysis, and figures can be found in the following github repository https://github.com/sotarotakano/MetabolicHierarchy. Data and code will be provided with corresponding DOI before publication.
Funding
This work was partially funded by a Human Frontier Science Program Young Investigator Award RGY0077/2016 to A.S. and R.M. A.S. was partially supported by the Spanish Ministry of Science and Innovation, under project PID2021-125478NA-100. S.T. was partially supported by Japan Society for the Promotion of Science KAKENHI grants (21K14778) and postdoctoral fellowship (18J01280). R.M. was partially supported by the Institute for Fermentation, Osaka (G-2018-3-028).
Conflict of interest statement. The authors declare no conflicts of interest.
References
- Aguilar-Rodríguez J, Payne JL, Wagner A. 2017. A thousand empirical adaptive landscapes and their navigability. Nat Ecol Evol. 1:45. [DOI] [PubMed] [Google Scholar]
- Aguilar-Rodríguez J, Wagner A. 2018. Metabolic determinants of enzyme evolution in a genome-scale bacterial metabolic network. Genome Biol Evol. 10:3076–3088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aidelberg G, Towbin BD, Rothschild D, Dekel E, Bren A, Alon U. 2014. Hierarchy of non-glucose sugars in Escherichia coli. BMC Syst Biol. 8:133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajic D, Sanchez A. 2020. The ecology and evolution of microbial metabolic strategies. Curr Opin Biotechnol. 62:123–128. [DOI] [PubMed] [Google Scholar]
- Bajić D, Vila JCC, Blount ZD, Sánchez A. 2018. On the deformability of an empirical fitness landscape by microbial evolution. Proc Natl Acad Sci U S A. 115:11286–11291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balakrishnan R, de Silva RT, Hwa T, Cremer J. 2021. Suboptimal resource allocation in changing environments constrains response and growth in bacteria. Mol Syst Biol. 17:e10597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barve A, Wagner A. 2013. A latent capacity for evolutionary innovation through exaptation in metabolic systems. Nature 500:203–206. [DOI] [PubMed] [Google Scholar]
- Basan M, Hui S, Okano H, Zhang Z, Shen Y, Williamson JR, Hwa T. 2015. Overflow metabolism in Escherichia coli results from efficient proteome allocation. Nature 528:99–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beg QK, Vazquez A, Ernst J, de Menezes MA, Bar-Joseph Z, Barabási A-L, Oltvai ZN. 2007. Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity. Proc Natl Acad Sci U S A. 104:12663–12668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belliveau NM, Barnes SL, Ireland WT, Jones DL, Sweredoski MJ, Moradian A, Hess S, Kinney JB, Phillips R. 2018. Systematic approach for dissecting the molecular mechanisms of transcriptional regulation in bacteria. Proc Natl Acad Sci U S A. 115:E4796–E4805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergman A, Siegal ML. 2003. Evolutionary capacitance as a general feature of complex gene networks. Nature 424:549–552. [DOI] [PubMed] [Google Scholar]
- Besnard F, Picao-Osorio J, Dubois C, Félix M-A. 2020. A broad mutational target explains a fast rate of phenotypic evolution. eLife 9:e54928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloxham B, Lee H, Gore J. 2022. Diauxic lags explain unexpected coexistence in multi-resource environments. Mol Syst Biol. 18:e10630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloxham B, Lee H, Gore J. 2023. Biodiversity is enhanced by sequential resource utilization and environmental fluctuations via emergent temporal niches. bioRxiv. 2023.02.17.529002. Available from: https://www.biorxiv.org/content/10.1101/2023.02.17.529002v1.abstract [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bordbar A, Monk JM, King ZA, Palsson BO. 2014. Constraint-based models predict metabolic and associated cellular functions. Nat Rev Genet. 15:107–120. [DOI] [PubMed] [Google Scholar]
- Chang C-Y, Bajic D, Vila J, Estrela S, Sanchez A. 2022. Emergent coexistence in multispecies microbial communities. Science 381(6655):343–348. [DOI] [PubMed] [Google Scholar]
- Chaumeil P-A, Mussig AJ, Hugenholtz P, Parks DH. 2019. GTDB-Tk: a toolkit to classify genomes with the genome taxonomy database. Bioinformatics 36:1925–1927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Groot DH, van Boxtel C, Planqué R, Bruggeman FJ, Teusink B. 2019. The number of active metabolic pathways is bounded by the number of cellular constraints at maximal metabolic rates. PLoS Comput Biol. 15:e1006858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dekel E, Alon U. 2005. Optimality and evolutionary tuning of the expression level of a protein. Nature 436:588–592. [DOI] [PubMed] [Google Scholar]
- de Visser JAGM, Hermisson J, Wagner GP, Ancel Meyers L, Bagheri-Chaichian H, Blanchard JL, Chao L, Cheverud JM, Elena SF, Fontana W, et al. 2003. Perspective: evolution and detection of genetic robustness. Evolution 57:1959–1972. [DOI] [PubMed] [Google Scholar]
- Dykhuizen DE, Dean AM, Hartl DL. 1987. Metabolic flux and fitness. Genetics 115:25–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebrahim A, Lerman JA, Palsson BO, Hyduke DR. 2013. COBRApy: cOnstraints-based reconstruction and analysis for python. BMC Syst Biol. 7:74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elena SF, Lenski RE. 2003. Evolution experiments with microorganisms: the dynamics and genetic bases of adaptation. Nat Rev Genet. 4:457–469. [DOI] [PubMed] [Google Scholar]
- Estrela S, Vila JCC, Lu N, Bajić D, Rebolleda-Gómez M, Chang C-Y, Goldford JE, Sanchez-Gorostiaga A, Sánchez Á. 2022. Functional attractors in microbial community assembly. Cell Syst. 13:29–42.e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falconer DS, Mackay TFC. 1996. Introduction to quantitative genetics. Harlow: Prentice Hall.
- Flamholz A, Noor E, Bar-Even A, Milo R. 2012. Equilibrator–the biochemical thermodynamics calculator. Nucleic Acids Res. 40:D770–D775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontana W, Schuster P. 1998. Shaping space: the possible and the attainable in RNA genotype-phenotype mapping. J Theor Biol. 194:491–515. [DOI] [PubMed] [Google Scholar]
- Geiler-Samerotte K, Sartori FMO, Siegal ML. 2019. Decanalizing thinking on genetic canalization. Semin Cell Dev Biol. 88:54–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldford JE, Hartman H, Smith TF, Segrè D. 2017. Remnants of an ancient metabolism without phosphate. Cell 168:1126–1134.e9. [DOI] [PubMed] [Google Scholar]
- Görke B, Stülke J. 2008. Carbon catabolite repression in bacteria: many ways to make the most out of nutrients. Nat Rev Microbiol. 6:613–624. [DOI] [PubMed] [Google Scholar]
- Goyal A, Dubinkina V, Maslov S. 2018. Multiple stable states in microbial communities explained by the stable marriage problem. ISME J. 12:2823–2834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gralka M, Pollak S, Cordero OX. 2022. Fundamental metabolic strategies of heterotrophic bacteria. bioRxiv: 2022.08.04.502823. Available from: https://www.biorxiv.org/content/10.1101/2022.08.04.502823v1.abstract [Google Scholar]
- Huerta-Cepas J, Serra F, Bork P. 2016. ETE 3: reconstruction, analysis, and visualization of phylogenomic data. Mol Biol Evol. 33:1635–1638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob F, Monod J. 1961. Genetic regulatory mechanisms in the synthesis of proteins. J Mol Biol. 3:318–356. [DOI] [PubMed] [Google Scholar]
- Kalyaanamoorthy S, Minh BQ, Wong TKF, von Haeseler A, Jermiin LS. 2017. ModelFinder: fast model selection for accurate phylogenetic estimates. Nat Methods. 14:587–589. [DOI] [PMC free article] [PubMed]
- Kremling A, Geiselmann J, Ropers D, de Jong H. 2015. Understanding carbon catabolite repression in Escherichia coli using quantitative models. Trends Microbiol. 23:99–109. [DOI] [PubMed] [Google Scholar]
- Lewis NE, Hixson KK, Conrad TM, Lerman JA, Charusanti P, Polpitiya AD, Adkins JN, Schramm G, Purvine SO, Lopez-Ferrer D, et al. 2010. Omic data from evolved E. coli are consistent with computed optimal growth from genome-scale models. Mol Syst Biol. 6:390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lozada-Chávez I, Janga SC, Collado-Vides J. 2006. Bacterial regulatory networks are extremely flexible in evolution. Nucleic Acids Res. 34:3434–3445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machado D, Andrejev S, Tramontano M, Patil KR. 2018. Fast automated reconstruction of genome-scale metabolic models for microbial species and communities. Nucleic Acids Res. 46:7542–7553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metropolis N, Rosenbluth AW. 1953. Equation of state calculations by fast computing machines. J Chem Phys. 21:1087.
- Monod J. 1942. Recherches sur la croissance des cultures bacteriennes. Paris: Hermann & Cie. [Google Scholar]
- Mori M, Hwa T, Martin OC, De Martino A, Marinari E. 2016. Constrained allocation flux balance analysis. PLoS Comput Biol. 12:e1004913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen L-T, Schmidt HA, von Haeseler A, Minh BQ. 2015. IQ-TREE: a fast and effective stochastic algorithm for estimating maximum-likelihood phylogenies. Mol Biol Evol. 32:268–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noor E, Flamholz A, Bar-Even A, Davidi D, Milo R, Liebermeister W. 2016. The protein cost of metabolic fluxes: prediction from enzymatic rate laws and cost minimization. PLoS Comput Biol. 12:e1005167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Notebaart RA, Szappanos B, Kintses B, Pál F, Györkei Á, Bogos B, Lázár V, Spohn R, Csörgő B, Wagner A, et al. 2014. Network-level architecture and the evolutionary potential of underground metabolism. Proc Natl Acad Sci U S A. 111:11762–11767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Brien EJ, Monk JM, Palsson BO. 2015. Using genome-scale models to predict biological capabilities. Cell 161:971–987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okano H, Hermsen R, Hwa T. 2021. Hierarchical and simultaneous utilization of carbon substrates: mechanistic insights, physiological roles, and ecological consequences. Curr Opin Microbiol. 63:172–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okano H, Hermsen R, Kochanowski K, Hwa T. 2020. Regulation underlying hierarchical and simultaneous utilization of carbon substrates by flux sensors in Escherichia coli. Nat Microbiol. 5:206–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orth JD, Conrad TM, Na J, Lerman JA, Nam H, Feist AM, Palsson BØ. 2011. A comprehensive genome-scale reconstruction of Escherichia coli metabolism–2011. Mol Syst Biol. 7:535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pacciani-Mori L, Giometto A, Suweis S, Maritan A. 2020. Dynamic metabolic adaptation can promote species coexistence in competitive microbial communities. PLoS Comput Biol. 16:e1007896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papp B, Pál C, Hurst LD. 2004. Metabolic network analysis of the causes and evolution of enzyme dispensability in yeast. Nature 429:661–664. [DOI] [PubMed] [Google Scholar]
- Perrin E, Ghini V, Giovannini M, Di Patti F, Cardazzo B, Carraro L, Fagorzi C, Turano P, Fani R, Fondi M. 2020. Diauxie and co-utilization of carbon sources can coexist during bacterial growth in nutritionally complex environments. Nat Commun. 11:3135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posfai A, Taillefumier T, Wingreen NS. 2017. Metabolic trade-offs promote diversity in a model ecosystem. Phys Rev Lett. 118:028103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poyatos JF. 2020. Genetic buffering and potentiation in metabolism. PLoS Comput Biol. 16:e1008185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price MN, Dehal PS, Arkin AP. 2008. Horizontal gene transfer and the evolution of transcriptional regulation in Escherichia coli. Genome Biol. 9:R4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richardson JB, Uppendahl LD, Traficante MK, Levy SF, Siegal ML. 2013. Histone variant HTZ1 shows extensive epistasis with, but does not increase robustness to, new mutations. PLoS Genet. 9:e1003733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutherford SL, Lindquist S. 1998. Hsp90 as a capacitor for morphological evolution. Nature 396:336–342. [DOI] [PubMed] [Google Scholar]
- Salvy P, Hatzimanikatis V. 2021. Emergence of diauxie as an optimal growth strategy under resource allocation constraints in cellular metabolism. Proc Natl Acad Sci USA. 118(8):e2013836118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samal A, Matias Rodrigues JF, Jost J, Martin OC, Wagner A. 2010. Genotype networks in metabolic reaction spaces. BMC Syst Biol. 4:30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäfer M, Pacheco AR, Künzler R, Bortfeld-Miller M, Field CM, Vayena E, Hatzimanikatis V, Vorholt JA. 2023. Metabolic interaction models recapitulate leaf microbiota ecology. Science 381:eadf5121. [DOI] [PubMed] [Google Scholar]
- Schluter D. 1996. Adaptive radiation along genetic lines of least resistance. Evolution 50:1766–1774. [DOI] [PubMed] [Google Scholar]
- Schmidt A, Kochanowski K, Vedelaar S, Ahrné E, Volkmer B, Callipo L, Knoops K, Bauer M, Aebersold R, Heinemann M. 2016. The quantitative and condition-dependent Escherichia coli proteome. Nat Biotechnol. 34:104–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuetz R, Kuepfer L, Sauer U. 2007. Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol Syst Biol. 3:119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuetz R, Zamboni N, Zampieri M, Heinemann M, Sauer U. 2012. Multidimensional optimality of microbial metabolism. Science 336:601–604. [DOI] [PubMed] [Google Scholar]
- Segrè D, Deluna A, Church GM, Kishony R. 2005. Modular epistasis in yeast metabolism. Nat Genet. 37:77–83. [DOI] [PubMed] [Google Scholar]
- Stadler BM, Stadler PF, Wagner GP, Fontana W. 2001. The topology of the possible: formal spaces underlying patterns of evolutionary change. J Theor Biol. 213:241–274. [DOI] [PubMed] [Google Scholar]
- Szappanos B, Fritzemeier J, Csörgő B, Lázár V, Lu X, Fekete G, Bálint B, Herczeg R, Nagy I, Notebaart RA, et al. 2016. Adaptive evolution of complex innovations through stepwise metabolic niche expansion. Nat Commun. 7:11607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Towbin BD, Korem Y, Bren A, Doron S, Sorek R, Alon U. 2017. Optimality and sub-optimality in a bacterial growth law. Nat Commun. 8:14123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuncil YE, Xiao Y, Porter NT, Reuhs BL, Martens EC, Hamaker BR. 2017. Reciprocal prioritization to dietary glycans by gut Bacteria in a competitive environment promotes stable coexistence. MBio. 8:e01068-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vitkup D, Kharchenko P, Wagner A. 2006. Influence of metabolic network structure and function on enzyme evolution. Genome Biol. 7:R39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner GP, Chiu C-H, Laubichler M. 2000. Developmental evolution as a mechanistic science: the inference from developmental mechanisms to evolutionary processes. Integr Comp Biol. 40:819–831. [Google Scholar]
- Wang Z, Goyal A, Dubinkina V, George AB, Wang T, Fridman Y, Maslov S. 2021. Complementary resource preferences spontaneously emerge in diauxic microbial communities. Nat Commun. 12:6661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, Xia K, Yang X, Tang C. 2019. Growth strategy of microbes on mixed carbon sources. Nat Commun. 10:1279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waschina S, D'Souza G, Kost C, Kaleta C. 2016. Metabolic network architecture and carbon source determine metabolite production costs. FEBS J. 283:2149–2163. [DOI] [PubMed] [Google Scholar]
- Wortel MT, Noor E, Ferris M, Bruggeman FJ, Liebermeister W. 2018. Metabolic enzyme cost explains variable trade-offs between microbial growth rate and yield. PLoS Comput Biol. 14:e1006010. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All code for simulations, data analysis, and figures can be found in the following github repository https://github.com/sotarotakano/MetabolicHierarchy. Data and code will be provided with corresponding DOI before publication.