Enhanced cell viscosity: A new phenotype associated with lamin A/C alterations

Summary

Lamin A/C is a well-established key contributor to nuclear stiffness and its role in nucleus mechanical properties has been extensively studied. However, its impact on whole-cell mechanics has been poorly addressed, particularly concerning measurable physical parameters. In this study, we combined microfluidic experiments with theoretical analyses to quantitatively estimate the whole-cell mechanical properties. This allowed us to characterize the mechanical changes induced in cells by lamin A/C alterations and prelamin A accumulation resulting from atazanavir treatment or lipodystrophy-associated LMNA R482W pathogenic variant. Our results reveal a distinctive increase in long-time viscosity as a signature of cells affected by lamin A/C alterations. Furthermore, they show that the whole-cell response to mechanical stress is driven not only by the nucleus but also by the nucleo-cytoskeleton links and the microtubule network. The enhanced cell viscosity assessed with our microfluidic assay could serve as a valuable diagnosis marker for lamin-related diseases.

Graphical abstract

Highlights

• •We explored the mechanical properties of cells with prelamin A accumulation
• •We showed an increase in cell viscosity upon prelamin A accumulation
• •The disruption of microtubule network reverses cell viscosity increase

Biological sciences; Biotechnology; Cell biology

Introduction

Lamin A/C is an intermediate filament underlying the nuclear envelope and a well-established key contributor to nuclear stiffness, chromatin organization, and gene expression.^1,2 Due to its links with both the nucleoskeleton and the cytoskeleton, lamin A/C is also a major piece of the mechanotransduction process, i.e., the conversion of mechanical stimuli into biochemical signals.^3,4 With regard to these fundamental and ubiquitous roles, lamin A/C alterations resulting from genetic or environmental factors induce diverse cellular features such as abnormal nuclear shape, proliferation defect, and premature senescence.^5,6,7 Genetic diseases due to pathogenic variants in LMNA, the gene encoding lamin A/C, are referred to as laminopathies. They are severe and clinically heterogeneous diseases either tissue specific like cardiomyopathies or multi-systemic like Hutchinson-Gilford progeria syndrome and type 2 familial partial lipodystrophy (FPLD2).^8,9,10

On account of their pivotal role in nuclear stiffness, the involvement of lamins in nucleus mechanical properties has been extensively studied through a variety of techniques applied to different cell types and different lamin modifications such as depletion or genetic variants.¹ Significant work has been conducted on cells with lamin A/C depletion.^{11,12,13,14,15} This defect partly reflects the common mechanism of laminopathies as complete haploinsufficiency is lethal in humans¹⁶ and heterozygous haploinsufficient variants are responsible for defects in striated muscle only (cardiomyopathies and EDMD).¹⁷ Few other studies have addressed the effect of missense mutations, mainly mutations involved in cardiomyopathies or progeria.^18,19,20,21 However, the diversity of approaches has resulted in a large panel of results that are rather difficult to compare.^3,22,23 In addition, the link between lamin A/C structural or functional changes and cell or tissue manifestations in the pathological context of laminopathies remains unclear. To a large extent, the impact of laminopathies on the whole-cell mechanical properties has been poorly described in terms of measurable physical mechanical parameters.

Here, the mechanical impact of two types of lamin A/C alterations was investigated: (1) the canonical FPLD2-associated lamin A/C R482W pathogenic variant, which induces an abnormal accumulation of the mutant prelamin A at the nuclear periphery due to a persistent farnesyl group^{24,25,26,27,28}; (2) an in vitro treatment with atazanavir, a HIV protease inhibitor known to induce senescence phenotypes associated to lamin A/C alterations.^29,30,31 To test the whole-cell response to mechanical stress, the microfluidic technique, largely applied to infer cellular mechanical properties, was implemented.^32,33,34 A microfluidic device designed to apply a compressive stress on cells by forcing them into constrictions was used to provide a quantitative dataset on the cell mechanics. The mechanical stress was applied over a few seconds to probe the intrinsic cell properties without inducing a major reorganization of cellular components. Regarding this aspect, the study differs from most previously reported experiments in which the mechanical stress is applied over longer times ranging from 10 s to a few minutes and the deformation is not tracked in the first 2 s.^35,36 Measurements of the cells’ entry times in constrictions were combined with a semi-automated image analysis routine and the application of a rheological model to extract the cells’ viscoelastic properties. The results showed that the main mechanical feature of cells displaying lamin A/C alterations, whether induced in vitro or by the R482W mutation, is an increase in the cell’s viscosity attributed to both nuclear and cytoskeleton networks. Moreover, a contribution of the microtubule network in this mechanical property was unraveled in cells with lamin A/C alterations.

Results

Atazanavir treatment drives a premature senescence phenotype in fibroblasts identical to that induced by lamin A/C R482W mutation

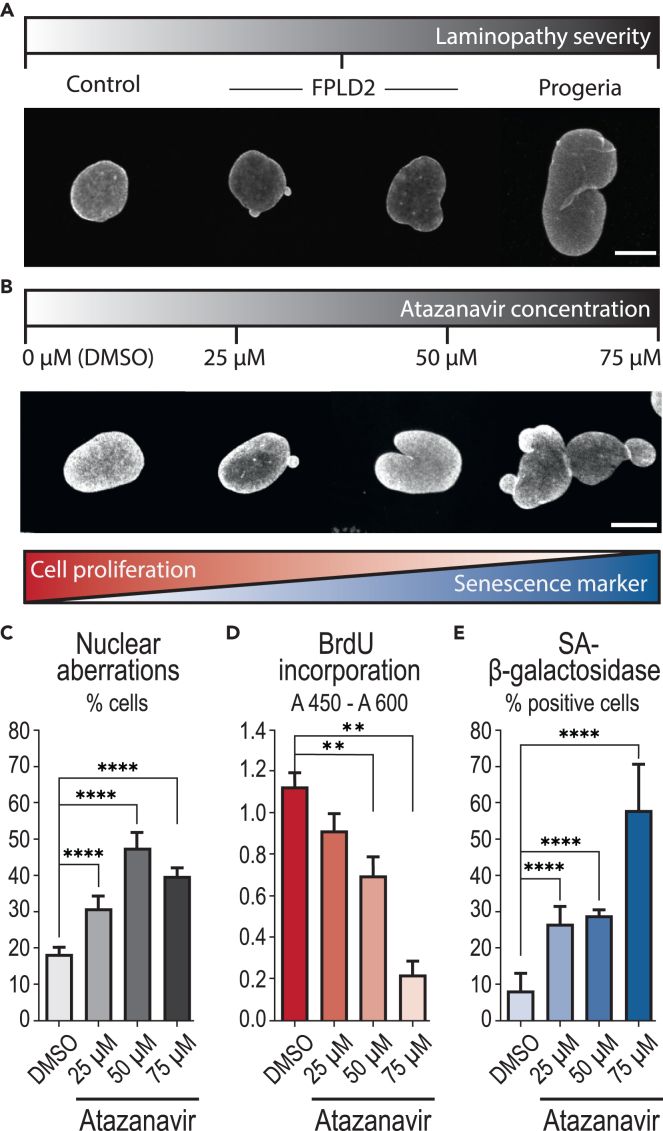
Two cell models characterized by lamin A/C alterations were selected to study cell viscoelastic property changes as compared to control cells: 1) skin fibroblasts issued from a healthy individual and treated with atazanavir, and 2) skin fibroblasts issued from two patients with FPLD2 carrying the canonical lamin A/C R482W mutation (patients 8 and 12 from Vatier et al.³⁷). Atazanavir treatment has been shown by us and others^27,31,38,39 to inhibit the activity of the mammalian protease ZMPSTE24 and to result in farnesylated prelamin A accumulation. This effect results ultimately in increased senescence, impaired proliferation capacity, and abnormal nuclei shape. The response of control fibroblasts to atazanavir was checked by studying the nuclear shape, proliferation capacity, and senescent markers. Cells were treated for 48 h with increasing concentrations of atazanavir, or incubated only with its solvent, DMSO, as a control. High levels of nuclear aberrations were observed and were similar to those observed in cells from patients with FPLD2 or from a patient with progeria carrying the LMNA G608G mutation (Figures 1A–1C). The impact of increasing atazanavir concentration was also confirmed on proliferation capacity by measuring bromodeoxyuridine incorporation, and on senescence level by estimating the cellular SA-beta-galactosidase activity (Figures 1D and 1E). From these data, the concentration of 50 μM was determined to efficiently drive senescence while avoiding impaired cell viability.

Figure 1.

Atazanavir treatment induces cellular phenotypes associated with premature senescence

Control fibroblasts were treated for 48 h with increasing doses of atazanavir or incubated with DMSO as a control.

(A and B) Representative images of nuclear aberrations (abnormal size or shape) observed in (A) control fibroblasts, fibroblasts from patients with FPLD2 carrying the LMNA R482W mutation, or from a patient with progeria, and (B) control fibroblasts treated with atazanavir. Nuclear envelope is stained using a lamin A/C-specific antibody. Scale bars: 10 μm.

(C) Percentage of cells displaying nuclear aberrations.

(D) Bromodeoxyuridine (BrdU) incorporation reporting cell proliferation ability.

(E) Percentage of SA-beta-galactosidase-positive cells identified as senescent. Data in (C–E) are represented as mean ± SD (standard deviation). Number of experiments: N ≥ 3 (C–E); number of analyzed cells: n ≥ 1000 (C) and ≥500 (E).

As a second step, we evaluated the impact of atazanavir treatment and FPLD2 mutation on cellular and nuclear volumes of cells in suspension to engineer constriction dimensions in the microfluidic device described hereafter. Both cells and nuclei were imaged using confocal microscopy (Figure S1A, Videos S1 and S2). Volumes were computed from the z-stacks of confocal images. Cell volumes of control fibroblasts treated with atazanavir increased by 37% (nuclei volumes by 13%) when compared to those of fibroblasts incubated with DMSO only. The volumes of fibroblasts from the 2 patients affected with FPLD2 (referred to as K and M) were compared to those of control cells and to those of fibroblasts from a patient affected with progeria, known to induce an increase in nuclear and cellular volumes.^40,41 As expected, both cellular and nuclear volumes of progeria cells were much larger than the others, whereas the volumes of FPLD2 cells and nuclei remained closer to those displayed by control cells (Figure S1).

Video S1. 3D-reconstructions of atazanavir-treated cells (left) and nuclei (right) labeled with CellBrite and Hoechst, respectively, related to Figure S1

Scales are in μm.

Video S2. Z-stacks of the confocal planes of cells (left) and nuclei (right) used for reconstructing the 3D-images from Video S1, related to Figure S1

Scale bar: 10 μm.

A two-height microfluidic device to infer the cell responses to mechanical constraint

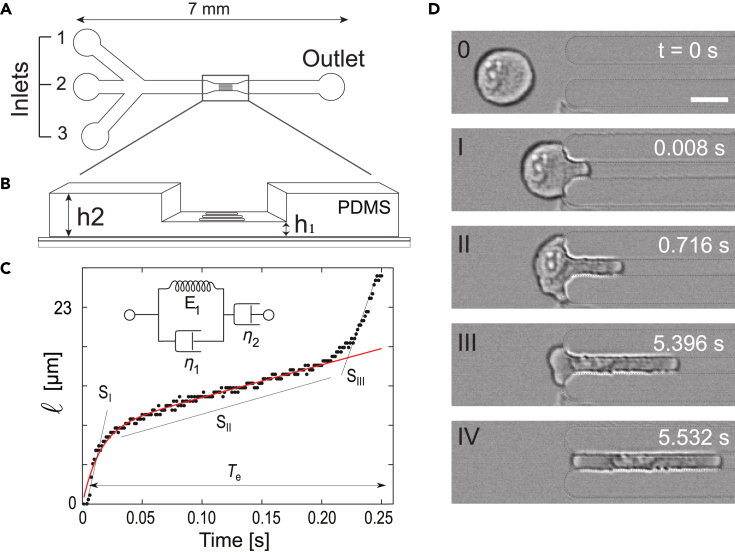
To investigate cell mechanical properties, we engineered a microfluidic device consisting of a wide channel with parallel constrictions dedicated to constraining cells (Figures 2A and 2B). An original feature of the device lies in the presence of two heights along the channel (Figure 2B): in the center of the device lies a region with constrictions of a 6 × 6 μm² cross section, which are small enough to squeeze both the cells and their nuclei. Before and after the central constrictions, the channel displays a 200-μm long section of a 6 × 300 μm² cross section. By applying a controlled pressure difference between inlet and outlet, cells are pushed through channels and deform to adopt a circular pancake shape (i.e., a disk of 6 μm in thickness). Then, they experience an additional lateral confinement when entering the constrictions. This device allows to observe the passage of tens of cells through the constrictions and, therefore, to quantitatively analyze the cell behavior. The dynamics of cell entry into the constrictions is measured by the temporal evolution of cell portion inside the constriction called cell tongue (Figure 2C and Video S3). This dynamics exhibits three different successive phases, I to III (Figure 2D) each being characterized by a specific linear increase in cell tongue length over time, i.e., a specific entry velocity. Once the cell has fully entered the constriction, its deformation is maximum and its transit through the constriction corresponds to phase IV (Figure 2D).

Figure 2.

Microfluidic device, data processing, and analysis

(A) Top-view schematics of the microfluidic device made of polydimethylsiloxane (PDMS). Inlets (1) and (3) are used for injecting buffer solutions while cells are injected through inlet (2). Controlled pressure drop is applied between inlets and outlet to push cells through constrictions.

(B) Zoomed 3D view of the constriction zone, with two different heights: h₂ for the main 300-μm wide channel and h₁ for the constrictions (length l, width w). l = 100 μm, w = h₁ = 6 μm, h₂ = 10 μm. The low-height region is 500 μm long in total, including the constrictions.

(C) Typical time evolution of the cell tongue length l(t). The curve is analyzed using two methods: i) It is decomposed into three linear parts, of slopes S_I to S_III, which correspond to the cell entry time T_e; ii) The first two parts of the curve are fitted (in red) using a rheological model which combines a Kelvin–Voigt solid (a spring of constant E₁ in parallel with a dashpot of viscosity η₁) in series with a dashpot of viscosity η₂ (see inset).

(D) Time-lapse of a 24-μm cell entering a constriction of width w. Scale bar: 15 μm.

Cells exposed to atazanavir treatment or carrying the lamin A/C R482W mutation display an increase in viscosity

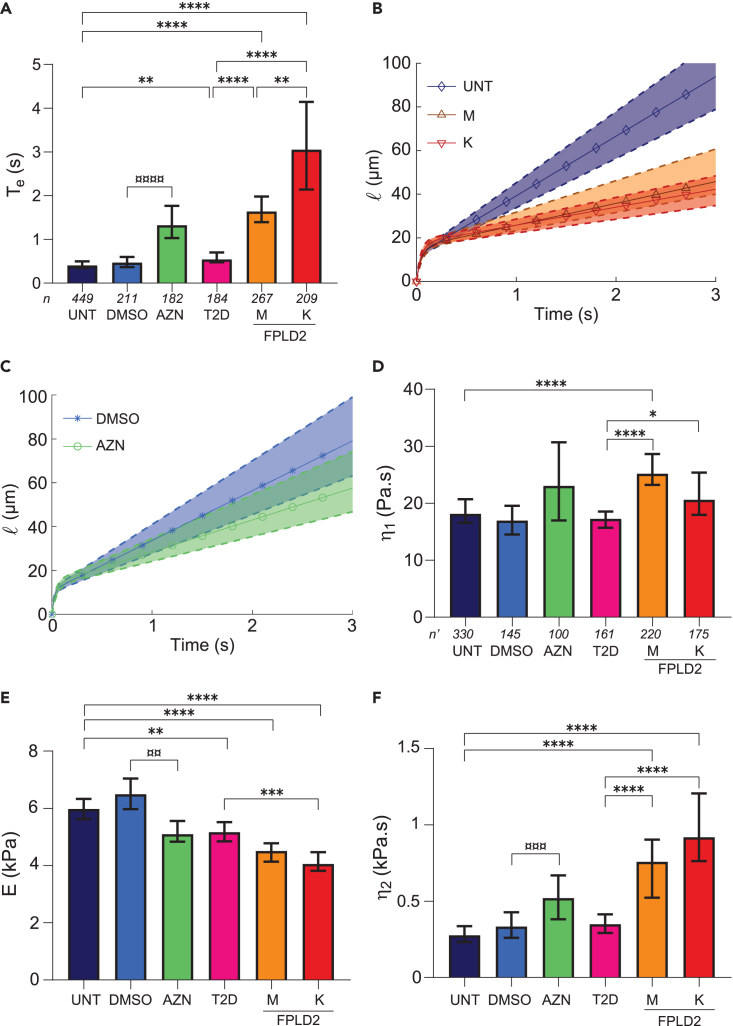
Time course curves of cell tongue length were analyzed in two ways: first, by determining the global entry time T_e, defined as the time to go from phase I to III, and the three cell entry velocities corresponding to the three slopes S_I to S_III, of the three phases; second, using a rheological model to fit phases I and II. Fibroblasts from the 2 patients with FPLD2 (named M and K) were compared to untreated control fibroblasts (UNT) and fibroblasts treated with atazanavir (AZN) to fibroblasts incubated with DMSO only (DMSO). As the major metabolic signs of FPLD2 are dyslipidemia and diabetes, we also used fibroblasts from a patient with dyslipidemia and diabetes but without lamin A/C alteration (patient 17 from Dutour et al.,⁴² named T2D hereafter) to validate that the assay specifically discriminates cells with lamin A/C alterations.

The entry times (T_e) of UNT and DMSO cells were similar (0.4 and 0.46 s), confirming that the DMSO used as atazanavir solvent had no effect on T_e. In contrast, the entry times of AZN, and M and K cells were at least 3 times longer than those of their respective controls (Figures 3A and S2A and Video S4). The entry time of T2D cells was slightly longer than that of UNT cells but significantly shorter than that of FPLD2 or AZN cells (Figures 3A and S2A). To check that these variations in entry times were not due to a cell volume effect, cells were sorted by volume. As expected, entry times were longer for larger cell volumes, but for comparable volumes, those of FPLD2 and AZN cells were systematically longer than those of their respective controls (Figure S2).

Figure 3.

Atazanavir treatment and lamin A/C R482W mutation alter cell rheological behavior

UNT: untreated control cells (control); DMSO: control cells incubated with DMSO (AZN control); AZN: control cells treated with atazanavir; T2D: cells from a patient with type 2 diabetes; M,K: cells from patients with FPLD2 carrying the LMNA R482W mutation.

(A) Entry time in 6x6-μm² constrictions T_e (median ±95% CI, Confidence Interval).

(B and C) Fits of tongue length l as a function of time t (t = 0 defined at cell contact with constriction), for (B) UNT, M and K cells, and (C) DMSO and AZN cells. Solid curves with symbols indicate the median fits; dashed upper and lower curves delineate the 95% CIs; the curves are plotted using median and CI values from Table 1 in Equation 1.

(D–F) Fit-extracted rheological parameters: long-time viscosity η₂ (D), short-time elastic modulus E (E), and viscosity η₁ (F). Medians ±95% CI are displayed. Significant differences: AZN vs. DMSO cells (¤), FPLD2 and T2D vs. UNT cells (∗). Number of experiments: N ≥ 3; n: number of analyzed cells (A); n': number of fitted curves (D–F).

Video S4. Entry and transit of fibroblasts in 6 × 6 μm2 constrictions: top) 24-μm untreated control cell, middle) 23-μm atazanavir-treated cell, bottom) 27-μm FPLD2 K cell, related to Figure 3A

Cells were observed in brightfield microscopy, the background with the image of the constrictions has been subtracted to enhance cell contrast. Time is indicated in sec. Scale bar: 10 μm.

The cell entry velocities of the three phases (slopes S_I–S_III) were slowed down for M and K cells compared to UNT cells, as well as for AZN cells compared to DMSO cells, in agreement with the observed increase in entry times (Figure S3). For T2D cells, the entry velocities were similar to those of UNT cells in phase I and II, and higher in phase III, indicating again that their response to mechanical stress is different from that of FPLD2 and AZN cells. Altogether, these results showed that entry times, overall or for the different phases, were longer for cells with lamin A/C alterations, indicating changes in their mechanical properties.

To confirm this assumption and quantitatively measure the cell mechanical properties, the Jeffreys rheological model was used as a complementary approach (⁴³, see STAR Methods). This rheological model considers the cell as a homogeneous viscoelastic material with viscoelastic properties like elastic modulus and viscosities which respectively represent its ability to resist to deformation and its deformation speed. The model was used to fit the first 2 entry phases I and II only because the differences in entry phase III could not be clearly attributed to a specific cell condition.

As the minimal pressure difference required to push cells through the constrictions was estimated and found relatively minor compared to the pressure difference applied during experiments, the model was simplified by considering the applied stress as constant. Assuming constant applied stress on the cell and volume conservation, the cell deformation during constriction entering, i.e., the cell tongue length, can be expressed as a function of the cell viscoelastic properties using the Jeffreys model.^35,43 The evolution of the cell tongue length l according to time t then reads as:

$$l\left(t\right)=\frac{R_{eff}\Delta P}{E}\left(1-e^{-\frac{E}{3\pi {\eta }_1}t}\right)+\frac{R_{eff}\Delta P}{3\pi {\eta }_2}t$$

where R_eff is the radius of an effective cylindrical constriction which circular cross section is equivalent to the square cross section of the constrictions used here, ΔP the applied pressure difference, E the elastic modulus of the cell, and η₁ and η₂ its short- and long-time viscosities. Following this model, at small deformations associated with short-time scale (phase I), a viscoelastic regime dominates which is controlled by the short-time viscosity η₁ and the elastic modulus E. At larger deformations and long-time scale (phase II), a linear viscous regime dominates controlled by the long-time viscosity η₂.

The cell tongue lengths obtained from experiments on individual cells were thus fitted using the Jeffreys model to derive their viscoelastic properties. Figures 3B and 3C display the fits for UNT vs. M and K cells, and for DMSO vs. AZN cells, respectively, plotted using the median and CI values of the viscoelastic properties. In phase I, the short-time viscosity η₁ tended to be higher in altered lamin A/C cells compared to their respective controls, and it was significantly different between FPLD2 cells and T2D cells (Figure 3D). The elastic modulus E, on the other hand, was lower in AZN and FPLD2 cells, by 22%–32% compared to their respective controls (Figure 3E). T2D cells also displayed a slightly lower elastic modulus suggesting that the changes are not related to lamin A/C alterations only. At long timescale, in phase II, UNT, DMSO, and T2D cells presented a comparable long-time viscosity η₂, while AZN and FPLD2 cells displayed an increase in η₂, by at least 50% (Figure 3F). Entry time T_e and viscosity η₂ showed a similar trend with an increase in cells carrying altered lamin A/C, suggesting that the entry time is mostly dominated by the long-time viscosity. All rheological parameters are summarized with T_e, in Table 1 (the corresponding dot plots are shown in Figures S2A and S4).

Table 1.

Entry time and rheological parameters (Median [95% CI])

	UNT	DMSO	AZN	T2D	M	K
Te (s)	0.40 [0.35–0.50]	0.46 [0.37–0.60]	1.30 [1.00–1.77]∗∗∗∗	0.54 [0.48–0.70]∗∗	1.60 [1.40–1.98]∗∗∗∗	3.05 [2.14–4.14]∗∗∗∗
η1 (Pa.s)	18 [17–21]	17 [15–20]	23 [16.6–31] ns	17 [16–19] ns	25 [23–29]∗∗∗∗	21 [18–25] ns
E (kPa)	6.0 [5.6–6.3]	6.5 [6.0–7.0]	5.1 [4.8–5.6]∗∗	5.2 [4.8–5.5]∗∗	4.5 [4.1–4.8]∗∗∗∗	4.1 [3.8–4.5]∗∗∗∗
η2 (Pa.s)	277 [232–336]	333 [260–428]	521 [381–668]∗∗∗	349 [292–413] ns	758 [522–904]∗∗∗∗	920 [762–1206]∗∗∗∗

Differences between AZN and DMSO cells, and T2D/M/K and UNT cells are indicated as: ns, non-significant; ∗∗, p < 0.01; ∗∗∗, p < 0.001; ∗∗∗∗, p < 0.0001.

With additional simplifications in the Jeffreys model (see STAR Methods for details), we obtained a scaling law between the entry time and the cell initial diameter, T_e = ν·L₀², which could be used to fit the T_e(L₀) datasets and derive the factor ν (see, for example, the fits for UNT and K cells in Figure S5A). The ν values normalized to that of UNT cells (ν/ν_UNT) behave almost identically to the η₂ ratios (η₂/η₂__UNT) obtained with the precise fits of the elongation curves (Figure S5B). Thus, the measurement of the cell entry time and its initial size seems appropriate to perform a first rapid comparison of the long-time viscosities between different cell types. This method constitutes a fast screening of cell populations to obtain a rough estimation of viscosity differences based on the sole measurement of the entry time and initial cell diameter.

We also applied a power-law fit to the curves as in the study by Davidson et al.³⁵ which derives a parameter equivalent to the long-time viscosity obtained with the Jeffreys model (see STAR Methods). This second approach provided results with a similar trend, though less marked (Figure S6). Typical elongation curves fitted with both models are displayed in Figure S7.

Taken altogether, our data highlight that lamin A/C alterations, induced either by atazanavir treatment or FPLD2-associated R482W mutation, are associated with a higher long-time cell viscosity. The short-time viscosity values, which are much lower than those of the long-time viscosity, are comparable to the viscosity values previously reported for cytoplasm.^44,45 This short-time viscosity is probably due to the formation of a bleb at the cell front when it contacts the constriction, a process that is expected not to depend on the nucleus (Figure S8). Importantly, using this approach, we were able to discriminate T2D cells, from a patient with type 2 diabetes, from FPLD2 cells, supporting that the mechanical phenotypes observed in phases I and II are related to LMNA pathogenic variants.

So far, the observed behavior corresponded to the whole-cell response, with the combined contributions of both the nucleus and the cytoplasmic content. The lamin A/C alterations induced changes not only in phase II which was presumably attributed to the deformation of the nucleus entering the constriction but also in phases I and III, associated with the entry of front and rear cytoplasm, suggesting that alterations in the nuclear envelope impact the response of the whole cell and not only of the nucleus. To determine which part could be attributed to changes in nucleus only, the intrinsic properties of isolated nuclei were investigated.

The lamin A/C-dependent whole-cell response to mechanical constraint does not depend exclusively on the nucleus

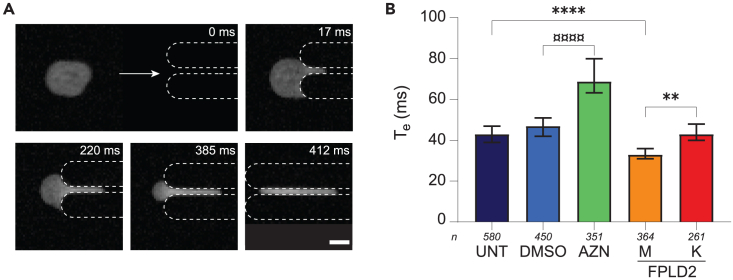
The same microfluidic experiments, albeit with 3 × 3 μm² squared constrictions, were performed on nuclei extracted from UNT, DMSO, AZN, and both FPLD2 cell lines. The nucleus tongue length was measured over time and the nucleus entry time T_e was extracted.

The entry of isolated nuclei in constrictions was much faster than that of whole cells, within a few hundreds of milliseconds, without distinct entry dynamics (Figure 4, Video S5). In accordance with the trend observed with whole cells, atazanavir treatment increased nucleus entry time by approximately 50% compared to incubation with DMSO, regardless of the nuclear volume (Figure S9A). Conversely, entry times of M and K nuclei were shorter than that of UNT ones, especially in the largest volume range (Figure S9B).

Figure 4.

Nucleus response differs from whole-cell response

(A) Time-lapse of a 20-μm nucleus entering (I–III) and transiting (IV) through a 3x3-μm² constriction. Nucleus is labeled with Hoechst. Scale bar: 10 μm.

(B) Entry time of isolated nuclei in constrictions T_e (median ±95% CI). Nuclei from UNT: untreated control cells (control); DMSO: control cells incubated with DMSO; AZN: control cells treated with atazanavir; M,K: cells from patients with FPLD2. Significant differences: AZN vs. DMSO nuclei (¤), FPLD2 and T2D vs. UNT nuclei (∗). Number of experiments: N ≥ 4; n: number of analyzed isolated nuclei.

Video S5. Entry and transit of a 20-μm nucleus in a 3 × 3 μm2 constriction, related to Figure 4

Nucleus is labeled with Hoechst and observed in epifluorescence microscopy. Time is indicated in msec. Scale bar: 10 μm.

Assuming the entry time of isolated nuclei is dominated by their viscosity, as observed in whole cells, the results show that isolated nuclei behavior did not reproduce the response of whole cells. We thus tested a possible role of the altered nucleus-cytoskeleton interplay in modifying the viscosity of whole cells in the context of lamin A/C alterations.

Increase of cell viscosity in response to lamin A/C alterations implies the microtubule network

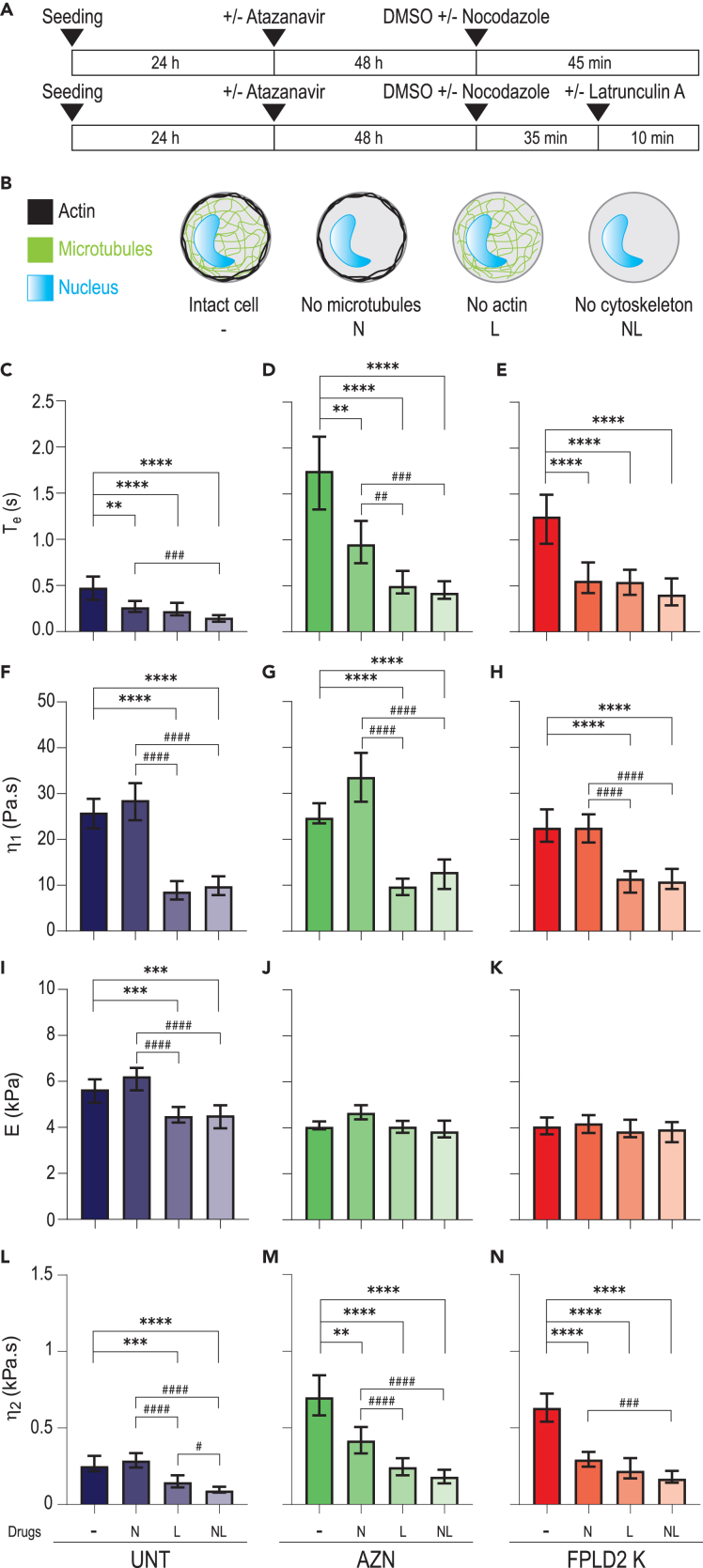
As actin and, to a lesser extent, microtubule networks are known to participate in cell viscoelastic properties, their contribution to cell responses was assessed by destabilizing actin and/or microtubule networks, using respectively latrunculin A or nocodazole treatment on UNT, AZN, and FPLD2 K cells (Figures 5A, 5B, and S10). Just as for cells with an intact cytoskeleton, three phases were distinguished and the entry time T_e and viscoelastic parameters (E, η₁, and η₂) were quantified (Figures 5C–5N; Table S1). As expected, cytoskeletal drugs induced significant changes in cell response. Globally, the destabilization of either microtubule or actin networks induced a large decrease in T_e, which remained higher for AZN and K cells than for control cells (Figures 5C–5E). Regarding the viscoelastic properties extracted by the rheological model, actin cytoskeleton disruption induced a significant decrease in viscosities and elastic modulus of control cells as expected from the literature (Figures 5F, 5I, and 5L). In FPLD2 and AZN cells, we observed the same impact on viscosities than in control cells, while no effect of actin disruption was noticed on the elastic modulus (Figures 5F–5N). Overall, even if AZN and FLPD2 cells are softer, their viscosity dominates their global behavior in the constrictions and significantly increases their entry time T_e.

Figure 5.

Actin and microtubule network destabilization accelerates cell entry into constrictions and decreases long-time viscosity in senescent cells

(A) Timeline protocol for cytoskeletal drug treatments: 72 h after seeding, cells, treated or not with atazanavir, are treated with nocodazole (45 min), latrunculin A (10 min), or both (35 min with nocodazole, then 10 min with both drugs).

(B) Sketched effect of drug treatments on cells, with nocodazole and/or latrunculin A leading to microtubule and/or actin destabilization. Control condition is incubation with drug solvent, DMSO.

(C–N) (C–E) Entry time in constrictions T_e and (F–N) fit-extracted rheological parameters of untreated control cells (UNT, dark blue), atazanavir-treated cells (AZN, green), and FPLD2 cells (FPLD2 K, red) upon drug treatments. Medians ±95% CIs are displayed. Significant differences: drug treatments vs. DMSO control (∗), and between drug treatments (^#). Number of experiments: N ≥ 3; number of analyzed cells: n ≥ 100 (C–E); number of fitted curves: n' ≥ 60 (F–N).

In response to microtubule network disruption only, short-time viscosity η₁ and the elastic modulus E were barely impacted regardless of the cell conditions (Figures 5F–5K). Conversely, the long-time viscosity η₂ was unchanged in UNT cells but significantly decreased by 50% or more in both AZN and K cells in response to microtubule destabilization (Figures 5L–5N). Therefore, this observation unravels an unexpected contribution of microtubules in the cellular viscosity of cells with lamin A/C alterations.

Finally, the effect of actin filaments and microtubules appears to be cumulative as destabilizing both actin and microtubule networks induced an approximately 70% decrease in entry time and long-time viscosity, regardless of cellular lamin A/C alterations. Altogether, our results suggest that the nucleus alone contributes, at most, by 30% to the viscous response of the whole cell, and that the effect of altered lamin A/C on cell viscosity mainly relies on cytoskeleton modifications.

Discussion

In the present study, microfluidic experiments combined with a theoretical analysis were performed to explore changes in whole-cell mechanical properties related to lamin A/C alterations caused either by atazanavir treatment or FPLD2-associated LMNA R482W mutation.

It is largely assumed that alterations of the lamin A/C protein impact the mechanical properties of the nucleus. As such, previous studies have focused on cell nuclei only and used viscoelastic fluid models to report changes in nuclear viscosity and elastic modulus. For instance, the decrease of both nuclear viscosity and elastic modulus has been shown in lamin A/C-depleted systems and in dilated cardiomyopathy-associated K219T mutation models.^35,36 Upon lamin A/C overexpression or in progeria-affected cells, an increased nuclear stiffness, a feature which can be interpreted as a higher elastic modulus, was reported.^18,46 In these studies, besides the fact that only nucleus changes were studied and that lamin A/C alterations were of different types, the observed timescale ranged from a few tens of seconds to a few minutes and the imposed deformation was usually limited to a few percent. In contrast, in our study, the dynamic response of the whole cells was assessed within at most a few seconds, and for high stresses and deformations (16.5 kPa pressure drop, 6 × 6 μm² confinement). In the Jeffreys model, the timescale of the experiment affects the values of the parameters: consistently, we obtained different elastic modulus and viscosities than those obtained by Davidson et al., who applied stresses over 10 s.³⁵ Regarding the high applied constraint, the aim is not to mimic physiological conditions such as deformations encountered in developing tissues or during cell migration like the migration of invasive cancer cells but to provide measurable responses allowing the quantification of differences in cell mechanical properties, according to nuclear cytoskeleton composition. With these experimental settings, we highlighted a decrease of the elastic modulus and an increase of both short-time and long-time viscosities upon lamin A/C alterations. We also performed a power-law fit of the elongation data, which is time invariant, and is thus complementary to the Jeffreys model. The trend of the prefactor in the power law is similar to the trend of the long-time viscosity in the Jeffreys model, confirming the impact of FPLD2-associated mutation and atazanavir treatment on this mechanical property. A relatively similar microfluidic assay was used by Lange et al., to derive what they called cell elasticity and fluidity from entry times in microconstrictions.⁴⁷ They described increased cell elasticity and decreased cell fluidity upon overexpression of wild-type lamin A, features which could correspond to increased elastic modulus and viscosity using our analysis method. With such analogy, the results of this study differ on the elastic modulus: this discrepancy could be due to a different impact of lamin A overexpression compared to abnormal lamin A expression. In addition, we cannot exclude that the cell elasticity in their model is not equivalent to the cell elastic modulus in ours.

Here, we showed that, in addition to the cell entry time, all three dynamic regimes of cell deformation were changed by lamin A/C alterations, with a significant slowdown of the second regime corresponding to an increase in cell viscosity. The changes in the viscous regime were not entirely reproduced with isolated nuclei, suggesting that the nucleus alone is not responsible for all changes observed in whole cells. Our results evaluate to 30%, at most, the nuclear contribution to the viscous response of the whole cell, and indicate that the cytoskeleton and its link with the nucleus play a major role in lamin A/C-dependent cell mechanical properties. The physical coupling between the cytoskeleton and the nuclear envelope is known to involve the linker of nucleoskeleton and cytoskeleton (LINC) complex and its connections to lamin A/C through KASH domain proteins.^48,49 Especially, the LINC complex plays a major role in the nuclear envelope-microtubule crosstalk.⁵⁰ However, this coupling can also result from direct interactions between cytoskeleton components and nuclear envelope proteins, such as microtubules which are linked to emerin.⁵¹

Our experiments point out that the viscosity of cells with lamin A/C alterations is significantly decreased upon disruption of the microtubule network, which is not the case in control cells as expected from the literature.^52,53 Several recent studies reported that microtubule network contributes to laminopathy pathophysiology in progeria and in dilated cardiomyopathies (DCM).^{20,21,54,55,56} This effect is mediated by an increase in alpha-tubulin acetylation when compared to control cells that induce an increased microtubule network stability.^55,57 Moreover, the inhibition of acetyltransferase protein 10 (NAT10), responsible for alpha-tubulin acetylation, improves cellular phenotype in progeria and DCM models reinforcing the potential role of microtubule network in laminopathies.^20,54,55 Finally, Leong et al. recently showed that the phenotype of mice models for LMNA-linked cardiac pathology results from microtubule cytoskeleton activity at the nuclear envelope and that the pathological phenotype can be reversed by the disruption of Nesprin 1-KASH domain that mediates the link between nuclear envelope and microtubule network.²¹ Here, we show that the increase in cell viscosity observed in laminopathic cells is reversed by microtubule destabilization suggesting that, as in striated muscle laminopathy, microtubule network contributes to the pathophysiology of the adipose tissue-related laminopathy. Consequently, this microtubule contribution to the pathophysiology should be considered as a common feature of different types of laminopathies. As this pathway is a potential target for treatment either by NAT10 inhibition or by disruption of the link between LINC and microtubules, lamin A-related lipodystrophy also is eligible to such therapeutic approaches.

The data presented here show that the actin network is involved in short- and long-time viscosities, both in control cells and in cells with lamin A/C alteration, whereas it has a contribution to the elastic modulus in control cells only. This suggests that the elastic modulus measured with our device might relate to additional cell components such as the intermediate filament vimentin known to regulate cell mechanical properties.^{58,59,60,61,62} Indeed, a recent study showed significant changes in vimentin distribution in lamin-deficient cells.¹⁵ These works suggest that vimentin organization might be affected in FPLD2 and AZN-treated cells and contribute to the observed changes in viscoelastic properties.

In the Jeffreys model, the cell is considered as a homogeneous material whereas the nucleus is known to be stiffer than the cytoplasm.⁶³ Nevertheless, this global approach of the cell is largely used and allowed us to investigate the mechanical properties of the whole structure constituted by the cytoplasm, the nucleus, and their physical links. Here, the model was used to fit the entry time of cells and extract rheological properties. Using this approach, the long-time viscosity η₂ measurements were situated around 1 kPa and the elastic modulus E displayed values around 5 kPa, both measurements being consistent with the range of values reported in the literature.^{35,64,65,66,67} Overall, the microfluidic test described here provides a quantitative estimation of the whole-cell mechanical properties and unveils a specific mechanical signature of cells affected by lamin A/C alterations, namely an increase of the long-time viscosity and a critical contribution of the microtubule network in the cell mechanical properties. Moreover, for the first time, we have provided data on changes in cell mechanical properties resulting from the canonical lamin A/C mutation responsible for the most frequent type of genetic lipodystrophy, whereas, up to now, most studies on laminopathies have focused on LMNA pathogenic variants involved in cardiomyopathy, myopathy, or progeria. In this specific laminopathy of the adipose tissue, the pathophysiology has been shown to involve prelamin A accumulation similar to progeria but to a lesser extent.^24,25,26,27 This prelamin A accumulation can be considered a determinant of changes in cell viscosity observed in our cellular model.

Our study could have several implications for the management of human diseases. First, by showing the uncovered role of microtubules in the regulation of cell mechanics upon lamin A/C alterations, our results point to new fields of investigations regarding the pathophysiology of laminopathies. Second, given that altered deformability and changes in mechanical properties are key determinants in cell pathophysiology, as previously shown in several situations including invasive cancers, our device constitutes a step toward potential new inexpensive and standardized biomarkers to be transferred into clinical practice. In particular, although further investigations are required in cells with different LMNA pathogenic variants, enhanced cell viscosity assessed by a microfluidic device could represent a useful diagnosis marker for laminopathic diseases.

Limitations of the study

The main limitation of this study is that we focused on testing a single LMNA pathogenic variant, R482W, while there are numerous LMNA variants reported with documented pathogenic effects. To strengthen our findings and explore potential correlations between whole-cell viscosity and disease severity, further studies comparing various mutants responsible for lipodystrophy and other tissue-specific laminopathies, such as cardiomyopathies, would be warranted.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
anti-lamin A/C mouse monoclonal antibody	Santa Cruz Biotechnology	Cat# sc-376248; RRID: AB_10991536
anti-α-tubulin mouse monoclonal antibody	Sigma-Aldrich	Cat# T5168; RRID: AB_477579
donkey anti mouse secondary antibody Alexa Fluor 488	Thermofisher	Cat# A21202; RRID: AB_141607
Hoechst 33342	Thermofisher	Cat# H3570
Texas Red™-X Phalloidin	Thermofisher	Cat# T7471
CellBrite™ Green	Biotum	Cat# 30021
SPY555-actin	Spirochrome	Cat# SC202
Chemicals, peptides, and recombinant proteins
Atazanavir	Sigma-Aldrich	Cat# SML1796
Latrunculin A	Sigma-Aldrich	Cat# L5163
Nocodazole	Sigma-Aldrich	Cat# 487928
Bovine Serum Albumin	Sigma-Aldrich	Cat# A3294
Pluronic®F-127	Sigma-Aldrich	Cat# P2443
IGEPAL	Sigma-Aldrich	Cat# I8896
PLL-PEG polymer	SuSoS AG	Cat# PLL(20)-g[3.5]PEG(5)
PDMS Sylgard 184	Dow Corning	Cat# DC184-1.1
Trichloro(1H,1H,2H,2H-perfluorooctyl)silane	Sigma-Aldrich	Cat# 448931
Critical commercial assays
Cell proliferation ELISA, BrdU (colorimetric) Kit	Roche Applied Science	Cat# 11647229001
Senescence β-Galactosidase Staining Kit	Cell Signaling	Cat# 9860
Experimental models: Cell lines
Human healthy fibroblasts	Coriell Institute	Cat# AG07095; RRID: CVCL_0N66
Human progeria fibroblasts	Coriell Institute	Cat# AG06917; RRID: CVCL_L613
Human FPLD2 fibroblasts (K and M)	Vatier et al.37	Patients 8 and 12
Human diabetic fibroblasts (T2D)	Dutour et al.42	Patient 17
Software and algorithms
FIJI	NIH	https://imagej.net/software/fiji/; RRID: SCR_002285
FIJI Non-Local Mean Denoising Plugin	Buades et al.73 Darbon et al.72	https://imagej.net/plugins/non-local-means-denoise/
FIJI Trackmate Plugin	Jaqaman et al.74	https://imagej.net/plugins/trackmate/
MATLAB	Mathworks	https://www.mathworks.com/products/matlab.html; RRID: SCR_001622
MATLAB Active Contour algorithm	Lankton and Tannenbaum75 Getreuer76	https://fr.mathworks.com/help/images/ref/activecontour.html
MATLAB Curve Fit function		https://fr.mathworks.com/help/curvefit/fit.html
Cell or nucleus tongue length measurement, cell and nucleus volume quantification (codes in MATLAB R2023a and FIJI)		https://zenodo.org/record/8251833
Prism 6.0	GraphPad	https://www.graphpad.com/scientific-software/prism/
Other
Pressure controller 1000 mbar	FLUIGENT	MFCS™-EZ 1000 mbar
High-speed camera	Photron	Fastcam Mini UX
High-speed camera	Phantom	VEO310
Table Top Spin Coater POLOS SPIN150i	SPS	Cat# 41096
Plasma Cleaner	Harrick Plasma	Cat# PDC-002
0.75-mm Punch	World Precision Instruments	Cat# 504529
Teflon tubing 0.012” ID / 0.030” OD	Scientific Commodities Inc.	Cat# BB311-30

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by Catherine Badens (catherine.badens@univ-amu.fr).

Materials availability

This study did not generate new unique reagents.

Experimental model and study participant details

Primary cells

Human fibroblasts from a healthy control (male, 2 yo) and a Progeria patient (male, age 3 yo) were purchased from Coriell Institute (Refs. AG07095, AG06917). The three other human fibroblast cell lines were issued from patients who were unrelated and gave their consent. Two female patients (36 and 41 yo) were affected with FPLD2 due to the c.1444C>T; R482W heterozygous pathogenic variant of the LMNA gene (patients 8 and 12 in Vatier et al.,³⁷ referred to as patients K and M, respectively). They presented similar symptoms such as peripheral lipoatrophy, fat accumulation in face and neck, muscular hypertrophy, fatty liver, hypertriglyceridemia, diabetes. Patient K had a more severe form of Dunnigan syndrome than patient M: lower amount of body fat, antecedent of acute pancreatitis at age 19, very severe insulin resistance, and diabetes was complicated by retinopathy and nephropathy. The third patient (male, 49 yo) was a diabetic patient who does not carry LMNA mutation (patient 17 in Dutour et al.,⁴² referred to as patient T2D) and who presented neuromuscular complaint, fatty liver, severe hypertriglyceridemia, and diabetes.

Method details

Cell culture conditions

Cells were cultured at 37°C under 5% CO₂ in low glucose Dulbecco Medium Eagle Modified (DMEM) supplemented with 15% fetal bovine serum (FBS) and 2 mM L-Glutamine (DMEM, FBS, L-Glutamine, Gibco), and used between passage 10 and 15. The cell lines were regularly tested for mycoplasma contamination.

Cell treatments and senescence assays, nucleus isolation

Cell treatments

Atazanavir (stock solution at 50 mM in DMSO; SML1796, Sigma-Aldrich) was added at varying concentrations from 25 to 75 μM to the cell medium of control cells for 48 h before analyzing senescence-associated phenotypes. Control cells were incubated with 50 μM atazanavir when performing microfluidic experiments. To induce the depolymerization of actin and/or microtubule networks, fibroblasts were treated with latrunculin A (stock solution at 1 mM in DMSO; L5163, Sigma-Aldrich) or nocodazole (stock solution at 50 mM in DMSO; 487928, Sigma-Aldrich). Cells were exposed to 200nM latrunculin A for 10 min, or 10 μM nocodazole for 45 min, or to both drugs (35 min nocodazole, then 10 min with latrunculin A and nocodazole), before being processed. For latrunculin A treatment, cells were incubated 35 min with DMSO prior to drug addition to keep 45 min total incubation with the carrier.

Senescence tests

Incorporation of 5-bromo-2’-deoxyuridine (BrdU): Cells were seeded on 96-well plate at a density of 10⁴ cells/well and BrdU was added to the cell culture medium 24 h before performing an ELISA assay following the manufacturer’s instructions (Cell proliferation ELISA, BrdU (colorimetric) Kit, Roche Applied Science). SA-β-galactosidase activity: Cells were seeded on glass coverslips (Lab-tek, SPL Life Sciences) coated with 100 μg/mL fibronectin (Sigma-Aldrich) and β-galactosidase activity was measured following the manufacturer’s instructions (Senescence β-Galactosidase Staining Kit, Cell Signaling Technology).

Nucleus isolation

Nuclei were isolated following an adapted protocol from Kidiyoor et al.⁶⁸ Adherent cells were incubated in H₂O MQ + IGEPAL 0.05% + Citric Acid 1% for 5 min at 37°C (IGEPAL, citric acid, Sigma-Aldrich). The flask was vigorously tapped to expel the nuclei. The flask content was harvested, and the nuclei were washed with 10 mL PBS, vortexed ∼ 10 s and centrifuged at 800 g for 5 min. The supernatant was removed and the nuclei in the pellet were resuspended in PBS + BSA 1%. Nuclei were extracted right before microfluidic experiments.

Fluorescence microscopy, cellular and nuclear volume quantification

Immunofluorescence

Immunofluorescence was performed on adhered cells after fixation with 4% PFA at room temperature (RT) for 10 min and permeabilization with 0.5% Triton® X-100 (Sigma-Aldrich) at RT for 10 min. After washing twice with PBS, saturation was performed with 1% BSA (37525, Thermofisher) for 30 min at RT. Cells were incubated with 150 ng/mL Hoechst 33342 (H3570, Thermofisher) for 15 min at RT prior to saturation with primary mouse anti-lamin A/C (1:1000, sc-376248, Santa Cruz) or anti-α-tubulin (1:1000, T5168, Sigma-Aldrich) antibodies for 1.5 h at 37°C. After washing twice with PBS 0.1% tween, samples were incubated with an appropriate secondary antibody coupled with Alexa Fluor 488 (Invitrogen) for 1 h at 37°C. When required, actin staining was performed at the same time using Texas Red™-X Phalloidin (1:100, T7471, Thermofisher). Samples were then washed twice with PBS and post-fixed for 10 min with 4% PFA, before mounting on slides with ProLong™ Diamond Antifade Mountant (Thermofisher).

Nuclear aberrations

Immunofluorescence staining of lamin A/C was performed on fixed adhered cells and nuclear aberrations were quantified as previously described.⁶⁹ Nuclear phenotypes were monitored using an ApoTome system (Zeiss), equipped with a 100× objective and a CCD camera (Axiocam MRm, Zeiss). Nuclear abnormality criteria were aberrant nuclear lamin A/C staining pattern, enlarged nucleus, and aberrant nucleus shape. At least 1000 cells were examined for each condition and the percentage of abnormal nuclei was calculated.

Cellular and nuclear volumes

Adhered cells were labeled for plasma membrane and DNA by incubation for 1 h with CellBrite™ Green (Biotum) and 5 mg/mL Hoechst (Invitrogen), respectively, then detached using 0.05% Trypsin-EDTA (25300-054, Gibco). Cells were resuspended in complete cell medium supplemented with 1 mM HEPES and deposited on glass coverslips coated with 0.1 mg/mL PLL-PEG (PLL(20)-g[3.5]PEG(5), SuSoS AG) in 10 mM HEPES pH 7.4 to prevent cell adhesion. Cells in suspension were subsequently observed on a confocal microscope (LSM 800 airyscan Axio Observer Z1 7, Zeiss) equipped with a 63× water objective (63x/1.20 W Korr UV VIS IR C-Apochromat, Zeiss). Z-stacks were acquired with a 0.5-μm z-step in fluorescence channels corresponding to Cell Brite and Hoechst labeling. FIJI software (ImageJ) was used for volume quantification using a home-made macro: 1) the z-stack was thresholded; 2) for each stack slice i the object (cell or nucleus) contour was determined and its area Area_i was measured (in μm²); 3) the volume was calculated by summing the slice volumes: V = Σ_iArea_i·δh, with δh = 0.5 μm (z-step between slices). Nuclei are wrinkled when cells are in suspension (Figure S1A and Video S2), as previously reported.^70,71 Here, the wrinkles were neglected in the estimation of the nuclear volumes.

Actin labeling in living cells

Adhered cells were incubated for 1 h at 37°C with SPY555-actin diluted at 1:2000 (Spirochrome, 1000x stock solution in DMSO) before being processed for microfluidic experiments (see below).

Microfluidic device fabrication

The microfluidic device is made of polydimethylsiloxane (PDMS, Dow Corning) and consists in a chamber assembled from a bottom PDMS-coated glass coverslip (defined as “bottom coverslip”) and a few mm-thick PDMS piece with drilled inlets/outlet (defined as “microchannel”).

Microchannel

The microchannel was fabricated from a master mold created on a silicon wafer using standard photolithography performed at PLANETE microfabrication facility of the laboratory (Figure S11). Three masks were used to create the mold: (1) alignment crosses, (2) main channel with micrometer-sized constrictions in the central part, and (3) main channel without constrictions. A negative tone resist (AR-N 4340, AllResist) was spin-coated at 4000 rpm for 1 min on the silicon wafer before a first soft baking step at 85°C for 2 min, followed by exposure to UV for 14 s using mask (1) positioned with an aligner (MJB4 aligner, Carl Suss). A post-exposure baking step was performed (95°C, 2 min) before the resist layer was developed with a developer (AR300-475, Allresist). Next, a thin 160-nm aluminum (Al) layer was deposited by sputtering. A lift-off step was performed overnight with a solvent (NMP, MicroChemicals) to remove the resist which had not been exposed to UV and the Al deposited on it, leaving only the alignment crosses. To enhance adhesion between the resist and the silicon wafer, the wafer was plasma-treated for 10 min before an adhesion promotion layer (Omnicoat™, MicroChemicals) was spin-coated (3000 rpm, 40 s) then baked (200°C, 1 min). Permanent Epoxy Negative Photoresist (SU8-2005, MicroChemicals) was spin-coated on the wafer (1500 rpm, 60 s) to obtain a 6-μm layer before soft baking (9°C, 2 min). The resist was then aligned with mask (2) using Al crosses and exposed to UV for 10 s. The resist-coated wafer was then post baked (95°C, 3 min), developed in SU8-Developer (DevSU8/4, MicroChemicals) to remove unpolymerized resist, washed abundantly with isopropanol, air-blown and hard baked (cured) at 150°C for 5-10 min to prevent the resist from cracking. The process was repeated with mask (3) to create a second 4-μm layer, with diluted SU8-2005 (90% v/v in cyclopentanone). After fabrication, the mold was treated once with silane Trichloro(1H,1H,2H,2H-perfluorooctyl)silane (448931, Sigma-Aldrich) to prevent the PDMS from sticking and subsequently damaging the constrictions. A mold is typically used at least ten times. A 10:1 mixture of PDMS and cross-linking agent (Sylgard 184, Dow Corning) was poured on the master mold. After degassing in a vacuum chamber for 30 min and curing at 80°C from 2 h up to overnight, the PDMS microchannel was peeled off from the mold.

Bottom coverslip

Glass coverslips were cleaned by sonication in acetone then in isopropanol, for 30 min each, washed in ethanol for 5 min, and rinsed abundantly with MilliQ water. Cleaned coverslips were stored in MilliQ water before use. A few drops of PDMS were poured onto a dried coverslip and spin-coated at 4000 rpm for 45 s before being cured at 80°C overnight.

Chip assembly

The three inlets and the outlet of the PDMS microchannel were drilled with a 0.75-mm punch (Biopsy Punch 504529, World Precision Instruments) prior to assemble the microfluidic chip by bonding the microchannel to the bottom coverslip via plasma treatment, followed by a curing step at 80°C overnight.

Microfluidic experiments

The experiments were performed on a microscope (IX71, Olympus) equipped with a 20x objective and high-speed cameras (Fastcam Mini UX, Photron and VEO310, Phantom) at 37°C. Prior to experiments, cells were cultured for 72 h (including 48 h of atazanavir treatment), to ensure ≈90% cell confluence. The microfluidic chip inlets and oulet were connected via Teflon tubing (0.012” inner diameter (ID) and 0.030” outer diameter (OD), BB311-30, Scientific Commodities Inc.) to a pressure controller (MFCS™-EZ 1000 mbar, FLUIGENT) that allows to fix the pressure drop between the inlets and outlet and thus the circulation of cells/nuclei in suspension. Microchannels were passivated with 10% Pluronic®F-127 (P2443, Sigma) in PBS for 1 h at room temperature. Inlets (1) and (3) were used to inject buffer solutions while cells/nuclei were injected with inlet (2) (see Figure 2A for a schematic view of the chip).

Cell experiments

Cells suspended in complete medium supplemented with 10 mM HEPES, 1% BSA (± cytoskeleton drugs) were injected in microchannels under a pressure drop of ΔP = 165 mbar (P_inlets = 170 mbar, P_oulet = 5 mbar). Cells were observed in brightfield and movies were acquired at frame rates varying from 125 to 1000 fps.

Isolated nucleus experiments

Isolated nuclei suspended in PBS with 1% BSA were injected into microchannels under a pressure drop of ΔP = 200 mbar (P_inlets = 205 mbar, P_oulet = 5 mbar). Nuclei were observed in epifluorescence and movies were acquired between 500 and 1000 fps.

Image processing and analysis

Cell analysis

Movies of cells were pre-processed using FIJI software to enhance contrast and segment the cells. To enhance cell contrast and remove constrictions (static in the movie), a median image from a few frames was computed and a new movie was produced by subtracting the median image. Using Non-Local Mean Denoising Plugin,^72,73 the background noise was removed while keeping the cell intact, which was then manually thresholded. Using Matlab software (MathWorks, r2018b version), a bounding box was fitted around the thresholded cell at each time point to measure the cell dimensions (length L along the flow axis and width w perpendicularly to it) over time.

Isolated nucleus analysis

Movies of nuclei were pre-processed using FIJI software, with automated tracking of individual nuclei using Trackmate.⁷⁴ Each track contained the X-Y positions of a nucleus centroid at each timepoint. Using the X-Y positions of the centroids, we defined an initial mask of 12×12 pixel² that evolved to perfectly fit the nucleus contour using the Active Contour method in Matlab.^75,76 Once the final contour was retrieved, the image was segmented and the bounding box analysis was performed such as for cells.

Cellular and nuclear volumes

Additionally, volumes of cells and isolated nuclei were computed from microfluidic images before contact with constrictions, assuming they have a "pancake" shape. The volume is computed as the projected area multiplied by the microfluidic channel height: V = area × h₁.

Tongue length analysis

Entry time and slope analysis

With a home-made Matlab routine, the time evolution of the tongue length l(t) was plotted and four parameters were manually determined: the entry time T_e (in seconds), defined as the time to fully enter a constriction, and three slopes S_I to S_III (in s⁻¹) corresponding to three distinct regimes displayed during the cell entry and considered as linear in a first approximation. To calculate the slopes, the first and last points of each regime were selected, and a tangent was automatically fitted that provided the slope value.

Rheological fit

Matlab fit function (MATLAB 2018) was used on the curves l(t), with expression a(1-exp(-bt)) + ct, where a, b, and c are fit parameters; the combination of these parameters provides the physical quantities defined in Equation 8. We performed a series of 6 fits of the experimental curves with a set of time intervals I_m = [0;m × T_e/10] with m = 4, . . . , 10, where T_e is the cell entry time. For each fit, we evaluated the corresponding physical parameters and R² chi-square values, and defined for each cell the following lists: (η₂^(m))_{m= 4,...,10}, (η₁^(m))_{m= 4,...,10}, (E^(m))_m=4,...,10 and (R^2(m))_m=4,...,10. We only retained fitted parameters whose corresponding fits had the maximal R² value that is larger than a critical threshold set at 0.85, i.e. those such that R²_I = max(R²_m)_m=4,...,10 > 0.85. We discarded too large values of η₂ > 10⁵ Pa.s, η₁ > 500 Pa.s and E > 70 kPa, threshold values one to two orders of magnitude larger than typical median values. We also discarded too low values of η₁ < 5 Pa.s and E < 0.7 kPa.

Rheological models

Here we show how we derive the elastic modulus and the viscosities of cells using a viscoelastic model. We follow a method laid out in previous works using micropipettes,^35,43 with adaptation for a squared cross-section constriction.

Constant pressure drop approximation

In Guevorkian et al.,⁴³ aspiration is performed using a cylindrical pipette of circular cross-section $\pi R_p^2$. Considering volume conservation (experimentally, the cell volume decreases at most by 20%), the aspiration force under a pressure drop ΔP between the exterior and the interior of the pipette reads as:

$$f=\pi R_p^2\left(\Delta P-\Delta P_c\right)\text{,}$$ (Equation 1)

where ΔP_c is the Laplace pressure, i.e. the critical pressure required to push cells through constrictions, which reads as:

$$\Delta P_c\approx 2\gamma \left(\frac{1}{R_{\mathrm{i}\mathrm{n}}}-\frac{1}{R_{\mathrm{o}\mathrm{u}\mathrm{t}}}\right)\text{,}$$ (Equation 2)

where the cell radii R_in = R_p and R_out correspond to the portion of the cell either inside (front of the cell) or outside (back of the cell) the constriction, respectively, and γ is the cortical surface tension.

Here we argue that the Laplace pressure ΔP_c can be neglected. Indeed, the cortical tension lies in the 5.10^-4 N.m^-1 (cortical tension in fibroblast cells^77,78), with upper values reported at 2.10^-3 N.m^-1 (dividing Hela cells⁷⁹), corresponding to ΔP_c in the 0.5 to 2 kPa range. In comparison, the applied pressure drop is ΔP = 165 mbar = 16.5 kPa, which is significantly larger than ΔP_c. Considering a more realistic geometry with a Laplace pressure given as in Bruus et al.⁸⁰ does not affect our conclusion. In addition, the validity of our approximation is verified a posteriori through the estimation of a capillary number based on the measurement of the cell viscosity. We point out that Dupire et al.,³⁴ who focused on the measurement of the surface tension, considered a significantly lower applied pressure. Therefore, in the rest of the manuscript we consider that:

$$f\approx \pi R_p^2\Delta P\text{.}$$ (Equation 3)

Jeffreys rheological model

The established literature^35,36,43 models the evolution of the deformation of various objects (from nuclei to cell aggregates) in micropipettes through the Jeffreys rheological model. The Jeffreys model results in the following time evolution of the aspirated tongue length:³⁵

$$l\left(t\right)=\frac{f}{k}\left(1-e^{-\frac{t}{\tau }}\right)+\frac{f}{{\mu }_2}t\text{,}$$ (Equation 4)

where f is the applied force, defined in Equation 1, k is a spring constant, τ is a relaxation time and μ₂ is the long-time viscosity. The first term in Equation 4 describes the short time behavior, during which the pressure force is balanced by the cell elastic forces. The cell yields after a characteristic time τ, which we can express in terms of a short-time viscosity μ₁ as τ = k/μ₁. The second term in Equation 4 describes the long-time behavior (before complete cell entrance is achieved) during which the pressure force is balanced by the viscous force due to a plug flow at the entrance of the capillary, leading to a linear increase of the regime strain with time. The stress/strain relationship of Equation 4 is commonly represented diagrammatically in terms of a Kelvin-Voigt element, i.e., a spring (k) and a dashpot (μ₁ = k/τ) in parallel, in series with a dashpot (μ₂).

Relation to rheology

Here we propose to map the spring k, viscoelastic time τ and viscosity μ₂ parameters defined in Equation 4 to a simplified model for the cell rheological properties. Following the literature,^35,43 we discuss the expected behavior of the cell considered as a homogeneous viscoelastic material under aspiration through a cylindrical constriction of radius R_p.

At short time scales, the aspiration force is balanced by the elastic deformation and is given by the following equation:

$$\frac{f}{A}=CE\frac{\delta }{R_p}\text{,}$$ (Equation 5)

where A = π R_p² is the cross-sectional area of the constriction, C is a geometrical factor approximately equivalent to 1,^35,43 E is the elastic modulus and δ is the elastic deformation at short times. We thus obtain f = π R_p E δ. The spring constant k is the coefficient between the applied force f and the extension δ, f = k·δ, leading to the relation:

$$k=\pi R_{p}E$$ (Equation 6)

At long time scales, the aspiration force is balanced by two dissipation forces. The first one arises from the viscous flow of the cell through the entrance of the constriction, such as the flow of a viscous fluid through a circular pore described by Sampson.⁸¹ The second source of dissipation arises from the resistance of the tongue slipping along the constriction wall. Combining both terms leads to:^43,82

$$f=3{\pi }^2{\eta }_2{R}_p\stackrel{\bullet }{l}+2\pi \xi R_p\stackrel{\bullet }{l}$$ (Equation 7)

where η₂ is the cell viscosity and ξ is the cell-wall friction coefficient. As in Refs.⁴³ and,³⁵ we can ignore the friction on the surface of the constriction: indeed, once the cell has fully entered into the constriction, its velocity (in the 50 μm.s^-1 range) is significantly larger than during the deformation phase. Identifying $\dot{\mathcal{l}}=f/{\mu }_2$ from the second term in Equation 4 leads to:

$${\mu }_2=3{\pi }^2{\eta }_2{R}_p$$ (Equation 8)

Inserting Equations 6 and 8 into Equation 4, we obtain the following relation of the cell tongue length as a function of the cell rheological properties:

$$l\left(t\right)=\frac{R_p\Delta P}{E}\left(1-e^{-\frac{E}{3\pi {\eta }_1}t}\right)+\frac{R_p\Delta P}{3\pi {\eta }_2}t$$ (Equation 9)

which is the expression that we use within the main text.

A key interest of Equation 9 is to provide a set of intensive mechanical properties that allows comparison between classes of cell types. For each cell type, we verified that the estimated mechanical parameters in Equation 9 did not vary for cells of different sizes.

Effective radius of the constriction

For a cylindrical pipette as in Guevorkian et al.,⁴³ the pipette radius R_p is used in Equation 1. In our case, the constrictions are rectangular instead of cylindrical and R_p is replaced by an effective radius R_eff that is the function of the height and width of the rectangular cross-section. Following Davidson et al.³⁵ and the theoretical study from Son,⁸³ we express the effective radius as:

$$R_{\mathrm{e}\mathrm{f}\mathrm{f}}^4=\frac{2}{\pi }\frac{w\times h_1^3}{{\left(1+h_1/w\right)}^2\times g^{\ast }\left(h_1/w\right)}\text{,}$$ (Equation 10)

where h₁ and w are the dimensions of the constriction cross-section and g∗ is a dimensionless function of the form:

$$g^{\ast }\left(x\right)={\left[{\left(1+\frac{1}{x}\right)}^2\left(1-\frac{192}{{\pi }^{5}x}\sum _{i=\mathrm{1,3,5}}^{\infty }\frac{\tanh \left(\frac{\pi }{2}ix\right)}{i^5}\right)\right]}^{-1}\text{.}$$ (Equation 11)

With w = h₁ = 6 μm, applying Equation 10 yields R_eff = 4.32 μm.

We point out that Equation 10 is not strictly exact in our case, since our geometry is off-centered in height, which is not exactly the case considered by Son.⁸³ Nonetheless, we expect R_eff to be a satisfactory approximation. In addition, in our study the constriction geometry is identical for all cell types and drug treatment; any approximation on the value of R_eff will not affect conclusions based on the comparisons of mechanical parameters between experiments.

A simple scaling law between cell initial length L0 and entry time Te allows for crossed comparisons of viscous moduli

Here we propose to extract a simple relation between the entry time T_e and the cell radius before entry that holds for sufficiently large cells. In this case T_e ≫ τ on average and, by neglecting the time spent in both phases I and III (see Figure 2C), the aspirated tongue length at time T_e derives from Equation 9 as:

$$l\left(T_e\right)\approx \frac{R_{\mathrm{e}\mathrm{f}\mathrm{f}}\Delta P}{E}+\frac{R_{\mathrm{e}\mathrm{f}\mathrm{f}}\Delta P}{3\pi {\eta }_2}{T}_e$$ (Equation 12)

Assuming the cell has a disk shape of diameter L₀ before entering the constriction, the initial volume V_i can be expressed as V_i = π (L₀/2)² h₁. Once fully entered in the constriction, the cell shape is approximately a parallelepiped of final length l(T_e) and final volume V_f ≈ l(T_e) w h₁. Considering the cell volume to be conserved, the final aspirated tongue length l(T_e) can be expressed in terms of L₀ as:

$$l\left(T_e\right)\approx \pi \frac{L_0^2}{4w}$$ (Equation 13)

Substituting the latter expression into Equation 12, we obtain, for large cells L₀/w ≫ 1, the following approximate scaling of the entry time T_e with the initial cell diameter (or initial length) L₀:

$$T_e\approx \frac{3{\pi }^2{\eta }_2}{4w{R}_{\mathrm{e}\mathrm{f}\mathrm{f}}\Delta P}{L}_0^2\text{.}$$ (Equation 14)

Equation 14 provides a rationale for fitting the relation between the experimental entry time T_e and the cell diameter L₀ through the following log-log scaling:

$${\log }_{10}\left(T_e\right)={\log }_{10}\left(\nu \right)+2{\log }_{10}\left(L_0\right)\text{.}$$ (Equation 15)

where we expect the quantity ν to be proportional to the long-time cell viscosity η₂ (see Figure S5).

The scaling law fit was applied to the T_e vs L₀ data using the nonlinear least-square solver from MATLAB (MATLAB 2018). We measured the value of ν for all cells whose experiment time is long enough (T_e > 10τ ≈ 0.3 s).

Alternative model: Power-law rheology

Following Refs.^18,35, we also evaluate the efficiency of a power-law fit of the tongue length data. We employ a similar fitting procedure to the one previously used for viscosity extraction, with a master curve:

$$\ell \left(t\right)={\ell }_0+\frac{t^{\alpha }}{A_{\alpha }}\text{,}$$ (Equation 16)

where l₀ corresponds to the very short-time elastic response and A_α is a quantity that corresponds to a non-Newtonian viscous coefficient (in the limit α = 1, A_α corresponds to a Newtonian viscosity). Inspired by the range of values measured in ref.³⁵, we set the value of the exponent to α = 0.5. We then observe that the relations between the 1/A_α prefactors in all cell types also correspond to the previously measured relations on η₂ (see Figure S8).

Quantification and statistical analysis

When indicated, N, n, and n’ are the number of experiments, of analyzed cells, and of fitted curves, respectively. Statistical calculations were performed using Prism 6.0 statistical software (GraphPad). Significant differences (p-values) are indicated with ∗(or #,¤): ∗, p < 0.05; ∗∗, p < 0.01; ∗∗∗, p < 0.001 ; ∗∗∗∗, p < 0.0001.

For experiments examining the proportions of cells with nuclear abnormalities or SA-β-galactosidase positive staining, data were averaged over at least 3 independent experiments (mean ± SD, standard deviation) and mean values were compared using the Fisher’s exact test and the Bonferroni post-hoc analysis to correct for multiple comparisons.

For BrdU incorporation, data were averaged over at least 3 independent experiments (mean ± SD) for each condition, and mean values were compared using the Kruskal-Wallis test followed by the Dunn’s multiple comparison post-hoc analysis when appropriate.

For nuclear and cellular volumes, the median values and 95% Confidence Intervals (CIs) were calculated from measurements on individual cells pooled from at least 2 independent experiments, and median values were compared using the Kruskal-Wallis test followed by the Dunn’s multiple comparison analysis.

Entry time, tongue length slopes, and rheological parameters derived from the fits of the tongue length curves all displayed non-Gaussian distributions. The median values were calculated with 95% CIs from individual cells pooled from at least 3 independent experiments, and data were compared using the Kruskal-Wallis test followed by the Dunn’s multiple comparison analysis.

Published: August 25, 2023

Data and code availability

• •All experimental generated data are available upon request from the lead contact.
• •All custom computer codes (measurement of cell or nucleus tongue length in constrictions, quantification of cell and nucleus volumes from confocal imaging) are available on a repository (see key resource table).
• •Any additional information required to reanalyze the data reported in this work paper is available from the lead contact upon request.