Siderophore-mediated iron partition promotes dynamical coexistence between cooperators and cheaters

Summary

Microbes shape their habitats by consuming resources and producing a diverse array of chemicals that can serve as public goods. Despite the risk of exploitation by cheaters, genes encoding sharable molecules like siderophores are widely found in nature, prompting investigations into the mechanisms that allow producers to resist invasion by cheaters. In this work, we presented the chemostat-typed “resource partition model” to demonstrate that dividing the iron resource between private and public siderophores can promote stable or dynamic coexistence between producers and cheaters in a well-mixed environment. Moreover, our analysis shows that when microbes not only consume but also produce resources, chemical innovation leads to stability criteria that differ from those of classical consumer resource models, resulting in more complex dynamics. Our work sheds light on the role of chemical innovations in microbial communities and the potential for resource partition to facilitate dynamical coexistence between cooperative and cheating organisms.

Graphical abstract

Highlights

• •Siderophore-mediated iron partition allows for the cooperator–cheater coexistence
• •The resource partition mechanism bypasses competitive exclusion
• •Chemical innovation leads to different stability criteria than classical models

Biological sciences; Biochemistry; Microbiology

Introduction

Theoretical ecology has long been fascinated by the intricate feedback between microbes and their microhabitats.¹ Central to this ecological feedback is the “chemical environment,” which includes the substances in the local environment that directly impact and are influenced by microbes.^2,3 Examples of such substances include essential “resources,” such as carbon, nitrogen, and oxygen, which are supplied to the extracellular environment and consumed by microorganisms to promote their own growth.^4,5,6 In theoretical ecology, the consumer-resource model has been employed for decades in studying this feedback, where the dimension of the chemical space has been demonstrated to be of key importance.⁷ For instance, MacArthur et al. validated the competitive exclusion principle (CEP), which asserts that the number of stably coexisting species cannot exceed the number of resources they are competing for.^8,9 Tilman et al. demonstrated that in a chemical space of dimension two, the zero-net growth isoclines and the consumption vector dictate the outcome of competition.¹⁰ Moreover, in a multi-species resource competition system with a minimal chemical dimension of three, Huisman et al. established that oscillatory and even chaotic dynamics could arise, allowing for dynamic coexistence that surpasses the upper limits of CEP.^11,12 Actually, despite numerous research efforts aimed at reconciling the conflict between CEP and the apparent biodiversity in nature, most of which include additional factors such as spatial or temporal heterogeneity,^13,14,15,16 a definitive answer has yet to be achieved.^17,18

Microorganisms have developed ways to overcome the upper limit of competitive exclusion. By leaking metabolic byproducts or actively producing and secreting secondary metabolites, cells can expand the chemical diversity of their habitats.^19,20 Such chemical innovations, in which microorganisms generate new chemical dimensions previously nonexistent in the environment, have profound implications for microbial ecology.^21,22 For example, cross-feeding through metabolic byproducts has been suggested to promote stable coexistence even with a single carbon source.²³ Meanwhile, the vast range of bacteriocins and antibiotics contributes to the chemical warfare among microorganisms.^24,25,26 Overall, microbial chemical innovations increase the chemical dimensions in the environment, raising the upper bounds of competitive exclusion.

However, the active production of secondary metabolites often requires microbial cooperation, such as various quorum sensing molecules that coordinate collective decision-making,²⁷ or niche-construction molecules such as siderophores or secretory proteases that serve as “public goods” to enhance the microenvironment for the entire population,^28,29,30 From a game theory perspective, secondary metabolites produced for cooperation bring “the tragedy of the commons”³¹: If a cheater strain can exploit public goods without contributing to their production, how can the cooperating strains that provide these extra chemical dimensions remain competitive?

Big questions in biology often have specific solutions in particular systems. The siderophore system, a diverse family of microbial secondary metabolites used for iron-scavenging, provides an excellent model to investigate the game between cooperators and cheaters and the ecological effect of self-generated chemical dimension.^32,33 Iron is one of the most limiting resources for microbes, required for crucial processes like energy metabolism and DNA synthesis.³⁴ However, the bioavailable iron concentration is orders of magnitude lower than what is required for normal microbial growth in most environments.^4,35 Most microorganisms acquire iron via siderophores, a type of small molecule with a strong iron-binding affinity.³⁶ Siderophores are secreted into the extracellular environment to chelate iron, and the iron-siderophore complex forms a new chemical dimension only absorbed by cells via corresponding membrane receptors.³⁷ However, siderophore production carries a metabolic cost that slows microbial growth, making siderophores a costly public good that may result in the “tragedy of the commons” in game theory: cheaters that do not invest in siderophore production but still benefit from the presence of siderophores can have a selective advantage over producers, leading to a decrease in overall siderophore production and potentially reducing the availability of iron for all microbes in the community.^38,39 Many theories have been proposed to explain the prevalence of siderophore synthesis pathways,^40,41 most of which entail spatial factors that facilitate kin selection or group selection.^42,43,44 Despite this, microorganisms actively produce siderophores of various types in well-mixing environments such as the ocean.^45,46

Recent experiments have suggested that private siderophores, which are accessible only to their producers, may be crucial for the survival of siderophore-producing microorganisms.⁴⁷ In many organisms, certain modifications during the multi-step process of siderophore production can transform the secretory molecules into a membrane-attached form.^47,48,49 This privatization of siderophores may shift the game between cooperators and cheaters toward the “snowdrift” scenario, where producers can benefit from their membrane-attached siderophores when diffusible siderophores are scarce. According to evolutionary game theory, the snowdrift scenario allows both cooperation and defection to persist at a stable equilibrium through negative frequency-dependent selection.⁵⁰ However, membrane-attached siderophores have a considerably lower diffusion radius in iron scavenging.^29,37 The marginal benefits conferred by membrane-attached siderophores have not been quantitatively assessed by ecological models, and it is unclear whether they provide cooperators with a sufficient advantage over cheaters. Many questions remain to be systematically explored through mathematical formulation, such as whether and how cooperators and cheaters can coexist, how different allocation strategies between membrane-attached and publicly shareable siderophores change the system dynamics, and which strategies might be optimal considering within- and between-species interactions. Furthermore, can siderophore-mediated iron competition help address a profound question in ecology: whether self-generated resource dimensions fundamentally change the properties of mathematical models about resource competition?

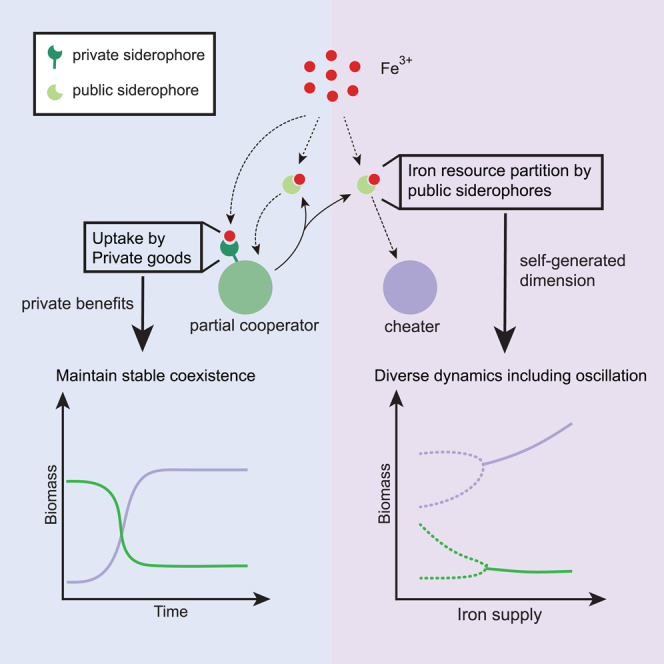
In this work, we employed a chemostat-type “resource partition model” to investigate the iron competition mediated by siderophores, accounting for the allocation of limited cellular resources between biomass accumulation and the production of membrane-attached (private) and publicly sharable (public) siderophores. By incorporating private siderophores into the resource allocation strategies, new classes of strategies emerge, including “partial cooperators,” who produce both types of siderophores, and “self-suppliers,” who only produce membrane-attached siderophores. Coexistence between the partial cooperators and the pure cheaters is made possible by private siderophores, by providing partial cooperators with a growth advantage over cheaters when public siderophores are scares. Notably, such coexistence between two species can occur via dynamical oscillation. Further stability analysis revealed that creating new resource dimensions by species, i.e., siderophore production in our model, modifies the stability criteria of the classical consumer-resource model, allowing for more diverse dynamics than the classical model. In summary, our model of iron competition suggests that the division of the iron resource by siderophores increases the upper bound of coexistence, and the privatization of siderophores in cellular strategies provides advantages to partial cooperators to achieve coexistence. Our analysis of the stability criteria revealed that microbial niche construction by creating new resource dimensions adds more dynamics than the classical model, which may contribute to the diversity and complexity of the microbial world.

Results

A resource partition model with trade-offs between growth and siderophore production

The consumer resource model is a widely used theoretical framework in ecology that simulates ecosystems with constant nutrient supplies and extensive mixings, such as lakes and oceans. However, in the microbial world, species not only consume resources but also produce them, which can be shared among the community, such as siderophores for iron scavenging. To investigate the ecological consequences of siderophore production and privatization, we developed a modified version of the consumer resource model that incorporates resource generation, which we refer to as the “resource partition model”. Our model is based on three assumptions:

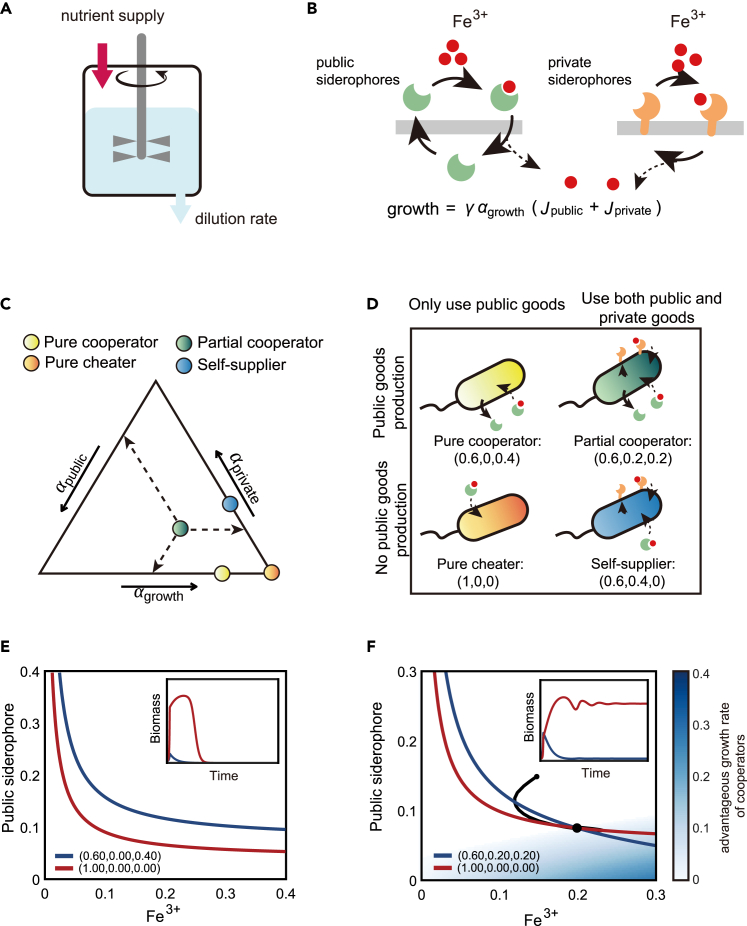
• 1.Chemostat-typed resource partitioning: we used a chemostat-type model, in which the volume is maintained constant by maintaining the same rate of in-and-out fluxes. Parameters about the concentration of iron in the influx $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}$, together with the dilution rate $d$, are referred to as “chemostat conditions” (Figure 1A). The chemical environment that cells directly face within the chemostat can be quantified by two variables: concentration of the iron ($R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}$) and of the public siderophores ($R_{\mathrm{s}\mathrm{i}\mathrm{d}}$). They serve as both “resources” for microbial growth; meanwhile, the public siderophore is also a “product” released by bacteria. We coined the term “resource partition model” to refer to models in which organisms generate more chemical dimensions than are supplied from the external influx, and partition the externally supplied resources by these secondary metabolites.
• 2.The growth rate scales linearly with the iron uptake rate: Assuming iron was the limiting resource, we set the growth rate to a value that linearly scales the total iron fluxes obtained via two types of siderophores: the flux from secreted public siderophores ($J_{\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}$, depicted on the left side of Figure 1B) and the flux from membrane-bound private siderophore ($J_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$, depicted on the right side of Figure 1B).
• 3.Trade-offs in resource allocation between growth and siderophore-production: Given the limited amount of proteins and energies in a microorganism, we assumed that there are trade-offs between different biological processes. In an iron-limited environment, we focused on resource partitioning into biomass accumulation and production of private and public siderophores. Each partition corresponds to an allocation strategy $\overrightarrow{\alpha }=\left({\alpha }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}},{\alpha }_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}},{\alpha }_{\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}\right)$, where ${\alpha }_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$ and ${\alpha }_{\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}$ denote the percentage of resources used to produce private and public siderophores, respectively, and ${\alpha }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$ donates the percentage of resources devoted to biomass accumulation. The summation of all allocations was fixed as ${\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}+{\alpha }_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}+{\alpha }_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}=1$. Various species may differ in their abilities to produce and scavenge siderophores, but different strains $\sigma$ only differ in their resource allocation strategies $\overrightarrow{\alpha }$.

Figure 1.

Privatization of siderophore enables the coexistence of partial cooperators and pure cheaters

(A) The schematic diagram of a chemostat model.

(B) The schematic diagram showing two iron uptake fluxes from the public siderophores (left) and private siderophores (right).

(C) The strategy space (the strategic phase diagram) by ternary plot, showing all resource allocation strategies $\overrightarrow{\alpha }=\left({\alpha }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}},{\alpha }_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}},{\alpha }_{\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}\right)$. The model has four typical strategies, distinguished according to whether to produce public siderophores and whether to use private siderophores. Pure cooperators (yellow) only produce and use public siderophores, while the pure cheater (orange) only use public siderophores and put all resources into ${\alpha }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$; partial cooperators (green) produce and use both public and private siderophores, while self-suppliers (blue) only produce private siderophores and use both public and private siderophores.

(D) The schematic illustration of the four typical strategies shown in (C).

(E and F) The growth contours in the chemical space, with the concentration of Fe³⁺ by the x axis and the concentration of public siderophore by the y axis. (E) shows the growth contours of a pure cooperator and the pure cheater, and (F) shows the growth contours of a partial cooperator and the pure cheater (color scheme same as that in (C) and (D)). The blue area represents a growth-advantageous zone in which the partial cooperator outperforms the pure cheater. Inserts are the biomass time-courses of species competing in the chemostat. The small black dot represents the beginning of the dynamical trajectory (black line).

Under this trade-off, all possible strategies for a species can be located in a ternary graph (Figure 1C). There are four types of typical strategies (Figures 1C and 1D): pure cooperators, pure cheaters, partial cooperators, and self-suppliers. Pure cooperators produce public siderophores but not private siderophores (${\alpha }_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}=0,{\alpha }_{\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}>0$), while the pure cheater allocates all resources to growth and exploits only the public siderophores (${\alpha }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}=1$). On the other hand, partial cooperators (${\alpha }_{\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}>0,{\alpha }_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>0$) and self-suppliers(${\alpha }_{\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}=0,{\alpha }_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>0$) have access to both public and private siderophores due to non-zero ${\alpha }_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$. The difference between the two strategies is that partial cooperators still produce public siderophores while self-suppliers do not. The characteristics of self-suppliers make them very similar to the “loner” in the work of Inglis et al.,⁵¹ but unlike the loner, the self-suppliers can still use public siderophores and may gain an advantage over the cooperators instead of being outcompeted. In the ternary graph (Figure 1C), pure cooperators’ strategies span the triangle’s base, while the pure cheater’s strategy locates on the right-vertex. The right side is occupied by self-suppliers, and each strategy contained within the triangle can be considered a partial cooperator.

With the three assumptions above, the microbe $\sigma$ with biomass concentration $m_{\sigma }$ and strategy ${\overrightarrow{\alpha }}_{\sigma }$ shapes its chemical environment in two ways:

• 1.Producing public siderophore with the out flux $ϵ\frac{m_{\sigma }}{r}{\alpha }_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}$, where $ϵ$ is the production coefficient of public siderophores, and the constant $r$ represents the biomass per cell volume (Details in SI). Assuming the public siderophores can be fully recycled for simplicity, the changing rate for $R_{\mathrm{s}\mathrm{i}\mathrm{d}}$ can be written as:

$$\frac{d{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}}{dt}=-d{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}+\sum _{\sigma }ϵ\frac{m_{\sigma }}{r}{\alpha }_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}\text{.}$$ (Equation 1)

• 2.Consuming iron by public siderophores and private siderophores.

For iron-uptake, the fluxes of $J_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$ and $J_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}$ take the Monod form with the environmental iron concentration $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}$. We also assumed that both fluxes linearly scale with the concentration of corresponding siderophores. Taken together, there are:

$$J_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}=\frac{v_{\mathrm{m}}{{\beta \alpha }_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}R}_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{K_{\mathrm{m}}+R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}\text{,}$$ (Equation 2)

$$J_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}=\frac{v_{\mathrm{l}}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}{R}_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{K_{\mathrm{l}}+R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}\text{.}$$ (Equation 3)

In the equations above, $v_{\mathrm{m}}$ and $v_{\mathrm{l}}$ are the rate coefficients for the two fluxes; $K_{\mathrm{m}}$ and $K_{\mathrm{l}}$ are the affinity coefficients of the two kinds of siderophores for intaking iron; $\beta$ is the efficiency coefficient of the private siderophores. In total, the changing rate for iron is written as:

$$\frac{d{R}_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{dt}=d\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}\right)-\sum _{\sigma }\frac{m_{\sigma }}{r}\left(J_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}+J_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}\right)\text{,}$$ (Equation 4)

It can be proved that other forms of iron uptake-fluxes do not qualitatively affect the result of this work (see STAR Methods, method details).

Meanwhile, the microbe $\sigma$ has its growth rate affected by its chemical environment $\left[R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{sid}\right]$ and allocation strategy ${\overrightarrow{\alpha }}_{\sigma }$ as:

$$g\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{sid},{\overrightarrow{\alpha }}_{\sigma }\right)=\gamma {\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\left(J_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}+J_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}\right)\text{,}$$ (Equation 5)

where $\gamma$ here represents the growth coefficient.

In this iron-partition model, the changing rate for the biomass for microbe $\sigma$ can be written as:

$$\frac{d{m}_{\sigma }}{dt}=m_{\sigma }·\left(g\left(R_{sid},R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},{\overrightarrow{\alpha }}_{\sigma }\right)-d\right)\text{.}$$ (Equation 6)

Privatization of siderophore enables the coexistence between partial cooperators and pure cheaters

Graphical approaches developed for consumer resource models allow for an intuitive assessment of ecological consequences in chemical space¹⁰ (Figure S1). This approach involves two elements: the growth contour, i.e., the zero net growth isoclines (ZNGI), and the consumption vector. By setting Equation 6 to zero for a single subpopulation, we obtained the growth contour. The growth contour shows all possible chemical environments $\left[R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{\mathrm{s}\mathrm{i}\mathrm{d}}\right]$ in which the microbe can achieve steady-state growth at the dilution rate. Any environment above the growth contour belongs to the “invisible zone,” where the microbe can invade.⁵²

This graphical approach provides an intuitive explanation of why pure cooperators and pure cheaters cannot coexist. To allow for stable coexistence between two strains, their respective growth contours must intersect, as denoted by the "∗" in Figure 1E. However, as shown in the figure, the growth contour of the pure cheater completely encloses that of the pure cooperator without any intersection. This is due to the fact that the pure cheater grows faster than the pure cooperator in any chemical environment, since they receive the same amount of iron influx via public siderophores $J_{\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}$, but the cooperator invests less in ${\alpha }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$ (for a rigorous proof, see STAR Methods, method details). Nonetheless, the pure cheater can only use public siderophores and cannot survive independently. Therefore, in our simulations, the pure cheater eventually takes over the entire population, causing its own extinction due to a lack of public siderophores. This phenomenon can be seen as analogous to the “tragedy of the commons.”

Investing in private siderophores can change the game. The transition from pure cooperators to partial cooperators enables the growth contours to intersect with those of pure cheaters, thereby allowing for coexistence (Figure 1F). In regions where the public siderophore is abundant but iron is scarce (upper-left region of Figure 1F filled in white), the cheater still retains a growth advantage over the partial cooperator; however, in regions where the public siderophore is scarce but free iron is abundant (lower-right region of Figure 1F filled in blue-green color), the partial cooperator gains a growth advantage over the pure cheater because their membrane siderophores sustain iron-dependent growth. Under this model setting, the game enters the regime of “snowdrift”⁵⁰: although producing siderophores incurs costs, cooperators gain by holding portions of them as private goods, particularly in environments where public siderophores are scarce.

Mathematically, it can be analytically proven that the presence of an intersection between the growth contours of strain 1 and strain 2, under the setting that strain 1 invests less in its own growth ${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}<{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\text{,}$ requires:

$${\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}\text{.}$$ (Equation 7)

Equation 7 shows that for any two strains to coexist, the strain that invests fewer resources in growth must invest more in private siderophores (details can be found in STAR Methods, method details).

Meanwhile, the non-zero biomass of two strains imposes constraints on the iron supply concentration $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}$ in that

$$R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }+\frac{1}{k_2}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }>R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}>R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }+\frac{1}{k_1}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }\text{.}$$ (Equation 8)

with $k_1=\frac{ϵ\gamma }{d}{\alpha }_{1,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$ , $k_2=\frac{ϵ\gamma }{d}{\alpha }_{2,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$.

Graphically, inequality Equation 8 requires the supply point [$R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}},0]$, located within the region bounded by the reverse extensions of the consumption vectors in the chemical space (see STAR Methods, method details).

However, the presence of an intersection between growth contours is just one necessary condition for coexistence. The feasibility of coexistence is further determined by how each strategy shapes the chemical environment for the entire community.⁵² In the system depicted in Figure 1F, where the partial cooperator stably coexists with the pure cheater (as demonstrated by the competition dynamics shown in the insert), the partial cooperator creates a chemical environment that is rich in public siderophores in the upper-left region of the chemical space where the cheater can invade. At the same time, the pure cheater cannot survive on its own and has no corresponding stable point, but its competition for iron reduces the abundance of the partial cooperator, causing an environment deficient in public siderophores to favor the partial cooperator. This interaction between the partial cooperator and the pure cheater resembles mutual invasion and allows for stable coexistence.⁵² However, it is worth noting that such stable coexistence occurs only under specific ranges of parameters of the iron influx $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}$ and the dilution rate $d$. The discovery of an area in the chemical space where the partial cooperator thrives prompted us to investigate whether other chemostat conditions would lead to more complex ecological dynamics.

The partial cooperators and cheaters can generate diverse ecological dynamics

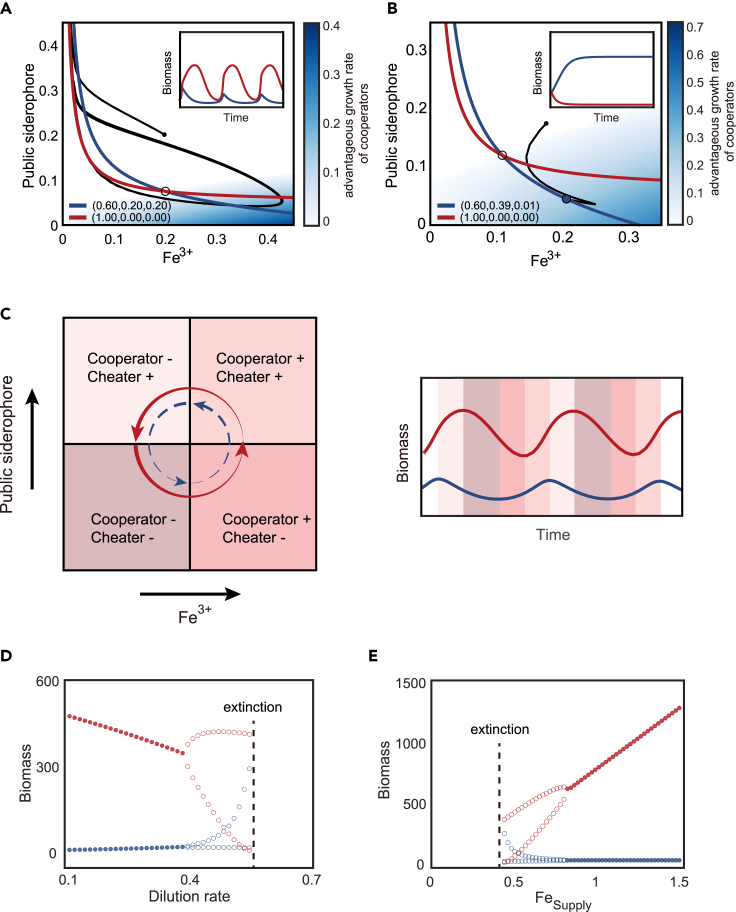
The classical consumer resource models have shown that oscillatory dynamics can emerge among at least three species that preferentially consume the resources for which they have intermediate requirements.^11,12 In this study, we were surprised to find that oscillations can occur between the partial cooperator and the pure cheater in the resource partition model, at intermediate levels of iron supply (Figure 2A). In contrast to the stable coexistence observed in Figure 1F, the partial cooperator generates an environment that is vulnerable to invasion by cheaters. The intersection of the two growth contours, therefore, becomes unstable and allows oscillation.

Figure 2.

The partial cooperators and cheaters generate diverse ecological dynamics

(A) The partial cooperators can oscillate with the cheater. In the chemical space, the intersection between the growth contours of a partial cooperator (blue) and a pure cheater (red) is represented by a black circle. The dynamical trajectory is represented by the small black dot with a black line. The background color indicates the growth-advantageous zone of partial cooperators over cheaters. The insert depicts the two species' competition dynamics.

(B) The partial cooperators can exclude the cheater. Same as (A), but the partial cooperators allocate more resources to private siderophores.

(C) The phase diagram illustrates the mechanism of oscillation shown in (A). In the left panel, the chemical space is divided into four regions with varying relative finesses (growth rate relative to dilution rate) between the cheater and the partial cooperators, denoted by the symbols + and -. The background color of the right panel corresponds to the regions in the chemical space depicted in the upper panel.

(D and E) Bifurcation diagrams for the system in (A) as the dilution rate (D) and the Fe³⁺ supply changes (E). Empty circles represent the minimum and maximum of the oscillation, while solid dots represent a steady state.

Figure 2C explains the oscillation visually with a phase diagram. The diagram shows that in the upper-left quadrant, where the public siderophore concentration is high and the iron concentration is low, the rapid proliferation of cheaters effectively eliminates partial cooperators (cooperator-, cheater+). As a result, the abundance of public siderophores decreases, which forces the system into the lower-left quadrant, where both partial cooperators and cheaters are scarce (cooperator−, cheater−). The decrease in total population promotes the recovery of iron concentration, allowing the system to enter the advantageous growth zone of partial cooperators in the lower-right quadrant, where public siderophores remain low, but iron is abundant. In this quadrant, partial cooperators resume positive growth by taking in iron influx through their private siderophores, while pure cheaters continue to decline (cooperator+, cheater−). As partial cooperators grow, the concentration of public siderophores also increases, inhibiting the decrease of pure cheaters and restoring their growth in the upper-right quadrant (cooperator+, cheater+). However, the continued growth of pure cheaters depletes iron, forcing partial cooperators into negative net growth again (cooperator−, cheater+). The preceding process generates oscillations, mostly owing to the private siderophores providing an advantageous growth zone for partial cooperators in the absence of public siderophores.

Another parameter region of interest is where the partial cooperators are able to outcompete the pure cheaters. When the partial cooperator is more capable of establishing a high-iron, low-public-siderophores environment, the dynamics become even more skewed in favor of the partial cooperators. For instance, if the steady-state environment formed by a partial cooperator goes outside the growth contour of pure cheaters, the partial cooperator can effectively exclude the pure cheater (Figure 2B).

As we scanned across the chemostat conditions, we found that the system underwent bifurcation into and out of oscillation. In the presence of one pure cheater and one partial cooperator, an increase in the dilution rate results in a Hopf bifurcation that drives the system from stable coexistence into oscillation (Figures 2D and 2E). Similarly, increasing the iron supply concentration can shift the oscillation into stable coexistence. The phase diagram of chemostat conditions (Figure S2) shows that a “better” environment, characterized by a low dilution rate or high iron supply, reduces the relative difference in growth between partial cooperators and cheaters, increasing the tendency of coexistence. Conversely, a harsher environment, characterized by a high dilution rate or low iron supply, increases the relative difference in growth between the two, thereby increasing the likelihood of oscillations and extinction.

The self-generated chemical dimension changes the stability criteria of classical consumer resource models

The oscillation observed between the pure cheater and the partial cooperator in our resource partition models suggests that the introduction of resource partition may alter the stability criteria of consumer resource models, as oscillatory dynamics in classical consumer resource models usually necessitate at least three species.^11,12 Therefore, in this section, we explore how the self-generated chemical dimension in our model affects the stability of the system.

We will now detail the general form of the resource partition model. Similar to Tilman’s model for the classical consumer resource model,¹⁰ microbes interacting with two resources $R_1$ and $R_2$ in the resource partition model can be represented by:

$$\frac{d{m}_i}{dt}=m_i\left(g_i\left(R_1,R_2\right)-d\right),\mathrm{f}\mathrm{o}\mathrm{r}i=\mathrm{1,2}$$ (Equation 9)

$$\frac{d{R}_j}{dt}=d\left(R_{j,\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-R_j\right)-\sum _{i=1}^2{m}_i{h}_{ij}\left(R_1,R_2\right)g_i\left(R_1,R_2\right),\mathrm{f}\mathrm{o}\mathrm{r}j=\mathrm{1,2}\text{,}$$ (Equation 10)

where $R_{j,\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}$ is the supply concentration of resource $j$, and $h_{ij}$ is the function describing the amount of resource $j$ impacted by microbe $i$ per biomass.

When $h_{ij}$ describes resource uptake and has a positive sign. Equations 9 and 10 above represent the classical consumer resource model. However, when at least one of the $h_{ij}$ describes resource production and exhibits a negative sign, the resulting equations represent the broader “resource partition model,” which exhibits different criteria for the stability of coexistence.

The stability of the fixed point (∗) can be deduced from the Routh-Hurwitz (RH) criterion.⁵³ From the Jacobian matrix of the model:

$$J=\left[\begin{array}{cccc}0& 0& v_{11}& v_{12}\\ 0& 0& v_{21}& v_{22}\\ -w_{11}& -w_{12}& -x_{11}& -x_{12}\\ -w_{21}& -w_{22}& -x_{21}& -x_{22}\end{array}\right]\text{,}$$ (Equation 11)

with

$$v_{ij}={\left(\frac{\partial \stackrel{.}{m_i}}{\stackrel{.}{\partial R_j}}\right)}^{\ast },w_{ij}=-{\left(\frac{\partial \stackrel{.}{R_i}}{\stackrel{.}{\partial m_j}}\right)}^{\ast },x_{ij}=-{\left(\frac{\partial \stackrel{.}{R_i}}{\stackrel{.}{\partial R_j}}\right)}^{\ast }\text{,}$$

For simplicity, we set the abbreviation as:

$$\begin{array}{c}{P}_1={\left({\partial }_{R_1}{g}_1\right)}^{\ast },P_2={\left({\partial }_{R_2}{g}_1\right)}^{\ast }\text{,}\\ P_3={\left({\partial }_{R_1}{g}_2\right)}^{\ast },P_4={\left({\partial }_{R_2}{g}_2\right)}^{\ast }\text{,}\\ c_{11}={\left(h_{11}\right)}^{\ast },c_{12}={\left(h_{21}\right)}^{\ast }\text{,}\\ c_{21}={\left(h_{12}\right)}^{\ast },c_{22}={\left(h_{22}\right)}^{\ast }\text{.}\end{array}$$ (Equation 12)

Here, $P$ can be interpreted as the growth rate dependency on “resources” at the fixed point, and $c_{ij}$ represents how microbe $i$ impacts resource $j$ at the fixed point.

So we have elements in the Jacobian matrix expressed as:

$$\begin{array}{cc}{v}_{11}=m_1^{\ast }{P}_1,& v_{12}=m_1^{\ast }{P}_2\\ v_{21}=m_2^{\ast }{P}_3,& v_{22}=m_2^{\ast }{P}_4\\ w_{11}=c_{11}d,& w_{12}=c_{12}d,\\ w_{21}=c_{21}d,& w_{22}=c_{22}d,\\ x_{11}=d,& x_{12}=0\\ x_{21}=m_1^{\ast }{c}_{21}{P}_1+m_2^{\ast }{c}_{22}{P}_3,& x_{22}=d+m_1^{\ast }{c}_{21}{P}_2+m_2^{\ast }{c}_{22}{P}_4\end{array}$$ (Equation 13)

At the steady state, ${g_1}^{\ast }={g_2}^{\ast }=d$. With definitions in Equations 12 and 13, the characteristic equation of eigenvalue $\lambda$ for the Jacobian matrix can be expressed as:

$${\lambda }^4+\left(x_{11}+x_{22}\right){\lambda }^3+\left(q_1+q_4+x_{11}{x}_{22}-x_{12}{x}_{21}\right){\lambda }^2+\left(x_{11}{q}_4+x_{22}{q}_1-x_{12}{q}_3-x_{21}{q}_2\right)\lambda +\left(q_1{q}_4-q_2{q}_3\right)=0\text{,}$$ (Equation 14)

the coefficients of this quartic equation are: $a_0=1$, $a_1=x_{11}+x_{22}$, $a_2=q_1+q_4-x_{12}{x}_{21}+x_{11}{x}_{22}\text{,}$ $a_3=q_4{x}_{11}-q_3{x}_{12}-q_2{x}_{21}+q_1{x}_{22}$, $a_4=-q_2{q}_3+q_1{q}_4$, with $q_i$ defined as:

$$\begin{array}{c}{q}_1=w_{11}{v}_{11}+w_{12}{v}_{21}\text{,}\\ q_2=w_{11}{v}_{12}+w_{12}{v}_{22}\text{,}\\ q_3=w_{21}{v}_{11}+w_{22}{v}_{21}\text{,}\\ q_4=w_{21}{v}_{12}+w_{22}{v}_{22}\text{.}\end{array}$$ (Equation 15)

The Routh-Hurwitz (RH) criterion states the necessary and sufficient condition for the stability of a dynamical system⁵³: for a quartic equation for the eigenvalue $\lambda$, $a_0{\lambda }^4+a_1{\lambda }^3+a_2{\lambda }^2+a_3\lambda +a_4=0$, if the fixed point for coexistence is stable, then the coefficients must satisfy: (1) $a_1>0$, (2) $a_4>0$, (3) $a_3>0$, (4) $a_1{a}_2{a}_3-a_1^2{a}_4-a_3^2>0$.

Based on the four RH criteria, we compared the difference between the classical consumer resource model and the resource partition model about their stabilities. Details on the comparison can be found in STAR Methods, analysis of the self-creating dimension section in method details.

First, the criteria (1) $a_1>0$ holds for both the classical consumer resource model and the iron-partition model.

Second, the criteria (2) $a_4>0$ is central to the classical model. By definitions in Equation 12, the original form $a_4=-q_2{q}_3+q_1{q}_4$ expands into:

$$a_4=d{m}_1^{\ast }{m}_2^{\ast }\left(c_{12}{c}_{21}-c_{11}{c}_{22}\right)\left(P_2{P}_3-P_1{P}_4\right)\text{,}$$ (Equation 16)

There are two possible situations for $\left(c_{12}{c}_{21}-c_{11}{c}_{22}\right)\left(P_2{P}_3-P_1{P}_4\right)>0$:

$$\begin{array}{cc}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}1\text{:}& \frac{P_2}{P_1}>\frac{P_4}{P_3},\frac{c_{11}}{c_{21}}<\frac{c_{12}}{c_{22}}\text{,}\end{array}$$ (Equation 17)

$$\begin{array}{cc}\mathrm{o}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}2\text{:}& \frac{P_2}{P_1}<\frac{P_4}{P_3},\frac{c_{11}}{c_{21}}>\frac{c_{12}}{c_{22}}\text{.}\end{array}$$ (Equation 18)

In the classical consumer resource model, these two inequalities can be interpreted as “each species must consume more of the one resource that more limits its own growth rate.”

In the resource partition model, using the iron-partition model at Equations 1, 2, 3, 4, 5, and 6 as an example, parameters in Equation 12 can be specified into:

$$\begin{array}{cc}{P}_1={\left({\partial }_{R_{\mathrm{s}\mathrm{i}\mathrm{d}}}{g}_1\right)}^{\ast }\text{,}& P_2={\left({\partial }_{R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{g}_1\right)}^{\ast }\text{,}\\ P_3={\left({\partial }_{R_{\mathrm{s}\mathrm{i}\mathrm{d}}}{g}_2\right)}^{\ast }\text{,}& P_4={\left({\partial }_{R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{g}_2\right)}^{\ast }\text{.}\\ c_{11}=-{\alpha }_{1,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}ϵ/r\text{,}& c_{12}=-{\alpha }_{2,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}ϵ/r\text{,}\\ c_{21}=1/\left({\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\gamma r\right)\text{,}& c_{22}=1/\left({\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\gamma r\right)\text{.}\end{array}$$ (Equation 19)

Then it can be proven that under the setting of ${{\alpha }_{1,\text{growth}}<\alpha }_{2,\text{growth}}$, the criteria (2) $a_4>0$ requires that:

$${{\alpha }_{1,\text{public}}>\alpha }_{2,\text{public}}\text{.}$$ (Equation 20)

In the iron-partition model, Equations 7 and 20 suggest that, if two strains should stably coexist, not only the strain that invests fewer resources in growth must invest more in private siderophores, but also play a more cooperative role.

The remaining two criteria, (3) $a_3>0$ and (4) $a_1{a}_2{a}_3-a_1^2{a}_4-a_3^2>0$, differentiate between the classical model and the iron-partition model. By definitions in Equations 12, 13, 14, and 15, equations for these two criteria are the additive or multiplicative combination of $a_4$ with other positive definite terms involving $c_{11}$ and $c_{12}$ (see STAR Methods, method details):

$$a_3=d\left(m_1^{\ast }\left(c_{11}{P}_1+c_{21}d{P}_2\right)+m_2^{\ast }\left(c_{12}{P}_3+c_{22}d{P}_4\right)\right)+\frac{a_4}{d}\text{.}$$ (Equation 21)

$$a_1{a}_2{a}_3-a_1^2{a}_4-a_3^2=\left(2d^3+a_3\right)\left(m_1^{\ast }\left(c_{11}{P}_1+d{c}_{21}{P}_2\right)\left(d+c_{21}{P}_2{m}_1^{\ast }\right)+m_2^{\ast }\left(c_{12}\left(d{P}_3+c_{21}{P}_1{P}_4{m}_1^{\ast }\right)+c_{22}\left(d^2{P}_4+P_2\left(c_{11}{P}_3+2d{c}_{21}{P}_4\right)m_1^{\ast }\right)\right)+{m_1^{\ast }}^2{c}_{22}{P}_4\left(c_{12}{P}_3+d{c}_{22}{P}_4\right)\right)\text{.}$$ (Equation 22)

In the classical consumer resource model, $c_{ij}$ describes the consumption of species $i$ on resource $j$, which is always positive. Consequently, once the criteria (2) $a_4>0$ holds, criteria (3) $a_3>0$ and criteria (4) $a_1{a}_2{a}_3-a_1^2{a}_4-a_3^2>0$ are satisfied automatically. Actually, the determination of the fixed point stability only depends on the tangent slope of the growth contours ($\frac{P_1}{P_2},\frac{P_3}{P_4}$) and the slope of the consumption vector ($\frac{c_{21}}{c_{11}},\frac{c_{22}}{c_{12}}$). If the criteria in Equations 17 and 18 are satisfied, the coexistence is stable as long as the supply vector locates within the sector area formed by the reverse extension of the two consumption vectors.

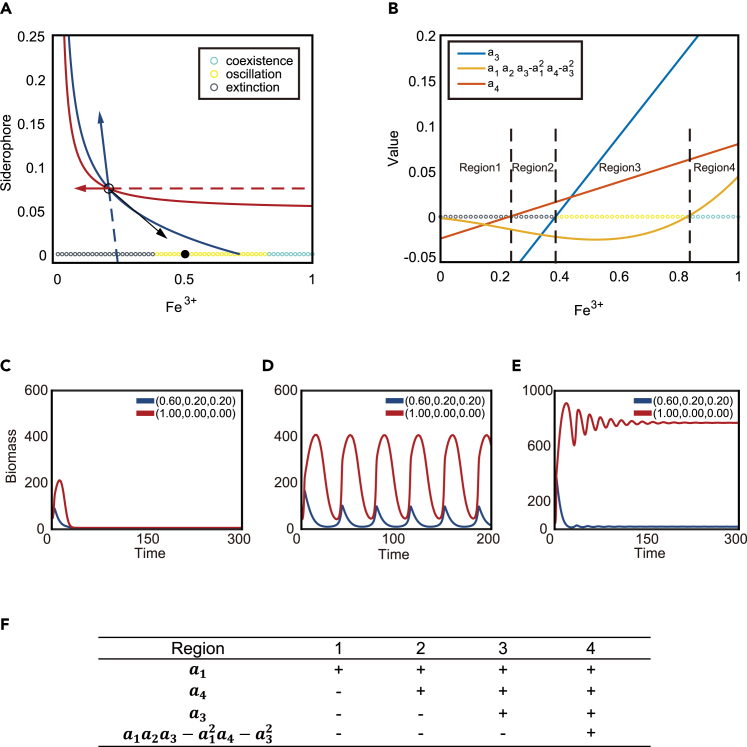
However, in the iron-partition model, simply fulfilling criteria (2) no longer guarantees the satisfaction of criteria (3) and (4). Even when Equations 17 and 18 are satisfied and the supply vector locates within the sector formed by consumption vectors, changes in the iron supply can still alter the stability of the growth contour intersection, causing the system to exhibit different forms of dynamics rather than stable coexistence. As shown in Figure 3A, in the chemical space, the growth contours of a partial cooperator and the pure cheater intersect. At the crossing point, the consumption vector of the partial cooperators points to the upper-left direction, suggesting it consumes iron while creating public siderophores. The consumption vector of the pure cheater points horizontally to the left, as it solely consumes iron without contributing to public siderophore. These sectors formed by two consumption vectors overlap a region on the iron-supply axis (x axis). Nevertheless, within this region of iron-supply, the stability of the fixed point changes: when the iron supply is low, the system still collapses to extinction even if the supply (black circles, Figure 3C) lies within the sector zone; oscillations begin as the iron supply increases (yellow circles, Figure 3D); and eventually, stable coexistence can be achieved when the iron supply is high (blue circles, Figure 3E).

Figure 3.

The self-generated dimension enables oscillation and coexistence

(A) The growth contours of a partial cooperator (blue) and the cheater (red), and their consumption vectors at the intersection. Different types of dynamics induced by different supplies of Fe³⁺ are indicated by the colors of the circles along the x axis. Black indicates the extinction of both species; yellow indicates oscillatory dynamics; and blue indicates steady-state coexistence.

(B) The values of the three stability criteria change as the iron supply increases along the x axis. The signs of three stability criteria divide the x axis into four regions, as indicated by the text.

(C–E) Exemplary time-courses of the three types of dynamics induced by different supplies of Fe³⁺, such as extinction (C), oscillation (D), and coexistence (E).

(F) The signs of all four stability criteria in the four regions shown in (B).

The collapse of the system in Figure 3C can be attributed to the changes in criteria (3) $a_3>0$. Due to the negative signs of $c_{11}$ and $c_{12}\text{,}$ the first term of $a_3$, $d\left(m_1^{\ast }\left(c_{11}{P}_1+c_{21}d{P}_2\right)+m_2^{\ast }\left(c_{12}{P}_3+c_{22}d{P}_4\right)\right)$ now has an uncertain sign. If $P_1={\left({\partial }_{R_1}{g}_1\right)}^{\ast }$ or $P_3={\left({\partial }_{R_1}{g}_2\right)}^{\ast }$ are sufficiently large, indicating that strains are highly sensitive to free iron, the first term might be negative, and is able to drive the whole equation of $a_3$ into the negative regime. Moreover, the sign of the first term also relies on $m_1^{\ast }$ and $m_2^{\ast }$, both of which are dependent on the iron-supply concentration. As shown in Region 2 in Figure 3B, the sign of $a_3$ remains negative when $a_4$ is positive, which contributes to the extinction of both species even when the iron supply falls within the sector formed by the reverse extension of consumption vectors (Figure 3C).

Similarly (see STAR Methods, method details), with negative $c_{11}$ and $c_{12}$, criteria (4) in the iron-partition model now has an uncertain sign, with complex dependence on $m_1^{\ast }$ and $m_2^{\ast }$. When criteria (4) remains negative (Region 3) while the other criteria are met (Region 3, Figure 3B), the fixed point remains unstable and the system oscillates.

In the classical model, due to the positive sign of $c_{11}$ and $c_{12}$, Region 2 and Region 3 in Figure 3F would not exist. As the existence of Region 2 and Region 3 is the result of negative $c_{11}$ and $c_{12}$, such extinction and oscillation dynamics are not exceptional. Two partial cooperators with distinct allocation strategies may also undergo similar transitions, with the dynamics experiencing extinction, oscillation, coexistence, and exclusion as the iron supply increases (Figure S3).

Comprehensive assessment of strategies under within-species and between-species competitions

In our model, different resource allocation strategies distinguish distinct strains within the same species, and their public siderophores can be shared. Species may differ in parameters such as the cost of siderophores and the growth coefficient. More importantly, we assumed that siderophores produced by different species cannot be shared. Based on these assumptions, we systematically assessed the competitiveness of strategies both within and between species.

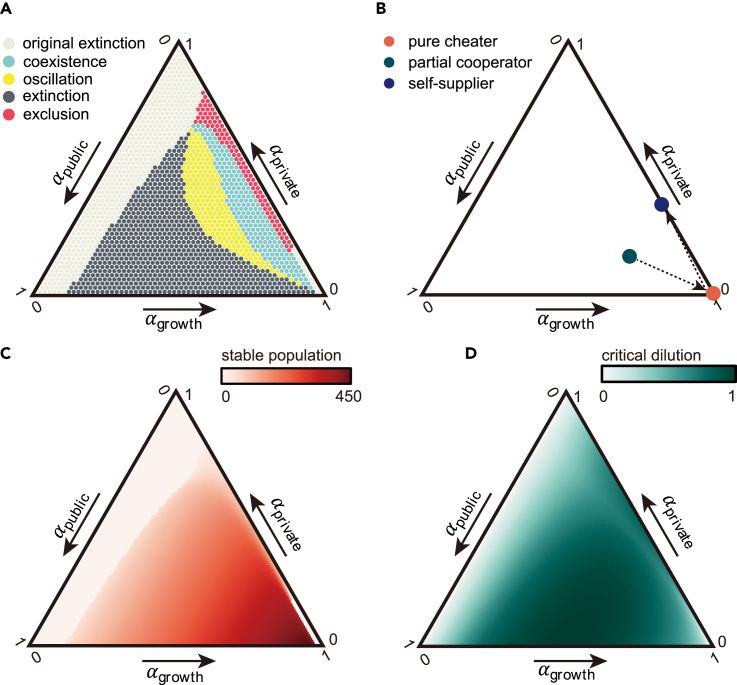
The competition between all potential strategies against the pure cheater of the same species reveals complex dynamics, as shown in the ternary plot of Figure 4A. While the pure cheater can trigger extinction for highly cooperative strains (high in ${\alpha }_{\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}$ and low in ${\alpha }_{\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$), partial cooperator strategies can stably or dynamically coexist with pure cheater strategies over a broad range of strategy space. This coexistence can exist across different parameters and public siderophore production and recycling sets, as demonstrated in Figures S5 and S6. Moreover, self-supplier strategies can even exclude the pure cheater. Our results suggest that increasing investment in public siderophores increases the likelihood of oscillations with the cheater, while increasing investment in private siderophores enhances the tendency of stable coexistence.

Figure 4.

Assessment of all possible strategies, by their interplay with cheaters, evolutionary stability, stable population, and critical dilution rate

(A) How different strategies interact with the pure cheater. Each strategy’s competition outcomes with the pure cheater are indicated by dot color in the ternary plot (light gray: non-viable by itself; deep gray: viable by itself but extinct with the cheater; yellow: oscillate with the cheater; blue: stably coexist with the cheater; red: exclude the cheater).

(B) The chain of invasion in the strategy space. For each arrow, the dot at the beginning of the arrow is the initial strategy that creates the steady-state environment, and the dot at the endpoint of the arrow indicates the strategy with the maximal growth rate in the formal environment. The endpoint of the whole invasion chain is the evolutionarily stable strategy that cannot be invaded by any other strategies. The path starts with a partial cooperator strategy(green dot, $\overrightarrow{\alpha }=\left(\mathrm{0.6,0.2},0.2\right)$), then directs to the pure cheater strategy(orange dot), and ends at the self-supplier strategy(blue dots, $\overrightarrow{\alpha }=\left(\mathrm{0.65,0.35},0\right)$).

(C) The stable population for different strategies when existing alone.

(D) The maximal dilution rate for non-zero biomass in a steady-state chemostat.

To evaluate a species’ non-invasive strategy, we used the invasion chain method.⁵⁴ Starting with an arbitrarily chosen strategy, we added strains with the highest growth rate in the existing chemical environment until no species could be added. As depicted in Figure 4B, the pure cheater has the highest growth rate in the environment shaped by the initial partial cooperator, but in the environment co-created by these two strains, the self-suppliers (${\alpha }_{\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}=0,{\alpha }_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>0$) have a growth advantage, allowing them to invade and create an environment devoid of public siderophores. In such an environment, only self-suppliers can survive, bringing the invasion chain to an end. Thus, within the same species, the self-supplier strategy is the most resistant against pure cheater strains and is “evolutionarily optimal” because it generates a chemical environment that cannot be invaded by other strategies. Additionally, the self-supplier strategy can establish a community with a lower initial population, benefiting the start of colonization (Figure S7).

However, in assessing the environmental resilience of a population, the self-supplier strategy is not always the most advantageous. For instance, when evaluating the steady-state population size of a single strain, strategies that closely resemble the pure cheater exhibit larger overall population sizes, as illustrated in Figure 4C. On the other hand, when considering the resilience of strains to harsher external conditions, pure cooperators demonstrate greater resistance to increased dilution, as demonstrated in Figure 4D.

When considering the competition between species utilizing different public siderophores, we found that strains investing more in public siderophores have a higher capacity for invading another species (Figure S4A), while strains investing less in private siderophores exhibit greater resistance to invasion by another species (Figure S4C). Interestingly, self-supplier strategies are not effective in either invasion or resistance, as revealed by the corresponding plots in Figures S4B and S4D. These findings suggest that the most successful strategy is highly dependent on the environmental context and the nature of the competition.

Discussion

Microbial diversity has been a long-standing area of interest in microbial ecology.³ While the range of species may be constrained by chemical parameters, microorganisms can expand this limit by generating chemical diversity in their microhabitat. In this study, we constructed a model of siderophore-mediated iron competition to address two broader questions: first, how can cooperators responsible for chemical diversity withstand extinction triggered by cheaters, and second, what are the ecological implications of microbes creating new chemical dimensions?

Addressing the first question, we proposed the privatization of siderophores as a “game changer” that provides partial cooperators an advantage over pure cheaters. By avoiding diffusion losses and cheater exploitation, this privatization strategy reflects a microbial instance of the “snowdrift” scenario in game theory.⁵⁰ While cheaters reap the benefits of public goods without contributing, cooperators prioritize access to the goods to gain advantages when public siderophores are scarce.⁵⁵ This instance shows that negative frequency-dependent selection in microbial communities can be mediated by siderophore production and consumption. Analytically, we derived that the necessary condition for coexistence is that the cooperators who invest more in public siderophores also invest more in private siderophores.

Answering the second question led us to develop an updated model for microbial interactions called the “resource partition model.” This model incorporates the idea that organisms not only consume but also actively produce resources. Furthermore, the public siderophore is not considered a “resource” until it forms a complex with ferric iron, which is the actual resource that microorganisms require. This adds another layer of meaning to the term “resource partition model”: externally supplied resources (iron) and microbe-generated resources (siderophore) interact to form the actual resources (iron-associated siderophores) that are taken up by the microorganisms.

Chemical innovation and resource partition

Microbes interact by influencing their shared environment.⁵⁶ Classical ecological models have mostly emphasized the “consumption” aspect of such influences.^57,58 With the rapid development of microbiology, it has become increasingly clear that bacteria have enormous potential to introduce new chemicals into their microhabitats, providing chemical innovations that shape their community interactions.⁵⁹ Siderophores are just one example of the many secondary metabolites that microbes actively produce for their own benefit. Other examples include antibiotics, bacteriocins, signaling molecules, and even bacterial vesicles, all of which can be considered as “chemical dimensions” generated by microbes.^1,26 A general ecological framework for such “self-generated dimensions” has yet to be established. The conventional consumer resource model provides intuitive coexistence criteria where species should preferentially consume the resource that limits their growth, and the consumption vectors clearly segregate supply conditions into zones of the same stability.^10,60 In contrast, in this “resource partition model,” due to the reversed direction of consumption vectors, there are additional parameter areas where the Routh-Hurwitz (RH) criterion can change signs. Consequently, in regions of steady-state equilibrium in the classical model, non-equilibrium dynamics become possible. Our analysis suggests that an ecosystem with “self-generated dimensions” tends to be more dynamic and complex.

Oscillation usually bridges two distinct states and often plays critical roles in various biological systems.⁶¹ Notably, the oscillation in our model differs from the oscillation in the work of Huisman et al., where the oscillation bridges the stable equilibrium and the chaos with higher-than-CEP dynamical coexistence.^11,12 In our model, the parameter region of oscillation locates between total extinction and stable coexistence between partial cooperators and cheaters. Oscillation here is more of a “danger zone”, indicating that the system is on the verge of collapse, similar to the early warning signatures of ecosystems.⁶² Indeed, our continuous equations assume that organisms can recover from arbitrarily small values, but the troughs of oscillatory dynamics increase the probability of stochastic extinction in natural systems.^63,64 Recent studies in game theory have detected oscillations when the environment is made explicit, showing that oscillatory dynamics prevent the extinction of cooperators.^65,66,67 Given the specificity of oscillatory dynamics in ecology and the propensity of resource partition models to enter the oscillation zone, it would be intriguing to explore the facilitative or destructive functions of oscillations in diverse ecological systems with chemical innovations.

Resource partitioning and cross-feeding are two mechanisms that enable microbes to increase the resource dimensions in their environment, enabling higher species diversity. While both byproducts and siderophores play crucial roles in microbial ecosystems, there are notable differences between these two mechanisms. Cross-feeding occurs primarily via passive leakage of metabolic byproducts that are no longer utilized by producers, while resource partitioning mediated by siderophores involves active competition among microbes for binding sites on the limiting iron. This competitive process results in different siderophore-iron complexes that serve as actual iron resources, which can only be absorbed by microorganisms possessing corresponding receptors. Furthermore, resource partitioning involves an additional level of complexity, as it requires the formation of distinct siderophore-iron complexes based on factors such as affinity and concentration. These characteristics distinguish resource partitioning from cross-feeding, highlighting the need for a nuanced understanding of microbial interactions and the mechanisms that underlie them.

Spatial factors, private goods, and adaption

Spatial factors were commonly considered in theoretical models to explain the coexistence mechanisms of cheaters and cooperators.^43,68,69 Structured habitats, such as soil and the human body, are typical in natural habitats. Even in weakly structured environments like the ocean, many microbes can construct structured environments by adhering to surfaces or assembling into groups.⁷⁰ It has been suggested that coexistence can be promoted by highly structured habitats, where the sharing of public goods is spatially limited to local cooperation.⁴³ However, in models with weakly structured or highly mixed habitats, the dissipation of public goods and the costs associated with their production impose losses and burdens on cooperators, still leading to the “tragedy of the commons.”⁷¹

In siderophore-mediated iron competition, privatization enables coexistence in homogeneous habitats. Although our model was specifically developed for certain species, such as marine microbes or actinomycetes, this public-private goods framework provides generalizable insights on the necessary conditions for coexistence: the organism that shares more must also preserve more. Furthermore, our results suggested that the partial cooperator might serve as a universal strategy of microbes, as it facilitates coexistence among different species. Recently, studies have discussed the private properties of “public goods,” converting them into a continuous metric (partially privatized public goods). Niehus et al. found that the privatized siderophores evolved to be upregulated.⁴⁸ The work of Lerch et al. discovered that when two public goods exist, a species producing a completely public good can exclude non-producers by partially privatizing another public good,⁷² and this ability is highly reliant on nutrient supply, underscoring the significance of environmental conditions for sustaining cooperation.

Several studies have bridged the microbial habitat with their goods’ private and public properties. Kummerli et al. revealed that the more structured the habitat, the more microbes utilize siderophores with high diffusibility.⁷³ Similarly, Garcia et al. found that bacteria living in more structured habitats encode more extracellular proteins with higher diffusibility.⁷⁴ These findings are consistent with the adaption of siderophore privatization proposed by our model and other works,^48,72 where the private portion is more advantageous in highly mixed environments.

Another microbial adaptation in iron competition involves the regulation of resource allocation strategies in response to the environment. For example, quorum sensing (QS) can regulate the degree of privatization of siderophores, such as in marine Vibrio harveyi, where cells produce more membrane-attached siderophores at low cell density and switch into more soluble siderophores at higher cell density.⁷⁵ By balancing the private and public benefits, QS regulation can promote cooperation and enhance the efficiency of resource utilization in microbial communities. In the future, more research is needed to identify the regulatory mechanisms underlying microbial cooperation in natural environments.

Besides the membrane-attached form, other forms of siderophore privatization, such as keeping siderophores intracellularly for relieving oxidative stress, have been proposed to confer cheater resistance.⁷⁶ We hypothesize that the division of the iron resource by siderophores provides a universal mechanism for “resource privatization”: numerous siderophores exist in the natural world, each with its specific receptors.^76,77 For a given type of siderophore, microorganisms with corresponding receptors can share it as a public good, whereas microbes without comparable receptors perceive it as inaccessible “private goods”.²⁹ Theoretical models suggest that the populations of different cooperators utilizing distinct siderophores can be regulated by their cheaters, similar to how parasites impose negative frequency selection.⁷⁸ Additionally, a model with multiple types of siderophores suggests that coexistence between cooperators and cheaters is possible if a “loner” uses a less efficient siderophore.⁵¹

In the future, it will be exciting to investigate iron interactions in a more realistic biological setting and systematically examine the ecological consequences of microbial chemical innovation. It would be interesting to explore the role of microbial chemical innovation in community dynamics and stability in different habitats. The results of such investigations could lead to the development of novel strategies for understanding, controlling, and predicting microbial community dynamics, with important applications in areas such as agriculture, medicine, and environmental management.

Limitations of the study

Our research highlights the role of siderophores in promoting dynamical coexistence through resource partitioning, yet we acknowledge several limitations that warrant discussion. First, our model system was a highly simplified chemostat model, with constant supply, constant dilution, and well-mixed environment. These assumptions may not fully capture the complexity of natural systems, where the environment is heterogeneous in both space and time. Second, to obtain analytical results, we only discussed the two-dimensional case and did not explore the effects of high-dimensional scenarios or multiple types of siderophores. Third, for convenience, our model made certain assumptions about species parameters, and these assumptions may not hold in all ecological contexts. While our study offers valuable insights into the principles of siderophore-mediated interactions, further expansion and refinement of our model are necessary to fully understand more complex systems. We believe that future studies could benefit from incorporating additional ecological factors, such as spatial structure, varying resource availability, and diverse microbial communities.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Raw and analyzed data	This paper	https://doi.org/10.5281/zenodo.8024261
Software and algorithms
Model and analysis source code	This paper	https://doi.org/10.5281/zenodo.8024261
Ggtern	Hamilton et al., 201879	http://www.ggtern.com/
Matlab 2021	MathWorks, Inc	https://www.mathworks.com/products/matlab.html; RRID: SCR_001622
R	R Core Team, 2013	https://www.r-project.org/; RRID: SCR_001905

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Zhiyuan Li (zhiyuanli@pku.edu.cn).

Materials availability

This study did not generate new unique reagents.

Method details

Description of the resource partition model

We utilized the chemostat-typed model to investigate the ecological interactions between iron-uptake strategies. In this simplified resource partition model, we made the following assumptions:

• 1.Iron is the primary growth-limiting resource, and the iron intaking rate linearly scales with the growth rate.
• 2.Siderophores can be recycled during the iron-uptake process, so in the equations, we excluded their consumption for simplicity. Actually, we also demonstrated that including siderophores consumption in the model does not qualitatively alter the results of this investigation (Figure S5).
• 3.“Species” in this work were represented by different parameters, such as $v_{\mathrm{m}}$, $K_{\mathrm{l}}$, $\gamma$, $\beta$, etc.; Within a species, different strains adopt different resource allocation strategies ${\overrightarrow{\alpha }}_{\sigma }=\left({\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}},{\alpha }_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}},{\alpha }_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}\right)$, which specifies the fraction of cellular proteins and energies devoted to the growth, private siderophores production, and public siderophores production, respectively. To represent the limited cellular resources, the summation of all components in ${\overrightarrow{\alpha }}_{\sigma }$ equals to one. By this measurement, behaviors can be quantified by elements of ${\overrightarrow{\alpha }}_{\sigma }$. For example, “cheating” is defined as not producing public siderophores (${\overrightarrow{\alpha }}_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}=0$).

Thereby, a continuous spectrum of strategies could be visualized in a ternary diagram, where we can define four major classes of strategies:

• •Pure cheater: ${\overrightarrow{\alpha }}_{\sigma }=\left(\mathrm{1,0,0}\right)$, where the strain does not produce any siderophore but allocates all resource budgets into growth.
• •Self-supplier: ${\overrightarrow{\alpha }}_{\sigma }=\left({\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}},1-{\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}},0\right)$, where the strain only produces private siderophores without secreting them. Self-suppliers can be considered as another type of cheater as it does not produce public siderophore but can utilize them.
• •Pure cooperator: ${\overrightarrow{\alpha }}_{\sigma }=\left({\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}},\mathrm{0,1}-{\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\right)$, where the strain only produces public siderophores without privatizing them.
• •Partial cooperator: ${\overrightarrow{\alpha }}_{\sigma }=\left({\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}},{\alpha }_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}},{\alpha }_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}\right)$, with all three fractions non-zero. In this case, the strain produces both public and private siderophores.

Following the assumptions above, resource competition dynamics between two strains 1 and 2 adopting strategies ${\overrightarrow{\alpha }}_1$ and ${\overrightarrow{\alpha }}_2$ can be expressed as the following:

$$\frac{d{m}_1}{dt}=m_1\left(g\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{\mathrm{s}\mathrm{i}\mathrm{d}},{\overrightarrow{\alpha }}_1\right)-d\right)$$ (Equation 23)

$$\frac{d{m}_2}{dt}=m_2\left(g\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{\mathrm{s}\mathrm{i}\mathrm{d}},{\overrightarrow{\alpha }}_2\right)-d\right)$$ (Equation 24)

$$\frac{d{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}}{dt}=\frac{m_1}{r}{\alpha }_{1,\text{public}}ϵ+\frac{m_2}{r}{\alpha }_{2,\text{public}}ϵ-d{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}$$ (Equation 25)

$$\frac{d{R}_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{dt}=d\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}\right)-\sum _{i=1}^2\frac{m_i}{r}I\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{\mathrm{s}\mathrm{i}\mathrm{d}},{\overrightarrow{\alpha }}_i\right)$$ (Equation 26)

The total iron intake rate is the summation of iron intake from both private and public sources:

$$I\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{\mathrm{s}\mathrm{i}\mathrm{d}},{\overrightarrow{\alpha }}_i\right)=J_{{\sigma }_i,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}+J_{{\sigma }_i,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}\text{,}$$ (Equation 27)

where $J_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$ and $J_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}$ are the uptake fluxes of iron from private and from public siderophores, respectively, which we assumed Monad forms as:

$$J_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}={\alpha }_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}\beta v_{\mathrm{m}}\frac{R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{K_{\mathrm{m}}+R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}\text{,}$$ (Equation 28)

$$J_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}=v_{\mathrm{l}}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}\frac{R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{K_{\mathrm{l}}+R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}\text{.}$$ (Equation 29)

$v_{\mathrm{m}}$ and $v_{\mathrm{l}}$ denote the intake rate coefficients, and we set $v_{\mathrm{m}}=v_{\mathrm{l}}=1$ for convenience. $\beta$ represents the efficiency of private siderophores’ production. $K_{\mathrm{m}}$ and $K_{\mathrm{l}}$ are the affinity constants for private siderophores and public siderophores. In this model, we set $K_{\mathrm{m}}>K_{\mathrm{l}}$ to show that public siderophores have advantages in acquiring iron. In the later section, we will prove that other forms of iron uptake yield to similar conclusions.

By the first assumption, the growth rate linearly scales with the total iron intake $I$, as well as the fraction of resources allocated to biomass accumulation ${\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$:

$$g\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{sid},{\overrightarrow{\alpha }}_{\sigma }\right)=\gamma {\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}I\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{\mathrm{s}\mathrm{i}\mathrm{d}},{\overrightarrow{\alpha }}_{\sigma }\right)\text{.}$$ (Equation 30)

Conditions for the stable coexistence

Growth contour for single strain

In this work, the two-dimensional “chemical space” is defined by the concentrations of iron and siderophores that directly impact cellular growth, as the ensembles of all possible $\left[R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{\mathrm{s}\mathrm{i}\mathrm{d}}\right]$.

The growth contour of strain $\sigma$ is defined as all $\left[R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{\mathrm{s}\mathrm{i}\mathrm{d}}\right]$ that meet $g\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{sid},{\overrightarrow{\alpha }}_{\sigma }\right)=d$ in the chemical space, equivalent to the zero net growth isoclines (ZNGI) in contemporary niche theory. For strain $\sigma$, we can obtain the growth contour from Equation 23 equals 0, leading to the following relation between $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}$ and $R_{\mathrm{s}\mathrm{i}\mathrm{d}}$ for the growth contour:

$$R_{\mathrm{s}\mathrm{i}\mathrm{d}}=\frac{\frac{d}{\gamma {\alpha }_{\sigma ,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}-\frac{v_{\mathrm{m}}{\beta \alpha }_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}{R}_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{K_{\mathrm{m}}+R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}}{\frac{v_{\mathrm{l}}{R}_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{K_{\mathrm{l}}+R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}}$$ (Equation 31)

Requirement for growth contours intersection

For multiple strains, the possible chemical environment allowing for stable coexistence must locate at the intersection of their growth contours, indicated by the “∗”.

Between two strains 1 and 2 adopting two strategies, the relationships between the intersection point $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }$ and $R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }$ follows:

$$R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }=\frac{v_{\mathrm{m}}\beta \left(K_{\mathrm{l}}+R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }\right)\left({\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}\right)}{v_{\mathrm{l}}\left(K_{\mathrm{m}}+R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }\right)\left({\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}-{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\right)}\text{.}$$ (Equation 32)

Given a certain dilution rate $d$, $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }$ and $R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }$ could be solved as a function of $d$:

$$R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }=\frac{-d{K}_{\mathrm{m}}\left({\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\right)}{d\left({\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\right)+\beta \gamma v_{\mathrm{m}}{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\left({\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}-{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}\right)}$$ (Equation 33)

$$R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }=-\left({\alpha }_{1,\text{growth}}{\alpha }_{1,\text{private}}-{\alpha }_{2,\text{growth}}{\alpha }_{2,\text{private}}\right)(K_{\mathrm{l}}\left({\alpha }_{1,\text{growth}}\left(\beta \gamma v_{\mathrm{m}}{\alpha }_{2,\text{growth}}\left({\alpha }_{1,\text{private}}-{\alpha }_{2,\text{private}}\right)+d\right)-d{\alpha }_{2,\text{growth}}\right)+{dK}_{\mathrm{m}}\left({\alpha }_{2,\text{growth}}-{\alpha }_{1,\text{growth}}\right){\left(\gamma v_{\mathrm{l}}{K}_{\mathrm{m}}{\alpha }_{1,\text{growth}}{\alpha }_{2,\text{growth}}\left({\alpha }_{1,\text{growth}}-{\alpha }_{2,\text{growth}}\right)\left({\alpha }_{1,\text{private}}-{\alpha }_{2,\text{private}}\right)\right)}^{-1}$$ (Equation 34)

From the solution and trajectory derived above, the presence of intersection points requires:

$${\alpha }_{1,\text{growth}}\ne {\alpha }_{2,\text{growth}},{\alpha }_{1,\text{private}}\ne {\alpha }_{2,\text{private}}\text{,}$$ (Equation 35)

so that the denominators of Equations 33 and 34 can be non-zero.

In the following analysis, we always assume that strategy 1 allocate less on its own growth than strategy 2, then we have the setting:

$${\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}-{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}>0\text{.}$$ (Equation 36)

If the intersection point for possible coexistence exists with realistic value ($R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }>0,R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }>0$), then the numerator of Equation 32 needs to be larger than zero too:

$${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>0\text{.}$$ (Equation 37)

Equation 37 is the condition for the presence of the intersection point.

By Equation 37 and with the setting ${\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}-{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}>0$., it is straightforward to conclude the extinction of the pure cooperator (strain 1) when conferring cheaters (strain 2): for a pure cooperator, ${\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}=0$, therefore ${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}<0$ for any none zero ${\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$. Therefore, coexistence is not possible for a pure cooperator with any other types of strategies, let alone cheaters.

Necessary condition for pairwise coexistence

If we set strategy 1 being a partial cooperator (${\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>0$, ${\alpha }_{1,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}>0$) and strategy 2 being a pure cheater $({\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}=1$), according to Equations 33, 34, 35, 36, and 37, the necessary condition for a positive $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }$ is:

$${\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}-{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>0$$ (Equation 38)

Therefore, ${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}<{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$, ${\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$ is required for the intersection point to exist, therefore is the necessary condition for coexistence. This requirement means that only the partial cooperators (${\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>0$) can possibly stably coexist with the pure cheater (${\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}=1$), while the pure cooperator goes to extinction when the cheater invades. More generally, for the possible coexistence between any pair of strains, the one that allocates fewer resources in growth must invest more in private siderophores.

Non-zero biomass of both strains

Stable coexistence between two strains also requires the positive biomass of both strains. At the possible steady state of coexistence, we can set Equations 25 and 26 equal to 0. Then, the solutions for $m_1^{\ast }$ and $m_1^{\ast }$ can be deduced as a function of the steady state concentrations of the iron $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }$ and the siderophore $R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }$:

$$m_1^{\ast }=r\frac{\frac{d}{ϵ}\frac{R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }}{{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}-\gamma {\alpha }_{2,\text{public}}\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }\right)}{\frac{{\alpha }_{1,\text{public}}}{{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}-\frac{{\alpha }_{2,\text{public}}}{{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}}\text{,}$$ (Equation 39)

$$m_2^{\ast }=r\frac{\gamma {\alpha }_{1,\text{public}}\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }\right)-\frac{d}{ϵ}\frac{R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }}{{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}}{\frac{{\alpha }_{1,\text{public}}}{{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}-\frac{{\alpha }_{2,\text{public}}}{{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}}\text{.}$$ (Equation 40)

For stable coexistence, $m_1^{\ast }$ and $m_2^{\ast }$ need to be positive.

As will be proved by the next section, under the setting that ${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}<{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$.the denominator of the formal two equations, $\frac{{\alpha }_{1,\text{public}}}{{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}-\frac{{\alpha }_{2,\text{public}}}{{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}>0$ for stable coexistence.

Therefore, in order for $m_1^{\ast }>0$, it requires that $\frac{d}{ϵ}\frac{R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }}{{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}-\gamma {\alpha }_{2,\text{public}}\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }\right)>0$. Similarly, $m_2^{\ast }>0$ requires $\gamma {\alpha }_{1,\text{public}}\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }\right)-\frac{d}{ϵ}\frac{R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }}{{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}>0$. Together, they lead to the requirement of supply concentration that:

$$R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }+\frac{1}{k_2}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }>R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}>R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }+\frac{1}{k_1}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }\text{,}$$ (Equation 41)

where $k_1=\frac{ϵ\gamma }{d}{\alpha }_{1,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$ , $k_2=\frac{ϵ\gamma }{d}{\alpha }_{2,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$.

In these graphical tools developed by Tilman et al.,⁸⁰ The consumption vector is defined as $\overrightarrow{C_i}=\left[\begin{array}{c}{\partial }_{m_i}\stackrel{.}{R_1}\\ {\partial }_{m_i}\stackrel{.}{R_2}\end{array}\right]$ for species $i$, whose slope indicates the consumption preference of species $i$. $k_1$ and $k_2$ are the slopes of the consumption vectors of strain 1 and strain 2, respectively. and $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }+\frac{1}{k_{\mathrm{i}}}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }$ is equal to the intersection of the reverse extension of the consumption vector of strain $i$ with the x-axis.

Taken together, $m_1^{\ast },m_2^{\ast }>0$ require the iron supply point, $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}\text{,}$ locates inside the sector spanned by the inverse extensions of supply vectors of two strains, just as the classical consumer resource model.

Nevertheless, the presence of growth contour intersection, and non-zero biomass of two strains at the intersection point, only provide necessary conditions for the coexistence. The stability of the possible coexistence points needs to be analyzed by the Jacobian matrix.

Analysis of the self-creating dimension

Unlike the classical consumer resource model where species utilizes externally-supplied resources, microbe in our model can access external iron resources more efficiently by producing public siderophores. In terms of chemical dimensions, the production of public goods implies that bacteria autonomously generate new resource dimensions (such as $\left[R_{sid}\right]$ in our model). This resource-generation behavior changes the sign of the consumption vector, and can further affect the stability criteria for the system compared to the classical consumer resource models.

In the following section, we first reviewed the classical consumer resource model (Tilman’s model) and its stability criteria, and further elucidated the updated stability criteria in the resource partition model, using the resource partition model in Equations 23, 24, 25, and 26 as example.

Stability criteria of resource partition model

Similar to a classical consumer resource model (represented by Tilman’s model), the generalized form of microbes interacting with two resources $R_1$ and $R_2$ can be represented as:

$$\frac{d{m}_i}{dt}=m_i\left(g_i\left(R_1,R_2\right)-d\right),\text{for}i=\mathrm{1,2}$$ (Equation 42)

$$\frac{d{R}_j}{dt}=d\left(R_{j,\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-R_j\right)-\sum _{i=1}^2{m}_i{h}_{ij}\left(R_1,R_2\right)g_i\left(R_1,R_2\right),\text{for}j=\mathrm{1,2}\text{,}$$ (Equation 43)

Where $R_{j,\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}$ is the supply concentration of resource $j$, and $h_{ij}$ is the function describing the amount of resource $j$ impacted by species $i$ per-biomass.

When $h_{ij}$ describes resource uptake and has a positive sign, Equations 42 and 43 above represent the classical consumer resource model.⁸⁰ When at least one of the $h_{ij}$ describes resource production and exhibit negative sign, these equations represents the broader “resource partition model” and exhibit different criteria on the stability of coexistence.

The graphical approach is composed of two elements: the growth contour, i.e. the zero net growth isoclines (ZNGI), and the consumption vector. ZNGI, i.e. the growth contour, is defined as all $\left[R_1,R_2\right]$ that meet $g\left(R_1,R_2\right)=d$. And consumption vectors $\overrightarrow{C_i}=-d\left[\begin{array}{c}{h}_{i1}\\ h_{i2}\end{array}\right]$ indicates the total consumption rate of resources per biomass of the species $i$ at the growth contour.

Assume that the growth contours of two species intersect at a fixed point $\left[R_1^{\ast },R_2^{\ast }\right]$. The resource supply vector $\overrightarrow{U}=d\left[\begin{array}{c}{R}_{1,\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-R_1^{\ast }\\ R_{2,\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-R_2^{\ast }\end{array}\right]$ points to the supply point $\left[R_{1,\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}},R_{2,\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}\right]$ from the fixed point. To balance $\overrightarrow{U}$, the summation of resource supply vector $\overrightarrow{U}$ and consumption vectors $\overrightarrow{C_1}$ and $\overrightarrow{C_2}$ equals to $0$: $m_1^{\ast }\overrightarrow{C_1}+m_2^{\ast }\overrightarrow{C_2}+\overrightarrow{U}=\overrightarrow{0}$.

For the fixed point to exist with non-zero biomass of strain 1 and 2, the resource supply vector needs to be located within the sector area formed by two consumption vectors $\overrightarrow{C_1}$ and $\overrightarrow{C_2}$. Nevertheless, the (1) existence of the intersection of two growth contours, and (2) supply vector locates within the angle of consumption vectors, are only necessary conditions for coexistence. The stability of coexistence needs to also be accessed by the eigenvalue of the Jacobian matrix of the fixed point.

At the fixed point (∗), the Jacobian matrix of the models above takes a general form:

$$J=\left[\begin{array}{cccc}0& 0& v_{11}& v_{12}\\ 0& 0& v_{21}& v_{22}\\ -w_{11}& -w_{12}& -x_{11}& -x_{12}\\ -w_{21}& -w_{22}& -x_{21}& -x_{22}\end{array}\right]\text{,}$$ (Equation 44)

with

$$v_{ij}={\left(\frac{\partial \stackrel{.}{m_i}}{\stackrel{.}{\partial R_j}}\right)}^{\ast },w_{ij}=-{\left(\frac{\partial \stackrel{.}{R_i}}{\stackrel{.}{\partial m_j}}\right)}^{\ast },x_{ij}=-{\left(\frac{\partial \stackrel{.}{R_i}}{\stackrel{.}{\partial R_j}}\right)}^{\ast }\text{.}$$

For simplicity, we set the abbreviation as:

$$\begin{array}{c}{P}_1={\left({\partial }_{R_1}{g}_1\right)}^{\ast },P_2={\left({\partial }_{R_2}{g}_1\right)}^{\ast }\text{,}\\ P_3={\left({\partial }_{R_1}{g}_2\right)}^{\ast },P_4={\left({\partial }_{R_2}{g}_2\right)}^{\ast }\text{,}\\ c_{11}={\left(h_{11}\right)}^{\ast },c_{12}={\left(h_{21}\right)}^{\ast }\text{,}\\ c_{21}={\left(h_{12}\right)}^{\ast },c_{22}={\left(h_{22}\right)}^{\ast }\text{,}\end{array}$$ (Equation 45)

so we have elements in the Jacobian matrix expressed as:

$$\begin{array}{cc}{v}_{11}=m_1^{\ast }{P}_1,& v_{12}=m_1^{\ast }{P}_2\\ v_{21}=m_2^{\ast }{P}_3,& v_{22}=m_2^{\ast }{P}_4\\ w_{11}=c_{11}d,& w_{12}=c_{12}d,\\ w_{21}=c_{21}d,& w_{22}=c_{22}d,\\ x_{11}=d,& x_{12}=0\\ x_{21}=m_1^{\ast }{c}_{21}{P}_1+m_2^{\ast }{c}_{22}{P}_3,& x_{22}=d+m_1^{\ast }{c}_{21}{P}_2+m_2^{\ast }{c}_{22}{P}_4\end{array}$$ (Equation 46)

At the steady state, ${g_1}^{\ast }={g_2}^{\ast }=d$. With definitions in Equations 23 and 24, the characteristic equation of eigenvalue $\lambda$ for the Jacobian matrix can be expressed as:

$${\lambda }^4+\left(x_{11}+x_{22}\right){\lambda }^3+\left(q_1+q_4+x_{11}{x}_{22}-x_{12}{x}_{21}\right){\lambda }^2+\left(x_{11}{q}_4+x_{22}{q}_1-x_{12}{q}_3-x_{21}{q}_2\right)\lambda +\left(q_1{q}_4-q_2{q}_3\right)=0\text{,}$$ (Equation 47)

the coefficients of this quartic equation are: $a_0=1$, $a_1=x_{11}+x_{22}$, $a_2=q_1+q_4-x_{12}{x}_{21}+x_{11}{x}_{22}\text{,}$ $a_3=q_4{x}_{11}-q_3{x}_{12}-q_2{x}_{21}+q_1{x}_{22}$, $a_4=-q_2{q}_3+q_1{q}_4$, with $q_i$ defined as:

$$\begin{array}{c}{q}_1=w_{11}{v}_{11}+w_{12}{v}_{21}\text{,}\\ q_2=w_{11}{v}_{12}+w_{12}{v}_{22}\text{,}\\ q_3=w_{21}{v}_{11}+w_{22}{v}_{21}\text{,}\\ q_4=w_{21}{v}_{12}+w_{22}{v}_{22}\text{.}\end{array}$$ (Equation 48)

The Routh-Hurwitz (RH) criterion states a necessary and sufficient condition for the stability of a dynamical system⁵³: for a quartic equation for the eigenvalue $\lambda$, $a_0{\lambda }^4+a_1{\lambda }^3+a_2{\lambda }^2+a_3\lambda +a_4=0$, The RH table were calculated as Table S2.

Along the “Values” column of Table S2, from term 0 to term 4, the number of sign changes equals the number of non-negative roots in Equation 24. As $a_0=1$, the RH table leads to four RH criteria: (1) $a_1>0$, (2) $a_4>0$, (3) $a_3>0$, (4) $a_1{a}_2{a}_3-a_1^2{a}_4-a_3^2>0$. Detailed derivations of the RH criterion on resource competition models can be found in the appendix of Tilman’s original literature.⁸⁰

In the following text, we will go through these four RH criteria, and compare the difference between the classical consumer resource model and the resource partition model. We use the resource partition model in Equations 23, 24, 25, and 26 as examples, which specifies the parameters in Equation 23 into:

$$\begin{array}{cc}{P}_1={\left({\partial }_{R_{\mathrm{s}\mathrm{i}\mathrm{d}}}{g}_1\right)}^{\ast }\text{,}& P_2={\left({\partial }_{R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{g}_1\right)}^{\ast }\text{,}\\ P_3={\left({\partial }_{R_{\mathrm{s}\mathrm{i}\mathrm{d}}}{g}_2\right)}^{\ast }\text{,}& P_4={\left({\partial }_{R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{g}_2\right)}^{\ast }\text{.}\\ c_{11}=-{\alpha }_{1,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}ϵ/r\text{,}& c_{12}=-{\alpha }_{2,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}ϵ/r\text{,}\\ c_{21}=1/\left({\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\gamma r\right)\text{,}& c_{22}=1/\left({\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\gamma r\right)\text{.}\end{array}$$ (Equation 49)

Note that $c_{11},c_{12}<0$ here, which is different from the classical consumer resource model, as the public siderophore were produced instead of consumed by microbes.

Comparison of the RH criteria

Next, we will compare the four RH criteria between the resource partition model and the classical model.

• (1)Criteria 1: ${\mathit{a}}_{\mathbf{1}}>\mathbf{0}$

With the corresponding parameters replaced by definitions in Equations 23, 24, and 25, $a_1=x_{11}+x_{22}$ turns into:

$$a_1=2d+c_{21}{P}_2{m}_1^{\ast }+c_{22}{P}_4{m}_2^{\ast }\text{.}$$ (Equation 50)

In both classical model and the resource partition model, $P$ denotes the growth rate dependency on “resources” and is always positive. Because all the terms on the right side are greater than or equal to zero, $a_1>0$ holds for both classical consumer resource model and the resource partition model (Equations 23, 24, 25, and 26).

• (2)Criteria 2: ${\mathit{a}}_{\mathbf{4}}>\mathbf{0}$

We discussed $a_4$ before $a_3$, as $a_4$ composed the second term of $a_3$. In the classical model, if criteria (2) $a_4>0$, then the criteria (3) $a_3>0$ holds automatically.

In both consumer resource and resource partition models, by definitions in Equation 25, the original form $a_4=-q_2{q}_3+q_1{q}_4$ expand into:

$$a_4=d{m}_1^{\ast }{m}_2^{\ast }\left(c_{12}{c}_{21}-c_{11}{c}_{22}\right)\left(P_2{P}_3-P_1{P}_4\right)\text{,}$$ (Equation 51)

There are two possible situations for $\left(c_{12}{c}_{21}-c_{11}{c}_{22}\right)\left(P_2{P}_3-P_1{P}_4\right)>0$:

$$\begin{array}{cc}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}1\text{:}& \frac{P_2}{P_1}>\frac{P_4}{P_3},\frac{c_{11}}{c_{21}}<\frac{c_{12}}{c_{22}}\text{,}\end{array}$$ (Equation 52)

$$\begin{array}{cc}\mathrm{o}\mathrm{r},\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}2& \frac{P_2}{P_1}<\frac{P_4}{P_3},\frac{c_{11}}{c_{21}}>\frac{c_{12}}{c_{22}}\text{.}\end{array}$$ (Equation 53)

The above requirements hold for both classical consumer resource and the resource partition model. Nevertheless, these two types of models interpret the requirements differently.

In the classical consumer resource model, for situation 1, $\frac{P_1}{P_2}>\frac{P_3}{P_4}$ means the growth of species 1 is more limited by resource 1 compared to species 2, and $\frac{c_{11}}{c_{21}}>\frac{c_{12}}{c_{22}}$ means species 1 also preferentially consumes resource 1 compared to species 2. Similarly, for situation 2, the growth of species 1 is more limited by resource 2, and also consumes more of resource 2. In combination, both possibilities suggest that a necessary condition for stable coexistence in the classical consumer resource model is that each species must consume more of the one resource which more limits its own growth rate.

This condition can be easily applied by the graphical tool for judging coexistence (Figure S1). When the supply point locates within the region bounded by the reverse extensions of the consumption vectors, the growth contours in Figure S1 show the example that species A and species B are more limited by $R_2$ and $R_1$, respectively. As the consumption vectors show that species A and species B preferentially consume more $R_1$ and $R_2$ respectively, species A and B can stably coexist.

In the resource partition model, we assumed ${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}<{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$. If situation 1 holds, $\frac{P_2}{P_1}>\frac{P_4}{P_3}$ means the growth of strain 1, relative to strain 2, is more limited by iron. Since two strains have the same influx rate through public siderophores, $J_{12}=J_{22}$ and $\frac{\partial \left(J_{11}+J_{12}\right)}{\partial R_{\mathrm{s}\mathrm{i}\mathrm{d}}}=\frac{\partial \left(J_{21}+J_{22}\right)}{\partial R_{\mathrm{s}\mathrm{i}\mathrm{d}}}$. $\frac{P_2}{P_1}>\frac{P_4}{P_3}$, i.e., $\frac{\frac{\partial \left(J_{11}+J_{12}\right)}{\partial R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}}{\frac{\partial \left(J_{11}+J_{12}\right)}{\partial R_{\mathrm{s}\mathrm{i}\mathrm{d}}}}>\frac{\frac{\partial \left(J_{21}+J_{22}\right)}{\partial R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}}{\frac{\partial \left(J_{21}+J_{22}\right)}{\partial R_{\mathrm{s}\mathrm{i}\mathrm{d}}}}$, further demands $J_{11}>J_{21}$, i.e., ${\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$. Note that $c_{11},c_{12}<0$, $\frac{c_{11}}{c_{21}}<\frac{c_{12}}{c_{22}}$ means $\left|\frac{c_{11}}{c_{21}}\right|>\left|\frac{c_{12}}{c_{22}}\right|$, that is, strain 1, relative to strain 2, produces proportionately more public siderophores. And $c_{12}{c}_{21}-c_{11}{c}_{22}=\frac{ϵ\left(\frac{{\alpha }_{1,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}}{{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}-\frac{{\alpha }_{2,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}}{{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}}\right)}{r^2\gamma }>0$ asks for ${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{1,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{2,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}>0$. Taken together, if the intersection point exists and situation 1 holds, under the assumption of

$${{\alpha }_{1,\text{growth}}<\alpha }_{2,\text{growth}}\text{,}$$ (Equation 54)

$a_4>0$ requires that:

$${{\alpha }_{1,\text{private}}>\alpha }_{2,\text{private}}\text{,}$$ (Equation 55)

$${{\alpha }_{1,\text{public}}>\alpha }_{2,\text{public}}\ge 0\text{.}$$ (Equation 56)

If situation 2 holds and the assumption of ${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}<{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$ applies, $\frac{P_2}{P_1}<\frac{P_4}{P_3}$ requires $J_{11}>J_{21}$, i.e., ${{\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}<\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$, which does not match the condition for the existence of intersection point ${\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$. This would prove that situation 2 does not hold under the setting ${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}<{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$.

Taken together, in the resource partition model, if two strains could stably coexist, the strain that gives more public goods and plays a more cooperative role (strain 1) must retain more private goods than the other strain (strain 2).

• (3)Criteria 3: ${\mathit{a}}_{\mathbf{3}}>\mathbf{0}$

With the corresponding items replaced by definitions in Equations 23, 24, and 25, the formula of $a_3$ turns into:

$$a_3=d\left(m_1^{\ast }\left(c_{11}{P}_1+c_{21}d{P}_2\right)+m_2^{\ast }\left(c_{12}{P}_3+c_{22}d{P}_4\right)\right)+m_1^{\ast }{m}_2^{\ast }\left(c_{12}{c}_{21}-c_{11}{c}_{22}\right)\left(P_2{P}_3-P_1{P}_4\right)\text{.}$$ (Equation 57)

The second term is linear with $a_4$ in criteria (2).

In the classical consumer resource model, the resource is supplied externally and consumed by species, thus each of the $c_{11},c_{12},c_{21},c_{22}>0$. The first term in the equation above, $d\left(m_1^{\ast }\left(c_{11}{P}_1+c_{21}d{P}_2\right)+m_2^{\ast }\left(c_{12}{P}_3+c_{22}d{P}_4\right)\right)$, is non-negative under the classical model. Thus, as long as criteria (2) $a_4>0$ is satisfied, $a_3>0$ holds.

In the resource partition model, however, the first term $d\left(m_1^{\ast }\left(c_{11}{P}_1+c_{21}d{P}_2\right)+m_2^{\ast }\left(c_{12}{P}_3+c_{22}d{P}_4\right)\right)$ is no longer guaranteed to be nonnegative, as $c_{11},c_{12}<0$. Therefore, the sign of $a_3$ could be negative even when the second term is positive (demonstrated by Region 2 in Figure 3B), adding a region of instability.

• (4)Criteria 4: ${\mathit{a}}_{\mathbf{1}}{\mathit{a}}_{\mathbf{2}}{\mathit{a}}_{\mathbf{3}}-{\mathit{a}}_{\mathbf{1}}^{\mathbf{2}}{\mathit{a}}_{\mathbf{4}}-{\mathit{a}}_{\mathbf{3}}^{\mathbf{2}}>\mathbf{0}$

After expansion and simplification, the equation in criteria (4) can be derived into the product of two terms:

$$a_1{a}_2{a}_3-a_1^2{a}_4-a_3^2=\left(2d^3+d{m}_1^{\ast }\left(c_{11}{P}_1+2d{c}_{21}{P}_2\right)+d{m}_2^{\ast }\left(c_{12}{P}_3+2d{c}_{22}{P}_4\right)+m_1^{\ast }{m}_2^{\ast }\left(c_{12}{c}_{21}-c_{11}{c}_{22}\right)\left(P_2{P}_3-P_1{P}_4\right)\right)\left(\left(c_{11}{P}_1+d{c}_{21}{P}_2\right)m_1^{\ast }\left(d+c_{21}{P}_2{m}_1^{\ast }\right)+\left(c_{12}\left(d{P}_3+c_{21}{P}_1{P}_4{m}_1^{\ast }\right)+c_{22}\left(d^2{P}_4+P_2\left(c_{11}{P}_3+2d{c}_{21}{P}_4\right)m_1^{\ast }\right)\right)m_2^{\ast }+c_{22}{P}_4\left(c_{12}{P}_3+d{c}_{22}{P}_4\right){m_1^{\ast }}^2\right)\text{.}$$ (Equation 58)

The first multiplier term $2d^3+d{m}_1^{\ast }\left(c_{11}{P}_1+2d{c}_{21}{P}_2\right)+d{m}_2^{\ast }\left(c_{12}{P}_3+2d{c}_{22}{P}_4\right)+m_1^{\ast }{m}_2^{\ast }\left(c_{12}{c}_{21}-c_{11}{c}_{22}\right)\left(P_2{P}_3-P_1{P}_4\right)$ is a linear combination of $a_3$ and $a_4$, which is non-negative when criteria (2) $a_4>0$ and criteria (3) $a_3>0$ holds.

Nevertheless, the second multiplier term differs in two types of models.

In the classical consumer resource model, with $c_{21},c_{22}>0$, the second multiplier term in Equation 34, $\left(c_{11}{P}_1+d{c}_{21}{P}_2\right)m_1^{\ast }\left(d+c_{21}{P}_2{m}_1^{\ast }\right)+\left(c_{12}\left(d{P}_3+c_{21}{P}_1{P}_4{m}_1^{\ast }\right)+c_{22}\left(d^2{P}_4+P_2\left(c_{11}{P}_3+2d{c}_{21}{P}_4\right)m_1^{\ast }\right)\right)m_2^{\ast }+c_{22}{P}_4\left(c_{12}{P}_3+d{c}_{22}{P}_4\right){m_1^{\ast }}^2$ is always non-negative.

In the resource partition model, with changed signs in $c_{11}$ and $c_{12}$, the sign of the second term $\left(c_{11}{P}_1+d{c}_{21}{P}_2\right)m_1^{\ast }\left(d+c_{21}{P}_2{m}_1^{\ast }\right)+\left(c_{12}\left(d{P}_3+c_{21}{P}_1{P}_4{m}_1^{\ast }\right)+c_{22}\left(d^2{P}_4+P_2\left(c_{11}{P}_3+2d{c}_{21}{P}_4\right)m_1^{\ast }\right)\right)m_2^{\ast }+c_{22}{P}_4\left(c_{12}{P}_3+d{c}_{22}{P}_4\right){m_1^{\ast }}^2$ cannot be indirectly inferred, and can still be negative even when the criteria (2) $a_4>0$ and criteria (3) $a_3>0$ holds, which contributes to the oscillatory dynamics (Region 3 in Figures 3 and S3).

Conditions for stable coexistence in our model

First, in the resource partition model of Equations 23, 24, 25, and 26, the presence of the co-existence point between two strains, with the setting

$${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}<{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\text{,}$$

requires

$${\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}>{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}\text{.}$$

Second, the non-zero biomass of two strains imposes constraints on the iron supply concentration $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}$, that

$$R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }+\frac{1}{k_2}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }>R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}>R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }+\frac{1}{k_1}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }$$

with $k_1=\frac{ϵ\gamma }{d}{\alpha }_{1,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$ , $k_2=\frac{ϵ\gamma }{d}{\alpha }_{2,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$.

Graphically, this inequality requires the supply point [$R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}$, 0] locating within the region bounded by the reverse extensions of the consumption vectors in the chemical space.

Third, the stability of the coexistence point is judged by the RH criterion. The criteria (2) $a_4>0$ also requires

$${{\alpha }_{1,\text{public}}>\alpha }_{2,\text{public}}\text{.}$$

If it were a classical consumer resource model, the satisfaction of the criteria (2) automatically grants the criteria (3) $a_3>0$ and criteria (4) $a_1{a}_2{a}_3-a_1^2{a}_4-a_3^2>0$. Actually, as the satisfaction of criteria (2) in a classical model does not impose constraints on biomass (Equations 28 and 29), an important property in a classical model is that the stability of the system can be kept as long as the supply point [$R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n},\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}$, 0] locates within the region bounded by the reverse extensions of the consumption vectors.

However, in the resource partition model, the self-creating dimension changes the sign of the coefficients $c_{11}$ and $c_{12}$. Under this situation, even when criteria (2) holds, criteria (3) and criteria (4) may still be violated. Due to the change in the sign of the coefficients $c_{11}$ and $c_{12}$, the occurrence of oscillations becomes possible, as well as exclusion and extinction, even when the supply point locates within the region bounded by the reverse extensions of the consumption vectors (Figures 3 and S3).

Impact of parameters and uptake forms

Siderophore consumption rate, cost, and affinity

Although we assumed in the main text that all public siderophores were recycled, modifying the model to allow the consumption of a portion of public siderophores does not affect the overall dynamics, including oscillation and stable coexistence. We also analyzed a modified version of Equation 25 with a consumption ratio parameter $p$ ranging from 0 to 1 to indicate the proportion of consumption of the public siderophores:

$$\frac{d{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}}{dt}=\sum _{i=1}^2\frac{m_i}{r}{\alpha }_{i,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}ϵ-p\sum _{i=1}^2\frac{m_i}{r}·I\left(R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}},R_{\mathrm{s}\mathrm{i}\mathrm{d}},{\overrightarrow{\alpha }}_i\right)-d{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}$$ (Equation 59)

As shown by Figure S5, the higher the consumption ratio $p$, the easier for the partial cooperator to exclude or stably coexist with the cheater.

We also checked how the increases of production cost, i.e., the decreases of $ϵ$, affect the systems’ dynamics. Intuitively, it becomes more difficult for the partial cooperator to coexist with the cheater (Figure S5).

We also examined the effect of affinity coefficients on the dynamics. Coexistence is possible over a wide range and becomes more likely in the oscillatory case as $K_l$ is smaller, which means the public siderophore has a much higher affinity for iron (Figure S6).

Forms of iron uptake fluxes

In our resource partition model, we assumed the Monad form of iron uptake. There can be other forms of iron uptake:

Possibility (1): $J_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}$ and $J_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}$ can take the following mass-action forms instead of Monad form:

$$J_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}=v_{\mathrm{m}}{\alpha }_{1,\text{private}}\beta R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}\text{,}$$ (Equation 60)

$$J_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}=v_{\mathrm{l}}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}{R}_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}\text{.}$$ (Equation 61)

Between strains adopting two strategies, at the possible intersection point, $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }$ and $R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }$ can be solved as:

$$R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }=\frac{-\beta v_{\mathrm{m}}\left({\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}{-\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}\right)}{v_{\mathrm{l}}\left({\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\right)}\text{.}$$ (Equation 62)

$$R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }=\frac{-d\left({\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\right)}{\beta \gamma v_{\mathrm{m}}{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\left({\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}-{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}\right)}\text{,}$$ (Equation 63)

Under this highly simplified form of iron-uptake fluxes, $R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }$ is a constant, and $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }$ is a linear function with respect to $d$. That is, as $d$ increases, the intersection point moves parallel to the $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}$-axis in the chemical space. It is obvious that ${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}<{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}$ is also the necessary condition for the intersection point to exist.

Possibility (2): When $J_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}$ takes the following sigmoidal form of siderophores-iron complex:

$$J_{\sigma ,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}=\frac{v_{\mathrm{m}}{\alpha }_{1,\text{private}}\beta R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{K_{\mathrm{m}}+R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}\text{,}$$ (Equation 64)

$$J_{\sigma ,\mathrm{p}\mathrm{u}\mathrm{b}\mathrm{l}\mathrm{i}\mathrm{c}}=\frac{v_{\mathrm{l}}{R}_{\mathrm{s}\mathrm{i}\mathrm{d}}{R}_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}{K_{\mathrm{l}}+R_{\mathrm{s}\mathrm{i}\mathrm{d}}{R}_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}}\text{,}$$ (Equation 65)

Between strains adopting two strategies, relationships between the intersection point $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }$ and $R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }$ follows:

$$R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }=\frac{-\beta K_{\mathrm{l}}{v}_{\mathrm{m}}\left({\alpha }_{1,\text{growth}}{\alpha }_{1,\text{private}}-{\alpha }_{2,\text{growth}}{\alpha }_{2,\text{private}}\right)}{v_{\mathrm{l}}{K}_{\mathrm{m}}\left({\alpha }_{1,\text{growth}}-{\alpha }_{2,\text{growth}}\right)+R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }\left(v_{\mathrm{l}}\left({\alpha }_{1,\text{growth}}-{\alpha }_{2,\text{growth}}\right)+\beta v_{\mathrm{m}}\left({\alpha }_{1,\text{growth}}{\alpha }_{1,\text{private}}-{\alpha }_{2,\text{growth}}{\alpha }_{2,\text{private}}\right)\right)}$$ (Equation 66)

Despite that the form of $R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }$ is relatively complex, from the setting ${\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}<0$, for a meaningful intersection to exist, Equation 37 also must be satisfied. The solutions for $R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }$ and $R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }$ can be solved as:

$$R_{\mathrm{s}\mathrm{i}\mathrm{d}}^{\ast }=-\frac{K_{\mathrm{l}}\left({\alpha }_{1,\text{growth}}{\alpha }_{1,\text{private}}-{\alpha }_{2,\text{growth}}{\alpha }_{2,\text{private}}\right)\left({\alpha }_{1,\text{growth}}\left(\beta \gamma v_{\mathrm{m}}{\alpha }_{2,\text{growth}}\left({\alpha }_{1,\text{private}}-{\alpha }_{2,\text{private}}\right)+d\right)-d{\alpha }_{2,\text{growth}}\right)}{K_{\mathrm{m}}\left({\alpha }_{1,\text{growth}}-{\alpha }_{2,\text{growth}}\right)\left({\alpha }_{1,\text{growth}}{\alpha }_{1,\text{private}}\left(\gamma v_{\mathrm{l}}{\alpha }_{2,\text{growth}}-d\right)+{\alpha }_{2,\text{growth}}{\alpha }_{2,\text{private}}\left(d-\gamma v_{\mathrm{l}}{\alpha }_{1,\text{growth}}\right)\right)}$$ (Equation 67)

$$R_{\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}}^{\ast }=-\frac{d{K}_{\mathrm{m}}\left({\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\right)}{d\left({\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}-{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\right)+\beta \gamma v_{\mathrm{m}}{\alpha }_{1,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}{\alpha }_{2,\mathrm{g}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{t}\mathrm{h}}\left({\alpha }_{1,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}-{\alpha }_{2,\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{t}\mathrm{e}}\right)}$$ (Equation 68)

The method of constructing the invasion chain

In obtaining Figure 4B, the simulated evolutionary process of strategies towards “evolutionarily optimal” can be expressed in the following steps:

• (1)Arbitrarily assign a strain $\sigma$ with strategy ${\overrightarrow{\alpha }}_{\sigma }$ as the initial strategy. This initial strategy is selected as (1,0,0) in Figure 4B. If this strain can survive stably in the given chemostat condition, then it creates a steady-state chemical environment.
• (2)Scan the whole strategy space for the “maximizing strategy” that maximizes growth rate under the current steady-state chemical environment. Then, the strain adopting this maximizing strategy is added to the system to invade. If the added strain can survive, the invasion is considered “successful”. The new chemical environment formed after adding new strains is used for another round of invasion (in the case of oscillatory coexistence, the environmental value of the instability point of the limit cycle is chosen).
• (3)A set of strategies are considered as “evolutionarily stable” when the steady-state environment created by strains adopting these strategies cannot be invaded by any other strategies, i.e., no maximizing strategies could be found outside of the current strategies.

The invasion chain is formed by repeating (2) for successive invasions, till an evolutionarily stable environment can be achieved.

Simulation and visualization

All simulations and most visualizations were performed on Matlab with original codes listed in Key resource table, and parameter sets were listed in Table S3. Ternary plots in the article were generated by the ggtern package in the R platform.⁷⁹

Published: July 20, 2023

Data and code availability

• •Simulation data have been deposited at Zenodo and are publicly available as of the date of publication. DOIs are listed in the key resources table.
• •All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.