Abstract
Pathogen population dynamics within individual hosts can alter disease epidemics and pathogen evolution, but our understanding of the mechanisms driving within-host dynamics is weak. Mathematical models have provided useful insights, but existing models have only rarely been subjected to rigorous tests, and their reliability is therefore open to question. Most models assume that initial pathogen population sizes are so large that stochastic effects due to small population sizes, so-called demographic stochasticity, are negligible, but whether this assumption is reasonable is unknown. Most models also assume that the dynamic effects of a host’s immune system strongly affect pathogen incubation times or “response times,” but whether such effects are important in real host-pathogen interactions is likewise unknown. Here we use data for a baculovirus of the gypsy moth to test models of within-host pathogen growth. By using Bayesian statistical techniques and formal model-selection procedures, we are able to show that the response time of the gypsy moth virus is strongly affected by both demographic stochasticity and a dynamic response of the host immune system. Our results imply that not all response-time variability can be explained by host and pathogen variability, and that immune system responses to infection may have important effects on population-level disease dynamics.
Keywords: within-host model, speed-of-kill, demographic stochasticity, baculovirus
Graphical Abstract
“Such degraded forms of Diptera are the connecting links between the true six-footed insects and the order of Arachnids (spiders, mites, ticks, etc.). The reader should compare the Nycteribia with the young six-footed moose-tick figured on page 559 of the Naturalist. Another spider-like fly is the Chionea valga […], which is a degraded Tipula, the latter genus standing near the head of the suborder Diptera. The Chionea, according to Harris, lives in its early stages in the ground like many other gnats, and is found early in the spring, sometimes crawling over the snow.” From “A Chapter on Flies (Concluded)” by A. S. Packard Jr. (The American Naturalist, 1869, 2:638-644).
Introduction
An understanding of within-host pathogen growth is critically important for predicting and responding to disease outbreaks, but achieving such an understanding is difficult without mechanistic mathematical models. The development of models of within-host population growth is therefore an important area of current research (Alizon and van Baalen 2008), but few existing models have been formally tested, and so their reliability is unknown. Here we use experimentally collected time-to-death data to test models of within-host pathogen growth for an insect virus by comparing the ability of different models to explain the time that it takes the virus to kill infected hosts.
Most within-host pathogen growth models are aimed at understanding the fluctuations in pathogen density that occur during chronic or acute infections (Antia et al. 1994; Alizon and van Baalen 2008; King et al. 2009). These fluctuations are often described using deterministic models, because deterministic models can be easily analyzed. An important assumption made by deterministic models is that pathogen populations are so large that there are no effects of demographic stochasticity, the variability in population growth that results from the timing of chance events such as reproduction or death (Borsuk and Lee 2009). A growing body of theoretical literature, however, suggests that stochastic events are important (Michael et al. 1998; Grant et al. 2008; Vaughan et al. 2012), suggesting in turn that deterministic models are insufficient for describing these dynamics.
Variability in susceptibility between hosts that results from differences in host genetics or condition is known to cause variation in within-host pathogen dynamics (van der Werf et al. 2011). Circumstantial evidence from the empirical literature, however, suggests that demographic stochasticity may also play an important role. First, the symptoms of many diseases only appear after relatively long incubation periods, suggesting that initial pathogen population sizes are small (Moury et al. 2007; Zwart et al. 2009a). Second, there is often high variability across hosts in within-host pathogen dynamics, even when pathogens are grown in closely related hosts under identical conditions (Mideo et al. 2008; Zwart et al. 2009a). Demographic stochasticity may therefore be an important source of variability in growth rates. What is needed then, is a formal test of whether models that allow for demographic stochasticity provide a better explanation for pathogen growth than do models that allow only for variability between hosts. Quantifying pathogen numbers within hosts when pathogen population sizes are small is often imprecise (Chandler 1998), but it is when population sizes are small that the effects of demographic stochasticity are most likely important. We therefore instead use incubation time data to test for the importance of demographic stochasticity. Our model-fitting procedure shows that demographic stochasticity does indeed play a crucial role in within-host pathogen growth.
Efforts to use stochastic models to make inferences about mechanisms determining pathogen population growth have a long history (Shortley 1965; Shortley and Wilkins 1965; Chang 1970). Early efforts estimated parameters using data on a disease’s incubation period or “response time,” the time between infection and the appearance of disease symptoms. This work, however, was based only on “birth-death” models, which assume that per capita pathogen clearance rates are constant. In many organisms, however, pathogen clearance rates instead change over time because of changes in the immune system during the period of infection. Because birth-death models do not allow for such dynamic changes in the immune system, they generally provide a poor fit to data (Armitage et al. 1965; Williams and Meynell 1967; Schach and Schach 1970).
More recent stochastic models have instead often included immune system dynamics, usually to describe HIV growth, and have compared model predictions either to patterns in within-host pathogen dynamics (Chao et al. 2004; Lin and Shuai 2010; Conway and Coombs 2011; Vaughan et al. 2012), or to changes in within-host pathogen diversity (Woo and Reifman 2012). Comparisons to data, however, have been carried out only for the purposes of qualitative model validation, not for parameter estimation or model comparison. Other researchers have instead neglected the dynamic effects of the immune system but have avoided poor fits to data by applying their models only to the first few days of infection, before the immune system has begun to have much effect. This latter approach requires reduced computing resources, and it has therefore been straightforward to compare models to data, using data on multiplicity of infection (Brown et al. 2006) or changes in pathogen diversity (Grant et al. 2008) in mice infected with typhoid (Salmonella enterica).
Nevertheless, neither approach directly addresses the questions prompted by Shortley’s work: does demographic stochasticity affect response times, and are response times affected by immune system dynamics? Answers to these questions are crucial for the further development of theories of the evolution of virulence, because response time is a key component of pathogen fitness (May and Anderson 1983). We therefore combined recent approaches, following the lead of HIV researchers in using models that allow for immune system dynamics and following the lead of mouse-typhoid researchers in using model-selection procedures to formally choose between models. To meet the significantly greater computing requirements of our models, we used a highly parallel computing environment, and we developed a new form of Markov chain Monte Carlo algorithm that takes advantage of this environment (Kennedy et al. 2014b). Because response-time data are sometimes insufficient to choose between models (Morgan and Watts 1980), we constrained the values of some parameters by using previously collected experimental data, while estimating other parameters directly from response-time data.
The baculovirus that we study is a nucleopolyhedrovirus of the gypsy moth, Lymantria dispar. Because baculoviruses are directly transmitted, fatal, and usually either species-specific or with narrow host ranges, they are widely used as environmentally benign insecticides (Moreau and Lucarotti 2007). In baculoviruses, response time is effectively equivalent to speed of kill, an important measure of efficacy when baculoviruses are used as insecticides. Our efforts to understand response times may therefore be helpful in efforts to use baculoviruses in pest management. Previous efforts to make inferences about mechanisms of baculovirus growth have in contrast used deterministic models (van Beek et al. 1988a), which often ignore relationships between speed of kill and probability of death, thereby requiring two separate models to analyze speed of kill and percent mortality. Our approach in contrast relates a particular baculovirus dose to both speed of kill and percent mortality, thereby using a single model to draw inferences from both types of data.
Methods
Study System
The gypsy moth is an invasive pest in North America that causes economic damage by periodically defoliating hardwood trees (Elkinton and Liebhold 1990). As in many forest insects, gypsy moth outbreaks are partly driven by a species-specific baculovirus, the Lymantria dispar nucleopolyhedrovirus (Dwyer et al. 2004). This virus is also used in gypsy moth control (Webb et al. 1999), but the evolutionary consequences of virus application are unknown. Because within-host pathogen growth is a crucial element in virus evolution, one of our aims is to develop a reliable model of within-host dynamics that can be used to understand the evolutionary consequences of microbial control programs.
Baculovirus infection begins when a larva consumes foliage contaminated by infectious particles or “occlusion bodies” released from the cadaver of a virus-killed conspecific (Cory and Myers 2003). In the alkaline environment of the gut, the pH-sensitive, outer protein coat dissolves (Adams and McClintock 1991). Viral proteins called “enhancins” then increase the permeability of the peritrophic membrane of the insect gut (Wang and Granados 1997; Peng et al. 1999), allowing virions to bind to epithelial cells of the midgut (Horton and Burand 1993). Infection is thus associated with damage to the peritrophic membrane (Rohrmann 2008), and so gut-cell sloughing increases as a response to virus challenge (Washburn et al. 2001). Larvae have many midgut cells (Baldwin and Hakim 1991), and so the number of suitable binding sites probably does not impose a severe limitation on midgut cell infection (van Beek et al. 1988a). Increased rates of cell sloughing, however, may nevertheless lead to a non-linear relationship between pathogen dose and the number of particles that successfully invade a host.
In infected midgut cells, virions bud from the cell membrane and enter the tracheal system, at which point systemic spread begins (Adams and McClintock 1991). Through the tracheal system, virions gain access to the hemolymph, where a particular virion’s fate depends on whether it first comes into contact with a host immune cell or with a host cell suitable for replication. If a virion contacts a host immune cell, or “hemocyte,” it is bound to the hemocyte (Washburn et al. 1996; Schmid-Hempel 2005; McNeil et al. 2010), an event that initiates a phenoloxidase cascade that destroys the virion and renders the hemocyte inactive (Ashida and Brey 1998; Trudeau et al. 2001). Interactions between virions and immune cells thus result in the destruction of both the virion and the immune cell. If a virion instead encounters a cell suitable for replication, it enters the cell and moves to the nucleus, where it begins to replicate (Rohrmann 2008). Newly formed virus particles then bud and detach from the cytoplasmic membrane of the cell, which allows them to find new cells to infect (Adams and McClintock 1991; Slack and Arif 2006). An important point is that insect immune systems lack clonal reproduction (Vilmos and Kurucz 1998), and so over the course of an infection, hemocytes likely become depleted. The depletion of these hemocytes thus results in a decline in the effectiveness of the immune system over time.
Some exposed larvae are able to clear all of the virions from their system and recover (Washburn et al. 1996), but in others, virion number increases from the presumably small number of particles consumed to a very large number, roughly 2 × 109 particles in the fourth-instar larvae (“instar” p larval developmental stage) that we use here (Shapiro et al. 1986). Though the precise mechanism that causes death is unknown, nearly all internal host tissue is converted into a virus-rich, fluid-like substance that pours out of larvae on rupture of the host integument by the action of viral encoded chitinases and cathepsins (Hawtin et al. 1997). The virus occlusion bodies are then available to infect additional larvae (Elkinton and Liebhold 1990).
Data Collection
To collect speed-of-kill data, we used egg masses from the New Jersey standard strain of gypsy moths (USDA-APHIS, Otis, MA), which are of low heterogeneity in susceptibility (Dwyer et al. 1997). Using this strain reduced differences between hosts, aiding our effort to determine whether demographic stochasticity is important to host response times. Because this population nevertheless includes at least modest variability between individuals, we included variability between individuals in our models.
Larvae were reared according to standard rearing protocols (app. A, “Rearing Methods”; apps. A and B available online). Fourth-instar larvae were then used in a “diet-plug” bioassay (Hughes and Wood 1986; Dwyer et al. 1997; Li and Bonning 2007) to determine mortality and speed of kill at five virus doses (app. A, “Bioassay”).
Model Construction
Because there is already an extensive literature on baculovirus pathogenesis, the goal of our model-fitting was not to identify novel mechanisms but instead to determine which known mechanisms have detectable effects on response times. Our statistical approach to solving this problem was to fit a range of different models to the data and to use formal model-selection criteria to choose the model that best explains the data.
Baculovirus biology suggests that the number of virus particles that initiates infections is probably small (Zwart et al. 2009a, 2009b), and so we used probabilistic models that inherently allow for demographic stochasticity. The models track the replication and destruction of virions, as well as the immune cells that are destroyed along with the virions. Our most complex model is then
| (1) |
| (2) |
| (3) |
| (4) |
Here is , where , and . Term is the number of virions, and is the number of immune cells at time . Term is the threshold number of virus particles at which host death occurs, and is the initial number of immune cells in the host. Virus replication then follows a logistic-growth model, with intrinsic rate of increase and carrying capacity . In practice, it is convenient to express as so that we instead estimate , which is the extent to which the carrying capacity exceeds the host-death threshold . Note that the model assumes host death occurs when the virus population reaches , but the assumption does not require that reaching is the cause of death. Virus removal depends on the massaction term , where is the rate at which virus-destruction events occur. We thus follow standard immune system models in assuming that virus-immune cell interactions can be modeled as predator-prey interactions, with the virus acting as the prey and the immune cell acting as the predator (Alizon and van Baalen 2008). An important difference from previous models, however, is that we assume that immune cells do not reproduce, to reflect the fact that insect hemocytes do not undergo clonal selection (Vilmos and Kurucz 1998). Nevertheless, because the model includes changes in the number of immune cells, it allows for a dynamic immune response.
The initial virus population size , the threshold virus population size for host death , and the initial immune-cell population size are likely to vary among insects, and we therefore treat them as random variables. Preliminary results indicated that the initial virus population that actually established inside an insect was a saturating function of the applied dose. Because randomness is introduced during the process of virus establishment, we described this initial population using a Poisson distribution with parameter , such that is dose and and are estimated parameters that account for the dosesaturation effect. Specifically, is the saturation value of the initial virus population, and is the dose at which half of the saturation value is reached.
To allow for variability between individuals, we assumed that the initial immune cell population and the threshold population size for host death followed lognormal distributions, with medians and variances estimated from the data. Lognormal distributions allow for separate adjustment of medians and variances while constraining the variables to be positive. Allowing for a nonzero variance in the number of immune cells is especially important, because it allows us to incorporate the effects of variability between hosts in immune system strength. The boundary conditions are thus
| (5) |
| (6) |
| (7) |
Note that in the above equations, we distinguish between the parameter , which is the median initial number of immune cells in a host, and the state variable , which is the realized initial number of immune cells. We similarly distinguish between the median threshold virus population at which a host dies and the realized threshold . These distinctions allow us to include the effects of stochastic variation between hosts in the initial number of immune cells and the threshold virus population size. All model parameters are listed in table 1.
Table 1:
List of the parameters, and parameter descriptions contained in the models
| Parameter | Parameter description |
|---|---|
|
| |
| Immune cell attack rate | |
| Virus growth rate | |
| Virus establishment asymptote | |
| Virus establishment half-saturation constant | |
| Median initial immune cell number | |
| Scale parameter of initial immune cell number | |
| Median threshold for host response | |
| Scale parameter of threshold for host response | |
| Virus carrying capacity | |
Our candidate models are then derived as follows. First, our most complex model (M1) is given by equations (1)–(7). Second, to produce a model in which host resources do not limit pathogen growth, we assumed that the virus carrying capacity is much greater than the threshold for host response (), so that there is no effect of resource depletion on pathogen growth. This causes the logistic terms to disappear from equation (2). We call this the “no-carrying-capacity” model (M2). Third, to produce a linear birth-death model, we began with M2 and we additionally fixed the number of immune cells at for all , so that the death rate is set to the constant value . Note that this model was first introduced by Shortley (1965), and so we call this the “Shortley birth-death” model (M3) (Chang 1970; Ercolani 1985). Fourth, by reparameterizing M1 according to and by assuming that dose , we produce a model in which virus establishment is a linear, nonsaturating function of dose. In practice, this is equivalent to rewriting equation (5) as . We call this the “linear virus colonization” model (M4). Fifth and sixth, we remove variability between hosts in immune system strength and in the threshold for response, respectively, by setting and to 0. These changes, in effect, replace equations (6) and (7) with, respectively, and . We call these latter two models the “identical immune system” (M5) and “identical response threshold” (M6) models, respectively. Seventh, we note that models including demographic stochasticity can be closely approximated by corresponding ordinary differential equation models, when population sizes are large (Renshaw 1991). We therefore constructed a model with no demographic stochasticity by assuming that virus population sizes are large enough to be tracked as continuous rather than discrete values. We then rewrite the probabilistic model as a set of differential equations, as in van Beek et al. (1988a). We call this the “no-demographic-stochasticity” model (M7). We emphasize, however, that this latter model does include stochasticity in the form of stochastic differences between hosts in immune system strength and the threshold for response. Transition probabilities for each of these models can be found in figure 1.
Figure 1:
Models considered. The most complex model (M1) contains all of the mechanisms hypothesized to be important for baculovirus growth in gypsy moth hosts. All other models are nested versions of this model, with the additional assumptions listed in the “Assumptions beyond model M1” column. Differences between M1 and all other models are shown either in boldface, representing a changed term, or in gray, representing a term that dropped out of the model.
Our main goal in fitting models to data was to infer the importance of different mechanisms in determining pathogen growth within hosts. We therefore compared the ability of our competing models to explain the data, such that the best model included only those mechanisms that could justifiably be included given the data. Although equations (1)–(7) include effectively every mechanism hypothesized to affect within-host dynamics of baculoviruses, it is possible that the effects of one or more of these mechanisms are weak enough that they can be neglected. Because we considered not just the most complex model but simpler models that successively left out mechanisms, we were able to quantify the importance of each mechanism (Burnham and Anderson 1998).
Bayesian Inference
We analyzed these models in a Bayesian statistical framework (Kennedy et al. 2014a; see app. A, “Fitting the Models to Data” for details), and we then compared our competing models using the deviance information criterion or DIC (Spiegelhalter et al. 2002). Smaller DIC values imply better models, and so if the DIC score of a simpler model is larger than that of a more complex model, the mechanism missing from the simpler model is likely to be important in understanding speed of kill. To aid in these comparisons, we present the score of each model, which is the difference between a model’s DIC score and the DIC score of the best model. There is no absolute cutoff for scores such that one model can be outright rejected in favor of another, but a rule of thumb proposed by Burnham and Anderson (1998) for interpreting differences in the Akaike Information Criterion (AIC) appears to work well for DIC as well (Spiegelhalter et al. 2002; Bolker 2008). According to this rule of thumb, a model with of <2 has substantial support, a model with between 3 and 7 has considerably less support, and a model with has very little support.
A crucial feature of DIC is that it allows us to include information from other data sets in model selection. This is important because estimating some of the model parameters from response-time data alone is very difficult (Morgan and Watts 1980). For example, unreasonably low estimates of the median threshold population size can produce reasonable speeds of kill if the estimate of the virus growth rate parameter is also very low. Shapiro et al. (1986), however, directly counted occlusion bodies to estimate that, for the developmental stage of the insects that we use here, , which we used to construct a prior distribution on . We likewise used literature data to include such information in the priors of many of the model parameters (app. A, “Prior Construction”), an increasingly common practice in ecological modeling (McCarthy and Masters 2005; Elderd et al. 2006; Bolker 2008).
The resulting posterior distribution includes information from our priors as well as information from our response-time data (Gelman et al. 2004). As we explain in more detail in appendix A, “Prior Construction,” however, our priors serve mostly to constrain parameters away from biologically unrealistic values such as extremely low median threshold pathogen population sizes and extremely low pathogen replication rates . Our informative priors, specifically for the threshold pathogen number at which death occurs , the number of pathogen particles that cross the gut barrier , and the pathogen replication rate are based on reliable data. Moreover, our main conclusions are not based on parameter estimates but are instead derived from model comparisons. By constraining our parameter estimates to biologically realistic values we ensure that our models are reasonable descriptions of pathogen growth in insect hosts, which in turn improves the reliability of our conclusions.
We additionally note that we used vague priors for the attack rate of immune cells and the median initial number of immune cells that describe the dynamics of the immune system. Our estimates of and thus depended almost entirely on the response-time data. We used identical priors for the models that include demographic stochasticity and for the model that does not. Our conclusion that response times are partly determined by demographic stochasticity and a dynamic immune system is thus not simply due to our use of informative priors for some parameters.
Qualitative Model Behavior
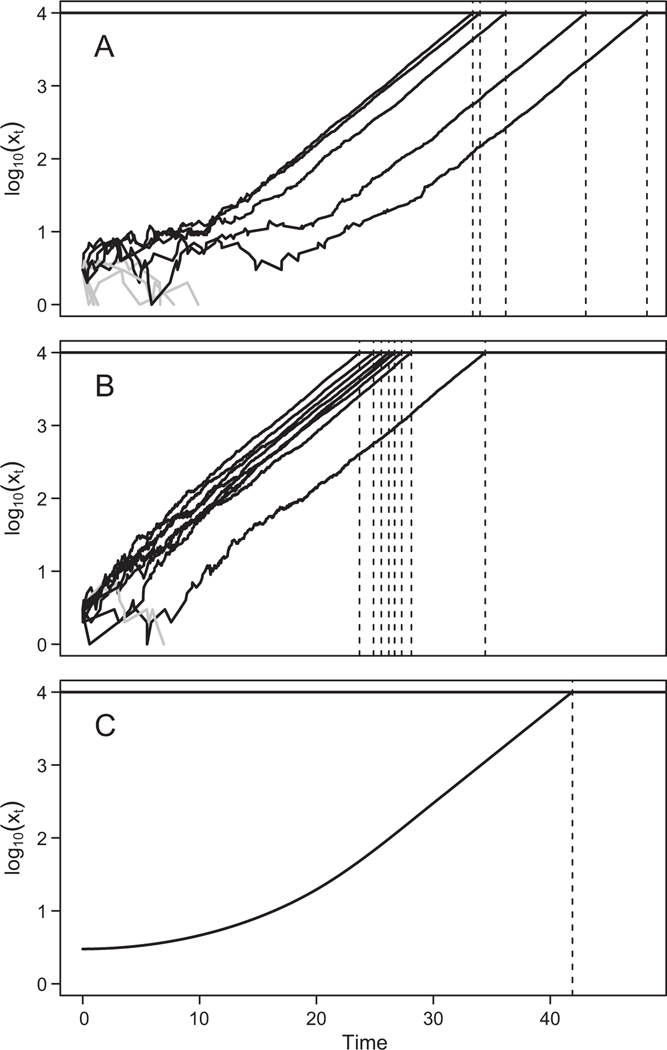
To illustrate the key biological differences between our models, here we focus on the behavior of three particular models that highlight the effects of a dynamic host immune response and of demographic stochasticity on response times. In figure 2A, we show multiple stochastic realizations of our most complex model (M1), equations (1)–(7), which allows for a dynamic immune system and demographic stochasticity. In B, we show realizations of the Shortley birth-death model (M3), which does not allow for a dynamic immune system but does allow for demographic stochasticity. In C, we show realizations of the no-demographic-stochasticity model (M7), which allows for a dynamic immune system but does not allow for demographic stochasticity. Realizations of the former two models were generated using the Gillespie algorithm (Doob 1945; Gillespie 1977), while realizations of the latter model were generated using the Euler method of numerical integration (as we explain in app. A, “Fitting the Models to Data,” our fitting routine required millions of realizations, and so for the stochastic models in the fitting routine, we used a hybrid simulation algorithm). When we fit the models to data, we allowed for variation in doses and in hosts, but because figure 2 is intended to highlight the conceptual differences between the models, in these simulations, dose and susceptibility are identical across hosts. Parameter values were also chosen to highlight these conceptual differences (realizations using more realistic parameter sets are in fig. B1; figs. A1, A2, B1, B2 available online). In figure 2, the black lines show realizations in which the virus population grew to high levels and killed the host, while the gray lines show realizations in which the virus population was cleared and the host recovered. Importantly, parameters and initial conditions within each panel are identical for all realizations, so that differences in trajectories are only the result of the timing of birth and death events, and thus demographic stochasticity. As a result, for this figure, the no-demographic-stochasticity model is effectively deterministic. Demographic stochasticity is then evident in the jaggedness of the trajectories for the first two models. As the figure highlights, demographic stochasticity plays a substantial role when pathogen populations are small, and the trajectories become increasingly smooth as the pathogen population grows. Demographic stochasticity therefore leads to variability between trajectories in the time it takes for the pathogen population to reach a size at which its population growth is effectively deterministic.
Figure 2:
Realizations of the most complex model (A), the Shortley birth-death model (B), and the no-demographic-stochasticity model (C). Each trajectory shows the pathogen population size inside a single simulated host. The gray trajectories show realizations in which the pathogen became extinct, so that the host recovers, while the black trajectories show realizations in which the pathogen overwhelms the host immune system, killing the host. Death occurs when the virus population reaches the upper threshold (solid horizontal line) at 104 virions, and the times of host deaths are marked on the horizontal axis (dotted vertical lines). Each panel shows 10 realizations of the respective models. Parameters and initial conditions for A and . Parameters and initial conditions for .
Comparing the most complex model (A) and the Shortley birth-death model (B) reveals that the models behave similarly late in an infection when the pathogen population is large but that they behave quite differently early in an infection when the pathogen population is small. For the most complex model, pathogen populations are maintained at low sizes for a relatively long period of time before the immune system is finally overwhelmed and the pathogen population begins to grow quickly. The Shortley birth-death model in contrast predicts that the pathogen population will usually begin to increase immediately. This difference occurs because in the Shortley birth-death model the history and current state of the population have no effect on whether the next event is a birth or a death, while in the most complex model, the relative probabilities of births and deaths change over time, because the host immune system is dynamic. That is, in the most complex model, the relative probability of the death of a virus particle is highest immediately after infection, but it decreases over time as the immune system becomes exhausted. Because the effects of demographic stochasticity are strongest when population sizes are small, and because the immune system keeps the virus population at low levels for long periods in the most complex model, the most complex model predicts that there will be a great deal of variation among trajectories. Response times in our data are highly variable, as is the case for many pathogens. Because the presence of a dynamic host immune system in the most complex model causes virus populations to be low for long periods, it allows the most complex model to provide a much better fit to the data than the Shortley birth-death model, which has only a static immune system. Because in figure 2 we temporarily assumed that there are no differences between hosts in the threshold virus population for host response or in immune system strength, the model without demographic stochasticity (M7) predicts that there will be no variation in response times (fig. B1 shows realizations of M7 that include those types of stochasticity). Although this is an extreme case, it usefully emphasizes the potential importance of demographic stochasticity in causing variation in response times.
Results
The data from this experiment are deposited in Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.04vh7 (Kennedy et al. 2014a).
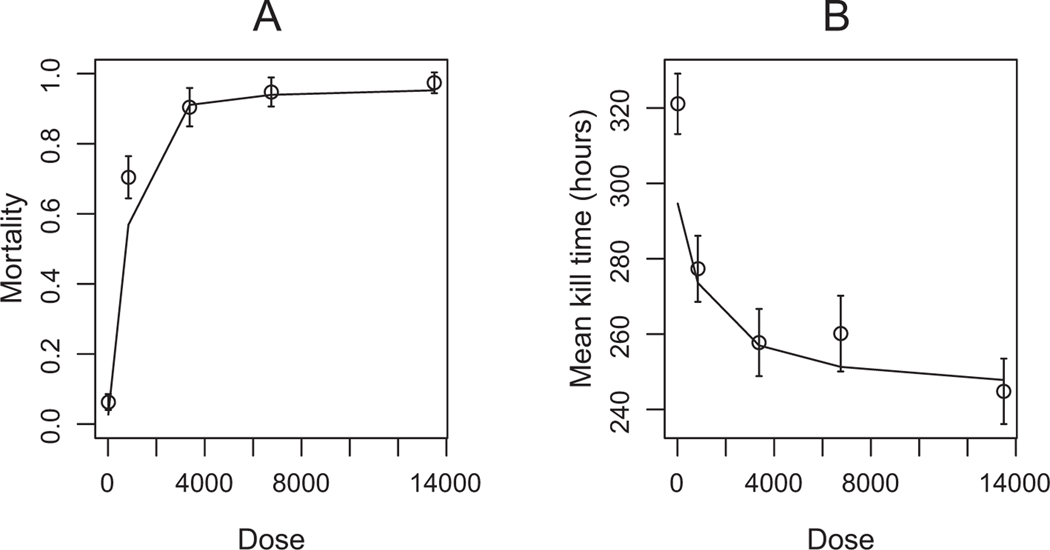
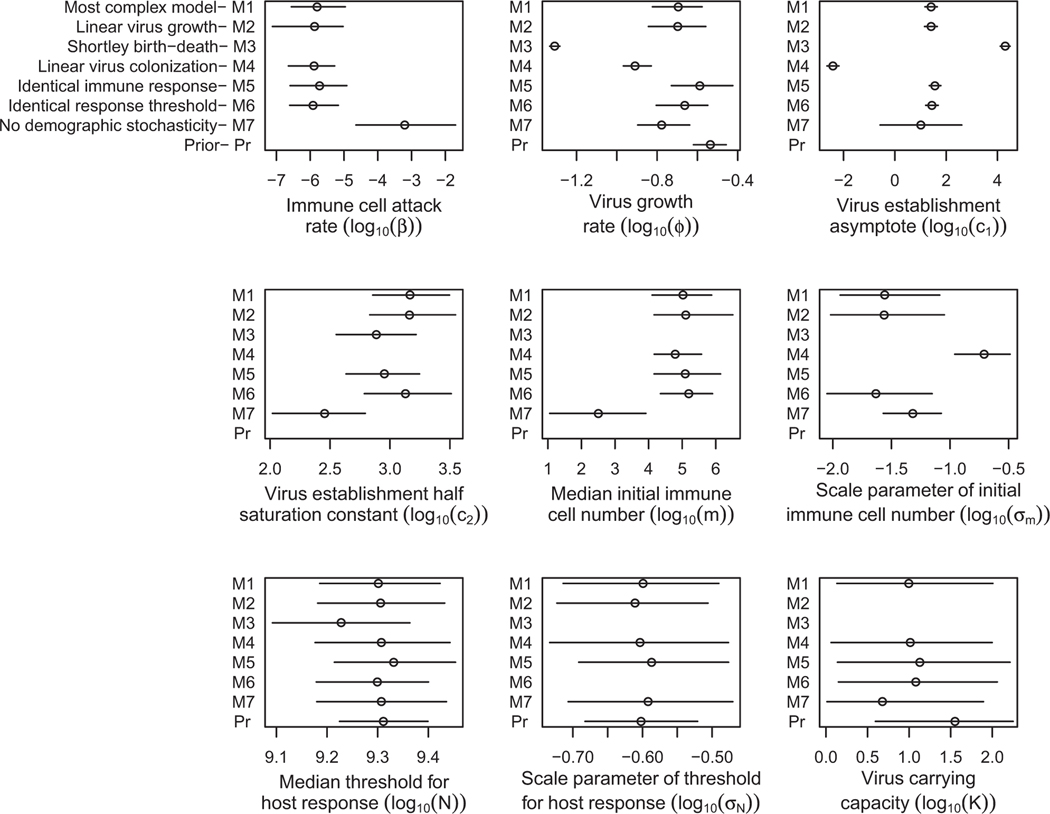
As is almost always the case in dose-response studies using baculoviruses (van Beek et al. 2000; Hodgson et al. 2001; Zwart et al. 2009a), our data show clear relationships between virus dose and host outcomes (fig. 3; app. A, “Generalized Linear Model (GLM) Analyses”). Higher virus doses caused higher mortality and faster deaths. Model selection using DIC showed that the best model is the linear virus growth model (M2), which includes demographic stochasticity, a nonlinear relationship between applied and effective dose, dynamic effects of the immune system, and variability between hosts, but not a carrying capacity for virus growth (table 2). Reassuringly, this model fits the data quite well (fig. 4A). Relative to this best model, the Shortley birth-death model (M3), the linear virus colonization model (M4), and the no-demographic-stochasticity model (M7) all fit the data much more poorly (table 2). The best model includes a dynamic host immune response, nonlinear virus colonization, and demographic stochasticity, whereas the poorly fitting models leave out one or more of these mechanisms, and so we conclude that these mechanisms all have strong effects on the distribution of host response times. Reasonable explanations for the data were also provided by the most complex model (M1), which differs from the best model in including a virus carrying capacity, as well as the identical immune system model (M5), and the identical response threshold model (M6). The strong showing of the latter two models suggests that the effects of variability between hosts in response thresholds and immune responses are not very strong. To quantify such effects, we used our parameter estimates (fig. 5) to calculate the coefficients of variation (CV) for both the initial number of immune cells and the threshold pathogen population size for our best model, the linear virus growth model (M2). The CV of is approximately 0.027, and the CV of is approximately 0.249. The small CV on and the modest CV on lend weight to our assertion that variability in speed of kill across hosts is not easily explained by variability among larvae, and we therefore conclude that demographic stochasticity in pathogen growth is important in generating variability in speed of kill.
Figure 3:
The relationship between host outcomes and virus dose, in the data and as predicted by the linear virus growth model (M2). The solid lines show the predictions of this model, the open circles show the data, and the error bars are ±2 SE of the mean. A, Relationship between host mortality and dose, with mortality increasing with dose. B, Relationship between kill time and dose, with earlier deaths occurring at higher doses.
Table 2:
Deviance information criterion (DIC) scores
| Model name | No. model parameters | pD | Mean deviance | ΔDIC |
|---|---|---|---|---|
|
| ||||
| M1: most complex model | 9 | 18.97 | 578.69 | 3.46 |
| M2: linear virus growth | 8 | 15.33 | 578.87 | 0 |
| M3: Shortley birth-death model | 5 | 2.86 | 786.12 | 194.79 |
| M4: linear virus colonization | 8 | 15.48 | 673.33 | 94.61 |
| M5: identical immune system | 8 | 20.42 | 584.13 | 10.35 |
| M6: identical response threshold | 8 | 18.79 | 579.68 | 4.27 |
| M7: no demographic stochasticity | 9 | −2.20 | 744.25 | 147.85 |
Note: The scores for each of the seven models considered. Following Spiegelhalter et al. (2002), pD = the mean deviance of the posterior minus the posterior deviance of the mean. The absolute DIC score is the sum of pD and the mean deviance. The model with the best DIC is highlighted in bold.
Figure 4:
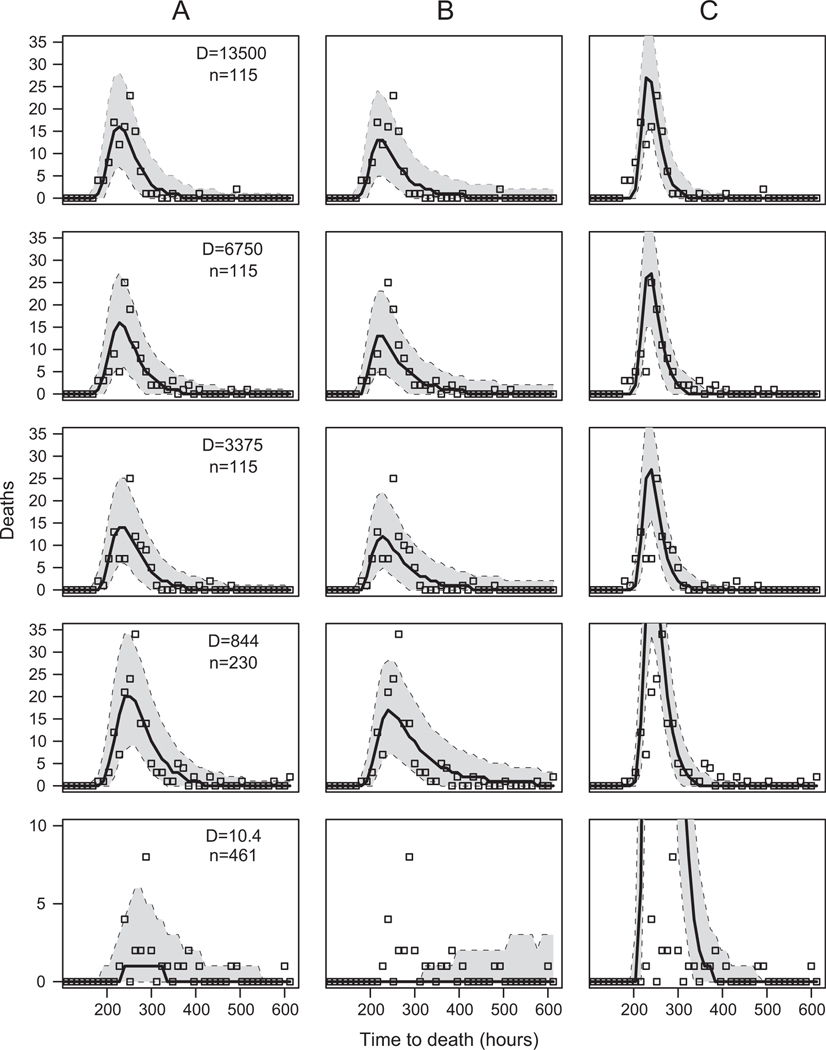
The fit of our models to the data. Each column shows the fit of a different model. A corresponds to the linear virus growth model (M2), which is the overall best model. B corresponds to the no-demographic-stochasticity model (M7). C corresponds to the Shortley birth-death model (M3). Each row shows a different virus dose D. To make model predictions, we sampled 105 parameter sets from the joint posterior distribution of the parameters, and we used each parameter set to simulate a set of response times. The median value of the number dying in each time bin is plotted as a solid black line, and the 99% envelope is encompassed by the dotted lines. The open squares are the data. The symbol D indicates the applied virus dose, and n is the number of exposed larvae.
Figure 5:
Marginal medians and 95% central credible intervals for each parameter of each model. The model numbers (M1–M7) are shown on the -axes, with the values of the parameters on the -axes. Each line shows the respective 95% central credible interval with a point denoting the median. Note that priors are not shown for the parameters with extremely vague priors (, , ), and for the parameters with a joint prior (, ). All priors can be found in appendix A (available online), “Prior Construction.” Lines are also missing for modelparameter combinations that do not exist. For model M3, and are individually nonidentifiable, and so their respective marginal posterior distributions are not shown. We additionally note that the value shown as the virus birth rate has a slightly different interpretation in the Shortley birth-death model (M3) than in the other models. As we explain in appendix A, “Prior Construction,” the quantity most comparable to the birth rate of the other models is the net virus replication rate , and so that is the value plotted in the panel labeled “Virus growth rate .” Finally, for the linear virus colonization model (M4), the parameter shown in the panel labeled “Virus establishment asymptote ” is actually , which is defined in the main text as . This difference likely explains why the estimate of this parameter is substantially lower than in the other models.
In addition to model selection, we also provide a visual comparison of the fit of the best model, the linear virus growth model (M2), as well as the Shortley birth-death model (M3) and the no-demographic-stochasticity model (M7). We include only these three models because the linear virus growth model (M2) represents our basic argument that the response time of the virus is driven by demographic stochasticity and a dynamic immune system, while the other two models represent the most important alternatives to this argument. Figure 4 shows that the nodemographic-stochasticity model (M7) does a poor job of explaining the data because, for this model, variability in response time can be explained only by differences between hosts. This model does a spectacularly poor job of reproducing response times at the lowest virus dose, because it predicts substantially lower mortality rates than what we observed. Even at higher doses, however, model M7 produces an overly flat distribution of response times, with too little mortality at the peak of each distribution and too much mortality in the right-hand tail (fig. 4). Model M7 thus does a poor job of reproducing the sharp peak of mortality and the extreme right-handed skew that are apparent at all doses, a failure that is perhaps easier to see when the fit of model M7 is compared to the fit of the linear virus growth model (M2), which includes demographic stochasticity.
The Shortley birth-death model (M3), which assumes a constant virus clearing rate and thus does not include the effects of a dynamic immune system, fails even more spectacularly at lower doses, drastically overpredicting mortality at the peak, and underpredicting mortality in the tails (fig. 4). The same effects are also present at higher doses, although they are not as striking. The Shortley birth-death model has long been criticized on the grounds that it predicts too little variability in response times relative to the variability seen in many data sets (Armitage et al. 1965; Schach and Schach 1970), and the model’s failure here is due to the same problem. A dynamic immune system, in contrast, allows the virus population to be maintained at low levels for highly variable periods of time (fig. 2). In the models that allow for a dynamic immune response and demographic stochasticity, the distribution of response times shows a sharp peak with an extreme right-handed skew, which leads to a much better fit to the data.
Insights can also be gained by examining the posterior estimates of the model parameters (fig. 5). First, the parameter estimates of the most complex model (M1), the linear virus growth model (M2), the identical immune system model (M5), and the identical immune response threshold model (M6) are all very similar. The relatively poor fits of models M5 and M6 (table 2) therefore suggest that small differences in the initial immune cell number (absent in M5) and in the threshold for host response (absent in M6) can have important effects on host response times. Second, our earlier conclusion that a virus carrying capacity is unimportant to explaining our response time data is further strengthened by the observation that the central credible intervals of the carrying capacity are large and similar for every model considered.
As Shortley (1965) pointed out, decreasing the net virus growth rate and the threshold for host response in linear birth-death models increases the variability in host response times. Our estimates of the virus growth rate and the median threshold for host response are quite a bit smaller for the Shortley birth-death model (M3) than for the other models (fig. 5). This observation thus strengthens our previous contention that a dynamic host immune system, missing from model M3, is important for generating the high level of variability seen in our response-time data.
Our best model (M2) and the no-demographic-stochasticity model (M7) provide very different estimates of the median number of initial immune cells (on the order of 100,000 for M2, but only 100–1,000 for model M7). Given that this latter model provides a much worse fit to the data, the difference in these estimates suggests that using model M7 alone would lead to the erroneous conclusion that gypsy moth larvae have only a small number of immune cells. Likewise, there is a substantial difference in the CV of the initial number of immune cells between these models (0.048 for M7 vs. 0.027 for M2). This difference in CV likely occurs because the no-demographic-stochasticity model (M7) relies entirely on differences between hosts to explain variability in response-time data and therefore overestimates the size of these differences. If demographic stochasticity is important in other host-pathogen systems, similar biases may exist in parameter estimates for many within-host models. The differences in parameter estimates between these two models thus illustrate that inference based on a badly fitting model may lead to incorrect conclusions. Additionally, the relatively high estimate of the CV of the initial number of immune cells in the no-demographic-stochasticity model (M7) and the nonzero estimate of this CV in our best model (M2) emphasize that demographic stochasticity plays an important role in determining response times, as does variability among hosts.
Discussion
We found that the model that best fits our data (M2) allows for demographic stochasticity. This is because virus population sizes early in infections are small, and so chance events have disproportionately large impacts on whether and when hosts die and recover. Previous efforts to make inferences about the processes driving the within-host growth of baculoviruses used only deterministic models (van Beek et al. 1988a), and therefore could not have detected such effects (but see van der Werf et al. 2011 for a stochastic model of baculovirus colonization). Although studies in other systems have shown that differences in disease dynamics can sometimes be explained by stochastic processes (Riley et al. 2003; Brown et al. 2006; Grant et al. 2008; Woo and Reifman 2012), many models assume that differences in pathogen dynamics between hosts are due only to differences in host genetics or condition (Antia et al. 1996; Ganusov et al. 2002; Andre et al. 2003; Mideo et al. 2008; Pepin et al. 2010). To our knowledge, we are the first to show that models with demographic stochasticity and differences between hosts provide a better fit to response-time data than do models lacking either of these sources of variability. Indeed, the Shortley birth-death model provides a very poor fit to response-time data in several host-pathogen systems, especially compared to models that allow for variability between hosts (Armitage et al. 1965; Chang 1970; Schach and Schach 1970). We likewise show that the model that allows for variability between hosts but not demographic stochasticity (M7) fits the data better than the Shortley birth-death model. Nevertheless, models with both variability between hosts and demographic stochasticity fit our data far better than models lacking either of these mechanisms, suggesting that both sources of variation are important. Our results therefore provide strong evidence that, for the gypsy moth virus, demographic stochasticity has an important effect on the response time of infected hosts. Additionally, differences between hosts affect response times, even though the magnitudes of these host differences are quite modest. Small differences between hosts can thus have detectable effects on host outcomes. Our results thus suggest that the outcome of infection might be difficult to predict both because of demographic stochasticity within hosts and because of small differences between hosts that cannot be measured precisely.
A stochastic model will almost inevitably provide a better fit to data than a deterministic model given the importance of stochasticity in population biology, but all of our models include some form of stochasticity. Comparisons of the best model to the identical response threshold model (M5), the identical immune system model (M6), and the no-demographic-stochasticity model (M7) show that both stochastic differences between hosts and stochastic variation in virus growth play roles in generating response times. Because M7 includes only stochastic differences between hosts, it cannot fully explain how the distribution of response times changes across virus doses, whereas the models that include demographic stochasticity can explain this aspect of the data. On the other hand, the models that neglect stochastic differences between hosts (M5 and M7) provide a substantially poorer fit than our best model (M2), which means that stochastic variation between hosts also plays a role in generating response times. Our general conclusion is thus that demographic stochasticity in within-host population growth is a neglected mechanism in studies of infectious diseases.
The crucial difference between our best model (M2) and the Shortley birth-death model (M3) is that our best model allows for dynamic effects of the immune system, demonstrating that changes in the immune system over time are important to understanding response-time data. Insect immune responses against viruses have long been presumed to be quite limited (Washburn et al. 1996; Strand 2008), and we therefore hope that our work will stimulate further research in insect immunology. More broadly, theory has strongly emphasized the role of dynamic immune responses on host-pathogen evolution (Antia et al. 1994; Hamilton et al. 2008; King et al. 2009), and models have shown that stochasticity may play an important role in pathogen dynamics within hosts (Grant et al. 2008; Vaughan et al. 2012; Woo and Reifman 2012). To our knowledge, however, we are the first to show that dynamic changes in an immune system can have a detectable effect on variation in host response times.
For nucleopolyhedroviruses like the gypsy moth pathogen, host death is required for transmission, and so variability in response time leads to variability in time to transmission. Variability in time to transmission can in turn have dramatic consequences for longer-term disease dynamics (Wearing et al. 2005). Because we have shown that dynamic host immune responses affect response times, it follows that immune responses can affect disease dynamics.
We found that the most complex model (M1) provided a poorer fit to the data than the linear virus growth model (M2), even though model M2 lacks resource limitation during virus growth. Given that the difference in DIC scores between these models is small, this conclusion might change if we had more data or different data, but it is nevertheless worth considering why there may be no resource limitation. For baculoviruses and other obligately lethal pathogens, there are likely trade-offs between the benefits that arise from keeping a host alive so that the pathogen can replicate and the benefits that arise from killing a host quickly so that the pathogen can spread. Indeed, there is empirical evidence that such trade-offs exist in baculoviruses (O’Reilly and Miller 1991; Hodgson et al. 2001; Cooper et al. 2002). Given this trade-off between pathogen production and transmission, it follows that there must be an optimal killing time (Ebert and Weisser 1997) that maximizes pathogen fitness. The lack of importance of resource limitation in our models thus suggests that the gypsy moth virus usually kills before host resources are completely exhausted. A rapid speed of kill may be beneficial because doses in the field are very high (D’Amico et al. 2005), which in combination with our finding that dose effects are nonlinear, implies that there is little benefit to producing additional virus particles. The optimal killing time may therefore occur well before host resources become limiting.
Although our data were collected for only a single host-pathogen system, our models are general. It is therefore at least possible that our results can be generalized to other host-pathogen systems. In particular, the greater complexity of the vertebrate immune system suggests that the immune-system effects that we see in the gypsy moth may be even stronger in vertebrates. Likewise, population bottlenecks are associated with transmission events in many host-pathogen systems (McGrath et al. 2001; Moury et al. 2007), suggesting that initial pathogen populations within hosts are small for many pathogens. Demographic stochasticity may thus be important in many infectious diseases.
The importance of demographic stochasticity means that individual responses to pathogens may be unpredictable even given extensive knowledge of host and pathogen genetics. Furthermore, selection is often assumed to be extremely efficient in pathogen populations, because population sizes are large and generation times are short relative to host generation times (Tooby 1982; Altizer et al. 2003; Ebert and Bull 2008). In the case of within-host growth, however, demographic stochasticity is effectively equivalent to genetic drift (Turner and Duffy 2008). The importance of demographic stochasticity in explaining our data thus suggests that drift may often overwhelm selection inside hosts, in turn implying that selection may be less effective than previously believed. One consequence of this effect is that deleterious alleles may be quite common in pathogen populations, despite the common assumption that pathogens have optimal phenotypes (Ewald 1994; Ebert 1998). An interesting question for further research is thus, how strong a selective force is needed to overwhelm drift in insect-baculovirus systems?
The small magnitude of host differences in our best-fitting model is surprising given that previous research has shown that differences between hosts play a strong role in virus transmission in gypsy moth populations in the field (Dwyer et al. 1997, 2000; Elderd et al. 2008). We emphasize again, however, that our host insects were derived from a lab colony of low variability (Dwyer et al. 1997), and we followed standard protocols by discarding larvae that did not consume the entire dose (Li and Bonning 2007). In nature, in contrast, larvae can sometimes detect and avoid infectious cadavers (Capinera et al. 1976), and variability in this trait appears to be heritable (Parker et al. 2010). The exclusion of such behaviors in our experiments may therefore explain why differences between hosts had only weak effects in our data.
We used response time data because response time is important for insect biocontrol and because such data are cheap, can be collected more easily, and can be measured more accurately than pathogen population sizes. The success with which these data allowed us to detect effects of demographic stochasticity and a dynamic immune system suggests that response times do indeed provide substantial information about within-host pathogen growth, despite the Morgan and Watts (1980) argument that response-time data are insufficient for model comparison. A key difference between their work and ours, however, is that we took a Bayesian approach to estimate our model parameters. This allowed us to use literature data to construct prior distributions, ensuring that our parameter estimates would be biologically reasonable. We emphasize, however, that our main conclusions come from the relative abilities of the models to explain our data rather than from our parameter estimates. Our main conclusions are thus not based solely on parameter estimates that reflect our choices of priors.
More direct measurements of within-host population sizes may allow powerful inferences about within-host population growth. Nevertheless, in gypsy moths and other small insects, a quantitative polymerase chain reaction requires destructive sampling (Mukawa and Goto 2008), and so time series of virus population sizes would still be unavailable. As a result, it may be difficult to distinguish demographic stochasticity from stochastic differences between hosts.
For baculoviruses in particular, response time data are very common. Most studies, however, report only median or mean survival times (Farrar and Ridgway 1998), making it difficult to use the data to choose between models. Nevertheless, we note that van Beek and colleagues (van Beek et al. 1988a, 1988b) have shown that within-host models can usefully describe variability in median survival time across treatments. By going beyond their approach to test our models with the entire distribution of survival times, we hope to have shown that more powerful conclusions can be drawn about the mechanisms driving within-host pathogen growth.
Supplementary Material
Acknowledgments
D.A.K. thanks the members of his dissertation committee, S. Allesina, J. Bergelson, M. Kreitman, and C. Pfister, for helpful comments on earlier drafts of the manuscript. G.D., V.D., and the experimental work were supported by National Institutes of Health (NIH) grant R01GM096655. V.D. was also supported by National Science Foundation grants DEB-1316334 and GEO-1211668. D.A.K. was supported by an Achievement Rewards for College Scientists fellowship while at the University of Chicago and by the Research and Policy for Infectious Disease Dynamics program of the Science and Technology Directorate, Department of Homeland Security, and the Fogarty International Center, NIH. We thank L. Hemerik, O. Restif, and one anonymous reviewer for comments that substantially improved the manuscript.
Literature Cited
- Adams J, and McClintock J. 1991. Baculoviridae. Nuclear polyhedrosis viruses. Pt. I. Nuclear polyhedrosis viruses of insects. Atlas of invertebrate viruses. CRC Press, Boca Raton, FL. [Google Scholar]
- Alizon S, and van Baalen M. 2008. Acute or chronic? within-host models with immune dynamics, infection outcome, and parasite evolution. American Naturalist 172:E244–E256. [DOI] [PubMed] [Google Scholar]
- Altizer S, Harvell D, and Friedle E. 2003. Rapid evolutionary dynamics and disease threats to biodiversity. Trends in Ecology and Evolution 18:589–596. [Google Scholar]
- Andre J, Ferdy J, and Godelle B. 2003. Within-host parasite dynamics, emerging trade-off, and evolution of virulence with immune system. Evolution 57:1489–1497. [DOI] [PubMed] [Google Scholar]
- Antia R, Levin B, and May R. 1994. Within-host populationdynamics and the evolution and maintenance of microparasite virulence. American Naturalist 144:457–472. [Google Scholar]
- Antia R, Nowak M, and Anderson R. 1996. Antigenic variation and the within-host dynamics of parasites. Proceedings of the National Academy of Sciences of the USA 93:985–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armitage P, Meynell G, and Williams T. 1965. Birth-death and other models for microbial infection. Nature 207:570–572. [DOI] [PubMed] [Google Scholar]
- Ashida M, and Brey P. 1998. Molecular mechanisms of immune responses in insects. Chapman & Hall, London. [Google Scholar]
- Baldwin K, and Hakim R. 1991. Growth and differentiation of the larval midgut epithelium during molting in the moth, Manduca sexta. Tissue and Cell 23:411–422. [DOI] [PubMed] [Google Scholar]
- Bolker B. 2008. Ecological models and data in R. Princeton University Press, Princeton, NJ. [Google Scholar]
- Borsuk M, and Lee D. 2009. Stochastic population dynamic models as probability networks. In Handbook of ecological modelling and informatics. WIT, Boston. [Google Scholar]
- Brown S, Cornell S, Sheppard M, Grant A, Maskell D, Grenfell B, and Mastroeni P. 2006. Intracellular demography and the dynamics of Salmonella enterica infections. PLoS Biology 4:2091–2098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnham K, and Anderson D. 1998. Model selection and inference: a practical information-theoretic approach. Springer, New York. [Google Scholar]
- Capinera J, Kirouac S, and Barbosa P. 1976. Phagodeterrency of cadaver components to gypsy moth larvae, Lymantria dispar. Journal of Invertebrate Pathology 28:277–279. [Google Scholar]
- Chandler D. 1998. Redefining relativity: quantitative PCR at low template concentrations for industrial and environmental microbiology. Journal of Industrial Microbiology and Biotechnology 21: 128–140. [Google Scholar]
- Chang P. 1970. Statistical models for animal survival time in mouse lymphoma. Biometrics 26:749–766. [PubMed] [Google Scholar]
- Chao D, Davenport M, Forrest S, and Perelson A. 2004. A stochastic model of cytotoxic T cell responses. Journal of Theoretical Biology 228:227–240. [DOI] [PubMed] [Google Scholar]
- Conway J, and Coombs D. 2011. A stochastic model of latently infected cell reactivation and viral blip generation in treated HIV patients. PLoS Computational Biology 7:e1102033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper V, Reiskind M, Miller J, Shelton K, Walther B, Elkinton J, and Ewald P. 2002. Timing of transmission and the evolution of virulence of an insect virus. Proceedings of the Royal Society B: Biological Sciences 269:1161–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cory J, Myers J. 2003. The ecology and evolution of insect baculoviruses. Annual Review of Ecology, Evolution, and Systematics 34:239–272. [Google Scholar]
- D’Amico V, Elkinton J, Podgwaite J, Buonaccorsi J, and Dwyer G. 2005. Pathogen clumping: an explanation for non-linear transmission of an insect virus. Ecological Entomology 30:383–390. [Google Scholar]
- Doob J. 1945. Markov chains: denumerable case. Transactions of the American Mathematical Society 58:455–473. [Google Scholar]
- Dwyer G, Dushoff J, Elkinton J, and Levin S. 2000. Pathogendriven outbreaks in forest defoliators revisited: building models from experimental data. American Naturalist 156:105–120. [DOI] [PubMed] [Google Scholar]
- Dwyer G, Dushoff J, and Yee S. 2004. The combined effects of pathogens and predators on insect outbreaks. Nature 430:341–345. [DOI] [PubMed] [Google Scholar]
- Dwyer G, Elkinton J, and Buonaccorsi J. 1997. Host heterogeneity in susceptibility and disease dynamics: tests of a mathematical model. American Naturalist 150:685–707. [DOI] [PubMed] [Google Scholar]
- Ebert D. 1998. Experimental evolution of parasites. Science 282: 1432–1435. [DOI] [PubMed] [Google Scholar]
- Ebert D, and Bull J. 2008. The evolution and expression of virulence. In Evolution in health and disease. 2nd ed. Oxford University Press, New York. [Google Scholar]
- Ebert D, and Weisser W. 1997. Optimal killing for obligate killers: the evolution of life histories and virulence of semelparous parasites. Proceedings of the Royal Society B: Biological Sciences 264: 985–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elderd B, Dukic V, and Dwyer G. 2006. Uncertainty in predictions of disease spread and public health responses to bioterrorism and emerging diseases. Proceedings of the National Academy of Sciences of the USA 103:15693–15697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elderd B, Dushoff J, and Dwyer G. 2008. Host-pathogen interactions, insect outbreaks, and natural selection for disease resistance. American Naturalist 172:829–842. [DOI] [PubMed] [Google Scholar]
- Elkinton J, and Liebhold A. 1990. Population dynamics of gypsy moth in North America. Annual Review of Entomology 35:571–596. [Google Scholar]
- Ercolani G. 1985. The relation between dosage, bacterial growth and time for disease response during infection of bean leaves by Pseudomonas syringae pv. phaseolicola. Journal of Applied Bacteriology 58:63–75. [Google Scholar]
- Ewald P. 1994. Evolution of infectious disease. Oxford University Press, New York. [Google Scholar]
- Farrar R. and Ridgway R. 1998. Quantifying time-mortality relationships for nuclear polyhedrosis viruses when survivors are present. Environmental Entomology 27:1289–1296. [Google Scholar]
- Ganusov V, Bergstrom C, and Antia R. 2002. Within-host population dynamics and the evolution of microparasites in a heterogeneous host population. Evolution 56:213–223. [DOI] [PubMed] [Google Scholar]
- Gelman A, Carlin J, Stern H, and Rubin D. 2004. Bayesian data analysis. 2nd ed. Chapman & Hall/CRC, Boca Raton, FL. [Google Scholar]
- Gelman A, and Rubin D. 1992. Inference from iterative simulation using multiple sequences. Statistical Science 7:457–472. [Google Scholar]
- Gillespie D. 1977. Exact stochastic simulation of coupled chemical reactions. Journal of Physical Chemistry 81:2340–2361. [Google Scholar]
- Grant A, Restif O, McKinley T, Sheppard M, Maskell D, and Mastroeni P. 2008. Modelling within-host spatiotemporal dynamics of invasive bacterial disease. PLoS Biology 6:757–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamilton R, Siva-Jothy M, and Boots M. 2008. Two arms are better than one: parasite variation leads to combined inducible and constitutive innate immune responses. Proceedings of the Royal Society B: Biological Sciences 275:937–945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawtin R, Zarkowska T, Arnold K, Thomas C, Gooday G, King L, Kuzio J, and Possee R. 1997. Liquefaction of Autographa californica nucleopolyhedrovirus-infected insects is dependent on the integrity of virus-encoded chitinase and cathepsin genes. Virology 238:243–253. [DOI] [PubMed] [Google Scholar]
- Hodgson D, Vanbergen A, Watt A, Hails R, and Cory J. 2001. Phenotypic variation between naturally co-existing genotypes of a lepidopteran baculovirus. Evolutionary Ecology Research 3:687–701. [Google Scholar]
- Horton H, and Burand J. 1993. Saturable attachment sites for polyhedron-derived baculovirus on insect cells and evidence for entry via direct membrane fusion. Journal of Virology 67:1860–1868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hughes P, and Wood H. 1986. In vivo and in vitro bioassay methods for baculoviruses. In The biology of baculoviruses. Vol. II. CRC, Boca Raton, FL. [Google Scholar]
- Kennedy D, Dukic V, and Dwyer G. 2014a. Data from: Pathogen growth in insect hosts: inferring the importance of different mechanisms using stochastic models and response time data. American Naturalist, Dryad Digital Repository, 10.5061/dryad.04vh7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy D, Dukic V, and Dwyer G. . 2014b. Combining principal component analysis with parameter line-searches to improve the efficacy of Metropolis-Hastings MCMC. Environmental and Ecological Statistics. doi: 10.1007/s10651-014-0297-0. [DOI] [Google Scholar]
- King A, Shrestha S, Harvill E, and Bjørnstad O. 2009. Evolution of acute infections and the invasion-persistence trade-off. American Naturalist 173:446–455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, and Bonning B. 2007. Evaluation of the insecticidal efficacy of wild type and recombinant baculoviruses. In Baculovirus and insect cell expression protocols. Humana, Totowa, NJ. [Google Scholar]
- Lin H, and Shuai J. 2010. A stochastic spatial model of HIV dynamics with an asymmetric battle between the virus and the immune system. New Journal of Physics 12:043051. [Google Scholar]
- May RM, and Anderson RM 1983. Epidemiology and genetics in the coevolution of parasites and hosts. Proceedings of the Royal Society B: Biological Sciences 219:281–313. [DOI] [PubMed] [Google Scholar]
- McCarthy M, and Masters P. 2005. Profiting from priorinformation in Bayesian analyses of ecological data. Journal of Applied Ecology 42:1012–1019. [Google Scholar]
- McGrath K, Hoffman N, Resch W, Nelson J, and Swanstrom R. 2001. Using HIV-1 sequence variability to explore virus biology. Virus Research 76:137–160. [DOI] [PubMed] [Google Scholar]
- McNeil J, Cox-Foster D, Gardner M, Slavicek J, Thiem S, and Hoover K. 2010. Pathogenesis of Lymantra dispar multiple nucleopolyhedrovirus (LdMNPV) in L. dispar and mechanisms of developmental resistance. Journal of General Virology 91:1590–1600. [DOI] [PubMed] [Google Scholar]
- Michael E, Grenfell B, Isham V, Denham D, and Bundy D. 1998. Modelling variability in lymphatic filariasis: macrofilarial dynamics in the Brugia pahangi-cat model. Proceedings of the Royal Society B: Biological Sciences 265:155–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mideo N, Barclay V, Chan B, Savill N, Read A, and Day T. 2008. Understanding and predicting strain-specific patterns of pathogenesis in the rodent malaria Plasmodium chabaudi. American Naturalist 172:E214–E238. [DOI] [PubMed] [Google Scholar]
- Moreau G, and Lucarotti C. 2007. A brief review of the past use of baculoviruses for the management of eruptive forest defoliators and recent developments on a sawfly virus in Canada. Forestry Chronicle 83:105–112. [Google Scholar]
- Morgan B, and Watts S. 1980. On modeling microbial infections. Biometrics 36:317–321. [PubMed] [Google Scholar]
- Moury B, Fabre F, and Senoussi R. 2007. Estimation of the number of virus particles transmitted by an insect vector. Proceedings of the National Academy of Sciences of the USA 104:17891–17896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukawa S, and Goto C. 2008. In vivo characterization of two granuloviruses in larvae of Mythimna separate (Lepidoptera: Noctuidae). Journal of General Virology 89:915–921. [DOI] [PubMed] [Google Scholar]
- O’Reilly D, and Miller L. 1991. Improvement of a baculovirus pesticide by deletion of the EGT gene. Nature Biotechnology 9:1086–1089. [Google Scholar]
- Parker B, Elderd B, and Dwyer G. 2010. Host behaviour and exposure risk in an insect-pathogen interaction. Journal of Animal Ecology 79:863–870. [DOI] [PubMed] [Google Scholar]
- Peng J, Zhong J, and Granados R. 1999. A baculovirus enhancin alters the permeability of a mucosal midgut peritrophic matrix from lepidopteran larvae. Journal of Insect Physiology 45:159–166. [DOI] [PubMed] [Google Scholar]
- Pepin K, Volkov I, Banavar J, Wilke C, and Grenfell B. 2010. Phenotypic differences in viral immune escape explained by linking within-host dynamics to host-population immunity. Journal of Theoretical Biology 265:501–510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plummer M, Best N, Cowles K, and Vines K. 2009. Coda: output analysis and diagnostics for MCMC. R package version 0.13–4. http://cran.r-project.org/packagepcoda. [Google Scholar]
- R Development Core Team. 2009. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. [Google Scholar]
- Renshaw E. 1991. Modeling biological populations in space and time. Cambridge University Press, Cambridge. [Google Scholar]
- Riley S, Donnelly C, and Ferguson N. 2003. Robust parameter estimation techniques for stochastic within-host macroparasite models. Journal of Theoretical Biology 225:419–430. [DOI] [PubMed] [Google Scholar]
- Rohrmann G. 2008. Baculovirus molecular biology. National Library of Medicine, Bethesda, MD. [Google Scholar]
- Schach E, and Schach S. 1970. On variability of survival times of mice inoculated with cancer cells. Biometrische Zeitschrift 12:14–24. [Google Scholar]
- Schmid-Hempel P. 2005. Evolutionary ecology of insect immune defenses. Annual Review of Entomology 50:529–551. [DOI] [PubMed] [Google Scholar]
- Shapiro M, Robertson J, and Bell R. 1986. Quantitative and qualitative differences in gypsy moth (Lepidoptera: Lymantriidae) nucleopolyhedrosis virus produced in different-aged larvae. Journal of Economic Entomology 79:1174–1177. [Google Scholar]
- Shortley G. 1965. A stochastic model for distributions of biological response times. Biometrics 21:562–582. [PubMed] [Google Scholar]
- Shortley G, and Wilkins J. 1965. Independent-action and birth-death models in experimental microbiology. Bacteriological Reviews 29:102–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slack J, and Arif B. 2006. The baculoviruses occlusion-derived virus: virion structure and function. Advances in Virus Research 69:99–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiegelhalter D, Best N, Carlin B, and van der Linde A. 2002. Bayesian measures of model complexity and fit. Journal of the Royal Statistical Society B: Statistical Methodology 64:583–639. [Google Scholar]
- Strand M. 2008. The insect cellular immune response. Insect Science 15:1–14. [Google Scholar]
- Tooby J. 1982. Pathogens, polymorphism, and the evolution of sex. Journal of Theoretical Biology 97:557–576. [DOI] [PubMed] [Google Scholar]
- Trudeau D, Washburn J, and Volkman L. 2001. Central role of hemocytes in Autographa californica M nucleopolyhedrovirus pathogenesis in Heliothis virescens and Helicoverpa zea. Journal of Virology 75:996–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner P, and Duffy S. 2008. Evolutionary ecology of multiple phage adsorption and infection. In Bacteriophage ecology: population growth, evolution, and impact of bacterial viruses. Cambridge University Press, Cambridge. [Google Scholar]
- van Beek N, Hughes P, and Wood H. 2000. Effects of incubation temperature on the dose-survival time relationship of Trichoplusia ni larvae infected with Autographa californica nucleopolyhedrovirus. Journal of Invertebrate Pathology 76:185–190. [DOI] [PubMed] [Google Scholar]
- van Beek N, Wood H, Angellotti J, and Hughes P. 1988a. Rate of increase and critical amount of nuclear polyhedrosis virus in lepidopterous larvae estimated from survival time assay data with a birth-death model. Archives of Virology 100:51–60. [DOI] [PubMed] [Google Scholar]
- van Beek N, Wood H, and Hughes P. 1988b. Quantitative aspects of nuclear polyhedrosis virus infections in lepidopterous larvae: the dose-survival time relationship. Journal of Invertebrate Pathology 51:58–63. [Google Scholar]
- van der Werf W, Hemerik L, Vlak J, and Zwart M. 2011. Heterogeneous host susceptibility enhances prevalence of mixed-genotype micro-parasite infections. PLoS Computational Biology 7: e1002097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughan T, Drummond P, and Drummond A. 2012. Within-host demographic fluctuations and correlations in early retroviral infection. Journal of Theoretical Biology 295:86–99. [DOI] [PubMed] [Google Scholar]
- Vilmos P, and Kurucz E. 1998. Insect immunity: evolutionary roots of the mammalian innate immune system. Immunology Letters 62:59–66. [DOI] [PubMed] [Google Scholar]
- Wang P, and Granados R. 1997. An intestinal mucin is the target substrate for a baculovirus enhancin. Proceedings of the National Academy of Sciences of the USA 94:6977–6982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Washburn J, Kirkpatrick B, and Volkman L. 1996. Insect protection against viruses. Nature 383:767. [Google Scholar]
- Washburn J, Wong J, and Volkman L. 2001. Comparative pathogenesis of Helicoverpa zea S nucleopolyhedrovirus in noctuid larvae. Journal of General Virology 82:1777–1784. [DOI] [PubMed] [Google Scholar]
- Wearing H, Rohani P, and Keeling M. 2005. Appropriate models for the management of infectious diseases. PLoS Medicine 2:e174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webb R, Thorpe K, Podgwaite J, Reardon R, White G, and Talley S. 1999. Efficacy of Gypchek against the gypsy moth (lepidoptera: Lymantriidae) and residual effects in the year following treatment. Journal of Entomological Science 34:404–414. [Google Scholar]
- Williams T, and Meynell G. 1967. Time-dependence and count-dependence in microbial infection. Nature 214:473–475. [DOI] [PubMed] [Google Scholar]
- Woo H, and Reifman J. 2012. A quantitative quasispecies theory-based model of virus escape mutation under immune selection. Proceedings of the National Academy of Sciences of the USA 109: 12980–12985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwart M, Hemerik L, Cory J, de Visser J, Bianchi F, Van Oers M, Vlak J, Hoekstra R, and Van der Werf W. 2009a. An experimental test of the independent action hypothesis in virus-insect pathosystems. Proceedings of the Royal Society B: Biological Sciences 276:2233–2242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwart M, van der Werf W, van Oers M, Hemerik L, van Lent J, de Visser J, Vlak J, and Cory J. 2009b. Mixed infections and the competitive fitness of faster-acting genetically modified viruses. Evolutionary Applications 2:209–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.