Inverse Probability Weights for Quasicontinuous Ordinal Exposures With a Binary Outcome: Method Comparison and Case Study

Abstract

Inverse probability weighting (IPW), a well-established method of controlling for confounding in observational studies with binary exposures, has been extended to analyses with continuous exposures. Methods developed for continuous exposures may not apply when the exposure is quasicontinuous because of irregular exposure distributions that violate key assumptions. We used simulations and cluster-randomized clinical trial data to assess 4 approaches developed for continuous exposures—ordinary least squares (OLS), covariate balancing generalized propensity scores (CBGPS), nonparametric covariate balancing generalized propensity scores (npCBGPS), and quantile binning (QB)—and a novel method, a cumulative probability model (CPM), in quasicontinuous exposure settings. We compared IPW stability, covariate balance, bias, mean squared error, and standard error estimation across 3,000 simulations with 6 different quasicontinuous exposures, varying in skewness and granularity. In general, CBGPS and npCBGPS resulted in excellent covariate balance, and npCBGPS was the least biased but the most variable. The QB and CPM approaches had the lowest mean squared error, particularly with marginally skewed exposures. We then successfully applied the IPW approaches, together with missing-data techniques, to assess how session attendance (out of a possible 15) in a partners-based clustered intervention among pregnant couples living with human immunodeficiency virus in Mozambique (2017–2022) influenced postpartum contraceptive uptake.

Abbreviations

ATE

average treatment effect

CBGPS

covariate balancing generalized propensity score

CPM

cumulative probability model

HIV

human immunodeficiency virus

HoPS+

Homens para Saúde Mais

IPW

inverse probability weight/weighting

MSE

mean squared error

npCBGPS

nonparametric covariate balancing generalized propensity score

OLS

ordinary least squares

OR

odds ratio

QB

quantile binning

sIPW

stabilized inverse probability weight/weighting

Inverse probability weighting (IPW), commonly used in causal analyses of observational data with binary exposures, has been extended to continuous exposures (1–4). It remains unclear, however, whether these extensions are appropriate for commonly encountered “quasicontinuous” exposures, including continuous exposures reported in rounded form (e.g., blood pressure); counts (e.g., numbers of completed intervention visits); and ordinal variables with numbers assigned to categories (e.g., depressive symptoms assessed via a psychometric scale). Because quasicontinuous exposures can have skewed distributions, be zero-inflated, suffer from exposure floor/ceiling effects, or not have interval scales, it is not clear whether recent methodological developments in IPW for continuous exposures apply to quasicontinuous exposures (2–8).

The Homens para Saúde Mais (HoPS+) Trial (Men for Health Plus Trial), a cluster-randomized trial of a partners-based intervention in seroconcordant expectant couples with human immunodeficiency virus (HIV) in Mozambique, illustrates one type of quasicontinuous exposure (9). The intervention includes couples counseling and skills sessions, peer support sessions, and joint couples HIV care, which may contribute to the primary outcomes (retention in care, treatment adherence, viral suppression, and parent-to-child HIV transmission). How intervention engagement, measured by the number of sessions attended, affects HoPS+ intervention arm primary outcomes is of interest.

Recent evidence suggests that treating continuous and quasicontinuous response variables as ordinal yields more robust analyses requiring fewer assumptions (10). We therefore explored the performance of 5 IPW methods for quasicontinuous exposures: ordinary least squares (OLS); covariate balancing generalized propensity score (CBGPS) (4); nonparametric covariate balancing generalized propensity score (npCBGPS) (4); quantile binning (QB) with 10, 15, and 20 bins (3); and a novel approach directly using a cumulative probability model (CPM) on a quasicontinuous exposure, analogous to fitting an ordinal logistic regression model to a continuous outcome (10). We compared the IPW methods under 6 exposure scenarios in simulated data and applied applicable methods to the HoPS+ Trial intervention arm (9).

METHODS

Estimand of interest

We were interested in estimating the average treatment effect (ATE)—the average effect of assigning everyone in the population to one exposure level versus another (6, 7). For continuous outcomes, the ATE is often expressed as a difference in mean potential outcomes: ATE(a, b) = E[Y(X = a)] – E[Y(X = b)], where E[Y(X = x)] is the expected outcome (Y) if all individuals had exposure (X) equal to x. For binary outcomes, the ATE may be expressed as an odds ratio (OR) of potential outcomes: ATE(a, b) = E[Y(X = a)]{1 − E[Y(X = b)]}/{E[Y(X = b)]{1 − E[Y(X = a)]}}, where E[Y(X = x)] is the probability that Y = 1 if X = x. The ATE can be similarly expressed as a marginal risk difference or risk ratio. With binary exposures, X = 0 or 1, and ATE(1, 0) is of interest. With quasicontinuous exposures, a large number of ATEs can exist.

Estimating the ATE using IPW

IPW creates a pseudopopulation in which the measured confounders (C) and exposure (X) are independent (6, 7). Weights are calculated on the basis of C and X, then applied during the ATE estimation process. We use an extension of IPW, stabilized inverse probability weighting (sIPW), which generates less extreme weights and hence less variable estimators (2):

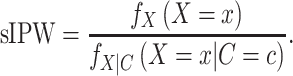For discrete exposures, the numerator, 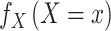, is each individual’s marginal probability (i.e., not conditional on covariates) of having experienced the observed exposure, and the denominator, 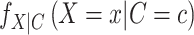, is each individual’s probability of having experienced the observed exposure conditional on their confounding covariates. For continuous exposures, the numerator and denominator are the estimated marginal and conditional density functions rather than probabilities.

Once calculated, weights can be used in weighted regressions to estimate ATEs. To estimate multiple ATEs for a continuous or quasicontinuous exposure, analysts can estimate E[Y | X = x] at several exposure values, creating a dose-response curve. Under the assumption that ATE(a, b) = ATE(c, d) if a − b = c − d on some scale, analysts can also estimate a single ATE via a weighted regression of Y on X. With a binary outcome, a single overall ATE for a 1-unit change in a continuous exposure X is often estimated using a weighted logistic regression that places a linearity constraint on the marginal log odds. The marginal structural model can therefore be written as logit{E[Y(X = x)]} = β₀ + β₁x. Estimates of the ATE using sIPW are consistent under the following conditions: 1) no unmeasured confounders (exchangeability), 2) a nonzero probability/density of each individual’s experiencing each exposure level (positivity), 3) each individual’s potential outcome for the exposure they experienced equaling their observed outcome (causal consistency), and 4) a properly specified weight-generating model (6, 7, 11, 12).

sIPW approaches

In our simulations and case study, we considered 5 potential sIPW approaches for quasicontinuous exposure variables: OLS, CBGPS, npCBGPS, QB, and CPM. OLS makes the often untenable assumption that the quasicontinuous exposure is normally distributed and uses the predicted marginal and conditional exposure densities for the sIPW numerator and denominator, respectively (2). The CBGPS methods attempt to optimize covariate balance by constraining the weighted correlations between all confounders and the exposure to equal 0 (4). Like OLS, standard (parametric) CBGPS assumes normal densities for the sIPW numerator and denominator, but it estimates the parameters of these densities using a method-of-moments framework that implements the zero-correlation constraint (4). In contrast, npCBGPS makes no distributional assumptions about the quasicontinuous exposure and uses an empirical likelihood approach to flexibly estimate the sIPW under the same constraint (4). QB bins the exposure into q quantiles; the numerator and denominator of the sIPW are then estimated using fitted probability mass functions derived, respectively, from marginal and conditional CPMs, also known as cumulative link models (13), fitted to the ordinal binned exposure quantiles (3). We used the proportional odds model, which uses a logit link function (14), although other link functions (e.g., probit or complementary log-log) can also be used. CPM extends QB by directly fitting a CPM to the quasicontinuous exposure without binning. Table 1 and Web Appendix 1 (available at https://doi.org/10.1093/aje/kwad085) present additional details on each approach.

Table 1.

Stabilized Inverse Probability Weighting Approaches for Quasicontinuous Ordinal Exposures With a Binary Outcome

Method	Description	Numerator	Denominator	Model SpecificationAssumptions a	Practical Considerations
OLS	Uses OLS to calculate the numerator and denominator for the sIPW based on predicted exposure density under the assumption of normality.	Normal probability density function with mean and variance equal to the estimated marginal mean and variance of the exposure, evaluated at the observed exposure level.	Normal probability density function with mean and variance equal to the conditional mean exposure and residual variance estimated from an OLS model regressing exposure X on confounder C, evaluated at the observed exposure level.	Treats the quasicontinuous exposure as normally distributed.	Computationally simple using most software packages.
CBGPS	Employs a method-of-moments framework that constrains the weighted correlation between all covariates and the exposure to equal 0. This constraint ensures covariate balance, at least as measured by this correlation.	Standard normal probability density function (i.e., mean = 0 and variance = 1), evaluated at the observed standardized (i.e., centered and scaled) exposure level.	Normal probability density function with mean and variance equal to the conditional mean and residual variance estimated using a method-of-moments estimator on the standardized X and C that constrains the weighted product of standardized X and C to be 0, evaluated at the observed standardized exposure level.	Treats the quasicontinuous exposure as normally distributed. Implicitly assumes that the best sIPW is one that forces covariate balance as measured by correlation.	Computationally simple using the CBPS package in R statistical software (21). We used the “just-identified” approach.
npCBGPS	Uses an empirical likelihood approach to estimate the sIPW while constraining the correlation between covariates and the exposure to equal 0.	Not explicitly specified.	Not explicitly specified. The sIPWs (numerator and denominator together) are simultaneously estimated as those that minimize the product of the weights under the constraints that the weights sum to the sample size, the weighted standardized means of X and C are 0, and the weighted correlation of standardized X and C are 0.	No distributional assumptions. Implicitly assumes that the best sIPW is one that forces covariate balance as measured by correlation.	Computationally more burdensome than other approaches; may fail to find a solution and may require specification of a tuning parameter. Available in the CBPS package in R statistical software (21). We used the “just-identified” approach. The sum of weights adds up to the size of the data set such that the average weight within the data set of interest equals 1.

Table continues

Table 1.

Continued

Method	Description	Numerator	Denominator	Model SpecificationAssumptions a	Practical Considerations
Quantile binning	Bins the exposure into q quantiles to create an approximately uniform exposure distribution with q levels and then calculates the denominator from a CPM (also known as the “cumulative link model”; the proportional odds model is a special case).	The marginal probability that an individual falls into their observed exposure quantile; this is the number of individuals with the binned exposure level divided by the sample size.	The conditional probability that an individual falls into their observed exposure quantile based on their covariates as estimated from a cumulative probability (e.g., proportional odds) model.	Treats all exposure values within the same bin as equivalent. The parallelism (e.g., proportional odds) assumption holds between covariates and the exposure.	Computationally simple using most software packages. Requires binning of quasicontinuous data and choosing the number of bins.
CPM	Uses the CPM without binning to calculate the numerator and denominator for the sIPW based on the predicted probability that each individual receives the exposure they received based on their covariates.	The marginal probability that an individual falls into their actual exposure level; this is the number of individuals with the exposure level divided by the sample size.	The conditional probability that an individual falls into their actual exposure level based on their covariates as estimated from a CPM.	The parallelism (e.g., proportional odds) assumption holds between covariates and the exposure.	Computationally simple using most software packages. Particularly straightforward using the rms package in R statistical software (21). Exposure cannot be truly continuous (i.e., there must be some ties in the data set).

Abbreviations: CBGPS, covariate balancing generalized propensity score; CPM, cumulative probability model; OLS, ordinary least squares; sIPW, stabilized inverse probability weight; npCBGPS, nonparametric covariate balancing generalized propensity score.

^a All weighting methods assume exchangeability, positivity, consistency, and a properly specified propensity score model.

SIMULATION STUDY

Data generation

To facilitate comparisons with existing literature, our simulations followed those of Naimi et al. (3), which explored IPW method performance in simulations with 2 different continuous exposures and a binary outcome. Keeping their conditionally and marginally normal and conditionally and marginally skewed exposures, we added a conditionally normal, marginally skewed exposure and changed all exposures from continuous to quasicontinuous. Web Appendix 2 provides additional data-generation details.

In summary, we generated 3,000 1,500-observation data sets matching the Naimi et al. mean values, variances, and distributions for variables that influenced both the exposures and the outcome: maternal age, paternal age, and parity (3, 15). While their simulations were based on singleton live birth data from Quebec, Canada (3, 16), the exposures in that and the current work were hypothetical. We then generated 3 exposure distributions based on 2 population means: the Naimi et al. mean (μ_a) and a modified version (μ_b) using a new version of maternal age that had the same mean and variance as the original but a skewed distribution (location-scale transformed gamma distribution) and increased correlation with the exposure (Web Appendix 2).

We used these mean values (μ_a and μ_b) as the basis for 3 continuous exposure distributions. Two exposures were conditionally normally distributed as X_a ~ 15 + μ_a + ε and X_b ~ 15 + μ_b + ε, with ε ∼ N(0, 2); X_a was marginally normally distributed, while X_b was marginally skewed. The third exposure, X_c, was conditionally and marginally skewed, created by first generating a Poisson variable with mean = variance = μ_a, then adding random error distributed N(0, 1) and setting negative values to 0 (3).

From the continuous exposures X_a, X_b, and X_c, we created 2 sets of quasicontinuous exposures by rounding to different levels of precision: X₁, X₂, and X₃ to the nearest tenth and X₄, X₅, and X₆ to the nearest integer. X₁–X₃ approximate a scenario where a continuous exposure variable is collected in a rounded form with ties (e.g., blood pressure, about 80–110 unique values), and X₄–X₆ approximate a scenario where an exposure variable has discrete orderable levels (e.g., completed intervention visits, about 8–15 unique values), as in the case study below. With each exposure’s transformation to quasicontinuous, normal distributions became approximately normal; we describe them below as “normal” for brevity.

For all 6 quasicontinuous exposures, we generated a binary outcome, Y, from a Bernoulli distribution with the log odds of success following the linear model:

The log ORs for the covariates, 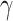, were the same for all 6 scenarios, but the intercept term, α_i, varied so that the marginal outcome probability was approximately constant at 0.08 (see Web Appendix 2) (3, 16).

Ascertainment of “truth”

As we noted above, 2 representations of the ATE may be of interest in studies with quasicontinuous exposures: a single-number summary of the effect of a 1-unit exposure increase and a dose-response curve with multiple points. We generated a distinct 4.5-million–observation reference population using the above-described approach to calculate both types of “truth.” To calculate the overall marginal log OR for a 1-unit exposure increase, we extended the limited marginal standardization approach used in the study by Naimi et al. (3, 17), using techniques suggested in the papers by Zhang (18) and Zhang et al. (19). First, for every exposure level (x) in the reference population, we calculated the marginal predicted outcome probability (the average predicted probability if everyone in the reference population maintained their original covariates but had exposure x), using the true outcome-generation formula. Then, maintaining the full number of rows (4.5 million) and thus the exposure distribution in the reference population, we fitted the marginal structural model logit{E[Y(X = x)]} = β₀ + β₁x, with E[Y(X = x)] the marginal predicted outcome probability at exposure x (described in the previous sentence), using logistic regression (allowing nonbinary outcome values). β₁ was the “true” overall marginal log OR. Following the method of Austin (20), we also calculated dose-response curve values—the marginal outcome probability if everyone in the reference population received 1 exposure level—at 9 deciles of each exposure, using the true outcome-generation formula.

IPW approach comparison

In each simulated data set, we calculated sIPWs for X₁, X₂, and X₃ using 7 weighting approaches (OLS; CBGPS; npCBGPS; QB with 10, 15, and 20 quantiles; and CPM), as well as an unweighted and otherwise unadjusted approach. For X₄, X₅, and X₆, we assessed all approaches except QB, since some of the simulated data sets had fewer than 10 unique exposure levels, rendering this approach unnecessary (Table 1, Web Table 1). For each set of weights, the denominator model used the same covariates as the exposure-generation model, with the same functional forms (Web Appendix 2). Thus, for exposures X₁, X₂, X₄, and X₅, the denominators for the OLS weights would have been correctly specified had we left the exposures continuous. For each exposure-sIPW combination, we fitted a weighted logistic regression model with the exposure as the sole predictor: logit(E[Y|X]) = β₀ + β₁X, with robust standard errors accounting for weighting (2). The fitted model generated a marginal log OR for a single-unit increase in exposure (β₁) and allowed us to create a dose-response curve showing the expected response probability at 9 exposure deciles (Web Table 2).

Within each simulated data set, we evaluated each weighting method for each exposure via the mean values and ranges of the sIPWs themselves (means far from 1 and/or extreme weights can result from nonpositivity and/or propensity score misspecification) (6, 7) and the number of absolute correlations greater than 0.10 between covariates and the exposure (covariate balance) (7, 8). For each exposure-sIPW combination, for the marginal log OR and each of the 9 dose-response–curve decile points, we then calculated the “within–data-set bias” of the estimator as the difference between the true and estimated β₁ (henceforth called “bias”).

We then constructed summary measures for each exposure-sIPW combination across all 3,000 simulated data sets. For both types of estimators (OR and dose-response curve), we calculated the mean squared error (MSE) as the mean of the squared biases (8, 17). For the marginal log OR, we also assessed the performance of our standard error estimates across all 3,000 data sets. We calculated the “standard error ratio” as the ratio of the average of the 3,000 β₁ robust standard errors to the empirical standard deviation of β₁ across all simulated data sets. We calculated the empirical coverage of the nominal 95% confidence interval as the proportion of simulated data sets where the 95% confidence interval included the “true” β₁.

For the analyses, we used R statistical software (version 4.1; R Foundation for Statistical Computing, Vienna, Austria) and the packages cobalt (version 4.3.1), rms (version 6.2.0), survey (version 4.1-1), and WeightIt (version 0.12.0) (21–24). We wrote de novo R code to calculate the QB and CPM sIPWs.

Simulation results

Across 3,000 simulations, all exposures exhibited the expected marginal and conditional distributions, with 69–117 exposure levels for X₁–X₃ and 8–17 exposure levels for X₄–X₆ (Figure 1; Web Tables 1–3; Web Figures 1–4) (3).

Figure 1.

Marginal and conditional exposure distributions across 3,000 simulated data sets based on singleton live births in Quebec, Canada, 1995--2005. Panels on the left (panel A, X₁; panel C, X₂; panel E, X₃, panel G, X₄; panel I, X₅; panel K, X₆), show the marginal distributions of 6 exposures. Panels on the right (panel B, X₁; panel D, X₂; panel F, X₃, panel H, X₄; panel J, X₅; panel L, X₆) show residuals from multiple linear regressions of the 6 exposures on the confounding covariates. Panels A, B, E, and F suggest that we successfully recreated the marginal and conditional exposure distributions from the study by Naimi et al. (3) for X₁ and X₃. For X₂, panel C shows that introducing a higher correlation between left-skewed maternal age and the exposure shifted the exposure mean upwards (from 16.96 to 23.74), increased the variance (from 2.16 to 3.37), and made the exposure marginally left-skewed. Panels G, I, and K show that with rounding to integers instead of tenths, X₄, X₅, and X₆ recreate the distributions of X₁, X₂, and X₃. The appearance of heteroskedasticity in panels D and J is due to the higher numbers of individuals with higher exposure levels. X₁: conditionally normal, marginally normal exposure rounded to the nearest tenth; X₂: conditionally normal, marginally skewed exposure rounded to the nearest tenth; X₃: conditionally skewed, marginally skewed exposure rounded to the nearest tenth; X₄: conditionally normal, marginally normal exposure rounded to the nearest integer; X₅: conditionally normal, marginally skewed exposure rounded to the nearest integer; X₆: conditionally skewed, marginally skewed exposure rounded to the nearest integer.

We examined the mean values and ranges of mean sIPWs and the number of absolute covariate-exposure correlations greater than 0.10 (of 7 possible correlations) across all simulations for OLS, CBGPS, npCBGPS, QB (with 10, 15, and 20 bins), and CPM under all 6 exposure scenarios (Table 2). For npCBGPS, the mean, minimum, and maximum npCBGPS weights were equal to 1 by design. The remaining weighting approaches generated mean weights very close to 1 across all scenarios, except for OLS and CBGPS weights in the scenario with a conditionally normal, marginally skewed exposure rounded to tenths (X₂). Across all exposure scenarios, npCBGPS (by design), QB, and CPM generated the smallest range of mean weights across simulations. Only the conditionally normal, marginally skewed exposure scenarios (X₂ and X₅) led to mean covariate imbalances that did not round to 0 across the simulated data sets. In these scenarios, CBGPS performed best, with npCBGPS, QB, and CPM being less prone to extreme covariate imbalance than OLS.

Table 2.

Mean (Range) Inverse Probability Weight and Covariate Balance Distributions From 3,000 Simulated Data Sets Based on Singleton Live Births in Quebec, Canada, 1995--2005

	Distribution, Rounding, and Exposure Status
	Conditional Distribution = Normal; Marginal Distribution = Normal		Conditional Distribution = Normal; Marginal Distribution = Skewed		Conditional Distribution = Skewed; Marginal Distribution = Skewed
Method	Rounding = Tenths; Exposure = X 1	Rounding = Integers; Exposure = X 4	Rounding = Tenths; Exposure = X 2	Rounding = Integers; Exposure = X 5	Rounding = Tenths; Exposure = X 3	Rounding = Integers; Exposure = X 6
Unweighted
No. of correlations > 0.1	4.03 (4–5)	4.04 (4–5)	4.22 (4–5)	5.72 (5–7)	4.16 (4–5)	4.18 (4–5)
Ordinary least squares
Mean stabilized weight	1.04 (1.02–1.09)	1.04 (0.01–36.20)	1.29 (1.18–5.69)	1.01 (0.02–10.70)	1.03 (1.01–1.07)	1.03 (0–29.10)
No. of correlations > 0.1	0.01 (0–3)	0.01 (0–3)	0.83 (0–7)	1.17 (0–3)	0.01 (0–2)	0 (0–2)
CBGPS
Mean stabilized weight	1.00 (0.99–1.12)	1.00 (0.01–113.00)	1.17 (0.96–1.80)	1.00 (0.01–16.80)	1.00 (1.00–1.15)	1.00 (0.01–40.90)
No. of correlations > 0.1	0 (0–0)	0 (0–0)	0.05 (0–2)	1.17 (0–3)	0 (0–0)	0 (0–0)
npCBGPS
Mean stabilized weight	1.00 (1–1)	1.00 (1–1)	1.00 (1–1)	1.00 (1–1)	1.00 (1–1)	1.00 (1–1)
No. of correlations > 0.1	0 (0–0)	0 (0–2)	0.82 (0–4)	1.16 (0–3)	0 (0–0)	0 (0–1)
Quantile binning
10 bins
Mean stabilized weight	1.00 (0.99–1.01)		0.97 (0.92–1.12)		1.00 (0.99–1.01)
No. of correlations > 0.1	0 (0–0)		0.61 (0–4)		0 (0–0)
15 bins
Mean stabilized weight	1.00 (0.99–1.01)		0.96 (0.92–1.15)		1.00 (0.99–1.01)
No. of correlations > 0.1	0 (0–0)		0.68 (0–4)		0 (0–0)
20 bins
Mean stabilized weight	1.00 (0.99–1.01)		0.96 (0.91–1.12)		1.00 (0.99–1.01)
No. of correlations > 0.1	0 (0–0)		0.71 (0–4)		0 (0–0)
Cumulative probability model
Mean stabilized weight	1.00 (0.99–1.01)	1.00 (0.04–11.60)	0.96 (0.91–1.15)	1.00 (0.12–6.44)	1.00 (0.99–1.01)	1.00 (0.07–14.80)
No. of correlations > 0.1	0 (0–0)	0 (0–1)	0.85 (0–3)	1.19 (0–3)	0 (0–0)	0 (0–0)

Abbreviations: CBGPS, covariate balancing generalized propensity score; npCBGPS, nonparametric covariate balancing generalized propensity score.

The bias and MSE of the marginal log OR are shown in Figure 2 (Web Table 4). All weighting strategies had low bias and MSE within the conditionally and marginally normal exposure scenarios (X₁ and X₄) and the conditionally and marginally skewed exposure scenarios (X₃ and X₆). In these 4 scenarios, although bias was slightly lower for OLS, CBGPS, and npCBGPS, MSE was slightly lower for QB and CPM. In the conditionally normal, marginally skewed exposure scenario rounded to tenths (X₂), npCBGPS had the lowest bias of the weighting strategies, but it also had a substantially larger MSE due to its higher variance; and QB and CPM tended to have the lowest MSE again. In the conditionally normal, marginally skewed exposure scenario rounded to integers (X₅), all weighting strategies performed poorly. The dose-response estimates yielded bias and MSE findings similar to those of the marginal log OR approach (Web Appendix 2; Web Figures 5 and 6). Despite its low bias, npCBGPS had the highest MSE in most scenarios, and QB and CPM tended to have slightly lower MSEs than OLS and CBGPS.

Figure 3.

Intervention session attendance in the Homens para Saúde Mais (HoPS+) Trial, Zambezia Province, Mozambique, 2017--2022. A) HoPS+ session attendance among female participants (n = 315); B) HoPS+ session attendance among male participants (n = 315).

Among sIPW approaches, the estimated standard errors for CPM and QB tended to be the most accurate (i.e., standard error ratios closest to 1) (Table 3). Confidence interval coverage was near the expected 0.95 level for all weighted estimators in all scenarios except the conditionally normal, marginally skewed scenarios (X₂ and X₅). With X₂, npCBGPS had good coverage (despite having the lowest standard error ratio, probably because of its low bias, as seen in Figure 2) followed by CPM, QB, OLS, and CBGPS (in that order). With X₅, all approaches had low coverage (86%–87%), presumably because of their bias (Figure 2). As expected, coverage was lowest in all scenarios for the unweighted estimate that failed to address confounding.

Table 3.

Standard Error Ratio and Coverage Across 3,000 Simulated Data Sets Based on Singleton Live Births in Quebec, Canada, 1995--2005

	Distribution, Rounding, and Exposure Status
	Conditional Distribution = Normal; Marginal Distribution = Normal		Conditional Distribution = Normal; Marginal Distribution = Skewed		Conditional Distribution = Skewed; Marginal Distribution = Skewed
Method	Rounding = Tenths; Exposure = X 1	Rounding = Integers; Exposure = X 4	Rounding = Tenths; Exposure = X 2	Rounding = Tenths; Exposure = X 5	Rounding = Integers; Exposure = X 3	Rounding = Tenths; Exposure = X 6
Unweighted
SE ratioa	0.991	0.998	1.020	1.025	0.996	0.982
Coverageb	0.855	0.864	0.813	0.815	0.863	0.865
Ordinary least squares
SE ratio	0.960	0.965	0.778	0.994	0.983	0.973
Coverage	0.946	0.948	0.915	0.861	0.946	0.944
CBGPS
SE ratio	0.969	0.973	0.814	0.995	0.991	0.979
Coverage	0.945	0.949	0.881	0.863	0.946	0.945
npCBGPS
SE ratio	0.871	0.887	0.669	0.986	0.963	0.961
Coverage	0.952	0.950	0.943	0.867	0.948	0.946
Quantile binning
10 bins
SE ratio	0.974		0.949		0.991
Coverage	0.942		0.922		0.942
15 bins
SE ratio	0.975		0.944		0.991
Coverage	0.942		0.925		0.943
20 bins
SE ratio	0.974		0.944		0.991
Coverage	0.944		0.927		0.943
Cumulative probability model
SE ratio	0.974	0.982	0.949	0.999	0.991	0.986
Coverage	0.944	0.948	0.929	0.867	0.943	0.947

Abbreviations: CBGPS, covariate balancing generalized propensity score; npCBGPS, nonparametric covariate balancing generalized propensity score; SE, standard error.

^a The SE ratio was the average SE (the average β₁ robust SE in each simulated model) divided by the empirical SE (the standard deviation of β₁ across all simulated data sets).

^b Coverage was the proportion of simulated data sets for which the 95% confidence interval included the “true” β₁ in each exposure scenario.

HoPS+ CASE STUDY

We applied sIPW methods to assess the dose-response relationship between intervention session attendance (out of a possible total of 15 sessions) and a secondary outcome, postpartum contraceptive uptake by female partners, in the HoPS+ Trial intervention arm (9). We included 315 (60% of 524) seroconcordant couples with HIV whose female partner was at least 12 months from a live birth on January 30, 2022, when the data were pulled, and had nonmissing data on postpartum contraceptive use (Web Figure 7). We conducted one analysis using female partner attendance as the exposure and another using male partner attendance as the exposure. We combined counseling and skills session attendance and peer support session attendance into 1 exposure variable, recognizing that this assumed that different types of sessions were interchangeable, which limits interpretation of the findings.

Outcome definition

Postpartum uptake of oral contraceptives reduces the incidence of short interpregnancy intervals and negative sequelae such as poor maternal and fetal outcomes (25, 26). It is an essential component of postpartum care for people living with HIV (27, 28). Postpartum contraceptive use at any point from birth to 12 months postpartum, while imprecise, was a useful case-study binary outcome.

Covariates

Participants from the HoPS+ Trial intervention arm constituted a prospectively enrolled cohort, clustered by clinical site. Web Figure 8 is a directed acyclic graph identifying covariates that may have confounded the relationship between intervention session attendance and postpartum contraceptive uptake: age, depressive symptoms, educational level, World Health Organization clinical stage, social support, partner HoPS+ engagement, and enrollment date (29, 30).

Figure 2.

Bias and mean squared error (MSE) of marginal log odds ratio estimates across 3,000 simulated data sets based on singleton live births in Quebec, Canada, 1995--2005. In each row, the gray shaded area shows a probability density function of the biases; the black circle shows the median bias; the thicker black bar shows the interquartile range of the biases; and the thinner black bar shows the range of 95% of biases across the simulated data sets. The right side of each panel shows the MSE, the mean of the squared bias (“true” β₁ minus estimated β₁) across all simulated data sets, for each stabilized inverse probability weighting (sIPW) approach. A) Conditionally normal, marginally normal exposure rounded to the nearest tenth (X₁); B) conditionally normal, marginally normal exposure rounded to the nearest integer (X₄); C) conditionally normal, marginally skewed exposure rounded to the nearest tenth (X₂); D) conditionally normal, marginally skewed exposure rounded to the nearest integer (X₅); E) conditionally skewed, marginally skewed exposure rounded to the nearest tenth (X₃); F) conditionally skewed, marginally skewed exposure rounded to the nearest integer (X₆). UW, unweighted; OLS, ordinary least squares; CBGPS, covariate balancing generalized propensity score; npCBGPS, nonparametric covariate balancing generalized propensity score; QB10, quantile binning with 10 bins; QB15, quantile binning with 15 bins; QB20, quantile binning with 20 bins; CPM, cumulative probability model.

Applied statistical analysis

Simulation studies support inclusion of a clustering variable as a fixed effect when generating continuous propensity scores and as a random effect in the outcome model for continuous treatments for calculation of consistent effect estimates (31). We therefore calculated the OLS, CBGPS, npCBGPS, and CPM sIPWs as described above—we omitted QB, since, with this 16-level exposure, it would be a near-duplication of CPM—with the above-mentioned covariates and clinical site included as a fixed effect. We imputed missing covariate data 25 times with an imputation model that accounted for the clustered nature of the data and included all baseline covariates and the outcome (32, 33). We then calculated sIPWs for each imputed data set and assessed covariate balance via sIPW means and ranges and absolute correlation coefficients across imputed data sets (7, 8, 22, 34). Finally, within each imputed data set, using weighted generalized linear mixed-effects models with a random effect for clinical site, we estimated the overall OR for the impact of attending an additional HoPS+ intervention session on postpartum contraceptive use. We estimated standard errors via a clustered bootstrap using 1,000 resamples of the 12 clusters, using all participants within each resampled cluster (31). OR and standard error estimates were then pooled across imputed data sets using Rubin’s rules (35). We fitted a total of 8 models, one for each combination of exposure (female partner attendance or male partner attendance) and sIPW type.

Case study results

Among the 315 eligible couples, female participants attended more intervention sessions (median, 13; interquartile range, 11–15) than males (median, 8; interquartile range, 3.5–11). The distribution of female attendance was highly skewed, whereas the distribution of male attendance was more uniform (Figure 3). Fewer than half (n = 129; 41%) of female participants used postpartum contraception (Table 4).

Table 4.

Baseline, Exposure, and Outcome Data From the HoPS+ Trial, by Sex, Zambezia Province, Mozambique, 2017–2022

	Sex
Data Type and Variable	Female (n = 315)		Male (n = 315)
	No.	%	No.	%
Baseline data
Age, yearsa	23.0 (19.5–27.0)		27.0 (24.0–32.0)
Missing	0	0	1	0.3
District
Pebane	103	32.7	103	32.7
Inhassunge	23	7.3	23	7.3
Namacurra	63	20.0	63	20.0
Mocubela	29	9.2	29	9.2
Maganja da Costa	26	8.3	26	8.3
Gilé	56	17.8	56	17.8
Quelimane	15	4.8	15	4.8
Relationship status
Living together	170	54.0	169	53.7
Single	79	25.1	79	25.1
Married	66	21.0	65	20.6
Missing	0	0	2	0.6
Education
None	50	15.9	19	6.0
Some primary school (grades 1–7)	210	66.7	161	51.1
Completed primary school (grade 7)	19	6.0	31	9.8
Some secondary school (grades 8–10)	24	7.6	61	19.4
Completed secondary school (grade 10)	8	2.5	21	6.7
College/higher education	4	1.3	21	6.7
Missing	0	0	1	0.3
Occupation
Farmer	152	48.3	129	41.0
Domestic worker	158	50.2	51	16.2
Trader	2	0.6	43	13.7
Fisher	0	0	60	19.0
Other	3	1.0	31	9.8
Missing	0	0	1	0.3
Perceived supporta	27.0 (24.0–28.0)		26.0 (24.0–28.0)
Missing	21	6.7	25	7.9
Needed supporta	30.0 (28.0–32.0)		31.0 (28.0–32.0)
Missing	26	8.3	28	8.9
PHQ-9 scorea	3.0 (0.5–7.0)		3.0 (0–7.0)
Missing	48	15.2	53	16.8

Table continues

Table 4.

Continued

	Sex
Data Type and Variable	Female (n = 315)		Male (n = 315)
	No.	%	No.	%
WHO HIV clinical stage
I	248	78.7	262	83.2
II	32	10.2	31	9.8
III	4	1.3	7	2.2
IV	1	0.3	1	0.3
Missing	30	9.5	14	4.4
Exposure data
No. of completed counseling and skills sessionsa	6 (5–6)		3 (1–5)
No. of completed peer sessionsa	8 (6–9)		5 (2–7)
Total no. of sessions attendeda	13.0 (11.0–15.0)		8.0 (3.5–11.0)
Outcome data
Postpartum contraceptive use
No	186	59.0	0	0
Yes	129	41.0	0	0

Abbreviations: HIV, human immunodeficiency virus; HoPS+, Homens para Saúde Mais; PHQ-9, Patient Health Questionnaire 9; WHO, World Health Organization.

^a Values are expressed as median (interquartile range).

Other than npCBGPS by design, CPM weighting generated a mean sIPW closest to 1 and the smallest range of mean sIPWs across the 25 imputed data sets for female attendance, whereas CBGPS did so for male attendance (Table 5, Web Figure 9). CBGPS generated the fewest absolute covariate-exposure correlations greater than 0.10 for both female and male attendance, and CPM generated the most (Table 5, Web Figure 9).

Table 5.

Method Characteristics and Likelihood of Female Postpartum Contraceptive Uptake in the HoPS+ Trial, Zambezia Province, Mozambique, 2017–2022

	Method
	OLS			CBGPS			npCBGPS			CPM
Sex and Model	Mean (Range) a	OR	95% CI	Mean (Range)	OR	95% CI	Mean (Range)	OR	95% CI	Mean (Range)	OR	95% CI
Female
sIPW	1.17 (1.16–1.19)			1.36 (1.25–1.50)			1.00 (1.00–1.00)			1.00 (0.99–1.02)
No. of correlations > 0.1b	3.0 (2–6)			0 (0–0)			3.1 (0–17)			8.1 (5–16)
+ 1 session		1.12	0.99, 1.26		1.18	0.98, 1.43		1.21	0.74, 1.99		1.05	0.94, 1.18
Male
sIPW	1.68 (1.56–1.80)			1.03 (0.98–1.31)			1.00 (1.00–1.00)			1.17 (1.07–1.31)
No. of correlations > 0.1	19.9 (15–26)			1.8 (1–4)			5.6 (1–17)			22.9 (18–26)
+ 1 session		1.04	0.91, 1.20		1.14	0.96, 1.35		1.07	0.81, 1.41		1.07	0.93, 1.22

Abbreviations: CBGPS, covariate balancing generalized propensity score; CI, confidence interval; CPM, cumulative probability model; HoPS+, Homens para Saúde Mais; npCBGPS, nonparametric covariate balancing generalized propensity score; OLS, ordinary least squares; OR, odds ratio; sIPW, stabilized inverse probability weight.

^a Mean value and range of mean sIPWs.

^b Number of covariate correlations greater than 0.1 (out of 44) across the 25 imputed data sets.

All models suggested that additional session attendance among female and male participants was associated with slightly increased odds of postpartum contraceptive use by female participants, but results were not statistically significant at the 0.05 level (Table 5). For female attendance, ORs ranged from 1.05 (CPM) to 1.21 (npCBGPS). For male attendance, ORs ranged from 1.04 (OLS) to 1.14 (CBGPS). For attendance by participants of both sexes, the npCBGPS approach generated the widest 95% confidence intervals, followed by CBGPS.

DISCUSSION

Although sIPW methods have been developed for continuous exposures, prior to our study there were few direct comparisons of these methods with quasicontinuous exposure data that may be skewed, bounded, discretized, or ordinal in nature. Using simulated and real data, we compared several sIPW approaches to estimate the ATE of a quasicontinuous exposure on a binary outcome.

Across simulated data sets, CBGPS and npCBGPS resulted in the best covariate balance. Furthermore, npCBGPS, which makes no distributional assumptions, tended to have the lowest median bias of all approaches. However, QB (with 10, 15, and 20 bins) and CPM generated lower MSEs than npCBGPS, CBGPS, and OLS in all simulation settings, particularly when the exposure was marginally skewed. This finding seems reasonable because OLS and CBGPS incorrectly assume that the quasicontinuous exposure is normally distributed, and npCBGPS (as other nonparametric methods do) probably sacrifices some efficiency by making no distributional assumptions. In contrast, CPM, and by extension QB, can be thought of as semiparametric approaches which make distributional assumptions, albeit much weaker than that of normality (10). CPM may have slightly outperformed QB in our simulations, and it does not require arbitrarily binning the exposure variable prior to analysis. In addition, across simulations, CPM generated weights closest to 1 and with narrower ranges than the other approaches (other than npCBGPS, which generates mean weights exactly equal to 1 by design). Despite some model misfit, it is worth highlighting that all IPW approaches outperformed unweighted analyses that ignored confounding. We did observe a setting (conditionally normal, marginally skewed exposure with few levels, X₅) in which none of the sIPW approaches had fully satisfactory results (i.e., all methods had median bias that was nonzero and confidence interval coverage below the nominal 95% level).

In our HoPS+ case study, we examined the impact of female and male partner session attendance on female postpartum contraceptive uptake. We applied OLS, CBGPS, npCBGPS, and CPM with clustered exposures after multiply imputing missing baseline covariate data. Because the truth was unknown in the case study, it was impossible to determine which sIPW approach was best. For analyses of female attendance, given the skewed nature of the exposure variable distribution, our simulation study favored using CPM. However, in the case study, CPM tended to result in worse covariate balance than OLS and (as expected) CBGPS and npCBGPS, suggesting that CBGPS or npCBGPS might be preferred, particularly for the analyses of male attendance, which had a less skewed distribution. It is possible that CPM performed poorly with regards to covariate balance because of model overfitting due to the inclusion of many covariates (44 degrees of freedom) (10). All approaches suggested effects with similar magnitudes and directions for the effect of female and male partner HoPS+ session attendance on postpartum contraceptive uptake.

Our simulations, which considered only correctly specified propensity score models and 6 exposure distributions, had several limitations and raise key questions for future research. First, there were only low levels of confounding and bias in the unweighted approach (not assessed in the study by Naimi et al. (3)). In future simulations, researchers should evaluate the sIPW methods under more extreme confounding and assess how each approach works under other exposure distributions and when key covariates are excluded from or incorrectly specified in sIPW calculation. Furthermore, while we implemented sIPWs through weighted marginal structural models (3, 11), investigators performing other simulations have considered propensity score covariate adjustment instead of weighting and have found decreased effect variability and mean squared error (8). Finally, although covariate balance has been described as a key metric for assessing how well sIPW removes the relationship between covariates and the exposure (7, 8), we found that it could be misleading in quasicontinuous exposures when the exposure is conditionally normal and marginally skewed. This finding requires further exploration.

Given that recent work has shown that ordinal regression models can be fitted to continuous outcome data without binning (3, 10), we considered whether CPM would work with continuous exposures. Although CPMs can compute conditional cumulative distribution functions with continuous exposure data, they do not easily yield the conditional probability density function estimates required for sIPW calculation, because there is only 1 observation in each level of any truly continuous exposure. Although smoothing techniques could estimate the conditional probability density function after fitting a CPM to continuous data (36), these approaches involve additional complexities that are likely to cancel out their potential benefits.

In conclusion, we demonstrated that various sIPW approaches can be appropriate when working with quasicontinuous exposures with many and few levels. We also implemented CPM, an extension of the QB approach (3) that does not require exposure binning prior to sIPW generation, which performed well with various exposure distributions. Finally, we implemented the approaches in a cluster-randomized study that included missing baseline covariates using freely available software (22, 23, 34).