Abstract
Background:
Automated segmentation of individual calf muscle compartments in 3D MR images is gaining importance in diagnosing muscle disease, monitoring its progression, and prediction of the disease course. Although deep convolutional neural networks have ushered in a revolution in medical image segmentation, achieving clinically acceptable results is a challenging task and the availability of sufficiently large annotated datasets still limits their applicability.
Purpose:
In this paper, we present a novel approach combing deep learning and graph optimization in the paradigm of assisted annotation for solving general segmentation problems in 3D, 4D, and generally n-D with limited annotation cost.
Methods:
Deep LOGISMOS combines deep-learning-based pre-segmentation of objects of interest provided by our convolutional neural network, FilterNet+, and our 3D multi-objects LOGISMOS framework (layered optimal graph image segmentation of multiple objects and surfaces) that uses newly designed trainable machine-learned cost functions. In the paradigm of assisted annotation, multi-object JEI for efficient editing of automated Deep LOGISMOS segmentation was employed to form a new larger training set with significant decrease of manual tracing effort.
Results:
We have evaluated our method on 350 lower leg (left/right) T1-weighted MR images from 93 subjects (47 healthy, 46 patients with muscular morbidity) by fourfold cross-validation. Compared with the fully manual annotation approach, the annotation cost with assisted annotation is reduced by 95%, from 8 hours to 25 minutes in this study. The experimental results showed average Dice similarity coefficient (DSC) of 96.56 ± 0.26% and average absolute surface positioning error of 0.63 pixels (0.44 mm) for the five 3D muscle compartments for each leg. These results significantly improve our previously reported method and outperform the state-of-the-art nnUNet method.
Conclusions:
Our proposed approach can not only dramatically reduce the expert’s annotation efforts but also significantly improve the segmentation performance compared to the state-of-the-art nnUNet method. The notable performance improvements suggest the clinical-use potential of our new fully automated simultaneous segmentation of calf muscle compartments.
I. Introduction
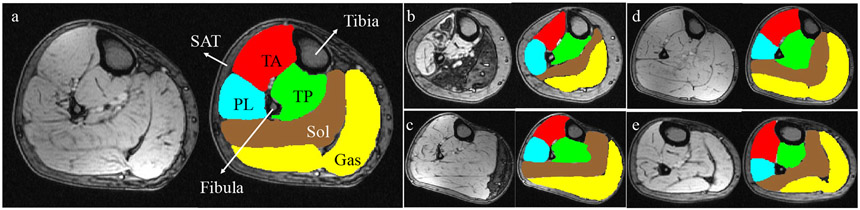
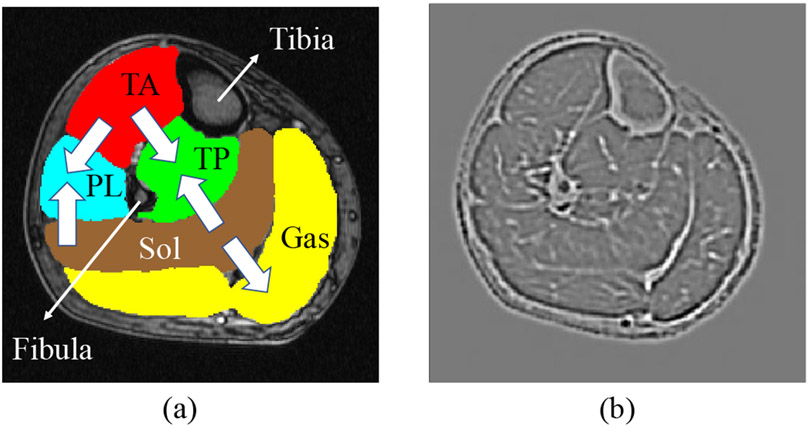
In humans, the muscles of the lower leg between the knee joint and the ankle support weight-bearing activities such as walking, running and jumping. Anatomically, this group is composed of five individual muscle compartments shown in Fig. 1(a): Tibialis Anterior (TA), Tibialis Posterior (TP), Soleus (Sol), Gastrocnemius (Gas) and Peroneal Longus (PL)1. Structural and volumetric changes of these compartments provide valuable information for the diagnosis, severity, and progression evaluation for various muscular diseases such as myotonic dystrophy type 1 (DM1), an inherited disorder characterized by progressive muscle weakness, myotonia, and dystrophic changes2. DM1 is the most common form of muscular dystrophy that begins in adulthood and causes severe fatty degeneration of calf muscle in most patients3. Magnetic resonance (MR), which offers non-invasive imaging of muscles with high sensitivity to dystrophic changes, has been widely used in the clinic for muscular disease diagnosis and follow-up evaluation3,4. Traditional structural assessment of multiple individual muscles invariably resorts to manual tracing5,6, which is arduous, time-consuming, and limiting in large research and clinical settings. Automated segmentation of multiple individual calf muscles is therefore essential for developing quantitative biomarkers of muscular disease diagnosis and progression.
Figure 1:
Examples of T1-weighted MR images of calf muscle cross sections and corresponding expert segmentations of TA, TP, Sol, Gas and PL. (a) Normal subject. (b-c) Patients with severe DM1. (d) Patient at risk for DM1 (PreDM1). (e) Patient with juvenile onset DM1 (JDM). Best viewed in color.
Past calf muscle segmentation research is relatively sparse. Valentinitsch et al.7 proposed a three-stage method using unsupervised multi-parametric k-means clustering to segment calf muscle regions and subcutaneous fat for determining subcutaneous adipose tissue (SAT) and inter-muscular adipose tissue (IMAT). Yao et al.8 combined deep learning with a dual active contour model to accurately locate the fascia lata and segment multiple tissue types for quantifying calf muscle and fat volumes. Amer et al.9 employed deep learning to segment the whole calf muscle region where IMAT and healthy muscle are classified afterward by deep convolutional auto-encoders. All these entire muscle-region segmentation methods are mainly proposed to separate muscle, SAT and IMAT for estimating fat infiltration into muscular dystrophies.
However, the segmentation of individual muscle compartments is more desirable for assessing the progression of different neuromuscular diseases10. For example, it has been shown that individual skeletal muscle may be affected differently by DM111. It is necessary to improve the efficiency and utility of muscle MRI as a marker of muscle pathology12.
Automated 3D segmentation of individual calf muscle compartments is challenging and attempts in this field are rare. As shown in Fig. 1(b-e), muscular dystrophy introduces substantial variations of shape, texture and grayscale appearance to a part of or the entire calf region in addition to the already existing substantial variations due to the flexible nature of the muscles and leg’s position in the scanner. Ghosh et al.13 fine-tuned a pre-trained AlexNet on 700 3D MR images to predict two parameters representing the contour of the leg muscles and achieved an average DSC of 0.85 ± 0.09. However, the network must be trained separately for each leg muscle and the whole method can not learn from the features while training all kinds of muscles together. Hiasa et al. 14 proposed a general automated segmentation of individual muscles by using Bayesian convolutional neural networks with the U-Net architecture. They achieved a DSC of 0.891 ± 0.016 and an average surface distance of 0.994 ± 0.230 mm over 19 muscles in the set of 20 CTs. The method can be used in the active-learning framework to achieve considerable reduction in manual annotation cost. Wong et al.15 proposed the presence-masking strategy that created labels from each label image across multiple datasets and then applied these masks to loss function during training to remove influence of unannotated classes. This strategy reduced the costs involved in manual annotations and resulted in a DSC of 0.706 – 0.905 for 6 muscle group segmentations in a partially labeled calf-muscle dataset containing 22 left calves acquired from healthy subjects. More recently, Guo et al.16 proposed a novel neighborhood relationship-aware fully convolutional network (FCN), called FilterNet, for automated segmentation of individual calf muscle compartments and reached an average DSC of 0.90 ± 0.01 on 40 T1-weighted 3D MR images of 11 healthy and 29 diseased subjects. This approach was used in clinical research12.
Although the aforementioned approaches reported acceptable segmentation performance by applying deep learning methods, several critical issues remained to be settled. 1) Availability of sufficiently large annotated datasets represents a bottleneck limiting their application, especially in large clinical settings where new data accumulates continuously. Annotation (manual tracing) of medical images is not only arduous and time-consuming but also requires costly specialty-oriented knowledge and skills. 2) There is still room for improvement of deep learning-based calf segmentation approaches. 3) Undesirable regional inaccuracies remain in the deep learning segmentation due to the lack of global-information-aware optimization.
Considering the complementary advantages of deep learning and graph-based methods, the nature of their combination is ideally suited for solving the above issues. Deep learning methods offer state-of-the-art accuracy in medical image segmentation although they are not explicitly topology-aware and significant annotation effort is needed for their training. Graph-based algorithms maintain pre-segmentation topology, deliver globally optimal solutions, and may be combined with efficient interactive adjudication if needed – but they lack a good way to guide the necessary graph construction and cost function design if starting from scratch; reasonable initialization is required. In this paper, we present a novel approach combining deep learning and graph optimization in the paradigm of assisted annotation to address these issues.
Compared with previously reported approaches, the contributions of our work can be summarized as follows.
Assisted annotation with efficient adjudication substantially decreases expert manual tracing effort when forming annotated training sets.
FilterNet+ extends the underlying FilterNet approach, significantly improves the segmentation performance and outperforms the state-of-the-art methods.
Deep LOGISMOS substantially improves the performance of 3D calf muscle compartment segmentation by utilizing FilterNet+ pre-segmentation and new machine-learned cost functions.
II. Methods
II.A. Assisted Annotation
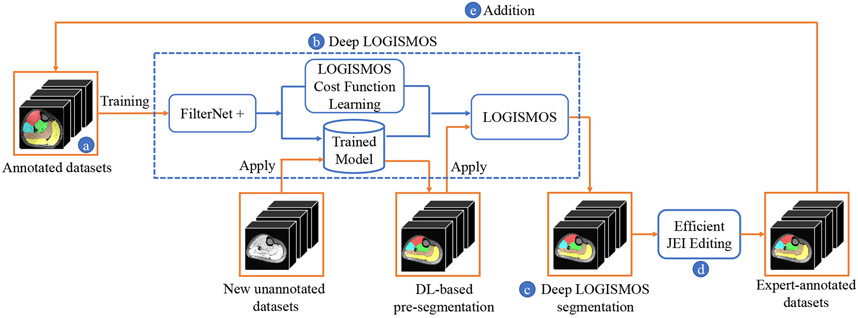
Fig. 2 shows the workflow of our assisted annotation approach that employs the iterative loop to achieve the best use of the existing and efficient way of adding new annotated datasets. This approach a) starts with a small training set, b) uses it to create the initial version of an automated calf segmentation method, c) employs this method to automatically segment additional unannotated images, some of which are likely segmented inaccurately at first. These automated segmentations are d) expert-corrected using Just-Enough-Interaction (JEI) functionality of LOGISMOS18 and combined with the previous training set, thus e) forming a new larger training set of expert-annotated images, which are iteratively used to create next versions of the automated calf segmentation method in step “b”. The assisted annotation steps (“b–e”) are repeated until the desired performance is achieved or all data are annotated.
Figure 2:
Workflow of the proposed Deep LOGISMOS segmentation framework in the scheme of assisted annotation. Processing steps in blue, datasets in orange. (a)–(e) modules correspond to steps given in Section II.A. Best viewed in color.
The process of creating new versions of the automated calf segmentation (step “b” above) relies on the following sub-steps in each iteration of the assisted annotation loop: 1) deep-learning based approximate pre-segmentation of calf muscle compartments; 2) deep-learning based design of LOGISMOS cost functions; 3) design of multi-object JEI for efficient editing of automatically-segmented calf compartments.
II.B. FilterNet+: DL-Based Pre-Segmentation
Pre-processing
The region of interest (ROI) was extracted by cropping data to the region of nonzero values corresponding to left and right legs. Z-score normalization was applied to intensities of all images of individual legs to reduce inter-subject variations. Because of the newly designed large variety of data augmentation and robust training, the bias field correction19 and right-left mirroring processing steps used in16 can be eliminated without performance degradation. All pre-processing steps were completely unsupervised and were automatically carried out without any user intervention.
FilterNet+
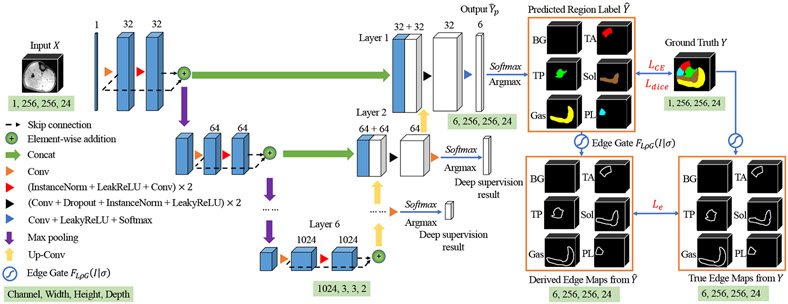
Fig. 3 illustrates the network architecture of FilterNet+. The success of previously reported original FilterNet16 was attributed to the enhancement of neighborhood relationship brought by the increased convolution receptive field, resolution-preserving skip connections and explicitly edge-aware regulation. FilterNet was extended to FilterNet+ by introducing three main novel contributions: 1) Network architecture adaptation to the properties of the calf muscle dataset – the networks was configured with a deeper topology to increase the receptive field size for more effective extraction of contextual information and, due to the initial resolution discrepancy between axes at the input image whose size and spacing is 256 × 256 × 24 and 0.7 × 0.7 × 7 mm respectively, we applied the kernel size of one for convolution and pooling operation along each axis until the feature map spacing became isotropic. As a result, adequate aggregation of spatial and contextual information is guaranteed; 2) Deeply-supervised nets (DSN)20 simultaneously minimize classification errors and improve the directness and transparency of the hidden layer learning process. As shown in Fig. 3, additional deep supervised layers along the expansive path and each deep supervision output are used for loss computation with a corresponding downsampled ground truth. This way, the supervised layers play a supervisory role in the process of training and guide the network to learn more precise residual information at different resolutions; 3) in order to constrain both the regional character and boundary positioning of the segmentation, we designed a new loss function that combines regional loss , multi-class cross-entropy loss , and edge loss during deeply supervised training. Given a network with deeply supervised layers ( in the proposed method), the training objective is to minimize loss across all resolutions:
| (1) |
where is the index number of a deeply supervised layer and is the loss of that layer. The index number increases with the decrease of the resolution and the supervised layer with highest resolution is set as 1 (the final layer in Fig. 3). The loss is designed as:
| (2) |
where , and are the dice similarity loss, multi-class cross-entropy loss and edge gate loss at layer , respectively. is an adjustable weight reflecting the strength of edge-aware regularizations through training and is a non-negative weighting coefficient to balance and . originates from DSC as in21:
| (3) |
where , is the predicted label for class from the softmax output, is one-hot encoding of the ground truth, represents voxels of the foreground in the segmentation map. Note that the ground truth at layer for loss computation is also downsampled correspondingly to match the resolution of the softmax output at that layer. Incorporation of dice loss is beneficial for the model to consider the loss information both locally and globally and as a result, improve the edge continuity between calf muscles. We conducted a line search for the value of the weighting coefficient and was selected as maximizing segmentation performance in validation experiments.
Figure 3:
The basic 3D FilterNet+ architecture. The input is a 256×256×24 3D image patch cropped from the whole 256×512×30 3D pre-processed image of one leg. The size of output is 6×256×256×24. The segmentations are optimized by , cross-entropy and edge constraints . The trainable edge gate learns the muscle compartment boundary-related parameter from and , used later as an image-learned component of the LOGISMOS cost function (Section II.C. and Fig. 4). Best viewed in color.
Edge gate loss is the differences (L1-norm) between the derived edge maps and the true edge maps which are generated by our 2D trainable convolution kernels, edge gate . is a trainable variant of a Laplacian of Gaussian filter (LoG) and can be used as a convolution in the network. It is defined as
| (4) |
where is the input image, and represent Laplacian and Gaussian smoothing operations, respectively, and is the learned parameter of the Gaussian kernel. * is the convolution operation and is a variant of non-linear hard tanh function that restricts the output into range [0, 1]:
| (5) |
The edge gate module was implemented by convolution layers with designed kernels inside the network. In the training process, kernel remains unchanged and kernel is updated with trainable parameter , initially set as 1. The edge gate can effectively extract valuable edge information from predicted region labels and ground truth to derive the edge maps. The edge gate loss is imposed to constrain the edge-based error to enhance the neighborhood relationships of calf muscle compartments and further improve topological correctness of the results. Importantly, the edge gate builds a linkage between Deep Learning and LOGISMOS. The linkage has an effect on the cost function of LOGISMOS to further improve its segmentation accuracy (Section II.C.).
Post-processing
Raw 3D object segmentation produced by the network shows local inaccuracies (small holes, coarse boundaries), which can be easily improved by simple post-processing refinement. Post-processing included two iterations of recursive Gaussian image filter () and hole filling by enforcing single-component connectivity of each segmented calf compartment. The refined FilterNet+ yielded approximate pre-segmentation of calf compartments, the performance of which was evaluated separately and was also further used for initialization and graph construction of the subsequent Deep LOGISMOS steps.
II.C. Deep LOGISMOS
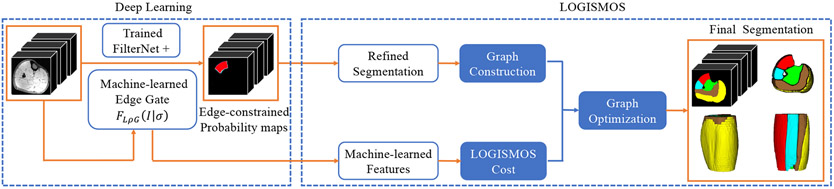
LOGISMOS (Layered Optimal Graph Image Segmentation for Multiple Objects and Surfaces) is a general approach for optimally segmenting multiple -D surfaces that mutually interact within and/or between objects22,23. Like other graph-search-based segmentation methods, the LOGISMOS approach first builds a graph that contains information related to the desired boundaries of the target objects in the input images and then searches the graph for a segmentation solution24. With the DL-based (FilterNet+) pre-segmentation, the remaining key issue is how to capture relevant information about the target object boundaries in a graph and how to search the graph for the optimal surfaces of the target objects. To perform simultaneous multi-compartment 3D segmentation of calf muscles, the main steps of LOGISMOS are: 1) 3D mesh is generated from DL-based pre-segmentation that gives useful information about the topological structures of the target objects and is considered the approximation to the (unknown) surfaces for target object boundaries by probability map thresholding and marching cubes algorithm. The triangulated mesh is computed to specify the structure of the base graph that defines the neighboring relations among voxels on the sought surfaces. 2) A weighted directed graph is built on the vectors of voxels in the image. Each such voxel vector corresponds to a list of nodes in the graph (graph columns) and is normal to the mesh surface at mesh vertices. 3) The cost function for LOGISMOS uses on-surface costs that emulate the unlikeness of the graph node residing on the desired surface. 4) A single multi-object graph is constructed by linking five specific-object subgraphs (each representing one muscle compartment), while incorporating geometric surface constraints and anatomical priors. 5) The graph construction scheme ensures that the sought optimal surfaces correspond to an optimal closed set in the weighted directed graph25 and the optimal solution is found by standard s-t cut algorithms as the closed set of nodes, one node per column, with a globally optimal total cost. Because steps (1, 2, 5) are all generic and the performance of LOGISMOS is mainly determined by steps (3 and 4), in this work, we mainly focus on initializing the graph by using DL-based pre-segmentation that serves as a good target-object shape prior and on designing relevant cost functions that determine accurate optimal surface localization, yielding the overall Deep LOGISMOS approach (Fig. 4).
Figure 4:
Schematic diagram of the Deep LOGISMOS method. Best viewed in color.
Graph construction
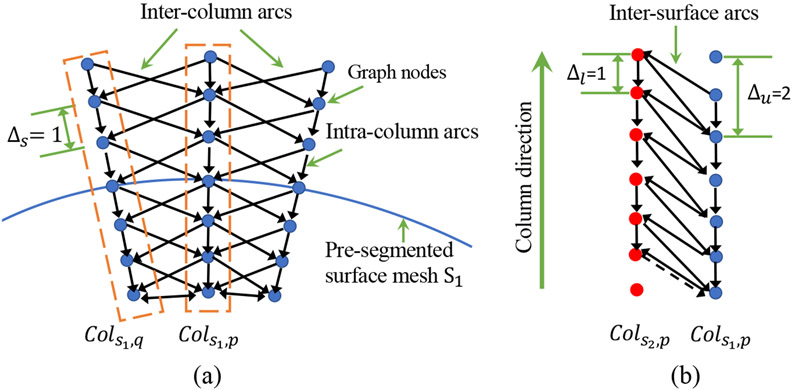
Fig. 5 illustrates the geometric constraints in graph construction of a single object and for two interacting objects. The smoothness constraint defines the maximum allowed difference between node locations in two neighboring columns of the same surface. Smaller causes the surface to be smoother. Surface separation constraints, and , determine the bounds of distances between two surfaces on the corresponding columns. More related work about graph construction can be found in18,22,23. Different from the traditional implementation that relies on interactively defined initial approximate segmentation, we overcame the manual-design limitations by using the FilterNet+ segmentation to initialize LOGISMOS. FilterNet+ pre-segmentation provides approximate segmentation of each calf muscle compartment as 3D mesh surfaces, defines their topology, and mutual relationships. Graph columns are constructed along the directions normal to the mesh surfaces. To incorporate the spatial relationships between muscle compartments as object separation constraints, the column orientations of subgraphs associated with individual compartments are specially designed as shown in Fig. 6(a), where the columns are built from inside to outside for TA and Sol, and outside to inside for TP, Gas and PL. This special orientation scheme utilizes anatomical prior knowledge about the muscle compartments to avoid formation of frustrating cycles26.
Figure 5:
Geometric constraints in graph construction. (a) Inter-column and intra-column arcs link graph nodes from columns built along the column direction through the pre-segmented surface mesh . Each mesh vertex is associated with a column of nodes and and represent the coordinates of the mesh vertices where columns are built. Columns located in the same triangle polygon are neighboring columns. The inter-column arcs are deployed between neighboring columns to enforce surface smoothness constraints . (b) Inter-surface arcs model the separation constraint between the two interacting surfaces and . The column from interacts with from and and restrict the minimum and maximum distances between the surface-connected nodes of the two columns, respectively. Best viewed in color.
Figure 6:
(a) Graph column orientations. (b) The machine-learned edge features by the trained edge gate from the original image. Best viewed in color.
Machine learning cost design
Let the cost of node on column of surface be , the total cost for a given surface function that chooses an on-surface node for each column is . The objective of segmentation is to find the optimal that globally minimizes . Designing appropriate cost functions is crucial for graph-based segmentation methods. The cost function , for each graph node, must reflect the likelihood that the sought target surface passes through that node. Intensity derivatives and inverse of image gradient magnitudes are typical for edge-based cost functions. An advanced version of edge-based cost function27 utilized a combination the first and second derivatives of the image intensity function. These cost functions are commonly human-expert designed and limit the accuracy of the segmentations. Machine learning derived cost functions are better suited for segmentation of objects with complex patterns. Here we used a cost function which is jointly learned from segmentation examples in combination with utilizing the independently learned FilterNet+ parameters. As shown in Fig. 3, the edge gate was trained globally on the predicted labels and the ground truth to derive edge maps which constrain the edge-based error in the loss function (Equation (2)). Since the optimized edge gate can effectively extract the edge-based information under the regional constraint, we adopt the edge features derived on the input calf images by the ultimate edge gate as the machine-learned features in the trained LOGISMOS cost function, i.e., . As shown in Fig. 6(b), the edge features by the trained edge gate effectively highlight the boundaries of multiple compartments of calf muscles. These cost values are then used by the min-cut/max-flow graph optimization algorithms to determine the locations of the optimal surfaces.
Deep LOGISMOS segmentation
The constructed graph in the LOGISMOS system integrates shape prior from the refined FilterNet+ pre-segmentation, object separation constraints, geometric smoothness constraints, and learned costs for each node by the newly machine-learned cost function design, and the globally optimized segmentation is guaranteed by the graph optimization. The final simultaneous segmentation of all 5 calf-muscle compartments is obtained by optimal hyper-surface detection in polynomial time22.
Just-Enough Interaction – Deep LOGISMOS+JEI
Deep LOGISMOS not only generates segmentations that outperform the state-of-the-art DL results, but also provides JEI capability not readily available in DL segmentation. When necessary refinements are needed to adjudicate results of the automated Deep LOGISMOS, JEI can be utilized by experts to guide the graph optimization process and thus efficiently improve the segmentations. The dynamic nature of the underlying algorithm is utilized to edit the segmentation result via interactive modification of local costs. Since JEI modifications, i.e., the user-defined segmentation-surface points and local cost modifications, directly interact with the underlying graph framework, the global optimality for every interaction is guaranteed and existing geometric constraints are still satisfied when handling multiple objects and surfaces. In practice, user interaction on one 2D slice is often enough to correct segmentation errors three-dimensionally in its neighboring 2D slices and thus reduce the amount of human effort. In addition, due to the existence of embedded inter-object constraints, in regions where multiple compartments are close to each other, editing is only needed on one compartment. More details about the design of the JEI architecture are covered in28. LOGISMOS+JEI approaches have been successfully applied in29,30 and are useful in reducing the inter-observer and intra-observer variability.
III. Experimental Methods
III. A. Data
Only 40 lower leg T1-weighted MR images from 40 subjects were initially available (11 healthy, 23 DM1, 2 pre-DM1, 4 Juvenile Onset DM1 or JDM), the same data set as reported in16. Over the course of a longitudinal DM1 study, some of the initial subjects were rescanned and new subjects added, with additional 135 MR images acquired with the same scanning parameters, increasing the annotated set size to 175 images of 350 lower legs from 93 subjects (47 healthy, 35 DM1, 6 Pre-DM1, 5 JDM). MR image size was 512×512×30, voxel size 0.7×0.7×7 mm, acquisition used the first echo of a 3-point Dixon gradient echo sequence, TR=150 ms, TE=3.5 ms, FOV=36 cm, bandwidth 224 Hz/pixel, scan time 156 s.
III.B. Independent standard
The initial set of 40 annotated MR datasets (80 legs) was fully manually traced by experts in 3D Slicer31 and each annotation took approximately 8 hours on average. This set was used for the initial stage of training Deep LOGISMOS to deliver decent automated segmentations of the five calf compartments. The remaining 135 MR datasets were sequentially segmented, their segmentations reviewed and – if needed – interactively corrected by experts using Deep LOGISMOS+JEI (Section II.C.), and served as additional training data used in the assisted annotation training loop (Fig. 2). The average time of reviewing and editing each 3D MR image used in the assisted annotation loop steps was approximately 25 minutes – expert effort decreased by 95%.
III.C. Experimental Setting
Multiple experiments were designed to compare the performance of the proposed method with nnUNet32 (state-of-the-art medical image segmentation framework) and two popular transformer-based approaches (TransUNet and Cotr) to demonstrate the contribution of our new approach. Similarly, to demonstrate the improvements achieved by assisted annotation, we compared performance on differently sized datasets (fully traced or assist-annotated). The following methods were compared, the numeric index specifies the number of training datasets used:
nnUNet_80: The nnUNet32 baseline approach, 40 subjects, 80 legs.
nnUNet_350: The nnUNet baseline approach using the fully-assisted annotation of 93 subjects, 350 legs.
TransUNet_80: The transformer-based TransUNet approach33, 40 subjects, 80 legs,
TransUNet_350: TransUNet approach using the fully-assisted annotation of 93 subjects, 350 legs.
CoTr_80: The transformer-based CoTr approach34, 40 subjects, 80 legs.
CoTr_350: CoTr approach using the fully-assisted annotation of 93 subjects, 350 legs.
FilterNet+_80: FilterNet+ approach, 40 subjects, 80 legs.
FilterNet+_350: FilterNet+ approach using the fully-assisted annotation datasets of 93 subjects, 350 legs.
DeepLOGISMOS_80: Deep LOGISMOS method using FilterNet+_80 results as pre-segmentation.
DeepLOGISMOS_350: Deep LOGISMOS method using FilterNet+_350 results as pre-segmentation.
To further assess the effectiveness of the machine-learned features by the trained edge gate, we compared the proposed method with manually designed traditional cost functions including 2nd image derivatives, Laplacian filter and Sobel edge detection filter.
Given a limited-size dataset, 4-fold cross-validation was used to evaluate the performance of each tested approach with the 4 groups created randomly at the subject level so that data (legs) from the same subject were never simultaneously used for both training and testing. That means that for a dataset of 80 (350) legs, training was based on 60 (262) legs and testing was done in 20 (88) legs, repeated 4 times.
Each image segmentation method design uses specific parameters that influence its behavior. In all tests, the same parameters were used in the corresponding steps of each method. In FilterNet+, to increase the robustness and generalization of the network, resizing and small patching are avoided. The input image patches have the same size (256×256×24) as the cropped ROI from the localized one-leg-area. A larger variety of data augmentation techniques including scaling, mirror, rotations, elastic deformation, multiple Gaussian operations, etc. are randomly applied to boost the training and prevent overfitting.
FilterNet+ training loss parameter was initially set as 0.001 and increased ten fold every 10 epochs, the batch size was 4. The initial learning rate of the Adam optimizer was 3 × 10−4. Training of FilterNet+ was improved by introducing the widely used strategies including dropout35, Kaiming initialization36 and Adam optimizer37,38. The learning rate was reduced by 5 when the monitored exponential moving average of the training loss stopped improving in 20 consecutive training epochs. To increase the robustness of the network predictions, in the inference steps, one image was mirrored along all valid axes in 3D space and the segmentation result was obtained by averaging all corresponding outputs from the 8 networks. FilterNet+ was implemented using PyTorch platform39 and trained on Nvidia Tesla V100 GPU with 32 GB memory. LOGISMOS graph columns consisted of 17 nodes spaced 0.35 mm apart. LOGISMOS smoothness constraints were set as 2 node-to-node distances, corresponding to 0.7 mm.
III.D. Quantitative Analysis
To comprehensively evaluate the segmentation performance and allow method-to-method comparisons, DSC and Jaccard Similarity Coefficient (JSC) evaluated region-based accuracy, absolute surface-to-surface distance (ASSD, in pixels) and relative surface-to-surface distance (RSSD, in pixels) assessed boundary-based accuracy. ASSD and RSSD measure the distances between the surface of the automated segmentation and the independent standard. Because of the order-of-magnitude difference between the XY plane in-slice resolution (0.7 mm) and the Z plane slice distance (7 mm), the surface-to-surface distances were calculated on the XY planes slice-by-slice. To allow meaningful comparisons, scores for ASSD and RSSD were calculated as
| (6) |
where is an application-specific parameter empirically chosen as 1.111 to reach approximate linearity and maximum score of 1.0 when the two surfaces match (at zero distance). Given the four indices: DSC, JSC, , and , the final comprehensive score was defined as
| (7) |
Higher indicates better comprehensive performance in the combined regional and boundary-positioning respect. Additionally, , was evaluated as the 95th percentile of the absolute distance between two surfaces of each compartment. Performance indices were averaged for left and right calf muscle compartments and reported as mean±standard deviation. For statistical comparisons between methods, paired t-tests were used, p value < 0.05 denoted statistical significance.
IV. Results
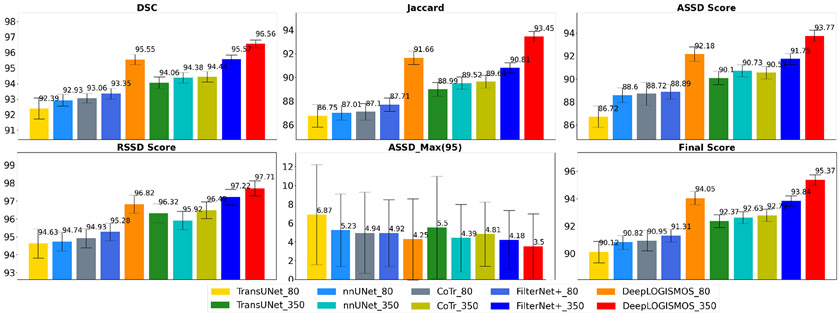
The performance comparisons of the ten tested methods are listed in Table 1 and also visualized in Fig. 7. Compared with nnUNet framework, FilterNet+ achieved significantly better results in terms of DSC, JSC, ASSD, RSSD, , as well as the comprehensive . Compared to FilterNet+_80, DeepLOGISMOS_80 offered yet additional tremendous improvement of all indices with statistical significance. In particular, ASSD and RSSD segmentation quality scores increased substantially after the LOGISMOS steps resulting in improved values of . On the 350-leg (93-subject) dataset obtained by assisted annotation, both the FilterNet+_350 and DeepLOGISMOS_350 outperformed the methods using 80-leg dataset while the advantages of FilterNet+ compared to nnUNet diminished. Notably, DeepLOGISMOS_80 was superior to all methods using the 350-leg dataset except for the DeepLOGISMOS_350. The performance increase with the smaller dataset attests to the effectiveness of our proposed DeepLOGISMOS method. Similarly, compared to Filter-Net+350 alone, DeepLOGISMOS_350 demonstrated overall improvements with consistent statistically significant differences. The 95th percentile of the ASSD values (), representing the locally most severe segmentation inaccuracies, also decreases significantly for all 5 segmented muscle compartments.
Table 1:
Evaluation indices for five calf muscle compartments from different segmentation methods and training datasets. * and ** denote results of paired t-tests vs. nnUNet_80, and nnUNet_350, respectively. See Section III.C. for details of the compared methods. Bolded values represent statistically significant improvements in comparison with the compared approaches.
| TransUNet_80 |
nnUNet_80 |
CoTr_80 |
FilterNet+_80 |
DeepLOGISMOS_80 |
|||||
|---|---|---|---|---|---|---|---|---|---|
| Mean±STD | p value* | Mean±STD | Mean±STD | p value* | Mean±STD | p value* | Mean±STD | p value* | |
| DSC (%) | 92.39±0.68 | ≪0.001 | 92.93±0.38 | 93.06±0.30 | ≪0.001 | 93.35±0.34 | 0.124 | 95.55±0.34 | ≪0.001 |
| Jaccard (%) | 86.75±0.96 | ≪0.001 | 87.01±0.62 | 87.1±0.69 | ≪0.001 | 87.71±0.56 | 0.115 | 91.66±0.57 | ≪0.001 |
| ASSD (pixel) | 1.50±1.38 | ≪0.001 | 1.18±0.78 | 1.15±1.36 | ≪0.001 | 1.15±0.77 | 0.579 | 0.80 ±0.75 | ≪0.001 |
| ASSD Score | 86.72±0.93 | ≪0.001 | 88.60±0.64 | 88.72±1.01 | ≪0.001 | 88.89±0.63 | 0.534 | 92.18±0.63 | ≪0.001 |
| RSSD (pixel) | 0.35±1.27 | ≪0.001 | −0.09±0.78 | 0.16±0.79 | ≪0.001 | −0.13±0.71 | 0.361 | 0.14±0.64 | ≪0.001 |
| RSSD Score | 94.63±0.81 | 0.02 | 94.74±0.53 | 94.93±0.53 | 0.008 | 95.28±0.49 | 0.135 | 96.83±0.50 | ≪0.001 |
| ASSDmax95 | 6.87±5.33 | ≪0.001 | 5.23±3.87 | 4.94±4.32 | ≪0.001 | 4.92±3.87 | 0.244 | 4.25±4.33 | ≪0.001 |
| Final Score | 90.12±0.78 | ≪0.001 | 90.82±0.50 | 90.95±0.75 | ≪0.001 | 91.31±0.47 | 0.178 | 94.05±0.48 | ≪0.001 |
| TransUNet_350 |
nnUNet_350 |
CoTr_350 |
FilterNet+_350 |
DeepLOGISMOS_350 |
|||||
| Mean±STD | p value** | Mean±STD | Mean±STD | p value** | Mean±STD | p value* | *Mean±STD | p value** | |
| DSC (%) | 94.06±0.37 | 0.007 | 94.38±0.34 | 94.44±0.35 | 0.60 | 95.57±0.27 | 0.050 | 96.56±0.26 | ≪0.001 |
| Jaccard (%) | 88.99±0.58 | 0.003 | 89.52±0.51 | 89.64±0.55 | 0.48 | 90.81±0.44 | 0.051 | 93.45±0.43 | ≪0.001 |
| ASSD (pixel) | 1.02±0.75 | 0.006 | 0.95 ±0.78 | 0.96±0.63 | 0.61 | 0.94 ±0.64 | 0.708 | 0.63 ±0.62 | ≪0.001 |
| ASSD Score | 90.10±0.59 | ≪0.001 | 90.73±0.53 | 90.57±0.54 | 0.35 | 91.75±0.48 | 0.909 | 93.77±0.48 | ≪0.001 |
| RSSD (pixel) | 0.14±0.70 | ≪0.001 | −0.13±0.81 | 0.16±0.60 | ≪0.001 | −0.19±0.63 | 0.014 | 0.07±0.58 | ≪0.001 |
| RSSD Score | 96.32±0.52 | 0.017 | 95.92±0.52 | 96.49±0.47 | ≪0.001 | 97.22±0.43 | 0.051 | 97.71±0.42 | ≪0.001 |
| ASSDmax95 | 5.50±5.46 | ≪0.001 | 4.39±3.57 | 4.81±3.42 | ≪0.001 | 4.18±3.15 | 0.049 | 3.50±3.46 | ≪0.001 |
| Final Score | 92.37±0.48 | 0.07 | 92.63±0.43 | 92.79±0.45 | 0.29 | 93.84±0.37 | 0.121 | 95.37±0.38 | ≪0.001 |
Figure 7:
Performance comparison for the segmentation of five calf muscle compartments from different experiments. Best viewed in color.
Table 2 shows the performance comparison between different cost functions in Deep LOGISMOS. Deep LOGISMOS using the machine-learned features by the trained edge gate outperformed other approaches that combined deep learning pre-segmentation and LOGISMOS with manually designed cost functions.
Table 2:
Evaluation indices for five calf muscle compartments from different cost functions in Deep LOGISMOS and training datasets. * and ** denote results of paired t-tests vs. EdgeGate_80, and EdgeGate_350, respectively. Bolded values represent statistically significant improvements in comparison with the compared approaches.
| Sobel_80 |
Laplacian_80 |
2nd Derivative_80 |
EdgeGate_80 |
||||
|---|---|---|---|---|---|---|---|
| Mean±STD | p value* | Mean±STD | p value* | Mean±STD | p value* | Mean±STD | |
| DSC (%) | 91.71±0.35 | ≪0.001 | 93.93±0.34 | ≪0.001 | 94.10±0.36 | ≪0.001 | 95.55±0.34 |
| Jaccard (%) | 84.86±0.55 | ≪0.001 | 88.75±0.57 | ≪0.001 | 89.06±0.60 | ≪0.001 | 91.66±0.57 |
| ASSD (pixel) | 1.39±0.76 | ≪0.001 | 1.10±0.74 | ≪0.001 | 1.04±0.78 | ≪0.001 | 0.80 ±0.75 |
| ASSD Score | 86.61±0.59 | ≪0.001 | 89.29±0.60 | ≪0.001 | 89.90±0.64 | ≪0.001 | 92.18±0.63 |
| RSSD (pixel) | −0.35±0.83 | ≪0.001 | 0.41±0.64 | ≪0.001 | 0.13±0.68 | 0.0367 | 0.14±0.64 |
| RSSD Score | 93.12±0.50 | ≪0.001 | 95.09±0.51 | ≪0.001 | 96.15±0.51 | 0.07 | 96.83±0.50 |
| ASSDmax95 | 4.54±3.42 | 0.27 | 5.11±3.86 | 0.0015 | 5.15±3.72 | ≪0.001 | 4.25±4.33 |
| Final Score | 89.08±0.45 | ≪0.001 | 91.76±0.46 | ≪0.001 | 92.3±0.50 | ≪0.001 | 94.05±0.48 |
| Sobel_350 |
Laplacian_350 |
2nd Derivative_350 |
EdgeGate_350 |
||||
| Mean±STD | p value** | Mean±STD | p value** | Mean±STD | p value** | Mean±STD | |
| DSC (%) | 94.06±0.37 | 0.007 | 95.53±0.27 | ≪0.001 | 95.69±0.28 | ≪0.001 | 96.56±0.26 |
| Jaccard (%) | 88.99±0.58 | 0.003 | 91.15±0.44 | ≪0.001 | 91.45±0.47 | ≪0.001 | 93.45±0.43 |
| ASSD (pixel) | 1.02±0.75 | 0.006 | 0.92 ±0.62 | ≪0.001 | 0.86±0.65 | ≪0.001 | 0.63 ±0.62 |
| ASSD Score | 90.10±0.59 | ≪0.001 | 91.45±0.48 | ≪0.001 | 92.00±0.51 | ≪0.001 | 93.77±0.48 |
| RSSD (pixel) | 0.14±0.70 | ≪0.001 | 0.34±0.60 | ≪0.001 | −0.021±0.63 | ≪0.001 | 0.07±0.58 |
| RSSD Score | 96.32±0.52 | 0.017 | 96.42±0.44 | ≪0.001 | 97.40±0.44 | ≪0.001 | 97.71±0.42 |
| ASSDmax95 | 5.50±5.46 | ≪0.001 | 4.38±3.25 | ≪0.001 | 4.46±3.22 | ≪0.001 | 3.50±3.46 |
| Final Score | 92.37±0.48 | 0.07 | 93.64±0.38 | ≪0.001 | 94.14±0.40 | ≪0.001 | 95.37±0.38 |
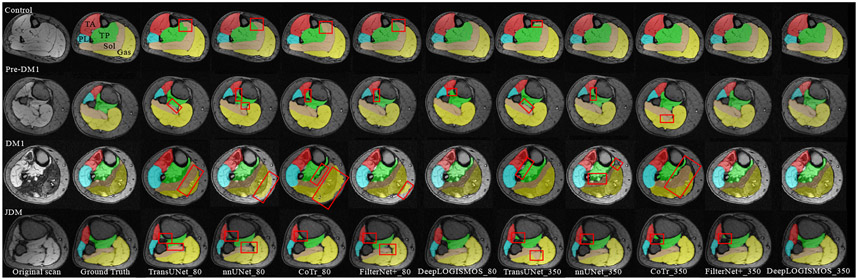
Fig. 8 displays four cross-sectional segmentation examples from images of four subjects – healthy control, Pre-DM1, DM1, and JDM. The comparisons show that the most advanced DeepLOGISMOS_350 avoids almost all of the segmentation inaccuracies present in the results of the other methods.
Figure 8:
Examples of segmentation overlaid with MR images. Each row shows a representative 2D cross-sectional slice from images of subjects with a given status (healthy/diseased). The red rectangles highlight regions with segmentation errors. In the control subject, the incorrect segmentation between TP and Sol in nnUNet_80 is mostly alleviated in FilterNet+_80 and corrected in DeepLOGISMOS_80. In the Pre-DM1 example, the shrunk TP segmentation in FilterNet+_80 is guided by DeepLOGISMOS_80 to the correct position at the boundaries. In the severe DM1 case, the infiltrates of Gas into the subcutaneous adipose tissue visible for both nnUNet and FilterNet+ methods is solved by the Deep LOGISMOS method. Similarly, in the JDM case, disconnected TP by FilterNet+ method is substantially alleviated by Deep LOGISMOS. Throughout all the examples, segmentation improvements are noticeable for each more advanced method from the nnUNet to Deep LOGISMOS methods in the same dataset, for which muscle compartments segmented are increasingly better agreeing with the ground truth. In the DM1 and JDM case, DeepLOGISMOS_80 even outperforms nnUNet_350 and FilterNet+_350. Best viewed in color.
Table 3 gives the average inference times for a typical 512×512×30 sized MR image by different methods. The high efficiency of Deep LOGISMOS+JEI utilizing assisted annotation suggests its high clinical-use potential. Importantly, since graph s-t cut optimization can be applied iteratively without restarting the optimization process from scratch, each JEI interaction used to regionally modify the respective local/regional graph costs generates new graph optimization solution iteratively and very efficiently in close-to-real time. The whole pipeline helps experts decrease time required to carefully 3D-annotate all 5 calf-muscle compartments on a volumetric MR image from 8 hours to 25 minutes.
Table 3:
Average inference times for a 512 × 512 × 30 sized MR image.
| Method | TransUNet | nnUNet | CoTr | FilterNet+ | Deep LOGISMOS |
|---|---|---|---|---|---|
| Time (s) | 10.80 | 3.14 | 13.64 | 4.69 | 11.83 |
V. Discussion
V.A. Ablation Study
Table 1 and Fig. 7 show the superiority of our deep learning method in comparison with the nnUNet method and the transformer-based methods. In agreement with the ablation study principles, the results are methodically ordered from the state-of-the-art results from the nnUNet framework, then introducing improvement in the FilterNet+_80 approach, combining FilterNet+ with LOGISMOS optimization, and finally proceeding further to employing assisted annotation to increase the training sizes in FilterNet+_350 and DeepLOGISMOS_350 approaches. Fig. 8 demonstrates that segmentation inaccuracies in the nnUNet method tend to be alleviated in FilterNet+. Deep LOGISMOS segmentations exhibit additional increases in accuracy, surface smoothness, and topologic superiority as shown in Fig. 8. For the DM1 subject, while the Gas compartment segmented by FilterNet+_80 still spreads into the surrounding tissue, this problem is resolved by DeepLOGISMOS_80 due to the addition of machine-learned features in the cost function (Section II.C.). Similarly, benefiting from LOGISMOS graph optimization, the disjoint TP segmentation in the JDM subject by FilterNet+ is corrected by the Deep LOGISMOS approach. Two main reasons may be causing the performance difference between TransUNet and Deep LOGISMOS: 1) Transformer-based methods usually require much more data than pure CNN models to achieve good accuracy, and 2) TransUNet encodes tokenized image patches by CNN layers and extracts global context from the input sequence of CNN feature map via the usage of Transformer – compared to the original U-Net model, low-level fine-grained details could be insufficient due to only a few layers of CNN if the model is not pre-trained well; in such a case, localization capabilities of the transformer frame and segmentation capabilities of the CNN layers may be limited and thus yield lower performance.
Table 2 assesses the effectiveness of the machine-learned features by the trained edge gate in LOGISMOS and shows that the three manually designed cost functions achieve different performance levels. FilterNet+ performance would degrade if the subsequent LOGISMOS used Sobel edge detector as its cost function, while employing the Laplacian filter would keep the performance at the same level. Although utilizing 2nd intensity derivatives of the image as the cost function improves FilterNet+ results, it is still outperformed by employing the edge gate. Obviously, the machine-learned derived cost functions are better suited for segmentation of objects with complex pattern.
The improvements of the observed segmentations are partly due to the creation of the larger dataset of 350 samples by manually refining (JEI) segmentation results of the dataset of 80 samples. The superiority of training on a larger dataset, indicating the effectiveness of assisted annotation, is further shown in FilterNet+_350 and DeepLOGISMOS_350 (Table 1, Fig. 7). LOGISMOS+JEI based assisted annotation, in the process of providing larger training datasets, dramatically reduces the annotation effort of human experts. In all four examples in Fig. 8, most of the errors in the earlier segmentation approaches are successfully resolved by FilterNet+_350 and DeepLOGISMOS_350.
V.B. Generalizability of combining Deep LOGISMOS and assisted annotation
The power of our work in combining deep learning pre-segmentation and graph-optimality seeking Deep LOGISMOS trained on data produced by efficient assisted annotation was demonstrated in the case of segmenting human calf muscle compartments on MRI. The combination of DL and LOGISMOS is not simply using the output of DL pre-segmentation as the input to LOGISMOS. DL and LOGISMOS have complementary roles. DL achieves state-of-the-art medical image pre-segmentation. LOGISMOS+JEI (graph-based method) achieves globally optimal solution that allows to efficiently refine segmentation results if needed. LOGISMOS itself lacks a good way to to guide the necessary graph construction and cost function design steps – it requires reasonable initialization. Therefore, the proposed Deep LOGISMOS combines the strengths and interlinks the two components as follows. 1) DL pre-segmentation provides useful topology and shape information for graph construction in LOGISMOS. 2) The machine-learned edge gate not only improves the accuracy of pure DL results but also impacts the cost function of LOGISMOS to further improve the LOGISMOS segmentation accuracy. As a result, globally optimal results are obtained effectively. 3) LOGISMOS provides JEI capability to optionally adjudicate segmentation results in close-to-real time. The overall performance of Deep LOGISMOS is improved compared to sole DL approaches.
Alternatively, other deep convolutional neural network architectures can be integrated into the Deep LOGISMOS framework to utilize information linkages between deep learning and graph optimization. Further strengthened by the inherently incorporated Deep LOGISMOS+JEI based assisted annotation (Fig. 2), its effectiveness and efficiency in reducing the annotation effort and optimizing the segmentation model are clearly visible from the achieved segmentation improvements (Section IV.). Note of course, that detailed understanding of LOGISMOS is not necessary to appreciate this work and the Deep LOGISMOS+JEI method used here for assisted annotation is not the only one applicable. The idea of training-segmentation-annotation iterative epochs can be generically incorporated into supervised learning methods or one can elect to employ suggested annotation approaches40. Given this inherent generalizability of Deep LOGISMOS and the assisted annotation paradigm, these strategies can be further integrated and the machine-learned deep segmentation features and the machine-learned LOGISMOS cost functions applied to various segmentation tasks to benefit both the segmentation processes and those leading to assisted annotations.
V.C. Future work
Although we showed that assisted annotation helps experts reduce the effort of manual tracing substantially (from 8 hours to 25 minutes per 3D image), the total time and effort of reviewing and editing a large dataset can not be neglected either. There are two promising directions to further relieve the annotation effort problem: active learning41 and quality assessment without ground truth. The approach of quality assessment without the ground truth focuses on further reducing the human effort in searching for small segmentation errors in a large 3D image by automatically locating likely segmentation errors on the volumetrically visualized object surfaces. Afterward, the identified likely-erroneous locations can be used as feedback to guide the network to prevent similar errors. As a result, the time of reviewing and editing the segmentations to produce new annotations can be significantly reduced. Sample-Incremental-Learning (SIL) can become a promising direction for large datasets and limited computation resources because SIL would help the models balance old and new data without retraining on all samples. Furthermore, due to the complementary advantages of DL and graph-based methods, potential interactions between the two components could be considered to additionally benefit the optimization process.
VI. Conclusion
A hybrid framework combining the main advantages of our convolutional neural network FilterNet+ with those of our graph-based LOGISMOS approach, further supported by Deep LOGISMOS+JEI assisted annotation, was reported. The presented comparative performance assessment demonstrated an improved performance obtained during simultaneous multi-compartment 3D segmentation of calf muscle compartments on 3D MRI. By maximizing the value of an original small dataset of fully annotated MR images of 80 lower legs, and by initially training a Deep LOGISMOS segmentation method on this small dataset, we have designed and employed an efficient assisted annotation strategy that decreased the average annotation time required to 3D-annotate 5 calf-muscle compartments on a volumetric 512×512×30 MR image from 8 hours to 25 minutes – a 95% reduction of human expert effort. Our Deep LOGISMOS method trained on a larger dataset of 350 assisted-annotated legs then outperformed all other tested deep learning and graph-optimization approaches in the region-based voxel labeling, boundary-based surface positioning, and the final comprehensive performance score. The experimental results showed an average Dice similarity coefficient (DSC) of 96.56 ± 0.26% and an average absolute surface positioning error of 0.63 pixels (0.44 mm) for the five 3D muscle compartments for each leg. These results significantly improve our previously reported method and outperform the state-of-the-art nnUNet method. The notable performance improvements suggest the clinical-use potential of our new fully automated simultaneous segmentation of calf muscle compartments.
Acknowledgment
This work was supported in part by the NIH grants R01EB004640 and R01-NS094387, and S10-OD025025. Eric Axelson’s contributions to data preparation and management are gratefully acknowledged.
Footnotes
Conflict of Interest
The authors have no relevant conflict of interest to disclose.
References
- 1.Yaman A, Ozturk C, Huijing PA, and Yucesoy CA, Magnetic resonance imaging assessment of mechanical interactions between human lower leg muscles in vivo, Journal of biomechanical engineering 135 (2013). [DOI] [PubMed] [Google Scholar]
- 2.Ranum LP and Day JW, Myotonic dystrophy: clinical and molecular parallels between myotonic dystrophy type 1 and type 2, Current neurology and neuroscience reports 2, 465–470 (2002). [DOI] [PubMed] [Google Scholar]
- 3.Wattjes MP, Kley RA, and Fischer D, Neuromuscular imaging in inherited muscle diseases, European radiology 20, 2447–2460 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ogier AC, Hostin M-A, Bellemare M-E, and Bendahan D, Overview of MR Image Segmentation Strategies in Neuromuscular Disorders, Frontiers in Neurology 12, 255 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Heskamp L, van Nimwegen M, Ploegmakers MJ, Bassez G, Deux J-F, Cumming SA, Monckton DG, van Engelen BG, and Heerschap A, Lower extremity muscle pathology in myotonic dystrophy type 1 assessed by quantitative MRI, Neurology 92, e2803–e2814 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Maggi L et al. , Quantitative muscle MRI protocol as possible biomarker in Becker muscular dystrophy, Clinical neuroradiology , 1–10 (2020). [DOI] [PubMed] [Google Scholar]
- 7.Valentinitsch A, Karampinos DC, Alizai H, Subburaj K, Kumar D, Link TM, and Majumdar S, Automated unsupervised multi-parametric classification of adipose tissue depots in skeletal muscle, Journal of Magnetic Resonance Imaging 37, 917–927 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yao J, Kovacs W, Hsieh N, Liu C-Y, and Summers RM, Holistic segmentation of intermuscular adipose tissues on thigh MRI, in International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 737–745, Springer, 2017. [Google Scholar]
- 9.Amer R, Nassar J, Bendahan D, Greenspan H, and Ben-Eliezer N, Automatic segmentation of muscle tissue and inter-muscular fat in thigh and calf MRI images, in International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 219–227, Springer, 2019. [Google Scholar]
- 10.Alizai H, Nardo L, Karampinos DC, Joseph GB, Yap SP, Baum T, Krug R, Majumdar S, and Link TM, Comparison of clinical semi-quantitative assessment of muscle fat infiltration with quantitative assessment using chemical shift-based water/fat separation in MR studies of the calf of post-menopausal women, European radiology 22, 1592–1600 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kornblum C, Lutterbey G, Bogdanow M, Kesper K, Schild H, Schr”oder R, and Wattjes MP, Distinct neuromuscular phenotypes in myotonic dystrophy types 1 and 2, Journal of neurology 253, 753–761 (2006). [DOI] [PubMed] [Google Scholar]
- 12.van der Plas E, Gutmann L, Thedens D, Shields RK, Langbehn K, Guo Z, Sonka M, and Nopoulos P, Quantitative muscle MRI as a sensitive marker of early muscle pathology in myotonic dystrophy type 1, Muscle & Nerve 63, 553–562 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ghosh S, Ray N, and Boulanger P , A structured deep-learning based approach for the automated segmentation of human leg muscle from 3D MRI, in 2017 14th Conference on Computer and Robot Vision (CRV), pages 117–123, IEEE, 2017. [Google Scholar]
- 14.Hiasa Y, Otake Y, Takao M, Ogawa T, Sugano N, and Sato Y, Automated muscle segmentation from clinical CT using Bayesian U-net for personalized musculoskeletal modeling, IEEE transactions on medical imaging 39, 1030–1040 (2019). [DOI] [PubMed] [Google Scholar]
- 15.Wong CK et al. , Training CNN Classifiers for Semantic Segmentation using Partially Annotated Images: with Application on Human Thigh and Calf MRI, arXiv preprint arXiv:2008.07030 (2020). [Google Scholar]
- 16.Guo Z, Zhang H, Chen Z, van der Plas E, Gutmann L, Thedens D, Nopoulos P, and Sonka M, Fully automated 3D segmentation of MR-imaged calf muscle compartments: neighborhood relationship enhanced fully convolutional network, Computerized Medical Imaging and Graphics 87, 101835 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.”Çiçek O, Abdulkadir A, Lienkamp SS, Brox T, and Ronneberger O, 3D U-Net: learning dense volumetric segmentation from sparse annotation, in International conference on medical image computing and computer-assisted intervention, pages 424–432, Springer, 2016. [Google Scholar]
- 18.Zhang H, Lee K, Chen Z, Kashyap S, and Sonka M, LOGISMOS-JEI: Segmentation using optimal graph search and just-enough interaction, in Handbook of Medical Image Computing and Computer Assisted Intervention, pages 249–272, Elsevier, 2020. [Google Scholar]
- 19.Tustison N and Gee J, N4ITK: Nick’s N3 ITK implementation for MRI bias field correction, Insight Journal 9 (2009). [Google Scholar]
- 20.Lee C-Y, Xie S, Gallagher P, Zhang Z, and Tu Z, Deeply-supervised nets, in Artificial intelligence and statistics, pages 562–570, PMLR, 2015. [Google Scholar]
- 21.Drozdzal M, Vorontsov E, Chartrand G, Kadoury S, and Pal C, The importance of skip connections in biomedical image segmentation, in Deep learning and data labeling for medical applications, pages 179–187, Springer, 2016. [Google Scholar]
- 22.Li K, Wu X, Chen DZ, and Sonka M, Optimal surface segmentation in volumetric images – a graph-theoretic approach, IEEE transactions on pattern analysis and machine intelligence 28, 119–134 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yin Y, Zhang X, Williams R, Wu X, Anderson DD, and Sonka M, LOGISMOS – layered optimal graph image segmentation of multiple objects and surfaces: cartilage segmentation in the knee joint, IEEE transactions on medical imaging 29, 2023–2037 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Oguz I, Bogunovi’c H, Kashyap S, Abr‘amoff M, Wu X, and Sonka M, LOGISMOS: A Family of Graph-Based Optimal Image segmentation methods, in Medical Image Recognition, Segmentation and Parsing, pages 179–208, Elsevier, 2016. [Google Scholar]
- 25.Wu X and Chen DZ, Optimal net surface problems with applications, in International Colloquium on Automata, Languages, and Programming, pages 1029–1042, Springer, 2002. [Google Scholar]
- 26.Delong A and Boykov Y, Globally optimal segmentation of multi-region objects, in 2009 IEEE 12th International Conference on Computer Vision, pages 285–292, IEEE, 2009. [Google Scholar]
- 27.Sonka M, Reddy GK, Winniford MD, and Collins SM, Adaptive approach to accurate analysis of small-diameter vessels in cineangiograms, IEEE transactions on medical imaging 16, 87–95 (1997). [DOI] [PubMed] [Google Scholar]
- 28.Zhang H, Kashyap S, Wahle A, and Sonka M, Highly modular multi-platform development environment for automated segmentation and just enough interaction, in MICCAI IMIC workshop, 2016. [Google Scholar]
- 29.Kashyap S, Oguz I, Zhang H, and Sonka M, Automated segmentation of knee MRI using hierarchical classifiers and just enough interaction based learning: data from osteoarthritis initiative, in International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 344–351, Springer, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kashyap S, Zhang H, Rao K, and Sonka M, Learning-based cost functions for 3-D and 4-D multi-surface multi-object segmentation of knee MRI: Data from the Osteoarthritis Initiative, IEEE Transactions on Medical Imaging 37 (5), 1103–1113, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fedorov A et al. , 3D Slicer as an image computing platform for the Quantitative Imaging Network, Magnetic resonance imaging 30, 1323–1341 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Isensee F et al. , nnU-Net: Self-adapting framework for U-Net-based medical image segmentation, arXiv preprint arXiv:1809.10486 (2018). [Google Scholar]
- 33.Chen J, Lu Y, Yu Q, Luo X, Adeli E, Wang Y, Lu L, Yuille AL, and Zhou Y, Transunet: Transformers make strong encoders for medical image segmentation, arXiv preprint arXiv:2102.04306 (2021). [Google Scholar]
- 34.Xie Y, Zhang J, Shen C, and Xia Y, Cotr: Efficiently bridging cnn and transformer for 3d medical image segmentation, in International conference on medical image computing and computer-assisted intervention, pages 171–180, Springer, 2021. [Google Scholar]
- 35.Srivastava N, Hinton G, Krizhevsky A, Sutskever I, and Salakhutdinov R, Dropout: a simple way to prevent neural networks from overfitting, The journal of machine learning research 15, 1929–1958 (2014). [Google Scholar]
- 36.He K, Zhang X, Ren S, and Sun J, Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification, in Proceedings of the IEEE international conference on computer vision, pages 1026–1034, 2015. [Google Scholar]
- 37.Kingma DP and Ba J, Adam: A method for stochastic optimization, arXiv preprint arXiv:1412.6980 (2014). [Google Scholar]
- 38.Bottou L, Large-scale machine learning with stochastic gradient descent, in Proceedings of COMPSTAT’2010, pages 177–186, Springer, 2010. [Google Scholar]
- 39.Paszke A, Gross S, Chintala S, Chanan G, Yang E, DeVito Z, Lin Z, Desmaison A, Antiga L, and Lerer A, Automatic differentiation in PyTorch, (2017). [Google Scholar]
- 40.Yang L, Zhang Y, Chen J, Zhang S, and Chen DZ, Suggestive annotation: A deep active learning framework for biomedical image segmentation, in International conference on medical image computing and computer-assisted intervention, pages 399–407, Springer, 2017. [Google Scholar]
- 41.Cohn DA, Ghahramani Z, and Jordan MI, Active learning with statistical models, Journal of artificial intelligence research 4, 129–145 (1996). [Google Scholar]