Abstract
Purpose:
To develop a unified deep-learning framework by combining an ultrafast Bloch simulator and a semisolid macromolecular magnetization transfer contrast (MTC)-MRF reconstruction for estimation of MTC effects.
Methods:
The Bloch simulator and MRF reconstruction architectures were designed with recurrent neural networks (RNN) and convolutional neural networks (CNN), evaluated with numerical phantoms with known ground-truths and cross-linked BSA phantoms, and demonstrated in the brain of healthy volunteers at 3T. In addition, the inherent MT ratio asymmetry effect was evaluated in MTC-MRF, chemical exchange saturation transfer (CEST), and relayed nuclear Overhauser enhancement (rNOE) imaging. A test-retest study was performed to evaluate the repeatability of MTC parameters, CEST, and rNOE signals estimated by the unified deep-learning framework.
Results:
Compared to a conventional Bloch simulation, the deep Bloch simulator for generation of the MTC-MRF dictionary or a training dataset reduced the computation time by 181-fold, without compromising MRF profile accuracy. The RNN-based MRF reconstruction outperformed existing methods in terms of reconstruction accuracy and noise robustness. Using the proposed MTC-MRF framework, for tissue parameter quantification, the test-retest study showed a high degree of repeatability in which the coefficients of variance were less than 7% for all tissue parameters.
Conclusion:
Bloch simulator-driven, deep-learning MTC-MRF can provide robust and repeatable multiple-tissue parameter quantification in a clinically feasible scan time on a 3T scanner.
Keywords: Deep-learning, MR fingerprinting, semisolid MT, CEST, APT, rNOE
1. INTRODUCTION
Saturation transfer (ST) MRI provides unique and flexible contrast mechanisms, including semisolid magnetization transfer contrast (MTC) and chemical exchange saturation transfer (CEST), which enable indirect detection of MR-invisible protons bound to macromolecules (e.g., semisolid proteins and lipid bilayers of myelin) or water-exchangeable solute protons (e.g., mobile proteins and peptides), respectively (1–4). MTC imaging is highly sensitive to demyelination, inflammation, and edema and has shown promise for evaluating white matter diseases, such as multiple sclerosis and traumatic brain injury (5–7). However, MTC measured by a conventional MT ratio (MTR) metric has a dependence on multiple parameters, including semisolid proton concentration, average exchange rate of bound water and exchangeable protons, and free water relaxation properties (8–10). In addition, the ratio is affected by imaging scan parameters, such as RF irradiation frequency, saturation field strength, and duration. To improve the specificity and reproducibility of MTC, quantitative MT imaging analysis procedures have been used to estimate intrinsic tissue properties that are independent of the choice of acquisition parameters, most commonly by fitting acquired MTC-weighted images to a biophysical two-pool exchange model (3, 11–13). However, the fitting-based approach is often computationally intensive, susceptible to being stuck at local minima, and dependent on the number of fitting parameters, initial fitting values, and boundary conditions, often leading to poor quantification accuracy and computational efficiency.
While MTC has a broad absorption line-shape of the semisolid macromolecule-bound protons over a wide range of frequencies, CEST contrast is based on RF irradiation applied at a frequency offset specific for certain exchangeable protons. Amide proton transfer (APT) is one type of CEST contrast for a large group of amide protons (-NH) with an average chemical shift of about 3.5 ppm downfield from water. APT-weighted MRI has shown great potential in the diagnosis of many pathologies, such as cancer, stroke, and neurodegenerative disease (14–29). When applying RF saturation at 3.5 ppm for APT imaging, however, free bulk water and semisolid macromolecular protons may also be saturated due to overlap in the chemical shift, leading to an inevitable interference with the desirable APT contrast. Although a conventional MTR asymmetry (MTRasym) analysis can largely remove symmetric, direct water saturation and MTC effects, the APT-weighted (APTw) signal, measured by the MTR asymmetry analysis, is still confounded by inherent MT asymmetry, both from the relayed nuclear Overhauser effect (rNOE) in mobile macromolecules upfield from water and asymmetry in the semisolid MTC (30–33). To make matters worse, the MTR asymmetry and/or rNOE effects are weighted by the choice of RF saturation parameters, thus, reducing the specificity of APTw contrast (16, 34–36).
Recently, fast and quantitative MTC and CEST imaging techniques have been proposed by integrating an RF saturation scheme with MR fingerprinting (MRF) (37–41). Various RF saturation parameters are applied, which create distinct signal evolutions for different tissue properties. For MRF reconstruction, a pattern-matching algorithm is typically needed to determine different tissue-type parameters against a pre-calculated dictionary created by Bloch simulations with a large range of tissue parameters (38). However, depending on the sequence type, the number of tissue properties, and the granularity of the tissue property values, the dimension or size of the dictionary is exponentially increased, which inevitably leads to an intensive computation time for dictionary generation and MRF reconstruction. To reduce the computational burden for MRF reconstruction, deep-learning-based reconstruction techniques have been developed by learning the mapping relationship between MRF signals and tissue properties (37, 39–43). To improve reconstruction accuracy and generalization performance, the training dataset must be highly sampled with a wide range of tissue parameter combinations, which is extremely computationally expensive. In addition, optimization of the MRF acquisition schedule is very important to accelerate data acquisition and improve accuracy of the tissue parameter estimation (43, 44). However, repeatedly generating a dictionary or training dataset for each MRF schedule tested incurs a very high and impractical computational cost. In this study, a unified deep-learning architecture that included an ultrafast Bloch simulator and tissue parameter reconstruction was developed to address the above-mentioned issues. A deep Bloch simulator was designed to generate a huge amount of training dataset in a short time. A hybrid deep-learning model combined with a recurrent neural network (RNN) and a convolutional neural network (CNN) was proposed to improve the accuracy of MTC-MRF reconstruction (water proton and semisolid macromolecular proton parameters, such as relaxation time, pool size ratio, and exchange rate). The performance of the hybrid neural network was evaluated on numerical phantoms with known ground-truths and cross-linked bovine serum albumin phantoms. The proposed framework was demonstrated on healthy volunteers and compared with previous reconstruction methods (40, 45), including a fully connected neural network (FCNN) and Bloch fitting approaches. In addition, a test-retest study was performed to evaluate the repeatability of the tissue parameters estimated from the deep-learning framework.
2. THEORY
The Bloch simulator and MTC-MRF reconstruction are based on a two-pool exchange model. The dependence of tissue and scan parameters is captured by forward and inverse models derived from two-pool Bloch equations (3, 40, 46).
2.1. Steady-state two-pool MTC model
The MTC process can be described by a two-pool exchange model, free bulk water proton (w) and semisolid macromolecular proton (m) pools. Two-pool signal profiles were generated with a pseudorandomized RF saturation and acquisition parameters consisting of RF saturation strength (B1), saturation time (Ts), frequency offset (Ω), repetition time (TR) or relaxation delay time (Td), as shown in Figs. 1A and B. A steady-state MTC signal assuming a long Ts and TR is derived as follows (3):
| [1] |
| [2] |
| [3] |
where T1m and T2m are respectively longitudinal relaxation time and transverse relaxation time of a semisolid macromolecular proton pool; kmw is the proton exchange rate from pool m to pool w; M0m is the equilibrium magnetization of a pool m; ωoff is the frequency offset of the RF saturation, defined as ωoff = γB0Ω with Ω in ppm; and ω1 is the RF saturation amplitude, defined as ω1 = γB1. M0w is the equilibrium magnetization of a pool w, T1w is longitudinal relaxation time and T2w is transverse relaxation time of free bulk water. Note that the ratio of semisolid macromolecular pool size to free water pool size (pool size ratio) was defined as F = 100% × (M0m/M0w), where M0w is set to 1. The RF absorption rate (Rrf), which is the rate of loss of the longitudinal magnetization of the semisolid macromolecule pool, is dependent on the super-Lorentzian lineshape (gm) as follows:
| [4] |
| [5] |
| [6] |
where Δmw is the radial frequency difference between the semisolid macromolecule and the free bulk water proton pools. Note that a positive Δmw corresponds to the MTC line-shape center shifted upfield from the water resonance, while a negative Δmw corresponds to the MTC line-shape shifted downfield. The on-resonance singularity problem of the super-Lorentzian lineshape was avoided by extrapolating signal (13, 47). The super-Lorentzian values were extrapolated from 1 kHz to the asymptotic limit and approximated by cubic spline method.
Figure 1.
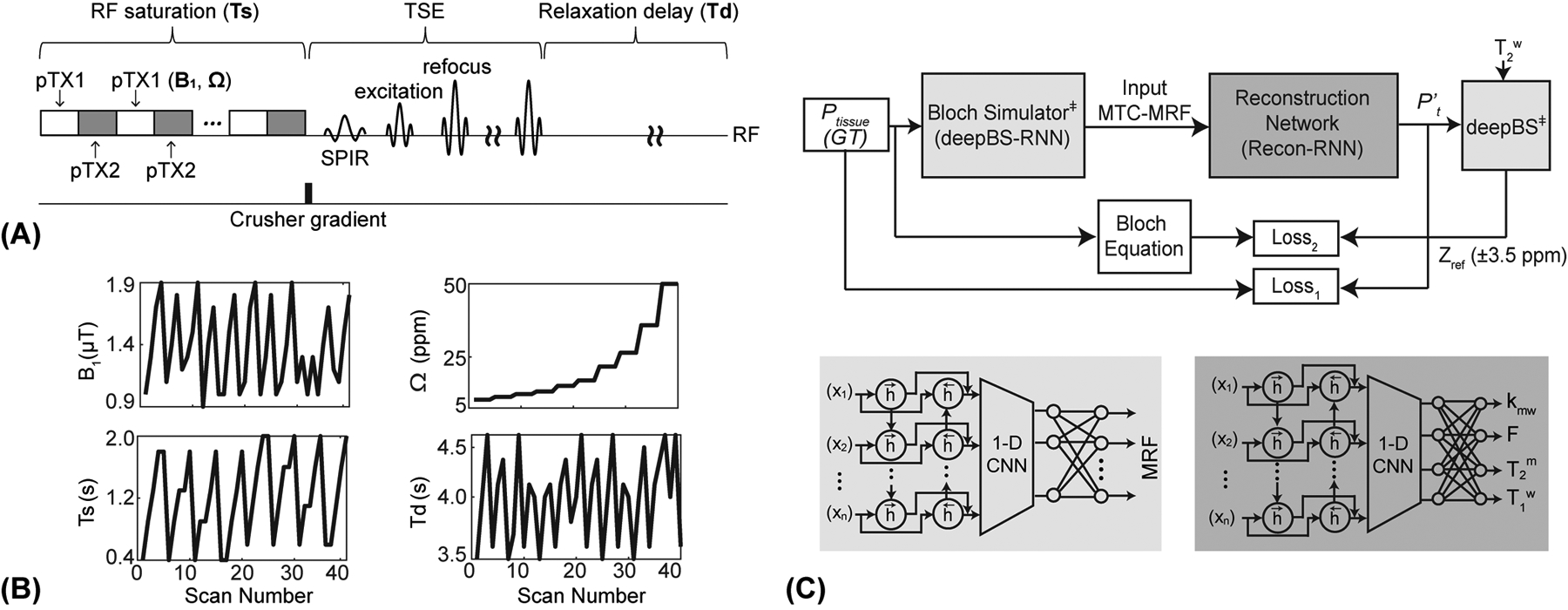
(A) An illustration of RF saturation-encoded MTC-MRF sequence. A two-channel parallel transmission (pTX) was used to achieve continuous RF saturation at a 100% duty cycle. A variable density under-sampling pattern with the elliptic-centric k-space ordering was used in a turbo spin-echo (TSE) sequence and a spectral pre-saturation with inversion recovery (SPIR) was used for fat-suppressed data acquisitions. (B) An example of B1, Ts, Ω, and Td schedule for an MRF image acquisition. (C) MTC-MRF framework consisting of a deep Bloch simulator (deepBS-RNN) and a reconstruction network (Recon-RNN). Pt represents ground-truth (GT) tissue parameters and P’t represents estimated tissue parameters from the Recon-RNN. The estimated tissue parameters (P’t) and acquired T2w are fed to the pre-trained deep Bloch simulator (deepBS) module as input to calculate baseline reference signals (Zref(±3.5 ppm) = 100% - MTC (±3.5 ppm)). ‡ indicates pre-trained neural networks.
2.2. Non-steady-state two-pool MTC model
For a non-steady-state (transient-state) signal evolution with short Ts and Td, the MTC signal () can be described by (34, 46, 48):
| [7] |
where:
| [8] |
| [9] |
in which Rrfm and Rrfw are the rate of loss of the longitudinal magnetization by semisolid macromolecules and water pools, respectively. For a series of transient MTC-MRF acquisitions, varied RF saturation and acquisition parameters are dynamically applied. The transient MTC-MRF signal evolution can be described as follows:
| [10] |
The relaxation delay time in the absence of RF irradiation allows the longitudinal magnetization recovery, determining an initial state of the magnetization for the next dynamic scan. To solve an inverse problem of the two-pool Bloch equation, a neural network architecture was designed to learn the non-linear relation between tissue properties and the MRF signal profiles derived from the analytical solution (Eq. [10]) of the transient MTC-MRF model.
3. METHODS
3.1. Bloch simulator network
A bi-directional long-short term memory (Bi-LSTM)-based RNN was combined with convolutional and dense layers for the Bloch simulator (deepBS-RNN). The network had sixty-four hidden memory units of Bi-LSTM as an input layer, one 1-D convolutional layer with 128 channels and two fully connected dense layers with 256 neurons in the middle, and one fully connected dense layers with 40 neurons as an output layer. For comparison of the performance of the deep-Bloch simulator, another Bloch simulator was designed using fully connected neural networks (deepBS-FCNN), which consisted of one fully connected input layer with five neurons, one fully connected output layer with forty neurons, and four fully connected layers with 128 neurons in the middle. During the training of the Bloch simulators, the errors of the network outputs were calculated using the L1-norm loss function between ground-truths and estimated MRF signal profiles, and then propagated back to the networks. The deep Bloch simulators were validated using a conventional two-pool Bloch simulation (BS) with ground-truths. The Bloch simulations were performed on MATLAB (MathWorks, Natick, MA) installed on a 64-bit Linux system (32-core, 3.75-GHz AMD processor and 512 GB of memory).
3.2. Reconstruction network
A reconstruction network using RNN (Recon-RNN) was designed with Bi-LSTM as an input layer, four 1-D convolutional layers and four fully connected layers to extract the feature from MTC-MRF signals as middle layers, and one fully connected layer at an output layer. The Bi-LSTM layer had 128 hidden memory units, each convolutional layer had 256 channels, each fully connected layer in middle had 512 neurons and the last fully connected layer had four neurons. ReLU activation function was used to add non-linearity after Bi-LSTM layer and each convolutional layer. A sigmoid activation function was used as the last activation function in the fully connected layer, and then, the output values (tissue parameters) were de-normalized in their maximum to minimum range: kmw: [100, 5] Hz; F: [17, 2] %; T2m: [100, 1] μs; and T1w: [3, 0.2] s. To evaluate the MTC asymmetry effect, an additional tissue parameter (Δmw: [4, 0] ppm) was estimated, hence the fully connected layer had five neurons at the output. Note that T1m was assumed to be 1 s due to a negligible contribution to the MTC signal (49). Mean squared errors between ground-truth values and estimated tissue parameters (N = 4 or 5) were calculated as the loss function (Loss1):
| [11] |
where Pt is the ground-truth and P’t is the tissue estimate. After de-normalization, the estimated tissue parameters and the T2 relaxation time of free bulk water (T2w) were fed to a two-pool Bloch equation module to calculate MTC signal intensities at ±3.5 ppm with a B1 of 1 μT and 1.5 μT. The second loss function (Loss2) was calculated by averaging of the sum of the squared difference between the ground-truth values and the estimated MTC signal intensities at 1 μT and 1.5 μT respectively. The overall loss function was defined as:
| [12] |
The hyper-parameter (λ = 30) empirically determined such that the two sub-loss functions had similar contributions to the total loss (40).
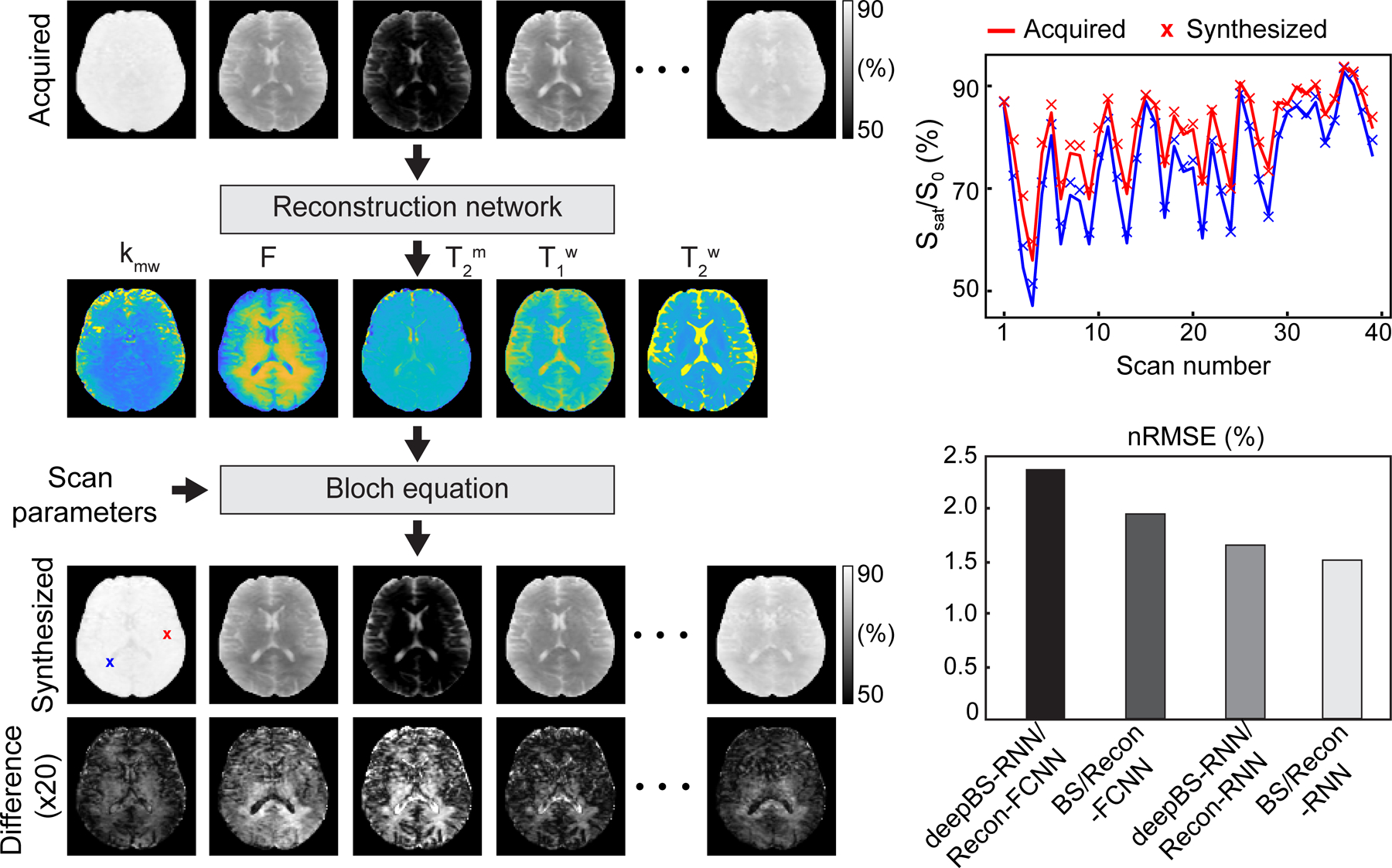
Recon-RNN used the pre-trained deepBS network within training loop to estimate Zref (±3.5 ppm) signals. The deepBS contained a Bi-LSTM layer as the input layer, six 1-D convolutional layers with sixty-four channels as middle layers, and one 1-D convolutional layer with one channel as an output layer. Batch normalization and dropout layers (dropout rate of 20%) were placed between the Bi-LSTM and the first convolutional layer. The adaptive moment estimation optimizer was adopted, with a learning rate of 10−5 and a batch size of 1000. The reconstruction performance of Recon-RNN was compared with a fully connected neural network (Recon-FCNN). Training and testing for the Bloch simulators and reconstruction networks were performed using TensorFlow on multiple NVIDIA RTX A6000, 48GB GPUs systems. The proposed network architecture is schematically shown in Fig. 1C.
3.3. Training dataset
Ground-truth MRF signals were generated using a two-pool Bloch simulation with a pseudo-randomized MRF schedule with 40 dynamic scans and a wide variety of tissue parameter combinations within the pre-defined ranges (section 3.2). The deep Bloch simulators (deepBS-RNN and deepBS-FCNN) were trained on a ten million ground-truth dataset, while the reconstruction networks (Recon-RNN and Recon-FCNN) were trained on a forty million dataset. White Gaussian noise was added to the training dataset to achieve a signal-to-noise ratio (SNR) of 46 dB. The SNR (= 10log10[s/σ]2) was defined as the ratio of signal (s) power to the noise (σ) power in decibels. Note that the SNR of 46 dB is equivalent to an imaging SNR (= μ/σ) of 188, calculated from the ratio of the average MRF signal intensity (μ = 0.78) over the standard deviation of the noise (σ = 0.0042) in normal white matter. To estimate the asymmetric MTC effect, both positive and negative frequency offsets were taken into account in the Bloch simulators and reconstruction networks. For simplicity, identical RF saturation field strength, duration, and relaxation delay time schedules were applied to both positive and negative frequency offset acquisitions, and thus, asymmetric MTC-MRF signal profiles with 80 dynamic scans were generated and fed to the reconstruction networks for training.
3.4. Test dataset
The reconstruction networks were tested and validated with Bloch equation-based numerical phantoms that had ground-truths. To evaluate the reconstruction accuracy for each of the tissue parameters, the numerical phantom that consisted of five compartments was constructed with five fixed values of one tissue parameter, while the other three tissue parameters were randomly selected in all five compartments. With the numerical phantom with a matrix size of 30 × 150 × 4 (tissue parameters) and the pre-defined MRF schedule, digital MTC-MRF images with a matrix size of 30 × 150 × 40 (dynamic scans) were synthesized using the Bloch simulation. To assess the generalization capability of the reconstruction networks across different noise levels in the test phase, the numerical phantom images were corrupted by additive Gaussian noise levels (SNR = 46, 45, and 42.5 and 40 dB) and these SNRs are equivalent to imaging SNRs (= μ/σ) of 188, 166, 125 and 95 respectively. Mean normalized root mean square error (nRMSE) values were calculated through Monte Carlo simulation. Within each iteration of the Monte Carlo simulation, Gaussian-distributed random noise was added to MTC-MRF signals with a fixed noise standard deviation. By repeating the random noise generation and MTC-MRF reconstruction for 200 times, nRMSE values from each iteration were calculated and averaged. The reconstruction accuracy was evaluated using the normalized root mean square error between the reconstructed quantitative maps and ground-truth maps, which was also used to assess the difference in reconstruction errors between the Recon-RNN and the Recon-FCNN methods. The accuracy of the deep Bloch simulator from in vivo test images was evaluated using two quantitative metrics, including peak signal-to-noise ratio (pSNR) and structural similarity index metrics (SSIM).
3.5. In vitro MRI experiments
A set of cross-linked bovine serum albumin (BSA, Sigma Aldrich, St Louis, MO, USA) samples was prepared to mimic the in vivo MTC pool. Samples of 10%, 15%, and 20% (w/w) BSA were dissolved in phosphate buffered saline (PBS) with pH adjusted to 7.3. All samples were placed in 50 ml Falcon tubes. Cross-linking was achieved by adding 25 μL of 25% glutaraldehyde solution. Prepared samples were stirred and allowed to sit overnight at 4 °C to ensure adequate cross-linking. Then, all samples were fixed in a 1.5% agarose gel (Sigma Aldrich, St Louis, MO, USA) in a plastic container. Imaging was performed on a 3T MRI system (Achieva dStream, Philips Healthcare, Best, The Netherlands) with a body coil for RF parallel transmission and a 32-channel head phased-array coil for reception. For MTC-MRF image acquisition, a pseudo-randomized RF saturation and acquisition schedule was applied. The MTC-MRF images were acquired with a multi-shot turbo spin-echo (TSE) sequence with a fat suppressed pre-pulse (spectral selective inversion recovery) (39, 40). The imaging parameters were FOV = 212 × 186 × 60 mm3, spatial resolution = 1.8 × 1.8 × 4 mm3, TE = 6 ms, turbo factor = 104, refocusing flip angle = 120°, and compressed sensing acceleration factor = 4 (2 × 2 in ky × kz direction) (50, 51). TRs were varied dynamically according to the MRF schedule pattern (e.g., Ts and Td). In addition, an unsaturated image was acquired for signal normalization. A pseudo-continuous RF saturation scheme with a 100% duty cycle was achieved using a time-interleaved, parallel RF transmission technique, enhancing saturation effects, and increasing degrees of freedom in the MRF schedule design. For B0 field correction, water saturation shift reference images (52) were acquired from -1.2 to 1.2 ppm (step size = 0.1 ppm) with a B1 of 0.5 μT and a 500-ms saturation duration and other scan parameters were identical to those used for MTC-MRF, as described above. To measure the water T2 relaxation time, a five-echo turbo gradient-spin-echo sequence was acquired with TEs from 20 ms to 100 ms in 20-ms steps and a TR of 3 s.
3.6. In vivo MRI experiments
Eleven healthy volunteers (four females and seven males, age: 37.5 ± 4.3 years) were recruited for the study after informed consent was obtained in accordance with IRB requirements. Among these, eight subjects were scanned in two sessions, at a median of 1.5 weeks apart to measure test-retest repeatability and reliability, remaining three subjects were scanned for analysis of MTC asymmetry. The 3D MTC-MRF, WASSR, and T2 map data were acquired with the same parameters used for the BSA phantom study. For APT and rNOE imaging, additional saturated images were acquired with the following scan parameters: Ω = 3.0, 3.5, 4.0 ppm for APT; Ω = -3.0, -3.5, -4.0 ppm for rNOE; B1 = 1 and 1.5 μT; Ts = 2s; and Td = 4 s.
3.7. APT# and rNOE# image analysis
APT# and rNOE# signals were calculated by subtracting the saturated (or labeled, Zlab) Z-spectra at 3.5 and -3.5 ppm, respectively, from the two-pool MTC reference spectra (Zref) (36):
| [13] |
| [14] |
in which Z(Δω) = Ssat(Δω)/S0, for in vivo studies, the baseline reference Z-spectra (Zref) were synthesized by solving the two-pool Bloch equation with the estimated tissue parameters from Recon-RNN and scan parameters. The labeled Z-spectra (Zlab) were experimentally acquired B0-corrected Z-spectra. Note that Zref(+3.5 ppm) and Zref(-3.5 ppm) are identical when the symmetric MTC model is considered (Δmw = 0), while Zref(-3.5 ppm) is lower than Zref(+3.5 ppm) when the asymmetric MTC model is considered, with the center of the semisolid resonance frequency shifted upfield from the water resonance (Δmw > 0) (31, 34). For comparison, APTw signals were obtained by subtracting the labeled Z-spectra at -3.5 ppm upfield, with respect to water, from that at +3.5 ppm (28):
| [15] |
3.8. Statistical analysis
Two regions of interest were carefully drawn on T2w images for white matter and gray matter regions (Supporting Information Fig. S1). The tissue parameters, MTC, APT#, and rNOE# signal intensities were statistically compared using a two-sided Student’s t-test. Statistical significance was considered at p < 0.05. Scan-rescan repeatability was assessed by the coefficient of variance (CoV) within subjects and between subjects. The within-subject CoV values were computed as the percentage ratio of standard deviation and mean (= STD / mean × 100%) calculated over scan 1 and scan 2 data for each subject, and then averaged across all subjects. The between-subject CoV values were computed as the percentage ratio of standard deviation and mean calculated over scan 1 data of all subjects and scan 2 data of all subjects, and then averaged across both scans. A CoV less than 10% was defined as indicative of excellent repeatability of tissue parameters, MTC, APT#, and rNOE# signals (53). The reliability of measurement was performed with intra class correlation coefficient (ICC), which was calculated for mean of two measurements, absolute-agreement, 2-way mixed-effects model as follows: , where MSR is mean square for rows, MSE is mean square for error, MSC is mean square for columns, n is number of subjects participated in test-retest study.
4. RESULTS
4.1. Evaluation of Bloch simulators
The performance of the deep Bloch simulators was benchmarked against ground-truth values from Bloch simulations, as shown in Fig. 2. The residual error signals were calculated by subtracting the ground-truth MRF profiles from the MRF profiles estimated from the deep Bloch simulators (Fig. 2A, bottom). The MTC-MRF profiles from the deep Bloch simulators were in agreement with the ground-truths, however, the deepBS-RNN showed slightly higher accuracy than the deepBS-FCNN. The root mean square error (RMSE) between the MRF profiles estimated from the deep Bloch simulators and the ground-truths were 0.51% for deepBS-RNN vs 0.53% for deepBS-FCNN (Fig. 2B). Importantly, the deep Bloch simulators achieved significantly higher computation efficiency (by a factor of ~181 for deepBS-RNN and ~570 for deepBS-FCNN) than the conventional Bloch simulation. Although the deepBS-RNN was slower than deepBS-FCNN (0.53 s vs. 0.17 s), both Bloch simulators required less than a second for the prediction of a 10k test dataset and were computationally efficient, compared to the conventional Bloch simulation (96 s). Therefore, the slightly more accurate deepBS-RNN method was further used in the reconstruction framework.
Figure 2.
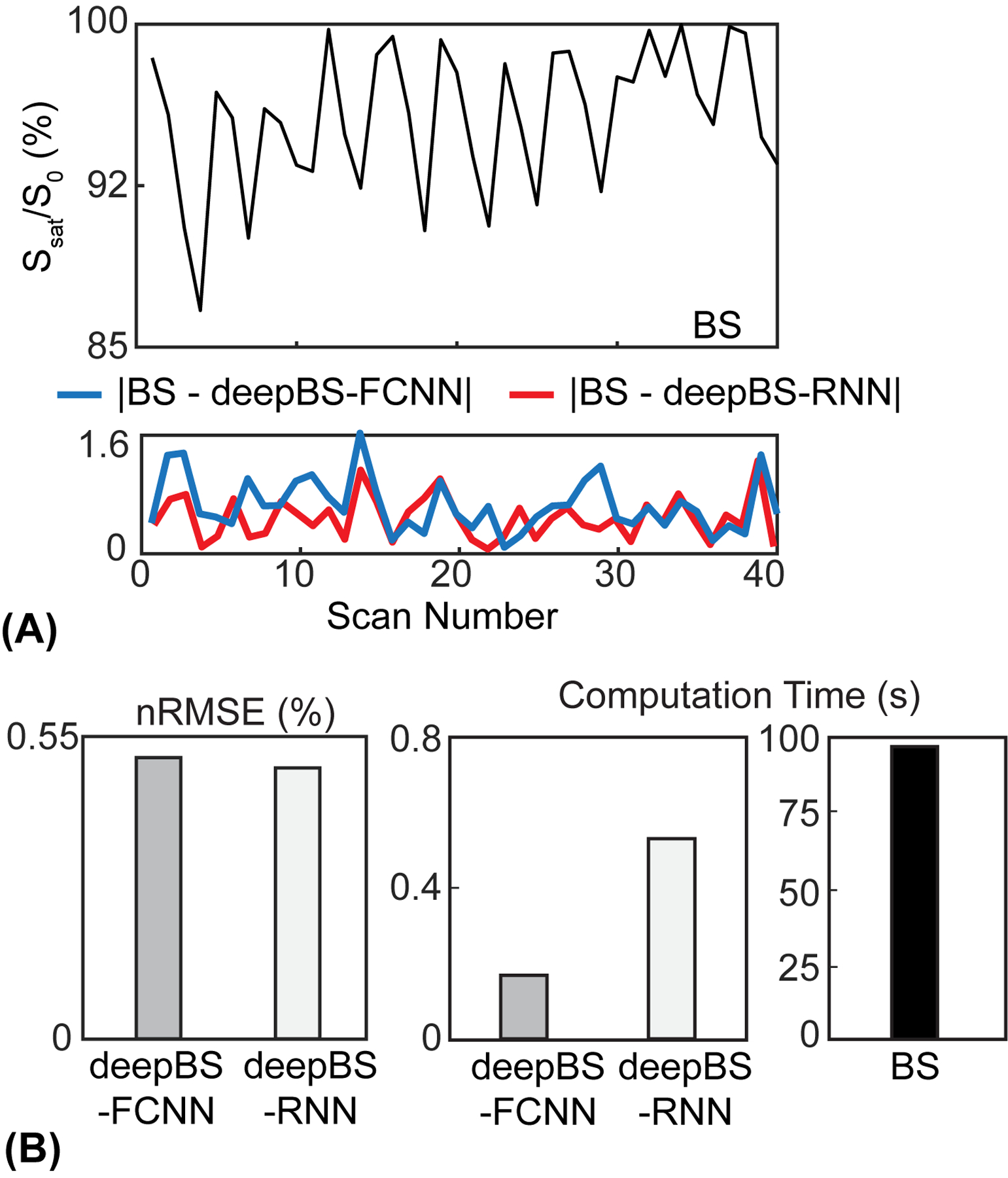
Evaluation of the performance of the deep Bloch simulators. (A) Top: Bloch simulation (BS) of Ssat/S0 and bottom: residual errors (absolute values of difference) between MTC-MRF profiles obtained from BS, deepBS-FCNN, and deepBS-RNN. Note that the saturation parameters used in the Bloch simulation are shown in Fig. 1B. (B) Comparison of the performance between deepBS-FCNN and deepBS-RNN for accuracy with nRMSE, and efficiency with computation time for a 10k test dataset.
4.2. Evaluation of reconstruction methods
The deep-learning MTC-MRF reconstruction methods were evaluated and validated using the numerical phantoms constructed by a two-pool Bloch simulation with a pseudo-randomized MRF schedule (Fig. 3A). The Recon-RNN was compared with the Recon-FCNN to evaluate the reconstruction accuracy under various SNR levels to demonstrate generalization performance with respect to noise levels. The proposed Recon-RNN method outperformed the existing Recon-FCNN method in tissue parameter quantification in terms robustness to noise (Fig. 3B). In addition, the Recon-RNN outperformed dictionary matching approaches (Supporting Information Fig. S2A) in terms of reconstruction accuracy and computational speed. The higher-performing Recon-RNN was further trained and tested to estimate the MTC asymmetric effect. The nRMSE values of the Recon-RNN for the asymmetric MTC effect were 8.5% for kmw, 3.1% for F, 1.5% for T2m, 1.1% for T1w, 3.4% for Δmw at an SNR of 46 dB. Figure 3C shows the cross-liked BSA phantom results. A variable RF saturation and acquisition schedule generated unique MTC signal profiles for the three compartments with different BSA concentrations.
Figure 3.
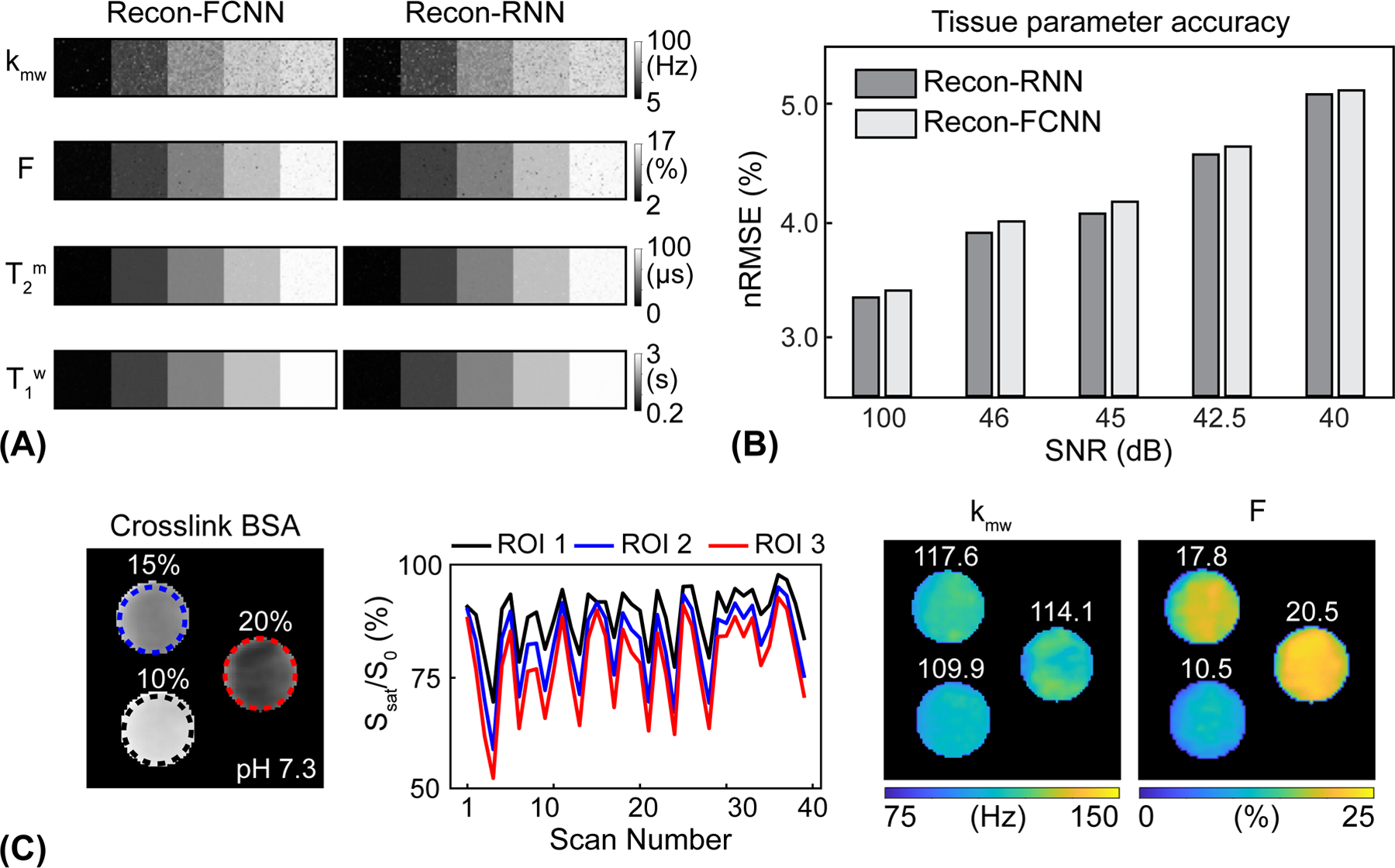
Evaluation of the performance of the deep-learning MRF reconstruction using Bloch equation-based numerical phantoms and BSA phantoms. (A) Tissue parameter maps estimated from the Recon-FCNN and Recon-RNN reconstruction networks. (B) Comparison of average reconstruction accuracy between Recon-FCNN and Recon-RNN across varied SNR levels. (C) Cross-linked BSA phantom validation experiments. kmw and F maps were estimated by deepBS-RNN/recon-RNN. The mean value of each ROI is shown in the insert (white).
The Recon-RNN-based estimated pool size ratio was proportional to the known BSA concentration (10.5 ± 1.4% for 10% BSA, 17.8 ± 2.0% for 15% BSA, and 20.5 ± 1.9% for 20% BSA). However, the estimated value is not necessarily equal to BSA concentration, since it depends on how many macromolecular protons are present and participate in MT process with water (54). Similar exchange rate values (109.9 ± 2.7 Hz for 10% BSA, 117.6 ± 3.8 Hz for 15% BSA, and 114.1 ± 5.1 Hz for 20% BSA) were estimated at constant pH 7.3.
4.3. In vivo MRI experiments
The Bloch simulator-driven, deep-learning reconstruction models were applied to the brains of healthy volunteers. Quantitative water and MTC parameter maps were successfully obtained in vivo using the conventional Bloch fitting, the deep-learning reconstruction models trained with two-pool Bloch simulations (BS/Recon-FCNN and BS/Recon-RNN), and the deep-learning reconstruction trained with the deep Bloch simulators (deepBS-RNN/Recon-RNN) as shown in Fig. 4. In addition, the maps obtained from the deepBS-RNN/Recon-RNN method were compared with a conventional dictionary matching approach (Supporting Information Fig. S2B). The dictionary matching method showed a poor reconstruction performance due to quantization errors from the discrete step size of the dictionary. The quantitative tissue parameter maps generated from the BS/Recon-RNN method were in good agreement with the results obtained from the deepBS-RNN/Recon-RNN method (mean pSNR = 30.3 dB and mean SSIM =0.96), but substantially reduced computation time for the generation of the training dataset by ~181-fold (106 h for Bloch simulation and 35 min for the deepBS-RNN to generate a forty million dataset). The total reconstruction time of the Recon-RNN for an image matrix of 256 × 256 × 9 × 40 was 3 min 33 s, while the reconstruction time of the conventional Bloch fitting approach and dictionary matching (size = 200k) approach was approximately 34 h and 19 min, respectively. In addition, APT# and rNOE# images were calculated by subtracting the saturated images at ±3.5 ppm from the symmetric (Δmw = 0) baseline reference images synthesized by solving a two-pool Bloch equation with estimated tissue parameters and scan parameters (Fig. 5). Good agreement was found between the synthetic images generated from the RNN-based reconstruction models trained with Bloch simulation (BS/Recon-RNN) and the deep Bloch simulator (deepBS-RNN/Recon-RNN). The pSNR and SSIM values of the MTC, APT#, and rNOE# images between the BS/Recon-RNN and the deepBS-RNN/Recon-RNN were all above 40 dB and 0.96, respectively. However, the MTC signal intensity estimated from the Bloch fitting approach was slightly higher than that from the deep-learning-based reconstruction methods and accordingly, lower APT# and rNOE# signal intensities were observed, particularly at 1.5 μT. Importantly, there were RF strength dependencies of the APT# and rNOE# signal intensities. At relatively low B1 (1 μT), the upfield rNOE# signal became more pronounced, compared to the downfield APT# signal. Table 1 summarizes the averaged tissue parameters, MTC, APT#, and rNOE# for gray matter and white matter regions, estimated from the RNN-based MRF reconstruction with symmetric MTC assumption (Δmw =0) (see also Supporting Information Table S1 for results from Bloch fitting, BS/Recon-FCNN, BS/Recon-RNN and deepBS/Recon-RNN methods). These tissue parameters and MTC, APT#, and rNOE# signals were significantly different between white matter and gray matter (p < 0.05), except for T2m. For quantitative performance comparison in in vivo, MRF images were synthesized with tissue parameters estimated from the different reconstruction methods and compared with experimentally acquired images, as shown in Fig. 6. The mean nRMSE values for the deepBS-FCNN/Recon-FCNN, BS/Recon-FCNN, deepBS-RNN/Recon-RNN, and BS/Recon-RNN were 2.4%, 2.0%, 1.7%, and 1.5%, respectively. The Recon-RNN overall outperformed the Recon-FCNN method, which is consistent with the numerical phantom result.
Figure 4.
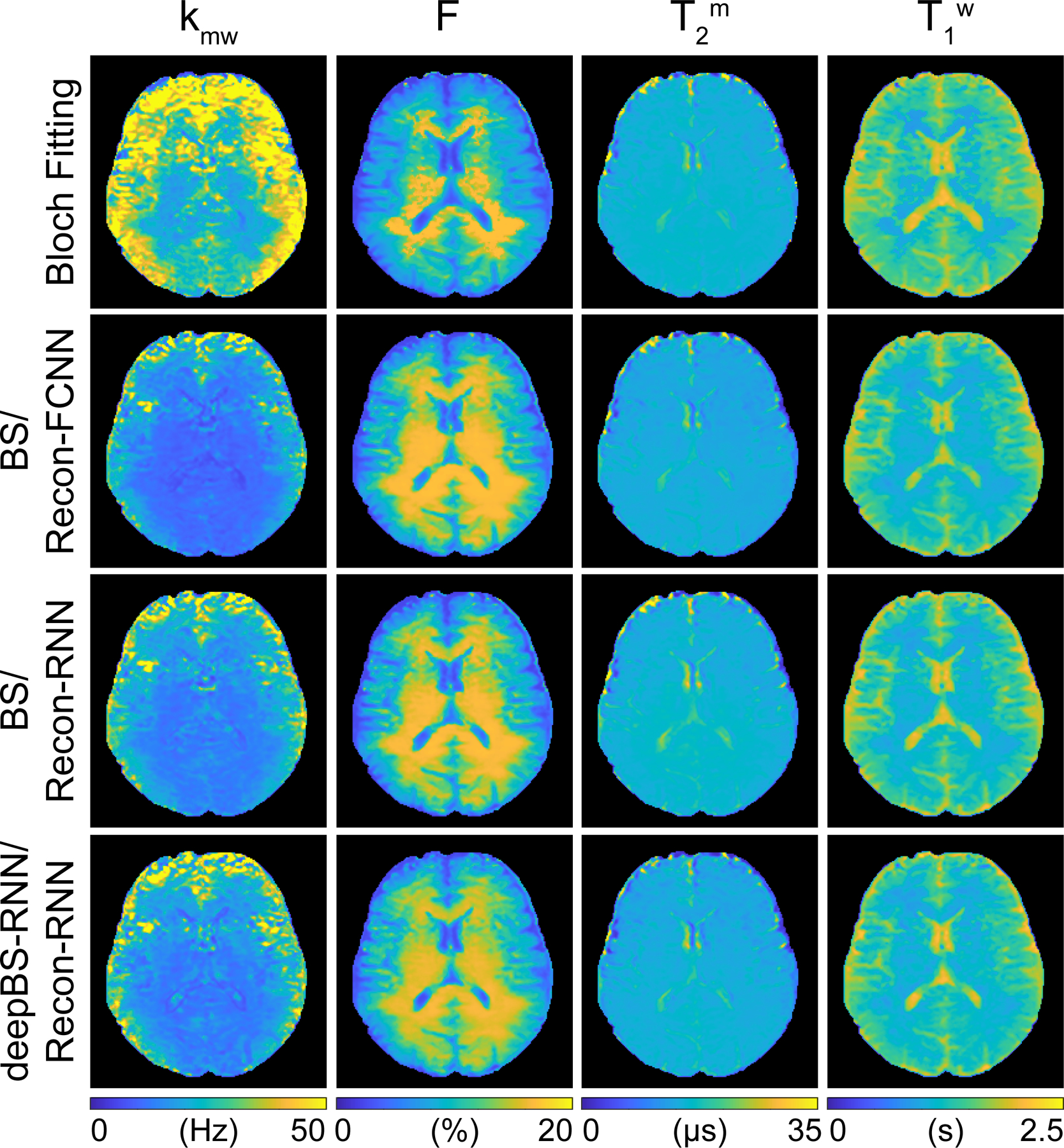
Quantitative MTC and water T1 maps of the human brain from a healthy volunteer. The tissue parameter maps were reconstructed from Bloch fitting, Bloch simulation (BS)-driven Recon-FCNN, BS-driven Recon-RNN, and deepBS-RNN-driven Recon-RNN.
Figure 5.
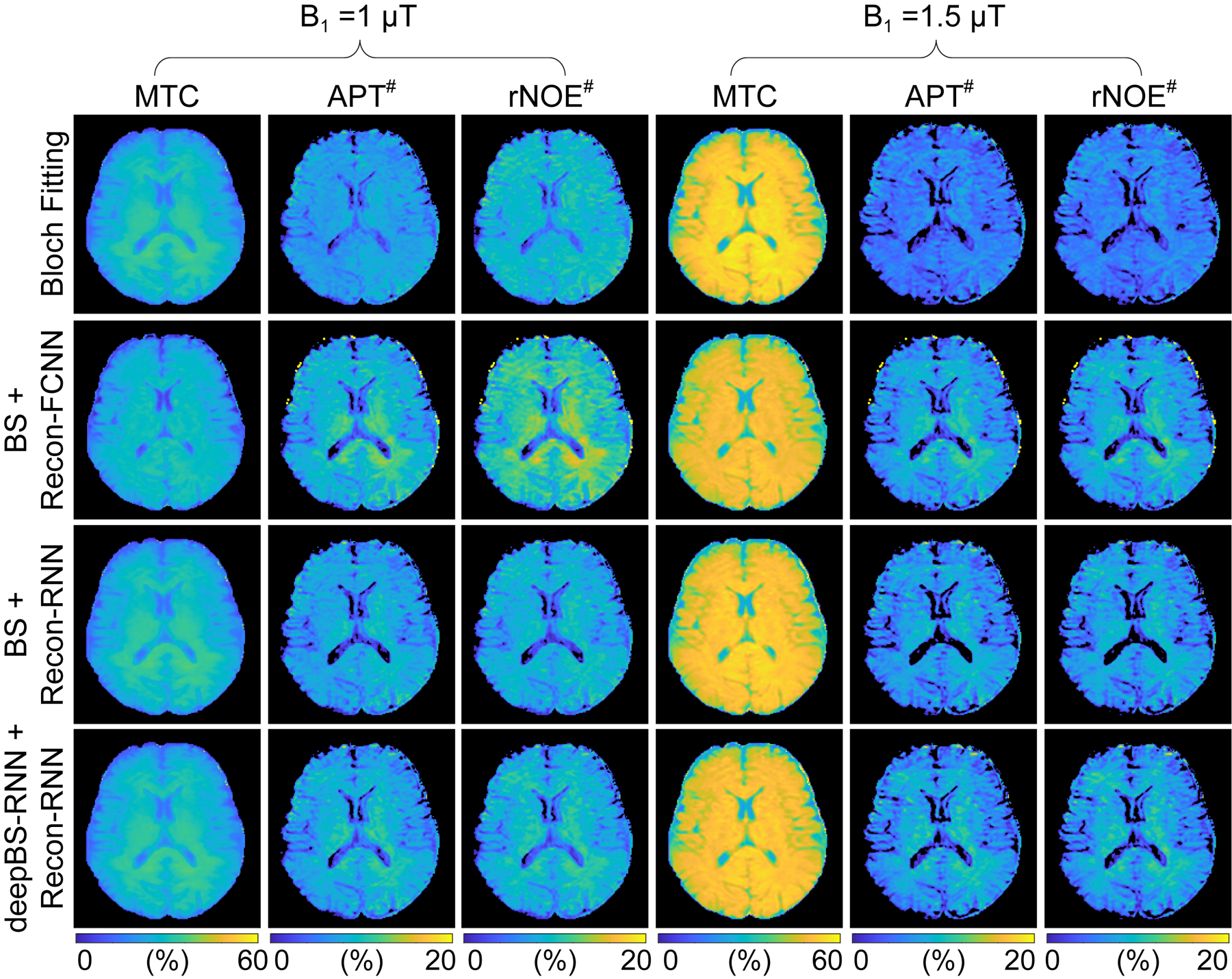
MTC, APT#, and rNOE# images from the brain of a healthy volunteer. The MTC images were synthesized with RF saturation strengths of 1 μT and 1.5 μT, an RF saturation time of 2 s, a relaxation delay time of 4 s, and a frequency offset of ±3.5 ppm. In this case, the semisolid MTC line-shape was assumed to be symmetric around water. The APT# and rNOE# images were calculated by subtracting acquired saturated images at +3.5 ppm and -3.5 ppm from the synthesized Zref(±3.5 ppm) images (= 100% - MTC(±3.5 ppm)), respectively.
Table 1.
Estimated semisolid MTC parameters, free bulk water T1 relaxation time, MTC at ±3.5 ppm, APT#, and rNOE# signal intensities (mean ± standard deviation and 95% confidence interval) obtained from Recon-RNN for white matter and gray matter of eight healthy volunteer human brain. Note that the Recon-RNN was trained with a forty million dataset synthesized from the RNN-based deep Bloch simulator (deepBS-RNN). Mean and standard deviations values were obtained across subjects.
| ROIs | kmw (Hz) | F (%) | T2m (μs) | T1w (s) | B1 = 1 μT | B1 = 1.5 μT | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MTC (%) |
APT# (%) |
rNOE# (%) | MTC (%) |
APT# (%) |
rNOE# (%) | ||||||
| WM | Mean ± STD | 14.6 ± 0.9 | 17.0 ± 0.6 | 14.6 ± 0.5 | 1.1 ± 0.1 | 35.6 ± 0.4 | 9.5 ± 0.5 | 11.7 ± 0.5 | 51.8 ± 0.5 | 9.0 ± 0.7 | 9.3 ± 0.6 |
| 95% CI | 14.1 – 15.1 | 16.7 – 17.3 | 14.4 – 14.9 | 1.1 – 1.2 | 35.4 – 35.8 | 9.2 – 9.8 | 11.4 – 12.0 | 51.5 – 52.0 | 8.6 – 9.4 | 8.9 – 9.6 | |
| GM | Mean ± STD | 19.8 ± 3.0 | 12.1 ± 1.3 | 14.9 ± 0.6 | 1.3 ± 0.1 | 32.9 ± 0.9 | 7.3 ± 0.9 | 9.3 ± 0.9 | 49.5 ± 1.2 | 6.1 ± 1.0 | 6.3 ± 1.1 |
| 95% CI | 18.2 – 21.5 | 11.4 – 12.9 | 14.5 – 15.2 | 1.2 – 1.4 | 32.4 – 33.4 | 6.9 – 7.8 | 8.8 – 9.7 | 48.8 – 50.1 | 5.6 – 6.6 | 5.7 – 6.9 | |
| p -value | < 0.01 | < 0.01 | 0.24 | < 0.01 | < 0.01 | < 0.01 | < 0.01 | < 0.01 | < 0.01 | < 0.01 | |
Figure 6.
Evaluation of the reconstruction performance. Synthesized MTC-MRF images were generated using the tissue parameter maps estimated from different reconstruction neural networks (deepBS-RNN/Recon-FCNN, BS/Recon-FCNN, deepBS-RNN /Recon-RNN and BS/Recon-RNN) and compared with acquired MTC-MRF images. Difference images (x 20) between the synthesized and the acquired images as well as quantitative reconstruction quality assessment with nRMSE are shown.
To evaluate the asymmetric MTC effect, MTC-MRF signal profiles were acquired at both positive frequency offsets (Ω+) and negative frequency offsets (Ω−), 80 dynamic scans in total. To display the MTC asymmetry effect, the MTC-MRF profile obtained from the negative frequency offsets was mirrored to the MTC-MRF profile from the positive frequency offsets, as shown in Fig. 7A. Although most of the MTC-MRF (Ω−) signal intensities were lower than the MTC-MRF (Ω+) due to asymmetric MTC effects around the water resonance frequency, some signal intensities were quite similar at certain scan numbers because the asymmetric effect is dependent on the frequency offset and other scan parameters, e.g., saturation B1 strength levels and durations. Figure 7B shows tissue parameter maps estimated from the RNN-based reconstruction with only MTC-MRF (Ω+) and with both MTC-MRF (Ω+) and (Ω−). Note that the asymmetric tissue parameter maps (asym MTC-MRF) were reconstructed from 40 MTC-MRF (Ω+) and 40 MTC-MRF (Ω−) images (80 dynamic scans in total), while the symmetric tissue parameter maps (sym MTC-MRF) were reconstructed from only 40 MTC-MRF (Ω+) images. The chemical shift center (Δmw) was found to be 2.8 ± 0.1 ppm and 2.6 ± 0.2 ppm for the white matter and gray matter, respectively.
Figure 7.
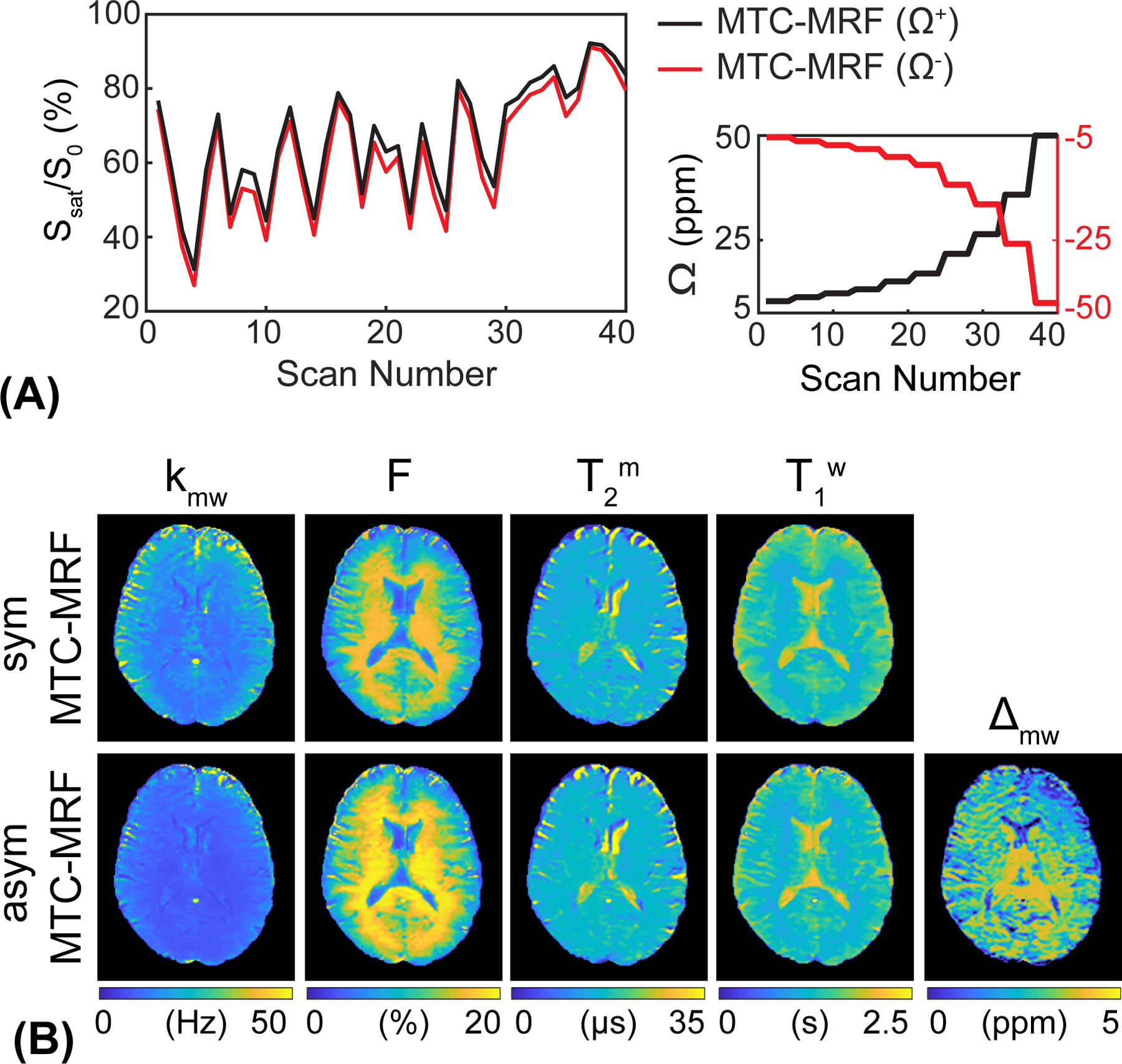
Comparison of MTC-MRF profiles and reconstruction maps with symmetric and asymmetric MTC effects. (A) MTC-MRF profiles obtained from positive frequency offsets (Ω+, black line) and negative frequency offsets (Ω−, red line). The negative frequency offset values were mirrored to the positive frequency offset values. (B) Tissue parameter maps reconstructed from the Recon-RNN with only positive frequency offsets (40 dynamic scans) and both positive and negative frequency offsets (80 dynamic scans) to evaluate the asymmetric MTC effect. The additional tissue parameter, Δmw, represents a chemical-shift center mismatch between free bulk water and semisolid macromolecules.
To investigate the asymmetric MTC effect on APT# and rNOE# images, asymmetric MTC images were synthetized using the tissue estimates from RNN-based reconstruction and scan parameters identical to those acquired in saturation images at ±3.5 ppm for APT# and rNOE# image calculation. The synthetic MTC images at ±3.5 ppm were generated with an assumption of asymmetric (Fig. 8A) and symmetric (Fig. 8B) MTC effects at RF saturation field strengths of 1 μT and 1.5 μT, respectively. With the assumption of the MTC asymmetry effect, overall MTC effects became more pronounced, which influenced APT# and rNOE# image contrast, as shown in Figs. 8D and 8E. Several important results were observed, including: (i) the rNOE# signal intensities with the asymmetric MTC effect were significantly lower than those with the symmetric MTC effect at 1 μT (p < 0.05) because the background baseline level (Zref = 100% - MTC) was lower when the asymmetric MTC component was added (also see Supporting Information Table S2); (ii) the broad MTC asymmetry also influenced downfield APT# signal intensities. The APT# signal intensities with the asymmetric MTC effect were higher than those with the symmetric MTC effects at the two RF saturation strength levels (p < 0.05) because the asymmetric super-Lorentzian lineshape signals spilled over into downfield frequency offsets from the water (Supporting Information Fig. S3); (iii) at 1 μT, the APTw signal intensities were all negative (-2.1 ± 0.2% for white matter and -1.9 ± 0.3% for gray matter) due to a large upfield rNOE#, while the APTw effect (-0.2 ± 0.3% for white matter and -0.3 ± 0.3% for gray matter) was more pronounced at 1.5 μT due to decreased rNOE# and/or asymmetric MTC effects.
Figure 8.
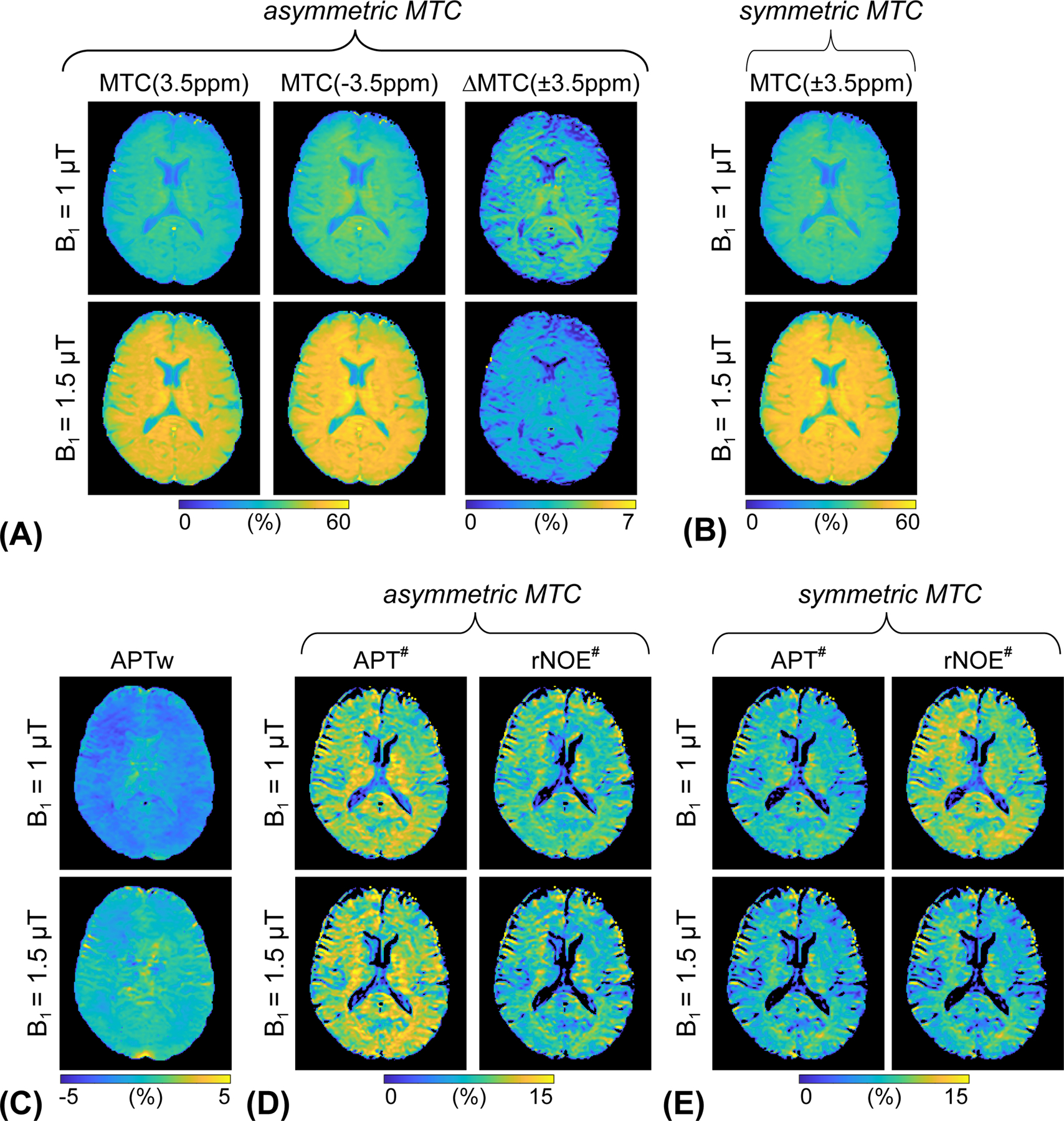
(A) Synthesized asymmetric MTC images at 3.5 ppm and -3.5 ppm, and corresponding difference images (= MTC(-3.5 ppm) - MTC(3.5 ppm)) and (B) synthesized symmetric MTC image at ±3.5 ppm at two different RF saturation strength levels. (C) APTw images calculated by MT ratio asymmetry analysis. (D) APT# and rNOE# images calculated with the asymmetric MTC effect. (E) APT# and rNOE# images calculated with the symmetric MTC effect
The repeatability of measurements by all reconstruction methods was evaluated by the test-retest study (Table 2). The within-subject CoV values for the deep-learning MRF reconstruction methods were less than 7% for all water and semisolid MTC parameters, and less than 10% for MTC, APT#, and rNOE# signals, indicating a high test-retest repeatability. The between-subject CoV values are reported in Supporting Information Table S3. The ICC values for test-retest reliability are presented in Supporting Information Table S4. An overall moderate reliability (ICC > 0.6) of the measurements was obtained.
Table 2.
Within-subject coefficient of variance (CoV) of the estimated semisolid MTC parameters, free bulk water T1 relaxation time, MTC at ±3.5 ppm, APT#, and rNOE# signal intensities obtained from Bloch fitting, BS/Recon-FCNN, BS/Recon-RNN and deepBS/Recon-RNN methods.
| Coefficient of Variance | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| kmw | F | T2m | T1w | B1 = 1 μT | B1 = 1.5 μT | ||||||
| MTC | APT# | rNOE# | MTC | APT# | rNOE# | ||||||
| Bloch Fitting | WM | 4.3% | 3.2% | 0.7% | 3.2% | 0.5% | 2.9% | 2.4% | 0.3% | 4.9% | 4.2% |
| GM | 5.8% | 2.7% | 1.2% | 2.0% | 1.0% | 4.1% | 2.9% | 0.8% | 5.8% | 6.9% | |
| BS/Recon-FCNN | WM | 2.1% | 1.1% | 1.0% | 2.1% | 0.8% | 1.8% | 1.7% | 0.7% | 2.9% | 2.8% |
| GM | 5.3% | 3.4% | 1.3% | 3.0% | 1.2% | 2.7% | 2.4% | 1.3% | 3.0% | 3.7% | |
| BS/Recon-RNN | WM | 2.5% | 1.4% | 0.8% | 2.1% | 0.7% | 3.0% | 2.5% | 0.6% | 4.8% | 4.2% |
| GM | 4.8% | 3.7% | 1.6% | 3.1% | 1.2% | 4.3% | 3.3% | 1.1% | 5.9% | 6.9% | |
| deepBS/Recon-RNN | WM | 4.2% | 1.4% | 1.1% | 1.6% | 0.5% | 2.7% | 2.1% | 0.5% | 4.1% | 3.0% |
| GM | 6.3% | 3.5% | 1.8% | 3.8% | 1.3% | 5.0% | 4.2% | 1.4% | 8.4% | 9.1% | |
5. DISCUSSION
High-resolution MRF that includes a multi-pool exchange model requires an extremely large dictionary or training dataset simulated with Bloch equations (40, 55). Furthermore, intensive Bloch simulation tasks are inevitable for MRF schedule optimization (44, 56). In this study, we developed a deep-learning-based Bloch simulator for ultrafast MRF dictionary or training data generation, and a recurrent neural network for semisolid macromolecular magnetization transfer contrast MRF reconstruction. For MRF training dataset generation, the deep Bloch simulator achieved a 181-fold reduction of the computation time compared to a conventional Bloch simulation. For MRF reconstruction, the deep-learning neural networks significantly reduced the reconstruction time without compromising reconstruction accuracy, ~570-fold reduction, compared to a Bloch equation-fitting approach without parallel computing. The proposed MRF reconstruction using recurrent neural networks outperformed the existing reconstruction methods, e.g., fully connected neural networks, Bloch fitting, and dictionary matching methods in terms of tissue parameter quantification accuracy. Importantly, the unified deep-learning framework, including an ultrafast Bloch simulator and MRF reconstruction provided a high degree of repeatability.
The deep Bloch simulator mimics a conventional Bloch simulation to generate dictionaries or training datasets for MRF reconstruction more efficiently. For the semisolid MTC pool, a super-Lorentzian lineshape was used. The super-Lorentzian lineshape model includes an integration term to consider all possible dipolar orientations, requiring intensive computation. However, the deep Bloch simulator was able to address this computational challenge. For example, the deep Bloch simulator took only 34 min to generate forty million training datasets for MRF reconstruction neural networks, while the conventional Bloch simulation took about 107 h. In addition, the deep Bloch simulator substantially reduced the training time for MRF reconstruction neural networks. During training of the reconstruction network (Fig. 1C), the baseline MTC signal (Zref) was calculated for the loss function per iteration. For training the reconstruction network, the reconstruction network with the deep Bloch simulator took about 70 min for each epoch (1,000 iterations), while the reconstruction network with the conventional Bloch simulation took about 4 days for each epoch and would take 6 months for 40 epochs. Furthermore, the deep Bloch simulator could be utilized to solve MRF sequence optimization problems. In MRF sequence optimization, a very large amount of MRF signal profiles must be simulated with updated tissue and scan parameters for each optimization iteration, which is computationally intensive (37). The Bloch simulator needs to be re-trained repeatedly for each MRF schedule tested, requiring intensive computation (about 27 hr per epoch, including training dataset generation and neural network training). However, the re-training of the Bloch simulator after each epoch during MRF optimization could be avoided if the RNN-based Bloch simulator is trained with various tissue parameters and scan parameters using a recently developed Only-Train-Once MR fingerprinting (OTOM) method (57, 58). The current deep Bloch simulator can be trained with a fixed duration of the MRF sequence (e.g., 40 dynamic scans), which is a limitation in the optimization of the number of dynamic scans for acquisition efficiency. However, the RNN-based OTOM framework can be trained only once and applied to different types of MRF schedule with various schedule lengths. Therefore, combining the deep Bloch simulator with the OTOM method can improve the generalization ability and optimize the number of dynamic scans, improving scan efficiency. For the evaluation of MTC asymmetry in vivo, for the sake of simplicity, positive and negative frequency offsets were symmetrically acquired, instead of fully mixing frequency offsets. These frequency offsets need to be chosen to improve quantification accuracy of the chemical shift center of the semisolid macromolecular proton pool.
Regarding the accuracy of the deep Bloch simulator, errors may propagate into the subsequent MRF reconstruction network during the training process and lead to a difference in final tissue parameter maps. However, it was observed that the RMSE were only 0.51% and 0.53% for deepBS-FCNN and -RNN, respectively, which are equivalent to the acquisition noise level (RMSE of 0.42% at SNR = 46 dB). In addition, through the Monte Carlo simulation study and the comparison study between BS-driven and deepBS-driven MRF reconstruction, the reconstruction neural networks were demonstrated to be robust to noise and errors introduced from the deep Bloch simulators. In some cases, different parameter values were found between different methods (e.g., Bloch fitting vs. neural network-based reconstruction or Recon-FCNN vs. Recon-RNN) which may cause concern for disease evaluation. However, the signal difference from the different methods would not affect detection of diseases-related contrast as long as consistent methodology is used when comparing healthy subjects with patients. In future work, the diagnostic accuracy of the deep-learning methods to identify pathology will be evaluated.
The proposed Recon-RNN framework is based on a hybrid network architecture in which the input RNN layers enable an understanding of the temporal behavior of MTC-MRF profiles, the intermediate CNN layer extracts important features from each MRF profile in the temporal domain, and the last fully connected dense layers comply the features from the previous CNN layers to form the final output (59–61). The hybrid architecture increased the reconstruction accuracy compared to the single FCNN model, while the reconstruction times were slightly longer mainly due to ReLU activation functions used in BiLSTM which is not currently supported by Computer Unified Device Architecture (CUDA) in TensorFlow environment (~3.5 min for Recon-RNN vs. 11 s for Recon-FCNN vs. ~34 h for Bloch equation fitting without parallel computing, for an image matrix of 256 × 256 × 9 × 40). Nevertheless, highly accurate and precise measurement of the semisolid MTC exchange rate is a very difficult task, as described previously (39, 40, 44), because the contribution of the MTC exchange rate to MR signals is very small and vulnerable to noise. Rather than improving the sensitivity and specificity of the exchange rate estimation in the reconstruction process, the development of proton exchange-sensitizing RF labeling strategies may be rather desirable (62–65). Using symmetric MTC, our estimated APT# and rNOE# signal intensities were slightly higher than the values reported previously (34), likely due to differences in RF saturation parameters and direct water saturation effect. The previous study acquired MTC data with a fixed B1 field strength of 2 μT and a saturation duration of 800 ms.
Several previous studies assumed a symmetric semisolid MTC effect because the semisolid macromolecular protons have a very broad RF absorption lineshape (13, 40, 56, 66). However, the MTC is caused by aliphatic protons and experimental data have shown clear asymmetry around the water resonance (31). When using asymmetry in the MTC background, a higher pool size ratio of white matter is estimated (Fig. 7B). Correspondingly, the MTC signal intensities at -3.5 ppm with asymmetric MTC were significantly higher than those with symmetric MTC, resulting in decreased rNOE# signal intensities. With the inclusion of an asymmetric MTC, the semisolid macromolecular proton pool had a chemical shift center about 2.8 ppm upfield from the water resonance for white matter, which is consistent with the results (~2.34 ppm for normal white matter) presented by Hua et al. (31). Regarding the super-Lorentzian lineshape, the on-resonance singularity was handled by extrapolating gm(Δω) from 1 kHz cut-off frequency to the asymptotic limit Δω → 0 (13, 47). However, the choice of the cut-off frequency may affect MTC signal estimation, particularly at -3.5 ppm, since the frequency offset of rNOE is very close to the chemical shift center (Δmw) of the semisolid macromolecular proton pool, as shown in Supporting Information Fig. S3. Alternatively, the singularity could be avoided by integrating power spectral density of RF pulse over frequencies (67).
Along with quantification accuracy, the repeatability of the measurement plays a vital role in establishing an imaging method suitable for a clinical study. The test-retest repeatability from the CoV analysis was excellent for all tissue parameters, MTC, APT#, and rNOE# signals estimated from the deep Bloch simulator-driven MTC-MRF framework.
6. CONCLUSIONS
We developed a deep-learning-based Bloch simulator for the ultrafast generation of MRF training datasets and a recurrent neural network for semisolid macromolecular magnetization transfer contrast MRF reconstruction. The deep Bloch simulator significantly reduced the computation time for the generation of training datasets compared to a conventional Bloch simulation. The recurrent neural-network-based MRF reconstruction demonstrated advantages in terms of tissue parameter quantification accuracy and computation efficiency. The test-retest study showed a high degree of repeatability of the proposed MTC-MRF framework in the brain and holds promise for assessing multiple tissue parameters simultaneously in a single scan.
Supplementary Material
Supporting Information Figure S1. ROIs were drawn on T2w images. Eight subjects (S1 - S8) were participated in the test-retest study, while three subjects (S9 - S11) were participated in the MTC asymmetry study. T2 maps are shown as references.
Supporting Information Figure S2. Comparison of the deepBS-RNN/Recon-RNN with the dictionary matching method. (A) Bloch equation-based numerical phantom results. The nRMSE values of the dictionary matching method were 18.9% for kmw, 6.2% for F, 2.5% for T2m, and 3.4% for T1w, while nRMSE values of the Recon-RNN were 9.1% for kmw, 2.4% for F, 1.1% for T2m, and 0.8% for T1w. (B) In vivo tissue parameter maps of a healthy volunteer brain. Note that the reconstruction accuracy of the dictionary matching approach depends directly on the resolution of the dictionary (size = 200k).
Supporting Information Figure S3. Semisolid absorption lineshapes (Lorentzian and Super-Lorentzian) with/without MTC asymmetry (e.g., Δmw = 3 ppm). The super-Lorentzian functions are extrapolated from two cut-off frequencies (ε = 1 kHz vs. 2 kHz) to model the semisolid macromolecular pool lineshape during on-resonance RF irradiation because the super-Lorentzian absorption lineshape has an on-resonance singularity (at Δw =0). With an asymmetric MTC, the lineshape center is shifted upfield from the water resonance, thus, the amplitude of the lineshape is increased at upfield frequency offsets but decreased at downfield frequency offsets (black vs. red for super-Lorentzian or green vs. blue for Lorentzian). Consequently, the shift can affect the overall MTC (or Zref), APT#, and NOE# signal intensities.
Supporting Information Table S1. Estimated semisolid MTC parameters, free bulk water T1 relaxation time, MTC at ±3.5 ppm, APT#, and rNOE# signal intensities (mean ± standard deviation and 95% confidence interval) obtained from Bloch fitting, BS/Recon-FCNN, BS/Recon-RNN and deepBS-RNN/Recon-RNN methods for white matter and gray matter of the human brain. Mean and standard deviations values were obtained across eight subjects participated in test-retest study.
Supporting Information Table S2. Effect of symmetric vs. asymmetric MTC on semisolid MTC parameters, free bulk water T1 relaxation time, MTC at +3.5 ppm, APT#, and rNOE# signal intensities (mean ± standard deviation) in white matter and gray matter of the healthy volunteer human brain. All quantitative tissue parameters and signal intensities were estimated using Recon-RNN. Mean and standard deviations values were obtained across three subjects participated in the study of asymmetric analysis.
Supporting Information Table S3. Between-subject coefficient of variance (CoV) of the estimated semisolid MTC parameters, free bulk water T1 relaxation time, MTC at ±3.5 ppm, APT#, and rNOE# signal intensities obtained from Bloch fitting, Recon-FCNN, and Recon-RNN methods.
Supporting Information Table S4. Intraclass correlation coefficient (ICC) of the estimated semisolid MTC parameters, free bulk water T1 relaxation time, MTC at ±3.5 ppm, APT#, and rNOE# signal intensities obtained from Bloch fitting, BS/Recon-FCNN, BS/Recon-RNN and deepBS-RNN/Recon-RNN methods. Mean ICC values were 0.6 ± 0.3, 0.6 ± 0.3, 0.6 ± 0.2 and 0.6 ± 0.1 corresponding to Bloch Fitting, BS/Recon-FCNN, BS/Recon-RNN and deepBS-RNN/Recon-RNN respectively.
ACKNOWLEDGMENTS
This work was supported, in part, by grants from the National Institutes of Health (R01EB029974, R01NS112242, R01AG069179, and P41EB031771). Under a license agreement between Philips and the Johns Hopkins University, Dr. van Zijl, Dr. Zhou, and the University are entitled to fees related to an imaging device used in the study discussed in this publication. Dr. van Zijl also is a paid lecturer for Philips and receives research support from Philips. This arrangement has been reviewed and approved by the Johns Hopkins University in accordance with its conflict of interest policies.
Footnotes
SUPPORTING INFORMATION
Additional Supporting Information may be found in the online version of this article.
Data Availability Statement
The source code is available at https://github.com/Heo-Group/DeepBS-MRF.
REFERENCES
- 1.Ward KM, Aletras AH, Balaban RS. A new class of contrast agents for MRI based on proton chemical exchange dependent saturation transfer (CEST). J Magn Reson 2000;143:79–87. [DOI] [PubMed] [Google Scholar]
- 2.Wolff SD, Balaban RS. Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn Reson Med 1989;10:135–144. [DOI] [PubMed] [Google Scholar]
- 3.Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med 1993;29:759–766. [DOI] [PubMed] [Google Scholar]
- 4.van Zijl PCM, Lam WW, Xu J, Knutsson L, Stanisz GJ. Magnetization Transfer Contrast and Chemical Exchange Saturation Transfer MRI. Features and analysis of the field-dependent saturation spectrum. Neuroimage 2018;168:222–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Iannucci G, Rovaris M, Giacomotti L, Comi G, Filippi M. Correlation of multiple sclerosis measures derived from T2-weighted, T1-weighted, magnetization transfer, and diffusion tensor MR imaging. AJNR Am J Neuroradiol 2001;22:1462–1467. [PMC free article] [PubMed] [Google Scholar]
- 6.Horsfield MA, Barker GJ, Barkhof F, Miller DH, Thompson AJ, Filippi M. Guidelines for using quantitative magnetization transfer magnetic resonance imaging for monitoring treatment of multiple sclerosis. J Magn Reson Imaging 2003;17:389–397. [DOI] [PubMed] [Google Scholar]
- 7.Sinson G, Bagley LJ, Cecil KM, Torchia M, McGowan JC, Lenkinski RE, McIntosh TK, Grossman RI. Magnetization transfer imaging and proton MR spectroscopy in the evaluation of axonal injury: correlation with clinical outcome after traumatic brain injury. AJNR Am J Neuroradiol 2001;22:143–151. [PMC free article] [PubMed] [Google Scholar]
- 8.Cercignani M, Bozzali M, Iannucci G, Comi G, Filippi M. Magnetisation transfer ratio and mean diffusivity of normal appearing white and grey matter from patients with multiple sclerosis. J Neurol Neurosurg Psychiatry 2001;70:311–317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Filippi M, Rocca MA, Rizzo G, Horsfield MA, Rovaris M, Minicucci L, Colombo B, Comi G. Magnetization transfer ratios in multiple sclerosis lesions enhancing after different doses of gadolinium. Neurology 1998;50:1289–1293. [DOI] [PubMed] [Google Scholar]
- 10.Henkelman RM, Stanisz GJ, Graham SJ. A multicenter measurement of magnetization transfer ratio in normal white matter. J Magn Reson Imaging 2000;11:568. [DOI] [PubMed] [Google Scholar]
- 11.Morrison C, Stanisz G, Henkelman RM. Modeling magnetization transfer for biological-like systems using a semi-solid pool with a super-Lorentzian lineshape and dipolar reservoir. J Magn Reson B 1995;108:103–113. [DOI] [PubMed] [Google Scholar]
- 12.Quesson B, Bouzier AK, Thiaudiere E, Delalande C, Merle M, Canioni P. Magnetization transfer fast imaging of implanted glioma in the rat brain at 4.7 T: interpretation using a binary spin-bath model. J Magn Reson Imaging 1997;7:1076–1083. [DOI] [PubMed] [Google Scholar]
- 13.Heo HY, Zhang Y, Lee DH, Hong X, Zhou J. Quantitative assessment of amide proton transfer (APT) and nuclear overhauser enhancement (NOE) imaging with extrapolated semi-solid magnetization transfer reference (EMR) signals: Application to a rat glioma model at 4.7 Tesla. Magn Reson Med 2016;75:137–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhou J, Heo HY, Knutsson L, van Zijl PCM, Jiang S. APT-weighted MRI: Techniques, current neuro applications, and challenging issues. J Magn Reson Imaging 2019;50:347–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Heo HY, Zhang Y, Burton TM, Jiang S, Zhao Y, van Zijl PCM, Leigh R, Zhou J. Improving the detection sensitivity of pH-weighted amide proton transfer MRI in acute stroke patients using extrapolated semisolid magnetization transfer reference signals. Magn Reson Med 2017;78:871–880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.van Zijl PCM, Yadav NN. Chemical exchange saturation transfer (CEST): What is in a name and what isn’t? Magn Reson Med 2011;65:927–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tee YK, Harston GW, Blockley N, Okell TW, Levman J, Sheerin F, Cellerini M, Jezzard P, Kennedy J, Payne SJ, Chappell MA. Comparing different analysis methods for quantifying the MRI amide proton transfer (APT) effect in hyperacute stroke patients. NMR Biomed 2014;27:1019–1029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sun PZ, Zhou J, Sun W, Huang J, van Zijl PCM. Detection of the ischemic penumbra using pH-weighted MRI. J Cereb Blood Flow Metab 2007;27:1129–1136. [DOI] [PubMed] [Google Scholar]
- 19.Heo HY, Tee YK, Harston G, Leigh R, Chappell MA. Amide proton transfer imaging in stroke. NMR Biomed 2022:e4734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhou J, Zaiss M, Knutsson L, Sun PZ, Ahn SS, Aime S, Bachert P, Blakeley JO, Cai K, Chappell MA, Chen M, Gochberg DF, Goerke S, Heo HY, Jiang S, Jin T, Kim SG, Laterra J, Paech D, Pagel MD, Park JE, Reddy R, Sakata A, Sartoretti-Schefer S, Sherry AD, Smith SA, Stanisz GJ, Sundgren PC, Togao O, Vandsburger M, Wen Z, Wu Y, Zhang Y, Zhu W, Zu Z, van Zijl PCM. Review and consensus recommendations on clinical APT-weighted imaging approaches at 3T: Application to brain tumors. Magn Reson Med 2022;88:546–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen L, Wei Z, Chan KWY, Cai S, Liu G, Lu H, Wong PC, van Zijl PCM, Li T, Xu J. Protein aggregation linked to Alzheimer’s disease revealed by saturation transfer MRI. Neuroimage 2019;188:380–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jiang S, Eberhart CG, Lim M, Heo HY, Zhang Y, Blair L, Wen Z, Holdhoff M, Lin D, Huang P, Qin H, Quinones-Hinojosa A, Weingart JD, Barker PB, Pomper MG, Laterra J, van Zijl PCM, Blakeley JO, Zhou J. Identifying Recurrent Malignant Glioma after Treatment Using Amide Proton Transfer-Weighted MR Imaging: A Validation Study with Image-Guided Stereotactic Biopsy. Clin Cancer Res 2019;25:552–561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zaiss M, Windschuh J, Goerke S, Paech D, Meissner JE, Burth S, Kickingereder P, Wick W, Bendszus M, Schlemmer HP, Ladd ME, Bachert P, Radbruch A. Downfield-NOE-suppressed amide-CEST-MRI at 7 Tesla provides a unique contrast in human glioblastoma. Magn Reson Med 2017;77:196–208. [DOI] [PubMed] [Google Scholar]
- 24.Harston GW, Tee YK, Blockley N, Okell TW, Thandeswaran S, Shaya G, Sheerin F, Cellerini M, Payne S, Jezzard P, Chappell M, Kennedy J. Identifying the ischaemic penumbra using pH-weighted magnetic resonance imaging. Brain 2015;138:36–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zu Z Towards the complex dependence of MTRasym on T1w in amide proton transfer (APT) imaging. NMR Biomed 2018;31:e3934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Park JE, Kim HS, Park SY, Jung SC, Kim JH, Heo HY. Identification of Early Response to Anti-Angiogenic Therapy in Recurrent Glioblastoma: Amide Proton Transfer-weighted and Perfusion-weighted MRI compared with Diffusion-weighted MRI. Radiology 2020:191376. [DOI] [PubMed] [Google Scholar]
- 27.Wen Q, Wang K, Hsu YC, Xu Y, Sun Y, Wu D, Zhang Y. Chemical exchange saturation transfer imaging for epilepsy secondary to tuberous sclerosis complex at 3 T: Optimization and analysis. NMR Biomed 2021;34:e4563. [DOI] [PubMed] [Google Scholar]
- 28.Zhou J, Payen J, Wilson DA, Traystman RJ, van Zijl PCM. Using the amide proton signals of intracellular proteins and peptides to detect pH effects in MRI. Nature Med 2003;9:1085–1090. [DOI] [PubMed] [Google Scholar]
- 29.Wang K, Wen Q, Wu D, Hsu YC, Heo HY, Wang W, Sun Y, Ma Y, Wu D, Zhang Y. Lateralization of temporal lobe epileptic foci with automated chemical exchange saturation transfer measurements at 3 Tesla. EBioMedicine 2023;89:104460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhou J, Hong X, Zhao X, Gao JH, Yuan J. APT-weighted and NOE-weighted image contrasts in glioma with different RF saturation powers based on magnetization transfer ratio asymmetry analyses. Magn Reson Med 2013;70:320–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hua J, Jones CK, Blakeley J, Smith SA, van Zijl PC, Zhou J. Quantitative description of the asymmetry in magnetization transfer effects around the water resonance in the human brain. Magn Reson Med 2007;58:786–793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Paech D, Burth S, Windschuh J, Meissner JE, Zaiss M, Eidel O, Kickingereder P, Nowosielski M, Wiestler B, Sahm F, Floca RO, Neumann JO, Wick W, Heiland S, Bendszus M, Schlemmer HP, Ladd ME, Bachert P, Radbruch A. Nuclear Overhauser Enhancement imaging of glioblastoma at 7 Tesla: region specific correlation with apparent diffusion coefficient and histology. PLoS One 2015;10:e0121220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhou Y, Bie C, van Zijl PCM, Yadav NN. The relayed nuclear Overhauser effect in magnetization transfer and chemical exchange saturation transfer MRI. NMR Biomed 2022:e4778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Heo HY, Zhang Y, Jiang S, Lee DH, Zhou J. Quantitative assessment of amide proton transfer (APT) and nuclear overhauser enhancement (NOE) imaging with extrapolated semisolid magnetization transfer reference (EMR) signals: II. Comparison of three EMR models and application to human brain glioma at 3 Tesla. Magn Reson Med 2016;75:1630–1639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Paech D, Zaiss M, Meissner JE, Windschuh J, Wiestler B, Bachert P, Neumann JO, Kickingereder P, Schlemmer HP, Wick W, Nagel AM, Heiland S, Ladd ME, Bendszus M, Radbruch A. Nuclear overhauser enhancement mediated chemical exchange saturation transfer imaging at 7 Tesla in glioblastoma patients. PLoS One 2014;9:e104181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Heo HY, Lee DH, Zhang Y, Zhao X, Jiang S, Chen M, Zhou J. Insight into the quantitative metrics of chemical exchange saturation transfer (CEST) imaging. Magn Reson Med 2017;77:1853–1865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Perlman O, Farrar CT, Heo HY. MR fingerprinting for semisolid magnetization transfer and chemical exchange saturation transfer quantification. NMR Biomed 2022:e4710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature 2013;495:187–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kang B, Kim B, Schar M, Park H, Heo HY. Unsupervised learning for magnetization transfer contrast MR fingerprinting: Application to CEST and nuclear Overhauser enhancement imaging. Magn Reson Med 2021;85:2040–2054. [DOI] [PubMed] [Google Scholar]
- 40.Kim B, Schar M, Park H, Heo HY. A deep learning approach for magnetization transfer contrast MR fingerprinting and chemical exchange saturation transfer imaging. Neuroimage 2020;221:117165. [DOI] [PubMed] [Google Scholar]
- 41.Perlman O, Ito H, Herz K, Shono N, Nakashima H, Zaiss M, Chiocca EA, Cohen O, Rosen MS, Farrar CT. Quantitative imaging of apoptosis following oncolytic virotherapy by magnetic resonance fingerprinting aided by deep learning. Nat Biomed Eng 2022;6:648–657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.McGivney DF, Boyacioglu R, Jiang Y, Poorman ME, Seiberlich N, Gulani V, Keenan KE, Griswold MA, Ma D. Magnetic resonance fingerprinting review part 2: Technique and directions. J Magn Reson Imaging 2020;51:993–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Perlman O, Zhu B, Zaiss M, Rosen MS, Farrar CT. An end-to-end AI-based framework for automated discovery of rapid CEST/MT MRI acquisition protocols and molecular parameter quantification (AutoCEST). Magn Reson Med 2022;87:2792–2810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kang B, Kim B, Park H, Heo HY. Learning-based optimization of acquisition schedule for magnetization transfer contrast MR fingerprinting. NMR Biomed 2022;35:e4662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Heo HY, Han Z, Jiang S, Schar M, van Zijl PCM, Zhou J. Quantifying amide proton exchange rate and concentration in chemical exchange saturation transfer imaging of the human brain. Neuroimage 2019;189:202–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Quesson B, Thiaudiere E, Delalande C, Chateil JF, Moonen CT, Canioni P. Magnetization transfer imaging of rat brain under non-steady-state conditions. Contrast prediction using a binary spin-bath model and a super-lorentzian lineshape. J Magn Reson 1998;130:321–328. [DOI] [PubMed] [Google Scholar]
- 47.Gloor M, Scheffler K, Bieri O. Quantitative magnetization transfer imaging using balanced SSFP. Magn Reson Med 2008;60:691–700. [DOI] [PubMed] [Google Scholar]
- 48.Heo HY, Zhang Y, Jiang S, Zhou J. Influences of experimental parameters on chemical exchange saturation transfer (CEST) metrics of brain tumors using animal models at 4.7T. Magn Reson Med 2019;81:316–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Morrison C, Henkelman RM. A model for magnetization transfer in tissues. Magn Reson Med 1995;33:475–482. [DOI] [PubMed] [Google Scholar]
- 50.Heo HY, Xu X, Jiang S, Zhao Y, Keupp J, Redmond KJ, Laterra J, van Zijl PCM, Zhou J. Prospective acceleration of parallel RF transmission-based 3D chemical exchange saturation transfer imaging with compressed sensing. Magn Reson Med 2019;82:1812–1821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Heo HY, Zhang Y, Lee DH, Jiang S, Zhao X, Zhou J. Accelerating chemical exchange saturation transfer (CEST) MRI by combining compressed sensing and sensitivity encoding techniques. Magn Reson Med 2017;77:779–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kim M, Gillen J, Landman BA, Zhou J, van Zijl PC. Water saturation shift referencing (WASSR) for chemical exchange saturation transfer (CEST) experiments. Magn Reson Med 2009;61:1441–1450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kakite S, Dyvorne H, Besa C, Cooper N, Facciuto M, Donnerhack C, Taouli B. Hepatocellular carcinoma: short-term reproducibility of apparent diffusion coefficient and intravoxel incoherent motion parameters at 3.0T. J Magn Reson Imaging 2015;41:149–156. [DOI] [PubMed] [Google Scholar]
- 54.Malyarenko DI, Zimmermann EM, Adler J, Swanson SD. Magnetization transfer in lamellar liquid crystals. Magn Reson Med 2014;72:1427–1434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cohen O, Huang S, McMahon MT, Rosen MS, Farrar CT. Rapid and quantitative chemical exchange saturation transfer (CEST) imaging with magnetic resonance fingerprinting (MRF). Magn Reson Med 2018;80:2449–2463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Perlman O, Herz K, Zaiss M, Cohen O, Rosen MS, Farrar CT. CEST MR-Fingerprinting: Practical considerations and insights for acquisition schedule design and improved reconstruction. Magn Reson Med 2020;83:462–478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kang B, Heo HY, Park H. Only-Train-Once MR Fingerprinting for Magnetization Transfer Contrast Quantification. Lect Notes Comput Sc 2022;13436:387–396. [Google Scholar]
- 58.Kang B, Singh M, Park H, Heo HY. Only-train-once MR fingerprinting for B(0) and B(1) inhomogeneity correction in quantitative magnetization-transfer contrast. Magn Reson Med 2023: 10.1002/mrm.29629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci U S A 1982;79:2554–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Schuster M, Paliwal KK. Bidirectional recurrent neural networks. Ieee T Signal Proces 1997;45:2673–2681. [Google Scholar]
- 61.Alzubaidi L, Zhang J, Humaidi AJ, Al-Dujaili A, Duan Y, Al-Shamma O, Santamaria J, Fadhel MA, Al-Amidie M, Farhan L. Review of deep learning: concepts, CNN architectures, challenges, applications, future directions. J Big Data 2021;8:53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Knutsson L, Xu J, Ahlgren A, van Zijl PCM. CEST, ASL, and magnetization transfer contrast: How similar pulse sequences detect different phenomena. Magn Reson Med 2018;80:1320–1340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Yadav NN, Jones CK, Hua J, Xu J, van Zijl PCM. Imaging of endogenous exchangeable proton signals in the human brain using frequency labeled exchange transfer imaging. Magn Reson Med 2013;69:966–973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Zu Z, Xu J, Li H, Chekmenev EY, Quarles CC, Does MD, Gore JC, Gochberg DF. Imaging amide proton transfer and nuclear overhauser enhancement using chemical exchange rotation transfer (CERT). Magn Reson Med 2014;72:471–476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Xu J, Yadav NN, Bar-Shir A, Jones CK, Chan KW, Zhang J, Walczak P, McMahon MT, van Zijl PCM. Variable delay multi-pulse train for fast chemical exchange saturation transfer and relayed-nuclear overhauser enhancement MRI. Magn Reson Med 2014;71:1798–1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lee DH, Heo HY, Zhang K, Zhang Y, Jiang S, Zhao X, Zhou J. Quantitative assessment of the effects of water proton concentration and water T1 changes on amide proton transfer (APT) and nuclear overhauser enhancement (NOE) MRI: The origin of the APT imaging signal in brain tumor. Magn Reson Med 2017;77:855–863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Asslander J, Gultekin C, Flassbeck S, Glaser SJ, Sodickson DK. Generalized Bloch model: A theory for pulsed magnetization transfer. Magn Reson Med 2022;87:2003–2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Figure S1. ROIs were drawn on T2w images. Eight subjects (S1 - S8) were participated in the test-retest study, while three subjects (S9 - S11) were participated in the MTC asymmetry study. T2 maps are shown as references.
Supporting Information Figure S2. Comparison of the deepBS-RNN/Recon-RNN with the dictionary matching method. (A) Bloch equation-based numerical phantom results. The nRMSE values of the dictionary matching method were 18.9% for kmw, 6.2% for F, 2.5% for T2m, and 3.4% for T1w, while nRMSE values of the Recon-RNN were 9.1% for kmw, 2.4% for F, 1.1% for T2m, and 0.8% for T1w. (B) In vivo tissue parameter maps of a healthy volunteer brain. Note that the reconstruction accuracy of the dictionary matching approach depends directly on the resolution of the dictionary (size = 200k).
Supporting Information Figure S3. Semisolid absorption lineshapes (Lorentzian and Super-Lorentzian) with/without MTC asymmetry (e.g., Δmw = 3 ppm). The super-Lorentzian functions are extrapolated from two cut-off frequencies (ε = 1 kHz vs. 2 kHz) to model the semisolid macromolecular pool lineshape during on-resonance RF irradiation because the super-Lorentzian absorption lineshape has an on-resonance singularity (at Δw =0). With an asymmetric MTC, the lineshape center is shifted upfield from the water resonance, thus, the amplitude of the lineshape is increased at upfield frequency offsets but decreased at downfield frequency offsets (black vs. red for super-Lorentzian or green vs. blue for Lorentzian). Consequently, the shift can affect the overall MTC (or Zref), APT#, and NOE# signal intensities.
Supporting Information Table S1. Estimated semisolid MTC parameters, free bulk water T1 relaxation time, MTC at ±3.5 ppm, APT#, and rNOE# signal intensities (mean ± standard deviation and 95% confidence interval) obtained from Bloch fitting, BS/Recon-FCNN, BS/Recon-RNN and deepBS-RNN/Recon-RNN methods for white matter and gray matter of the human brain. Mean and standard deviations values were obtained across eight subjects participated in test-retest study.
Supporting Information Table S2. Effect of symmetric vs. asymmetric MTC on semisolid MTC parameters, free bulk water T1 relaxation time, MTC at +3.5 ppm, APT#, and rNOE# signal intensities (mean ± standard deviation) in white matter and gray matter of the healthy volunteer human brain. All quantitative tissue parameters and signal intensities were estimated using Recon-RNN. Mean and standard deviations values were obtained across three subjects participated in the study of asymmetric analysis.
Supporting Information Table S3. Between-subject coefficient of variance (CoV) of the estimated semisolid MTC parameters, free bulk water T1 relaxation time, MTC at ±3.5 ppm, APT#, and rNOE# signal intensities obtained from Bloch fitting, Recon-FCNN, and Recon-RNN methods.
Supporting Information Table S4. Intraclass correlation coefficient (ICC) of the estimated semisolid MTC parameters, free bulk water T1 relaxation time, MTC at ±3.5 ppm, APT#, and rNOE# signal intensities obtained from Bloch fitting, BS/Recon-FCNN, BS/Recon-RNN and deepBS-RNN/Recon-RNN methods. Mean ICC values were 0.6 ± 0.3, 0.6 ± 0.3, 0.6 ± 0.2 and 0.6 ± 0.1 corresponding to Bloch Fitting, BS/Recon-FCNN, BS/Recon-RNN and deepBS-RNN/Recon-RNN respectively.
Data Availability Statement
The source code is available at https://github.com/Heo-Group/DeepBS-MRF.


