Summary:
Electronic health record (EHR) data are increasingly used for biomedical research, but these data have recognized data quality challenges. Data validation is necessary to use EHR data with confidence, but limited resources typically make complete data validation impossible. Using EHR data, we illustrate prospective, multi-wave, two-phase validation sampling to estimate the association between maternal weight gain during pregnancy and the risks of her child developing obesity or asthma. The optimal validation sampling design depends on the unknown efficient influence functions of regression coefficients of interest. In the first wave of our multi-wave validation design, we estimate the influence function using the unvalidated (phase 1) data to determine our validation sample; then in subsequent waves, we re-estimate the influence function using validated (phase 2) data and update our sampling. For efficiency, estimation combines obesity and asthma sampling frames while calibrating sampling weights using generalized raking. We validated 996 of 10,335 mother-child EHR dyads in 6 sampling waves. Estimated associations between childhood obesity/asthma and maternal weight gain, as well as other covariates, are compared to naïve estimates that only use unvalidated data. In some cases, estimates markedly differ, underscoring the importance of efficient validation sampling to obtain accurate estimates incorporating validated data.
Keywords: generalized raking, measurement error, obesity, two-phase sampling, weight gain
1. Introduction
There is great interest in using electronic health record (EHR) data as a cost-effective resource to support biomedical research. A growing number of studies relying on data extracted from the EHR are appearing in the medical literature. These articles, however, are showing up alongside others that highlight concerns of data quality and potentially misleading findings from analyses using EHR data that do not properly address data quality issues (e.g., Floyd et al. (2012)). To fully realize the potential of EHR data for biomedical research, widely recognized problems of data accuracy and completeness must be addressed.
Computerized data checks are necessary but not sufficient for quality data. Validation, in which trained personnel thoroughly compare EHR-derived data with the original source documents (e.g., paper medical charts or the entire EHR itself for a patient), is best practice for ensuring data quality (Duda et al., 2012). However, full validation of EHR data is costly and time-consuming, and is generally not possible for large or multi-center cohorts. Instead, investigators may validate sub-samples of patient records. This validation sample can be used to inform researchers of the errors in their data and their phenotyping algorithms. Data from the validation sub-samples can then be used with unvalidated data from the full EHR to adjust analyses and improve estimation (Huang et al., 2018; Giganti et al., 2020).
Since researchers have limited funds, it is important to maximize the information obtained from data validation. The efficiency of estimators using validated EHR data can be improved with carefully designed validation sampling strategies. The literature on two-phase sampling is relevant (Breslow and Chatterjee, 1999). In our setting, phase 1 consists of EHR data available on all subjects and phase 2 consists of the subset of records that were selected for validation. Optimal two-phase designs have been studied for settings where there is an expensive explanatory variable that is only measured in the phase 2 subsample (McIsaac and Cook, 2014; Tao et al., 2020; Han et al., 2021b); in our case, the validated value of an EHR-derived variable can be thought of as this expensive variable. Optimal two-phase designs rely on phase 1 data that are correlated with the expensive explanatory variable of interest; in our case, the unvalidated variable is often a good surrogate for the validated value, which can help with designing efficient validation samples. However, with EHR data, there are typically errors across multiple variables (Giganti et al., 2020), which complicates sampling designs and subsequent analyses that incorporate the validated data.
Generalized raking, also known as survey calibration, is a robust and efficient way to obtain estimates that incorporate data from both phase 1 and phase 2 , even with multiple error-prone variables (Deville et al., 1993; Oh et al., 2021b). Generalized raking estimators, which include members of the class of optimally efficient augmented inverse probability weighted estimators (Robins et al., 1994; Lumley et al., 2011), tilt weights using auxiliary information available in the phase 1 sample. Optimal sampling designs for generalized raking estimators are not easily derived, but the optimal design for the inverse probability weighted (IPW) estimator, based on Neyman allocation (Neyman, 1938), is typically a good design for a generalized raking estimator (Chen and Lumley, 2022). However, the optimal design depends on parameters that are usually unknown without previous data collection.
The necessity of prior data to design optimal sampling strategies has led to multi-wave sampling schemes. McIsaac and Cook (2015) proposed multi-wave sampling strategies and illustrated two-wave sampling in a setting with a binary outcome and an error-prone binary covariate. Data from the first wave was used to adaptively estimate parameters needed to design the optimal phase 2 sample, and the second wave sampled based on this estimated optimal design. Others have also considered similar two-wave sampling strategies for different settings (Chen and Lumley, 2020; Han et al., 2021b). Multi-wave sampling has shown a remarkable ability to yield sampling designs that are nearly as efficient as the optimal sampling design, and therefore have the potential to optimize resources in practice.
In this manuscript, we describe our experience designing and implementing a multi-wave validation study with EHR data to estimate the associations between maternal weight gain during pregnancy and risks of childhood obesity and asthma. To our knowledge, this is the first implementation of a multi-wave sampling design to address data quality issues in the EHR. Other novel developments in this paper include the application of functional principal components analyses to estimate maternal weight gain during pregnancy and to initiate data quality checks (Yao et al., 2005); the implementation of a multi-frame analysis to combine results across two independent validation samples targeting our two endpoints (Metcalf and Scott, 2009); and estimation via generalized raking techniques, with multiply imputed influence functions to estimate the optimal auxiliary variable Han, 2016, Oh et al. 2021a). The use of these methods allows us to obtain efficient estimates that address data quality concerns across many EHR variables while making minimal assumptions.
2. Maternal Pregnancy Weight and Child Health
2.1. Background
Maternal obesity and excessive weight gain during pregnancy have been associated with childhood obesity (Heslehurst et al., 2019) and childhood asthma (Forno et al., 2014). However, small sample sizes have limited the ability to study the complex nature of these associations: for example, to ascertain population sub-group effects, especially by race/ethnicity. Hence, there is growing interest in conducting large epidemiological studies using EHR data to evaluate the association between maternal gestational weight gain and child health outcomes. However, data obtained from EHRs suffer from quality issues, necessitating data validation.
2.2. Primary and Secondary Analysis Models
Of primary interest is the association between maternal weight change during pregnancy, , and time from birth to childhood obesity, . We do not observe in all children; follow - up is censored at the first of child’s date of last visit or 6th birthday. Let be the time to censoring, be the censored-failure time, and be the indicator childhood obesity is observed. Other covariates, Z, include BMI at conception, age at delivery, race, ethnicity, cesarean delivery, diabetes, smoking during pregnancy, history of depression, insurance status, marital status, number of prior children, whether child was singleton, estimated gestational age, and child sex. We assume that and are independent conditional on . Our primary model is a priori specified as the Cox model, , with the hazard of obesity at time conditional on and , and an unspecified baseline hazard function. Of primary interest is estimating .
Of secondary interest is the association between maternal weight change during pregnancy and childhood asthma. Given challenges making definitive diagnoses in very young children, we only consider asthma diagnoses during ages 4 and 5 years; the subset of children in the obesity study who have data between their fourth and sixth birthdays are included in these analyses. Our secondary analysis model is a priori specified as a logistic regression model with the outcome asthma (yes/no). The primary exposure is maternal weight change during pregnancy, and covariates are maternal BMI at conception, maternal age at delivery, maternal race, maternal ethnicity, cesarean delivery, maternal diabetes, smoking during pregnancy, insurance status, estimated gestational age, child sex, and maternal asthma. To simplify presentation, we do not mathematically define variables for the secondary analysis.
Instead of observing , our phase 1 data consist of error-prone versions of these variables, denoted , and auxiliary variables, , that are not directly included in the outcome model but may provide useful information for sampling or weighting. Our strategy is to validate a phase 2 sample of records so that we know for this sample. Before we get to that, we first describe the phase 1 data.
3. Phase 1 Data
3.1. EHR Data Sources
We received data from all mothers in the Vanderbilt University Medical Center EHR who gave birth between December 2005 to August 2019 and could be linked with children whose data were also in the EHR. Mother-child dyads were included if the child had at least one pair of height-weight measurements after 2 years of age, the mother had at least one height measurement, and the mother had at least one weight measurement during the year preceding pregnancy up to delivery date. A total of mother-child dyads were included in the study as the phase 1 sample. The asthma sub-study included 7,053 (68%) of these dyads.
Study investigators received data tables extracted from the EHR including demographics, ICD-9/ICD-10 diagnoses, labs, medications, encounters, and insurance data. Childhood obesity was defined as body mass index th percentile based on age and sex according to the U.S. Centers for Disease Control and Prevention growth curves between ages 2 to 5 years (up until 6th birthday) (Flegal and Cole, 2013). The date of obesity was defined as the first date where a child met the obesity endpoint. Children were not eligible to be classified as having obesity before age 2. Childhood asthma and maternal diagnoses of asthma, diabetes, gestational diabetes, and depression were determined using ICD-9 or ICD10 codes and based on published Phecodes (Wu et al. 2019). Additional details regarding data management and cleaning of the phase 1 data are in Web Appendix A.
3.2. Deriving Maternal Weight Change
Maternal weight change per week during pregnancy is ideally computed as the weight immediately preceding delivery minus the weight at the time of conception divided by the length of the pregnancy. There are several challenges with calculating this exposure. First, the date of conception, which is difficult to obtain in the best designed studies, was not readily extractable from the EHR data. Second, although most women in our study had multiple (median of 9) weight measurements, the weight just before giving birth or at the date of conception was often not known. To overcome the former problem, we start by assuming that conception occurred 273 days before delivery for all women. This initial assumption of a 273-day gestational period is obviously an oversimplification; the actual duration of pregnancy is addressed in our phase 2 validation. To overcome the latter problem of sparse weight measurements, we estimated maternal weight trajectories fit using functional principal components analyses (FPCA) and then extracted the estimated maternal weights at conception and delivery from these models. The FPCA permits the borrowing of information across mothers while fitting a mother-specific weight trajectory. Our FPCA analysis was based on Karhunen-Loève expansion (Ramsay and Silverman, 2007) and an estimation technique proposed by Yao et al. (2005) that incorporates measurement error. Details are in Web Appendix B. The phase 1 exposure of interest, the maternal weight gain per week during pregnancy was given by , where and are the estimated weights at conception and the day before delivery for mother .
4. Phase 2 Data Validation
The previous section describes how we derived the phase 1 data from the EHR. This section describes the data validation procedures to obtain phase 2 data on a probabilistic sample of mother-child records.
Data used to derive all outcomes, the primary exposure, and all covariates were validated by a single research nurse. Data were validated by a thorough review of the EHR. It is important to recognize that the phase 1 EHR data were extracted by programmers and that variables used in phase 1 analyses were constructed computationally. In contrast, during data validation, the nurse looked through the complete EHR, including data not readily extracted and free text fields, to validate, and in some cases, find data. For example, estimated gestational age could not be readily extracted by programmers from the EHR and was not in the phase 1 data; however, this information is in the EHR and was able to be extracted by the nurse. Number of prior children and marital status were similarly not in the phase 1 data but extracted by the nurse. Other desired variables (e.g., smoking during pregnancy) were approximated in the phase 1 sample using readily available data (e.g., any history of smoking prior to delivery), but were more accurately obtained from a thorough review of the EHR. Values were either verified as correct (i.e., matching the phase 1 value), replaced with the correct value, or removed if deemed to be an error but no replacement was found.
Although we refer to these manually abstracted data as the validated data, they may still contain errors. The nurse may have made mistakes or the correct diagnosis may not be in the EHR because it was not entered or missed by health care providers. In our analyses, we assume that validated data are of higher quality than data algorithmically extracted from the EHR, and the validated data are considered the reference standard.
More details about phase 2 data validation are in Web Appendix C. Of note, because mother-child dyads could have a large number of weight and height measurements, we used FPCA to prompt validation. In addition to reviewing a sample of measurements around critical time points, the nurse validated all weights outside the FPCA-derived 95% confidence band of the estimated weight trajectory for a woman. After chart review, the estimated maternal weight changes during pregnancy for each woman selected for validation were again estimated using FPCA, but incorporating the updated data. The estimated gestation period was also entered as part of the phase 2 validation, which typically resulted in a new date of conception; the timing of weight measurements was adjusted accordingly.
Figure 1 shows a de-identified example. Five weight measurements were flagged as outside the FPCA 95% confidence band based on phase 1 data (left panel), so the nurse checked weights corresponding to those dates. The weight above the 95% confidence band was found to be incorrect, whereas the weights below the confidence bands were verified as correct. The estimated gestational age based on the chart review was 259 days. The weight trajectory was then re-estimated for this mother (right panel). The validated weight change per week was then re-computed as .
Figure 1.
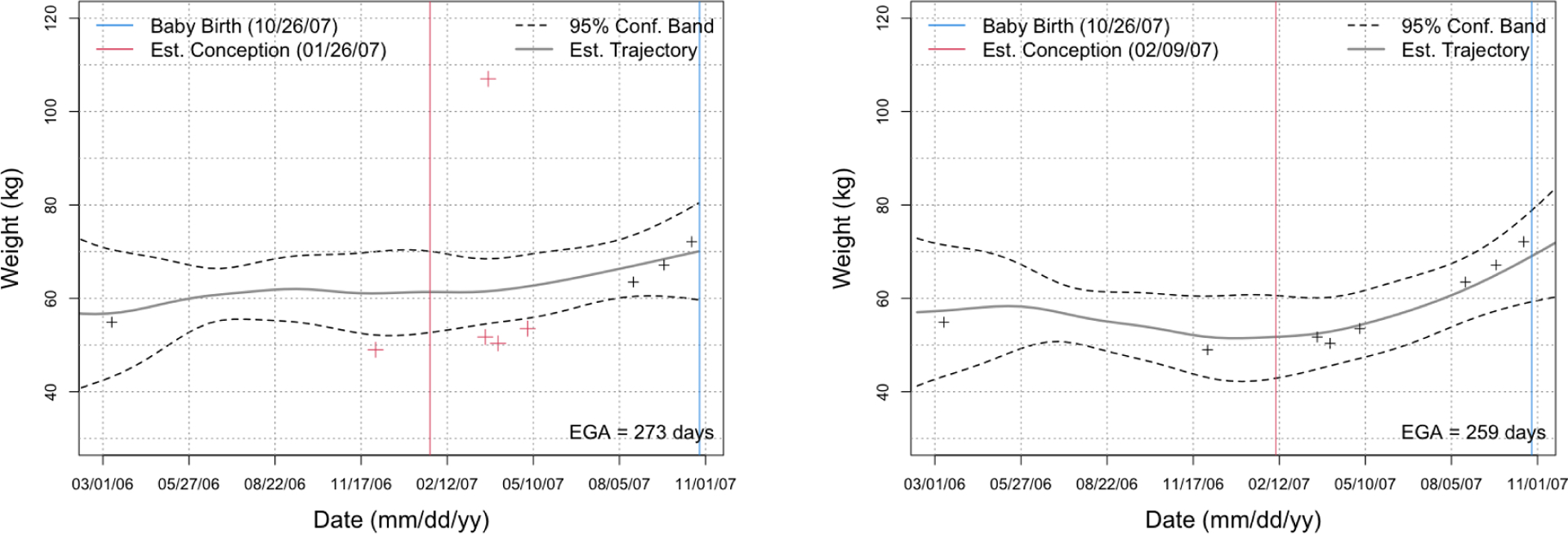
The estimated weight trajectory and 95%-confidence band derived using FPCA for one of the mothers based on phase 1 (left) and phase 2 (right) data; dates have been shifted for de-identification. Red crosses in the left panel were identified as potential outliers and were manually validated. After validation, we updated the weight trajectory (right panel); the outlier weight > 100 kg was found to be erroneous and removed.
5. Multi-Wave Phase 2 Validation Design
Here we describe our phase 2 sampling design. We had resources to validate 1000 mother-child dyads. We targeted the first three-fourths of our validation sample to optimize efficiency of the primary (obesity) analysis and the remaining to optimize the secondary (asthma) analysis. Figure 2 provides an overview. A few key concepts are first reviewed.
Figure 2.
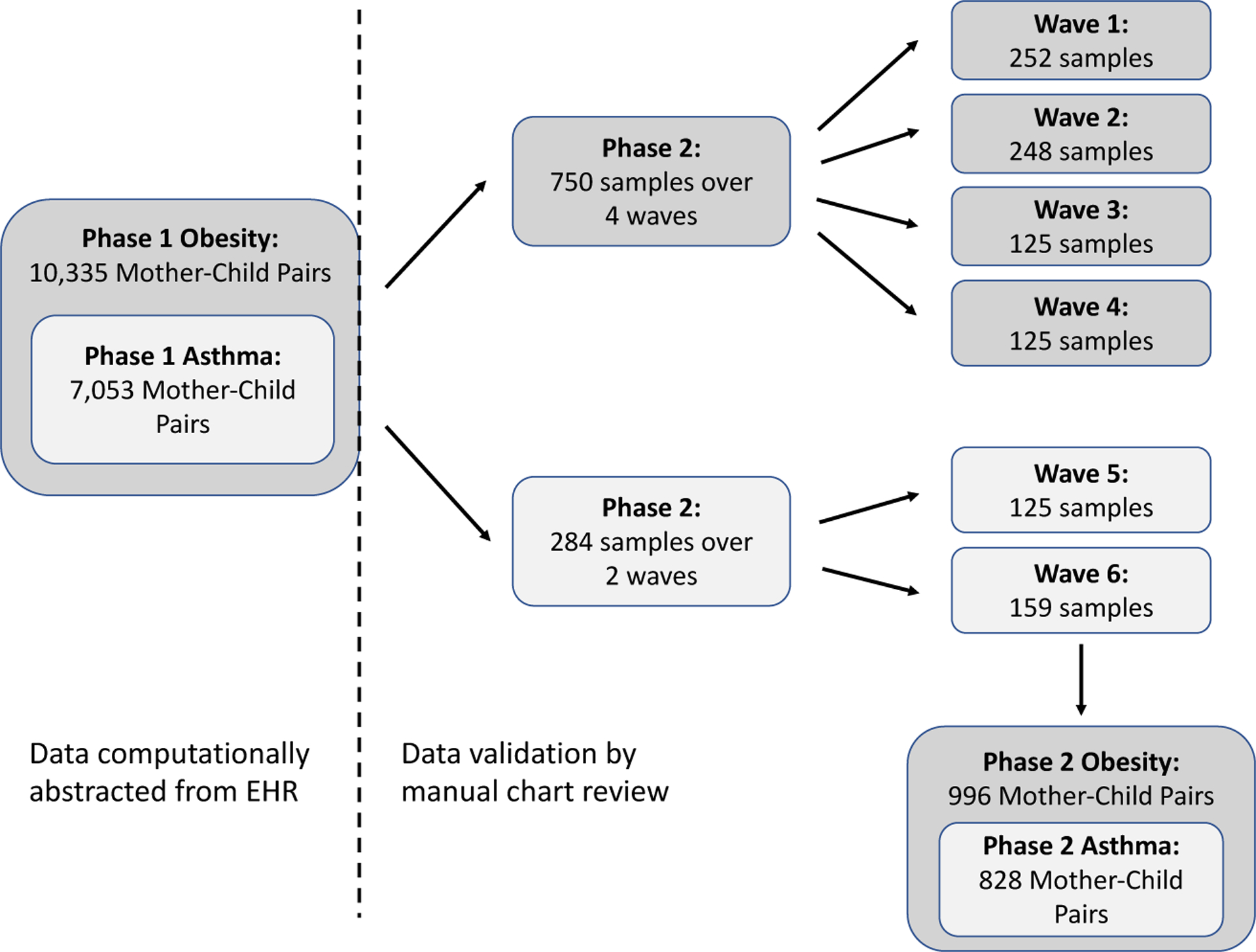
Schematic of multi-wave sampling strategy for data validation in the childhood obesity study and the childhood asthma sub-study. The numbers do not sum to 996 because of overlap of 38 records sampled for both the obesity and asthma studies.
5.1. Generalized raking
We perform analyses combining phase 1 and phase 2 data using generalized raking. Generalized raking, also known as survey calibration, is well-known in the survey sampling literature (Deville et al., 1993), but only recently has been recognized in the biostatistics literature as a practical approach to obtain augmented IPW estimators (Lumley et al., 2011). In brief, generalized raking calibrates the sampling weights with an auxiliary variable (or vector of auxiliary variables) available in the phase 1 data such that the new calibrated weights are as close as possible to the original sampling weights but under the constraint that the sum of the auxiliary variable in the re-weighted phase 2 data is equal to its known sum in the phase 1 data. This approach improves efficiency over IPW estimators if the auxiliary variable is correlated with the variable of interest, with efficiency gains growing with increasing correlation (Oh et al., 2021a). In our setting, the primary goal is to estimate a regression coefficient, specifically the log hazard ratio, , and the most efficient auxiliary variable is the expected efficient influence function for , denoted (Breslow et al. 2009). This variable relies on unknown parameters, but a good estimate of it may be the influence function for fit to the error-prone phase 1 data, denoted . An even better estimate might be the influence function for fit to multiply imputed estimates of the validated data (Han, 2016; Han et al., 2021a), specifically, , where represent the th imputation of for imputation replications. The imputation model is constructed from the phase 2 sample. How well approximate affects how well and approximate the expected efficient influence function.
More precisely, let and be the parameter defined by the population Cox partial likelihood score equation such that . Let be the indicator that record is in the phase 2 sample, and let denote the sampling probability, with . The IPW estimator, , is the solution to . The generalized raking estimator, , is the solution to , where is chosen to minimize for some distance measure subject to the constraint that , where is an estimate of the expected efficient influence function for , either or . Here we use .
5.2. Stratification, Neyman Allocation, and Multi-wave Sampling
For an IPW estimator, the optimal stratified sampling strategy is Neyman allocation (Neyman, 1938). Although not necessarily optimal for generalized raking, the loss of efficiency when using raking with a Neyman allocation design versus the theoretically optimal design is minimal (Chen and Lumley, 2022). Neyman allocation is also fairly straightforward to implement. Given a set of strata, Neyman allocation samples proportional to the number of observations in the strata times the standard deviation of the variable of interest in the strata. Since the log hazard ratio estimator from the Cox model is asymptotically equivalent to the sum of influence functions, Neyman allocation in our setting is to sample proportional to the product of the number of records in a stratum times the standard deviation of the influence function for the target coefficient in that stratum Amorim et al. 2021). Again, we do not know the true influence function, but we can estimate it from phase 1 data, and as we collect phase 2 data, we can update estimates of it and adjust our sampling accordingly.
Following the adaptive multi-wave sampling approach by McIsaac and Cook (2015), we divided our phase 2 sample into multiple waves. In wave 1, we estimate the influence function of with . We then allocate , the sample size of the first wave of our phase 2 sample, across the set of strata in wave 1 via Neyman allocation,
| (1) |
where is the population size of stratum and is the estimated standard deviation of in stratum . For the th sampling wave , we determine the desired set of strata , which may be the same as , or individual strata can be split into 2 or more smaller strata. We use the phase 2 data to fit the target model using the validated data and directly estimate the influence function of interest. We then estimate the sample design with Neyman allocation for the total cumulative validated sample size , where is the size of the th wave of validation sampling. The strategy for the th wave is then to sample the difference between the derived optimal allocation for a stratum and the number already sampled in that stratum. Specifically, for each , the Neyman allocation for a stratum is given by
| (2) |
where is the estimated standard deviation in stratum of the influence function using data already validated, i.e., where is the cumulative indicator that data have been validated by wave . If a stratum is determined to have been oversampled relative to its optimal allocation in the current wave (i.e., ), that stratum is closed to further sampling and Neyman allocation is recalculated for the total number to be validated in the remaining strata.
In our case, since the cost of validation is essentially equivalent across records, we can further improve precision by carefully choosing sampling strata. In general, creating strata based on both the outcome and the exposure jointly can result in more efficient designs (Breslow and Chatterjee, 1999). More strata are generally more efficient than fewer strata (Lumley, 2010). In addition, the most efficient stratification is one where Neyman allocation suggests to sample approximately equal numbers from each stratum (Sarndal et al., 2003). Put together, our general sampling strategy was to stratify on both the primary exposure and outcome together and to choose a fair number of strata such that the number of records sampled in each stratum based on Neyman allocation was approximately equal. After each sampling wave, we re-calculated the influence function based on the phase 2 data, re-computed the optimal number to be sampled with this updated influence function, divided large strata following the principle that optimality is achieved by sampling approximately equal numbers from strata, and then selected the next wave’s sample based on this updated stratification / allocation. We note in subsequent waves strata can be split, but for the final post-stratification weights to be well-defined, strata cannot be merged. Note also that the number of sampling waves does not need to be a priori specified.
5.3. Multi-wave sampling for obesity endpoint
Our phase 2 sample for the obesity endpoint validated 750 paired records over a total of four sampling waves. Strata were created based on phase 1 data including the childhood obesity event indicator, the censored-failure time (time to childhood obesity or censoring), and the exposure of interest (estimated maternal weight change during pregnancy). We fit a simplified Cox model to the phase 1 data with the outcome time-to-obesity, the exposure of interest, and covariates BMI at conception, maternal diabetes, maternal age at delivery, child sex, child ethnicity, and child race. From this model, we computed the estimated influence function for the maternal weight gain log hazard ratio for each mother-child dyad. This influence function was then used to create the wave 1 sampling design, where strata boundaries were chosen such that the Neyman allocation was similar across strata.
For wave 1 of our phase 2 sample, we started with 21 strata based on seven combinations of obesity/follow-up (censored in ages [2,5) years, censored in ages [5,6), obesity in ages [2,2.5), obesity in ages [2.5,3), obesity in ages [3,4), obesity in ages [4,5), and obesity in ages [5,6)) and three categories for mother’s estimated weight change during pregnancy (, and , where 5.14 and 20.5 were the 5th and 95th percentiles for weight change in phase 1 data). These strata choices make intuitive sense: records with more influence on the hazard ratio are those in the tails of the exposure and those experiencing the event, particularly early into follow-up (Lawless, 2018). Our plan was to validate 250 records in wave 1; due to rounding, we sampled 252. Unfortunately, we had an error in our code which was not discovered until we began planning our wave 2 sample. This error led us to sample more than was optimal from records with maternal weight gains outside the 5th and 95th percentiles; without this coding error, our wave 1 strata would likely have been based on less extreme weight gain percentiles, e.g., perhaps the 10th and 90th percentiles.
Table 1 shows the final strata, the population total in each stratum , the number sampled from each stratum in each wave , and the total number sampled from each stratum . Note that since wave 1 had fewer strata than the final number of strata (21 vs. 33), some of the original strata that were subsequently divided are represented by multiple rows. (For example, 8 records were sampled in wave 1 from the original stratum B; these 8 were distributed in some manner across final strata 2–4, not just from final stratum 2.)
Table 1.
Multi-wave Sampling Design for Childhood Obesity Endpoint
| Original Strata | Final Strata | Obesity | Follow-up Time (yrs) | Maternal Gestational Weight Gain (kg) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 0 | (2, 5] | ⩽ 5.14 | 190 | 7 | 0 | 0 | 0 | 7 |
| B | 2 | 0 | (2, 5] | (5.14, 12] | 1904 | 8 | 21 | 7 | 3 | 24 |
| 3 | 0 | (2, 5] | (12, 16] | 1356 | 28 | 0 | 34 | |||
| 4 | 0 | (2, 5] | (16, 20.5] | 526 | 27 | 37 | ||||
| C | 5 | 0 | (2, 5] | > 20.5 | 177 | 8 | 2 | 3 | 0 | 13 |
| D | 6 | 0 | (5, 6] | ⩽ 5.14 | 208 | 14 | 18 | 1 | 0 | 33 |
| E | 7 | 0 | (5, 6] | (5.14, 8.6] | 429 | 16 | 22 | 0 | 0 | 25 |
| 8 | 0 | (5, 6] | (8.6, 12] | 1478 | 15 | 5 | 13 | 39 | ||
| 9 | 0 | (5, 6] | (12, 14] | 846 | 18 | 21 | 20 | 44 | ||
| 10 | 0 | (5, 6] | (14, 16] | 563 | 22 | 40 | ||||
| 11 | 0 | (5, 6] | (16, 20.5] | 588 | 22 | 8 | 35 | |||
| F | 12 | 0 | (5,6] | (20.5, 24.3] | 154 | 17 | 19 | 0 | 0 | 32 |
| 13 | 0 | (5,6] | > 24.3 | 71 | 24 | 0 | 0 | 28 | ||
| G | 14 | 1 | (2, 2.5] | ⩽ 5.14 | 49 | 17 | 0 | 0 | 0 | 17 |
| H | 15 | 1 | (2, 2.5] | (5.14, 10] | 140 | 20 | 19 | 16 | 3 | 28 |
| 16 | 1 | (2, 2.5] | (10, 12] | 126 | 8 | 1 | 22 | |||
| 17 | 1 | (2, 2.5] | (12, 16] | 205 | 12 | 8 | 5 | 29 | ||
| 18 | 1 | (2, 2.5] | (16, 20.5] | 76 | 3 | 14 | ||||
| I | 19 | 1 | (2, 2.5] | > 20.5 | 33 | 17 | 0 | 0 | 0 | 17 |
| J | 20 | 1 | (2.5, 3] | ⩽ 5.14 | 13 | 12 | 0 | 0 | 0 | 12 |
| K | 21 | 1 | (2.5, 3] | (5.14, 12] | 129 | 12 | 13 | 0 | 2 | 19 |
| 22 | 1 | (2.5, 3] | (12, 20.5] | 129 | 15 | 0 | 1 | 24 | ||
| L | 23 | 1 | (2.5, 3] | > 20.5 | 19 | 12 | 0 | 0 | 0 | 12 |
| M | 24 | 1 | (3, 4] | ⩽ 5.14 | 21 | 10 | 0 | 0 | 0 | 10 |
| N | 25 | 1 | (3, 4] | (5.14, 12] | 175 | 13 | 25 | 0 | 5 | 20 |
| 26 | 1 | (3, 4] | (12, 20.5] | 203 | 3 | 4 | 30 | |||
| O | 27 | 1 | (3, 4] | > 20.5 | 28 | 13 | 0 | 0 | 0 | 13 |
| P | 28 | 1 | (4, 5] | ⩽ 5.14 | 22 | 9 | 0 | 0 | 0 | 9 |
| Q | 29 | 1 | (4, 5] | (5.14, 20.5] | 261 | 10 | 19 | 0 | 4 | 33 |
| R | 30 | 1 | (4, 5] | > 20.5 | 24 | 11 | 4 | 0 | 0 | 15 |
| S | 31 | 1 | (5, 6] | ⩽ 5.14 | 14 | 8 | 0 | 0 | 0 | 8 |
| T | 32 | 1 | (5, 6] | (5.14, 20.5] | 167 | 8 | 2 | 3 | 4 | 17 |
| U | 33 | 1 | (5,6] | > 20.5 | 11 | 10 | 0 | 0 | 0 | 10 |
| Total | 10335 | 252 | 248 | 125 | 125 | 750 |
is the population size in stratum is the number sampled from the stratum in wave is the number sampled from the stratum in wave 2 , and and are defined similarly. is the total number sampled from stratum over all waves of the phase 2 validation sampling.
Upon receiving the wave 1 validation data, we fit a weighted Cox model to the validated data (weights equal to the inverse of the sampling probabilities) to obtain influence functions and estimate their standard deviations in each of our strata. This Cox model included phase 2 data for the outcome, the exposure of interest, and nearly all covariates specified for our final model. (The model did not include the singleton indicator and dichotomized a few of our categorical covariates.) For wave 2, we chose to validate an additional 248 records bringing our total validated to 500. We used the updated estimates of the standard deviation of the influence function in each stratum and (correctly) applied Neyman allocation for a total sampled of 500. From this, we learned we had over-sampled from some strata in wave 1. For example, the optimal number to be sampled from original stratum A (obesity = 0, follow-up ∈ (2,5], and weight change ) after wave 1 was 6 , but we had already sampled 7 . In contrast, the estimated optimal number to be sampled from original stratum E (obesity=0, follow-up ∈(5,6], weight change ∈ (5.14,20.5], i.e., the union of final strata 7–11 in Table 1) was 105; in wave 1 we had sampled 16 from this stratum meaning in wave 2 we would need to sample 89. Since optimal strata boundaries would sample approximately equal numbers from each stratum after applying Neyman allocation, we further divided strata. Specifically, prior to sampling for wave 2 we divided 4 strata into 9 new strata (stratum E was split into 3 strata), making a total of 26 strata. Neyman allocation was used to decide the optimal way to sample 500 records from these 26 strata. Nine of these new strata, which included a total of 108 records sampled in wave 1 , had already been over-sampled (i.e., Neyman allocation for stratum for ), so these strata were closed, and Neyman allocation was re-computed to determine how to allocate 392 records (=500–108) across the 17 (= 26–9) open strata. The number sampled from each stratum in wave 2 is given in column .
The process was repeated after collecting wave 2 validation data to select which records to sample in wave 3 and then again after collecting wave 3 validation data to select which records to sample in wave 4 . For wave 3 there were a total of 30 strata and for wave 4 we expanded to 33 strata. Additional details can be inferred from Table 1.
5.4. Multi-wave sampling for asthma endpoint
We applied a similar multi-wave sampling strategy for the asthma study. Strata were chosen based on phase 1 data for child asthma status and maternal weight gain during pregnancy. Recall that those in the asthma study were a subset of those in the obesity study . Of the 750 records already validated for the obesity study, 582 met inclusion criteria for the asthma study. Our strategy was to 1) to use this already collected phase 2 data to build an imputation model for the validated data, 2) to impute “validated data” from that model for all mother-child records that had not been validated, 3) to fit a working analysis model to the complete data from which the influence function for the maternal weight gain log odds ratio was obtained, 4) to repeat this across multiple imputations to obtain the average influence function per mother-child dyad, and 5) to perform Neyman allocation based on these estimated average influence functions, refining strata so the allocation was approximately balanced across strata. Details are in Web Appendix D.
Table 2 shows strata for the validation sample targeted for the asthma study. Wave 1 for the asthma study (5th overall sampling wave) sampled 125 dyads across five strata. After completing this validation wave, the process was repeated, combining all phase 2 validated data across the 5 prior waves to re-estimate the average multiply imputed influence function for the maternal weight gain log odds ratio, which was then used to target our 6th and final sampling wave. Unlike the obesity sampling, we had not over-sampled from any strata. However, strata were split, creating ten strata from which similar numbers were sampled.
Table 2.
Multi-wave Sampling Design for Childhood Asthma Endpoint
| Original Strata | Final Strata | Asthma | Maternal Gestational Weight Gain (kg) | ||||
|---|---|---|---|---|---|---|---|
| A | 1 | 0 | < 5 | 306 | 31 | 27 | 31 |
| 2 | 0 | [5, 10) | 1251 | 4 | 31 | ||
| B | 3 | 0 | [10, 12) | 1520 | 16 | 16 | 20 |
| 4 | 0 | [12, 15) | 1681 | 13 | 25 | ||
| C | 5 | 0 | [15, 19.5) | 1105 | 24 | 21 | 34 |
| 6 | 0 | ⩾ 19.5 | 459 | 23 | 34 | ||
| D | 7 | 1 | < 8 | 115 | 23 | 11 | 23 |
| 8 | 1 | [8, 12) | 278 | 13 | 24 | ||
| E | 9 | 1 | [12, 17] | 240 | 31 | 4 | 27 |
| 10 | 1 | ⩾ 17 | 98 | 27 | 35 | ||
| Total | 7053 | 125 | 159 | 284 |
is the population size in stratum is the number sampled from the stratum in wave is the number sampled from the stratum in wave 2 , and is the total number sampled from stratum over both waves of the phase 2 validation sampling.
Our plan was to use all validated records meeting inclusion criteria for both the obesity and asthma analyses. Thus, in each of the 6 waves of the phase 2 sample, we validated all variables needed for both analyses. Thus, we could combine these two separate sampling frames using the approach of Metcalf and Scott (2009). This approach requires that the samples from the two frames be independent. Hence, records already sampled for validation for the obesity study were eligible for sampling in the asthma study. There was some overlap between sampled records. If a pair of records had already been validated as part of the obesity sampling, we did not re-validate data, but used the already validated data and made note of the double-sampling for our analyses. Given we had resources to validate 1000 records, we selected 284 records for our final wave sample, knowing that there would be some overlap. It turned out that 38 of these 284 (13%) had already been validated, so the total number of unique mother-child dyads validated across the two sampling designs was 996.
6. Analysis of Mother-Child Health Outcomes Data
6.1. Analysis Approach
To obtain valid estimates that are efficient and properly quantify uncertainty, we need to account for the multiple sampling frames used to select records in our analyses. To do this, we follow the approach of Metcalf and Scott (2009). Specifically, the records that were in both sampling frames (i.e., the 7,053 records in the asthma study) were included twice in a combined sampling frame and weights were adjusted accordingly. Let be the sampling probability for record in the obesity frame (i.e., defined by the final strata in Table 1). Similarly, let be the sampling probability for record in the asthma frame (i.e., defined by the final strata in Table 2). The subset of 3,282 records in the obesity frame but not the asthma frame received a weight of . The 7,053 records in both frames that were duplicated in the combined frame received weights of and , respectively. We set so that the weight assigned to the unit did not depend on the sample in which it was drawn. Treating the original sampling frames as super-strata and preserving the original (independent) designs of the two frames, the usual IPW sandwich variance estimator with these weights properly accounts for duplication of records in this multi-frame dataset (Metcalf and Scott, 2009). A similar approach was applied for the asthma endpoint.
Generalized raking estimators potentially improve the efficiency of the multi-frame IPW estimator by calibrating the weights using estimates of the efficient influence function of the target regression parameter. Calibration was based on either the naïve influence function or on the multiply imputed influence function (Han,2016); the resulting estimators are referred to as RakingNv and RakingMI, respectively. The naïve influence function was extracted from the Cox model based on only the error-prone phase 1 data. The multiply imputed influence function was based on the following procedure: 1) using phase 2 data, fit a model for the validated variables conditional on the unvalidated variables; 2) using this model, impute “validated data” for all phase 1 records (including those in the phase 2 sample); 3) fit the full Cox model to the fully imputed “validated data” and obtain the estimated influence function for each record; 4) repeat steps 2 and 3 multiple (in our case 100) times; 5) for each observation, compute the average of the estimated multiply imputed influence functions; 6) use this average influence function to calibrate weights. The performance of the RakingNv versus RakingMI estimators depends on how much error is in the phase 1 data and how well the phase 2 data can be imputed. Analyses were performed using the R package survey.
6.2. Error Rates
Table 3 summarizes phase 1 and unweighted phase 2 data for study variables. In the phase 1 sample, 18% of f our phase 2 sample, where 42% were found to meet the obesity definition. Of the 996 validated records, childhood obesity was misclassified only 6 times (0.6%). In the subset of phase 1 records in the asthma study, 10% had asthma between ages 4–5 years. The asthma outcome had higher rates of misclassification than the obesity outcome: 10.4% of children in the phase 2 sample had their asthma diagnosis misclassified with positive predictive value (PPV) of 0.57 and negative predictive value (NPV) of 0.97 .
Table 3.
Characteristics of phase 1 and unweighted phase 2 samples, and discrepancies.
| Variable | Phase 1 N = 10, 335 |
Phase 2a n = 996 |
Percent Errorb | Discrepancy |
|---|---|---|---|---|
| Child obesity | 17.9% | 42.0% | 0.6 | PPV=0.998, NPV=0.991 |
| Time to event/censoring (age, yrs) | 4.3 (2.9, 6.0)c | 4.8 (3.0, 6.0) | 4.7 | 1.0 (range 0.04, 1.8) |
| Maternal weight gain (kg/wk) | 0.30 (0.26, 0.38) | 0.30 (0.22, 0.41) | 100 | −0.02 (range −0.66, 0.93) |
| Maternal BMI (kg/m2) | 25.9 (22.6, 30.5) | 27.9 (23.8, 33.1) | 100 | 0.13 (range −6.8, 8.6) |
| Maternal age (yrs) | 28.0 (23.5, 32.3) | 27.4 (23.0, 31.8) | 0 | – |
| Maternal race | 5.4 | |||
| White | 61.8% | 56.8 | PPV=0.952, NPV=0.962 | |
| Black | 23.1% | 29.7 | PPV=0.986, NPV=0.993 | |
| Asian | 6.9% | 4.0 | PPV=0.904, NPV=0.998 | |
| Other/Unknown | 8.2% | 9.4 | PPV=0.778, NPV=0.966 | |
| Maternal ethnicity, Hispanic | 14.9% | 14.9% | 1.1 | PPV=0.948, NPV=0.996 |
| Maternal diabetes | 10.9 | |||
| None | 83.3% | 89.4 | PPV=0.991, NPV=0.553 | |
| Gestational | 13.7% | 6.7 | PPV=0.420, NPV=0.992 | |
| Type 1 or 2 | 3.0% | 3.9 | PPV=0.472, NPV=0.977 | |
| Cesarean delivery | 36.2% | 38.2% | 1.3 | PPV=0.989, NPV=0.986 |
| Child sex, male | 52.7% | 55.4% | 0.4 | PPV=0.995, NPV=0.998 |
| Maternal depression | 8.9% | 10.9% | 13.5 | PPV=0.376, NPV=0.926 |
| No private insurance | 45.9% | 67.6% | 24.3 | PPV=0.941, NPV=0.580 |
| Singleton | 98.1% | 97.3% | 1.2 | PPV=0.992, NPV=0.826 |
| Maternal smoking | 6.3% | 13.2% | 11.8 | PPV=0.618, NPV=0.897 |
| Marriedd | – | 51.8% | – | – |
| Number prior live birthsd | – | 0.5 (0, 1) | – | – |
| Gestational aged (wks) | – | 39.1 (38.1, 40.3) | – | – |
| Child asthmae | 10.4% | 13.0% | 10.4 | PPV=0.570, NPV=0.973 |
| Maternal asthmae | 7.8% | 11.0% | 4.5 | PPV=0.827, NPV=0.968 |
Not meant to represent the study populations. Children diagnosed with obesity and asthma were intentionally over-sampled in phase 2 .
Percentage of phase 2 values that did not match phase 1 value.
Median (25th percentile, 75 th percentile) are reported for continuous variables unless range is noted.
Marital status, number of prior live births, and estimated gestational age were not available in the phase 1 data. Gestational age was assumed to be 39 weeks for computing maternal weight gain per week.
Child asthma and maternal asthma are only shown for the in phase 1 and in phase 2 meeting the inclusion criteria for the asthma sub-study.
The estimated maternal weight gain per week during pregnancy was different from that estimated in phase 1 data for all mothers in the phase 2 sample, primarily due to corrections in the length of pregnancy. The median discrepancy between maternal weight gain was 19.6 grams/week, ranging from −655 to 933 g/ wk; 93% of validated records had discrepancies under 100 g/ wk. Similarly, the estimated BMI at conception was different from that in phase 1 data for all mothers in the phase 2 sample with median (range) of discrepancy 0.13(−6.8 to 8.6)kg/m2. Other variables with high levels of misclassification were maternal diabetes (10.9%), smoking during pregnancy (11.8%), maternal depression (13.5%), and insurance status (24.3%). In contrast, misclassification was fairly low for race (5.4%), ethnicity (1.1%), cesarean delivery (1.3%), child sex (0.4%), singleton (1.2%), and maternal asthma (4.5%).
6.3. Regression Results
Holding all other factors constant, a child from a woman who gained 250 grams more per week during pregnancy (i.e., 9.75 kg in added weight over a normal 39 week pregnancy) had an estimated 30% increased hazard of obesity before age 6 (hazard ratio [HR] = 1.30;95% CI 1.14–1.48) based on the multi-frame generalized raking estimator incorporating the phase 2 validation data and raking with the naïve influence function. For comparison, a model using only the unvalidated phase 1 data estimated a 24% increased hazard of obesity (HR = 1.24; 95% CI 1.14–1.36). Table 4 shows log hazard ratio estimates and standard errors for all variables for the various estimators. The estimated log hazard ratio for maternal weight gain during pregnancy was fairly similar across all estimators. Raking the multi-frame IPW estimator with either the naïve or multiply imputed influence function led to a 33% decrease in the variance of the estimated log hazard ratio for maternal weight gain.
Table 4.
Estimated log hazard ratios for childhood obesity and log odds ratios for childhood asthma () and standard errors based on various data and estimators. IPW=inverse probability weighted estimator; RakingNv=generalized raking with the naive influence function; RakingMI=generalized raking with the multiply imputed influence function.
| Log hazard ratios for childhood obesity | ||||||||
|---|---|---|---|---|---|---|---|---|
| Phase 1 | IPW | RakingNv | RakingMI | |||||
| SE | SE | SE | SE | |||||
| Maternal weight gain (kg/wk) | 0.87 | 0.18 | 1.17 | 0.33 | 1.06 | 0.27 | 1.00 | 0.26 |
| Maternal BMI (5 kg/m2) | 0.28 | 0.02 | 0.32 | 0.03 | 0.32 | 0.03 | 0.32 | 0.03 |
| Maternal age (10 yrs) | −0.05 | 0.04 | 0.15 | 0.11 | 0.15 | 0.11 | 0.15 | 0.11 |
| Maternal race, Black | −0.03 | 0.06 | −0.24 | 0.14 | −0.24 | 0.14 | −0.24 | 0.14 |
| Maternal race, Asian | 0.24 | 0.11 | 0.08 | 0.25 | 0.10 | 0.25 | 0.10 | 0.25 |
| Maternal race, other/unknown | 0.41 | 0.08 | 0.04 | 0.17 | 0.04 | 0.17 | 0.04 | 0.17 |
| Maternal ethnicity, Hispanic | 0.72 | 0.06 | 0.95 | 0.15 | 0.95 | 0.14 | 0.94 | 0.14 |
| Maternal diabetes, gestational | 0.12 | 0.06 | −0.54 | 0.22 | −0.54 | 0.22 | −0.54 | 0.22 |
| Maternal diabetes, type 1/2 | 0.13 | 0.12 | −0.19 | 0.27 | −0.15 | 0.26 | −0.15 | 0.26 |
| Cesarean delivery | 0.12 | 0.05 | 0.17 | 0.10 | 0.17 | 0.10 | 0.17 | 0.10 |
| Child sex, male | 0.12 | 0.05 | −0.15 | 0.10 | −0.15 | 0.10 | −0.14 | 0.10 |
| Maternal depression | 0.08 | 0.08 | −0.19 | 0.18 | −0.17 | 0.18 | −0.16 | 0.18 |
| No private insurance | 0.18 | 0.05 | 0.60 | 0.14 | 0.59 | 0.14 | 0.59 | 0.14 |
| Singleton | 0.44 | 0.21 | −0.00 | 0.33 | 0.03 | 0.32 | 0.02 | 0.32 |
| Maternal smoking | 0.32 | 0.10 | 0.48 | 0.17 | 0.46 | 0.17 | 0.46 | 0.17 |
| Married | 0.32 | 0.13 | 0.31 | 0.13 | 0.31 | 0.13 | ||
| Number prior live births | −0.07 | 0.05 | −0.08 | 0.05 | −0.08 | 0.05 | ||
| Gestational age (wks) | 0.03 | 0.02 | 0.03 | 0.02 | 0.03 | 0.02 | ||
| Log odds ratios for childhood asthma | ||||||||
| Phase 1 | IPW | RakingNv | RakingMI | |||||
| SE | SE | SE | SE | |||||
| Maternal weight gain (kg/wk) | −0.54 | 0.31 | 0.48 | 0.73 | 0.25 | 0.74 | 0.26 | 0.74 |
| Maternal BMI (5 kg/m2) | 0.10 | 0.03 | 0.10 | 0.07 | 0.09 | 0.07 | 0.10 | 0.07 |
| Maternal age (10 yrs) | −0.18 | 0.07 | −0.07 | 0.18 | −0.08 | 0.17 | −0.08 | 0.17 |
| Maternal race, Black | 0.71 | 0.09 | 1.25 | 0.26 | 1.28 | 0.25 | 1.28 | 0.25 |
| Maternal race, Asian | −0.34 | 0.22 | 0.76 | 0.53 | 0.78 | 0.52 | 0.79 | 0.52 |
| Maternal race, other/unknown | 0.05 | 0.19 | 0.49 | 0.36 | 0.45 | 0.36 | 0.45 | 0.36 |
| Maternal ethnicity, Hispanic | −0.09 | 0.14 | 0.20 | 0.30 | 0.25 | 0.30 | 0.25 | 0.30 |
| Maternal diabetes, gestational | −0.38 | 0.14 | −2.43 | 0.54 | −2.33 | 0.53 | −2.33 | 0.53 |
| Maternal diabetes, type 1/2 | 0.10 | 0.20 | 0.51 | 0.50 | 0.53 | 0.48 | 0.54 | 0.48 |
| Cesarean delivery | 0.16 | 0.08 | −0.15 | 0.21 | −0.14 | 0.21 | −0.14 | 0.21 |
| Child sex, male | 0.47 | 0.08 | 0.70 | 0.21 | 0.73 | 0.21 | 0.73 | 0.21 |
| No private insurance | 0.11 | 0.09 | 0.90 | 0.28 | 0.90 | 0.28 | 0.90 | 0.28 |
| Maternal smoking | −0.44 | 0.24 | 0.31 | 0.28 | 0.28 | 0.28 | 0.29 | 0.28 |
| Maternal asthma | 0.70 | 0.12 | 0.75 | 0.27 | 0.72 | 0.26 | 0.71 | 0.26 |
| Gestational age (wks) | −0.07 | 0.03 | −0.07 | 0.03 | −0.07 | 0.03 | ||
An additional analysis raking with the naive influence function suggested that the relationship between maternal weight gain during pregnancy and childhood obesity was non-linear , with a fairly constant hazard of obesity for women who gained under 11–12 kg during pregnancy, but increasing hazards thereafter; no such non-linear relationship was seen using the phase 1 data alone . Details are in Web Appendix E.
Smoking and insurance status were quite error-prone in the phase 1 data, and their relationships with childhood obesity were stronger using the validated data and raking analyses. Some apparent associations with childhood obesity in the phase 1 data were no longer seen (i.e., 95% CI for crossing 0) in the raking results. The loss of association may have been due to decreased precision when incorporating validation data (e.g., cesarean section), attenuation (e.g., Asian race), or inclusion of other variables (e.g., phase 1 association with singleton status may have been confounded with gestational age). Gestational diabetes appeared protective in the raked analyses but not in analyses using only the phase 1 data.
Similar analyses were performed to estimate odds ratios for our asthma outcome (Table 4). In analyses based only on phase 1 data, the estimated beta coefficient of asthma for maternal weight gain during pregnancy was −0.54 . Generalized raking estimates were in the opposite direction: 0.25 (raking with naïve influence function) and 0.26 (raking with multiply imputed influence function). In terms of a 250 g/ wk difference in weight gain, these correspond to odds ratios of 0.88 (95% CI 0.75–1.02) with phase 1 data only and 1.07 (95% CI 0.74–1.53) raking with the naïve influence function. Although both estimates would fail to conclude that maternal weight gain during pregnancy is associated with an increased risk of childhood asthma, the naïve estimator is weakly suggestive of a protective effect, whereas the raked estimators provide no evidence of an association. The raking estimators suggested a stronger association between childhood asthma and Black race, male sex, and public insurance than was seen using the unvalidated EHR data; these are known risk factors for childhood asthma. Longer gestational age was associated with a lower odds of asthma in the raking analyses; no such estimate could be computed using the phase 1 data alone.
7. Discussion
We have described our experience implementing a multi-wave validation study to address EHR data quality and obtain efficient estimates of the association between maternal gestational weight gain and diagnoses of childhood obesity and asthma. Our multi-wave sampling approach targeted records for validation based on information learned in prior sampling waves. Although we and others have demonstrated the efficiency of multi-wave sampling with extensive simulations (McIsaac and Cook, 2015; Chen and Lumley, 2020; Han et al., 2021b), to our knowledge this is the first implementation of such a design.
We obtained estimates using a novel generalized raking procedure that efficiently combined validation data across multiple sampling waves within two sampling frames with the larger, error-prone EHR data. The resulting augmented IPW estimators addressed complicated error structures across multiple variables in a robust manner that reliably approximates estimates had the entire phase 1 sample been validated. Other analysis approaches could have been employed - in particular, multiple imputation, where one imputes the “validated data” using models built in the phase 2 subsample (Giganti et al., 2019). However, multiple imputation estimators may be biased if the imputation model is misspecified, which is a real concern in our setting given that there were over a dozen error-prone variables. Our raking analyses that attempted to improve efficiency by calibrating weights with multiply imputed influence functions also required substantial imputation; however, consistency of these estimators did not depend on correct specification of the imputation model (Han, 2016).
We also employed a modern FPCA approach to estimate maternal gestational weight gain and to prompt chart reviews. This approach was critical for producing reliable estimates of mothers’ weight trajectories in the presence of sparse data and measurement error. The information extracted from the estimated trajectories and used for analysis (i.e., each mother’s average weight gain per week during pregnancy) was admittedly simple; other components of the FPCA weight trajectory are being considered in on-going analyses. However, this summary measure was chosen for primary analyses because of its simplicity, ease of interpretation, and scientific relevance based on discussions with a pediatrician and a group of women who met with us as part of a community-engagement process.
Our results suggest that greater maternal weight gain during pregnancy is associated with increased risk of childhood obesity but not asthma. Our primary estimate for the obesity analysis was similar to the estimate that simply analyzed the error-prone EHR data. This is despite our discovery during validation of several variables with appreciable error, including the primary exposure. In contrast, the difference between estimates using our methods with validated data and only using the error-prone EHR data were much more substantial for the asthma analysis. This is likely due in part to differences in the accuracy of the EHR-derived phenotypes for childhood obesity (> 99% PPV) versus childhood asthma (57% PPV). However, both models demonstrated substantive changes for other associations between analyses that ignored versus incorporated validation data. And in an additional analysis, we found a sensible, non-linear relationship between maternal weight gain and the hazard of childhood obesity that was not seen using the error-prone EHR data alone.
Although the Cox model was a priori specified, it may be of interest to know how results would have differed had we used a different model, for example an accelerated failure time (AFT) model. In short, the multi-wave sampling procedures would have been identical to those described above, except Neyman allocation would have been based on the influence function for the relevant coefficient from the AFT model. Although not optimal, our sampling strategy designed for a Cox model was likely quite efficient for an AFT model. For example, the correlation between the influence functions for the maternal weight gain coefficients using the error-prone data for the Cox model and a log-normal model was strong, –0.96 (correlation is negative because a higher hazard corresponds to a shorter time-to-event). Generalized raking can be easily applied with an AFT model. For example, the coefficient for maternal weight gain from a log-normal model with weights calibrated with the naïve estimate of the AFT parameter influence function based on error-prone phase 1 data was –0.54 (standard error of 0.125). Holding all other variables constant, this implies that the child from a woman who gained an extra 250 grams per week during pregnancy had a 12.6% (95% CI 7.1, 17.8%) decrease in the geometric mean time until obesity. For comparison, the coefficient for maternal weight gain from a log-normal model without calibration (i.e., using inverse probability weights) was −0.59 (standard error 0.159 ); hence, generalized raking resulted in a 38% decrease in the variance of the estimator.
The vast majority of EHR validation studies reported in the biomedical literature validate sub-optimal subsamples (most employ simple random or case-control sampling) and do not incorporate validation data into analyses, other than simply reporting estimates of data quality (e.g., PPV). There are bias-variance trade-offs between naïve analyses of phase 1 data versus those that incorporate validation data, and in some cases, the decreased precision of estimates using validation data may outweigh the increased bias of using unvalidated data. Though we can hope that errors in EHR data yield estimates with minimal bias, we cannot know this until we actually validate data, examine error rates, and directly calculate their impact on estimates. The impact that poor data quality can have on results has been observed time and again to be potentially substantial (Floyd et al., 2012, Giganti et al., 2020).
We learned several lessons from our multi-wave validation study. First, adaptive sampling designs provide an important chance to recover from a poorly chosen first sampling wave. Second, we learned that it takes quite a bit of time between receiving validation data from one wave to design the next wave. Upon receiving validation data we needed to perform data quality checks, de-identify data, re-run FPCA analyses, re-fit regression models to estimate influence functions, re-compute Neyman allocation, and then meet as a team to discuss whether and how to divide strata. Keeping track of interim datasets also became tedious. To alleviate some of these challenges we have developed an package, optimall, which performs Neyman allocation, allows easy splitting of strata, and keeps track of various datasets in an efficient manner. This package also implements integer-valued Neyman allocation Wright, 2017), which provides exact optimality for a fixed sample size (i.e., avoids rounding issues) and was employed in later waves of our validation sampling.
When there are two parameters of interest (e.g., maternal gestational weight gain coefficients for childhood obesity and asthma), it is not possible to design a validation study that is simultaneously optimal for both. We focused three-fourths of our validation sample to optimize estimation of the parameter of primary interest; however, we sacrificed some precision for estimating the primary parameter to improve estimation of a parameter of secondary interest. More research in optimizing designs for multiple parameters is warranted.
Our study has potential limitations beyond those already mentioned. The phase 1 sample may be unrepresentative because it only included mother-child dyads that could be linked; our validation did not investigate whether some dyads were inappropriately excluded. Our analyses assumed that the validated data were correct, which may not always be the case. There are many other challenges to using EHR data that go beyond what one can glean from data validation (e.g., confounding, sparse or erratic data capture, and poor follow-up). In particular, although our study addressed a setting where a variable was completely missing in phase 1 and found in phase 2 (e.g., estimated gestational age), we did not address a setting where there was missing data in a subsample of records, both in phase 1 and phase 2; presumably standard methods for addressing missing data (e.g., multiple imputation) could be employed on top of those presented here.
In conclusion, we applied innovative designs and analyses to address data quality issues across multiple variables in the EHR to efficiently estimate associations between a mother’s weight gain during pregnancy and her child’s risks of developing obesity and asthma. With the rapid growth of secondary-use data for biomedical research, sampling designs and analysis methods of this nature will be increasingly important.
Supplementary Material
Acknowledgements
This work was funded in part bythe Patient Centered Outcomes Research Institute (R-160936207) and the National Institutes of Health (R01AI131771, UL1TR002243).
Footnotes
Supporting Information
Web Appendices referenced in Sections 3, 4, and 5, as well as analysis code, are available with this paper at the Biometrics website on Wiley Online Library.
Data Availability Statement
The data that support the findings in this paper are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.
References
- Amorim G, Tao R, Lotspeich S, Shaw PA, Lumley T, and Shepherd BE (2021). Two-phase sampling designs for data validation in settings with covariate measurement error and continuous outcome. Journal of the Royal Statistical Society, A, 184:1368–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breslow NE and Chatterjee N (1999). Design and analysis of two-phase studies with binary outcome applied to Wilms tumour prognosis. Applied Statistics, 48:457–468. [Google Scholar]
- Breslow NE, Lumley T, Ballantyne CM, Chambless LE, and Kulich M (2009). Improved Horvitz-Thompson estimation of model parameters from two-phase stratified samples: applications in epidemiology. Statistics in Biosciences, 1:32–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen T and Lumley T (2020). Optimal multiwave sampling for regression modeling in two-phase designs. Statistics in Medicine, 39(30):4912–4921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen T and Lumley T (2022). Optimal sampling for design-based estimators of regression models. Statistics in Medicine, 41(8):1482–1497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deville JC, Sarndal CE, and Sautory O (1993). Generalized raking procedures in survey sampling. Journal of the American Statistical Association, 88(423):1013–1020. [Google Scholar]
- Duda SN, Shepherd BE, Gadd CS, Masys DR, and McGowan CC (2012). Measuring the quality of observational study data in an international HIV research network. PLOS One, 7:e33908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flegal KM and Cole TJ (2013). Construction of LMS parameters for the Centers for Diseases Control and Prevention 2000 Growth Charts. National health statistics reports; no 63. Hyattsville, MD: National Center for Health Statistics. [PubMed] [Google Scholar]
- Floyd JS, Heckbert SR, Weiss NS, Carrell DS, and Psaty BM (2012). Use of administrative data to estimate the incidence of statin-related rhabdomyolysis. Journal of the American Medical Association, 307:1580–1582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forno E, Young OM, Kumar R, Simhan H, and Celedón JC (2014). Maternal obesity in pregnancy, gestational weight gain, and risk of childhood asthma. Pediatrics, 134:e535–e546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giganti MJ, Shaw PA, Chen G, Bebawy SS, Turner MM, Sterling TR, and Shepherd BE (2020). Accounting for dependent errors in predictors and time-to-event outcomes using electronic health record, validation samples, and multiple imputation. Annals of Applied Statistics, 14:1045–1061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giganti MJ, Shepherd BE, Caro-Vega Y, Luz PM, Rebeiro PF, Maia M, Julmiste G, Cortes C, McGowan CC, and Duda SN (2019). The impact of data quality and source data verification on epidemiologic inference: a practical application using HIV observational data. BMC Public Health, 19:1748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han K, Lumley T, and Shaw PA (2021a). Combining multiple imputation with raking of weights in the setting of nearly-true models. Statistics in Medicine, 40(30):6777–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han K, Lumley T, Shepherd BE, and Shaw PA (2021b). Two-phase analysis and study design for survival models with error-prone exposures. Statistical Methods in Medical Research, 30:857–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han P (2016). Combining inverse probability weighting and multiple imputation to improve robustness of estimation. Scandinavian Journal of Statistics, 43(1):246–260. [Google Scholar]
- Heslehurst N, Vieira R, Akhter Z, and et al. (2019). The association between maternal body mass index and child obesity: A systematic review and meta-analysis. PLOS Medicine, 16:e1002817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J, Duan R, Hubbard RA, Wu Y, Moore JH, Xu H, and Chen Y (2018). Pie: A prior knowledge guided integrated likelihood estimation method for bias reduction in association studies using electronic health records data. Journal of the American Medical Informatics Association, 25:345–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawless J (2018). Two-phase outcome-dependent studies for failure times and testing for effects of expensive covariates. Lifetime Data Analysis, 24:28–44. [DOI] [PubMed] [Google Scholar]
- Lumley T (2010). Complex Surveys: a guide to analysis using R. John Wiley & Sons. [Google Scholar]
- Lumley T, Shaw PA, and Dai JY (2011). Connections between survey calibration estimators and semiparametric models for incomplete data. International Statistical Review, 79:200–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIsaac MA and Cook RJ (2014). Response-dependent two-phase sampling designs for biomarker studies. The Canadian Journal of Statistics, 42 (2):268–284. [Google Scholar]
- McIsaac MA and Cook RJ (2015). Adaptive sampling in two-phase designs: a biomarker study for progression in arthritis. Statistics in Medicine, 34:2899–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metcalf P and Scott A (2009). Using multiple frames in health surveys. Statistics in Medicine, 28:1512–1523. [DOI] [PubMed] [Google Scholar]
- Neyman J (1938). Contributing to the theory of sampling human populations. Journal of the American Statistical Association, 33:101–116. [Google Scholar]
- Oh EJ, Shepherd BE, Lumley T, and Shaw PA (2021a). Improved generalized raking estimators to address dependent covariate and failure-time outcome error. Biometrical Journal, 63:1006–1027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oh EJ, Shepherd BE, Lumley T, and Shaw PA (2021b). Raking and regression calibration: Methods to address bias from correlated covariate and time-to-event error. Statistics in Medicine, 40(3):631–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay JO and Silverman BW (2007). Applied functional data analysis: methods and case studies. Springer. [Google Scholar]
- Robins JM, Rotnitzky A, and Zhao LP (1994). Estimation of regression coefficients when some regressors are not always observed. Journal of the American Statistical Association, 89(427):846–866. [Google Scholar]
- Sarndal CE, Swensson B, and Wretman J (2003). Model assisted survey sampling. Springer. [Google Scholar]
- Tao R, Zeng D, and Lin DY (2020). Optimal designs of two-phase studies. Journal of the American Statistical Association, 115(532):1946–1959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright T (2017). Exact optimal sample allocation: more efficient than Neyman. Statistics & Probability Letters, 129:50–57. [Google Scholar]
- Wu P, Gifford A, Meng X, Li X, Campbell H, Varley T, Zhao J, Carroll R, Bastarache L, Denny JC, Theodoratou E, and Wei WQ (2019). Mapping ICD-10 and ICD-10-CM codes to phecodes: Workflow development and initial evaluation. JMIR Med Inform, 7:e14325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao F, Müller H-G, and Wang J-L (2005). Functional data analysis for sparse longitudinal data. Journal of the American Statistical Association, 100(470):577–590. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings in this paper are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.


