Abstract
Open-source, publicly available neuroimaging datasets—whether from large-scale data collection efforts or pooled from multiple smaller studies—offer unprecedented sample sizes and promote generalization efforts. Releasing data can democratize science, increase the replicability of findings, and lead to discoveries. Partly due to patient privacy, computational, and data storage concerns, researchers typically release preprocessed data with the voxelwise time series parcellated into a map of predefined regions, known as an atlas. However, releasing preprocessed data also limits the choices available to the end-user. This is especially true for connectomics, as connectomes created from different atlases are not directly comparable. Since there exist several atlases with no gold standards, it is unrealistic to have processed, open-source data available from all atlases. Together, these limitations directly inhibit the potential benefits of open-source neuroimaging data. To address these limitations, we introduce Cross Atlas Remapping via Optimal Transport (CAROT) to find a mapping between two atlases. This approach allows data processed from one atlas to be directly transformed into a connectome based on another atlas without the need for raw data access. To validate CAROT, we compare reconstructed connectomes against their original counterparts (i.e., connectomes generated directly from an atlas), demonstrate the utility of transformed connectomes in downstream analyses, and show how a connectome-based predictive model can generalize to publicly available data that was processed with different atlases. Overall, CAROT can reconstruct connectomes from an extensive set of atlases—without needing the raw data—allowing already processed connectomes to be easily reused in a wide range of analyses while eliminating redundant processing efforts. We share this tool as both source code and as a stand-alone web application (http://carotproject.com/).
Keywords: functional connectivity, brain-behavior associations, dataset harmonization, optimal transport
1. Introduction
A connectome—a matrix describing the connectivity between any pair of brain regions—is a popular approach used to model the brain as a graph-like structure (Sporns et al., 2004; Bassett and Bullmore, 2006; Bullmore and Sporns, 2009). They are created by parcellating the brain into distinct areas using an atlas (i.e., the nodes of a graph) and estimating the connections between these regions (i.e., the edges of a graph). A wide range of works demonstrates the value of connectomics in studying individual differences in brain function (Elliott et al., 2019; Dubois and Adolphs, 2016), associating brain-behavior associations (Sui et al., 2020; Jiang et al., 2019; Beaty et al., 2018), and understanding brain alterations in neuropsychiatric disorders (Yan et al., 2019). Overall, connectomes have high potential as a biomarker of various phenotypic information.
Nevertheless, the need for an atlas to create a connectome hinders comparisons across studies and replication and generalization efforts. Different atlases divide the brain into different regions of varying size and topology. Thus, connectomes created from different atlases are not directly comparable. In other words, simply comparing the results from two independent studies that use different atlases is challenging. Further, several atlases exist with no gold standards (Arslan et al., 2018), and more are being developed yearly. Currently, no solutions exist to extend previous results and potential biomarkers to a connectome generated from a different atlas, limiting the broader use of potential connectome-based biomarkers.
Transforming an existing connectome into one generated from a different atlas would help these efforts and increase the utility of existing connectomes. For example, large-scale projects—like the Human Connectome Project (HCP) (Van Essen et al., 2013), the Adolescent Brain Cognitive Development (ABCD) study (Casey et al., 2018), and the UK Biobank (Sudlow et al., 2015)—share fully processed connectomes. However, the released connectomes for each project are based on different atlases, preventing these datasets from being combined without reprocessing data from thousands of participants. Smaller labs might not have the resources to store and reprocess these data from scratch (Horien et al., 2021). Finally, due to privacy concerns of being able to identify a participant based on unprocessed data, some datasets are only released as fully processed connectomes (Yan et al., 2019). Critically, in this case, it is not possible to go to the data to create connectomes from another atlas. Thus, algorithms to map and transform connectomes have applications for preserving participant privacy and democratizing data access, as well as improving the generalizability of scientific findings.
To this aim, we propose Cross Atlas Remapping via Optimal Transport (CAROT), which uses optimal transport theory, or the mathematics of converting a probability distribution from one set to another, to find an optimal mapping between two atlases. CAROT is designed for functional connectomes based on functional magnetic imaging (fMRI) data. It allows a connectome constructed from one atlas to be directly transformed into a connectome based on a different atlas without needing to access or preprocess the raw data. We define raw data as data in any form other than fully preprocessed timeseries from an atlas, which is the final form of the data used to create a connectome. Fully preprocessed timeseries from an atlas have several benefits over other intermediate forms derived from a connectomic processing pipeline. As these data consist of only 200 – 500 timeseries, they require less storage than voxel-wise or vertex-wise preprocessed data in common space (1 – 3 MB compared to 500 – 1000 MB per individual). These data are also not identifiable if privacy concerns exist.
First, in a training sample with fMRI time series data from two different atlases, we find a mapping by solving the Monge–Kantorovich transportation problem (Kantorovich, 1942). Then, by employing this optimal mapping, time series data based on the first atlas (from individuals independent of the training data) can be reconstructed into connectomes based on the second atlas without ever needing to be preprocessed. To validate CAROT, we compare reconstructed connectomes against their original counterparts (i.e., connectomes generated directly from an atlas), demonstrate the utility of transformed connectomes in downstream analyses, and show how a connectome-based predictive model can be generalized to publicly available data preprocessed with different atlases. Overall, CAROT can reconstruct connectomes from an extensive set of atlases without ever needing the raw data—enabling comparison across connectome-based results from different atlases and the reuse of already processed connectomes in a wide range of downstream analyses.
This work builds upon two conference papers presented at the 2021 and 2022 International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI) (Dadashkarimi et al., 2021, 2022). The conference papers present our initial results using optimal transport to map and transform connectomes from different atlases. We expand our previous results by presenting an extensive set of validation studies, increasing the number of atlases and datasets tested, and sharing this tool as source code and a stand-alone web application (http://carotproject.com/).
2. Theory and calculations
2.1. Optimal transport
The optimal transport problem solves how to transport resources from one location to another while minimizing the cost C (Tolstoi, 1930; Hitchcock, 1941; Koopmans, 1949; Gangbo and McCann, 1996). It has been used for contrast equalization (Delon, 2004), image matching (Li et al., 2013), image watermarking (Mathon et al., 2014), text classification (Huang et al., 2016), and music transportation (Flamary et al., 2016). Optimal transport is one of the few methods that provides a well-defined distance metric when the supports of the distributions are different. Other mapping approaches, such as Kullback–Leibler divergence, do not make this guarantee.
The original formulation of the optimal transport problem is known as the Monge problem. Assuming we have some resources in location and some other resources in location , we specify weight vectors and over these resources and define matrix as a measure of pairwise distances between points and comparable points . The Monge problem aims to solve the following optimizing problem (Monge, 1781):
| (1) |
where the push forward operator indicates that mass from moves towards assuming that weights absorbed in . An assignment problem when the number of elements in the measures is not equal is a special case of this problem, where each point in can be assigned to several points in .
As a generalization of the Monge problem, the Kantorvich relaxation solves the mass transportation problem using a probabilistic approach in which the amount of mass located at potentially dispatches to several points in the target (Kantorovich, 1942). An admissible solution for Kantorvich relaxation is defined as indicating the amount of mass being transferred from location to by :
| (2) |
where represents a vector of all 1’s. An optimum solution is obtained by solving the following problem for a given (Rubner et al., 2000):
| (3) |
While a unique solution is not guaranteed (Peyré et al., 2019), an optimal solution exists (see proof in Birkhoff (1946); Bertsimas and Tsitsiklis). Kantorovich and Monge’s problems are equivalent under certain conditions (see proof in Brenier (1991)).
2.2. Cross Atlas Remapping via Optimal Transport (CAROT)
CAROT operates by transforming time series data from one atlas (labeled the source atlas) into time series from an unavailable atlas (labeled the target atlas). This transformation is a spatial mapping between the two atlases. Next, the corresponding functional connectomes can be estimated using standard approaches (e.g., full or partial correlation). Transforming the time series data rather than connectomes themselves has two benefits. First, this results in a lower dimensional mapping, which is more robust to estimate. Second, connectomes can be constructed with standard methods (like correlation), guaranteeing properties like semi-positive definite. Direct mapping between connectomes may not guarantee this property.
Formally, let us assume we have training time series data consisting of time points from the same individuals but from two different atlases (atlas with regions and atlas with regions). Additionally, let and to be the vectorized brain activity at single time point based on atlases and , respectively. We normalize these vectors, to sum up to one using the softmax function, as we are only concerned about the mass. For a fixed cost matrix , which measures the pairwise distance between regions in and , we aim to find a mapping that minimizes transportation cost between and :
| (4) |
in which is vectorized version of such that the ’s element of is equal to and is defined as:
 |
(5) |
represents the optimal way of transforming the brain activity data from regions into regions. Thus, by applying to every timepoint from the time series data of the source atlas, we can estimate the time series data of the target atlas. As solving this large linear program is computationally hard (Dantzig, 1983), we use the entropy regularization, which gives an approximation solution with the complexity of for Peyré et al. (2019), and instead solve the following:
| (6) |
Specifically, we use the Sinkhorn algorithm—an iterative solution for Equation 6 (Altschuler et al., 2017)—to find . For training data with participants and time points per participant, first, we estimate the optimal mapping , independently, for time point for a given participant using Equation 6. Next, we average overall time points and participants to produce a single optimal mapping in the training data (e.g., ).
For the cost matrix , we used a distance metric (labeled functional distance) that is based on the similarity of pairs of time series from the different atlases:
| (7) |
where and are time series from and and is Spearman correlation between them. To increase a reliable estimation of , we calculate the time series correlation independently for each individual in the training data and average over these correlations. The functional distance was used over Euclidean distance between nodes for two main reasons: (i) functional distance does not require having access to the atlas or node locations, which provides greater flexibility should an unknown and unavailable atlas be used, and (ii) spatial proximity in the brain does not guarantee a similar function. For example, the medial prefrontal nodes of the default mode network are more correlated with nodes in the posterior cingulate cortex than other nodes in the frontal lobe. Nevertheless, we formally compare the performance of functional and Euclidean distances.
3. Material and methods
3.1. Evaluation datasets
We evaluated CAROT on six prominent functional atlases from the literature using three datasets, the Human Connectome Project (HCP), the REST-Meta-MDD Consortium, and the Yale Low-Resolution Controls Dataset.
3.1.1. Atlases
The Shen atlas (Shen et al., 2013) was created using functional connectivity data from 45 adult participants. The 268-node atlas was constructed using a group-wise spectral clustering algorithm (derived from the N-cut algorithm) and covers the entire cortex, sub-cortex, and cerebellum. The Craddock atlas (Craddock et al., 2012) was created using functional connectivity data from 41 adult participants. The 200-node atlas was constructed using an N-cut algorithm and covers the entire cortex, sub-cortex, and cerebellum. The Schaefer atlas (Schaefer et al., 2018) was created using functional connectivity data from 744 adult participants from the Genomics Superstruct Project (Holmes et al., 2015). The 400-node atlas was constructed using a gradient-weighted Markov Random Field (gwMRF) model, covering only the cortex. The Brainnetome atlas (Fan et al., 2016) was created using structural connectivity data from 40 adult participants from the HCP. The 246-node atlas was constructed using a tractography-based approach and covers the cortex and sub-cortex. While it was created with structural connectivity, the Brainnetome atlas is suited for functional studies. The Dosenbach atlas(Dosenbach et al., 2010) was created from meta-analyses of task-related fMRI studies and consists of 160 nodes that cover the cortex, cerebellum, and a few sub-cortical nodes. The Power atlas (Power et al., 2011) was created by combining the meta-analytical approach of the Dosenbach atlas with areal boundary detection based on functional connectivity data. The 264-node atlas covers the cortex, sub-cortex, and cerebellum.
3.1.2. HCP participants
We used behavioral and functional imaging data from this data set as previously described (Gao et al., 2019). We restricted our analyses to those subjects who participated in all nine fMRI conditions (seven tasks, two rest), whose mean frame-to-frame displacement was less than 0.1mm and whose maximum frame-to-frame displacement was less than 0.15mm, and for whom IQ measures were available (n=515; 241 males; ages 22–36+). The HCP minimal preprocessing pipeline was used on these data, which includes artifact removal, motion correction, and registration to common space (Glasser et al., 2013). All subsequent preprocessing was performed in BioImage Suite (Joshi et al., 2011) and included standard preprocessing procedures, including removal of motion-related components of the signal; regression of mean time courses in white matter, cerebrospinal fluid, and gray matter; removal of the linear trend; and low-pass filtering.
3.1.3. REST-meta-MDD
Fully processed data was downloaded from http://rfmri.org/REST-meta-MDD. Full details about the dataset have been previously published elsewhere (Yan et al., 2019). We used data from 21 of the 24 sites. Two sites were removed due to a large imbalance between male and female participants (i.e., < 30% male or female; sites 2 and 12). One site was removed as self-reported sex was not provided (site 4). Briefly, the data was processed as follows. First, the initial 10 volumes were discarded, and slice-timing correction was performed. Then, the time series of images for each subject were realigned using a six-parameter linear transformation. After realignment, individual T1-weighted images were co-registered to the mean functional image using a six-degrees-of-freedom linear transformation without re-sampling and then segmented into gray matter, white matter, and cerebrospinal fluid. Finally, transformations from individual native space to MNI space were computed with the Diffeomorphic Anatomical Registration Through Exponentiated Lie algebra (DARTEL) tool. To minimize head motion confounds, the Friston 24-parameter model was regressed from the data. Scrubbing (removing time points with FD>0.2mm) was also utilized to verify results using an aggressive head motion control strategy. Other sources of spurious variance (global, white matter, and CSF signals) were also removed from the data through linear regression. Additionally, linear trend were included as a regressor to account for drifts in the blood oxygen level dependent (BOLD) signal. Temporal bandpass filtering (0.01–0.1Hz) was performed on all time series.
3.1.4. Yale participants
In addition, we used resting-state data collected from 100 participants at the Yale School of Medicine. This dataset included 50 females (age=33.3±12.3) and 50 males (age=34.9±10.1) with eight functional scans (48 minutes total). The dataset and processing details can be found in (Scheinost et al., 2014). Briefly, standard preprocessing procedures were applied to these data. Structural scans were skull stripped using an optimized version of the FMRIB’s Software Library (FSL) pipeline. Slice time and motion correction were performed in SPM8. The remainder of image preprocessing was performed in BioImage Suite. The data was cleaned by regressing nuisance variables (motion parameters, drift terms, and the mean time courses of the white matter, cerebrospinal fluid, and gray matter signals) and band-pass filtering) and was nonlinearly registered to the MNI template.
3.1.5. Generating connectomes
After processing, the Shen, Schaefer, Craddock, Brainnetome, Power, and Dosenbach atlases were applied to the preprocessed fMRI data to create mean time series for each node. For each atlas and dataset, connectomes were generated by calculating the Pearson’s correlation between each pair of these mean time series and then tasking the Fisher transform of these correlations. Connectomes reconstructed by CAROT were also generated using Pearson’s Correlation.
3.2. Evaluation overview
We performed several evaluations of CAROT. First, we performed a baseline evaluation of CAROT, investigating the similarity of the original and reconstructed connectomes, the impact of free parameters (e.g., the number of participants used to train CAROT), and the number of available source atlases. Second, we investigated how reconstructed connectomes perform in standard downstream analyses (i.e., do reconstructed connectomes give similar neuroscience results as the original connectomes?). Finally, we present a real-world evaluation of how CAROT can generalize a preexisting connectome-based predictive model when data from the required atlas is unavailable.
3.3. Baseline evaluation of CAROT
3.3.1. Similarity between the original and reconstructed connectomes
We compared reconstructed connectomes to their original counterparts using HCP data. We partitioned our data into a 25/75 split, where 25% of the individuals are used to estimate the optimal mapping and 75% are used to evaluate the reconstructed connectomes. Reconstructed connectomes were created using single and multiple source atlases. To evaluate the similarity between CAROT-reconstructed and original connectomes, the upper triangles of the connectomes were vectorized and correlated with Spearman’s rank correlation. We also present the mean square error (MSE) and the Forbenius norm between CAROT-reconstructed and original connectomes.
3.3.2. Comparison with k-nearest neighbor mapping
Given the similarities between the optimal transport problem and the k-nearest neighbor problem, we compared CAROT to a simplified approach based on mapping the atlas pairs using k-nearest neighbors, where and . We tested Euclidean and functional distances for this approach.
3.3.3. Evaluation of free parameters
We investigated the sensitivity of CAROT to the number of time points and number of participants used to find the mappings and the value of in the Sinkhorn approximation. Using the same 25/75 split of the HCP participants for training and testing as above, we varied the number of time points used from 100 to 1100 in increments of 100, the number of participants from 100 to 515 in increments of 100, and from 0.01 to 10 in increments of 1.
3.3.4. Extending CAROT for multiple atlases
A vital drawback of the single-source optimal transport is that it relies on a single pair of source and target atlases (i.e., one source atlas and one target atlas), which ignores additional information when multiple source atlases exist. As preprocessed data is often released with time series data from multiple atlases (Yan et al., 2016), we investigated using these additional data to better reconstruct connectomes from an unavailable atlas. Previously, in a conference proceeding (Dadashkarimi et al., 2022), we combined information from multiple source atlases by using a larger cost matrix generated from stacking the set of region centers in each source atlas. In general, assume we have paired time-series, from the same person, but from different source atlases with a total of regions (where from source atlas with regions, with regions, .., with regions) and a target atlas with regions, lets define and to be the distribution of brain activity at single time point based on atlases and :
| (8) |
, and is based on the similarity of pairs of time series from nodes and from different atlases. Equation 6 can then be solved using this new cost matrix .
However, this approach is time-consuming to solve. Instead, we applied CAROT to transform time series data from source atlases into the time series data for the target atlas. This process results in different estimates of the target atlas’s time series data. Next, the transformed time series data were averaged across all source atlases, improving the estimated time series data of the source atlas. Finally, a single connectome for the target atlas was created (Fig. 1). Further, we investigated the impact of using a smaller number of source atlases by only including k random source atlases when creating a connectome for the target atlas. This process was repeated with 100 iterations over .
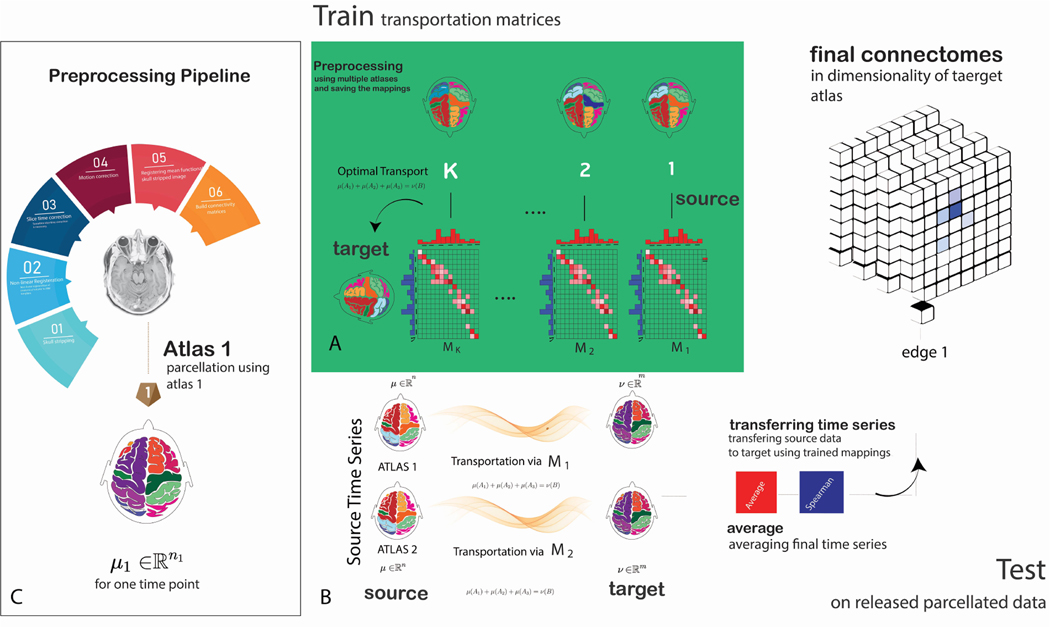
Fig. 1:
Schematic of CAROT: A) During training, CAROT transforms time series fMRI data from multiple source atlases to a target atlas to obtain transportation mappings. Mappings between the source and target atlases are found by employing optimal transport and solving Monge–Kantorovich transportation problem using the Sinkhorn approximation. The solution provides a transformation that maps the brain activity parcellated using the source atlas to brain activity parcellated based on the target atlas. B) During testing, for each pair of source and target atlases and a single time point in the time series data, the offline solutions are used, and time series and functional connectomes accordingly will be reconstructed in the desired target atlas. Results from several pairs of source and target atlases can be combined to improve the quality of the final reconstructed connectome. C) A standard image preprocessing pipeline to create functional connectomes.
3.3.5. Generalizing mappings across datasets
We investigated if CAROT mappings trained in one dataset generalize to other datasets. In other words, we tested if CAROT can be trained once (for example, using the HCP) and then applied to any new datasets without the need to rerun CAROT (for example, the Yale dataset). First, we trained CAROT using only the HCP dataset. Then, we reconstructed connectomes using the Yale dataset using these . Spearman’s rank correlation between the upper triangles of the connectomes was used to assess the similarity between the reconstructed and original connectomes.
3.4. Evaluation of downstream analyses
3.4.1. Consistency of aging results
We tested whether the reconstructed connectomes produced consistent neuroscience results compared to the original connectomes. First, we used 25% of the HCP participants to train CAROT. Next, using the original and reconstructed connectomes for the remaining 75% of participants, we calculated the association between connectomes and age using mass uni-variate, edge-wise correlations. Results were thresholded at , corrected for multiple comparisons using the Network-based Statistic (NBS) (Zalesky et al., 2010). To assess whether the overlap of the significant edges found using the original and reconstructed connectomes was statistically significant (i.e., edge-level), we calculated the probability of the overlap being due to chance using the hypergeometric cumulative distribution:
where is the probability of drawing up to of a possible items in drawings without replacement from a group of objects. The p-value for the significance of overlap is then calculated as . We also assess the similarity of results at the node-level by summing over all significant edges for a node (i.e., the network theory measure degree) and correlating these maps for results from the original and reconstructed connectomes.
3.4.2. IQ prediction
To show that meaningful brain-phenotype association are retained in reconstructed connectomes, we used reconstructed connectomes to predict fluid intelligence using connectome-based predictive modeling (CPM) (Shen et al., 2017). We partitioned the HCP dataset into three groupings: , consisting of 25% of the participants; , consisting of 50% of the participants; and, , consisting of the final 25% of the participants. In , we trained CAROT for each source and target atlas pair. We then applied the learned on and to estimate connectomes for each target atlas, resulting in seven connectomes for each atlas (five reconstructed connectomes based on a single source atlas, one reconstructed connectome based on all source atlases, and the original connectome). Finally, we trained a CPM model of fluid intelligence for each set of connectomes using and tested this model in . Fluid intelligence was quantified using a 24-item version of the Penn Progressive Matrices test. Spearman correlation between observed and predicted values was used to evaluate prediction performance. This procedure was repeated with 100 random splits of the data into three groups.
3.4.3. Identification rate
We investigated if the individual uniqueness of connectomes is retained in reconstructed connectomes by identifying individuals scanned on repeated days (Finn et al., 2015). As mentioned above, we used the HCP data and a 25/75 split to create reconstructed connectomes based on all available source atlases. In an iterative process, one individual’s connectome was selected from the target set and compared against each of the connectivity matrices in the database to find the matrix that was maximally similar. Spearman correlation between the target connectome and each in the database was used to assess similarity. A score of 1 was assigned if the predicted identity matched the true identity, or 0, if it did not. Each target connectome was tested against the database in an independent trial. Connectomes generated from the day 1 resting-state data were used as the target set, and connectomes generated from the day 2 resting-state data were used as the database. We performed this identification procedure for the original and reconstructed connectomes independently. We used permutation testing to generate a null distribution to determine if identification rates were achieved at above-chance levels. Specifically, participants’ identities were randomly shuffled and identification was performed with these shuffled labels. Identification rates obtained using the correct labels were then compared to this null distribution to determine significance.
3.5. Real-world evaluation
In this evaluation, we generalized a sex classification model (using 100 adults collected at the Yale School of Medicine and created with the Shen atlas) to the REST-Meta-MDD dataset (Yan et al., 2016), which only provides preprocessed time series data from the Dosenbach, Power, and Craddock atlases. First, we trained the sex classification model using the Yale dataset’s resting-state data from 100 individuals (50 males). We trained a -penalized logistic regression model with 10-fold cross-validation to classify self-reported sex. Then, we used estimated from the HCP to transform the publicly available preprocessed data (i.e., time series data from the Dosenbach, Power, and Craddock atlases) from the REST-Meta-MDD dataset into the Shen atlas. Data from each source atlas were combined to create a single connectome based on the Shen atlas for the 1005 (585 females) health controls. Finally, the sex classification model created in the Yale dataset was applied to these reconstructed Shen connectomes.
3.6. Data availability
All datasets used in this study are open-source: HCP (ConnectomeDB database, https://db.humanconnectome.org), REST-meta-MDD (http://rfmri.org/REST-meta-MDD), and Yale dataset (http://fcon_1000.projects.nitrc.org/indi/retro/yale_lowres.html). BioImage Suite tools used for processing can be accessed at (https://bioimagesuiteweb.github.io/). bCAROT and associated canonical mappings are on GitHub (https://github.com/dadashkarimi/carot). The Python Optimal Transport (POT) toolbox is available at https://pythonot.github.io/.
4. Results
4.1. Baseline evaluation of CAROT
4.1.1. Reconstructed connectomes are similar to original connectomes
As shown in Table 1, the correlation between the reconstructed connectomes and their original counterparts depends on the atlas pairing, with more similar atlases appearing to have higher correlations. For instance, a strong correlation is seen while transforming data from the Craddock atlas to the Shen atlas (, ). Both atlases are based on clustering time series fMRI data using variants of the N-cut algorithm. In contrast, a weaker correlation exists for transforming data from the Dosenbach atlas (which was constructed based on a meta-analysis of task activations) to the Shen atlas (, ). Table S1 and Table S2 shows the similarity between reconstructed and original connectomes using MSE and the Frobenius norm. Finally, the similarity between the reconstructed and original connectomes was much lower when using Euclidean distance (Fig. S1)
Table 1:
Spearman correlation between reconstructed connectomes and original connectomes for each source-target pair. Presented results show mean ± standard deviation over 100 iterations of randomly splitting the data into training and testing sets.
| Shen | Schaefer | Craddock | Brainnetome | Power | Dosenbach | |
|---|---|---|---|---|---|---|
| Shen | 0.46 ±0.010 | 0.55 ±0.001 | 0.42 ±0.003 | 0.36 ±0.030 | 0.39 ±0.004 | |
| Schaefer | 0.31 ±0.001 | 0.38 ±0.010 | 0.38 ±0.001 | 0.33 ±0.010 | 0.34 ±0.002 | |
| Craddock | 0.48 ±0.010 | 0.54 ±0.010 | 0.51 ±0.003 | 0.43 ±0.002 | 0.43 ±0.001 | |
| Brainnetome | 0.17 ±0.003 | 0.23 ±0.003 | 0.23 ±0.002 | 0.19 ±0.004 | 0.18 ±0.002 | |
| Power | 0.24 ±0.002 | 0.35 ±0.003 | 0.32 ±0.001 | 0.29 ±0.070 | 0.32 ±0.002 | |
| Dosenbach | 0.24 ±0.001 | 0.32 ±0.003 | 0.28 ±0.020 | 0.28 ±0.001 | 0.28 ±0.010 |
4.1.2. Comparison with k-nearest neighbor mapping
Results using a k-nearest neighbor mapping with are shown in Table for Euclidean distance and Table functional distance. Results using a k-nearest neighbor mapping with are shown in Table for Euclidean distance and Table functional distance. In all cases, results are worse than CAROT.
4.1.3. Using multiple atlases improves CAROT
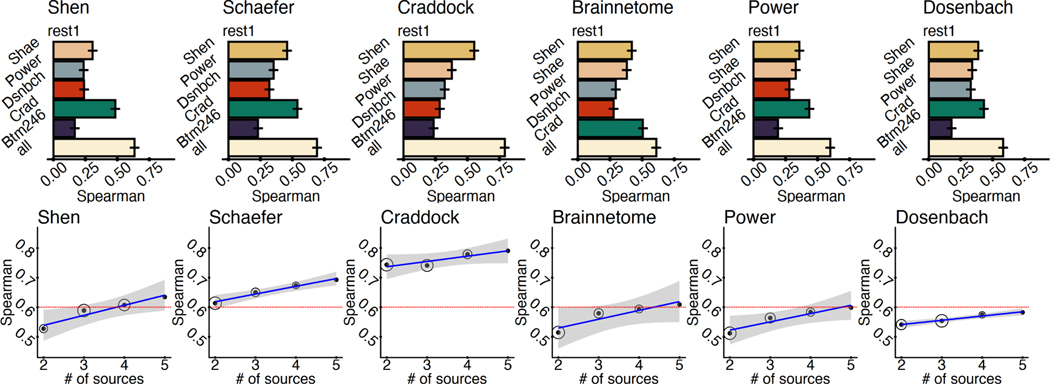
Overall, we observed a considerable improvement when including data from multiple source atlases. In every case, using all available data produced more similar connectomes to their original counterparts (all ; Fig. 2). For most atlases, explained variance is more than tripled using CAROT with multiple source atlases compared to using a single source atlas. As shown in Fig. 2, while the similarity between reconstructed and original connectomes increases as the number of source atlases increases, strong correlations (e.g., ) can be observed with as little as two or three source atlases, suggesting that a small number of atlases may be sufficient for most applications. Results from averaging time series data were similar to the procedure presented in (Dadashkarimi et al., 2022). Fig. S2 and Fig. S3 shows the similarity between reconstructed and original connectomes using MSE and the Frobenius norm.
Fig. 2:
Using multiple source atlases improves the similarity of reconstructed connectomes. A) The Spearman’s rank correlation between the reconstructed connectomes and connectomes generated directly with the target atlases are shown for each pair of source and target atlas as well as reconstructed connectomes using all of the source atlases. Using all source atlases produces higher-quality reconstructed connectomes for each target atlas. Error bars are generated from 100 iterations of randomly splitting the data into 25% for training and 75% for testing. B) For each target atlas, increasing the source atlases increases the similarity of reconstructed and original connectomes. For most atlases, a Spearman’s correlation of (red line) can be achieved by using fewer than five source atlases (i.e., all available source atlases). Circle size represents the variability of the correlation over 100 iterations of splitting the data into training and testing sets.
4.1.4. CAROT is insensitive to parameter choices
No clear pattern of performance change was observed across the tested parameter range, suggesting that CAROT is not affected by the number of frames and participants, and the range of (Fig. S4 ). However, using only 100 participants and 100 time points significantly reduced the processing time from 2,975 s to 467s ().
4.1.5. Mappings generalize across datasets
When applying the mapping trained in the HCP dataset to the Yale dataset, we observed a strong correspondence between the reconstructed connectomes and their original counterparts with (Shen: ; Schaefer: ; Craddock: ; Brainnetome: ; Power: ; Dosenbach: ). Notably, these correlations are in the same range as those observed when we applied these mappings to the HCP data (i.e., the same dataset used for training the mappings). Together, these results exhibit that mappings can be trained in one dataset and applied to another.
4.2. Evaluation of reconstructed connectomes in downstream analyses
4.2.1. Similar patterns of aging are found with reconstructed connectomes
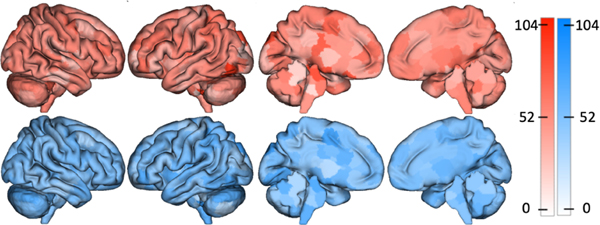
At the edge level, the reconstructed connectomes for all atlases produced aging results that significantly overlapped with the results from using the original connectomes (). Similarly, node-level correlations were all significant (, ). Fig 3 shows a representative example of node-level results between the reconstructed and original connectomes for the Shen atlas.
Fig. 3:
Reconstructed connectomes give similar aging results as the original connectomes. The top row shows the nodes with the largest number of edges significantly associated with age for original connectomes from the HCP created with the Shen atlas. The bottom row shows the same but using reconstructed Shen connectomes. These spatial maps correlate at , suggesting that analyses with the reconstructed connectomes produce comparable neuroscientific insights as analyses with the original connectomes.
4.2.2. Reconstructed connectomes predict IQ
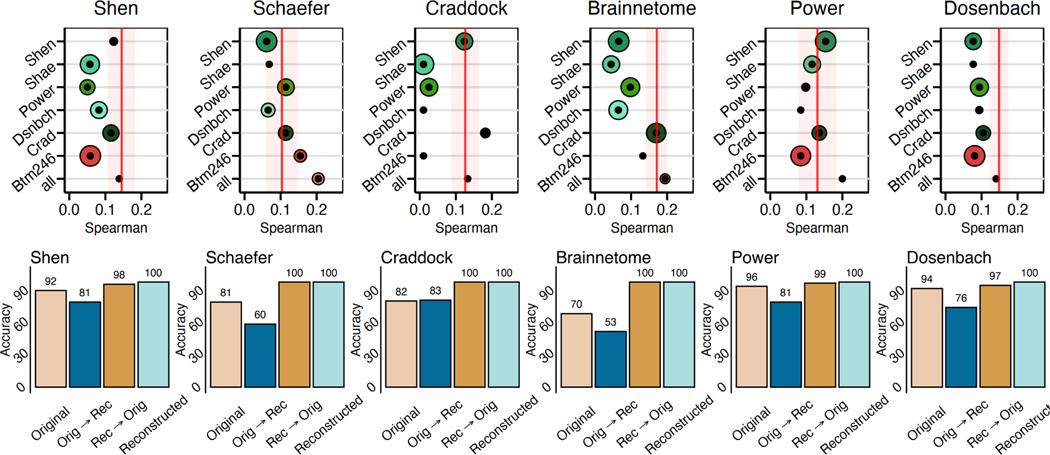
In all cases, connectomes reconstructed using all source atlases performed as well in prediction (i.e., similar correlations between observed and predicted values) as the original connectomes (Fig 4A). The reconstructed connectomes using all source atlases performed better than the original connectomes for the Schaefer and Power atlases. As these atlases displayed the lowest initial prediction (see the red vertical line in Fig 4A), incorporating information from atlases that better predict IQ increases the ability of the reconstructed Schaefer and Power atlases to predict IQ. Similar to other analyses, connectomes reconstructed from a single atlas varied in prediction performance depending on the combination of source and target atlases.
Fig. 4:
Reconstructed connectomes behave the same as original connectomes in downstream analyses. A) The reconstructed connectomes retain sufficient individual differences to predict IQ using connectome-based predictive modeling. In all cases, reconstructed connectomes based on all available source atlases (bottom circle) predicted IQ with a similar or better correlation between the observed and predicted values than the original connectome (red line). Size of the circle represents the variance of prediction performance of 100 iterations of 10-fold cross-validation. B) The reconstructed connectomes retain sufficient individual uniqueness to identify individuals using the reconstructed connectomes.
4.2.3. Reconstructed connectomes are unique to an individual
For all analyses, the identification of individuals from their connectomes demonstrated a high success rate that was significantly greater than chance (5%; ; based on permutation testing). (Fig. 4B). Reconstructed connectomes performed slightly better than the originals (original connectomes: mean rate=79%; reconstructed connectomes: mean rate=90%). Overall, these results suggest that the reconstructed connectomes retain similar levels of individual differences as their original connectome counterparts.
4.3. CAROT facilitates external validation of connectome-based predictive models
Overall, the sex classification model demonstrated significant classification accuracy in the Yale dataset (Accuracy=60.5% 6%; Naive model accuracy=50%; ; ). and the REST-Meta-MDD dataset (Accuracy=66.5%; Naive model accuracy=52.3%; ; ) when using the reconstructed connectomes. To better contextualize this result, we created connectomes for the Dosenbach, Power, and Craddock atlases in the Yale dataset, created a sex classification model for connectome type, and generalized these models to the REST-Meta-MDD dataset. The generalization accuracy of reconstructed connectomes (Shen: 66.5%) was numerically superior to the generalization accuracies based on original connectomes (Dosenbach: 59.6%, Power: 59.0%, and Craddock: 64.5%), suggesting that using CAROT and reconstructed connectomes perform as well as original connectomes in generalizing a preexisting predictive model.
4.4. Software availability and implementation
To facilitate open science and the broader adoption of CAROT, we have created http://carotproject.com/. This web application allows end-users to convert time series data from the Shen, Schaefer, Craddock, Brainnetome, Power, and Dosenbach atlases to connectomes for any of the other atlases. As a web application, it works without software installation and across multiple platforms (e.g., Windows, Linux, MacOS, Android). The only requirement is a modern web browser, such as Google Chrome. Please note that any data used on http://carotproject.com/ remains on the local computer and is never uploaded or stored on a remote server. In addition, we provide the CAROT software and associated canonical mapping as opensource at https://github.com/dadashkarimi/carot/.
Specifically, we provide functionality: (i) to generate the cost matrix based on the functional distance for time series data from two different atlases; (ii) to generate the mapping between two atlases based on the cost matrix defined above; and (iii) to convert time series data from one or more source atlases to connectomes based on a target atlas. In addition, we provide canonical mappings based on the HCP data to map between every pair of the Shen, Schaefer, Craddock, Brainnetome, Power, and Dosenbach atlases. Based on the results present here, these mappings should work in other datasets, saving researchers the need to regenerate these mappings for themselves. We will look to provide mappings between additional atlases as they become available. CAROT is implemented in Python 3, building on the Python Optimal Transport (POT) toolbox (Flamary and Courty, 2017).
5. Discussion and conclusions
Neuroimaging is at a crossroads, facing a need to increase replication efforts and use larger-than-ever samples (Yarkoni, 2009; Szucs and Ioannidis, 2020; Marek et al., 2022). These are tough challenges for functional connectomics, where connectomes created from different atlases are incomparable. As such, processed connectomes or connectomic results from different atlases must be reprocessed from raw data. Here, we introduced and validated CAROT, a method that will allow us to overcome the limitation of not being able to combine connectomes and results from different atlases. CAROT allows functional connectomes from different atlases to be transformed into a standard atlas and combined in downstream analyses. CAROT relies on optimal transport to find a frame-to-frame mapping of fMRI time series data used to create functional connectomes for a missing atlas. We show that these reconstructed connectomes are highly similar to the original ones and perform similarly in downstream analyses. Specifically, reconstructed connectomes retain sufficient individual differences to predict IQ and uniqueness to identify individuals. Finally, we provide a real-world example of how a connectome-based predictive model (based on the Shen atlas) can be generalized to open-source, preprocessed data that was not processed with the Shen atlas.
Critically, the mappings between connectomes are general to the dataset used to create the mappings. As such, a single set of canonical or gold-standard mappings can be trained with one dataset and distributed to work in new datasets without retraining the mappings. Accordingly, we have released initial mappings based on the HCP data to map between every pair of the Shen, Schaefer, Craddock, Brainnetome, Power, and Dosenbach atlases as part of our software. We hope that CAROT and http://carotproject.com/ will save researchers time and effort by eliminating data reprocessing and increasing the ease of performing mega-analysis and external validation efforts.
Across analyses, we show that CAROT produces reconstructed connectomes that achieve similar results in IQ prediction and fingerprinting as connectomes created directly from the data. This observation holds across a range of atlases that differ in their construction and constituent brain regions. While atlas pairs that are more similar in terms of their construction and coverage produced better pair-wise mappings (e.g., the Craddock and Shen atlases were created with N-cut algorithms and cover the cortex, sub-cortex, and cerebellum (Shen et al., 2013; Craddock et al., 2012) ), using multiple source atlases is even better. Likely, combining transformed time series averages out the minor idiosyncrasies in the individual mappings between atlas pairs, producing more stable results. Overall, when using multiple source atlases, CAROT is robust to differences between the source and target atlases.
While including all available data generated the most similar connectomes, a strong correspondence between reconstructed and original connectomes was observed when as few as 2 or 3 different source atlases were used. This suggests that an exhaustive list of every possible atlas does not need to be released but rather only including a few different atlases could vastly increase the utility of any released preprocessed data. Balancing the utility of released data and the effort to release it is a delicate task. If the data is not in a convenient form for end-users, it will not be used and if the effort is too high to share data, data will not be shared. We believe that CAROT can help balance these considerations by increasing the utility of the shared data with only a slight increase in effort for sharing the data.
Given that multiple source atlases produce more robust results, we encourage future studies to release preprocessed data from a few atlases. Not only does this increase the chances that the needed atlas is available for an end-user, but it also better facilitates the use of the data when the needed atlas is unavailable. Some open-source datasets release data from multiple atlases (e.g., REST-Meta-MDD). That CAROT performs better with multiple altases may be relevant for large-scale projects, like ABCD and UK Biobank, that share raw data and curated releases. Given that these datasets range in the several thousands of participants, curated data from multiple atlases further facilitates the use of this data by smaller labs and research groups with a more expansive range of atlases and tools. Additionally, CAROT may help with connectome-based meta analyses, of which there are few, by allowing results to be pooled across studies. Coordinate-based meta analyses are popular for task activation and brain morphometry studies (Laird et al., 2005; Yarkoni et al., 2011; Eickhoff et al., 2009) and are possible as most neuroimaging studies rely on a common template (i.e., the MNI template). This common template allows for spatial comparisons and pooling of results across different studies.
There are a few notable strengths and limitations of CAROT. First, CAROT appears to be robust to the choices of algorithmic parameters such as the number of fMRI frames, the sample size used for training, the choice of cost matrix, and the equation used to solve the optimal transport problem. We showed that the method is not sensitive to parameter search in part due to the large amount of spatial and temporal autocorrelation in fMRI data (Shinn et al., 2021), which allows something as complex as a connectome to be compactly parameterized. In an earlier MICCAI work (Dadashkarimi et al., 2022), we solved more complex joint optimization problems across all atlases. In this work, we instead average the resulting time series from CAROT. The averaging approach is less time-consuming and produces similar results. The main use case of CAROT is to harmonize connectomes across shared data. While there are some scenarios where CAROT would be useful for labs using their own datasets (e.g., the voxel/vertice-wise processed data is lost or delete), most will be able to directly calculate a connectome from the raw data.
Future work includes generalizing CAROT to other functional time series data—such as electroencephalography (EEG), functional near-infrared spectroscopy (fNIRS), or even widefield CA2+ imaging data in mice (Lake et al., 2020)—where spatial and temporal autocorrelation patterns will be different. One limitation is that since CAROT is based on time series data, it is only appropriate for functional connectomes. Nevertheless, the ”missing atlas” problem also exists for structural connectomes, for which no solution exists. Hence, the problem still exists for studies looking to uncover structure-function relationships at the connectome level. However, perhaps CAROT based on Euclidean distance rather than functional distance may be a reasonable approach to map between atlases used to create structural connectomes as well as map between different atlases used in morphometric analyses (such as the Desikan-Killiany and Destrieux atlases used in FreeSurfer). While we tested CAROT with an extensive range of atlases, we could not test CAROT in every functional atlas, as there are many. Nevertheless, given the range in atlas size (200–500 nodes) and atlas coverage (whole-brain and cortical only), we expect CAROT to work well for modern atlases not tested here and look to update CAROT when a new generation of brain atlases emerges.
In sum, CAROT allows a connectome generated based on one atlas to be directly transformed into a connectome based on another without needing raw data. These reconstructed connectomes are similar to and, in downstream analyses, behave like the original connectomes created from the raw data. Using CAROT on preprocessed open-source data will increase its utility, accelerate the use of big data, and help make generalization and replication efforts easier.
Supplementary Material
6. Acknowledgments
This work was supported by NIMH R01 MH121095, NSF (IIS-1845032), ONR (N00014-19-1-2406), and Tata. Data were provided in part by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; U54 MH091657) and funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University. Data was also provided by the REST-meta-MDD Consortium Data Sharing, which was supported by the National Key R&D Program of China (2017YFC1309902), the National Natural Science Foundation of China (81671774, 81630031, 81471740 and 81371488), the 13th Five-year Informatization Plan (XXH13505) of Chinese Academy of Sciences, Beijing Municipal Science & Technology Commission (Z161100000216152, Z171100000117016, Z161100002616023 and Z171100000117012), Department of Science and Technology, Zhejiang Province (2015C03037) and the National Basic Research (973) Program (2015CB351702). The remainder of the data used in this study were provided by the Philadelphia Neurodevelopmental Cohort (Principal Investigators: Hakon Hakonarson and Raquel Gur; phs000607.v1.p1). Support for the collection of the data sets was provided by grant RC2MH089983 awarded to Raquel Gur and RC2MH089924 awarded to Hakon Hakonarson.
Footnotes
Connectomes created from different atlases are not directly comparable, limiting generalization efforts
We introduce cross Atlas Remapping via Optimal Transport (CAROT)
CAROT reconstructs connectomes from different atlases without needing raw data
Reconstructed connectomes are highly similar to the original connectomes
Reconstructed connectomes behave the same in downstream analyses
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Altschuler J, Weed J, Rigollet P, 2017. Near-linear time approximation algorithms for optimal transport via sinkhorn iteration. arXiv preprint arXiv:1705.09634.
- Arslan S, Ktena SI, Makropoulos A, Robinson EC, Rueckert D, Parisot S, 2018. Human brain mapping: A systematic comparison of parcellation methods for the human cerebral cortex. NeuroImage 170, 5–30. doi: 10.1016/j.neuroimage.2017.04.014. segmenting the Brain. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Bullmore E, 2006. Small-world brain networks. The Neuroscientist 12, 512–523. [DOI] [PubMed] [Google Scholar]
- Beaty RE, Kenett YN, Christensen AP, Rosenberg MD, Benedek M, Chen Q, Fink A, Qiu J, Kwapil TR, Kane MJ, et al. , 2018. Robust prediction of individual creative ability from brain functional connectivity. Proceedings of the National Academy of Sciences 115, 1087–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertsimas D, Tsitsiklis J,. Introduction to linear optimization, athena scientific, 1997.
- Birkhoff G, 1946. Tres observaciones sobre el algebra lineal. Univ. Nac. Tucuman, Ser. A 5, 147–154. [Google Scholar]
- Brenier Y, 1991. Polar factorization and monotone rearrangement of vector-valued functions. Communications on pure and applied mathematics 44, 375–417. [Google Scholar]
- Bullmore E, Sporns O, 2009. Complex brain networks: graph theoretical analysis of structural and functional systems. Nature reviews neuroscience 10, 186–198. [DOI] [PubMed] [Google Scholar]
- Casey B, Cannonier T, Conley MI, Cohen AO, Barch DM, Heitzeg MM, Soules ME, Teslovich T, Dellarco DV, Garavan H, et al. , 2018. The adolescent brain cognitive development (abcd) study: imaging acquisition across 21 sites. Developmental cognitive neuroscience 32, 43–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craddock RC, James GA, Holtzheimer III PE, Hu XP, Mayberg HS, 2012. A whole brain fmri atlas generated via spatially constrained spectral clustering. Human brain mapping 33, 1914–1928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dadashkarimi J, Karbasi A, Scheinost D, 2021. Data-driven mapping between functional connectomes using optimal transport, in: de Bruijne M, Cattin PC, Cotin S, Padoy N, Speidel S, Zheng Y, Essert C. (Eds.), Medical Image Computing and Computer Assisted Intervention – MICCAI 2021, Springer International Publishing, Cham. pp. 293–302. [Google Scholar]
- Dadashkarimi J, Karbasi A, Scheinost D, 2022. Combining multiple atlases to estimate data-driven mappings between functional connectomes using optimal transport, in: Wang L, Dou Q, Fletcher PT, Speidel S, Li S. (Eds.), Medical Image Computing and Computer Assisted Intervention – MICCAI 2022, Springer Nature Switzerland, Cham. pp. 386–395. [Google Scholar]
- Dantzig GB, 1983. Reminiscences about the origins of linear programming, in: Mathematical Programming The State of the Art. Springer, pp. 78–86. [Google Scholar]
- Delon J, 2004. Midway image equalization. Journal of Mathematical Imaging and Vision 21, 119–134. [Google Scholar]
- Dosenbach NUF, Nardos B, Cohen AL, Fair DA, Power JD, Church JA, Nelson SM, Wig GS, Vogel AC, Lessov-Schlaggar CN, Barnes KA, Dubis JW, Feczko E, Coalson RS, Pruett JR Jr, Barch DM, Petersen SE, Schlaggar BL, 2010. Prediction of individual brain maturity using fMRI. Science 329, 1358–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubois J, Adolphs R, 2016. Building a science of individual differences from fmri. Trends in Cognitive Sciences 20, 425–443. doi: 10.1016/j.tics.2016.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickhoff SB, Laird AR, Grefkes C, Wang LE, Zilles K, Fox PT, 2009. Coordinate-based activation likelihood estimation meta-analysis of neuroimaging data: A random-effects approach based on empirical estimates of spatial uncertainty. Human Brain Mapping 30, 2907–2926. doi: 10.1002/hbm.20718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliott ML, Knodt AR, Cooke M, Kim MJ, Melzer TR, Keenan R, Ireland D, Ramrakha S, Poulton R, Caspi A, Moffitt TE, Hariri AR, 2019. General functional connectivity: Shared features of resting-state and task fmri drive reliable and heritable individual differences in functional brain networks. NeuroImage 189, 516–532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan L, Li H, Zhuo J, Zhang Y, Wang J, Chen L, Yang Z, Chu C, Xie S, Laird AR, et al. , 2016. The human brainnetome atlas: a new brain atlas based on connectional architecture. Cerebral cortex 26, 3508–3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn ES, Shen X, Scheinost D, Rosenberg MD, Huang J, Chun MM, Papademetris X, Constable RT, 2015. Functional connectome finger-printing: identifying individuals using patterns of brain connectivity. Nature neuroscience 18, 1664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flamary R, Courty N, 2017. Pot python optimal transport library. [DOI] [PubMed]
- Flamary R, Févotte C, Courty N, Emiya V, 2016. Optimal spectral transportation with application to music transcription. arXiv preprint arXiv:1609.09799.
- Gangbo W, McCann RJ, 1996. The geometry of optimal transportation. Acta Mathematica 177, 113–161. [Google Scholar]
- Gao S, Greene AS, Constable RT, Scheinost D, 2019. Combining multiple connectomes improves predictive modeling of phenotypic measures. NeuroImage 201, 116038. doi: 10.1016/j.neuroimage.2019.116038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, Van Essen DC, Jenkinson M, 2013. The minimal preprocessing pipelines for the human connectome project. NeuroImage 80, 105–124. doi: 10.1016/j.neuroimage.2013.04.127. mapping the Connectome. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hitchcock FL, 1941. The distribution of a product from several sources to numerous localities. Journal of mathematics and physics 20, 224–230. [Google Scholar]
- Holmes AJ, Hollinshead MO, O’Keefe TM, Petrov VI, Fariello GR, Wald LL, Fischl B, Rosen BR, Mair RW, Roffman JL, Smoller JW, Buckner RL, 2015. Brain genomics superstruct project initial data release with structural, functional, and behavioral measures. Scientific Data 2. doi: 10.1038/sdata.2015.31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horien C, Noble S, Greene AS, Lee K, Barron DS, Gao S, O’Connor D, Salehi M, Dadashkarimi J, Shen X, et al. , 2021. A hitchhiker’s guide to working with large, open-source neuroimaging datasets. Nature human behaviour 5, 185–193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang G, Quo C, Kusner MJ, Sun Y, Weinberger KQ, Sha F, 2016. Supervised word mover’s distance, in: Proceedings of the 30th International Conference on Neural Information Processing Systems, pp. 4869–4877. [Google Scholar]
- Jiang R, Calhoun VD, Fan L, Zuo N, Jung R, Qi S, Lin D, Li J, Zhuo C, Song M, Fu Z, Jiang T, Sui J, 2019. Gender Differences in Connectome-based Predictions of Individualized Intelligence Quotient and Sub-domain Scores. Cerebral Cortex 30, 888–900. URL: 10.1093/cercor/bhz134, doi: 10.1093/cercor/bhz134,arXiv:https://academic.oup.com/cercor/article-pdf/30/3/888/330114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi A, Scheinost D, Okuda H, Belhachemi D, Murphy I, Staib LH, Papademetris X, 2011. Unified framework for development, deployment and robust testing of neuroimaging algorithms. Neuroinformatics 9, 69–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kantorovich L, 1942. On the transfer of masses (in russian), in: Doklady Akademii Nauk, pp. 227–229. [Google Scholar]
- Koopmans TC, 1949. Optimum utilization of the transportation system. Econometrica: Journal of the Econometric Society, 136–146.
- Laird AR, Lancaster JL, Fox PT, 2005. BrainMap: The social evolution of a human brain mapping database. Neuroinformatics 3, 065–078. doi: 10.1385/ni:3:1:065. [DOI] [PubMed] [Google Scholar]
- Lake EMR, Ge X, Shen X, Herman P, Hyder F, Cardin JA, Higley MJ, Scheinost D, Papademetris X, Crair MC, Constable RT, 2020. Simultaneous cortex-wide fluorescence ca2 imaging and whole-brain fmri. Nature Methods 17, 1262–1271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li P, Wang Q, Zhang L, 2013. A novel earth mover’s distance methodology for image matching with gaussian mixture models, in: Proceedings of the IEEE International Conference on Computer Vision, pp. 1689–1696. [Google Scholar]
- Marek S, Tervo-Clemmens B, Calabro FJ, Montez DF, Kay BP, Hatoum AS, Donohue MR, Foran W, Miller RL, Hendrickson TJ, Malone SM, Kandala S, Feczko E, Miranda-Dominguez O, Graham AM, Earl EA, Perrone AJ, Cordova M, Doyle O, Moore LA, Conan GM, Uriarte J, Snider K, Lynch BJ, Wilgenbusch JC, Pengo T, Tam A, Chen J, Newbold DJ, Zheng A, Seider NA, Van AN, Metoki A, Chauvin RJ, Laumann TO, Greene DJ, Petersen SE, Garavan H, Thompson WK, Nichols TE, Yeo BTT, Barch DM, Luna B, Fair DA, Dosenbach NUF, 2022. Reproducible brain-wide association studies require thousands of individuals. Nature doi: 10.1038/s41586-022-04492-9. [DOI] [PMC free article] [PubMed]
- Mathon B, Cayre F, Bas P, Macq B, 2014. Optimal transport for secure spread-spectrum watermarking of still images. IEEE Transactions on Image Processing 23, 1694–1705. [DOI] [PubMed] [Google Scholar]
- Monge G, 1781. Mémoire sur la théorie des déblais et des remblais. Histoire de l’Académie Royale des Sciences de Paris. [Google Scholar]
- Peyré G, Cuturi M, et al. , 2019. Computational optimal transport: With applications to data science. Foundations and Trends in Machine Learning 11, 355–607. [Google Scholar]
- Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel AC, Laumann TO, Miezin FM, Schlaggar BL, et al. , 2011. Functional network organization of the human brain. Neuron 72, 665–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubner Y, Tomasi C, Guibas LJ, 2000. The earth mover’s distance as a metric for image retrieval. International journal of computer vision 40, 99–121. [Google Scholar]
- Schaefer A, Kong R, Gordon EM, Laumann TO, Zuo XN, Holmes AJ, Eickhoff SB, Yeo BT, 2018. Local-global parcellation of the human cerebral cortex from intrinsic functional connectivity mri. Cerebral cortex 28, 3095–3114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheinost D, Finn ES, Tokoglu F, Shen X, Papademetris X, Hampson M, Constable RT, 2014. Sex differences in normal age trajectories of functional brain networks. Human Brain Mapping 36, 1524–1535. doi: 10.1002/hbm.22720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X, Finn ES, Scheinost D, Rosenberg MD, Chun MM, Papademetris X, Constable RT, 2017. Using connectome-based predictive modeling to predict individual behavior from brain connectivity. nature protocols 12, 506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen X, Tokoglu F, Papademetris X, Constable RT, 2013. Groupwise whole-brain parcellation from resting-state fmri data for network node identification. Neuroimage 82, 403–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinn M, Hu A, Turner L, Noble S, Achard S, Anticevic A, Scheinost D, Constable RT, Lee D, Bullmore ET, Murray JD, 2021. Spatial and temporal autocorrelation weave human brain networks. bioRxiv doi: 10.1101/2021.06.01.446561. [DOI]
- Sporns O, Chialvo DR, Kaiser M, Hilgetag CC, 2004. Organization, development and function of complex brain networks. Trends in cognitive sciences 8, 418–425. [DOI] [PubMed] [Google Scholar]
- Sudlow C, Gallacher J, Allen N, Beral V, Burton P, Danesh J, Downey P, Elliott P, Green J, Landray M, et al. , 2015. Uk biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS medicine 12, e1001779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sui J, Jiang R, Bustillo J, Calhoun V, 2020. Neuroimaging-based individualized prediction of cognition and behavior for mental disorders and health: Methods and promises. Biological Psychiatry 88, 818–828. URL: https://www.sciencedirect.com/science/article/pii/S0006322320301116,doi: 10.1016/j.biopsych.2020.02.016. neuroimaging Biomarkers of Psychological Trauma. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szucs D, Ioannidis JP, 2020. Sample size evolution in neuroimaging research: An evaluation of highly-cited studies (1990–2012) and of latest practices (2017–2018) in high-impact journals. NeuroImage 221, 117164. doi: 10.1016/j.neuroimage.2020.117164. [DOI] [PubMed] [Google Scholar]
- Tolstoi A, 1930. Methods of finding the minimal total kilometrage in cargo transportation planning in space. TransPress of the National Commissariat of Transportation 1, 23–55. [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K, Consortium WMH, et al. , 2013. The wu-minn human connectome project: an overview. Neuroimage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan CG, Chen X, Li L, Castellanos FX, Bai TJ, Bo QJ, Cao J, Chen GM, Chen NX, Chen W, Cheng C, Cheng YQ, Cui XL, Duan J, Fang YR, Gong QY, Guo WB, Hou ZH, Hu L, Kuang L, Li F, Li KM, Li T, Liu YS, Liu ZN, Long YC, Luo QH, Meng HQ, Peng DH, Qiu HT, Qiu J, Shen YD, Shi YS, Wang CY, Wang F, Wang K, Wang L, Wang X, Wang Y, Wu XP, Wu XR, Xie CM, Xie GR, Xie HY, Xie P, Xu XF, Yang H, Yang J, Yao JS, Yao SQ, Yin YY, Yuan YG, Zhang AX, Zhang H, Zhang KR, Zhang L, Zhang ZJ, Zhou RB, Zhou YT, Zhu JJ, Zou CJ, Si TM, Zuo XN, Zhao JP, Zang YF, 2019. Reduced default mode network functional connectivity in patients with recurrent major depressive disorder. Proceedings of the National Academy of Sciences 116, 9078–9083. doi: 10.1073/pnas.1900390116, arXiv:https://www.pnas.org/content/116/18/9078.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan CG, Wang XD, Zuo XN, Zang YF, 2016. Dpabi: data processing & analysis for (resting-state) brain imaging. Neuroinformatics 14, 339–351. [DOI] [PubMed] [Google Scholar]
- Yarkoni T, 2009. Big correlations in little studies: Inflated fMRI correlations reflect low statistical power—commentary on vul et al. (2009). Perspectives on Psychological Science 4, 294–298. doi: 10.1111/j.1745-6924.2009.01127.x. [DOI] [PubMed] [Google Scholar]
- Yarkoni T, Poldrack RA, Nichols TE, Essen DCV, Wager TD, 2011. Large-scale automated synthesis of human functional neuroimaging data. Nature Methods 8, 665–670. doi: 10.1038/nmeth.1635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky A, Fornito A, Bullmore ET, 2010. Network-based statistic: Identifying differences in brain networks. NeuroImage 53, 1197–1207. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All datasets used in this study are open-source: HCP (ConnectomeDB database, https://db.humanconnectome.org), REST-meta-MDD (http://rfmri.org/REST-meta-MDD), and Yale dataset (http://fcon_1000.projects.nitrc.org/indi/retro/yale_lowres.html). BioImage Suite tools used for processing can be accessed at (https://bioimagesuiteweb.github.io/). bCAROT and associated canonical mappings are on GitHub (https://github.com/dadashkarimi/carot). The Python Optimal Transport (POT) toolbox is available at https://pythonot.github.io/.