Epithelial tissue confinement inhibits cell growth and leads to volume-reducing divisions

John Devany; Martin J Falk; Liam J Holt; Arvind Murugan; Margaret L Gardel

doi:10.1016/j.devcel.2023.05.018

. Author manuscript; available in PMC: 2023 Sep 27.

Published in final edited form as: Dev Cell. 2023 Jun 19;58(16):1462–1476.e8. doi: 10.1016/j.devcel.2023.05.018

Epithelial tissue confinement inhibits cell growth and leads to volume-reducing divisions

John Devany ^1,^3,⁴, Martin J Falk ^1,³, Liam J Holt ², Arvind Murugan ^1,³, Margaret L Gardel ^1,^3,^4,^5,^6,^*

PMCID: PMC10528006 NIHMSID: NIHMS1910865 PMID: 37339629

SUMMARY

Cell proliferation is a central process in tissue development, homeostasis, and disease, yet how proliferation is regulated in the tissue context remains poorly understood. Here, we introduce a quantitative framework to elucidate how tissue growth dynamics regulate cell proliferation. Using MDCK epithelial monolayers, we show that a limiting rate of tissue expansion creates confinement that suppresses cell growth; however, this confinement does not directly affect the cell cycle. This leads to uncoupling between rates of cell growth and division in epithelia and, thereby, reduces cell volume. Division becomes arrested at a minimal cell volume, which is consistent across diverse epithelia in vivo. Here, the nucleus approaches the minimum volume capable of packaging the genome. Loss of cyclin D1-dependent cell-volume regulation results in an abnormally high nuclear-to-cytoplasmic volume ratio and DNA damage. Overall, we demonstrate how epithelial proliferation is regulated by the interplay between tissue confinement and cell-volume regulation.

In brief

Devany et al. show that cell growth and division respond to different cues in epithelia. They find that cell growth rate is constrained by tissue growth rate and that growth-arrested cells can continue to reduce their volume by division until reaching a minimum size.

Graphical Abstract

graphic file with name nihms-1910865-f0008.jpg

INTRODUCTION

Regulation of cell proliferation is a central question for understanding tissue development, growth, and homeostasis.^1,2 In contrast to the exponential proliferation of isolated cells,^3,4 multicellular tissue requires tight coupling between cell proliferation and tissue growth.⁵ One proposed mechanism for regulating proliferation in epithelia is the so-called process of “contact inhibition of proliferation” (henceforth referred to as contact inhibition) where cell proliferation becomes highly restricted due to spatial constraints imposed by the tissue.^5,6 The disruption of contact inhibition results in cell overproliferation and altered tissue architecture.^7–9 Therefore, contact inhibition is thought to play a key role in maintaining tissue homeostasis and preventing tumor formation.^5,10 However, because contact inhibition is regulated through multiple signaling pathways and largely unknown parameters, we currently lack a framework for understanding the process across diverse tissues. This is evident from the literature where contact inhibition is described as dependent on cell density,¹¹ adhesion signaling,^6,8 and mechanical stress.^5,12 As these variables are difficult to manipulate independently, it remains unclear how tissue geometry and growth dynamics impact division and growth of constituent cells.

Cell proliferation is the process by which an individual cell grows and progresses through the cell cycle to divide and produce two daughter cells. The regulation of proliferation in isolated mammalian cells has been studied in detail identifying many key mechanisms.^13–16 Cell proliferation in the tissue context is similar in some ways: for example, most of the variation in cell-cycle length occurs in the G1 phase of the cell cycle,^13,17 and cell growth can occur normally during cell-cycle inhibition.^18,19 However, there appear to be different regulatory mechanisms acting in each context. For example, single cells grow by a similar amount of volume each cell cycle independent of their birth volume, an “adder” behavior.^13,14 In contrast, mouse epidermal tissue shows a cell-size checkpoint preventing small cells from entering S phase, meaning that smaller cells grow more than larger cells, a “sizer” behavior.¹⁷ Due to limited in vivo data, it remains unclear whether this is a consequence of tissue specific behavior in the skin or could reflect a difference in regulation between single cells and epithelial tissue. Several lines of evidence suggest the latter is true. For instance, the cell-cycle duration can be on the scale of weeks or months in vivo,²⁰ challenging established dilution-based mechanisms of cell-cycle regulation.^15,16 Further, prior work has shown a possible switch to size-dependent regulation of the cell cycle in cell-culture models of epithelial tissue.^21,22 However, we lack a systematic study that examines how tissue-scale growth dynamics impact regulation of cell volume and growth in epithelia.

To understand how cell proliferation is regulated in epithelia, we first performed a meta-analysis of cell-size data and found that epithelial cell volumes are remarkably consistent and highly context dependent. The cell volume in epithelial tissue in vivo is always smaller than single cells in culture. However, we could recapitulate the in vivo cell volume using a cell-culture model of epithelial tissue formation, indicating that tissue-scale phenomena impact cell-volume regulation. To quantitatively examine this, we employed model epithelial tissues with varied growth rates. We then introduced a general framework to quantify how tissue-scale growth dynamics constrain cell growth, providing a measure of “tissue confinement.” We show that increasing tissue confinement reduces cell growth and YAP/TAZ signaling but does not impact the cell-cycle duration directly. Instead, cell-cycle duration is strongly correlated with cell volume. There is a sharp cell-cycle arrest at a cell volume of ~1,000 μm³, consistent with cell volume found in vivo. In both epithelial and single-cell contexts, cell-volume regulation is well described by a “G1 sizer model” with a tunable growth rate. In epithelia, cyclin D1 protein levels are strongly cell-volume dependent and overexpression of cyclin D1 reduces the minimal cell volume. This suggests that the levels of cyclin D1 controls volume-dependent cell-cycle arrest. We see that abnormally small cells display DNA damage as these cells approach a physical limit where the nucleus approaches the volume occupied by the fully compacted genome. This suggests that, in addition to mediating cell-cycle arrest during contact inhibition, cell-volume regulation pathways are critical for maintaining epithelial homeostasis. Overall, we demonstrate the general mechanisms of cell growth and division regulation in epithelia, which may provide insight into proliferative processes in tissue development, homeostasis, and disease.

RESULTS

Epithelial cell volume is context dependent

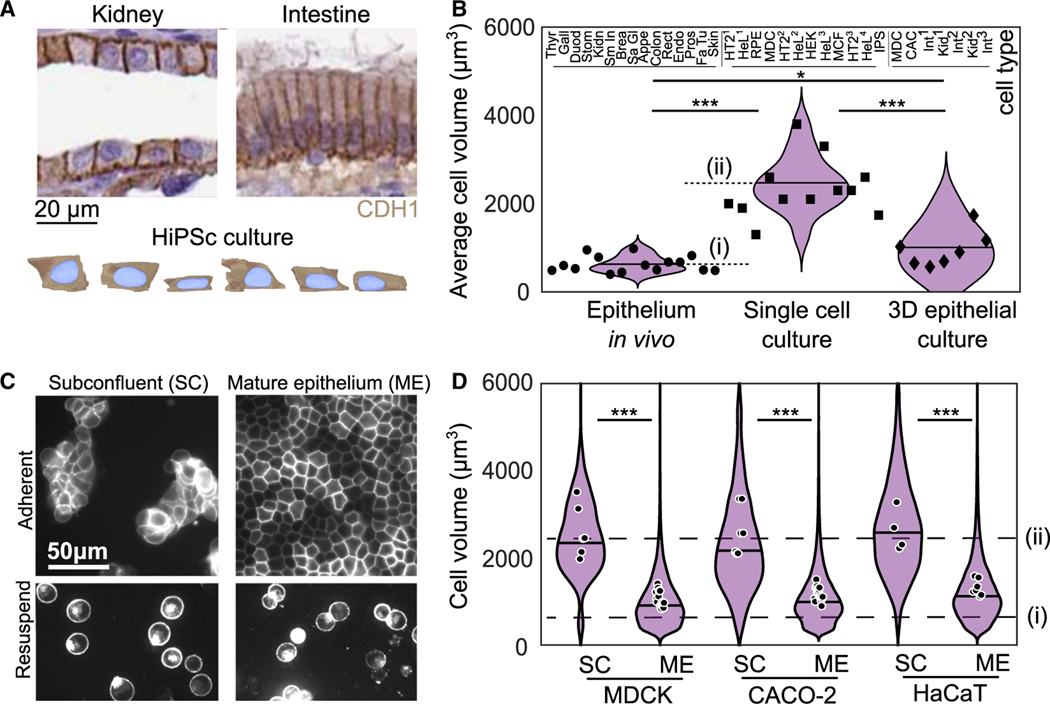
To screen for varied cell-volume regulation in epithelial tissue, we systematically compared cell volume from different tissues in vivo and cell-culture models (Table S1). We compiled these data from available sources including histology sections from the Human Protein Atlas (Figure 1A),²³ 3D segmentation data from Allen Cell Institute (Figure 1A),^24,25 and published cell-volume measurements.^13,26–40 When cell-volume measurements weren’t available, we estimated cell volume by identifying cells perpendicular to the tissue slice and then measuring their length and width. We confirmed that this provides an accurate estimation of volume from benchmarking against full 3D imaging (Figure S1). Across 15 tissue types in the Human Protein Atlas, we find the volume of epithelial cells is surprisingly consistent, with a narrow distribution of 630 ± 180 μm³ (Figure 1B, circles). By comparison, the volume across 12 types of isolated epithelial or epithelial-like cells is consistently measured to be severalfold larger, with a volume of 2,330 ± 650 μm³ (Figure 1B, squares).^{13,29,31,35,36,38,40} Interestingly, the volumes of epithelial cells cultured in 3D more closely matched those in vivo, with a mean of 1,020 ± 520 μm³ (Figure 1B, diamonds).^{26–28,30,32,33,37} These data suggest that epithelial cell volume is strongly influenced by the tissue environment.

Figure 1. — (A) Histology sections published by the Human Protein Atlas showing E-cadherin (CDH1) staining kidney and intestine (duodenum) tissue (image credit: Human Protein Atlas) and human induced pluripotent stem cell (HiPSc) segmentation data from Allen Cell Institute (available from allencell.org/3d-cell-viewer). In all images cells are displayed in cross-sectional view with the apical-basal axis vertical.

(B) Cell volume from 15 tissues *in vivo* (circles), 12 published measurements from cell lines cultured as single cells (squares), and 7 measurements from 3D epithelial cell cultures (diamonds). Each data point is the average cell size from >50 cells for a given cell type. Measurement details available in Table S1. Dashed lines show the average cell volumes from epithelium *in vivo* (i) and in single-cell culture (ii).

(C) (Top) Images of MDCK cells with fluorescently labeled cell membranes (stargazin-gfp) in subconfluent colonies (SCs) and mature epithelium (ME). (Bottom) Cells under each condition are also shown after being treated with trypsin for 10 min and resuspended.

(D) Cell volume in SC and ME for MDCK, CaCo-2 and HaCaT cell lines. Violins show the distribution of cell volumes pooled from all experiments, solid line shows median of this cell-volume distribution, and points show the mean volume of each experimental replicate. Dashed lines show the average cell volumes from epithelium *in vivo* (i) and in single-cell culture (ii) from (B) $(n = cells [N = experiments], n_{MDCK - sc} = 5, 884 [N = 6], n_{MDCK - ME} = 25, 863 [N = 17], n_{CACO 2 - sc} = 3, 408 [N = 6], n_{CACO 2 - ME} = 59, 817 [N = 16], n_{HaCaT - SC} = 12, 704 [N = 4], n_{HaCaT - ME} = 31, 454 [N = 6])$ . *p < 0.05, ***p < 0.001 from comparison of experimental or sample means. See also Figures S2–S4 and Table S1.

To test this hypothesis, we studied several different epithelial cell lines (Madin-Darby canine kidney [MDCK], Caco-2, and HaCaT) to measure the cell volume in either subconfluent colonies (SCs) or mature epithelium (ME). Controlling cell-plating density allowed for the formation of SCs, each composed of 50–1,000 cells or a nearly confluent monolayer on collagen gels (see STAR Methods). After the initial plating, cell dynamics drive changes in cell density, shape, and speed over the next 1–2 days⁴¹; we define ME as the time at which these properties stop changing in time (see STAR Methods and Figure S3). Cell boundaries were visualized with a fluorescently tagged membrane protein (stargazin-green flourescent protein [GFP] [CACNG2-GFP] or stargazin-halotag) (Figure 1C). To facilitate measurement of cell volume, cells were trypsinized, resuspended, and then imaged (Figure 1C; Figure S1; see STAR Methods). When in SCs, the cell volume of all three epithelial cell types is ~2,800 μm³ (Figure 1D, SC), consistent with the mean value of single cells in Figure 1B (Figure 1D, dashed line [ii]). Further, we found that ME culture conditions reduced the cell volume by 60% to plateau at ~1,000 μm³ (Figures S2B–S2D), a volume similar to cell volumes measured in vivo (Figures 1B and 1D, dashed line [i]). We performed the same experiment on two cell lines that do not form coherent colonies, retinal pigment epithelial cells (RPE-1) and mouse embryonic fibroblasts (MEFs) and did not see volume reduction (Figure S3). This suggests this context-dependency of cell volume may be specific to epithelium. Together, these data suggest that contact inhibition qualitatively changes cell-volume regulation across diverse epithelia.

Cell-volume reduction occurs through division in the absence of cell growth

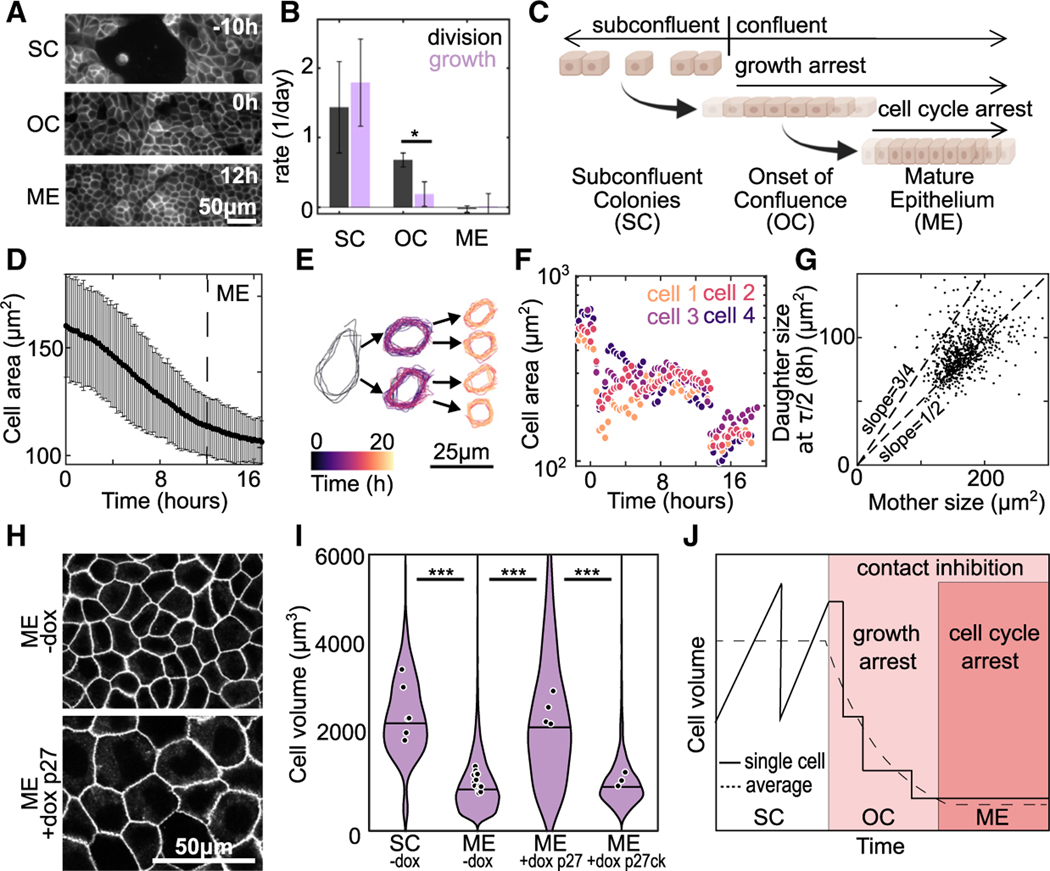
To query how cell growth and division rates change during the transition from SC to ME, live-cell imaging was used to monitor changes in cell volume and number. The data were aligned such that $t = 0$ h denotes the onset of confluence (OC). For all earlier times, cells are in SC. By $t > 12$ h cell movement has ceased, and density is constant; we denote this as a ME (Figure 2A). We first consider cell division and growth rates for $t < < 0$ h (SC), $t \sim 0$ h (OC), and $t ≫ 0$ h (ME). We prepared cells in each condition and performed bulk measurements. Cell-division rate, obtained by cell-counting measurements, was completely arrested in the ME but only suppressed by ~40% at OC, as compared with SC (Figure 2B, black bars). By contrast, the cell growth rate, determined from changes in protein concentration over time (see STAR Methods), was suppressed almost entirely at OC (Figure 2B, purple bars). These data indicate suppression of cell growth and division are not tightly coupled during the transition from subconfluent to confluent tissue. Instead, cell growth is suppressed acutely at OC whereas division is only impacted in later stages (Figure 2C). In single cells, cell growth and division are coupled to maintain a constant volume.¹⁶ In contrast, a division rate exceeding the growth rate should result in cell-volume reduction.

To test this hypothesis, we measured the cell area between $t = 0$ and 18 h during the transition from OC to ME. Over this time, the cell height remained constant, such that changes in cell area were accurate indicators of cell volume (Figure S2G). The average cell area from a population of ~1,000 cells decreased by ~50% from OC ( $t = 0$ h) to ME (Figure 2D). To determine the mechanism driving changes in cell volume we performed single-cell tracking. Cells that divided near the beginning of the experiment ( $t = 0$ h) were identified and tracked through the experiment. Individual cell trajectories showed that the cell-volume reduction occurred by successive cell-division events in the absence of cell growth (Figures 2E and 2F). Indeed, across a large population of mother-daughter cell pairs, the cell area of a daughter cell 8 h (~1/2 cell-cycle time, t) post cell division remained approximately half that of the mother cell area (Figure 2G). This indicates minimal cell growth during the cell cycle. This is in stark contrast with subconfluent cells, in which a cell grows at a constant rate and doubles in volume prior to division into two daughter cells.¹³ For single cells, we would expect the cell to grow by ~50% at 8 h post division, resulting in a slope of ~3/4 (Figure 2G, dashed line).

To demonstrate that cell division is necessary for cell volume to decrease, experiments similar to those in Figure 2A were performed with a Tet-On p27 1–176 MDCK cell line to artificially arrest the cell cycle by induction of a degradation resistant mutant of the human p27 (CDKN1B) cell-cycle inhibitor in the presence of doxycycline.⁴² In the absence of dox (−dox), the volume decreased in ME compared with SC, similar to our previous experiments (Figures 2H and 2I). Addition of doxycycline at OC prevented cell-volume decrease in ME (ME +dox p27), and the volume of these cells remained similar to that of SC (Figures 2H and 2I). Induction of a defective p27 mutant that does not arrest the cell cycle (+dox p27ck)⁴³ had no effect on cell volume in ME (Figure 2I). Together, these data demonstrate that temporal uncoupling of cell growth and cell division result in cell-volume reduction during formation of mature epithelial tissue. At the OC, cell growth is highly suppressed and cell volume reduces by division in absence of cell growth (Figure 2J). Then at later times the cell cycle also becomes arrested, and cells reach a final cell volume that is comparable to epithelium in vivo. We next sought to understand regulation of cell growth and cycle in the epithelium.

Tissue confinement regulates cell growth

The acutely cell-suppressed growth rate observed at the OC suggests that tissue and cell growth rates are strongly coupled. Therefore, we defined a quantitative framework to study cell proliferation within expanding colonies to better understand this coupling. We first considered that changes in tissue and colony size are governed by cell proliferation and migration of cells outward into free space. We refer to these increases in tissue area as tissue growth. Our hypothesis is that the product of all growth of cells cannot exceed the total growth of tissue, such that cell growth and tissue growth occur at the same rate in normal epithelial tissue. When the tissue forms a confluent monolayer at the OC, tissue growth stops, and, consequently, cell growth must arrest. But even if tissue expansion becomes limited earlier, for example, by the rate of cell migration at the tissue margin, cell growth will begin to be suppressed.

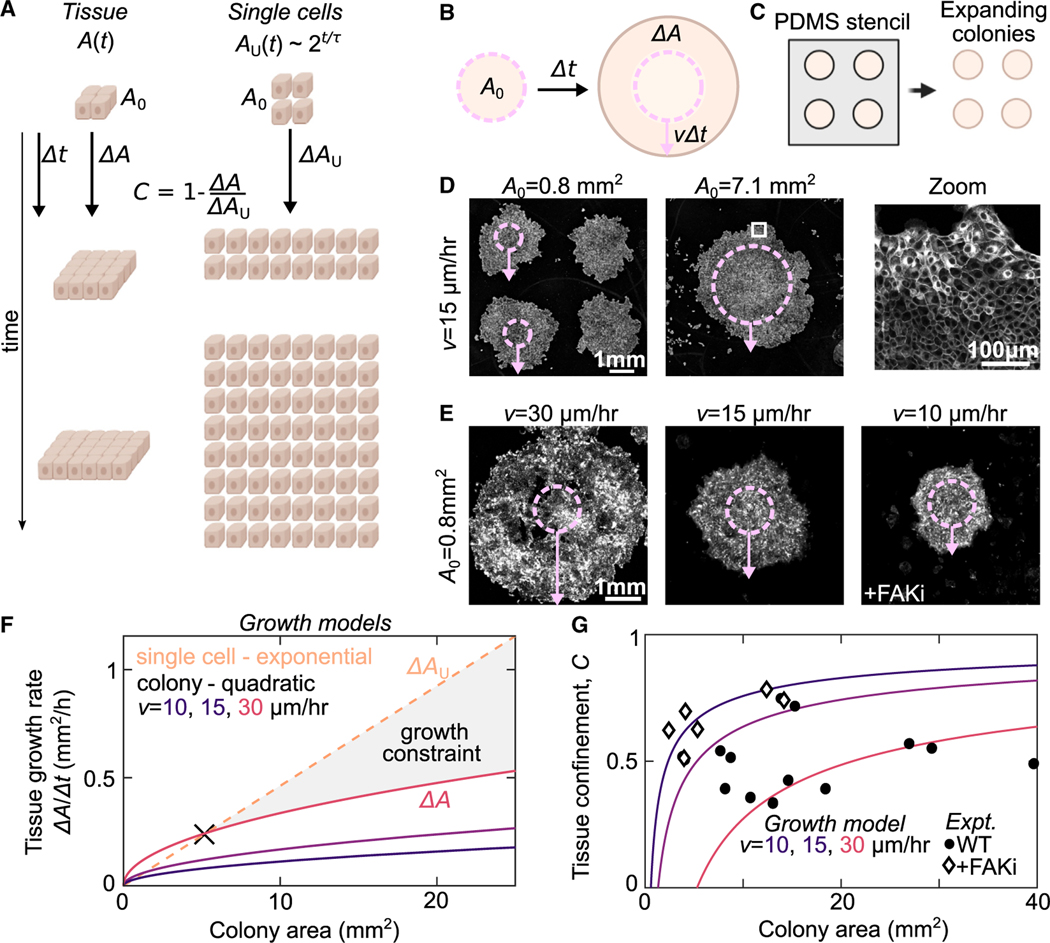
To test this hypothesis, we introduce a thought experiment to compare growth dynamics within a multicellular tissue with the exponential growth dynamics of a population of unconstrained individual cells. The area of a multicellular tissue with initial area $A_{0}$ grows over a time interval $Δ t$ by an amount $Δ A$ . Then, consider that this tissue $A_{0}$ is broken up into individual cells that proliferate over the same time interval (Figure 3A). The total area of the hypothetical ensemble of single cells grows exponentially, such that the total time-dependent area is described by $A_{U} (t) \sim 2^{t / τ}$ , where $τ$ is the average cell-cycle time. The deviation of the tissue growth from this hypothetical maximum exponential growth rate is a quantitative measure of the constraints that changes in tissue area place on cell proliferation. For a specific tissue area, $A^{'}$ , if the ratio of the tissue growth rate to the unconfined growth rate: ${\frac{d A}{d t} |}_{A^{'}} / {\frac{d A_{U}}{d t} |}_{A^{'}}$ is less than 1, then the tissue growth dynamics constrain cell growth. We then define the tissue confinement $C (A^{'}) = 1 - {\frac{d A}{d t} |}_{A^{'}} / {\frac{d A_{U}}{d t} |}_{A^{'}}$ such that there is no confinement effect $(C = 0)$ when single cells and tissues have identical growth dynamics and $C = 1$ when tissue growth rate is zero as in a fully confluent tissue.

We explored our tissue confinement model in the context of large, circular colonies of MDCK cells, chosen for their well-characterized growth dynamics and the ability to control their area.^22,44 Circular colonies of variable area $A_{0}$ from ~1 to 7 mm² were formed by seeding the cells in a polydimethylsiloxane (PDMS) stencil atop a glass coverslip (Figures 3B and 3C). The stencil was then released to allow for colony expansion for $Δ t = 48$ h (Figure 3D). Importantly, the average colony expansion is determined by radial migration speed $v$ of cells at the periphery to increase the colony radius by $v Δ t$ (Figure 3B, arrow). Consistent with previous studies, the radial expansion rate was independent of colony area (Figure 3D; Figures S4A–S4C). This results in a tissue growth rate that scales quadratically with colony area (see STAR Methods). For a given colony area, variation in $v$ provides additional control over colony growth rate (Figure 3E). Under control conditions, $v$ varied between experiments from 15 to 30 μm/h (Figure S4C). This tissue growth rate was reduced by inhibiting cell migration by a focal adhesion kinase inhibitor (FAKi) (Figure S4C). Thus, variations in both the initial colony area and edge velocity allowed us to investigate our model over a wide range of tissue growth rates.

We generated model curves of the expected colony growth rates for the ranges of areas and edge velocities observed experimentally (Figure 3F, solid lines). These rates were then compared with those expected for exponential growth of single cells, using the experimentally measured doubling time of 15 h (Figure 3F, dashed line). For small areas, exponential growth is smaller than the theoretical growth rate of the expanding colony (Figure 3F); here tissue-scale growth dynamics do not constrain cell proliferation. This is the behavior for SC. By contrast, for large areas, expanding colony growth rates become substantially lower than the exponential growth of single cells (e.g., Figure 3F, gray-shaded region). Here, tissue growth dynamics constrain cell proliferation. The colony area when exponential growth and quadratic growth rates are equal demarks the transition between these two regimes and, here, $C = 0$ (Figure 3F, black X). For each given growth model, the confinement $C$ is plotted as a function of colony area (Figure 3G, lines). Confinement was determined from experimental data with varying $A_{0}$ and $v$ (Figure 3G, points). These experimental conditions then provide a means to systematically examine cell behavior in varied $C$ from <0.25 to ~0.8. Thus, our tissue confinement framework provides a quantitative method to assess how tissue-scale growth dynamics are expected to constrain growth of single cells.

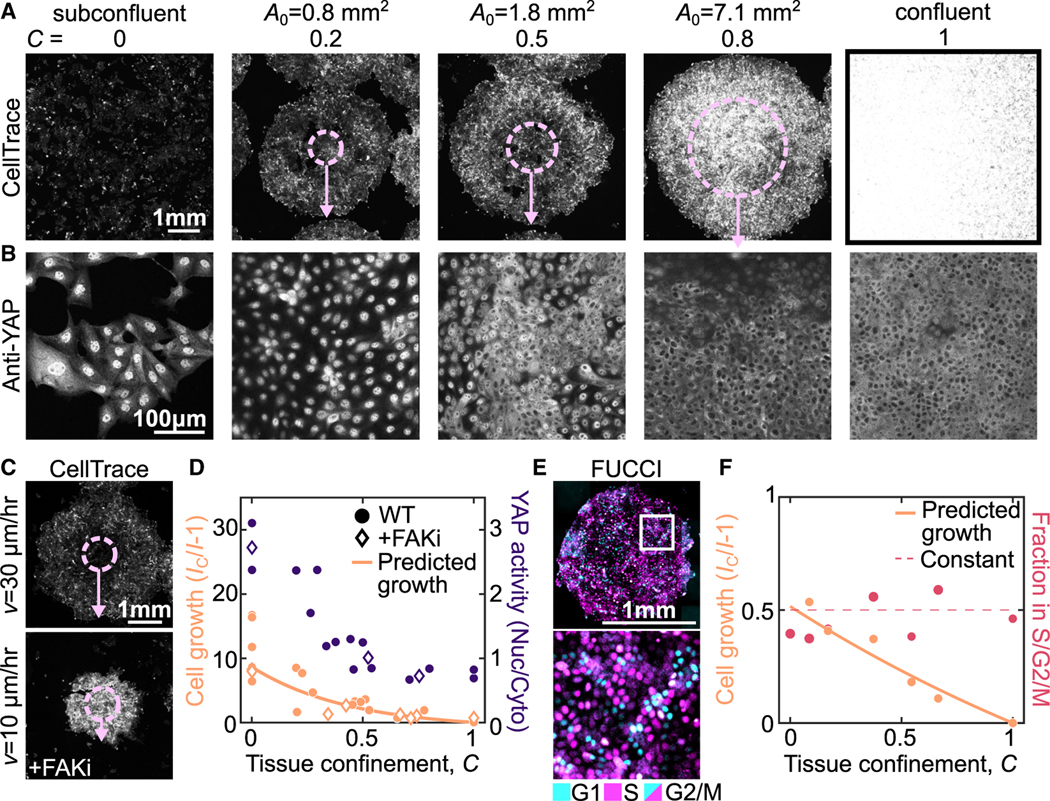
To test the utility of this framework, we measured cell growth and signaling in tissues with varied levels of confinement. To query cell growth, we labeled the cells at $t = 0$ with CellTrace, a fluorescent dye that reports on increases in cell volume by its dilution (i.e., more growth leads to lower cell intensity) (see STAR Methods). The total growth is determined from the CellTrace images by the ratio of intensity $\frac{l (t = 0)}{l (t = Δ t)} - 1 = \frac{V o l (t = Δ t)}{V o l (t = 0)} - 1 = Δ V o l$ . Since the growth rate of confluent monolayers is close to zero (Figure 2B), the intensity of the confluent monolayer $I_{C} \sim I (t = 0)$ , can be used as the standard to compare to the intensity $I$ of expanding colonies (Figure 4A, $C = 1$ ). This allows for determination of the growth rate by $I_{C} / I - 1$ . For $Δ t = 48$ h, subconflucent cells show a 10-fold CellTrace dilution consistent with the cells doubling every 15 h (Figure 4A, $C = 0$ ). We then used expanding colonies with varied $A_{0}$ to explore intermediate levels of confinement from 0.2 to 0.8. In smaller colonies with $C = 0.2$ , cell growth was already suppressed to <50% that of subconfluent conditions. By $C = 0.6$ , growth was restricted to <10% that of the subconfluent cells, and was suppressed to nearly zero by $C = 0.8$ (Figure 4A). Changes in growth can also be modulated by changing the velocity of colony expansion at the edges, which can be achieved by perturbing cell migration. In our experiments, we observed that differences in migration rate significantly impacted the cell growth, as predicted by our modeling (Figure 4C). In all conditions, the intensity was remarkably uniform across the tissue suggesting that the growth regulation mechanism is a tissue-scale phenomenon (Figure S6E).

Figure 4. — (A and B) Images of Cell Trace (A) and YAP (B) at $Δ t = 48$ h in expanding colonies with initial size, $A_{0}$ , varying from 0.8 to 7.1 mm², subconfluent colonies and confluent conditions. In (A), overlay shows initial colony size $A_{0}$ (dashed circle) and expansion $v Δ t$ (arrow). Note different scale bars in (A) and (B).

(C) CellTrace images of expanding monolayers with $A_{0} = 0.8$ mm at $Δ t = 48$ h in the presence and absence of 500 nM PND1186 (+FAKi) to illustrate the effect of changes in $v Δ t$ .

(D) Quantification of cell growth and YAP signaling at varying tissue confinements with $Δ t = 48$ h across multiple experiments. Each data point is an average of multiple colonies from one experiment (see STAR Methods). YAP activity is determined by the nuclear-to-cytoplasmic ratio of anti-YAP intensity, quantified for >150 cells in each experiment. Growth is plotted against the time averaged confinement and YAP activity is plotted against the final confinement. Data are from 6 independent experiments (cell growth) and 3 independent experiments (YAP activity).

(E) MDCK FUCCI cells in expanding colony with $A_{0} = 1.8$ mm² and $Δ t = 12$ h.

(F) Quantification of cell growth and fraction of cells in the S/G2/M cell-cycle states as a function of the average tissue confinement. Each data point is quantified from >3 colonies in a single experiment with $A_{0} = 0.8$ , 1.8, or 7.1 mm² and $Δ t = 12$ h. Data are from 2 independent experiments. See also Figure S11.

To query cell growth signaling under confinement, we also performed immunostaining against yes-associated protein 1 (YAP1). YAP is a transcription factor implicated in regulating cell proliferation during contact inhibition.^6,45,46 When YAP is active, it is localized to the nucleus; when inactive, YAP is localized to the cytoplasm. We see in the conditions with lower confinement, a greater fraction of YAP is localized to the nucleus, whereas around $C = 0.5$ it becomes more localized to the cytoplasm (Figure 4B). This suggests that YAP activity is regulated in response to changes in tissue confinement (Figure 4B). Taken together, all of our experimental data from colonies with varying size and edge velocity (Figure 3G) identify a systematic decrease in cell growth and YAP signaling as a function of confinement (Figure 4D, points). Moreover, the predicted growth from the definition of tissue confinement is consistent with the experimental data (Figure 4D, line). All of these data demonstrate the rapid suppression of cell growth at low levels of confinement.

At the OC, the cell-division rate remains similar to subconfluent cells despite the increased confinement (Figure 2B); this suggests that tissue confinement may not immediately affect the cell cycle. To query the cell cycle, we performed the expanding colony experiments with MDCK cells expressing the pip-degron fluorescent ubiquitination cell-cycle indicator (FUCCI MDCK)⁴⁷ to measure the fraction of cells in S/G2/M in model tissues with varying levels of confinement. We restrict our analysis to short expansion times $(Δ t = 12 h)$ before cells have reached the ME state and arrested the cell cycle. In contrast to cell growth (Figure 4F, peach), the cell-cycle fraction is insensitive to tissue confinement (Figure 4F, red). Instead, the fraction of cells in S/G2/M is constant (Figure 4F, dashed line). Together with our data showing similar division rate at the OC and in subconfluent cells (Figures 2B and 2F) this suggests that no change in the cell cycle with confinement. These data identify the qualitatively different impact of confinement on cell cycle and growth. Thus, the transient uncoupling between cell division and growth rate observed in Figure 2B is consistent with a rapid increase in confinement at the OC.

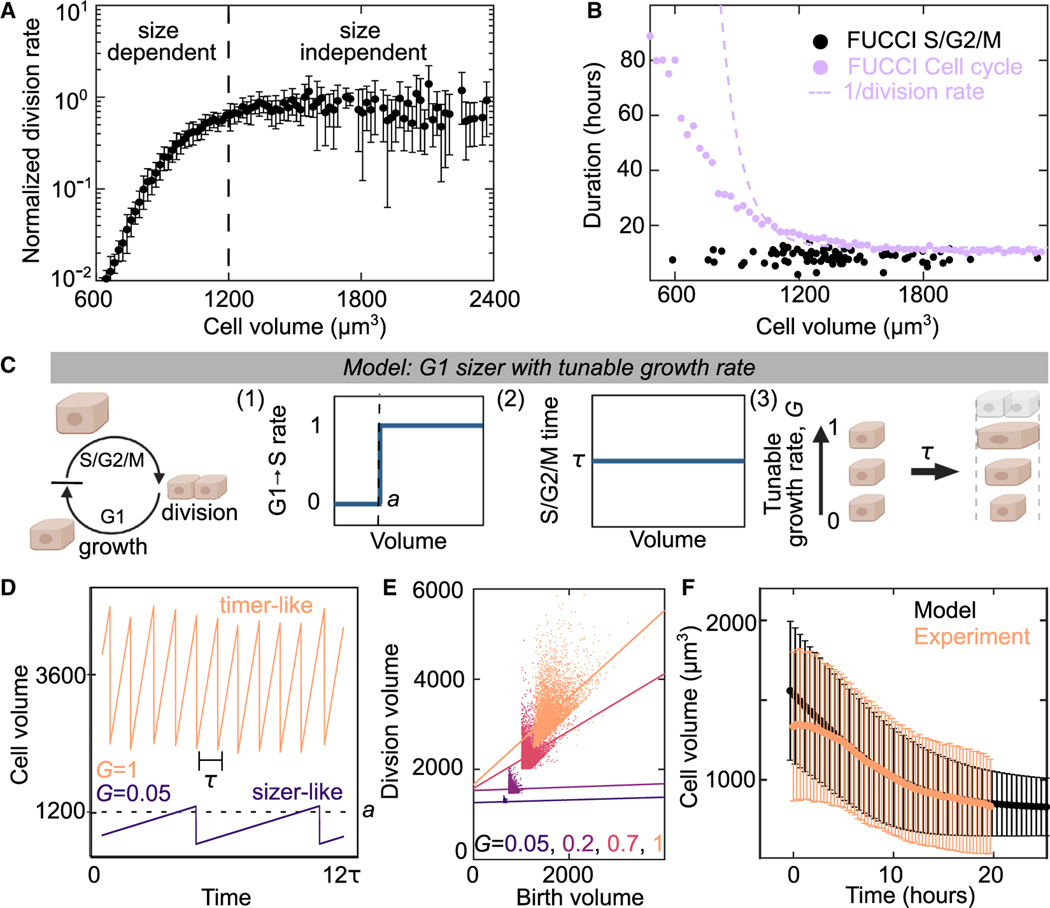
A G1 sizer arrests the cell cycle in confined epithelium

We next examined how the cell cycle arrests in monolayers at the later stages of contact inhibition. After confinement reduces the growth rate, cell volume decreases through successive cell division until the cell cycle becomes arrested (Figure 2J). Previous work has shown that cell-cycle regulation can be volume dependent for in vivo epithelium.¹⁷ To examine if cell division is regulated by cell volume in our data, we measured how the cell division rate varied as a function of cell volume by tracking individual division events. We estimate volumes from the cell area multiplied by the typical cell height of 6.5 ± 1.5 μm (Figure S2G, mean ± SD). Above a volume of 1,300 μm³, the cell-division rate is independent of volume (Figure 5A). However, the division rate sharply decreases for smaller volumes. This trend is observed across a range of experimental conditions and two epithelial cell types, indicating that it is a robust feature of cell-volume regulation in confluent epithelial tissue (Figure S5). We then used FUCCI MDCK cells to look more closely at the cell-cycle regulation for large and small cells. From the FUCCI data, we obtained the S/G2/M duration by tracking single-cell trajectories and saw that the duration of the S/G2/M phases is 10 h and independent of cell volume (Figure 5B). In the same data, the duration of the entire cell cycle was estimated by measuring the fraction of cells in each cell-cycle phase (see STAR Methods). We see that the cell-cycle duration rapidly increases for smaller cells (Figure 5B, purple data). The division rate in Figure 5A can also be used to estimate cell-cycle duration and shows a similar trend (Figure 5B, dashed line). Together, these data indicate an increased duration of the G1 phase for smaller cells. This is consistent with previous results that volume-dependent cell-cycle regulation occurs at the G1-S transition.^1,13,17

Motivated by this data, we developed a simple “G1 sizer” model of volume-dependent exit from G1 with a tunable growth rate (Figure 5C).^17,48 In the model, we simulate an ensemble of cells that grow at a constant rate, have two cell-cycle phases G1 and S/G2/M, and divide into two daughter cells with half the mother volume. We added additional features based on experimental observations: (1) there is a sharp volume threshold of the G1-S transition rate and below this minimal volume $a$ , the transition rate is zero, (2) cells have an S/G2/M duration of $τ = 10$ h independent of cell volume, and (3) a variable cell growth rate $G$ that is normalized to vary from 0 for no growth to 1 for growth in the unconfined condition. Due to rule (2), the minimum cell-cycle time is $τ$ h and cells will grow by a minimum of $G_{τ}$ before each division. When $G_{τ} ≫ a$ , cells are large compared with $a$ and the G1-S transition proceeds quickly. In this regime, the cell-cycle regulation is volume independent (timer-like) with a time $τ$ between cell divisions (Figure 5D, $G = 1$ ; Figures S6A–S6C). However, when the growth rate is suppressed such that $G_{τ} ≪ a$ , additional time is required to relieve the volume constraint of the G1-S transition (1) (Figure 5D, $G = 0.05$ ; Figures S6A–S6C). In this regime, the cell-cycle regulation is highly volume dependent (sizer-like). We tested several simplifying assumptions of our model by performing additional simulations and consistently see this behavior (Figures S6D–S6H).

Plotting the cell volume at division as a function of cell volume at birth for a range of growth rates shows that the model transitions smoothly from volume-dependent to volume-independent behavior as a function of growth rate (Figure 5E, Figures S6E–S6H). Volume-dependent cells divide at the same volume and show no correlation between birth volume and division volume (Figure 5E, dashed lines for $G = 0.05$ and 0.2). This contrasts with volume-independent cells which show a correlation between birth volume and division volume (Figure 5E, dashed lines for $G = 0.7$ and 1).^13,16,17,49 These different behaviors also occur in distinct cell-volume ranges consistent with previous work showing that large, rapidly growing, single cells are more volume independent¹³ and small, slowly growing cells, in vivo are volume dependent.¹⁷

Having developed an understanding of the model at constant or near-constant growth rates, we tested if the model could also predict the cell-volume distributions found in the experiments of monolayer formation and maturation in Figure 2B. We simulate monolayer formation in our model by a rapid quench of cell growth rate from 1 to 0 at $t = 0$ and measure the cell-volume distribution over time (Figure 5F). The simulation results (Figure 5F, black) are consistent with those of the experiment (Figure 5F, peach). This suggests that the G1 sizer model together with an understanding of how confinement impacts cell growth (Figure 4F) is sufficient to explain transitions in volume of isolated cells to those in epithelial tissue.

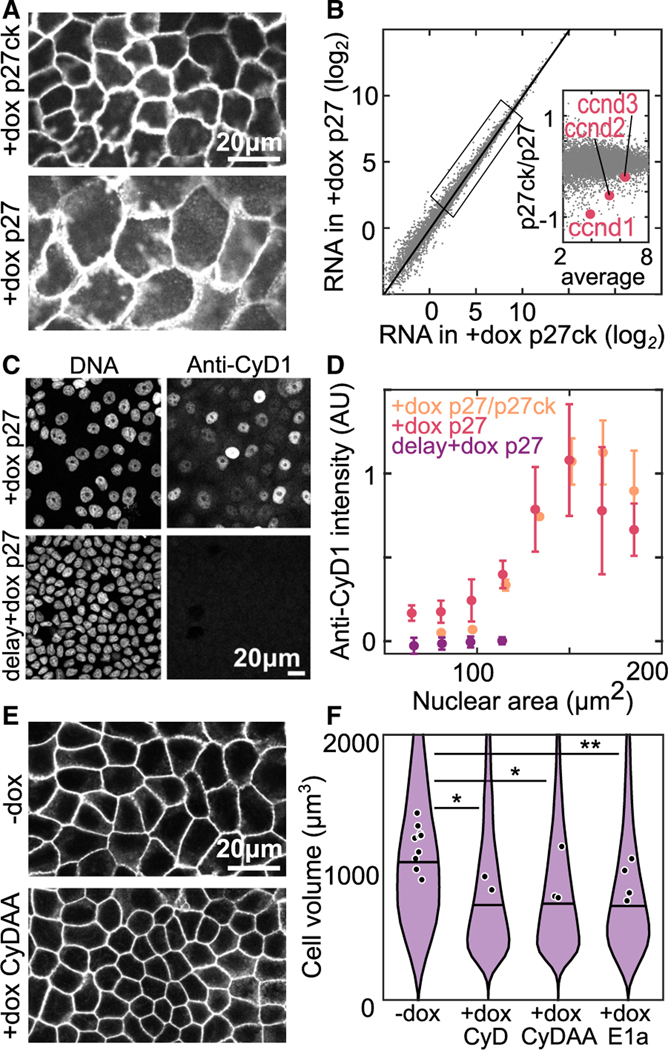
Volume-dependent cyclin D downregulation leads to cell-cycle arrest

To investigate molecular mechanisms of volume-dependent cell-cycle control, we took advantage of our Tet-inducible cell lines to manipulate cell volume in confluent monolayers. We prepared monolayers at the OC with Tet-On p27 and Tet-On p27ck cells. Prior to the experiment, cells were synchronized in G1 with palbociclib and at $t = 0$ , we added doxycycline (+dox) to induce expression. After 5 days, both monolayers are in a cell cycle and growth-arrested ME state, but the +dox p27ck cells are 40% the volume of +dox p27 cells (Figures 2I and 6A). RNA sequencing identified almost no differences in the steady-state transcriptome of these samples (Figure 6B). However, close examination identified several weak signatures (Figures S7E–S7J) including a slight downregulation of cyclins D1, D2, and D3 in the smaller contact-inhibited cells (Figure 6B, inset). The G1/S transition has a steep dependence on cyclin D concentration,⁵⁰ so it is possible that small changes in cyclin D concentration are sufficient to arrest the cell cycle. Furthermore, cyclin D is strongly post transcriptionally regulated by degradation.⁵¹ To check if this difference in RNA abundance leads to changes in protein levels, we looked at cyclin D1 (cyD1) protein levels via immunofluorescence in ME formed with Tet-On p27 cells (+dox p27) and co-cultures including Tet-On p27ck cells (+dox p27/p27ck). Since p27 is known to interact with cyclin D, we tested if its overexpression did not change the cyclin D1 levels by inducing p27 after ME formation (delay +dox p27). Interestingly, we found significant differences in cyclin D1 abundance, with nearly undetectable levels in cells with a nuclear area <100 μm², corresponding to a cell volume of 1,100 μm³ (Figure 6C; Figure S7D). We observed that the intensity of cyD1 drops rapidly with decreasing nuclear area, corresponding to a decreasing cell volume (Figure 6D; Figure S7D). The same trend was seen for all monolayer preparations, suggesting that the cyclin D1 level is regulated by a volume-dependent pathway. This suggests that in addition to transcriptional changes in cyclin D, additional volume-dependent post transcriptional regulation occurs, possibly as reported in other contexts.^51,52

Figure 6. — (A) Cell membranes of Tet-On p27 and Tet-On p27ck MDCK cells in ME + 4 days; dox added at $t = 0$ h.

(B) RNA sequencing data from monolayers prepared in (A). Data are averaged transcripts per million from 3 experimental replicates. Inset: zoom in of genes in indicated box, cyclin D genes expression levels are highlighted in red.

(C) DNA staining and anti-cyclin D1 (cyD1) immunofluorescence staining in MDCK monolayers at ME + 3 days. Dox is added at either $t = 0$ (+dox p27) or at $t = ME + 2$ days (delay +dox p27).

(D) Quantification of anti-cyD1 intensity from immunostaining data as a function of nuclear area. Intensity is normalized in each experiment to a maximum value of 1. P27/p27ck are monolayers with a mixture of Tet-On p27 and Tet-On p27ck cells. $(N_{+dox} = 4, 564 [3], N_{Delay+dox} = 7, 515 [2], N_{p 27 / p 27 ck} = 11, 080 [4])$ .

(E) Labeled cell membranes in Tet-On cyclin D1 T286A T288A (CyDAA) MDCK monolayers at ME + 3 days without dox (−dox) or with dox added at $t = 0$ (+dox CyDAA).

(F) Cell volume measured in resuspended Tet-On cyclin D1, Tet-On cyclin D T286A T288A, and Tet-On 12sE1a cells at ME + 3 days without dox (−dox) or with dox added at $t = 0$ (+dox CyD, +dox CyDAA, +dox E1a). $(n_{−dox} = 13, 513 [N = 10], n_{CyD} = 7, 240 [N = 2], n_{CydAA} = 9, 092 [N = 3], n_{E 1 a} = 6, 457 [N = 4])$ (*p < 0.05, **p < 0.01 from comparison of experimental means). See also Figures S9 and S10.

To test if decreased cyclin D levels are required to arrest the cell cycle, we overexpressed cyclin D1 in contact-inhibited cells. We used Tet-On cyclin D1-GFP (CyD) or Tet-On Cyclin D1 T286A T288A-GFP (CyDAA, a degradation resistant mutant) cells and induced the expression of additional cyclin D1 at OC. We then looked at the cell volume 3 days later, after it had reached a plateau. We observed that overexpression of either CyD or CyDAA leads to decrease in minimal cell volume in ME, compared with control (−dox) (Figures 6E and 6F). Therefore, restoring cyclin D1 in small cells is sufficient to initiate the cell cycle. This suggests that the depletion of cyclin D is necessary for volume-dependent arrest of the cell cycle. We also overexpressed the viral oncoprotein E1a, which is known to bind with and inactivate Rb pocket proteins and activate the G1/S transition.⁵³ Cells that overexpressed E1a also showed decreased volume, suggesting that cyclin D depletion arrests the cell cycle by inhibiting the G1/S transition (Figure 6F).

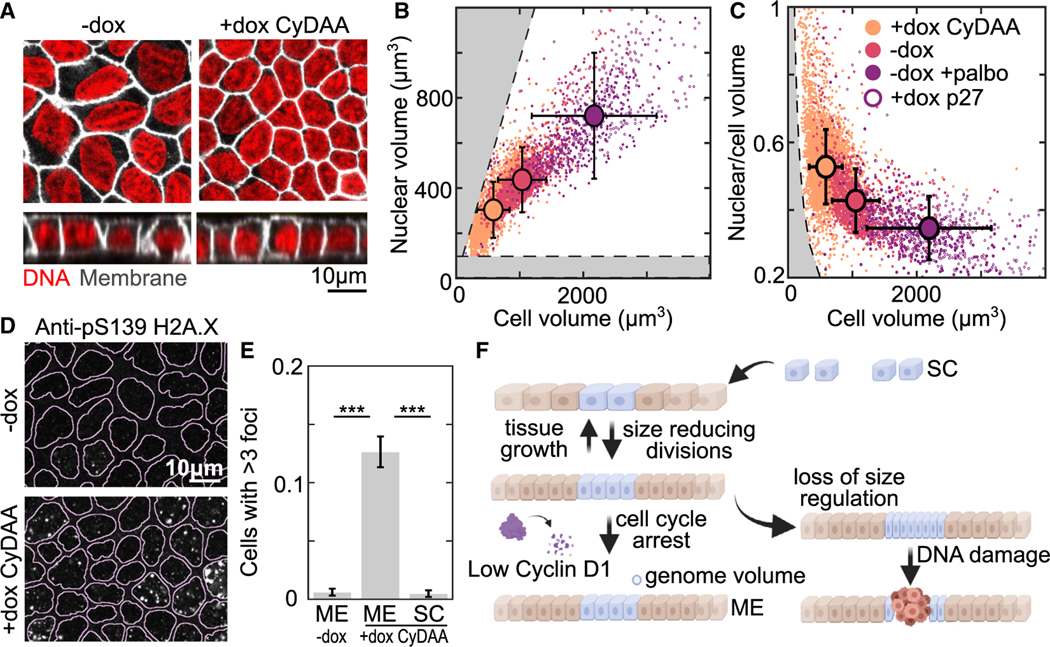
Cell-cycle arrest occurs near cell volume minimum set by the genome volume

We next wanted to understand why the cell cycle normally arrests at a volume of ~1,000 μm³. A possible constraint on cell volume comes from the volume occupied by the genome. As the cell volume decreases, the nucleus gets smaller and chromatin gets more compact.³⁸ A simple estimate suggests low chromatin concentrations of ~5% by volume in an average subconfluent mammalian cell $({Vol}_{nuc} \sim 1 / 3 {Vol}_{cell} \sim 800 {μm}^{3} {vs Vol}_{genome} \sim 40 {μm}^{3})$ .⁵⁴ However, the concentration would increase several fold as cell volume reduces and the total chromatin per cell remains constant. Previous measurements of chromosome volume by TEM and AFM have shown that the volumes of a full set of chromosomes are approximately 50– 100 μm^355,56 and 50% chromatin by volume,⁵⁷ thus setting a lower limit on cell volume. When we stained both the DNA and cell membrane, we observed that the abnormally small Tet-On CyDAA cells appear to have an unusually large nucleus relative to the cell size (Figure 7A). This was surprising given that typically there is a tight scaling relationship between cell volume and nuclear volume.³⁸ Comparing the cell volume against the nuclear volume for epithelium prepared under our previously described conditions, we observe this scaling relationship except in the Tet-On CyDAA cells in the presence of doxycycline (Figure 7B, peach). Instead, we observe that the ratio of nuclear to cell volume is rapidly increasing as cell volume decreases below 1,000 μm³ (Figure 7C) and approaches regions where DNA compaction exceeds chromosomal compaction or where nuclear volume exceeds cell volume (Figures 7B and 7C, gray). We hypothesized that increasing chromatin concentration could disrupt normal chromatin function, leading to DNA damage. In CyDAA overexpressing cells in ME we observed phospho-H2A.X foci indicating locations of DNA damage (Figures 7D and 7E). Importantly, there was no DNA damage in CyDAA overexpressing cells in SC or WT cells in ME. This suggests that normal cells arrest near a cell volume minimum but outside the range where DNA damage occurs frequently. DNA damage is known to arrest the cell cycle through Rb/cyclin D-independent mechanisms,⁵⁸ preventing further volume reduction. Therefore, in epithelia, proliferative homeostasis is maintained by an interplay between cell growth in proportion to tissue constraints and cell-volume-dependent G1/S regulation which arrests the cell cycle near a minimum volume (Figure 7F).

Figure 7. — (A) Nuclear (red, Spy650-DNA) and membrane (white, Stargazin-halotag) staining of Tet-On cyclin D1 T286A T288A MDCK cell monolayers at ME + 3 days without dox (−dox) or with dox added at $t = 0$ (+dox CyDAA).

(B and C) Plots comparing nuclear volume and cell volume measured from 3D imaging in conditions from (A) (−dox, +dox CyDAA) or in cell-cycle-inhibited conditions (−dox +palbo) or Tet-On p27 cells (+dox p27). +palbo is 1 μM palbociclib. (B) shows the correlation between the cell and nuclear volumes, while (C) show the ratio of these volumes. Gray regions indicate when nuclear volume is larger than cell volume (B, top left) or when chromatin density is higher than chromosomes (B, bottom; C, left). Error bars show SD of data $(N_{- dox} = 1, 405 [2], N_{+dox cyDAA} = 4, 207 [2], N_{- dox + Palbo} = 390 [1], N_{+dox p27} = 324 [1])$ .

(D) Monolayers in the same conditions as (A) immunostained for pS139 H2A.X (yH2A.X). Lines overlayed on images show nuclear segmentation from DNA staining.

(E) Quantification of pS139 H2A.X foci from conditions in (D). Bar is the mean fraction of cells with >3 foci between 3 experimental replicates. Error bar is SD of experiment means $(n_{ME−dox} = 5, 813 [N = 3], n_{ME + dox CydAA} = 9, 127 [N = 3], n_{SC + dox CydAA} = 2, 470 [N = 3])$ .

(F) schematic summarizing cell-volume regulation in epithelium. (***p < 0.001 from comparison of experimental means).

DISCUSSION

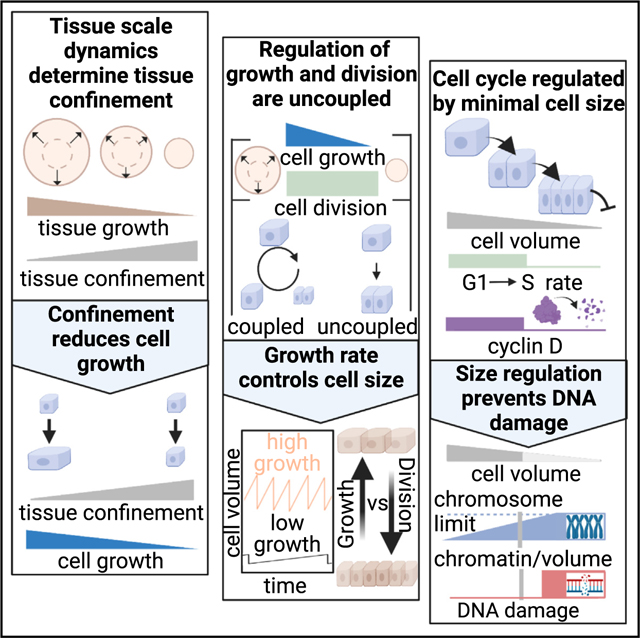
While growth and division are balanced in to maintain a constant cell volume, we observe that in the context of epithelial tissue, growth and division rates can respond to different cues, which leads to transient changes in cell volume during contact inhibition of proliferation. The tissue growth dynamics regulate cell growth, whereas cell division is regulated solely by cell volume. Differences in these two rates drive changes in cell volume depending on the tissue environment. In single cells, the environment places no constraint on cell growth, leading to high growth rates and large cell volume. In contrast, in MEs, tissue growth rates are low and reduce cell volume to a minimum. In this regime, cell-volume regulation is critical for maintaining cell homeostasis and preventing DNA damage. The consistency in cell-volume distributions across diverse epithelial cell types (Figure 1B) suggests that our models should be broadly applicable to understand contact inhibition and cell-volume regulation across diverse biological systems.

Canonically, growth factor signaling is thought to be the main pathway to control and coordinate proliferation.^59,60 We identify an independent role for tissue confinement in controlling cell growth. While we exploited model tissues with a particular type of growth dynamics driven by edge migration, these ideas can be easily extended to arbitrary systems so long as the tissue growth dynamics can be readily characterized (Figures S4F–S4M). One limitation of our analysis was that we considered the tissue averaged behavior. These monolayers show nonuniform expansion and variations in cell height and density (Figure S4E), which we expect leads to spatial variations in confinement. Additionally, tissue growth is driven by diverse processes, including migration, tissue buckling or mechanical stretch,^61,62 all of which would reduce tissue confinement. Importantly, in tissue homeostasis, cells also constantly turnover, which we think can be incorporated into our framework by considering cell exit from the tissue as locally reducing spatial constraints.^13,20,59,63 A more comprehensive study that considers nonuniform confinement driven by different processes is required to understand confinement in vivo.

Previous work has implied that cell growth and YAP/TAZ signaling in epithelium are regulated by mechanical stress.^{5,12,22,64,65} Our framework provides a means to isolate the roles of physical constraints on cell growth regulation. Importantly, confinement is a geometric quantity readily determined from timelapse microscopy. Our data show that confinement is a strong predictor of growth and YAP/TAZ activity, demonstrating the utility of our model to study the mechanisms underlying epithelial growth control. However, future work will be needed to connect our findings to classical contact inhibition pathways. Our work and others implicate the hippo pathway as a key mechanism,^7,12 but future work is needed to determine the relationships between tissue confinement, growth, and mechano-transduction. Importantly, the contributions from mechanical forces, cadherin adhesions, and growth factor accessibility need to be carefully dissected individually while monitoring cell and tissue growth to determine the underlying mechanisms. Additionally, our measurements of growth in Figure 4 were limited to changes in cell volume; however, there are cases where the density of biomass in the cell changes,^66–68 and understanding how protein density, synthesis, and degradation are regulated during contact inhibition could be an interesting direction for future research.

Our observation of a transition between volume-dependent and independent behaviors in epithelia may explain prior observations of volume regulation in mammalian cells.^13,17,69 In our computational model, we find that a volume-dependent G1/S transition gives rise to both sizer-like and timer-like behaviors of cell-volume regulation at low and high growth rates, respectively (Figure 5E). Other cell types also show large changes in cell volume due to growth arrest and volume-dependent proliferation.^18,70–73 Future work may identify if these processes can be understood using the same framework as contact-inhibited epithelia. In single cells, feedback mechanisms lead to compensation in the cell-cycle duration during growth arrest,^14,50 but growth and cell cycle appear more independent in epithelium and the examples above. Future work will be required to understand how these feedback mechanisms are regulated in different contexts. Furthermore, the molecular mechanisms of G1 sizer regulation have remained elusive.^17,69,74 By experimentally manipulating cell volume, we showed that cyclin D1 regulation underlies G1 sizer behavior in epithelium. Cyclin D1 is strongly post transcriptionally regulated by degradation,⁵¹ suggesting that upstream kinase localization or activity may function in the volume-sensing pathway. Our observations may lead to future work to connect cyclin D1 regulation directly to cell-volume sensing. It will be important to understand how cyclin D1 levels are regulated in response to cell volume. Other work suggests potential mechanisms like changes in the proteome,^75,76 nuclear size, or surface area to volume ratio of the cell.^16,69

Finally, below the minimal volume set by cyclin D1 regulation, significant changes in nuclear-to-cytoplasmic ratio and DNA damage occur, suggesting an important role of volume regulation in maintaining epithelial cell homeostasis. Cancers that are driven by mutations in genes implicated in cell-volume regulation, such as small cell cancer, may show volume dependent DNA damage leading to additional mutations. Examining the source of this DNA damage and the changes in nuclear-to-cytoplasmic ratio will be an interesting avenue for future research. It may be possible to connect these results to other studies looking at how nuclear-to-cytoplasmic ratio is determined by proteome composition^77–79 and how DNA damage responds to cell compression⁸⁰ and examine the limits of nuclear volume in more detail. Alongside recent work that shows that very large cells become nonfunctional,^19,75,76 the lower bound set by the genome volume establishes a range of cell volumes for viable diploid mammalian cells from ~ 200 to 10,000 μm³, similar to the range observed across different cell types.⁵⁴ Overall, our framework for understanding of the proliferative behaviors in epithelium provides a basis for studying development, homeostasis, and disease in complex epithelial tissues across diverse biological contexts.

Limitations of the study

While the phenomena presented here generalize to several cell lines tested, future work is required to understand the application of this framework in vivo. In experiments looking at cell growth, we only examined the average behavior to show the overall effects of tissue confinement; however, there may be interesting effects at smaller scales. To determine growth rates, we used CellTrace to measure changes in cell volume, but measurements of protein production and density of protein within the cell can provide further insight into the process of tissue confinement. Due to the scope of this paper, we were only able to perform a limited set of experiments looking at molecular mechanisms. This leaves considerable room for future studies on the molecular mechanisms controlling growth arrest in epithelial due to confinement, transmission of confinement signals across the tissue scale, and how cell volume leads to cyclin D regulation and cell-cycle arrest. Our experiments looking at DNA damage were limited, and future work is required to find the mechanism causing the increase in DNA damage at low cell volumes, to understand how DNA damage triggers cell-cycle arrest in this context, and to determine what happens if DNA damage response is blocked.

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Margaret Gardel (gardel@uchicago.edu).

Materials availability

Plasmids will be deposited to addgene prior to publication. Cell lines are available from the lead contact upon request without restriction.

Data and code availability

RNA sequencing data have been deposited at Gene Expression Omnibus (GEO) and are publicly available as of the date of publication. Accession numbers are listed in the key resources table. Imaging data and histology measurements have been deposited at figshare and are publicly available as of the date of publication. Due to data size contraints imaging datasets are limited to a single experimental replicate. Additional data will be provided by the lead contact upon request. DOIs are listed in the key resources table. This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table. All original code has been deposited at Github and is publicly available as of the date of publication. DOIs are listed in the key resources table. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Cell culture and lines

All cells were maintained at 37C and 5% CO2. Cells were passaged using 0.25% trypsin EDTA every 2–3 days. Cells were checked for mycoplasma by Hoechst staining. MDCK, CACO-2 and MEF cells were cultured in Dulbecco’s modified eagle medium (DMEM) high glucose supplemented with 2mM L-glutamine and 10% FBS. HaCaT cells were maintained in low calcium high glucose DMEM prepared from calcium-free DMEM powder supplemented with 40 μM calcium-chloride, 2 mM L-glutamine and 10% calcium depleted FBS using Chelex-100. RPE-1 cells were maintained in 1:1 high glucose DMEM:F12k supplemented with 2mM glutamine and 10% FBS. Tet inducible gene expression was done with 200ng/ml doxycycline in all indicated experiments (+dox).

Stargazin-halotag Caco-2 and MDCK cells were produced by lentiviral infection of CACO-2 and MDCK cells by a WPT-Stargazin-halotag construct packaged in 293T cells by a second-generation lentiviral system with pHR1–8.2-deltaR and a VSV-G pseudotyping plasmid (gifts from M. Rosner). Viral supernatant was collected at 24, 48 and 72 h after transfection then concentrated ~30x using Amicon Ultra-15 Centrifugal Filter Unit (100kDa) or concentrated ~30x by peg precipitation (Marino et al., 2003). Cells (~50,000 cells a in 6cm diameter dish) were treated overnight with 300ul of concentrated virus in 2ml of media supplemented with 8μg/ml polybrene. Positive cells were isolated using a BD FACSAria^™ III cell sorter. FUCCI MDCK cells were produced by lentiviral infection with virus of pLenti-PGK-Neo-PIP-FUCCI packaged and infected the same way. Cells were then selected using 800 μg/ml G418. pLenti-PGK-Neo-PIP-FUCCI was a gift from Jean Cook. Tet-on mEmerald-P27 1–176 (human CDKN1B 1–176; NCBI Reference Sequence: NP_004055.1), snaptag-P27ck 1–176, Cyclin D1-mEmerald, Cyclin D1 T286A T288A-mEmerald (subcloned from RRID: Addgene_11181), mKate-T2a-12sE1a (subcloned from RRID: Addgene_18742) cells were produced using the Lenti-X Tet-On 3G system. DNA above were subcloned into the Tre3g vector. Lentiviral particles were packaged in 293T cells transfected with pHR1–8.2-deltaR and a VSV-G. Cells were infected with lentivirus with both the EF1a-Tet-on-3g and Tre3g plasmids above using the infection protocol above then selected using 2 μg/ml puromycin and 800 μg/ml G418.

METHOD DETAILS

Epithelial monolayer cultures

For all experiments unless indicated otherwise, monolayers were formed on 2mg/ml collagen I gels (~200um thick) formed on top of a coverglass substrate (see Collagen gel substrate preparation section for more detail). For monolayer samples to reach the OC state after ~12 h and ME at ~36 h cells were seeded onto collagen gels at high density (~80,000 cells/cm2). For SC samples a low density of cells (~8,000 cells/cm2) were plated on the same substrates and cells were measured at time points before reaching OC. Cells were added on top of the gel in a volume of 100–200ul and allowed to adhere for 5–10 min before adding 1.5ml to the culture dish containing the coverslip and gel. Culture media was changed once each day.

Expanding colony assay

Expanding colonies were prepared using published methods modified as follows.⁴⁴ 4.4 grams of 10:1 PDMS (silgard) was cast in a 10cm petri dish and cured at 70C overnight. A piece of PDMS ~20×20 mm was cut out then a set of holes was cut into the PDMS using a leather hole punch of 1mm,1.5mm or 3mm (Nuhank 0795787181775). The PDMS was washed in 70% ethanol for 5 min repeated 3 times then milli-Q water 3 times and allowed to dry. Cover slips were coated with collagen 1 by incubating them on 100ul of 0.2mg/ml collagen in 0.02M acetic acid for 1 h in a petri dish. Coverslips were washed with 1xPBS 3 times then with MQ water 3 times and allowed to dry completely. Dry PMDS and coverslips were stuck together ensuring that no air bubbles remain between the surfaces. Cells were seeded in the well (2000 cells/mm2) and allowed to adhere for 5–10 min before adding 2ml of media to the petri dish. Colonies were left overnight then the PDMS was removed to allow colonies to expand. The initial colony size under these conditions at the time of PDMS removal was measured and used as the initial size for subsequent analysis. Each experiment included a subconfluent and confluent sample as exponential and non-growing controls to ensure that results could be compared across experiments. After the desired time delay samples were either fixed and imaged or fixed, permeabilized, immunostained and imaged according to methods below.

BCA assay

BCA assay was performed using the Pierce^™ BCA Protein Assay Kit according to the manufactures protocol. Samples were prepared by plating cells in two duplicate samples at a density which would reach confluence after 8 h (60,000 cells/cm²), after 24 h (30,000 cells/cm²) and to remain subconfluent (3,000 cells/cm²). Cells were lysed at 24 h (ME,OC,SC) and 48 h (ME+24hr, OC+24hr SC+24hr) on ice with 500μl of 1x RIPA buffer. All samples were collected and stored frozen for up to 2 days, then run in cuvettes with 100ul of lysate and 2ml of BCA reagent. Samples were left for 2 h at room temperature and the absorbance was measured using an Ultrospec 2100 pro UV/Visible spectrophotometer within 10 min.

A control sample where a collagen coated glass without cells was prepared, cultured, and lysed under identical conditions to the samples and the absorbance was subtracted from all samples. This absorbance was not negligible in subconfluent samples (~50ug/ml collagen vs ~100 ug/ml protein) and was required for accurate determination of growth rate. Then the growth rate, $G$ , was calculated from the protein concentrations, $C$ , by the change in protein concentration normalized by the initial protein concentration $G = (C_{f} - C_{i}) / C_{i}$ .

To measure the total cell division, samples prepared under the same conditions were trypsinized at the same time points and counted to determine the number of cells. Then the division rate, $D$ , was calculated from the cell numbers, $N$ , by the change in cell number normalized by the initial cell number $D = (N_{f} - N_{i}) / N_{i}$

CellTrace labeling

Cells were labeled using CellTrace according to the manufacturer’s protocol. Cells were resuspended in PBS (10⁶ cells in 1 ml) and cell trace was added at 1μM for 15 min at 37C. Then cells were pelleted and resuspended in media and either directly used for experiments or cultured under normal conditions for 1 day before use.

To measure growth using CellTrace the prepared cells were seeded according to the expanding monolayers protocol above and a subconfluent and confluent control using seeding densities in the epithelial monolayer culture section above. The cells were grown under normal culture conditions until the indicated time point then fixed and imaged or fixed, permeabilized and immunostained according to the immunostaining protocol below. Images were taken of all samples and controls under identical imaging settings at the same time, then an average intensity of the confluent control was used as an intensity corresponding to no cell growth. The average intensity was measured for all other conditions and the growth was computed using the following formula: $\frac{I (confluent)}{I (sample)} - 1 = \frac{V o l (t = Δ t)}{V o l (t = 0)} - 1 = Δ V o l$ . The subconfluent condition showed intensity consistent with the known doubling time of MDCK cells under the experimental conditions.

Immunostaining

For halotag labeling, 30nM halotag JF 646 or 549 solution was added for 1 h before fixation. Just before fixation cells were washed once in 1xPBS. Cells were fixed in 4% PFA in 1xPBS for 15 min at room temperature. Cells were blocked and permeabilized in 1xTBS, 0.3% triton-X 100, 2%BSA solution for 1 h. Antibody solutions were prepared in 1xTBS 0.3% triton-X 100 2%BSA using 1:400 anti-Cyclin D1, 1:100 anti-YAP, 1:400 anti-Phospho-Histone H2A.X. Samples were incubated in primary antibody overnight at 4C. Samples were washed 3 times in 1xPBS then incubated in 1xTBS 0.3% triton-X 100 2%BSA and secondary antibody for 1 h. In conditions with DNA staining SPY650 DNA was added during the secondary staining step according to the manufacturer’s protocol at 1x concentration. Samples were washed 3 times for 5 min in 1xPBS then mounted on a slide in prolong gold antifade mounting media – non curing (Invitrogen), sealed and imaged.

Fluorescence microscopy

For time lapse imaging cells were imaged on an inverted epi-fluorescence microscope (Nikon TI-E, Nikon, Tokyo, Japan) with a 20x plan fluor multi-immersion objective. images were acquired at 10-min intervals in GFP, 642 and transmitted light channels using standard filter sets (Ex 490/30, Em 525/30, Ex 640/30, DAPI/FITC/TRITC/cy5 cube) (Chroma Technology, Bellows Falls, VT). For halotag labeling, 30nM halotag JF 646 or 549 solution was added for 1 h before imaging. Samples were mounted on the microscope in a humidified stage top incubator maintained at 37C and 5% CO₂. Images were acquired on either a Photometrics Coolsnap HQv2 CCD camera (Photometrics, Tucson, AZ) or Andor Zyla 4.2 CMOS camera (Andor Technology, Belfast, UK).

Cell volume measurement samples in resuspension were imaged on an inverted spinning disk confocal microscope (Nikon TI-E) with laser lines at 491, 561 and 642 and suitable emission filters (Chroma Technology). Images were acquired using a 40x plan fluor oil immersion objective (NA 1.3) and Andor Zyla 4.2 CMOS camera (Andor Technology, Belfast, UK). Images were acquired at room temperature within 1 h of cell resuspension.

All other imaging was done using a point scanning confocal microscope (Ziess Airyscan LS980) with laser lines at 491,561,642 and an adjustable emission filter suitable for fluorophores that were imaged. Cell trace images were acquired using a 5x air objective (NA 0.16), YAP images were acquired using a 20x air objective (NA 0.8), Immunostaining images were acquired using a 40x oil immersion objective (NA 1.3).

RNA sequencing

Cells were treated with 1mm Palbociclib for 16 h then replated on collagen gels to make 3 monolayers from each condition. All monolayers were cultured together in a 10cm petri dish with 10ml of media containing 100ng/ml doxycycline. Media was replaced each day for 5 days. Then 2 monolayers from each condition were lysed, pooled and total RNA was collected using a NucleoSpin RNA kit. 1 monolayer from each condition was labeled with JF 646 halotag and imaged, then cells were resuspended for volume measurements as described above. Volume distributions corresponding to each RNA seq experiment are available in Figure S7E. RNA samples were submitted to the University of Chicago Genomics Facility. RNA quality and quantity was assessed using the Agilent bio-analyzer (RNA Integrity Number from 9.4 to 10). Strand-specific RNA-SEQ libraries were prepared using an TruSEQ mRNA RNA-SEQ library protocol (Illumina provided). Library quality and quantity was assessed using the Agilent bio-analyzer and libraries were sequenced using an Illumina NovaSEQ6000 (illumine provided reagents and protocols) with ~60M PE reads/sample. Alignments were made to the canine genome (Canis_lupus_familiaris.CanFam3.1) by psudeoalignment using Kallisto 0.46.1 (Bray et al., 2016).⁸² between 62.2 and 69.2% of reads were mapped with two technical replicates per experiment a total of $n_{p 27_1} = 28049196$ $n_{p 27_2} = 28117815$ $n_{p 27_3} = 28012202$ $n_{p 27 ck_1} = 28212157$ $n_{p 27 ck_2} = 27961694$ $n_{p 27 ck_3} = 27964407$ reads. Technical replicates were highly similar so they were averaged before further analysis. Data were then processed using iDEP 0.91(Ge et al., 2018)⁸³ to measure differential gene expression and the Wnt homepage was use to determine a list of Wnt target genes (“Wnt Target genes | The Wnt Homepage,” n.d.).⁸⁴

Silane modification of glass coverslips

Glass coverslips were modified using the following protocol based on previously described methods (Zhu et al., 2012).⁸⁵ Coverslips were first cleaned by sonication in 70% and 100% ethanol solutions then dried with compressed air. We placed coverslips in a staining rack and submerged the rack in a solution of 2% (3-Aminopropyl)trimethoxysilane (APTMS) 93% propanol and 5% DI water for 10 min at room temperature while stirring. Staining racks were removed and washed in DI water 5 times then placed in a 37C incubator for 6–12 h to allow the water to dry and amino-silane layer to cure. The staining racks were then submerged in 1% glutaraldehyde in DI water for 30 min while stirring. The coverglass was washed 3 times for 10 min in distilled water, air dried and stored at room temperature. Activated coverslips were stored under vacuum and used within 6 months of preparation.

Collagen gel preparation

10x PBS, milli-Q water, a 5mg/ml collagen stock and 1M NaOH were mixed to generate a polymerization mix with 1xPBS and 2 mg/ml collagen at pH ~7. 70uL of the polymerization mix was added on to a 22×22mm coverslip modified with aminosilane according to the protocol above and quickly spread to coat the surface using a pipette tip. Samples were transferred to a humidified incubator at 37C to polymerize for 20 min. After polymerization gels were washed 3 times in 1x PBS and it was verified that gels were still intact and adhered to the glass by a tissue culture microscope.

Cell volumes measurements

Resuspended - Cells were plated as monolayers for indicated times. Just before making volume measurements the cells were resuspended by adding 0.25% trypsin EDTA solution to the cells. Resuspending cells from ME conditions required partial physical disruption of the monolayer using a pipette tip. Cells were resuspended in 35μl of media containing 30nM JF646 and incubated for 5–15 min before adding to a thin channel prepared by sticking a coverslip to a glass slide using double stick tape. Cells were imaged immediately with spinning disk confocal microscopy. We verified that samples showed no changes in cell volume measured over time up to 1 h and performed all measurements within this time window. Cells were imaged at the middle plane so that the radius of the cell could be measured. The cross-sectional area was used to estimate the radius which was used to calculate the volume of the cell. It was verified that this provided a comparable measurement to 3D segmentation of cells in the monolayer (Figure S1).

3D Images- Monolayers were stained using JF 549 halotag ligand and imaged using an airyscan LSM 980. Z-stacks spanning the height of the cell were imaged. The height of the monolayer was determined at each point by identifying maxima of the intensity corresponding to labeling at the top and bottom membrane of the cell. The membrane label averaged across the middle 5 planes of the cell was used to determine the area of the cell in the XY plane and this value is multiplied with the average cell height contained within this region to give the cell volume. A similar process was repeated with nuclei images to measure the nuclear volume.

Cross-sectional Images- 3D images were acquired above and displayed as projections in the YZ plane. Images were opened in imageJ and the width and height of individual cells was measured from these cross sectional images. The same method was applied to histology sections where cells oriented perpendicular to the tissue section were first identified then the width and height of these cells was measured. The volume was estimated by the width squared times the height of each individual cell.

These measurements are compared with 3D images for MDCK cells and show similar mean values (Figure S1). We also note that changes in mitotic fraction can have some impact on the average cell volume of any population measure. This is important when comparing single cells to tissues in vivo or ME. Cultured cells will typically contain a much larger fraction of cycling cells (~50% vs ~1%), cycling cells can be up to 2 times larger than G1 arrested cells, but this would not be sufficient to explain the 4 fold difference in cell volume observed in the data.

Image segmentation

Images of cell membranes were segmented using custom MATLAB code. The main algorithm performs initial segmentation using the Phase Stretch Transform algorithm developed by the Asghari and Jalali (H and JalaliBahram, 2015).⁸⁶ Phase stretch images were thresholded and skeletonized to obtain cell outlines. Broken edges in the skeleton were repaired using a modified implementation of edgelink developed by Peter Kovesi (“Peter’s Functions for Computer Vision,” n.d.).⁸⁷ Segmentation code is available on GitHub.

Cell tracking

Cell tracking was performed using established particle tracking methods applied as follows (Crocker and Grier, 1996).⁸⁸ Cell centers were determined by taking the centroid of each segmented cell area generated as described above in Segmentation. The particle trajectories were compiled from these position measurements using SimpleTracker, a MATLAB function developed by Jean-Yves Tinevez (“simpletracker,” n.d.).⁸⁹

FUCCI analysis

Cells were imaged in GFP and RFP channels similar to above methods using timelapse imaging. Images of FUCCI markers and cell boundaries were segmented using Phase Stretch Transform in Matlab as described above. Each cell was identified using the cell boundaries and was determined to be GFP or RFP positive by measuring the intensity contained within the segmented images of each nuclear marker. The percent of cells in G1 was determined by taking the ratio of cells identified as only GFP positive to the cells identified as GFP positive, RFP positive and positive for both markers. To determine duration of S/G2/M phase the cell cycle state was measured along the cell trajectory and points where the cell switched from G1 to S and then back to G1 were identified. Then the time between these events was measured to give the duration. To determine the full cell cycle duration the fraction of cells in S and G2/M phase was measured and along with the S/G2/M phase duration was used to estimate the cell cycle duration by CC duration = S phase duration/S phase fraction (i.e. if 10% of cells are in S/G2/M which lasts 10 h, cells spend 9 times longer on average in G1 and the duration of the cell cycle is likely ~100 h)

Division rate measurement

We identified cell divisions by finding pairs of cells which appear adjacent to each other in a frame after both cells were not present in the previous frame. We further filter out cells which are not of similar size to one another. We confirmed by inspection that this gives us a subset set of cells which have divided in the previous frame with few false positives. We then find the mother cell by looking several frames back for a cell near the centroid of the pair of daughter cells. We compare the number of cells of a given size which are detected to divide compared to the total number of cells of that size to get a probability of division. This process is repeated for the entire time series with a total number of division events typically >500. However, because not all division events are detected, this process give the relative division rate as a function of size. The division rate is determined by the change in cell density over time at early time points and the plateau value of the relative division rate is set to match this value.

Quantification of H2ax staining

Foci were segmented using a phase stretch transform-based method and an intensity threshold based on the intensity of the dimmest foci measured manually. The cell nuclei were segmented using methods above and the number of foci in each nucleus was quantified.

Simulation growth models

Growth curves were generated from growth models of exponentially proliferating cells with doubling time $τ (A (t) = 2^{t / τ}, dA (t) / dt = \log (2) / τ * 2^{t / τ} = A (t) * \log (2) / τ)$ and of a circle with an expanding radius $(r (t) = v^{*} t, A (t) = π^{*} v^{2 *} t^{2}, dA (t) / dt = 2^{*} π^{*} v 2^{*} t = 2^{*} v^{*} sqrt (π^{*} A))$ . Confinement curves are calculated from the ratio of these rates as defined in the main text.

G1-sizer model

Our phenomenological model of cell size control is a “G1 sizer”, which posits that exit from G1 is controlled by a size-dependent function. Based on the sharp drop-off in the G1 exit rate seen in the log-plot of experimental data in Figure 5A, we assume that the rate is a constant $k ≫ 1$ above a critical size $a$ and 0 below that size. Following G1-exit, division proceeds in time $τ$ .

As discussed in the main text, this model has two regimes: one of slow growth ( $G_{τ} ≪ a$ ), and one of fast growth ( $G_{τ} ≫ a$ ). Switching to non-dimensional units where $a = 1$ and $τ = 1$ , we can derive results for time-averaged single-cell quantities, including average area, average time between divisions, and confinement. This can be done for both the fast- and slow-growth limits. In the following expressions, < > indicates an average over time for a single cell.

In the fast-growth limit with growth rate $G$ , cells never interact with the size-threshold a, and hence have a constant division time set by the mean length of G1 plus the length of S/G2/M. This means a confinement of 0, and an average size $s$ proportional to $G$ . To summarize:

< s > = 1.5 (1 + 1 / k) G; < t_{d i v} > = (1 + 1 / k); C = 0.

In the slow-growth limit with growth rate $G$ , cells are almost exclusively below the size-threshold, and hence have division time set by the mean length of G1, plus the length of S/G2/M, plus the time it takes to grow up to the size threshold. Solving for the division time yields the following expressions:

< s > = .75 (1 + G (1 + 1 / k)); < t_{d i v} > = \frac{1}{2} (1 + 1 / k + 1 / G); C = 1 - \frac{1 + 1 / k}{\frac{1}{2} (1 + 1 / k + 1 / G) .}

These expressions are verified against numerical results ( Figures S6A–S6C).

Numerical simulation of G1-Sizer model

In order to further understand the implications of the phenomenological G1-sizer model in a tissue context, we implemented a stochastic agent-based simulation of growing cell monolayers. In this simulation, each cell carries an index i, as well as two quantities a_i and p_i, representing the size and cell cycle phase respectively. Time and size are in non-dimensional units during the simulation and are converted to dimensional units for analysis after the simulation. We do this by associating 1 unit of simulation time to be the length of a typical S phase (~10 h), and 1 unit of simulation size to be the volume at which it is seen experimentally that cells transition from a size-dependent to a size-independent division rate (~1200 um³). We run our simulations with constant timesteps dt of.005. In the specific use case of Figure 5E, we verified that the results obtained with a timestep of.0005 were not quantitatively different from those generated at $dt = .005$ .

At every step in the simulation, growth of cells is advanced by changing each $a_{i}$ by an amount $G^{*} dt$ , where $G$ is the growth rate of the cell. $G$ is in principle a function of the parameters of the cell itself, such as a_i and p_i, as well as global parameters such as the total number of cells N and the total area of cells A. We observed similar results in a model with exponential single-cell growth (Figures S6G and S6H).

Division of cells is regulated by a size-dependent probability of entrance into S-phase. For most simulations, we use a step function for the S-entrance probability, due to its simplicity and qualitative similarity to the experimentally measured S-entrance probability. If a cell exceeds an area of 1, it enters S at a rate of 3, at which point its phase variable $p_{i}$ is set to a value of 1/dt. At every step in the simulation, the phase variable $p_{i}$ decreases by 1, and once $p_{i}$ reaches 0, the cell’s S/G2/M phase is completed. In some simulations (Figures S6E and S6F) we use a rate function based on a logistic fit to the experimental data. In either case, following stochastic initiation, each cell experiences S/G2/M phase as being a deterministic time of 1. We choose a G1 exit rate of 3 so that the average total time of the cell-cycle in the size-independent regime is matched between simulation and experiment. At the point that a cell exits M, the cell’s size a_i is reduced by a factor of 2, and an additional new cell is created with size a_i/2.

These two elements—size-dependent S entrance, and growth of cells—constitute the core of how we advance single-cell trajectories through time. We examine the implications of this framework in two categories of simulations—ensemble simulations, and single-cell simulations. In single-cell simulations, we track the trajectory of only one cell, following only one daughter cell after division. In ensemble simulations, we track a whole population of cells, and the growth rate can therefore depend on quantities like N, the total number of cells in the population.

In Figure 5D, we show example single-cell trajectories with two different constant growth rates $G$ . To exhibit timer-like behavior, we simulated cells with a growth rate $g = 1.6$ . To demonstrate sizer-like behavior, we simulated cells with a growth rate $G = 0.1$ . In this particular set of simulations, the S entrance rate was set to 10, to more clearly demonstrate the differences between the two growth regimes. Cells are initialized with a size uniformly drawn from 1 to 2, and a phase $p_{i}$ that is either 50% uniformly distributed between 0 and 1/dt, or 50% $p_{i} = - 1$ . Trajectories are simulated for 50 units of simulation time, though only a small fraction is shown of those trajectories.

In Figure 5E, we use single-cell simulations to look at the relation between cell size immediately post-division versus immediately pre-division in the subsequent round as a function of growth rate. We did this for 4 growth rates $G = 1.0$ , 0.7, 0.2, and 0.05. Each growth rate was simulated with 400 simulation replicates, each run for 40 units of simulation time. We initialize each simulation with $p_{i} = - 1$ , and a random size uniformly distributed between 1 and 2, and allow cells to grow with $g = 1$ for 10 units of simulation time before switching to the simulation specific growth rate. After another 10 units of simulation time, we begin recording the size of a cell immediately post-division, and immediately pre-division. Confinement values are estimated as $1 - \frac{# d i v i s i o n s o b s e r v e d}{# d i v i s i o n s e x p e c t e d}$ .

In Figure 5F, we show results from an ensemble simulation of cells. Ensembles are initialized from 4 cells with sizes uniformly drawn from 1 to 2, and then normalized such that they have total area 8. Cell phases are either 20% uniformly distributed between 0 and 1/dt, or 80% $p_{i} = - 1$ . We first allow the cells to expand in an unconstrained way, i.e. we grow each cell in our simulation with a growth rate $G$ , which is drawn for each cell and each time point from a uniform distribution with support between.9 and 1.1. When the ensemble of cells collectively exceeds a critical total size, we quench all their growth rates to 0, and therefore only division occurs from beyond that time point, which we set to be $t = 0$ . We perform these simulations for three different critical total sizes 500, 1200, and 4700, with 20, 10, and 5 simulation replicates respectively. After the critical size is reached, we can track the ensemble distribution of areas as a function of time, which we do for 4 units of simulation time, corresponding to 48 h of real time. We did not notice any significant differences in the distributions as a function of the total size at which we quench the growth rate.

QUANTIFICATION AND STATISTICAL ANALYSIS

For individual experiments the number of samples and replicates are indicated in the figure caption. Significance was determined by a paired-sample t-test of experimental means with p<0.05 indicating a significant result. p-values for individual experiments are indicated in the figure captions.

Supplementary Material

Supplemental Information

NIHMS1910865-supplement-Supplemental_Information.pdf^{(6MB, pdf)}

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies

Anti-cyclin D1	Cell Signaling Technologies	Cat# 55506; RRID: AB_2827374
Anti-Phospho-Histone H2A.X (Ser139)	Cell Signaling Technologies	Cat# 9718; RRID:AB_2118009
Anti-Yap1	Santa Cruz Biotechnology	Cat# 101199; RRID: AB_1131430

Bacterial and virus strains

Stellar Competent E. coli	Clontech	Cat# 636766

Chemicals, peptides, and recombinant proteins

PND 1186	Tocris	Cat# 6891
(3-Aminopropyl)trimethoxysilane	Sigma-Aldrich	Cat# 281778
CellTrace Far Red	Invitrogen	Cat# C34572
Cell Mask Deep Red	Invitrogen	Cat# C10046
Cell Mask Orange	Invitrogen	Cat# C10045
Coverslips, 22 mm x 22 mm	Fisher	Cat# 50–189-9787
DMEM-L-glut, high-glucose	Fisher/Mediatech	Cat# MT10–013-CVEA
DPBS without Ca Mg	Fisher/Mediatech	Cat# MT21–031-CVEA
Trypsin 0.25%	Fisher/Mediatech	Cat# MT25–053CIEA
RIPA buffer (150 mM NaCl, 5mM EDTA, 50mM Tris, 1% NP40, 0.5% sodium deoxycholate, 0.1% sodium dodecyl sulfate)	This paper	N/A
Janelia Fluor 646 halotag ligand	Promega	Cat# GA1120
Janelia Fluor 549 halotag ligand	Promega	Cat# GA1110
Fugene HD	Promega	Cat# E2311
SNAP-Cell^® 505-Star	New England Biolabs	Cat# S9103S
SNAP-Cell^® TMR-Star	New England Biolabs	Cat# S9105S
Polybrene	EMD Millipore	Cat# TR-1003-G
PD 0332991 (Palbociclib)	Cayman Chemical	Cat# 16273
Collagen I, rat tail	Corning	Cat# 354236
Glutaraldehyde 70%	Fisher	Cat# 16360
Paraformaldehyde 16%	Fisher	Cat# 15710
calcium-free DMEM powder	US Biological	Cat# 09800
Puromycin Dihydrochloride	Fisher	Cat# A1113803
SYLGARD^™ 184 Silicone Elastomer Kit	Dow	Cat# 1673921
Corning^™ F12K Medium	Corning	Cat# MT10025CV
Chelex 100	Simga	Cat# C7901
Doxycycline hyclate (dox)	Fisher	Cat# AC446060050

Critical commercial assays

NucleoSpin RNA Purification Kit	Macherey Nagel	Cat# 740955
Pierce^™ BCA Protein Assay Kit	Thermo Scientific	Cat# 23225

Deposited data

Imaging data	This paper	Figshare: https://doi.org/10.6084/m9.figshare.22231219
RNA sequencing data	This paper	GEO: GSE227906
Histology analysis	This paper	Figshare: https://doi.org/10.6084/m9.figshare.22231219
Simulation Data	This paper	Zenodo: https://doi.org/10.5281/zenodo.7632621
Dog reference genome NCBI build 3.1, CanFam3.1	NCBI	https://www.ncbi.nlm.nih.gov/assembIy/GCF_000002285.3/
human protein atlas CDH1 histology	Human Protein Atlas	https://www.proteinatlas.org/ENSG00000039068-CDH1
Allen cell 3D cell viewer	Allen Cell	https://www.allencell.org/3d-cell-viewer.html

Experimental models: Cell lines

MDCK	Laboratory of W. James Nelson (Stanford)	RRID: CVCL_0422
HaCaT	Laboratory of Yu-Ying He (University of Chicago)	RRID: CVCL_0038
CACO-2	ATTC	HTB-37; RRID: CVCL_0025
Mouse Embryonic Fibroblasts (MEF)	Laboratory of Mary Beckerle (University of Utah)	N/A
HEK 293T	ATTC	CRL-3216; RRID: CVCL_0063
hTERT-RPE-1	Laboratory of Wallace Marshall (UCSF)	RRID: CVCL_4388

Oligonucleotides

Primers for cloning and sequencing, see Table S2	This Paper	N/A

Recombinant DNA

pHR1–8.2-delta-R	Laboratory of Marsha Rosner (University of Chicago)	N/A
pCMV-VSV-G	Laboratory of Marsha Rosner (University of Chicago)	N/A
pLenti-PGK-Neo-PIP-FUCCI	Addgene	RRID: Addgene_118616
pWPT-Stargazin-Halotag	This paper	N/A
pLVX-Tre3g-mEmerald-p27–1-176	This paper	N/A
pLVX-Tre3g-snap-p27ck-1–176	This paper	N/A
pLVX-Tre3g-mEmerald-ccnd1	This paper	N/A
pLVX-Tre3g mEmerald-ccnd1 T286A T288A	This paper	N/A
pcDNA cyclin D1 HA	Addgene	RRID: Addgene_11181
pLVX-Tre3g mKate2-T2a-12sE1a	This paper	N/A
pBabe 12S E1A	Addgene	RRID: Addgene_18742
pLVX-Tre3g	Takara Lenti-X^™ Tet-On^® 3G Inducible Expression System	Cat# 631363
pLVX-EF1a-Tet3G	Takara Lenti-X^™ Tet-On^® 3G Inducible Expression System	Cat# 631363

Software and algorithms

ImageJ	National Institutes of Health	https://imagej.nih.gov/ij/Snapgene.com
Snapgene Software	GSL Biotech LLC
Metamorph	Molecular Devices	Moleculardevices.com
Image analysis code	This paper	https://github.com/Gardel-lab/Devany2023DevCell
Simulation code	This paper	https://github.com/falkma/tissueconfinement-simulations
Matlab	Mathworks	https://www.mathworks.com/

Open in a new tab

Highlights.

In epithelia, regulation of cell growth and cycle are not directly coupled
Cell growth rate is regulated by tissue-scale growth dynamics
Cell cycle in epithelia is described by G1 sizer model with a tunable growth rate
Volume of cells in epithelia is near a minimum set by genome volume

ACKNOWLEDGMENTS

The authors would like to thank Jan M. Skotheim and Boris Shraiman for helpful discussions. This work was funded by NIH RO1 GM104032 to M.L.G. L.J.H. was funded by NIH R01 GM132447 and R37 CA240765, the American Cancer Society Cornelia T Bailey Research Award, and the NIH Director’s Transformative research award TR01 NS127186. J.D. was supported by the Grainger and Harper Fellowships provided by University of Chicago. M.J.F. was supported by DMR-2239801. A.M. was supported by the Simons Foundation. This work was partially supported by the UChicago Materials Research Science and Engineering Center (NSF DMR-2011864). The authors would like to acknowledge The University of Chicago Functional Genomics (RRID: SCR_019196) for processing RNA sequencing samples. Graphical abstract and Figures 2C, 3A, 5C, 7F, and S1A were created with BioRender.com.

INCLUSION AND DIVERSITY

We support inclusive, diverse, and equitable conduct of research. One or more of the authors of this paper self-identifies as a member of the LGBTQIA + community.

Footnotes

SUPPLEMENTAL INFORMATION

Supplemental information can be found online at https://doi.org/10.1016/j.devcel.2023.05.018.

DECLARATION OF INTERESTS

The authors declare no competing interests.

REFERENCES

1.Murray AW, and Hunt T. (1993). The Cell Cycle: An Introduction (Oxford University Press; ). [Google Scholar]
2.Nurse P. (2000). A long twentieth century of the cell cycle and beyond. Cell 100, 71–78. 10.1016/S0092-8674(00)81684-0. [DOI] [PubMed] [Google Scholar]
3.Broach JR (2012). Nutritional control of growth and development in yeast. Genetics 192, 73–105. 10.1534/genetics.111.135731. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Scott M, and Hwa T. (2011). Bacterial growth laws and their applications. Curr. Opin. Biotechnol 22, 559–565. 10.1016/j.copbio.2011.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Irvine KD, and Shraiman BI (2017). Mechanical control of growth: ideas, facts and challenges. Development 144, 4238–4248. 10.1242/dev.151902. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.McClatchey AI, and Yap AS (2012). Contact inhibition (of proliferation) redux. Curr. Opin. Cell Biol 24, 685–694. 10.1016/j.ceb.2012.06.009. [DOI] [PubMed] [Google Scholar]
7.Fomicheva M, and Macara IG (2020). Genome-wide CRISPR screen identifies noncanonical NF-kB signaling as a regulator of density-dependent proliferation. eLife 9. e63603. 10.7554/eLife.63603. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Kim N-G, Koh E, Chen X, and Gumbiner BM (2011). E-cadherin mediates contact inhibition of proliferation through Hippo signaling-pathway components. Proc. Natl. Acad. Sci. USA 108, 11930–11935. 10.1073/pnas.1103345108. [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Leontieva OV, Demidenko ZN, and Blagosklonny MV (2014). Contact inhibition and high cell density deactivate the mammalian target of rapamycin pathway, thus suppressing the senescence program. Proc. Natl. Acad. Sci. USA 111, 8832–8837. 10.1073/pnas.1405723111. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Mendonsa AM, Na T-Y, and Gumbiner BM (2018). E-cadherin in contact inhibition and cancer. Oncogene 37, 4769–4780. 10.1038/s41388-018-0304-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Ibar C, Kirichenko E, Keepers B, Enners E, Fleisch K, and Irvine KD (2018). Tension-dependent regulation of mammalian Hippo signaling through LIMD1. J. Cell Sci 131. jcs214700. 10.1242/jcs.214700. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Pan Y, Heemskerk I, Ibar C, Shraiman BI, and Irvine KD (2016). Differential growth triggers mechanical feedback that elevates Hippo signaling. Proc. Natl. Acad. Sci. USA 113. E6974–E6983. 10.1073/pnas.1615012113. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Cadart C, Monnier S, Grilli J, Sá ez PJ, Srivastava N, Attia R, Terriac E, Baum B, Cosentino-Lagomarsino M, and Piel M. (2018). Size control in mammalian cells involves modulation of both growth rate and cell cycle duration. Nat. Commun 9, 3275. 10.1038/s41467-018-05393-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Tan C, Ginzberg MB, Webster R, Iyengar S, Liu S, Papadopoli D, Concannon J, Wang Y, Auld DS, Jenkins JL, et al. (2021). Cell size homeostasis is maintained by CDK4-dependent activation of p38 MAPK. Dev. Cell 56. 1756.e7–1769.e7. 10.1016/j.devcel.2021.04.030. [DOI] [PubMed] [Google Scholar]
15.Zatulovskiy E, Zhang S, Berenson DF, Topacio BR, and Skotheim JM (2020). Cell growth dilutes the cell cycle inhibitor Rb to trigger cell division. Science 369, 466–471. 10.1126/science.aaz6213. [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Zatulovskiy E, and Skotheim JM (2020). On the molecular mechanisms regulating animal cell size homeostasis. Trends Genet. 36, 360–372. 10.1016/j.tig.2020.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Xie S, and Skotheim JM (2020). A G1 sizer coordinates growth and division in the mouse epidermis. Curr. Biol 30, 916–924.e2. 10.1016/j.cub.2019.12.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Neufeld TP, de la Cruz AF, Johnston LA, and Edgar BA (1998). Coordination of growth and cell division in the Drosophila wing. Cell 93, 1183–1193. 10.1016/S0092-8674(00)81462-2. [DOI] [PubMed] [Google Scholar]
19.Neurohr GE, Terry RL, Lengefeld J, Bonney M, Brittingham GP, Moretto F, Miettinen TP, Vaites LP, Soares LM, Paulo JA, et al. (2019). Excessive cell growth causes cytoplasm dilution and contributes to senescence. Cell 176, 1083–1097.e18. 10.1016/j.cell.2019.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Sender R, and Milo R. (2021). The distribution of cellular turnover in the human body. Nat. Med 27, 45–48. 10.1038/s41591-020-01182-9. [DOI] [PubMed] [Google Scholar]
21.Puliafito A, Primo L, and Celani A. (2017). Cell-size distribution in epithelial tissue formation and homeostasis. J. R. Soc. Interface 14. 20170032. 10.1098/rsif.2017.0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Puliafito A, Hufnagel L, Neveu P, Streichan S, Sigal A, Fygenson DK, and Shraiman BI (2012). Collective and single cell behavior in epithelial contact inhibition. Proc. Natl. Acad. Sci. USA 109, 739–744. 10.1073/pnas.1007809109. [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Uhlén M, Fagerberg L, Hallström BM, Lindskog C, Oksvold P, Mardinoglu A, Sivertsson Å, Kampf C, Sjöstedt E, Asplund A, et al. (2015). Proteomics. Tissue-based map of the human proteome. Science 347, 1260419. 10.1126/science.1260419. [DOI] [PubMed] [Google Scholar]
24.Dataset accessed through 3D Cell Viewer: Allen Institute for Cell Science (2018). hiPSC Single-cell Image Dataset. Available from https://www.allencell.org/3d-cell-viewer.html.
25.Chen J, Ding L, Viana MP, Lee H, Sluezwski MF, Morris B, Hendershott MC, Yang R, Mueller IA, and Rafelski SM (2020). The Allen Cell and Structure Segmenter: a new open source toolkit for segmenting 3D intracellular structures in fluorescence microscopy images. Preprint at bioRxiv. 10.1101/491035. [DOI]
26.Elamin E, Jonkers D, Juuti-Uusitalo K, van IJzendoorn S, Troost F, Duimel H, Broers J, Verheyen F, Dekker J, and Masclee A. (2012). Effects of ethanol and acetaldehyde on tight junction integrity: in vitro study in a three dimensional intestinal epithelial cell culture model. PLoS One 7. e35008. 10.1371/journal.pone.0035008. [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Engelberg JA, Datta A, Mostov KE, and Hunt CA (2011). MDCK cystogenesis driven by cell stabilization within computational analogues. PLoS Comput. Biol 7. e1002030. 10.1371/journal.pcbi.1002030. [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Goldspink DA, Rookyard C, Tyrrell BJ, Gadsby J, Perkins J, Lund EK, Galjart N, Thomas P, Wileman T, and Mogensen MM (2017). Ninein is essential for apico-basal microtubule formation and CLIP-170 facilitates its redeployment to non-centrosomal microtubule organizing centres. Open Biol. 7, 160274. 10.1098/rsob.160274. [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Guo M, Pegoraro AF, Mao A, Zhou EH, Arany PR, Han Y, Burnette DT, Jensen MH, Kasza KE, Moore JR, et al. (2017). Cell volume change through water efflux impacts cell stiffness and stem cell fate. Proc. Natl. Acad. Sci. USA 114. E8618–E8627. 10.1073/pnas.1705179114. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Karve SS, Pradhan S, Ward DV, and Weiss AA (2017). Intestinal organoids model human responses to infection by commensal and Shiga toxin producing Escherichia coli. PLoS One 12. e0178966. 10.1371/journal.pone.0178966. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Leung E, Kim JE, Askarian-Amiri M, Finlay GJ, and Baguley BC (2014). Evidence for the existence of triple-negative variants in the MCF-7 breast cancer cell population. Biomed Res. Int 2014, 836769. 10.1155/2014/836769. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.de Medeiros G, Ortiz R, Strnad P, Boni A, Maurer F, and Liberali P. (2021). Multiscale light-sheet organoid imaging framework. Nat. Commun 13, 4864. 10.1101/2021.05.12.443427. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Morizane R, Lam AQ, Freedman BS, Kishi S, Valerius MT, and Bonventre JV (2015). Nephron organoids derived from human pluripotent stem cells model kidney development and injury. Nat. Biotechnol 33, 1193–1200. 10.1038/nbt.3392. [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Padovan-Merhar O, Nair GP, Biaesch AG, Mayer A, Scarfone S, Foley SW, Wu AR, Churchman LS, Singh A, and Raj A. (2015). Single mammalian cells compensate for differences in cellular volume and DNA copy number through independent global transcriptional mechanisms. Mol. Cell 58, 339–352. 10.1016/j.molcel.2015.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Park K, Millet LJ, Kim N, Li H, Jin X, Popescu G, Aluru NR, Hsia KJ, and Bashir R. (2010). Measurement of adherent cell mass and growth. Proc. Natl. Acad. Sci. USA 107, 20691–20696. 10.1073/pnas.1011365107. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Perez-Gonzalez NA, Rochman ND, Yao K, Tao J, Le M-TT, Flanary S, Sablich L, Toler B, Crentsil E, Takaesu F, et al. (2019). YAP and TAZ regulate cell volume. J. Cell Biol 218, 3472–3488. 10.1083/jcb.201902067. [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Schutgens F, Rookmaaker MB, Margaritis T, Rios A, Ammerlaan C, Jansen J, Gijzen L, Vormann M, Vonk A, Viveen M, et al. (2019). Tubuloids derived from human adult kidney and urine for personalized disease modeling. Nat. Biotechnol 37, 303–313. 10.1038/s41587-019-0048-8. [DOI] [PubMed] [Google Scholar]
38.Viana MP, Chen J, Knijnenburg TA, Vasan R, Yan C, Arakaki JE, Bailey M, Berry B, Borensztejn A, Brown JM, et al. (2021). Robust integrated intracellular organization of the human iPS cell: where, how much, and how variable. Preprint at bioRxiv. 10.1101/2020.12.08.415562. [DOI]
39.Yao K, Rochman ND, and Sun SX (2020). CTRL - a label-free artificial intelligence method for dynamic measurement of single-cell volume. J. Cell Sci 133. jcs245050. 10.1242/jcs.245050. [DOI] [PMC free article] [PubMed] [Google Scholar]
40.Zhao L, Kroenke CD, Song J, Piwnica-Worms D, Ackerman JJH, and Neil JJ (2008). Intracellular water-specific MR of microbead-adherent cells: the HeLa cell intracellular water exchange lifetime. NMR Biomed. 21, 159–164. 10.1002/nbm.1173. [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Devany J, Sussman DM, Yamamoto T, Manning ML, and Gardel ML (2021). Cell cycle-dependent active stress drives epithelia remodeling. Proc. Natl. Acad. Sci. USA 118. e1917853118. 10.1073/pnas.1917853118. [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Sherr CJ, and Roberts JM (1999). CDK inhibitors: positive and negative regulators of G1-phase progression. Genes Dev. 13, 1501–1512. 10.1101/gad.13.12.1501. [DOI] [PubMed] [Google Scholar]
43.Vlach J, Hennecke S, and Amati B. (1997). Phosphorylation-dependent degradation of the cyclin-dependent kinase inhibitor p27. EMBO J. 16, 5334–5344. 10.1093/emboj/16.17.5334. [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Heinrich MA, Alert R, LaChance JM, Zajdel TJ, Košmrlj A, and Cohen DJ (2020). Size-dependent patterns of cell proliferation and migration in freely-expanding epithelia. eLife 9. e58945. 10.7554/eLife.58945. [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Aragona M, Panciera T, Manfrin A, Giulitti S, Michielin F, Elvassore N, Dupont S, and Piccolo S. (2013). A mechanical checkpoint controls multicellular growth through YAP/TAZ regulation by actin-processing factors. Cell 154, 1047–1059. 10.1016/j.cell.2013.07.042. [DOI] [PubMed] [Google Scholar]
46.Zheng Y, and Pan D. (2019). The hippo signaling pathway in development and disease. Dev. Cell 50, 264–282. 10.1016/j.devcel.2019.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
47.Grant GD, Kedziora KM, Limas JC, Cook JG, and Purvis JE (2018). Accurate delineation of cell cycle phase transitions in living cells with PIP-FUCCI. Cell Cycle 17, 2496–2516. 10.1080/15384101.2018.1547001. [DOI] [PMC free article] [PubMed] [Google Scholar]
48.Heldt FS, Lunstone R, Tyson JJ, and Novák B. (2018). Dilution and titration of cell-cycle regulators may control cell size in budding yeast. PLoS Comput. Biol 14. e1006548. 10.1371/journal.pcbi.1006548. [DOI] [PMC free article] [PubMed] [Google Scholar]
49.Amir A. (2014). Cell size regulation in bacteria. Phys. Rev. Lett 112, 208102. 10.1103/PhysRevLett.112.208102. [DOI] [Google Scholar]
50.Fan Y, and Meyer T. (2021). Molecular control of cell density-mediated exit to quiescence. Cell Rep. 36, 109436. 10.1016/j.celrep.2021.109436. [DOI] [PMC free article] [PubMed] [Google Scholar]
51.Alao JP (2007). The regulation of cyclin D1 degradation: roles in cancer development and the potential for therapeutic invention. Mol. Cancer 6, 24. 10.1186/1476-4598-6-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
52.Masamha CP, and Benbrook DM (2009). Cyclin D1 degradation is sufficient to induce G1 cell cycle arrest despite constitutive expression of cyclin E2 in ovarian cancer cells. Cancer Res. 69, 6565–6572. 10.1158/0008-5472.CAN-09-0913. [DOI] [PubMed] [Google Scholar]
53.Whyte P, Williamson NM, and Harlow E. (1989). Cellular targets for transformation by the adenovirus E1A proteins. Cell 56, 67–75. 10.1016/0092-8674(89)90984-7. [DOI] [PubMed] [Google Scholar]
54.Milo R, and Phillips R. (2015). Cell Biology by the Numbers (Garland Science). 10.1201/9780429258770. [DOI]
55.Fritzsche W, and Henderson E. (1996). Volume determination of human metaphase chromosomes by scanning force microscopy. Scanning Microsc. 10, 103–108. [PubMed] [Google Scholar]
56.Heslop-Harrison JS, Leitch AR, Schwarzacher T, Smith JB, Atkinson MD, and Bennett MD (1989). The volumes and morphology of human chromosomes in mitotic reconstructions. Hum. Genet 84, 27–34. 10.1007/BF00210666. [DOI] [PubMed] [Google Scholar]
57.Ou HD, Phan S, Deerinck TJ, Thor A, Ellisman MH, and O’Shea CC (2017). ChromEMT: visualizing 3D chromatin structure and compaction n interphase and mitotic cells. Science 357. eaag0025. 10.1126/science.aag0025. [DOI] [PMC free article] [PubMed] [Google Scholar]
58.Shaltiel IA, Krenning L, Bruinsma W, and Medema RH (2015). The same, only different – DNA damage checkpoints and their reversal throughout the cell cycle. J. Cell Sci 128, 607–620. 10.1242/jcs.163766. [DOI] [PubMed] [Google Scholar]
59.Liang J, Balachandra S, Ngo S, and O’Brien LE (2017). Feedback regulation of steady-state epithelial turnover and organ size. Nature 548, 588–591. 10.1038/nature23678. [DOI] [PMC free article] [PubMed] [Google Scholar]
60.Schlessinger J, and Ullrich A. (1992). Growth factor signaling by receptor tyrosine kinases. Neuron 9, 383–391. 10.1016/0896-6273(92)90177-F. [DOI] [PubMed] [Google Scholar]
61.Cowin SC (2004). Tissue growth and remodeling. Annu. Rev. Biomed. Eng 6, 77–107. 10.1146/annurev.bioeng.6.040803.140250. [DOI] [PubMed] [Google Scholar]
62.Guillot C, and Lecuit T. (2013). Mechanics of epithelial tissue homeostasis and morphogenesis. Science 340, 1185–1189. 10.1126/science.1235249. [DOI] [PubMed] [Google Scholar]
63.Mesa KR, Kawaguchi K, Cockburn K, Gonzalez D, Boucher J, Xin T, Klein AM, and Greco V. (2018). Homeostatic epidermal stem cell self-renewal is driven by local differentiation. Cell Stem Cell 23, 677–686.e4. 10.1016/j.stem.2018.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
64.Shraiman BI (2005). Mechanical feedback as a possible regulator of tissue growth. Proc. Natl. Acad. Sci. USA 102, 3318–3323. 10.1073/pnas.0404782102. [DOI] [PMC free article] [PubMed] [Google Scholar]
65.Streichan SJ, Hoerner CR, Schneidt T, Holzer D, and Hufnagel L. (2014). Spatial constraints control cell proliferation in tissues. Proc. Natl. Acad. Sci. USA 111, 5586–5591. 10.1073/pnas.1323016111. [DOI] [PMC free article] [PubMed] [Google Scholar]
66.Knapp BD, Odermatt P, Rojas ER, Cheng W, He X, Huang KC, and Chang F. (2019). Decoupling of rates of protein synthesis from cell expansion leads to supergrowth. Cell Syst. 9, 434–445.e6. 10.1016/j.cels.2019.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
67.Miettinen TP, Ly KS, Lam A, and Manalis SR (2022). Single-cell monitoring of dry mass and dry mass density reveals exocytosis of cellular dry contents in mitosis. eLife 11. e76664. 10.7554/eLife.76664. [DOI] [PMC free article] [PubMed] [Google Scholar]
68.Venkova L, Vishen AS, Lembo S, Srivastava N, Duchamp B, Ruppel A, Williart A, Vassilopoulos S, Deslys A, Garcia Arcos JM, et al. (2022). A mechano-osmotic feedback couples cell volume to the rate of cell deformation. eLife 11. e72381. 10.7554/eLife.72381. [DOI] [PMC free article] [PubMed] [Google Scholar]
69.Xie S, Swaffer M, and Skotheim JM (2022). Eukaryotic cell size control and its relation to biosynthesis and senescence. Annu. Rev. Cell Dev. Biol 38, 291–319. 10.1146/annurev-cellbio-120219-040142. [DOI] [PubMed] [Google Scholar]
70.Homem CCF, Steinmann V, Burkard TR, Jais A, Esterbauer H, and Knoblich JA (2014). Ecdysone and mediator change energy metabolism to terminate proliferation in drosophila neural stem cells. Cell 158, 874–888. 10.1016/j.cell.2014.06.024. [DOI] [PubMed] [Google Scholar]
71.Li Y, Liu D, López-Paz C, Olson BJ, and Umen JG (2016). A new class of cyclin dependent kinase in Chlamydomonas is required for coupling cell size to cell division. eLife 5. e10767. 10.7554/eLife.10767. [DOI] [PMC free article] [PubMed] [Google Scholar]
72.Liao Y, and Rust MJ (2021). The circadian clock ensures successful DNA replication in cyanobacteria. Proc. Natl. Acad. Sci. USA 118. e2022516118. 10.1073/pnas.2022516118. [DOI] [PMC free article] [PubMed] [Google Scholar]
73.Lum JJ, Bauer DE, Kong M, Harris MH, Li C, Lindsten T, and Thompson CB (2005). Growth factor regulation of autophagy and cell survival in the absence of apoptosis. Cell 120, 237–248. 10.1016/j.cell.2004.11.046. [DOI] [PubMed] [Google Scholar]
74.Zhurinsky J, Leonhard K, Watt S, Marguerat S, Bähler J, and Nurse P. (2010). A coordinated global control over cellular transcription. Curr. Biol 20, 2010–2015. 10.1016/j.cub.2010.10.002. [DOI] [PubMed] [Google Scholar]
75.Cheng L, Chen J, Kong Y, Tan C, Kafri R, and Björklund M. (2021). Size-scaling promotes senescence-like changes in proteome and organelle content. Preprint at bioRxiv. 10.1101/2021.08.05.455193. [DOI]
76.Lanz MC, Zatulovskiy E, Swaffer MP, Zhang L, Ilerten I, Zhang S, You DS, Marinov G, McAlpine P, Elias JE, and Skotheim JM (2021). Increasing cell size remodels the proteome and promotes senescence. Preprint at bioRxiv. 10.1101/2021.07.29.454227. [DOI] [PMC free article] [PubMed]
77.Deviri D, and Safran SA (2022). Balance of osmotic pressures determines the nuclear-to-cytoplasmic volume ratio of the cell. Proc. Natl. Acad. Sci. USA 119. e2118301119. 10.1073/pnas.2118301119. [DOI] [PMC free article] [PubMed] [Google Scholar]
78.Lemière J, Real-Calderon P, Holt LJ, Fai TG, and Chang F. (2022). Control of nuclear size by osmotic forces in Schizosaccharomyces pombe. eLife 11. e76075. 10.7554/eLife.76075. [DOI] [PMC free article] [PubMed] [Google Scholar]
79.Rollin R, Joanny J-F, and Sens P. (2022). Cell size scaling laws: a unified theory. Preprint at bioRxiv. 10.1101/2022.08.01.502021. [DOI]
80.Shah P, Hobson CM, Cheng S, Colville MJ, Paszek MJ, Superfine R, and Lammerding J. (2021). Nuclear deformation causes DNA damage by increasing replication stress. Curr. Biol 31, 753–765.e6. 10.1016/j.cub.2020.11.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
81.Marino MP, Luce MJ, and Reiser J. (2003). Small- to Large-Scale Production of Lentivirus Vectors. In Lentivirus Gene Engineering Protocols Methods in Molecular Biology^™., Federico M, ed. (Humana Press; ), pp. 43–55. 10.1385/1-59259-393-3:43. [DOI] [PubMed] [Google Scholar]
82.Bray NL, Pimentel H, Melsted P, and Pachter L. (2016). Near-optimal probabilistic RNA-seq quantification. Nat. Biotechnol 34, 525–527. 10.1038/nbt.3519. [DOI] [PubMed] [Google Scholar]
83.Ge SX, Son EW, and Yao R. (2018). iDEP: an integrated web application for differential expression and pathway analysis of RNA-Seq data. BMC Bioinformatics 19, 534. 10.1186/s12859-018-2486-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
84.Wnt Target genes | The Wnt Homepage. https://web.stanford.edu/group/nusselab/cgi-bin/wnt/target_genes.
85.Zhu M, Lerum MZ, and Chen W. (2012). How To Prepare Reproducible, Homogeneous, and Hydrolytically Stable Aminosilane-Derived Layers on Silica. Langmuir 28, 416–423. 10.1021/la203638g. [DOI] [PMC free article] [PubMed] [Google Scholar]
86.H A, and Jalali Bahram. (2015). Edge detection in digital images using dispersive phase stretch transform. J. Biomed. Imaging 10.1155/2015/687819. [DOI] [PMC free article] [PubMed]
87.Peter’s Functions for Computer Vision. https://peterkovesi.com/matlabfns/.
88.Crocker JC, and Grier DG (1996). Methods of Digital Video Microscopy for Colloidal Studies. J. Colloid Interface Sci 179, 298–310. 10.1006/jcis.1996.0217. [DOI] [Google Scholar]
89.Tinevez J-Y simpletracker.Version 1.5.1. June 19 2019. https://www.mathworks.com/matlabcentral/fileexchange/34040-simpletracker.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplemental Information

NIHMS1910865-supplement-Supplemental_Information.pdf^{(6MB, pdf)}

Data Availability Statement

[R1] 1.Murray AW, and Hunt T. (1993). The Cell Cycle: An Introduction (Oxford University Press; ). [Google Scholar]

[R2] 2.Nurse P. (2000). A long twentieth century of the cell cycle and beyond. Cell 100, 71–78. 10.1016/S0092-8674(00)81684-0. [DOI] [PubMed] [Google Scholar]

[R3] 3.Broach JR (2012). Nutritional control of growth and development in yeast. Genetics 192, 73–105. 10.1534/genetics.111.135731. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R4] 4.Scott M, and Hwa T. (2011). Bacterial growth laws and their applications. Curr. Opin. Biotechnol 22, 559–565. 10.1016/j.copbio.2011.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R5] 5.Irvine KD, and Shraiman BI (2017). Mechanical control of growth: ideas, facts and challenges. Development 144, 4238–4248. 10.1242/dev.151902. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R6] 6.McClatchey AI, and Yap AS (2012). Contact inhibition (of proliferation) redux. Curr. Opin. Cell Biol 24, 685–694. 10.1016/j.ceb.2012.06.009. [DOI] [PubMed] [Google Scholar]

[R7] 7.Fomicheva M, and Macara IG (2020). Genome-wide CRISPR screen identifies noncanonical NF-kB signaling as a regulator of density-dependent proliferation. eLife 9. e63603. 10.7554/eLife.63603. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] 8.Kim N-G, Koh E, Chen X, and Gumbiner BM (2011). E-cadherin mediates contact inhibition of proliferation through Hippo signaling-pathway components. Proc. Natl. Acad. Sci. USA 108, 11930–11935. 10.1073/pnas.1103345108. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R9] 9.Leontieva OV, Demidenko ZN, and Blagosklonny MV (2014). Contact inhibition and high cell density deactivate the mammalian target of rapamycin pathway, thus suppressing the senescence program. Proc. Natl. Acad. Sci. USA 111, 8832–8837. 10.1073/pnas.1405723111. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R10] 10.Mendonsa AM, Na T-Y, and Gumbiner BM (2018). E-cadherin in contact inhibition and cancer. Oncogene 37, 4769–4780. 10.1038/s41388-018-0304-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R11] 11.Ibar C, Kirichenko E, Keepers B, Enners E, Fleisch K, and Irvine KD (2018). Tension-dependent regulation of mammalian Hippo signaling through LIMD1. J. Cell Sci 131. jcs214700. 10.1242/jcs.214700. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R12] 12.Pan Y, Heemskerk I, Ibar C, Shraiman BI, and Irvine KD (2016). Differential growth triggers mechanical feedback that elevates Hippo signaling. Proc. Natl. Acad. Sci. USA 113. E6974–E6983. 10.1073/pnas.1615012113. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R13] 13.Cadart C, Monnier S, Grilli J, Sá ez PJ, Srivastava N, Attia R, Terriac E, Baum B, Cosentino-Lagomarsino M, and Piel M. (2018). Size control in mammalian cells involves modulation of both growth rate and cell cycle duration. Nat. Commun 9, 3275. 10.1038/s41467-018-05393-0. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] 14.Tan C, Ginzberg MB, Webster R, Iyengar S, Liu S, Papadopoli D, Concannon J, Wang Y, Auld DS, Jenkins JL, et al. (2021). Cell size homeostasis is maintained by CDK4-dependent activation of p38 MAPK. Dev. Cell 56. 1756.e7–1769.e7. 10.1016/j.devcel.2021.04.030. [DOI] [PubMed] [Google Scholar]

[R15] 15.Zatulovskiy E, Zhang S, Berenson DF, Topacio BR, and Skotheim JM (2020). Cell growth dilutes the cell cycle inhibitor Rb to trigger cell division. Science 369, 466–471. 10.1126/science.aaz6213. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R16] 16.Zatulovskiy E, and Skotheim JM (2020). On the molecular mechanisms regulating animal cell size homeostasis. Trends Genet. 36, 360–372. 10.1016/j.tig.2020.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R17] 17.Xie S, and Skotheim JM (2020). A G1 sizer coordinates growth and division in the mouse epidermis. Curr. Biol 30, 916–924.e2. 10.1016/j.cub.2019.12.062. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] 18.Neufeld TP, de la Cruz AF, Johnston LA, and Edgar BA (1998). Coordination of growth and cell division in the Drosophila wing. Cell 93, 1183–1193. 10.1016/S0092-8674(00)81462-2. [DOI] [PubMed] [Google Scholar]

[R19] 19.Neurohr GE, Terry RL, Lengefeld J, Bonney M, Brittingham GP, Moretto F, Miettinen TP, Vaites LP, Soares LM, Paulo JA, et al. (2019). Excessive cell growth causes cytoplasm dilution and contributes to senescence. Cell 176, 1083–1097.e18. 10.1016/j.cell.2019.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] 20.Sender R, and Milo R. (2021). The distribution of cellular turnover in the human body. Nat. Med 27, 45–48. 10.1038/s41591-020-01182-9. [DOI] [PubMed] [Google Scholar]

[R21] 21.Puliafito A, Primo L, and Celani A. (2017). Cell-size distribution in epithelial tissue formation and homeostasis. J. R. Soc. Interface 14. 20170032. 10.1098/rsif.2017.0032. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] 22.Puliafito A, Hufnagel L, Neveu P, Streichan S, Sigal A, Fygenson DK, and Shraiman BI (2012). Collective and single cell behavior in epithelial contact inhibition. Proc. Natl. Acad. Sci. USA 109, 739–744. 10.1073/pnas.1007809109. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R23] 23.Uhlén M, Fagerberg L, Hallström BM, Lindskog C, Oksvold P, Mardinoglu A, Sivertsson Å, Kampf C, Sjöstedt E, Asplund A, et al. (2015). Proteomics. Tissue-based map of the human proteome. Science 347, 1260419. 10.1126/science.1260419. [DOI] [PubMed] [Google Scholar]

[R24] 24.Dataset accessed through 3D Cell Viewer: Allen Institute for Cell Science (2018). hiPSC Single-cell Image Dataset. Available from https://www.allencell.org/3d-cell-viewer.html.

[R25] 25.Chen J, Ding L, Viana MP, Lee H, Sluezwski MF, Morris B, Hendershott MC, Yang R, Mueller IA, and Rafelski SM (2020). The Allen Cell and Structure Segmenter: a new open source toolkit for segmenting 3D intracellular structures in fluorescence microscopy images. Preprint at bioRxiv. 10.1101/491035. [DOI]

[R26] 26.Elamin E, Jonkers D, Juuti-Uusitalo K, van IJzendoorn S, Troost F, Duimel H, Broers J, Verheyen F, Dekker J, and Masclee A. (2012). Effects of ethanol and acetaldehyde on tight junction integrity: in vitro study in a three dimensional intestinal epithelial cell culture model. PLoS One 7. e35008. 10.1371/journal.pone.0035008. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R27] 27.Engelberg JA, Datta A, Mostov KE, and Hunt CA (2011). MDCK cystogenesis driven by cell stabilization within computational analogues. PLoS Comput. Biol 7. e1002030. 10.1371/journal.pcbi.1002030. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R28] 28.Goldspink DA, Rookyard C, Tyrrell BJ, Gadsby J, Perkins J, Lund EK, Galjart N, Thomas P, Wileman T, and Mogensen MM (2017). Ninein is essential for apico-basal microtubule formation and CLIP-170 facilitates its redeployment to non-centrosomal microtubule organizing centres. Open Biol. 7, 160274. 10.1098/rsob.160274. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R29] 29.Guo M, Pegoraro AF, Mao A, Zhou EH, Arany PR, Han Y, Burnette DT, Jensen MH, Kasza KE, Moore JR, et al. (2017). Cell volume change through water efflux impacts cell stiffness and stem cell fate. Proc. Natl. Acad. Sci. USA 114. E8618–E8627. 10.1073/pnas.1705179114. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R30] 30.Karve SS, Pradhan S, Ward DV, and Weiss AA (2017). Intestinal organoids model human responses to infection by commensal and Shiga toxin producing Escherichia coli. PLoS One 12. e0178966. 10.1371/journal.pone.0178966. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R31] 31.Leung E, Kim JE, Askarian-Amiri M, Finlay GJ, and Baguley BC (2014). Evidence for the existence of triple-negative variants in the MCF-7 breast cancer cell population. Biomed Res. Int 2014, 836769. 10.1155/2014/836769. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R32] 32.de Medeiros G, Ortiz R, Strnad P, Boni A, Maurer F, and Liberali P. (2021). Multiscale light-sheet organoid imaging framework. Nat. Commun 13, 4864. 10.1101/2021.05.12.443427. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R33] 33.Morizane R, Lam AQ, Freedman BS, Kishi S, Valerius MT, and Bonventre JV (2015). Nephron organoids derived from human pluripotent stem cells model kidney development and injury. Nat. Biotechnol 33, 1193–1200. 10.1038/nbt.3392. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R34] 34.Padovan-Merhar O, Nair GP, Biaesch AG, Mayer A, Scarfone S, Foley SW, Wu AR, Churchman LS, Singh A, and Raj A. (2015). Single mammalian cells compensate for differences in cellular volume and DNA copy number through independent global transcriptional mechanisms. Mol. Cell 58, 339–352. 10.1016/j.molcel.2015.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] 35.Park K, Millet LJ, Kim N, Li H, Jin X, Popescu G, Aluru NR, Hsia KJ, and Bashir R. (2010). Measurement of adherent cell mass and growth. Proc. Natl. Acad. Sci. USA 107, 20691–20696. 10.1073/pnas.1011365107. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] 36.Perez-Gonzalez NA, Rochman ND, Yao K, Tao J, Le M-TT, Flanary S, Sablich L, Toler B, Crentsil E, Takaesu F, et al. (2019). YAP and TAZ regulate cell volume. J. Cell Biol 218, 3472–3488. 10.1083/jcb.201902067. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R37] 37.Schutgens F, Rookmaaker MB, Margaritis T, Rios A, Ammerlaan C, Jansen J, Gijzen L, Vormann M, Vonk A, Viveen M, et al. (2019). Tubuloids derived from human adult kidney and urine for personalized disease modeling. Nat. Biotechnol 37, 303–313. 10.1038/s41587-019-0048-8. [DOI] [PubMed] [Google Scholar]

[R38] 38.Viana MP, Chen J, Knijnenburg TA, Vasan R, Yan C, Arakaki JE, Bailey M, Berry B, Borensztejn A, Brown JM, et al. (2021). Robust integrated intracellular organization of the human iPS cell: where, how much, and how variable. Preprint at bioRxiv. 10.1101/2020.12.08.415562. [DOI]

[R39] 39.Yao K, Rochman ND, and Sun SX (2020). CTRL - a label-free artificial intelligence method for dynamic measurement of single-cell volume. J. Cell Sci 133. jcs245050. 10.1242/jcs.245050. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R40] 40.Zhao L, Kroenke CD, Song J, Piwnica-Worms D, Ackerman JJH, and Neil JJ (2008). Intracellular water-specific MR of microbead-adherent cells: the HeLa cell intracellular water exchange lifetime. NMR Biomed. 21, 159–164. 10.1002/nbm.1173. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R41] 41.Devany J, Sussman DM, Yamamoto T, Manning ML, and Gardel ML (2021). Cell cycle-dependent active stress drives epithelia remodeling. Proc. Natl. Acad. Sci. USA 118. e1917853118. 10.1073/pnas.1917853118. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R42] 42.Sherr CJ, and Roberts JM (1999). CDK inhibitors: positive and negative regulators of G1-phase progression. Genes Dev. 13, 1501–1512. 10.1101/gad.13.12.1501. [DOI] [PubMed] [Google Scholar]

[R43] 43.Vlach J, Hennecke S, and Amati B. (1997). Phosphorylation-dependent degradation of the cyclin-dependent kinase inhibitor p27. EMBO J. 16, 5334–5344. 10.1093/emboj/16.17.5334. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R44] 44.Heinrich MA, Alert R, LaChance JM, Zajdel TJ, Košmrlj A, and Cohen DJ (2020). Size-dependent patterns of cell proliferation and migration in freely-expanding epithelia. eLife 9. e58945. 10.7554/eLife.58945. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R45] 45.Aragona M, Panciera T, Manfrin A, Giulitti S, Michielin F, Elvassore N, Dupont S, and Piccolo S. (2013). A mechanical checkpoint controls multicellular growth through YAP/TAZ regulation by actin-processing factors. Cell 154, 1047–1059. 10.1016/j.cell.2013.07.042. [DOI] [PubMed] [Google Scholar]

[R46] 46.Zheng Y, and Pan D. (2019). The hippo signaling pathway in development and disease. Dev. Cell 50, 264–282. 10.1016/j.devcel.2019.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R47] 47.Grant GD, Kedziora KM, Limas JC, Cook JG, and Purvis JE (2018). Accurate delineation of cell cycle phase transitions in living cells with PIP-FUCCI. Cell Cycle 17, 2496–2516. 10.1080/15384101.2018.1547001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R48] 48.Heldt FS, Lunstone R, Tyson JJ, and Novák B. (2018). Dilution and titration of cell-cycle regulators may control cell size in budding yeast. PLoS Comput. Biol 14. e1006548. 10.1371/journal.pcbi.1006548. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R49] 49.Amir A. (2014). Cell size regulation in bacteria. Phys. Rev. Lett 112, 208102. 10.1103/PhysRevLett.112.208102. [DOI] [Google Scholar]

[R50] 50.Fan Y, and Meyer T. (2021). Molecular control of cell density-mediated exit to quiescence. Cell Rep. 36, 109436. 10.1016/j.celrep.2021.109436. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R51] 51.Alao JP (2007). The regulation of cyclin D1 degradation: roles in cancer development and the potential for therapeutic invention. Mol. Cancer 6, 24. 10.1186/1476-4598-6-24. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R52] 52.Masamha CP, and Benbrook DM (2009). Cyclin D1 degradation is sufficient to induce G1 cell cycle arrest despite constitutive expression of cyclin E2 in ovarian cancer cells. Cancer Res. 69, 6565–6572. 10.1158/0008-5472.CAN-09-0913. [DOI] [PubMed] [Google Scholar]

[R53] 53.Whyte P, Williamson NM, and Harlow E. (1989). Cellular targets for transformation by the adenovirus E1A proteins. Cell 56, 67–75. 10.1016/0092-8674(89)90984-7. [DOI] [PubMed] [Google Scholar]

[R54] 54.Milo R, and Phillips R. (2015). Cell Biology by the Numbers (Garland Science). 10.1201/9780429258770. [DOI]

[R55] 55.Fritzsche W, and Henderson E. (1996). Volume determination of human metaphase chromosomes by scanning force microscopy. Scanning Microsc. 10, 103–108. [PubMed] [Google Scholar]

[R56] 56.Heslop-Harrison JS, Leitch AR, Schwarzacher T, Smith JB, Atkinson MD, and Bennett MD (1989). The volumes and morphology of human chromosomes in mitotic reconstructions. Hum. Genet 84, 27–34. 10.1007/BF00210666. [DOI] [PubMed] [Google Scholar]

[R57] 57.Ou HD, Phan S, Deerinck TJ, Thor A, Ellisman MH, and O’Shea CC (2017). ChromEMT: visualizing 3D chromatin structure and compaction n interphase and mitotic cells. Science 357. eaag0025. 10.1126/science.aag0025. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R58] 58.Shaltiel IA, Krenning L, Bruinsma W, and Medema RH (2015). The same, only different – DNA damage checkpoints and their reversal throughout the cell cycle. J. Cell Sci 128, 607–620. 10.1242/jcs.163766. [DOI] [PubMed] [Google Scholar]

[R59] 59.Liang J, Balachandra S, Ngo S, and O’Brien LE (2017). Feedback regulation of steady-state epithelial turnover and organ size. Nature 548, 588–591. 10.1038/nature23678. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R60] 60.Schlessinger J, and Ullrich A. (1992). Growth factor signaling by receptor tyrosine kinases. Neuron 9, 383–391. 10.1016/0896-6273(92)90177-F. [DOI] [PubMed] [Google Scholar]

[R61] 61.Cowin SC (2004). Tissue growth and remodeling. Annu. Rev. Biomed. Eng 6, 77–107. 10.1146/annurev.bioeng.6.040803.140250. [DOI] [PubMed] [Google Scholar]

[R62] 62.Guillot C, and Lecuit T. (2013). Mechanics of epithelial tissue homeostasis and morphogenesis. Science 340, 1185–1189. 10.1126/science.1235249. [DOI] [PubMed] [Google Scholar]

[R63] 63.Mesa KR, Kawaguchi K, Cockburn K, Gonzalez D, Boucher J, Xin T, Klein AM, and Greco V. (2018). Homeostatic epidermal stem cell self-renewal is driven by local differentiation. Cell Stem Cell 23, 677–686.e4. 10.1016/j.stem.2018.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R64] 64.Shraiman BI (2005). Mechanical feedback as a possible regulator of tissue growth. Proc. Natl. Acad. Sci. USA 102, 3318–3323. 10.1073/pnas.0404782102. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] 65.Streichan SJ, Hoerner CR, Schneidt T, Holzer D, and Hufnagel L. (2014). Spatial constraints control cell proliferation in tissues. Proc. Natl. Acad. Sci. USA 111, 5586–5591. 10.1073/pnas.1323016111. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R66] 66.Knapp BD, Odermatt P, Rojas ER, Cheng W, He X, Huang KC, and Chang F. (2019). Decoupling of rates of protein synthesis from cell expansion leads to supergrowth. Cell Syst. 9, 434–445.e6. 10.1016/j.cels.2019.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R67] 67.Miettinen TP, Ly KS, Lam A, and Manalis SR (2022). Single-cell monitoring of dry mass and dry mass density reveals exocytosis of cellular dry contents in mitosis. eLife 11. e76664. 10.7554/eLife.76664. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R68] 68.Venkova L, Vishen AS, Lembo S, Srivastava N, Duchamp B, Ruppel A, Williart A, Vassilopoulos S, Deslys A, Garcia Arcos JM, et al. (2022). A mechano-osmotic feedback couples cell volume to the rate of cell deformation. eLife 11. e72381. 10.7554/eLife.72381. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R69] 69.Xie S, Swaffer M, and Skotheim JM (2022). Eukaryotic cell size control and its relation to biosynthesis and senescence. Annu. Rev. Cell Dev. Biol 38, 291–319. 10.1146/annurev-cellbio-120219-040142. [DOI] [PubMed] [Google Scholar]

[R70] 70.Homem CCF, Steinmann V, Burkard TR, Jais A, Esterbauer H, and Knoblich JA (2014). Ecdysone and mediator change energy metabolism to terminate proliferation in drosophila neural stem cells. Cell 158, 874–888. 10.1016/j.cell.2014.06.024. [DOI] [PubMed] [Google Scholar]

[R71] 71.Li Y, Liu D, López-Paz C, Olson BJ, and Umen JG (2016). A new class of cyclin dependent kinase in Chlamydomonas is required for coupling cell size to cell division. eLife 5. e10767. 10.7554/eLife.10767. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R72] 72.Liao Y, and Rust MJ (2021). The circadian clock ensures successful DNA replication in cyanobacteria. Proc. Natl. Acad. Sci. USA 118. e2022516118. 10.1073/pnas.2022516118. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R73] 73.Lum JJ, Bauer DE, Kong M, Harris MH, Li C, Lindsten T, and Thompson CB (2005). Growth factor regulation of autophagy and cell survival in the absence of apoptosis. Cell 120, 237–248. 10.1016/j.cell.2004.11.046. [DOI] [PubMed] [Google Scholar]

[R74] 74.Zhurinsky J, Leonhard K, Watt S, Marguerat S, Bähler J, and Nurse P. (2010). A coordinated global control over cellular transcription. Curr. Biol 20, 2010–2015. 10.1016/j.cub.2010.10.002. [DOI] [PubMed] [Google Scholar]

[R75] 75.Cheng L, Chen J, Kong Y, Tan C, Kafri R, and Björklund M. (2021). Size-scaling promotes senescence-like changes in proteome and organelle content. Preprint at bioRxiv. 10.1101/2021.08.05.455193. [DOI]

[R76] 76.Lanz MC, Zatulovskiy E, Swaffer MP, Zhang L, Ilerten I, Zhang S, You DS, Marinov G, McAlpine P, Elias JE, and Skotheim JM (2021). Increasing cell size remodels the proteome and promotes senescence. Preprint at bioRxiv. 10.1101/2021.07.29.454227. [DOI] [PMC free article] [PubMed]

[R77] 77.Deviri D, and Safran SA (2022). Balance of osmotic pressures determines the nuclear-to-cytoplasmic volume ratio of the cell. Proc. Natl. Acad. Sci. USA 119. e2118301119. 10.1073/pnas.2118301119. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R78] 78.Lemière J, Real-Calderon P, Holt LJ, Fai TG, and Chang F. (2022). Control of nuclear size by osmotic forces in Schizosaccharomyces pombe. eLife 11. e76075. 10.7554/eLife.76075. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R79] 79.Rollin R, Joanny J-F, and Sens P. (2022). Cell size scaling laws: a unified theory. Preprint at bioRxiv. 10.1101/2022.08.01.502021. [DOI]

[R80] 80.Shah P, Hobson CM, Cheng S, Colville MJ, Paszek MJ, Superfine R, and Lammerding J. (2021). Nuclear deformation causes DNA damage by increasing replication stress. Curr. Biol 31, 753–765.e6. 10.1016/j.cub.2020.11.037. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R81] 81.Marino MP, Luce MJ, and Reiser J. (2003). Small- to Large-Scale Production of Lentivirus Vectors. In Lentivirus Gene Engineering Protocols Methods in Molecular Biology^™., Federico M, ed. (Humana Press; ), pp. 43–55. 10.1385/1-59259-393-3:43. [DOI] [PubMed] [Google Scholar]

[R82] 82.Bray NL, Pimentel H, Melsted P, and Pachter L. (2016). Near-optimal probabilistic RNA-seq quantification. Nat. Biotechnol 34, 525–527. 10.1038/nbt.3519. [DOI] [PubMed] [Google Scholar]

[R83] 83.Ge SX, Son EW, and Yao R. (2018). iDEP: an integrated web application for differential expression and pathway analysis of RNA-Seq data. BMC Bioinformatics 19, 534. 10.1186/s12859-018-2486-6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R84] 84.Wnt Target genes | The Wnt Homepage. https://web.stanford.edu/group/nusselab/cgi-bin/wnt/target_genes.

[R85] 85.Zhu M, Lerum MZ, and Chen W. (2012). How To Prepare Reproducible, Homogeneous, and Hydrolytically Stable Aminosilane-Derived Layers on Silica. Langmuir 28, 416–423. 10.1021/la203638g. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R86] 86.H A, and Jalali Bahram. (2015). Edge detection in digital images using dispersive phase stretch transform. J. Biomed. Imaging 10.1155/2015/687819. [DOI] [PMC free article] [PubMed]

[R87] 87.Peter’s Functions for Computer Vision. https://peterkovesi.com/matlabfns/.

[R88] 88.Crocker JC, and Grier DG (1996). Methods of Digital Video Microscopy for Colloidal Studies. J. Colloid Interface Sci 179, 298–310. 10.1006/jcis.1996.0217. [DOI] [Google Scholar]

[R89] 89.Tinevez J-Y simpletracker.Version 1.5.1. June 19 2019. https://www.mathworks.com/matlabcentral/fileexchange/34040-simpletracker.

PERMALINK

Epithelial tissue confinement inhibits cell growth and leads to volume-reducing divisions

John Devany

Martin J Falk

Liam J Holt

Arvind Murugan

Margaret L Gardel

SUMMARY

In brief

Graphical Abstract

INTRODUCTION

RESULTS

Epithelial cell volume is context dependent

Figure 1. Epithelial cell size is consistent across tissues but context dependent.

Cell-volume reduction occurs through division in the absence of cell growth

Figure 2. Division during growth arrest at the onset of confluence leads to cell-size reduction.

Tissue confinement regulates cell growth

Figure 3. Tissue confinement quantifies how tissue-scale growth dynamics constrain cell growth.

Figure 4. Tissue confinement determines cell growth rate and signaling.

A G1 sizer arrests the cell cycle in confined epithelium

Figure 5. A G1 sizer arrests the cell cycle.

Volume-dependent cyclin D downregulation leads to cell-cycle arrest

Figure 6. Low cyclin D causes cell-cycle arrest in small cells.

Cell-cycle arrest occurs near cell volume minimum set by the genome volume

Figure 7. Cells arrest near a minimum size set by genome volume.

DISCUSSION

Limitations of the study

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Materials availability

Data and code availability

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Cell culture and lines

METHOD DETAILS

Epithelial monolayer cultures

Expanding colony assay

BCA assay

CellTrace labeling

Immunostaining

Fluorescence microscopy

RNA sequencing

Silane modification of glass coverslips

Collagen gel preparation

Cell volumes measurements

Image segmentation

Cell tracking

FUCCI analysis

Division rate measurement

Quantification of H2ax staining

Simulation growth models

G1-sizer model

Numerical simulation of G1-Sizer model

QUANTIFICATION AND STATISTICAL ANALYSIS

Supplementary Material

Highlights.

ACKNOWLEDGMENTS

INCLUSION AND DIVERSITY

Footnotes

REFERENCES

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases