Higher-order multi-shell diffusion measures complement tensor metrics and volume in gray matter when predicting age and cognition

Abstract

Recent advances in diffusion-weighted imaging have enabled us to probe the microstructure of even gray matter non-invasively. However, these advanced multi-shell protocols are often not included in large-scale studies as they significantly increase scan time. In this study, we investigated whether one set of multi-shell diffusion metrics commonly used in gray matter (as derived from Neurite Orientation Dispersion and Density Imaging, NODDI) provide enough additional information over typical tensor and volume metrics to justify the increased acquisition time, using the cognitive aging framework in the human hippocampus as a testbed. We first demonstrated that NODDI metrics are robust and reliable by replicating previous findings from our lab in a larger population of 79 younger (20.41 ± 1.89 years, 46 females) and 75 older (73.56 ± 6.26 years, 45 females) adults, showing that these metrics in the hippocampal subfields are sensitive to age and memory performance. We then asked how these subfield specific hippocampal NODDI metrics compared with standard tensor metrics and volume in predicting age and memory ability. We discovered that both NODDI and tensor measures separately predicted age and cognition in comparable capacities. However, integrating these modalities together considerably increased the predictive power of our logistic models, indicating that NODDI and tensor measures may be capturing independent microstructural information. We use these findings to encourage neuroimaging data collection consortiums to include a multi-shell diffusion sequence in their protocols since existing NODDI measures (and potential future multi-shell measures) may be able to capture microstructural variance that is missed by traditional approaches, even in studies exclusively examining gray matter.

1. Introduction

Magnetic Resonance Imaging (MRI) studies have been very valuable in non-invasively detecting structural changes associated with behavior, cognition, function, and pathology. While there are a range of MRI techniques that can capture different types of information, acquisition time is always at a premium in any study. It is challenging to determine which acquisition protocols to include in a study while finding the best balance between scan time and information received. Structural Magnetic Resonance Imaging (sMRI) techniques like T1-weighted, T2-weighted, and Fluid Attenuated Inversion Recovery (FLAIR) imaging have been crucial in understanding the anatomical alterations that the brain experiences, both in research and clinical contexts (Brans et al., 2010; Dekaban and Sadowsky, 1978; Hedman et al., 2011; Ho et al., 1980; Jernigan et al., 2001; Morrison and Hof, 1997; Peter R., 1979; Raz et al., 2004; Taki et al., 2011; van Haren et al., 2008). For example, being able to trace the outline and subsequently calculate the volume of the hippocampus using T1-weighted images has been extremely valuable when studying diseases like Alzheimer’s (Fox and Freeborough, 1997). However, while these techniques can detect useful macrostructural properties like regional volume and cortical thickness, dramatic changes like gross atrophy or cortical thinning likely follow a myriad of more subtle microstructural changes that cannot be detected by standard T1- and T2-weighted imaging and their analogs (Jack et al., 2018). Cytoarchitectural properties like dendritic complexity, glial density, and cellular characteristics may be more reflective of individual differences in cognitive and pathological identities. Observing these microstructural characteristics in the brain non-invasively had been a major challenge to the field until recent advances in MRI technology.

Diffusion-weighted imaging (DWI) (Stejskal and Tanner, 1965) is increasingly becoming a key solution to this problem, given its ability to provide a range of quantitative measures describing neural microstructure within only minutes of acquisition (Johansen-Berg and Behrens, 2014). Until recently, DWI was almost exclusively associated with the characterization of white matter. Diffusion tensor metrics and tractography revealed how important features like axonal integrity, myelination, and specific structural connections change through healthy and pathological conditions and how they influence cognitive performance and other behavior (Assaf and Pasternak, 2008; Sasson et al., 2010; Thomason and Thompson, 2011; Madden et al., 2012). Given this, diffusion imaging has been considered a general microstructural probe as the geometry, organization, and morphology of any tissue type influences the diffusion signal. More recently, studies have been conducted using diffusion metrics to investigate gray matter microstructure (Aggarwal et al., 2015; Assaf, 2019; Budde and Annese, 2013; Colgan et al., 2016; Köhncke et al., 2021; Radhakrishnan et al., 2020; Venkatesh et al., 2020). However, the ratio of current publications that use diffusion MRI to study white matter vs gray matter is a striking 5:1, perhaps because early modeling algorithms could not accommodate the cytoarchitectural complexity of gray matter, and DWI used to provide poor image resolution in gray matter sub-structures (Assaf, 2019; Nazeri et al., 2020). Recent advances in both diffusion image acquisition and analysis techniques may be able to resolve some of these issues (Frank, 2001; Jones, 2004; Papadakis et al., 1999).

A promising acquisition technique has been multi-shell DWI, which acquires scans at multiple gradient strengths (b-values). These images can then be analyzed using biophysically plausible models like Neurite Orientation Dispersion and Density Imaging (NODDI) (Zhang et al., 2012), which yield microstructural metrics that correspond to “intracellular”, “extracellular” and free water sources of the diffusion signal across tissue types. While NODDI may be well-suited to characterize the cytoarchitectural properties of gray matter, it has been seldom utilized to do so, especially in large-scale studies which usually only collect single-shelled diffusion data, and any multi-shelled data is collected in a much smaller sample size (Beekly et al., 2004; Petersen et al., 2010). This is mainly because increasing the number of shells can double or triple scan time (depending on the number of shells added), which can be a valuable commodity, especially when studying sensitive populations. The counterargument for including additional DWI shells may be strengthened if the advantage of models that need multi-shelled acquisitions (specifically in studying gray matter microstructure) can be documented, as proposed here.

In this study, we asked whether one such model utilizing multi-shell diffusion protocols, NODDI, can generate metrics that provide enough additional information over traditional tensor and volume metrics to justify the added acquisition time. To simplify this question and directly determine the value of NODDI metrics over the other metrics in a test case, we observed the effect of aging in the hippocampal subfields, and the relationship of this phenomenon with two popular hippocampal-dependent memory tasks. We first reproduced prior results from our lab and others (Radhakrishnan et al., 2020; Venkatesh et al., 2020) in a larger study population showing that NODDI metrics are sensitive to aging-related microstructural differences in hippocampal subfields and that differences in these NODDI metrics may be associated with cognitive decline. Our central question beyond this replication was how the hippocampal NODDI metrics compare to traditional tensor metrics and volume when predicting age or cognitive performance.

We found that NODDI metrics and tensor/volume metrics predicted age and cognition in similar capacities. However, integrating these modalities together significantly increased the predictive power of both our age and cognition models, suggesting that these methods may be capturing different types of information. We use these results to urge neuroimaging data collection consortiums to include acquisitions in their protocol that allow the calculation of NODDI metrics- i.e., multi-shell sequences, as they might be able to capture independently valuable information complementary to the more conventional measures.

2. Methods

2.1. Participants

Participants were recruited from the University of California, Riverside, and surrounding communities. Before enrollment, participants were screened for neurological conditions (e.g., depression, stroke, etc.) and scanner-related contraindications (e.g., claustrophobia, pregnancy, etc.). After scanning, sixteen of the 170 participants were excluded based on data segmentation issues and/or registration artifacts. The final sample consisted of 79 younger adults (20.41 ± 1.89 years, 46 females) and 75 older adults (73.56 ± 6.26 years, 45 females) (Table 3.1). All participants provided informed consent before participation in this study and were compensated for their time. All experimental procedures were approved by the University of California, Riverside Review Board.

Table 3.1:

Demographics and cognitive test scores. *Rows in blue indicate p<0.05 in a t-test between young and old groups.

	Young	Old
N	79	75
Age*	20.41 ± 1.89	73.56 ± 6.26
Female (%)	58.2%	60%
Education	13.98 ± 2.26	14.56 ± 2.30
RAVLT Immediate*	11.29 ± 2.50	8.30 ± 3.02
RAVLT Delay*	10.68 ± 3.00	7.67 ± 3.40
MST LDI*	0.83 ± 0.50	1.12 ± 0.57
MST REC	2.67 ± 0.94	2.97 ± 0.72

2.2. Cognitive testing

All participants completed a battery of neuropsychological tests to evaluate their cognitive abilities. We assessed participants’ memory using the Rey Auditory Verbal Learning Test (RAVLT) (Rey, 1941) and the two-choice Mnemonic Similarity Test (MST) (Kirwan and Stark, 2007; Stark et al., 2019, 2013). The RAVLT has three components: 5 presentations of the same 15-word list with immediate recall, a second immediate recall test following an interference list of 15 new words, and a final delayed recall of the initial list after 15 minutes. The RAVLT Delay score reflects the final recall score, on a scale of 0 to 15.

The MST is a modified recognition memory task that was designed to tax “pattern separation” processes in an explicit attempt to rely on hippocampal processing and its link to the hippocampus has been validated in a wide range of domains (see Stark et al., 2019 for review). In the MST, participants viewed 128 images of everyday objects during an incidental encoding phase. During the test phase, participants were shown repeated images, novel foils, and items that were similar to, but not the same as studied images. On each trial, participants had to judge them as either “old” (repeated targets) or “new” (novel foils and similar lures) using a two-choice button press. A lure discrimination index (LDI) was calculated using signal detection theory as the discrimination d’ between repeated targets and similar lures (Kirwan and Stark, 2007; Stark et al., 2015). A traditional recognition measure was calculated as the d’ between repeated targets and novel foils. Participants who had >20% omitted trials or an extremely poor recognition score (greater than 2.5 standard deviations from the mean [REC < 0.5]) were excluded. The final sample size for the MST analyses was 78 younger adults (20.41 ± 1.89 years, 46 females) and 69 older adults (74.04 ± 6.35 years, 35 females).

2.3. MR Image Acquisition

The participants were scanned using a Siemens Prisma 3T MRI scanner (Siemens Healthineers, Malvern, PA), fitted with a 32-channel receive-only head coil. Fitted padding was used to minimize head movements.

T1W:

A T1-weighted magnetization-prepared rapid gradient echo (MP-RAGE) scan was acquired with the following parameters: echo time (TE)/repetition time (TR) = 2.72/2400 ms, 208 axial slices, GRAPPA acceleration factor = 2, and in 0.8mm isotropic resolution.

DWI:

Axial diffusion-weighted echo-planar images were acquired in both anterior-posterior and posterior-anterior phase encodings with b = 1500 s/mm² and b = 3000 s/mm² applied in 64 orthogonal directions each with the following parameters: TE/TR = 102/3500 ms, FOV = 212 x 182 mm, 64 axial slices, Acquisition time = 10 minutes and 57 seconds, multi-band acceleration factor = 4 and in 1.7 mm isotropic resolution. Twelve images with no diffusion weighting (b = 0; half in each encoding direction) were also collected.

2.4. Diffusion data preprocessing

All preprocessing steps employed MRtrix3 (Tournier et al., 2012) (www.mrtrix.org) commands or used Mrtrix3 scripts that linked external software packages. Physiological noise arising from thermal motion of water molecules in the brain was first removed (Veraart et al., 2016), followed by removal of Gibbs ringing artifacts (Kellner et al., 2016), eddy current correction (Andersson and Sotiropoulos, 2016), motion correction (Andersson et al., 2003), susceptibility-induced distortion correction (Skare and Bammer, 2009) and bias field correction (Tustison et al., 2014). The image intensity was then normalized across subjects in the log domain (Raffelt et al., 2012). Images with no diffusion weighting (b=0) were extracted and averaged to aid with structural registration.

2.5. Structural data processing

Each participant’s structural image was nonlinearly co-registered to the average of their respective preprocessed b0 images using the ANTS Registration SyN algorithm with a b-spline transform (Avants et al., 2008; Tustison and Avants, 2013). Registration was manually checked to ensure accuracy, and DWI-registered T1w images were used for the rest of the analyses. The T1-weighted images were then processed using FMRIPREP version 20.2.1 (Esteban et al., 2018; Gorgolewski et al., 2011). Each volume was corrected for intensity non-uniformity using N4 Bias Field Correction from Advanced Normalization Tools (ANTS v2.3.4) (Tustison et al., 2010). The images were then skull stripped using the OASIS template. Brain surfaces were reconstructed using recon-all from FreeSurfer v7 (Dale et al., 1999) and the brain mask estimated previously was refined with a custom variation of the method to reconcile ANTs-derived and FreeSurfer-derived segmentations of the cortical gray-matter of Mindboggle (Klein et al., 2017). The hippocampus was previously hand-segmented on a template image into 3 subregions: a combined dentate gyrus and CA3 (combined due to resolution constraints; DG/CA3), CA1, and subiculum, based on our previous work (Stark and Stark, 2017). As the hippocampal atlas was in template space, spatial normalization to the ICBM 152 Nonlinear Asymmetrical template version 2009c (Fonov et al., 2009) was performed through nonlinear registration with ANTs, using brain-extracted versions of both T1w volume and template and using ANTs MultiLabel resampling technique. Regional volume was calculated by transforming the masks back to subject space and calculating the number of voxels encompassing each subfield multiplied with the image resolution. Brain tissue segmentation of cerebrospinal fluid (CSF), white-matter (WM), and gray-matter (GM) was performed on the brain-extracted T1w using FAST from FSL v6.0.

2.6. Deriving diffusion metrics

All diffusion metrics were estimated in native space. Given the concerns about estimating tensor metrics from multi-shell data and diffusion being non-Gaussian at high b values, we calculated tensor metrics only from the b=1500 shells. A weighted least squares (WLS) approach was first used to fit the diffusion tensor to the log signal, using weights based on empirical signal intensities (Basser et al., 1994). We repeated the weighted least squares with weights determined by the signal predictions from the previous step (Veraart et al., 2013). We then generated maps of the following tensor-derived parameters: the mean apparent diffusion coefficient (ADC, sometimes also referred to as Mean Diffusivity or MD), fractional anisotropy (FA), axial diffusivity (AD, same as principal eigen value), and radial diffusivity (RD, equal to mean of the two non-principal eigen values) (Westin, 1997).

While these traditional tensor metrics are widely used, they were not originally designed to capture the complex cytoarchitectural properties of gray matter. Hence, we derived higher-order multi-compartment metrics using data from all shells using the Neurite Orientation Dispersion and Density Imaging (NODDI) (Zhang et al., 2012) model in the Microstructure Diffusion Toolbox (Harms et al., 2017). NODDI’s metrics are tissue type agnostic and can readily be used in gray matter as it characterizes diffusion within each voxel as a combination of intracellular, extracellular, and CSF-based components. Here, we focus on three NODDI-derived parameters: the neurite density index (NDI), the orientation dispersion index (ODI), and the fractional isotropy (FISO). The NDI measures intracellular volume fraction and is calculated as the proportion of the voxel expressing unhindered diffusion along a given set of sticks, and restricted diffusion perpendicular to the same set of sticks. The ODI is a measure of tortuosity coupling an intracellular and extracellular space and models the extracellular space as hindered, gaussian anisotropic diffusion (very similar to, and hence highly correlated with, the tensor-derived FA). The amount of isotropic free volume within a voxel is measured by FISO and is usually proportional to the amount of CSF in a voxel. The intrinsic diffusivity was set to 1.7 μm² ms⁻¹. Note that if this intrinsic diffusivity values is suboptimal for gray matter as suggested by some prior work (Guerrero et al., 2019), it would be expected to overestimate absolute NDI values but have minimal effect on the age group differences of interest. Because there was no significant age group difference in the number of voxels that may have insufficient signal to accurately estimate the NODDI metrics (i.e., voxels with NDI > 0.99; (Emmenegger et al., 2021), no thresholding was applied. Outputs were transformed into atlas space where diffusion metrics in each of the hippocampal subfields were calculated by averaging the parameter maps using AFNI (Cox, 1996).

2.7. Statistical Analyses

All statistical analyses were performed in Python’s Scipy (Jones et al., 2001) or GraphPad Prism 9.1.0. Age group differences in diffusion metrics were computed using Student’s two-tailed t-tests (Student, 1908). Relationships between diffusion metrics and age or cognition scores were evaluated using ordinary least squares regression. Absolute subfield values are reported here unless stated otherwise. All diffusion parameters were evaluated independently given the high correlation within the diffusion metrics themselves (Supplementary figure S1). No nuisance covariates were included in the model and subfield volumes were not adjusted for head size to keep consistent with other metrics. In separate, but related work, we tested the efficacy of using an ANCOVA-based hippocampal volume correction and failed to find any effect and so did not include it here.

Statistical p-values were corrected for multiple comparisons using the Holm-Sidak test (Holm, 1979), unless running tests with a priori hypotheses. Receiver operating characteristic (ROC) curves and their corresponding areas under the curve (AUC) were calculated using statsmodels (Seabold and Perktold, 2010). ROC curves were used to quantify the ability of these diffusion metrics to predict age or cognitive performance, and additional information about these tests is provided under the respective results sections.

2.8. Data and code availability

Raw and preprocessed data supporting the findings of this study would be available upon reasonable request, made via email to the corresponding author (CS). The code used for analysis is in a GitHub repository (https://github.com/StarkLabUCI/NODDiffusion_ROCs) which will be made available upon acceptance for publication.

3. Results

We had previously shown that NDI of the DG/CA3 was increased in older adults and was negatively associated with RAVLT Delay (n = 38) (Radhakrishnan et al., 2020). We first reproduced these results in a larger population before diving into more complex analyses.

3.1. NDI of all hippocampal subfields is increased in older adults

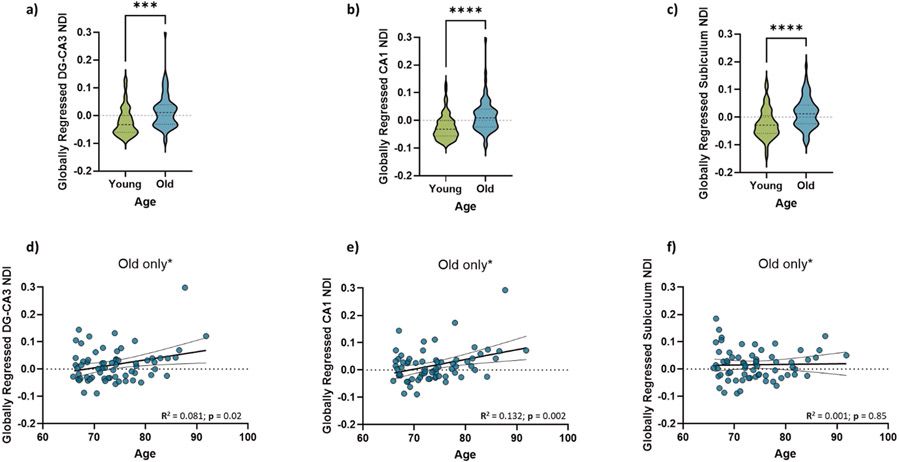
With this larger sample size, we found that the NDI of all the hippocampal subfields was greater in the older group as compared to the younger group (Two-sample t-test. DG/CA3: t = 5.30, p < 0.0001; CA1: t = 4.32, p < 0.0001; Subiculum: t = 4.10, p<0.0001). Moreover, the NDI of the DG/CA3 and CA1 subfields increased with age within the older subpopulation alone (Linear regression. DG/CA3: R² = 0.09, p = 0.04; CA1: R² = 0.179, p = 0.002; Subiculum: R² = 0.025, p = 0.277). Because of the lack of variance in age in the younger population and the absence of middle-aged data, we could not perform correlations with age in just the young group or across the lifespan, in a meaningful way. The relationship between all diffusion metrics studied and age can be found in Supplementary Tables S1 and S2.

We next asked whether these diffusion metrics followed a different pattern with age compared to the global average. To determine whether these relationships had any sort of selectivity towards the hippocampal subfields and were not just a consequence of age-related global gray matter decline, we modeled the subfield-specific NDI linearly against the average whole-brain gray matter NDI as described in our previous study (Radhakrishnan et al., 2020). The residuals of this highly correlated model were quantified as the “globally regressed” NDI for each subfield. Post global regression, we found that the older adults not only still had higher hippocampal NDI, but the globally regressed NDI for older adults was also largely positive, while that for the younger adults was largely negative. This suggests that younger adults have a hippocampal NDI that is well below the whole brain average, while older adults have a hippocampal NDI above the global average (Figure 1; Two-sample t-test. DG/CA3: t = 3.89, p = 0.0002; CA1: t = 4.63, p < 0.0001; Subiculum: t = 4.28, p<0.0001), consistent with a focused age-related NDI increase in the hippocampal subfields. The globally regressed NDI was also positively correlated with age within the older subpopulation in the DG/CA3 and CA1, but not in the subiculum. (Figure 1; Linear regression. DG/CA3: R² = 0.081, p = 0.019; CA1: R² = 0.132, p = 0.002; Subiculum: R² = 0.005, p = 0.847). To ensure that nothing about our sample was driving the observed effect and that any deviation from normality might be altering our results, we performed 1000 random samplings of 70% of our data. The resulting slopes were entirely consistent with our regression-based confidence intervals.

Figure 1:

(a-c) Hippocampal NDI is significantly greater in older adults as compared to young adults- for all three hippocampal subfields. Moreover, the NDI of the DG/CA₃ (d) and CA₁ (e) linearly increases with age within the older subpopulation, while that of the subiculum (f) does not.

We found no differences between hemispheric metrics for all subfields. The NDI was greater in biologically male participants compared to biologically female participants for all subfields (Two-sample t-test. DG/CA3: t = 2.04, p = 0.043; CA1: t = 2.036, p = 0.044; Subiculum: t = 3.74, p = 0.0003), but the previously described age effects remained significant after controlling for sex.

3.2. Hippocampal NDI is negatively associated with RAVLT Delay, and more weakly with the LDI

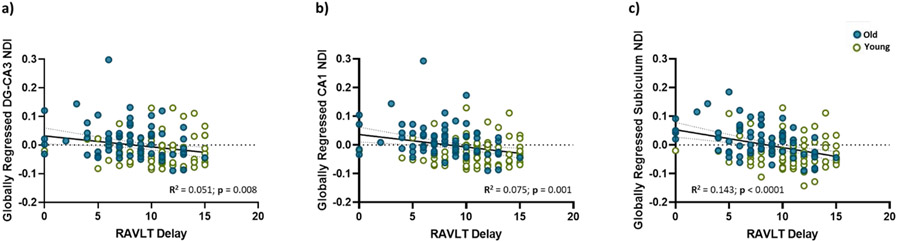
We were also able to replicate our previous finding that the hippocampal subfield NDI was negatively correlated with RAVLT performance, even after factoring in age as a regressor. While previously (Radhakrishnan et al., 2020), we observed reliable correlations in only the DG/CA3, here the NDI of all hippocampal subfields was negatively correlated with RAVLT delay, both before and after global regression, suggesting that this relationship in the hippocampus may not be a general brain-wide phenomenon (Figure 2). Within the older subpopulation, age was not significantly correlated with RAVLT Delay. However, the NDI of all hippocampal subfields still trended towards a negative relationship with the RAVLT delay in both the younger age group (Linear regression. DG/CA3: R² = 0.059, p = 0.007; CA1: R² = 0.075, p = 0.001; Subiculum: R² = 0.143, p < 0.0001) as well as the older age group (Linear regression. DG/CA3: R² = 0.054, p = 0.05; CA1: R² = 0.080, p = 0.021; Subiculum: R² = 0.195, p = 0.0002), with the subiculum NDI having the strongest relationship in both groups, suggesting that this relationship was beyond just an effect of age, and that hippocampal subfield NDI might be capable of capturing individual differences associated with cognition. The relationship between all diffusion metrics studied and RAVLT performance can be found in Supplementary Table S3.

Figure 2:

Globally regressed NDI is negatively associated with RAVLT Delay in all three hippocampal subfields, in both the younger and older groups, with the subiculum NDI having the strongest relationship with RAVLT performance. Green dots indicate the younger adults (18 – 29 years), while blue dots represent the older adults (65 – 92 years).

A more selective and weaker relationship was found between performance in the MST, as measured by the LDI, and the NDI of the hippocampal subfields. While the raw NDI of both the DG/CA3 and subiculum were negatively associated with LDI (Linear regression. DG/CA3: R² = 0.030, p = 0.043; CA1: R² = 0.021, p = 0.087; Subiculum: R² = 0.1, p = 0.0002), this relationship was only weakly significant in the subiculum after global regression (Linear regression. DG/CA3: R² = 0.002, p = 0.557; CA1: R² = 0.007, p = 0.346; Subiculum: R² = 0.03, p = 0.0434). As in the previous analysis, we performed 1000 samplings of 70% of our data for both RAVLT delay and LDI, and all resulting slopes were consistent with our confidence intervals. Interestingly, none of the raw diffusion metrics were significantly correlated with LDI (Supplementary Table S4).

3.3. Tensor, NODDI, and volumetric measures of hippocampal subfields can all successfully predict age group

The results in sections 3.1 and 3.2 reproduce previously reported findings in a larger dataset and establish that the relationships between age, NDI, and cognition are reliable and consistent. We next wanted to assess how NDI and other NODDI metrics compare to tensor metrics and coarse volume in their relationships with age and cognition. Note that some hippocampal diffusion metrics like AD and ADC were not correlated with their global averages, so we used only raw diffusion metrics (not globally regressed) for the rest of the study to be consistent across metrics.

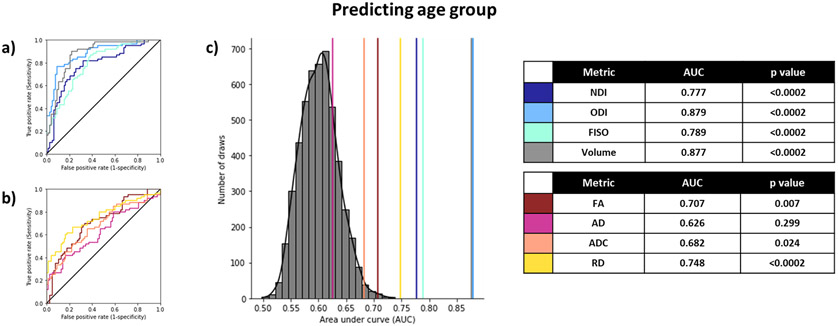
As an initial test, we sought to determine how well the various diffusion and volumetric measures from the hippocampus could classify participants into their age groups. To do this, we used ROC curves to evaluate the performance of each metric in accurately distinguishing between young and old groups. We calculated the AUC for each measure, by passing in the metric for each subfield split by hemisphere (for a total of 6 input features) and fitting a logistic regression model to derive the ROC and consequently predict the age group. We used hemisphere-specific metrics instead of bilateral ones simply because they generated the greatest AUC for most metrics (Supplementary Table S5). Since the input features were highly collinear (Supplementary Figure S1), we used the newton conjugate gradient method (Buckley, 1978; Knoll and Keyes, 2004) for optimization to prevent a non-Hessian matrix error. To calculate the null distribution and estimate the p-value, we conducted a permutation analysis by randomly shuffling the old/young labels and estimating the AUC over 5000 iterations using the volumetric input features (since the null distributions would essentially remain equivalent across all metrics). We found that most metrics studied could successfully distinguish between young and old age groups well above chance with just the six inputs from that metric in each hippocampal subfield alone (Figure 3), with the ODI and volume yielding the highest AUCs. All NODDI metrics and volume outperformed the tensor metrics. Given the difference in age between the groups and considering that aging causes very dramatic changes in the brain, it is unsurprising that all metrics, even volume, are sensitive to these changes.

Figure 3:

Using diffusion and structural metrics of the hippocampal subfields to predict age group. All metrics can successfully predict age group, with ODI, volume, and RD being the best predictors and AD being the worst predictor (a-b). The histogram represents the null distribution (random permutation of old/young labels), and the colored lines represent the AUC of each of the metrics from all 6 subfields (c). After Holm-Sidak correction for multiple comparisons, p-values < 0.0253 are considered statistically significant.

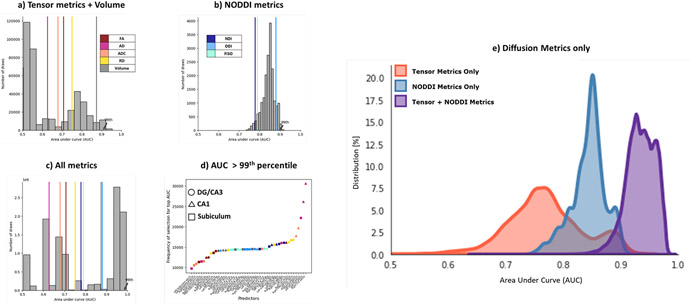
We then asked whether we could achieve higher prediction accuracy inputting a specific combination of these metrics, instead of a single metric from all subfields, and whether having the NODDI metrics posed any advantage over just the tensor metrics and volume in predicting age group. To answer this, we calculated the AUC for each combination of 6 input features from either a) a composite of tensor metrics and volume [${}_6^{30}C=593,775$ combinations] b) NODDI metrics [${}_6^{18}C=18,564$ combinations] or c) a composite of all metrics studied i.e., volume, tensor, and NODDI metrics [${}_6^{48}C=12,271,512$ combinations] (Figure 4 a-c). We found that the 99^th percentile of the AUC distribution from permuting over just the NODDI metrics (0.90) was comparable with that sampled from the tensor metrics and volume (0.91). However, the 99^th percentile of the AUC distribution of combinations of all metrics was significantly higher at 0.98. More specifically, the 99^th percentile of the Tensor metrics + Volume distribution was equal to the 57.57^th percentile of the All metrics distribution, while the 99^th percentile of the just NODDI distribution was equal to 57.38^th percentile of the All metrics distribution. To isolate this and understand it more completely, we then asked which individual features were most often contributing to the highest AUC values (> 99^th percentile) over all the combinations (Figure 4d). Within these best-performing combinations, we found all metrics and all subfields were consistently represented. Note that the distributions were non-Gaussian when volume was included in the selection features, due to the lack of collinearity of volume with the other metrics while using the newton conjugate gradient optimization algorithm (Supplementary Figure S1). The results remained consistent even after removing volume from the combinations and considering only the diffusion metrics (Figure 4e).

Figure 4:

A combination of all metrics results in the highest AUC peaks, compared to just the tensor metrics and volume or the NODDI metrics. Histograms represent the AUCs generated following an exhaustive n-choose-6 analysis to determine how well various combinations of 6 Region x Metric regressors could model age group. (a) Analysis of only the traditional tensor and volume metrics; (b) Analysis of only the NODDI metrics; and (c) Analysis of all metrics combined. The colored lines represent the AUCs of each metric from all 6 subfields. (d) Plot of the frequency of selection of a given Region x Metric combination in the top AUCs (above 99^th percentile) in the All metrics analysis. e) Histogram of distribution of AUCs with only combinations of the diffusion metrics (no volume included).

3.4. A combination of NODDI, tensor metrics, and volume predict RAVLT performance better than any of them alone

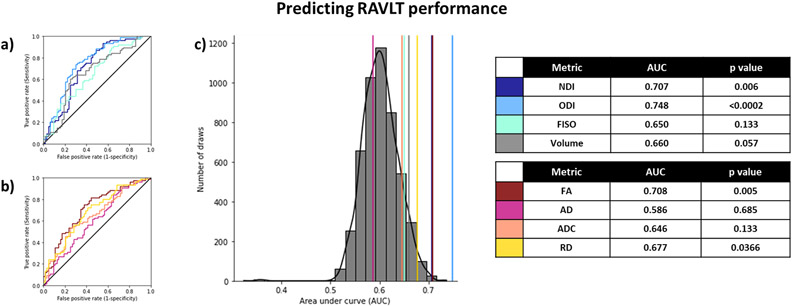
We then repeated the same analysis as the previous section, this time for predicting RAVLT delay. We binarized the RAVLT score at a threshold of 9, such that all those who scored higher than 9 were considered “high performing”, and those who scored 9 or below were considered “low performing”, consistent with previous findings for these age groups (Stark et al., 2013, 2010). Binarizing the RAVLT in this way also helped reduce noise that might arise from screener differences or individual participants having “off” days (it is more likely that a binarized RAVLT score would remain consistent over multiple testing days, compared to the continuous score, speaking to its robustness). While calculating the AUC for predicting high/low RAVLT delay this way in the entire subpopulation, using each metric from all 6 subfield features, we found that ODI, NDI, and FA were the best predictors of RAVLT performance (Figure 5).

Figure 5:

Using diffusion and structural metrics of the hippocampal subfields to predict RAVLT performance (<9). ODI, NDI, and FA were the best predictors of RAVLT performance. The histogram (c) represents the null distribution (randomly permuting the high/low RAVLT labels), and the colored lines represent the AUC of each of the metrics from all 6 subfields. After Holm-Sidak correction for multiple comparisons, p-values < 0.0253 are considered statistically significant.

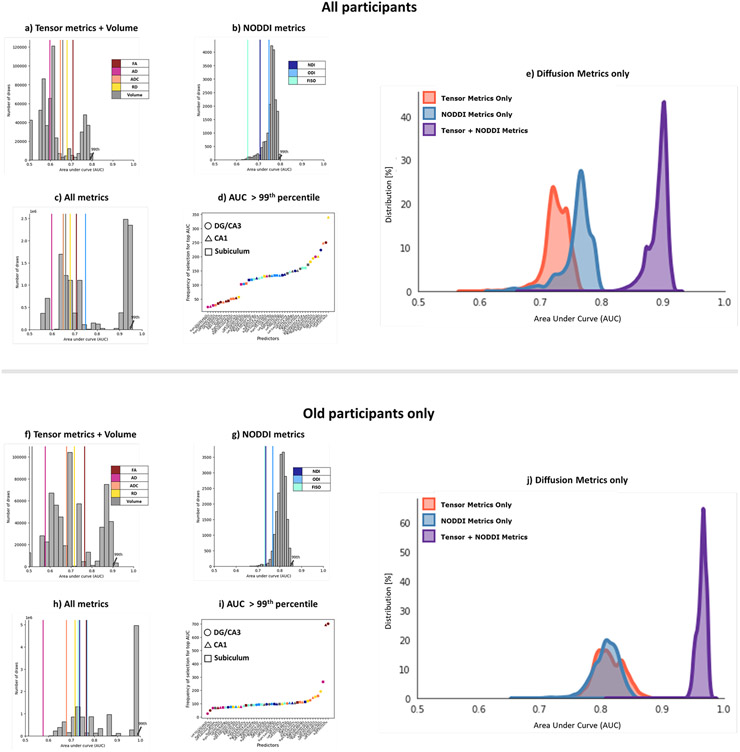
We next performed the same ${}_6^{48}C$ analysis of all possible combinations of metrics. Notably, when examining AUCs resulting from combinations of only NODDI metrics and AUCs resulting from only tensor+volume metrics, we observed similar distributions with AUCs at the 99^th percentile of 0.79 and 0.78 respectively. However, when combinations of NODDI and Tensor metrics + volume metrics were included, we observed a distribution with the AUC at the 99^th percentile = 0.95 (Figure 6), and the AUCs of the separate distributions were both equal to about the ~57^th percentile of the all metrics distribution. This indicates that NODDI and Tensor metrics + volume, while correlated, contain independent aspects of variance that are useful in modeling RAVLT performance. As expected from these results, the input features that most frequently contributed to the top AUCs spanned all metrics and all subfields. This effect remained even when observing the diffusion metrics alone, without volume.

Figure 6:

Combining NODDI and tensor metrics results in a significantly higher AUC after selecting for best-performing features in predicting high/low RAVLT performance, as compared to just traditional measures or just NODDI measures both when examining the full study population (a-e) and when examining only the older subpopulation (f-j). (a, f) Analysis of only the traditional tensor and volume metrics; (b, g) Analysis of only the NODDI metrics; and (c, h) Analysis of all metrics combined. Histograms represent the distribution of AUCs generated following an exhaustive n-choose-6 analysis to determine how well various combinations of 6 Region x Metric regressors could model high/low RAVLT group. The colored lines represent the AUCs of each metric from all 6 subfields. (d, i) Plot of the frequency of selection of a given Region x Metric combination in the top AUCs (above 99^th percentile) in the All metrics analysis. e, j) Histogram of distribution of AUCs with only combinations of the diffusion metrics (no volume included).

Given the correlation between age and RAVLT performance, it is certainly possible that our prediction of RAVLT status is driven by our ability to predict age group. To assess whether these metrics were capturing cognitive differences beyond just a function of age, we repeated this analysis separately in the younger and older subpopulations. In the older group, we found that these results were just as reliable (99th percentile of AUC distribution with Tensor metrics + Volume: 0.90; NODDI metrics: 0.85; All metrics: 0.98). The peak AUCs of all conditions were greater when predicting RAVLT delay in just the older group compared to the entire study sample. Notably, the features that contributed to the highest AUCs here were not in the same order as with the entire sample size but still appeared to span across all metrics and subfields evenly. In the younger group, we found that combining the metrics did not result in a significantly higher AUC distribution over just the tensor metrics or NODDI metrics (99th percentile of AUC distribution with Tensor metrics + Volume: 0.72; NODDI metrics: 0.71; All metrics: 0.70), possibly due to the low number of poor performers (75% of the high-performing RAVLT participants belong to the younger age group), or because these metrics weren’t sensitive to microstructural properties that contributed to low RAVLT delay at a young age.

3.5. A combination of NODDI and tensor metrics predicts MST performance better than either of them alone

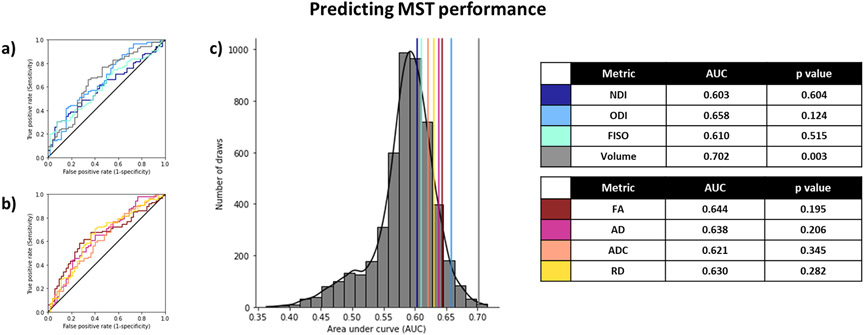
We also found similar results when predicting MST performance, as relayed by the LDI. Here, we binarized the LDI at a threshold of 1.25, to match the proportion used in our RAVLT analysis. We found that the AUCs for predicting high/low LDI were lower overall than the corresponding high/low RAVLT or age group (Figure 7) when restricting ourselves to individual metrics from all 6 subfields. Interestingly, only volume predicted MST scores better than chance.

Figure 7:

Using diffusion and structural metrics of the hippocampal subfields to predict LDI (<1.25). Only volume could predict MST performance slightly better than chance. The histogram represents the null distribution (randomly permuting the high/low labels), and the colored lines represent the AUC of each of the metrics from all 6 subfields. After Holm-Sidak correction for multiple comparisons, p-values < 0.0253 are considered statistically significant.

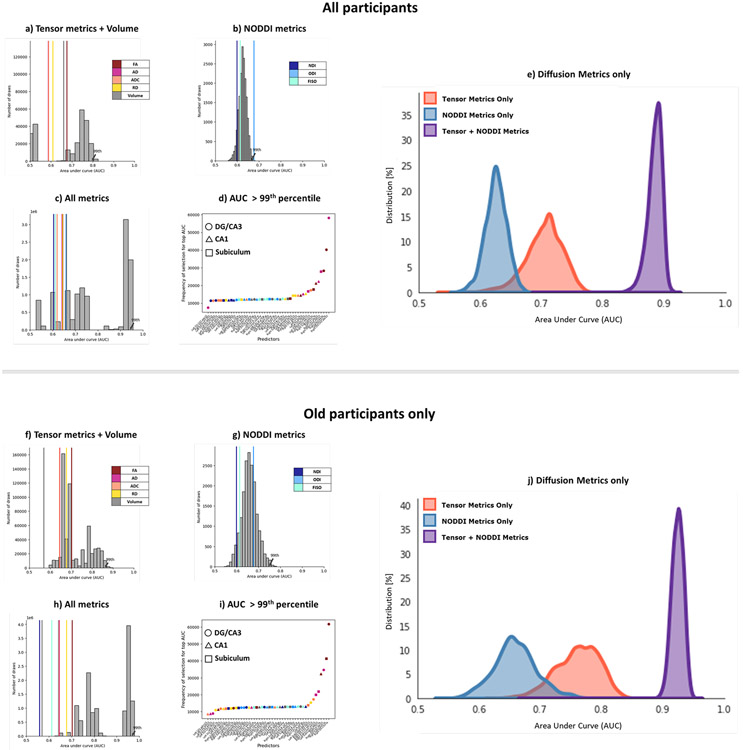
Turning to the n-choose-6 permutations, we observed a familiar pattern. The 99th percentile of the AUC distribution obtained from using just the NODDI metrics or just the Tensor metrics + Volume were 0.67 and 0.80, respectively, but using All metrics resulted in a bimodal distribution with a 99th percentile AUC of 0.94 (Figure 8), again with the separate distributions having their 99^th percentile equal to below the 60^th percentile in the complete distribution. As with RAVLT delay, the most informative input features spanned all metrics across all subfields. We were also able to reproduce these results in just the older subgroup (99th percentile of AUC distribution with Tensor metrics + Volume: 0.86; NODDI metrics: 0.75; All metrics: 0.97). As with RAVLT performance, combining the metrics did not help the AUC in the younger subgroup (99th percentile of AUC distribution with Tensor metrics + Volume: 0.73; NODDI metrics: 0.77; All metrics: 0.69). These results again indicate that while NODDI and traditional tensor metrics can be correlated with each other, they provide unique information and contributions to the variance that can be used to model memory performance.

Figure 8:

Combining NODDI and tensor metrics results in a significantly higher AUC after selecting for best-performing features in predicting high/low MST performance, as compared to just traditional measures or just NODDI measures, in both the full study population (a-e), as well as in the older subpopulation (f-j). (a, f) Analysis of only the traditional tensor and volume metrics; (b, g) Analysis of only the NODDI metrics; and (c, h) Analysis of all metrics combined. Histograms represent the distribution of AUCs generated following an exhaustive n-choose-6 analysis to determine how well various combinations of 6 Region x Metric regressors could model high/low RAVLT group. The colored lines represent the AUCs of each metric from all 6 subfields. (d, i) Plot of the frequency of selection of a given Region x Metric combination in the top AUCs (above 99^th percentile) in the All metrics analysis. e, j) Histogram of distribution of AUCs with only combinations of the diffusion metrics (no volume included).

4. Discussion

In this study, we show that at least one model of multi-shelled diffusion-weighted imaging (NODDI) can provide significant benefits in determining aging-associated microstructural differences in the hippocampal subfields and their cognitive consequences, when used in conjunction with tensor and volume measures. We first reproduced our previous studies in a larger sample size (about three-fold of that reported in our prior publications) showing that the NODDI metric NDI is increased in older adults, and this increase may be partially driving aging-associated memory decline. The ability to reproduce these effects across independent populations and study centers speaks to the robustness and reliability of these relationships, which is a major concern in neuroimaging research (Poldrack et al., 2017).

We also found that NDI increases with age within the older population alone (ages 65 – 92) in the DG-CA3 and CA1, but not in the subiculum. However, the negative relationship between NDI and RAVLT performance was strongest in the subiculum in both the entire study population as well as the older subgroup alone, potentially suggesting a subfield-specific pattern of NDI differentially associating with cognition at the outset of aging. The other hippocampal diffusion metrics derived from both NODDI and the tensor models had selective relationships with age and RAVLT delay and LDI across the subfields (see supplementary material) that are consistent with prior reports in the literature (Fukutomi et al., 2019; Mortimer et al., 2004; Müller et al., 2005; Nazeri et al., 2015; Nobis et al., 2019; Yassa et al., 2011). These similar results across subfields may, at least in part, be due to inherent smoothing when transforming between high-resolution ROI segmentations (1mm³) and lower resolution diffusion images (1.7mm³), performing the segmentations using only T1-weighted images (Wisse et al., 2021), or using diffusion data that is not ideally suited to subfield work but is in higher resolution than what is often used. Moreover, our prediction models rely on highly correlated input features, across both metrics and subfields, which puts us at risk of overfitting data. While we theorize that differences in segmentation would not change the main findings of this study, future work examining differences as a function of methodological details would be valuable. Our finding of reliable whole hippocampal effects but little in the way of subfield-specific effects should not be taken as evidence of absence of subfield differentiation, although it does suggest that many studies can be effectively conducted without specific attention to the subfields (or without meticulous attention to the methodological details). Moreover, because we did not observe anything that would suggest a cancelation of effects via opposing patterns across subfields, future work using lower resolutions and even more blending of signals across subfields can still make clear contributions at the level of the hippocampus itself.

Also consistent with several previous studies (Aggarwal et al., 2015; Assaf, 2019; Leuze et al., 2014; Truong et al., 2014), we found that even the most basic diffusion metrics like FA and RD were sensitive to age and cognitive measures. They could detect specific microstructural properties of gray matter and were mainly better than volume in detecting individual cognitive differences. Interestingly, relationships between these diffusion metrics and aging/cognition were largely independent of hippocampal volume. Moreover, despite being highly correlated with each other, none of the diffusion metrics were associated with volume in any of the subfields. These observations suggest that hippocampal microstructure as relayed by the diffusion metrics, and macrostructure measured by subfield volume, could represent independent processes in normal aging.

Not only could diffusion metrics be reliably used in gray matter to make inferences about aging and cognition, we also found that including NODDI metrics greatly improved the ability of our statistical models to predict age and cognition. We find that a combination of NODDI and tensor measures consistently result in better age group predictions than either modality by itself. Interestingly, when using ROC analysis to predict memory performance, we observed that while combinations of just tensor metrics and volume, or just NODDI metrics yielded laudable AUCs, combining the tensor metrics, volume, and NODDI metrics could result in a near-perfect prediction model. Additionally, when predicting both RAVLT and MST performance, this effect only got stronger when looking within just the older subpopulation (resulting in AUCs of over 0.98). This enhancement could be because the neurobiological properties that help define cognitive performance are more likely to be consistent under the common effect of aging, as compared to a much wider age range.

The increase in the predictive power of the model in the older group also demonstrates that these metrics could be capturing neurobiological properties that go beyond just the dramatic effect of age and might be sensitive to individual differences within this age group as well. This could be attributed to the idea that NODDI and tensor metrics may be capturing related but neurobiologically distinct properties associated with aging. The ability of NODDI to separate intracellular and extracellular spaces might result in sensitivity to properties like inflammation and cellularity (Garcia-Hernandez et al., 2020 ; Yi et al., 2019) that complement tensor measures of anisotropy and diffusivity. While the biological implications of these diffusion metrics require much more examination, the inability of just volume to be a relatively strong predictor of cognition in both the entire population as well as just the older adults emphasizes that aging-associated cognitive decline is a function of more microstructural changes.

The ability of the combined diffusion metrics to successfully predict LDI (Figure 8) despite none of them being correlated directly with the measure also raises an important question about how we approach relationships between neuroimaging measures and cognition. Different patterns of cytoarchitecture could result in the exact same value for certain diffusion metrics but might not result in the exact same value for all diffusion metrics.

Most prior works attempting to tie implicit neurobiological properties with diffusion imaging have tended to look at these relationships separately within each metric. However, as demonstrated in this paper, treating these varied diffusion metrics as a unique “signature” for each participant can generate more specific models that can predict behavior successfully. However, even with such a method, extreme caution must be taken when speculating on the neurobiological implications of these diffusion metrics.

The results in this paper collectively present a strong case in support of including multi-shelled diffusion sequences that allow analysis like NODDI modelling in study protocols, despite the increase in acquisition time. The full diffusion sequence here required ~16 minutes to acquire both phase-encoding directions. However, excellent results are still possible with diffusion data from one phase encoding and only b0 images from the reverse (or a separate phase map), reducing the acquisition time to ~9 minutes. Adding just a single shell and a modest number of directions over typical DTI protocols allowed for NODDI analyses that generated metrics that immensely improved the predictive power of our model, suggesting that combining higher-order models with tensor metrics could uncover large effects not discernible by either analysis technique alone. Of course, including multi-shell acquisition protocols also opens up analysis to other complex models (even those yet to be created) that could be more sensitive to specific microstructural properties in gray matter. We posit that these results observed in hippocampal aging likely extend to other domains of interest. Researchers studying the microstructural mechanisms of both healthy developmental stages, as well as various neuropsychiatric illnesses, could benefit from implementing NODDI in their protocols. In such studies, however, it is important to identify the “domain of validity” where both the assumptions and interpretations of these diffusion metrics are accurate (Lampinen et al., 2019), as diffusion indices tend to be very context-specific. Seemingly similar changes in diffusion metrics may have different anatomical implications across pathologies, age groups, and even across brain regions. For example, we report consistent and reproducible increases in hippocampal NDI with age. However, the NDI of other regions, especially white matter, have been shown to decrease with age with similar associated cognitive decline (Merluzzi et al., 2016). Moreover, conditions like schizophrenia and bipolar disorder present decreased levels of hippocampal NDI, with potentially very different neurobiological implications (Nazeri et al., 2017). More research examining gray matter microstructure using these methods across the whole brain, in both the healthy lifespan and disease, can help in developing powerful signatures for both developmental milestones as well as neurological illnesses. This is another reason we advocate for the inclusion of multi-shell acquisition schemes, that allow for analysis like NODDI modelling, in large-scale data collection efforts.

Of note, NODDI is not the only analysis technique made possible with multiple shells. We use NODDI here as one example of a multi-shell technique and demonstrate that it can improve sensitivity to specific microstructural properties related to aging and cognition. An interesting question for future research is the extent to which other multi-shell (e.g., diffusion kurtosis imaging (Steven et al., 2014), multiple Q-shell imaging (Descoteaux et al., 2011)) or even single-shell (e.g., bi-tensor models (Pasternak et al., 2009), Q-ball imaging (Tuch, 2004), constrained spherical deconvolution (Nath et al., 2020)) models perform similarly to NODDI. However, this will first require validation of these approaches in gray matter as they have been designed to improve sensitivity to white matter microstructure. We speculate that the advantages of NODDI observed here (and potentially observed with related multi-shell or single-shell bi-tensor models) may be because it separately estimates free water diffusion. In line with this view, our group has previously shown that single tensor metrics are worse at predicting age after accounting for free diffusion by excluding voxels with low tissue content (i.e., those with high free diffusion) (Venkatesh et al, 2020). This suggests that single-tensor metrics are significantly influenced by free diffusion, which may reflect partial volume effects or neurodegeneration in aging. Of note, NODDI outperformed both the tensor metrics even after accounting for free water when predicting age and memory performance, supporting an advantage for multi-shell approaches as shown in the current study. Studies that compare metrics derived from such techniques to the metrics used in this paper may reveal valuable information on the right analysis technique to use for a given context.

While our spatial resolution is close to its optimum for a 3T scanner, one could argue that the extra time required to scan the additional shell could instead be utilized elsewhere- like in increasing angular resolution. Previous studies have explored the effects of different acquisition schemes on both single-shell and multi-shell metrics in white matter and have consistently shown that the value of adding extra directions begins to taper off at around n(directions) = ~60 for a single shell (Li et al., 2020; Schilling et al., 2018; Tournier et al., 2013). The acquisition scheme used in this study was optimized for these observations and included 64 directions. Increasing scan times, even by small amounts, result in many issues in studies involving children or participants with neurological conditions. To accommodate for research where long scan times are not feasible, more work that examines the benefits of additional shells over additional directions (angular resolution) or higher spatial resolution is required as advantages of these acquisition schemes have been demonstrated in white matter. Moreover, since the data presented here are cross-sectional, we cannot conclude that NODDI metrics would display the same advantage when studying the temporal dynamics of phenomena like aging. Longitudinal studies and studies monitoring interventions (Eaton-Rosen et al., 2015; Kamiya et al., 2020; Radhakrishnan et al., 2021) could greatly enhance our understanding of the benefits of these metrics.

Another limitation is that our models binarize age and continuous cognitive measures, so we cannot evaluate whether NODDI metrics would complement tensors and volume so clearly when predicting absolute age and cognition. However, these binarized cognitive scores are far more robust than the continuous scores, and much less prone to noise or sample bias. Though this study is fairly well-balanced by sex, it is also important to acknowledge the role of other demographic differences (like race and socioeconomic status) often rising from volunteer and selection biases in most human neuroimaging studies.

In conclusion, we have demonstrated that NODDI measures complement tensor metrics and volume when capturing age and cognition related information. The extra diffusion-weighted shell needed for NODDI provided predictive and neurobiologically relevant information that are ancillary to but seemingly distinct from what the tensor measures provide. NODDI metrics offer obvious value beyond and/or in conjunction with traditional tensor and volumetric measures when studying gray matter microstructure and might even be able to explain individual differences in cognition or behavior.

Highlights:

• Diffusion metrics from multi-shell sequences are reliable and sensitive to gray matter microstructure.

• NODDI complements traditional tensor and volume measures when predicting age and cognition.

• NODDI metrics greatly improve the predictive power of models estimating individual differences.