Deriving confidence intervals for mutation rates across a wide range of evolutionary distances using FracMinHash

Abstract

Sketching methods offer computational biologists scalable techniques to analyze data sets that continue to grow in size. MinHash is one such technique to estimate set similarity that has enjoyed recent broad application. However, traditional MinHash has previously been shown to perform poorly when applied to sets of very dissimilar sizes. FracMinHash was recently introduced as a modification of MinHash to compensate for this lack of performance when set sizes differ. This approach has been successfully applied to metagenomic taxonomic profiling in the widely used tool sourmash gather. Although experimental evidence has been encouraging, FracMinHash has not yet been analyzed from a theoretical perspective. In this paper, we perform such an analysis to derive various statistics of FracMinHash, and prove that although FracMinHash is not unbiased (in the sense that its expected value is not equal to the quantity it attempts to estimate), this bias is easily corrected for both the containment and Jaccard index versions. Next, we show how FracMinHash can be used to compute point estimates as well as confidence intervals for evolutionary mutation distance between a pair of sequences by assuming a simple mutation model. We also investigate edge cases in which these analyses may fail to effectively warn the users of FracMinHash indicating the likelihood of such cases. Our analyses show that FracMinHash estimates the containment of a genome in a large metagenome more accurately and more precisely compared with traditional MinHash, and the point estimates and confidence intervals perform significantly better in estimating mutation distances.

One strategy scientists use when analyzing large data sets is to create a low-dimensional “sketch” or “fingerprint” of their data that allows fast, but approximate answers to their query of interest. Such sketching-based approaches in recent years have been successfully applied to a variety of genomic and metagenomic analysis tasks, due in large part to such methods incurring low computational burden when applied to large data sets. For example, Mash (Ondov et al. 2016) is a MinHash (Broder 1997)-based approach that was used to characterize the similarity between all pairs of RefSeq genomes in <30 CPU h. Such efficiency gains are due primarily to sketching-based approaches recording a small subsample (or modification thereof) of the data in such a fashion that some distance metric or similarity measure is approximately preserved, a process called a locality sensitive hashing scheme. In bioinformatics, this has resulted in improvements to error correction (Miclotte et al. 2015; Sahlin and Medvedev 2021), assembly (Birol et al. 2009; Chin and Khalak 2019; Ghosh and Kalyanaraman 2019; Ekim et al. 2021), alignment (Jain et al. 2018; Li 2018), clustering (Zhang et al. 2014; Crusoe et al. 2015; Koslicki and Zabeti 2019; Pierce et al. 2019), classification (Breitwieser et al. 2018; LaPierre et al. 2019, 2020), and so on. Importantly, the accuracy and efficiency of sketching approaches can frequently be characterized explicitly, allowing practitioners to balance between efficiency improvements and accuracy. Often, these theoretical guarantees dictate that certain sketching approaches are well suited only to certain kinds of data. For example, MinHash, which is used in many of the aforementioned applications, has been shown to be particularly well suited to quantify the similarity of sets of roughly the same size but falters when sets of very different sizes are compared (Koslicki and Zabeti 2019). This motivated the introduction of the containment MinHash, which used a MinHash sketch of the smaller set, with an additional probabilistic data structure (a Bloom filter) (Bloom 1970) to store the larger set. Although this improved speed and accuracy, this approach can become quite inconvenient for large sets owing to requiring a bloom filter to be created for the larger of the two sets.

To ameliorate this, an approach called the FracMinHash was recently introduced (Irber 2020; Irber et al. 2022) that uses a MinHash hash selection approach but allows sketch size to scale naturally with the size of the underlying data, similar to ModHash dynamic scaling (Broder 1997). These properties allow both Jaccard and containment estimation between FracMinHash sketches, extending the computational advantages of MinHash sketches beyond similar-sized genome comparisons to sequencing data sets of all types. Most notably, FracMinHash enables large-scale metagenome analyses, including genomic and metagenomic similarity assessment, metagenomic taxonomic classification, streaming database searches, and outbreak detection via genomic surveillance (Pierce et al. 2019; Viehweger et al. 2021). FracMinHash sketching is implemented in a software package called sourmash (Brown and Irber 2016). Independently, and more recently, the same concept of FracMinHash was introduced with the name universe minimizer (Ekim et al. 2021).

Although there is ample computational evidence for the superiority of FracMinHash compared with the classic MinHash, particularly when comparing sets of different sizes, no theoretical characterization about the accuracy and efficiency of the FracMinHash approach has yet been given. In this paper, we address this missing characterization of accuracy and efficiency by deriving a number of theoretical guarantees. In particular, we show that the FracMinHash approach, as originally introduced, requires a slight modification in order to become an unbiased estimator of the containment index (in terms of expected value). After this, we characterize the statistics of this unbiased estimator and derive an asymptotic normality result for FracMinHash. This in turn allows us to derive confidence intervals and hypothesis tests for this estimator when considering a simple mutation model (which is related to the commonly used average nucleotide identity [ANI] score). We also characterize the likelihood of experiencing an edge case when analyzing real data, which allows us to provide a level of confidence along with the estimated containment index. Finally, we support the theoretical results with additional experimental evidence and compare our approach to the frequently used Mash distance (Ondov et al. 2016). Many of these theoretical findings have already been implemented into the sourmash (Brown and Irber 2016) computational package (see https://github.com/sourmash-bio/sourmash/pull/1967 and https://github.com/sourmash-bio/sourmash/pull/2032).

Methods

In this section, we describe theoretical analyses of the containment index using FracMinHash. For the sake of continuity from a reader's perspective, we have included proofs of all theorems in the Supplemental Materials (Sec. A.3).

FracMinHash and its statistics

We begin by formally defining a FracMinHash sketch by slightly modifying the definition of Irber et al. (2022). We aim to compare two sequences by computing the containment index from their corresponding FracMinHash sketches.

Definitions and preliminaries

We recall the definition of FracMinHash given by Irber et al. (2022). Given two arbitrary sets A and B, which are subsets of a domain Ω, the containment index C(A, B) is defined as $C\left(A,B\right):={\displaystyle \frac{\left|A\cap B\right|}{\left|A\right|}}$. Let h be a perfect hash function h : Ω → [0, H] for some H ∈ ℝ. For a scale factor s, where 0 ≤ s ≤ 1, a FracMinHash sketch of a set A is defined as follows:

$$\mathbf{F}\mathbf{R}\mathbf{A}{\mathbf{C}}_s\left(A\right)=\left\{h\left(a\right)\mid a\in A\mathrm{and}h\left(a\right)\le Hs\right\}.$$ (1)

The scale factor s is an easily tunable parameter that can modify the size of the sketch. Using this FracMinHash sketch, we define the FracMinHash estimate of the containment index ${\hat{C}}_{\mathrm{frac}}\left(A,B\right)$ as follows:

$${\hat{C}}_{\mathrm{frac}}\left(A,B\right):={\displaystyle \frac{\left|\mathbf{F}\mathbf{R}\mathbf{A}{\mathbf{C}}_s\left(A\right)\cap \mathbf{F}\mathbf{R}\mathbf{A}{\mathbf{C}}_s\left(B\right)\right|}{\left|\mathbf{F}\mathbf{R}\mathbf{A}{\mathbf{C}}_s\left(A\right)\right|}.}$$ (2)

Simply speaking, we want to compute ${\hat{C}}_{\mathrm{frac}}\left(A,B\right)$ because the sketches are considerably smaller than the original sets A and B, and we want ${\hat{C}}_{\mathrm{frac}}\left(A,B\right)$ to accurately approximate C(A, B).

For notational simplicity, let us define X_A: = |FRAC_s(A)|. We observe that if one views h as a uniformly distributed random variable, we have that X_A is distributed as a binomial random variable: $X_A\sim Binom\left(\left|A\right|,s\right)$. In practice, hashing libraries use a large enough hash value space (i.e., 2⁶⁴) and well-enough hash functions that the assumptions on h are mostly valid. Furthermore, if $A\cap B\ne \mathrm{\varnothing }$, where both A and B are nonempty sets and one is not a subset of the other, then $X_{A\mathrm{\setminus }B}$ and $X_{A\cap B}$ are independent when the probability of success, s, is strictly smaller than one. Using these notations, the expectation of ${\hat{C}}_{\mathrm{frac}}\left(A,B\right)$ is given by Theorem 1, recapitulated from Irber et al. (2022) for completeness.

Theorem 1.

For 0 < s < 1, if A and B are two nonempty sets such that $A\mathrm{\setminus }B$ and $A\cap B$ are nonempty, the following holds:

$$E\left[{\hat{C}}_{frac}\left(A,B\right){𝟙}_{\left|\mathbf{F}\mathbf{R}\mathbf{A}{\mathbf{C}}_s\left(A\right)\right|>0}\right]={\displaystyle \frac{\left|A\cap B\right|}{\left|A\right|}\left(1-{\left(1-s\right)}^{\left|A\right|}\right).}$$

In light of Theorem 1, we note that ${\hat{C}}_{\mathrm{frac}}\left(A,B\right)$ is not an unbiased estimate of C(A, B): The expected value of ${\hat{C}}_{\mathrm{frac}}\left(A,B\right)$ is not equal to C(A, B). This may explain the observations of Irber (2020) that showed the uncorrected version in Equation 2 leads to suboptimal performance for short sequences (e.g., viruses). However, for sufficiently large |A| and s, the bias factor (1 − (1 − s)^|A|) is sufficiently close to one. Alternatively, if |A| is known (or estimated, e.g., by using HyperLogLog or the estimate in Sec. A.6) (Flajolet et al. 2007), then

$$C_{\mathrm{frac}}\left(A,B\right):={\displaystyle \frac{\left|\mathbf{F}\mathbf{R}\mathbf{A}{\mathbf{C}}_s\left(A\right)\cap \mathbf{F}\mathbf{R}\mathbf{A}{\mathbf{C}}_s\left(B\right)\right|}{\left|\mathbf{F}\mathbf{R}\mathbf{A}{\mathbf{C}}_s\left(A\right)\right|\left(1-{\left(1-s\right)}^{\left|A\right|}\right)}{𝟙}_{\left|\mathbf{F}\mathbf{R}\mathbf{A}{\mathbf{C}}_s\left(A\right)\right|>0}}$$ (3)

is an unbiased estimate of the containment index C(A, B). Throughout the rest of the paper, we will refer to the debiased C_frac(A, B) as the fractional containment index.

Mean and variance of C_frac(A, B)

The expectation of C_frac(A, B) is as follows.

Theorem 2.

For 0 < s < 1, if A and B are two distinct sets such that $A\mathrm{\setminus }B$ and $A\cap B$ are nonempty, the expectation of C_frac(A, B) is given by

$$E\left[C_{frac}\left(A,B\right)\right]={\displaystyle \frac{\left|A\cap B\right|}{\left|A\right|}.}$$ (4)

Proof.

This follows directly from Equation 3 and Theorem 1.

We now turn to determining the variance of C_frac(A, B). Ideally, we can do so by using the multivariate probability mass function of $X_{A\cap B}$ and $X_{A\mathrm{\setminus }B}$. However, we found that doing so does not result in a closed-form formula. Therefore, we use Taylor expansions to approximate the variance.

Theorem 3.

For $n=\left|A\cap B\right|$ and $m=\left|A\mathrm{\setminus }B\right|$ where both m and n are nonzero, a first-order Taylor series approximation gives

$$Var\left[{\hat{C}}_{frac}\left(A,B\right)\right]\approx {\displaystyle \frac{mn\left(1-s\right)}{s{\left(m+n\right)}^3}.}$$

Using the results of Theorem 3 and Equation (3), we have the variance of C_frac(A, B) as follows.

Corollary 1.

For $n=\left|A\cap B\right|$ and $m=\left|A\mathrm{\setminus }B\right|$, where both m and n are nonzero, a first-order Taylor series approximation gives

$$Var\left[C_{frac}\left(A,B\right)\right]\approx {\displaystyle \frac{mn\left(1-s\right)}{s{\left(m+n\right)}^3{\left(1-{\left(1-s\right)}^{\left|A\right|}\right)}^2}.}$$

Proceeding in the same fashion, we can obtain series approximations of arbitrarily high order owing to the binomial distribution having finite central moments of arbitrary order. However, we found that the higher-order expansion derivations are tedious and long, whereas the results obtained using first-order approximation are both simple and accurate enough in practice.

Asymptotic normality of C_frac(A, B)

We next prove that C_frac(A, B) is asymptotically normal. We use the delta method (Agresti 2012) combined with the De Moivre–Laplace theorem, which guarantees asymptotic normality of $X_{A\cap B}$ and $X_{A\mathrm{\setminus }B}$, and because $g\left(x,y\right)={\displaystyle \frac{x}{x+y}}$ is a function that is twice differentiable, setting $x=X_{A\cap B}$ and $y=X_{A\mathrm{\setminus }B}$ satisfies all requirements of using the delta method on g(x, y), which gives us the following result:

Theorem 4.

For $g\left(x,y\right)={\displaystyle \frac{x}{x+y}}$, $n=\left|A\cap B\right|$ and $m=\left|A\mathrm{\setminus }B\right|$, where both m and n are nonzero,

$$\sqrt{n+m}\left(g\left(X_{A\cap B},X_{A\mathrm{\setminus }B}\right)-g\left(n,m\right)\right)\underset{n,m\to \mathrm{\infty }}{\overset{\mathcal{D}}{\to }}\mathcal{N}\left(0,{\displaystyle \frac{mn\left(1-s\right)}{{\left(m+n\right)}^{3}s}}\right).$$

We note that additional statistical quantities can easily be derived. For example, in Supplemental Material Section A.5, we provide concentration inequalities that show theoretically how little C_frac(A, B) deviates from its expected value. Supplemental Material Section A.6 provides a simple way to calculate the number of distinct k-mers from a given sketch. Lastly, Supplemental Material Section A.7 shows how to compute (and debias) a Jaccard estimate from FracMinHash sketches.

Statistics of C_frac(A, B) under simple mutation model

In the previous section, we introduced C_frac(A, B) and derived its statistics. In this section, we use these results and connect C_frac(A, B) to a biologically meaningful quantity: the average nucleotide identity (ANI) and mutation rate. We do this by assuming a simple mutation model, in which each nucleotide of some sequence S is independently mutated at a fixed rate, p, resulting in the mutated sequence S′, which has an expected ANI of 1 − p with S. This model was recently introduced by Blanca et al. (2022), where it was quantified how this mutation process affects the k-mers in S.

Before mentioning the details of the mutation model, it is important to note that there are other models of evolution, for example, TK4 and TK5 models (Takahata and Kimura 1981), the general time reversible (GTR) model (Tavaré 1984), and Sueoka's model (Sueoka 1995). These vary in the number of parameters used, as well as the degree of complexity. In this work, we consider the simple mutation model because (1) the statistics of k-mers under this model are already well explored, and (2) it allows us to connect C_frac(A, B) and mutation rate p directly, which would not be the case if we considered one of these more nuanced models. The mutation model we use, even though simple enough to be mathematically tractable, is more realistic that the Poisson model assumed by Mash (Ondov et al. 2016), which assumes that all k-mers are mutated independently, where in reality, one point mutation can affect up to k number of k-mers. Our experiments reveal that even in case of real genomes, where the lengths of two sequences can be widely dissimilar and clearly the assumptions of the simple mutation model are violated, our approach can accurately determine the mutation rate (and ANI) between two real-world sequences.

Preliminaries

Here, we closely follow the exposition contained in the work by Blanca et al. (2022). Let L > 0 be a natural number that denotes the number of k-mers in some string S. A k-span K_i is the range of integers [i, i + k − 1], which denotes the set of indices of the sequence S where a k-mer resides. Fix a mutation rate p, where 0 < p < 1. The simple mutation model considers each position in i = 1, …, L + k − 1 and, with probability p, marks it as mutated. A mutation at location i affects the k-spans K_{max (1,i−k+1)}, …, K_i. Let N_mut be a random variable defined to be the number of affected/mutated k-spans. We use q = 1 − (1 − p)^k to express the probability that a k-span is mutated. Note that 1 − p corresponds precisely to the expected ANI between a sequence S and its mutated counterpart S′.

Given a nonempty sequence S on the alphabet {A, C, T, G} and a k-mer size such that each k-mer in S is unique, let A represent the set of all k-mers in S, and let L = |S| − k + 1. Now, we apply the simple mutation model to S via the following: If for any i ∈ [1, …, L + k − 1], this index is marked as mutated, let $S_i^{\mathrm{\prime }}$ be some nucleotide in $\left\{A,C,T,G\right\}\mathrm{\setminus }\left\{S_i\right\}$; otherwise, let $S_i^{\mathrm{\prime }}=S_i$. Let B represent the set of k-mers of S′, and we assume that S′ does not contain repeated k-mers either. In summary, A denotes the set of k-mers of a sequence S, and B denotes the set of k-mers of a sequence S′ derived from S using the simple mutation model with no spurious matches. Note that given a sufficiently large k-mer size, these assumptions will be satisfied in most practical scenarios.

We also recall the definition of a confidence interval. Given a distribution and a parameter of interest τ, a (1 − α)-CI is an interval that contains τ with probability 1 − α. Given 0 < α < 1, we define $z_{\alpha }={\mathit{\Phi }}^{-1}\left(1-\alpha /2\right)$, where Φ⁻¹ is the inverse CDF of the standard Gaussian distribution.

Expectation and variance of C_frac(A, B)

We notice that $\left|A\mathrm{\setminus }B\right|=\left|B\mathrm{\setminus }A\right|=N_{\mathrm{mut}}$ and that $\left|A\cap B\right|=L-N_{\mathrm{mut}}$. We note that the results in Theorem 3, Corollary 1, and Theorem 4 above still hold for a fixed N_mut. However, assuming a simple mutation model, N_mut is not a fixed quantity but, rather, a random variable. Therefore, the analyses so far only connect C_frac(A, B) to a fixed N_mut, as we have only considered the randomness from the FracMinHash sketching process so far. To quantify the impact of the mutation rate p on C_frac(A, B), we now consider the randomness introduced by both the FracMinHash sketching process and the mutation process simultaneously.

Let $\mathcal{P}=\left({\mathit{\Omega }}_1,{\mathcal{F}}_1,{\mathbf{P}}_1\right)$ and $\mathcal{S}=\left({\mathit{\Omega }}_2,{\mathcal{F}}_2,{\mathbf{P}}_2\right)$ be the probability spaces corresponding to the mutation and FracMinHash sketching random processes, respectively. Here, $\mathit{\Omega },\mathcal{F}$, and P denote the sample space, the sigma-algebra on the sample space, and the probability measure, respectively. We will use the subscript $\mathcal{P},\mathcal{S}$ to indicate the product probability space, for example, $E_{\mathcal{P},\mathcal{S}}[\cdot ]$ and $\mathrm{Va}{\mathrm{r}}_{\mathcal{P},\mathcal{S}}[\cdot ]$. Hence, we assume that the mutation process and the process of taking a FracMinHash sketch are independent. Before proceeding with the analysis, we make a note that the expectation and variance of N_mut under the simple mutation model with no spurious matches have been investigated by Blanca et al. (2022). As such, we already know $E_{\mathcal{P}}\left[N_{\mathrm{mut}}\right]$, $\mathrm{Va}{\mathrm{r}}_{\mathcal{P}}\left[N_{\mathrm{mut}}\right]$, and $E_{\mathcal{P}}\left[N_{\mathrm{mut}}^2\right]$ and will use these results directly (Table 1; see Blanca et al. 2022).

Table 1.

The percentage of experiments that resulted in the true mutation rate falling within the 95% confidence interval given in Theorem 8 when using various mutation rates across multiple k-mer sizes and L values

Theorem 5.

For 0 < s < 1, if A and B are respectively distinct sets of k-mers of a sequence S and a sequence S′ derived from S under the simple mutation model with mutation probability p such that $A\cap B$ is nonempty, then the expectation of C_frac(A, B) in the product space $\mathcal{P},\mathcal{S}$ is given by

$$E_{\mathcal{P},\mathcal{S}}\left[C_{frac}\left(A,B\right)\right]={\left(1-p\right)}^k,$$ (5)

where$\mathcal{P}=\left({\mathit{\Omega }}_1,{\mathcal{F}}_1,{\mathbf{P}}_1\right)$ and $\mathcal{S}=\left({\mathit{\Omega }}_2,{\mathcal{F}}_2,{\mathbf{P}}_2\right)$ are the probability spaces corresponding to the mutation and FracMinHash sketching random processes, respectively.

To show how the expected value of C_frac(A, B) (considering both the random processes) reacts to the mutation rate p and the k-mer size k, we show $E_{\mathcal{P},\mathcal{S}}\left[C_{\mathrm{frac}}\left(A,B\right)\right]$ in a heatmap in Figure 1. The heatmap shows that the expected value of the containment index decreases with a larger mutation rate and a larger k-mer size. This means that in the lighter cells (such as k = 20, P = 0.001), a small scale factor would suffice to find shared k-mers in two sketches, whereas in the darker cells (such as k = 100, P = 0.1), even a scale factor of 1.0 may not be sufficient because all k-mers are mutated. Consequently, a safe and meaningful choice of the scale factor s depends on the choices of p and k, which we discuss in more detail later in this section.

Figure 1.

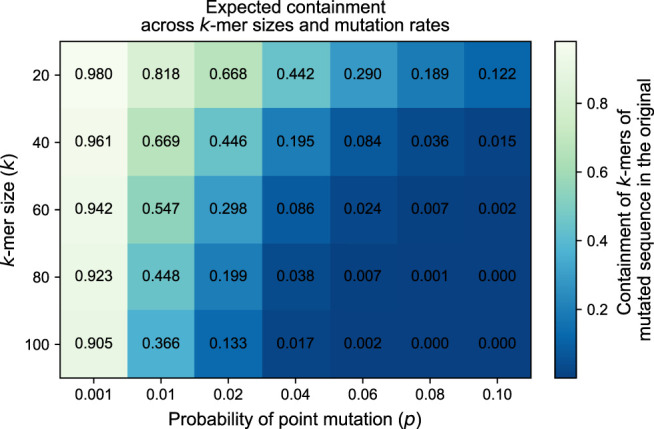
$E_{\mathcal{P},\mathcal{S}}\left[C_{\mathrm{frac}}\left(A,B\right)\right]={\left(1-p\right)}^k$ across different mutation rates and k-mer sizes. Darker cells indicate a smaller value. The expected containment decreases with a larger mutation rate and a larger k-mer size. This ideal case indicates that even a scale factor of s = 1 will be insufficient for large enough k sizes and P values.

Next, we turn to the more challenging task of calculating the variance of C_frac(A, B) in the product space $\mathcal{P},\mathcal{S}$.

Theorem 6.

For 0 < s < 1, if A and B are, respectively, distinct sets of k-mers of a sequence S and a sequence S′ derived from S under the simple mutation model with mutation probability p such that $A\cap B$ is nonempty, then the variance of C_frac(A, B) in the product space $\mathcal{P},\mathcal{S}$ is given by

$$\underset{\mathcal{P},\mathcal{S}}{\mathrm{Var}}\left[C_{frac}\left(A,B\right)\right]={\displaystyle \frac{\left(1-s\right)}{s{L}^3{\left(1-{\left(1-s\right)}^L\right)}^2}\left(L{E}_{\mathcal{P}}\left[N\right]-E_{\mathcal{P}}\left[N^2\right]\right)+{\displaystyle \frac{1}{L^2}\underset{\mathcal{P}}{\mathrm{Var}}\left(N_{mut}\right),}}$$ (6)

where $\mathcal{P}=\left({\mathit{\Omega }}_1,{\mathcal{F}}_1,{\mathbf{P}}_1\right)$ and $\mathcal{S}=\left({\mathit{\Omega }}_2,{\mathcal{F}}_2,{\mathbf{P}}_2\right)$ are the probability spaces corresponding to the mutation and FracMinHash sketching random processes, respectively.

With the results of Theorem 5, we now have a point estimate of the mutation rate p given C_frac(A, B), which is simply p = 1 − C_frac(A, B)^1/k. We next derive a hypothesis test for C_frac(A, B) to capture the variability around the point estimate and later turn it into a confidence interval.

Hypothesis test and confidence interval

We observe that the marginal of C_frac(A, B) with respect to the mutation process is simply $1-{\displaystyle \frac{N_{\mathrm{mut}}}{L}}$ . Using the results of Blanca et al. (2022), we note that N_mut is asymptotically normally distributed when the mutation rate p and k-mer length k are independent of L, and L is sufficiently large. In Theorem 4, we showed that C_frac(A, B) is normally distributed for a fixed N_mut. Therefore, considering the randomness from both the FracMinHash sketching and the mutation model independently, C_frac(A, B) is asymptotically normal when all conditions are met. Using the statistics derived earlier, we obtain the following hypothesis test for C_frac(A, B).

Theorem 7.

Let 0 < s < 1, and let A and B be two distinct sets of k-mers, respectively, of a sequence S and a sequence S′ derived from S under the simple mutation model with mutation probability p, such that $A\cap B$ is nonempty.

Also, let 0 < α < 1, and let C_low and C_high be defined as follows:

$$C_{\mathrm{low}}={\left(1-p\right)}^k-z_{\alpha }\sqrt{{\displaystyle \frac{\left(1-s\right)}{s{L}^3\left(1-{\left(1-s\right)}^2\right)}\left(L{E}_p\left[N_{\mathrm{mut}}\right]-E_p\left[N_{\mathrm{mut}}^2\right]\right)+{\displaystyle \frac{1}{L^2}\underset{p}{\mathrm{Var}}\left(N_{\mathrm{mut}}\right)}}}$$

$$C_{\mathrm{high}}={\left(1-p\right)}^k+z_{\alpha }\sqrt{{\displaystyle \frac{\left(1-s\right)}{s{L}^3\left(1-{\left(1-s\right)}^2\right)}\left(L{E}_p\left[N_{\mathrm{mut}}\right]-E_p\left[N_{\mathrm{mut}}^2\right]\right)+{\displaystyle \frac{1}{L^2}\underset{p}{\mathrm{Var}}\left(N_{\mathrm{mut}}\right)}}}.$$

Then, the following holds as L → ∞ and when p and k are independent of L:

$$\mathrm{Pr}\left[C_{\mathrm{low}}\le C_{\mathrm{frac}}\left(A,B\right)\le C_{\mathrm{high}}\right]=1-\alpha .$$

We can turn this hypothesis test into a confidence interval for the mutation rate p as follows.

Theorem 8.

Let A and B be two distinct sets of k-mers, respectively of a sequence S and a sequence S′ derived from S under the simple mutation model with mutation rate p, such that $A\cap B$ is nonempty. Let $E_{p_{\mathrm{fixed}}}\left[X\right]$ and $\mathrm{Va}{\mathrm{r}}_{p_{\mathrm{fixed}}}\left[X\right]$ denote the expectation and variance of a given random variable X under the randomness from the mutation process with fixed mutation rate p_fixed, respectively. Then, for fixed α, s, k, and an observed C_frac(A, B), there exists an L large enough such that there exist unique solutions p = p_low and p = p_high to the following equations, respectively,

$$\begin{array}{rl}& C_{\mathrm{frac}}\left(A,B\right)={\left(1-p_{\mathrm{low}}\right)}^k\\ & +z_{\alpha }\sqrt{{\displaystyle \frac{\left(1-s\right)}{s{L}^3{\left(1-{\left(1-s\right)}^L\right)}^2}\left(L{E}_{p_{\mathrm{low}}}\left[N_{\mathrm{mut}}\right]-E_{p_{\mathrm{low}}}\left[N_{\mathrm{mut}}^2\right]\right)+{\displaystyle \frac{1}{L^2}\underset{p_{\mathrm{low}}}{\mathrm{Var}}\left(N_{\mathrm{mut}}\right)}}},\end{array}$$

$$\begin{array}{rl}& C_{\mathrm{frac}}\left(A,B\right)={\left(1-p_{\mathrm{high}}\right)}^k\\ & -z_{\alpha }\sqrt{{\displaystyle \frac{\left(1-s\right)}{s{L}^3{\left(1-{\left(1-s\right)}^L\right)}^2}\left(L{E}_{p_{\mathrm{high}}}\left[N_{\mathrm{mut}}\right]-E_{p_{\mathrm{high}}}\left[N_{\mathrm{mut}}^2\right]\right)+{\displaystyle \frac{1}{L^2}\underset{p_{\mathrm{high}}}{\mathrm{Var}}\left(N_{\mathrm{mut}}\right)}}},\end{array}$$

such that the following holds:

$$\underset{L\to \mathrm{\infty }}{lim}\mathrm{Pr}\left[p_{\mathrm{low}}\le p\le p_{\mathrm{high}}\right]=1-\alpha .$$

Setting parameters correctly: likelihood of pathological corner cases

In practice, one disadvantage of sketching techniques is that the size of the sketch (here controlled via the scale factor s) may be too small to distinguish between highly similar or dissimilar sequences. For example, given a small mutation rate p, one may need a very large scale factor, and so sketch, to be able to distinguish between a sequence and the mutated version. Similarly, if the mutation rate p is high and/or a large k size is used, it is possible that FracMinHash may report a containment value of zero, even though the true value is nonzero, yet small. These “corner cases” are precisely the ones in which the confidence interval given by Theorem 8 will likely fail. One of these pathological cases shows up when there is nothing common between the two FracMinHash sketches FRAC_s(A) and FRAC_s(B). We observe that this occurs when $X_{A\cap B}=0$. Now $X_{A\cap B}$ is distributed as a binomial distribution Binom(n, s), where $n=\left|A\cap B\right|=L-N_{\mathrm{mut}}$, so the probability of the intersection being empty with respect to the sketching process is

$$\mathrm{P}{\mathrm{r}}_{\mathcal{S}}\left[X_{A\cap B}=0\right]={\left(1-s\right)}^{L-N_{\mathrm{mut}}}.$$

Ideally, we would be able to directly calculate $E_{\mathcal{P}}\left[\mathrm{P}{\mathrm{r}}_{\mathcal{S}}\left[X_{A\cap B}=0\right]\right]$, the expected probability of this corner case happening. The challenge in doing so is that we do not have a closed-form representation of the probability mass function (PMF) of N_mut. As a workaround, we developed a dynamic programming algorithm (presented in Supplemental Material Sec. A.4) to compute Pr[N_mut = x] given the parameters L and p.

Using this PMF, we can easily compute $E_{\mathcal{P}}\left[\mathrm{P}{\mathrm{r}}_{\mathcal{S}}\left[X_{A\cap B}=0\right]\right]$, which is the likelihood of the corner case that we observe nothing common between two sequences purely by chance. The remaining pathological case occurs when p ≠ 0 and yet FRAC_s(A) = FRAC_s(B) (i.e., the sketches are not large enough to distinguish between A and B). Similar to before, we have

$$\mathrm{P}{\mathrm{r}}_{\mathcal{S}}\left[X_{A\mathrm{\setminus }B}=0,X_{B\mathrm{\setminus }A}=0\right]=\mathrm{P}{\mathrm{r}}_{\mathcal{S}}\left[X_{A\mathrm{\setminus }B}=0\right]\mathrm{P}{\mathrm{r}}_{\mathcal{S}}\left[X_{B\mathrm{\setminus }A}=0\right]={\left(1-s\right)}^{2N_{\mathrm{mut}}},$$

and hence, by calculating $E_{\mathcal{P}}\left[{\left(1-s\right)}^{2N_{\mathrm{mut}}}\right]$ using the PMF of N_mut, we can obtain the likelihood of the latter pathological case. Here, $A\mathrm{\setminus }B$ and $B\mathrm{\setminus }A$ are disjoint sets, allowing us to use the independence of $X_{A\mathrm{\setminus }B}$ and $X_{B\mathrm{\setminus }A}$. We assume both $A\mathrm{\setminus }B$ and $B\mathrm{\setminus }A$ are nonempty.

It is important to note the importance to characterize these “corner cases” as without them, a user would be unable to determine if the observed containment index of, say, zero is owing to the sequences under consideration being highly diverged or else the scale factor chosen is much too small. These equations have been implemented into sourmash (Brown and Irber 2016) for precisely this purpose: to help practitioners assess if containment estimates of zero or one are owing to parameter settings (e.g., scale value too high/low) or else are biologically meaningful.

Results

FracMinHash accurately estimates containment index for sets of very different sizes

We first show that FracMinHash can estimate the true containment index better than MinHash when the sizes of two sets are dissimilar. For this experiment, we compared FracMinHash with the popular MinHash implementation tool Mash (Ondov et al. 2016). We took a Staphylococcus genome from the GAGE data set (Salzberg et al. 2012) and selected a subsequence that covers C% of the whole genome in terms of number of bases, added this sequence to a metagenome, and calculated the containment of Staphylococcus in this “super metagenome.” The metagenome we used is a WGS metagenome sample consisting of ∼1.3G bases. We used a scale factor of 0.005 for FracMinHash, and we set the number of hash functions for Mash at 4000, because Mash works reasonably well with even only 1000 hash functions to find the containment of Staphylococcus genome in the unaltered metagenome. We picked 0.005 because it generates small enough sketch sizes to be computationally inexpensive and, at the same time, ensures that the likelihoods of the corner cases are minimal.

We repeated this setup for different values of C and compared the containment index calculated by Mash and FracMinHash in Figure 2. We show the mean values for multiple runs with different seeds in the figure and use the error bars to show the standard deviation. Mash primarily reports MinHash Jaccard index, so we converted the Jaccard into containment by counting the number of distinct k-mers using brute force.

Figure 2.

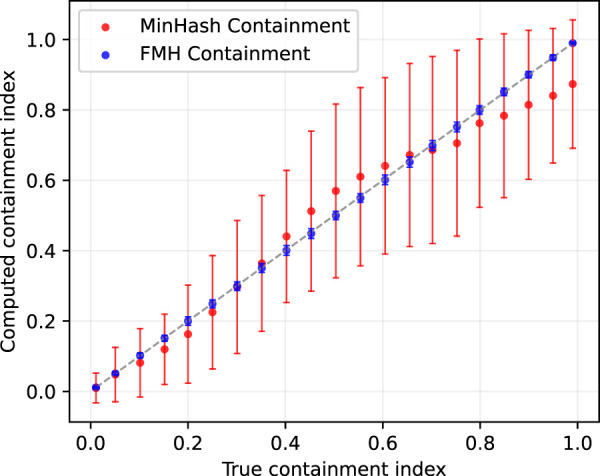
True versus estimated containment index for both the Mash and FracMinHash approaches for two sets with dissimilar sizes. The containment index of a Staphylococcus genome is computed when C% of this genome is inserted into an assembled metagenome. Error bars indicate standard deviation over hash seed values.

Figure 2 illustrates that although Mash and FracMinHash both faithfully estimate the true containment index, the FracMinHash approach more accurately estimates the containment index as this index increases in value. In addition, the estimate is more precise as shown by the size of the error bars on the estimates. This is likely because although Mash and FracMinHash both use a sketch of size 4000 for the Staphylococcus genome, Mash uses the same fixed value of 4000 when forming a sketch for the metagenome, whereas FracMinHash selects a sketch size that scales with the size of the metagenome. This can be seen most starkly when the metagenome is significantly larger than the query genome.

FracMinHash gives accurate confidence intervals around mutation rates

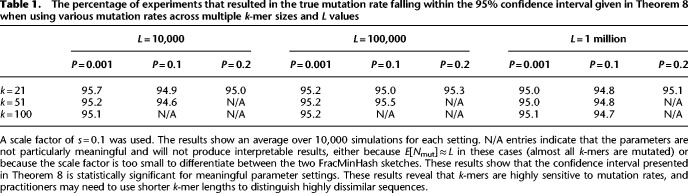
Next, we show that the confidence interval from Theorem 8 for the mutation rate p is statistically sound and works well in practice. To do so, we performed 10,000 simulations of sequences of length L = 10,000, 100,000, and 1 million that underwent the simple mutation model with P = 0.001, 0.1, and 0.2. We then used a scale factor of s = 0.1 when calculating p_low and p_high for a 95% confidence interval and repeated this for k-mer sizes of 21, 51, and 100. Table 1 records the percentage of experiments that resulted in p_low ≤ p ≤ p_high and shows that the confidence intervals indeed are ∼95%. Results with other scale factors are presented in Supplemental Tables S1 and S2.

In some of these settings (indicated with N/A) shown in Table 1, we skipped the experiment because these do not yield a meaningful result. Mostly, like the darkest cells in Figure 1, these are cases in which all or almost all k-mers are mutated, and consequently, we observe a zero containment, leading to undefined results. In the other cases, the number of shared k-mers is too small to use a scale factor of 0.1 and find a representative number of shared k-mers in the FracMinHash sketch, again resulting in a zero containment. To better understand these settings, we listed the expected number of nonmutated k-mers (studied by Blanca et al. 2022) in Supplemental Table S3: only a 10% of which is expected to end up in the sketch, which explains the N/A entries in Table 1.

FracMinHash more accurately estimates mutation distance

On simulated data

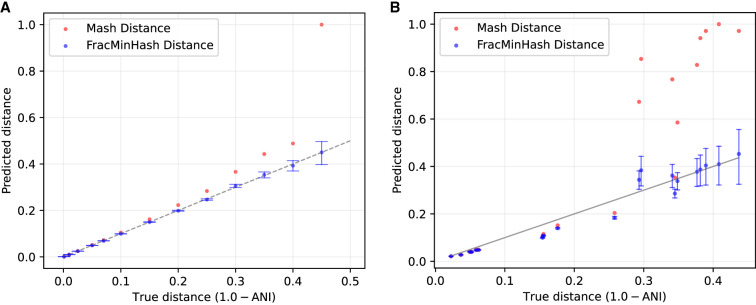
We finally compare the Mash estimate and FracMinHash estimate (given as a confidence interval) of mutation rates. For this experiment, we simulated point mutations in the aforementioned Staphylococcus genome at a mutation rate p and then calculated the distance of the original Staphylococcus genome with this mutated genome using both Mash and the interval given by Theorem 9. The results are shown in Figure 3A. This plot shows that Mash overestimates the mutation rate by a noticeable degree, with increasing inaccuracy as the mutation distance increases. This is likely because of the Mash distance assuming a Poisson model for how mutations affect k-mer occurrences, which has been shown to be violated when considering a point mutation model. In contrast, the point estimate given by Theorem 9 is fairly close to the true mutation rate, and the confidence interval accurately entails the true mutation rate.

Figure 3.

Mash distances and FracMinHash estimates of evolutionary distance (given in terms of one minus the average nucleotide identity [ANI]) between an original and a mutated Staphylococcus genome with introduced point mutations at a known rate (A) and between pairs of real bacterial genomes (B). Error bars indicate the confidence intervals surrounding the FracMinHash estimate calculated using Theorem 8. To obtain the FracMinHash estimates, k-mer size k = 21 and scale factor s = 0.1 were used.

On real data

We next present pairwise mutation distances between a collection of real genomes using both Mash and the interval in Theorem 8. To make a meaningful comparison, it is important to compute the true mutation distance (or equivalently, the ANI) between a pair of genomes. For this purpose, we used OrthoANI (Lee et al. 2016), a fast ANI calculation tool. From among 199,000 bacterial genomes downloaded from NCBI, we randomly filtered out pairs of genomes so that the pairwise ANI ranges from 0.5 to one. For visual clarity, we kept at most three pairs of genomes for any ANI interval of width 5%. We used 4000 hash functions to run Mash, and set L = (|A| + |B|)/2 for the confidence intervals in Theorem 9, where |A| and |B| denote the numbers of distinct k-mers in the two genomes in a pair. The results are presented in Figure 3B.

Clearly, Mash overestimates the mutation distance, particularly for moderate to high distances. In contrast, the confidence intervals given by Theorem 8 perform significantly better. It is noticeable that the confidence intervals are not as accurate as in the case of a simulated genome (presented in Fig. 3A). This is natural because in this real setup, the sizes of the genomes are very dissimilar, have repeats, and very easily violate the simplifying assumptions of the simple mutation model. Nonetheless, these results show the usefulness of the proposed approach even when the model assumptions are violated.

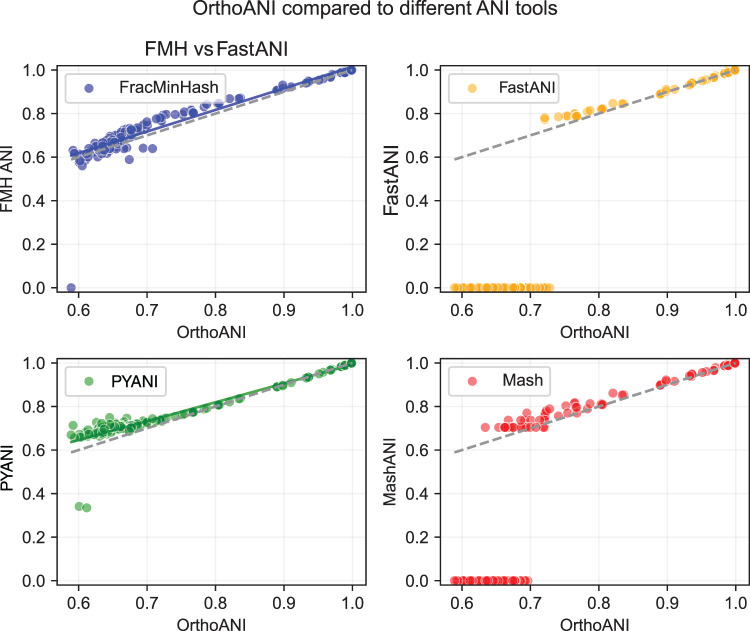
We conclude this section by computing ANI using FracMinHash sketches (k = 21, s = 0.1) and a few other well-known tools: namely, Mash (Ondov et al. 2016), PYANI (Pritchard et al. 2016), and FastANI (Jain et al. 2018). To build the set of genomes for this experiment, we first selected representative genomes from 10 species with the largest number of genomes in GTDB-rs207 (seven bacteria and three archaea) (Parks et al. 2022). Then, we built an “evolutionary path” for each of these “anchor” genomes by selecting three nonrepresentative genomes sharing each taxonomic rank, for example, three genomes in the same genus but different species, three in the same family but different genus, etc. We computed pairwise ANI from the “anchor” representative genome to each of these genomes using all methods. Using this approach allows the usage of real genomes across a range of ANI values. The results are shown in Figure 4. Like the previous set of figures, we again plotted the ANI computed using OrthoANI (Lee et al. 2016) on the x-axis.

Figure 4.

Pairwise ANI estimation among a selection of genomes from the GTDB database. The dashed line represents ANI computed using OrthoANI. The solid blue and green lines show the least-squares fit for the ANI scores computed using FracMinHash and PYANI, respectively. Mash and FastANI both have many zeroed-out values, and therefore, the least-squares fit is not shown for these two.

As above, Mash cannot reliably differentiate genomes at ANI <70%. In addition, as most ANI tools are recommended for use only at >75%–80% ANI, the lack of meaningful ANI values <75% for FastANI is expected. In the 80%–100% range, all tools correlate well with OrthoANI (shown in dashed gray), with least-squares fits for FracMinHash and PYANI in blue and green, respectively. However, both PYANI and FracMinHash correlate with OrthoANI quite well even <80% ANI, with FracMinHash performing slightly better in this low range. From 60%–80% ANI, FracMinHash had a Pearson correlation coefficient with OrthoANI of 0.79, whereas PYANI had a correlation of 0.69 with OrthoANI.

Discussion

In contrast to classic MinHash, which uses a fixed sketch size, FracMinHash automatically scales the size of the sketch based on the size of the input data. This has the advantage of facilitating an accurate comparison of sets of very different sizes, extending sketch-based comparisons to metagenomic data sets, including streaming-based analyses and large-scale database searches. Given that a user has control over what percentage of the data to keep in the sketch (in terms of s), reasonable estimates can be made about sketch sizes a priori, and trade-offs can be used to prevent large sketch sizes while maintaining sufficient resolution for search. One particularly attractive feature of FracMinHash is its analytical tractability: As we have shown, it is relatively straightforward to characterize the performance of FracMinHash, derive its statistics, and study how it interacts with a simple mutation model. Given these advantages, it seems reasonable to favor FracMinHash in situations in which sets of differing sizes are being compared or else when fast and accurate estimates of mutation rates are desired (particularly for moderate to high mutation rates). We believe that using FracMinHash can enable fast metagenomic binning by discarding genomes irrelevant to a metagenomic sample (based on low containment scores), let users filter genomes from a reference database using ANI thresholds, allow practitioners to use the confidence intervals with taxonomic tree and sample bootstrap phylogenies off of the taxonomy, and realize many other useful applications.

This paper focuses on theoretical analyses using the containment index, primarily because deriving confidence intervals around the mutation rate from the Jaccard index proved to be mathematically intractable. We still showed how to obtain a point estimate of the mutation rate using an observed Jaccard index. These analyses are included in the Supplemental Materials: theoretical analysis (Sec. A.7), derivation of a point estimate of mutation rate (and ANI) using the Jaccard index (Sec. A.8), and results on the utility of this point estimate (Supplemental Fig. S1).

Software availability

A Python-based implementation of the algorithms and theorems we derive is freely available at GitHub (https://github.com/KoslickiLab/mutation-rate-ci-calculator). The results presented in this paper can be reproduced using the code at GitHub (https://github.com/KoslickiLab/FracMinHash-reproducibles). All code in these GitHub repositories is also available as Supplemental Material.

Competing interest statement

The authors declare no competing interests.