A general framework of nonparametric feature selection in high-dimensional data

Abstract

Nonparametric feature selection for high-dimensional data is an important and challenging problem in the fields of statistics and machine learning. Most of the existing methods for feature selection focus on parametric or additive models which may suffer from model misspecification. In this paper, we propose a new framework to perform nonparametric feature selection for both regression and classification problems. Under this framework, we learn prediction functions through empirical risk minimization over a reproducing kernel Hilbert space. The space is generated by a novel tensor product kernel, which depends on a set of parameters that determines the importance of the features. Computationally, we minimize the empirical risk with a penalty to estimate the prediction and kernel parameters simultaneously. The solution can be obtained by iteratively solving convex optimization problems. We study the theoretical property of the kernel feature space and prove the oracle selection property and Fisher consistency of our proposed method. Finally, we demonstrate the superior performance of our approach compared to existing methods via extensive simulation studies and applications to two real studies.

1 ∣. INTRODUCTION

With fast technological advances in modern medicine, biomedical studies that collect complex data with a large number of features are becoming the norm. High-dimensional feature selection is an essential tool to allow using such data for disease prediction or precision medicine, for instance, to discover a subset of biomarkers that can predict treatment response to chronic disorders or to determine predictive biomarkers for effective management of patient healthcare. Accurately identifying the subset of true important features and building an individualized treatment outcome prediction model is even more crucial and challenging in modern medicine and personalized healthcare. Specifically, in a motivating study presented in Section 4 (Trivedi et al., 2016), the goal is to identify behavioral and biological markers that can predict treatment response in patients affected by major depressive disorder (MDD) to guide clinical care. Treatment responses for mental disorders are inadequate, and considerable heterogeneity is observed, in part because of a lack of knowledge on predictive markers that are informative of heterogeneous treatment effects. It is desirable to create a biosignature of treatment response for MDD by selecting and combining informative markers among a comprehensive candidate pool of clinical, behavioral, neuroimaging, and electrophysiology measures.

High-dimensional feature selection has been extensively studied for a linear model or generalized linear models in the past decades, and many methods have been developed including Lasso (Tibshirani, 1996), smoothly clipped absolute deviation (Fan and Li, 2001), and minimax concave penalty (Zhang, 2010). In these parametric models, the importance of individual features is characterized by non-null coefficients associated with them, so proper penalization can identify non-null coefficients with the probability tending to one when the sample size increases. However, parametric model assumptions are likely to be incorrect for many biomedical data due to potential higher order interactions among feature variables. In fact, applying these approaches to any simple transformation of feature variables may lead to very different feature selection results.

More recently, increasing efforts have been devoted to high-dimensional feature selection when parametric assumptions, especially linearity assumptions, do not hold. Various approaches were proposed to select features based on measuring certain marginal dependency (Guyon and Elisseeff, 2003; Fan and Lv, 2008; Fan et al., 2011; Song et al., 2012; Yamada et al., 2014; Urbanowicz et al., 2018). For example, the nonparametric association between each feature and outcome was used for screening (Fan and Lv (2008); Fan et al. (2011); Song et al. (2012). Li et al. (2012) adopted a robust rank correlation screening method based on the marginal Kendall correlation coefficient. Yamada et al. (2014) considered a feature-wise kernelized Lasso, namely HSICLasso, for capturing nonlinear dependency between features and outcomes. In this approach, after a Lasso-type regression of an output kernel matrix on each feature-wise kernel matrix, nonimportant features with small marginal dependence in terms of a Hilbert–Schmidt independence criterion (HSIC) would be removed. However, all methods based on marginal dependence may fail to select true important variables since marginal dependency does not necessarily imply the significance of a feature when other features are also included for prediction, which is the case even for a simple linear model.

Alternatively, other approaches were proposed to relax parametric model assumptions and perform feature selection and prediction simultaneously. Lin and Zhang (2006) proposed Component Selection and Smoothing Operator (COSSO) to perform penalized variable selection based on smoothing spline ANOVA. Ravikumar et al. (2009) studied feature selection in a sparse additive model (SpAM), which assumed an additive model but allowed arbitrary nonparametric smoothers such as approximation in a reproducing kernel Hilbert space (RKHS) for each individual component function. Huang et al. (2010) considered spline approximation in the same model and adopted an adaptive group Lasso method to perform feature selection. Wu and Stefanski (2015) also proposed a kernel-based variable selection method as an extension of the additive model via local polynomial smoothing using a backfitting algorithm. Although COSSO, SpAM, and Wu and Stefanski (2015) allowed nonlinear prediction from each feature, they still imposed restrictive additive model structures, possible with some higher order interactions. To allow arbitrary interactions among the features and perform a fully nonparametric prediction, Allen (2013) and Stefanski et al. (2014) proposed a procedure in which the feature input was constructed in a Gaussian RKHS in order to perform nonparametric prediction. Different weights were used for different features in the constructed Gaussian kernel function so that a larger weight implied higher importance of the corresponding feature variable. However, due to high nonlinearity in the kernel function, estimating the weights was numerically unstable even when the dimension of the features was moderate. Finally, Yang et al. (2016) and Rosasco et al. (2013) considered model-free variable selection by examining the partial derivatives of regression functions with respect to each feature variable. Although theoretically an unimportant feature should yield a zero derivative, estimating the partial derivatives in a high-dimensional setting is known to be numerically unstable and such methods cannot be applied to noncontinuous feature variables.

In this paper, we propose a general framework to perform nonparametric high-dimensional feature selection. We consider a general loss function, which includes both regression models and classification as special cases. To perform nonparametric prediction, we construct a novel RKHS based on a tensor product of kernels for individual features. The constructed tensor product kernel, as discussed in Gao and Wu (2012), can handle any high-order nonlinear relationship between the features and outcome and any high-order interactions among the features. More importantly, each feature kernel depends on a nonnegative parameter which determines the feature importance, so for feature selection, we further introduce a $l_1$-penalty of these parameters in the estimation. Computationally, coordinate descent algorithms are used for updating parameters and each step involves simple convex optimization problems. Thus, our algorithm is numerically stable and can handle high-dimensional features easily. Theoretically, we first derive the approximation property of the proposed RKHS and characterize the complexity of the unit ball in this space in terms of bracket covering numbers. We then show that the estimated prediction function from our approach is consistent, and, moreover, we show that under some regularity conditions the important features can be selected with the probability tending to one.

The rest of the paper is organized as follows. In Section 2, we introduce our proposed regularized tensor product kernel and lay out a penalized framework for both estimation and feature selection. We then provide detailed computational algorithms to solve the optimization problem. In Section 3, two simulation studies for regression and classification problems are conducted and we compare our method to existing methods. Applications to a microarray study and a depression study are given in Section 4. We conclude the paper with some discussion in Section 5.

2 ∣. METHOD

Suppose data are obtained from $n$ independent subjects and consist of $({\mathbf{X}}_i,Y_i),i=1,\dots ,n$, where we let $\mathbf{X}$ denote $p_n$-dimensional feature variables and $Y$ be the outcome which can be continuous, binary, or ordinal. Our goal is to use the data to learn a nonparametric prediction function, $f(\mathbf{X})$, for the outcome $Y$.

We learn $f(\mathbf{X})$ through a regularized empirical risk minimization by assuming $f(\cdot )$ belongs to an RKHS associated with a kernel function, $\kappa (\mathbf{X},\tilde{\mathbf{X}})$, which will be described later. Specifically, if we denote the RKHS generated by $\kappa (\mathbf{X},\tilde{\mathbf{X}})$ by ${\mathscr{H}}_{\kappa }$, equipped with norm $\Vert \cdot {\Vert }_{{\mathscr{H}}_{\kappa }}$, then the empirical regularized risk minimization on RKHS for estimating $f(\mathbf{X})$ solves the following optimization problem:

$$\underset{f}{\text{min}}{\mathbf{P}}_{n}l(Y,f(\mathbf{X}))+{\gamma }_n\Vert f{\Vert }_{{\mathscr{H}}_{\kappa }}^2,$$ (1)

where $l(y,f)$ is a prespecified nonnegative and convex loss function to quantify the prediction performance, ${\mathbf{P}}_n$ denotes the empirical measure from $n$ observations, that is, ${\mathbf{P}}_{n}g(Y,\mathbf{X})=n^{-1}{\sum }_{i=1}^{n}g(Y_i,{\mathbf{X}}_i)$, and ${\gamma }_n$ is a tuning parameter to control the complexity of $f$. For a continuous outcome, $l(y,f)$ is often chosen to be an $L_2$-loss given as ${(y-f)}^2$, while, for a binary outcome, it can be one of the large-margin losses such as $\text{exp}(-yf)$ in Adaboost since it yields the same classifier as the Bayesian classifier (Bartlett, 2006). There are many choices of kernel functions for $\kappa (\cdot ,\cdot )$ so that the estimated $f(\mathbf{X})$ is nonlinear. One of the most commonly used kernel functions in machine learning is the Gaussian kernel function given by $\kappa (\mathbf{X},\tilde{\mathbf{X}})=\text{exp}(-{\Vert \mathbf{X}-\tilde{\mathbf{X}}\Vert }^2∕{\sigma }^2)$ for some bandwidth $\sigma$, where $\Vert \cdot \Vert$ is the Euclidean norm. To handle high-dimensional features, SpAM is considered as an additive kernel function by assuming $\kappa (\mathbf{X},\tilde{\mathbf{X}})={\sum }_{j=1}^{p_n}\text{exp}(-{\mid X_j-{\tilde{X}}_j\mid }^2∕{\sigma }^2)$. In the kernel iterative feature extraction procedure, the kernel function is defined as ${\kappa }_{\omega }(\mathbf{X},\tilde{\mathbf{X}})=\text{exp}\{-{\sum }_{j=1}^{p_n}{{\omega }_j(X_j-{\tilde{X}}_j)}^2∕{\sigma }^2\}$, where ${\omega }_j,j=1,..,p_n$, are the additional weights to determine the feature importance.

To achieve the goal of both nonparametric prediction and feature selection, we propose a tensor product kernel as follows. For any given nonnegative vector $\lambda ={({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n)}^{⊺}$, we define a $\lambda$-regularized kernel function as

$${\kappa }_{\lambda ,{\sigma }_n}(\mathbf{X},\tilde{\mathbf{X}})=\prod _{m=1}^{p_n}\{1+{\lambda }_m{\kappa }_n(X_m,{\tilde{X}}_m)\},$$ (2)

where ${\kappa }_n(x,y)=\text{exp}\{-{(x-y)}^2∕2{\sigma }_n^2\}$ with a predefined bandwidth ${\sigma }_n$ in $ℛ$. There are two important observations for this new kernel function. First, it is the product of a univariate kernel function for each feature variable, which is given by $1+{\lambda }_m{\kappa }_n(X_m,{\tilde{X}}_m)$. Thus, the RKHS generated by ${\kappa }_{\lambda ,{\sigma }_n}$ is equivalent to the tensor product of the RKHS generated by each feature-specific space. Second, each univariate kernel function is essentially the same as the Gaussian kernel function when ${\lambda }_m\ne 0$. Consequently, the resulting tensor product space is the same as the RKHS generated by the multivariate Gaussian kernel function from all features whose ${\lambda }_m\mathrm{s}$ are nonzero. Therefore, the closure for the RKHS generated by ${\kappa }_{\lambda ,{\sigma }_n}$ consists of all functions that only depend on feature variables for which ${\lambda }_m\ne 0$. In other words, nonnegative parameters, ${\lambda }_m$, completely capture and regularize the contribution of each feature $X_m$. In this way, feature selection can be achieved by estimating the regularization parameters, ${\lambda }_m\mathrm{s}$, in the kernel function. In Web Figure 1, we present a tensor-product kernel function in a two-dimensional space with different choices of ${\lambda }_1$ and ${\lambda }_2$. When increasing ${\lambda }_1$ (or ${\lambda }_2$ ) from zero to some positive number, the kernel function along $X_1$ (or $X_2$) direction becomes nonflat, indicating that such a kernel function can capture nontrivial functional form along this direction.

More specifically, using the proposed kernel function, we let ${\mathscr{H}}_{\lambda ,{\sigma }_n}$ denote the RKHS corresponding to ${\kappa }_{\lambda ,{\sigma }_n}$ so we aim to minimize

$$\begin{gathered} L_n(\lambda ,f)\equiv {\mathbf{P}}_{n}l\{Y,f(\mathbf{X})\}+{\gamma }_{1n}\Vert f{\Vert }_{{\mathscr{H}}_{\lambda ,{\sigma }_n}}^2+{\gamma }_{2n}P(\lambda ) \\ \text{subject to}M\ge {\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{p_n}\ge 0, \end{gathered}$$ (3)

where $M$ is a prespecified large constant. $P(\lambda )={\sum }_{m=1}^{p_n}P({\lambda }_m)={\sum }_{m=1}^{p_n}{\lambda }_{m}I({\lambda }_m<M∕2)$, which is a truncated Lasso, and ${\gamma }_{1n}$, ${\gamma }_{2n}$ are tuning parameters. Here, we include an $l_1$ penalization term on the regularization vector to perform feature selection and restrict ${\lambda }_m$ to be bounded. The latter bound is useful for numerical convergence to avoid the situation that some ${\lambda }_m$ can diverge. Since our RKHS contains a constant and based on the representation theory (Aronszajn, 1950) for RKHS, solution for (3) takes the form

$$f(\mathbf{X})=\sum _{i=1}^n{\alpha }_i{\kappa }_{\lambda ,{\sigma }_n}(\mathbf{X},{\mathbf{X}}_i)$$ (4)

and

$$\Vert f{\Vert }_{{\mathscr{H}}_{\lambda ,{\sigma }_n}}^2={\alpha }^T{\mathbf{K}}_{\lambda ,{\sigma }_n}\alpha ,$$ (5)

where $\alpha ={({\alpha }_1,\dots ,{\alpha }_n)}^T$ and ${\mathbf{K}}_{\lambda ,{\sigma }_n}$ is an $n\times n$ matrix with entry ${\kappa }_{\lambda ,{\sigma }_n}({\mathbf{X}}_i,{\mathbf{X}}_j)$. Then the optimization becomes solving

$$\begin{gathered} \underset{{\alpha }_1,\dots ,{\alpha }_n,\lambda }{\text{min}}{\mathbf{P}}_{n}l\left\{Y,\sum _{i=1}^n{\alpha }_i{\kappa }_{\lambda ,{\sigma }_n}(\mathbf{X},{\mathbf{X}}_i)\right\} \\ +{\gamma }_{1n}{\alpha }^T{\mathbf{K}}_{\lambda ,{\sigma }_n}\alpha +{\gamma }_{2n}\sum _{m=1}^{p_n}{\lambda }_{m}I({\lambda }_m<M∕2) \\ \text{subject to}M\ge {\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{p_n}\ge 0. \end{gathered}$$ (6)

We iterate between $\alpha$ and $\lambda$ to solve the above optimization problem. At the $k$th iteration,

$$\begin{gathered} {\alpha }^{k+1}=\underset{\alpha }{\text{min}}{n}^{-1}\sum _{j=1}^{n}l\left\{Y_j,\sum _{i=1}^n{\alpha }_i{\kappa }_{{\lambda }^k,{\sigma }_n}({\mathbf{X}}_j,{\mathbf{X}}_i)\right\} \\ +{{\gamma }_{1n}\alpha }^{⊺}{\mathbf{K}}_{{\lambda }^k,{\sigma }_n}\alpha \end{gathered}$$ (7)

$$\begin{gathered} {\lambda }^{k+1}=\underset{0\le \lambda \le M}{\text{min}}{n}^{-1}\sum _{j=1}^{n}l\left\{Y_j,\sum _{i=1}^n{\alpha }_i^{k+1}{\kappa }_{\lambda ,{\sigma }_n}({\mathbf{X}}_j,{\mathbf{X}}_i)\right\} \\ +{{\gamma }_{1n}({\alpha }^{k+1})}^{⊺}{\mathbf{K}}_{\lambda ,{\sigma }_n}{\alpha }^{k+1} \\ +{\gamma }_{2n}\sum _{m=1}^{p_n}{\lambda }_{m}I({\lambda }_m<M∕2). \end{gathered}$$ (8)

Since the loss function is a convex loss, the optimization in (7) is a convex minimization problem, so many optimization algorithms can be applied. To solve (8) for $\lambda$, we adopt a coordinate descent algorithm to update each ${\lambda }_q(q=1,2,\dots ,p_n)$ in turn. Specifically, to obtain ${\lambda }_q^{k+1}$, we fix ${\lambda }_1^{k+1},{\lambda }_2^{k+1},\dots ,{\lambda }_{q+1}^k,{\lambda }_{q+2}^k,\dots ,{\lambda }_{p_n}^k$ and then after simple calculation, the objective function takes the following form:

$$\underset{{\lambda }_q\ge 0}{\text{min}}\frac{1}{n}\sum _{i=1}^{n}g(a_{iq}+b_{iq}{\lambda }_q)+d_q{\lambda }_q,$$ (9)

where $g(a_{jq}+b_{jq}{\lambda }_q)$ is equal to $l\{Y_j,{\sum }_{i=1}^n{\alpha }_i^{k+1}{\kappa }_{\lambda ,{\sigma }_n}({\mathbf{X}}_j,{\mathbf{X}}_i)\}$ as a function of ${\lambda }_q$, and $a_{iq},b_{iq},d_q’\mathrm{s}$ are constants. By the construction of ${\kappa }_{\lambda ,{\sigma }_n}$, $g(\cdot )$ is a differentiable and convex function so each step in the coordinating descent algorithm is a constrained convex minimization problem in a bounded interval, which is easy to solve.

ALGORITHM 1 Algorithm for learning

$$\begin{array}{cc}\hfill & \mathrm{Input}:\text{Data}(\mathbf{X},\mathbf{Y});\text{Regularization prarameter}{\gamma }_{1n}\text{and}{\gamma }_{2n};\hfill \\ \hfill & \text{Former updating results},{\widehat{\alpha }}^k,{\widehat{\lambda }}^k,{\widehat{f}}_{{\widehat{\lambda }}^k};\hfill \\ \hfill & \mathbf{Initialize}\text{For regression},{\widehat{\lambda }}_0=0;\text{For classification},\hfill \\ \hfill & {\widehat{\lambda }}_0=(0,\dots ,1,\dots ,0),\text{where all elements equal to}0,\text{expect}\hfill \\ \hfill & \text{the one having largest margin correlation with outcome}.\hfill \\ \hfill & \mathbf{Iterate}\text{until convergence}\hfill \\ \hfill & (\delta =\text{abs}\{L_n({\widehat{\lambda }}^{k+1},{\widehat{f}}_{{\widehat{\lambda }}^{k+1}})-L_n({\widehat{\lambda }}^k,{\widehat{f}}_{{\widehat{\lambda }}^k})\}\le c_1,\hfill \\ \hfill & e={\Vert {\widehat{\lambda }}^{k+1}-{\widehat{\lambda }}^k\Vert }_1\le c_2,\text{where}{c}_1\text{and}{c}_2\text{arge given cut}\hfill \\ \hfill & \text{points}):\hfill \\ \hfill & (\mathrm{i})\text{Update}{\widehat{\alpha }}^{k+1}\text{for fix}{\widehat{\lambda }}^k,\text{which can be solved explicitly for}\hfill \\ \hfill & \text{regression and via fminsearch function for classification}.\hfill \\ \hfill & (\text{ii})\text{Update}{\widehat{\lambda }}^{k+1}\text{for fixed}{\widehat{\alpha }}^{k+1}\text{via the coordinate descent}\hfill \\ \hfill & \text{algorithm}.\hfill \\ \hfill & (\text{iii})\delta =\text{abs}\{L_n({\widehat{\lambda }}^{k+1},{\widehat{f}}_{{\widehat{\lambda }}^{k+1}})-L_n({\widehat{\lambda }}^k,{\widehat{f}}_{{\widehat{\lambda }}^k})\}\text{and}\hfill \\ \hfill & e={\Vert {\widehat{\lambda }}^{k+1}-{\widehat{\lambda }}^k\Vert }_1.\hfill \\ \hfill & \mathrm{Output}:{\widehat{\alpha }}^{k+1},{\widehat{\lambda }}^{k+1},{\widehat{f}}_{{\widehat{\lambda }}^{k+1}}.\hfill \end{array}$$

At the convergence after $k$ iterations, the final prediction function is given as

$${\widehat{f}}_{{\lambda }^{k+1}}(\mathbf{X})=\sum _{i=1}^n{\alpha }_i^{k+1}{\kappa }_{{\lambda }^{k+1},{\sigma }_n}(\mathbf{X},{\mathbf{X}}_i).$$ (10)

For the classification problem, the classification rule is

$$\text{sign}\left\{{\widehat{f}}_{{\lambda }^{k+1}}(\mathbf{X})\right\}=\text{sign}\left\{\sum _{i=1}^n{\alpha }_i^{k+1}{\kappa }_{{\lambda }^{k+1},{\sigma }_n}(\mathbf{X},{\mathbf{X}}_i)\right\}.$$ (11)

We give details of our algorithm in Algorithm 1.

Remark 1. When updating $\alpha$ iteratively for regression, it can be solved in a closed form as ${\widehat{\alpha }}^{k+1}={({\mathbf{K}}_{{\widehat{\lambda }}^k,{\sigma }_n}^{⊺}{\mathbf{K}}_{{\widehat{\lambda }}^k,{\sigma }_n}+n{\gamma }_{1n}{\mathbf{K}}_{{\widehat{\lambda }}^k,{\sigma }_n})}^{-1}{\mathbf{K}}_{{\widehat{\lambda }}^k,{\sigma }_n}^{⊺}\mathbf{Y}$. For classification, we apply the one-step Newton method for updating. Tuning parameters in the algorithm are chosen via cross-validation over a grid of $2^{-15},2^{-13},\dots ,2^{13},2^{15}$. Although the kernel bandwidth, ${\sigma }_n$, can also be tuned, to save computation cost, we follow Jaakkola et al. (1999) to set it to be the median value of the paired distances. Following the same analysis as in Wright (2015), since $g$-function in (9) is convex and is twice continuously differentiable, if we further assume that it is strictly convex and has bounded second derivatives in a neighborhood of the minimizer for $\lambda$ in Step (ii), say $𝒩$, then the distance between the updated ${\lambda }_q$ and its convergent value can be bounded by a mulitiplier of the distance for the previous ${\lambda }_q$. In addition, this multiplication factor is approximately $\text{abs}[1-{\{{\max }_{\lambda \in 𝒩}{\sum }_i{g}^{″}(a_{iq}+b_{iq}{\lambda }_q)\}}^{-1}\{{\text{min}}_{\lambda \in 𝒩}{\sum }_i{g}^{″}(a_{iq}+b_{iq}{\lambda }_q)\}]$ so is less than one when $\lambda$ is sufficiently close to its convergent value. That is, the whole coordinate descent algorithm has a linear convergence rate in a local neighborhood of the minimizer for $\lambda$. Finally, since it is possible that the proposed algorithm will converge to a local minimum, we suggest to start with a few initial values and consider the algorithm to converge once the objective function does not change more than a given threshold. In practice, we may also compare the prediction error from our algorithm with the ones from other methods such as SpAM or random forest, so it will give additional assurance when these errors are comparable.

Remark 2. In the Supporting Information accompanying this paper, we provide details for the properties of the proposed kernel function including its universal approximation property and complexity of the unit ball in its induced RKHS. Furthermore, we provide regularity conditions to show that our proposed prediction function leads to the best prediction performance asymptotically. We also establish the oracle property of variable selection using the proposed method in an ultra-high dimensional setting, that is, when the dimension of the feature variables grows exponentially as a function of the sample size.

3 ∣. SIMULATION STUDY

We conducted two simulation studies, one for a regression problem with continuous $Y$ and the other for classification with binary $Y$. In the first simulation study, we considered a continuous outcome model with a total number of $p$ correlated feature variables, which were generated from a multivariate normal distribution, each with mean zero and variance one. Furthermore, $X_1,X_2,X_3,X_4$ were correlated with $corr(X_1,X_2)=0.4$, $corr(X_1,X_3)=-0.3$, $corr(X_2,X_3)=0.5$ and $corr(X_3,X_4)=0.2$, while the others were all independent. The outcome variable, $Y$, was simulated from a nonlinear model

$$Y=0.9X_5^3+4X_1{X}_2{X}_3+2.3\text{exp}(-X_3)+4X_4+ϵ,$$ (12)

where $ϵ\sim N(0,1)$. Thus, $X_1$ to $X_5$ were important variables but not any others. In the second simulation study, $X$ were generated similarly but with some different correlations: $corr(X_1,X_2)=-0.2$, $corr(X_1,X_4)=0.2$, $corr(X_2,X_3)=0.5$, $corr(X_2,X_4)=0.3$, and $corr(X_3,X_4)=-0.4$ The binary outcome, $Y$, with values −1 and 1, was generated from a Bernoulli distribution with the probability of being one given by

$${\left\{1+e^{-0.25+(X_2-1.1X_3+{0.3X{}_4)}^3}\right\}}^{-1},$$ (13)

so only $X_2$ to $X_4$ were important variables. Since many biomedical applications (as well as our application in this work) have small to moderate sample sizes, in both simulation studies, we considered sample size $n=100$, 200, and 400 and varied the feature dimension from $p=200$, 400 to 1000. Each simulation setting was repeated 500 times.

For each simulated data, we used the proposed method to learn the prediction function. Initial values, tuning parameters, and the optimization package used for the binary case are chosen as in Remark 1 of Section 2, where threefold cross-validation was used for selecting the tuning parameters. The bound of regularized parameter $M$ was chosen to be 10⁵. We also centered the continuous outcome and reweighted class label controlled to be balanced before iteration to make numerically stable. We reported the true positive rates, true negative rates, and the average number of the selected variables for feature selection. We also reported the prediction errors or misclassification rates using large and independent validation data. For comparison, we compared our proposed method with HSICLasso and SpAM since both methods were able to estimate nonlinear functions in high-dimensional settings. In addition, we also compared the performance with LASSO in the first simulation study and $l_1$-SVM in the second simulation study, in order to study the impact due to model misspecification. In the simulations, our algorithm usually converged within 400 iterations for the continuous outcome and within 100 iterations for the binary outcome.

The results based on 500 replicates are summarized in Tables 1 and 2. From these tables, we observe that for a fixed dimension the performance of our method improves as sample size $n$ becomes large in terms of the improved true positive and true negative rates for feature selection as well as decreasing prediction errors. In almost all cases, our true negative rate is close to 100%, which shows that noise variables can be identified with a very high chance. As expected, the performance deteriorates as the dimensionality increases. Interestingly, our method continues to select only a small number of feature variables. Comparatively, HSICLasso selected many more noise variables and had larger prediction errors, while SpAM also tended to select more features than our method. The performance of these methods becomes much worse when the feature dimension is 1000.

TABLE 1.

Results from the simulation study with a continuous outcome

(a) Summary of feature selection performance
		Proposed method			HSICLasso			SpAM			LASSO
$\mathit{p}$	$\mathit{n}$	TPR	TNR	Avg#	TPR	TNR	Avg#	TPR	TNR	Avg#	TPR	TNR	Avg#
100	100	60.9%	97.3%	5.6	81.5%	78.5%	24.5	99.6%	34.6%	67.1	98.8%	1.3%	98.8
	200	71.2%	99.0%	4.5	98.0%	60.4 %	42.5	100.0%	4.4%	95.8	100.0%	0.1%	99.9
	400	82.7%	98.4%	5.7	99.6 %	78.0 %	25.8	100.0%	0.3%	99.7	100.0%	0.1%	99.9
200	100	57.2%	98.7%	5.5	75.6%	88.8%	25.6	99.1%	63.0%	77.1	84.0%	52.2%	97.5
	200	66.6%	99.5%	4.2	94.0%	75.2%	53.1	100.0%	33.7%	134.1	99.1%	0.0%	198.6
	400	78.1%	99.4%	5.0	99.8 %	84.2%	35.8	100.0%	5.4%	189.5	100.0%	0.12%	199.8
400	100	47.3%	99.3%	5.2	68.5%	90.4%	41.5	98.2%	80.8%	80.8	79.4%	76.4%	97.1
	200	65.0%	99.7%	4.5	86.3%	89.0%	47.6	100.0%	62.1%	154.6	90.7%	51.4%	196.6
	400	73.1%	99.8%	4.4	99.7%	87.6%	54.0	100.0%	34.0%	265.8	99.1%	0.7%	397.3
1000	100	40.7%	99.7%	5.0	56.0%	91.8%	84.5	93.7%	92.2%	82.6	73.6%	90.6%	97.2
	200	61.2%	99.9%	4.5	78.2%	98.6%	18.4	99.9%	84.2%	162.0	85.5%	80.7%	196.1
	400	70.7%	99.9%	4.0	99.4%	91.0%	94.9	100.0%	68.7%	316.4	94.5%	60.7%	395.6

(b) Summary of prediction errors
$\mathit{p}$	$\mathit{n}$	Proposed method	HSICLasso	SpAM	LASSO
100	100	7.405 (0.527)	7.695 (0.291)	6.985 (0.291)	41.663 (11.325)
	200	5.929 (0.950)	7.323 (0.098)	7.299 (0.389)	9.508 (0.575)
	400	4.424 (0.777)	7.115 (0.053)	6.868 (0.292)	7.840 (0.183)
200	100	7.567 (0.493)	7.603 (0.286)	6.672 (0.336)	10.176 (0.794)
	200	6.623 (0.412)	7.313 (0.130)	6.404 (0.279)	44.464 (9.125)
	400	5.661(0.580)	6.946 (0.054)	6.767 (0.305)	9.370 (0.433)
400	100	7.920 (0.670)	8.001 (0.284)	6.815 (0.399)	9.091 (0.532)
	200	7.008 (0.346)	7.563 (0.233)	6.222 (0.218)	10.151 (0.722)
	400	6.444 (0.199)	7.061 (0.049)	6.079 (0.192)	40.190 (6.402)
1000	100	8.215 (0.764)	8.638 (0.263)	7.067 (0.372)	8.851 (0.406)
	200	7.324 (0.368)	7.539 (0.252)	6.214 (0.242)	8.871 (0.379)
	400	6.818 (0.250)	7.376 (0.068)	5.870 (0.161)	9.652 (0.429)

Note: In (a), “TPR” is the true positive rate, “TNR” is the true negative rate, and “Avg#” is the average number of the selected variables from 500 replicates. In (b), the numbers are the mean squared errors from prediction, and the numbers within parentheses are the median absolute deviations from 500 replicates.

TABLE 2.

Results from the simulation study with a binary outcome

(a) Summary of feature selection performance
		Proposed method			HSICLasso			SpAM			${\mathit{l}}_1$-SVM
$\mathit{p}$	$\mathit{n}$	TPR	TNR	Avg#	TPR	TNR	Avg#	TPR	TNR	Avg#	TPR	TNR	Avg#
100	100	74.7%	99.0%	3.3	71.1%	79.4%	22.1	64.5%	89.6%	12.1	76.2%	75.1%	26.5
	200	83.9%	99.9%	2.6	80.7%	89.7%	12.4	53.4%	98.9%	2.6	92.5%	80.4%	21.8
	400	86.0%	99.9%	2.6	87.8%	90.3%	12.1	50.6%	99.9%	1.5	98.8%	71.3%	30.8
200	100	70.4%	99.3%	3.5	71.3%	80.1%	41.3	63.6%	91.2%	19.2	71.3%	85.4%	31.0
	200	84.1%	99.8%	2.9	78.3%	95.0 %	12.2	54.5%	98.7%	4.1	90.7%	80.2%	41.8
	400	87.0%	100.0%	2.7	83.1 %	96.5%	9.3	50.6%	99.9%	1.6	89.3%	73.4%	55.0
400	100	68.5%	99.5%	3.9	70.9%	79.4%	84.0	63.7%	92.8%	30.6	65.9%	86.7%	54.7
	200	84.5%	99.9%	3.0	76.9%	95.5 %	20.2	57.7%	98.3%	8.3	87.0%	91.0%	38.1
	400	87.0%	100.0%	2.6	79.6 %	98.9%	6.8	51.9%	100.0%	1.8	99.1%	82.3%	73.0
1000	100	61.3%	99.8%	4.1	72.2%	77.4%	227.4	61.0%	95.7 %	45.0	58.4%	90.3 %	98.9
	200	86.3%	99.9%	3.3	75.5 %	95.9 %	43.6	54.3%	98.9 %	12.8	79.4%	91.4%	87.4
	400	87.7%	100.0%	2.8	73.9 %	99.6 %	6.6	50.0%	100.0%	1.9	96.8%	90.1 %	101.6

(b) Summary of misclassification errors
$\mathit{p}$	$\mathit{n}$	Proposed method	HSICLasso	SpAM	${\mathit{l}}_1$-SVM
100	100	0.314 (0.017)	0.345 (0.028)	0.343 (0.018)	0.359 (0.032)
	200	0.290 (0.009)	0.307 (0.012)	0.312 (0.002)	0.305 (0.011)
	400	0.283 (0.004)	0.292 (0.012)	0.297 (0.002)	0.292 (0.007)
200	100	0.316 (0.019)	0.351 (0.042)	0.344 (0.034)	0.352 (0.031)
	200	0.280 (0.008)	0.302 (0.015)	0.302 (0.003)	0.321 (0.028)
	400	0.270 (0.004)	0.282 (0.014)	0.297 (0.002)	0.326 (0.025)
400	100	0.331 (0.024)	0.372 (0.047)	0.369 (0.046)	0.390 (0.031)
	200	0.286(0.010)	0.319 (0.018)	0.311 (0.003)	0.327 (0.026)
	200	0.277 (0.004)	0.288 (0.014)	0.305 (0.001)	0.295 (0.010)
1000	100	0.352 (0.027)	0.397 (0.037)	0.390 (0.036)	0.416 (0.027)
	200	0.287 (0.008)	0.335 (0.024)	0.315 (0.003)	0.381 (0.020)
	400	0.277 (0.004)	0.294 (0.008)	0.305 (0.001)	0.353 (0.016)

Note: See Table 1.

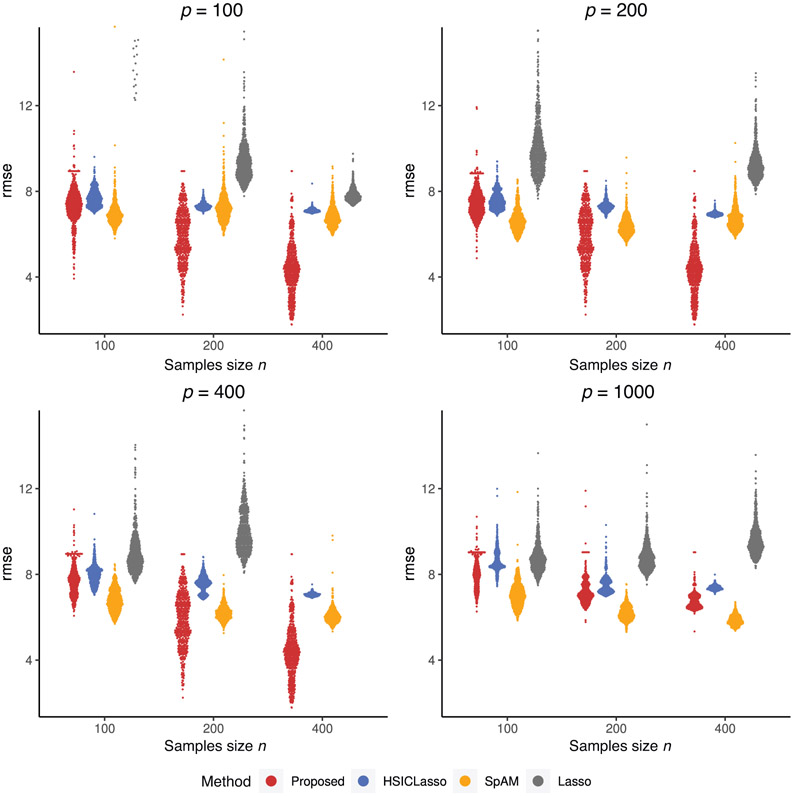
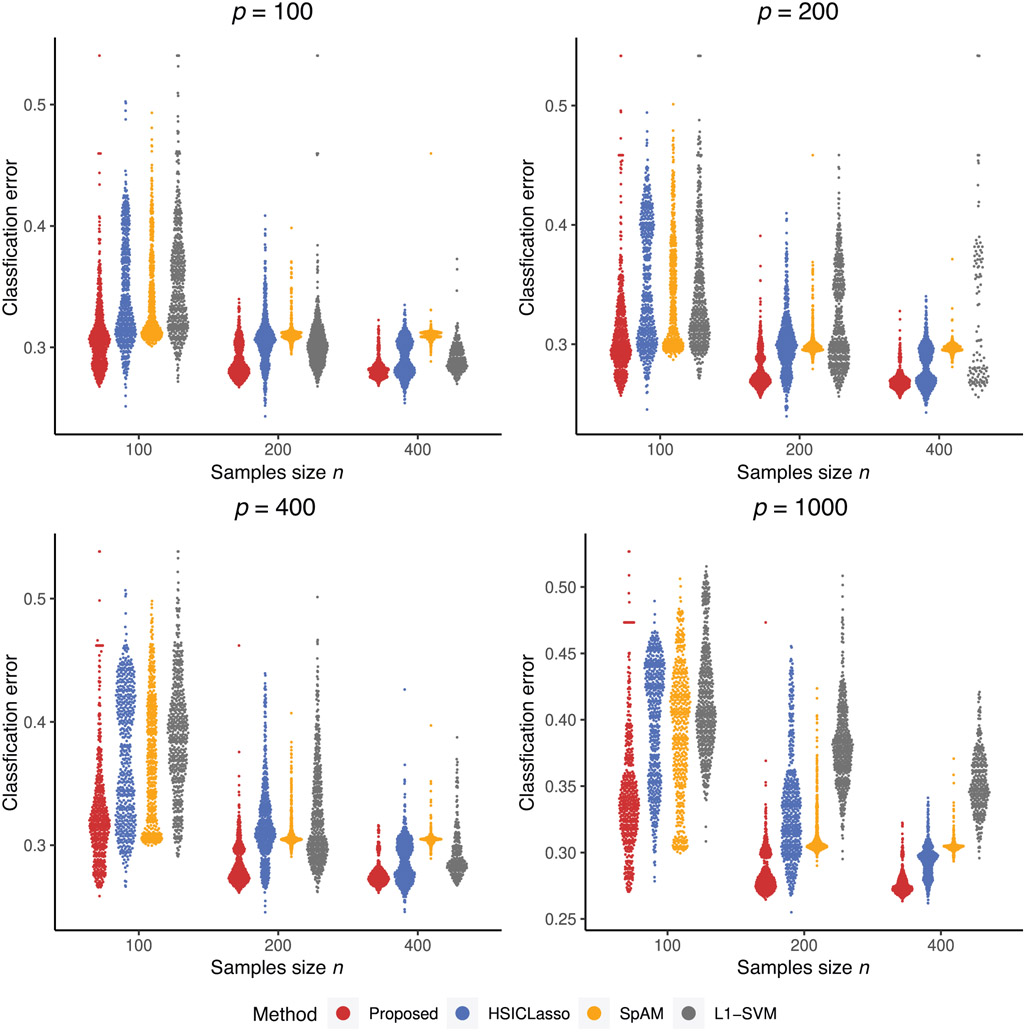
Clearly, LASSO and $l_1$-SVM did not yield reasonable variable selection results and their prediction errors are much higher due to model misspecification. We also give violin plots to visualize the prediction performance of 500 replications in Figures 1 and 2. Since Lasso cannot provide stable prediction errors, its prediction errors from many replicates are out of the bound as shown in Figure 1. Figures 1 and 2 further confirm that our method is superior to all other methods, even when the dimension is as large as 1000 and the sample size is as small as $n=100$, which is of similar size as our real data analysis example in Section 5. In the Supporting Information, we conducted an additional simulation study that had a similar setting to the first simulation study but allowed the dependence between the important and unimportant variables. Our method remains to perform better than the other methods.

FIGURE 1. Violin plots of prediction errors for continuous outcome.

Note: The plots give the distribution of prediction errors among four competing methods. The comparing methods from left to right in each plot are our proposed method, HSICLasso, SpAM, and Lasso. This figure appears in color in the electronic version of this article, and any mention of color refers to that version

FIGURE 2. Violin plots of misclassification errors for binary outcome.

Note: The plots give the distribution of misclassification rates among four competing methods. The comparing methods from left to right in each plot are our proposed method, HSICLasso, SpAM, and $l_1$-SVM. This figure appears in color in the electronic version of this article, and any mention of color refers to that version

4 ∣. APPLICATION

4.1 ∣. Application to microarray study of eye disease in animals

We applied our proposed method to analyze a gene expression study in Scheetz et al. (2006). This study analyzed microarray RNAs of eye disease from 120 male rats, containing the expression levels from about 31,000 gene probes. Gene TRIM32 is known to cause Bardet–Biedl syndrome (Chiang et al., 2006) but is responsible for less than half of cases. Therefore, identifying other genes associated with TRIM32 can help to identify additional novel disease genes, which provide a more complete gene signature to understand the disease mechanisms. The biological rationale behind this is that there is an evolutionary advantage in linking the expression of functionally related genes to the same biological system for which their function is needed. As a note, the association analysis between the causal gene and other genes using the same dataset has also been considered in Scheetz et al. (2006) and Huang et al. (2010).

Since the expression value for TRIM 32 was skewed due to some extreme values, we dichotomized TRIM32 based on whether it was overexpressed as compared to a reference sample in the dataset. We further restricted our feature variables to the top 1000 probe sets that were most correlated with TRIM32, while the analysis using all 31,000 probes was presented in the Supporting Information. All feature variables were on a log-scale and standardized in the analysis. To examine the performance of our method, we randomly divided the whole sample so that 70% was used for training and the rest was used for testing. This random splitting was then repeated 500 times to obtain reliable results. For each training data, we used threefold cross-validation to choose tuning parameters. We also applied HSICLasso, SpAM, and $l_1$-SVM for comparison.

The analysis results are shown in Table 3. We notice that our method gives almost the same classification error as $l_1$-SVM, which is the smallest on average. However, our method selects a much smaller set of feature variables with an average of five variables. SpAM selects 13 variables on average, but its classification error is higher. In Table 3, we also report the top 10 most-frequently selected features among all 500 replications for each method. We notice that some features such as Fbxo7 and LOC102555217 were selected by at least three methods. In addition, Gene Sirt 3 was identified by all three nonlinear feature selection methods, but not $l_1$-SVM, indicating some possible nonlinear relationship between Sirt 3 and TRIM32. In the Supporting Information, we provide a figure to reveal the nonlinear relationship between Sirt 3 and Fbxo7. We applied our method to analyze the whole sample and obtained a training error of 21.9% along five genes identified (Fbxo7, Plekha6, Nfatc4, 1375872, and 1388656), which were all selected as the top 10 genes in the previous random splitting experiment. As a note, the average prediction errors when using only the top five feature variables were in turn 0.345, 0.344, 0.344, 0.367, and 0.294, indicating that each individual feature itself was not sufficient to achieve the best prediction.

TABLE 3.

Top 10 Most selected genes for each method with a summary of feature selection results in the real data application based on 500 random splittings

	Proposed method	HSICLasso	SpAM	${\mathit{l}}_1$-SVM
Top 10 most selected genes	Fbxo7 (67.5%)	Ska1 (76.6%)	1388491 (46.2%)	1376747 (99.1%)
	Plekha6 (47.3%)	Sirt3 (76.2%)	Fbxo7 (37.8%)	1390538 (98.9%)
	LOC102555217 (24.5%)	Ddx58 (76.2%)	Slco1c1 (36.6%)	RragB (98.6%)
	Nfatc4 (22.7%)	1371610 (76.0%)	Stmn1 (35.4%)	Atl1 (97.9%)
	1390538 (20%)	LOC100912578 (73.2%)	1373944 (32.4%)	Fbxo7 (97.3%)
	1375872 (20%)	Ttll7 (70.4%)	Ufl1 (32.2%)	Plekha6 (95.1%)
	RGD1306148 (13.4%)	Decr1 (70.4%)	LOC100912578 (31.0%)	1375872 (94.8%)
	Sirt3 (11.6%)	Mff (68.0%)	LOC100911357 (28.6%)	RGD1306148 (94.1%)
	Prpsap2 (11.4%)	Pkn2 (67.0%)	LOC102555217 (26.8%)	Ska1 (93.6%)
	1388656 (10.2%)	Taf11 (65.0%)	Sirt3 (22.4%)	LOC102555217 (93.2%)
min #	2	1	1	7
max #	13	1000	26	990
avg #	5.1	250.3	12.3	448.7
Classification error	0.286 (0.057)	0.293 (0.046)	0.316 (0.057)	0.283 (0.058)

Note: For the top 10 most selected genes part, the numbers within parentheses are the frequencies to be selected in 500 random splittings. The genes also selected by the proposed method are highlighted in boldface. The last four rows give the summary of feature selection results. The numbers are the means of misclassification rates from 500 replicates. The numbers within parentheses are the median absolute deviations from 500 replicates. “min#” is the minimum number of the selected features, “max#” is the maximum number of the selected features, and “avg.#” is the average number of the selected features. This table appears in color in the electronic version of this article, and any mention of color refers to that version.

4.2 ∣. Application to the EMBARC study

In the second application, we applied our method to the Establishing Moderators and Biosignatures of Antidepressant Response for Clinical Care (EMBARC) study (Trivedi et al., 2016), which aimed to create a biosignature from clinical and biological markers to improve the response rates for MDD as well as to guide clinical care for patients. The study recruited early onset (< 30 years) chronic or recurrent MDD patients, and the study medication was Sertraline (an antidepressant). A comprehensive array of biomarkers was collected from participants: functional magnetic resonance imaging (fMRI) was used to assess key amygdala-anterior cingulate cortex circuitry implicated in implicit emotion processing and regulation under task and to collect functional connectivity measures under resting state (a total of 232 variables including the region of interest [ROI] biomarkers measuring regional brain activation under tasks and functional connectivity during rest); an electroencephalogram was used to measure brain signals at several power spectral bands (e.g., alpha and theta power and loudness dependence of auditory evoked potential [LDAEP], a total of 11 variables); and structural MRI was used to collect diffusion tensor imaging white matter measures (two variables). Other measures included demographics, quick inventory of depressive symptomatology (QIDS score), and behavioral phenotyping that measures psychomotor slowing, cognitive control (particularly posterror behavioral adjustments), working memory performance, and reward responsiveness. Details of the study measures were reported elsewhere (Trivedi et al., 2016).

Our study sample included 111 randomized patients. The outcome we considered was the treatment responder status assessed by a trained clinician (36 responders and 75 nonresponders). Due to a large number of candidate feature variables (266 variables) compared to the sample size, it was essential to select features that can best predict patient response to create the biosignature. We standardized all the feature variables before fitting the model and treatment assignment was included as a feature variable. To further examine the performance of our method, we randomly divided the whole sample so that 70% was used for training and the rest was used for testing. We repeated 500 times of random splittings to obtain reliable results. We used threefold cross-validation to choose tuning parameters. We compared with HSICLasso, SpAM, and $l_1$-SVM as in the simulation studies.

The analysis results are shown in Table 4. Our proposed method has the smallest mean and median classification error among all the comparison methods. Regarding feature selection, our proposed method gives the sparsest results with only 3.36 variables selected, on average, among 500 replications. However, all the other three methods selected more than 40 variables with larger classification errors. The topmost selected variables by our method include age, behavioral phenotypes (e.g., reaction time under various behavioral tasks), and neuroimaging biomarkers (e.g., mean activation in ROIs under various tasks). Moreover, one task fMRI measure (i.e., mean activation of subgenual cingulate ROI under the conflict adaptation task) was chosen both by our method and SpAM, but not $l_1$-SVM, which indicates that there could be a nonlinear relationship between this moderator and the outcome. More interestingly, there are some overlaps regarding the features selected by the proposed method and $l_1$-SVM, but our proposed method has a much smaller prediction error compared to $l_1$-SVM. This indicates that the proposed method successfully identified some predictors that have nonlinear relationships, which improves the classification error compared to a linear model. Note that the marginal classification errors for the top five features selected by our method range from 0.381 to 0.419, which are higher than the classification error when they are all included in our prediction method. These results provide empirical evidence to support using behavioral and neuroimaging measures to predict depression treatment responses, which has been suggested in theoretical models of depression biotypes (Williams, 2017).

TABLE 4.

Top 10 most selected markers for each method with a summary of feature selection results in the real data application based on 500 random splittings

	Proposed method	HSICLasso	SpAM	${\mathit{l}}_1$-SVM
Top 10 Most selected markers	Task.median.reaction.time. mean (40.4%)	Right.insula.perfusion.std (91.6%)	Dorsal.cingulate.conflict.adaptation. activation.mean (78.4%)	Task.median.reaction.time.mean (86.9%)
	Conflict.reaction.time.effect.mean (31.6%)	Left.Insula…Right.Insula.resting.coupling. (90.2%)	A/B choice test accuracy (77.2%)	Conflict.reaction.time.effect.mean (85.6%)
	Conflict.adaptation.reaction.time.effect.mean (26.0%)	RightAmygdala…Subgenual.cingulate.resting.coupling.mean (89.4%)	RightAmygdala…Subgenual.cingulate.resting.coupling.mean (68.8%)	Conflict.reaction.time.effect.mean (84.9%)
	Task.median.reaction.time.std (25.0%)	Left.insula.conflict.activation.std (88.6%)	Left.Insula…Right.Insula.resting.coupling. (76.0%)	Task.median.reaction.time.std (83.6%)
	Rabbit test reaction time (21.2%)	Ventral.striatum..seed..to.Perigenual.cingulate.coupling.anticipation.std (86.2%)	Left.ventral.striatum–Pregenual.cingulate.resting.coupling.mean (66.2%)	Age (81.9%)
	Age (17.6%)	Right..Insula…posterior.cingulate.resting.coupling.mean (85.4%)	Left.amygdala.perfusion.mean (65.2%)	Rabbit test reaction time (80.6%)
	Subgenual.cingulate.conflict.adaptation.activation.mean (11.2%)	Left.insula.conflict.activation.std (84.6%)	BP_w0_1924 (64.6%)	Gratton test reaction time (79.6%)
	Left.insula.conflict.activation.std (8.6%)	Ventral.striatum..seed..to.Perigenual.cingulate.coupling.anticipation.std (84.0%)	Rabbit test reaction time (63.8%)	Conflict.adaptation.reaction.time.effect.std (72.5%)
	Gratton test reaction time (7.2%)	Left.ventral.striatum.outcome.mean (83.2%)	Left.ventral.striatum.outcome.mean (62.0%)	Flanker test reaction time (71.8%)
	Right.ventral.striatum.outcome.std (5.6%)	Dorsal.anterior.cingulate.outcome.mea (82.6%)	Subgenual.cingulate.conflict.adaptation.activation.mean (58.0%)	Conflict.reaction.time.effect.std (69.9%)
min #	0	2	25	2
max #	32	267	140.6	266
avg #	3.36	140.6	41.2	41.6
Mean of classification error	0.346 (0.045)	0.356 (0.058)	0.412 (0.065)	0.441 (0.123)
Median of classification error	0.324	0.325	0.417	0.412

Note: See Table 3. This table appears in color in the electronic version of this article, and any mention of color refers to that version.

5 ∣. DISCUSSION

In this work, we have proposed a general framework for nonparametric feature selection for both regression and classification in high-dimensional settings. We introduced a novel tensor product kernel for empirical risk minimization. This kernel led to fully nonparametric estimation for the prediction function but allowed the importance of each feature to be captured by a nonnegative parameter in the kernel function. Our approach is computationally efficient because it iteratively solves a convex optimization problem in a coordinate descent manner. We have shown that the proposed method has theoretical oracle property for variable selection. The superior performance of the proposed method was demonstrated via simulation studies and a real data application with a large number of feature variables.

We considered the $l_2$ loss function for regression and the exponential loss function for classification as examples, respectively. Clearly, the proposed framework applies to feature selection under many different loss functions in the machine learning field. Another extension is to incorporate structures of feature variables in constructing the kernel function. For example, in integrative data analysis, feature variables arise from many different domains such as clinical domain, DNA, RNA, imaging, and nutrition. It will be interesting to construct a hierarchical kernel function, which can not only identify feature variables within each domain but also identify important domains at the same time. Furthermore, our theoretical results can be extended to not only derive the oracle selection of the important feature variables but also obtain the convergence rate of the prediction error.

Our framework of nonparametric feature selection can be generalized to perform feature selection when estimating individualized treatment rules. We can adapt loss functions used for learning treatment rules in our proposed method to simultaneously accomplish nonparametric variable selection and discover optimal individualized treatment rules. Extensions to categorical outcomes and multistage treatment rule estimation can also be considered.

DATA AVAILABILITY STATEMENT

The microarray data are publicly available and see Scheetz et al. (2006). The data for the Establishing Moderators and Biosignatures of Antidepressant Response for Clinical Care study and the research tools used in the preparation of this manuscript were obtained from the National Institute of Mental Health (NIMH) Data Archive (NDA). NDA is a collaborative informatics system created by the National Institutes of Health to provide a national resource to support and accelerate research in mental health. Dataset identifier(s): NIMH Data Archive Collection ID=2199. This manuscript reflects the views of the authors and may not reflect the opinions or views of the NIH or of the Submitters submitting original data to NDA.