Bayesian combinatorial MultiStudy factor analysis

Abstract

Mutations in the BRCA1 and BRCA2 genes are known to be highly associated with breast cancer. Identifying both shared and unique transcript expression patterns in blood samples from these groups can shed insight into if and how the disease mechanisms differ among individuals by mutation status, but this is challenging in the high-dimensional setting. A recent method, Bayesian Multi-Study Factor Analysis (BMSFA), identifies latent factors common to all studies (or equivalently, groups) and latent factors specific to individual studies. However, BMSFA does not allow for factors shared by more than one but less than all studies. This is critical in our context, as we may expect some but not all signals to be shared by BRCA1-and BRCA2-mutation carriers but not necessarily other high-risk groups. We extend BMSFA by introducing a new method, Tetris, for Bayesian combinatorial multi-study factor analysis, which identifies latent factors that any combination of studies or groups can share. We model the subsets of studies that share latent factors with an Indian Buffet Process, and offer a way to summarize uncertainty in the sharing patterns using credible balls. We test our method with an extensive range of simulations, and showcase its utility not only in dimension reduction but also in covariance estimation. When applied to transcript expression data from high-risk families grouped by mutation status, Tetris reveals the features and pathways characterizing each group and the sharing patterns among them. Finally, we further extend Tetris to discover groupings of samples when group labels are not provided, which can elucidate additional structure in these data.

1. Introduction.

Breast cancer incidence is strongly associated with family history, suggesting a link between breast cancer risk and genetic factors. Mutations in the BRCA1 and BRCA2 genes are now well-known to increase risk of breast cancer, but more than half of families with multiple cases are not carriers for mutations in either of these genes (Pouliot et al., 2017), and for many, it is not known what genes drive this hereditary risk. It is also not yet well-understood if and how mechanisms of this disease differ by mutation status. Pouliot et al. (2017) addressed these questions in a transcript expression dataset of women from high-risk families with BRCA1 mutations, BRCA2 mutations, and neither. They identified transcripts that are differentially expressed in lymphoblastoid cell lines derived across women from these groups, shedding insight into how mutation status may affect breast cancer susceptibility and development.

However, genes often act together in complex and coordinated ways, which can be overlooked by analyses that consider each transcript marginally. The unsupervised identification of latent factors can be particularly useful for uncovering patterns of transcript expression or other types of signal in a high-dimensional setting. However, there has been limited work on formal statistical approaches to unsupervised learning for multiple groups or datasets. This is crucial for several analyses, where the data are divided by the presence of group structure, as well as for analyses that consider data from multiple studies. For example, analyses are often carried out using systematic collections of genomic data generated over time in different laboratories and/or with different techniques. Methods that jointly analyze multiple groups or studies can identify what signal is shared by some or all of the studies, and what signal is specific to an individual study. This offers the opportunity to distinguish biological and technological variation, as well as to characterize different studies by the signals they contain. These types of analyses are not unique to high-throughput biology. Methods to identify replicable patterns across heterogeneous settings are valuable to many disciplines.

Here, we use the terms “studies” and “groups” exchangeably, to refer to any categorically-valued label of the samples. We refer to groups in our application, but use studies when describing the methods, for ease of reference of earlier contributions. Roy et al. (2021) introduced Perturbed Factor Analysis (PFA), which models groups as sharing a common factor structure perturbed by unique multiplicative effects. PFA allows for potentially large differences among groups, but only explicitly estimates factors shared by all. By contrast, De Vito et al. (2021) developed a Bayesian multi-study factor analysis methodology (BMSFA) that assumes an additive factor structure in which each factor is either common to all studies or unique to a single study. However, in our context, it is important to also identify factors only shared by subsets of studies. For example, there is likely to be substantial signal shared by groups with BRCA1 and BRCA2 mutations, but not other groups. In more general applications, we might similarly expect the subset of studies using the same experimental techniques and/or generated from the same laboratory to share latent factors.

In this work, we introduce a Bayesian combinatorial multi-study factor analysis method, which extends BMSFA (De Vito et al., 2021) to learn latent factors shared by any subset of studies. We do so by using the Indian Buffet Process (Ghahramani and Griffiths, 2006) to model the shared ownership of factors across multiple studies, which encourages sparsity. We thus refer to our method as Tetris, since the matrix indicating factor ownership resembles patterns from the Tetris video game. We estimate parameters using a Metropolis-within-Gibbs sampling algorithm tuned to ensure feasibility in $p\gg n$ settings. We test Tetris through a broad range of simulations, and we highlight Tetris’s utility not only in dimension reduction but also in covariance estimation. We further extend Tetris to discover groupings of observations when the group structure is not explicitly provided, and evaluate this extension in additional simulations. Finally, we apply Tetris with and without this extension to the transcript expression data from Pouliot et al. (2017) to uncover the patterns of expression shared by and unique among the different groups of mutation status.

2. Methods.

2.1. Model and Estimation.

We consider $S$ studies with the same $P$ variables. Study $s$ has $n_s$ subjects and $P$-dimensional centered data vector ${\mathbf{x}}_{is}$ with $i=1,\dots ,n_s$. Our model is

$${\mathbf{x}}_{is}=\mathbf{\Lambda }{\mathit{A}}_s{\mathit{l}}_{is}+{\mathit{e}}_{is}.$$ (1)

If $K$ is the total number of factors (including common, study-specific, and partially shared), then $\mathbf{\Lambda }$ is a $P\times K$ factor loadings matrix and ${\mathit{l}}_{is}$ are $K\times 1$ latent factors.

The $K\times K$ study-level factor indicator matrix ${\mathit{A}}_s$ is our key element to estimate the pattern of partial sharing of factors. This matrix consists of all 0s, except for the diagonal entries, which are either 1 or 0. The $k$th diagonal entry of ${\mathit{A}}_s$ is 1 whenever the $k$th factor is present in study $s$, so the product $\mathbf{\Lambda }{\mathit{A}}_s{\mathit{l}}_{is}$ will include the corresponding elements. Hence, for study $s,{\mathit{A}}_s$ controls which factors are included or not in the model.

We denote by $𝒜$ the overall $S\times K$ factor indicator matrix whose $s$th row consists of the $K$ diagonal entries of ${\mathit{A}}_s$. If the $k$th column of $𝒜$ consists of all 1 s, the $k$th factor is a common factor; if it consists of exactly a single 1, this is a study-specific factor; and if it consists of more than one 1 and at least one 0, this is a partially shared factor.

Our prior model builds on BMSFA (De Vito et al., 2021) wherein the latent factors are ${\mathit{l}}_{is}\sim {𝒩}_K\left(0,{\mathit{I}}_k\right)$, and the error terms are ${\mathit{e}}_{is}\sim {𝒩}_P\left(0,{\mathbf{\Psi }}_s\right)$ for ${\mathbf{\Psi }}_s=diag\left({\psi }_{s1}^2,\dots ,{\psi }_{sP}^2\right)$. In turn, the elements of this matrix are ${\psi }_{sp}^{-2}\sim \mathrm{\Gamma }\left(a_{\psi },b_{\psi }\right)$. For the loading matrix $\mathbf{\Lambda }$, we use the multiplicative gamma process shrinkage prior (Bhattacharya and Dunson, 2011) to encourage factors with decreasing norm, i.e., for each loading matrix element, ${\mathrm{\Lambda }}_{pk}\sim 𝒩(0,{\omega }_{pk}^{-1}{\tau }_k^{-1})$ with ${\tau }_k={\prod }_{l=1}^k{\delta }_l,$ ${\omega }_{pk}\sim \mathrm{\Gamma }\left(\frac{\nu }{2},\frac{\nu }{2}\right),{\delta }_1\sim \mathrm{\Gamma }\left(a_1,1\right)$ and ${\delta }_l\sim \mathrm{\Gamma }\left(a_2,1\right)$ for $l\ge 2$.

The study-level factor indicator matrices ${\mathit{A}}_s$, which are jointly summarized by the overall factor indicator matrix $𝒜$, allow us to estimate factors shared by any subset of studies. To avoid having to select the number of factors ahead of time, and to avoid the explicit assessment of all combinatorial possibilities, we place an Indian Buffet Process prior on $𝒜$.

The IBP (Ghahramani and Griffiths, 2006) is a probability distribution defined over infinite binary matrices, specifically matrices that have a finite number of rows and an infinite number of columns. In our case, each row represents a study, and each column represents a factor; as described earlier, an entry of 1 indicates that a given factor is shared by the corresponding study. Although the number of columns is infinite, the expected number of columns whose entries are not all 0 is finite. This expectation increases with the number of rows (i.e., studies). Hence, using this prior on $𝒜$ implies that we will automatically be performing dimension selection, without having to use heuristic post-hoc measures to determine the number of factors. The resulting patterns of 1s and 0s in this matrix resemble the patterns of fallen Tetris blocks, giving our method its name.

We specifically choose to use the two-parameter generalization of the IBP (Knowles and Ghahramani, 2007). In the regular one-parameter model, a single parameter $\alpha$ governs both the expected number of non-zero columns and the expected sparsity of each column. However, in the two-parameter version, $\alpha$ governs the expected sparsity of the total matrix, whereas $\alpha$ and $\beta$ together govern the expected number of columns. The resulting effect is that for fixed $\alpha$, small values of $\beta$ are more likely to result in factors shared by larger numbers of studies (i.e., more common factors, and factors shared by large subsets), whereas large values of $\beta$ are more likely to result in factors shared by small numbers of studies (i.e., more study-specific factors, and factors shared by small subsets). This is a desirable property in our setting because data may fall at either end of the spectrum.

The multiplicative gamma process shrinkage prior on $\mathrm{\Lambda }$ has previously been used in contexts where the property of increasing shrinkage allowed the number of factors to be chosen via truncation, such as in Bhattacharya and Dunson (2011), De Vito et al. (2021), and Roy et al. (2021). Because the IBP prior allows the factors to be automatically selected, truncation is unnecessary. However, the shrinkage prior and IBP prior together result in a faster effective rate of increasing shrinkage across the columns, which encourages a greater amount of signal in a smaller number of factors. We provide a simple illustrative example in Supplementary Materials Section A. We further note that the shrinkage prior and IBP prior can be thought of as working together by imposing sparsity in two different senses. Namely, the IBP prior imposes exact sparsity through the binary presence or absence of factors in each study, whereas the shrinkage prior encourages the shrinkage of loading entries arbitrarily close to zero.

Our model implies that the marginal distribution of each observation is

$${\mathit{x}}_{is}\sim 𝒩\left(0,\mathbf{\Lambda }{\mathit{A}}_s{\mathbf{\Lambda }}^T+{\mathbf{\Psi }}_s\right).$$ (2)

If study $s$ contained only common or study-specific factors, we could rewrite $\mathbf{\Lambda }{\mathit{A}}_s{\mathbf{\Lambda }}^T$ as the sum of the common loading matrix covariance (the covariance of the loading matrix when subsetted only to common factors) and the study-specific loading matrix covariance (the covariance of the loading matrix when subsetted only to the study-specific factors). This corresponds exactly to the covariance matrix decomposition of BMSFA. In the more general model described by Tetris, we can analogously decompose $\mathbf{\Lambda }{\mathit{A}}_s{\mathbf{\Lambda }}^T$ as the sum of loading matrix covariances corresponding to each “type” of factor, e.g. common factors, factors specific to study $s$, factors shared exactly by study 2 and study $s$, and so on. In this way, Tetris more flexibly characterizes the covariance of each study as a sum of terms corresponding to distinct sharing patterns.

To sample from the posterior distributions using these priors and our model, we develop a computationally efficient Metropolis-within-Gibbs sampler based primarily on the work in De Vito et al. (2021), Knowles and Ghahramani (2007), and Doshi-Velez et al. (2009). The specific sampler steps are in Supplementary Materials Section B. We implement the sampler and perform all subsequent analyses in the statistical software package R version 4.0 (R Core Team, 2021).

2.2. Recovery of Factor Indicator Matrix and Loading Matrix.

In our Metropolis-within-Gibbs sampler, the number of factors can change dynamically from iteration to iteration in the chain. This means that the MCMC samples of the factor indicator matrix $𝒜$ and of the loading matrix $\mathrm{\Lambda }$ can have varying dimensions across iterations. Recovering point estimates of these quantities requires post-processing on the sampler output.

To recover $𝒜$, we recommend the following approach, which we use in all results presented in this work. First, we define a distance $d\left({𝒜}_i,{𝒜}_j\right)$ between two sampled matrices ${𝒜}_i,{𝒜}_j$ as the minimum number of $0\to 1$ or $1\to 0$ “flips” needed to change all the entries of ${𝒜}_i$ to those of ${𝒜}_j$ (or, symmetrically, from ${𝒜}_j$ to ${𝒜}_i$) over all possible permutations of their columns. Intuitively, this counts the number of differences between the two matrices under the best possible “alignment” of their columns, since the ordering of the columns (which correspond to factors) is not itself meaningful. Note, therefore, that if two matrices ${𝒜}_i^1,{𝒜}_i^2$ are identical except for the ordering of their columns, $d\left({𝒜}_i^1,{𝒜}_j\right)=d\left({𝒜}_i^2,{𝒜}_j\right)$ for any other matrix ${𝒜}_j$. If ${𝒜}_i$ and ${𝒜}_j$ have a different number of active factors, we take the matrix having fewer factors and pad it with columns of all 0s to match the dimension of the other. We can express the computation of the distance formally as

$$\underset{\mathit{L},\mathit{R}}{\mathrm{m}\mathrm{i}\mathrm{n}}\mathrm{T}\mathrm{r}(\mathit{L}\mathit{M}\mathit{R}),$$

where each $M_{kl}$ is the number of flips between the $k$th column of ${𝒜}_i$ and the $l$th column of ${𝒜}_j$, and $\mathit{L},\mathit{R}$ represent left and right permutation matrices respectively. This can be efficiently computed using the Hungarian Algorithm, as implemented in the library clue (Hornik, 2005).

We compute these distances between every pair of post-burn-in MCMC samples, and then select the MCMC sample that contains the largest number of other MCMC samples within a radius $r$. We choose $r$ as whichever is larger between the 0.05th quantile of all distances and the number of studies $S$. The motivation for this upper bound on the radius is to allow each study to change one entry, but other options could be used instead. Overall, we can think of this selection process as choosing the sampled $𝒜$ matrix that defines the highest density neighborhood when chosen as the center. Ties are broken first by selecting the matrix with fewest factors, and if there are still ties, then by selecting the matrix with highest probability under the IBP prior.

It should be noted that, in the worst case, this procedure scales quadratically in the number of post-burn-in MCMC samples, because the distance is computed between every pair of such samples. Furthermore, the time required for each distance computation scales linearly in the number of studies $S$ and cubically with the number of factors $K$. In practice, however, it is common for values of ${𝒜}_i$ to re-appear many times throughout the chain of MCMC samples, which allows the corresponding computations to be stored and re-used. As such, the worst-case scaling is unlikely to occur. We found this procedure to be computationally tractable for the settings considered in this work, and describe more detailed results on computational timing in Supplementary Materials Section C.

To summarize the uncertainty around this point estimate of $𝒜$, we generalize the idea of credible balls from the Bayesian clustering context. Following Wade et al. (2018), we define the credible ball of radius $ϵ$ for point estimate $\widehat{𝒜}$ as

$$B_{ϵ}(\widehat{𝒜})=\{𝒜:d(𝒜,\widehat{𝒜})\le ϵ\}.$$

Then we define a level $1-\alpha$ credible ball as $B_{{ϵ}^{\mathrm{*}}}(\widehat{𝒜})$ with ${ϵ}^{\mathrm{*}}$ the smallest $ϵ\ge 0$ such that

$$\mathrm{P}\mathrm{r}(B_{ϵ}(\widehat{𝒜})|\mathit{X})\ge 1-\alpha$$

for data $\mathit{X}$. In practice, we can approximate this quantity using the MCMC output as $\frac{1}{M}{\sum }_{m=1}^M\mathbf{1}(d({𝒜}^m,\widehat{𝒜})\le ϵ)$, if there are $M$ iterations post-burn-in and ${𝒜}^m$ represents the $m$-th such sampled matrix. This allows us to summarize a set of plausible values for $𝒜$.

Next, to recover $\mathbf{\Lambda }$, we first need sampler output where $𝒜$ is exactly the same across all iterations; otherwise, it is not meaningful to construct a single estimate of $\mathbf{\Lambda }$, since there would not be a single set of factors for the columns of $\mathbf{\Lambda }$ to correspond to. Hence, after recovering the point estimate $\widehat{𝒜}$, we propose to rerun the MCMC with $𝒜$ fixed to this estimate, while updating all the remaining parameters as previously. Note that because updating $𝒜$ is the most computationally expensive step of the sampler, rerunning the MCMC with $𝒜$ fixed only represents minor additional time (see Supplementary Materials Section C for details).

In factor analysis, loading matrices are not unique since they are only identifiable up to rotations. Different draws of $\mathbf{\Lambda }$ from iteration to iteration could correspond to a different rotation of the same parameter. Thus, to estimate $\mathbf{\Lambda }$, we cannot simply take, say, the posterior median of all $\mathbf{\Lambda }$ draws in this new chain. However, quantities that involve squaring $\mathbf{\Lambda }$ are invariant to rotation. We can produce point estimates of the study-specific covariance matrices ${\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_s$ as the mean values of $\mathbf{\Lambda }{\mathit{A}}_s{\mathbf{\Lambda }}^T$ over the chain for each $s$, and then choose $\stackrel{\mathbf{ˆ}}{\mathbf{\Lambda }}$ that minimizes the distance from these estimates over all studies, i.e.

$$\stackrel{\mathbf{ˆ}}{\mathbf{\Lambda }}={\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}_{\mathbf{\Lambda }}\sum _s{\parallel {\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_s-\mathbf{\Lambda }{\stackrel{\mathit{ˆ}}{\mathit{A}}}_s{\mathbf{\Lambda }}^T\parallel }_2^2.$$

We perform this optimization numerically using the low-storage BFGS algorithm as implemented in the library nloptr version 1.2.2.2 (Johnson, 2020; Nocedal, 1980; Liu and Nocedal, 1989).

Once we have point estimates for both $𝒜$ and $\mathbf{\Lambda }$, we can also use the credible ball for $\widehat{𝒜}$ to characterize uncertainty about how a particular factor of interest is shared across studies. If we are interested in, say, factor $i$ of the point estimate, we can compute the congruence coefficient (Lorenzo-Seva and Ten Berge, 2006) between our point estimate’s loadings for factor $i$ and the loadings of every factor in every MCMC iteration corresponding to a value of $𝒜$ in the credible ball. We assume that every factor whose congruence coefficient with factor $i$ exceeds a certain threshold represents the same factor as factor $i$. We can then examine the set of sharing patterns for all such factors to describe the variability in sharing pattern for this factor. This challenge is unique to our context. We illustrate it, as well as one way to select the threshold for the congruence coefficient, in Section 4.3.

Characterizing the uncertainty of $\mathbf{\Lambda }$ is challenging due to the previously described identifiability issues. Simply using the MCMC samples to summarize credible intervals for each entry would ignore the potential for rotation from iteration to iteration. A better approach would be to compute, for each MCMC iteration $i$, an estimate ${\stackrel{\mathbf{ˆ}}{\mathbf{\Lambda }}}_i$ as described above using the study-specific covariances constructed from the MCMC samples at iteration $i$. This generates a set of plausible values of $\mathbf{\Lambda }$. It should be noted, however, that because the second sampler run conditions on a point estimate of $𝒜$, the level of uncertainty portrayed is conditional on $𝒜$. When appropriate, it is more straightforward and reliable to instead characterize the unconditional uncertainty of the study-specific covariances $\mathbf{\Lambda }{\mathit{A}}_s{\mathbf{\Lambda }}^T$, because they are invariant to rotation and therefore their values at each iteration can be summarized directly from the MCMC samples in the initial sampler run.

2.3. Extension to Clustering.

Tetris as described thus far assumes that the study labels are known, i.e. for each observation ${\mathit{x}}_i$, we know to which study $z_i\in \{1,\dots ,S\}$ it belongs. This is a reasonable assumption for many applications, such as when data are known to come from different laboratories, batches, or experimental conditions, or when established groups such as breast cancer mutation status are of interest. However, in other applications, we may suspect or know a grouping structure is present but lack access to the study labels. Even if study labels are known, we might still be interested in whether there is an additional grouping structure that offers an alternative explanation of how signal is shared among the observations. For example, in our breast cancer application, there could plausibly be other groupings of samples, related or not to mutation status, that could reveal additional structure in the data.

To this end, we develop an extension to Tetris that treats the study labels $z_i$ as latent variables and estimates these values as part of the algorithm. In other words, this extension simultaneously clusters the data and estimates the factors and their sharing pattern. We assume that the total number of studies $S$ is known, and set the prior on $z_i$ as the categorical distribution with equal probability of belonging to each study, i.e. $p_s=\frac{1}{S}$ for study $s$. We randomly initialize $z_i$, and update these values in each iteration using a Gibbs sampling step. Details are in Supplementary Materials Section B. This also covers scenarios where the labels $z_i$ may be known for some but not all samples, i.e. the semi-supervised case. Technically, extensions are straightforward in an MCMC setting, as one simply needs to fix the known $z_i$. Practically, this can be used to support classification of samples from unknown groups when some of the group labels are known for other samples.

These extensions can be thought of as a combinatorial multi-study mixture of factor analyzers. Ghahramani et al. (1996) first introduced mixtures of factor analyzers as Gaussian mixtures where the covariance structure is modeled via factor analysis. There have been numerous extensions of this work since then. For example, McNicholas and Murphy (2008) presented a family of parsimonious Gaussian mixture models, one special case of which assumes a common loadings matrix but unconstrained uniquenesses across clusters. This is analogous to our model if we only allowed common factors. Conversely, Murphy, Viroli and Gormley (2020) introduced a mixture of infinite factor analyzers that assumes cluster-specific loading matrices, each with automatic dimension selection using the same multiplicative gamma process shrinkage prior as our model. Notably, this approach also simultaneously clusters the data while estimating these cluster-specific parameters. This, then, is analogous to our model if we only allowed study-specific factors. Our extension thus introduces a new mixture of factor analyzers that allows for the possibilities of common, partially shared, and study-specific loadings components.

3. Simulations.

3.1. Simulation Design.

We evaluated our method in four different simulated scenarios, with a range of parameters encompassing similar dimensionality, sample size, and number of studies as our real data application. In brief, the first scenario specifically assesses Tetris’s ability to differentiate signal that is partially shared from the signal that is common to all studies. The second scenario is designed to test Tetris’s performance as the data dimensions, loading matrix sparsity, and number of partially shared factors are systematically varied. The third scenario evaluates Tetris’s performance when the number of studies is greatly increased. Finally, the fourth scenario is designed to mimic the breast cancer transcript expression data in order to most closely assess how Tetris would perform on our data of interest. We also evaluated the clustering extension on this last scenario. These scenarios are loosely based on those used to evaluate BMSFA (De Vito et al., 2021), and modified to study partially shared factors. We use “partially shared” to refer to factors belonging to multiple, but not all, studies.

In all of the following scenarios, each combination of settings was simulated ten times, and Tetris was run with a total of 10,000 iterations and a burn-in of 8,000 iterations. These iterations were sufficient for convergence and good mixing. For choice of hyperparameters, we used $\alpha =1.25S$, capped no lower than 5 and no greater than 10, where $S$ is the number of studies, and $\beta =1$ for the IBP prior on $𝒜$. For the shrinkage prior on $\mathbf{\Lambda }$, following BMSFA (De Vito et al., 2021) and the recommendations of Durante (2017), we used $a_1=2.1,a_2=3.1$, and $\nu =3$. Finally, for the prior on the variance, again following BMSFA (De Vito et al., 2021), we used $a_{\psi }=1$ and $b_{\psi }=0.3$.

3.1.1. Scenario 1: Structurally Distinct Common and Partially Shared Signals.

In the first scenario, we simulated four studies with $n_s$ observations and $p$ variables from ${\mathit{X}}_s\sim ℳ𝒱𝒩\left(0,{\mathbf{\Sigma }}_{\mathit{s}}\right)$, with ${\mathbf{\Sigma }}_s=\mathbf{\Lambda }{\mathit{A}}_s{\mathbf{\Lambda }}^T+{\mathbf{\Psi }}_s$. We fixed three common factors and three factors shared by the first two studies, as well as one study-specific factor per study.

The non-zero elements of $\mathrm{\Lambda }$ were drawn from $𝒥(-1,1)$. For the columns corresponding to the common factors, their locations were chosen uniformly at random among the first $\frac{p}{2}$ rows (i.e., these loadings only involved the first half of the variables). For the columns corresponding to the partially shared factors, their locations were chosen uniformly at random among the last $\frac{p}{2}$ rows (i.e., these loadings only involved the second half of the variables). This was designed to create structural distinction between the common and partially shared factors. The locations of the non-zero elements for columns corresponding to study-specific factors were not restricted, and were selected uniformly at random over all rows. The number of non-structurally-zero locations of the loading matrix was set to result in a sparsity of 80%.

${\mathrm{\Psi }}_s$ is a diagonal matrix where each element is drawn from $𝒥(0,0.5)$. We set the dimension of the data $\left(n_s,p\right)$ to our $p\gg n_s$ setting (10, 60). The dimension of $\mathbf{\Lambda }$ is (60, 10).

3.1.2. Scenario 2: Inference on Dimension, Sparsity, and Number of Partially Shared Factors.

In the second scenario, we simulated four studies with $n_s$ samples and $p$ variables from ${\mathit{X}}_s\sim ℳ𝒱𝒩\left(0,{\mathbf{\Sigma }}_s\right)$, where ${\mathbf{\Sigma }}_s=\mathbf{\Lambda }{\mathit{A}}_s{\mathbf{\Lambda }}^T+{\mathbf{\Psi }}_s$. Each non-zero element of $\mathrm{\Lambda }$ was drawn from $𝒥(-1,1)$, and their locations in the matrix were selected uniformly at random. ${\mathrm{\Psi }}_s$ is a diagonal matrix where each element is drawn from $𝒥(0,0.5)$. All simulations in this scenario have three common factors and one study-specific factor per study.

We then varied three parameters: the dimension of the data, where $\left(n_s,p\right)$ is set to one of (60, 10),(35, 35), and (10, 60) to correspond to the $p\ll n_s,p=n_s$, and $p\gg n_s$ settings; the sparsity of the loading matrix, which is one of 20%, 50%, and 80%; and the number of partially shared factors, which is either zero, one (shared by the first two studies), or two (both shared by the first two studies). Thus, the dimensions of $\mathbf{\Lambda }$ are either $(p,7)$, $(p,8)$, or $(p,9)$. In total, we considered all 27 combinations of these parameters under this scenario.

3.1.3. Scenario 3: Large Number of Studies.

In the third scenario, we adapted the second scenario to consider the case where the data consists of 16 studies. We used the $p\gg n_s$ (i.e. $\left(n_s,p\right)=(10,60)$) and 80% sparsity setting, and varied the number of partially shared factors as 0 or 1. When there is one partially shared factor, that factor is shared by the first eight studies. Accordingly, the dimension of $\mathbf{\Lambda }$ is (60, 19) or (60, 20).

3.1.4. Scenario 4: Based on Breast Cancer Transcript Expression Application.

In the fourth scenario, we generated data to mimic the breast cancer transcript expression dataset both when analyzed as three groups (BRCA1 mutations, BRCA2 mutations, and neither), and as six groups (the aforementioned three groups crossed with affected status, i.e. whether or not each individual was diagnosed with breast cancer).

To generate data in the three-group setting, we first ran single-study factor analysis with the multiplicative gamma process shrinkage prior (Bhattacharya and Dunson, 2011) on the dataset subsetted to 370 genes (see Section 4 for more details). We then took the final post-burn-in MCMC sample of the loadings matrix as our ground truth $\mathbf{\Lambda }$ parameter. Next, we conducted exploratory analyses with these factors and the three mutation status groups to determine a reasonable ground-truth value of $𝒜$. Ultimately, we chose to simulate from 8 factors with the following sharing pattern:

$$𝒜=\left(\begin{array}{llllllll}0& 1& 1& 1& 0& 0& 0& 1\\ 1& 1& 1& 1& 1& 0& 0& 0\\ 1& 1& 1& 1& 0& 1& 1& 0\end{array}\right).$$

This corresponds to three common factors, one partially shared factor, and four study-specific factors. Finally, we generated ${\mathbf{\Psi }}_s$ as a diagonal matrix where each element is drawn from $𝒥(0,0.5)$. We then simulated the three groups from ${\mathit{X}}_s\sim ℳ𝒱𝒩\left(0,{\mathbf{\Sigma }}_s\right)$ for ${\mathbf{\Sigma }}_s=\mathbf{\Lambda }{\mathit{A}}_s{\mathbf{\Lambda }}^T+{\mathbf{\Psi }}_s$, with $p,n_s$ matching the observed values of the data, i.e. $p=370$ and $n_1=37,n_2=50$, and $n_3=34$. Accordingly, the dimension of $\mathbf{\Lambda }$ is (370, 8).

To generate data under the six-group setting, we used the same ground truth $\mathbf{\Lambda }$ parameter but conducted exploratory analyses between the factors and the six groups (mutation status crossed with affected status) to determine the form of $𝒜$. Ultimately, we chose 11 factors with the following sharing pattern:

$$𝒜=\left(\begin{array}{lllllllllll}0& 1& 1& 1& 0& 0& 0& 0& 0& 0& 1\\ 1& 1& 1& 1& 1& 0& 0& 1& 1& 0& 0\\ 1& 1& 1& 1& 0& 1& 1& 1& 1& 0& 1\\ 0& 1& 1& 1& 1& 0& 0& 0& 0& 0& 1\\ 0& 1& 1& 1& 1& 0& 0& 0& 1& 1& 0\\ 1& 1& 1& 1& 0& 1& 1& 1& 1& 1& 0\end{array}\right)$$

This corresponds to three common factors, and the rest partially shared. Hence, the dimension of $\mathbf{\Lambda }$ is (370, 11). We then generated ${\mathbf{\Psi }}_s$ and subsequently simulated ${\mathit{X}}_s$ as described for the three-group setting, but now with six groups such that $n_1=11,n_2=26,n_3=18,n_4=32,n_5=17$, and $n_6=17$.

3.2. Evaluation Metrics.

We evaluate the accuracy of our simulation results on both loading matrix covariances and study covariances, using the $\mathrm{R}\mathrm{V}$ coefficient (Abdi, 2007). For two positive semi-definite matrices $S$ and $T$, the $\mathrm{R}\mathrm{V}$ is defined as

$$RV(S,T)=\frac{\mathrm{T}\mathrm{r}(S^{T}T)}{\sqrt{\mathrm{T}\mathrm{r}(S^{T}S)\mathrm{T}\mathrm{r}\left(T^{T}T\right)}},$$ (3)

and takes on a value between 0 and 1, where a value closer to 1 indicates greater similarity between the two matrices.

3.2.1. Loading Matrix Covariances.

We quantified the similarity between the true and estimated full loading matrix covariance $\mathrm{\Lambda }{\mathrm{\Lambda }}^T$ using RV. The quantity $\mathrm{\Lambda }{\mathrm{\Lambda }}^T$ can be interpreted as summarizing relationships among variables for a hypothetical study containing all the factors found across any of the observed studies.

We also quantified the similarity between the true and estimated common loading matrix covariance ${\mathrm{\Lambda }}_C{\mathrm{\Lambda }}_C^T$, where ${\mathrm{\Lambda }}_C$ represents the loading matrix subsetted to just the common factors, using the RV coefficient. This assesses how well specifically the common signal among all studies was recovered.

3.2.2. Study Covariances.

We reconstructed the study-specific covariance matrix of study $s$ as ${\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_{s,\mathit{Tetris}}=\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}{\stackrel{\mathit{ˆ}}{\mathit{A}}}_s{\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}}^T$, following the result in Equation 2. We then computed the RV coefficient between this matrix and the structural component of the true covariance matrix ${\mathrm{\Sigma }}_s=\mathrm{\Lambda }{A}_s{\mathrm{\Lambda }}^T$ used to generate the data, i.e. the covariance matrix with noise subtracted. As a comparison, we applied the same procedure to estimates obtained from BMSFA, from single-study factor analysis (FA) using the multiplicative gamma process shrinkage prior (Bhattacharya and Dunson, 2011), and from PFA (Roy et al., 2021).

BMSFA separately estimates a common loading matrix and a study-specific loading matrix for each study. We ran BMSFA and obtained estimates of each loading matrix using default parameters as implemented in the MSFA package (De Vito et al., 2021). We then reconstructed the covariance matrix for each study ${\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_{s,BMSFA}$ as the sum of the common loading matrix covariance and the study-specific loading matrix covariance. When using FA, which only supports the analysis of one study at a time, we considered each study independently and estimated ${\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_{s,FA}=\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}{\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}}^T$, that is, the estimated loading matrix covariance. We used FA with default parameters as implemented in MSFA. Unlike the others, PFA models group differences through multiplicative, rather than additive, perturbations. We ran the fully Bayesian version of PFA with default parameters and post-processed the loading matrix as recommended by author A. Roy via personal communication. We then estimated ${\stackrel{\mathrm{ˆ}}{\mathrm{\Sigma }}}_{s,PFA}$ as ${\hat{Q}}_s^{-1}(\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}\hat{E}{\stackrel{\mathrm{ˆ}}{\mathrm{\Lambda }}}^T){({\hat{Q}}_s^{-1})}^T$, where $Q_s$ is the perturbation matrix representing the multiplicative effects on study $s$ and $E$ represents the variance of the latent factors. As recommended by personal communication, we summarized $Q_s,E$ via posterior means.

3.3. Simulation Results.

We first examine the results of the Scenario 1 simulation to highlight Tetris’s ability to clearly and consistently discriminate between common and partially shared signal when there are important structural differences between the two. We use “common” to refer to signal shared by all the studies under consideration, and “partially shared” to refer to signal shared by more than one but not all of the studies. In this particular simulation, the partially shared factors are all shared by the first two (out of four) studies. The structural differences between the common and partially shared factors are that the features involved in the common factors and the features involved in the partially shared factors are disjoint and exhaustive. Note that the study-specific factors for each of the four studies may span the entire set of features.

Tetris differentiated between the common and partially shared signal by correctly identifying high loadings on the appropriate sets of features in both types of signal. As an illustration, this can be visually seen in the heatmaps of the estimated common and partially shared loading matrix covariances, as compared to the heatmaps of the true common and partially shared loading matrix covariances (Figure 1A). The common loading matrix covariance is the covariance of the loading matrix when subsetted only to the common factors, and analogously so for the partially shared loading matrix covariance. In the interest of space, we are showcasing results from the run with sixth best performance out of ten (as measured by RV coefficient) in an effort to be representative. Nevertheless, we obtained similar results across the other runs. This demonstrates that Tetris can capture and differentiate common and partially shared signals across multiple studies.

FIG 1.

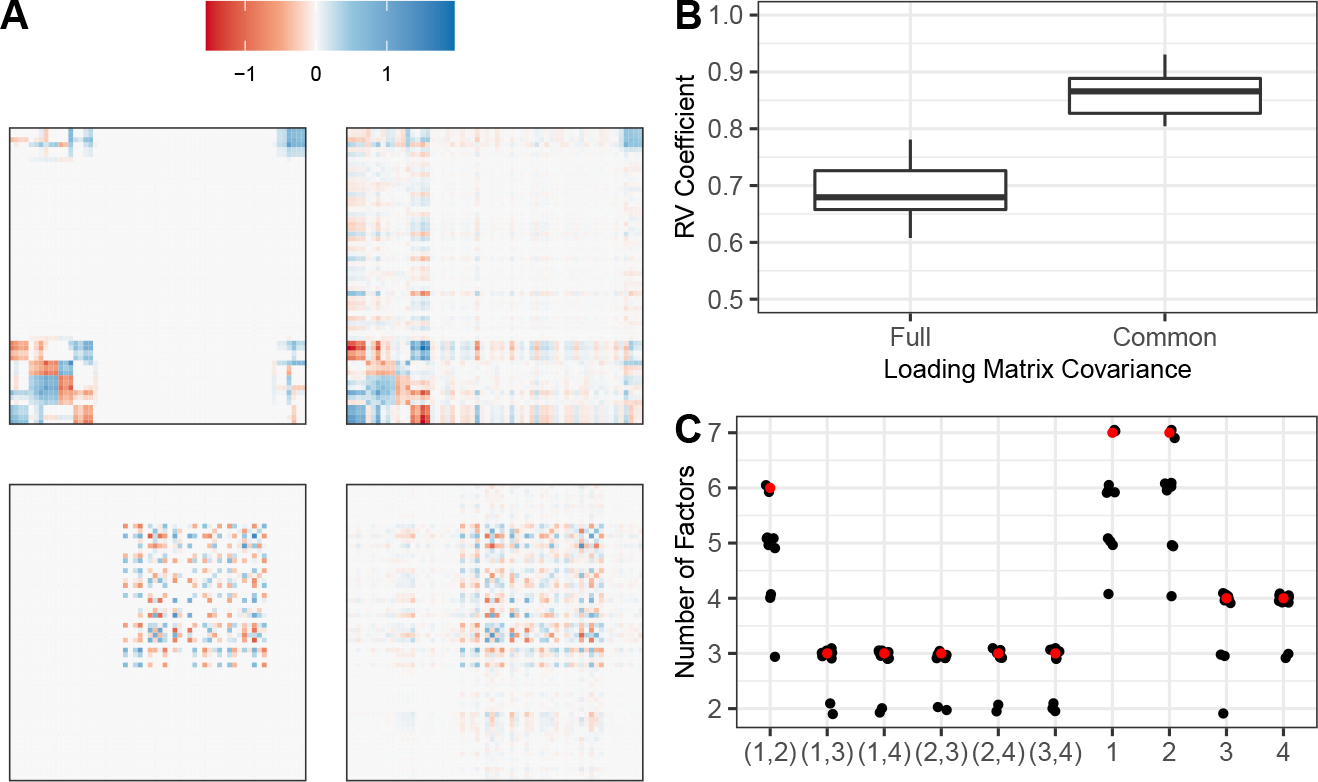
(A) Comparison of heatmaps for the true (left) and estimated (right) partially shared loading covariance (top) and common loading covariance (bottom). Results shown are based on a single dataset generated using the Scenario 1 simulation, where there are structural differences between the common and partially shared factors. (B) RV coefficients for the full loading matrix covariance and common loading matrix covariance for the Scenario 1 simulation. (C) Number of factors shared by each pair of studies $i$ and $j$, indicated by $(i,j)$, and the number of total factors belonging to study $i$, indicated by $i$. Estimated values are in black (with jitter, for visual clarity) and ground-truth values are in red.

We can also quantify the accuracy of our parameter estimation by looking at the RV coefficients for the full and common loading matrix covariances (Figure 1B). The full loading matrix covariance can be interpreted as the loading matrix covariance corresponding to a hypothetical study containing all the factors found across all studies. Intuitively, this quantity summarizes all relationships among variables across the studies. Analogously, the common loading matrix covariance can be thought of as summarizing the structure common to all the studies. For both the full and common loading matrix covariance, the RV coefficients are stable and high over all runs, confirming that Tetris estimated these parameters well. Finally, we summarize Tetris’s ability to estimate the factor sharing pattern $𝒜$ by comparing the estimated and true number of factors that should be shared by each pair of studies (Figure 1C). Although some runs underestimated exactly how many factors should be shared by the first two studies, Tetris consistently captured that these two studies, and not any other pair, share a high degree of signal, and overall closely recovered the true sharing pattern.

Next, to understand how robust Tetris is under varied settings and without such clear structural differences across factors, we examine the results from the Scenario 2 simulation. The RV coefficients for the full and common loading matrix covariances are shown for all tested sparsities and dimensionalities in the case with two partially shared factors (Figure 2), demonstrating Tetris’s ability to estimate the loading matrix covariance under a wide range of settings. The results with zero and one partially shared factor respectively are similar, and are included in Supplementary Materials Section D. In general, the RV coefficient improves with decreasing sparsity of the loading matrix, and is also generally higher for the $p=n_s$ or $p\ll n_s$ cases than for the $p\gg n_s$ cases. As might be expected, the RV coefficient is higher for the common loading matrix covariances than for the full loading matrix covariances, which can be attributed to the ability to borrow strength across studies. However, even in challenging settings, Tetris remains robust and continues to have reasonable RV coefficients for both quantities.

FIG 2.

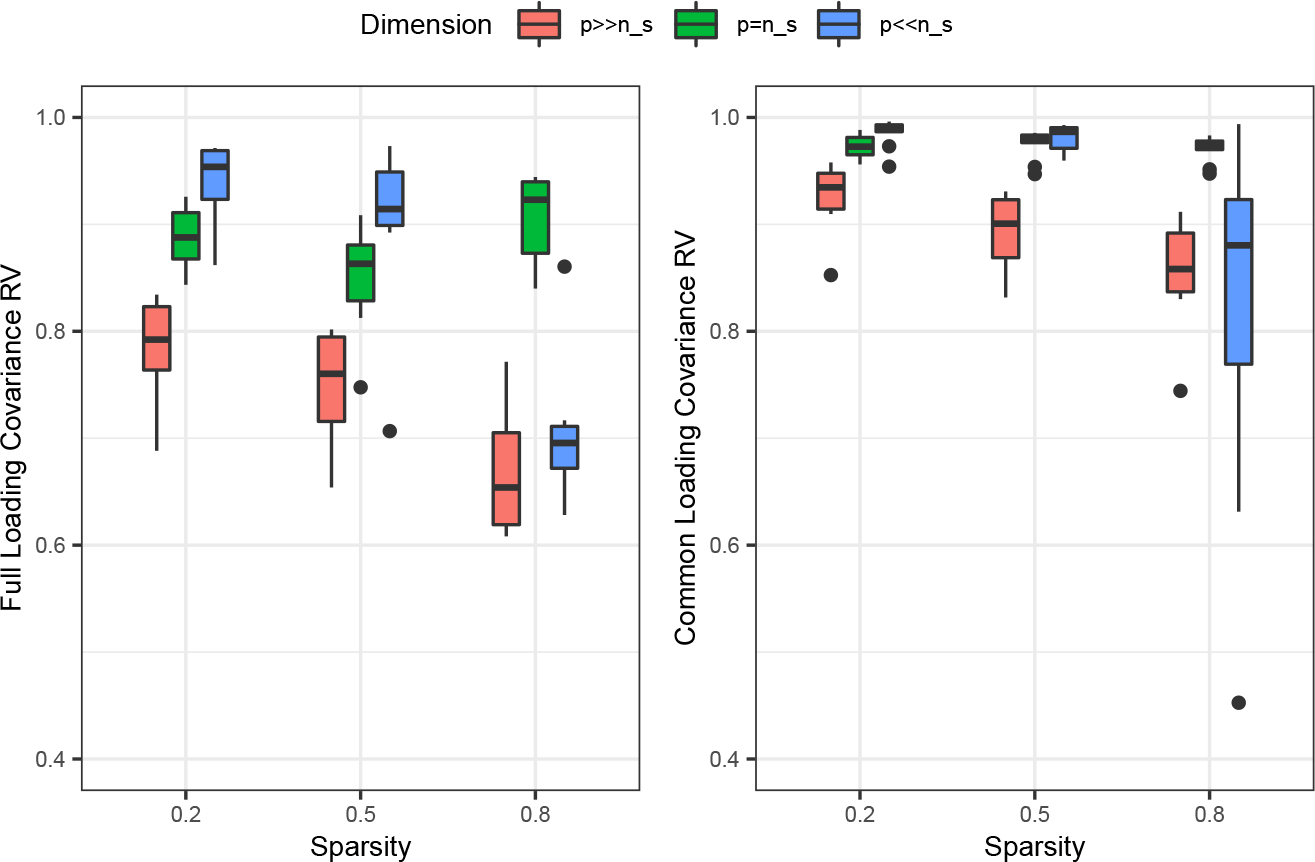
RV coefficients for the full loading matrix covariance (left) and common loading matrix covariance (right) across varying sparsity and data dimension in the Scenario 2 simulations.

We also examine how well Tetris estimated $𝒜$. We compare the estimated number of factors shared by every study to the true values for the $p\gg n_s$ setting with varying sparsity and number of partially shared factors (Figure 3). Again, we find that estimation improves with decreasing sparsity, but overall Tetris is able to capture the factor sharing patterns well across the board. Results for the other settings are in the Supplementary Materials Section D. They are similar to those shown here, though it should be noted that Tetris did tend to identify somewhat too parsimonious solutions specifically in the high-sparsity, $p\ll n_s$ conditions.

FIG 3.

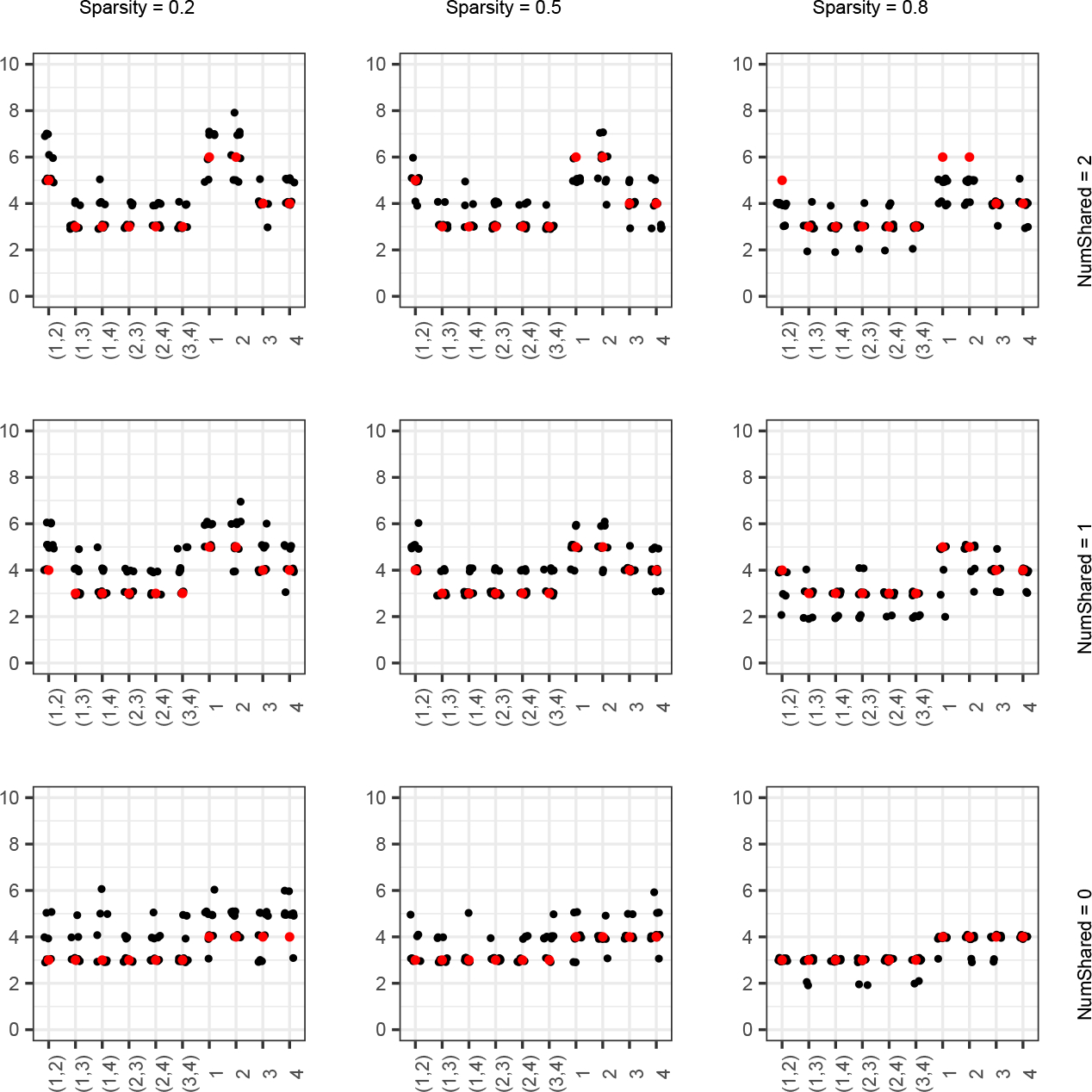
Number of factors shared by each pair of studies $i$ and $j$, indicated by $(i,j)$, and the number of total factors belonging to study $i$, indicated by $i$, for the $p\gg n_s$ ns simulations in Scenario 2, with varying sparsity and number of partially shared factors. Estimated values are in black (with jitter, for visual clarity) and ground-truth values are in red.

An important, related note is that occasionally, in $p\ll n_s$ or $p=n_s$ settings with high sparsity, Tetris found a solution with zero factors in most or all of the studies. In other words, all the variance of the data in each study with zero factors is explained by the study-specific noise ${\mathbf{\Psi }}_s$. This occurred in five runs out of the total 270 Scenario 2 simulations. When examining these runs, we found in three out of five of them that those particular realizations of the simulated datasets were equally well-described by a noise-only model as by the data-generating model via a test (Supplementary Materials Section E). Hence, Tetris found a reasonable and parsimonious description of the data in those cases. We excluded these five results from the figures presented here because it is not meaningful to consider $\mathrm{\Lambda }$ or $𝒜$ when no factors are present. Nevertheless, this finding shows that when a factor model is not needed to describe the data, Tetris can report this result accordingly.

Thus far, we have shown that Tetris can accurately estimate the loading matrix and the factor sharing pattern, which can be thought of as multi-study parameters. However, we can also demonstrate that Tetris’s approach to multi-study estimation has important advantages even when the main quantities of interest are study-specific. In particular, we examine Tetris’s ability to recover study-specific signal, by leveraging the common, study-specific, and applicable partially shared loadings for each study to reconstruct their covariance matrices. We compute the RV coefficients between the reconstructed covariance matrices for each study with the true data-generating covariance matrices in order to assess the accuracy of Tetris’s estimates. We also obtain covariance estimates for each study using BMSFA, PFA, and single-study factor analysis (FA).

Tetris recovers these study-specific covariance matrices well, with the median RV coefficient for each study remaining above 0.70 in each of the 27 parameter combinations tested. In most cases, the median RV coefficient is much higher than 0.70. We show results across varying sparsity and number of partially shared factors in the $p\gg n_s$ setting (Figure 4); results for $p=n_s$ and $p\ll n_s$ are in Supplementary Materials Section D. As we have seen before with the loading matrix covariances, the RV coefficients for Tetris’s estimates improve with decreasing loading matrix sparsity and decreasing data dimensionality. In general, Tetris outperforms PFA, BMSFA, and FA across the parameter settings examined. There are some studies in high- or medium-sparsity cases in the $p\gg n_s$ setting where PFA performs indistinguishably well as Tetris or better. However, Tetris’s results are better than PFA’s on all other cases in the $p\gg n_s$ setting, and nearly across the board in the $p=n_s$ and $p\ll n_s$ settings, including under high sparsity. The fact that Tetris is able to outperform single-study FA shows that joint analysis of multiple studies can improve inference of studies on the study-specific level. The fact that Tetris outperforms BMSFA and often PFA further shows that partially shared signal, rather than only common and/or study-specific signal, can be critical to more accurate estimation. These findings both support the premise of our multi-study, shared factor approach, and suggest that Tetris has utility in covariance estimation.

FIG 4.

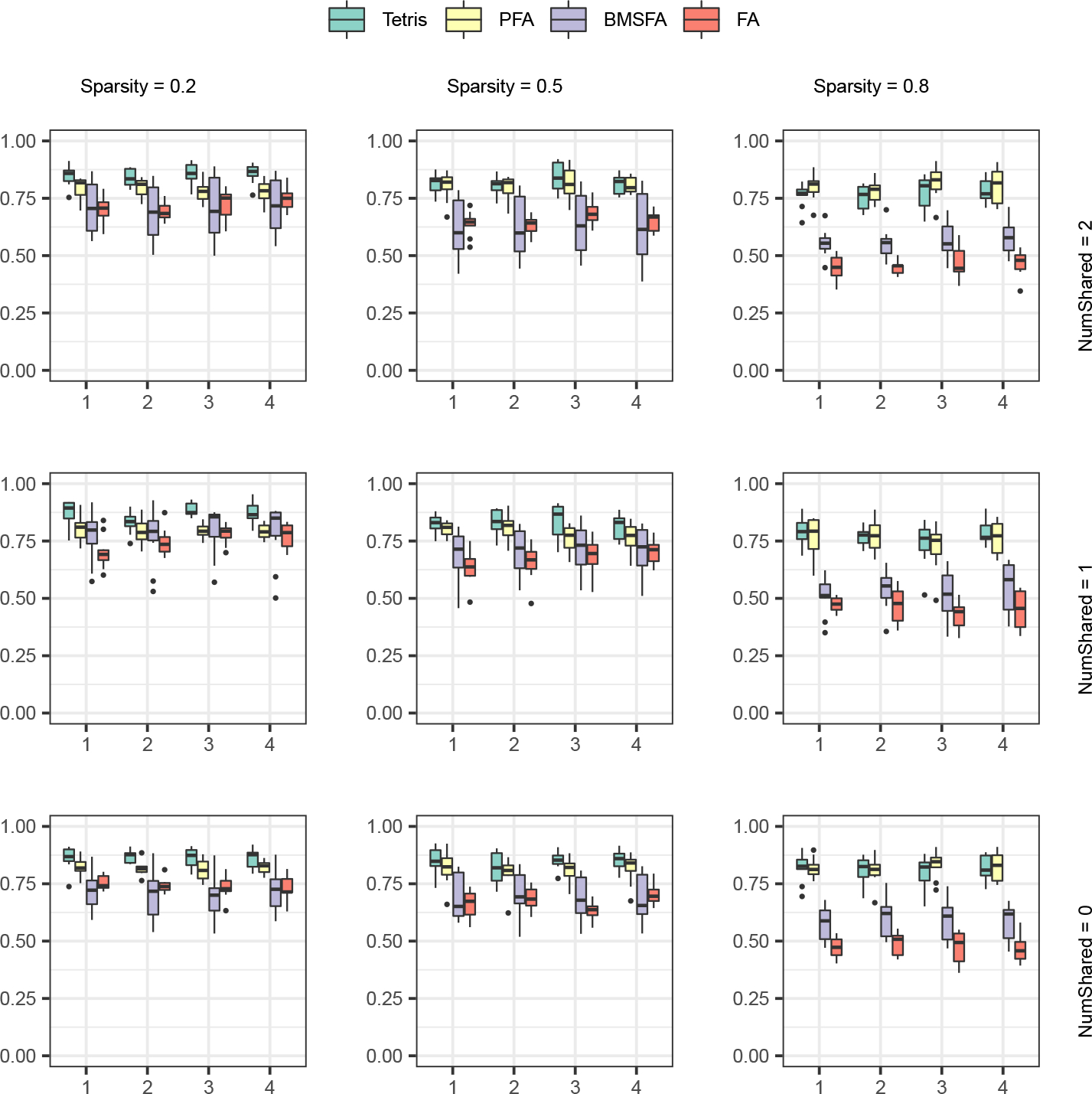
$RV$ coefficients for study-specific covariances across varying sparsities and numbers of partially shared factors in the $p\gg n_s$ setting of Scenario 2.

The findings we have discussed so far focus on the case with four studies, but in practice it is also interesting to consider a setting where a much larger number of studies is available. In the Scenario 3 simulation, we examine 16 studies in the $p\gg n_s$ setting and assess the accuracy of both the loading matrix covariances and the study-specific covariances. As with the Scenario 2 simulation, we find that the full and common loading matrix covariances are estimated reasonably well across all sparsity settings (Supplementary Materials Section D), with performance again improving as sparsity decreases. We further find that the sharing patterns are well-recovered, albeit with a tendency to sometimes overestimate the number of factors (Supplementary Materials Section D).

We also examine the study-specific covariances (Supplementary Materials Section D). We find that Tetris clearly outperforms BMSFA, PFA, and FA in both the low-sparsity and medium-sparsity conditions, and performs similarly to PFA in the high-sparsity conditions. These results demonstrate that even with a large number of studies, Tetris retains the ability to accurately estimate study-specific covariance matrices with competitive performance as compared to existing approaches.

Finally, in Scenario 4, we apply Tetris to our highest-dimensional case, which is simulated data that mimics the breast cancer transcript expression dataset and is generated using loadings from an exploratory single-study factor analysis of these data. We consider two settings: three studies (mimicking the three mutation statuses) and six studies (mimicking the three mutation statuses crossed by affected status). Although this simulation is more challenging due to its higher dimensionality, Tetris still recovers both the full and common loading matrix covariances with high RV coefficients (Figure 5A). Tetris also estimates the factor sharing pattern well (Figure 5C). Lastly, when comparing the estimated study-specific covariances from Tetris to those from BMSFA, FA, and PFA, Tetris yields the best RV coefficients by a fairly large margin for every study in every case (Figure 5B). Overall, these results show that Tetris accurately captures signal and substantially outperforms competing approaches when the ground-truth parameters are derived from data. This further motivates Tetris as a useful tool to apply to our gene expression data of interest.

FIG 5.

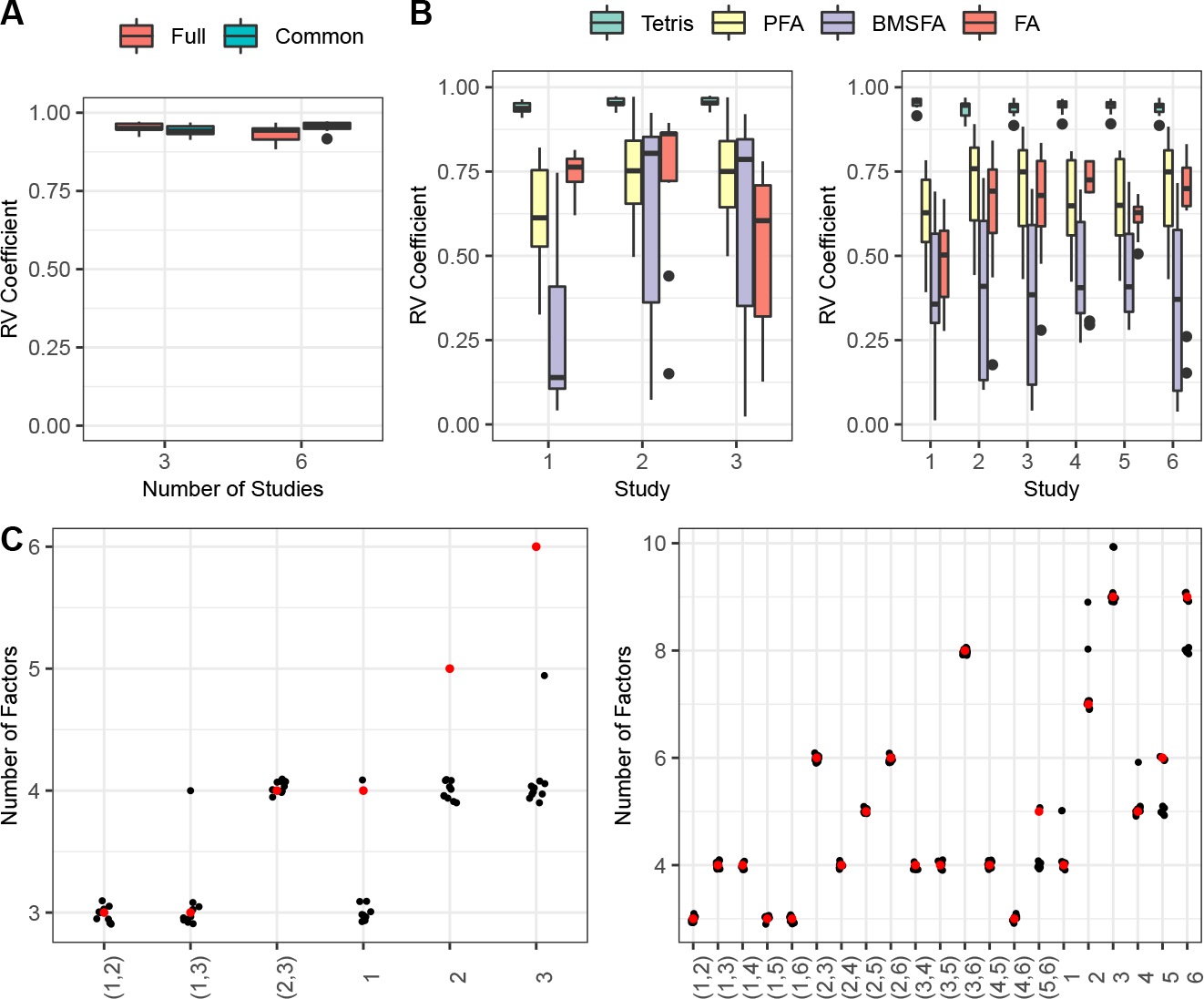
(A) RV coefficients for full and common loading matrix covariances in the Scenario 4 simulations. (B) RV coefficients for the study-specific covariance matrices in the Scenario 4 simulations. (C) Number of factors shared by each pair of studies $i$ and $j$, indicated by $(i,j)$, and the number of total factors belonging to study $i$, indicated by $i$, for the Scenario 4 simulations. Estimated values are in black (with jitter, for visual clarity) and ground-truth values are in red.

We also evaluated the clustering extension of Tetris in the Scenario 4 simulated datasets, by running this extension with $S=3$ and $S=6$ respectively for the three-study and six-study settings with all study labels removed and cluster labels initialized at random. We then compared the labels of the modal clustering to the true study labels to assess performance. In the case of the 3-study datasets, Tetris was able to identify perfect clustering in four out of ten runs: the modal clustering each time separated the samples of the three studies exactly. For the other six runs, Tetris found a collapsed, two-study solution (i.e. one study was kept empty) in which two groups were combined into one. In the case of the 6-study datasets, in three of the runs, Tetris perfectly separated the samples into the six groups. In five of the other runs, Tetris found a collapsed, five-study solution in which two of the groups were combined into one. In another run, Tetris found a four-study solution in which three groups were combined into one, and in the last run, Tetris found a three-study solution where one group matched up with an original study, one group combined three studies, and the remaining group combined two studies. This greater variation and tendency towards collapse can be attributed to the more complex sharing pattern present among the six groups, as well as the higher within-study dimensionality $\frac{p}{n_s}$. Nevertheless, despite the collapsed solutions, each sample was always ultimately assigned the same cluster as the other samples of the same ground-truth label, except for just two runs where each time just one sample was out of place. Hence, these results show that even in this challenging setting, Tetris still identifies an interpretable clustering with strong separation based on ground-truth signal.

4. Application to RNA-seq Data.

4.1. Data.

We applied Tetris to RNA-sequencing gene expression data from the immortalized lymphoblastoid cell lines of women at high risk for breast cancer reported by Pouliot et al. (2017). Their experiment produced a total of 121 samples: 37 from subjects with a germline BRCA1 mutation, 50 from subjects with a germline BRCA2 mutation, and 34 from subjects with a strong family history of breast cancer but no BRCA1 or BRCA2 mutation. We refer to these as BRCA1, BRCA2, and BRCAX samples, respectively. Not all subjects in the study were affected by breast cancer. There were 11 affected among the BRCA1 samples, 18 affected among the BRCA2 samples, and 17 affected among the BRCAX samples.

We considered two main ways to define the group structure in the context of these data. Firstly, we defined BRCA1, BRCA2, and BRCAX carrier status as the three groups. Secondly, we defined six groups by further stratifying each of these genotype categories (BRCA1, BRCA2, and BRCAX) into those affected and unaffected. We refer to these as analysis by genotype, and analysis by genotype and affected status respectively. In both, we preprocessed the data by transforming transcripts per million (TPM) as ${\mathrm{l}\mathrm{o}\mathrm{g}}_2(TPM+1)$ for approximate normality.

To control computational time, we limited our analysis to a set of transcripts likely to contain signal differentiating our conditions of interest. In particular, we identified the top 500 differentially expressed transcripts among the three genotype categories by fitting univariate models (equivalent to a three-class ANOVA) for each transcript with limma version 3.46.0 (Ritchie et al., 2015). We then further restricted attention to the subset of these transcripts whose total counts across all samples are in the upper quartile of all transcripts. This resulted in a final set of 370 transcripts. This step further contributes to meeting the normality assumption.

We did not perform any additional preprocessing of the data, such as batch adjustment (Zhang, Parmigiani and Johnson, 2020). The data may thus retain some batch structure. Batch effects that are confounded with the conditions investigated will likely result in condition-specific factors. Finally, when applying Tetris, we set the IBP hyperparamters to $\alpha =3.75,\beta =1$ for the 3-group case and $\alpha =7.5,\beta =1$ for the 6-group case. All other hyperparameters were set as described for the simulations.

4.2. Analysis by Genotype.

When considering three groups (the genotype categories BRCA1, BRCA2, and BRCAX), Tetris finds a total of 8 factors (Figure 6), all of which are common. This suggests that the differences among these three groups were not large enough to be explained by study-specific or partially shared factors. This result is not necessarily surprising, given that each group contains both individuals with and without cancer, and thus the heterogeneity within each group may be larger than the variation differentiating these groups.

FIG 6.

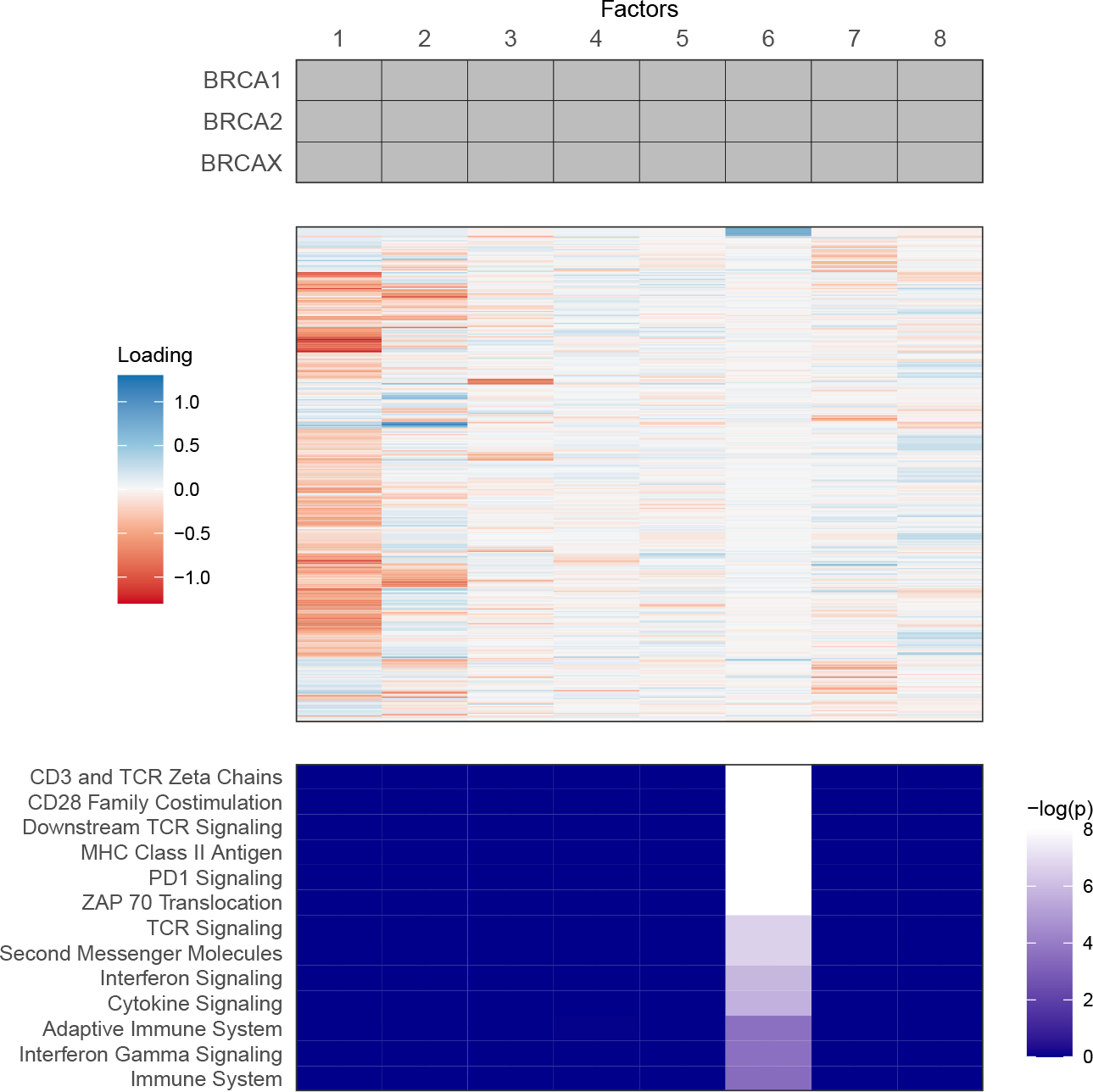
Visual summary of sharing pattern (top), factor loadings (middle), and pathway analysis (bottom) for the analysis by genotype. Each column corresponds to the same factor through the three panels. Transcripts (rows) in the heatmap of loadings are clustered by their TPMs across all samples. Enrichment p-values have been remapped with the Benjamini-Hochberg method. Pathway names are abbreviated, with an identifying table in Supplementary Materials Section F.

Our results show that several of these factors, particularly 1 and 2, have large loadings in absolute magnitude for many different transcripts. By contrast, other factors, especially 6, only have a few large loadings, suggesting more concentrated signal in a smaller set of transcripts. To begin interpreting these factors, we explored gene set enrichment (Subramanian et al., 2005) using point estimates of the factor loadings. This analysis asks whether gene sets representing known biological classes and pathways are displaying higher or lower factor loadings compared to the distribution of loadings in the set formed by all other genes. We used gene sets from reactome.org, and assessed enrichment with the library RTopper version 1.36.0 (Marchionni, 2013).

Factor 6 was the only factor to have significant ($p<0.05$ after Benjamini-Hochberg correction) gene set enrichment. These gene sets are shown in Figure 6, along with sets enriched with $p<0.25$ after Benjamini-Hochberg correction, a visualization threshold motivated by the small sample sizes of our studies. There is a great deal of overlap among these enriched sets. Many of these sets are related to immune signaling pathways (e.g. PD1, TCR) and antigen presentation in immune system processes, suggesting an essential role for these processes in lymphoblastoid cells across all genotype conditions.

For comparison, we analyzed this data with BMSFA, which identifies common and study-specific, but not partially shared, factors. BMSFA found a total of 16 factors, including five common factors, two study-specific factors for BRCA1, three study-specific factors for BRCA2, and six study-specific factors for BRCAX (Supplementary Materials Section G). Similar to Tetris’s findings, some of BMSFA’s common factors have large loadings, in magnitude, across many transcripts. This is true for some of the study-specific factors as well, with others having only a few large loadings in a smaller set of transcripts.

We compare each of Tetris’s factors to BMSFA’s factors (Supplementary Materials Section G) using the congruence coefficient (Lorenzo-Seva and Ten Berge, 2006), i.e. the uncentered correlation between the two vectors of factor loadings. All five of BMSFA’s common factors show strong similarity to five of Tetris’s factors, which are all common. This suggests a fair degree of concordance between the two analyses. Two of BMSFA’s study-specific factors (8 and 11, which are specific to BRCA2 and BRCAX respectively) have moderate similarity to Tetris’s factor 4, but the others are not similar to any of Tetris’s factors. Overall, Tetris appears to have found a sparser solution than BMSFA in terms of number of factors.

Finally, we also analyzed this data with PFA, which identifies common factors that are then perturbed by study-specific multiplicative effects. PFA found a total of 21 factors, and we again compare these factors to Tetris’s by examining the congruence coefficients (Supplementary Materials Section G). Some of PFA’s factors, such as 2 and 11, have relatively high similarity with some of Tetris’s factors, suggesting a clear one-to-one correspondence in those cases. However, most have weak similarities across multiple of Tetris’s factors. This again implies that Tetris may have found a more parsimonious solution than PFA in terms of the total number of factors.

Although all of PFA’s factors can be interpreted as common, this method additionally estimates perturbation matrices that quantify each study’s deviations from the common signal. The differences between every pair of studies $l,j$ can be summarized with a divergence statistic $d_{lj}$ computed using these perturbation matrices (Roy et al., 2021). We compute the divergence statistics here, and find small values for all pairs: $d_{BRCA1,BRCA2}\approx 4.2\times {10}^{-4},d_{BRCA1,BRCAX}\approx 3.9\times {10}^{-4}$, and $d_{BRCA2,BRCAX}\approx 1.5\times {10}^{-4}$. This suggests that only very small differences are present between groups, which is consistent with Tetris’s finding of all common factors.

4.3. Analysis by Genotype and Affected Status.

Next, we examine the results of further stratifying the groups into the six combinations of genotype and affected status (Figure 7). We find a total of 28 factors, of which 14 are common, seven are study-specific (one for each group, and a total of two for BRCA1 affected), and the rest are partially shared. Of the partially shared factors, it is notable that two are shared by all BRCA1 and BRCA2 subgroups, and one is shared by both BRCAX subgroups. This suggests the presence of signal shared by BRCA1 and BRCA2 individuals that is distinct from signal among BRCAX individuals, regardless of affected status. These patterns were not found in the analysis by genotype, possibly because revealing their presence required stratifying by affected status to remove the extra within-group variation. Interestingly, there are also several partially shared factors that are shared by all groups but one (factors 15, 16, and 17). These suggest there may be particular structural differences between BRCA2 unaffected individuals, as well as BRCA1 unaffected individuals, and the rest of the groups.

FIG 7.

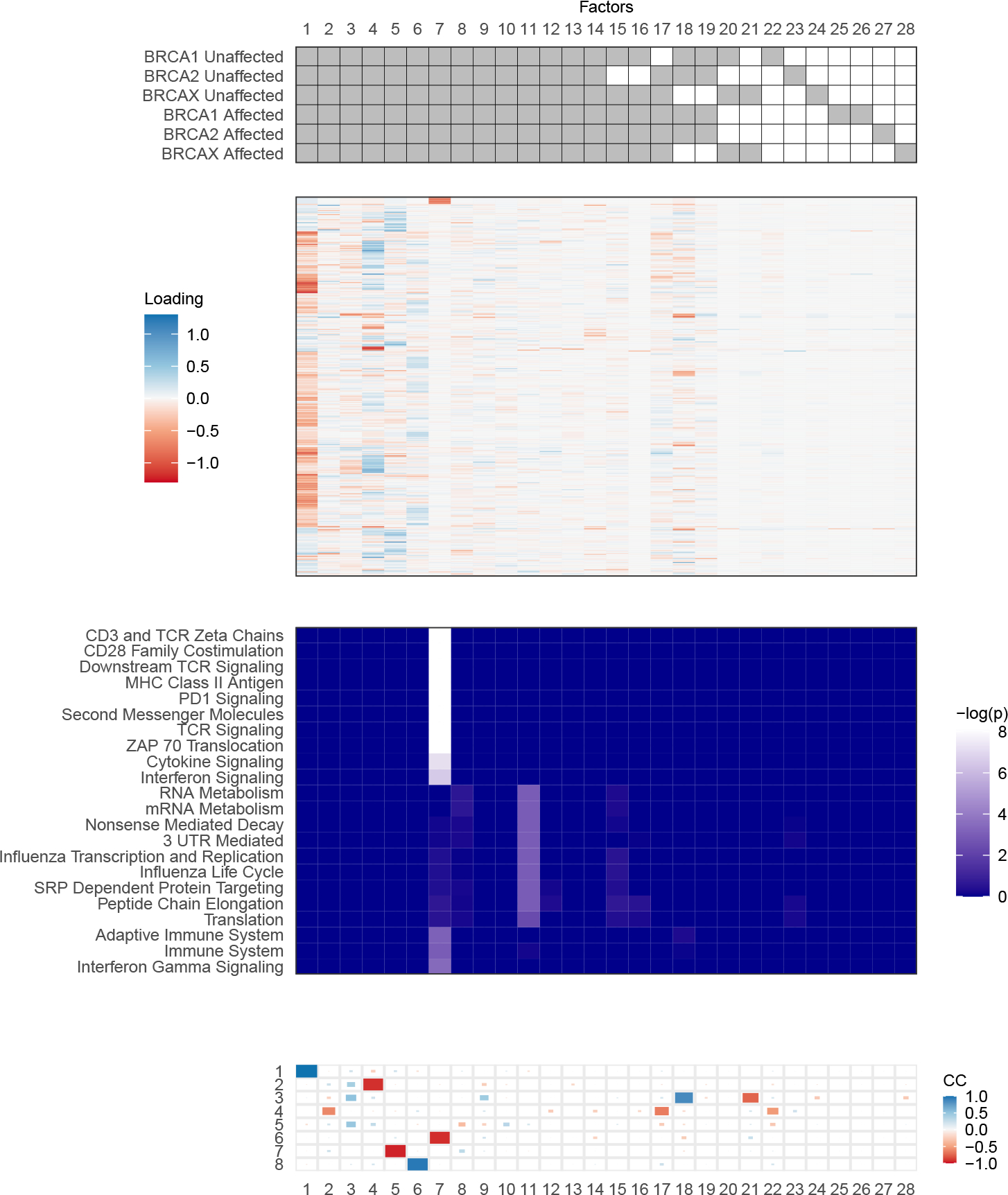
Visual summary of sharing patterns (top), factor loadings (second), pathway analysis (third), and congruence coefficients with analysis by genotype (bottom) for the analysis by genotype and affected status. Each column corresponds to the same factors through the three panels. Transcripts (rows) in the heatmap of loadings are clustered by their raw counts across all samples. Enrichment p-values have been corrected with the Benjamini-Hochberg method. Pathway names are abbreviated, with an identifying table in the Supplementary Materials Section F.

We compared these factors to those identified in the analysis by genotype using congruence coefficients (Figure 7). Five of the common factors have very strong similarities with those from the analysis by genotype, suggesting reasonable concordance between these two analyses. Interestingly, two of the partially shared factors from the more stratified analysis (18 and 21) had moderate similarities with common factor 3 from the analysis by genotype. Factor 18 is shared by all BRCA1 and BRCA2 subgroups, and factor 21 is shared by both BRCAX subgroups. This further supports the idea that there may be signal with relatively subtle deviations between BRCA1/BRCA2 and BRCAX individuals, such that the distinction could only be detected with the stratification of these groups by affected status. The remaining other factors, including about half of the common factors, were not similar to any of the eight factors found in the analysis by genotype, implying that substantially more signal, and/or a less sparse solution, has been found under stratification.

We again investigated the loadings with the pathway analysis, and found one factor (7) to be significantly enriched for pathways. Notably, this factor has a very high congruence coefficient with factor 6 from the analysis by genotype, which was also significantly enriched for pathways. The pathways that came up in this analysis overlapped those previously identified, relating primarily to immune system processes and signaling. Although not exceeding the 0.05 threshold, there was some additional enrichment for metabolism and other pathways in factor 11, another common factor. A subset of these also appears in factor 15, shared by all but BRCA2 unaffected, again not exceeding the significance threshold. These enrichments may speculatively suggest avenues for further investigation.

We further examine these loadings by comparing factor loadings to the transcripts that Pouliot et al. (2017) found initially to be differentially expressed among various subgroups. Their analysis considers each transcript marginally while we explore broader coordinated changes. Nonetheless, it is interesting to explore correspondences. For example, they identify a transcript associated with the gene GUK1 to differentiate BRCA1 and BRCA2 samples from BRCAX samples, and we similarly find this same transcript to have very high loadings on factor 18, shared by all BRCA1 and BRCA2 subgroups. Hence both our analysis and the original analysis suggest this gene may be particularly relevant for both BRCA1 and BRCA2 samples regardless of affected status. Independently, this gene has been previously implicated in pituitary tumors (da Rocha et al., 2006).

There are also cases in which our results do not correspond directly to the Pouliot et al. (2017) differential expression analysis, and instead may be adding additional perspective. In particular, we sometimes identify broader signal sharing. For instance, Pouliot et al. (2017) identified transcript ENST00000494862, associated with the gene HDLBP, to differentiate BRCA1 and BRCA2 samples from the rest. We find high loadings for this transcript on two common factors, namely 4 and 13, suggesting that this gene is involved in transcriptional programs active across all six groups. In other cases, our results suggest potentially more complex roles may be played by genes previously determined to be differentially expressed. For example, Pouliot et al. (2017) found a transcript associated with the gene EEF2 to differentiate BRCA1 and BRCA2 individuals from BRCAX individuals. This gene is of interest because past work has shown overexpression of EEF2 in many cancer types, including breast cancer (Oji et al., 2014). Our analysis found high loadings for this transcript on factors 4, 14, and 15; the former two are both common, and the latter is shared by all but BRCA2 unaffected. Hence, our results suggest that this gene may be involved in signal shared by all samples, while also playing a role not seen in BRCA2 unaffected samples.

The credible ball for the factor sharing matrix allows us to characterize uncertainty about which groups share these factors of interest. This requires examining the sharing patterns for factors appearing in sufficiently probable draws of the pattern sharing matrix that are similar to these factors of interest. To this end, we consider each factor separately. We focus on the credible ball around the best estimate of $𝒜$ and examine the MCMC draws of the loading matrices associated with the pattern sharing matrices within the credible ball. We identify matrices containing another sufficiently similar factor. Among all such draws, we then examine the sharing patterns for those factors to quantify how frequently each possible sharing pattern was observed, thus capturing uncertainty.

We measure similarity of factors using the congruence coefficient. To determine whether a given factor has a sufficiently large congruence coefficient with the point estimate of the loadings of the factor of interest, we first create a reference distribution of congruence coefficients by generating factor loadings samples via a conditional MCMC with $𝒜$ fixed to its point estimate. For each such MCMC iteration, we take the maximum absolute congruence coefficient between the point estimate of the loadings of the factor of interest, and all factors with the same sharing pattern. We consider the resulting set of absolute congruence coefficients to represent the reference distribution to calibrate similarity between our factor of interest and others. When we examine the MCMC samples within the credible ball, we identify the maximum absolute congruence coefficient between any factor and our factor of interest’s point estimate, and consider it sufficiently similar if the absolute congruence coefficient is larger than the 0.05th quantile of our reference distribution.

We carried out this procedure for some of the factors of interest from the analysis above: 4, 13, 14, and 15. Factor 4, which had high loadings for both HDLBP and EEF2, appeared in 35% of the credible ball samples, but every time it did appear, it was a common factor. This suggests a fairly high degree of uncertainty associated with this factor’s existence, since more than half of the samples associated with the credible ball do not contain a similar factor. Nevertheless, there is high certainty that if this factor exists, it is common and not, for instance, partially shared by BRCA1 and BRCA2 subgroups. Factor 13, which also had a high loading on HDLBP, appeared in 71% of credible ball samples, and was a common factor in the vast majority of these. However, in 0.2% of these samples, this factor was shared by all but BRCA1 unaffected. This suggests that factor 13 has a relatively high degree of certainty associated with its existence, and a very high degree of certainty associated with being a common factor, but that there may be some noise or very weak signal regarding the involvement of the BRCA1 unaffected group.

Factors 14 and 15 both had high loadings for EEF2. Factor 14 appeared in 95% of the credible ball samples and was a common factor in every one, implying a high degree of certainty both for its existence and sharing pattern. Factor 15 appeared in 90% of the credible ball samples, which is also a high proportion, shared by all but BRCA2 unaffected in nearly every sample. However, in 0.6% of the samples, this factor was shared by all but BRCA2 unaffected and BRCAX affected, and in 0.1% of the samples, this factor was common. Hence, this factor is associated with a high degree of certainty in its sharing pattern, but this factor could arise from noise or potentially weak signal in the groups it is involved with.

It should be clarified that our findings are not in direct conflict with the Pouliot et al. (2017) original analysis. It may very well be the case that HDLBP and/or EEF2 are differentially expressed between BRCA1 and BRCA2 subgroups. Instead, our results suggest that even if these genes are differentially expressed, there is signal, also shared by BRCAX subgroups, strongly involving this gene. In the case of EEF2, the detected differential expression may be related to the observed differences between the BRCA2 unaffected group from the rest. This analysis potentially contributes to a more nuanced understanding of the roles of both of these genes.

We also ran BMSFA on this set of six groups (Supplementary Materials Section G) for comparison. BMSFA found a total of 22 factors: five common factors; two factors each specific to BRCA1 unaffected and BRCA2 unaffected, respectively; three factors each specific to BRCAX unaffected, BRCA2 affected, and BRCAX affected, respectively; and four factors specific to BRCA1 affected. When comparing BMSFA’s factor loadings to Tetris’s factor loadings by congruence coefficient (Supplementary Materials Section G), we find that four of BMSFA’s five common factors have high similarity with four of Tetris’s common factors. The remaining common factor of BMSFA has high similarity with Tetris’s factors 18 and 21, which are partially shared by all BRCA1 and BRCA2 subgroups, and by all BR-CAX subgroups, respectively. This is suggestive of signal that may be very similar between BRCA1/BRCA2 and BRCAX samples, but with some deviations between the two. Because BMSFA can only identify common or study-specific factors, this signal may then have been summarized as common, whereas Tetris is able to distinguish the two with its more flexible pattern sharing model.

Similarly, some of BMSFA’s study-specific factors have moderate similarities with one or more of Tetris’s factors. For example, BMSFA’s factor 15, specific to BRCA1 affected, has moderate similarity with Tetris’s factor 15, which is shared by all but BRCA2 unaffected. It is possible that this signal is truly shared by BRCA1 affected and additional, but not all, of the other groups, as Tetris’s results suggest, but BMSFA would not have been able to describe such a finding. This again shows how Tetris allows for more flexible and detailed descriptions of signal sharing than BMSFA.

Finally, we also ran PFA on these six groups. PFA found 22 factors, which we compared to Tetris’s factors (Supplementary Materials Section G). There were no pairs of factors with clear one-to-one correspondences between methods. Instead, several of Tetris’s common factors were weakly to moderately similar to many of PFA’s factors. In turn, nearly half of PFA’s factors were weakly similar to multiple of Tetris’s factors, often spanning several different sharing patterns. Overall, this suggests that while much of the same signal may be encapsulated between the two approaches, decomposing that signal into factors is quite different. This is not surprising given the major structural distinctions in how group deviations are defined in the two models.

We also computed the divergence statistics for every pair of groups. Similar to the results in the analysis by genotype, these values were very small for each pair, on the order of 10⁻⁴ or 10⁻⁵. This again suggests minimal differences between every pair of groups. This is now in contrast to Tetris’s results, in which half of the factors are partially shared or study-specific, implying substantial structural differences among the groups. Such findings help illustrate the utility of Tetris. Whereas PFA may be particularly useful in settings where the common signal is of primary interest, Tetris can yield more interpretable and meaningful results when the scientific questions pertain to the differences, especially potentially shared differences, among groups.

4.4. Clustering.

We also applied the clustering extension of Tetris to these data with all study labels removed to investigate whether any additional structure can be detected. The samples were all centered by the overall mean. We set the total number of potential studies to 10 and initialized the clusters via uniform random assignment of the samples. The modal clustering assignment found by Tetris is shown in Supplementary Materials Section G. The ten clusters were essentially collapsed into three, with the remaining seven empty, where one cluster contained most of the BRCA2 affected samples, about half of the BRCAX affected samples, and a handful of others; one cluster contained just a single BRCA2 affected sample; and the last contained all other samples. This suggests some structure distinguishing BRCA2 affected samples and some of the BRCAX affected samples from the rest. Similarly, this result also implies that the single sample assigned to its own cluster may be an outlier in some way.

It should be noted that structure may be somewhat challenging to identify in these data through traditional means. For example, we also applied PCA to these data, treating it as a single study, and plotted the first two PCs in Supplementary Materials Section G. While there appears to be some separation of BRCAX samples from the rest, the distinction of the three or six labeled subgroups are not obvious from this reduction. Hence, Tetris is picking up on signal that could otherwise be difficult to find.

5. Discussion.

We presented Tetris, the first multi-study factor analysis method that investigates factors shared by any subset of studies or conditions. We tested Tetris on a range of simulations and demonstrated its accuracy in estimating model parameters and distinguishing common, study-specific, and partially shared signal. This decomposition of signal offers a precise way to quantify wholly or partially shared information across studies, avoiding the otherwise common practice of running separate analyses on each study and subjectively integrating the results, and offering a more principled form of joint dimension reduction that directly estimates each factor and its membership across studies. Moreover, our use of the Indian Buffet Process prior results in automatic dimension selection, without ad-hoc post-processing steps. We also present an extension of Tetris for when study labels are not known, which allows for simultaneous clustering and estimation of factor structure.

We further highlighted how this flexible approach to joint estimation allows Tetris to borrow strength across studies and recover study-specific covariance matrices more accurately than standard single-study factor analysis. Thus, our approach offers an opportunity to leverage multiple studies to improve analysis even for research questions pertaining to a single study. Since Tetris also outperformed BMSFA and often PFA on study-specific covariance estimation, we have demonstrated that permitting partial sharing of factors can result in substantial improvements over the sole consideration of common and/or study-specific factors.

Our approach is similarly effective in jointly analyzing multivariate data collected in multiple conditions. We applied Tetris to gene expression datasets to jointly identify signal among women with known genetic risk for breast cancer. The identification of partially shared factors provided a more detailed understanding of how signal is partitioned across the multiple groups, which would have been lost if only common and group-specific factors were estimated. For example, we recovered instances of signal sharing between samples from women with BRCA1 and BRCA2 germline mutations that were not present in those without the mutations, even though there were other factors common to all. This analysis recapitulated known biology by identifying signal related to genes previously associated with breast cancer. By specifically implicating these genes in factors shared by a subset of groups, our analysis then suggests novel hypotheses about whether these genetic mechanisms may be particularly relevant for certain conditions. Finally, by applying the clustering extension of Tetris to these data, we found potential additional structure suggesting subsets of BRCA2 and BR-CAX affected samples that may be distinguished from the rest. Hence, we have shown how Tetris can be successfully employed in the unsupervised analysis of complex, multi-study or multi-group data. This is useful for a wide range of applications beyond genomics, such as epidemiology, nutrition, and sociology.

One of the key goals of our inference is the factor membership indicator matrix $𝒜$. Summarization of MCMC output for $𝒜$ is an open challenge. We suggest to consider point estimates based on defining a distance and identifying the point defining the neighborhood with highest density. To do so, we proposed a novel distance for comparing binary matrices of this nature, and drew a connection with the Hungarian Algorithm to compute it efficiently. There are many possible alternative options to summarize the MCMC samples of $𝒜$ with a single point estimate. For example, the maximum a posteriori value could be selected, where the posterior density $f(𝒜|\mathit{X})$ for data $\mathit{X}$ is approximated using importance sampling or variational inference. There is also a wider literature of Bayesian model averaging (Hoeting et al., 1998) and Bayesian model selection (Chipman et al., 2001) that could be considered and adapted to this problem, including approaches based on Bayes factors (Berger and Pericchi, 1996), Bayesian information criteria (Chen and Chen, 2008), and techniques from reversible jump MCMC (Lopes and West, 2004). For our purposes, we found our chosen approach was simple and achieved strong results. We also adapted the idea of credible balls (Wade et al., 2018) from Bayesian clustering to express regions of uncertainty around our point estimate. This offers an important summary of uncertainty that is useful not only in our specific context, but in any model considering infinite binary matrices such as those in the Indian Buffet Process.

Simultaneous factorization of multiple matrices sharing common structure is an area of active research. Preference between PFA, BMSFA, and Tetris may vary depending on the context of the practical applications. Specifically, PFA might be most useful in contexts where multiple studies are believed to have very strong common structure, and where investigators have limited interest in explicitly estimating study-specific factor loadings. For example, this could be the case in an application where the goal is to remove numerous and small batch effects, which are not of direct interest, from common signal. BMSFA might instead be most applicable when both the common and study-specific structure are of particular interest, when the batch effects are strong and potentially confounded with study, and when partially shared structure is not likely to exist. An example might be when each study is based in a different subpopulation, and it is important to understand the unique contributions from each subpopulation. Finally, through Tetris, we contribute an approach that is most useful when partially shared structure is plausible, and when explicit estimates of each type of signal are desired. This might be the case if we expect subsets of our studies to share commonalities without being identical. For example, in our gene expression case study, we expect some similarities between BRCA1 and BRCA2 samples. We might then be interested in answering questions about what all groups share, what is unique to each group, and what BRCA1 and BRCA2 samples might share that does not belong to BRCAX samples.

In summary, Tetris demonstrates that it is viable to perform flexible joint unsupervised analyses of multiple high-dimensional studies, identifying common, study-specific, and partially shared structure. Multi-study unsupervised analyses are underutilized, despite the fact that the multi-study setting offers a unique foundation for both stabilizing and validating the signal identified. We hope that this work will support a broader application of multi-study methods in unsupervised learning applications.