Abstract
Wide field of view microscopy that can resolve 3D information at high speed and spatial resolution is highly desirable for studying the behaviour of freely moving model organisms. However, it is challenging to design an optical instrument that optimises all these properties simultaneously. Existing techniques typically require the acquisition of sequential image snapshots to observe large areas or measure 3D information, thus compromising on speed and throughput. Here, we present 3D-RAPID, a computational microscope based on a synchronized array of 54 cameras that can capture high-speed 3D topographic videos over an area of 135 cm2, achieving up to 230 frames per second at spatiotemporal throughputs exceeding 5 gigapixels per second. 3D-RAPID employs a 3D reconstruction algorithm that, for each synchronized snapshot, fuses all 54 images into a composite that includes a co-registered 3D height map. The self-supervised 3D reconstruction algorithm trains a neural network to map raw photometric images to 3D topography using stereo overlap redundancy and ray-propagation physics as the only supervision mechanism. The resulting reconstruction process is thus robust to generalization errors and scales to arbitrarily long videos from arbitrarily sized camera arrays. We demonstrate the broad applicability of 3D-RAPID with collections of several freely behaving organisms, including ants, fruit flies, and zebrafish larvae.
Keywords: parallelized microscopy, camera array, computational microscopy, behavioral imaging, self-supervised learning, 3D imaging
1. Introduction
Quantifying behavior and locomotion of freely-moving organisms, such as the fruit fly and zebrafish, is essential in many applications, including neuroscience [1–3], developmental biology [4], disease modeling [5, 6], drug discovery [7, 8], and toxicology [9–13]. Particularly for high-throughput screening, it is desirable to monitor tens or hundreds of organisms simultaneously, thus requiring high-speed imaging over large fields of view (FOVs) at high spatial resolution, ideally in 3D. Such an imaging system would allow researchers to bridge the gap between microscopic phenotypic expression and multi-organism behavior across more macroscopic scales, such as shoaling [14, 15], courtship and aggression behaviors [16, 17], exploration [18, 19], and hunting [19–23].
Common approaches for behavioral recording utilize 2D wide-field microscopes at low-magnification to cover as large a FOV as possible. However, due to space-bandwidth product (SBP) limitations of conventional optics [24, 25], standard imaging systems have to accept a tradeoff between image resolution and FOV. Techniques that enhance SBP to facilitate high-resolution imaging over large areas, such as Fourier ptychography (FP) [26] and mechanical sample translation [27, 28], often require multiple sequential measurements, which compromises imaging speed and throughput. Approaches that perform closed-loop mechanical tracking to record single organisms freely moving in 2D with scanning mirrors [29] or moving cameras [19] do not scale to multiple organisms.
Conventional wide-field techniques also lack 3D information, which potentially precludes observation of important behaviors, such as vertical displacement and out-of-plane tilt changes in zebrafish larvae [23, 30, 31] and 3D limb coordination and kinematics in various insects [32–35]. Commonly used 3D microscopy techniques such as diffraction tomography [36, 37], light sheet microscopy [38, 39], and optical coherence tomography [40–42], are not well-suited for behavioral imaging, since they often require multiple sequential measurements for 3D estimation and inertia-limited scanners that sacrifice speed. Furthermore, while such techniques can achieve micrometer-scale resolutions, they typically have millimeter-scale FOVs rather than the multi-centimeter-scale FOVs necessary for imaging freely-moving organisms. Thus, these techniques are typically limited to imaging one immobilized organism at a time (e.g., embedded in agarose, tethered [34, 35], or paralyzed).
Camera array-based imaging systems have also been proposed to increase SBP and overall throughput [43–47]; however, none of these prior approaches have demonstrated scalable, high-speed, high-resolution, wide-FOV, 3D imaging. In particular, several of these approaches were designed for 2D macroscopic photographic applications, which face challenges for miniaturization for microscopy applications, or feature a primary objective lens that limits the maximum achievable SBP. Macroscale 3D imaging techniques such as time-of-flight LiDAR [48], coherent LiDAR [49–51], structured light [52], stereo vision [53], and active stereo vision techniques [54] have throughputs typically limited to 10s of megapixels (MPs) per second and have millimeter-scale spatial resolution.
Here, we present 3D Reconstruction with an Array-based Parallelized Imaging Device (3D-RAPID), a new computational 3D microscope based on an array of 9×6 = 54 synchronized cameras, capable of acquiring continuous high-speed video of dynamic 3D topographies over a 135-cm2 lateral FOV at 10s of micrometer 3D spatial resolution and at spatiotemporal data rates exceeding 5 gigapixels (GPs) per second (Fig. 1). We demonstrate three operating modes, which can be flexibly chosen depending on whether to prioritize speed (up to 230 frames per second (fps)) or spatial SBP (up to 146 MP/frame). We also present a new scalable 3D reconstruction algorithm that, for each synchronized snapshot, simultaneously forms a globally-consistent photometric composite and a coregistered 3D height map based on a ray-based physical model. The 3D reconstruction itself trains aspatiotemporally-compressed convolutional neural network (CNN) that maps multi-ocular inputs to the 3D topographies, using ray propagation physics and consistency in the overlapped regions as the only supervision. Thus, after computational reconstruction of just a few video frames (<20), 3D-RAPID can rapidly generate photometric composites and 3D height maps for the remaining video frames non-iteratively.
Fig. 1.
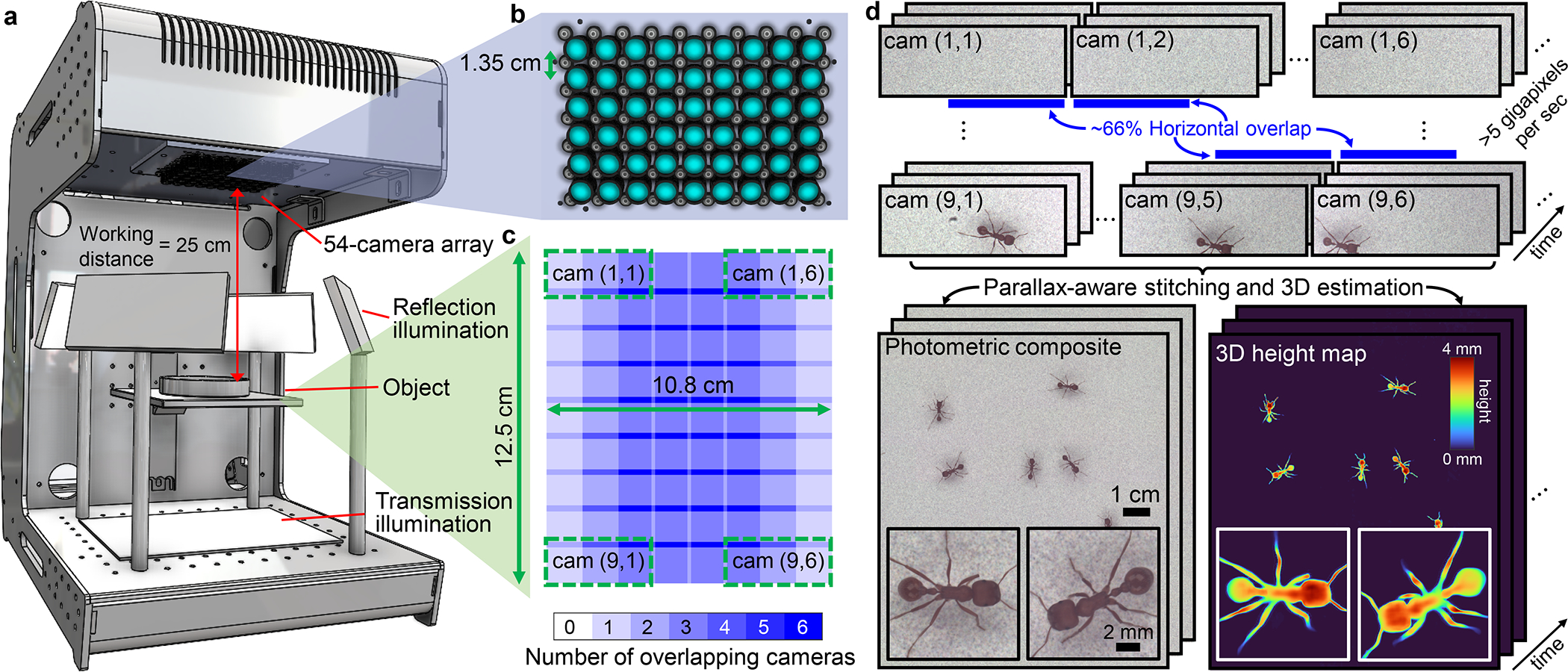
Overview of 3D-RAPID. a, Computational microscope setup, consisting of a 9×6 = 54 array of finite-conjugate imaging systems, jointly recording across a 135-cm2 area. LED arrays serve as the illumination source, both in transmission and reflection. b, 9×6 array of cameras and lenses. c, Overlap map of the object plane, demonstrating roughly 66% horizontal overlap redundancy between neighboring cameras (and minimal overlap in the vertical dimension). Four example camera FOVs are denoted with green dotted boxes, identified by (row,column) coordinates. d, The MCAM captures 54 synchronized videos at >5-GP/sec throughputs, which are stitched to form a high-speed video sequence of globally-consistent composites and the corresponding 3D height maps.
3D-RAPID thus solves a longstanding problem in the field of behavioral imaging of freely moving organisms that previously only admitted low-throughput solutions. To our knowledge, prior to our work, there was no imaging system that could sustainably image at such high spatiotemporal throughputs (>5 GP/sec) in 3D. We demonstrated the broad applicability of 3D-RAPID in three model organisms: zebrafish, fruit flies, and ants. In particular, the large FOV of 3D-RAPID enabled imaging of multiple freely behaving organisms in parallel, while the dynamic 3D reconstructions and high spatial resolution and imaging speeds enabled 3D tracking of fine features, such as ant leg joints during exploration, zebrafish larva eye orientation during feeding, and fruit fly pose while grooming.
2. High-throughput 3D video with 3D-RAPID
2.1. 3D-RAPID hardware design
The 3D-RAPID hardware is based on a multi-camera array microscope (MCAM) architecture [47, 55], consisting of 54 synchronized micro-camera units spaced by 13.5 mm and tiled in a 9×6 configuration. Each micro-camera captures up to 3120 × 4208 pixels (1.1-μm pitch), for a total of ~700 megapixels per snapshot. The data is transmitted to computer memory via PCIe at ~5 GB/sec. We axially positioned the lenses (Supply Chain Optics, f = 26.23 mm) to obtain a magnification of M ≈ 0.11, leading to ~66% overlap in the sample plane field of view (FOV) between cameras adjacent along the longer camera dimension (Fig. 1c), so that almost every point in the synthesized ~12.5×10.8-cm2 is viewed at least twice.. This overlap redundancy enables 3D estimation using stereoscopic parallax cues. The sample is illuminated in transmission or reflection using planar arrays of white LEDs covered by diffusers (Fig. 1a).
2.2. Tradeoff space of lateral resolution, FOV, and frame rate
3D-RAPID has flexibility to downsample or crop sensors or use fewer cameras to increase the frame rate. The overall data throughput is limited by the slower of two factors: the data transfer rate from the sensors to the computer RAM (~5 GB/sec) or the sensor readout rate, both functions of the sensor crop shape and downsample factor. Streaming all 54 cameras without downsampling or cropping runs into the data transfer rate-limited frame rate of ~7 fps. To achieve higher frame rates, we present results with a 1536×4096 sensor crop using either 4×, 2×, or no downsampling, allowing 230, 60, or 15 fps frame rates, respectively, while maintaining roughly the same throughput of ~5 GP/sec (Table 1). While excluding half of the sensor rows nearly eliminates FOV overlap in the vertical dimension, the benefits are two-fold: increased frame rate and reduced rolling shutter artifacts (see Methods 5.1).
Table 1.
The three imaging configurations.
| Downsample factor | 1× (none) | 2× | 4× |
|---|---|---|---|
|
| |||
| Per-camera dims | 1536×4096 | 768×2048 | 384×1024 |
| Composite dims | 13000×11250 | 6500×5625 | 3250×2810 |
| Composite SBP | 146.3 MP | 36.6 MP | 9.1 MP |
| Frame rate | 15 fps | 60 fps | 230 fps |
| Exposure | 20 ms | 5 ms | 2.5 ms |
| Raw pixel rate | 5.1 GP/sec | 5.1 GP/sec | 4.9 GP/sec |
| Composite pixel rate | 2.2 GP/sec | 2.2 GP/sec | 2.1 GP/sec |
| Image pixel pitch | 9.6 μm | 19.2 μm | 38.4 μm |
2.3. Seamless image registration, stitching, and 3D estimation
For each video frame, the 3D-RAPID algorithm fuses the 54 synchronously acquired images, via gradient descent using a pixel-intensity-based loss, into a continuous, seamless, expanded-FOV composite image, and simultaneously estimates a coregistered 3D height map (Fig. 2a). In fact, these two tasks are intimately related – to form a high-quality registration, it is necessary to account for parallax distortions induced by height deviations from a planar sample scene that would otherwise thwart simple registration using homographic transformations (Fig. 2b) [1, 56]. To achieve this, the algorithm starts with calibration of the 6-degree-of-freedom poses (, roll, pitch, yaw), camera distortions, and intensity variations by registering and stitching 54 images of a flat, patterned target (Methods 5.3). Estimating the 3D height map of the sample of interest relative to this calibration plane is tantamount to rendering the images registerable using homographies (Fig. 2b). In particular, the per-pixel deformation vectors that undo the parallax shifts (i.e., orthorectify the images) have magnitudes that are directly proportional to the per-pixel heights, (i.e., the height map), given by [1]
| (1) |
where is the effective focal length of the lens, is the linear magnification, is the apparent 2D position of the object in the pixel (before orthorectification), is the vanishing point to which all lines perpendicular to the sample plane appear to converge, and is the 2D orthorectification vector pointing towards the vanishing point (Fig. 2b). can be determined from the camera pose, as the point in the sample plane that intersects with the perpendicular line that passes through the principal point in the thin lens model. The orthorectification vectors , and therefore the height map, for each object position can be determined by registering images (via photometric pixel values) from different perspectives. The accuracy of the height map thus depends on the object having photometrically textured (i.e., not uniform) surfaces that enable unique image registration, a condition satisfied by all model organisms we imaged.
Fig. 2.
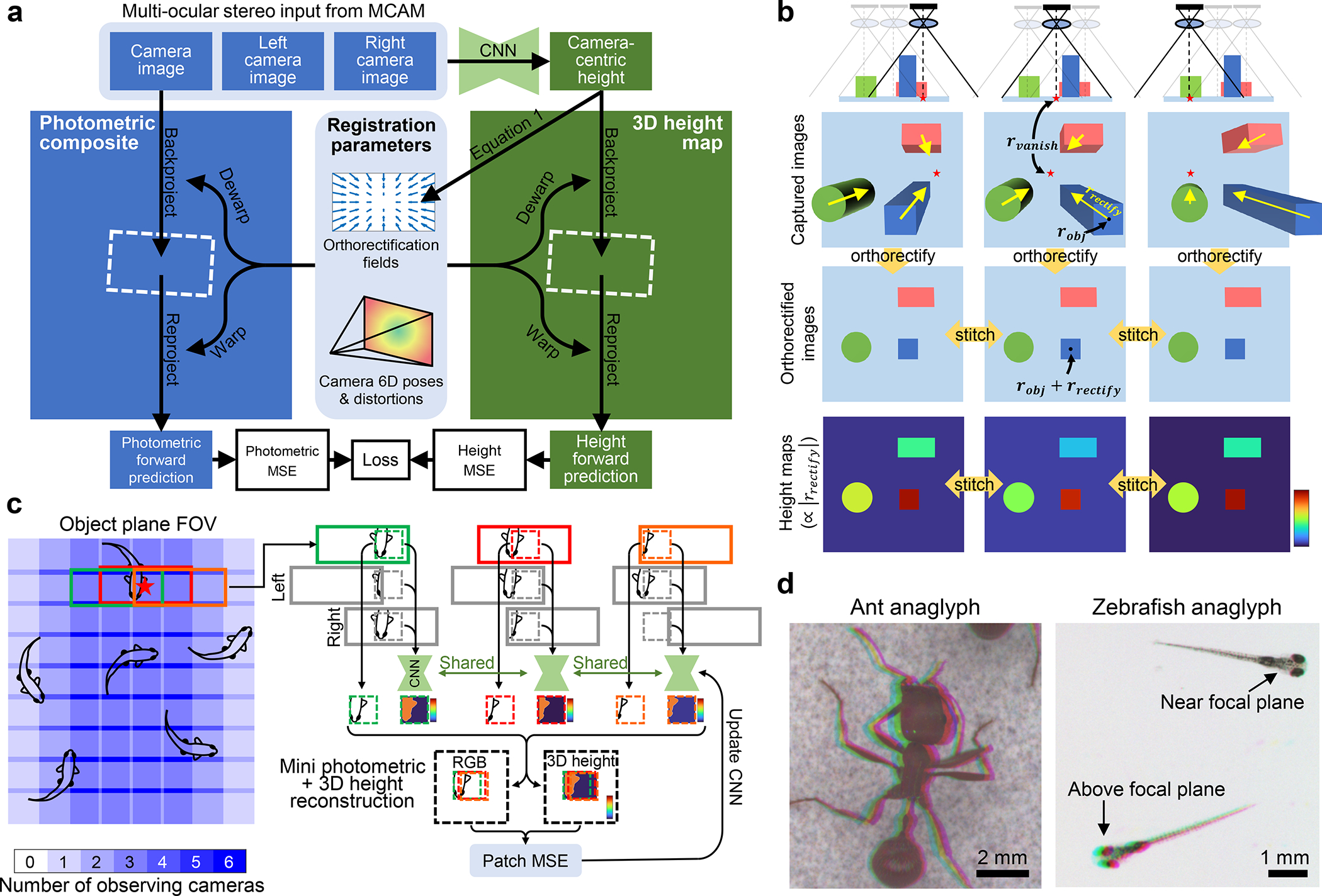
Computational 3D reconstruction and stitching algorithm for 3D-RAPID. a, The algorithm starts with raw RGB images (only one shown for clarity), along with coregistered images from the cameras to left and right, as CNN inputs. CNN generates camera-centric height maps, which in turn dictate orthorectification fields (see b and Eq. 1). Orthorectificaton fields and camera poses + distortions constitute registration parameters, dictating where and how each image should be backprojected in the stitched photometric composite and 3D height map. The backprojection step is then reversed (reprojection) to form forward predictions of the RGB images and camera-centric height maps. Errors (photometric MSE and height MSE) guide the optimization of the CNN. b, The physical ray model, intuitively showing how orthorectification facilitates stitching of non-telecentric images and height maps. c, The patch-based joint training/stitching/3D reconstruction algorithm. At each gradient descent iteration, random coordinates are chosen (red star); all cameras that view a given point are isolated. A patch is cropped out from each camera image surrounding the randomly sampled point, along with the corresponding left/right camera images to serve as the multi-ocular stereo inputs to the CNN to predict the patch height map. These patches undergo the procedure outlined in a to form a mini photometric and 3D height reconstructions to update the CNN. Zeros are assigned to stereo input pixels when unavailable (e.g., at the edge of the object plane FOV), to preserve convolutionality when applying the CNN to the entire camera images to generate the full-size reconstructions. d, Analyphs, whereby the three stereo inputs are color-coded as RGB channels, showing the parallax that is used to estimate 3D.
Thus, the optimization problem is to jointly register all 54 images using the pixel-wise photometric loss, using the orthorectification maps (which are directly proportional to the height maps via Eq. 1) as the deformation model on top of the fixed, pre-calibrated camera parameters, including distortions (Fig. 2a,b). In practice, since viewpoint-dependent photometric appearance can affect image registration, we also employed normalized high-pass filtering to standardize photometric appearance (Methods 5.2 and Supplementary Sec. S3.5).
2.4. Spatiotemporally-compressed 3D video via physics-supervised learning
Instead of optimizing the height maps directly, we reparameterized them as the output of an encoder-decoder CNN that takes the multi-view stereo images as inputs. This reparameterization has two interpretations, depending on whether we emphasize the CNN or the ray-based physical model. First, the CNN can be thought to act entirely as a training-data-free regularizer (i.e., deep image prior (DIP) [3]) that safeguards against 3D reconstruction artifacts that may otherwise arise from practical deviations from modeling assumptions that thwart image registration [1]. For example, using the CNN as a regularizer can be useful when the sample has a different appearance when viewed from different angles, which can be caused by uneven illumination, angle-dependent scattering responses, or varying pixel responses. Since we wish to reconstruct hundreds to thousands of 3D video frames, it would be prohibitively slow to independently reconstruct every video frame, with or without CNNs. Thus, we use one shared DIP, with each frame encoded by the raw multi-ocular stereo photometric inputs.
Thus, the second interpretation is one of physics-supervised learning, in which the image registration of the overlapped MCAM image frames, governed by a ray-based thin lens physical model (Eq. 1), provides the physics-based supervision that guides the CNN training (Fig. 2a,c). The CNN can then be used to generalize to other MCAM data, both spatially (other micro-cameras) and temporally (other video frames).
This dual interpretation of our CNN-regularized, physics-supervised learning approach reveals several advantages. First, since we employ a fully-convolutional CNN, we can optimize on arbitrarily-sized image patches (Fig. 2c) that can fit in GPU memory, and then perform non-iterative forward inference on arbitrarily-large full-size images (Fig. S4). Thus, our proposed approach is scalable and generalizable to arbitrarily many cameras, each with arbitrarily many pixels, for arbitrarily many video frames. For implementation details on patch-based training, see Sec. 2.5, Fig. 2c, and Supplementary Sec. S3. Second, the CNN enforces a spatiotemporally-compressed representation of the 3D height map videos, thus avoiding the need to iteratively optimize each frame individually. Third, this spatiotemporal compression reduces the chances of overfitting, as there are far fewer CNN parameters than height map pixels across all video frames. Furthermore, the CNN implicitly enforces consistency across space and time, thus, for example, avoiding variance induced by independent optimization runs on different frames. Fourth, our approach has an inherent fail-safe against generalization errors, unlike other deep learning-based approaches, since the ground truth is always available via the overlap redundancy and the physical model.
2.5. Patch-based learning from multi-ocular stereo inputs
While Fig. 2a summarizes the ideal joint 3D reconstruction, stitching, and training method, in practice we are constrained by GPU memory. Thus, we train the CNN using a random patch sampling approach (Fig. 2c). Briefly, at each optimization iteration, we sample (batch size) random points within the composite FOV (one shown in Fig. 2c). All cameras viewing each point are selected, from which patches surrounding that point are extracted from each camera view. Thereafter, these groups of selected patches independently undergo the procedure outlined in Fig. 2a. Once CNN training is done, the backprojection step in Fig. 2a is carried out for each full temporal frame to create the stitched RGBH 3D reconstructions (Fig. S4). For more implementation details, see Supplementary Sec. S3.
3. Results
3.1. 3D-RAPID system characterization
Our 3D-RAPID system has a full-pitch lateral resolution of ~25 μm and DOF of ~9.4 mm, based on imaging a USAF resolution target and translating a patterned target axially (see Supplementary Sec. S1). We validated the height precision and accuracy of our 3D-RAPID system by imaging precisely machined (to within 0.3 μm) gauge blocks (Mitutoyo). As expected, accuracy and precision of the reconstructed height improve at higher spatial resolution, which facilitates more accurate measurement of parallax shifts (Supplementary Sec. S5). Specifically, we achieved sub-20 μm accuracy and precision in the 15-fps configuration, and ~37 μm accuracy and ~74 μm precision in the 230-fps configuration. See Supplementary Sec. S1 for detailed characterization.
3.2. Zebrafish larvae (Danio rerio)
We applied 3D-RAPID to several 10-sec videos of zebrafish larvae (Danio rerio) freely swimming in a large 97 mm × 130 mm open arena using the 60-fps and 230-fps configurations (Table 1) across three separate experiments, the first of which was on 10-dpf fish feeding on microcapsule food particles (AP100) (Supplementary Videos 1 (60 fps), 2 (230 fps), and 3 (60 fps with tracking)). Fig. 3 and Extended Data Fig. 1 summarize the results for the 60-fps video of the 10-dpf fish feeding on AP100, most of which are floating at or near the water surface (Extended Data Fig. 1b). We tracked all 40 fish using a simple particle-tracking algorithm (Methods 5.4; Supplementary Video 3). The high throughput of 3D-RAPID allowed us to observe fine detail over a very wide FOV, capturing multiple rapid feeding events (~10s of ms), as shown in Fig. 3b,c. From the photometric images, we can see that the larvae turn their bodies laterally so that their ventrally positioned mouths can access the overhead floating food. We also observe eye convergence once the larvae identify and approach the target [20–22]. The eye angles rapidly deconverge after food capture (Fig. 3e,f). The older fish (20 dpf) exhibit similar eye behavior when feeding on brine shrimp (Supplementary Videos 4, 5).
Fig. 3.
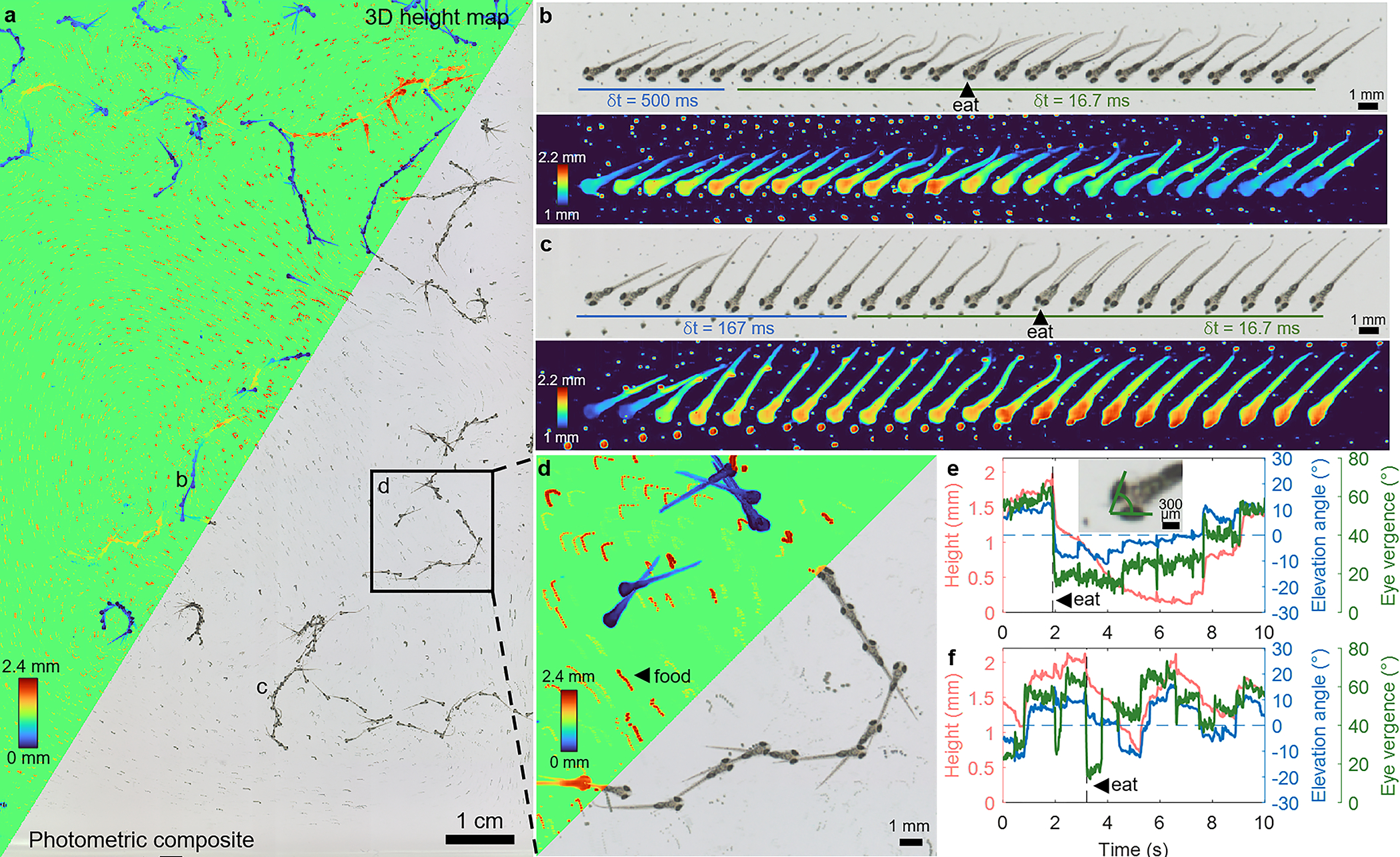
Zebrafish larvae (10 dpf) swimming in an open arena with interspersed microcapsulated food particles (AP100), acquired at 60 fps for 10 sec (Supplementary Videos 1,3). a, 3D height map and photometric composites of the zoomed-out FOV, projected across every 50th temporal frame (0.83 sec) to highlight dynamics. The height map assigns an arbitrary value to the otherwise empty background. b, Photometric and height map frames of a single tracked fish feeding on AP100. The first 5 frames are spaced by 500 ms while the remaining frames are spaced by 16.7 ms (the full frame rate). e, The same fish’s head height, elevation angle (pitch), and eye vergence angle (illustrated in inset) throughout the 10-sec video. c,f, Another example of a zebrafish feeding event. Note the change in eye vergence before and after the feeding event in both b and c. d, A zoomed-in region of a, showing 3 individual larvae in varying states of activity. The small red tracks are the drifting and floating AP100 food particles. Population-level analysis is summarized in Extended Data Fig. 1.
The 3D information enabled by our technique reveals how the larvae axially approach their targets from below, including their head heights and elevation (pitch) angles during these feeding events (Fig. 3b,c,e,f) [23]. The larvae’s head height matches that of the targeted food particle during ingestion (see also Supplementary Videos 1, 2, 4, 5), offering validation of our technique.
In addition to making organism-level observations, the high throughput of 3D-RAPID enabled us to make population-level inferences by aggregating height and elevation angle information for all 40 individually-tracked larvae for all in-frame time points. The results show a roughly linear trend between height and elevation angle (Extended Data Fig. 1a), which can be explained based on the mobility constraints defined by the length of the larvae and the water depth. For example, if the head is at the bottom of the arena, then the elevation angle must be negative. Assuming a larval length of and a water depth of , these geometric constraints on the elevation angle, , for a fish at height, , are
| (2) |
which are plotted in Extended Data Fig. 1a. This offers additional validation of the accuracy of our 3D height maps. We also estimated the probability distributions of the heights of the larvae and the food particles (Extended Data Fig. 1b), both of which are bimodal. Predominantly, the larvae dwell at the bottom of the arena, only occasionally venturing upwards for food.
We also analyzed population-level correlations between eye vergence angle (Methods 5.4), a property observable in the photometric images, and the fish height and elevation angle, which are derived from our 3D height maps (Extended Data Fig. 1c,d), across fish (one stationary fish excluded). Specifically, we used a linear mixed-effects model, where height or elevation angle is the fixed effect and dependence among images from the same fish are accounted for as random effects. Analyses of variance suggest that while fish height is not a statistically significant linear predictor of eye vergence angle , fish elevation angle is (p < 10−5). This is consistent with the fact that when the fish is swimming upwards, it is likely focusing on a food particle close to the surface. On the other hand, the fish can still be close to the surface following a feeding event, immediately after which the eyes deconverge (Fig. 3b,c,e,f).
With the 230-fps configuration, we can trade off spatial resolution to temporally resolve higher-speed zebrafish larval locomotion. For example, compare the beginning of Supplementary Videos 6 and 7, which feature rapidly swimming zebrafish larvae, captured at 60 fps and 230 fps. Similarly, we can resolve the 4D fish dynamics as it attempts to swallow a live brine shrimp (Supplementary Videos 4 (60 fps) and 5 (230 fps)).
3.3. Fruit flies (Drosophila hydei)
Next, we applied 3D-RAPID to image 50 freely exploring adult fruit flies (Drosophila hydei) under the 60-fps (Supplementary Videos 8 and 10) and 230-fps (Supplementary Video 9) configurations. Fig. 4 and Extended Data Fig. 2 summarize the results for the 60-fps configuration for six individual flies exhibiting various grooming behaviors. Supplementary Video 10 shows tracking of all 50 flies. The 3D height map reveals changes in fly height and body tilt as the flies transition between different grooming behaviors. In Fig. 4b, as the fly transitions between grooming with its hindlegs and forelegs, the abdomen moves up and down, respectively. When a middle leg joins the grooming (Fig. 4b, arrowheads), there is a subtle change in abdomen height relative to head height. In Fig. 4c, our method correctly predicts an elevated height as one fly climbs atop another. At 2.5 sec, the fly’s height drops, consistent with the straightened leg joints. A similar body tilt trend is observed for foreleg vs. hindleg grooming in this fly, as well as in Fig. 4d, e, and f. In Fig. 4f, we see another instance of the fly’s leg joints fully extended at 1.767 sec, resulting in a reduced overall height. Further, we observe that the abdomen takes on a different relative height during abdominal grooming compared to hindleg grooming. Finally, in Fig. 4g, although the fly is grooming its forelegs throughout the video, it reduces its overall height after 1 sec, consistent with its extended leg posture.
Fig. 4.
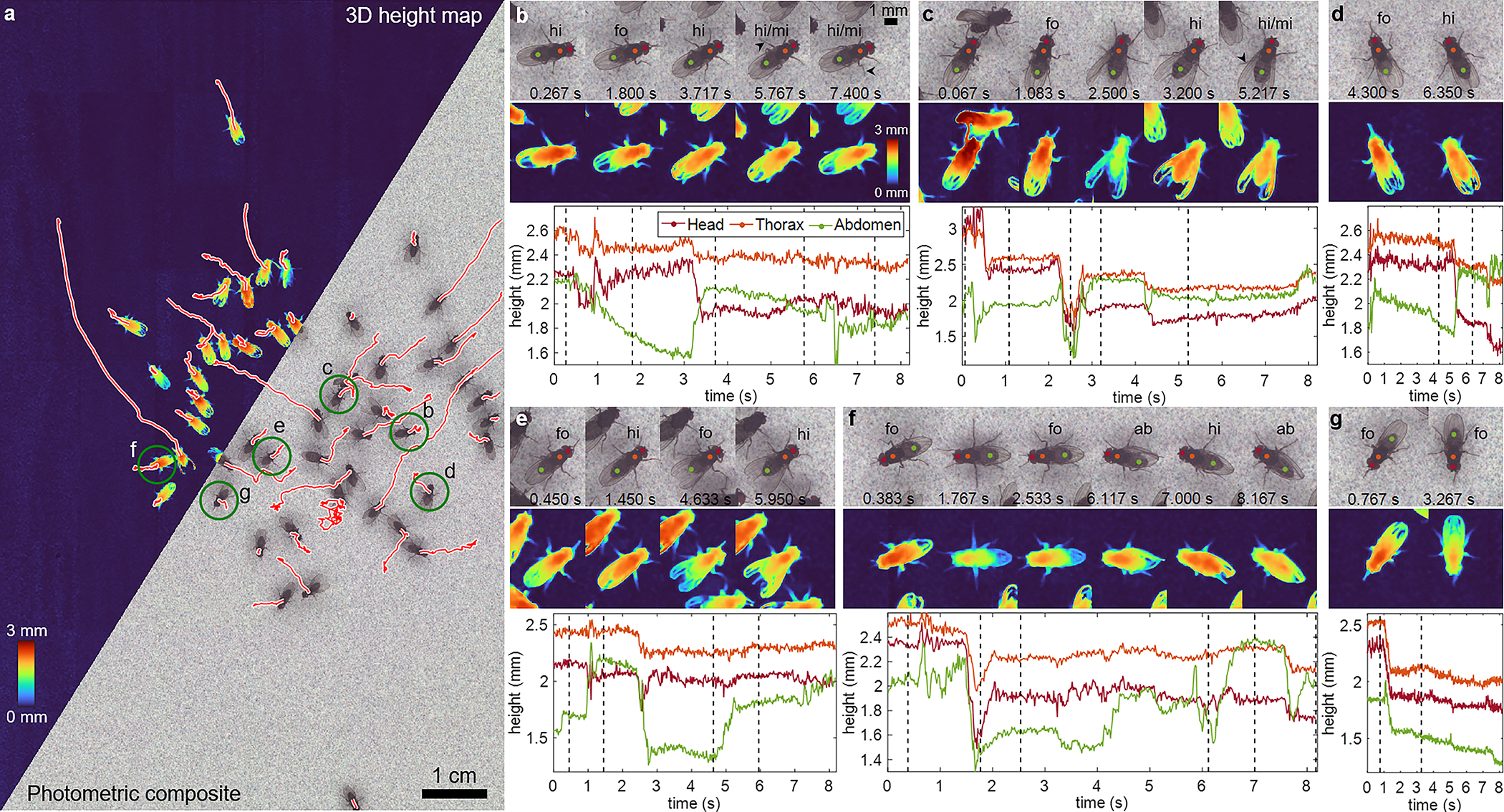
Adult fruit flies freely moving across a flat, noise-patterned surface, acquired at 60 fps for 8 sec (Supplementary Videos 8,10). a, 3D height map and photometric composites of the zoomed-out FOV. The white-outlined red lines are the trajectories the 50 flies take. The green-circled flies are analyzed in the other figure panels. b, Select photometric and height map frames of a single tracked fly, exhibiting several grooming behaviors (hi = hindleg grooming, fo = foreleg or head grooming, mi = mid leg participation, ab = abdominal grooming). The time points of the frames are indicated by dotted lines in the plot below, which in turn highlights the changing heights of the head, thorax, and abdomen for the different grooming actions. c-g, The same information for 5 additional flies. Population-level analysis is summarized in Extended Data Fig. 2.
To analyze population trends, we annotated video frames across flies flies with one of five behaviors: hindleg grooming, foreleg/head grooming, abdomen grooming, standing still, and walking (Extended Data Fig. 2). Flies that exited the FOV were excluded. We tested for cross-behavioral differences in heights of the head, thorax, and abdomen using three separate linear categorical mixed-effects models, accounting for random effects due to correlations among video frames from the same fly. Analyses of variance suggest that behavior groups are a statistically significant predictor of the heights of the head (p < 10−7), thorax (p < 10−16), and abdomen (p < 10−62).
3.4. Harvester ants (Pogonomyrmex barbatus)
We also imaged freely exploring red harvester ants (Pogonomyrmex barbatus) under the 60-fps (Supplementary Video 11) and 230-fps (Supplementary Video 12) configurations. The 60-fps results are summarized in Fig. 5. We used the dynamic 3D reconstructions to track the femur-tibia joints of all six legs of an individual ant (Fig. 5b,c; Methods 5.4), providing information about the kinematics of ant locomotion. The joint trajectories are plotted in Fig. 5c, showing that the high-frequency (~3–4 Hz) oscillations from walking kinematics are anti-correlated between left and right legs. This frequency remains relatively constant throughout the ant’s journey. Further, the forelegs and hindlegs on the same side of the body are correlated, but anti-correlated with the mid legs on the same side of the body. These behaviors are consistent with the well-known alternating tripod gait pattern in ants [33, 59, 60], which persists even as the curvature of ant trajectory changes.
Fig. 5.
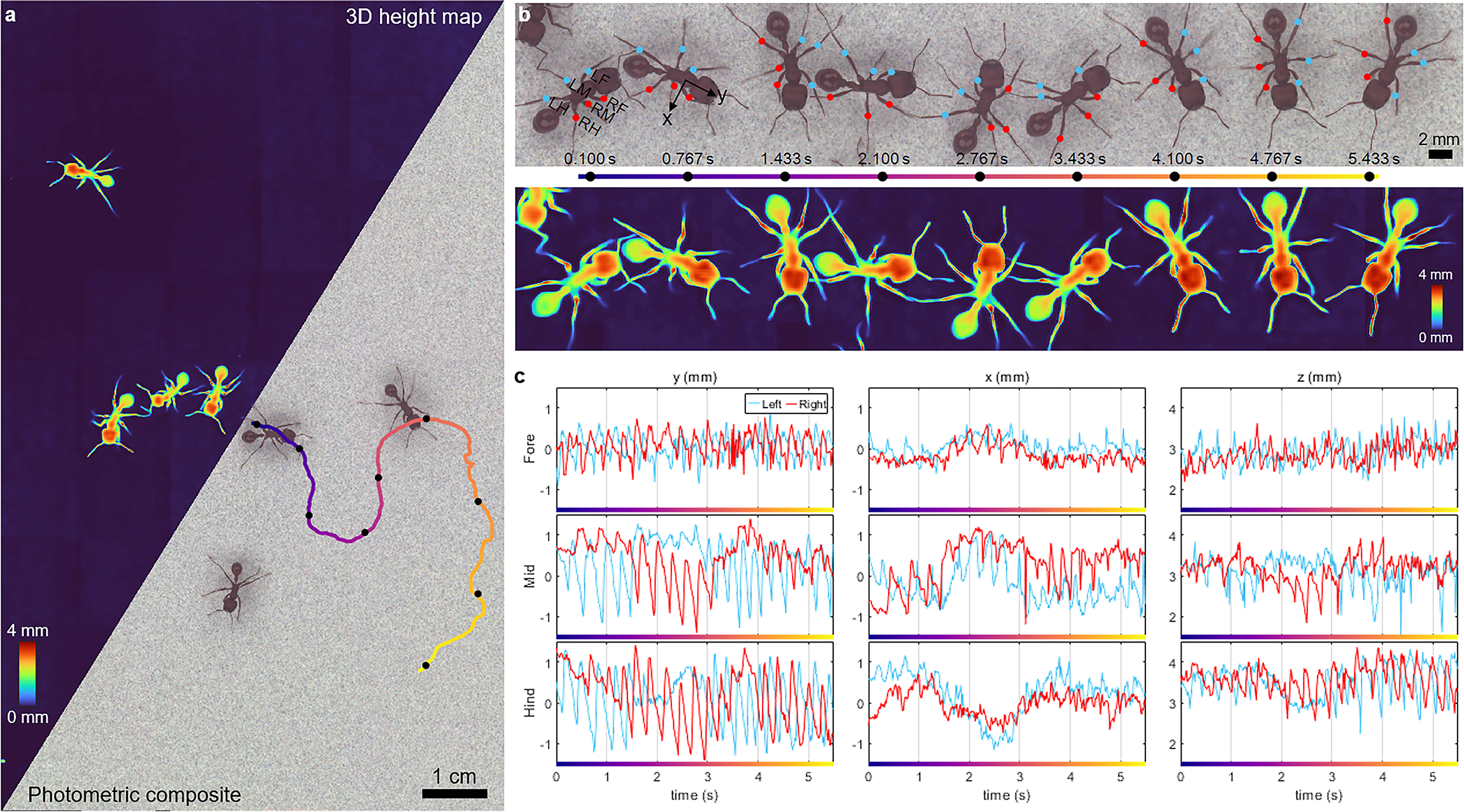
Harvester ants freely moving across a flat, noise-patterned surface, acquired at 60 fps for 10 sec (Supplementary Videos 11–12). a, Photometric composite and 3D height map of the zoomed-out FOV. One of the ants’ trajectories is color-coded by time, progressing from blue to red over a 5.5-sec duration, and is analyzed in b and c. b, Temporal snapshots of a single tracked ant along the trajectory in a. The blue and red dots are the femur-tibia joints for the ant’s 6 legs (L = left, R = right, F = foreleg, M = middle leg, H = hindleg). c, The 3D positions of the femur-tibia joints over the 5.5-sec trajectory. The lateral dimensions (xy) are defined relative to the ant’s orientation, as illustrated in b.
We also observe changes in lower-frequency gait patterns as the ant makes multiple turns throughout its exploration. In the first ~1.5 sec, as the ant is turning right, we see a reduced oscillation amplitude in the mid and hindlegs on the right side in both the and directions; however, for the direction, we see the opposite trend (see Fig. 5b for the ant-centric coordinate system). Between 1.5 and 3 sec, as the ant is turning left, we see the opposite motions as in the first 1.5 sec – the oscillation amplitudes in the mid and hindlegs on the left are reduced in both the and directions, while amplitude of the right mid leg motion in the x direction is reduced. From 3 to 4.5 sec, the ant once again is turning right and we see similar trends as in the first 1.5 sec. Overall, this reduction in motion in and on the side of the ant corresponding to the direction the ant is turning is consistent with prior knowledge [59]. Interestingly, the amplitudes of the foreleg oscillations on both the left and right sides in both and remain relatively constant throughout the entire 5.5 sec, suggesting a lesser role in the biomechanics of changing directions.
Finally, we observe a low-frequency oscillation (with a period of ~4 sec) in the direction for all 6 legs that is correlated with the curvature of the ant’s trajectory. Unlike the high-frequency (3–4 Hz) walking kinematics, which are anti-correlated between left and right, these low-frequencies are correlated between left and right legs, suggesting left-right coordination when the ant is turning. These low-frequencies in the direction further are correlated between the forelegs and mid legs, but anti-correlated with the hindlegs.
4. Discussion
We have presented 3D-RAPID, a new computational microscope with a unique capability of dynamic topographic 3D imaging at 10s-of-μm resolution, over >130-cm2 FOV at throughputs exceeding 5 GP/sec. To handle this high data throughput, we devised an efficient, end-to-end, physics-supervised, CNN-based, joint 3D reconstruction and stitching algorithm that scales to arbitrarily long videos and arbitrarily sized camera arrays. Thus, 3D-RAPID fills a unique niche, enabling scientists to study several unconstrained, freely-behaving model organisms in parallel at high speed and high resolution over a very large FOV.
3D-RAPID differs from other camera array-based techniques [43–47] in several ways, due to the dense camera packing requirements necessitated by the high magnifications associated with microscopy. Some approaches alleviate this challenge by first magnifying to an intermediate image plane. However, the primary objective’s intrinsic SBP would limit the total throughput. Instead, our approach tiles CMOS sensors on a common PCB, which is connected to a single FPGA for unified data routing. This allows for extremely tight packing and scalability by simply adding more sensors. To our knowledge, 3D-RAPID is the 3D imaging system with the highest sustained throughput to date.
While we have presented several convincing 3D behavioral imaging demonstrations, there are several avenues for improvement. The hardware parameters could be adjusted to improve the 3D height reconstruction accuracy, which depends on how accurately parallax shifts can be detected to match features from different cameras (see Supplementary Sec. S5). Furthermore, since the reconstruction algorithm is agnostic to the contrast mechanism, it would also be possible to incorporate, for example, fluorescence to correlate behaviors with molecular signatures. Finally, throughput could be improved beyond 5 GP/sec by alleviating data transfer bottlenecks.
In summary, we have presented 3D-RAPID as a new platform for studying the behavior of multiple freely-moving organisms at high speed and resolution over a very wide area. We expect our technique to be broadly applicable to elucidate new behavioral phenomena, not only in zebrafish, fruit flies, and ants, but also other model organisms such as tadpoles and nematodes.
5. Methods
5.1. Temporal synchronization of the camera array
Ideally, all sensor pixels should be fully synchronized with a global shutter, not only within each sensor, but also across sensors. This would ensure that between different views of the same object, after accounting for camera poses, the only discrepancies are due to parallax shifts and not sample motion. For example, if two camera views of a moving object with zero height were desynchronized, lateral motion could be interpreted as a parallax shift, leading to an erroneous height estimate. In practice, each of our sensors exhibits a rolling shutter, whereby only a single pixel value can be read out at a given time for a given sensor, row by row from the top-left to bottom-right corner in a raster scan pattern. This means that the bottom of a given sensor is captured later than the top of the sensor immediately below. However, across independent sensors, this rolling shutter readout pattern is synchronized to within 10 μs, limited by the serial communication interface (I2C with a 100-kHz clock).
To mitigate the rolling shutter effects, we employed two strategies. First, we cropped the sensors so that there is only significant overlap in the horizontal dimension for stitching, in which the desynchronization is much less severe. Second, we calculated that with exposures of 2.5 ms for 4× downsampling, 5 ms for 2× downsampling, and 20 ms for no downsampling, artifacts would be minimal. For a detailed discussion and calculations, see Supplementary Sec. S4.
5.2. Achieving robustness to illumination variation
Since the optimization metric of our approach is the mean square per-pixel photometric error, we would achieve optimal performance when the sample has a camera-independent photometric appearance. This condition would require not only uniform response across all pixels of all cameras, but also that the sample is isotropically emanating light in all directions. The latter property is in practice difficult to achieve, requiring either perfectly diffuse illumination or a diffusely scattering sample, regardless of the illumination direction. In addition to the regularizing effects of the CNN/DIP, we employed two additional strategies to reduce the effects of camera-dependent appearance. First, as part of the camera pose pre-calibration procedure, we also jointly optimized per-camera second-order 2D polynomials (with cross terms) to correct the slowly-varying image intensity variation (whether caused by uneven illumination or camera response), using the same photometric stitching loss. Thus, the pre-calibration step not only ensures geometric consistency of the 54 images, but also photometric continuity. For more details, see Methods 5.3, below.
Second, for terrestrial organisms illuminated in reflection, we employed a two-step optimization process, where we first optimize the CNN to register the images using the RGB intensities. In the second step, we continue optimizing the CNN, except this time registering normalized high-pass-filtered versions of the photometric images, which reduces illumination-induced differences in photometric appearance and emphasizes edges (Supplementary Sec. S3.5). This two-step procedure effectively removes artifacts in the 3D height maps that would otherwise result from camera-dependent photometric appearances.
5.3. Camera calibration: pose, distortion, & intensity variation
The first step in the 3D estimation pipeline was to calibrate the cameras’ geometric and photometric properties. Specifically, the geometric properties include their 6D pose (3D position + 3D orientation) and second-order radial distortions (e.g., pincushion or barrel distortions). The photometric properties include the pixel intensity variations both within individual cameras and across different cameras. These may arise due to vignetting, uneven illumination, pixel response variation, or angle-dependent scattering of the sample. To estimate the calibration parameters, we imaged a flat, epi-illuminated, homogeneously-patterned calibration target with the MCAM and registered the resulting 54 images, enforcing both geometric and photometric consistency in the overlapped regions.
The calibration procedure follows the optimization procedure outlined in Fig. 2a, excluding the height map-related orthorectification portion. In particular, let and be two vectors representing the ideal 2D spatial coordinates of the camera pixels – that is, a 2D rectangular grid of equally-spaced points (e.g., 1536×4096). Next, let be an image deformation operation that maps from the ideal camera coordinates to a common global coordinate space (the object plane), parameterized by the camera parameters, . See Supplementary Sec. 1 of Ref. [1] for specific implementation details of . Let be the camera parameters for the ith camera, so that
| (3) |
represents the (de)warped coordinates of the ith camera in a common object plane.
Let be a vector of the same length as and , indicating the measured photometric intensity at every pixel coordinate for the ith camera. Although the debayered images have 3 color channels, here, for simplicity, we assume a single-channel image. Further, let be a photometric correction operation, parameterized by , so that
| (4) |
represents the photometrically-adjusted intensity values for the camera. The dependence on and indicates that the photometric correction is spatially-varying. Specifically, we used a second-order polynomial correction,
| (5) |
where represents element-wise multiplication and . In sum, assuming and are optimized, then represents the corrected camera data, accounting for distortion and photometric variation.
Next, let be three vectors representing the flattened concatenation of for all . We then initialize a blank matrix, , representing the stitched reconstruction, into which we backproject the collection of points,
| (6) |
with interpolation, as and are continuously valued. When specific coordinates are visited more than once, the values are averaged. The result of Eq. 6 is an estimate of the stitched composite for a given set of . To update these parameters, we form a forward prediction from by reprojecting back into the camera spaces, as follows:
| (7) |
should match when the camera images are well-registered and the corrected photometric intensities match in overlapped regions. Thus, we minimize the error metric,
| (8) |
with respect to via gradient descent. Since the image target is homogeneous, we also include a regularization term,
| (9) |
which enforces a homogeneous reconstruction. Here, the standard deviation (stdev) is taken across all the pixels in one image.
Finally, we apply the calibrated parameters, , to each frame of the videos of the freely-moving organisms. To homogenize the background in the case of zebrafish, which uses transmission illumination instead of the epiilluminated calibration target, we apply a second calibration step that only optimizes the photometric correction parameters, , using the maximum projection of the video across time, which eliminates all moving objects.
5.4. Organism tracking and pose determination
To track the fruit flies, zebrafish larvae, and harvester ants, we first thresholded the photometric composites to segment each organism and compute each of their centroids across all video frames. We then employed a simple particletracking algorithm, matching the organisms by finding the closest centroid in the subsequent video frame. In the case of clashing match proposals, we assigned matches that minimized the sum of the total absolute lateral displacements. To track the ants’ 6 femur-tibia joints, we incorporated the observation that the joint heights are local maxima in the 3D height maps for segmentation, and employed a similar particle-tracking algorithm.
To determine the orientation of the organisms, we performed principal component analysis (PCA) on the thresholded pixel coordinates and took the first principal component (PC) as the organism’s orientation. In the case of zebrafish, we used the height map coordinates to perform PCA in 3D, thereby allowing us to compute the elevation angles in Fig. 3. We resolved the sign ambiguity of the PC either by enforcing the dot products of PCs of the tracked organism in consecutive frames to be positive, or by computing the relative displacement between the unweighted centroid and the intensity-weighted centroid and forcing the PC to point in the same direction.
The fish eye vergence angles were estimated by thresholding the green channel of the photometric intensity images to identify the eyes. The orientations of the eyes were estimated using the <monospace>regionprops</monosapce> command in MATLAB, which finds the angle of the major axis of the ellipse with the equivalent second moments. The vergence angle is then computed as the angle between the two eyes.
5.5. Biological samples and data acquisition
Zebrafish stocks were bred and maintained following Duke University Institutional Animal Care Use Committee guidelines and as previously described [1]. Zebrafish were stored at 28°C with daily feeding and water changes, and cycled through 14 hours of light and 10 hours of darkness per day. Free swimming fish were imaged at larval stages between 5 dpf and 20 dpf. Specifically, zebrafish larvae were transferred from culture chambers using a transfer pipette to a clear plastic imaging arena (with lateral inner dimensions 97 mm × 130 mm), which was filled with system water a few mm deep. The arena was then placed on the sample stage of the MCAM system. The z position of the stage was adjusted such that the zebrafish larvae were all within the DOF of the lenses. The system was left undisturbed with the LED illumination panels turned on for at least 5 minutes to allow the zebrafish to acclimate, after which multiple MCAM videos were acquired using a custom Python script. After video acquisition, the arena was removed and replaced with a flat patterned calibration target. We focused the target with the z stage using a Laplacian-based sharpness metric and captured a single frame (all 54 cameras), which would serve to calibrate the camera poses and distortions for all videos captured during that imaging session.
The wild-type red harvester ants and fruit flies (available from various vendors on Amazon) were maintained at room temperature. When ready for imaging, we positioned and focused a flat patterned calibration target, which serves two purposes: 1) for camera calibration, just as for the zebrafish videos described in the previous paragraph, and 2) to serve as a flat substrate for the ants and fruit flies to walk upon. The patterned target, although not required, serves as a global reference in the 3D height maps. Alternatively, the substrate could be monochrome/featureless or transparent (e.g., a glass sheet), as was the case for the zebrafish imaging configuration, in which case the 3D height map would assign an arbitrary height value to the background without affecting the 3D accuracy of the organisms themselves.
The ants or fruit flies were inserted into a Falcon tube and released onto the center of the flat substrate, after which we immediately ran the same custom Python script to acquire MCAM videos. If necessary, the insects were re-collected in the tubes and re-released into the arena for repeated imaging. After video acquisition, we acquired a single frame of the calibration target alone, just as we did after zebrafish video acquisition.
Extended Data
Extended Data Fig. 1.
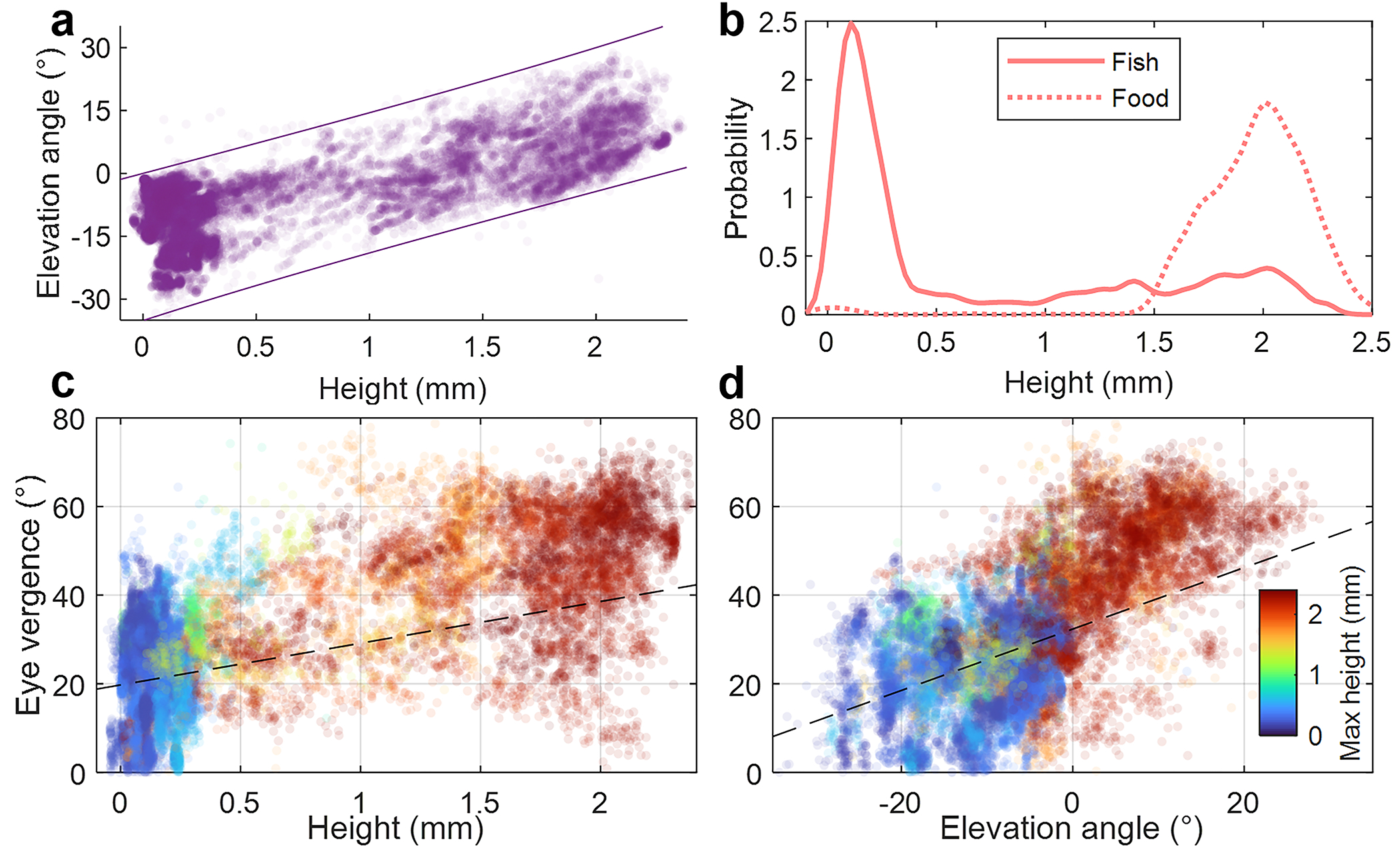
Population-level analysis of the zebrafish larvae featured in Fig. 3 and Supplementary Videos 1,3. a Fish head height vs. elevation angle for all 40 fish over time. Lines define the approximate physical limits due to geometric fish mobility constraints. b Kernel density estimates of the height distributions of the zebrafish and AP100 food particles. Eye vergence vs. head height (c) and vs. elevation angle (d) plots are color-coded by the maximum height the fish attained in the 10-sec video. Fixed effect components of the linear mixed-effects regression lines are plotted (p = 0.33 and p < 10−5) for c and d, respectively.
Extended Data Fig. 2.
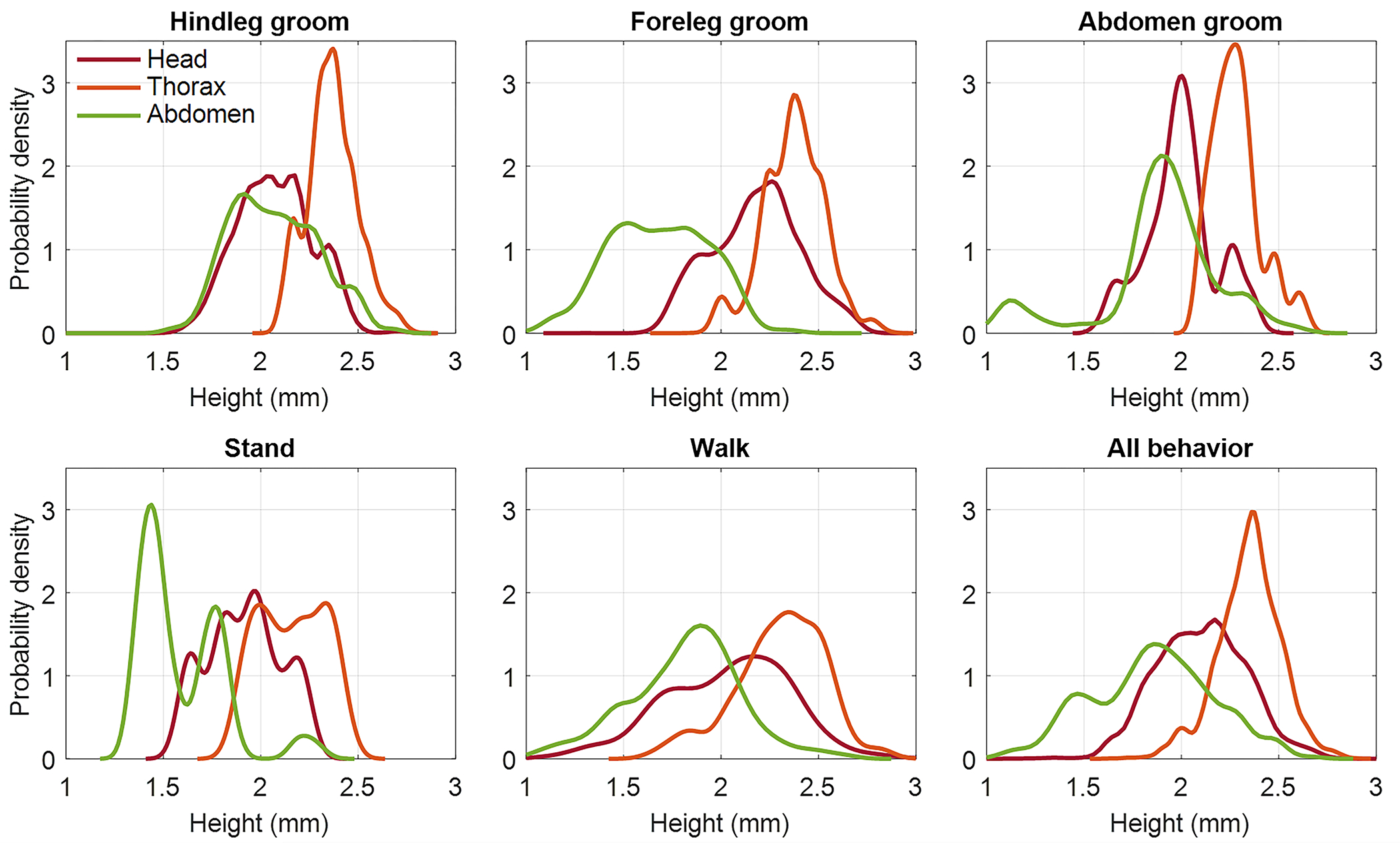
Population-level analysis of the adult fruit flies featured in Fig. 4 and Supplementary Videos 8,10. The six plots show kernel densities of the heights of the head, thorax, and abdomen for various behaviors. Differences of head (p < 10−7), thorax (p < 10−16), and abdomen (p < 10−62) heights across behaviors are statistically significant (n = 43 flies).
Supplementary Material
Acknowledgements
We would like to thank Kristin Branson, Srinivas Turaga, Timothy Dunn, Archan Chakraborty, and Maximilian Hoffmann for their helpful feedback on the manuscript. Research reported in this publication was supported by the Office of Research Infrastructure Programs (ORIP), Office Of The Director, National Institutes Of Health of the National Institutes Of Health and the National Institute Of Environmental Health Sciences (NIEHS) of the National Institutes of Health under Award Number R44OD024879 (MH, JP, TD, PR, VS, MZ, JPB, AB, GH), the National Cancer Institute (NCI) of the National Institutes of Health under Award Number R44CA250877 (MH, JP, TD, PR, VS, MZ, JPB, AB, GH), the National Institute of Biomedical Imaging and Bioengineering (NIBIB) of the National Institutes of Health under Award Number R43EB030979 (MH, JP, TD, PR, VS, MZ, JPB, AB, GH), the National Science Foundation under Award Number 2036439 (MH, JP, TD, PR, VS, MZ, JPB, AB, GH), and the Duke Coulter Translational Partnership Award (KCZ, KK, RH).
Footnotes
Competing interests
RH and MH are cofounders of Ramona Optics, Inc., which is commercializing multi-camera array microscopes. MH, JP, TD, PR, VS, CBC, MZ, JPB, and GH are or were employed by Ramona Optics, Inc. during the course of this research. KCZ is a consultant for Ramona Optics, Inc. The remaining authors declare no competing interests.
Code availability
Code will be available at https://github.com/kevinczhou/3D-RAPID.
Data availability
Data will be available at https://doi.org/10.7924/r4db86b1q.
References
- [1].Bellen HJ, Tong C, Tsuda H: 100 years of drosophila research and its impact on vertebrate neuroscience: a history lesson for the future. Nature Reviews Neuroscience 11(7), 514–522 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Oliveira RF: Mind the fish: zebrafish as a model in cognitive social neuroscience. Frontiers in neural circuits 7, 131 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Kalueff AV, Stewart AM, Gerlai R: Zebrafish as an emerging model for studying complex brain disorders. Trends in pharmacological sciences 35(2), 63–75 (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Dreosti E, Lopes G, Kampff AR, Wilson SW: Development of social behavior in young zebrafish. Frontiers in neural circuits 9, 39 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Pandey UB, Nichols CD: Human disease models in drosophila melanogaster and the role of the fly in therapeutic drug discovery. Pharmacological reviews 63(2), 411–436 (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Sakai C, Ijaz S, Hoffman EJ: Zebrafish models of neurodevelopmental disorders: past, present, and future. Frontiers in molecular neuroscience 11, 294 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].MacRae CA, Peterson RT: Zebrafish as tools for drug discovery. Nature reviews Drug discovery 14(10), 721–731 (2015) [DOI] [PubMed] [Google Scholar]
- [8].Maitra U, Ciesla L: Using drosophila as a platform for drug discovery from natural products in parkinson’s disease. Medchemcomm 10(6), 867–879 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Hirsch HV, Mercer J, Sambaziotis H, Huber M, Stark DT, Torno-Morley T, Hollocher K, Ghiradella H, Ruden DM: Behavioral effects of chronic exposure to low levels of lead in drosophila melanogaster. Neurotoxicology 24(3), 435–442 (2003) [DOI] [PubMed] [Google Scholar]
- [10].Bambino K, Chu J: Zebrafish in toxicology and environmental health. Current topics in developmental biology 124, 331–367 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Rihel J, Prober DA, Arvanites A, Lam K, Zimmerman S, Jang S, Haggarty SJ, Kokel D, Rubin LL, Peterson RT, et al. : Zebrafish behavioral profiling links drugs to biological targets and rest/wake regulation. Science 327(5963), 348–351 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].McCarroll MN, Gendelev L, Kinser R, Taylor J, Bruni G, Myers-Turnbull D, Helsell C, Carbajal A, Rinaldi C, Kang HJ, et al. : Zebrafish behavioural profiling identifies gaba and serotonin receptor ligands related to sedation and paradoxical excitation. Nature communications 10(1), 1–14 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Mathias JR, Saxena MT, Mumm JS: Advances in zebrafish chemical screening technologies. Future medicinal chemistry 4(14), 1811–1822 (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Wright D, Krause J: Repeated measures of shoaling tendency in zebrafish (danio rerio) and other small teleost fishes. Nature Protocols 1(4), 1828–1831 (2006) [DOI] [PubMed] [Google Scholar]
- [15].Harpaz R, Nguyen MN, Bahl A, Engert F: Precise visuomotor transformations underlying collective behavior in larval zebrafish. Nature communications 12(1), 1–14 (2021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Dankert H, Wang L, Hoopfer ED, Anderson DJ, Perona P: Automated monitoring and analysis of social behavior in drosophila. Nature methods 6(4), 297–303 (2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Robie AA, Seagraves KM, Egnor SR, Branson K: Machine vision methods for analyzing social interactions. Journal of Experimental Biology 220(1), 25–34 (2017) [DOI] [PubMed] [Google Scholar]
- [18].Dunn TW, Mu Y, Narayan S, Randlett O, Naumann EA, Yang C-T, Schier AF, Freeman J, Engert F, Ahrens MB: Brain-wide mapping of neural activity controlling zebrafish exploratory locomotion. Elife 5, 12741 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Johnson RE, Linderman S, Panier T, Wee CL, Song E, Herrera KJ, Miller A, Engert F: Probabilistic models of larval zebrafish behavior reveal structure on many scales. Current Biology 30(1), 70–82 (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Bianco IH, Kampff AR, Engert F: Prey capture behavior evoked by simple visual stimuli in larval zebrafish. Frontiers in systems neuroscience 5, 101 (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Patterson BW, Abraham AO, MacIver MA, McLean DL: Visually guided gradation of prey capture movements in larval zebrafish. Journal of Experimental Biology 216(16), 3071–3083 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Muto A, Kawakami K: Prey capture in zebrafish larvae serves as a model to study cognitive functions. Frontiers in neural circuits 7, 110 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Bolton AD, Haesemeyer M, Jordi J, Schaechtle U, Saad FA, Mansinghka VK, Tenenbaum JB, Engert F: Elements of a stochastic 3d prediction engine in larval zebrafish prey capture. ELife 8, 51975 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Lohmann AW: Scaling laws for lens systems. Applied optics 28(23), 4996–4998 (1989) [DOI] [PubMed] [Google Scholar]
- [25].Park J, Brady DJ, Zheng G, Tian L, Gao L: Review of biooptical imaging systems with a high space-bandwidth product. Advanced Photonics 3(4), 044001 (2021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Zheng G, Horstmeyer R, Yang C: Wide-field, high-resolution Fourier ptychographic microscopy. Nature Photonics 7(9), 739–745 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Kumar N, Gupta R, Gupta S: Whole slide imaging (wsi) in pathology: current perspectives and future directions. Journal of Digital Imaging 33, 1034–1040 (2020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Borowsky AD, Glassy EF, Wallace WD, Kallichanda NS, Behling CA, Miller DV, Oswal HN, Feddersen RM, Bakhtar OR, Mendoza AE, Molden DP, Saffer HL, Wixom CR, Albro JE, Cessna MH, Hall BJ, Lloyd IE, Bishop JW, Darrow MA, Gui D, Jen K-Y, Walby JAS, Bauer SM, Cortez DA, Gandhi P, Rodgers MM, Rodriguez RA, Martin DR, McConnell TG, Reynolds SJ, Spigel JH, Stepenaskie SA, Viktorova E, Magari R, Wharton J, Keith A., Qiu J., Bauer TW: Digital whole slide imaging compared with light microscopy for primary diagnosis in surgical pathology a multicenter, double-blinded, randomized study of 2045 cases. Archives of pathology & laboratory medicine 144(10), 1245–1253 (2020) [DOI] [PubMed] [Google Scholar]
- [29].Grover D, Katsuki T, Greenspan RJ: Flyception: imaging brain activity in freely walking fruit flies. Nature methods 13(7), 569–572 (2016) [DOI] [PubMed] [Google Scholar]
- [30].Ehrlich DE, Schoppik D: Control of movement initiation underlies the development of balance. Current Biology 27(3), 334–344 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Ehrlich DE, Schoppik D: A primal role for the vestibular sense in the development of coordinated locomotion. Elife 8 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Akitake B, Ren Q, Boiko N, Ni J, Sokabe T, Stockand JD, Eaton BA, Montell C: Coordination and fine motor control depend on drosophila trpγ. Nature communications 6(1), 1–13 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Shamble PS, Hoy RR, Cohen I, Beatus T: Walking like an ant: a quantitative and experimental approach to understanding locomotor mimicry in the jumping spider myrmarachne formicaria. Proceedings of the Royal Society B: Biological Sciences 284(1858), 20170308 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Günel S, Rhodin H, Morales D, Campagnolo J, Ramdya P, Fua P: Deepfly3d, a deep learning-based approach for 3d limb and appendage tracking in tethered, adult drosophila. Elife 8, 48571 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Lobato-Rios V, Ramalingasetty ST, Özdil PG, Arreguit J, Ijspeert AJ, Ramdya P: Neuromechfly, a neuromechanical model of adult drosophila melanogaster. Nature Methods 19(5), 620–627 (2022) [DOI] [PubMed] [Google Scholar]
- [36].Wolf E: Three-dimensional structure determination of semi-transparent objects from holographic data. Optics Communications 1(4), 153–156 (1969) [Google Scholar]
- [37].Chowdhury S, Chen M, Eckert R, Ren D, Wu F, Repina N, Waller L: High-resolution 3D refractive index microscopy of multiple-scattering samples from intensity images. Optica 6(9), 1211–1219 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Chen B-C, Legant WR, Wang K, Shao L, Milkie DE, Davidson MW, Janetopoulos C, Wu XS, Hammer JA, Liu Z, et al. : Lattice light-sheet microscopy: imaging molecules to embryos at high spatiotemporal resolution. Science 346(6208) (2014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Patel KB, Liang W, Casper MJ, Voleti V, Li W, Yagielski AJ, Zhao HT, Perez Campos C, Lee GS, Liu JM, Philipone E, Yoon AJ, Olive KP, Coley SM, Hillman EMC: High-speed light-sheet microscopy for the in-situ acquisition of volumetric histological images of living tissue. Nature Biomedical Engineering (2022). 10.1038/s41551-022-00849-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Huang D, Swanson EA, Lin CP, Schuman JS, Stinson WG, Chang W, Hee MR, Flotte T, Gregory K, Puliafito CA, et al. : Optical coherence tomography. Science 254(5035), 1178–1181 (1991) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Zhou KC, Qian R, Dhalla A-H, Farsiu S, Izatt JA: Unified k-space theory of optical coherence tomography. Advances in Optics and Photonics 13(2), 462–514 (2021) [Google Scholar]
- [42].Zhou KC, McNabb RP, Qian R, Degan S, Dhalla A-H, Farsiu S, Izatt JA: Computational 3d microscopy with optical coherence refraction tomography. Optica 9(6), 593–601 (2022) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Wilburn B, Joshi N, Vaish V, Talvala E-V, Antunez E, Barth A, Adams A, Horowitz M, Levoy M: High performance imaging using large camera arrays. In: ACM SIGGRAPH 2005 Papers, pp. 765–776 (2005) [Google Scholar]
- [44].Brady DJ, Gehm ME, Stack RA, Marks DL, Kittle DS, Golish DR, Vera E, Feller SD: Multiscale gigapixel photography. Nature 486(7403), 386–389 (2012) [DOI] [PubMed] [Google Scholar]
- [45].Lin X, Wu J, Zheng G, Dai Q: Camera array based light field microscopy. Biomedical optics express 6(9), 3179–3189 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Fan J, Suo J, Wu J, Xie H, Shen Y, Chen F, Wang G, Cao L, Jin G, He Q, et al. : Video-rate imaging of biological dynamics at centimetre scale and micrometre resolution. Nature Photonics 13(11), 809–816 (2019) [Google Scholar]
- [47].Thomson E, Harfouche M, Konda P, Seitz CW, Kim K, Cooke C, Xu S, Blazing R, Chen Y, Jacobs WS, et al. : Gigapixel behavioral and neural activity imaging with a novel multi-camera array microscope. bioRxiv (2021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Jiang Y, Karpf S, Jalali B: Time-stretch lidar as a spectrally scanned time-of-flight ranging camera. Nature photonics 14(1), 14–18 (2020) [Google Scholar]
- [49].Riemensberger J, Lukashchuk A, Karpov M, Weng W, Lucas E, Liu J, Kippenberg TJ: Massively parallel coherent laser ranging using a soliton microcomb. Nature 581(7807), 164–170 (2020) [DOI] [PubMed] [Google Scholar]
- [50].Rogers C, Piggott AY, Thomson DJ, Wiser RF, Opris IE, Fortune SA, Compston AJ, Gondarenko A, Meng F, Chen X, et al. : A universal 3d imaging sensor on a silicon photonics platform. Nature 590(7845), 256–261 (2021) [DOI] [PubMed] [Google Scholar]
- [51].Qian R, Zhou KC, Zhang J, Viehland C, Dhalla A-H, Izatt JA: Video-rate high-precision time-frequency multiplexed 3d coherent ranging. Nature Communications 13(1), 1476 (2022). 10.1038/s41467-022-29177-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Geng J: Structured-light 3d surface imaging: a tutorial. Advances in Optics and Photonics 3(2), 128–160 (2011) [Google Scholar]
- [53].Aguilar J-J, Torres F, Lope M: Stereo vision for 3d measurement: accuracy analysis, calibration and industrial applications. Measurement 18(4), 193–200 (1996) [Google Scholar]
- [54].Scharstein D, Szeliski R: High-accuracy stereo depth maps using structured light. In: 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2003. Proceedings., vol. 1, p. (2003). IEEE [Google Scholar]
- [55].Harfouche M, Kim K, Zhou KC, Konda PC, Sharma S, Thomson EE, Cooke C, Xu S, Kreiss L, Chaware A, et al. : Multi-scale gigapixel microscopy using a multi-camera array microscope. arXiv preprint arXiv:2212.00027 (2022) [Google Scholar]
- [56].Kumar R, Anandan P, Hanna K: Direct recovery of shape from multiple views: A parallax based approach. In: Proceedings of 12th International Conference on Pattern Recognition, vol. 1, pp. 685–688 (1994). IEEE [Google Scholar]
- [57].Zhou KC, Cooke C, Park J, Qian R, Horstmeyer R, Izatt JA, Farsiu S: Mesoscopic photogrammetry with an unstabilized phone camera. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 7535–7545 (2021) [Google Scholar]
- [58].Ulyanov D, Vedaldi A, Lempitsky V: Deep image prior. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 9446–9454 (2018) [Google Scholar]
- [59].Zollikofer C: Stepping patterns in ants-influence of speed and curvature. The Journal of experimental biology 192(1), 95–106 (1994) [DOI] [PubMed] [Google Scholar]
- [60].Reinhardt L, Blickhan R: Level locomotion in wood ants: evidence for grounded running. Journal of Experimental Biology 217(13), 2358–2370 (2014) [DOI] [PubMed] [Google Scholar]
References
- [1].Westerfield M: The zebrafish book: a guide for the laboratory use of zebrafish. http://zfin.org/zfinfo/zfbook/zfbk.html (2000) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be available at https://doi.org/10.7924/r4db86b1q.


