Abstract
Human epidermal growth factor receptor 2 positive (HER2+) breast cancer is frequently treated with drugs that target the HER2 receptor, such as trastuzumab, in combination with chemotherapy, such as doxorubicin. However, an open problem in treatment design is to determine the therapeutic regimen that optimally combines these two treatments to yield optimal tumor control. Working with data quantifying temporal changes in tumor volume due to different trastuzumab and doxorubicin treatment protocols in a murine model of human HER2+ breast cancer, we propose a complete framework for model development, calibration, selection, and treatment optimization to find the optimal treatment protocol. Through different assumptions for the drug–tumor interactions, we propose ten different models to characterize the dynamic relationship between tumor volume and drug availability, as well as the drug–drug interaction. Using a Bayesian framework, each of these models are calibrated to the dataset and the model with the highest Bayesian information criterion weight is selected to represent the biological system. The selected model captures the inhibition of trastuzumab due to pre-treatment with doxorubicin, as well as the increase in doxorubicin efficacy due to pre-treatment with trastuzumab. We then apply optimal control theory (OCT) to this model to identify two optimal treatment protocols. In the first optimized protocol, we fix the maximum dosage for doxorubicin and trastuzumab to be the same as the maximum dose delivered experimentally, while trying to minimize tumor burden. Within this constraint, optimal control theory indicates the optimal regimen is to first deliver two doses of trastuzumab on days 35 and 36, followed by two doses of doxorubicin on days 37 and 38. This protocol predicts an additional 45% reduction in tumor burden compared to that achieved with the experimentally delivered regimen. In the second optimized protocol we fix the tumor control to be the same as that obtained experimentally, and attempt to reduce the doxorubicin dose. Within this constraint, the optimal regimen is the same as the first optimized protocol but uses only 43% of the doxorubicin dose used experimentally. This protocol predicts tumor control equivalent to that achieved experimentally. These results strongly suggest the utility of mathematical modeling and optimal control theory for identifying therapeutic regimens maximizing efficacy and minimizing toxicity.
Keywords: Optimal control theory, Model selection, Model calibration, Uncertainty quantification, Tumor growth model, Chemotherapy model
1. Introduction
In the United States, breast cancer is the second most common type of cancer in women [1]. Breast tumors that overexpress the human epidermal growth factor receptor 2 (HER2) are referred to as HER2 + cancers and are typically treated with drugs that target the HER2 receptor, such as the monoclonal antibody trastuzumab [2,3]. Trastuzumab binds with the HER2 receptor, downregulating the HER2 protein and reducing cell proliferation [3]. Importantly, HER2 + drugs are often given in combination with chemotherapies to increase response rates [4–7]. However, the optimal manner in which to combine these two classes of drugs is not well-studied and currently an important open problem in treatment design. In pre-clinical models of HER2 + cancer, trastuzumab has been shown to not only inhibit tumor growth, but also alter tumor-associated angiogenesis [8–10]. Furthermore, sequencing experiments have revealed that combining trastuzumab and the chemotherapy doxorubicin could yield either additive or synergistic effects [11,12]. Results from [12] demonstrated that the order in which the drugs are delivered affects the treatment outcome; in particular, administering trastuzumab prior to doxorubicin improved the outcome.
In clinical studies, combination trastuzumab and chemotherapy results in longer time to disease progression, longer survival, and a 20 percent reduction in the risk of death when compared to chemotherapy alone [4]. However, there was a concomitant increase in cardiac toxicity when combining trastuzumab and anthracyclines (e.g., doxorubicin) [5,6]. While the cardiac damage induced by trastuzumab does not appear to be dose dependent and it is reversible in the majority of the patients [5,7], doxorubicin cardiotoxicity is cumulative, dose dependent, and irreversible [7]. Thus, methods to optimize treatment regimens for HER2 + breast cancer are desperately needed so that tumor control can be maximized while simultaneously minimizing toxicity.
We have recently employed mathematical models to characterize and optimize combination trastuzumab and paclitaxel for the treatment of HER2 + breast cancer [13,14]. In particular, we developed a system of three ordinary differential equations to model tumor response to the combination of trastuzumab and paclitaxel [13]. This system was calibrated using in vitro, time-resolved microscopy data of BT474 HER2 + breast cancer cells. The data demonstrated that changing the order of treatments, while keeping the same total drug dose, significantly altered the treatment outcome. The model showed an increase in treatment efficacy when trastuzumab is administered prior to paclitaxel, and that trastuzumab accelerates the cytotoxic effects of paclitaxel. Though these are important observations, the experimental system and mathematical model did not account for the interactions between the drugs and the microenvironment (e.g., blood vessels, immune system, and different cell types) and only focused on cellular interactions. Subsequently, we performed in vivo experiments to determine the effects of the tumor microenvironment on the order in which the treatments were administered [12]. In that study the delivery of trastuzumab was inhibited due to the reduction in vascular density caused by pre-treatment with doxorubicin [15], a phenomenon that is extremely difficult to replicate through in vitro experiments. In present effort, we develop a system of ordinary differential equations that is able to reproduce the data obtained in [12]. Of course, there are many, more complex models, available in the literature designed to capture the effects of treatments on breast cancer cells [16–19]. Indeed, there are now mature reviews available on tumor growth models [20–28].
For example, Norton et al. developed a 3D, agent-based model of triple negative breast cancer cells to capture the spatio-temporal distribution of cells in primary tumors. The authors performed in silico simulations of MDA-MD-231 cells, assigning values found in the literature to the parameters in the model, and tested different drug efficacies on killing cancer stem cells. Their results indicated that even if the drug successfully eliminates all cancer stem cells, the regression of the tumor may be very slow (approximately 750 days after the treatment) [16]. Bianca et al. proposed a system of ten ordinary differential equations to model the competition between immune and tumor cells under the action of a vaccine. In particular, they model a cellular vaccine, called Triplex, that can avoid the development of breast cancer [19]. The model tracks the number of vaccine cells, cancer cells, tumor associated antigens, Plasma B cells, thymus cytotoxic lymphocytes, thymus helper lymphocytes, antibodies, interleukins 2 and 12, and antigen presenting cells. The authors simulated the tumor growth for the control and under two vaccination protocols: early (only three 4-weeks cycles at the beginning of the experiment) and chronic (lifelong 4-weeks cycles). Their results indicated that the early vaccination delays the onset of tumor, but the tumor eventually growth, while the chronic protocol is able to completely prevent tumor growth [19]. It is important to note that in the above examples, in which elegant mathematical models of tumor growth and response are developed, it is very difficult to obtain the requisite data to calibrate all parameters from such models. Thus, in the present effort, we focus on building parsimonious models that can be intimately integrated with readily-available experimental data, to make predictions that can be practically tested.
Given a mathematical model that can accurately recapitulate the temporal development of a tumor, it can then be used to systematically optimize treatment protocols, potentially leading to improved outcomes while decreasing side effects. Optimal control theory (OCT) is the branch of mathematics that aims to minimize some criterion (e.g., tumor volume) imposed on a dynamic system (e.g., tumor cells growing over time) subject to constraints (e.g., maximum allowed drug dose) and control functions (e.g., drug delivered over time). When applied to cancer, OCT can be used to (for example) minimize the amount of drug [29,30], define the best treatment protocol in the presence of resistant cells [31], and define the optimal combination protocol [32]. Swan and Vincent combined the effect of multiple drugs into a single drug for the treatment of multiple myeloma [29]. The goal was to minimize the amount of drug used while maintaining a target tumor burden. When compared to clinical data, the accumulated amount of drug in the optimized protocol is 1/40 of the standard protocol. Martin et al. studied how the presence of drug resistant cells can affect chemotherapy outcome [31]. By assuming that the tumor already has resistant cells on the first day of therapy, they demonstrated that an aggressive treatment protocol may not the best option if the goal is to maximize survival time. In particular, they found that treatment protocols that keep a higher tumor burden are optimal for Gompertz tumor growth and close to optimal for exponential and logistic growth, indicating that it may not be necessary to know the precise tumor growth characteristic before scheduling the drugs. Cho and Levy incorporated not only chemotherapy resistance, but also included resistance to targeted drugs, competition between cancer and healthy cells, and the effects of spatial heterogeneity on drug delivery [32]. According to their model, as the competition between tumor and healthy cells increases, the efficacy of the target drug increases. The authors found that the order between the drugs (as also observed in [12]) and the duration of each drug treatment, is dependent on the competition between tumor and healthy cells and on the ratio of resistance to each drug. These studies indicate the great promise of employing mathematical modeling to guide and optimize the treatment of cancer.
In the present effort, we develop a family of tumor growth models that incorporate the effects of doxorubicin and trastuzumab. Following the principles of the Occam Plausibility Algorithm (OPAL; [33–36]) we perform a Bayesian calibration to infer the model parameters of every model, and select the most parsimonious model from the set that describes the data obtained in [12]. After the model is selected, we then apply optimal control theory on this model to solve two problems: (1) achieve tumor control as quickly as possible when using the same total dose as employed in our experiments, and (2) minimize the total dose of doxorubicin to achieve the tumor control observed in our experiments. We hypothesize that the solution of the optimal control problem will be a treatment protocol (i.e., sequence of order, dose, and timing of the drugs) different than the ones tested in our experiments [12]. In this way, we developed a methodology capable of identifying therapeutic regimens capable of maximizing efficacy and minimizing dose.
2. Methods
2.1. Murine model
As details are described elsewhere [12], here we present only the salient details. We have previously measured tumor size changes as function of time and treatment (Table 1) in a murine model of HER2 + breast cancer. BT474 cells were obtained from American Type Culture Collection (ATCC, Manassas, VA). On day 0, nude athymic female mice were subcutaneously implanted with a 0.72 mg, 60-day release, 17β-estradiol pellet (Innovative Research of America, Sarasota, FL). Approximately 24 h later, 107 BT474 cells in serum-free media with 20% growth factor-reduced Matrigel were injected subcutaneously into the flank of 42 mice. The experiments began 35 days after implantation when the tumor volume reached 228.79 ± 20.31 mm3 (mean ± standard error) [12].
Table 1.
The six different treatment schedules for doxorubicin and trastuzumab we employed in a previous study [12] to generate the data for the present study. Each treatment is represented by the following symbol: saline (✩, 100 μl), doxorubicin (○, 1.5 mg/kg diluted to 100 μl), and trastuzumab (×, 10 mg/kg, diluted to a total volume of 100 μL). The number of mice per group is represented by n.
| Group | Day |
|||
|---|---|---|---|---|
| 35 | 36 | 38 | 39 | |
|
| ||||
| ✩ | ✩ | ✩ | ||
| ✩ | ✩ | ○ | ||
| × | × | ✩ | ||
| ○ | × | × | ||
| × | × | ○ | ||
| ⊗ | ⊗ | |||
On the days noted in Table 1, mice received an intraperitoneal injection of trastuzumab (10 mg/kg, diluted to a total volume of 100 μL), and/or a tail vein injection of doxorubicin (1.5 mg/kg diluted to 100 μl), while control mice received saline (100 μl) injections. Tumor size was measured using calipers once a week before therapy, and three times per week after treatment starts. There were seven animals per group for each treatment schedule in Table 1.
2.2. Mathematical models
We developed two families of models: one is a three-constituent family, while the other is a four-constituent family. The three-constituent family characterizes the tumor temporal dynamics by directly accounting for the effects of doxorubicin and trastuzumab. In the four-constituent family, we include another equation to capture the increase in reactive oxygen species (ROS) due to treatment [37,38] which can indirectly lead to tumor cell death, rather than the direct effects of the drugs. The main drug mechanism considered in both families is that treatment with doxorubicin increases the oxidative stress which can cause mitochondrial damage and cell death in endothelial cells [39]. As endothelial cells line blood vessels and help to regulate the exchange of materials into and out of the extravascular space, their destruction can limit the delivery of trastuzumab if doxorubicin is given before trastuzumab [12]. This mechanism is incorporated in our models through the trastuzumab delivery inhibition term. In experimental protocols where trastuzumab is given first, its vascular remodeling properties [10] can improve tumor perfusion and therefore the subsequent vascular delivery of doxorubicin [12]. We model this effect by the increase in treatment efficacy when trastuzumab is delivered prior to doxorubicin. Thus, our modeling assumptions are based on current experimental evidence. In the following subsections we detail each of these model families.
2.2.1. Three-constituent model
We propose a system of ordinary differential equations that capture the temporal evolution of tumor volume , as well the availability of doxorubicin and trastuzumab and their effects on . We assume that the tumor volume increases according to the growth rate, , which we model as either exponential or logistic, depending on the choice of the proliferation function. If the proliferation function is exponential, we assume that the tumor is able to grow without any limiting factor during the experiment. However, if the proliferation function is logistic, we assume that some limiting factors (e.g., nutrient and/or space availability) limit the maximum tumor size. We hypothesize that the availability of doxorubicin increases proportionally to the dose delivery function, , and that it decays at the rate, . The availability of trastuzumab also increased proportionally to the dose delivery function, , with a decay rate of, . (Note that “drug availability” is normalized by the concentration of a single dose of what was delivered in our experiment, so that a “drug availability” value of 1 represents the dose of a single, experimentally delivered injection.) In experiments performed in mice (as the one presented in [15]), that treatment with doxorubicin was shown to significantly decrease the total vascular density. We hypothesize that the reduction in vascular density subsequently reduces the delivery of trastuzumab [40]. Thus, the availability of trastuzumab will be reduced if an animal is pre-treated with doxorubicin. We incorporated this effect by multiplying the dose delivery function of trastuzumab by a penalty term. This penalty term takes the form of , where characterizes the inhibition of trastuzumab delivery by doxorubicin. We define our penalty term in a way that its effect will decrease as the availability of doxorubicin decreases. The net growth rate of the tumor, which is the balance between the proliferation and death terms, decreases due to an increase in the death rate caused by doxorubicin , trastuzumab , and the interaction between the two drugs [12]. With these assumptions, the model takes the following form:
| (1) |
where the proliferation function is
| (2) |
or
| (3) |
In Eq. (3), is the carrying capacity (i.e., the maximum volume that the tumor can reach). In Eq. (1), we assume that the drugs affect proliferative cells. If the proliferation function is an exponential model, each term is uncoupled if we distribute the function . However, if is a logistic growth, only the proliferating cells will be affected. This is based on the assumption that both doxorubicin and trastuzumab affect tumor cells only when they are proliferating. In Eq. (1), the doxorubicin and trastuzumab dose delivery functions, and , respectively, are defined as:
| (4) |
| (5) |
where and are the doxorubicin and trastuzumab daily doses, respectively, and are the doxorubicin and trastuzumab days of treatment, respectively, and are the doxorubicin and trastuzumab number of treatments, respectively, and is the Dirac delta function. (Note that, going forward, we normalize and by the daily experimental dose so that ). From Eqs. (1)–(3) we construct four models:
2.2.2. Four-constituent model
Multiple mechanisms of anti-tumor action have been identified for trastuzumab [41] and doxorubicin [42]. Importantly, their combination has been linked to increased treatment efficacy, as well as increased risk of cardiovascular damage [43,44]. The increase in treatment efficacy is partially attributable to an increase in reactive oxygen species (ROS) within HER2 + cells [45]. In normal cells, ROS are generated during mitochondrial oxidative phosphorylation and are essential for many fundamental biological processes (e.g., modulation of cell survival, cell death, differentiation, cell signaling, and the production of inflammation factors) [46,47]. ROS production is increased by both chemo- and radiotherapy [48], and dysregulated ROS levels can damage cellular proteins, lipids, and DNA, triggering cell death. As both trastuzumab and doxorubicin increase ROS levels, our goal was to determine if incorporating this phenomenon into our model would yield a better description of the observed, treatment induced, changes in tumor volume. Thus, even though we do not have measured data regarding ROS, we extend the system described by Eqs. (1) – (3) to include the excess cellular concentration of ROS. This addition potentially provides a superior representation of the tumor’s response to doxorubicin and trastuzumab. Specifically, the four-constituent model, in addition to characterizing , and , captures the temporal evolution of the ROS concentration, . The equations that represent the availability of doxorubicin and trastuzumab are the same as presented in Eq. (1). In Eq. (1), we replace the decrease of tumor volume by doxorubicin by its decrease due to . We also assume that the rate of tumor volume decay increases proportionally to the interaction between trastuzumab and . The dynamics of the , are determined by the balance between its natural decay and its production which is directly proportional to the availability of doxorubicin and trastuzumab which produce ROS at a rates and , respectively. The ROS concentration increases at a rate when these two drugs are combined. Incorporating ROS dynamics allows the model to explore different tumor responses to drugs than those allowed by the three-constituent models. For example, if we assume a low value for the ROS decay and a low rate of increase in ROS due to the drugs and , this will result in a delayed tumor response. With these assumptions on ROS production, decrease, and effects on tumor, we arrive at the following four-constituent model:
| (6) |
As it is not clear a priori if all the terms in Eq. (6) are required, we systematically remove specific terms to yield the following set of six models:
4CEM1, four-constituent exponential model (i.e., Eqs. (6) and (2)), with ,
4CEM2, four-constituent exponential model (i.e., Eqs. (6) and (2)), with ,
4CEM3, four-constituent exponential model (i.e., Eqs. (6) and (2)), with ,
4CLM1, 4CEM1 with logistic growth (i.e., replacing Eq. (2) for Eq. (3)),
4CLM2, 4CEM2 with logistic growth (i.e., replacing Eq. (2) for Eq. (3)),
4CLM3, 4CEM3 with logistic growth (i.e., replacing Eq. (2) for Eq. (3)).
Table 2 presents the parameters, definitions, and priors. The priors are taken to be uniform distributions with the ranges determined by reasonable estimate of their minimum and maximum values, , max). Table 3 summarizes the set of models developed from the three and four constituent models. The check mark indicates if a particular variable or parameter is present in the model. We note that all the models include the functions (tumor volume), (doxorubicin availability), and (trastuzumab availability). Similarly, every model contains the parameters: (tumor growth rate), (doxorubicin decay rate), (trastuzumab decay rate), and (inhibition of trastuzumab delivery by doxorubicin).
Table 2.
Parameter’s definitions and priors (in units of inverse hours, h−1, and millimeters cubed, mm3).
| Parameter | Meaning | Prior |
|---|---|---|
|
| ||
| Growth rate | ||
| Death rate by trastuzumab | ||
| Death rate by doxorubicin | ||
| Death rate by drug interaction | ||
| Carrying capacity | ||
| Doxorubicin decay rate | ||
| Trastuzumab decay rate | ||
| Trastuzumab delivery inhibition by doxorubicin | ||
| Death rate by ROS | ||
| Death rate by ROS and trastuzumab combined effects | ||
| ROS decay rate | ||
| ROS production rate by doxorubicin | ||
| ROS production rate by trastuzumab | ||
| ROS production rate by drug interaction | ||
Table 3.
The model family developed to reproduce the observed tumor growth measurements under treatment with doxorubicin and trastuzumab. The variables , , and , and the parameters , and are present in every model. The four-constituent models (4C) have one extra variable, the reactive oxygen species . The last column indicates the number of parameters (#P) in each model.
| Model | Parameter |
#P | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||
| 3CEM0 | ✓ | ✓ | 6 | ||||||||
|
| |||||||||||
| 3CLM0 | ✓ | ✓ | ✓ | 7 | |||||||
| 3CEM | ✓ | ✓ | ✓ | 7 | |||||||
|
| |||||||||||
| 3CLM | ✓ | ✓ | ✓ | ✓ | 8 | ||||||
| 4CEM1 | ✓ | ✓ | ✓ | ✓ | 8 | ||||||
| 4CEM2 | ✓ | ✓ | ✓ | ✓ | 8 | ||||||
| 4CEM3 | ✓ | ✓ | ✓ | ✓ | 8 | ||||||
|
| |||||||||||
| 4CLM1 | ✓ | ✓ | ✓ | ✓ | ✓ | 9 | |||||
| 4CLM2 | ✓ | ✓ | ✓ | ✓ | ✓ | 9 | |||||
| 4CLM3 | ✓ | ✓ | ✓ | ✓ | ✓ | 9 | |||||
2.3. Bayesian model calibration and selection
We calibrate every model in the set to find the most parsimonious (i.e., the model that optimally balances the number of free parameters with the fitting error) to represent every experimental scenario. We assume that the differences between experimental scenarios are due to different treatment protocols, and assume that any biological heterogeneity is captured by the uncertainty in the model parameters. The goal is to select one model that can represent a wide range of treatment scenarios, so that it can be used to predict the results of new treatment protocols. (Note that this is different from some of our previous efforts [35,36], wherein we focused on patient/scenario specific model parameters, and not testing new treatment protocols.)
The calibration and selection framework used here is a simplified version of the Occam Plausibility Algorithm (OPAL; [33–36]). The main difference from the original OPAL framework is that we are computing the Bayesian information criterion (BIC) instead of the model plausibility. (Please see Supplemental Material for details on the difference between the two approaches.) In Fig. 1, we summarize the main steps of this framework. We start by defining the model set (where the refers to the ten models in Table 3). Each model , has its own vector of parameters . The model parameters are calibrated using the experimental data from all treatment protocols. To account for the data uncertainties and model inadequacy, the models are calibrated via a Bayesian framework defined as:
| (7) |
| (8) |
where is the experimental data, is the prior knowledge about the model parameters, is the likelihood that the data is observed for a given set of parameters, is a normalizing factor, and is the posterior distribution of the parameters. Assuming that the data is normally distributed, the likelihood is:
| (9) |
where is the number of treatment groups (here ; see Table 1), is the number of measurements in each group, is the output of the model (i.e., tumor volume over time), and is the variance of the total error (i.e., the sum of the variance of the model uncertainties and the model inadequacy).
Fig. 1.
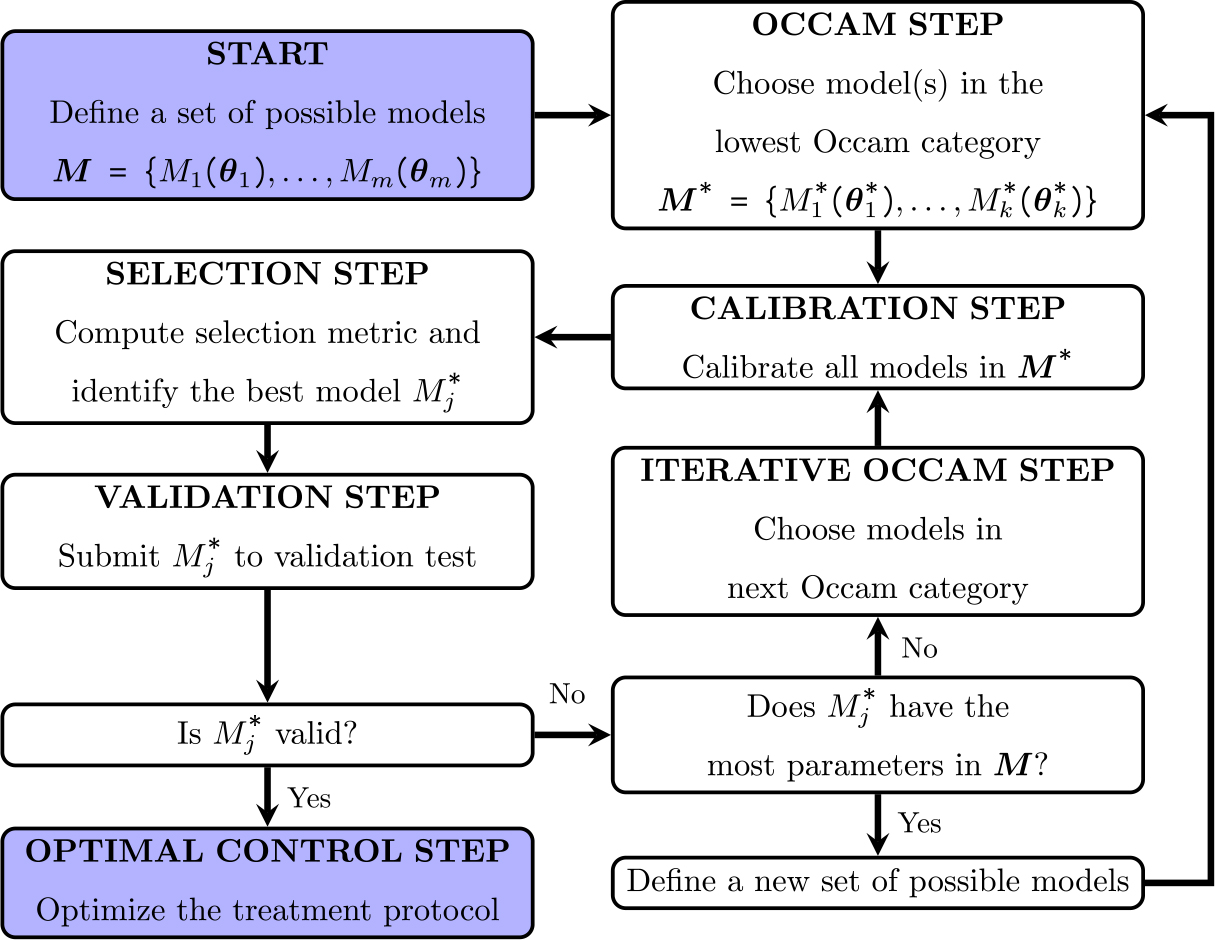
Model calibration and selection framework. We start with a set of possible models . Every model is calibrated using the experimental data, and the Bayesian information criterion (BIC) is calculated for each calibration. The model with the highest BIC model weight is selected, and if the average mean percent error is considered acceptable (i.e., lower than a defined threshold), the model is approved to be used in the optimal control step.
Following the calibration of every model, we compute the BIC:
| (10) |
where is the number of parameters in model is the number of data points, and is the set of parameters that maximize the likelihood of model . The model with the lowest BIC is the one with the highest likelihood (among models with the same number of parameters) and thus, it is the best model to represent the data. As it is difficult to intuit the difference between models BIC, we compute the Bayesian information criterion model weights [49,50] as:
| (11) |
where is the lowest BIC among the model in the same Occam category, and is the number of models in the same Occam category. The sum of all model weights is 1, and can be interpreted as the probability that model is the best model to capture the dynamics of the experimental data [50]. Thus, the model with the highest BIC weight is selected. If the mean absolute percent error between the model output and the experimental data is below a defined threshold, the model is defined as valid. We iterate over all Occam categories in search of a valid model. In the case where we cannot find a valid model (i.e., we reach the bottom right box of the framework presented in Fig. 1), we would need to define a new set of models. If a valid model is selected, it is used in the optimal control step (described in detail in the next section) to find the optimal treatment protocol (which can be a protocol that has yet to be tested experimentally). We also computed the Pearson correlation coefficient (PCC) and the concordance correlation coefficient (CCC), which measures the linear relationship and agreement, respectively, between the measured data and the model output [51].
2.4. Optimal control theory
Consider a model describing the tumor volume over time given as:
| (12) |
where describes the growth of a tumor that is being treated with doxorubicin and trastuzumab (see Supplementary Material for the optimal control derivation employing the selected valid model). In our optimization problem, the goals are: (1) to find the best way to distribute the maximum allowed doses of these two drugs such as that the tumor burden during treatment (i.e., the integral of the tumor volume during the treatment interval) is minimized; and (2) to minimize the doxorubicin dose while maintaining the tumor burden obtained experimentally. With the first goal in mind, we minimize the following objective function:
| (13) |
where and are the first and last day that the treatment can be delivered, respectively. This optimization problem is subject to the following trastuzumab and doxorubicin restrictions:
| (14) |
| (15) |
where and are the total dose of trastuzumab and doxorubicin, respectively, delivered in our experiment. Note that in this formulation of the optimal control problem, we are allowing the time of the treatment and the daily dose to change, while keeping doxorubicin and trastuzumab total doses and maximum daily doses the same as the ones considered in our experiments. In the second OCT problem (described next), we seek to maintain tumor control while minimizing total dose, which has important implications of limiting undesirable side effects due to drug toxicity.
In the second goal of the OCT problem, we minimize the following objective function:
| (16) |
subject to Eq. (14) and
| (17) |
where is the minimum experimental tumor burden. Through Eqs. (14), (16), and (17), we are minimizing the doxorubicin dose, thus reducing treatment toxicity, while achieving the same tumor control as the best experimental protocol. By minimizing the total doxorubicin dose, we are implicitly reducing unwanted toxicities due to the drugs. These can be quite serious in nature [52], including increased likelihood of hospitalization, cardiac damage, leukemia, and even death [53]. Thus, the importance of developing a practical, mathematical methodology to optimize tumor control while simultaneously minimizing toxicity, is difficult to overstate.
2.5. Numerical implementation
The model calibration and selection framework (presented in Fig. 1) and the optimal control problem are both implemented in Python. The models (i.e., the systems of ordinary differential equations defined by Eqs. (1) and (6)) are solved via a fourth order Runge–Kutta method [54]. We employ a Markov Chain Monte Carlo (MCMC) sampling method to compute the posterior density (see, e.g., [55,56]). The MCMC method is available in the package PyMC3 [57]. The optimal control problem is solved via the package GEKKO [58]. The code itself, as a well as a description of how to use it, is provided at https://github.com/reidwyde/trazdox.
3. Results
3.1. Model calibration and selection
Using the priors defined in Table 2, and following the framework presented in Fig. 1, we calibrate each model to the six experimental scenarios. Table 4 presents the mean absolute percent error between the measured and calibrated models over the six experimental scenarios, and the BIC weight for each Occam category (a “category” is the set of models with the same number of parameters). The BIC model weight is normalized between 0 and 1; thus, it will be zero for some model. As the logistic models are considerably better in fitting the data than the exponential models, the BIC model weights of models containing the logistic growth term are higher. (For example, the BIC of model 3CEM is 1418, while the BIC of model 3CLM0 is 1401. Computing the BIC model weight using Eq. (11), the w(BIC) of model 3CLM0 is 1, while the w(BIC) of model 3CEM is 0.) We present the MAPE just for the model with the highest BIC model weight in each Occam category. Among all the models tested, 3CLM0 (three-constituent logistic model without death rate by doxorubicin) had the lowest mean absolute percent error, 25.29 ± 15.37% (mean ± standard deviation), and a CCC and PCC of 0.92 ± 0.05 and 0.96 ± 0.04, respectively. Thus, model 3CLM0 is selected as the best model to reproduce the six experimental scenarios.
Table 4.
Bayesian Information Criterion weight, w(BIC), of models with the same number of parameters, and mean absolute percent error (MAPE) of the models with the highest w(BIC). The model with the lowest error is the three-constituent logistic model without death rate by doxorubicin (3CLM0).
| Model | Parameters | w(BIC) | MAPE (%) |
|---|---|---|---|
|
| |||
| 3CEM0 | 6 | n/a | 28.51 ± 17.24 |
|
| |||
| 3CLM0 | 7 | 1.00 | 25.29 ± 15.37 |
| 3CEM | 7 | 0.00 | |
|
| |||
| 3CLM | 8 | 1.00 | 29.06 ± 21.78 |
| 4CEM1 | 8 | 0.00 | |
| 4CEM2 | 8 | 0.00 | |
| 4CEM3 | 8 | 0.00 | |
|
| |||
| 4CLM1 | 9 | 0.44 | |
| 4CLM2 | 9 | 0.10 | |
| 4CLM3 | 9 | 0.46 | 28.47 ± 21.42 |
Fig. 2, displays the scatter plots and distributions of the parameters. The model has a negative correlation between tumor growth rate and carrying capacity , where the higher tumor growth rate leads to smaller carrying capacity. A positive correlation is observed between the trastuzumab decay rate and the death rate due trastuzumab , which indicates that, the faster the drug decays, the stronger its action. We note that correlations between model parameters, can help simplify the model [36]. In general, if two parameters are correlated, one could define one parameter as function of the other, and thus reduce the number of model parameters needed to be calibrated. In the present case, we could define as , where the value of is the outcome of the function , which has as an argument. (Note that the challenge then becomes to identify the function that captures this correlation.)
Fig. 2.
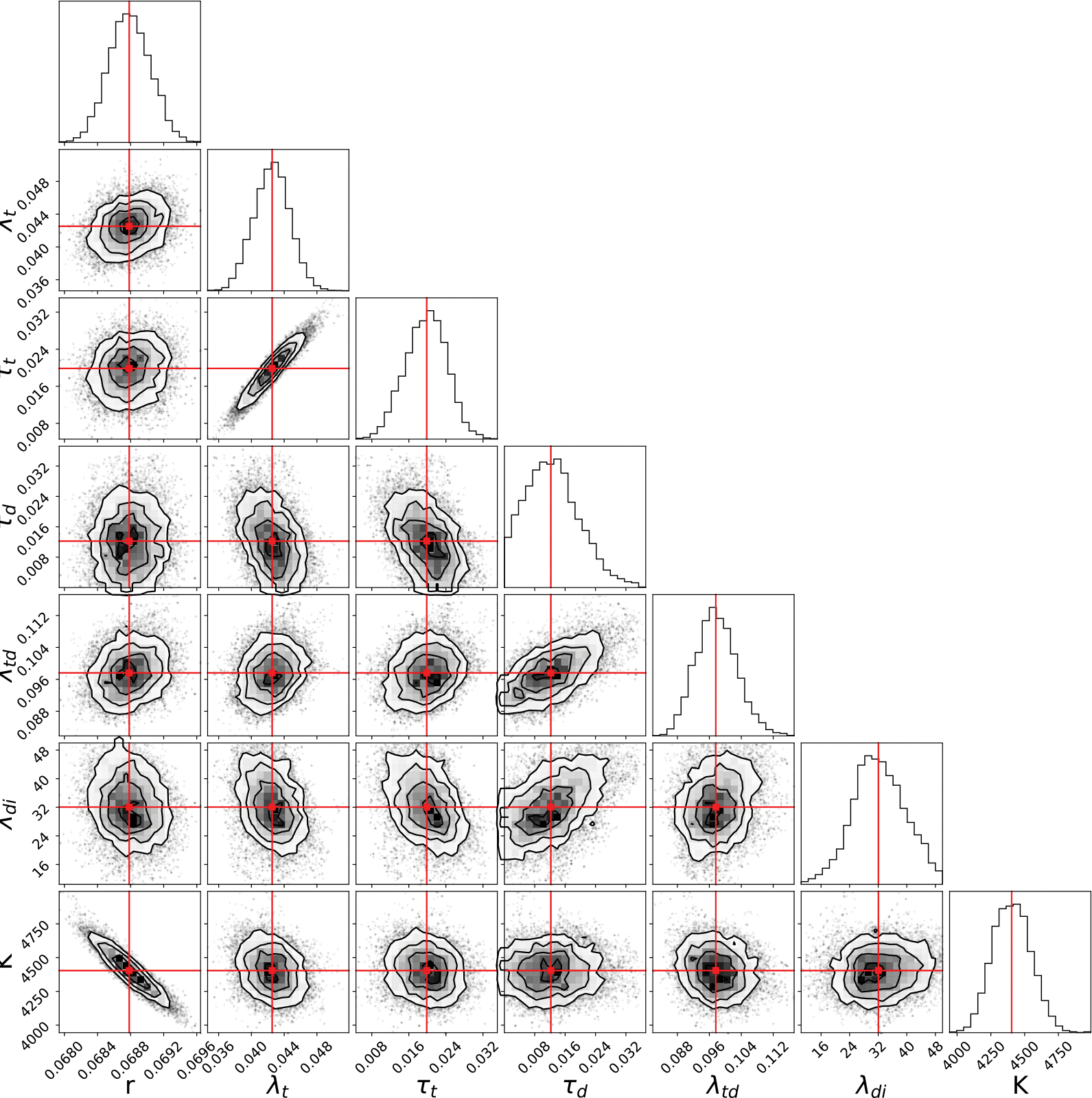
Distributions of the 3CLM0 parameters. Each scatter plot represents the correlation between two model parameters, and the top figure in each row shows the histogram of the parameter distribution. The strongest correlations are: a negative correlation between the tumor growth and carrying capacity (i.e., and , respectively), and a positive correlation between the trastuzumab decay rate and the death rate due by trastuzumab (i.e., and , respectively). The red line represents the median of each parameter distribution.
From the posterior distributions presented in Fig. 2, we sample 200 sets of parameters and run the 3CLM0 model forward in time to generate time courses of tumor volume and drug availability. Fig. 3 displays both the temporal change in tumor volume measured during the experiments and the output of the calibrated model. Note that there the time courses are very similar between the control animals (panel (a)) and the doxorubicin only animals (panel (b)), during the 68 days of this experiment. The best experimental protocol (i.e., the one that leads to the lowest total tumor burden) is the one shown in panel (f). (Please see Supplemental Material for the mean and standard deviation of the temporal change in tumor volume for each experimental scenario.) We compute the mean absolute percent error (MAPE) for each treatment protocol, and the average MAPE of the tumor volume among the six treatment protocols is 25.29 ± 15.37%. The lowest MAPE is for the tumors treated only with trastuzumab (panel (c)), 8.30 ± 7.91%. In panel (f), the tumor is treated with doxorubicin and trastuzumab at days 35 and 38. This protocol emerged as the best treatment protocol in that it leads to the largest reduction in tumor burden among the six scenarios tested experimentally. The MAPE in this scenario is 51.45±74.67%; note that this value is artificially inflated because, as the tumor volume decreases, small errors in tumor volume generate high percent errors. More specifically, as the tumor volume approaches zero, even a small overprediction in tumor volume will cause a large average error. Consider, for example, panel (f) in which the tumor volume ranges between 5 and 300 mm3. If we have an absolute error of 10 mm3 over the whole model simulation, this would lead to an absolute percent error of 3.33% for the 300 mm3 tumor, but a 200% error for the 5 mm3 tumor. Computing the mean of these two time points, the MAPE is 101.66%. This indicates how errors in regions where the tumor volume is quite small would artificially inflate the value of MAPE. Thus, we present the CCC and the PCC to as an additional way to summarize the quality of the prediction. Importantly, this scenario, panel (f), has a CCC = 0.98 and a PCC = 0.99, demonstrating a high agreement between the data and the model solution. (Please, see Supplemental Material for a comparison of these results with a leave-one-out calibration.)
Fig. 3.
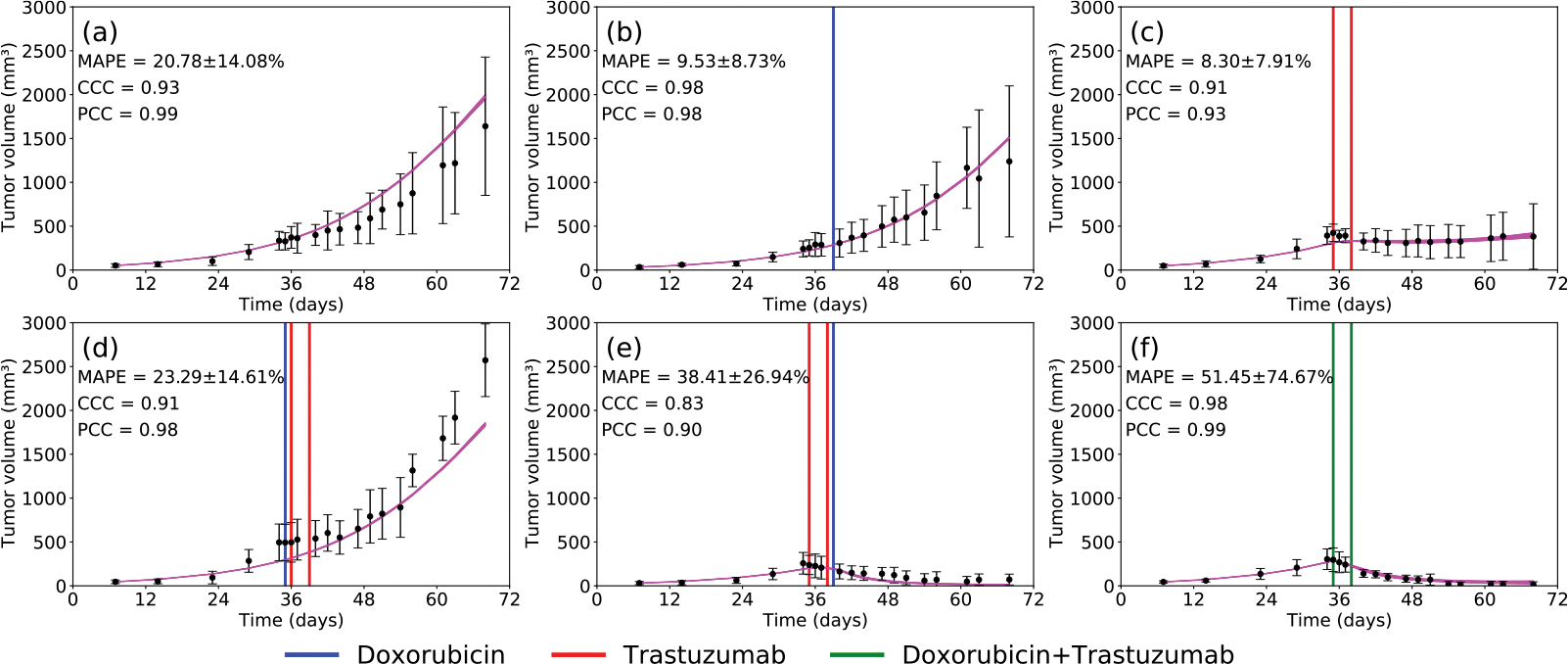
Temporal evolution of the experimentally measured tumor volume (black; error bars represent the standard deviation) and the 3CLM0 (magenta) in the following scenarios: (a) control (b) doxorubicin (c) trastuzumab (d) doxorubicin 24 h prior to trastuzumab (e) trastuzumab 24 h prior to doxorubicin (f) trastuzumab + doxorubicin. The mean absolute percent error is 22.77 ± 11.84%. The vertical lines indicate the day each drug was delivered; doxorubicin in blue, trastuzumab in red, and doxorubicin + trastuzumab in green.
In Fig. 4, we present the drug availability estimated by model 3CLM0 in the same scenarios shown in Fig. 3. However, as no drug was delivered to the control (Fig. 3(a)), we are showing drug availability only for the five scenarios in which the tumor received treatment. In panel (a), when only doxorubicin is administered on day 39, it is possible to observe a single pulse increase in its availability due to the single dose delivered. In panel (b), it is possible to observe the two increases in trastuzumab availability due to its delivery on days 35 and 38. The inhibition effect modeled by the parameter is noticeable in panels (c) and (e). In panel (c), the initial delivery of doxorubicin on day 35 blocks the increase in trastuzumab availability on days 36 and 39. Similarly, in panel (e), the first dose of doxorubicin on day 35 also inhibits the second dose of trastuzumab on day 38. Only the increase in trastuzumab availability due to the first dose of trastuzumab on day 35 is observed in panel (e). In panel (d), as both trastuzumab injections are given on days 35 and 38, before doxorubicin (administered on day 39), there is an observable increase in trastuzumab availability. Note that nonlinear effects in the drug terms (e.g., the inhibition of trastuzumab delivery) occurs only when doxorubicin is delivered before trastuzumab. As trastuzumab is delivered before doxorubicin in panel (d), the nonlinear term from 3CLM0 does not affect the drug availability.
Fig. 4.
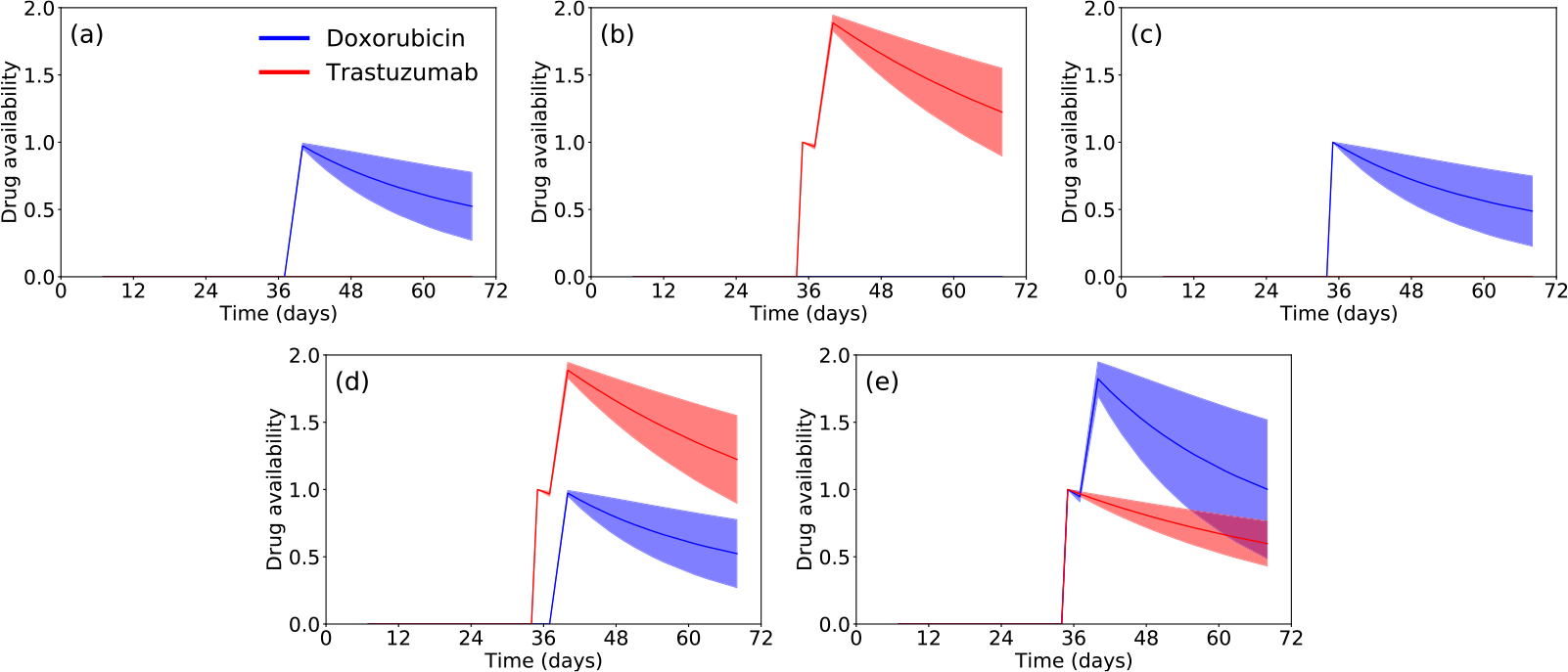
Temporal evolution of doxorubicin (blue) and trastuzumab (red) availabilities for model 3CLM0 in the following scenarios: (a) doxorubicin (b) trastuzumab (c) doxorubicin 24 h prior to trastuzumab (d) trastuzumab 24 h prior to doxorubicin (e) trastuzumab + doxorubicin. The effects of trastuzumab delivery inhibition by doxorubicin, modeled by the parameter , can be observed in (c), and for the second trastuzumab dose in (e). In these scenarios, the current doxorubicin availability blocks the increase of trastuzumab availability as in panel (c), where there is no trastuzumab availability, and in panel (e) where the effects of the second trastuzumab dose is blocked.
3.2. Optimal treatment protocol
Following model calibration and selection, we derive the optimal control formulation for the model with the highest BIC weight, 3CLM0 (see Supplementary Material for the derivation). After sampling 200 values of each parameter from the posteriors obtained during the calibration with 3CLM0 (shown in Fig. 2), we find the optimal treatment protocol that maximally reduces the tumor burden (see Eq. (13)) subject to not exceeding the total drug dose delivered experimentally. In our simulations, the treatment was allowed to start at day 35. For all 200 samples, the optimal control problem converged to the same solution (see Fig. 5): two doses of trastuzumab (on days 35 and 36), followed by two doses of doxorubicin (on days 37 and 38). With this treatment protocol, compared to the best experimental protocol (i.e., trastuzumab and doxorubicin delivered on days 35 and 38, as shown in Fig. 3(f)), we are able to reduce the tumor burden (i.e., the integral of the tumor volume during the treatment interval) by 45.34%. Moreover, we compare the time to reach 30%, 50%, and 100% of the response achieved by the best experimental protocol to the corresponding times predicted to be achieved by the optimized protocol. The optimized protocol reaches the 30% reduction time point 0.6 days earlier than the best experimental protocol, the 50% reduction time point 2.25 days earlier, and the 100% reduction time point on day 59 (the tumor does not actually achieve 100% reduction when using the best experimental protocol).
Fig. 5.
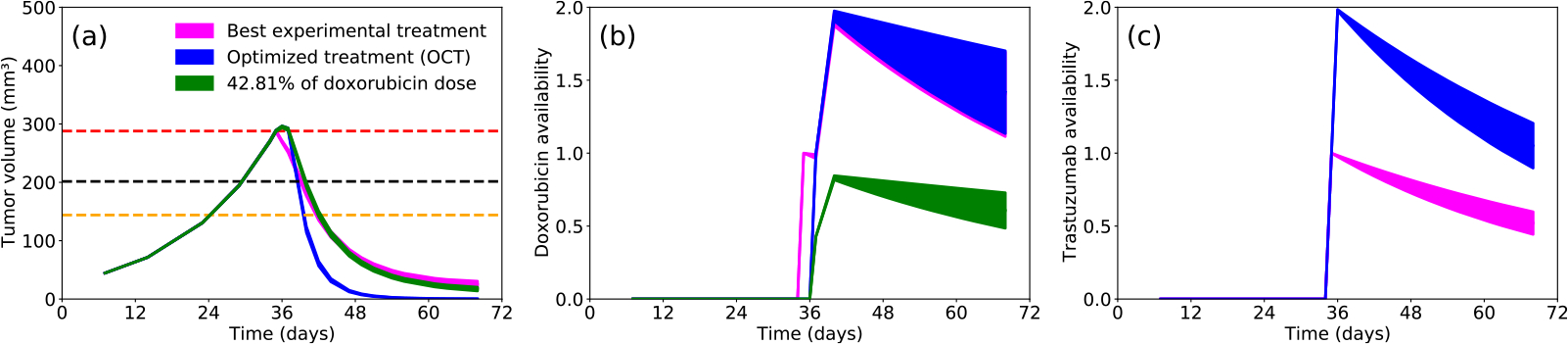
Temporal evolution of the 3CLM0 model using the best experimental protocol (magenta), the 3CLM0 model using the optimal computationally designed protocol with same total drug dose (blue), and the 3CLM0 model using the optimal computationally designed protocol with a 42.81% reduction in total doxorubicin dose (green). The results of the different treatment protocols are compared for (a) the tumor volume dynamics, (b) doxorubicin availability, and (c) trastuzumab availability. In panel (a), the red line indicates the tumor volume at the first day of treatment (day 35), the black line indicates a 30% reduction in tumor volume, and the orange line indicates a 50% reduction in treatment volume. The optimized protocol (blue) reaches the 30% reduction time point 0.6 days earlier than the best experimental protocol (magenta), the 50% reduction time point 2.25 days earlier, and the 100% reduction time point on day 59 (note that the best experimental protocol does not ever achieve a 100% reduction in tumor size). The green line demonstrates that the optimized treatment protocol is able to achieve the same tumor control as the best experimental protocol, but using only 42.81% of the doxorubicin dose employed in the experiment. In panel (c), the blue line overlaps with the green line, as we kept the same trastuzumab protocol. Note also how the best experimental treatment protocol yields approximately half of the trastuzumab availability as compared to the computationally optimized protocol.
Using the optimized treatment protocol, we also determined if it was possible to achieve the same tumor control as the best experimental protocol—but with a reduction in the total dose of doxorubicin. We found that is possible to reduce the amount of doxorubicin delivered to 42.81% of the experimental dose (Fig. 5(b)) while maintaining the same tumor burden (Fig. 5(a)). Importantly, note how, in Fig. 5(c), the trastuzumab availability can reach a value of 2.0 when using the optimized protocol with a reduced doxorubicin dose. However, when using the best experimental protocol, trastuzumab availability can only reach a value of 1.0 as the first dose of doxorubicin inhibits trastuzumab delivery.
4. Discussion
We have developed a family of models to capture the effects of combination trastuzumab and doxorubicin on tumor growth to optimize the outcome of this combination therapy while minimizing the amount of cytotoxic therapy necessary to achieve tumor control. These models were calibrated using experimental data from a murine model of human HER2 + breast cancer [12]. According to our 68 days of data, doxorubicin does not have a direct effect on the tumor as demonstrated by no change in tumor growth kinetics between the control group and the doxorubicin-treated tumors. This can be seen when comparing the growth curves of the control (Fig. 3a) and doxorubicin treated animals (Fig. 3b), and it is reported in [12,59,60]. In particular, Howard et al. collected data from in vitro experiments where different doxorubicin concentrations delivered to BT474 cells [60]. Their results indicate that, during the 600 h that the authors collected the data, low concentrations of doxorubicin do not affect the number of tumor cells. These data led us to develop the different members of the model set, including: (1) if an exponential or logistic growth function should represent the data, (2) if doxorubicin directly reduces tumor growth, and (3) if the addition of a reactive oxygen species (ROS) improves the ability of the model to capture drug delivery and (subsequently) effect on tumor growth.
The OPAL framework selected 3CLM0 (which does not account for the effects of doxorubicin on the tumor) as the model that best describes the experimental data. The 3CLMO model is able to describe the experimental data by accounting for a key effect of doxorubicin. Recall that doxorubicin increases oxidative stress which can cause mitochondrial damage and cell death in endothelial cells [39]. As endothelial cells line blood vessels and help to regulate the exchange of materials into and out of the extravascular space, their destruction can limit the delivery of trastuzumab if doxorubicin is given before trastuzumab [12]. This mechanism is incorporated in the 3CLM0 model through the term describing the inhibition of trastuzumab delivery. In protocols where trastuzumab is given first, its vascular remodeling properties [10] can improve tumor perfusion and thus the vascular delivery of doxorubicin [12]. We model this effect by the increase in treatment efficacy when trastuzumab is delivered before doxorubicin. Model 3CLM0 was able to most faithfully reproduce the experimental results and achieved a mean absolute percent error 25.29±15.37%, and a CCC and PCC of 0.92±0.05 and 0.96±0.04, respectively. The high CCC between our model and the data indicates that these phenomena can be captured by our model and that this could explain the different treatment outcomes observed with different ordering of the two therapies.
In [13], we defined a single model to reproduce the data obtained in experiments combining trastuzumab and paclitaxel. The tumor size was assumed to follow a logistic growth function, while trastuzumab was assumed to reduce the tumor growth rate. The present effort represents a significant extension of the first by testing 10 different models to determine which is best able to represent the effects of combination trastuzumab and doxorubicin on tumor growth. We tested both exponential and logistic growth functions, with the logistic growth function selected as the one best able to capture the tumor growth. In the current model, trastuzumab also reduces the tumor growth rate. In both studies, trastuzumab is delivered in combination with a chemotherapy; paclitaxel in [13] and doxorubicin in the present study. Similarly, in both studies, we observed a synergistic effect when the chemotherapies were delivered with trastuzumab. Furthermore, in [13], the experiments were done in vitro, where the effects of the drug on the vasculature could not be observed. Thus, in [13], paclitaxel reduces the tumor carrying capacity, while in the current model, doxorubicin reduces the proliferation rate and inhibits trastuzumab delivery.
Following the development and calibration of a tumor growth model that can capture the dynamics observed from experiments, our goal was to optimize the delivery of both drugs. Using the model that best reproduced the experimental data, we optimized the order and duration of both drugs. In the interest of increasing treatment efficacy without increasing its toxicity, the amount of drug delivered was kept the same as in the experiments. The optimal protocol was to deliver trastuzumab before doxorubicin, similar to that found experimentally. However, by reducing the interval between the administration of the two drugs, the optimal protocol reduced the total tumor burden by 45.34% compared to the best experimental outcome. (Note that the optimal protocol is different than the ones tested in [12].) Furthermore, in addition to achieving tumor reductions at earlier time points (Fig. 5), the optimal protocol was able to achieve 100% tumor reduction—something not achieved in the experimental group. Alternatively, in our second optimization problem, we were able to use our methodology to achieve the same experimental tumor control using only 42.81% of the doxorubicin dose used in the experimental studies.
The results of our optimization generate clear hypotheses for treatment protocols that can be directly tested experimentally, thereby providing an experimental–computational approach for rigorously identifying candidate therapeutic regimens. The optimal protocol found in our optimization agrees with the results presented in [13]; namely, that the highest overall tumor reduction is when trastuzumab is delivered before the chemotherapy. The importance of dose, timing, and order is also reflected in the clinical literature. For example, Gullo et al. analyzed the data from 506 patients that received combination trastuzumab and chemotherapy and demonstrated that initiating trastuzumab within 12 weeks of diagnosis resulted in superior outcomes than longer than 12 weeks [61]. Furthermore, chemotherapy in combination with trastuzumab proved to yield superior outcomes than either of them used alone [4,62]. In particular, the combination of the two drugs leads to longer time to disease progression, a higher rate of objective response, a longer duration of response, a lower death rate at 1 year, longer survival, and a 20 percent reduction in the risk of death. However, it is impossible to determine the optimal dose, order, and timing in standard clinical trials—there are simply too many options and not enough patients and resources to systematically test all possible combinations. We believe that the present study outlines and demonstrates a practical methodology to identify candidate therapeutic regiments hypothesized to outperform standard treatment protocols.
From a modeling perspective, we could have used more complex model as the ones presented in [26,63,64]. However, the data collected from the experiments presented here would not be enough to calibrate such models. As our current model yielded an average CCC of 0.92 between experimental data and model output, we believe that the necessary increase in the number of parameters that would be required to include additional mechanisms of the drug action is not justified. We stress that our modeling goal is not to comprehensively characterize all processes at all spatial and temporal scales. Rather, we focus on first-order effects related to well-established hallmarks of cancer [65–67] including proliferation, death, and drug-related tumor growth inhibition and cell death. By employing the most parsimonious model possible, it becomes practical to calibrate it with quantitative data that is readily-available from experimental or clinical setting. Thus, the innovation in our contribution is not from developing the most comprehensive model; rather it is on integrating experimental data with practical mathematical models that can make testable predictions—in the present case, about which therapeutic regimens are optimal.
From an experimental perspective, our treatment optimization scheme only made use of drug doses employed in the murine studies. While this increases the reliability of our model predictions, it does limit the investigation of treatment outcomes achieved with higher doses. However, employing a higher drug dose will also yield an increase in toxicity. It may be possible to account for and limit the associated increase in drug toxicity by incorporating an additional penalty (or two if both drugs are considered) in the objective function. Such a new term would be similar to the current one in Eq. (13); however, instead of being a function of the tumor volume, , it would be function of some measurement of drug toxicity (e.g., total drug dose delivered, death of healthy cells, or a surrogate for cardiotoxicity). Another limitation of the current approach is that we do not explicitly account for resistant tumor cells. As described in [31,32], the appearance of resistant tumor cell phenotypes can have a significant effect on the order, duration, and dose of the treatment to achieve optimal control. To solve these limitations, additional data (e.g., different drug doses, effects on the healthy cells, increased number of treatment days) are necessary to develop a mathematical model that can capture these phenomena. Further experiments are necessary to confirm, or improve, the optimized treatment protocol.
5. Conclusions
We developed 10 mathematical models to capture tumor growth under different doxorubicin and trastuzumab treatment protocols. These models were calibrated to the data obtained through in vivo experiments in a murine model of HER2 + breast cancer. The model with the highest Bayesian Information Criteria weight is a three-constituent model, 3CLM0, that assumes logistic tumor growth and that doxorubicin acts maximally on the tumor only in the presence of trastuzumab. Two notable features of the model are its ability to capture inhibition of trastuzumab due to pre-treatment with doxorubicin, as well as the increase in doxorubicin efficacy due to pre-treatment with trastuzumab. It is precisely the ability of our model to capture these phenomena so accurately that allow us to apply optimal control theory to identify optimal therapeutic regimens. In particular, using optimal control theory to optimize the treatment protocol of the selected model (i.e., model 3CLM0), we identified a treatment protocol that predicts we can reduce the overall tumor burden by approximately 45% more than the experimental protocol while using the same total drug dose. Additionally, we were also able to use optimal control theory to identify a second treatment protocol that predicts we can achieve the same tumor reduction as the experiments, but with less than half of the doxorubicin dose. These results strongly indicate that integrating mathematical models of tumor growth and treatment response with model selection and optimal control theory provides a rigorous and practical framework for identifying therapeutic regimens capable of maximizing efficacy while simultaneously minimizing toxicity.
Supplementary Material
Acknowledgments
We thank the American Cancer Society Grant RSG-18-006-01-CCE and the National Institute of Health for funding via R01CA240589 and U24CA226110. We thank the Cancer Prevention and Research Institute of Texas for support through CPRIT RR160005. T.E.Y. is a CPRIT Scholar in Cancer Research. We also thank the Texas Advanced Computing Center for providing high-performance computing resources. E.A.B.F.L. would like to thank Dr. J. Tinsley Oden for his mentorship and his contributions to the fields of computational and applied engineering that are fundamental to this work.
Footnotes
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Contribution for the Special Issue. “A Special Issue in Honor of the Lifetime Achievements of J. Tinsley Oden”.
References
- [1].Tarver T, Cancer facts & figures 2012. american cancer society (acs) atlanta, ga: American cancer society, 2012, p. 66, pdf. available from (2012). [Google Scholar]
- [2].Nahta R, Esteva FJ, Her2 therapy: molecular mechanisms of trastuzumab resistance, Breast Cancer Res. 8 (6) (2006) 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Spector NL, Blackwell KL, Understanding the mechanisms behind trastuzumab therapy for human epidermal growth factor receptor 2–positive breast cancer, J. Clin. Oncol. 27 (34) (2009) 5838–5847. [DOI] [PubMed] [Google Scholar]
- [4].Slamon DJ, Leyland-Jones B, Shak S, Fuchs H, Paton V, Bajamonde A, Fleming T, Eiermann W, Wolter J, Pegram M, et al. , Use of chemotherapy plus a monoclonal antibody against her2 for metastatic breast cancer that overexpresses her2, New England J. Med. 344 (11) (2001) 783–792. [DOI] [PubMed] [Google Scholar]
- [5].Guarneri V, Lenihan DJ, Valero V, Durand J-B, Broglio K, Hess KR, Michaud LB, Gonzalez-Angulo AM, Hortobagyi GN, Esteva FJ, Long-term cardiac tolerability of trastuzumab in metastatic breast cancer: the md anderson cancer center experience, J. Clin. Oncol. 24 (25) (2006) 4107–4115. [DOI] [PubMed] [Google Scholar]
- [6].Martin M, Esteva FJ, Alba E, Khandheria B, Pérez-Isla L, García-Sáenz JÁ, Marquez A, Sengupta P, Zamorano J, Minimizing cardiotoxicity while optimizing treatment efficacy with trastuzumab: review and expert recommendations, Oncologist 14 (1) (2009) 1–11. [DOI] [PubMed] [Google Scholar]
- [7].Chintalgattu V, Khakoo AY, Mechanisms of cardiac dysfunction associated with cancer therapeutics, in: Translational Cardiology, Springer, 2012, pp. 291–316. [Google Scholar]
- [8].Zhang A, Shen G, Zhao T, Zhang G, Liu J, Song L, Wei W, Bing L, Wu Z, Wu Q, Augmented inhibition of angiogenesis by combination of her2 antibody cha21 and trastuzumab in human ovarian carcinoma xenograft, J. Ovarian Res. 3 (1) (2010) 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Kumar R, Yarmand-Bagheri R, The role of her2 in angiogenesis, in: Seminars in Oncology, Vol. 28, Elsevier, 2001, pp. 27–32. [DOI] [PubMed] [Google Scholar]
- [10].Izumi Y, Xu L, Di Tomaso E, Fukumura D, Jain RK, Herceptin acts as an anti-angiogenic cocktail, Nature 416 (6878) (2002) 279–280. [DOI] [PubMed] [Google Scholar]
- [11].Montemurro F, Valabrega G, Aglietta M, Trastuzumab-based combination therapy for breast cancer, Expert Opin. Pharmacother. 5 (1) (2004) 81–96. [DOI] [PubMed] [Google Scholar]
- [12].Sorace AG, Quarles CC, Whisenant JG, Hanker AB, McIntyre JO, Sanchez VM, Yankeelov TE, Trastuzumab improves tumor perfusion and vascular delivery of cytotoxic therapy in a murine model of her2+ breast cancer: preliminary results, Breast Cancer Res. Treat. 155 (2) (2016) 273–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Jarrett AM, Shah A, Bloom MJ, McKenna MT, Hormuth DA, Yankeelov TE, Sorace AG, Experimentally-driven mathematical modeling to improve combination targeted and cytotoxic therapy for her2+ breast cancer, Sci. Rep. 9 (1) (2019) 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Jarrett AM, Bloom MJ, Godfrey W, Syed AK, Ekrut DA, Ehrlich LI, Yankeelov TE, Sorace AG, Mathematical modelling of trastuzumab-induced immune response in an in vivo murine model of her2+ breast cancer, Math. Med. Biol. J. IMA 36 (3) (2019) 381–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Fung AS, Lee C, Yu M, Tannock IF, The effect of chemotherapeutic agents on tumor vasculature in subcutaneous and orthotopic human tumor xenografts, BMC Cancer 15 (1) (2015) 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Norton K-A, Wallace T, Pandey NB, Popel AS, An agent-based model of triple-negative breast cancer: the interplay between chemokine receptor ccr5 expression, cancer stem cells, and hypoxia, BMC Syst. Biol. 11 (1) (2017) 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Jarrett AM, Hormuth DA, Adhikarla V, Sahoo P, Abler D, Tumyan L, Schmolze D, Mortimer J, Rockne RC, Yankeelov TE, Towards integration of 64cu-dota-trastuzumab pet-ct and mri with mathematical modeling to predict response to neoadjuvant therapy in her2+ breast cancer, Sci. Rep. 10 (1) (2020) 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Wu C, Hormuth D, Lorenzo G, Jarrett A, Pineda F, Howard FM, Karczmar G, Yankeelov TE, Towards patient-specific optimization of neoadjuvant treatment protocols for breast cancer based on image-guided fluid dynamics, IEEE Trans. Biomed. Eng. (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Bianca C, Chiacchio F, Pappalardo F, Pennisi M, Mathematical modeling of the immune system recognition to mammary carcinoma antigen, in: BMC Bioinformatics, Vol. 13, Springer, 2012, pp. 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Metzcar J, Wang Y, Heiland R, Macklin P, A review of cell-based computational modeling in cancer biology, JCO Clin. Cancer Inf. 2 (2019) 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Oden JT, Lima EA, Almeida RC, Feng Y, Rylander MN, Fuentes D, Faghihi D, Rahman MM, DeWitt M, Gadde M, et al. , Toward predictive multiscale modeling of vascular tumor growth, Arch. Comput. Methods Eng. 23 (4) (2016) 735–779. [Google Scholar]
- [22].Yin A, Moes DJA, van Hasselt JG, Swen JJ, Guchelaar H-J, A review of mathematical models for tumor dynamics and treatment resistance evolution of solid tumors, CPT: Pharm. Syst. Pharmacol. 8 (10) (2019) 720–737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Dogra P, Butner JD, Chuang Y.-l., Caserta S, Goel S, Brinker CJ, Cristini V, Wang Z, Mathematical modeling in cancer nanomedicine: a review, Biomed. Microdevices 21 (2) (2019) 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Gallasch R, Efremova M, Charoentong P, Hackl H, Trajanoski Z, Mathematical models for translational and clinical oncology, J. Clin. Bioinf. 3 (1) (2013) 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Kazerouni AS, Gadde M, Gardner A, Hormuth IIDA, Jarrett AM, Johnson KE, Lima EA, Lorenzo G, Phillips C, Brock A, et al. , Integrating quantitative assays with biologically based mathematical modeling for predictive oncology, Iscience 23 (12) (2020) 101807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Hormuth DA, Phillips CM, Wu C, Lima EA, Lorenzo G, Jha PK, Jarrett AM, Oden JT, Yankeelov TE, Biologically-based mathematical modeling of tumor vasculature and angiogenesis via time-resolved imaging data, Cancers 13 (12) (2021) 3008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Wu C, Lorenzo G, Hormuth DA, Lima EA, Slavkova KP, DiCarlo JC, Virostko J, Phillips CM, Patt D, Chung C, et al. , Integrating mechanism-based modeling with biomedical imaging to build practical digital twins for clinical oncology, Biophys. Rev. 3 (2) (2022) 021304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Rockne RC, Hawkins-Daarud A, Swanson KR, Sluka JP, Glazier JA, Macklin P, Hormuth DA, Jarrett AM, Lima EA, Oden JT, et al. , The 2019 mathematical oncology roadmap, Phys. Biol. 16 (4) (2019) 041005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Swan GW, Vincent TL, Optimal control analysis in the chemotherapy of igg multiple myeloma, Bull. Math. Biol. 39 (3) (1977) 317–337. [DOI] [PubMed] [Google Scholar]
- [30].Colli P, Gomez H, Lorenzo G, Marinoschi G, Reali A, Rocca E, Optimal control of cytotoxic and antiangiogenic therapies on prostate cancer growth, Math. Models Methods Appl. Sci. 31 (07) (2021) 1419–1468. [Google Scholar]
- [31].Martin R, Fisher M, Minchin R, Teo K, Optimal control of tumor size used to maximize survival time when cells are resistant to chemotherapy, Math. Biosci. 110 (2) (1992) 201–219. [DOI] [PubMed] [Google Scholar]
- [32].Cho H, Levy D, The impact of competition between cancer cells and healthy cells on optimal drug delivery, Math. Model. Nat. Phenom. 15 (2020) 42. [Google Scholar]
- [33].Farrell K, Oden JT, Faghihi D, A bayesian framework for adaptive selection, calibration, and validation of coarse-grained models of atomistic systems, J. Comput. Phys. 295 (2015) 189–208. [Google Scholar]
- [34].Oden JT, Babuška I, Faghihi D, Predictive Computational Science: Computer Predictions in the Presence of Uncertainty, American Cancer Society, 2017, pp. 1–26. [Google Scholar]
- [35].Lima EABF, Oden JT, Hormuth IIDA, Yankeelov TE, Almeida RC, Selection, calibration, and validation of models of tumor growth, Math. Models Methods Appl. Sci. 26 (12) (2016) 2341–2368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Lima EABF, Oden JT, Wohlmuth B, Shahmoradi A, Hormuth IIDA, Yankeelov TE, Scarabosio L, Horger T, Selection and validation of predictive models of radiation effects on tumor growth based on noninvasive imaging data, Comput. Methods Appl. Mech. Engrg. 327 (2017) 277–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Asensio-López MC, Soler F, Pascual-Figal D, Fernández-Belda F, Lax A, Doxorubicin-induced oxidative stress: The protective effect of nicorandil on hl-1 cardiomyocytes, PLoS One 12 (2) (2017) e0172803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Mohan N, Shen Y, Endo Y, ElZarrad MK, Wu WJ, Trastuzumab, but not pertuzumab, dysregulates her2 signaling to mediate inhibition of autophagy and increase in reactive oxygen species production in human cardiomyocytes, Mol. Cancer Ther. 15 (6) (2016) 1321–1331. [DOI] [PubMed] [Google Scholar]
- [39].Ismail MB, Rajendran P, AbuZahra HM, Veeraraghavan VP, Mangiferin inhibits apoptosis in doxorubicin-induced vascular endothelial cells via the nrf2 signaling pathway, Int. J. Mol. Sci. 22 (8) (2021) 4259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Murata T, Yamawaki H, Yoshimoto R, Hori M, Sato K, Ozaki H, Karaki H, Chronic effect of doxorubicin on vascular endothelium assessed by organ culture study, Life Sci. 69 (22) (2001) 2685–2695. [DOI] [PubMed] [Google Scholar]
- [41].Jaques R, Xu S, Matsakas A, Evaluating trastuzumab in the treatment of her2 positive breast cancer, Histol. Histopathol. (2020) 18221. [DOI] [PubMed] [Google Scholar]
- [42].Cappetta D, De Angelis A, Sapio L, Prezioso L, Illiano M, Quaini F, Rossi F, Berrino L, Naviglio S, Urbanek K, Oxidative stress and cellular response to doxorubicin: a common factor in the complex milieu of anthracycline cardiotoxicity, Oxid. Med. Cell. Longev. 2017 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Wilkinson EL, Sidaway JE, Cross MJ, Cardiotoxic drugs herceptin and doxorubicin inhibit cardiac microvascular endothelial cell barrier formation resulting in increased drug permeability, Biol. Open 5 (10) (2016) 1362–1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Ewer MS, Ewer SM, Troponin i provides insight into cardiotoxicity and the anthracycline-trastuzumab interaction, J. Clin. Oncol. 28 (25) (2010) 3901–3904. [DOI] [PubMed] [Google Scholar]
- [45].Khalil HS, Langdon SP, Kankia IH, Bown J, Deeni YY, Nrf2 regulates her2 and her3 signaling pathway to modulate sensitivity to targeted immunotherapies, Oxid. Med. Cell. Longev. 2016 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Abdal Dayem A, Hossain MK, Lee SB, Kim K, Saha SK, Yang G-M, Choi HY, Cho S-G, The role of reactive oxygen species (ros) in the biological activities of metallic nanoparticles, Int. J. Mol. Sci. 18 (1) (2017) 120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Ray PD, Huang B-W, Tsuji Y, Reactive oxygen species (ros) homeostasis and redox regulation in cellular signaling, Cell. Signal. 24 (5) (2012) 981–990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Wang J, Yi J, Cancer cell killing via ros: to increase or decrease, that is the question, Cancer Biol. Ther. 7 (12) (2008) 1875–1884. [DOI] [PubMed] [Google Scholar]
- [49].Schwarz G, Estimating the dimension of a model, Ann. Statist. (1978) 461–464. [Google Scholar]
- [50].Wagenmakers E-J, Farrell S, Aic model selection using akaike weights, Psych. Bull. Rev. 11 (1) (2004) 192–196. [DOI] [PubMed] [Google Scholar]
- [51].Lawrence I, Lin K, A concordance correlation coefficient to evaluate reproducibility, Biometrics (1989) 255–268. [PubMed] [Google Scholar]
- [52].Nyrop KA, Deal AM, Shachar SS, Basch E, Reeve BB, Choi SK, Lee JT, Wood WA, Anders CK, Carey LA, et al. , Patient-reported toxicities during chemotherapy regimens in current clinical practice for early breast cancer, Oncologist 24 (6) (2019) 762–771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].McAndrew N, DeMichele A, Neoadjuvant chemotherapy considerations in triple-negative breast cancer, J. Target. Therapies Cancer 7 (1) (2018) 52. [PMC free article] [PubMed] [Google Scholar]
- [54].Butcher JC, The Numerical Analysis of Ordinary Differential Equations: Runge–Kutta and General Linear Methods, Wiley-Interscience, 1987. [Google Scholar]
- [55].Roberts GO, Rosenthal JS, et al. , General state space markov chains and mcmc algorithms, Probab. Surv. 1 (2004) 20–71. [Google Scholar]
- [56].Gelman A, Rubin DB, et al. , Inference from iterative simulation using multiple sequences, Statist. Sci. 7 (4) (1992) 457–472. [Google Scholar]
- [57].Salvatier J, Wiecki TV, Fonnesbeck C, Probabilistic programming in python using pymc3, PeerJ Comput. Sci. 2 (2016) e55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Beal L, Hill D, Martin R, Hedengren J, Gekko optimization suite, Processes 6 (8) (2018) 106. [Google Scholar]
- [59].Sharmin S, Rahaman M, Martorell M, Sastre-Serra J, Sharifi-Rad J, Butnariu M, Bagiu IC, Bagiu RV, Islam MT, et al. , Cytotoxicity of synthetic derivatives against breast cancer and multi-drug resistant breast cancer cell lines: a literature-based perspective study, Cancer Cell Int. 21 (1) (2021) 1–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Howard GR, Jost TA, Yankeelov TE, Brock A, Quantification of long-term doxorubicin response dynamics in breast cancer cell lines to direct treatment schedules, PLoS Comput. Biol. 18 (3) (2022) e1009104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Gullo G, Walsh N, Fennelly D, Bose R, Walshe J, Tryfonopoulos D, O’Mahony K, Hammond L, Silva N, McDonnell D, et al. , Impact of timing of trastuzumab initiation on long-term outcome of patients with early-stage her2-positive breast cancer: the one thousand her2 patients project, Br. J. Cancer 119 (3) (2018) 374–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Sawaki M, Taira N, Uemura Y, Saito T, Baba S, Kobayashi K, Kawashima H, Tsuneizumi M, Sagawa N, Bando H, et al. , Randomized controlled trial of trastuzumab with or without chemotherapy for her2-positive early breast cancer in older patients, J. Clin. Oncol. 38 (32) (2020) 3743–3752. [DOI] [PubMed] [Google Scholar]
- [63].Jarrett AM, Lima EA, Hormuth DA, McKenna MT, Feng X, Ekrut DA, Resende ACM, Brock A, Yankeelov TE, Mathematical models of tumor cell proliferation: a review of the literature, Exp. Rev. Anticancer Ther. 18 (12) (2018) 1271–1286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Fritz M, Lima EA, Tinsley Oden J, Wohlmuth B, On the unsteady darcy–forchheimer–brinkman equation in local and nonlocal tumor growth models, Math. Models Methods Appl. Sci. 29 (09) (2019) 1691–1731. [Google Scholar]
- [65].Hanahan D, Weinberg RA, The hallmarks of cancer, Cell 100 (2000) 57–70. [DOI] [PubMed] [Google Scholar]
- [66].Hanahan D, Weinberg RA, Hallmarks of cancer: The next generation, Cell 144 (2011) 646–674. [DOI] [PubMed] [Google Scholar]
- [67].Hanahan D, Hallmarks of cancer: new dimensions, Cancer Discov. 12 (1) (2022) 31–46. [DOI] [PubMed] [Google Scholar]
- [68].Lenhart S, Workman JT, Optimal Control Applied To Biological Models, Chapman and Hall/CRC, 2007. [Google Scholar]
- [69].Schättler H, Ledzewicz U, Optimal Control for Mathematical Models of Cancer Therapies, Springer, 2015. [Google Scholar]
- [70].Prudencio E, Cheung SH, Parallel adaptive multilevel sampling algorithms for the bayesian analysis of mathematical models, Int. J. Uncertain. Quantif. 2 (3) (2012). [Google Scholar]
- [71].Prudencio EE, Schulz KW, The parallel C++ statistical library ‘QUESO’: Quantification of uncertainty for estimation, simulation and optimization, in: Euro-Par 2011: Parallel Processing Workshops, Springer, 2012, pp. 398–407. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


