Skip to main content
PMC home page
Oxford University Press logoLink to Oxford University Press
. 2023 Aug 25;133(656):3136–3152. doi: 10.1093/ej/uead069

Males at the Tails: How Socioeconomic Status Shapes the Gender Gap

David Autor 1, David Figlio 2, Krzysztof Karbownik 3, Jeffrey Roth 4, Melanie Wasserman 5,✉
PMCID: PMC10558139  PMID: 37808479

Abstract

We document that the female advantage in childhood behavioural and academic outcomes is driven by gender gaps at the extremes of the outcome distribution. Using unconditional quantile regression, we show that family socioeconomic status particularly influences boys’ relative to girls’ outcomes at the lower tails of the outcome distribution, precisely where gender gaps are most pronounced. These relationships are not explained by school or neighbourhood factors, or parents’ differential treatment of boys. The disproportionate effect of socioeconomic status on boys at the tails substantially contributes to the gender gap in high school dropout.

Women now outpace men in many measures of educational achievement, including the propensity to graduate from high school, enrol in post-secondary education and graduate from college. In 2010, for example, the high school graduation rate among US women was 87%, while it was 81% among US men (Murnane, 2013).1 These female-favourable gaps have motivated a burgeoning literature examining their potential determinants, with recent papers tracing the evolution of gender disparities during childhood (Buchmann and DiPrete, 2006; DiPrete and Jennings, 2012; Lundberg, 2017; Autor et al., 2019). While realised gender gaps in adult educational outcomes are large, a wrinkle in the examination of the precursor childhood gender gaps is that these differences are on average relatively modest. For example, among US eighth grade students during the 2000s, boys and girls exhibited modest differences in their mean test scores, with boys maintaining a small advantage in math and girls maintaining a more robust advantage in reading (Pope and Sydnor, 2010; Bertrand and Pan, 2013). In behavioural outcomes, where boys have long experienced a higher incidence of disciplinary problems than girls, the average female-favourable gap is larger (Jacob, 2002; Bertrand and Pan, 2013; Autor et al., 2019). However, in the Florida public school system that we study here, the gender gap in school absences is only 0.45 percentage points, with the average boy and girl both attending more than 94% of school days.

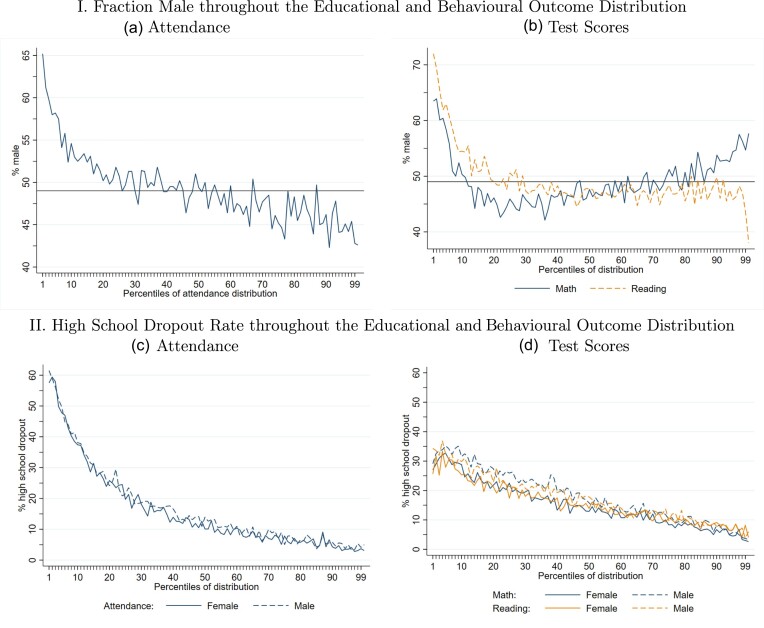
In this paper, we document and analyse two patterns that jointly help explain why modest mean gaps between boys and girls in early academic and behavioural outcomes translate into large differences in realised educational attainment. We first show that female-favourable gaps in behavioural and academic outcomes during childhood—where present—stem largely from the overrepresentation of boys in the lower tails of the academic and behavioural outcome distributions. This is visible in the upper two panels of Figure 1, which plots the fraction of students who are boys at each percentile of the academic and behavioural outcome distributions among children born in Florida in 1992–3 who attended Florida public schools in grades 5 to 8. Evident from this figure is the substantial overrepresentation of boys in the bottom quintile of attendance rates (panel (a)) and reading and math scores (panel (b)). Boys make up 49% of the sample (the dark horizontal line in each panel). But at the 10th percentile of the attendance and reading score distributions, boys comprise 55% of the population, and their overrepresentation rises convexly at lower percentiles. For math test scores, males are overrepresented at both the lower and upper tails of the distribution, yielding a small mean math advantage for boys.

Fig. 1.

Fig. 1.

Open in a new tab

Males at the Tails.

Note: These plots use data for birth cohorts 1992 and 1993 for whom we can observe both high school graduation outcomes as well as intermediate educational outcomes. The intermediate outcomes are attendance rate, mathematics test scores and reading test scores, all recorded for grades 5 to 8. Panel (a) plots the fraction male in each percentile of the attendance (averaged grades 5 to 8 attendance) distribution. Panel (b) plots the fraction male in each percentile of the test score (averaged grades 5 to 8 test scores) distributions separately for mathematics (solid navy line) and reading (dashed orange line). Panel (c) plots the fraction of high school dropouts at each attendance percentile (averaged grades 5 to 8 attendance) separately for females (solid navy line) and males (dashed navy line). Panel (d) plots the fraction of high school dropouts at each test score percentile (averaged grades 5 to 8 test scores) separately for females (solid lines) and males (dashed lines) and by testing domain (dark navy for mathematics and light orange for reading).

These childhood lower tail behavioural and academic outcomes are highly predictive of subsequent high school dropout. As shown in Figures 1(c) and 1(d), high school dropouts are drawn disproportionately from the lower tails of the test score and attendance distributions. Children at the 10th percentile of the math and reading score distributions are almost four times as likely to leave high school without a degree as those at the 90th percentile. Poor attendance in school is even more predictive: the dropout ratio among 10th percentile attendees exceeds that of 90th percentile attendees by a factor of six.

Figures 1(c) and 1(d) additionally reveal the second pattern that undergirds our analysis: boys and girls at the lower tails of the behavioural and academic distributions have a similar likelihood to drop out of high school; thus, conditional on childhood school performance, there is only a small remaining gender gap in high school dropout. These two patterns—boys and girls at the tails have comparable dropout rates, but boys are substantially overrepresented at the tails—suggest that better understanding why males are overrepresented at the lower tails of the childhood outcome distribution may help to illuminate why they are more prone to high school dropout.

This paper tests the hypothesis that boy-girl differences in tail outcomes stem in part from differential susceptibility of boys to adverse child-rearing conditions—specifically, that lower family socioeconomic status differentially raises the prevalence of adverse outcomes among boys relative to girls at the tails. Because these tail outcomes are determinative of high school dropout, this differential sensitivity could help explain the large average gender gap in dropout. Our analysis employs the universe of Florida birth records for years 1992–2000, matched to public school test score and disciplinary outcomes, and the unconditional quantile regression method of Firpo et al. (2009) to assess the effect of childhood environmental influences—families, neighbourhoods and schools—on the gender gap throughout the distribution of behavioural and academic outcomes.

We provide three main insights. First, we show that the differential negative association between family disadvantage (proxied by socioeconomic status (SES)) and school outcomes of boys relative to girls is concentrated in precisely the parts of the distribution where gender gaps are most pronounced. These relationships are evident from unconditional quantile regressions, and they are robust to including controls for correlated environmental factors. Second, by extrapolating the effects of family environment on the gender gap in grade-school behavioural and academic outcomes to high school dropout and on-time graduation decisions, we show that a substantial fraction of the gender gap in high school outcomes can potentially be explained by the differential effect of family SES on boys’ medium-run outcomes. For the lowest decile of the behavioural outcome distribution, a one-SD (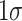Inline graphic) increase in family SES—equivalent to the difference between a family with a married high school graduate mother and a family with an unmarried high school dropout mother—would predict more than a 40% reduction in the decile-specific gender gap in high school dropout. Third, we document that the differential association between SES and boys’ outcomes is unlikely to be driven by low-SES parents investing less in the human capital of boys relative to girls. When examining individual components of family SES, we find that boys are differentially responsive to family financial and human capital resources. In addition, having a mother who is married at birth—a proxy for male role models in the home—particularly benefits boys relative to girls, especially at the lower tails of the outcome distribution.

We also test four alternative explanations for our findings. First, we assess whether boys are more likely than girls to be born to disadvantaged families. Second, we examine whether family SES differentially affects boys’ neonatal health throughout the distribution. From these tests, we conclude that family environment does not exert a meaningful differential effect on boys’ relative to girls’ initial conditions, as measured both by their initial allocation to family types and by their health at birth—consistent with the supposition that its impact on outcomes arises postnatally. Third, we document that other childhood environmental factors—schools and neighbourhoods—account for a small portion of the differential effects of family environment on boys at the tails. Finally, we show that within-family sibling spillovers—specifically the gender of one’s younger sibling—are not meaningful mediators of the disproportionate relationship between family SES and boys’ outcomes.

Our paper contributes to a growing literature examining gender gaps in educational outcomes. First, our paper complements prior work that characterises gender gaps throughout educational outcome distributions, which has primarily focused on the male advantage in mathematics. Gender gaps in math (favouring males) are largest at the upper end of the achievement distribution in the United States (Ellison and Swanson, 2010; Fryer and Levitt, 2010; Robinson and Lubienski, 2011) and Italy (Contini et al., 2017). Robinson and Lubienski (2011) further documented that gender gaps in reading (favouring females) are largest at the bottom of the achievement distribution. Using administrative data, our paper confirms the previously documented patterns and additionally documents that the well-known female advantage in behavioural outcomes is driven by lower tail gaps.

We additionally contribute to the literature that explores the childhood determinants of gender gaps in educational outcomes. To date, this literature has focused on explaining conditional mean differences between boys and girls. Closely related papers are Bertrand and Pan (2013), Aucejo and James (2019) and Autor et al. (2019), who found that growing up in a more disadvantaged family environment disproportionately harms boys’ childhood outcomes, including disciplinary infractions, standardised test scores and high school graduation rates.2 In Australia, Cobb-Clark and Moschion (2017) and Le and Nguyen (2018) reported Oaxaca-Blinder decompositions of gender gaps throughout the test score distribution, but their results regarding the differential return to family background were inconclusive. We provide novel evidence that the disproportionate association between family disadvantage and adverse outcomes among boys are concentrated at the lower tails of academic and behavioural outcome distributions, precisely where the female advantage is most pronounced.

1. Data and the Empirical Approach

1.1. Florida Birth Certificates Linked to School Records

Our data come from the universe of Florida birth certificates for years 1992–2000 linked to public school records from the 2002-03 through 2009-10 school years (Figlio et al., 2014). For each year that a child attends a Florida public school, our data report the child’s Florida Comprehensive Assessment Test standardised math and reading scores, daily absences and suspensions for grades 3 through 8. To measure behavioural outcomes, we compute a ‘combined attendance rate’ by totalling the number of absences and suspensions in a given academic year, dividing by the number of school days in the year and subtracting this absence rate from one.3 We account for the higher rates of absences and suspensions during middle school relative to elementary school by normalising each child’s combined attendance rate by the average rate in their grade. To reduce computational demands of the quantile regression models, we average grade 3 through 8 outcomes, so each child contributes one observation to the analysis for each outcome.4

We construct a family SES index from a principal components analysis of demographic variables reported on the child’s birth certificate: maternal education, age, marital status and Medicaid receipt at birth (Online Appendix Table A.1). Neighbourhood SES is computed by aggregating the family SES index to the zip code of birth level (excluding the child’s own family). School quality comes from the Florida Department of Education’s school-level gain scores, which measure schools’ estimated average contribution to student outcomes. For each school, we average the 2002–13 gain scores, then compute its percentile rank in the Florida public school distribution. We assign each child the cumulative quality of schools attended from grades 3 through 8 (Autor et al., 2016). The main sample comprises all children born in Florida 1994–2000 who attended Florida public schools. To assess the relationship between childhood behavioural and academic outcomes and high school completion, we analyse children born in 1992 and 1993, for whom we observe high school graduation outcomes. Online Appendix Tables A.2 and A.3 present summary statistics.

1.2. Empirical Framework

Below we outline an empirical framework for assessing the causal effect of family SES on the gender gap in children’s educational outcomes throughout the distribution, which follows Havnes and Mogstad (2015). The assumptions required for causal identification in our non-experimental setting are restrictive, and hence the reader may prefer to view the estimated relationships as associations. We believe that the framework is nevertheless constructive for clarifying which factors would undermine causal inference, and that the estimates are informative under either a causal or associational interpretation.

Let 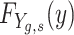Inline graphic represent the cumulative distribution function of educational outcome Y for children with gender 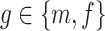Inline graphic, whose family SES at the time of the children’s birth is 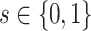Inline graphic, where one denotes the family is high SES and zero denotes the family is low SES.5 First we construct the distributional contrast 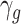Inline graphic, which captures for children of gender g, the difference in the shares from high- and low-SES backgrounds who score above a given outcome level y:

1.2.

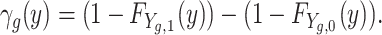This quantity will be positive if a higher fraction of high-SES than low-SES children of gender g score above level y.

Since family SES is not randomly assigned to children, 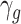Inline graphic will incorporate differences between children, not only due to SES, but also due to the correlation of SES and other child and environmental characteristics. For this reason, 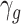Inline graphic does not reflect the quantile treatment effect of SES on the outcomes of children of gender g. We can write 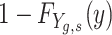Inline graphic as the sum of two distributions, 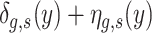Inline graphic, which allows us to write:

1.2.

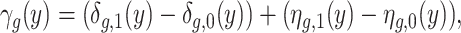where 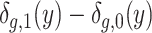Inline graphic is the effect of SES on the share of children of gender g who score above level y, while 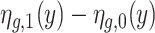Inline graphic is the difference in the latent distributions of the outcome among children of gender g born to high- and low-SES families. In our definition of 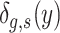Inline graphic, we include both the direct effect of family SES and the indirect effect of SES that may operate through other correlated channels, such as schools and neighbourhoods.

The difference-in-differences contrast is as follows:

1.2.

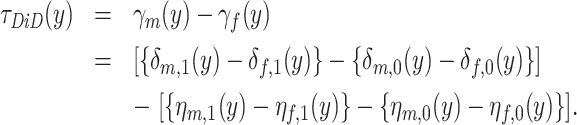The first bracketed expression is the effect of SES on the share of boys relative to girls who score above outcome level y. The second bracketed expression contains the potentially confounding difference in the latent distributions of the outcome among high- and low-SES children. In addition, it includes the potentially confounding difference in the latent distributions of the outcome among boys and girls of a given SES level. Isolating the effect of SES on the gender gap in outcomes throughout the distribution requires the following two assumptions.

Assumption 1.

The latent gender gap in  Inline graphic  is independent of SES. Hence, Inline graphic  for all y.

Under this assumption, the double difference of the shares of high-SES boys and girls relative to low-SES boys and girls who score above outcome level y eliminates the bias terms. This assumption does not require that the latent distribution of educational outcomes is independent of SES for either sex. Rather, akin to the standard parallel trend assumption in a differences-in-differences setting (augmented for a quantile setting), this assumption requires that any gender difference in latent outcomes is independent of SES and hence can be eliminated by differencing the gender gap across SES levels. We acknowledge that this is a strong assumption. In Section 2.3, we provide supporting evidence, but we cannot definitively test it. Specifically, we find that SES has little effect on gender gaps in initial conditions—as measured by neonatal health—throughout the distribution. We cannot rule out, however, the presence of sex-specific gene expression or that our neonatal health metrics do not adequately capture latent outcomes.6

If SES were perfectly observed in our data then Assumption 1 would be sufficient to isolate the effect of SES on the gender gap throughout the distribution. In practice, we proxy SES with detailed information from birth certificates.7 Even under Assumption 1, using a proxy for SES could lead to a spurious correlation between the gender gap in 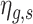Inline graphic and the proxy, if there is gender imbalance among family types. This would potentially confound the effect of SES on the gender gap with the non-random assignment of genders to family types. This confound is eliminated with the following assumption, the validity of which we test in Section 2.3.

Assumption 2.

The gender of children is as good as randomly assigned to family SES.

Bringing this empirical approach to the data, we construct the following contrast:

1.2.

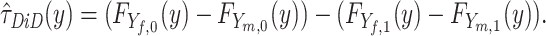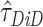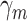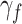The estimand Inline graphic corresponds to differences in shares of children scoring above each educational outcome level. To convert these shares into quantile treatment effects, we employ the method developed by Firpo et al. (2009) to estimate unconditional quantile regression using the recentred influence function (RIF). This approach estimates the quantile treatment effect by contrasting Inline graphic and Inline graphic and scaling this contrast by the kernel density of the joint distribution of SES and the outcome at a given y. Thus, the RIF analysis recovers the quantile treatment effect by inverting the cumulative distribution function of the outcome variable in the neighbourhood of a given y.

2. Family Environment and the Gender Gap throughout the Distribution

2.1. Family SES and Boys’ Tail Outcomes

We estimate baseline gender gaps using the specification:

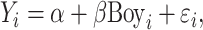2.1. (1)

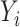where Inline graphic is an academic or behavioural outcome for child i and 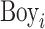Inline graphic is an indicator for a male child. To characterise the gender gap throughout the outcome distribution, we replace the dependent variable in (1) with the recentred influence function for each quantile of the outcome distribution.

Next we incorporate the interaction of child gender and family environment into the specification:

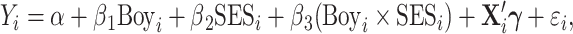2.1. (2)

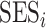where Inline graphic is an index of the family’s socioeconomic status at birth and 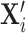Inline graphic is a vector of other controls; and we again replace the dependent variable with the recentred influence function. The coefficient 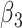Inline graphic on the interaction term 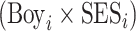Inline graphic permits the relationship between family SES and outcomes to differ by child sex.8

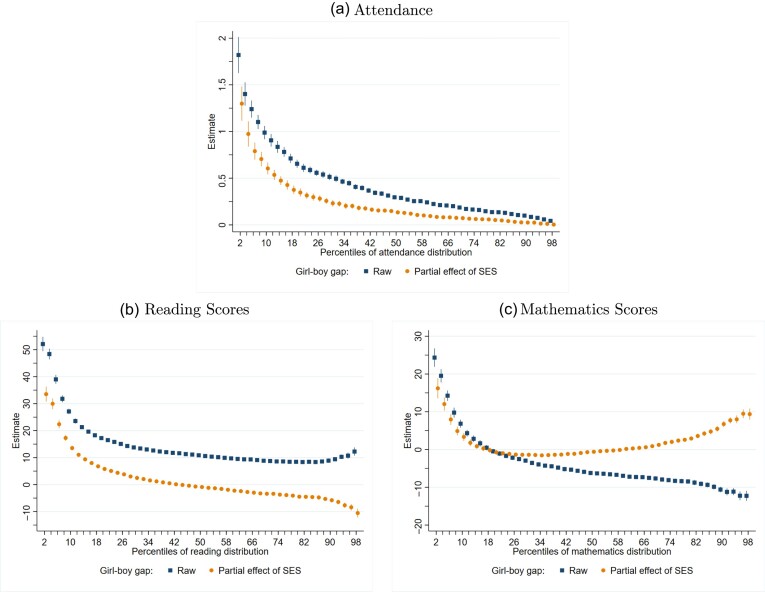
The first outcome we consider is attendance in grade school, a behavioural outcome. On average, girls are absent 5.1% of school days while boys are absent 5.6% of school days (Online Appendix Table A.3). This mean difference masks considerable heterogeneity in the gender gap throughout the attendance distribution. Figure 2(a) reveals this heterogeneity by plotting the raw gender gap (which we have reversed for expositional purposes to be the girl-boy gap) at 50 percentiles of the attendance distribution.9 The positive gender gap indicates that boys have a lower attendance rate (higher absence rate) at every point in the distribution. Relevant to our analysis and consistent with Figure 1, the female-favourable gender gap in attendance is considerably larger at the lower tail of the distribution. At the 10th percentile, boys miss 0.99 percentage points more school days than do girls (Online Appendix Table A.4). This gap shrinks monotonically as one moves upward in the distribution. The gap at the 90th percentile of 0.10 percentage points is one-tenth as large as that at the 10th percentile. Online Appendix Figure A.1 replicates the results with an attendance rate that only relies on absences (excludes suspensions, which for most students take on a value of zero). The gender gap in attendance as well as the effect of SES on the gender gap continue to be most pronounced at the lower tail of the outcome distribution.

Fig. 2.

Fig. 2.

Open in a new tab

Effect of SES on the Gender Gap throughout the Distribution.

Note: The sample is individuals born between 1994 and 2000 in Florida, attending Florida public schools and having non-missing attendance and test score outcomes. The graphs plot girl-boy gender gaps (navy squares) and the differential effects of SES on boys (orange circles) for every other percentile of the attendance (panel (a)), reading test score (panel (b)) and mathematics test score (panel (c)) distributions. Dependent variables are multiplied by 100. The estimates are from RIF regressions (Firpo et al., 2009) and implemented using the rifreg command in Stata. Each scatterplot series contains 49 estimates. Raw gender gap estimates come from regressing one of the three outcome variables on a Boy indicator and multiplying these coefficients by 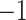Inline graphic. Partial effects of SES are the coefficients on Boy × SES interaction terms from a regression of one of the three outcome variables on the Boy indicator, SES index, interaction between Boy and SES (the plotted coefficients of interest), race/ethnicity indicators, month-of-birth indicators, year-of-birth indicators and birth order indicators. Spikes represent 95% confidence intervals based on bootstrapped SEs with 200 replications.

To characterise the effects of family SES on the gender gap throughout the attendance distribution, we estimate unconditional quantile regressions corresponding to (2), which we plot for 50 percentiles. The coefficients on the interaction term 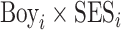Inline graphic plotted in Figure 2(a) indicate that the differential effect of family environment on boys’ attendance rates is largest at the lower end of the distribution, precisely where the gender gap is most pronounced. As the female advantage in attendance attenuates, the estimated effect of family SES on the gender gap also declines. We estimate that a 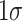Inline graphic lower SES predicts an increase in the 10th percentile boy-girl gap in absences by 0.60 percentage points. At the median, this effect is only 0.13 percentage points, and at the 90th percentile, it is a mere 0.03 percentage points.

These estimated effects can be compared to the observed gender gaps at these percentiles, equal to 0.99, 0.30 and 0.10, respectively. The estimates imply that a 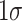Inline graphic decline in SES is predicted to expand the lower-tail (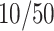Inline graphic) gender gap in attendance by roughly two-thirds of its observed magnitude. Similar to Autor et al. (2019), we find a substantial differential effect of family SES on boys’ behavioural outcomes on average as well. The OLS coefficient on the interaction of boy and family SES is positive and highly significant, at 0.25 percentage points. The quantile estimates reported here reveal that this mean effect is driven almost entirely by the lower half of the distribution. A 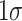Inline graphic rise in SES is predicted to close the lower-tail 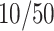Inline graphic boy-girl attendance gap by 0.47 percentage points while compressing the upper tail 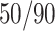Inline graphic gap by only 0.10 percentage points.

The estimates for the academic outcomes—reading and math scores—tell a more nuanced story. For reading, there is a female advantage, both on average and throughout the distribution. The female-favourable gap in reading test scores plotted in Figure 2(b) largely mirrors that for attendance. The gender gap in reading narrows from 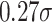Inline graphic at the 10th percentile to 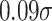Inline graphic at the 90th percentile of the score distribution (Online Appendix Table A.5). As with attendance, we estimate that boys differentially benefit from a more advantaged family environment. At the 10th percentile, a 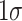Inline graphic increase in the family SES index corresponds to a 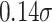Inline graphic closure of the gender gap in reading, or half of the raw gap.

Math test scores report a small mean male advantage of 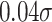Inline graphic (Online Appendix Table A.6). This mean difference stems from boys outperforming girls above approximately the 20th percentile of the score distribution. Meanwhile, there is a substantial male disadvantage in math scores below the 20th percentile. As depicted Figure 2(c), family SES exerts a differential effect on boys’ versus girls’ math scores, but this effect is non-monotone throughout the outcome distribution. At the tails of the distribution, boys differentially benefit from higher family SES, while in the middle of the distribution, family SES confers a slight differential benefit to girls.

In summary, for all three outcomes, the differential effect of SES on boys is amplified at the lower tail of the distribution, precisely where there are large female-favourable gaps.

2.2. Tail Outcomes and Gender Gaps in Educational Achievement

What do the effects of family environment on the gender gap throughout the childhood outcome distribution imply for the gender gap in high school graduation? We conduct a mediation analysis in order to assess the ramifications of family environment for the gender gap in high school outcomes. Specifically, we scale our unconditional quantile estimates of family environment on the gender gap in academic and behavioural outcomes by the relationship between each outcome and high school dropout/completion. First, we estimate the relationship between intermediate (attendance, reading scores, math scores) and high school outcomes (on-time graduation and dropout), using a cubic specification:

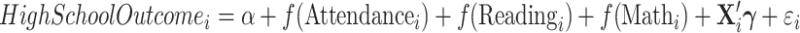2.2. (3)

with the 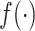Inline graphic cubic polynomials of intermediate academic and behavioural outcomes. The regression results confirm the robust predictive power of all three elementary/middle school outcomes for high school completion (Online Appendix Table A.7).10

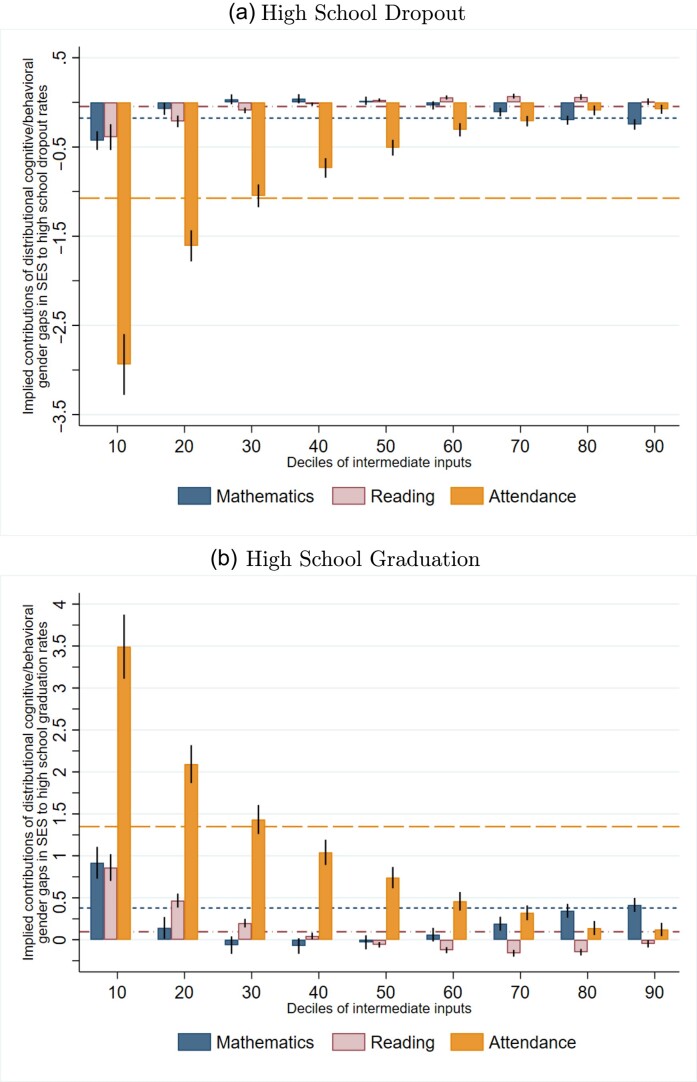
Next, we multiply the quantile-specific estimates of the coefficient on 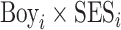Inline graphic from (2) by the marginal effect on the high school outcome from (3), corresponding to the value at the same quantile of the intermediate outcome. The results of this extrapolation exercise are presented in Figure 3, where the bars denote the implied effect of a 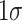Inline graphic increase in family environment on the gender gap in high school outcomes through its effects on the gender gap in math, reading and attendance, respectively. In our setting, a 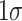Inline graphic shift represents, for example, shifting from growing up in a family with a mother who is an unmarried high school dropout to one in which the mother is a married high school graduate.

Fig. 3.

Fig. 3.

Open in a new tab

Implications for the Gender Gap in High School.

Note: The graphs depict an extrapolation of the intermediate attendance and test score results for high school dropout (panel (a)) and high school graduation (panel (b)). We first estimate the relationship between high school dropout or graduation and a cubic polynomial in attendance, reading test scores and math test scores in grades 5 to 8, additionally controlling for gender, SES, race/ethnicity, month-of-birth dummies, year-of-birth dummies, birth order dummies and an interaction between SES and Boy. We compute marginal effects of attendance, reading scores and math scores on the two high school outcomes, separately at each decile (10 to 90) of these independent variables’ distributions. Separately, we compute unconditional quantile effects of Boy × SES for 10 to 90 deciles from our main specifications as described in Figure 2. This figure plots the implied effects of a one-SD change in the SES index (1.51) on high school dropout or high school graduation, operating through the differential effect of SES on boys relative to girls (Boy × SES interaction) at each decile of the distribution of intermediate inputs. Each bar represents the decile-specific effect of a one-SD change in SES obtained by multiplying the marginal effect of a given intermediate input (attendance, mathematics or reading) and the Boy × SES coefficient for this input. Attendance is depicted using medium orange color, mathematics is depicted using dark navy color, and reading is depicted using light maroon color. The dashed lines represent the contribution of family SES to the gender gap through its average effect on attendance (medium orange), mathematics (dark navy) and reading (light maroon). For high school graduation, the implied contributions of the mean effects are 1.35, 0.38 and 0.10 for attendance, mathematics and reading, respectively. For high school dropout, the implied contributions of the mean effects are −1.07, −0.18 and −0.05 for attendance, mathematics and reading, respectively. SEs are obtained by bootstrapping the procedure 200 times.

An increase in family SES closes the gender gap in dropping out of high school primarily through its effects on attendance (panel (a)). This is due to the substantial differential association between family environment and boys’ attendance—particularly at the lower tail of the distribution—and the sizeable predictive relationship between elementary/middle school attendance and high school dropout.11 A shift in family environment would not meaningfully close the gender gap in high school outcomes through its effects on math or reading test scores. At the 10th percentile of the attendance distribution, we observe that a 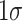Inline graphic increase in family SES would, however, predict a 2.9-percentage-point, or 43%, reduction in the decile-specific gender gap in high school dropout through attendance alone.12 When we instead focus on the implications of family SES for the gender gap in high school dropout rates through its mean effect on attendance, the contribution is just 1.07 percentage points. Focusing on average effects thus obscures the substantial explanatory power of SES at the lower tail. Logically, this contribution is much smaller higher in the distribution, where family environment makes little contribution to gender gaps in childhood school outcomes (Figure 2).

The results for on-time high school graduation are comparable. At the lowest deciles, a 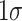Inline graphic increase in family environment predicts a decline of 3.5 percentage points, or 29%, of the decile-specific gender gap, again operating primarily through its effects on attendance. In contrast, shifts in family environment predict a mere 1.35-percentage-point closure of the gender gap in high school graduation, through its mean differential effect on boys’ attendance.

2.3. Testing Alternative Explanations

2.3.1. Family SES and the gender gap in at-birth health

While it is not possible to test the validity of Assumption 1—that the gender gap in potential outcomes is independent of family SES throughout the outcome distribution—we provide evidence that gender gaps in initial conditions are unlikely to vary with family SES. Using (2), we examine the relationship between family SES and neonatal health. There is almost no economically meaningful relationship between family SES and the gender gap in birth weight (Online Appendix Table A.9). The mean effect is a precisely estimated zero, whereas the estimated quantile effects range between plus and minus 1%. To interpret the magnitude of this relationship, we draw on the fact that, using the same Florida data as employed here, Figlio et al. (2014) found that a 10% increase in birth weight generates a 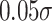Inline graphic gain in children’s academic outcomes. Our point estimates for the effect of SES on the gender gaps in birth weight 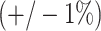Inline graphic are an order of magnitude smaller than this effect, implying that any confounding influence of SES on birth weight could add no more than 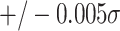Inline graphic to the gender gap in academic outcomes. This is minute relative to the effects we estimate in Figure 2. The conclusion is similar for the specification examining a neonatal health index.

We also directly test the sensitivity of our main results to the inclusion of controls for birth weight and the neonatal health index and their interactions with 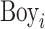Inline graphic. These additional controls have almost imperceptible effects on the estimated relationship between family SES and the gender gap in academic and behavioural outcomes throughout the distribution (Online Appendix Figure A.2). The lack of an association between family SES and gender gaps at birth is consistent with our assumption that the effect of family SES manifests after birth. The data, however, do not allow us to test whether latent gender differences that are correlated with SES—but not detectable at birth—subsequently lead to gender-divergent outcomes. Finally, Online Appendix Figure A.3 shows that children with moderate or severe disabilities are not driving our results.

2.3.2. Exogeneity of gender

We also show that the differential allocation of boys and girls among family types is unlikely to explain our findings. We estimate the relationship between child gender and family SES using the specification:

2.3.2.

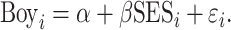In the full sample of children born in Florida, family SES is not correlated with the probability that a newborn child is male (Online Appendix Table A.10). In our analysis sample, which matches births to schooling records, we note that there is a small, positive and statistically significant relationship between the likelihood a child is male and family SES. A 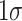Inline graphic increase in SES is associated with a 0.007 increase in the fraction of male children. Given its statistical significance, we benchmark the economic magnitude of this relationship in two ways, both of which indicate that it is unlikely to bias our results.

First, we compare the relationship to sex ratios in the literature. Our coefficient of 0.007 shifts the sex ratio from the sample mean of 1.022 to 1.036. This is within the range of the biological norm in the white US population, which does not exhibit sex selective behaviour (Almond and Edlund, 2008; Almond and Sun, 2017).

Second, we examine the sensitivity of our main results to the imbalance of male children throughout the family SES distribution by implementing the Lee (2009) bounding approach. As an upper (lower) bound, we assume that the excess gender is positively (negatively) selected and drop children from the excess gender throughout the SES distribution who are the highest (lowest) performing. We then re-estimate (2) using the upper and lower bound samples (Online Appendix B). In the lower half of the distribution, for all outcomes, we observe that the lower bounds are within our original confidence intervals (Online Appendix Figure A.4). In the upper half of the distribution, the lower bounds are a bit below the 95% confidence intervals of the original point estimates, indicating that we may slightly overestimate the differential effects of family SES. The upper bounds for all outcomes amplify the 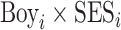Inline graphic coefficients at the lower tails, implying that our main results may understate the differential benefits of family SES for boys.

3. Mechanisms for Boys’ Responsiveness

3.1. Correlated Environmental Factors

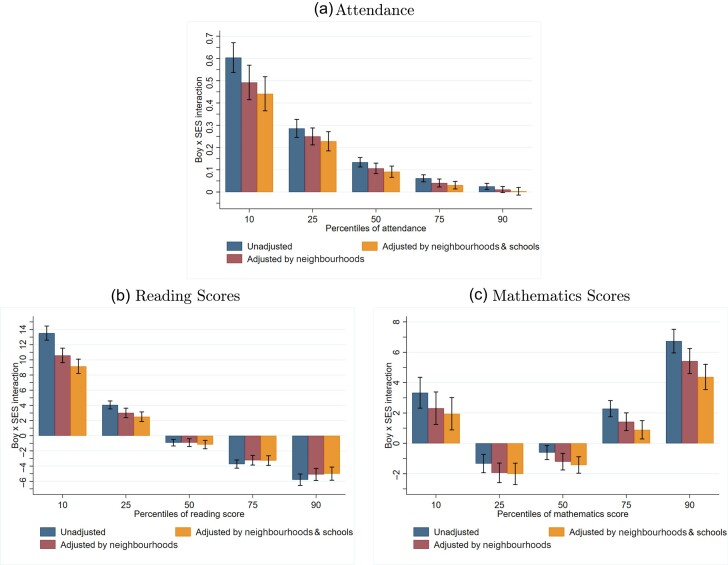
We first evaluate whether other environmental factors that are correlated with family SES, such as childhood neighbourhood characteristics and school quality, explain the differential effects of SES on boys at the lower tails. We modify (2) by including controls for a child’s neighbourhood SES at birth, their school quality and the interactions of these attributes with 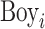Inline graphic. Although we account for overall school quality, we cannot test whether boys face different achievement expectations and disciplinary standards within schools (Kinsler, 2011; Alan et al., 2018). Figure 4 plots the interaction term 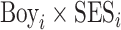Inline graphic with and without these controls (coefficients are in Online Appendix Tables A.11, A.12 and A.13). The inclusion of school and neighbourhood controls modestly reduces the differential effect of family SES on boys’ attendance, suggesting that these are meaningful channels through which family SES affects behavioural outcomes. More than two-thirds of the unadjusted effect of SES remains at the 10th, 25th and 50th percentiles (panel (a)), implying that there is a substantial remaining effect of SES on the gender gap, even controlling for school quality and neighbourhood characteristics. Similarly, the effect of family SES on the gender gap in math and reading scores is only modestly attenuated by these additional environmental controls (panels (b) and (c)).

Fig. 4.

Fig. 4.

Open in a new tab

The Role of Schools and Neighbourhoods in the Gender Gap throughout the Distribution.

Note: The sample is individuals born between 1994 and 2000 in Florida, attending Florida public schools and having non-missing attendance and test score outcomes. These graphs plot the coefficients on the interaction of Boy × SES without additional Boy × other environmental factors (dark navy bars) as well as with the addition of the Boy × neighbourhood SES measure (medium maroon bars) or both Boy × neighbourhood SES measure and Boy × school quality (light orange bars). Each graph plots estimates from 15 unconditional quantile regressions, estimated using RIF regressions (Firpo et al., 2009) and implemented using the rifreg command in Stata. The quantiles of interest are 10, 25, 50, 75 and 90. Panel (a) presents results for attendance, panel (b) presents results for reading test scores and panel (c) presents results for mathematics test scores. Dependent variables are multiplied by 100. Estimates represented by dark navy bars come from regressing one of the three outcome variables on the Boy indicator, SES index, interaction between those two (plotted parameter of interest), school quality, neighbourhood SES index, race/ethnicity indicators, month-of-birth indicators, year-of-birth indicators and birth order indicators. Estimates represented by medium maroon bars include the same set of control variables, but further add Boy × neighbourhood SES index interaction. Estimates represented by light orange bars further add Boy × school quality interaction. Whiskers represent 95% confidence intervals based on bootstrapped SEs with 200 replications.

3.2. Differential Treatment by Families

To test whether families’ differential treatment of boys and girls contributes to boys’ disproportionate responsiveness to family SES, we use the one parental decision observed in our data: children’s school quality. We characterise a child’s grade 1 and grade 6 schools by their gain scores and a child’s high school by its gain score, on-time graduation rate and dropout rate. Online Appendix Table A.14 shows that boys, on average, attend elementary, middle and high schools of lower quality. Furthermore, boys attend high schools with higher dropout rates and lower on-time graduation rates than their female counterparts. While these results show quantitatively small differences in parental treatment of boys and girls, we provide two pieces of evidence that this pattern is unlikely to explain the differential responsiveness of boys to family environment.13 First, there is only a small relationship between family SES and the gender gap in school quality. Second, the differential effect of family SES on boys’ outcomes changes little when we control for school quality in our main specifications (Online Appendix Tables A.11, A.12 and A.13).

3.3. Differential Sensitivity to Family Resources

Our main interpretation of the findings above is that boys are differentially sensitive to household inputs. In Online Appendix Tables A.15, A.16 and A.17 we examine how each component of the SES index affects the gender gap in educational outcomes. Having a mother who is married at birth—a proxy for male role models in the home—confers additional benefits to boys relative to girls, particularly at the lower tails of the outcome distribution. It is also possible that boys are differentially vulnerable to a scarcity of parental time, emotional and financial resources due to gender differences in non-cognitive skills, including boys’ lower rates of socioemotional skills and lesser ability to delay gratification (Bertrand, 2011). Although we do not directly observe these non-cognitive traits in our data, we find that boys’ outcomes are differentially responsive to other subcomponents of the SES index, such as income and maternal education.

Another aspect of family environment that could differentially affect boys and girls is the gender of their siblings (Butcher and Case, 1994; Peter et al., 2018; Brenøe, 2021). This effect could arise from direct interactions or differential parental resource allocation through sibling spillovers (Black et al., 2021; Karbownik and Özek, 2021). We investigate whether boys’ responsiveness to family environment is due to the differential effects of younger sibling gender. Online Appendix Figure A.5 shows that additional controls for younger sibling gender and its interaction with own gender do not alter the differential effects of family SES on boys’ outcomes, suggesting that sex-specific sibling spillovers are unlikely to mediate the main results.

4. Conclusion

Leveraging rich longitudinal data, we document and analyse two patterns that help explain why modest mean gaps between boys and girls in early academic and behavioural outcomes translate into large differences in educational attainment: first, female-favourable gaps in childhood outcomes are driven by a preponderance of boys at the lower tails of the respective outcome; and, second, conditional on these outcomes, there is only a small remaining gender gap in high school dropout. Using unconditional quantile regression, we find that family disadvantage is associated with differentially poor outcomes of boys at low quantiles, thus proximately contributing to the gender gap at the tails of the distribution. These tail differences mediate gender gaps in high school non-completion. Family SES is correlated with other environmental attributes, such as neighbourhood SES and school quality, but these correlates explain only a modest portion of boys’ differential responsiveness to family environment. Regarding mechanisms, boys’ response at the tails is unlikely due to parents’ differential educational choices for boys and girls. We do find that, conditional on financial and educational resources, having a mother who is married at birth differentially benefits boys. While we cannot directly analyse outcomes after high school, the disproportionate association between family SES and childhood outcomes among the lowest performing boys, paired with the predictive power of behavioural outcomes for high school completion, positions family environment as a potentially important contributor to gender gaps in long-term educational achievement—and likely adult earnings as well.

Supplementary Material

uead069_Online_Appendix
Click here for additional data file. (1.4MB, pdf)

Notes

The authors were granted an exemption to publish their data because access to the data is restricted. However, the authors provided a simulated or synthetic dataset that allowed the Journal to run their codes. The synthetic/simulated data and codes are available on the Journal website. They were checked for their ability to generate all tables and figures in the paper, but the synthetic/simulated data are not designed to reproduce the same results. The replication package for this paper is available at the following address: https://doi.org/10.5281/zenodo.8234223.

We thank seminar participants at University of California at Davis. Autor acknowledges support from the Russell Sage Foundation (Grant #85-12-07). Figlio and Roth acknowledge support from the National Science Foundation and the Institute for Education Sciences (CALDER grant), and Figlio acknowledges support from the National Institute of Child Health and Human Development and the Bill and Melinda Gates Foundation. Wasserman acknowledges support from the National Institute on Aging, Grant #T32-AG000186. We are grateful to the Florida Departments of Education and Health for providing the de-identified, matched data used in this analysis. The conclusions expressed in this paper are those of the authors and do not represent the positions of the Florida Departments of Education and Health or those of our funders. This project has been ruled exempt by the Northwestern University and University of Florida Institutional Review Boards.

Footnotes

1

In Florida, our paper’s focus, graduation rates in 2018/9 were 90% for women and 84% for men.

2

For college attendance, employment and earnings, Chetty et al. (2016) found that boys differentially benefit from growing up in a higher income family. These longer-run effects documented using US administrative data stand in contrast with findings from Danish administrative data (Brenøe and Lundberg, 2018) and US survey data (Lei and Lundberg, 2020).

3

Total absences include excused and unexcused absences, which are not separately reported in the data.

4

Results are similar when analysing combined attendance without normalisation and when separately analysing each grade.

5

We use a discrete SES measure for expositional clarity. The measure in our analysis is continuous.

6

Research on gene-SES interactions is inconclusive (e.g., Figlio et al., 2017 found null effects while Ronda et al., 2022 found small positive effects). To the extent that gene expression is sex specific, these gender differences tend to be smaller than the gene-SES gradient (Ronda et al., 2022).

7

We are unable to observe certain parental behaviours such as maternal labour supply.

8

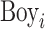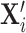We find similar results with specifications that include interactions between Inline graphic and all covariates Inline graphic.

9

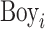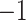We estimate an RIF regression of (1) and plot the coefficients on Inline graphic multiplied by Inline graphic.

10

The vector 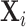Inline graphic includes demographic/socioeconomic controls and 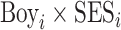Inline graphic. The results are invariant to including all controls interacted with gender.

11

The marginal effect of attendance on high school outcomes is smaller in magnitude at the lower tail of the attendance distribution (Online Appendix Table A.7). Because of the substantial differential effect of SES on boys’ attendance at the lower tail of the attendance distribution, however, the overall contribution of SES to the gender gap in high school outcomes through attendance remains larger at the lower tail.

12

Online Appendix Table A.8 reports decile-specific gender gaps. Specifically, we take the high school dropout rate at each percentile of the gender-specific attendance distribution. This differs from Figure 1(c), which computes the gender gap in high school dropout at each percentile of the pooled boy-girl attendance distribution.

13

It is likely that parents choose children’s grade 1 schools, but middle and high schools could be jointly decided by parents and children or the result of earlier educational outcomes.

Contributor Information

David Autor, MIT & NBER, USA.

David Figlio, University of Rochester & NBER, USA.

Krzysztof Karbownik, Emory University & NBER, USA.

Jeffrey Roth, University of Florida, USA.

Melanie Wasserman, UCLA & NBER, USA.

Additional Supporting Information may be found in the online version of this article:

Online Appendix

Replication Package

References

  1. Alan  S., Ertac  S., Mumcu  I. (2018). ‘Gender stereotypes in the classroom and effects on achievement’, The Review of Economics and Statistics, vol. 100(5), pp. 876–90. [Google Scholar]
  2. Almond  D., Edlund  L. (2008). ‘Son-biased sex ratios in the 2000 United States census’, Proceedings of the National Academy of Sciences, vol. 105(15), pp. 5681–2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Almond  D., Sun  Y. (2017). ‘Son-biased sex ratios in 2010 US census and 2011-2013 US natality data’, Social Science & Medicine, vol. 176, pp. 21–4. [DOI] [PubMed] [Google Scholar]
  4. Aucejo  E.M., James  J. (2019). ‘Catching up to girls: Understanding the gender imbalance in educational attainment within race’, Journal of Applied Econometrics, vol. 34(4), pp. 502–25. [Google Scholar]
  5. Autor  D., Figlio  D., Karbownik  K., Roth  J., Wasserman  M. (2016). ‘School quality and the gender gap in educational achievement’, American Economic Review, vol. 106, pp. 289–95. [Google Scholar]
  6. Autor  D., Figlio  D., Karbownik  K., Roth  J., Wasserman  M. (2019). ‘Family disadvantage and the gender gap in behavioral and educational outcomes’, American Economic Journal: Applied Economics, vol. 11(3), pp. 338–81. [Google Scholar]
  7. Bertrand  M. (2011). ‘New perspectives on gender’, in (Card  D., Ashenfelter  O., eds.), Handbook of Labor Economics, vol. 4, pp. 1543–90., Amsterdam: Elsevier. [Google Scholar]
  8. Bertrand  M., Pan  J. (2013). ‘The trouble with boys: Social influences and the gender gap in disruptive behavior’, American Economic Journal: Applied Economics, vol. 5(1), pp. 32–64. [Google Scholar]
  9. Black  S., Breining  S., Figlio  D., Guryan  J., Karbownik  K., Skyt Nielsen  H., Roth  J., Simonsen  M. (2021). ‘Sibling spillovers’, Economic Journal, vol. 131(633), pp. 101–28. [Google Scholar]
  10. Brenøe  A.A. (2021). ‘Brothers increase women’s gender conformity’, Journal of Population Economics, vol. 35, pp. 1859–96. [Google Scholar]
  11. Brenøe  A.A., Lundberg  S. (2018). ‘Gender gaps in the effects of childhood family environment: Do they persist into adulthood?’, European Economic Review, vol. 109, pp. 42–62. [Google Scholar]
  12. Buchmann  C., DiPrete  T.A. (2006). ‘The growing female advantage in college completion: The role of family background and academic achievement’, American Sociological Review, vol. 71(4), pp. 515–41. [Google Scholar]
  13. Butcher  K., Case  A. (1994). ‘The effect of sibling sex composition on women’s education and earnings’, Quarterly Journal of Economics, vol. 109(3), pp. 531–63. [Google Scholar]
  14. Chetty  R., Hendren  N., Lin  F., Majerovitz  J., Scuderi  B. (2016). ‘Childhood environment and gender gaps in adulthood’, American Economic Review, vol. 106, pp. 282–8. [Google Scholar]
  15. Cobb-Clark  D., Moschion  J. (2017). ‘Gender gaps in early educational achievement’, Journal of Population Economics, vol. 30(4), pp. 1093–134. [Google Scholar]
  16. Contini  D., Tommaso  M.L.D., Mendolia  S. (2017). ‘The gender gap in mathematics achievement: Evidence from Italian data’, Economics of Education Review, vol. 58, pp. 32–42. [Google Scholar]
  17. DiPrete  T.A., Jennings  J.L. (2012). ‘Social and behavioral skills and the gender gap in early educational achievement’, Social Science Research, vol. 41(1), pp. 1–15. [DOI] [PubMed] [Google Scholar]
  18. Ellison  G., Swanson  A. (2010). ‘The gender gap in secondary school mathematics at high achievement levels: Evidence from the American mathematics competitions’, Journal of Economic Perspectives, vol. 24(2), pp. 109–28. [Google Scholar]
  19. Figlio  D., Freese  J., Karbownik  K., Roth  J. (2017). ‘Socioeconomic status and genetic influences on cognitive development’, Proceedings of the National Academy of Sciences, vol. 114(51), pp. 13441–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Figlio  D.N., Guryan  J., Karbownik  K., Roth  J. (2014). ‘The effects of poor neonatal health on children’s cognitive development’, American Economic Review, vol. 104(12), pp. 3921–55. [DOI] [PubMed] [Google Scholar]
  21. Firpo  S., Fortin  N.M., Lemieux  T. (2009). ‘Unconditional quantile regressions’, Econometrica, vol. 77(3), pp. 953–73. [Google Scholar]
  22. Fryer  R.G., Levitt  S.D. (2010). ‘An empirical analysis of the gender gap in mathematics’, American Economic Journal: Applied Economics, vol. 2(2), pp. 210–40. [Google Scholar]
  23. Havnes  T., Mogstad  M. (2015). ‘Is universal child care leveling the playing field?’, Journal of Public Economics, vol. 127, pp. 100–14. [Google Scholar]
  24. Jacob  B.A. (2002). ‘Where the boys aren’t: Non-cognitive skills, returns to school and the gender gap in higher education’, Economics of Education Review, vol. 21, pp. 589–98. [Google Scholar]
  25. Karbownik  K., Özek  U. (2021). ‘Setting and good example? Examining sibling spillovers in educational achievement using a regression discontinuity design’, Journal of Human Resources, doi: 10.3368/jhr.58.5.0220-10740R1. [Google Scholar]
  26. Kinsler  J. (2011). ‘Understanding the black-white school discipline gap’, Economics of Education Review, vol. 30(6), pp. 1370–831. [Google Scholar]
  27. Le  H.T., Nguyen  H.T. (2018). ‘The evolution of the gender test score gap through seventh grade: New insights from Australia using unconditional quantile regression and decomposition’, IZA Journal of Labor Economics, vol. 7, pp. 1–42. [Google Scholar]
  28. Lee  D.S. (2009). ‘Training, wages, and sample selection: Estimating sharp bounds on treatment effects’, The Review of Economic Studies, vol. 76, pp. 1071–102. [Google Scholar]
  29. Lei  Z., Lundberg  S. (2020). ‘Vulnerable boys: Short-term and long-term gender differences in the impacts of adolescent disadvantage’, Journal of Economic Behavior and Organization, vol. 178, pp. 424–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lundberg  S. (2017). ‘Father absence and the educational gender gap’, Discussion Paper 10814, Institute of Labor Economics. [Google Scholar]
  31. Murnane  R.J. (2013). ‘U.S. high school graduation rates: Patterns and explanations’, Journal of Economic Literature, vol. 51(2), pp. 370–422. [Google Scholar]
  32. Peter  N., Lundborg  P., Mikkelsen  S., Webbink  D. (2018). ‘The effect of a sibling’s gender on earnings and family formation’, Labour Economics, vol. 54, pp. 61–78. [Google Scholar]
  33. Pope  D.G., Sydnor  J.R. (2010). ‘Geographic variation in the gender differences in test scores’, Journal of Economic Perspectives, vol. 24(2), pp. 95–108. [Google Scholar]
  34. Robinson  J.P., Lubienski  S.T. (2011). ‘The development of gender achievement gaps in mathematics and reading during elementary and middle school: Examining direct cognitive assessments and teacher ratings’, American Educational Research Journal, vol. 48(2), pp. 268–302. [Google Scholar]
  35. Ronda  V., Agerbo  E., Bleses  D., Mortensen  P.B., Borglum  A., Mors  O., Rosholm  M. (2022). ‘Family disadvantage, gender, and the returns to genetic human capital’, Scandinavian Journal of Economics, vol. 124(2), pp. 550–78. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

uead069_Online_Appendix
Click here for additional data file. (1.4MB, pdf)

Articles from Economic Journal (London, England) are provided here courtesy of Oxford University Press

RESOURCES