Abstract
Genetic studies on yield and yield quality are becoming benchmarks for farmers and industry in selecting and developing varieties. Evaluations that combine various stability statistics can provide more accurate information to select the ideal genotype. This study aims to identify the effect of genotype by environment interactions (GEIs) for yield and yield quality, to select high yield and stable sweet potato genotypes, as well as to select superior genotypes based on yield and yield quality. Three different environments in West Java, Indonesia, were used to test the sweet potato genotypes using a randomized block design that was repeated three times. Highly significant effects of sweet potato genotypes (G), environments (E), and GEIs were observed for yield and yield quality. The Combined ANOVA showed that GEIs effect contributed 54.88% for yield, 40.01% for sweetness, 10.46% for moisture content, 68.80% for tuber diameter, and 72.57% for tuber length from the sum of square. Five most high and stable yield on sweet potato genotypes identified by all measures, includes G4, G6, G7, G31, and G32. Genotype by yield*traits (GYT) selected seven genotypes that have superior in yield and yield quality, they were G7, G15, G4, G20, G6, G31, and G14. Based on stability measurements and GYT biplots, the genotypes G4, G6, G7, and G31 are in both slices. So that the four genotypes have high, stable yields, and have a good combination of traits for yield quality. Our findings can be used for improvement cultivation involving partner companies, partner institutions, and farmers, and the selected genotypes can be release as superior varieties candidate.
Keywords: Genotypes stability index (GSI), Production, Stability, Sweet potato
1. Introduction
Sweet potato (Ipomoea batatas [L.] Lam) is a commodity that has high commercial value. In Indonesia, many food industries have made sweet potatoes as their main raw material, especially in the West Java province [1]. The development of the food industry has resulted in a high demand for certain varieties/genotypes. However, the amount of demand is not proportional to the supply. Some of the reasons for this were (i) many varieties grown by farmers, but not according to industry standards, (ii) varieties that comply with industrial standards have decreased quality and productivity. According to Maulana et al. [2], the decline in sweet potato production was caused by several factors, including continuous land use without crop rotation, then continuous use of seeds without replanting. Therefore, new high yielding varieties are needed and in accordance with industry standards.
Multi-environments trials play an important role in selecting the superior genotypes in different locations. In multi-environments testing, genotypes are usually evaluated at several years, locations, and growing seasons. The development of new commercial genotypes, high yielding, and stable under a variety of environmental conditions is the main objective of plant breeding programs. The interpretation of genotypes performance is usually always influenced by large GEIs [[3], [4], [5], [6]]. The effect of GEIs decreases the relationship between genotype and phenotypic values, and also makes it difficult for breeders to select superior genotypes [[6], [7], [8]]. Therefore, interpreting GEIs in multilocation tests is very helpful in determining the stability of genotypes in diverse environments, or adaptive to specific environments [[8], [9], [10], [11]]. Numerous methods have been suggested to analyze GEIs, adaptability and stability of genotypes under diverse environmental conditions. Including parametric and non-parametric measurements, and visual measurements such as AMMI and GGE biplot [[12], [13], [14], [15], [16]]. Each of these measurements can complement each other for investigating and interpreting GEIs and genotype stability, ultimately leading to fairly clear information about these interactions as genotype sensitivity to the test environment [4,[17], [18], [19]].
Selection of stable and high yielding genotypes requires effective method of evaluation [5,10]. Multi-environment evaluation is a critical step in plant breeding programs that aims to select the ideal genotype in a wide range of environments. A method of evaluation that combines a variety parameter of stability could provide more accurate information to select the stable and high yielding genotype [6,10,13,20].
Each stability measure has its own advantages and disadvantages in explaining the phenomenon of the GEIs. Therefore, most breeding programs now integrate some of statistical measurements [10,13,20,21]. Planting the stable and high yield genotype in a diverse environments is one approach to increase sweet potato production in the country. Recently, a selection method has been developed to obtain superior genotypes based on a combination of yields and other traits, namely genotype by yield*traits (GYT) [22]. This method was considered effective in selecting genotypes based on a combination of many traits. Several researchers have succeeded in selecting superior genotypes using GYT biplots, including sweet potato [23], red spring wheat [24], durum wheat [25], barley [26], and sesame [27]. The use of this method will be improved the accuracy of genotypic selection based on multiple traits. The purpose of this study were to identify the effect of genotype by environment interactions (GEIs) for yield and yield quality, to select high yield and stable sweet potato genotypes, as well as to select superior genotypes based on yield and yield quality.
2. Materials and methods
2.1. Plant material and experimental design
The genetic materials used include 30 new breeding genotypes, and three commercial varieties as checks. These genotypes were the result of open pollination, where only the female parent was known. These tubers were previously selected based on tuber production in the initial growth phase, and based on preference level of the community and farmers.
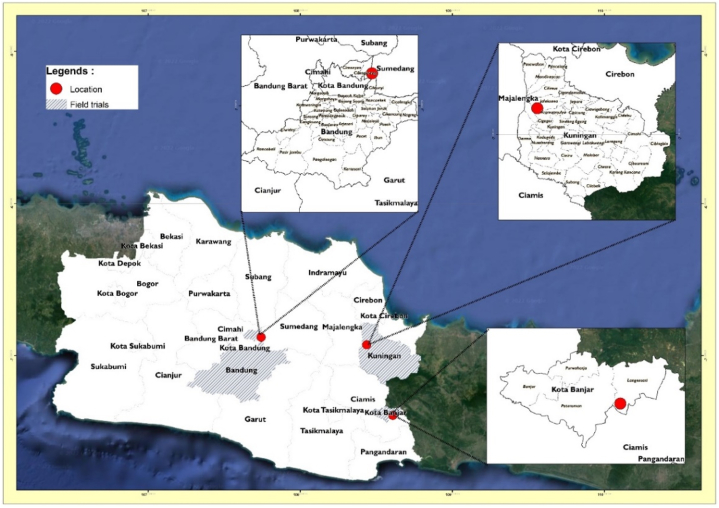
Field experiments were conducted in three environments in West Java, Indonesia: Kuningan (L1), Bandung (L2), and Banjar (L3). Information about the field trials presented in Table 1 and Fig. 1. The experiments were carried out using a randomized block design planting in three replications. Fertilization was applied using chicken dung at the rate of 5 tons ha−1 and NPK at 200 kg/ha in each location.
Table 1.
Variations across three environments during experiment.
| Kuningan | Bandung | Banjar | |
|---|---|---|---|
| Coordinates | 6°55′45.7″S 108°26′12.0″E | 6°52′45.5″S 107°44′36.8″E | 7°23′34.3″S 108°36′32.5″E |
| Altitudes (m.a.s.l.) | 782 | 753 | 16 |
| Type of agro-climate | B·II.2 | A.II.2 | B·II.3 |
| Temperature (OC) | |||
| Min. | 24.59 | 26.11 | 24.58 |
| Max. | 26.18 | 26.66 | 26.69 |
| Mean | 25.20 | 26.41 | 25.37 |
| Dry months per year (month) | 3–7 | 3–7 | 3–7 |
| Wet months per year (month) | 5–9 | 5–9 | 3–4 |
| Annual rainfall (mm) | 1.500–2.500 | >2.500 | 1.500–2.500 |
| Rainfall (mm/month) | |||
| Min. | 14.77 | 18.61 | 11.09 |
| Max. | 26.47 | 23.34 | 24.06 |
| Mean | 20.88 | 20.38 | 17.91 |
| Humidity (%) | |||
| Min. | 83.72 | 80.76 | 77.98 |
| Max. | 85.68 | 84.77 | 85.26 |
| Mean | 84.59 | 82.31 | 83.31 |
| Soil Parameters | |||
| pH H2O | 6.68 | 6.02 | 6.74 |
| C-Organic (%) (C) | 1.12 | 3.38 | 1.11 |
| Total Nitrogen (%) (N) | 0.18 | 0.21 | 0.12 |
| C/N | 6.22 | 16.01 | 9.25 |
| P2O5 HCl 25% (mg/100 g) | 90.5 | 1.87 | 66.7 |
| Potassium (K) | 0.21 | 1.02 | 0.18 |
Fig. 1.
Maps of multi-locations trial in West Java, Indonesia.
2.2. Data collection
The observed traits was tuber yield per plot and yield quality. The data were collected at the time of harvest. The weight (kg) of sample obtained from a 3 × 5 m2 plot of each genotype. Data was converted to ton ha−1.
2.3. Data analysis
An estimation of the GEIs was carried out for all genotypes. The statistical model for combined ANOVA of the environments was as follows:
| (1) |
where Yefgh is the value in plot h of genotype e, and the value in location f of each replication g; μ is the grand mean; Ge is the influence of genotype e; Ef is the influence of the location; GEef is the influence of interaction between genotype e and location f; Rg(f) is the influence of replicate g on location f; Bh(g) is the influence of repeat g on plot h; and εefgh is the influence error of genotype e in plot h and repeat g of location f, respectively.
Identification of the stable genotypes based on combined stability measurement using parametric and non-parametric stability components. Linear regressions following [28] method. Based on this component, genotype is indicated stable if a regression slope (bi) of 1 and a variance deviation (S2di) of 0. The mean variance component (θi) was estimated according to Ref. [29] with the formula:
| (2) |
The GE variance component (θ(i)) was calculated according to Ref. [30] as:
| (3) |
Wricke's ecovalence (Wi2) was calculated according to Ref. [31] as:
| (4) |
Shukla's stability variance was calculated according to Ref. [32] as:
| (5) |
and the coefficient of variance (CVi) was calculated according to Ref. [33] as:
| (6) |
where xij = yield of genotype i in location j; = yield of genotype i; = average yield of location j; = average overall yield; p and q = the number of genotypes and environments, respectively; and SDg = standard deviation of a genotype mean across locations.
Stability nonparametric (S(i)) components were applied according to Refs. [34,35] with the formula:
| (7) |
| (8) |
| (9) |
| (10) |
where rij = rank in location j from genotype i; = mean rank across all locations for each genotype; and N = the number of environments. Stability parameters (NP(i)) were calculated according to Ref. [36] as:
| (11) |
| (12) |
| (13) |
| (14) |
where = rank of genotype ‘I’ in location ‘j’ based on adjusted data; = median rank of adjusted data; Mdi = same parameter obtained from the unadjusted data; N = number of an location. Kang's nonparametric stability measure (KR) was assessed according to Ref. [37]. In this method, the yield performance and stability variance to identify stable and high-yielding genotypes were given weightings of 1. To calculate the parametric and nonparametric statistics, the online software STABILITYSOFT [38] was used. To select and to compare high yield based on combined analysis, the results of parametric and non-parametric stability measurements were grouped using hierarchical cluster analysis (dendrogram) based on the stability rank of each parameter. Dendrogram was estimated using SPSS v19 software [39].
Identification of stable genotypes using AMMI following the formula of [40]:
| (15) |
where: Yijk is the yield in location j from genotype i of replication k, is the average of grand yield, Gi is the influence of genotype i, Ej is the influence of the location j, λk is the value of primer component k, αik and γjk were the vector score for the genotype i and location j to component k, ρijr is a mistake from genotype i and location j. ASV, then, was estimated following the study of [41]:
| (16) |
Were: ss IPCA1, ss IPCA2 were the sum of square in IPCA 1 and 2, which shows the score of the main component because of the high contribution in genotype by location interactions. IPCA1 and IPCA2 were the first and second from IPCA scores for each genotype from the AMMI analysis.
The value of the Genotype Stability Index (GSI) of each sweet potato genotype was calculated based on the gth genotype rank in three environments based on ASV Rank (RASV) and gth genotype rank based on the average yield in three environments (RAY) with the following equation:
| (17) |
The model for GGE biplot following [42] with the formula:
| (18) |
where Ῡef; μe; βf; k; λg; αeg and γfh; εef are the performance in location ‘f’ from genotype ‘e’; overall average yield; the influence of location ‘f’; number of primer components; the singular value from primer component ‘g’; value of genotype ‘e’ and location ‘f’ for primer component ‘g’; and the error of the genotype ‘e’ in location ‘f’, respectively.
To select the best sweet potato genotype based on multi-traits (yield and yield quality), we used genotype by yield*traits (GYT) measurement. The formula of genotype by yield*traits (GYT) follows [22]. To calculate GYT, we used the R program software v3.6.3 [43].
3. Results
3.1. Genotype by environment interactions on yield and yield quality of sweet potato
The yield and yield quality of 33 sweet potato genotypes at three locations were evaluated. The results of the combined ANOVA showed that genotype, environment, and GEIs had a significant effect on the variation in the yield and yield quality of each genotype tested. The six new sweet potato genotypes had higher yields than all check varieties (Rancing, AC-putih, and Ayamurasaki). Kuningan (L1) had a higher average yield than other locations (29.10 ton ha−1). The mean yield of the sweet potatoes ranged from 7.71 to 40.27 ton ha−1 (Table 2). Average yields ranged from 1.78 ton ha−1 (L2) to 77.79 ton ha−1 (L1), while the average yield at the three locations was 25.18 ton ha−1. On sweetness level there were no genotypes that exceeded rancing, but there were six genotypes that exceeded two check varieties (AC-putih and Ayamurasaki). The moisture content (MC) trait was preferred which has a smaller value, in this study there were three genotypes that had a lower value than all check varieties, namely F1(2)Kuput (58.63%), F1(2)NK102 (56.67%), and F1 (7)GKAW(58.37%).
Table 2.
Combined variance analysis on 33 sweet potato in three environments.
| Source | df | Yield (tons.ha−1) |
Sweetness (oBrix) |
Moisture Content (%) |
Tuber Diameter (cm) |
Tuber Length (cm) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SS | %TSS | SS | %TSS | SS | %TSS | SS | %TSS | SS | %TSS | |||||||
| Genotypes (G) | 32 | 17656.00 | ** | 34.41 | 48.90 | ** | 39.66 | 5969.00 | ** | 88.72 | 139.80 | ** | 32.79 | 812.00 | * | 26.33 |
| Environments (E) | 2 | 2643.00 | * | 5.15 | 237.40 | * | 19.34 | 35.00 | * | 0.52 | 7.40 | * | 1.74 | 4.00 | ns | 0.13 |
| Block (E) | 6 | 2850.00 | ** | 5.55 | 12.20 | ns | 0.99 | 20.00 | ns | 0.30 | 2.90 | ns | 0.68 | 30.00 | ns | 0.97 |
| GEIs | 64 | 28157.00 | ** | 54.88 | 491.20 | ** | 40.01 | 704.00 | ** | 10.46 | 276.30 | ** | 64.80 | 2238.00 | ** | 72.57 |
| Error | 192 | 3506.00 | * | 310.10 | * | 409.00 | * | 205.60 | * | 3086.00 | * | |||||
| Mean | 25.18 | 8.73 | 65.78 | 5.08 | 18.67 | |||||||||||
| SD | 13.58 | 2.26 | 4.85 | 1.46 | 4.50 | |||||||||||
| CV (%) | 16.99 | 13.88 | 1.78 | 20.52 | 28.28 | |||||||||||
*p < 0.05; **p < 0.01; SD = Standard Deviation; CV = Coefficient of Variations; SS = Sum of Square; GEIs = Genotype-by-environment interactions.
In the tuber length trait, there were no genotypes that exceeded the three checks, but there were 25 genotypes that exceeded AC-putih and Ayamurasaki. The tuber length is in the range of 11.67 cm–29.20 cm, where Bandung has the highest average length (18.77 cm) and the lowest is Kuningan (18.47 cm). There were also no genotypes that exceeded three checks in tuber diameter, but there were five genotypes that exceeded Rancing and Ayamurasaki. Sweet potato diameter was in the range of 2.73 cm–8.00 cm, where Banjar had the highest average diameter (5.27 cm) and Bandung (4.87 cm). The difference in yield and yield quality between each genotype is very significant. The highly significant effect of the trial site and the tested genotypes was reflected in the significance of the GEIs for yield and yield quality. The each factor contributes differently to sweet potato variability, location (E) contributed 5.15% for yield, 19.34% for sweetness, 0.52% for MC, and 1.74% for tuber diameter; genotype (G) contributed 34.41% for yield, 39.66% for sweetness, 88.72% for MC, 32.79% for tuber diameter, and 26.33% for tuber length; and their interactions (GEIs) contributed 54.88% for yield, 40.01% for sweetness, 10.46% for MC, 68.80 for tuber diameter, and 72.57% for tuber length from the sum of square (Table 2). The results showed that GEIs had the greatest influence on yield, sweetness, tuber length, and tuber diameter. While in MC trait, the effect of GEIs showed the greatest contribution after genotype. In multi-environment testing, the emergence of GEIs requires researchers to conducted stability analysis. In this case, the stability analysis was only carried out on the yield. Yield stability is one of the traits taken into consideration for the release of varieties in Indonesia.
3.2. Combined stability measurement of yield of sweet potato genotypes
The results of the yield stability and rank stability were presented based on parametric measurements in Table 3 and Table 4, and non-parametric measurements in Table 5 and Table 6. Based on the four tables, each measurement shows a difference in evaluating the yield stability of the sweet potato genotypes. The high significantly of the main effect of genotypes and GEIs on yields (p < 0.01), showed that the yield was the first parameter to evaluated the sweet potato genotypes tested. In this study, genotypes G20, G15, G6, G4 and G7 had the highest and G17, G10, G8, G28 and G29 had the lowest mean yields across three environments (Table 3). Genotype G1 with regression coefficient (bi) = 1 is the most stable. Genotypes with a regression coefficient of bi > 1, i.e. G3, G4, G6, G7, G11, G14, G15, G16, G19, G20, G21, G24, G26, G31, and G32, showed that the yield performance above an average overall yield, as well as adapt to a specific favorable environment; meanwhile, the other genotypes that had the bi < 1 and the lowest yield, were less adapted to various test environments or had specific adaptations to the unfavorable environment. At the regression deviation (S2di), the genotypes that had high yields (more than the overall mean yield) had the highest variance ranks. Based on these measurements, G3 with the ranking of 3 and 4, G4 with the ranking of 4 and 7, and G32 with the ranking of 8 and 5 in mean yield and S2di, respectively, had a better combination of yield and stability statistics. Other several measurements that select the same most stable genotype, i.e. G6 by KR and CVi. G23 by S(1), S(2), S(3), S(6), NP(1), NP(2), NP(4), Wi2, σ2ᵢ, and θ₍ᵢ₎ (Table 5, Table 6). The Wi2, σ2ᵢ, and θ₍ᵢ₎ measures had the same rank's of stable for all genotypes (Table 5).
Table 3.
Parametric stability analysis of 33 sweet potato in three environments.
| Code | Genotypes | Y | Wᵢ2 | σ2ᵢ | s2dᵢ | bᵢ | CVi | θ₍ᵢ₎ | θᵢ |
|---|---|---|---|---|---|---|---|---|---|
| G1 | F1(3)NK102 | 25.04 | 397.69 | 137.47 | 56.81 | 1.00 | 92.03 | 112.33 | 126.72 |
| G2 | F1(3)NIR B | 24.49 | 185.98 | 62.35 | 24.77 | 0.84 | 72.31 | 114.68 | 90.34 |
| G3 | F1(4)C2J-01 | 33.27 | 1000.77 | 351.46 | 142.75 | 1.06 | 91.35 | 105.64 | 230.38 |
| G4 | F1(5)KUPUT | 35.70 | 150.00 | 49.58 | 14.15 | 1.32 | 67.23 | 115.08 | 84.15 |
| G5 | F1(21)NK102 | 21.66 | 80.05 | 24.76 | 10.16 | 0.87 | 75.25 | 115.85 | 72.13 |
| G6 | F1(1)HAR | 35.82 | 103.94 | 33.23 | 5.02 | 1.37 | 67.21 | 115.59 | 76.23 |
| G7 | F1(2)KUPUT | 35.04 | 202.06 | 68.05 | 23.55 | 1.27 | 68.69 | 114.50 | 93.10 |
| G8 | F1(15)T3 | 16.37 | 353.26 | 121.70 | 44.24 | 0.71 | 111.24 | 112.82 | 119.09 |
| G9 | F1(7)KUMEROT | 19.12 | 344.96 | 118.76 | 49.12 | 0.95 | 113.91 | 112.92 | 117.66 |
| G10 | F1(18)KUMEROT | 9.39 | 197.03 | 66.27 | 0.08 | 0.37 | 69.12 | 114.56 | 92.24 |
| G11 | F1(36)HAR | 27.18 | 123.87 | 40.30 | 15.59 | 1.17 | 80.03 | 115.37 | 79.66 |
| G12 | F1(4)BRAS2 | 24.57 | 377.59 | 130.34 | 53.58 | 0.93 | 89.04 | 112.55 | 123.27 |
| G13 | F1(1.15)NAR | 20.48 | 235.21 | 79.81 | 27.77 | 0.71 | 79.80 | 114.13 | 98.80 |
| G14 | F1(1.3)NAR | 33.35 | 312.57 | 107.26 | 33.45 | 1.40 | 80.35 | 113.27 | 112.09 |
| G15 | F1(2)NK102 | 38.13 | 286.44 | 97.99 | 22.59 | 1.51 | 72.70 | 113.56 | 107.60 |
| G16 | F1(7)CDG-01 | 28.95 | 262.49 | 89.49 | 33.16 | 1.25 | 84.59 | 113.83 | 103.49 |
| G17 | F1(6)SITAK | 7.71 | 244.70 | 83.18 | 0.22 | 0.30 | 69.21 | 114.03 | 100.43 |
| G18 | F1(17)KUMEROT | 22.02 | 204.18 | 68.80 | 24.33 | 0.74 | 73.80 | 114.48 | 93.46 |
| G19 | F1(14)LAD | 21.73 | 193.73 | 65.09 | 27.67 | 1.01 | 94.07 | 114.59 | 91.67 |
| G20 | F1(18)T3 | 40.27 | 2481.32 | 876.82 | 300.77 | 1.87 | 118.65 | 89.23 | 484.85 |
| G21 | F1(43)HAR | 30.93 | 391.85 | 135.40 | 53.73 | 1.18 | 81.49 | 112.40 | 125.72 |
| G22 | F1(14)GKAW | 26.75 | 234.59 | 79.60 | 33.43 | 0.97 | 76.25 | 114.14 | 98.69 |
| G23 | F1(2)AMBEU | 19.71 | 51.67 | 14.69 | 4.10 | 0.79 | 71.92 | 116.17 | 67.25 |
| G24 | F1(10)HAR | 25.78 | 195.05 | 65.56 | 27.14 | 1.10 | 84.39 | 114.58 | 91.89 |
| G25 | F1(5)CDRA-02 | 19.49 | 523.16 | 181.99 | 64.06 | 0.61 | 99.74 | 110.94 | 148.29 |
| G26 | F1(2)Ayamurasaki | 28.68 | 252.57 | 85.97 | 30.68 | 1.27 | 86.16 | 113.94 | 101.78 |
| G27 | F1(38)HAR | 21.86 | 254.85 | 86.78 | 34.23 | 0.83 | 84.97 | 113.91 | 102.17 |
| G28 | F1(7)GKAW | 16.80 | 155.51 | 51.53 | 17.38 | 0.74 | 91.32 | 115.02 | 85.10 |
| G29 | F1(23)LAD | 18.85 | 251.00 | 85.42 | 31.45 | 0.75 | 91.72 | 113.96 | 101.51 |
| G30 | F1(30)CIA | 19.14 | 370.71 | 127.89 | 41.54 | 0.60 | 87.40 | 112.63 | 122.09 |
| G31 | Rancing | 31.12 | 154.54 | 51.19 | 14.22 | 1.33 | 77.80 | 115.03 | 84.93 |
| G32 | AC Putih | 31.48 | 78.53 | 24.22 | 5.25 | 1.29 | 72.15 | 115.87 | 71.87 |
| G33 | Ayamurasaki | 20.16 | 205.00 | 69.09 | 28.71 | 0.91 | 94.89 | 114.47 | 93.60 |
Table 4.
Rank's of parametric and non-parametric stability analysis of 33 sweet potato in three environments.
| Code | Genotypes | Y | Wᵢ2 | σ2ᵢ | s2dᵢ | bi | CVi | θ₍ᵢ₎ | θᵢ |
|---|---|---|---|---|---|---|---|---|---|
| G1 | F1(3)NK102 | 16 | 30 | 30 | 30 | 16 | 27 | 30 | 4 |
| G2 | F1(3)NIR B | 18 | 9 | 9 | 14 | 22 | 8 | 9 | 25 |
| G3 | F1(4)C2J-01 | 7 | 32 | 32 | 32 | 14 | 25 | 32 | 2 |
| G4 | F1(5)KUPUT | 4 | 6 | 6 | 7 | 6 | 2 | 6 | 28 |
| G5 | F1(21)NK102 | 22 | 3 | 3 | 6 | 21 | 11 | 3 | 31 |
| G6 | F1(1)HAR | 3 | 4 | 4 | 4 | 4 | 1 | 4 | 30 |
| G7 | F1(2)KUPUT | 5 | 13 | 13 | 12 | 9 | 3 | 13 | 21 |
| G8 | F1(15)T3 | 31 | 26 | 26 | 26 | 29 | 31 | 26 | 8 |
| G9 | F1(7)KUMEROT | 28 | 25 | 25 | 27 | 18 | 32 | 25 | 9 |
| G10 | F1(18)KUMEROT | 32 | 12 | 12 | 1 | 32 | 4 | 12 | 22 |
| G11 | F1(36)HAR | 13 | 5 | 5 | 9 | 12 | 15 | 5 | 29 |
| G12 | F1(4)BRAS2 | 17 | 28 | 28 | 28 | 19 | 23 | 28 | 6 |
| G13 | F1(1.15)NAR | 23 | 17 | 17 | 17 | 28 | 14 | 17 | 17 |
| G14 | F1(1.3)NAR | 6 | 24 | 24 | 23 | 3 | 16 | 24 | 10 |
| G15 | F1(2)NK102 | 2 | 23 | 23 | 11 | 2 | 9 | 23 | 11 |
| G16 | F1(7)CDG-01 | 11 | 22 | 22 | 21 | 10 | 19 | 22 | 12 |
| G17 | F1(6)SITAK | 33 | 18 | 18 | 2 | 33 | 5 | 18 | 16 |
| G18 | F1(17)KUMEROT | 19 | 14 | 14 | 13 | 27 | 10 | 14 | 20 |
| G19 | F1(14)LAD | 21 | 10 | 10 | 16 | 15 | 28 | 10 | 24 |
| G20 | F1(18)T3 | 1 | 33 | 33 | 33 | 1 | 33 | 33 | 1 |
| G21 | F1(43)HAR | 10 | 29 | 29 | 29 | 11 | 17 | 29 | 5 |
| G22 | F1(14)GKAW | 14 | 16 | 16 | 22 | 17 | 12 | 16 | 18 |
| G23 | F1(2)AMBEU | 25 | 1 | 1 | 3 | 24 | 6 | 1 | 33 |
| G24 | F1(10)HAR | 15 | 11 | 11 | 15 | 13 | 18 | 11 | 23 |
| G25 | F1(5)CDRA-02 | 26 | 31 | 31 | 31 | 30 | 30 | 31 | 3 |
| G26 | F1(2)Ayamurasaki | 12 | 20 | 20 | 19 | 8 | 21 | 20 | 14 |
| G27 | F1(38)HAR | 20 | 21 | 21 | 24 | 23 | 20 | 21 | 13 |
| G28 | F1(7)GKAW | 30 | 8 | 8 | 10 | 26 | 24 | 8 | 26 |
| G29 | F1(23)LAD | 29 | 19 | 19 | 20 | 25 | 26 | 19 | 15 |
| G30 | F1(30)CIA | 27 | 27 | 27 | 25 | 31 | 22 | 27 | 7 |
| G31 | Rancing | 9 | 7 | 7 | 8 | 5 | 13 | 7 | 27 |
| G32 | AC Putih | 8 | 2 | 2 | 5 | 7 | 7 | 2 | 32 |
| G33 | Ayamurasaki | 24 | 15 | 15 | 18 | 20 | 29 | 15 | 19 |
Table 5.
Non-parametric stability analysis of 33 sweet potato in three environments.
| Code | Genotypes | S⁽1⁾ | S⁽2⁾ | S⁽³⁾ | S⁽⁶⁾ | NP⁽1⁾ | NP⁽2⁾ | NP⁽³⁾ | NP⁽⁴⁾ | KR |
|---|---|---|---|---|---|---|---|---|---|---|
| G1 | F1(3)NK102 | 13.00 | 103.33 | 17.22 | 1.67 | 7.75 | 0.46 | 0.54 | 0.72 | 46.00 |
| G2 | F1(3)NIR B | 7.17 | 42.92 | 7.69 | 1.16 | 6.00 | 0.19 | 0.47 | 0.43 | 27.00 |
| G3 | F1(4)C2J-01 | 15.33 | 171.33 | 22.35 | 1.65 | 13.00 | 0.45 | 0.58 | 0.67 | 39.00 |
| G4 | F1(5)KUPUT | 5.67 | 25.67 | 2.91 | 0.57 | 8.25 | 0.30 | 0.33 | 0.21 | 10.00 |
| G5 | F1(21)NK102 | 4.17 | 10.92 | 2.15 | 0.72 | 5.25 | 0.22 | 0.35 | 0.27 | 25.00 |
| G6 | F1(1)HAR | 13.33 | 134.67 | 20.20 | 1.70 | 5.25 | 0.39 | 0.38 | 0.67 | 7.00 |
| G7 | F1(2)KUPUT | 9.33 | 57.67 | 7.69 | 0.93 | 6.25 | 0.38 | 0.38 | 0.41 | 18.00 |
| G8 | F1(15)T3 | 8.67 | 51.00 | 14.57 | 2.10 | 8.25 | 1.00 | 1.03 | 0.83 | 57.00 |
| G9 | F1(7)KUMEROT | 17.67 | 192.67 | 34.00 | 2.71 | 11.50 | 0.68 | 0.69 | 1.04 | 53.00 |
| G10 | F1(18)KUMEROT | 4.00 | 13.67 | 7.45 | 2.00 | 7.25 | 2.38 | 1.61 | 0.73 | 44.00 |
| G11 | F1(36)HAR | 8.33 | 43.00 | 6.29 | 0.98 | 5.50 | 0.32 | 0.36 | 0.41 | 18.00 |
| G12 | F1(4)BRAS2 | 11.17 | 81.58 | 13.41 | 1.48 | 7.50 | 0.33 | 0.53 | 0.61 | 45.00 |
| G13 | F1(1.15)NAR | 9.83 | 67.58 | 18.02 | 2.09 | 8.00 | 0.94 | 0.73 | 0.87 | 40.00 |
| G14 | F1(1.3)NAR | 15.50 | 145.58 | 23.93 | 2.14 | 9.75 | 0.54 | 0.58 | 0.85 | 30.00 |
| G15 | F1(2)NK102 | 9.00 | 49.00 | 6.00 | 0.90 | 9.00 | 0.36 | 0.43 | 0.37 | 25.00 |
| G16 | F1(7)CDG-01 | 10.67 | 81.33 | 10.61 | 1.13 | 10.00 | 0.36 | 0.47 | 0.46 | 33.00 |
| G17 | F1(6)SITAK | 13.50 | 173.58 | 56.30 | 4.27 | 7.50 | 4.25 | 1.04 | 1.46 | 51.00 |
| G18 | F1(17)KUMEROT | 8.67 | 46.00 | 10.62 | 1.69 | 6.25 | 0.44 | 0.64 | 0.67 | 33.00 |
| G19 | F1(14)LAD | 8.83 | 50.92 | 12.47 | 1.71 | 7.00 | 0.74 | 0.66 | 0.72 | 31.00 |
| G20 | F1(18)T3 | 18.67 | 225.67 | 34.72 | 2.56 | 13.25 | 0.59 | 0.71 | 0.96 | 34.00 |
| G21 | F1(43)HAR | 11.00 | 89.00 | 11.36 | 1.15 | 10.25 | 0.39 | 0.47 | 0.47 | 39.00 |
| G22 | F1(14)GKAW | 11.17 | 82.92 | 16.31 | 1.67 | 6.25 | 0.48 | 0.56 | 0.73 | 30.00 |
| G23 | F1(2)AMBEU | 2.50 | 4.25 | 0.96 | 0.42 | 3.50 | 0.17 | 0.36 | 0.19 | 26.00 |
| G24 | F1(10)HAR | 11.17 | 78.92 | 16.61 | 2.04 | 7.25 | 0.56 | 0.60 | 0.78 | 26.00 |
| G25 | F1(5)CDRA-02 | 14.50 | 154.25 | 28.48 | 2.65 | 12.25 | 0.65 | 0.77 | 0.89 | 57.00 |
| G26 | F1(2)Ayamurasaki | 12.00 | 87.33 | 13.79 | 1.58 | 9.25 | 0.41 | 0.54 | 0.63 | 32.00 |
| G27 | F1(38)HAR | 10.50 | 72.25 | 12.57 | 1.68 | 8.50 | 0.43 | 0.54 | 0.61 | 41.00 |
| G28 | F1(7)GKAW | 15.50 | 153.58 | 31.24 | 2.24 | 6.25 | 0.72 | 0.55 | 1.05 | 38.00 |
| G29 | F1(23)LAD | 9.67 | 59.33 | 13.69 | 2.00 | 10.50 | 0.52 | 0.81 | 0.74 | 48.00 |
| G30 | F1(30)CIA | 10.17 | 85.58 | 17.41 | 1.86 | 7.00 | 0.53 | 0.69 | 0.69 | 54.00 |
| G31 | Rancing | 10.17 | 66.25 | 7.72 | 0.97 | 6.50 | 0.45 | 0.28 | 0.39 | 16.00 |
| G32 | AC Putih | 14.50 | 150.25 | 24.70 | 1.92 | 5.25 | 0.42 | 0.31 | 0.79 | 10.00 |
| G33 | Ayamurasaki | 10.67 | 68.67 | 18.73 | 2.36 | 7.75 | 0.88 | 0.77 | 0.97 | 39.00 |
Table 6.
Rank's of non-parametric stability analysis of 33 sweet potato in three environments.
| Code | Genotypes | S⁽1⁾ | S⁽2⁾ | S⁽³⁾ | S⁽⁶⁾ | NP⁽1⁾ | NP⁽2⁾ | NP⁽³⁾ | NP⁽⁴⁾ | KR | SR | AR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | F1(3)NK102 | 24 | 24 | 21 | 14 | 18 | 18 | 16 | 19 | 27 | 364 | 21.41 |
| G2 | F1(3)NIR B | 5 | 5 | 7 | 10 | 6 | 2 | 12 | 8 | 11 | 180 | 10.59 |
| G3 | F1(4)C2J-01 | 29 | 30 | 26 | 13 | 32 | 17 | 19 | 14 | 20 | 376 | 22.12 |
| G4 | F1(5)KUPUT | 4 | 4 | 3 | 2 | 21 | 4 | 3 | 2 | 2 | 110 | 6.47 |
| G5 | F1(21)NK102 | 3 | 2 | 2 | 3 | 2 | 3 | 4 | 3 | 7 | 129 | 7.59 |
| G6 | F1(1)HAR | 25 | 25 | 25 | 18 | 2 | 10 | 7 | 14 | 1 | 181 | 10.65 |
| G7 | F1(2)KUPUT | 11 | 11 | 8 | 5 | 7 | 9 | 8 | 7 | 5 | 160 | 9.41 |
| G8 | F1(15)T3 | 7 | 10 | 18 | 26 | 21 | 31 | 31 | 25 | 32 | 404 | 23.76 |
| G9 | F1(7)KUMEROT | 32 | 32 | 31 | 32 | 30 | 26 | 25 | 31 | 30 | 458 | 26.94 |
| G10 | F1(18)KUMEROT | 2 | 3 | 6 | 22 | 14 | 32 | 33 | 20 | 25 | 284 | 16.71 |
| G11 | F1(36)HAR | 6 | 6 | 5 | 7 | 5 | 5 | 6 | 6 | 5 | 144 | 8.47 |
| G12 | F1(4)BRAS2 | 20 | 19 | 15 | 11 | 16 | 6 | 13 | 12 | 26 | 315 | 18.53 |
| G13 | F1(1.15)NAR | 13 | 14 | 23 | 25 | 20 | 30 | 27 | 27 | 23 | 352 | 20.71 |
| G14 | F1(1.3)NAR | 30 | 26 | 27 | 27 | 26 | 22 | 20 | 26 | 12 | 346 | 20.35 |
| G15 | F1(2)NK102 | 10 | 8 | 4 | 4 | 24 | 8 | 9 | 4 | 7 | 182 | 10.71 |
| G16 | F1(7)CDG-01 | 17 | 18 | 10 | 8 | 27 | 7 | 10 | 9 | 16 | 261 | 15.35 |
| G17 | F1(6)SITAK | 26 | 31 | 33 | 33 | 16 | 33 | 32 | 33 | 29 | 409 | 24.06 |
| G18 | F1(17)KUMEROT | 7 | 7 | 11 | 17 | 7 | 15 | 22 | 14 | 16 | 247 | 14.53 |
| G19 | F1(14)LAD | 9 | 9 | 13 | 19 | 12 | 28 | 23 | 18 | 14 | 279 | 16.41 |
| G20 | F1(18)T3 | 33 | 33 | 32 | 30 | 33 | 24 | 26 | 29 | 18 | 426 | 25.06 |
| G21 | F1(43)HAR | 19 | 23 | 12 | 9 | 28 | 11 | 11 | 10 | 20 | 302 | 17.76 |
| G22 | F1(14)GKAW | 20 | 20 | 19 | 15 | 7 | 19 | 18 | 21 | 12 | 282 | 16.59 |
| G23 | F1(2)AMBEU | 1 | 1 | 1 | 1 | 1 | 1 | 5 | 1 | 9 | 115 | 6.76 |
| G24 | F1(10)HAR | 20 | 17 | 20 | 24 | 14 | 23 | 21 | 23 | 9 | 288 | 16.94 |
| G25 | F1(5)CDRA-02 | 27 | 29 | 29 | 31 | 31 | 25 | 28 | 28 | 32 | 473 | 27.82 |
| G26 | F1(2)Ayamurasaki | 23 | 22 | 17 | 12 | 25 | 12 | 14 | 13 | 15 | 287 | 16.88 |
| G27 | F1(38)HAR | 16 | 16 | 14 | 16 | 23 | 14 | 15 | 11 | 24 | 312 | 18.35 |
| G28 | F1(7)GKAW | 30 | 28 | 30 | 28 | 7 | 27 | 17 | 32 | 19 | 358 | 21.06 |
| G29 | F1(23)LAD | 12 | 12 | 16 | 22 | 29 | 20 | 30 | 22 | 28 | 363 | 21.35 |
| G30 | F1(30)CIA | 14 | 21 | 22 | 20 | 12 | 21 | 24 | 17 | 31 | 375 | 22.06 |
| G31 | Rancing | 14 | 13 | 9 | 6 | 11 | 16 | 1 | 5 | 4 | 162 | 9.53 |
| G32 | AC Putih | 27 | 27 | 28 | 21 | 2 | 13 | 2 | 24 | 2 | 211 | 12.41 |
| G33 | Ayamurasaki | 17 | 15 | 24 | 29 | 18 | 29 | 29 | 30 | 20 | 366 | 21.53 |
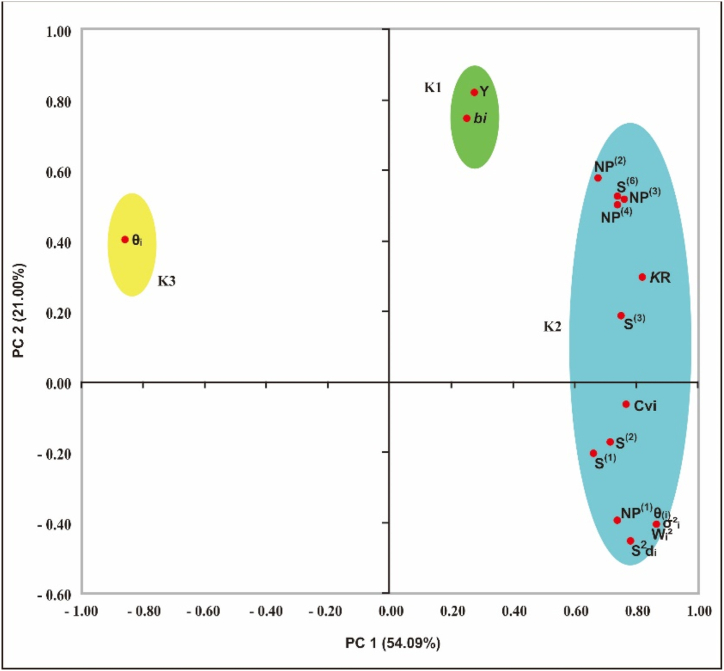
Fig. 1 presents the biplot of Principal component analysis (PCA), which shows the relationship between each measurement in a clear group. The resulting variation from the first PC with eigenvalues >1 for yield, parametric and non-parametric measures was 89.33% of the total variation. The first two components have the highest eigenvalues, so a biplot diagrams for the yield and stability measures was drawn based on PC1 and PC2 (Fig. 2). Fig. 2 shows the stability measurements were classified into two main groups for yield: (1) K1, which included yield (Y) and bi stability measure, (2) K2, which included S(1), S(2), S(3), S(6), NP(1), NP(2), NP(3), NP(4), KR, CVi, S2di, and θ₍ᵢ₎ stability measures. By contrast, the stability measure θᵢ was separate from all groups, being in quadrants 2.
Fig. 2.
Biplot of PCA for interpreting the relationships between non-parametric and parametric stability measurements, and yield on 33 sweet potato genotypes in three environments of West Java, Indonesia.
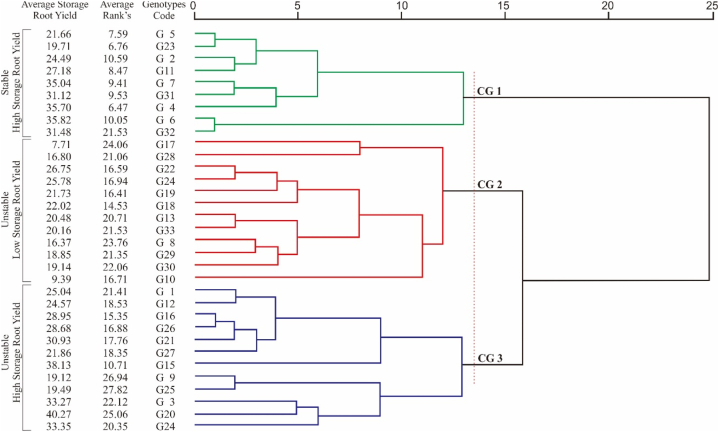
Dendrogram was used to classify the genotypes tested into clear clusters. Fig. 3 separates the sweet potato genotypes into three main clusters. The first cluster (CG 1) consisted of genotypes G2, G4, G5, G6, G7, G11, G23, G31, and G32, which had a higher average yield and had low average stability ranks. They were the stable genotypes with high yields. The second group (CG 2) comprised of genotypes, G8, G10, G13, G17, G18, G19, G22, G24, G28, G29, G30, and G33, which were unstable genotypes and had low yields and highest average rank; The third group (CG 3) consisted of genotypes G1, G3, G9, G12, G14, G15, G16, G20, G21, G25, G26, and G27, which were unstable genotypes but had high yields and highest average rank.
Fig. 3.
Dendrogram of yield on 33 sweet potato genotype based on stability rank's.
3.3. The yield stability of sweet potato genotype based on biplot analysis using AMMI, genotype stability index (GSI), and GGE biplot
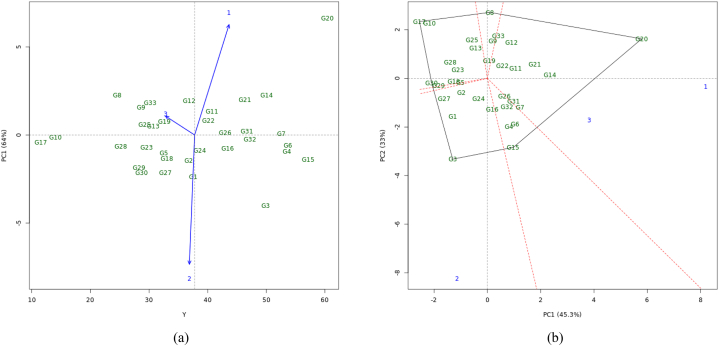
Fig. 4 shows the results of stability analysis used AMMI (Fig. 4a) and GGE biplots (Fig. 4b). In Fig. 4a, the horizontal line shows zero interaction with the environment (PCA1). Sweet potato genotypes close to the line have a small GEIs effect or stable. The vertical center line represents the average value of sweet potato yield. Genotypes on the right-hand side have higher yields (above the overall average) compared to those on the left-hand side.
Fig. 4.
Biplot analysis of the yield stability in three environments of West Java, Indonesia (a) stability genotypes based on AMMI Model for the PC1 score; (b) stability genotypes based on GGE biplot analysis; 1 = Kuningan, 2 = Bandung, and 3 = Banjar; PC: principle component.
There were 15 genotypes showed higher yields than the others, although only ten (10) genotypes were seen to be close to the stability line, i.e. G3, G4, G6, G7, G15, G16, G20, G26, G31 and G32 (Fig. 4a). Bandung (L2) has a positive PC1 score and a long environmental vector, indicating that there was a small GEIs. Nearly all of the genotypes performed well at this location (L2). Genotypes G7, G26, and G31 showed a high degree of stability and has low environmental effect, with PC1 values close to zero and Kuningan (L1) was the most preferred location. Banjar (L3) has a small PC1 and a large PC2, indicating that this location has a large environmental effect, so that the difference of yield between each genotype tested was biased. The best locations for genotype selection were L1 (Kuningan) and L2 (Bandung), because of the high yield stability. The genotypes with high yields were genotypes G3 and G20.
In Table 7, the information on genotype stability index (GSI) testing was presented. In this test, the genotype that has a small GSI value was a stable genotype with high yields. The results of GSI showed that there were several genotypes that was declared stable and high yields, i.e. G6, G4, G32, G15, G7, G31, and G11. The seven genotypes had the smallest GSI values and had yield above the overall average (>25.18 ton ha−1).
Table 7.
Stability analysis based on AMMI Stability Value (ASV) and Genotypes Stability Index (GSI).
| Code | Genotypes | IPCAg [1] | IPCAg [2] | ASV | RASV | AY | RAY | GSI | RGSI |
|---|---|---|---|---|---|---|---|---|---|
| G1 | F1(3)NK102 | 1.95 | 1.34 | 2.92 | 30 | 25.04 | 16 | 46 | 27 |
| G2 | F1(3)NIR B | 1.18 | −1.16 | 1.95 | 15 | 24.49 | 18 | 33 | 14 |
| G3 | F1(4)C2J-01 | 3.27 | −1.47 | 4.59 | 32 | 33.27 | 7 | 39 | 23 |
| G4 | F1(5)KUPUT | 0.75 | −0.63 | 1.18 | 6 | 35.70 | 4 | 10 | 2 |
| G5 | F1(21)NK102 | 0.83 | 0.55 | 1.23 | 7 | 21.66 | 22 | 29 | 8 |
| G6 | F1(1)HAR | 0.49 | −0.11 | 0.66 | 3 | 35.82 | 3 | 6 | 1 |
| G7 | F1(2)KUPUT | −0.05 | −1.49 | 1.49 | 10 | 35.04 | 5 | 15 | 5 |
| G8 | F1(15)T3 | −1.85 | −0.71 | 2.57 | 26 | 16.37 | 31 | 57 | 32 |
| G9 | F1(7)KUMEROT | −1.27 | 1.82 | 2.49 | 25 | 19.12 | 28 | 53 | 30 |
| G10 | F1(18)KUMEROT | 0.10 | −0.39 | 0.42 | 1 | 9.39 | 32 | 33 | 15 |
| G11 | F1(36)HAR | −1.10 | 0.68 | 1.62 | 11 | 27.18 | 13 | 24 | 7 |
| G12 | F1(4)BRAS2 | −1.57 | −1.79 | 2.76 | 29 | 24.57 | 17 | 46 | 28 |
| G13 | F1(1.15)NAR | −0.41 | −1.88 | 1.96 | 16 | 20.48 | 23 | 39 | 24 |
| G14 | F1(1.3)NAR | −1.84 | 0.06 | 2.45 | 24 | 33.35 | 6 | 30 | 11 |
| G15 | F1(2)NK102 | 1.13 | 1.04 | 1.82 | 12 | 38.13 | 2 | 14 | 4 |
| G16 | F1(7)CDG-01 | 0.61 | 1.96 | 2.12 | 21 | 28.95 | 11 | 32 | 13 |
| G17 | F1(6)SITAK | 0.34 | −0.35 | 0.56 | 2 | 7.71 | 33 | 35 | 19 |
| G18 | F1(17)KUMEROT | 1.09 | −1.34 | 1.98 | 17 | 22.02 | 19 | 36 | 20 |
| G19 | F1(14)LAD | −0.62 | 1.63 | 1.83 | 13 | 21.73 | 21 | 34 | 16 |
| G20 | F1(18)T3 | −5.42 | 0.73 | 7.27 | 33 | 40.27 | 1 | 34 | 17 |
| G21 | F1(43)HAR | −1.62 | −1.68 | 2.74 | 28 | 30.93 | 10 | 38 | 21 |
| G22 | F1(14)GKAW | −0.68 | −1.84 | 2.05 | 20 | 26.75 | 14 | 34 | 18 |
| G23 | F1(2)AMBEU | 0.57 | 0.27 | 0.80 | 4 | 19.71 | 25 | 29 | 9 |
| G24 | F1(10)HAR | 0.71 | 1.64 | 1.89 | 14 | 25.78 | 15 | 29 | 10 |
| G25 | F1(5)CDRA-02 | −0.49 | −2.87 | 2.95 | 31 | 19.49 | 26 | 57 | 33 |
| G26 | F1(2)Ayamurasaki | −0.10 | 2.04 | 2.05 | 18 | 28.68 | 12 | 30 | 12 |
| G27 | F1(38)HAR | 1.74 | 0.45 | 2.36 | 23 | 21.86 | 20 | 43 | 25 |
| G28 | F1(7)GKAW | 0.53 | 1.18 | 1.38 | 8 | 16.80 | 30 | 38 | 22 |
| G29 | F1(23)LAD | 1.51 | 0.88 | 2.19 | 22 | 18.85 | 29 | 51 | 29 |
| G30 | F1(30)CIA | 1.75 | −1.36 | 2.69 | 27 | 19.14 | 27 | 54 | 31 |
| G31 | Rancing | −0.18 | 1.47 | 1.49 | 9 | 31.12 | 9 | 18 | 6 |
| G32 | AC Putih | 0.19 | 0.89 | 0.92 | 5 | 31.48 | 8 | 13 | 3 |
| G33 | Ayamurasaki | −1.50 | 0.46 | 2.05 | 19 | 20.16 | 24 | 43 | 26 |
| L1 | Kuningan | −5.68 | 3.81 | 29.10 | |||||
| L2 | Bandung | 6.65 | 2.35 | 24.58 | |||||
| L3 | Banjar | −0.97 | −6.17 | 21.86 |
IPCAg = Interaction Principal Component Axis Genotype; ASV = AMMI Stability Value; RASV = Rank of ASV; AY = Average Yield; RAY = Rank of Average Yield; GSI = Genotype Stability Index; RGSI = Rank of GSI.
Illustrated of genotype and environmental performance was presented in Fig. 4b. Genotype G20 shows the highest yields at two locations (L1 and L3), while G3 shows the highest yields at the L2 (Bandung). Genotypes G11, G22, and G26 show high stability in yields, as reflected in their low PC2 and close to zero in Fig. 4b. Our results suggest that the genotypes with the highest yields did not show broad adaptability in the various test environments. Referring to the PC1 and PC2 scores, 78.3% was calculated by the interactions of G, E, and GEIs. Genotypes G3, G17, and G20 showed high of interaction. L2 is very different from other locations. Biplots showed the highest yields in genotypes G3, G15, G4, G1, G6, G32, and G24 which were grouped by location and approached the original graph (0.0). Genotypes G17, G10, G25, G28, and G30 were in the low yield group (Fig. 4b). Genotypes that are closer to the origin axis show better stability. Based on this measure, genotypes G4, G6, G11, G19, G22, G24, G26, G31, G7, and G32 have high yield and stable.
3.4. Genotype selection based on multiple traits using genotype by Yield*Traits (GYT) measurement
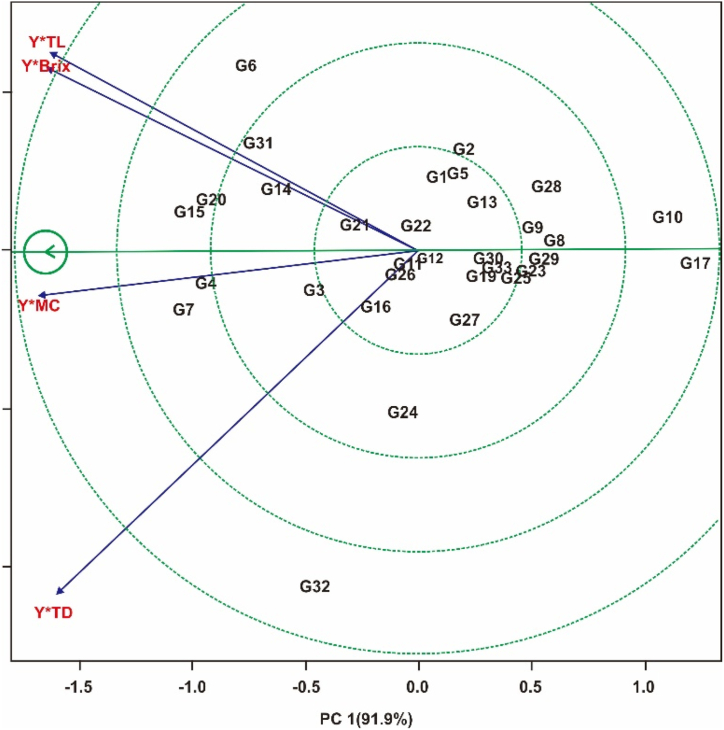
Fig. 5 represents the polygon display of the 'best ranking of genotypes' from the GYT biplot resulting from the combination of yields and yield quality of 33 honey sweet potato genotypes in multi-environment trials. The GYT biplot accounts for 96.5% of the total variation. The combination of yields with yield quality on the GYT biplot tends to have a positive correlation. Based on this biplot, the genotypes are ordered graphically based on the combination of traits tested. The most obvious correlations are: positive correlation between Y*TL and Y*Brix; and between Y*MC and Y*TD, because they are in the same quadrant and have an acute angle (<90°). Fig. 5 also shows the rank's of the genotypes tested based on the combination of yield and yield quality. The best genotype sequences tested based on proximity to the ideal point (arrows in small circles), they were: G7> G15> G4> G20> G6> G31> G14. In contrast, G17, G10, G8 and G28 were ranked lowest.
Fig. 5.
The display of ‘the best genotypes rank' from the GYT biplot resulting from the combination of yields and yield quality on 33 honey sweet potato in multi-environment trials.
4. Discussion
The main factors in the selection of varieties in each location were differences in genotype and environment. Multi-locations testing should be carried out to obtain superior varieties of sweet potatoes that were adapt at various growing environments. In our study, the combined ANOVA showed that GEIs effect contributed 54.88% for yield, 40.01% for sweetness, 10.46% for MC, 68.80 for tuber diameter, and 72.57% for tuber length from the sum of square (Table 2). The large of GEIs effect was responds to environmental rather than genotype factors [20,44]. The existence of a significant effect from genotype, environment, and GEIs indicates that the three causes variations in sweet potato yields in the three test environments. Kuningan (L1) is the location that has the highest average yield of the genotypes tested. This location has more sandy soil conditions compared to other locations. Banjar (L3) is the location with the lowest average yield. This location showed a higher clay content. While the L2 location has a more balanced of sand and clay contents than other locations, so that the average yield produced at this location is quite high. In this case, the average rainfall during the trial was not determine of sweet potato yield. Sweet potato does require adequate water intake during its infancy. However, if the soil contains more clay, the water will be retained in the soil and the tuber will be rot. Therefor, we recommend don't to plant sweet potatoes on land with high clay content during the rainy season.
Sweet potato generally needs adequate water during the growing cycle [45]. Management of water supply has an impact on optimal sweet potato yields [46]. In this study, all three environments had sufficient average rainfall for the growth of sweet potatoes (Table 1). However, different test environments lead to variations in the yield performance of the genotypes tested between locations. Kuningan (L1) is the best environment in terms of average yield, but Bandung (L2) is the suitable environment as a test location (favorable). Banjar (L3) is a location that has a small GEIs effect (PC1 was close to zero) (Table 7), so the impact on the variation in yield performance for each genotype was also small [40]. However, this environment has a higher clay content, so the sweet potato yields will be unoptimal.
The yield of sweet potato was mainly affected by GEIs (54.88%). Mustamu et al. [47] reported the same results that the effect of GEIs was greater on differences in yield performance of the sweet potato genotypes in Indonesia. The emergence of GEIs in multi-environment testing makes plant breeding programs inefficient [5]. The percentage of the genotype (34.41%) was lower than that of GEIs (54.88%) effects, this indicates that there was a significant difference in yield performance between each genotype in each environment [4]. In addition, the magnitude of the GEIs effect causes the yield ranking of each genotype in each location was different, so that an adaptive genotypes was selected for specific environment [5,18,19]. According to Jamshidmoghaddam [48], the large of variation in the growth environment that affects crop yields causes the appearance of GEIs. Some researchers reported the comparison of the GGE biplot and AMMI measurements were useful for the evaluation of GEIs under multi-locations [15,21,[49], [50], [51]].
Several stability measurements have been widely used to test the adaptability and yield performance of genotypes. We used parametric and non-parametric measurements in this study. According to Becker [52], the stability measurements relate to one of concepts of stability, i.e. static and dynamic stability. The use of PCA biplots generated from the first two PCs, can be describe the relationship between stability measurements (non-parametric and parametric) and its relation to the concept of stability (Fig. 2).
The PCA biplot showed that the θᵢ separated from the other groups (Fig. 2). These measure was related to concept of static stability. Some researchers also found the concept of static stability including for the Stability index (SI) and ASV in rice [53], and for the bi and S2di measurements in barley [19]. Several studies also shown negative correlation between this measure with others measurements. We found that S(1), S(2), S(3), S(6), NP(1), NP(2), NP(3), NP(4), KR, CVi, S2di, and θ₍ᵢ₎ were in the one group (K2), and they were represented of static stability. In other studies [20], reported the static concept for the S(1), S(2), S(3), S(6), NP(1), NP(2), NP(3), NP(4), S2di, Wi2, σ2ᵢ, and KR measurements in barley genotypes. The biplot also showed that the bi measure and yield (Y) were in the same group (K1). Hence, this measure (bi) represented a concept of dynamic stability. The genotypes selected according to this measures (bi) shows the average stability. However, they were may not has better yield performance than genotypes responsive to favorable environments. Wi2, σ2ᵢ, and θ₍ᵢ₎ gave similar ranking for all tested genotypes, so they were has the same power to classifying the genotypes stability in diverse environments. Therefore, we can use one of them to measure the stable genotypes [4].
The stability measurement used in this study is not yet clear. Some measurements show stability for some genotypes, but not for other. This is one of the problems in the GEIs studies [4,19,54]. The information regarding GEIs can be identified through multivariate analysis. One method to extract GEIs and distribute stable genotypes into the same groups qualitatively was cluster analysis [19,20]. In this study, cluster analysis separated 33 sweet potato genotypes into three main clusters (Fig. 3). The first cluster (G1) contained high yielding genotypes with the sum of rank's (SR) stability measurements ranged from 115 to 211, indicating that this group has stability in diverse environments. Also, the genotypes with high-yield performance (G4, G6, G7, G11,G31, and G32) were in this cluster. The genotypes that had low yields, grouped in second cluster (G2). The all genotypes in this cluster, have highest sum rangks of stability parameters (247–409). The genotypes that have high and intermediate yield were in the third cluster (G3). Some genotypes in this cluster have such high yield ranks (G3, G14, G15, G16, G20, G21, and G26), with the ranking of 7, 6, 2, 11, 1, 10, and 12 in average yield, which had a higher value of stability measurements (SR from 182 to 426) and identified as unstable genotypes (Table 3, Table 4, Table, 5, and Table 6).
In this study, the AMMI, GSI, and GGE Biplot was also used to identify the distribution of the tested genotypes in three environments. Based on AMMI, 10 genotypes were identified to have close proximity to the stability line (Fig. 4a), i.e. G3, G4, G6, G7, G15, G16, G20, G26, G31 and G32. According to Refs. [40,55], genotypes that are close to the stability line on the AMMI 1 biplot and were in the right-hand position indicate that they have high yield and stability in various test environments [53]. also reported has succeeded selected rice genotypes had high and stable yields with AMMI measurement. The GSI, confirmed the seven genotypes that have high and stable yields in three environments, namely G6, G4, G32, G15, G7, G31, and G11 (Table 7). Several researchers succeeded in selecting stable genotypes with this measure on sweet potato [1,56]. The GGE biplot also selects several stable genotypes with high yields including G4, G6, G11, G19, G22, G24, G26, G31, G7, and G32 (Fig. 4b). Several researchers have also succeeded in selecting stable genotypes with GGE biplot on sweet potato [47], upland cotton [57], maize hybrid [51], rice [58], and barley [20].
The combination of various stability analysis methods (Parametric, non-parametric, AMMI, GSI, and GGE Biplot) shows that five genotypes identified as having high and stable yields in various environments, i.e. G4, G6, G7, G31, and G32. They where can be used as new superior genotypes. For specific environments, selection should be made for each genotype based on yield performance. Therefore, evaluations that combine various stability statistics can provide more accurate information to select the ideal genotype.
The results of GYT biplot measurements on the combination of yield traits and yield quality showed that the polygons account for 96.5% of the total variation (Fig. 5). This shows that the variations that occurred are the influence of the traits tested, while the rest are influenced by other factors. The yield-traits combinations that have the most striking correlations are: positive correlation between Y*TL and Y*Brix; and between Y*MC and Y*TD. Yield-traits combinations in the same quadrant shows a strong correlation between these combinations [23,25]. In Fig. 5, a high correlation were observed between Y*TL and Y*Brix, indicating that their combination will be suitable for selecting high-performing genotypes for these traits. Fig. 5 shows the ranking of the best genotypes tested based on yield-traits combinations. They were: G7 > G15 > G4 > G20 > G6 > G31 > G14. In contrast, G17, G10, G8, and G28 rank the poorest. According to Yan and Frégeau-reid [22] and Mohammadi [25], the genotype that is closest to the ideal point is the best genotype. Based on these appearances, G7, G15, G4, G20, G6, G31, and G14 were the best genotypes showing the highest average values. In the yield stability test, five genotypes were identified as having stable yields and high yields, namely: G4, G6, G7, G31, and G32. Judging from the results of both measurements (stability measurements and GYT biplot), G4, G6, G7, and G31 were in the selected genotype slices. This shows that the four genotypes have stable yields, high yields, and also have a good combination of traits for the yield quality. Hence, that the four were considered superior and have excellent potential to be developed in terms of yield and yield quality.
5. Conclusions
The stable and high yielding of sweet potato genotypes in West Java, Indonesia can be determined in this study. Highly significant effects of sweet potato genotypes (G), environments (E), and GEIs were observed for yield and yield quality. The Combined ANOVA showed that GEIs effect contributed 54.88% for yield, 40.01% for sweetness, 10.46% for MC, 68.80 for tuber diameter, and 72.57% for tuber length from the sum of square. Combined various stability measurements (Parametric, non-parametric, AMMI, GSI, and GGE biplot) identified five genotypes that were declared stable and high yield in three environments, i.e. G4, G6, G7, G31, and G32. Genotype by yield*traits (GYT) selected seven genotypes that have superior in yield and yield quality, they were G7, G15, G4, G20, G6, G31, and G14. Based on stability measurements and GYT biplots, the genotypes G4, G6, G7, and G31 are in both slices. So that the four genotypes have high, stable yields, and have a good combination of traits for yield quality. They where can be proposed as candidates for new superior varieties of sweet potato. The results in terms of adaptability and stability are valid for the predictable environmental components of locations, but need to be validated in evaluations involving different agricultural years for the unpredictable environmental factors.
Funding statement
This research was funded by RISPRO LPDP, Ministry of Finance of the Republic of Indonesia to Prof. Dr. Sc.Agr. Agung Karuniawan, Ir., M.Sc.Agr. from Faculty of Agriculture, Universitas Padjadjaran (UNPAD) (Contract number: 27/UN6.R/Kep/PL/2014) and The APC was funded by Universitas Padjadjaran (UNPAD).
Author contribution statement
Haris Maulana: Conceived and design the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Eso Solihin and Acep Atma Wijaya: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Lucyana Trimo and Syarif Hidayat: Performed the experiments; Wrote the paper.
Hari Hariadi: Contributed reagens, materials, analysis tools or data; Wrote the paper.
Suseno Amien and Dedi Ruswandi: Conceived and design the experiments; Wrote the paper.
Agung Karuniawan: Conceived and design the experiments; Contributed reagens, materials, analysis tools or data; Wrote the paper.
Data availability statement
Data included in article/supp. material/referenced in article.
Additional information
No additional information is available for this paper.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Appreciation is also given to Rector of Universitas Padjadjaran (UNPAD) for providing research facilities. A highly appreciation is also dedicated to Universitas Padjadjaran for the post-doctoral grant awarded to Haris Maulana (Contract number: 2990/UN6.3.1/TU.00/2022).
References
- 1.Maulana H., Dewayani S., Solihin M.A., Arifin M., Amien S., Karuniawan A. Yield stability dataset of new orange fleshed sweet potato (Ipomoea batatas L. (lam)) genotypes in West Java, Indonesia. Data Br. 2020;32 doi: 10.1016/j.dib.2020.106297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Maulana H., Nugroho D.M., Trimo L., Karuniawan A. Proceedings of SABRAO 13th Congress and International Congress. IPB Press; Bogor: 2016. Participatory selection of sweet potato based on farmers preferences in banjar city. [Google Scholar]
- 3.Pour-Aboughadareh A., Khalili M., Poczai P., Olivoto T. Stability indices to deciphering the genotype-by-environment interaction (GEI) effect : an applicable review for use in plant breeding programs. Plants. 2022;11:1–24. doi: 10.3390/plants11030414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vaezi B., Pour-Aboughadareh A., Mehraban A., Hossein-Pour T., Mohammadi R., Armion M., Dorri M. The use of parametric and non-parametric measures for selecting stable and adapted barley lines. Arch. Agron Soil Sci. 2017;64:597–611. doi: 10.1080/03650340.2017.1369529. [DOI] [Google Scholar]
- 5.Maulana H., Nafi'ah H.H., Solihin E., Ruswandi D., Arifin M., Amien S., Karuniawan A. Combined stability analysis to select stable and high yielding sweet potato genotypes in multi-environmental trials in West Java, Indonesia. Agric. Nat. Resour. 2022;56:761–772. doi: 10.34044/j.anres.2022.56.4.10. [DOI] [Google Scholar]
- 6.Wicaksana N., Maulana H., Yuwariah Y., Ismail A., Ruswandi Y.A.R., Ruswandi D. Selection of high yield and stable maize hybrids in mega-environments of Java island, Indonesia. Agronomy. 2022;12:1–18. doi: 10.3390/agronomy12122923. [DOI] [Google Scholar]
- 7.Andrade M.I., Ricardo J., Naico A., Alvaro A., Makundo G.S., Low J., Ortiz R., Gruneberg W.J. Release of orange-fleshed sweetpotato (Ipomoea batatas [L.] Lam.) cultivars in Mozambique through an accelerated breeding scheme. J. Agric. Sci. 2016;2016:1–11. doi: 10.1017/S002185961600099X. [DOI] [Google Scholar]
- 8.Maulana H., Maxiselly Y., Yuwariah Y., Ruswandi D. Heritability and selection using GGE biplots and the Sustainability Index (SI) of maize mutants under different cropping systems in upland. Sustainability. 2023;15:1–22. doi: 10.3390/su15086824. 6824. [DOI] [Google Scholar]
- 9.Shahzad K., Qi T., Guo L., Tang H., Zhang X., Wang H., Qiao X., Zhang M., Zhang B., Feng J., Iqbal M.S., Wu J., Xing C. Adaptability and stability comparisons of inbred and hybrid cotton in yield and fiber quality traits. Agronomy. 2019;9:1–16. doi: 10.3390/agronomy9090516. [DOI] [Google Scholar]
- 10.Ruswandi D., Syafii M., Wicaksana N., Maulana H., Ariyanti M., Indriani N.P., Suryadi E., Supriatna J., Yuwariah Y. Evaluation of high yielding maize hybrids based on combined stability analysis , sustainability index , and GGE biplot. BioMed Res. Int. 2022;2022:1–12. doi: 10.1155/2022/3963850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wijaya A.A., Maulana H., Susanto G.W.A., Sumardi D., Amien S., Ruswandi D., Karuniawan A. Grain yield stability of black soybean lines across three agroecosystems in West Java , Indonesia. Open Agric. 2022;7:749–763. doi: 10.1519/opag-2022-0137. [DOI] [Google Scholar]
- 12.Abate F., Mekbib F., Dessalegn Y. Association of different parametric and non parametric stability models in durum wheat (Triticum turgidum Desf .) genotypes. Int. J. Plant Soil Sci. 2015;7:192–201. doi: 10.9734/IJPSS/2015/15568. [DOI] [Google Scholar]
- 13.Karuniawan A., Maulana H., Ustari D., Dewayani S., Solihin E., Solihin M.A., Amien S., Arifin M. Yield stability analysis of orange - fleshed sweet potato in Indonesia using AMMI and GGE biplot. Heliyon. 2021;7 doi: 10.1016/j.heliyon.2021.e06881. 1, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ruswandi D., Azizah E., Maulana H., Ariyanti M., Nuraini A. Selection of high - yield maize hybrid under different cropping systems based on stability and adaptability parameters. Open Agric. 2022;7:161–170. doi: 10.1515/opag-2022-0073. [DOI] [Google Scholar]
- 15.Filio Y.L., Maulana H., Aulia R., Suganda T., Ulimaz T.A., Aziza V., Concibido V., Karuniawan A. Evaluation of Indonesian butterfly pea (Clitoria ternatea L .) using stability analysis and sustainability index. Sustainability. 2023;15:1–14. doi: 10.3390/su15032459. 2459. [DOI] [Google Scholar]
- 16.Susanto G.W.A., Maulana H., Putri P.H., Purwaningrahayu R.D., Wijaya A.A., Sekti B.A., Karuniawan A. Stability analysis to select the stable and high yielding of black soybean (Glycine max (L.) Merril) in Indonesia. Int. J. Agron. 2023;2023:1–4. doi: 10.1155/2023/7255444. [DOI] [Google Scholar]
- 17.Goksoy A.T., Sincik M., Erdogmus M., Ergin M., Aytac S., Gumuscu G., Gunduz O., Keles R., Bayram G., Senyingit E. The parametric and non-parametric stability analyses for interpreting genotype by environment interaction of some soybean genotypes. Turkish J. F. Crop. 2019;24:28–38. doi: 10.17557/tjfc.562637. [DOI] [Google Scholar]
- 18.Farshadfar E., Sabaghpour S.H., Zali H. Comparison of parametric and non-parametric stability statistics for selecting stable chickpea (Cicer arietinum L.) genotypes under diverse environments. Aust. J. Crop. Sci. 2012;6:514–524. [Google Scholar]
- 19.Khalili M., Pour-aboughadareh A. Parametric and non-parametric measures for evaluation yield stability and adaptability in barley doubled haploid lines. J. Agric. Sci. Technol. 2016;18:789–803. [Google Scholar]
- 20.Vaezi B., Pour-Aboughadareh A., Mohammadi R., Mehraban A., Pour-Hossein T., Koohkan E., Gasemi S., Moradkhani H., Siddique K.H.M. Integrating different stability models to investigate genotype x environment interactions and identify stable and high-yielding barley genotypes. Euphytica. 2019;215:1–18. doi: 10.1007/s10681-019-2386-5. [DOI] [Google Scholar]
- 21.Amien S., Maulana H., Ruswandi D., Nurjanah S. Stevia (Stevia rebaudiana B.) genotypes assessment for leaf yield stability through genotype by environment interactions, AMMI, and GGE biplot analysis. Sabrao J. Breed. Genet. 2022;54:767–779. doi: 10.54910/sabrao2022.54.4.8. [DOI] [Google Scholar]
- 22.Yan W., Frégeau-reid J. Genotype by yield*trait (GYT) biplot : a novel approach for genotype selection based on multiple traits. Sci. Rep. 2018;8:1–10. doi: 10.1038/s41598-018-26688-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Karuniawan A., Maulana H., et al. Storage root yield and sweetness level selection for new honey sweet potato (Ipomoea batatas [L.] Lam) Open Agric. 2021;6:329–345. doi: 10.1515/opag-2021-0219. [DOI] [Google Scholar]
- 24.Merrick L.F., Glover K.D., Yabwalo D., Byamukama E. Use of genotype by yield * trait (GYT) analysis to select hard red spring wheat with elevated performance for agronomic and disease resistance traits, Crop Breeding. Genet. Genomics. 2020;2:1–18. [Google Scholar]
- 25.Mohammadi R. Genotype by yield*trait biplot for genotype evaluation and trait profiles in durum wheat. Cereal Res. Commun. 2019;47:541–551. doi: 10.1556/0806.47.2019.32. [DOI] [Google Scholar]
- 26.Karahan T., Akgün I. Selection of barley (Hordeum vulgare) genotypes by GYT (genotype × yield × trait) biplot technique and its comparison with GT (genotype × trait) Appl. Ecol. Environ. Res. 2020;18:1347–1359. [Google Scholar]
- 27.Boureima S., Yaou A. Genotype by yield*trait combination biplot approach to evaluate sesame genotypes on multiple traits basis. Turkish J. F. Crop. 2019;24:237–244. [Google Scholar]
- 28.Eberhart S.A., Russell W.A. Stability parameters for comparing varieties. Crop Sci. 1966;6:36–40. doi: 10.2135/cropsci1966.0011183x000600010011x. [DOI] [Google Scholar]
- 29.Plaisted R.L., Peterson L.C. A technique for evaluating the ability of selection to yield consistently in different locations or seasons. Am. Potato J. 1959;36:381–385. [Google Scholar]
- 30.Plaisted R.L. A shorter method for evaluating the ability of selections to yield consistently over locations. Am. Potato J. 1960;37:166–172. [Google Scholar]
- 31.Wricke G. Übereine Methode zur Erfassung der ökologischen Streubreite in Feldversuchen. Zeitschrift für Pflanzenzüchtung. 1962;47:92–96. [Google Scholar]
- 32.Shukla G.K. Some statistical aspects of partitioning genotype-environmental components of variability. Heredity. 1972;29:237–245. doi: 10.1038/hdy.1972.87. [DOI] [PubMed] [Google Scholar]
- 33.Francis T.R., Kannenberg L.W. Yield stability studies in short-season maize: I. A descriptive method for grouping genotypes. Can. J. Plant Sci. 1978;5:1029–1034. [Google Scholar]
- 34.Nassar R., Huhn M. Studies on estimation of phenotypic stability : tests of significance for nonparametric measures of phenotypic stability. Biometrics. 1987;43:45–53. [Google Scholar]
- 35.Huehn M. Nonparametric measures of phenotypic stability. Part 1 : Theory, Euphytica. 1990;47:189–194. [Google Scholar]
- 36.Thennarasu K. PJ School, IARI; New Delhi, India.: 1995. On Certain Non-parametric Procedures for Studying Genotype-Environment Interactions and Yield Stability, PhD Thesis. [Google Scholar]
- 37.Kang M.S. A rank-sum method for selecting high-yielding, stable corn genotypes. Cereal Res. Commun. 1988;16:113–115. [Google Scholar]
- 38.Pour-aboughadareh A., Yousefian M., Moradkhani H., Poczai P., Siddique K.H.M. Stabilitysoft : a new online program to calculate parametric and non-parametric stability statistics for crop traits. Apllications Plant Sci. 2019;7:1–6. doi: 10.1002/aps3.1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yim O., Ramdeen K.T. Hierarchical cluster analysis: comparison of three linkage measures and application to psychological data. Quant. Methods Psychol. 2015;11:8–21. doi: 10.20982/tqmp.11.1.p008. [DOI] [Google Scholar]
- 40.Gauch H.G. A simple protocol for AMMI analysis of yield trials. Crop Sci. 2013;53:1860–1869. doi: 10.2135/cropsci2013.04.0241. [DOI] [Google Scholar]
- 41.Purchase J.L., Hatting H., van Deventer C.S. Genotype × environment interaction of winter wheat (Triticum aestivum L .) in South Africa : II. Stability analysis of yield performance. S. Afr. J. Plant Soil. 2000;17:101–107. doi: 10.1080/02571862.2000.10634878. [DOI] [Google Scholar]
- 42.Yan W., Tinker N.A. Biplot analysis of multi-environment trial data : principles and applications. Can. J. Plant Sci. 2006;86:623–645. [Google Scholar]
- 43.R Core team R. R Foundation for Statistical Computing; Vienna: 2018. A Language and Environment for Statistical Computing.https://www.r-project.org [Google Scholar]
- 44.Zerner M.C.A., Rebetzke G.J.B., Gill G.S.A. Genotypic stability of weed competitive ability for bread wheat (Triticum aestivum) genotypes in multiple environments. Crop Pasture Sci. 2016;67:695–702. doi: 10.1071/CP15198. [DOI] [Google Scholar]
- 45.Lestari S.U., Ricky I.H. Dual-purpose assessment for sweetpotato. AGRIVITA J. Agric. Sci. 2015;37:123–129. doi: 10.17503/Agrivita-2015-37-2-p123-129. [DOI] [Google Scholar]
- 46.Alam M.J., Al Mahmud A., Gaber A., Hossain A. Energy efficiency and water use indices for sweet potato (Ipomoea batatas L.) production under subtropical climatic conditions of Bangladesh. J. Water Clim. Chang. 2023;14:576–589. doi: 10.2166/wcc.2023.401. [DOI] [Google Scholar]
- 47.Mustamu Y.A., Tjintokohadi K., Gruneberg W.J., Karuniawan A., Ruswandi D. Selection of superior genotype of sweet-potato in Indonesia based on stability and adaptability. Chil. J. Agric. Res. 2018;78:461–469. doi: 10.4067/S0718-58392018000400461. [DOI] [Google Scholar]
- 48.Jamshidmoghaddam M., Pourdad S.S. Genotype x environment interactions for seed yield in rainfed winter safflower (Carthamus tinctorius L .) multi-environment trials in Iran. Euphytica. 2013;190:357–369. doi: 10.1007/s10681-012-0776-z. [DOI] [Google Scholar]
- 49.Persaud R., Saravanakumar D., Persaud M. Identification of resistant cultivars for sheath blight and use of AMMI models to understand genotype and environment interactions. Plant Dis. 2019:1–8. doi: 10.1094/PDIS-12-18-2301-RE. [DOI] [PubMed] [Google Scholar]
- 50.Ruswandi D., Syafii M., Maulana H., Ariyanti M., Indriani N.P., Yuwariah Y. GGE biplot analysis for stability and adaptability of maize hybrids in Western Region of Indonesia. Int. J. Agron. 2021;2021:1–9. doi: 10.1155/2021/2166022. [DOI] [Google Scholar]
- 51.Yousaf M.I., Akhtar N., Mumtaz A., Shehzad A., Arshad M., Shoaib M., Mehboob A. Yield stability studies in indigenous and exotic maize hybrids under genotype by environment interaction. Pakistan J. Bot. 2021;53:941–948. doi: 10.30848/PJB2021-3(41. [DOI] [Google Scholar]
- 52.Becker H.C., Leon J. Stability analysis in plant breeding. Plant Breed. 1988;101:1–23. [Google Scholar]
- 53.Bose L.K., Jambhulkar N.N., Pande K., Singh O.N. Use of AMMI and other stability statistics in the simultaneous selection of rice genotypes for yield and stability under direct-seeded conditions. Chil. J. Agric. Res. 2014;74:3–9. doi: 10.4067/S0718-58392014000100001. [DOI] [Google Scholar]
- 54.Ahmadi J., Vaezi B., Shaabani A., Khademi K., Ourang S.F. Non-parametric measures for yield stability in grass pea (Lathyrus sativus L.) advanced lines in semi warm regions. J. Agric. Sci. Technol. 2015;17:1825–1838. [Google Scholar]
- 55.Gauch H.G., Piepho H.P., Annicchiarico P. Statistical analysis of yield trials by AMMI and GGE : further considerations. Crop Sci. 2008;48:866–889. doi: 10.2135/cropsci2007.09.0513. [DOI] [Google Scholar]
- 56.Chalwe A., Chiona M., Sichilima S., Njovu J., Chama C., Ndhlovu D. Genotype stability index for root yield and tolerance to sweetpotato weevil cylas puncticolis : a tool for identifying climate smart varieties. Open Agric. 2017;2:166–174. doi: 10.1515/opag-2017-0017. [DOI] [Google Scholar]
- 57.Abro S., Rizwan M., Rajput M.T., Sial M.A.L.I., Deho Z.A. Evaluation of upland cotton genotypes for stability over different locations using AMMI and GGE biplot analysis. Pakistan J. Bot. 2022;54:1733–1739. doi: 10.30848/PJB2022-5(1. [DOI] [Google Scholar]
- 58.Inabangan-Asilo M.A., Swamy B.P.M., Amparado A.F., Descalsota-Empleo G.I.L., Arocena E.C., Reinke R. Stability and G × E analysis of zinc-biofortified rice genotypes evaluated in diverse environments. Euphytica. 2019;215:1–17. doi: 10.1007/s10681-019-2384-7. 2019. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data included in article/supp. material/referenced in article.