Aggregated Molecular Phenotype Scores: Enhancing Assessment and Visualization of Mass Spectrometry Imaging Data for Tissue-Based Diagnostics

Abstract

Mass spectrometry imaging (MSI) has gained increasing popularity for tissue-based diagnostics due to its ability to identify and visualize molecular characteristics unique to different phenotypes within heterogeneous samples. Data from MSI experiments are often assessed and visualized using various supervised and unsupervised statistical approaches. However, these approaches tend to fall short in identifying and concisely visualizing subtle, phenotype-relevant molecular changes. To address these shortcomings, we developed aggregated molecular phenotype (AMP) scores. AMP scores are generated using an ensemble machine learning approach to first select features differentiating phenotypes, weight the features using logistic regression, and combine the weights and feature abundances. AMP scores are then scaled between 0 and 1, with lower values generally corresponding to class 1 phenotypes (typically control) and higher scores relating to class 2 phenotypes. AMP scores, therefore, allow the evaluation of multiple features simultaneously and showcase the degree to which these features correlate with various phenotypes. Due to the ensembled approach, AMP scores are able to overcome limitations associated with individual models, leading to high diagnostic accuracy and interpretability. Here, AMP score performance was evaluated using metabolomic data collected from desorption electrospray ionization MSI. Initial comparisons of cancerous human tissues to their normal or benign counterparts illustrated that AMP scores distinguished phenotypes with high accuracy, sensitivity, and specificity. Furthermore, when combined with spatial coordinates, AMP scores allow visualization of tissue sections in one map with distinguished phenotypic borders, highlighting their diagnostic utility.

Graphical Abstract

INTRODUCTION

The accurate identification of different tissue phenotypes is crucial for early diagnosis, successful tumor removal, and treatment of disease. Achieving this has been challenging due to the spatially complex nature of tissues, especially tumors, which gives rise to both intra-tumoral and inter-tumoral heterogeneity.^1,2 Historically, the manual evaluation of stained or labeled sections of tissue by highly trained histopathologists has been the gold standard for diagnosis. However, hematoxylin and eosin (H&E) stains only provide morphological information and may not fully resolve tissue types, especially when changes are primarily molecular in nature.^3,4 For example, poorly differentiated breast cancer can be difficult to distinguish with this approach.⁵ Furthermore, H&E staining can also be time-consuming, subjective, and ultimately delay patient care. Therefore, the need for an improved approach that combines molecular and spatial distributions with tissue morphology has become apparent. Mass spectrometry imaging (MSI) has thus emerged as a powerful approach to address these needs.^6–10

MSI-based techniques rely on sampling regions of interest by using an ionization probe that feeds directly to a mass spectrometer. Notably, ambient ionization sampling techniques allow for the direct analysis of complex samples under atmospheric pressure and require minimal sample preparation, thereby allowing for rapid data collection.^7,11 To identify intrinsic patterns in the resulting datasets, unsupervised statistical approaches are often applied, which utilize the m/z features detected to assess trends without prior biological knowledge. Due to the large size of MSI datasets, it is common to implement dimension reduction techniques, such as principal component analysis (PCA), t-distributed stochastic neighbor embedding (t-SNE), or non-negative matrix factorization (NMF) as a pre-processing step. Dimension reduction is often followed by clustering techniques, such as hierarchical clustering, k-means clustering, or Gaussian mixture modeling to segment pixels into groups with similar feature profiles. Once clusters are assigned, tissue sections are often visualized by creating ion images where pixels are colored according to their cluster. Comparison of cluster localization to pathologist-annotated slides has revealed that these approaches can identify highly relevant clusters that correspond to regions of the tissue that have different biochemical or biological properties, such as different cell types or different stages of disease.^12–19

While unsupervised approaches aim to unveil natural patterns in the data, supervised approaches are often used to select features associated with phenotypes of interest. This can be achieved by either applying univariate methods, such as an ANOVA or t-test, to directly characterize the relationship between a given feature and phenotype, or by using multivariate approaches, such as random forest (RF) or linear discriminant analysis (LDA), to highlight features that are important for phenotypic classification.^20–22 For example, supervised approaches have been used to identify diagnostic lipid and metabolic signatures of human cancerous tissues, including brain,²³ breast,^24,25 thyroid,²⁶ gastric,²⁷ ovarian,²⁸ and others.^20,29–31 With these approaches, ion images are frequently made by coloring pixels based on feature abundance for features that were found to be statistically significant or influential on model performance. Alternatively, tissue sections can be summarized in a single image by coloring pixels based on phenotypic predictions or predicted class probabilities provided by models.^27,32

Although the benefits of using MSI data for tissue diagnosis and visualization are apparent, there are still limitations in the outlined statistical approaches. While unsupervised techniques have the benefit of requiring minimal a priori knowledge, the resulting clusters may not correspond to phenotypic differences. Further, because pixels are colored categorically, rigid borders will exist between clusters in ion images, failing to capture any gradual molecular changes. These limitations may be circumvented by utilizing a supervised approach, where specific differences between phenotypes can be assessed based on sample annotations and tissue sections are visualized based on feature abundances or model output. However, assessing feature abundances often involves plotting only a few features at a time, which is not only time-consuming but also makes it difficult to holistically understand the molecular landscape of a tissue section. To make visualizations more concise, categorical phenotypic classifications or classification probabilities from predictive models may be used. However, relying solely on classification output may overlook subtle variations and nuanced molecular changes within the tissue. For example, while a histopathologist may identify unusual or rare features in a tissue section, classification-based visualizations may indicate that a tissue is normal with no further indication of anomalies that may be relevant to disease management and prognosis, e.g., detection of inflammation or precancerous lesions.³³ To this end, we have developed aggregated molecular phenotype (AMP) scores, which allow for concurrent visualization of phenotype-associated features while picking up on subtle molecular changes.

An AMP score is a value between 0 and 1 that summarizes the aggregated molecular information of a single sample or pixel in a MSI experiment. These scores are defined for pairwise phenotype comparisons with low scores indicating that a given pixel has molecular characteristics matching the user-defined class 1 phenotype (often control) and high scores correlating with the user-defined class 2 phenotype. To calculate AMP scores, we utilized an ensemble feature selection approach to identify features differing between the two phenotypes, weighted these features using logistic regression, and then applied a custom function to combine feature abundances with their respective weights for each sample or pixel. A threshold value of 0.5 was utilized for binary classification of these scores, with scores closer to 0.5 suggesting that a pixel shares molecular characteristics of both phenotypes. Once calculated, AMP scores were then combined with the location coordinates for each pixel to create one image of a tissue section. This image represents all features (or molecules) of interest and illustrates how the molecular landscape changes spatially (Figure 1).

Figure 1.

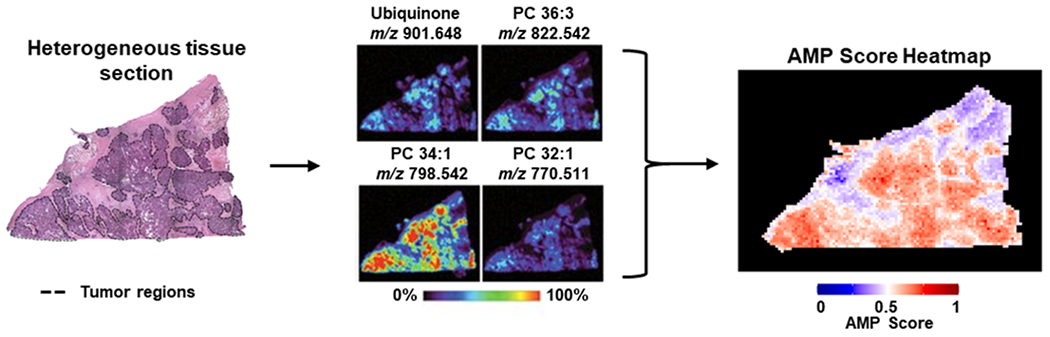
Example AMP score heatmaps for a heterogeneous tissue sample. On the left, a H&E slide is shown for a HGSC tissue sample with tumor areas outlined in dashed black lines. In the middle, an example of how tissue sections may be visualized with traditional MSI approaches is shown, with feature abundances across the tissue area visualized individually. On the right, the same tissue section is visualized using AMP scores, which summarizes signal across all features and greatly reduces the number of images.

In this paper, we utilized metabolomic data from three previously published studies to demonstrate how AMP scores are calculated and evaluate their performance.^24,26,28 Namely, in the first evaluation, we analyzed AMP scores for homogeneous tissue sections from follicular thyroid adenoma (FTA), a benign thyroid tumor vs papillary thyroid carcinoma (PTC),²⁶ the most common type of thyroid cancer. In our next comparison, we assessed normal breast (NB) vs invasive ductal carcinoma (IDC), the most common type of breast cancer tissue to evaluate margins.²⁴ Three different ovarian tissues, normal ovarian tissue (NO), borderline ovarian tumor (BOT), and high-grade serous carcinoma (HGSC), were evaluated in the final comparison to understand how each pairwise assessment would perform, especially when our class 1 was not a control but a less severe disease case (i.e., BOT vs HGSC).²⁸ These analyses illustrated the high predictive power of AMP scores with class 1 samples having substantially lower scores compared to class 2 samples. The ability to distinguish phenotypes was further showcased in AMP score heatmap visualizations, which distinguished tissue borders and identified regions of normal and diseased tissue. Further, we compared these results to classification and visualization using LDA posterior probabilities, which highlighted the method’s ability to detect gradual changes (Supporting Information). Overall, these results suggest that AMP scores can be used as a powerful approach to visualize and diagnose tissue sections from MSI.

METHODS

Descriptions of the datasets used can be found in the Supporting Information.

Overview of AMP Score Calculation Pipeline.

AMP scores were calculated by first filtering and normalizing the data. The data were then split into training and testing sets, where distinguishing features were selected and AMP score parameters were calculated using the training data. Finally, AMP scores were calculated for the testing data for evaluation. An overview of this pipeline is shown in Figure 2. A description of the data pre-processing can be found in the Supporting Information, and all other steps are described below.

Figure 2.

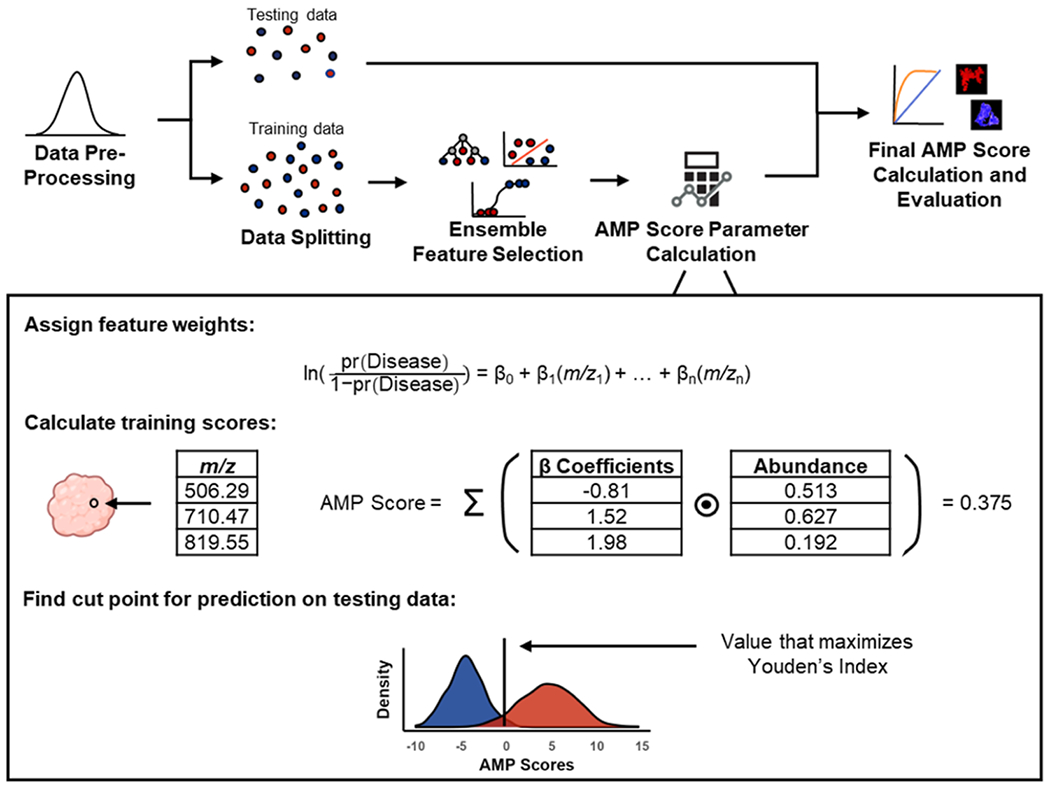
Pipeline for AMP score calculation. Data are first filtered and normalized before being split into testing and training sets. Features distinguishing phenotypes are selected using ensemble feature selection with Lasso regression, random forest, and support vector machine. Selected features are weighted using logistic regression and preliminary AMP scores are calculated for each pixel in the training data by multiplying the abundance of selected features by their respective weights and then summing. Following preliminary scoring, the value that maximizes Youden’s index is calculated, which is later used to scale the testing data. Finally, AMP scores are calculated for the testing data, predictions are made, and scores are plotted for visualization across tissue sections.

Data Splitting.

To evaluate the performance of the AMP scores, we followed the standard practice of data splitting in machine learning by first training the scoring system on a subset of the data and then applying it to an independent testing set. For each pairwise comparison, homogeneous samples were randomly split into training and testing sets using a 2:1 ratio. Splitting was done at the sample level to ensure independence between the training and testing sets. Heterogeneous samples were withheld as an additional validation set to visualize phenotype borders.

Ensemble Feature Selection.

To identify features that distinguish between phenotypes, we leveraged an ensemble feature selection approach. In this approach, features were initially selected by applying the least absolute shrinkage and selection operator (Lasso) regression, RF, and support vector machine (SVM) to the training data. Details of these methods, their associated parameters, and their implementation are discussed below:

1. Lasso regression is a method that selects features by imposing a penalty on the size of the regression coefficients, shrinking them toward zero, and resulting in a sparse model that retains only the most important features.³⁴ Lasso analysis was performed in R (v4.2.1) using the glmnet package.³⁵ For each pairwise comparison, the optimal value for lambda, which controls the strength of the regularization applied, was obtained using 5-fold cross-validation with the function “cv.glmnet”. After selecting the lambda value, Lasso logistic regression was performed using the “glmnet” function, and all features with a non-zero coefficient were retained.

2. RF ranks features based on how much their inclusion in a forest of decision trees decreases the impurity of predictions quantified using the Gini Index, with features yielding the highest decrease in impurity being considered the most important.³⁶ To determine these features, RF models were constructed for each pairwise comparison using the randomForest package in R. Each model was built using the function “randomForest” and consisted of 1000 decision trees, where the number of variables to use as candidates at each split point was equal to the square root of the number of features.³⁷ Once a model was constructed, the out-of-bag error rates were noted, and features were ranked using the “importance” function. The bottom ~10% of features were then removed from the data, the model was reconstructed, and the out-of-bag errors were reassessed. This process was repeated iteratively until the out-of-bag error began to increase, suggesting that all current features were useful for distinguishing phenotypes.

3. SVM with a linear kernel was employed for feature selection by examining the coefficients of the decision boundary, indicating the importance of each feature in predicting the classification outcome.³⁸ SVM analysis was conducted using scikit-learn in Python (v3.9.7).³⁹ Models were first constructed using the “SVC” function with a linear kernel and C = 1. To evaluate model performance, 5-fold cross-validation was performed on the training data using the “cross_val_scores” function, and top features were identified using the “coef_” function. The bottom ~10% of features were then removed from the data, the model was reconstructed, and cross-validation performance was reassessed. This process was repeated iteratively until model performance began to decrease, suggesting all current features were useful for distinguishing phenotypes.

Features were determined to be important and included in the AMP score calculation if selected by at least two of the three models.

AMP Score Parameter Calculation.

After selecting significant features that distinguish phenotypes of interest, the next step was to assign a weight to each feature. To achieve this, training data was filtered down to just the selected features, and logistic regression was performed in R using the “glm” function with the abundances of features as independent variables and the phenotype group as the dependent variable. From this model, each feature was assigned a β coefficient. Preliminary AMP scores were then calculated for each individual pixel by multiplying the β coefficient of each selected feature by the feature’s abundance and then summing all of these values. From these preliminary AMP scores, the optimal threshold value for distinguishing the two phenotypes was chosen by finding the value that maximized Youden’s Index, which is defined as the sum of sensitivity and specificity minus 1.⁴⁰ This was done using the “cutpointr” function from the R package cutpointr, which utilizes bootstrapping methodology to identify the value that maximizes a given metric.⁴¹

Final AMP Score Calculation and Evaluation.

Unscaled AMP scores for testing data were calculated for each pixel using the same approach as the training data, which included multiplying the β coefficient of all features selected by at least two of the three models by their associated abundance and then summing all products for each pixel. Testing scores were then scaled between 0 and 1, with all scores below the optimal threshold value determined by the training data ranging between 0 and 0.5 and all scores above the threshold value occurring between 0.5 and 1. All pixels with a score less than 0.5 were predicted to be from class 1 samples, while pixels with a score greater than or equal to 0.5 were predicted to be from class 2 samples. Predicted phenotype labels were then compared to true pixel labels from pathology, and accuracy, sensitivity, and specificity were calculated using functions from the R package caret. Receiver operator characteristic curves were also calculated using the ‘roc’ function from the R package pROC.⁴² To assess differences between class 1 and class 2 AMP scores, the function “t.test” was used.

Violin plots, boxplots, and AMP score heatmaps were then made in R using the package ggplot2 to compare results.⁴³ AMP score heatmaps were created by first plotting each pixel according to its x and y coordinates and then coloring based on the AMP score value.

RESULTS AND DISCUSSION

AMP scores were developed in this work to enhance MSI data visualization by assessing multiple features and molecular changes simultaneously, including the gradation of borderline phenotypes. Assigning AMP scores for datasets of interest had several main steps, as shown in Figure 2. These steps included the following: (1) removing noise and normalizing the data, (2) splitting the data into training and testing sets, (3) applying ensemble feature selection to select significant features (or molecules) distinguishing the phenotypes of interest from the training data, (4) using selected features to calculate AMP score parameters, and (5) leveraging parameters from the training data to calculate AMP scores for the testing data and applying the phenotypic predictions to individual pixels.

As AMP scores are calculated solely on selected features, it is imperative to implement a robust feature selection method. For this reason, we opted for an ensemble feature selection approach, which was preferred due to its ability to overcome the limitations and biases associated with individual selection methods.⁴⁴ In our ensemble, we included Lasso, RF, and SVM as they each have different underlying assumptions and are therefore likely to capture unique patterns in the data.^34,36,38,44 A breakdown of the overlap between the three methods is shown in Figure S1. While these selection approaches were able to identify distinguishing features for this study, other selection methods, such as elastic net or ridge regression, may be better suited for different comparisons and could also be easily incorporated into the AMP score pipeline. Moreover, incorporating additional selection methods into the feature selection ensemble may result in a more stable feature list by ameliorating the biases of individual selection methods.

Once features were selected, weights for the selected features were determined. Because a key component of AMP score calculation is multiplying feature abundances with their respective weights, it was crucial that feature weights were directional, so that high feature abundances associated with class 1 or control phenotype result in lower AMP scores, while high abundance features correlating with class 2 phenotype provide higher AMP scores. To achieve this, we assigned β coefficients to each feature using logistic regression. This method was preferred over other feature weighting methods, such as information gain, due to the weights being signed and easily interpretable.⁴⁵ However, we do recognize that some datasets may not meet the underlying assumptions for logistic regression, and consequently, other weighting methods may be more appropriate. As such, identifying a nonparametric way to generate signed weights is a focus of future work.

After β coefficients were assigned to each feature, we subsequently calculated preliminary AMP scores for the training data. The purpose of doing this was to identify the optimal cutoff score for distinguishing the two phenotypes in each comparison, which would later be used to scale the AMP scores for the testing data. To choose a cutoff, the score value that maximized Youden’s Index was chosen. This specific statistic was maximized over other potential performance measures, such as accuracy because it considers both the true positive rate (sensitivity) and the true negative rate (specificity), making it a comprehensive measure of dichotomous diagnostic performance.^46,47 Once all parameters were determined, AMP scores were calculated for the testing data. To do this, the testing data was first filtered down to the selected features. The abundance for each feature was multiplied by its respective weight at each pixel, and all the resulting products were summed. However, since AMP score ranges varied for the different comparisons, we scaled all AMP scores between 0 and 1, with the cutoff value determined from the training dataset to 0.5. This allowed for easier, consistent interpretation both within and across comparisons.

To assess the AMP score calculations, three different MSI studies with normal, benign, and cancerous human tissue sections were evaluated (Figure 3). For all studies, the number of pixels used for training far exceeded the number of input features (e.g., 23,657 pixels and 738 features in the NB vs IDC comparison). This characteristic supported the decision to conduct analysis using machine learning methods (Lasso regression, RF, and SVM). It was also observed that following ensemble feature selection, the dimensions of each dataset decreased substantially, with 87.5 to 98.0% of the overall features removed prior to AMP score calculation. This reduction resulted in 40 features for the FTA vs PTC tissue comparison, 92 for NB vs IDC, 17 for NO vs BOT, 18 for NO vs HGSC, and 44 for BOT vs HGSC. When the AMP scores were calculated from these features and assessed on the testing data, they showcased a high predictive power, with class 1 samples having significantly lower scores than class 2 samples (p < 2.2 × 10⁻¹⁶ across all comparisons). We also observed high sensitivity and specificity across all studies with all metrics above 92.7%, which is visualized in receiver operating characteristic curves (Figures 3 and S2). This balance of sensitivity and specificity was observed across comparisons having markedly different pixel ratios. For example, the NB vs IDC comparison involved considerably more IDC pixels than NB. This is a result of many NB tissue samples being primarily composed of fat, limiting the number of pixels that could be extracted from epithelial cells.²⁴ Despite this imbalance, AMP performed comparably to other comparisons. These results suggest that a generalized AMP pipeline offers balanced performance. Importantly, the parameters could be tuned to favor sensitivity (i.e., disease detection) or specificity depending upon clinical considerations regarding the consequences of false-negatives versus false-positives.

Figure 3.

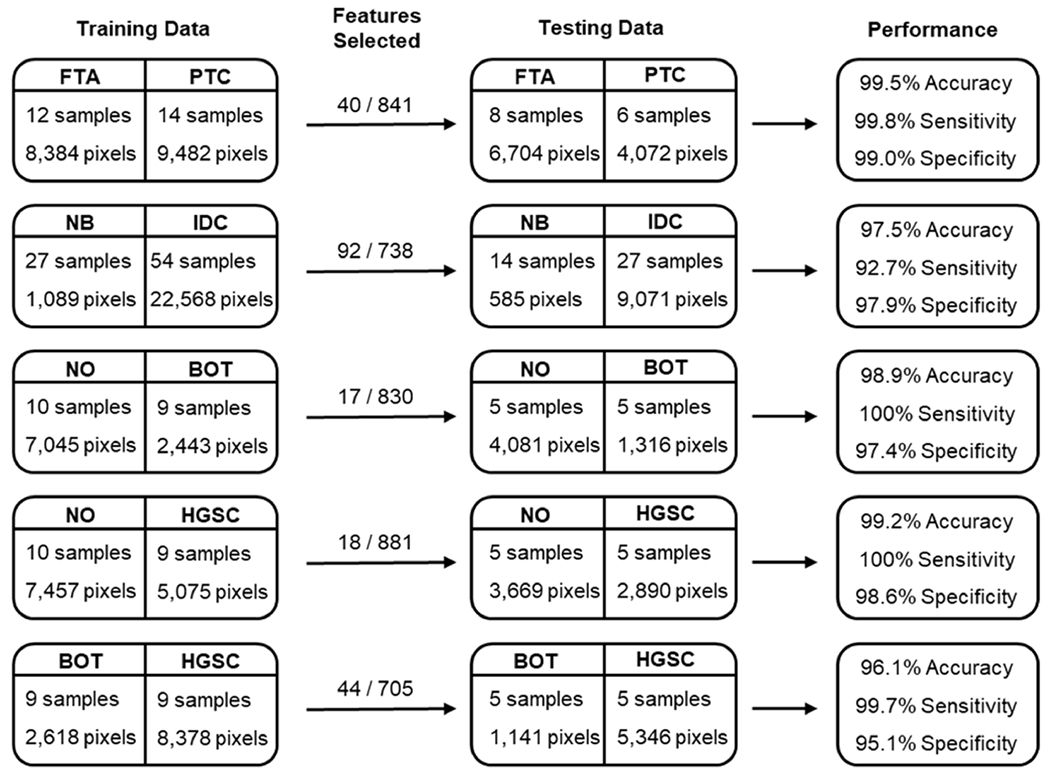
Summary of data used for the AMP score calculation and validation and overall performance for each pairwise comparison. The number of features selected as significant for each study is also noted versus the total number of features evaluated. From top to bottom: FTA vs PTC, NB vs IDC, NO vs BOT, NO vs HGSC, and BOT vs HGSC.

While the ability to differentiate phenotypes can be summarized as approximately equal across comparisons, as shown by the metrics in Figure 3, the distribution of AMP scores across pixels varied (Figure 4). In each comparison, the distributions were separated by phenotype, with the greatest separations in AMP scores between the NO vs HGSC and NO vs BOT comparisons. Interestingly, in the normal/benign vs cancerous comparisons (top four plots), the distribution for cancerous pixels was wider than the distribution of pixels for the normal/control This wider distribution may be due to diseased samples having different degrees of progression and thereby leading to more variable molecular profiles compared to control samples. In particular, the distribution of BOT samples appears somewhat bimodal. Since BOTs have the potential to develop into low-grade serous carcinoma, we hypothesize that this split may correspond to samples that are progressing in severity.²⁸ This trend is further supported in the BOT vs HGSC distributions (bottom plot), where we see BOT is once again bimodal, with the smaller mode having AMP scores closer to HGSC. When comparing the AMP score distribution of HGSC in the NO vs HGSC comparison to the BOT vs HGSC comparison, we also can see that the distribution is much narrower in the BOT vs HGSC comparison. This result may suggest that the molecular features that differentiate HGSC samples from BOT samples are expressed more consistently in HGSC samples than the features that differentiate NO and HGSC samples. While the comparisons in this study mainly focused on various healthy and disease phenotypes from human tissue, the BOT vs HGSC comparison showed that the AMP score pipeline is not specific to normal/benign vs disease cases. Therefore, we believe that AMP scores may be useful for assessing disease severity, identifying mechanisms of pathogenesis, and selecting prognostic markers. To further explore this capability, future steps include characterizing the relationship between patient metadata and AMP scores to determine if correlations exist between scores and patient outcomes or other clinical measurements.

Figure 4.

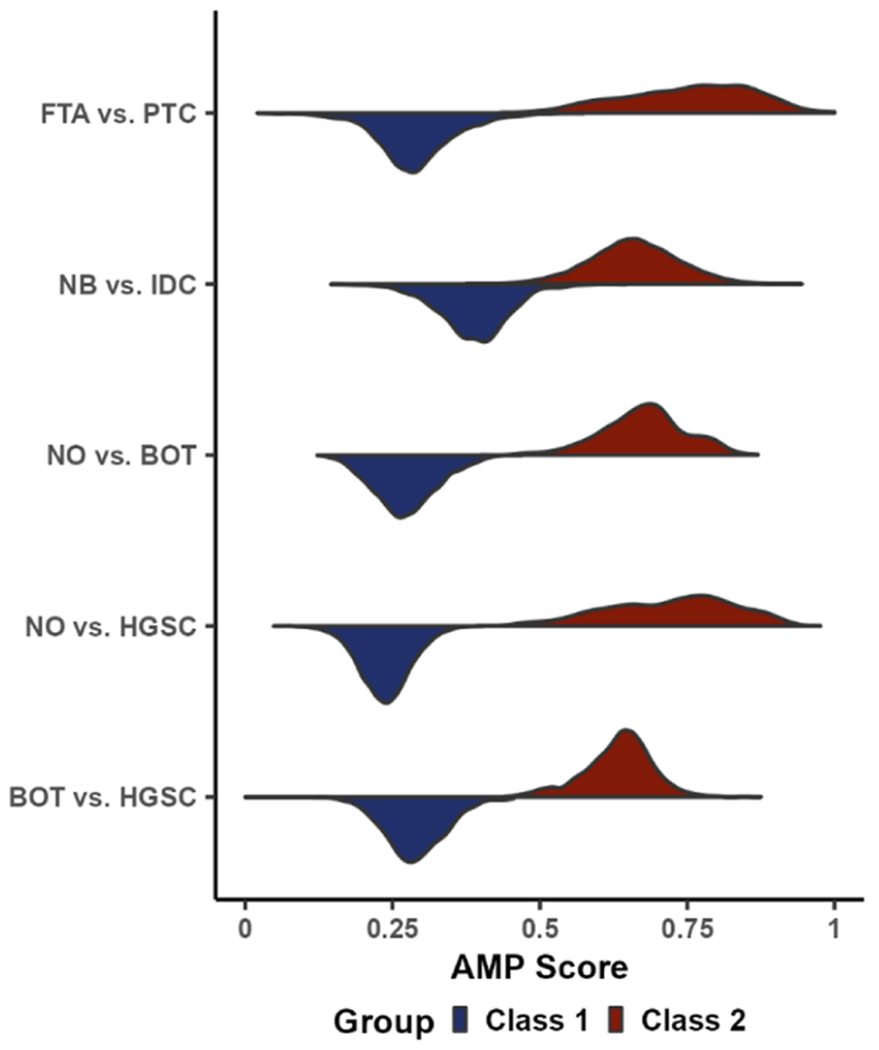
Violin plot showing the density of AMP scores for each pairwise comparison split by phenotype.

To gain more information on the phenotype classifications, we also evaluated the AMP score distributions at the individual sample level (Figure 5). Again, there was a strong distinction between the different phenotypes, with samples from class 1 phenotypes being closer to zero and class 2 samples being closer to one. Interestingly, all misclassified pixels had an intermediate AMP score, with the lowest score from the true class 2 pixels being 0.374 and the highest score from the true class 1 pixels being 0.645 (Figure 5A–E). An exception to the otherwise high prediction accuracy is sample 7 in the NO/HGSC comparison (Figure 5C), which had over half of the pixels misclassified. This sample only consisted of 20 total pixels and therefore had very little influence on the overall prediction performance of the testing data. However, this result may also suggest that this sample should be further examined by pathology to confirm its phenotype. Additionally, when comparing the sample distributions within each pairwise phenotype comparison to one another, there is considerable variation, particularly for class 2 phenotypes. This reveals that rather than reflecting the overall phenotype distributions from Figure 4, individual samples or pixels may contribute more heavily to certain parts of the distributions. This trend is best observed when considering the HGSC data in the NO vs HGSC comparison, where the distribution of all pixels is quite wide (Figure 4), but the individual sample distributions are much narrower and almost completely in distinct interquartile ranges (Figure 5C).

Figure 5.

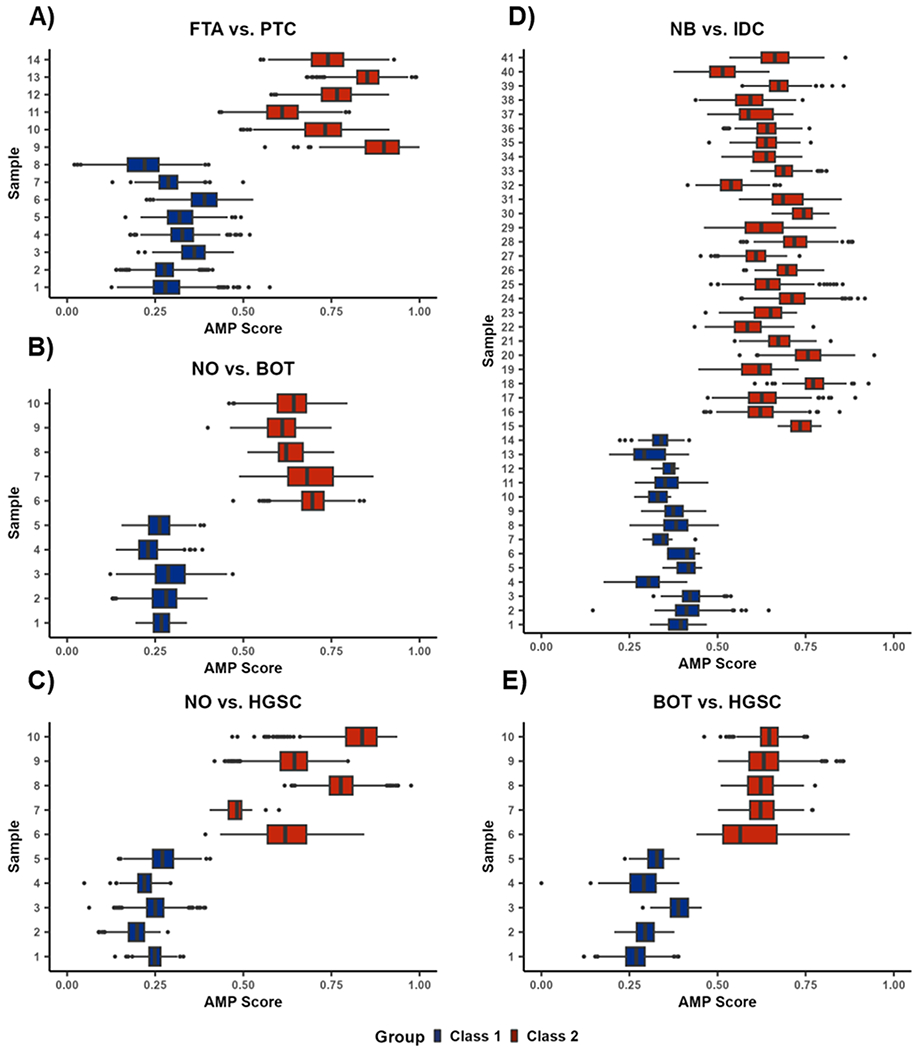
AMP score distributions by sample for (A) FTA vs PTC, (B) NO vs BOT, (C) NO vs HGSC, (D) NB vs IDC, and (E) BOT vs HGSC. Each individual box and whisker plot shows the distribution of AMP scores across all pixels within a sample. Outlier points are defined as observations more than 1.5 times the interquartile range away from the upper or lower quartile.

Beyond binary classifications, AMP scores were also evaluated for their continuous scoring of phenotypes and visualization of margins in the tissue sections. The ability of AMP score heatmaps to capture overall molecular patterns was demonstrated in both the homogeneous (Figure 6) and heterogeneous samples (Figure 7). In homogeneous tissue sections, the phenotype of each sample was readily apparent from the AMP score heatmaps (Figure 6). For both class 1 and class 2 samples for the FTA vs PTC, NO vs BOT, and BOT vs HGSC comparisons, AMP scores remain relatively consistent throughout the entire diseased or control tissue areas. Notably, pixels with intermediate AMP scores are frequently located near the tissue border. As the presented tissue sections were extracted to only show homogeneous regions, pixels near the tissue borders in these images likely represent areas near phenotypic changes. These intermediate pixels also match the outliers seen in Figure 5. This suggests that intermediate scores may indicate transition regions where tissue shares molecular characteristics with both phenotypes. To further assess this possibility, predictions were made on a few heterogeneous tissue samples to see how scores changed near phenotypic borders (Figure 7). Specifically, we assessed two HGSC tissues and one IDC tissue, each having accompanying H&E slides with tumorous areas outlined in black. Comparing AMP score heatmaps to these annotations, we see that AMP score heatmaps were able to successfully identify tumorous areas, highlighting the utility of AMP scores for distinguishing phenotypes. Once again, in all three plots, pixels located at the border of normal and cancerous tissue had intermediate scores, suggesting that molecular differences between phenotypes occur gradually, with transition regions sharing molecular characteristics of both tissue types (Figure 7D). To ensure that this border reflected biological changes and not faulty model output, we assessed a subset of mass spectra corresponding to pixels across this transition region. This comparison, which is presented in the Supporting Information, provided further evidence that the transition region shares characteristics of both tissue phenotypes. This result is consistent with the work done by Woolman et al., which showed that molecular borders are not as sharp as the morphometric borders identified with microscopy and that a gradient of cancer-like metabolic states may be observed near cancerous tissue regions.⁴⁸ To determine if the ability to detect these transition regions is unique to our method, we also applied LDA for both prediction and visualization. This analysis, which is reported in the Supporting Information, revealed that while LDA had comparable prediction accuracy, it favored outputting extreme probabilities and therefore failed to capture transition spaces.

Figure 6.

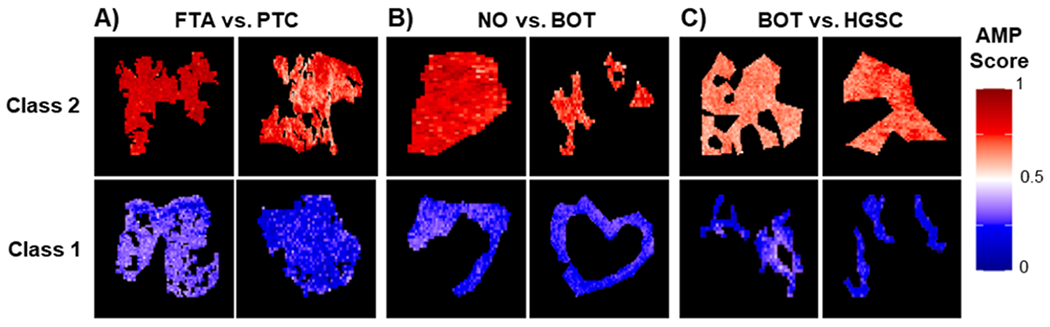
Example AMP score heatmaps for select (A) FTA vs PTC, (B) NO vs BOT, and (C) BOT vs HGSC homogeneous tissues. For each tissue section, individual pixels are colored by their respective AMP score with lower scores shown in blue, midrange scores in white, and higher scores in red.

Figure 7.

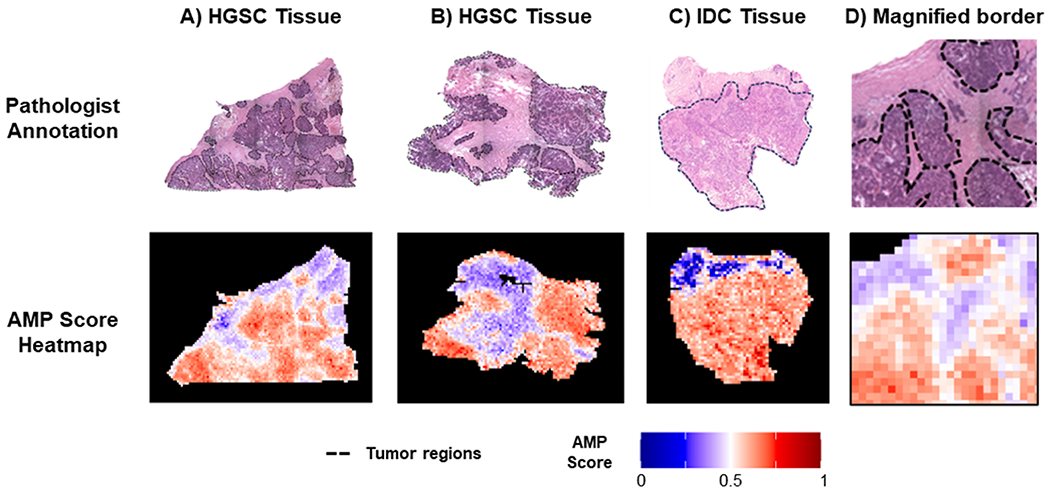
Comparison of AMP score heatmaps for heterogeneous tissues to annotated H&E slides, for example, HGSC tissue shown in (A,B), IDC tissue in (C), and a magnified border region from (A) in (D). On the H&E slides, tissue outlined in black corresponds to tumorous areas with healthy tissue in the other regions.

CONCLUSIONS

In this study, we developed an AMP score pipeline to assess phenotypic differences in MSI data. We assessed these scores using data from three previous studies examining differences in normal, benign, and cancerous human tissue. Using the different studies, we first illustrated how AMP scores can improve tissue diagnostics by providing precise phenotypic predictions, as demonstrated by the high accuracy, sensitivity, and specificity observed across comparisons. In addition to providing accurate predictions, AMP score heatmaps highlight their ability to concisely visualize tissue sections in a phenotype-relevant way. For example, at phenotype borders, intermediate AMP scores were observed, suggesting that these regions may have a combination of characteristics similar to both phenotypes. This finding provides insight into the molecular changes that take place as malignancies spread, as well as further informs decision-making in surgical settings as physicians can choose to be more or less aggressive around these borders based on the nature of the disease.⁴⁹

To improve upon our described work, we aim to expand the AMP score pipeline in future work to improve its usability and increase the number of possible use cases. While the outlined steps for AMP score calculation are somewhat complex, we believe this pipeline has the potential to be fully automated through the auto-selection model parameters. As such, we hope to disseminate our work into a user-friendly interface. Additionally, we hope to expand the AMP scoring framework to accommodate multiple classifications as there may be scenarios where more than two phenotypes are suspected. Achieving this thus far has proven computationally difficult as the directionality of beta coefficients and other common signed feature weighting methods only accommodate two classes. However, we believe an adapted scoring system could be implemented for these cases by comparing all potential phenotypes to a control and using some form of similarity scoring. Finally, since AMP scores are calculated before being combined with spatial information, the AMP scoring framework is also applicable to different biofluids, such as urine and blood, for patient classification. Thus, future work will include evaluating these different scenarios to define other AMP score use cases.