Driving forces of the complex formation between highly charged disordered proteins

Significance

Charged disordered proteins are abundant in the cell, especially in the nucleus, and oppositely charged molecules can form high-affinity disordered complexes. Such interactions can exhibit surprising behavior, such as increased affinity with increasing temperature, but a detailed characterization of the underlying thermodynamic driving forces has been lacking. Combining single-molecule FRET (Förster resonance energy transfer), calorimetry, and analytical polymer theory, we dissect the thermodynamics of the disordered high-affinity complex between two highly charged disordered proteins and find that the release of counterions is an essential entropic contribution to binding. Our results also demonstrate the formation of higher-order complexes at high protein concentrations, and provide a quantitative experimental and theoretical framework for elucidating the interactions of charged disordered biomolecules and synthetic polyelectrolytes.

Abstract

Highly disordered complexes between oppositely charged intrinsically disordered proteins present a new paradigm of biomolecular interactions. Here, we investigate the driving forces of such interactions for the example of the highly positively charged linker histone H1 and its highly negatively charged chaperone, prothymosin α (ProTα). Temperature-dependent single-molecule Förster resonance energy transfer (FRET) experiments and isothermal titration calorimetry reveal ProTα-H1 binding to be enthalpically unfavorable, and salt-dependent affinity measurements suggest counterion release entropy to be an important thermodynamic driving force. Using single-molecule FRET, we also identify ternary complexes between ProTα and H1 in addition to the heterodimer at equilibrium and show how they contribute to the thermodynamics observed in ensemble experiments. Finally, we explain the observed thermodynamics quantitatively with a mean-field polyelectrolyte theory that treats counterion release explicitly. ProTα-H1 complex formation resembles the interactions between synthetic polyelectrolytes, and the underlying principles are likely to be of broad relevance for interactions between charged biomolecules in general.

Intrinsically disordered proteins (IDPs) can bind to many different cellular targets and are thus abundant in molecular interaction hubs (1–3). The underlying interaction mechanisms and the extent of disorder in IDP complexes cover a remarkably broad spectrum. For some IDPs, binding is coupled to folding and results in complexes with a well-defined three-dimensional structure (4). In other cases, some disorder is retained in the bound state (5, 6). For instance, IDPs often employ short secondary structure elements, small linear motifs, or even single-site modifications or side chains to engage interaction partners (7, 8). As a result, large parts of the chain can remain disordered. In extreme cases, one or both partners fully retain their structural disorder after binding, a mechanism that is particularly common for highly charged IDPs interacting with each other or with nucleic acids (9–13). We have recently identified such an example, the complex between the two human IDPs prothymosin α (ProTα) and linker histone H1 (13). ProTα and H1 carry large opposite net charges (−44 and +53, respectively) and associate into a heterodimer with picomolar to nanomolar affinity in the physiological range of salt concentrations, yet they retain their disorder in the complex. ProTα acts as a chaperone of H1 (14) and enables the dissociation of H1 from nucleosomes despite the extreme affinity of the H1-nucleosome complex (15).

The surprising absence of structure formation and of structured interaction interfaces in such disordered complexes raises the question of how the underlying thermodynamic driving forces for binding differ from the classical paradigms of interactions for folded proteins (16–18). In many respects, the interactions between highly charged naturally occurring biopolymers are reminiscent of the complexation between synthetic polyelectrolytes (9, 19–22). However, for synthetic systems, it has been challenging to experimentally probe the properties of small oligomers with well-defined stoichiometry separately from their phase separation by complex coacervation (23). The preparative biochemical methods and single-molecule spectroscopy available for biological polyelectrolytes provide an opportunity for closing this gap. Here, we dissect the thermodynamic driving forces involved in the formation of the dimer and the ternary complexes of ProTα and H1 under conditions where phase separation does not occur. We show that in spite of the high affinity, the interaction is enthalpically unfavorable and instead driven by the entropy gain from counterion release, as suggested for polyelectrolyte complexation (9, 19, 21, 22, 24–27).^* Considering the abundance of charges in IDPs and other biomolecules in the cell, the thermodynamic characteristics of the ProTα-H1 interaction are likely to resemble those of many biomolecular binding processes.

Results

High Affinity Despite Unfavorable Enthalpy.

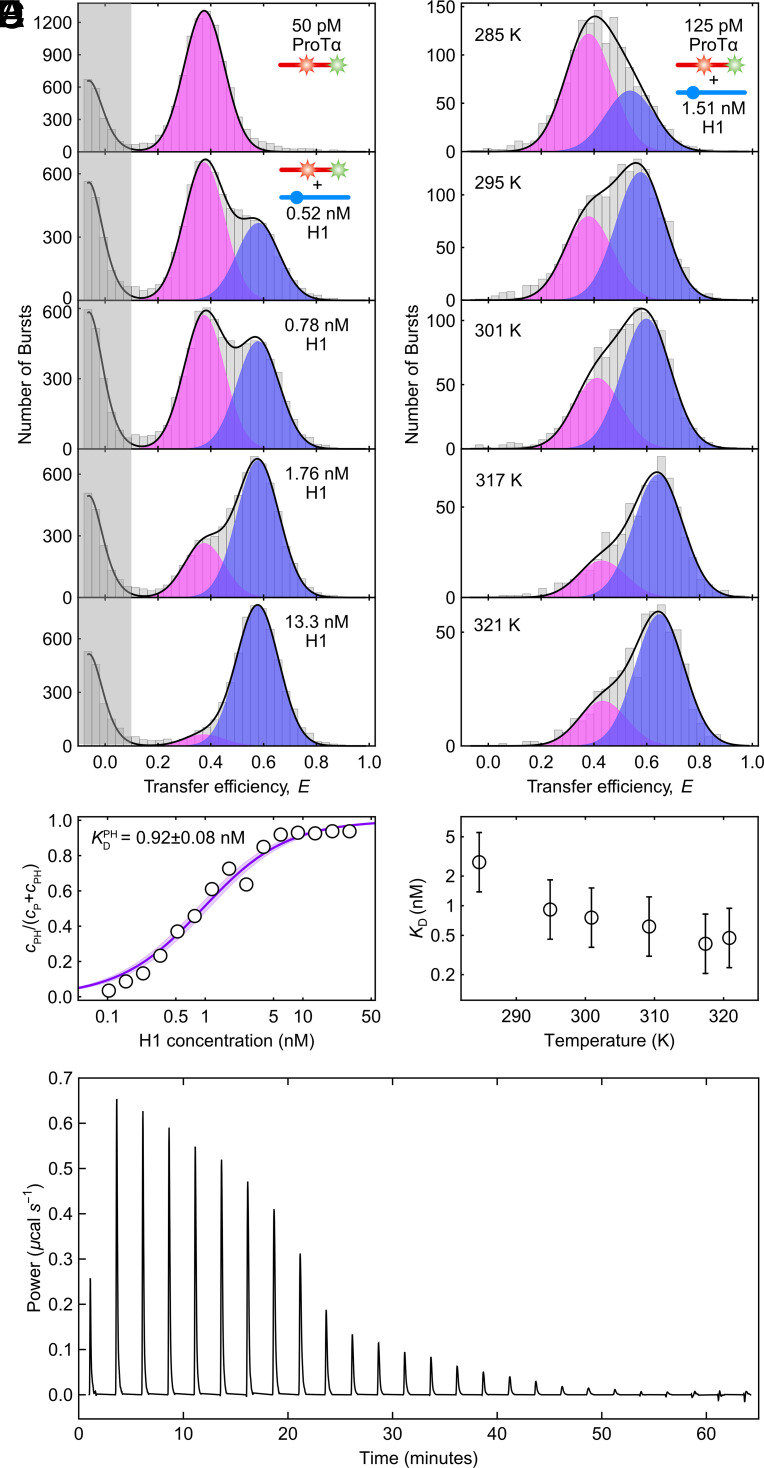
The most striking feature of the ProTα-H1 complex is that the two IDPs bind to each other with picomolar to nanomolar affinity in the physiological ionic strength range, although they both remain disordered in the complex (13, 28). To enable measurements at the very low protein concentrations where the equilibrium between monomers and the dimer of ProTα (P) and H1 (H) can be monitored, we use single-molecule Förster resonance energy transfer (FRET) on freely diffusing molecules with confocal detection (29–33). ProTα labeled with donor and acceptor fluorophores (Alexa Fluor 488 and 594, respectively) at positions 56 and 110 exhibits a FRET efficiency of 0.37 ± 0.03 at a monovalent salt concentration^† of 208 mM. Upon titrating picomolar concentrations of labeled ProTα with increasing concentrations of unlabeled H1, we observe a second population corresponding to the ProTα-H1 dimer (PH) (Fig. 1A). Owing to the mutual charge screening of the two oppositely charged IDPs, ProTα is more compact in the complex (13), resulting in a higher transfer efficiency of 0.56 ± 0.03. The equilibrium fraction of PH as a function of H1 concentration allows us to determine the equilibrium dissociation constant, $K_{\mathrm{D}}^{\mathrm{PH}}$ (Fig. 1B). $K_{\mathrm{D}}^{\mathrm{PH}}$ increases from ${2.1}_{-0.8}^{+1.1}$ pM at 165 mM (13) to ${1.2}_{-0.6}^{+1.2}$ nM at 208 mM monovalent salt concentration.

Fig. 1.

The high-affinity binding between H1 and ProTα is endothermic. (A) Transfer efficiency histograms of 50 pM ProTα E56C/D110C labeled with Alexa Fluors 488 and 594 in the presence of increasing concentrations of unlabeled H1 (see the legend) at 208 mM monovalent salt concentration, globally fit with two Gaussian peak functions for the unbound (magenta) and bound (blue) ProTα populations, respectively (sum: black lines). (B) Representative example showing the bound fraction of labeled ProTα as a function of the H1 concentration fitted with a binding isotherm (solid line), in this case yielding an equilibrium dissociation constant of K_D = 0.92 ± 0.08 nM (shaded band: 90% CI). (C) Transfer efficiency histograms of 125 pM ProTα E56C/D110C labeled with Alexa Fluor 488/594 in the presence of 1.51 nM unlabeled H1 at 208 mM monovalent salt concentration, measured at different temperatures and fitted with two Gaussian peak functions for the unbound (magenta) and bound (blue) ProTα populations, respectively (sum: black lines). (D) The resulting temperature-dependent K_D shows rising affinity with increasing temperature, thus endothermic binding. Error bars represent a conservative systematic error of a factor of 2 on K_D (SI Appendix). (E) ITC thermogram, showing differential power as a function of time upon titrating ProTα into H1 at 208 mM monovalent salt concentration, which confirms endothermic binding.

To assess the role of enthalpic and entropic contributions to the binding process, we investigated the temperature dependence of $K_{\mathrm{D}}^{\mathrm{PH}}$. We measured transfer efficiency histograms of picomolar concentrations of labeled ProTα in the presence of a fixed concentration of unlabeled H1 close to $K_{\mathrm{D}}^{\mathrm{PH}}$ between 283.5 K and 331 K (Fig. 1C). The temperature dependence reveals another remarkable feature of the PH complex: The equilibrium fraction of PH increases with increasing temperature, i.e., higher temperature favors binding (Fig. 1D). Correspondingly, ProTα-H1 complex formation must be associated with a thermodynamically unfavorable, positive enthalpy change, ΔH^PH > 0. This conclusion is confirmed by isothermal titration calorimetry (ITC), which shows the signature of an endothermic reaction (Fig. 1E), as observed previously (34). Since ΔH^PH > 0, ProTα-H1 binding must be entropically driven. This behavior contrasts with many high-affinity protein interactions, for which the enthalpy of binding is often favorable (17, 35). Notably, an unfavorable enthalpic contribution has also been observed for complex coacervation (10, 36, 37), indicating that the driving forces for phase separation of polyelectrolytes and for the formation of the ProTα-H1 dimer are closely related. The origin of the entropically dominated driving force of ProTα-H1 binding thus deserves closer investigation.

Counterion Release Entropy Is a Strong Driving Force for ProTα-H1 Binding.

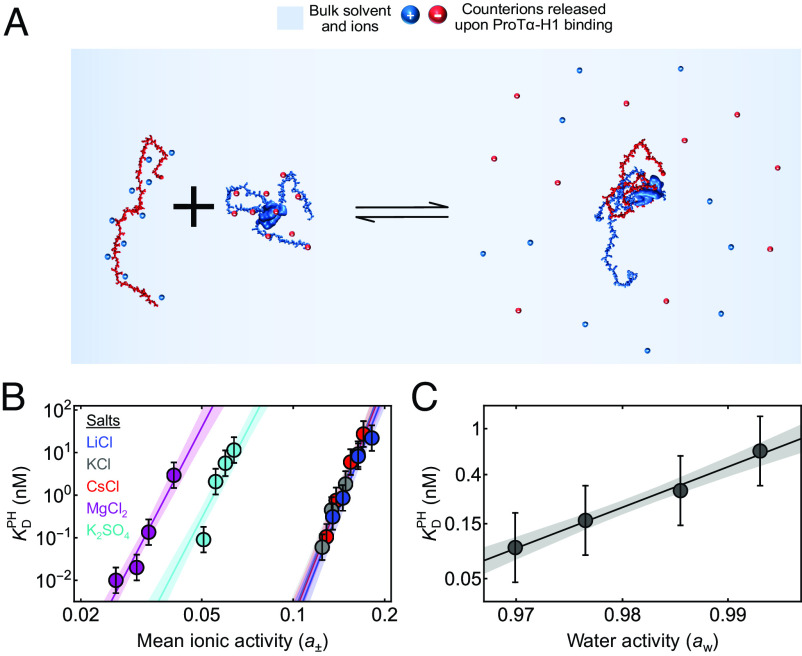
Naively, it might be tempting to envision the driving force for binding between oppositely charged macromolecules in terms of simple Coulomb attraction between them. However, in this case, the process should be exothermic, in contrast to what we observe for H1 and ProTα. This simple picture ignores the essential role of counterions, present in the solution to ensure electroneutrality, and some of which associate with polyelectrolytes due to Coulomb attraction (19, 24). The presence of ions can extensively modulate biomolecular conformations, dynamics, and recognition (38–40), but the effects become particularly pertinent when two polyelectrolyte chains associate (be they biological or synthetic): Counterions are released into solution as charge interactions form between the chains, which results in a gain in translational entropy owing to the dilution of the ions into the bulk solution (Fig. 2A). This favorable counterion release entropy has been suggested to be a key driving force for polyelectrolyte complexation (24, 41–43). To quantify the contribution of counterions, Record and Lohman (24) developed an approach based on the principles of coupled equilibria between biomolecular binding and counterion release. In our case, unbound ProTα and H1 are associated with their counterions to attain charge neutrality; upon H1 binding to ProTα, $n_{-}$ of the previously associated monovalent anions (${\mathrm{A}}^{-}$) and $n_{+}$ of the monovalent cations (${\mathrm{C}}^{+}$) are released:

$$\begin{array}{c}\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{T}\alpha +\mathrm{H}1\rightleftharpoons \mathrm{P}\mathrm{r}\mathrm{o}\mathrm{T}\alpha -\mathrm{H}1+n_{+}{\mathrm{C}}^{+}+n_{-}{\mathrm{A}}^{-}.\hfill \end{array}$$ [1]

Fig. 2.

Effects of ion and water activities on ProTα-H1 binding. (A) Schematic of ProTα binding to H1 associated with counterion release. (B) Equilibrium dissociation constant for ProTα-H1 binding, $K_{\mathrm{D}}^{\mathrm{PH}}$, at different mean ionic activities (a_±) of various salts (see the legend for color code). The data are fitted globally to obtain the number of monovalent and/or divalent ions released upon ProTα-H1 complex formation (see SI Appendix for details). The solid lines represent the fit, and the shaded regions represent 90% CIs. (C) $K_{\mathrm{D}}^{\mathrm{PH}}$ at 208 mM monovalent salt concentration as a function of water activity (a_w), varied by changing the concentration of the osmolyte triethylene glycol (SI Appendix). The solid line represents a fit with Eq. 4 for estimating the apparent number of water molecules released upon ProTα-H1 complex formation (shaded band: 90% CI). All error bars represent a conservative systematic error of a factor of 2 on K_D (SI Appendix).

However, $n_{+}$ and $n_{-}$ can usually not be observed directly. Instead, we probe the apparent equilibrium

$$\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{T}\alpha +\mathrm{H}1\stackrel{K_{\mathrm{D}}^{\mathrm{PH}}}{\rightleftharpoons }\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{T}\alpha -\mathrm{H}1.$$ [2]

Record and Lohman (24) related the dependence of the corresponding observed equilibrium dissociation constant, $K_{\mathrm{D}}^{\mathrm{PH}}$, on the mean ionic activity of the participating ions, a_±, to the total number of counterions released, $\mathrm{\Delta }n$:

$$\mathrm{\Delta }n=n_{+}+n_{-}\approx \frac{d\log K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}}}{d\log a_{\pm }}.$$ [3]

For H1 binding to ProTα, this dependence on salt concentration is remarkably strong: $K_{\mathrm{D}}^{\mathrm{PH}}$ increases by six orders of magnitude (from ${2.1}_{-0.8}^{+1.1}$ pM to 4 ± 2 μM) between 165 mM and 340 mM monovalent salt (13, 28). Eq. 3 yields a release of 18 ± 1 monovalent counterions upon complex formation (13, 28), an unusually large number compared to other biomolecular systems (24, 44).

To assess the effect of the chemical identity of the counterions and their charge on the process, we extended this analysis to other chloride salts of monovalent cations (LiCl and CsCl) as well as divalent cations and anions [K₂(SO₄) ad MgCl₂] (Fig. 2B). Effects of ions on polyelectrolyte complexation and biomolecular recognition can be complex, including the coupling of ion-specific conformational transitions to binding (45), differential ion uptake and release (46), and the ion-driven modulation of hydration effects (47). In the simplest scenario, however, the total number of anionic and cationic charges that are released upon binding to warrant charge neutrality is independent of the valence and identity of the counterions—this indeed seems to be the case for the binding of ProTα to H1: For the monovalent salts tested, the results are independent of chemical identity (Fig. 2B), suggesting that their interactions with the protein are nonspecific. For the divalent salts, the total number of released ions should be lower than for monovalent salts. Indeed, we observe a reduced slope for the dependence of log $K_{\mathrm{D}}^{\mathrm{PH}}$ vs. log a_± for salts with divalent cations or anions (Fig. 2B). From a global fit of the dependencies of $K_{\mathrm{D}}^{\mathrm{PH}}$ on mean ionic activity for all five salts with a generalization of Eq. 3 (SI Appendix), we obtain 18 ± 1 for the sum of positive and negative charges released upon binding (Fig. 2B), respectively, consistent with our previous estimate of 18 ± 1 monovalent counterions released (13, 28). A general caveat of this analysis lies in the assumption that the extent of counterion adsorption is independent of salt concentration (24), which may not be fully realistic for flexible polyelectrolytes (48). Nevertheless, we can conclude that a large number of counterions is released when H1 binds to ProTα, and the resulting gain in their translational entropy is a driving force of complex formation (24, 41, 42).

Another contribution to binding processes originates from hydration (24, 49–51). These effects are more difficult to interpret mechanistically (52), but we assessed the role of water in ProTα-H1 complex formation by varying the water activity, a_w, with a neutral small-molecule osmolyte, triethylene glycol (53) (SI Appendix), and measuring its influence on $K_{\mathrm{D}}^{\mathrm{PH}}$. Formally, this result can be expressed in terms of the number of water molecules released upon complex formation, ${\mathrm{\Delta }n}_{\mathrm{w}}$, according to (51, 53)

$$\mathrm{\Delta }{n}_{\mathrm{w}}\approx \frac{d\log K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}}}{d\log a_{\mathrm{w}}},$$ [4]

yielding ${\mathrm{\Delta }n}_{\mathrm{w}}$ = 80 ± 5 (Fig. 2C). For comparison, for folded proteins binding specifically to their cognate double-stranded DNA targets, ${\mathrm{\Delta }n}_{\mathrm{w}}$ is considerably larger, typically with hundreds and up to ~1,000 water molecules released upon complex formation (47, 53–55). The lower value of ${\mathrm{\Delta }n}_{\mathrm{w}}$ for ProTα-H1 binding is not entirely surprising since the IDPs remain highly hydrated owing to the disordered nature of the complex (13). Relating ${\mathrm{\Delta }n}_{\mathrm{w}}$ to simple thermodynamic quantities is complicated by the many degrees of freedom involved in hydration processes (52), but the free energy gain from the entropy of dilution is expected to be low because of the high bulk concentration of water (~55.5 M).

A final contribution to consider is configurational entropy of the polypeptide chains, which can play an important thermodynamic role in binding reactions of IDPs, for instance, if they are coupled to folding (56). In the case of H1 and ProTα, however, both IDPs retain their disorder and chain dynamics in the bound state (13), and the chains undergo only a minor compaction (Fig. 1A and SI Appendix, Fig. S1). Other degrees of freedom may contribute (18) but are difficult to identify unequivocally and are likely to be model-dependent. Based on a simple Gaussian chain model and a compaction by 23% in terms of end-to-end distance for ProTα at 208 mM monovalent salt concentration (SI Appendix, Fig. S1), we estimate a total change in configurational free energy of ~0.5 k_BT upon binding, assuming similar compaction for both ProTα and H1; this contribution is negligible compared to the total free energy of binding of ~20 k_BT.

Altogether, we thus conclude that counterion release entropy is likely to be a strong thermodynamic driving force for PH formation, as for polyelectrolyte complexation of synthetic systems (24, 41, 42), whereas changes in chain entropy of the IDPs are negligible for such a highly disordered complex. Contributions from hydration to the free energy of binding are likely to be relevant (57) but difficult to dissect into enthalpic and entropic contributions experimentally.

Resolving Ternary Complex Formation at Higher Protein Concentrations.

So far, we have focused on the dimerization equilibrium P + H ⇌ PH, which describes the interaction between H1 and ProTα at picomolar and low nanomolar protein concentrations in the physiological ionic-strength range (13, 28). However, several observations indicate the existence of larger oligomers. First, transfer efficiencies and hydrodynamic radii for ProTα-H1 complexes were found to exhibit a continuous and progressive shift at large excess of one of the binding partners (13). Second, the interaction kinetics of H1 and ProTα are protein concentration-dependent and deviate from two-state behavior at high nanomolar protein concentrations and above (28), a signature of the formation of ternary complexes, such as ProTα₂-H1 (PPH) and ProTα-H1₂ (PHH) (58). The presence of ternary complexes also explains the fast exchange between bound and unbound states when the reaction is probed at the micromolar concentrations required for NMR spectroscopy (28). Third, molecular simulations demonstrate that the disordered nature of the complex facilitates the formation of higher-order oligomers (13, 15, 28). To probe the properties of ternary complexes more directly, we reasoned that since the interactions are charge-driven, reducing the salt concentration should further increase the affinity and decrease the kinetic exchange rates for the ternary complexes and might thus enable the detection of ternary complexes at equilibrium.

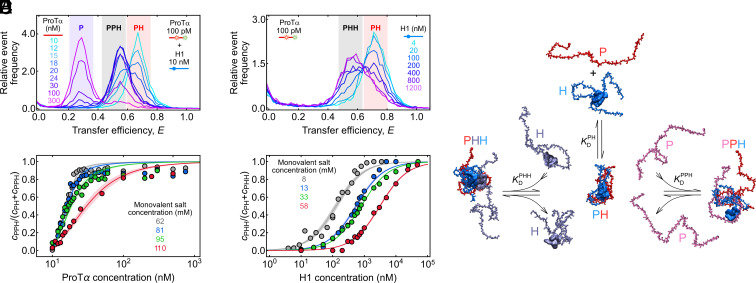
The existence of species beyond monomers and dimers does indeed become obvious in single-molecule titration experiments at low salt and elevated concentrations of unlabeled protein as distinct subpopulations in the transfer efficiency histograms (Fig. 3 A and B). For instance, we mixed 10 nM unlabeled ProTα and H1 each at 62 mM monovalent salt concentration and doped it with 70 pM labeled P as a probe that partitions between all ProTα-containing species and reports on their equilibrium fractions (Fig. 3A). Initially, a single population corresponding to the ProTα-H1 dimer is observed. If P + H ⇌ PH was the only contributing process, adding excess unlabeled P would simply cause a decrease in the observed equilibrium fraction of PH and an increase in the fraction of P. Instead, the decrease in the fraction of PH is accompanied by the appearance of a separate population with a transfer efficiency between those of PH and P. This new population reaches its maximum at a P:H stoichiometry of ~2:1, as expected for the ternary complex PPH. Adding even higher excess of P decreases the fraction of PPH, concomitant with an increase in the fraction of unbound P. From the fractions of PH and PPH, we obtain $K_{\mathrm{D}}^{\mathrm{P}\mathrm{P}\mathrm{H}}$ = ${0.7}_{-0.4}^{+0.7}$ nM for the reaction PPH ⇌ PH + P (Fig. 3C).

Fig. 3.

Resolving ternary complexes with single-molecule spectroscopy at equilibrium. (A) Overlay of transfer efficiency histograms of 100 pM ProTα E56C/D110C labeled with Alexa Fluors 488/594 at 62 mM monovalent salt concentration in the presence of 10 nM unlabeled H1, with increasing concentrations of unlabeled ProTα (see legend), showing the formation of the PPH ternary complex as a separate peak. The red-, gray-, and purple-shaded regions indicate the peaks corresponding to PH, PPH, and unbound P, respectively. (B) Overlay of transfer efficiency histograms of 100 pM ProTα E56C/D110C labeled with Alexa Fluors 488/594 at 8 mM monovalent salt concentration, with increasing concentrations of unlabeled H1 (see legend), showing the formation of the PHH ternary complex as a separate peak. The red- and gray-shaded regions indicate the peaks corresponding to PH and PHH, respectively. (C and D) Fraction of ternary complexes, PPH (C) or PHH (D), as a function of unlabeled ProTα (C) or H1 concentration (D) at different monovalent salt concentrations (see legend) from the type of titrations shown in A and B. Solid lines represent fits with binding isotherms (SI Appendix); shaded regions indicate 90% CIs. (E) Schematic of ProTα (red, pink) and H1 (blue, purple) forming the PH dimer and PHH and PPH ternary complexes, using snapshots from coarse-grained simulations (59).

Analogously, we can populate the ternary complex PHH in experiments with an excess of H1. Fig. 3B shows a titration starting from 70 pM labeled ProTα saturated with 3 nM unlabeled H1 at a monovalent salt concentration of 8 mM (originating from the buffer alone), which results in a single population corresponding to the ProTα-H1 dimer. Upon adding more unlabeled H1, however, an additional population with lower transfer efficiency appears and increases with H1 concentration, corresponding to PHH. From the H1-dependent fraction of PHH, we obtain $K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}\mathrm{H}}$ = ${0.12}_{-0.06}^{+0.12}$ μM for the reaction PHH ⇌ PH + H (Fig. 3D). These titration experiments thus not only allow us to resolve the ternary complexes PPH and PHH at equilibrium but also to quantify their stability.

With this approach, we can also probe the sensitivity of $K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}\mathrm{H}}$ and $K_{\mathrm{D}}^{\mathrm{P}\mathrm{P}\mathrm{H}}$ to salt concentration and assess the role of counterion release for ternary complex formation (Fig. 4A). For both $K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}\mathrm{H}}$ and $K_{\mathrm{D}}^{\mathrm{P}\mathrm{P}\mathrm{H}}$, the highest experimentally accessible salt concentrations are limited by the decreasing separation between dimers and ternary complexes in the transfer efficiency histograms, which prevents assignment of the different species at high salt (Fig. 3 A and B); for $K_{\mathrm{D}}^{\mathrm{P}\mathrm{P}\mathrm{H}}$, the lowest accessible salt concentrations were limited by complex coacervation of ProTα and H1 occurring even at nanomolar protein concentrations (60). Nevertheless, extrapolating the salt concentration dependencies of $K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}}$, $K_{\mathrm{D}}^{\mathrm{P}\mathrm{P}\mathrm{H}}$, and $K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}\mathrm{H}}$ affords a systematic comparison of the free energies of formation for PH (${\mathrm{\Delta }G}^{\mathrm{P}\mathrm{H}}$), PPH (${\mathrm{\Delta }G}^{\mathrm{P}\mathrm{P}\mathrm{H}}$), and PHH (${\mathrm{\Delta }G}^{\mathrm{P}\mathrm{H}\mathrm{H}}$). Across the experimentally accessible range, the absolute values of the free energies follow the order $\left|\mathrm{\Delta }{G}^{\mathrm{PH}}\right|$ >$\left|\mathrm{\Delta }{G}^{\mathrm{PPH}}\right|$ >$\left|\mathrm{\Delta }{G}^{\mathrm{PHH}}\right|$; i.e., PH is most stable, followed by PPH and PHH (Fig. 4A).

Fig. 4.

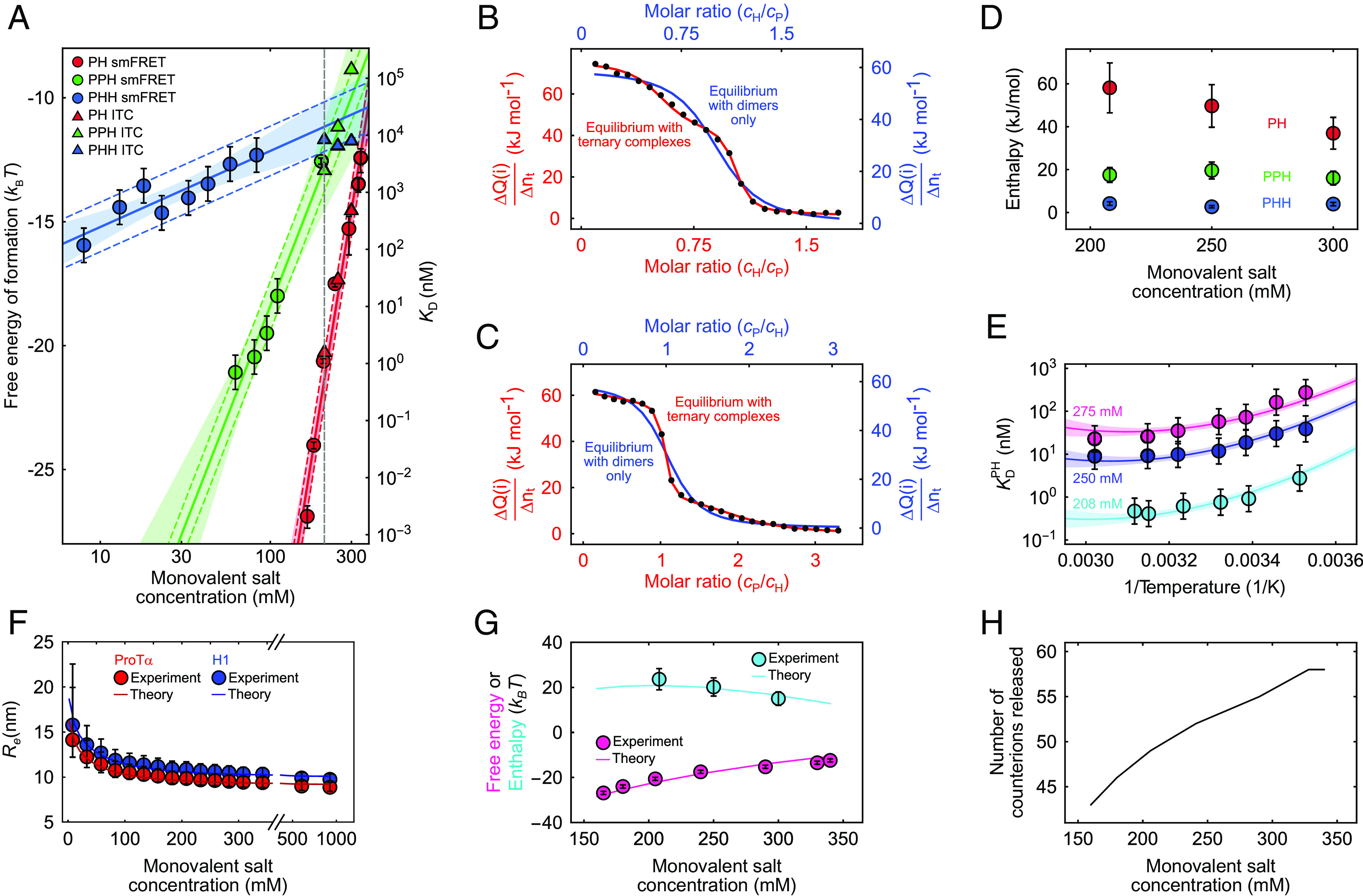
Thermodynamics of ProTα-H1 binding including ternary complex formation. (A) Free energies and dissociation constants of forming PH dimers (red) and the ternary complexes PPH (green) and PHH (blue) from single-molecule FRET (circles; including previously published data (13, 59)) and ITC (triangles; see SI Appendix, Fig. S2, for titrations) as a function of monovalent salt concentration and fits with Eq. 3 (or analogous for PPH and PHH, solid lines; shaded bands: 90% CIs). Error bars on single-molecule data for PH are from Borgia et al. (13); for PHH and PPH, error bars represent a conservative systematic error of a factor of 2 on K_D (SI Appendix). Colored dashed lines represent ±1 k_BT from the fit lines, the upper bound estimated for the perturbation from dye labeling (59). The vertical dashed gray line indicates a monovalent salt concentration of 208 mM. (B and C) Integrated power from ITC per molar amount of injected titrant (ΔQ/Δn_t; black points for each injection i) as a function of the molar ratio of both proteins, upon titrating H1 into ProTα (B) and ProTα into H1 (C) at 208 mM monovalent salt concentration. The data in (B) and (C) are globally fitted either with a 1:1 binding model (blue line and blue axis labels) or with a model including PHH and PPH ternary complexes (red line and axis labels) (see SI Appendix for details; note that the molar ratio is a fit parameter and thus slightly different for the two analyses). (D) Enthalpies of forming PH (red), PPH (green), and PHH (blue) from the ITC analysis (B and C and SI Appendix, Fig. S2) as a function of monovalent salt concentration. Error bars of ±20% are from the constraints on the protein concentrations used in fitting (SI Appendix, Table S2). (E) Temperature dependence of ProTα-H1 dissociation constants from single-molecule FRET measurements, shown as Van ‘t Hoff plots, at 208 mM (cyan), 250 mM (blue), and 275 mM (magenta) monovalent salt concentration. Error bars represent a conservative systematic error of a factor of 2 on K_D (SI Appendix). All three datasets are fitted globally with the integral form of the Van ‘t Hoff equation (solid lines; SI Appendix), with the heat capacity change upon binding as a shared fit parameter (SI Appendix; shaded bands: 90% CIs). (F) Salt dependence of the average end-to-end distance, $R_e$, for ProTα (red circles) and H1 (blue circles). $R_e$ for ProTα was measured using single-molecule FRET; for H1, it is approximated using the scaling exponents for ProTα (see SI Appendix for details). Error bars are estimated from a conservative systematic error of ±0.03 on transfer efficiencies. The blue and red lines show $R_e$ for ProTα and H1, respectively, using the theory for single isolated polyelectrolyte chains (see SI Appendix for details). (G) Comparison of the experimental free energy (magenta circles) and enthalpy (cyan circles) of ProTα-H1 complex formation as a function of monovalent salt concentration with those estimated from the theory of polyelectrolyte complexation (magenta and cyan lines for enthalpy and free energy, respectively; see SI Appendix for details). Error bars on experimental free energy and enthalpy as in (A) and (D). (H) The number of counterions released upon PH formation from the theory of polyelectrolyte complexation (see SI Appendix for details).

The slopes of the three salt concentration dependencies, however, are very different. Using Eq. 1, we can estimate the numbers of counterions released upon formation of PPH and PHH, yielding values of 8 ± 1 and 1.3 ± 0.3, respectively (Fig. 4A), much lower than the value of 18 ± 1 for PH formation. Evidently, the largest charge compensation and counterion release occurs during formation of PH, corresponding to the largest driving force among the three complexes. The ProTα-H1 dimer has a nominal net charge of +9 owing to the higher net charge of H1 (+53) compared to ProTα (−44); adding another ProTα chain thus yields substantial further charge compensation and counterion release. In contrast, adding H1 to the dimer is electrostatically much less favorable and leads to little counterion release. Extrapolation to 208 mM monovalent salt concentration (Fig. 4A) yields values of the dissociation constants of $K_{\mathrm{D}}^{\mathrm{P}\mathrm{P}\mathrm{H}}=3_{-2}^{+14}$ μM and $K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}\mathrm{H}}={13}_{-9}^{+26}$ μM. The presence of ternary complexes^‡ must thus be taken into account for the quantitative interpretation of any experiment performed in the micromolar protein concentration range.

Quantifying Enthalpic Contributions in ProTα-H1 Complex Formation.

Calorimetric measurements are considered the gold standard of thermodynamic analysis because they afford the direct measurement of binding enthalpies (61). However, since ITC cannot directly detect how many or which molecular species contribute, the accurate interpretation of the measured reaction heats requires an appropriate model comprising all equilibria involved. A semiempirical analysis of ITC measurements under conditions where both coacervation and soluble complex formation contribute have previously been used to infer positive enthalpies of ion pairing between polyelectrolytes (10, 36, 37). Here, we take the thermodynamic analysis one step further by performing measurements at sufficiently low protein concentrations so that phase separation does not contribute (60) and by explicitly accounting for the binding equilibria of dimers and ternary complexes of H1 and ProTα. Our detailed dissection of the ProTα-H1 interaction based on single-molecule FRET experiments over a wide range of protein and salt concentrations now allows us to approach such a complete thermodynamic analysis of ITC measurements. We performed ITC experiments at three different KCl concentrations corresponding to monovalent salt concentrations of 208 mM, 250 mM, and 300 mM, each with ProTα as a titrant (material injected) and H1 as a titrand (material in the sample cell) and vice versa (Fig. 4 B and C and SI Appendix, Fig. S2). Quantitative analysis of ITC measurements at lower salt concentrations was impeded by liquid–liquid phase separation (60).

The ITC titrations measured at 208 mM monovalent salt concentration, when fitted with a binding model involving only dimer formation, P + H ⇌ PH, yield apparent micromolar dissociation constants (34) (SI Appendix, Fig. S2 and Table S1) but show obvious deviations from the experimental data, reflecting the inadequacy of the model (Fig. 4 B and C and SI Appendix, Fig. S2). This result is not unexpected since the ITC measurements require micromolar protein concentrations, where both the dimer and the ternary complexes need to be considered. At 208 mM monovalent salt concentration, e.g., we expect that for 15 μM H1 and 45 μM ProTα, ~84% of the complexes are PPH. We thus include all three coupled equilibria, P + H ⇌ PH, PH + P ⇌ PPH, and PH + H ⇌ PHH, with their corresponding dissociation constants and reaction enthalpies $K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}}$ and ${\mathrm{\Delta }H}^{\mathrm{P}\mathrm{H}}$, $K_{\mathrm{D}}^{\mathrm{P}\mathrm{P}\mathrm{H}}$ and ${\mathrm{\Delta }H}^{\mathrm{P}\mathrm{P}\mathrm{H}}$, and $K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}\mathrm{H}}$ and ${\mathrm{\Delta }H}^{\mathrm{P}\mathrm{H}\mathrm{H}}$, respectively, as fit parameters, in a global analysis of the ITC measurements (see SI Appendix for details). We constrain the dissociation constants to be in agreement with the values extrapolated from the single-molecule data (binding free energies within ~1 k_BT, Fig. 4A and SI Appendix, Table S2) and obtain a good fit at all salt concentrations (Fig. 4 A–C and SI Appendix, Fig. S2). Taking into account ternary complex formation thus reconciles the apparent discrepancy between $K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}}$ obtained from single-molecule FRET (13, 28) and ITC (34) (Fig. 4A and SI Appendix, Fig. S2).

Our ITC analysis yields positive values for ${\mathrm{\Delta }H}^{\mathrm{P}\mathrm{H}}$, ${\mathrm{\Delta }H}^{\mathrm{P}\mathrm{P}\mathrm{H}}$, and ${\mathrm{\Delta }H}^{\mathrm{P}\mathrm{H}\mathrm{H}}$; thus, not only dimerization but also ternary complex formation must be entropically driven. ${\mathrm{\Delta }H}^{\mathrm{P}\mathrm{H}}$ is the largest among the three reaction enthalpies and decreases with monovalent salt concentration, from 58 ± 12 kJ mol⁻¹ at 208 mM to 35 ± 7 kJ mol⁻¹ at 300 mM (Fig. 4D). Electrostatic interactions, be they counterion accumulation near charged side chains of H1 and ProTα, or attraction between charged side chains in H1 and ProTα, are per se exothermic. However, if counterion condensation is more exothermic than the electrostatic attraction between the two IDPs, then the overall complex formation process can be endothermic. This hypothesis is compatible with the decrease in ${\mathrm{\Delta }H}^{\mathrm{P}\mathrm{H}}$ with increasing salt concentration, where charge screening is expected to attenuate the exothermicity of the underlying microscopic processes. Additional contributions may originate from ion-water interactions (41). In summary, while counterion release entropy is a strong overall driving force for ProTα-H1 complex formation, the enthalpy of binding is likely to be determined by competing differential side chain–ion and side chain–side chain interactions.

To complete the thermodynamic characterization of ProTα-H1 binding, we extended our analysis to the temperature dependence of $K_{\mathrm{D}}^{\mathrm{P}\mathrm{H}}$ from the single-molecule FRET measurements at different salt concentrations (Figs. 1 C and D and 4E). The resulting Van ‘t Hoff plots show a small yet consistent curvature for all datasets, indicating a temperature dependence of ${\mathrm{\Delta }H}^{\mathrm{P}\mathrm{H}}$ and the reaction entropy, ${\mathrm{\Delta }S}^{\mathrm{P}\mathrm{H}}$. The corresponding change in heat capacity upon binding, ${\mathrm{\Delta }C}_{\mathrm{p}}$, can be obtained from a fit with the integrated form of the Van ‘t Hoff equation (SI Appendix). Using ${\mathrm{\Delta }H}^{\mathrm{P}\mathrm{H}}$ from the ITC measurements^§, we fit all datasets with ${\mathrm{\Delta }C}_{\mathrm{p}}$ as a global fit parameter, yielding a value of −1.6 ± 0.3 kJ mol⁻¹ K⁻¹ (Fig. 4E). Identifying the molecular origins of ${\mathrm{\Delta }C}_{\mathrm{p}}$ is far from trivial, with potential contributions from different factors, including a differential temperature dependence of hydration for charged side chains and ions (62), but the small value of ${\mathrm{\Delta }C}_{\mathrm{p}}$ is typical of biomolecular binding and contrasts with the larger values associated with protein folding (63), where hydrophobic interactions are expected to make a larger contribution. The nonzero ${\mathrm{\Delta }C}_{\mathrm{p}}$ reflects some entropy–enthalpy compensation across different salt concentrations, resulting in a modest sensitivity of ${\mathrm{\Delta }G}^{\mathrm{P}\mathrm{H}}$ to temperature, in contrast to the dramatic sensitivity of ${\mathrm{\Delta }G}^{\mathrm{P}\mathrm{H}}$ to salt concentration. We can thus conclude that at the physiological temperature of 37 °C, PH complex formation is enthalpically unfavorable over a broad range of salt concentrations, up to ~350 mM, and counterion release is an important entropic driving force.

A Polymer Model of Polyelectrolyte Dimer Formation.

We employed an analytical polyelectrolyte model incorporating counterion condensation and uniform expansion (64–66), based on the Edwards–Muthukumar Hamiltonian (48, 67–69), to quantitatively describe the driving forces of the ProTα-H1 interaction. This theory of polyelectrolyte complexation takes into account conformational properties of the individual IDPs, IDP-associated counterions, and salt ions free in solution, resulting in various contributing free energy components: the translational entropy of IDP-associated and free counterions (referred to as F₁ and F₂, respectively, in SI Appendix); the electrostatic free energy due to the spatial correlations between free ions (F₃); the energy of ion-pairing for chain-counterion and interchain charge interactions (F₄); and the conformational free energy of the IDPs (F₅). For two complexing IDPs characterized by their respective degrees of polymerization and net charges (N₁, N₂, and N_c1, N_c2, respectively), intra- and interchain excluded-volume interaction strengths (w₀) as well as local dielectric mismatch parameters (δ₀ for chain-counterion and δ₁₂ for chain–chain ion-pairing), the total free energy is self-consistently minimized with respect to chain dimensions and the number of adsorbed counterions, and this is done for different salt concentrations for the complexed state and the unbound states (64, 65) (see SI Appendix for details).

While free salt ions have an ideal-gas-like entropy in the system volume (F₂), bound counterions have substantially reduced translational entropy (F₁) since they are assumed to remain confined to a cylindrical volume along the chain contour. The electrostatic free energy among the free ions (F₃) is captured by a parametrically corrected Debye–Hückel theory using a multiplicative factor, Λ (see SI Appendix, Fig. S3 for details). There is a gain in ion-pairing energy (F₄) due to counterion condensation on the chains as well as from interchain ion-pairing. IDPs with charged segments contribute to the configurational entropy, excluded-volume interactions, and screened Coulomb interactions (F5). Upon chain complexation, counterions associated with the complexed parts of the chains are assumed to be released into the system volume, gaining translational entropy, while the dangling uncomplexed parts of the longer chain retain their adsorbed counterions.

Although the model takes into account the entropy and enthalpy of counterions and their interactions with the protein chains, and thus charge renormalization, it lacks an explicit description of charge patterning (18, 70) and charge regulation in terms of side chain pK_a shifts (71, 72), and it also uses a parametric correction for the free energy of ionic correlations instead of a formal description of this correlation energy (73) as a function of salt concentration. Charge regulation is likely to be negligible in the salt concentration range where we studied ProTα-H1 complex formation experimentally (see SI Appendix for details and SI Appendix, Fig. S4) (74, 75) and is therefore inconsequential for the interpretation of theoretical thermodynamic estimates; however, the estimates of the single-chain dimensions are slightly affected at low salt concentrations (see SI Appendix for details and SI Appendix, Fig. S4). The uniform net charge density assumed in the theory is likely to limit its applicability to highly charged polyelectrolytic sequences such as ProTα and H1. Hydration effects and solvent degrees of freedom (57, 62, 76) are beyond the scope of this type of theory. Nevertheless, the implicit solvent model of our approach accounts for some hydration effects in the enthalpic terms describing the protein–protein and protein–ion interactions, primarily by considering a local dielectric constant near the protein surface that can be different from the bulk, as supported by fluorescence spectroscopy with polarity-sensitive probes (77, 78); the theory approximates the distance dependence of the dielectric constant as a step function and assumes ion pairing to be represented by fixed dipoles as a simple approximation. Furthermore, the dielectric mismatch parameter serves as a single mean-field parameter that comprises two microscopic aspects of ion-pairing: a local dielectric constant and the effective dipole length, so it does not allow either parameter to be determined independently (see SI Appendix for details).

We parameterized the theory based on the experimental salt concentration-dependent observables—chain dimensions of ProTα and H1 and thermodynamic parameters for complex formation of ProTα-H1—using a sequential approach. An estimate of w₀ was obtained from the single-chain dimensions at high salt, where charge interactions are screened, and constraints on δ₀ were estimated based on the chain dimensions and their experimental uncertainty at low salt; subsequently, using the estimated value of w₀, we fitted the experimental thermodynamic observables (enthalpy and free energy of complexation) by systematically varying δ₀ (within the constraints from the previous step), δ₁₂, and Λ (see SI Appendix for details).

The resulting polymer model captures the thermodynamics of complex formation, both in terms of the reaction enthalpy and free energy for different salt concentrations (Fig. 4G), as well as the salt concentration-dependent chain dimensions (Fig. 4F) with only four adjustable parameters, w₀, δ₀, δ₁₂, and Λ. In line with our simple estimate for a Gaussian chain above, the change in configurational entropy of the chains upon binding (ΔF₅, SI Appendix, Fig. S3) makes a negligible contribution to the total free energy. The total enthalpy is determined by the balance between the Coulomb energy of ion-pair formation (F₄) and the enthalpic part of the free energy from correlations between free ions (F₃). With increasing salt concentration, more counterions are released upon IDP complex formation (Fig. 4H), but the decreasing entropy gain of each released ion owing to the larger bulk salt concentration compensates this effect and moderates the overall entropic driving force from counterion release at high salt (SI Appendix, Fig. S3). The decrease in enthalpy as a function of salt concentration resulting from the reduction in the number of bound ion pairs is offset by the increase in energy gain from more pronounced correlations between the free ions at higher salt concentrations (SI Appendix, Fig. S3). By considering the effect of the local dielectric environment on the electrostatic energy of ion pair formation, it becomes apparent that the entropy gain from the released counterions (ΔF₂) is the primary thermodynamic driving force (SI Appendix, Fig. S3).

Discussion

Most high-affinity protein complexes involve enthalpic and entropic contributions that are both favorable (17, 35). The high-affinity disordered complex between H1 and ProTα stands in contrast to this behavior: Its binding is entropically driven, with a large unfavorable enthalpy of similar magnitude as the total free energy of complex formation. Our results suggest that counterion-release entropy is a strong driving force for PH complex formation. This finding highlights the importance of counterions in interactions involving highly charged biomacromolecules and leads to behavior such as increasing affinity with temperature (Figs. 1C and 4E). Polyelectrolyte interactions of this kind abound in the cell, especially in the nucleus, where charged IDPs and nucleic acids are key players in chromatin structure and transcriptional regulation (15, 28, 79–81).

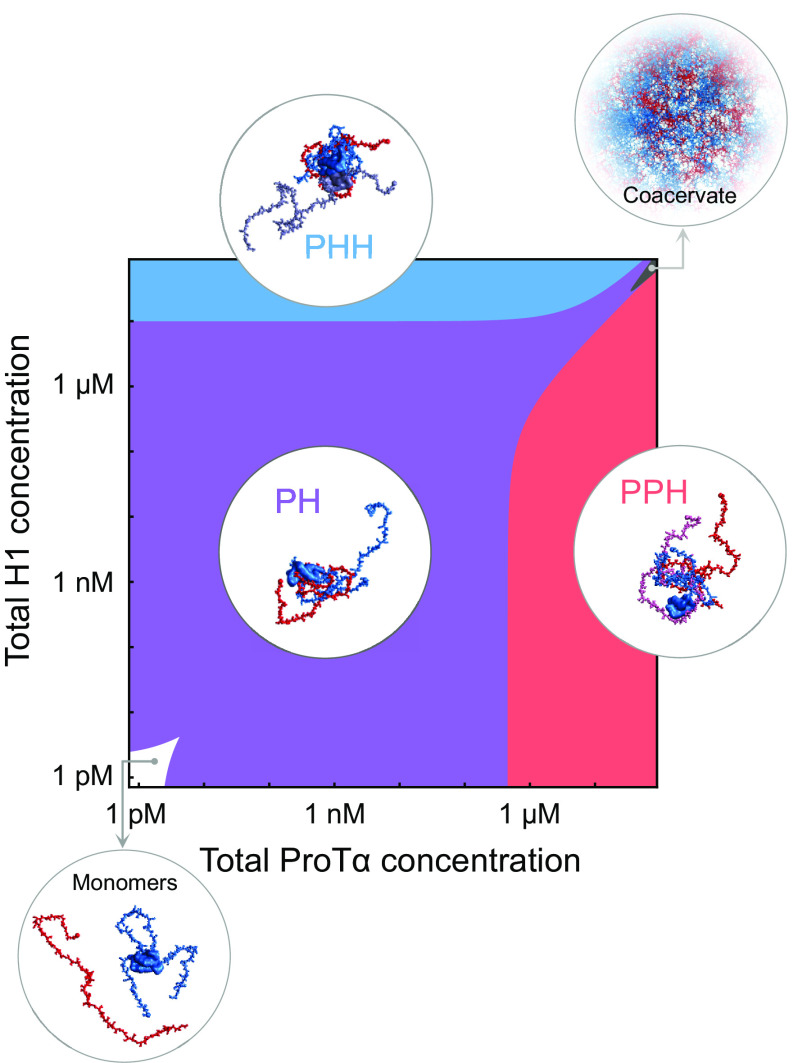
Much of the behavior we observe here for H1 and ProTα is reminiscent of synthetic polyelectrolytes (36, 37, 41, 42, 82), especially the important role of counterion release entropy (42, 82) and the endothermic character of the interaction (36, 37). However, a key aspect of our results is that we unambiguously detect and quantify the presence of stoichiometrically defined soluble complexes between H1 and ProTα—the PH dimer and the two ternary complexes PPH and PHH—afforded by the ability of single-molecule spectroscopy to identify different molecular species as distinct subpopulations (29–32). Only at near charge-balanced stoichiometry and above tens of micromolar protein concentrations does phase separation set in at physiological salt concentrations (Fig. 5) (60). For synthetic polyelectrolytes, as well as some biomolecular systems such as gelatin, indications for the presence of soluble complexes from experiments have been reported (36, 37, 83, 84), but the unambiguous detection and characterization of species such as dimeric and trimeric complexes has remained elusive, presumably owing to the low critical concentrations for the coacervation of binary mixtures of oppositely charged polyelectrolytes (21, 85) and the lack of experimental methods required for investigating the ultralow polyelectrolyte concentrations where the association equilibria for the formation of dimers and ternary complexes can be probed. Correspondingly, the formation of well-defined oligomeric polyelectrolyte complexes has primarily been investigated via simulations and theory (42, 57, 64, 65, 82, 86), and small soluble complexes such as dimers have been postulated to be a first step of polyelectrolyte complexation preceding coacervation (37, 83, 84, 87). Considering the obvious parallels between highly charged IDPs and synthetic polyelectrolytes, the dimers and ternary complexes of ProTα and H1 are thus likely to resemble the small soluble complexes of synthetic polyelectrolytes. Our single-molecule approach is expected to be extendable to synthetic polyelectrolytes and would facilitate their quantitative investigation, including their mechanistic role in coacervation.

Fig. 5.

Diagram of assembly states formed by H1 and ProTα as a function of protein concentrations at 165 mM monovalent salt. The colored regions indicate the predominant oligomeric species. If both protein concentrations are in the low picomolar range or below (white area), ProTα and H1 are predominantly monomeric. In the purple, blue, and red regions, ProTα-H1 (PH), ProTα-H1₂ (PHH), and ProTα₂-H1 (PPH) are the predominant oligomeric species, respectively. The dark gray region at high concentrations of both proteins indicates conditions where phase separation by complex coacervation occurs (57). Note that the re-entrant boundaries for complex coacervation are approximate. The other regions are calculated based on the equilibrium dissociation constants $K_{\mathrm{D}}^{\mathrm{PH}}$, $K_{\mathrm{D}}^{\mathrm{PPH}}$, and $K_{\mathrm{D}}^{\mathrm{PHH}}$ at 165 mM salt (SI Appendix, Eqs. S1–S3). Snapshots of complexes and the dense phase are based on simulations (13, 59).

Another parallel to the behavior of synthetic polyelectrolytes is the thermodynamic signature we observe for the formation of ProTα-H1 oligomers, especially its endothermicity, which requires a pronounced entropic driving force to yield a strong interaction. A positive interaction enthalpy has previously been reported for synthetic polyelectrolytes, but the need to separate the contributions of small oligomers from coacervation complicates quantitative modeling (36, 37). Here, we demonstrate that such modeling is feasible for H1 and ProTα since phase separation is absent under our experimental conditions, and independent information on the stabilities and thus concentrations of the contributing dimer and ternary complexes is available from single-molecule measurements. Obviously, both the dimer and the ternary complexes need to be accounted for in the quantitative analysis of binding experiments at micromolar protein concentrations, where they are substantially populated at physiologically relevant salt concentrations. This insight resolves the orders-of-magnitude discrepancy between the affinity of the PH complex obtained from single-molecule experiments and the apparent affinities inferred from ITC if an inadequate model involving only dimer formation is assumed (34). Ternary complex formation also reconciles the fast exchange between bound and unbound states observed in NMR experiments at high micromolar concentrations with the high affinity of ProTα-H1 complex formation (28). The underlying mechanism of competitive substitution (88) may also be involved in transcriptional regulation (15).

We rationalize our results with concepts from the field of synthetic polyelectrolytes (13, 28, 31, 36, 37, 42, 64, 65, 82, 83, 87), in particular a minimal mean-field theory that treats a salt-moderated balance between Coulomb energy of bound ion pairs and free-ion entropy, and accounts for counterion adsorption and release (64, 65). Recent theoretical considerations based on the temperature dependence of the relative permittivity of bulk water suggest the relevance of solvent entropy for polyelectrolyte interactions related to the reorientational entropy of the dipolar solvent associated with ion-pair formation (57). Our theoretical approach indicates substantial counterion condensation on the chains, potentially amplified by a reduced dielectric constant near the polypeptide chain (48, 89, 90), which is expected to render solvent orientation effects small compared to the entropy gain from counterion release. One way of testing and refining the parameters used in the current theoretical framework might be all-atom molecular dynamics simulations (60, 62, 91). The modular nature of the theory would in principle also allow aspects such as charge patterning and charge regulation (92, 93) to be incorporated explicitly.

Our results may further contribute to a quantitative understanding of polyelectrolyte complex coacervation by complementing theories for phase separation that explicitly account for polyelectrolyte-associated counterions (36, 94–96) but do not yet account for the diversity of soluble complexes in the dilute phase. From the perspective of kinetics (97), the formation of small oligomers or clusters may be the earliest steps of phase separation, and for subsaturated solutions of several RNA-binding proteins that undergo homotypic phase separation, a heterogeneous distribution of clusters ranging from tens or hundreds of molecules to mesoscale assemblies has been observed (98). A continuum of such assemblies may thus provide a link between the small oligomers we observe here and phase separation. However, in contrast to homotypic cluster formation, in heterotypic systems such as ProTα and H1, not only the absolute but also the relative concentrations are crucial for cluster formation. In such systems, higher-order oligomers may define the phase boundaries, particularly for reentrant phase separation (99). It will be an interesting topic of future research whether an analogous broad range of heterotypic oligomers and clusters exists for systems like H1 and ProTα that undergo complex coacervation.

With counterion release entropy as a principle driving force for polyelectrolyte complex formation, the affinity between chains can potentially become extremely large since the number of counterions adsorbed on a polyelectrolyte chain increases with the number of charged groups and thus the degree of polymerization (48, 64, 66). The cellular milieu is rife with highly charged flexible biopolymers, such as nucleic acids (100), inorganic polyphosphate (101), and highly charged IDPs (13), and high-affinity interactions as well as complex coacervation can result without the need for interactions encoded by folded domains. Considering the combinatorial possibilities of complexes that can arise from such polyelectrolyte molecules in a cell, an obvious question is the origin of specificity in such interactions. Specificity can arise from distinct patterns of spatial and temporal localizations and concentrations of interaction partners such that the likelihood of a specific pair of such molecules forming a complex is maximized. Other regulatory processes, such as posttranslational modifications, to which IDPs are particularly amenable, as well as patterning of charged residues, can also contribute (18, 102, 103). Polyelectrolyte interactions are likely to often act in synergy with structured domains and motifs, a combination that is widespread in nucleic acid-binding proteins (104). Polyelectrolyte interactions and counterion release as a driving force are thus likely to be of general importance for biomolecular interactions (19, 24, 51, 105), and understanding the underlying mechanisms will be essential for quantifying intracellular communication.

Material and Methods

Proteins were recombinantly expressed in Escherichia coli, purified, and labeled for single-molecule FRET experiments as described previously (13, 28, 77). The details of single-molecule experiments and the experimental setup have been described before (13, 28, 106). Calorimetry experiments were performed on a MicroCal iTC200 calorimeter. See SI Appendix for detailed descriptions on protein expression, purification, labeling, single-molecule FRET, and calorimetry experiments and analysis, and a description of the theory.

Supplementary Material

Appendix 01 (PDF)

Dataset S01 (XLSX)

Dataset S02 (XLSX)

Dataset S03 (XLSX)

Dataset S04 (XLSX)

Dataset S05 (XLSX)

Dataset S06 (XLSX)

Dataset S07 (XLSX)

Dataset S08 (XLSX)

Dataset S09 (XLSX)

Data, Materials, and Software Availability

Code for analysis of single-molecule and computational data has been deposited in GitHub (https://github.com/SchulerLab/Fretica.git) (107). All other data are included in the manuscript and/or supporting information.