Mechanistic modeling projections of antibody persistence after homologous booster regimens of COVID‐19 vaccine Ad26.COV2.S in humans

Abstract

Mechanistic model‐based simulations can be deployed to project the persistence of humoral immune response following vaccination. We used this approach to project the antibody persistence through 24 months from the data pooled across five clinical trials in severe acute respiratory syndrome coronavirus‐2 (SARS‐CoV‐2)‐seronegative participants following vaccination with Ad26.COV2.S (5 × 10¹⁰ viral particles), given either as a single‐dose or a homologous booster regimen at an interval of 2, 3, or 6 months. Antibody persistence was quantified as the percentage of participants with detectable anti‐spike binding and wild‐type virus neutralizing antibodies. The projected overall 24‐month persistence after single‐dose Ad26.COV2.S was 70.5% for binding antibodies and 55.2% for neutralizing antibodies, and increased after any homologous booster regimen to greater than or equal to 89.9% for binding and greater than or equal to 80.0% for neutralizing antibodies. The estimated model parameters quantifying the rates of antibody production attributed to short‐lived and long‐lived plasma cells decreased with increasing age, whereas the rate of antibody production mediated by long‐lived plasma cells was higher in women relative to men. Accordingly, a more pronounced waning of antibody responses was predicted in men aged greater than or equal to 60 years and was markedly attenuated following any homologous boosting regimen. The findings suggest that homologous boosting might be a viable strategy for maintaining protective effects of Ad26.COV2.S for up to 24 months following prime vaccination. The estimation of mechanistic modeling parameters identified the long‐lived plasma cell pathway as a key contributor mediating antibody persistence following single‐dose and homologous booster vaccination with Ad26.COV2.S in different subgroups of recipients stratified by age and sex.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Anti‐severe acute respiratory syndrome coronavirus‐2 (SARS‐CoV‐2) antibodies are detectable for up to 9 months following vaccination with single‐dose Ad26.COV2.S and are robustly increased after homologous boosting. Data are limited, however, characterizing the long‐term antibody persistence after homologous boosting with Ad26.COV2.S.

• WHAT QUESTION DID THIS STUDY ADDRESS?

We used mechanistic model‐based simulations to project the percentages of SARS‐CoV‐2‐seronegative participants with quantifiable antibodies at 24 months (antibody persistence) following vaccination with Ad26.COV2.S (5 × 10¹⁰ viral particles) given either as a single‐dose or homologous booster regimen at an interval of 2, 3, or 6 months.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

Antibody persistence following any homologous booster was increased relative to a single‐dose regimen equaling to greater than or equal to 89.9% for binding and greater than or equal to 80.0% for neutralizing antibodies. The most pronounced decline in antibody persistence was projected for men aged greater than or equal to 60 years and was attenuated after any homologous booster regimen.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

Quantifiable antibody levels could be used to inform definitions of long‐term antibody‐based correlates of protection in the setting of Ad26.COV2.S vaccination.

INTRODUCTION

Deployment of vaccines has had a global impact on mitigating the coronavirus disease‐2019 (COVID‐19) pandemic caused by the spread of severe acute respiratory syndrome coronavirus‐2 (SARS‐CoV‐2), with an estimated global mortality reduction of 79% during the first year of vaccination. ¹ However, waning of vaccine protection and reduced vaccine effectiveness in the setting of new SARS‐CoV‐2 variants support recommendations for booster doses, ² , ³ and uncertainties remain regarding the durability of protection and optimal booster timing. ² , ⁴

A single dose of adenovirus type 26 (Ad26)‐vectored vaccine Ad26.COV2.S (JCOVDEN; Janssen Biotech) administered at 5 × 10¹⁰ viral particles (vp) elicited detectable binding and neutralizing antibodies through greater than or equal to 6 months post‐immunization. ⁵ Homologous boosting with Ad26.COV2.S rapidly and robustly increased binding and neutralizing antibody levels, with stronger booster‐elicited immunity obtained with a longer interval between primary and booster doses. ⁵ The efficacy of single‐dose and homologous booster regimens of Ad26.COV2.S was subsequently determined in randomized, placebo‐controlled, phase III trials. ⁶ , ⁷ Single‐dose Ad26.COV2.S (5 × 10¹⁰ vp) was 56.3% effective in preventing moderate to severe‐critical COVID‐19 beginning greater than or equal to 14 days after vaccination through median 121 days of follow‐up (ENSEMBLE). ⁶ Furthermore, homologous boosting with Ad26.COV2.S at 2 months was 75.2% effective in preventing moderate to severe‐critical COVID‐19 beginning greater than or equal to 14 days post‐boost through median 36 days of follow‐up (ENSEMBLE2). ⁷ In addition, the correlate analyses of single‐dose Ad26.COV2.S and two‐dose messenger RNA (mRNA‐1273) vaccine demonstrated statistical associations between day 29 post‐vaccination binding and neutralizing antibody levels and vaccine efficacy up to 4 months following immunization. ⁸ , ⁹ Uncertainties remain, however, regarding the long‐term durability of humoral immunity and the utility of quantifiable antibody levels as correlates of protection (CoP) in predicting vaccine efficacy beyond 4 months following vaccination with single‐dose and homologous boosting regimens of Ad26.COV2.S.

Mechanistic modeling can be used to characterize the dynamics of humoral immune response following vaccination, ¹⁰ , ¹¹ , ¹² and to project antibody persistence over a longer time frame. ¹³ We recently used mechanistic model‐based simulations to quantify antibody persistence over 24 months from clinical trial data curated through 8 months in SARS‐CoV‐2‐seronegative participants vaccinated with single‐dose Ad26.COV2.S (5 × 10¹⁰ vp). ¹³ The projected 24‐month persistence was 81.1% for binding antibodies and 80.4% for neutralizing antibodies. ¹³ Antibody responses were projected to decline over time, with the most pronounced waning projected in men and older adults. ¹³ Consistent with this, regional surveillance data showed waning effectiveness of single‐dose Ad26.COV2.S (5 × 10¹⁰ vp) in reducing the risk of COVID‐19 from 74.8% at 1 month to 59.4% at 5 months post‐vaccination, ¹⁴ supporting the use of a booster dose to counter the waning efficacy of primary vaccination.

In this study, we used a mechanistic modeling approach to characterize the time course of antibody responses from pooled clinical trial data collected through 15 months in SARS‐CoV‐2‐seronegative participants following vaccination with one or two doses of Ad26.COV2.S (5 × 10¹⁰ vp). We used mechanistic model‐based simulations to project the antibody persistence (defined as the percentage of participants with quantifiable antibodies) following vaccination with single‐dose Ad26.COV2.S (5 × 10¹⁰ vp) or a homologous booster dose given at an interval of 2, 3, or 6 months. Building on a previous mechanistic modeling study that projected a more pronounced waning of antibody persistence in men and older adults following single‐dose Ad26.COV2.S, ¹³ our main focus was to project the antibody persistence in subgroups of Ad26.COV2.S recipients, stratified by age and sex.

METHODS

Data collection

A pooled dataset was generated using the data from participants randomized into five clinical trials of Ad26.COV2.S: phase I–IIa COV1001 (NCT04436276), phase I COV1002 (NCT04509947), phase II COV2001 (NCT04535453), phase III COV3001 (NCT04505722), and phase III COV3009 (NCT04614948). Vaccination regimens included a single dose (prime at day 1), booster at 2 months (prime at day 1 and booster at days 25–70), booster at 3 months (prime at day 1 and booster at days 70–130), and booster at 6 months (prime at day 1 and booster at day >130). All participants were SARS‐CoV‐2‐seronegative at the time of prime; when SARS‐CoV‐2 infection occurred, participants were withdrawn from the analysis at that point. All studies were approved by institutional review boards. Participants provided written informed consent, which included the possibility of further testing and evaluation. The trials adhered to the Declaration of Helsinki principles and Good Clinical Practice guidelines. Further information on clinical studies used in the analysis can be found in prior publications. ⁵ , ⁶ , ⁷ , ¹⁵ , ¹⁶

Blood samples for determining binding and neutralizing antibody biomarkers of humoral immunity (see next section) were collected pre‐vaccination on day 1 (immunization) in all studies, and on days 8, 15, 29, 57, 71, 85, 183, 190, 211, 183, 239, 366, 372, 393, and 421 in COV1001; days 15, 29, 57, 71, 85, 239, and 366 in COV1002; days 15, 29, 57, 64, 71, 85, 92, 99, 113, 169, 176, 197, 204, 225, 393, and 421 in COV2001; days 29 and 71, and week 24 in COV3001; and days 29, 57, and 71 in COV3009.

Immunogenicity assays

Wild‐type virus neutralizing assay

A wild‐type virus (Victoria/1/2020) microneutralization assay performed by Public Health England was used to quantify neutralizing antibodies capable of inhibiting live virus infection. The neutralizing titer of a serum sample was calculated as the reciprocal serum dilution corresponding to the 50% maximal inhibitory concentration (IC₅₀). Assay values were determined as IC₅₀ 58 (lower limit of quantification [LLOQ]) and 12,800 (upper limit of quantification [ULOQ]).

Spike protein enzyme‐linked immunosorbent assay

Concentrations of binding antibodies specific to the pre‐fusion conformation of SARS‐CoV‐2 spike protein were quantified by spike protein enzyme‐linked immunosorbent assay (S‐ELISA). A stabilized pre‐fusion spike protein ([2P], Δfurin, T4 foldon, and His‐Tag), was derived from the first clinical isolate of the Wuhan strain (Wuhan, 2019, whole genome sequence NC_045512). Assay LLOQ and ULOQ were 50.3 and 58,158.1 EU/mL, respectively.

In both assays, seropositivity was defined as sera above LLOQ. Further information about the assays was previously published, ¹³ , ¹⁵ and is provided in Appendix S1.

Exploratory analyses

We explored the relative contributions of short‐lived and long‐lived plasma cells in antibody production following homologous boosting with Ad26.COV2.S by comparing the geometric mean ratios of binding and neutralizing antibody levels at peak (maximum plasma concentration [C_max]) and at days 140–160 (C_th) from second peak (the longest follow‐up timepoint in all regimens) across regimens. The relative reduction was calculated as 1 – C_th/C_max. For this comparison, values below LLOQ were imputed to LLOQ.

Data from participants with both S‐ELISA and wild‐type virus neutralizing assay (wtVNA) measurements collected at the same time were used to explore the relationship between binding and neutralizing antibody levels and to determine the most suitable mathematical function to link S‐ELISA and wtVNA observations during model building. The log‐transformed ratio of wtVNA to S‐ELISA measurements over time was explored to evaluate the presence of temporal changes.

Structural model

The structural model (Figure 1) considered the key elements of humoral immune response ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁷ : the antigen (Ag, Spike [S]‐protein), the memory B cells (M₁), germinal centers (M₂), the short‐lived plasma cells (SLPCs), the long‐lived plasma cells (LLPCs), the antibody in serum (Ab), and the antibody in peripheral sites (P). The relationship between vaccine dosing and antigen effects on antibody response was described using a virtual antigen compartment based on a K‐PD (kinetics of drug action) model as follows ¹⁸ :

$$\frac{\mathrm{dAg}}{\mathrm{d}t}=-{\mathrm{k}}_{\mathrm{Ag}}·\mathrm{Ag}$$ (1)

where k _Ag denotes the first‐order equilibration rate constant depicting the apparent nonspecific decay of S‐protein over time following vaccination. ¹⁰

FIGURE 1.

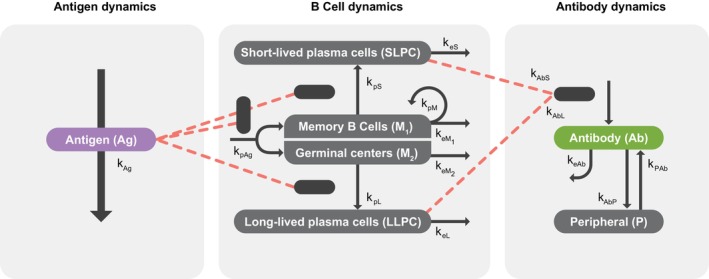
Schematic of the mechanistic model for humoral immune response following a single dose regimen or a homologous booster regimen of Ad26.COV2.S in severe acute respiratory syndrome coronavirus‐2 (SARS‐CoV‐2)‐seronegative participants. Modified from “Quantifying Antibody Persistence After a Single Dose of COVID‐19 Vaccine Ad26.COV2.S in Humans Using a Mechanistic Modeling and Simulation Approach” by A. Dari et al., 2023, Clinical Pharmacology & Therapeutics, Feb;113(2):380–389. IC₅₀, 50% maximal inhibitory concentration; S‐ELISA, spike protein enzyme‐linked immunosorbent assay; wtVNA, wild‐type virus neutralizing assay.

Two proliferation terms were used to describe the time course of B cell responses generated directly through memory B cell formation (M ₁) and germinal center (GC, [M₂]) pathways. ¹⁷ The memory B cell pathway is assumed to mediate the vaccine‐induced production of SLPCs, ¹⁹ , ²⁰ as evidenced by data in nonhuman primates showing faster peak response after second versus first dose of Ad26.COV2.S. ¹⁷ The GC pathway is assumed to predominantly mediate the production of LLPC, and was considered relevant for explaining the slower peak response following the first dose of Ad26.COV2.S and the sustained antibody concentrations following single‐dose and two‐dose regimens of Ad26.COV2.S. ¹⁷ The dual pathway dynamics of B cell responses is summarized as follows:

$$\begin{array}{c}\frac{\mathrm{d}{M}_1}{\mathrm{d}t}=\left({\mathrm{k}}_{p\mathrm{Ag}}·\mathrm{Ag}+{\mathrm{k}}_{\mathit{pM}}·M_1\right)\left(1-\frac{M_1}{N_1}\right)\hfill \\ -\left[{\mathrm{k}}_{\mathrm{pS}}·\mathrm{Ag}+{\mathrm{k}}_{e{M}_1}\right]·M_1\hfill \end{array}$$ (2)

$$\frac{\mathrm{d}{M}_2}{\mathrm{d}t}=\left({\mathrm{k}}_{\mathrm{pAg}}·\mathrm{Ag}\right)\left(1-\frac{M_2}{N_2}\right)-\left[{\mathrm{k}}_{\mathrm{pL}}·\mathrm{Ag}+{\mathrm{k}}_{e{M}_2}\right]·M_2$$ (3)

where a rate constant k_pAg denotes the antigen‐dependent production of memory B cells and GCs which differentiate into SLPCs and LLPCs, respectively; N ₁ and N ₂ denote the maximum growth levels of M₁ and M₂, respectively; a first‐order rate constant k_pM denotes antigen‐independent production of memory B cells ¹² , ²¹ ; and k_eM1 and k_eM2 denote the first‐order rate constants of antigen‐independent elimination of memory B cells through M₁ and M₂, respectively.

The production of SLPCs and LLPCs is assumed to be a second‐order process determined by the amount of antigen, the memory B cells and GCs available, and the differentiation rates of memory B cells into SLPCs (k_pS) and GCs into LLPCs (k_pL) ¹⁰ , ¹³ , ²² :

$$\frac{\mathrm{d}S}{\mathrm{d}t}={\mathrm{k}}_{\mathrm{pS}}·\mathrm{Ag}·M_1-{\mathrm{k}}_{\mathrm{eS}}·S$$ (4)

$$\frac{\mathrm{d}L}{\mathrm{d}t}={\mathrm{k}}_{\mathrm{pL}}·\mathrm{Ag}·M_2-{\mathrm{k}}_{\mathrm{eL}}·L$$ (5)

where k_eS and k_eL denote the first‐order elimination rate constants of SLPC and LLPC, respectively, assuming differential half‐life durations for SLPC (days) versus LLPC (months or years). ²¹ , ²² , ²³ The dynamics of serum antibody production was described as a linear combination of production due to the amount of SLPCs and LLPCs, and antibody disposition was characterized by a first‐order elimination and linear distribution to a nonspecific peripheral compartment:

$$\frac{\mathrm{dAb}}{\mathrm{d}t}={\mathrm{k}}_{\mathrm{AbS}}·S+{\mathrm{k}}_{\mathrm{AbL}}·L-{\mathrm{k}}_{\mathrm{eAb}}·\mathrm{Ab}-{\mathrm{k}}_{\mathrm{AbP}}·\mathrm{Ab}+{\mathrm{k}}_{\mathrm{PAb}}·P$$ (6)

$$\frac{\mathrm{dP}}{\mathrm{d}t}={\mathrm{k}}_{\mathrm{AbP}}·\mathrm{Ab}-{\mathrm{k}}_{\mathrm{PAb}}·P$$ (7)

where k_AbS and k_AbL denote the first‐order production rate constants of antibodies from SLPCs and LLPCs, respectively; k_eAb denotes the first‐order elimination rate constant of serum antibodies; k_AbP denotes the nonspecific distribution to a peripheral compartment; and k_PAb denotes the return of antibodies from the peripheral to the serum compartment.

S‐ELISA measures the IgG isotype, whereas wtVNA measures all isotypes with a neutralizing function. In seronegative participants, the wtVNA measurement after the first vaccination includes both IgM and IgG, subsequently a significant decline of IgM occurs. ²⁴ Thus, an exponential decay of IgM over time was added to the IgG isotype of neutralizing antibodies when describing the longitudinal ratio of S‐ELISA to wtVNA:

$${\mathrm{Ab}}_{\text{wtVNA}}/\mathrm{Ab}=\beta +\mathit{IgM}·\exp \left(-{\mathrm{k}}_{\mathrm{IgM}}·\text{time}\right)$$ (8)

where Ab is obtained from Equation 6 and denotes the binding antibodies; β denotes the constant ratio between IgG neutralizing and binding antibodies; IgM represents the baseline contribution of neutralizing IgM to the ratio of IgG neutralizing to binding antibodies; and k_IgM denotes a first‐order decaying rate constant of IgM. Finally, a linear relationship between neutralizing and binding antibody measurements independent of time and in the log domain was assumed (see Exploratory analyses):

$${\log }_{10}\left({\mathrm{Ab}}_{\text{wtVNA}}\right)=\alpha ·{\log }_{10}\left(\mathrm{Ab}\right)$$ (9)

where α denotes a slope, while no intercept could be estimated.

Model parameters

The estimated parameters were k_eL, k_AbS, k_AbL, k_pM, N ₂ , α, β, IgM, and k_IgM. Other parameters were fixed based on literature ¹⁰ , ¹¹ , ¹³ , ²⁵ or tested through sensitivity analysis: k_pS and k_pL assumed the same value; N ₁ was fixed to a mean value obtained from eight of 12 successful runs where only initial estimates were randomly changed and estimated a biologically plausible value for N ₁ . Fixing N ₁ resolved the observed high uncertainty in parameter estimates. Interindividual variability (IIV) was estimated on k_AbS and k_AbL (Appendix S1). In contrast to the mechanistic modeling study of single‐dose Ad26.COV2.S, ¹³ the increasing model complexity precluded IIV estimation on k_pM. An additive error model incorporating different variance estimates for S‐ELISA and wtVNA assays was used to quantify the residual unexplained variability after logarithmic transformation of measured antibodies (Appendix S1).

Covariate analysis

The effects of age, body weight, sex, race, and country were evaluated. As described previously, ¹³ the levels of categorical covariates representing less than 10% of the total (<30 participants) were grouped with other categories. The covariate screening was performed using graphical assessment and stepwise linear regression of the relationships between the empirical Bayesian estimates of random effects and covariates. Statistically significant covariates (p < 0.01) and/or covariates with a coefficient of determination r ² > 0.10 with model parameters were further tested one‐by‐one in nonlinear mixed‐effects modeling to evaluate their suitability for the model through a forward‐inclusion (p < 0.01) and backward‐elimination (p < 0.005) process (Appendix S1).

Model evaluation

Several models were evaluated to identify the most appropriate model for describing the time course of data. For each nested model, the improvement in fit was assessed by the likelihood ratio test (p ≤ 0.01), based on the change in the minimum objective function value. ²⁶ , ²⁷ The reduction in IIV and residual variability, the precision and correlation in parameter estimates, diagnostic goodness‐of‐fit plots, visual predictive checks (VPCs), ²⁸ and shrinkage were used to evaluate the model. Modeling software is described in Supplementary Materials.

Mechanistic model‐based simulations

Population simulations were conducted using the final model with pooled S‐ELISA and wtVNA data. For each of the four vaccination regimens with Ad26.COV2.S (5 × 10¹⁰ vp; i.e., single‐dose, homologous boosting at 2, 3, and 6 months), the time course of binding and neutralizing antibodies at baseline and every 4 weeks up to 24 months after vaccination was simulated for a cohort of 250,000 participants. The uncertainty around the fixed‐effect parameter estimates, the random effect distribution, and the residual error were considered. The sex covariate was coded using 1:1 ratio. Age was sampled from the age distribution in the analysis dataset and was implemented as a continuous covariate in the model, although the simulation results are displayed as a categorical covariate.

Antibody persistence at the individual level was defined as the time from vaccination until the last measurement remained above the LLOQ before two consecutive monthly measurements below the LLOQ. Antibody persistence at the population level was defined as the percentage of antibody persistence at the individual level computed at defined timepoints (i.e., 8, 12, 18, and 24 months).

Computer software

Modeling analysis was conducted using the nonlinear mixed effect modeling software NONMEM 7.4.3 (ICON plc). The NONMEM analysis was performed in a validated environment, based on Good Automated Manufacturing Practice and in accordance with 21 CFR Part 11 and Good Clinical Practice regulations. The Fortran compiler was Intel Fortran 64 Compiler Professional, version 11.1. Perl‐speaks‐NONMEM (PsN, version 4.7.0, [http://psn.sourceforge.net/docs.php]) was used to execute NONMEM when appropriate. The first‐order conditional estimation with interaction method was used for all model runs. Data management, exploratory analyses, diagnostic graphics, and post‐processing of the data and NONMEM outputs as well as simulations were performed using statistical software R (version 3.4.1, The R Project for Statistical Computing, [www.r‐project.org]), embedded in RStudio (version 1.2.1335‐1).

RESULTS

Population

Data were available for up to 15 months and included 5608 S‐ELISA samples from 978 participants (median age 55 years [range, 18–84]) and 1882 wtVNA samples from a subset of 375 participants (median age 47 years [range, 18–80]). Sex distribution was balanced across S‐ELISA and wtVNA assays. Table S1 summarizes participant demographics by assay type.

Exploratory analyses

S‐ELISA and wtVNA geometric mean levels

The geometric mean peak of binding antibodies following primary (single‐dose) vaccination was 543 EU/mL and increased 3.24‐fold after boosting at 2 months (1760 EU/mL), 3.79‐fold after boosting at 3 months (2056 EU/mL), and 4.92‐fold after boosting at 6 months (2674 EU/mL). On days 140–160 from second peak, the binding antibody geometric mean concentrations were 343 EU/mL after single‐dose, and 606 EU/mL, 810 EU/mL, and 1407 EU/mL after boosting at 2, 3, and 6 months, respectively. The relative reduction was 36.8% after single‐dose, and 65.6%, 60.6%, and 47.4% after boosting at 2, 3, and 6 months, respectively. Similar trends were observed for the neutralizing antibody titer (Appendix S1).

Correlation between S‐ELISA and wtVNA datasets

The relationship between log‐transformed S‐ELISA and wtVNA data was linear, with an estimated slope (α) of 0.732 (log₁₀(IC₅₀)/log₁₀(EU/mL)) (95% confidence interval [CI]: 0.691–0.773). The relationship deviated from the identity line (Figure 2a), indicating that the wtVNA signal is less than proportional to the S‐ELISA signal. The log‐transformed wtVNA to S‐ELISA ratio over time shows larger values at early visits (Figure 2b), indicating that other neutralizing isotypes were captured by wtVNA (e.g., IgM).

FIGURE 2.

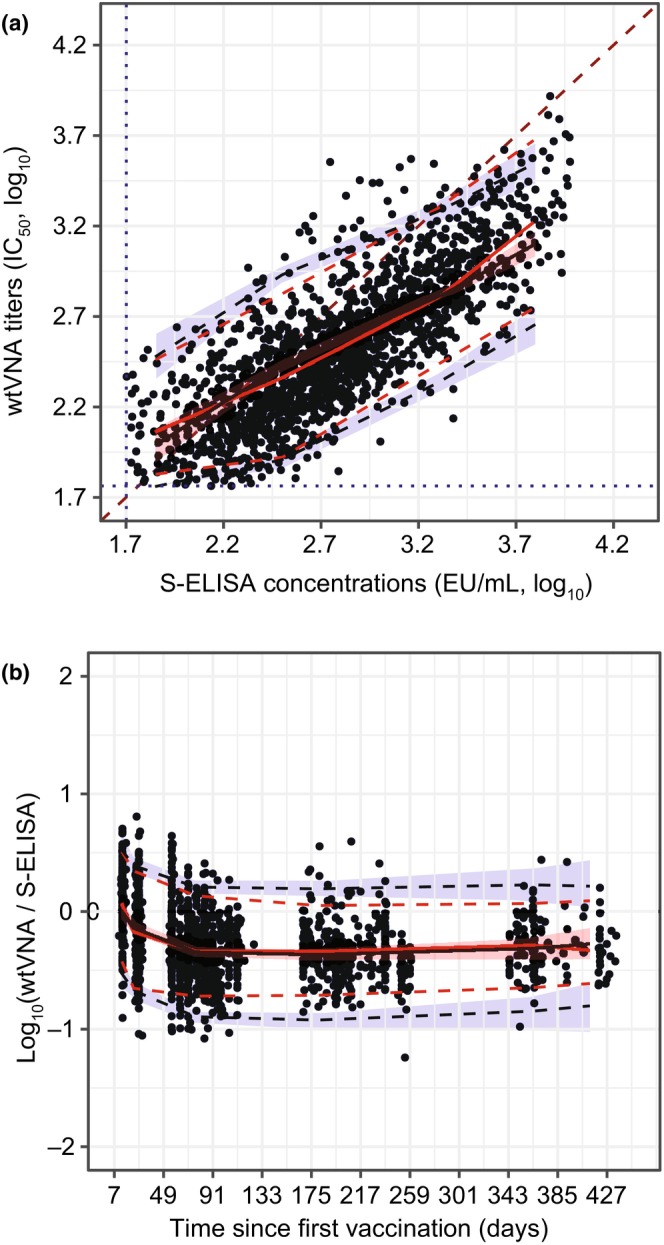
Exploratory analyses with S‐ELISA and wtVNA datasets. Correlation between the log‐transformed wtVNA titers and S‐ELISA concentrations (a). The log‐transformed wtVNA to S‐ELISA ratio by time since primary vaccination (b). Black dots represent observed data. Continuous red lines represent median; dashed red lines represent the 5th and 95th percentiles of the observed data. Black continuous line is the median of simulated data and red shaded area represent 95% CIs. Blue dashed lines and blue shaded area represent the 5th and 95th percentiles of the simulated data and 95% CIs, respectively. A dark red dashed line represents the identity line (Panel a only). The blue dotted lines represent LLOQ for S‐ELISA and wtVNA assays (Panel a only). CI, confidence interval; IIV, interindividual variability; LLOQ, lower limit of quantification; S‐ELISA, spike protein enzyme‐linked immunosorbent assay; wtVNA, wild‐type virus neutralization assay.

Model parameters and covariate effects

Table 1 shows the mechanistic model parameters and statistically significant covariates. All parameters were estimated with adequate precision (relative standard error, ≤46%). The rate of antibody production mediated by SLPCs decreased by 23% from the 5th (23 years) to the 95th (84 years) percentile of age distribution, and the rate of antibody production mediated by LLPCs decreased by 64% for the same age range. The rate of antibody production mediated by LLPCs was 81.6% higher in women relative to men (95% CI: 53.6%–110.0%).

TABLE 1.

Fixed and estimated parameter values and significant covariate effects from the mechanistic model of the humoral immune response after a single dose of Ad26.COV2.S (5 × 10¹⁰ vp) and homologous booster doses given at 2, 3, and 6 months post‐prime.

Parameter	Unit	Assay	Estimate	95% CI
Ad26 antigen decay, kAg	day−1	S‐ELISA	0.065	Fixed 10 , 13
Mem B production rate (antigen‐dependent, kpAg)	Cells/vp/day	S‐ELISA	1	Fixed 13
Mem B production rate (antigen‐independent, kpM)	day−1	S‐ELISA	0.0167	0.0121 to 0.0213
B cell decay in M 1 and M 2 (keM1 and keM2)	year−1	S‐ELISA	0	Fixed due to short follow‐up
Maximum B cell produced (memory B pathway, N 1)	Cells	S‐ELISA	10.7 ∙ 104	Fixed to the mean value of multiple runs
Maximum B cell produced (GC pathway, N 2)	Cells	S‐ELISA	0.129 ∙ 104	(0.033 to 0.225) ∙ 104
SLPC production rate – B cell dependent, kpS	day−1/vp	S‐ELISA	0.5 ∙ 10−5	Fixed based on sensitivity analysis
SLPC elimination half‐life, keS	day−1	S‐ELISA	0.578	Fixed 11 , 13
LLPC production rate – B cell dependent, kpL	day−1/vp	S‐ELISA	0.5 ∙ 10−5	Fixed based on sensitivity analysis
LLPC elimination half‐life, keL	year−1	S‐ELISA	19.1 ∙ 10−4	(15.2 to 23.0) ∙ 10−4
Ab production rate by SLPC, (kAbS for median age of 55 years)	day−1 ∙ (EU/mL)/cells	S‐ELISA	3.01	2.60 to 3.42
Ab production rate by LLPC, kAbL (median age of 55 years and male)	day−1 ∙ (EU/mL)/cells	S‐ELISA	0.394	0.143 to 0.645
Central‐to‐peripheral rate, kAbP	day−1	S‐ELISA	0.2075	Fixed 13 , 25
Peripheral‐to‐central rate, kPAb	day−1	S‐ELISA	0.2716	Fixed 13 , 25
Ab decay rate, keAb	day−1	S‐ELISA	0.0556	Fixed 13 , 25
Slope – S‐ELISA to wtVNA linear relationship, α	log10(IC50 titer)/log10((EU/mL))	wtVNA	0.732	0.691 to 0.773
Constant ratio between neutralizing and binding IgG, β	IC50 titer/(EU/mL)	wtVNA	3.85	2.27 to 5.43
IgM contribution at baseline – S‐ELISA to wtVNA ratio, IgM	IC50 titer/(EU/mL)	wtVNA	6.10	2.98 to 9.22
IgM exponential decay rate, kIgM	day−1	wtVNA	0.0368	0.00858 to 0.065
Age (continuous, KAbS_AGE) – decrease for age 55 years	–	S‐ELISA	−0.221	−0.421 to −0.0211
Age (continuous, KAbL_AGE) – decrease for age 55 years	–	S‐ELISA	−0.867	−1.06 to −0.677
Sex (kAbL_SEX) – increase for female (1 + estimate)	–	S‐ELISA	0.816	0.536 to 1.10
Interindividual variability			CV a (%)	Shrinkage b (%)
On kAbL		S‐ELISA	126	20.8
On kAbS		S‐ELISA	127	18.9
Proportional error c		S‐ELISA	21	15.6
		wtVNA	23.8	4.48

Abbreviations: Ab, antibody; CV, coefficient of variation; CI, confidence interval, GC, germinal center; IC₅₀, 50% maximal inhibitory concentration; LLPC, long‐lived plasma cells; SLPC, short‐lived plasma cells; S‐ELISA, spike protein enzyme‐linked immunosorbent assay; vp, viral particles; wtVNA, wild‐type virus neutralization assay.

^a CV% derived as sqrt(exp(ω²)‐1).

^b Shrinkage as reported in the final model output.

^c Proportional error refers to original values (i.e., additive error on log‐transformed values).

S‐ELISA and wtVNA observations plotted against population‐predicted and individual‐predicted values showed a normal random scatter around the identity line (Figures S1A and S2A). Conditional weighted residuals plotted against population‐predicted S‐ELISA and wtVNA observations and versus time confirmed the adequacy of our model (Figures S1B and S2B). As evidenced by VPC, the mechanistic model adequately described the time course and associated variability of S‐ELISA (Figure 3) and wtVNA (Figure S3) data for up to 15 months post prime.

FIGURE 3.

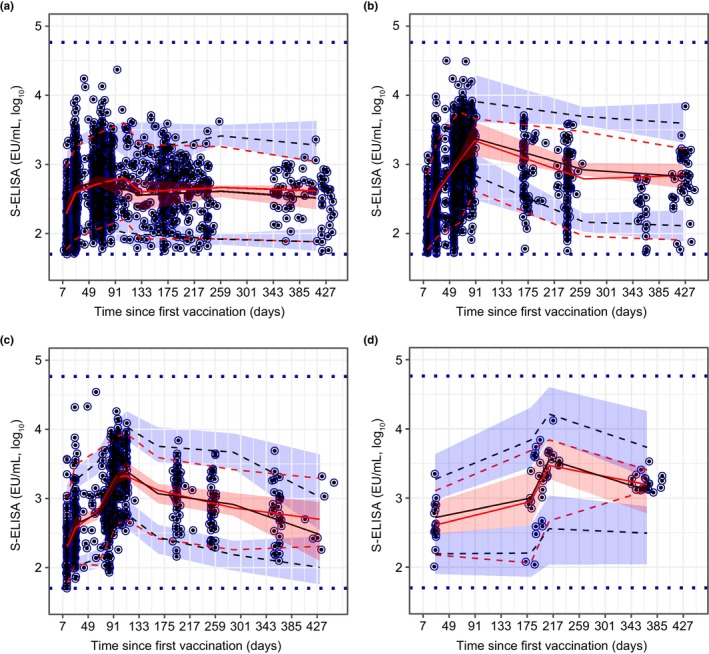
Visual predictive check of the mechanistic model for binding antibody responses after single‐dose Ad26.COV2.S (5 × 10¹⁰ vp) (a), homologous booster dose at 2 months post prime (b), homologous booster dose at 3 months post prime (c), and homologous booster dose at 6 months post prime (d). Blue dots represent observed data (log₁₀ transformed). Continuous red lines represent the median of the observed data; dashed red lines represent the 5th and 95th percentiles of observed data. Black continuous lines represent the median of simulated data; red shaded area represents 95% CIs of simulated data. Blue dashed lines represent the 5th and 95th percentiles of simulated data; blue shaded area represents 95% CIs of simulated data. Horizontal blue dashed lines represent the assay‐specific LLOQ and ULOQ values. CI, confidence interval; LLOQ, lower limit of quantification; S‐ELISA, spike protein enzyme‐linked immunosorbent assay; ULOQ, upper limit of quantification.

Projected persistence of humoral immune responses

The projected percentages of participants with quantifiable binding antibody concentrations at 24 months (antibody persistence) was 70.5% following single‐dose Ad26.COV2.S and greater than or equal to 89.9% following any homologous booster regimen (Table 2). The projected neutralizing antibody persistence at 24 months was 55.2% following single‐dose Ad26.COV2.S and greater than or equal to 80.0% following any homologous booster regimen (Table S2).

TABLE 2.

Projected percentages of SARS‐CoV‐2‐seronegative participants with measurable S‐ELISA concentrations (persistence of binding antibody responses) up to 24 months after administration of a single‐dose regimen and multiple homologous booster regimens of Ad26.COV2.S (5 × 10¹⁰ vp), and observed antibody persistence at 8 and 12 months after primary vaccination with Ad26.COV2.S.

Treatment regimen	Predicted		Observed
	Time	Predicted % above LLOQ for the overall population	Actual time, a Bin range	Observed % above LLOQ (95% CI), b N
Single dose	Day 239	93.5%	Day 237 (230, 245]	100% (90.4%, 100%), 36
Single dose	12 months	87.9%	Day 370 (350, 390]	91.7% (75.8%, 96.8%), 32
Single dose	18 months	80.0%
Single dose	24 months	70.5%
Booster dose (D1, D57)	Day 239	99.9%	Day 239 (230, 245]	98.9% (93.9%, 99.9%), 89
Booster dose (D1, D57)	12 months	97.6%	Day 358 (350, 390]	83.3% (64.1%, 93.3%), 24
Booster dose (D1, D57)	18 months	94.3%
Booster dose (D1, D57)	24 months	89.9%
Booster dose (D1, D85)	Day 239	100%	Day 254 (245, 260]	100% (91.4%, 100%), 41
Booster dose (D1, D85)	12 months	98.2%	Day 360 (350, 390]	100% (88.6%, 100%), 30
Booster dose (D1, D85)	18 months	94.7%
Booster dose (D1, D85)	24 months	90.4%
Booster dose (D1, D183) c	Day 239	95.6%	Day 205 (190, 217]	100% (83.2%, 100%), 19
Booster dose (D1, D183) c	12 months	95.6%	Day 365 (350, 390]	100% (81.6%, 100%), 17
Booster dose (D1, D183)	18 months	93.9%
Booster dose (D1, D183)	24 months	90.8%

Abbreviations: CI, confidence interval; D1, day 1; D57, day 57; D85, day 85; D183, day 183; LLOQ, lower limit of quantification; S‐ELISA, spike protein enzyme‐linked immunosorbent assay.

^a “Actual time” is chosen as the closest to the nominal simulated time (Time). “Bin range” refers to the lowest excluded value up to the largest included value of the range. Manual binning was used instead of actual visits to account for the heterogeneity of planned visits across studies. The following bins were defined: [0,21], (21,35], (35,67], (67,85], (85,113], (113,176], (176,190], (190,217], (217, 230], (230, 245], (245, 260], (260, 300], (300, 350], (350, 390], and (390, 440].

^b 95% CI for binomial probabilities based on Wilson's method.

^c Given the large time range for binning, additional samples of the same participant were included in the computations of sample size for the 6‐month booster arms. N = number of samples per bin in the final analysis dataset (8‐month and 12‐month timepoints only).

Although longer intervals between prime and boost resulted in higher peak antibody responses post boost (see Exploratory analyses), the projected binding antibody persistence at 24 months was similar after boosting at 2, 3, and 6 months (Table 2). There was a good agreement between observed and predicted percentages of quantifiable S‐ELISA concentrations (Table 2). Small differences between observed and predicted wtVNA titers could be explained by the sample size in the 6‐month booster arms (n = 15), and by the larger weight of single‐dose data in the interval between primary and booster vaccination (n = 158) given large assay variability.

Similar overall persistence of binding and neutralizing antibodies at 24 months was observed for different boosting regimens (Figure 4). Any homologous booster given between 2 and 6 months post‐prime was predicted to attenuate the waning of binding and neutralizing antibody persistence through 24 months in all subgroups stratified by age and sex (Figure 4). The most pronounced attenuation in antibody waning was predicted for men aged greater than or equal to 60 years: the projected 24‐month persistence following single‐dose Ad26.COV2.S was 50.7% for S‐ELISA and 34.3% for wtVNA, and increased to greater than or equal to 79.7% for S‐ELISA and greater than or equal to 64.7% for wtVNA after any booster regimen. A higher loss of neutralizing antibody persistence was projected within the longer boosting interval (6 months vs. 2 or 3 months; Figure 4b).

FIGURE 4.

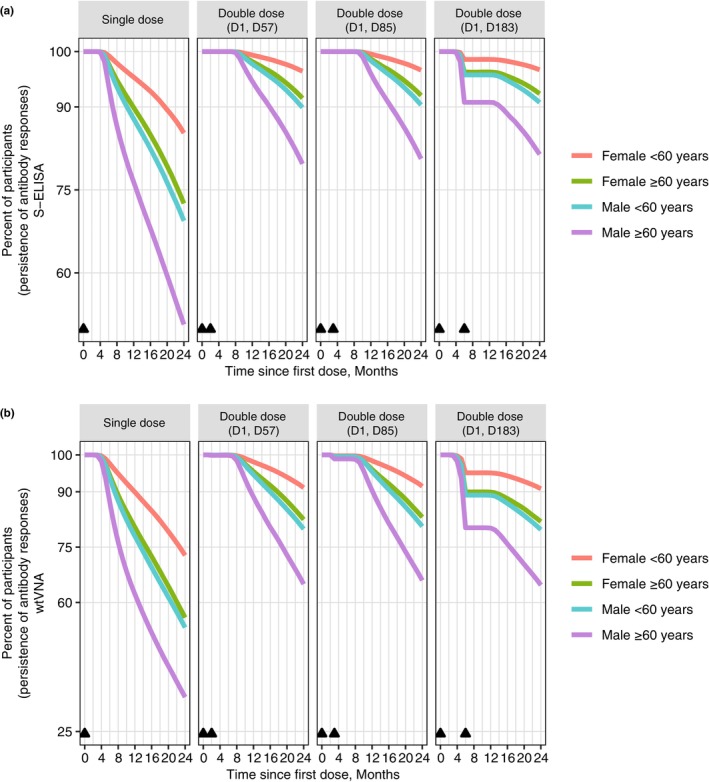
Projected persistence of binding and neutralizing antibody responses stratified by age and sex. S‐ELISA (a). wtVNA (b). Triangles indicate the immunization visit; D1 = day 1, D57 = day 57, D85 = day 85, and D183 = day 183. S‐ELISA, spike protein enzyme‐linked immunosorbent assay; wtVNA, wild‐type virus neutralization assay.

DISCUSSION

The mechanistic model adequately described the time course of binding and neutralizing antibody responses in SARS‐CoV‐2‐seronegative participants across five clinical trials and through 15 months following vaccination with single‐dose Ad26.COV2.S (5 × 10¹⁰ vp) or homologous boosting at 2, 3, or 6 months post‐prime.

Binding and neutralizing antibody responses were projected to wane through 24 months following vaccination with single‐dose Ad26.COV2.S. According to the model predictions, antibody persistence through 24 months was increased following any homologous boosting regimen: the binding antibody persistence was 70.5% after single‐dose Ad26.COV2.S and greater than or equal to 89.9% after boosting; similarly, the neutralizing antibody persistence was 55.2% after single‐dose Ad26.COV2.S and greater than or equal to 80.0% after boosting. These findings are in line with clinical data showing greater antibody response with homologous and heterologous boosting following Ad26.COV2.S prime compared to single‐dose Ad26.COV2.S. ²⁹ By contrast, modeling of trial data from individuals vaccinated with two doses of mRNA vaccine projected a decline in IgG response of greater than 99% relative to peak through 8 months, ³⁰ and of 98% relative to peak through 1 year post‐first dose. ³¹

Men aged greater than or equal to 60 years were predicted to show the most pronounced waning of antibody persistence, in line with the mechanistic modeling simulations stratified by age and sex in the context of single‐dose Ad26.COV2.S. ¹³ This subgroup was also projected to show the most pronounced reduction in waning following any booster. Covariate analyses revealed an inverse relationship between age and the rate of antibody production mediated by SLPCs and LLPCs, whereas women showed significantly higher rates of antibody production mediated by LLPCs relative to men. These findings are consistent with age and sex differences in vaccine‐induced humoral immunity, ¹³ , ²⁴ , ³² and with modeling results estimating a more marked waning immunity in men and older adults following heterologous vaccination with ChAdOx1/BNT162b2 or two doses of BNT162b2. ³¹

The current mechanistic model incorporated two proliferation terms of B cell dynamics to account for differential mechanisms mediating the production of SLPCs and LLPCs through the memory B cell and GC pathways, respectively. ¹⁷ This modeling framework helped us explain the observed antibody time course following vaccination with Ad26.COV2.S. For instance, the relative reduction (1 – C_th/C_max) increased from single‐dose (36.8%) relative to any booster regimen (47.4%–65.6%). The model assumes that a higher peak after any boosting was driven primarily by the production of SLPCs through the antigen‐independent production memory B cell term (M ₁ ), and to a lesser extent by LLPCs that showed a moderate increase after boosting, as exemplified by the illustration (Figure 5). As the decay rate of SLPCs was constant in the model, the faster relative antibody reduction after the second compared to the first peak indicated greater contribution of SLPC production to second peak formation. However, the observed lower relative reduction of binding antibodies after boosting at 6 months (47.4%), relative to 2 months (65.6%) and 3 months (60.6%), could be explained by longer observation period afforded by late boosting that purportedly allowed for GC‐dependent LLPC maturation over time. This finding might reflect differential increases in B cell growth mediated by GC versus memory B cell pathways, and supports modification of the previously published mechanistic model ¹³ by including two proliferation terms to account for differential dynamics of SLPC versus LLPC production. The model predictions regarding the time course of the memory B cell pathway are in line with the observations of steep decreases in antibody levels following the second dose of mRNA vaccine, ³³ accelerated projected declines in antibody levels following the second peak in the context of mRNA and adenovirus‐vectored vaccines, ¹⁷ , ³¹ and the relevance of reactivated memory B cells for rapid antibody production after exposure to an additional vaccine dose. ³⁴

FIGURE 5.

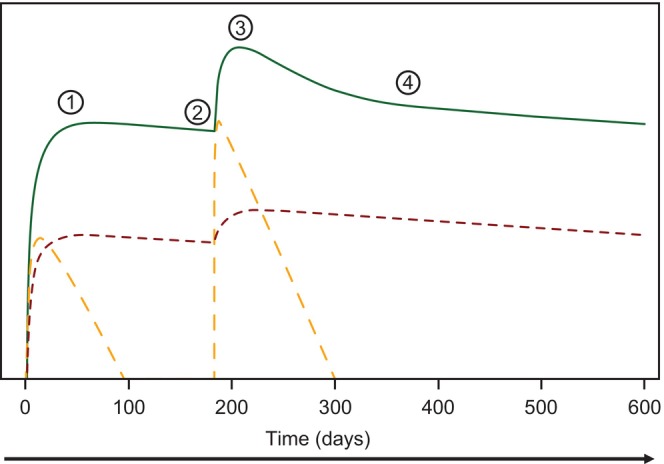
A sketch illustrating relative contributions of antibody production attributed to short‐lived plasma cells and long‐lived plasma cells to the first and second peak of log‐transformed binding antibody levels following a prime with Ad26.COV2.S (5 × 10¹⁰ vp) and a homologous booster given at 6 months post‐prime. Red dotted line illustrates the contribution to the antibody concentrations in the plasma due to long‐lived plasma cell production. Orange dotted line illustrates the contribution to the antibody concentrations in the plasma due to short‐lived plasma cell production. ① = C_max after single (first) dose; ② = pre‐booster dose, C_th; ③ = C_max after booster dose; ④ = long‐term antibody concentrations at 140–160 days after second peak, C_th. C_max, maximum plasma concentration.

In addition to age, sex, and length of boosting interval, antibody response to SARS‐CoV‐2 vaccination is influenced by boosting regimen and prior SARS‐CoV‐2 exposure. Heterologous boosting with mRNA vaccine after Ad26.COV2.S prime results in a greater increase in antigen‐specific antibody levels compared to homologous boosting, ²⁹ whereas SARS‐CoV‐2‐recovered and ‐naive individuals show distinct patterns of antibody response after mRNA vaccination. ²⁴ , ³⁴ Previous SARS‐CoV‐2 infection is predicted to influence IgG response for up to 1 year following vaccination. ³¹ In SARS‐CoV‐2‐naïve recipients, a third dose of mRNA vaccine is associated with slower IgG waning for up to 5 months relative to the second dose. ³⁵ , ³⁶ Future studies could focus on investigating differences in antibody persistence between SARS‐CoV‐2‐recovered and ‐naïve individuals in the context of homologous and heterologous boosters involving Ad26.COV2.S.

Our study carries implications for informing research focused on establishing antibody‐based CoP following immunization with Ad26.COV2.S or mRNA vaccine. ⁸ , ⁹ Our findings suggest that above‐LLOQ wtVNA and S‐ELISA values could be used to inform definitions of long‐term CoP in Ad26‐vectored vaccine platform.

At the time of the model building longitudinal data collected on assays which measure neutralizing antibody biomarkers against variants of concern (VoC) were not available. The current approach, where two different assays were pooled and a log‐transformed ratio of wtVNA to S‐ELISA measurements over time was established, supports the hypothesis that the structural model could also be used to fit data of VoC. Moreover, the high correlation between the S‐ELISA and wtVNA, especially at later timepoints, suggests that once the fold‐change of the VoC compared to the original variant and the correlation coefficient between assays are defined, the antibody persistence for VoC could be predicted. However, the generalizability of our findings to different SARS‐CoV‐2 variants requires further research.

Notably, the complexity of our model and its high number of fixed parameters allowed for IIV estimation only on k_AbS and k_AbL. Consequently, observed covariate effects are linked to SLPC and LLPC pathways, rather than to direct effects on the two antibody production parameters. Furthermore, the precision of model extrapolations for a booster dose administered beyond 6 months remains unknown, especially considering the limited number of data points with longer post‐boost intervals.

The current model approach can be positioned between a very complex approach, as the quantitative system pharmacology (QSP) models, ³⁷ , ³⁸ , ³⁹ , ⁴⁰ , ⁴¹ and a simpler one, as the empirical models (i.e., power law or exponential models) ⁴² widely used in vaccine development. The mechanistic modeling approach presented in the current work has four advantages: (1) it constitutes a step forward with respect to predictability compared to the empirical models, (2) is less complex than a QSP model but accounts for the key elements of the immune response, (3) is informed by the available clinical data, and finally, (4) uses the nonlinear mixed effect modeling methodology, which not only allows to describe the biological system of interest and its intersubject variability, but also enables to evaluate the effect of different covariates on the estimated parameter outcomes.

The knowledge acquired during this research and tested on the Ad26.COV2.S vaccine should not be considered to provide only information to this specific case. More and more vaccines are developed also for therapeutic use, and the mechanistic modeling approach presented here might contribute to accelerate the development programs by contributing to the dose selection decision and quantifying the persistence of immunogenicity, comparison among vaccines once the same assays and study design are considered, or even, the duration of protection if a humoral response correlate of protection is established.

In conclusion, a homologous booster of Ad26.COV2.S (5 × 10¹⁰ vp) administered between 2 and 6 months was projected to increase the persistence of binding and neutralizing antibody responses relative to a single‐dose vaccination through 24 months post‐prime. Similar rates of 24‐month persistence were projected for the homologous boosting regimens administered at an interval of 2, 3, or 6 months, and were greater than or equal to 89.9% for binding and greater than or equal to 80.0% for neutralizing antibodies. Antibody persistence following a single dose of Ad26.COV2.S was projected to decline over time. The most pronounced waning was projected for men aged greater than or equal to 60 years and was markedly attenuated following the administration of any homologous booster. These findings suggest that homologous boosting might be a viable strategy for maintaining protective effects of the Ad26.COV2.S vaccination for up to 2 years in different subgroups of recipients stratified by age and sex.

AUTHOR CONTRIBUTIONS

A.D. and J.J.P.R. wrote the manuscript. M.L.G., K.H., J.R.G., and J.S. designed the research. M.L.G., K.H., J.R.G., and J.S. performed the research. A.D, P.J., and J.J.P.R. analyzed the data. M.N. and Y.I. contributed new reagents/analytical tools.

FUNDING INFORMATION

This project has been funded in whole or in part with federal funds from the Department of Health and Human Services, Administration for Strategic Preparedness and Response, Biomedical Advanced Research and Development Authority, under Other Transaction Agreement HHSO100201700018C.

CONFLICT OF INTEREST STATEMENT

A.D., Y.I., M.N., M.L.G., J.S., K.H., J.R.G., and J.J.P.R. are employees of Janssen Research & Development (a Johnson & Johnson company) and may hold stock in Johnson & Johnson. P.J. is a paid consultant of Johnson & Johnson.

DATA ACCESSIBILITY STATEMENT

The data sharing policy of the Sponsor is available at https://www.janssen.com/clinical‐trials/transparency. As noted on this site, requests for access to the study data can be submitted through Yale Open Data Access (YODA) Project site at http://yoda.yale.edu.

Supporting information

Appendix S1

Dari A, Jacqmin P, Iwaki Y, et al. Mechanistic modeling projections of antibody persistence after homologous booster regimens of COVID‐19 vaccine Ad26.COV2.S in humans. CPT Pharmacometrics Syst Pharmacol. 2023;12:1485‐1498. doi: 10.1002/psp4.13025