Propensity score analysis for a semi-continuous exposure variable: a study of gestational alcohol exposure and childhood cognition

Abstract

Propensity score methodology has become increasingly popular in recent years as a tool for estimating causal effects in observational studies. Much of the related research has been directed at settings with binary or discrete exposure variables with more recent work involving continuous exposure variables. In environmental epidemiology, a substantial proportion of individuals is often completely unexposed while others may experience heavy exposure leading to an exposure distribution with a point mass at zero and a heavy right tail. We suggest a new approach to handle this type of exposure data by constructing a propensity score based on a two-part model and show how this model can be used to more reliably adjust for covariates of a semi-continuous exposure variable. We also consider the case when a misspecified propensity score is used in a regression adjustment and derive an explicit form of the bias. We show that the potential bias gets smaller as the estimated propensity score gets closer to the true expectation of the exposure variable given a set of observed covariates. While this result pertains to a more general setting, we use it to evaluate the potential bias in settings in which the true exposure has a semi-continuous structure. We also evaluate and compare the performance of our proposed method through simulation studies relative to a simpler linear regression-based propensity score for a continuous exposure variable as well as through direct covariate adjustment. Overall, we find that using a propensity score constructed via a two-part model significantly improves the regression estimate when the exposure variable is semi-continuous in nature. Specifically when the proportion of non-exposed subjects is high and the effects of covariates on exposure and outcome are strong, the proposed two-part propensity score method outperforms the more standard competing methods. We illustrate our method using data from the Detroit Longitudinal Cohort Study in which the exposure variable reflects gestational alcohol exposure featuring zero values and a long tail.

1 |. INTRODUCTION

1.1 |. Background and literature review

Environmental epidemiologists often seek to assess the impact of a potentially toxic exposure on a health outcome, while adjusting statistically for possible confounders. Failure to account for the effect of the confounders can result in biased effect estimates that either overstate or obscure the true causal effect of the exposure. In practice, regression models that include potential confounders are most commonly used to adjust for the effects of confounding variables. However, particularly when the number of potential confounders is large, it can be difficult to determine whether the regression model relating the exposure variable and confounding variables to the outcome has been correctly specified (Austin, 2011). Use of a propensity score has become a popular alternative strategy to reduce or eliminate the effects of confounding in observational settings (Austin, 2011; Rosenbaum & Rubin, 1983).

A propensity score is typically obtained via a regression analysis in which the exposure is modelled as a function of potential confounding variables. Propensity score methodology was originally developed to estimate the causal effect of a binary exposure variable (Rosenbaum & Rubin, 1984, 1985) and consequently propensity scores have typically been based on binary regression models. Imbens (1999), Imai and van Dyk (2004) and Hirano and Imbens (2004) broadened this framework to accommodate continuous exposure variables and coined the term the generalized propensity score for such settings. (Hirano & Imbens, 2004; Imai & van Dyk, 2004; Imbens, 1999). With a continuous exposure variable, Hirano and Imbens (2004) define the generalized propensity score for a particular individual as the conditional density function of the exposure model given covariates, including potential confounders, evaluated at the observed exposure and covariate values. In contrast, Imai and van Dyk (2004) define the generalized propensity score to be the entire conditional density function of the treatment. Such propensity score-based methods allow practitioners to estimate a full dose–response function rather than simply the average treatment effect (Fichera et al., 2016; Moodie & Stephens, 2012). Zhao et al. (2020) evaluated these two methods for estimation of the full dose–response function and explored the performance of two extensions they proposed to improve the robustness of analyses based on the generalized propensity score (Zhao et al., 2020).

Generalized propensity scores have been used in settings involving continuous exposure variables related to labour earnings (Bia & Mattei, 2008; Imai & van Dyk, 2004), medical expenditure (Imai & van Dyk, 2004; Zhao et al., 2020), and birth weight (Zhang et al., 2016), among others.

In environmental and behavioural epidemiology, exposure may refer to chemical exposures, pollution or personal use of substances, such as alcohol, tobacco or illicit drugs. A number of challenging problems can arise in such settings. Often, the exposure variable is semi-continuous in that the data may feature a large proportion of individuals who have not been exposed at all. The exposure distribution may also have a long right tail due to a small number of individuals with very high exposure. Examples are ubiquitous and include counts of cigarettes smoked per day in a population made up of smokers and non-smokers (Wang & Heitjan, 2008), concentrations of toxins in environmental epidemiology where levels below the detection limit are recorded as zero (Choi & Hwang, 2018), and alcohol intake per day in a population made up of drinkers and non-drinkers (Choi & Hwang, 2018). Other settings include health services research (Neelon et al., 2015), studies of the microbiome (Chai et al., 2018), when modelling functional ability in chronic diseases (Su et al., 2015) and when modelling occlusion therapy in the treatment of childhood amblyopia (Moodie & Stephens, 2012). One strategy for modelling the effects of such exposure variables is to discretize them. In the present setting, for example, we could classify subjects as having zero, low, moderate or high exposure. While this can address confounding, this strategy is not appropriate when scientific interest lies in a parsimonious characterization of the dose–response effect. In environmental risk assessment, for instance, the goal is often to identify the specific exposure level associated with a specified risk above a background level (Crump, 1984). In the project funded by the National Institutes of Health in the United States that motivates our work, investigators seek to understand whether there are levels of gestational alcohol exposure that are not associated with clinically significant risks of adverse developmental effects for the children. Study findings could have important implications for the diagnosis and treatment of affected children.

Semi-continuous variables can be viewed as arising from two distinct processes: (i) a binary process, reflecting whether or not the subject was exposed, and (ii) a continuous process, determining the level of exposure given that some exposure occurred. Two-part models have been developed to handle such data. Often the binary component is modelled via logistic regression, and a log transformation is applied to model the continuous part using standard linear regression (Smith et al., 2017). As an alternative to two-part models, analysts often fit a standard generalized linear model with a log link to ensure that the predicted values are not negative (Smith et al., 2017). Several researchers have compared the performance of two-part models with various classical approaches in settings that involve semi-continuous response variables. While findings are context dependent, two-part models often exhibit better performance (Duan et al., 1983; Madden et al., 2000; Smith et al., 2017). Smith et al. (2017) found that the standard generalized linear models are not appropriate when data are zero-heavy. Specifically, they reported that inferences based on standard generalized linear models incurred increased bias, lower than nominal coverage, and increased type I error rates in settings with non-negligible proportions of individuals with zero values (Smith et al., 2017).

Despite the recent interest in generalized propensity scores, there has been relatively little work examining modelling issues with zero-inflated exposure variables. Imai and van Dyk (2004) argued that generalized propensity scores can be used to establish causal effects in observational studies when the exposure has a mixture of zeros and continuously distributed positive values, but did not explore this issue further. Naimi et al. (2014) explored a variety of approaches for modelling the propensity score for normal and contaminated Poisson exposure variables and investigated the sensitivity of misspecification of propensity score models within the framework of inverse probability weighted estimating functions. Specifically, they constructed inverse probability weights using: a normal distribution, a normal distribution with heteroscedastic variance, a gamma distribution, a t-distribution and using a quantile binning approach. These authors found that when the exposure variable is zero-inflated, all of these methods yielded slightly biased estimators with the gamma and quantile binning approach giving the best estimators (Naimi et al., 2014).

In this paper, we propose use of a two-part model for the construction of a generalized propensity score for a semi-continuous exposure variable. Unlike the existing methods, our method allows covariates to act differently on the exposure indicator (exposed vs. unexposed) and the extent of exposure among those who are exposed. Given the known problems of inferences based on standard generalized linear models when the response variable is semi-continuous, application of a two-part modelling approach to propensity score construction would seem to be a more appealing approach for propensity score construction in this setting. We evaluate and compare the performance of the proposed method with the established generalized propensity score approach (Imai & van Dyk, 2004).

The seminal work by Rosenbaum and Rubin (1983) showed that once the propensity score is estimated, effects of confounding can be eliminated through propensity score matching, stratification or covariance adjustment in regression. We focus on covariate adjustment using the propensity score estimated by the two-part model. We derive an explicit functional form of the bias that arises when a misspecified propensity score is used in covariate adjustment. In our simulation studies, we calculate this bias for settings where the exposure variable is governed by a two-part model but the propensity score is estimated by ordinary least square regression as it is suggested in generalized propensity score approach.

The remainder of this article is organized as follows. In the following sub-section we introduce the motivating study which explores the relationship between prenatal alcohol exposure and cognitive function in children from the Detroit Longitudinal Cohort study. In Section 2, we introduce notation and describe how to estimate the two-part generalized propensity score. We then provide the explicit form of bias associated with use of a misspecified propensity score as a covariate in regression adjustment. Section 3 describes and reports on a simulation study designed to evaluate the performance of the proposed method relative to methods based on a naive unadjusted analysis, conventional linear regression and the generalized propensity score approach. In Section 4, we apply these methods to the Detroit Longitudinal Cohort Study. In Section 5 we discuss the strengths and limitations of the proposed methods, and outline areas warranting further research.

1.2 |. The Detroit study of foetal alcohol exposure

While evidence from animal models and epidemiological studies has linked prenatal alcohol exposure (PAE) to a broad range of cognitive and behavioural deficits (Jacobson et al., 2011; Lewis et al., 2016; Mattson et al., 1997) the exact nature of the dose–response effect is not well understood. In particular, there is virtually no information in the scientific literature regarding the levels of PAE associated with an increased risk of clinically significant adverse effects. It is widely know that women should stop drinking during pregnancy, but there remain important scientific questions regarding whether or not low-level exposures will result in adverse developmental effects, and more generally about the dose–response effects. Insights into these questions could have important clinical implications for the diagnosis and treatment of affected children. Moreover this critical public health question cannot be addressed by studies that have used samples of children identified in clinics and referred to specialists for assessment since in such cases the level of maternal alcohol use, and hence gestational alcohol exposure has not been quantified.

The Detroit Longitudinal Cohort study is a large prospective study of children with a broad range of prenatal alcohol exposure levels, who were followed from birth through age 19 years (Jacobson et al., 2004). Four hundred and eighty pregnant, African-American, inner-city women were interviewed about their alcohol use during pregnancy using a timeline follow-back interview (Jacobson et al., 2002). Data from each visit regarding maternal alcohol consumption were summarized in terms of daily alcohol intake (standard drinks or ounces of absolute alcohol (AA)/day) averaged across pregnancy.

For this paper, we analysed data for a single outcome measure, the Wechsler Intelligence Scales for Children (3rd edition) (WISC-III) Freedom from Distractibility Index, for the 337 children who participated in the 7-year follow-up assessment of this cohort in the presence of a broad set of potential confounding variables covariates (see Tables 1 and 2). Figure 1 displays the relation between the outcome variable and the log of prenatal alcohol exposure. The figure shows a long-tailed exposure distribution, even after transformation to the log scale. Given that 23.8% of the women reported no alcohol use during pregnancy, characterizing this variable as two distinct processes (i.e. one determining whether the mother consumed alcohol, the other determining the actual level if alcohol was consumed), is theoretically appealing and provides a richer description than a model with a single function. It is also reasonable to suspect that covariates might operate differently in terms of predicting whether or not a mother consumes alcohol, as compared to the amount of alcohol used by those who consumed it. Indeed, initial exploratory analysis revealed that prenatal marijuana exposure and gravidity were strong predictors of whether or not a woman drank alcohol during pregnancy but were not predictors of the amount consumed by those who reported drinking at least some alcohol.

TABLE 1.

Summary statistics of continuous covariates in the Detroit Longitudinal Cohort study (N=232)

	Mean	SD
Gestational age at recruitment (weeks)	23.8	7.5
Number of prenatal visits	5.8	3.0
Smoking during pregnancy (cigarettes/day)	9.5	11.2
Prenatal marijuana exposure (days/month)	0.9	2.9
Prenatal cocaine exposure (days/month)	1.0	2.9
Prenatal opiate exposure (days/month)	0.2	1.0
Biological mother’s education (years)	11.8	1.6
Biological mother’s verbal IQ (PPVT score)	71.7	11.7
Beck Depression Inventory at 6-month postpartum follow-up	11.2	7.5
Age of a child at 7-year follow-up visit (years)	7.9	0.3
Socioeconomic status at age 7-year follow-upa	26.2	10.4
Primary caregiver’s verbal IQ (PPVT score)at 7-year follow-up	72.9	12.5
HOME score at 7-year follow-up	33.7	6.9
Beck Depression Inventory at 7-year follow-up	8.3	7.4
Number of stressful events at 7-year follow-upb	10.2	5.5
Perceived life stress at 7-year follow-upb	36.7	27.8

^aHollingshead Four Factor Index of Social Status (Hollingshead, 2011)

^bLife Events Scale (Holmes and Rahe, 1967)

TABLE 2.

Summary statistics of categorical covariates in the Detroit Longitudinal Cohort

	N	%
Marital status
Biological mother’s
Married	19	8.2
Not married	213	91.8
Primary care giver’s at 7-year follow-up
Married	205	88.4
Not married	27	11.6
Parity
0	88	37.9
1	63	27.2
2	51	22.0
3	17	7.3
4	8	3.4
>=5	5	2.2
Gravidity
1	39	16.8
2	53	22.8
3	47	20.3
4	33	14.2
>=5	60	25.8

FIGURE 1.

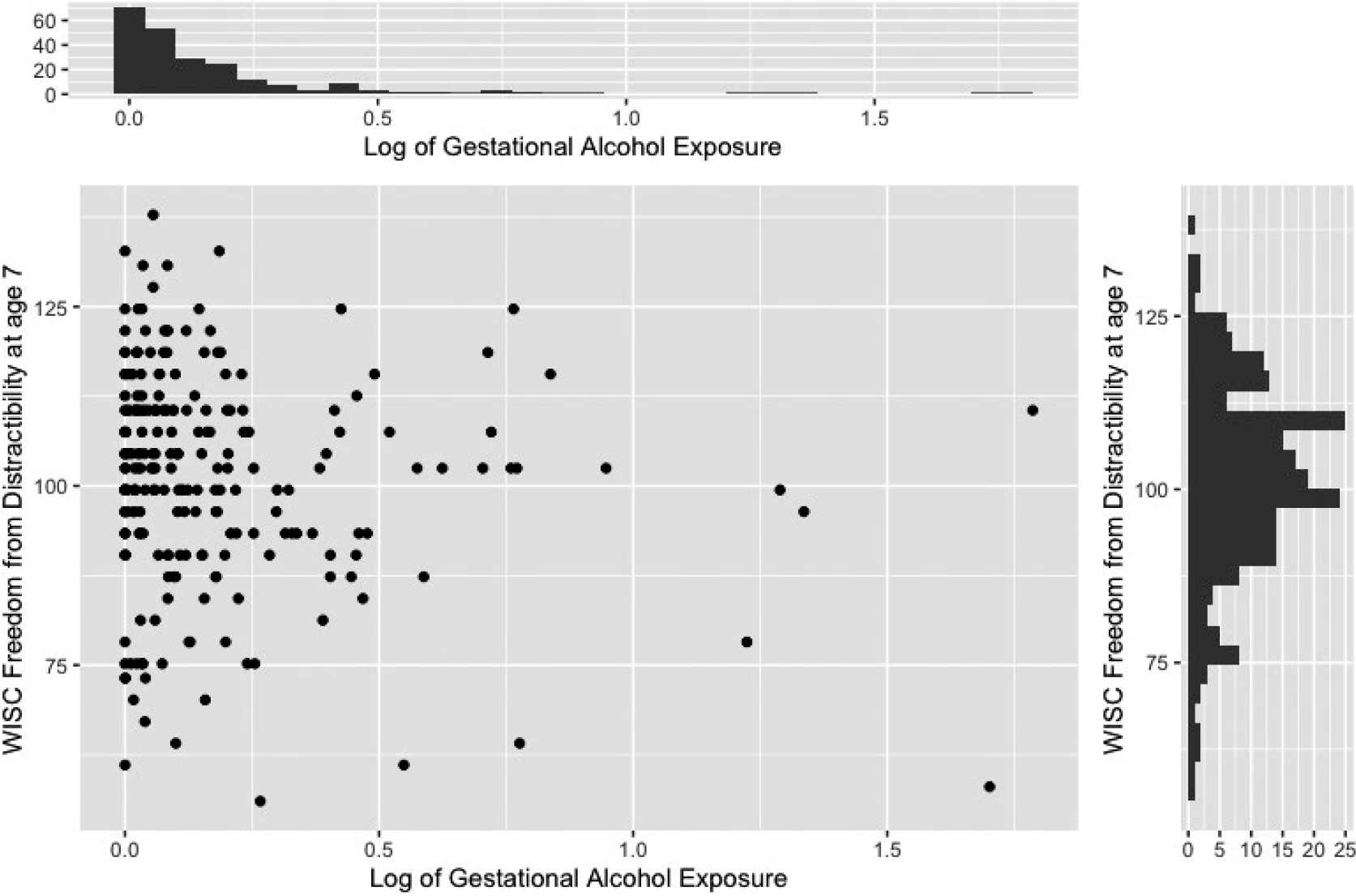
The relation between the Wechsler Intelligence Scale for Children (WISC) Freedom from Distractibility Score at age 7 and log of gestational alcohol exposure

2 |. PROPENSITY SCORE ADJUSTMENT WITH SEMI-CONTINUOUS EXPOSURE

We consider the case in which the goal is to model the causal effect of a semi-continuous exposure variables $X$ on an outcome $Y$ in the presence of a set of confounding variables $Z={\left(Z_1,\dots ,Z_p\right)}^{\prime }$. The effect of confounding can be addressed by regressing the quantitative exposure on the set of observed covariates as it is suggested by Imai and van Dyk (2004). Specifically, the propensity score can be estimated using ordinary least squares (OLS) regression. Then the predicted mean of $\mathrm{X}$ obtained from a model predicting $X$ given all confounding variables $Z$ can be used as the estimated propensity score in the outcome model:

$$Y_i={\eta }_0+{\eta }_1{X}_i+{\eta }_2{S}_i^{\mathrm{*}}+{ϵ}_i$$ (1)

where $S_i^{\mathrm{*}}$ is the estimated propensity score for subject $i$. In the next subsection, we introduce a two-part generalized propensity score for the settings where the exposure variable has a substantial proportion of zero values. In this approach, the semi-continuous exposure variable is considered as arising from two distinct processes: a binary part (exposed vs. not exposed) and a continuous part (characterizing the extent of exposure among those exposed).

2.1. A two-part generalized propensity score model

Consider a non-negative semi-continuous variable $X$ with a point mass at zero and a density characterizing the probability distribution of non-zero values on the positive real line. Let $Z={\left(Z_1,\dots ,Z_p\right)}^{\prime }$ denote a $p\times 1$ set of covariates and consider a two-part model for characterizing the association between $Z$ and $X$. Specifically, if $X^{+}=I(X>0)$ indicates a positive value for $X$, we let $\pi \left(Z\right)=E\left(X^{+}\mid Z\right)$ and consider a binary regression model defined by the link function $g(\cdot )$ mapping the interval [0, 1] onto the real line and setting $g\left(\pi \left(Z;{\alpha }_1\right)\right)={\bar{Z}}^{\prime }{\alpha }_1$ where $\bar{Z}={\left(1,Z^{\prime }\right)}^{\prime }$ and ${\alpha }_1={\left({\alpha }_{10},{\alpha }_{11},\dots ,{\alpha }_{1p}\right)}^{\prime }$. In what follows we use the canonical logistic link function in which case ${\alpha }_{1j},j=0,1,\dots ,p$, are log odds ratios.

We also let $P\left(X\le x\mid X^{+}=1,Z;{\alpha }_2\right)=F^{+}\left(x\mid Z;{\alpha }_2\right)$ denote the cumulative distribution function for the positive part of $X,X\mid X>0$, given $Z$, which we take to be indexed by a $(p+1)\times 1$ parameter ${\alpha }_2$. The full distribution for $X$ is therefore indexed by $\alpha ={\left({\alpha }_1^{\prime },{\alpha }_2^{\prime }\right)}^{\prime }$. A key requirement of the model for $X\mid X^{+}=1$ given $Z$ is that it involve a simple way to compute $E\left(X\mid X^{+}=1,Z;{\alpha }_2\right)=\mu \left(Z;{\alpha }_2\right)$. One approach would be to adopt a generalized linear model, but any non-negative distribution can be used. Ultimately we may compute

$$E(X\mid Z;\alpha )=\pi \left(Z;{\alpha }_1\right)\mu \left(Z;{\alpha }_2\right)$$ (2)

as the marginal mean for $X\mid Z$ based on the two-part model formulation. For example, we consider a logistic model for $X^{+}\mid Z$ and let

$$\mathrm{l}\mathrm{o}\mathrm{g}\left(\pi \left(Z;{\alpha }_1\right)/\left(1-\pi \left(Z;{\alpha }_1\right)\right)\right)={\bar{Z}}^{\prime }{\alpha }_1,$$ (3)

while any location-scale regression model can be adopted for $X\mid X>0,Z$. These models are specified by setting

$$\mathrm{l}\mathrm{o}\mathrm{g}X=\eta +\sigma R$$ (4)

where $\eta ={\bar{Z}}^{\prime }\gamma$ is the linear predictor, $\sigma$ is a dispersion parameter, and $R$ is an error term which has any standard distribution on the real line; we write ${\alpha }_2={\left({\gamma }^{\prime },\sigma \right)}^{\prime }$. We assume $R$ are independently distributed with $R\perp Z$. If $R\sim N(0,1)$ for example this implies a log-normal regression model for which $\mu \left(Z;{\alpha }_2\right)=\mathrm{e}\mathrm{x}\mathrm{p}({\bar{Z}}^{\prime }\gamma +{\sigma }^2/2)$. Together the two models based on (3) and (4) give an expression for (2) as

$$E(X\mid Z;\alpha )=\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{t}({\bar{Z}}^{\prime }{\alpha }_1)\cdot \mathrm{e}\mathrm{x}\mathrm{p}({\bar{Z}}^{\prime }\gamma +{\sigma }^2/2)$$ (5)

where $\mathrm{e}\mathrm{x}\mathrm{p}\mathrm{i}\mathrm{t}\left(\mathrm{u}\right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{u}\right)/(1+\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{u}\left)\right)$.

With a sample of observations on $n$ independent individuals, we introduce a subscript $i$ to label individuals and write the data for fitting the semi-continuous propensity score as $\left\{\left(X_i,Z_i\right),i=1,\dots ,n\right\}$. The full likelihood for $\alpha$ based on this sample is,

$$L\left(\alpha \right)\propto \prod _{i=1}^n{\left[P\left(X_i^{+}=0\mid Z_i;{\alpha }_1\right)\right]}^{1-X_i^{+}}[P\left(X_i^{+}=1\mid Z_i;{\alpha }_1\right)d{F}^{+}{(X_i\mid X_i^{+}=1,Z_i;{\alpha }_2]}^{X_i^{+}}$$ (6)

where $d{F}^{+}\left(x\mid X_i^{+}=1,Z_i;{\alpha }_2\right)=f\left(x\mid X_i^{+}=1,Z_i;{\alpha }_2\right)dx$. Note that (6) can be factored as $L\left(\alpha \right)=L_1\left({\alpha }_1\right)L_2\left({\alpha }_2\right)$ where

$$L_1\left({\alpha }_1\right)\propto \prod _{i=1}^n{\left[1-\pi \left(Z_i;{\alpha }_1\right)\right]}^{1-X_i^{+}}[\pi {(Z_i;{\alpha }_1]}^{X_i^{+}}$$ (7)

and

$$L_2\left({\alpha }_2\right)\propto \prod _{i=1}^{n}d{F}^{+}{\left(X_i\mid Z_i;{\alpha }_2\right)}^{X_i^{+}}$$ (8)

which can be maximized separately as they are functionally independent. Then substitution of $\widehat{\alpha }$ into (2.2) yields the estimated propensity score $S_i=E\left(X_i\mid Z_i;\widehat{\alpha }\right)$ for individuals $i,i=1\dots ,n$. We make the stable unit treatment value assumption, which posits that $Y_i$, the response by the ith subject under exposure $X=x$, is not affected by what exposures are received by other subjects (Hernán & Robins, 2006; Winship & Morgan, 1999). We also assumed weak unconfoundedness (Hirano & Imbens, 2004).

Instead of including an extensive list of potential confounders in the primary regression analysis, we address the confounding effect of the covariates via covariate adjustment using the propensity score $S_i$. We fit a linear regression model of the response over the exposure variable and the propensity score. We then fit the response model by controlling for $S_i$ in

$$Y_i={\beta }_0+{\beta }_1{X}_i+{\beta }_2{S}_i+\tau R_i$$ (9)

$R_i$ are assumed to be independent and identically distributed with mean zero and variance one, $i=1,\dots ,\dots ,n$ and we also assume $R_i\perp \left(X_i,S_i\right),i=1,\dots ,n$. Note also that the purpose of adjusting for the propensity score is to render $X_i\perp Z_i\mid S_i$.

2.2 |. Bias associated with using a misspecified propensity score as a regression covariate

In this sub-section, we derive a formula of the limiting bias of an estimator of an exposure effect when a propensity score is used via regression adjustment but is estimated based on a misspecified propensity score model. While our general result facilitates the calculation of the asymptotic bias for any type of misspecified propensity score model, we use our result to explore the consequences of using a standard generalized propensity score based on a linear regression model when the confounder–exposure relationship is governed by a two-part model.

As before, $X$ denotes the exposure variable and $\mathbf{Z}$ represents the $p\times 1$ vector of confounding variables. We denote $\mathbf{W}\left(\mathbf{Z}\right)$ to be a $q\times 1$ function of the confounders. If we let $\mathbf{V}={\left(1,X,{\mathbf{W}}^{\prime }\left(\mathbf{Z}\right)\right)}^{\prime }$ be a $(q+2)\times 1$ vector of covariates and $\mathit{\theta }={\left({\theta }_0,{\theta }_1,{\mathit{\theta }}_2^{\prime }\right)}^{\prime }$ be a $(q+2)\times 1$ vector of parameters, we can consider a linear model of the form:

$$Y={\theta }_0+{\theta }_{1}X+{\theta }_2{}^{\prime }\mathit{W}\left(\mathit{Z}\right)+E$$ (10)

where we assume $(X,\mathbf{Z})\perp \perp E$ and $E\sim N\left(0,{\sigma }^2\right)$. We assume that a possibly misspecified propensity score has been computed from a model for $X$ given all of the covariates $\mathbf{Z}$ and We denote this propensity score by

$$\widehat{\mu }=\mu (\mathbf{Z};\widehat{\mathit{\alpha }}).$$

Then we regress the continuous outcome $Y$ on the semi-continuous exposure variable $X$ and the estimated assumed propensity score obtained from the assumed model:

$$Y={\beta }_0+{\beta }_{1}X+{\beta }_2\mu \left(\mathbf{Z};\widehat{\alpha }\right)+ϵ,$$ (11)

under the assumption $(X,\mu (\mathbf{Z});\widehat{\alpha })⫫ϵ$ with $ϵ\sim N\left(0,{\tau }^2\right)$; We let $\mathit{\beta }={\left({\beta }_0,{\beta }_1,{\beta }_2\right)}^{\prime }$ and assume that estimates are obtained as follows. Let $\stackrel{-}{\mathbf{V}}=(1,X,\mu (\mathbf{Z}){)}^{\prime }$. The contribution to the score equation for $\mathit{\beta }$ from a single individual based on (2.11) is

$$\mathbf{U}(Y,X,\mu (Z);\mathit{\beta })=\stackrel{-}{\mathbf{V}}(\mathbf{Y}-{\stackrel{-}{\mathbf{V}}}^{\prime }\beta )$$

and $\widehat{\mathit{\beta }}$ is consistent for the solution to $E\{\mathbf{U}(Y,X,\mathbf{Z};\mu (\mathbf{Z}),\beta )\}=0$ where the expectation is taken with respect to true distribution involving $Y,X,\mathbf{Z}$ (Rotnitzky & Wypij, 1994; White, 1982). We show in the Appendix that the explicit form of the asymptotic bias of the estimator ${\widehat{\beta }}_1$ for ${\theta }_1$ can be expressed as

$${\beta }_1={\theta }_1+\frac{{\mathit{\theta }}_2^{\prime }[\mathit{\eta }(\mathit{Z})-\mathit{\varphi }(\mathit{Z})\text{corr}(E(X\mid \mathit{Z})\mu (\mathit{Z}))\sqrt{V(E(X\mid \mathit{Z}))/V(\mu (\mathit{Z}))}]}{\text{var}(X)-\text{var}(E(X\mid \mathit{Z})){\text{corr}}^2(E(X\mid \mathit{Z}),(\mu (\mathit{Z})))},$$ (12)

where, $\mathit{\eta }(\mathbf{Z})={\left({\eta }_1(\mathbf{Z}),{\eta }_1(\mathbf{Z}),\dots ,{\eta }_q(\mathbf{Z})\right)}^{\prime }$ where ${\eta }_j(\mathbf{Z})=\mathrm{cov}\left(E(X\mid \mathbf{Z}),W_j(\mathbf{Z})\right),j=1,\dots ,q$, and $\mathit{\varphi }(\mathbf{Z})=\left({\varphi }_1(\mathbf{Z}),{\varphi }_2(\mathbf{Z}),\dots ,{\varphi }_q(\mathbf{Z}{)}^{\prime }\right.$ where $\left.{\varphi }_j(\mathbf{Z})=\mathrm{cov}(\mu (\mathbf{Z})),W_j(\mathbf{Z})\right),j=1,\dots ,q$.

From (2.12), we see that the correct solution is ${\theta }_1$, so the propensity score-based estimation will be consistent when the second term in (2.12) is zero. The bias will be smaller as the assumed propensity score model gets closer to characterizing the true conditional expectation of $X\mid Z$. Through (2.12) the bias can be seen to depend on the effect of covariates on the continuous outcome $Y$ as well as the covariance between $\mathbf{W}(Z)$, $E(X\mid \mathbf{Z})$ and $E(\mu (\mathbf{Z}))$ and related variances.

3 |. EMPIRICAL STUDIES OF FINITE SAMPLE PROPERTIES

In Section 2, we derived an expression for the limiting bias of an estimator of an exposure effect when a propensity score is used via regression adjustment but it is estimated based on a misspecified propensity score model. The purpose of this derivation is to examine the sensitivity of causal inference to the validity of the propensity score model, and in particular to lay the foundation for the empirical studies that follow relating to the two-part model and its importance with semi-continuous exposure data.

Here we conduct simulation studies to investigate the finite sample performance of the propensity score adjustment based on the two-part model for the exposure variable. We consider $Z={\left(Z_1,Z_2\right)}^{\prime }$ where we let $Z_1$ and $Z_2$ be standard normal with $E\left(Z_k\right)=0$ and $\mathrm{v}\mathrm{a}\mathrm{r}\left(Z_k\right)=1,k=\mathrm{1,2}$.

We specify the distribution for the semi-continuous exposure variable using the framework of Section 2.1. We let $(\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t})(\pi (Z))={\alpha }_{10}+{\alpha }_{11}{Z}_1+{\alpha }_{12}{Z}_2$ where ${\alpha }_{11}=\mathrm{l}\mathrm{o}\mathrm{g}2$ and ${\alpha }_{12}=0$ and solve for ${\alpha }_{10}$ in order to set the marginal probability $P\left(X^{+}=1\right)=p^{\circ }$ is at a desired level. We then consider a log-normal regression model as in Equation (4) where we set $\bar{Z}={\left(1,Z_1,Z_2\right)}^{\prime }$ in Equation (4) to ${\gamma }_1=0.5,{\gamma }_2=0.5,{\gamma }_0=1.8$; we set $\sigma =0.5$. Here, we specified the regression coefficients to ensure that covariates operate differently in terms of predicting whether or not a subject is exposed, versus the amount of exposure for subjects who are exposed.

We also explore the performance of procedure based on fitting a log-normal model when the true distribution for exposed individuals follows a Weibull regression model. Specifically we generate positive exposure levels according to $\log X={\eta }^{\mathrm{*}}+\varphi R^{\mathrm{*}}$ where ${\eta }^{\mathrm{*}}={\bar{Z}}^{\prime }{\gamma }^{\mathrm{*}}$ is the linear predictor, $\varphi$ is a dispersion parameter, and $R^{\mathrm{*}}$ is an error term. We assume $R^{\mathrm{*}}$ has extreme value distribution which implies a Weibull regression model.

We generated the outcome variable using various known functions of the covariates and exposure variable. In particular, we follow the simulation studies described by Imai and van Dyk (2004). First we constructed an additive model of the form:

$$Y_1={\theta }_0+{\theta }_{1}X+{\theta }_2\sum _{k=1}^K{\lambda }_k^{{\kappa }_k{Z}_k}$$ (13)

and a multiplicative model of the from:

$$Y_2={\theta }_0^{\mathrm{*}}+{\theta }_1^{\mathrm{*}}X+{\theta }_2^{\mathrm{*}}\sum _{k=1}^K{\lambda }_k{Z}_k.$$ (14)

In both models the coefficient vector for covariates is represented by $\lambda =\left({\lambda }_1,\dots ,{\lambda }_p\right)$, the constants ${\theta }_2$ and ${\theta }_2^{\mathrm{*}}$ determine the relative influence of the exposure and the covariates on the continuous outcome, and each component of $\kappa =\left({\kappa }_1,\dots ,{\kappa }_p\right)$ is 1.

We considered scenarios in which 25% or 50% of subjects are unexposed. For each scenario, we carried out a naive unadjusted analysis, a conventional covariate adjustment, an analysis in which we adjusted for the generalized propensity score function via Gaussian linear regression (Imai & van Dyk, 2004) and finally our proposed propensity function based on a two-part model. We evaluate the performance of our method in two settings, one where the exposure levels for exposed individuals follow a log-normal regression model and one where it follows a Weibull regression model. For each parameter setting we simulated 1000 datasets of size $n=500$, a number comparable to the sample size of 480 in our motivating cohort study. We recorded the average estimate across the 1000 datasets, the empirical bias, the empirical standard error, the average model-based standard error and the empirical coverage probability. Tables 3 and 4 display the results to facilitate a comparison of the estimators based on the two-part generalized propensity score with the methods above for the additive and multiplicative outcome models. We find that use of the two-part propensity score model significantly improves the regression estimate when the exposure variable is semi-continuous in nature. Even in cases when the assumptions of the direct regression model are appropriate (i.e. additive models with a constant treatment effect), using a conventional generalized propensity score with regression adjustment produced estimators with substantial bias compared to estimators based on the two-part model propensity score. Moreover, our simulation results demonstrate that use of the two-part propensity score model is increasingly important as the per cent of unexposed individuals increases. When the continuous exposure data are generated from an alternative error distribution within the location-scale family of models the model describe in Equation (4) is misspecified. Figure 2 shows the bias resulting from each method of regression adjustment for the scenario in which 50% of the subjects are unexposed and the positive exposure values are generated from log-normal distribution. Similarly, Figure 3 shows the bias for the scenario where 50% of the subjects are unexposed and the positive exposure values arise from a Weibull regression model. It is clear that the two-part propensity score model leads to better performance than the alternative approaches when the true propensity score model involves an extreme value error distribution.

TABLE 3.

Empirical results for estimators of causal effect of each additional unit exposure on outcome for the scenario where $P(X=0)=0.25$

Method	Log-normal				Weibull
	EBIAS	ESE	ASE	ECP	EBIAS	ESE	ASE	ECP
Additive outcome model
Unadjusted	0.83	0.24	0.16	0.05	0.77	0.22	0.17	0.05
Regression adjustment	0.3	0.18	0.13	0.34	0.27	0.18	0.14	0.47
Generalized propensity score	0.3	0.18	0.16	0.53	0.27	0.18	0.17	0.66
Propensity score based on two-part model	0.0	0.15	0.15	0.96	0.01	0.16	0.15	0.97
Multiplicative outcome model
Unadjusted	−0.98	0.23	0.17	0.03	−0.99	0.23	0.17	0.03
Regression adjustment	−0.43	0.19	0.14	0.1	−0.45	0.2	0.14	0.1
Generalized propensity score	−0.43	0.19	0.14	0.12	−0.45	0.2	0.15	0.11
Propensity score based on two-part model	0.0	0.09	0.07	0.95	0	0.1	0.08	0.96

^aEBIAS: Empirical bias

^bESE: Empirical standard error

^cASE: Asymptotic standard error

^dECP: Empirical coverage probability

TABLE 4.

Empirical results for estimators of causal effect of each additional unit exposure on outcome for the scenario where $P(X=0)=0.50$

Method	Log-normal				Weibull
	EBIAS	ESE	ASE	ECP	EBIAS	ESE	ASE	ECP
Additive outcome model
Unadjusted	1.18	0.26	0.23	0.01	0.82	0.23	0.16	0.05
Regression adjustment	0.44	0.23	0.18	0.27	0.30	0.17	0.13	0.32
Generalized propensity score	0.44	0.23	0.23	0.48	0.30	0.17	0.16	0.53
Propensity score based on two-part model	0.00	0.22	0.21	0.97	0.00	0.15	0.14	0.96
Multiplicative outcome model
Unadjusted	−1.39	0.23	0.19	0.00	−0.97	0.23	0.17	0.03
Regression adjustment	−0.63	0.24	0.18	0.03	−0.42	0.18	0.14	0.10
Generalized propensity score	−0.63	0.24	0.19	0.04	−0.42	0.18	0.14	0.11
Propensity score based on two-part model	0.00	0.13	0.10	0.95	0.00	0.08	0.07	0.95

^aEBIAS: Empirical bias

^bESE: Empirical standard error

^cASE: Asymptotic standard error

^dECP: Empirical coverage probability

FIGURE 2.

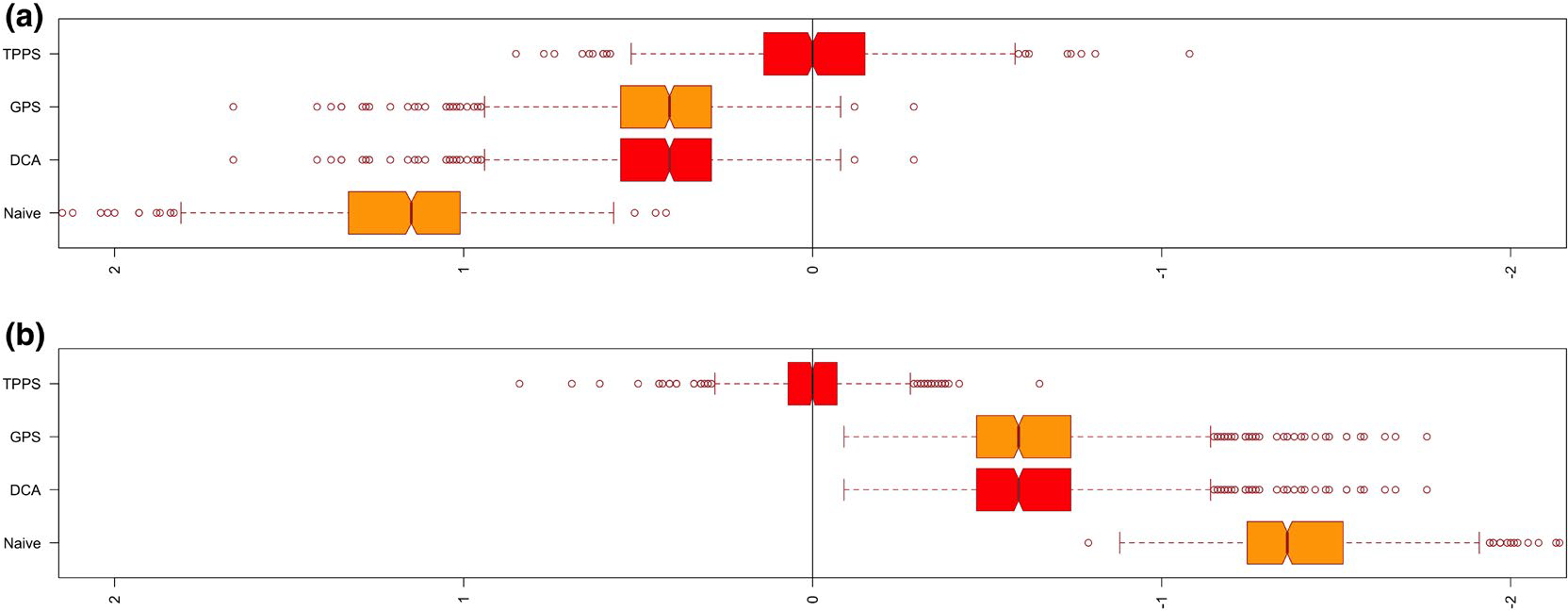
Bias of regression adjustment methods from the simulation study where the true propensity score is generated from log-normal distribution. A, Additive outcome model; B, Multiplicative outcome model. Naive, Unadjusted model; DCA, Direct covariate adjustment; GPS, Generalized propensity score; TPPS, Two-part propensity score

FIGURE 3.

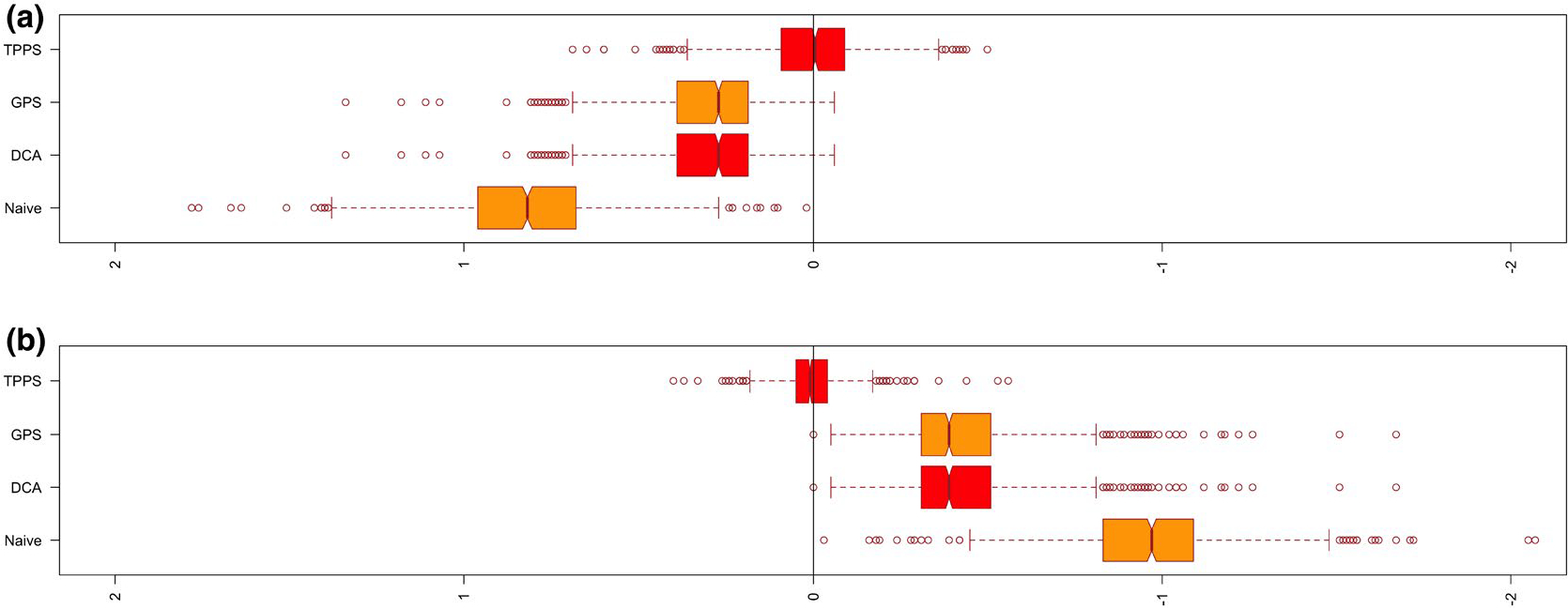
Bias of regression adjustment methods from the simulation study where the true propensity score involves extreme value error distribution. A, Additive outcome model; B, Multiplicative outcome model. Naive, Unadjusted model; DCA, Direct covariate adjustment; GPS, Generalized propensity score; TPPS, Two-part propensity score

We also considered scenarios where we varied the percentage of unexposed subjects, the effect of $Z_1$ on the exposure status, the effect of $Z_2$ on the extent of exposure among exposed individuals and the effect of covariates on the continuous outcome $Y_1$ and $Y_2$. We thus constructed 8 different scenarios for the two outcome models. Table S1–S2 provided in the supplementary material compares the performance of the two-part generalized propensity score with the methods above for the additive and multiplicative outcome models for the scenarios considered above. These results also showed that improvement offered by our method as the per cent of subjects who are not exposed increases in the sample and the effects of covariates $Z_1$ and $Z_2$ on the exposure variable and the outcome variables become stronger.

4 |. APPLICATION

We evaluated the performance of our method using data from the Detroit Longitudinal Cohort study. We focus on the subset of 232 subjects with complete data since our purpose is to illustrate the use of propensity score estimation for long-tailed, semi-continuous prenatal alcohol exposure variables. In practice, it would be important to incorporate appropriate strategies for handling missing data. However, further discussion on this issue is beyond the scope of this paper. The effect of observed covariates on the association between prenatal alcohol exposure and the continuous outcome variable, the WISC Freedom from Distractibility measure at age 7 years was examined using four methods: (1) conventional regression adjustment, (2) covariate adjustment using the generalized propensity score, (3) covariate adjustment using a two-part generalized propensity score and (4) adjustment using a two-part generalized propensity score via stratification (5 and 10 strata).

For the two-part propensity score method, we first modelled the probability of drinking any alcohol during pregnancy on all covariates using logistic regression. We then modelled the conditional distribution of the log of alcohol consumption given all covariates using Gaussian linear regression. The covariates, which are listed in Table 1 and 2, were selected because they are expected to affect child outcomes and also to be likely to correlate with prenatal alcohol exposure. If these variables are left uncontrolled, they could confound the estimated exposure effect on the outcome in question. We included covariates that may be unrelated to the exposure but related to the outcome in the propensity score model. It has been reported that inclusion of these variables increases the precision of the estimated exposure effect without increasing bias (Brookhart et al., 2006). To evaluate the relation of these covariates to the quantity of alcohol consumed by the mother during pregnancy, we computed the absolute values of the Pearson correlations between each covariate and the exposure variable for those cases in which the mother used alcohol during pregnancy (Fong et al., 2018). We found that the correlation between the exposure and each covariate was reduced substantially after conditioning on the propensity score, indicating that the covariate balance is significantly improved. We further evaluated the balance of covariates by employing the graphical method suggested by Imai and van Dyk (2004). Figure 4(a) shows the standard normal quantile plot of the t-statistics obtained by regressing each covariate on the exposure variable using linear or logistic regression for continuous and indicator covariates respectively. The magnitude of the t-statistics shows an obvious lack of balance. Figure 4(b) shows the magnitude of t-statistics after we control for the estimated propensity score. The figure shows the substantial reduction in the t-statistics obtained by conditioning on the estimated propensity score. These figures are constructed including the square of the prenatal visit and gestational age variables. Inclusion of the square of these variables in the estimation of the propensity score improves the balance. The WISC Freedom from Distractibility Index was then regressed on the prenatal alcohol exposure variable and the estimated propensity score to estimate the average effect of prenatal alcohol exposure on the response. We conducted regression diagnostics for the outcome model to assess whether there is evidence that we need to expand the main effects model. There was insufficient evidence to reject the adequacy of the linearity assumption. (See diagnostic plots provided in the supplementary material). We tested our model for a possible interaction between the prenatal alcohol exposure and the propensity score. To fit this model, we centred the exposure variable and the propensity score so that the coefficient of the exposure variable represents the effect of a one unit increase in the logarithm of the volume of alcohol consumed per day during pregnancy. It turns out that there was no significant interaction between the exposure variable and the propensity score. To allow for the possibility of a more complex relationship between the propensity score and the response, we fitted a generalized additive model. In this model we let the exposure effect and the effect of propensity score vary smoothly. Figure 5 illustrates the smooth curves for the prenatal alcohol exposure and the estimated propensity score. We did not find evidence of a non-linear relationship between the estimated propensity score and the response.

FIGURE 4.

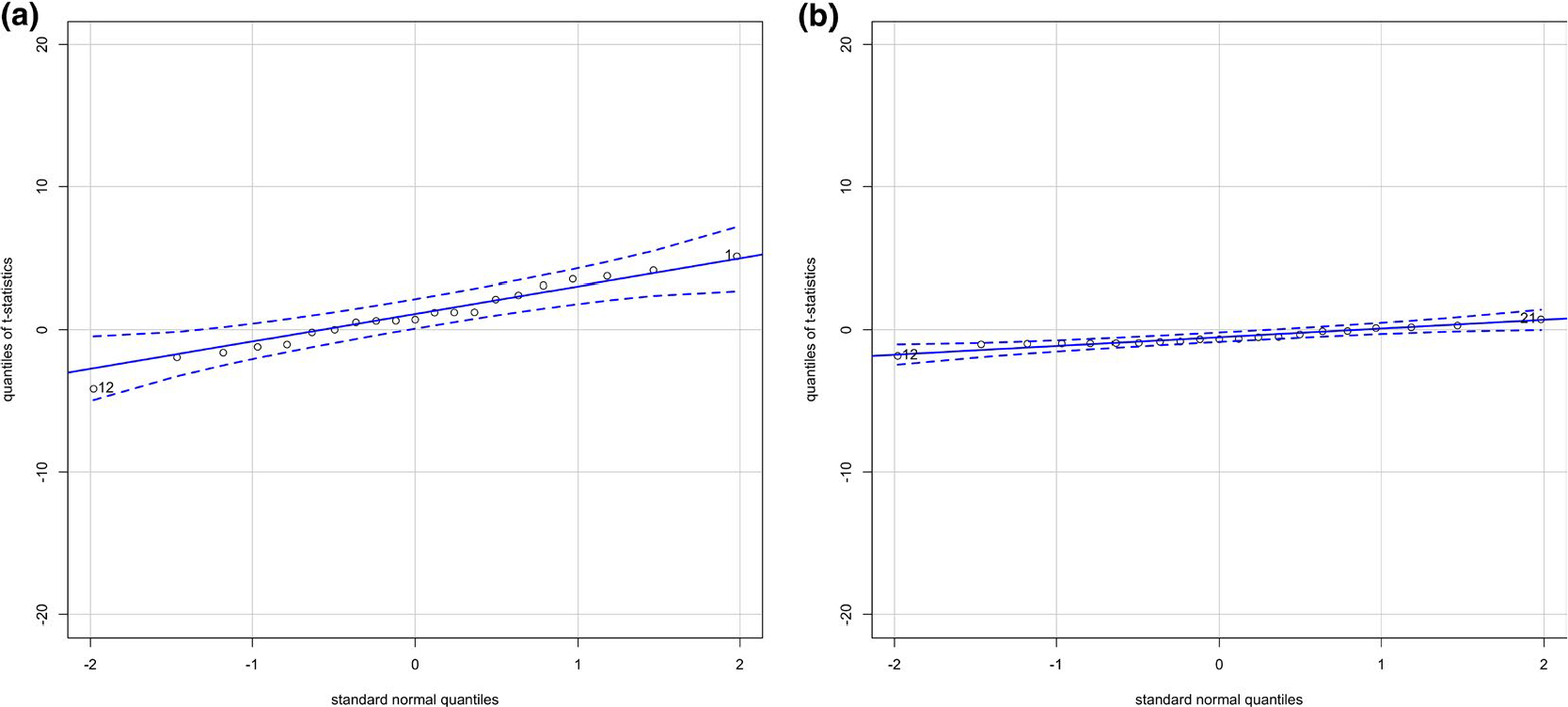
Standard normal quantile plots of t-statistics for the coefficient of log of gestational alcohol exposure in the models predicting each covariate including the square of the number of prenatal visits and the gestational age at screening, (a) Without controlling for the estimated propensity score and (b) Controlling for the estimated propensity score

FIGURE 5.

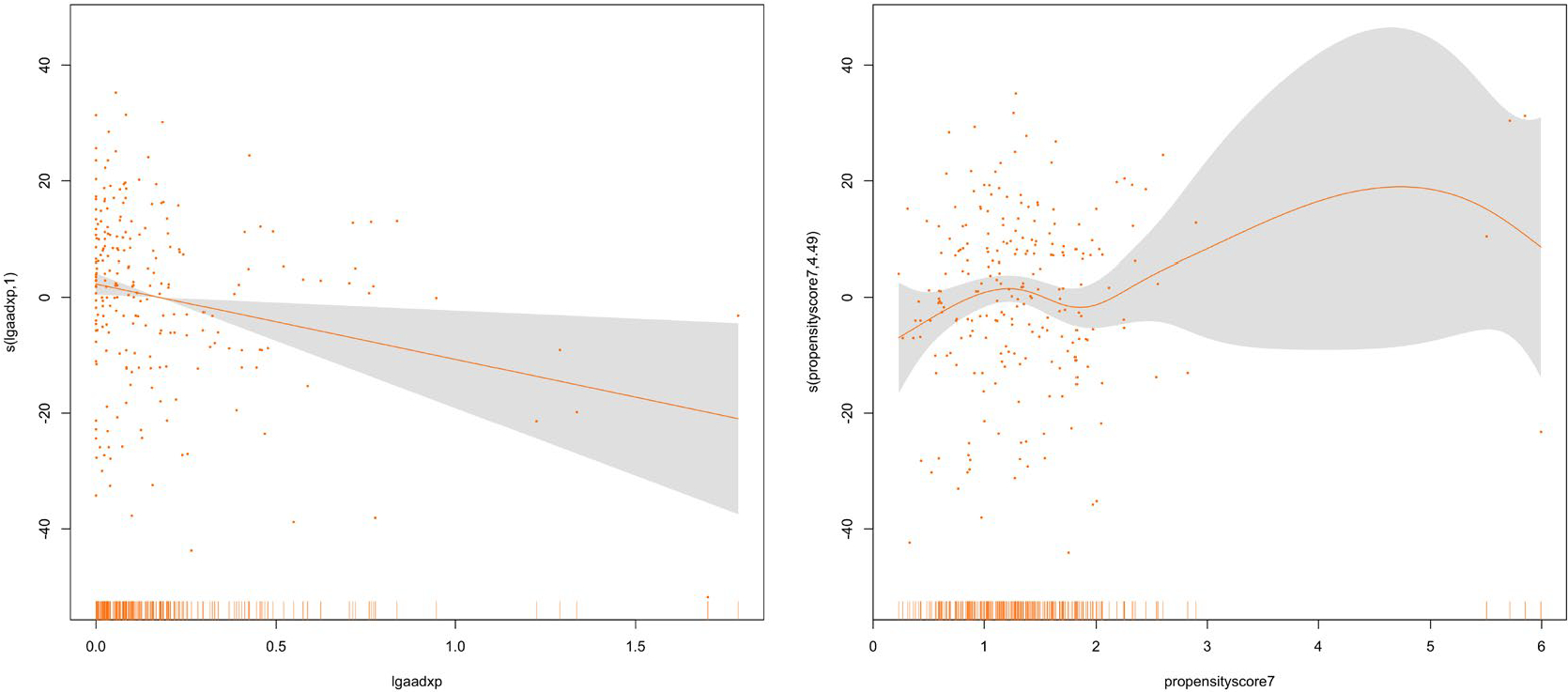
Generalized Additive Model (GAM) plots showing the partial effects of log of gestational alcohol exposure and the estimated propensity score on the Wechsler Intelligence Scale for Children (WISC) Freedom from Distractibility Score at age 7

As an alternative to regression adjustment, we considered stratification on the estimated propensity score. Specifically, we considered the unexposed as one category and the quartiles of the continuous value as defining four more categories to create five strata. We then create four indicator variables with each one indicating a distinct quartile of the positive exposure variable, and regress on these along with the exposure variable itself. To assess the sensitivity of stratification schemes, we repeated the same process with 10 strata.

Table 5 presents the results from the methods based on unadjusted regression analysis, the covariate-adjusted regression model, the regression model adjusted for the generalized propensity score, the regression adjusted for the two-part propensity score and the adjusting for the two-part propensity score via stratification (5 and 10 strata). With the exception of the unadjusted regression method and the stratification with five strata, all of the methods provided very similar estimates, indicating that the WISC Freedom from Distractibility score decreases as the amount of alcohol consumption during pregnancy increases. Adjusting for the estimated propensity score via stratification using five strata tends to result in a smaller effect size than did estimates obtained using other adjustment methods. Indeed the estimated effect size obtained via stratification using five strata is closer to the effect size obtained from the unadjusted analysis. This finding highlights the importance of creating adequate number of strata when adjusting via stratification. Table 6 presents the regression estimates and standard errors from the two-part model. Even though some covariates operated differently in terms of predicting whether or not a mother consumes alcohol, as compared to the amount of alcohol used by those who consumed it, the parameter estimates were fairly similar for the logistic model and for the log-normal model. This reflects the fact that the percentage of zeros was not large enough, and the correlation between the estimated generalized propensity score and the estimated generalized two-part propensity score was quite strong $(\rho =0.83)$; hence, the estimated propensity score was primarily driven by the non-zero values.

TABLE 5.

Estimated effects of prenatal alcohol exposure on the WISC Freedom based on six models: (1) an unadjusted model, (2) a model using traditional covariate adjustment via linear regression, (3) a model using the generalized propensity score, (4) the proposed two-part generalized propensity score, (5) two-part generalized propensity score via stratification (5 strata) and (6) two-part generalized propensity score via stratification (10 strata)

Method	Average causal effect	SE
Unadjusted model	−7.90	3.65
Covariate-adjusted model	−11.21	4.43
Generalized propensity score	−11.21	4.29
Two-part generalized propensity score	−11.89	5.03
Two-part generalized propensity score via stratification (5 strata)	−8.50	3.96
Two-part generalized propensity score via stratification (10 strata)	−11.04	4.11

TABLE 6.

Estimates for the effects of each of the components of the two-part model

	P(Xi > 0)		E(ln(Xi) | Xi > 0)
	Estimate	Standard error	Estimate	Standard error
Intercept	0.3823	6.100	3.142	2.804
Gestational age at recruitment (week)	0.008	0.035	0.016	0.016
Number of prenatal visits	0.063	0.088	−0.100	0.041
Smoking during pregnancy (cigarettes/day)	0.113	0.039	0.031	0.009
Prenatal marijuana exposure (days/month)	0.336	0.220	−0.014	0.033
Prenatal cocaine exposure (days/month)	−0.074	0.094	−0.044	0.038
Prenatal opiate exposure (days/month)	−0.050	0.248	0.316	0.101
Biological mother’s education (years)	0.196	0.166	0.106	0.072
Biological mother’s verbal IQ (PPVT score)	−0.029	0.056	−0.023	0.027
Beck Depression Inventory at 6-month postpartum follow-up	−0.010	0.042	0.000	0.016
Age of a child at 7-year follow-up (years)	−0.000	0.002	−0.002	0.000
Socioeconomic status at age 7-year follow-up	0.023	0.027	0.018	0.011
Primary caregiver’s verbal IQ (PPVT score)at 7-year follow-up	0.016	0.057	0.003	0.026
HOME score at 7-year follow-up	−0.063	0.041	0.018	0.017
Beck Depression Inventory at 7-year follow-up	0.029	0.050	0.047	0.019
Number of stressful events at 7-year follow-up	0.191	0.115	0.037	0.043
Perceived life stress at 7-year follow-up	−0.020	0.024	−0.016	0.009
Biological mother’s marital status	−0.401	0.750	0.213	0.408
Primary care giver’s marital status at 7-year follow-up	−0.109	0.636	−0.273	0.303
Parity	−0.6705	0.338	0.131	0.122
Gravidity	0.3653	0.215	0.016	0.016

As suggested by a referee, we extend our analysis and examine the estimation of full dose–response function using a more flexible approach suggested by Zhao et al. (2020). Specifically, we fit a smooth coefficient model using R package ‘mgcv’ (Wood, 2017) to predict the response variable as a smooth function of the prenatal alcohol exposure and a smooth function of the estimated propensity score along with their interaction through a tensor product smooth. We then estimated the dose–response by averaging predicted values over the empirical distribution of the propensity score, for a set of equally spaced values of exposure. A comparison of this model fit compared with the one that omitted the tensor product term suggests that adding the interaction did not significantly improve model fit (p–value = 0.10). However it is important to note that because only partial ranges of the propensity score values were observed for most exposure levels, the power to detect an interaction effect was low. Similarly, it means that when we estimated the dose–response curve by averaging over the empirical distribution of propensity score values, the results were subject to bias because they involved extrapolation outside the range of observed data. Indeed, confidence intervals were very wide for the resulting predicted dose–response. Zhao et al. (2020) found a similar issue with their application and recommended caution in such settings.

5 |. DISCUSSION

In this paper, we developed a propensity score methodology for use with a semi-continuous exposure/treatment variable. In particular, our strategy allows researchers to estimate causal effects after adjustment for potential confounding variables based on an estimated propensity score rather than on a large number of potential confounders when the exposure/treatment variable includes both a large number of non-drinking mothers and continuously distributed levels of alcohol consumption. Our approach also allows covariates to operate differently in terms of predicting whether or not the subject is exposed, as compared to the level of exposure. We evaluate and compare our method with conventional covariate adjustment and the generalized propensity score method.

In our simulations we observed that the use of the propensity score based on a two-part model as an additional covariate can successfully reduce bias relative to standard regression adjustment and the generalized propensity score method in all scenarios considered here. Our simulation results suggested that when the exposure variable is semi-continuous, a propensity score based on a two-part model provides a better alternative to both conventional regression adjustment and a generalized propensity score. Our work and that of a number of other authors suggests that propensity score methodologies can be sensitive to model misspecification. In this paper, we derived an explicit expression for the asymptotic bias in the estimator of the causal parameter arising from use of a misspecified propensity score. Specifically, we calculated the asymptotic bias associated with using the generalized propensity score in settings where the exposure variable is semi-continuous in nature and a two-part regression model is more appropriate. We found that the asymptotic bias was aligned with the empirical bias from the simulation studies as expected (Table S1–S2). The expression for the asymptotic bias from the misspecified propensity score model generalizes the findings of Hade and Lu (2014), who investigated the impact of using estimated propensity score in lieu of the true propensity score, which is, of course, necessary in such applications. We emphasize that while our derivations were carried out primarily to investigate the importance of two-part models for semi-continuous exposure data, they offer general insight into the impact of propensity score model specification. We evaluate the performance of our method when there is some form of model misspecification. Specifically, we explore the performance of the log-normal model when the true propensity score model involves a Weibull regression model. We found that even in this misspecified setting, our method performs better than the other approaches considered here.

We estimated the average effect of prenatal alcohol exposure on the WISC Freedom from Distractibility at age 7 using four methods: (1) conventional regression adjustment, (2) covariate adjustment using the generalized propensity score, (3) covariate adjustment using a two-part generalized propensity score and (4) adjustment using a two-part generalized propensity score via stratification (5 and 10 strata). All methods agreed that the WISC Freedom from Distractibility score decreases as the amount of alcohol consumption during pregnancy increases. Even though stratification is more flexible way to adjust for the propensity score, our results underlined that creating smaller number of strata may cause bias on the estimated effect size.

In our response model we assumed a linear relationship between the estimated propensity score and the response. As noted by Schafer and Kang (2008), it is important to check the assumption that the propensity score is linearly related to the response. To assess the need for a more complex relationship between the propensity score and the response, we tested our model for a possible interaction between the propensity score and the exposure variable. Furthermore, we fit a smooth coefficient model by including a smooth estimated propensity score. We found no evidence of non-linear relationship between the propensity score and the outcome.

In this paper, we extended the use of generalized propensity score to settings where the exposure variable is semi-continuous in nature. Specifically, we use the mean obtained from the two-part model as the estimated propensity score to generalize the propensity score method suggested by Imai and van Dyk (2004). However, one can consider to use two elements of the two-part propensity score separately in the outcome model and facilitate causal inference regarding the effects of any alcohol consumption and the incremental change in the volume of alcohol consumed. As a future research, we are exploring approaches for propensity scores for multivariate exposure data.

As in many studies involving environmental exposures, a complication for our application was the very long tail of the prenatal alcohol exposure distribution. In practice we have found that it works well to use a log transformation of alcohol to reduce the effect of outliers when predicting the developmental outcomes, but this approach complicates construction of the propensity score based on two-part models. To overcome this complication we used a smooth function of the propensity score using the R package ‘mgcv’ (Wood, 2017) rather than a linear function of the propensity score function. Missing data are another complication that needs to be addressed in our data application. For the purpose of this paper we have conducted a complete case analysis yielding a sample of 232 subjects. However, in practice, it will be important to properly take account of missing data since complete case analysis involving the propensity score produces biased causal inference unless the data are missing completely at random (D’Agostino & Rubin, 2000).

It is also important to point out that our application involves a cohort of socio-economically disadvantaged women, who were asked to provide sensitive information regarding their exposure to alcohol and other substances of abuse in pregnancy. For this reason, there can be a concern regarding under-reporting. This concern is ameliorated in part by the fact that study investigators used a state-of-the-art timeline follow-back interview method, which has been validated in relation to levels of fatty acid ethyl esters in meconium samples (Bearer et al., 2003) and successfully predicted a broad range of developmental outcomes (Jacobson et al., 2002; Lindinger et al., 2016). There were also other sources of information regarding prenatal exposure, including toxicological screens performed during pregnancy that can identify women who used cocaine or other substances but denied using them when interviewed (Jacobson et al., 2002). Developing analytical strategies to take account of these kinds of issues is part of our ongoing work on the project.

APPENDIX A

BIAS FROM A MISSPECIFIED PROPENSITY SCORE IN REGRESSION

Let $\mathbf{Z}$ be an $r\times 1$ vector of confounders and $\mathbf{W}(\mathbf{Z})$ be a $q\times 1$ function of these. If we let $\mathbf{V}={\left(1,X,{\mathbf{W}}^{\prime }(\mathbf{Z})\right)}^{\prime }$ be a $(q+2)\times 1$ vector of covariates and $\mathit{\theta }={\left({\theta }_0,{\theta }_1,{\theta }_2{}^{\prime }\right)}^{\prime }$ be a $(q+2)\times 1$ vector of parameters, we can consider a linear model of the form:

$$Y={\theta }_0+{\theta }_{1}X+{\mathit{\theta }}_{\mathbf{2}}^{\prime }\mathbf{W}(\mathbf{Z})+E$$ (A1)

where we assume $(X,\mathbf{Z})\perp \perp E$ and $E\sim N\left(0,{\sigma }^2\right)$. Now consider a propensity score estimated based on a linear model for $X|\mathbf{Z}$ with estimation of the regression coefficients via using ordinary least squares (OLS) to give an estimate:

$$\widehat{\mu }=\mu (\mathbf{Z};\widehat{\mathit{\alpha }})$$

We then regress on $Y$ on $X$ and the true propensity score, we fit a linear model

$$Y={\beta }_0+{\beta }_{1}X+{\beta }_2\mu (\mathbf{Z};\stackrel{\mathit{ˆ}}{\mathit{\alpha }})+ϵ$$ (A2)

under the assumption $(X,\mu (\mathbf{Z};\mathit{\alpha }))\perp \perp \epsilon$ with $ϵ\sim N\left(0,{\tau }^2\right)$. We aim to derive the limiting value of the estimator of $\mathit{\beta }={\left({\beta }_0,{\beta }_1,{\beta }_2\right)}^{\prime }$ from fitting (A2), when the linear propensity score is misspecified. To do so, we let $\stackrel{-}{\mathbf{V}}=(1,X,\mu (\mathbf{Z}){)}^{\prime }$ and $\mu (\mathbf{Z})=E(X\mid \mathbf{Z};\mathit{\alpha })$ and write the least squares equations for $\beta$ in vector form with the contribution from single individual given by

$$\mathbf{U}(Y,X,\mu (\mathbf{Z});\mathit{\beta })=\stackrel{-}{\mathbf{V}}(Y-{\stackrel{-}{\mathbf{V}}}^{\prime }\mathit{\beta })$$ (A3)

Note that $\widehat{\mathit{\beta }}$ is consistent for $\beta$, the solution to $E\{\mathbf{U}(Y,X,\mathbf{Z};\mu (\mathbf{Z}),\mathit{\beta })\}=0$, where the expectation is taken with respect to true distribution involving $Y,X,\mathbf{Z}$. We evaluate this expectation in stages in the following subsections.

A.1. The expectation with respect to $\mathit{Y}\mid \mathit{X},\mathit{Z}$

We first take the expectation with respect to $\mathrm{Y}$ given $\mathrm{X},\mathbf{Z}$ so require

$$E_Y\{\mathbf{U}(Y,X,\mu (\mathbf{Z};\mathit{\beta })\mid X,\mathbf{Z})\}=E_{Y\mid X,\mathbf{Z}}\{\stackrel{-}{\mathbf{V}}(Y-{\stackrel{-}{\mathbf{V}}}^{\prime }\mathit{\beta })\mid X,\mathbf{Z}\}$$

This gives elements,

$$\mathbf{D}(\stackrel{-}{\mathbf{V}})(E\left(Y∣X,\mathbf{Z};\mathit{\theta }\right)-{\stackrel{-}{\mathbf{V}}}^{\prime }\mathit{\beta }),$$ (A4)

where $\mathbf{D}(\stackrel{-}{\mathbf{V}})=\frac{\partial {\stackrel{-}{\mathbf{V}}}^{\prime }\mathit{\beta }}{\partial \beta }$

A.2. The expectation with respect to $\mathit{X}\mid \mathit{Z}$

The next step requires computation of $E\{\mathbf{D}(\stackrel{-}{\mathbf{V}})[E(Y\mid X,\mathbf{Z};\theta )-{\stackrel{-}{\mathbf{V}}}^{\prime }\mathit{\beta }]\mid \mathbf{Z}\}$. We give the form of each entry in this 3 × 1 vector explicitly as follows:

$$\begin{array}{r}{\theta }_0+{\theta }_{1}E(X\mid \mathbf{Z})+{\mathit{\theta }}_2^{\prime }\mathbf{W}(\mathbf{Z})-\left({\beta }_0+{\beta }_{1}E(X\mid \mathbf{Z})+{\beta }_2\mu (\mathbf{Z})\right)=0\\ {\theta }_{0}E(X\mid \mathbf{Z})+{\theta }_{1}E\left(X^2\mid \mathbf{Z}\right)+{\mathit{\theta }}_2^{\prime }E((X\mid \mathbf{Z})\mathbf{W}(\mathbf{Z}))-\left({\beta }_{0}E(X\mid \mathbf{Z})+{\beta }_{1}E\left(X^2\mid \mathbf{Z}\right)+{\beta }_{2}E(X\mid \mathbf{Z})\mu (\mathbf{Z})\right)=0\\ {\theta }_0\mu (\mathbf{Z})+{\theta }_{1}E(X\mid \mathbf{Z})\mu (\mathbf{Z})+{\mathit{\theta }}_2^{\prime }(\mu (\mathbf{Z})\mathbf{W}(\mathbf{Z}))-({\beta }_0\mu (\mathbf{Z})+{\beta }_{1}E(X\mid \mathbf{Z})\mu (\mathbf{Z})+{\beta }_2\mu (\mathbf{Z}{)}^2)=0\end{array}$$

The Expectation with Respect to $\mathbf{Z}$ From the first line of (A5) we get

$${\theta }_0+{\theta }_{1}E(X)+{\mathit{\theta }}_2^{\prime }E(\mathbf{W}(\mathbf{Z}))-\left({\beta }_0+{\beta }_{1}E(X)+{\beta }_{2}E(\mu (\mathbf{Z}))\right)=0$$ (A6)

From the second line we get

$$\begin{array}{l}{\theta }_{0}E(X)+{\theta }_{1}E\left(X^2\right)+{\mathit{\theta }}_2^{\prime }[\mathit{\eta }(\mathbf{Z})+E(X)E(\mathbf{W}(\mathbf{Z}))]\\ -\left({\beta }_{0}E(X)+{\beta }_{1}E\left(X^2\right)+{\beta }_2[\mathrm{cov}(E(X\mid \mathbf{Z}),\mu (\mathbf{Z}))+E(X)E(\mu (\mathbf{Z}))]\right)=0\end{array}$$ (A7)

where $\mathit{\eta }(\mathbf{Z})={\left({\eta }_1(\mathbf{Z}),{\eta }_1(\mathbf{Z}),\dots ,{\eta }_q(\mathbf{Z})\right)}^{\prime }$ where ${\eta }_j(\mathbf{Z})=\mathrm{cov}\left(E(X\mid \mathbf{Z}),W_j(\mathbf{Z})\right),j=1,\dots ,q$.

From the last line of (A5) we get

$$\begin{array}{l}{\theta }_{0}E(\mu (Z))+{\theta }_1[\mathrm{cov}(E(X\mid \mathbf{Z})\mu (\mathbf{Z}))+E(X)E(\mu (\mathbf{Z}))]+{\mathit{\theta }}_2^{\prime }[\mathit{\varphi }(\mathbf{Z})+E(\mu (\mathbf{Z}))E(\mathbf{W}(\mathbf{Z}))]\\ -({\beta }_{0}E(\mu (\mathbf{Z}))+{\beta }_1[\mathrm{cov}(E(X\mid \mathbf{Z})\mu (\mathbf{Z}))+E(X)E(\mu (\mathbf{Z}))]+{\beta }_{2}E(\mu (\mathbf{Z}{)}^2))=0\end{array}$$ (A8)

where $\mathit{\varphi }(\mathbf{Z})={\varphi }_1(\mathbf{Z}),{\varphi }_2(\mathbf{Z}),\dots ,{\varphi }_q(\mathbf{Z})$ where ${\varphi }_j(\mathbf{Z})=\mathrm{cov}\left(\mu (\mathbf{Z}),W_j(\mathbf{Z})\right),j=1,\dots ,q$. Solve equation (A6) to get ${\beta }_0$ :

$${\beta }_0={\theta }_0+{\theta }_{1}E(X)+{\mathit{\theta }}_2^{\prime }E(\mathbf{W}(\mathbf{Z}))-{\beta }_{1}E(X)-{\beta }_{2}E(\mu (Z))$$

We next replace ${\beta }_0$ in (A7) to get

$$\begin{array}{l}{\theta }_{0}E(X)+{\theta }_{1}E(X^2)+{\mathit{\theta }}_2^{\prime }\left[\mathit{\eta }(\mathit{Z})+E(X)E(\mathit{W}(\mathit{Z}))\right]\\ -(E(X)({\theta }_0+{\theta }_{1}E(X)+{\mathit{\theta }}_2^{\prime }E(\mathit{W}(\mathit{Z}))-{\beta }_{1}E(X)\\ -{\beta }_{2}E(\mu (\mathit{Z})))+{\beta }_{1}E(X^2)+{\beta }_2\left[\text{cov}(E(X\mid \mathit{Z}),\mu (\mathit{Z}))+E(X)E(\mu (\mathit{Z}))\right])=0\end{array}$$

$$\begin{array}{l}{\theta }_{0}E(X)+{\theta }_{1}E(X^2)+{\mathit{\theta }}_2^{\prime }\left[\mathit{\eta }(\mathit{Z})+E(X)E(\mathit{W}(\mathit{Z}))\right]\\ -({\theta }_{0}E(X)+{\theta }_{1}E{(X)}^2+{\mathit{\theta }}_2^{\prime }E(\mathit{W}(\mathit{Z}))E(X)-{\beta }_{1}E{(X)}^2\\ -{\beta }_{2}E(\mu (\mathit{Z})))E(X)+{\beta }_{1}E(X^2)+{\beta }_2\left[\text{cov}(E(X\mid \mathit{Z}),\mu (\mathit{Z}))+E(X)E(\mu (Z))\right]=0\end{array}$$

$$\begin{array}{l}{\theta }_{0}E(X)+{\theta }_{1}E(X^2)+{\mathit{\theta }}_2^{\prime }\text{cov}(E(X\mid \mathit{Z}),\mathit{W}(\mathit{Z}))+{\mathit{\theta }}_2^{\prime }E(X)E(\mathit{W}(\mathit{Z}))\\ -{\theta }_{0}E(X)-{\theta }_{1}E{(X)}^2-{\mathit{\theta }}_2^{\prime }E(\mathit{W}(\mathit{Z})E(X)+{\beta }_{1}E{(X)}^2\\ +{\beta }_{2}E(\mu (\mathit{Z}))E(X)-{\beta }_{1}E(X^2)-{\beta }_2\text{cov}(E(X\mid \mathit{Z}),\mu (\mathit{Z}))-{\beta }_{2}E(X)E(\mu (\mathit{Z}))=0\end{array}$$

$$\begin{array}{l}{\theta }_1[E(X^2)-E{(X)}^2]+{\mathit{\theta }}_2^{\prime }\eta (\mathit{Z})-{\beta }_1[E{(X)}^2-E{(X)}^2]\\ -{\beta }_2\text{cov}(E(X\mid \mathit{Z}),\mu (\mathit{Z}))=0\end{array}$$ (A9)

Likewise replace ${\beta }_0$ in equation (A8) to obtain a simplified expression in ${\beta }_1$ and ${\beta }_2$

$$\begin{array}{l}{\theta }_{0}E(\mu (\mathbf{Z}))+{\theta }_1[\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z}))+E(X)E(\mu (\mathbf{Z})))]+{\mathit{\theta }}_2^{\prime }[\mathit{\varphi }(\mathbf{Z})+E(\mu (\mathbf{Z}))E(\mathbf{W}(\mathbf{Z}))]\\ -\left[\left(E(\mu (\mathbf{Z}))\left({\theta }_0+{\theta }_{1}E(X)+{\mathit{\theta }}_2^{\prime }E(\mathbf{W}(\mathbf{Z}))-{\beta }_{1}E(X)-{\beta }_{2}E(\mu (\mathbf{Z}))\right)\right.\right.\\ +{\beta }_1[\mathrm{cov}(E(X\mid \mathbf{Z})\mu (\mathbf{Z}))+E(X)E(\mu (\mathbf{Z}))]+{\beta }_{2}E(\mu (\mathbf{Z}{)}^2))0]=0\end{array}$$

$$\begin{array}{l}{\theta }_{0}E(\mu (\mathbf{Z}))+{\theta }_1\mathrm{cov}\left(E((X\mid \mathbf{Z})\mu (\mathbf{Z}))+{\theta }_{1}E(X)E(\mu (\mathbf{Z}))\right)+{\mathit{\theta }}_2^{\prime }\mathit{\varphi }(\mathbf{Z})+{\mathit{\theta }}_2^{\prime }E(\mu (\mathbf{Z}))E(\mathbf{W}(\mathbf{Z}))\\ -{\theta }_{0}E(\mu (\mathbf{Z}))-{\theta }_{1}E(X)E(\mu (\mathbf{Z}))-{\mathit{\theta }}_2^{\prime }E(\mathbf{W}(\mathbf{Z}))E(\mu (\mathbf{Z}))+{\beta }_{1}E(X)E(\mu (\mathbf{Z}))+{\beta }_{2}E(\mu (\mathbf{Z}){)}^2\\ -{\beta }_1\mathrm{cov}(E(X\mid \mathbf{Z})\mu (\mathbf{Z}))-{\beta }_{1}E(X)E(\mu (\mathbf{Z}))-{\beta }_2(E(\mu (\mathbf{Z}{)}^2))=0\end{array}$$

$$\begin{array}{l}{\theta }_1\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z})))+{\mathit{\theta }}_2^{\prime }\mathit{\varphi }(\mathbf{Z})\\ -{\beta }_1\mathrm{cov}(E(X\mid \mathbf{Z})\mu (\mathbf{Z}))-{\beta }_2[E(\mu (\mathbf{Z}{)}^2)-E(\mu (\mathbf{Z}{)}^2)]=0\end{array}$$

Solve for ${\beta }_2$ we obtain

$${\beta }_2=\frac{\left[\left({\theta }_1-{\beta }_1\right)(\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z})))]+{\mathit{\theta }}_2^{\prime }\mathit{\varphi }(\mathbf{Z})\right]}{V(\mu (Z))}$$

Replacing ${\beta }_2$ in (A9) we obtain

$$\begin{array}{l}{\theta }_{1}V(X)+{\mathit{\theta }}_2^{\prime }\mathit{\eta }(\mathbf{Z})-{\beta }_{1}V(X)\\ -\left[\frac{\left[\left({\theta }_1-{\beta }_1\right)(\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z}))))\right]+{\mathit{\theta }}_2^{\prime }\mathit{\varphi }(\mathbf{Z})}{V(\mu (\mathbf{Z}))}\right]\mathrm{cov}(E(X\mid \mathbf{Z}),\mu (\mathbf{Z}))=0\end{array}$$

Re-organize terms:

$$\begin{array}{l}{\theta }_{1}V(X)+{\mathit{\theta }}_2^{\prime }\mathit{\eta }(\mathbf{Z})-\{{\theta }_1[\frac{\mathrm{cov}(E(X\mid \mathbf{Z}),\mu (\mathbf{Z}))}{V(\mu (\mathbf{Z}))}]+{\mathit{\theta }}_2^{\prime }[\frac{\varphi (\mathbf{Z})}{V(\mu (\mathbf{Z}))}]\}\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z})))\\ ={\beta }_1[V(X)-\frac{(\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z})))\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z}))))}{V(\mu (\mathbf{Z}))}]\end{array}$$

The whole expression can be re-written as:

$${\theta }_1[V(X)-\left[\frac{\mathrm{cov}(E(X\mid \mathbf{Z}),\mu (\mathbf{Z}))\mathrm{cov}(E(X\mid \mathbf{Z}),\mu (\mathbf{Z}))}{V(\mu (\mathbf{Z}))}\right]]$$ (A)

$$+{\mathit{\theta }}_2^{\prime }[\mathit{\eta }(\mathbf{Z})-\frac{\mathit{\varphi }(\mathbf{Z})\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z})))}{V(\mu (\mathbf{Z}))}]$$ (B)

$$={\beta }_1[V(X)-\frac{\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z}))\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z})))}{V(\mu (\mathbf{Z}))}]$$ (C)

Term (A) can be re-written as

$$\begin{array}{l}{\theta }_1\left[V(X)-V(E(X\mid \mathbf{Z})){\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}^2(E(X\mid \mathbf{Z}),(\mu (\mathbf{Z})))\right]\\ ={\theta }_1\left[V(X)\left[1-{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}^2(E(X\mid \mathbf{Z}),(\mu (\mathbf{Z})))\right]+E(V(X\mid \mathbf{Z})){\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}^2(E(X\mid \mathbf{Z}),(\mu (\mathbf{Z})))\right]\end{array}$$

And term (C) can be re-written as:

$${\beta }_1\left[V(X)\left[1-{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}^2(E(X\mid \mathbf{Z})\mu (\mathbf{Z}))\right]+E(V(X\mid \mathbf{Z})){\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}^2(E(X\mid \mathbf{Z}),\mu (\mathbf{Z}))\right]$$

So the whole expression can be written as:

$$\begin{array}{l}{\theta }_1\left[V(X)-V(E(X\mid \mathbf{Z})){\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}^2(E(X\mid \mathbf{Z}),(\mu (\mathbf{Z})))\right]\\ +{\mathit{\theta }}_2^{\prime }[\mathit{\eta }(\mathbf{Z})-\frac{\mathit{\varphi }(\mathbf{Z})\mathrm{cov}(E((X\mid \mathbf{Z})\mu (\mathbf{Z})))}{V(\mu (\mathbf{Z}))}]\\ ={\beta }_1\left[V(X)-V(E(X\mid \mathbf{Z})){\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}^2(E(X\mid \mathbf{Z}),(\mu (\mathbf{Z})))\right]\end{array}$$

We can re-express this as

$${\beta }_1={\theta }_1+\frac{{\mathit{\theta }}_2^{\prime }[\mathit{\eta }(\mathbf{Z})-\mathit{\varphi }(\mathbf{Z})\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}(E(X\mid \mathbf{Z})\mu (\mathbf{Z}))\sqrt{\frac{V(E(X\mid \mathbf{Z}))}{V(\mu (\mathbf{Z}))}}]}{V(X)-V(E(X\mid \mathbf{Z})){\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}^2(E(X\mid \mathbf{Z}),(\mu (\mathbf{Z})))}$$

To help interpret this expression, it is helpful to define $\rho$ to represent the correlation between the propensity score, $\mu (\mathbf{Z})$ and the true expected value of $X$ given $Z$, namely:

$$\rho =\mathrm{corr}\left(E\left(X∣\mathbf{Z}\right),\mu \left(\mathbf{Z}\right)\right).$$

In this case, we can rewrite the last expression as follows:

$${\beta }_1={\theta }_1+\frac{{\mathit{\theta }}_2^{\prime }[\mathit{\eta }(\mathbf{Z})-\mathit{\varphi }(\mathbf{Z})\rho \sqrt{\frac{V(E(X\mid \mathbf{Z}))}{V(\mu (\mathbf{Z}))}}]}{V(X)-V(E(X\mid \mathbf{Z})){\rho }^2}.$$