Adaptive RAxML-NG: Accelerating Phylogenetic Inference under Maximum Likelihood using Dataset Difficulty

Abstract

Phylogenetic inferences under the maximum likelihood criterion deploy heuristic tree search strategies to explore the vast search space. Depending on the input dataset, searches from different starting trees might all converge to a single tree topology. Often, though, distinct searches infer multiple topologies with large log-likelihood score differences or yield topologically highly distinct, yet almost equally likely, trees. Recently, Haag et al. introduced an approach to quantify, and implemented machine learning methods to predict, the dataset difficulty with respect to phylogenetic inference. Easy multiple sequence alignments (MSAs) exhibit a single likelihood peak on their likelihood surface, associated with a single tree topology to which most, if not all, independent searches rapidly converge. As difficulty increases, multiple locally optimal likelihood peaks emerge, yet from highly distinct topologies. To make use of this information, we introduce and implement an adaptive tree search heuristic in RAxML-NG, which modifies the thoroughness of the tree search strategy as a function of the predicted difficulty. Our adaptive strategy is based upon three observations. First, on easy datasets, searches converge rapidly and can hence be terminated at an earlier stage. Second, overanalyzing difficult datasets is hopeless, and thus it suffices to quickly infer only one of the numerous almost equally likely topologies to reduce overall execution time. Third, more extensive searches are justified and required on datasets with intermediate difficulty. While the likelihood surface exhibits multiple locally optimal peaks in this case, a small proportion of them is significantly better. Our experimental results for the adaptive heuristic on 9,515 empirical and 5,000 simulated datasets with varying difficulty exhibit substantial speedups, especially on easy and difficult datasets ($\mathbf{53}\mathbf{\%}$ of total MSAs), where we observe average speedups of more than $\mathbf{10}\times$. Further, approximately $\mathbf{94}\mathbf{\%}$ of the inferred trees using the adaptive strategy are statistically indistinguishable from the trees inferred under the standard strategy (RAxML-NG).

Introduction

Phylogenetic tree inference addresses the problem of finding the binary tree that best explains the sequence data, typically given in the form of a multiple sequence alignment (MSA). To infer trees, various techniques and methods have been developed, such as distance-based approaches (e.g. neighbor joining; Saitou and Nei 1987), maximum parsimony (MP) (Fitch 1971), maximum likelihood (ML) (Felsenstein 1981), and Bayesian inference (BI) methods (Yang and Rannala 1997; Mau et al. 1999). ML and BI methods rely on the phylogenetic likelihood function, which implements an explicit statistical model of sequence evolution. Computing the likelihood score of a given, single candidate tree already constitutes a computationally expensive task. ML and BI analyses are time- and resource-intensive because hundreds of thousands of likelihood computations are performed on a large number of distinct tree topologies. Here, we focus on developing adaptive heuristics for ML-based phylogenetic inference. Analogous techniques could be developed for MP, BI, and potentially also NJ.

In addition to the computational burden associated with the likelihood function itself, ML inference is known to be an NP-hard problem (Roch 2006) as the number of possible topologies exponentially increases with the number of sequences. Since the brute-force evaluation of all possible tree topologies is not computationally feasible, there exists a plethora of inference tools which deploy different heuristics to find a tree with what has been globally accepted in the field as a sufficiently “good” likelihood score. In fact, heuristics are involved in all distinct phases of the ML tree search, including: (i) the construction of the starting tree(s) upon which one initiates the search, (ii) the underlying strategy for topological alterations (e.g. Nearest Neighbor Interchange [NNI] or Subtree Prune and Regraft [SPR] moves) to efficiently search the vast tree space, (iii) the optimization techniques applied to continuous parameters of the evolutionary model (e.g. branch lengths and substitution rates between states), and (iv) the stopping criteria to terminate the tree search (St John 2016). Some of the most widely used tools for ML tree inference are RAxML (Stamatakis 2014), RAxML-NG (Kozlov et al. 2019), IQ-TREE 2 (Minh et al. 2020), FastTree 2 (Price et al. 2010), and PhyML (Guindon et al. 2010).

Heuristics, evidently, do not guarantee that one will find the globally optimal tree. Empirical observations (Morrison 2007; Stamatakis 2011; Morel et al. 2020) suggest that, on certain datasets, independent ML tree searches converge to a single—or topologically highly similar—tree(s), while on other datasets, they yield multiple topologically highly distinct trees with almost identical likelihood scores. In the latter case, standard phylogenetic significance tests, for example the tree topology tests implemented in IQ-TREE 2 (Naser-Khdour et al. 2019), usually report no statistically significant difference among the majority of the inferred, highly contradicting, topologies. Thus, “easy” MSAs exhibit a single, well-distinguishable, globally optimal peak on their likelihood surface, associated with a single tree topology. In contrast, “difficult” MSAs exhibit a rugged likelihood surface, with multiple locally optimal and statistically indistinguishable peaks emerging from contradicting topologies.

This MSA behavior is quantified by the Pythia tool (Haag et al. 2022a), which uses machine learning methods to estimate the difficulty of analyzing a given MSA prior to ML tree inference (more details in “Difficulty Prediction” section). The estimated difficulty parameter is a real number between $0.0$ and $1.0$ used to reflect the degree of ruggedness on the respective likelihood surface. Easy MSAs, with a difficulty score close to $0.0$, exhibit a single globally optimal peak on their likelihood surface, while difficult ones, with a score closer to $1.0$, exhibit multiple locally optimal peaks. The difficulty score does not only capture these two extreme cases but also the entire spectrum of intermediate cases. Therefore, one can roughly identify MSAs as easy, intermidiate, and hard-to-analyze.

Here, we introduce an adaptive ML tree search heuristic based on Pythia’s difficulty prediction and implement it in RAxML-NG. Our new adaptive RAxML-NG tool modifies the thoroughness of the tree search strategy, as well as additional heuristic search parameters (e.g. the number of distinct starting trees or the maximum subtree reinsertion radius of SLOW-SPR moves), as a function of the predicted difficulty. We introduce two new mechanisms for faster and more efficient exploration of the tree space so that the first phase of topological moves can be terminated earlier: NNI rounds and the $1\mathrm{\%}$ ML convergence interval. We provide a detailed description of the new algorithm and the underlying mechanisms in “Related Work” and “Algorithm” sections.

Our main goal is to deploy Pythia's difficulty score for informing the adaptive tree search heuristic under ML. To this end, we compare the standard and adaptive RAxML-NG versions in terms of topological accuracy and ML score of the respective output trees. We conduct experiments with a sufficiently large number of empirical and simulated datasets. Furthermore, our datasets are also representative of the difficulty distributions in phylogenetic data repositories such as TreeBASE (Piel et al. 2009) or RAxML Grove (Höhler et al. 2021). To simplify the experimental setup, we executed RAxML-NG and adaptive RAxML-NG in sequential execution mode only.

Our experimental results (“Results” section) yield substantial speedups, on 9,515 empirical and 5,000 simulated datasets with varying difficulty, capturing the whole difficulty spectrum. The average speedup ranges between $1.8\times$ for intermediate datasets and up to $16\times$ for easy and difficult datasets. The overall accumulated speedup achieved over all datasets is approximately $3.4\times$. Further, in about $94\mathrm{\%}$ of the cases, the output ML trees from standard and adaptive RAxML-NG are statistically indistinguishable. Future directions including potential parallelization strategies for adaptive RAxML-NG are discussed in “Conclusions and Future Work” section. All MSAs we used for our experiments, are available for download at https://cme.h-its.org/exelixis/material/raxml_adaptive_data.tar.gz.

Related Work

ML Tree Search Heuristics

The likelihood function has both discrete and continuous parameters. The tree topology and the specific model of sequence evolution constitute discrete parameters, while the branch lengths of the input tree, the substitution rates between the characters/states, the equilibrium frequencies, and the α shape parameter of the Γ model of rate heterogeneity (Yang 2014) are continuous parameters. RAxML-NG optimizes the continuous parameters, with respect to the likelihood score, using the Newton–Raphson method for the branch lengths and other numerical optimization routines for the remaining parameters. This software optimizes all continuous parameters iteratively, repeating the process for multiple rounds until either a numerical threshold is reached or no further changes are applied to the parameter values. ML inference tools typically split the optimization of continuous parameters into the Branch-Length Optimization (BLO) and the Model-Parameter Optimization (MPO) routines. The latter refers to any other continuous parameter except for branch lengths. Both, standard and adaptive RAxML-NG use the exact same framework to optimize continuous parameters.

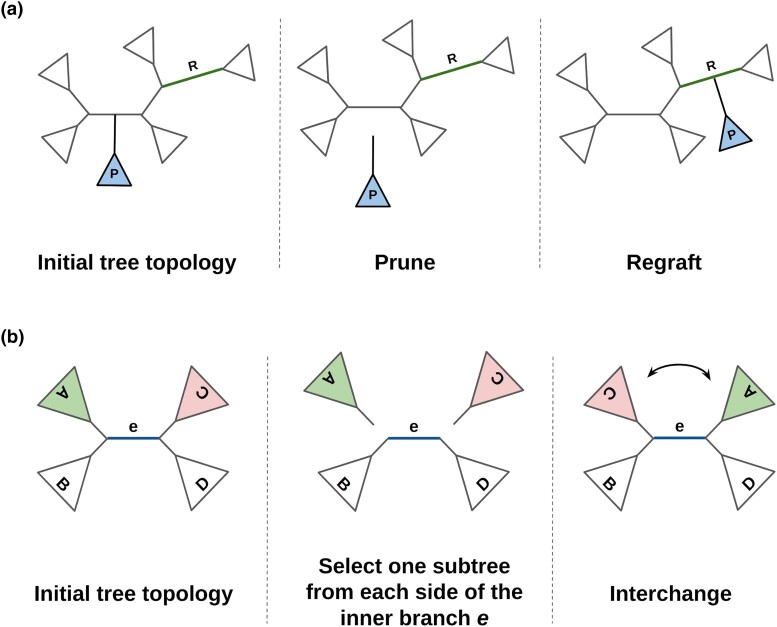
Standard RAxML-NG exclusively explores the vast tree space via SPR moves (Fig. 1a). The tree search heuristic is based on the greedy hill-climbing algorithm previously introduced in RAxML (Stamatakis 2014), with minor modifications (Kozlov 2018). Initially, the algorithm stores pointers to all inner nodes of the initial comprehensive tree topology (starting tree). For every pointer in the list, RAxML-NG prunes the corresponding subtree from the, thus far, best-scoring tree, and evaluates its possible reinsertions into neighboring branches, up to a certain maximum distance (reinsertion radius) from the pruning branch. The move that yields the highest likelihood improvement, if such a move exists, is accepted and the algorithm proceeds to the next element in the node list. When SPR moves for all pointers/nodes have been evaluated, and therefore all corresponding subtrees have been pruned and regrafted once, the SPR round is completed. There are two types of SPR rounds in adaptive RAxML-NG. During Fast SPR rounds, adaptive RAxML-NG evaluates each alternative tree topology that results from an SPR move, using the existing branch lengths, while in Slow SPR rounds, the lengths of the three adjacent branches around the insertion node are reoptimized. Further, in Slow SPR rounds the 20 top-scoring topologies are stored in a list BT. At the end of the round, all trees in BT undergo a full BLO and the best tree is used as initial tree for the next SPR round. The distinction between Fast and Slow SPR rounds is a feature of both RAxML and RAxML-NG. The implementation of Fast and Slow SPR rounds, differs among standard and adaptive RAxML-NG versions. However, the optimization of the adjacent branches around the insertion node remains the same in both versions.

Fig. 1.

a) An SPR move example. The subtree P is pruned from the initial comprehensive tree and regrafted into branch R. b) An example of an NNI move around an inner branch e. Two subtrees, one from each side of the inner branch, are selected, pruned, and interchanged. The NNI move is a special case of the SPR move.

In addition to SPR moves, our adaptive RAxML-NG vesion also uses NNI moves (Fig. 1b) for tree space exploration. While NNI-based heuristics are more prone to becoming stuck in local optima, the main motivation for including NNI moves is that they might be sufficient to attain trees with good scores for easy datasets with a low difficulty score. The NNI algorithm is analogous to the NNI round implementation in RAxML v8.2 (-f J option). The search starts from an inner branch and compares the three alternative NNI topologies in terms of their likelihood score. For computing the likelihood, adaptive RAxML-NG optimizes the five branches which are most affected by an NNI move. Once an NNI evaluation has been executed, the algorithm accepts the topology with the highest likelihood score and proceeds to the adjacent inner branches. When all inner branches have been visited once, the algorithm returns to the initial inner branch and repeats the process for multiple iterations, until it reaches an NNI-optimal tree (i.e. a tree where the application of any additional NNI move will not further improve the likelihood score).

Difficulty Prediction

Pythia (developed in our research group) is a Gradient Boosted Tree Regressor^a trained to predict the difficulty of a phylogenetic analysis of an MSA prior to initiating ML-based tree inferences. In Haag et al. (2022a), the inference difficulty of empirical MSAs is defined and calculated by conducting 100 ML tree searches on each dataset using RAxML-NG. For each dataset, the plausible tree set (PTS) is extracted, that is, the inferred ML trees that are not significantly worse than the best-scoring ML tree under any statistical significance test implemented in IQ-TREE 2. Next, the Robinson–Foulds (RF) distances (Robinson and Foulds 1981) are calculated between all pairs of trees in the ML tree set and in the PTS. The definition of the difficulty score is based on the proportion of plausible trees, the number of unique tree topologies in the ML tree set as well as in the PTS, and the average relative RF-distances among trees in the PTS.

Next, Pythia was trained and tested by using the calculated difficulty scores aforementioned. There are eight features that represent each MSA as an 8D data point. Six of them are simple and fast-to-compute as they rely on MSA attributes (e.g. the proportion of gaps or the Bollback Multinomial metric; Bollback 2002). Pythia calculates the two remaining features by conducting 100 MP searches, which are orders of magnitude faster to compute than ML searches. The two features extracted from these 100 MP trees are (i) the proportion of unique tree topologies in the MP tree set and (ii) the average relative RF-distances between all pairs of MP trees. More details about the definition of the difficulty score can be found in the Supplementary material and the original Pythia publication (Haag et al. 2022a).

Heuristics, Difficulty, and Phylogenetic Signal

Properly evaluating and comparing different heuristics/tools constitutes a challenging task when introducing novel heuristics. According to a recent comparative study (Höhler et al. 2022), there is no standard set of benchmark data for assessing/comparing different tools. Most performance and accuracy studies typically use ad hoc benchmark dataset collections. These collections sometimes exhibit specific properties that might even yield contradictory results (see examples further below). In this section, we examine some major issues reported in the preprint by Höhler et al. in relation to previous studies as well. We outline the connection between the difficulty score of an MSA and the respective convergence speed of the ML heuristic, as well as the accuracy and robustness of the result.

FastTree 2 is one of the fastest and most widely used tools for ML inference. The tool applies a combination of “linear SPR” moves under MP and ML-NNI moves thereby achieving linear run time complexity with respect to the number of taxa ($O(n)$). The results in the FastTree 2 paper (Price et al. 2010) indicate that the tool is 100–1,000 times faster than PhyML and RAxML (version 7.2.1), but the trees inferred by the latter tools are substantially more accurate, due to the thoroughness of their tree search heuristics. This rather discouraging result concerning the inference quality of FastTree 2 is also confirmed by an independent study (Zhou et al. 2017), in which the authors found that RAxML, IQ-TREE (Nguyen et al. 2014), and PhyML perform similarly in terms of topological accuracy on single-gene datasets, while FastTree 2 performs substantially worse. In contrast to the aforementioned studies, the results from a third comparative study between RAxML (version $\mathrm{7.2.6}$) and FastTree 2 only (Liu et al. 2011) show that, although RAxML generally infers topologically more accurate trees than FastTree 2, the differences diminish as the sites-over-taxa ratio decreases. A similar observation was also made by Höhler et al.^b

A similar pattern was described in Morel et al. (2020) when analyzing SARS-CoV-2 data. Due to the comparatively low nucleotide substitution rate of SARS-CoV-2 (van Dorp et al. 2020), the four MSAs analyzed are characterized by a high proportion of invariable sites, and the patterns-over-taxa ratio is equal to or less than 1. Morel et al. conducted 100 ML tree searches using RAxML-NG and generated the PTS. In all four MSAs, the independent searches yielded 100 distinct tree topologies, and the PTS comprised more than $70\mathrm{\%}$ of the 100 ML trees. The average relative RF-distance between all pairs of ML trees was approximately $0.78$, implying topologically highly distinct trees.

The inconsistent conclusions in the aforementioned studies can potentially be explained by reflecting on the concept of the difficulty score. Starting from the latter study, the 100 output ML trees with contradicting topologies imply an extremely rugged likelihood surface that exhibits a plethora of local optima. This hypothesis is confirmed by calculating the difficulty score of the full SARS-CoV-2 dataset with a score of $0.84$, the dataset is categorized as “hopeless-to-analyze”. In other words, analyzing such dataset will not yield a single strictly bifurcating tree, that is, a clear peak. Additional indications for a high degree of difficulty could also be the sites-over-taxa (SoT), and patterns-over-taxa (PoT) ratios of an MSA, which are also used by Pythia as prediction features. First, Rosenberg and Kumar (2001) concluded that, the higher the SoT ratio of a dataset, the stronger the phylogenetic signal, and thus more accurate the results should be. This observation provides a sufficient explanation for the results of the aforementioned study by Liu et al.: as the number of taxa grows, the SoT ratio of the MSA decreases and the difficulty increases. Hence, both RAxML and FastTree 2 infer (potentially) distinct locally optimal trees with similar likelihood scores, an observation also made by Höhler et al. Further, the first Figure in Höhler et al. preprint establishes a strong negative correlation between the PoT ratio and the difficulty of empirical MSAs, showing that the difficulty decreases substantially when the PoT ratio exceeds 10. These results provide an additional explanation for the high difficulty of the SARS-CoV-2 dataset. In the same study, RAxML-NG and IQ-TREE 2 perform substantially better than FastTree 2 in terms of topological accuracy for empirical datasets with difficulty scores ranging between $0.2$ and $0.6$ (easy-to-intermediate), which is in agreement with the results of the two other studies (Price et al. 2010; Zhou et al. 2017). For easy datasets with a difficulty score below $0.2$, FastTree 2 performs similarly in terms of likelihood score and topological accuracy.

Algorithm

For our experiments, we collected 10,389 empirical MSAs from TreeBASE (Piel et al. 2009) and 5,000 simulated MSAs with varying degree of difficulty. We begin by dividing datasets into three classes: (i) easy datasets with a difficulty score below $0.3$, (ii) intermediate datasets with a difficulty between $0.3$ and $0.7$, and (iii) difficult datasets with a difficulty above $0.7$. Our adaptive RAxML-NG tree search heuristic is based upon three observations derived from the discussion in “Difficulty Prediction” and “Heuristics, Difficulty, and Phylogenetic Signal” sections.

1. The majority of independent ML tree searches on easy MSAs converges to a single, or topologically highly similar, tree(s). Moreover, fast and thorough heuristics (FastTree 2 and standard RAxML-NG) perform similarly in terms of topological accuracy and likelihood score, especially when the difficulty score is close to 0.

2. Independent ML tree searches on difficult MSAs yield topologically highly distinct trees, with most of them being equally likely and, therefore, statistically indistinguishable. Fast and thorough heuristics perform similarly in this difficulty range, albeit only in terms of likelihood score. Overanalyzing such datasets is hopeless, and thus it suffices to quickly infer only a few out of the many almost equally likely topologies, to reduce overall execution time.

3. On datasets of intermediate difficulty, thorough heuristics yield statistically better ML trees than superficial ones; faster heuristics are more prone to become stuck in local optima and, therefore, yield suboptimal trees. In general, intermediate MSAs exhibit fewer peaks on their likelihood surface than the difficult ones. While the corresponding likelihood surfaces exhibit multiple peaks on intermediate datasets, only a small proportion of these peaks is significantly better. Thus, more extensive search strategies yield significantly better results.

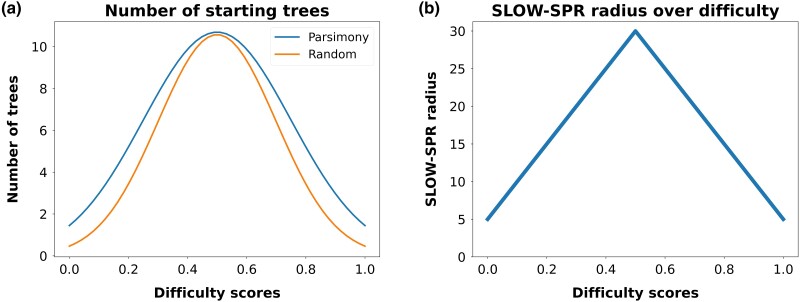
The thoroughness of the tree space exploration conducted by RAxML-NG is determined by two factors, which are (i) the number of independent tree searches that are executed and (ii) the thoroughness of each individual search. Regarding the number of independent tree searches, by default, RAxML-NG executes ML tree inferences on 10 random and 10 MP starting trees. In adaptive RAxML-NG, though, we modify the number of independent tree inferences based on the difficulty score of the input MSA. The functions to determine the number of random/MP starting trees depending on the respective difficulty score in adaptive RAxML-NG are shown in Fig. 2a. Both functions are Gaussian curves with a peak of 10 trees when the difficulty score is $0.5$. For each input MSA, adaptive RAxML-NG computes the respective number of random and parsimony starting trees that are determined by the two curves/functions in Fig. 2a. We intentionally set a wider curve for the number of MP starting trees, such that the heuristic uses more MP than random starting trees on easy and difficult datasets. This procedure is based on an observation made by Morel et al. (2020) on a difficult-to-analyze SARS-CoV-2 dataset (see “Heuristics, Difficulty, and Phylogenetic Signal” section). The authors observed that tree searches initiated on parsimony starting trees consistently yielded phylogenies with substantially better log-likelihood scores.

Fig. 2.

a) Number of random and MP starting trees that are initiated by the adaptive RAxML-NG as a function of the difficulty score. b) SLOW-SPR radius parameter over difficulty score.

Regarding the second factor, which is the thoroughness of each individual tree search, we modify the Slow SPR radius parameter (i.e. the maximum distance between pruning and regrafting points in a slow SPR round), a parameter which directly determines the number of alternative topologies explored per SPR round. Figure 2b shows the function to determine the Slow SPR radius setting depending on the MSA difficulty. We use a triangle function, starting from a radius of 5 when the difficulty score is either 0 or 1 and a peak radius of 30 for a difficulty of $0.5$.^c

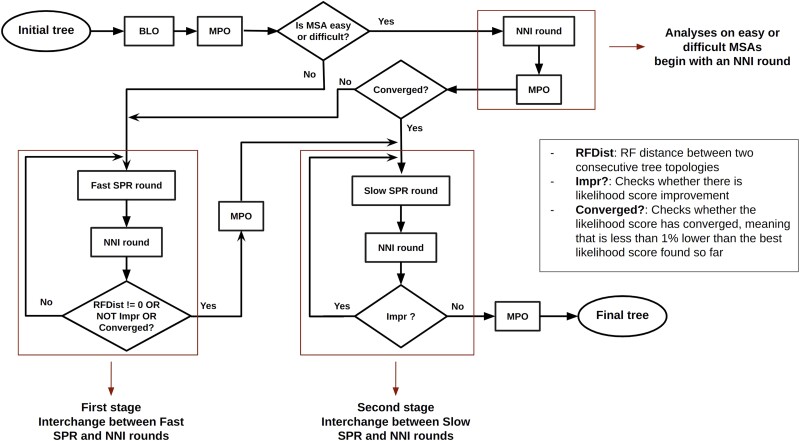
Standard RAxML-NG exclusively searches the tree space via SPR moves. Generally, the advantage of using NNI instead of SPR moves for tree searches, is that the time complexity of the heuristic is reduced from $O(n^2)$ to $O(n)$, where n is the number of taxa (Heath and Ramakrishnan 2010). On the other hand, NNI-based heuristics are more likely to become stuck in local optima and therefore infer suboptimal trees. We trade speed for accuracy by deploying a combination of SPR and NNI moves. In our adaptive heuristic, every SPR Round (either Fast or Slow) is followed by an NNI round (see “ML Tree Search Heuristics” section). The process is divided into two stages. During the first stage, Fast SPR rounds alternate with NNI rounds, until either the RF distance between two consecutive tree topologies is zero^d or the likelihood score improvement is below a user-defined threshold (Haag et al. 2022b). In the second stage, Slow SPR rounds alternate with NNI rounds until the likelihood score improvement threshold is reached again. Note that the algorithm optimizes the branch lengths (BLO) and model parameters (MPO) of the starting tree before entering the first stage. At the end of each stage, the algorithm only reoptimizes the model parameters, since local and full BLOs are already part of the SPR and NNI rounds.

Finally, we introduce a new criterion for early termination of the first stage of the heuristic. We use the log-likelihood score of the best ML tree inferred so far by the already completed tree inferences, as a reference score to define a $1\mathrm{\%}$ ML convergence interval. We assume that the first stage of the tree search has converged when the log-likelihood score of the current tree is less than $1\mathrm{\%}$ worse than this reference score. We observed that alternating between SPR and NNI moves yields a higher convergence speed (i.e. log-likelihood improvement over execution time) than relying exclusively on SPR rounds as the standard version of RAxML-NG does. For easy and difficult MSAs, adaptive RAxML-NG begins with an NNI round followed by MPO, as the probability to already converge when only using these two routines in those difficulty score ranges is comparatively high. In fact, around $70\mathrm{\%}$ of tree searches conducted on easy and difficult empirical/simulated MSAs converged by only applying an NNI round, followed by MPO. We provide the workflow of the adaptive RAxML-NG heuristic in Fig. 3; the full pseudocode is available in the Supplementary material.

Fig. 3.

Workflow of a single adaptive RAxML-NG tree inference. Standard RAxML-NG, on the other hand, conducts three stages of SPR rounds. The first stage comprises SPR rounds “on fast mode.” The second and third stages are series of Fast and Slow SPR rounds, respectively. The sole criterion to terminate a stage in standard RAxML-NG is the log-likelihood score improvement. Further, Fast and Slow SPR rounds differ between the standard and adaptive versions of RAxML-NG, although their basic principles remain the same (Kozlov 2018).

Results

As mentioned in “Algorithm” section, we conducted experiments on 10,389 empirical and 5,000 simulated MSAs. Regarding the simulated MSAs, we sampled 4,500 of the already simulated DNA datasets used in the preprint by Höhler et al. and also generated an additional 500 simulated amino-acid datasets (see Supplementary material for details). We will refer to these MSAs as RAxML Grove simulated (RGS) datasets.

For each empirical and simulated MSA, we executed both the standard and adaptive RAxML-NG versions in sequential mode. Due to the large number of MSAs, we set an execution time limit of 24 h for standard and adaptive RAxML-NG. When tree searches with both RAxML-NG versions terminate within this prespecified time interval, the experiment for the corresponding MSA is considered successful and we continue with further evaluations/comparisons. Otherwise, the dataset is discarded from downstream analysis.

We compare the two RAxML-NG versions based on: (i) the log-likelihood score (LH) of the output trees, (ii) the relative RF distance between them, (iii) the results from IQ-TREE 2 significance tests, and (iv) execution times. Regarding the significance tests, we consider the two output ML trees to be statistically indistinguishable, and therefore none of them to be significantly worse, if the corresponding standard RAxML-NG/adaptive RAxML-NG tree pair passes all seven statistical tests implemented in IQ-TREE 2. This approach is very conservative, but circumvents the discussion about the appropriateness of distinct statistical significance tests. In case all tests are passed, we assign the label PASSED to the respective pair of trees. On the other hand, if any of the tests fails to establish statistical connection, we assign the label FAILED to the pair. Finally, there are some cases in which the execution of IQ-TREE 2 was unsuccessful due to unfavorable MSA properties (duplicated sequences or sequences only comprising gaps) or due to some invalid characters in taxon names, which triggered errors in IQ-TREE 2 when importing the trees inferred by RAxML-NG. Those MSAs were also discarded from the results.

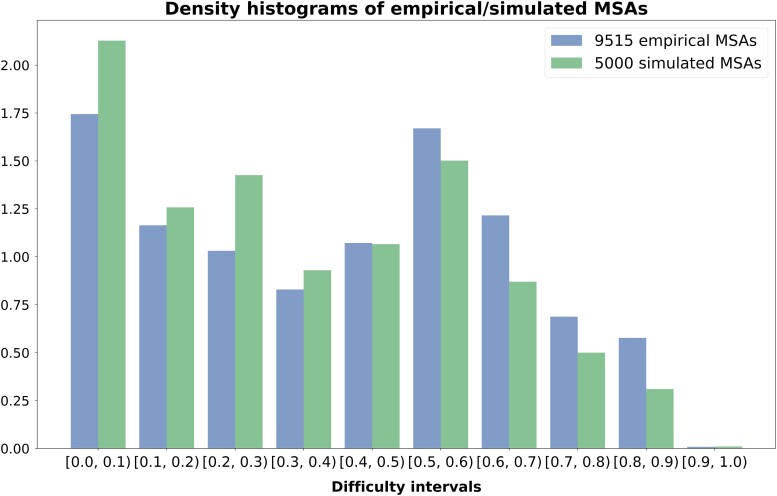
Due to this filtering, we present results for 9,515 empirical and 5,000 simulated MSAs.^e In these datasets, the execution of standard and adaptive RAxML-NG versions was within 24 h of runtime and all IQ-TREE 2 significance tests were successfully executed, either establishing a statistical connection between the pair of trees (label PASSED) or not (label FAILED). Figure 4 illustrates the distributions (density plots) of empirical/simulated datasets over ten difficulty intervals. We observe that the proportion of datasets with a difficulty score above $0.9$ is comparatively low. This is also an observation made by Höhler et al. on TreeBASE and RGS datasets, which is associated with the definition of the difficulty score per se. More information regarding the datasets used can be found in the Supplementary material.

Fig. 4.

Density histograms showing the distribution of empirical/simulated MSAs on 10 difficulty intervals.

We ran our experiments on the Haswell/URZ Cluster, located at the Computing Center of the University of Heidelberg. It consists of 224 nodes with Intel Haswell CPUs (E5-2630v3 running at 2.40 GHz). Each node contains two CPUs and each CPU has eight physical cores. The operating system is CentOS Linux 7 (Core).

Comparing the Log-Likelihood Scores

For the sake of simplicity, we will refer to the output ML tree inferred for a given MSA by standard RAxML-NG as the standard tree, and to the tree inferred by adaptive RAxML-NG as the adaptive tree. We define the absolute log-likelihood difference (LD) between the scores of standard and adaptive tree as:

$$\mathrm{LD}={\mathrm{LH}}_S-{\mathrm{LH}}_A,$$

where ${\mathrm{LH}}_S$ is the LH of the standard tree and ${\mathrm{LH}}_A$ of the adaptive tree for a given MSA. The LD metric is measured in log-likelihood units (LHUs). Evidently, in cases where the adaptive tree has a higher score, the LD metric is negative. In $96.3\mathrm{\%}$ of empirical and $99.9\mathrm{\%}$ of simulated MSAs, the LD metric is below 2 LHUs. In this way, either the adaptive tree has a lower LH score (but not by more than 2 LHUs), or has a higher LH score than the standard tree. Figures S1 and S2 in the Supplementary material summarize the LD metrics over all empirical and simulated MSAs.

We further define the relative LH difference (RLD) as:

$$RLD=\frac{{\mathrm{LH}}_S-{\mathrm{LH}}_A}{|{\mathrm{LH}}_S|}$$

Again, in cases where the adaptive tree has a higher score, the RLD is negative. The results from our experiments indicate that:

• For $98.9\mathrm{\%}$ of the empirical datasets (9,408 out of 9,515 MSAs), the RLD is below ${10}^{-3}$. In the remaining $1.1\mathrm{\%}$, the RLD does not exceed $0.02$.

• For $99.9\mathrm{\%}$ of the simulated datasets (4,997 out of 5,000 MSAs), the RLD is below ${10}^{-3}$. In the remaining 3 datasets, the RLD does not exceed $0.01$.

We can therefore claim that, in $99\mathrm{\%}$ of all cases, adaptive RAxML-NG performs similarly, or even better, than the standard version in terms of log-likelihood score. The RLD provides an intuition about the proximity of the two scores, even in cases where the absolute LH difference appears to be high. For example, in empirical dataset 11762_4, we observe the highest log-likelihood difference of 5,237.10047 LHU among all MSAs for the standard-adaptive tree pair. The RLD metric, however, is only $0.003$.

Significance Tests and Topological Similarity

Figure 5 summarizes the results of the IQ-TREE 2 significance tests conducted on all standard-adaptive tree pairs. The best-scoring tree of each pair serves as the reference tree, and the hypothesis tested is whether the second tree is significantly worse under any of the statistical significance tests available in IQ-TREE 2. In approximately $94\mathrm{\%}$ of the cases, the two trees are statistically indistinguishable, while in $0.84\mathrm{\%}$ of the cases, adaptive RAxML-NG infers significantly better trees.

Fig. 5.

Results of IQ-TREE 2 significance tests. For $95\mathrm{\%}$ of the datasets, the inferred standard and adaptive trees are statistically indistinguishable. For approximately $1\mathrm{\%}$ of the datasets, adaptive RAxML-NG infers significantly better trees.

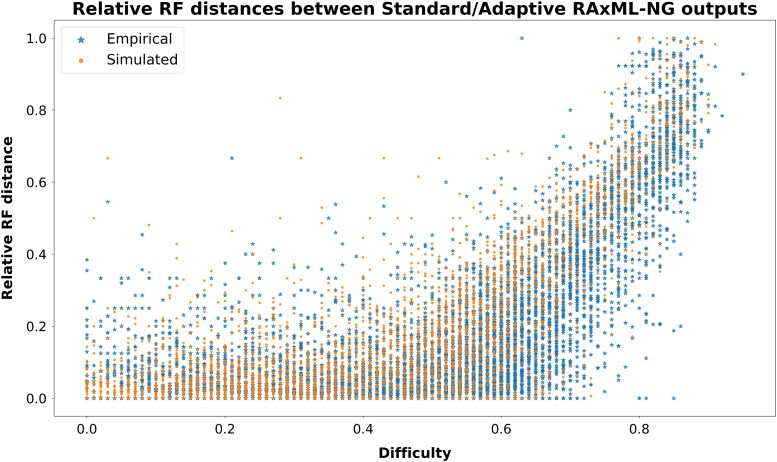
Figure 6 illustrates the relative RF distances between the two best trees found in all standard-adaptive tree pairs. We observe that, for datasets with a difficulty score below $0.5$, the majority of pairs exhibits a relative RF distance below $0.2$. This implies that the standard and adaptive version of RAxML-NG infer topologically similar trees on datasets with sufficient phylogenetic signal.

Fig. 6.

Relative RF distances between the two trees in all standard-adaptive tree pairs.

Speedups

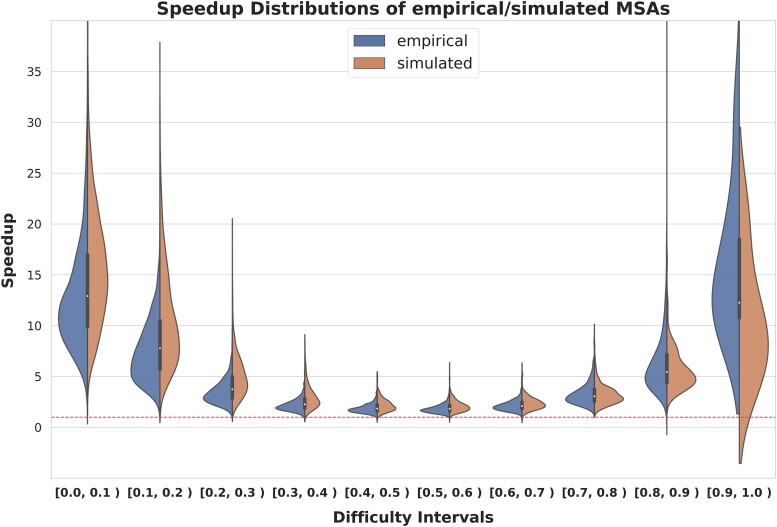
For each dataset, we calculate the speedup by dividing the execution time of standard RAxML-NG by the execution time of adaptive RAxML-NG. Figure 7 summarizes the speedup distributions for empirical and simulated datasets over ten difficulty intervals. As expected, the results indicate substantial speedups (exceeding $5\times$) on easy and difficult datasets, since the number of independent tree searches performed by adaptive RAxML-NG is lower for these difficulty intervals.

Fig. 7.

Speedup distributions for empirical/simulated datasets over 10 difficulty intervals. The dashed line at the bottom corresponds to a speedup of 1.

We further define the Per-search Speedup (PS) to be:

$$\mathrm{PS}=\frac{T_S/N_S}{T_A/N_A}$$

where $T_S$ and $T_A$ are the overall execution times of standard and adaptive RAxML-NG, and $N_S$ and $N_A$ are the number of independent tree searches conducted by each RAxML-NG version, respectively. In Table 1, we provide analogous statistics, the average value, and the standard deviation, for the overall and per-search speedup distribution over 10 difficulty intervals.

Table 1.

Average value and standard deviation of speedups and per-search speedups over 10 difficulty intervals.

	Empirical				Simulated
Difficulty	Av.S	Std.S	Av.PS	Std.PS	Av.S	Std.S	Av.PS	Std.PS
$[0.0,0.1)$	12.58	4.77	1.55	0.5	16.06	6.02	1.96	0.81
$[0.1,0.2)$	7.48	3.08	1.88	0.57	10.71	4.74	2.72	1.05
$[0.2,0.3)$	3.48	1.15	1.82	0.49	5.13	2.17	2.69	1.02
$[0.3,0.4)$	2.2	0.61	1.79	0.46	3.02	1.2	2.44	0.87
$[0.4,0.5)$	1.85	0.45	1.84	0.44	2.2	0.63	2.18	0.61
$[0.5,0.6)$	1.84	0.47	1.83	0.47	2.1	0.54	2.09	0.53
$[0.6,0.7)$	2.15	0.55	1.81	0.42	2.36	0.63	2.0	0.5
$[0.7,0.8)$	3.29	1.09	1.8	0.49	3.24	0.97	1.75	0.42
$[0.8,0.9)$	6.43	3.48	1.85	0.75	5.71	2.01	1.68	0.45
$[0.9,1.0)$	16.06	6.69	2.7	0.85	10.8	5.46	1.95	0.74

Av.S, average speedup; Std.S, standard deviation of speedups; Av.PS, average Per-search speedup; Std.PS, standard deviation of Per-search speedup.

Finally, we calculate the overall run time for standard RAxML-NG by summing over the execution times of all standard RAxML-NG invocations. We calculate the overall run time for adaptive RAxML-NG analogously. We define the accumulated speedup to be the ratio of the overall accumulated execution times of the two versions. The accumulated speedup on empirical data is $3.11\times$ and on simulated data is $4.27\times$.

Conclusions and Future Work

We designed, implemented, and tested an adaptive version of RAxML-NG. We imported Pythia into the tree inference pipeline and modified the number of independent tree searches, as well as the thoroughness of the search heuristic, based on the predicted difficulty for the input MSA. For the vast majority of MSAs, our adaptive version performs equally well as the standard RAxML-NG version with respect to tree inference accuracy. As expected, the lower the difficulty score of the dataset, the higher the topological similarity between the two ML trees inferred from the standard and adaptive versions is. We achieve substantial overall and per-search speedups in our adaptive version, in particular on easy and difficult MSAs.

By introducing Pythia into the phylogenetic inference pipeline, we provide users with an a priori estimate of the expected robustness of the final result, since the difficulty score directly reflects the amount of phylogenetic signal in the input MSA. The benefits of analyzing easy MSAs with our adaptive version are both the substantial speedups and the robustness of the final result. On the other hand, users should be aware that any individual tree inferred on difficult MSAs with a rugged likelihood surface is most likely noninformative. On difficult MSAs, adaptive RAxML-NG executes a fast heuristic to quickly infer only a few, out of the many equally likely, yet incongruent, topologies. In such cases, the software issues a warning in the standard program output, informing the users about the insufficient quality of phylogenetic signal in the input MSA.

Regarding future work, our first aim is to efficiently parallelize the adaptive RAxML-NG version, by deploying a fine-grained parallelization scheme for the first ML inference on the first starting tree, and then either coarse-grained or automatic parallelization for the subsequent inferences on the remaining starting trees. The idea is to utilize more computational resources for the first ML inference such as to quickly establish a reference ML score and determine the $1\mathrm{\%}$ likelihood convergence interval, which will be used by the subsequent inferences for an early termination of the first stage. Next, we intend to implement checkpointing in various phases of the tree search to improve user-friendliness in adaptive RAxML-NG. Lastly, we aim to test alternative heuristic tree search strategies so that we can design and implement improved heuristic approaches in adaptive RAxML-NG to further refine likelihood scores and reduce runtime.

Supplementary Material

Supplementary material is available at Molecular Biology and Evolution online.

Data Availability

GNU GPL at https://github.com/togkousa/raxml-ng/tree/adaptive