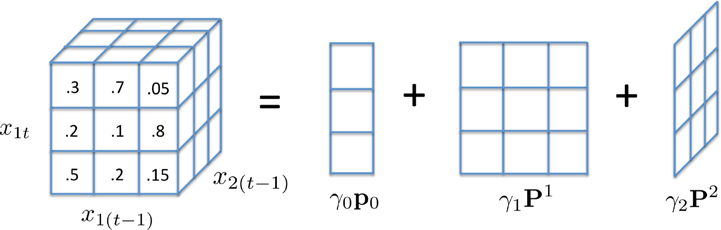The Convex Mixture Distribution: Granger Causality for Categorical Time Series

Abstract

We present a framework for learning Granger causality networks for multivariate categorical time series based on the mixture transition distribution (MTD) model. Traditionally, MTD is plagued by a nonconvex objective, non-identifiability, and presence of local optima. To circumvent these problems, we recast inference in the MTD as a convex problem. The new formulation facilitates the application of MTD to high-dimensional multivariate time series. As a baseline, we also formulate a multi-output logistic autoregressive model (mLTD), which while a straightforward extension of autoregressive Bernoulli generalized linear models, has not been previously applied to the analysis of multivariate categorial time series. We establish identifiability conditions of the MTD model and compare them to those for mLTD. We further devise novel and efficient optimization algorithms for MTD based on our proposed convex formulation, and compare the MTD and mLTD in both simulated and real data experiments. Finally, we establish consistency of the convex MTD in high dimensions. Our approach simultaneously provides a comparison of methods for network inference in categorical time series and opens the door to modern, regularized inference with the MTD model.

1. Introduction.

Granger causality [17] is a popular framework for assessing the relationships between time series, and has been widely applied in econometrics, neuroscience, and genomics, amongst other fields. Given two time series $x$ and $y$, the idea is to use the temporal structure of the data to assess whether the past values of one, say $x$, are predictive of future values of the other, $y$, beyond what the past of $y$ can predict alone; if so, $x$ is said to Granger cause $y$. Recently, the focus has shifted to inferring Granger causality networks from multivariate time series data, with the goal of uncovering a sparse set of Granger causal relationships amongst the individual univariate time series. Building on the typical autoregressive framework for assessing Granger causality, the majority of approaches for inferring Granger causal networks have focused on real-valued Gaussian time series using the vector autoregressive model (VAR) with sparsity inducing penalties [19, 42]. More recently, this approach has been extended to non-Gaussian data such as multivariate point processes using sparse Hawkes processes [48], count data using autoregressive Poisson generalized linear models [18], or even time series with heavy tails using VAR models with elliptical errors [36]. In contrast, inferring networks for multivariate categorical time series under this paradigm has received less attention.

Multivariate categorical time series arise naturally in many domains. For example, we might have health states from various indicators for a patient over time, voting records for a set of politicians, action labels for players on a team, social behaviors for kids in a school, or musical notes in an orchestrated piece. There are also many datasets that can be viewed as binary multivariate time series based on the presence or absence of an action for some set of entities. Furthermore, in some applications, collections of continuous-valued time series are each quantized into a small set of discrete values, like the weather data from multiple stations [12], wind data [39], stock returns [32], or sales volume for a collection of products [10]. Our work develops both interpretable and computationally efficient methodology for Granger causality network estimation in such cases using sparse penalties [19, 42]. Existing approaches to modeling categorical series both do not scale to higher dimensional series and also lack Granger causal interpretability, hampering their ability to estimate large Granger causality networks. We first discuss the specific drawbacks of existing approaches and then introduce the contributions of our proposed framework.

The mixture transition distribution (MTD) model [4, 39], originally proposed for parsimonious modeling of higher order Markov chains, can provide an approach to modeling multivariate categorical time series [10, 32, 49]. The MTD model reduces each categorical interaction to a standard single dimensional Markov transition probability table. While alluring due to its elegant construction and intuitive interpretation, widespread use of the MTD model has been limited by a non-convex objective with many local optima, a large number of parameter constraints, and unknown identifiability conditions [32, 49, 3]. For these reasons, the few applications of the MTD model to multivariate time series have looked at a maximum of three or four time series. To bypass the limitations of MTD, autoregressive generalized linear models have been advocated for categorical time series. In particular, autoregressive generalized linear binomial models are often used for the special case of two categories per series [18, 2]. While their multinomial-output extension to a larger number of states per series has not been widely adopted, they have been applied to the univariate time series case [24].

We refer to the autoregressive multinomial GLM as the mixture logistic transition distribution (mLTD). The mLTD model uses a logistic function to bypass parameter constraints, results in a convex objective, and has well-known identifiability conditions. However, these advantages of mLTD come at the cost of reduced interpretability, mainly because the transition distribution in mLTD depends nonlinearly on the model parameters. Recently, a constrained autoregressive probit model that improves interpretability has been proposed [32]. However, the probit model is both non-convex and inference is computationally intensive, limiting applications to higher dimensional series. As such, one is still torn between a computational and interpretability tradeoff. Methods for learning Granger causality networks among general time series based on transfer entropy or directed information have been proposed. In particular, the empirical estimator [37] and the context tree weighting estimator [23] for directed information are specifically applicable to categorical time series. However, consistency guarantees of these estimators are derived under the pairwise (group-wise) Markov assumption, and implementing these algorithms can be computationally intensive.

We address these issues by going back to the interpretable MTD framework and showing how one can improve its computational drawbacks. In particular, we recast inference in the MTD model as a convex problem through a novel re-parameterization. We further develop a regularized estimation framework for identifying Granger causality for multivariate categorical time series. We also establish, for the first time, conditions for identifiability in the MTD model and compare the identifiability conditions for MTD and mLTD models. We find that while the identifiability conditions for the MTD model are given by a non-convex set, we may easily enforce the constraints using our convex re-parameterization by augmenting the likelihood with appropriate convex penalties. We then develop efficient projected gradient and Frank-Wolfe algorithms for optimizing the penalized convex MTD objective. Our projected gradient algorithm depends on a Dykstra splitting method for projection onto the constraint sets of the MTD model. This computational approach for MTD enables this model to be applied to large, modern datasets for the first time. Importantly, the computational insights we provide carry over to the suite of other applications of MTD models, such as higher-order Markov chains, beyond the multivariate categorical time series which are the focus herein.

As a comparison benchmark we also develop a penalized mLTD model for Granger causality in multivariate Markov chains. While straightforward, the application of the penalized mLTD framework to multivariate categorical time series with more than two categories is new. We compare MTD and mLTD methods under multiple simulation conditions and use the MTD method to uncover Granger causality structure in both music [27] and iEEG brain recording [9] data sets. Finally, we also establish, for the first time, consistency of the convex MTD in high dimensions, which facilitates future theoretical developments in this area.

2. Categorical Time Series and Granger Causality.

2.1. Granger Causality.

Let $x_t=\left(x_{1t},\dots ,x_{dt}\right)\in 𝒳$ denote a $d$-dimensional categorical random variable indexed by time where $𝒳=\left({𝒳}_1\times {𝒳}_2\times \cdots \times {𝒳}_d\right)$, with ${𝒳}_i$ denoting the set of possible values of $x_{it}$. Let $m_i=\left|{𝒳}_i\right|$ be the cardinality of set ${𝒳}_i$, i.e., the number of categories that series $i$ may take. A length $T$ multivariate categorical time series is the sequence $X=\left\{x_1,\dots ,x_t,\dots ,x_T\right\}$.

An order $k$ multivariate Markov chain models the transition probability between the categories at lagged times $t-1,\dots ,t-k$ and those at time $t$ using a transition probability distributions:

$$p\left(x_t|x_{t-1},\dots \right)=p\left(x_t|x_{t-1},\dots ,x_{t-k}\right).$$ (2.1)

Due to the complexity of fully parameterizing this transition distribution, it is common to simplify the model and assume that the categories at time $t$ are conditionally independent of one another given the past realizations:

$$p\left(x_t|x_{t-1},\dots ,x_{t-k}\right)=\prod _{i=1}^{d}p\left(x_{it}|x_{t-1},\dots ,x_{t-k}\right).$$ (2.2)

For simplicity, we assume $k=1$, but stress that all models and results equally apply to higher orders of $k$. By the decomposition assumption (2.2), the problem of estimation and inference can be divided into independent subproblems over each series $i$. Using this decomposition, we define Granger non-causality for two categorical time series $x_i$ and $x_j$ as follows.

Definition 2.1.

Time series $x_j$ is not Granger causal for time series $x_i$ iff $\forall t$,

$$\begin{gathered} p(x_{it}|x_{1(t-1)},\dots ,x_{j(t-1)},\dots ,x_{d(t-1)})= \\ p\left(x_{it}|x_{1(t-1)},\dots ,x_{(j-1)(t-1)},x_{(j+1)(t-1)},\dots ,x_{d(t-1)}\right). \end{gathered}$$

Definition 2.1 states that $x_{jt}$ is not Granger causal for time series $x_{it}$ if the probability that $x_{it}$ is in any state at time $t$ is conditionally independent of the value of $x_{j(t-1)}$ at time $t-1$ given the values of all other series $x_{k(t-1)},$ $k\ne i,j$, at time $t-1$. Definition 2.1 is natural since it implies that if $x_{jt}$ does not Granger cause $x_{it}$, then knowing $x_{j(t-1)}$ does not help predicting the future state of series $i,$ $x_{it}$. For real-valued data, classical definitions of Granger non-causality generally state that the conditional mean, in homoskedastic models, or conditional variance, in heteroskedastic models, of $x_{it}$ do not depend on the past values $x_{j(t-1)}$. Thus, Definition 2.1 is a generalization of the classical case to multivariate categorical data, where notions like conditional mean and variance are less applicable. The same definition has been considered before, for example, in [14].

2.2. Tensor Representation for Categorical Time Series.

Each individual conditional distribution in Equation (2.2) can be represented as a conditional probability tensor ${\tilde{\mathbf{P}}}^i$ with $d+1$ modes of dimension $m_i\times m_1\times \cdots \times m_d$. Each entry of the tensor is given by

$${\tilde{\mathbf{P}}}_{x_{it},x_{1(t-1)},\dots ,x_{d(t-1)}}^i=p\left(x_{it}|x_{1(t-1)},\dots ,x_{d(t-1)}\right).$$ (2.3)

Definition 2.1 may be stated equivalently using the language of tensors: $x_j$ does not Granger cause $x_i$ if all subtensors along the mode associated with $x_j$ are equal. Specifically,

$${\tilde{\mathbf{P}}}_{1:m_i,1:m_1,\dots ,x_{j(t-1)}=1,\dots ,1:m_d}^i=\cdots ={\tilde{\mathbf{P}}}_{1:m_i,1:m_1,\dots ,x_{j\left(t-1\right)}=m_j,\dots ,1:m_d}^i.$$ (2.4)

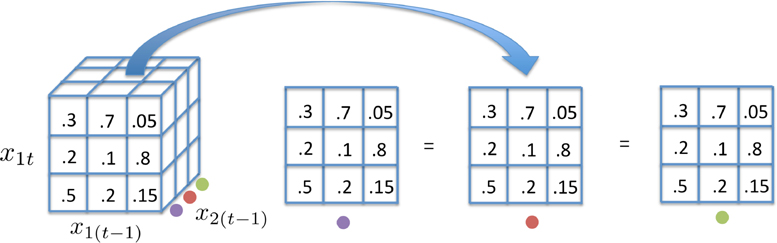
This subtensor view of Granger non-causality in categorical time series is displayed graphically in Figure 1.

Figure 1.

Illustration of Granger non-causality in an example with $d=2$ and $m_1=m_2=3$. Since the tensor represents conditional probabilities, the columns of the front face of the tensor, the vertical $x_{1t}$ axis, must sum to one. Here, $x_2$ is not Granger causal for $x_1$ since each slice of the conditional probability tensor along the $x_2$ mode is equal.

The tensor interpretation suggests a naive penalized likelihood method for Granger non-causality selection in categorical time series: perform penalized maximum likelihood estimation of the conditional probability tensor with a penalty that enforces equality among the subtensors of each mode. While we have explored the above approach in low dimensions, e.g. for $d\le 5$, memory, and in turn, computational requirements for storing the complete probability tensor become infeasible for even moderate dimensions since ${\tilde{\mathbf{P}}}^i$ has $m_i\times m_1\times \cdots \times m_d$ entries. Other authors have modeled the conditional probability distribution of Markov chains using a Bayesian nonparametric higher order singular value decomposition [41] that adaptively shrinks the number of parameters needed to represent the high-dimensional tensor. We take an alternative approach and, instead, in Sections 2.3 and 2.4, present tensor parameterizations where the number of parameters needed to represent the full conditional probability tensor grows linearly with $d$. We establish Granger non-causality conditions and associated penalized likelihood methods for estimation under these parameterizations in Sections 3 and 4, respectively.

In specifying our models, and throughout the remainder of the paper, we focus on a single conditional of $x_{it}$ given $x_{t-1}$ in Equation (2.2). For notational simplicity, we drop the $i$ index.

2.3. The MTD Model.

The MTD model as in [39] provides an elegant and intuitive parameterization of a high-order Markov chain. Here, we extend this model to the case of multiple time series, and model the multivariate Markov transition as a convex combination of pairwise transition probabilities. The MTD model is given by:

$$p\left(x_{it}|x_{1(t-1)},\dots ,x_{d(t-1)}\right)={\gamma }_0{p}_0\left(x_{it}\right)+\sum _{j=1}^d{\gamma }_j{p}_j\left(x_{it}|x_{j(t-1)}\right),$$ (2.5)

where $p_0$ is a probability vector, $p_j(.|\cdot )$ is a pairwise transition probability table between $x_{j(t-1)}$ and $x_{it}$ and $\gamma =\left({\gamma }_0,{\gamma }_1,\dots ,{\gamma }_d\right)$ is a $d+1$ dimensional probability distribution such that ${\mathbf{1}}^T\gamma =1$ with ${\gamma }_j\ge 0,$ $j=0,\dots ,d$. We let the matrix ${\mathbf{P}}^j\in {\mathbb{R}}^{m_i\times m_j}$ denote the pairwise transition probability ${\mathbf{P}}_{x_{it},x_{j(t-1)}}^j=p_j\left(x_{it}|x_{j(t-1)}\right)$. Thus, ${\mathbf{1}}^T{\mathbf{P}}^j={\mathbf{1}}^T,$ ${\mathbf{P}}_{lk}^j\ge 0,l=1,\dots ,m_i,$ $k=1,\dots ,m_j$. We also let ${\mathbf{p}}^0\in {\mathbb{R}}^{m_i}$ denote the intercept, where ${\mathbf{p}}_{x_{it}}^0=p_0\left(x_{it}\right)$. While past formulations of the MTD model neglect the $p_0$ intercept term, we show below that the intercept is crucial for model identifiability and, consequently, Granger causality inference. Finally, we note that the MTD model may be extended by adding interaction terms for pairwise effects [4], such as $p_{jk}\left(x_{it}|x_{j(t-1)},x_{k(t-1)}\right)$, though we focus our presentation on the simple case above.

2.4. The mLTD Model.

The multinomial logistic transition distribution model (mLTD) is given by:

$$p\left(x_{it}|x_{1(t-1)},\dots ,x_{d(t-1)}\right)=\frac{\exp \left({\mathbf{z}}_{x_{it}}^0+\sum _{j=1}^d{\mathbf{Z}}_{x_{it},x_{j(t-1)}}^j\right)}{\sum _{x^{\prime }\in {𝒳}_i}\exp \left({\mathbf{z}}_{x^{\prime }}^0+\sum _{j=1}^d{\mathbf{Z}}_{x^{\prime },x_j(t-1)}^j\right)},$$ (2.6)

where ${\mathbf{Z}}^j\in {\mathbb{R}}^{m_i\times m_j}$ and ${\mathbf{z}}^0\in {\mathbb{R}}^{m_i}$. The probit model in [32] is not a natural fit for inferring Granger causality networks both due to the non-convexity of the probit model and the non-convex constraints imposed on the ${\mathbf{Z}}^j$ matrices. Note that, like the MTD model, the mLTD model naturally allows adding interaction terms, though we focus again on the simple case above.

2.5. Comparing MTD and mLTD Models.

Both MTD and mLTD models represent the full conditional probability tensor using individual matrices for each $x_j$ series, ${\mathbf{P}}^j$ for MTD and ${\mathbf{Z}}^j$ for mLTD. However, how these matrices are composed and restrictions on their domains differ substantially between the two models. The MTD model is a convex combination of pairwise probability tables, whereas mLTD is a nonlinear function of the unrestricted ${\mathbf{Z}}^j\mathrm{s}$. MTD may thus be thought of as a linear tensor factorization method for conditional probability tensors, where the tensor is created by summing probability table slices along each dimension. This interpretation of MTD is displayed graphically in Figure 2.

Figure 2.

Schematic of the MTD factorization of the conditional probability tensor $p\left(x_{1t}|x_{1(t-1)},x_{2(t-1)}\right)$ for $d=2$ time series and $m=3$ categories.

3. Convexity, Identifiability and Granger Causality.

In this section, we first introduce a novel re-parameterization of the MTD model that renders the log likelihood of the MTD model convex. The convex formulation alone opens up an array of possibilities for the MTD framework beyond our multivariate categorical time series focus, eliminating the primary barrier to adoption of this model, i.e., non-convexity and associated computationally demanding inference procedures. The proposed change-of-variables also allows us to derive both novel identifiability conditions for the MTD model and Granger causality restrictions that hold for both MTD and mLTD models. The non-identifiability of the MTD model was first pointed out by [28], but no explicit conditions or general framework for identifiability were given. We show that while the identifiability conditions for MTD are non-convex, they may be enforced implicitly by adding an appropriate convex penalty to the convex log-likelihood objective. The proofs of all results are given in the Supplementary Material.

3.1. Convex MTD.

Maximum likelihood estimator for the MTD model under the $(\gamma ,\mathbf{P})$ parameterization is defined by the non-convex optimization problem:

$$\begin{gathered} \underset{\mathbf{P},\gamma }{\mathrm{minimize}}-\sum _{t=1}^T\log \left({\gamma }_0{\mathbf{p}}_{x_{it}}^0+\sum _{j=1}^d{\gamma }_j{\mathbf{P}}_{x_{it},x_{j(t-1)}}^j\right) \\ \text{subject}\text{to}{\mathbf{1}}^T{\mathbf{P}}^j={\mathbf{1}}^T,{\mathbf{P}}^j\ge 0,\forall j{\mathbf{1}}^T\gamma =1,\gamma \ge 0. \end{gathered}$$ (3.1)

The log-likelihood surface is highly non-convex, following from the multiplication of ${\gamma }_j$ and ${\mathbf{P}}^j$ in the log term. It also contains many local optima due to the general non-identifiability. Indeed, the set of equivalent models forms a non-convex region in the $(\gamma ,\mathbf{P})$ parameterization (i.e., the convex combination of equivalent models is not necessarily another equivalent model). This limitation may lead to many non-convex shaped ridges and sets of equal probability.

Fortunately, the optimization problem in (3.1) may be recast as a convex program using the re-parameterization ${\mathbf{Z}}^j={\gamma }_j{\mathbf{P}}^j$ and ${\mathbf{z}}^0={\gamma }_0{\mathbf{p}}^0$. Using this reparameterization, we can rewrite the factorization of the conditional probability tensor for MTD in Equation (2.5) as

$$p\left(x_{it}|x_{1(t-1)},\dots ,x_{d(t-1)}\right)={\mathbf{z}}_{x_{it}}^0+\sum _{j=1}^d{\mathbf{Z}}_{x_{it}{x}_{j(t-1)}}^j.$$ (3.2)

The full optimization problem for maximum log-likelihood including constraints then becomes:

$$\begin{gathered} \underset{\mathbf{Z},\gamma }{\mathrm{minimize}}-\sum _{t=1}^T\log \left({\mathbf{z}}_{x_{it}}^0+\sum _{j=1}^d{\mathbf{Z}}_{x_{it}{x}_{j(t-1)}}^j\right) \\ \text{subject}\text{to}{\mathbf{1}}^T{\mathbf{Z}}^j={\gamma }_j{\mathbf{1}}^T,{\mathbf{Z}}^j\ge 0,\forall j{\mathbf{1}}^T\gamma =1,\gamma \ge 0. \end{gathered}$$ (3.3)

Problem (3.3) is convex since the objective function is a linear function composed with a log function and only involves linear equality and inequality constraints [6].

The ${\mathbf{Z}}^j$ reparameterization in Equation (3.2) also provides clear intuition for why the MTD model may not be identifiable. Since the probability function is a linear sum of ${\mathbf{Z}}^j$s, one may move probability mass around, taking mass from some ${\mathbf{Z}}^j$ and moving to some ${\mathbf{Z}}^k,$ $k\ne j$ or ${\mathbf{z}}^0$, while keeping the conditional probability tensor constant. These sets of equivalent MTD parameterizations have the following appealing property:

Proposition 3.1.

The set of MTD parameters, $\mathbf{Z}$, that yield the same factorized conditional distribution $p\left(x_{it}|x_{(t-1)}\right)$ forms a convex set.

Taken together, the convex reparameterization and Proposition 3.1 imply that the convex function given in Equation (3.3) has no local optima, and that the globally optimal solution to Problem (3.3) is given by a convex set of equivalent MTD models.

3.2. Identifiability.

3.2.1. Identifiability for the MTD Model.

The re-parameterization of the MTD model in terms of ${\mathbf{Z}}^j$s, instead of ${\gamma }_j$ and ${\mathbf{P}}^j$, combined with the introduction of an intercept term, allows us to explicitly characterize identifiability conditions for the MTD model.

Theorem 3.2.

Every MTD distribution has a unique parameterization where the minimal element in each row of ${\mathbf{P}}^j$ (and thus ${\mathbf{Z}}^j$) is zero for all $j$.

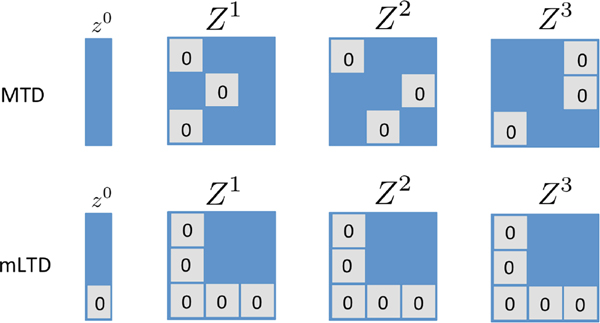
The intuition for this result is simple: any excess probability mass on a row of each ${\mathbf{Z}}^j$ may be pushed onto the same row of the intercept term ${\mathbf{z}}^0$ without changing the full conditional probability. This operation may be done until the smallest element in each row is zero, but no more without violating the positivity constraints of the pairwise transitions. The identifiability condition in Theorem 3.2 also offers an interpretation of the parameters in the MTD model. Specifically, the element ${\mathbf{Z}}_{mn}^j$ denotes the additive increase in probability that $x_{it}$ is in state $m$ given that $x_{j(t-1)}$ is in state $n$. Furthermore, the ${\gamma }_j$ parameters now represent the total amount of probability mass in the full conditional distribution explained by categorical variable $x_j$, providing an interpretable notion of dependence in categorical time series. The mLTD model, however, does not readily suggest a simple and interpretable notion of dependence from the ${\mathbf{Z}}^j$ matrix due to the non-linearity of the link function. The identifiability conditions are displayed pictorially in Figure 3.

Figure 3.

Schematic displaying the identifiability conditions for the MTD model (top) and the mLTD model (bottom) for an example with $d=3$ and $m_1=m_2=m_3=3$. Identifiability for MTD requires a zero entry in each row of ${\mathbf{Z}}^j$, while for mLTD the first column and last row must all be zero. In MTD the columns of each ${\mathbf{Z}}^j$ must also sum to the same value, and must sum to one across all ${\mathbf{Z}}^j$.

Unfortunately, the necessary constraint set for identifiability specified in Theorem 3.2 is a non-convex set since the locations of the zero elements in each row of ${\mathbf{Z}}^j$ are unknown. Naively, one could search over all possible locations for the zero element in each row of each ${\mathbf{Z}}^j$; however, this quickly becomes infeasible as both $m$ and $d$ grow. Instead, we add a penalty term $\mathrm{\Omega }\left(\mathbf{Z}\right)$, or prior, that biases the solution towards the uniqueness constraints. This regularization also aids convergence of optimization since the maximum likelihood solution without identifiability constraints is not unique. Letting

$$L_{\text{MTD}}(\mathbf{Z})=-\sum _{t=1}^T\log \left({\mathbf{z}}_{x_{it}}^0+\sum _{j=1}^p{\mathbf{Z}}_{x_{it}{x}_{j(t-1)}}^j\right),$$ (3.4)

the regularized estimation problem is given by

$$\begin{gathered} \underset{\mathbf{Z},\gamma }{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}{L}_{\mathrm{M}\mathrm{T}\mathrm{D}}(\mathbf{Z})+\lambda \mathrm{\Omega }(\mathbf{Z}) \\ \text{subject}\text{to}{\mathbf{1}}^T{\mathbf{Z}}^j={\gamma }_j{\mathbf{1}}^T,{\mathbf{Z}}^j\ge 0,\forall j,{\mathbf{1}}^T\gamma =1,\gamma \ge 0. \end{gathered}$$ (3.5)

Theorem 3.3.

For any $\lambda >0$ and $\mathrm{\Omega }\left(\mathbf{Z}\right)$ that does not depend on ${\mathbf{z}}^0$ and is increasing with respect to the absolute value of entries in ${\mathbf{Z}}^j$, the solution to the problem in Equation (3.5) is contained in the set of identifiable MTD models described in Theorem 3.2.

Intuitively, by penalizing the entries of the ${\mathbf{Z}}^j$ matrices, but not the intercept term, solutions will be biased to having the intercept contain the excess probability mass, rather than the ${\mathbf{Z}}^j$ matrices. Thus, even with a very small penalty, we constrain the solution space to the set of identifiable models. Theorem 3.3 characterizes an entire class of regularizers that enforce the identifiability constraints for MTD. As we explain in Section 4.1, a simple choice for $\mathrm{\Omega }\left(\mathbf{Z}\right)$ is a regularizer that also selects for Granger causality.

3.2.2. Identifiability for the mLTD Model.

The non-identifiability of multinomial logistic models is also well-known, as is the non-identifiability of generalized linear models with categorical covariates. Combining the standard identifiability restrictions for both settings gives the following result.

Proposition 3.4.

([1]) Every mLTD has a unique parameterization such that first column and last row of ${\mathbf{Z}}^j$ are zero for all $j$ and the last element of ${\mathbf{z}}^0$ is zero.

These conditions are displayed pictorially in Figure 3. Under the identifiability constraints for both MTD and mLTD models, at least one element in each row must be zero. For MTD this zero may be in any column, while for mLTD the zero may, without loss of generality, be placed in the first column of each row. For mLTD, the last row of ${\mathbf{Z}}^j$ must also be zero due to the logistic output (one category serves as the ‘baseline’); in MTD, instead, each column of ${\mathbf{P}}^j$ must sum to one.

3.3. Granger Causality in MTD and mLTD.

Under the ${\mathbf{Z}}^j$ parameterization for MTD and mLTD specification of Equation (2.6), we have the following simple result for Granger non-causality conditions:

Proposition 3.5.

In both the MTD model of Equation (3.2) and the mLTD model of Equation (2.6), time series $x_j$ is Granger non-causal for time series $x_i$ if and only if the columns of ${\mathbf{Z}}^j$ are all equal. Furthermore, all equivalent MTD model parameterizations give the same Granger causality conclusions.

Intuitively, if all columns of ${\mathbf{Z}}^j$ are equal, the transition distribution for $x_{it}$ does not depend on $x_{j(t-1)}$. This result for mLTD and MTD models is analogous to the general Granger non-causality result for the slices of the conditional probability tensor being constant along the $x_{j(t-1)}$ mode being equal. Based on Proposition 3.5, we might select for Granger non-causality by penalizing the columns of ${\mathbf{Z}}^j$ to be the same. While this approach is potentially interesting, a more direct, stable method takes into account the conditions required for identifiability of the ${\mathbf{Z}}^j$ under both models.

Under the identifiability constraints for both MTD and mLTD given in Theorems 3.2 and Proposition 3.4, respectively, $x_j$ is Granger non-causal for $x_i$ if and only if ${\mathbf{Z}}^j=0$ (a special case of all columns being equal). For both MTD and mLTD models this fact follows from each row having at least one zero element; for all the columns to be equal, as stated in Proposition 3.5, all elements in each row must also be equal to zero. Taken together, if we enforce the identifiability constraints, we may uniquely select for Granger non-causality by encouraging some ${\mathbf{Z}}^j$ to be zero.

4. Granger Causality Selection.

We now turn to procedures for inferring Granger non-causality statements from observed multivariate categorical time series. In Section 3, we derived that if ${\mathbf{Z}}^j=0$, then $x_j$ is Granger non-causal for $x_i$ in both MTD and mLTD models. To perform model selection, we take a penalized likelihood approach and present a set of penalty terms that encourage ${\mathbf{Z}}^j=0$, while maintaining convexity of the overall objective. The final parameter estimates automatically satisfy the identifiability constraints for MTD. We also develop an analogous penalized criterion for selecting Granger causality in the mLTD model.

4.1. Model Selection in MTD.

We now explore penalties that encourage the ${\mathbf{Z}}^j$ matrices to be zero. Under the $\left({\mathbf{P}}^j;{\gamma }_j\right)$ parameterization, this is equivalent to encouraging the ${\gamma }_j$ to be zero. We first introduce an $L_0$ penalized problem in terms of the original ${\gamma }_j$ parameterization, and then show how convex relaxations of the $L_0$ norm on ${\gamma }_j$ lead to natural convex penalties on ${\mathbf{Z}}^j$. Ideally, we would solve the penalized $L_0$ problem:

$$\begin{gathered} \underset{\mathbf{Z},\gamma }{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}{L}_{\mathrm{M}\mathrm{T}\mathrm{D}}(\mathbf{Z})+\lambda {∥{\gamma }_{1:d}∥}_0 \\ \text{subject}\text{to}{\mathbf{1}}^T{\mathbf{Z}}^j={\gamma }_j{\mathbf{1}}^T,{\mathbf{Z}}^j\ge 0\forall j,{\mathbf{1}}^T\gamma =1,\gamma \ge 0, \end{gathered}$$ (4.1)

where $\lambda \ge 0$ is a regularization parameter and ${∥{\gamma }_{1:d}∥}_0$ is the $L_0$ norm over the weights; the intercept weight ${\gamma }_0$ is not regularized. The $L_0$ penalty simply counts the number of non-zero ${\gamma }_j$, which is equivalent to the number of non-zero ${\mathbf{Z}}^j$. This results in a non-convex objective. Instead, we develop alternative convex penalties suited to model selection in MTD. Importantly, we require that any such penalty, $\mathrm{\Omega }\left(\mathbf{Z}\right)$, fall in the intersection of two penalty classes: 1) $\mathrm{\Omega }\left(\mathbf{Z}\right)$ must be a convex relaxation to the $L_0$ norm in Problem (4.1) to promote sparse solutions and 2) $\mathrm{\Omega }\left(\mathbf{Z}\right)$ must satisfy the conditions of Theorem 3.3 to ensure the final parameter estimates satisfy the MTD identifiability constraints. We propose and compare two penalties that satisfy these criteria.

Our first proposal is the standard $L_1$ relaxation, as in lasso regression, which simply sums the absolute values of ${\gamma }_j$. This penalty encourages soft-thresholding, where some estimated ${\gamma }_j$ are set exactly to zero while others are shrunk relative to the estimates from the unpenalized objective. Note that due to the non-negativity constraint, the $L_1$ norm on ${\gamma }_{1:d}$ is simply given by ${\sum }_{j=1}^d{\gamma }_j$. If ${\gamma }_0$ were included in the $L_0$ regularization, the $L_1$ relaxation would fail due to the $\gamma$ simplex constraints $1^T\gamma =1,$ $\gamma \ge 0$ so the $L_1$ norm would always be equal to one over the feasible set [35]. Our addition of an unpenalized intercept to the MTD model allows us to sidestep this issue and leverage the sparsity promoting properties of the $L_1$ penalty for model selection in MTD. The $L_1$ regularized MTD problem is thus given by

$$\begin{gathered} \underset{\mathbf{Z},\gamma }{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}{L}_{\mathrm{M}\mathrm{T}\mathrm{D}}(\mathbf{Z})+\lambda \sum _{j=1}^d{\gamma }_j \\ \text{subject}\text{to}{\mathbf{1}}^T{\mathbf{Z}}^j={\gamma }_j{\mathbf{1}}^T,{\mathbf{Z}}^j\ge 0,\forall j,{\mathbf{1}}^T\gamma =1,\gamma \ge 0. \end{gathered}$$ (4.2)

Equation (4.2) may be rewritten solely in terms of the ${\mathbf{Z}}^j$s by noting that ${\gamma }_j=\frac{1}{m_j}{1}^T{\mathbf{Z}}^{j}1$. Defining ${\tilde{z}}^T=(\mathrm{v}\mathrm{e}\mathrm{c}{\left({\mathbf{Z}}^1\right)}^T,\dots ,\mathrm{v}\mathrm{e}\mathrm{c}{\left({\mathbf{Z}}^d\right)}^T)$, and assuming, for simplicity of presentation, $\left|{𝒳}_i\right|=m\forall i$, we can rewrite the MTD constraints as

$$\left(I_d\otimes A\right)\tilde{z}=0,{\mathbf{1}}^T\tilde{z}=m,\tilde{z}\ge 0,$$

where

$$A=\left(\begin{array}{ccccc}{\mathbf{1}}_m^T& -{\mathbf{1}}_m^T& 0& 0& \cdots \\ 0& {\mathbf{1}}_m^T& -{\mathbf{1}}_m^T& 0& \cdots \\ \cdots & \cdots & \ddots & ⋮& ⋮\\ 0& 0& \cdots & {\mathbf{1}}_m^T& -{\mathbf{1}}_m^T\end{array}\right),$$ (4.3)

and $I_d$ is a $d$-dimensional identity matrix. This gives the final penalized optimization problem only in terms of ${\mathbf{Z}}^j$ as

$$\begin{gathered} \underset{\mathrm{Z}}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}{L}_{\mathrm{M}\mathrm{T}\mathrm{D}}(\mathbf{Z})+\lambda \sum _{i=1}^d\frac{1}{m}{\mathbf{1}}^T{\mathbf{Z}}^j\mathbf{1} \\ \text{subject}\text{to}\left(I_d\otimes A\right)\tilde{z}=0,{\mathbf{1}}^T\tilde{z}=m,\tilde{z}\ge 0. \end{gathered}$$ (4.4)

Writing the $L_1$ penalized problem in this form shows that the $L_1$ penalty increases with the absolute value of the entries in ${\mathbf{Z}}^j$ and does not penalize the intercept; it thus satisfies the conditions of Theorem 3.3. As a result, the solution to the problem given in Equation (4.4) automatically satisfies the MTD identifiability constraints. Furthermore, the solution will lead to Granger causality estimates since many of the ${\mathbf{Z}}^j\mathrm{s}$ will be zero due to the $L_1$ penalty.

Another natural convex relaxation of the objective in Equation (4.1) is given by a group lasso penalty on each ${\mathbf{Z}}^j$ [47]. The relaxation is derived by writing the $L_0$ norm as a rank constraint in terms of ${\mathbf{Z}}^j$, which is then relaxed to a group lasso. Specifically, assume all time series have the same number of categories, i.e., $m_j=m\forall j$. Due to the equality and non-negativity constraints,

$$\begin{gathered} {∥{\gamma }_{1:d}∥}_0={∥\left({\mathbf{1}}^T\mathrm{v}\mathrm{e}\mathrm{c}\left({\mathbf{Z}}^1\right),\dots ,{\mathbf{1}}^T\mathrm{v}\mathrm{e}\mathrm{c}\left({\mathbf{Z}}^d\right)\right)∥}_0 \\ =\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left({\mathbf{Q}}^T\mathbf{Q}\right) \\ =\mathrm{rank}\left(\mathbf{Q}\right), \end{gathered}$$

where

$$\mathbf{Q}=\left(\begin{array}{cccc}\mathrm{v}\mathrm{e}\mathrm{c}\left({\mathbf{Z}}^1\right)& 0& \dots & 0\\ 0& \mathrm{v}\mathrm{e}\mathrm{c}\left({\mathbf{Z}}^2\right)& \dots & 0\\ 0& \dots & \ddots & ⋮\\ 0& \dots & \dots & \mathrm{v}\mathrm{e}\mathrm{c}\left({\mathbf{Z}}^d\right)\end{array}\right).$$

Thus, we can use the nuclear norm on $\mathbf{Q}$ as a convex relaxation of ${∥{\gamma }_{1:d}∥}_0$. Furthermore, the nuclear norm of $\mathbf{Q}$ is given by the sum of Frobenius norms of ${\mathbf{Z}}^j$. More specifically, denoting by $\parallel \cdot {\parallel }_{\mathrm{*}}$ the nuclear norm and by $\parallel \cdot {\parallel }_F$ the Froebenius norm,

$$\parallel \mathbf{Q}{\parallel }_{\mathrm{*}}=\sum _{j=1}^d{∥{\mathbf{Z}}^j∥}_F=\sum _{j=1}^d\sqrt{\mathrm{tr}({({\mathbf{Z}}^j)}^T({\mathbf{Z}}^j))}.$$

This group lasso penalty gives the final problem

$$\begin{gathered} \underset{\mathbf{Z}}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}{L}_{\mathrm{M}\mathrm{T}\mathrm{D}}(\mathbf{Z})+\lambda \sum _{j=1}^d{∥{\mathbf{Z}}^j∥}_F \\ \text{subject}\text{to}\left(I_d\otimes A\right)\tilde{z}=0,{\mathbf{1}}^T\tilde{z}=m,\tilde{z}\ge 0. \end{gathered}$$ (4.5)

Here, we penalize ${\mathbf{Z}}^j$ directly, rather than indirectly via ${\gamma }_j$. The group lasso penalty drives all elements of ${\mathbf{Z}}^j$ to zero together, such that the optimal solution sets some ${\mathbf{Z}}^j$ to be all zero. This effect naturally coincides with our conditions of Granger non-causality that all elements of ${\mathbf{Z}}^j=0$. The group lasso penalty also satisfies the conditions of Theorem 3.3 since the $L_2$ norm is increasing with respect to each element in ${\mathbf{Z}}^j$ and the intercept is not penalized. Thus, solutions to Problem (4.5) automatically enforce the MTD identifiability constraints.

The group lasso penalty tends to favor larger groups [20]. When the time series have different number of categories, the sizes of the coefficient matrices ${\mathbf{Z}}^j$s are different. In this case, one can use penalties that scale with the group size, for example, $\lambda {\sum }_{j=1}^d\sqrt{m_j}{\parallel {\mathbf{Z}}^j\parallel }_F$. For simplicity, we focus on the case where all time series have the same number of categories hereafter, and omit the dependence of the penalty on group sizes.

4.2. Model Selection in mLTD.

To select for Granger causality in the mLTD model, we add a group lasso penalty to each of the ${\mathbf{Z}}^j$ matrices, similar to Equation (4.5), leading to the following optimization problem:

$$\begin{gathered} \underset{\mathbf{Z}}{\mathrm{minimize}}\sum _{t=1}^T{\mathbf{z}}_{x_{it}}^0+\sum _{j=1}^d{\mathbf{Z}}_{x_{it}{x}_{j(t-1)}}^j \\ +\log \left(\sum _{x^{\prime }\in {𝒳}_i}\exp \left({\mathbf{z}}_{x^{\prime }}^0+\sum _{j=1}^d{\mathbf{Z}}_{x^{\prime }{x}_{j(t-1)}}^j\right)\right)+\lambda \sum _{j=1}^d{\Vert {\mathbf{Z}}^j\Vert }_F \\ \text{subject}\text{to}{\mathbf{Z}}_{1:m_i,1}^j=0,{\mathbf{Z}}_{m_i,1:m_j}^j=0\forall j\text{.} \end{gathered}$$ (4.6)

For two categories, $m_i=2\forall i$, this problem reduces to sparse logistic regression for binary time series, which was recently studied theoretically [18]. As in the MTD case, the group lasso penalty shrinks some ${\mathbf{Z}}^j$ entirely to zero.

5. Optimization.

Here we present fast proximal algorithms for fitting both penalized MTD and mLTD models. The convex formulation invites new optimization routines for fitting MTD models since many options exist for solving problems with convex objectives with linear equality and inequality constraints. In the Supplementary Material, we present alternative MTD solvers based on Frank-Wolfe [22] and Majorization-Minimization (MM) [21], and discuss their trade-offs. Both Frank-Wolfe and MM algorithms for MTD take elegant and simple forms. Furthermore, the MM algorithm for the non-penalized convex Problem 3.2 is equivalent to an EM algorithm for the MTD model in the original non-convex parameterization of Problem 3.1. As a byproduct, this equivalence shows that the EM algorithm under the non-convex parameterization converges to a global optima. Here we focus on proximal algorithms since the MM algorithm for MTD is applicable only to the non-penalized MTD objective and Frank-Wolfe converges slowly relative to proximal gradient for the dimensions we consider; see the Supplementary Material for more details.

For the mLTD model, we perform gradient steps with respect to the mLTD likelihood followed by a proximal step with respect to the group lasso penalty. This leads to a gradient step of the smooth likelihood followed by separate soft group thresholding [33] on each ${\mathbf{Z}}^j$.

For the MTD model, our proximal algorithm reduces to a projected gradient algorithm [33]. Projected gradient algorithms take steps along the gradient of the objective, and then project the result onto the feasible region defined by the constraints. Compared to other MTD optimization methods, our projected gradient algorithm under the ${\mathbf{Z}}^j$ parameterization is guaranteed to reach the global optima of the MTD log-likelihood. The gradient of the regularized MTD model with respect to entries in ${\mathbf{Z}}^j$ over the feasible set is given by

$$\frac{dL}{d{\mathbf{Z}}_{x^{\prime }{x}^{″}}^j}=\sum _{t=1}^T{1}_{\left\{x_{it}=x^{\prime },x_{j(t-1)}=x^{″}\right\}}\frac{1}{{\mathbf{Z}}_{x_{it}}^0+\sum _{j=1}^d{\mathbf{Z}}_{x_{it}{x}_{j(t-1)}}^j}+\lambda \frac{d\mathrm{\Omega }}{d{\mathbf{Z}}_{x^{\prime }{x}^{″}}^j}.$$ (5.1)

For the $L_1$ norm, $\mathrm{\Omega }\left(\mathbf{Z}\right)$ is not differentiable when an element in any ${\mathbf{Z}}^j$ is zero. For the $L_2$ group norm, $\mathrm{\Omega }\left(\mathbf{Z}\right)$ is not differentiable when every element in at least one ${\mathbf{Z}}^j$ is zero. However, the MTD constraints enforce that ${\mathbf{Z}}^j\ge 0$. Since the point of non-differentiability for the $L_2$ norm in our case occurs when elements are identically zero, we modify the constraints so that ${\mathbf{Z}}^j\ge ϵ$ for some small $ϵ$ when using the group penalty. This allows us to ignore non-differentiability issues, and instead take gradient steps directly along the penalized MTD objective.

Following the notation from the end of Section 4.1, let the set $C=\left\{\tilde{z}|\tilde{z}\ge ϵ,\left(I_d\otimes A\right)\tilde{z}=\right.\left.0,1^T\tilde{z}=m\right\}$ denote the modified MTD constraints with respect to the ${\mathbf{Z}}^j$ parameterization. We perform projected gradient descent by taking a step along the regularized MTD gradient of Equation (5.1) and then project the result onto $C$. Specifically, the algorithm iterates the following recursion starting at iteration $k=0$:

$${\tilde{z}}^{k+1}={𝒫}_C\left({\tilde{z}}^k-{\delta }_k\frac{dL}{d\tilde{z}}\right),$$ (5.2)

where ${\delta }_k$ is a step size chosen by line search [33]. For ease of presentation, here we have written the projected gradient steps in terms of the vectorized variables $\tilde{z}$, rather than the ${\mathbf{Z}}^j$ matrices. The ${𝒫}_C\left(x\right)$ operation is the projection of a vector $x$ onto the modified MTD constraint set $C$:

$$\begin{gathered} \underset{z}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}\parallel z-x{\parallel }_2^2 \\ \text{subject}\text{to}z\ge ϵ,\left(I_d\otimes A\right)z=0,1^{T}z=m, \end{gathered}$$

with $ϵ=0$ for the $L_1$ penalty and $ϵ>0$ but small for the group lasso penalty. While this is a standard quadratic program for which we may use the dual method [16] as, e.g. implemented in the R quadratic programming package quadprog [43], we have found that standard solvers may scale poorly as the number of time series $d$ become large. To mitigate this inefficiency, here we develop a fast projection algorithm based on Dykstra’s splitting algorithm [7] that harnesses the particular structure of the constraint set for much faster projection, as described in Section 5.1.

5.1. Dykstra’s Splitting Algorithm for Projection onto the MTD Constraints.

The set $C$ may be written as the intersection of two simpler sets: $C=S\cap B$, where $S$ is the simplex constraint set of the first column of each ${\mathbf{Z}}^j$ matrix and the non-negativity constraint for all entries of ${\mathbf{Z}}^j$. Specifically,

$$S=\left\{{\left\{{\mathbf{Z}}^j\in {ℝ}^{m\times m}\right\}}_{j=0}^d|\sum _{j=0}^d\sum _{i=1}^m{\mathbf{Z}}_{i1}^j=1,{\mathbf{Z}}^j\ge 0\forall j\right\}.$$ (5.3)

On the other hand, $B={\cup }_{j=1}^d{B}_j$, where $B_j$ is the constraint set that all columns in ${\mathbf{Z}}^j$ sum to the same value:

$$B_j=\left\{{\mathbf{Z}}^j\in {\mathbb{R}}^{m\times m}|A\mathrm{v}\mathrm{e}\mathrm{c}\left({\mathbf{Z}}^j\right)=\mathbf{0}\right\},$$ (5.4)

where the matrix $A$ is given in Equation (4.3). Dykstra’s algorithm alternates between projecting onto the simplex constraints $S$ and the equal column sums $B$ by iterating the following steps. Let $w^0=x,u^0=v^0=0$. Denote by ${𝒫}_S$ the projection onto the set $S$ and by ${𝒫}_B$ the projection onto the set $B$. Dykstra’s algorithm amounts to the following iterations starting with $l=0$:

$$y^l={𝒫}_S\left(w^l+u^l\right)$$

$$u^{l+1}=w^l+u^l-y^l$$

$$w^l={𝒫}_B\left(y^l+v^l\right)$$

$$v^{l+1}=y^l+v^l-w^l.$$

The ${𝒫}_S$ projection may be split into a simplex projection for the constraint ${\sum }_{j=0}^d{\sum }_{i=1}^m{\mathbf{Z}}_{i1}^j=1,{\mathbf{Z}}_{i1}^j\ge 0\forall i,j$ and a non-negativity constraint ${\mathbf{Z}}_{ni}^j\ge 0\forall i,j$ and $n>1$. We perform the simplex projection in $\left(dm\right)\mathrm{l}\mathrm{o}\mathrm{g}\left(dm\right)$ time using the algorithm of [13]; the non-negativity projection is simply thresholding elements at zero and is performed in linear time. The ${𝒫}_B$ linear projection is performed separately for each ${\mathbf{Z}}^j$:

$${𝒫}_{B_j}\left(x\right)=\left(I-\left(A{\left(A{A}^T\right)}^{-1}{A}^T\right)\right)x,$$ (5.5)

where $\left(I-\left(A{\left(A{A}^T\right)}^{-1}{A}^T\right)\right)$ may be precomputed so the per-iteration complexity for the full $B$ projection is $d{m}^4$ since $A$ is a $(m-1)\times m^2$ matrix. Importantly, this projection scheme harnesses the structure of the constraint set by splitting the projections into components that admit fast and simple low-dimensional projections. The full projection algorithm is given in Algorithm 5.2.

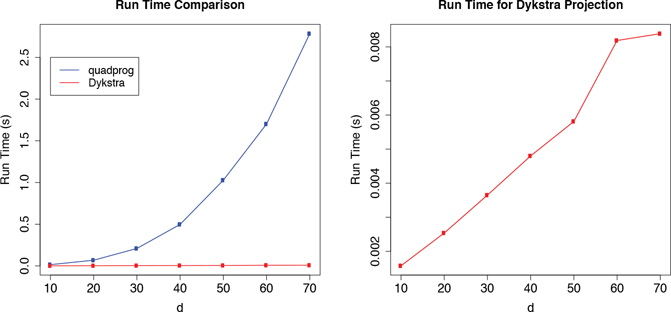
We compare projection times of the Dykstra algorithm to the active set method of [16] implemented in the R package quadprog [43]. The Dykstra projection for the MTD constraints was implemented in C++. Elements of ${\mathbf{Z}}^j$ were drawn independently from a normal distribution with standard deviation .7 and then projected onto $C$. Average run times across 10 random realizations for $d\in (10,20,30,40,50,60,70)$ series and $m=5$ categories are displayed in Figure 4. The Dykstra algorithm was run until iterates changed by less than 10⁻¹⁰. For each run, the elementwise maximum difference between the Dykstra projection and the quadprog projection was always on the scale of 10⁻¹⁰. Across this range of $d$, the quadprog runtime appears to scale quadratically in $d$, with a total run time on the scale of seconds for $d\ge 20$. The Dykstra projection method, however, appears to scale near linearly in this range with run times on the order of milliseconds. We also performed experiments with differing standard deviations for the independent draws of ${\mathbf{Z}}^j$ and observed very similar results.

Figure 4.

(left) A runtime comparison of the quadprog projection method and the Dykstra projection method on a range of time series dimensions. (right) A zoom in of only the compute time of the Dykstra method.

Algorithm 5.1.

Projected gradient algorithm for MTD using Dykstra projections.

Initialize ${\mathbf{Z}}^{(0)}\forall j$

$k=0$

while ${\mathbf{Z}}^{(k)}$ not converged do

compute $\nabla L\left({\mathbf{Z}}^{(k)}\right)$ via Equation 5.1

determine ${\gamma }^k$ by line search [33]

${\mathbf{Z}}^{(k+1)}=\mathrm{Dykstra}MTD\left({\mathbf{Z}}^{(k)}+{\gamma }^k\nabla L\left({\mathbf{Z}}^{(k)}\right)\right)$

end while

return ${\mathbf{Z}}^{(k)}$

5.2. Comparing Model Selection and Optimization in MTD and mLTD.

Approaches to model selection in MTD and mLTD models are conceptually similar; both add regularizing penalties to enforce elements in ${\mathbf{Z}}^j$ to zero. However, these two approaches differ in practice. We explore the differences in selecting for Granger causality between these two approaches via extensive simulations in Section 7.

Both MTD and mLTD models take gradient steps followed by a proximal operation. In the mLTD model, this proximal operation is given by soft thresholding on the elements of ${\mathbf{Z}}^j$. In the MTD optimization the proximal operation reduces to a projection onto the MTD constraint set. Importantly, due to the restricted domain of the MTD parameter set, the normally non-smooth penalty terms become smooth over the constraint set and we thus include them in the gradient step. In mLTD, the soft threshold proximal operation is performed in linear time while in MTD the projection is performed by iteratively using the Dykstra algorithm, where each step of the Dykstra algorithm is performed in log-linear time.

Algorithm 5.2.

DykstraMTD: Dykstra algorithm for projection onto the MTD constraints.

$z={\left({\left({\mathbf{z}}^0\right)}^T,\mathrm{vec}{\left({\mathbf{Z}}^1\right)}^T,\dots ,\mathrm{vec}{\left({\mathbf{Z}}^d\right)}^T\right)}^T$

Let $S$ be the ordered indices of $z$ whose elements belong in the first column of some ${\mathbf{Z}}^j,j>0$ or in ${\mathbf{z}}^0$

Let ($j$) refer to ordered indices of $z$ whose elements belong to ${\mathbf{Z}}^j\forall j$.

$w_0=z$

$u_0=v_0=0$

$l=0$

while $w^l$ not converged do

$y_S^l=\mathrm{Simplex}\text{Projection}\left(w_S^l+p_S^l\right)$ via [13]

$y_{\backslash S}^l=\text{Positive}\text{Threshold}\left(w_{\backslash S}^l+u_{\backslash S}^l\right)$

$u^{l+1}=w_l+u_l-y_l$

$w_{(0)}^k=y_{(0)}^l+v_{(0)}^l$

for $j=l:d$ do

$w_{(j)}^l=P_{B_j}\left(y_{(j)}^l+v_{(j)}^l\right)$ via Equation 5.5

end for

$v^{(l+1)}=y^l+q^l-w^l$

$l=l+l$

end while

return $w^l$

6. Estimation Consistency of MTD Model.

In this section, we establish an upper bound for estimation error of MTD parameters under the group lasso penalty. Analogous results can be obtained for the standard lasso penalty.

We first note that the MTD likelihood is of the same form as a multinomial GLM model with identity link, i.e., with probability modeled as linear combination of covariates. However, the dependence in the time series and the identity link create additional technicalities in the proof, and we will use newly developed concentration and entropy results in the dependent sample setting to overcome these difficulties.

We begin by stating the assumptions. Recall that $X=\left\{x_1,\dots ,x_t,\dots ,x_T\right\}$ is a Markov chain with state space $𝒳$. The transition kernel is given by (2.2) and (2.5). As in [34], we say that $X$ is $\phi$-irreducible, if there exists a non-zero $\sigma$-finite measure $\phi$ on $𝒳$ such that for all $A\subset 𝒳$ with $\phi \left(A\right)>0$ and for all $x\in 𝒳$, there exists a positive integer $n$ such that $P^n(x;A)>0$. Here, $P^n(x;\cdot )$ is the distribution of $x_n$ given $x_0=x$. Our first assumption concerns the nature of the data generating model and is rather mild.

Assumption 1.

$X$ is aperiodic and $\phi$-irreducible, and has a unique stationary distribution $\pi$.

For the ease of presentation, we will write the MTD likelihood as a multinomial model with identity link. Let $I\{\cdot \}$ be the indicator function. Define $W_{t0}={\left(W_{t0}^1,\dots ,W_{t0}^m\right)}^{\mathrm{\top }}\in {\mathbb{R}}^m$ where $W_{t0}^l=I\left\{x_{it}=l\right\}$, and hence $W_{t0}$ indicates the state of time series $i$ at time $t$. We define $W_{tj}={\left({\left(W_{tj}^1\right)}^{\mathrm{\top }},\dots ,{\left(W_{tj}^m\right)}^{\mathrm{\top }}\right)}^{\mathrm{\top }}\in {\mathbb{R}}^{m^2}$, for each $j\in \{1,\dots ,d\}$, where $W_{tj}^l={\left(W_{tj}^{l1},\dots ,W_{tj}^{lm}\right)}^{\mathrm{\top }}$ and $W_{tj}^{lk}=I\left\{x_{it}=l,x_{j(t-1)}=k\right\}$. Hence, $W_{tj}$ indicates both the state of time series $i$ at time $t$ and the state of time series $j$ at time $t-1$. Define a new covariate vector $W\in {\mathbb{R}}^{m+d{m}^2}$ as $W_t={\left(W_{t0}^{\mathrm{\top }},W_{t1}^{\mathrm{\top }},\dots ,W_{td}^{\mathrm{\top }}\right)}^{\mathrm{\top }}$. We note that each component of $W$ can take values only in {0, 1}, and denote the possible values of $W$ as $𝒲$. The MTD model can then be written as

$$p\left(x_{it}|x_{t-1}\right)=W_t^{\mathrm{\top }}{\beta }^0,$$ (6.1)

where ${\beta }^0\in {\mathbb{R}}^{m+d{m}^2}$ is the coefficient of interest defined in terms of $\mathbf{Z}$’s. Specifically, for a general set of MTD parameters, we let ${\beta }_0={\mathbf{Z}}^0,$ ${\beta }_j=\mathrm{v}\mathrm{e}\mathrm{c}\left({\mathbf{Z}}^j\right)$ for $j\in \{1,\dots ,d\}$ and define $\beta ={\left({\beta }_0^{\mathrm{\top }},{\beta }_1^{\mathrm{\top }},\dots ,{\beta }_d^{\mathrm{\top }}\right)}^{\mathrm{\top }}$. In other words, the first $m$ components correspond to the intercept and each subsequent consecutive $m^2$ components correspond to a transition matrix. The superscript 0 denotes the true parameter value.

Denote the group lasso penalty by $\mathrm{\Omega }(\beta )={\sum }_{j=1}^d{∥{\beta }_j∥}_2={\sum }_{j=1}^d{∥{\mathbf{Z}}^j∥}_F$, where the intercept is left unpenalized. The MTD optimization problem can be written as

$${\mathrm{minimize}}_{\beta }\left\{-\frac{1}{T}\sum _{t=1}^T\log \left(W_t^{\top }\beta \right)+\lambda \mathrm{\Omega }(\beta )\right\},$$ (6.2)

$$\text{subject}\text{to}\left(I_d\otimes A\right){\beta }_{1:d}=0,m{\mathbf{1}}^{\top }{\beta }_0+\sum _{j=1}^d{\mathbf{1}}^{\top }{\beta }_j=m,\beta \ge 0.$$ (6.3)

Let $R_n$ and $R$ be the empirical and conditional expected negative log-likelihood risks, respectively

$$R_n(\beta )=-\frac{1}{T}\sum _{t=1}^T\log \left(W_t^{\top }\beta \right);R(\beta )=-\frac{1}{T}\sum _{t=1}^T\mathbb{E}\left[\log \left(W_t^{\top }\beta \right)|{𝒜}_{t-1}\right],$$ (6.4)

where ${𝒜}_t$ is the $\sigma$-algebra generated by $x_1,\dots ,x_t$. Furthermore, let $S$ denote the active set of ${\beta }^0$, i.e., $S=\left\{j:j>0,{\beta }_j^0\ne 0\right\}$ and $S^c$ denote its complement in $\{1,\dots ,d\}$. We define ${\mathrm{\Omega }}^{+}(\beta )={\sum }_{j\in S}{∥{\beta }_j∥}_1$ and ${\mathrm{\Omega }}^{-}(\beta )={\sum }_{j\in S^c}{∥{\beta }_j∥}_1$. With this formulation, we are now ready to state the next assumptions.

Assumption 2.

For all $W\in 𝒲$ such that $W^T{\beta }^0\ne 0,W^T{\beta }^0\ge c(T,d)$ for some function $c$ that only depends on $T$ and $d$. Moreover, we assume that

$$\frac{\left|S\right|}{c^2(T,d)}\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}(d){\mathrm{l}\mathrm{o}\mathrm{g}}^3\left(T\right)}{T}}=o\left(1\right).$$ (6.5)

Assumption 3.

Define a semi-norm $\tau (\cdot )$ as $\tau (\beta )=\sqrt{{\beta }^{\mathrm{\top }}{\mathbb{E}}_{\pi }\left[W_t{W}_t^{\mathrm{\top }}\right]\beta }$. For a stretching factor $L\ge 1$, define

$${\mathrm{\Gamma }}_{\mathrm{\Omega }}(L,S,\tau )={\left(\underset{\beta }{\mathrm{m}\mathrm{i}\mathrm{n}}\left\{\tau \left(\beta \right):\beta \in ℬ,{∥{\beta }_0∥}_1+{\mathrm{\Omega }}^{+}\left(\beta \right)=1,{\mathrm{\Omega }}^{-}\left(\beta \right)\le L\right\}\right)}^{-1},$$ (6.6)

$${\varphi }^2(L,S,\tau )={\mathrm{\Gamma }}_{\mathrm{\Omega }}^{-2}(L,S,\tau )\left|S\right|,$$ (6.7)

where $ℬ$ is the set of all $\beta$ that can be written as a scaled difference between two vectors that satisfy the MTD model constraints and identifiability constraints. We assume that for some $L\ge 1,{\varphi }^2(L,S,\tau )\ge c_1$ for some constant $c_1$.

Assumption 2 states that the transition probabilities are either 0 or bounded away from 0 by some quantity that only depends on the sample size and dimension. We further assume that this quantity is larger than the estimation error, which we will derive later. It ensures that when the parameter estimates are close to the true value, the likelihoods are also close. This in general may not be the case, as log(⋅) is unbounded when its argument approaches 0 and is not Lipschitz-continuous. Assumption 3 is a compatibility condition, often used in establishing estimation consistency of lasso-type estimators [8]. It is slightly weaker than the restricted eigenvalue condition which is also commonly used. Intuitively, this assumption requires that inactive groups are not too correlated with the active ones. The requirement that $\beta \in ℬ$ constrains the inherent co-linearity among the covariates.

Due to the Markovian structure, the design ${\left(W_t\right)}_{t=1}^T$ has to be treated as random, yet the compatibility constant is defined using population quantities. Hence, we need to show that the sample version of compatibility constant converges to its population counterpart defined in Assumption 3. To this end we use concentration results for Markov chains developed in [34] based on spectral methods.

A key quantity for the concentration results is the pseudo spectral gap of the chain [34]. We re-state the relevant definitions here for completeness. Let $L^2\left(\pi \right)$ be the Hilbert space of complex valued measurable functions on $𝒳$ that are square integrable with respect to $\pi$. We equip $L^2\left(\pi \right)$ with the inner product $⟨f,g{⟩}_{\pi }=\int f{g}^{\mathrm{*}}d\pi$. Define a linear operator $\mathbf{P}$ on $L^2\left(\pi \right)$ as $\left(\mathbf{P}f\right)\left(x\right)={\mathbb{E}}_{P(x,\cdot )}\left(f\right)$, which is induced from the transition kernel $P$. The spectrum of a chain is defined as

$$S_2=\{\lambda \in \mathbb{C}:(\lambda \mathbf{I}-\mathbf{P}{)}^{-1}\text{does}\text{not}\text{exist}\text{as}\text{a}\text{bounded}\text{linear}\text{operator}\text{on}{L}^2(\pi )\}.$$ (6.8)

If $\mathbf{P}$ is a self-adjoint operator, the spectral gap is defined as

$$\gamma =\left\{\begin{array}{ll}1-\mathrm{s}\mathrm{u}\mathrm{p}\left\{\lambda :\lambda \in S_2,\lambda \ne 1\right\}& \text{if}\text{eigenvalue}1\text{has}\text{multiplicity}1,\\ 0& \text{otherwise.}\end{array}\right.$$ (6.9)

The self-adjointness of $\mathbf{P}$ corresponds to the reversibility of the Markov chain with transition kernel $P$. In general, the chain specified by the MTD model may not be reversible. In this case, define the time reversal of $P$ as the transition kernel

$$P^{\mathrm{*}}(x,y)=\frac{P(y,x)}{\pi \left(x\right)}\pi (y).$$ (6.10)

Then, the induced linear operator ${\mathbf{P}}^{\mathrm{*}}$ is the adjoint of $\mathbf{P}$ on $L^2\left(\pi \right)$. Note that when the chain is indeed reversible, we have ${\mathbf{P}}^{\mathrm{*}}=\mathbf{P}$. Finally, the pseudo spectral gap of $\mathbf{P}$ is defined as

$${\gamma }_{ps}=\underset{k\ge 1}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{\gamma ({({\mathbf{P}}^{\mathrm{*}})}^k{\mathbf{P}}^k)/k\right\},$$ (6.11)

where $\gamma ({({\mathbf{P}}^{\mathrm{*}})}^k{\mathbf{P}}^k)$ denotes the spectral gap of the self-adjoint operator ${({\mathbf{P}}^{\mathrm{*}})}^k{\mathbf{P}}^k$. See Section 3.1 in [34] for additional discussion on the pseudo spectral gap. We make the following assumption on the pseudo spectral gap:

Assumption 4.

The pseudo spectral gap ${\gamma }_{ps}$ satisfies $|S|\sqrt{\mathrm{l}\mathrm{o}\mathrm{g}\left(d\right)/T{\gamma }_{ps}}=o(1)$.

This assumption requires that as $d$ grows, the pseudo spectral gap of the chain does not approach 0 too fast. For a uniformly ergodic chain, the pseudo spectral gap is closely related to its mixing time, and this assumption requires that the mixing time does not grow too large. If ${\gamma }_{ps}$ is lower bounded by some constant, Assumption 4 reduces to an assumption on the dimension and sparsity relative to the sample size. Methods have been proposed to estimate the pseudo spectral gap [44], which can be used to assess the validity of this assumption empirically.

We are now ready to state our main theorem on the estimation error of the MTD model.

Theorem 6.1.

(Estimation error) Let $0<\delta <1$. Suppose that there exists $M_{\mathrm{m}\mathrm{a}\mathrm{x}}\ge 0and{\lambda }_{ϵ}$ such that for all $0\le M\le M_{\mathrm{m}\mathrm{a}\mathrm{x}}$

$$\underset{\beta :{∥{\beta }_0-{\beta }_0^0∥}_1+\mathrm{\Omega }\left(\beta -{\beta }^0\right)\le M}{\mathrm{s}\mathrm{u}\mathrm{p}}\left|\left(R_n\left(\beta \right)-R\left(\beta \right)\right)-\left(R_n\left({\beta }^0\right)-R\left({\beta }^0\right)\right)\right|\le {\lambda }_{ϵ}M,$$ (6.12)

and

$$\frac{32{\lambda }_{ϵ}(1+\delta {)}^2|S|}{{\delta }^2{\varphi }^2(1/(1-\delta ),S,\tau )}\le M_{\mathrm{m}\mathrm{a}\mathrm{x}}.$$ (6.13)

Take $\lambda \ge 8{\lambda }_{ϵ}/\delta$. Then, under Assumption 1 and Assumption 4, for sufficiently large $T$, we have that

$${∥{\hat{\beta }}_0-{\beta }_0^0∥}_1+\mathrm{\Omega }(\hat{\beta }-{\beta }^0)\le \frac{4\lambda (1+\delta {)}^2|S|}{\delta {\varphi }^2(\frac{1}{1-\delta },S,\tau )}.$$ (6.14)

Furthermore, under Assumption 3, the RHS is upper bounded by $C\left(\delta \right)\lambda \left|S\right|$ where $C\left(\delta \right)$ is a constant depending on $\delta$.

This theorem states that the estimation error defined in terms of $\mathrm{\Omega }(\cdot )$ is closely related to ${\lambda }_{ϵ}$. The next lemma quantifies the magnitude of ${\lambda }_{ϵ}$.

Lemma 6.2.

Under Assumption 2 and Assumption 3, we can take ${\lambda }_{ϵ}$ and $M_{\mathrm{m}\mathrm{a}\mathrm{x}}$ to satisfy (6.12) and (6.13), and

$${\lambda }_{ϵ}=O_p\left(\frac{1}{c(T,d)}\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}\left(d\right){\mathrm{l}\mathrm{o}\mathrm{g}}^3\left(T\right)}{T}}\right),M_{\mathrm{m}\mathrm{a}\mathrm{x}}=O(c(T,d)).$$ (6.15)

Combining Theorem 6.1 and Lemma 6.2, we have the following corollary.

Corollary 6.3. Under Assumptions 1–4, we have that

$${∥{\hat{\beta }}_0-{\beta }_0^0∥}_1+\mathrm{\Omega }(\hat{\beta }-{\beta }^0)=O_p\left(\frac{\left|S\right|}{c(T,d)}\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}\left(d\right){\mathrm{l}\mathrm{o}\mathrm{g}}^3\left(T\right)}{T}}\right).$$ (6.16)

If the minimal nonzero transition probability is large enough so that $1/c(T,d)=O\left(1\right)$, we get a convergence rate of $O_p\left(|S|\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}\left(d\right){\mathrm{l}\mathrm{o}\mathrm{g}}^3\left(T\right)}{T}}\right)$. Compared with the classical results on the estimation error of lasso (see, for example, [5]), we have an extra $\mathrm{l}\mathrm{o}\mathrm{g}\left(T\right)$ term. This is due to a concentration result in the dependent data setting [40]. Investigating whether this log factor can be removed would be an interesting question for future research.

Based on the estimation error bound, one can consider a thresholded version of the MTD estimator to achieve variable selection consistency. The thresholding step helps eliminating false positives, without the stringent irrepresentable condition, which is required for variable selection consistency of the lasso [30]. Specifically, we can use a threshold of $c_t\sqrt{\frac{\mathrm{l}\mathrm{o}\mathrm{g}\left(d\right)\mathrm{l}\mathrm{o}\mathrm{g}3\left(T\right)}{T}}$ for some appropriately chosen $c_t$. If we additionally assume that the minimal signal strength is of order larger than the estimation error bound, we can achieve variable selection consistency asymptotically.

7. Experiments.

We study the performance of our approaches to Granger causality detection in categorical time series. First, we compare penalized mLTD and MTD methods across multiple simulated data scenarios in Section 7.1. In Section 7.2 we apply our penalized MTD method to detect Granger causal connectivity between musical elements in a music dataset of Bach chorales and in Section 7.3 between iEEG sensors during seizures in an awake canine.

7.1. Simulated Data.

We perform a set of simulation experiments to compare the MTD and mLTD model selection methods. Specifically, we compare the MTD group lasso, $L_1$-MTD, and mLTD group lasso methods on simulated categorical time series generated from a sparse MTD model, a sparse mLTD model and a sparse latent vector autoregressive model (VAR) with quantized outputs. In the sparse VAR setting, we also compare the three proposed methods to a penalized VAR fit using the ordinal categorical variables. For all experiments, we consider time series of length $T\in (200,400,800,1600)$, $d\in (15,25)$, and number of categories $m\in (\mathrm{2,3},\mathrm{4,5},6)$. We first explain the details of each simulation condition and then discuss the results.

Sparse MTD.

For the MTD model, we randomly generate parameters by ${\gamma }_{ij}\sim \frac{z_{ij}{\varphi }_{ij}}{{\sum }_{l=1}^d{z}_{il}{\varphi }_{il}}$ where ${\varphi }_i\sim \mathrm{D}\mathrm{i}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{h}\mathrm{l}\mathrm{e}\mathrm{t}\left(\alpha \right)$ and $z_{ij}\sim \mathrm{B}\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{a}\mathrm{l}\left(\delta \right)$. We let $\delta =.15,$ $\alpha =5$. Columns of ${\mathbf{P}}^{ij}$ are generated according to ${\mathbf{P}}_{:l}^{ij}\sim \mathrm{D}\mathrm{i}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{h}\mathrm{l}\mathrm{e}\mathrm{t}(\gamma )$ with $\gamma =.7$. (Note that here we have added a superscript $i$ to $\mathbf{P}$ to specifically indicate the $j$ to $i$ interaction, whereas previously we dropped the $i$ index for notational simplicity by assuming we were just looking at the series $i$ term.) To ensure that the columns are not close to identical in ${\mathbf{P}}^{ij}$ (which would imply Granger non-causality), ${\mathbf{P}}^{ij}$ is sampled until the average total variation norm between the columns is greater than some tolerance $\rho$. This ensures that non-causality occurs only when ${\mathbf{P}}^{ij}$ are zero, and not due to equal columns in the simulation. For our simulations, we set $\rho =.3$. A lower value of $\rho$ makes it more difficult to learn the Granger causality graph since some true interactions might be extremely weak.

Sparse mLTD.

For the mLTD model, the nonzero ${\mathbf{Z}}^{ij}$ parameters are generated by ${\mathbf{Z}}_{lk}^{ij}\sim z_{ij}N\left(0,{\sigma }_Z^2\right)$ where $z_{ij}\sim \mathrm{B}\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{a}\mathrm{l}\left(\delta \right)$ with $\delta =.15$.

Sparse Latent VAR.

To examine data generated from neither of the models considered, we simulate data from a continuous time series $y_t\in {\mathbb{R}}^d$ according to a sparse VAR(1):

$$y_t=A{y}_{t-1}+{ϵ}_t,$$ (7.1)

where ${ϵ}_t\sim N\left(0,{\sigma }^2{I}_d\right)$. The sparse matrix A is generated by first sampling entries $B_{ij}\sim N\left(0,{\sigma }_A^2\right)$ and then setting $A_{ij}=B_{ij}{z}_{ij}$, where $z_{ij}\sim \mathrm{B}\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{a}\mathrm{l}\left(\delta \right)$ with $\delta =.15$. We then quantize each dimension, $y_{it}$, into $m$ categories to create a categorical time series $x_{it}$. For example, when $m=3,$ $x_{it}=1$ if $y_{it}$ is in the (0,.33) quantile of $\left\{y_{i1},\dots y_{iT}\right\}$, and so forth.

Results.

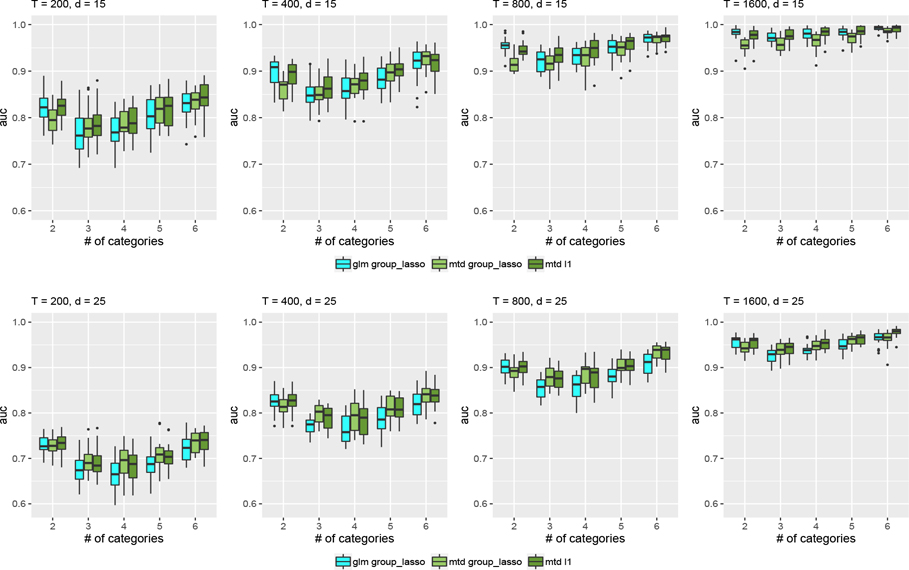
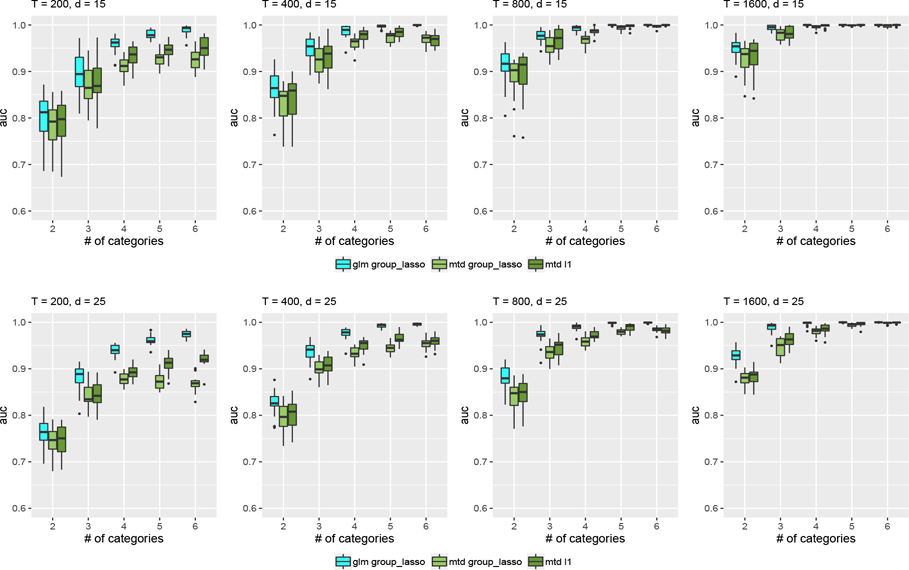
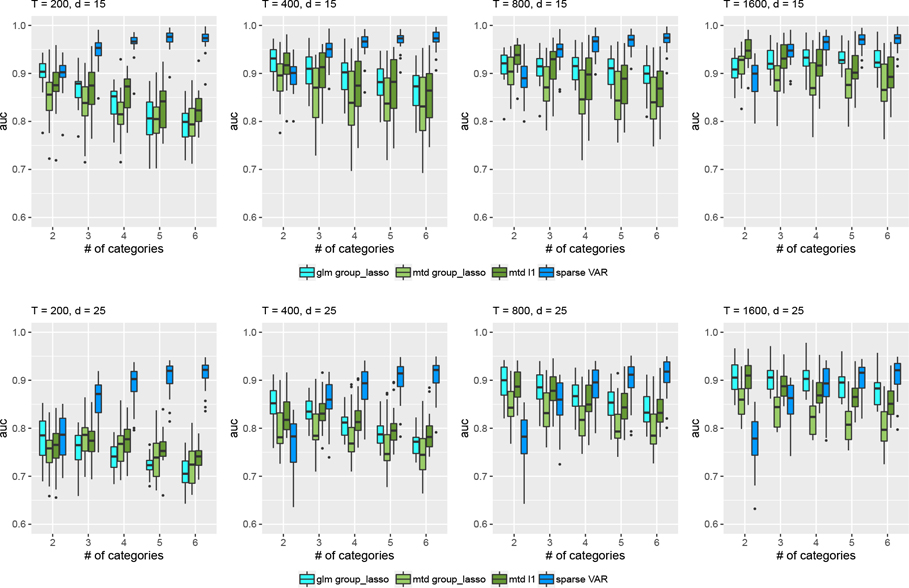
For all methods — MTD $L_1$, MTD group lasso, and mLTD group lasso — we compute the true positive rate and false positive rate over a grid of $\lambda$ values, and trace out the ROC curve. We then compute the area under the ROC curve. The results are displayed as boxplots across 20 simulation runs in Figures 5, 6, and 7 for the categorical time series generated by MTD, mLTD, and latent VAR, respectively. We note that the mLTD group lasso model performs best when the data are generated from a mLTD, and likewise the MTD $L_1$ and MTD group lasso perform better when the data are generated from a MTD. As pointed out in [20], when the groups are homogeneous in the sense that most coefficients in the active group are nonzero, group lasso tends to perform well. This is the case in the MTD model as the coefficients in nonzero ${\mathbf{P}}^{ij}$ are generated from a Dirichlet distribution. However, this principle is less applicable when the data are generated from a mLTD model as we have model misspecification. MTD with either group lasso or lasso penalty tries to find the best MTD approximation to the true data generating mechanism. Interestingly, for data generated from mLTD, we see improved performance as a function of the number of categories $m$ for all $T$ and $d$ settings, while for MTD performance starts high, dips and goes back up with increasing $m$. This is probably due to the simulation conditions, as in both MTD and mLTD models Granger causality can be quantified as the difference between the columns of ${\mathbf{Z}}^{ij}$. When there are more categories, there is higher probability under our simulation conditions that there will be some columns with large deviation from other columns in ${\mathbf{Z}}^{ij}$. This leads to improved Granger causality detection when it exists. Furthermore, we notice that in general the performances of all three methods are better when the data are generated from a mLTD model compared to a MTD model. This is again related to the simulation conditions. In the MTD model, the columns of ${\mathbf{Z}}^{ij}$ are generated from a Dirichlet distribution with values constrained between 0 and 1, and the differences among columns are in general smaller than those in the mLTD model where the coefficients are generated using a normal distribution. Thus the connections among time series in the sense of Granger causality are weaker in the MTD model than the mLTD model. The difference in the signal strengths is illustrated in Figure SM3 in the Supplementary Material.

Figure 5.

AUC for data generated by a sparse MTD process. Boxplots over 20 simulation runs.

Figure 6.

AUC for data generated by a sparse mLTD process. Boxplots over 20 simulation runs.

Figure 7.

AUC for data generated by a sparse latent VAR process. Boxplots over 20 simulation runs.

In the latent VAR simulation, the MTD $L_1$ and the mLTD methods have comparable performance, and both outperform the MTD group lasso approach. However, under model misspecfication, the relative performance of these methods might depend on how well they approximate the true data generating mechanism. There is also evidence of worsened performance for all three methods as the quantization of the latent VAR processes becomes finer, and the number of categories increases. This might be due to the increased extent of model misspecification. We additionally compare the proposed methods to a sparse VAR fit, where we use the ordinal categorical variables directly. We observe that when the number of categories is small, our proposed methods perform similarly to the sparse VAR approach, as not much information is lost by ignoring the order. However, as the number of categories increases, sparse VAR approach performs better by taking the order into account.

As expected, across all simulation conditions and estimation methods increasing the sample size $T$ leads to improved performance while increasing the dimension $d$ worsens performance.

We additionally present the median ROC curves in the Supplementary Material, along with points on the ROC curves chosen by cross-validation and BIC. In general, our numerical experiments indicate that the values of the tuning parameter selected by cross-validation tend to over-select edges, which has been observed in previous studies [29]. This highlights the importance of the thresholding step to reduce false positives. In contrast, BIC tends to give a large tuning parameter and results in an overly sparse graph when the sample size is small compared to the dimension; however, its performance improves considerably with large sample sizes.

7.2. Music Data Analysis.

We analyze Granger causality connections in the ‘Bach Choral Harmony’ data set available at the UCI machine learning repository [27] (https://archive.ics.uci.edu/ml/datasets/Bach+Chorales). This data set, which has been used previously [38, 15], consists of 60 chorales for a total of 5665 time steps. At each time step, 15 unique discrete events are recorded. There are 12 harmony notes, {C, C#, D, F#, D#, E, F, G, G#, A, A#, B}, that take values either ‘on’ (played) or ‘off’ (not played), i.e., $x_{jt}\in \left\{\mathrm{0,1}\right\}$ for $j\in \{1,\dots ,12\}$. There is a ‘meter’ category taking values in $\{1,\dots ,5\}$, where lower numbers indicate less accented events and higher numbers higher accented events. There is also the ‘pitch class of the base note’, taking 12 different values and a ‘chord’ category. We group all chords that occur less than 200 times into one group, giving a total of 12 chord categories.

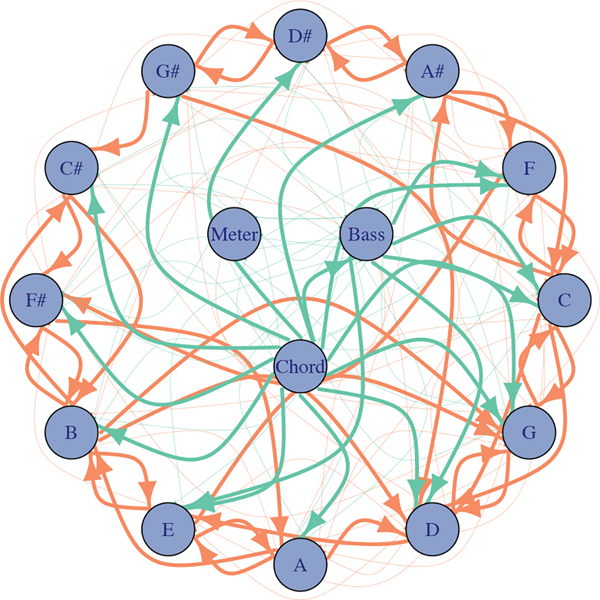
We apply the sparse MTD model for Granger causality selection. As the sample size is relatively small compared to the number of time series and number of categories per series, we choose the tuning parameter $\lambda$ by five-fold cross validation over a grid of $\lambda$ values. However, since cross-validation tends to over-select Granger causality relationships, we threshold the $\gamma$ weights at .01. The estimated resulting Granger causality graph is plotted in Figure 8. To aide in the presentation of our structural analysis below, we bold all edges with $\gamma$ weight magnitudes greater than .06.

Figure 8.

The Granger causality graph for the ‘Bach Choral Harmony’ data set using the penalized MTD method. The harmony notes are displayed around the edge in a circle corresponding to the circle of fifths. Orange links display directed interactions between the harmony notes while green links display interactions to and from the ‘bass’, ‘chord’, and ‘meter’ variables.

The harmony notes in the graph are displayed in a circle corresponding to the circle of fifths; the circle of fifths is a sequence of pitches where the next pitch in the circle is found seven semitones higher or lower, and it is a common way of displaying and understanding relationships between pitches in western classical music. Plotting the graph in this way shows substantially higher connections with respect to sequences on this circle. For example, moving both clockwise and counter-clockwise around the circle of fifths we see strong connections between adjacent pitches, and in some cases strong connections between pitches that are two hops away on the circle of fifths. Strong connections to pitches far away on the circle of fifths are much rarer. Together, the results suggest that in these chorales there is strong dependence in time between pitches moving in both the clockwise and counter-clockwise direction on the circle of fifths.

We also note that the ‘chord’ category has very strong outgoing connections implying it has strong Granger causality relationship with all harmony pitches. This result is intuitive, as it implies that there is strong dependence between what chord is played at time step $t$ and what harmony notes are played at time step $t+1$. The ‘bass’ pitch is also influenced by ‘chord’ and tends to both influence and be influenced by most harmony pitches. Finally, we note that the ‘meter’ category has much fewer and weaker incoming and outgoing connections, capturing the intuitive notion that the level of accentuation of certain notes does not really relate to what notes are played.

As mentioned in Section 3.2.1, the MTD model is much more appropriate than the mLTD model for this type of exploratory Granger causality analysis: The $\gamma$ weights intuitively describe the amount of probability mass that is accounted for in the conditional probability table, giving an intuitive notion of dependence between categorical variables. In the mLTD model, in contrast, there is not as an intuitive interpretation of ‘link strength’ between two categorical variables due to the non-linearity of the softmax function. For this reason, it is not clear how to define the strength of interaction and dependence given a set of estimated ${\mathbf{Z}}^{ij}$ parameters. We still attempted to draw such a comparison. We chose to use the normalized $L_2$ norm of each ${\mathbf{Z}}^{ij}$ matrix, $\frac{∥{\mathbf{Z}}^{ij}∥}{\sqrt{m_i}\sqrt{m_j}}$, as a measure of connection strength in the mLTD model. However, this metric does not have a direct interpretation with respect to the conditional probability tensor. Due to these interpretational difficulties, we present the results of the mLTD Bach analysis in the Supplementary Material. We note here that the final graph shows some of the structure of the MTD analysis: strong connections between chord and the harmony notes and some strong connections between notes on the circle of fifths. However, in general, the resulting graph is much less sparse and interpretable than the MTD graph.

7.3. Functional Connectivity in Canine iEEG.

We analyze functional connectivity among intracranial electroencephalogram (iEEG) sensors during seizures in an awake canine [11]. The data was collected from a single canine undergoing seizures and is available at ieeg.org [9]. Recent time series segmentation of iEEG data around seizure events has shown that different discrete dynamic states are active before, during, and after a seizure onset [45, 11]. We analyze Granger causal connectivity between the iEEG recording channels at the level of these discrete dynamic states, providing a Granger causal analysis at a more abstract level. Specifically, we segment the continuous measurements into nominal categorical states using a Markov switching autoregressive model. This analysis illustrates which channel’s dynamic states are predictive of another channel’s states.

Each of 18 iEEG recordings from a single dog contains $d=16$ channels and $T=20000$ time points corresponding to a two minute window around a seizure event. The time series for each channel was segmented into a categorical time series with $m=5$ states using a Markov switching autoregressive model of multiple time series [46, 45]. See the Supplementary Material for details on the segmentation model and procedure.

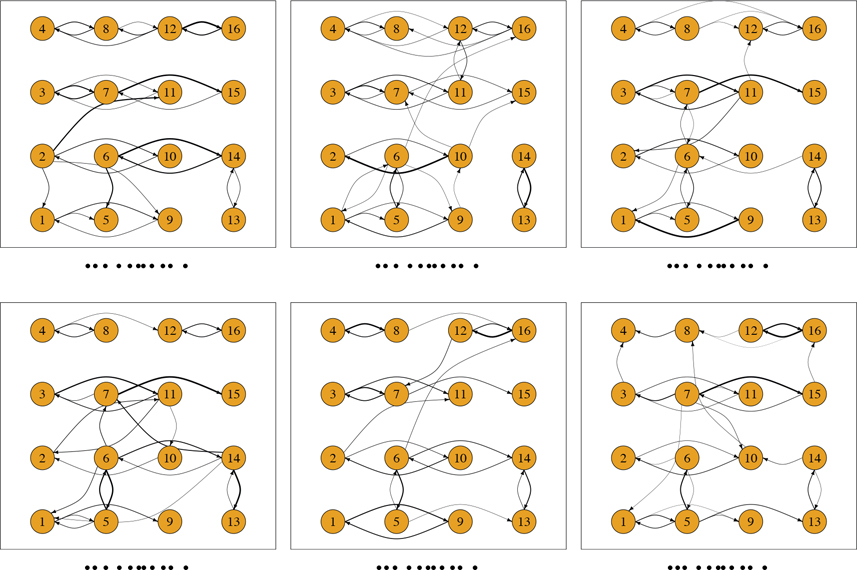
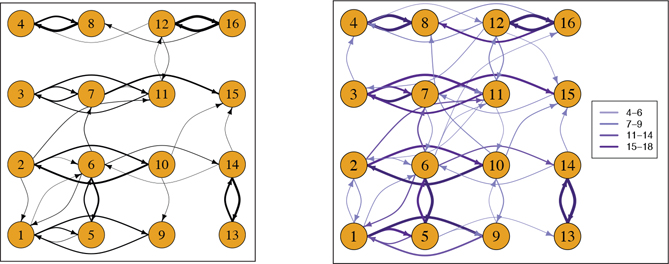
We separately apply our sparse MTD model to the resulting iEEG multivariate categorical time series from 18 different seizure events. For each seizure, the hyperparameter $\lambda$ was varied over 800 values sampled uniformly between 0.01 and 100000. As the sample size is large, the final model was selected by the Bayesian information criterion (BIC). The resulting estimated graphs for six representative seizure events are shown in Figure 9. For aided interpretability, only edges that contribute more than 1% of the total conditional probability tensor are displayed. In Figure 10 we display two graphs that summarize Granger causality across all 18 seizures. In the first, we compute the average edge weight across all seizures and threshold the final graph at 0.5%. In the second, for each edge we display the number of times that edge is included across all seizures.

Figure 9.

Granger causality graphs estimated from a sparse MTD model across six different seizure events for canine iEEG data.

Figure 10.

(left) Graph weighted by the average across 18 siezures and (right) graph weighted and colored by the number of edge inclusions across 18 seizures.

The graphs in Figures 9 and 10 indicate persistent shared structure across seizures. The four nodes in the same row represent a strip of four electrodes that were placed along the anterior-posterior direction. There were two parallel strips of four electrodes on each hemisphere. Most connections appear horizontally across the sensor locations, corresponding to anterior-posterior connections among regions within the same strip, which should be close both spatially and functionally. The few vertical connections are between adjacent rows, which represent connections between strips next to each other. Some groups of edges like 1 → 9, 14 → 13, 13 → 14, 3 → 7, 7 → 3, 4 → 8, 8 → 4, 12 → 16, 16 → 12 and others, appear in at least fifteen of the seizure graphs, showing the persistence in some Granger causal connectivity across different seizure events. Future work aims to assess the clinical significance of these findings. But, at a high level, we have identified that AR states, that capture the frequency content in individual channel signals, are correlated across time in a structured and sparse manner during seizure events.

8. Discussion.

We have proposed a novel convex framework for the MTD model, as well as two penalized estimation strategies that simultaneously promote sparsity in Granger causality estimation and constrain the solution to an identifiable space. We have also introduced the mLTD model as a baseline for multivariate categorical time series that although straightforward, has not been explored in the literature. Novel identifiability conditions for the MTD have been derived and compared to those for the mLTD model. Finally, we have developed both projected gradient and Frank-Wolfe algorithms for the MTD model that harnesses the new convex formulation. For the projected gradient optimization, we also developed a Dykstra projection method to quickly project onto the MTD constraint set, allowing the MTD model to scale to much higher dimensions. Our experiments demonstrate the utility of both the MTD and mLTD model for inferring Granger causality networks from categorical time series, even under model misspecification.

There are a number of potential directions for future work. Consistency of high dimensional autoregressive GLMs with univariate natural parameters for each series has been recently established [18]. With less stringent parametric assumptions, the MTD model offers a more flexible framework than autoregressive GLMs. To handle this additional flexibility, we need additional assumptions on the Gram matrix and the spectral properties of the process when deriving an upper bound for the estimation error. We also have an extra $\mathrm{l}\mathrm{o}\mathrm{g}\left(T\right)$ factor in the upper bound compared to the results for lasso-type estimators in the independent data setting. This log factor also appears in [18]. Whether it can be removed or not would be an interesting question for future research. Further theoretical comparison between mLTD and MTD is also important. For example, to what extent may a mLTD distribution be represented by an MTD one, and vice versa; or, to what extent are both models consistent for Granger causality estimation under model misspecification? Our simulation results suggest that both methods perform well under model misspecification but more general theoretical results are certainly needed. Our sparse MTD framework also presents a simple approach to sparsity estimation under simplex constraints. As mentioned in Section 4.1, typically $L_1$ penalties are avoided under simplex constraints since the sum is constrained to equal one. Many authors have proposed a variety of non-convex sparsity regularizers that demand more involved optimization routines [35]. Inspired by our work with MTD, a simple solution is to leave some of the important coefficients known to be in the model unpenalized. For instance, treasury bonds in a sparse portfolio optimization [26] or large background clusters in sparse clustering and density estimation [25, 35].

It would also be interesting to explore other regularized MTD objectives, such as the nuclear norm on ${\mathbf{Z}}^j$ when the number of categories per time series is large. This penalty would both select for sparse dependencies, while simultaneously sharing information about transitions within each ${\mathbf{Z}}^j$. While we have considered sparsity in $\gamma$, in other applications including categorical time series with large state-spaces, such as language modeling, the entries within each ${\mathbf{Z}}^j$ might be sparse. Comparing the projected gradient and Frank-Wolfe algorithms in these sparse, large state-space settings would be interesting. Another possible extension includes the hierarchical group lasso over lags for higher order Markov chains [31] to automatically obtain the order of the Markov chain. Overall, the methods presented herein open many new opportunities for analyzing multivariate categorical time series both in practice and theoretically.