The Utility of Mixed Effects Models in the Evaluation of Complex Genomic Traits In Vitro

Abstract

In pharmacogenomic studies, the use of human liver microsomes as a model system to evaluate the impact of complex genomic traits (i.e., linkage-disequilibrium patterns, coding, and non-coding variation, etc.) on efficiency of drug metabolism is challenging. To accurately predict the true effect size of genomic traits requires large richly sampled datasets representative of the study population. Moreover, the acquisition of this data can be labor-intensive if the study design or bioanalytical methods are not high throughput, and it is potentially unfeasible if the abundance of sample needed for experiments is limited. To overcome these challenges, we developed a novel strategic approach using non-linear mixed effects models (NLME) to determine enzyme kinetic parameters for individual liver specimens using sparse data. This method can facilitate evaluation of the impact that complex genomic traits have on the metabolism of xenobiotics in vitro when tissue and other resources are limited. In addition to facilitating the accrual of data, it allows for rigorous testing of covariates as sources of kinetic parameter variability. In this in silico study, we present a practical application of such an approach using previously published in vitro cytochrome P450 (CYP) 2D6 data and explore the impact of sparse sampling, and experimental error on known kinetic parameter estimates of CYP2D6 mediated formation of 4-hydroxy-atomoxetine in human liver microsomes.

SIGNIFICANCE STATEMENT

This study presents a novel non-linear mixed effects model (NLME)-based framework for evaluating the impact of complex genomic traits on saturable processes described by a Michaelis-Menten kinetics in vitro using sparse data. The utility of this approach extends beyond gene variant associations, including determination of covariate effects on in vitro kinetic parameters and reduced demand for precious experimental material.

Introduction

Pharmacogenomic studies remain a key precision medicine tool for evaluating the impact of genetic variability on drug disposition (Woodcock & Lesko, 2009; Reynolds, 2012; Peck, 2018; Huang et al., 2022). Major innovations in DNA sequencing technologies now enable exploration and discovery of previously unidentified polymorphisms and complex genomics traits (Schwarz et al., 2019). Despite these advancements, measuring the effect of often rare and/or coinciding genetic variants on drug disposition remains challenging due to either sample size restrictions and/or the inability to distinguish causal variants from others. This is further complicated by interindividual variability in drug-metabolizing enzyme expression associated with other intrinsic factors (i.e., age, sex, disease state, etc.) and extrinsic factors (i.e., diet, concomitant drug use, and environmental exposures) which are known to impact metabolic activity (Parkinson et al., 2004). There are several methods by which human pharmacokinetic (PK) parameters can be predicted from preclinical pharmacokinetic data and/or in vitro (Obach et al., 1997). Of these methods, in vitro to in vivo extrapolation using human liver microsomes (HLMs) provides a convenient system for evaluating the impact of genetic variants on drug metabolism and in vivo pharmacokinetics.

Variation in genes encoding drug-metabolizing enzymes can produce altered catalytic activity in several ways (Nagar et al., 2021), including amino-acid substitutions that lead to perturbations in protein structure, stability and/or function, modifications of regulatory elements that control gene transcription, and nucleotide insertions and/or deletions that alter gene translation. The downstream impact that genetic variability has on enzymatic activity can be assessed experimentally by estimating the Michaelis-Menten parameters (K_m), and maximum velocity (V_max) (catalytic rate constant $\times$ [E], where E = enzyme abundance) in vitro and comparing the intrinsic clearance (V_max/K_m) values for tissues from donors exhibiting combinations of reference and variant alleles. However, to accurately predict the true effect size of genetic variation on intrinsic clearance (CL_int) at a population level using HLMs often requires large richly sampled datasets representative of the study population in question (Mohatt et al., 2007; LaPierre et al., 2021), and accumulating this data can be labor-intensive and time-consuming if the study design and bioanalytical methods are not high-throughput. An efficient and commonly employed method to address this involves pooling individual HLMs by genotype and comparing the pool's CL_int estimates to a reference group by fitting experimental data using a Michaelis-Menten model (McDonald et al., 2009; Flora & Tracy, 2012; Shirasaka et al., 2016). Although this method provides robust estimates of kinetic parameters, relevant information about the sample population such as between-subject variability and its correlation with known intrinsic or extrinsic factors is lost. Alternatively, another commonly used in vitro approach approximates individual CL_int by evaluating metabolite formation or parent drug depletion at singular sub-saturating substrate concentrations (Dalton et al., 2020) ([S] ≪ K_m); this generally allows for a larger number of individuals to be included in the data analysis, and the retention of covariate information. However, this approach does not provide robust estimates of the underlying kinetic parameters (V_max and K_m) that ultimately determine CL_int, and as a result, there is a loss in mechanistic understanding of the impact that genetic variation has on drug-metabolizing enzyme function.

Population pharmacokinetic/pharmacodynamic (PD) models are powerful tools that use a non-linear-mixed effects modeling approach to study both population and individual-level PK and PD relationships in vivo (Sheiner and Beal, 1980; Bonate, 2005; Sheiner et al., 2015; Bhavatharini et al., 2022). Additionally, the impact of known covariates (i.e., intrinsic and extrinsic factors) on PK parameters (e.g., CL and V) can be incorporated into population PKPD models and quantified as “fixed-effects,” while known sources of unexplained variability (e.g., individual subjects) can be quantified as “random effects”. One key advantage of population PKPD models is the ability to estimate individual PK parameters based on a complete profile of the entire population instead of its individuals; thus, sparse data can be used at the individual level to generate meaningful estimates of both fixed and random effects. Although top-down approaches are not designed to provide a mechanistic understanding of factors that impact PK parameters, a population-based approach using non-linear mixed-effects modeling in vitro can answer these questions while maintaining the previously mentioned advantage of sparse sampling at the individual level; its utility in this regard has been demonstrated extensively in the fields of agronomy and ecology (Archontoulis and Miguez, 2015; Oddi et al., 2019). In this article, we further explore the utility of non-linear mixed-effects models and their practical application in the field of pharmacogenomics, for estimating individual level and population-level Michaelis-Menten kinetic parameters (V_max and K_m) of known cytochrome P450 (CYP) 2D6 variants using a sparse strategic sampling approach. We also explore the utility of mixed effects models for hypothesis testing and characterization of complex genomic traits.

Materials and Methods

Virtual Population Design

A virtual population (n = 9000) consisting of individuals across 9 CYP2D6 genotype groups (*1/*1, *1/*2, *1/*2x2, *1/*4, *2/*2, *2/*3, *2/*4, *4/*41, and *4/*5; 1000 subjects per group) was simulated in silico using R (v4.2.0). Individual microsomal V_max and K_m values were generated randomly and centered by genotype around mean estimates extracted from previously published work (Dinh et al., 2016). Within-group standard deviation for each parameter was fixed at 25% of the extracted mean estimate to simulate the variability observed in in vitro population studies.

In Silico Study Design

In silico experiments were conducted to simulate CYP2D6 mediated formation of 4-hydroxy-atomoxetine (4-OH-ATX) in human liver microsomes using atomoxetine as a probe substrate. Michaelis-Menten kinetics were simulated across substrate concentrations ranging between 0 and 2000 µM using V_max and K_m parameters obtained from individuals in the virtual population. Two types of sampling designs were employed to define substrate concentrations used to generate the Michaelis-Menten profiles: rich and sparse designs. Rich design experiments were conducted using nine overlapping atomoxetine (ATX) incubation concentrations per subject (for extensive and ultra-rapid metabolizers) or 16 overlapping ATX incubation concentrations per subject (for intermediate and poor metabolizers). To determine an optimal sparse design sampling scheme, a pilot study was conducted at the outset to explore the lower limit of a randomized sampling approach. In this pilot study, individuals of a virtual population (n = 21) were randomly assigned to either a 2 or 3 pt sampling scheme with concentrations that were randomly selected across a fixed range (1–100 uM). Results from that study revealed that a 3 pt sampling scheme, where substrate concentration landed above, near, and below the population K_m values, performed the best, whereas 2-point sampling schemes gave the least accurate estimates and were subject to a high degree of model shrinkage (data not shown). Based on these results, for the study at hand, the sparse design experiments used 3–4 staggered incubation concentrations (below, near, and above anticipated K_m value) per subject, with both designs covering similar concentration ranges, depending on the genotype. Residual error was added to simulated data using a constant coefficient of variation structure, where the observed metabolic rate (V_obs) for the i^th individual at the j^th substrate incubation concentration is described by eq. 1. The residual errors (ε_i) were normally distributed with a mean of 0 and a standard deviation (σ) set at the following values: 0, 0.05, 0.10, or 0.2.

Model Development

In silico population modeling was performed in R (v4.2.0) using the NLME (Pinheiro and Bates, 2000) mixed-effects modeling package and supporting packages for data manipulation and graphics. The final model was built by fitting a structural (base) model and a random-effects model with covariates. The structure of the base model was derived from the Michaelis-Menten equation with modifications to V_max and K_m to incorporate both fixed- and random-effects. Product formation rate for the i^th individual at the j^th substrate incubation concentration, defined as (V_ij), was modeled as a function of a Φ_i and substrate concentration (S_i) plus residual error (ε_ij); where Φ_i is a matrix of parameters (Φ_1i and Φ_2i) each being vectors of fixed and random effects whose sum equates to the predicted individual-level estimates of V_max and K_m, respectively (eq. 2). Specifically, individual estimates of V_max (Φ_1i) and K_m (Φ_2i) were defined as the sum of a typical population value for V_max (θ_{1, Vmax}) or K_m (θ_{2, Km}), a fixed covariate effect based on individual CYP2D6 genotype (X_{1i, Genotype Vmax} or X_{2i, Genotype Km}) and an individual specific random effect on both V_max and K_m (η_1i, and η_2i, respectively) (eq. 3). X_{1i, genotype Vmax} and X_{2i, genotype Km} were incorporated as additive fixed-effects under the assumption that they do not depend on the magnitude of the typical value (reference group); rather, they deviate from the typical value by a fixed magnitude. An additive variation was used to describe between-subject variability under the assumption that random effects are distributed evenly across a parameter estimate after accounting for the fixed genotype effect. Individual level random effects (η_i) and residual error (ε_ij) were assumed to be normally distributed with a mean of 0 and ε_ij having a variance of σ². V_max and K_m were assumed to be uncorrelated (independent), therefore variance (${\psi }_i)$ for η_i was structured as a diagonal matrix with covariance set to 0. In scenarios in which the underlying kinetic parameters are log-normally distributed in the population an alternate structure for incorporating random-effects into the model is to use exponential variation as described in eq. 4, where θ_{1, Vmax} and θ_{1, Km} represent the typical population value for V_max and K_m; θ_{2, Vmax} and θ_{2, Km} represent the fixed effect of each genotype on V_max and K_m; X_i,Genotype represents a binary categorical covariate denoting the presence or absence of a specific genotype (0 = no, 1 = yes); and η_1i and η_2i represent individual random-effects on V_max and K_m, respectively.

CL_int estimates were calculated as the quotient of V_max/K_m, with population level intrinsic clearance defined as (θ_{1, Vmax})/(θ_{2, Km}), genotype level defined as (X_{1i, Genotype Vmax} + θ_{1, Vmax})/(X_{2i, Genotype Km} + θ_{2, Km}) and individual level intrinsic clearance defined by Φ_1i/Φ_2i as described in eq. 5.

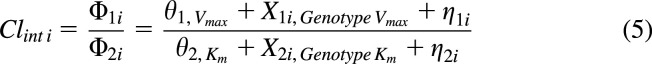Selection of the appropriate covariates and error model were based on Akaike criterion (AIC), F-tests (ANOVA), diagnostic plots, and the precision of the parameter estimate (95% confidence intervals, relative standard error). The final model was weighted using a power residual error structure.

Model Evaluation

CL_int sensitivity was assessed by comparing standardized residuals (Pearson) values for each CYP2D6 genotype across all experimental designs and conditions (rich and sparse designs, 0%–20% coefficient of variation [CV]). Standardized residuals were calculated using eq. 6, where the Pearson residual (R_p,ijk) of the i^th genotype, and the j^th experimental condition for the k^th parameter is equal to the difference between the predicted (P_ijk) estimate of the i^th genotype for the j^th condition and expected value for the k^th parameter divided by the square-root of the expected value for the k^th parameter for the i^th genotype.

Additionally, non-parametric bootstrap analysis based on a total of 120 generated datasets (ten re-sampled populations per experimental condition) was performed to evaluate the precision of the final model parameters. Mean parameter estimates and 95% confidence intervals for each condition were summarized by genotype. Confidence intervals (CIs) were calculated using eq. 7, where CI is equal to the mean value of the sample population ($\overline{x}$) plus or minus the t-score at significance level α (0.05) for N-1 degrees of freedom, $t_{\left(\frac{\alpha }{2}\right),\left(N-1\right)}$ multiplied by the standard error of the sample population mean $S_{\overline{x}.}$

Substrate Depletion Model

An alternative, and mathematically equivalent, method of estimating intrinsic clearance and Michaelis-Menten parameters is by monitoring depletion of parent drug rather than metabolite formation. Here, we assume (1) reaction rate (v), which is the change in substrate concentration over time (d[S]_t/dt), is equal to the change in product formation over time (−d[P]_t/dt) at steady-state, and (2) product formation represents the sum of all metabolic formation clearance pathways for the parent in the system. Reaction rate (v) can be modeled as a substrate dependent hyperbolic relationship defined by a theoretical first-order depletion rate constant observed at infinitesimally low substrate concentrations (k_dep[S]→0) and the K_m, where k_dep[S]→0 is equal to intrinsic clearance (eq. 8). Similar to the Michaelis-Menten equation, a population approach can be applied by re-parameterizing this model to include fixed and random effects (eq. 9). The depletion rate for the i^th individual at the j^th substrate incubation concentration, defined as (v_ij), can be modeled as a function of a Φ_i and substrate concentration (S_i) plus residual error (ε_ij), where Φ_i is a matrix of parameters (Φ_1i and Φ_2i) each being vectors of fixed and random effects whose sum equates to the predicted individual-level estimates of V_max and K_m, respectively.

Results

Virtual Population Characteristics

A summary of the model development workflow can be found in Fig. 1. To generate a virtual population, reported V_max and K_m estimates from 21 HLM donors (Dinh et al., 2016) were used as a proxy to assign Michaelis-Menten values. Average V_max and K_m values across individuals from a total of nine genotype groups were used as the mean estimates for their respective virtual group. A summary of the extracted parameter estimates can be found in Supplemental Table 1. Within-group variability was simulated (n = 1000 per genotype group) using randomly selected and normally distributed values with a standard deviation of 25% of the mean reported genotype group estimate for both V_max and K_m (Fig. 2). Setting the standard deviation for the underlying distribution of the Michaelis-Menten parameters (V_max and K_m) for each genotype to 25% of the original estimate provided a 707-fold range in V_max values (3.47–2457 pmol/min/mg protein) and a 464-fold range in K_m values (0.26–120.53 µM) across the virtual population (n = 9000). Additionally, at 25% CV, within-group variability of Michaelis-Menten parameters exhibited a sixfold range for each CYP2D6 genotype. Population geometric means for V_max and K_m were 181.29 pmol/min/mg protein, and 2.74 μM, respectively. A comparison of the virtual mean estimates and standard deviation for V_max and K_m values versus the actual mean estimate along with their ranges can be found in Supplemental Tables 2 and 18. The experimental population was generated by randomly sampling the virtual population with a total of ten individuals per genotype group (n = 90); a summary of parameter estimates for the sample population (experimental population) can be found in Table 1.

Fig. 1.

NLME model development workflow. UM, EM, IM, and PM in the experimental design represent ultra-rapid metabolizer (UM), extensive metabolizer (EM), intermediate metabolizer (IM), and poor metabolizer (PM), respectively.

Fig. 2.

Distribution of Michaelis-Menten parameters for virtual population (n = 9000) stratified by CYP2D6 genotype. (B) K_m represents the Michaelis-Menten constant, and (A) V_max represents maximal 4-OH atomoxetine formation (pmol/min/mg protein) by CYP2D6 in human liver microsomes.

TABLE 1.

Summary of parameter estimates for sample population

CYP2D6 Genotype	Vmax (pmol/min/mg protein)	Km (μM)	n
*1/*1	373.70 ± 62.84	1.53 ± 0.26	10
*1/*2	495.81 ± 83.38	1.47 ± 0.25	10
*1/*2x2	1486.38 ± 249.95	1.92 ± 0.32	10
*1/*4	288.84 ± 48.57	0.97 ± 0.16	10
*2/*2	265.65 ± 44.67	4.84 ± 0.81	10
*2/*3	264.60 ± 44.5	1.39 ± 0.23	10
*2/*4	101.09 ± 17	1.77 ± 0.30	10
*4/*41	32.57 ± 5.48	5.64 ± 0.95	10
*4/*5	12.99 ± 2.18	72.9 ± 12.26	10

V_max and K_m values represent mean ± standard deviation of each genotype group.

In Silico Experiments

To evaluate the utility of estimating Michaelis-Menten parameters using a non-linear mixed effects modeling approach with a minimal dataset, two in silico experimental designs (rich design, and sparse design) were evaluated against one another. Due to substantial differences in parameter estimates across genotype groups, to characterize the full kinetic profile of 4-OH-ATX formation in vitro, ATX incubation concentrations for extensive metabolizer (EM; *1/*1, *1/*2, *1/*4, *2/*2, *2/*3, and *2/*4) and ultra-rapid metabolizers (UM; *1/*2x2) ranged from 0.1–100 μM, while ATX incubation concentrations for intermediate metabolizers (IM; *4/*41) and poor metabolizers (PM; *4/*5) ranged from 1–2000 μM (Fig. 3). Additionally, each experimental design was subjected to 4 levels of experimental error: 0, 5, 10, and 20% CV (Fig. 4).

Fig. 3.

Illustration of rich sampling design (9–16 points per subject) versus strategic sparse sampling design (3–4 points per subject) for two subjects with the same genotype and no experimental error (0% CV). (A–C) Rich, sparse 4-point, and sparse 3-point experimental designs for extensive and ultra-rapid metabolizers; (D–F) designs for intermediate and poor metabolizers. Black line represents the non-linear least-squares Michaelis-Menten fit for the genotype group.

Fig. 4.

Illustration of experimental error scenarios for three subjects with the same genotype. Black line represents the non-linear least-squares Michaelis-Menten fit for the genotype group.

Model Optimization

A Michaelis-Menten structural model was used to characterize the hyperbolic relationship between the initial reaction rate (V₀) of 4-OH-ATX formation and ATX substrate concentration (S). When fixed covariate effects and individual-level random effects (eqs. 2 and 3) were both incorporated into the model there was improvement in model fit when compared with the base model alone for both rich and sparse sampling designs (ANOVA, p < 0.0001). Additive, proportional, combined (additive + proportional), and power structures were used to model residual error (data not shown). The power residual error structure was selected because it provided the greatest improvement across Akaike information criterion, Bayesian information criterion, and log-likelihood, in addition to eliminating heteroscedastic patterns in residual plots (Supplemental Tables 3–10). Final UM/EM models and IM/PM models stratified by condition are shown in Fig. 5. Summary tables for all models and experimental conditions can be found in the supplementary data (Supplemental Tables 11–14). Model diagnostic plots and the complete code used to perform the data analysis can be found in the supplemental information.

Fig. 5.

In silico NLME predicted Michaelis-Menten fits of 4-hydroxy-atomoxetine formation using human liver microsomes by CYP2D6 extensive metabolizers (*1/*1, *1/*2, *1/*4, *2/*2, *2/*3, and *2/*4), ultra-rapid metabolizers (*1/*2x2), intermediate (*4/*41), and poor metabolizers (*4/*5) across all experimental conditions (sparse 3–4 pt, 0%–20% CV).

Model Evaluation

Sensitivity analysis was conducted to determine the impact of experimental design on parameter estimates (V_max and K_m). Both V_max and K_m estimates were within 2-fold of the reference value across all experimental design conditions (Supplemental Figs. 1 and 2). Additionally, extracted estimates of intrinsic clearance (V_max/K_m) were also evaluated for sensitivity to experimental conditions. Overall, intrinsic clearance estimates for all CYP2D6 genotype groups across each experimental condition were within 2-fold of reference values and the magnitude of the standardized residual (R_p, P = Pearson) of estimated intrinsic clearance from reference values for each group fell within an acceptable range (−2 < R_p< 2) across all conditions (Supplemental Fig. 3); with *1/*2 being the only notable exception for sparse 3 and 4 pt 20% CV sampling designs (R_p = −2.4 and −2.3, respectively). To assess the sensitivity of the model to individuals within the sample population (n = 90 subjects), bootstrap analysis was performed on the original virtual population (n = 9000 subjects), which yielded 10 re-sampled populations datasets for each experimental design and condition (n = 120 new datasets). Each dataset was fit to the final non-linear mixed effects covariate model and fixed effects on V_max and K_m for each CYP2D6 genotype were extracted. Bootstrapped parameter estimates and 95% confidence intervals for V_max and K_m across all conditions for each CYP2D6 genotype are plotted in Supplemental Figs. 4 and 5; tabulated summaries can be found in the supplemental data (Supplemental Tables 15–17). In summary, bootstrapped Michaelis-Menten estimates and their 95% confidence intervals fell within 80%–125% of reference values for the majority of experimental designs and conditions, specifically 88% and 98% of designs for K_m and V_max, respectively. Sparsely sampled designs with high residual error (20% CV) most frequently fell out of this range for K_m (13% of designs) yet infrequently for V_max (<1% of designs). All bootstrapped parameter estimates (and confidence intervals) were within 2-fold of their respective reference values.

Discussion

The concept of conducting population analysis in vitro using human liver microsomes as a model system has been demonstrated previously (Belle et al., 2000) where non-linear mixed effects modeling was used as a tool to identify human CYPs involved in the deethylation of phenacetin to acetaminophen. A two-enzyme non-linear mixed effects kinetic model was fit to a sparse data set, generated from incubations containing human liver microsomes (n = 19) and phenacetin. Variability in CYP1A2 activity was found to correlate with inter-HLM V_max variability, and when CYP1A2 activity was included in the model as a covariate the coefficient of variation improved from 70% to 39%. A noted limitation of that study was a potential data set bias due to the experimental design favoring the identification of the low K_m1 enzyme (CYP1A2) and lacking the optimum design needed to identify the high K_m2 enzyme (CYP2C19). In a subsequent study (Bogacka et al., 2017) this concept was expanded upon by exploring how a categorical factor with covariate information can be a design variable combined with other design factors. Bogacka et al. demonstrated how incorporating optimum design strategies into experimental planning can lead to substantial savings and concluded that optimized designs can be equally efficient using less experimental material than is needed in standard practice or, if a similar experimental effort is allowed, can achieve higher efficiency.

Our analysis demonstrates that the incorporation of genotype as a categorical factor with covariate information in conjunction with a dynamic strategic sampling approach can allow for accurate measurement of metabolic kinetic parameters using 50%–70% fewer primary data than conventional experimental designs. Our strategic sampling approach, using sparse data at the individual level staggered in a manner to create rich data at the covariate level, provided accurate estimates of kinetic parameters associated with CYP2D6 genotype; with a geometric mean percent error of 2.61% (range 0%–9.33%) for V_max and 4.39% (range 0%–55.7%) for K_m across all experimental designs and conditions, when compared with the published estimates. Bootstrap analysis further supported the efficacy of the strategic sampling approach, with mean parameter values and their 95% confidence intervals falling within 80%–125% of published estimates for most experimental designs and condition (88% and 98% of conditions for K_m and V_max, respectively). Additionally, there were minimal differences in parameter estimates and sensitivity to condition between sparse 3 pt and 4 pt sampling strategies, even with experimental errors as high as 10% CV.

In a scenario where metabolic products have not been (or cannot be) characterized, our approach can still be used by adjusting the experimental design to monitor the elimination of the parent drug and switching from a Michaelis-Menten structural model to a substrate depletion model (eq. 8); which has been previously identified as a mathematically equivalent means for monitoring intrinsic clearance of the parent compound in vitro (Nath and Atkins, 2006). Similarly, a non-linear mixed effects model can be applied to estimate kinetic parameters (V_max, and K_m) across a substrate concentration range to approximate intrinsic clearance (k_{depl([S]→0)}) at the individual level (eq. 9). Although modeling in vitro data using a substrate depletion approach is not the focus of this study, the principles remain the same, hence, provides a suitable example for the broad applicability of our method.

While our strategic sampling approach does not leverage optimal design estimators (Fedorov and Leonov, 2013) which statistically determine the best experimental design by using an iterative search algorithm that seeks to minimize the covariance of the parameter estimates for a specified model using optimality criterion (i.e., D and E-optimality), it provides a practical example of how such an approach can be applied empirically, solely based off a sampling range that would be used in a conventionally designed in vitro study. It is important to note that a priori knowledge of a genotype-effect (in vitro or in vivo) is not required when deciding which genotype to include as a covariate in this model, when the goal of a study is to test whether there is a significant difference in activity between a particular variant compared with the reference allele. This is particularly useful for exploratory analysis or hypothesis testing purposes. Moreover, the incorporation of random effects not only allows us to estimate between-subject variability, but also quantify and attribute sources of variability (i.e., inter-day, inter-instrument, and between-analyst variability) many of which are factors unaccounted for when conducting in vitro studies (Piehowski et al., 2013). This additional benefit also provides an opportunity to probe complex characteristics of experimental data, such as an interaction between fixed-effects, and hierarchical random-effect structures (Pinheiro and Bates, 2000) (crossed or nested-random effect designs); both of which could be informative tools for identifying causal variants/conditions found in complex genomic traits (Slatkin, 2008; Goddard et al., 2016; Favé et al., 2018) (i.e., haplotype synergy and gene-environment interactions).

A notable limitation of the sparse sampling approach is its sensitivity to high experimental error (≥20% CV), particularly in the estimation of K_m, where the initial sample population estimates of K_m were over-predicted, leading to underestimation of intrinsic clearance. The overprediction of K_m was not readily apparent in the bootstrap analysis, suggesting that its occurrence is a phenomenon specific to that sample population. The bootstrap analysis confirms that a 20% CV leads to a decrease in the precision of the K_m estimate; an observation that is more apparent for the 3 pt and 4 pt sampling conditions. This is presumably because variability in the K_m region of the Michaelis-Menten curve can lead to significant changes in the predicted reaction rate, and consequently, the estimated K_m value. Inclusion of more points across the full Michaelis-Menten profile may help anchor and/or center K_m estimates under high variability conditions, as evidenced by the greater precision observed for the rich design models. Additionally, it is assumed that the sampling range needed to capture the full kinetic profile for each genotype is generally known; that may not always be the case. Scenarios where the K_m values for a particular genotype vary drastically from the typical population value warrant adjustments in the sampling range to maximize profile coverage. Finally, the frequencies of an existing gene variant may differ from sub-population to sub-population due to exogenous factors (i.e., genetic drift, population bottlenecks, and founders’ effects); therefore, estimates of population level fixed effects will be heavily dependent on the sub-population they are estimated from, which may not always reflect the total population.

Conclusions

In summary, this study highlights the utility of non-linear mixed effects models as a population based in vitro approach for characterizing the impact of pharmacogenes on the underlying kinetic parameters that influence xenobiotic metabolism. Introducing CYP2D6 genotype as a categorical covariate in our NLME model allowed for an estimation of the impact that each genetic variant had on Michaelis-Menten parameters (V_max and K_m) as fixed-effects and provided a means for assessing between-subject variability. Additionally, we provide a method for empirically designing a sampling strategy that can generate robust estimates of covariate effects using sparse data at the individual level. Altogether, we envision significant utility for this approach, not only as an exploratory tool for identifying covariates of interest with in vitro studies, but also as a quantitative tool for providing a mechanistic understanding of how genetic variation impacts xenobiotic metabolism at a molecular level.

Abbreviations

4-OH-ATX

4-hydroxy-atomoxetine

ATX

atomoxetine

CI

confidence interval

CL

clearance

CL_int

intrinsic clearance

CV

coefficient of variation

CYP

cytochrome P450

HLM

human liver microsome

K_m

Michaelis-Menten constant

NLME

non-linear mixed effects model

PD

pharmacodynamic

PK

pharmacokinetic

V

volume of distribution

V_max

maximum velocity

Authorship Contributions

Participated in research design: Alade, Nath, Isoherranen, Thummel.

Performed data analysis: Alade.

Wrote or contributed to the writing of the manuscript: Alade, Nath, Isoherranen, Thummel.