Abstract
Background:
The opioid epidemic has been ongoing for over 20 years in the United States. As opioid misuse has shifted increasingly towards injection of illicitly produced opioids, it has been associated with HIV and hepatitis C transmission. These epidemics interact to form the opioid syndemic.
Methods:
We obtain annual county-level counts of opioid overdose deaths, treatment admissions for opioid misuse, and newly diagnosed cases of acute and chronic hepatitis C and newly diagnosed HIV from 2014–2019. Aligned with the conceptual framework of syndemics, we develop a dynamic spatial factor model to describe the opioid syndemic for counties in Ohio and estimate the complex synergies between each of the epidemics.
Results:
We estimate three latent factors characterizing variation of the syndemic across space and time. The first factor reflects overall burden and is greatest in southern Ohio. The second factor describes harms and is greatest in urban counties. The third factor highlights counties with higher than expected hepatitis C rates and lower than expected HIV rates, which suggests elevated localized risk for future HIV outbreaks.
Conclusions:
Through the estimation of dynamic spatial factors, we are able to estimate the complex dependencies and characterize the synergy across outcomes that underlie the syndemic. The latent factors summarize shared variation across multiple spatial time series and provide new insights into the relationships between the epidemics within the syndemic. Our framework provides a coherent approach for synthesizing complex interactions and estimating underlying sources of variation that can be applied to other syndemics.
Keywords: Bayesian, factor model, HIV, hepatitis C, opioid misuse, overdose, spatio-temporal, syndemic
Background
The opioid epidemic in the United States (U.S.) was declared a public health emergency in 2017 but has been ongoing for over 20 years [1]. The epidemic has caused substantial morbidity and mortality [2, 3]. In 2021, more than 100,000 people died of overdose in the U.S., with most deaths involving opioids [4]. With increases in injection of illicitly produced opioids (i.e., heroin and fentanyl), opioid misuse has increasingly been associated with HIV and hepatitis C (HCV) transmission. Together, these epidemics – fatal and non-fatal overdose, HIV, and HCV – interact synergystically as a syndemic [5] within specific social, temporal, and geographic contexts [6, 7]. These synergistic relationships can be used to help inform public health responses [5].
In Ohio, the opioid syndemic is particularly severe. Ohio had the fourth highest age-adjusted overdose death rate in the U.S. in 2019 at 38.3 per 100,000 residents, almost double the national rate [8]. Concurrently from 2014 to 2018, Ohio experienced a four-fold increase in acute HCV infections [9] with rates approximately 40% above the national average [10]. However, Ohio has yet to see injection drug-related HIV outbreaks on the scale of neighboring states Indiana [11, 12], Kentucky [13, 14], and West Virginia [15, 16].
The underlying driver of the syndemic is opioid misuse, but estimating opioid misuse at a population level is challenging because no single data source fully captures the problem [17, 18]. Instead, we are able to more easily observe the health outcomes related to misuse, such as overdose death, treatment admissions, and HIV and HCV cases, which form the opioid syndemic and are monitored by ongoing public health surveillance. Each outcome is driven by prevalence of opioid misuse in the community and the local drug use environment. The phrase drug use environment includes the socio-cultural environment, local drug supply, prevalence of infectious diseases, density of the injection networks, and availability of treatment and harm reduction resources. As with misuse, it is difficult to fully capture this complex environment at the spatio-temporal scales of interest.
While some of aspects of opioid misuse and the drug use environment may be partially characterized with observable covariates, it is often challenging to explicitly model the complex and dynamic dependencies between epidemics. To date, methods applied to analyze syndemics have been limited in their ability to formally capture such complex dependencies [7]. However, these dependencies are of epidemiologic interest to describe the syndemic and guide future investigations into the specific conditions that lead to variation in how the syndemic is experienced across different places and times. These analytical goals are generally applicable to the modeling of syndemics but take on additional importance for examining the opioid syndemic because of the inability to observe the set of underlying drivers of the syndemic.
One statistical tool for understanding common, unobserved drivers of a set of outcomes in communities is the spatial factor model [19, 20]. Spatial factor models were developed for multivariate spatial data when the focus is not primarily on the outcomes themselves but, instead, on the underlying hidden processes (i.e., latent factors) that drive the observable outcomes. Conceptually, factor models are similar to latent trait [21], structural equation [22], and shared component models [23] that are used in other applications. When change over time is of interest, longitudinal [21] and dynamic [24] factor models may be used. Spatio-temporal factor models have typically focused on estimation of dynamic factors and spatial loadings [25, 26, 27, 28], which reflect spatially homogeneous longitudinal processes that may have heterogeneous spatial effects. More recently, models have been developed to estimate location-specific dynamic factors (i.e., latent factors that themselves vary over space and time) [29], which more closely align to the assumptions in our setting and will serve as our modeling foundation in this paper.
Dynamic factor models are particularly useful for studying syndemics. Implicit in the definition of syndemic is the belief that there is synergy, or underlying dependence, between multiple epidemics. Factor models provide a statistical machinery for extracting and describing that dependence across all or subsets of the epidemics. Within the context of the opioid syndemic, it is even more relevant as we theoretically believe the epidemics result from unobservable common causes. If we only looked at a single epidemic or outcome, we may be misled by outcome specific variation or error that is not directly related to the underlying common factors. In the factor model framework, we use factors to identify and synthesize variation that is common to multiple outcomes from that which is specific to each individual outcome. The factors then tell the collective story of the syndemic of outcomes, while the outcome specific variation can suggest locations where other unrelated processes might be influencing that outcome only. While the primary goal of the analysis is to extract the common underlying factors of the syndemic, location-specific departures from the joint patterns observed elsewhere can be informative and suggest emerging patterns that may warrant further investigation. For example, a location with higher overdose death rates than expected based on a collection of syndemic outcomes may suggest an especially potent drug supply in that location.
The objective of this study is to describe the opioid syndemic in Ohio from 2014 to 2019 using a dynamic spatial factor model. Doing so will highlight complex dependencies between the overlapping epidemics of the syndemic and estimate hidden drivers of the outcomes that can be used to help inform future epidemiologic investigation.
Methods
Data
We base our syndemic model on multiple sources of surveillance data that are routinely monitored by state agencies. We characterize the syndemic using four outcomes: overdose deaths involving opioids, treatment admissions for opioid use disorder, total cases of HCV, and new diagnoses of HIV. For each outcome of interest, we obtain annual county-level counts for each of Ohio’s 88 counties from 2014 to 2019, which is the most recent completely available 6-year period. We obtain annual population estimates from the Ohio Public Health Data Warehouse [30], which curates estimates from the National Center for Health Statistics, to enable the calculation of rates.
We obtain publicly available county-level counts of overdose deaths involving opioids from the Ohio Public Health Data Warehouse Ohio Resident Mortality Data [30], maintained by the Ohio Department of Health (ODH). We include all resident deaths where poisoning from any opioid is mentioned on the death certificate, which includes ICD-10 multiple cause of death codes T40.0-T40.4 and T40.6. Deaths are indexed to the county of residence of the decedent. We also obtain county-level counts of treatment admissions via a data use agreement from the Ohio Department of Mental Health and Addiction Services. Treatment admissions include any residential, intensive outpatient, or outpatient treatment for opioid misuse and are indexed to the patient’s county of residence. Counts reflect unique patients and do not include healthcare encounters for treatment of overdose or other complications due to misuse. In this analysis, treatment admissions serve as a proxy for opioid use disorder diagnoses. Data are broken down into two age groups but are only used in total here. State policy requires censoring of counts between 1 and 9, which we account for within the model.
We also include county-level counts of HCV and HIV cases to capture infectious disease dimensions of the syndemic. Both counts are collected and publicly reported by ODH. Due to county-level variation and substantial under-reporting of acute HCV cases, we use the total count of HCV cases, which provides the best indicator of trends in the burden of infections. The total count includes both newly diagnosed acute and newly diagnosed chronic cases. We also use counts of newly diagnosed HIV infections to assess trends in HIV. A new diagnosis of HIV is defined as a person with a diagnosis of HIV and not AIDS, a diagnosis of HIV and an AIDS diagnosis within 12 months, or concurrent diagnoses of HIV and AIDS. Cases are indexed to the county of residence at the time of diagnosis.
Statistical Considerations
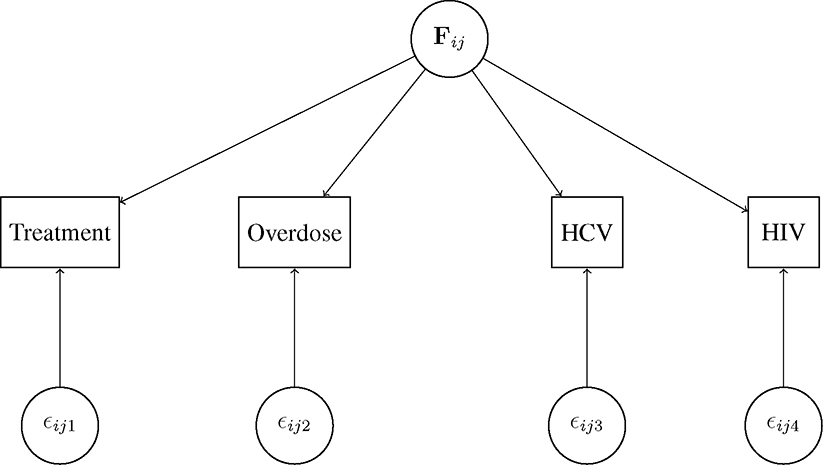
We take an exploratory approach using a dynamic spatial factor analysis following the conceptual diagram in Figure 1. In this framework, we assume a vector of spatio-temporal factors, F, characterizes the unobserved common processes that drive each epidemic and induce dependence between epidemics. While not explicitly estimating unobserved drivers like opioid misuse, this model will allow us to decompose the syndemic into a set of spatio-temporal factors that will help to illuminate complex patterns that can guide future investigations and enhance epidemiologic knowledge of the syndemic. Our framework serves as a bridge between the multivariate statistical problem of modeling a syndemic and the theoretical problem that the opioid syndemic is driven by common unobservable processes.
Figure 1:
Conceptual diagram of the model for location in year . HCV=hepatitis C virus. HIV=human immunodeficiency virus.
Let be the observed count for outcome in year in county . In our case, we have outcomes (treatment, death, HCV, and HIV). We assume a spatial rates model [31]:
| (1) |
where is the relative risk of outcome in year for county compared to the expected count standardized to the state-level rate in 2014 . That is, where is the total population in county in year and is the overall state rate of outcome in 2014 (i.e., ). The adjustment for censoring [32] of treatment counts is shown in the eAppendix.
Let denote the -dimensional vector of dynamic spatial factors at location in year . These factors estimate the common underlying processes, or shared variation, across the outcomes of the syndemic. In this paper, we use . We assume the following generalized linear model to relate to relative risk for the observed outcomes:
| (2) |
We define factor loadings for outcome , as the column of the matrix . To ensure identifiability, is constrained to be lower triangular with entries of 1 on the main diagonal. The factor loadings determine how each factor relates to each outcome and reflects the multivariate relationships common across locations and years. We assume is an error term to account for uncorrelated heterogeneity and overdispersion. That is, is outcome-specific variation that is not explained by the common factors.
In general, the selection of the dimension of the factors and the construction of the matrix will be application specific. The number of factors must be less than the number of outcomes and can be selected by an optimization of model fit or theoretical considerations. Likewise, there are identifiability constraints on the specification of the factor loadings , but as long as those constraints are met [33, 34], the loadings can be specified to ease interpretation of the factors or align with theoretical understanding. Here, we choose a specification of that leads to factors that are epidemiologically meaningful within our application.
The model parameters of primary interest are the dynamic spatial factors. From Equation 2. we note that is shared across each outcome as it lacks an outcome specific subscript . Thus characterizes the shared latent processes that drive the set of outcomes and describe the interrelationships that define the syndemic. The vector of factors is dynamic and spatial as it varies over time for each county. Let denote the element of and assume an intrinsic conditional autoregressive model of spatial correlation [35, 36] with an autoregressive of order 1 (AR(1)) temporal dependence structure. We assume for (i.e., 2014):
| (3) |
and for :
| (4) |
where , is a mean for factor at year is an autoregressive parameter for factor is a variance, and is the vector of factor for all counties excluding county in year . We let be an indicator of whether counties and are neighbors (i.e., share a boundary) and be the total number of neighbors for county . This structure implies within each factor the value for a particular county is correlated with its value the previous year and the values of its neighboring counties. Since the intrinsic conditional autoregressive model is an improper probability distribution, we enforce a necessary centering constraint so it is a valid process model [35].
We fit the model within the Bayesian paradigm and must specify prior distributions for all unknown parameters. In general, we use weakly informative prior distributions for all parameters. As mentioned above, the factor loadings matrix is constrained to be lower triangular for identifiability. For the non-constrained element of , we assume for . Constrained elements of are fixed at 1 for and 0 for . For each of the time-varying factor mean parameters , we assume independent uniform prior distributions on the real line. Each autoregressive parameter is assigned an independent Uniform(0,1) distribution. Finally, all variance parameters and are given independent inverse gamma prior distributions with shape and scale parameters equal to 0.5. We fit the model using a Markov chain Monte Carlo algorithm implemented in nimble [37] in R for 500,000 iterations. We discard the first 250,000 iterations as burn-in and thin the remaining samples by 50. We assess convergence visually using trace plots. Computation took approximately 8 hours using the DEAC cluster [38]. Code is available in the eAppendix.
This project was reviewed and deemed exempt by the Wake Forest University Institutional Review Board.
Results
In Table 1, we present descriptive statistics of the observed county rates of each outcome per 100,000 residents over the course of the study period. For summary purposes, treatment rates are computed by assuming censored counts equal 5. Throughout the six year study period, median treatment rates increased each year and the rate in 2019 was almost 2.5 times the rate in 2014. For both death and HCV rates, the median increases to a peak in 2016 and 2017 with slight declines at the end of the study period, although median rates still exceeded those in 2014. Median rates of HIV remained fairly constant throughout the six years studied. Observed log rate ratios for each outcome are shown in eFigure 1, standardized to expected state-level rates for each outcome in 2014.
Table 1:
Median (first quartile, third quartile) observed county rates of each outcome per 100,000 residents from 2014–2019. Observed treatment rates are computed by assuming censored counts are equal to 5.
| Year | Treatment | Death | HCV | HIV |
|---|---|---|---|---|
|
| ||||
| 2014 | 90.4 (54.8, 117.7) | 13.9 (9.2, 20.1) | 97.8 (54.7, 140.1) | 2.5 (0.0, 5.2) |
| 2015 | 108.8 (71.8, 163.7) | 16.9 (11.1, 24.6) | 127.4 (80.0, 193.5) | 2.6 (0.0, 4.7) |
| 2016 | 137.6 (88.8, 198.1) | 23.6 (11.9, 32.0) | 162.0 (106.3, 232.4) | 2.4 (0.0, 5.0) |
| 2017 | 161.3 (111.9, 226.6) | 27.7 (14.6, 41.4) | 149.9 (108.3, 215.7) | 2.8 (1.0, 5.9) |
| 2018 | 195.6 (129.0, 274.1) | 21.9 (12.5, 29.2) | 132.8 (95.9, 183.6) | 2.6 (0.0, 6.4) |
| 2019 | 224.5 (148.2, 347.9) | 19.3 (11.2, 34.1) | 113.3 (80.9, 153.7) | 2.8 (0.0, 5.1) |
The parameters of primary interest are the dynamic spatial factors that characterize the synergy and shared variation of the epidemics that compose the syndemic. Posterior mean estimates of the three factors are shown in Figure 2. Since 2014 was used as a baseline, estimates of the factors are relative to 2014. That is, a value of 0 corresponds to the state average value in 2014. Posterior estimates of the loadings are shown in Table 2, which provide necessary context for interpreting the factor estimates. The loadings illustrate the relative contribution of each outcome to each factor and also the constraints applied to .
Figure 2:
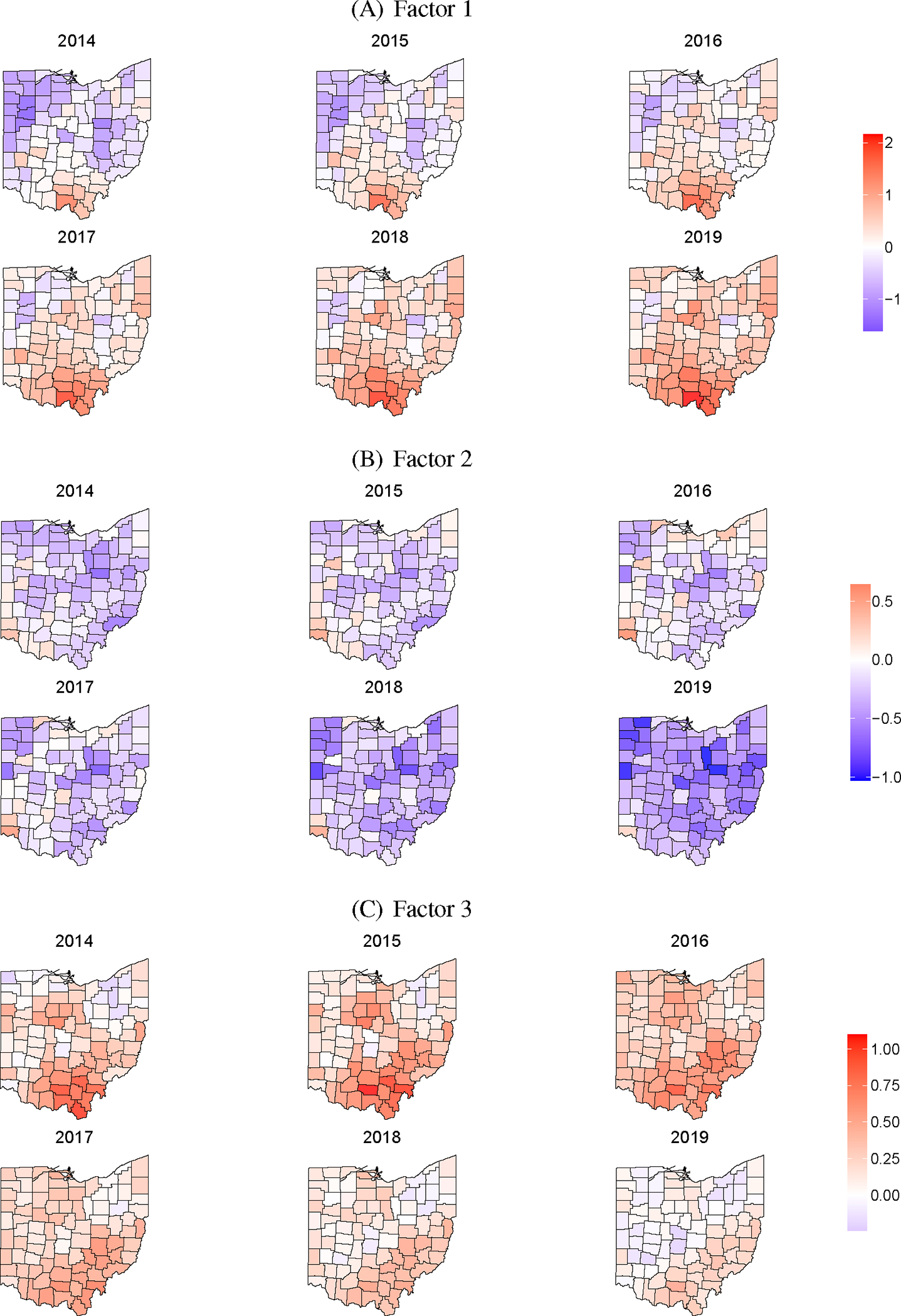
Posterior mean estimates of the three latent factors from 2014–2019.
Table 2:
Posterior mean estimates and 95% credible intervals for the factor loadings on each outcome for each of the three factors.
| Outcome | Factor 1 | Factor 2 | Factor 3 |
|---|---|---|---|
|
| |||
| Treatment | 1.00 | 0 | 0 |
| Death | 0.68 (0.55, 0.81) | 1.00 | 0 |
| HCV | 0.58 (0.46, 0.69) | 0.77 (0.62, 0.94) | 1.00 |
| HIV | 0.38 (0.08, 0.69) | 2.03 (1.55, 2.57) | −1.93 (−2.45, −1.40) |
Figure 2(A) gives the posterior mean estimates of Factor 1. Based on Table 2, the first factor characterizes variation shared by all four outcomes with the most weight on treatment, death, and HCV. We can interpret this factor as the overall latent burden of the syndemic over space and time, which reflects shared variation across all four outcomes. That is, Factor 1 estimates an underlying hidden process that is related to all of the outcomes. In general, we see temporally increasing trends across the state. In the first 3 years, above average counties are mostly concentrated in the southern portion of the state. As the time series advances, estimates across most of the state shift to above the baseline average with the largest estimates still concentrated in southern Ohio. The maps of Factor 1 generally align with the current understanding of the geographic burden of the opioid syndemic in Ohio, providing a degree of qualitative validity.
The posterior mean estimates of Factor 2 appear in Figure 2(B). From Table 2, we see that Factor 2 is composed of shared variation from the harms of opioid misuse (death, HCV, and HIV) and is particularly weighted towards HIV. Practically, we are able to use Factor 2 to describe counties where rates of harms are above or below what would be expected based on the joint relationship across outcomes after accounting for Factor 1. That is, Factor 2 highlights counties where the harms are disproportionate to what would be expected given the number of treatment admissions. The general temporal trend of Factor 2 is increasing through 2016 and then decreasing through the end of the time series. Spatially, above average areas are primarily concentrated in the state’s largest cities, Cincinnati (southwest), Columbus (central), and Cleveland (northeast). While the general burden is concentrated in rural southern Ohio, rates of harms are higher in the state’s urban counties, particularly overdose death and HIV. This is also likely due to higher rates of treatment in southern Ohio relative to the rates of harm in that part of the state and thus below average estimates of Factor 2. This is also apparent by examining the observed and estimated log standardized rate ratios in eFigures 1 and 2.
In Figure 2(C), we show the posterior mean estimates of Factor 3. Factor 3 is positively associated with HCV and negatively associated with HIV (Table 2). This reflects remaining shared variation between HCV and HIV that is not already accounted for in Factors 1 and 2. That is, Factor 3 is greater for counties where rates of HCV exceed what would be expected, but HIV rates are below expected. This factor provides an interesting epidemiologic construct because HCV is often used as an early warning proxy for the potential of HIV outbreaks. Essentially, Factor 3 is highlighting counties at risk of but not yet experiencing HIV outbreaks. The general temporal trend in Factor 3 is similar to the other factors with increases followed by decreases. Spatially, the largest estimates of Factor 3 are in southern and southeastern Ohio, which is the Appalachian region of the state. As seen in eFigures 1 and 2, this region has some of the highest rates of HCV in the state but below average rates of HIV, which suggests that networks exist for transmission of injection-related infectious diseases, even if HIV has yet to penetrate those networks.
The trends in the estimated factors described above can also be seen in eFigure 3. In eFigure 3, we plot each county’s time series for the posterior mean of each factor. County time series are colored by region, as defined in eFigure 4, to further highlight the geographic trends illustrated by the maps of the estimates.
We highlight seven counties in Figure 3 to illustrate the general themes discussed above. For Factor 1, we see the Appalachian counties (Scioto, Jackson, Pike) and Montgomery (Dayton) have the highest estimates. Franklin (Columbus) and Hamilton (Cincinnati) are closer to the state average. Focusing on harms illustrated by Factor 2, the urban counties (Hamilton, Montgomery, Franklin) have the highest values which peak around 2016. In 2017, estimates for Factor 2 also increase for Pike and Scioto counties. Finally for Factor 3, all of the urban counties are below the state average while the Appalachian counties are above the state average. These counties are known to have a high burden of HCV and have been identified as being at high risk of an HIV outbreak [39]. We also note that Delaware, a wealthy county outside of Columbus, is below the state average for all three factors.
Figure 3:
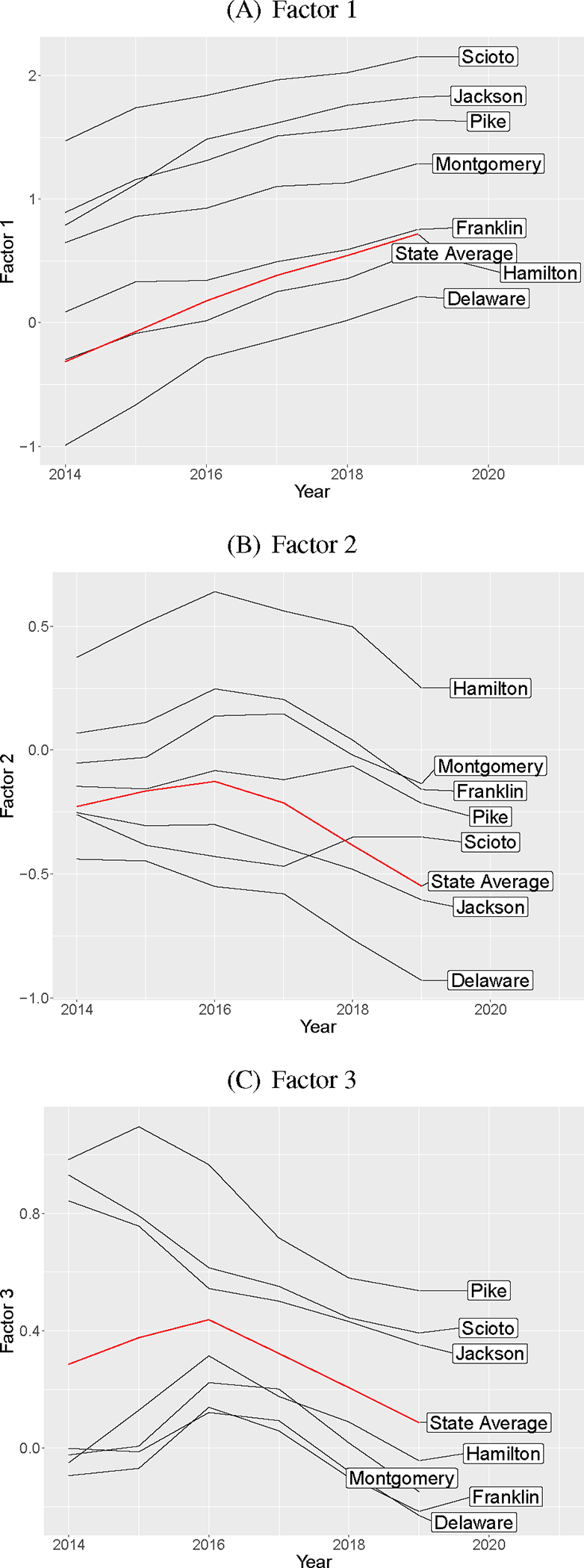
Posterior mean estimates of each of the factors over time for selected counties.
Finally, we can also extract useful meaning from the uncorrelated heterogeneity and show posterior mean estimates of the random effect in eFigure 5. These estimates characterize residual variation that is unique to each outcome. For treatment, there are not particularly strong patterns. For death, we see larger estimates in the southwest and northeast corners of the state. These correspond to the Cincinnati/Dayton and Cleveland areas, respectively. Both of these regions saw high death rates, particularly from 2015–2017, due to the influx of illicit fentanyl and carfentanyl which was initially centered in urban areas. As these changes in the drug market were unrelated to the other outcomes considered, the associated increases in the death rates are reflected as uncorrelated heterogeneity in the model. Looking at HCV, rates are slightly higher in the north central region of the state than would be suggested by levels of the other outcomes considered. Finally for HIV, rates are higher in the state’s major cities: Cincinnati (southwest), Columbus (central), and Cleveland (northeast). This is not particularly surprising as these areas likely have more sexual transmission of HIV and would be less correlated with the rest of the outcomes of the opioid syndemic.
Discussion
In this paper, we develop a dynamic spatial factor model for the opioid syndemic in Ohio counties. Through the estimation of dynamic spatial factors, we are able to estimate the complex dependencies and characterize the synergy across outcomes that underlies the syndemic. By examining the sources of shared variation across outcomes, we can extract useful epidemiologic insights to help better understand the complexities of the syndemic and guide future investigations. Our model also enables us to identify uncorrelated heterogeneity which suggests the presence of variation unique to specific outcomes and not shared across the syndemic.
Our approach is particularly useful for describing complex epidemiologic phenomena like the opioid syndemic. The syndemic is fundamentally driven by unobservable community processes related to misuse of opioids and the drug use environment. Since we cannot directly observe these processes of interest, we glean our epidemiologic insights from the set of related outcomes that constitute the syndemic. While one may be able to infer a picture similar to that given by Factor 1, it is challenging, if not impossible, to manually synthesize multiple spatio-temporal time series to uncover the relationships brought out by our model. This challenge only increases as the number of time series or the size of the spatial field increases. Instead, the dynamic factor model provides a principled approach for synthesizing shared information across time series into a lower dimensional set of factors. It also provides flexibility to construct factors through the specification of the loadings that are theory driven and epidemiologically meaningful. Our approach simplifies the complexity of the problems and illuminates insights that would otherwise be missed by simply examining the observed data.
Our descriptive analysis can motivate several future investigations to better understand the opioid syndemic and its spatio-temporal heterogeneity. We observe the highest overall burdens of the syndemic in southern Ohio as illustrated by Factor 1. These counties would be ideal places to study opioid misuse and the general impact of the syndemic on rural communities. In fact, there are existing studies doing just that [40]. We also found areas with excess rates of harm due to the syndemic as illustrated by Factor 2, particularly around Cincinnati, Columbus, and Cleveland. Future work may want to explore whether there is adequate access to, awareness of, and uptake of harm reduction services among people who misuse opioids in those communities. The results also suggest that while the overall burden may be highest in rural areas of the state, it is also critical to remember to adequately address the needs in more urban areas, which may differ from those in rural areas. Finally, Factor 3 highlights counties that are not experiencing HIV outbreaks currently but are at high risk given their observed increased rates of HCV. These counties should be targeted for harm reduction programs focusing on the prevention and treatment of infectious diseases, such as syringe service programs and rapid HIV testing. Such targeted efforts can help prevent injection-related HIV outbreaks like those seen in neighboring Indiana [11, 12], Kentucky [13, 14], and West Virginia [15, 16].
Our analysis has a few limitations. All data used in the analysis are surveillance data collected by the state of Ohio and can be subject to reporting biases. In particular, death counts are based on information reported on death certificates which can contain systematic errors [41]. There are also limitations to and variations in the detection and reporting of infectious diseases like HIV and HCV. Because the analysis uses newly diagnosed total HCV, some chronic cases may have been acquired in the past and be less relevant to the current syndemic. However, we believe most HCV cases are linked to the growth of injection drug use in the state. In addition, it is likely that a substantial proportion of HIV cases are not related to injection, which may impact the results and lead to a stronger signal in more urban areas. However, a strength of this analysis is that we focus on shared variation across all of the outcomes, which may help to mitigate bias or error unique to any single outcome.
In conclusion, we have developed an approach for syndemic modeling using a dynamic spatial factor model. Our approach is particularly useful for the opioid syndemic because the underlying drivers of the syndemic are not easily observable. Through estimation of latent factors, we are able to summarize shared variation across multiple spatial time series and use the resulting estimates to gain new insights into the relationships between the epidemics within the syndemic. Our framework provides a coherent approach for synthesizing information and estimating underlying sources of variation that can be used to inform future investigations and interventions to mitigate harms of the opioid syndemic.
Supplementary Material
Acknowledgement:
Computations were performed using the Wake Forest University (WFU) High Performance Computing Facility, a centrally managed computational resource available to WFU researchers including faculty, staff, students, and collaborators. These data were provided by the Ohio Department of Health. The Department specifically disclaims responsibility for any analyses, interpretations, or conclusions.
Funding:
Research reported in this publication was supported by the National Institute On Drug Abuse of the National Institutes of Health under Award Number R01DA052214. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Footnotes
No conflicts of interest
Contributor Information
David Kline, Department of Biostatistics and Data Science, Division of Public Health Sciences, Wake Forest School of Medicine, Winston-Salem, North Carolina.
Lance A. Waller, Department of Biostatistics and Bioinformatics, Rollins School of Public Health, Emory University, Atlanta, Georgia
Erin McKnight, Division of Adolescent Medicine, Nationwide Children’s Hospital, Columbus, Ohio; Department of Pediatrics, College of Medicine, The Ohio State University, Columbus, Ohio.
Andrea Bonny, Division of Adolescent Medicine, Nationwide Children’s Hospital, Columbus, Ohio; Department of Pediatrics, College of Medicine, The Ohio State University, Columbus, Ohio.
William C. Miller, Division of Epidemiology, College of Public Health, The Ohio State University, Columbus, Ohio
Staci A. Hepler, Department of Statistical Sciences, College of Arts and Sciences, Wake Forest University, Winston-Salem, North Carolina
Data Accessibility:
The authors do not have permission to share treatment admission data used in this study. The data are available via data use agreement with the Ohio Department of Mental Health and Addiction Services. Overdose death, HCV, and HIV data are publicly available from the Ohio Department of Health. Computer code for the analysis is available online.
References
- [1].Gostin Lawrence O, Hodge James G, Noe Sarah A. Reframing the Opioid Epidemic as a National Emergency JAMA. 2017;318:1539–1540. [DOI] [PubMed] [Google Scholar]
- [2].Rudd RA, Seth P, David F, Scholl L. Increases in Drug and Opioid-Involved Overdose Deaths - United States, 2010–2015 MMWR. Morbidity and mortality weekly report. 2016. [DOI] [PubMed] [Google Scholar]
- [3].Zibbell JE, Igbal K, Patel RC, et al. Increases in Hepatitis C Virus Infection Related to Injection Drug Use among Persons Aged 30 Years - Kentucky, Tennessee, Virginia, and West Virginia, 2006–2012 MMWR. 2015;64:453–458. [PMC free article] [PubMed] [Google Scholar]
- [4].Ahmad FB, Cisewski JA, Rossen LM, Sutton P. Provisional Durg Overdose Death Counts https://www.cdc.gov/nchs/nvss/vsrr/drug-overdose-data.htm 2022. [Google Scholar]
- [5].Perlman DC, Jordan AE. The Syndemic of Opioid Misuse, Overdose, HCV, and HIV: Structural-level Causes and Interventions. Current HIV/AIDS reports. 2018;15:96–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Merill Singer, Scott Clair. Syndemics and Public Health: Reconceptualizing Disease in Bio-Social Context Medical Anthropology Quarterly. 2003;17:423–441. [DOI] [PubMed] [Google Scholar]
- [7].Shrestha Shikhar, Bauer Cici XC, Hendricks Brian, Stopka Thomas J . Spatial Epidemiology: An Empirical Framework for Syndemics Research Social Science & Medicine. 2020:113352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].CDC/NCHS, National Vital Statistics System, Mortality. 2019 Drug Overdose Death Rates | Drug Overdose | CDC Injury Center https://www.cdc.gov/drugoverdose/deaths/2019.html 2020. [Google Scholar]
- [9].Ohio Department of Health. Hepatitis Surveillance Program Data Reported through 5/13/2019 Online; accessed 5-November-2019 2019. [Google Scholar]
- [10].Division of Viral Hepatitis, National Center for HIV/AIDS, Viral Hepatitis, STD, and TB Prevention. Online; accessed 9-November-2019 2019.
- [11].Conrad Caitlin, Bradley Heather M, Broz Dita, et al. Community Outbreak of HIV Infection Linked to Injection Drug Use of Oxymorphone - Indiana, 2015 MMWR. Morbidity and mortality weekly report. 2015;64:443–444. [PMC free article] [PubMed] [Google Scholar]
- [12].Gonsalves Gregg S, Crawford Forrest W. Dynamics of the HIV Outbreak and Response in Scott County, IN, USA, 2011–15: A Modelling Study The Lancet HIV. 2018;5:e569–e577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Campo-Flores Jeanne Whalen and Arian. Jump in HIV Cases Among Drug Users Seen in Northern Kentucky Wall Street Journal. 2018. [Google Scholar]
- [14].HIV Cases Increasing in Louisville. https://louisvilleky.gov/news/hiv-cases-increasing-louisville.
- [15].Paul McClung R., Atkins Amy D, Kilkenny Michael, et al. Response to a Large HIV Outbreak, Cabell County, West Virginia, 2018–2019 American Journal of Preventive Medicine. 2021;61:S143–S150. [DOI] [PubMed] [Google Scholar]
- [16].Bradley Heather, Hogan Vicki, Agnew-Brune Christine, et al. Increased HIV Diagnoses in West Virginia Counties Highly Vulnerable to Rapid HIV Dissemination through Injection Drug Use: A Cautionary Tale Annals of Epidemiology. 2019;34:12–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Schuler Megan S, Griffin Beth Ann, Cerdá Magdalena, McGinty Emma E., Elizabeth A. Stuart. Methodological Challenges and Proposed Solutions for Evaluating Opioid Policy Effectiveness Health Services and Outcomes Research Methodology. 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Sullivan Patrick S, Bradley Heather M, del Rio Carlos, Rosenberg Eli S.. The Geography of Opioid Use Disorder: A Data Triangulation Approach Infectious Disease Clinics of North America. 2020;34:451–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Wall MM, Wang F. Generalized Common Spatial Factor Model Biostatistics (Oxford, England). 2003;4:569–582. [DOI] [PubMed] [Google Scholar]
- [20].Hepler Staci, McKnight Erin, Bonny Andrea, Kline David. A Latent Spatial Factor Approach for Synthesizing Opioid-Associated Deaths and Treatment Admissions in Ohio Counties Epidemiology. 2019;30:365–370. [DOI] [PubMed] [Google Scholar]
- [21].Dunson David B. Bayesian Methods for Latent Trait Modelling of Longitudinal Data Statistical Methods in Medical Research. 2007;16:399–415. [DOI] [PubMed] [Google Scholar]
- [22].Muthen B, Asparouhov T. Bayesian Structural Equation Modeling: A More Flexible Representation of Substantive Theory. Psychological methods. 2012;17:313–35. [DOI] [PubMed] [Google Scholar]
- [23].Knorr-Held Leonhard, Best Nicola G.. A Shared Component Model for Detecting Joint and Selective Clustering of Two Diseases Journal of the Royal Statistical Society: Series A (Statistics in Society). 2001;164:73–85. [Google Scholar]
- [24].Tihomir Asparouhov, Hamaker Ellen L, Muthén Bengt. Dynamic Structural Equation Models Structural Equation Modeling: A Multidisciplinary Journal. 2018;25:359–388. [Google Scholar]
- [25].Lopes Hedibert Freitas, Gamerman Dani, Salazar Esther. Generalized Spatial Dynamic Factor Models Computational Statistics & Data Analysis. 2011;55:1319–1330. [Google Scholar]
- [26].Ippoliti L, Valentini P, Gamerman D. Space-Time Modelling of Coupled Spatiotemporal Environmental Variables Journal of the Royal Statistical Society: Series C (Applied Statistics). 2012;61:175–200. [Google Scholar]
- [27].Bai Jushan, Wang Peng. Identification and Bayesian Estimation of Dynamic Factor Models Journal of Business & Economic Statistics. 2015;33:221–240. [Google Scholar]
- [28].Xiaoyi Han, Lung-Fei Lee. Bayesian Analysis of Spatial Panel Autoregressive Models with Time-Varying Endogenous Spatial Weight Matrices, Common Factors, and Random Coefficients Journal of Business & Economic Statistics. 2016;34:642–660. [Google Scholar]
- [29].Leorato Samantha, Mezzetti Maura. A Bayesian Factor Model for Spatial Panel Data with a Separable Covariance Approach Bayesian Analysis. 2021;16:489–519. [Google Scholar]
- [30].Ohio Public Health Data Warehouse. Ohio Resident Mortality Data 2020. [Google Scholar]
- [31].Cressie Noel, Perrin Olivier, Thomas-Agnan Christine. Likelihood-Based Estimation for Gaussian MRFs Statistical Methodology. 2005;2:1–16. [Google Scholar]
- [32].Famoye Felix, Wang Weiren. Censored Generalized Poisson Regression Model Computational Statistics and Data Analysis. 2004;46:547–560. [Google Scholar]
- [33].Tabrizi Elham, Samani Ehsan Bahrami, Ganjali Mojtaba. A Note on the Identifiability of Latent Variable Models for Mixed Longitudinal Data Statistics & Probability Letters. 2020;167:108882. [Google Scholar]
- [34].Papastamoulis Panagiotis, Ntzoufras Ioannis. On the Identifiability of Bayesian Factor Analytic Models Statistics and Computing. 2022;32:23. [Google Scholar]
- [35].Banerjee Sudipto., Carlin Bradley P, Gelfand Alan E. Hierarchical Modeling and Analysis for Spatial Data. Boca Raton, Fla.: Chapman & Hall/CRC; 2004. [Google Scholar]
- [36].Besag Julian. Spatial Interaction and the Statistical Analysis of Lattice Systems Journal of the Royal Statistical Society. Series B (Methodological). 1974;36:192–236. [Google Scholar]
- [37].de Valpine P, Turek D, Paciorek CJ, Anderson-Bergman C, Temple Lang D, Bodik R. Programming with Models: Writing Statistical Algorithms for General Model Structures with NIMBLE Journal of Computational and Graphical Statistics. 2017;26:403–417. [Google Scholar]
- [38].Information Systems, Wake Forest University. WFU High Performance Computing Facility 2021. [Google Scholar]
- [39].Van Handel MM, Rose CE, Hallisey EJ, et al. County-Level Vulnerability Assessment for Rapid Dissemination of HIV or HCV Infections among Persons Who Inject Drugs, United States Journal of Acquired Immune Deficiency Syndrome. 2016;73:323–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Jenkins Richard A, Whitney Bridget M, Nance Robin M, et al. The Rural Opioid Initiative Consortium Description: Providing Evidence to Understand the Fourth Wave of the Opioid Crisis Addiction Science & Clinical Practice. 2022;17:38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Slavova S, O’Brien DB, Creppage K, et al. Drug Overdose Deaths: Let’s Get Specific. Public health reports. 2015;130. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The authors do not have permission to share treatment admission data used in this study. The data are available via data use agreement with the Ohio Department of Mental Health and Addiction Services. Overdose death, HCV, and HIV data are publicly available from the Ohio Department of Health. Computer code for the analysis is available online.