Development of an adaptive clinical web-based prediction tool for kidney replacement therapy in children with chronic kidney disease

Abstract

Clinicians need improved prediction models to estimate time to kidney replacement therapy (KRT) for children with chronic kidney disease (CKD). Here, we aimed to develop and validate a prediction tool based on common clinical variables for time to KRT in children using statistical learning methods and design a corresponding online calculator for clinical use. Among 890 children with CKD in the Chronic Kidney Disease in Children (CKiD) study, 172 variables related to sociodemographics, kidney/cardiovascular health, and therapy use, including longitudinal changes over one year were evaluated as candidate predictors in a random survival forest for time to KRT. An elementary model was specified with diagnosis, estimated glomerular filtration rate and proteinuria as predictors and then random survival forest identified nine additional candidate predictors for further evaluation. Best subset selection using these nine additional candidate predictors yielded an enriched model additionally based on blood pressure, change in estimated glomerular filtration rate over one year, anemia, albumin, chloride and bicarbonate. Four additional partially enriched models were constructed for clinical situations with incomplete data. Models performed well in cross-validation and the elementary model was then externally validated using data from a European pediatric CKD cohort. A corresponding user-friendly online tool was developed for clinicians. Thus, our clinical prediction tool for time to KRT in children was developed in a large, representative pediatric CKD cohort with an exhaustive evaluation of potential predictors and supervised statistical learning methods. While our models performed well internally and externally, further external validation of enriched models is needed.

Graphical Abstract

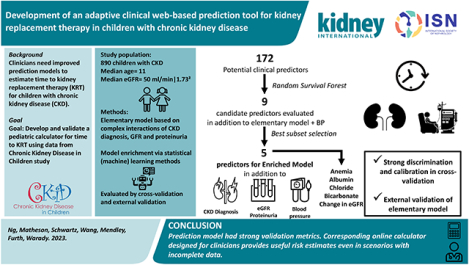
Lay Summary

We aimed to construct a prediction tool for doctors to estimate when children with chronic kidney disease (CKD) might require kidney replacement therapy (KRT). Using statistical (machine) learning methods, we analyzed 172 common clinical variables from 890 children with CKD in North America as predictors of time to KRT to identify the best model. The optimal model included type of CKD, eGFR, proteinuria, blood pressure, anemia, albumin, chloride, and bicarbonate; additional models were constructed to accommodate incomplete data. The tool performed well in testing and the simplest model was externally validated in a European pediatric CKD cohort. By integrating two complementary statistical learning methods with the rich CKiD database, we developed a powerful predictive tool that is adaptive to scenarios with incomplete data. We further designed a corresponding online calculator that is simple to use and provides valid predictions to guide clinical planning and treatment for pediatric CKD patients.

Introduction

Chronic kidney disease (CKD) in children precedes end stage kidney disease (ESKD)^1,2, and disease severity and rate of progression are heterogeneous and based on many factors^3,4. Identifying clinical profiles associated with varying rates of CKD progression and predicting time to kidney replacement therapy (KRT), defined as dialysis or kidney transplant, is clinically useful for stratifying patient risk, as well as for preparatory efforts by clinicians, patients and their families. Decades of research in children and adults demonstrated that underlying CKD etiology, glomerular filtration rate (GFR) levels at early stages of disease, and proteinuria are strong predictors of progression to ESKD^3–8, and these variables were used to construct previously proposed pediatric risk prediction models^3,4 using data from the Chronic Kidney Disease in Children (CKiD) study.

We recently demonstrated weak calibration of the adult Kidney Failure Risk Equation (KFRE) when applied to children with CKD which highlighted the need for improved pediatric-specific calculators⁹. In 2015, we presented a multivariable model to estimate times to first occurrence of KRT or a 50% decline in GFR in children with CKD³. Inclusion of the latter event can weaken inference because it is a surrogate endpoint of disease progression rather than a clinical endpoint. While surrogate endpoints like GFR decline can be useful in randomized clinical trials¹⁰, the clinical endpoint of KRT alone is superior. In addition, this model required complete data for 5 or 9 predictors for valid prediction which may not always be clinically available. In 2017, we proposed a simpler model⁴ based on a larger dataset combining CKiD and European Study Consortium for Chronic Kidney Disorders Affecting Pediatric Patients (ESCAPE) cohorts¹¹. This equation used only underlying CKD etiology (hereafter, referred to as “diagnosis”), estimated GFR (eGFR), and proteinuria but was limited because the prediction was a composite of the surrogate endpoint of 50% eGFR decline or KRT and it did not incorporate BP, a well-recognized risk factor for disease progression.

The availability of new equations to estimate GFR¹², updated pediatric blood pressure (BP) guidelines¹³, more data within CKiD focused on KRT as a clinical endpoint² and powerful machine learning methods^14,15 presented a timely opportunity to enhance KRT-specific risk prediction for children with CKD under treatment by pediatric nephrologists. For improved clinical use, a new proposed model should provide valid estimates even if some predictors are missing or not available and be conveniently accessible online.

The purpose of this analysis was to construct and validate a suite of predictive models for time to KRT for children with CKD based on commonly available clinical data, statistical learning methods, and parametric survival models. Statistical learning methods were used to assess commonly measured candidate predictors and to specify equations to address clinical instances of incomplete data. Lastly, we developed a web-based tool to interpret these complex equations for clinical applications.

Methods

Study population

Initiated in 2005, the CKiD study is a longitudinal cohort of children with CKD and eGFR <90/ml/min|1.73m² at entry from 56 clinical sites in the United States and Canada. Participants contributed data at annual study visits, including biomarkers of CKD severity, cardiovascular and metabolic health, questionnaires for general health, medical history, and sociodemographic characteristics. All participants and families provided informed consent/assent, and the study protocols were approved by local institutional review boards. A complete description of the study design has been previously published.¹⁶

Time scale and outcome

The time origin for this analysis was the second study visit (i.e., Visit 2) in order to evaluate and identify longitudinal predictors of KRT incidence (i.e. risk factor changes over the first study year). For this analysis, 890 of 1098 participants contributed the first two study visits prior to KRT with complete data and were included for analysis (exclusions: 146 had no follow-up data; 47 missed Visit 2 (time origin); 15 initiated KRT prior to time origin; see Supplementary Figure S1). The primary outcome was the time to first occurrence of KRT. Date of dialysis or transplant was extracted from medical records, or participant/family-reported with confirmation. Participants who were event-free at the last available study visit were considered censored. Administrative censoring was performed at 10 years due to limited data availability.

Predictors

Supplementary Table S1 presents all candidate predictors evaluated for the prediction model. These included sociodemographic (sex, age, maternal education, household income, family history of kidney disease), CKD severity (U25 eGFR, urine protein:creatinine ratio [UPCR], years with CKD, anemia, BP stage based on 2017 American Academy of Pediatrics [AAP] guidelines¹³), birth history (prematurity, low birth weight, small for gestational age), laboratory markers (metabolic, blood and lipid panels), and medication use (antihypertensive therapy, alkali therapy, growth hormone, among many others). For time-varying variables, we also investigated change over approximately 1 year from Visit 1 to Visit 2 (i.e., divided by the duration in years for annualized change) for continuous variables and for binary variables (i.e., diagnoses, therapy use), the four different possible responses between two visits (no/no; no/yes; yes/no; yes/yes).

CKD diagnosis type (glomerular or non-glomerular), U25 eGFR¹², and UPCR were considered essential variables a priori for the simplest “elementary” model^2–4. A full list of diagnoses is presented in Supplementary Table S2. All serum and urine biomarkers were measured centrally (University of Rochester, PI: GJ Schwartz), except for bicarbonate which was measured locally.

Statistical methods

Prediction model development process

Briefly, the development of the clinical KRT prediction models comprised three steps, followed by a cross-validation step. The first step was to develop an elementary model using the most fundamental established predictors of KRT: eGFR, UPCR and diagnosis. Various functional forms of these variables were tested in a parametric survival model. The second step was to identify the best additional candidate predictors out of 172 selected CKiD variables using a random survival forest (RSF). The third step brought the first two together, exploring an enriched set of models based on adding the important variables identified from the RSF to the elementary model. Lastly, the entire three-step process was validated using 10-fold cross-validation.

Parametric survival models

Elementary and enriched parametric survival models used the generalized gamma (GG) family and maximum likelihood methods to estimate predicted time to KRT¹⁷. The GG distribution is defined by 3 parameters: location (β; linked to the median), scale (σ; linked to the interquartile ratio) and shape (κ; linked to the positions of the first and third quartiles relative to the median¹⁸), and is denoted as GG(β, σ, κ). All predictors were allowed to modify the location parameter; type of CKD diagnosis (described below) was allowed to additionally modify the scale and shape. These models were used to estimate the time at which the 10^th, 25^th and 50^th percentiles for a given profile are expected to experience KRT.

Functional form of CKD diagnosis, eGFR, and UPCR for development of the elementary prediction model

To develop the elementary model, we first investigated classification of diagnoses. We previously reported distinct risk functions for those with glomerular non-hemolytic uremic syndrome (HUS) diagnoses, HUS diagnoses, and non-glomerular diagnoses². Since we did not have sufficient data for HUS-specific prediction (n=48), we fit two GG models with HUS combined with glomerular diagnoses and then non-glomerular diagnoses. This approach determined which diagnostic group those with HUS resembled in terms of time to KRT. The Akaike’s Information Criterion (AIC) values were 1490.287 and 1479.916, respectively, indicating that HUS disease should be grouped together with non-glomerular diagnoses.

To flexibly model eGFR and UPCR as continuous variables (natural log-transformed) and overcome limitations associated with broad groupings of GFR and UPCR by category for predictive modeling, we investigated three continuous functional forms of each variable (linear, natural cubic spline, and linear spline, with a single knot at 45 ml/min|1.73m² for eGFR or 0.5 mg/mgCr for UPCR), along with interactions of diagnosis with eGFR and/or UPCR. This analysis compared 36 models (=3² functional forms × 2² interaction possibilities); the model with the lowest AIC was selected as the elementary model, enabling prediction with the minimum number of variables and serving as the foundation for subsequent enriched models incorporating more predictors.

Random survival forest to identify candidate predictors

To broadly evaluate a pool of variables for enhancement of the elementary model, we used RSF, a supervised statistical learning method designed to classify outcomes (with censoring) using regression trees¹⁹ (randomForestSRC package in R). In brief, RSF is a bootstrapped regression tree method to identify variables most closely associated with progression to KRT as candidate predictors, including potentially identifying predictors not previously known or suspected to be important. Two key metrics assessed the value of each predictor: variable importance (VIMP), which evaluates how much classification error would be introduced if the predictor were unavailable; and minimal depth of the maximal subtree, which evaluates how early in the branching process a variable is generally selected. We used 1000 trees in each forest and the number of variables explored per node was $⌈\sqrt{172}⌉$, or 14 variables.

Development of enriched models

To build upon the elementary model which included diagnosis, eGFR, and UPCR as predictors, we a priori decided to include blood pressure (categorized as a binary variable defined as normal vs. elevated/Stage 1/Stage 2 according to AAP guidelines¹³) in all enriched models as a modifier of the location parameter, since it was previously identified as a key clinical variable associated with CKD progression^20–22. Beyond these four variables, we investigated 9 additional candidate predictors (modifying the location parameter) using best subset selection, a supervised statistical learning method that evaluates all possible combinations of predictors to identify sets of variables that yield the lowest AIC (a measure of training error and goodness-of-fit)¹⁵. A total of 512 (= 2⁹) models were evaluated including the null (elementary + BP) model in this procedure. The model with the lowest AIC in the best subset analysis was selected for use as the fully enriched model.

Evaluation of models

For internal model validation, we also calculated optimism-corrected c-statistic for discrimination²³ and the Greenwood-Nam-D’Agostino (GND) goodness-of-fit test^24,25 for calibration comparing 2-year and 5-year risk of KRT (with at least 5 events per bin²⁵ and the χ² critical value has n bins −1 degrees of freedom). The GND null hypothesis is that the observed risk equals the predicted risk; lower values of the test statistic indicate improved calibration. These metrics were compared across models from elementary to fully enriched in which we expected validation measures to improve with additional predictors. We also compared model fit for nested models relative to the elementary model and enriched model using likelihood ratio tests (LRTs).

Cross-validation and external validation

We conducted 10-fold cross-validation of the entire model-building process^26,27. In this procedure, 10 random samples comprising 90% of the data were used to develop the elementary and enriched model with the concatenation of the remaining 10% per fold used to evaluate model fit. In the model development stage of the cross-validation, we executed the same three-step process described above so the results from the functional forms of elementary model predictors, the RSF, and best subset selection were allowed to vary. For the concatenation of the excluded data, standardized residual times from the model were compared to the standard exponential distribution to evaluate over-fitting (full details in Supplement)² and calibration curves with slope (based on a regression without an intercept) using the GND method. Significance testing was not included because cross-validation sets are not independent.

External validation of the elementary model used data from the ESCAPE cohort which was part of Furth et al.⁴ To account for regional differences in KRT initiation^28,29, the outcome of KRT or eGFR<20ml/min|1.73m² was used (which is about the GFR at which KRT is initiated in this North American population). We assessed standardized residual times, calculated Harrell’s c-statistic and performed the GND test (full description in the Supplement) estimated the calibration slope (based on a regression without an intercept). Statistical significance was assessed at p<0.05.

All analyses and graphs were conducted in R 3.6.3 (R Core Team, Vienna, Austria).

Results

Cohort description

Table 1 describes the demographic and clinical characteristics of the cohort at the time origin, approximately 1 year after the baseline visit. In this sample, the median age was 11.4 years [interquartile range (IQR): 6.7, 15.3] years, 63% were boys, and 21% were of self- or parentalreported Black race. Only 48 participants (5%) had a diagnosis of HUS, and 21% had glomerular, non-HUS diagnoses; the remainder had non-glomerular diagnoses (74%). The median eGFR at the time origin was 50.4 ml/min|1.73m² [IQR: 35.0, 64.6] and the median UPCR was 0.32 mg/mgCr [IQR: 0.13, 1.00]. There was substantial heterogeneity in change of these biomarkers in the year between study entry and the time origin: the median change per year was 1.3% decline in eGFR and 1.3% increase in UPCR, but the IQR for eGFR was −10.3% to +7.8% per year, and was −32.6% to +51.4% per year for UPCR. The median duration of follow-up was 5.2 [IQR: 2.2, 7.9] years and 29% initiated KRT (56% dialysis and 44% kidney transplant). The cumulative incidence function of KRT is presented in Supplementary Figure S2.

Table 1.

Clinical and demographic characteristics of 890 CKiD participants at the time origin (i.e., second study visit). Longitudinal data of progression was characterized by the annualized percent change in GFR and proteinuria between the first and second study visit. Median [IQR] or n (%).

Characteristics	Median [IQR] or n (%) n= 890
Demographics and clinical history
Age, years	11.4 [6.7, 15.3]
Male sex	557 (63%)
Self- or parental reported Black race	187 (21%)
Hispanic ethnicity	121 (14%)
Abnormal birth historya	261 (30%)
Kidney disease characteristics, severity and progression
CKD diagnosis
Glomerular, hemolytic uremic syndrome (HUS)	48 (5%)
Glomerular, non-HUS	186 (21%)
Non-glomerular, non-CAKUT	159 (18%)
Non-glomerular, CAKUT	497 (56%)
Age at disease onset
Present at birth	605 (69%)
<1 year old	41 (5%)
1–5 years old	73 (8%)
6–10 years old	73 (8%)
≥11 years old	89 (10%)
Years with CKD	7.9 [4.5, 12.4]
U25eGFR, ml/min|1.73m2	50.4 [35.0, 64.6]
1-year annualized % change in U25eGFR	−1.3% [−10.3%, +7.8%]
Urine protein/creatinine (UPCR), mg/mgCr	0.32 [0.13, 1.00]
1-year annualized % change in UPCR	+ 1.3% [−32.6%, +51.4%]
Elevated blood pressure, Stage 1 or 2 hypertension	331 (37%)
Laboratory measures
Serum albumin, g/dL	4.4 [4.2, 4.6]
Serum potassium, mmol/L	4.4 [4.1, 4.7]
Serum phosphate, mg/dL	4.6 [4.0, 5.0]
Serum chloride, mmol/L	104 [102, 107]
Serum bicarbonate, mmol/L	23 [21, 25]
Total cholesterol, mg/dL	169 [147, 191]
Anemia	228 (27%)
Follow-up and outcomes
Duration of follow-up, years	5.2 [2.2, 7.9]
Total duration of follow-up, years	4596.8
Any kidney replacement therapy	261 (29%)
Dialysis	147 (17%)
Transplant	114 (13%)

^aDefined as premature birth or small for gestational age or low birthweight (birthweight < 2500g)

Development of the elementary parametric survival model for prediction

Supplementary Table S3 presents the AIC for the parametric models investigating the functional forms of diagnosis, eGFR, and UPCR. The best model included eGFR with a linear spline at 45 ml/min|1.73m² with an interaction with diagnosis, UPCR with a linear spline at 0.5 mg/mgCr, and diagnosis modifying the location parameter, as well as diagnosis modifying both the scale and shape parameters (AIC= 1476.477). This elementary model represents the fewest variables required to predict time to KRT and was substantially lower than the null model with no covariates (AIC= 2021.164).

Random survival forest and development of enriched models

Figure 1 depicts the most important variables by VIMP and minimal depth of the maximal subtree from the RSF analysis; variables towards the top and right are stronger predictors. The results identified eGFR and UPCR as the most important predictors of KRT, affirming our prior decision to build the elementary model around these variables. The next set of important variables included annual change in UPCR, albumin, phosphate, potassium, and chloride. The third set of important variables included annual change in eGFR, bicarbonate, calcium, hematocrit, red blood cell count, anemia, and initiation of erythropoietin stimulating agent (ESA). These were conceptually grouped as markers of CKD progression (change in eGFR and proteinuria over the past year), markers of CKD comorbidities: anemia (since hematocrit, erythrocyte count, present anemia, persistent anemia, and ESA use may be summarized by a single diagnosis); hypoalbuminemia (serum albumin), and metabolic derangement (bicarbonate, chloride, phosphate, potassium, calcium); for a total of 9 additional variables. Supplementary Table S4 presents the full rankings of the top variables.

Figure 1.

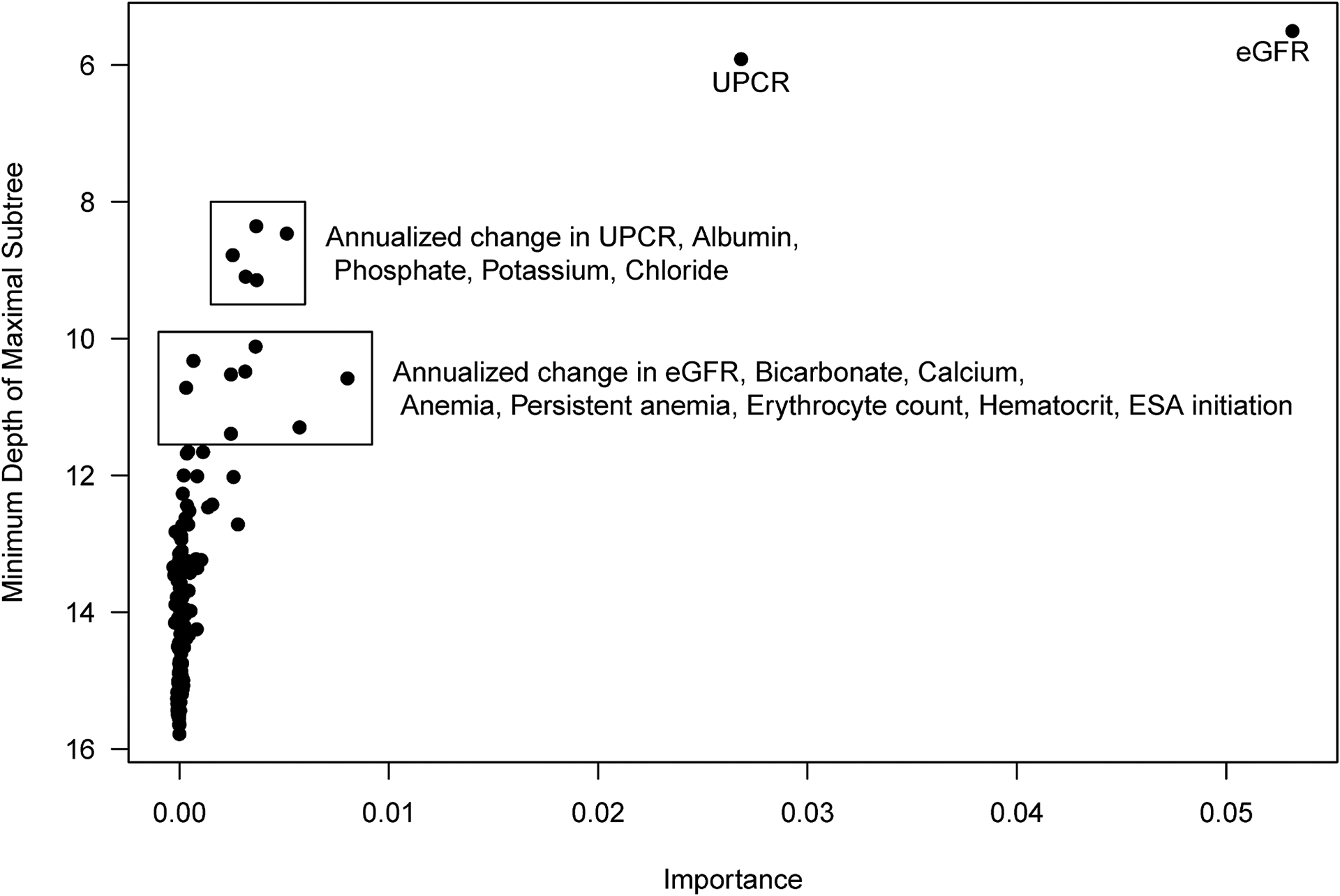
Results from random survival forest plotting metrics of predictive value (minimum depth of maximal subtree versus variable importance) to identify candidate predictors for parametric survival models. Minimum depth of maximal subtree indicates how early in the branching process a predictor is selected, on average; smaller values correspond to earlier selection and thus greater predictive value (y-axis is descending). Importance measures how much prediction error is introduced by randomly permuting the values of a predictor within the dataset; larger values indicate more such error, attributing greater importance to the correct ordering of the values. Groups of variables are denoted and variables listed were included in best subset selection methods of parametric survival models.

Best subset selection was used to evaluate which combination of these 9 additional candidate variables yielded the best predictive model by AIC. Supplementary Figure S3 presents AIC values for the 512 (= 2⁹) models evaluated. The elementary model was the base model (AIC= 1476.477); adding BP as a binary variable (i.e., normal vs. elevated, Stage 1 or Stage 2 hypertension) yielded an AIC of 1471.702. Substantial improvements in minimum AIC were observed as models included up to 5 additional variables, while models with combinations of 6 or more additional variables yielded higher (worse) AIC than the best model with 5 additional variables. This enriched model included annual change in eGFR, anemia, albumin, chloride and bicarbonate in addition to eGFR, UPCR, diagnosis, and BP stage.

Table 2 presents the coefficients for the GG model parameters and model fit statistics and calibration for the elementary model, the enriched model, and four partially enriched models, for circumstances in which data may be unavailable. The evaluation of each model was the test error quantified by AIC and this decreased with the inclusion of additional variables. Enriched models had significantly better fit relative to the elementary model by LRT; the fully enriched model had significantly better fit than less enriched models, with the exception of Partially Enriched Model 4 (p= 0.080). There was improved discrimination in the enriched models (c-statistic= 0.868 for the elementary model to 0.880 for Partially Enriched Model 4 and the enriched model). The GND test statistic for 2-year risk decreased from 2.201 (elementary) to 1.526 (Partially Enriched Model 4) and for 5-year risk decreased from 4.123 (elementary) to 2.643 (enriched) and there were no significant differences between predicted and observed risk. The integration of these models into a unified adaptive tool is presented as a decision tree in Figure 2, describing logic based on available data that leads to the model with the lowest AIC.

Table 2.

Summary of parametric survival generalized gamma models for elementary, partially enriched and fully enriched models, including coefficients and model fit statistics. The unit of analysis were models with model fit and calibration described at the bottom.

		Partially enriched models
Parameter	Elementary (eGFR, UPCR, diagnosis only)	PE Model 1 (Elementary + BP + ΔGFR)	PE Model 2 (Elementary + BP + Anemia)	PE Model 3 (Elementary + BP + lab values)	PE Model 4 (Elementary + BP + Anemia + lab values)	Enriched (All predictors)
β
Intercept	2.8624	2.8993	2.9967	3.7450	4.4095	4.4493
Per 1 log increase in (eGFR/45)	2.0868	1.9511	1.9769	2.1789	2.0944	1.9837
Per 1 log increase in (eGFR/45)×(eGFR ≥ 45)	−1.0758	−1.0091	−1.1370	−1.3874	−1.4511	−1.4158
Glomerular non-HUS vs. Non-glom/HUS	−0.1532	−0.0718	−0.0511	−0.1071	−0.0231	0.0268
Per 1 log increase in (eGFR/45) × Glom non-HUS	1.0386	0.8132	0.9807	0.6812	0.7360	0.6275
Per 1 log increase in (eGFR/45)×(eGFR ≥ 45) × Glom non-HUS	−1.2154	−1.0010	−1.0714	−0.5795	−0.6282	−0.5253
Per 1 log increase in (UPCR/0.5)	−0.1959	−0.2123	−0.2127	−0.1720	−0.1984	−0.1968
Per 1 log increase in (UPCR/0.5) × (UPCR ≥ 0.5)	−0.3146	−0.2721	−0.2566	−0.2102	−0.1803	−0.1759
Elevated BP/hypertension vs. normal BP		−0.2229	−0.2337	−0.2242	−0.2339	−0.2282
Per 1 increase in Δ( log(eGFR)) per year		0.4349				0.3934
Anemia vs. no anemiaa			−0.3617		−0.3162	−0.3033
Per 1 unit increase in albumin, mg/dLb				0.3802	0.3168	0.3172
Per 1 unit increase in chloride, mmol/Lb				−0.0235	−0.0248	−0.0255
Per 1 unit increase in CO2, mmol/Lb				0.0005	−0.0074	−0.0071
σ
Intercept	0.7440	0.7454	0.7441	0.7204	0.7242	0.7262
Glomerular non-HUS vs. Non-glom/HUS	0.2627	0.1744	0.2521	0.2426	0.2172	0.1390
K
Intercept	0.4253	0.3888	0.3513	0.4467	0.4163	0.3914
Glomerular non-HUS vs. Non-glom/HUS	−0.0005	0.2204	0.1023	0.0768	0.1367	0.2787
Model fit and calibration
AIC	1476.48	1470.09	1457.68	1456.72	1446.15	1445.06
Likelihood ratio test
Compared to elementary	Ref	0.006	<0.001	<0.001	<0.001	<0.001
Compared to enriched	<0.001	<0.001	<0.001	<0.001	0.080	Ref
Optimism-corrected c-statistic	0.865	0.866	0.874	0.871	0.875	0.875
Greenwood-Nam-D’Agostino test statistic
At 2 years with 4 bins (${\chi }_3^2$)	2.201	2.213	2.237	2.318	1.526	1.903
p-value	0.53	0.53	0.52	0.51	0.68	0.59
At 5 years with 6 bins (${\chi }_5^2$)	4.123	5.022	4.827	4.231	3.518	2.643
p-value	0.53	0.41	0.44	0.52	0.62	0.75

^aAnemia defined as current low hemoglobin.

^bLaboratory-measured serum biomarkers from renal panel.

Figure 2.

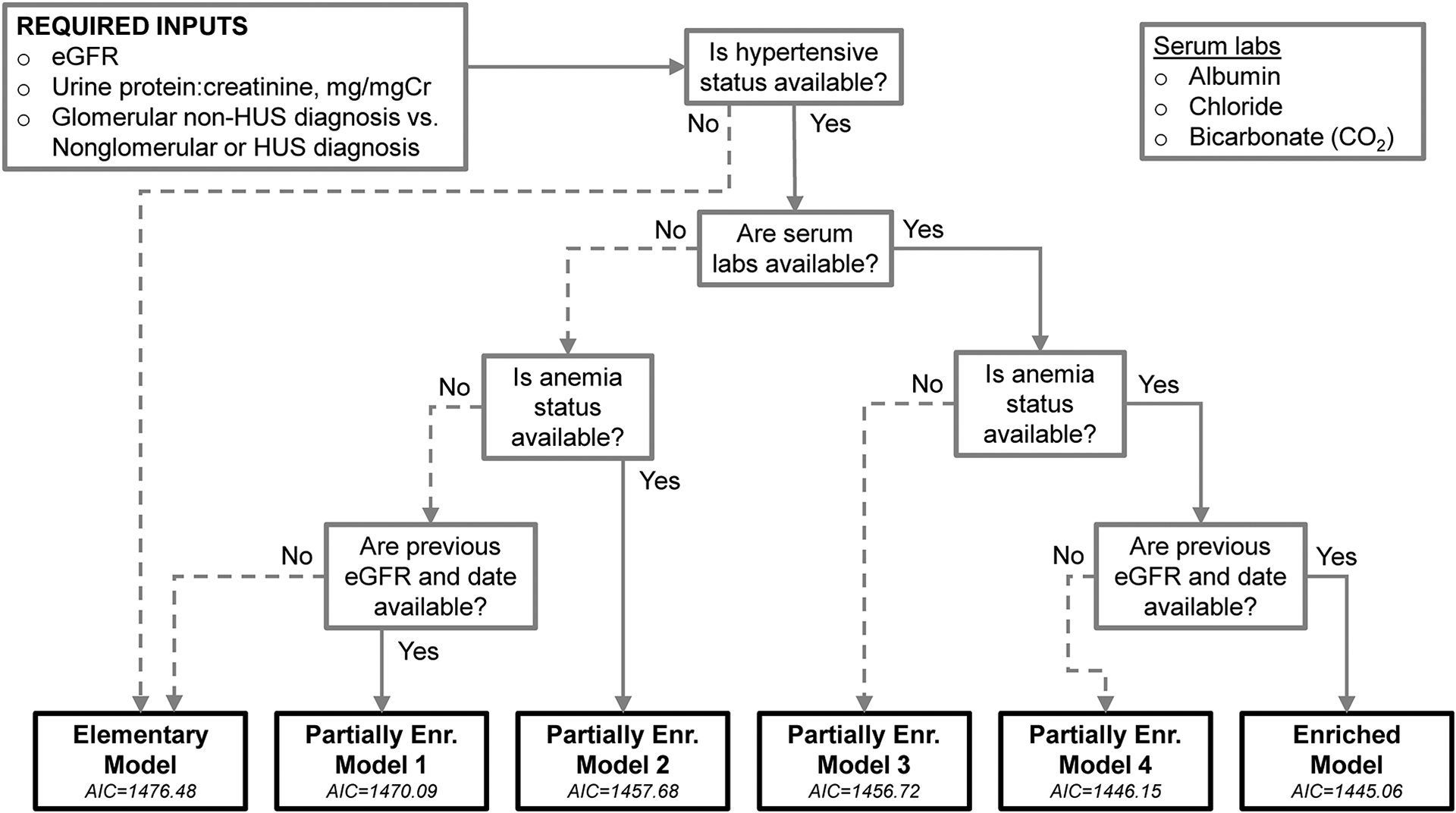
Decision tree describing adaptive approach for model based on availability of data for use in the online calculator. Akaike’s Information Criterion (AIC) statistics for each model are presented and correspond to improved penalized model fit (i.e., lower corresponds to lower error).

Cross-validation and external validation results

Figure 3 presents results from the cross-validation of the fully enriched model. Figure 3a presents the calibration plot for bins of predicted 5-year estimated risk which was very close to the observed risk (i.e., 1- KM(t)) and the c-statistic for the cross-validation sample was 0.868. The calibration slope was 1.019 (slope for perfect agreement= 1) and was very close to the average calibration slopes over the 10-fold calibration (1.017). The survival function of expected standardized residual times closely aligned with the standard exponential distribution (Figure 3b). Cross-validation of the elementary model was similar in terms of calibration, discrimination (c-statistic= 0.861) and standardized residual times.

Figure 3.

Model validation assessment based on 10-fold cross-validation of model building process for the Enriched Model including calibration plot depicting observed risk on predicted risk from at 5-year risk of kidney replacement therapy (3a) and survival function of standardized residual times for participants (3b). The calibration plot demonstrates close correspondence between observed and predicted 5-year risk and the survival function aligns closely with the expected standard exponential for strong model fit.

To externally validate the elementary model using European ESCAPE data (descriptive statistics in Supplementary Table S5 and cumulative incidence in Supplementary Figure S4), the GND test for 5-year risk did not demonstrate significant differences between the predicted risk and observed risk (${\chi }_4^2$ = 6.926; p= 0.140), the calibration slope was 0.996 (95%CI: 0.903, 1.088, p= 0.90), and the c-statistic was 0.854 (95%CI: 0.835, 0.873) indicating strong discrimination. The standardized residual times were congruent with the standard exponential distribution. Full results and further interpretation are in Supplementary Figure S5.

Enhancement of risk prediction by model enrichment

Figure 4 presents a visual comparison of the Elementary Model (based on diagnosis, GFR and UPCR) and Partially Enriched Model 1 (Elementary Model with current BP stage and GFR from the previous year) of predicted median times to KRT to demonstrate the enhanced risk prediction provided by blood pressure and longitudinal GFR as additional predictors. This hypothetical profile is a patient with non-glomerular or HUS diagnosis, current GFR= 30 ml/min|1.73m² and UPCR= 2mg/mgCr corresponding to the elementary model variables: the median predicted time to KRT (y-axis) is 3.3 years (black horizontal line); this estimate does not incorporate GFR from 1 year ago (x-axis) and is thus invariant to it. The light and dark grey lines describe the predicted median time to KRT using Partially Enriched Model 1 across a range of GFR values from 1 year ago, if the patient had normal BP or elevated BP/hypertension , respectively. The elementary model prediction was in between the lines contrasting BP categories, which is reasonable when BP data is not available. The predicted time to KRT was longer for normal BP compared to elevated BP/hypertension reflecting the well-established relationship of accelerated CKD progression with higher BP. In addition, for Partially Enriched Model 1, the time to KRT was shorter when the annual GFR decline was faster. This reflects higher risk associated with accelerated progression over the course of 1 year.

Figure 4.

Comparison of Elementary Model with Partially Enriched Model 1 including blood pressure and longitudinal GFR. The example profile is a child with non-glomerular or HUS diagnosis, a current GFR of 30 ml/min|1.73m² and a urine protein:creatinine ratio (UPCR) of 2 mg/mgCr. The y-axis represents the median predicted time to KRT and the x-axis represents GFR from one year ago with the dashed line indicating no change. The three lines represent different models: the elementary model (light grey) is constant across previous GFR, and the partially enriched model 1 (dark grey) is depicted by blood pressure status (normal or elevated).

Online tool for clinical use

Because individual predictions are not easily derived without specialized software, we developed an accompanying accessible online clinical tool to estimate times to KRT for individual patients. This tool requires input of U25 eGFR, UPCR, and diagnosis but additional optional variables can be entered (if available) for improved estimates. The best model (i.e., lowest AIC) based on available data computes the estimated time to KRT following the logic described in Figure 2. Estimated times are provided for the 10^th, 25^th and 50^th percentiles in years rounded to the nearest month, with an upper limit of 10 years. The output provides the time by which the p^th percentile of children with the same profile will experience KRT. For instance, if a patient has a U25 eGFR of 60, UPCR of 0.8 mg/mgCr, glomerular diagnosis, hypertension, anemia, albumin level of 4.5, chloride level of 105, CO2 level of 22, and experiences a 10% annual decline in eGFR, the output would state that 10% of children with this profile are expected to initiate KRT within 2.5 years, 25% within 5.1 years, and 50% within 10.1 years (>10 years). R code of all models for this hypothetical profile is provided (Supplementary Appendix 1). The online calculator is available at: https://ckid-gfrcalculator.shinyapps.io/CKiD_KRT_Risk/.

Discussion

In this paper, we propose a predictive tool to estimate time to KRT initiation for children with CKD. This model is based on the largest observational cohort of children with CKD in North America and predicts the clinically meaningful outcome of KRT initiation rather than a composite outcome including KRT and accelerated disease progression. The predictors evaluated are commonly measured clinical variables, and multiple models allow for an adaptive prediction of risk depending on availability of patient data. Cross-validation of the model-building process and the external validation in a European cohort of the elementary model demonstrated strong discrimination and calibration and gives confidence that this suite of six unified models (presented in a corresponding online tool) will help with risk stratification as well as for dialysis and transplant planning for children.

The model development capitalized on statistical learning methods: the RSF agnostically evaluated candidate predictors and best subset selection evaluated all possible combinations to specify the optimal models. Crucially, our models were also informed by clinical insight, previous literature, and the culmination of numerous CKiD-specific risk factor studies. It was somewhat surprising that BP was not identified as a key predictor in the RSF analysis, but because of its established importance in CKD progression^{11,20–22,30} it was included in the enriched models. BP is routinely assessed as part of clinic care so its inclusion is broadly applicable, although we encourage careful measurement for valid estimates of BP percentiles and classification of BP¹³.

Major strengths of the study included a population with a wide spectrum of kidney function at study entry and centrally measured biomarkers as predictors. Furthermore, CKiD collected data from 2005 and there are now enough observed KRT events to develop a robust predictive model for a clinical endpoint, which overcomes previous limitations of models based on a weaker surrogate endpoint of GFR decline. In addition, this analysis used the latest U25 GFR estimating equations¹² and updated AAP BP guidelines¹³. The longitudinal data collection offered an opportunity to explore the predictive value of annual measurements (specifically, between the first and second visit). The rich longitudinal data was a major feature of this analysis, although only annual GFR change was identified in the RSF and included in two enriched models.

Using an adaptive approach based on six models overcame a limitation of previous risk calculators requiring complete data³. Even if data are limited, clinicians should be confident of a good prediction of KRT risk using only elementary predictors. Additional data will enhance risk prediction, as evidenced by improvement in training error rate for partially and fully enriched models. The custom-designed online calculator translates multiple underlying GG models into a simple user interface. This adaptive tool provides an interpretable output of estimated median times to KRT initiation: in the absence of other data, a reasonable estimate for individual patients is the 50^th (average) percentile. To provide estimated variability, we report the 10^th and 25^th percentiles. For many profiles, there could be substantial variability in the percentiles and we note that the risk prediction is not deterministic.

While we dealt with independent variables from a purely predictive framework, rather than etiologic or causal perspective, many predictors are established etiologic risk factors for pediatric CKD progression, including diagnosis⁷, eGFR^3,4, proteinuria^6,31,32, blood pressure^{20–22,30,33}, anemia^34–36 and bicarbonate³⁷. Chloride, which was included in two partially enriched models and the fully enriched model, represents a metabolic derangement that is likely linked to bicarbonate, but future work should investigate chloride as a risk factor for CKD progression.

We caution about interpreting the Table 2 coefficients directly. In general, negative values indicate shorter time to KRT (increased risk) and positive values denote longer time to KRT (protective). However, when looking at the GFR coefficient, the intertwined relationship between GFR and diagnosis (which also modifies the scale and shape parameters) obfuscates direct interpretation of any one individual coefficient. In addition to interaction, linear splines for GFR and proteinuria further complicate coefficient interpretation. We provide R code for readers wishing to explore these models further (Supplementary Appendix 1), but we emphasize that the goal was to develop the best prediction tool that offered the lowest test error quantified by AIC. While it may be useful to inspect the coefficients for face validity, the primary unit of evaluation was the prediction model itself.

There are important limitations to this analysis. We were not able to estimate diagnosis-specific risk beyond two broad diagnostic categories, nor could we incorporate response to specific therapies, for example treatments for glomerular diseases like FSGS, lupus nephritis or atypical HUS. Second, while CKiD offers broad representation of a pediatric CKD population, extreme patient characteristics (compared to Table 1) may yield invalid estimates. Third, we were only able to externally validate the elementary models but cross-validation methods demonstrated sound calibration, discrimination and model fitting for the enriched models. Other potentially important predictors, such as ambulatory blood pressure^22,30 and uric acid³⁸, did not have complete data for analysis; though these may also not be as readily available clinically.

In summary, using data from the CKiD study, we developed a predictive tool for time to KRT to aid clinical decision making and KRT planning in children and adolescents with CKD. We presented a series of equations to predict time to KRT based on routinely measured data in an adaptive way and designed a website for applied use by clinicians managing children with kidney diseases. While this predictive model was internally validated using cross-validation methods and with an external validation of the elementary model, future studies are necessary for additional external validation of the enriched models in other pediatric CKD cohorts.

Supplementary Material

1

Description of cross-validation and external validation methods.

Supplementary Table S1. List of variables evaluated in random survival forest analysis to identify potential predictive candidates in subsequent parametric survival models to predict time to kidney replacement therapy.

Supplementary Table S2. Distribution of specific chronic kidney disease diagnoses represented in the study population (n= 890).

Supplementary Table S3. Akaike Information Criterion (AIC) values as a measure of test error from different functional forms of GFR, proteinuria and interactions with diagnosis as modifiers of the location parameter (β) in generalized gamma parametric survival model.

Supplementary Table S4. Ranking of variables from random survival forest according to top 20 minimal depth of maximal subtree classification and top 20 variable importance.

Supplementary Table S5. Descriptive characteristics of the ESCAPE cohort used for external validation.

Supplementary Figure S1. Cohort flow diagram of those with no follow-up time, prevalent kidney replacement therapy event prior to time origin, and those with missed visits at the time origin.

Supplementary Figure S2. Kaplan-Meier estimates of cumulative incidence of kidney replacement therapy in the CKiD cohort.

Supplementary Figure S3. Results from best subset selection of top 9 variables identified from random survival forest analysis presenting Akaike information criterion (AIC) on best subset models with additional variables (2⁹= 512, including the elementary model as the null model).

Supplementary Figure S4. Kaplan-Meier estimates of cumulative incidence of ESKD in the ESCAPE cohort.

Supplementary Figure S5. Results and interpretation from external validation of elementary model using data from the ESCAPE study including calibration plot depicting observed risk on predicted risk from at 5-year risk of kidney replacement therapy and survival function of standardized times of residuals for participants.

Supplementary Appendix 1. R Code of models presented in Table 2 and used in the online clinical calculator for a hypothetical patient profile.

Supplementary Appendix 2. Content from online clinical calculator describing model purpose, use, strengths and limitations designed for clinicians.

Supplementary Table S6. List of principal site investigators of the Chronic Kidney Disease in Children (CKiD) cohort study.

Data sharing statement

CKiD data is available upon request at the NIDDK Repository: https://repository.niddk.nih.gov/studies/ckid/

Analytic datasets and R programs for this analysis is available upon request to the corresponding author (dng@jhu.edu).