Significance
The continued circulation of many endemic viruses relies on escape mutations, which help the virus avoid the hosts’ immunity and spread in the population. Frequent mutations make escape easier, yet they also increase the chance of harmful mutations to the virus. By treating both the evolving viral population and responding immune system on equal footing, we show that the breadth of viral strains identified by a set of immune cells determines whether it is beneficial for the virus to mutate fast and explore antigenic space, or to exploit its position by increasing its population size with limited mutations. We place influenza-A in the range of broad cross-reactivity where viral population growth is fast but mutations are rare.
Keywords: coevolution, immune system, evolution of mutation rate, viral evolution, evolution of virulence
Abstract
Antigenic variation is the main immune escape mechanism for RNA viruses like influenza or SARS-CoV-2. While high mutation rates promote antigenic escape, they also induce large mutational loads and reduced fitness. It remains unclear how this cost–benefit trade-off selects the mutation rate of viruses. Using a traveling wave model for the coevolution of viruses and host immune systems in a finite population, we investigate how immunity affects the evolution of the mutation rate and other nonantigenic traits, such as virulence. We first show that the nature of the wave depends on how cross-reactive immune systems are, reconciling previous approaches. The immune-virus system behaves like a Fisher wave at low cross-reactivities, and like a fitness wave at high cross-reactivities. These regimes predict different outcomes for the evolution of nonantigenic traits. At low cross-reactivities, the evolutionarily stable strategy is to maximize the speed of the wave, implying a higher mutation rate and increased virulence. At large cross-reactivities, where our estimates place H3N2 influenza, the stable strategy is to increase the basic reproductive number, keeping the mutation rate to a minimum and virulence low.
RNA viruses like influenza or SARS-Cov-2 are subject to a constant antigenic evolution driven by their hosts’ immune pressure and fueled by their remarkably high mutation rates (1–4). Although immune memories in hosts are geared toward reinfections and possible variants (5–7) this constant evolution allows viruses to evade immunity, leading to repeated epidemics and reinfections. The recent SARS-Cov-2 outbreak has shown that the management of infectious diseases remains a global health challenge and is now a major public concern in the face of an increased ecosystem disruption (8–10). In these conditions, predicting the emergence of future variants is essential to inform vaccine strain selection, improve collective immunity and lift the burden imposed on healthcare systems.
These challenges have led to the development of theoretical methods to predict influenza antigenic evolution (11–13). However, these approaches do not inform about the evolution of nonantigenic traits like virulence or the mutation rate itself, while these traits clearly influence the future state of the viral and host populations. On the other hand, extensive epidemiological literature describes host-pathogen coevolution in pathogens not escaping immunity (14–18). While bridges between this literature and population genetics models have long been built to predict the evolution of parasite virulence (19, 20), they have only recently been extended to study virulence evolution in antigenically evolving viruses (21). These approaches showed that in populations of infinite size, antigenic escape promotes higher transmission rates and virulence than expected for pathogens at an endemic equilibrium. However, antigenic adaptation is mostly driven by stochastic birth, death, and mutation events occurring in the most well-adapted individuals (22, 23), which are typically in small numbers. Thus, finite-size demographic effects are crucial to accurately describe antigenically evolving pathogens (24–27). It remains unclear how antigenic escape in a coevolving system of viruses and antibodies, coupled with finite size demography, constrains the evolution of nonantigenic traits, such as the mutation rate or the virulence.
To model antigenic escape it is convenient to describe both the host immune memories and the viral strains as living in the same antigenic space (21, 24, 27, 28), corresponding to a space of molecular similarity, also called “shape space” (29). This construction is not just conceptual: Dimensionality reduction of hemagglutination inhibition data can be used to build low dimensional manifolds on which influenza and hosts antibodies coevolve (30–32). While mapping influenza evolution in this shape space has been used to describe evolutionary modes of influenza (27, 33, 34), it remains unclear how this regime influences the evolution of nonantigenic traits such as the mutation rate of viruses.
In this work, we describe with a SI(R) formalism (15, 35) for the coevolution of a finite population of viruses and immune systems of infected hosts, in an effective one dimensional antigenic space. The model generates a traveling wave for the number of viruses, which escapes from a continuously adapting immune system. Our first finding is that, depending on the model parameters, the antigenic wave crosses over between two well-characterized regimes. Among those parameters, the ability of antibodies to recognize pathogens similar to the already encountered ones, called immune cross-reactivity or cross-immunity, plays a key role. A narrow cross-reactivity leads to a Fisher–Kolmogorov–Petrovsky–Piskunov (FKPP) traveling wave (36), while, for a large one, the wave converges to a linear-fitness wave dominated by finite-size effects (25, 37), with a smooth cross-over between the two. These regimes result in very different scalings of the macroscopic properties of the wave, such as its speed. They also affect the evolutionary stability of nonantigenic traits. To investigate this effect, we derive a simple and general relation for the evolutionary stability of viral parameters, which displays two qualitatively different behaviors depending on the regimes. We then apply these results to study the evolution of the viral mutation rate on the one hand, and of the virulence on the other. We discuss how the evolutionarily stable states are strongly impacted by cross-reactivity.
Results
A. Model of Coevolving Pathogens and Immune Systems.
We start by defining and analyzing a mathematical model of pathogen-immune dynamics. We consider the evolution of a pathogen in a one-dimensional antigenic space with density (Fig. 1A, red line), where denotes position in that space. Immune protections are also assigned positions in that space, so that protections are close to the viruses they recognize. While the antigenic space is believed to have higher dimensions (38), theoretical work has shown that the effective evolution of the resulting traveling wave of escaping viruses is “canalized” into a one-dimensional track (34), provided that we ignore possible speciation events (27, 33, 39). This picture is overall consistent with influenza data that show a low-dimensional reduction of the viral evolutionary trajectory from hemagglutination inhibition assays (30).
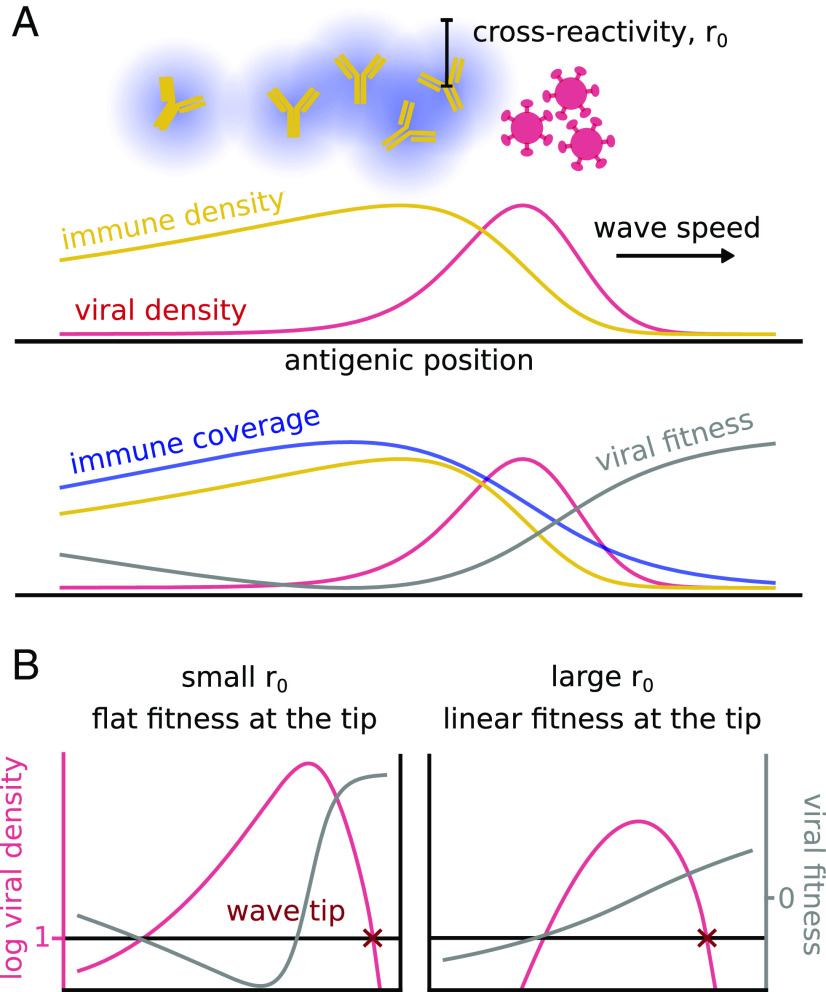
Fig. 1.
Two types of antigenic waves controlled by cross-reactivity. (A) Typical traveling wave dynamics of a population of viruses (in red) escaping the immune system (in blue), Eqs. 1 and 5. In the Bottom panel, the immune coverage and the viral fitness are also drawn. The increase of fitness in the back of the wave does not give rise to a second wave as the virus is extinct in that region. (B) Differences between the two regimes of small and large cross-reactivity. The plots show the viral density (in red) under two different fitness profiles (in yellow). They highlight the phenomenological difference between the two regimes.
We assume that mutations act continuously and in an unbiased way on the antigenic space so that, in the limit of infinitely small mutations happening at a rate , the density of infected hosts effectively diffuses with constant , where is the typical step covered by a mutation in the antigenic space. This continuous model approximates any arbitrary discrete mutational model provided that a random amino acid mutation in the antigenic sites of the pathogen is unlikely to induce a large change in hemagglutination inhibition titer, or equivalently in the antigenicity of the strain. For influenza, in spite of rare mutations inducing large antigenic jumps (30, 40), the typical number of amino acid mutations happening in the hemagglutinin antigenic sites before observing a substantial change in antigenicity is closer to 15 substitutions (12). In this regime and for similar pathogens, a continuous approximation is accurate enough.
Following standard SI(R) modeling, we denote by the pathogen transmission rate in the absence of immunity, its virulence and the recovery rate. An important quantity is the reproductive ratio, , corresponding to the mean number of transmissions infectious individuals cause in an unprotected population, before they recover or die. We define the effective growth rate of a viral strain at position as , where is the susceptibility of the population to that strain, defined below. This leads to the following stochastic differential equation for the viral evolution:
| [1] |
We consider an effective, population-averaged effect of the immune systems of the hosts onto the virus (27). The immune protection is described by a function (Fig. 1A, blue line), which is the probability density of immune receptors in a random host. We consider hosts, each with immune protections drawn at random from . Upon infection by , the host acquires a new immune protection at , which replaces one of its protections at random. This results in the following population-wide dynamics:
| [2] |
where is the total number of infected hosts.
To estimate the susceptibility , we assume that a protection at position provides protection against nearby pathogens, with a probability that decays exponentially with characteristic length , called cross-reactivity range. This allows us to define the immune coverage as
| [3] |
which is the probability that a random protection from a random host is effective against (Fig. 1 A, green curve). The susceptibility is then just the probability that none of the protections of a random host is effective against :
| [4] |
B. Deterministic Approximation.
Eqs. 1–4 describe the coevolutionary dynamics of pathogens and immune protections. Because escape mutants of the pathogen are subject to random extinctions due to genetic drift in their early days, one should not ignore demographic noise for all population sizes. To simplify the computational load yet account for the effect of small numbers, we use a deterministic version of Eq. 1 where viruses stop spreading when :
| [5] |
where if and otherwise. This approximation is known to provide traveling wave results in excellent agreement with fully stochastic agent–based simulations in various models of rapidly adapting populations (22, 27, 37). Details about simulations of this equation are given in Section A. We checked that our results are consistent with a full stochastic approach, Section B.
Note that in general, has units of an inverse antigenic distance. We will show that results depend very weakly on (SI Appendix, Text and Fig. S1). Nevertheless, to fix the scale of in an interpretable way, we set , so that roughly represents the average number of infected hosts in its mutation class (i.e., within a bin of size ). We then set , which corresponds to one individual per class. The cross-reactivity parameter can be interpreted as the number of mutations that a virus needs to acquire to escape an immune protection.
Table 1.
List of free parameters of the model
| Viral mutation rate | Viral transmission rate | ||
| Mutational step | Receptor cross-reactivity | ||
| Virulence | Number of hosts | ||
| Recovery rate | Protections per host |
Table 2.
Main quantities of the model
| , Eq. 1 | Density of infected hosts |
| , Eq. 2 | Density of immune receptors |
| , Eq. 3 | Coverage of the receptors |
| , Eq. 4 | Susceptibility |
| Viral growth rate | |
| Maximal viral growth rate | |
| Mutation diffusion coef. | |
| Reproductive ratio | |
| Speed of the viral wave | |
| Viral growth rate at the wave tip | |
| Slope of growth rate at the tip | |
| Notation shorthand | |
| growth-to-escape dimensionless ratio |
C. Cross-Reactivity Drives Different Regimes of Antigenic Evolution.
The coupled system of Eqs. 1 and 2 admits a traveling wave solution, where the viral population is a moving bump followed by the immune system (Fig. 1A). This dynamics is known to be driven mainly by the few individuals the front of the wave (22, 23): Mutations generate new strains at more favorable antigenic positions ahead of the wave, where the hosts’ immune systems provide less protection. As a consequence, they grow faster than strains in the bulk of the wave, which is under stronger immune pressure. This process is controlled by the few individuals at the front tip and therefore is intrinsically stochastic.
There are two different limits depending on the shape of the viral fitness at the tip of the wave, as illustrated in Fig. 1B. For small cross-reactivities of the immune protections, viral strains at the tip feel no immune pressure at all. The fitness profile is thus locally constant. As we will see in detail, the wave dynamics in this regime corresponds to the classical FKPP traveling wave (36), where stochastic effects do not play an important role.
At large , the immune coverage extends all the way to the tip of the wave, where viral strains experience a local gradient of fitness. This case, where stochastic events at the wave tip drive its motion, has been also well characterized in previous works (25, 37). In general, varying allows us to interpolate smoothly between the two regimes.
These two different behaviors are not just of technical interest. As we will see, they result in different parameter dependencies for the speed of the wave and imply markedly different evolutionarily stable states for nonantigenic traits such as the mutation rate or the virulence. While previous work on the evolutionary stability of such traits has focused on the FKPP regime (21), here, we treat the general case.
D. The Cross-Over Results in Different Wave Speed Dependencies.
We assume that Eq. 5 admits a stationary solution in the frame moving with constant speed , so that all quantities depend on the reduced variable :
| [6] |
The dynamics of the wave is driven by its behavior around the wave tip , defined by , where we assume the fitness is locally linear, . This is a strong approximation which neglects everything that happens away from the tip, but, as shown below, it works extremely well, confirming the idea that the individuals at maximal fitness are the main drivers of evolution (23). In that regime, Eq. 6 may be solved exactly in the vicinity of . The continuity condition between the and parts of the solution yields the relation (SI Appendix, Text A1):
| [7] |
where , and is the largest zero of the Airy function. We verified numerically that this relation is satisfied for both the deterministic equation with a cutoff, Eq. 5, and the original stochastic equation, Eq. 1 (Fig. 2A). This relation connects the wave speed with the value of the fitness, , and its derivative, , at the tip in a very general way, without assuming any specific behavior of the immune system. It can be potentially applied to every system showing traveling waves and a locally linearizable fitness at the tip. However, it is only implicit, since the position of the fitness tip itself needs to be computed from the model parameters in order to evaluate and . A second implicit equation for and may be obtained by imposing the normalization condition on the solution to Eq. 6, where is the number of infected hosts.
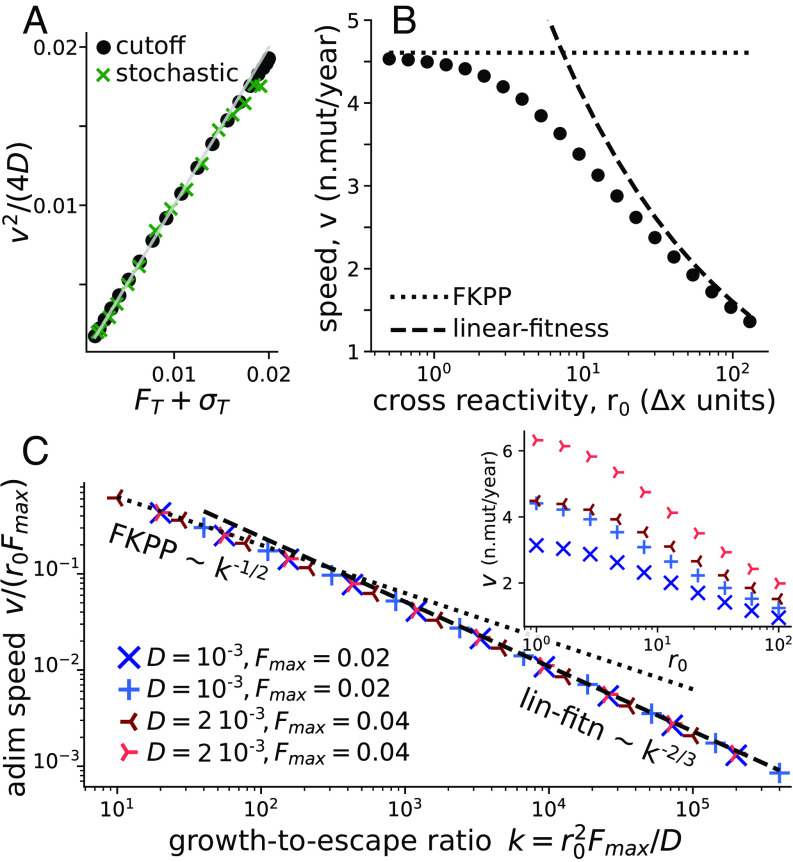
Fig. 2.
Wave speed. (A) Numerical check of Eq. 7 relating speed and fitness profile at the tip of the wave, for both the stochastic model and its deterministic approximation with a cutoff (Eq. 5). The gray line is identity. Each point is defined by the values of speed, fitness, and selection at the tip of the numerical solutions of our model. Different points are different values of and fixed values of the other parameters: , , , , (B) Wave speed as a function of the cross-reactivity, showing the cross-over between the FKPP and linear-fitness regime. In the two extreme regimes, analytical predictions can be explicitly obtained (Eq. 8 for the dotted line and SI Appendix, Eq. S24 for the dashed one). Same simulation parameters as (A). (C) Inset: speed vs cross-reactivity for different values of in n.mutations day and in day. The main plot shows the collapse of these curves as a function of the growth-to-escape ratio . The dashed and dotted lines are the theoretical predictions for the FKPP and linear fitness regimes.
A special case is given by the regime of “small” cross-reactivity (Fig. 1B, Left) where the fitness at the tip is maximal, and its derivative . Then Eq. 7 is sufficient to determine the speed, giving back the classical expression for FKPP waves:
| [8] |
Fig. 2B shows how the wave speed of our model converges to this limit (dotted line) for decreasing .
In the opposite limit of a linear fitness profile, (Fig. 1B, Right), the normalization condition can be expressed analytically (25, 37, 41), leading to the following approximated formula for the speed (SI Appendix, Text A2 for a full expansion):
| [9] |
The fitness profile may be obtained by integrating Eq. 2. The stationarity condition of zero mean fitness, , gives an additional relation between and , . The gradient then reads . This creates a closed system of 2 implicit equations that allows us to estimate and . The speed obtained numerically converges to that solution in the large regime (Fig. 2B, dashed line).
To better understand the dependency of the cross-over on the model parameters, we introduce the natural dimensionless parameter . It is equal to the ratio of two timescales: the typical time it takes a single virus to escape immunity by antigenic drift, and the characteristic doubling time in the absence of immunity. We call this quantity the “growth-to-escape ratio.” As Fig. 2C shows, the normalized speed collapses as a function of for a wide range of parameter values. The cross-over takes place around . In particular, a larger diffusion coefficient helps the virus to be well ahead of the immune coverage, which corresponds to the FKPP regime. By contrast, a large cross-reactivity increases the immune coverage and pushes the system toward the linear-fitness regime.
E. The Evolutionarily Stable Strategy has a Cross-Over between Maximizing the Speed and the Reproductive Ratio.
From this section on, we tackle the main question of this manuscript: understanding the evolutionarily stable strategies of the viral population under immune pressure. The first step is to ask whether a mutant competing with a resident population can displace it. Consider a mutant strain with slightly different parameters than the resident one. The evolution of its number, , is given by Eq. 5. In the early days of this mutant, the resident strain is at stationary state, and that the mutant is too rare to contribute to the immune receptor density .
We assume that the fate of the mutant is determined by its behavior at the tip of the wave, where the fitness profile is approximately linear. Then, as we show in SI Appendix, Text C1, the mutant population evolves in the moving frame as , with growth rate:
| [10] |
where and , with , and where the mutant parameters are indicated with a prime and is the speed of the resident population. The mutant invades if and only if .
As expected, when the mutant is phenotypically identical to the resident, , , , then Eq. 7 implies , meaning that the mutant has no advantage or disadvantage. We tested the validity of the invasion condition for mutants of and in SI Appendix, Text and Fig.S2. Note that this stability relation depends only on the fitness and the selection coefficient at the tip, without specific details of our immune framework. This implies that it can be extended to other models.
Eq. 10 allows us to see how the best viral strategy radically depends on the considered regime. In the FKPP limit (small ), the condition becomes , or equivalently with : The best strategy is to maximize the speed of adaptation. In the linear-fitness regime (large ), the fitness in the bulk of the wave dominates Eq. 10, yielding the condition or equivalently : The best strategy is to maximize the reproductive ratio.
We can use Eq. 10 to derive evolutionarily stable points of the population in all regimes. Consider phenotypic continuous variables over which the evolutionary process acts, so that , , and so on. The growth rate of an invading mutant, Eq. 10, depends on both the phenotypes of the resident and invading population, . A stable point must satisfy for all perturbations . Since , this implies , which can be rewritten as (SI Appendix, Text C1):
| [11] |
We will now use this condition to study the evolutionary stability of two distinct quantities independently: the mutation rate (next two sections) and the virulence (last section).
F. Evolutionary Stability of Mutation Rate Under Mutational Load Trade-Off.
The mutation rate plays a key role for antigenic escape. By raising it, the ability of the virus to escape immune protection increases, as shown by the positive dependency of the wave speed on (Eqs. 8 and 9). However, a majority of mutations occurring in viruses are not affecting antigenic traits and generically decrease the intrinsic fitness of the strain (42–44). The larger the total mutation rate, the more these deleterious mutations accumulate and decrease the pathogen’s infectivity, possibly leading to viral extinction. In fact, increasing mutation rates is a widely used antiviral strategy (45). To account for this trade-off between the harmful effect of mutations and the benefits of antigenic escape, we let the infectivity depend on the rate of deleterious mutations per transmission as . In SI Appendix, Text B, we derive this relation from the balance between mutation and selection (43, 46, 47) in an epidemiological context, using an approach similar to ref. 48. The two rates and are assumed to scale both with the global mutation rate, so that they are linearly related, . This implies , with .
Using Eq. 11 with as the only phenotypic control parameter , yields an implicit expression for the evolutionarily stable state:
| [12] |
In the two extreme limits and , we obtain explicit expressions that give us two different scalings between the normalized diffusion coefficient, and the normalized scaling factor: for FKPP, and for linear fitness (SI Appendix, Text C2). Note that may be interpreted as the inverse of the time it takes for a single strain to escape an immune protection by antigenic diffusion, while may be interpreted as the number of deleterious mutations accrued during that time.
These expressions are compared to numerical simulations of the evolutionary stability in Fig. 3A, and confirm the scaling relation . We also tested the validity of the general stability condition, Eq. 12, for both the stochastic model and its deterministic approximation with a cutoff (SI Appendix, Text, Fig.S3).
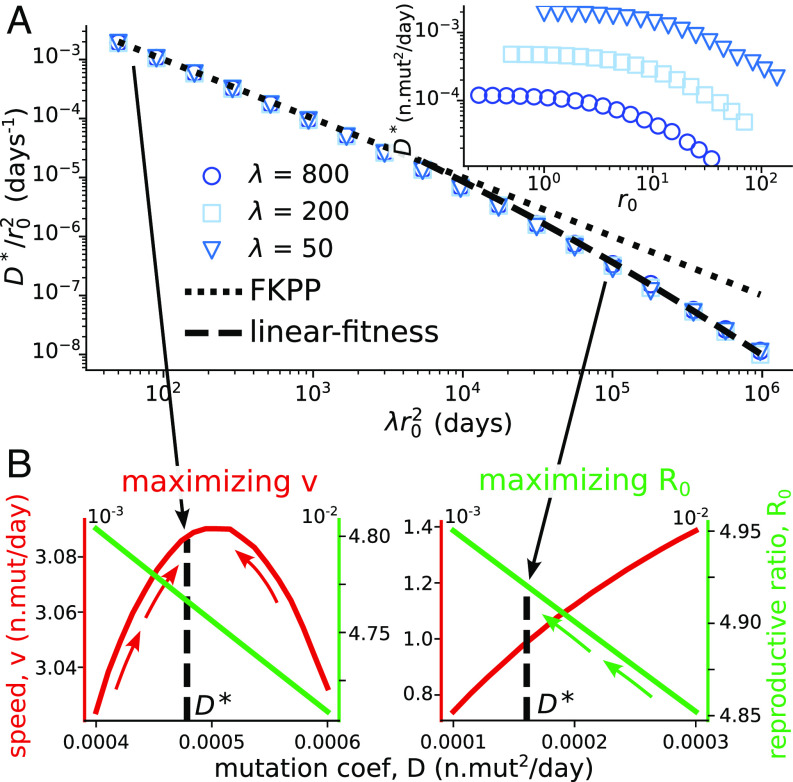
Fig. 3.
Evolutionary stability of the mutation rate. (A) Evolutionarily stable mutation coefficient , rescaled by , as a function of the rescaled coefficient . The dotted and dashed lines show the FKPP and linear-fitness predictions valid for small and large (SI Appendix, Text 3B). Used parameters: , , , . The value of shown in the legend is in days/n.mutations. Inset: same simulations plotted without rescaling. (B) Wave speed and reproductive ratio as a function of the mutation coefficient for two extreme cross-reactivities: , at . The evolutionarily stable coefficient is indicated with the black line. It tends to maximize the speed for small , and the reproductive ratio for large .
Fig. 3B shows the different behavior of the viral strategy depending on the value of discussed in the previous section: It tends to be the one that maximizes the speed for small , and the reproductive ratio for large .
G. Application to H3N2 Evolution.
We can apply the predictions from our model for the mutational trade-off to data obtained for the strain H3N2 of influenza infections. Some of the parameters of the model can be fixed from data and their values are well-established in literature. Recall that we have set . The reproductive ratio is set to , the recovery rate to d, and the virulence to , which is negligible compared with the recovery rate. We consider those parameters as fixed and we explore our model by varying the remaining ones, whose estimate is more indirect and less precise. The number of receptors per host, , is both difficult to estimate and specific to the particular modeling choice. However, we observed that results depend very weakly on its choice in the range –. The effective population of hosts can be difficult to estimate, and we considered two reasonable choices .
We are left with three parameters to fix: the cross-reactivity in units of mutational steps , the deleterious mutation rate , and the diffusion coefficient (or equivalently ). The substitution rate of nonsynonymous mutations in antigenically interacting regions of the virus, which can be identified with the wave speed in units of antigenic effects year-pagination (24, 49, 50), imposes an implicit relation between these parameters. In addition, the condition of evolutionary stability, Eq. 12, imposes another constraint. This leaves us with one degree of freedom, which we chose to control through the deleterious mutation rate, .
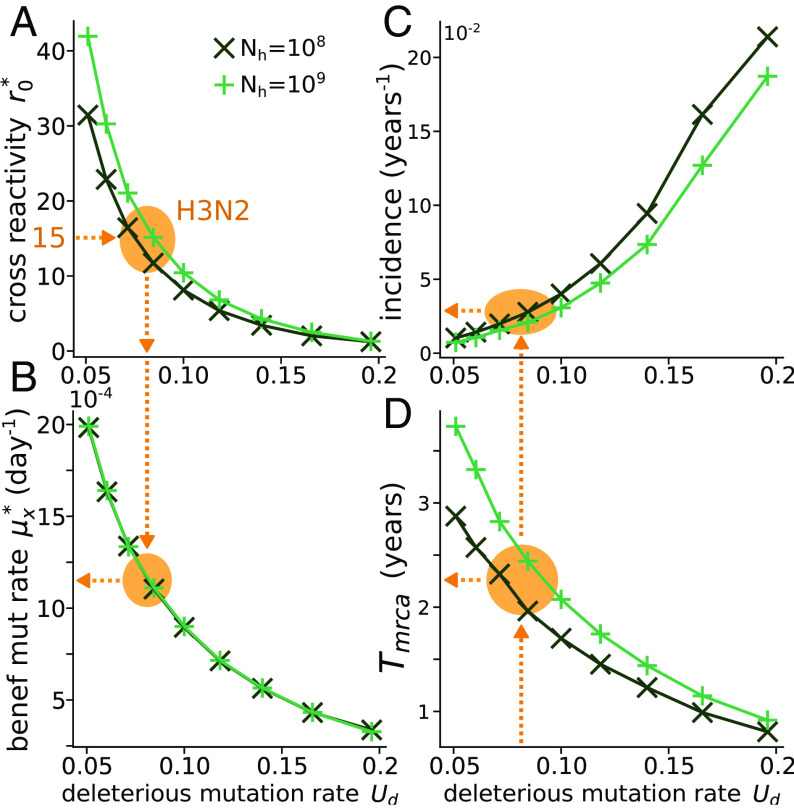
Figs. 4 A,B shows the values of the two parameters and obtained by imposing the two conditions discussed above for different given values of (see Section D for details on how and are evaluated). Hemagglutination experiments with immunized ferrets show that the minimal number of antigenic mutations before escaping immunity can be of order 1–5 (30, 40), while epidemiological models (12, 24) estimate the cross-reactivity to be around 14–15. This discrepancy stems from the fact that antigenic effects are heterogeneous, and while there exist rare mutations leading to immune escape, the majority of mutations are unlikely to induce a sizable change in the strain’s antigenicity. Therefore, as opposed to controlled experiments on ferrets, the typical number of mutations observed between two successive epidemic strains is larger than the minimal number of antigenic mutations needed to escape immunity. From the left panel of Fig. 4 starting from , we can estimate deleterious mutation per genome per transmission event, which is consistent with an independent estimate of (48). Using the right panel of Fig. 4, this value of in turn leads to an estimate for the beneficial mutation rate antigenic mutations per day.
Fig. 4.
Application to the H3N2 influenza strain. Evolutionarily stable values of the (A) cross-reactivity and (B) antigenic mutation rate as a function of the rate of deleterious mutations , for fixed values of the parameters , day, , , and specified in the legend, with the additional constraint y, as fixed by empirical estimation. The orange arrows are the predictions of our model assuming using the empirical estimate which implies . Panels (C) and (D) show the incidence and the time from the most recent common ancestor.
These numbers allow us to determine the regime of evolution of the virus. We estimate , suggesting that H3N2 evolves in the linear fitness regime as has been assumed in other work, e.g., refs. 27 and 24. While our analysis is very similar to these earlier works, we do not hypothesize a linear fitness regime to study H3N2 evolution. We show that H3N2 evolves in this regime under an evolutionary stability constraint balancing antigenic escape and deleterious mutations. This observation provides, with no additional fitting parameters, a justification for this early hypothesis.
We tested if other observables predicted by the model were consistent with empirical estimates. Fig. 4C shows the incidence, defined as the fraction of infected people in a given time: . The H3N2 strain infects of the population each year (24, 51), while our model predicts . Fig. 4 D shows the average time from the most recent common ancestor, which can be computed as the time the wave takes to reach its tip, , where (27, 41). Our numerical estimates predict 2–2.5 y, versus empirical estimates of (33). For both quantities, our model captures the correct order of magnitude, recapitulating the overall features of influenza evolution with minimal ingredients.
H. Evolutionary Stability of Virulence Under Transmission Trade-Off.
We now turn to the application of our stability condition to the evolution of the virulence . Recall that according to the classical argument (which ignores immune escape and waves), virulence should evolve to maximize the viral reproductive ratio (14, 17). If is an increasing but concave function of , there exists a tradeoff between the opposing needs to increase transmissibility and to decrease virulence.
By contrast, applying Eq. 11 with gives us the following condition for the evolutionarily stable virulence:
| [13] |
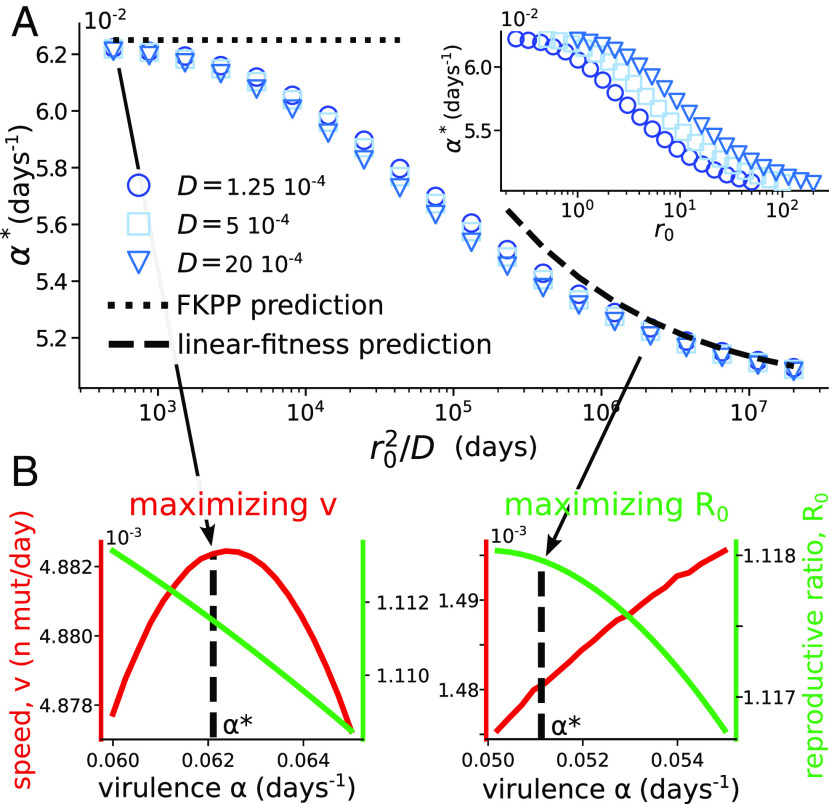
To check the validity of this relation, we numerically looked for the evolutionarily stable value of the virulence as a function of , for the commonly used concave function (Fig. 5A). The numerical results are consistent with Eq. 13 (SI Appendix, Text and Fig.S4), and show a collapse of as a function of .
Fig. 5.
Evolutionary stability of virulence. (A) Evolutionarily stable virulence as a function of the diffusion-escape time . Transmissibility has the form . The dotted and dashed lines show the two limits of FKPP and linear fitness (SI Appendix, Text 3C). Parameters: , , , . The values of in the legend are in n.mutations/d. Inset: same simulations shown as a function of the nonrescaled variables. (B) Wave speed and reproductive ratio as a function of the virulence for two different cross-reactivities, and , and .
As we expect from previous arguments, the evolutionary endpoint maximizes the speed of the wave in the FKPP regime of low cross-reactivity (), consistent with a previous analysis (21). By contrast, the reproductive ratio is maximized in the linear-fitness regime of high cross-reactivity, consistent with the classical result in the absence of escape. The two limit cases are illustrated in Fig. 5B.
Fig. 5A also implies that short cross-reactivities favor the evolution of higher virulence.
This result holds for every concave function . This highlights the importance of correctly estimating the quantitative effect of immunity for predicting the evolution of nonantigenic traits.
Discussion
The relevance of propagating waves for describing the continual dynamics of viral escape from immunity according to the “Red Queen” hypothesis has long been recognized, but using two seemingly contradictory mathematical paradigms. The FKPP wave, originally introduced to describe the spatial spreading of beneficial mutations (36), was shown to emerge in simple models of joint viral-immune dynamics along an antigenic dimension (52). The fitness-wave model was proposed to model the evolution of RNA viruses with an infinite reservoir of beneficial mutations (25). Shifting immunity was then proposed as a mechanism for such a reservoir in models of viral-immune coevolution (27, 33). The two descriptions lead to markedly different predictions for the rate of adaptation and its dependence upon the antigenic mutation rate and host population size. We have explicitly shown that these two descriptions correspond to limiting cases of the same model, reconciling apparently incompatible approaches.
These two limits may be understood intuitively as follows. In the regime of low cross-reactivity, where the FKPP wave description holds, the fittest variants at the tip of the wave grow in an almost entirely susceptible host population. They all have comparable growth rates, and so do variants with additional escape mutations, which only confer a negligible advantage until hosts start getting infected in large numbers. By contrast, in the regime of high cross-reactivity, where the fitness-wave description is valid, even the most advanced escape mutants face a partially immune host population. This implies that additional escape mutations at the tip have an immediate growth advantage over their ancestors, driving the evolution of the virus.
Applying our theory to the evolution of H3N2 influenza, by plugging parameter estimates along with the additional assumption that the viral mutation rate is evolutionarily stable, we are able to recover the empirical estimates of the incidence rate and the time from the most recent common ancestor, which have not been used in the fitting procedure. We argued that H3N2 falls in the linear-fitness regime, where cross-reactivity is relatively large. This implies that the new variants driving influenza evolution are still largely subject to the hosts’ collective immunity, albeit a bit less so that they retain a small fitness advantage to the majority of circulating strains. This is consistent with the observation that emerging variants have a moderate effective reproductive number relative to the basic one (49). We may expect the evolution of SARS-CoV-2 to fall in the same regime as it settles in its endemic state.
We showed that our model is able to capture key features of influenza evolution, and allows us to estimate both evolutionary and epidemiological quantities such as the antigenic mutation rate and the incidence rate. However, this model oversimplifies several aspects of influenza evolution and notably ignores the rare mutations capable of inducing large jumps in the antigenic space (30, 40). While our continuous model is a simple approximation to influenza evolution, we believe that a more detailed treatment of its mutational process (53) could provide a more accurate estimation of the parameters presented in this paper, and would also allow for the estimation of yet inaccessible parameters such as the rate and the size of large antigenic jumps. While in the current state our simulations does not give us philogenies, it would be interesting to compare observations with the results of a more detailed version of the model allowing for genealogy reconstruction, e.g., particular the succession of clades bursting from the trunk of the tree, as seen in the data.
We showed that the cross-over between high and low cross-reactivity has a strong impact of the evolution of nonantigenic traits. In the low cross-reactivity regime, the ESS maximizes the speed of the wave (the rate of adaptation), consistent with (21): Strains that get ahead at the tip of the wave outcompete slower ones. In the high cross-reactivity regime, however, the ESS maximizes the reproductive number. Intuitively, all strains are under strong immune pressure, so that their effective growth rate is close to 0, with a minute growth advantage for the most advanced immune-escape strains; any intrinsic fitness advantage (larger ) is likely to fix in the bulk of the wave, regardless of the wave’s speed. This last conclusion differs from that of ref. 21, where it was argued that the speed of the wave was maximized in the ESS regardless of the extent of cross-immunity. This discrepancy may be explained by the different assumptions about the dynamical regime. In this paper, we specifically looked for strict steady-state solutions (in the moving frame of the wave), while ref. 21 also considered oscillatory solutions, which emerge in the high cross-reactivity limit (where we claim the fitness-wave solution holds). One limitation of our approach is that it ignores the possible effect of such oscillations. However, oscillations also lead to near population collapse, and may not survive a full stochastic setting where extinction is likely. Which dynamical regime is relevant for real viruses remains an interesting question for future research.
Our results have several implications for the evolution of nonantigenic traits. The suggestion that respiratory viruses may be in the linear-fitness regime implies that their mutation rate should evolve toward low values to minimize their mutational load, at the expense of their ability to escape immunity. More broadly, our result that is maximized in the linear-fitness regime implies that antigenic and nonantigenic evolutions are decoupled, suggesting that previous arguments that ignored antigenic escape may still be valid. We also predict that viruses for which there is more cross-immunity should evolve to be less virulent.
Materials and Methods
A. Deterministic Simulation with a Cutoff.
Eqs. 2–5 are simulated using the Euler–Maruyama method. The code can be found at the following repository: https://github.com/statbiophys/viral_coevo. Time and space are discretized with resolution and , respectively (note that is a “parameter” of the algorithm for solving the continuous equation and should not be confused with ). We choose small compared to both and the width of the wave (the second condition between checked a posteriori), and then set to satisfy the Courant-Friedrichs-Lewy condition, .
The one-dimensional antigenic space is simulated with periodic boundary conditions, with a box size larger than the immune persistence . Previous passages are erased by setting to zero ahead of the wave. In some regimes, the immune protection cannot be sufficient to prevent individuals at the back of the wave to grow again, creating a secondary wave. Since the behavior of the primary wave is not affected and secondary waves can create numerical instabilities, we artificially impose perfect immunity () at the back of the wave.
For large cross-reactivities , some initial conditions may lead to oscillations occurring around the stationary state of the wave (21), leading to extinctions when a cutoff is imposed. To start close to the stationary wave solution, we initialize as a skewed Gaussian: , where the normalization coefficient is chosen to obtain an incidence rate of : . The immune protection is initialized as , where if and otherwise, , and is chosen such that . To study the stationary state, we first simulate for some time 100–1,000 d without the cutoff (), and some time 200–20,000 d with the cutoff (the larger the , the longer the equilibration time).
B. Stochastic Simulation.
The stochastic simulation of Eqs. 1–4 uses a hybrid deterministic-stochastic approach. The bulk of the wave, characterized by very large numbers where demographic noise is negligible, is treated deterministically, while the front is simulated stochastically. We fix a threshold on the number of infected people ( for Fig. 2, for Fig. 3, for Fig. 5). If , we update its value at each time step following the following stochastic prescription, which appropriately models demographic noise. Each individual can mutate with probability , generating a binomial number of mutations to the right at , and a similarly distributed number to the left at . Numbers are then updated as . Growth is then implemented by updating , with .
C. Evolutionary Stability Simulations.
To simulate the evolution of populations with nonantigenic mutations, we consider a two-dimensional system , where is the phenotypic parameter over which evolution is acting (i.e., or in the two examples considered in this paper). We then assume that the system diffuses slowly with coefficient in the second dimension, and the full simulated equation reads:
where the demographic noise can be treated fully or through a cutoff as in Eq. 5. The diffusion coefficient is chosen to be as small as possible, so that the dynamics of the wave will be much faster than the evolutionary time scale over which changes, and that the simulation converge to an evolutionarily stable state well peaked in . The dimension is discretized with step . After the simulation has converged, we take as the evolutionary end point .
D. Imposing Evolutionary Stability and Speed of the Wave for the H3N2 Study.
Here, we detail the method for getting and , all other parameters (, , , , ) being fixed, by using the following two relations: y, and evolutionary stability.
The pseudoalgorithm for finding these two values is the following:
-
1.
Choose an initial guess for .
-
2.
Find that matches the speed condition through nested iteration:
-
a.Choose an initial guess .
-
b.Calculate the speed with .
-
c.Update , where is the target value, and is a learning rate. Go to b.
-
a.
-
3.
Run an evolutionary simulation where is left free as in Section C, now with , with fixed. Call the resulting evolutionarily stable point.
-
4.
Update and go back to 2.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
The study was supported by the European Research Council Consolidator Grant 724208 and ANR-19-CE45-0018 “RESP-REP” from the Agence Nationale de la Recherche and Deutsche Forschung Gesselschaft grant CRC 1310 “Predictability in Evolution.”
Author contributions
V.C., A.M., T.M., and A.M.W. designed research; performed research; contributed new reagents/analytic tools; analyzed data; and wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Contributor Information
Thierry Mora, Email: thierry.mora@phys.ens.fr.
Aleksandra M. Walczak, Email: aleksandra.walczak@phys.ens.fr.
Data, Materials, and Software Availability
There are no data underlying this work. The software for the numerical simulations and for reproducing the figures can be found at https://github.com/statbiophys/viral_coevo (54).
Supporting Information
References
- 1.Belshaw R., Gardner A., Rambaut A., Pybus OG Pacing a small cage: Mutation and RNA viruses. Trends Ecol. Evol. 23, 188–193 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sanjuán R., Nebot M. R., Chirico N., Mansky L. M., Belshaw R., Viral mutation rates. J. Virol. 84, 9733–9748 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Duffy S., Why are RNA virus mutation rates so damn high? PLoS Biol. 16, e3000003 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Peck K. M., Lauring A. S., Complexities of viral mutation rates. J. Virol. 92, e01031-17 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chardès V., Vergassola M., Walczak A. M., Mora T., Affinity maturation for an optimal balance between long-term immune coverage and short-term resource constraints. Proc. Natl. Acad. Sci. U.S.A. 119, e2113512119 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shlomchik M. J., Luo W., Weisel F., Linking signaling and selection in the germinal center. Immunol. Rev. 288, 49–63 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Viant C., et al. , Antibody affinity shapes the choice between memory and germinal center B cell fates. Cell 183, 1298–1311.e11 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jones K. E., et al. , Global trends in emerging infectious diseases. Nature 451, 990–993 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jones B. A., et al. , Zoonosis emergence linked to agricultural intensification and environmental change. Proc. Natl. Acad. Sci. U.S.A. 110, 8399–8404 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Salkeld D. J., Padgett K. A., Jones J. H., Antolin M. F., Public health perspective on patterns of biodiversity and zoonotic disease. Proc. Natl. Acad. Sci. U.S.A. 112, E6261 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Neher R. A., Bedford T., Daniels R. S., Russell C. A., Shraiman B. I., Prediction, dynamics, and visualization of antigenic phenotypes of seasonal influenza viruses. Proc. Natl. Acad. Sci. U.S.A. 113, E1701–E1709 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Łuksza M., Lässig M., A predictive fitness model for influenza. Nature 507, 57–61 (2014). [DOI] [PubMed] [Google Scholar]
- 13.Morris D. H., et al. , Predictive modeling of influenza shows the promise of applied evolutionary biology. Trends Microbiol. 26, 102–118 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.May R. M., Anderson R. M., Parasite–host coevolution. Parasitology 100, S89–S101 (1990). [DOI] [PubMed] [Google Scholar]
- 15.Anderson R. M., May R. M., Infectious Diseases of Humans: Dynamics and Control (Oxford University Press, Oxford/New York, 1992). [Google Scholar]
- 16.Mideo N., Alizon S., Day T., Linking within- and between-host dynamics in the evolutionary epidemiology of infectious diseases. Trends Ecol. Evol. 23, 511–517 (2008). [DOI] [PubMed] [Google Scholar]
- 17.Alizon S., Hurford A., Mideo N., Van Baalen M., Virulence evolution and the trade-off hypothesis: History, current state of affairs and the future. J. Evol. Biol. 22, 245–259 (2009). [DOI] [PubMed] [Google Scholar]
- 18.Lion S., Metz J. A. J., Beyond R0 maximisation: On pathogen evolution and environmental dimensions. Trends Ecol. Evol. 33, 458–473 (2018). [DOI] [PubMed] [Google Scholar]
- 19.Day T., Gandon S., Applying population-genetic models in theoretical evolutionary epidemiology. Ecol. Lett. 10, 876–888 (2007). [DOI] [PubMed] [Google Scholar]
- 20.Gandon S., Day T., Metcalf C. J. E., Grenfell B. T., Forecasting epidemiological and evolutionary dynamics of infectious diseases. Trends Ecol. Evol. 31, 776–788 (2016). [DOI] [PubMed] [Google Scholar]
- 21.Sasaki A., Lion S., Boots M., Antigenic escape selects for the evolution of higher pathogen transmission and virulence. Nat. Ecol. Evol. 6, 51–62 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hallatschek O., The noisy edge of traveling waves. Proc. Natl. Acad. Sci. U.S.A. 108, 1783–1787 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Desai M. M., Fisher D. S., Beneficial mutation-selection balance and the effect of linkage on positive selection. Genetics 176, 1759–1798 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rouzine I. M., Rozhnova G., Antigenic evolution of viruses in host populations. PLoS Pathog. 14, e1007291 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tsimring L. S., Levine H., Kessler D. A., RNA virus evolution via a fitness-space model. Phys. Rev. Lett. 76, 4440–4443 (1996). [DOI] [PubMed] [Google Scholar]
- 26.Minayev P., Ferguson N., Incorporating demographic stochasticity into multi-strain epidemic models: Application to influenza A. J R. Soc. Interface 6, 989–996 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Marchi J., Lässig M., Walczak A. M., Mora T., Antigenic waves of virus–immune coevolution. Proc. Natl. Acad. Sci. U.S.A. 118, e2103398118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gog J. R., Grenfell B. T., Dynamics and selection of many-strain pathogens. Proc. Natl. Acad. Sci. U.S.A. 99, 17209–17214 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Segel L. A., Perelson A. S., Shape space: An approach to the evaluation of cross-reactivity effects, stability and controllability in the immune system. Immunol. Lett. 22, 91–99 (1989). [DOI] [PubMed] [Google Scholar]
- 30.Smith D. J., et al. , Mapping the antigenic and genetic evolution of influenza virus. Science 305, 371–376 (2004). [DOI] [PubMed] [Google Scholar]
- 31.Bedford T., et al. , Integrating influenza antigenic dynamics with molecular evolution. eLife 3, e01914 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fonville J. M., et al. , Antibody landscapes after influenza virus infection or vaccination. Science 346, 996–1000 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Yan L., Neher R. A., Shraiman B. I., Phylodynamic theory of persistence, extinction and speciation of rapidly adapting pathogens. eLife 8, e44205 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bedford T., Rambaut A., Pascual M., Canalization of the evolutionary trajectory of the human influenza virus. BMC Biol. 10, 38 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kermack W. O., McKendrick A. G., Walker G. T., A contribution to the mathematical theory of epidemics. Proc. R. Soc. London. Ser. A 115, 700–721 (1927). [Google Scholar]
- 36.Fisher R. A., The wave of advance of advantageous genes. Ann. Eugen. 7, 355–369 (1937). [Google Scholar]
- 37.Cohen E., Kessler D. A., Levine H., Front propagation up a reaction rate gradient. Phys. Rev. E 72, 066126 (2005). [DOI] [PubMed] [Google Scholar]
- 38.Perelson A. S., Oster G. F., Theoretical studies of clonal selection: Minimal antibody repertoire size and reliability of self-non-self discrimination. J. Theor. Biol. 81, 645–670 (1979). [DOI] [PubMed] [Google Scholar]
- 39.Marchi J., Lässig M., Mora T., Walczak A. M., Multi-lineage evolution in viral populations driven by host immune systems. Pathogens 8, 115 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Koel B. F., et al. , Substitutions near the receptor binding site determine major antigenic change during influenza virus evolution. Science 342, 976–979 (2013). [DOI] [PubMed] [Google Scholar]
- 41.Neher R. A., Hallatschek O., Genealogies of rapidly adapting populations. Proc. Natl. Acad. Sci. U.S.A. 110, 437–442 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gabriel W., Lynch M., Burger R., Muller’s ratchet and mutational meltdowns. Evolution 47, 1744–1757 (1993). [DOI] [PubMed] [Google Scholar]
- 43.Bull J. J., Sanjuán R., Wilke C. O., Theory of lethal mutagenesis for viruses. J. Virol. 81, 2930–2939 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Silander O. K., Tenaillon O., Chao L., Understanding the evolutionary fate of finite populations: The dynamics of mutational effects. PLoS Biol. 5, e94 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Swanstrom R., Schinazi R. F., Lethal mutagenesis as an antiviral strategy. Science 375, 497–498 (2022). [DOI] [PubMed] [Google Scholar]
- 46.Kimura M., Maruyama T., The mutational load with epistatic gene interactions in fitness. Genetics 54, 1337 (1966). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Haigh J., The accumulation of deleterious genes in a population—Muller’s ratchet. Theor. Popul. Biol. 14, 251–267 (1978). [DOI] [PubMed] [Google Scholar]
- 48.Koelle K., Rasmussen D. A., The effects of a deleterious mutation load on patterns of influenza A/H3N2’s antigenic evolution in humans. eLife 4, e07361 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Biggerstaff M., Cauchemez S., Reed C., Gambhir M., Finelli L., Estimates of the reproduction number for seasonal, pandemic, and zoonotic influenza: A systematic review of the literature. BMC Infect. Dis. 14, 480 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Einav T., Gentles L. E., Bloom J. D., Snapshot: Influenza by the numbers. Cell 182, 532 (2020). [DOI] [PubMed] [Google Scholar]
- 51.Wen F. T., Malani A., Cobey S., The potential beneficial effects of vaccination on antigenically evolving pathogens. Am. Nat. 199, 223–237 (2022). [DOI] [PubMed] [Google Scholar]
- 52.Sasaki A., Evolution of antigen drift/switching: Continuously evading pathogens. J. Theor. Biol. 168, 291–308 (1994). [DOI] [PubMed] [Google Scholar]
- 53.Good B. H., Rouzine I. M., Balick D. J., Hallatschek O., Desai M. M., Distribution of fixed beneficial mutations and the rate of adaptation in asexual populations. Proc. Natl. Acad. Sci. U.S.A. 109, 4950–4955 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Mazzolini A., Chardès V., Mora T., Walczak A. M., viral\_coevo. GitHub. https://github.com/statbiophys/viral_coevo. Accessed 12 July 2023.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
There are no data underlying this work. The software for the numerical simulations and for reproducing the figures can be found at https://github.com/statbiophys/viral_coevo (54).