Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Oct 19;145(43):23620–23629. doi: 10.1021/jacs.3c07628

Combining Force Fields and Neural Networks for an Accurate Representation of Chemically Diverse Molecular Interactions

Alexey Illarionov †, Serzhan Sakipov †, Leonid Pereyaslavets †, Igor V Kurnikov †, Ganesh Kamath †,*, Oleg Butin †, Ekaterina Voronina †,@, Ilya Ivahnenko †, Igor Leontyev †, Grzegorz Nawrocki †, Mikhail Darkhovskiy †, Michael Olevanov †,&, Yevhen K Cherniavskyi †, Christopher Lock †,∇, Sean Greenslade †, Subramanian KRS Sankaranarayanan §,∥, Maria G Kurnikova ‡, Jeffrey Potoff ⊥, Roger D Kornberg #, Michael Levitt #, Boris Fain †,*
PMCID: PMC10623557  PMID: 37856313

Abstract

graphic file with name ja3c07628_0006.jpg

A key goal of molecular modeling is the accurate reproduction of the true quantum mechanical potential energy of arbitrary molecular ensembles with a tractable classical approximation. The challenges are that analytical expressions found in general purpose force fields struggle to faithfully represent the intermolecular quantum potential energy surface at close distances and in strong interaction regimes; that the more accurate neural network approximations do not capture crucial physics concepts, e.g., nonadditive inductive contributions and application of electric fields; and that the ultra-accurate narrowly targeted models have difficulty generalizing to the entire chemical space. We therefore designed a hybrid wide-coverage intermolecular interaction model consisting of an analytically polarizable force field combined with a short-range neural network correction for the total intermolecular interaction energy. Here, we describe the methodology and apply the model to accurately determine the properties of water, the free energy of solvation of neutral and charged molecules, and the binding free energy of ligands to proteins. The correction is subtyped for distinct chemical species to match the underlying force field, to segment and reduce the amount of quantum training data, and to increase accuracy and computational speed. For the systems considered, the hybrid ab initio parametrized Hamiltonian reproduces the two-body dimer quantum mechanics (QM) energies to within 0.03 kcal/mol and the nonadditive many-molecule contributions to within 2%. Simulations of molecular systems using this interaction model run at speeds of several nanoseconds per day.

Introduction

Molecular modeling has been promising to augment, enhance, or even replace experimentation in a wide range of fields and applications. Recognition of the increasing importance of these models led to the award of the 2013 Nobel Prize in Chemistry to Martin Karplus, Michael Levitt, and Arieh Warshel “for the development of multiscale models for complex chemical systems.”1 Over 50 years later, wide-coverage accurate polarizable force fields, accurate solvation energies, and accurate predictions of protein–ligand binding energies are still considered to be unrealized “holy grails” of computational chemistry that are unreachable for several more decades.2 This article describes a path toward reaching these goals.

The basic tenet of statistical physics is that given the correct total energy (the Hamiltonian) of a system, with proper and sufficient sampling, any desired property can then be derived. In principle, computational quantum mechanics (QM) can determine the energy of any collection of atoms and molecules. However, as ab initio methods scale as the number of atoms ∼N3 (DFT3,4) or ∼N7 (CCSD(T)5,6), in practice, it is not possible to compute even a single snapshot of systems of interest (∼400 to 108 atoms), much less a fully thermodynamically averaged ensemble. To overcome the intractable computational limit of QM, scientists have replaced quantum energies and forces with much faster and immensely better-scaling (N log(N)) analytical7−14 or, more recently, neural network15−18 approximations of QM called force fields (FF), which are propagated via Newton’s laws of motion.

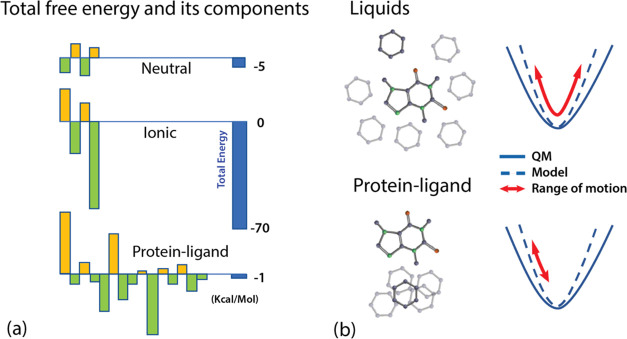
Another and somewhat underappreciated challenge of modeling a wide range of molecular systems, aspects of which we and others have touched on previously,19,20 is the necessity of the models to have a high degree of accuracy. As illustrated in Figure 1a, the overall free energy is a sum of much larger offsetting subcomponents, and it is their interplay and shifting partial cancellations that create dynamic behavior (e.g., life) at room temperature and pressure.

Figure 1.

Figure 1

Open in a new tab

(a) Schematic representation of the scale of the entropic and enthalpic components (yellow, green) of three types of molecular systems compared with their sum, i.e., the total free energy (blue). The first two represent solvation of neutral atoms and ions, and the last represents the binding free energy for a ligand in a protein. Neutral ensembles are the least challenging14 as their energy components are the smallest. Ionic systems are similar to neutral ones, but their energies are an order of magnitude higher. The protein–ligand systems are the most difficult: the interactions are many, varied, and strong, and the desired final accuracy is very small (∼0.5 kcal/mol for relative binding free energy between two ligands). (b) Illustration of why models need to be accurate for all possible orientations in protein–ligand systems. In liquids, there is significant mixing about the minima, and model energy errors, if properly centered, have a chance to average out. In protein–ligand systems functional groups assume and maintain a priori orientations, and the energy errors in the sampled subspace may not average to zero.

This demand for accuracy is particularly stringent for protein–ligand interactions because the energies between interacting ligand and protein functional groups and water are very diverse and frequently quite strong. Furthermore, as shown in Figure 1b, because the system is a liquid crystal and its phase space is constrained, the errors in potential energy surface (PES) approximations will not average out as in a liquid, and the models must therefore be accurate at all distances and orientations. Consequently, the accuracy of each component of a useful prediction of the free energy of ligand binding must be significantly higher than the desired “chemical” accuracy of the final answer (∼±0.5 kcal/mol). The components’ agreement with quantum mechanics can be as narrow as the uncertainty of the underlying ab initio calculations.21 This is a significant challenge.

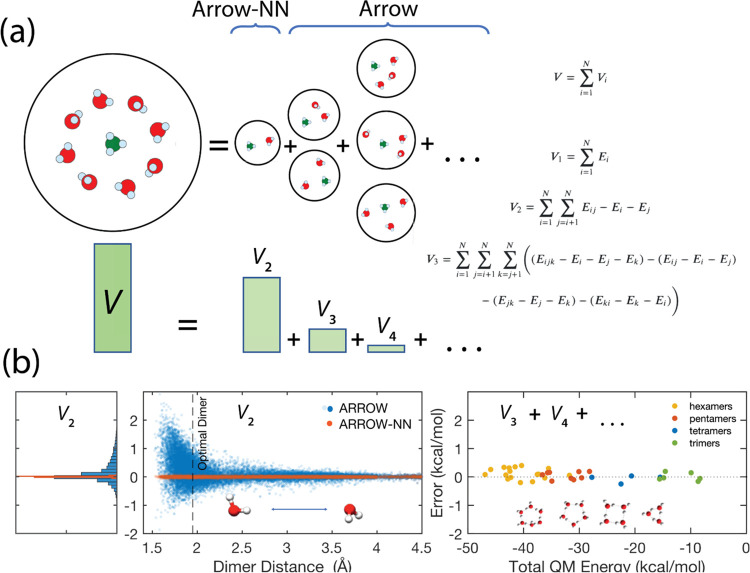
Most of the current approaches to Newtonian molecular models are roughly grouped into three categories. The first category, one that has a rich history and has been in active development for over a decade, are ultra-accurate potentials parametrized from first principles developed for water and/or a limited set of molecular species.22−24 These models frequently employ explicit representations25 of each term of the many-body inductive expansion (see Figure 3), and, in the short range, reproduce the QM PES for dimers and multimers exquisitely well.24 However, the methodology used in these models has not yet been successfully generalized to arbitrary and wide-ranging descriptions of the full chemical space. One of the reasons is the combinatorial growth of potential training sets that will be needed for parametrizing the 3, 4, etc.—body terms for arbitrary molecules and their combinations. Additional reasoning can be found in Section SI 6.

Figure 3.

Figure 3

Open in a new tab

(a) Graphical representation of the many-body expansion. (b) Center and left: the 2-body energy error vs intermolecular distance for a water dimer and as a histogram. (b) Right: the nonadditive many-body error for water multimers vs their total QM intermolecular energy. The many-body errors are below 0.5 kcal/mol or 1% of total energy, and below 3% of the many-body contributions. The bottom left and center panels show the accuracy of an analytical 2-body approximation (ARROW, MAE = 0.3 kcal/mol) plotted vs intermolecular distance for a water dimer in blue, and a neural net augmented interaction model (ARROW-NN) in orange-brown. The representation becomes purely analytical at distances >5 Å. The accuracy of ARROW-NN across the full dimer interaction range (MAE = 0.014 kcal/mol) is on par with the best underlying QM uncertainty. Water is used as a specific example, and analogous results are seen in all molecular ensembles.

There has recently been an explosion of rich and creative work in the second category of representations of the QM potential energy surfaces: encoding the atomic interactions via neural networks.15,18,26−29 While these approaches30−33 have been very good and rapidly improving, NN-based models are unable to incorporate effects that traditional physics has been built to represent: e.g., a response to an external electric field, the ability to extrapolate from 2 or 3 molecules to arbitrarily many,11,13,14,34−36 and a proper treatment and truncation of long-range interactions.19,37−39 Furthermore, the accuracy of the reproduction of intermolecular potentials by NN-based models has plateaued at ∼1 kcal/mol.40,41

The third, original, and the most widely used category of molecular interaction models are wide-coverage analytical force fields whose functional terms try to mimic components of the QM interactions.7,42−45 Within the polarizable subcategory, most models are (partially) parametrized by fitting to experimental data,13,36,46 and some, e.g., ARROW FF, are based purely on ab initio QM calculations.11,14,47 Although the ARROW FF has successfully predicted solvation and hydration energies of neutral molecules to within chemical accuracy,14 this group’s application of the ARROW force field to protein–ligand complexes48 has uncovered major deficiencies in describing strong interactions in these systems. As we have previously noted, “The ARROW FF is likely at the limit of complexity feasible for a wide-coverage analytical force field,”14 and a fresh approach is needed.

Guided by the advantages and the pitfalls of the above three approaches, we describe the construction of a wide-coverage accurate molecular interaction hybrid model,49 which is ab initio parametrized, describes a wide range of chemical functional groups, and is both computationally tractable and accurate enough to achieve reliable quantitative predictions. As realized by us50 and other groups,51,52 combining NNs and analytical expressions is the obvious next step in reproducing the QM PES.

The analytical part of the hybrid model is the ARROW14 FF because it faithfully describes polarization and electrostatics. This permits an accurate (Figure 3b right) approximation of the full inductive many-body expansion by performing monomer and, with appropriate decomposition,53 dimer QM calculations only, and thus bypassing the explicit many-body inductive description that models in the first category need to create. It also enables the hybrid model to more properly respond to external electric fields and to inherit appropriate and advantageous long-range treatment and truncation. At the same time, we understand and illustrate here that at short range (Figures 3b and 4), one needs special machinery for extra accuracy, and we add it to the 2-body intermolecular term, which is by far the largest and the most inaccurate one. The mechanism for doing this is inspired by the third category: the correction is encoded in a perceptron,54 an object which is quickly trained, well behaved with insufficient data, highly flexible, and computationally efficient. Finally, to enhance sensitivity and accuracy, we decouple the description of inter- and the much stronger intramolecular interactions.

Figure 4.

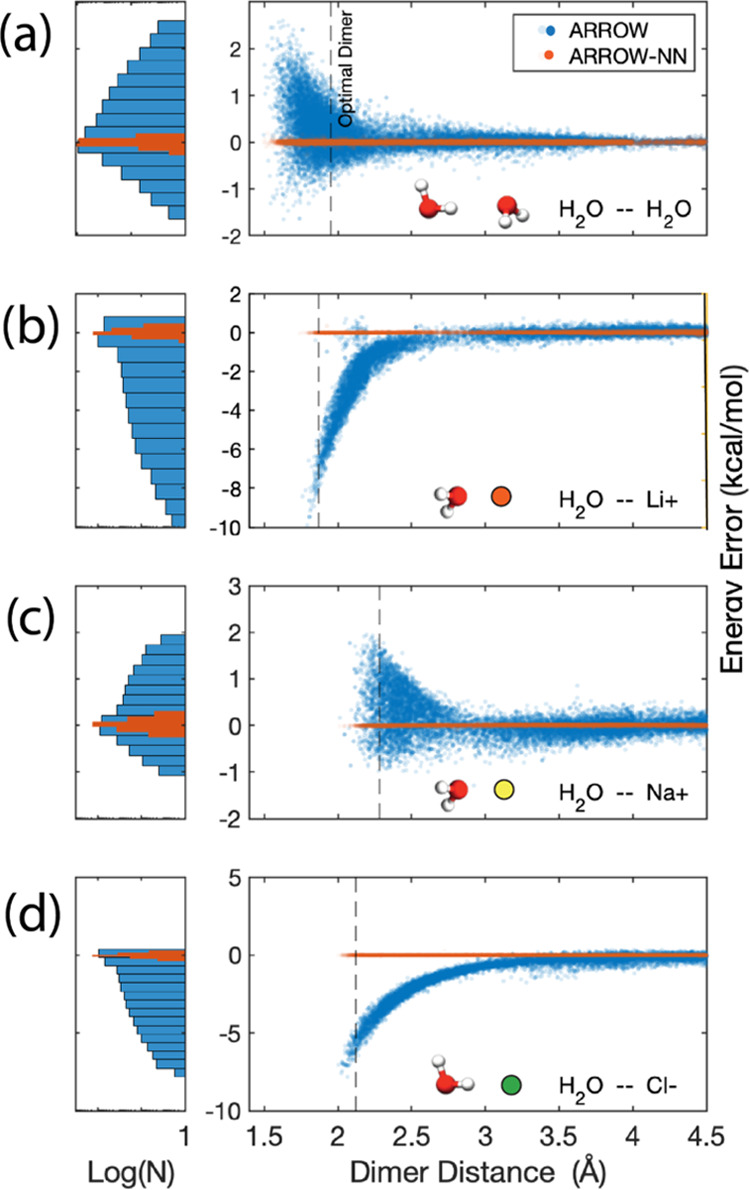
Figure 4

Open in a new tab

ARROW and ARROW-NN 2-body energy accuracy for (a) a water dimer, (b) water–lithium cation Li+: H2O, (c) water–sodium cation Na+: H2O, and (d) water–chloride anion Cl–: H2O. The histograms are in log units to amplify the distributions. In the strongly interacting region of close approach, the analytical model (ARROW) has significant errors >5 kcal/mol. ARROW-NN has excellent accuracy for all distances.

Based on our experience and on the use of ARROW as the base model, we make several additional choices that we think are advantageous: (a) the 2-body correction is not separable with respect to the interacting atoms (i.e., it is the property of the pair or pair-specific) and (b) the perceptron term is atom typed in the same way as the underlying force field. This correction is inherently not separable. It is already unreasonable to expect a convenient behavior such as Newtonian separability in the short range. It is more unlikely to be able to obtain it in a correction where the underlying “physical” model has already extracted the simplifying combination rules. Our construction makes the pair-interaction-specific neural net more economical because it is not tasked with encoding all of the chemical space. It allows the model to be incrementally augmented by the NN term in distinct small slices of the chemical interaction space with a relatively small training set of structures and energies. Finally, it results in a greater accuracy of the reproduction of the 2-body QM and therefore total energies. The main drawback is the amount of bookkeeping required to keep track of the multitude of neural nets and pair types. These choices reflect the practical trade-offs required for generating a wide-coverage molecular model that computes free energy observables to within chemical accuracy.

Interaction Model

The underlying analytical model—ARROW—has been described and benchmarked in previous publications.11,14,20,48,50 It is an ab initio parametrized polarizable force field containing representations for charge penetration, multipolar electrostatic and exchange–repulsion interactions, as well as anisotropic polarization. The atomic parameters are typed according to the chemical groups and atomic environments. The treatment of the dispersion interaction in the intermediate range follows55 with a crossover at 4 Å from the vacuum form to a screened asymptotic coefficient of 0.5 × C6 of vacuum. The bonded interactions follow the MMFF94, QMPFF.11,56 Further details on ARROW and its parametrization are provided in Section SI 3 and discussed previously.14

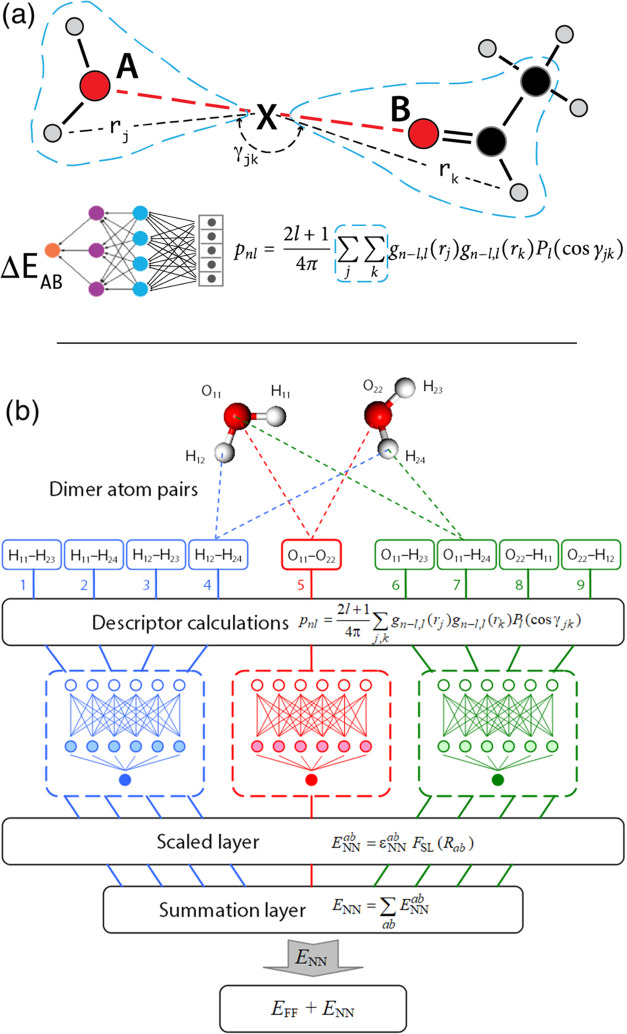
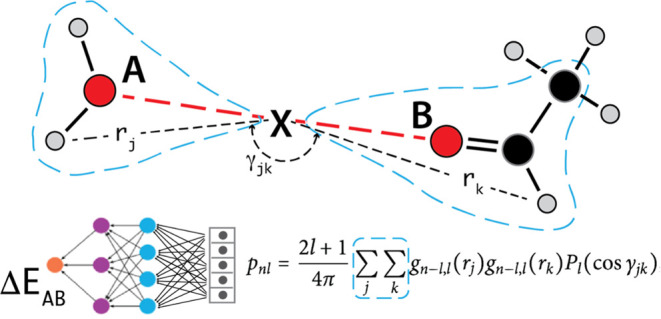
In this work, we construct the neural network term to augment the intermolecular interactions only.11,14,20,48,50 In contrast to the prevailing practice of partitioning the potential energy onto individual atoms,16,26,57,58 we partition the energy onto interacting pairs of atoms (A–B).59,60 A representative diagram of the fingerprint of an interacting pair is shown in Figure 2a.61 To encode the pair interaction A–B, we use atom pair symmetry functions (APSF) centered at the midpoint X between A and B (A–X–B). The atoms included into the fingerprint summations are neighbors of both A and B. We use either a bond distance (e.g., d = 1 for including nearest bonded neighbors of A and B only, or d = 2 for select terminal atoms to break the rotational degeneracy) or a membership cutoff distance (neighbors of A and B within some distance from either A or B) criteria for neighborhood membership. The interaction fingerprint is produced by expanding the atomic density neighboring X via an orthonormal basis set, consisting of spherical Bessel functions for the radial basis,58 and the usual spherical harmonics for the angular triples (atom-X atom). The midpoint construction geometrically symmetrizes the interaction fingerprint with respect to the permutation A ↔ B. The generated descriptors couple the intermolecular energy to the relative orientation as well as to the monomer distortions of the two molecules. The midpoint construction is also computationally economical as every term in the summation must contain X (see Figure 2a and Sections SI 1.1 and 1.2).

Figure 2.

Figure 2

Open in a new tab

(a) Diagram of the intermolecular interaction fingerprint. A and B are the interacting atoms, X is located at the midpoint between A and B, and the atom pair symmetry functions (APSF) are atomic symmetry functions centered at X. The location of X automatically symmetrizes the construction with respect to the A ↔ B permutation. The APSF summations (blue dashed lines) are over neighborhoods of both A and B. The fingerprint is fed into an [AB] specific neural network to produce an energy correction to the ARROW interaction energy between A and B (ΔEAB) EARROW-NN = EFF + ENN. (b) Diagram of the neural network term for pair interactions between two water molecules. Each pair interaction fingerprint is fed into its corresponding trained neural network (e.g., HH, HO, and OO in this case). The output is then smoothly truncated by a TensorFlow λ-layer to zero beyond a cutoff distance. All of the individual pair energy contributions are then summed to a final dimer energy correction ΔENN, which is then added to the energy EFF output by the analytical force field to produce the total energy.

The fingerprints are then input into a collection of corresponding pair-typed perceptrons (Figure 2b) and the outputs are summed. As analytical force field errors are largest at a close range, and as NN fingerprint computational demands grow as distance squared, we taper the NN correction beyond a chosen distance between atoms A and B (4 to 6 Å), beyond which the interactions are computed by ARROW alone. Rather than relying on the built-in decay of radial symmetry functions,26,62 we append a TensorFlow λ-layer to the network to smoothly force the outputs to zero beyond the cutoff distance. More details on the neural network interaction model and its training are in Sections SI 1.2 and 1.3.

Like in most analytical force fields, the NN correction for the pair of atoms is further subdivided by their atomic types. For example, instead of encoding a general interaction correction for chemical elements: NN (Carbon ↔ Nitrogen), we fine-grain the interaction corrections according to the chemical environments: NN (Aromatic Carbon ↔ Amide Nitrogen). As noted above, this typification has several significant advantages. It breaks up the full chemical interaction space into much smaller training subgroups so that model improvement is realized in segments and avoids a precompute of all possible intermolecular interactions. It permits the resulting total hybrid accuracy of representation of the interaction to be exceedingly high (in our experience, essentially on the order of convergence accuracy of the QM method chosen for the training set). Furthermore, because the amount of encoded information is limited, and because the fingerprint itself does not need to encode the chemical environment (“type”) but only the relative orientation and bonded distortion of the interaction, it allows for a smaller and therefore faster set of neural networks than ones in current practice.15,63,64 Finally, it is simply convenient and helpful for triage and prioritization of NN augmentation to have the NN correction have the same typification as the underlying analytical FF. Drawbacks of the intermolecular, type-segmented representation are the lack of a natural extension to bond-breaking and significant bookkeeping.

Results: 2-Body Energies

In this section, water is used as a convenient illustration only, and analogous results are seen in all molecular ensembles (Figure 4 and Section SI 4). The total potential energy of a collection of molecules may be represented by a many-body expansion,65 as illustrated in Figure 3a. One of the main goals of designing ARROW was to obtain excellent agreements for the many-body inductive nonadditive components (V3, V4, ···) of the intermolecular energy. As we have shown in previous work14 and in Figure 3b(right) and Section SI 4, for ARROW, this is indeed so: the inductive nonadditive components are accurate to less than 1% of the total energy. The required degree of accuracy of the 2-body energies (V2), touched on above and illustrated in Figure 1, was unexpected,48 and improving them is the main point of this manuscript.

Figure 3b (left, center) shows the distribution of 2-body errors vs intermolecular distance for 88K water dimers selected from MD and PIMD trajectories at room temperature and pressure. The blue dots are produced by the ARROW FF. At close range, a significant proportion of conformations deviate from QM energies by almost 1 kcal/mol. For ionic systems, as shown in Figure 4b–d, the analytical dimer energy error increases to as much as 10 kcal/mol.

The augmentation of the 2-body term with neural nets produces a dramatic improvement. The dark orange dots in Figure 3b (left, center) and Figure 4 show the deviation of the energies produced by the hybrid model, where the neural net term is fitted to the residual error of the analytical force field (EQM – EFF). In each case, the accuracy of the hybrid model is essentially equal to that of QM methods at the highest level of theory. For the H2O dimer it is 0.02 kcal/mol, and for the ion–water systems, it is Li-water 0.035 kcal/mol, Cl-water 0.018 kcal/mol, and Na-water 0.018 kcal/mol.

The flexibility of feed-forward perceptrons that enable such remarkable combined accuracy imposes a training set size penalty. While an ARROW pair interaction is training-test-saturated with 2–3 K dimer calculations (see the SI in ref (14)), the hybrid FF + NN model demands an order of magnitude more: 10–80 K dimers per interaction in our current systems. Figure SI 2 shows the training-test convergence for a representative system.

Results: Molecular Ensemble Predictions

Molecular simulations were performed with in-house MD software (Arbalest) as has been described in previous publications14,20,48 as well as in Section SI 5. We have previously20 highlighted the necessity of including nuclear quantum effects for precise predictions, and all computations below are done at the PIMD8 level of NQE.

Because the original ARROW14 water model was already of high quality both neat and as a solvent, the ARROW-NN water properties were not a major focus. As expected, they are similar and slightly better than ARROW.14 The hybrid 2-body energies are displayed in Figure 3 (left, center) and 4a, and further details on the properties of ARROW-NN water can be found in Section SI 5.1. Our requirements for water14 are the same as for all other molecular species, and while we do not expect its neat properties to be as perfect as in dedicated models,25,66 they are still very good.

The hybrid model is most useful in augmenting and correcting the most challenging, strong and/or limited mobility intermolecular interactions. Ionic hydration is a suitable and important showcase, and so we present the simulation results of the ubiquitous hydration of table salt. The dimer 2-body energies are shown in Figure 4c,d and are extremely accurate. The many-body contributions for ion-(H2O)N multimers are within 2% of the total multimer energy (SI Figure 1), which shows that ARROW and polarization physics are doing an excellent job. Although a better description of the many-body and field-induced dispersion is undoubtedly necessary for some systems, for the class of systems and molecules considered here, the inductive and implicit treatment of many-body effects is sufficient.67−70 Because single ion experiments are difficult and the results are thought to be inaccurate, we compare our predictions with the much more reliable data of hydration of salts (Table SI 5). The free energy results are given in Table 1 and are within 1% of the true experimental values. Considering that these values have been calculated starting purely from CCSD(T) quality ab initio data absent any empirical adjustments and without a host of approximations usually present in QM or QM-MM studies, this is a remarkable agreement.

Table 1. Hydration of Salts as Predicted by ARROW-NN.

salt expt. hydration (kcal/mol) ARROW-NN (kcal/mol)
LiCl –198.9 ± 2.9 –201.23 ± 0.79
NaCl –173.4 ± 3.3 –176.74 ± 0.64
Open in a new tab

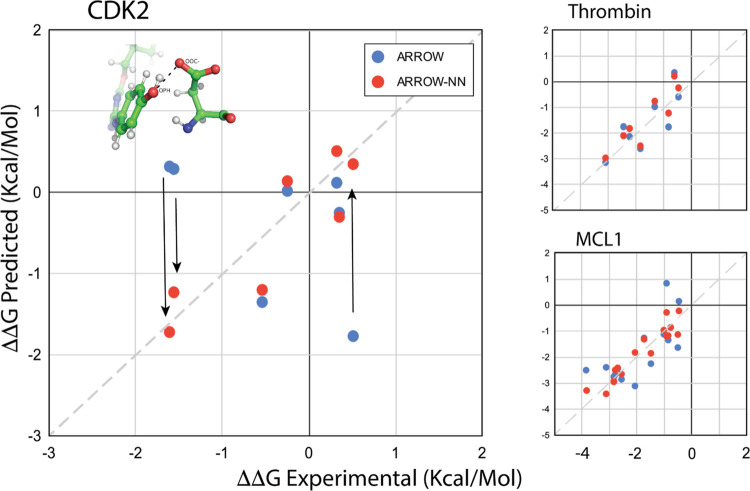
Finally, we apply the hybrid ARROW-NN model to determine the relative free energies of binding of ligands to proteins. These are highly complex systems: they contain many diverse ligand–ligand, ligand–pocket, and pocket–pocket interactions that demand a more accurate representation, and the ligand–protein complex and the protein itself are liquid crystals with limited mobility (Figure 1). Previously,48 we had extensively analyzed three systems (CDK2, MCL1, and Thrombin) with the goal of definitively isolating force field errors from sampling deficiencies. In two of the systems (MCL1 and Thrombin), ARROW performed well, and in a third (CDK2) serious force field deficiencies were uncovered in describing strong interactions involving the charged ASP87. Here we have described the ligand–protein, ligand–water, and protein–protein (within 6A of the binding pocket) interactions by ARROW-NN and repeated the benchmark48 calculations. The multiple details of alchemical transformations and other protocols are discussed at length in ref (48). The results are shown in Figure 5 and are summarized in Table SI 6. For the thrombin and the MCL1 systems, ARROW-NN performs slightly better than the original ARROW (Table SI 6), which was already within chemical accuracy. The CDK2 system is worthy of highlighting. It contains a key set of interactions, namely, ones between ASP87 (PDB 1OI9 residue numbering) and (phenol/chlorobenzene/benzamide) fragments present in some of the ligands, which are exceedingly difficult to describe accurately with conventional analytical functions. Considering the magnitudes of the energies of some of these contacts (phenol-acetate −31.56 kcal/mol, NMA-acetate −28.89 kcal/mol, phenol-water −6.8 kcal/mol, NMA-water −8.09 kcal/mol, acetate-water −21.28 kcal/mol), one sees that the final relative binding free energy (∼2 kcal/mol) is arrived at through the cancellations and differences of many values that are an order of magnitude greater (see Figure 1a). Of all interactions in all three ligand–protein systems, the ones present in CDK2 ASP87 ↔ phenol, ASP87 ↔ H2O, and phenol ↔ H2O had the largest discrepancies between the ARROW FF and QM, and therefore benefited the most from being described by ARROW-NN. The arrows in Figure 5 show the dramatic improvement in free energy predictions for ligands involved in these interactions. Numerically, the correlation goes from −0.5 → 0.88 and the MAE from 0.81 → 0.33 kcal/Mol. Section SI 5.2 as well as48 lay out the protein–ligand binding calculations, protocols, and the CDK2 system analysis in significantly more detail.

Figure 5.

Figure 5

Open in a new tab

Summary of relative binding affinity predictions for protein–ligand systems. The results in blue are computed with the ARROW force field,48 and the results in red are computed with ARROW-NN. Thrombin, MCL1: ARROW-NN predictions are slightly better than the already good ARROW ones. CDK2: inset is an illustration of one of the interactions (ASP87/acetate ↔ phenol) that benefited the most by being described by ARROW-NN. The values are in Table SI 6.

Discussion

In this paper, we describe the design of, and predictions made by a hybrid analytical-perceptron model of intermolecular interactions. In previous work we14 concluded that although an analytical approximation is able to accurately predict free energies of solvation of neutral organic molecules, such a model is at or close to the limit of reasonable complexity. We have now shown that an addition of a perceptron-based, pair-specific energy component to a polarizable wide-coverage force field is a natural and acceptable compromise between obtaining a very good agreement between the model and the reference QM energies and providing a general framework that describes the vast variety of chemical interaction space.

Encoding the intermolecular interactions separately from intramolecular ones enables us to decouple from the much stronger intramolecular energy range of chemistry, which can overwhelm an accurate description of the physics and energetics of interacting molecules. The Parinello-like encoding26 naturally and accurately describes the relative orientations of the interacting atom pairs, as well as the coupling of the intermolecular interaction to the intramolecular monomer perturbations. Splitting the interaction pairs into FF-like chemical types allows us to employ much smaller neural networks and atomic neighborhoods, as the network does not need to recognize types. It also permits us to encode and correct the intermolecular interaction space piece by piece instead of needing to precompute the whole vast universe of everything vs everything for convergence.

In a departure from current efforts to encode the full interaction via neural nets,18,40,41 we chose to preserve as much analytical physics as possible. Although in principle, one can correct any analytical model, the inherited physics of ARROW, specifically polarization, enables parametrization of the model on QM-computable sets of molecules (e.g., dimers) and ensures adequate transferability to large numbers of molecules (bulk). The traditional “physics” terms naturally and properly respond to external perturbations such as an applied electric field, and they also permit the full model to be properly truncated at long range, which is necessary for efficient and accurate simulation.37,39 But in the regime of close molecular approach, where simplifying assumptions used to represent quantum mechanics with Newtonian analytical formulas (separability of interactions, manageable functional forms) begin to break down, neural nets are a natural choice to encode the difficult 2-body remainder. The proposed combination of an analytical polarizable force field with an intermolecular 2-body neural net short-range correction is a fast and accurate representation of the intermolecular potential energy surface for the majority of molecular ensembles.71 Admittedly, a full NN augmentation of the chemical interaction space in the manner we propose will require an intimidating amount of QM calculations. Nonetheless, because the model parameters are extracted from dimer computations only, with only occasional multimer energies as a check, this effort is far more scalable than other similar efforts that employ multimers.29,52,72

The model described here is able to achieve chemical accuracy for a range of previously intractable challenges—protein–ligand and ionic solvation—without any empirical adjustments to experimental values and based purely on first-principles computations. It must be noted that an important class of nanosystems containing extended conjugated complexes,67 as well as full protein conformations,73 will need a much better description of the dispersion interaction. Furthermore, the effect of strong electric fields on the dispersion interaction may also need to be probed further68 and potentially be included into the functional form(s).

Here, we showcase not only a proof of concept but a fully enabled computational suite able to handle proteins, free energy perturbation calculations, and enhanced sampling. By combining sufficient accuracy and wide chemical coverage, the hybrid analytical-perceptron model achieves the long-awaited goal of running accurate molecular simulations for many molecular systems of arbitrary size and varied chemical composition at speeds equivalent to those of polarizable models: several nanoseconds per day or more. This approach will finally allow in silico experiments to tackle and quantitatively solve important real-world problems and challenges.

Acknowledgments

The authors wish to thank NeoTX, InterX, Paul T. Marinelli, Asher Nathan, Robert Harow, and Jeffrey Kletzel for support; Zohar Nussinov and Hulda Chen for useful discussions. Work performed at the Center for Nanoscale Materials, a U.S. Department of Energy Office of Science User Facility, was supported by the U.S. DOE, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. MK research was supported by NIH R01NS083660 and NSF MCB-1818213.

Data Availability Statement

The scripts, tools, and data used in this work are available from the corresponding authors and InterX Inc. upon request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.3c07628.

  • Details of the molecular descriptors; neural network construction; generation and implementation in molecular dynamics package; description of procedure for generating test and training sets; description of the ARROW force field, simulation details, and free energy calculations; tables for the predictions of the relative binding free energies for ligands with proteins (CDK2, MCL1, and thrombin) (PDF)

The authors declare the following competing financial interest(s): B.F., L.P., S.S., I.K., G.K. have filed a non-provisional patent application ARTIFICIAL INTELLIGENCE-BASED MODELING OF MOLECULAR SYSTEMS GUIDED BY QUANTUM MECHANICAL DATA. 18/136,621 on 9/1/2022 in the name of InterX Inc. a subsidiary of NeoTX Therapeutics LTD. The other authors declare no competing interests.

Notes

The scripts, binaries, tools, and data needed to reproduce the data presented in this article are available on GitHub in a conda package https://github.com/freecurve/interx_arrow-nn_suite

Supplementary Material

ja3c07628_si_001.pdf (547.3KB, pdf)

References

  1. Hodak H. The Nobel Prize in Chemistry 2013 for the Development of Multiscale Models of Complex Chemical Systems: A Tribute to Martin Karplus, Michael Levitt and Arieh Warshel. J. Mol. Biol. 2014, 426 (1), 1–3. 10.1016/j.jmb.2013.10.037. [DOI] [PubMed] [Google Scholar]
  2. Houk K. N.; Liu F. Holy Grails for Computational Organic Chemistry and Biochemistry. Acc. Chem. Res. 2017, 50 (3), 539–543. 10.1021/acs.accounts.6b00532. [DOI] [PubMed] [Google Scholar]
  3. Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136 (3B), B864–B871. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  4. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140 (4A), A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  5. Čížek J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 1966, 45 (11), 4256–4266. 10.1063/1.1727484. [DOI] [Google Scholar]
  6. Crawford T. D.; Schaefer H. F. III. An Introduction to Coupled Cluster Theory for Computational Chemists. In Reviews in Computational Chemistry; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2007; pp 33–136. [Google Scholar]
  7. Levitt M.; Lifson S. Refinement of Protein Conformations Using a Macromolecular Energy Minimization Procedure. J. Mol. Biol. 1969, 46 (2), 269–279. 10.1016/0022-2836(69)90421-5. [DOI] [PubMed] [Google Scholar]
  8. Warshel A.; Levitt M.; Lifson S. Consistent Force Field for Calculation of Vibrational Spectra and Conformations of Some Amides and Lactam Rings. J. Mol. Spectrosc. 1970, 33 (1), 84–99. 10.1016/0022-2852(70)90054-8. [DOI] [Google Scholar]
  9. Levitt M. Molecular Dynamics of Native Protein. I. Computer Simulation of Trajectories. J. Mol. Biol. 1983, 168 (3), 595–617. 10.1016/S0022-2836(83)80304-0. [DOI] [PubMed] [Google Scholar]
  10. Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25 (9), 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
  11. Donchev A. G.; Galkin N. G.; Illarionov A. A.; Khoruzhii O. V.; Olevanov M. A.; Ozrin V. D.; Pereyaslavets L. B.; Tarasov V. I. Assessment of Performance of the General Purpose Polarizable Force Field QMPFF3 in Condensed Phase. J. Comput. Chem. 2008, 29 (8), 1242–1249. 10.1002/jcc.20884. [DOI] [PubMed] [Google Scholar]
  12. Vanommeslaeghe K.; Hatcher E.; Acharya C.; Kundu S.; Zhong S.; Shim J.; Darian E.; Guvench O.; Lopes P.; Vorobyov I.; Mackerell A. D. Jr CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2010, 31 (4), 671–690. 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ponder J. W.; Wu C.; Ren P.; Pande V. S.; Chodera J. D.; Schnieders M. J.; Haque I.; Mobley D. L.; Lambrecht D. S.; DiStasio R. A. Jr; Head-Gordon M.; Clark G. N. I.; Johnson M. E.; Head-Gordon T. Current Status of the AMOEBA Polarizable Force Field. J. Phys. Chem. B 2010, 114 (8), 2549–2564. 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Pereyaslavets L.; Kamath G.; Butin O.; Illarionov A.; Olevanov M.; Kurnikov I.; Sakipov S.; Leontyev I.; Voronina E.; Gannon T.; Nawrocki G.; Darkhovskiy M.; Ivahnenko I.; Kostikov A.; Scaranto J.; Kurnikova M. G.; Banik S.; Chan H.; Sternberg M. G.; Sankaranarayanan S. K. R. S.; Crawford B.; Potoff J.; Levitt M.; Kornberg R. D.; Fain B. Accurate Determination of Solvation Free Energies of Neutral Organic Compounds from First Principles. Nat. Commun. 2022, 13 (1), 414 10.1038/s41467-022-28041-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Miksch A. M.; Morawietz T.; Kästner J.; Urban A.; Artrith N. Strategies for the Construction of Machine-Learning Potentials for Accurate and Efficient Atomic-Scale Simulations. Mach. Learn.: Sci. Technol. 2021, 2 (3), 031001 10.1088/2632-2153/abfd96. [DOI] [Google Scholar]
  16. Smith J. S.; Nebgen B. T.; Zubatyuk R.; Lubbers N.; Devereux C.; Barros K.; Tretiak S.; Isayev O.; Roitberg A. E. Approaching Coupled Cluster Accuracy with a General-Purpose Neural Network Potential through Transfer Learning. Nat. Commun. 2019, 10 (1), 2903 10.1038/s41467-019-10827-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. von Lilienfeld O. A.; Burke K. Retrospective on a Decade of Machine Learning for Chemical Discovery. Nat. Commun. 2020, 11 (1), 4895 10.1038/s41467-020-18556-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Behler J.; Csányi G. Machine Learning Potentials for Extended Systems: A Perspective. Eur. Phys. J. B 2021, 94 (7), 142 10.1140/epjb/s10051-021-00156-1. [DOI] [Google Scholar]
  19. Shirts M. R.; Mobley D. L.; Chodera J. D.; Pande V. S. Accurate and Efficient Corrections for Missing Dispersion Interactions in Molecular Simulations. J. Phys. Chem. B 2007, 111 (45), 13052–13063. 10.1021/jp0735987. [DOI] [PubMed] [Google Scholar]
  20. Pereyaslavets L.; Kurnikov I.; Kamath G.; Butin O.; Illarionov A.; Leontyev I.; Olevanov M.; Levitt M.; Kornberg R. D.; Fain B. On the Importance of Accounting for Nuclear Quantum Effects in Ab Initio Calibrated Force Fields in Biological Simulations. Proc. Natl. Acad. Sci. U.S.A. 2018, 115 (36), 8878–8882. 10.1073/pnas.1806064115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Burns L. A.; Marshall M. S.; Sherrill C. D. Appointing Silver and Bronze Standards for Noncovalent Interactions: A Comparison of Spin-Component-Scaled (SCS), Explicitly Correlated (F12), and Specialized Wavefunction Approaches. J. Chem. Phys. 2014, 141 (23), 234111 10.1063/1.4903765. [DOI] [PubMed] [Google Scholar]
  22. Herman K. M.; Xantheas S. S. An Extensive Assessment of the Performance of Pairwise and Many-Body Interaction Potentials in Reproducing Ab Initio Benchmark Binding Energies for Water Clusters N = 2 – 25. Phys. Chem. Chem. Phys. 2023, 25, 7120–7143. 10.1039/D2CP03241D. [DOI] [PubMed] [Google Scholar]
  23. Bukowski R.; Szalewicz K.; Groenenboom G. C.; van der Avoird A. Predictions of the Properties of Water from First Principles. Science 2007, 315 (5816), 1249–1252. 10.1126/science.1136371. [DOI] [PubMed] [Google Scholar]
  24. Paesani F.; Bajaj P.; Riera M. Chemical Accuracy in Modeling Halide Ion Hydration from Many-Body Representations. Adv. Phys.: X 2019, 4 (1), 1631212 10.1080/23746149.2019.1631212. [DOI] [Google Scholar]
  25. Medders G. R.; Babin V.; Paesani F. Development of a “First-Principles” Water Potential with Flexible Monomers. III. Liquid Phase Properties. J. Chem. Theory Comput. 2014, 10 (8), 2906–2910. 10.1021/ct5004115. [DOI] [PubMed] [Google Scholar]
  26. Behler J.; Parrinello M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98 (14), 146401 10.1103/PhysRevLett.98.146401. [DOI] [PubMed] [Google Scholar]
  27. Yao K.; Herr J. E.; Toth D. W.; Mckintyre R.; Parkhill J. The TensorMol-0.1 Model Chemistry: A Neural Network Augmented with Long-Range Physics. Chem. Sci. 2018, 9 (8), 2261–2269. 10.1039/C7SC04934J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Poltavsky I.; Tkatchenko A. Machine Learning Force Fields: Recent Advances and Remaining Challenges. J. Phys. Chem. Lett. 2021, 12 (28), 6551–6564. 10.1021/acs.jpclett.1c01204. [DOI] [PubMed] [Google Scholar]
  29. Zhang Y.; Hu C.; Jiang B. Accelerating Atomistic Simulations with Piecewise Machine-Learned Ab Initio Potentials at a Classical Force Field-like Cost. Phys. Chem. Chem. Phys. 2021, 23 (3), 1815–1821. 10.1039/D0CP05089J. [DOI] [PubMed] [Google Scholar]
  30. Unke O. T.; Chmiela S.; Sauceda H. E.; Gastegger M.; Poltavsky I.; Schütt K. T.; Tkatchenko A.; Müller K.-R. Machine Learning Force Fields. Chem. Rev. 2021, 121 (16), 10142–10186. 10.1021/acs.chemrev.0c01111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Behler J. Four Generations of High-Dimensional Neural Network Potentials. Chem. Rev. 2021, 121 (16), 10037–10072. 10.1021/acs.chemrev.0c00868. [DOI] [PubMed] [Google Scholar]
  32. Musil F.; Grisafi A.; Bartók A. P.; Ortner C.; Csányi G.; Ceriotti M. Physics-Inspired Structural Representations for Molecules and Materials. Chem. Rev. 2021, 121 (16), 9759–9815. 10.1021/acs.chemrev.1c00021. [DOI] [PubMed] [Google Scholar]
  33. Keith J. A.; Vassilev-Galindo V.; Cheng B.; Chmiela S.; Gastegger M.; Müller K.-R.; Tkatchenko A. Combining Machine Learning and Computational Chemistry for Predictive Insights Into Chemical Systems. Chem. Rev. 2021, 121 (16), 9816–9872. 10.1021/acs.chemrev.1c00107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Piquemal J.-P.; Chevreau H.; Gresh N. Toward a Separate Reproduction of the Contributions to the Hartree-Fock and DFT Intermolecular Interaction Energies by Polarizable Molecular Mechanics with the SIBFA Potential. J. Chem. Theory Comput. 2007, 3 (3), 824–837. 10.1021/ct7000182. [DOI] [PubMed] [Google Scholar]
  35. Khoruzhii O.; Butin O.; Illarionov A.; Leontyev I.; Olevanov M.; Ozrin V.; Pereyaslavets L.; Fain B.. Polarizable Force Fields for Proteins. In Protein Modelling; Náray-Szabó G., Ed.; Springer International Publishing: Cham, 2014; pp 91–134. [Google Scholar]
  36. Lemkul J. A.; Huang J.; Roux B.; MacKerell A. D. Jr An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev. 2016, 116 (9), 4983–5013. 10.1021/acs.chemrev.5b00505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103 (19), 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
  38. Popelier P. L. A.; Joubert L.; Kosov D. S. Convergence of the Electrostatic Interaction Based on Topological Atoms. J. Phys. Chem. A 2001, 105 (35), 8254–8261. 10.1021/jp011511q. [DOI] [Google Scholar]
  39. Yonetani Y. Liquid Water Simulation: A Critical Examination of Cutoff Length. J. Chem. Phys. 2006, 124 (20), 204501 10.1063/1.2198208. [DOI] [PubMed] [Google Scholar]
  40. Glick Z. L.; Metcalf D. P.; Koutsoukas A.; Spronk S. A.; Cheney D. L.; Sherrill C. D. AP-Net: An Atomic-Pairwise Neural Network for Smooth and Transferable Interaction Potentials. J. Chem. Phys. 2020, 153 (4), 044112 10.1063/5.0011521. [DOI] [PubMed] [Google Scholar]
  41. Metcalf D. P.; Koutsoukas A.; Spronk S. A.; Claus B. L.; Loughney D. A.; Johnson S. R.; Cheney D. L.; Sherrill C. D. Approaches for Machine Learning Intermolecular Interaction Energies and Application to Energy Components from Symmetry Adapted Perturbation Theory. J. Chem. Phys. 2020, 152 (7), 074103 10.1063/1.5142636. [DOI] [PubMed] [Google Scholar]
  42. Weiner S. J.; Kollman P. A.; Nguyen D. T.; Case D. A. An All Atom Force Field for Simulations of Proteins and Nucleic Acids. J. Comput. Chem. 1986, 7 (2), 230–252. 10.1002/jcc.540070216. [DOI] [PubMed] [Google Scholar]
  43. Hermans J.; Berendsen H. J. C.; Van Gunsteren W. F.; Postma J. P. M. A Consistent Empirical Potential for Water–protein Interactions. Biopolymers 1984, 23 (8), 1513–1518. 10.1002/bip.360230807. [DOI] [Google Scholar]
  44. Brooks B. R.; Bruccoleri R. E.; Olafson B. D.; States D. J.; Swaminathan S.; Karplus M. CHARMM: A Program for Macromolecular Energy, Minimization, and Dynamics Calculations. J. Comput. Chem. 1983, 4 (2), 187–217. 10.1002/jcc.540040211. [DOI] [Google Scholar]
  45. Jorgensen W. L.; Swenson C. J. Optimized Intermolecular Potential Functions for Amides and Peptides. Structure and Properties of Liquid Amides. J. Am. Chem. Soc. 1985, 107 (3), 569–578. 10.1021/ja00289a008. [DOI] [Google Scholar]
  46. Ewig C. S.; Berry R.; Dinur U.; Hill J.-R.; Hwang M.-J.; Li H.; Liang C.; Maple J.; Peng Z.; Stockfisch T. P.; Thacher T. S.; Yan L.; Ni X.; Hagler A. T. Derivation of Class II Force Fields. VIII. Derivation of a General Quantum Mechanical Force Field for Organic Compounds. J. Comput. Chem. 2001, 22 (15), 1782–1800. 10.1002/jcc.1131. [DOI] [PubMed] [Google Scholar]
  47. Gresh N.; Cisneros G. A.; Darden T. A.; Piquemal J.-P. Anisotropic, Polarizable Molecular Mechanics Studies of Inter- and Intramolecular Interactions and Ligand–Macromolecule Complexes. A Bottom-Up Strategy. J. Chem. Theory Comput. 2007, 3 (6), 1960–1986. 10.1021/ct700134r. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Nawrocki G.; Leontyev I.; Sakipov S.; Darkhovskiy M.; Kurnikov I.; Pereyaslavets L.; Kamath G.; Voronina E.; Butin O.; Illarionov A.; Olevanov M.; Kostikov A.; Ivahnenko I.; Patel D. S.; Sankaranarayanan S. K. R. S.; Kurnikova M. G.; Lock C.; Crooks G. E.; Levitt M.; Kornberg R. D.; Fain B. Protein-Ligand Binding Free-Energy Calculations with ARROW—A Purely First-Principles Parameterized Polarizable Force Field. J. Chem. Theory Comput. 2022, 18 (12), 7751–7763. 10.1021/acs.jctc.2c00930. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Boris F.; Leonid P.; Ganesh K.; Igor K.; Serzhan S.. Artificial intelligence-based modeling of molecular systems guided by quantum mechanical data. U.S. Patent US18/136,621, 2022.
  50. Pereyaslavets L.; Fain B.; Kamath G.. System and Method for Determining Material Properties of Molecular Systems from an Ab-Initio Parameterized Force-Field. US20230129485A1, 2023.
  51. Inizan T. J.; Plé T.; Adjoua O.; Ren P.; Gökcan H.; Isayev O.; Lagardère L.; Piquemal J.-P. Scalable Hybrid Deep Neural Networks/polarizable Potentials Biomolecular Simulations Including Long-Range Effects. Chem. Sci. 2023, 14 (20), 5438–5452. 10.1039/D2SC04815A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Yang L.; Li J.; Chen F.; Yu K. A Transferrable Range-Separated Force Field for Water: Combining the Power of Both Physically-Motivated Models and Machine Learning Techniques. J. Chem. Phys. 2022, 157 (21), 214108 10.1063/5.0128780. [DOI] [PubMed] [Google Scholar]
  53. Misquitta A. J.; Podeszwa R.; Jeziorski B.; Szalewicz K. Intermolecular Potentials Based on Symmetry-Adapted Perturbation Theory with Dispersion Energies from Time-Dependent Density-Functional Calculations. J. Chem. Phys. 2005, 123 (21), 214103 10.1063/1.2135288. [DOI] [PubMed] [Google Scholar]
  54. McCulloch W. S.; Pitts W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5 (4), 115–133. 10.1007/BF02478259. [DOI] [PubMed] [Google Scholar]
  55. Fiedler J.; Walter M.; Buhmann S. Y. Effective Screening of Medium-Assisted van Der Waals Interactions between Embedded Particles. J. Chem. Phys. 2021, 154 (10), 104102 10.1063/5.0037629. [DOI] [PubMed] [Google Scholar]
  56. Halgren T. A. Merck Molecular Force Field. I. Basis, Form, Scope, Parameterization, and Performance of MMFF94. J. Comput. Chem. 1996, 17 (5–6), 490–519. 10.1002/(sici)1096-987x(199604)17:5/63.0.co;2-p. [DOI] [Google Scholar]
  57. Bartók A. P.; Kondor R.; Csányi G. On Representing Chemical Environments. Phys. Rev. B 2013, 87 (18), 184115 10.1103/PhysRevB.87.184115. [DOI] [Google Scholar]
  58. Kocer E.; Mason J. K.; Erturk H. Continuous and Optimally Complete Description of Chemical Environments Using Spherical Bessel Descriptors. AIP Adv. 2020, 10 (1), 015021 10.1063/1.5111045. [DOI] [Google Scholar]
  59. Jose K. V. J.; Artrith N.; Behler J. Construction of High-Dimensional Neural Network Potentials Using Environment-Dependent Atom Pairs. J. Chem. Phys. 2012, 136 (19), 194111 10.1063/1.4712397. [DOI] [PubMed] [Google Scholar]
  60. Kabylda A.; Vassilev-Galindo V.; Chmiela S.; Poltavsky I.; Tkatchenko A. Efficient Interatomic Descriptors for Accurate Machine Learning Force Fields of Extended Molecules. Nat. Commun. 2023, 14 (1), 3562 10.1038/s41467-023-39214-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Fain B.Molecular Interactions Lapham’s Quarterly XV 7 (2), .
  62. Smith J. S.; Isayev O.; Roitberg A. E. ANI-1: An Extensible Neural Network Potential with DFT Accuracy at Force Field Computational Cost. Chem. Sci. 2017, 8 (4), 3192–3203. 10.1039/C6SC05720A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. von Lilienfeld O. A.; Müller K.-R.; Tkatchenko A. Exploring Chemical Compound Space with Quantum-Based Machine Learning. Nat. Rev. Chem. 2020, 4 (7), 347–358. 10.1038/s41570-020-0189-9. [DOI] [PubMed] [Google Scholar]
  64. Artrith N.; Butler K. T.; Coudert F.-X.; Han S.; Isayev O.; Jain A.; Walsh A. Best Practices in Machine Learning for Chemistry. Nat. Chem. 2021, 13 (6), 505–508. 10.1038/s41557-021-00716-z. [DOI] [PubMed] [Google Scholar]
  65. Stone A.The Theory of Intermolecular Forces; OUP: Oxford, 2013. [Google Scholar]
  66. Li C.; Paesani F.; Voth G. A. Static and Dynamic Correlations in Water: Comparison of Classical Ab Initio Molecular Dynamics at Elevated Temperature with Path Integral Simulations at Ambient Temperature. J. Chem. Theory Comput. 2022, 18 (4), 2124–2131. 10.1021/acs.jctc.1c01223. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Ambrosetti A.; Ferri N.; DiStasio R. A. Jr; Tkatchenko A. Wavelike Charge Density Fluctuations and van Der Waals Interactions at the Nanoscale. Science 2016, 351 (6278), 1171–1176. 10.1126/science.aae0509. [DOI] [PubMed] [Google Scholar]
  68. Kleshchonok A.; Tkatchenko A. Tailoring van Der Waals Dispersion Interactions with External Electric Charges. Nat. Commun. 2018, 9 (1), 3017 10.1038/s41467-018-05407-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Karimpour M. R.; Fedorov D. V.; Tkatchenko A. Quantum Framework for Describing Retarded and Nonretarded Molecular Interactions in External Electric Fields. Phys. Rev. Res. 2022, 4 (1), 013011 10.1103/PhysRevResearch.4.013011. [DOI] [Google Scholar]
  70. Karimpour M. R.; Fedorov D. V.; Tkatchenko A. Molecular Interactions Induced by a Static Electric Field in Quantum Mechanics and Quantum Electrodynamics. J. Phys. Chem. Lett. 2022, 13 (9), 2197–2204. 10.1021/acs.jpclett.1c04222. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Al-Hamdani Y. S.; Nagy P. R.; Zen A.; Barton D.; Kállay M.; Brandenburg J. G.; Tkatchenko A. Interactions between Large Molecules Pose a Puzzle for Reference Quantum Mechanical Methods. Nat. Commun. 2021, 12 (1), 3927 10.1038/s41467-021-24119-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Zhang Y.; Hu C.; Jiang B. Embedded Atom Neural Network Potentials: Efficient and Accurate Machine Learning with a Physically Inspired Representation. J. Phys. Chem. Lett. 2019, 10 (17), 4962–4967. 10.1021/acs.jpclett.9b02037. [DOI] [PubMed] [Google Scholar]
  73. Stöhr M.; Tkatchenko A. Quantum Mechanics of Proteins in Explicit Water: The Role of Plasmon-like Solute-Solvent Interactions. Sci. Adv. 2019, 5 (12), eaax0024 10.1126/sciadv.aax0024. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja3c07628_si_001.pdf (547.3KB, pdf)

Data Availability Statement

The scripts, tools, and data used in this work are available from the corresponding authors and InterX Inc. upon request.

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES