Three approaches to supervised learning for compositional data with pairwise logratios

ABSTRACT

Logratios between pairs of compositional parts (pairwise logratios) are the easiest to interpret in compositional data analysis, and include the well-known additive logratios as particular cases. When the number of parts is large (sometimes even larger than the number of cases), some form of logratio selection is needed. In this article, we present three alternative stepwise supervised learning methods to select the pairwise logratios that best explain a dependent variable in a generalized linear model, each geared for a specific problem. The first method features unrestricted search, where any pairwise logratio can be selected. This method has a complex interpretation if some pairs of parts in the logratios overlap, but it leads to the most accurate predictions. The second method restricts parts to occur only once, which makes the corresponding logratios intuitively interpretable. The third method uses additive logratios, so that K−1 selected logratios involve a K-part subcomposition. Our approach allows logratios or non-compositional covariates to be forced into the models based on theoretical knowledge, and various stopping criteria are available based on information measures or statistical significance with the Bonferroni correction. We present an application on a dataset from a study predicting Crohn's disease.

1. Introduction

Compositional data are data in the form of components, or parts, of a whole, where the relative values of the parts are of interest, not their absolute values. John Aitchison [1–3] pioneered the use of the logratio transformation as a valid, (subcompositionally) coherent way to analyse compositional data. Coherence means that, if the set of parts is extended or reduced, the relationships between the common parts remain constant, whereas their relative values do change because of the differing sample totals. Ratios of parts, however, are invariant with respect to the normalization (closure) of the data and these form the basis of Aitchison's approach to compositional data analysis, often referred to as CoDA.

Since ratios are themselves compared on a ratio scale, and are usually highly right-skew, they are log-transformed to an interval scale. Hence, the basic concept and data transformation in CoDA is the logratio, with the simplest being the logarithm of a pairwise ratio, for example, for two parts A and B: $\log (A/B)=\log (A)-\log (B)$. This study is concerned with such pairwise logratios, denoted henceforth exclusively by the abbreviation LR – logratios, in general, will not be abbreviated. The challenge is to choose a set of LRs that effectively replaces the compositional dataset and are at the same time substantively meaningful to the practitioner as well as having a clear interpretation. Once the transformation to LRs is performed, analysis, visualization and inference carry on as before, but always taking into account the interpretation in terms of ratios.

For a composition consisting of J parts, a set of J−1 LRs contains the whole information of the composition, as long as each part participates in at least one LR [23]. When the number of parts is large (in biological applications often larger than the number of cases), some form of selection of fewer than J−1 LRs is convenient or even necessary prior to subsequent statistical analysis. Greenacre [22,23] developed an unsupervised learning method based on a stepwise selection of the LRs that explained the maximum percentage of logratio variance in the composition itself, where ‘explained’ is in the linear regression sense. In this article, we are interested rather in supervised learning, that is, selecting LRs that best explain or predict a target variable. Two bivariate supervised approaches have been proposed [15,52] to find the LRs which are most related to a qualitative target variable. In these approaches, each chosen LR does not take into account the explanatory power of the remaining chosen LRs. More recently, the authors in Ref. [6] have extended the idea to the penalized regression approach and to a continuous target variable. In this paper, we present three alternative stepwise supervised learning methods to select the LRs that make a net contribution to explaining a dependent variable in a generalized linear model, as an alternative to the hybrid approach by [29] with much the same aim. As opposed to [29], the dependent variable can be of any kind supported by generalized linear models, including binary (Bernouilli), continuous, or count (Poisson) variables. The selection method for the LRs is the standard one in stepwise regression with forward selection, geared to deal with three distinct compositional problems. The conceptual simplicity of stepwise regression coupled with that of LRs can be appealing to applied researchers without a sophisticated statistical background, compared to the approaches in [6,29], and is yet flexible enough to accommodate three variants which fit different research objectives and to introduce the researcher's judgement in LR choice.

In the first variant, any LR is eligible to belong to the model. This approach will generally lead to the best predictive power but the LRs can be difficult to interpret if they overlap [30]. It is thus inappropriate when the main or only objective is LR interpretation. In the second variant, only LRs involving pairs of parts that do not overlap are eligible – thus if $\log (A/B)$ is selected, A and B are excluded from any other ratios. This leads to a simpler interpretation of the LRs as trade-off effects between pairs of parts on the dependent variable. The third variant aims at identifying a subset of parts (i.e. a subcomposition) with the highest explanatory power, by selecting a reduced set of additive logratios (ALRs). Several stopping criteria are possible for these three variants, optimising information measures or ensuring significance of the logratios with the Bonferroni correction. All variants allow the researcher to see the explanatory power of several candidate logratios and modify the LR entered at a given step from his or her expert knowledge, as incorporated into the selection process in [20,48,55]. This includes the possibility to force the inclusion of certain logratios or non-compositional variables from the start. All variants are best evaluated by means of cross-validation: the model that is finalized at the last step is estimated on a hold-out data set in order to get unbiased estimates, p-values and prediction accuracy figures.

This article adds to the literature on variable selection in explanatory compositions: first, the compositional developments using regularized regression, including Lasso and related methods, for example [5,10,35–37,39,40,50,51]; second, the unsupervised methods that aim at finding an optimal subcomposition, for example [31]; third, the discriminative balance approach [46,56] identifies ratios between two or three parts in a supervised problem; fourth, the selbal approach [49,51] selects two subcompositions, one positively related to the dependent variable and one negatively related, and computes the logratio of the geometric mean of the first over the second as predictor (this has been generalized to more than one logratio by [18]); fifth and finally, additional approaches such as using amalgamations [25,45], investigator-driven search of LRs [53], kernel-based nonparametric regression and classification [32], relative-shift regression [34], data augmentation [19], principal balances derived from partial least squares [42], the nearest-single-balance-shift approach [43], and Bayesian methods [58].

The article is organized as follows, we first state the problem of stepwise regression in the context of LRs. We next describe the three variants of the algorithm, each geared to solve a specific problem. We next present an application to one of the data sets used by [49]. The last section concludes with a discussion.

2. Compositional stepwise regression

2.1. Compositions and their logratios

A J-part composition can be defined as an array of strictly positive numbers called parts, for which ratios between them are considered to be relevant [44]: $\mathbf{x}=(x_1,x_2,\dots ,x_J)$, with $x_j>0$ for $j=1,2,\dots ,J$. Notice that an alternative definition of a composition, which is more realistic in practice, is to define it as consisting of non-negative numbers, thus admitting zeros and using alternative methods that do not rely on ratios, yet approximate logratio methods very closely – see, for example, [21,25].

Focusing on strictly positive parts, logarithms of ratios are more statistically tractable than ratios, and Aitchison [1] presented the first comprehensive treatment of compositions by means of logratios, using the additive logratio transformation (ALR) in which J−1 LRs are computed with the same denominator or reference part, which is assumed here, without loss of generality, to be the last part:

$$\log \left(\frac{x_j}{x_J}\right)=\log (x_j)-\log (x_J),j=1,2,\dots ,J-1.$$ (1)

This can easily be generalized to any of the possible $J(J-1)/2$ LRs between any two parts [2,22]:

$$\log \left(\frac{x_j}{x_{j^{\prime }}}\right)=\log (x_j)-\log (x_{j^{\prime }}),j=1,2,\dots ,j^{\prime }-1,j^{\prime }=2,3,\dots ,J.$$ (2)

The inherent dimensionality of a composition is J−1, which means that $J(J-1)/2-(J-1)$ LRs are redundant and only J−1 LRs can participate in a statistical model. Greenacre [22,23] showed that taking exactly J−1 LRs in such a way that each part participates in at least one LR, always leads to a non-redundant selection. But even J−1 is too large a number when the composition has many parts, and the aim of this article is to select a subset of fewer LRs that is optimal in some sense.

The most general form of a logratio is the log-contrast, which can be expressed as:

$$\left[\begin{array}{cccc}{\alpha }_1& {\alpha }_2& \cdots & {\alpha }_J\end{array}\right]\left[\begin{array}{c}\log (x_1)\\ \log (x_2)\\ ⋮\\ \log (x_J)\end{array}\right]={\mathit{\alpha }}^{\mathsf{\text{T}}}\log (\mathbf{x}),\mathrm{where}\sum _{j=1}^J{\alpha }_j={\mathit{\alpha }}^{\mathsf{\text{T}}}\mathbf{1}=0.$$ (3)

A LR is a special case with one value in the coefficient vector $\mathit{\alpha }$ equal to 1 and another equal to $-1$, corresponding to the numerator and denominator parts, respectively, and the remaining coefficients equal to zero.

Other ways of computing logratios involving more than two parts have been suggested [12,14,16,41] with the requirement of orthogonality of the $\mathit{\alpha }$ vectors in the log-contrasts, which has implications for the logratio's interpretation [30] as shown below. Notice that two LRs can also have mutually orthogonal $\mathit{\alpha }$ vectors if they do not overlap, that is, if no part participates in both LRs. For instance, in a four-part composition, the LRs $\log (x_1/x_2)$ and $\log (x_3/x_4)$ have the orthogonal $\mathit{\alpha }$ vectors $[1,-1,0,0]$ and $[0,0,1,-1]$ respectively.

The LRs can be used as dependent, predicted by non-compositional variables [13], or as explanatory, to predict a non-compositional outcome [4], which should be continuous in a linear regression model. The extension from a linear model to a generalized linear model is straightforward. For instance, if the dependent variable is a count, a Poisson regression can be specified, or if the dependent variable is binary, a logit model can be specified [8]. In this article, we are concerned with using LRs as explanatory variables.

2.2. Stepwise regression

Logratio selection in linear or generalized linear models belongs to the domain of statistical learning [33], and, more precisely, supervised statistical learning, because the selection is made with the purpose of optimising the explanatory power or the predictive accuracy with respect to an external response variable. Stepwise regression is one of the earliest forms of supervised statistical learning and can be adapted both to linear and generalized linear models. The forward selection method of stepwise regression is especially interesting due to its ability to handle any number of LRs, even if J−1 is larger than the sample size, and is described simply as:

• In the first step, the algorithm selects the LR leading to the lowest residual sum of squares, or its generalization for both linear models and generalized linear models, $-2\times \log (\mathrm{likelihood})$, abbreviated as −2logLik, which is called deviance for some specific models, such as the logit model that we consider in the application section.

• In the second and subsequent steps, the algorithm adds to the equation the LR leading to the strongest reduction in the residual sum of squares or in −2logLik, one LR at a time.

Since adding an LR always decreases −2logLik, a stopping criterion is needed in order not to reach the trivial solution with J−1 LRs which would imply that no selection has been made. This is achieved by means of adding a penalty to −2logLik as a function of the number of selected LRs. The many possibilities available to introduce such a penalty makes the stepwise approach very flexible. Let m be the number of parameters estimated in the model and n the sample size. The most popular penalties are:

• the Akaike information criterion (AIC), which minimizes $-2\mathrm{logLik}+2m$;

• the Bayesian information criterion (BIC), which minimizes $-2\mathrm{logLik}+\log (n)m$.

Notice that $\log (n)>2$ for n>7, so that the BIC criterion will generally lead to more parsimonious models with fewer LRs than the AIC criterion. For example, if n = 500, the penalty is 6.215 m.

Another possibility is to set the penalty in such a way that an additional LR is introduced into the model only if it is statistically significant at a given significance level. At first sight, this could be achieved if the penalty factor equals the quantile of the ${\chi }^2$ distribution with 1 degree of freedom and tail area equal to the significance level. For example, ensuring that the added LRs are significant at 5% is equivalent to a penalty equal to 3.841 m.

However, this approach is flawed because of multiple testing. Since J−1 non-redundant LRs are simultaneously being tested for inclusion, the significance level has to be defined in more strict terms in order to account for the accumulation of risks arising from multiple testing. A popular criterion is the conservative Bonferroni correction which implies using the ${\chi }^2$ quantile with a tail area equal to the significance level divided by J−1. For the commonly encountered J and n values, this criterion usually leads to the strongest penalty (and thus to the smallest set of selected LRs and the highest model parsimony). For example, if J−1 = 10, the relevant tail area is 0.005, the ${\chi }^2$ quantile is 7.879 and the procedure minimizes $-2\mathrm{logLik}+7.879$ m.

It is well-known that estimates and t-values are biased upwards in absolute value when using stepwise regression, because the variables included are those with the highest values for the particular sample [7,28,54]. For the same reason, p-values are too low (risking to make the Bonferroni correction insufficient) and prediction intervals too narrow. It is also hardly surprising that goodness of fit measures are overestimated when the data are used to find the model which optimizes them. The whole issue falls under the umbrella of failing to take model uncertainty into account [7]. The problem is made more serious when samples are small, the number of variables is large, and the number of steps in the stepwise procedure is large.

This requires shrinkage methods or independent testing of the final model with a fresh cross-validation sample. If the original sample is large enough, it is possible to split it randomly, roughly two-thirds being used to run the stepwise regression (training part) and one-third to validate the final model (test part). However, gathering fresh data provides a more convincing argument for the model, as it extends the range of time and space settings under which the model is valid [7].

Even after validation, it must be taken into account that many models may have a similar fit to the data and the procedure has only found one of them [54]. The problem is compounded when there is strong collinearity [28] and makes stepwise regression appropriate for predictive and exploratory purposes, but not for theory testing. The final model cannot be interpreted as if it were prespecified [28].

Having said this, many learning methods for compositional data use stepwise algorithms due to their wide acceptance and conceptual simplicity [22,23,29,31,49,51], and the existence of several solutions with similar goodness of fit and the need for cross-validation are shared by even the most sophisticated statistical learning methods.

2.3. Introducing expert knowledge in stepwise regression

Expert knowledge can be a crucial complement to data-driven statistical learning for compositional data [23,53], serving to overcome the inherent limitations of the stepwise method, by reducing the number of data-driven steps. In this respect, the user should be able to:

• force certain theoretically relevant LRs into the regression equation;

• discard LRs with a nonsensible effect sign according to theory [28];

• force certain theoretically relevant non-compositional covariates into the regression equation;

• choose among LRs with approximately the same significance or AIC/BIC improvements.

With respect to the last of the above-mentioned options, there are already three published studies [20,48,55] where the expert with domain knowledge has interacted with the statistical algorithm to make choices of LRs from a list of those competing to enter. The idea in the present context is to present the expert with the ‘top 20’ LRs, say, in decreasing order of importance in the modelling, that is increasing order of −2logLik. Those at the top often have very little difference between them statistically, and the expert can agree with the optimal one but could also, at the expense of a slightly worse fit, choose an LR lower down the list which has a preferred interpretation or a higher theoretical relevance.

The three studies cited above all operate in an unsupervised mode. That is, they are not concerned with modelling or predicting a response but rather with substituting the full set of LRs with a smaller set that accounts for most of the logratio variance while approximating the multivariate structure of the data as closely as possible. Nevertheless, notice that the second study [48] cited above does have a supervised learning flavour, since the LRs are chosen not to explain total logratio variance between samples, but logratio variance between four groups of samples. In other studies focused on choosing sets of ALRs [27,57], there are often competing choices of the denominator parts that lead to similar results, where again the expert can make a reasoned choice based on substantive considerations.

If there are non-compositional continuous or categorical variables that are substantively relevant and statistically predictive of the response, they can be introduced into the model first, and then the LRs are introduced as before to explain the residuals. For the ALR variant of our method, the choice of initial LR can also be made by the expert who wants to force a particular reference part in the ALRs, based on domain knowledge. Whichever the intervention of the user, the final model should then be cross-validated in the same way as described in Section 4.5.

3. The logratio selection algorithms

In this section, we propose three variants of the forward stepwise selection algorithm for generalized linear models, each geared towards solving a specific compositional problem. At the final step, any of them will yield an equation of the form:

$$g(y)={\beta }_{00}+\sum _{j{j}^{\prime }}{\beta }_{j{j}^{\prime }}\log \left(\frac{x_j}{x_{j^{\prime }}}\right),$$ (4)

where the summation term contains at most J−1 non-redundant logratios, ${\beta }_{00}$ is the intercept term and g is the link function of the generalized linear model.

3.1. Unrestricted search

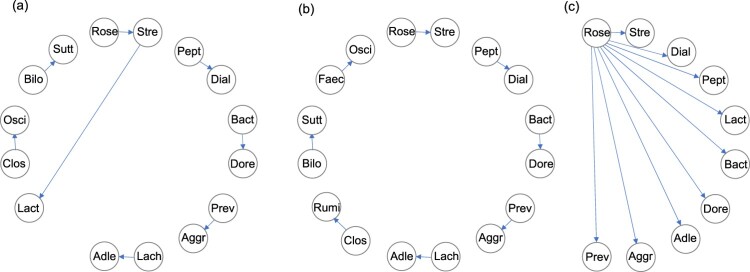
The first algorithm is a straightforward adaption of the unsupervised stepwise selection algorithm [23] to a supervised setting. Any non-redundant LRs may be selected by the algorithm. This implies that if $\log (C/B)$ and $\log (C/A)$ have already been selected, then $\log (B/A)$ is excluded, since $\log (B/A)=\log (C/A)-\log (C/B)$ and would not contribute to explain variance or improve predictions. More importantly, redundancy implies that many models lead to the same predictions and goodness of fit. Selecting $\log (B/A)$ and $\log (C/B)$ leads to the same predictions as $\log (C/B)$ and $\log (C/A)$ and as $\log (B/A)$ and $\log (C/A)$. It also leads to the same expression of the regression equation as a single log-contrast of $\log (A)$, $\log (B)$ and $\log (C)$ (see Section 3.4). Rather than different models, they are three reformulations of the same and only model [9], the choice among which is absolutely irrelevant for all intents and purposes. Faced with this situation, the stepwise algorithm provides only one solution. This argument can be extended to any set of LRs with parts forming a cycle in a graph, which indicates redundancy (see [22,23]) – the chosen LRs have to form an acyclic graph (examples are shown in Figure 2 in the application).

Figure 2.

Directed acyclic graphs (DAGs) visualizing the ratios selected in the three stepwise approaches (according to the Bonferroni penalty, the right-hand panels in Tables 1–3). Arrows point from the denominator to the numerator in every case. In each graph, the LR at the top (Stre/Rose) is the first one selected and the ratios introduced in the following steps are shown in a clockwise direction. (a) Unrestricted search, showing an overlap of Stre; 15 parts included. (b) Restricted to non-overlap; 16 parts included. (c) ALR selection; 10 parts included, which define a subcomposition, and the only graph out of the three that is connected.

The final solution of this algorithm may be a combination of overlapping and non-overlapping pairs of parts. For example, supposing there are J = 7 parts, denoted by A, B, C, D, E, F, G. The stepwise algorithm might, for instance, select $\log (B/A)$, $\log (C/B)$ and $\log (G/F)$. The pair G/F does not overlap with any other (i.e. the parts F and G participate in only one LR) while the pairs B/A and C/B overlap in part B.

The parameter interpretation in models combining overlapping and non-overlapping LRs is all but intuitive [9,30]. In the above example with the selection $\log (B/A)$, $\log (C/B)$ and $\log (G/F)$ in the model, the interpretation would be as follows, taking into account that the effects of the explanatory variables have to be interpreted keeping all other variables constant [9]. The coefficient associated with $\log (G/F)$ is interpreted as increasing G at the expense of decreasing F, while keeping the mutual ratios of A, B and C constant. Since $\log (G/F)$ does not overlap with the remaining LRs, its interpretation is not affected and its coefficient expresses a trade-off between only the numerator and denominator parts.

Of course, it can be the case that both G and F increase in absolute terms at different rates. However, in relative terms, i.e. compositionally speaking, there will still be a trade-off. The coefficient associated with $\log (B/A)$ is interpreted as increasing B at the expense of decreasing A, while keeping constant both C relative to B and G relative to F. Keeping the ratio of C over B constant means that C changes by the same factor as B. Thus, the coefficient associated to $\log (B/A)$ is interpreted as increasing B and C by a common factor at the expense of decreasing A, in relative terms. Likewise, the coefficient associated to $\log (C/B)$ is interpreted as increasing C at the expense of decreasing B, while keeping the ratios of B over A and G over F constant. Keeping the ratio of B over A constant means that A decreases by the same factor as B. Thus, the coefficient associated with $\log (C/B)$ is interpreted as increasing C while decreasing A and B by a common factor. As a result, the effects of overlapping LRs do not correspond to the effects of the trade-offs between the numerator and denominator parts. On the one hand, this requires exercising great care in the interpretation task, and on the other, it deviates from the objective of choosing LRs that lead to simple interpretation.

Nevertheless, the present variant of the algorithm selects the LRs that contribute the most to predictive power, overlapping or not. If the purpose of the researcher is only to make predictions, then interpretation may not be essential and this variant may be the best choice. An interpretational trick that does not involve the LRs is provided in Section 3.4.

This method variant can be related to the approach in Ref. [6] which similarly makes an unrestricted selection of LRs based on penalized regression. The following two variants of the method make for simpler interpretations of the effects of each LR.

3.2. Search for non-overlapping pairwise logratios

In this variant of the algorithm, the stepwise search is restricted to at most J/2 (if J is even) or $(J-1)/2$ (if J is odd) LRs with non-overlapping parts. This limitation may yield a lower predictive power in some applications but may be very welcome for high-dimensional compositions where parsimony is a must. Since they are non-overlapping, the K/2 selected LRs will involve exactly K parts. This approach has some important advantages:

• It is easily interpreted. Non-overlapping LRs have orthogonal $\mathit{\alpha }$ coefficient vectors in Equation (3) by construction. They are thus an exception to the often-quoted problems when interpreting LRs as explanatory variables [30]. For this reason, their effects on the dependent variable can be interpreted in a straightforward manner in terms of trade-offs between only the numerator and the denominator parts [30], as intended when building the LRs.

• It tends to reduce collinearity among the LRs, which is an important issue in stepwise methods.

• It is faster, as it continuously removes LRs from the set of feasible choices.

Each non-overlapping LR can also be considered to be a balance up to a multiplicative scalar, which brings this variant of the algorithm close to the discriminative-balance approach in [46], where ratios between two or three parts are selected in a supervised problem.

3.3. Search for additive logratios in a subcomposition

This algorithm draws from the fact that a subcomposition with K parts can be fully represented by K−1 LRs as long as each part participates in at least one LR [23] and that any logratio selection fulfilling this criterion has identical predictions and goodness of fit [9]. This includes the additive logratios (ALRs) with any part of the subcomposition in the denominator and the remaining K−1 parts in the numerator, which makes for a shorter search of candidate LRs and makes the interpretation easier. Thus, this algorithm searches for the K-part subcomposition with the highest explanatory power by fixing the denominator part of the LR determined in the first step and then bringing in additional parts as numerators of the LRs entering subsequently.

The effects of the selected set of ALRs in the model in the final linear model are not interpretable as trade-offs between pairs of parts [30] but an alternative simple rule for interpretation is given in [9]: to interpret the ALR effects as those of increasing the part in the numerator while decreasing all other parts in the subcomposition by a common factor. The common denominator of the ALRs has an associated effect equal to the sum of all coefficients with a reversed sign.

In our previous 7-part example, suppose that $\log (B/G)$ and $\log (A/G)$ are chosen:

$$g(y)=b_{00}+b_{AG}\log (A/G)+b_{BG}\log (B/G).$$ (5)

The estimated coefficient $b_{AG}$ is the effect of increasing A while decreasing B and G by a common factor, the coefficient $b_{BG}$ is the effect of increasing B while decreasing A and G by a common factor, and $(-b_{AG}-b_{BG})$ shows the effect of increasing G while decreasing B and A by a common factor.

As stated previously, this algorithm that results in an equation with ALR predictors, also results in identifying a subcomposition. If the researcher prefers other parameter interpretations, the resulting subcomposition can be fitted into the regression model in a subsequent step using the researcher's favourite type of logratio transformation, including those with orthogonal $\mathit{\alpha }$ vectors in Equation (3).

This algorithm has similar objectives as the approaches of the regularized-regression family [35,37,50], which also aim at selecting a subcomposition to explain the non-compositional dependent variable. It is also related to the selbal approach [49], which selects two subcompositions, one positively related to the dependent variable and one negatively related, and computes the logratio of the geometric mean of the first over the second as predictor. The selbal algorithm constrains the effects of all parts to be equal within the numerator and denominator sets.

Our approach can also be understood as a supervised equivalent of the algorithm presented by [31], which is a backward stepwise procedure searching for the subcomposition containing the highest possible percentage of total logratio variance of the original composition. Notice the difference between ‘containing’ and ‘explaining’ variance – contained variance is the contribution to the total logratio variance, where the contributions of each part in the composition are summed to get the total, whereas explained variance is in the regression sense, where a part can not only explain its own contribution to the variance but also contributions due to intercorrelations with other parts.

3.4. Reexpression as a single log-contrast

The final model in any of the three approaches can be expressed as a log-contrast of the logarithms of all involved parts, whose coefficients add up to zero.

For instance, the equivalent log-contrast to in Equation (5) has the ${\alpha }_j$ coefficients in:

$$b_{AG}\log (A)+b_{BG}\log (B)+(-b_{AG}-b_{BG})\log (G).$$ (6)

This log-contrast can be interpreted as a whole: increasing the parts with positive ${\alpha }_j$ log-contrast coefficients at the expense of decreasing the parts with negative ${\alpha }_j$ log-contrast coefficients leads to an increase in the dependent variable, parts with higher coefficients in absolute value being more important.

All three methods are available in the new release of the package easyCODA [22] in R [47], using function STEPR, with options method=1 (unrestricted search) method=2 (non-overlapping search) and method=3 (search for a subcomposition by selecting ALRs). The user can specify how many steps the algorithm will proceed, or select a stopping criterion, either BIC or Bonferroni. Theoretically relevant LRs or covariates can be forced into the regression equation at step 0. The selection can also be made one single step at a time, where the researcher is presented with a list of LRs that are competing to enter the model, from which either the statistically optimal one is chosen or a slightly less optimal one with a more interesting and justified substantive meaning and interpretation.

4. Application

4.1. Data

The three approaches to logratio selection are applied to a data set relating Crohn's disease to the microbiome of a group of patients in a pediatric cohort study [17,49]. The 662 patients with Crohn's disease (coded as 1) and the 313 without any symptoms (coded as 0) are analysed. The operational taxonomic unit (OTU) table was agglomerated to the genus level, resulting in a matrix with J = 48 genera and a total sample size n = 662 + 313 = 975. All the genera but one had some zeros, varying from 0.41% to 79.38% and overall the zeros accounted for 28.8% of the values in the $975\times 48$ table of OTU counts. Among the available zero-replacement methods, for comparability purposes with [49], the zeros were substituted with the geometric Bayesian multiplicative replacement method [38].

Since the dependent variable is binary, the appropriate member of the generalized linear model family is the logit model, with the probability p of Crohn's disease expressed as the logit (log-odds) $\log (\frac{p}{1-p})$. Positive regression coefficients would indicate associations with a higher incidence of Crohn's disease. For the particular case of logit models, the deviance equals −2logLik. As recommended by Ref. [28], prior to any stepwise procedure, we tested an intercept-only model against a model with J−1 LRs, rejecting the intercept-only model ( ${\chi }^2=407.1$ with 47 degrees of freedom).

The same data set has been analysed using the selbal approach [49], which contrasts two subcompositions of genera $S_1$ and $S_2$ in a single variable equal to the log-transformed ratio of the respective geometric means. Thus the coefficients of the parts for each subcomposition are the same, resulting in the following log-contrast as a predictor of the incidence of Crohn's disease, where the positive and negative coefficients apply respectively to the 8 parts of $S_1$ in the numerator and the 4 parts of $S_2$ in the denominator (abbreviations of the genera are used – see the Appendix for the list of full names):

$$\begin{array}{rl}& 0.2041\log (\mathrm{Dial})+0.2041\log (\mathrm{Dore})+0.2041\log (\mathrm{Lact})+0.2041\log (\mathrm{Egge})\\ & +0.2041\log (\mathrm{Aggr})+0.2041\log (\mathrm{Adle})+0.2041\log (\mathrm{Stre})+0.2041\log (\mathrm{Osci})\\ & -0.4082\log (\mathrm{Rose})-0.4082\log (\mathrm{Clos})-0.4082\log (\mathrm{Bact})-0.4082\log (\mathrm{Pept})\end{array}$$

4.2. Results with the complete data set

For comparability with [49] we first run the analysis on the complete dataset, leaving the crucial cross-validation step for Section 4.5. The results for our three approaches, with the stopping criterion set to optimise BIC are in the left panel of Tables 1 to 3. The function which is being optimised is deviance +6.8824 m. Table 1 shows the unrestricted solution. Variables are ordered according to entry in the stepwise algorithm.

Table 1.

Estimates of the final model with the first approach (unrestricted stepwise search). Ratios have been inverted, where necessary, to make all coefficients positive.

	BIC penalty			Bonferroni penalty
Ratio	Estimate	s.e.	p-value	Estimate	s.e.	p-value
Stre/Rose	0.3059	0.0320	$<0.0001$	0.3022	0.0315	$<0.0001$
Dial/Pept	0.1378	0.0235	$<0.0001$	0.1618	0.0218	$<0.0001$
Dore/Bact	0.2436	0.0376	$<0.0001$	0.2393	0.0372	$<0.0001$
Aggr/Prev	0.1025	0.0221	$<0.0001$	0.1008	0.0220	$<0.0001$
Adle/Lach	0.1107	0.0275	$<0.0001$	0.1158	0.0273	$<0.0001$
Lact/Stre	0.1489	0.0371	$<0.0001$	0.1482	0.0364	$<0.0001$
Osci/Clos	0.1645	0.0429	0.0001	0.1688	0.0426	$<0.0001$
Sutt/Bilo	0.0889	0.0247	0.0003	0.0873	0.0246	0.0004
Clot/Pept	0.0712	0.0264	0.0070
BIC	932.03			932.55

Table 3.

Estimates of the final model with the third approach (subcomposition search with ALR). Ratios have been left with the fixed denominator part, hence positive and negative coefficients.

	BIC penalty			Bonferroni penalty
Ratio	Estimate	s.e.	p-value	Estimate	s.e.	p-value
Stre/Rose	0.1488	0.0444	0.0008	0.1415	0.0438	0.0012
Dial/Rose	0.1354	0.0267	$<0.0001$	0.1407	0.0262	$<0.0001$
Pept/Rose	−0.1909	0.0331	$<0.0001$	−0.2065	0.0324	$<0.0001$
Lact/Rose	0.1547	0.0404	$<0.0001$	0.1420	0.0397	0.0003
Bact/Rose	−0.2859	0.0521	$<0.0001$	−0.2792	0.0481	$<0.0001$
Dore/Rose	0.2252	0.0483	$<0.0001$	0.2021	0.0439	$<0.0001$
Adle/Rose	0.1477	0.0375	$<0.0001$	0.1511	0.0360	$<0.0001$
Aggr/Rose	0.1381	0.0332	$<0.0001$	0.1378	0.0328	$<0.0001$
Prev/Rose	−0.0905	0.0260	0.0005	−0.0920	0.0258	0.0004
Osci/Rose	0.1551	0.0439	0.0004
Clos/Rose	−0.2140	0.0723	0.0031
BIC	964.44			967.42

There is an overlap of the genus Stre in steps 1 and 6, which will cause complications in the interpretation. In the second version of the algorithm, then, the selected LRs differ from the sixth step onward, with very small increases in the BIC, shown in Table 2.

Table 2.

Estimates of the final model with the second approach (non-overlapping LRs). Ratios have been inverted, where necessary, to make all coefficients positive.

	BIC penalty			Bonferroni penalty
Ratio	Estimate	s.e.	p-value	Estimate	s.e.	p-value
Stre/Rose	0.2377	0.0294	$<0.0001$	0.2444	0.0291	$<0.0001$
Dial/Pept	0.1570	0.0221	$<0.0001$	0.1702	0.0217	$<0.0001$
Dore/Bact	0.2322	0.0379	$<0.0001$	0.2272	0.0371	$<0.0001$
Aggr/Prev	0.1026	0.0223	$<0.0001$	0.1087	0.0222	$<0.0001$
Adle/Lach	0.1077	0.0279	0.0001	0.1139	0.0276	$<0.0001$
Rumi/Clos	0.2511	0.0660	0.0001	0.2553	0.0642	$<0.0001$
Sutt/Bilo	0.0728	0.0248	0.0033	0.0844	0.0245	0.0006
Osci/Faec	0.1220	0.0346	0.0004	0.1088	0.0333	0.0011
Lact/Turi	0.0864	0.0295	0.0034
Egge/Euba	0.0792	0.0303	0.0091
BIC	937.92			939.64

Since non-overlapping LRs have orthogonal $\mathit{\alpha }$ vectors, their interpretation is according to the logratio formulation [30]. That is, the incidence of Crohn's disease is significantly associated with an increase in the relative abundance of each numerator genus at the expense of a decrease in the relative abundance of the respective denominator genus.

The third approach identifies the set of ALRs, shown in Table 3, where there is a much bigger increase in the BIC. The first LR selected, identical to the first ones in the previous results, determines the denominator part of them all. The algorithm selects 11 ALRs as a 12-part subcomposition. This subcomposition of 12 genera may be transformed into the practitioner's favourite logratio representation without changing the predictions or goodness of fit of the model as long as 11 logratios are used [9]. A convenient example of the former is to rerun the final model with a different part in the ALR denominator. This makes it possible to obtain the missing standard error and p-value in the log-contrast corresponding to the denominator part in the original run (Rose in the first row of Table 4). The remaining estimates and standard errors in Table 4 do not change. Each coefficient can be interpreted as the effect on the dependent variable (i.e. the log-odds of having Crohn's disease) of increasing the part in the numerator while decreasing all other parts in the subcomposition by a common factor. For instance, according to the coefficient of Stre/Rose in Table 3, the likelihood of Crohn's disease increases with increases in the genus Stre, at the expense of joint decreases in Dial, Pept, Lact, Bact, Dore, Adle, Aggr, Prev, Osci, Clos and Rose.

Table 4.

Estimates of the final model with the third approach and an alternative denominator (subcomposition search with ALR).

	BIC penalty			Bonferroni penalty
Ratio	Estimate	s.e.	p-value	Estimate	s.e.	p-value
Rose/Stre	−0.3237	0.0425	$<0.0001$	−0.3375	0.0383	$<0.0001$
Dial/Stre	0.1354	0.0267	$<0.0001$	0.1407	0.0262	$<0.0001$
Pept/Stre	−0.1909	0.0331	$<0.0001$	−0.2065	0.0324	$<0.0001$
Lact/Stre	0.1547	0.0404	$<0.0001$	0.1420	0.0397	0.0003
⋮	⋮	⋮	⋮	⋮	⋮	⋮
Prev/Stre	−0.0905	0.0260	0.0005	−0.0920	0.0258	0.0004
Osci/Stre	0.1551	0.0439	0.0004
Clos/Stre	−0.2140	0.0723	0.0031
BIC	964.44			967.42

If the model is not used merely for prediction, significance of the logratios becomes important. The right panel of Tables 1 to 4 presents the results using a penalty equivalent to forcing the selected LRs to be significant at 0.05 with the Bonferroni inequality: deviance +10.7130 m. This has led to selecting one fewer LR for the first approach and two fewer LRs for the second and third approaches. Given the large sample size, BIC also employs a substantial penalty to the deviance and this is why results are barely affected in this particular application.

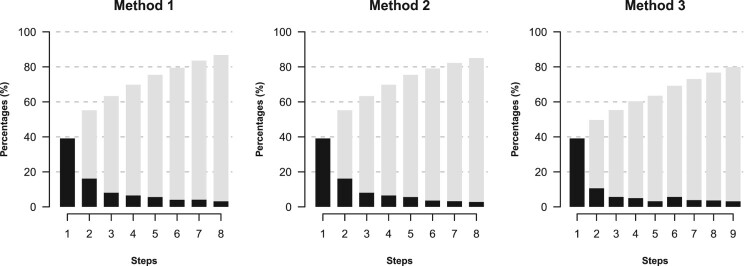
Figure 1 shows three plots of the sequence of certain diagnostics for the three algorithms. The null deviance of this application is equal to 1223.9, and if a complete set of J−1 logratios is used as predictors, which can be LRs, ALRs or other logratio transformations, the residual (or ‘unexplained’) deviance is 816.8. This means that 1223.9−816.8 = 407.1 units of deviance is the best that can be accounted for by the LRs. Using this maximum of 407.1 as 100%, each LR entering at each step is accounting for a part of that maximum, expressed as a percentage. In Figure 1, the grey bars show the increasing percentages at each step, which would eventually reach 100%. The black bars show the incremental amounts, in a type of scree plot.

Figure 1.

Scree-type plots showing incremental amounts (black bars) at each step and cumulative amounts (gray bars) at each step of the three respective algorithms. The values are percentages of the maximum achievable deviance that can be accounted for by using a complete set of J−1 = 47 LRs in the logistic regression.

4.3. Interpretational tools

A convenient way of summarizing the selected LRs of the three algorithms in each of the Tables 1–3 is in the form of a directed acyclic graph (DAG), where the parts are vertices and the LRs are defined by the edges [22,23], with each arrow pointing to the numerator part (Figure 2, showing the solutions for the Bonferroni penalty). The ALRs in Figure 2(c) define a connected DAG, which is why they are equivalent to the complete explanatory power of a subcomposition [23].

All models can be interpreted when converted into the corresponding log-contrast [9] as a function of the log abundances constrained to a zero sum of the ${\alpha }_j$ coefficients. Log-contrasts can easily be obtained, for instance, from the right panel in Tables 1–3. This is essential for the unrestricted approach for which the LRs have no easy interpretation on their own. Coefficients can be arranged in descending order for convenience.

In the unrestricted approach the log-contrast is:

$$\begin{array}{rl}& 0.2393\log (\mathrm{Dore})+0.1688\log (\mathrm{Osci})+0.1618\log (\mathrm{Dial})+1540\log (\mathrm{Stre})\\ & +0.1482\log (\mathrm{Lact})+0.1158\log (\mathrm{Adle})+0.1008\log (\mathrm{Aggr})+0.0873\log (\mathrm{Sutt})\\ & -0.0873\log (\mathrm{Bilo})-0.1008\log (\mathrm{Prev})-0.1158\log (\mathrm{Lach})-0.1618\log (\mathrm{Pept})\\ & -0.1688\log (\mathrm{Clos})-0.2393\log (\mathrm{Bact})-0.3022\log (\mathrm{Rose})\end{array}$$

Thus, the likelihood of Crohn's disease increases with increases in the genera Dore, Osci, Dial, Stre, Lact, Adle, Aggr and Sutt at the expense of decreases in Rose, Bact, Clos, Pept, Lach, Prev and Bilo.

In the non-overlapping LR approach, the numerator and denominator parts have ${\alpha }_j$ coefficients of equal value and reversed sign in the log-contrast:

$$\begin{array}{rl}& 0.2553\log (\mathrm{Rumi})+0.2444\log (\mathrm{Stre})+0.2272\log (\mathrm{Dore})+0.1702\log (\mathrm{Dial})\\ & +0.1139\log (\mathrm{Adle})+0.1088\log (\mathrm{Osci})+0.1087\log (\mathrm{Aggr})+0.0844\log (\mathrm{Sutt})\\ & -0.0844\log (\mathrm{Bilo})-0.1087\log (\mathrm{Prev})-0.1088\log (\mathrm{Faec})-0.1139\log (\mathrm{Lach})\\ & -0.1702\log (\mathrm{Pept})-0.2272\log (\mathrm{Bact})-0.2444\log (\mathrm{Rose})-0.2553\log (\mathrm{Clos})\end{array}$$

Thus, the likelihood of Crohn's disease increases with increases in the genera Rumi, Stre, Dore, Dial, Adle, Osci, Aggr and Sutt at the expense of decreases in Clos, Rose, Bact, Pept, Lach, Faec, Prev and Bilo.

In the ALR approach in Table 3, coefficients of the numerator parts can be taken directly from the estimates, and the coefficient of the denominator part is the sum of all coefficients with a reversed sign and can also be taken from Table 4:

$$-(0.1415+0.1407-0.2065\cdots -0.0920)=-0.3375$$

The log-contrast is:

$$\begin{array}{rl}& 0.2021\log (\mathrm{Dore})+0.1511\log (\mathrm{Adle})+0.1420\log (\mathrm{Lact})+0.1415\log (\mathrm{Stre})\\ & +0.1407\log (\mathrm{Dial})+0.1378\log (\mathrm{Aggr})-0.0920\log (\mathrm{Prev})-0.2065\log (\mathrm{Pept})\\ & -0.2792\log (\mathrm{Bact})-0.3375\log (\mathrm{Rose})\end{array}$$

Thus, the likelihood of Crohn's disease increases with increases in the genera Dore, Adle, Lact, Stre, Dial and Aggr, at the expense of decreases in Rose, Bact, Pept, and Prev.

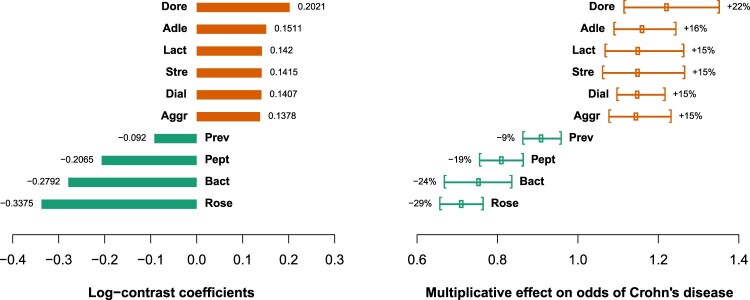
Figure 3 plots the above coefficients for the ALR approach with the Bonferroni penalty as well as the multiplicative effects after exponentiating the coefficients and expressed as percentage effects. The 95% bootstrap confidence intervals of these multiplicative effects are shown graphically, based on 1000 bootstrap samples, and the 2.5% and 97.5% percentiles of the bootstrapped estimates of the log-contrast coefficients. It can be seen that none cross the threshold of 1, which represents the hypothesis of no effect for each term of the log-contrast.

Figure 3.

Estimated log-contrast coefficients (left) and their conversion to multiplicative effects and 95 % bootstrap confidence intervals (right).

4.4. Introduction of expert knowledge

Because of space considerations, from this section on, we focus on the ALR subcomposition search approach. Under this approach, in the 9th step, the algorithm reports the Egge genus as the second best choice additional part in the subcomposition after Prev. Since Egge is present in the subcomposition by Ref. [49], while Prev is not, a researcher might want to force the logratio with Egge in the numerator instead of Prev as in Table 3 (Table 5). We see that the subcomposition under the BIC penalty (left panel) has changed and the Osci and Clos genera have dropped out and the Egge and Sutt genera have been substituted, at the expense of only a slight increase in the BIC value as compared to Table 3. In this way, more than one solution can be presented to the user to choose from.

Table 5.

Estimates of the final model with subcomposition search where the ALR Egge/Rose was forced into the equation at the 9th step.

	BIC penalty			Bonferroni penalty
Ratio	Estimate	s.e.	p-value	Estimate	s.e.	p-value
Stre/Rose	0.1362	0.0451	0.0025	0.1055	0.0438	0.0161
Dial/Rose	0.1283	0.0267	$<0.0001$	0.1270	0.0263	$<0.0001$
Pept/Rose	−0.2087	0.0326	$<0.0001$	−0.2045	0.0321	$<0.0001$
Lact/Rose	0.1363	0.0399	0.0006	0.1265	0.0390	0.0012
Bact/Rose	−0.3659	0.0554	$<0.0001$	−0.3165	0.0486	$<0.0001$
Dore/Rose	0.1847	0.0450	$<0.0001$	0.1685	0.0445	0.0002
Adle/Rose	0.1341	0.0367	0.0003	0.1329	0.0364	0.0003
Aggr/Rose	0.1249	0.0333	0.0002	0.1246	0.0322	0.0001
Egge/Rose	0.0823	0.0329	0.0125	0.0905	0.0320	0.0046
Prev/Rose	−0.0923	0.0268	0.0006
Sutt/Rose	0.0964	0.0329	0.0034
BIC	967.50			972.18

4.5. Results with separate training and test subsamples

The previous sections presented the results on the full sample for the sake of comparability with [49]. However, a much better way to proceed, which we recommend to all users of the approaches proposed in this article, is to hold a part of the sample out for testing and validation. In this section, a Bernouilli random variable was generated with probability 0.4 indicating units belonging to the test part, while the remaining units were assigned to the training part on which the stepwise procedure was run. Table 6 shows the unbiased coefficients of the model of the last step in the training sample estimated from the test sample (ALR subcomposition approach). It must be noted that BIC does no longer have to be better when applying the BIC penalty. In this particular case, the Bonferroni approach leads to a better BIC value on the test sample. BIC values in Tables 3 and 6 are not comparable because they are computed from different samples.

Table 6.

Estimates of the final model with the third approach (subcomposition search with ALR). Test sample.

	BIC penalty			Bonferroni penalty
Ratio	Estimate	s.e.	p-value	Estimate	s.e.	p-value
Lact/Rose	0.1533	0.0581	0.0083	0.1887	0.0572	0.0010
Dial/Rose	0.1930	0.0423	$<0.0001$	0.2098	0.0406	$<0.0001$
Pept/Rose	−0.1268	0.0511	0.0131	−0.1110	0.0480	0.0208
Adle/Rose	0.1200	0.0602	0.0464	0.1345	0.0528	0.0108
Bilo/Rose	−0.0751	0.0438	0.0862	−0.0758	0.0378	0.0451
Dore/Rose	0.2305	0.0799	0.0039
Faec/Rose	−0.0466	0.0666	0.4848
Osci/Rose	0.0406	0.0752	0.5894
Clos/Rose	−0.1978	0.1165	0.0895
Egge/Rose	0.0813	0.0549	0.1387
Coll/Rose	−0.0031	0.0455	0.9463
BIC	417.05			397.16
Accuracy (+ cases)	87.8%			88.5%
Accuracy (− cases)	58.1%			50.4%
Overall accuracy	78.6%			76.8%

Under the Bonferroni approach (right panel of Table 6), all parts except Bilo were also present in the full-sample analysis (Table 3) and all ALRs are statistically significant at 5%. The estimation on a separate test sample makes it possible to get not only unbiased p-values but also unbiased predictive accuracy figures. The model predicts 88.5% of cases with Crohn's disease correctly as such, and 50.4% of cases without Crohn's disease correctly as such. Overall predictive accuracy is 76.8%. An unbiased log-contrast can be obtained from the estimates on the test sample in the right panel of Table 6:

$$\begin{array}{rl}& 0.2098\log (\mathrm{Dial})+0.1887\log (\mathrm{Lact})+0.1345\log (\mathrm{Adle})\\ & -0.0758\log (\mathrm{Bilo})-0.1110\log (\mathrm{Pept})-0.3462\log (\mathrm{Rose})\end{array}$$

Thus, the likelihood of Crohn's disease increases with increases in the genera Dial, Lact, and Adle, at the expense of decreases in Rose, Pept and Bilo. The differences between this log-contrast and that presented in Section 4.3 stress the importance of cross-validation.

Under the BIC approach (left panel of Table 6), four different parts appear compared to the full-sample analysis (Bilo, Coll, Egge and Faec), and some ALRs are not statistically significant, although they had been significant in the training sample due to the downward bias of p-values in that part of the data. The model predicts 87.8% of cases with Crohn's disease correctly, and 58.1% of cases without Crohn's disease. Overall predictive accuracy is 78.6%. In this case the BIC penalty leads to a better predictive accuracy as compared to the Bonferroni penalty, at the expense of including some ALRs whose relevance is uncertain.

Table 6 thus presents an example in which the significance of LRs in the training sample is confirmed in the test sample (right panel) and an example of the opposite (left panel). The actual strength of cross-validation is the chance given to the researcher to identify parameter estimates which behave differently in the test sample compared to the training sample, particularly those that perform less well.

4.6. Exploring model stability using the bootstrap

The bootstrap performed in Figure 3 only takes into account the estimation uncertainty [28]. In order to take into account the uncertainty associated to model selection, the whole stepwise procedure can be submitted to the bootstrap procedure. The following simulation exercise was performed, reported here for Method 3 (that is, choosing a subcomposition via the selection of ALRs). The complete data set was bootstrapped 100 times and for each bootstrap sample, Method 3 with the Bonferroni penalty was applied and the chosen subcomposition recorded. In doing so, the researcher becomes aware that subcompositions vary in size and some of the genera in the right-hand panel in Table 3 are not consistently selected as parts in the subcomposition, while some absent parts in Table 3 are selected in a sizeable proportion of bootstrap samples.

The 20 most often selected genera in the 100 bootstrap samples are, in descending order: Rose (100%), Dial (96%), Pept (95%), Bact (76%), Dore (75%), Lact (69%), Aggr (59%), Adle (58%), Stre (54%), Bilo (37%), Acti (36%), Prev (35%), Osci (30%), Clos (30%), Egge (29%), Sutt (27%), Clot (18%), Lach (15%), Coll (13%), and Rumi (12%). The numbers of ALRs selected in the bootstrap samples vary from 5 to 15, with 90% of them between 6 and 12. This shows that there is indeed a potentially wide variability in the number of ALRs selected by this method, which translates to a corresponding variability in the size of the selected subcompositions. The right hand panel in Table 3 and the bootstrap results show that, with the exception of Prev (35%, see above), all the selected genera in Section 4.2 are in more than 50% of the bootstrap samples.

5. Conclusion and discussion

The main strength of this article is its conceptual and practical simplicity. Compared to many competing supervised statistical learning methods for compositional data, it yields an actual equation whose predictors the user can actually see, which makes it ultimately possible to introduce modifications based on expert knowledge. The method is very flexible in allowing several types of dependent variables (for the time being, continuous, Poisson and binary), several stopping criteria, and three approaches each geared towards a particular objective, namely prediction, interpretation and subcomposition analysis. The selected LRs are readily interpretable for the latter two modalities, while a log-contrast is interpretable for all. Last but not least, the method will likely appear familiar to many applied researchers without a sophisticated statistical background, who may gather courage to use and understand it.

The possibility to take advantage of the user's judgement in order to select meaningful albeit statistically suboptimal LRs has already been developed for unsupervised learning [22,23]. In supervised learning, this can also include forcing non-compositional controls into the model and can be a way out of the limitations of purely data-driven approaches [20,48,55]. The possibility has been shown in the application section by forcing in a part that had been found to be relevant in the previous study by [49]. This has led to two alternative subcompositions for the user to choose from, in Tables 3 and 5.

Daunis-i Estadella et al. [11] compare our approach with the selbal approach [49], principal balances derived from partial least squares [42] and penalized regression from LRs [6]. Our approach and especially the third variant of the algorithm, leads to identifying similar predictive parts as selbal and penalized regression from LRs, while balances derived from partial least squares tend to identify a much larger number of parts.

The results of stepwise regression are indeed sample-dependent and biased. The way out is to perform cross-validation and apply the model that is finalized at the last step to a hold-out data set, if one is available. As a second option, the sample can be split in two subsamples for training and testing purposes, respectively. Estimates, tests and predictions obtained with the cross-validation sample are unbiased. The user is encouraged to perform cross-validation whenever applying stepwise methods and has to be reminded that even after cross-validation, the approach is exploratory by nature and the final model cannot be assumed to be correct, but at most one out of many models fitting the data about as well and with about the same predictive accuracy. This drawback is common to all statistical learning methods. An extension of our approach is then possible to other supervised learning techniques such as classification and regression trees and random forests, where cross-validation is routinely applied. At each step, an LR can be selected to maximize the success of the prediction of the response variable, based on cross-validation. As we have done in the context of generalized linear models, the stepwise selection can again take place using any of the three selection methods. Introducing other cross-validation methods into our approach is the subject of ongoing research. Another future development is to include logratios that involve amalgamated (summed) parts as in [24,26].

The particular example used in this article has a medium-sized number of parts compared to many compositional datasets used in the past in different fields. However, the method needs to be trialled in more diverse scenarios, especially in the case of very high-dimensional “omics” and microbial datasets, where CoDA is being regularly used nowadays. The stepwise selection of logratios is not a particularly fast algorithm for large numbers of variables, although the third version with ALRs is more scalable than the rest. All three variants start with a search through $J(J-1)/2$ LRs, which is problematic if J is very large, in the hundreds or even the thousands. For the ALR approach in Method 3, it could be that the approach presented in [27] can be used as an alternative to isolate a suitable ALR transformation, by choosing the reference part to give an ALR transformation that is the most isometric, that is, as close to the exact logratio geometry as possible. This greatly facilitates the algorithm, since the stepwise searches are only of order J, whereas for Methods 1 and 2, they are of order $J^2/2$. This is the subject of ongoing research.

Appendix. List of genera abbreviations and full names

• Acti: Actinomyces

• Adle: Adlercreutzia

• Aggr: Aggregatibacter

• Bact: Bacteroides

• Bilo: Bilophila

• Clos: Clostridiales

• Clot: Clostridium

• Coll: Collinsella

• Dial: Dialister

• Dore: Dorea

• Egge: Eggerthella

• Euba: Eubacterium

• Faec: Faecalibacterium

• Lach: Lachnospira

• Lact: Lactobacillales

• Osci: Oscillospira

• Pept: Peptostreptococcaceae

• Prev: Prevotella

• Rose: Roseburia

• Rumi: Ruminococcaceae

• Stre: Streptococcus

• Sutt: Sutterella

• Turi: Turicibacter

Funding Statement

This work was supported by the Spanish Ministry of Science and Innovation/AEI/10.13039/501100011033 and by ERDF A way of making Europe [grant number PID2021-123833OB-I00]; the Spanish Ministry of Health (Ministerio de Sanidad, Consumo y Bienestar Social) [grant number CIBERCB06/02/1002]; and the Government of Catalonia (Generalitat de Catalunya) [grant number 2017SGR656].

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data and software availability

The Crohn data set is available in the R package selbal.

All methods will be available in the new release of the easyCODA package [22] in R [47], which is already pre-released on RForge and can be installed as follows:

$$\begin{array}{rl}& \mathtt{\text{install.packages}}\\ & \mathtt{\text{("easyCODA", repos="http://R-Forge.R-project.org")}}.\end{array}$$

The R code for reproducing these results is available on GitHub at https://github.com/michaelgreenacre/CODAinPractice