Abstract
In many applications, it is of interest to assess the relative contribution of features (or subsets of features) toward the goal of predicting a response — in other words, to gauge the variable importance of features. Most recent work on variable importance assessment has focused on describing the importance of features within the confines of a given prediction algorithm. However, such assessment does not necessarily characterize the prediction potential of features, and may provide a misleading reflection of the intrinsic value of these features. To address this limitation, we propose a general framework for nonparametric inference on interpretable algorithm-agnostic variable importance. We define variable importance as a population-level contrast between the oracle predictiveness of all available features versus all features except those under consideration. We propose a nonparametric efficient estimation procedure that allows the construction of valid confidence intervals, even when machine learning techniques are used. We also outline a valid strategy for testing the null importance hypothesis. Through simulations, we show that our proposal has good operating characteristics, and we illustrate its use with data from a study of an antibody against HIV-1 infection.
Keywords: variable importance, statistical inference, machine learning, targeted learning
1. Introduction
In many scientific problems, it is of interest to assess the contribution of features toward the objective of predicting a response, a notion that has been referred to as variable importance. Various approaches for quantifying variable importance have been proposed in the literature. In recent applications, variable importance has often been taken to reflect the extent to which a given algorithm makes use of particular features in rendering predictions (Breiman, 2001; Lundberg and Lee, 2017; Fisher et al., 2018; Murdoch et al., 2019). In this case, the goal is thus to characterize a fixed algorithm. While this notion of variable importance can help provide greater transparency to otherwise opaque black-box prediction tools (Guidotti et al., 2018; Murdoch et al., 2019), it does not quantify the algorithm-agnostic relevance of features for the sake of prediction. Thus, a feature that holds great value for prediction may be deemed unimportant simply because it plays a minimal role in the given algorithm. This motivates the consideration of approaches in which the focus is instead on measuring the population-level predictiveness potential of features, which we can refer to as intrinsic variable importance. By definition, any measure of intrinsic variable importance should not involve the external specification of a particular prediction algorithm.
Traditionally, intrinsic variable importance has been considered in the context of simple population models (e.g., linear models) (see, e.g., Grömping, 2006; Nathans et al., 2012). For such models, both the prediction algorithm and the associated variable importance measure (VIM) are easy to compute from model outputs and straightforward to interpret. Common VIMs based on simple models include, for example, the difference in R2 and deviance values based on (generalized) linear models (Nelder and Wedderburn, 1972; Grömping, 2006). However, overly simplistic models can lead to misleading estimates of intrinsic variable importance with little population relevance. In an effort to improve prediction performance, complex prediction algorithms, including machine learning tools, have been used as a substitute for algorithms resulting from simple population models. Many variable importance measures have been proposed for specific algorithms (see, e.g., reviews of the literature in Wei et al., 2015, Fisher et al., 2018, and Murdoch et al., 2019), with a particularly rich literature on variable importance for random forests (see, e.g., Breiman, 2001; Strobl et al., 2007; Ishwaran, 2007; Grömping, 2009) and neural networks (see, e.g., Garson, 1991; Bach et al., 2015; Shrikumar et al., 2017; Sundararajan et al., 2017). Several recent proposals aim to describe a broad class of fixed algorithms (LeDell et al., 2015; Ribeiro et al., 2016; Benkeser et al., 2018; Lundberg and Lee, 2017; Aas et al., 2019). However, while some measures have been recently described for algorithm-independent variable importance (see, e.g., van der Laan, 2006; Lei et al., 2017; Williamson et al., 2020), there has been limited work on developing broad frameworks for algorithm-independent variable importance with corresponding theory for inference using machine learning tools.
In this article, we seek to circumvent the limitations of model-based approaches to assessing intrinsic variable importance. We provide a unified nonparametric approach to formulate variable importance as a model-agnostic population parameter, that is, a summary of the true but unknown data-generating mechanism. The VIMs we consider are defined as a contrast between the predictiveness of the best possible prediction function based on all available features versus all features except those under consideration. We allow predictiveness to be defined arbitrarily as relevant and appropriate for the task at hand, as we illustrate in several examples. In this framework, once a measure of predictiveness has been selected, estimation of VIM values from data can be carried out similarly as for any other statistical parameter of interest. This task involves estimation of oracle prediction functions based on all the features or various subsets of features, and the use of machine learning algorithms is advantageous for maximizing prediction performance for this purpose. Because we consider variable importance as a summary of the data-generating mechanism rather than a property of any particular prediction algorithm, its definition and implementation does not hinge on the use of any particular prediction algorithm. This perspective contrasts with the model-based approach, where the probabilistic population-level mechanism that generates data and the algorithm that makes predictions based on data are usually entangled.
In Williamson et al. (2020), we focused on an application of the proposed framework to infer about a model-agnostic R2-based variable importance, for which we described a nonparametric efficient estimator. We also presented the construction of valid confidence intervals and hypothesis tests for features with some importance but found it challenging to assess features with zero-importance. Here, we propose a general framework to study general predictiveness measures and propose a valid strategy for hypothesis testing. Our framework allows us to tackle cases involving complex predictiveness measures (e.g., defined in terms of counterfactual outcomes or involving missing data). It can be used to describe the importance of groups of variables as easily as individual variables. Our framework formally incorporates the use of machine learning tools to construct efficient estimators and perform valid statistical inference. We emphasize that the latter is especially important if high-impact decisions will be made on the basis of the resulting VIM estimates.
This article is organized as follows. In Section 2, we define variable importance as a contrast in population-level oracle predictiveness and provide simple examples. In Section 3, we construct an asymptotically efficient VIM estimator for a large class of measures using flexibly estimated prediction algorithms (e.g., predictive models constructed via machine learning methods) and provide a valid test of the zero-importance null hypothesis. These results allow us to analyze nonparametric extensions of common measures, including the area under the receiver operating characteristic curve (AUC) and classification accuracy. In Section 4, we explore an extension to deal with more complex predictiveness measures. In Section 5, we illustrate the use of the proposed approach in numerical experiments and detail its operating characteristics. Finally, we study the importance of various HIV-1 viral protein sequence features in predicting resistance to neutralization by an antibody in Section 6, and provide concluding remarks in Section 7. All technical details as well as results from additional simulation studies and data analyses can be found in the Supplementary Material.
2. Variable importance
2.1. Data structure and notation
Suppose that observations Z1, …, Zn are drawn independently from a data-generating distribution P0 known only to belong to a rich (nonparametric) class of distributions. For concreteness, suppose that Zi = (Xi, Yi), where is a covariate vector and is the outcome. Here, and denote the sample spaces of X and Y, respectively. Below, we will use the shorthand notation E0 to refer to expectation under P0.
We denote by the index set of the covariate subgroup of interest, and for any p-dimensional vector w, we refer to the elements of w with index in ℓ and not in ℓ as wℓ and w−ℓ, respectively. We also denote by and the sample space of Xs and X−s, respectively. Finally, we consider a rich class of functions from to endowed with a norm , and define the subset for all u, satisfying u−s = v−s} of functions in whose evaluation ignores elements of the input x with index in s. In all examples we consider, we will take to be essentially unrestricted up to regularity conditions. Common choices include the class of all P0-square-integrable functions from to endowed with L2(P0)-norm , and of all bounded functions from to endowed with the supremum norm .
2.2. Oracle predictiveness and variable importance
We now detail how we define variable importance as a population parameter. Suppose that V(f, P) is a measure of the predictiveness of a given candidate prediction function when P is the true data-generating distribution, with large values of V(f, P) implying high predictiveness. Examples of predictiveness measures — including those based on R2, deviance, the area under the ROC curve, and classification accuracy — are discussed in detail in Section 2.3. If the true data-generating mechanism P0 were known, a natural candidate prediction function would be any P0-population maximizer f0 of predictiveness over the class :
| (1) |
This population maximizer can be viewed as the oracle prediction function within under P0 relative to V. In particular, the definition of f0 depends on the chosen predictiveness measure and on the data-generating mechanism. It can also depend on the choice of function class, although in contexts we consider this is not the case as long as is sufficiently rich. It is often true that f0 is the underlying target of machine learning-based prediction algorithms or a transformation thereof, which facilitates the integration of machine learning tools in the estimation of f0. The oracle predictiveness V(f0, P0) provides a measure of total prediction potential under P0. Similarly, defining the oracle prediction function f0,s that maximizes V(f, P0) over all , the residual oracle predictiveness V(f0,s, P0) quantifies the remaining prediction potential after exclusion of covariate features with index in s.
We define the population-level importance of the variable (or subgroup of variables) Xs relative to the full covariate vector X as the amount of oracle predictiveness lost by excluding Xs from X. In other words, we consider the VIM value defined as
| (2) |
By construction, we note that . Whether or not the loss in oracle predictiveness is sufficiently large to confer meaningful importance to a given subgroup of covariates depends on context. Once more, we emphasize that the definition of ψ0,s involves the oracle prediction function within , and if is large enough, this definition is agnostic to this choice.
2.3. Examples of predictiveness measures
We now illustrate our definition of variable importance by listing common VIMs that are in this framework. As we will see, the conditional mean plays a prominent role in the examples below. This is convenient since μ0 is the implicit target of estimation for many standard machine learning algorithms for predictive modeling.
Example 1: R2
The R2 predictiveness measure is defined as , where we set , the variance of Y under P0. This measure quantifies the proportion of variability in Y explained by f(X) under P0. Since μ0 is the unrestricted minimizer of the mean squared error mapping , the optimizer of V(f, P0) is given by f0 = μ0 as long as .
Example 2: deviance
When Y is binary, the deviance predictiveness measure is defined as
where is the marginal success probability of Y under P0. This measure quantifies in a Kullback-Leibler sense the information gain from using X to predict Y relative to the null model that does not use X at all. Again, because the conditional mean μ0 is the unconstrained population maximizer of the average log-likelihood, we find the optimizer of to be f0 = μ0 for any rich enough . This result similarly holds for a multinomial extension of deviance.
Example 3: classification accuracy
An alternative predictiveness measure in the context of binary outcomes is classification accuracy, defined as . This measure quantifies how often the prediction f(X) coincides with Y, and is commonly used in classification problems. As shown in the Supplementary Material, the Bayes classifier is the unconstrained maximizer of , and so, f0 = b0 as long as .
Example 4: area under the ROC curve
The area under the receiver operating characteristic curve (AUC) is another popular predictiveness measure for use when Y is binary. The AUC corresponding to f is given by , where (X1, Y1) and (X2, Y2) represent independent draws from P0. As shown in the Supplementary Material, the unrestricted maximizer of is the population mean μ0, so that once more f0 = μ0 provided .
In all examples above, the unrestricted oracle prediction function f0 equals or is a simple transformation of the conditional mean function μ0. The unrestricted oracle prediction function f0,s based on all covariates except those with index in s is obtained similarly but with μ0 replaced by .
3. Estimation and inference
3.1. Plug-in estimation
In our framework, the variable importance of Xs relative to X under P0, denoted ψ0,s, is a population parameter. Thus, assessing variable importance reduces to the task of inferring about ψ0,s from the available data. More formally, our goal is to construct a nonparametric (asymptotically) efficient estimator of ψ0,s using independent observations Z1, …, Zn from P0. Definition (2) suggests considering the plug-in estimator
| (3) |
where Pn is the empirical distribution based on Z1, …, Zn, and fn and fn,s are estimators of the population optimizers f0 and f0,s, respectively. Often, fn and fn,s are obtained by building a predictive model for outcome Y using all features in X or only those features in X−s, respectively — this might be done, for example, using tree-based methods, deep learning, or other machine learning algorithms, including tuning via cross-validation. Using flexible learning techniques to construct fn and fn,s minimizes the risk of systematic bias due to model misspecification.
As an illustration of the form of the resulting plug-in estimates, we note that, in the case of classification accuracy (Example 3), the VIM estimate is given by , where fn and fn,s are estimates of the oracle prediction functions f0 and f0,s, respectively. Sensible estimates of f0 and f0,s are given by
where μn and μn,s are estimates of conditional mean functions μ0 and μ0,s, respectively. We provide the explicit form of ψn,s for all examples in the Supplementary Material.
The simplicity of the plug-in construction makes it particularly appealing. However, the literature on semiparametric inference and targeted learning suggests that such naively constructed plug-in estimators may fail to even be consistent at rate n−1/2, let alone efficient, if they involve nuisance functions — in this case, f0 and f0,s — that are flexibly estimated. This phenomenon is due to the fact that excess bias is often inherited by the plug-in estimator from the nuisance estimators. Generally, this fact would motivate the use of debiasing procedures, such as the one-step correction or targeted maximum likelihood estimation (see, e.g., Pfanzagl, 1982; van der Laan and Rose, 2011). However, in Williamson et al. (2020) we noted the intriguing fact that the plug-in estimator of the R2 VIM did not require debiasing, being itself already efficient. Below, we show that the same holds true for a large class of VIMs. These plug-in estimators therefore benefit from a combination of simplicity and statistical optimality.
3.2. Large-sample properties
We now study conditions under which ψn,s is an asymptotically linear and nonparametric efficient estimator of the VIM value ψ0,s, and we describe how to conduct valid inference on ψ0,s. Below, we explicitly focus on inference for the oracle predictiveness value based on the plug-in estimator , since results can readily be extended to the residual oracle predictiveness value and thus to the VIM value ψ0,s. The behavior of vn can be studied by first decomposing
| (4) |
where . Each term on the right-hand side of (4) can be studied separately to determine the large-sample properties of vn. The first term is the contribution from having had to estimate the second argument value P0. The third term is a difference-of-differences remainder term that can be expected to tend to zero in probability at a rate faster than n−1/2 under some conditions. We must pay particular attention to the second term, which represents the contribution from having had to estimate the first argument value f0. A priori, we may expect this term to dominate since the rate at which fn – f0 tends to zero (in suitable norms) is generally slower than n−1/2 when flexible learning techniques are used. However, because f0 is a maximizer of over , we may reasonably expect that
for any smooth path through f0 at ϵ = 0, and thus that there is no first-order contribution of to the behavior of vn − v0. Under regularity conditions, this indeed turns out to be the case, and thus, if fn − f0 does not tend to zero too slowly, the second term will be asymptotically negligible.
Our first result will make use of several conditions requiring additional notation. Below, we define the linear space of finite signed measures generated by . For any , say R = c(P1 – P2), we refer to the supremum norm , where F1 and F2 are the distribution functions corresponding to P1 and P2, respectively. Furthermore, we denote by the Gâteaux derivative of at P0 in the direction , and define the random function , where δz is the degenerate distribution on {z}. For any , we also denote by fP any P-population maximizer of over . Finally, we define the following sets of conditions, classified as being either deterministic (A) or stochastic (B) in nature:
-
(A1)
(optimality) there exists some constant C > 0 such that, for each sequence such that , for each j large enough;
-
(A2)(differentiability) there exists some constant δ > 0 such that for each sequence and satisfying that and , it holds that
-
(A3)
(continuity of optimization) for each ;
-
(A4)
(continuity of derivative) is continuous at f0 relative to for each ;
-
(B1)
(minimum rate of convergence);
-
(B2)
(weak consistency);
-
(B3)
(limited complexity) there exists some P0-Donsker class such that .
Theorem 1. If conditions (A1)–(A2) and (B1)–(B3) hold, then vn is an asymptotically linear estimator of v0 with influence function equal to , that is,
under sampling from P0. If conditions (A3)–(A4) also hold, then ϕ0 coincides with the nonparametric efficient influence function (EIF) of at P0, and so, vn is nonparametric efficient.
This result implies, in particular, that the plug-in estimator vn of v0 is often consistent as well as asymptotically normal and efficient. A similar theorem applies to the study of the estimator of residual oracle predictiveness v0,s upon replacing instances of fn, f0 and by fn,s, f0,s and in the conditions above, and denoting the resulting influence function by ϕ0,s. Thus, under the collection of all such conditions, the estimator ψn,s of the VIM value ψ0,s is asymptotically linear with influence function and nonparametric efficient. If and , this suggests that the asymptotic variance of can be estimated by
and that is an interval for ψ0,s with asymptotic coverage 1−α, where z1−α/2 denotes the (1−α/2)th quantile of the standard normal distribution. This procedure is summarized in Algorithm 1. We discuss settings in which ψ0,s = 0 (and therefore ) in Section 3.4.
Algorithm 1.
Inference on VIM value ψ0,s (valid in non-null settings)
| 1: | construct estimators fn of f0 and fn,s of f0,s; |
| 2: | construct empirical distribution estimator Pn of P0; |
| 3: | compute estimator of ψ0,s; |
| 4: | compute estimator |
| of the asymptotic variance of . |
Condition (A1) ensures that there is no first-order contribution that results from estimation of f0. As indicated above, this condition can generally be established as a consequence of the optimality of f0. However, in each particular problem, appropriate regularity conditions on P0 and must be determined for this condition to hold. We have provided details for Examples 1–4 in the Supplementary Material, though we summarize our findings here. In Example 1, we have that as long as , and so, condition (A1) holds with and taken to be either the L2(P0) or supremum norm. In Example 2, provided that all elements of are bounded between γ and 1 − γ for some and that , then condition (A1) holds with and taken to be either the L2(P0) or supremum norm. In Example 3, condition (A1) holds for C = 4κ and the supremum norm provided the classification margin condition holds for some 0 < κ < ∞ and all t small. Similarly, in Example 4, condition (A1) holds for with and the supremum norm provided the margin condition holds for some 0 < κ < ∞ and all t small, where X1 and X2 are independent draws from P0.
Condition (A2) is a form of locally uniform Hadamard differentiability of at P0 in a neighborhood of f0. It can be readily verified in Examples 1–4; in fact, in Examples 1–3, this condition holds for any δ > 0. Condition (A3) requires that the optimizer fP vary smoothly in P around P0, and is often straightforward to verify when fP has a closed analytic form. Condition (A4) instead requires that the Hadamard derivative of at P0 vary smoothly in f around f0. Condition (B1) requires that f0 be estimated at a sufficiently fast rate in order for second-order terms to be asymptotically negligible, while condition (B2) states that a particular parameter-specific functional of fn must tend to the corresponding evaluation of f0, and is thus implied by consistency of fn with respect to some norm under which this functional is continuous. Condition (B3) restricts the complexity of the algorithm used to generate fn. We note that conditions (B1)–(B3) depend not only on the predictiveness measure chosen and on the true data-generating mechanism but also on properties of the estimator of the oracle prediction function.
3.3. Implementation based on cross-fitting
Condition (B3) puts constraints on the complexity of the algorithm used to generate fn. This condition is prone to violations when flexible machine learning tools are employed, as discussed in Zheng and van der Laan (2011) and Chernozhukov et al. (2018), for example. However, it can be eliminated by dividing the entire dataset into two parts (say, training and testing sets), estimating f0 using the training data, and then evaluating the predictiveness measure on the test data. This readily extends to K-fold cross-fitting. To construct a cross-fitted estimator in the current context, we begin by randomly partitioning the dataset into K subsets of roughly equal size. Setting aside one such subset, we construct an estimator fk,n of f0 based on the bulk of the data, and then store , where Pk,n is the empirical distribution estimator based on the data set aside. We note that fk,n and Pk,n are therefore estimated using non-overlapping subsets of the data. After repeating this operation for each of the K subsets, we finally construct the cross-fitted estimator of v0.
To describe the large-sample behavior of , we require an adaptation of the previously defined conditions (B1) and (B2) to the context of cross-fitted estimators. Below, the random function gk,n is defined identically as gn but with fn replaced by fk,n.
(B1’) (minimum rate of convergence) for each k ∈ {1, …, K};
(B2’) (weak consistency) for each k ∈ {1, …, K}.
The resulting cross-fit estimator enjoys desirable large-sample properties under weaker conditions than those imposed on vn, as the theorem below states. In particular, condition (B3), which in practice limits the complexity of machine learning tools used to estimate f0, is no longer required.
Theorem 2. If conditions (A1)–(A2) and (B1’)–(B2’) hold, then is an asymptotically linear estimator of v0 with influence function equal to , that is,
under sampling from P0. If conditions (A3)–(A4) also hold, then is nonparametric efficient.
The cross-fitted construction can be used to obtain an improved estimator of v0,s as well, thereby resulting in a cross-fitted estimator of the VIM value ψ0,s. Cross-fitting can also be used to obtain an improved estimator of the asymptotic variance . We summarize this construction in Algorithm 2, and provide the explicit form of for Examples 1–4 in the Supplementary Material. As before, Theorem 2 readily provides conditions under which is an asymptotically linear and nonparametric efficient estimator of v0,s, and so, under which is an asymptotically linear and nonparametric efficient estimator of the VIM value ψ0,s. Based on these theoretical results as well as numerical experiments, we recommend this implementation whenever machine learning tools are used to estimate f0 and f0,s.
Algorithm 2.
Cross-fitted inference on VIM value ψ0,s (valid in non-null settings)
| 1: | generate by sampling uniformly from {1, …, K} with replacement, and for j = 1, …, K, denote by Dj the subset of observations with index in ; |
| 2: | for k = 1, …, K do |
| 3: | using only data in ∪j≠kDj, construct estimators fk,n of f0 and fk,n,s of f0,s; |
| 4: | using only data in Dk construct empirical distribution estimator Pk,n of P0; |
| 5: | with , compute and |
| 6: | end for |
| 7: | compute estimator of ψ0,s; |
| 8: | compute estimator of the asymptotic variance of . |
3.4. Inference under the zero-importance null hypothesis
When ψ0,s = 0, in which case the variable group considered has null importance, the influence function of ψn,s is identically zero. In these cases, even after standardization, ψn,s generally does not tend to a non-degenerate law. As such, deriving an implementable test of the null hypothesis ψ0,s = 0 or a confidence interval valid even when ψ0,s = 0 is difficult. In such cases, standard Wald-type confidence intervals and tests based on will typically have incorrect coverage or type I error, as illustrated in numerical simulations reported in Williamson et al. (2020) While in parametric settings n-rate inference is possible under this type of degeneracy, this is not expected to be the case in nonparametric models, because the second-order contribution from estimation of f0 and f0,s will generally have a rate slower than n−1.
We note that, although ψn,s has degenerate behavior under the null, each of vn and vn,s are asymptotically linear with non-degenerate (but possibly identical) influence functions. Except for extreme cases in which the entire set of covariates has null predictiveness, we may leverage this fact to circumvent null degeneracy via sample-splitting. Indeed, if vn and vn,s are constructed using different subsets of the data, then the resulting estimator ψn,s is asymptotically linear with a non-degenerate influence function even if ψ0,s = 0 so that a valid Wald test of the strict null H0 : ψ0,s = 0 versus H1 : ψ0,s > 0 can be constructed using ψn,s and an estimator of the standard error of ψn,s. Of course, the same holds for the corresponding cross-fitted procedures, as we consider below. We emphasize here that sample-splitting and cross-fitting are distinct operations with distinct goals. Sample-splitting is used to ensure valid inference under the zero-importance null hypothesis, whereas cross-fitting is used to eliminate the need for Donsker class conditions, which otherwise limit how flexible the learning strategies for estimating the oracle prediction functions can be. Sample-splitting and cross-fitting can be used simultaneously — Figure 1 provides an illustration of the subdivision of a dataset when equal subsets are used for sample-splitting and six splits are used for cross-fitting.
Figure 1:
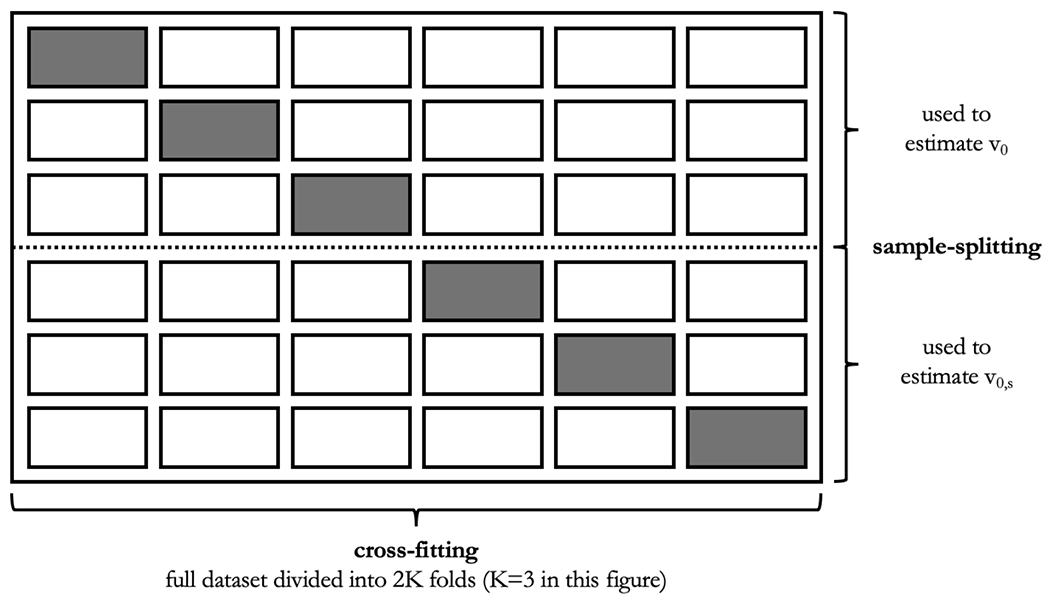
Illustration of dataset subdivision when sample-splitting and cross-fitting are used simultaneously for valid inference under the zero-importance hypothesis (sample-splitting) without requiring Donsker class conditions (cross-fitting). Each row represents the entire dataset with a different subset singled out (in grey) as testing set. To estimate v0, the top three rows are used. In each such row, f0 is estimated using data in the white cells, and v0 is estimated using the resulting estimate of f0 and data in the grey cells. Row-specific estimates of v0 are then averaged. The process is repeated for estimating v0,s but instead using the bottom three rows and estimating f0,s rather than f0.
In practice, a group of variables may be considered scientifically unimportant even when ψ0,s is nonzero but small, yet such grouping would be deemed statistically significant in large enough samples. For this reason, given a threshold β > 0, it may be more scientifically appropriate to consider testing the β-null H0 : ψ0,s ∈ [0, β] versus its complement alternative H1 : ψ0,s > β. The β-null approaches the strict null as β decreases to 0. The idea of sample-splitting also allows us to tackle β-null testing. Suppose that mutually exclusive portions of the dataset, say of respective sizes n—ns and ns, are used to construct and . Suppose further that and are consistent estimators of and , respectively. Then, provided v0 > 0, we may consider rejecting the β-null hypothesis H0 in favor of its complement H1 if and only if
| (5) |
where and z1−α is the (1 − α)th quantile of the standard normal distribution. The implementation of the resulting test, including computation of the corresponding p-value, is summarized in Algorithm 3. Its validity is guaranteed under conditions of Theorem 2 directly applied on the split used to estimate v0 and modified appropriately (by replacing instances of fn, f0 and by fn,s, f0,s and in all conditions) to the split used to estimate v0,s. We note that, although there is no degeneracy under the β-null whenever ψ0,s ∈ (0, β), sample-splitting is still required for proper type I error control since the strict null ψ0,s = 0 is contained in the β-null and must therefore be guarded against. We emphasize here that the use of distinct subsets of the data is critical for constructing and . If instead ψ0,s = 0 and and were constructed using the same data, the behavior of any testing procedure based on an estimator κn,s of the standard error of ψn,s would depend on the relative rates of convergence to zero of both ψn,s and κn,s. In particular, this would lead to either uncontrolled type I error or type I error tending to zero depending on the procedures used to obtain fn and fn,s. Inference based on a cross-fitted version of this sample-split procedure is described in Algorithm 3.
The above testing procedure can be readily inverted to yield a one-sided confidence interval for ψ0,s. Specifically, under regularity conditions and provided v0 > 0 the random interval contains ψ0,s with probability no less than 1 − α asymptotically, even when ψ0,s = 0. Then, rejecting the null hypothesis H0 is equivalent to verifying that zero is contained in this one-sided interval. A two-sided confidence interval is instead given by . While the latter interval has the advantage of giving both a lower and upper bound on possible values for ψ0,s supported by the data, using it for testing purposes necessarily results in a reduction in power since the null value of ψ0,s is at the edge of the parameter space.
4. Extensions to more complex settings
In all examples studied thus far, the primary role P plays in V(f, P) is to indicate the population with respect to which a particular measure of prediction performance should be averaged. In these
Algorithm 3.
Sample-split, cross-fitted inference on VIM value ψ0,s
| 1: | generate by sampling uniformly from {1, …, 2K} with replacement, and for j = 1, …, 2K, denote by Dj the set of observations with index in and ; |
| 2: | for k = 1, …, 2K do |
| 3: | using only data in , construct estimators fk,n of f0 and fk,n,s of f0,s; |
| 4: | using only data in Dk, construct estimator Pn,k of P0; |
| 5: | if k is odd, compute and ; |
| 6: | if k is even, compute and ; |
| 7: | end for |
| 8: | compute , and estimator of ψ0,s; |
| 9: | compute , and estimator of the variance of ; |
| 10: | to test vs at level 1−α, reject H0 in favor of H1 iff with and Φ the standard normal distribution function. |
cases, is well-defined on discrete probability measures and sufficiently smooth so that is in first order a linear estimator in view of the functional delta method. However, there are other examples in which this requirement may not be true. In these examples, V(f, P) involves P in a complex manner beyond some form of averaging, rendering V(f, P) undefined for discrete P, let alone Hadamard differentiable. Complex predictiveness measures often arise when the sampling mechanism precludes from observation the ideal data unit on which a (possibly simpler) predictiveness measure is defined, and identification formulas must therefore be established to express predictiveness in terms of the observed data-generating distribution.
As a concrete illustration, we begin with an example from the causal inference literature. As before, we denote by Y and X the outcome of interest and a covariate vector, respectively. We suppose that larger values of Y correspond to better clinical outcomes, and consider a binary intervention A ∈ {0, 1}. A given treatment rule for assigning the value of A based on X can be adjudicated, for example, on the basis of the population mean outcome that would arise if everyone in the population were treated according to f. We can consider the ideal data structure to be , where for each a ∈ {0, 1}, Y(a) denotes the counterfactual outcome corresponding to the intervention that deterministically sets A = a. The ideal-data predictiveness of f is then . In contrast, the observed data structure is Z ≔ (X, A, Y) ~ P0, and we must find some observed-data predictiveness measure V such that to establish identification and proceed with estimation and inference. Defining the outcome regression , it is not difficult to verify that
provides a valid identification of under standard causal identification conditions. We note that this predictiveness measure involves P through more than simple averaging, as the outcome regression QP also appears in the definition of V(f, P). Unless the distribution of X is discrete under P, QP is ill-defined on the empirical distribution Pn, thus violating conditions (A1) and (A4) defined in Section 3. We also remark that, in this example, the moniker ‘prediction function’ is not entirely fitting for f, which represents a treatment rule and maps into the treatment (rather than outcome) space. Nevertheless, the proposed framework for variable importance remains applicable, underscoring the fact that it is sufficiently flexible to unify a large swath of variable importance problems. Restrictions imposed on the data structure and on the properties of the prediction function in Section 2 were largely for the sake of concreteness.
The simple plug-in approach described in Section 3 may fail in applications with more complex predictiveness measures. In such cases, we can instead employ a more general strategy based on nonparametric debiasing techniques to make valid inference about V(f0, P0). For each , we denote by fP any optimizer of over , and define the parameter mapping so that v0 can be expressed as . If is an estimator of P0, the plug-in estimator generally fails to be asymptotically linear unless was purposefully constructed to ensure that it is indeed so. This happens because the plug-in estimator generally suffers from excessive bias whenever flexible learning techniques have been used, for example, because V*(P0) involves local features of P0 (e.g., the conditional mean or density function) — see Pfanzagl (1982) and van der Laan and Rose (2011). This fact renders the use of debiasing approaches necessary. In contrast, the one-step estimator
where ϕn is the nonparametric EIF of V* at , is nonparametric efficient (Pfanzagl, 1982) under regularity conditions. Alternatively, the framework of targeted minimum loss-based estimation describes how to convert into a revised estimator such that is itself nonparametric efficient without the need for further debiasing (van der Laan and Rose, 2011). Similarly as in Section 3, cross-fit versions of these debiasing procedures (see, e.g., Zheng and van der Laan, 2011; Chernozhukov et al, 2018) can be used to improve performance when flexible estimation algorithms are used.
The generic approach above relies on deriving the nonparametric EIF of V*. The definition of V* involves P in various ways, including through the P-optimal prediction function fP. While in our examples fP has a simple closed-form expression, this may not always be so. This fact can greatly complicate the derivation of the required EIF. However, as we shall see, the optimality of fP often implies that fP does not contribute to the nonparametric EIF of .
Before stating a formal result to this effect, we introduce a regularity condition. Below, refers to the subset of all functions in L2(P0) that have mean zero under P0.
-
(A5)There exists a dense subset of such that, for each and regular univariate parametric submodel through P0 at ϵ = 0 and with score for ϵ equal to h at ϵ = 0 (see, e.g., Bickel et al, 1998), the following conditions hold, with f0,ϵ denoting fP0,ϵ:
-
(A5a)(second-order property of predictiveness perturbations) holds;
-
(A5b)(differentiability) the mapping is differentiable in a neighborhood of ϵ = 0;
-
(A5c)(richness of function class) the optimizer f0,ϵ is in for small enough ϵ.
-
(A5a)
Condition (A5a) essentially requires the pathwise derivative of at P0 to be insensitive to infinitesimal perturbations of f around f0. In such case, the difference-in-differences term appearing in the condition can indeed be expected to be second-order in ϵ. Condition (A5b) will generally hold provided the functionals and are sufficiently smooth around f0 and P0, respectively. Finally, condition (A5c) requires that be sufficiently rich around f0 so that, for a dense collection of paths through P0, contains f0,ϵ for small enough ϵ.
Theorem 3. Provided condition (A5) holds, if is pathwise differentiable at P0 relative to the nonparametric model , then so is , and the two parameters have the same EIF.
This theorem indicates that, under a regularity condition, the computation of the nonparametric EIF ϕ0 can be done treating fP as fixed at f0, thereby simplifying considerably this calculation. This fact is also useful because for a fixed prediction function f the parameter will often have already been studied in the literature, thereby circumventing the need for any novel derivation. Armed with this observation, we revisit the motivating example we presented in this section, and also consider an additional example involving missing data.
Example 5: mean outcome under a binary intervention rule
As described above, in this example, the ideal-data parameter of interest, , can be identified by the observed-data parameter when the observed data unit consists of . The map is maximized over the unrestricted class by the intervention rule , and over its subset by , where we define Q0,s pointwise as . Furthermore, the parameter is pathwise differentiable at a distribution P0 if, for example, occurs P0-almost surely. The nonparametric EIF of at P0 is given by
where we define the propensity score for each a ∈ {0, 1}. Thus, under regularity conditions, the one-step debiased estimator
of v0 is nonparametric efficient, where Qn and gn are estimators of Q0 and g0, respectively, and fn is defined pointwise as . The one-step debiased estimator of v0,s is defined similarly, with fn replaced by any appropriate estimator of f0,s, such as with Qn,s(a, x) obtained by flexibly regressing outcome Qn(a, x) onto X−s for each a ∈ {0, 1}.
Example 6: Classification accuracy under outcome missingness
Suppose the ideal-data structure consists of and the predictiveness measure of interest based on this ideal data structure is the classification accuracy measure, , described in Example 3. Suppose that the outcome Y is subject to missingness, so that the observed data structure is Z ≔ (X, Δ, U), where Δ is the indicator of having observed the outcome Y, and we have defined U ≔ ΔY. The observed-data predictiveness measure
equals the ideal-data accuracy measure provided that (a) Δ and Y are independent given X, and (b) for P-almost every value x. In other words, the provided identification holds provided the outcome is missing at random (relative to X), and there is no subpopulation of patients (as defined by the value of X) for which the outcome can never be observed. Defining , the unrestricted optimizers f0 and f0,s are given pointwise by and . Finally, the nonparametric EIF of at P0 is given by
where we now have defined the nuisance parameters and , so that Q0(x) is no more than a simple transformation of π0(x). Under regularity conditions, the one-step debiased estimator
of v0 is nonparametric efficient, where gn and πn are consistent estimators of g0 and π0, and we define fn and Qn pointwise as and . The one-step debiased estimator of v0,s is defined identically except that all instances of fn are replaced by fn,s, which we define pointwise as , with πn,s representing an appropriate estimator of , obtained, for example, by flexibly regressing outcome πn(X) onto X−s.
5. Numerical experiments
5.1. Simulation setup
We now present empirical results describing the performance of our proposed plug-in VIM estimator. In all cases, our simulated dataset included independent replicates of (X, Y), where X is a covariate vector with independent components X1, …, Xp each following a standard normal distribution and a binary outcome Y following a Bernoulli distribution with success probability Φ(β01x1 + … + β0pxp) conditional on X = x, where Φ is the standard normal distribution function. In Scenario 1, we set p = 2 and β0 = (2.5, 3.5), whereas in Scenario 2, we took p = 4 and β0 = (2.5, 3.5, 0, 0); thus, in all cases, the first two features had nonzero importance and the remaining features (if any) had zero importance. In this specification, Y follows a probit model. For each scenario considered, we generated 1000 random datasets of size n ∈ {100, 500, 1000, …, 4000}, and considered the importance of both X1 and X2 in Scenario 1 and the importance of X2 and X3 in Scenario 2. In each scenario, we considered VIMs based on classification accuracy (Example 3) and the area under the ROC curve (Example 4). The true values of these VIMs implied by the data-generating mechanisms considered under Scenarios 1 and 2 are provided in Table 1. All analyses were performed using our R package vimp and may be reproduced using code available online (see details in the Supplementary Material). Since results were similar for accuracy and AUC, we only display results for accuracy here but provide results for AUC in the Supplementary Material.
Table 1:
Approximate values of ψ0,s in the numerical experiments.
| Feature of interest | ||||
|---|---|---|---|---|
| Importance measure | X 1 | X 2 | X 3 | X 4 |
| Accuracy | 0.136 | 0.236 | 0 | 0 |
| Area under the ROC curve | 0.105 | 0.221 | 0 | 0 |
In Scenario 1, we investigate the finite-sample properties of our proposal in a setting in which all features are truly important. We also use this setting to explore the effect of cross-fitting when using flexible estimators of f0 and f0,s. Specifically, we compare the performance of our estimation procedure with and without five-fold cross-fitting when using the following estimators of f0 and f0,s: a correctly specified (parametric) probit regression model; a generalized additive model (GAM; Hastie and Tibshirani, 1990, implemented in the R package mgcv); random forests (RF; Breiman, 2001, implemented in the R package ranger); and the Super Learner (SL; van der Laan et al, 2007, implemented in the R package SuperLearner). The latter estimator is a particular implementation of stacking (Wolpert, 1992) with favorable finite-sample and asymptotic performance guarantees (van der Laan et al., 2007). For the Super Learner, we used a library consisting of gradient boosted trees (Friedman, 2001, implemented in the R package xgboost), GAMs (implemented in the R package gam), and random forests, each with the default tuning parameter choices, in addition to parametric probit regression, with five-fold cross-validation to determine the optimal convex combination of these learners that minimizes the cross-validated negative log-likelihood risk. The resulting optimal convex combination of these individual algorithms is the Super Learner-based conditional mean estimator we adopt in any case where the Super Learner was fit. The tuning parameters considered for each algorithm are provided in the Supplementary Material. We do not use sample-splitting, since the results of Section 3 are valid under the alternative. We use Algorithm 2 to compute the cross-fitted point and standard error estimators for the importance of X1 and X2, from which we computed nominal 95% Wald-type confidence intervals. We then computed the empirical bias scaled by n1/2, the empirical variance scaled by n, the empirical coverage of confidence intervals, and the width of these intervals.
In Scenario 2, we study the properties of our proposal under the null hypothesis. In this case, we used sample-splitting since the importance of X3 and X4 is zero. We again ran both cross-fitted and non-cross-fitted implementations, and considered the same learning strategies as in Scenario 1, with one exception: in this case, we added the lasso (Tibshirani, 1996, implemented in the R package glmnet) to the library of candidate learners in the Super Learner. As before, we computed point estimates and nominal 95% Wald-type confidence intervals but also obtained p-values for the null hypothesis using the sample-splitting procedure of Algorithm 3. We then computed the empirical bias scaled by n1/2, the empirical variance scaled by n, the empirical coverage of confidence intervals, and the rejection probability for the proposed hypothesis test.
5.2. Primary empirical results
In Figure 2, we display the results of the experiment conducted under Scenario 1, in which both features have nonzero importance. For ease of visualization, we only display the results for X2; the results for X1 are similar and available in the Supplementary Material. In the top-left panel, we observe that the bias of the proposed estimators decreases to zero at rate faster than n1/2 for all non-cross-fitted estimators except those based on random forests and Super Learner, whereas it does so for all cross-fitted estimators. This reflects the need for cross-fitting in cases where the Donsker class conditions of Theorem 1 may fail to hold. The top-right panel shows that the variance of all estimators is approximately proportional to n. In the bottom-left panel, we observe that coverage of nominal 95% confidence intervals increases to the nominal level with increasing sample size for all cases except the non-cross-fitted estimators based on random forests and Super Learner. In the bottom-right panel, we see that the width of these intervals decreases with increasing sample size, as expected.
Figure 2:
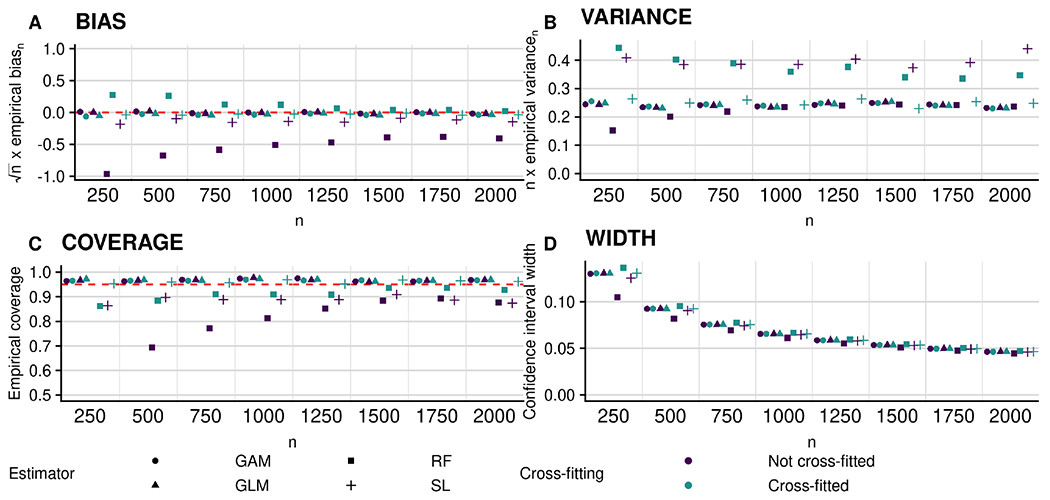
Performance of plug-in estimators for estimating (non-zero) importance of X2 in terms of accuracy under Scenario 1 (all features have non-zero importance). Clockwise from top left: empirical bias of the proposed plug-in estimator scaled by n1/2; empirical variance scaled by n; empirical coverage of nominal 95% confidence intervals; and average width of these intervals. Circles, triangles, squares and plus symbols denote estimators based on the use of generalized additive models (GAMs), probit regression (GLM), random forests (RF), and the Super Learner (SL), respectively. Blue and green symbols denote non-cross-fitted and cross-fitted estimators, respectively.
In Figure 3, we display the results pertaining to null feature X3 in the experiments conducted under Scenario 2. Here, it appears that the bias vanishes at a rate faster than n−1/2 for both the cross-fitted and non-cross-fitted estimators (top-left panel), but that the variance of the non-cross-fitted estimators tends to increase with increasing sample size, especially for the more flexible learning algorithms (top-right panel). We observe that empirical coverage is near the nominal level at all sample sizes (bottom-left panel). Finally, we see that the type I error of the proposed hypothesis test is controlled at the nominal level for all cross-fitted procedures, but not so for their non-cross-fitted counterparts, yielding an inflated type I error in that case (bottom-right panel). In the Supplementary Material, we present results for the non-null feature X2, which show that power of the proposed test is large for all sample sizes considered here.
Figure 3:
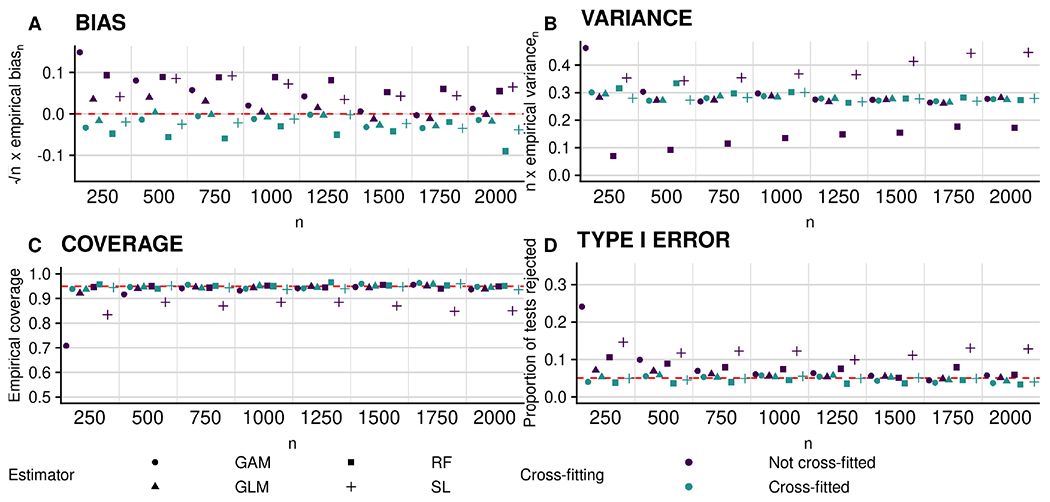
Performance of plug-in estimators for estimating (zero) importance of X3 in terms of accuracy under Scenario 2. Clockwise from top left: empirical bias of the proposed plug-in estimator scaled by n1/2; empirical variance scaled by n; empirical coverage of nominal 95% confidence intervals; and empirical type I error of the proposed hypothesis test. Circles, triangles, squares and plus symbols denote estimators based on the use of generalized additive models (GAMs), probit regression (GLM), random forests (RF), and the Super Learner (SL), respectively. Blue and green symbols denote non-cross-fitted and cross-fitted estimators, respectively.
This simulation study suggests that the estimation and inferential procedures proposed, including our null testing approach, have good practical performance and are properly calibrated, as suggested by theory. Our findings suggest that cross-fitting is critical when flexible algorithms are used, in which case the estimation procedure without cross-fitting performs poorly while its cross-fitted counterpart instead shows good performance. This is the case both for point and interval estimation, as we explicitly show in the Supplementary Material. When correctly-specified parametric regression models are implemented, both procedures (with and without cross-fitting) perform similarly well. This reflects the fact that when parametric estimators are used, condition (B3) is typically satisfied and cross-fitting is then not needed.
5.3. Additional empirical results
In the Supplementary Material, we present results for additional features under Scenarios 1 and 2, observing similar patterns to those presented in Figures 2 and 3. We also consider pairing a non-cross-fitted standard error estimator with the cross-fitted estimation procedure, observing reduced coverage compared to the cross-fitted standard error estimator of Algorithm 2. Finally, we present results from additional investigations scrutinizing the performance of our proposal in higher dimensions, both with and without correlated features. We found, in small samples, that the presence of many independent null features results in an increased bias in the estimation of the importance of non-null features, with a corresponding decrease in empirical interval coverage. However, this inflated bias and undercoverage dissipate as the sample size increases. A similar pattern was seen in the presence of correlated null features. This suggests that greater dimensionality indeed increases the difficulty of the statistical problem at hand, but that correlation between features does not exacerbate this challenge beyond rendering more difficult the interpretation of the population VIM values.
6. Studying an antibody against HIV-1 infection
Broadly neutralizing antibodies (bnAbs) against HIV-1 neutralize a large fraction of genetic variants of HIV-1. Two harmonized, placebo-controlled randomized trials were conducted to evaluate VRC01, a promising bnAb, for its ability to prevent HIV-1 infection (Corey et al, 2021). A secondary objective was to assess how VRC01 prevention efficacy depends on amino acid (AA) sequence features of HIV-1. Because there are thousands of AA features, the statistical analysis plan for addressing this objective requires first restricting attention to a subset of AA features that putatively affect prevention efficacy. Given the underlying assumption that VRC01 prevents infection via in vivo neutralization, a useful approach may be to rank AA features based on their estimated VIM for predicting in vitro neutralization — whether or not an HIV-1 virus is sensitive to neutralization by VRC01 — and select only the top-ranked features for further analyses.
In an effort to determine these important AA features, we analyzed the HIV-1 envelope (Env) AA sequence features of 611 publicly-available HIV-1 Env pseudoviruses made from blood samples of HIV-1 infected individuals (Magaret et al, 2019). All analyses accounted for the geographic region of the infected individuals. Among AA sequence features, approximately 800 individual features and 13 groups of features were of interest, e.g., polymorphic AA positions in Env AA that comprise the VRC01 antibody footprint to which VRC01 binds. These groups of features are described more fully in the Methods section of Magaret et al. (2019). There, we focused on a definition of variable importance as the difference in nonparametric R2, and used as outcome an indicator of whether or not the 50% inhibitory concentration (IC50, defined as the concentration of VRC01 necessary to neutralize 50% of viruses in vitro, with large values of the IC50 indicating that the virus was resistant to neutralization; Montefiori, 2009) was right-censored. However, the AMP trials have identified the 80% inhibitory concentration (IC80) as a possible biomarker of prevention efficacy, with 75.4% estimated efficacy against the most sensitive viruses (IC80 < 1). Since many observations in our dataset are missing IC80 values, we use as outcome the binary indicator that IC50 < 1. Here, analyzing the same data set, we compare results based on the outcome of Magaret et al. (2019) with a variable importance analysis based on classification accuracy and AUC and the AMP-based outcome IC50 < 1. We consider a marginal VIM value, evaluating the intrinsic importance of each feature group of interest relative to geographic confounding variables – this can be achieved by considering the full feature vector in (2) to be simply the geographic confounders plus the feature group of interest. We provide a replication of Magaret et al. (2019) using a harmonized outcome in the Supplementary Material.
We used the Super Learner with a large library of candidate learners to estimate the involved regression functions. These learners included the lasso, random forests, and boosted decision trees, each with varying tuning parameters. Details on our library of learners are described in the Supplementary Material. Our resulting estimator is the convex combination of the candidate estimators, where we used five-fold cross-validation to determine the convex combination that minimized the negative log-likelihood risk. Finally, to make inference on the VIM values considered, we used the sample-split cross-fitted method (Algorithm 3) studied in the simulations under Scenario 2.
In Figure 4, we display the results of this analysis and the feature groups of interest. The top-ranked feature groups do not differ much between different VIMs but the magnitude of both importance and p-values depends greatly on the measure chosen. Both VIMs result suggest that the CD4 binding sites, the VRC01 binding footprint, sites with sufficient exposed surface area (ESA sites), sites with residues that co-vary with the VRC01 binding footprint (co-varying sites), and sites for indicating N-linked glycosylation (glycosylation sites) are the five most important groups. The finding that CD4 binding sites are in the most important groups across VIMs matches our expectations from basic science experiments that have identified AA substitutions at CD4 binding sites that altered VRC01 neutralization sensitivity. This result is in line with Magaret et al. (2019). Based on our proposed hypothesis test, we computed p-values for a test of the strict null hypothesis (that is, β = 0) for each group. We found that AA features in the CD4 binding sites (group 2), VRC01 binding footprint (group 1), ESA sites (group 3), co-varying sites (group 5), and glycosylation sites (group 8) had p-values of 6.98 × 10−9, 8.14 × 10−9, 1.69 × 10−7, 4.66 × 10−6, and 8.07 × 10−6, respectively, based on AUC (denoted by stars in Figure 4). Based on these analyses, AA features in these groups may be prioritized for the forthcoming trial data analyses. Additionally, taking the set of top-ranked features above a minimum threshold may help to narrow the set of gp160 AA sequence features to pre-specify for the analysis of the AMP trial data sets. Our recommendation, nonetheless, is to analyze all feature sets in secondary or supporting analysis of the AMP trial data sets to ensure that the results generated are comprehensive.
Figure 4:
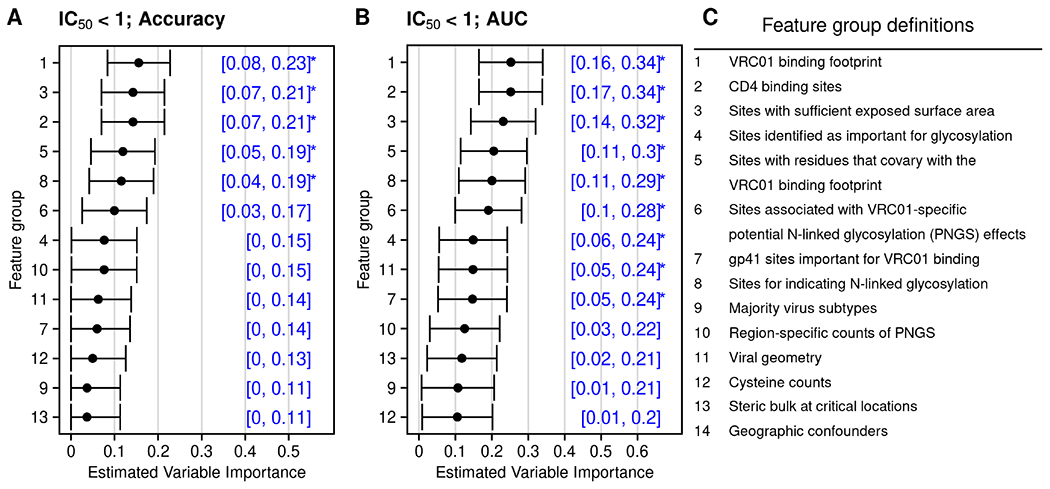
Variable importance measured by accuracy (panel A) and AUC (panel B) for the groups defined in panel C. Stars denote importance deemed statistically significantly different from zero at the 0.0038 (0.05 / 13) level.
7. Discussion
We have proposed a general model-agnostic framework for statistical inference on population-level VIMs. These measures are summaries of the true data-generating mechanism, defined as a contrast between the predictiveness of the best possible prediction function based on all available features versus all features but those under consideration. We found that plug-in estimators of these VIMs are asymptotically linear and nonparametric efficient under regularity conditions. Through examples, we showed that many simple and commonly used VIMs fall within this framework. We found in numerical experiments that our proposed cross-fitted VIM estimator enjoys good operating characteristics, and that these characteristics match our theoretical expectations. More complex predictiveness measures and sampling scenarios, including missing data, may also be analyzed within our proposed framework, though these cases typically require more effort, including the computation of an influence function. Interpretation of the estimated VIMs depends on the application, and may include considering the ranked VIM values, or considering features with VIM values above some scientifically meaningful threshold.
Defining the importance of individual features in cases with large amounts of correlation is challenging. In practice, we recommend making use of any available background scientific knowledge either to group variables that are expected to be highly correlated or to develop an appropriate causal model. In settings where this knowledge is lacking, it may be useful to consider, for example, unsupervised methods to cluster variables before assessing variable importance; however, further work is needed to determine how to preserve inferential validity with any such procedure. One alternative approach to handling correlated features is to consider marginal importance, wherein each feature in turn could be considered as the ‘full set of covariates’ and its importance could be assessed relative to the null feature vector; if there are concerns about confounding factors, these can constitute the ‘null feature vector’ and each feature could be added to the potential confounders. A second alternative approach is to use measures like the Shapley Population VIM (SPVIM; Williamson and Feng, 2020). Since SPVIM is defined as the average increase in predictive power from including a particular feature in all possible subsets of the remaining features, use of this approach comes at the cost of significantly increased complexity.
The inferential procedures following Theorems 1 and 2 can be used whenever it is known a priori that the features of interest have non-zero importance. We note that, as an alternative, a nonparametric bootstrap scheme could be used in which f0 and f0,s are not re-estimated over bootstrap samples but rather fixed at their original estimates. The use of this bootstrap is illustrated in the Supplementary Material, where it is shown to yield similar results as the inferential procedures described in this paper. If the features of interest may have zero importance, inference should generally be conducted using sample-splitting, as described in Section 3.4. There, we propose confidence intervals valid even when a feature of interest has zero importance and a test of the zero-importance hypothesis. Our numerical results suggest that the resulting test controls type I error rate at the desired level. However, since our procedure involves sample-splitting without data reuse, it does not fully exploit the information available in the data, and may possibly be improved upon. Use of the bootstrap in this context is complicated by the need to re-estimate f0 and f0,s. Developing a more powerful test of the null importance hypothesis is an important unresolved need. This objective could be achieved, on one hand, by considering modifications of our current approach, including averaging results over multiple splits of the dataset or choosing split sizes more judiciously, or on the other hand, by utilizing more complex analytical tools, including approximate higher-order influence functions. These ideas are being pursued in ongoing research.
Supplementary Material
Acknowledgments
This work was supported by NIH grants F31AI140836, R01AI029168, R01HL137808, UM1AI068635, and S10OD028685. The opinions expressed in this article are those of the authors and do not necessarily represent the official views of the NIH.
Appendix A. Special case: standardized V-measures
Beyond smoothness requirements, the results presented in Section 3 do not impose much structure on the predictiveness measure. However, as is often the case that the predictiveness measure has the form with
for some symmetric function , where is a fixed constant, is Hadamard differentiable, and the expectation defining V1 is over the distribution of independent draws (X1, Y1), …, (Xm, Ym) from P. In this case, the plug-in estimator V1(fn, Pn) of V1(f0, P0) is a V-statistic of degree m (Hoeffding, 1948), whereas the denominator V2(P0) does not depend on f0 and typically serves as a normalization constant. As such, we refer to any predictiveness measure of this form as a standardized V-measure. We note that each example presented in Section 2.3 is a standardized V-measure, defined respectively by:
a = 1, , , m = 1;
a = 1, , , m = 1;
a = 0, , V2(P) = 1, m = 1;
a = 0, , V2(P) = P (Y = 1) P (Y = 0), m = 2.
This is useful to note because whenever V is a standardized V-measure, the influence function ϕ0 of V(fn, Pn) can be described more explicitly. Specifically, its pointwise evaluation ϕ0(z) at a given observation value z = (x, y) is given by
with denoting the Gâteaux derivative of V2 at P0 in the direction h = δz − P0. Except for the influence function of the normalization estimator V2(Pn), which is typically straightforward to compute, this is an explicit form. In Examples 1–4, the influence function of V(fn, Pn) can thus be derived respectively as:
;
;
;
where here we have used the shorthand notation , , , , and . Furthermore, for standardized V-measures, condition (A2) is often easier to verify. For example, if m = 1, then it holds trivially since V1(f, P), the only component of V(f, P) involving f, is linear in P.
Footnotes
Software and supplementary material
We implement the methods discussed above in the R package vimp and the Python package vimpy, both available on CRAN and PyPI, respectively. Additional technical details are available in the supplementary material. All results may be reproduced using code available on GitHub at https://github.com/bdwilliamson/vimp_supplementary. The data from Section 6 are available at https://github.com/benkeser/vrc01/tree/1.0.
References
- Aas K, Jullum M, and Løland A (2019). Explaining individual predictions when features are dependent: More accurate approximations to Shapley values. arXiv:1903.10464. [Google Scholar]
- Bach S, Binder A, Montavon G, Klauschen F, Müller K, and Samek W (2015). On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS One 10(7), e0130140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benkeser D, Mertens A, Arnold B, Colford J, Hubbard A, Jumbe N, and van der Laan M (2018). A machine learning-based approach for estimating and testing associations with multivariate outcomes. arXiv:1803.04877. [DOI] [PubMed] [Google Scholar]
- Bickel P, Klaasen C, Ritov Y, and Wellner J (1998). Efficient and Adaptive Estimation for Semiparametric Models. Springer. [Google Scholar]
- Breiman L (2001). Random forests. Machine Learning 45(1), 5–32. [Google Scholar]
- Chernozhukov V, Chetverikov D, Demirer M, Duflo E, Hansen C, Newey W, and Robins J (2018). Double/debiased machine learning for treatment and structural parameters. [Google Scholar]
- Corey L, Gilbert P, Juraska M, Montefiori D, Morris L, Karuna S, Edupuganti S, Mgodi N, deCamp A, Rudnicki E, et al. (2021). Two randomized trials of neutralizing antibodies to prevent HIV-1 acquisition. New England Journal of Medicine 384 (11), 1003–1014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher A, Rudin C, and Dominici F (2018). All models are wrong but many are useful: variable importance for black-box, proprietary, or misspecified prediction models, using model class reliance. arXiv:1801.01489. [Google Scholar]
- Friedman J (2001). Greedy function approximation: a gradient boosting machine. Annals of Statistics 29(5), 1189–1232. [Google Scholar]
- Garson D (1991). Interpreting neural network connection weights. Artificial Intelligence Expert. [Google Scholar]
- Grömping U (2006). Relative importance for linear regression in r: the package relaimpo. Journal of Statistical Software. [Google Scholar]
- Grömping U (2009). Variable importance in regression: linear regression versus random forest. The American Statistician 63(4), 308–319. [Google Scholar]
- Guidotti R, Monreale A, Ruggieri S, Turini F, Giannotti F, and Pedreschi D (2018). A survey of methods for explaining black box models. ACM Computer Surveys 51 (5), 93:1–93:42. [Google Scholar]
- Hastie T and Tibshirani R (1990). Generalized Additive Models, Volume 43. CRC Press. [DOI] [PubMed] [Google Scholar]
- Hoeffding W (1948). A class of statistics with asymptotically normal distribution. The Annals of Mathematical Statistics 19(3), 293–325. [Google Scholar]
- Ishwaran H (2007). Variable importance in binary regression trees and forests. Electronic Journal of Statistics 1, 519–537. [Google Scholar]
- LeDell E, Petersen M, and van der Laan M (2015). Computationally efficient confidence intervals for cross-validated area under the ROC curve estimates. Electronic Journal of Statistics. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei J, G’Sell M, Rinaldo A, Tibshirani R, and Wasserman L (2017). Distribution-free predictive inference for regression. Journal of the American Statistical Association. [Google Scholar]
- Lundberg S and Lee S-I (2017). A unified approach to interpreting model predictions. In Advances in Neural Information Processing Systems. [Google Scholar]
- Magaret C, Benkeser D, Williamson B, Borate B, Carpp L, et al. (2019). Prediction of VRC01 neutralization sensitivity by HIV-1 gp160 sequence features. PLoS Computational Biology 15(4), e1006952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montefiori D (2009). Measuring HIV neutralization in a luciferase reporter gene assay. In: Prasad VR, Kalpana GV (eds) HIV Protocols. Methods in Molecular Biology 485, 395–405. [DOI] [PubMed] [Google Scholar]
- Murdoch W, Singh C, Kumbier K, Abbasi-Asl R, and Yu B (2019). Interpretable machine learning: definitions, methods, and applications. arXiv:1901.04592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nathans L, Oswald F, and Nimon K (2012). Interpreting multiple linear regression: A guidebook of variable importance. Practical Assessment, Research & Evaluation 17(9). [Google Scholar]
- Nelder J and Wedderburn R (1972). Generalized linear models. Journal of the Royal Statistical Society, Series A 135 (3), 370–384. [Google Scholar]
- Pfanzagl J (1982). Contributions to a general asymptotic statistical theory. Springer. [Google Scholar]
- Ribeiro M, Singh S, and Guestrin C (2016). Why should I trust you?: Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1135–1144. [Google Scholar]
- Shrikumar A, Greenside P, and Kundaje A (2017). Learning important features through propagating activation differences. arXiv:1704.02685. [Google Scholar]
- Strobl C, Boulesteix A, Zeileis A, and Hothorn T (2007). Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinformatics 8(1), 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sundararajan M, Taly A, and Yan Q (2017). Axiomatic attribution for deep networks. arXiv:1703.01365. [Google Scholar]
- Tibshirani R (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, Series B, 267–288. [Google Scholar]
- van der Laan M (2006). Statistical inference for variable importance. The International Journal of Biostatistics 2(1). doi: 10.2202/1557-4679.1008. [DOI] [Google Scholar]
- van der Laan M, Polley E, and Hubbard A (2007). Super learner. Statistical Applications in Genetics and Molecular Biology 6(1), Online Article 25. [DOI] [PubMed] [Google Scholar]
- van der Laan M and Rose S (2011). Targeted learning: causal inference for observational and experimental data. Springer Science & Business Media. [Google Scholar]
- Wei P, Lu Z, and Song J (2015). Variable importance analysis: a comprehensive review. Reliability Engineering & System Safety 142, 399–432. [Google Scholar]
- Williamson B and Feng J (2020). Efficient nonparametric statistical inference on population feature importance using Shapley values. In Proceedings of the 37th International Conference on Machine Learning, Volume 119 of Proceedings of Machine Learning Research, pp. 10282–10291. [PMC free article] [PubMed] [Google Scholar]
- Williamson B, Gilbert P, Carone M, and Simon N (2020). Nonparametric variable importance assessment using machine learning techniques. Biometrics 77, 9–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolpert D (1992). Stacked generalization. Neural Networks 5(2), 241–259. [Google Scholar]
- Zheng W and van der Laan M (2011). Cross-validated targeted minimum-loss-based estimation. In Targeted Learning, pp. 459–474. Springer. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


