Individual Data Protected Integrative Regression Analysis of High-Dimensional Heterogeneous Data

Abstract

Evidence-based decision making often relies on meta-analyzing multiple studies, which enables more precise estimation and investigation of generalizability. Integrative analysis of multiple heterogeneous studies is, however, highly challenging in the ultra high-dimensional setting. The challenge is even more pronounced when the individual-level data cannot be shared across studies, known as DataSHIELD contraint. Under sparse regression models that are assumed to be similar yet not identical across studies, we propose in this paper a novel integrative estimation procedure for data-Shielding High-dimensional Integrative Regression (SHIR). SHIR protects individual data through summary-statistics-based integrating procedure, accommodates between-study heterogeneity in both the covariate distribution and model parameters, and attains consistent variable selection. Theoretically, SHIR is statistically more efficient than the existing distributed approaches that integrate debiased LASSO estimators from the local sites. Furthermore, the estimation error incurred by aggregating derived data is negligible compared to the statistical minimax rate and SHIR is shown to be asymptotically equivalent in estimation to the ideal estimator obtained by sharing all data. The finite-sample performance of our method is studied and compared with existing approaches via extensive simulation settings. We further illustrate the utility of SHIR to derive phenotyping algorithms for coronary artery disease using electronic health records data from multiple chronic disease cohorts.

1. Introduction

1.1. Background

Synthesizing information from multiple studies is crucial for evidence-based medicine and policy decision making. Meta-analyzing multiple studies allows for more precise estimates and enables investigation of generalizability. In the presence of heterogeneity across studies and high-dimensional predictors, such integrative analysis however is highly challenging. An example of such integrative analysis is to develop generalizable predictive models using electronic health records (EHR) data from different hospitals. In addition to high-dimensional features, EHR data analysis encounters privacy constraints in that individual patient data (IPD) typically cannot be shared across local hospital sites, which makes the challenge of integrative analysis even more pronounced. Breach of Privacy arising from data sharing is in fact a growing concern in general for scientific studies. Recently, Wolfson et al. (2010) proposed a generic individual-information protected integrative analysis framework, named DataSHIELD, that transfers only summary statistics¹ from each distributed local site to the central site for pooled analysis. Conceptually highly valued by research communities (see, e.g., Jones et al. 2012; Doiron et al. 2013), the DataSHIELD facilitates multi-study integrative analysis when IPD pooled meta-analysis is not feasible due to ethical and/or legal restrictions (Gaye et al. 2014). In the low-dimensional setting, a number of statistical methods have been developed for distributed analysis that satisfy the DataSHIELD constraint (see, e.g., Chen et al. 2006; Wu et al. 2012; Liu and Ihler 2014; Lu et al. 2015; Huang and Huo 2015; Han and Liu 2016; He et al. 2016; Zöller, Lenz, and Binder 2018; Duan et al. 2019, 2020). Distributed high-dimensional regression have largely focused on settings without between-study heterogeneity as detailed in Section 1.2. To the best of our knowledge, no existing distributed learning methods can effectively handle both high-dimensionality and the presence of model heterogeneity across the local sites.

1.2. Related Work

In the context of high-dimensional regression, several recently proposed distributed inference approaches can be potentially used for integrative analysis under the DataSHIELD constraint. Specifically, Tang, Zhou, and Song (2016), Lee et al. (2017), and Battey et al. (2018) proposed distributed inference procedures aggregating the local debiased LASSO estimators (Zhang and Zhang 2014; Van de Geer et al. 2014; Javanmard and Montanari 2014). By including debiasing procedure in their pipelines, the corresponding estimators can be used for inference directly. Lee et al. (2017) and Battey et al. (2018) proposed to further truncate the aggregated dense debiased estimators to achieve sparsity; see also Maity, Sun, and Banerjee (2019). Though this debiasing-based strategy can be extended to fit for our heterogeneous modeling assumption, it still loses statistical efficiency due to the failure to account for the heterogeneity of the information matrices across different sites. In addition, the use of debiasing procedure at local sites incurs additional error for estimation, as detailed in Section 4.4.

Lu et al. (2015) and Li et al. (2016) proposed distributed approaches for ${\ell }_2$-regularized logistic and Cox regression. However, their methods requires equential communications between local sites and the central machine, which may be time and resource consuming. Chen and Xie (2014) proposed to estimate high dimensional parameters by first adopting majority voting to select a positive set and then combining local estimation of the coefficients belonging to this set. Wang, Peng, and Dunson (2014) proposed to aggregate the local estimators through their median values rather than their mean, shown to be more robust to poor estimation performance of local sites with insufficient sample size (Minsker 2019). More recently, Wang et al. (2017) and Jordan, Lee, and Yang (2019) presented a communication-efficient surrogate likelihood framework for distributed statistical learning that only transfers the first-order summary statistics, that is, gradient between the local sites and the central site. Fan, Guo, and Wang (2019) extended their idea and proposed two iterative distributed optimization algorithms for the general penalized likelihood problems. However, their framework, as well as others summarized in this paragraph, is restricted to homogeneous scenarios and cannot be easily extended to the settings with heterogeneous models or covariates.

1.3. Our Contributions

In this article, we fill the methodological gap of high-dimensional distributed learning methods that can accommodate cross-study heterogeneity by proposing a novel data-Shielding High-dimensional Integrative Regression (SHIR) method under the DataSHIELD constraints. While SHIR can be viewed as analogous to the integrative analysis of debiased local LASSO estimators, it achieves debiasing without having to perform debiasing for the local estimators. SHIR solves LASSO problem only once in each local site without requiring the inverse Hessian matrices or the locally debiased estimators and only needs one turn in communication. Statistically, it serves as the tool for the integrative model estimation and variable selection, in the presence of high dimensionality and heterogeneity in model parameters across sites. In addition, under the ultra-high dimensional regime where p can grow exponentially with the total sample size N, we demonstrate that SHIR can achieve the same error rates asymptotically as the ideal estimator based on the IPD pooled analysis, denoted by IPDpool, and attain consistent variable selection. Such properties are not readily available in the existing literature and some novel technical tools are developed for the theoretical verification. We also show theoretically that SHIR is statistically more efficient than the approach based on integrating and thresholding locally debiased estimators (see, e.g., Lee et al. 2017; Battey et al. 2018). Results from our numerical studies confirm that SHIR performs similarly to the ideal IPDpool estimator outperforms the other methods.

1.4. Outline of the Paper

The rest of this article is organized as follows. We introduce the settings in Section 2 and describe SHIR, our proposed approach in Section 3. Theoretical properties of the SHIR estimator are studied in Section 4. We derive the upper bound for its prediction and estimation risks, compare it with the existing approach, and show that the errors incurred by aggregating derived data is negligible compared to the statistical minimax rate. When the true model is ultra-sparse, SHIR is shown to be asymptotically equivalent to the IPDpool estimator and achieves sparsistency. Section 5 compares the performance of SHIR to existing methods through simulations. We apply SHIR to derive classification models for coronary artery disease (CAD) using EHR data from four different disease cohorts in Section 6. Section 7 concludes the paper with a discussion. Technical proofs of the theoretical results and additional numerical results are provided in the supplementary material.

2. Problem Statement

Throughout, for any integer $d,[d]=\{1,\dots ,d\}$. For any vector $\mathbf{x}={\left(x_1,x_2,\dots ,x_d\right)}^{\top }\in {ℝ}^d$ and index set $𝓢=\left\{j_1,\dots ,j_k:j_1<\cdots <j_k\right\}\subseteq [d]$, ${\mathbf{x}}_{𝓢}={\left(x_{j_1},\dots ,x_{j_k}\right)}^{\top }$, ${\mathbf{x}}_{-1}={\left(x_2,\dots ,x_d\right)}^{\top }$, $\Vert \mathbf{x}{\Vert }_q$ denotes the ${\ell }_q$ norm of $\mathbf{x}$ and $\Vert \mathbf{x}{\Vert }_{\infty }={\max }_{j\in [d]}\left|x_j\right|$. Suppose there are $M$ independent studies and $n_m$ subjects in the $m\text{th}$ study, for $m=1,\dots ,M$. For the $i\text{th}$ subject in the $m\text{th}$ study, let $Y_i^{(\text{m})}$ and ${\mathbf{X}}_i^{(\text{m})}$, respectively, denote the response and the $p$-dimensional covariate vector, ${\mathbf{D}}_i^{(\text{m})}={\left(Y_i^{(\text{m})},{\mathbf{X}}_i^{(\text{m})\top }\right)}^{\top }$, ${\mathbf{Y}}^{(\text{m})}={\left(Y_1^{(\text{m})},\dots ,Y_{n_m}^{(\text{m})}\right)}^{\top }$, and ${\mathbb{X}}^{(\text{m})}={\left({\mathbf{X}}_1^{(\text{m})},{\mathbf{X}}_2^{(\text{m})},\dots ,{\mathbf{X}}_{n_m}^{(\text{m})}\right)}^{\top }$. We assume that the observations in study $m$, ${𝓓}^{(\text{m})}=\left\{{\mathbf{D}}_i^{(\text{m})},i=1,\dots ,n_m\right\}$, are independent and identically distributed. Without loss of generality, assume that ${\mathbf{X}}_i^{(\text{m})}$ includes 1 as the first component and ${\mathbf{X}}_{i,-1}^{(\text{m})}$ has mean $\mathbf{0}$. Define the population parameters of interests as

$${\mathit{\beta }}_0^{(\text{m})}=\underset{{\mathit{\beta }}^{(\text{m})}}{\mathrm{argmin}}{𝓛}_m\left({\mathit{\beta }}^{(\text{m})}\right),\text{where}$$

$${𝓛}_m\left({\mathit{\beta }}^{(\text{m})}\right)=\text{E}\left\{f\left({\mathit{\beta }}^{(\text{m})\top }{\mathbf{X}}_i^{(\text{m})},Y_i^{(\text{m})}\right)\right\},$$

$${\mathit{\beta }}^{(\text{m})}={\left({\beta }_1^{(\text{m})},{\beta }_2^{(\text{m})},\dots ,{\beta }_p^{(\text{m})}\right)}^{\top }$$

for some specified loss function $f$. Let ${\mathit{\beta }}_j={\left({\beta }_j^{(1)},\dots ,{\beta }_j^{(\text{M})}\right)}^{\top }$, ${\mathit{\beta }}^{(•)}={\left({\mathit{\beta }}^{(1)\top },\dots ,{\mathit{\beta }}^{(\text{M})\top }\right)}^{\top }$, and ${\mathit{\beta }}_{0j}$, ${\mathit{\beta }}_0^{(•)}$ denote the true values of ${\mathit{\beta }}_j$, ${\mathit{\beta }}^{(•)}$. We consider the ultra-high dimensional setting, where the covariate dimension $p$ could grow in an exponential rate of the sample size $N=\sum _{m=1}^M{n}_m$.

For each $j$, we follow the typical meta-analysis to decompose ${\beta }_j^{(\text{m})}$ as ${\beta }_j^{(\text{m})}={\mu }_j+{\alpha }_j^{(\text{m})}$ with ${\mathit{\alpha }}_j={\left({\alpha }_j^{(1)},\dots ,{\alpha }_j^{(\text{M})}\right)}^{\top }$ and we set ${\mathbf{1}}_{M\times 1}^{\top }{\mathit{\alpha }}_j=0$ for identifiability. Here, ${\mu }_j$ represents average effect of the covariate $X_j$ and ${\mathit{\alpha }}_j$ captures the between-study heterogeneity of the effects. Let $\mathit{\mu }={\left({\mu }_1,\dots ,{\mu }_p\right)}^{\top }$, ${\mathit{\alpha }}^{(•)}={\left({\mathit{\alpha }}^{(1)\top },\dots ,{\mathit{\alpha }}^{(\text{M})\top }\right)}^{\top }$, ${\mathit{\alpha }}_{-1}^{(•)}={\left({\mathit{\alpha }}_{-1}^{(1)\top },\dots ,{\mathit{\alpha }}_{-1}^{(\text{M})\top }\right)}^{\top }$, and ${\mathit{\mu }}_0$ and ${\mathit{\alpha }}_0^{(•)}$ be the true values of $\mathit{\mu }$ and ${\mathit{\alpha }}^{(•)}$, respectively. Consider the empirical global loss function

$$\widehat{𝓛}\left({\mathit{\beta }}^{(•)}\right)=N^{-1}\sum _{m=1}^M{n}_m{\widehat{𝓛}}_m\left({\mathit{\beta }}^{(\text{m})}\right),\text{where}$$

$${\widehat{𝓛}}_m\left({\mathit{\beta }}^{(\text{m})}\right)=n_m^{-1}\sum _{i=1}^{n_m}f\left({\mathit{\beta }}^{(\text{m})\top }{\mathbf{X}}_i^{(\text{m})},Y_i^{(\text{m})}\right),m=1,\dots ,M$$

Minimizing $\widehat{𝓛}\left({\mathit{\beta }}^{(•)}\right)$ is obviously equivalent to estimating ${\mathit{\beta }}^{(\text{m})}$ using ${𝓓}^{(\text{m})}$ only. To improve the estimation of ${\mathit{\beta }}_0^{(•)}$ by synthesizing information from ${𝓓}^{(•)}$ and overcome the high dimensionality, we employ penalized loss functions, $\widehat{𝓛}\left({\mathit{\beta }}^{(•)}\right)+\lambda \rho \left({\mathit{\beta }}^{(•)}\right)$, with the penalty function $\rho (\cdot )$ designed to leverage prior structure information on ${\mathit{\beta }}_0^{(•)}$. Under the prior assumption that ${\mathit{\mu }}_0$ is sparse and ${\mathit{\alpha }}_{0,-1}^{(1)},\dots ,{\mathit{\alpha }}_{0,-1}^{(\text{M})}$ are sparse and share the same support, we impose a mixture of LASSO and group LASSO penalty: $\rho \left({\mathit{\beta }}^{(•)}\right)=\sum _{j=2}^p\left|{\mu }_j\right|+{\lambda }_g\sum _{j=2}^p{\Vert {\mathit{\alpha }}_j\Vert }_2$, where ${\lambda }_g\ge 0$ is a tuning parameter. Similar penalty has been used in Cheng, Lu, and Liu (2015). Our construction differs slightly from that of Cheng, Lu, and Liu (2015) where ${\Vert {\mathit{\alpha }}_{j,-1}\Vert }_2$ was used instead of ${\Vert {\mathit{\alpha }}_j\Vert }_2$. This modified penalty leads to two main advantages: (i) the estimator is invariant to the permutation of the indices of the $M$ studies; and (ii) it yields better theoretical estimation error bounds for the heterogeneous effects. Then an idealized IPDpool estimator for ${\mathit{\beta }}_0^{(•)}$ can be obtained as

$$\begin{gathered} {\widehat{\mathit{\beta }}}_{\text{IPDpool}}^{(•)}=\underset{{\mathit{\beta }}^{(•)}}{\mathrm{argmin}}\widehat{𝓠}\left({\mathit{\beta }}^{(•)}\right),\text{where} \\ \widehat{𝓠}\left({\mathit{\beta }}^{(•)}\right)=\widehat{𝓛}\left({\mathit{\beta }}^{(•)}\right)+\lambda \rho \left({\mathit{\beta }}^{(•)}\right), \end{gathered}$$ (1)

for some tuning parameter $\lambda \ge 0$. However, the IPDpool estimator is not feasible under the DataSHIELD constraint. Our goal is to construct an alternative estimator that attains the same efficiency as ${\widehat{\mathit{\beta }}}_{\text{IPDpool}}^{(•)}$ asymptotically but only requires sharing summary data. When $p$ is small, the sparse meta analysis (SMA) approach by He et al. (2016) achieves this goal via estimating ${\mathit{\beta }}^{(•)}$ as ${\widehat{\mathit{\beta }}}_{\text{SMA}}^{(•)}={\mathrm{argmin}}_{{\mathit{\beta }}^{(•)}}{\widehat{Q}}_{\text{SMA}}\left({\mathit{\beta }}^{(•)}\right)$, where ${\widehat{Q}}_{\text{SMA}}\left({\mathit{\beta }}^{(•)}\right)=N^{-1}\sum _{m=1}^M{\left({\mathit{\beta }}^{(\text{m})}-{\breve{\mathit{\beta }}}^{(\text{m})}\right)}^{\top }{\breve{\mathbb{V}}}_m^{-1}\left({\mathit{\beta }}^{(\text{m})}-{\breve{\mathit{\beta }}}^{(\text{m})}\right)+\lambda \rho \left({\mathit{\beta }}^{(•)}\right)$, ${\breve{\mathit{\beta }}}^{(\text{m})}={\mathrm{argmin}}_{{\mathit{\beta }}^{(\text{m})}}{\widehat{𝓛}}_m\left({\mathit{\beta }}^{(\text{m})}\right)$ and ${\breve{\mathbb{V}}}_m={\left\{n_m^{-1}{\nabla }^2{\widehat{𝓛}}_m\left({\breve{\mathit{\beta }}}^{(\text{m})}\right)\right\}}^{-1}$. The SMA method is DataSHIELD since only derived statistics ${\breve{\mathit{\beta }}}^{(\text{m})}$ and ${\breve{\mathbb{V}}}_m$ are shared in the integrative regression. The SMA estimator attains oracle property when $p$ is relatively small but fails for large $p$ due to the failure of ${\breve{\mathit{\beta }}}^{(\text{m})}$.

3. Data-SHIR

3.1. SHIR Method

In the high-dimensional setting, one may overcome the limitation of the SMA approach by replacing ${\breve{\mathit{\beta }}}^{(\text{m})}$ with the regularized LASSO estimator,

$${\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}=\underset{{\mathit{\beta }}^{(\text{m})}}{\mathrm{argmin}}{\widehat{𝓛}}_m\left({\mathit{\beta }}^{(\text{m})}\right)+{\lambda }_m{\Vert {\mathit{\beta }}_{-1}^{(\text{m})}\Vert }_1$$ (2)

However, aggregating $\left\{{\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})},m\in [M]\right\}$ is problematic with large $p$ due to their inherent biases. To overcome the bias issue, we build the SHIR method motivated by SMA and the debiasing approach for LASSO (see, e.g., Van de Geer et al. 2014) yet achieve debiasing without having to perform debiasing for $M$ local estimators. Specifically, we propose the SHIR estimator for ${\mathit{\beta }}_0^{(•)}$ as ${\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(•)}={\mathrm{argmin}}_{{\mathit{\beta }}^{(•)}}{\widehat{Q}}_{\text{SHIR}}\left({\mathit{\beta }}^{(•)}\right)$, where

$$\begin{gathered} {\widehat{Q}}_{\text{SHIR}}\left({\mathit{\beta }}^{(•)}\right)=N^{-1}\sum _{m=1}^M{n}_m\left\{{\mathit{\beta }}^{(\text{m})\top }{\widehat{\mathrm{ℍ}}}_m{\mathit{\beta }}^{(\text{m})}-2{\mathit{\beta }}^{(\text{m})\top }{\widehat{\mathbf{g}}}_m\right\} \\ +\lambda \rho \left({\mathit{\beta }}^{(•)}\right), \end{gathered}$$ (3)

${\widehat{\mathrm{ℍ}}}_m={\nabla }^2{\widehat{𝓛}}_m\left({\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}\right)$ is an estimate of the Hessian matrix and ${\widehat{\mathbf{g}}}_m={\widehat{\mathrm{ℍ}}}_m{\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}-\nabla {\widehat{𝓛}}_m\left({\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}\right)$. Our SHIR estimator ${\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(•)}$ satisfy the DataSHIELD constraint as ${\widehat{Q}}_{\text{SHIR}}\left({\mathit{\beta }}^{(•)}\right)$ depends on ${𝓓}^{(\text{m})}$ only through summary statistics ${\widehat{𝓓}}_m=\left\{n_m,{\widehat{\mathrm{ℍ}}}_m,{\widehat{\mathbf{g}}}_m\right\}$, which can be obtained within the $m^{\text{th}}$ study, and requires only one round of data transfer from local sites to the central node.

With $\left\{{\widehat{\mathrm{ℍ}}}_m,{\widehat{\mathbf{g}}}_m,m=1,\dots ,M\right\}$, we may implement the SHIR procedure using coordinate descent algorithms (Friedman, Hastie, and Tibshirani 2010) along with reparameterization. Let

$${\widehat{Q}}_{\text{SHIR}}\left(\mathit{\mu },{\mathit{\alpha }}^{(•)}\right)={\widehat{𝓛}}_{\text{SHIR}}\left(\mathit{\mu },{\mathit{\alpha }}^{(•)}\right)+\lambda \rho \left(\mathit{\mu },{\mathit{\alpha }}^{(•)};{\lambda }_g\right),$$

where $\rho \left(\mathit{\mu },{\mathit{\alpha }}^{(•)};{\lambda }_g\right)={\Vert {\mathit{\mu }}_{-1}\Vert }_1+{\lambda }_g{\Vert {\mathit{\alpha }}_{-1}^{(•)}\Vert }_{2,1},{\Vert {\mathit{\alpha }}_{-1}^{(•)}\Vert }_{2,1}=\sum _{j=2}^p{\Vert {\mathit{\alpha }}_j\Vert }_2$ and

$$\begin{gathered} {\widehat{𝓛}}_{\text{SHIR}}\left(\mathit{\mu },{\mathit{\alpha }}^{(•)}\right)=N^{-1}\sum _{m=1}^M{n}_m\{\left({\mathit{\mu }}^{\top }+{\mathit{\alpha }}^{(\text{m})\text{T}}\right){\widehat{\mathrm{ℍ}}}_m\left(\mathit{\mu }+{\mathit{\alpha }}^{(\text{m})}\right) \\ -2{\widehat{\mathbf{g}}}_m^{\top }\left(\mathit{\mu }+{\mathit{\alpha }}^{(\text{m})}\right)\}. \end{gathered}$$

Then the optimization problem in Equation (3) can be reparameterized and represented as:

$$\begin{gathered} \left({\widehat{\mathit{\mu }}}_{\text{SHIR}},{\widehat{\mathit{\alpha }}}_{\text{SHIR}}^{(•)}\right)={\mathrm{argmin}}_{\left(\mathit{\mu },{\mathit{\alpha }}^{(•)}\right)}{\widehat{Q}}_{\text{SHIR}}\left(\mathit{\mu },{\mathit{\alpha }}^{(•)}\right), \\ \text{s.t.}{\mathbf{1}}_{M\times 1}^{\top }{\mathit{\alpha }}_j=0,j\in [p], \end{gathered}$$

and ${\widehat{\mathit{\beta }}}_{\text{SHIR}}$ is obtained with the transformation: ${\beta }_j^{(\text{m})}={\mu }_j+{\alpha }_j^{(\text{m})}$ for every $j\in [p]$. The above procedure is presented in Algorithm A1 in Section A.5 of the supplementary material.

Remark 1.

The first term in ${\widehat{Q}}_{\mathrm{SHIR}}\left({\mathit{\beta }}^{(•)}\right)$ is essentially the second-order Taylor expansion of $\widehat{𝓛}\left({\mathit{\beta }}^{(•)}\right)$ at the local LASSO estimators ${\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(•)}$. The SHIR method can also be viewed as approximately aggregating local debiased LASSO estimators without actually carrying out the standard debiasing process. To see this, let ${\widehat{Q}}_{\text{dLASSO}}\left({\mathit{\beta }}^{(•)}\right)=N^{-1}\sum _{m=1}^M{n}_m{\left({\mathit{\beta }}^{(\text{m})}-{\widehat{\mathit{\beta }}}_{\text{dLASSO}}^{(\text{m})}\right)}^{\top }{\widehat{\mathrm{ℍ}}}_m\left({\mathit{\beta }}^{(\text{m})}-{\widehat{\mathit{\beta }}}_{\text{dLASSO}}^{(\text{m})}\right)+\lambda \rho \left({\mathit{\beta }}^{(•)}\right)$, where ${\widehat{\mathit{\beta }}}_{\text{dLASSO}}^{(\text{m})}$ is the debiased LASSO estimator for the $m^{\text{th}}$ study with

$${\widehat{\mathit{\beta }}}_{\text{dLASSO}}^{(\text{m})}={\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}-{\widehat{\mathbf{\text{Θ}}}}_m\nabla {\widehat{𝓛}}_m\left({\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}\right),\text{for}m=1,\dots ,M,$$ (4)

and ${\widehat{\mathbf{\text{Θ}}}}_m$ is a regularized inverse of ${\widehat{\mathrm{ℍ}}}_m$. We may write

$$\begin{gathered} {\widehat{Q}}_{\text{dLASSO}}\left({\mathit{\beta }}^{(•)}\right) \\ =N^{-1}\sum _{m=1}^M\{n_m\left[{\mathit{\beta }}^{(\text{m})\top }{\widehat{\mathrm{ℍ}}}_m{\mathit{\beta }}^{(\text{m})}-2{\mathit{\beta }}^{(\text{m})\top }{\widehat{\mathrm{ℍ}}}_m{\widehat{\mathit{\beta }}}_{\text{dLASSO}}^{(\text{m})}\right] \\ +C_m\}+\lambda \rho \left({\mathit{\beta }}^{(•)}\right) \\ \approx N^{-1}\sum _{m=1}^M\left\{n_m\left[{\mathit{\beta }}^{(\text{m})\top }{\widehat{\mathrm{ℍ}}}_m{\mathit{\beta }}^{(\text{m})}-2{\mathit{\beta }}^{(\text{m})\top }{\widehat{\mathbf{g}}}_m\right]+C_m\right\} \\ +\lambda \rho \left({\mathit{\beta }}^{(•)}\right) \\ ={\widehat{Q}}_{\text{SHIR}}\left({\mathit{\beta }}^{(•)}\right)+N^{-1}\sum _{m=1}^M{C}_m \end{gathered}$$

where we use ${\widehat{\mathbf{\text{Θ}}}}_m{\widehat{\mathrm{ℍ}}}_m\approx \mathbb{I}$ in the above approximation and the term

$$\begin{gathered} C_m=n_m{\left\{{\widehat{\mathrm{ℍ}}}_m{\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}-{\widehat{\mathrm{ℍ}}}_m{\widehat{\mathbf{\text{Θ}}}}_m\nabla {\widehat{𝓛}}_m\left({\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}\right)\right\}}^{\top } \\ \left\{{\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}-{\widehat{\mathbf{\text{Θ}}}}_m\nabla {\widehat{𝓛}}_m\left({\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}\right)\right\} \end{gathered}$$

does not depend on ${\mathit{\beta }}^{(•)}$. We only use ${\widehat{\mathbf{\text{Θ}}}}_m{\widehat{\mathrm{ℍ}}}_m\approx \mathbb{I}$ heuristically above to show a connection between our SHIR estimator and the debiased LASSO, but the validity and asymptotic properties of the SHIR estimator do not require obtaining any ${\widehat{\mathbf{\text{Θ}}}}_m$ or establishing a theoretical guarantee for ${\widehat{\mathbf{\text{Θ}}}}_m{\widehat{\mathrm{ℍ}}}_m$ being sufficiently close to $\mathbb{I}$.

Remark 2.

Compared with existing debiasing-based methods (Lee et al. 2017; Battey et al. 2018), the SHIR approach is both computationally and statistically efficient. It does not rely on the debiased statistics (4) and achieves debiasing without calculating ${\widehat{\mathbf{\text{Θ}}}}_m$, which can only be estimated well under strong conditions (Van de Geer et al. 2014; Janková and Van De Geer 2016).

3.2. Tuning Parameter Selection

The implementation of SHIR requires selection of three sets of tuning parameters, $\left\{{\lambda }_m,m\in [M]\right\}$, $\lambda$ and ${\lambda }_g$. We select $\left\{{\lambda }_m,m\in [M]\right\}$ for the LASSO problem locally via the standard $K$-fold cross-validation (CV). Selecting $\lambda$ and ${\lambda }_g$ needs to balance the tradeoff between the model’s degrees of freedom, denoted by $\mathrm{DF}\left(\lambda ,{\lambda }_g\right)$, and the quadratic loss in ${\widehat{Q}}_{\text{SHIR}}\left({\mathit{\beta }}^{(•)}\right)$ It is not feasible to tune $\lambda$ and ${\lambda }_g$ via the CV since individual-level data are not available in the central site. We propose to select $\lambda$ and ${\lambda }_g$ as the minimizer of the generalized information criterion (GIC) (Wang and Leng 2007; Zhang, Li, and Tsai 2010), defined as

$$\mathrm{GIC}\left(\lambda ,{\lambda }_g\right)=\mathrm{Deviance}\left(\lambda ,{\lambda }_g\right)+{\gamma }_N\text{DF}\left(\lambda ,{\lambda }_g\right),$$

where ${\gamma }_N$ is some prespecified scaling parameter and

$$\begin{gathered} \text{Deviance}\left(\lambda ,{\lambda }_g\right)=N^{-1}\sum _{m=1}^M{n}_m\{{\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(\text{m})\top }\left(\lambda ,{\lambda }_g\right){\widehat{\mathrm{ℍ}}}_m{\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(\text{m})}\left(\lambda ,{\lambda }_g\right) \\ -2{\widehat{\mathbf{g}}}_m^{\text{T}}{\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(\text{m})}\left(\lambda ,{\lambda }_g\right)\}. \end{gathered}$$

Following Zhang, Li, and Tsai (2010) and Vaiter et al. (2012), we define $\mathrm{DF}\left(\lambda ,{\lambda }_g\right)$ as the trace of

$${\left[{\partial }_{{\widehat{𝓢}}_{\mu },{\widehat{𝓢}}_{\alpha }}^2{\widehat{Q}}_{\text{SHIR}}\left({\widehat{\mathit{\mu }}}_{\text{SHIR}},{\widehat{\mathit{\alpha }}}_{\text{SHIR}}^{(•)}\right)\right]}^{-1}\left[{\partial }_{{\widehat{𝓢}}_{\mu },{\widehat{𝓢}}_{\alpha }}^2{\widehat{𝓛}}_{\text{SHIR}}\left({\widehat{\mathit{\mu }}}_{\text{SHIR}},{\widehat{\mathit{\alpha }}}_{\text{SHIR}}^{(•)}\right)\right],$$

where ${\widehat{𝓢}}_{\mu }=\left\{j:{\widehat{\mu }}_{\text{SHIR},j}\left(\lambda ,{\lambda }_g\right)\ne 0\right\}$, ${\widehat{𝓢}}_{\alpha }=\left\{j:{\Vert {\widehat{\mathit{\alpha }}}_{\text{SHIR},j}\left(\lambda ,{\lambda }_g\right)\Vert }_2\ne 0\right\}$, the operator ${\partial }_{{\widehat{𝓢}}_{\mu },{\widehat{𝓢}}_{\alpha }}^2$ is defined as the second order partial derivative with respect to ${\left({\mathit{\mu }}_{{\widehat{𝓢}}_{\mu }}^{\top },{\mathit{\alpha }}_{{\widehat{𝓢}}_{\alpha }}^{(2)\top },\dots {\mathit{\alpha }}_{{\widehat{𝓢}}_{\alpha }}^{(\text{M})\top }\right)}^{\top }$, after plugging ${\mathit{\alpha }}^{(1)}=-\sum _{m=2}^M{\mathit{\alpha }}^{(\text{m})}$ into ${\widehat{Q}}_{\text{SHIR}}\left(\mathit{\mu },{\mathit{\alpha }}^{(•)}\right)$ or ${\widehat{𝓛}}_{\text{SHIR}}\left(\mathit{\mu },{\mathit{\alpha }}^{(•)}\right)$.

Remark 3.

As discussed in Kim, Kwon, and Choi (2012), ${\gamma }_N$ can be chosen depending on the goal with commonly choices including ${\gamma }_N=2/N$ for AIC (Akaike 1974), ${\gamma }_N=\log N/N$ for BIC (Bhat and Kumar 2010), ${\gamma }_N=\log \log p\log N/N$ for modified BIC (Wang, Li, and Leng 2009) and ${\gamma }_N=2\log p/N$ for RIC (Foster and George 1994). We used the BIC with ${\gamma }_N=\log N/N$ in our numerical studies.

Remark 4.

For linear models, it has been shown that the proper choice of ${\gamma }_N$ guarantees GIC’s model selection consistency under various divergence rates of the dimension $p$ (Kim, Kwon, and Choi 2012). For example, for fixed $p$, GIC is consistent if $N{\gamma }_N\to \infty$ and ${\gamma }_N\to 0$. When $p$ diverges in polynomial rate $N^{\xi }$, then GIC is consistent provided that ${\gamma }_N=\log N/N$ (BIC) if $0<\xi <1/2$; ${\gamma }_N=\log \log p\log N/N$ (modified BIC) if $0<\xi <1$. When $p$ diverges in exponential rate $O\left(\exp \left(\kappa N^{\xi }\right)\right)$ with $0<v<\xi$, GIC is consistent as ${\gamma }_N=N^{v-1}$. These results can be naturally extended to more general log-likelihood functions.

4. Theoretical Results

In this section, we present theoretical properties of ${\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(•)}$ for $\rho \left({\mathit{\beta }}^{(•)}\right)=\rho \left({\mathit{\beta }}^{(•)}\right)$ but discuss how our theoretical results can be extended to other sparse structures in Section 7. In Sections 4.2 and 4.3, we derive theoretical consistency and equivalence for the prediction and estimation risks of the SHIR, under high dimensional sparse model and smooth loss function $f$. In Section 4.4, we compare the risk bounds for SHIR with an estimator derived based on those of the debiasing-based aggregation approaches (Lee et al. 2017; Battey et al. 2018). In addition, Section 4.5 shows that the SHIR achieves sparsistency, that is, variable selection consistency, for the nonzero sets of ${\mathit{\mu }}_0$ and ${\mathit{\alpha }}_0^{(•)}$. We begin with some notation and definitions that will be used throughout the article.

4.1. Notation and Definitions

Let $o\{\alpha (n)\}$, $O\{\alpha (n)\}$, $\omega \{\alpha (n)\}$, $\text{Ω}\{\alpha (n)\}$ and $\text{Θ}\{\mathit{\alpha }(n)\}$ respectively represent the sequences that grow in a smaller, equal/ smaller, larger, equal/larger and equal rate of the sequence $\alpha (n)$. Similarly, let $o_{\text{P}}$, $O_{\text{P}}$, ${\omega }_{\text{P}}$, ${\text{Ω}}_{\text{P}}$ and ${\text{Θ}}_{\text{P}}$ represent each of the corresponding rates with probability approaching 1 as $n\to \infty$.

For any vector ${\mathit{v}}_0\in {ℝ}^d$, denote the ${\ell }_2$-ball around ${\mathit{v}}_0$ with radius $r>0$ as ${𝓑}_r\left({\mathit{v}}_0\right)=\left\{\mathit{v}\in {ℝ}^d:{\Vert \mathit{v}-{\mathit{v}}_0\Vert }_2\le r\right\}$. Following Vershynin (2018), we define the sub-Gaussian norm of a random variable $X$ as $\Vert X{\Vert }_{{\psi }_2}:={\sup }_{q\ge 1}{q}^{-1/2}{\left(\text{E}|X{|}^q\right)}^{1/q}$ and for any random vector $\mathit{X}={\left(X_1,\dots ,X_d\right)}^{\top }$, its sub-Gaussian norm defined as $\Vert \mathit{X}{\Vert }_{{\psi }_2}={\sup }_{\mathit{v}\in {𝓑}_1(\mathbf{0})}{\Vert {\mathit{v}}^{\top }\mathit{X}\Vert }_{{\psi }_2}$. For any symmetric matrix $\mathbb{X}$, let ${\text{Λ}}_{\min }(\mathbb{X})$ and ${\text{Λ}}_{\max }(\mathbb{X})$ denote its minimum and maximum eigenvalue, respectively. For $a\in ℝ$, denote by $\mathrm{sign}(a)$ the sign of $a$, and for event $𝓔$, denote by $\mathbf{I}(𝓔)$ the indicator for $𝓔$. Denote by ${𝓢}_{\mu }=\left\{j:{\mu }_{0j}\ne 0\right\}$, ${𝓢}_{\alpha }=\left\{j:{\Vert {\mathit{\alpha }}_{0j}\Vert }_2\ne 0\right\}$, ${𝓢}_0={𝓢}_{\mu }\cup {𝓢}_{\alpha }$, ${𝓢}_{\text{full}}=\left\{{𝓢}_{\mu },{𝓢}_{\alpha }\right\}$, $s_{\mu }=\left|{𝓢}_{\mu }\right|$, $s_{\alpha }=\left|{𝓢}_{\alpha }\right|$ and $s_0=\left|{𝓢}_0\right|$. Let $f_1^{\prime }(a,y)=\partial f(a,y)/\partial a$ and $f_1^{″}(a,y)={\partial }^{2}f(a,y)/\partial a^2$. Also, let $\mathrm{ℍ}\left({\mathit{\beta }}^{(•)}\right)=N^{-1}\mathrm{bdiag}\left\{n_1{\mathrm{ℍ}}_1\left({\mathit{\beta }}^{(1)}\right),n_2{\mathrm{ℍ}}_2\left({\mathit{\beta }}^{(2)}\right),\dots ,n_M{\mathrm{ℍ}}_M\left({\mathit{\beta }}^{(\text{M})}\right)\right\}$, $\widehat{\mathrm{ℍ}}=\mathrm{ℍ}\left({\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(•)}\right)$, ${\overline{\mathrm{ℍ}}}_m\left({\mathit{\beta }}^{(\text{m})}\right)=\text{E}\left[{\mathrm{ℍ}}_m\left({\mathit{\beta }}^{(\text{m})}\right)\right]$, and ${\overline{\mathrm{ℍ}}}_m={\overline{\mathrm{ℍ}}}_m\left({\mathit{\beta }}_0^{(\text{m})}\right)$. Finally, we introduce the compatibility condition $\left({𝓒}_{\text{comp}}\right)$ as below.

Definition 1 (Compatibility Condition $\left({𝓒}_{\text{comp}}\right)$.

The Hessian matrix $\mathrm{ℍ}\left({\mathit{\beta }}^{(•)}\right)$ and the index set $𝓢$ satisfy the Compatibility Condition, if for all ${\left({\mathit{\mu }}_{\text{Δ}}^{\top },{\mathit{\alpha }}_{\text{Δ}}^{(•)\top }\right)}^{\top }={\left({\mathit{\mu }}_{\text{Δ}}^{\top },{\mathit{\alpha }}_{\text{Δ}}^{(1)\top },\dots ,{\mathit{\alpha }}_{\text{Δ}}^{(\text{M})\top }\right)}^{\top }\in 𝓒(t,𝓢)$ with any constant $t>0$, there exists a constant ${\varphi }_0\left\{t,𝓢,\mathrm{ℍ}\left({\mathit{\beta }}^{(•)}\right)\right\}$ such that,

$$\begin{gathered} {\left({\Vert {\mathit{\mu }}_{\text{Δ}}\Vert }_1+{\lambda }_g{\Vert {\mathit{\alpha }}_{\text{Δ}}^{(•)\top }\Vert }_{2,1}\right)}^2\le N^{-1}\sum _{m=1}^M{n}_m\left|𝓢\right|\Vert {\mathrm{ℍ}}_m^{1/2}\left({\mathit{\beta }}^{(\text{m})}\right) \\ \left({\mathit{\mu }}_{\text{Δ}}+{\mathit{\alpha }}_{\text{Δ}}^{(\text{m})}\right){\Vert }_2^2/{\varphi }_0\left\{t,𝓢,\mathrm{ℍ}\left({\mathit{\beta }}^{(•)}\right)\right\}, \end{gathered}$$

where $𝓒(t,𝓢)=\{{\left({\mathit{u}}^{\top },{\mathit{v}}^{(•)\top }\right)}^{\top }={\left({\mathit{u}}^{\top },{\mathit{v}}^{(1)\top },\dots ,{\mathit{v}}^{(\text{M})\top }\right)}^{\top }:{\mathit{v}}^{(1)}+\cdots +{\mathit{v}}^{(\text{M})}=\mathbf{0},{\Vert {\mathit{u}}_{{𝓢}^c}\Vert }_1+{\lambda }_g{\Vert {\mathit{v}}_{{𝓢}^c}^{(•)}\Vert }_{2,1}\le t\left({\Vert {\mathit{u}}_{𝓢}\Vert }_1+{\lambda }_g{\Vert {\mathit{v}}_{𝓢}^{(•)}\Vert }_{2,1}\right)\}$, and ${\varphi }_0\left\{t,𝓢,\mathrm{ℍ}\left({\mathit{\beta }}^{(•)}\right)\right\}$ represents the compatibility constant of $\mathrm{ℍ}\left({\mathit{\beta }}^{(•)}\right)$ on the set $𝓢$.

4.2. Prediction and Estimation Consistency

To establish theoretical properties of the SHIR estimators in terms of estimation and prediction risks, we first introduce some sufficient conditions. Throughout the following analysis, we assume that $n_m=\text{Θ}(N/M)$ for $m\in [M]$ and ${\lambda }_g=\text{Θ}\left(M^{-1/2}\right)$

Condition 1.

There exists an absolute constant ${\varphi }_0>0$ such that for all ${\delta }_1=\text{Θ}\left\{{\left(s_{0}M\log p/N\right)}^{1/2}\right\}$, ${\mathit{\beta }}^{(•)}={\left({\mathit{\beta }}^{(1)\top },\dots ,{\mathit{\beta }}^{(\text{M})\top }\right)}^{\top }$ satisfying ${\mathit{\beta }}^{(\text{m})}\in {𝓑}_{{\delta }_1}\left({\mathit{\beta }}_0^{(\text{m})}\right)$, the Hessian matrices $\mathrm{ℍ}\left({\mathit{\beta }}^{(•)}\right)$ and the index set ${𝓢}_0$ satisfy ${𝓒}_{\text{comp}}$ (Definition 1) with compatibility constant ${\varphi }_0\left\{t,{𝓢}_0,\mathrm{ℍ}\left({\mathit{\beta }}^{(•)}\right)\right\}\ge {\varphi }_0$.

Condition 2.

For all $m\in [M]$, $X_{ij}^{(\text{m})}{f}_1^{\prime }\left({\mathit{\beta }}_0^{(\text{m})\text{T}}{\mathbf{X}}_i^{(\text{m})},Y_i^{(\text{m})}\right)$ is sub-Gaussian, that is, there exists some positive constant $\kappa =\text{Θ}(1)$ such that ${\Vert X_{ij}^{(\text{m})}{f}_1^{\prime }\left({\mathit{\beta }}_0^{(\text{m})\top }{\mathbf{X}}_i^{(\text{m})},Y_i^{(\text{m})}\right)\Vert }_{{\psi }_2}<\kappa$. In addition, there exists $B>0$ such that ${\max }_{m\in [M],i\in \left[n_m\right]}{\Vert {\mathbf{X}}_i^{(\text{m})}\Vert }_{\infty }\le B$.

Condition 3.

There exists positive $C_L=\text{Θ}(1)$ such that $\left|f_1^{″}(a,y)-f_1^{″}(b,y)\right|\le C_L|a-b|$ for all $a,b\in \mathrm{ℝ}$.

Remark 5.

Condition 1 is in a similar spirit as the restricted eigenvalue or restricted strong convexity condition introduced by Negahban et al. (2012). The first part of Condition 2 controls the tail behavior of $X_{ij}^{(\text{m})}{f}_1^{\prime }(a,y)$ so that the random error $\nabla {\widehat{𝓛}}_m\left({\mathit{\beta }}_0^{(\text{m})}\right)$ can be bounded properly and the method could be benefited from the group sparsity of ${\mathit{\alpha }}^{(•)}$ (Huang and Zhang 2010). This condition can be easily verified for sub-Gaussian design and an extensive class of models, for example, the logistic model. In addition, the condition ${\max }_{m\in [M],i\in \left[n_m\right]}{\Vert {\mathbf{X}}_i^{(\text{m})}\Vert }_{\infty }\le B$ holds for bounded design with $B=\text{Θ}(1)$ and for subGaussian design with $B=\text{Θ}\left[{\{\log (pN)\}}^{1/2}\right]$ Condition 3 assumes a smooth function $f$ to guarantee that the empirical Hessian matrix ${\nabla }^2{\widehat{𝓛}}_m\left({\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}\right)$ is close enough to ${\nabla }^2{\widehat{𝓛}}_m\left({\mathit{\beta }}_0^{(\text{m})}\right)$, and the term ${\widehat{\mathbf{g}}}_m=\left[{\widehat{ℍ}}_m{\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}-\nabla {\widehat{𝓛}}_m\left({\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}\right)\right]$ is close enough to $\left[{\nabla }^2{\widehat{𝓛}}_m\left({\mathit{\beta }}_0^{(\text{m})}\right){\mathit{\beta }}_0^{(\text{m})}-\nabla {\widehat{𝓛}}_m\left({\mathit{\beta }}_0^{(\text{m})}\right)\right]$.

The following Proposition 1 illustrates that for sub-Gaussian weighted design with regular Hessian matrix, Condition 1 (Compatibility Condition) holds with probability approaching 1. This can be viewed as an extension of the existing results, that is, sub-Gaussian design and linear model with lasso penalty (Rivasplata 2012), to our case with nonlinear model and the mixture penalty. We present the proof of Proposition 1 in Section A.1 of the supplementary material.

Proposition 1.

Assume that $s_0=o\{N/(M\log p)\}$ and Condition 3 holds. Assume in addition that there exists absolute constants ${\kappa }_x$, $C_x>0$, such that for all $m\in [M]$, $C_x^{-1}\le {\text{Λ}}_{\min }\left({\overline{\mathrm{ℍ}}}_m\right)\le {\text{Λ}}_{\max }\left({\overline{\mathrm{ℍ}}}_m\right)\le C_x$, ${\max }_{\mathbf{x}\in {𝓑}_1(\mathbf{0})}\text{E}{\left[{\mathbf{x}}^{\top }{\mathbf{X}}_i^{(\text{m})}\right]}^4\le C_x$ and for any ${\delta }_1=\text{Θ}\left\{{\left(s_{0}M\log p/N\right)}^{1/2}\right\}$ and ${\mathit{\beta }}^{(\text{m})}\in {𝓑}_{{\delta }_1}\left({\mathit{\beta }}_0^{(\text{m})}\right)$, ${\Vert {\mathbf{X}}_i^{(\text{m})}{\left\{f_1^{″}\left({\mathit{\beta }}^{(\text{m})\top }{\mathbf{X}}_i,Y_i^{(\text{m})}\right)\right\}}^{1/2}\Vert }_{{\psi }_2}\le {\kappa }_x$. Then we have that, Condition 1 is satisfied with probability approaching 1.

Remark 6.

As an important example in practice, it is not hard to verify that, for logistic models with $f(a,y)=ya-\log \left(1+e^a\right)$, and sub-Gaussian covariates ${\mathbf{X}}_i^{(\text{m})}$, the key assumption on the weighted design required in Proposition 1, ${\Vert {\mathbf{X}}_i^{(\text{m})}{\left\{f_1^{″}\left({\mathit{\beta }}^{(\text{m})\text{T}}{\mathbf{X}}_i,Y_i^{(\text{m})}\right)\right\}}^{1/2}\Vert }_{{\psi }_2}\le {\kappa }_x$, is satisfied.

We further assume in Condition 4 that the local LASSO estimators achieve the minimax optimal error rates to a logarithmic scale (Raskutti, Wainwright, and Yu 2011; Negahban et al. 2012).

Condition 4.

The local estimators satisfy that ${\max }_{m\in [M]}\Vert {\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}-{\mathit{\beta }}_0^{(\text{m})}{\Vert }_1=O_{\text{P}}\left\{s_0{\left(\log p/n_m\right)}^{1/2}\right\}$, and ${\max }_{m\in [M]}\Vert {\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}-{\mathit{\beta }}_0^{(\text{m})}{\Vert }_2\asymp {\max }_{m\in [M]}\Vert {\mathbb{X}}^{(\text{m})}\left({\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}-{\mathit{\beta }}_0^{(\text{m})}\right){\Vert }_2=O_{\text{P}}\left\{{\left(s_0\log p/n_m\right)}^{1/2}\right\}$.

Remark 7.

Extensive literatures, such as Van de Geer et al. (2008), Bühlmann and Van De Geer (2011), and Negahban et al. (2012), have established a complete theoretical framework regarding to this property. See, for example, Negahban et al. (2012), in which Condition 4 can be proved for strongly convex loss function $f$.

Next, we present the risk bounds for the SHIR including the prediction risk ${\Vert {\widehat{\mathrm{ℍ}}}^{1/2}\left({\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(•)}-{\mathit{\beta }}_0^{(•)}\right)\Vert }_2$ and estimation risk ${\Vert {\widehat{\mathit{\mu }}}_{\text{SHIR}}-{\mathit{\mu }}_0\Vert }_1+{\lambda }_g{\Vert {\widehat{\mathit{\alpha }}}_{\text{SHIR}}^{(•)}-{\mathit{\alpha }}_0^{(•)}\Vert }_{2,1}$.

Theorem 1 (Risk bounds for the SHIR).

Under Conditions 1–4, there exists $\lambda =\text{Θ}\left({\{(\log p+M)/N\}}^{1/2}+B{s}_{0}M\log p/N\right)$ and ${\lambda }_g=\text{Θ}\left(M^{-1/2}\right)$ such that

$$\begin{gathered} {\Vert {\widehat{\mathrm{ℍ}}}^{1/2}\left({\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(•)}-{\mathit{\beta }}_0^{(•)}\right)\Vert }_2=O_{\text{P}}({\left\{s_0(\log p+M)/N\right\}}^{1/2} \\ +B{s}_0^{3/2}M\log p/N); \end{gathered}$$

$$\begin{gathered} {\Vert {\widehat{\mathit{\mu }}}_{\text{SHIR}}-{\mathit{\mu }}_0\Vert }_1+{\lambda }_g{\Vert {\widehat{\mathit{\alpha }}}_{\text{SHIR}}^{(•)}-{\mathit{\alpha }}_0^{(•)}\Vert }_{2,1} \\ =O_{\text{P}}\left(s_0{\{(\log p+M)/N\}}^{1/2}+B{s}_0^{2}M\log p/N\right). \end{gathered}$$

Note that, in Theorem 1, the rate of the penalty coefficient for $\sum _{j=2}^p{\Vert {\mathit{\alpha }}_j\Vert }_2$ is $\lambda {\lambda }_g=\text{Θ}\left[{\{(\log p+M)/NM\}}^{1/2}+B{M}^{1/2}{s}_0\log p/N\right]$. The second term in each of the upper bounds of Theorem 1 is the error incurred by aggregation noise of derived data instead of raw data. These terms are asymptotically negligible under sparsity as $s_0=o\left({\{N(\log p+M)\}}^{1/2}/[BM\log p]\right)$. Then ${\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(•)}$ achieves the same error rate as the ideal estimator ${\widehat{\mathit{\beta }}}_{\text{IPDpool}}^{(•)}$ obtained by combining raw data as shown in the following section, and is nearly rate optimal.

4.3. Asymptotic Equivalence in Prediction and Estimation

Under specific sparsity assumptions, we show the asymptotic equivalence, with respect to prediction and estimation risks, of the SHIR and the ideal IPDpool estimator ${\widehat{\mathit{\beta }}}_{\text{IPDpool}}^{(•)}$ or alternatively defined as

$$\begin{gathered} \left({\widehat{\mathit{\mu }}}_{\text{IPDpool}},{\widehat{\mathit{\alpha }}}_{\text{IPDpool}}^{(•)}\right)=\underset{\left(\mathit{\mu },{\mathit{\alpha }}^{(•)}\right)}{\mathrm{argmin}}\widehat{𝓛}\left(\mathit{\mu },{\mathit{\alpha }}^{(•)}\right)+\tilde{\lambda }\rho \left(\mathit{\mu },{\mathit{\alpha }}^{(•)};{\lambda }_g\right), \\ \text{s.t.}{\mathbf{1}}_{M\times 1}^{\top }{\mathit{\alpha }}_j=0,j\in [p], \end{gathered}$$

where $\tilde{\lambda }$ is a tuning parameter.

Theorem 2.

(Asymptotic Equivalence) Under assumptions in Theorem 1 and assume $s_0=o\left({\{N(\log p+M)\}}^{1/2}/[BM\log p]\right)$, there exists $\tilde{\lambda }=\text{Θ}{\{(\log p+M)/N\}}^{1/2}$ and ${\lambda }_g=\text{Θ}\left(M^{-1/2}\right)$ such that the IPDpool estimator ${\widehat{\mathit{\beta }}}_{\text{IPDpool}}^{(•)}$ satisfies

$$\begin{gathered} {\Vert {\widehat{\mathrm{ℍ}}}^{1/2}\left({\widehat{\mathit{\beta }}}_{\text{IPDpool}}^{(•)}-{\mathit{\beta }}_0^{(•)}\right)\Vert }_2=O_{\text{P}}\left({\left\{s_0(\log p+M)/N\right\}}^{1/2}\right); \\ {\Vert {\widehat{\mathit{\mu }}}_{\text{IPDpool}}-{\mathit{\mu }}_0\Vert }_1+{\lambda }_g{\Vert {\widehat{\mathit{\alpha }}}_{\text{IPDpool}}^{(•)}-{\mathit{\alpha }}_0^{(•)}\Vert }_{2,1} \\ =O_{\text{P}}\left(s_0{\{(\log p+M)/N\}}^{1/2}\right). \end{gathered}$$

Furthermore, for some ${\lambda }_{\text{Δ}}=o(\tilde{\lambda })$, the IPDpool and the SHIR defined by (3) with $\lambda =\tilde{\lambda }+{\lambda }_{\text{Δ}}$ are equivalent in prediction and estimation in the sense that

$$\begin{gathered} {\Vert {\widehat{\mathrm{ℍ}}}^{1/2}\left({\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(•)}-{\mathit{\beta }}_0^{(•)}\right)\Vert }_2\le \Vert {\widehat{\mathrm{ℍ}}}^{1/2}({\widehat{\mathit{\beta }}}_{\text{IPDpool}}^{(•)} \\ -{\mathit{\beta }}_0^{(•)}){\Vert }_2+o_{\text{P}}\left({\left\{s_0(\log p+M)/N\right\}}^{1/2}\right); \\ {\Vert {\widehat{\mathit{\mu }}}_{\text{SHIR}}-{\mathit{\mu }}_0\Vert }_1+{\lambda }_g{\Vert {\widehat{\mathit{\alpha }}}_{\text{SHIR}}^{(•)}-{\mathit{\alpha }}_0^{(•)}\Vert }_{2,1}\le {\Vert {\widehat{\mathit{\mu }}}_{\text{IPDpool}}-{\mathit{\mu }}_0\Vert }_1 \\ +{\lambda }_g{\Vert {\widehat{\mathit{\alpha }}}_{\text{IPDpool}}^{(•)}-{\mathit{\alpha }}_0^{(•)}\Vert }_{2,1}+o_{\text{P}}\left(s_0{\{(\log p+M)/N\}}^{1/2}\right). \end{gathered}$$

Theorem 2 demonstrates the asymptotic equivalence between ${\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(•)}$ and ${\widehat{\mathit{\beta }}}_{\text{IPDpool}}^{(•)}$ with respect to estimation and prediction risks, and hence implies the optimality of the SHIR. Specifically, when $s_0=o\left({\{N(\log p+M)\}}^{1/2}/[BM\log p]\right)$, the excess risks of ${\widehat{\mathit{\beta }}}_{\text{SHIR}}^{(•)}$ compared to ${\widehat{\mathit{\beta }}}_{\text{IPDpool}}^{(•)}$ are of smaller order than those of IPDpool, that is, the minimax optimal rates (up to a logarithmic scale) for multi-task learning of high-dimensional sparse model (Huang and Zhang 2010; Lounici et al. 2011). Similar equivalence results was given in Theorem 4.8 of Battey et al. (2018) for the truncated debiased LASSO estimator. However, to the best of our knowledge, in the existing literatures, such results have not been established yet for the LASSO-type estimators obtained directly from a sparse regression model. Compared with Battey et al. (2018), our result does not require the Hessian matrix ${\widehat{\mathrm{ℍ}}}_m$ to have a sparse inverse since we do not actually rely on the debiasing of ${\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}$. Consequently, the proofs of Theorem 2 are much more involved than those in Battey et al. (2018). The new technical skills are developed and presented in detail in the supplementary material.

4.4. Comparison With the Debiasing-based Strategy

To compare to existing approaches, we next consider an extension of the debiased LASSO-based procedures proposed in Lee et al. (2017) and Battey et al. (2018) to incorporating between study heterogeneity. Specifically, at the $m\text{th}$ site, we derive the debiased LASSO estimator ${\widehat{\mathit{\beta }}}_{\text{dLASSO}}^{(\text{m})}$ as defined in (4) and send it to the central site, where ${\widehat{\mathbf{\text{Θ}}}}_m$ is obtained via nodewise LASSO (Javanmard and Montanari 2014). At the central site, compute ${\widehat{\mathit{\mu }}}_{\text{dLASSO}}=M^{-1}\sum _{m=1}^M{\widehat{\mathit{\beta }}}_{\text{dLASSO}}^{(\text{m})}$, ${\widehat{\mathit{\alpha }}}_{\text{dLASSO}}^{(\text{m})}={\widehat{\mathit{\beta }}}_{\text{dLASSO}}^{(\text{m})}-{\widehat{\mathit{\mu }}}_{\text{dLASSO}}$ and ${\widehat{\mathit{\alpha }}}_{\text{dLASSO}}^{(•)}={\left({\widehat{\mathit{\alpha }}}_{\text{dLASSO}}^{(1)},\dots ,{\widehat{\mathit{\alpha }}}_{\text{dLASSO}}^{(\text{M})}\right)}^{\top }$. The final estimator for $\mathit{\mu }$ and $\mathit{\alpha }$ can be obtained by thresholding ${\widehat{\mathit{\mu }}}_{\text{dLASSO}}$ and ${\widehat{\mathit{\alpha }}}_{\text{dLASSO}}^{(•)}$ as ${\widehat{\mathit{\mu }}}_{\text{L\&B}}={𝓣}_{\mu }\left({\widehat{\mathit{\mu }}}_{\text{dLASSO}};{\tau }_1\right)$ and ${\widehat{\mathit{\alpha }}}_{\text{L\&B}}^{(•)}={𝓣}_{\alpha }\left({\widehat{\mathit{\alpha }}}_{\text{dLASSO}}^{(•)};{\mu }_2\right)$, by Lee et al. (2017) and Battey et al. (2018), where

$$\begin{gathered} {𝓣}_{\mu }\left(\mathit{\mu };{\tau }_1\right)={\left\{{\mu }_1,{\mu }_2^{h_{+}}\left({\tau }_1\right),\dots ,{\mu }_p^{h_{+}}\left({\tau }_1\right)\right\}}^{\top }\text{or} \\ {\left\{{\mu }_1,{\mu }_2^{s_{+}}\left({\tau }_1\right),\dots ,{\mu }_p^{s_{+}}\left({\tau }_1\right)\right\}}^{\top } \\ {𝓣}_{\alpha }\left({\mathit{\alpha }}^{(•)};{\tau }_2\right)=\mathrm{vec}\left\{{\left[{\mathit{\alpha }}_1,{\mathit{\alpha }}_2^{h_{+}}\left({\tau }_2\right),\dots {\mathit{\alpha }}_p^{h_{+}}\left({\tau }_2\right)\right]}^{\top }\right\}\text{or} \\ \mathrm{vec}\left\{{\left[{\mathit{\alpha }}_1,{\mathit{\alpha }}_2^{s_{+}}\left({\tau }_2\right),\dots {\mathit{\alpha }}_p^{s_{+}}\left({\tau }_2\right)\right]}^{\top }\right\}, \end{gathered}$$

for any vector $\mathbf{x}={\left(x_1,\dots ,x_d\right)}^{\top }$ and constant $\tau$, ${\mathbf{x}}^{h_{+}}=\mathbf{x}I\left(\Vert \mathbf{x}{\Vert }_2>\tau \right)$ and ${\mathbf{x}}^{s_{+}}=\mathbf{x}\left(1-\Vert \mathbf{x}{\Vert }_2^{-1}\tau \right)I\left(\Vert \mathbf{x}{\Vert }_2>\tau \right)$ respectively denote the hard and soft thresholded counterparts of $\mathbf{x}$, and $\mathrm{vec}(\mathbb{A})$ vectorize the matrix $\mathbb{A}$ by column.

The error rates of $\left\{{\widehat{\mathit{\mu }}}_{\text{L\&B}},{\widehat{\mathit{\alpha }}}_{\text{L\&B}}^{(•)}\right\}$ can be derived by extending Lee et al. (2017) and Battey et al. (2018). We outline the results below and provide details in Section A.3.4 of the supplementary material. Denote by ${\overline{\mathrm{ℍ}}}_m\left({\mathit{\beta }}^{(\text{m})}\right)=\text{E}\left[{\mathrm{ℍ}}_m\left({\mathit{\beta }}^{(\text{m})}\right)\right]$, ${\overline{\mathrm{ℍ}}}_m={\overline{\mathrm{ℍ}}}_m\left({\mathit{\beta }}_0^{(\text{m})}\right)$, ${\overline{\mathbf{\text{Θ}}}}_m={\left\{{\overline{\theta }}_{mj\ell }\right\}}_{p\times p}={\overline{\mathrm{ℍ}}}_m^{-1}$ and $s_1={\max }_{m\in [M]j\in [p]}\left|\left\{\ell \ne j:{\overline{\theta }}_{mj\ell }\ne 0\right\}\right|$. Then in analog to Theorem 1, one can obtain that

$${\Vert {\widehat{\mathit{\mu }}}_{\text{L\&B}}^{(•)}-{\mathit{\mu }}_0\Vert }_1+{\lambda }_g{\Vert {\widehat{\mathit{\alpha }}}_{\text{L\&B}}^{(•)}-{\mathit{\alpha }}_0^{(•)}\Vert }_{2,1}$$ (5)

$$=O_{\text{P}}\left(s_0{\{(\log p+M)/N\}}^{1/2}+B{s}_0\left(s_0+s_1\right)M\log p/N\right),$$ (6)

where $B$ is as defined in Condition 2. Compared with the error rates of SHIR as presented in Theorem 1, $\left\{{\widehat{\mathit{\mu }}}_{\text{L\&B}},{\widehat{\mathit{\alpha }}}_{\text{L\&B}}^{(•)}\right\}$ shares the same “first term”, $s_0{\{(\log p+M)/N\}}^{1/2}$, representing the error of an individual-level empirical process. However, its second term incurred by data aggregation can be larger than that of SHIR as $s_1=\omega \left(s_0\right)$, which could happen due to the complex design in practice.

In addition, SHIR could be more efficient than the debiasing-based strategy even when the impact of the additional error term, which depends on $s_1$ in (6), is asymptotically negligible. Consider the setting when all ${\mathit{\beta }}^{(\text{m})}$’s are the same, that is, ${\mathit{\beta }}^{(\text{m})}=\mathit{\beta }$, and $p$ is moderate or small so that the regularization is unnecessary and the maximum likelihood estimator (MLE) for $\mathit{\beta }$ is feasible and asymptotically Gaussian. In this case, SHIR can be viewed as the inverse variance weight estimation with asymptotic variance ${\mathbf{\Sigma }}_{\text{SHIR}}={\left\{\sum _{m=1}^M{n}_m{\overline{\mathbf{\text{Θ}}}}_m^{-1}\right\}}^{-1}$, while the debiasing-based approach outputs an estimator of variance ${\mathbf{\Sigma }}_{\text{L\&B}}=M^{-2}\sum _{m=1}^M{n}_m^{-1}{\overline{\mathbf{\text{Θ}}}}_m$. It is not hard to show that ${\mathbf{\text{Σ}}}_{\text{SHIR}}⪯{\mathbf{\text{Σ}}}_{\text{L\&B}}$, where the equality holds only if all ${\overline{\mathbf{\text{Θ}}}}_m$’s are in certain proportion. Thus, SHIR is strictly more efficient than debiasing-based approach under the low-dimensional setting with heterogeneous ${\overline{\mathbf{\text{Θ}}}}_m$, which commonly arises in metaanalysis as the distributions of ${\mathbb{X}}^{(\text{m})}$’s are typically heterogeneous across the local sites. In the high-dimensional setting, similarly, SHIR is expected to benefit from the “inverse variance weight” construction, and our simulation results in Section 5 support this point.

4.5. Sparsistency

In this section, we present theoretical results concerning the variable selection consistency of the SHIR. We begin with some extra sufficient conditions for the sparsistency result.

Condition 5.

For all ${\delta }_2=\text{Θ}\left\{{\left(s_{0}M\log p/N\right)}^{1/2}\right\}$ and ${\mathit{\beta }}^{(\text{m})}$ satisfying ${\mathit{\beta }}^{(\text{m})}\in {𝓑}_{{\delta }_2}\left({\mathit{\beta }}_0^{(\text{m})}\right)$, there exists $C_{\min }=\text{Θ}(1)$ such that ${\text{Λ}}_{\min }\left\{{\mathrm{ℍ}}_{m,{𝓢}_0}\left({\mathit{\beta }}^{(\text{m})}\right)\right\}>C_{\min }$, where ${\mathrm{ℍ}}_{m,{𝓢}_0}\left({\mathit{\beta }}^{(\text{m})}\right)$ denotes the submatrix of ${\mathrm{ℍ}}_m\left({\mathit{\beta }}^{(\text{m})}\right)$ with its rows and columns corresponding to ${𝓢}_0$.

Condition 6.

For all ${\delta }_3=\text{Θ}\left\{{\left(s_{0}M\log p/N\right)}^{1/2}\right\}$ and ${\mathit{\beta }}^{(•)}={\left({\mathit{\beta }}^{(1)\top },\dots ,{\mathit{\beta }}^{(\text{M})\top }\right)}^{\top }$ satisfying ${\mathit{\beta }}^{(\text{m})}\in {𝓑}_{{\delta }_3}\left({\mathit{\beta }}_0^{(\text{m})}\right)$, the weighted design matrix $\mathbb{W}\left({\mathit{\beta }}^{(•)}\right)$ satisfies the Irrepresentable Condition ${𝓒}_{\text{Irrep}}$ on ${𝓢}_{\text{full}}$ with parameter $ϵ>0$, where $\mathbb{W}\left({\mathit{\beta }}^{(•)}\right)$ is defined in Section A.2 and ${𝓒}_{\text{Irrep}}$ is given in Definition A2 of the supplementary material.

Condition 7.

Let $v=\min \{{\min }_{j\in {𝓢}_{\mu }}\left|{\mu }_{0j}\right|,M^{-1/2}{\min }_{j\in {𝓢}_{\alpha }}{\Vert {\mathit{\alpha }}_{0j}\Vert }_2\}$. For the $ϵ$ defined in Condition 6, $[\{s_0(\log p+M)/N{\}}^{1/2}+B{s}_0^{3/2}M\log p/N]/(vϵ)\to 0$, as $N\to \infty$.

Remark 8.

Conditions 5–7 are sparsistency assumptions similar to those of Zhao and Yu (2006) and Nardi et al. (2008). Condition 5 requires the eigenvalues for the covariance matrix of the weighted design matrix corresponding to ${𝓢}_0$ to be bounded away from zero, so that its inverse behaves well. Condition 6 adopts the commonly used Irrepresentable Condition (Zhao and Yu 2006) to our mixture penalty setting. Roughly speaking, it requires that the weighted design corresponding to ${𝓢}_{\text{full}}$ cannot be represented well by the weighted design for ${𝓢}_{\text{full}}^c$. Compared to Nardi et al. (2008), ${𝓒}_{\text{Irrep}}$ is less intuitive but essentially weaker. We justify such condition on several common correlation structures and compare it with Zhao and Yu (2006) in Section A.2 of the supplementary material. Condition 7 assumes that the minimum magnitude of the coefficients is large enough to make the nonzero coefficients recognizable. It requires essentially weaker assumption on the minimum magnitude than local LASSO (Zhao and Yu 2006). This is because we leverage the group structure of ${\mathit{\beta }}_0^{(\text{m})}$’s to improve the efficiency of variable selection.

Theorem 3.

(Sparsistency) Let ${\widehat{𝓢}}_{\mu }=\left\{j:{\widehat{\mu }}_{\text{SHIR},j}\ne 0\right\}$ and ${\widehat{𝓢}}_{\alpha }=\left\{j:{\Vert {\widehat{\mathit{\alpha }}}_{\text{SHIR},j}\Vert }_2\ne 0\right\}$. Denote by the event ${𝓞}_{\mu }=\left\{{\widehat{𝓢}}_{\mu }={𝓢}_{\mu }\right\}$ and ${𝓞}_{\alpha }=\left\{{\widehat{𝓢}}_{\alpha }={𝓢}_{\alpha }\right\}$. Under Conditions 1–7 and assume that

$$\lambda =o\left(v/s_0^{1/2}\right)\text{and}$$

$$\lambda ={ϵ}^{-1}\omega \left({\{(\log p+M)/N\}}^{1/2}+B{s}_{0}M\log p/N\right),$$

we have $\text{P}\left({𝓞}_{\mu }\cap {𝓞}_{\alpha }\right)\to 1$ as $N\to \infty$.

Theorem 3 establishs the sparsistency of SHIR. When $s_0=o\left({\{N(\log p+M)\}}^{1/2}/[BM\log p]\right)$, Condition 7 turns out to be $vϵ=\omega \left({\left\{s_0(\log p+M)/N\right\}}^{1/2}\right)$, the corresponding sparsistency assumption for the IPDpool estimator. In contrast, a similar condition, which could be as strong as $vϵ=\omega \left\{{\left(s_{0}M\log p/N\right)}^{1/2}\right\}$, is required for the local LASSO estimator (Zhao and Yu 2006). Compared with the local one, our integrative analysis procedure can recognize smaller signal under some sparsity assumptions. In this sense, the structure of ${\mathit{\beta }}_0^{(•)}$ helps us to improve the selection efficiency over the local LASSO estimator. Different from the existing work, we need carefully address the mixture penalty $\rho$ and the aggregation noise of the SHIR, which introduce technical difficulties to our theoretical analysis.

In both Theorems 2 and 3, we allow $M$, the number of studies, to diverge while still preserving theoretical properties. The growing rate of $M$ is allowed to be

$$M=\min \left(o\left\{{(N/\log p)}^{1/2}/\left(B{s}_0\right)\right\},o\left\{N/{\left(B{s}_0\log p\right)}^2\right\}\right)$$

for the equivalence result in Theorem 2 and

$$M=\min \left(o\left\{Nϵv/\left(B{s}_0^{3/2}\log p\right)\right\},o\left\{N{(ϵ\nu )}^2/s_0\right\}\right)$$

for the sparsistency result in Theorem 3.

5. Simulation Study

We present simulation results in this section to evaluate the performance of our proposed SHIR estimator and compare it with several other approaches. The simulation codes are available at https://github.com/moleibobliu/SHIR. Let $M\in \{4,8\}$ and $p\in \{100,800,1500\}$ and set $n_m=n=400$ for each $m$. For each configuration, we summarize results based on 200 simulated datasets. We consider three data-generating mechanisms:

1. Sparse precision and correctly specified model (strong and sparse signal): Across all studies, let ${𝓢}_{\mu }=\{1,2,\dots ,6\}$ for $\mathit{\mu },{𝓢}_{\alpha }=\{3,4,\dots ,8\}$ for $\mathit{\alpha },𝓢={𝓢}_{\mu }\cup {𝓢}_{\alpha }$ and ${𝓢}^c=[p]\backslash 𝓢$. For each $m\in [M]$, we generate ${\mathbf{X}}^{(\text{m})}$ from a zero-mean multivariate normal distribution with covariance ${\text{ℂ}}^{(\text{m})}$, where ${\text{ℂ}}_{{𝓢}^c{𝓢}^c}^{(\text{m})}={ℝ}_{p-8}\left(r_m\right)$, ${\text{ℂ}}_{{𝓢}^c𝓢}^{(\text{m})}={ℝ}_{p-8}\left(r_m\right){\mathbf{\text{Γ}}}_{p-8,8}\left(r_m,15\right)$, ${\text{ℂ}}_{𝓢𝓢}^{(m)}={\mathbb{I}}_8+{\mathbf{\text{Γ}}}_{p-8,8}^{\top }\left(r_m,15\right){ℝ}_{p-8}\left(r_m\right){\mathbf{\text{Γ}}}_{p-8,8}\left(r_m,15\right)$, ${\mathbb{I}}_q$ denotes the $q\times q$ identity matrix, ${ℝ}_q(r)$ denotes the $q\times q$ correlation matrix of AR(1) with correlation coefficient $r$, ${\mathbf{\text{Γ}}}_{q_1,q_2}\left(r,s_1\right)$ denotes the $q_1\times q_2$ matrix with each of its column having randomly picked $s_1$ entries set as $r$ or $-r$ in random and the remaining being 0, and $r_m=0.4(m-1)/M+0.15$. Given ${\mathbf{X}}^{(\text{m})}$, we generate $Y^{(\text{m})}$ from the logistic model $P\left(Y^{(\text{m})}=1\mid {\mathbf{X}}^{(\text{m})}\right)=\mathrm{expit}\left\{{\mathbf{X}}_{{𝓢}_{\mu }}^{(\text{m})\top }{\mathit{\mu }}_{{𝓢}_{\mu }}+{\mathbf{X}}_{{𝓢}_{\alpha }}^{{(\text{m})}^{\top }}{\alpha }_{{𝓢}_{\alpha }}^{(\text{m})}\right\}$ with ${\mathit{\mu }}_{{𝓢}_{\mu }}=0.5{(1,-1,1,-1,1,-1)}^{\top }$ and ${\mathit{\alpha }}_{{𝓢}_{\alpha }}^{(m)}=0.35{(-1)}^m\cdot {(1,1,1,-1,-1,-1)}^{\top }$.

2. Sparse precision and correctly specified model (weak and sparse signal): Use the same data-generation mechanism as in (i) but relatively weak signals ${\mathit{\mu }}_{{𝓢}_{\mu }}=0.2{(1,-1,1,-1,1,-1)}^{\top }$ and ${\mathit{\alpha }}_{{𝓢}_{\alpha }}^{(m)}=0.15{(-1)}^m\cdot {(1,1,1,-1,-1,-1)}^{\top }$.

3. Sparse precision and correctly specified model (strong and dense signal): Use the same mechanism as in (i) but denser supports: ${𝓢}_{\mu }=\{1,2,\dots ,18\}$, and ${𝓢}_{\alpha }=\{7,8,\dots ,24\}$, and more heterogeneous coefficients across the sites (see their specific values in Section A.5 of the supplementary material).

4. Sparse precision and correctly specified model (weak and dense signal): Use the same mechanism as in (iii) but weaker signals (see Section A.5 of the supplementary material).

5. Dense precision and wrongly specified model: Let $𝓢=\{1,2,\dots ,5\}$, ${𝓢}^{\prime }=\{6,\dots ,50\}$, and ${𝓢}^{″}=[p]\backslash \left(𝓢\cup {𝓢}^{\prime }\right)$. For each $m\in [M]\text{,}$, we generate ${\mathbf{X}}^{(m)}$ from zero-mean multivariate normal with covariance matrix ${\text{ℂ}}^{(\text{m})}$, where ${\text{ℂ}}_{\left({𝓢}^{\prime }\cup {𝓢}^{″}\right)\left({𝓢}^{\prime }\cup {𝓢}^{″}\right)}^{(m)}=\mathrm{bdiag}\left\{{ℝ}_{45}\left(r_m\right),{ℝ}_{p-50}\left(r_m\right)\right\}$, ${\text{ℂ}}_{𝓢{𝓢}^{″}}^{(\text{m})}=\mathbf{0},{\text{ℂ}}_{{𝓢}^{\prime }𝓢}^{(\text{m})}={ℝ}_{45}\left(r_m\right){\mathbf{\text{Γ}}}_{45,5}\left(r_m,45\right)$ and ${\text{ℂ}}_{𝓢𝓢}^{(\text{m})}={\mathbb{I}}_5+{\mathbf{\text{Γ}}}_{45,5}^{\top }\left(r_m,45\right){ℝ}_{45}\left(r_m\right){\mathbf{\text{Γ}}}_{45,5}\left(r_m,45\right)$. Given ${\mathbf{X}}^{(\text{m})}$, we generate $Y^{(\text{m})}$ from a logistic model with $P\left(Y^{(\text{m})}=1\mid {\mathbf{X}}^{(m)}\right)=\mathrm{expit}\left\{\sum _{j=1}^5\left\{0.25+0.15{(-1)}^m\right\}\left\{X_j^{(\text{m})}+0.2{\left(X_j^{(\text{m})}\right)}^3\right\}+0.1\sum _{j=1}^4{X}_j^{(\text{m})}{X}_{j+1}^{(\text{m})}\right\}$.

Across all settings, the distributions of ${\mathbf{X}}^{(\text{m})}$ and model parameters of $Y^{(\text{m})}\mid {\mathbf{X}}^{(\text{m})}$ differ across the $M$ sites, which mimic the heterogeneity of the covariates and models. The heterogeneity of ${\mathbf{X}}^{(\text{m})}$ is driven by the study-specific correlation coefficient $r_m$ in its covariance matrix ${\text{ℂ}}^{(m)}$. Under Settings (i)–(iv), the fitted logistic loss corresponds to the likelihood under a correctly specified model with the support of $\mathit{\mu }$ and that of ${\mathit{\alpha }}^{(\text{m})}$ overlapping but not exactly the same. Under Setting (v), the fitted loss corresponds to a misspecified model but the true target parameter ${\mathit{\beta }}^{(\text{m})}$ remains approximately sparse with only first 5 elements being relatively large, 45 close to zero and remaining exactly zero. For each $j\in 𝓢$, there are 15 nonzero coefficients on average in the $j\text{th}$ column of the precision ${\mathbf{\Theta }}_m$ under Settings (i)–(iv), and 45 nonzero coefficients under Setting (v). So we can use Settings (i)–(iv) to simulate the scenario with sparse precision on the active set and use Setting (v) to simulate relatively dense precision.

For each simulated dataset, we obtain the SHIR estimator as well as the following alternative estimators: (a) the IPDpool estimator ${\widehat{\mathit{\beta }}}_{\text{IPDpool}}^{(•)}={\mathrm{argmin}}_{{\mathit{\beta }}^{(•)}}\widehat{𝓠}\left({\mathit{\beta }}^{(•)}\right)$; (b) the SMA estimator (He et al. 2016), following the sure independent screening procedure (Fan and Lv 2008) that reduces the dimension to $n/(3\log n)$ as recommended by He et al. (2016); and (c) the debiasing-based estimator ${\widehat{\mathit{\beta }}}_{\text{L\&B}}^{(•)}$ as introduced in Section 4.4, denoted by ${\text{Debias}}_{\text{L\&B}}$. For ${\widehat{\mathit{\beta }}}_{\text{L\&B}}^{(•)}$, we used the soft thresholding to be consistent with the penalty used by IPDpool, SMA and SHIR. We used the BIC to choose the tuning parameters for all methods.

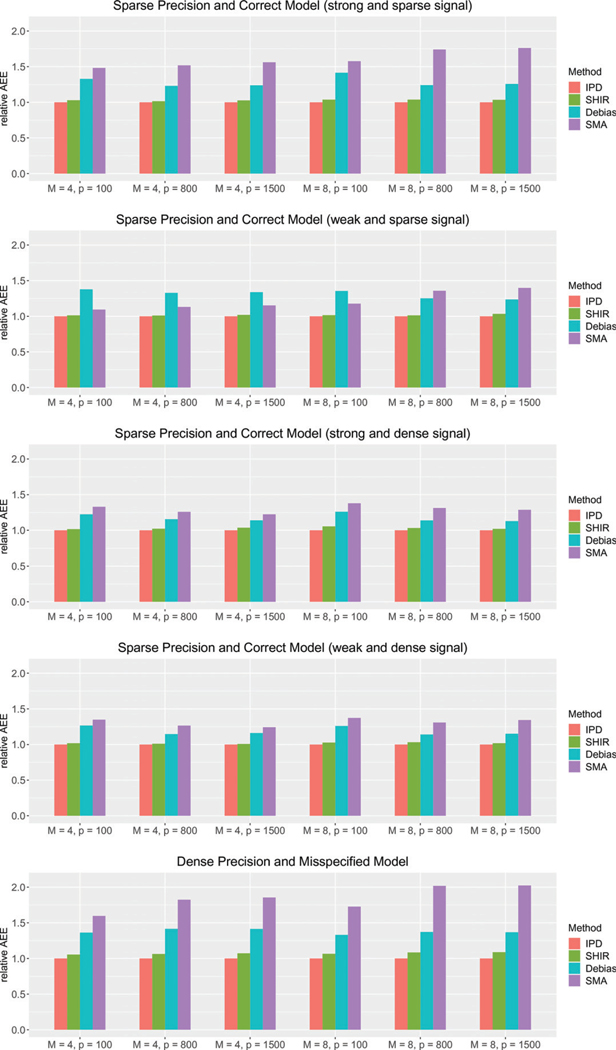
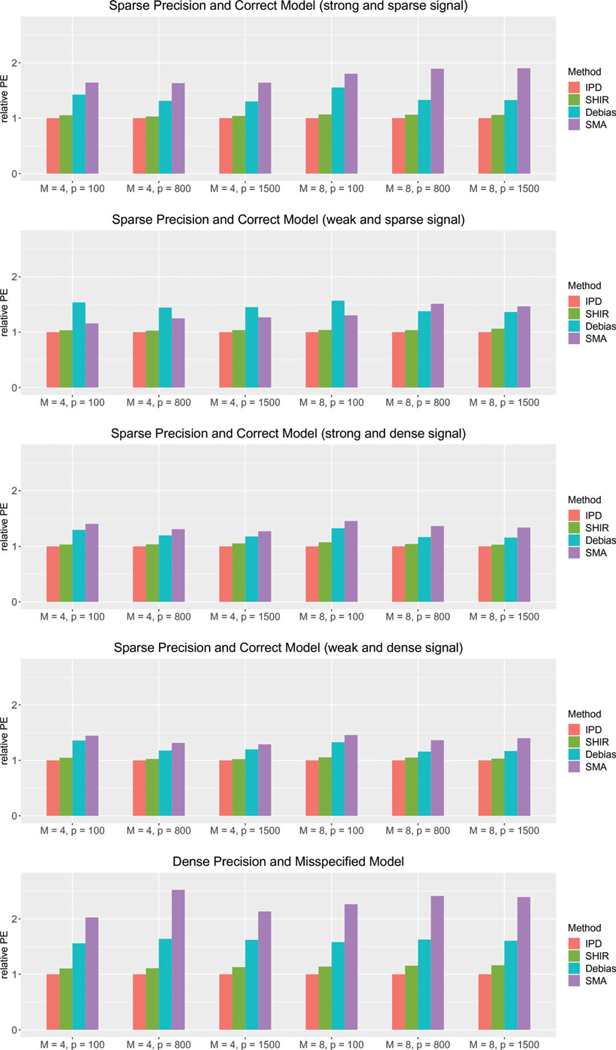
In Figures 1 and 2, we present the relative average absolute estimation error (rAEE), ${\Vert {\mathit{\beta }}^{(•)}-{\mathit{\beta }}_0^{(•)}\Vert }_1$, and the relative prediction error (rPE), ${\Vert \mathbb{X}\left({\mathit{\beta }}^{(•)}-{\mathit{\beta }}_0^{(•)}\right)\Vert }_2$, for each estimator compared to the IPDpool estimator, respectively. Consistent with the theoretical equivalence results, the SHIR estimator attains very close estimation and prediction accuracy as those of theidealizedIPDpoolestimator,withrPEandrAEEaround1.03 under Setting (i), 1.02 under (ii), 1.04 under (iii), 1.03 under (iv), and 1.07 under (v). The SHIR estimator is substantially more efficient than the SMA under all the settings, with about 45% reduction in both AEE and PE on average. This can be attributed to the improved performance of the local LASSO estimator ${\widehat{\mathit{\beta }}}_{\text{LASSO}}^{(\text{m})}$ over the MLE ${\breve{\mathit{\beta }}}^{(\text{m})}$ on sparse models. The superior performance is more pronounced for large $p$ such as 800 and 1500, because the screening procedure does not work well in choosing the active set, especially in the presence of correlations among the covariates. Compared with ${\text{Debias}}_{\text{L\&B}}$, SHIR also demonstrates its gain in efficiency. Specifically, relative to SHIR, ${\text{Debias}}_{\text{L\&B}}$ has 15% ~ 29% higher AEE and 18% − 42% higher PE under the five settings. This is consistent with our theoretical results presented in Section 4.4 that SHIR has smaller error compared to ${\text{Debias}}_{\text{L\&B}}$ due to the heterogeneous Hessians and aggregation errors. In addition, compared to Settings (i)–(iv), the excessive error of ${\text{Debias}}_{\text{L\&B}}$ is larger in Setting (v) where the the inverse Hessian ${\overline{\mathbf{\Theta }}}_m$ is relatively dense. This is consistent with conclusion in Section 4.4.

Figure 1.

The relative average absolute estimation error (AEE) of IPDpool (IPD), SHIR, ${\text{Debias}}_{\text{L\&B}}$ (Debias) and SMA compared to those of IPDpool underdifferent $M\in \{4,8\}$, $p\in \{100,800,1500\}$ and data-generation mechanisms (i)–(v) introduced in Section 5.

Figure 2.

The relative prediction error (PE) of IPDpool (IPD), SHIR, ${\text{Debias}}_{\text{L\&B}}$ (Debias), and SMA compared to those of IPDpool under different $M\in \{4,8\}$, $p\in \{100,800,1500\}$ and data-generation mechanisms (i)–(v) introduced in Section 5.

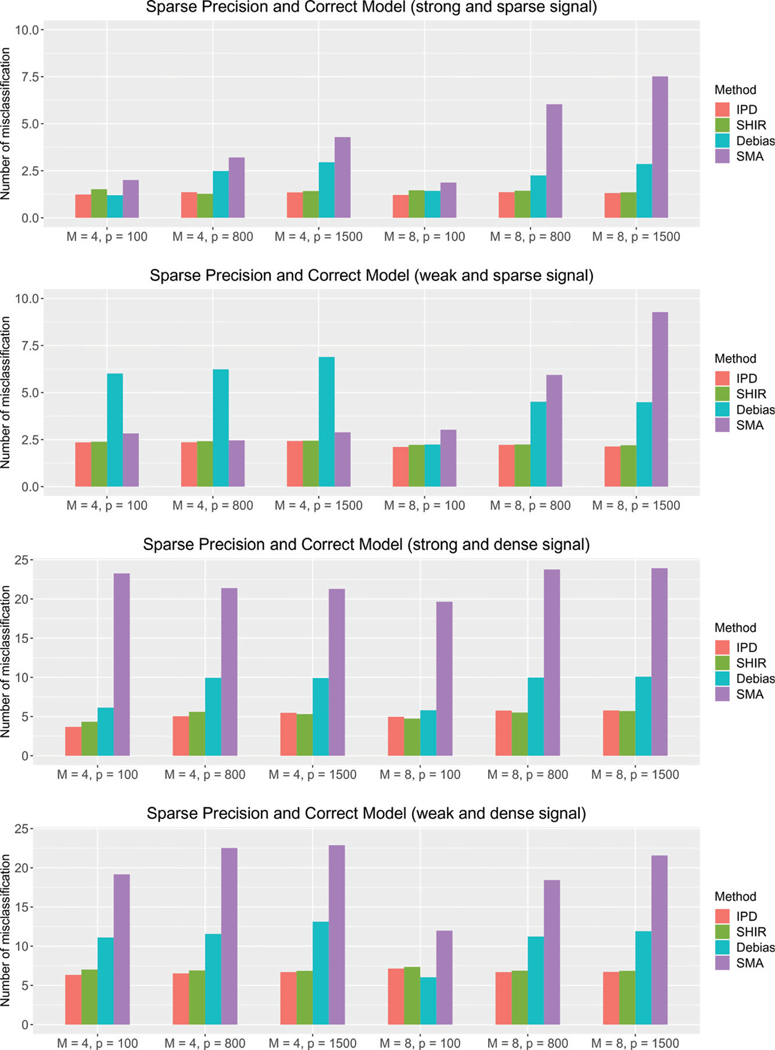
In Figure 3, we present the average number of misclassifications on the support of ${\mathit{\beta }}^{(•)}$, that is, $\sum _{j=1}^{p}I\left({\widehat{\mathit{\beta }}}_j=0\right)\ne I\left({\mathit{\beta }}_{0,j}=0\right)$ for $\widehat{\mathit{\beta }}$ obtained via different methods under Settings (i)–(iv) where the model for $Y$ is correctly specified. SMA performs poorly and has more misclassification numbers under nearly all the settings, specially for $p=800,1500$ and dense signals. Both IPDpool and SHIR have good support recovery performance with the misclassification numbers below 2.5 under all settings with sparse signal, and below 7.5 under those with dense signal. These two methods attain similar misclassification numbers with the absolute differences less than 0.8 across all settings. Compared to IPDpool and SHIR, ${\text{Debias}}_{\text{L\&B}}$ has significantly worse performance for all the settings with $p\in \{800,1500\}$. For weak signal, $M=4$ and $p\in \{800,1500\}$, the misclassification numbers of ${\text{Debias}}_{\text{L\&B}}$ are about two to four times as large as those of IPDpool and SHIR. For strong signal or $M=8$, the gap between ${\text{Debias}}_{\text{L\&B}}$ and SHIR is still visible though a bit smaller. For example, under Setting (i) with $M=8$, ${\text{Debias}}_{\text{L\&B}}$ has about 60% more misclassifications than SHIR when $p=800$, and 110% more misclassifications when $p=1500$ on average. In Figures A1 and A2 of the supplementary material, we present the average true positive rate (TPR) and false discovery rate (FDR) for recovering the support of ${\mathit{\beta }}^{(•)}$. When $p=100$, the estimator ${\text{Debias}}_{\text{L\&B}}$ tends to have smaller FDR than those of SHIR. However, this is achieved at the expense of substantially lower TPR. On the other hand, when $p$ is larger $(p\in \{800,1500\})$, SHIR attains lower FPR than ${\text{Debias}}_{\text{L\&B}}$ while attaining higher or comparable TPR. In summary, SHIR achieves similar performance as IPDpool and better performance than ${\text{Debias}}_{\text{L\&B}}$ in support recovery.

Figure 3.

The average number of misclassifications on $\left\{l\left({\beta }_j\ne 0\right),j=1,\dots ,p\right\}$ based on IPDpool (IPD), SHIR, ${\text{Debias}}_{\text{L\&B}}$ (Debias), and SMA under different $M\in \{4,8\}$, $p\in \{100,800,1500\}$ and data-generation mechanisms (i)–(iv) introduced in Section 5.

6. Application to EHR Phenotyping in Multiple Disease Cohorts

Linking EHR data with biorepositories containing “-omics” information has expanded the opportunities for biomedical research (Kho et al. 2011). With the growing availability of these high-dimensional data, the bottleneck in clinical research has shifted from a paucity of biologic data to a paucity of high-quality phenotypic data. Accurately and efficiently annotating patients with disease characteristics among millions of individuals is a critical step in fulfilling the promise of using EHR data for precision medicine. Novel machine learningbased phenotyping methods leveraging a large number of predictive features have improved the accuracy and efficiency of existing phenotyping methods (Liao et al. 2015; Yu et al. 2015).

While the portability of phenotyping algorithms across multiple patient cohorts is of great interest, existing phenotyping algorithms are often developed and evaluated for a specific patient population. To investigate the portability issue and develop EHR phenotyping algorithms for CAD useful for multiple cohorts, Liao et al. (2015) developed a CAD algorithm using a cohort of rheumatoid arthritis (RA) patients and applied the algorithm to other disease cohorts using EHR data from Partner’s Healthcare System. Here, we performed integrative analysis of multiple EHR disease cohorts to jointly develop algorithms for classifying CAD status for four disease cohorts including type 2 diabetes mellitus (DM), inflammatory bowel disease (IBD), multiple sclerosis (MS), and RA. Under the DataSHIELD constraint, our proposed SHIR algorithm enables us to let the data determine if a single CAD phenotyping algorithm can perform well across four disease cohorts or disease specific algorithms are needed.

For algorithm training, clinical investigators have manually curated gold standard labels on the CAD status used as the response $Y$, for $n_1=172\text{DM}$ patients, $n_2=230\text{IBD}$ patients, $n_3=105\text{MS}$ patients, and $n_4=760\text{RA}$ patients. There are a total of $p=533$ candidate features including both codified features, narrative features extracted via natural language processing (NLP) (Zeng et al. 2006), as well as their two-way interactions. Examples of codified features include demographic information, lab results, medication prescriptions, counts of International Classification of Diseases (ICD) codes and Current Procedural Terminology (CPT) codes. Since patients may not have certain lab measurements and missingness is highly informative, we also create missing indicators for the lab measurements as additional features. Examples of NLP terms include mentions of CAD, current smoking (CSMO), nonsmoking (NSMO) and CAD related procedures. Since the count variables such as the total number of CAD ICD codes are zero-inflated and skewed, we take $\log (x+1)$ transformation and include $\mathbf{I}(x>0)$ as additional features for each count variable $x$.

For each cohort, we randomly select 50% of the observations to form the training set for developing the CAD algorithms and use the remaining 50% for validation. We trained CAD algorithms based on SHIR, ${\text{Debias}}_{\text{L\&B}}$ and SMA. Since the true model parameters are unknown, we evaluate the performance of different methods based on the prediction performance of the trained algorithms on the validation set. We consider several standard accuracy measures including the area under the receiver operating characteristic curve (AUC), the brier score defined as the mean squared residuals on the validation data, as well as the $F$-score at threshold value chosen to attain a false-positive rate of 5% ($F_{5\%}$) and 10% ($F_{10\%}$), where the $F$-score is defined as the harmonic mean of the sensitivity and positive predictive value. The standard errors of the estimated prediction performance measures are obtained by bootstrapping the validation data. We only report results based on tuning parameters selected with BIC as in the simulation studies but note that the results obtained from AIC are largely similar in terms of prediction performance. Furthermore, to verify the improvement of the performance by combining the four datasets, we include the LASSO estimator for each local dataset (Local) as a comparison.

In Table 1, we present the estimated coefficients for variables that received nonzero coefficients by at least one of the included methods. Interestingly, all integrative analysis methods set all heterogeneous coefficients to zero, suggesting that a single CAD algorithm can be used across all cohorts although different intercepts were used for different disease cohorts. The magnitude of the coefficients from SHIR largely agree with the published algorithm with most important features being NLP mentions and ICD codes for CAD as well as total number of ICD codes which serves as a measure of healthcare utilization. The SMA set all variables to zero except for age, nonsmoker and the NLP mentions and ICD codes for CAD, while ${\text{Debias}}_{\text{L\&B}}$ has more similar support to SHIR.

Table 1.

Detected variables and magnitudes of their fitted coefficients for homogeneous effect $\mu$.

Variable	${\text{Debias}}_{\text{L\&B}}$	SHIR	SMA
Prescription count of statin	0.14	0.07	0
Age	0.09	0.26	0.28
Total ICD counts	−0.38	−0.75	0
NLP count of CAD	0.97	1.34	0.81
NLP count of CAD procedure related concepts	0	0.02	0
NLP count of nonsmoker	−0.07	−0.25	− 0.42
NLP count of nonsmoker > 0	−0.53	0	0
NLP count of current-smoker	0	−0.03	0
NLP count of CAD related diagnosis or procedure ≥ 1	0.06	0.05	0
ICD count for CAD	1.00	0.67	0.35
CPT count for stent or CABG	0	0.05	0
CPT count for echo	0	−0.10	0
ICD count for CAD × CPT count for echo	0	−0.04	0
NLP count of non-smoker × Oncall	0.09	0	0
NLP count of CAD × NLP count of possible-smoker	0	−0.02	0

NOTE: $\text{A}\times \text{B}$ denotes the interaction term of variables A and B. The $\log (x+1)$ transformation is taken on the count data and the covariates are normalized.

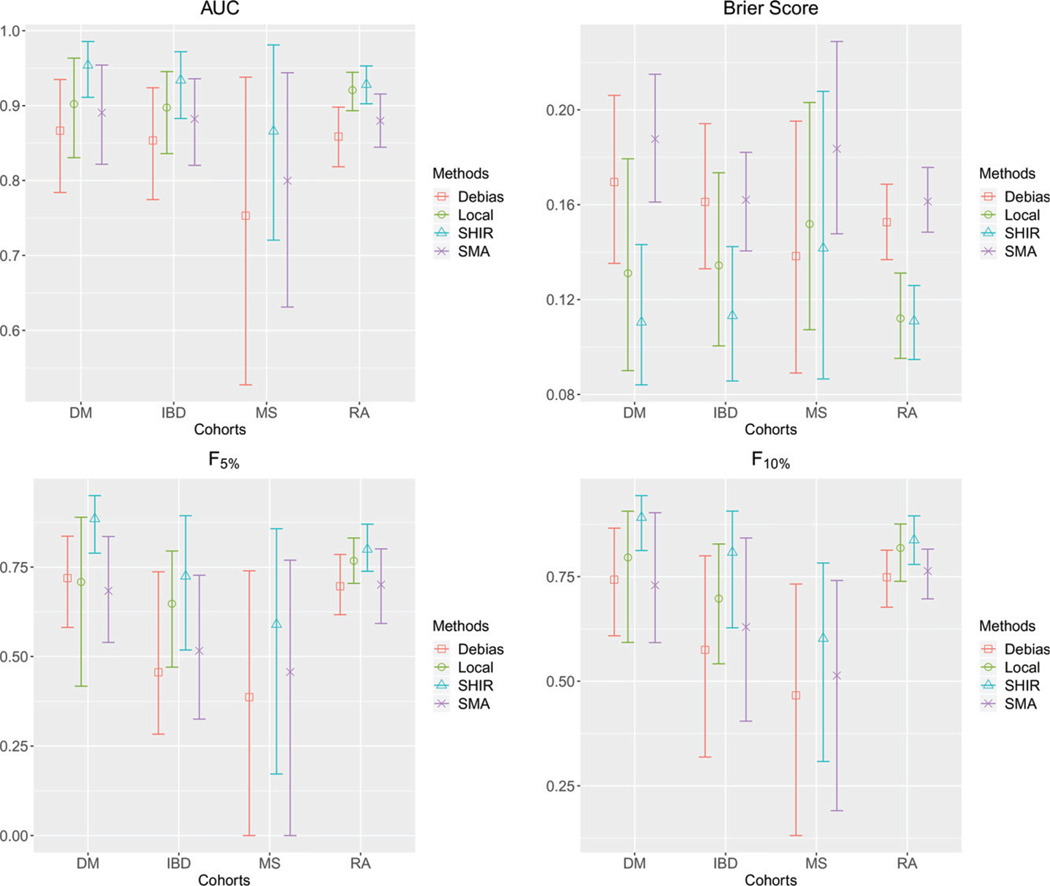
The point estimates along with their 95% bootstrap confidence intervals of the accuracy measures are presented in Figure 4. The results suggest that SHIR has the best performance across all methods, nearly on all datasets and across all measures. Among the integrative methods, SMA and ${\text{Debias}}_{\text{L\&B}}$ performed much worse than SHIR on all accuracy measures. For example, the AUC with its 95% confidence interval of the CAD algorithm for the RA cohorts trained via SHIR, SMA and ${\text{Debias}}_{\text{L\&B}}$ is respectively 0.93 (0.90,0.95), 0.88 (0.84,0.92), and 0.86 (0.82,0.90). Compared to the local estimator, SHIR also performs substantially better. For example, the AUC of SHIR and Local for the IBD cohort is 0.93 (0.88,0.97) and 0.90 (0.84,0.95). The difference between the integrative procedures and the local estimator is more pronounced for the DM cohort with AUC being around 0.95 for SHIR and 0.90 for the local estimator trained using DM data only. The local estimator fails to produce an informative algorithm for the MS cohort due to the small size of the training set. These results again demonstrate the power of borrowing information across studies via integrative analysis.

Figure 4.

The mean and 95% bootstrap confidence interval of AUC, Brier Score, $F_{5\%}$ and $F_{10\%}$ of ${\text{Debias}}_{\text{L\&B}}$, Local, SHIR and SMA on the validation data from the four studies.

7. Discussion

In this article, we proposed a novel approach, the SHIR, for integrative analysis of high dimensional data under the DataSHIELD framework, where only summary statistics are allowed to be transferred from the local sites to the central node to protect the individual-level data. As we demonstrated via both theoretical analyses and numerical studies, the SHIR estimator is considerably more efficient than the estimators obtained based on the debiasing-based strategies considered in literatures (Lee et al. 2017; Battey et al. 2018). Also, our method accommodates heterogeneity among the design matrices, as well as the coefficients of the local sites, which is not adequately handled under the ultra high-dimensional regime in existing literature. Our approach only solves the LASSO problem once in each local site without requiring the computation of ${\widehat{\mathbf{\Theta }}}^{(\text{m})}$ or debiasing. Note that, SHIR aims at an ${\ell }_1/{\ell }_2$-consistent estimation and is not asymptotically unbiased. Consequently, it cannot be directly used for hypothesis testing or confidence interval construction, for example, Caner and Kock (2018a,b). Future work lies on developing statistical approaches for such purposes under DataSHIELD, high-dimensionality and heterogeneity. In addition, sparsistency of our estimator relies on the Irrepresentable Condition (Condition 6) that has been commonly used in the literature (see, e.g.,Yuan and Lin 2006; Nardi et al. 2008), but its rigorous verification for random design or nonlinear models is technically highly challenging. To achieve variable selection consistency without such condition, one may use non-concave (group) sparse penalty like group adaptive lasso (Wang and Leng 2008) or group bridge (Zhou and Zhu 2010) in our framework.

For the choice of penalty, in the current article, we focus primarily on the mixture penalty, $\rho \left({\mathit{\beta }}^{(•)}\right)=\sum _{j=2}^p\left|{\mu }_j\right|+{\lambda }_g\sum _{j=2}^p{\Vert {\mathit{\alpha }}_j\Vert }_2$. Nevertheless, other penalty functions, such as group lasso (Huang and Zhang 2010) and hierarchical lasso (Zhou and Zhu 2010), can be incorporated into our framework provided that they effectively leverage certain prior knowledge. Similar techniques used for deriving the theoretical results of SHIR with the mixture penalty can be used for other penalty functions, with some technical details varying according to different choices on $\rho (\cdot )$. See Section A.4 of the supplementary material for further justifications.

For the consistency result in Theorem 1, SHIR requires $s_0=o\left\{{(N/M\log p)}^{1/2}\right\}$. Although this sparsity assumption is already weaker than those in the existing literature (Battey et al. 2018, e.g.) as shown in Section 4.4, it may be strong in practical applications. For example, ${(N/M\log p)}^{1/2}\approx 7$ in the EHR example which suggests that the sparsity assumption may not hold. Nevertheless, the resulting SHIR algorithm appear to perform well in terms of out-of-sample classification accuracy. On the other hand, it is of interests to explore the possibilities of relaxing such assumption. One potential way is to use multiple rounds of communications such as Fan, Guo, and Wang (2019). Detailed analysis of this approach warrants future research.