Abstract
Brain function is characterized by a convolution of various biochemical and physiological processes, raising the interest whether resting-state functional connectivity derived from hemodynamic scales shows underlying metabolic synchronies. Increasing evidence suggests that metabolic connectivity based on glucose consumption associated PET recordings may serve as a marker of cognitive functions and neuropathologies. However, to what extent fMRI-derived resting-state brain connectivity can also be characterized based on dynamic fluctuations of glucose metabolism and how metabolic connectivity is influenced by [18F]FDG pharmacokinetics remains unsolved.
Simultaneous PET/MRI measurements were performed in a total of 26 healthy male Lewis rats. Simultaneously to resting-state fMRI scans, one cohort (n = 15) received classical bolus [18F]FDG injections and dynamic PET images were recorded. In a second cohort (n = 11) [18F]FDG was constantly infused over the entire functional PET/MRI scans. Resting-state fMRI and [18F]FDG-PET connectivity was evaluated using a graph-theory based correlation approach and compared on whole-brain level and for a default-mode network-like structure. Further, pharmacokinetic and tracer uptake influences on [18F]FDG-PET connectivity results were investigated based on the different PET protocols.
By integrating simultaneous resting-state fMRI and dynamic [18F]FDG-PET measurements in the rat brain, we identified homotopic correlations between both modalities, suggesting an underlying synchrony between hemodynamic processes and glucose consumption.
Furthermore, the presence of the prominent resting-state default-mode network-like structure was not only depicted on a functional scale but also from dynamic fluctuations of [18F]FDG. In addition, the present findings demonstrated strong pharmacokinetic and tracer uptake dependencies of [18F]FDG-PET connectivity outcomes.
This study highlights the application of dynamic [18F]FDG-PET to study cognitive brain functions and to decode underlying brain networks in the resting-state. Thereby, PET-derived connectivity outcomes indicated strong dependencies on tracer application regimens and subsequent time-varying tracer pharmacokinetics.
Keywords: Simultaneous PET/fMRI, fPET, Resting-state brain networks, Connectomics
1. Introduction
Resting-state functional magnetic resonance imaging (rs-fMRI) is widely used to investigate brain functional connectivity (Biswal et al., 1995). Studying functional brain networks and network organizations relies on estimations of brain connectivity mainly by applying correlational approaches. Using rs-fMRI, temporal correlations of blood-oxygen-level-dependent (BOLD) signals are calculated to describe functional networks at rest (Greicius et al., 2003; Fox et al., 2005) since low-frequency (0.01–0.1 Hz) fluctuations of BOLD signals are considered reflective of neuronal activity (Biswal et al., 1995; Logothetis et al., 2001). However, BOLD-derived correlations of spatially distinct brain regions reflect only hemodynamic changes, including cerebral blood flow, blood volume and oxygen consumption (Buxton, 2002, 2009).
Although rs-fMRI studies contribute tremendously to the understanding of functional neurological mechanisms, [18F]fluorodeoxyglucose ([18F] FDG) Positron Emission Tomography (PET) represents one of the first methods used to describe inter-regional metabolic-derived relationships among brain areas (Horwitz et al., 1984; Metter et al., 1984). In contrast to the vascular-weighted BOLD effect, [18F]FDG-PET measures cellular glucose consumption and can uncover the metabolic basis of neuronal and glial activities, which are more directly related to the underlying neurophysiological basis of brain functions (Phelps et al., 1979). Despite the widespread use of rs-fMRI over [18F]FDG-PET, metabolic connectivity has emerged as a complementary approach to decode brain connectivity (Di and Biswal, 2012; Riedl et al., 2016). However, the underlying neurophysiological mechanisms of metabolic brain connectivity remain to be investigated.
Using simultaneous PET/MRI in rats, we previously demonstrated that spatial independent component analysis (ICA) identified complementary metabolic and functional brain circuits to process somatosensory input (Wehrl et al., 2013). Furthermore, others reported that metabolic connectivity has the potential as a promising biomarker for determining the progression of neurodegenerative diseases and appropriate treatment strategies (Eckert et al., 2007; Feigin et al., 2007).
Indeed, inter-subject correlations between metabolic rates derived from glucose consumption may provide additional information regarding functional connectivity (Wehrl et al., 2013; Di et al., 2017); however, the similarities and differences in connectivity outcomes and brain networks between rs-fMRI and [18F]FDG-PET remain largely unknown. A major issue in most metabolic connectivity studies is the restriction to static PET acquisitions without any temporal resolution. Furthermore, correlation analyses to decode metabolic connectivity have typically been carried out across subjects, limiting network analyses to only group levels rather than an individual level. Therefore, whether and how fMRI-derived resting-state functional connectivity is associated with an underlying synchrony in brain metabolism must be clarified. Recently, Passow and colleagues investigated temporal fluctuations of brain glucose uptake using dynamic [18F] FDG-PET measurements and reported close relationships between functional connectivity and metabolic activity (Passow et al., 2015). However, these findings are inconsistent with the data demonstrated by Tomasi et al. describing very different connectivity patterns emerging from temporal functional and metabolic connectivity (Tomasi et al., 2017).
We hypothesize that these controversial findings may reflect influences of tracer application-dependent uptake patterns, temporal resolution and non-simultaneous acquisitions of the PET and fMRI datasets on the observed metabolic connectivity outcomes.
To investigate rs-fMRI and [18F]FDG-PET brain connectivity correlates and to test the hypothesis of tracer application dependent connectivity measurements, we performed simultaneous PET/MRI. The measurements were performed by applying two different tracer administration regimens, including a single bolus injection and a constant infusion of [18F]FDG, in 26 healthy rats to compare temporal functional connectivity and dynamic [18F]FDG-PET connectivity based on different pharmacokinetic properties. While tracer availability decreases over time using a bolus injection, a constant infusion allows the maintenance of a stable plasma supply of [18F]FDG. Therefore, a continuous tracer infusion protocol has the advantage of increased sensitivity to brain-state changes since glucose metabolism may not be at equilibrium over the full imaging time (Villien et al., 2014). Additionally, the simultaneous PET/MRI approach enabled highly spatially and temporally correlated data acquisition. The combination of a traditional correlation-based method and a graph theory-based analysis of spatially distinct brain regions was used to assess associations between dynamic [18F]FDG-PET connectivity and functional connectivity derived from BOLD-fMRI on whole-brain and default-mode network-like (DMN-like) levels. Finally, dependencies between glucose consumption, tracer kinetics and hemodynamic neuro-vascular parameters among brain network organizations are discussed.
2. Material and methods
2.1. Animals
Healthy male Lewis rats were purchased from Charles River Laboratories (Charles River Laboratories, Sulzfeld, Germany) and were maintained under specific pathogen-free conditions. Rats (n = 26) weighing 315 ± 36 g and aged 11–13 weeks were used for all experiments. Fifteen rats were assigned to the bolus injection cohort and 11 rats were assigned to the constant infusion cohort. The animal procedures were conducted in accordance with German federal regulations regarding the use and care of experimental animals and were approved by local authorities (Regierungspräsidium Tübingen; permit number R8/16).
2.2. Animal preparation
Rats were fasted 6 h prior to the imaging experiments. For anesthesia induction, the rats were placed in a knock-out box and 3% isoflurane evaporated in regular air was delivered. After negative reflex testing, the isoflurane level was reduced to 2%. Bodyweights were examined and baseline capillary blood glucose levels were obtained. An intravenous (i.v.) catheter with a 30-G needle was placed in one of the tail veins to allow [18F]FDG tracer administration. After catheter placement, the animals were positioned inside the PET/MR system using dedicated animal holders. A rectal temperature probe was inserted to monitor and maintain body temperature at 36.5 ± 1 °C, and the respiration rate was monitored via a pressure sensitive breathing pad. For measurement conditions isoflurane level was reduced to 1.3% in regular air. At the end of each simultaneous PET/MR scan post-measurement capillary blood glucose levels were collected.
2.3. Simultaneous PET/MRI imaging
Simultaneous [18F]FDG-PET/MRI was applied on 26 animals. For magnetic resonance image acquisition on a small animal 7 T BioSpec (Bruker BioSpin MRI), a linearly polarized radiofrequency coil with an inner diameter of 72 mm (Bruker BioSpin MRI) for transmission was used in combination with a four-channel rat brain coil (Bruker BioSpin MRI) for reception. Using magnetic resonance localizer images, the brain of each rat was centered in the PET/MRI field of view (FOV). In addition to anatomical T2 TurboRARE images (TE: 67.11 ms, TR: 1800 ms, FOV: 40 × 32 × 32 mm3, image size: 160 × 128 × 128 px, Rare factor: 28, averages: 1), whole brain covering T2*-weighted gradient echo EPI sequences (TE: 18 ms, TR: 2500 ms, 0.25 mm isotropic in plane resolution, FoV 25 × 23 mm2, image size: 92 × 85 × 20 px, slice thickness: 0.8 mm, 20 slices) were acquired. Before fMRI data acquisition the local field homogeneity has been optimized using acquired field maps and shimming. To acquire [18F]FDG-PET simultaneously with MRI, a small animal PET insert was installed inside the MR scanner as described previously (Wehrl et al., 2013). For the bolus injection cohort, [18F]FDG (31.5 MBq) was injected over a period of 30 s. At the same time, the simultaneous PET/MRI scan was started and 60-min EPI BOLD scans and PET emission scans were obtained. For the constant infusion cohort, simultaneously to 80 min EPI BOLD scans, rats were continuously i. v. infused with [18F] FDG in saline solution (dose at infusion start: 148 MBq) at a constant infusion rate of 8 μl/min. Coincidence event PET data were recorded and saved in list-mode format. Raw list-mode data were reconstructed using an in house-written ordered-subsets expectation maximization 2D (OSEM-2D) algorithm.
For dynamic PET scan analysis of both groups, list mode data were reconstructed in 1-min frames resulting in 60 frames for the bolus injection group and 80 frames for the constant infusion group, respectively. Due to initial low count rates resulting from the constant infusion approach, the first 20 frames (i.e., 20 min) were omitted for analysis of the constant infusion cohort.
2.4. [18F]FDG production
[18F]Fluorine was prepared as [18F]fluoride by the PETtrace cyclotron (GE Healthcare, Uppsala, Sweden) using [18O]water (Rotem, Leipzig, Germany) via the 18O(p,n)18F nuclear reaction.
The PET tracer [18F]FDG was synthesized in a TRACERlab MXFDG synthesizer (GE Healthcare, Liege, Belgium) using mannose triflate (ABX, Radberg, Germany) and previously established protocols (Hamacher et al., 1986). Quality control was performed in accordance with GOP guidelines.
2.5. Data preprocessing and analysis
Simultaneous PET/MRI data preprocessing was performed as previously described (Wehrl et al., 2013) using SPM 12 (Wellcome Trust Centre for Neuroimaging) on MATLAB (MathWorks). Briefly, a group-average image atlas was generated by realignment of individual PET images resulting from summed frames over the entire PET scan time. The anatomical T2 TurboRARE MR images of all subjects were realigned and averaged to generate a corresponding MR template. Both PET and MR atlases were finally coregistered. BOLD-fMRI data were motion-corrected and coregistered to the corresponding MR atlas.
PET data were processed similarly to the fMRI data. To account for differences in the spatial resolution between the fMRI and PET methods, all functional imaging data were smoothed with a Gaussian kernel of 1.5 mm full width half maximum (FWHM). A kernel size of 1.5 mm represents the approximate spatial resolution of the PET insert.
2.5.1. Graph theory-based connectivity analysis
To extract whole-brain time-course-derived data from PET and fMRI scans, the preprocessed functional images were segmented into 26 bilateral (52 total) anatomically relevant brain regions based on the Schiffer rat brain atlas (Schiffer et al., 2006) and coregistered to the PET and MR atlases. The ROI time series were defined as the average over the time series of the voxels in the defined brain region:
| (1) |
where is the delineated brain ROI, is the number of voxels in the ROI, and is the time series of voxel .
Selected ROIs from the Schiffer rat brain atlas, their position on correlation matrices, abbreviations and ROI sizes are listed in Supplementary Tables 1 and 2 For the connectivity analysis, Pearson’s r correlation coefficient between each pair of ROIs was calculated based on their time series for all individual scans using an in-house-written algorithm based on Matlab (MathWorks). The data were subjected to a normalization step to correct for non-intrinsic correlations generated by factors such as increasing [18F]FDG-PET tracer uptake or MR scanner drifts. Exemplary signal time courses are presented in Supplementary Fig. 1.
For global normalization, a whole-brain mean value of the measured signal was determined at each time point and the value of each ROI was then divided by its respective whole-brain mean. Pearson’s r correlation coefficients were computed between every pair of the 52 ROIs, resulting in 2704 correlations:
| (2) |
where is the number of samples, and are the single samples, and and are the arithmetical sample means.
The calculated correlation coefficients were then averaged across subjects. Averaging was initially carried out by Fisher Z-transforming the correlation coefficients obtained using equation (2):
| (3) |
Computed Fisher values were averaged across subjects, and the mean values were inversely transformed back to the interval [−1, 1].
This process resulted in a correlation matrix , where the element indicated the strength of the correlation between the brain regions and . The diagonal was set to zero to exclude self-correlations.
Furthermore, only correlations exhibiting a p-value less than 0.05 were considered relevant, and correlations with a p-value equal to or greater than 0.05 were set to zero. The p-values were computed using Student’s t distribution.
Therefore, a matrix of p-values to test the hypothesis of no correlation against the alternative that a nonzero correlation exists was generated. Each element of the p-value matrix is the p-value for the corresponding element of the correlation matrix. If the p-value between and was less than 0.05, then the correlation coefficient was considered significantly different from zero.
In addition, static scan correlation matrices were generated for the 10-min PET frames ranging from 50 to 60 min of the bolus injection cohort scans. PET signals resulting from the 10-min frames were determined in each ROI for the 15 animals of the bolus injection cohort, resulting in 15 different PET signal values for every region. Additionally, a whole-brain mean value was computed for each scan, reflecting the total [18F]FDG brain uptake for the individual rats, which was used for normalization. Correlation coefficients for the 15 normalized PET signal values were computed as described above.
For better visualization of the relevant positive and negative correlations between ROIs, selected matrices were converted into tertiary matrices. Tertiary matrices display connectivity more qualitatively by indicating positive and negative edges, which were determined by a certain threshold, but not correlation strength. The selected thresholds were and for positive and negative correlations, respectively (Aiello et al., 2015). All positive correlations above the threshold were set to a value of −1, whereas a value of 1 was assigned to the negative correlations below the set threshold. Correlation coefficient values between −0.25 and 0.25 were set to zero.
The analysis based on computed correlation matrices aimed to determine several methodological aspects of simultaneously acquired functional and [18F]FDG-PET group-level connectivity data and to assess similarities both qualitatively and quantitatively. Therefore, intraclass correlation (ICC) analysis was performed to investigate within-scan consistency, and Sörensen-Dice indices were used to compute the level of connectivity overlap between the fMRI data and the two PET cohorts.
2.5.2. Intraclass correlation (ICC)
For weighted matrices, similarities were determined using intraclass correlations (ICCs). ICC is an inferential statistical method applied to data divided into different groups and reflects similarity between units belonging to the same group (Chicchetti, 1994). In the present study, the observed correlations between the same pair of ROIs under three sliding time windows of 40 min each were defined as a single group.
Three sliding time windows for the PET and fMRI scans were set for the bolus injection cohort from 0 to 40, 10 to 50 and 20–60 min. Since the first 20 min of the constant infusion scans needed to be excluded due to low count rates, the sliding time windows were adapted and set from 20 to 60, 30 to 70 and 40–80 min. The following formula was used to compute the ICC coefficients:
| (4) |
where is the subject mean square of the correlation coefficients, is the error mean square of the correlation coefficients, and is the number of measurements.
The following interpretation was employed for the computed ICC values (Chicchetti, 1994):
ICC less than 0.40 – poor
ICC between 0.40 and 0.59 – fair
ICC between 0.60 and 0.74 – good
ICC between 0.75 and 1.00 – excellent
2.5.3. Sörensen-Dice index
To quantify the similarities between the fMRI and PET or the bolus injection cohort and constant infusion cohort matrices, the Sörensen-Dice index (DSC) of the respective tertiary matrices for total, positive and negative edges was calculated. This method computes the level of overlap by dividing the number of identical observations between two samples by the total number of observations:
| (5) |
where is the number of observations in dataset A, is the number of observations in dataset B, and is the number of observations that datasets A and B have in common. Therefore, for every pair of compared matrices, the Sörensen-Dice coefficient was determined by considering all edges of the two matrices.
To further expand the analysis, the absolute mean correlation strengths and the numbers of coinciding total, positive and negative correlations (edges) were calculated for the matrices obtained from fMRI, the bolus injection PET cohort and the constant infusion PET cohort.
2.5.4. Linear regression between correlation strength and [18F]FDG uptake ratios
To evaluate the dependency of correlation strength outcomes on [18F] FDG uptake ratios between two brain regions, scatter plots showing the relationship between the mean correlation strengths and the mean [18F] FDG uptake ratios were computed. The scatter plots were calculated for the bolus injection and constant infusion cohorts. Therefore, 52 × 51 correlation values (correlation of one region with itself = 1) were plotted against the respective [18F]FDG uptake ratios of two brain regions. The [18F]FDG uptake ratios between two brain regions were computed by dividing the lower uptake value by the higher uptake value. Based on the obtained scatter plots, linear regression was performed using the three highest mean positive correlation strength values in 6 consecutive [18F] FDG uptake ratio intervals (0.40–0.50, 0.50–0.60, 0.60–0.70, 0.70–0.80, 0.80–0.90, and 0.90–1.00).
3. Results
3.1. Rs-fMRI and dynamic [18F]FDG-PET connectivity comparison implies whole-brain connectivity synchrony between hemodynamics and glucose consumption
To identify associations of functional connectivity with an underlying synchrony of dynamic [18F]FDG signal fluctuations, averaged correlation matrices (Pearson’s correlation) based on functional and dynamic [18F] FDG-PET correlations were computed (Fig. 1). To extract whole-brain time course-derived data from fMRI and [18F]FDG-PET scans of the bolus injection (Fig. 1A) and constant infusion (Fig. 1B) cohorts, motion-corrected functional images were segmented into 26 bilateral anatomically relevant brain regions and aligned on the correlation matrices according to the Schiffer rat brain atlas listing (Schiffer et al., 2006). The respective brain regions selected for connectivity analysis are presented in Supplementary Table 1. Figures.
Fig. 1. Whole-brain functional and [18F]FDG-PET graph theory-based connectivity.
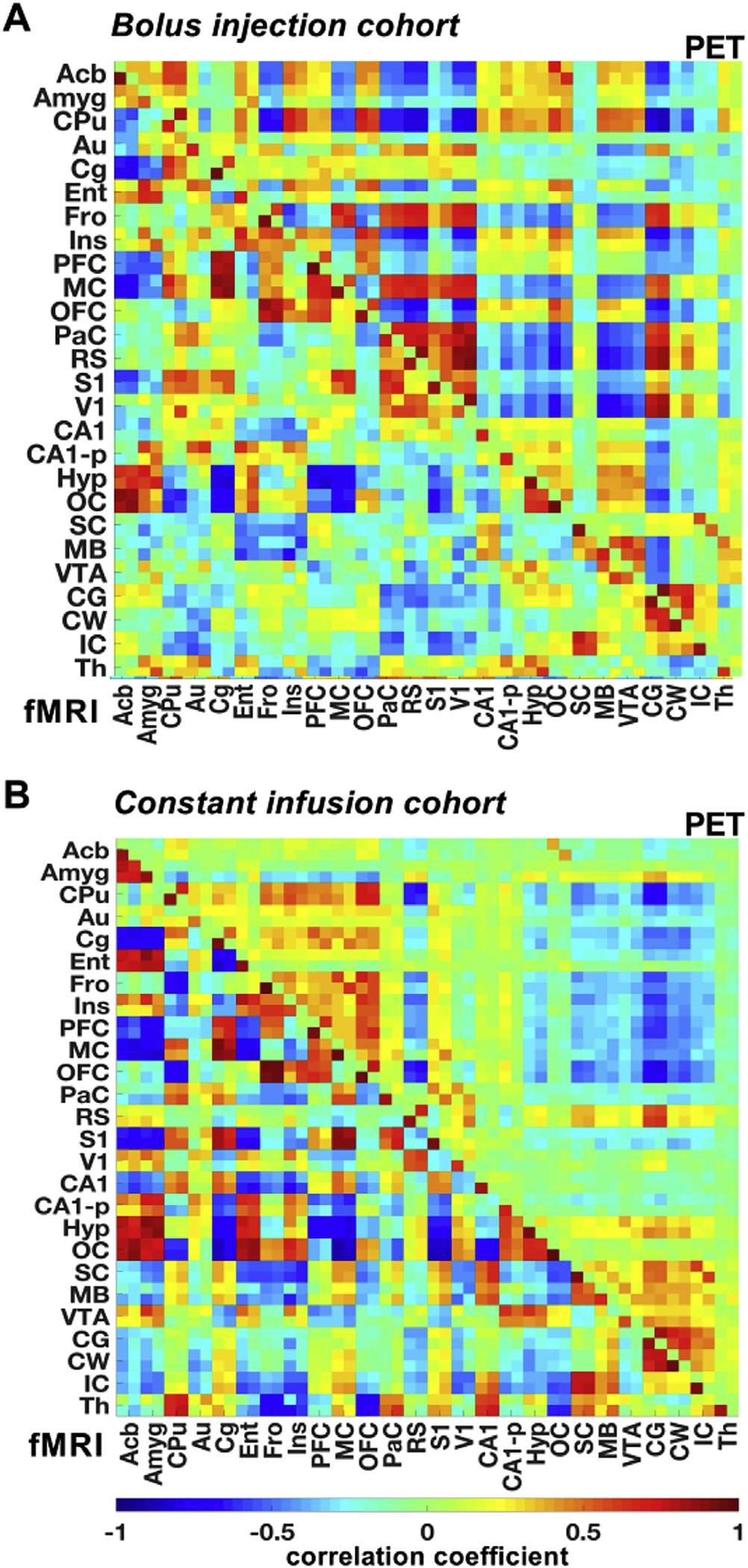
Whole-brain group-mean Pearson’s r correlation coefficient matrices were computed for the fMRI and [18F]FDG-PET data of the (A) bolus injection and (B) the constant infusion cohorts. The color scale represents the strengths of correlations. Correlation coefficients with p-values ≥ 0.05 were set to 0. The respective brain ROIs and their abbreviations are listed in Supplementary Table 1. Bolus injection cohort (N = 15); constant infusion cohort (N = 11).
Based on the correlation matrices displayed in Fig. 1, tertiary correlation matrices highlighting only mutual fMRI- and PET-derived edges of both cohorts were generated to illustrate overlapping functional and PET-derived correlations (Fig. 2A). Both the bolus injection and constant infusion cohort results indicated abundant positive correlations centered along the diagonal of the matrices. Mutual positive correlations were detected between pairs of contralateral brain regions. The correlation coefficients of the various regions were arranged based on their anatomical proximity. Most positive edges were found to be situated near the matrix diagonal where the correlation coefficients of anatomically nearby regions were located. In contrast, negative correlations were observed between anatomically distant cortical and subcortical brain regions.
Fig. 2. Correlation synchrony based on fMRI and dynamic PET data.
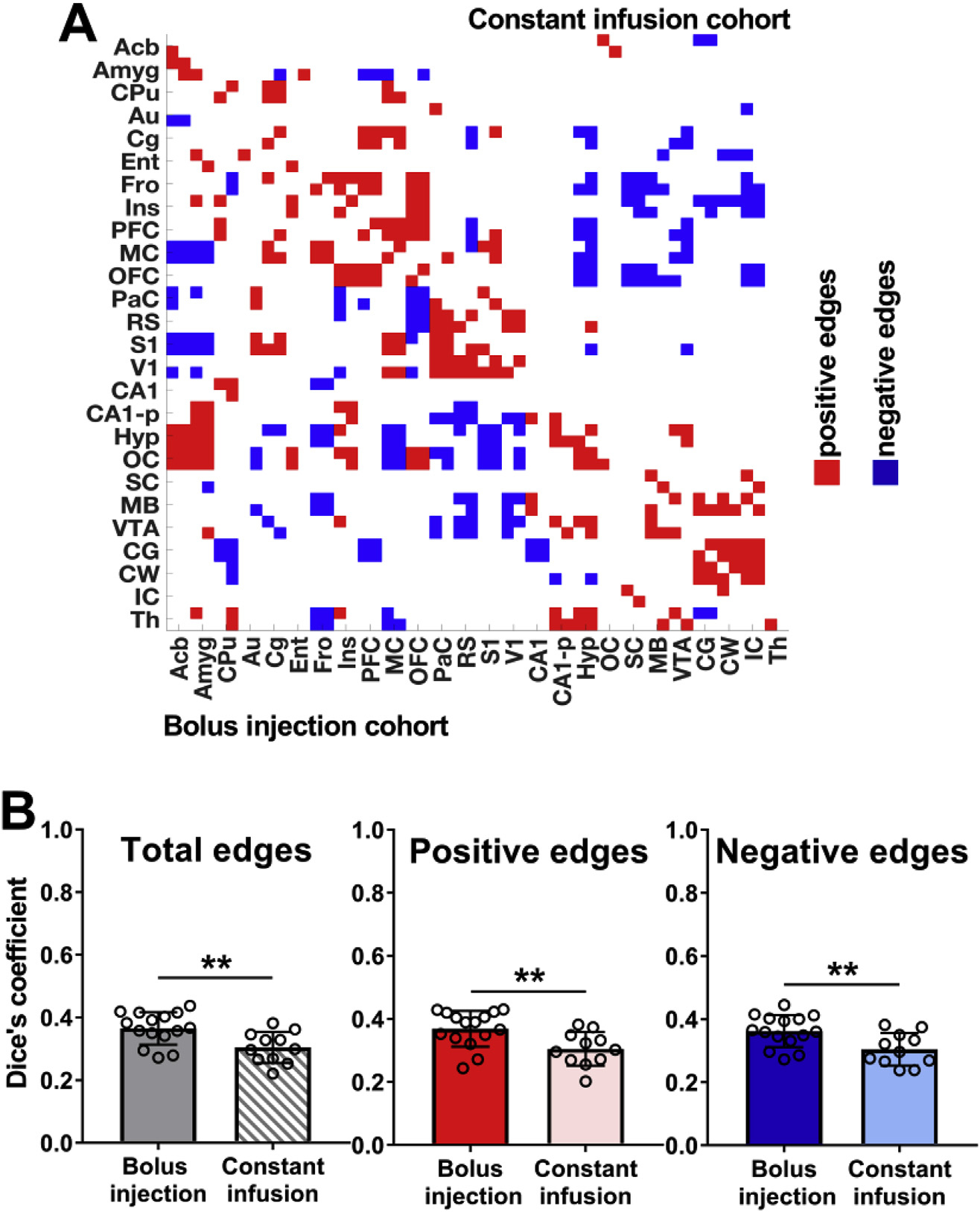
(A) Tertiary group-mean matrices of the bolus injection cohort versus the constant infusion cohort indicate common functional and dynamic [18F]FDG-PET correlations; red shows common positive edges (r > 0.25) and blue shows common negative edges (r < −0.25). (B) Dice coefficients indicate similarities for total, positive and negative edges between weighted group-mean functional and dynamic [18F] FDG-PET correlations in both cohorts. The respective brain ROIs and their abbreviations are listed in Supplementary Table 1. Bolus injection cohort (N = 15); constant infusion cohort (N = 11). The error bars represent standard deviations. ** represents p-values < 0.01.
For example, in both cohorts the hypothalamus (Hyp) was negatively correlated with the frontal cortex (Fro), motor cortex (MC) and the somatosensory cortex (S1). Further, in the bolus injection cohort the midbrain (MB) was negatively correlated with the auditory cortex (Au), frontal cortex (Fro), the retrosplenial cortex (RS) and the visual cortex (V1). In the constant infusion cohort, the MB depicted also negative correlations towards cortical structures such as the entorhinal cortex (Ent), frontal cortex (Fro), insular cortex (Ins) and the orbitofrontal cortex (OFC).
Three distinct positive clusters were identified from the correlation matrix. The largest cluster depicting an accumulation of mutual positive edges was detected between the frontal (Fro), insular (Ins), prefrontal (PFC), motor (MC) and orbitofrontal (OFC) cortices.
The second cluster showing a large number of common positive edges consisted of the parietal (PaC), retrosplenial (RS), somatosensory (S1) and visual (V1) cortices. The cerebellar gray (CG) and white matter (CW) and the superior (SC) and inferior (IC) colliculi constituted a third cluster of common positive edges. Various cortical areas, including the PFC, MC, OFC, PaC, RS, S1, and V1, were characterized by many common positive edges between each other but regularly formed common negative edges with other brain structures, including the hypothalamus (Hyp), hippocampus (CA1, CA1-p), superior colliculus (SC), midbrain (MB) and the ventral tegmental area (VTA).
Despite forming similar edge clusters, which were also detected when comparing fMRI and statically reconstructed [18F]FDG-PET data (Supplementary Fig. 2), the common edges of the constant infusion cohort indicated lower similarity between correlations of both modalities, which was validated by computing Dice’s coefficients between fMRI- and PET-derived correlations of both cohorts (Fig. 2B). In this study, the constant infusion cohort showed significantly reduced similarities between total edges (bolus injection: DSC = 0.37 ± 0.05; constant infusion: DSC = 0.30 ± 0.05; p = 5.97*10−3), positive edges (bolus injection: DSC = 0.37 ± 0.06; constant infusion: DSC = 0.31 ± 0.05; p = 8.03*10−3) and negative edges (bolus injection: DSC = 0.36 ± 0.05; constant infusion: DSC = 0.30 ± 0.05; p = 8.55*10−3) compared to the bolus injection group.
3.2. A default-mode network-like structure emerges from both hemodynamic and surrogate metabolic scales
Weighted correlation matrices of brain regions containing the default-mode network-like (DMN-like) structure were computed for the [18F]FDG-PET and fMRI data (Fig. 3) to assess how [18F]FDG-PET connectivity and functional connectivity behave in a defined resting-state network. Both the bolus injection (Fig. 3A) and constant infusion (Fig. 3B) cohorts demonstrated similar functional and hemodynamic network patterns of positive correlations within the DMN-like architecture. However, the subsystem centered on the medial prefrontal cortex (PFC) exhibiting strong surrogate metabolic and functional correlations to the cingulate (Cg), motor (MC) and orbitofrontal cortices (OFC) was more pronounced in the constant infusion cohort (Fig. 3B).
Fig. 3. Functional and [18F]FDG-PET correlations within the DMN-like network.
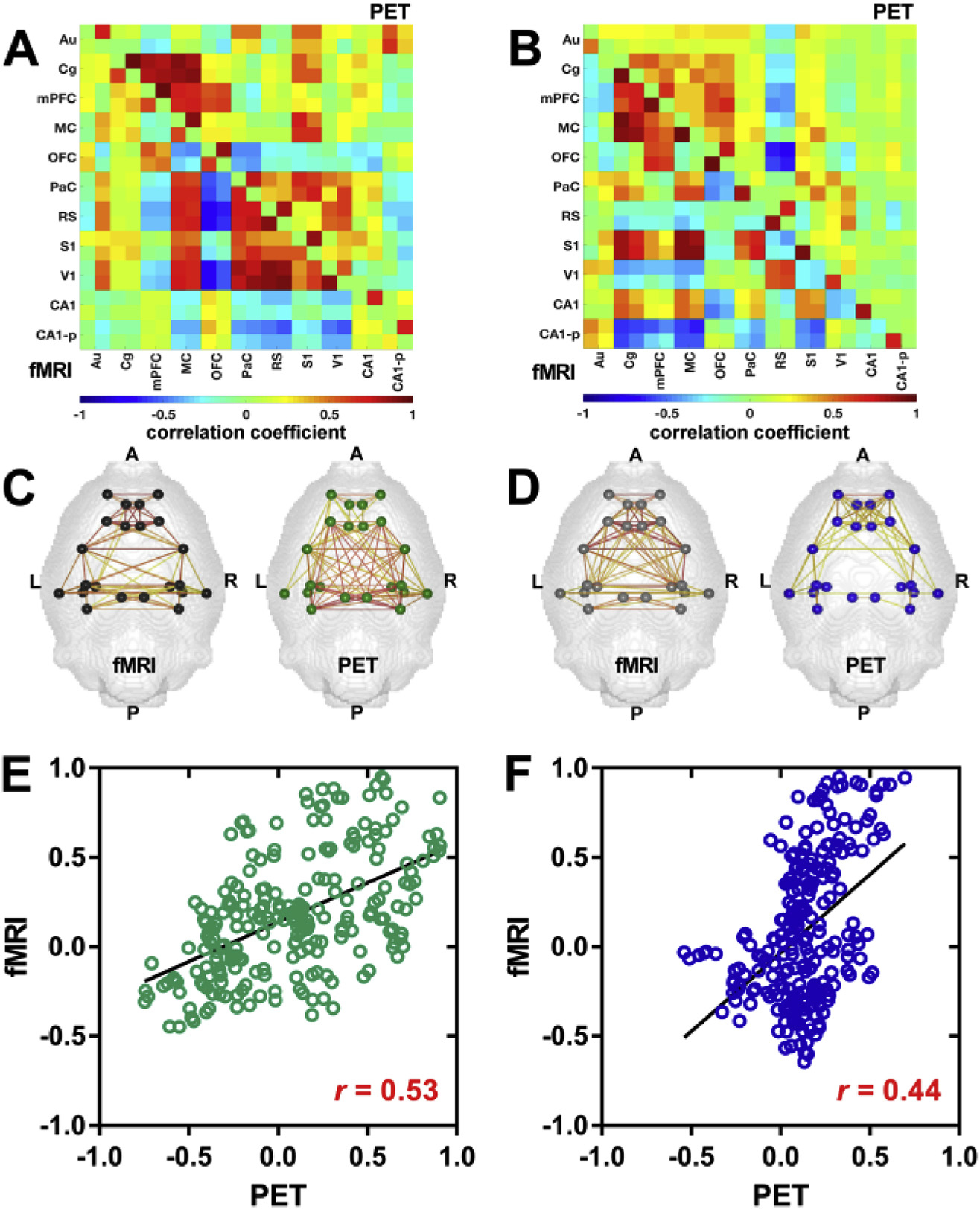
Group-mean Pearson’s r correlation coefficient matrices of the DMN-like structure were computed for the fMRI and [18F]FDG-PET data of the (A) bolus injection and (B) constant infusion cohorts. Correlation coefficients with p-values ≥ 0.05 were set to 0. Positive correlations (r ≥ 0.25) are displayed within regions of the DMN-like structure for (C) the bolus injection and (D) constant infusion cohorts. Colored nodes represent the different brain regions involved in the DMN-like structure. Colored lines indicate positive correlation between two nodes. The color scale represents the strengths of correlations. Scatter plots of pair-wise correlations between brain regions (averaged across subjects) containing the DMN-like structure and linear fits were computed for (E) the bolus injection and (F) constant infusion cohorts. The correlation value represents Pearson’s correlation coefficient r. The different brain ROIs containing the DMN-like structure and their abbreviations are listed in Supplementary Table 2. Bolus injection cohort (N = 15); constant infusion cohort (N = 11).
Complementary, the second subsystem centered on the retrosplenial cortex (RS) showing strong correlations to the somatosensory (S1), visual (V1) and parietal cortices (PaC) on both fMRI- and PET-derived scales was more distinct in bolus injection cohort (Fig. 3A). This was further illustrated by positive correlations (r ≥ 0.25) displayed as connecting lines between the different anatomical nodes comprising the DMN-like structure.
The anterior-posterior organization of the DMN-like connectivity was similar with both imaging modalities in the bolus injection (Fig. 3C) and constant infusion (Fig. 3D) cohorts. Notably, with constant tracer infusion, the posterior subsystem centered on the retrosplenial cortex (RS) exhibited slightly less PET-derived connections compared to functional and bolus injection-derived PET correlations.
To quantify the similarities among functional and [18F]FDG-PET matrices of the bolus injection (Fig. 3E) and constant infusion cohorts (Fig. 3F), Pearson’s r correlations between each pair of matrices were calculated. The functional fMRI and [18F]FDG-PET matrices of the bolus injection cohort showed higher correlations (r = 0.53; p < 0.001) compared to the matrices of the constant infusion cohort (r = 0.44; p < 0.001). Overall, the network organizations and correlation patterns derived from both fMRI and [18F]FDG-PET data suggest noticeable similarities. Brain regions comprising the DMN-like structure are presented in Supplementary Table 2.
3.3. Temporal synchronization of rs-fMRI and [18F]FDG-PET data
Due to technical characteristics of rs-fMRI and [18F]FDG-PET acquisitions, the two datasets possess different temporal resolutions (fMRI: 2.5 s; [18F]FDG-PET: 60 s), that prohibit the exact temporal correlation of hemodynamic and dynamic [18F]FDG-PET connectivity outcomes. To synchronize the temporal resolution of fMRI and PET data, the fMRI time courses were binned into 60 s time frames according to the temporal resolution of the [18F]FDG-PET data. Pearson’s r correlation matrices based on the binned fMRI dataset were computed for the DMN-like structure of the bolus injection cohort to compare the similarity between temporally synchronized fMRI and PET data (Fig. 4). The typical functional DMN-like connectivity patterns described above can also be derived from the binned fMRI data (Fig. 4A), since the correlation matrix derived from the binned dataset is qualitatively identical to the original fMRI matrix.
Fig. 4. Temporal synchronization of fMRI and PET data.
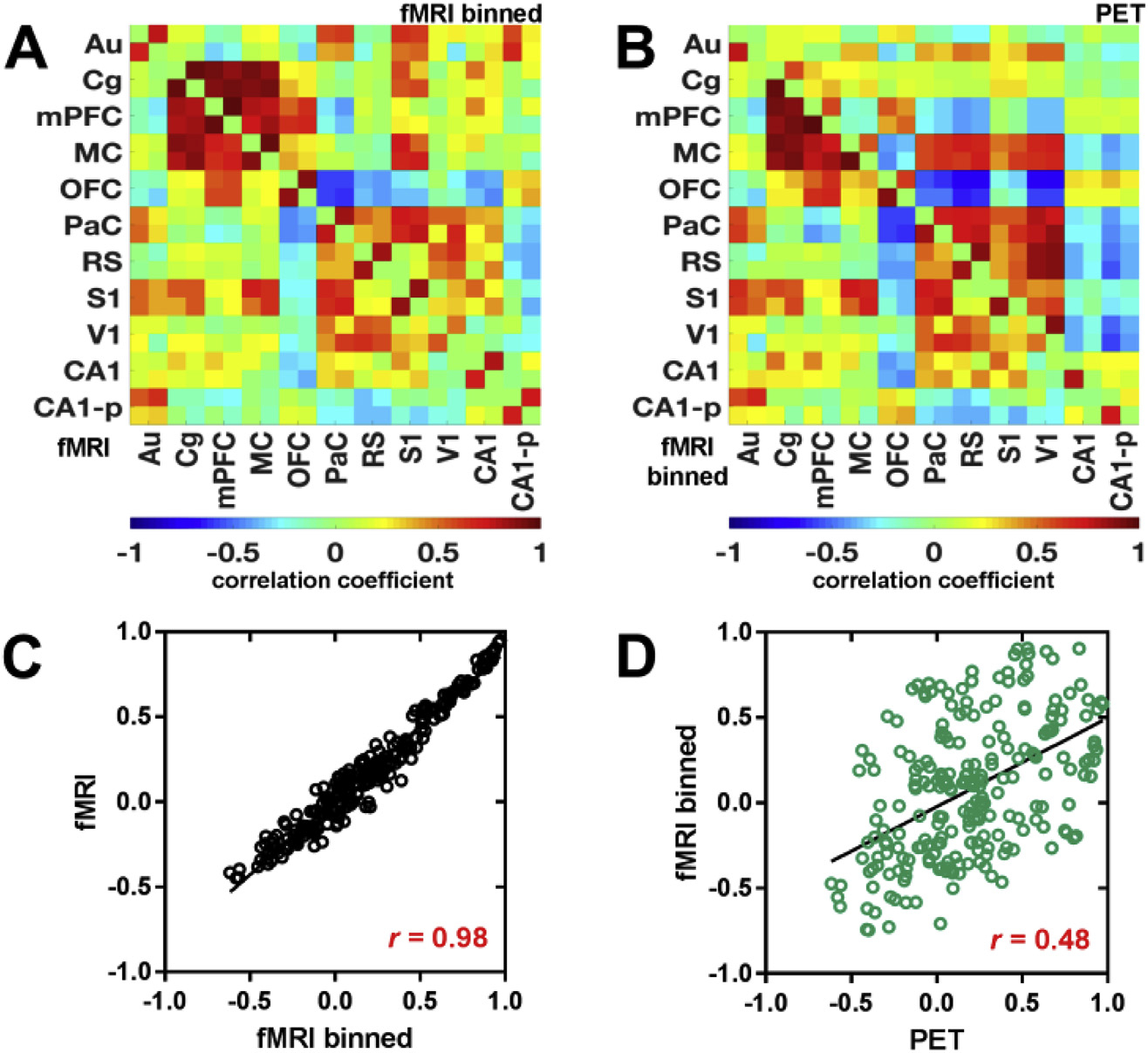
fMRI time course data of the bolus injection cohort were binned to the temporal resolution of the PET data (1 min) and Pearson’s r correlation coefficient matrices were computed for the DMN-like structure. Resulting matrices were compared to (A) the original fMRI data and the (B) the [18F]FDG-PET data. Scatter plots of pair-wise correlations between brain regions (averaged across subjects) containing the DMN-like structure and linear fits were computed for (C) the comparison between original fMRI and binned fMRI data, as well as for (D) the comparison between binned fMRI and [18F]FDG-PET data. The correlation value represents Pearson’s correlation coefficient r. The different brain ROIs containing the DMN-like structure and their abbreviations are listed in Supplementary Table 2. (N = 15).
Thus, the common connectivity pattern between the binned fMRI shows temporally synchronized underlying [18F]FDG-PET correlations (Fig. 4B).
To quantify the similarities among regular and binned fMRI matrices (Fig. 4C) and binned fMRI and PET matrices (Fig. 4D), Pearson’s r correlations between each pair of matrices were calculated. The regular fMRI and the binned fMRI matrices depicted a very higher correlation of 0.98, while the correlation value between fMRI and PET matrices was not impacted by the fMRI binning (r = 0.48), suggesting the presence of brain connectivity also on slow temporal scales in the minute range. Similar findings were detected for the constant infusion cohort (Supplementary Fig. 3). Brain regions comprising the DMN-like structure are presented in Supplementary Table 2.
3.4. Dynamic [18F]FDG connectivity indicates tracer kinetic dependencies
Fig. 5 shows functional and dynamic [18F]FDG-PET-derived connectivity matrices of the bolus injection and constant infusion cohorts at different time intervals.
Fig. 5. Dynamic [18F]FDG-PET connectivity.
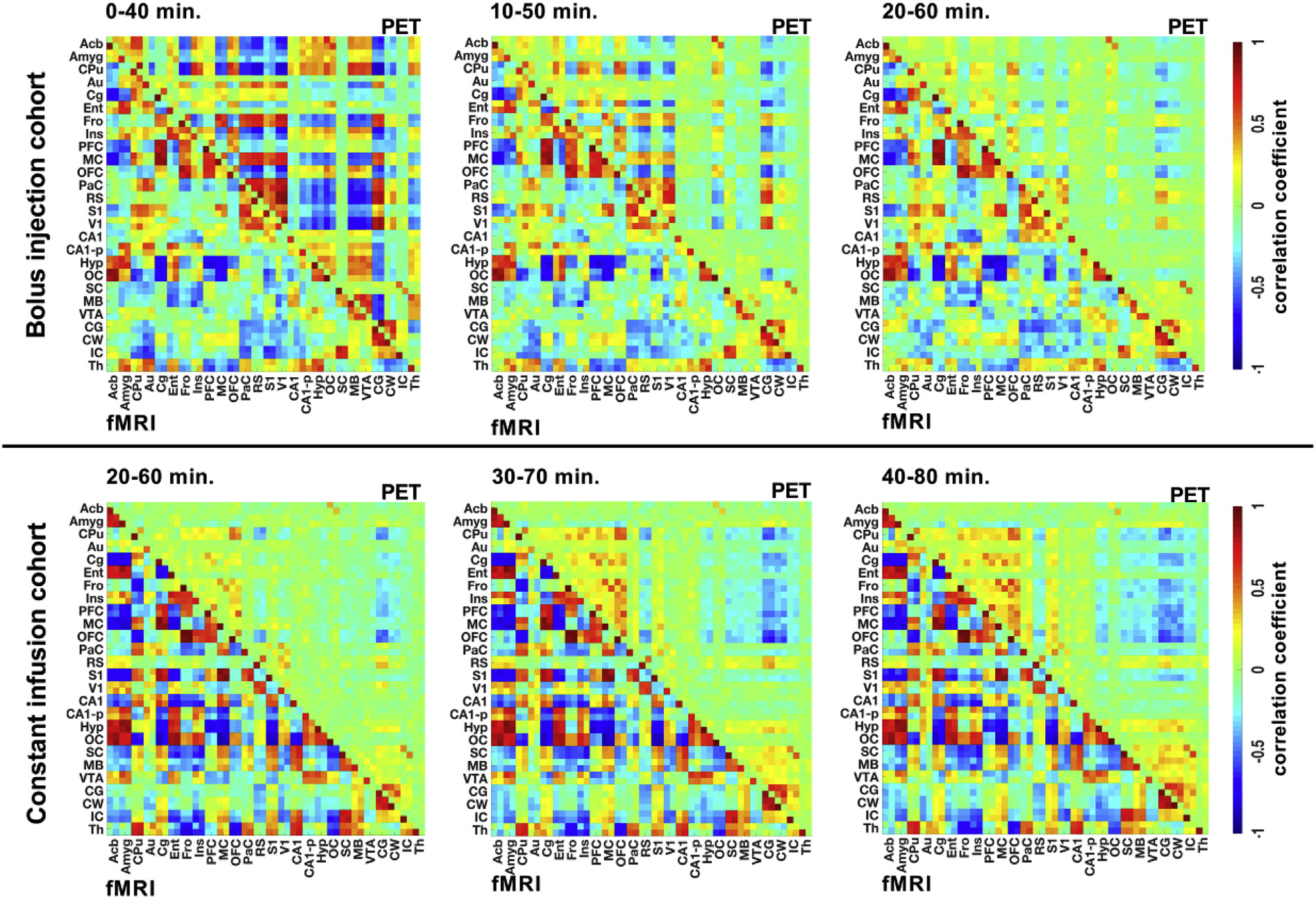
Pearson’s r correlation coefficient matrices were computed for the fMRI and [18F]FDG-PET data of the bolus injection and constant infusion cohorts at three different time intervals of 40 min (bolus injection cohort: 0–40 min, 10–50 min, and 20–60 min; constant infusion cohort: 20–60 min, 30–70 min, and 40–80 min). The color scale represents the strengths of correlations. Correlation coefficients with p-values ≥ 0.05 were set to 0. The different brain ROIs and their abbreviations are listed in Supplementary Table 1 p ≥ 0.05. Bolus injection cohort (N = 15); constant infusion cohort (N = 11).
In contrast to the stability of the BOLD-fMRI-derived functional connectivity over time, clear changes in [18F]FDG-PET connectivity based on the investigated time window were observed in both cohorts. While strong correlations were detected in the 0–40-min time window, the PET-based connectivity decreased towards the 10–50-min time window and further decreased to the 20–60-min time window after bolus injection. In contrast, PET-based connectivity in the constant infusion cohort increased from 20–60 min to 30–70 min and remained stable from 40 to 80 min.
The observed differences between stable functional connectivity and time-varying dynamic [18F]FDG-PET connectivity were quantitatively supported by only minor changes in the computed absolute correlation strengths (Fig. 6A) of functional connectivity in both cohorts (bolus injection cohort: 0.476 ± 0.084, 0.458 ± 0.093 and 0.450 ± 0.117; constant infusion cohort: 0.464 ± 0.119, 0.470 ± 0.125 and 0.437 ± 0.111). However, the PET-based correlation strength of the bolus injection cohort decreased significantly (p = 4.674*10−6) from 0 to 40 min (0.319 ± 0.116) to 10–50 min (0.188 ± 0.100) and further decreased in the 20–60-min time window (0.118 ± 0.092; p = 1.134*10−3), whereas constant infusion resulted in increased connectivity strengths from 20 to 60 (0.100 ± 0.049) to 30–70 (0.138 ± 0.111; p = 0.174) and 40–80 (0.148 ± 0.139; p = 0.326) minutes.
Fig. 6. Quantitative dynamic correlation characteristics.
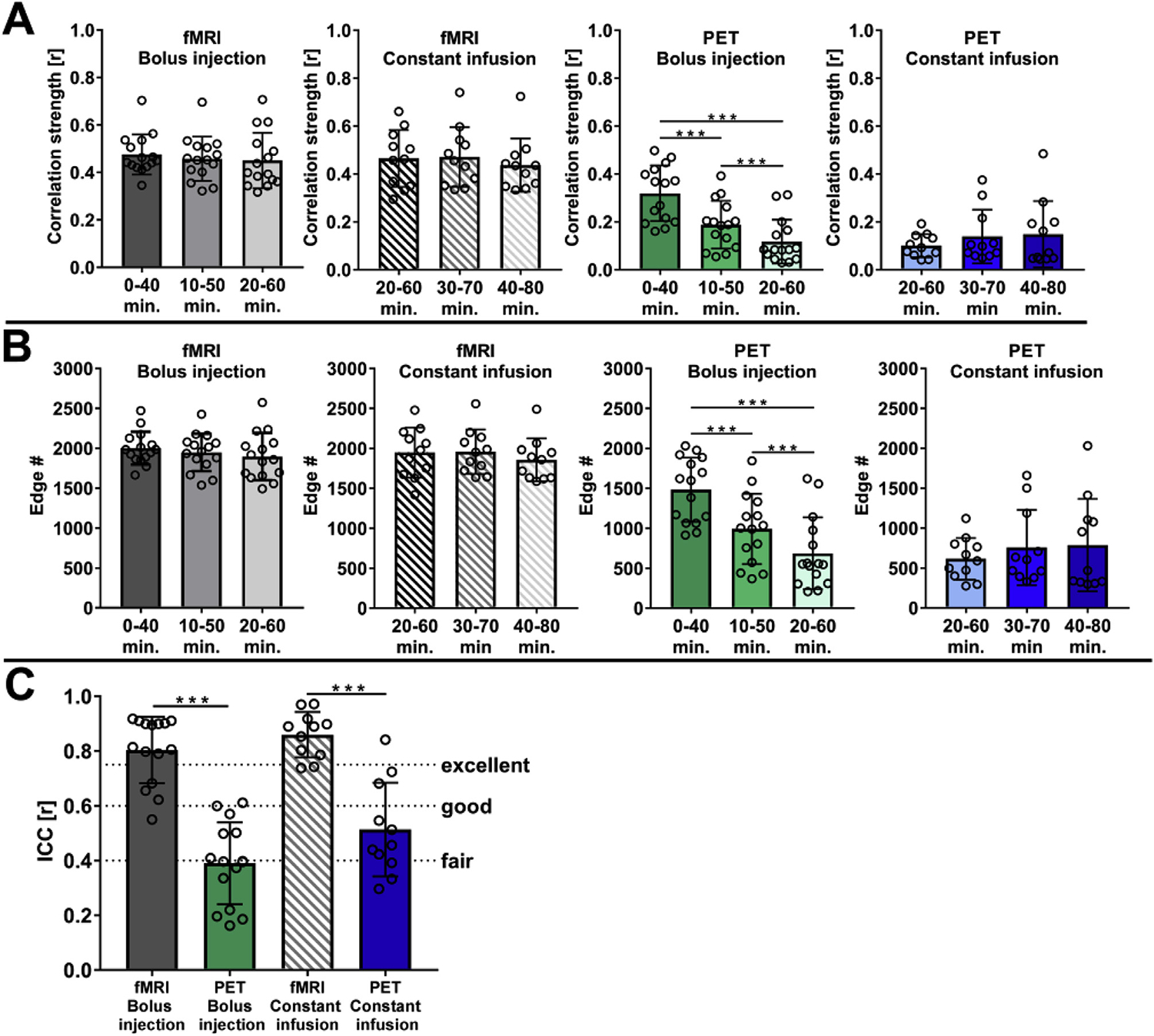
(A) The mean correlation strengths and (B) edge numbers of functional and [18F]FDG-PET correlations were calculated for the bolus injection and constant infusion cohorts at three 40-min time intervals (bolus injection cohort: 0–40 min, 10–50 min, and 20–60 min; constant infusion cohort: 20–60 min, 30–70 min, and 40–80 min). (C) Intraclass correlations were calculated to describe within-scan consistency between functional and [18F]FDG-PET correlation matrices obtained for the three mentioned time intervals. Intraclass correlations are interpreted as r < 0.40: poor correlation, 0.40 ≤ r < 0.59: fair correlation, 0.60 ≤ r < 0.75: good correlation, and r ≥ 0.75: excellent correlation. The error bars represent standard deviations. Bolus injection cohort (N = 15); constant infusion cohort (N = 11). *** represents p-values < 0.001.
These findings were further supported by the quantified edge numbers (Fig. 6B) for the respective cohorts and time windows. While the edge numbers for functional connectivity in both cohorts remained stable (bolus injection cohort: 2001 ± 207, 1947 ± 235 and 1895 ± 296; constant infusion cohort: 1949 ± 314, 1958 ± 278 and 1857 ± 268), the bolus injection cohort exhibited significant decreases (p = 2.07*10−6) in edge numbers from the 0–40 min time window (1482 ± 402) compared to 10 50 min (992 ± 439) and the 20–60-min time window (687 ± 450). In contrast to the bolus injection cohort, constant infusion resulted in increased edge numbers over time (20–60 min: 616 ± 261, 30–70 min: 758 ± 471; p = 0.202 and 40–80 min: 787 ± 578; p = 0.307).
The within-scan consistency of changes in correlation strengths and edge numbers was ultimately summarized as low (ICC = 0.39 ± 0.15) after bolus injection and fair (ICC = 0.51 ± 0.17) with constant infusion for PET-derived connectivity, whereas functional connectivity showed excellent within-scan consistency in both cohorts (bolus injection: ICC = 0.80 ± 0.12; constant infusion: ICC = 0.86 ± 0.08) (Fig. 6C). In contrast to the differences of [18F]FDG-PET connectivity outcomes between both cohorts, the functional between-group connectivity depicted good similarities (ICC: 0.65; Dice: 0.61) (Supplementary Fig. 4).
3.5. PET-derived correlation strengths depend on [18F]FDG tracer uptake ratios
The relationship between correlation strengths and [18F]FDG tracer uptake ratios was computed to elucidate the impact of tracer uptake similarities on the correlation strength measurements between two brain regions (Fig. 7). Computed scatter plots indicating the dependencies of Pearson’s correlation coefficients on [18F]FDG uptake ratios of two respective brain regions are shown for the bolus injection (Fig. 7A) and the constant infusion (Fig. 7B) cohorts. In both cohorts, the scatter plots depict the requirement for high [18F]FDG uptake ratios to obtain strong positive and negative correlation coefficients. However, high [18F]FDG uptake ratios did not ultimately cause strong correlation coefficients since both cohorts presented weak correlation coefficients in the range of 0.25 < r < −0.25 between regions with high [18F]FDG uptake ratios. Notably, the constant infusion cohort was characterized by a wider range of [18F]FDG uptake ratios (0.37–0.98) compared to the bolus injection group (0.57–0.99).
Fig. 7. [18F]FDG-PET correlation strength is tracer uptake-dependent.
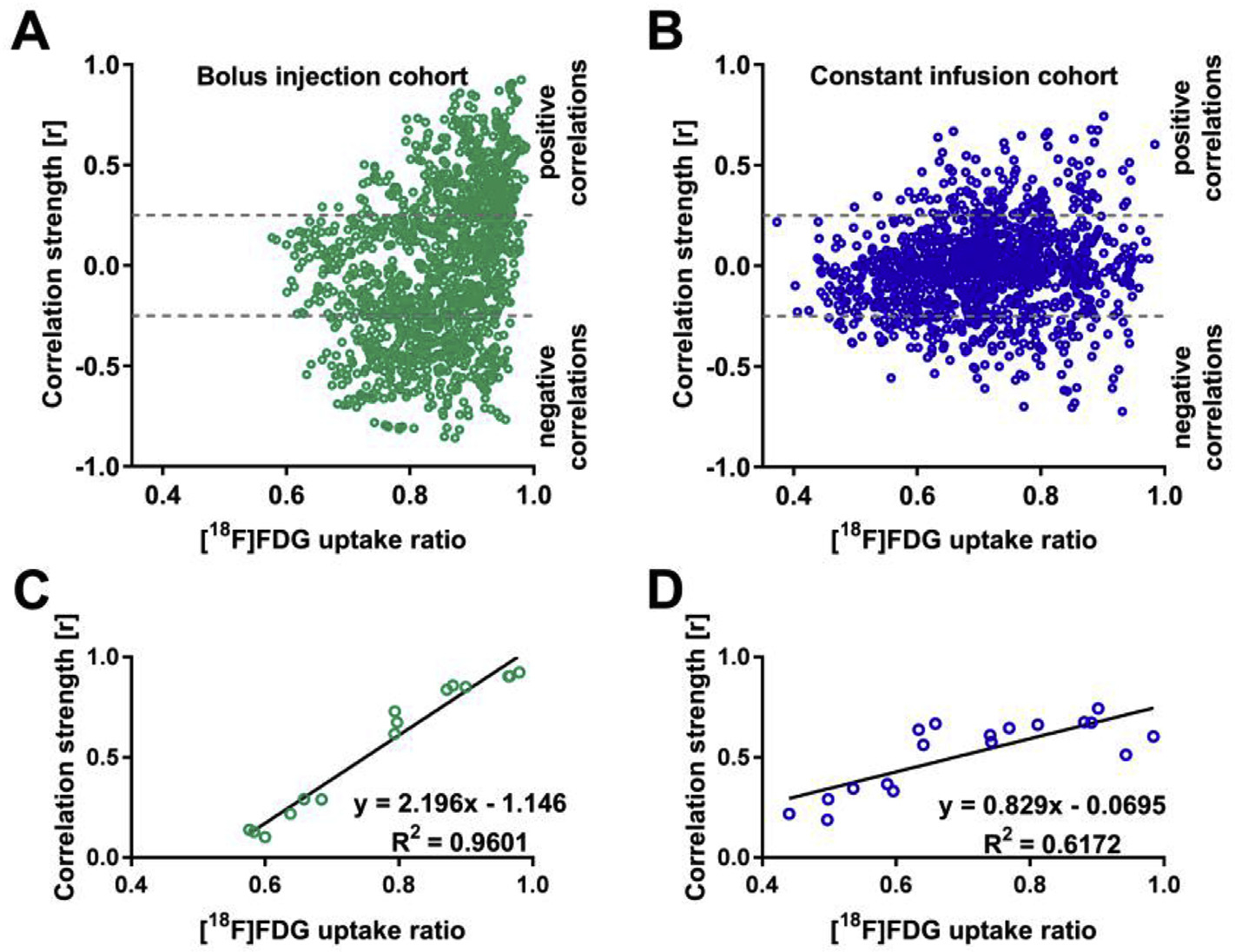
The dependencies of correlation coefficient strengths on the [18F]FDG uptake ratios of the respective brain areas are shown in scatter plots for the bolus injection cohort (A) and the constant infusion cohort (B). The three highest positive correlations for six [18F]FDG uptake ratio intervals (0.40–0.50, 0.50–0.60, 0.60–0.70, 0.70–0.80, 0.80–0.90, and 0.90–1.00) were selected for linear regression analysis for (C) the bolus injection and (D) constant infusion cohorts. Bolus injection cohort (N = 15); constant infusion cohort (N = 11).
Linear regression analysis of the three strongest positive correlations of six consecutive [18F]FDG uptake ratio intervals (0.40–0.50, 0.50–0.60, 0.60–0.70, 0.70–0.80, 0.80–0.90, and 0.90–1.00) for the bolus injection (Fig. 7C) and the constant infusion cohorts (Fig. 7D) confirmed the scatter plot-derived descriptions. The R2 values were 0.96 for positive correlations in the bolus injection cohort and 0.62 for positive correlations in the constant infusion cohort.
4. Discussion
Investigations of brain network structures have become a major focus in the field of neuroscience, especially in cognitive neuroscience (Pessoa, 2014). However, due to the structural and functional complexity of the brain, interpretations of network connectivity remain elusive (Horwitz, 2014). Therefore, utilizing a combination of imaging modalities that characterize different biochemical and physiological parameters of brain function may provide further insights into brain connectomics. The current study evaluated the association between BOLD-fMRI functional and dynamic [18F]FDG-PET derived resting-state connectivity based on simultaneous PET/MRI measurements in rodents. For the first time, we focused on glucose metabolism-associated [18F]FDG-PET tracer uptake and dynamic influences on whole-brain and DMN-like approximate metabolic connectivity measurements. Unlike previous studies in humans investigating similarities between fMRI and [18F]FDG-PET (Aiello et al., 2015; Di et al., 2017; Tomasi et al., 2017), the major strengths of our study, which was performed in a preclinical setting, were the maximal reduction of inter-individual differences due to the inclusion of homogenous cohorts and the implementation of simultaneous acquisitions to provide optimal spatial, temporal and physiological correlations between both modalities (Judenhofer et al., 2008; Wehrl et al., 2013). Utilizing this powerful experimental setting, we showed that the whole-brain correlation matrices calculated for resting-state fMRI and dynamically reconstructed [18F]FDG-PET data had similar clustering patterns exhibiting a modular architecture. Evaluation of the connectivity within the DMN-like structure revealed further synchrony between functional and [18F]FDG-PET connectivity in a distinct resting-state network.
The presence of PET-derived connectivity developing on slower time scales was further confirmed by modulating the fMRI temporal resolution, which allowed a direct comparison to the temporal dynamics of glucose metabolism associated correlations.
By analyzing the development of functional and PET-derived correlations, time-varying tracer dynamic dependencies of [18F]FDG correlations were identified, while functional connectivity remained stable. Providing a constant supply of [18F]FDG the time-varying correlation characteristics were reduced. The mean correlation strengths and edge numbers depicted stronger functional correlations in BOLD-fMRI-derived versus [18F]FDG-PET-derived connectivity. Furthermore, the [18F]FDG-derived peak correlation strengths increased linearly with higher tracer uptake ratios between respective brain regions for both positive and negative correlations. Conclusively, we found great similarities between dynamic [18F]FDG-PET and functional connectivity. By varying the [18F] FDG pharmacokinetics using different tracer applications, we identified the tracer administration regimens as a major driving forces for dynamic [18F]FDG-PET-derived connectivity outcomes.
4.1. PET/MRI analogies of resting-state brain connectivity
The correlation clusters identified for functional and dynamic [18F] FDG-PET connectivity correspond well with previously identified functional resting-state whole-brain networks in rodents (D’Souza et al., 2014; Bukhari et al., 2018). Further reports using binary network analysis (Liang, King et al. 2011, 2012) or ICA-based correlation analysis of fMRI data (Hutchison et al., 2010; Becerra et al., 2011; Jonckers et al., 2011) support these findings.
Based on the mentioned studies on functional connectivity in the rodent brain, our previous study comparing ICA-derived functional and metabolic somatosensory circuits (Wehrl et al., 2013) together with the present findings on fully connected connectivity networks indicate a certain similarity between functional and metabolic network information.
The PET-derived connectivity, in this case using [18F]FDG as a surrogate marker for glucose metabolism, was characterized by overall weaker connectivity strengths and lower edge numbers compared to the corresponding values obtained using fMRI. However, the observation of [18F]FDG-PET correlation modules was found to be closely related to functional connectivity networks (using fMRI) and indicates that fundamental information regarding brain networks is coded in dynamic fluctuations of brain energy consumption measured by [18F]FDG-PET. The underlying [18F]FDG-PET connectivity was further demonstrated by temporal assimilation of the fMRI data, which confirmed the presence of resting-state brain connectivity even at slower temporal scales in the range of minutes. This observation contradicts the common sense that fMRI-based functional connectivity can be derived only from low frequency fluctuations on a temporal scale of seconds and suggests that fluctuations on different temporal scales contribute to the connectivity outcome. Physiologically, an underlying synchrony between the BOLD contrast used in fMRI studies and glucose consumption in the brain can be expected since the resting brain derives most of its energy via oxidative phosphorylation (Shulman et al., 2001), leading to a similar ratio of oxygen consumption and glucose utilization. However, the results from human studies are not consistent. Several studies have reported only minor similarities between functional and metabolic connectivity (Di et al., 2017; Tomasi et al., 2017). On the other hand, positive correlations of elevated aerobic glycolysis with functional networks have also been reported (Vaishnavi et al., 2010).
A primary limitation of human studies is the large age range of subjects included in these studies since several studies have reported age-dependent changes in structural covariance (Zielinski et al., 2010; Montembeault et al., 2012; Spreng and Turner, 2013), possibly influencing the similarity outcome of functional and metabolic connectivity. The identification of strong positive correlations within the DMN-like structure using [18]FDG-PET provides further evidence for hemodynamic and metabolic analogies on brain connectivity levels.
Multiple functional networks have been described in the rat brain that are homologous to those reported in humans (Lu et al., 2012; Raichle, 2015; Sierakowiak et al., 2015). However, the DMN is probably the most extensively described resting-state network structure and may have evolutionary significance, functioning as an “intelligence oversight” system remaining alert to protect the subject from environmental dangers (Lu et al., 2012; Raichle, 2015). The necessary default and nonstop coherent activity may explain the high baseline demand for cerebral blood flow as well as metabolic activity (Raichle et al., 2001) as reflected by both functional and metabolic correlations within the rodent DMN-like structure in this study. The presence of a metabolically active DMN-like network in rats, which is fairly similar to its functional human counterpart, is important since several trials of human neurodegenerative pathologies have reported altered metabolic connectivity within the DMN (Raichle, 2015; Spetsieris et al., 2015; Sala et al., 2017). The present study identified the existence of a DMN-like network derived from dynamic metabolic information, which may contribute significantly to the development of resting-state brain connectivity as a tool to understand cognitive impairment on a translational level and as a potential diagnostic marker for early detection of brain pathologies.
4.2. Tracer application dependencies on dynamic [18F]FDG-PET-derived connectivity
By applying two different [18F]FDG-PET tracer administration regimes characterized by their individual pharmacokinetic properties, strong tracer uptake dependencies on connectivity outcomes were observed. While a standard bolus injection of [18F]FDG results in high K1/k2 values in the first 10–20 min (Alf et al., 2013), a constant infusion of [18F]FDG leads to a K1/k2 equilibrium after 20–30 min post infusion start (Villien et al., 2014).
To our knowledge, this is the first preclinical study evaluating the influence of [18F]FDG tracer kinetics and uptake patterns by varying the tracer pharmacokinetics using a standard bolus injection as well as a constant infusion of [18F]FDG. Recently, Tomasi et al. (Tomasi et al., 2017) reported prominent metabolic correlations in the early phase of bolus injection-based dynamic [18F]FDG-PET measurements. Our data from the bolus injection cohort support these findings, and further specify the dependency of [18F]FDG signal correlations on glucose transport rates K1 and k2 varying over the time course of PET measurements.
In contrast to the bolus protocol, the [18F]FDG-derived connectivity obtained by constant [18F]FDG infusion led to stable correlation readouts once glucose transport rates reached equilibrium. Given that [18F]FDG was infused at a constant rate during PET acquisition, the freely available [18F]FDG level for metabolism at rest was different from that with bolus-injected [18F]FDG and remained nearly constant (Villien et al., 2014). Notably, the rate constant of [18F]FDG transport from the blood to the brain (K1) is smaller than the rate constant for transport back from the brain to the blood (k2), but both K1 and k2 are greater than the rate constant for phosphorylation of [18F]FDG (k3) (Sokoloff et al., 1977; Reivich et al., 1985).
Accordingly, the metabolic rate is slow compared to blood-brain exchange, and due to the constant infusion of [18F]FDG, its availability is not limited by tracer supply to the brain through the circulation, unlike with bolus injection. Therefore, [18F]FDG-PET connectivity derived via constant tracer infusion can be considered a result of K1/k2-dependent uptake characteristics. Due to the constant tracer infusion perfusion influences on the [18F]FDG-PET signal that may cause hemodynamic contributions in the PET-based correlation outcome via bolus injection can be excluded. This is further supported by the linear relationship between correlation strength and [18F]FDG uptake ratios. Although strong positive and negative correlations were detected regardless of the [18F]FDG uptake ratio, the strongest correlations were detected between brain regions with similar [18F]FDG uptake values, which is consistent with the energy demand of brain connectivity (Tomasi et al., 2013; Passow et al., 2015).
To further decode the influence of tracer dynamics and uptake characteristics on connectivity readouts, alternatively labeled glucose analogs such as 3-fluoro-3-deoxy-D-glucose or [15O]-labeled 2-deoxy-D-glucose with different pharmacokinetic and metabolic properties compared to 2-fluor-2-deoxy-D-glucose, which was used in this study, may provide promising results. Due to the steady-state characteristics of constant tracer infusion, this method may reflect a more dynamic approach and probably results in higher temporal resolution. To determine brain function in multiple biochemical and neurophysiological states, simultaneously acquired data must be assessed preclinically and in human studies with homogenous cohorts, and improved comparative analysis strategies must be developed. Studies including additional time scales (e.g., PET/MRI/EEG) may yield additional insight.
4.3. Technical considerations
Despite its numerous advantages brain connectivity outcomes are not without limitations of interpretation and confounding factors. Observed effects are usually interpreted on network levels, but without supporting data from for example cognitive or behavioral data. Thus, obtained results may be easily over-interpreted. Hence, several aspects need to be considered when interpreting the presented data.
The first confounding factor is the use of isoflurane as anesthesia suppressing neuronal activity, reducing cerebral metabolism and acting as a dose dependent vasodilator for the cerebrovascular system. This results in a higher baseline cerebral blood flow and volume that can increase the amplitude of cerebrovascular fluctuations causing stronger correlation readouts for the fMRI data (Williams et al., 2010). Even though isoflurane levels were kept at minimum levels, the contrary effects of isoflurane on BOLD-fMRI and [18F]FDG-PET signals need to be considered for data interpretation. However, anesthesia is a general concern in preclinical settings which is hardly to circumvent. The α2-agonist medetomidine producing dose-dependent sedation, analgesia, muscle relaxation and anxiolysis has been proposed as an alternative for isoflurane anesthesia for rodent fMRI studies (Weber et al., 2006; Zhao et al., 2008). Unfortunately, medetomidine causes increased blood glucose levels (Wehrl et al., 2013) hampering its use for [18F]FDG-PET measurements.
Another confounding factor may be the different group sizes, since the p-value based significance of correlations depends not only on the correlation strengths but also on and the underlying sample sizes. This could negatively influence the comparison of correlations between the two cohorts and explain the observed minor differences on a functional level. However, the observed differences on a surrogate metabolic level were remarkably strong. Here, varying signal to noise variations of both application protocols could further contribute to differences in the dynamic [18F]FDG-PET connectivity profiles.
5. Conclusion
To date, most clinical and preclinical metabolic connectivity studies have been performed using static [18F]FDG-PET scans. This type of analysis is limited to group-level investigations and does not include temporal information, which is necessary to investigate a possible synchrony between time course-derived hemodynamic fMRI- and PET-derived metabolic signal fluctuations. Our first aim was to examine a possible underlying synchrony of hemodynamic fluctuations and glucose uptake on whole-brain and resting-state network levels using simultaneous dynamic [18F]FDG-PET/fMRI acquisitions characterized by very precise temporal, spatial and physiological correlations for each subject. Furthermore, we sought to describe the influences of tracer kinetics and uptake characteristics on dynamic [18F]FDG-PET connectivity readouts. The similarities between the identified functional and [18F]FDG-PET connectivity clusters on a whole-brain level and the distinct DMN-like structure reflected further evidence of their related information.
By applying bolus or constant infusion tracer administration protocols that are characterized by different pharmacokinetic properties, our data demonstrate tracer application and consecutive time-varying uptake dependencies of PET-derived whole-brain connectivity readouts. We identified that [18F]FDG-PET data acquired during constant infusion is more dominated by the metabolic component of the kinetics compared to a classical bolus injection. Therefore, the application of fPET via constant infusion of [18F]FDG may be more suitable than a classical bolus injection to evaluate metabolic connectivity. Based on our findings further work will concentrate on the evaluation of resting-state networks based on multitracer approaches targeting also different neurotransmitter systems.
Supplementary Material
Acknowledgements
We acknowledge PD Dr. Gerald Reischl (Department of Preclinical Imaging and Radiopharmacy, Werner Siemens Imaging Center, Eberhard Karls University Tuebingen) for producing the PET radiotracer [18F]FDG. Furthermore, we gratefully acknowledge Dr. Julia Mannheim, Dr. Rebecca Rock and Ines Wickertsheim (Department of Preclinical Imaging and Radiopharmacy, Werner Siemens Imaging Center, Eberhard Karls University Tuebingen) for their technical and administrative support. This study is also part of the PhD thesis of Mario Amend.
Funding
The research was funded by the German Ministry of Education and Research (BMBF, grant number 01GQ1415), the IZKF-Juniorgrant (2209–0-0) for Functional and Metabolic Brain Imaging of the Medical Faculty for HFW, the DFG Emmy-Noether Grant “Multiscalar monitoring of small animal brain activity using combined PET/MR/EEG” (WE 5795/2–1) to HFW, and the National Institutes of Health (NIH R01 DA038895) to BBB.
Footnotes
Conflicts of interest
The authors declare no conflict of interest.
Appendix A. Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.neuroimage.2019.04.034.
References
- Aiello M, Salvatore E, Cachia A, Pappata S, Cavaliere C, Prinster A, Nicolai E, Salvatore M, Baron JC, Quarantelli M, 2015. Relationship between simultaneously acquired resting-state regional cerebral glucose metabolism and functional MRI: a PET/MR hybrid scanner study. Neuroimage 113, 111–121. [DOI] [PubMed] [Google Scholar]
- Alf MF, Martic-Kehl MI, Schibli R, Kramer SD, 2013. FDG kinetic modeling in small rodent brain PET: optimization of data acquisition and analysis. EJNMMI Res. 3, 61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becerra L, Pendse G, Chang PC, Bishop J, Borsook D, 2011. Robust reproducible resting state networks in the awake rodent brain. PLoS One 6 (10), e25701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS, 1995. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson. Med. 34 (4), 537–541. [DOI] [PubMed] [Google Scholar]
- Bukhari Q, Schroeter A, Rudin M, 2018. Increasing isoflurane dose reduces homotopic correlation and functional segregation of brain networks in mice as revealed by resting-state fMRI. Sci. Rep. 8 (1), 10591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton RB, 2002 and 2009. Introduction to Functional Magnetic Resonance Imaging: Principles and Techniques. Cambridge University Press. [Google Scholar]
- Chicchetti DV, 1994. Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology. Psychol. Assess. 6 (4), 284–290. [Google Scholar]
- D’Souza DV, Jonckers E, Bruns A, Kunnecke B, von Kienlin M, Van der Linden A, Mueggler T, Verhoye M, 2014. Preserved modular network organization in the sedated rat brain. PLoS One 9 (9), e106156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di X, Biswal BB, 2012. Metabolic brain covariant networks as revealed by FDG-PET with reference to resting-state fMRI networks. Brain Connect. 2 (5), 275–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di X, Gohel S, Thielcke A, Wehrl HF, Biswal BB, 2017. Do all roads lead to Rome? A comparison of brain networks derived from inter-subject volumetric and metabolic covariance and moment-to-moment hemodynamic correlations in old individuals. Brain Struct. Funct. 222 (8), 3833–3845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert T, Tang C, Eidelberg D, 2007. Assessment of the progression of Parkinson’s disease: a metabolic network approach. Lancet Neurol. 6 (10), 926–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feigin A, Kaplitt MG, Tang C, Lin T, Mattis P, Dhawan V, During MJ, Eidelberg D, 2007. Modulation of metabolic brain networks after subthalamic gene therapy for Parkinson’s disease. Proc. Natl. Acad. Sci. U. S. A. 104 (49), 19559–19564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME, 2005. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci. U. S. A. 102 (27), 9673–9678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Krasnow B, Reiss AL, Menon V, 2003. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc. Natl. Acad. Sci. U. S. A. 100 (1), 253–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamacher K, Coenen HH, Stocklin G, 1986. Efficient stereospecific synthesis of no-carrier-added 2-[18F]-fluoro-2-deoxy-D-glucose using aminopolyether supported nucleophilic substitution. J. Nucl. Med. 27 (2), 235–238. [PubMed] [Google Scholar]
- Horwitz B, 2014. The elusive concept of brain network. Comment on “Understanding brain networks and brain organization” by Luiz Pessoa. Phys. Life Rev. 11 (3), 448–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horwitz B, Duara R, Rapoport SI, 1984. Intercorrelations of glucose metabolic rates between brain regions: application to healthy males in a state of reduced sensory input. J. Cereb. Blood Flow Metab. 4 (4), 484–499. [DOI] [PubMed] [Google Scholar]
- Hutchison RM, Mirsattari SM, Jones CK, Gati JS, Leung LS, 2010. Functional networks in the anesthetized rat brain revealed by independent component analysis of resting-state FMRI. J. Neurophysiol. 103 (6), 3398–3406. [DOI] [PubMed] [Google Scholar]
- Jonckers E, Van Audekerke J, De Visscher G, Van der Linden A, Verhoye M, 2011. Functional connectivity fMRI of the rodent brain: comparison of functional connectivity networks in rat and mouse. PLoS One 6 (4), e18876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judenhofer MS, Wehrl HF, Newport DF, Catana C, Siegel SB, Becker M, Thielscher A, Kneilling M, Lichy MP, Eichner M, Klingel K, Reischl G, Widmaier S, Rocken M, Nutt RE, Machulla HJ, Uludag K, Cherry SR, Claussen CD, Pichler BJ, 2008. Simultaneous PET-MRI: a new approach for functional and morphological imaging. Nat. Med. 14 (4), 459–465. [DOI] [PubMed] [Google Scholar]
- Liang Z, King J, Zhang N, 2011. Uncovering intrinsic connectional architecture of functional networks in awake rat brain. J. Neurosci. 31 (10), 3776–3783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang Z, King J, Zhang N, 2012. Anticorrelated resting-state functional connectivity in awake rat brain. Neuroimage 59 (2), 1190–1199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Pauls J, Augath M, Trinath T, Oeltermann A, 2001. Neurophysiological investigation of the basis of the fMRI signal. Nature 412 (6843), 150–157. [DOI] [PubMed] [Google Scholar]
- Lu H, Zou Q, Gu H, Raichle ME, Stein EA, Yang Y, 2012. Rat brains also have a default mode network. Proc. Natl. Acad. Sci. U. S. A. 109 (10), 3979–3984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metter EJ, Riege WH, Kuhl DE, Phelps ME, 1984. Cerebral metabolic relationships for selected brain regions in healthy adults. J. Cereb. Blood Flow Metab. 4 (1), 1–7. [DOI] [PubMed] [Google Scholar]
- Montembeault M, Joubert S, Doyon J, Carrier J, Gagnon JF, Monchi O, Lungu O, Belleville S, Brambati SM, 2012. The impact of aging on gray matter structural covariance networks. Neuroimage 63 (2), 754–759. [DOI] [PubMed] [Google Scholar]
- Passow S, Specht K, Adamsen TC, Biermann M, Brekke N, Craven AR, Ersland L, Gruner R, Kleven-Madsen N, Kvernenes OH, Schwarzlmuller T, Olesen RA, Hugdahl K, 2015. Default-mode network functional connectivity is closely related to metabolic activity. Hum. Brain Mapp. 36 (6), 2027–2038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pessoa L, 2014. Understanding brain networks and brain organization. Phys. Life Rev. 11 (3), 400–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phelps ME, Huang SC, Hoffman EJ, Selin C, Sokoloff L, Kuhl DE, 1979. Tomographic measurement of local cerebral glucose metabolic rate in humans with (F-18)2-fluoro-2-deoxy-D-glucose: validation of method. Ann. Neurol. 6 (5), 371–388. [DOI] [PubMed] [Google Scholar]
- Raichle ME, 2015. The brain’s default mode network. Annu. Rev. Neurosci. 38, 433–447. [DOI] [PubMed] [Google Scholar]
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL, 2001. A default mode of brain function. Proc. Natl. Acad. Sci. U. S. A. 98 (2), 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reivich M, Alavi A, Wolf A, Fowler J, Russell J, Arnett C, MacGregor RR, Shiue CY, Atkins H, Anand A, et al. , 1985. Glucose metabolic rate kinetic model parameter determination in humans: the lumped constants and rate constants for [18F]fluorodeoxyglucose and [11C]deoxyglucose. J. Cereb. Blood Flow Metab. 5 (2), 179–192. [DOI] [PubMed] [Google Scholar]
- Riedl V, Utz L, Castrillon G, Grimmer T, Rauschecker JP, Ploner M, Friston KJ, Drzezga A, Sorg C, 2016. Metabolic connectivity mapping reveals effective connectivity in the resting human brain. Proc. Natl. Acad. Sci. U. S. A. 113 (2), 428–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sala A, Caminiti SP, Presotto L, Premi E, Pilotto A, Turrone R, Cosseddu M, Alberici A, Paghera B, Borroni B, Padovani A, Perani D, 2017. Altered brain metabolic connectivity at multiscale level in early Parkinson’s disease. Sci. Rep. 7 (1), 4256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schiffer WK, Mirrione MM, Biegon A, Alexoff DL, Patel V, Dewey SL, 2006. Serial microPET measures of the metabolic reaction to a microdialysis probe implant. J. Neurosci. Methods 155 (2), 272–284. [DOI] [PubMed] [Google Scholar]
- Shulman RG, Hyder F, Rothman DL, 2001. Lactate efflux and the neuroenergetic basis of brain function. NMR Biomed. 14 (7–8), 389–396. [DOI] [PubMed] [Google Scholar]
- Sierakowiak A, Monnot C, Aski SN, Uppman M, Li TQ, Damberg P, Brene S, 2015. Default mode network, motor network, dorsal and ventral basal ganglia networks in the rat brain: comparison to human networks using resting state-fMRI. PLoS One 10 (3), e0120345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokoloff L, Reivich M, Kennedy C, Des Rosiers MH, Patlak CS, Pettigrew KD, Sakurada O, Shinohara M, 1977. The [14C]deoxyglucose method for the measurement of local cerebral glucose utilization: theory, procedure, and normal values in the conscious and anesthetized albino rat. J. Neurochem. 28 (5), 897–916. [DOI] [PubMed] [Google Scholar]
- Spetsieris PG, Ko JH, Tang CC, Nazem A, Sako W, Peng S, Ma Y, Dhawan V, Eidelberg D, 2015. Metabolic resting-state brain networks in health and disease. Proc. Natl. Acad. Sci. U. S. A. 112 (8), 2563–2568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spreng RN, Turner GR, 2013. Structural covariance of the default network in healthy and pathological aging. J. Neurosci. 33 (38), 15226–15234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomasi D, Wang GJ, Volkow ND, 2013. Energetic cost of brain functional connectivity. Proc. Natl. Acad. Sci. U. S. A. 110 (33), 13642–13647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomasi DG, Shokri-Kojori E, Wiers CE, Kim SW, Demiral SB, Cabrera EA, Lindgren E, Miller G, Wang GJ, Volkow ND, 2017. Dynamic brain glucose metabolism identifies anti-correlated cortical-cerebellar networks at rest. J. Cereb. Blood Flow Metab. 37 (12), 3659–3670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaishnavi SN, Vlassenko AG, Rundle MM, Snyder AZ, Mintun MA, Raichle ME, 2010. Regional aerobic glycolysis in the human brain. Proc. Natl. Acad. Sci. U. S. A. 107 (41), 17757–17762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villien M, Wey HY, Mandeville JB, Catana C, Polimeni JR, Sander CY, Zurcher NR, Chonde DB, Fowler JS, Rosen BR, Hooker JM, 2014. Dynamic functional imaging of brain glucose utilization using fPET-FDG. Neuroimage 100, 192–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber R, Ramos-Cabrer P, Wiedermann D, van Camp N, Hoehn M, 2006. A fully noninvasive and robust experimental protocol for longitudinal fMRI studies in the rat. Neuroimage 29 (4), 1303–1310. [DOI] [PubMed] [Google Scholar]
- Wehrl HF, Hossain M, Lankes K, Liu CC, Bezrukov I, Martirosian P, Schick F, Reischl G, Pichler BJ, 2013. Simultaneous PET-MRI reveals brain function in activated and resting state on metabolic, hemodynamic and multiple temporal scales. Nat. Med. 19 (9), 1184–1189. [DOI] [PubMed] [Google Scholar]
- Williams KA, Magnuson M, Majeed W, LaConte SM, Peltier SJ, Hu X, Keilholz SD, 2010. Comparison of alpha-chloralose, medetomidine and isoflurane anesthesia for functional connectivity mapping in the rat. Magn. Reson. Imaging 28 (7), 995–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao F, Zhao T, Zhou L, Wu Q, Hu X, 2008. BOLD study of stimulation-induced neural activity and resting-state connectivity in medetomidine-sedated rat. Neuroimage 39 (1), 248–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zielinski BA, Gennatas ED, Zhou J, Seeley WW, 2010. Network-level structural covariance in the developing brain. Proc. Natl. Acad. Sci. U. S. A. 107 (42), 18191–18196. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


