Summary
Lateral inhibition is a central principle for sensory system function. It is thought to operate by the activation of inhibitory neurons that restrict the spatial spread of sensory excitation. Much work on the role of inhibition in sensory systems has focused on visual cortex; however, the neurons, computations, and mechanisms underlying cortical lateral inhibition remain debated, and its importance for visual perception remains unknown. Here, we tested how lateral inhibition from PV or SST neurons in mouse primary visual cortex (V1) modulates neural and perceptual sensitivity to stimulus contrast. Lateral inhibition from PV neurons reduced neural and perceptual sensitivity to visual contrast in a uniform subtractive manner, whereas lateral inhibition from SST neurons more effectively changed the slope (or gain) of neural and perceptual contrast sensitivity. A neural circuit model identified spatially extensive lateral projections from SST neurons as the key factor, and we confirmed this with direct subthreshold measurements of a larger spatial footprint for SST versus PV lateral inhibition. Together, these results define cell-type specific computational roles for lateral inhibition in V1, and establish their unique consequences on sensitivity to contrast, a fundamental aspect of the visual world.
Introduction
Lateral inhibition is a core concept for sensory coding. It was discovered in the retina, where neural responses to small spots of light decreased when spatially adjacent regions were simultaneously illuminated1. This narrows the region of visual space in which stimuli elicit spikes from single neurons. Evidence for lateral inhibition shaping neural responses has since been found across sensory systems2–7. Nevertheless, the importance of lateral inhibition for sensory perception remains questioned, particularly from studies of primary visual cortex (V1).
One question concerns the perceptual effects of lateral inhibition in V1. Much work in V1 shows that lateral inhibition is unnecessary to explain several aspects of neural selectivity for stimuli in the central portion of the receptive field (RF)8. However, just like retinal neurons, V1 neurons improve their spatial sensitivity during costimulation of the RF plus the surrounding regions of space9–13. This modulation (or surround suppression14) is due to inhibition suppressing excitation within V110,11,15,16. Remarkably, it is not known how lateral inhibition from a distant site in V1 affects perceptual sensitivity for stimuli appearing only in the RF.
A second question concerns how perceptual effects of lateral inhibition depend on cell types. Surround suppression in mouse V1 relies on somatostatin (SST) positive inhibitory neurons15,17,18, but the spatial scale of SST inhibition driving these effects remains unresolved19. Further, SST neurons strongly inhibit both excitatory neurons and parvalbumin (PV) interneurons20–22, which could counteract SST mediated suppression. PV neurons themselves show larger spatial integration than excitatory neurons10,15,23,24, and could also be involved in lateral suppression of excitation. Remarkably, the relationship between cell-type specific lateral inhibition and perception is unknown. To clarify this, it would be beneficial to activate lateral inhibition from PV or SST neurons independent from stimulus drive, and then measure how these activations propagate through V1 circuitry and affect stimulus perception. One possibility is that distant PV or SST neurons equally suppress excitation in the RF and equally alter perceptual sensitivity; an alternative is that anatomical and circuit properties of PV versus SST neurons confer unique consequences for perceptual sensitivity.
A third question concerns the computational role of lateral inhibition in V1. Several studies have examined computational roles for local inhibition (i.e., inhibition activated near the excitatory neurons that are driven by the visual stimulus). Moderate, sustained activation of local PV neurons (but not SST neurons) causes a divisive scaling of excitatory neuron responses to stimuli of different orientations25–28. Divisive scaling of the response curve –termed gain modulation–adjusts neural sensitivity without diminishing selectivity, a key neural computation underlying a variety of contextual effects29–31. Crucially, it is not known if scaling of V1 neural responses leads to scaling of perceptual responses. Furthermore, these prior studies were restricted to interactions within the local network; no studies have probed the computational role of lateral inhibition on both neural and perceptual response curves. This is important to clarify because lateral interactions among cortically (and retinotopically) distant sites have long been conjectured as a mechanism for behavioral and contextual modulation of perceptual sensitivity across the visual field32,33.
Here we tested how lateral inhibition from distant PV or SST neurons in mouse V1 modulates neural and perceptual sensitivity to stimulus contrast. Driving PV neurons reduced perceptual sensitivity uniformly across all contrasts, consistent with a subtractive shift of the psychometric contrast response curve. On the other hand, driving SST neurons caused a stronger divisive change of the contrast response curve. These perceptual effects of PV and SST lateral inhibition were mirrored by changes in neural contrast sensitivity on the same trials. A neural circuit model identified lateral projections from distal SST neurons as a key factor driving divisive scaling of response curves. Patch-clamp recordings directly confirmed a larger spatial footprint for SST versus PV lateral inhibition in awake V1. Together, these results define cell-type specific computational roles for lateral inhibition in V1, and establish their unique consequences on perception.
Results
SST lateral inhibition controls the slope of psychometric contrast sensitivity.
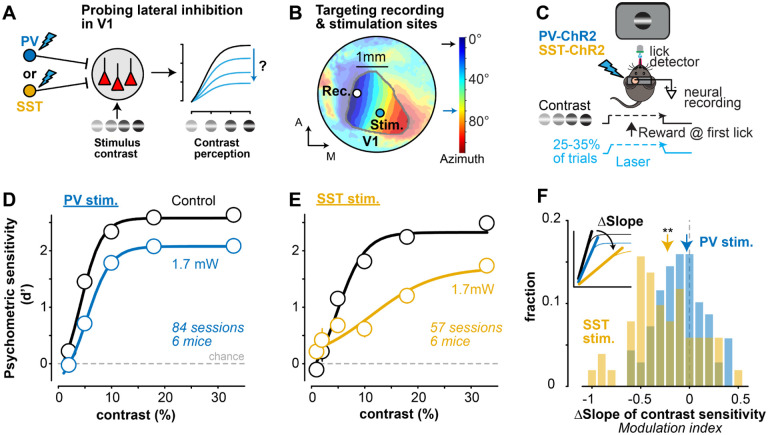
To probe the perceptual effects of PV versus SST lateral inhibition, we trained water-restricted, head-fixed stationary mice to perform a visual detection task34,35. We expressed channelrhodopsin (ChR2) in PV or SST neurons by crossing Ai32 mice with PV- or SST-cre mice (abbreviated as PV-ChR2 or SST-ChR2 mice). Mice learned to report detection of small Gabor gratings appearing in discrete locations in the visual field. We focused on blocks of trials where the stimulus appeared at the vertical meridian (defined as 0∘ azimuth) in the binocular region of greatest visual sensitivity34,36. Visual stimuli appeared at multiple contrasts (0–33%) so that we could probe how lateral inhibition impacted psychometric contrast sensitivity (Fig. 1A). V1 sites for silicon probe neural recordings and laser stimulation were precisely targeted in every experiment using hemodynamic imaging, per our prior studies37. Recording sites in V1 targeted the retinotopic location of the detected gratings (Fig. 1B, C; Fig. S1) while the laser spot (~0.3 mm in width; Fig. S1) was positioned far away from the recording site (~0.8 mm) and stimulated neurons with spatial receptive fields 70° away from the detected gratings (Fig. S1), a distance much larger than excitatory neuron RF size23. On a randomized subset of trials (25–33%), we activated PV or SST neurons at this distal location using moderate laser power (1.7 mW) that modulated behavioral performance without abolishing it. Moderate and sustained laser activation lasted for the duration of the visual stimulus, as in prior studies of local inhibition28,38. This experimental design allowed us to isolate the effects of lateral inhibitory drive from stimulus drive, and then measure how lateral inhibition from distinct inhibitory neurons transforms neural and perceptual sensitivity to contrast.
Figure 1. SST lateral inhibition controls the slope of psychometric contrast sensitivity A.
Experimental design to probe how lateral inhibition from PV (blue) or SST (gold) neurons in primary visual cortex (V1) affects neural and perceptual contrast sensitivity.
B. Example hemodynamic response map of horizontal visual space (azimuth, colorbar). Visual field sign (Methods) used to delimit V1 (contour) and target recording sites (0°) and laser stimulation (70°, ~0.8 mm away from recording site) in every experiment. See Fig. S1 for laser spot size (~0.3mm) and recording locations across experiments.
C. SST- or PV-cre x Ai32 channelrhodopsin (ChR2) mice were trained to detect static Gabor gratings (location ) at multiple contrasts (0–33%). PV or SST neurons were activated on 25% or 33% of trials with a laser ramp (1.7mW at peak) during grating appearance. Neural activity was recorded simultaneously from the V1 retinotopic site corresponding to grating location (as in B).
D. Psychometric contrast sensitivity (d’) in PV-ChR2 mice (6 mice, 84 sessions) for interleaved control (black) and PV inhibition trials (blue). Mean ± SEM, fit with a sigmoidal equation (Methods).
E. Same as D for SST-ChR2 mice (6 mice, 57 sessions).
F. SST stimulation significantly decreased the slope of the contrast response curve (−0.23 ± 0.26, median ± MAD; , Wilcoxon signed-rank test), but PV stimulation did not . Change in slope quantified as modulation index (MI), defined as difference between control and laser conditions (inset) divided by sum (see Methods). Histogram shows distributions of Ml calculated per session (same sessions in D, E). Changes not explained by differences in false alarms, pupil dynamics, or other behavioral factors in PV vs SST mice (Fig. S2).
PV stimulation diminished detectability of all contrasts in a uniform subtractive manner; however, SST stimulation resulted in a divisive scaling of the slope of the contrast sensitivity function. We quantified these effects in individual sessions by calculating a psychometric slope modulation index (MI), defined as the difference in contrast response function slopes for control and laser trials, divided by their sum (Fig. 1F). SST stimulation significantly decreased the slope of psychometric sensitivity (Fig. 1F; ), but PV stimulation did not . These different forms of SST vs PV modulation were clear when sorted by contrast, and were not explained simply by overall differences in behavioral performance or by differences in pupil area (linked to arousal39) or pupil position across groups (Fig. S2). Thus, lateral inhibition from SST neurons was more effective in driving divisive gain modulation of the contrast sensitivity function.
Cell-type specific lateral inhibition adjusts neural contrast sensitivity during perception
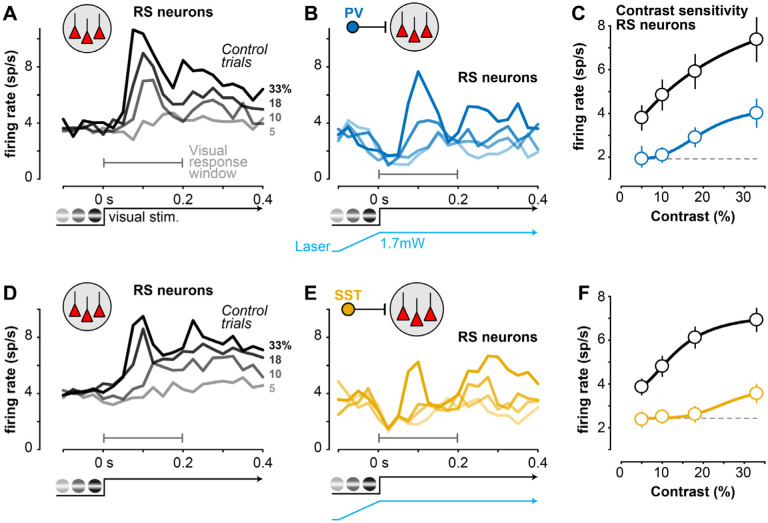
Are these perceptual changes in contrast sensitivity mirrored by changes in V1 neural activity? We performed extracellular silicon probe recordings in V1 during the task, and found that lateral inhibition controlled the contrast sensitivity of putative excitatory neurons. We optically targeted recordings to the retinotopic site of the visual stimulus, and stimulated PV or SST neurons far away (0.8 mm) from the retinotopic representation of the visual stimulus (Fig. 1B). We classified neurons with broad waveforms as regular spiking (RS) putative excitatory neurons (Methods; Fig. S3C), and focused on those with contrast dependent responses measured in control conditions (Fig. 2; r2 > 0.25 with Naka-Rushton fit; 312/657 or 47% of neurons in both PV and SST mice). Distal activation of PV or SST neurons reduced the visually-evoked transient response of RS neurons, but in different ways: PV stimulation reduced spiking by a similar factor across contrasts (Fig. 2C), while SST activation more effectively reduced low and medium contrast responses to near baseline levels (Fig. 2F), more consistent with a change in slope. We further dissected these average effects session-by-session to determine the strength and correlation of neural and behavioral contrast sensitivity.
Figure 2. Cell-type specific lateral inhibition adjusts neural contrast sensitivity during perception A.
Average responses of V1 putative excitatory regular spiking (RS) neurons during contrast detection (sorted by contrast, right) in PV-ChR2 mice (4 mice, 26 sessions). Recordings at V1 retinotopic location of stimulus (Fig. 1B).
B. Same sessions and neurons as A during interleaved trials of distal PV stimulation, sorted by contrast.
C. Contrast response curve (mean ± SEM) during control (black) and PV stimulation (blue, gray-dashed line shows firing rate at lowest contrast). Response calculated during visual response window (first 0.2 s after stimulus in A and B).
D-F. Same as A-C, for SST-ChR2 mice (n = 146 RS neurons; 4 mice, 18 sessions).
SST inhibition drives correlated reduction of neural and perceptual contrast sensitivity
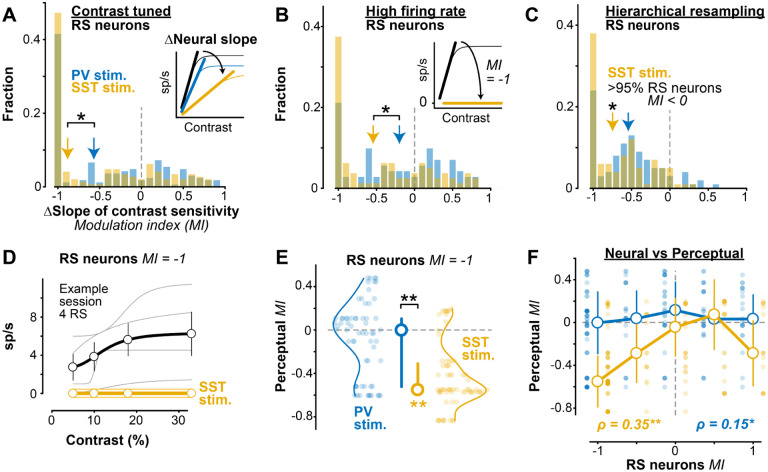
For all contrast tuned RS neurons recorded in the task, we first measured how contrast response functions changed with PV or SST distal inhibition, then compared this to the perceptual effects on the same trials. We again defined a modulation index (MI) to quantify changes in the slope of the RS neuron contrast response functions on control versus laser trials (Fig. 3A, inset). As suggested from the average responses, SST stimulation reduced the slope of contrast response functions in larger fractions of individual RS neurons than PV stimulation (Fig. 3A;). To control for potential “floor effects” (i.e., unreliable slope estimates in weakly responsive neurons), we next examined only neurons with high firing rates (those firing more than the population median, >3 spikes/s). Again, SST stimulation evoked larger reductions in the slope of contrast sensitivity than PV stimulation ; further, a large fraction of these neurons (38%) became completely insensitive to contrast during SST stimulation (MI = −1; Fig. 3B inset), a significantly greater fraction than during PV stimulation (21%; SST vs. PV, . These effects were not due to overrepresentation of contrast tuned neurons with high firing rates in individual recordings or mice: a hierarchical bootstrapping approach40 that resampled evenly across mice and sessions still revealed greater reductions in the slope of contrast sensitivity for RS neurons during SST stimulation (Fig. 3C).
Figure 3. SST activation simultaneously reduces neural and perceptual contrast sensitivity A.
SST stimulation significantly decreased contrast response function slope (inset) in contrast tuned RS neurons (−0.88 ± 0.54 MI, median ± MAD, 146 RS neurons; , Wilcoxon signed rank test), and significantly more than did PV stimulation ( excitatory neurons; PV vs SST, , 1 -tail Wilcoxon rank-sum test).
B. Same as A for RS neurons with high firing rate (> 3 spikes/s, population median). Larger slope decrease with SST (−0.54 ± 0.53 MI, 80 RS neurons) versus PV stimulation (−0.20 ± 0.50 MI, 71 RS neurons; PV vs SST, . Inset shows schematic for neurons that become contrast insensitive (MI = −1) with SST stimulation (38% of neurons with SST stimulation; 21% of neurons with stimulation; , Fisher’s exact test).
C. Hierarchical bootstrapping verified robustness of RS slope changes. SST stimulation significantly decreased the slope of RS neurons of bootstrapped samples had a decrease in slope), but distal PV stimulation did not significantly decrease the slope of RS neurons .
D. Response of 4 example simultaneously recorded RS neurons with a neural slope MI = −1 during distal SST stimulation. Spiking activity decreased to 0 across contrasts (individual curves offset from 0 for visualization). Corresponding behavioral slope MI = −0.57. Mean ± SEM.
E. The corresponding perceptual MI for neural MI = −1 (68 RS neurons during SST stimulation, 64 RS neurons during PV stimulation). Significant decrease in perceptual MI with SST stimulation (−0.55 ± 0.24 MI, median ± MAD; , Wilcoxon signed-rank test), but not PV stimulation ( . Median ± IQR.
F. Changes in neural and perceptual slope of contrast sensitivity more strongly correlated during SST stimulation , Spearman’s rank correlation) than distal PV stimulation .
We further examined how loss of contrast sensitivity in RS neurons varied with perceptual effects. Remarkably, in sessions where SST stimulation evoked complete loss of contrast sensitivity in RS neurons (MI = −1, example in Fig. 3D), there was a simultaneous and significant decrease of perceptual contrast sensitivity (Fig. 3E; ), with no such effect during PV stimulation . We expanded this approach to examine modulation of all contrast tuned RS neurons (not just those with total loss of contrast sensitivity). We found that SST stimulation drove significantly correlated reductions in both neural and perceptual contrast sensitivity slopes (Fig. 3F; ), with a weaker relationship during PV stimulation . In other words, lateral SST inhibition drove stronger reduction in the gain of contrast tuning of RS neurons, and this also drove stronger reduction in the gain of perceptual sensitivity to the same stimuli on the same trials. We next turned to a computational model to probe potential mechanisms driving these effects of PV versus SST lateral inhibition.
Network model with long-range SST projections replicates contrast tuning effects
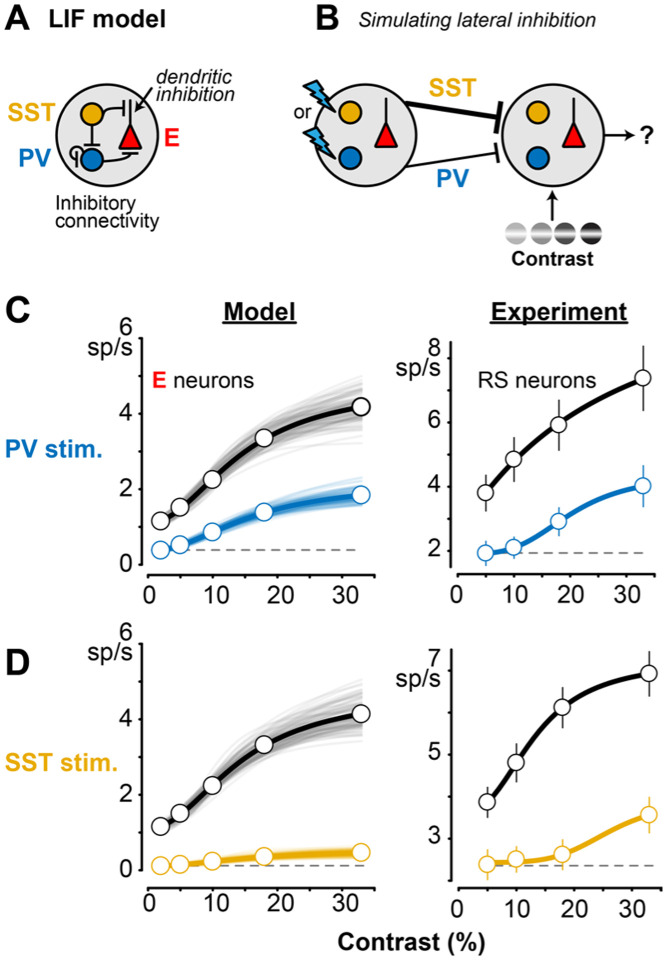
We wondered if differing control of contrast sensitivity was due to the subcellular location of PV versus SST inhibition, or due to the larger spatial extent of SST versus PV projections, as suggested by recent experiments41,42. We constructed a leaky integrate-and-fire (LIF) circuit model of excitatory (E), PV, and SST neurons based on prior studies43 and updated this model in three key ways (Fig. 4A, B). First, we updated the inhibitory connectivity probabilities and weights to match recent experimental data20,21. Second, we approximated SST dendritic inhibition by including an interaction term between excitation and SST inhibition44; this approach captures arithmetic operations of dendritic inhibition in pyramidal neurons45. Third, we updated the spatial extent of SST projections to reflect greater spatial influence of SST inhibition41,46, particularly relevant in V1 where most SST neurons are Martinotti cells with extensive lateral axons47. This V1 model was set up as a 1mm2 grid, with “visual” spiking (provided by an external thalamic layer) arriving in a 0.2 mm region of the grid (Gaussian distribution, see Methods). We simulated “optogenetic” activation in silico by injecting a conductance into PV or SST neurons ~0.8mm away from the site receiving visual input. The model parameters were fit to the spontaneous and visually-evoked firing rates of single unit activity recorded in RS (putative E) cells and both PV and SST neurons (detailed later) in control conditions (Methods). This simple model replicated the overall experimental effects of lateral PV versus SST stimulation on E neurons (Fig. 4C, D; model at left, experiments at right).
Figure 4. LIF network model replicates effects of PV or SST stimulation on contrast tuning A.
Conductance-based leaky integrate-and-fire (LIF) network model with PV, SST, and excitatory (E) neurons. SST dendritic inhibition of E neurons (arrow) modeled as multiplicative interaction with excitation per prior studies (see Results). Excitatory connectivity (Methods) not shown here to highlight inhibitory connectivity.
B. Within a 1mm2 grid of neurons, a 0.2mm patch received contrastmodulated “visual” input from an external thalamic layer (right), while PV or SST neurons away were directly activated to mimic lateral inhibition (left). The model included a higher probability for longrange SST versus PV projections (thicker line), per experimental data (Results).
C. Effects of distal PV stimulation in the model (left) and in the experiment (right, replotted from Fig. 2C). Uniform decreases in E across all contrasts.
D. Same as C for distal SST stimulation.
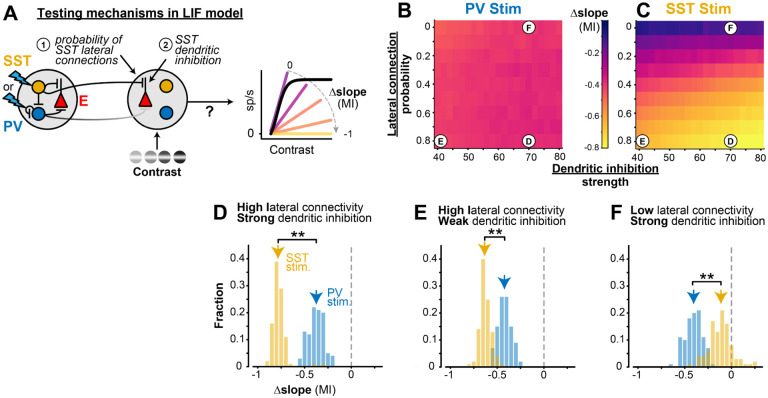
Using this simple circuit model, we varied either the strength of SST dendritic inhibition, or the spatial extent of SST connectivity, to disentangle two potential mechanisms mediating the effects of SST lateral inhibition (Fig. 5A). We found that a higher probability of SST lateral connections strongly modulated the slope of contrast sensitivity (Fig. 5C, top to bottom), while the strength of dendritic inhibition played a smaller role (Fig. 5C, left to right). We ran multiple instances of the model in three fixed regimes (Fig. 5D–F), and found that a high probability of lateral SST connectivity drove the greater changes in the slope of contrast sensitivity (Fig. 5D), even when dendritic SST inhibition was weakened (Fig. 5E). However, with a low probability of lateral SST connectivity, strong dendritic inhibition by itself was unable to change the slope of contrast sensitivity during SST stimulation (Fig. 5F). In all three of these model iterations, the effects of lateral PV stimulation were unaffected by changes in SST projection probability or dendritic strength (Fig. 5B, D-F). These findings identify long-range projections of SST neurons as a potentially critical factor for the effects of lateral inhibition on the slope (or gain) of contrast sensitivity.
Figure 5. Long-range SST projections in LIF network model control slope of contrast sensitivity A.
The probability of SST lateral connections and SST dendritic inhibition strength was varied in the model to identify the source of the slope change with distal SST stimulation.
B. Heat maps showing the average (100 iterations) slope MI of E neurons during distal PV stimulation for varied long-range SST projection probabilities ( p’sST) and SST dendritic inhibition strengths (; see Methods). MI is constant during distal PV stimulation with any lateral connection probability or dendritic inhibition strength. Letters on heatmaps indicate various SST dendritic integration strengths and long-range SST probabilities depicted in D-F.
C. Same as B for distal SST stimulation. Slope changes during distal SST stimulation are largely dependent on SST lateral connection probability (vertical gradient). Slope changes slightly varied with SST dendritic inhibition strength.
D. For high SST lateral projection probability (p’SST =0.8) and high SST dendritic inhibition strength ), distal SST stimulation had larger divisive effects (−0.78 ± 0.05 Ml, median ± MAD) than distal PV stimulation on E neurons across contrasts -tail Wilcoxon rank-sum test).
E. For high SST lateral projection probability (p’SST = 0.8) and low SST dendritic inhibition strength ), distal SST stimulation has larger divisive effects than distal PV stimulation on E neurons . These effects are smaller than when the strength of SST dendritic inhibition is high (D).
F. For low SST lateral projection probability (p’sst = 0) and high SST dendritic inhibition strength , distal SST stimulation had a smaller divisive effect (−0.11 ± 0.09 MI) than distal PV stimulation , indicating longrange SST projections are essential for eliciting strong divisive effects.
Do we find experimental evidence for a larger spatial footprint of SST activity? We reasoned that if SST neurons have a larger spatial extent of projections than PV neurons, SST neurons may spike more readily when stimulated at sites distal to the recording, potentially by direct activation of dendrites or long-range axons48–51. We tested these predictions in awake mice (outside of the task) by first identifying PV and SST neurons with brief square pulses (0.04s) of light directly at the recording site (“optotagging”52; Fig. S3), then moving stimulation to a distal site (0.8mm away, as in behavioral experiments). Local stimulation in PV-ChR2 mice rapidly increased population activity of fast-spiking (FS) putative PV inhibitory neurons (identified by waveform) and suppressed RS activity (Fig. S4A). The majority of FS neurons (n = 368) were also significantly optogenetically driven (n = 203 tagged PV+), while the statistically non-driven FS units (n = 165) were likely PV neurons that were themselves suppressed by driven PV units (Fig. S3D), consistent with strong self-inhibition among V1 PV neurons20,21. Local stimulation in SST-ChR2 mice identified significantly driven SST units (n = 52), and this strongly suppressed both RS (n = 784) and FS (n = 177) neurons (Fig. S4B). These effects on firing rates were present at the laser power used during the behavioral task, and increased at higher laser intensities at the recording site (Fig. S5).
When we stimulated at the distal site far away from the recording, in SST-ChR2 mice we measured significant increases in local spiking of SST+ units at the recording site (Fig. S4D; Fig. S5D). On the other hand, in PV-ChR2 mice, we never observed local FS units that increased spiking with distal stimulation (Fig. S4C; Fig. S5C). The increase in local SST activity with brief square laser pulses at a distant V1 site is consistent with antidromic activation of SST neurons that have long-range axonal projections, although we cannot exclude the possibility that a larger spread of SST dendrites also contributes to their activation. Importantly, RS (presumably excitatory) units were always suppressed at the recording site in these experiments, and both RS and FS neurons were always suppressed with SST stimulation during the task (Fig. S6), indicating the overall suppressive effect of lateral inhibition with no evidence of disinhibition of RS neurons. These overall suppressive effects of lateral SST stimulation could be due to withdrawal of excitation, increased inhibition, or a combination of both9,10,16,49. We next sought direct evidence for changes in synaptic excitation and inhibition in excitatory neurons during distal activation of SST versus PV neurons.
Synaptic inhibition from SST neurons underlies changes in contrast sensitivity
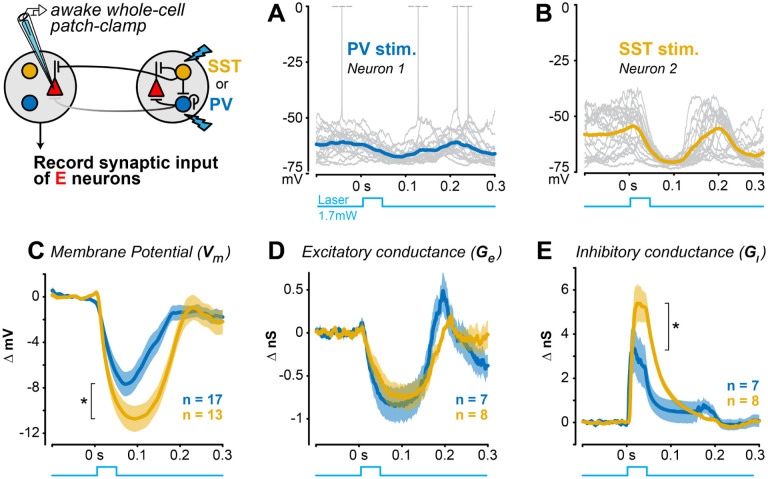
Whole-cell patch-clamp recordings revealed that distal SST stimulation evoked greater hyperpolarization than PV stimulation, and this was due to elevated inhibitory conductance in excitatory neurons. We performed both current and voltage clamp recordings in awake mice since anesthesia suppresses SST neuron activity15 and severely compromises the spatial and temporal functions of cortical inhibition during awake visual processing53–55. We first found that distal SST stimulation evoked significantly stronger hyperpolarization of membrane potential than distal PV stimulation (Fig. 6A–C). We then performed voltage clamp experiments to determine if this greater hyperpolarization was due to reduced excitation, elevated inhibition, or a combination of the two. Distal PV or SST stimulation both reduced excitatory conductance, but to a similar degree (Fig. 6D). However, there was significantly greater inhibitory conductance evoked by distal SST versus PV stimulation (Fig. 6E), despite dendritic SST inhibition being further from the electrode than somatic PV inhibition. These effects were not due to differences in recording quality or electrical access in PV versus SST recordings (Methods). Within each neuron, the net suppression was significantly more intense with distal SST (−3.7 ± 1.5nS) than PV stimulation (−1.9 ± 1.2nS;, Kolmogorov-Smirnov test). This combination of conductance effects likely underlies the stronger membrane potential hyperpolarization seen with distal SST stimulation. Taken together, these subthreshold recordings identify withdrawal of excitation and elevated synaptic inhibition in local excitatory neurons as a potential mechanism to adjust the slope of contrast sensitivity. We returned to the LIF model to test if directly modulating synaptic inhibition controls the slope of the contrast sensitivity in excitatory neurons.
Figure 6. Stronger lateral inhibition from distal SST versus PV neurons A.
Example current clamp recording of membrane potential from an RS neuron during distal PV stimulation in awake V1 (20 trials). Spikes truncated at 0 mV.
B. Same as A for an example RS neuron during distal SST stimulation.
C. Distal SST stimulation causes greater hyperpolarization of excitatory neurons , mean ± SEM, 13 RS neurons; mean ΔVm from 0–0.2s) than distal PV stimulation excitatory neurons; , 1-tail Wilcoxon rank-sum test).
D. Distal PV or SST stimulation decreased excitatory conductance to a similar degree (PV stim: neurons; SST stim: RS neurons; ; mean from ).
E. Inhibitory conductance significantly larger with distal SST versus PV stimulation (SST stim: neurons; stim: neurons; ; mean from ).
We found that the intensity of inhibition in the V1 circuit model was the key factor driving changes in slope of contrast sensitivity of E neurons. We systematically varied the effective intensity of inhibition by moving the site of “optogenetic” stimulation in silico. During local stimulation directly at the site of “visual” input (where both PV and SST inhibitory connections to E neurons were prevalent), the slope of contrast sensitivity strongly decreased with stimulation of either PV or SST neurons (Fig. S7). However, as we moved the stimulation site towards distal locations, the effects of PV stimulation on the slope of contrast sensitivity rapidly decreased since the lateral connectivity of PV neurons to local E neurons also decreased. However, distal SST stimulation retained the ability to decrease the slope of contrast sensitivity because of the stronger lateral connectivity of SST to E neurons (Fig. S7). We confirmed these observations in the model with three additional experiments. First, local optogenetic stimulation of either PV or SST neurons (at the recording site driven by the visual stimulus) decreased the contrast sensitivity slope of RS neurons, both to a similar degree (Fig. S7E). Second, local stimulation of PV or SST neurons evoked similar amounts of hyperpolarization and inhibitory conductance (Fig. S8). Third, local PV stimulation also significantly decreased the slope of perceptual contrast sensitivity (−0.53 ± 0.41 Ml, median ± MAD, , Wilcoxon sign-rank test), much more than distal PV stimulation did (−0.03 ± 0.20 Ml; Fig. 1D). Taken together, the model and experiments show that when excitatory neurons receive strong inhibition –regardless of the presynaptic source– this divisively scales the neural and perceptual sensitivity to contrast. However, SST neurons possess a unique ability to modulate contrast sensitivity across large regions of cortical and visual space, potentially by virtue of their more extensive lateral inhibitory footprint.
Discussion
Here we have established that lateral inhibition in V1 exerts direct effects on neural and perceptual sensitivity to stimulus contrast. Lateral inhibition from SST neurons caused greater divisive scaling of perceptual response curves than did PV lateral inhibition. The perceptual effects of SST lateral inhibition were correlated with the strength of divisive modulation in putative excitatory neuron responses on those same trials. A simple circuit model predicted long-range SST inhibition as a key driver of these effects, as confirmed with direct measurement of a larger spatial footprint of SST versus PV synaptic inhibition. Taken together, our findings establish a mechanistic basis for cell-type specific computations performed by lateral inhibition in V1. These operations flexibly modulate behavioral sensitivity to contrast across large regions of the visual field.
Driving PV and SST neurons far from the site of visual input altered perception in unique ways. PV lateral inhibition uniformly reduced contrast sensitivity but preserved its steepness. SST lateral inhibition more effectively scaled down sensitivity to low and medium contrast, linearizing the dynamic range56. Importantly, the behaviorally relevant visual stimulus did not itself confound the effects of driving distant PV or SST neurons. These two modes of lateral inhibition provide flexible ways to control behavioral sensitivity to visual contrast spanning extensive retinotopic space (~70° in our experiments). On the other hand, driving either SST or PV neurons directly at the retinotopic site of visual input (where both SST and PV connections to excitatory neurons are dense) invariably caused divisive effects on perceptual responses, consistent with prior studies of local inhibition on contrast perception57 and neural selectivity25,28,58,59. Although some studies have shown that local SST inhibition preceding visual input can cause subtractive effects on V1 firing rates27,60, divisive effects on firing rates dominate when visual excitation and local SST inhibition overlap in time25,26, as was the case here. Taken together, our results show how the perceivability of visual stimuli can be adjusted with distinct computations via cell-type specific lateral inhibition. These operations in V1 could be readily accessed by top-down inputs.
The cell-type specific effects of lateral inhibition depended on its spatial footprint. Using a V1 circuit model, we found that the critical feature driving greater divisive scaling of excitatory firing by SST rather than PV neurons was the reach and strength of inhibition, not its subcellular location (SST dendritic inhibition vs PV somatic inhibition). Preserving lateral projections of SST neurons but eliminating their dendritic effects still produced greater divisive scaling of excitatory neuron firing. We confirmed this critical feature with direct measurements of hyperpolarization driven by synaptic inhibition from distal SST neurons in awake mice. Further, we were able to resolve these differences even though dendritic SST inhibition is electrotonically attenuated compared to somatic PV inhibition. Our direct measurements of a larger spatial footprint for SST inhibition provide experimental confirmation of theoretical predictions19. Three additional pieces of experimental evidence support our findings. First, SST neurons in V1 fire most strongly to large visual stimuli (>70°)15, and are involved in synchronizing long-range (>0.5mm) visual oscillations61, both consistent with the spatial scale of effects on perception shown here. Second, most SST neurons in V1 are Martinotti subtypes defined by their extensive lateral axonal arbors20,47. Third, in slices of auditory cortex, the functional spatial footprint of SST inhibition also extends further than PV inhibition, and this lateral inhibition underlies the sharpness frequency tuning41. To our knowledge, our findings are the first to directly measure the subthreshold extent of cell-type specific lateral inhibition in awake V1, and identify this as a key mechanism enabling adjustment of perceptual sensitivity.
Lateral inhibition in mouse V1 suppressed firing of local excitatory and PV neurons, consistent with stabilized supralinear network architecture16,62–65. Our measurements of both cell-type specific spiking and subthreshold synaptic activity provide deeper insights for this framework. Activating distant PV neurons suppressed excitatory neuron firing and elicited a “paradoxical” decrease in the firing of local PV neurons, likely due to the combined loss of local excitation and increase of direct inhibition among PV neurons16,21. However, subthreshold recordings revealed that even without local PV neuron spiking, distal PV activation was visible as increased inhibitory conductance in local excitatory neurons. Similarly, SST lateral inhibition strongly suppressed both local excitatory and PV neuron firing, but local SST neurons were not suppressed. This along with more extensive lateral SST projections likely contributed to the greater inhibition of local excitatory neurons, and greater scaling of perceptual contrast sensitivity. These findings highlight that lateral interactions in realistic networks with multiple inhibitory neuron subtypes can support both “paradoxical” suppression of some inhibitory neurons but activation of others66, leading to differing impact on stimulus responses and behavior.
Our findings carry some limitations that can be addressed with future investigations. Firstly, we focused here on the divisive aspects of modulation because these have been most consistently implicated in prior studies of local inhibition, and revealed that SST rather than PV lateral inhibition causes relatively greater divisive modulation. However, this does not imply that SST lateral inhibition is purely divisive, or that PV lateral inhibition is purely subtractive – both aspects co-occur, and likely contribute to neural22,28,31 and perceptual57 modulation, an important topic for future studies. Second, for experimental clarity we drove distant PV or SST neurons optogenetically, but without also driving them visually. Future work could explore effects of suppressing lateral inhibition67 as well as detailing its recruitment during spatially extensive visual stimulation. Finally, we focused on PV and SST neurons since they are the main sources of synaptic inhibition of cortical excitatory neurons20,21. It will be interesting to see if other interneuron subtypes gate lateral interactions we observed here, and to examine how lateral interactions are recruited by cortical and subcortical inputs in a variety of visual spatial tasks.
Methods
Experimental model and subject details
All experimental procedures were approved by the Institutional Animal Care and Use Committee (IACUC) at the Georgia Institute of Technology.
Subject details
B6 PV[cre] (RRID: IMSR_JAX:017320) or Sst-IRES-Cre (RRID: IMSR_JAX:013044) mice crossed with Ai32(RCL-ChR2(H134R)/EYFP) (RRID: IMSR_JAX:024109) mice (crossed mice referred to as PV-ChR2 or SST-ChR2 respectively in this study) were used to optogenetically activate either PV or SST inhibitory neurons. Mice were individually housed under reverse light cycle and bred in house.
| Mouse strain | n = mice | n = behavior sessions | n = behavioral extracellular recordings | n = extracellular recordings no behavior | n = intracellular recordings |
|---|---|---|---|---|---|
| PV-ChR2 | 16 (2 female) | 84 | 26 (distal); 25(local) | 34 (distal); 63(local) | 17 (current clamp); 11(voltage clamp) |
| SST-ChR2 | 14 (4 female) | 57 | 18 (distal); 18(local) | 24 (distal); 52(local) | 13 (current clamp); 13(voltage clamp) |
Implant surgeries
Details of headplate / cranial window implants are described previously34,35,37,68. Briefly, 4–10-week-old male and female SST- or PV-ChR2 mice were chronically implanted with a stainless steel headplate with recording chamber (11 mm diameter) and a cranial window (5 mm diameter, intact skull prep) during isoflurane anesthesia (3% induction, 1–2% maintenance). The cranial window was placed over the visual cortex to map the retinotopy and visual cortices through hemodynamic measurements (see Intrinsic Signal Imaging). Mice recovered for 3 days after implantation before experimentation.
Intrinsic signal imaging
Intact intrinsic signal imaging (ISI) method details are described previously37. Briefly, mice were anesthetized (0.7–1% maintenance) and sedated (10−5 mg/kg Chlorprothixene) then head-fixed and positioned in front of 2 monitors spanning 150° (horizontal) by 48° (vertical) of the visual field. Contact lenses (3 mm diameter) were inserted to maintain ocular clarity during imaging. A camera was positioned over the cranial window and focused to ~0.5 mm below the vasculature. Green (525 nm) and red (700 nm) light were used to image vasculature and hemodynamic responses to visual stimuli drifting across the visual field. Azimuth (horizontal) and elevation (vertical) retinotopic maps were constructed from the hemodynamic responses. The visual field sign map was calculated from the sine angle difference between the azimuth and elevation maps, and used to delimit the extent of primary visual cortex (V1). Subject-specific retinotopic maps of V1 were used to target extracellular electrophysiological recordings and optogenetic stimulation. Optically targeted sites were confirmed via electrophysiological receptive field mapping (See “Recordings: Receptive field mapping”).
Retinotopically targeted laser stimulation
Prior to laser stimulation experiments, mice were briefly anesthetized and a small cortical site (0.1 – 0.3 mm) was either thinned to translucency, or opened into a small craniotomy over a retinotopically targeted site in V1. Mice recovered for >3 hours, and the skull was sealed between experiments by covering the site with an elastic polymer (Kwik-cast).
A blue laser (~473 nm) was used for optogenetic stimulation in PV- or SST-ChR2 mice. Using custom optics, the laser was focused to a spot that restricted most of the power to the target site (Gaussian profile, 0.33mm full-width at half-max with 1.7mW power). Areas around the thinned skull / craniotomy were covered with opaque polymer (Kwik-cast) or dental cement (Metabond) to further restrict light spread.
A galvanometer precisely positioned the laser spot to retinotopic locations of V1 using ISI maps aligned to vasculature landmarks. In most experiments we stimulated V1 far away from the representation of detected stimulus (stimulus at 0°, laser at 70°; 0.8 mm apart; Fig. 1). This experimental design isolates the effects of lateral inhibition from stimulus-driven activity. In a few experiments we also tested effects of laser stimulation directly at the recording site / V1 site representing the visual stimulus (Figs. S3- S5, S7, S8). Details of optogenetic stimulation during the behavioral task are described below (“Visual detection task with optogenetic perturbation”).
Identification of laser-activated PV and SST neurons
After every electrophysiological experiment the laser was positioned directly over the recording site to measure single unit responses to brief (~40 ms duration) laser pulses. This allowed us to statistically identify ChR2 expressing PV or SST neurons (“optotagging”52; Fig. S3). In some experiments, these brief pulses were also repeated at the distant manipulation site (Fig. S4; Fig. S5). Laser intensity in optotagging experiments was 0.5, 1.7, or 6.5 mW at the surface of the skull. These experiments allowed us to ensure that the moderate power we used during behavioral experiments (1.7 mW) avoided “paradoxical” or disinhibitory effects63,69 while also only modulating performance, rather than abolishing it (as we34,35 and others70–72 have shown with higher laser powers).
Visual detection task with optogenetic perturbation
Water-restricted PV- and SST- ChR2 mice were trained to report visual detection by licking for water rewards (as detailed in prior studies34,35,68. Mice were head-fixed and stationary inside a plastic tube in front of 2 monitors spanning 160° in azimuth (from −37.8° to 115.8°; vertical meridian defined as 0°) and 48° in elevation (from −18.6° to 29.4°; horizontal meridian defined as 0°). Visual stimuli (static Gabor grating, ) appeared without cueing and only after an enforced period of no licking (randomized per trial and drawn from a uniform distribution spanning 0.5s – 7s). The first lick during grating presentation (1s response window) triggered water delivery. Visual stimuli appeared at a single location in blocks of 10–30 trials, either in the binocular (0°) or the monocular (70°) visual field. Our main analysis here was restricted to trial blocks with binocular stimuli and recordings in binocular V1. Michaelson contrast of the binocular stimuli ranged from 1–33% (typically sampling 4 contrasts) to capture the psychometric performance curve. 0% contrast stimuli were used to probe the false alarm rate. On a fraction (25–33%) of trials PV or SST neurons in monocular (~70°)V1 were activated using a blue laser (~473 nm, 1.7 mW measured at the surface of the skull). The laser started ramping 0.1s before the appearance of the visual stimulus, and reached peak intensity at visual stimulus onset. The laser persisted throughout the duration of the visual stimulus. Visual stimuli (and laser stimulation, if present) terminated at the first lick on correct trials, or at the end of the response window (1 s) on incorrect trials. We analyzed the perceptual effects of optogenetic perturbations through either a thinned skull (6 PV-ChR2 mice, 30 sessions; 4 SST-ChR2 mice, 19 sessions) or craniotomy during recordings (6 PV-ChR2 mice, 54 sessions; 6 SST-ChR2 mice, 38 sessions). We observed no difference in the changes in psychometric slope of the contrast response curve for the thinned skull versus craniotomy preparation for distal SST stimulation (thinned skull, slope MI = −0.15 ± 0.31, median ± MAD; craniotomy, slope MI = −0.15 ± 0.31;, 1-tail Wilcoxon rank-sum test), or distal PV stimulation (thinned skull, slope MI = −0.16±0.20; craniotomy, slope MI = −0.01 ± 0.19; ). Behavioral data from all sessions were therefore combined in Fig. 1.
Perceptual performance analysis was primarily restricted to detection of stimuli presented in the binocular visual field to probe how PV or SST activation in site in V1 (monocular V1) not receiving task-relevant visual stimuli may influence perceptual behaviors. Perceptual performance was quantified using the sensitivity index d’ and response criterion (c)73 :
| (1) |
| (2) |
where Z represents the inverse of the normal cumulative distribution (MATLAB function, norminv). Task-irrelevant probe stimuli (5% contrast bars, 0.1s duration, 0.3s ISI, 9° width, appearing across randomly selected azimuth positions) were presented throughout the session, but not analyzed here; probe stimuli did not affect perceptual performance35. Mice typically performed hundreds of trials of detection in multiple spatial locations per day (307 ± 9 trials, mean ± SEM).
Pupillometry analysis
We simultaneously recorded pupil position and diameter (a proxy for arousal39,74,75) during all behavioral sessions. A camera (Imaging source DMK 21Bu04.H) with zoom lens (Navitar 7000) coupled with an infrared filter (Mightex, 092/52×0.75) was placed ~22 cm from the animal’s right eye. The eye was illuminated by a near-infrared LED (Mightex, SLS-02008-A). Video files were acquired using the Image Acquisition Toolbox in MATLAB with custom code. ~74 pixels in each frame of the video was equal to 1 mm. We focused analysis on a high-quality subset of these sessions (Fig. S2; 3 PV-ChR2 mice, 27 sessions; 4 SST-ChR2 mice, 28 sessions).
Pupil position and area were acquired and analyzed as previously described34,35,68. Δ Pupil area was calculated as the percent deviation from the mean Δ Pupil , where A is the area in pixels and is the average area across all frames in a video. Δ Pupil position (in azimuth) was calculated as Δ Pupil , where x is position in degrees and xAvg is average pupil position across all frames in a video. The pupil position in degrees was calculated assuming the eye was a sphere using the equation , where m is the position in mm, d is the diameter of the eye (~3.4 mm) based on a previous study76. Laser trials were subtracted from control trials to determine if pupil position or pupil area was different between the two conditions. Importantly, there were no differences in pupil metrics for PV versus SST mice (Fig. S2).
Recordings: Visual detection behavior
A small craniotomy (0.1 – 0.3 mm) was performed in either binocular (~0.5 mm anterior to lambda, ~2.5 – 3 mm lateral to central) or monocular V1(~0.5 mm anterior to lambda, ~2–2.5 mm lateral to central). Craniotomy sites were confirmed with ISI and receptive field mapping. Mice recovered for at least 3 hours before recording. After recordings the recording chamber was covered with an elastic polymer (KwikCast) to preserve the skull and craniotomy health between consecutive recording days (2–5 days). Recordings were performed using multi-site silicon electrodes (NeuroNexus A1 132) consisting of a single shank with 32 linear channels. Electrodes were inserted ~1 mm below the cortical surface. During visual detection behavior, targeted recordings were performed in binocular V1(0–20°) while optogenetically stimulating PV or SST neurons in monocular V1 (~70°).
Recordings: Receptive field mapping
After every recording the receptive field of the recording site was mapped by presenting vertical flashing bars one at a time (9° in width, duration 0.1s, inter-stimulus interval 0.3s, 5–100% contrast; randomized position) that tiled the entire visual display. These mapping sessions were used to confirm retinotopy identified by ISI (Fig. S1).
Whole-cell patch-clamp recordings
We performed whole-cell current clamp (n = 30 neurons) or voltage clamp (n = 24 neurons) recordings from regular spiking (RS) putative excitatory neurons in awake mice as detailed in past studies53,77. RS identity was determined by spike width and spike frequency adaptation to current pulses. We simultaneously optogenetically stimulated PV or SST neurons, either at a site ~0.8 mm distant from the recorded neuron (exactly as described above, see “Retinotopically targeted laser stimulation”), or directly at the recording site. The differing effects of distal PV versus SST stimulation were not explained by differences in the quality of electrical access. Series resistance was comparable across groups, both in current clamp (PV: 33.9 ± 2.9 MΩ, n=17; SST: 33.1 ± 2.9 MΩ, n=13, ) and voltage clamp recordings (after partial compensation, PV: 19.1 ± 1.9 MΩ, SST: 25.6 ± 2.2 MΩ, mean ±SEM, ).
PV and SST neuron identification and laser stimulation (optotagging)
Extracellular spikes were sorted using KlustaViewa Suite or Kilosort78,79. To identify PV or SST neurons, we measured the short latency responses to a strong brief laser pulse (0.04 s, 6.5 mW) positioned over the recording site and used the stimulus-associated spike latency test (“SALT”)52. Neurons that increased their activity rapidly (<10 ms) during the pulse were identified as tagged PV or SST neurons in PV-ChR2 or SST-ChR2 mice respectively. All neurons were additionally identified by waveform width and classified as fast-spiking (FS) putative PV neurons (narrow width) or regular-spiking (RS) putative excitatory neurons (broad width), per prior studies23,34,35,68. Optotagged PV neurons had narrow waveforms and were combined with non-tagged FS neurons for analysis (Fig. S3).
Perceptual contrast sensitivity analysis
The sensitivity index (d’) was measured across contrasts for control (no laser) and stimulation (PV or SST) conditions. A Boltzmann’s sigmoidal equation was fit to the data points to generate psychometric contrast response curves:
| (3) |
where A1 is the minimum d’, A2 is the maximum d’, x is the contrast, x50 is the contrast to reach 50% of the max d’, and dx is the steepness of the curve. The data was fit using the MATLAB function fit. From the Boltzmann’s sigmoidal fit, we quantified the maximum d’ (A2) and slope at the steepest point. A modulation index (MI) for the slopes was defined as and used to calculate how PV or SST stimulation modulated the slope of the contrast sensitivity function relative to no laser (control).
Neural contrast sensitivity analysis
To quantify neural contrast responses during perceptual behavior, the firing rate of RS neurons was calculated in the first 0.2s following stimulus onset for each contrast. We followed a similar strategy as behavioral data to estimate contrast response functions for firing rates, then assessed changes in the fit parameters during PV or SST lateral inhibition. Contrast response curves were fitted with Naka-Rushton equations80 :
| (4) |
where Rm is the max firing rate, x is the contrast, n is the steepness, x50 is the contrast at 50% of the max firing, and b is the minimum firing rate. Only RS neurons that had clear contrast tuning and were well fit to the Naka-Rushton equation (r2 > 0.25) were included in analysis (146 RS neurons in SST-ChR2 mice, 166 RS neurons in PV-ChR2 mice). A modulation index (MI) was defined the same way as perceptual analysis and used to calculate the relative changes in slope (slope at steepest point of the curve fits) elicited by PV or SST stimulation. We performed additional controls (Fig. 3B, C) to measure changes only in high firing RS neurons (>3 spikes/s), and also used a hierarchical bootstrapping method (100 samples) to confirm effects were not solely due to particular mice or sessions40.
Neural and perceptual correlation analysis
We assessed the strength of correlation between neural and perceptual changes to contrast sensitivity on the same trials. We calculated the changes in slope of the contrast sensitivity functions (MI, as described above), then calculated Spearman’s rank correlation coefficient between the neural Ml and perceptual MI acquired during the same sessions (Fig. 3F; neural activity binned between −1 and 1, bin size = 0.5). Similar results were obtained without binning (distal PV stimulation, ; distal SST stimulation, .
Local and distal stimulation neural activity analysis
We measured the RS, FS, and SST responses to a brief laser pulse (0.04s duration, 0.5 – 6.5 mW) during local stimulation (recording and manipulation sites are the same) and distal stimulation (recording and manipulations sites are ~0.8 mm apart) in V1. We calculated a modulation index of firing rates to measure the magnitude of change:
| (5) |
(baseline taken from the pre-stimulus laser period).
Statistical analysis
In general, non-parametric Wilcoxon rank sum tests (unpaired data) or signed rank tests (paired data) were performed, unless otherwise noted. Significance was defined at , unless noted. No strategies were employed for randomization of subjects, recordings, data collection, or analysis. Statistical analysis details are described in HYPERLINK Table S1.
Circuit model: Network construction
A leaky-integrate-and-fire (LIF) spiking neural network model of the V1 circuit was used to test the effects of long-range SST projections and nonlinear dendritic integration on cell type-specific lateral inhibition. The basic construction of the network was based on prior models of cortical excitatory and SST and PV inhibitory cell types43,81. It consisted of excitatory, PV, and SST neurons uniformly distributed on a 1 × 1 mm2 two-dimensional surface with periodic boundary conditions.
All neurons were modelled as conductance-based leaky integrate-and-fire (LIF) neurons. The membrane potential of the th neuron is described by
| (6) |
where the last term is only included for excitatory neurons. Here is the membrane capacitance, is the leak conductance, , and are the synaptic conductances from excitatory, PV, and SST neurons, respectively, is the resting membrane potential, and are the reversal potentials of the excitatory and inhibitory synapses, and is a constant determining the strength of dendritic integration effects, as in prior studies44. The first four terms on the right-hand side of Eq. 6 represent the leak current and the synaptic currents from excitatory, PV, and SST inputs, while the last term involving the product of and describes the interaction of excitatory and SST synaptic inputs within the dendrite (see below).
The synaptic conductances evolve according to
| ;(7) |
where and are excitatory and inhibitory synaptic time constants and , and are synaptic weights of synapses to population (where is the cell type of neuron ) from excitatory, PV, and SST neurons, respectively. , and are sums of Dirac delta functions representing incoming spike trains from excitatory, PV, and SST neurons, respectively. Neuron model parameters are based on the model by El-Boustani and Sur43 and are in the physiological range82,83.
Connection probabilities between neurons of each cell type were derived from published neuroanatomical data20,21. The density of connections from type to type is given by whose values are listed in Table 1. We also incorporated long-range projections which are controlled by the parameters . Specifically, each directed pair of neurons from type to type was connected with a probability which depends on their distance ,
Table 1:
Table of connection densities. The parameter determines the relative density of connections from neurons of type to neurons of type . Values were based on prior study20.
| Exc | PV | SST | ||
|---|---|---|---|---|
| Exc | 0.06 | 0.42 | 0.3 | |
| PV | 0.35 | 0.39 | 0 | |
| SST | 0.23 | 0.18 | 0 | |
| ;(8) |
Here is the cutoff distance given by 0.2 mm controls the overall connectivity density of the network, and and are normalization parameters given by and , respectively. There are a total of projections from a neuron of type to neurons of type , where is the total number of neurons in the network of type . Among the projections, are short-range and are long-range.
Circuit model: Long-range projections
The parameters control the proportion of long-range excitatory, PV, and SST projections. Experimental evidence suggests that SST long-range projections are more prominent compared to those of PV neurons41. Excitatory and SST neurons were given a high probability of long-range projections , while PV neurons were assumed to have a smaller long-range probability is varied between 0 and 0.8 to examine the effect of long-range SST projections.
Circuit model: Dendritic integration
PV neurons form perisomatic synapses on excitatory pyramidal cells, while SST neuron synapses target pyramidal cell dendrites46,84–86. The point-neuron LIF model implements SST dendritic inhibition of excitatory neurons by incorporating interactions of excitatory and SST inhibitory synaptic inputs that occur in the dendrites87. This approach has been validated against experimental data and a multicompartment biophysical mode87,88. Eq. (6) mimics dendritic integration of excitatory synaptic inputs and SST inhibitory inputs via the multiplicative term , while PV inputs sum linearly with excitatory inputs (mimicking linear somatic integration of excitation and inhibition). The parameter determines the strength of the effect of dendritic inhibition on excitation. Generally, this parameter depends on the distances of the excitatory (E) and inhibitory (I) synapses from one another, and from the soma44,45. For example, E and I synapses on opposite ends of the dendrites have low interaction strength ( values −8 cm2), but and I synapses proximal to each other but distant from the soma have much higher interaction strength ( values 20cm2; all values from Fig. 4 in prior study88). Using the estimated surface area of the neuron, we converted this range into values of −80 to 200 for our point models.
For simplicity, it was assumed that all excitatory and SST synapses interact with a single constant representing the average dendritic effect propagated to the soma and spike initiation site. We begin by assuming (conservatively within the range of Li et al44) and and tune a subset of parameters so that the spontaneous firing rates and evoked response without ChR2 stimulation approximately matched the data (see Circuit Model: Parameter Fitting). The parameter was then varied in the range of 40–80 to explore the impact of dendritic inhibition on scaling the contrast dependence of firing rate. This range was chosen as it represents the values at which the spontaneous and evoked firing rates are within a realistic range (given the fixed parameter values in Tables 1 and 2). Because positive values of result in stronger inhibition to excitatory neurons, the total inhibition from SST to excitatory neurons depends on a combination of and . Decreasing to values below 40 excessively weakens the strength of SST inhibition to excitatory neurons, leading to unrealistically high responses. For example, when , firing rates for high contrast grating responses were 10 -fold higher ( 75 spikes/s) than experimental data ( 7 spikes/s). However, one of our main results (Fig. 5) is that the dendritic integration term is not necessary to replicate the divisive effects of SST inhibition; even when the effect is restored by increasing (not shown here). Thus, choosing evoked 7 – 10 spikes/s for high contrast responses, matching the control experimental results. Conversely, increasing dendritic effects beyond our upper bound of suppressed excitatory neurons to an unrealistic degree: responses during the simulated ChR2 activation of SST neurons dropped to 0.1–0.3 spikes/s, 10-fold lower than the experimental range (2–4 spikes/s), and increasing further suppresses the rates.
Table 2:
Table of physiological parameters of the leaky integrate-and-fire (LIF) neuron models.
| Parameter | Description | Value | Units |
|---|---|---|---|
| membrane capacitance | 0.25 | ||
| leak potential | −70 | ||
| threshold potential | −40 | ||
| reset potential | −65 | ||
| refractory period | 5 | ||
| reversal potential for excitatory synapses | 0 | ||
| reversal potential for inhibitory synapses | −75 | ||
| excitatory synaptic time constant | 6 | ||
| inhibitory synaptic time constant | 20 |
Circuit model: Simulating visual input and ChR2 stimulation
In all simulation conditions, the V1 network receives spontaneous inputs from 1,000 Poisson-spiking neurons with firing rate . Each neuron in the V1 circuit receives incoming excitatory connections from the Poisson neurons with synaptic weight for neurons of type . SST neurons receive an additional inhibitory connections with synaptic weight . This is because SST neurons receive no other inhibitory input in this simple 3 neuron network, but experimental evidence suggests that they receive inhibitory inputs from multiple sources20.
Visual stimulation is implemented by an external thalamic layer consisting of 1,000 neurons with inhomogeneous Poisson firing statistics, also uniformly distributed on a 1 mm × 1 mm surface. Each neuron in the thalamic layer projects to excitatory and PV+ neurons within a lateral distance of 0.2 mm with density . At visual stimulus onset, the firing rates of the external thalamic layer neurons are activated with a spatiotemporal Gaussian pattern with spatial and temporal . The firing rate peaks 0.1 s after stimulus onset with a peak average firing rate of which depends on the contrast of the visual stimulus by the relation:
| ;(9) |
We model ChR2 activation of inhibitory cell types by stochastically injecting a conductance with a time-dependent rate to all neurons of the target cell type inside a circular area with radius 0.3mm (matching experiments, Fig. 2; Fig. 4). The rate of activation is linearly ramped up starting from 0.1s before the visual stimulus onset at a rate such that it reaches 1000 Hz at the visual stimulus onset time, again matching experiments. The rate is then held constant for 0.3s, after which the ChR2 activation is turned off and the rate set to zero.
In most simulations, the center of the laser stimulus was located at a maximal distance ~0.71 mm from the peak of the visual stimulus (except in Fig. S7 that measured the distance dependence of the effects). When targeting SST neurons, we assume that a randomly selected proportion of SST cells outside the targeted area also receive stimulation due to activation of long-range axonal or dendritic projections. Parameters related to external inputs are given in Table 3.
Table 3:
Table of parameter values used in network simulations.
| Parameter | Description | Value | Units |
|---|---|---|---|
| Spontaneous input rate | 2 | ||
| Synaptic weight of spontaneous excitatory inputs to Exc | 13.5 | ||
| Synaptic weight of spontaneous excitatory inputs to Exc | 12.0 | ||
| Synaptic weight of spontaneous excitatory inputs to SST | 12.0 | ||
| Synaptic weight of spontaneous inhibitory inputs to SST | 3.0 | ||
| Synaptic weight from thalamic layer to Exc neurons | 2.0 | ||
| Synaptic weight from thalamic layer to PV neurons | 1.0 | ||
| Visual input parameter | 4 | ||
| Visual input parameter | 30 | ||
| Contrast nonlinearity parameter | 16 | ||
| ChR2 quantal conductance for PV | 15 | ||
| ChR2 quantal conductance for SST | 1.3 | ||
| Synaptic weight from Exc to Exc | 1.2 | ||
| Synaptic weight from Exc to PV | 0.1 | ||
| Synaptic weight from Exc to SST | 0.1 | ||
| Synaptic weight from PV to Exc | 1.5 | ||
| Synaptic weight from PV to PV | 1.5 | ||
| Synaptic weight from SST to Exc | 0.8 | ||
| Synaptic weight from SST to PV | 0.8 | ||
| Strength of dendritic interaction between E and SST inputs in E neurons | 70 | ||
| Connectivity density parameter | 0.2 | - | |
| External connectivity density parameter | 0.05 | - | |
| Proportion of long-range Exc projections | 0.8 | - | |
| Proportion of long-range PV projections | 0.2 | - | |
| Proportion of long-range SST projections | 0.7 | - |
Circuit model: Parameter fitting
We adapted the neuron model parameters from a prior study43 (Table 2). Parameters relating to spontaneous inputs, visual stimulus, and synaptic weights were tuned within a physiologically plausible range to fit the model to the observed spontaneous firing rates and contrast curves measured in experiments. This was achieved with a combination of gradient descent minimizing the root mean square error of the average firing rates of each condition (spontaneous, contrasts 2–33%), followed by slight hand-tuning to capture both spontaneous and stimulus-driven regimes. The ChR2 conductance parameters were chosen so that the total degree of inhibition was similar to the observed data for PV and SST stimulation with nominal parameters.
Circuit model: Stimulation Details
PyNEST v. 3.389 and NESTML v. 5.2.090 were used to perform simulations.
bioRxiv preprint doi: https://doi.org/10.1101/2023.11.10.566605; this version posted November 14, 2023. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license.
Supplementary Material
Acknowledgements
We thank members of the Haider lab for feedback. This work was supported by the Alfred P. Sloan Foundation’s Minority Ph.D. (MPHD) Program Fellowship (to J.D.R.), the National Institute of General Medical Sciences (T32GM142616 to Z.M.), the National Eye Institute (R00 EY030840 to H.C.), Alfred P. Sloan Foundation Fellowships in Neuroscience (to B.H and H.C.), the Whitehall Foundation (to B.H.), National Institute of Neurological Disorders and Stroke and NIH BRAIN Initiative (NS107968, NS109978 to B.H.), and the Simons Foundation (SFARI 600343, B.H.).
Inclusion and Diversity Statement
We worked to ensure sex balance in the selection of non-human subjects. One or more of the authors of this paper self-identifies as an underrepresented ethnic minority in science. One or more of the authors of this paper received support from a program designed to increase minority representation in science. The author list of this paper includes contributors from the location where the research was conducted who participated in the data collection, design, analysis, and/or interpretation of the work.
Footnotes
Declaration of interests
The authors declare no competing interests.
Data and Code Availability
All data structures and code that generated each figure will be publicly available at DOI 10.6084/m9.figshare.24517960 upon publication and linked from the corresponding author’s institutional webpage upon publication.
References
- 1.Hartline H. K. Visual receptors and retinal interaction. Science 164, 270–278, doi: 10.1126/science.164.3877.270 (1969). [DOI] [PubMed] [Google Scholar]
- 2.Fan L. Z. et al. All-Optical Electrophysiology Reveals the Role of Lateral Inhibition in Sensory Processing in Cortical Layer 1. Cell 180, 521–535 e518, doi: 10.1016/j.cell.2020.01.001 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Isaacson J. S. & Scanziani M. How inhibition shapes cortical activity. Neuron 72, 231–243, doi: 10.1016/j.neuron.2011.09.027 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sachdev R. N., Krause M. R. & Mazer J. A. Surround suppression and sparse coding in visual and barrel cortices. Front Neural Circuits 6, 43, doi: 10.3389/fncir.2012.00043 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Whitesell J. D., Sorensen K. A., Jarvie B. C., Hentges S. T. & Schoppa N. E. Interglomerular lateral inhibition targeted on external tufted cells in the olfactory bulb. J Neurosci 33, 1552–1563, doi: 10.1523/JNEUROSCI.3410-12.2013 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lakunina A. A., Nardoci M. B., Ahmadian Y. & Jaramillo S. Somatostatin-Expressing Interneurons in the Auditory Cortex Mediate Sustained Suppression by Spectral Surround. J Neurosci 40, 3564–3575, doi: 10.1523/JNEUROSCI.1735-19.2020 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Studer F. & Barkat T. R. Inhibition in the auditory cortex. Neurosci Biobehav Rev 132, 61–75, doi: 10.1016/j.neubiorev.2021.11.021 (2022). [DOI] [PubMed] [Google Scholar]
- 8.Priebe N. J. & Ferster D. Inhibition, spike threshold, and stimulus selectivity in primary visual cortex. Neuron 57, 482–497, doi: 10.1016/j.neuron.2008.02.005 (2008). [DOI] [PubMed] [Google Scholar]
- 9.Ozeki H., Finn I. M., Schaffer E. S., Miller K. D. & Ferster D. Inhibitory stabilization of the cortical network underlies visual surround suppression. Neuron 62 578–592, doi: 10.1016/j.neuron.2009.03.028 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Haider B. et al. Synaptic and network mechanisms of sparse and reliable visual cortical activity during nonclassical receptive field stimulation. Neuron 65, 107–121, doi: 10.1016/j.neuron.2009.12.005 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pecka M., Han Y., Sader E. & Mrsic-Flogel T. D. Experience-dependent specialization of receptive field surround for selective coding of natural scenes. Neuron 84, 457–469, doi: 10.1016/j.neuron.2014.09.010 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Vinje W. E. & Gallant J. L. Natural stimulation of the nonclassical receptive field increases information transmission efficiency in V1. J Neurosci 22, 2904–2915 doi: 10.1523/JNEUROSCI.22-07-02904.2002 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vinje W. E. & Gallant J. L. Sparse coding and decorrelation in primary visual cortex during natural vision. Science 287, 1273–1276, doi: 10.1126/science.287.5456.1273 (2000). [DOI] [PubMed] [Google Scholar]
- 14.Angelucci A. et al. Circuits and Mechanisms for Surround Modulation in Visual Cortex. Annu Rev Neurosci 40, 425–451, doi: 10.1146/annurev-neuro-072116-031418 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Adesnik H., Bruns W., Taniguchi H., Huang Z. J. & Scanziani M. A neural circuit for spatial summation in visual cortex. Nature 490, 226–231, doi: 10.1038/nature11526 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Adesnik H. Synaptic Mechanisms of Feature Coding in the Visual Cortex of Awake Mice. Neuron 95, 1147–1159 e1144 doi: 10.1016/j.neuron.2017.08.014 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ferguson K. A. et al. VIP interneurons regulate cortical size tuning and visual perception. Cell Rep 42, 113088, doi: 10.1016/j.celrep.2023.113088 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nienborg H. et al. Contrast dependence and differential contributions from somatostatin- and parvalbumin-expressing neurons to spatial integration in mouse V1. J Neurosci 33, 11145–11154, doi: 10.1523/JNEUROSCI.5320-12.2013 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dipoppa M. et al. Vision and Locomotion Shape the Interactions between Neuron Types in Mouse Visual Cortex. Neuron 98, 602–615 e608, doi: 10.1016/j.neuron.2018.03.037 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Campagnola L. et al. Local connectivity and synaptic dynamics in mouse and human neocortex. Science 375, eabj5861, doi: 10.1126/science.abj5861 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Pfeffer C. K., Xue M. S., He M., Huang Z. J. & Scanziani M. Inhibition of inhibition in visual cortex: the logic of connections between molecularly distinct interneurons. Nat Neurosci 16, 1068–U1130, doi: 10.1038/nn.3446 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cottam J. C., Smith S. L. & Hausser M. Target-specific effects of somatostatin-expressing interneurons on neocortical visual processing. J Neurosci 33, 19567–19578, doi: 10.1523/JNEUROSCI.2624-13.2013 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Niell C. M. & Stryker M. P. Highly selective receptive fields in mouse visual cortex. J Neurosci 28, 7520–7536, doi: 10.1523/JNEUROSCI.0623-08.2008 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhuang J. et al. Layer 4 in primary visual cortex of the awake rabbit: contrasting properties of simple cells and putative feedforward inhibitory interneurons. J Neurosci 33, 11372–11389, doi: 10.1523/JNEUROSCI.0863-13.2013 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lee S. H., Kwan A. C. & Dan Y. Interneuron subtypes and orientation tuning. Nature 508, E1–2, doi: 10.1038/nature13128 (2014). [DOI] [PubMed] [Google Scholar]
- 26.Atallah B. V., Scanziani M. & Carandini M. Atallah et al. reply. Nature 508, E3, doi: 10.1038/nature13129 (2014). [DOI] [PubMed] [Google Scholar]
- 27.El-Boustani S., Wilson N. R., Runyan C. A. & Sur M. El-Boustani et al. reply. Nature 508, E3–4, doi: 10.1038/nature13130 (2014). [DOI] [PubMed] [Google Scholar]
- 28.Atallah B. V., Bruns W., Carandini M. & Scanziani M. Parvalbumin-expressing interneurons linearly transform cortical responses to visual stimuli. Neuron 73, 159–170, doi: 10.1016/j.neuron.2011.12.013 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ferguson K. A. & Cardin J. A. Mechanisms underlying gain modulation in the cortex. Nat Rev Neurosci 21, 80–92, doi: 10.1038/s41583-019-0253-y (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Haider B. & McCormick D. A. Rapid neocortical dynamics: cellular and network mechanisms. Neuron 62 171–189, doi: 10.1016/j.neuron.2009.04.008 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Silver R. A. Neuronal arithmetic. Nat Rev Neurosci 11, 474–489, doi: 10.1038/nrn2864 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stettler D. D., Das A., Bennett J. & Gilbert C. D. Lateral connectivity and contextual interactions in macaque primary visual cortex. Neuron 36, 739–750, doi: 10.1016/s0896-6273(02)01029-2 (2002). [DOI] [PubMed] [Google Scholar]
- 33.Gilbert C. D., Hirsch J. A. & Wiesel T. N. Lateral interactions in visual cortex. Cold Spring Harb Symp Quant Biol 55, 663–677, doi: 10.1101/sqb.1990.055.01.063 (1990). [DOI] [PubMed] [Google Scholar]
- 34.Speed A., Del Rosario J., Burgess C. P. & Haider B. Cortical State Fluctuations across Layers of V1 during Visual Spatial Perception. Cell Rep 26, 2868–2874 e2863, doi: 10.1016/j.celrep.2019.02.045 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Speed A., Del Rosario J., Mikail N. & Haider B. Spatial attention enhances network, cellular and subthreshold responses in mouse visual cortex. Nat Commun 11, 505, doi: 10.1038/s41467-020-14355-4 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.van Beest E. H. et al. Mouse visual cortex contains a region of enhanced spatial resolution. Nat Commun 12, 4029, doi: 10.1038/s41467-021-24311-5 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nsiangani A. et al. Optimizing intact skull intrinsic signal imaging for subsequent targeted electrophysiology across mouse visual cortex. Sci Rep 12, 2063, doi: 10.1038/s41598-02205932-2 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lee S. H. et al. Activation of specific interneurons improves V1 feature selectivity and visual perception. Nature 488, 379–383, doi: 10.1038/nature11312 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.McGinley M. J., David S. V. & McCormick D. A. Cortical Membrane Potential Signature of Optimal States for Sensory Signal Detection. Neuron 87, 179–192, doi: 10.1016/j.neuron.2015.05.038 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Saravanan V., Berman G. J. & Sober S. J. Application of the hierarchical bootstrap to multi-level data in neuroscience. Neuron Behav Data Anal Theory 3 (2020). [PMC free article] [PubMed] [Google Scholar]
- 41.Kato H. K., Asinof S. K. & Isaacson J. S. Network-Level Control of Frequency Tuning in Auditory Cortex. Neuron 95, 412–423 e414, doi: 10.1016/j.neuron.2017.06.019 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Funk C. M. et al. Role of Somatostatin-Positive Cortical Interneurons in the Generation of Sleep Slow Waves. J Neurosci 37, 9132–9148, doi: 10.1523/JNEUROSCI.1303-17.2017 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.El-Boustani S. & Sur M. Response-dependent dynamics of cell-specific inhibition in cortical networks in vivo. Nat Commun 5, 5689, doi: 10.1038/ncomms6689 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Li S. et al. Dendritic computations captured by an effective point neuron model. Proc Natl Acad Sci U S A 116, 15244–15252, doi: 10.1073/pnas.1904463116 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hao J., Wang X. D., Dan Y., Poo M. M. & Zhang X. H. An arithmetic rule for spatial summation of excitatory and inhibitory inputs in pyramidal neurons. Proc Natl Acad Sci U S A 106, 21906–21911, doi: 10.1073/pnas.0912022106 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Tremblay R., Lee S. & Rudy B. GABAergic Interneurons in the Neocortex: From Cellular Properties to Circuits. Neuron 91, 260–292, doi: 10.1016/j.neuron.2016.06.033 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Scala F. et al. Layer 4 of mouse neocortex differs in cell types and circuit organization between sensory areas. Nat Commun 10, 4174, doi: 10.1038/s41467-019-12058-z (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Li N., Chen T. W., Guo Z. V., Gerfen C. R. & Svoboda K. A motor cortex circuit for motor planning and movement. Nature 519, 51–56, doi: 10.1038/nature14178 (2015). [DOI] [PubMed] [Google Scholar]
- 49.Sato T. K., Haider B., Hausser M. & Carandini M. An excitatory basis for divisive normalization in visual cortex. Nat Neurosci 19, 568–570, doi: 10.1038/nn.4249 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sato T. K., Hausser M. & Carandini M. Distal connectivity causes summation and division across mouse visual cortex. Nat Neurosci 17, 30–32, doi: 10.1038/nn.3585 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Petreanu L., Huber D., Sobczyk A. & Svoboda K. Channelrhodopsin-2-assisted circuit mapping of long-range callosal projections. Nat Neurosci 10, 663–668, doi: 10.1038/nn1891 (2007). [DOI] [PubMed] [Google Scholar]
- 52.Kvitsiani D. et al. Distinct behavioural and network correlates of two interneuron types in prefrontal cortex. Nature 498, 363–366, doi: 10.1038/nature12176 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Haider B., Hausser M. & Carandini M. Inhibition dominates sensory responses in the awake cortex. Nature 493, 97–100 doi: 10.1038/nature11665 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Kimura R. et al. Curtailing effect of awakening on visual responses of cortical neurons by cholinergic activation of inhibitory circuits. J Neurosci 34, 10122–10133, doi: 10.1523/JNEUROSCI.0863-14.2014 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Vaiceliunaite A., Erisken S., Franzen F., Katzner S. & Busse L. Spatial integration in mouse primary visual cortex. J Neurophysiol 110, 964–972, doi: 10.1152/jn.00138.2013 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Pouille F., Marin-Burgin A., Adesnik H., Atallah B. V. & Scanziani M. Input normalization by global feedforward inhibition expands cortical dynamic range. Nat Neurosci 12, 1577–1585, doi: 10.1038/nn.2441 (2009). [DOI] [PubMed] [Google Scholar]
- 57.Cone J. J., Scantlen M. D., Histed M. H. & Maunsell J. H.R. Different Inhibitory Interneuron Cell Classes Make Distinct Contributions to Visual Contrast Perception. eNeuro 6, doi: 10.1523/ENEURO.0337-18.2019 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Ingram T. G. J., King J. L. & Crowder N. A. Divisive Inhibition Prevails During Simultaneous Optogenetic Activation of All Interneuron Subtypes in Mouse Primary Visual Cortex. Front Neural Circuits 13, 40, doi: 10.3389/fncir.2019.00040 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Shapiro J. T., Michaud N. M., King J. L. & Crowder N. A. Optogenetic Activation of Interneuron Subtypes Modulates Visual Contrast Responses of Mouse V1 Neurons. Cereb Cortex 32, 1110–1124, doi: 10.1093/cercor/bhab269 (2022). [DOI] [PubMed] [Google Scholar]
- 60.Wilson N. R., Runyan C. A., Wang F. L. & Sur M. Division and subtraction by distinct cortical inhibitory networks in vivo. Nature 488, 343–348, doi: 10.1038/nature11347 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Veit J., Hakim R., Jadi M. P., Sejnowski T. J. & Adesnik H. Cortical gamma band synchronization through somatostatin interneurons. Nat Neurosci 20, 951–959, doi: 10.1038/nn.4562 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Rubin D. B., Van Hooser S. D. & Miller K. D. The stabilized supralinear network: a unifying circuit motif underlying multi-input integration in sensory cortex. Neuron 85, 402–417, doi: 10.1016/j.neuron.2014.12.026 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sanzeni A. et al. Inhibition stabilization is a widespread property of cortical networks. Elife 9, doi: 10.7554/eLife.54875 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Sadeh S. & Clopath C. Inhibitory stabilization and cortical computation. Nat Rev Neurosci 22, 21–37, doi: 10.1038/s41583-020-00390-z (2021). [DOI] [PubMed] [Google Scholar]
- 65.Moore A. K., Weible A. P., Balmer T. S., Trussell L. O. & Wehr M. Rapid Rebalancing of Excitation and Inhibition by Cortical Circuitry. Neuron 97, 1341–1355 e1346, doi: 10.1016/j.neuron.2018.01.045 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Litwin-Kumar A., Rosenbaum R. & Doiron B. Inhibitory stabilization and visual coding in cortical circuits with multiple interneuron subtypes. J Neurophysiol 115, 1399–1409, doi: 10.1152/jn.00732.2015 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Phillips E. A. & Hasenstaub A. R. Asymmetric effects of activating and inactivating cortical interneurons. Elife 5, doi: 10.7554/eLife.18383 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Del Rosario J. et al. Diminished Cortical Excitation and Elevated Inhibition During Perceptual Impairments in a Mouse Model of Autism. Cerebral Cortex 31, 3462–3474, doi: 10.1093/cercor/bhab025 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Li N. et al. Spatiotemporal constraints on optogenetic inactivation in cortical circuits. Elife 8, doi: 10.7554/eLife.48622 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Glickfeld L. L., Histed M. H. & Maunsell J. H. Mouse primary visual cortex is used to detect both orientation and contrast changes. J Neurosci 33, 19416–19422, doi: 10.1523/JNEUROSCI.3560-13.2013 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Resulaj A., Ruediger S., Olsen S. R. & Scanziani M. First spikes in visual cortex enable perceptual discrimination. Elife 7, doi: 10.7554/eLife.34044 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Zatka-Haas P., Steinmetz N. A., Carandini M. & Harris K. D. Sensory coding and the causal impact of mouse cortex in a visual decision. Elife 10, doi: 10.7554/eLife.63163 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Green D. M. & Swets J. A. Signal detection theory and psychophysics. (R. E. Krieger Pub. Co., 1974). [Google Scholar]
- 74.Reimer J. et al. Pupil Fluctuations Track Fast Switching of Cortical States during Quiet Wakefulness. Neuron 84, 355–362, doi: 10.1016/j.neuron.2014.09.033 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Vinck M., Batista-Brito R., Knoblich U. & Cardin J. A. Arousal and locomotion make distinct contributions to cortical activity patterns and visual encoding. Neuron 86, 740–754, doi: 10.1016/j.neuron.2015.03.028 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Burgess C. P. et al. High-Yield Methods for Accurate Two-Alternative Visual Psychophysics in Head-Fixed Mice. Cell Rep 20, 2513–2524, doi: 10.1016/j.celrep.2017.08.047 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Williams B. et al. Spatial modulation of dark versus bright stimulus responses in the mouse visual system. Curr Biol 31, 4172–4179 e4176, doi: 10.1016/j.cub.2021.06.094 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Steinmetz N. A. et al. Neuropixels 2.0: A miniaturized high-density probe for stable, long-term brain recordings. Science 372, 258-+, doi:ARTN eabf458810.1126/science.abf4588 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Rossant C. et al. Spike sorting for large, dense electrode arrays. Nat Neurosci 19, 634–641, doi: 10.1038/nn.4268 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Naka K. I. & Rushton W. A. S-potentials from colour units in the retina of fish (Cyprinidae). J Physiol 185, 536–555, doi: 10.1113/jphysiol.1966.sp008001 (1966). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Yger P., El Boustani S., Destexhe A. & Fregnac Y. Topologically invariant macroscopic statistics in balanced networks of conductance-based integrate-and-fire neurons. J Comput Neurosci 31, 229–245, doi: 10.1007/s10827-0100310-z (2011). [DOI] [PubMed] [Google Scholar]
- 82.Vogels T. P. & Abbott L. F. Signal propagation and logic gating in networks of integrate-and-fire neurons. Journal of Neuroscience 25, 10786–10795, doi: 10.1523/Jneurosci.3508-05.2005 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Kumar A., Schrader S., Aertsen A. & Rotter S. The high-conductance state of cortical networks. Neural Comput 20, 1–43, doi:DOI 10.1162/neco.2008.20.1.1 (2008). [DOI] [PubMed] [Google Scholar]
- 84.Rudy B., Fishell G., Lee S. & Hjerling-Leffler J. Three Groups of Interneurons Account for Nearly 100% of Neocortical GABAergic Neurons. Dev Neurobiol 71, 45–61, doi: 10.1002/dneu.20853 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Kisvarday Z. F., Beaulieu C. & Eysel U. T. Network of GABAergic large basket cells in cat visual cortex (area 18): implication for lateral disinhibition. J Comp Neurol 327, 398–415, doi: 10.1002/cne.903270307 (1993). [DOI] [PubMed] [Google Scholar]
- 86.Silberberg G. & Markram H. Disynaptic inhibition between neocortical pyramidal cells mediated by Martinotti cells. Neuron 53, 735–746, doi: 10.1016/j.neuron.2007.02.012 (2007). [DOI] [PubMed] [Google Scholar]
- 87.Gidon A. & Segev I. Principles governing the operation of synaptic inhibition in dendrites. Neuron 35, 330–341, doi: 10.1016/j.neuron.2012.05.015 (2012). [DOI] [PubMed] [Google Scholar]
- 88.Li S. T. et al. Dendritic computations captured by an effective point neuron model. P Natl Acad Sci 116, 15244–15252 doi: 10.1073/pnas.1904463116 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Eppler J. M., Helias M., Muller E., Diesmann M. & Gewaltig M. O. PyNEST: A Convenient Interface to the NEST Simulator. Front Neuroinform 2, 12, doi: 10.3389/neuro.11.012.2008 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Plotnikov D. et al. NESTML: a modeling language for spiking neurons. arxiv, doi:arXiv:1606.02882 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data structures and code that generated each figure will be publicly available at DOI 10.6084/m9.figshare.24517960 upon publication and linked from the corresponding author’s institutional webpage upon publication.