A method for comparing multiple imputation techniques: a case study on the U.S. National COVID Cohort Collaborative

Abstract

Healthcare datasets obtained from Electronic Health Records have proven to be extremely useful for assessing associations between patients’ predictors and outcomes of interest. However, these datasets often suffer from missing values in a high proportion of cases, whose removal may introduce severe bias. Several multiple imputation algorithms have been proposed to attempt to recover the missing information under an assumed missingness mechanism. Each algorithm presents strengths and weaknesses, and there is currently no consensus on which multiple imputation algorithm works best in a given scenario. Furthermore, the selection of each algorithm’s parameters and data-related modeling choices are also both crucial and challenging.

In this paper we propose a novel framework to numerically evaluate strategies for handling missing data in the context of statistical analysis, with a particular focus on multiple imputation techniques. We demonstrate the feasibility of our approach on a large cohort of type-2 diabetes patients provided by the National COVID Cohort Collaborative (N3C) Enclave, where we explored the influence of various patient characteristics on outcomes related to COVID-19. Our analysis included classic multiple imputation techniques as well as simple complete-case Inverse Probability Weighted models. Extensive experiments show that our approach can effectively highlight the most promising and performant missing-data handling strategy for our case study. Moreover, our methodology allowed a better understanding of the behavior of the different models and of how it changed as we modified their parameters.

Our method is general and can be applied to different research fields and on datasets containing heterogeneous types.

Introduction

While electronic health records (EHRs) are a rich data source for biomedical research, these systems are not implemented uniformly across healthcare settings and significant data may be missing due to healthcare fragmentation and lack of interoperability between siloed EHRs [1][2].

Removal of cases with missing data may introduce severe bias in the subsequent analysis [3]; with the goal of reducing bias primarily, and improving precision secondarily, imputation of the missing information is often performed prior to statistical analysis.

Imputation of missing data has been debated since the 1980s, when Rubin’s seminal work [4] presented Multiple Imputation (MI) as an imputation strategy for statistical analysis. Based on Bayesian theory-motivated underpinnings [5][6], MI allows the natural variation in the data to be emulated in addition to accounting for uncertainty due to the missing values in the subsequent inferences. In practice, the objective of MI is to construct valid inference for the estimated quantity of interest [7] rather than being able to predict the true missing values with the greatest accuracy, which is the typical aim of imputation models applied in machine-learning contexts where the focus is on predictive analysis [8].

Since the introduction of MI, several MI algorithms have been proposed and successfully deployed in many different domains to avoid information loss before the application of standard statistical methods for causal inference [9][10] as well as machine learning techniques for predictive modeling [11][12].

However, there is no consensus on which MI algorithm works best under different scenarios. Aside from the choice of the MI strategy to be used (see section Literature review), the choice of the specific imputation algorithm and of its input parameter settings, as well as modeling decisions - such as the way datasets with heterogeneous types (categorical, numeric, binary) are handled - are also both crucial and challenging. The appropriateness of including outcome variables in the imputation model also remains difficult to determine. For example, in a prior predictive study [11] the target (outcome) variable was omitted during imputation with the aim of avoiding bias in imputation results for variables highly correlated with the outcome. However, other works [13][14] recommended the inclusion of the outcome variables during imputation to accommodate potential confounding explicitly and obtain more reliable estimates.

In this paper, we consider statistical inference problems in the medical/clinical context, where missing values may affect the validity of the statistical estimates, if not properly handled. More precisely, we focus on situations where (potentially adjusted) associations between patient characteristics and an outcome of interest need to be inferred. In this context, we propose a method for evaluating and comparing several MI techniques, with the aim of choosing the most appropriate and performant approach for processing the original (incomplete) dataset and compute inferential quantities in retrospective clinical studies. While we focus on the evaluation of MI algorithms, the method is general enough to be applied to any missing-data handling strategy.

To show the effectiveness and the practicality of the evaluation approach, we used as a case study a cohort of patients with diabetes (type-2 diabetes) infected with COVID-19 provided by the National COVID Cohort Collaborative (N3C) Enclave (see Material and Methods). The same patient-cohort was previously filtered to remove cases with missing values and the obtained (complete) cohort was analyzed to assess associations between hospital events (hospitalization, invasive mechanical ventilation, and death) and crucial descriptors of patients with diabetes. Results of this analysis are reported in [15]. By limiting the analysis to complete cases, Wong et al. lost 42% of available cases, thereby reducing the power of the estimator (subsection Case study: associations between descriptors of patients with diabetes and COVID-19 hospitalization events). In the literature, strategies such as Inverse Probability Weighting (IPW, [16][17], subsection Literature review) have been proposed to recover from the limits of complete-case analysis by including a “missingness model” for the probabilities that each variable’s values are missing into the overall analysis. However, frequently-applied implementations of these strategies, i.e., without augmentation approaches [16], may prove ineffective when a high number of cases exhibit missing values. Imputation of missing data instead allows all cases to be used for computing potentially more reliable statistical estimates.

To guide the choice of the MI model and of its specification, we used our MI evaluation method to choose among the MI methods available from the N3C Platform.

Further, given its generality, we were able to apply the evaluation method to also assess the comparative performance of broader families of IPW models, comparing them to MI algorithms. In our case study, comparison with complete-case analysis confirmed the performance-based preference of multiple imputation over IPW models; such conclusions may not necessarily apply to augmented IPW approaches that make use of all available data (including incomplete cases with some modeled variables non-missing; for more on these so-called ‘doubly-robust’ IPW methods, see [17]) . To obtain actionable results, we finally used the most valid and performant (MI imputation) algorithms as determined by our evaluation method to compute odds ratios (and confidence intervals) describing associations between patient predictors and hospital events.

Of note, in [18] we applied our evaluation method to choose the most valid MI strategy to estimate a treatment effect while adjusting for other, potentially confounding, variables (subsection Generalizability of the evaluation method to different scenarios, [18]). This is another practical example showing that our evaluation approach can be applied on a broad range of heterogeneous (clinical) datasets to compare different strategies and methods for handling missing data while performing statistical analysis.

The paper is organized as follows. In the Background section we first describe the case study we used to show the feasibility of the evaluation method (subsection Case study: associations between descriptors of patients with diabetes and potential COVID-19 hospitalization events), and we next detail the MI strategy and its underlying theories (subsection Multiple Imputation), followed by a brief literature review (subsection Literature review). Next, section Evaluation method details our evaluation framework. The following section Experimental material and methods firstly reports the data source used for our experiments and implementation details (subsection Data source and implementation details). Finally, we detail the algorithms evaluated on our use cases and their experimental settings (subsection Evaluated algorithms and settings); we conclude with Results, Discussion and Conclusions, and Highlights.

Highlights.

• We propose an evaluation framework for comparing the validity of multiple imputation algorithms in a range of retrospective clinical studies where the need is to compute statistical estimates.

• While we focused on multiple imputation techniques, the generality of the method allows us to evaluate any missing-data handling strategy (e.g., IPW [16]), beyond those performing data imputation.

• The application of the evaluation method on a large cohort of patients from the N3C Enclave has shed some light on the following issues regarding the application of MI algorithms:

  • inclusion of the outcome variable in the imputation model: when choosing MI algorithms exploiting parametric univariate/multivariate estimators, the inclusion of the outcome variables in the imputations model can provide a better control for confounders. When applied to our clinical problem/dataset, MI algorithms exploiting estimators based on machine learning (RF) had the opposite behavior and tended to be biased by the inclusion of the outcome variables. However, caution is warranted here, as whether inclusion/exclusion of the outcome variable is best practice strongly depends on the properties of the data at hand. Indeed, the effect we observed on the output of RF-based models was likely due to the strong relationships between the outcome variables and the predictors. When using a different dataset where these relationships are stronger or weaker, the effect of the outcome inclusion may become either stronger or weaker, respectively. Therefore, our “universal” guideline is to use our evaluation model to improve understanding of whether the outcome should be included for a particular application.
  • conversion of heterogeneous data types to homogeneous data types by one hot encoding: when working on data types containing numeric and categorical predictors, some MI algorithms (e.g., Amelia and Mice with Bayesian or pmm univariate imputation algorithm) convert categorical variables into numeric type, thus introducing a severe bias [51], and reducing the validity of the obtained estimates. A solution to avoid this is to one-hot-encode categorical variables, therefore obtaining a set of binary predictors, whose scale and variability is however completely different from that of continuously-valued numeric variables. Testing under the setting where all variables (even numeric ones) are one-hot-encoded to obtain homogeneous predictors did not improve results. In particular, RF based MI algorithms seem the most stable with respect to data type heterogeneity, and this is due to their ability to handle mixed data types by design. Therefore, when heterogeneous datasets must be treated, our “universal” guideline is to use imputation algorithms, e.g., RF-based methods, handling mixed data types by design.
  • univariate imputation order: when exploiting iterative univariate imputations (Mice and missRanger), the imputation order may have an impact on performance. The comparison of the imputation order according to either increasing or decreasing number of missing values showed only a slight impact on bias. This implies that, under a reasonable number of iterations, the MI algorithms can reach convergence and the univariate imputation order may have no particular effect on the obtained results. On the other hand, considering that we found no evidence in literature that allows to choose one order with respect to the other, when limited computational costs are available and hamper the computation of a large number of multiple imputations, our “universal” guideline is to use our evaluation method to both check whether the univariate imputation order has any effect on the validity of the obtained estimates and, if this is the case, to also choose the most effective one from among the orders.
  • number of multiple imputations: to choose the number of multiple imputations, Von Hippel’s rule of thumb [40] would surely be a good choice. However, when dealing with large datasets, such a number of imputations can be prohibitive both from a time and memory perspective. For this reason, we would suggest performing a sensitivity analysis that starts with a low number of imputations (e.g. m=5 as suggested by Rubin [4]) and then proceeds towards large values until the evaluation measures stabilize. This process would also allow gaining additional insights about the behavior of different algorithms.

Aim:

To propose an evaluation framework for comparing and contrasting different approaches for handling heterogeneous data missingness in the context of statistical analysis applied to real-world datasets.

Background

Case study: associations between descriptors of patients with diabetes and potential COVID-19 hospitalization events

We apply our methods to a previously published case study [15] on patients with type 2 diabetes mellitus with data from the N3C. We used two logistic regression (LR) models and one Cox Survival (CS) model to evaluate the association between glycemic control measured by HbA1c¹ and outcomes of acute COVID-19 infection, including mortality (hazards estimated by assuming a CS model), mechanical ventilation (odds estimated by an LR model), and hospitalization (odds estimated by an LR model). The study aimed at understanding the role of patients’ factors such as body mass index (BMI), race, and ethnicity on COVID-19 outcomes [20][21][22][23]. Before running the LR and CS estimation steps, BMI was grouped according to the World Health Organization classification [24][25]² that categorizes adults over 20 years of age as underweight (BMI < 18.5kg/m2), normal weight (18.5 ≤ BMI < 25kg/m2), overweight ( 25 ≤ BMI < 30kg/m2), class I obesity (30 ≤ BMI < 35kg/m2), class II obesity (35 ≤ BMI < 40kg/m2), and class III obesity (BMI ≥ 40kg/m2) and the grouped variable was one-hot-encoded, so that the following estimators could accommodate non-linear relationships between BMI and any of the three outcomes. Grouping and one-hot-encoding was also applied for the other numeric predictor variables (HbA1c and age). Table 1 reports details about the complete list of predictors, their type, the grouping of numeric variables, and the distribution of cases across all the predictors. Note that categorical predictors were also one-hot-encoded (Race³, Ethnicity⁴, Gender⁵) before the LR and CS analysis to explicitly investigate the influence of the different categories.

Table 1:

The variables in the Wong et al. dataset [15], their type and their representation in the logistic regression and Cox-survival model. Numeric variables (age, BMI, Hba1c) were grouped and one-hot-encoded, while categorical variables (Gender, Ethnicity, and Race) were one-hot-encoded. To avoid collinearity, when one-hot-encoding a predictor variable, the binary predictor representing the largest group was left out for reference (marked with “used for reference” in the table). For each predictor group, the table also reports the percentage of missing cases, if any.

Predictor Group and predictor type	Predictor	percentage of missing values	all cases
Number of cases (%)			56123 (100%)
Gender One-hot-encoded categorical variable	Male		49%
	Female (used for reference)		51%
Age Grouped and one-hot-encoded numeric variable			61.88 ± 0.06 [18,89]
	age < 40		7%
	40 ≤ age < 50		11%
	50 ≤ age < 60		22%
	60 ≤ age < 70 (used for reference)		28%
	70 ≤ age < 80		22%
	age ≥ 80		10%
BMI Grouped and one-hot-encoded numeric variable		29%	33.25 ± 0.04 [12.13,79.73]
	BMI < 20		1%
	20 ≤ BMI < 25		8%
	25 ≤ BMI < 30		18%
	30 ≤ BMI < 35 (used for reference)		18%
	35 ≤ BMI < 40		12%
	BMI ≥ 40		13%
Race One-hot-encoded categorical variable	White (used for reference)	15%	55%
	Other		1%
	Black		26%
	Asian		3%
Ethnicity One-hot-encoded categoric variable	Hispanic	12%	16%
	Not hispanic (used for reference)		73%
Hba1c Grouped and one-hot-encoded numeric variable			7.58 ± 0.01 [4.1,19.3]
	Hba1c < 6		17%
	6 ≤ Hba1c < 7 (used for reference)		30%
	7 ≤ Hba1c < 8		21%
	8 ≤ Hba1c < 9		12%
	9 ≤ Hba1c < 10		07%
	Hba1c ≥ 10		12%
Comorbidities Binary variables; 1 = has comorbidity 0 = does not have comorbidity	MI		13%
	CHF		23%
	PVD		21%
	Stroke		17%
	Dementia		5%
	Pulmonary		31%
	liver mild		16%
	liver severe		3%
	Renal		30%
	Cancer		14%
	Hiv		1%
Treatments Binary variables; 1 = has comorbidity 0 = does not have comorbidity	Metformin		26%
	dpp4		5%
	sglt2		5%
	Glp		7%
	Tzd		1%
	Insulin		25%
	Sulfonylurea		9%

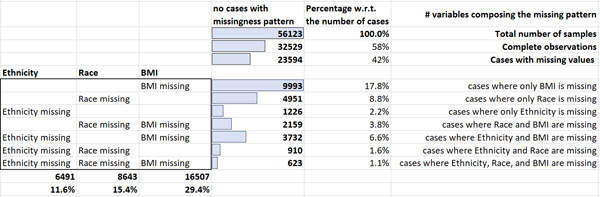
This study had several limitations. First, it was only conducted using complete cases for whom data on height and weight were present to calculate BMI. In particular, 16,507/56,123 (29.4%) of cases were excluded due to missing BMI. Also, race and ethnicity information was missing for a significant proportion of cases; to avoid their removal, the authors introduced missing indicators for race and ethnicity as two additional categories that represented uncertain information and that were one-hot-encoded as were the other race and ethnicity categories⁶.

In particular 8,643/56,123 (15.4%) of patients had missing data on race, 6,491/56,123 (11.6%) had missing data on ethnicity. This accounted for a total of 23,594/56,123 (42%) of samples containing missing or uncertain information. (Figure 1 shows details about the missing data patterns and the number of missing values per variable.)

Figure 1:

The presumed MAR missing data patterns in the Wong et al. [15] dataset.

In the Wong et al. cohort [15] the predictors were assumed to be, at best, Missing at Random (section Multiple Imputation), as suggested by Little’s test [27], whose p-value (p<0.0001) supported rejecting the null hypothesis of Missing Completely at Random (section Multiple Imputation) missingness. Therefore, the listwise-deletion performed in the original analysis (i.e., restriction analysis to “complete cases”) had not only reduced the sample size and the statistical power of the estimator, but may have inadvertently introduced bias in the resulting inferences. Therefore, we repeated the statistical analysis described in [15], after a previous step where we imputed missing data in BMI⁷, Ethnicity, and Race predictor variables.

Multiple Imputation

In the remainder of this paper, given a complete dataset $X\in R^{Nxd}$ (containing $N$ points represented by $d$ fully observed predictors) the statistical estimates (the log odds and log hazard scales), their variance, standard error, and confidence interval estimates will be referred to as $q_i,{var}_i,{se}_i$, and, ${ci}_i$, where the subscript $i\in \{1,...,d\}$ will index the predictor variable. The notation used throughout the paper is summarized in Table 2. Here, we assume that the effect of each covariate on the outcome is of interest, however if only a subset of effects are of interest and the remaining covariates are used for purposes of control, the methods remain virtually unchanged.

Table 2:

The notation used in the paper.

Parameter Name	Meaning
$N$	number of cases (sample points)
$d$	number of predictors
$X\in R_{ }^{Nxd}$	a dataset containing $N$ cases, each described by $d$ predictors
$q_i,{var}_i,{se}_i,{ci}_i$	the estimate (its variance, standard error, and confidence interval) computed on $X\in R_{ }^{Nxd}$ by a statistical estimator for the $i^{th}$ predictor variable $\left(foreachi\in \left\{1,...,d\right\}\right)$.
$Q=\left[q_i\right]$, $VAR=\left[{var}_i\right]$, $SE=\left[{se}_i\right]$, $CI=\left[{ci}_i\right]$, for each $i\in \left\{1,...,d\right\}$	The vector of all the estimates (their variance, standard error, and confidence interval) computed over all the predictors in a dataset $X\in R_{ }^{Nxd}$
$m$	number of multiple imputations
$\widehat{X^{\left(j\right)}}\in R_{ }^{Nxd}$	The j-th imputed set
$\widehat{q_i^{\left(j\right)}},\widehat{{var}_i^{\left(j\right)}},\widehat{{se}_i^{\left(j\right)}},\widehat{{ci}_i^{\left(j\right)}}$ for each $i\in \left\{1,...,d\right\}$	the estimate (its variance, standard error, and confidence interval) for the $i^{th}$ predictor $\left(i\in \left\{1,...,d\right\}\right)$ of the the j-th imputed set $\widehat{X^{\left(j\right)}}\in R_{ }^{Nxd}$
$\widehat{Q^{\left(j\right)}}=\left[\widehat{q_i^{\left(j\right)}}\right]$ $\widehat{{VAR}^{\left(j\right)}}=\left[\widehat{{var}_i^{\left(j\right)}}\right]$ $\widehat{{SE}^{\left(j\right)}}=\left[\widehat{{se}_i^{\left(j\right)}}\right]$ $\widehat{{CI}^{\left(j\right)}}=\left[\widehat{{ci}_i^{\left(j\right)}}\right]$ for each $i\in \left\{1,...,d\right\}$	The vector of all the estimates (their variance, standard error, and confidence interval) computed over all the predictors in the the j-th imputed set $\widehat{X^{\left(j\right)}}\in R_{ }^{Nxd}$.
$\widehat{q_i},\widehat{{var}_i},\widehat{{se}_i},\widehat{{ci}_i}$ for each $i\in \left\{1,...,d\right\}$	the pooled estimate (its variance, standard error, and confidence interval) obtained by an MI strategy for the $i^{th}$ predictor variable in $X\in R_{ }^{Nxd}$ by applying Rubin’s rule (Rubin et al 1987).
$\widehat{Q}=\frac{1}{m}{\sum }_{j=1}^m\widehat{Q^{\left(j\right)}}=\left[\widehat{q_i}\right]$, for each $i\in \{1,...,d\}$	The vector of the pooled estimates (one estimate per predictor variable) computed by an MI imputation strategy using $m$ imputations
$\widehat{W}=\frac{1}{m}{\sum }_{j=1}^m\widehat{{VAR}^{\left(j\right)}}\approx W_{\mathrm{\infty }}$ $\widehat{W}=\left[\widehat{W_i}\right]$, for each $i\in \{1,...,d\}$	$\widehat{W}$ is the vector of within imputation variances obtained with $m$ imputations (one within imputation variance per predictor variable). $\widehat{W}$ is an estimate of $W_{\mathrm{\infty }}$, the true within imputation variance when $m\to \mathrm{\infty }$
$\widehat{B}=\frac{1}{m-1}{\sum }_{j=1}^m{\left(\widehat{Q^{\left(j\right)}}-\widehat{Q}\right)}^2\approx B_{\mathrm{\infty }}$ $\widehat{B}=\left[\widehat{B_i}\right]$, for each $i\in \{1,...,d\}$	$\widehat{B}$ is the vector of between imputation variances obtained with $m$ imputations (one within imputation variance per predictor variable). $\widehat{B}$ is an estimate of $B_{\mathrm{\infty }}$, the true between imputation variance when $m\to \mathrm{\infty }$
$\widehat{T}=\widehat{W}+(1+\frac{1}{m})\widehat{B}\approx T_{\mathrm{\infty }}$	$\widehat{T}$ is the total variance that estimates the true total variance, $T_{\mathrm{\infty }}$ when $m\to \mathrm{\infty }$
$A$	The number of amputations of the complete dataset
$\underset{\_}{Q}=\frac{1}{A}{\sum }_{a=1}^A\widehat{Q\left(a\right)}=\left[\underset{\_}{q_i}\right]\approx E\left[\widehat{Q}\right]$ for each $i\in \{1,...,d\}$	The vector with the averages of the MI estimates across all the amputations, that approximates the (vector of) expected values of the MI estimates for each predictor

When data exhibit missing values, the data may be assumed to be Missing Completely At Random (MCAR), Missing At Random (MAR), or Missing Not At Random (MNAR) [28][29][30][31]. When the data are deemed MCAR the missing observations are considered to constitute a (completely) random subset of all observations; in other words, the probability of being missing is uniform across all cases or, simply said, there is no relationship between the missing values and any other values considered for analysis, whether observed or missing. This implies that the missing and observed data values will have similar distributions. Consequently, apart from the obvious loss of information, the deletion of cases with missing values (generally referred to as “listwise deletion” or complete case analysis) may be a viable choice if the number of fully observed cases is sufficient to obtain sufficiently reliable estimates.

MAR data, in contrast, entail systematic differences between the underlying distributions for cases exhibiting missing values for certain variables and cases with fully observed values for the same set of variables, but these underlying differences can be entirely explained by observed values in other variables (thus MCAR can be viewed as a more restrictive special case of MAR). In this case the probability of being missing is the same only within groups defined by the observed data (i.e., cases with missing values occur ‘at random’ within strata or latent groups determined by observed variable values), which means that there are relationships between missing and observed values, and these relationships may be exploited by modeling, to include proper data imputation techniques that adequately model such relationships to yield valid inferences about targeted quantities in the presence of missing data.

In contrast to MCAR data, for MAR data the removal of cases with missing values can not only affect statistical power [3], but it also may introduce non-negligible if not severe bias [32][33]. Indeed, for MAR data Little and Rubin [32] showed that the bias in the estimated mean for a given variable increases with the difference between the true underlying means of the observed and missing cases, in tandem with the proportion of the cases exhibiting missing values. Schafer and Graham [33] reported simulation studies where the removal of cases with missing values introduces bias under both MAR and MNAR missingness.

MNAR data is present when the data meets neither MCAR nor MAR assumptions due to underlying relationships, wherein missingness depends on unobserved data (thus MAR can be viewed as a restrictive special case of MNAR where dependence on unobserved data no longer holds). In this case, missingness is not at random, and it must be explicitly modeled to avoid some bias in the subsequent inferences [34][35]. As MNAR is empirically unverifiable and, in fact, non-identifiable from observed data [35], it follows that for any specific model of a MNAR mechanism to be adopted within an analysis, it must be postulated using domain-expert-driven assumptions. Given this context-specific aspect of MNAR modeling, we consider it outside the scope of this paper (aimed at proposing a generic evaluation framework for methods accommodating MAR missingness in EHR-based data). It requires domain-specific scientifically defensible assumptions in order to posit specific MNAR mechanisms, as they are empirically indistinguishable from specific MAR mechanisms that could yield an empirical (joint) distribution similar in all other respects, once given a set of observed data. Sensitivity analysis frameworks or other model-postulation-assessment methods are therefore necessarily specific to the scientific domain of a particular research question, and thus beyond the scope of this work; that said, such approaches should be routinely used to stress-test findings as a way to assess any (MI or IPW) missing-data techniques under a particular MNAR assumption.

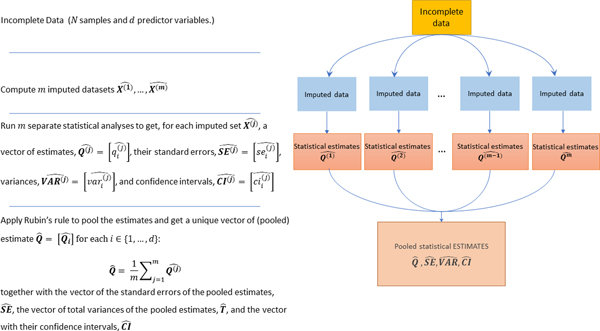
When an (univariate or multivariate) MI strategy is chosen for imputing the missing values prior to conducting the analysis, the following three steps are consecutively applied (sketched in Figure 2).

Figure 2:

Schematic diagram of the pipeline used to obtain pooled estimates when applying a MI strategy. The incomplete dataset is imputed $\mathit{m}$ times, where the value of $\mathit{m}$ can be defined in order to maximize the efficiency of the MI estimator (see Appendix A); each imputed dataset is individually processed to compute separate inferences; all the inferences are pooled by Rubin’s rule [4] to get the pooled estimates ($\widehat{\mathit{Q}}$), their total variances ($\widehat{\mathit{V}\mathit{A}\mathit{R}}$) and standard errors ($\widehat{\mathit{S}\mathit{E}}$) and their confidence intervals ($\widehat{\mathit{C}\mathit{I}}$). In the figure, we use the superscript $\mathit{j}$ to index the imputations number ($\mathit{j}\in \left\{1,\dots ,\mathit{m}\right\}$) and the subscript $\mathit{i}$ to index the predictor variable in the dataset (see Table 2 for a detailed list of all the notations used throughout the paper).

• (1) An (univariate or multivariate) imputation algorithm containing some randomness is used to impute the dataset a number $m$ of times, therefore obtaining a set of $m$ imputed sets, $\widehat{X^{\left(1\right)}},...,\widehat{X^{\left(j\right)}},...,\widehat{X^{\left(m\right)}}$ , where the superscript $j\in \{1,...,m\}$ will be used in the remaining part of this work to index the imputation number.

• (2) Each of the $m$ imputed datasets is then individually analyzed to obtain a vector $\widehat{Q^{\left(j\right)}}=\left[\widehat{q_i^{\left(j\right)}}\right]$ of estimates for each predictor variable (indexed by the subscript $i\in \{1,...,d\}$), their variances, $\widehat{{VAR}^{\left(j\right)}}=\left[\widehat{{var}_i^{\left(j\right)}}\right]$, standard errors, $\widehat{{SE}^{\left(j\right)}}=\left[\widehat{{se}_i^{\left(j\right)}}\right]$, and confidence intervals $\widehat{{CI}^{\left(j\right)}}=\left[\widehat{{ci}_i^{\left(j\right)}}\right]$.

• (3) the $m$ estimates are then pooled by Rubin’s rule [4] to obtain the final pooled inference as the mean of the estimates across all the imputations, $\widehat{Q}=\frac{1}{m}{\sum }_{j=1}^m\widehat{Q^{\left(j\right)}}$and its total variance, $\widehat{T}=\widehat{W}+(1+\frac{1}{m})\widehat{B}$, where $\widehat{W}=\frac{1}{m}{\sum }_{j=1}^m\widehat{{VAR}^{\left(j\right)}}\approx W_{\infty }$ is the estimate of the (true) within imputation variance (that would be obtained when $m\to \infty$) and $\widehat{B}=\frac{1}{m-1}{\sum }_{j=1}^m{\left(\widehat{Q^{\left(j\right)}}-\widehat{Q}\right)}^2\approx B_{\infty }$ is the estimate of the (true) between imputation variance (when $m\to \infty$). $\widehat{T}\approx T_{\infty }$ is an estimate of the true variance obtained when $m\to \infty$.

While easy to define in principle, the specification of a multiple imputation pipeline is not easy, and several open issues remain to be clarified. First, beside the arduous choice of the imputation algorithm, its application settings are also both crucial and challenging. This choice depends on the data structure, the data-generating mechanism, the inferential model, and the scientific question at hand. Unfortunately, the different algorithms and their different application settings may result in completely different estimates, therefore raising doubts about the reliability of the MI estimates.

Second, there does not exist a clear and well-defined theory that allows the optimal number $m$ of multiple imputations to be chosen. Indeed, several researchers [36][37] have supported Rubin’s empirical results [4] according to which 3 to 10 imputations usually suffice to obtain reliable estimates. However, more recent research studies [38][39] experimentally showed that the number of multiple imputations should be set to larger values (e.g. $m\ge 20$), which is now computationally more feasible than it was several decades ago. In our settings, $m$ was chosen in order to maximize the efficiency of the multiple imputation estimator (see Appendix A), by applying Von Hippel’s [40] rule of thumb, according to which a number of imputations comparable or higher than the percentage of cases that are incomplete is a reasonable setting. In our case-study, this criterion would require setting $m=42$; however, since the definition of $m$ is controversial and no well-accepted rule has been defined, we used the evaluation pipeline we are proposing to also experiment with the value $m=5$ suggested by Rubin and set as default by many packages (section Results). This allowed the stability of the computed estimates to be assessed with respect to the value of $m$.

Literature review

Statistical analysis of incomplete (missing) data is gaining a lot of interest in the research community.

To this aim, classic approaches such as simple complete-case IPW [16] limit the statistical analyses to the subset of complete cases weighted by their inverse probability of containing missing values. Since this probability is often unknown, it is typically estimated by using a logistic regression model that is fitted on the complete predictors and with outcome given by an indicator of each case containing at least one missing value. Though effective in several contexts, when a complex missingness pattern is present in the data and many predictors contain missing values, or when many cases are incomplete, IPW models tend to have a significant power loss due to the high number of cases being dropped; beyond the scope of this paper, the degree of power loss when using augmented IPW approaches leveraging all available data, e.g., [41], would warrant separate lines of research.

In these contexts, (multiple) data imputation strategies have often proven their effectiveness. In particular, MI algorithms can broadly be classified into three categories:

1. parametric multivariate MI imputation techniques exploiting a Joint Modeling (JM) approach [7][37];

2. univariate imputation methods exploiting a Fully Conditional Specification (FCS) strategy [28];

3. machine learning-based (e.g., missForest [42]) or deep-learning based MI strategies (e.g., MI via autoencoder models [43] – e.g. MIDA [44], or stacked deep denoising-autoencoders [45], or Generative Adversarial Networks [46] – e.g. GAIN [47] or MisGAN [48]).

Multivariate MI techniques exploiting a JM imputation strategy assume a joint distribution for all variables in the data and generate imputations for values in all variables by drawing from the implied conditional (predictive) distributions of the variables with missing values [37]. The multivariate JM strategy adheres to Rubin’s theoretical foundations [4] and its empirical computational time costs are significantly lower than those required by univariate FCS imputation algorithms; however, it is often challenging to specify a joint underlying distributional model, and this particularly happens when dealing with high-dimensional datasets and/or datasets characterized by mixed variable types (including binary and categorical types). For these reasons, some of the most popular algorithms exploiting a multivariate-JM strategy (e.g., “norm”, the classic MI multivariate imputation function implemented in R language [37], PROC MI [49], and Amelia [50] - subsection Evaluated algorithms and settings), simplify the problem by assuming an underlying multivariate Gaussian distribution, and dealing with categorical variables by converting then to numeric (integer) variables. Besides implicitly imposing an ordering between categories this can lead to bias [51]. To avoid any simplifying assumptions about the joint distribution, flexible nonparametric techniques have been proposed [7] that obtain effective imputation results by modeling the joint distribution through advanced Bayesian techniques. However, they incur high computational costs, hampering their practicability on high-dimensional, complex datasets such as those recently available from medical EHR studies.

FCS approaches exploit a univariate imputation approach where a conditional distribution (generally the normal distribution) is defined for each variable with missing values given all the other variables. This allows designing an iterative procedure where missing values are imputed variable-by-variable, akin to a Gibbs sampler. The most representative among MI algorithms using the FCS strategy is Mice [52] (subsection Evaluated algorithms and settings); it initially imputes the missing data in each variable by using a simple hot-deck-imputation technique (the mean/mode of observed values), and then imputes each incomplete variable by a separate model that exploits the values precedingly imputed from the other variables to “chain” all the univariate imputations. By default, Mice uses predictive mean matching (pmm, [28]) for imputing missing values in numeric data, logistic regression and polytomous logistic regression for binary data or categorical data. However, its version using classification and regression trees (CART, [53][54]) has also achieved promising results [55], as CART and regression trees are more-flexible estimation procedures. Other flexible machine-learning and deep-learning-based imputation techniques show promise as well.

MissForest [42] is a notable such procedure. It imputes missing values by applying a univariate FCS strategy, where variables with missing values are imputed by using RFs [56] for either regression (integer- or real-valued variables) or classification (binary or categorical variables). MissForest was presented as an imputation method to be applied for predictive modeling, where a unique imputation of missing data is generally produced before training any subsequent classifier on the imputed data. However, an MI version of MissForest was proposed in missRanger, where a final refinement step is added that applies pmm⁸ to both avoid outliers and recover the natural data variability (subsection Evaluated algorithms and settings).

Given the success of deep-learning techniques in a variety of fields, several authors have designed flexible deep, neural-network-based imputation models that showed promise in the presence of complex data [8]. In particular, two recent advances in the context of deep-neural networks are particularly suited for the task of (multiple) data imputation: denoising autoencoders (for MI) [43][44][45] and Generative Adversarial Networks (GANs) [46][47][48].

Autoencoders are unsupervised neural networks that compute an informative lower-dimensional representation of the input data. They are generally characterized by an hourglass shaped architecture, composed of two modules: an encoder-module and a decoder-module that share a bottleneck layer. The encoder-module processes the input layer to produce a lower dimensional representation of the input data in the so-called bottleneck layer; the decoder module processes the output of the bottleneck layer (the lower dimensional input representation) to obtain an output layer that best reconstructs the input data. After being trained by a loss function that measures the difference between the input and the output layers, the autoencoder can be used to process input samples to retrieve their lower dimensional representations in the bottleneck layer. In practice, an autoencoder is a neural network model trained to learn the identity function of the input data. Denoising autoencoders intentionally corrupt the input data (by randomly turning some of the input values to zero) in order to prevent the networks from learning the identity function, but rather a useful low-dimensional representation of the input data. Given a sample with missing values, denoising autoencoders are naturally suitable for producing MI data because they can simply be run several times by using different random initializations. A classic example of algorithm using denoising autoencoder for MI is MIDA [44]⁹.

GANs [46][47][48] are other neural-network models generally used for generative modeling, that is to output new examples that could have plausibly been drawn from the original dataset.

GANs allow reformulating the generative model as a supervised learning problem with two sub-modules: a generator-module that is trained to generate new examples, and the discriminator-module that is trained to classify examples as either real (i.e., from the domain to be learnt) or fake (generated). The two models are trained together in an “adversarial” game, until the discriminator-module is fooled about half of the time, meaning that the generator-module is generating plausible examples. GAIN [47] and MisGAN [48] are two recent examples of MI algorithms that utilize GANs. Given an input dataset with missing values, both of them first add noise and fill the missing values with some hot-deck imputation technique or constant values.

Next, GAIN [47] employs an imputer-generator module that is trained to produce plausible imputations of the missing data. The generator is adversarially trained to fool a discriminator that determines which entries in the completed data were actually observed and which were imputed.

MisGAN [48] instead uses a generator-module that is trained to generate both plausible imputation values and the missingness masks that mark the imputed values. This generator is adversarially trained to fool a discriminator that solely works on the masked-output of the generator to recognize a valid imputation. Both GAIN and MisGAN can be used to generate MIs by using several runs of the GAN model with varying initial noise and/or imputations of the missing values.

Machine-learning and deep-learning based MI methods have three main advantages over traditional multivariate-JM and univariate-FCS MI models. First, they are more flexible and do not need any underlying data distribution to be specified. Second, they are naturally designed to deal with mixed data-types. Third, they can uncover more complex, nonlinear relationships between variables and are able to exploit them to improve the validity of the computed imputations. Deep-learning based MI methods are further characterized by their documented ability to impute complex, high-dimensional data. Moreover, once trained, the computational time of deep-learning based models is much lower than that required by univariate-FCS algorithms (e.g., MICE) and univariate machine-learning based algorithms (e.g., missForest).

These advantages are however counterbalanced by crucial points, often hampering the practicability of deep-learning based MI techniques; indeed, the hyperparameter tuning of deep-learning based models is difficult and crucial, and slightly different model architectures can result in dramatically different results. Unfortunately, few details are provided in the literature about hyperparameter tuning and architectural choices, and their consequences for the performance of imputation methods. For this reason, their choice is generally limited to predictive modeling contexts, where the choice of the best architecture and hyperparameter values may be simply guided by the prediction performance.

Further, while considering recently proposed non-MI and MI methods using deep-learning models to handle simulated MNAR data [57][58], one encounters a lack of transparency in how deep architectures encode the missingness mechanism assumptions. Indeed, the proposed models tacitly adopt the (unidentifiable) MAR/MNAR assumptions, akin to failing to accommodate how two- and higher-way interactions among discrete sets of patient-level predictors might impact outcomes and analytic features deemed crucial by clinicians in most settings.

This inability to accommodate clinically-valid joint variable distributions with explainable distinctions between MAR and MNAR, together with implementation challenges, highlight that the proper setting of deep-learning models in the context of MI is still lacking a grounded theoretical basis, whose definition would require additional research.

Evaluation method

In statistical inference contexts, the goal of MI is to obtain statistically valid inferences from incomplete data. In other words, given a statistical model of interest (e.g., an LR estimator or a CS model), an imputation algorithm should ultimately allow the analyst to obtain estimates as similar as possible to those that the statistical model would provide if the data were complete.

Unfortunately, there is no rule of thumb for choosing an imputation model based on the problem at hand, the amount of missingness, or the missingness pattern.

However, following the guidelines in Van Buuren’s seminal work [28], when the number of complete cases has a reasonable cardinality, an MI algorithm may be evaluated by comparing the inferences (i.e., statistical estimates) obtained on the dataset containing fully observed data (complete dataset obtained by listwise deletion) to those computed by pooling all the MI estimates obtained on an amputated version of the complete dataset, where amputation refers to the process that synthetically generates missing values in a dataset [59]. Of course the comparison should be performed by using a properly designed evaluation pipeline exploiting solid evaluation measures. Such an MI evaluation pipeline is still lacking in literature.

Therefore, this paper proposes an MI evaluation framework that leverages Van Buuren’s guidelines and proposes a set of evaluation measures that are pooled across multiple amputated datasets.

The application of our approach allows numerical evaluation of the validity of any imputation model and its various application settings given the specific problem at hand. After testing a set of imputation algorithms (and/or their different application settings) the user can comparatively analyze the obtained numeric evaluations and choose the most appropriate imputation algorithm to be applied to the original (incomplete) dataset.

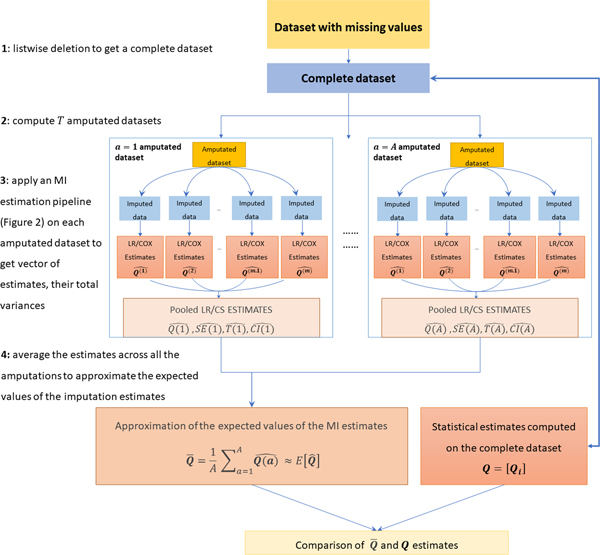
In practice, given a statistical estimator of interest, we propose to numerically evaluate a specific MI algorithm by applying the steps sketched in Figure 3:

Figure 3:

Schematic diagram of the pipeline used to evaluate one MI algorithm across A multiple amputation settings. The following steps are applied: 1) listwise deletion is used to produce a complete dataset on which a vector of estimates to be used as “gold standard” is computed; 2) a number A of amputated datasets is computed by using an amputation algorithm that reproduces the same missingness pattern in the original dataset; 3) An MI estimation pipelines (see Figure 2) are applied to get A pooled estimates, their total variances, standard errors and confidence intervals; 4) averaging the A estimates the expected value of the MI estimates are approximated and compared to the gold standard estimates computed on the complete dataset (step 1).

(step 1) starting from the original dataset with missing values, obtain a complete dataset by listwise deletion and apply the statistical estimator of interest to compute “gold standard” estimates;

(step 2) produce $A$ amputated versions of the complete dataset by reproducing the same (MCAR or MAR) missingness observed in the original dataset (for details about the best value for parameter $A$ see section Results, while a discussion about proper approaches for reproducing MCAR or MAR missingness is reported below);

(step 3) process each amputated dataset by applying the MI estimation pipeline detailed in Section Multiple Imputation (sketched in Figure 2) to obtain a vector of MI estimates (both point estimates and uncertainty estimates such as standard errors or confidence intervals) based on the statistical analysis of interest (one estimate per predictor variable in the dataset);

(step 4) average each MI estimate across all the amputations to obtain a vector approximating the expected value of the MI estimate for all the predictor variables in the dataset. Finally, compare the gold standard estimates (obtained on the complete dataset) to the expected values of the MI estimates by using the numeric evaluation measures detailed below.

Before detailing the evaluation method, an important note about the above step-2 is due. Reproduction of MCAR missingness in the complete dataset is simple and requires producing the same missingness proportions by sampling from uniform distributions.

On the other hand, data amputation to simulate a MAR mechanism is challenging and few works are available in literature [59] that describe different methodologies for producing simulated MAR data. The critical task is the estimation of the distribution describing the missingness in one variable conditioned on the other variables. The literature review in this context highlights that the method proposed by Shouten et al. [59] is promising and has been observed to be a reliable approach for emulating the MAR missingness characterizing a given dataset. Moreover, Shouten et al. support their results with extensive simulations showing the effectiveness of the produced amputations. Therefore, we produced MAR missingness by using the function “ampute”, available from the MICE package R, which implements the techniques of Shouten et al.¹⁰.

We must further note that it is possible for the subset of complete data to systematically differ from the original (incomplete) data that have “real” missingness, so that any amputation procedure would not be able to reproduce the exact missingness pattern. However, this numerical approach of evaluating imputation methods still has merit as an evaluative technique, as it provides empirical evidence of the ability of imputation approaches to handle observable missingness patterns in a given dataset.

Hereafter, we report the details about the evaluation method and the evaluation metrics we are using to compare the gold standard estimates to the MI estimates. Figure 4 reports a more detailed overview of the steps we are applying and considers the more general situation when more than one statistical estimator is applied, where each estimator computes inferences related to a specific outcome of interest (as an example, in our use case we had three outcomes of interest and three respective statistical estimators). In particular, for each outcome variable (statistical estimator) the following steps are applied to evaluate an MI algorithm:

Figure 4:

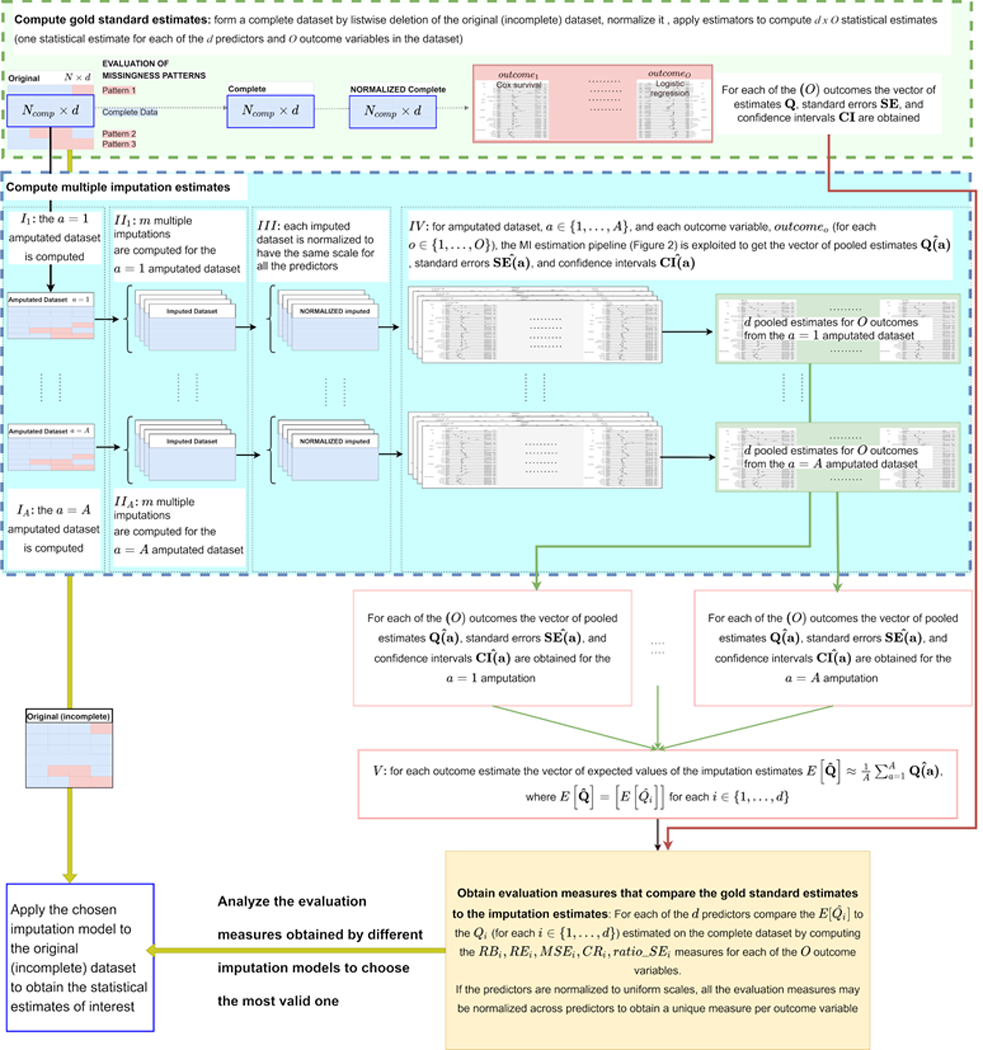
Schematic diagram of the pipeline used to evaluate a multiple imputation algorithm. [TOP light green BOX: compute gold standard estimates] Listwise deletion is used to create a “complete” dataset where all the values are observed; the predictor variables in the complete dataset are normalized to obtain uniform scales across different predictors; statistical estimators (in our experiments they were two logistic regression models and one Cox survival model) are applied to compute statistical estimates describing the influence of the available predictors on O outcome variables (in our experiments they were O = 3 outcomes describing the hospitalization event, the invasive ventilation event, and patients’ survival). [BOTTOM light blue BOX: compute MI estimates] $\left({\mathit{I}}_1,\dots ,{\mathit{I}}_{\mathit{A}}\right)$ From the complete dataset, A amputated dataset are computed; $\left({\mathit{I}\mathit{I}}_1,\dots ,{\mathit{I}\mathit{I}}_{\mathit{A}}\right)$ each amputated dataset is imputed $\mathit{m}$ times by the MI algorithm under evaluation and (III) each imputed dataset is normalized (as done in the TOP BOX for the complete dataset) to obtain uniform scales across all the predictors in all the imputed datasets and in the complete dataset. (IV) Each imputed-normalized dataset is processed by the O statistical estimators and Rubin’s rule [4] is applied to pool the estimates across the m imputations. (V) The pooled estimates obtained for each outcome and predictor variable are averaged across the A simulations (1 simulation per amputated dataset) to approximate the expected values of the estimate for each predictor and outcome. [YELLOW BOX: compare the gold standard estimates to the imputation estimates] The evaluation measures detailed in Section “Evaluation method” are computed for comparing the computed estimates to the gold standard estimates computed on the complete-normalized dataset (for each of the predictors and outcome variables). Of note, the normalization of the (complete and imputed) dataset predictors to a unique scale before the estimation would allow averaging all the evaluation measures across all the predictors. For each imputation algorithm under evaluation, the depicted pipeline provides a set of evaluation measures that can be analyzed to choose the most valid and performant algorithm for handling the data missingness. The chosen algorithm can be finally applied to the original (incomplete) dataset to obtain reliable statistical estimates.

• 1) Obtain gold standard statistical estimates (and their confidence intervals) on a complete dataset [light green box on top of Figure 4]. To this aim, listwise deletion is applied on the original (incomplete) dataset to get the complete dataset $X\in R^{N\times d}$ (composed by $N$ complete cases and $d$ predictor variables). The complete dataset is then normalized to have predictors with the same scale, and the estimator of interest is applied to get a vector of statistical estimates for each predictor variable in the dataset $i\in \{1,...,d\}$. Note that the dataset normalization step is not mandatory but it ensures obtaining statistical estimates (and evaluation measures) characterized by the same scale. This is a useful characteristic when having multiple predictors in the input dataset (as shown in section Results).

  Hereafter, the vector of gold standard statistical estimates will be referred to as $Q=\left[q_i\right]$ and the corresponding vector of confidence intervals will be $CI=\left[q_i^{min},q_i^{max}\right]=\left[{CI}_i\right]$.

• 2) Obtain the expected values of the MI estimates [light-blue box in Figure 4 and pseudo-code sketched in Algorithm 1 below]. To this aim, the following steps are applied:

  1. Compute $A$ amputations of the complete dataset (step I). Hereafter, we will refer to the a^th amputated dataset as $\widehat{X^{\left(a\right)}}\left(a=1,...,A\right).$
     At this stage, the MI estimation pipeline (section Multiple Imputation and Figure 2) is applied to each of the $A$ amputated datasets. More precisely, on the $a$^th $\left(a\in \{1,...,A\}\right)$ amputated dataset:
  2. the MI algorithm under evaluation is applied to compute $m$ imputations;
  3. each imputed dataset is normalized as done on the complete dataset (light-green box in Figure 4) to obtain predictors with the same scale;
  4. the statistical estimator of interest is applied on each imputed-normalized dataset and Rubin’s rule is used to pool all the estimates and obtain an imputation estimate. This allows to compute the vector of estimates $\widehat{Q\left(a\right)}=\left[\widehat{q_i\left(a\right)}\right]$, the vector of standard errors, $\widehat{SE\left(a\right)}=\left[{se}_i\left(a\right)\right]$,¹¹ and the vector of the 95% confidence interval estimates, $\widehat{CI\left(a\right)}=\left[{ci}_i\left(a\right)\right]$^{12 $\left(i\in \{1,...,d\}\right)$} for the $a$t^h amputated dataset. The vector is composed of the imputation estimates for each of the $d$ predictors in the dataset.
  5. For each predictor variable, average all the estimates across the $A$ amputated datasets to obtain a vector approximating the expected value of the MI estimate $E\left[\widehat{Q}\right]$. The vector $E\left[\widehat{Q}\right]$ is estimated as: $\underset{\_}{Q}=\left[\underset{\_}{q_i}\right]=\frac{1}{A}{\sum }_{a=1}^A\widehat{Q\left(a\right)}\approx E\left[\widehat{Q}\right]$.
• 3) Compare the gold standard estimates to the MI estimates [yellow-box in Figure 4]: the inferences obtained on the complete data ($Q=\left[q_i\right]$ - step 1) are compared to those obtained on each of the amputated datasets $\left(\widehat{Q\left(a\right)}=\left[\widehat{q_i\left(a\right)}\right],i\in \{1,...,d\}\right)$ by computing the evaluation measures described below (some of which are listed in [23] by considering a unique amputated dataset). In particular, considering the vectors containing all the predictor estimates, we compute:

  • the raw bias vector $RB=\left[{rb}_i\right](i\in \{1,...,d\left\}\right)=\underset{\_}{Q}-Q\approx E\left[\widehat{Q}\right]-Q$, where ${rb}_i$ is the raw bias for the $i^{th}$predictor variable, whose sign may be observed across all the predictor variables to understand whether the multiple imputation has the effect of globally underestimating or overestimating the true estimates. This information is complemented by the estimate ratio (ER), $ER=\left[{er}_i\right](i\in \{1,...,d\left\}\right)=\frac{\underset{\_}{Q}}{Q}\approx \frac{E\left[\widehat{Q}\right]}{Q}$, ${er}_i$ being the estimate ratio for the $i^{th}$predictor variable, and by the vector containing the expected value of the Mean Squared Error (MSE) of the estimate, where again ${mse}_i$ refers to the $i^{th}$predictor: $MSE=\left[{mse}_i\right]=\frac{1}{A}{\sum }_{a=1}^A{\left(\widehat{Q\left(a\right)}-Q\right)}^2\approx E\left[{\left(\widehat{Q}-Q\right)}^2\right]$.
  • the coverage rate (cr_i) for the $i^{th}$predictor variable is the proportion over all the $A$ amputations of the confidence intervals $\widehat{{ci}_i\left(a\right)}=$ $($for each $a\in \{1,...,A\})$ that contain the true estimate $q_i$. The actual rate should be equal to or exceed the nominal rate (95%). If ${cr}_i$ falls below the nominal rate, the method is too optimistic, leading to higher rates of false positives. A ${cr}_i$ too low (e.g., below 90 percent for a nominal 95% interval) indicates low reliability. On the other hand, a ${cr}_i$ too high (e.g., 0.99 for a 95% confidence interval) may indicate that the confidence intervals of the pooled estimates $\widehat{{ci}_i\left(a\right)}$ are too wide, which means that the MI method could be inefficient. In this case, the analysis of average standard error of each pooled estimates, $\widehat{{se}_i\left(a\right)}$, and the ratio of the standard errors of the pooled and true estimates $\mathit{r}\mathit{a}\mathit{t}\mathit{i}\mathit{o}{\mathit{s}\mathit{e}}_{\mathit{i}}=\frac{\widehat{{se}_i\left(a\right)}}{{se}_i\left(a\right)}$ may inform about the effective reliability of a high ${cr}_i$ value. In practice, high values of ${cr}_i$ are consistent with standard errors $\widehat{{se}_i}$ of the MI estimate being lower or comparable to the standard error of the true estimate (i.e., $ratio{se}_i\le 1$). To obtain such a result, the number of imputations must be sufficiently high to guarantee that the variance of the MI estimate is mainly dominated by the variance of the statistical estimator (evaluated by the within imputation variance).

• 4) Choose the most valid and performant MI algorithm and use it to compute statistical estimates from the original (incomplete) datasets: having applied steps 1 to 3 by using different MI imputation algorithms and (eventually) their different application settings, the obtained numerical evaluation measures can be comparatively analyzed to choose the most valid MI imputation model for the problem at hand. The chosen model can then be applied to the original (incomplete) datasets to obtain the desired MI estimates.

Algorithm 1.

Pseudo-code of the algorithm used to obtain the expected values of the MI estimates from the A = 25 amputations

We note that, when considered by itself, each of the numeric measures described above provides limited information about the validity of the MI algorithm being evaluated. However, when considered together, the evaluation measures we are proposing provide a full picture about the capability of each MI algorithm to provide estimates approximating the gold standard estimates computed on the complete set.

The proposed evaluation measures are general and can be used under different scenarios (subsection Generalizability of the evaluation method to different scenarios) where statistical estimators providing estimates, standard error of the estimate, and confidence intervals must be applied.

We used the proposed procedure to evaluate the validity of the estimates computed by IPW models and to compare them to those computed by MI algorithms (subsection Evaluated algorithms and settings and section Results).

Note that until the past decade, several methods amputated the complete data and then compared the application of different imputation algorithms by using the RMSE (or NRMSE) between the true values and the imputed values. However, research has clarified that such metrics may not give a full picture of the comparisons and sometimes can be even misleading and may lead to unreliable conclusions [60]. Moreover, when redesigned for assessing MI datasets, they are usually computed by considering the mean across all the imputations, which results in an opaque metric with an uncertain statistical meaning that ignores the uncertainty of imputations.

Experimental material and methods

Data source and implementation details

The dataset used in this study was provided by the N3C Enclave. The N3C receives, collates, and harmonizes EHR data from 72 sites across the US. With data from over 14 million patients with COVID-19 or matched controls, the N3C Platform (funded by NIH/NCATS, powered by Palantir Foundry©2021, Denver, CO) provides one of the largest and most representative datasets for COVID-19 research in the US [61][62][63].

The rationale, design, infrastructure, and deployment of N3C, and the characterization of the adult [62] and pediatric [63] populations have been previously published. Continuously updated data are provided by health care systems to N3C and mapped to the OMOP common data model¹³ for authorized research.

N3C data has been used in multiple studies to better understand the epidemiology of COVID-19 and the impact of the disease on health and healthcare delivery [15][64][65][66][67][68].

All the code for the analysis was implemented on the Palantir platform leveraging the Foundry operating system¹⁴. The platform enables groups of users to share code workbooks. Each code workbook is organized as a directed acyclic network of communicating nodes; each node can be written in SQL, Python/Pyspark, or R/SparkR code. The input and output of each node must be formatted in the form of a table (tabular dataframe) or a dataset (a collection of tables/dataframes).

For consistency, all the IPW [13] and imputation algorithms used in our experiments (subsection Evaluated algorithms and settings) are implemented in R packages, available from the CRAN repository. These included Amelia (version 1.7.6,[50]¹⁵), Mice (version 3.8.0, [52]¹⁶), and missRanger (version 2.1.3, [42]¹⁷).

Evaluated algorithms and settings

To demonstrate the feasibility and practicability of our evaluation method, we conducted a series of experiments where IPW models were compared to MI techniques for obtaining statistical estimates on the use-case presented in subsection Case study: associations between descriptors of patients with diabetes and potential COVID-19 hospitalization events.

The IPW models varied both the method used to compute the probability of missing values and the predictors used to estimate it. More precisely, for estimation of the non-missingness probability we compared the usage of logistic regression models and RFs [56]. With regards to the predictor variables used to estimate the missingness probability, we compared the inclusion/exclusion of the outcome variables in the prediction model. Moreover, in line with the LR models applied by Wong et al. [15], we also compared the usage of numeric variables (age and HbA1c) to the setting where numeric variables are binned and then one-hot-encoded.

The MI algorithms were chosen among those that 1) obtained good performance as reported by literature studies and by preliminary experiments; 2) were freely available as R/SparkR or python/pySpark packages (programming languages supported by the N3C Palantir secure analytics platform) and did not have technical constraints that hampered their application in the N3C Palantir secure analytics platform; 3) had a memory/time complexity supporting the computation on a large dataset within the N3C Palantir secure analytics platform.

Among the feasible packages we chose three R packages that applied different strategies (FCS imputation, JM imputation, or machine-learning based imputation) and were based on different theoretical grounds and assumptions ¹⁸.

Among the chosen imputation models, two imputation algorithms, Amelia [50] and Mice [52], exploit, respectively, a multivariate-JM strategy and an univariate-FCS strategy where an underlying normal distribution is assumed; the third method (missRanger [42]) is a representative of more-flexible machine-learning-based imputation approaches. All the methods are described in the section Literature review.

In the following we describe their different specifications and compare them by using the evaluation method proposed in this paper (section Evaluation method).

In its default settings, for each variable with missing values, Mice uses the observed part to fit either a predictive mean matching (pmm, for numeric variables), or a logistic regression (for binary variables), or a polytomous regression (for categorical variables) model and then predicts the missing part by using the fitted model.

Mice also provides the ability to use a Bayesian estimator for imputing numeric variables. To perform an exhaustive comparison, we therefore compared the performance of Mice with default settings (referred to as Mice-default in the following) with those of a Mice using univariate Bayesian estimators (hereafter denoted with Mice-norm) and run on a version of the dataset where all the categorical variables are one-hot-encoded to convert them to a numeric type.

This choice is coherent with the study from [15], where authors performed their analysis by 1) one-hot-encoding categorical variables (e.g. “Race”), and 2) binning continuous variables (BMI, age, and HbA1c) and then one-hot-encoding the resulting binned variables. As aforementioned, using such representation in an imputation setting essentially results in a fuzzy imputation, where each imputation run is allowed to choose multiple categories for each sample. We thus aimed to understand if one-hot-encoding both numeric and categorical variables could positively or negatively affect the obtained results. Experimenting this setting with Mice-default resulted in the application of a logistic regression model for each binned variable to be imputed. We use Mice-logreg to denote the Mice algorithm run on samples expressed by one-hot-encoded variables imputed via LR models. For exhaustiveness of comparison we also used the application of Mice-norm under this setting.

Independent from the univariate imputation models used, all the Mice algorithms iterate their univariate imputations over all the variables with missing values by following a pre-specified variable imputation order (increasing or decreasing number of missing values), and then restart the iteration until a stopping criterion is met, or a maximum number of user-specified iterations is reached. Iteration is used because each model refines the previous imputations by exploiting the better quality data from the previous imputation. In our experiments, due to the high dimensionality, we set the maximum number of iterations equal to 21 and tested the application of Mice when the univariate imputation order was given by the increasing and the decreasing number of missing values.

The missRanger algorithm (hereafter denoted as missRanger) is a fast R implementation of the missForest algorithm, which applies the same univariate, iterative imputation schema used by Mice, where the main difference is in the usage of the RF model for each univariate imputation. Note that, in between the consecutive variable imputations, missRanger allows using the pmm estimator (section Literature review). In this way, for each imputed value in variable $v$, pmm finds the nearest $k$ predictions for the observed data in $v$, randomly chooses one of the $k$ nearest predictions, and then uses the corresponding observed value as the imputed value. The application of pmm avoids imputing with values not present in the original data (e.g., a value less than zero in variables with non-negative valued variables); it also raises the variance in the resulting conditional distributions to a realistic level.

In our experiments, due to the high sample cardinality, we used 50 trees per RF, allowed a maximum number of iterations equal to 21, tested the application of missRanger by using the univariate imputation order given by the increasing and the decreasing number of missing values, and we also compared the behavior of the algorithm when pmm is avoided (missRanger no-pmm), or when it is applied with 3 or 5 donors (values suggested by authors of missRanger themselves). Further, for allowing an exhaustive comparison to the setting where all the variables are binarized, we also tested the application of missRanger under the scheme when categorical and binned numeric variables are one-hot-encoded.

The Amelia algorithm uses the Expectation Maximization algorithm presented in [50] to estimate the parameters underlying the distribution behind the complete observations, from which the imputed values are drawn. In case of categorical data, Amelia uses a one-hot-encoding strategy, which essentially reverts to fuzzy imputations for categorical variables. Similar to what was done for the other evaluated algorithms, we also experimented after binning and one-hot-encoding numeric variables.

In Table 3 we detail the 44 different MI specifications we compared when using the three imputation algorithms (Mice, missRanger, and Amelia) and (1) considering/neglecting the outcome variables in the imputation model, (2) one-hot-encoding numeric and categorical predictors or keeping their natural type, (3) varying the univariate imputation order (for the missRanger and the Mice methods), (4) varying the number of pmm donors in missRanger.

Table 3:

MI algorithms, their (default and evaluated) settings and the advantages and drawbacks evidenced by our experiments. Overall, we compared 44 different MI algorithms. They are four different specifications of Mice-default and Mice-logreg (using/avoiding the outcome variables in the imputation model and trying the imputation order given by the increasing/decreasing number of missing values), eight different specifications of MIce-Norm (where we also compared the usage of numeric variables - BMI/hba1c/age - versus the imputation and usage of one-hot-encoded binned numeric variables), four specifications of Amelia (using/avoiding the outcome variables in the MI model and using/one-hot encoding binned numeric variables) and 24 different specifications of missRanger (using/avoiding the outcome variables in the MI model and using/one-hot encoding binned numeric and categorical variables, using the imputation order provided by the increasing/decreasing order of missing values, and testing three different options for the pmm donors).

MI algorithm $(\mathit{m}=5,42)$	Mice-default (4 different specifications)	Mice-norm (8 different specifications)	Mice-logreg (4 different specifications)	missRanger	Amelia (4 different specifications)
Univariate / multivariate imputation model	univariate imputation by: pmm (continuous predictor) LR (binary predictors) polR (categorical predictors)	univariate imputation by Bayesian estimator	univariate imputation by LR	univariate imputation via RF	multivariate estimation of the distribution underlying the observed data via EM
Univariate imputation order	Increasing number of missing values (monotone order) Decreasing number of missing values (Reverse monotone order)				Multivariate imputation model
Use outcomes in the imputation model	TRUE / FALSE
One-hot-encoding of categorical predictors	FALSE (default)	TRUE (default)	TRUE (default)	FALSE (default) TRUE	TRUE (default)
One-hot-encoding of binned numeric predictors	FALSE (default)	FALSE (default) TRUE	TRUE (default)	FALSE (default) TRUE	FALSE (default) TRUE
pmm donors	3 donors	-	-	no pmm, 3 donors, 5 donors
Maximum number of iterations	21
notable ADVANTAGES and DRAWBACKS	ADVANTAGES: 1) usage of ad-hoc univariate imputation models based on predictor type 2) collinearities in predictor data are detected and reported to allow users to repair the problem	ADVANTAGES: 1) collinearities in predictor data are detected and reported to allow users to repair the problem	ADVANTAGES: 1) collinearities in predictor data are detected and reported to allow users to repair the problem	ADVANTAGES: 1) deals with heterogeneous data types 2) low variance when predictive mean matching is not used 3) application of pmm avoids generation of values outside the original data distribution DRAWBACKS: 1) RFs may take many iterations to converge when non informative predictors are provided	ADVANTAGES: 1) identifies collinearities that may alter results 2) faster than Mice and missRanger when working on datasets having large dimensionality DRAWBACKS: 1) when data collinearities are detected, the predictors causing the collinearities are not reported. In this case, the matrix is singular and Amelia crashes

Results

When evaluating the various missing-data handling algorithms (subsection Evaluated algorithms and settings), we considered the same patients’ cohort detailed in [15], we obtained a complete dataset by listwise deletion, and we run our evaluation pipeline by using $A=25$ amputated datasets, where we simulated MAR missingness with similar missingness patterns.

The value A = 25 was empirically set as a tradeoff between the computational memory/time complexity supported by the N3C Platform and the stability of the obtained results. To choose it, we started by a low number of amputated datasets (A = 5) and we increased it until we noted no appreciable changes of the computed measures. With additional computational power, a higher number of amputated datasets would be suggested to guarantee robustness of the obtained results.

For the evaluation, we defined a statistical estimation pipeline that reproduces the analysis in [15].

More precisely, a first step of variable binarization¹⁹ was applied to have comparable scales across predictors (both in the imputed and in the complete dataset) and the normalized dataset was then used to run two LR models and one CS model to understand the influence of the available predictors on the hospitalization event, invasive ventilation – i.e. mechanical ventilation, and patient survival. These analyses constituted the scientific analyses of interest in the motivating study and thus served as the basis for evaluating the different missing-data handling approaches. In particular, the regression parameters estimated by these three models (i.e. the log odds/hazard ratios) served as the targets of estimation. We treated the parameter estimates computed on the complete dataset (and their associated standard errors and confidence intervals – top left forest plots in Supplementary Figures S4, S5, and S6) as the gold standard estimates, and compared the parameter estimates computed by using the amputated data to these gold standard estimates.

The evaluation schema presented in this work was used to compare the validity of the considered IPW and MI algorithms under their different specifications (subsection Evaluated algorithms and settings). As a result, for each algorithm we obtained evaluation measures for $d=38$ binarized predictor variables and $O=3$ estimates. Thanks to the predictor binarization step mentioned above, the obtained statistical estimates and therefore the computed evaluations ($RB=\left[{rb}_i\right],MSE=\left[{mse}_i\right],ER=\left[{er}_i\right],CR=\left[{cr}_i\right],i\in \{1,...,d\}$) were expressed in the same scale and could be averaged over all the $d$ predictors and then over the $O$ outcomes. This allowed obtaining for each imputation algorithm (and its specification) representative average RB, MSE, ER, and CR measures.

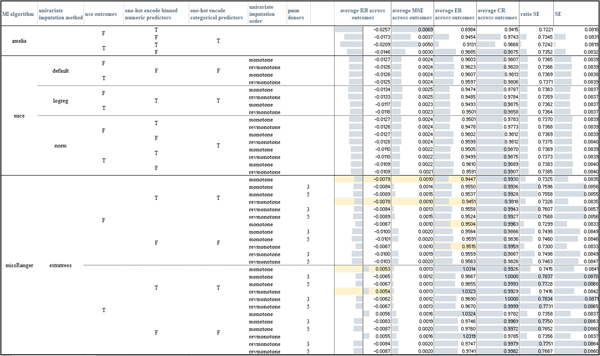
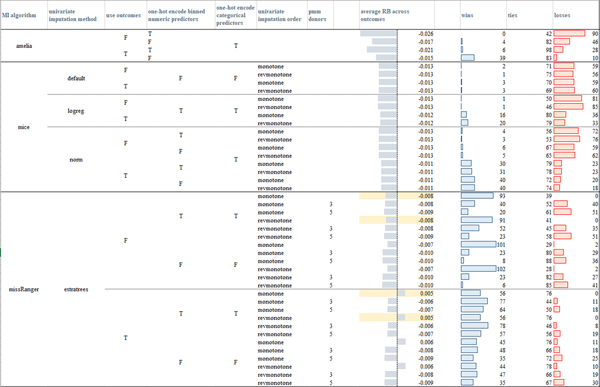
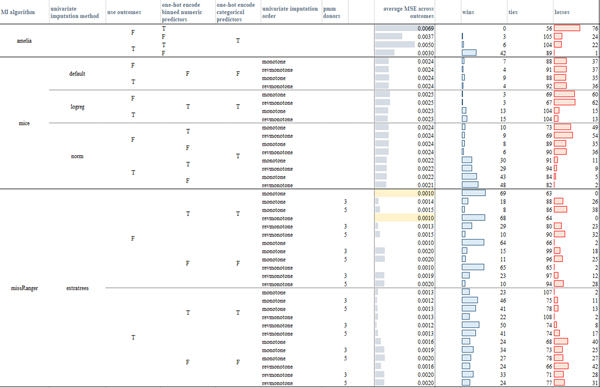
In Figure 5 we provide a visual comparison of the computed average evaluations, where the number of imputations (m = 42) was chosen according to Von Hippel’s rule of thumb [40] (Appendix A). To assess the significance of the comparison between different (IPW and MI) algorithms, we applied the two-sided Wilcoxon signed-rank test at the 95% confidence (p-value < 0.05). For the sake of exhaustiveness, the win-tie-loss tables resulting from comparisons of the RB, MSE, ER, CR evaluation measures obtained by the different models over each outcome variable and by using m = 42 and m = 5 imputations are reported in, respectively, the Supplementary files S1.xlsx, S2xlsx.

Figure 5:

Average measures obtained by the tested imputation algorithms across the three outcomes (the table is also made available in Supplementary file S1 – sheet “mean_measures_m42”) when MAR missingness is simulated in the amputated datasets. For the RB and MSE measures the highlighted cells mark the models that had less losses according to the paired Wilcoxon rank-sum tests computed over the three outcomes. For the CR measure, all the models, but the (non-augmented) IPW model (where the probability of data being missing was computed by an RF including the outcome variables in the model) had comparable performance. missRanger with no pmm achieves the lowest standard error estimate (indeed the ratio SE measures - column “ratio SE” - is the lowest, as also confirmed by the paired Wilcoxon rank-sign test), IPW models obtain a standard error greater than the one computed on the unweighted dataset.

Observing the results, it is clear that in our case study IPW approaches yield systematically less valid inferences. This may be due to the fact that IPW estimates the missingness probability by using only fully observed predictors, whereas MI uses all variables to estimate the conditional probabilities from which imputations are drawn. As a result, when the missingness pattern is complex and several and/or crucial variables contain missing values, as it is often the case in EHR data, the estimation of the inverse probability weights can thus only exploit a limited (less informative) set of predictors [16].

Moreover, the complex missingness patterns that characterize EHR data often result in many individuals with at least one missing value. In these cases, inverse probability weighting may exhibit extreme power loss as too many rows need to be dropped.

With regards to the comparison of the imputation algorithms, all but four missRanger models (with no pmm and considering the outcome variables) obtained negative RB values and corresponding ER measures lower than one, meaning that all the models but missRanger (with no pmm and considering the outcome variables in the imputation model) underestimated the log-odds computed on the complete dataset (per p-value < 0.05). When comparing the results achieved by the algorithms exploiting iterative univariate FCS imputation strategies (Mice and missRanger models), we note that the visiting order had a slight impact only in the case of missRanger, where the order given by the decreasing number of missing values produced lower RB distributions when compared to Amelia, Mice, and other missRanger algorithm settings (see the average RB values for the three outcomes in Figure 5 and the sum of the wins, ties, losses over the three outcomes in, respectively, Figure S1 and in the more detailed, per-outcome, colored win-tie-loss tables in Supplementary file S1.slsx). The slight behavioral differences among the two imputation orders suggested that the iterative procedure effectively reaches convergence.

On the other hand, the usage of the outcome variables in the imputation models did have an effect on the resulting evaluation measures. Amelia, Mice-norm, and Mice-logreg all achieved better results when the outcome variables were included in the imputation model (lower absolute RB and lowest MSE, p-value < 0.05, Figures 8, Supplementary Figures S1 and S2, and Supplementary file S1.xlsx). Mice under the default settings appeared more robust with respect to the inclusion of the outcome variables. The behavior of missRanger with respect to the inclusion of the outcome variables strongly depended on the usage of the pmm estimator. Indeed, when pmm was used, the inclusion of the outcome achieved better results (p-value < 0.05); when pmm was not used, the inclusion of the outcome variables produced worse results (p-value < 0.05). Summarizing, all algorithms that used parametric approaches were improved by inclusion of the outcome variables, while algorithms solely based on RF classifier models were biased by the inclusion of the outcome.

Regarding the coverage rates (CR), all the models but one (Amelia with no outcome variables and one-hot-encoded binned numeric variables, first row in Figure 5) obtained values greater than the nominal rate (0.95), with a confidence interval lower than that obtained on the true estimates (the ratio SE measures are always lower than one).

When the imputation models used one-hot-encoded (binned) numeric variables, only Amelia models seemed to be strongly impacted by an increase in the absolute values of the RB measure and of the MSE values and a decrease in the standard error. On the other hand, missRanger showed lower absolute values of RB and MSE measures when one-hot encoding of categorical and binned numeric variables was performed (Figures 5, Supplementary Figures S1 and S2, and Supplementary file S1.xlsx).

Overall, the missRanger algorithms using no pmm and one-hot-encoding both categorical and binned numeric variables produced the most reliable results; they also achieved the lowest average standard errors, even when compared to the standard error obtained on the complete dataset (as shown by the ratio SE values, p-value < 0.05, Figure 5 and Supplementary file S1.xlsx). With regards to the two other algorithms, among all the tested Mice models, Mice-norm with outcome variables achieved the lowest (absolute values of the) RB and MSE values (Figures 8, Supplementary Figures S1 and S2), outperforming also all the Amelia models; for Amelia, the inclusion of the outcome variables produced the best results.

When analyzing the results obtained by using only $m=5$ imputations (Supplementary file S2.xlsx), the conclusions drawn from the comparative evaluation measures over the 44 MI algorithms were similar. However, when comparing the evaluation measures obtained by each model on the $m=42$ versus $m=5$ imputations, we noted that a higher number of imputations tended to result in a lower variability of the evaluation measures with respect to different algorithm specifications, such as the usage of one-hot-encoded variables or the inclusion/deletion of the outcome variables in the prediction model. In other words, the higher the number of imputations, the higher the stability of the MI algorithm. This is particularly true for the missRanger algorithm.

Having chosen the settings with best performance for each of the three algorithms we then ran them on the full dataset by computing $m=42$ imputations. In this way, we obtained the odds estimates shown in Supplementary Figures S4 (Hospitalization event), S5 (Invasive ventilation event), and S6 (Cox survival estimate).

To show the feasibility and practicality of our evaluation method on different missingness mechanisms, while also providing a further assessment of the compared algorithms, we also run experiments by simulating MCAR and MNAR missingness. For coherence with the MAR experiments, we therefore performed the following two experiments, where we amputated the BMI, Race, and Ethnicity predictors to produce, respectively, the 30%, the 15%, and the 15% of MCAR and MNAR missing values.

Practicality of the evaluation method on different missingness mechanisms

For producing MCAR missingness the values to be amputated were randomly chosen by sampling from the uniform distribution. While MAR amputation maintains the proportion of cases with at least one missing value unaltered (42% in our case study - section Case study: associations between descriptors of patients with diabetes and potential COVID-19 hospitalization events), MCAR amputation produces random missingness patterns, resulting in different proportions of cases with at least one missing value across the amputations, i.e. therefore different numbers, $m$, of multiple imputations per dataset. In particular, on the average of the amputations we drew, the proportion of cases with at least one missing value was (average ± standard error) 49% ± 2%, which is on average 1.5 times higher than that of MAR simulations. This boils down to a higher number of multiple imputations with respect to the MAR experiments ($m=$ 49 ± 2 imputations [40], Appendix A). Moreover, considering that the relationships between missing and observed data are not guaranteed in MCAR, it may be more difficult for the data imputation algorithm to estimate the imputation values. Indeed, all the algorithms we experimented needed more iterations to reach convergence; however, the computed evaluation metrics were comparable to those computed for MAR amputations, and also the behavior of the different models was confirmed (Figure 6 and Supplementary file S3_MCAR.xlsx). This may suggest that, in this specific case study, the subset of complete cases remaining after amputation may suffice to describe the underlying data distribution; in other words, independent from the data being MAR or MCAR, the analysis of the observed data allows estimating the latent underlying relationships between predictors to recover the missing information.

Figure 6:

Average absolute value of the RB measures obtained by the tested imputation algorithms across the 38 predictors and the three outcomes (the table is also made available in Supplementary file S3_MCAR – sheet “mean_measures_m42”) when MCAR missingness is simulated in the amputated datasets.

To produce MNAR missingness we simulated the scenario where not-critical values for the BMI, race, and ethnicity variables are sometimes not recorded by clinicians. In practice, for BMI, race, and ethnicity we still removed, respectively, the 30%, 15%, and 15% of values. However, we created dependencies between the outcome variable and BMI by randomly choosing the 95% of the values to be removed among those in the BMI range [20–30]. The remaining 5% of the values were randomly chosen. For race and ethnicity we proceeded in the same way and used as less crucial categories the most frequent “White” category (for the race predictor) and “Not Hispanic or Latino” category (for the ethnicity predictor). Statistical hypothesis tests (p-value < 0.05) showed that this simulated amputation indeed generated strong dependencies both between the values in the outcome variables and the missingness indicator in the three predictors (BMI, race, and ethnicity) and, curiously, also among the missingness indicators of the three predictors themselves.

Moreover, we must highlight that, as it happens for MCAR amputation, the percentage of cases with at least one missing value obtained for the amputated dataset by producing MNAR missingness is different from the one in the original (incomplete) dataset (on average ± standard error equals 44.5% ± 0.5%). The comparative evaluation measures are shown in Figure 7 (detailed results are reported in Supplementary file S4_MNAR.xlsx). Under the MNAR scenario both the average absolute RB, the MSE, and the ER measure suggest that the simple missRanger algorithm with no pmm (i.e. the base missForest imputation algorithm) avoiding the inclusion of the outcome in the imputation model is the most accurate MI algorithm. This is probably due to the capability of the RF-based regressor used by the missForest/missRanger algorithm of uncovering the hidden mechanism and the relationships behind this particular data missingness in the predictors. Notably, when the outcome variables are included in the missRanger imputation model, the application of the pmm estimator is needed to obtain effective results. This suggests that the inclusion of the outcome variable may cause overfitting (boiling down to inflated imputation values) when using machine-learning based imputation algorithms. In this case, the imputed values must be corrected by the subsequent application of a pmm estimator, which guarantees that the final imputed values belong to the predictor distribution in the original dataset (section Literature review). This last example shows that our evaluation framework allows gaining hints about the behavior of a missing data handling strategy when different application settings are used.

Figure 7:

Average absolute value of the RB measures obtained by the tested imputation algorithms across the 38 predictors and the three outcomes (the table is also made available in Supplementary file S4_MNAR – sheet “mean_measures_m42”) when MNAR missingness is simulated in the amputated datasets.

Generalizability of the evaluation method to different scenarios

The evaluation method and evaluation metrics we are proposing are generalizable to different datasets, contexts, and scenarios.

Of course, depending on the problem at hand, any researcher may decide to favor one evaluation metric with respect to the others. As an example, besides the case study presented in subsection Case study: associations between descriptors of patients with diabetes and potential COVID-19 hospitalization events, we applied our evaluation method in a context where we wanted to estimate the effect of a primary exposure (usage of metformin treatment in patients with diabetes) while adjusting for other variables that may act as confounders [18]. In this context, the original data contained MAR missing values in the BMI (24%), race (15%), and ethnicity (7%) predictors, with 30% of cases having at least one missing value. To choose a proper imputation model, we applied our evaluation process. More precisely, we obtained a complete dataset by listwise deletion, we adjusted it by IPW, and we used a statistical estimator to estimate the gold-standard treatment-effect on the adjusted cohort. Next, for each MI algorithm under evaluation, we amputated the complete dataset multiple times by producing MAR missingness and we analyzed each amputated dataset as described in [69] to obtain MI-estimates of the treatment-effect on adjusted cohorts. Averaging all the MI treatment-effect estimates across all the amputations we obtained the expected value of the MI treatment-effect estimates. We next computed the numeric evaluation measures proposed in section Evaluation method to compare the gold-standard treatment effect estimates to the expected values of the MI treatment-effect estimates. In this context, we considered as the most important evaluation metrics the raw bias (whose absolute value we desired to be as little as possible), the ratio between the standard errors of the estimates (which we required to be as little as possible), and the coverage rate (which we required to be as high as possible). This is because in our context we wanted to identify the MI algorithms that could provide reliable inference for the treatment-effect. In other words, treatment-effects estimates as protective (or dangerous) on the gold-standard (complete) dataset, should also result as protective (or dangerous) when estimated by the MI algorithm. Under this specific scenario Mice-default and missRanger obtained comparable results. Between the two, we decided to use the missRanger algorithm because it obtained lower standard errors of the imputation estimates (p < 0.05); this guaranteed higher stability when running the estimation pipeline multiple times to evaluate different balancing scenarios. By using missRanger we therefore followed the algorithm proposed in [69] to process the original (incomplete) dataset and obtained pooled estimates on adjusted cohorts.

In the previously mentioned case, the treatment variable was of key scientific interest, while the others were used as adjustment factors; therefore we simply observed and compared the evaluation measures computed for the treatment variable across different MI algorithms. When instead all the predictor variables (or a subset of variables) in the dataset are of interest, since we propose to normalize the dataset, all estimates are on the same scale. We can therefore average each evaluation measure across the different predictors (of interest) and obtain unique $RB,MSE,ER,CR$ values characterizing the estimates of interest computed by applying the specific imputation method to the specific outcome variable. We observe that each MI algorithm is well characterized by the $RB$,$MSE,ER,CR$ vectors that contain, respectively, the ${rb}_i,{mse}_i,{er}_i$ and ${cr}_i$ measures for each predictor variable in the dataset. Therefore, given a measure of interest (e.g., RB), its vector can be seen as a distribution characterizing the specific MI algorithm. The distribution characterizing an MI algorithm can therefore be compared to the RB vector characterizing a second MI algorithm by the Wilcoxon paired rank sign test.

The cohort used in [18] comprises patients with diabetes described by a set of predictors (demographic, laboratory and comorbidity descriptors) similar to the one used in our main analysis.

In [70] we used our evaluation scheme to choose the most valid imputation model to be applied on a dataset comprising 1,135,973 patients who had experienced acute COVID-19, on which we wanted to evaluate the relationships between manifestations associated with post-acute sequelae of SARS-CoV2 Infection (PASC) and new-onset of psychiatric sequelae. In this case, patients were described by demographic variables (age, gender, BMI, race, ethnicity, length of hospital stay if applicable) and by a set of 178 Human Phenotype Ontology (HPO) terms [71] that represent PASC-associated manifestations. Each term is represented by a binary variable (1 if that symptom/manifestation has been declared by the clinician for the patient, 0 otherwise). The dataset contained MAR missingness in age, BMI, ethnicity, and race predictors per assumptions adopted following domain-expert input.

A preliminary version of this work was completed prior to the availability of the evaluation code presented here and our initial application of different MI methods produced divergent results, leading to our decision to work on a complete dataset (see preprint at [72]). For the final version of this work [70], we applied our framework and determined that Amelia and missRanger obtained comparable results, with missRanger showing higher stability of imputation values.

Discussion and Conclusions

In this work we presented a novel method to numerically evaluate (imputation) algorithms for handling missing data in the context of statistical analysis. The method is general and can be used in different research fields and with real-world datasets containing heterogeneous types. It allows different missing data handling strategies to be compared. Different application settings can be evaluated to determine the most appropriate and performant approach to be applied on any given dataset. The method is based on a robust evaluation pipeline and exploits well-grounded evaluation measures. Its application allows an informed choice of the proper imputation model (and the corresponding settings) to be used for the problem at hand. This avoids reverting to the often ‘default’ choice of removing cases with missing values, which may substantially reduce the number of available cases, therefore reducing the power of the following statistical estimators. A further advantage of the method relies in the fact that it can also be used to study the behavior of any missing data handling strategy with respect to their different settings or with respect to the different missingness mechanisms (MAR, MCAR, and MNAR) that may be assumed to have yielded the observed data.

To show the practicability of our method we analyzed a large cohort of patients with type 2 diabetes infected by COVID-19. The dataset, which contained a postulated MAR missingness affecting a high proportion (42%) of cases, was used in a previous work to perform a complete case analysis to identify associations between crucial predictors and three COVID-19 outcomes (hospitalization, invasive mechanical ventilation, death). By using the dataset we conducted thorough investigations to both answer computational and statistical questions about MI techniques, by also comparing them to commonly-applied forms of IPW models, and to validate our previous clinical results [15].

From a computational and statistical point of view, we were interested in understanding the differences between different specifications of (univariate and multivariate) multiple imputation techniques exploiting either flexible machine-learning based approaches [42] or parametric approaches [50][52] as the core model.

The comparison between complete-case IPW and imputation models showed that, in our use-case, MI techniques performed systematically better, probably due to the decrease in power caused by the high proportion of cases (42%) that must be dropped from the weighted, complete-case analysis performed by the (non-augmented) IPW algorithm. Our approach allows researchers to make considerations about the amount of missingness above which imputation should be applied with caution. In these regards, no universal limit has been defined yet in literature, though the work from Jakobsen et al. [29] concentrates on methods for handling missing data in randomized clinical trials and, based both on an extensive literature study, group discussions, and experience-in-the-field, suggests avoiding imputation when the proportions of missing data are large on important variables. In particular, when the proportions of missingness in predictors exceed, e.g., the 40% authors suggest to just report the results of the (eventually weighted) complete case analysis and then clearly discuss the resulting interpretative limitations of the trial results. Indeed, as also noted by Clark and Altman [73] if the proportions of missing data are large on crucial variables, then the obtained estimates may only be considered as hypothesis generating results.

We agree with suggestions from both Jakobsen et al. [29] and Clark and Altman [73]; however, we considered that other factors are relevant in this context. Indeed, the cardinality/dimensionality of the available complete cases, the number of variables in the dataset, and the complexity of the problem at hand should also be considered when evaluating whether the proportion of cases with missing values is too high. On one hand, when the overall number of cases is limited and the number of variables is high, even lower proportions of missingness (e.g., 20%) may raise concerns because the available complete cases may not be enough to fully represent the underlying data distribution. On the other hand, when a large cohort is available, higher proportions of missingness (as high as 30%−40%) may carry enough informative content. Indeed, when we applied our evaluation method to our use-case dataset (that contains a large cohort of complete cases and a limited number of predictors) and compared the validity of estimates computed by IPW or multiple imputation algorithms, we showed that Jakobsen’s et al. missingness thresholds (proportions of missingness as high as 30%−40%) may be sensible when the available complete cases carry enough information about the underlying (MAR) data structure. In any case, when the proportion of missingness is large (e.g., the 20%), we would suggest using our evaluation method to check the validity of data imputation models.

Obviously, a rare exception to this problem would be if it is relatively certain that the data are MCAR, because of the ignorability of this type of missingness; this scenario seems, however, rare in biomedical research.

Our comparative evaluation highlighted that MI models exploiting machine-learning techniques, in this case RFs, tend to obtain the most reliable estimates and the lowest standard errors. Further, they produced more reliable estimates when the outcome variables were not considered during the imputation. This behavior is opposite to models assuming an underlying multivariate distribution (FCS and JM models), which yielded results comparable to machine learning-based models when considering the outcome variable during imputation. Additionally, the standard errors they obtained were always appropriately higher, better resembling the natural uncertainty in the data. The usage of one-hot-encoded categorical or binned numerical variables had no impact in the overall performance.

The aforementioned results were confirmed when the number of imputations was reduced to $m$ = 5 (default value suggested by [4]), though in this case different algorithm specifications had a greater impact on the obtained evaluation measures. This result may suggest that Von Hippel’s rule of thumb is a good way to guarantee robustness with respect to different algorithm specifications. However, considering our previous research [11], we would strongly suggest starting with Rubin’s default value and then analyzing the behavior of the imputation model as the number of imputations increases to a value that is at least as high as the percent of missing cases. This would allow a researcher to assess the robustness of the obtained inferences. Therefore, since the fuzzy imputation resulting from one-hot-encoding may cause bias due to incoherent imputations, when possible we suggest avoiding one-hot-encoding.

In summary, exploiting the proposed MI-evaluation framework, we observe that, on our specific problem, missRanger (with no pmm application, no outcome variables in the imputation model, and without one-hot-encoding of categorical or binned numeric variables) is the most reliable imputation model. We applied this approach to impute the available samples m = 42 times and then estimate pooled odds ratios (Supplementary Figures S4, S5, S6) which were compared by experts to those reported in Wong et al. [15]. For the sake of visual comparison we also computed pooled estimates by using Mice-Norm (with outcome variables in the imputation model) and Amelia (with outcome variables in the imputation model).

From a clinical standpoint, the results we obtained validated those presented in Wong et al. [15], where we investigated the relationships between HbA1c, BMI, demographics, medications, and comorbidities and the severity of COVID-19 infection outcomes. In all analyses, the primary findings of the study that risk of hospitalization increased with worsening levels of glycemic control, but that the risk of death plateaued at HbA1c >8 and ventilator or extracorporeal membrane oxygenation use plateaued at HbA1c>9 remained consistent. The findings from the present study strengthen the robustness of the primary findings in Wong et al. [15] and reduce the risk of severe bias due to the removal of cases with missing values [3][32][33].

There were some minor differences from the original report in the comparison of the effect of covariates on the risk of death, namely HIV was associated with a statistically significant decrease and cancer with a statistically significant increase in death in the MI data sets. When modeling the odds ratio (ORs) for ventilation or extracorporeal membrane oxygenation (ECMO), there was also a statistically significant increased risk with dementia or severe liver disease, a significantly decreased risk with Sodium-glucose Cotransporter-2 (SGLT2) inhibitors, and no significant difference with sulfonylurea use in the imputed data sets. There was a small but statistically significant increase of hospitalization with pulmonary or peripheral vascular disease seen in the analysis using the imputed data set that was not seen with the complete data.

Of note, while in this paper we detailed the application of our evaluation method on a specific EHR-based dataset and for solving a clinical research question that did not require patient adjustment (via matching or weighing), in [18] we applied it to evaluate different MI algorithms to estimate the effect of a primary exposure while adjusting for other variables that may act as confounds (subsection Generalizability of the evaluation method to different scenarios). This shows that our evaluation approach can be applied to a broad range of (clinical) datasets to compare different strategies and methods to handle missing data while performing statistical analysis.

The evaluation measures described above provide a further advantage. In particular, we remind that in situations when the proportion of missingness is not so high as to raise caution, a proper number of multiple imputations may be chosen based on the proportion of missingness (as detailed in section Appendix A) to maximize the statistical efficiency of the MI estimator. As a result, the RB, MSE, ER, CR measures should only depend on the validity of the specific MI algorithm being used. On the other hand, when either the dataset is particularly complex, or it has high cardinality/dimensionality so that the computational costs of MI algorithms hamper the computation of a proper number of multiple imputations, the RB, MSE, ER, and CR measures could be worse for predictors whose imputation is problematic, due to their complexity and/or their high percentage of missingness. In this case, the analysis of the evaluation measures obtained by each predictor could be used to discard variables whose imputation is too problematic.

Our future work will be aimed at using the proposed evaluation method to perform a thorough comparison of different ways to deal with missing data when performing a statistical analysis. In particular, we will also consider cases when a single imputation strategy is preferred, by considering several contexts, scenarios, and datasets. As an example, we might consider interaction/effect modification cases, where, e.g., variables with missing data are multiplicative in their impact.

Table 4:

Dataset statistics for all the 56,123 patients (column “all cases”), hospitalized patients (column “hospitalized cases”) and non-hospitalized patients (column “non-hospitalized cases”). Column p-value reports, for each predictor, the p-value for the null hypothesis of a Pearson correlation test between the binary predictor and the outcome variable (Hospitalization event).

Hospitalization event
Predictor Group	Predictor	% of missing values	all cases		hospitalized cases	non-hospitalized cases		p-value
Number of cases (%)			56123 (100%)	25399 (45%)			30725 (55%)
Gender	Male		49%	23%			26%	< 0.0001
	Female (used for reference)		51%	22%			29%	< 0.0001
Age			61.88 ± 0.06 [18,89]	63.7 ± 0.09 [18,89]			60.39 ± 0.08 [18,89]	< 0.0001
	age < 40		7%	3%			4%	< 0.0001
	40 ≤ age < 50		11%	4%			7%	< 0.0001
	50 ≤ age < 60		22%	9%			14%	< 0.0001
	60 ≤ age < 70 (used for reference)		28%	13%			15%	~ 0.4257
	70 ≤ age < 80		22%	11%			11%	< 0.0001
	age ≥ 80		10%	6%			4%	< 0.0001
BMI		29%	33.25 ± 0.04 [12.13,79.73]	32.87 ± 0.06 [12.4,79.73]			33.62 ± 0.06 [12.13,78.98]	< 0.0001
	BMI < 20		1%	1%			0%	< 0.0001
	20 ≤ BMI < 25		8%	5%			4%	< 0.0001
	25 ≤ BMI < 30		18%	9%			9%	~ 0.0104
	30 ≤ BMI < 35 (used for reference)		18%	8%			10%	< 0.0001
	35 ≤ BMI < 40		12%	5%			7%	< 0.0001
	BMI ≥ 40		13%	6%			7%	~ 0.0574
Race	White (used for reference)	15%	55%	23%			32%	< 0.0001
	Other		1%	0%			1%	~ 0.1463
	Black		26%	14%			12%	< 0.0001
	Asian		3%	1%			2%	~ 0.0032
Ethnicity	Hispanic	12%	16%	8%			8%	< 0.0001
	Not hispanic (used for reference)		73%	33%			40%	< 0.0001
Hba1c			7.58 ± 0.01 [4.1,19.3]	7.78 ± 0.01 [4.1,19.3]			7.41 ± 0.01 [4.1,18.7]	< 0.0001
	Hba1c < 6		17%	8%			9%	~ 0.4878
	6 ≤ Hba1c < 7 (used for reference)		30%	12%			18%	< 0.0001
	7 ≤ Hba1c < 8		21%	09%			12%	< 0.0001
	8 ≤ Hba1c < 9		12%	06%			6%	< 0.0001
	9 ≤ Hba1c < 10		07%	04%			3%	< 0.0001
	Hba1c ≥ 10		12%	07%			5%	< 0.0001
Comorbidities	MI		13%	8%			5%	< 0.0001
	CHF		23%	14%			9%	< 0.0001
	PVD		21%	12%			9%	< 0.0001
	Stroke		17%	10%			7%	< 0.0001
	Dementia		5%	3%			2%	< 0.0001
	Pulmonary		31%	15%			16%	< 0.0001
	liver mild		16%	7%			8%	< 0.0001
	liver severe		3%	2%			01%	< 0.0001
	Renal		30%	18%			12%	< 0.0001
	Cancer		14%	7%			07%	< 0.0001
	Hiv		1%	0%			1%	~ 0.5856
Treatments	Metformin		26%	8%			18%	< 0.0001
	dpp4		5%	2%			3%	< 0.0001
	sglt2		5%	2%			3%	< 0.0001
	Glp		7%	2%			5%	< 0.0001
	Tzd		1%	0%			1%	< 0.0001
	Insulin		25%	14%			11%	< 0.0001
	Sulfonylurea		9%	03%			6%	< 0.0001

Table 5:

Dataset statistics for all the 56,123 patients (column “all cases”), patients who were treated with invasive ventilation (column “cases with invasive ventilation”) and were not treated with invasive ventilation (column “cases without invasive ventilation”). Column p-value reports, for each predictor, the p-value for the null hypothesis of a Pearson correlation test between the binary predictor and the outcome variable (Invasive ventilation event).

Invasive ventilation event
Predictor Group	predictor	% of missing values	all cases	cases with invasive ventilation	cases without invasive ventilation	p-value
Number of cases (%)			56123 (100%)	3623 (6.6%)	52500 (93.4%)
Gender	Male		49%	4%	0.45%	< 0.0001
	Female (used for reference)		51%	3%	0.48%	< 0.0001
Age			61.88 ± 0.06 [18,89]	64.22 ± 0.21 [19,89]	61.72 ± 0.06 [18,89]	< 0.0001
	age < 40		7%	0%	7%	< 0.0001
	40 ≤ age < 50		11%	0%	11%	< 0.0001
	50 ≤ age < 60		22%	1%	21%	~ 2e-04
	60 ≤ age < 70 (used for reference)		28%	2%	26%	< 0.0001
	70 ≤ age < 80		22%	2%	20%	< 0.0001
	age ≥ 80		10%	1%	9%	~ 0.4262
BMI		29%	33.25 ± 0.04 [12.13,79.73]	33.44 ± 0.18 [13,77.41]	33.24 ± 0.04 [12.13,79.73]	~ 0.5314
	BMI < 20		1%	0%	0%	~ 2e-04
	20 ≤ BMI < 25		8%	1%	7%	~ 0.496
	25 ≤ BMI < 30		18%	1%	17%	~ 0.538
	30 ≤ BMI < 35 (used for reference)		18%	1%	17%	~ 0.6923
	35 ≤ BMI < 40		12%	1%	11%	~ 0.1574
	BMI ≥ 40		13%	1%	12%	~ 0.5489
Race	White (used for reference)	15%	55%	3%	52%	< 0.0001
	Other		1%	0%	1%	~ 1e-04
	Black		26%	2%	24%	< 0.0001
	Asian		3%	0%	3%	~ 0.1976
Ethnicity	Hispanic	12%	16%	1%	15%	< 0.0001
	Not hispanic (used for reference)		73%	5%	68%	< 0.0001
Hba1c			7.58 ± 0.01 [4.1,19.3]	7.83 ± 0.04 [4.1,18.3]	7.56 ± 0.01 [4.1,19.3]	< 0.0001
	Hba1c < 6		17%	1%	16%	~ 0.3225
	6 ≤ Hba1c < 7 (used for reference)		30%	2%	29%	< 0.0001
	7 ≤ Hba1c < 8		21%	1%	20%	~ 0.1481
	8 ≤ Hba1c < 9		12%	1%	11%	< 0.0001
	9 ≤ Hba1c < 10		7%	1%	6%	< 0.0001
	Hba1c ≥ 10		12%	1%	11%	< 0.0001
Comorbidities	MI		13%	1%	12%	< 0.0001
	CHF		23%	2%	21%	< 0.0001
	PVD		21%	2%	19%	< 0.0001
	Stroke		17%	1%	16%	< 0.0001
	Dementia		5%	0%	5%	~ 0.269
	Pulmonary		31%	2%	29%	~ 0.0013
	liver mild		16%	1%	15%	~ 0.4166
	liver severe		3%	0%	3%	< 0.0001
	Renal		30%	3%	27%	< 0.0001
	Cancer		14%	1%	13%	~ 0.0186
	Hiv		1%	0%	1%	~ 0.6854
Treatments	Metformin		26%	1%	25%	< 0.0001
	dpp4		5%	0%	5%	< 0.0001
	sglt2		5%	0%	5%	< 0.0001
	Glp		7%	0%	7%	< 0.0001
	Tzd		1%	0%	1%	~ 0.0272
	Insulin		25%	2%	23%	< 0.0001
	Sulfonylurea		9%	0%	9%	< 0.0001

Table 6:

Dataset statistics for all the 56,123 patients (column “all cases”), patients who died (column “death”) and who survived (column “survival”). Column p-value reports, for each predictor, the p-value for the null hypothesis of a Pearson correlation test between the binary predictor and the outcome variable (death event).

Death event
Predictor Group	predictor	% of missing values	sample distribution	death	Survival	p-value
Number of cases (%)			56123 (100%)	2865 (5.1%)	53258 (94.9%)
Gender	Male		49%	3%	46%	< 0.0001
	Female (used for reference)		51%	2%	49%	< 0.0001
Age			61.88 ± 0.06 [18,89]	71.34 ± 0.21 [20,89]	61.38 ± 0.06 [18,89]	< 0.0001
	age < 40		7%	0%	7%	< 0.0001
	40 ≤ age < 50		11%	0%	11%	< 0.0001
	50 ≤ age < 60		22%	1%	22%	< 0.0001
	60 ≤ age < 70 (used for reference)		28%	1%	27%	< 0.0001
	70 ≤ age < 80		22%	2%	20%	< 0.0001
	age ≥ 80		10%	1%	9%	< 0.0001
BMI		29%	33.25 ± 0.04 [12.13,79.73]	31.47 ± 0.18 [12.4,74.91]	33.36 ± 0.04 [12.13,79.73]	< 0.0001
	BMI < 20		1%	0%	0%	< 0.0001
	20 ≤ BMI < 25		8%	1%	7%	< 0.0001
	25 ≤ BMI < 30		18%	1%	17%	~ 0.0029
	30 ≤ BMI < 35 (used for reference)		18%	1%	17%	~ 0.0114
	35 ≤ BMI < 40		12%	0%	12%	~ 7e-04
	BMI ≥ 40		13%	1%	12%	< 0.0001
Race	White (used for reference)	15%	55%	3%	52%	~ 0.0452
	Other		1%	0%	1%	~ 0.77
	Black		26%	1%	25%	~ 0.0385
	Asian		3%	0%	3%	~ 0.8894
Ethnicity	Hispanic	12%	16%	1%	15%	~ 0.6093
	Not hispanic (used for reference)		73%	0.04%	0.69%	~ 0.6093
Hba1c			7.58 ± 0.01 [4.1,19.3]	7.55 ± 0.04 [4.2,18]	7.58 ± 0.01 [4.1,19.3]	~ 0.3272
	Hba1c < 6		17%	1%	16%	~ 0.833
	6 ≤ Hba1c < 7 (used for reference)		30%	1%	29%	~ 0.0522
	7 ≤ Hba1c < 8		21%	1%	20%	~ 0.2162
	8 ≤ Hba1c < 9		12%	1%	12%	< 0.0001
	9 ≤ Hba1c < 10		07%	0%	7%	~ 0.3081
	Hba1c ≥ 10		12%	1%	11%	~ 6e-04
Comorbidities	MI		13%	1%	12%	< 0.0001
	CHF		23%	2%	21%	< 0.0001
	PVD		21%	2%	19%	< 0.0001
	Stroke		17%	1%	16%	< 0.0001
	Dementia		5%	1%	4%	< 0.0001
	Pulmonary		31%	2%	29%	< 0.0001
	liver mild		16%	1%	15%	~ 0.7307
	liver severe		3%	0%	3%	< 0.0001
	Renal		30%	3%	27%	< 0.0001
	Cancer		14%	1%	13%	< 0.0001
	Hiv		1%	0%	1%	~ 0.0048
Treatments	Metformin		26%	1%	25%	< 0.0001
	dpp4		5%	0%	5%	~ 0.0217
	sglt2		5%	0%	5%	< 0.0001
	Glp		7%	0%	7%	< 0.0001
	Tzd		1%	0%	1%	~ 0.0029
	Insulin		25%	2%	23%	< 0.0001
	Sulfonylurea		9%	0%	9%	< 0.0001

Statement of Significance.

Problem:

Missing data is a problem affecting many research contexts. Imputation of missing data has been debated since the 1980s, when Rubin’s seminal work presented multiple imputation as a key imputation strategy, given its ability to emulate the natural variation in data.

What is Already Known:

Considering that multiple imputation strategies have produced promising results in many fields, numerous biomedical/clinical research works have applied them to analyze patient data extracted from (electronic) health records. However, there are no established rules of thumb for choosing an effective multiple imputation method and adopting appropriate assumptions and chosen-method specifications required for its implementation.

What this paper adds:

We propose an evaluation framework for comparing the validity and performance of multiple imputation algorithms in the context of retrospective clinical studies that assess potential associations between patients’ predictors and outcomes of interest. As a case study, we used the proposed evaluation method to compare different versions of a selection of the most frequently used multiple imputation methods over a cohort of patients with diabetes (type-2 diabetes) provided by the National COVID Cohort Collaborative (N3C). Besides the clinical usefulness of the obtained results, for each algorithm we evaluated various specifications, such as the inclusion/exclusion of the outcome variables in the imputation model, and the ways in which categorical data are treated, among others. In addition to testing the usefulness of the evaluation framework, the results allowed us to gain a better understanding of the behavior of the compared algorithms. The generality of the evaluation approach allows it to be applied for assessing any collection of (multiple) imputation procedures, including recently proposed deep learning techniques, as well as any strategy and algorithm for handling missing data in the context of statistical analysis, beyond those designed for data imputation.

ABBREVIATIONS

EHR

Electronic Health Record

MI

Multiple Imputation

LR

Logistic Regression (model)

CS

Cox Survival (model)

BMI

Body Mass Index

N3C

National COVID Cohort Collaborative

MCAR

Missing Completely At Random

MAR

Missing At Random

MNAR

Missing Not At Random

FCS

Fully Conditional Specification

JM

Joint Modeling

MIDA

Multiple Imputation using Denoising Autoencoders

GAN

Generative Adversarial Networks

GAIN

Generative Adversarial Imputation Networks

CART

Classification And Regression Trees

RF

Random Forest (classifier)

pmm

predictive mean matching (model)

RB

Raw Bias

ER

Estimate Ratio

MSE

Mean Squared Error

SE

Standard Error

CR

Coverage Rate

OR

odds ratio

ECMO

Extracorporeal membrane oxygenation

SGLT2

Sodium-glucose Cotransporter-2

IPW

Inverse Probability Weighting

Appendix A. Defining the number $\mathit{m}$of multiple imputations

The minimum number of imputation is chosen by considering the statistical efficiency of the estimates obtained after imputation [4][37]. The relative efficiency RE of an estimator (e.g. logistic regression model or cox-survival model) exploiting m multiple imputations may be evaluated as the ratio of the total variance obtained with m imputations, $T_m$, compared to the total variance when$m\to \infty ,T_{\infty }$. Rubin [4] showed that this ratio is:

$$RE=\frac{T_m}{T_{\mathrm{\infty }}}=1+\frac{1}{m}{\gamma }_0$$

where ${\gamma }_0$ is the Fraction of Missing Information FMI = B/(W + B), with W representing within imputation variance and B representing between imputation variance [14]. From the above equation we get the percent loss of efficiency which should be minimized:

$$\frac{T_m}{T_{\mathrm{\infty }}}=1+\frac{1}{m}{\gamma }_0\Rightarrow \frac{T_m-T_{\mathrm{\infty }}}{T_{\mathrm{\infty }}}=\frac{1}{m}{\gamma }_0=\frac{1}{m}FMI$$

Therefore, the value of m should be chosen so that $\frac{1}{m}FMI$ becomes negligible or as small as it is feasible. White et al. [14] suggest using, for example, $\frac{1}{m}FMI<0.05$, that is, they require a maximum percent loss in efficiency lower than the 5 percent. Of course, this computation requires estimating the FMI due to the missing values, which on the other side would require trying different values for m, computing the pooled estimates and their FMI. A faster way is to use an upper bound of the FMI, that White et al. [14] conservatively estimated as the fraction of incomplete cases. This led to Von Hippel’s rule of thumb [40] that the number of imputations should be similar to the percentage of cases that are incomplete, which means we are requiring the maximum percent loss in efficiency lower than 1 percent. Unfortunately, when the sample size is high, such a low maximum percent loss in efficiency would result in demanding, and often impractical computational costs. Besides, as noted also in [14] this estimate may not be appropriate, because it also depends on the data and the problem at hand. Indeed, several other state-of-the-art definitions of FMI and different experimental results proposing estimates for the number of multiple imputations have been shown in literature. As an example, Graham [38] studied the loss in power when small numbers of imputed datasets are used. They recommended that at least 20 imputed datasets are needed to restrict the loss of power when testing a relationship between variables. Bodner [39] proposed the following guidelines after a simulation study using different values for the FMI to determine the number of imputed datasets. For FMIś of 0.05, 0.1, 0.2, 0.3, 0.5 the following number of imputed datasets are needed: ≥3, 6, 12, 24, 59, respectively.

We refer interested readers to Van Buuren’s book [28] for a brief description of different approaches.