Abstract
Coarse-grained force fields (CG FFs) such as the Martini model entail a predefined, fixed set of Lennard-Jones parameters (building blocks) to model virtually all possible nonbonded interactions between chemically relevant molecules. Owing to its universality and transferability, the building-block coarse-grained approach has gained tremendous popularity over the past decade. The parametrization of molecules can be highly complex and often involves the selection and fine-tuning of a large number of parameters (e.g., bead types and bond lengths) to optimally match multiple relevant targets simultaneously. The parametrization of a molecule within the building-block CG approach is a mixed-variable optimization problem: the nonbonded interactions are discrete variables, whereas the bonded interactions are continuous variables. Here, we pioneer the utility of mixed-variable particle swarm optimization in automatically parametrizing molecules within the Martini 3 coarse-grained force field by matching both structural (e.g., RDFs) as well as thermodynamic data (phase-transition temperatures). For the sake of demonstration, we parametrize the linker of the lipid sphingomyelin. The important advantage of our approach is that both bonded and nonbonded interactions are simultaneously optimized while conserving the search efficiency of vector guided particle swarm optimization (PSO) methods over other metaheuristic search methods such as genetic algorithms. In addition, we explore noise-mitigation strategies in matching the phase-transition temperatures of lipid membranes, where nucleation and concomitant hysteresis introduce a dominant noise term within the objective function. We propose that noise-resistant mixed-variable PSO methods can both improve and automate parametrization of molecules within building-block CG FFs, such as Martini.
1. Introduction
Atomically detailed molecular dynamics (MD) simulations provide great insights into the structure and dynamics of biomolecular and other soft matter systems, but larger time and length scales often require a coarse-grained (CG) description. In coarse-graining, a group of atoms is mapped into one bead or supra-atom. Coarse-grained descriptions achieve computational efficiency by reducing degrees of freedom while preserving relevant aspects. This not only allows for bridging larger time and length scales but also enhances our understanding of the fundamental physics underlying the molecular processes within biological cells. For example, it can enable fundamental insights into phenomena like the self-organization of lipid membranes and the formation of characteristic thermodynamic phases, including liquid-ordered, liquid-disordered, and gel phases.1−3 Systematic coarse-graining approaches such as inverse Boltzmann and inverse Monte Carlo approaches4,5 as well as force-matching approaches6,7 parametrize coarse-grained force fields by reproducing the structural part of the partition function of the fine-grained system by either matching relevant radial distribution functions or (combined) forces within the fine-grained system. However, because the partition function only describes a single thermodynamic state point at equilibrium, i.e., a unique combination of pressure and temperature values, systematically parametrized “bottom-up” coarse-grained force fields are not suited to describe phase transitions over a wider temperature range. Phase transitions or phase diagrams can, however, be optimally modeled using coarse-grained force fields based on the alternative Statistical Associating Fluid Theory (SAFT) parametrization approach, which uses a scaled Lennard-Jones interaction potential whose functional form (the exponent) is uniquely adapted for each interaction type.8,9 However, the main practical problem of all of these coarse-grained force fields is their lack of chemical transferability; i.e., inclusion of a new molecule (interaction type) within the system would require reparameterization of all of the existing interaction parameters.
The Martini coarse-grained force field10,11 is a building-block force field (FF); i.e., common chemical groups are parametrized as basic building blocks, which can be combined to build up any existing molecule. These basic building blocks of Martini, the beads, are parametrized top-down and reproduce the thermodynamic properties of the chemical groups they model, such as partitioning free energies in liquid–liquid systems, while complete molecules are parametrized with a combination of top-down (experimental data) and bottom-up (atomistic simulation). Such a parametrization enables the qualitative simulation of phase transitions as well as phase segregation in lipid membranes while simultaneously conserving molecular compatibility (transferability) by describing all nonbonded interactions with the same 12–6 Lennard-Jones potential form. However, a major drawback compared to other systematic coarse-grained approaches is that parametrization of molecules in Martini can be highly complex and often involves the selection and fine-tuning of a large number of parameters (e.g., bead types and bond lengths) to optimally match multiple relevant targets simultaneously. A task that is time-consuming when done by human labor. Additionally, it is not always obvious which parameters have to be changed in what manner to enhance a certain behavior, particularly when cooperative processes are involved. While the choice of individual bead types can be made using chemical intuition, still a sizable subset of combined possibilities exists. Importantly, parametrization of bonded and nonbonded parameters should be optimally performed simultaneously since bonded and nonbonded interactions are not independent—they are directly influencing each other via the density of interactions.12,13 Recent versions of the Martini force fields such as Martini 3 rebalanced the density of interactions by introducing an even larger number of possible interaction types, thereby rendering the parametrization of molecules, often a nontractable problem, to common users. Automation of coarse-graining is thus critical, especially in the construction of large databases of molecules. Automation offers a solution to address the challenge of force-field development, which typically involves collaboration among multiple researchers working on interdependent parameters. By automating the process, a clear, structured, and reproducible flowchart-based hierarchy is established, providing an overview of how the parametrization is conducted and which objectives are targeted. Moreover, the same objectives can be used for a wide range of molecules in the same family, thereby increasing the consistency of the force field even when the development is carried out in different laboratories. The automation approach therefore facilitates collaborations by allowing researchers to focus on selecting a set of relevant objectives and assigning importance or weights to each objective. These objectives, along with their individual weights, define the force field’s philosophy. Furthermore, automation empowers collaborations to prioritize two key aspects: the generation and provision of reference data for the objectives at hand and the design of analysis tools to quantitatively assess how each objective is addressed within the automation pipeline. By automating the parametrization process, collaborators can allocate their efforts toward obtaining high-quality reference data that accurately represent the desired objectives. Simultaneously, they can focus on developing comprehensive analysis tools that enable thorough quantitative evaluation, ensuring the effectiveness of the automation pipeline in achieving the defined objectives. This collaborative approach maximizes the efficiency, reliability, and reproducibility of the parametrization process while facilitating a deeper understanding of the force field’s performance.
Earlier works on automated parametrization for building-block FFs focused on optimizing bonded interactions only.14−16 For example, a method such as PyCGTOOL generates coarse-grained model parameters from atomistic simulation trajectories by using a user-provided mapping. However, it does not perform parameter optimization; instead equilibrium values and force constants are generated by Boltzmann inversion.14 No other targets are used. The SwarmCG method performs parameter optimization with traditional PSO and targets only bond length and angle distributions, as well as bilayer dimensions.16 The melting temperature is used only in validation after optimization. Nonbonded parameters are not being optimized, although a previous SwarmCG implementation17 could also perform optimization of continuous nonbonded parameters. No bead assignment is proposed, which is problematic for molecule parametrization in building-block FFs, as explained further down. Other approaches that addressed both the automation of mapping as well as the parametrization of bonded and nonbonded parameters solely focused on small molecules and rather provide an initial guess than an optimized parametrization.18,19 In Auto-Martini, bead type selection is done via ALOGPS20,21 partitioning prediction of fragments.18 Bonded parameters use generic values without any optimization. The approach from Potter et al. is similar to Auto-Martini but features an improved mapping scheme, and nonbonded interactions are derived in a similar fashion, bond lengths are taken from relaxed atomistic structures, and the force constants use generic values.19 We note that fast methods such as Auto-Martini and the method from Potter et al. could be used as a complementary approach to CGCompiler by providing an initial mapping as well as an initial nonbonded/bonded parameter guess for CGCompiler. Automation schemes exist also for systematic coarse-graining approaches.22,23
Particle swarm optimization (PSO) is a powerful computational method used to optimize problems by iteratively improving candidate solutions based on a defined objective function. Compared to evolutionary optimization methods such as genetic algorithms, PSO offers advantages in efficiently finding global optima within high-dimensional continuous spaces due to its vectorial search direction. PSO has been successfully employed in various coarse-grained (CG) parametrization tasks, as demonstrated in previous studies.15−17,24,25
PSO is primarily designed for continuous variables, making it well-suited for optimizing structure-based coarse-grained (CG) models where bonded and nonbonded parameters can be chosen from a continuum of values. However, in building-block models like Martini, the nonbonded parameters are predefined and discrete, representing different interaction levels. Consequently, the parametrization of molecules in a building-block CG force field becomes a mixed-variable optimization problem.
When using PSO for parametrization in building-block models, a transformation from the continuous space to the discrete space of force-field parameters is necessary. This transformation introduces cumulative rounding errors, which can potentially affect the quality of the parametrization, especially in larger molecules. Therefore, additional evaluation and reparametrization steps are often required to ensure the optimal performance of the force field.
It is crucial to parametrize both bonded and nonbonded interactions simultaneously since they are not independent and their optimization should be performed in a coordinated manner.13 By considering their interplay during the parametrization process, the resulting force field can better capture the complex behavior of molecules in the system.
To address the limitations of existing PSO approaches, we employ a mixed-variable PSO scheme (mv-PSO) for parametrization. This approach allows for the simultaneous optimization of both discrete parameters (representing nonbonded interactions) and continuous parameters (representing bonded interactions), enhancing the accuracy and reliability of the parametrization process.
Furthermore, due to the chaotic nature of MD simulations, observables measured in MD simulations are subject to noise. Since standard PSO was designed for deterministic objective functions, straightforward application to noisy optimization problems is error prone, because the algorithm can no longer correctly identify global and personal best solutions when noise levels are similar to differences between objective function values.26 Noise-mitigation strategies are particularly important when thermodynamic data are utilized as targets, as these are notoriously expensive to estimate accurately in MD simulations, even when employing CG models. Particularly problematic is the targeting of phase transition temperatures, which involve a first-order phase transition and are thus subject to nucleation and concomitant hysteresis.
In this work, we pioneer the application of mixed-variable particle swarm optimization in automated parametrization of molecules within the Martini 3 coarse-grained force field by matching both structural (e.g., RDFs) and thermodynamic data (phase-transition temperatures). The important advantage of this approach is that both bonded and nonbonded interactions are simultaneously optimized while conserving the search efficiency of vector guided particle swarm methods over other metaheuristic search methods such as genetic algorithms. In addition, we explore noise-mitigation strategies in matching the phase transition temperatures, where nucleation and concomitant hysteresis introduce a dominant noise term within the objective function. To the best of our knowledge, the impact of noisy objective function values has not been previously addressed in the context of applying PSO for CG parametrization. The manuscript is structured in the following way: Section 2 describes the mixed-variable PSO algorithm and parametrization procedure. As an example, we parametrized the linker region of sphingolipids, a biological highly relevant class of lipid molecules, that constitutes approximately 30 mol % of the plasma membrane lipids27 but has not been updated for Martini 3, yet. Details of the simulated molecules, systems, and observables are given in Section 3. Results are presented in Section 4, followed by conclusions in Section 5.
2. CG Molecule Parametrization via Mixed-Variable Particle Swarm Optimization
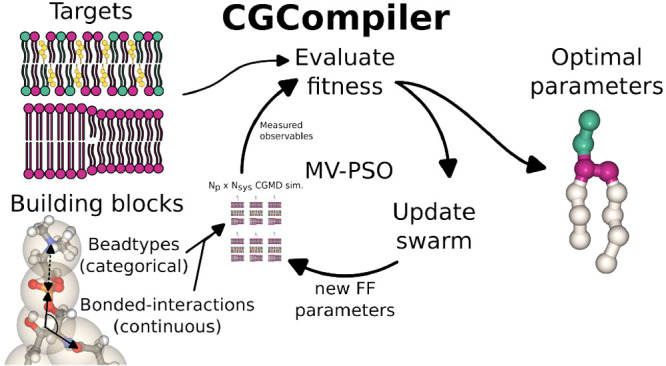
With CGCompiler we present a Python package that streamlines CG molecule parametrization. It employs mixed-variable particle swarm optimization to simultaneously optimize categorical (bead type) and continuous (bonds, angles, dihedrals, ...) variables. Therefore, CGCompiler is particularly well suited for, but not limited to, parametrization tasks in CG FFs that follow a building-block approach. To enable the application of the building-block approach also to larger molecular fragments, consisting of more than one CG bead, the method allows for optimization of shared building blocks in different molecules, e.g., the headgroup, linker, or tails of lipids.
Molecule parametrization in Martini 3 follows three steps: (i) choice of mapping and bead sizes; (ii) assignment of chemical bead types; (iii) choice of bonded terms and assignment of bonded parameters.11 While a mapping from atomistic to the CG model and the set of of bonded terms have to be predefined, the algorithm presented here optimizes bead size, chemical bead type, and bonded parameters simultaneously.
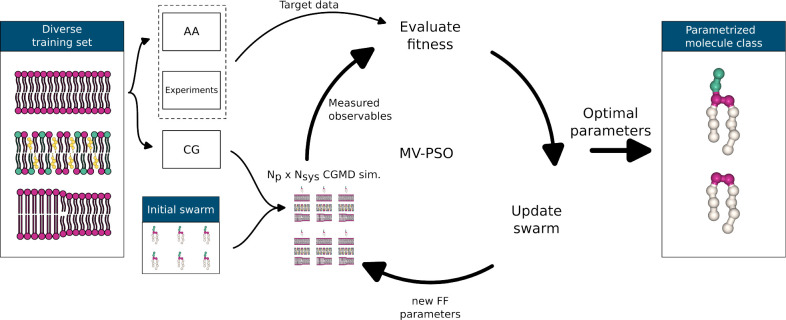
The parametrization workflow is shown in Figure 1. For a given parametrization task, the user provides or generates the target data and creates a set of CG training systems that allow measurement of the target observables. In the initial iteration, the optimization algorithm generates a number Np, i.e., the swarm size, of candidate solutions with random FF parameters and runs MD simulations for each candidate solution and each training system. Candidate solutions are then scored by how well the parametrization targets are reproduced. By utilizing the swarm’s knowledge of the fitness landscape, candidate solutions are updated and a new cycle of MD simulations, analyses, and fitness evaluations starts. This is repeated until a termination criterion is fulfilled. Due to noise in the objective function evaluation, the selection of the true best parameters can only be done with a certain probability. Therefore, the set of the best, statistically equal candidate solutions undergoes a screen-to-the-best procedure, which either provides one solution that is significantly better than the rest or reduces the field of viable candidate solutions further, on which more expensive evaluation simulations would be performed.
Figure 1.
Parametrization workflow. (i) Set of training systems from which the target properties can be extracted. (ii) Target data acquired from atomistic simulations and experiments. (iii) Initial swarm generated with FF parameters randomly selected from a predefined range of feasible parameters. (iv) All candidate solutions simulated in all training systems. The target observables are measured and compared to the target data; i.e., the fitness of the candidate solutions is estimated. New candidate solutions are generated by utilizing the swarm’s knowledge of the fitness landscape. (v) Step iv repeated until a termination criterion is fulfilled. (vi) Screen-to-the best procedure yielding the optimized set of FF parameters.
2.1. Mixed-Variable Particle Swarm Optimization
In the original PSO algorithm for continuous optimization problems in a D-dimensional parameter space, particle i has a position vector Xi = (x1i, ..., xDi) and a velocity Vi = (v1i, ..., vDi).28 At each iteration t the velocity and position are updated by
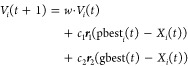 |
1 |
| 2 |
where pbesti(t) is the personal best position of particle i and gbest(t) is the best position found by the whole swarm. w is an inertia weight, which balances global vs local search. The coefficients c1 and c2 are balancing personal vs social experience. r1 and r2 are vectors with random numbers. In the mv-PSO algorithm that is utilized in our work, the position vector of a particle takes a hybrid form, where Z dimensions encode continuous variables and V dimensions encode categorical variables.29
| 3 |
The continuous and categorical parts of the position vector are updated separately.
2.1.1. Continuous Reproduction Method
In classical PSO the swarm can get trapped in local optima and therefore prematurely converge.29 To promote diversity while maintaining good convergence efficiency, Wang et al. proposed an altered continuous reproduction scheme, where particle i learns from the best position of a randomly selected particle.29 In order to guide the swarm toward improved solutions, the pool of pbest to choose from only consists of solutions whose fitness is superior to pbesti(t) .
| 4 |
2.1.2. Categorical Reproduction Method
Values of categorical variables are assigned according to a probability. Initial probabilities are given by
| 5 |
where nj is the number of available
values for the jth variable. To leverage the swarm’s
knowledge of good solutions,
only the superior half of the sorted swarm is utilized in updating
the probabilities of available categorical values. To avoid premature
extinction of the available values, a lower limit is assigned for Probj,n. If Probj,n falls
below that lower limit, Probj,n is set to that threshold value, and all
probabilities are renormalized such that ∑nProbj,n = 1.
The categorical update method is shown in Algorithm 2.
2.1.3. Cost Function
Molecule parametrization is typically a multiobjective optimization problem (MOP). A simple way to scalarize a MOP is by linear weighting. The scalarized optimization problem is solved by minimizing the cost, which is given by
| 6 |
where wo is an objective weight, fo the objective cost function, and x the parameter vector. The objective weights can be used to balance the importance of the utilized parametrization targets. The weights are set by the user. Setting weights might require some intuition about the parametrized molecule, quality of target data, etc.
Each objective can have a different objective cost function fo. New objective cost functions can be added by the user easily. In its present form, the parametrization algorithm uses two distinct objective cost functions. For single valued observables, such as area per lipid, membrane thickness, melting temperature, and solvent accessible surface area (SASA), the objective cost function is defined as
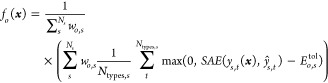 |
7 |
where ys(x) is the
observed value in training system s, given the FF
parameters x. ŷs is the target value. Ns is the number of training systems that
is used for the current parametrization objective. When using average
bond lengths or angles, Ntypes,s is the number of bond or angle types being parametrized. The
deviation from the target is calculated by the scaled absolute error 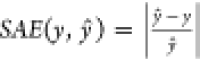 . With
error tolerance Etolo,s, uncertainties in target
data can be accounted for. Each training system has an additional
weight wo,s, which can be used in the case of differences in target data
quality or similar cases. Generally these are set to 1.
. With
error tolerance Etolo,s, uncertainties in target
data can be accounted for. Each training system has an additional
weight wo,s, which can be used in the case of differences in target data
quality or similar cases. Generally these are set to 1.
For observables that are given in the form of distributions, such as bond lengths, angles, or radial distribution functions (RDFs), the objective cost function is given by
| 8 |
where ϕ(x) is the observed distribution, given the FF parameters x. ϕ̂ is the target distribution. The earth mover’s distance EMD(ϕ(xs,t), ϕ̂s,t) is a measure of the distance between the two distributions.30
2.2. Noise Mitigation Strategies for PSO
PSO was designed for deterministic objective functions. Due to the chaotic nature of MD simulations, hereby measured observables are subject to noise. With noise in objective functions, the selection of the true best solutions is not guaranteed. Since solutions that are identified as the best attract the swarm toward regions of interest in parameter space, noise can misguide the swarm and therefore deteriorate PSO performance.
2.2.1. Resampling
Resampling is a widely applied strategy for noise mitigation within an objective function. Relatively simple resampling methods are equal resampling (PSO-ER), extended equal resampling (PSO-EER), and equal resampling with allocation to top-N solutions (PSO-ERN).31 These simpler methods are regularly outperformed by state-of-the-art resampling methods, such as optimal computing budget allocation (PSO-OCBA),32 but the quality of results depends on the specific optimization problem and noise levels.26,31 OCBA aims to maximize the probability of correctly selecting good solutions. This is done by first allocating a primary computational budget equally to all current solutions to estimate their cost means and variances. A secondary budget is then sequentially allocated to solutions with lower means and higher variances to improve the fitness estimations of potentially good solutions. For efficient secondary budget allocation at least 5 primary evaluations should be executed for mean and variance estimation.33 This might make application of OCBA prohibitively expensive for regular CG molecule parametrization tasks. Based on the observation that most observables utilized in the multiobjective optimization of the sphingomyelin (SM) linker region have a low variance and only a few suffer from a larger variance (cf. Figure S5), we hypothesize that in the molecule parametrization task at hand, one primary objective function evaluation is sufficient to differentiate potentially good solutions from bad solutions, but to maximize the probability of correctly selecting the true best solution, the accuracy of the fitness estimates has to be increased. Therefore, we propose a somewhat pragmatic approach that salvages the core idea of OCBA, i.e., allocate additional computational budgets to where it is the most useful (low mean and high variance). At each iteration, our resampling method involves one full objective function evaluation of the current solutions. The current solutions are then ranked by their fitness, and for the best N solutions, only the observables that have significant variance are reevaluated.
2.2.2. Set of Statistically Equivalent Solutions
Even with noise mitigation, at the end of an optimization run, there will be a number of solutions with very similar scores. While in a deterministic setting, the global best position is determined by
| 9 |
where 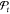 is the set of all positions that
have been
visited by the swarm up to iteration t, with noise
in the objective function no solution can be declared the best with
100% certainty.26 With the screen-to-the-best procedure of Boesel et al.34 a set of
positions
is the set of all positions that
have been
visited by the swarm up to iteration t, with noise
in the objective function no solution can be declared the best with
100% certainty.26 With the screen-to-the-best procedure of Boesel et al.34 a set of
positions 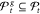 can be
selected, such that the true global
best solution gbest is contained in
can be
selected, such that the true global
best solution gbest is contained in 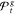 with probability of at least 1 –
α (with 0 < α < 1).26
with probability of at least 1 –
α (with 0 < α < 1).26
For solutions 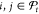 , f̅i and Si2 denote the sample mean and sample variance of
objective
function values. The elementary steps of the screen-to-the-best procedure
are
, f̅i and Si2 denote the sample mean and sample variance of
objective
function values. The elementary steps of the screen-to-the-best procedure
are
-
1.Compute Wij,
where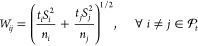
10 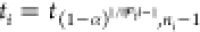 and tβ,ν is the β quantile of the t distribution with
ν degrees of freedom
and tβ,ν is the β quantile of the t distribution with
ν degrees of freedom -
2.
Set
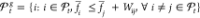
-
3.
Return
Wij is the half-width of pooled t-confidence intervals on the difference between the scores of solutions i and j.26 Therefore, the procedure entails a pairwise comparison of solutions and determines if differences of the sample averaged scores are statistically significant.26
3. Example Application: Sphingolipid Linker Parametrization
As an example application of CGCompiler, we reparametrize the linker region of sphingomyelin in Martini 3.11Figure 2 depicts the CG models of two sphingolipids, sphingomyelin, and ceramide. Except for the differing headgroup, the two CG models share the same parameters, following Martini’s building-block approach.
Figure 2.
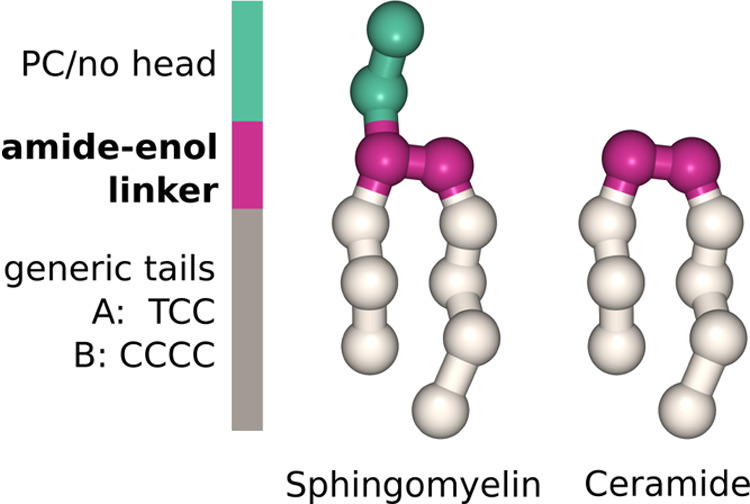
CG description of sphingomyelin and ceramide.
3.1. Simulation Details
The Python package is based on evo-MD.35 All simulations were performed with GROMACS 2020.4 and 2021.436 and analyzed with in-house Python scripts that are utilizing MDAnalysis,37,38 LiPyphilic,39 SciPy,40 and pyemd, which is a Python wrapper for Pele and Werman’s EMD implementation.41,42 Visualization was done with NGLview.43
3.1.1. Atomistic Models
All atomistic models were simulated using the CHARMM3644−46 force field. Table 1 provides details about the atomistic target systems. Initial configurations of the membrane systems were generated with the CHARMM-GUI membrane builder.47−49 Following energy minimization and equilibration, all systems were simulated with a 2 fs time step. Bonds of hydrogen atoms were constrained employing the LINCS algorithm.50 van der Waals forces were gradually switched off between 1.0 and 1.2 nm. The PME algorithm51 was used for electrostatic interactions. Temperature coupling was done via the velocity rescale algorithm52 with a coupling time τt = 1.0 ps. System pressures were held at 1 bar by using the Parinello–Rahman barostat53 with a coupling time τp = 5.0 ps. Pressure coupling was applied isotropically for aqueous solutions and semi-isotropically for membrane systems.
Table 1. Atomistic Target System Detailsa.
| system | lipids | no. of TIP3P | no. of NA | no. of CL | T/K | simul time/ns |
|---|---|---|---|---|---|---|
| DPSM128 328 K | 128 SSM | 5120 | 328.15 | 150 | ||
| POPC SSM CHOL | 100 POPC 100 SSM 100 CHL1 | 9000 | 18 | 18 | 321.15 | 300 |
In the naming scheme of the CHARMM FF, SSM and CHL1 denote sphingomyelin (18:0) and cholesterol, respectively.
3.1.2. Coarse-Grained Models
All coarse-grained models were simulated using the Martini 311 force field. DPSM denotes SM(16:0) and SM(18:0) in the Martini FF, as the current tail models do not differentiate between the two. β version 14 of the Martini 3 cholesterol parameters was used.54,55 Initial configurations of membrane systems were generated with the Python script insane.py.56 Details of the employed training systems are listed in Table 2. All systems were energy minimized and equilibrated with the current version of DPSM, which made the Martini 2 model of sphingomyelin compatible with Martini 3. During the particle swarm optimization each system was equilibrated with the candidate FF parameters in two stages, with time steps of 2 and 20 fs, respectively. For all coarse-grained production simulations, a time step of 20 fs was used. Nonbonded interactions were cut off at 1.1 nm. For electrostatic interactions, the reaction-field method was used with a dielectric constant of 15 and the reaction-field dielectric constant was set to infinity.
Table 2. Coarse-Grained Training System Details.
| system | lipids | no. of W | no. of NA | no. of CL | T/K |
|---|---|---|---|---|---|
| DPSM128 328 K | 128 DPSM | 1177 | 328.15 | ||
| DPSM256 biphasic | 256 DPSM half gel/half liquid | 2300 | 26 | 26 | 286, 291, 296, 301, 303, 305, 307, 308, 309, 310, 311, 316, 321, 326 |
| POPC SSM CHOL | 96 POPC 96 DPSM 96 CHOL | 2124 | 23 | 23 | 321.15 |
Temperature coupling was obtained via the velocity rescale algorithm52 with a coupling time τt = 1.0 ps. System pressures were held at 1 bar by using the Parinello–Rahman barostat53 with a coupling time τp = 12.0 ps. Pressure coupling was applied isotropically for aqueous solutions and semi-isotropically for membrane systems. In simulations for melting temperature estimation anisotropic pressure coupling was employed, using the Berendsen barostat57 with a coupling time τp = 4.0 ps.
4. Results
Our aim was the development of an automatization framework for molecule parametrization in building-block force fields. As an example, we parametrized the sphingolipid linker region. Section 4.1 shows the results of the parametrization with CGCompiler using a simple noise-mitigation strategy. Since noise-mitigation strategies can only reduce the effects of noise when selecting the true best solution, the best statistically equivalent solutions generated during the mv-PSO run are subsequently screened-to-the-best, as described in Section 2.2.2.
4.1. Parameterization of the Sphingolipid Linker Region
Table 3 shows the observables and their weights used in the parametrization. The observable weights wo were chosen pragmatically such that no single contribution dominates the overall cost. System specific observable weights wo,s are usually either 0 or 1, depending on whether the observable is evaluated in a certain system. The choice of 0.25 for membrane thickness and APL in the POPC/SSM/CHOL system stems from the fact that no experimental data were available for these observables in this composition. Instead data from atomistic simulations was used. To reflect Martini’s emphasis on experimental data, the weights for the AA simulation data were lowered in this case. The swarm size was 64. Noise-mitigation was done by reevaluating the melting temperature of the 16 best candidate solutions of the current iteration 12 times; i.e., results were obtained with noise-mitigation setting mv-PSO-R16 (cf. Section 4.2). Tm is the major contribution to cost variance, but the employed Tm estimation method is good for differentiating good from bad solutions; i.e., it has an accuracy of a few K. Other observables were only evaluated once, and area per lipid (APL) fluctuations were the second largest cause of cost variance. For more details on noise-mitigation efficacy, see Section 4.2.
Table 3. Weights of Observables wo and System Specific Observable Weights wo,s for Optimization Run 1.
| observable | w0 | wo,DPSM128 | wo,DPSM256 | wo,POPC SSM CHOL |
|---|---|---|---|---|
| bond length dist | 1 | 1 | 0 | 1 |
| angle dist | 100 | 1 | 0 | 1 |
| dHH | 500 | 1 | 0 | 0.25 |
| APL | 1000 | 1 | 0 | 0.25 |
| Tm | 250 | 0 | 1 | 0 |
| RDF COM DPSM-CHOL | 1 | 0 | 0 | 1 |
All results shown include the complete set
of the best statistically
equivalent candidate solutions  that remained
after two rounds of the screen-to-the-best
procedure (cf. Section 2.2.2). This set contains 18 candidate solutions.
that remained
after two rounds of the screen-to-the-best
procedure (cf. Section 2.2.2). This set contains 18 candidate solutions.
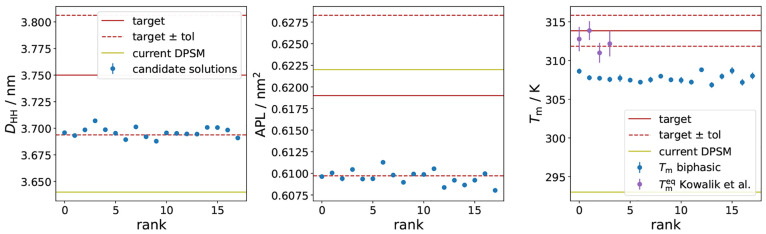
4.1.1. Improved Reproduction of Membrane Properties
Figure 3 shows thickness, average area per lipid, and melting temperature of pure DPSM membranes for the set of statistically equal candidate solutions that remained after the second screen-to-the-best procedure performed after reevaluating the initial set 20 times. All new candidate solutions outperform the current DPSM model regarding thickness. The average area per lipid of the current model is closer to the target value, but most of the candidate solutions are within the tolerance of 1.5% deviation. In general, thickness and APL are inversely correlated, increasing one will always result in decreasing the other; therefore, with both values inside the tolerance, the new models represent a better balance of thickness and APL. It is important to note that, in the comparison, SM(18:0) was used as the atomistic target. The current tail model of the Martini FF represents both SM(16:0) and SM(18:0). The CHARMM model for SM(16:0) exhibits a reduced thickness when compared to SM(18:0).45 It is therefore not unexpected that the Martini DPSM models show a reduced thickness compared to SM(18:0).
Figure 3.
Thickness, average area per lipid, and melting temperature for the set of statistically equal candidate solutions that remained after the second screen-to-the-best procedure performed after reevaluating the initial set 20 times.
While the melting temperatures estimated with the biphasic approach, which is used during optimization for performance reasons, are not within the specified tolerance regime of 2 K but ≈5–6 K below the target value and ≈3–4 K below the lower target threshold, the new models are greatly improved compared to the current model, which was 20 K off target. Notably, the estimation of Tm is approach-dependent. Estimations using the alternative, reversible melting approach with slow melting rates, based on Kowalik et al.58 and Sun and Böckmann59 (see the Supporting Information (SI) for further details), which requires a very large computational budget (as done here; total simulation time for one Tm estimation > 90 μs), show an even better agreement with the experimental melting temperature.
The biphasic approach performed here utilizes a bilayer that is half gel and half liquid. The gel phase is fabricated by quenching to a temperature well below the melting temperature, and the gel phase system is combined with a pre-equilibrated liquid system. The combined system is then equilibrated, with thermostats set to different temperatures for the two phases. As quenching and equilibration can take up to several hundreds of nanoseconds, reconstructing the starting structure for every candidate solution would significantly increase the computational cost of a PSO run. Therefore, starting structures for this procedure were generated with the current DPSM parameters beforehand and equilibrated by using the parameters of each candidate solution. While equilibration of the fluid phase is generally fast, this certainly is not the case for the gel phase. Considering that an unequilibrated phase is inherently less stable, the presence of an equilibrated liquid phase alongside an unequilibrated gel phase may lead to a slight systematic underestimation of the melting temperature (Tm).60 However, this potential underestimation can be anticipated and taken into account during the analysis.
The equilibrium melting rate approach does not suffer from the potential problem of unequally equilibrated phases. To minimize bias caused by the quenched starting structures used in this approach, for each validated candidate solution, eight different starting conformations were generated.
4.1.2. Structural Properties of the Parametrized Sphingomyelin Models
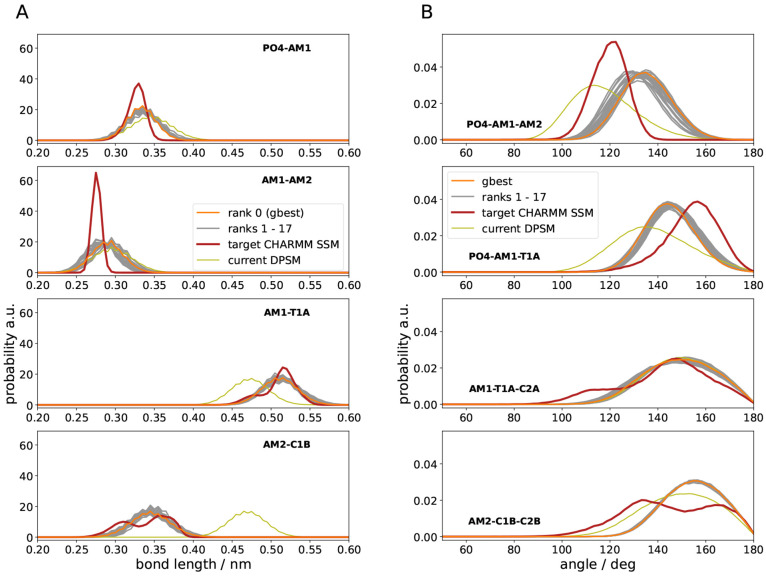
Figure 4 shows the distributions of the newly parametrized
bonds and angles for the candidate solutions in  . The atomistic target distributions are
matched reasonably well in all cases. Some finer details of the atomistic
model, such as double peaks or extensive shoulders, cannot be matched
in the CG model. The parametrization philosophy of Martini 3 adopts
a size–shape concept, where bond lengths are determined based
on the molecular volume of the atomistic fragment mapped by the beads,
rather than simply centers of mass. This complication further underscores
the necessity of employing multiobjective optimization algorithms
to achieve effective molecule parametrization.
. The atomistic target distributions are
matched reasonably well in all cases. Some finer details of the atomistic
model, such as double peaks or extensive shoulders, cannot be matched
in the CG model. The parametrization philosophy of Martini 3 adopts
a size–shape concept, where bond lengths are determined based
on the molecular volume of the atomistic fragment mapped by the beads,
rather than simply centers of mass. This complication further underscores
the necessity of employing multiobjective optimization algorithms
to achieve effective molecule parametrization.
Figure 4.
Validation of targets
from rerun simulations for the set  . (A) Bond length distributions. (B) Angle
distributions.
. (A) Bond length distributions. (B) Angle
distributions.
The solvent accessible surface
area (SASA) is commonly used to
further compare the molecular volumes and shapes between CG and AA
models.11,61Figure 5 shows the SASA values of  in comparison to the AA and current CG
DPSM models. The SASAs are computed for the linker beads AM1 and AM2,
as well as all supra-atoms that are directly connected to the linker,
i.e., beads PO4, T1A, and C1B, as these connections are also parametrized.
With SASA values of ≈6.24 nm2 all newly parametrized
CG models show a better reproduction of the AA value (5.24 nm2) compared to the current model (6.45 nm2), but
with discrepancy of ≈19% all SASA values remain grossly too
high. It appears that solely reparametrizing the linker region is
not enough to fix this issue. Furthermore, using SASA directly as
a target in the high-throughput optimization scheme is not necessarily
beneficial since a specific SASA value is not a unique representation
of a certain shape. Therefore, comparisons of solvent accessible surface
areas between AA and CG models are most helpful when done by simultaneous
visual inspection. For automated parametrization, however, more detailed
shape descriptors should be used.
in comparison to the AA and current CG
DPSM models. The SASAs are computed for the linker beads AM1 and AM2,
as well as all supra-atoms that are directly connected to the linker,
i.e., beads PO4, T1A, and C1B, as these connections are also parametrized.
With SASA values of ≈6.24 nm2 all newly parametrized
CG models show a better reproduction of the AA value (5.24 nm2) compared to the current model (6.45 nm2), but
with discrepancy of ≈19% all SASA values remain grossly too
high. It appears that solely reparametrizing the linker region is
not enough to fix this issue. Furthermore, using SASA directly as
a target in the high-throughput optimization scheme is not necessarily
beneficial since a specific SASA value is not a unique representation
of a certain shape. Therefore, comparisons of solvent accessible surface
areas between AA and CG models are most helpful when done by simultaneous
visual inspection. For automated parametrization, however, more detailed
shape descriptors should be used.
Figure 5.
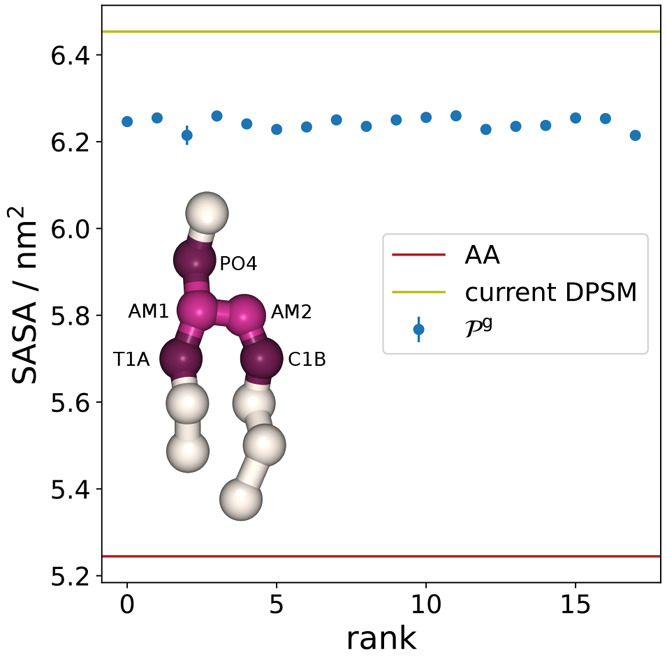
Solvent accessible surface area of the linker and beads connected directly to it. Beads involved in the SASA calculation are highlighted.
4.1.3. Force Field Parameters
Nonbonded Interactions
Due to the polar nature of the linker region of sphingolipids, only the chemical types of the P-block of the Martini 3 FF were eligible. As groups of 3 or 4 heavy atoms were combined into supra-atoms in the specified mapping, bead sizes small (S) and regular (default) could be chosen by the algorithm. Both bead sizes were permitted for both interaction sites, to allow for some wiggle room, even though 4 heavy atoms are grouped together into supra-atom AM1 and 3 into AM2. A slight miscount of mapped atoms is not uncommon in Martini; e.g., the mapping of the NC3 bead is actually 6-to-1.10 Generally, eligible bead types should be chosen with Martini rules in mind. Martini’s pragmatic philosophy allows for some freedom to match certain properties more accurately, but the bead type should not deviate strongly from the chemical identity of the molecule fragment.11
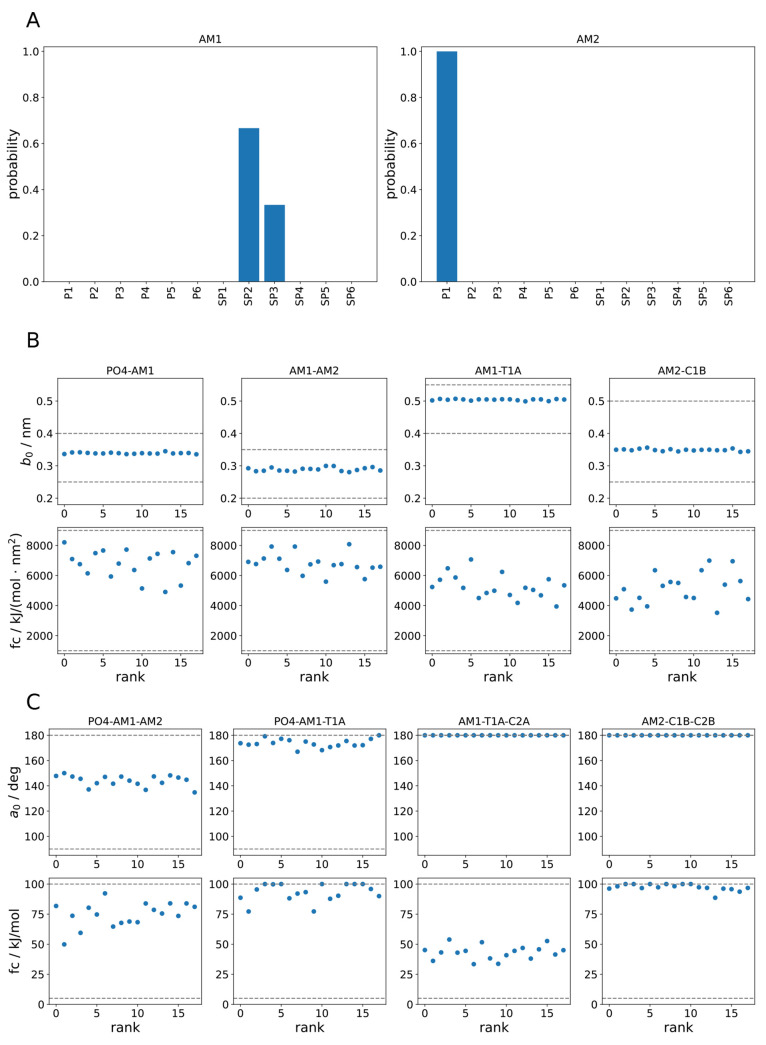
One feature of the mixed-variable approach is that the optimization procedure directly yields a probability distribution of bead types, cf. Figure 6A. While for the interaction site AM2 there is clear consensus on the bead type, for AM1 only the size (small) is clearly determined, but there is some ambiguity regarding the interaction strength. The reduced size of one of the beads seems to be warranted, given the still too high SASA values shown above, and is also inline with the new Martini 3 models of glycerolipids.11 It is also worth mentioning that the chemical bead types chosen by our algorithm match the expected assignment suggested by Martini 3.
Figure 6.
Force field parameters
of the set of statistically equivalent solutions  for the
sphingolipid linker region. (A)
Bead probability distributions. (B) Bond parameters. Dashed lines
are the upper and lower parameter limits. (C) Angle parameters. Dashed
lines are upper and lower parameter limits. The equilibrium angles
of AM1–T1A–C2A and AM2–C1B–C2B are not
varied during optimization. They are fixed at 180°.
for the
sphingolipid linker region. (A)
Bead probability distributions. (B) Bond parameters. Dashed lines
are the upper and lower parameter limits. (C) Angle parameters. Dashed
lines are upper and lower parameter limits. The equilibrium angles
of AM1–T1A–C2A and AM2–C1B–C2B are not
varied during optimization. They are fixed at 180°.
A converged “degenerate” probability distribution of bead types is the result of two or more bead types having indistinguishable effects on fitness. This can be caused by noise levels being larger than the fitness differences, or the employed set of observables and training systems is lacking the necessary discriminatory power. Both issues can be remedied in postoptimization screening but should optimally be addressed during optimization. As the former option would merely improve selection from the pool of generated candidate solutions, the latter would potentially allow the generation of truly better solutions.
Additionally, for both nonbonded and bonded FF parameters, diversity can be caused by the fact that the objective cost function for single valued observables (eq 7) has an error tolerance to accommodate for uncertainties in target data. With respect to these observables, different parametrizations with different “phenotypes” can have the same objective cost, as long as they are within the specified tolerances.
Bonded Interactions
Table 4 lists the range of permitted bond parameters
used in the optimization. The resulting bonded parameters of 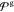 are shown in Figure 6. For equilibrium
bond lengths b0 there is little variation
among different candidate
solutions. This strong consensus suggests that the optimization has
converged and that small changes in equilibrium bond length are linked
to significant cost changes. The situation for the force constants
is quite different. The values fluctuate over a relatively large range,
compared to the predefined domain of permitted values. The measured
bond length distributions (Figure 4A) show that these seemingly substantial differences
in force constant values have only minor effects on the molecule’s
behavior.
are shown in Figure 6. For equilibrium
bond lengths b0 there is little variation
among different candidate
solutions. This strong consensus suggests that the optimization has
converged and that small changes in equilibrium bond length are linked
to significant cost changes. The situation for the force constants
is quite different. The values fluctuate over a relatively large range,
compared to the predefined domain of permitted values. The measured
bond length distributions (Figure 4A) show that these seemingly substantial differences
in force constant values have only minor effects on the molecule’s
behavior.
Table 4. Bonded Interactions: GROMACS Function Type, Permitted Parameter Ranges for Equilibrium Bond Length/Angle, and Corresponding Force Constants.
| bond | GROMACS bond funct type | b0/nm | fc/[(kJ/mol)/nm2] |
|---|---|---|---|
| PO4–AM1 | 1 | 0.25–0.40 | 1000–9000 |
| AM1–AM2 | 1 | 0.20–0.35 | 1000–9000 |
| AM1–T1A | 1 | 0.40–0.55 | 1000–9000 |
| AM2–C1B | 1 | 0.25–0.50 | 1000–9000 |
| angle | GROMACS angle funct type | a0/deg | fc/(kJ/mol) |
|---|---|---|---|
| PO4–AM1–AM2 | 2 | 90–180 | 5–100 |
| PO4–AM1–T1A | 2 | 90–180 | 5–100 |
| AM1–T1A–C2A | 2 | 180 | 5–100 |
| AM2–C1B–C2B | 2 | 180 | 5–100 |
The situation for the angle FF parameters is similar. The equilibrium values show smaller variances than the force constants compared to their respective domain sizes of applicable values. Again, the differences in FF parameters have little effect on the observed distributions (cf. Figure 4B). Notably, the optimal force constants for the angles of PO4–AM1–T1A and AM2–-C1B–C2B were close to or at the maximum of their permitted ranges. Further optimization was therefore likely hindered, and a wider range should have been chosen.
In a similar
vein to the discussion surrounding nonbonded parameters,
the relatively wide range of force constants in 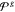 indicates
that additional metrics or training
systems could be employed to further optimize the overall performance
of candidate solutions while maintaining the quality of the employed
observables. For instance, exploring lipids in environments other
than a bilayer, which induce different lipid conformations, could
benefit from a candidate solution with a lower angle force constant
to allow for increased conformational variation.
indicates
that additional metrics or training
systems could be employed to further optimize the overall performance
of candidate solutions while maintaining the quality of the employed
observables. For instance, exploring lipids in environments other
than a bilayer, which induce different lipid conformations, could
benefit from a candidate solution with a lower angle force constant
to allow for increased conformational variation.
4.2. Noise-Mitigation Improvement of Quality of Parametrized Models
We investigated whether the simple noise-mitigation strategy described in Section 2.2.1 can improve the quality of the solutions found by the algorithm. The swarm size, training systems, observables, and weights are the same as in Section 4.1. We tested three different resampling allocation settings and compared these to the mv-PSO without noise mitigation. Each optimization run was given a fixed computational budget of 16128 MD simulation slots. One simulation slot equates to roughly 1.25 h on 6 physical cores of an Intel Cascade Lake Platinum 9242 CPU. Therefore, each optimization run had a cost of 120960 core-h. Using 12 nodes, each with two of the said CPUs, the wall time for one run was roughly 4.4 days. One should note that optimization runs were given a fixed number of iterations for comparability. In a normal parametrization task, optimization would be stopped after convergence is reached, which would have significantly reduced the computational cost. Furthermore, the required computational cost of a parametrization strongly depends on the observables that are used. In the presented example, the estimation of the melting temperature requires a comparatively large amount of sampling, especially when noise mitigation is applied.
With the given number of MD simulation slots, a swarm size of 64 particles, and 3 training systems required for one full objective function evaluation, this amounts to 84 iterations for the mv-PSO without resampling (named mv-PSO-R0). In the optimization runs with resampling, an initial computational budget of 64 × 3 = 192 MD simulation slots was used for one full objective function evaluation of each particle, and a second equally sized computational budget was allocated to reevaluate the melting temperature (the target observable with the largest variance) of the best 16, best 32, or all 64 candidate solutions of the current iteration. For brevity, we will refer to these as mv-PSO-R16, mv-PSO-R32, and mv-PSO-R64. Due to the fixed computational budget, for each particle involved in resampling, Tm was reevaluated 12, 6, or 3 times. As half of the total computational budget was used for resampling, the number of iterations was set to 42 in these runs.
From the literature on PSO noise mitigation,31,62 we draw the expectation that which of the resampling, or no resampling, strategies is the best depends on the level of noise. If noise levels are very low, the additional number of possible iterations, when resampling is avoided, could lead to better solutions. For intermediate noise levels, initial fitness evaluation results in a sufficient differentiation of good and bad solutions; i.e., overall sorting is roughly correct, and the focus on improving sorting of the very best solutions is most helpful. In the case of even higher noise levels, initial sorting would be vastly incorrect and a larger fraction of the swarm needs to be resampled to achieve satisfactory overall sorting. As a consequence, the sorting quality of the very top would be degraded as there is less computational budget allocated here.
The true quality of
a candidate solution is not necessarily reflected
by the cost estimated during an optimization run, as there is some
uncertainty in estimates of target observables other than Tm, and the confidence level of the Tm estimation with different resampling settings differs
vastly. Therefore, validation is required. As we are mostly interested
in the quality verification of the best solutions, the first step
of the screen-to-the-best procedure from Boesel et al.34 can be used to select the statistically equivalent
set of candidate solutions. For mv-PSO-R16 the set 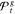 contains 69 candidate solutions. Due to
the increased uncertainty in mv-PSO-R32 and mv-PSO-R64, their respective
sets
contains 69 candidate solutions. Due to
the increased uncertainty in mv-PSO-R32 and mv-PSO-R64, their respective
sets 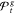 contain hundreds of candidate solutions.
To keep the computational cost for validation manageable, we selected
only the 72 best solutions of these optimization runs for validation.
As there are no variance estimates in the optimization run without
resampling, the selection procedure is not applicable. Again, the
72 best solutions from the optimization run were selected for validation.
All candidate solutions chosen for validation were fully (all training
systems and all observables) reevaluated 20 times. The resulting rerun
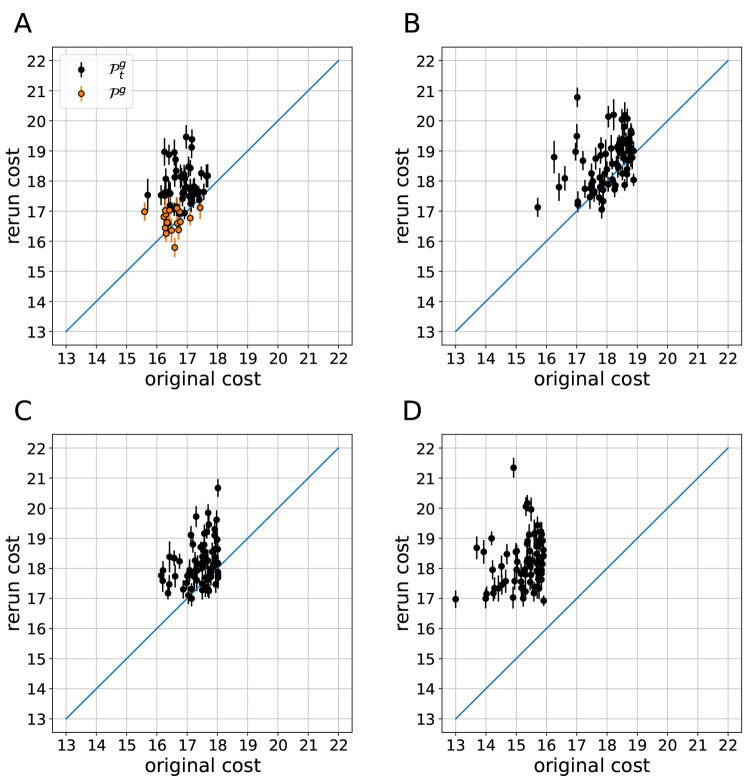
cost vs the originally estimated cost is shown in Figure 7. Clearly, mv-PSO-R16 gave
the best results, while the quality of the best solutions in the three
other cases did not differ much. Furthermore, the fact that for all
selected candidate solutions of mv-PSO-R0 the rerun cost estimate
is substantially higher than the original cost estimate indicates
that these original estimates are particularly favorable. While there
are also candidate solutions with substantial differences in original
and rerun cost for the resampling systems, in this case mostly caused
by APL fluctuations, these are much less frequent and there is much
better correlation between original and rerun cost (Pearson correlation
coefficient 0.21 vs 0.64, for mv-PSO-R0 and mv-PSO-R16, respectively).
contain hundreds of candidate solutions.
To keep the computational cost for validation manageable, we selected
only the 72 best solutions of these optimization runs for validation.
As there are no variance estimates in the optimization run without
resampling, the selection procedure is not applicable. Again, the
72 best solutions from the optimization run were selected for validation.
All candidate solutions chosen for validation were fully (all training
systems and all observables) reevaluated 20 times. The resulting rerun
cost vs the originally estimated cost is shown in Figure 7. Clearly, mv-PSO-R16 gave
the best results, while the quality of the best solutions in the three
other cases did not differ much. Furthermore, the fact that for all
selected candidate solutions of mv-PSO-R0 the rerun cost estimate
is substantially higher than the original cost estimate indicates
that these original estimates are particularly favorable. While there
are also candidate solutions with substantial differences in original
and rerun cost for the resampling systems, in this case mostly caused
by APL fluctuations, these are much less frequent and there is much
better correlation between original and rerun cost (Pearson correlation
coefficient 0.21 vs 0.64, for mv-PSO-R0 and mv-PSO-R16, respectively).
Figure 7.
Comparison
of cost estimated during the optimization run and average
cost estimated from repeated reruns of  (A) and the 72 best
candidate solutions
(B–D). Error bars are standard errors. (A) Original cost: 16
particles resampled, 1 + 12 Tm samples.
(B) Original cost: 32 particles resampled, 1 + 6 Tm samples. (C) Original cost: 64 particles resampled,
1 + 3 Tm samples. (D) No resampling during
optimization but twice as many iterations.
(A) and the 72 best
candidate solutions
(B–D). Error bars are standard errors. (A) Original cost: 16
particles resampled, 1 + 12 Tm samples.
(B) Original cost: 32 particles resampled, 1 + 6 Tm samples. (C) Original cost: 64 particles resampled,
1 + 3 Tm samples. (D) No resampling during
optimization but twice as many iterations.
Our interpretation of these results is the following: The noise level is low enough so that even without noise mitigation, the sorting of candidate solutions is correct in a coarser sense and the swarm is guided toward the “correct” vicinity in parameter space. Yet, noise levels are substantial enough, so that the resolution of finer cost differences is impeded. Only the concentrated allocation of the resampling budget on the top 16 solutions lowers the cost estimation errors sufficiently, such that improved candidate solutions can be found.
4.3. Validation: Phase Behavior of Binary Sphingomyelin–Cholesterol Membranes
To discern the universality of the parametrization,
we conducted a validation test on a target that was not included in
the optimization process. Specifically, we assessed whether the optimized
model (ranked 0 within the set  ) could accurately
replicate the phase behavior
of binary sphingomyelin–cholesterol membranes. Experimental
results show that below Tm, increasing
cholesterol content fluidizes the otherwise frozen systems.63 For very low cholesterol concentrations the
system remains in the gel phase (So);
at around 10 mol % there is a transition to coexistence of gel and
liquid ordered (Lo) domains; and above
≈30 mol % there is a (So + Lo)/Lo transition.63 As can be seen in Figure 8 the optimized model correctly reproduces
the experimental findings, while systems simulated with the current
DPSM model are always in the fluid phase, regardless of the cholesterol
concentration. These findings therefore highlight the robust universality
and transferability of the parametrization acquired with GCCompiler.
) could accurately
replicate the phase behavior
of binary sphingomyelin–cholesterol membranes. Experimental
results show that below Tm, increasing
cholesterol content fluidizes the otherwise frozen systems.63 For very low cholesterol concentrations the
system remains in the gel phase (So);
at around 10 mol % there is a transition to coexistence of gel and
liquid ordered (Lo) domains; and above
≈30 mol % there is a (So + Lo)/Lo transition.63 As can be seen in Figure 8 the optimized model correctly reproduces
the experimental findings, while systems simulated with the current
DPSM model are always in the fluid phase, regardless of the cholesterol
concentration. These findings therefore highlight the robust universality
and transferability of the parametrization acquired with GCCompiler.
Figure 8.
Phase
behavior of binary sphingomyelin–cholesterol membranes. T = 300 K. Production simulations were performed at 1 μs.
Snapshots are from the last frame. To help with the nucleation of
the gel phase, all systems were pre-equilibrated for 50 ns at 290
K (CGCompiler result) or 270 K (original DPSM). (A) CGCompiler optimized
(rank 0 of  ). (B) Current
DPSM.
). (B) Current
DPSM.
5. Discussion and Conclusion
We have illustrated how to apply mixed-variable particle swarm optimization for automated CG molecule parametrization. As an example application, we parametrized the sphingolipid linker region for the Martini 3 FF. The newly parametrized sphingomyelin model reproduces important target observables accurately, including the melting temperature, which was ≈20 K off target before and is now within ≈2 K of the experimental reference. Notably, reproduction of experimental melting temperatures had been historically problematic in Martini lipid models.64
The mixed-variable approach offers a major advantage when parametrizing molecules for building-block force fields. Due the explicit use of building blocks, every candidate model is a valid parametrization in the given FF. Otherwise, changing nonbonded interaction parameters of the FF’s building blocks breaks the validity of their parametrization. Candidate solutions generated by a continuous treatment of nonbonded interactions have to be converted to a valid FF model, followed by additional validation of this model.
A drawback of the mixed-variable treatment is that some advanced improvements to PSO, such as the fuzzy parameter tuning of Nobile et al.,65 are not directly applicable to mv-PSO, because in the categorical representation there is no similarity metric, which is utilized in the PSO parameter tuning. This could be overcome by using discrete ordered representation for nonbonded interactions instead of the categorical treatment.
One of the great benefits of automated parametrization algorithms is the simultaneous optimization against multiple structural and thermodynamic target data. As thermodynamic observables can be expensive to estimate accurately in MD simulations, formal consideration of noise in objective function values is an important conceptual improvement. As demonstrated, optimization with applied noise mitigation produced significantly better solutions and the utilized screen-to-the-best procedure provides a systematic approach to the postoptimization selection of the best model.
Although we have demonstrated the adverse effects of objective function value noise on the sorting and performance of PSO, it is important to note that the nondeterministic nature of particle swarm optimization necessitates multiple repetitions of full optimization runs to confidently determine the most effective noise-mitigation setting. Achieving a high level of confidence in identifying the optimal approach would require a significant number of iterations. Furthermore, the “ground truth”, i.e., the true score of a candidate parametrization, is unknown; hence, a large amount of validation simulations would be required. This is not feasible due to a high computational cost. Rigorous development and testing of noise-mitigation strategies should not be done with objective function evaluations that require costly MD simulations and are therefore beyond the scope of this work. Moreover, the additionally gained insight would only be of moderate value. The PSO literature has shown that under significant noise PSO performance is degraded and performance differences between resampling methods for noise mitigation are problem- and noise-level-dependent. Generally, noise-mitigation methods employing OCBA perform the best under various circumstances,31,66 but its sequential secondary budget allocation puts constraints on the parallelization of the parametrization algorithm. Still, its integration into the parametrization pipeline should be explored in the future.
Together with the general benefits of automation, the conceptual advantages presented here will further facilitate rigorous CG molecule parametrization. The CGCompiler Python package that comes with our method is tailor-made for parametrization tasks in building-block FFs, such as Martini. Also larger building blocks, i.e., a molecule class with shared regions, can be parametrized simultaneously. Our approach is not limited to lipid parametrization but can be applied to any kind of molecule. CGCompiler can be easily adapted to the needs of a specific parametrization task. Implementing new observables is not much different from writing Python functions for analyzing MD data. Importantly, our automation platform eases collaborations between individual researchers since a clear overview of the parametrization flow is provided. This also renders force-field reproducibility as well as retrospective force-field corrections, such as corrections to the targets (e.g., improved atomistic force-fields or simulation settings) or inclusion of additional targets rather straightforward.
The here-presented study focuses on method development, and the sphingolipid linker parametrization was merely a test case. The parameters of the headgroup and lipid tails, predefined in our study, are still actively improved/(re)parametrized by the core developers.11 Once these final parameters are released, reparametrization of the linker may be necessary, ideally with an even broader set of training systems, including liquid-ordered–liquid-disordered phase behavior.
Properly defining the set of feasible bead type choices, for the fragments that are to be optimized with CGCompiler, is a crucial step in the parametrization of a molecule. In the Martini FF, bead type assignment is based on partitioning data of isolated beads,10 and as of Martini 3 also partitioning of whole molecules and miscibility data are considered.11 The Martini 3 supporting material lists defaults bead type choices.11 For more accurate bead type assignment proximity and connectivity, effects between fragments need to be considered, and perturbations around the default solution are therefore allowed.11 In complex cases, bead type selection can become nontrivial when several proximity effects are present in a molecule.11 The use of target data other than the free energies of transfer is recommended and regularly employed54,61,67−71 when refining bead type choices. In our proof of concept parametrization, we have chosen to use the full range of P-block beads to showcase the capabilities of the algorithm. As the free energy of transfer was not explicitly part of the loss function, this choice could have possibly resulted in a deviation of free energies of transfer on the order of a few kJ/mol per linker fragment. As the final best bead type choices closely match the default bead type choices, this is not an issue for the optimized CG model of sphingomyelin. In a normal parametrization run and when a fragment’s partitioning and miscibility behavior is encoded by the choice of possible bead types and not explicitly part of the loss function, it is recommended to restrict the set of feasible bead types more narrowly. Otherwise, if applicable to the molecule that is to be parametrized, researchers should consider including the free energy of transfer into the loss function, either by calculating the free energy of transfer for the whole molecule or by making use of partitioning data for individual fragments.
In order to achieve fully automated molecule parametrization in high-throughput applications, the development of an automated mapping and selection of bonded terms remains a crucial component. Currently, mapping and parameter optimization are separate tasks, but integrating an automated mapping scheme into the parametrization pipeline could be facilitated prior to employing mixed-variable particle swarm optimization, utilizing CGCompiler. The choice of bonded parameters not only influences the accuracy of the model but also impacts the simulation stability. Various strategies, such as the use of virtual sites, restricted bending potentials, and hinge and “divide and conquer” constructions,68,72 have been previously described to address instability. Additionally, careful consideration of constraints is necessary to ensure simulation stability and prevent artificial temperature gradients.73,74 These aspects should be incorporated as essential steps in a future fully automated parametrization pipeline.
Reweighting of CG trajectories could be an interesting route to decrease the computational effort required for parametrization,75−77 particularly in a high-throughput setting. However, this currently is not part of CGCompiler for the following reason. The applicability of reweighting critically depends on the overlap of the original and the reweighted trajectory.75,76 As the candidate solutions in the swarm at a given iteration can have rather different potentials, it is unknown beforehand how many candidate solutions reweighting can be applied and how many new CG trajectories have to be generated. As CGCompiler is intended to be used with a high degree of parallelization on compute clusters, where a compute job runs on a fixed hardware allocation, not having to run a simulation for some of the candidate solutions does not directly result in decreased usage of a computational budget. For reweighting to be of use, an adaptive scheduling algorithm would be required, which could be implemented in future versions of CGCompiler.
When the number of optimized parameters is linearly increased, the search space grows exponentially, which negatively affects convergence of the optimization algorithm. In the study presented here, 2 categorical (nonbonded) and 14 continuous (bonded) parameters were optimized simultaneously. In a recent reparametrization of PC lipid tails16 77 bonded parameters were calibrated using a different flavor of PSO. As both parametrizations required only moderate swarm sizes and number of iterations for convergence, we expect that our PSO approach can be used for the parametrization of larger molecules as well. However, for very large molecules with several hundreds or even thousands of unique parameters, parametrization with CGCompiler or similar approaches likely becomes unfeasible. On one hand standard PSO in general is not the method of choice to tackle such large scale optimization problems (LSOPs).78 On the other hand, even if the PSO part of CGCompiler would be replaced by an optimization algorithm more suitable for an LSOP, the number of required function evaluations, i.e., MD simulations, likely remains too large to be of practical use in a molecule parametrization task.
No matter the number of parameters that are co-optimized, in order to lessen the computational cost, convergence can be facilitated by restricting the search space. Optimization with CGCompiler must then be performed on an initial, close guess rather than scanning a broad parameter range. Such an initial guess can be constructed either manually by following the Martini 3 rule book or by an automated tool. (Auto-Martini18 and the method of Potter et al.19 would need to be adapted for Martini 3, in order to be used in such a parametrization pipeline.) A restriction of search space that is not too narrow will not hinder discovery of good solutions, as parameters that are very far away from the standard Martini rules are not of interest anyway. Bond lengths that are very different from the atomistic reference would result in misshaped molecules. Very different bead types would result, for example, in incorrect partitioning behavior. In principle, these unwanted regions of the search space are filtered out by the cost function, but they can be excluded beforehand to save computational effort. A narrower search space restriction is expected to be more important when the number of parameters is large.
Another future prospect is the advancement of true nonscalarized multiobjective optimization, which eliminates the need for user-defined weights on the targets within the objective function. However, it can also be argued that these user-defined weights, which reflect the importance of targets based on intuition, experience, or additional knowledge, along with the predefined set of relevant structural and thermodynamic targets for the CG force field, encompass what is commonly known as the “force field’s philosophy”. In this sense, the user-defined weights embody the guiding principles that shape the force field.
Acknowledgments
K.S.S. and H.J.R. thank the NWO Vidi Scheme, The Netherlands, (Project No. 723.016.005) for funding this work. H.J.R thanks the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) for funding this work under Germany’s Excellence Strategy—EXC 2033-390677874-RESOLV. K.S.S. and H.J.R. thank the Leibniz Association for funding through the SAW grant “Controlling and Switching of Function of Peptide and Protein based BioSurfaces: From Fundamentals to Applications”. K.S.S. and H.J.R. gratefully acknowledge the computing time granted by the Resource Allocation Board and provided on the supercomputer Lise and Emmy at NHR@ZIB and NHR@Göttingen as part of the NHR infrastructure. The calculations for this research were conducted with computing resources under Project nip00054. K.S.S. and H.J.R. gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu for funding this project by providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS Supercomputer JUWELS at Jülich Supercomputing Centre (JSC). P.C.T.S. acknowledges the support of the French National Center for Scientific Research (CNRS) and the funding from a research collaboration agreement with PharmCADD. L.M. acknowledges funding by the Institut National de la Santé et de la Recherche Médicale (INSERM).
Data Availability Statement
The CGCompiler Python package is available at https://github.com/kaistroh/CGCompiler-lipids. A Gromacs topology file of the final sphingomyelin can be downloaded from the Martini Database server79 (https://mad.ibcp.fr).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.3c00637.
Methods to estimate melting temperature; additional plots regarding noise; sphingomyelin–cholesterol 2d center-of-mass radial distribution functions; DPSM Gromacs topology file (PDF)
Author Present Address
⊥ Laboratory of Biology and Modeling of the Cell, École Normale Supérieure de Lyon, Université Claude Bernard Lyon 1, CNRS UMR 5239 and Inserm U1293, 46 Allée d’Italie, 69007 Lyon, France
The authors declare no competing financial interest.
Supplementary Material
References
- Risselada H. J.; Marrink S. J. The molecular face of lipid rafts in model membranes. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 17367–17372. 10.1073/pnas.0807527105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada J.; Mark A. E. Simulation of gel phase formation and melting in lipid bilayers using a coarse grained model. Chem. .Phys. Lipids 2005, 135, 223–244. 10.1016/j.chemphyslip.2005.03.001. [DOI] [PubMed] [Google Scholar]
- Risselada H. J.; Marrink S. J. The freezing process of small lipid vesicles at molecular resolution. Soft Matter 2009, 5, 4531–4541. 10.1039/b913210d. [DOI] [Google Scholar]
- Lyubartsev A. P.; Laaksonen A. Calculation of effective interaction potentials from radial distribution functions: A reverse Monte Carlo approach. Phys. Rev. E 1995, 52, 3730. 10.1103/PhysRevE.52.3730. [DOI] [PubMed] [Google Scholar]
- Lyubartsev A. P. Multiscale modeling of lipids and lipid bilayers. Eur. Biophys. J. 2005, 35, 53–61. 10.1007/s00249-005-0005-y. [DOI] [PubMed] [Google Scholar]
- Izvekov S.; Parrinello M.; Burnham C. J.; Voth G. A. Effective force fields for condensed phase systems from ab initio molecular dynamics simulation: A new method for force-matching. J. Chem. Phys. 2004, 120, 10896–10913. 10.1063/1.1739396. [DOI] [PubMed] [Google Scholar]
- Izvekov S.; Voth G. A. A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B 2005, 109, 2469–2473. 10.1021/jp044629q. [DOI] [PubMed] [Google Scholar]
- Lafitte T.; Apostolakou A.; Avendaño C.; Galindo A.; Adjiman C. S.; Müller E. A.; Jackson G. Accurate statistical associating fluid theory for chain molecules formed from Mie segments. J. Chem. Phys. 2013, 139, 154504. 10.1063/1.4819786. [DOI] [PubMed] [Google Scholar]
- Papaioannou V.; Lafitte T.; Avendaño C.; Adjiman C. S.; Jackson G.; Müller E. A.; Galindo A. Group contribution methodology based on the statistical associating fluid theory for heteronuclear molecules formed from Mie segments. J. Chem. Phys. 2014, 140, 054107. 10.1063/1.4851455. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; de Vries A. H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- Souza P. C. T.; Alessandri R.; Barnoud J.; Thallmair S.; Faustino I.; Grünewald F.; Patmanidis I.; Abdizadeh H.; Bruininks B. M. H.; Wassenaar T. A.; Kroon P. C.; Melcr J.; Nieto V.; Corradi V.; Khan H. M.; Domański J.; Javanainen M.; Martinez-Seara H.; Reuter N.; Best R. B.; Vattulainen I.; Monticelli L.; Periole X.; Tieleman D. P.; de Vries A. H.; Marrink S. J. Martini 3: a general purpose force field for coarse-grained molecular dynamics. Nat. Methods 2021, 18, 382–388. 10.1038/s41592-021-01098-3. [DOI] [PubMed] [Google Scholar]
- Alessandri R.; Souza P. C. T.; Thallmair S.; Melo M. N.; de Vries A. H.; Marrink S. J. Pitfalls of the Martini Model. J. Chem. Theory Comput. 2019, 15, 5448–5460. 10.1021/acs.jctc.9b00473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risselada H. J. Martini 3: a coarse-grained force field with an eye for atomic detail. Nat. Methods 2021, 18, 342–343. 10.1038/s41592-021-01111-9. [DOI] [PubMed] [Google Scholar]
- Graham J. A.; Essex J. W.; Khalid S. PyCGTOOL: Automated Generation of Coarse-Grained Molecular Dynamics Models from Atomistic Trajectories. J. Chem. Inf. Model. 2017, 57, 650–656. 10.1021/acs.jcim.7b00096. [DOI] [PubMed] [Google Scholar]
- Empereur-Mot C.; Pesce L.; Doni G.; Bochicchio D.; Capelli R.; Perego C.; Pavan G. M. Swarm-CG: Automatic Parametrization of Bonded Terms in MARTINI-Based Coarse-Grained Models of Simple to Complex Molecules via Fuzzy Self-Tuning Particle Swarm Optimization. ACS Omega 2020, 5, 32823–32843. 10.1021/acsomega.0c05469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Empereur-mot C.; Pedersen K. B.; Capelli R.; Crippa M.; Caruso C.; Perrone M.; Souza P. C. T.; Marrink S. J.; Pavan G. M. Automatic Optimization of Lipid Models in the Martini Force Field Using SwarmCG. J. Chem. Inf. Model. 2023, 63, 3827–3838. 10.1021/acs.jcim.3c00530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Empereur-mot C.; Capelli R.; Perrone M.; Caruso C.; Doni G.; Pavan G. M. Automatic multi-objective optimization of coarse-grained lipid force fields using SwarmCG. J. Chem. Phys. 2022, 156, 024801. 10.1063/5.0079044. [DOI] [PubMed] [Google Scholar]
- Bereau T.; Kremer K. Automated Parametrization of the Coarse-Grained Martini Force Field for Small Organic Molecules. J. Chem. Theory Comput. 2015, 11, 2783–2791. 10.1021/acs.jctc.5b00056. [DOI] [PubMed] [Google Scholar]
- Potter T. D.; Barrett E. L.; Miller M. A. Automated Coarse-Grained Mapping Algorithm for the Martini Force Field and Benchmarks for Membrane–Water Partitioning. J. Chem. Theory Comput. 2021, 17, 5777–5791. 10.1021/acs.jctc.1c00322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tetko I. V.; Tanchuk V. Y.; Villa A. E. P. Prediction of n-Octanol/Water Partition Coefficients from PHYSPROP Database Using Artificial Neural Networks and E-State Indices. J. Chem. Inf. Comput. Sci. 2001, 41, 1407–1421. 10.1021/ci010368v. [DOI] [PubMed] [Google Scholar]
- Tetko I. V.; Tanchuk V. Y. Application of Associative Neural Networks for Prediction of Lipophilicity in ALOGPS 2.1 Program. J. Chem. Inf. Comput. Sci. 2002, 42, 1136–1145. 10.1021/ci025515j. [DOI] [PubMed] [Google Scholar]
- Rühle V.; Junghans C.; Lukyanov A.; Kremer K.; Andrienko D. Versatile Object-Oriented Toolkit for Coarse-Graining Applications. J. Chem. Theory Comput. 2009, 5, 3211–3223. 10.1021/ct900369w. [DOI] [PubMed] [Google Scholar]
- Mirzoev A.; Lyubartsev A. P. MagiC: Software Package for Multiscale Modeling. J. Chem. Theory Comput. 2013, 9, 1512–1520. 10.1021/ct301019v. [DOI] [PubMed] [Google Scholar]
- Bejagam K. K.; Singh S.; An Y.; Deshmukh S. A. Machine-Learned Coarse-Grained Models. J. Phys. Chem. Lett. 2018, 9, 4667–4672. 10.1021/acs.jpclett.8b01416. [DOI] [PubMed] [Google Scholar]
- Bejagam K. K.; Singh S.; An Y.; Berry C.; Deshmukh S. A. PSO-Assisted Development of New Transferable Coarse-Grained Water Models. J. Phys. Chem. B 2018, 122, 1958–1971. 10.1021/acs.jpcb.7b10542. [DOI] [PubMed] [Google Scholar]
- Taghiyeh S.; Xu J. A new particle swarm optimization algorithm for noisy optimization problems. Swarm Intell. 2016, 10, 161–192. 10.1007/s11721-016-0125-2. [DOI] [Google Scholar]
- van Meer G.; Voelker D. R.; Feigenson G. W. Membrane lipids: where they are and how they behave. Nat. Rev. Mol. Cell Biol. 2008, 9, 112–124. 10.1038/nrm2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eberhart R.; Kennedy J.. A new optimizer using particle swarm theory. MHS’95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science; IEEE, 1995. 10.1109/MHS.1995.494215. [DOI]
- Wang F.; Zhang H.; Zhou A. A particle swarm optimization algorithm for mixed-variable optimization problems. Swarm Evol. Comput. 2021, 60, 100808. 10.1016/j.swevo.2020.100808. [DOI] [Google Scholar]
- Rubner Y.; Tomasi C.; Guibas L. J. The Earth Mover’s Distance as a Metric for Image Retrieval. Int. J. Comput. Vision 2000, 40, 99–121. 10.1023/A:1026543900054. [DOI] [Google Scholar]
- Rada-Vilela J.; Johnston M.; Zhang M. Population statistics for particle swarm optimization: Resampling methods in noisy optimization problems. Swarm Evol. Comput. 2014, 17, 37–59. 10.1016/j.swevo.2014.02.004. [DOI] [Google Scholar]
- Pan H.; Wang L.; Liu B. Particle swarm optimization for function optimization in noisy environment. Appl. Math. Comput. 2006, 181, 908–919. 10.1016/j.amc.2006.01.066. [DOI] [Google Scholar]
- Chen C.-H.; Lin J.; Yücesan E.; Chick S. E. Simulation Budget Allocation for Further Enhancing the Efficiency of Ordinal Optimization. Discrete Event Dyn. Syst. 2000, 10, 251–270. 10.1023/A:1008349927281. [DOI] [Google Scholar]
- Boesel J.; Nelson B. L.; Kim S.-H. Using Ranking and Selection to “Clean up” after Simulation Optimization. Oper. Res. 2003, 51, 814–825. 10.1287/opre.51.5.814.16751. [DOI] [Google Scholar]
- Methorst J.; van Hilten N.; Risselada H. J.. Inverse design of cholesterol attracting transmembrane helices reveals a paradoxical role of hydrophobic length. bioRxiv (Biophysics), 2021. https://doi.org/10.1101/2021.07.01.450699.
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Michaud-Agrawal N.; Denning E. J.; Woolf T. B.; Beckstein O. MDAnalysis: A toolkit for the analysis of molecular dynamics simulations. J. Comput. Chem. 2011, 32, 2319–2327. 10.1002/jcc.21787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gowers R.; Linke M.; Barnoud J.; Reddy T.; Melo M.; Seyler S.; Domański J.; Dotson D.; Buchoux S.; Kenney I.; Beckstein O.. MDAnalysis: A Python Package for the Rapid Analysis of Molecular Dynamics Simulations. Proceedings of the 15th Python in Science Conference; SciPy, 2016. 10.25080/Majora-629e541a-014. [DOI]
- Smith P.; Lorenz C. D. LiPyphilic: A Python Toolkit for the Analysis of Lipid Membrane Simulations. J. Chem. Theory Comput. 2021, 17, 5907–5919. 10.1021/acs.jctc.1c00447. [DOI] [PubMed] [Google Scholar]
- Virtanen P.; Gommers R.; Oliphant T. E.; Haberland M.; Reddy T.; Cournapeau D.; Burovski E.; Peterson P.; Weckesser W.; Bright J.; van der Walt S. J.; Brett M.; Wilson J.; Millman K. J.; Mayorov N.; Nelson A. R. J.; Jones E.; Kern R.; Larson E.; Carey C. J.; Polat İ.; Feng Y.; Moore E. W.; VanderPlas J.; Laxalde D.; Perktold J.; Cimrman R.; Henriksen I.; Quintero E. A.; Harris C. R.; Archibald A. M.; Ribeiro A. H.; Pedregosa F.; van Mulbregt P.; Vijaykumar A.; Bardelli A. P.; Rothberg A.; Hilboll A.; Kloeckner A.; Scopatz A.; Lee A.; Rokem A.; Woods C. N.; Fulton C.; Masson C.; Häggström C.; Fitzgerald C.; Nicholson D. A.; Hagen D. R.; Pasechnik D. V.; Olivetti E.; Martin E.; Wieser E.; Silva F.; Lenders F.; Wilhelm F.; Young G.; Price G. A.; Ingold G.-L.; Allen G. E.; Lee G. R.; Audren H.; Probst I.; Dietrich J. P.; Silterra J.; Webber J. T.; Slavič J.; Nothman J.; Buchner J.; Kulick J.; Schönberger J. L.; de Miranda Cardoso J. V.; Reimer J.; Harrington J.; Rodríguez J. L. C.; Nunez-Iglesias J.; Kuczynski J.; Tritz K.; Thoma M.; Newville M.; Kümmerer M.; Bolingbroke M.; Tartre M.; Pak M.; Smith N. J.; Nowaczyk N.; Shebanov N.; Pavlyk O.; Brodtkorb P. A.; Lee P.; McGibbon R. T.; Feldbauer R.; Lewis S.; Tygier S.; Sievert S.; Vigna S.; Peterson S.; More S.; Pudlik T.; Oshima T.; Pingel T. J.; Robitaille T. P.; Spura T.; Jones T. R.; Cera T.; Leslie T.; Zito T.; Krauss T.; Upadhyay U.; Halchenko Y. O.; Vazquez-Baeza Y. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. 10.1038/s41592-019-0686-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pele O.; Werman M.. Fast and robust Earth Mover’s Distances. 2009 IEEE 12th International Conference on Computer Vision; IEEE, 2009. 10.1109/ICCV.2009.5459199 [DOI]
- Pele O.; Werman M.. A Linear Time Histogram Metric for Improved SIFT Matching. Computer Vision–ECCV 2008; Springer: Berlin, Heidelberg, 2008; pp 495–508. 10.1007/978-3-540-88690-7_37. [DOI] [Google Scholar]
- Nguyen H.; Case D. A.; Rose A. S. NGLview–interactive molecular graphics for Jupyter notebooks. Bioinformatics 2018, 34, 1241–1242. 10.1093/bioinformatics/btx789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klauda J. B.; Venable R. M.; Freites J. A.; O’Connor J. W.; Tobias D. J.; Mondragon-Ramirez C.; Vorobyov I.; MacKerell A. D.; Pastor R. W. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J. Phys. Chem. B 2010, 114, 7830–7843. 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venable R. M.; Sodt A. J.; Rogaski B.; Rui H.; Hatcher E.; MacKerell A. D.; Pastor R. W.; Klauda J. B. CHARMM All-Atom Additive Force Field for Sphingomyelin: Elucidation of Hydrogen Bonding and of Positive Curvature. Biophys. J. 2014, 107, 134–145. 10.1016/j.bpj.2014.05.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang E.; Klauda J. B. Molecular Dynamics Simulations of Ceramide and Ceramide-Phosphatidylcholine Bilayers. J. Phys. Chem. B 2017, 121, 10091–10104. 10.1021/acs.jpcb.7b08967. [DOI] [PubMed] [Google Scholar]
- Jo S.; Lim J. B.; Klauda J. B.; Im W. CHARMM-GUI Membrane Builder for Mixed Bilayers and Its Application to Yeast Membranes. Biophys. J. 2009, 97, 50–58. 10.1016/j.bpj.2009.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu E. L.; Cheng X.; Jo S.; Rui H.; Song K. C.; Dávila-Contreras E. M.; Qi Y.; Lee J.; Monje-Galvan V.; Venable R. M.; Klauda J. B.; Im W. CHARMM-GUI Membrane Builder toward realistic biological membrane simulations. J. Comput. Chem. 2014, 35, 1997–2004. 10.1002/jcc.23702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J.; Cheng X.; Swails J. M.; Yeom M. S.; Eastman P. K.; Lemkul J. A.; Wei S.; Buckner J.; Jeong J. C.; Qi Y.; Jo S.; Pande V. S.; Case D. A.; Brooks C. L.; MacKerell A. D.; Klauda J. B.; Im W. CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field. J. Chem. Theory Comput. 2016, 12, 405–413. 10.1021/acs.jctc.5b00935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C.; Fraaije J. G. E. M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle mesh Ewald: An N· log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- Bussi G.; Donadio D.; Parrinello M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Borges-Araújo L.; Borges-Araújo A. C.; Ozturk T. N.; Ramirez-Echemendia D. P.; Fábián B.; Carpenter T. S.; Thallmair S.; Barnoud J.; Ingólfsson H. I.; Hummer G.; Tieleman D. P.; Marrink S. J.; Souza P. C. T.; Melo M. N. Martini 3 Coarse-Grained Force Field for Cholesterol. J. Chem. Theory Comput. 2023, 19, 7387–7404. 10.1021/acs.jctc.3c00547. [DOI] [PubMed] [Google Scholar]
- Borges-Araújo L.; Borges-Araújo A.; Ozturk T.; Ramirez-Echemendia D. P.; Fábián B.; Carpenter T. S.; Thallmair S.; Barnoud J.; Ingólfsson H. I.; Hummer G.; Tieleman D. P.; Marrink S. J.; Souza P. C. T.; Melo M. N.. Parameterization of cholesterol for the Martini 3 coarse grained force field. 2023; https://github.com/Martini-Force-Field-Initiative/M3-Sterol-Parameters, accessed on 2023-06-09. [DOI] [PubMed]
- Wassenaar T. A.; Ingólfsson H. I.; Böckmann R. A.; Tieleman D. P.; Marrink S. J. Computational Lipidomics with insane: A Versatile Tool for Generating Custom Membranes for Molecular Simulations. J. Chem. Theory Comput. 2015, 11, 2144–2155. 10.1021/acs.jctc.5b00209. [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
- Kowalik B.; Schubert T.; Wada H.; Tanaka M.; Netz R. R.; Schneck E. Combination of MD Simulations with Two-State Kinetic Rate Modeling Elucidates the Chain Melting Transition of Phospholipid Bilayers for Different Hydration Levels. J. Phys. Chem. B 2015, 119, 14157–14167. 10.1021/acs.jpcb.5b05501. [DOI] [PubMed] [Google Scholar]
- Sun L.; Böckmann R. A. Membrane phase transition during heating and cooling: molecular insight into reversible melting. Eur. Biophys. J. 2018, 47, 151–164. 10.1007/s00249-017-1237-3. [DOI] [PubMed] [Google Scholar]
- Coppock P. S.; Kindt J. T. Determination of Phase Transition Temperatures for Atomistic Models of Lipids from Temperature-Dependent Stripe Domain Growth Kinetics. J. Phys. Chem. B 2010, 114, 11468–11473. 10.1021/jp104529m. [DOI] [PubMed] [Google Scholar]
- Borges-Araújo L.; Souza P. C. T.; Fernandes F.; Melo M. N. Improved Parameterization of Phosphatidylinositide Lipid Headgroups for the Martini 3 Coarse-Grain Force Field. J. Chem. Theory Comput. 2022, 18, 357–373. 10.1021/acs.jctc.1c00615. [DOI] [PubMed] [Google Scholar]
- Rada-Vilela J.; Johnston M.; Zhang M. Deception, blindness and disorientation in particle swarm optimization applied to noisy problems. Swarm Intell. 2014, 8, 247–273. 10.1007/s11721-014-0098-y. [DOI] [Google Scholar]
- Keyvanloo A.; Shaghaghi M.; Zuckermann M. J.; Thewalt J. L. The Phase Behavior and Organization of Sphingomyelin/Cholesterol Membranes: A Deuterium NMR Study. Biophys. J. 2018, 114, 1344–1356. 10.1016/j.bpj.2018.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada J.; Mark A. E. Simulation of gel phase formation and melting in lipid bilayers using a coarse grained model. Chem. Phys. Lipids 2005, 135, 223–244. 10.1016/j.chemphyslip.2005.03.001. [DOI] [PubMed] [Google Scholar]
- Nobile M. S.; Cazzaniga P.; Besozzi D.; Colombo R.; Mauri G.; Pasi G. Fuzzy Self-Tuning PSO: A settings-free algorithm for global optimization. Swarm Evol. Comput. 2018, 39, 70–85. 10.1016/j.swevo.2017.09.001. [DOI] [Google Scholar]
- Rada-Vilela J.; Johnston M.; Zhang M. Population statistics for particle swarm optimization: Hybrid methods in noisy optimization problems. Swarm Evol. Comput. 2015, 22, 15–29. 10.1016/j.swevo.2015.01.003. [DOI] [Google Scholar]
- Melo M. N.; Ingólfsson H. I.; Marrink S. J. Parameters for Martini sterols and hopanoids based on a virtual-site description. J. Chem. Phys. 2015, 143, 243152. 10.1063/1.4937783. [DOI] [PubMed] [Google Scholar]
- Alessandri R.; Barnoud J.; Gertsen A. S.; Patmanidis I.; de Vries A. H.; Souza P. C. T.; Marrink S. J. Martini 3 Coarse-Grained Force Field: Small Molecules. Adv. Theory Simul. 2022, 5, 2100391. 10.1002/adts.202100391. [DOI] [Google Scholar]
- Alessandri R.; Thallmair S.; Herrero C. G.; Mera-Adasme R.; Marrink S. J.; Souza P. C. T.. A Practical Guide to Recent Advances in Multiscale Modeling and Simulation of Biomolecules; American Institute of Physics (AIP): Melville, NY, 2023; pp 1–34. 10.1063/9780735425279. [DOI] [Google Scholar]
- Uusitalo J. J.; Ingólfsson H. I.; Akhshi P.; Tieleman D. P.; Marrink S. J. Martini Coarse-Grained Force Field: Extension to DNA. J. Chem. Theory Comput. 2015, 11, 3932–3945. 10.1021/acs.jctc.5b00286. [DOI] [PubMed] [Google Scholar]
- Vazquez-Salazar L. I.; Selle M.; de Vries A. H.; Marrink S. J.; Souza P. C. T. Martini coarse-grained models of imidazolium-based ionic liquids: from nanostructural organization to liquid–liquid extraction. Green Chem. 2020, 22, 7376–7386. 10.1039/D0GC01823F. [DOI] [Google Scholar]
- Bulacu M.; Goga N.; Zhao W.; Rossi G.; Monticelli L.; Periole X.; Tieleman D. P.; Marrink S. J. Improved Angle Potentials for Coarse-Grained Molecular Dynamics Simulations. J. Chem. Theory Comput. 2013, 9, 3282–3292. 10.1021/ct400219n. [DOI] [PubMed] [Google Scholar]
- Fábián B.; Thallmair S.; Hummer G. Optimal Bond Constraint Topology for Molecular Dynamics Simulations of Cholesterol. J. Chem. Theory Comput. 2023, 19, 1592–1601. 10.1021/acs.jctc.2c01032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thallmair S.; Javanainen M.; Fábián B.; Martinez-Seara H.; Marrink S. J. Nonconverged Constraints Cause Artificial Temperature Gradients in Lipid Bilayer Simulations. J. Phys. Chem. B 2021, 125, 9537–9546. 10.1021/acs.jpcb.1c03665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norgaard A. B.; Ferkinghoff-Borg J.; Lindorff-Larsen K. Experimental Parameterization of an Energy Function for the Simulation of Unfolded Proteins. Biophys. J. 2008, 94, 182–192. 10.1529/biophysj.107.108241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li D.-W.; Brüschweiler R. Iterative Optimization of Molecular Mechanics Force Fields from NMR Data of Full-Length Proteins. J. Chem. Theory Comput. 2011, 7, 1773–1782. 10.1021/ct200094b. [DOI] [PubMed] [Google Scholar]
- Carmichael S. P.; Shell M. S. A New Multiscale Algorithm and Its Application to Coarse-Grained Peptide Models for Self-Assembly. J. Phys. Chem. B 2012, 116, 8383–8393. 10.1021/jp2114994. [DOI] [PubMed] [Google Scholar]
- Gad A. G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch Comput. Method E 2022, 29, 2531–2561. 10.1007/s11831-021-09694-4. [DOI] [Google Scholar]
- Hilpert C.; Beranger L.; Souza P. C. T.; Vainikka P. A.; Nieto V.; Marrink S. J.; Monticelli L.; Launay G. Facilitating CG Simulations with MAD: The MArtini Database Server. J. Chem. Inf. Model. 2023, 63, 702–710. 10.1021/acs.jcim.2c01375. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The CGCompiler Python package is available at https://github.com/kaistroh/CGCompiler-lipids. A Gromacs topology file of the final sphingomyelin can be downloaded from the Martini Database server79 (https://mad.ibcp.fr).